PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1 [975576]: Đồ thị hàm số 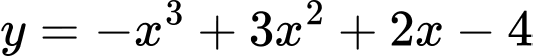 cắt trục tung tại điểm
cắt trục tung tại điểm
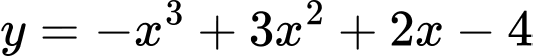 cắt trục tung tại điểm
cắt trục tung tại điểm A, 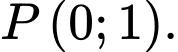
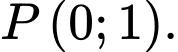
B, 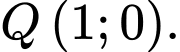
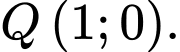
C, 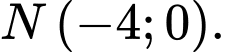
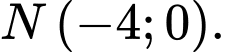
D, 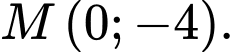
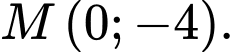
Giao điểm của đồ thị hàm số với trục tung có hoành độ 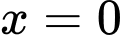
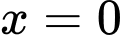
Cho 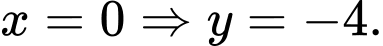
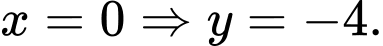
Vậy tọa độ giao điểm là 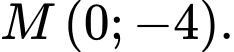
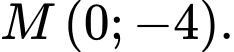
Chọn D.
Đáp án: D
Câu 2 [378331]: Đồ thị hàm số 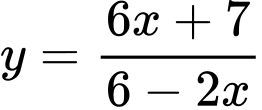 có đường tiệm cận đứng, đường tiệm cận ngang lần lượt là.
có đường tiệm cận đứng, đường tiệm cận ngang lần lượt là.
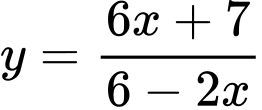 có đường tiệm cận đứng, đường tiệm cận ngang lần lượt là.
có đường tiệm cận đứng, đường tiệm cận ngang lần lượt là. A, 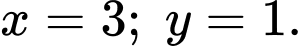
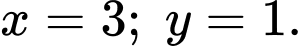
B, 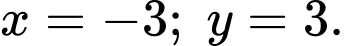
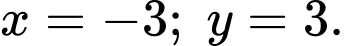
C, 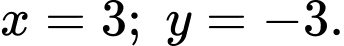
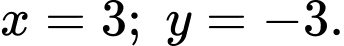
D, 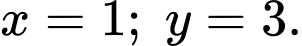
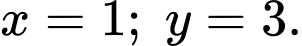
Phương pháp:
Hàm số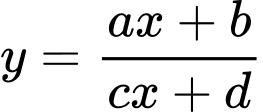 có tiệm cận đứng
có tiệm cận đứng 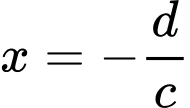 và tiệm cận ngang
và tiệm cận ngang 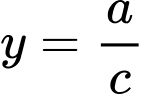
Cách giải:
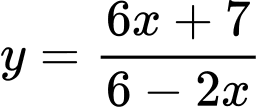 có tiệm cận đứng
có tiệm cận đứng 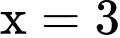 và tiệm cận ngang
và tiệm cận ngang 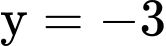 Đáp án: C
Đáp án: C
Hàm số
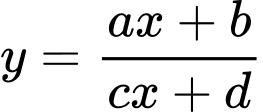 có tiệm cận đứng
có tiệm cận đứng 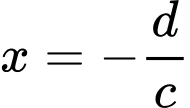 và tiệm cận ngang
và tiệm cận ngang 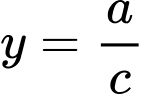
Cách giải:
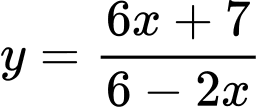 có tiệm cận đứng
có tiệm cận đứng 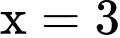 và tiệm cận ngang
và tiệm cận ngang 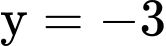 Đáp án: C
Đáp án: C
Câu 3 [185130]: Cho hàm số 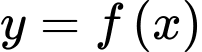 có bảng biến thiên như sau:
có bảng biến thiên như sau:
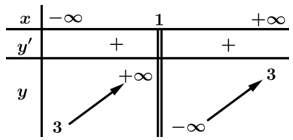
Tiệm cận đứng của đồ thị hàm số đã cho có phương trình là
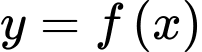 có bảng biến thiên như sau:
có bảng biến thiên như sau:
Tiệm cận đứng của đồ thị hàm số đã cho có phương trình là
A, 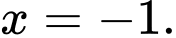
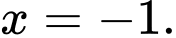
B, 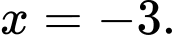
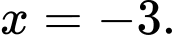
C, 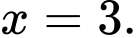
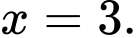
D, 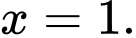
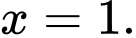
Từ đồ thị ta thấy 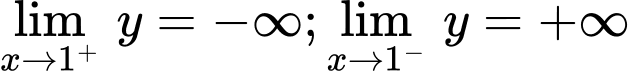
Vậy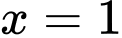 là tiệm cận đứng của đồ thị hàm số. Đáp án: D
là tiệm cận đứng của đồ thị hàm số. Đáp án: D
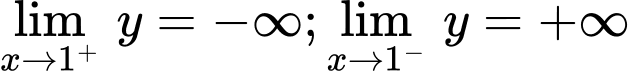
Vậy
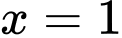 là tiệm cận đứng của đồ thị hàm số. Đáp án: D
là tiệm cận đứng của đồ thị hàm số. Đáp án: D
Câu 4 [503005]: Cho hàm số 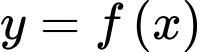 có đồ thị như hình bên.
có đồ thị như hình bên.
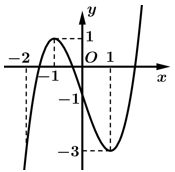
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
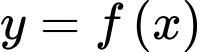 có đồ thị như hình bên.
có đồ thị như hình bên.
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A, 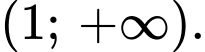
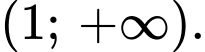
B, 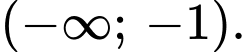
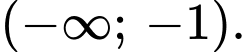
C, 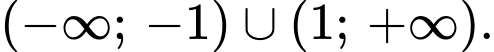
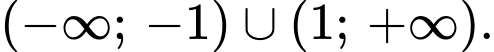
D, 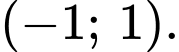
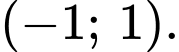
Chọn đáp án D.
Dựa vào đồ thị ta thấy hàm số đã cho nghịch biến trên khoảng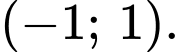 Đáp án: D
Đáp án: D
Dựa vào đồ thị ta thấy hàm số đã cho nghịch biến trên khoảng
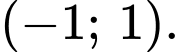 Đáp án: D
Đáp án: D
Câu 5 [502013]: Đường thẳng 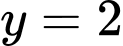 là tiệm cận ngang của đồ thị hàm số nào sau đây
là tiệm cận ngang của đồ thị hàm số nào sau đây
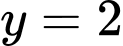 là tiệm cận ngang của đồ thị hàm số nào sau đây
là tiệm cận ngang của đồ thị hàm số nào sau đây A, 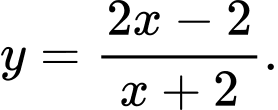
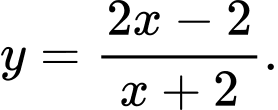
B, 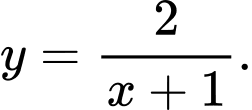
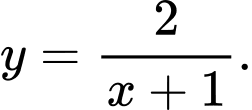
C, 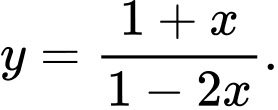
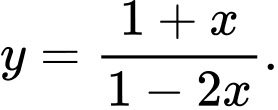
D, 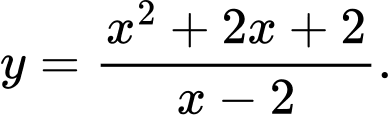
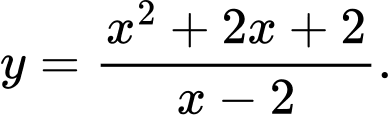
Chọn đáp án A.
Để tìm tiệm cận ngang của hàm số, ta sẽ tính giới hạn của hàm số tại vô cùng. Thực hiện như sau:
A. Đúng. Vì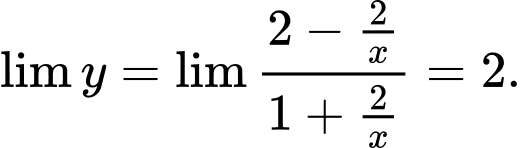 Nên
Nên 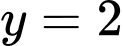 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
B. Sai. Vì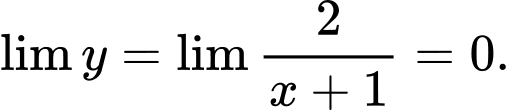 Nên
Nên 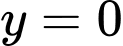 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
C. Sai. Vì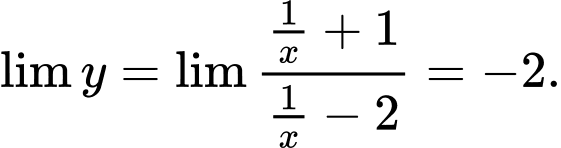 Nên
Nên 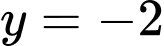 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
D. Sai. Vì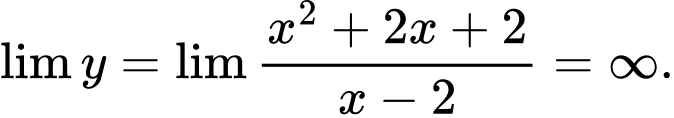 Nên hàm số không có tiệm cận ngang.
Đáp án: A
Nên hàm số không có tiệm cận ngang.
Đáp án: A
Để tìm tiệm cận ngang của hàm số, ta sẽ tính giới hạn của hàm số tại vô cùng. Thực hiện như sau:
A. Đúng. Vì
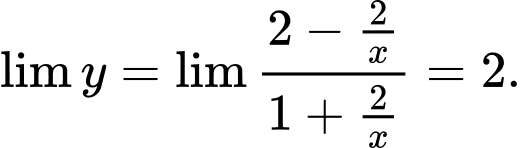 Nên
Nên 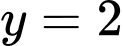 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
B. Sai. Vì
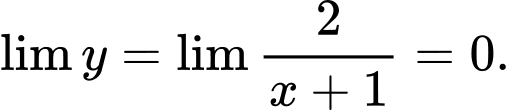 Nên
Nên 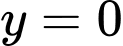 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
C. Sai. Vì
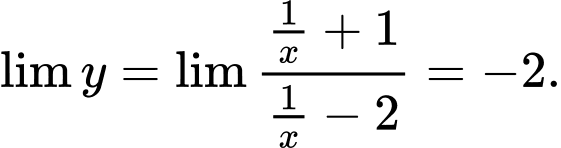 Nên
Nên 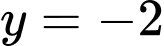 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
D. Sai. Vì
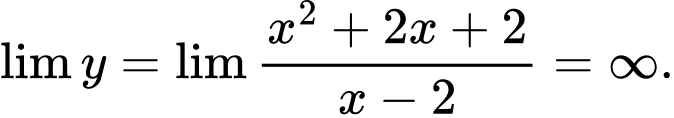 Nên hàm số không có tiệm cận ngang.
Đáp án: A
Nên hàm số không có tiệm cận ngang.
Đáp án: A
Câu 6 [547064]: Bảng biến thiên dưới đây là của hàm số nào?
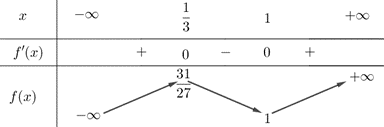

A, 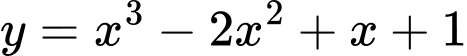 .
.
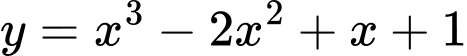 .
.B, 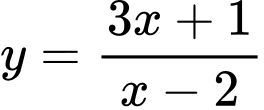 .
.
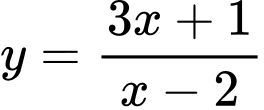 .
.C, 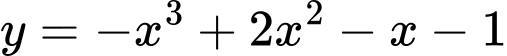 .
.
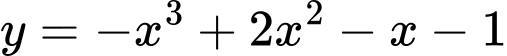 .
. D, 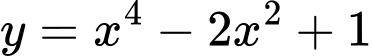 .
.
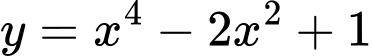 .
.
Chọn A.
Dựa vào bảng biến thiên, ta thấy hàm số xác định trên và có 2 điểm cực trị.
và có 2 điểm cực trị.
Mặt khác ta có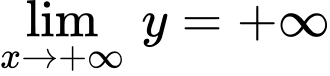
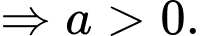
Vậy hàm số thỏa bảng biến thiên trên là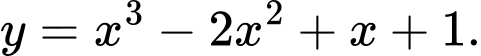 Đáp án: A
Đáp án: A
Dựa vào bảng biến thiên, ta thấy hàm số xác định trên
 và có 2 điểm cực trị.
và có 2 điểm cực trị.
Mặt khác ta có
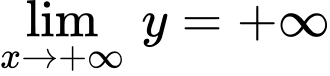
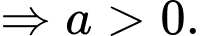
Vậy hàm số thỏa bảng biến thiên trên là
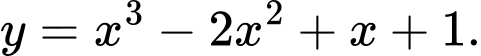 Đáp án: A
Đáp án: A
Câu 7 [16450]: Cho hàm số 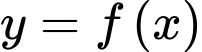 có bảng biến thiên như sau
có bảng biến thiên như sau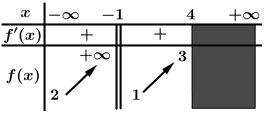
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
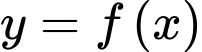 có bảng biến thiên như sau
có bảng biến thiên như sau
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A, 4.
B, 1.
C, 2.
D, 3.
Đáp án C
Từ bảng biến thiên ta có
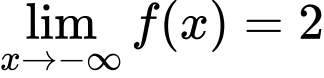 nên đường thẳng
nên đường thẳng 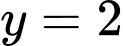 là đường tiệm cận ngang của đồ thị hàm số.
là đường tiệm cận ngang của đồ thị hàm số.
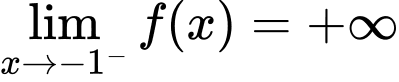 nên đường thẳng
nên đường thẳng 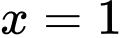 là đường tiệm cận đứng của đồ thị hàm số.
là đường tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có 2 đường tiệm cận. Đáp án: C
Từ bảng biến thiên ta có
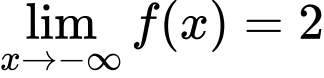 nên đường thẳng
nên đường thẳng 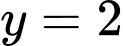 là đường tiệm cận ngang của đồ thị hàm số.
là đường tiệm cận ngang của đồ thị hàm số. 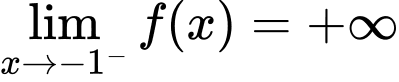 nên đường thẳng
nên đường thẳng 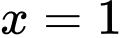 là đường tiệm cận đứng của đồ thị hàm số.
là đường tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có 2 đường tiệm cận. Đáp án: C
Câu 8 [378484]: Đồ thị trong hình vẽ là đồ thị của hàm số: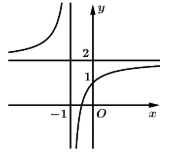

A, 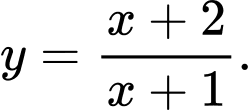
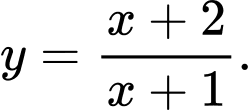
B, 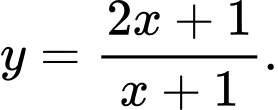
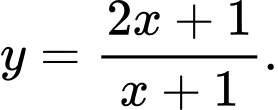
C, 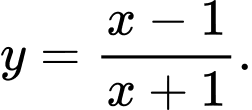
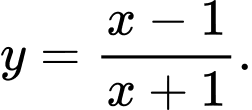
D, 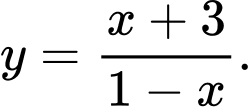
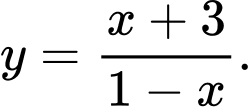
Ta có:
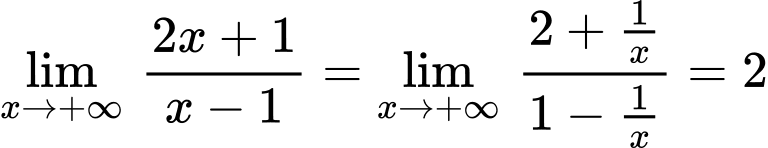 .
.
Suy ra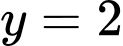 là đường tiệm cận ngang của đồ thị hàm số
là đường tiệm cận ngang của đồ thị hàm số 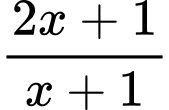
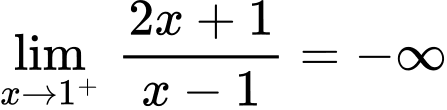 . Vì
. Vì
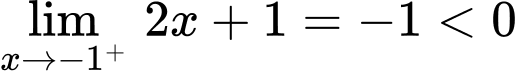 ;
; 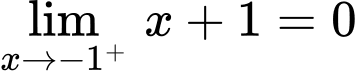 và
và 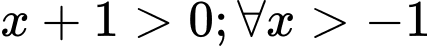 .
.
Suy ra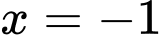 là đường tiệm cận đứng của đồ thị hàm số
là đường tiệm cận đứng của đồ thị hàm số 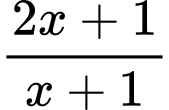 .
.
Dựa vào đồ thị hàm số đã cho, ta thấy hàm số đã cho có đường tiệm cận đứng là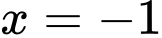 và đường tiệm cận ngang là
và đường tiệm cận ngang là 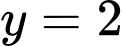 .
.
Nên hàm số cần tìm là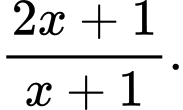
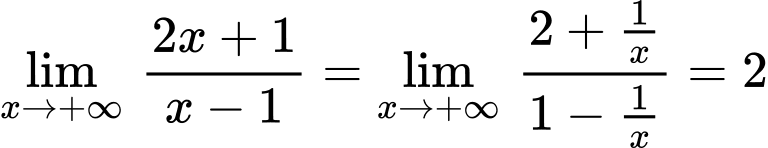 .
.
Suy ra
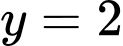 là đường tiệm cận ngang của đồ thị hàm số
là đường tiệm cận ngang của đồ thị hàm số 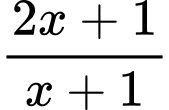
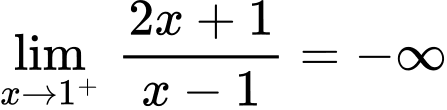 . Vì
. Vì 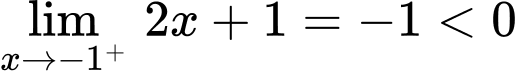 ;
; 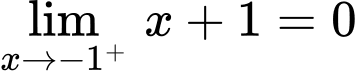 và
và 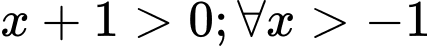 .
.
Suy ra
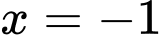 là đường tiệm cận đứng của đồ thị hàm số
là đường tiệm cận đứng của đồ thị hàm số 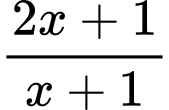 .
.
Dựa vào đồ thị hàm số đã cho, ta thấy hàm số đã cho có đường tiệm cận đứng là
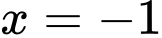 và đường tiệm cận ngang là
và đường tiệm cận ngang là 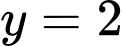 .
.
Nên hàm số cần tìm là
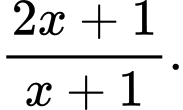
Chọn đáp án B.
Đáp án: B
Câu 9 [774160]: Cho hàm số 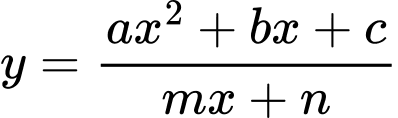 có đồ thị như hình vẽ bên.
có đồ thị như hình vẽ bên.
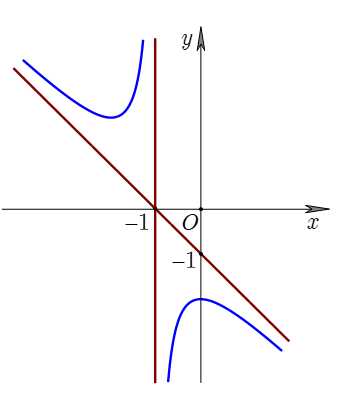
Tiệm cận xiên của đồ thị hàm số đã cho là
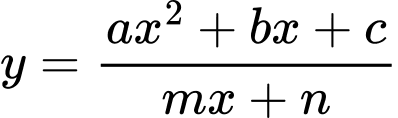 có đồ thị như hình vẽ bên.
có đồ thị như hình vẽ bên.
Tiệm cận xiên của đồ thị hàm số đã cho là
A, 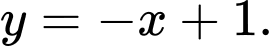
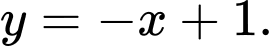
B, 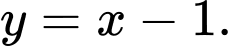
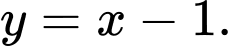
C, 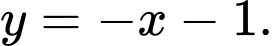
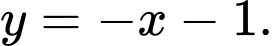
D, 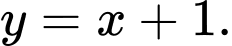
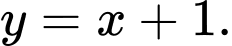
Chọn đáp án C.
Giả sử đường tiệm cận xiên của hàm số có dạng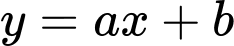
Quan sát đồ thị, ta thấy đường tiệm cận xiên đi qua 2 điểm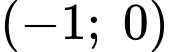 và
và 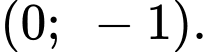
Từ đó, ta có hệ phương trình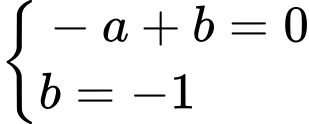
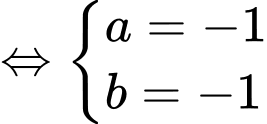
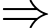 phương trình đường tiệm cận xiên là
phương trình đường tiệm cận xiên là 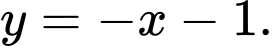 Đáp án: C
Đáp án: C
Giả sử đường tiệm cận xiên của hàm số có dạng
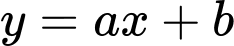
Quan sát đồ thị, ta thấy đường tiệm cận xiên đi qua 2 điểm
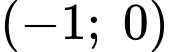 và
và 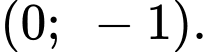
Từ đó, ta có hệ phương trình
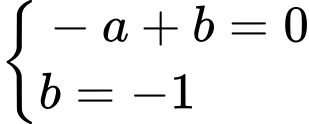
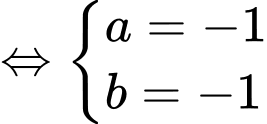
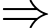 phương trình đường tiệm cận xiên là
phương trình đường tiệm cận xiên là 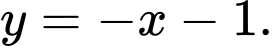 Đáp án: C
Đáp án: C
Câu 10 [544308]: Đồ thị của hàm số nào dưới đây có tiệm cận ngang?
A, 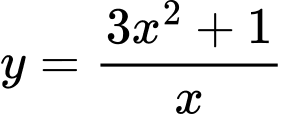 .
.
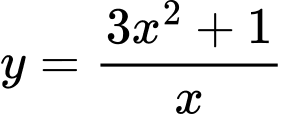 .
.B, 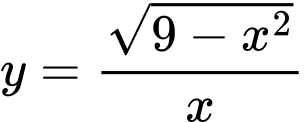 .
.
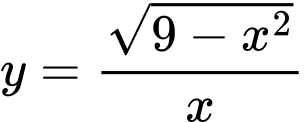 .
.C, 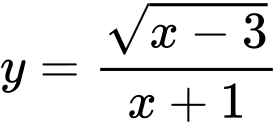 .
.
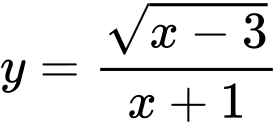 .
. D, 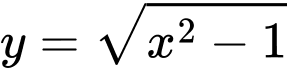 .
.
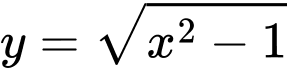 .
.
Chọn C.
Xét hàm số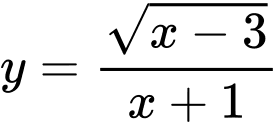 có tập xác định
có tập xác định 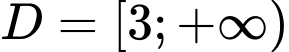 .
.
Ta có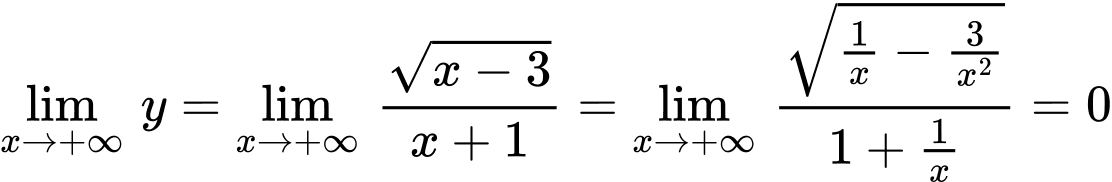 .
.
Do đó đồ thị hàm số có tiệm cận ngang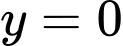 . Đáp án: C
. Đáp án: C
Xét hàm số
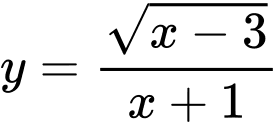 có tập xác định
có tập xác định 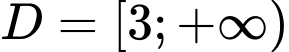 .
.
Ta có
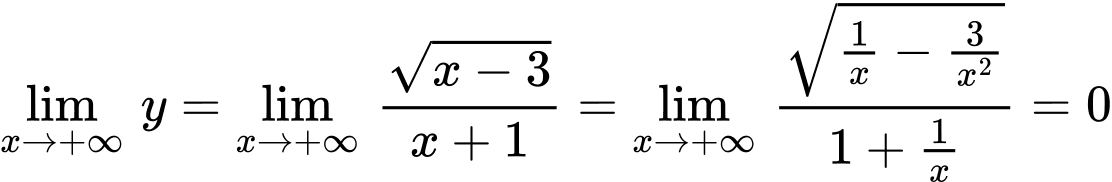 .
.
Do đó đồ thị hàm số có tiệm cận ngang
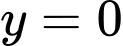 . Đáp án: C
. Đáp án: C
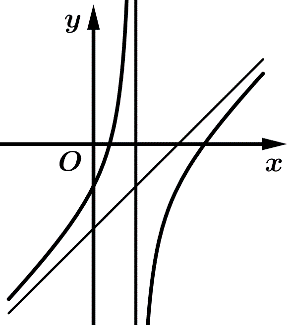
Câu 11 [383010]: Đồ thị trong hình vẽ là đồ thị của hàm số nào trong các hàm số dưới đây?

A, 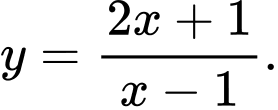
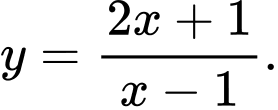
B, 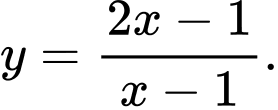
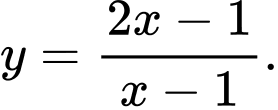
C, 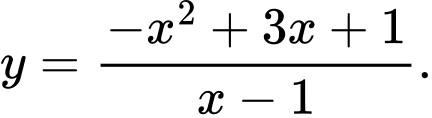
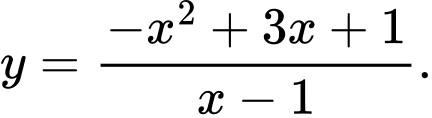
D, 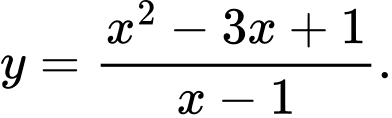
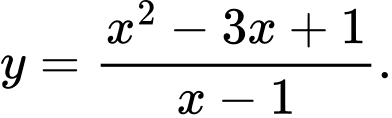
Chọn đáp án D.
Dựa vào hình dạng đồ thị ta thấy hàm số đã cho là hàm số bậc hai trên bậc nhất. Do đó, loại A, B.
Hàm số đã cho không có cực trị và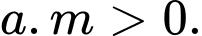 Do đó, loại C. Đáp án: D
Do đó, loại C. Đáp án: D
Dựa vào hình dạng đồ thị ta thấy hàm số đã cho là hàm số bậc hai trên bậc nhất. Do đó, loại A, B.
Hàm số đã cho không có cực trị và
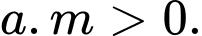 Do đó, loại C. Đáp án: D
Do đó, loại C. Đáp án: D
Câu 12 [358587]: Phương trình đường tiệm cận xiên của đồ thị hàm số 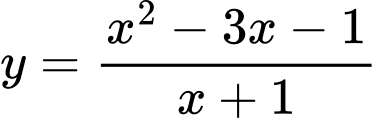 là
là
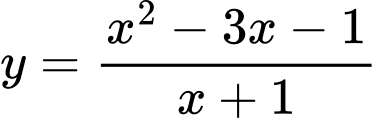 là
là A, 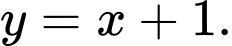
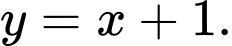
B, 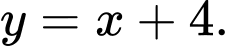
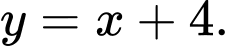
C, 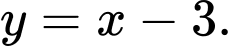
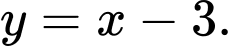
D, 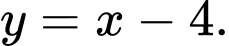
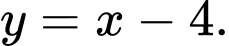
HD: Phương trình tiệm cận xiên của ĐTHS là: 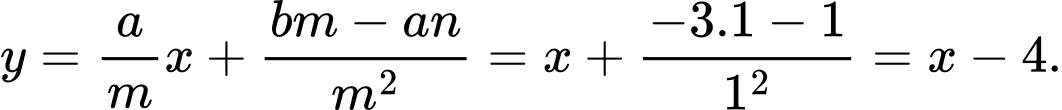 Chọn D. Đáp án: D
Chọn D. Đáp án: D
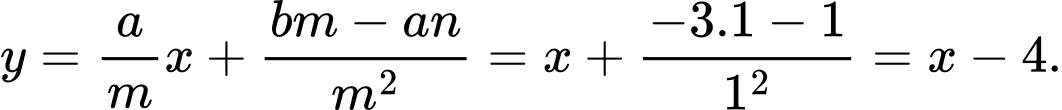 Chọn D. Đáp án: D
Chọn D. Đáp án: D PHẦN II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a),b),c),d) ở mỗi câu học sinh chọn đúng hoặc sai.
Câu 13 [774161]: Xét hàm số bậc ba 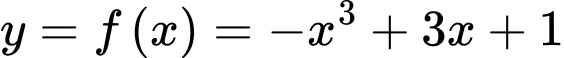 trên
trên 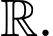
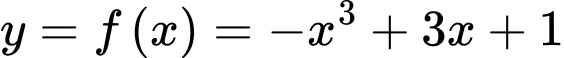 trên
trên 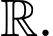
a) Đúng.
b) Sai.
Xét hàm số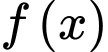 trên
trên 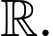
Ta có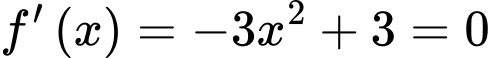
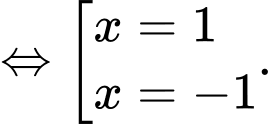
Bảng biến thiên
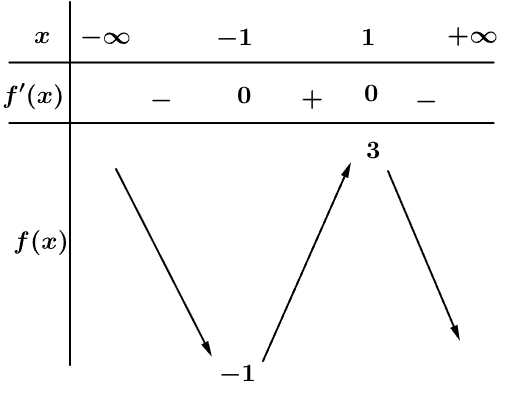
Từ bảng biến thiên, suy ra hàm số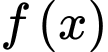 nghịch biến trên khoảng
nghịch biến trên khoảng 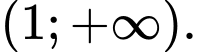
c) Sai.
Dựa vào bảng biến thiên của phần b) suy ra giá trị cực đại của hàm số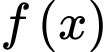 bằng 3.
bằng 3.
d) Sai.
Dựa vào bảng biến thiên của phần b), ta suy ra tọa độ hai điểm cực trị của hàm số là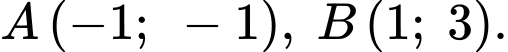
Suy ra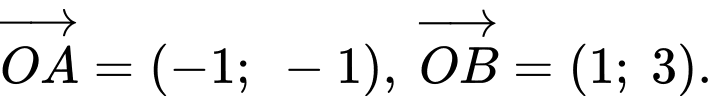
Công thức tính nhanh diện tích tam giác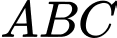 khi biết
khi biết 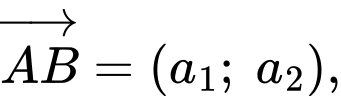
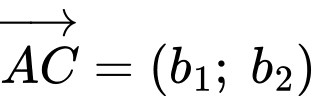 là
là
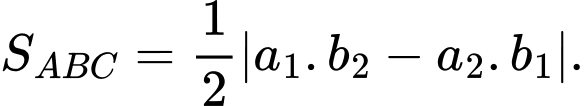
Áp dụng công thức trên, ta có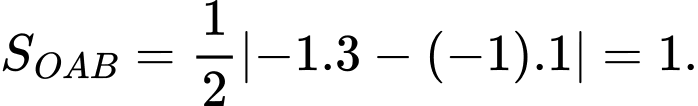
b) Sai.
Xét hàm số
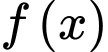 trên
trên 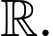
Ta có
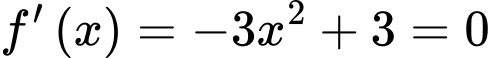
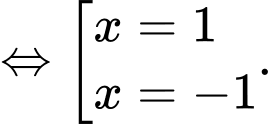
Bảng biến thiên

Từ bảng biến thiên, suy ra hàm số
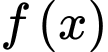 nghịch biến trên khoảng
nghịch biến trên khoảng 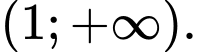
c) Sai.
Dựa vào bảng biến thiên của phần b) suy ra giá trị cực đại của hàm số
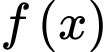 bằng 3.
bằng 3.
d) Sai.
Dựa vào bảng biến thiên của phần b), ta suy ra tọa độ hai điểm cực trị của hàm số là
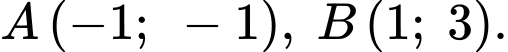
Suy ra
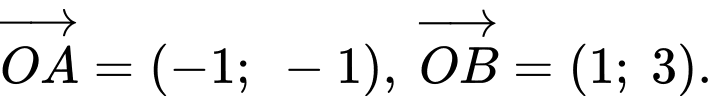
Công thức tính nhanh diện tích tam giác
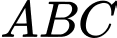 khi biết
khi biết 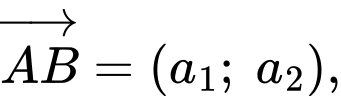
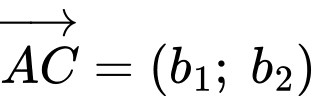 là
là
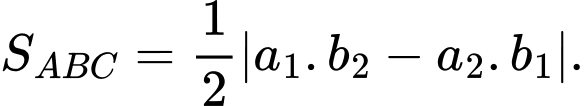
Áp dụng công thức trên, ta có
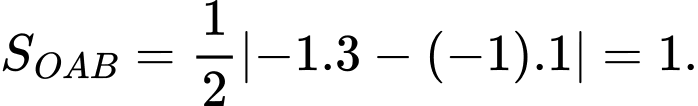
Câu 14 [713213]: Cho hàm số 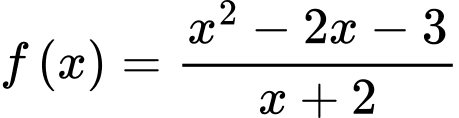 có đồ thị
có đồ thị 
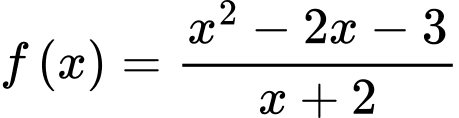 có đồ thị
có đồ thị 
a) Đúng.
TXĐ của hàm số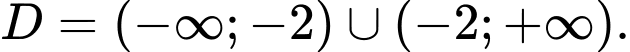
Ta có: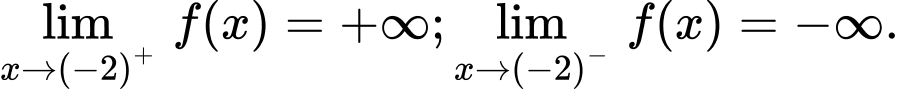
Suy ra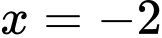 là đường tiệm cận đứng của đồ thị hàm số.
là đường tiệm cận đứng của đồ thị hàm số.
b) Sai.
Ta có: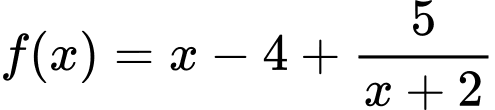 ;
; 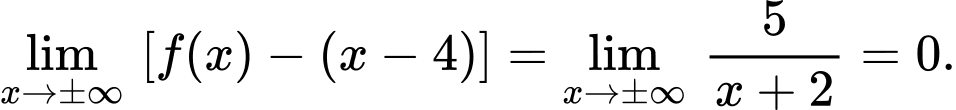
Suy ra đường thẳng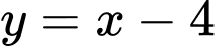 là tiệm cận xiên của đồ thị hàm số.
là tiệm cận xiên của đồ thị hàm số.
c) Đúng.
Tọa độ giao điểm của hai đường tiệm cận của đồ thị hàm số là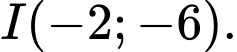
d) Sai.
Đường tiệm cận xiên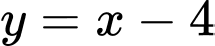 của đồ thị hàm số cắt trục hoành tại điểm
của đồ thị hàm số cắt trục hoành tại điểm 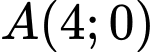 , cắt trục tung tại điểm
, cắt trục tung tại điểm 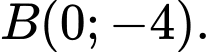
Đường tiệm cận xiên của đồ thị hàm số tạo với hai trục tọa độ tam giác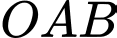 có diện tích
có diện tích 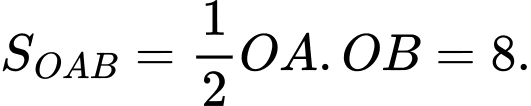
TXĐ của hàm số
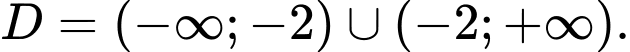
Ta có:
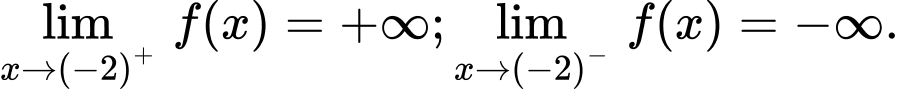
Suy ra
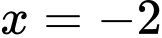 là đường tiệm cận đứng của đồ thị hàm số.
là đường tiệm cận đứng của đồ thị hàm số.b) Sai.
Ta có:
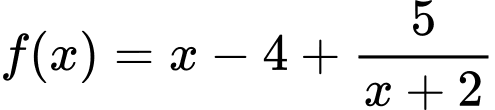 ;
; 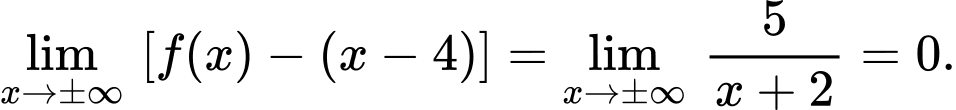
Suy ra đường thẳng
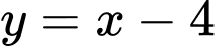 là tiệm cận xiên của đồ thị hàm số.
là tiệm cận xiên của đồ thị hàm số.c) Đúng.
Tọa độ giao điểm của hai đường tiệm cận của đồ thị hàm số là
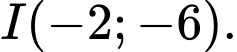
d) Sai.
Đường tiệm cận xiên
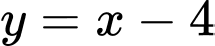 của đồ thị hàm số cắt trục hoành tại điểm
của đồ thị hàm số cắt trục hoành tại điểm 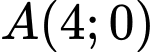 , cắt trục tung tại điểm
, cắt trục tung tại điểm 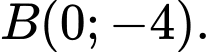
Đường tiệm cận xiên của đồ thị hàm số tạo với hai trục tọa độ tam giác
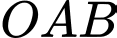 có diện tích
có diện tích 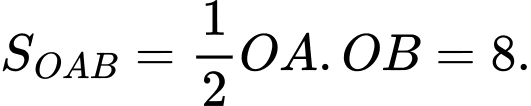
Câu 15 [708368]: Số lượng xe máy điện bán được của một cửa hàng bán xe máy điện trong địa bàn thành phố Vinh trong tháng thứ x được tính theo công thức 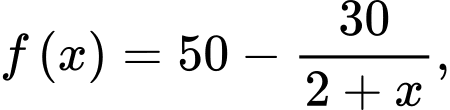 trong đó
trong đó 
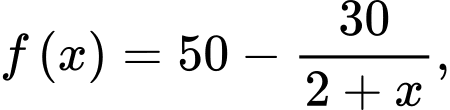 trong đó
trong đó 
a) SAI.
Vì tiệm cận đứng của đồ thị hàm số là đường thẳng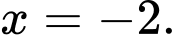
b) SAI.
Vì số lượng xe máy điện của cửa hàng được bán ra trong tháng đầu là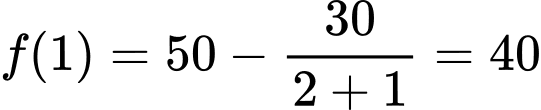 (xe).
(xe).
c) ĐÚNG.
Vì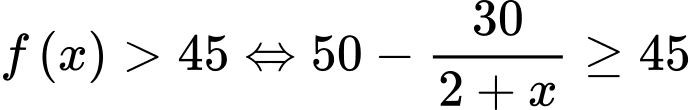
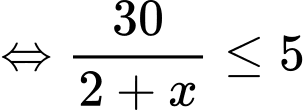
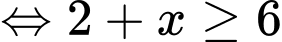
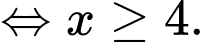
Suy ra để số lương xe bán ra trong tháng đạt mức từ 45 xe trở lên thì phải từ tháng thứ tư trở đi.
d) ĐÚNG.
Vì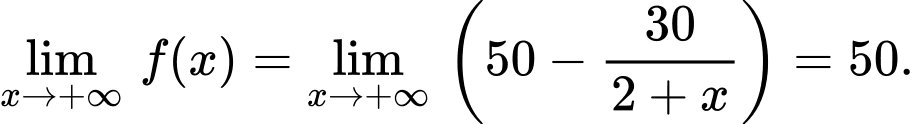
Suy ra tiệm cận ngang của đồ thị hàm số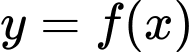 là đường thẳng
là đường thẳng 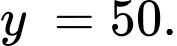
Vậy khi x càng lớn thì số lượng xe bán ra càng tiến gần đến mức 50 xe một tháng.
Vì tiệm cận đứng của đồ thị hàm số là đường thẳng
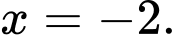
b) SAI.
Vì số lượng xe máy điện của cửa hàng được bán ra trong tháng đầu là
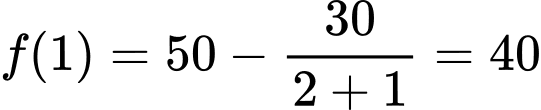 (xe).
(xe).c) ĐÚNG.
Vì
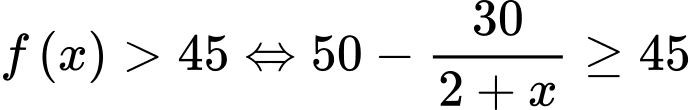
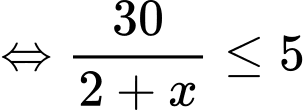
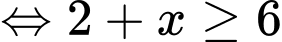
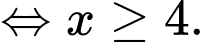
Suy ra để số lương xe bán ra trong tháng đạt mức từ 45 xe trở lên thì phải từ tháng thứ tư trở đi.
d) ĐÚNG.
Vì
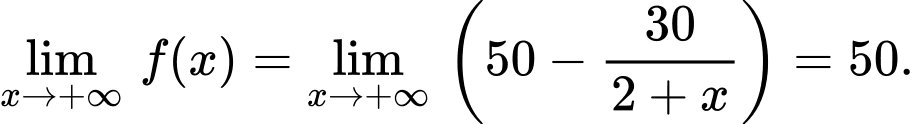
Suy ra tiệm cận ngang của đồ thị hàm số
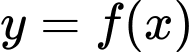 là đường thẳng
là đường thẳng 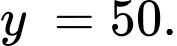
Vậy khi x càng lớn thì số lượng xe bán ra càng tiến gần đến mức 50 xe một tháng.
Câu 16 [774162]: Nhân dịp Tết Trung thu, bác Oanh làm các đèn lồng cho con. Mỗi đèn bác dùng một sợi dây đồng dài 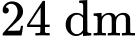 cắt thành 3 đoạn để uốn làm khung đèn. Đoạn thứ nhất bác uốn thành hình vuông
cắt thành 3 đoạn để uốn làm khung đèn. Đoạn thứ nhất bác uốn thành hình vuông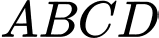 có cạnh bằng
có cạnh bằng  Để làm đáy, hai đoạn còn lại có độ dài bằng nhau uốn thành các đường gấp khúc
Để làm đáy, hai đoạn còn lại có độ dài bằng nhau uốn thành các đường gấp khúc 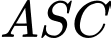 và
và 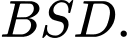 Khung đèn sau khi hoàn thiện có hình dạng là một hình chóp chóp tứ giác đều
Khung đèn sau khi hoàn thiện có hình dạng là một hình chóp chóp tứ giác đều 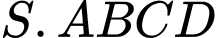 và bề mặt ngoài của đèn được dán giấy màu để trang trí (xem các mối nối, dán là không đáng kể). Khi đó ta có:
và bề mặt ngoài của đèn được dán giấy màu để trang trí (xem các mối nối, dán là không đáng kể). Khi đó ta có:
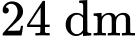 cắt thành 3 đoạn để uốn làm khung đèn. Đoạn thứ nhất bác uốn thành hình vuông
cắt thành 3 đoạn để uốn làm khung đèn. Đoạn thứ nhất bác uốn thành hình vuông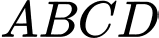 có cạnh bằng
có cạnh bằng  Để làm đáy, hai đoạn còn lại có độ dài bằng nhau uốn thành các đường gấp khúc
Để làm đáy, hai đoạn còn lại có độ dài bằng nhau uốn thành các đường gấp khúc 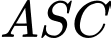 và
và 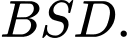 Khung đèn sau khi hoàn thiện có hình dạng là một hình chóp chóp tứ giác đều
Khung đèn sau khi hoàn thiện có hình dạng là một hình chóp chóp tứ giác đều 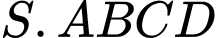 và bề mặt ngoài của đèn được dán giấy màu để trang trí (xem các mối nối, dán là không đáng kể). Khi đó ta có:
và bề mặt ngoài của đèn được dán giấy màu để trang trí (xem các mối nối, dán là không đáng kể). Khi đó ta có: 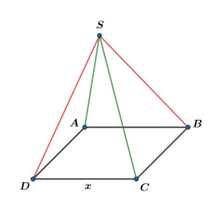
Minh họa chiếc đèn tạo thành như hình trên, với
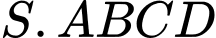 là hình chóp tứ giác đều có đáy
là hình chóp tứ giác đều có đáy 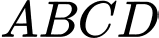 là hình vuông cạnh bằng
là hình vuông cạnh bằng 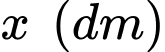 và các mặt bên là các tam giác cân.
và các mặt bên là các tam giác cân.a) Đúng.
Vì
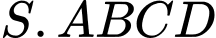 là hình chóp tứ giác đều nên
là hình chóp tứ giác đều nên 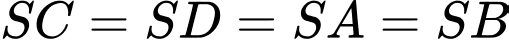
Khi đó ta có
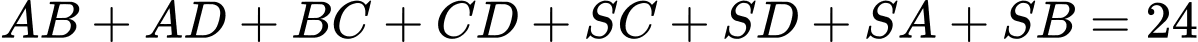
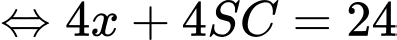


Vậy độ dài cạnh bên của khung đèn bằng
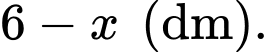
b) Đúng.
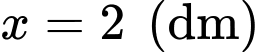 suy ra
suy ra 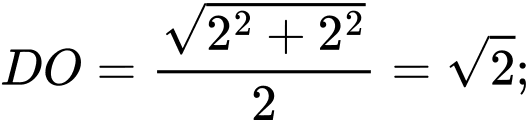
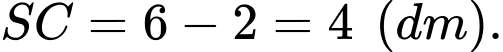
Gọi
 Khi đó
Khi đó 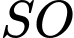 là đường cao của khung đèn.
là đường cao của khung đèn.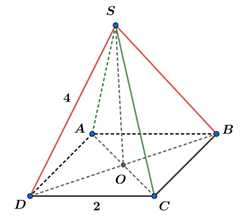
Áp dụng định lý Pytago trong tam giác vuông
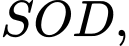 ta có
ta có 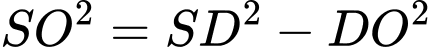
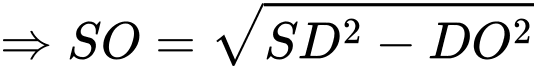
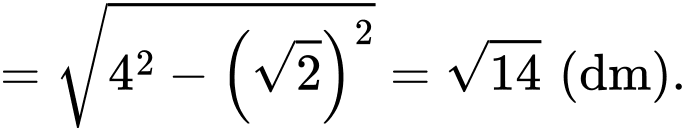
c) Đúng.
Hình chóp tứ giác có 8 cạnh, do đó, khi 8 cạnh của cái lồng đèn này bằng nhau thì độ dài mỗi cạnh là
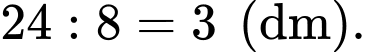
Khi đó diện tích cần dán giấy màu bằng diện tích hình vuông cộng với diện tích của 4 hình tam giác đều (cạnh bằng 3) và bằng
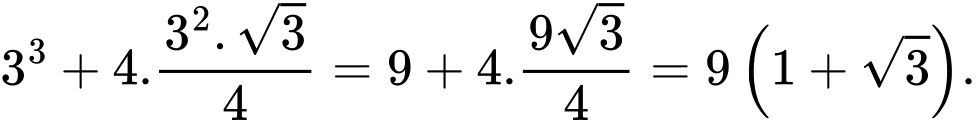
d) Đúng.
Ta có độ dài cạnh đáy bằng
 và độ dài cạnh bên là
và độ dài cạnh bên là 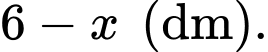 Để tính thể tích của đèn, ta cần tìm được chiều cao của đèn chính là
Để tính thể tích của đèn, ta cần tìm được chiều cao của đèn chính là 
Làm tương tự như phần b) ta có
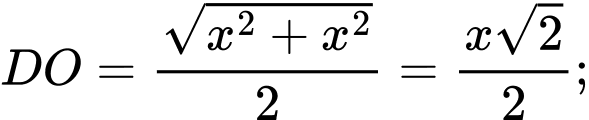
Áp dụng định lý Pytago trong tam giác vuông
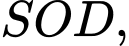 ta có
ta có 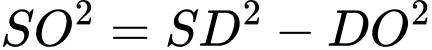
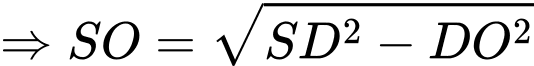
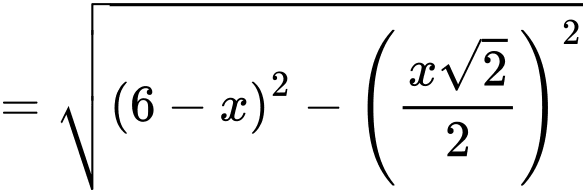
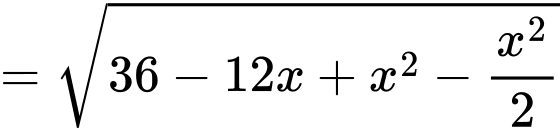
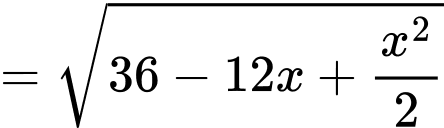
Suy ra thể tích phần không gian của đèn là
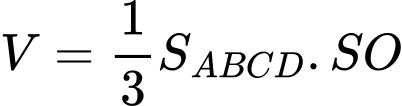
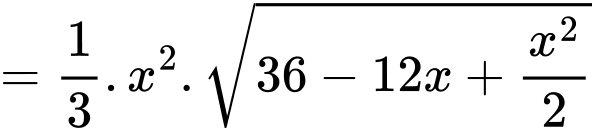
Để tìm ra
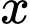 để
để 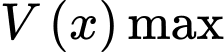 ta có thể dùng 2 cách sau:
ta có thể dùng 2 cách sau:Cách 1: Sử dụng máy tính casio
Cách 2: Khảo sát hàm số
Khảo sát hàm số
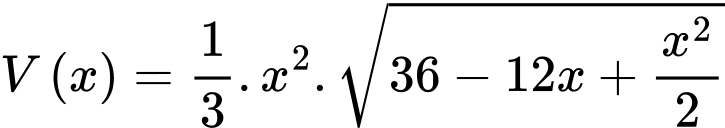 trên khoảng
trên khoảng 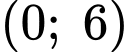
Ta có
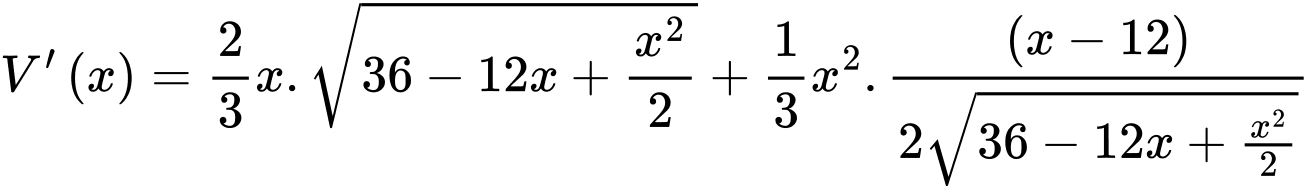
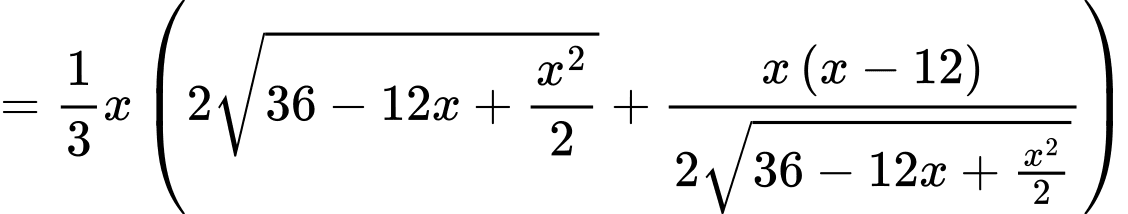
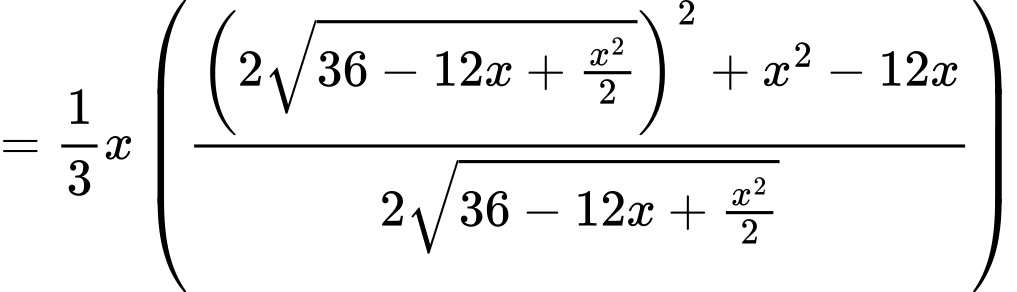
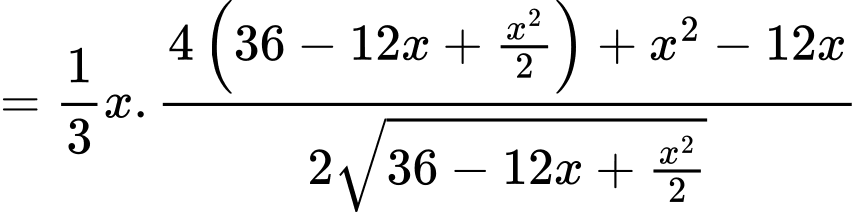
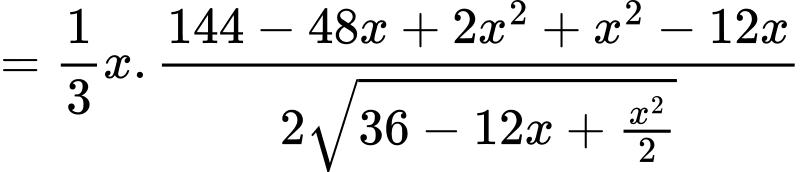
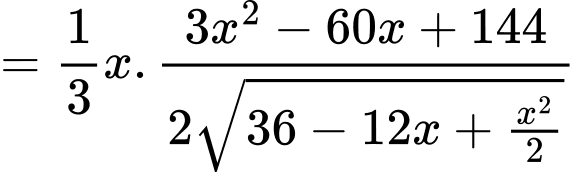
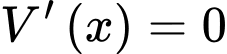
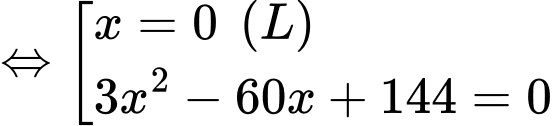
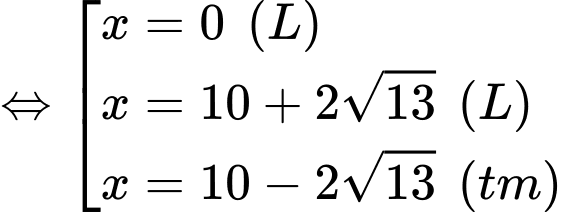
Bảng biến thiên:
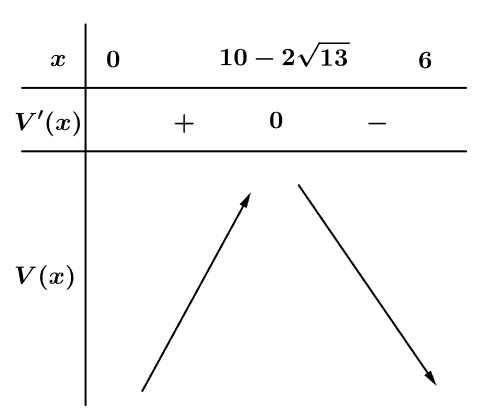
Vậy thể tích phần không gian của đèn lồng lớn nhất khi
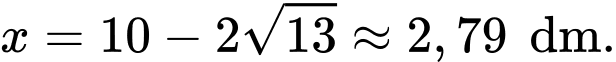
PHẦN III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 17 đến câu 22.
Câu 17 [774163]: Một nhà máy sản xuất ấm đun nước điện thực hiện một nghiên cứu để kiểm soát chi phí. Họ phát hiện ra rằng để sản xuất 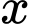 ấm đun nước mỗi ngày thì chi phí cho mỗi ấm đun nước được mô phỏng bằng hàm số
ấm đun nước mỗi ngày thì chi phí cho mỗi ấm đun nước được mô phỏng bằng hàm số 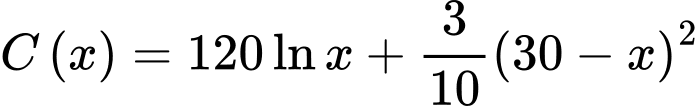 (đơn vị nghìn đồng). Biết rằng mỗi ngày nhà máy sản xuất ít nhất 10 ấm đun nước. Hỏi nhà máy nên sản xuất bao nhiêu ấm đun nước để chi phí cho mỗi ấm nước là nhỏ nhất?
(đơn vị nghìn đồng). Biết rằng mỗi ngày nhà máy sản xuất ít nhất 10 ấm đun nước. Hỏi nhà máy nên sản xuất bao nhiêu ấm đun nước để chi phí cho mỗi ấm nước là nhỏ nhất?
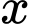 ấm đun nước mỗi ngày thì chi phí cho mỗi ấm đun nước được mô phỏng bằng hàm số
ấm đun nước mỗi ngày thì chi phí cho mỗi ấm đun nước được mô phỏng bằng hàm số 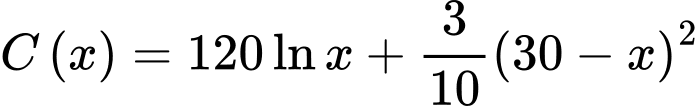 (đơn vị nghìn đồng). Biết rằng mỗi ngày nhà máy sản xuất ít nhất 10 ấm đun nước. Hỏi nhà máy nên sản xuất bao nhiêu ấm đun nước để chi phí cho mỗi ấm nước là nhỏ nhất?
(đơn vị nghìn đồng). Biết rằng mỗi ngày nhà máy sản xuất ít nhất 10 ấm đun nước. Hỏi nhà máy nên sản xuất bao nhiêu ấm đun nước để chi phí cho mỗi ấm nước là nhỏ nhất?
Điền đáp án: 20.
Xét hàm số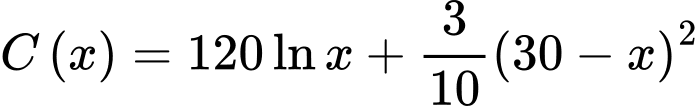 trên nửa khoảng
trên nửa khoảng 
Ta có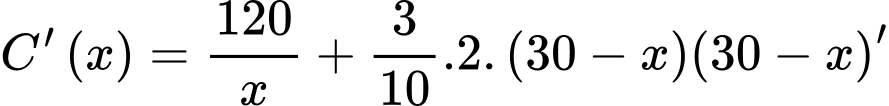
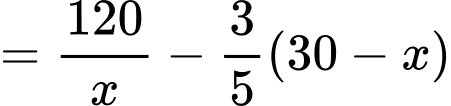
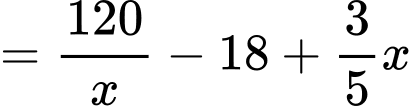
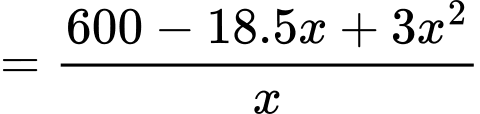
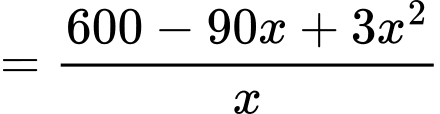
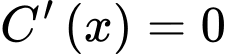
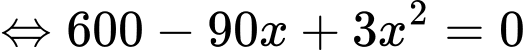
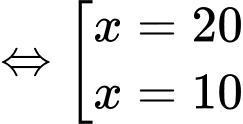
Bảng biến thiên:
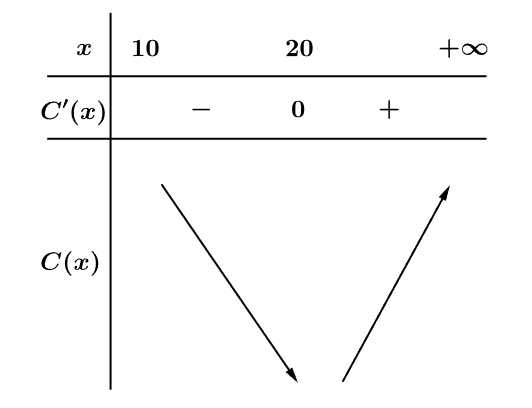
Dựa vào bảng biến thiên, suy ra nhà máy nên sản xuất 20 ấm đun nước mỗi ngày để chi phí cho mỗi ấm nước là nhỏ nhất.
Xét hàm số
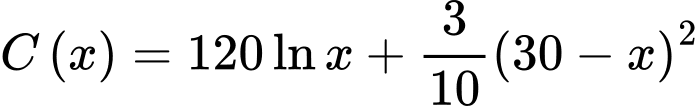 trên nửa khoảng
trên nửa khoảng 
Ta có
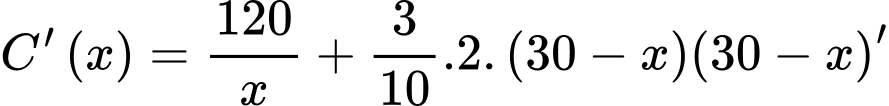
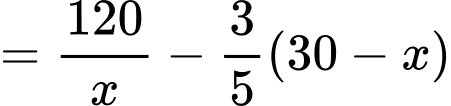
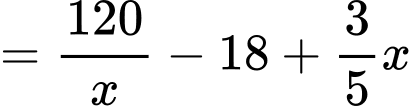
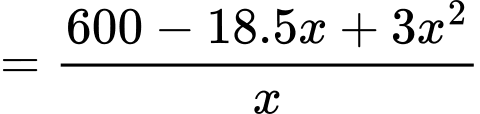
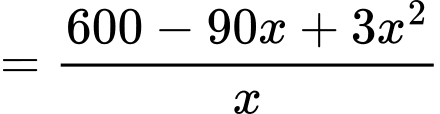
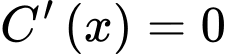
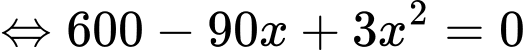
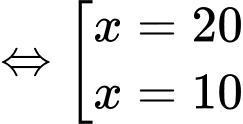
Bảng biến thiên:

Dựa vào bảng biến thiên, suy ra nhà máy nên sản xuất 20 ấm đun nước mỗi ngày để chi phí cho mỗi ấm nước là nhỏ nhất.
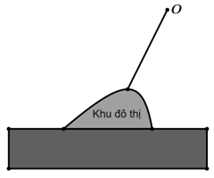
Câu 18 [774166]: Ở ngoài vịnh biển, ngoài xa có một hòn đảo nhỏ. Người ta tiến hành lấn biển để xây một khu đô thị và làm một tuyến cáp treo nối khu đô thị và hòn đảo để phát triển du lịch. Xét trong hệ toạ độ 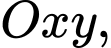 với đơn vị tương ứng 1 km có hòn đảo ở
với đơn vị tương ứng 1 km có hòn đảo ở  thì đường bao của phần đất lấn biển có dạng một phần của đồ thị hàm số
thì đường bao của phần đất lấn biển có dạng một phần của đồ thị hàm số 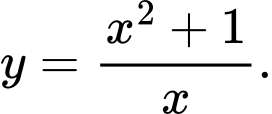 Giả sử tuyến cáp treo được thiết kế nối đảo với đường bao của khu đô thị với độ dài ngắn nhất. Độ dài tuyến cáp treo là bao nhiêu km (làm tròn kết quả đến hàng phần mười).
Giả sử tuyến cáp treo được thiết kế nối đảo với đường bao của khu đô thị với độ dài ngắn nhất. Độ dài tuyến cáp treo là bao nhiêu km (làm tròn kết quả đến hàng phần mười).
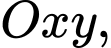 với đơn vị tương ứng 1 km có hòn đảo ở
với đơn vị tương ứng 1 km có hòn đảo ở  thì đường bao của phần đất lấn biển có dạng một phần của đồ thị hàm số
thì đường bao của phần đất lấn biển có dạng một phần của đồ thị hàm số 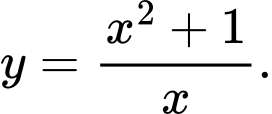 Giả sử tuyến cáp treo được thiết kế nối đảo với đường bao của khu đô thị với độ dài ngắn nhất. Độ dài tuyến cáp treo là bao nhiêu km (làm tròn kết quả đến hàng phần mười).
Giả sử tuyến cáp treo được thiết kế nối đảo với đường bao của khu đô thị với độ dài ngắn nhất. Độ dài tuyến cáp treo là bao nhiêu km (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 2,2.
Gọi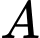 là điểm thuộc đường bao của khu đô thị. Nên suy ra
là điểm thuộc đường bao của khu đô thị. Nên suy ra 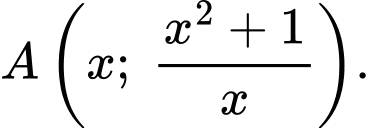
Giả sử độ dài của cáp treo là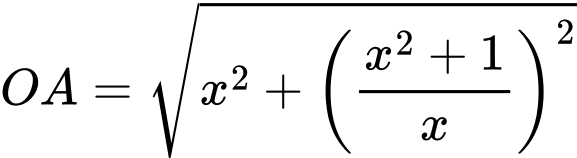 vì độ dài cáp treo là ngắn nhất nên ta cần tìm
vì độ dài cáp treo là ngắn nhất nên ta cần tìm 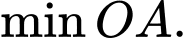
Xét hàm số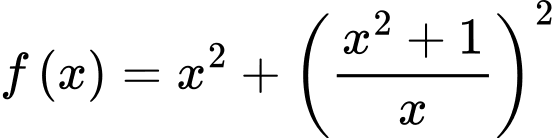 trên khoảng
trên khoảng 
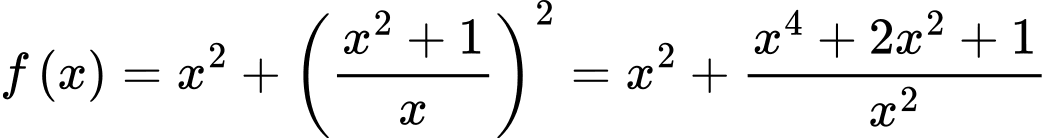
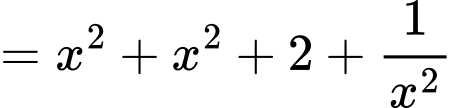
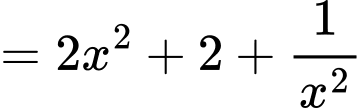
Ta có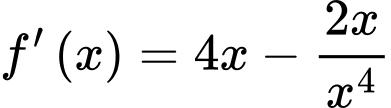
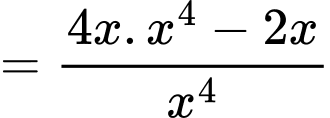
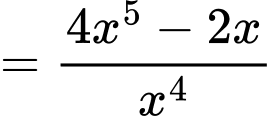
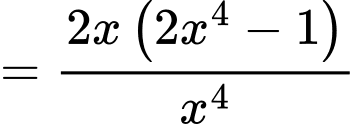
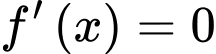
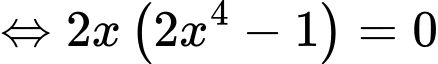
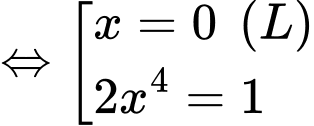
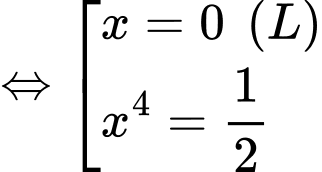
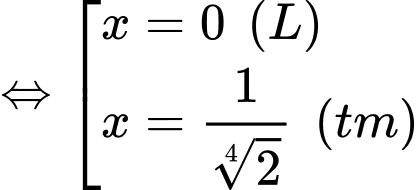
Bảng biến thiên
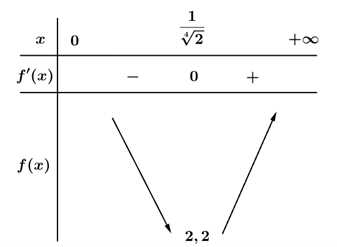
Từ bảng biến thiên, ta suy ra độ dài tuyến cáp treo là 2,2 km.
Gọi
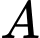 là điểm thuộc đường bao của khu đô thị. Nên suy ra
là điểm thuộc đường bao của khu đô thị. Nên suy ra 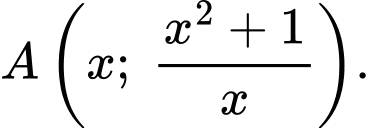
Giả sử độ dài của cáp treo là
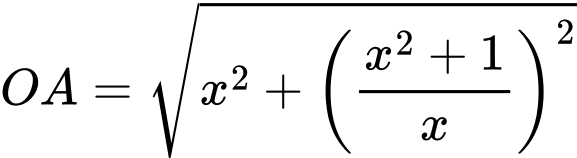 vì độ dài cáp treo là ngắn nhất nên ta cần tìm
vì độ dài cáp treo là ngắn nhất nên ta cần tìm 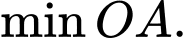
Xét hàm số
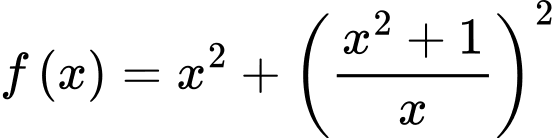 trên khoảng
trên khoảng 
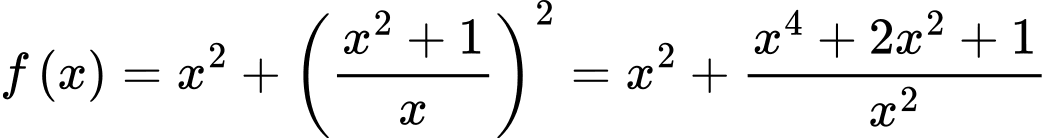
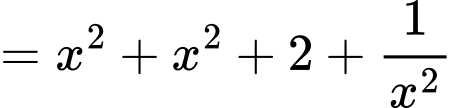
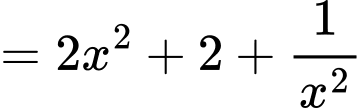
Ta có
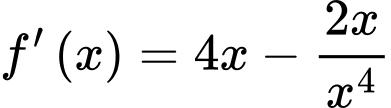
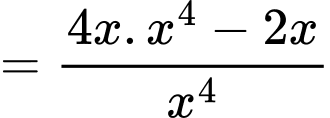
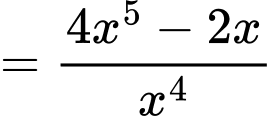
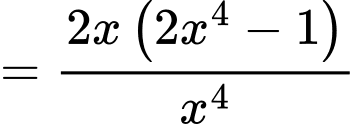
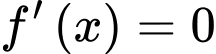
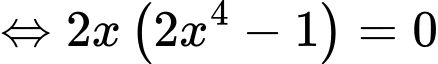
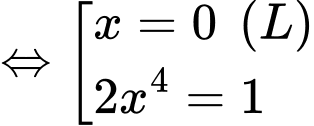
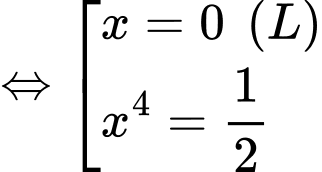
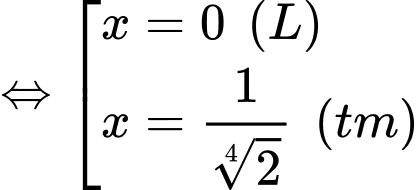
Bảng biến thiên

Từ bảng biến thiên, ta suy ra độ dài tuyến cáp treo là 2,2 km.
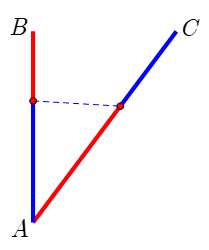
Câu 19 [774169]: Chào đón năm mới  Thành phố trang trí đèn led cho biểu tượng hình chữ
Thành phố trang trí đèn led cho biểu tượng hình chữ  được ghép từ các thanh
được ghép từ các thanh 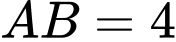 m,
m, 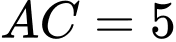 m sao cho tam giác
m sao cho tam giác 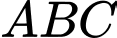 vuông tại
vuông tại 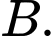 Để tăng hiệu ứng, các kỹ sư đã thiết kế một chuỗi led chạy từ
Để tăng hiệu ứng, các kỹ sư đã thiết kế một chuỗi led chạy từ 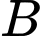 xuống
xuống 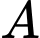 với vận tốc
với vận tốc 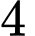 m/phút và một chuỗi led chạy từ
m/phút và một chuỗi led chạy từ 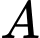 lên
lên  với vận tốc
với vận tốc  m/phút. Sau khi đóng nguồn điện thì cả hai chuỗi led đồng thời xuất phát. Hỏi sau bao nhiêu giây từ thời điểm đóng nguồn điện thì khoảng cách giữa hai điểm sáng đầu tiên của hai chuỗi led là nhỏ nhất?
m/phút. Sau khi đóng nguồn điện thì cả hai chuỗi led đồng thời xuất phát. Hỏi sau bao nhiêu giây từ thời điểm đóng nguồn điện thì khoảng cách giữa hai điểm sáng đầu tiên của hai chuỗi led là nhỏ nhất?
 Thành phố trang trí đèn led cho biểu tượng hình chữ
Thành phố trang trí đèn led cho biểu tượng hình chữ  được ghép từ các thanh
được ghép từ các thanh 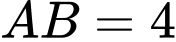 m,
m, 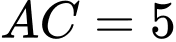 m sao cho tam giác
m sao cho tam giác 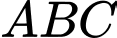 vuông tại
vuông tại 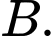 Để tăng hiệu ứng, các kỹ sư đã thiết kế một chuỗi led chạy từ
Để tăng hiệu ứng, các kỹ sư đã thiết kế một chuỗi led chạy từ 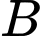 xuống
xuống 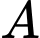 với vận tốc
với vận tốc  m/phút và một chuỗi led chạy từ
m/phút và một chuỗi led chạy từ  lên
lên  với vận tốc
với vận tốc  m/phút. Sau khi đóng nguồn điện thì cả hai chuỗi led đồng thời xuất phát. Hỏi sau bao nhiêu giây từ thời điểm đóng nguồn điện thì khoảng cách giữa hai điểm sáng đầu tiên của hai chuỗi led là nhỏ nhất?
m/phút. Sau khi đóng nguồn điện thì cả hai chuỗi led đồng thời xuất phát. Hỏi sau bao nhiêu giây từ thời điểm đóng nguồn điện thì khoảng cách giữa hai điểm sáng đầu tiên của hai chuỗi led là nhỏ nhất?
Điền đáp án: 16.
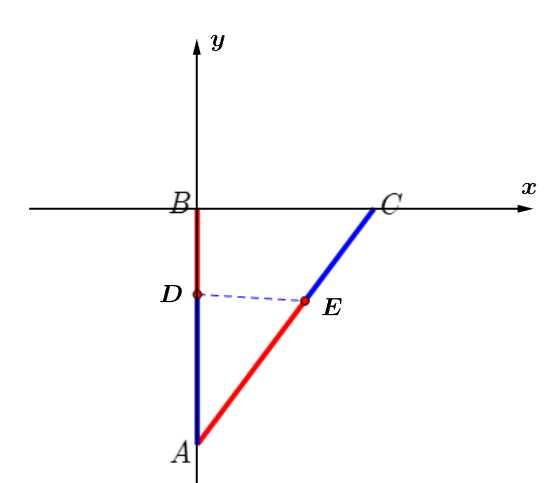
Vì tam giác vuông tại
vuông tại 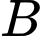 nên ta ghép hệ trục tọa độ
nên ta ghép hệ trục tọa độ 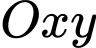 như hình vẽ, với
như hình vẽ, với 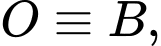
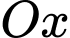 trùng với
trùng với 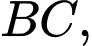 trục
trục 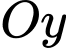 trùng với cạnh
trùng với cạnh  (mỗi đơn vị trên trục là 1 m).
(mỗi đơn vị trên trục là 1 m).
Khi đó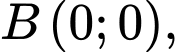
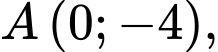
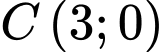
Gọi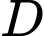 điểm sáng đầu tiên của chuỗi led
điểm sáng đầu tiên của chuỗi led 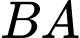 và
và 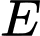 điểm sáng đầu tiên của chuỗi led
điểm sáng đầu tiên của chuỗi led 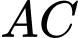 sau khi đóng nguồn điện.
sau khi đóng nguồn điện.
Vì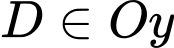 và chuỗi led chạy từ
và chuỗi led chạy từ 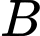 xuống
xuống 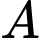 với vận tốc
với vận tốc 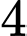 m/phút nên
m/phút nên 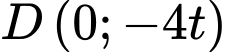 với
với 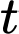 là thời gian được tính bằng phút.
là thời gian được tính bằng phút.
Vì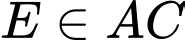 và chuỗi led chạy từ
và chuỗi led chạy từ 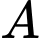 lên
lên  với vận tốc
với vận tốc 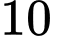 m/phút nên
m/phút nên 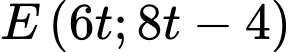 với
với 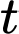 là thời gian được tính bằng phút.
là thời gian được tính bằng phút.
Ta có khoảng cách giữa hai điểm sáng đầu tiên của hai chuỗi led là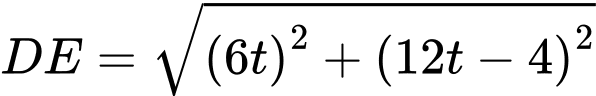

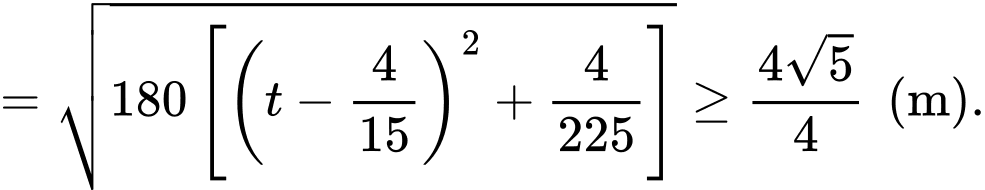
Dấu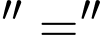 xảy ra khi
xảy ra khi 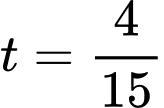 phút
phút 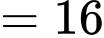 giây.
giây.
Vậy sau 16 giây từ thời điểm đóng nguồn điện thì khoảng cách giữa hai điểm sáng đầu tiên của hai chuỗi led là nhỏ nhất.

Vì tam giác
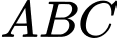 vuông tại
vuông tại 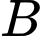 nên ta ghép hệ trục tọa độ
nên ta ghép hệ trục tọa độ 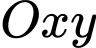 như hình vẽ, với
như hình vẽ, với 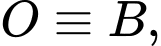
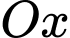 trùng với
trùng với 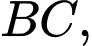 trục
trục 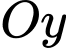 trùng với cạnh
trùng với cạnh  (mỗi đơn vị trên trục là 1 m).
(mỗi đơn vị trên trục là 1 m).
Khi đó
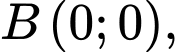
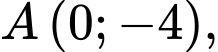
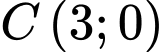
Gọi
 điểm sáng đầu tiên của chuỗi led
điểm sáng đầu tiên của chuỗi led 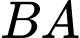 và
và 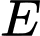 điểm sáng đầu tiên của chuỗi led
điểm sáng đầu tiên của chuỗi led 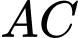 sau khi đóng nguồn điện.
sau khi đóng nguồn điện.
Vì
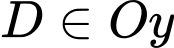 và chuỗi led chạy từ
và chuỗi led chạy từ 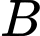 xuống
xuống 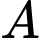 với vận tốc
với vận tốc 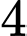 m/phút nên
m/phút nên 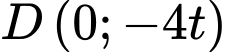 với
với 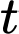 là thời gian được tính bằng phút.
là thời gian được tính bằng phút.
Vì
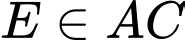 và chuỗi led chạy từ
và chuỗi led chạy từ 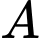 lên
lên  với vận tốc
với vận tốc 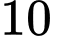 m/phút nên
m/phút nên 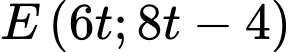 với
với 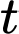 là thời gian được tính bằng phút.
là thời gian được tính bằng phút.
Ta có khoảng cách giữa hai điểm sáng đầu tiên của hai chuỗi led là
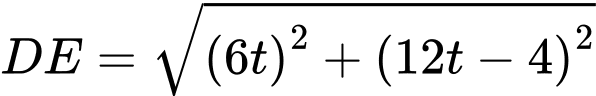

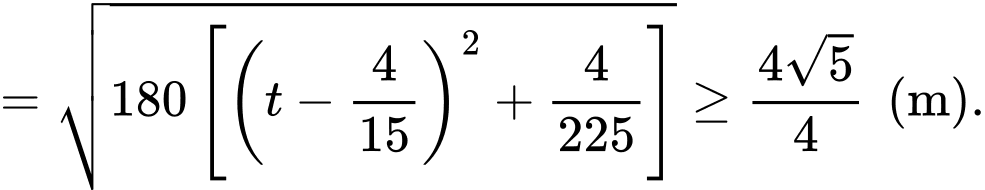
Dấu
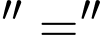 xảy ra khi
xảy ra khi 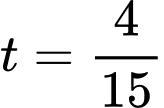 phút
phút 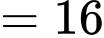 giây.
giây.
Vậy sau 16 giây từ thời điểm đóng nguồn điện thì khoảng cách giữa hai điểm sáng đầu tiên của hai chuỗi led là nhỏ nhất.
Câu 20 [358940]: Có hai xã 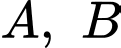 cùng ở một bên bờ sông Lam, khoảng cách từ hai xã đó đến bờ sông lần lượt là
cùng ở một bên bờ sông Lam, khoảng cách từ hai xã đó đến bờ sông lần lượt là 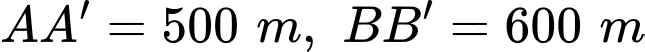 và người ta đo được
và người ta đo được 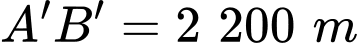 (Hình 37). Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông Lam cho người dân hai xã. Để tiết kiệm chi phí, các kĩ sư cần phải chọn vị trí
(Hình 37). Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông Lam cho người dân hai xã. Để tiết kiệm chi phí, các kĩ sư cần phải chọn vị trí 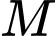 của trạm cung cấp nước sạch đó trên đoạn
của trạm cung cấp nước sạch đó trên đoạn 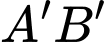 sao cho tổng khoảng cách từ hai xã đến vị trí
sao cho tổng khoảng cách từ hai xã đến vị trí  là nhỏ nhất. Hãy tìm giá trị nhỏ nhất của tổng khoảng cách đó (làm tròn kết quả đến hàng đơn vị của mét).
là nhỏ nhất. Hãy tìm giá trị nhỏ nhất của tổng khoảng cách đó (làm tròn kết quả đến hàng đơn vị của mét).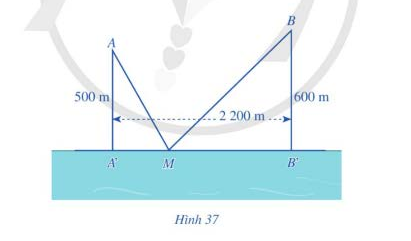
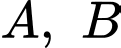 cùng ở một bên bờ sông Lam, khoảng cách từ hai xã đó đến bờ sông lần lượt là
cùng ở một bên bờ sông Lam, khoảng cách từ hai xã đó đến bờ sông lần lượt là 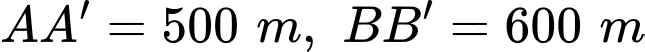 và người ta đo được
và người ta đo được 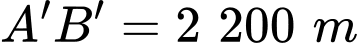 (Hình 37). Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông Lam cho người dân hai xã. Để tiết kiệm chi phí, các kĩ sư cần phải chọn vị trí
(Hình 37). Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông Lam cho người dân hai xã. Để tiết kiệm chi phí, các kĩ sư cần phải chọn vị trí 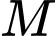 của trạm cung cấp nước sạch đó trên đoạn
của trạm cung cấp nước sạch đó trên đoạn 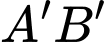 sao cho tổng khoảng cách từ hai xã đến vị trí
sao cho tổng khoảng cách từ hai xã đến vị trí 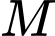 là nhỏ nhất. Hãy tìm giá trị nhỏ nhất của tổng khoảng cách đó (làm tròn kết quả đến hàng đơn vị của mét).
là nhỏ nhất. Hãy tìm giá trị nhỏ nhất của tổng khoảng cách đó (làm tròn kết quả đến hàng đơn vị của mét).
Điền đáp án: 2460.
Đặt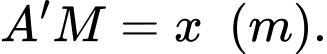
Suy ra: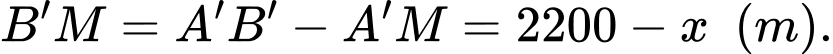
Rõ ràng,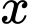 phảithỏa mãn điều kiện
phảithỏa mãn điều kiện 
Áp dụng định lí Pythagore ta tính được: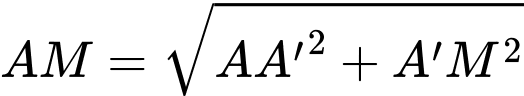
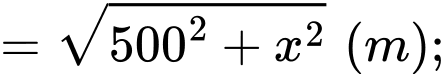
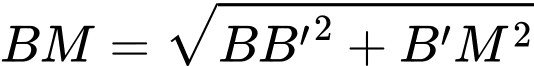
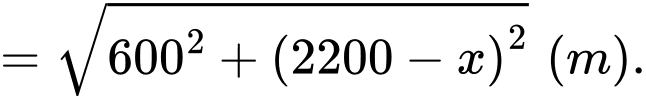
Tổng khoảng cách từ hai vị trí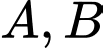 đến vị trí
đến vị trí 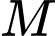 là:
là: 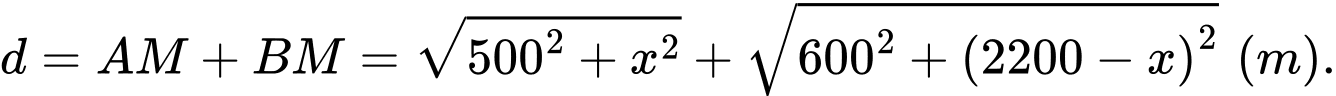
Xét hàm số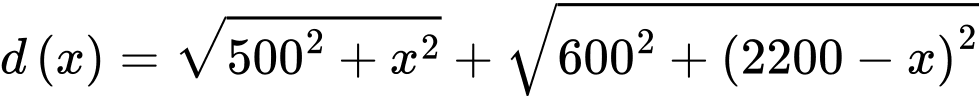 với
với 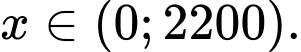
Ta có: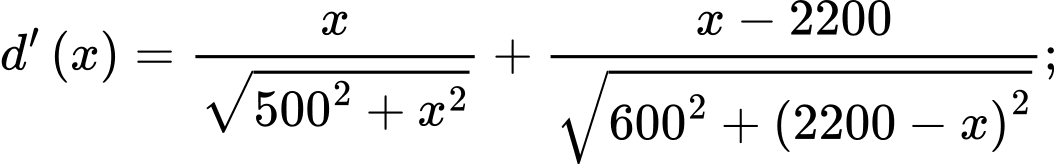 Trên khoảng
Trên khoảng 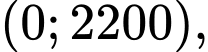 ta thấy
ta thấy 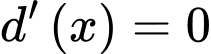 khi
khi 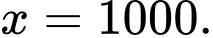
Bảng biến thiên:
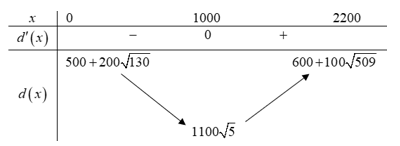
Dựa vào bảng biếnthiên, ta thấy hàm số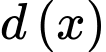 đạt giá trị nhỏ nhất bằng
đạt giá trị nhỏ nhất bằng 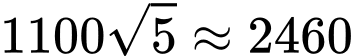 khi
khi 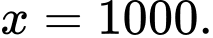
Vậy giá trị nhỏ nhất của tổng khoảng cách cần tìm là 2460 m.
Đặt
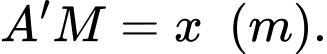
Suy ra:
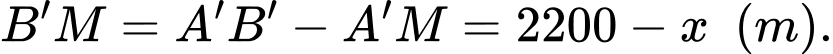
Rõ ràng,
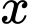 phảithỏa mãn điều kiện
phảithỏa mãn điều kiện 
Áp dụng định lí Pythagore ta tính được:
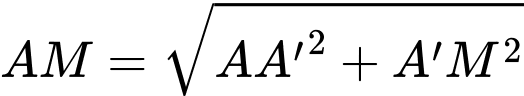
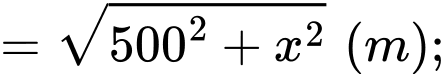
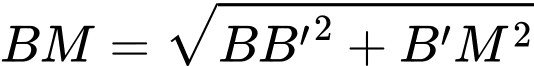
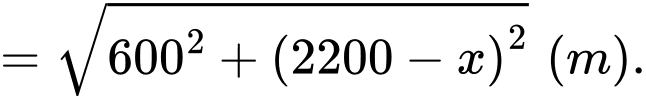
Tổng khoảng cách từ hai vị trí
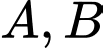 đến vị trí
đến vị trí 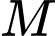 là:
là: 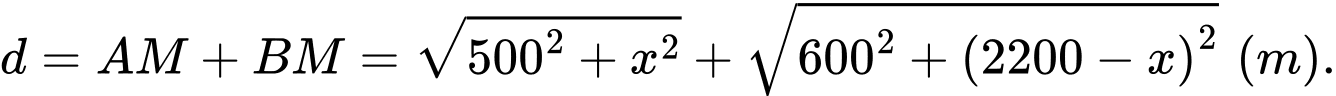
Xét hàm số
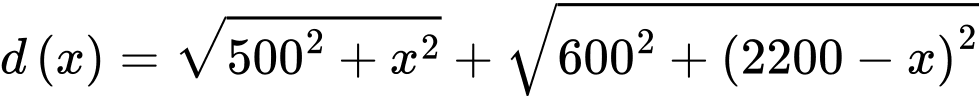 với
với 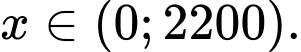
Ta có:
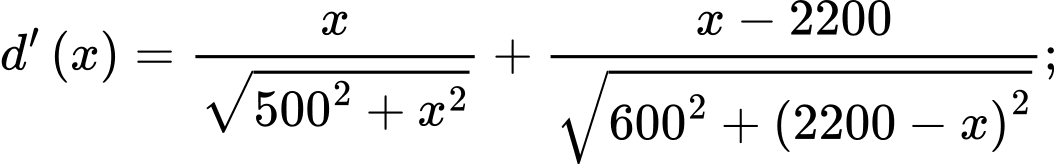 Trên khoảng
Trên khoảng 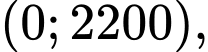 ta thấy
ta thấy 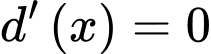 khi
khi 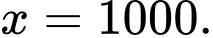
Bảng biến thiên:

Dựa vào bảng biếnthiên, ta thấy hàm số
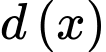 đạt giá trị nhỏ nhất bằng
đạt giá trị nhỏ nhất bằng 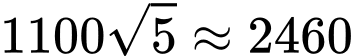 khi
khi 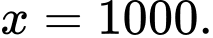
Vậy giá trị nhỏ nhất của tổng khoảng cách cần tìm là 2460 m.
Câu 21 [774172]: Trong hệ toạ độ 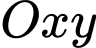 (đơn vị mỗi trục là feet (ft)), người ta dùng hàm số bậc ba
(đơn vị mỗi trục là feet (ft)), người ta dùng hàm số bậc ba 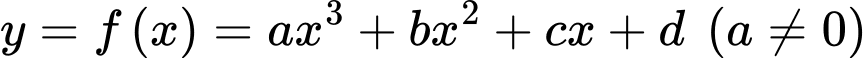 trên đoạn
trên đoạn 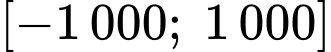 để mô phỏng một đoạn đường cao tốc. Giả sử bằng cách đo đạc ta có
để mô phỏng một đoạn đường cao tốc. Giả sử bằng cách đo đạc ta có 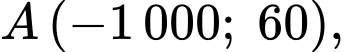
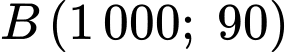 và giao điểm của đồ thị hàm số
và giao điểm của đồ thị hàm số 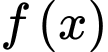 với trục tung cách gốc toạ độ 50 ft (xem hình vẽ). Biết độ dốc tại một điểm
với trục tung cách gốc toạ độ 50 ft (xem hình vẽ). Biết độ dốc tại một điểm 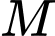 trên con đường bằng với
trên con đường bằng với 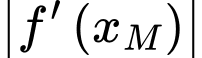 và độ dốc tại điểm
và độ dốc tại điểm 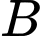 là
là 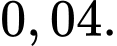 Hỏi độ dốc tại điểm
Hỏi độ dốc tại điểm 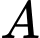 trên con đường bằng bao nhiêu?
trên con đường bằng bao nhiêu?
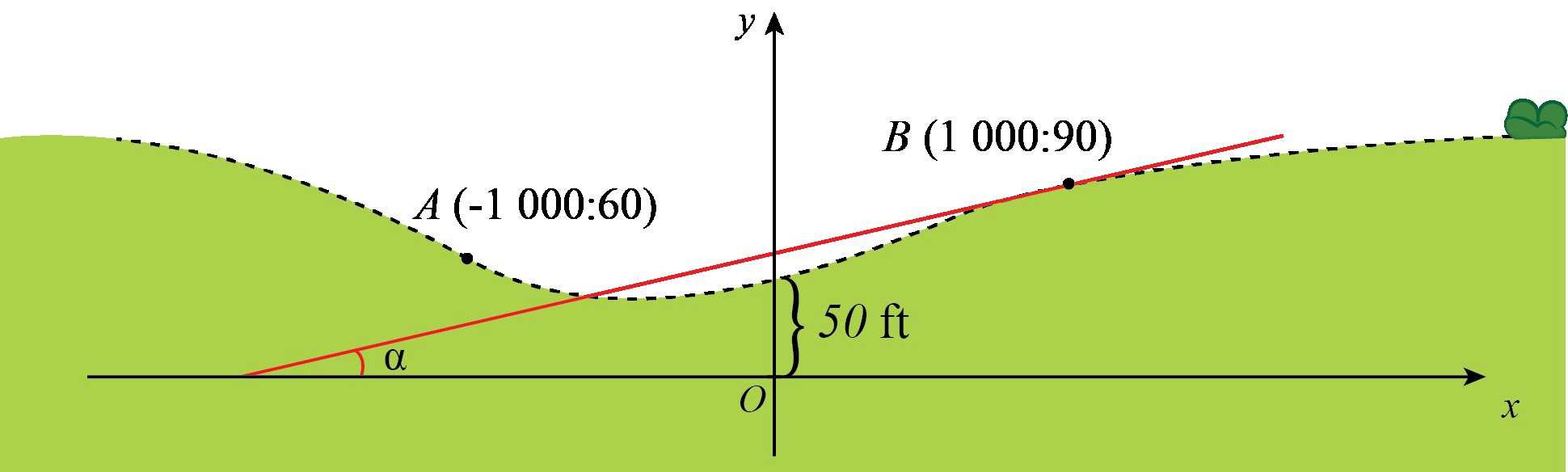
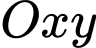 (đơn vị mỗi trục là feet (ft)), người ta dùng hàm số bậc ba
(đơn vị mỗi trục là feet (ft)), người ta dùng hàm số bậc ba 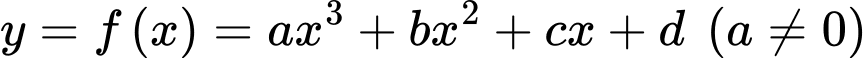 trên đoạn
trên đoạn 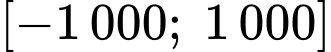 để mô phỏng một đoạn đường cao tốc. Giả sử bằng cách đo đạc ta có
để mô phỏng một đoạn đường cao tốc. Giả sử bằng cách đo đạc ta có 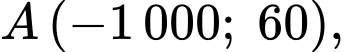
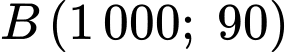 và giao điểm của đồ thị hàm số
và giao điểm của đồ thị hàm số 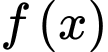 với trục tung cách gốc toạ độ 50 ft (xem hình vẽ). Biết độ dốc tại một điểm
với trục tung cách gốc toạ độ 50 ft (xem hình vẽ). Biết độ dốc tại một điểm 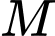 trên con đường bằng với
trên con đường bằng với 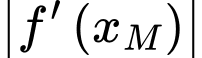 và độ dốc tại điểm
và độ dốc tại điểm 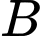 là
là 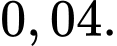 Hỏi độ dốc tại điểm
Hỏi độ dốc tại điểm 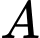 trên con đường bằng bao nhiêu?
trên con đường bằng bao nhiêu?
Điền đáp án: 0,06.
Vì độ dốc tại một điểm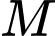 trên con đường bằng với
trên con đường bằng với 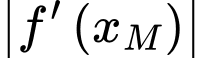 do đó độ dốc tại điểm
do đó độ dốc tại điểm 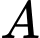 trên con đường bằng
trên con đường bằng 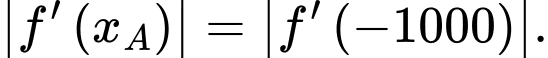 Do đó, để tính được
Do đó, để tính được 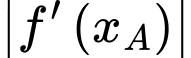 ta cần đi tìm hàm số
ta cần đi tìm hàm số 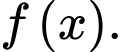
Ta có đồ thị hàm số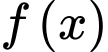 đi qua điểm
đi qua điểm 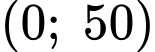
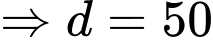
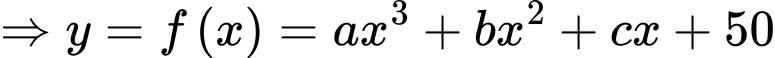
Tiếp nữa, đồ thị hàm số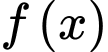 đi qua hai điểm
đi qua hai điểm 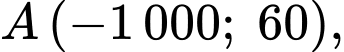
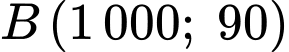 nên ta có hệ phương trình
nên ta có hệ phương trình 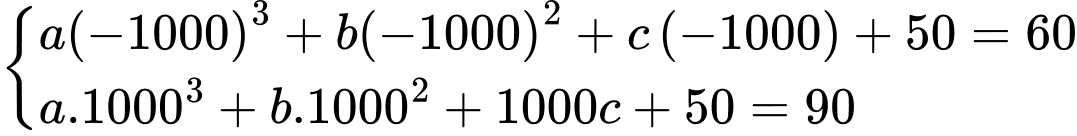
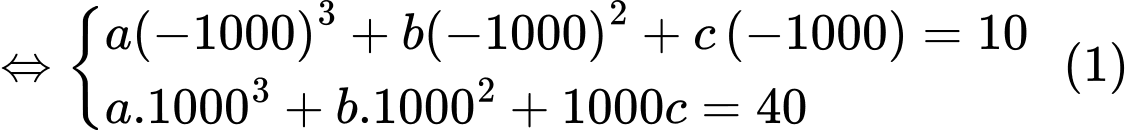
Ta có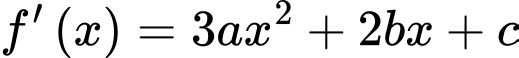
Theo giả thiết: độ dốc tại điểm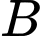 là 0,04
là 0,04 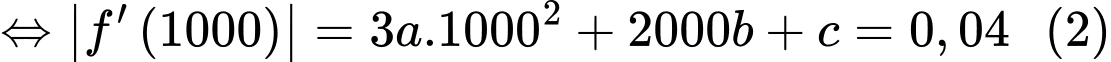
Từ (1) và (2) ta được một hệ phương trình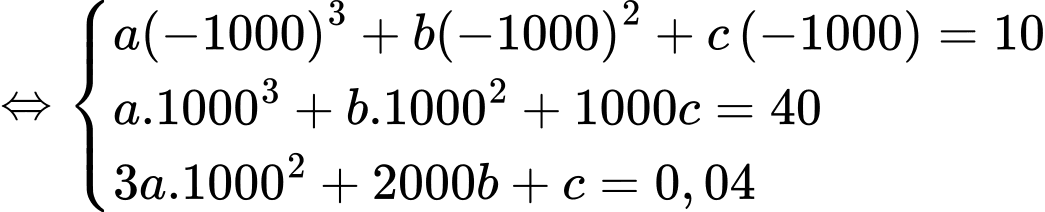
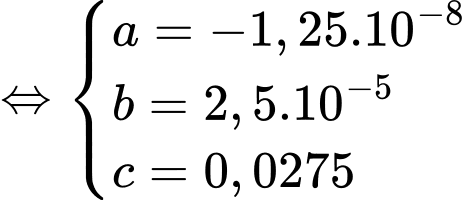
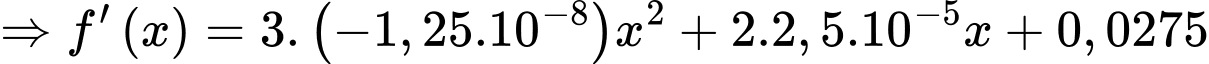
Vậy độ dốc tại điểm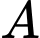 trên con đường bằng
trên con đường bằng 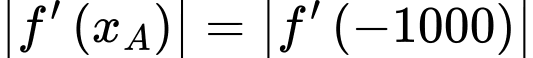
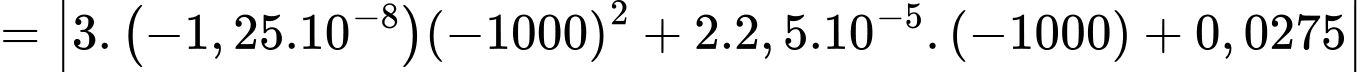
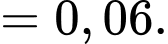
Vì độ dốc tại một điểm
 trên con đường bằng với
trên con đường bằng với 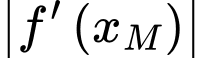 do đó độ dốc tại điểm
do đó độ dốc tại điểm 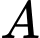 trên con đường bằng
trên con đường bằng 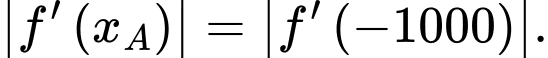 Do đó, để tính được
Do đó, để tính được 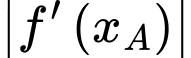 ta cần đi tìm hàm số
ta cần đi tìm hàm số 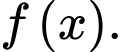
Ta có đồ thị hàm số
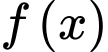 đi qua điểm
đi qua điểm 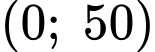
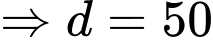
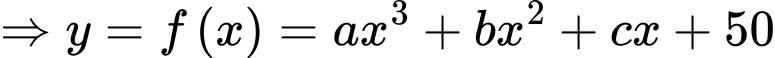
Tiếp nữa, đồ thị hàm số
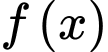 đi qua hai điểm
đi qua hai điểm 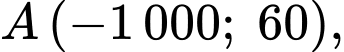
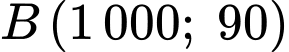 nên ta có hệ phương trình
nên ta có hệ phương trình 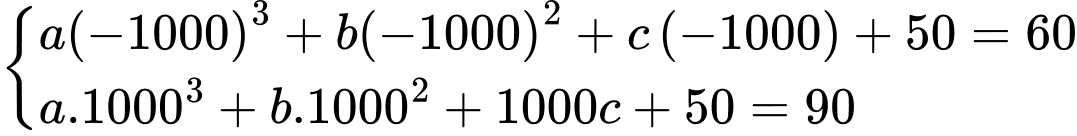
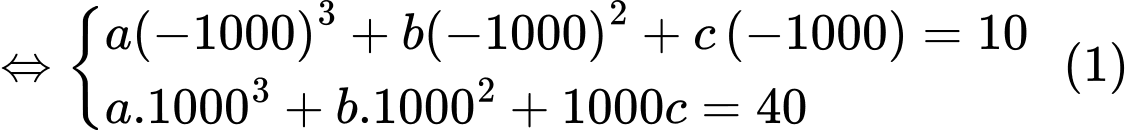
Ta có
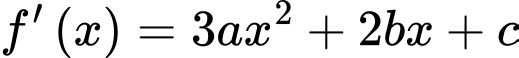
Theo giả thiết: độ dốc tại điểm
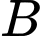 là 0,04
là 0,04 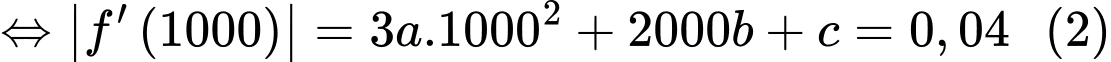
Từ (1) và (2) ta được một hệ phương trình
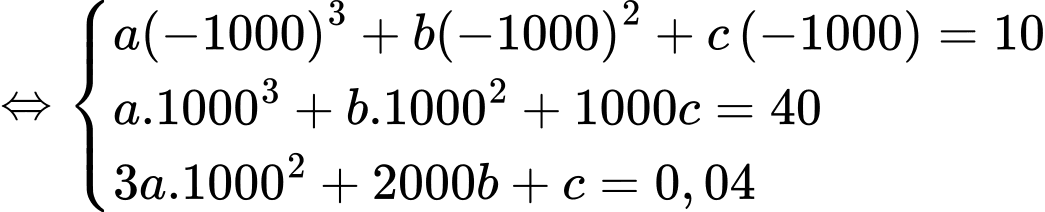
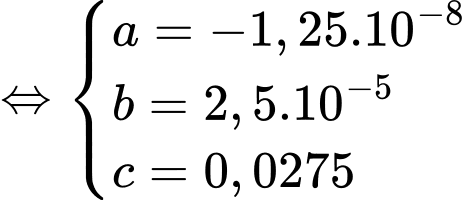
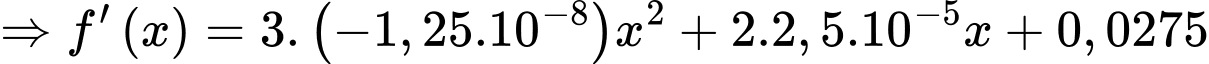
Vậy độ dốc tại điểm
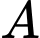 trên con đường bằng
trên con đường bằng 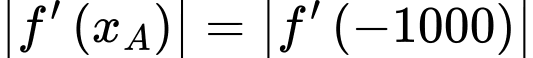
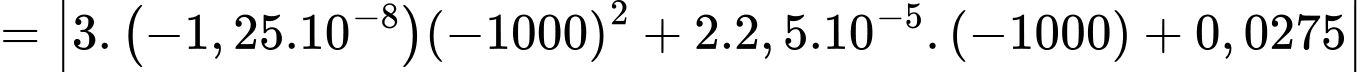
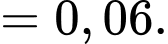
Câu 22 [390555]: Bạn Nam có thể chèo thuyền với vận tốc  và có thể đi bộ với vận tốc
và có thể đi bộ với vận tốc  Hiện tại Nam đang ở vị trí A trên bờ hồ bán kính 2 km. Nam sẽ chèo thuyền đến điểm C, sau đó đi bộ quanh bờ đến điểm B đối diện với A (như hình vẽ). Thời gian dài nhất bạn Nam đi từ A đến C rồi đến B là bao nhiều phút?. Viết kết quả làm tròn đến hàng đơn vị.
Hiện tại Nam đang ở vị trí A trên bờ hồ bán kính 2 km. Nam sẽ chèo thuyền đến điểm C, sau đó đi bộ quanh bờ đến điểm B đối diện với A (như hình vẽ). Thời gian dài nhất bạn Nam đi từ A đến C rồi đến B là bao nhiều phút?. Viết kết quả làm tròn đến hàng đơn vị. 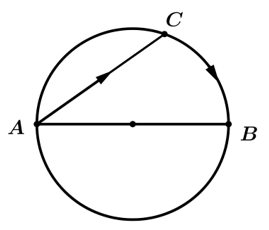
 và có thể đi bộ với vận tốc
và có thể đi bộ với vận tốc  Hiện tại Nam đang ở vị trí A trên bờ hồ bán kính 2 km. Nam sẽ chèo thuyền đến điểm C, sau đó đi bộ quanh bờ đến điểm B đối diện với A (như hình vẽ). Thời gian dài nhất bạn Nam đi từ A đến C rồi đến B là bao nhiều phút?. Viết kết quả làm tròn đến hàng đơn vị.
Hiện tại Nam đang ở vị trí A trên bờ hồ bán kính 2 km. Nam sẽ chèo thuyền đến điểm C, sau đó đi bộ quanh bờ đến điểm B đối diện với A (như hình vẽ). Thời gian dài nhất bạn Nam đi từ A đến C rồi đến B là bao nhiều phút?. Viết kết quả làm tròn đến hàng đơn vị. 
Đáp số:……………………………
Quãng đường Nam đi là: 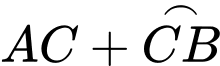
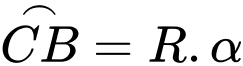
Gọi tâm hồ là
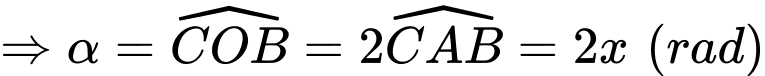
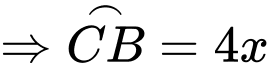
Ta có: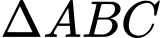 có
có  là đường kính của đường tròn ngoại tiếp tam giác
là đường kính của đường tròn ngoại tiếp tam giác
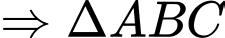 vuông tại
vuông tại 
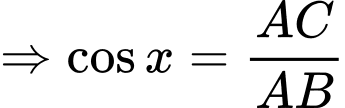

Tổng thời gian Nam đi là: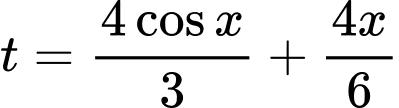 (giờ)
(giờ)
Xét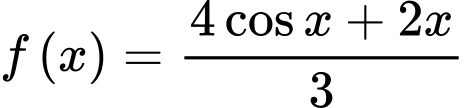 với
với 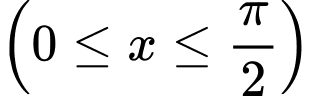
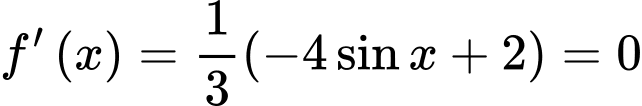
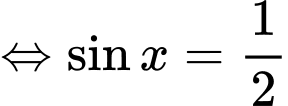
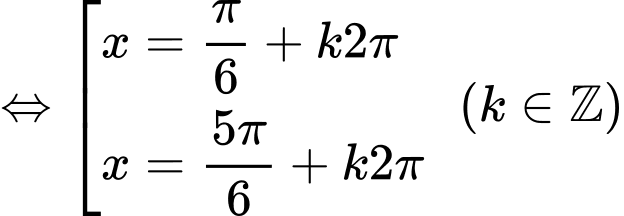
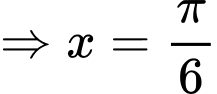
Ta bấm máy, nhận thấy bạn Nam đi từ A đến B với khoảng thời gian lớn nhất tại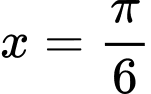 và
và 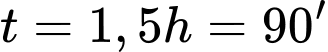
Đáp án: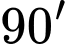
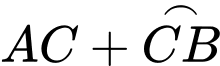
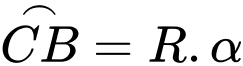
Gọi tâm hồ là

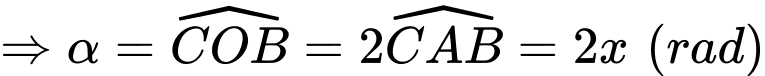
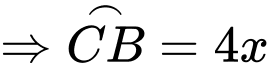
Ta có:
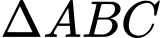 có
có  là đường kính của đường tròn ngoại tiếp tam giác
là đường kính của đường tròn ngoại tiếp tam giác 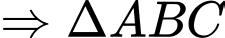 vuông tại
vuông tại 
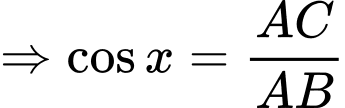

Tổng thời gian Nam đi là:
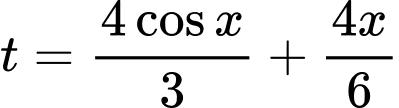 (giờ)
(giờ)Xét
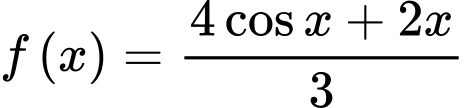 với
với 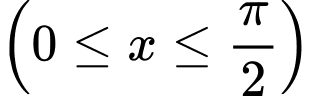
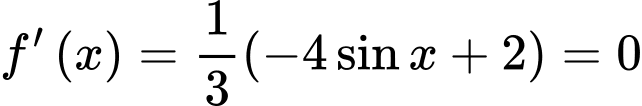
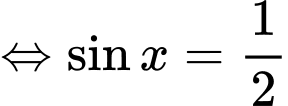
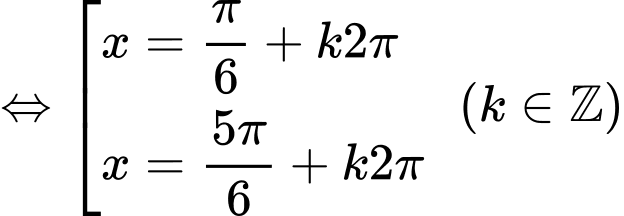
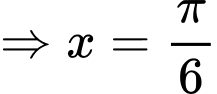
Ta bấm máy, nhận thấy bạn Nam đi từ A đến B với khoảng thời gian lớn nhất tại
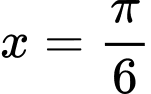 và
và 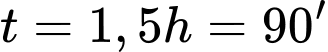
Đáp án: