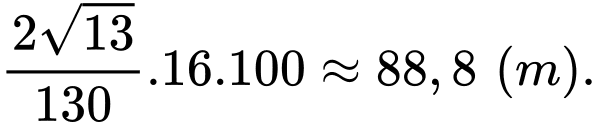PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1 [809908]: Đồ thị hàm số 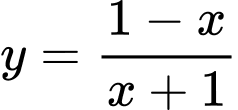 cắt trục
cắt trục  tại điểm có tọa độ là
tại điểm có tọa độ là
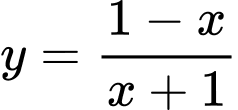 cắt trục
cắt trục 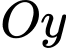 tại điểm có tọa độ là
tại điểm có tọa độ là A, 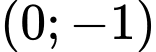 .
.
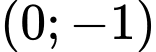 .
.B, 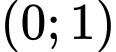 .
.
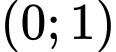 .
.C, 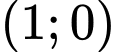 .
.
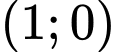 .
.D, 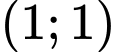 .
.
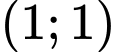 .
.
Chọn B.
Cho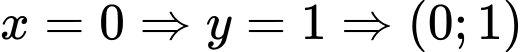 là giao điểm của đồ thị với trục tung. Đáp án: B
là giao điểm của đồ thị với trục tung. Đáp án: B
Cho
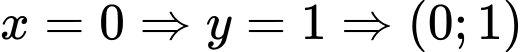 là giao điểm của đồ thị với trục tung. Đáp án: B
là giao điểm của đồ thị với trục tung. Đáp án: B
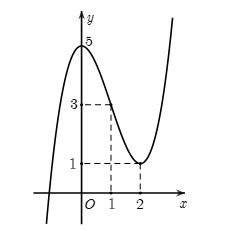
Câu 2 [11538]: Đường cong như hình vẽ là đồ thị của hàm số nào?

A, 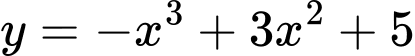 .
.
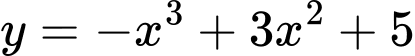 .
.B, 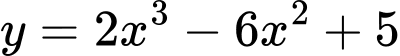 .
.
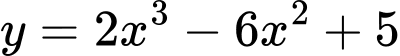 .
.C, 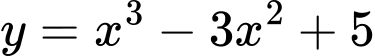 .
.
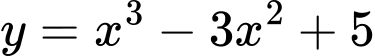 .
.D, 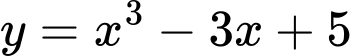 .
.
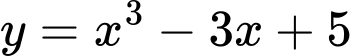 .
.
Chọn đáp án C.
Phương pháp:
+) Dựa vào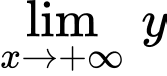 xác định dấu của hệ số a và loại đáp án.
xác định dấu của hệ số a và loại đáp án.
+) Dựa vào các điểm đồ thị hàm số đi qua xác định đáp án đúng.
Cách giải:
Đồ thị hàm số đã cho là hàm đa thức bậc ba có do
do 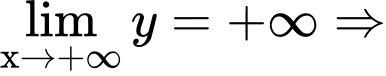 Loại đáp án A .
Loại đáp án A .
Đồ thị hàm số đi qua điểm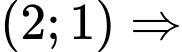 Loại các đáp án
Loại các đáp án  và
và 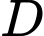 .
Đáp án: C
.
Đáp án: C
Phương pháp:
+) Dựa vào
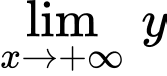 xác định dấu của hệ số a và loại đáp án.
xác định dấu của hệ số a và loại đáp án.
+) Dựa vào các điểm đồ thị hàm số đi qua xác định đáp án đúng.
Cách giải:
Đồ thị hàm số đã cho là hàm đa thức bậc ba có
 do
do 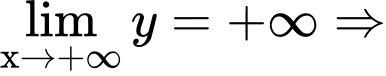 Loại đáp án A .
Loại đáp án A . Đồ thị hàm số đi qua điểm
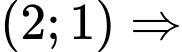 Loại các đáp án
Loại các đáp án 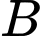 và
và 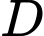 .
Đáp án: C
.
Đáp án: C
Câu 3 [522398]: Cho hàm số 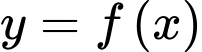 có bảng biến thiên như sau:
có bảng biến thiên như sau:
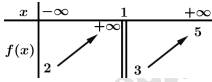
Tổng số tiệm cận ngang và số tiệm cận đứng của đồ thị hàm số đã cho là
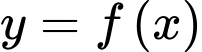 có bảng biến thiên như sau:
có bảng biến thiên như sau:
Tổng số tiệm cận ngang và số tiệm cận đứng của đồ thị hàm số đã cho là
A, 4.
B, 1.
C, 3.
D, 2.
Ta có 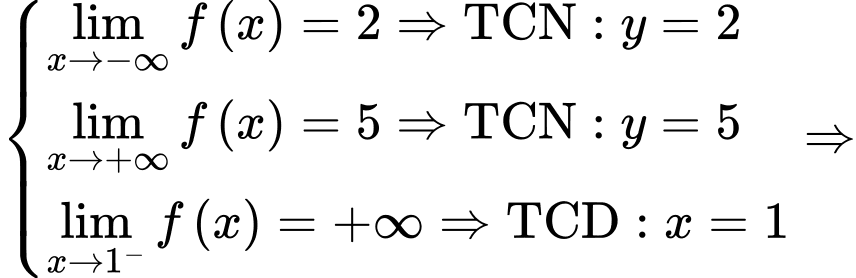 Chọn C.
Đáp án: C
Chọn C.
Đáp án: C
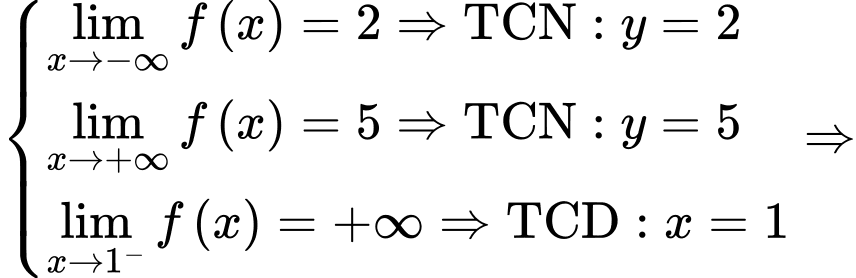 Chọn C.
Đáp án: C
Chọn C.
Đáp án: C
Câu 4 [801835]: Hàm số 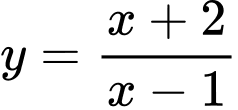 nghịch biến trên khoảng nào dưới đây?
nghịch biến trên khoảng nào dưới đây?
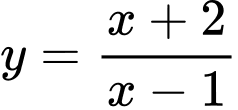 nghịch biến trên khoảng nào dưới đây?
nghịch biến trên khoảng nào dưới đây? A, 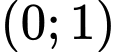 .
.
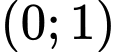 .
.B, 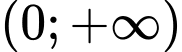 .
.
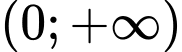 .
.C, 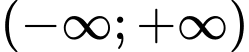 .
.
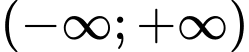 .
.D, 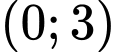 .
.
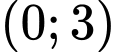 .
.
Chọn A.
Ta có TXĐ: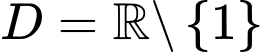 .
.
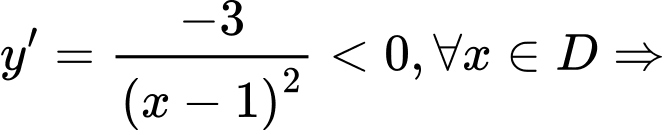 hàm số nghịch biến trên
hàm số nghịch biến trên  và
và 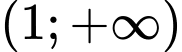 . Đáp án: A
. Đáp án: A
Ta có TXĐ:
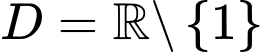 .
.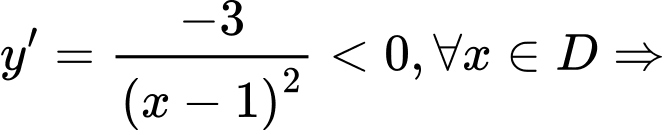 hàm số nghịch biến trên
hàm số nghịch biến trên  và
và 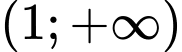 . Đáp án: A
. Đáp án: A
Câu 5 [382491]: Điểm uốn của đồ thị hàm số 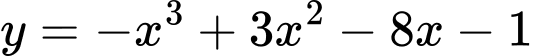 có tung độ bằng:
có tung độ bằng:
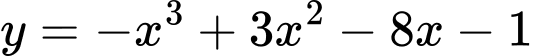 có tung độ bằng:
có tung độ bằng: A, 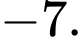
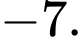
B, 

C, 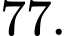
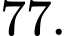
D, 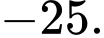
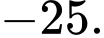
Ta có: 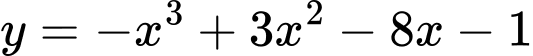
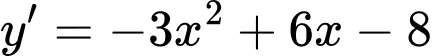
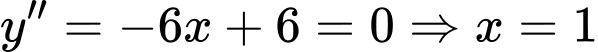
Khi đó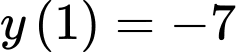
Vậy điểm uốn của đồ thị hàm số có tung độ bằng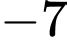 .
Đáp án: A
.
Đáp án: A
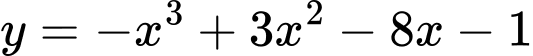
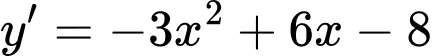
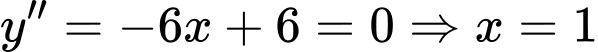
Khi đó
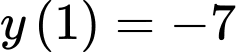
Vậy điểm uốn của đồ thị hàm số có tung độ bằng
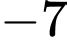 .
Đáp án: A
.
Đáp án: A
Câu 6 [307290]: Cho hàm số 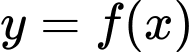 xác định trên
xác định trên  liên tục trên mỗi khoảng
xác định và có bảng biến thiên như sau
liên tục trên mỗi khoảng
xác định và có bảng biến thiên như sau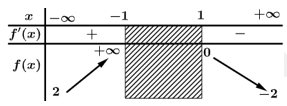
Tính tổng của số đường tiệm cận đứng và ngang của đồ thị hàm số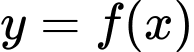 ?
?
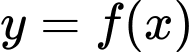 xác định trên
xác định trên  liên tục trên mỗi khoảng
xác định và có bảng biến thiên như sau
liên tục trên mỗi khoảng
xác định và có bảng biến thiên như sau
Tính tổng của số đường tiệm cận đứng và ngang của đồ thị hàm số
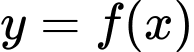 ?
? A, 1.
B, 4.
C, 3.
D, 2.
Chọn C
Từ bảng biến thiên, ta có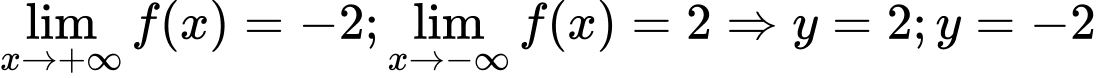 là 2 tiệm cận ngang của đồ thị hàm số
là 2 tiệm cận ngang của đồ thị hàm số
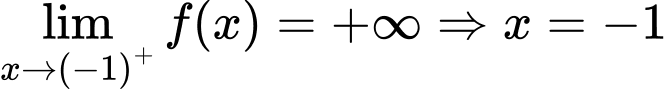 là tiệm cận đứng
là tiệm cận đứng
Vậy đồ thị hàm số có 3 tiệm cận. Đáp án: C
Từ bảng biến thiên, ta có
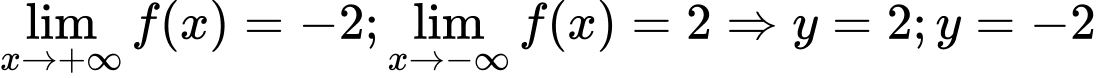 là 2 tiệm cận ngang của đồ thị hàm số
là 2 tiệm cận ngang của đồ thị hàm số
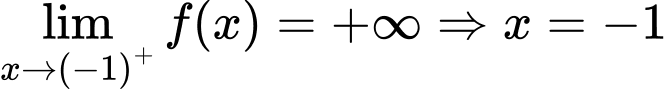 là tiệm cận đứng
là tiệm cận đứng
Vậy đồ thị hàm số có 3 tiệm cận. Đáp án: C
Câu 7 [506275]: Tâm đối xứng của đồ thị hàm số 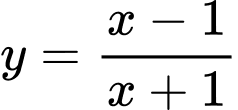 có tọa độ là
có tọa độ là
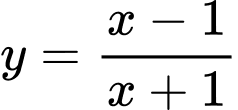 có tọa độ là
có tọa độ là A, 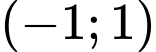 .
.
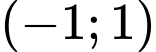 .
.B, 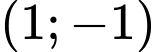 .
.
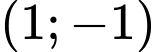 .
.C, 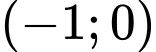 .
.
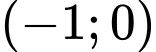 .
.D, 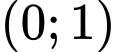 .
.
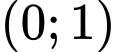 .
.
Chọn đáp án A.
Vì tiệm cận đứng của đồ thị hàm số là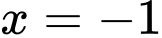 .
.
Tiệm cận ngang của đồ thị hàm số là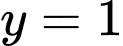 .
.
Tâm đối xứng của đồ thị hàm số là giao điểm của hai đường tiệm cận là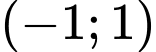 . Đáp án: A
. Đáp án: A
Vì tiệm cận đứng của đồ thị hàm số là
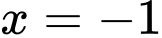 .
.Tiệm cận ngang của đồ thị hàm số là
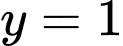 .
.Tâm đối xứng của đồ thị hàm số là giao điểm của hai đường tiệm cận là
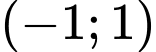 . Đáp án: A
. Đáp án: A
Câu 8 [9253]: Hàm số nào sau đây nghịch biến trên 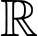 ?
?
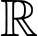 ?
? A, 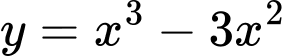 .
.
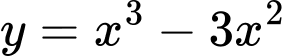 .
.B, 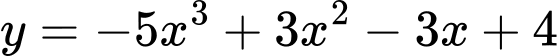 .
.
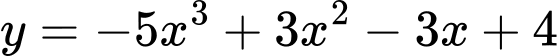 .
.C, 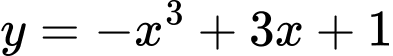 .
.
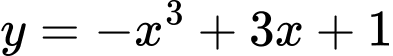 .
.D, 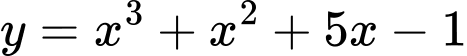 .
.
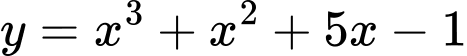 .
.
Chọn đáp án B.
Dễ nhận thấy hàm số có đạo hàm luôn âm cần hệ số đầu tiên âm, nên chỉ có thể là đáp án C hoặc B. Để ý tại B có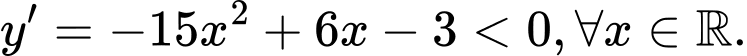 Đáp án: B
Đáp án: B
Dễ nhận thấy hàm số có đạo hàm luôn âm cần hệ số đầu tiên âm, nên chỉ có thể là đáp án C hoặc B. Để ý tại B có
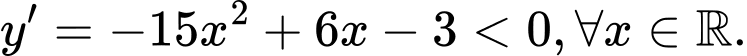 Đáp án: B
Đáp án: B
Câu 9 [383012]: Đường cong ở hình vẽ bên là đồ thị của hàm số 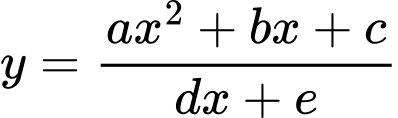 với
với 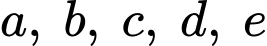 là các số thực. Mệnh đề nào dưới đây đúng?
là các số thực. Mệnh đề nào dưới đây đúng?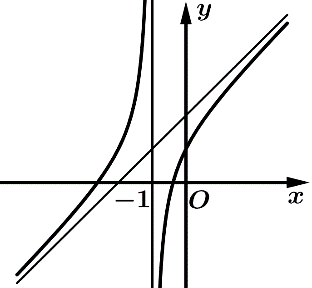
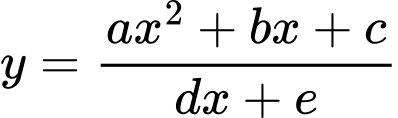 với
với 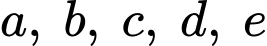 là các số thực. Mệnh đề nào dưới đây đúng?
là các số thực. Mệnh đề nào dưới đây đúng?
A, 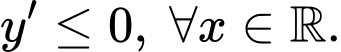
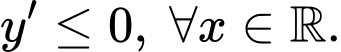
B, 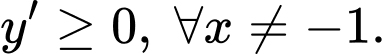
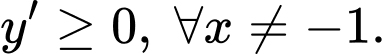
C, 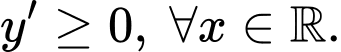
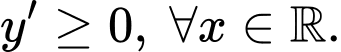
D, 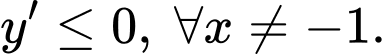
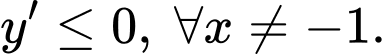
Dựa vào đồ thị hàm số dễ thấy hàm số đồng biến trên khoảng xác định
Chọn đáp án B Đáp án: B
Chọn đáp án B Đáp án: B
Câu 10 [601767]: Cho hàm số 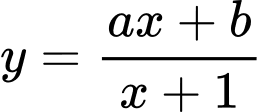 có đồ thị như hình vẽ dưới đây:
có đồ thị như hình vẽ dưới đây:
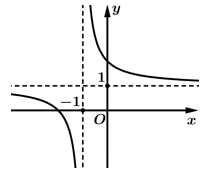
Tìm khẳng định đúng trong các khẳng định sau.
 có đồ thị như hình vẽ dưới đây:
có đồ thị như hình vẽ dưới đây: 
Tìm khẳng định đúng trong các khẳng định sau.
A, 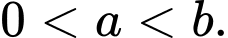
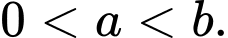
B, 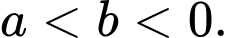
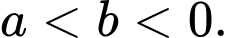
C, 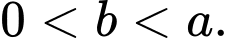
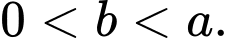
D, 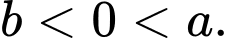
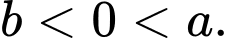
Chọn A
Dựa vào đồ thị, ta có:
+) Tiệm cận ngang: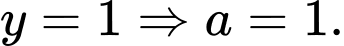
+) Đồ thị cắt trục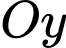 tại điểm có tung độ lớn hơn
tại điểm có tung độ lớn hơn 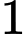 nên
nên 
Vậy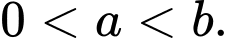 Đáp án: A
Đáp án: A
Dựa vào đồ thị, ta có:
+) Tiệm cận ngang:
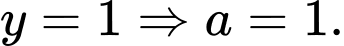
+) Đồ thị cắt trục
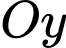 tại điểm có tung độ lớn hơn
tại điểm có tung độ lớn hơn 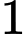 nên
nên 
Vậy
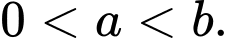 Đáp án: A
Đáp án: A
Câu 11 [501644]: Số đường tiệm cận của đồ thị hàm số 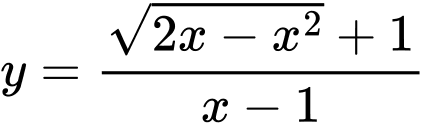 là
là
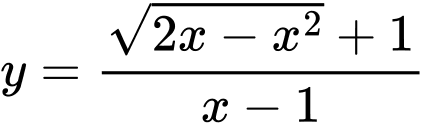 là
là A, 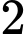
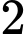
B, 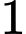
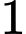
C, 

D, 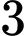
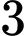
Chọn B
Tập xác định của hàm số là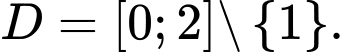
Do đó đồ thị hàm số không có đường tiệm cận ngang.
Ta có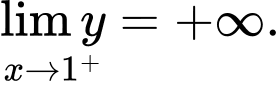 Suy ra
Suy ra 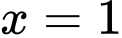 là đường tiệm cận đứng.
là đường tiệm cận đứng.
Vậy đồ thị hàm số đã chỉ có duy nhất 1 đường tiệm cận. Đáp án: B
Tập xác định của hàm số là
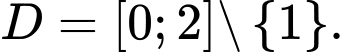
Do đó đồ thị hàm số không có đường tiệm cận ngang.
Ta có
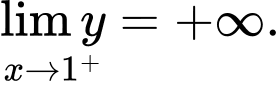 Suy ra
Suy ra 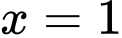 là đường tiệm cận đứng.
là đường tiệm cận đứng. Vậy đồ thị hàm số đã chỉ có duy nhất 1 đường tiệm cận. Đáp án: B
Câu 12 [382822]: Tâm đối xứng của đồ thị hàm số 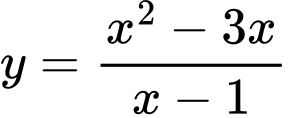 có toạ độ là
có toạ độ là
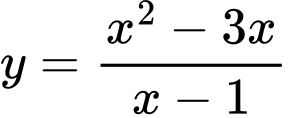 có toạ độ là
có toạ độ là A, 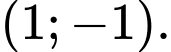
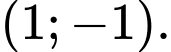
B, 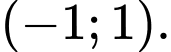
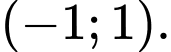
C, 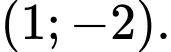
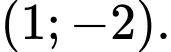
D, 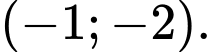
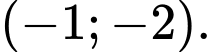
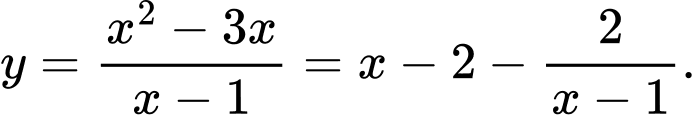
Đồ thị hàm số
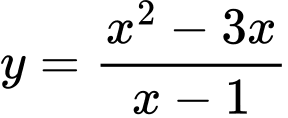 có TCĐ
có TCĐ 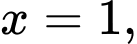 TCX
TCX 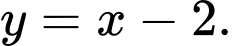
Vậy tâm đối xứng của đồ thị hàm số
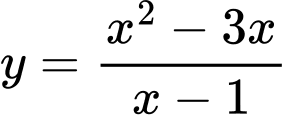 có toạ độ là
có toạ độ là 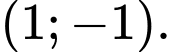 Đáp án: A
Đáp án: A PHẦN II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a),b),c),d) ở mỗi câu học sinh chọn đúng hoặc sai.
Câu 13 [774173]: Cho hàm số 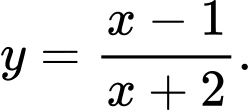
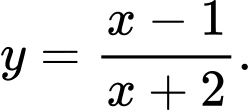
a) Sai.
Tập xác định: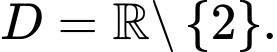
Ta có công thức tính nhanh đạo hàm cho hàm phân thức có dạng: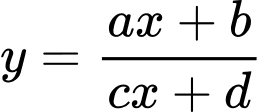 thì
thì 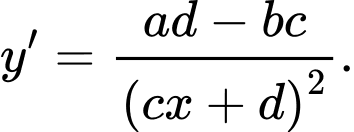
Áp dụng công thức trên, ta có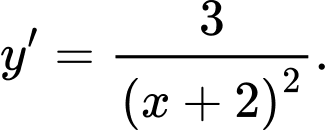
b) Sai.
Vì đồ thị hàm số đã cho có tiệm cận đứng là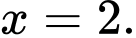
c) Sai.
Vì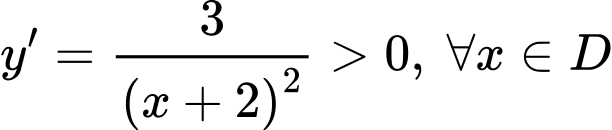 nên suy ra hàm số đồng biến trên tập xác định.
nên suy ra hàm số đồng biến trên tập xác định.
d) Đúng.
Mệnh đề ở phần d) tương đương với có 4 cặp giá trị nguyên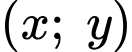 thỏa mãn hàm số
thỏa mãn hàm số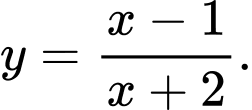
Ta có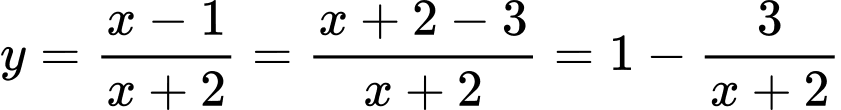
Do đó, để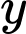 là giá trị nguyên thì
là giá trị nguyên thì 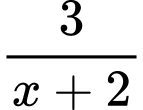 nguyên
nguyên 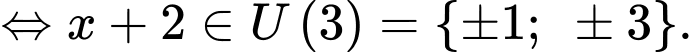
+) Với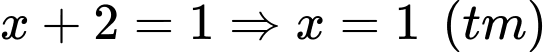
+) Với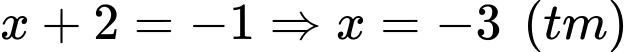
+) Với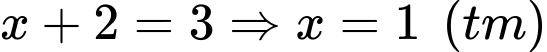
+) Với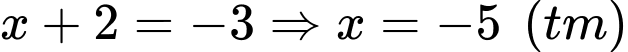
Vậy có tất cả 4 cặp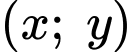 nguyên thuộc vào đồ thị hàm số đã cho.
nguyên thuộc vào đồ thị hàm số đã cho.
Tập xác định:
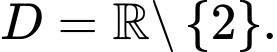
Ta có công thức tính nhanh đạo hàm cho hàm phân thức có dạng:
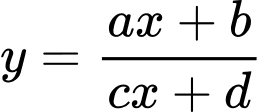 thì
thì 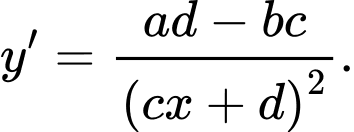
Áp dụng công thức trên, ta có
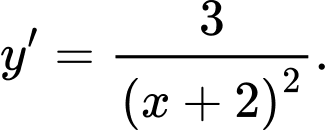
b) Sai.
Vì đồ thị hàm số đã cho có tiệm cận đứng là
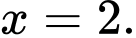
c) Sai.
Vì
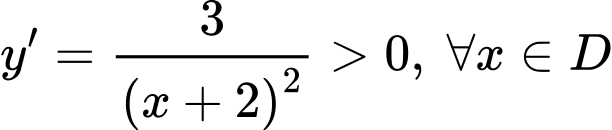 nên suy ra hàm số đồng biến trên tập xác định.
nên suy ra hàm số đồng biến trên tập xác định.
d) Đúng.
Mệnh đề ở phần d) tương đương với có 4 cặp giá trị nguyên
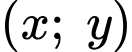 thỏa mãn hàm số
thỏa mãn hàm số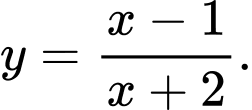
Ta có
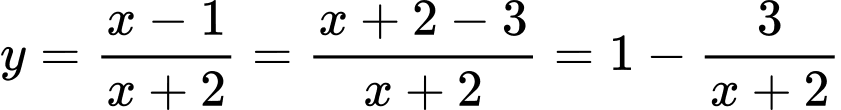
Do đó, để
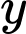 là giá trị nguyên thì
là giá trị nguyên thì 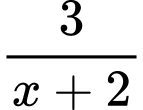 nguyên
nguyên 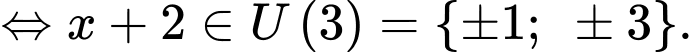
+) Với
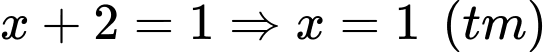
+) Với
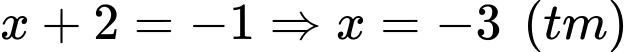
+) Với
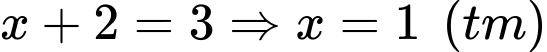
+) Với
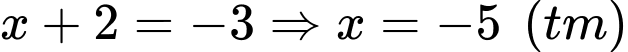
Vậy có tất cả 4 cặp
 nguyên thuộc vào đồ thị hàm số đã cho.
nguyên thuộc vào đồ thị hàm số đã cho.
Câu 14 [708365]: Cho hàm số 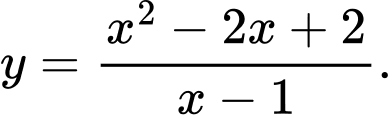 Các mệnh đề sau đúng hay sai?
Các mệnh đề sau đúng hay sai?
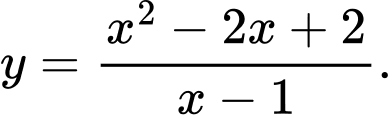 Các mệnh đề sau đúng hay sai?
Các mệnh đề sau đúng hay sai?
a) Ta có : 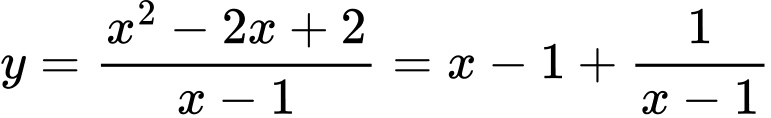
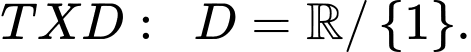
Đạo hàm của hàm số là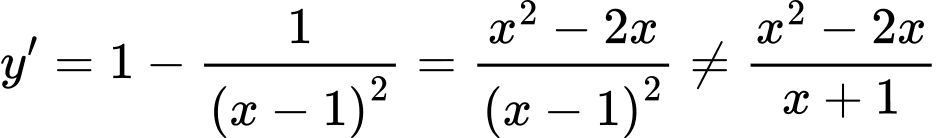
 a) SAI.
a) SAI.
b)

BBT:
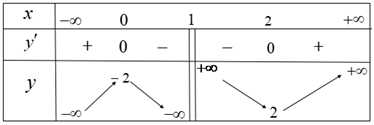
Từ BBT ta có: Giá trị cực đại của hàm số bằng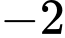
 b) ĐÚNG.
b) ĐÚNG.
c) Tiệm cận xiên của đồ thị hàm số đã cho là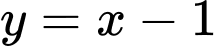 đi qua điểm
đi qua điểm 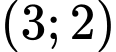
 c) ĐÚNG.
c) ĐÚNG.
d) Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số đã cho có dạng:
Vì đi qua các điểm
đi qua các điểm 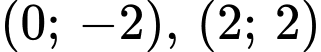 nên ta có :
nên ta có : 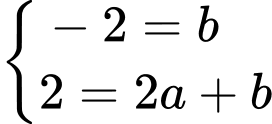
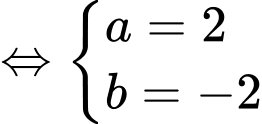
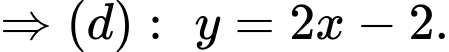
Suy ra d) ĐÚNG.
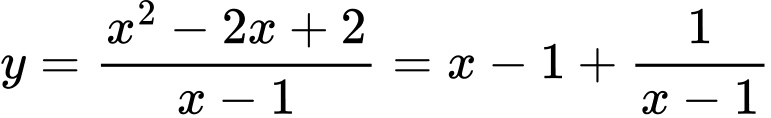
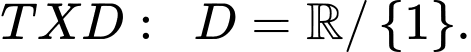
Đạo hàm của hàm số là
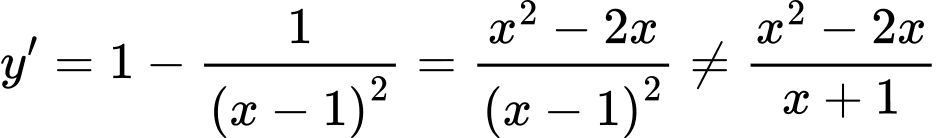
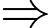 a) SAI.
a) SAI.
b)
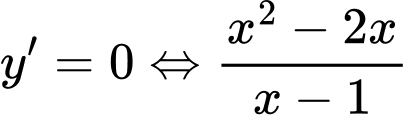

BBT:

Từ BBT ta có: Giá trị cực đại của hàm số bằng
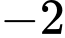
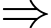 b) ĐÚNG.
b) ĐÚNG.
c) Tiệm cận xiên của đồ thị hàm số đã cho là
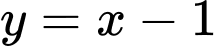 đi qua điểm
đi qua điểm 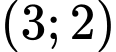
 c) ĐÚNG.
c) ĐÚNG.
d) Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số đã cho có dạng:

Vì
 đi qua các điểm
đi qua các điểm 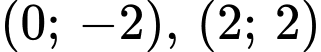 nên ta có :
nên ta có : 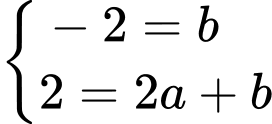
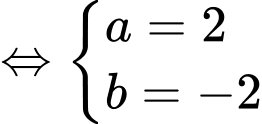
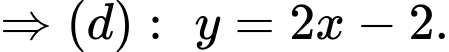
Suy ra d) ĐÚNG.
Câu 15 [715973]: Một bể chứa 3000 lít nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng độ 25 gam muối cho một lít nước với tốc độ 20 lít/phút.
a) Đúng.
Đổi 1 giờ = 60 phút.
Khối lượng muối sau khi bơm 60 phút là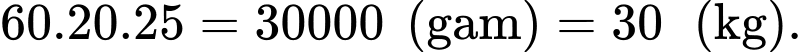
b) Đúng.
Thể tích lượng nước bơm vào bể sau thời gian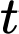 phút là
phút là 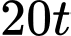 (lít)
(lít)
 Thể tích lượng nước trong bể sau thời gian
Thể tích lượng nước trong bể sau thời gian 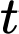 phút là:
phút là: 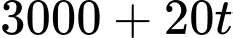 (lít)
(lít)
c) Sai.
Sau thời gian bơm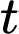 phút thì khối lượng muối trong bể là
phút thì khối lượng muối trong bể là 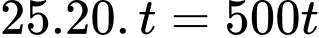 (gam)
(gam)
 Nồng độ muối trong bể sau khi bơm được
Nồng độ muối trong bể sau khi bơm được 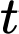 phút là
phút là 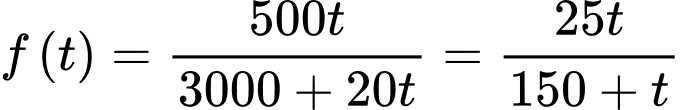 (gam/lít)
(gam/lít)
 Đường tiệm cận ngang của đồ thị hàm số
Đường tiệm cận ngang của đồ thị hàm số 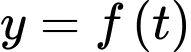 là
là 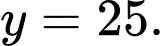
d) Đúng.
Ta có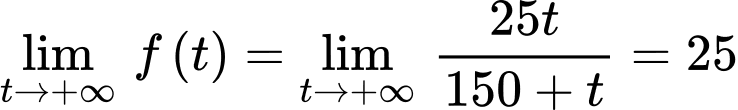 nên khi
nên khi  càng lớn thì nồng độ muối trong bể tiến gần đến 25 gam/lít.
càng lớn thì nồng độ muối trong bể tiến gần đến 25 gam/lít.
Đổi 1 giờ = 60 phút.
Khối lượng muối sau khi bơm 60 phút là
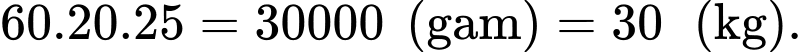
b) Đúng.
Thể tích lượng nước bơm vào bể sau thời gian
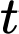 phút là
phút là 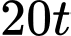 (lít)
(lít)
 Thể tích lượng nước trong bể sau thời gian
Thể tích lượng nước trong bể sau thời gian 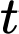 phút là:
phút là: 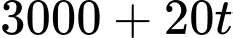 (lít)
(lít)
c) Sai.
Sau thời gian bơm
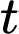 phút thì khối lượng muối trong bể là
phút thì khối lượng muối trong bể là 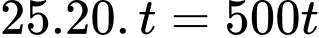 (gam)
(gam)
 Nồng độ muối trong bể sau khi bơm được
Nồng độ muối trong bể sau khi bơm được  phút là
phút là 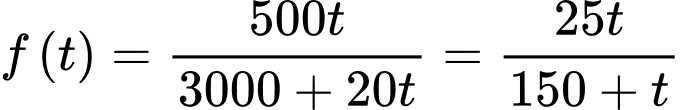 (gam/lít)
(gam/lít)
 Đường tiệm cận ngang của đồ thị hàm số
Đường tiệm cận ngang của đồ thị hàm số 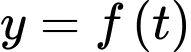 là
là 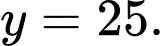
d) Đúng.
Ta có
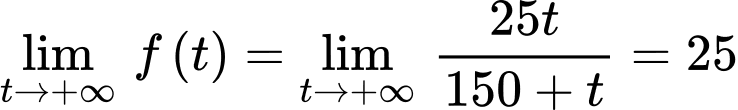 nên khi
nên khi  càng lớn thì nồng độ muối trong bể tiến gần đến 25 gam/lít.
càng lớn thì nồng độ muối trong bể tiến gần đến 25 gam/lít.
Câu 16 [713215]: Giả sử số lượng quần thể nấm men tại môi trường nuôi cấy trong phòng thí nghiệm được mô hình hóa bằng hàm số 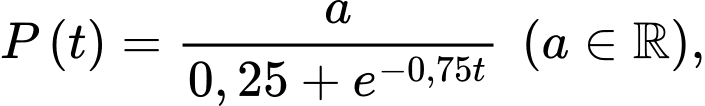 trong đó thời gian
trong đó thời gian 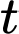 được tính bằng giờ. Tốc độ sinh trưởng của quần thể nấm men ở thời điểm
được tính bằng giờ. Tốc độ sinh trưởng của quần thể nấm men ở thời điểm 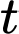 được tính theo công thức
được tính theo công thức 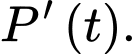 Biết rằng tại thời điểm ban đầu (
Biết rằng tại thời điểm ban đầu (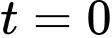 ) quần thể có 20 con.
) quần thể có 20 con.
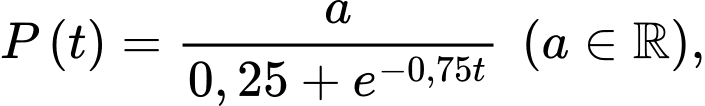 trong đó thời gian
trong đó thời gian 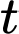 được tính bằng giờ. Tốc độ sinh trưởng của quần thể nấm men ở thời điểm
được tính bằng giờ. Tốc độ sinh trưởng của quần thể nấm men ở thời điểm 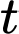 được tính theo công thức
được tính theo công thức 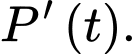 Biết rằng tại thời điểm ban đầu (
Biết rằng tại thời điểm ban đầu (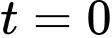 ) quần thể có 20 con.
) quần thể có 20 con.
a) Sai.
Ta có: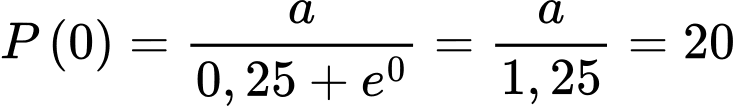
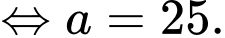
b) Đúng.
Ta có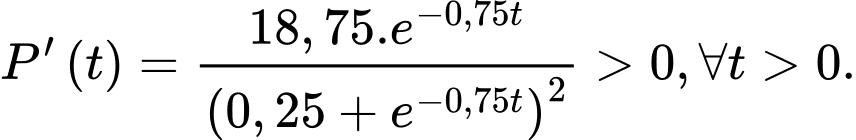
Suy ra số lượng quần thể nấm men được nuôi cấy luôn tăng.
c) Sai. Ta lại có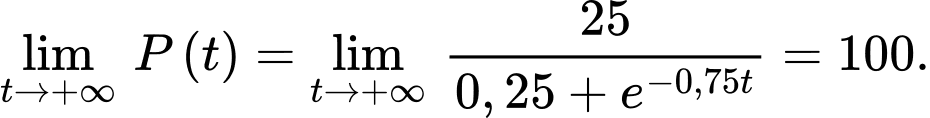 Do đó, số lượng quần thể nấm men tăng nhưng không vượt quá
Do đó, số lượng quần thể nấm men tăng nhưng không vượt quá 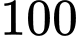 , nên không thể tăng lên vô cùng được.
, nên không thể tăng lên vô cùng được.
d) Đúng.
Đặt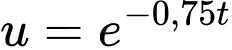
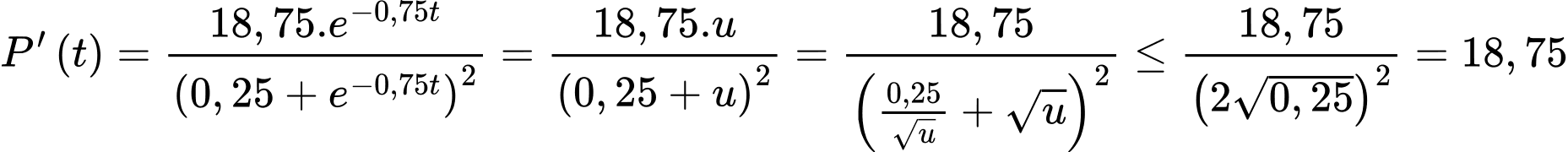 con/giờ
con/giờ
Ở đây ta áp dụng bất đẳng thức Cosi: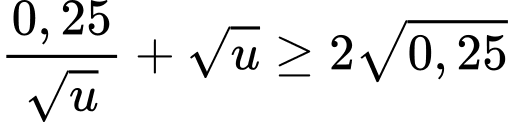
Đạt được khi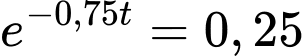
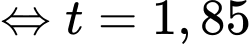 giờ.
giờ.
Ta có:
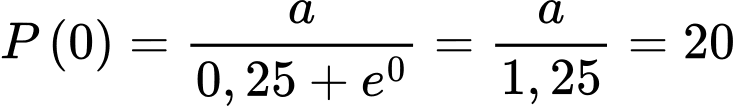
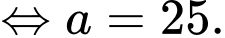
b) Đúng.
Ta có
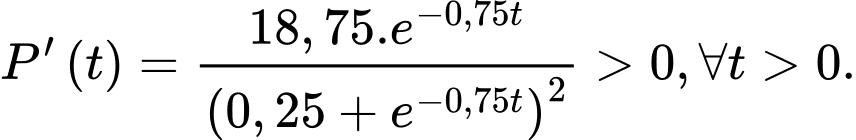
Suy ra số lượng quần thể nấm men được nuôi cấy luôn tăng.
c) Sai. Ta lại có
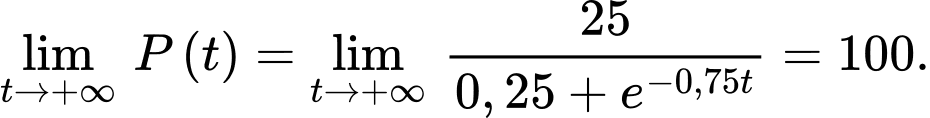 Do đó, số lượng quần thể nấm men tăng nhưng không vượt quá
Do đó, số lượng quần thể nấm men tăng nhưng không vượt quá 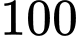 , nên không thể tăng lên vô cùng được.
, nên không thể tăng lên vô cùng được.d) Đúng.
Đặt
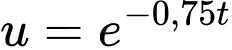
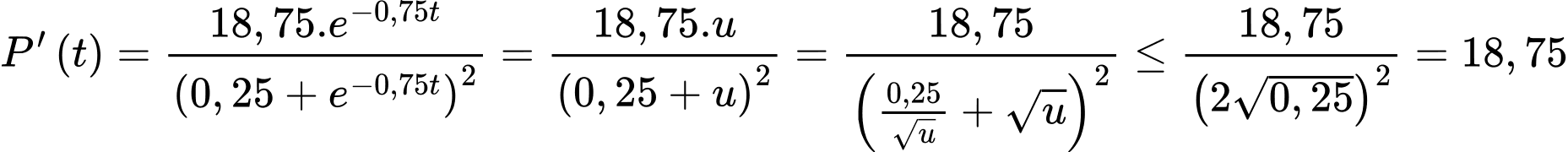 con/giờ
con/giờỞ đây ta áp dụng bất đẳng thức Cosi:
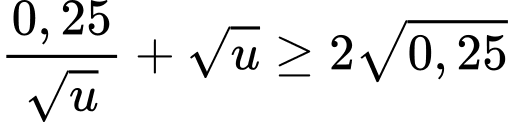
Đạt được khi
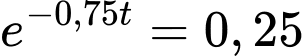
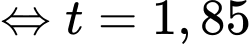 giờ.
giờ. PHẦN III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 17 đến câu 22.
Câu 17 [774176]: Cho hàm số 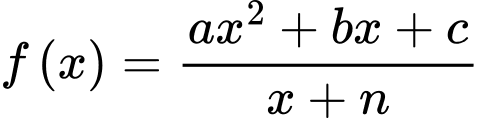 xác định trên
xác định trên 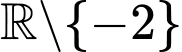 và có bảng biến thiên như sau:
và có bảng biến thiên như sau:
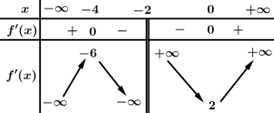
Tính giá trị của
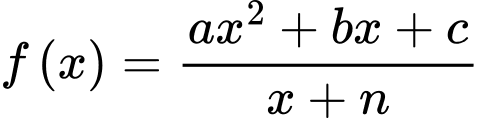 xác định trên
xác định trên 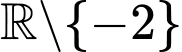 và có bảng biến thiên như sau:
và có bảng biến thiên như sau:
Tính giá trị của

Điền đáp án: 3.
Ta có: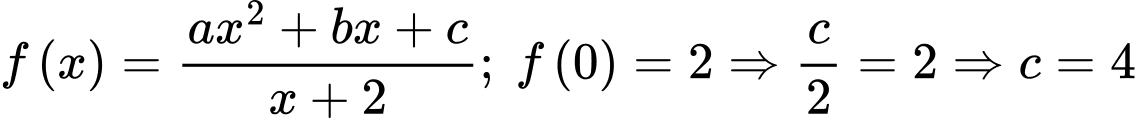
Do đó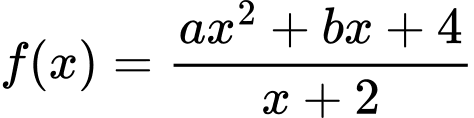
Phương trình đường thẳng qua hai điểm cực trị là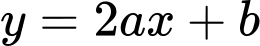
Ta có: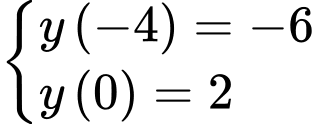
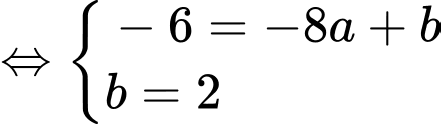
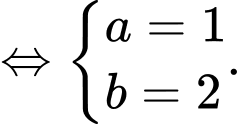
Vậy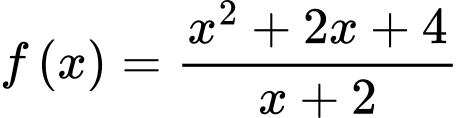
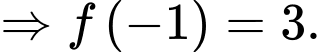
Ta có:
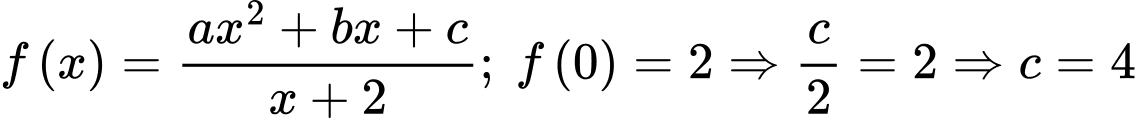
Do đó
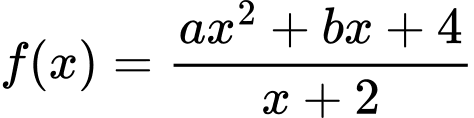
Phương trình đường thẳng qua hai điểm cực trị là
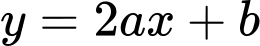
Ta có:
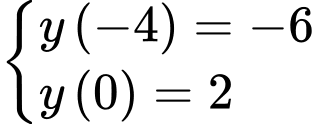
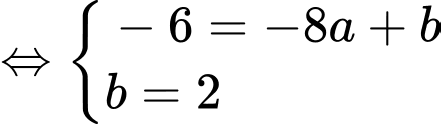
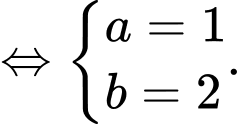
Vậy
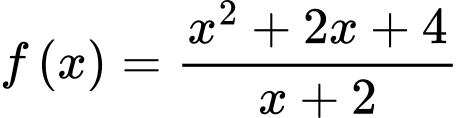
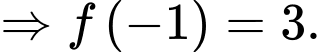
Câu 18 [774178]: Giả sử chi phí đặt hàng và vận chuyển  (đơn vị: triệu đồng) của một linh kiện được sử dụng trong sản xuất một sản phẩm được xác định bởi công thức:
(đơn vị: triệu đồng) của một linh kiện được sử dụng trong sản xuất một sản phẩm được xác định bởi công thức: 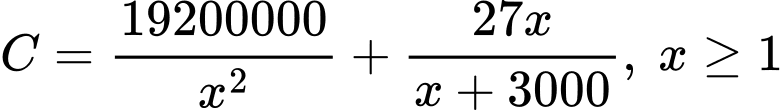 trong đó
trong đó 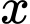 là số linh kiện được đặt hàng và vận chuyển. Tìm
là số linh kiện được đặt hàng và vận chuyển. Tìm 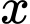 để chi phí đặt hàng và vận chuyển cho mỗi linh kiện trên là nhỏ nhất?
để chi phí đặt hàng và vận chuyển cho mỗi linh kiện trên là nhỏ nhất?
 (đơn vị: triệu đồng) của một linh kiện được sử dụng trong sản xuất một sản phẩm được xác định bởi công thức:
(đơn vị: triệu đồng) của một linh kiện được sử dụng trong sản xuất một sản phẩm được xác định bởi công thức: 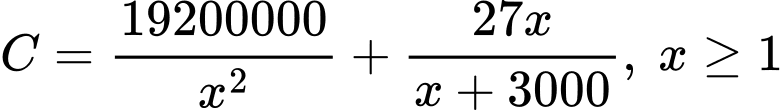 trong đó
trong đó 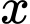 là số linh kiện được đặt hàng và vận chuyển. Tìm
là số linh kiện được đặt hàng và vận chuyển. Tìm 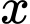 để chi phí đặt hàng và vận chuyển cho mỗi linh kiện trên là nhỏ nhất?
để chi phí đặt hàng và vận chuyển cho mỗi linh kiện trên là nhỏ nhất?
Điền đáp án: 2400.
Khảo sát hàm số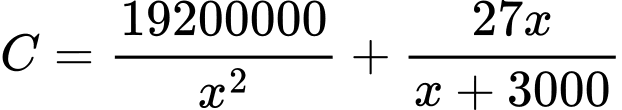 trong nửa khoảng
trong nửa khoảng 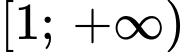
Ta có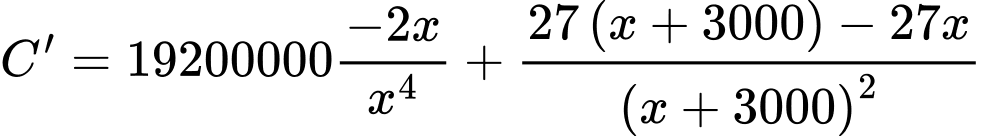
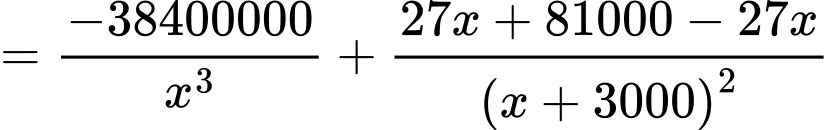
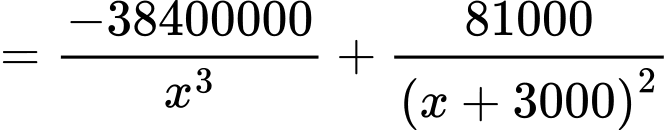
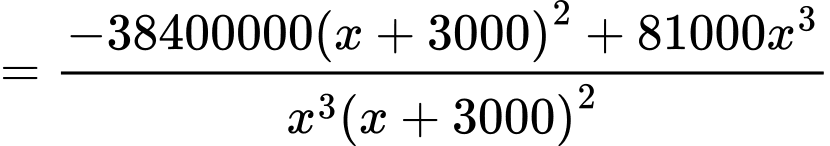
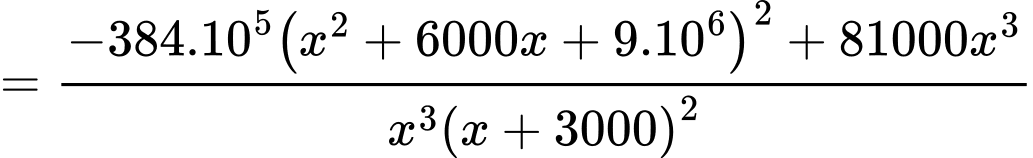
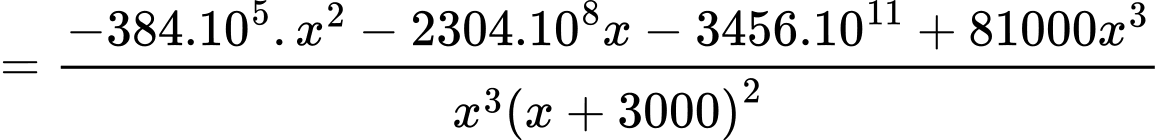
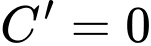
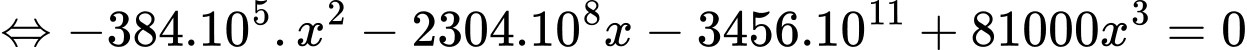
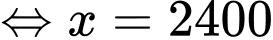
Bảng biến thiên
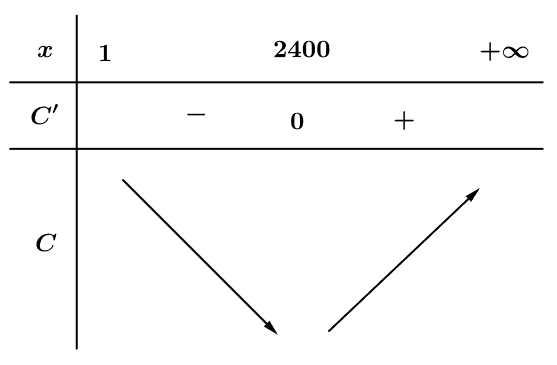
Vậy để chi phí đặt hàng và vận chuyển cho mỗi linh kiện trên là nhỏ nhất thì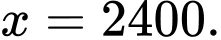
Khảo sát hàm số
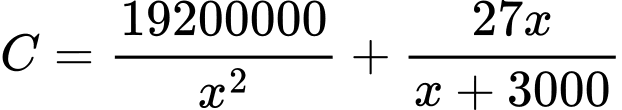 trong nửa khoảng
trong nửa khoảng 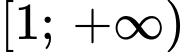
Ta có
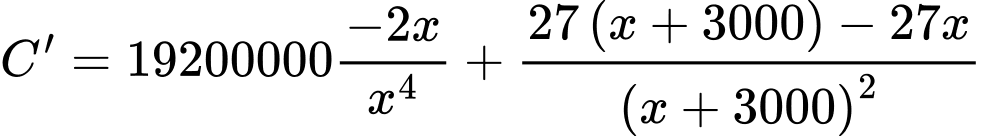
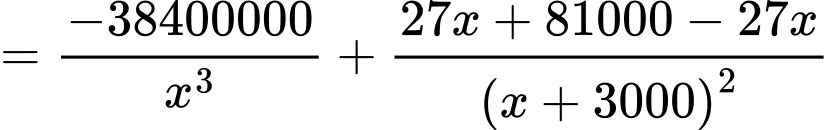
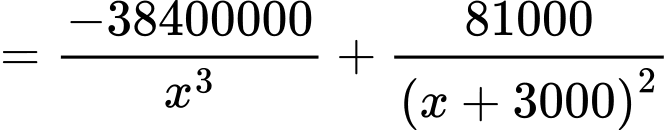
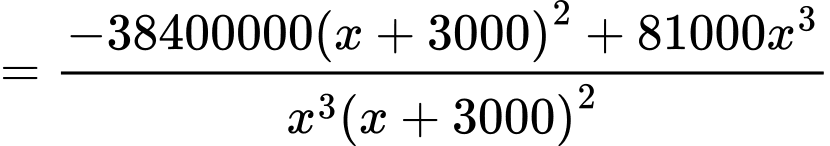
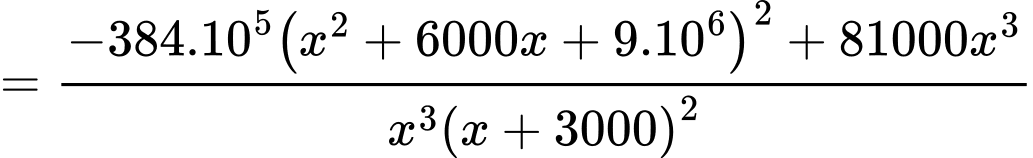
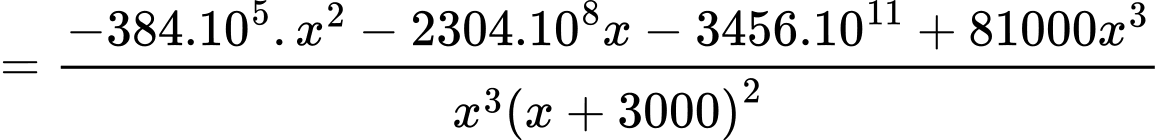
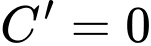
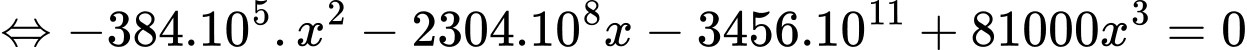
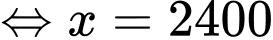
Bảng biến thiên

Vậy để chi phí đặt hàng và vận chuyển cho mỗi linh kiện trên là nhỏ nhất thì
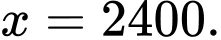
Câu 19 [774180]: Một nhà máy sản xuất 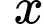 sản phẩm trong mỗi tháng. Chi phí sản xuất
sản phẩm trong mỗi tháng. Chi phí sản xuất 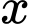 sản phẩm được cho bởi hàm chi phí
sản phẩm được cho bởi hàm chi phí 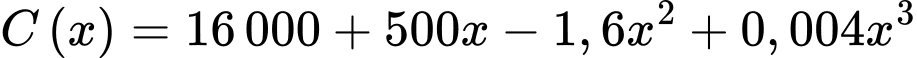 (nghìn đồng). Biết giá bán của của mỗi sản phẩm là một hàm số phụ thuộc vào số lượng sản phẩm
(nghìn đồng). Biết giá bán của của mỗi sản phẩm là một hàm số phụ thuộc vào số lượng sản phẩm 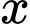 và được cho bởi công thức
và được cho bởi công thức 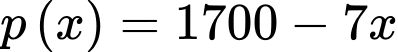 (nghìn đồng). Hỏi mỗi tháng nhà máy nên sản xuất bao nhiêu sản phẩm để lợi nhuận thu được là lớn nhất? Biết rằng kết quả khảo sát thị trường cho thấy sản phẩm sản xuất ra sẽ được tiêu thụ hết.
(nghìn đồng). Hỏi mỗi tháng nhà máy nên sản xuất bao nhiêu sản phẩm để lợi nhuận thu được là lớn nhất? Biết rằng kết quả khảo sát thị trường cho thấy sản phẩm sản xuất ra sẽ được tiêu thụ hết.
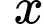 sản phẩm trong mỗi tháng. Chi phí sản xuất
sản phẩm trong mỗi tháng. Chi phí sản xuất 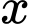 sản phẩm được cho bởi hàm chi phí
sản phẩm được cho bởi hàm chi phí 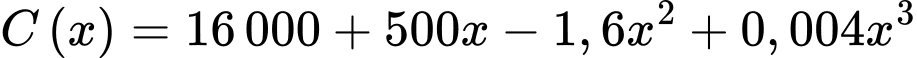 (nghìn đồng). Biết giá bán của của mỗi sản phẩm là một hàm số phụ thuộc vào số lượng sản phẩm
(nghìn đồng). Biết giá bán của của mỗi sản phẩm là một hàm số phụ thuộc vào số lượng sản phẩm 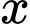 và được cho bởi công thức
và được cho bởi công thức 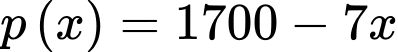 (nghìn đồng). Hỏi mỗi tháng nhà máy nên sản xuất bao nhiêu sản phẩm để lợi nhuận thu được là lớn nhất? Biết rằng kết quả khảo sát thị trường cho thấy sản phẩm sản xuất ra sẽ được tiêu thụ hết.
(nghìn đồng). Hỏi mỗi tháng nhà máy nên sản xuất bao nhiêu sản phẩm để lợi nhuận thu được là lớn nhất? Biết rằng kết quả khảo sát thị trường cho thấy sản phẩm sản xuất ra sẽ được tiêu thụ hết.
Điền đáp án: 100.
Ta có giá bán của mỗi sản phẩm là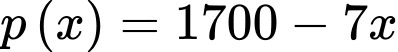 (nghìn đồng) (vì giá bán của mỗi sản phẩm phải là 1 số dương nên
(nghìn đồng) (vì giá bán của mỗi sản phẩm phải là 1 số dương nên 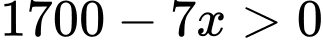
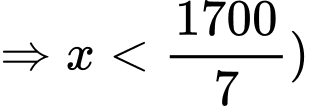
Suy ra giá bán của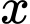 sản phẩm là
sản phẩm là 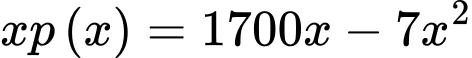 (nghìn đồng)
(nghìn đồng)
Ta có lợi nhuận thu được của nhà máy khi bán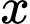 sản phẩm là
sản phẩm là
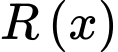 = Doanh thu – Chi phí sản xuất
= Doanh thu – Chi phí sản xuất
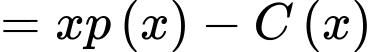
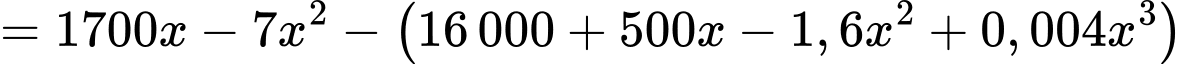
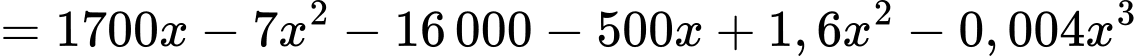
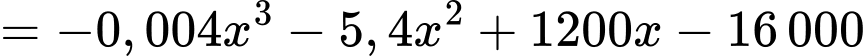
Xét hàm số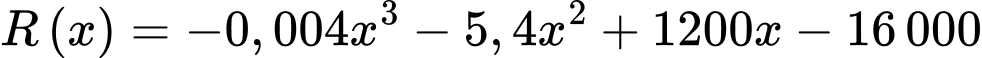 trên khoảng
trên khoảng 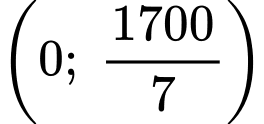
Ta có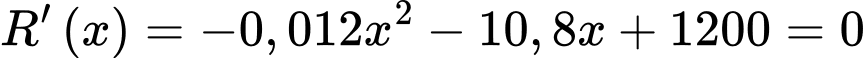
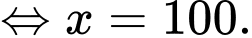
Bảng biến thiên
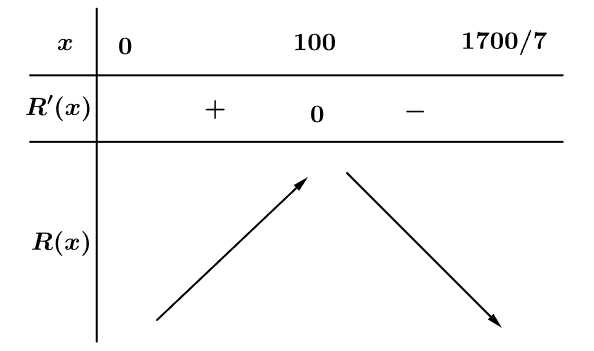
Dựa vào bảng biến thiên, suy ra nhà máy nên sản xuất 100 sản phẩm để thu được lợi nhuận lớn nhất.
Ta có giá bán của mỗi sản phẩm là
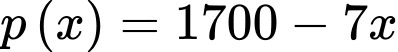 (nghìn đồng) (vì giá bán của mỗi sản phẩm phải là 1 số dương nên
(nghìn đồng) (vì giá bán của mỗi sản phẩm phải là 1 số dương nên 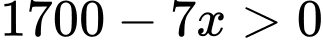
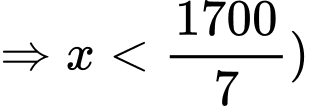
Suy ra giá bán của
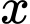 sản phẩm là
sản phẩm là 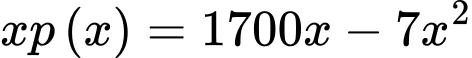 (nghìn đồng)
(nghìn đồng)
Ta có lợi nhuận thu được của nhà máy khi bán
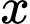 sản phẩm là
sản phẩm là
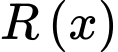 = Doanh thu – Chi phí sản xuất
= Doanh thu – Chi phí sản xuất
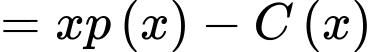
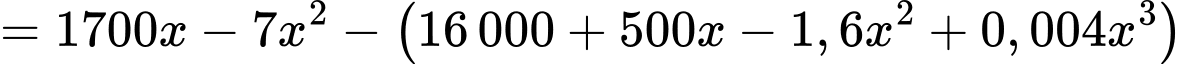
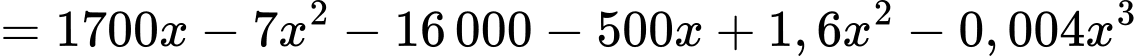
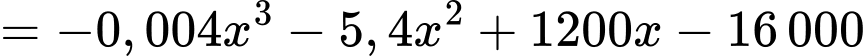
Xét hàm số
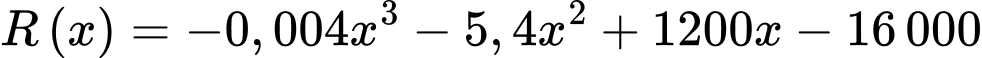 trên khoảng
trên khoảng 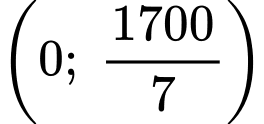
Ta có
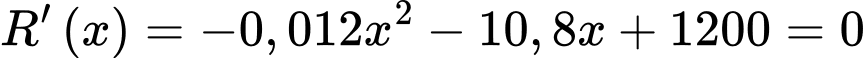
Bảng biến thiên

Dựa vào bảng biến thiên, suy ra nhà máy nên sản xuất 100 sản phẩm để thu được lợi nhuận lớn nhất.
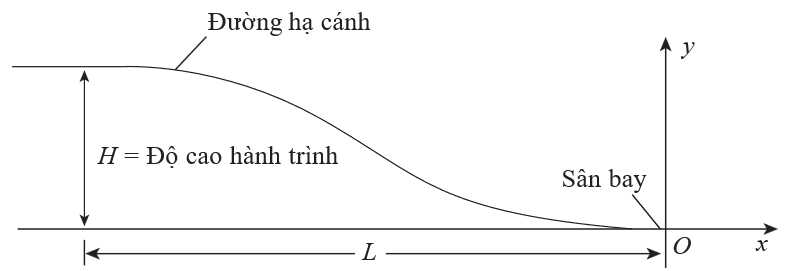
Câu 20 [774181]: Một máy bay đang bay ở độ cao 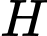 khi bắt đầu hạ cánh xuống một đường băng sân bay cách máy bay một khoảng
khi bắt đầu hạ cánh xuống một đường băng sân bay cách máy bay một khoảng 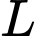 theo phương ngang, như hình vẽ. Giả sử đường bay hạ cánh của máy bay là đồ thị của một hàm đa thức bậc ba
theo phương ngang, như hình vẽ. Giả sử đường bay hạ cánh của máy bay là đồ thị của một hàm đa thức bậc ba 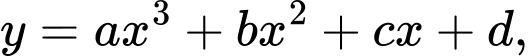 trong đó
trong đó 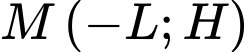 và
và  là 2 điểm cực trị của đồ thị hàm số.
là 2 điểm cực trị của đồ thị hàm số.
Biết rằng tại vị trí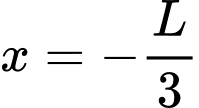 thì máy bay có độ cao là 2590 mét. Tính
thì máy bay có độ cao là 2590 mét. Tính 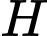 (đơn vị mét).
(đơn vị mét).
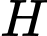 khi bắt đầu hạ cánh xuống một đường băng sân bay cách máy bay một khoảng
khi bắt đầu hạ cánh xuống một đường băng sân bay cách máy bay một khoảng 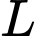 theo phương ngang, như hình vẽ. Giả sử đường bay hạ cánh của máy bay là đồ thị của một hàm đa thức bậc ba
theo phương ngang, như hình vẽ. Giả sử đường bay hạ cánh của máy bay là đồ thị của một hàm đa thức bậc ba 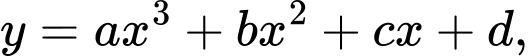 trong đó
trong đó 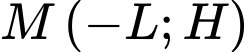 và
và  là 2 điểm cực trị của đồ thị hàm số.
là 2 điểm cực trị của đồ thị hàm số.
Biết rằng tại vị trí
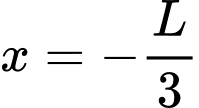 thì máy bay có độ cao là 2590 mét. Tính
thì máy bay có độ cao là 2590 mét. Tính 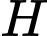 (đơn vị mét).
(đơn vị mét).
Điền đáp án: 9990.
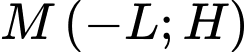 và
và  là 2 điểm cực trị của đồ thị hàm số nên
là 2 điểm cực trị của đồ thị hàm số nên 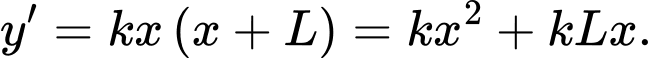
Ta có: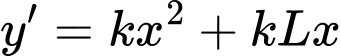
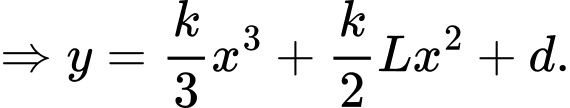
Đồ thị hàm số đi qua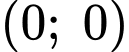 nên
nên 
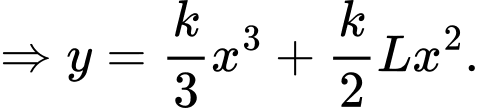
Đồ thị hàm số đi qua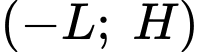 nên
nên 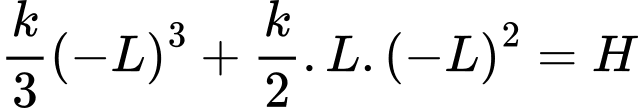
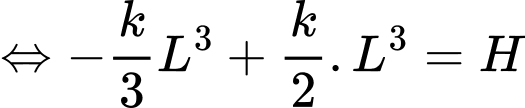
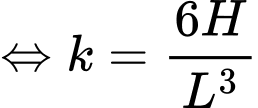
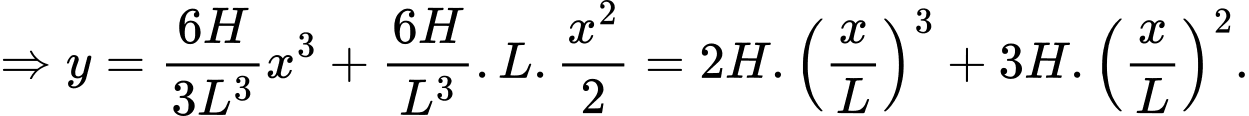
Ta có: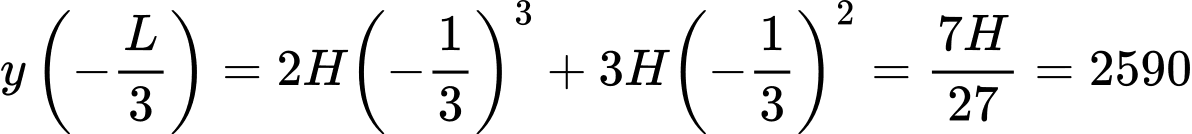
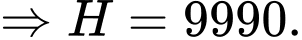
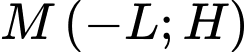 và
và  là 2 điểm cực trị của đồ thị hàm số nên
là 2 điểm cực trị của đồ thị hàm số nên 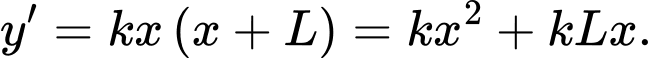
Ta có:
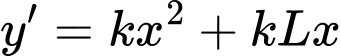
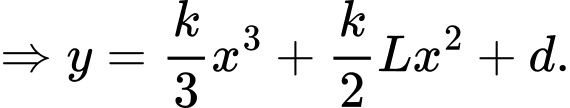
Đồ thị hàm số đi qua
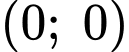 nên
nên 
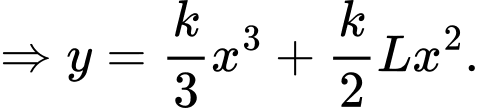
Đồ thị hàm số đi qua
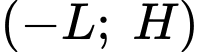 nên
nên 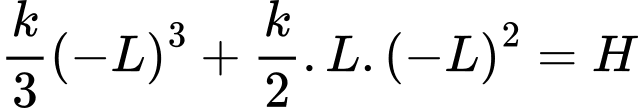
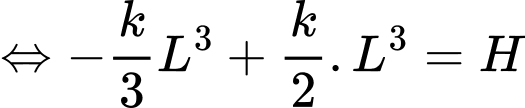
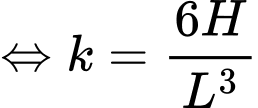
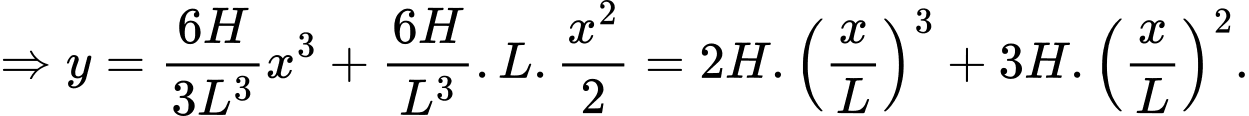
Ta có:
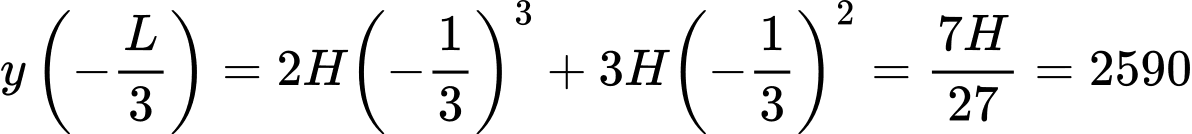
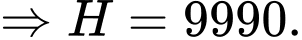
Câu 21 [703160]: Đường đi của một khinh khí cầu được gắn trong hệ trục tọa độ là một phần của đường cong bậc hai trên bậc nhất có đồ thị cắt trục hoành tại hai điểm có tọa độ là 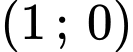 và
và 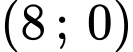 với đơn vị trên hệ trục tọa độ là
với đơn vị trên hệ trục tọa độ là 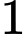 km.
km.
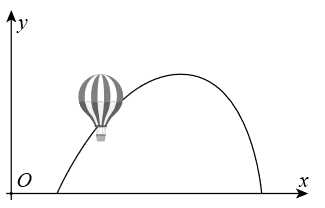
Biết rằng điểm cực đại của đồ thị hàm số là điểm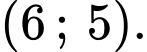 Hỏi khi khí cầu đi qua điểm cực đại và cách mặt đất
Hỏi khi khí cầu đi qua điểm cực đại và cách mặt đất 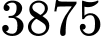 m thì khí cầu cách gốc tọa độ theo phương ngang bao nhiêu? (đơn vị: km).
m thì khí cầu cách gốc tọa độ theo phương ngang bao nhiêu? (đơn vị: km).
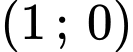 và
và 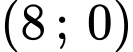 với đơn vị trên hệ trục tọa độ là
với đơn vị trên hệ trục tọa độ là 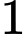 km.
km.
Biết rằng điểm cực đại của đồ thị hàm số là điểm
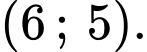 Hỏi khi khí cầu đi qua điểm cực đại và cách mặt đất
Hỏi khi khí cầu đi qua điểm cực đại và cách mặt đất 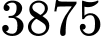 m thì khí cầu cách gốc tọa độ theo phương ngang bao nhiêu? (đơn vị: km).
m thì khí cầu cách gốc tọa độ theo phương ngang bao nhiêu? (đơn vị: km).
Điền đáp án: 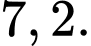
Cách 1:
Gọi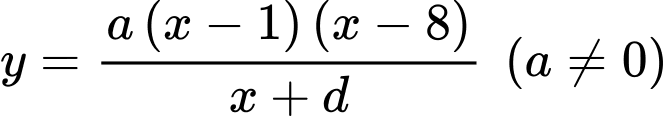 là đường đi của khinh khí cầu.
là đường đi của khinh khí cầu.
Khi đó, phương trình đường thẳng đi qua 2 điểm cực trị là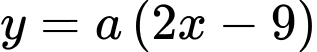 , phương trình đường thẳng này đi qua điểm
, phương trình đường thẳng này đi qua điểm 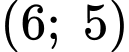 suy ra
suy ra 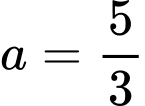
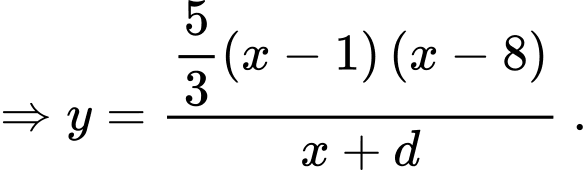
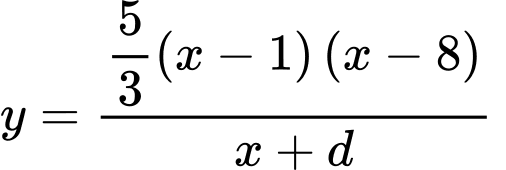 đi qua điểm
đi qua điểm 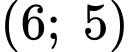 nên
nên 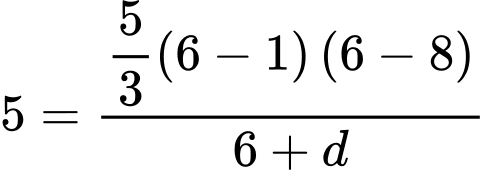
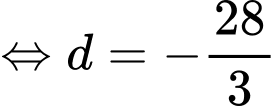
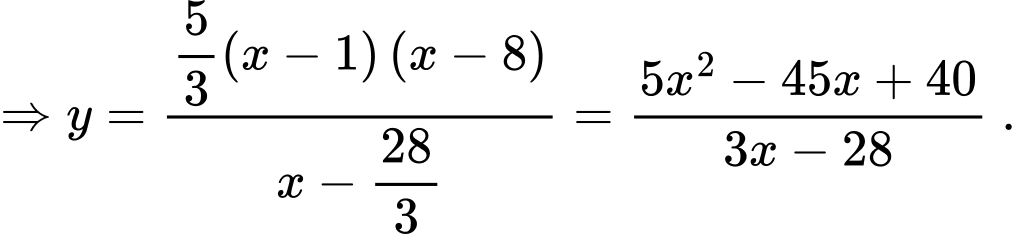
Cách 2:
Gọi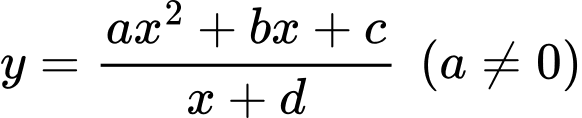 là đường đi của khinh khí cầu.
là đường đi của khinh khí cầu.
Khi đó: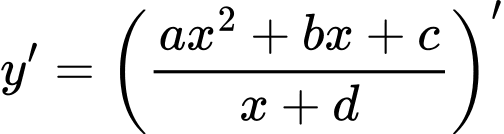
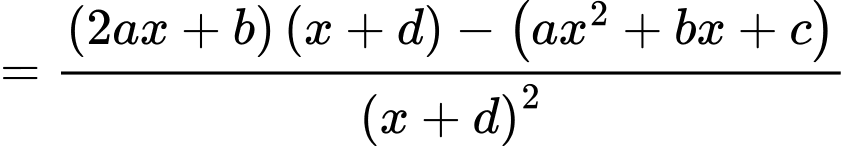
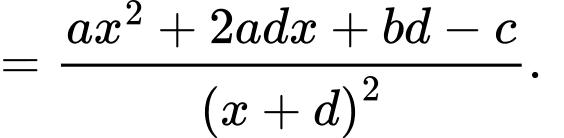
Ta có: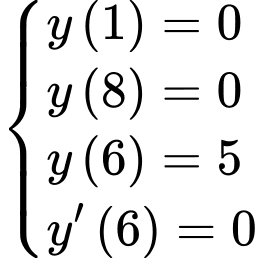
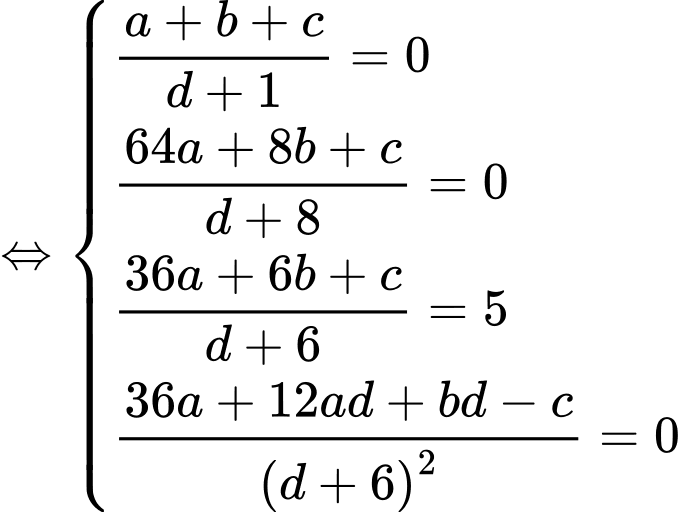
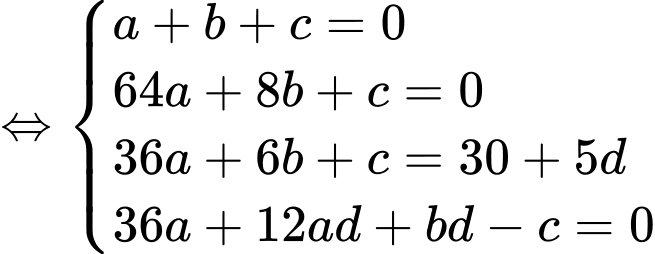
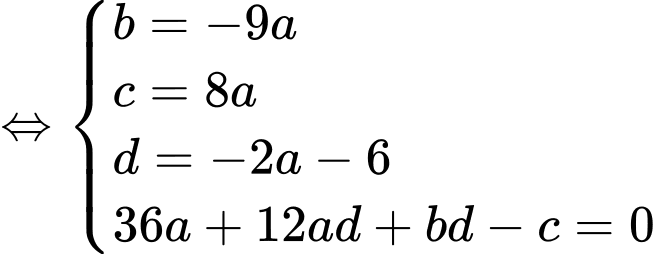
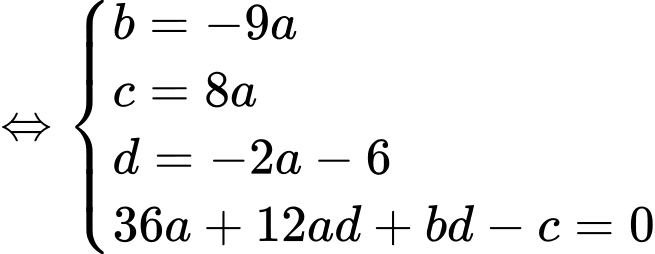
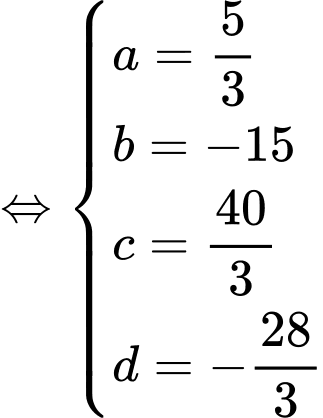
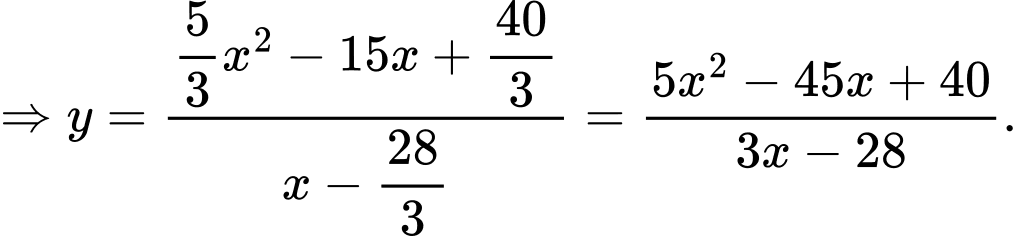
Ta có:
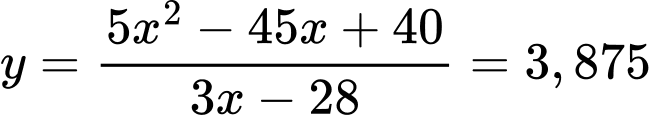
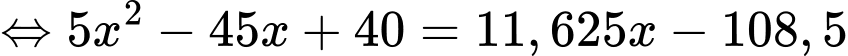
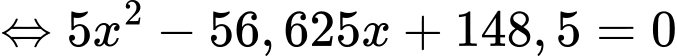
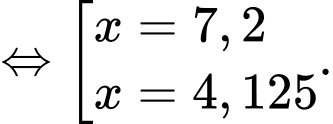
Vậy khi khí cầu đi qua điểm cực đại và cách mặt đất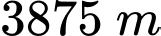 thì khí cầu cách gốc tọa độ theo phương ngang
thì khí cầu cách gốc tọa độ theo phương ngang 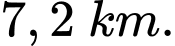
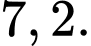
Cách 1:
Gọi
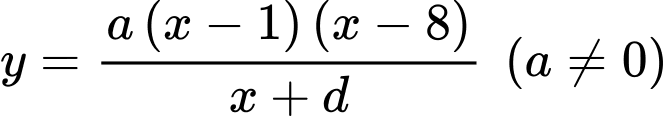 là đường đi của khinh khí cầu.
là đường đi của khinh khí cầu. Khi đó, phương trình đường thẳng đi qua 2 điểm cực trị là
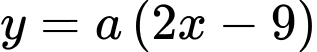 , phương trình đường thẳng này đi qua điểm
, phương trình đường thẳng này đi qua điểm 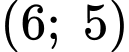 suy ra
suy ra 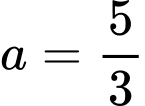
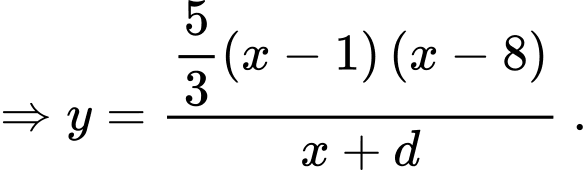
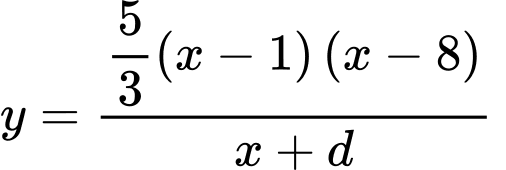 đi qua điểm
đi qua điểm 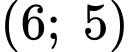 nên
nên 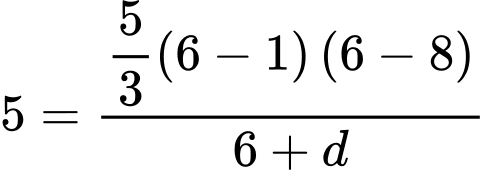
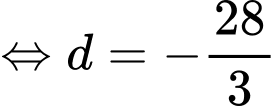
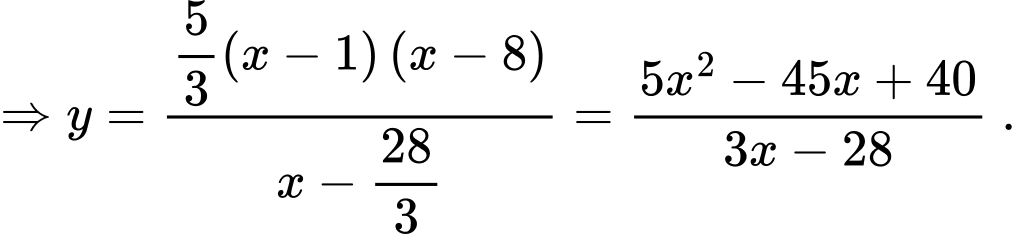
Cách 2:
Gọi
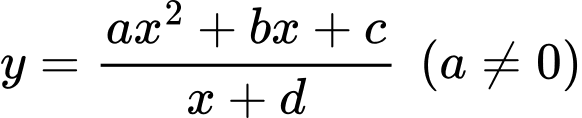 là đường đi của khinh khí cầu.
là đường đi của khinh khí cầu. Khi đó:
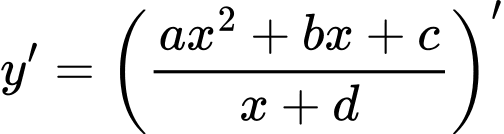
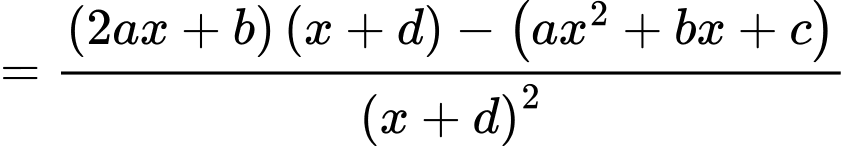
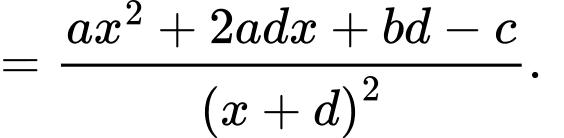
Ta có:
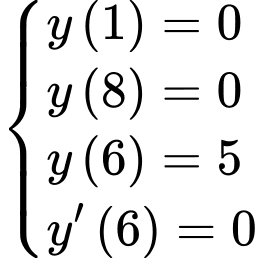
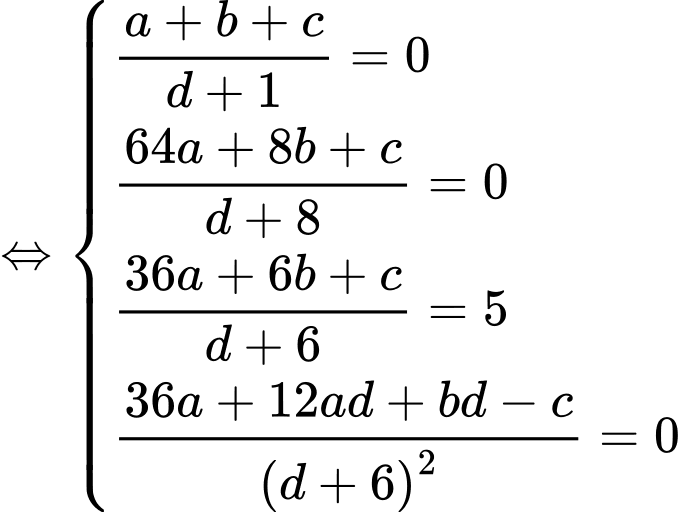
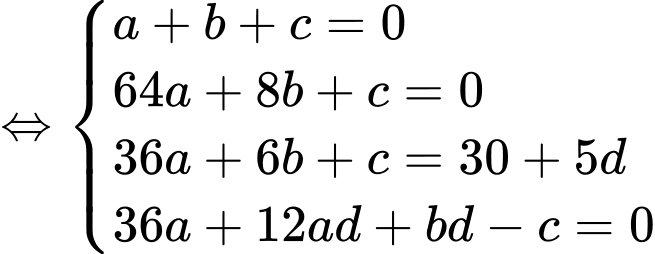
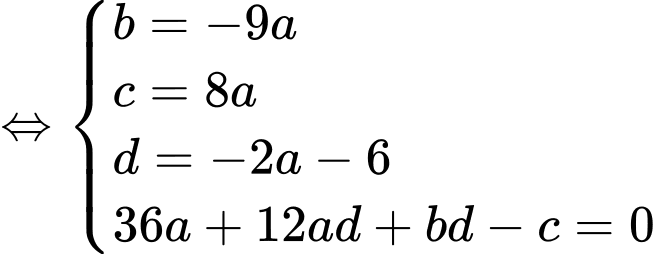
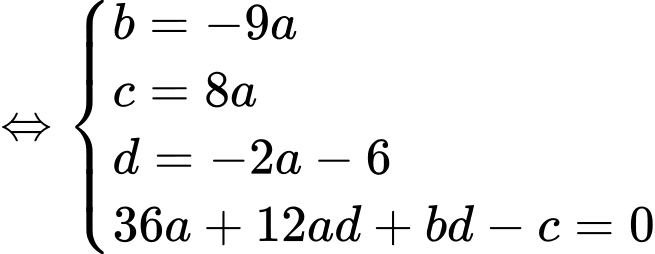
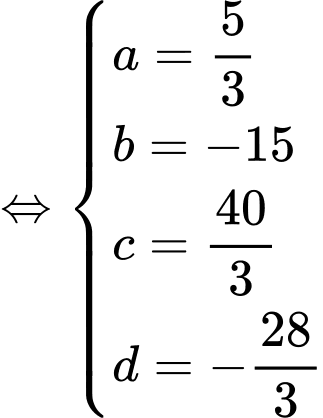
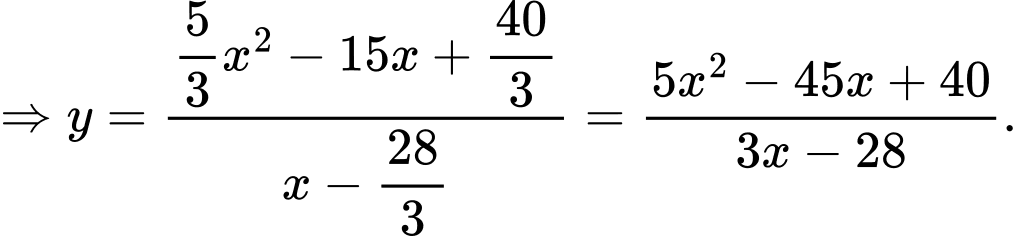
Ta có:
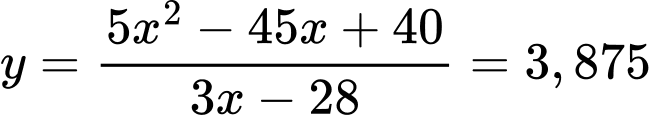
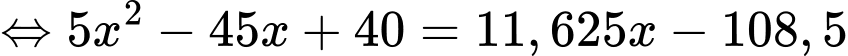
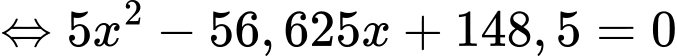
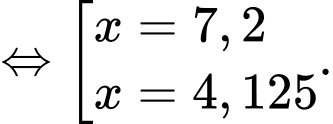
Vậy khi khí cầu đi qua điểm cực đại và cách mặt đất
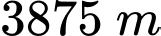 thì khí cầu cách gốc tọa độ theo phương ngang
thì khí cầu cách gốc tọa độ theo phương ngang 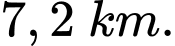
Câu 22 [384770]: Một hồ nước nhân tạo được xây dựng trong một công viên giải trí. Trong mô hình minh hoạ bên, nó được giới hạn bởi các trục toạ độ và đồ thị của hàm số 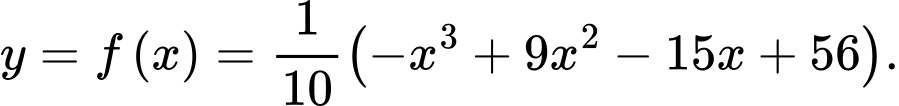 Đơn vị đo độ dài trên mỗi trục toạ độ là
Đơn vị đo độ dài trên mỗi trục toạ độ là 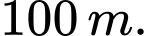 Trong công viên có một con đường chạy dọc theo đồ thị hàm số
Trong công viên có một con đường chạy dọc theo đồ thị hàm số 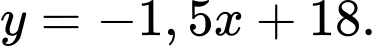 Người ta dự định xây dựng bên bờ hồ một bến thuyền đạp nước Khoảng cách từ bến thuyền đến con đường này là ngắn nhất la bao nhiêu mét?Viết kết quả làm tròn đến hàng phần chục?
Người ta dự định xây dựng bên bờ hồ một bến thuyền đạp nước Khoảng cách từ bến thuyền đến con đường này là ngắn nhất la bao nhiêu mét?Viết kết quả làm tròn đến hàng phần chục?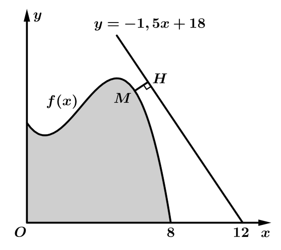
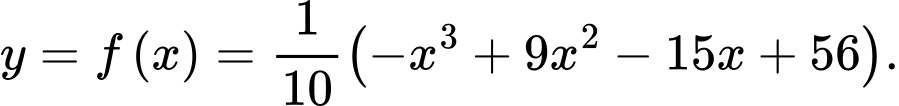 Đơn vị đo độ dài trên mỗi trục toạ độ là
Đơn vị đo độ dài trên mỗi trục toạ độ là 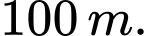 Trong công viên có một con đường chạy dọc theo đồ thị hàm số
Trong công viên có một con đường chạy dọc theo đồ thị hàm số 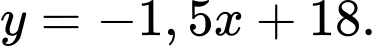 Người ta dự định xây dựng bên bờ hồ một bến thuyền đạp nước Khoảng cách từ bến thuyền đến con đường này là ngắn nhất la bao nhiêu mét?Viết kết quả làm tròn đến hàng phần chục?
Người ta dự định xây dựng bên bờ hồ một bến thuyền đạp nước Khoảng cách từ bến thuyền đến con đường này là ngắn nhất la bao nhiêu mét?Viết kết quả làm tròn đến hàng phần chục?
Gọi 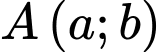
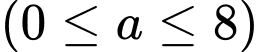 là điểm tượng trưng cho bến thuyền trên bờ hồ.
là điểm tượng trưng cho bến thuyền trên bờ hồ.
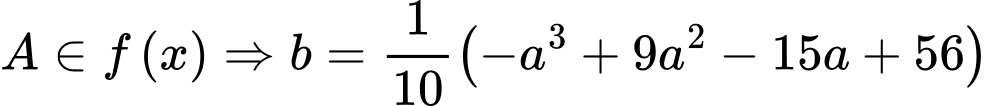 (1)
(1)
Khoảng cách từ bến thuyền đến con đường là: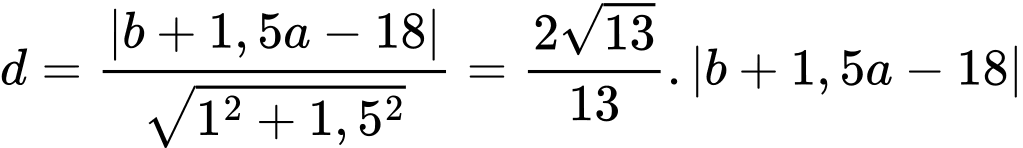 (2)
(2)
Từ (1) và (2), ta có: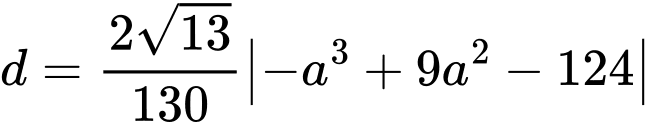
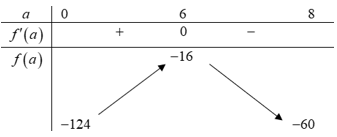
Đặt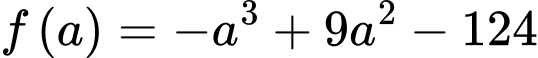 với
với 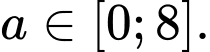
Có: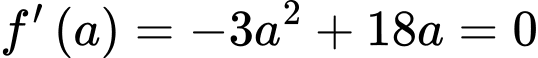
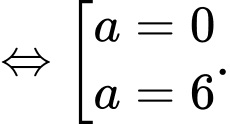
Bảng biến thiên:
Để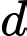 ngắn nhất
ngắn nhất 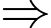 Hàm số
Hàm số 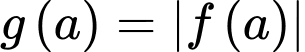 đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất.
Dựa vào bảng biến thiên, suy ra giá trị nhỏ nhất của là 16 khi
là 16 khi 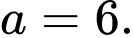
Vậy khoảng cách ngắn nhất từ bến thuyền đến con đường là: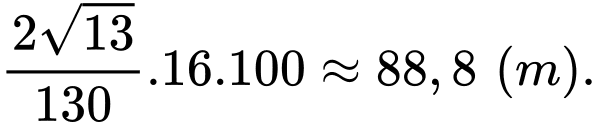
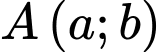
 là điểm tượng trưng cho bến thuyền trên bờ hồ.
là điểm tượng trưng cho bến thuyền trên bờ hồ.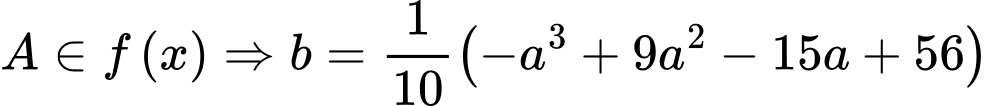 (1)
(1)Khoảng cách từ bến thuyền đến con đường là:
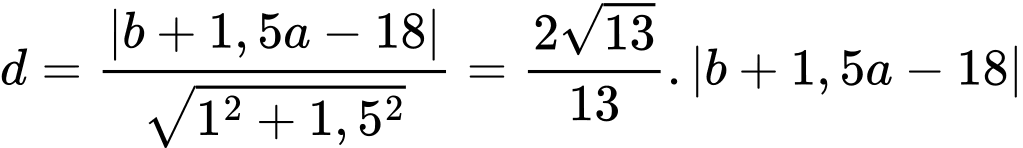 (2)
(2)Từ (1) và (2), ta có:
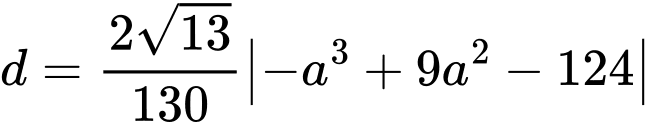
Đặt
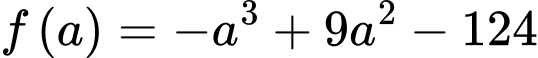 với
với 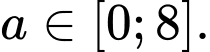
Có:
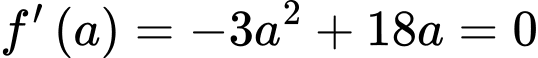
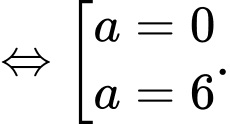
Bảng biến thiên:

Để
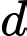 ngắn nhất
ngắn nhất  Hàm số
Hàm số 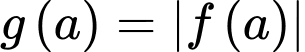 đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất.Dựa vào bảng biến thiên, suy ra giá trị nhỏ nhất của
 là 16 khi
là 16 khi 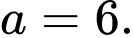
Vậy khoảng cách ngắn nhất từ bến thuyền đến con đường là: