PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
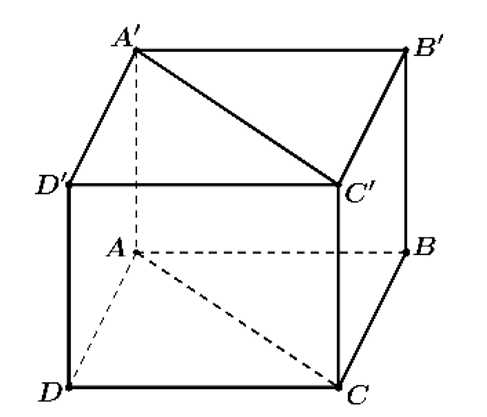
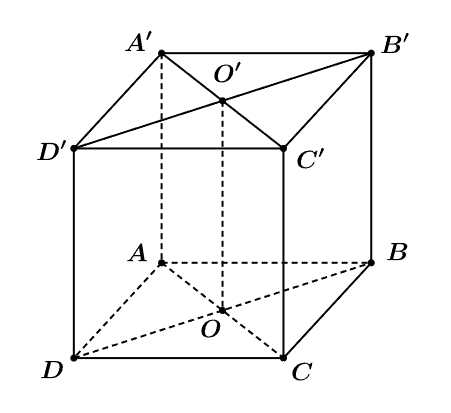
Câu 1 [708359]: Trong không gian cho hình hộp  (như hình vẽ). Khẳng định nào sau đây là sai?
(như hình vẽ). Khẳng định nào sau đây là sai?
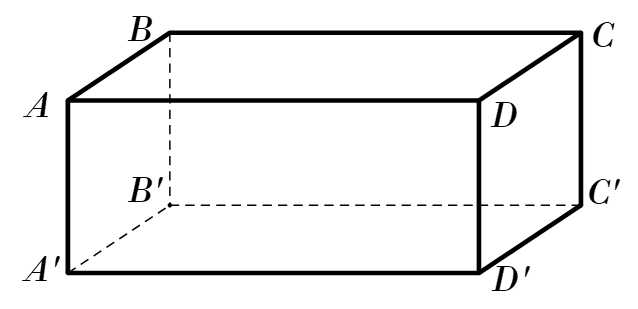
 (như hình vẽ). Khẳng định nào sau đây là sai?
(như hình vẽ). Khẳng định nào sau đây là sai?
A, 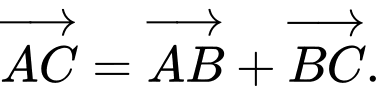
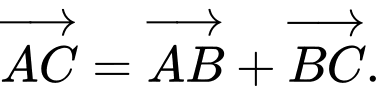
B, 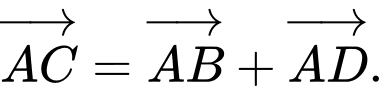
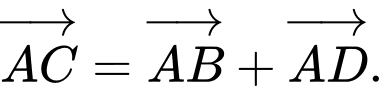
C, 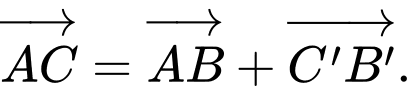
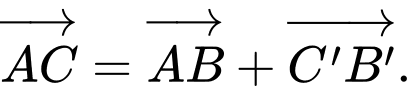
D, 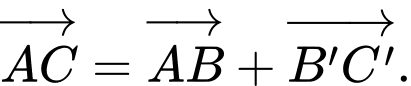
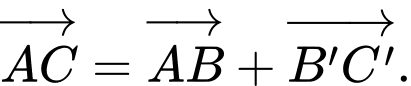
Chọn đáp án C.
Theo quy tắc cộng 2 vectơ. A và D đúng.
Quy tắc hình bình hành. B đúng. Đáp án: C
Theo quy tắc cộng 2 vectơ. A và D đúng.
Quy tắc hình bình hành. B đúng. Đáp án: C
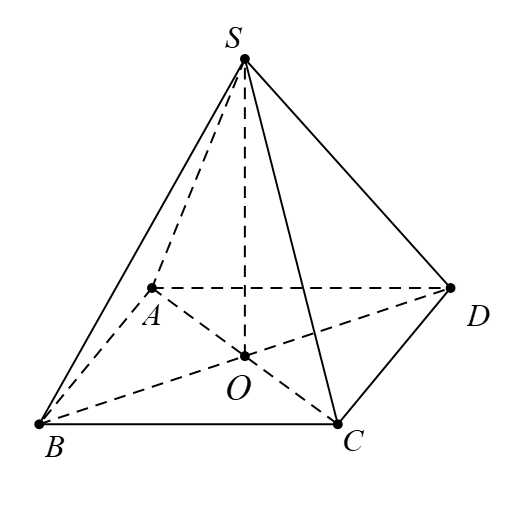
Câu 2 [715745]: Cho hình chóp  có đáy là hình bình hành tâm
có đáy là hình bình hành tâm  Tính tổng
Tính tổng 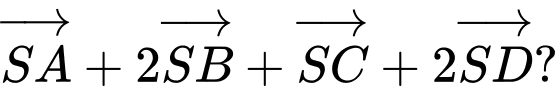
 có đáy là hình bình hành tâm
có đáy là hình bình hành tâm  Tính tổng
Tính tổng 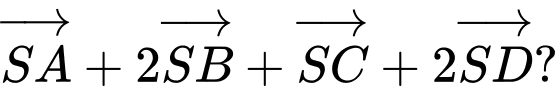
A, 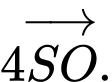
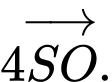
B, 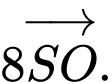
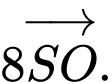
C, 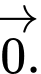
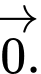
D, 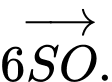
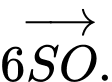
Chọn đáp án D.
Ta có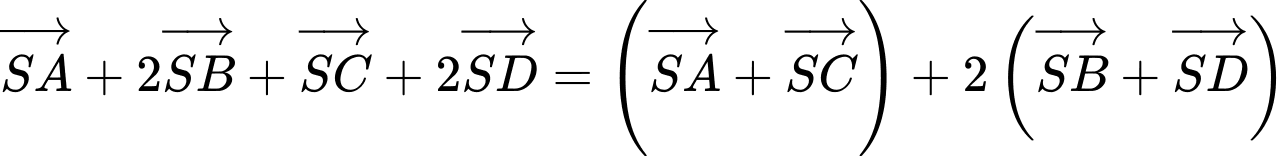
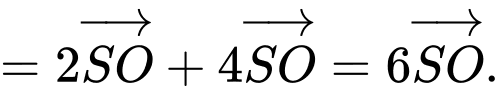 Đáp án: D
Đáp án: D

Ta có
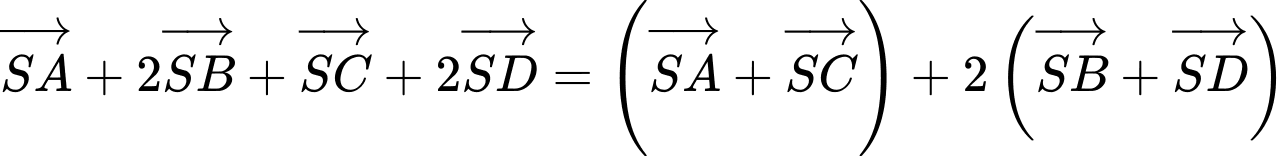
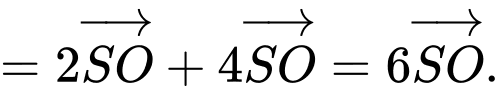 Đáp án: D
Đáp án: D
Câu 3 [774235]: Cho lập phương  có độ dài mỗi cạnh bằng 1. Tính độ dài của vectơ
có độ dài mỗi cạnh bằng 1. Tính độ dài của vectơ 
 có độ dài mỗi cạnh bằng 1. Tính độ dài của vectơ
có độ dài mỗi cạnh bằng 1. Tính độ dài của vectơ 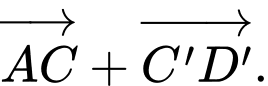

A, 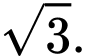
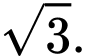
B, 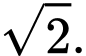
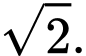
C, 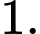
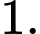
D, 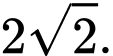
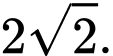
Chọn đáp án C.
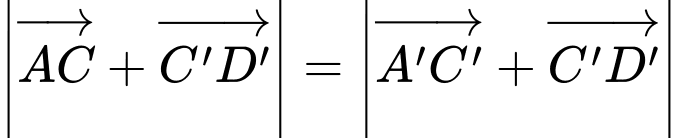
 Đáp án: C
Đáp án: C
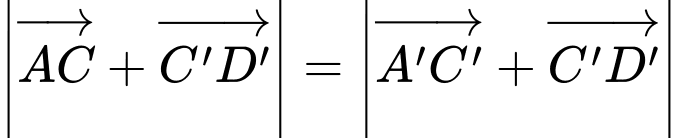
 Đáp án: C
Đáp án: C
Câu 4 [380263]: Cho hình chóp tứ giác đều 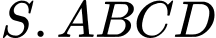 có tất cả các cạnh bằng
có tất cả các cạnh bằng 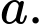 Góc giữa hai vectơ
Góc giữa hai vectơ  và
và 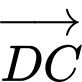 là?
là?
 có tất cả các cạnh bằng
có tất cả các cạnh bằng 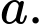 Góc giữa hai vectơ
Góc giữa hai vectơ  và
và 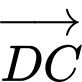 là?
là? A, 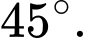
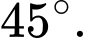
B, 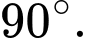
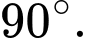
C, 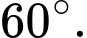
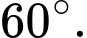
D, 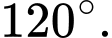
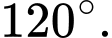

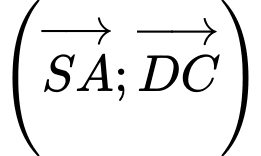
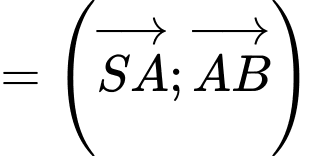
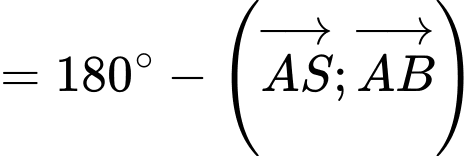

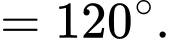 Đáp án: D
Đáp án: D
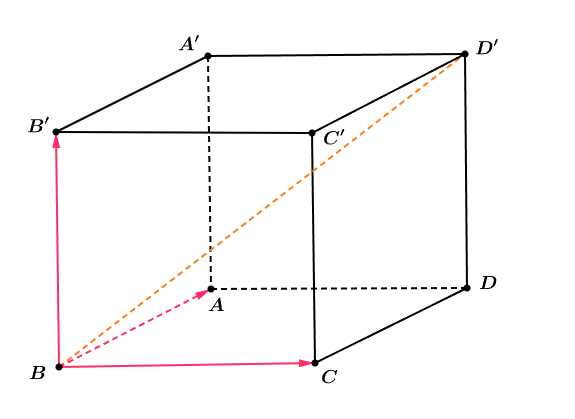
Câu 5 [717136]: Cho hình hộp 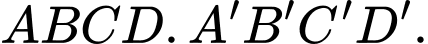 Vectơ
Vectơ 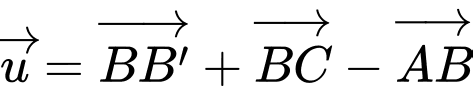 bằng vectơ nào dưới đây?
bằng vectơ nào dưới đây?
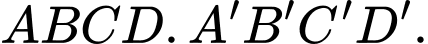 Vectơ
Vectơ 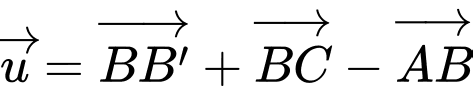 bằng vectơ nào dưới đây?
bằng vectơ nào dưới đây? A, 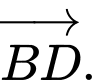
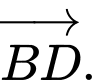
B, 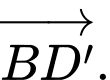
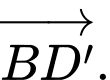
C, 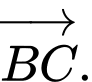
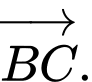
D, 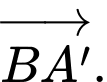
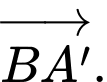
Chọn đáp án B.
Ta có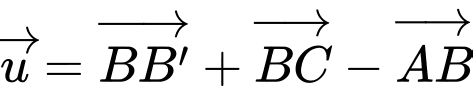
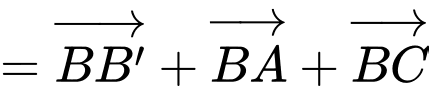
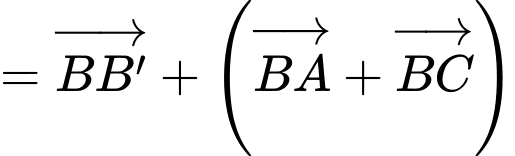
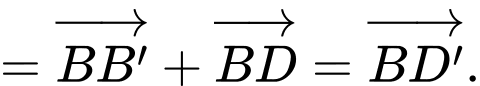 Đáp án: B
Đáp án: B

Ta có
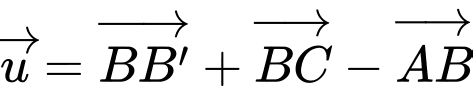
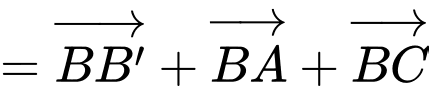
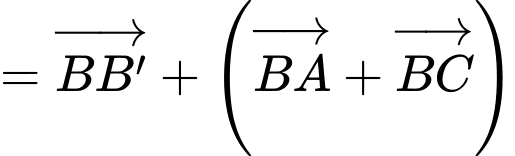
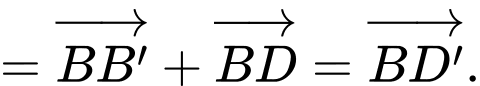 Đáp án: B
Đáp án: B
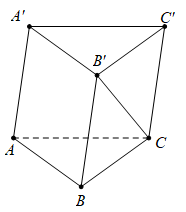
Câu 6 [975603]: Cho hình lăng trụ  Đặt
Đặt 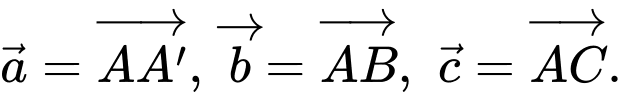 Hãy biểu diễn vectơ
Hãy biểu diễn vectơ  theo các vectơ
theo các vectơ 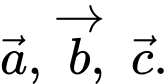
 Đặt
Đặt 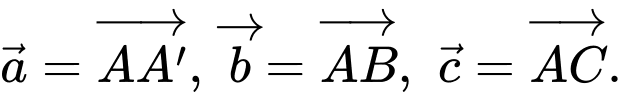 Hãy biểu diễn vectơ
Hãy biểu diễn vectơ 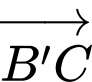 theo các vectơ
theo các vectơ 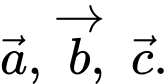
A, 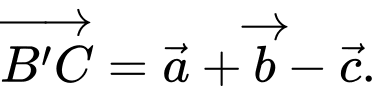
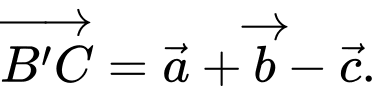
B, 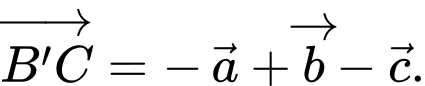
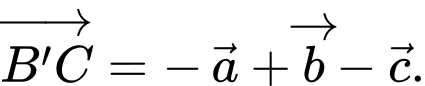
C, 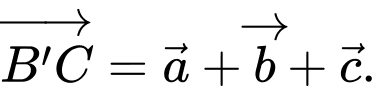
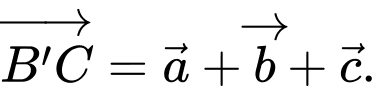
D, 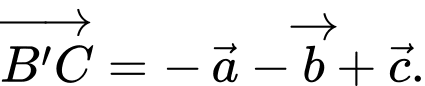
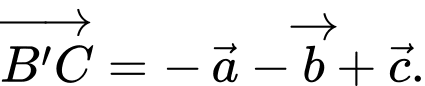
HD: Ta có:
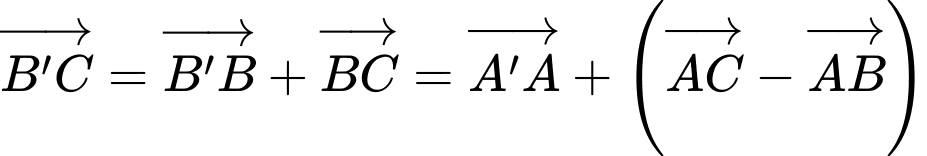
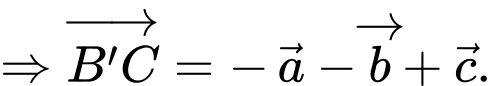 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
Câu 7 [715747]: Cho hình lập phương 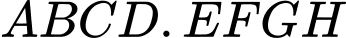 có cạnh bằng
có cạnh bằng  . Giá trị của
. Giá trị của 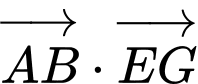 bằng
bằng
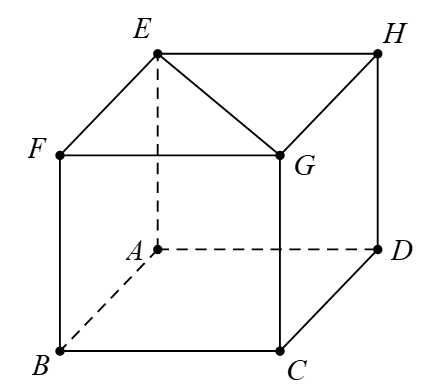
 có cạnh bằng
có cạnh bằng  . Giá trị của
. Giá trị của  bằng
bằng
A, 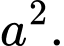
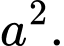
B, 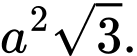
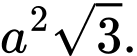
C, 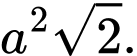
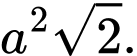
D, 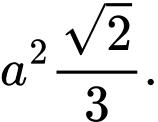
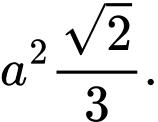
Chọn đáp án A.
Ta có:
Vì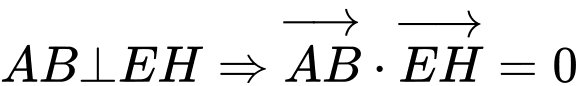
Vậy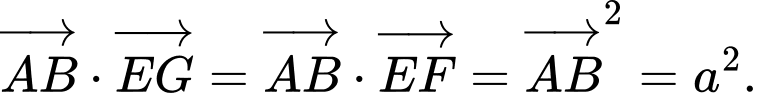 Đáp án: A
Đáp án: A
Ta có:

Vì
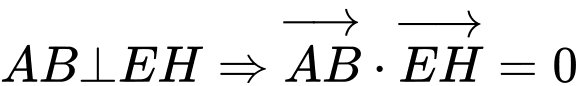
Vậy
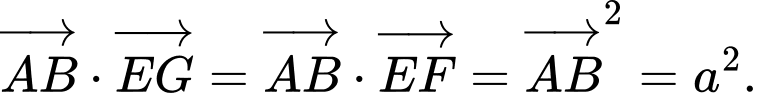 Đáp án: A
Đáp án: A
Câu 8 [717140]: Cho tứ diện đều 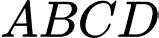 có cạnh bằng
có cạnh bằng  Tính
Tính 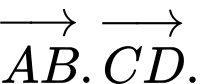
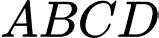 có cạnh bằng
có cạnh bằng 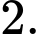 Tính
Tính 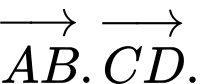
A, 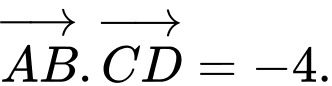
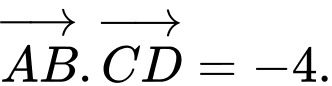
B, 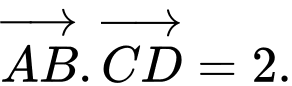
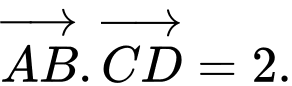
C, 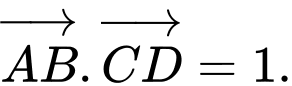
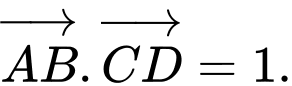
D, 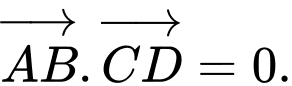
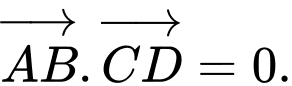
Chọn đáp án D.
Vì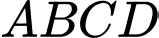 là tứ diện đều nên các tam giác
là tứ diện đều nên các tam giác 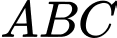 và
và 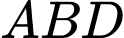 là các tam giác đều.
là các tam giác đều.
Khi đó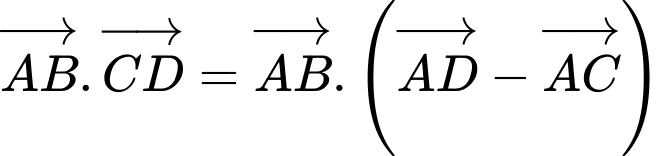
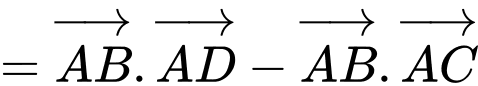
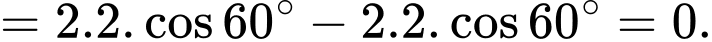 Đáp án: D
Đáp án: D

Vì
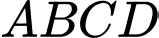 là tứ diện đều nên các tam giác
là tứ diện đều nên các tam giác 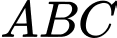 và
và 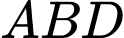 là các tam giác đều.
là các tam giác đều.
Khi đó
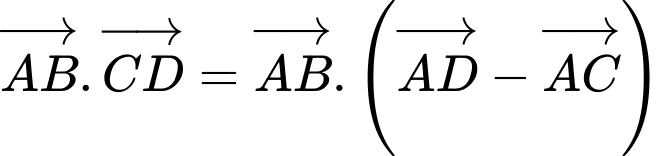
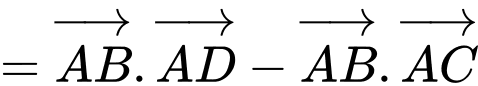
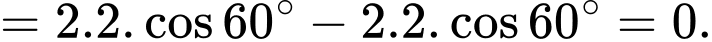 Đáp án: D
Đáp án: D
Câu 9 [774236]: Cho hình lập phương  có cạnh bằng
có cạnh bằng 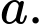 Gọi
Gọi  là tâm hình vuông
là tâm hình vuông 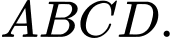 Đặt
Đặt 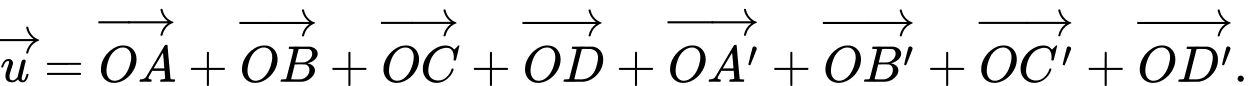 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng?
 có cạnh bằng
có cạnh bằng  Gọi
Gọi  là tâm hình vuông
là tâm hình vuông  Đặt
Đặt 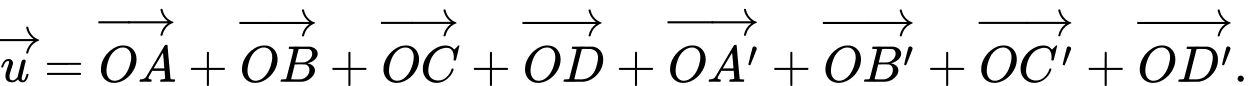 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng? A, 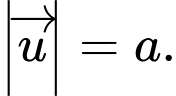
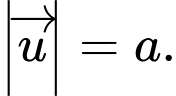
B, 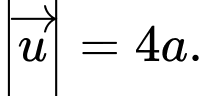
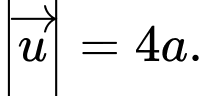
C, 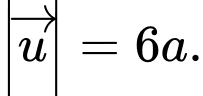
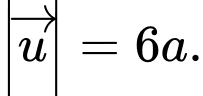
D, 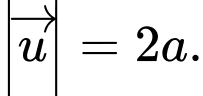
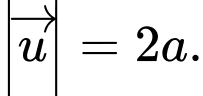
Chọn đáp án B.
Vì là tâm hình vuông
là tâm hình vuông  nên
nên 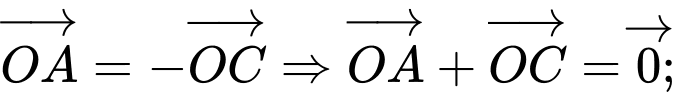
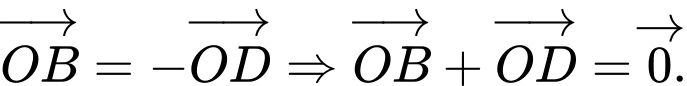
Gọi là tâm của hình vuông
là tâm của hình vuông  Dễ thấy
Dễ thấy 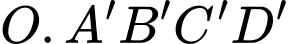 là hình chóp tứ giác đều từ đó áp dụng quy tắc trung tuyến, ta chứng minh được
là hình chóp tứ giác đều từ đó áp dụng quy tắc trung tuyến, ta chứng minh được 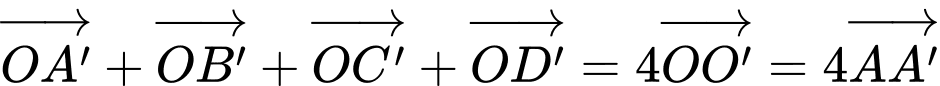
Suy ra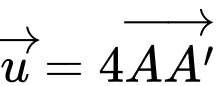
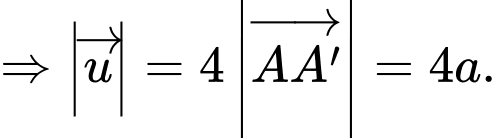 Đáp án: B
Đáp án: B

Vì
 là tâm hình vuông
là tâm hình vuông  nên
nên 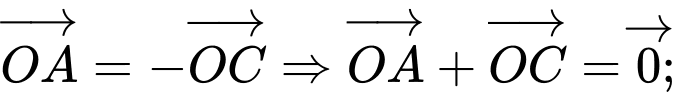
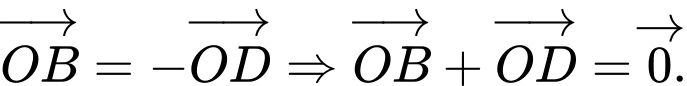
Gọi
 là tâm của hình vuông
là tâm của hình vuông  Dễ thấy
Dễ thấy 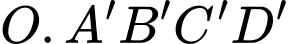 là hình chóp tứ giác đều từ đó áp dụng quy tắc trung tuyến, ta chứng minh được
là hình chóp tứ giác đều từ đó áp dụng quy tắc trung tuyến, ta chứng minh được 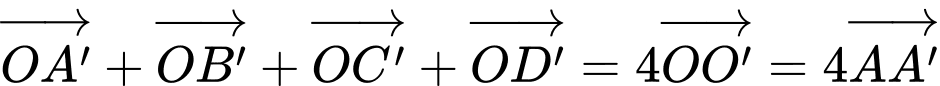
Suy ra
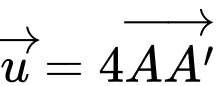
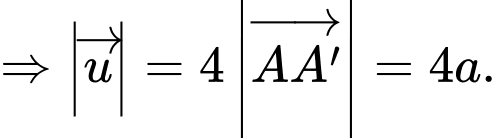 Đáp án: B
Đáp án: B
Câu 10 [541115]: Trong không gian 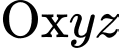 , cho hai vectơ
, cho hai vectơ 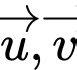 tạo với nhau góc
tạo với nhau góc 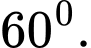 Biết rằng
Biết rằng 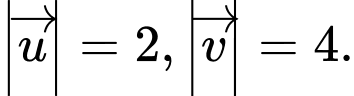 Tính
Tính 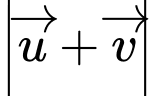
 , cho hai vectơ
, cho hai vectơ 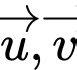 tạo với nhau góc
tạo với nhau góc 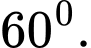 Biết rằng
Biết rằng 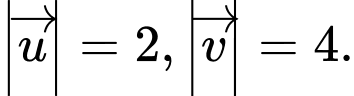 Tính
Tính 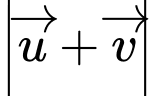
A, 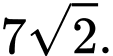
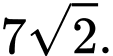
B, 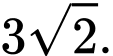
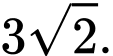
C, 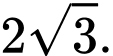
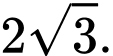
D, 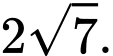
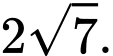
Có 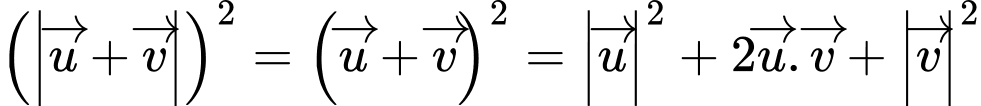
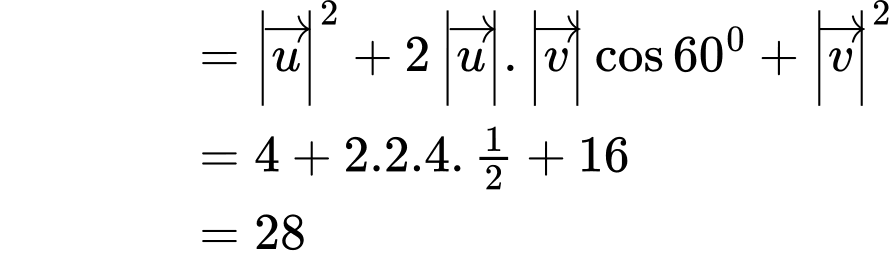
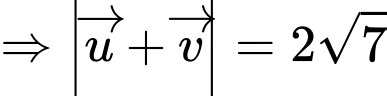
Chọn đáp án D. Đáp án: D
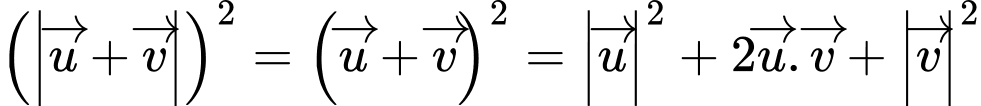
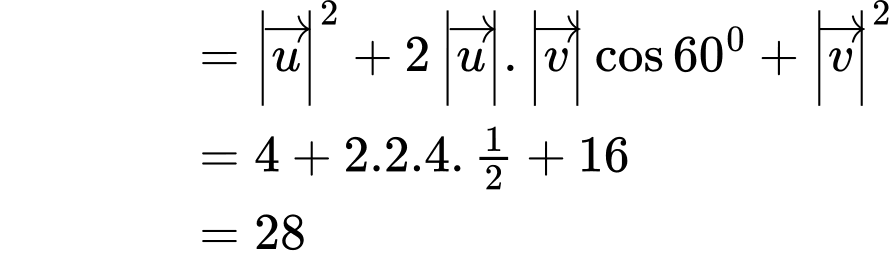
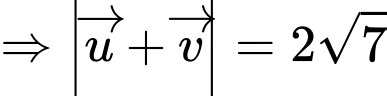
Chọn đáp án D. Đáp án: D
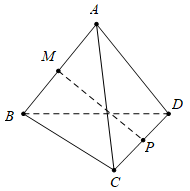
Câu 11 [975610]: Cho tứ diện 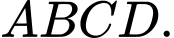 Gọi
Gọi 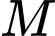 và
và 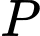 lần lượt là trung điểm của các cạnh
lần lượt là trung điểm của các cạnh  và
và 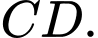 Đặt
Đặt 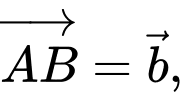
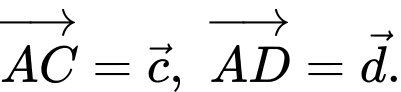 Khẳng định nào sau đây là đúng?
Khẳng định nào sau đây là đúng?
 Gọi
Gọi  và
và 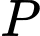 lần lượt là trung điểm của các cạnh
lần lượt là trung điểm của các cạnh  và
và 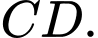 Đặt
Đặt 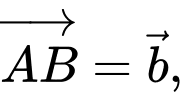
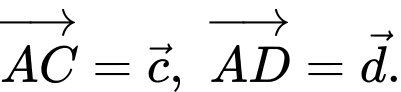 Khẳng định nào sau đây là đúng?
Khẳng định nào sau đây là đúng? A, 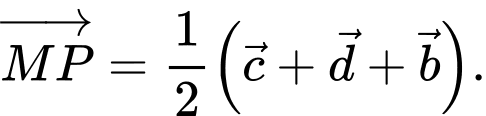
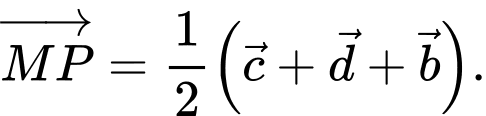
B, 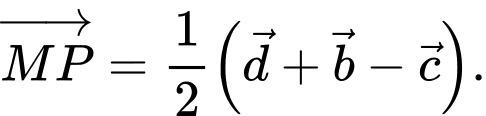
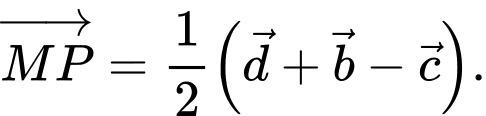
C, 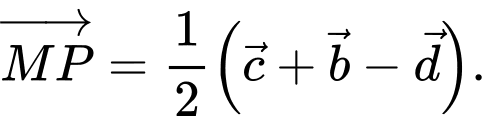
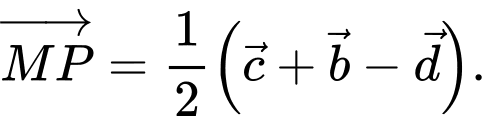
D, 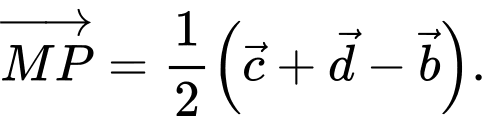
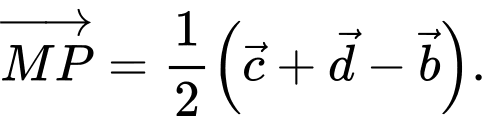
HD: Ta có:
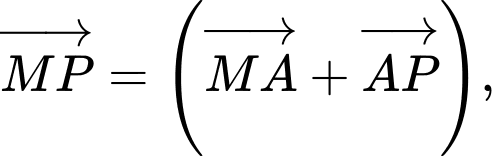 mặt khác
mặt khác 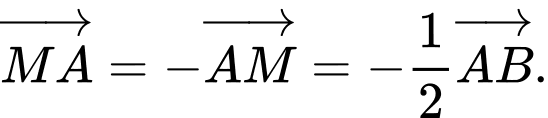
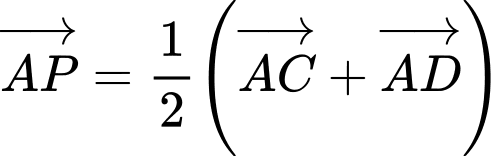 ( tính chất trung điểm)
( tính chất trung điểm) Do đó
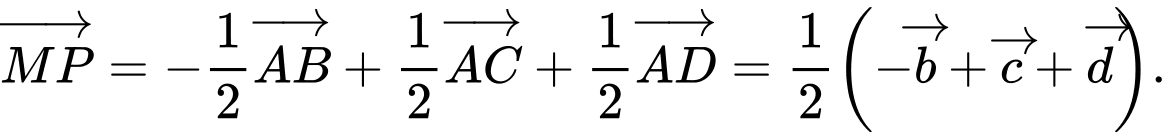 Chọn D. Đáp án: D
Chọn D. Đáp án: D
Câu 12 [379536]: Cho hình chóp 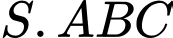 có
có 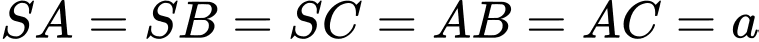 và
và 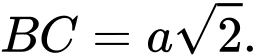 Tính tích vô hướng
Tính tích vô hướng 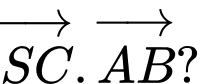
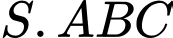 có
có 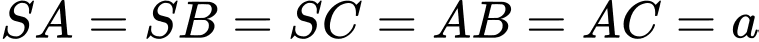 và
và 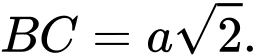 Tính tích vô hướng
Tính tích vô hướng 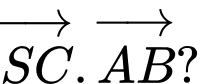
A, 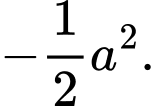
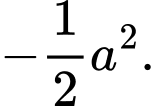
B, 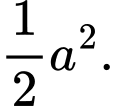
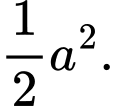
C, 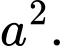
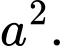
D, 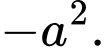
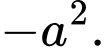
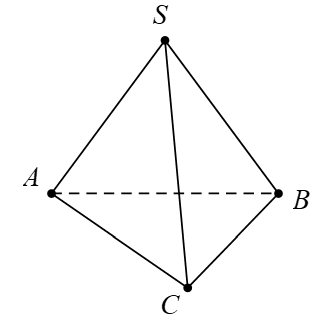
Tam giác
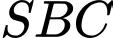 vuông tại
vuông tại 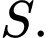
Khi đó:
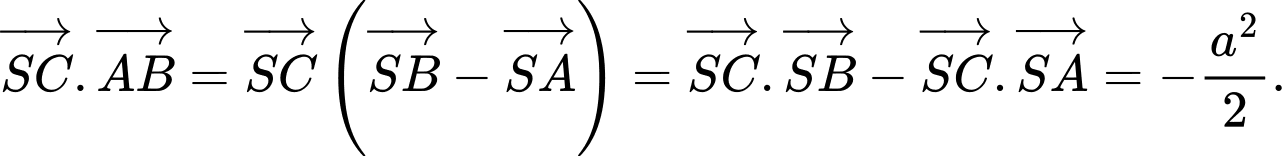 Chọn A. Đáp án: A
Chọn A. Đáp án: A PHẦN II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a),b),c),d) ở mỗi câu học sinh chọn đúng hoặc sai.
Câu 13 [681585]: Cho hình chóp  có
có  và
và  Các mệnh đề sau đúng hay sai?
Các mệnh đề sau đúng hay sai?
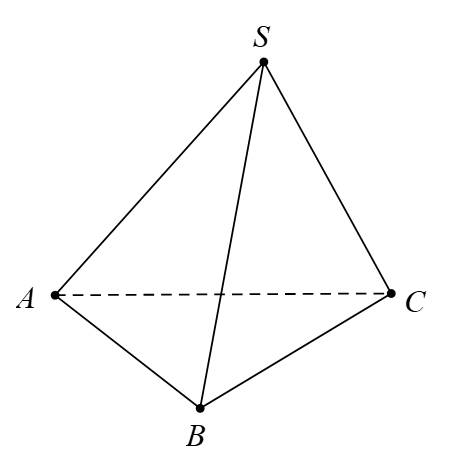
 có
có  và
và  Các mệnh đề sau đúng hay sai?
Các mệnh đề sau đúng hay sai?
– Theo quy tắc ba điểm, ta có:
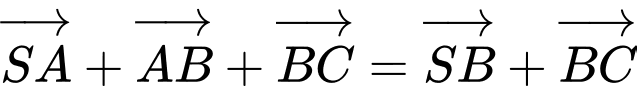
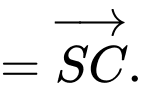 Do đó, ý a) đúng.
Do đó, ý a) đúng.
– Ta có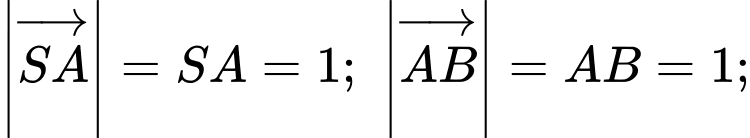
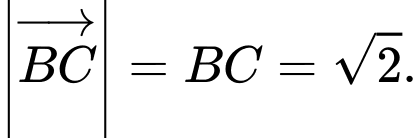 Do đó, ý b) sai.
Do đó, ý b) sai.
– Từ giả thiết, ta thấy tam giác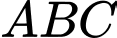 vuông tại
vuông tại 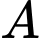 và tam giác
và tam giác 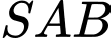 đều.
đều.
Do đó,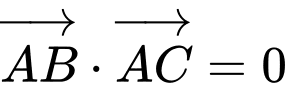 và
và 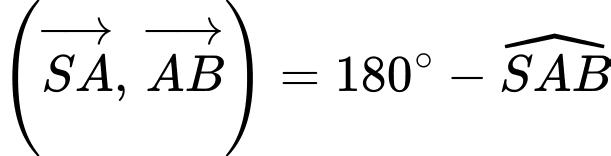
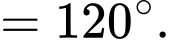
Ta có: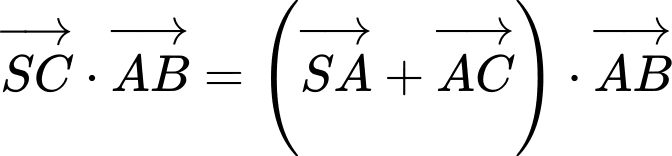
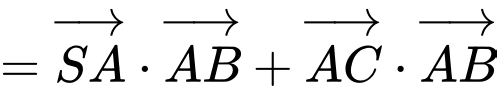
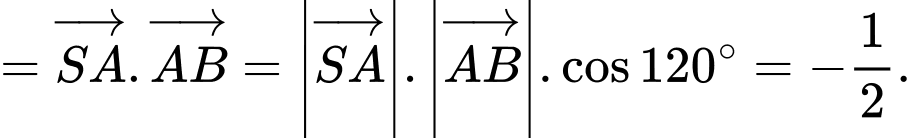 Do đó, ý c) sai.
Do đó, ý c) sai.
– Ta có: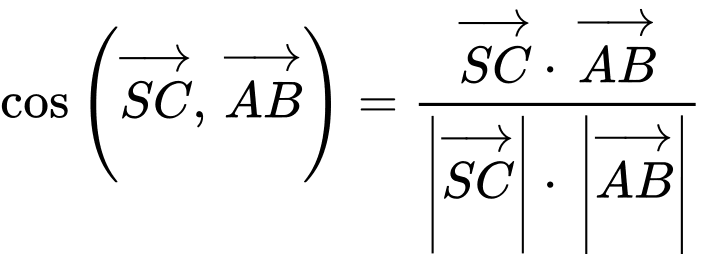
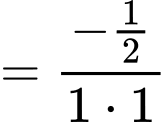
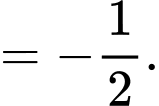
Vậy ý d) sai.
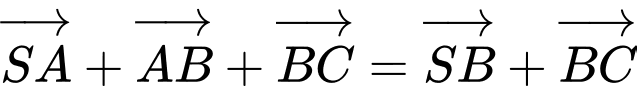
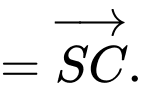 Do đó, ý a) đúng.
Do đó, ý a) đúng.– Ta có
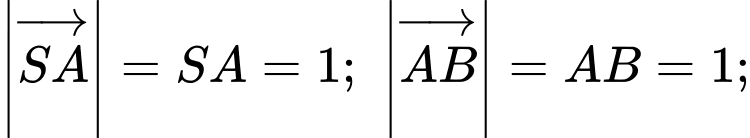
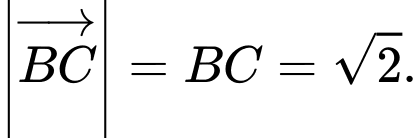 Do đó, ý b) sai.
Do đó, ý b) sai. – Từ giả thiết, ta thấy tam giác
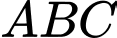 vuông tại
vuông tại 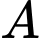 và tam giác
và tam giác 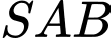 đều.
đều. Do đó,
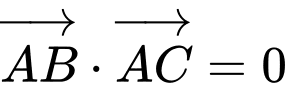 và
và 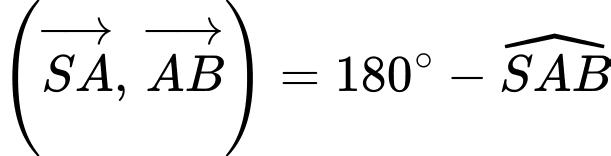
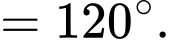
Ta có:
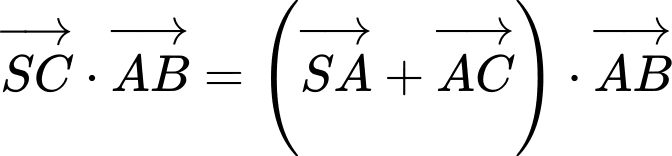
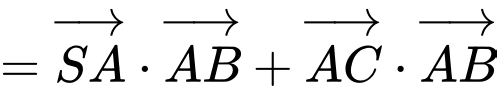
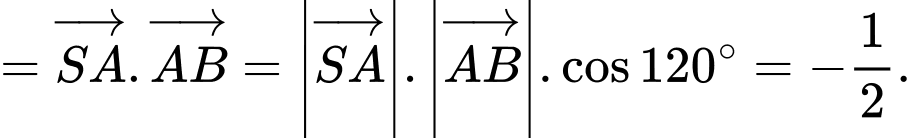 Do đó, ý c) sai.
Do đó, ý c) sai. – Ta có:
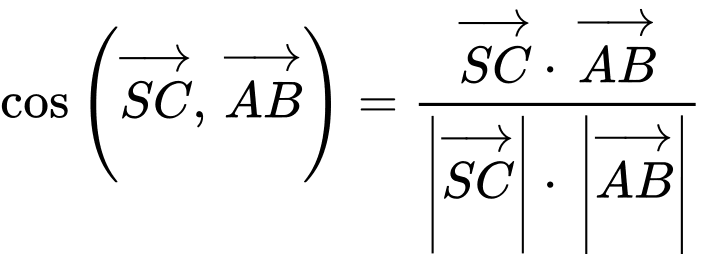
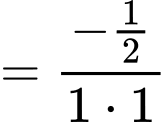
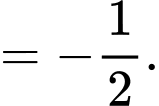
Vậy ý d) sai.
Câu 14 [599606]: Cho tứ diện 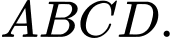 Gọi
Gọi 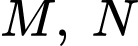 lần lượt là trung điểm của
lần lượt là trung điểm của 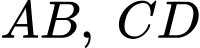 và
và  là trung điểm của
là trung điểm của 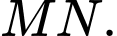 Gọi
Gọi  là trọng tâm của tam giác
là trọng tâm của tam giác  (Hình vẽ). Các mệnh đề sau đúng hay sai?
(Hình vẽ). Các mệnh đề sau đúng hay sai?
 Gọi
Gọi 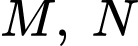 lần lượt là trung điểm của
lần lượt là trung điểm của 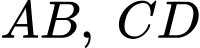 và
và 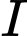 là trung điểm của
là trung điểm của 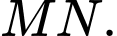 Gọi
Gọi  là trọng tâm của tam giác
là trọng tâm của tam giác  (Hình vẽ). Các mệnh đề sau đúng hay sai?
(Hình vẽ). Các mệnh đề sau đúng hay sai?
a) Đúng.
Do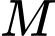 là trung điểm của đoạn thẳng
là trung điểm của đoạn thẳng  nên
nên 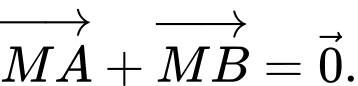
b) Đúng.
Ta có: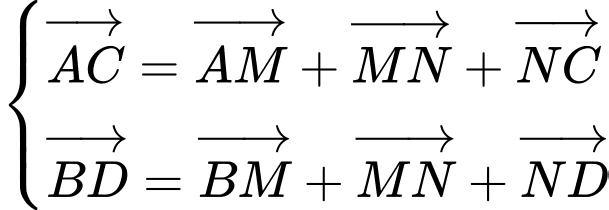
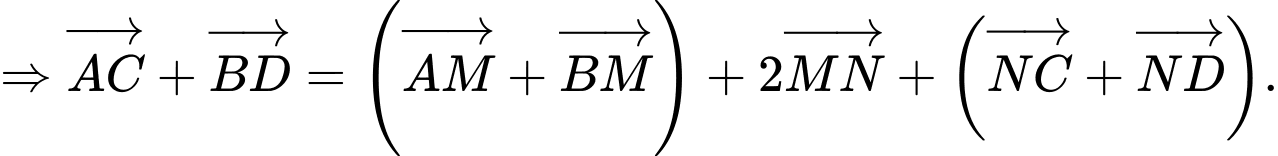
Vì lần lượt là trung điểm của
lần lượt là trung điểm của 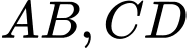 nên
nên 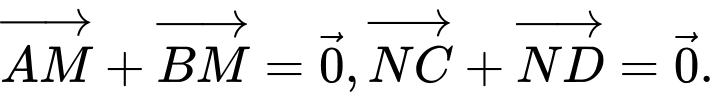
Do đó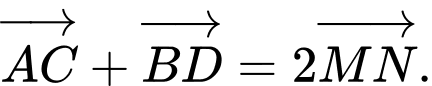
c) Đúng.
Ta có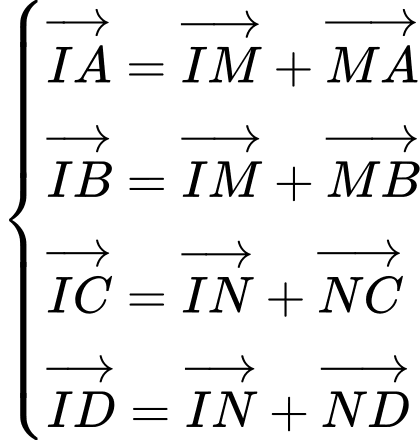
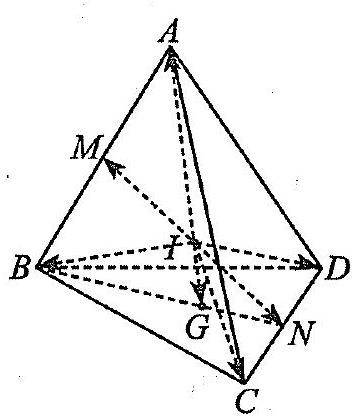
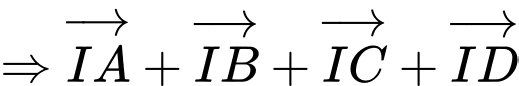
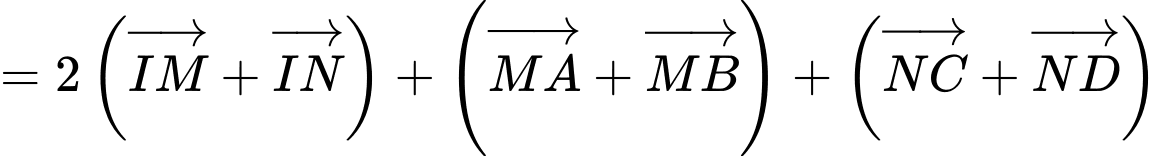
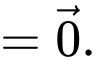
d) Sai.
Do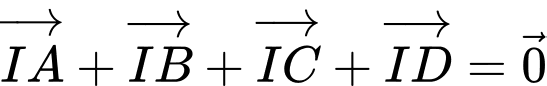 nên
nên
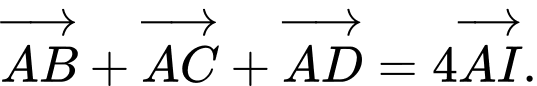
Mặt khác, vì là trọng tâm của tam giác
là trọng tâm của tam giác  nên
nên 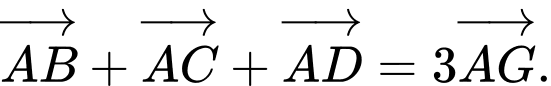
Suy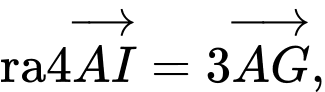 suy ra
suy ra 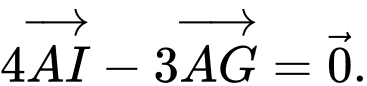
Do
 là trung điểm của đoạn thẳng
là trung điểm của đoạn thẳng  nên
nên 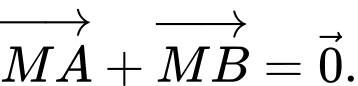
b) Đúng.
Ta có:
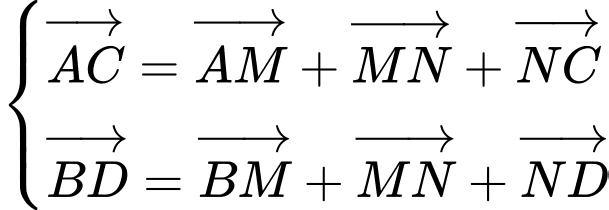
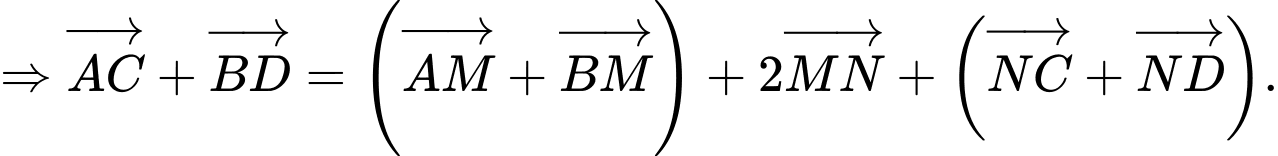
Vì
 lần lượt là trung điểm của
lần lượt là trung điểm của  nên
nên 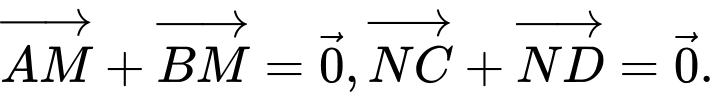
Do đó
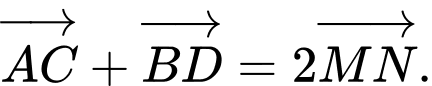
c) Đúng.
Ta có
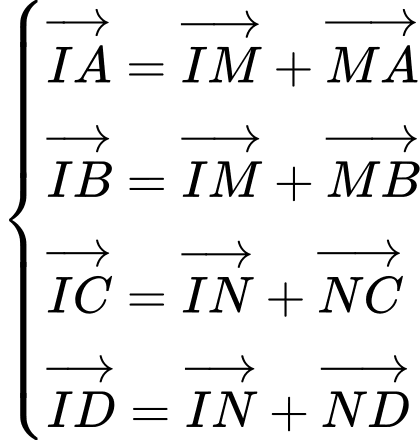

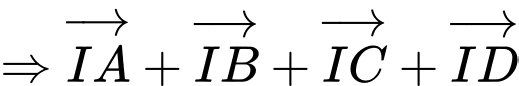
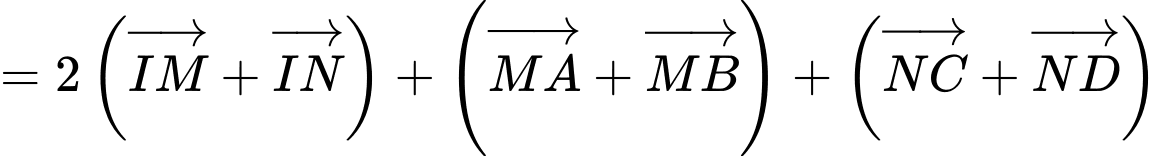
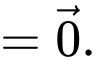
d) Sai.
Do
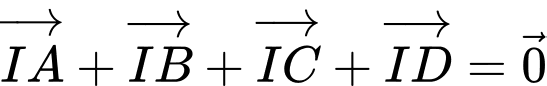 nên
nên 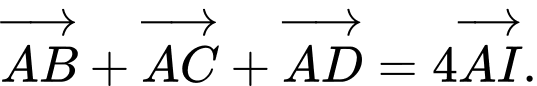
Mặt khác, vì
 là trọng tâm của tam giác
là trọng tâm của tam giác  nên
nên 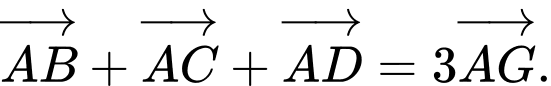
Suy
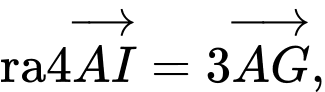 suy ra
suy ra 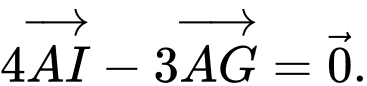
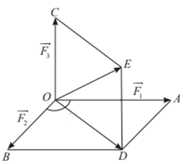
Câu 15 [774237]: Một vật nặng  được kéo từ ba hướng như hình vẽ và chịu tác dụng của 3 lực
được kéo từ ba hướng như hình vẽ và chịu tác dụng của 3 lực 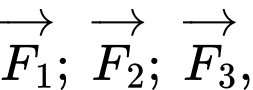 có độ lớn lần lượt là
có độ lớn lần lượt là 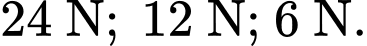 Biết góc tạo bởi 2 lực
Biết góc tạo bởi 2 lực 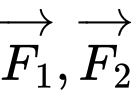 là
là 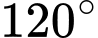 và lực thứ ba vuông góc với hai lực đầu tiên. Lấy các điểm
và lực thứ ba vuông góc với hai lực đầu tiên. Lấy các điểm 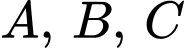 sao cho
sao cho 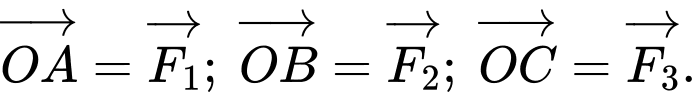 Dựng các hình bình hành
Dựng các hình bình hành  và
và  như hình vẽ.
như hình vẽ.
 được kéo từ ba hướng như hình vẽ và chịu tác dụng của 3 lực
được kéo từ ba hướng như hình vẽ và chịu tác dụng của 3 lực 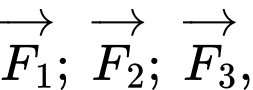 có độ lớn lần lượt là
có độ lớn lần lượt là 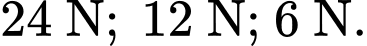 Biết góc tạo bởi 2 lực
Biết góc tạo bởi 2 lực 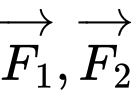 là
là 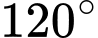 và lực thứ ba vuông góc với hai lực đầu tiên. Lấy các điểm
và lực thứ ba vuông góc với hai lực đầu tiên. Lấy các điểm 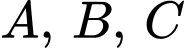 sao cho
sao cho 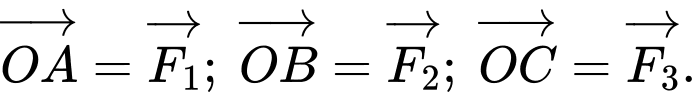 Dựng các hình bình hành
Dựng các hình bình hành 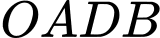 và
và 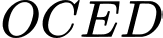 như hình vẽ.
như hình vẽ.
a) Sai: Theo quy tắc hình bình hành, ta có: 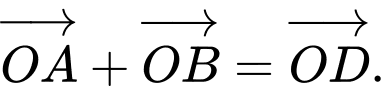
b) Đúng: Theo quy tắc hình bình hành, ta có: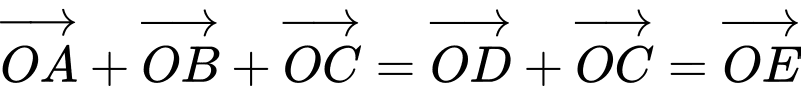 .
.
c) Sai: Ta có: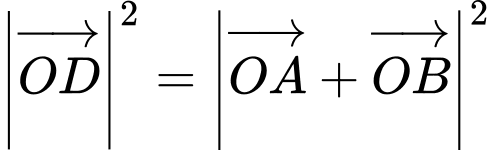
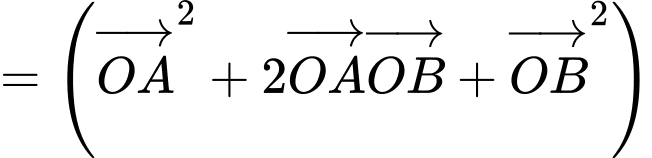
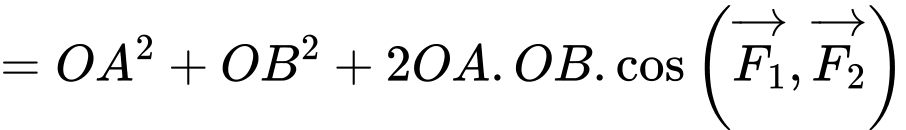 Suy ra:
Suy ra: 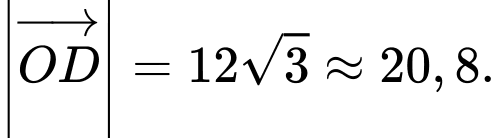
d) Đúng: Độ lớn hợp lực tác dụng vào vật O là:
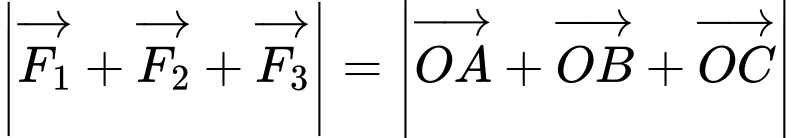
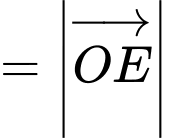
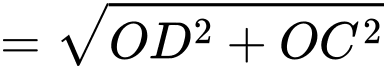
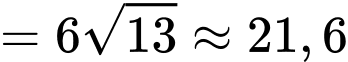 N.
N.
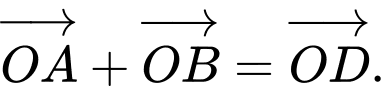
b) Đúng: Theo quy tắc hình bình hành, ta có:
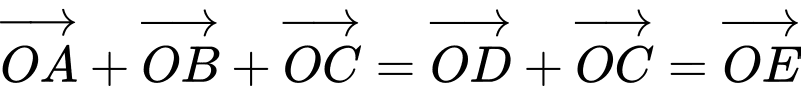 .
.c) Sai: Ta có:
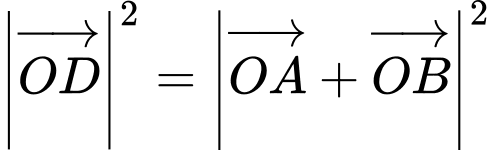
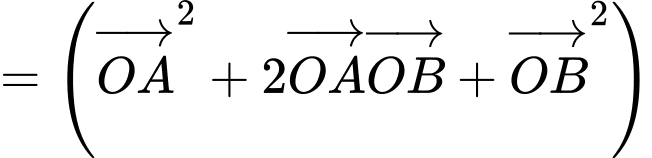
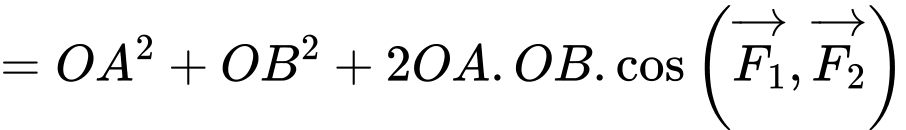 Suy ra:
Suy ra: 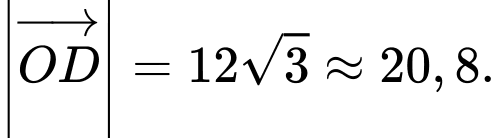
d) Đúng: Độ lớn hợp lực tác dụng vào vật O là:
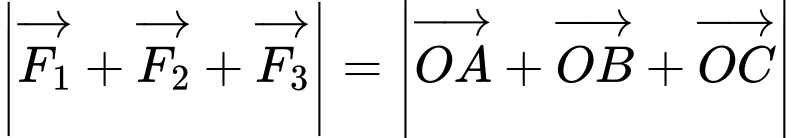
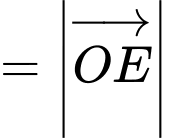
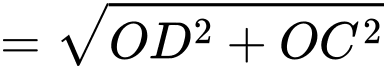
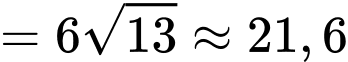 N.
N.
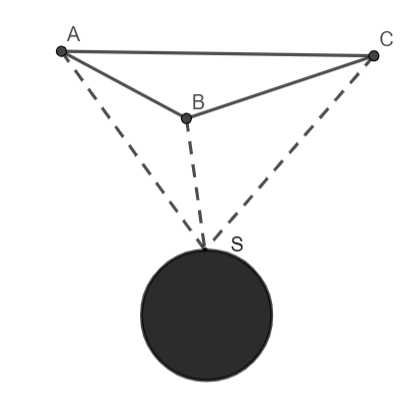
Câu 16 [774241]: Một chiếc đĩa kim loại khối lượng 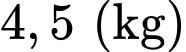 được treo bởi ba sợi dây không dãn
được treo bởi ba sợi dây không dãn  sao cho
sao cho 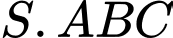 là hình chóp đều có
là hình chóp đều có 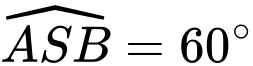 (hình vẽ). Khối lượng dây không đáng kể; lực căng của mỗi sợi dây
(hình vẽ). Khối lượng dây không đáng kể; lực căng của mỗi sợi dây  đặt tại điểm
đặt tại điểm 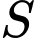 tương ứng là
tương ứng là 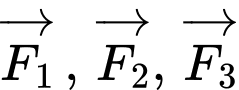 có độ lớn bằng nhau. Biết
có độ lớn bằng nhau. Biết 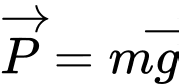 là trọng lực tác dung lên vật, với
là trọng lực tác dung lên vật, với  là gia tốc rơi tự do có độ lớn
là gia tốc rơi tự do có độ lớn 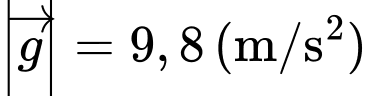 và m là khối lượng của vật có đơn vị kg.
và m là khối lượng của vật có đơn vị kg.
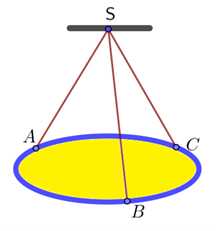
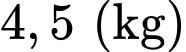 được treo bởi ba sợi dây không dãn
được treo bởi ba sợi dây không dãn  sao cho
sao cho 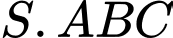 là hình chóp đều có
là hình chóp đều có 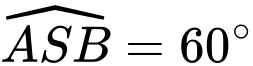 (hình vẽ). Khối lượng dây không đáng kể; lực căng của mỗi sợi dây
(hình vẽ). Khối lượng dây không đáng kể; lực căng của mỗi sợi dây  đặt tại điểm
đặt tại điểm 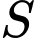 tương ứng là
tương ứng là 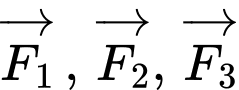 có độ lớn bằng nhau. Biết
có độ lớn bằng nhau. Biết 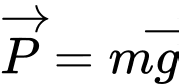 là trọng lực tác dung lên vật, với
là trọng lực tác dung lên vật, với  là gia tốc rơi tự do có độ lớn
là gia tốc rơi tự do có độ lớn 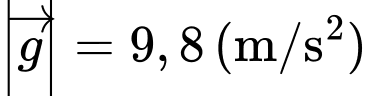 và m là khối lượng của vật có đơn vị kg.
và m là khối lượng của vật có đơn vị kg.
a) Ta có 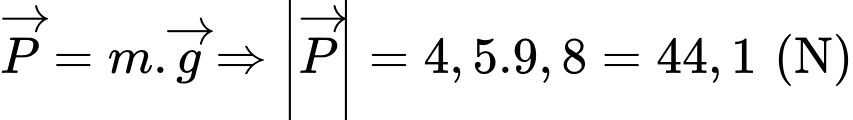 . Vậy mệnh đề đã cho sai.
. Vậy mệnh đề đã cho sai.
b) Trọng lực của hệ vật đặt tại điểm
của hệ vật đặt tại điểm  được phân tích thành ba lực
được phân tích thành ba lực 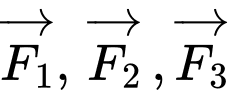 nên
nên 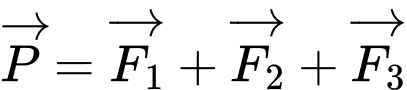 . Vậy mệnh đề đã cho đúng.
. Vậy mệnh đề đã cho đúng.
c) Ta có hình chóp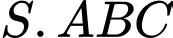 là hình chóp đều và có
là hình chóp đều và có 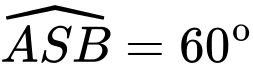 nên
nên 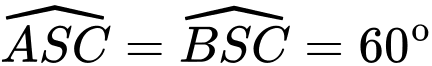 . Lại có véc tơ
. Lại có véc tơ 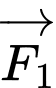 cùng hướng với véc tơ
cùng hướng với véc tơ  , véc tơ
, véc tơ 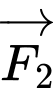 cùng hướng với véc tơ
cùng hướng với véc tơ 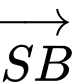 , véc tơ
, véc tơ 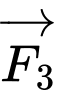 cùng hướng với véc tơ
cùng hướng với véc tơ 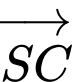 nên
nên 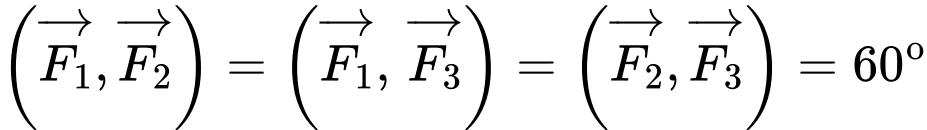 .
.

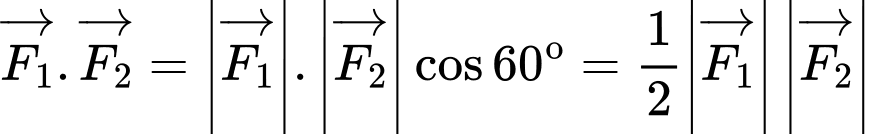 ;
; 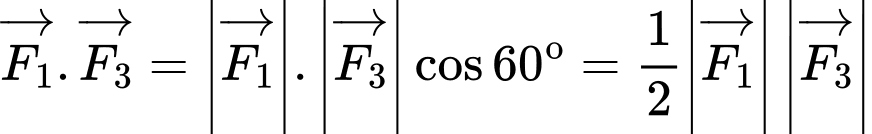 .
.
Mà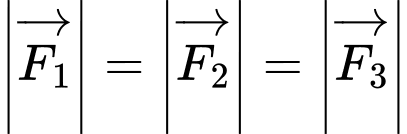 nên
nên 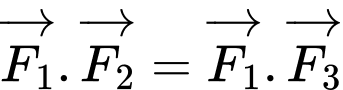 . Vậy mệnh đề đã cho đúng.
. Vậy mệnh đề đã cho đúng.
d) Ta có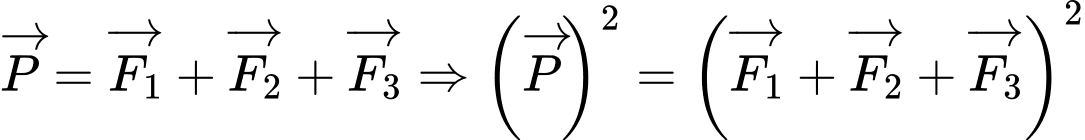
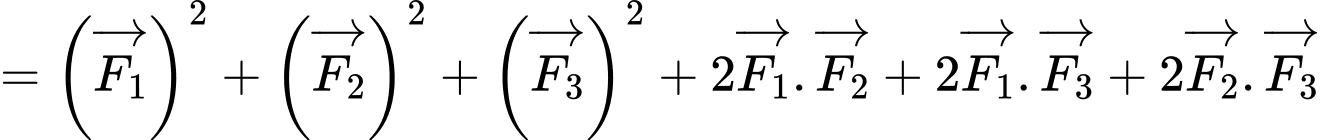
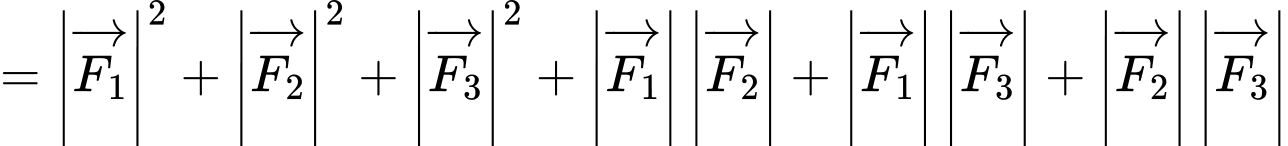
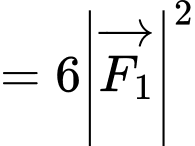
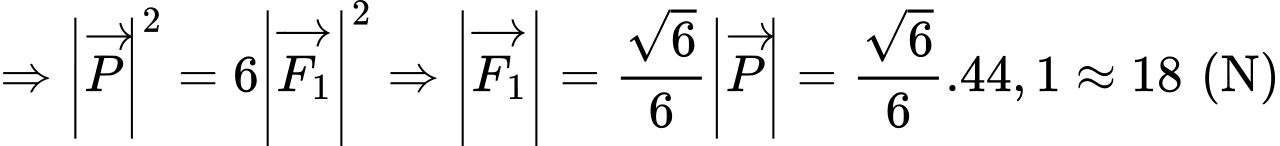 .
.
Vậy mệnh đề đã cho sai.
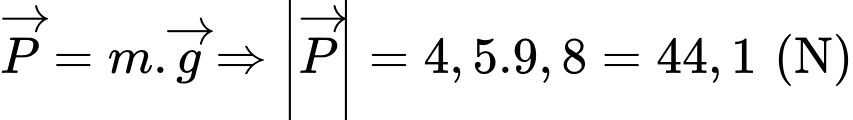 . Vậy mệnh đề đã cho sai.
. Vậy mệnh đề đã cho sai.
b) Trọng lực
 của hệ vật đặt tại điểm
của hệ vật đặt tại điểm 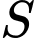 được phân tích thành ba lực
được phân tích thành ba lực 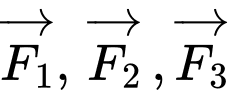 nên
nên 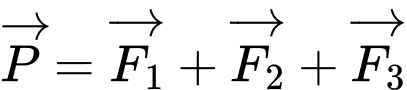 . Vậy mệnh đề đã cho đúng.
. Vậy mệnh đề đã cho đúng.
c) Ta có hình chóp
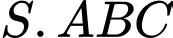 là hình chóp đều và có
là hình chóp đều và có 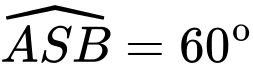 nên
nên 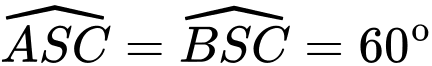 . Lại có véc tơ
. Lại có véc tơ  cùng hướng với véc tơ
cùng hướng với véc tơ  , véc tơ
, véc tơ 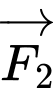 cùng hướng với véc tơ
cùng hướng với véc tơ 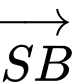 , véc tơ
, véc tơ 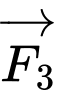 cùng hướng với véc tơ
cùng hướng với véc tơ 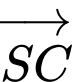 nên
nên 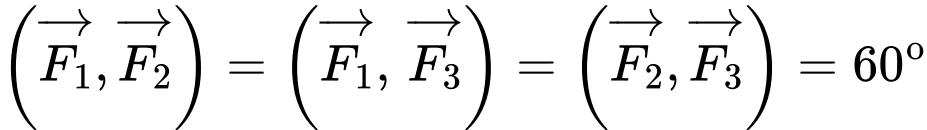 .
.

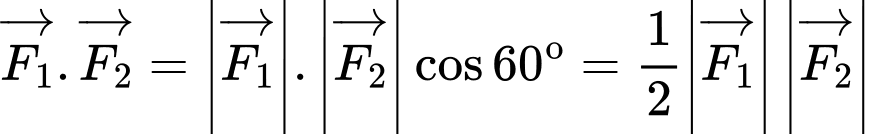 ;
; 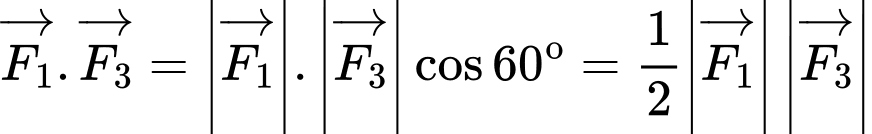 .
.
Mà
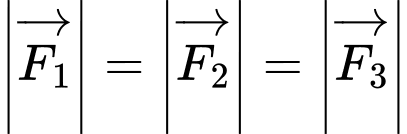 nên
nên 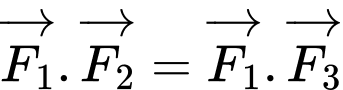 . Vậy mệnh đề đã cho đúng.
. Vậy mệnh đề đã cho đúng.
d) Ta có
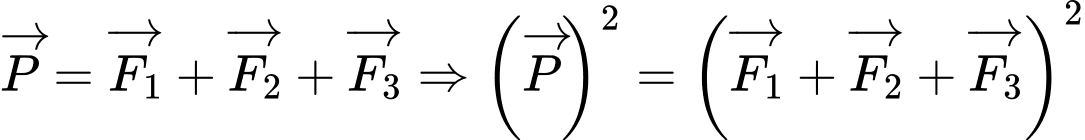
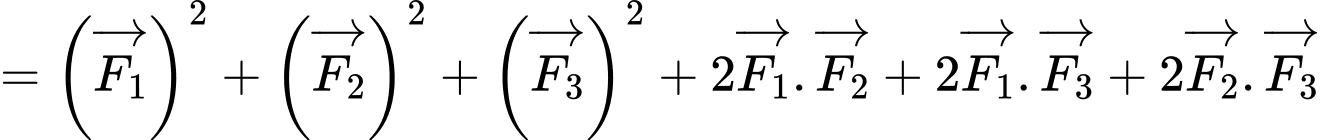
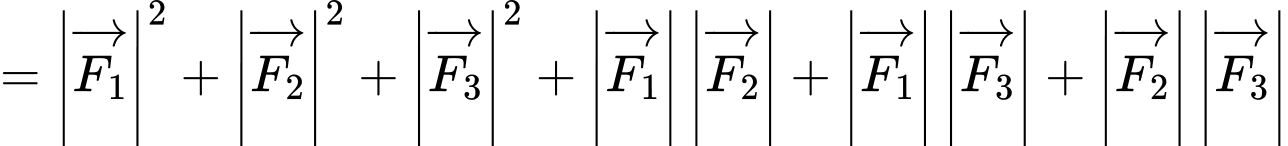
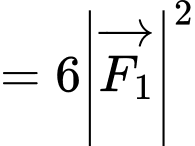
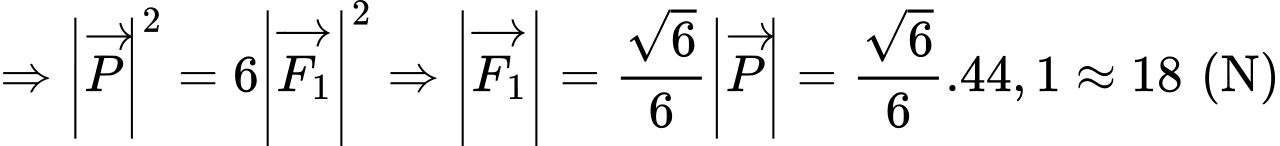 .
. Vậy mệnh đề đã cho sai.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 17 đến câu 22.
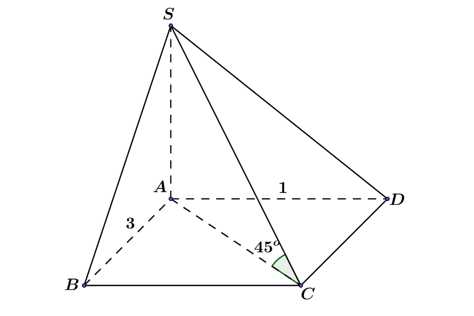
Câu 17 [717149]: Cho hình chóp  có cạnh đáy
có cạnh đáy  là hình chữ nhật. Biết
là hình chữ nhật. Biết 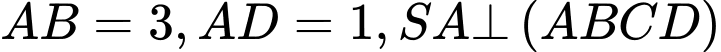 và
và 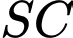 tạo với mặt đáy một góc
tạo với mặt đáy một góc 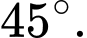 Tích vô hướng của hai vectơ
Tích vô hướng của hai vectơ 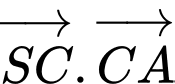 bằng bao nhiêu?
bằng bao nhiêu?
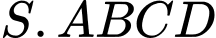 có cạnh đáy
có cạnh đáy 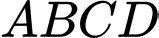 là hình chữ nhật. Biết
là hình chữ nhật. Biết 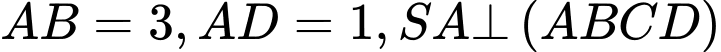 và
và 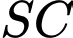 tạo với mặt đáy một góc
tạo với mặt đáy một góc 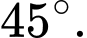 Tích vô hướng của hai vectơ
Tích vô hướng của hai vectơ 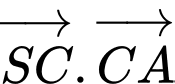 bằng bao nhiêu?
bằng bao nhiêu?
Điền đáp án: -10.
Góc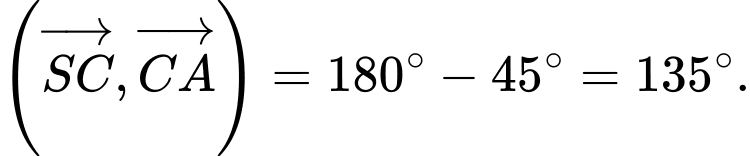
Ta có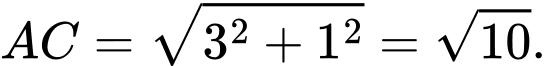
Tam giác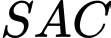 vuông tại
vuông tại  , có:
, có: 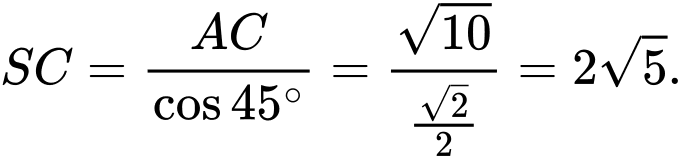
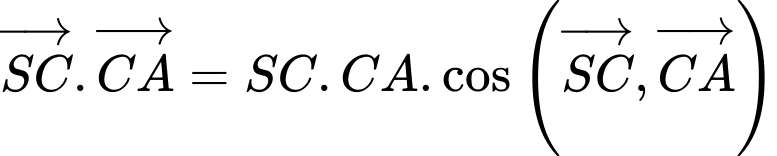

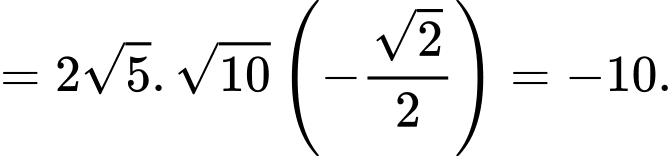

Góc
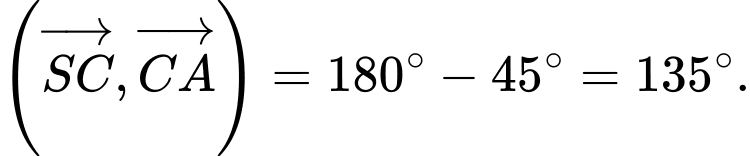
Ta có
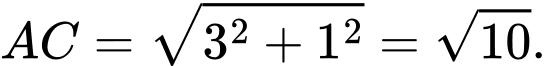
Tam giác
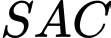 vuông tại
vuông tại 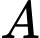 , có:
, có: 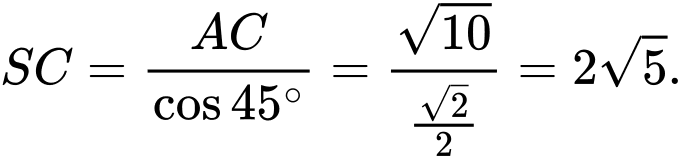
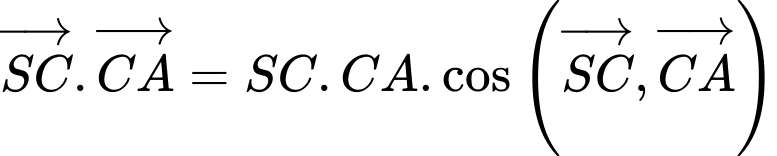

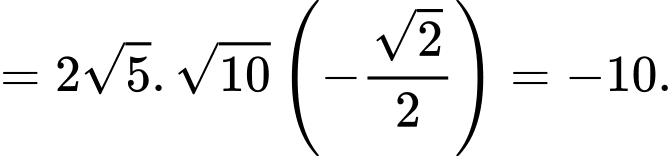
Câu 18 [379554]: Cho hình hộp chữ nhật  có
có 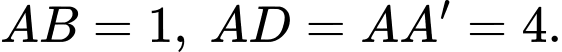 Độ dài của vectơ
Độ dài của vectơ 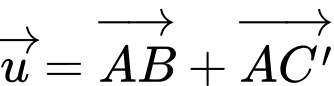 bằng bao nhiêu?
bằng bao nhiêu?
 có
có 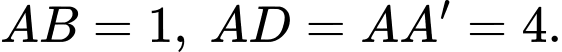 Độ dài của vectơ
Độ dài của vectơ 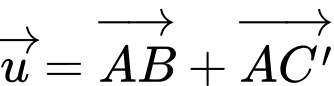 bằng bao nhiêu?
bằng bao nhiêu? 
Gọi
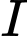 là trung điểm của
là trung điểm của 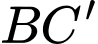 ta có:
ta có: 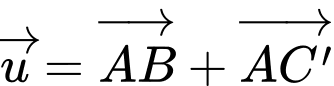
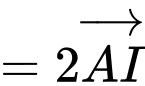
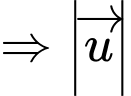
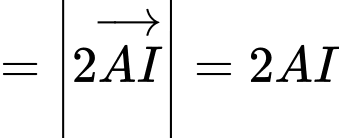
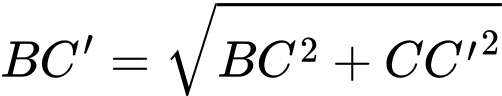
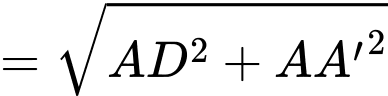
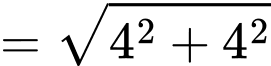
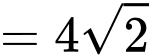
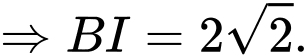
Ta có
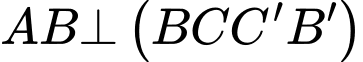
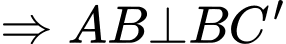
 vuông tại
vuông tại 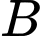
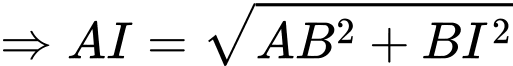
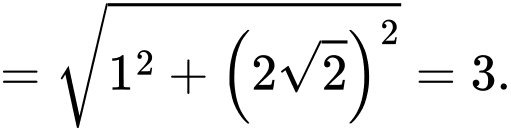
Vậy
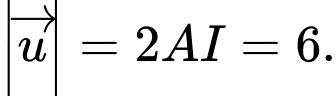
Câu 19 [681562]: Cho vectơ 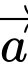 và
và 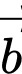 thỏa mãn
thỏa mãn 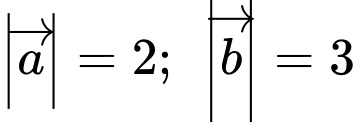 và
và 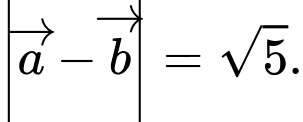 Tính giá trị của
Tính giá trị của 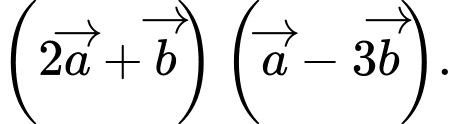
 và
và 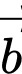 thỏa mãn
thỏa mãn 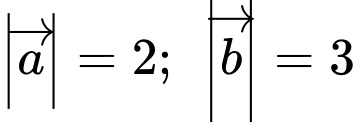 và
và 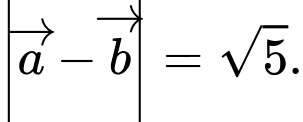 Tính giá trị của
Tính giá trị của 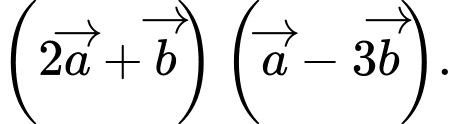
Ta có 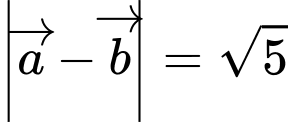
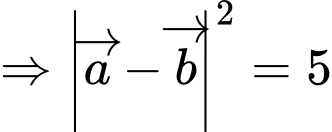
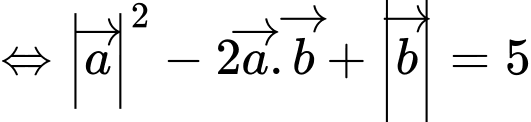
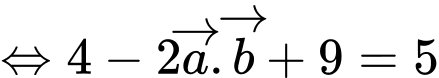
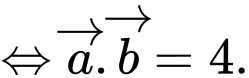
Ta có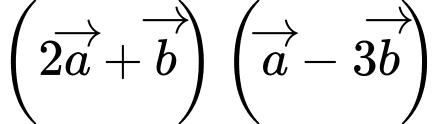
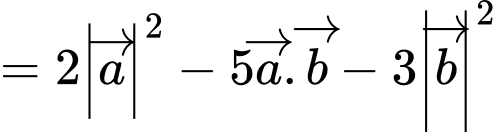
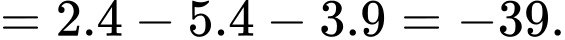
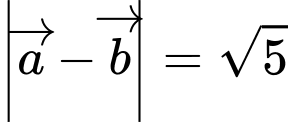
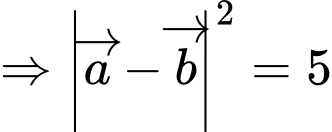
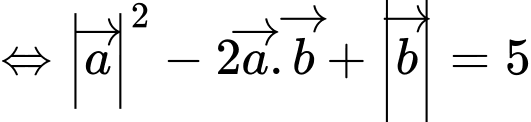
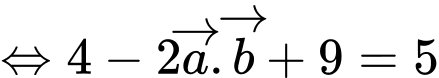
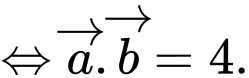
Ta có
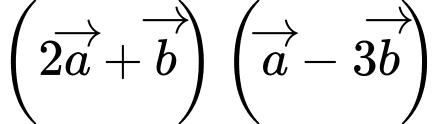
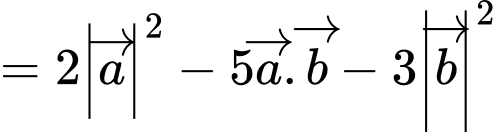
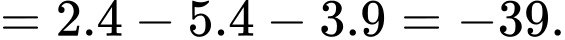
Câu 20 [708373]: Một quả cầu sắt nặng 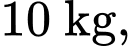 được treo bởi 3 sợi xích bằng nhau và vuông góc với nhau đôi một tại 3 điểm trên giá đỡ ( như hình vẽ)
được treo bởi 3 sợi xích bằng nhau và vuông góc với nhau đôi một tại 3 điểm trên giá đỡ ( như hình vẽ)
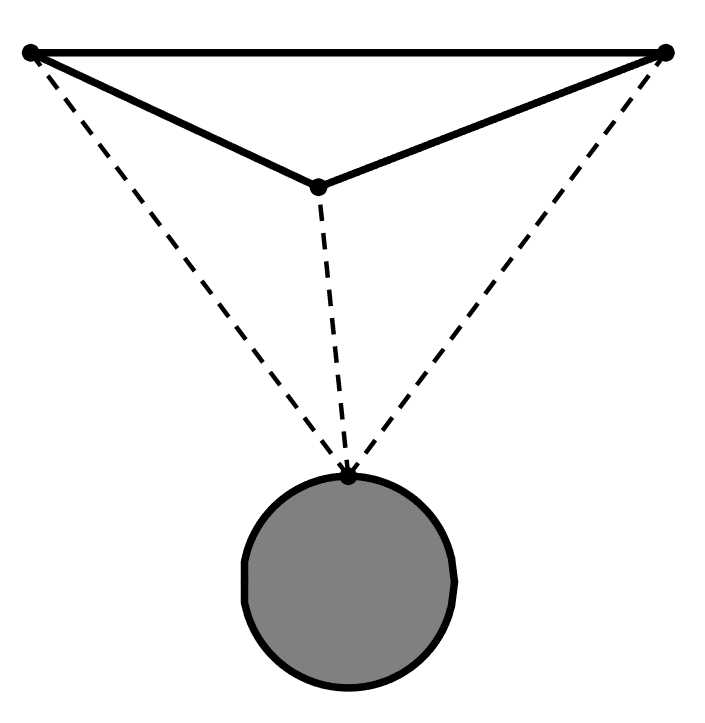
Biết rằng trọng lực của một vật được tính theo công thức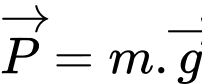 với
với 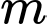 là khối lượng của vật,
là khối lượng của vật, 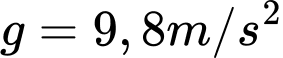 là gia tốc trọng trường.Tính lực căng của mỗi sợi xích (kết quả làm tròn đến hàng phần mười của Niu-tơn).
là gia tốc trọng trường.Tính lực căng của mỗi sợi xích (kết quả làm tròn đến hàng phần mười của Niu-tơn).
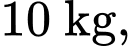 được treo bởi 3 sợi xích bằng nhau và vuông góc với nhau đôi một tại 3 điểm trên giá đỡ ( như hình vẽ)
được treo bởi 3 sợi xích bằng nhau và vuông góc với nhau đôi một tại 3 điểm trên giá đỡ ( như hình vẽ)
Biết rằng trọng lực của một vật được tính theo công thức
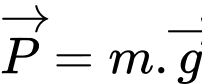 với
với 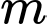 là khối lượng của vật,
là khối lượng của vật, 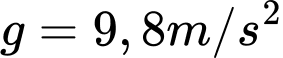 là gia tốc trọng trường.Tính lực căng của mỗi sợi xích (kết quả làm tròn đến hàng phần mười của Niu-tơn).
là gia tốc trọng trường.Tính lực căng của mỗi sợi xích (kết quả làm tròn đến hàng phần mười của Niu-tơn).
Điền đáp án: 56,6
Độ lớn của trọng lực tác động lên qủa cầu sắt là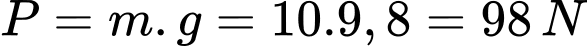
Hợp lực của 3 dây xích là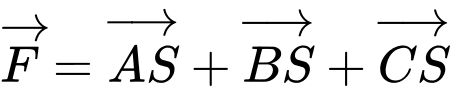 để vật đứng yên ta có
để vật đứng yên ta có 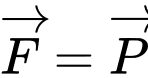
Khi đó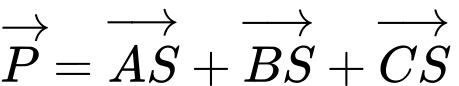
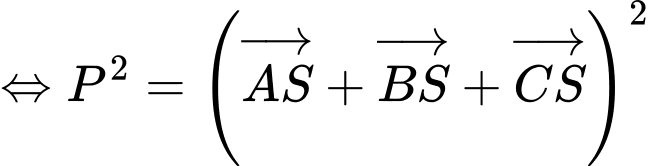
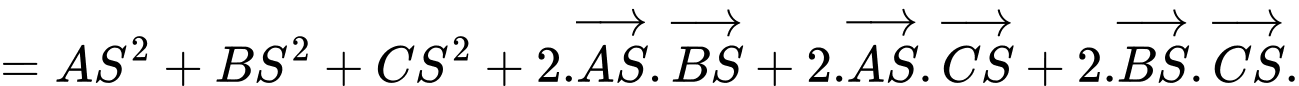
Do 3 sợi xích bằng nhau và vuông góc với nhau nên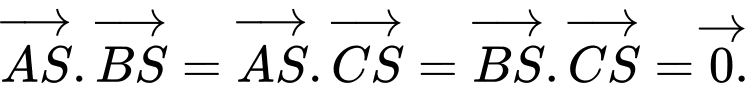
Do đó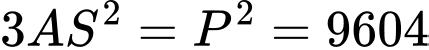
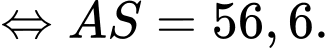
Vậy lực căng của mỗi sợi dây xích là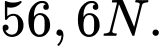

Độ lớn của trọng lực tác động lên qủa cầu sắt là
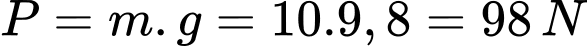
Hợp lực của 3 dây xích là
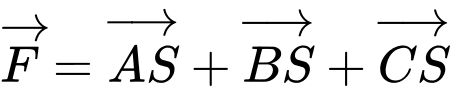 để vật đứng yên ta có
để vật đứng yên ta có 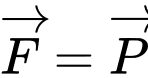
Khi đó
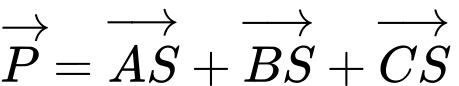
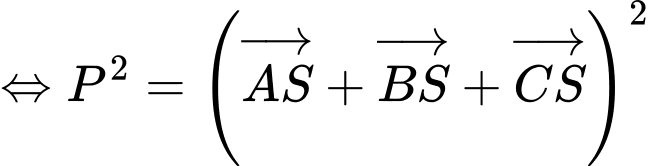
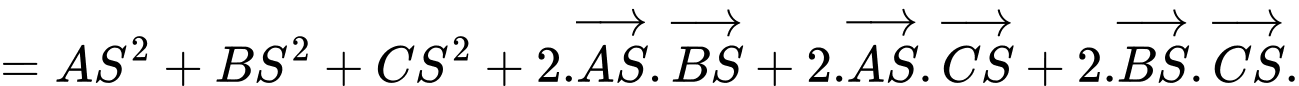
Do 3 sợi xích bằng nhau và vuông góc với nhau nên
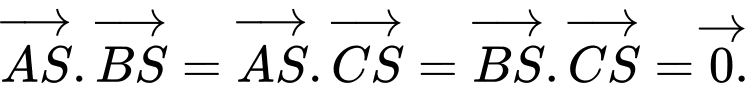
Do đó
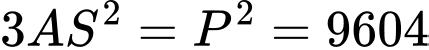
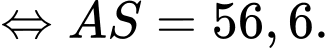
Vậy lực căng của mỗi sợi dây xích là
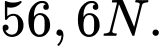
Câu 21 [681592]: Cho tứ diện  Gọi
Gọi  là các điểm lần lượt thuộc các cạnh
là các điểm lần lượt thuộc các cạnh 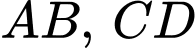 sao cho
sao cho 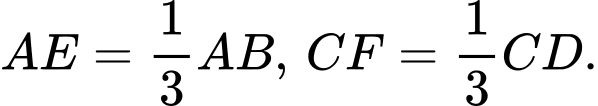 Khi biểu diễn vectơ
Khi biểu diễn vectơ 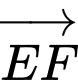 theo ba vectơ
theo ba vectơ 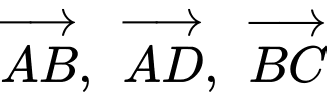 ta được:
ta được: 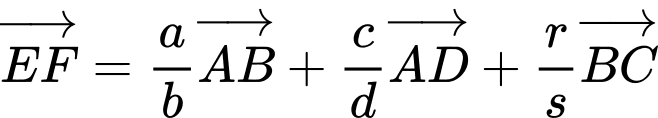 (với
(với 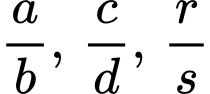 là các phân số tối giản và
là các phân số tối giản và 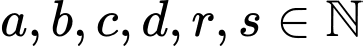 ). Ta tính được giá trị của biểu thức
). Ta tính được giá trị của biểu thức 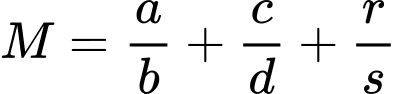 bằng
bằng 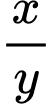 (với
(với 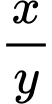 là phân số tối giản và
là phân số tối giản và 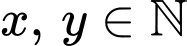 ). Khi đó, giá trị của biểu thức
). Khi đó, giá trị của biểu thức 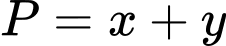 bằng bao nhiêu?
bằng bao nhiêu?
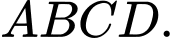 Gọi
Gọi 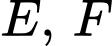 là các điểm lần lượt thuộc các cạnh
là các điểm lần lượt thuộc các cạnh 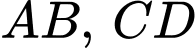 sao cho
sao cho 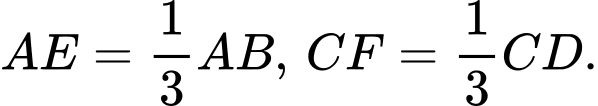 Khi biểu diễn vectơ
Khi biểu diễn vectơ 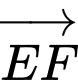 theo ba vectơ
theo ba vectơ 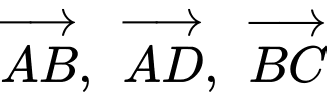 ta được:
ta được: 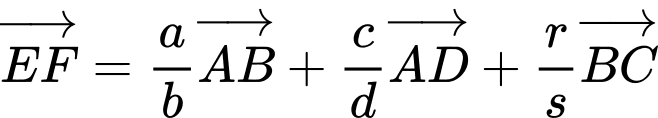 (với
(với 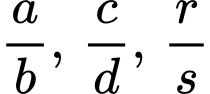 là các phân số tối giản và
là các phân số tối giản và 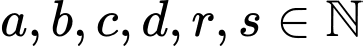 ). Ta tính được giá trị của biểu thức
). Ta tính được giá trị của biểu thức 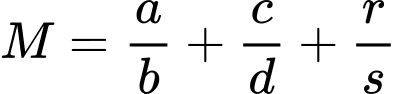 bằng
bằng 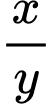 (với
(với 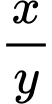 là phân số tối giản và
là phân số tối giản và 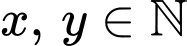 ). Khi đó, giá trị của biểu thức
). Khi đó, giá trị của biểu thức 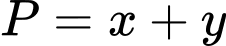 bằng bao nhiêu?
bằng bao nhiêu? 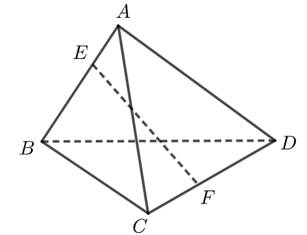
Ta có:
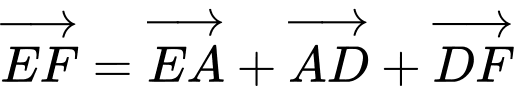
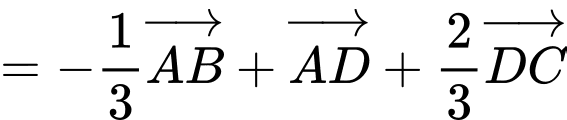
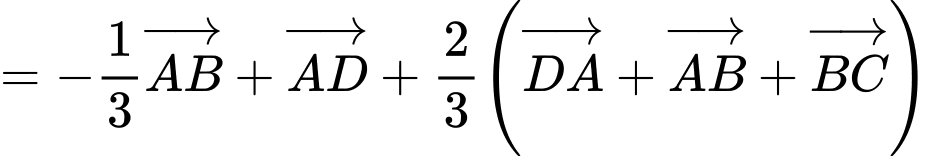
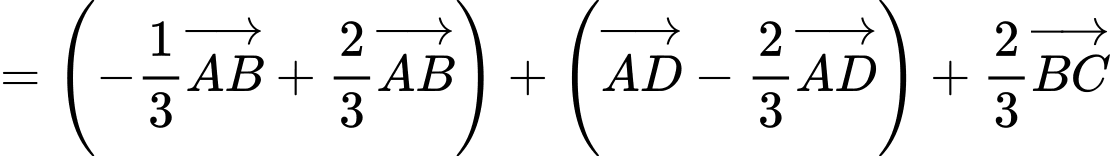
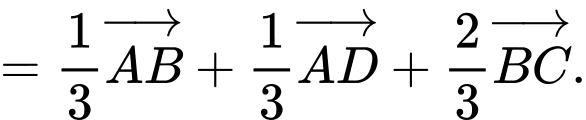
Khi đó,
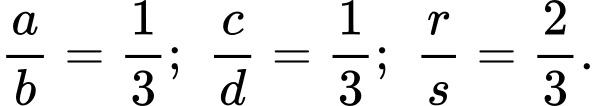
Do đó,
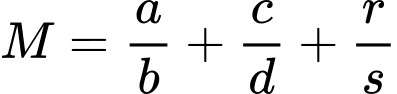
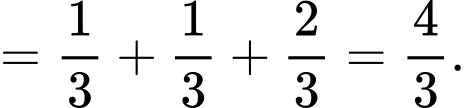 Suy ra
Suy ra 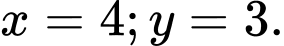
Vậy
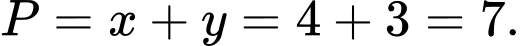
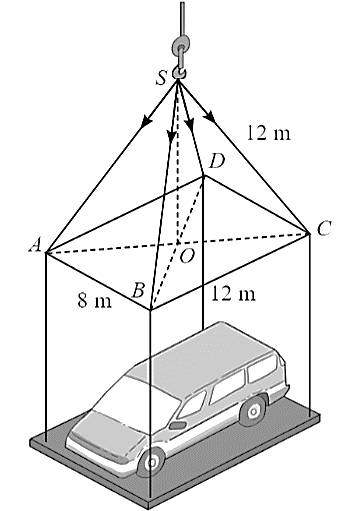
Câu 22 [684131]: Độ lớn của các lực căng trên mỗi sợi dây cáp trong hình dưới đây bằng bao nhiêu Newton? Biết rằng khối lượng xe là 1500 kg, gia tốc là 9,8 m/s2, khung nâng có khối lượng 300 kg và có dạng hình chóp 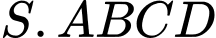 với đáy
với đáy 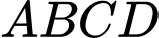 là hình chữ nhật tâm
là hình chữ nhật tâm 
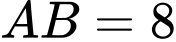 m,
m, 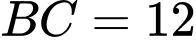 m,
m,  m và
m và 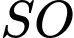 vuông góc với
vuông góc với 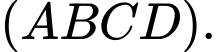 Làm tròn kết quả đến hàng đơn vị của Newton.
Làm tròn kết quả đến hàng đơn vị của Newton.
 với đáy
với đáy  là hình chữ nhật tâm
là hình chữ nhật tâm 
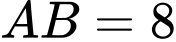 m,
m, 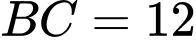 m,
m,  m và
m và 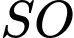 vuông góc với
vuông góc với 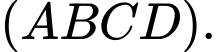 Làm tròn kết quả đến hàng đơn vị của Newton.
Làm tròn kết quả đến hàng đơn vị của Newton.
Ta có 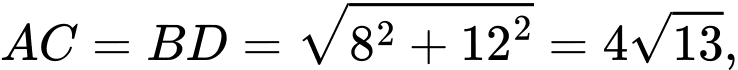
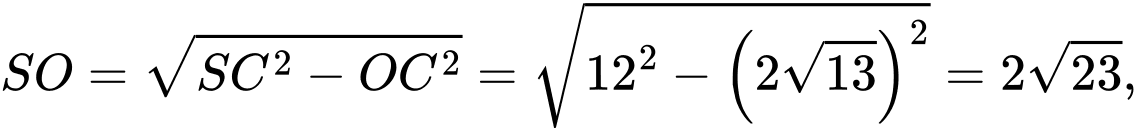
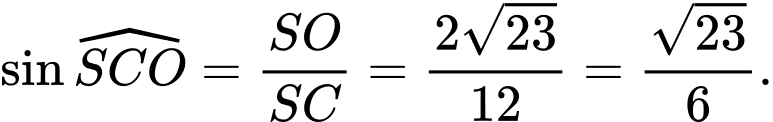
Gọi là độ lớn của trọng lực xe và khung sắt nâng.
là độ lớn của trọng lực xe và khung sắt nâng.
Ta có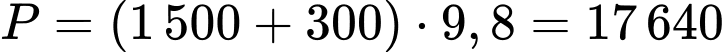 (N).
(N).
Gọi là độ lớn của lực căng trên mỗi sợi cáp.
là độ lớn của lực căng trên mỗi sợi cáp.
Ta chứng minh được suy ra
suy ra 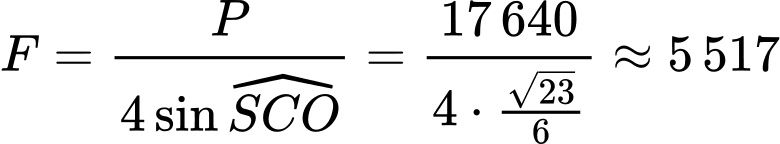 (N).
(N).
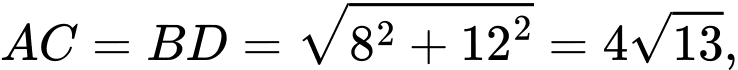
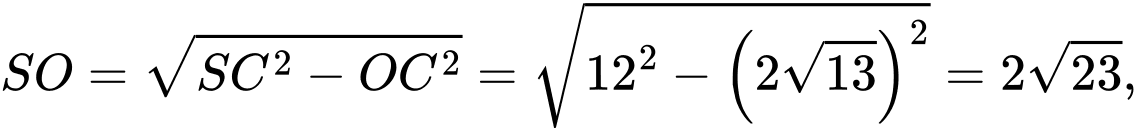
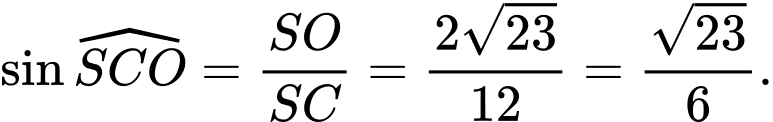
Gọi
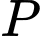 là độ lớn của trọng lực xe và khung sắt nâng.
là độ lớn của trọng lực xe và khung sắt nâng.
Ta có
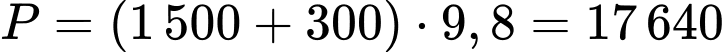 (N).
(N).
Gọi
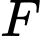 là độ lớn của lực căng trên mỗi sợi cáp.
là độ lớn của lực căng trên mỗi sợi cáp.
Ta chứng minh được
 suy ra
suy ra 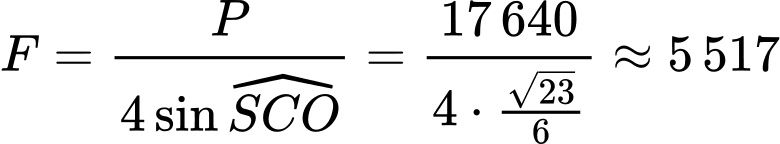 (N).
(N).