PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1 [808651]: Cho hàm số 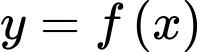 có bảng biến thiên như hình vẽ
có bảng biến thiên như hình vẽ
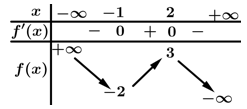
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
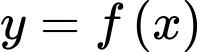 có bảng biến thiên như hình vẽ
có bảng biến thiên như hình vẽ
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A, 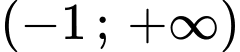 .
.
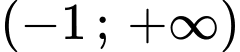 .
.B, 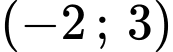 .
.
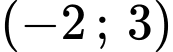 .
.C, 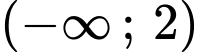 .
.
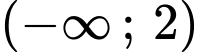 .
.D, 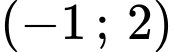 .
.
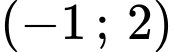 .
.
Chọn D
Dựa vào bảng biến thiên ta thấy hàm số đã cho đồng biến trên khoảng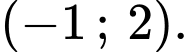 Đáp án: D
Đáp án: D
Dựa vào bảng biến thiên ta thấy hàm số đã cho đồng biến trên khoảng
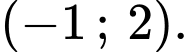 Đáp án: D
Đáp án: D
Câu 2 [909049]: Cho hàm số 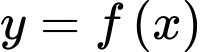 có bảng biến thiên như sau:
có bảng biến thiên như sau: 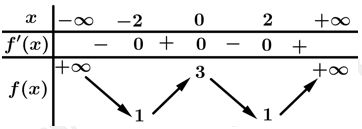
Giá trị cực đại của hàm số đã cho là
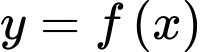 có bảng biến thiên như sau:
có bảng biến thiên như sau: 
A, 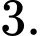
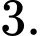
B, 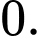
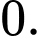
C, 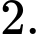
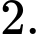
D, 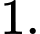
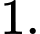
Chọn đáp án A.
Dựa vào bảng biến thiên, ta thấy tại giá trị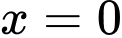 hàm số đổi dấu từ (+) sang (-) nên
hàm số đổi dấu từ (+) sang (-) nên 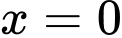 là cực đại của hàm số, suy ra
là cực đại của hàm số, suy ra 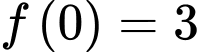 là giá trị cực đại của hàm số đã cho.
Đáp án: A
là giá trị cực đại của hàm số đã cho.
Đáp án: A
Dựa vào bảng biến thiên, ta thấy tại giá trị
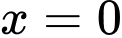 hàm số đổi dấu từ (+) sang (-) nên
hàm số đổi dấu từ (+) sang (-) nên 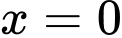 là cực đại của hàm số, suy ra
là cực đại của hàm số, suy ra 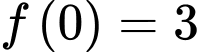 là giá trị cực đại của hàm số đã cho.
Đáp án: A
là giá trị cực đại của hàm số đã cho.
Đáp án: A
Câu 3 [378242]: Cho hàm số bậc ba 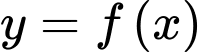 có đồ thị là đường cong trong hình bên.
có đồ thị là đường cong trong hình bên.
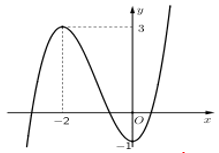
Giá trị cực đại của hàm số đã cho là
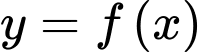 có đồ thị là đường cong trong hình bên.
có đồ thị là đường cong trong hình bên. 
Giá trị cực đại của hàm số đã cho là
A, 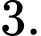
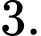
B, 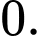
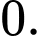
C, 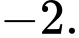
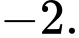
D, 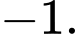
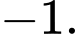
Chọn A
Giá trị cực đại của hàm số đã cho là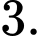 Đáp án: A
Đáp án: A
Giá trị cực đại của hàm số đã cho là
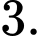 Đáp án: A
Đáp án: A
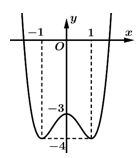
Câu 4 [511846]: Cho hàm số 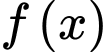 có đồ thị như hình vẽ. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
có đồ thị như hình vẽ. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
 có đồ thị như hình vẽ. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
có đồ thị như hình vẽ. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A, 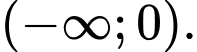
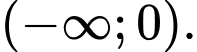
B, 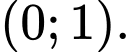
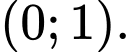
C, 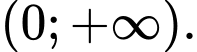
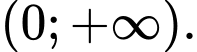
D, 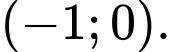
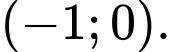
Chọn đáp án B.
Dựa vào hình vẽ, suy ra hàm số đã cho nghịch biến trên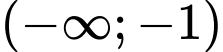 và
và 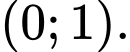 Đáp án: B
Đáp án: B
Dựa vào hình vẽ, suy ra hàm số đã cho nghịch biến trên
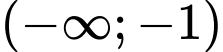 và
và 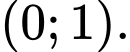 Đáp án: B
Đáp án: B
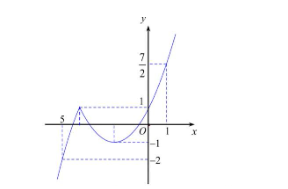
Câu 5 [297507]: Cho hàm số 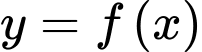 đồ thị như hình vẽ dưới đây.Gọi
đồ thị như hình vẽ dưới đây.Gọi 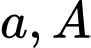 lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của
lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của 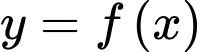 trên đoạn
trên đoạn 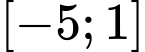 . Giá trị
. Giá trị 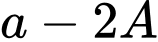 bằng
bằng
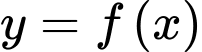 đồ thị như hình vẽ dưới đây.Gọi
đồ thị như hình vẽ dưới đây.Gọi 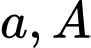 lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của
lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của 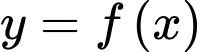 trên đoạn
trên đoạn 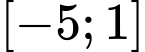 . Giá trị
. Giá trị 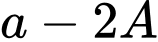 bằng
bằng
A, 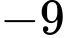 .
.
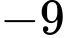 .
.B, 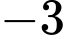 .
.
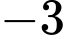 .
.C, 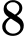 .
.
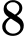 .
.D, 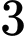 .
.
 .
.
Chọn A
Từ đồ thị suy ra 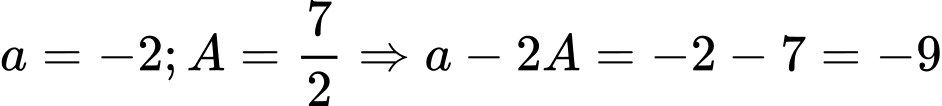 Đáp án: A
Đáp án: A
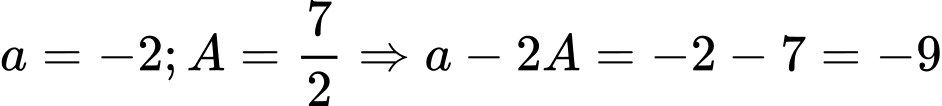 Đáp án: A
Đáp án: A
Câu 6 [809932]: Gọi 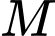 và
và 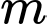 lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số 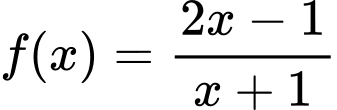 trên đoạn
trên đoạn 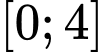 . Giá trị
. Giá trị 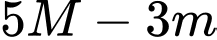 bằng
bằng
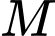 và
và 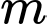 lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số 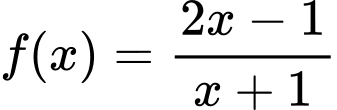 trên đoạn
trên đoạn 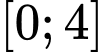 . Giá trị
. Giá trị 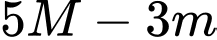 bằng
bằng A, 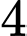
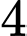
B, 

C, 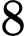
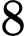
D, 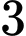
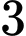
Chọn B
Hàm số xác định và liên tục trên đoạn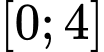 .
.
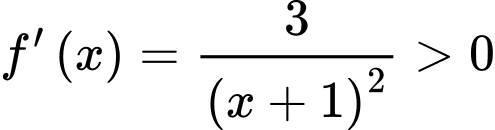 ,
, nên
nên  ,
, 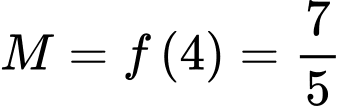
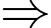
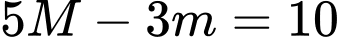 . Đáp án: B
. Đáp án: B
Hàm số xác định và liên tục trên đoạn
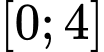 .
.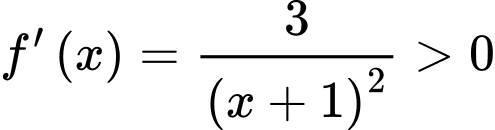 ,
, nên
nên  ,
, 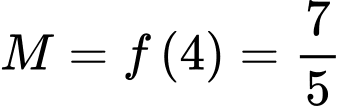
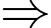
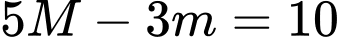 . Đáp án: B
. Đáp án: B
Câu 7 [503591]: Hàm số nào sau đây đồng biến trên 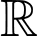 ?
?
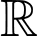 ?
? A, 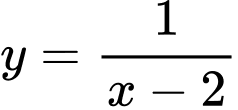 .
.
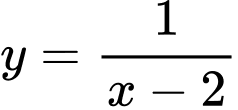 .
.B, 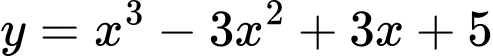 .
.
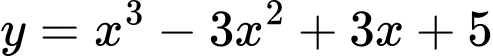 .
.C, 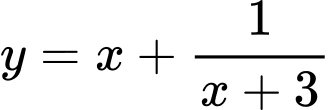 .
.
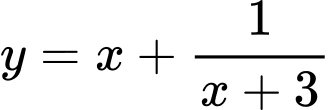 .
.D, 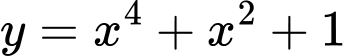 .
.
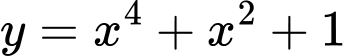 .
.
Chọn đáp án B. Đáp án: B
Câu 8 [377862]: Cho hàm số 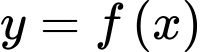 có đạo hàm
có đạo hàm 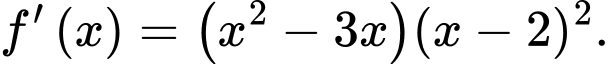 Hàm số
Hàm số 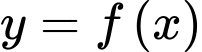 nghịch biến trên khoảng nào dưới đây?
nghịch biến trên khoảng nào dưới đây?
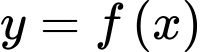 có đạo hàm
có đạo hàm 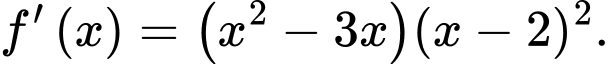 Hàm số
Hàm số 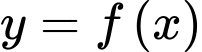 nghịch biến trên khoảng nào dưới đây?
nghịch biến trên khoảng nào dưới đây? A, 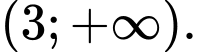
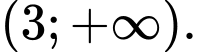
B, 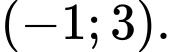
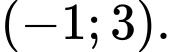
C, 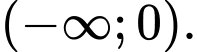
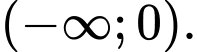
D, 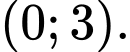
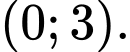
Phương pháp:
Lập bảng biến thiên
Cách giải: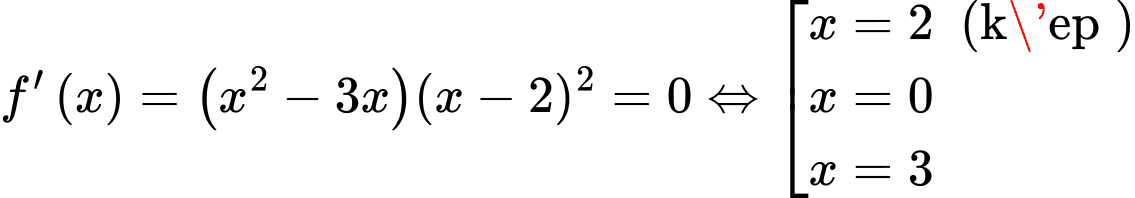
Suy ra hàm số nghịch biến trên khoảng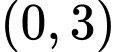
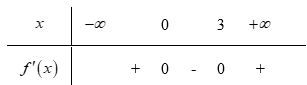 Đáp án: D
Đáp án: D
Lập bảng biến thiên
Cách giải:
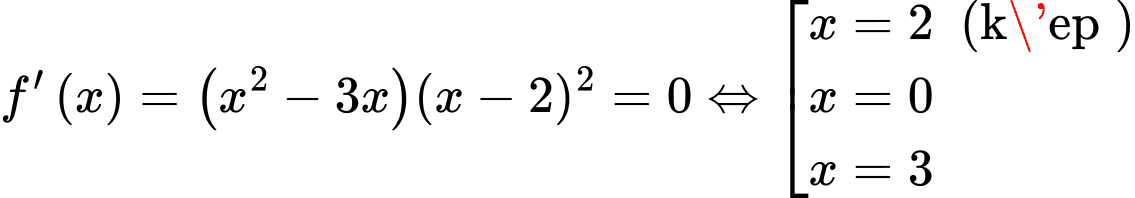
Suy ra hàm số nghịch biến trên khoảng
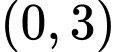
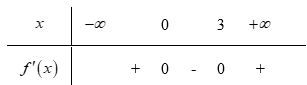 Đáp án: D
Đáp án: D
Câu 9 [599334]: Cho hàm số 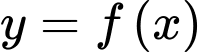 có đạo hàm trên
có đạo hàm trên  thoả mãn
thoả mãn 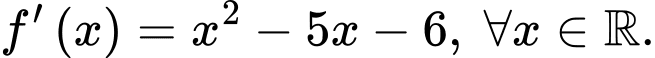 Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng dưới đây?
Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng dưới đây?
 có đạo hàm trên
có đạo hàm trên  thoả mãn
thoả mãn 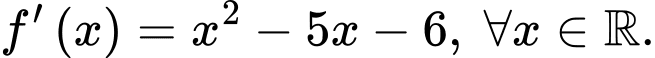 Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng dưới đây?
Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng dưới đây?
A, 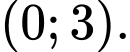
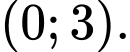
B, 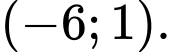
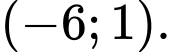
C, 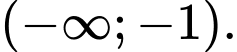
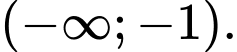
D, 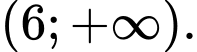
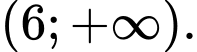
Tập xác định: 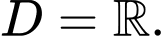
Ta có: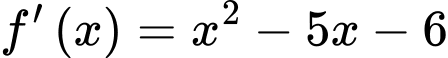 ;
; 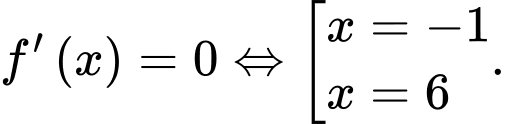
Bảng xét dấu:
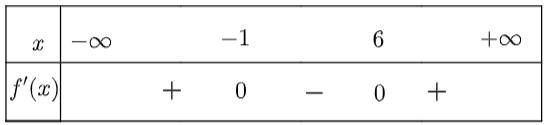
Do đó hàm số nghịch biến trên khoảng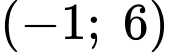 và đồng biến trên các khoảng
và đồng biến trên các khoảng 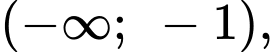
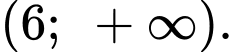
Ta có nên hàm số cũng nghịch biến trên khoảng
nên hàm số cũng nghịch biến trên khoảng 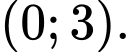 Chọn A
Đáp án: A
Chọn A
Đáp án: A
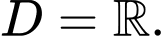
Ta có:
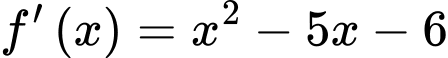 ;
; 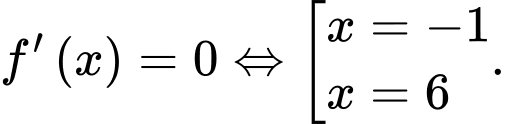
Bảng xét dấu:

Do đó hàm số nghịch biến trên khoảng
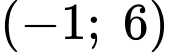 và đồng biến trên các khoảng
và đồng biến trên các khoảng 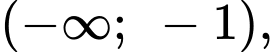
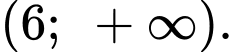
Ta có
 nên hàm số cũng nghịch biến trên khoảng
nên hàm số cũng nghịch biến trên khoảng 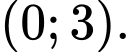 Chọn A
Đáp án: A
Chọn A
Đáp án: A
Câu 10 [597937]: Hàm số nào sau đây không có cực trị
A, 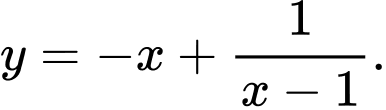
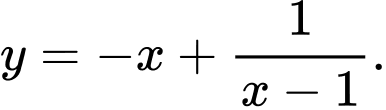
B, 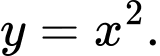
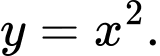
C, 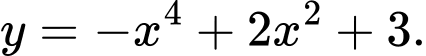
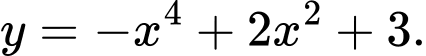
D, 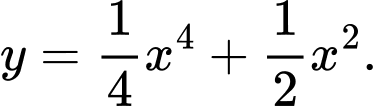
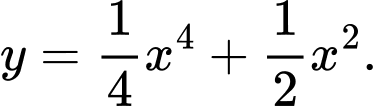
Xét hàm số 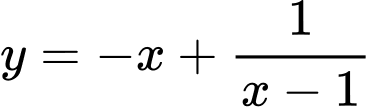 có
có 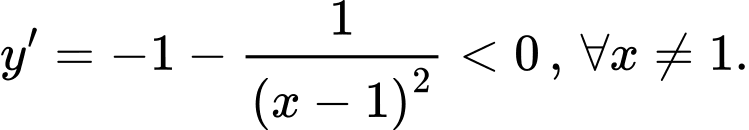 Suy ra hàm số không có cực trị. Chọn A. Đáp án: A
Suy ra hàm số không có cực trị. Chọn A. Đáp án: A
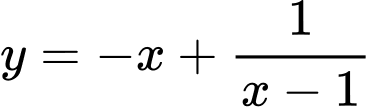 có
có 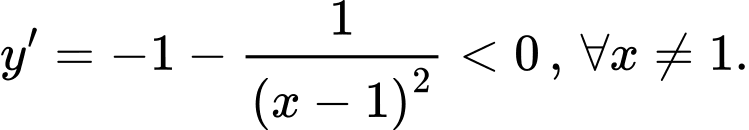 Suy ra hàm số không có cực trị. Chọn A. Đáp án: A
Suy ra hàm số không có cực trị. Chọn A. Đáp án: A
Câu 11 [544722]: Cho hàm số 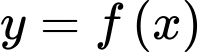 có đạo hàm
có đạo hàm 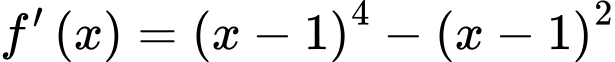 trên
trên 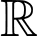 . Số điểm cực trị của hàm số
. Số điểm cực trị của hàm số
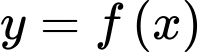 có đạo hàm
có đạo hàm 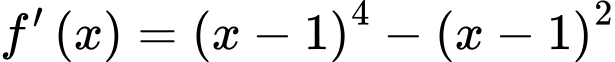 trên
trên 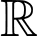 . Số điểm cực trị của hàm số
. Số điểm cực trị của hàm số A, 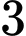 .
.
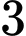 .
.B, 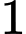 .
.
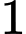 .
. C, 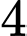 .
.
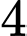 .
.D, 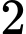 .
.
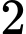 .
.
Chọn D.
Ta có 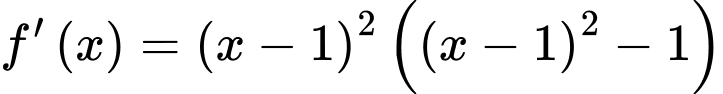
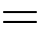
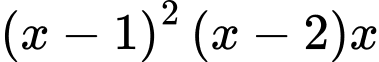
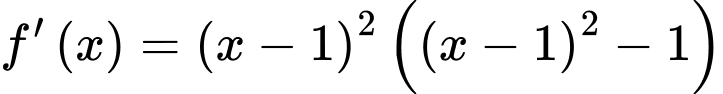
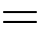
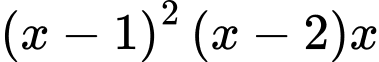
Ta có 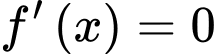 có hai nghiệm phân biệt và
có hai nghiệm phân biệt và 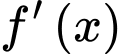 đổi dấu là
đổi dấu là 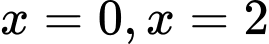 .
.
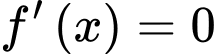 có hai nghiệm phân biệt và
có hai nghiệm phân biệt và 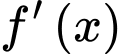 đổi dấu là
đổi dấu là 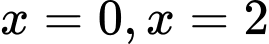 .
. Số điểm cực trị của hàm số là 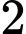 .
.
Đáp án: D 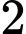 .
.
Câu 12 [681567]: Cho hàm số 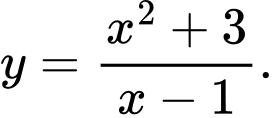 Khẳng định nào sau đây là đúng?
Khẳng định nào sau đây là đúng?
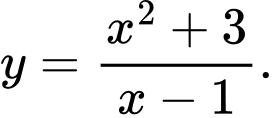 Khẳng định nào sau đây là đúng?
Khẳng định nào sau đây là đúng? A, Hàm số đã cho đạt cực đại tại 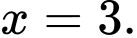
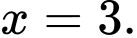
B, Hàm số đã cho có hai cực trị thỏa mãn 

C, Hàm số đã cho đạt cực tiểu tại 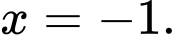
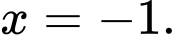
D, Giá trị cực tiểu của hàm số đã cho bằng -2.
TXĐ của hàm số là 
Ta có: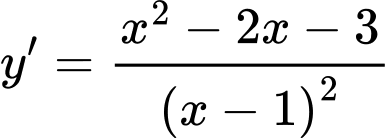 ;
;  hoặc
hoặc 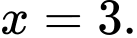
Bảng biến thiên của hàm số như sau:
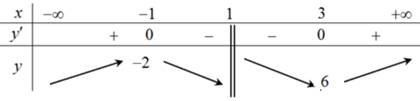
Căn cứ vào bảng biến thiên, ta thấy hàm số đạt cực đại tại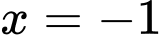 , giá trị cực đại
, giá trị cực đại 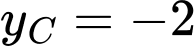 ; đạt cực tiểu tại
; đạt cực tiểu tại 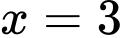 , giá trị cực tiểu
, giá trị cực tiểu 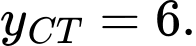 Chọn B. Đáp án: B
Chọn B. Đáp án: B

Ta có:
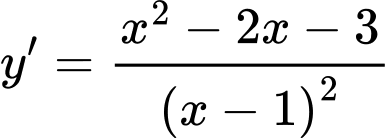 ;
;  hoặc
hoặc 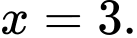
Bảng biến thiên của hàm số như sau:

Căn cứ vào bảng biến thiên, ta thấy hàm số đạt cực đại tại
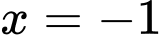 , giá trị cực đại
, giá trị cực đại 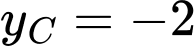 ; đạt cực tiểu tại
; đạt cực tiểu tại 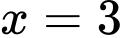 , giá trị cực tiểu
, giá trị cực tiểu 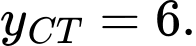 Chọn B. Đáp án: B
Chọn B. Đáp án: B PHẦN II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a),b),c),d) ở mỗi câu học sinh chọn đúng hoặc sai.
Câu 13 [774107]: Cho hàm số 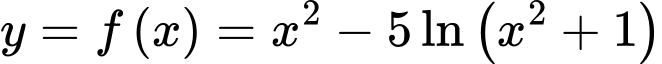
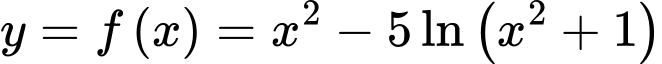
a) Đúng.
Vì điều kiện xác định của hàm số đã cho là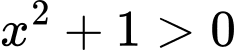 thỏa mãn với mọi
thỏa mãn với mọi 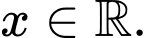
b) Sai.
Ta có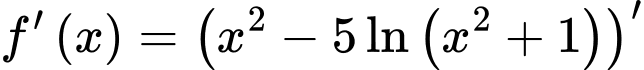
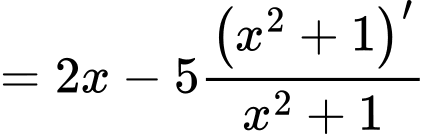
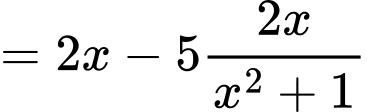
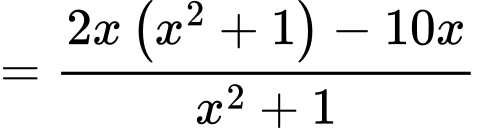
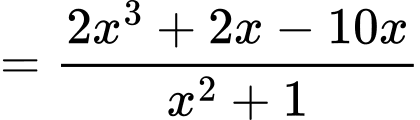
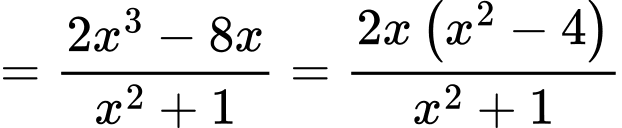
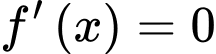
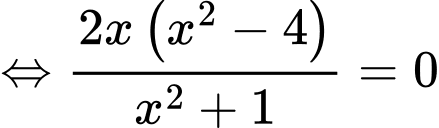
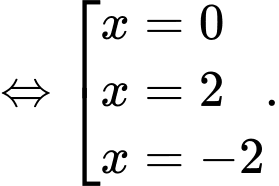
Vậy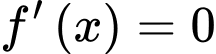 có 3 nghiệm phân biệt trên tập
có 3 nghiệm phân biệt trên tập 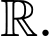
c) Đúng.
Tiếp tuyến của đồ thị hàm số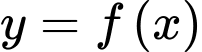 tại điểm có hoành độ
tại điểm có hoành độ 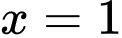 có hệ số góc là
có hệ số góc là 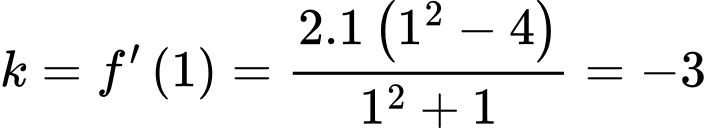
d) Đúng.
Khảo sát hàm số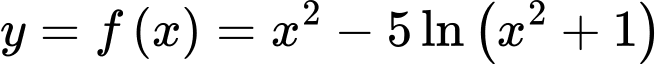 trên
trên 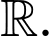
Dựa vào kết quả phần b) ta có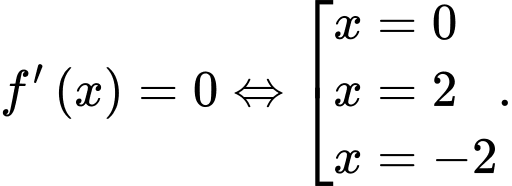
Bảng biến thiên:
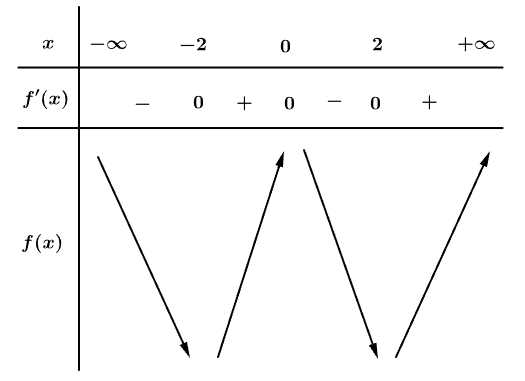
Dựa vào bảng biến thiên, ta thấy hàm số đã cho đồng biến trên khoảng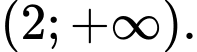
Vì điều kiện xác định của hàm số đã cho là
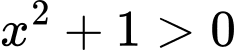 thỏa mãn với mọi
thỏa mãn với mọi 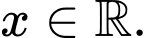
b) Sai.
Ta có
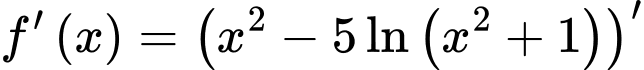
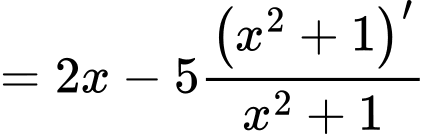
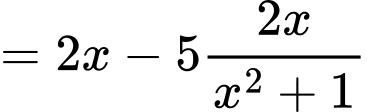
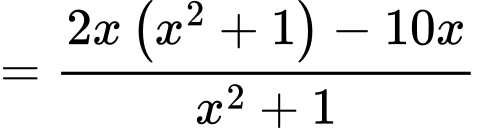
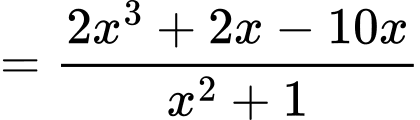
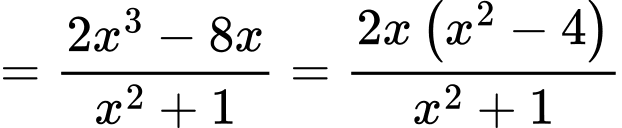
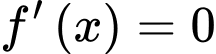
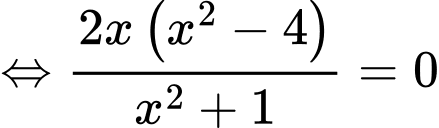
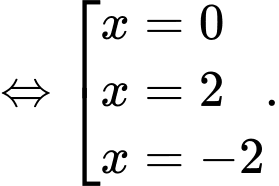
Vậy
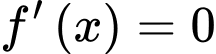 có 3 nghiệm phân biệt trên tập
có 3 nghiệm phân biệt trên tập 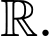
c) Đúng.
Tiếp tuyến của đồ thị hàm số
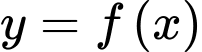 tại điểm có hoành độ
tại điểm có hoành độ 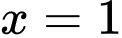 có hệ số góc là
có hệ số góc là 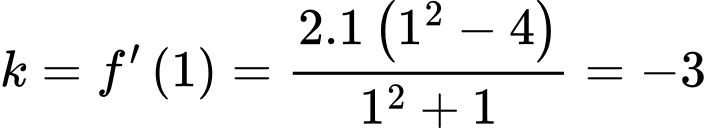
d) Đúng.
Khảo sát hàm số
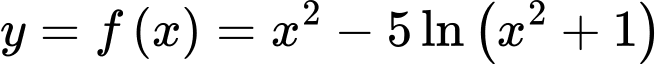 trên
trên 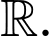
Dựa vào kết quả phần b) ta có
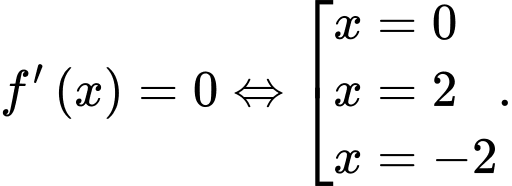
Bảng biến thiên:

Dựa vào bảng biến thiên, ta thấy hàm số đã cho đồng biến trên khoảng
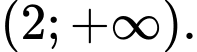
Câu 14 [774109]: Cho hàm số 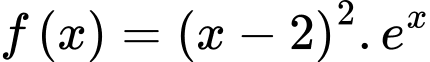
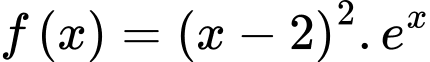
a) Sai.
Thay lần lượt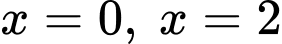 vào hàm số, ta được
vào hàm số, ta được 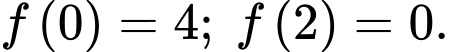
b) Đúng.
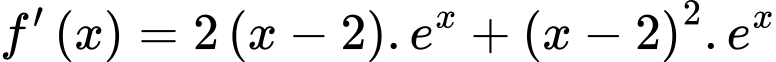
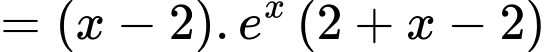
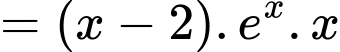
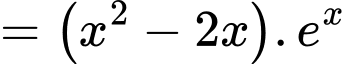
c) Đúng.
Từ kết quả phần b) ta có
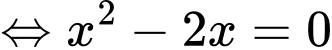
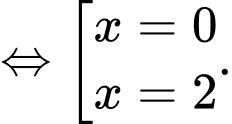
Vậy phương trình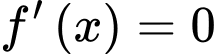 có hai nghiệm phân biệt trên
có hai nghiệm phân biệt trên 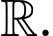
d) Sai.
Khảo sát hàm số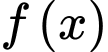 trên
trên 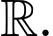
Từ kết quả thu được từ phần c) ta được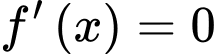
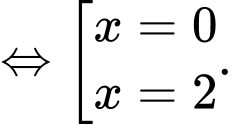
Bảng biến thiên
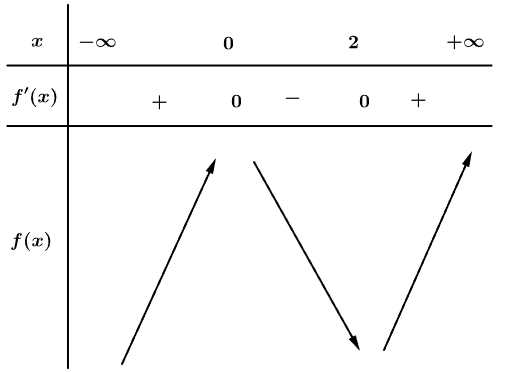
Dựa vào bảng biến thiên, ta suy ra giá trị cực tiểu của hàm số là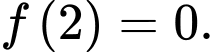
Thay lần lượt
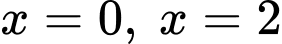 vào hàm số, ta được
vào hàm số, ta được 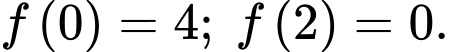
b) Đúng.
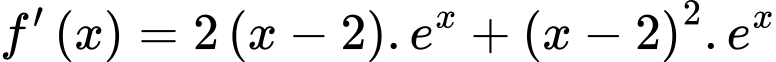
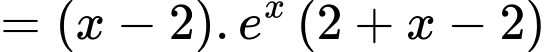
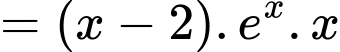
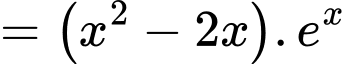
c) Đúng.
Từ kết quả phần b) ta có

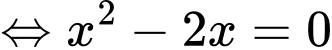
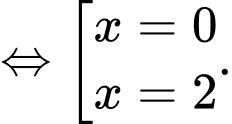
Vậy phương trình
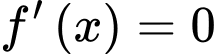 có hai nghiệm phân biệt trên
có hai nghiệm phân biệt trên 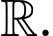
d) Sai.
Khảo sát hàm số
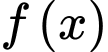 trên
trên 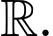
Từ kết quả thu được từ phần c) ta được
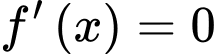
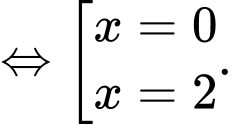
Bảng biến thiên

Dựa vào bảng biến thiên, ta suy ra giá trị cực tiểu của hàm số là
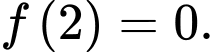
Câu 15 [599608]: Một vật chuyển động theo quy luật 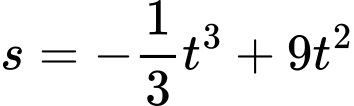 với t (giây,
với t (giây, 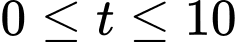 ) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và s (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó.
) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và s (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó.
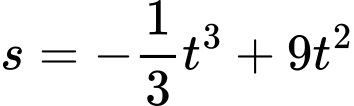 với t (giây,
với t (giây, 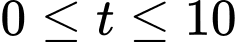 ) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và s (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó.
) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và s (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó.
a) Đúng. Quãng đường vật chuyển động được trong 6 giây đầu tiên là: 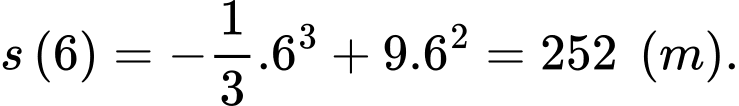
b) Sai. Ta có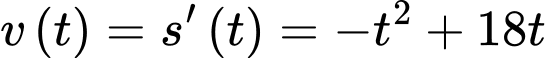
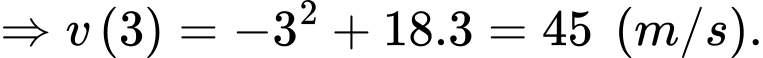
Vậy sau 3 giây vận tốc của vật đạt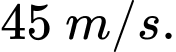
c) Sai. Ta có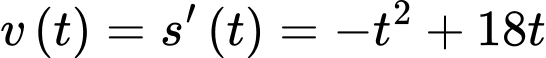
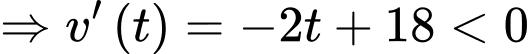
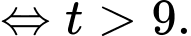
Vậy vận tốc của vật giảm từ giây thứ 9 đến giây thứ 10.
d) Đúng. Ta có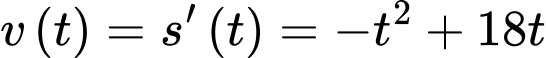
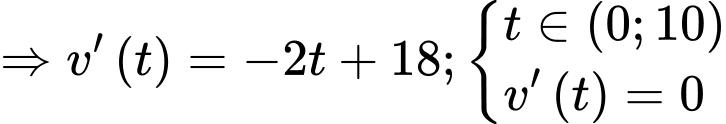
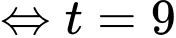
Tính được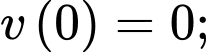
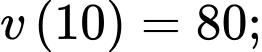
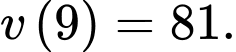
Vậy kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được là 81 m/s,
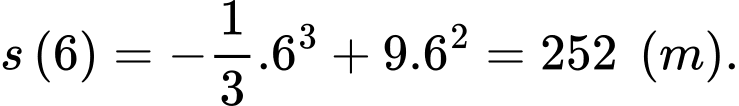
b) Sai. Ta có
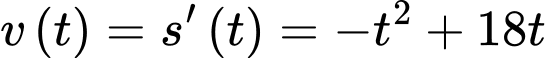
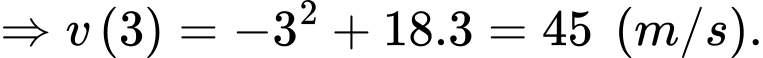
Vậy sau 3 giây vận tốc của vật đạt
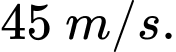
c) Sai. Ta có
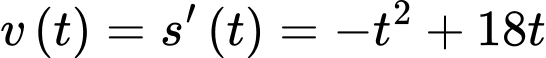
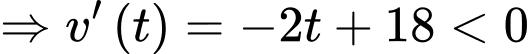
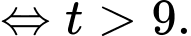
Vậy vận tốc của vật giảm từ giây thứ 9 đến giây thứ 10.
d) Đúng. Ta có
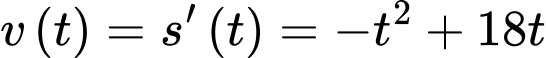
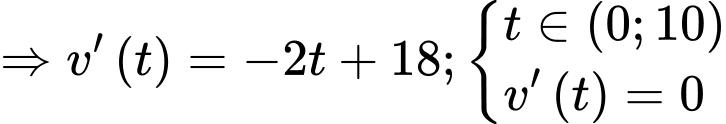
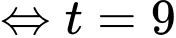
Tính được
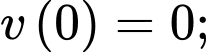
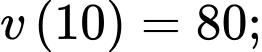
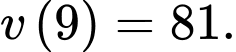
Vậy kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được là 81 m/s,
Câu 16 [774110]: Ông A sử dụng hết  kính để làm bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Gọi chiều rộng của bể cá là
kính để làm bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Gọi chiều rộng của bể cá là  và chiều cao của bể cá là
và chiều cao của bể cá là 
 kính để làm bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Gọi chiều rộng của bể cá là
kính để làm bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Gọi chiều rộng của bể cá là  và chiều cao của bể cá là
và chiều cao của bể cá là 
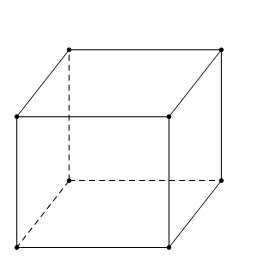
a) Sai. Vì: Chiều dài bể cá gấp đôi chiều rộng nên ta gọi chiều rộng, chiều dài, chiều cao của bể cá lần lượt là
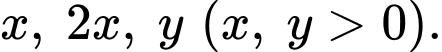
Thể tích của bể cá là:
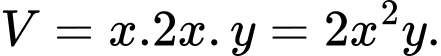
b) Sai. Vì: Ta sẽ tìm mối quan hệ giữa
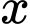 và
và 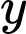 dựa vào diện tích phần lắp kính:
dựa vào diện tích phần lắp kính: 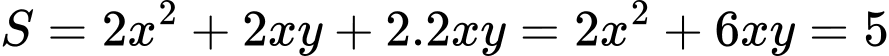
c) Đúng. Vì: Rút
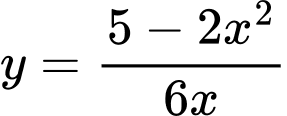 (với
(với  ) ta có:
) ta có: 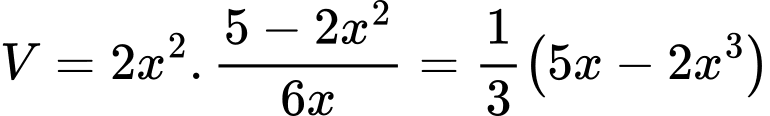
Xét hàm số
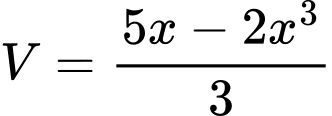 với
với  ta có:
ta có: 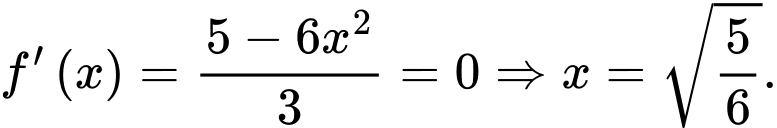
Lập BBT suy ra
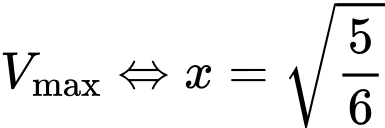
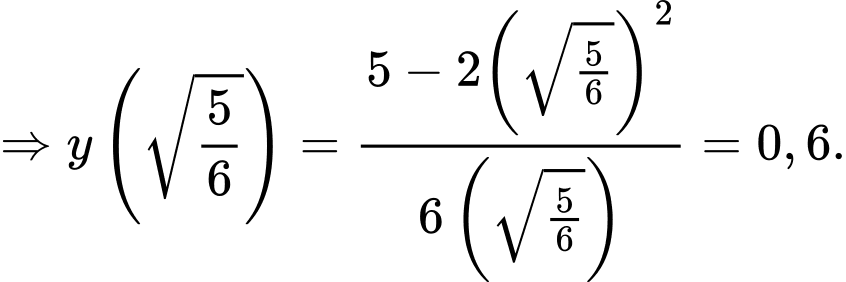
d) Sai. Vì:
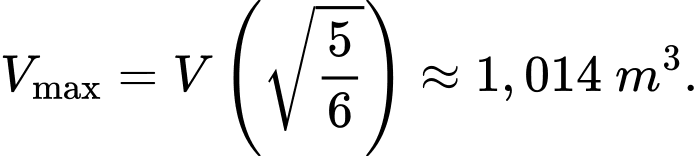
PHẦN III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 17 đến câu 22.
Câu 17 [681561]: Biết đồ thị hàm số 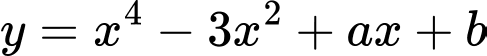 nhận điểm
nhận điểm 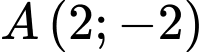 là một điểm cực trị. Tính
là một điểm cực trị. Tính 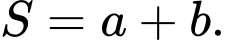
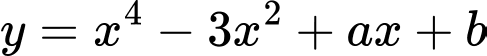 nhận điểm
nhận điểm 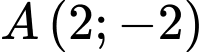 là một điểm cực trị. Tính
là một điểm cực trị. Tính 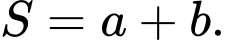
Ta có: 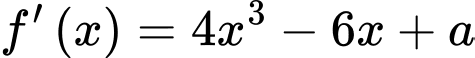
Vì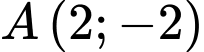 là một điểm cực trị của đồ thị hàm số
là một điểm cực trị của đồ thị hàm số 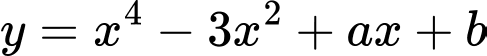 nên ta có:
nên ta có:
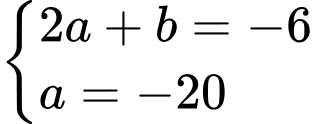
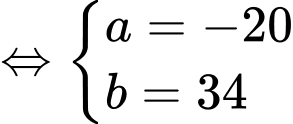 (thử lại thấy thoả mãn)
(thử lại thấy thoả mãn)
Vậy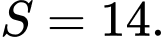
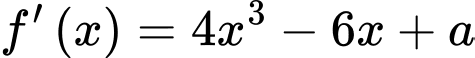
Vì
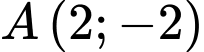 là một điểm cực trị của đồ thị hàm số
là một điểm cực trị của đồ thị hàm số 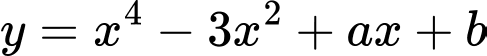 nên ta có:
nên ta có: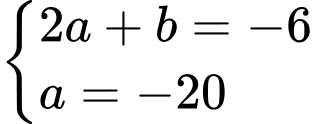
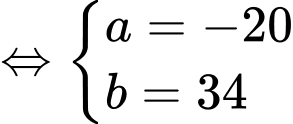 (thử lại thấy thoả mãn)
(thử lại thấy thoả mãn)Vậy
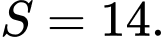
Câu 18 [774111]: Thể tích nước của một bể bơi sau 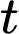 phút bơm được tính theo công thức
phút bơm được tính theo công thức 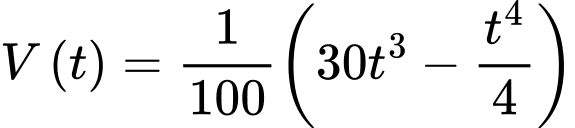
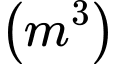 với
với 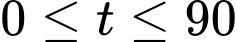 . Tốc độ bơm nước ở thời điểm
. Tốc độ bơm nước ở thời điểm 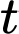 được tính theo công thức
được tính theo công thức 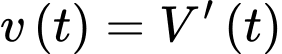 (
(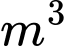 /phút). Tại một thời điểm
/phút). Tại một thời điểm 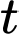 nào đó thì tốc độ bơm nước là lớn nhất, hãy tính tốc độ bơm nước lớn nhất đó theo đơn vị
nào đó thì tốc độ bơm nước là lớn nhất, hãy tính tốc độ bơm nước lớn nhất đó theo đơn vị 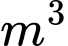 /phút.
/phút.
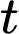 phút bơm được tính theo công thức
phút bơm được tính theo công thức 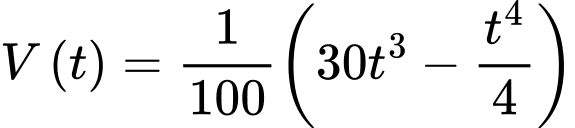
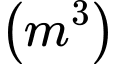 với
với 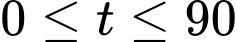 . Tốc độ bơm nước ở thời điểm
. Tốc độ bơm nước ở thời điểm 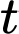 được tính theo công thức
được tính theo công thức 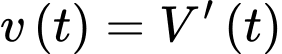 (
(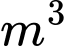 /phút). Tại một thời điểm
/phút). Tại một thời điểm 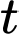 nào đó thì tốc độ bơm nước là lớn nhất, hãy tính tốc độ bơm nước lớn nhất đó theo đơn vị
nào đó thì tốc độ bơm nước là lớn nhất, hãy tính tốc độ bơm nước lớn nhất đó theo đơn vị 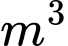 /phút.
/phút.
Ta có 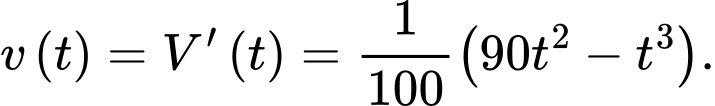
Suy ra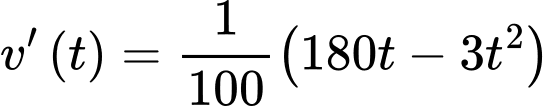 ;
; 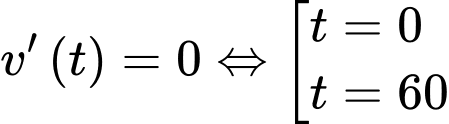 .
.
Bảng biến thiên
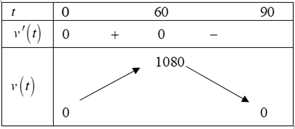 Từ bảng biến thiên ta thấy: Tốc độ bơm nước lớn nhất bằng
Từ bảng biến thiên ta thấy: Tốc độ bơm nước lớn nhất bằng 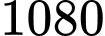
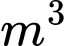 /phút, tại thời điểm
/phút, tại thời điểm 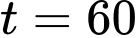 phút.
phút.
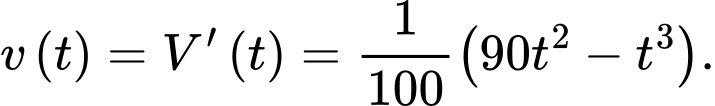
Suy ra
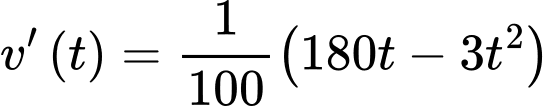 ;
; 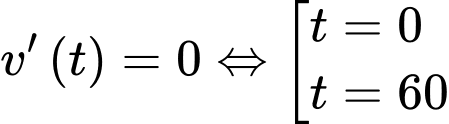 .
.Bảng biến thiên

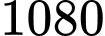
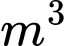 /phút, tại thời điểm
/phút, tại thời điểm 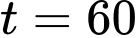 phút.
phút.
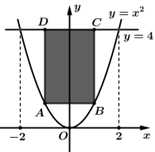
Câu 19 [774114]: Cho hình chữ nhật 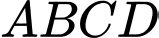 có hai đỉnh di động trên đồ thị hàm số
có hai đỉnh di động trên đồ thị hàm số 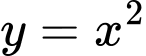 trên khoảng
trên khoảng 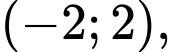 hai đỉnh còn lại nằm trên đường thẳng
hai đỉnh còn lại nằm trên đường thẳng 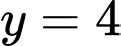 (như hình vẽ). Tìm diện tích lớn nhất của hình chữ nhật
(như hình vẽ). Tìm diện tích lớn nhất của hình chữ nhật 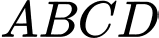 (kết quả làm tròn đến hàng phần trăm).
(kết quả làm tròn đến hàng phần trăm).
 có hai đỉnh di động trên đồ thị hàm số
có hai đỉnh di động trên đồ thị hàm số 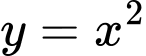 trên khoảng
trên khoảng 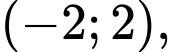 hai đỉnh còn lại nằm trên đường thẳng
hai đỉnh còn lại nằm trên đường thẳng 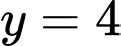 (như hình vẽ). Tìm diện tích lớn nhất của hình chữ nhật
(như hình vẽ). Tìm diện tích lớn nhất của hình chữ nhật 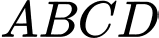 (kết quả làm tròn đến hàng phần trăm).
(kết quả làm tròn đến hàng phần trăm).
Sau đó, diện tích là 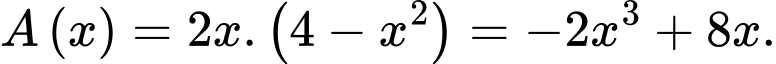 Chúng ta muốn giá trị lớn nhất của
Chúng ta muốn giá trị lớn nhất của 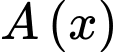 khi
khi 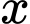 nằm trong
nằm trong 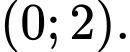
Đặt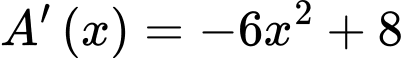 ta được
ta được 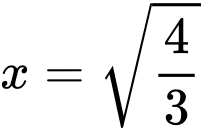 là giá trị cực trị duy nhất. Kiểm tra giá trị này và hai điểm đầu mút, ta có
là giá trị cực trị duy nhất. Kiểm tra giá trị này và hai điểm đầu mút, ta có 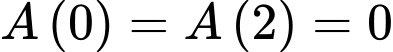 và
và 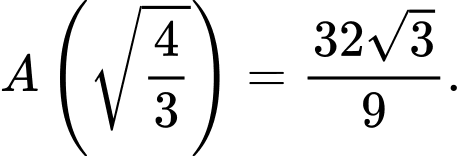
Do đó, diện tích lớn nhất bằng: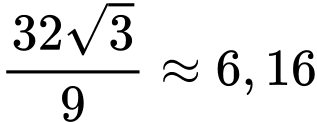
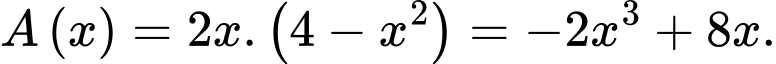 Chúng ta muốn giá trị lớn nhất của
Chúng ta muốn giá trị lớn nhất của 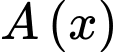 khi
khi 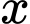 nằm trong
nằm trong 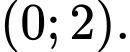
Đặt
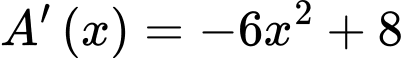 ta được
ta được 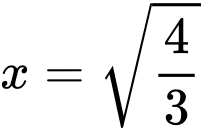 là giá trị cực trị duy nhất. Kiểm tra giá trị này và hai điểm đầu mút, ta có
là giá trị cực trị duy nhất. Kiểm tra giá trị này và hai điểm đầu mút, ta có 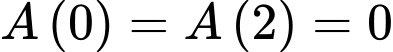 và
và 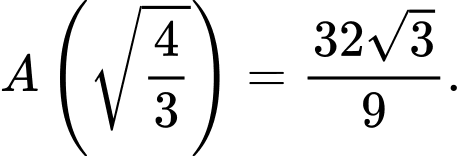
Do đó, diện tích lớn nhất bằng:
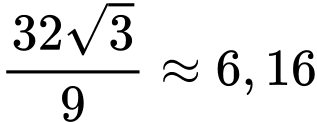
Câu 20 [774117]: Một xí nghiệp 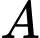 chuyên cung cấp sản phẩm
chuyên cung cấp sản phẩm 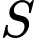 cho nhà phân phối
cho nhà phân phối 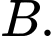 Hai bên thỏa thuận rằng, nếu đầu tháng
Hai bên thỏa thuận rằng, nếu đầu tháng 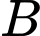 đặt hàng
đặt hàng 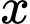 tạ sản phẩm
tạ sản phẩm 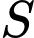 thì giá bán mỗi tạ sản phẩm
thì giá bán mỗi tạ sản phẩm 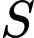 là
là 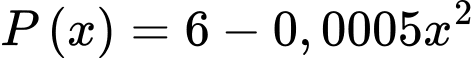 (triệu đồng)
(triệu đồng) 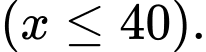 Chi phí
Chi phí 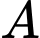 phải bỏ ra cho
phải bỏ ra cho 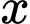 tạ sản phẩm
tạ sản phẩm 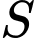 trong một tháng là
trong một tháng là 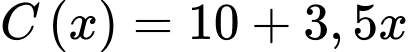 (triệu đồng) và mỗi sản phẩm bán ra bên
(triệu đồng) và mỗi sản phẩm bán ra bên 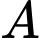 phải chịu thêm mức thuế là
phải chịu thêm mức thuế là 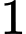 triệu đồng. Hỏi trong một tháng bên
triệu đồng. Hỏi trong một tháng bên 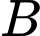 đặt bao nhiêu tạ sản phẩm
đặt bao nhiêu tạ sản phẩm 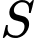 thì bên
thì bên 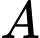 thu được lợi nhuận lớn nhất (kết quả làm tròn đến hàng phần chục).
thu được lợi nhuận lớn nhất (kết quả làm tròn đến hàng phần chục).
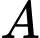 chuyên cung cấp sản phẩm
chuyên cung cấp sản phẩm 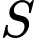 cho nhà phân phối
cho nhà phân phối 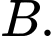 Hai bên thỏa thuận rằng, nếu đầu tháng
Hai bên thỏa thuận rằng, nếu đầu tháng 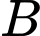 đặt hàng
đặt hàng 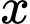 tạ sản phẩm
tạ sản phẩm 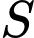 thì giá bán mỗi tạ sản phẩm
thì giá bán mỗi tạ sản phẩm  là
là 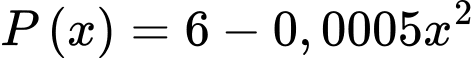 (triệu đồng)
(triệu đồng)  Chi phí
Chi phí  phải bỏ ra cho
phải bỏ ra cho 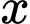 tạ sản phẩm
tạ sản phẩm 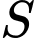 trong một tháng là
trong một tháng là 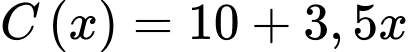 (triệu đồng) và mỗi sản phẩm bán ra bên
(triệu đồng) và mỗi sản phẩm bán ra bên 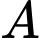 phải chịu thêm mức thuế là
phải chịu thêm mức thuế là 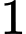 triệu đồng. Hỏi trong một tháng bên
triệu đồng. Hỏi trong một tháng bên 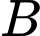 đặt bao nhiêu tạ sản phẩm
đặt bao nhiêu tạ sản phẩm 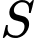 thì bên
thì bên 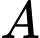 thu được lợi nhuận lớn nhất (kết quả làm tròn đến hàng phần chục).
thu được lợi nhuận lớn nhất (kết quả làm tròn đến hàng phần chục).
Lợi nhuận mà 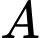 thu được khi
thu được khi 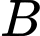 đặt
đặt 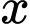 sản phẩm là
sản phẩm là
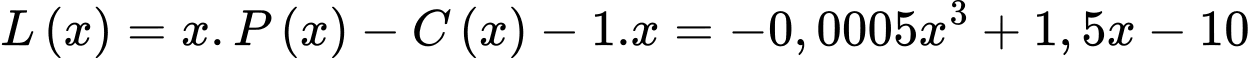 .
.
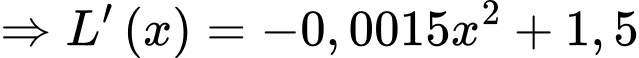 ,
, 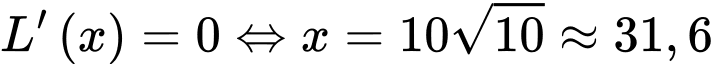 .
.
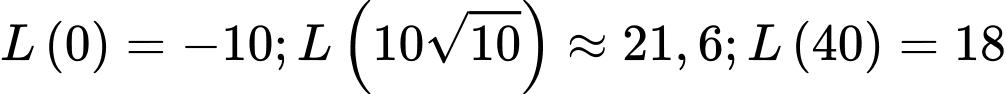 .
.
Vậy để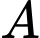 có lợi nhuận lớn nhất thì
có lợi nhuận lớn nhất thì 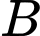 cần đặt khoảng
cần đặt khoảng 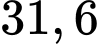 tạ sản phẩm
tạ sản phẩm 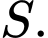
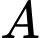 thu được khi
thu được khi 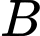 đặt
đặt 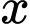 sản phẩm là
sản phẩm là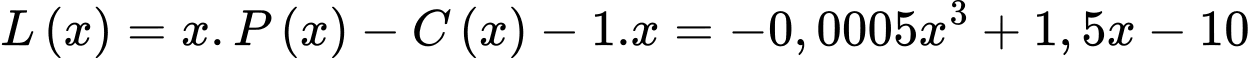 .
.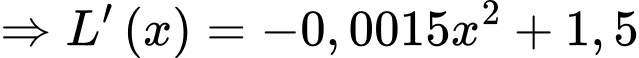 ,
, 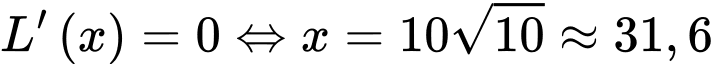 .
.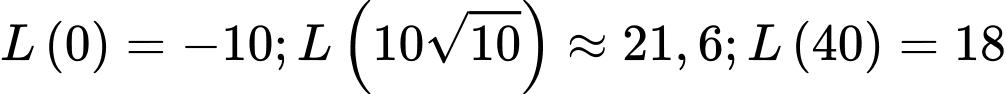 .
.Vậy để
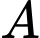 có lợi nhuận lớn nhất thì
có lợi nhuận lớn nhất thì 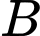 cần đặt khoảng
cần đặt khoảng 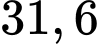 tạ sản phẩm
tạ sản phẩm 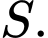
Câu 21 [774121]: Điện trở của một dây dẫn đối với dòng điện chạy qua nó tỉ lệ thuận với chiều dài của nó và tỉ lệ nghịch với diện tích tiết diện của nó. Do đó, điện trở 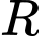 của một dây dẫn có chiều dài
của một dây dẫn có chiều dài 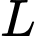 và bán kính
và bán kính 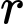 là
là 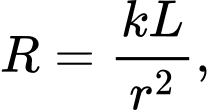 trong đó
trong đó 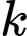 là một hằng số dương. Một dây dẫn thẳng dài có chiều dài
là một hằng số dương. Một dây dẫn thẳng dài có chiều dài 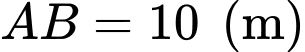 và bán kính
và bán kính 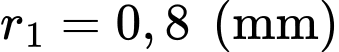 kéo dài từ
kéo dài từ 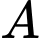 đến
đến 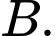 Một dây dẫn thẳng thứ hai có bán kính nhỏ hơn
Một dây dẫn thẳng thứ hai có bán kính nhỏ hơn 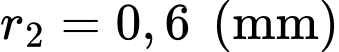 được nối giữa điểm
được nối giữa điểm 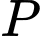 bất kì trên
bất kì trên  và điểm
và điểm  cách
cách 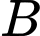 một khoảng
một khoảng 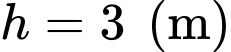 sao cho
sao cho 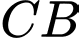 vuông góc với
vuông góc với  (xem hình vẽ). Tìm giá trị của góc
(xem hình vẽ). Tìm giá trị của góc 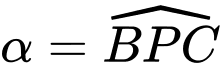 (rad) để tối thiểu hóa tổng điện trở của đường dẫn
(rad) để tối thiểu hóa tổng điện trở của đường dẫn 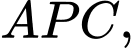 tức là tổng điện trở của dây dẫn
tức là tổng điện trở của dây dẫn 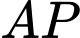 và
và 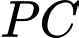 là nhỏ nhất (viết kết quả làm tròn đến hàng phần trăm).
là nhỏ nhất (viết kết quả làm tròn đến hàng phần trăm).
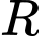 của một dây dẫn có chiều dài
của một dây dẫn có chiều dài 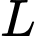 và bán kính
và bán kính 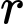 là
là 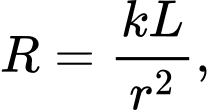 trong đó
trong đó 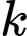 là một hằng số dương. Một dây dẫn thẳng dài có chiều dài
là một hằng số dương. Một dây dẫn thẳng dài có chiều dài 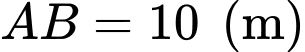 và bán kính
và bán kính 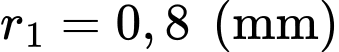 kéo dài từ
kéo dài từ 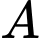 đến
đến 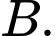 Một dây dẫn thẳng thứ hai có bán kính nhỏ hơn
Một dây dẫn thẳng thứ hai có bán kính nhỏ hơn 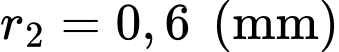 được nối giữa điểm
được nối giữa điểm 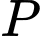 bất kì trên
bất kì trên  và điểm
và điểm  cách
cách 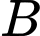 một khoảng
một khoảng 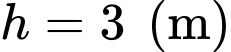 sao cho
sao cho 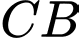 vuông góc với
vuông góc với  (xem hình vẽ). Tìm giá trị của góc
(xem hình vẽ). Tìm giá trị của góc 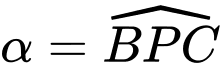 (rad) để tối thiểu hóa tổng điện trở của đường dẫn
(rad) để tối thiểu hóa tổng điện trở của đường dẫn 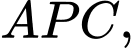 tức là tổng điện trở của dây dẫn
tức là tổng điện trở của dây dẫn 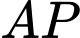 và
và 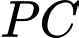 là nhỏ nhất (viết kết quả làm tròn đến hàng phần trăm).
là nhỏ nhất (viết kết quả làm tròn đến hàng phần trăm).
Điền đáp án: 0,97
Xét tam giác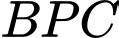 vuông tại
vuông tại 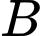 ta có:
ta có:
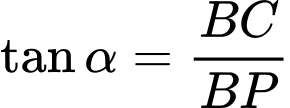
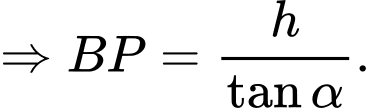
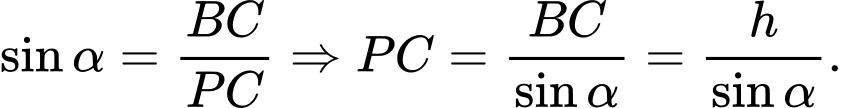
Khi đó: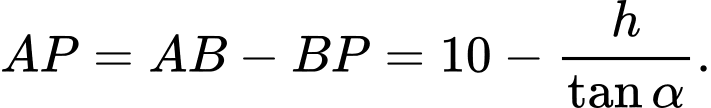
Tổng điện trở của đường dẫn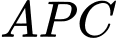 là
là

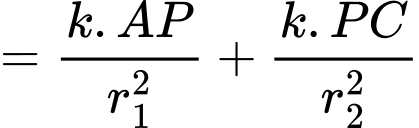
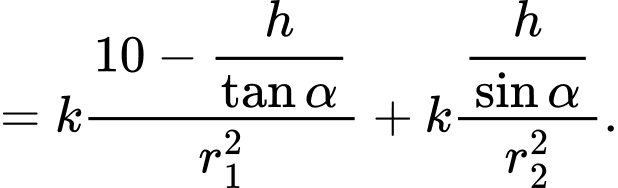
Xét hàm số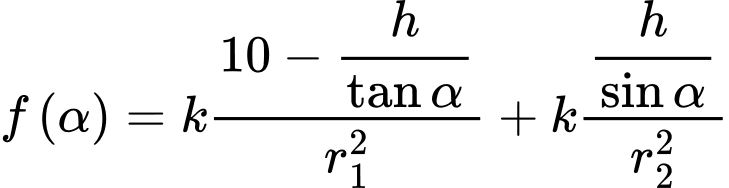 với
với 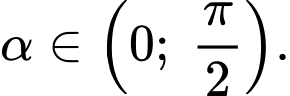
Ta có: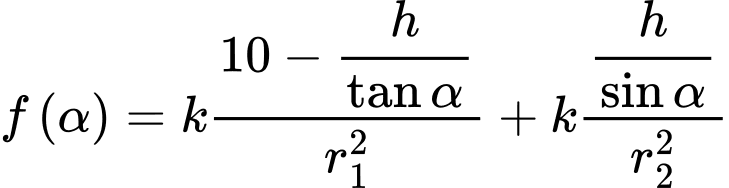
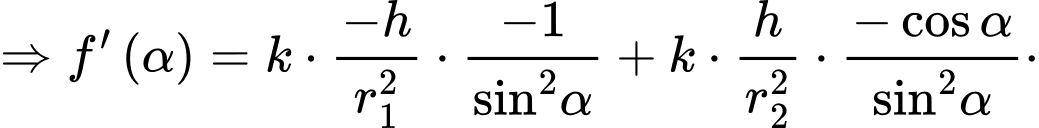
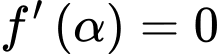
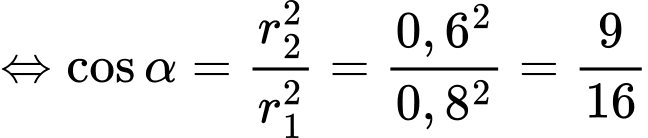
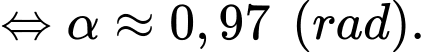
Bảng biến thiên:
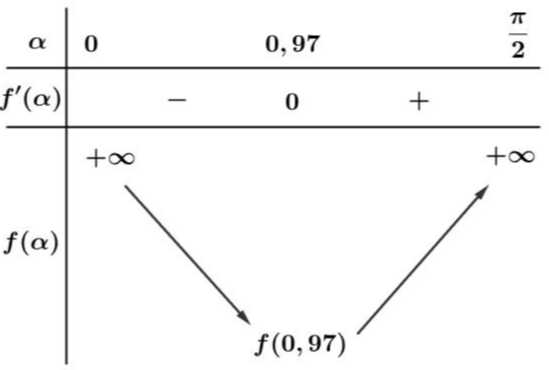
Dựa vào bảng biến thiên ta có: Tổng điện trở của dây dẫn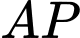 và
và 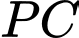 là nhỏ nhất khi
là nhỏ nhất khi 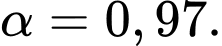
Xét tam giác
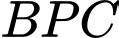 vuông tại
vuông tại 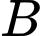 ta có:
ta có: 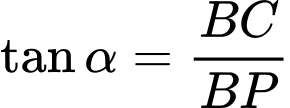
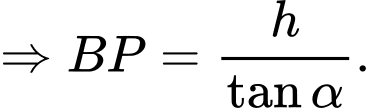
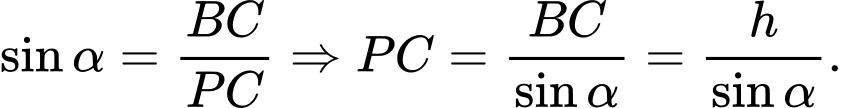
Khi đó:
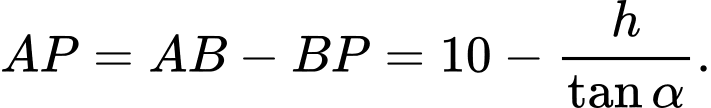
Tổng điện trở của đường dẫn
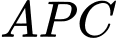 là
là 
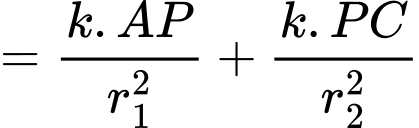
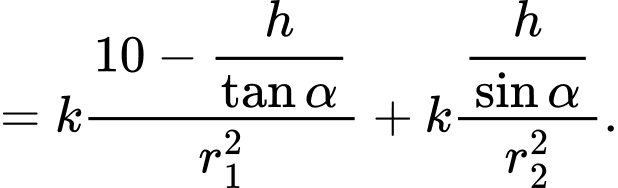
Xét hàm số
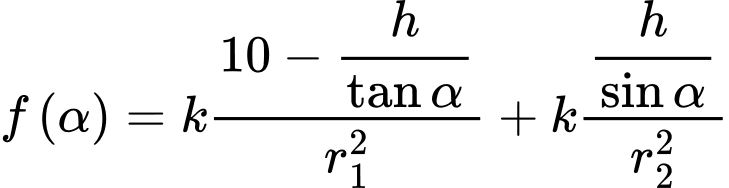 với
với 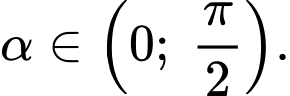
Ta có:
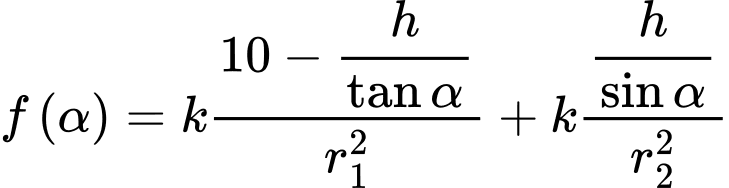
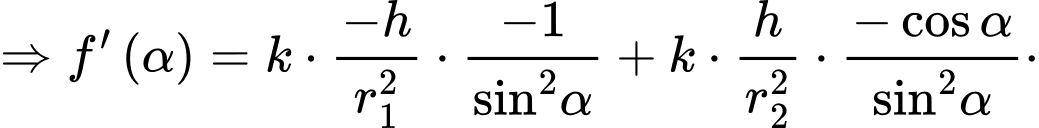
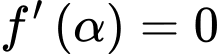
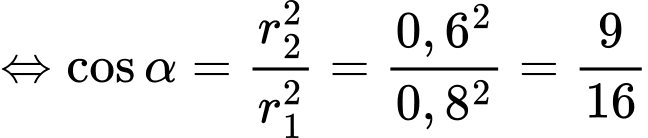
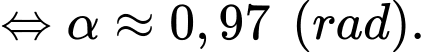
Bảng biến thiên:

Dựa vào bảng biến thiên ta có: Tổng điện trở của dây dẫn
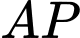 và
và 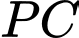 là nhỏ nhất khi
là nhỏ nhất khi 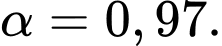
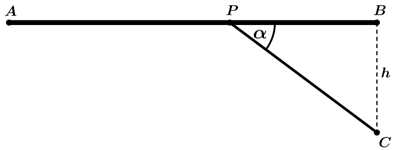
Câu 22 [774123]: Một nhiếp ảnh gia đang chụp ảnh một bức tranh treo trong phòng trưng bày nghệ thuật. Chiều cao của bức tranh là 120 cm. Ống kính máy ảnh thấp hơn 30 cm so với mép dưới của bức tranh (như hình vẽ). Máy ảnh nên đặt cách bức tranh bao nhiêu cm để góc tạo bởi ống kính máy ảnh (góc 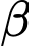 trong hình vẽ) là lớn nhất (viết kết quả làm tròn đến hàng đơn vị).
trong hình vẽ) là lớn nhất (viết kết quả làm tròn đến hàng đơn vị).
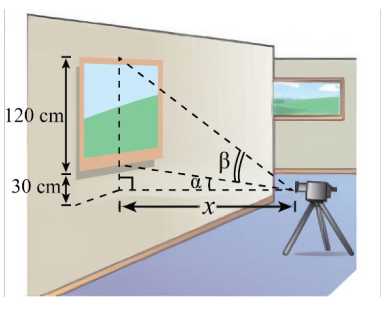
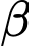 trong hình vẽ) là lớn nhất (viết kết quả làm tròn đến hàng đơn vị).
trong hình vẽ) là lớn nhất (viết kết quả làm tròn đến hàng đơn vị). 
Điền đáp án: 67.
Gọi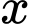 là khoảng cách từ máy ảnh đến bức tranh khi đó:
là khoảng cách từ máy ảnh đến bức tranh khi đó: 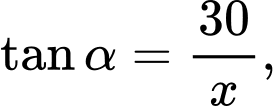
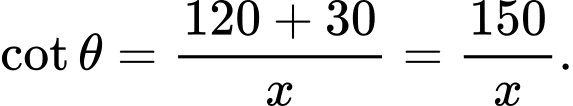
Dựa vào hình vẽ ta có: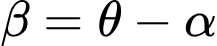
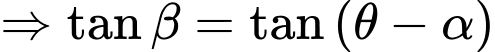
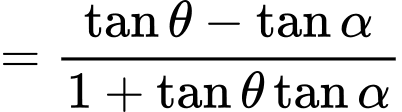
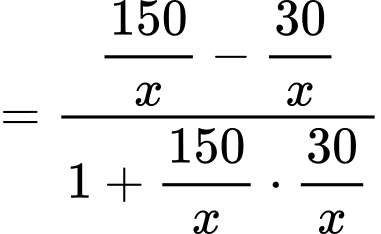
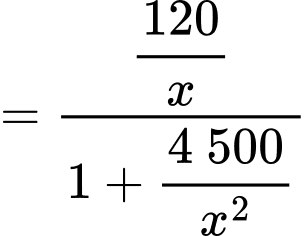
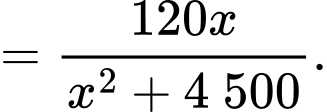
Xét hàm số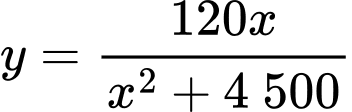 với
với 
Cách 1: Ta có: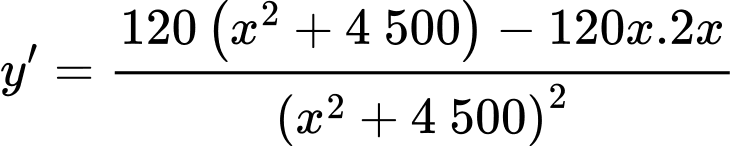
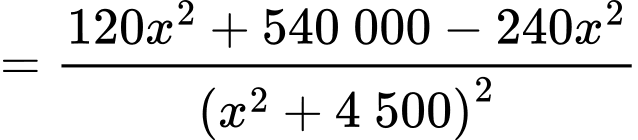
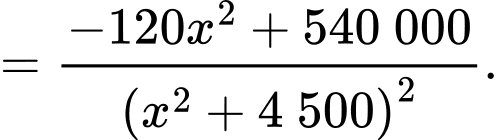
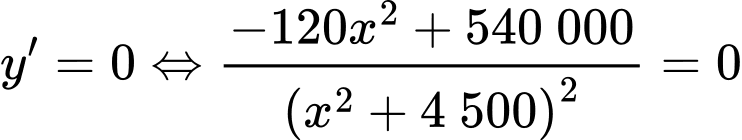
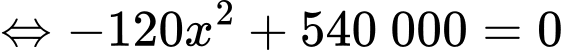
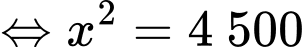
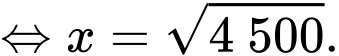
Bảng biến thiên:
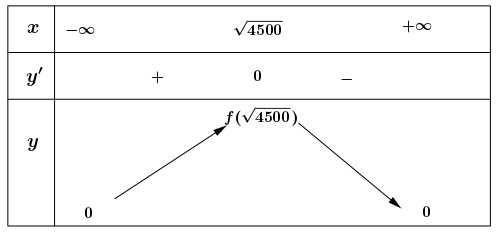
Dựa vào bảng biến thiên ta có: Máy ảnh nên đặt cách bức tranh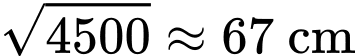 để góc tạo bởi ống kính máy ảnh
để góc tạo bởi ống kính máy ảnh 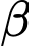 trong hình vẽ là lớn nhất.
trong hình vẽ là lớn nhất.
Cách 2: Áp dụng định lý Cô-si cho 2 số không âm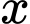 và
và 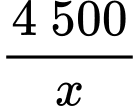 ta có:
ta có: 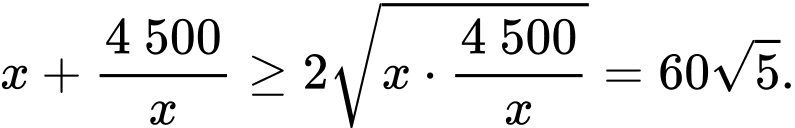
Khi đó: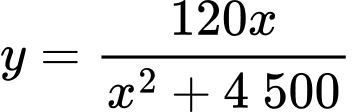
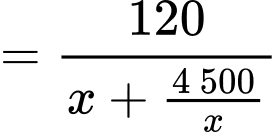
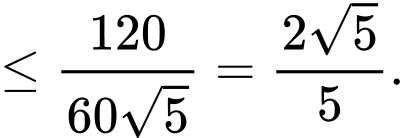
Dấu bằng xảy ra khi: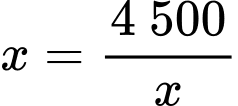 hay
hay 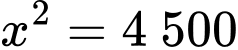
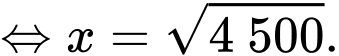
Vậy máy ảnh nên đặt cách bức tranh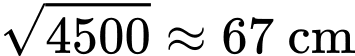 để góc tạo bởi ống kính máy ảnh
để góc tạo bởi ống kính máy ảnh 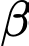 trong hình vẽ là lớn nhất.
trong hình vẽ là lớn nhất.
Gọi
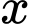 là khoảng cách từ máy ảnh đến bức tranh khi đó:
là khoảng cách từ máy ảnh đến bức tranh khi đó: 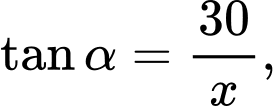
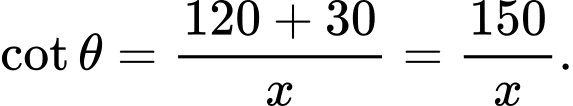
Dựa vào hình vẽ ta có:
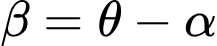
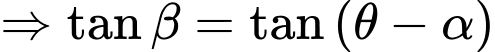
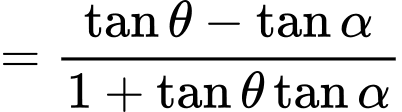
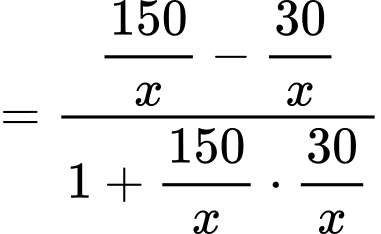
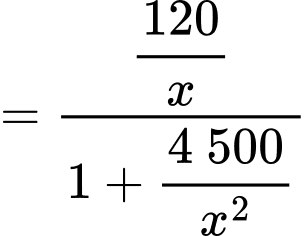
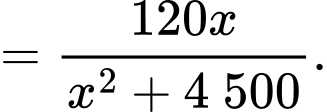
Xét hàm số
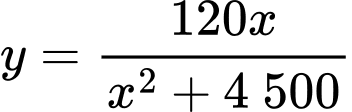 với
với 
Cách 1: Ta có:
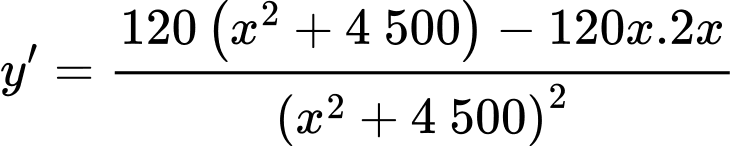
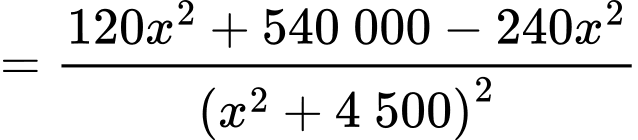
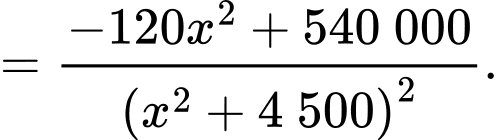
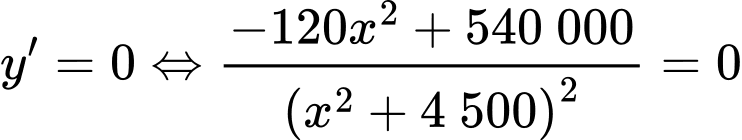
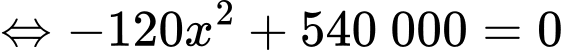
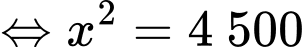
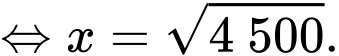
Bảng biến thiên:

Dựa vào bảng biến thiên ta có: Máy ảnh nên đặt cách bức tranh
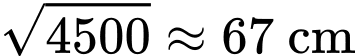 để góc tạo bởi ống kính máy ảnh
để góc tạo bởi ống kính máy ảnh 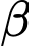 trong hình vẽ là lớn nhất.
trong hình vẽ là lớn nhất.Cách 2: Áp dụng định lý Cô-si cho 2 số không âm
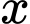 và
và 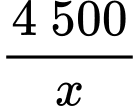 ta có:
ta có: 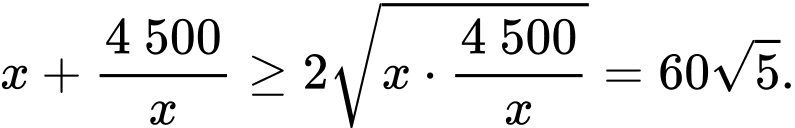
Khi đó:
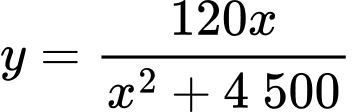
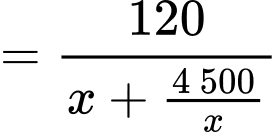
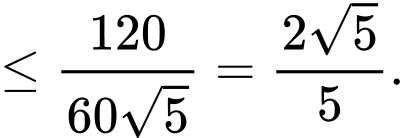
Dấu bằng xảy ra khi:
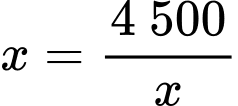 hay
hay 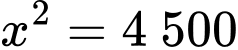
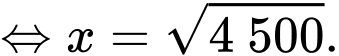
Vậy máy ảnh nên đặt cách bức tranh
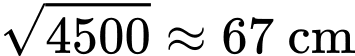 để góc tạo bởi ống kính máy ảnh
để góc tạo bởi ống kính máy ảnh 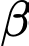 trong hình vẽ là lớn nhất.
trong hình vẽ là lớn nhất.