PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1 [358978]: Cho vectơ 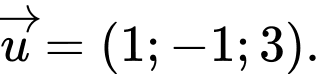 Toạ độ của vectơ
Toạ độ của vectơ 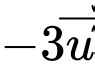 là:
là:
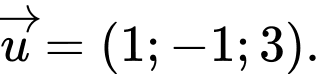 Toạ độ của vectơ
Toạ độ của vectơ 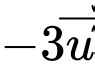 là:
là: A, 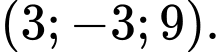
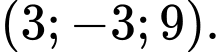
B, 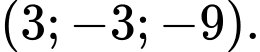
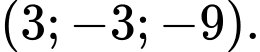
C, 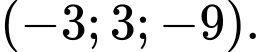
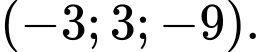
D, 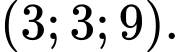
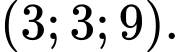
Toạ độ của vectơ 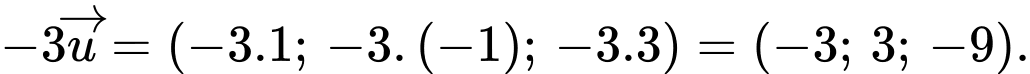 Chọn C. Đáp án: C
Chọn C. Đáp án: C
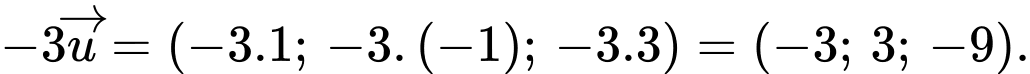 Chọn C. Đáp án: C
Chọn C. Đáp án: C
Câu 2 [543551]: Trong không gian 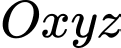 , cho
, cho 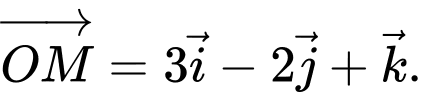 Điểm
Điểm 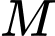 có tọa độ là
có tọa độ là
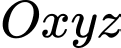 , cho
, cho 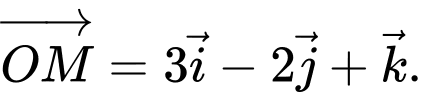 Điểm
Điểm 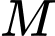 có tọa độ là
có tọa độ là A, 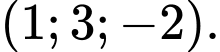
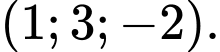
B, 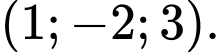
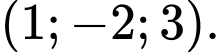
C, 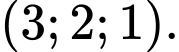
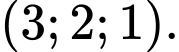
D, 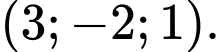
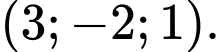
Chọn đáp án D.
Dựa vào phần lý thuyết trong sách Cấp tốc tốt nghiệp môn Toán học (trang 87) ta dễ dàng suy ra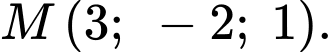 Đáp án: D
Đáp án: D
Dựa vào phần lý thuyết trong sách Cấp tốc tốt nghiệp môn Toán học (trang 87) ta dễ dàng suy ra
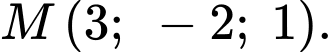 Đáp án: D
Đáp án: D
Câu 3 [543558]: Trong không gian 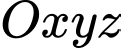 , cho hai điểm
, cho hai điểm 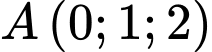 và
và 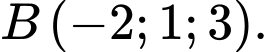 Tọa độ của vectơ
Tọa độ của vectơ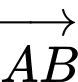 là
là
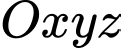 , cho hai điểm
, cho hai điểm 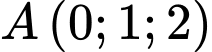 và
và 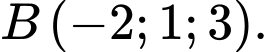 Tọa độ của vectơ
Tọa độ của vectơ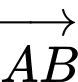 là
là A, 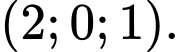
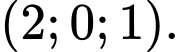
B, 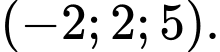
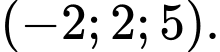
C, 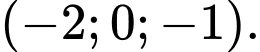
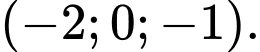
D, 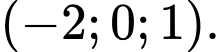
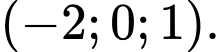
Chọn D
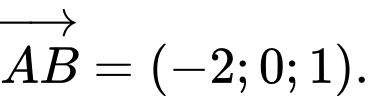 Đáp án: D
Đáp án: D
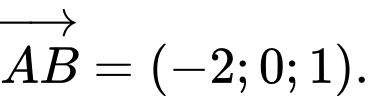 Đáp án: D
Đáp án: D
Câu 4 [543651]: Trong không gian 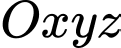 cho điểm
cho điểm 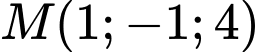 , xác định tọa độ vecto
, xác định tọa độ vecto 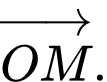
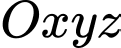 cho điểm
cho điểm 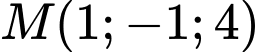 , xác định tọa độ vecto
, xác định tọa độ vecto 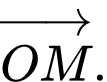
A, 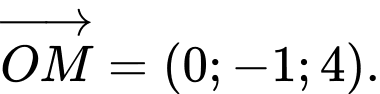
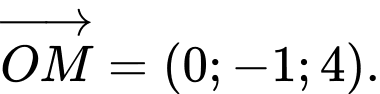
B, 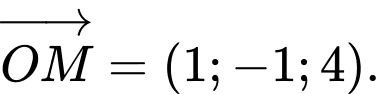
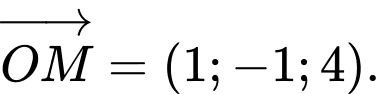
C, 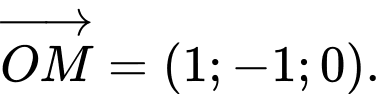
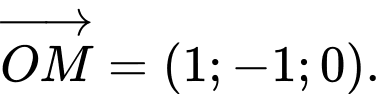
D, 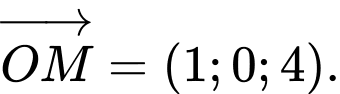
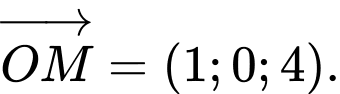
Ta có 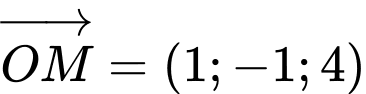 . Đáp án: B
. Đáp án: B
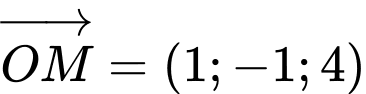 . Đáp án: B
. Đáp án: B
Câu 5 [543205]: Trong không gian với hệ tọa độ Oxyz, cho hai điểm 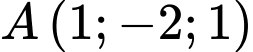 và
và 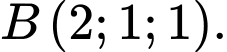 Đoạn
Đoạn  có
độ dài bằng
có
độ dài bằng
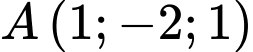 và
và 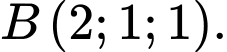 Đoạn
Đoạn  có
độ dài bằng
có
độ dài bằng A, 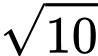 .
.
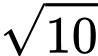 .
. B,  .
.
 .
.C, 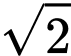 .
.
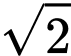 .
. D, 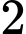 .
.
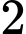 .
.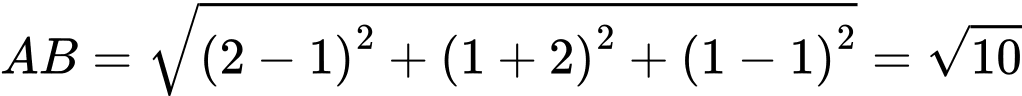 . Đáp án: A
. Đáp án: A
Câu 6 [541554]: Trong không gian 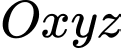 , cho
, cho 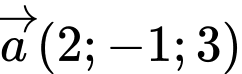 ,
, 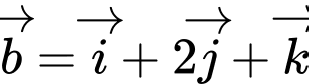 . Toạ độ véctơ
. Toạ độ véctơ 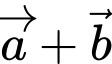 là
là
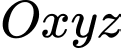 , cho
, cho 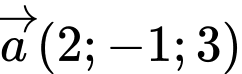 ,
, 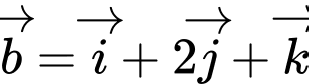 . Toạ độ véctơ
. Toạ độ véctơ 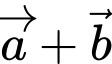 là
là A, 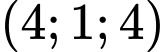 .
.
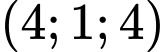 .
.B, 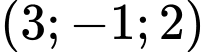 .
.
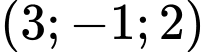 .
.C, 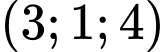 .
.
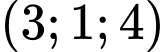 .
.D, 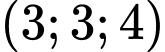 .
.
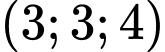 .
.
Ta có 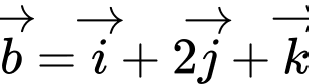 nên
nên 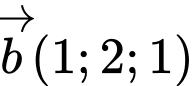 .
.
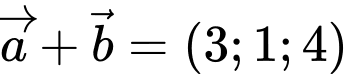 . Đáp án: C
. Đáp án: C
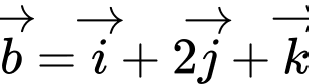 nên
nên 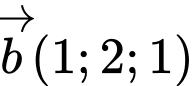 .
.
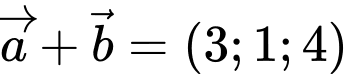 . Đáp án: C
. Đáp án: C
Câu 7 [399918]: Trong không gian 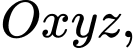 cho điểm
cho điểm 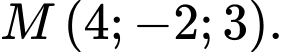 Tọa độ của điểm
Tọa độ của điểm 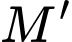 đối xứng với
đối xứng với 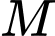 qua mặt phẳng
qua mặt phẳng 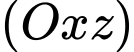 là
là
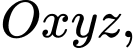 cho điểm
cho điểm 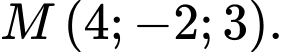 Tọa độ của điểm
Tọa độ của điểm 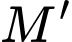 đối xứng với
đối xứng với 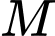 qua mặt phẳng
qua mặt phẳng 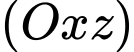 là
là A, 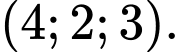
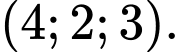
B, 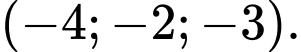
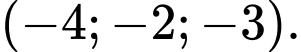
C, 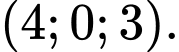
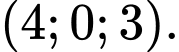
D, 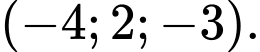
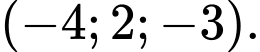
Chọn A
Hình chiếu vuông góc của điểm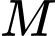 lên mặt phẳng
lên mặt phẳng 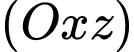 là điểm
là điểm 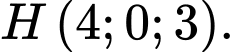
Khi đó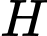 là trung điểm của
là trung điểm của 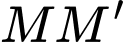 suy ra
suy ra 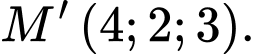 Đáp án: A
Đáp án: A
Hình chiếu vuông góc của điểm
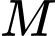 lên mặt phẳng
lên mặt phẳng 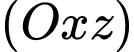 là điểm
là điểm 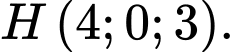
Khi đó
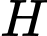 là trung điểm của
là trung điểm của 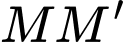 suy ra
suy ra 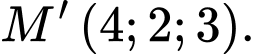 Đáp án: A
Đáp án: A
Câu 8 [755444]: Trong không gian với hệ tọa độ 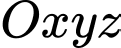 cho
cho 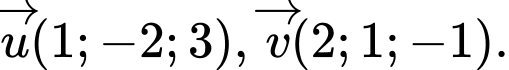 Tích vô hướng của hai véc tơ đã cho bằng:
Tích vô hướng của hai véc tơ đã cho bằng:
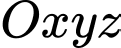 cho
cho 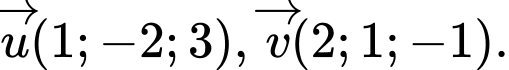 Tích vô hướng của hai véc tơ đã cho bằng:
Tích vô hướng của hai véc tơ đã cho bằng: A, 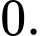
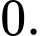
B, 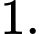
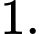
C, 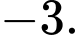
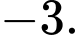
D, 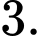
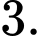
Áp dụng công thức tích vô hướng của 2 véc tơ ta có 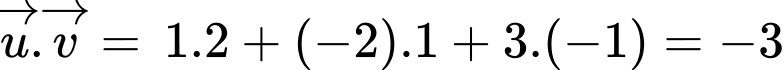 Đáp án: C
Đáp án: C
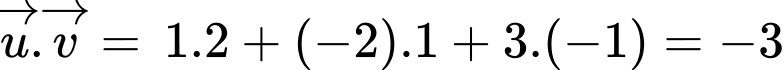 Đáp án: C
Đáp án: C
Câu 9 [755153]: Trong không gian 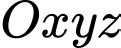 , cho hai điểm
, cho hai điểm 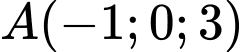 và
và 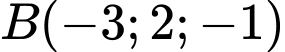 . Toạ độ trung điểm của AB là
. Toạ độ trung điểm của AB là
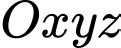 , cho hai điểm
, cho hai điểm 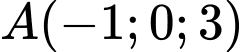 và
và 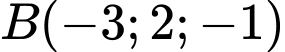 . Toạ độ trung điểm của AB là
. Toạ độ trung điểm của AB là A,
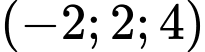 .
.
B,
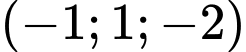 .
.
C,
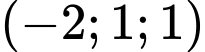 .
.
D,
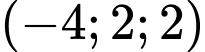 .
.
Chọn C.
Áp dụng công thức toạ độ trung điểm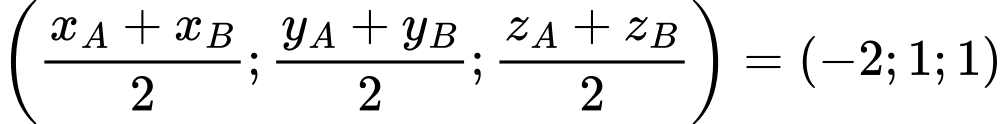 Đáp án: C
Đáp án: C
Áp dụng công thức toạ độ trung điểm
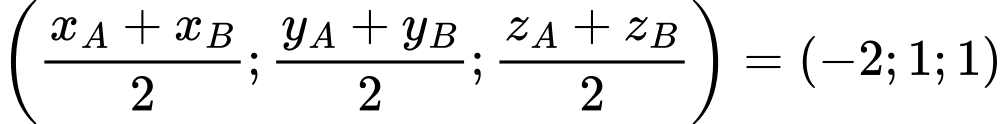 Đáp án: C
Đáp án: C
Câu 10 [541700]: Trong không gian với hệ tọa độ 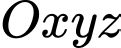 cho hai vectơ
cho hai vectơ 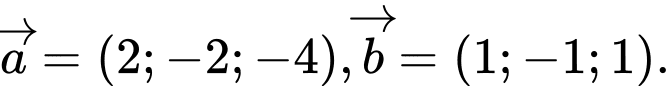 Mệnh đề nào dưới đây là sai?
Mệnh đề nào dưới đây là sai?
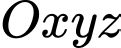 cho hai vectơ
cho hai vectơ 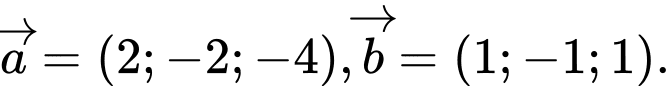 Mệnh đề nào dưới đây là sai?
Mệnh đề nào dưới đây là sai? A, 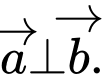
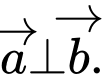
B, 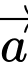 và
và 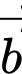 cùng phương.
cùng phương.
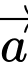 và
và 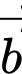 cùng phương.
cùng phương.C, 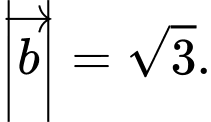
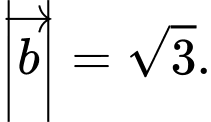
D, 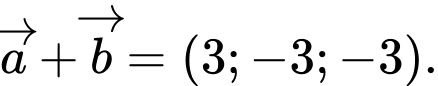
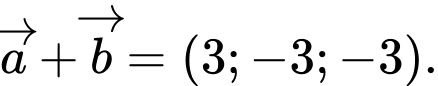
Ta có 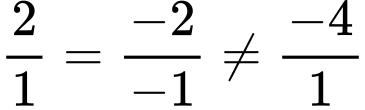 nên
nên 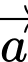 và
và 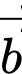 không cùng phương.
không cùng phương.
Vậy mệnh đề B là sai. Đáp án: B
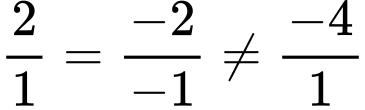 nên
nên 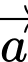 và
và 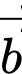 không cùng phương.
không cùng phương.Vậy mệnh đề B là sai. Đáp án: B
Câu 11 [543803]: Trong không gian 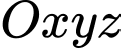 , cho hai véc tơ
, cho hai véc tơ 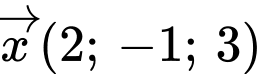 và
và 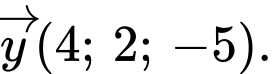 Toạ độ của véc tơ
Toạ độ của véc tơ 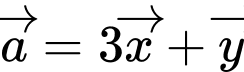 là
là
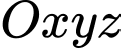 , cho hai véc tơ
, cho hai véc tơ 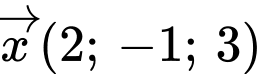 và
và 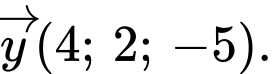 Toạ độ của véc tơ
Toạ độ của véc tơ 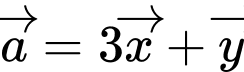 là
là A, 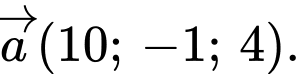
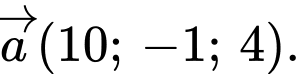
B, 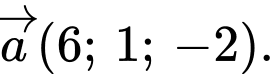
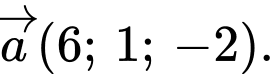
C, 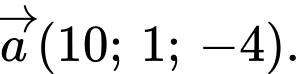
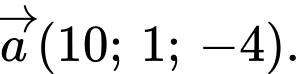
D, 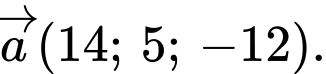
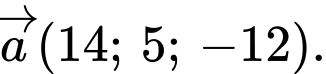
Ta có 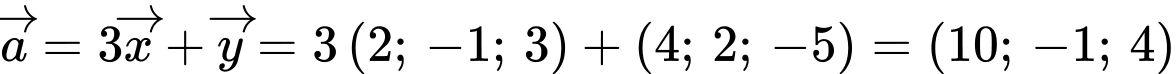 . Đáp án: A
. Đáp án: A
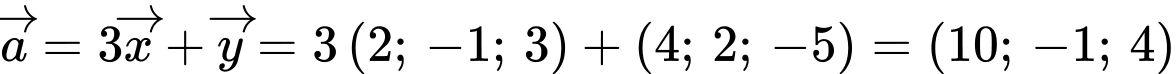 . Đáp án: A
. Đáp án: A
Câu 12 [398653]: Trong không gian 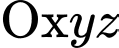 cho
cho 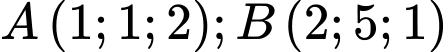 và điểm
và điểm 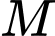 thuộc trục
thuộc trục 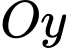 sao cho tam giác
sao cho tam giác 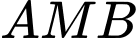 vuông tại
vuông tại 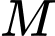 . Tính diện tích của tam giác
. Tính diện tích của tam giác 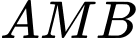
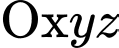 cho
cho 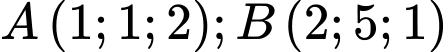 và điểm
và điểm 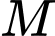 thuộc trục
thuộc trục 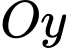 sao cho tam giác
sao cho tam giác 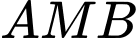 vuông tại
vuông tại 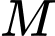 . Tính diện tích của tam giác
. Tính diện tích của tam giác 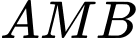
A, 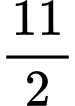 .
.
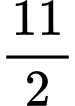 .
.B, 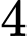 .
.
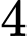 .
.C, 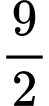 .
.
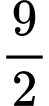 .
.D, 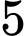 .
.
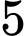 .
.
Do 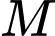 thuộc
thuộc 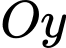 , gọi
, gọi 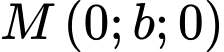 .Khi đó Ta có
.Khi đó Ta có 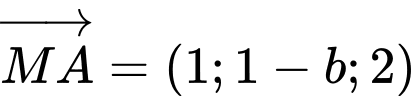 và
và 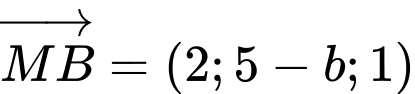 .
Tam giác
.
Tam giác 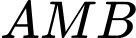 vuông nên
vuông nên 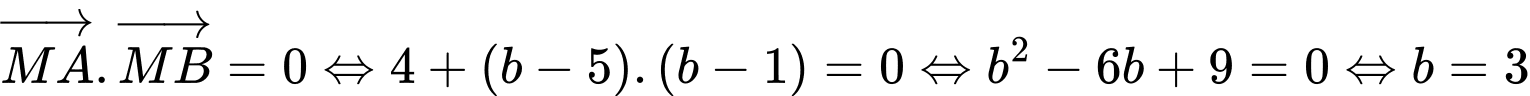
 . Diện tích tam giác
. Diện tích tam giác 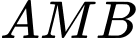 =
=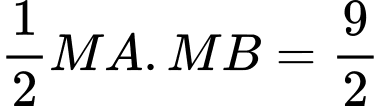 . Đáp án: C
. Đáp án: C
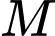 thuộc
thuộc 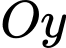 , gọi
, gọi 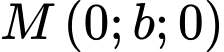 .Khi đó Ta có
.Khi đó Ta có 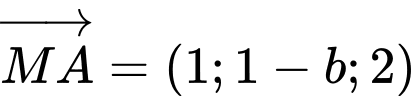 và
và 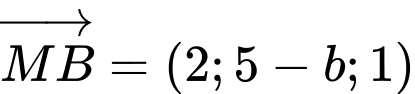 .
Tam giác
.
Tam giác 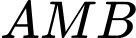 vuông nên
vuông nên 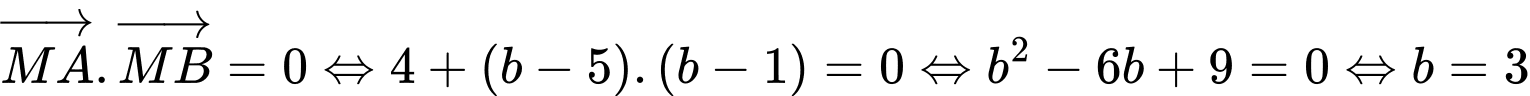
 . Diện tích tam giác
. Diện tích tam giác 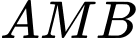 =
=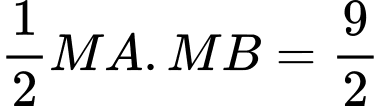 . Đáp án: C
. Đáp án: C PHẦN II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a),b),c),d) ở mỗi câu học sinh chọn đúng hoặc sai.
Câu 13 [716842]: Trong không gian tọa độ 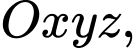 cho ba điểm
cho ba điểm 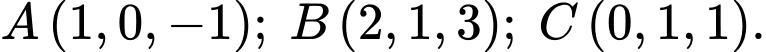
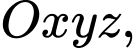 cho ba điểm
cho ba điểm 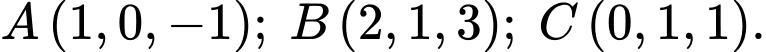
a) Đúng.
Ta có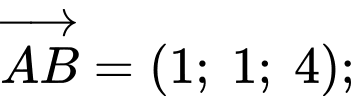
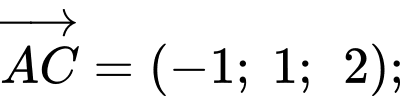
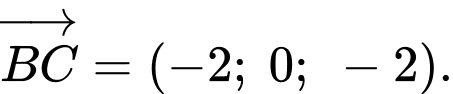
Suy ra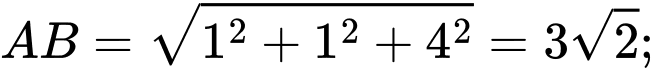
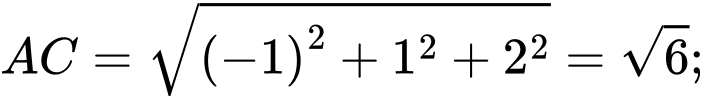
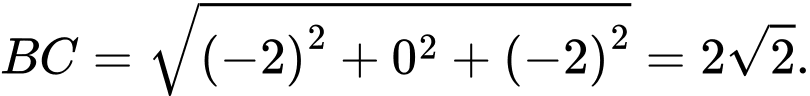
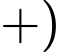 Chu vi của
Chu vi của 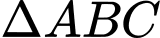 là
là 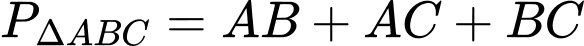
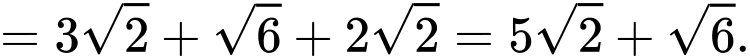
b) Đúng.
Gọi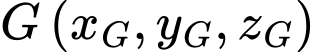 là tọa độ trọng tâm của
là tọa độ trọng tâm của 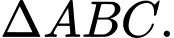
Ta có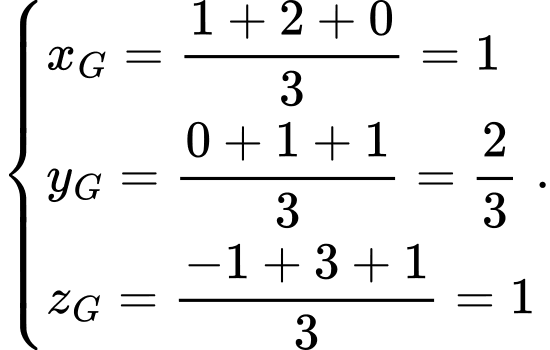 Vậy
Vậy 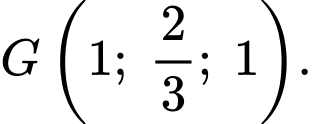
c) Sai.
Ta có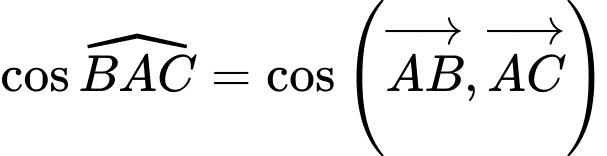
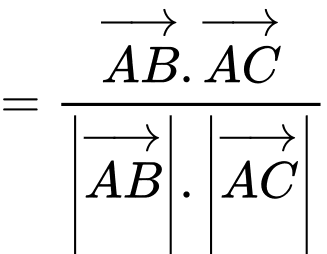
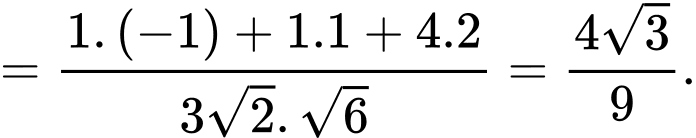
d) Đúng.
Ta có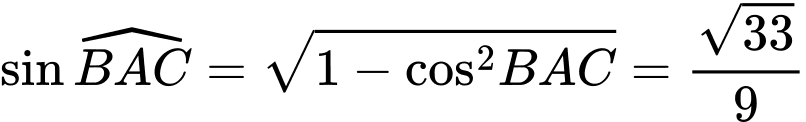
Suy ra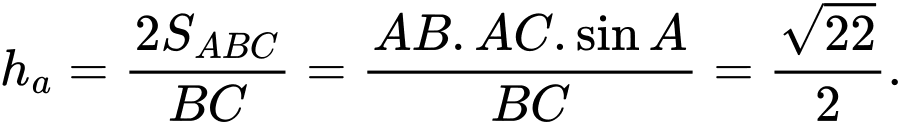
Ta có
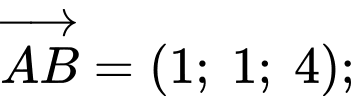
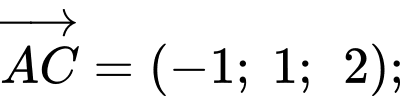
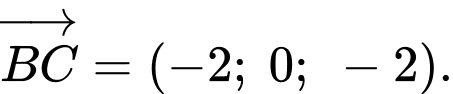
Suy ra
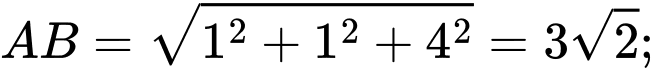
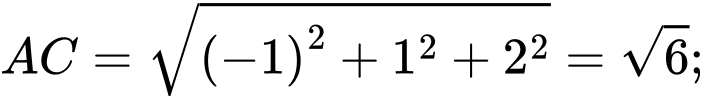
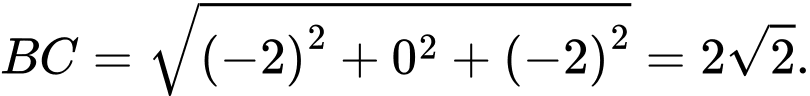
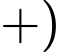 Chu vi của
Chu vi của 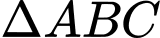 là
là 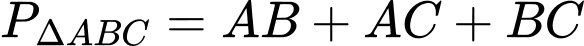
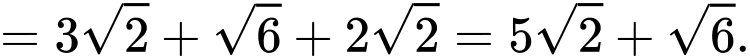
b) Đúng.
Gọi
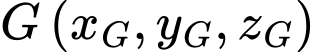 là tọa độ trọng tâm của
là tọa độ trọng tâm của 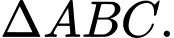
Ta có
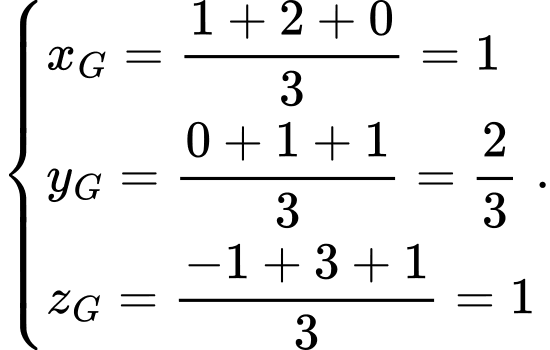 Vậy
Vậy 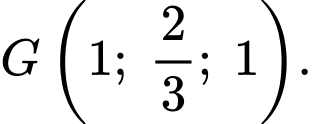
c) Sai.
Ta có
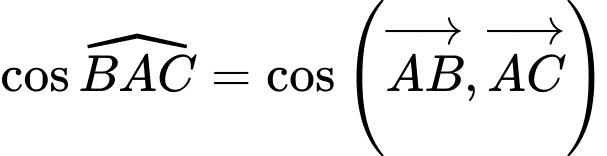
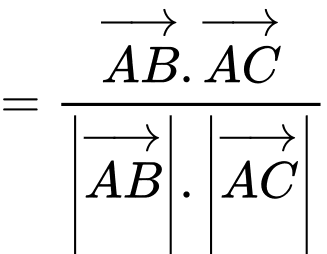
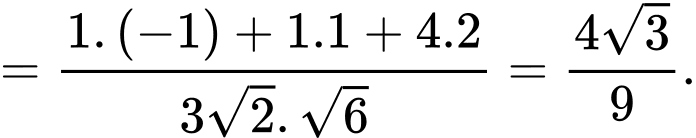
d) Đúng.
Ta có
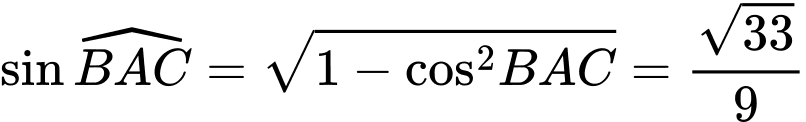
Suy ra
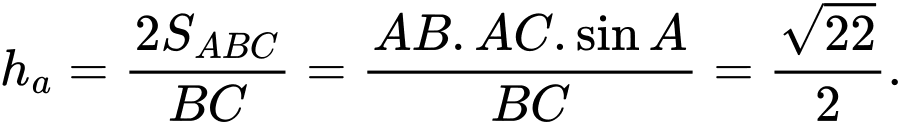
Câu 14 [775016]: Trong hệ toạ độ 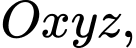 cho các điểm
cho các điểm 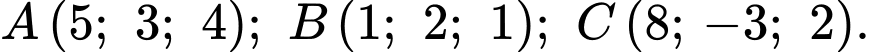 Gọi
Gọi 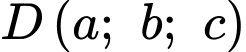 là chân đường phân giác trong kẻ từ đỉnh
là chân đường phân giác trong kẻ từ đỉnh 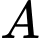 của tam giác
của tam giác 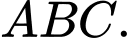
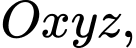 cho các điểm
cho các điểm 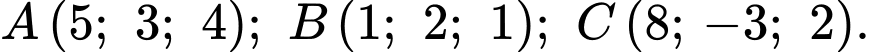 Gọi
Gọi 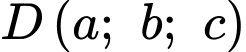 là chân đường phân giác trong kẻ từ đỉnh
là chân đường phân giác trong kẻ từ đỉnh 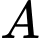 của tam giác
của tam giác 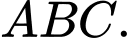
a) Đúng.
Áp dụng công thức tính toạ độ trọng tâm tam giác, ta suy ra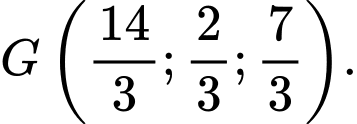
b) Sai.
Ta có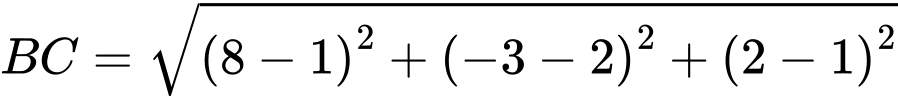
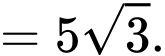
c) Đúng.
Ta có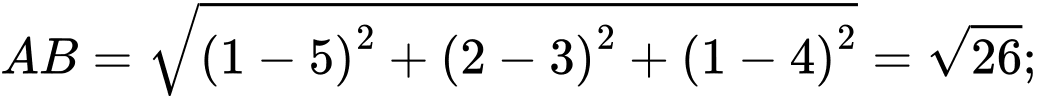
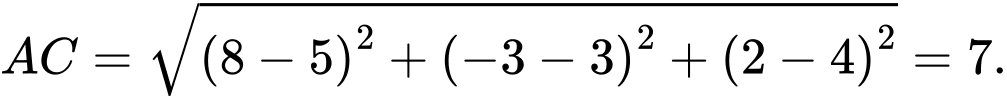
Nhận thấy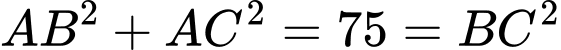 nên tam giác
nên tam giác 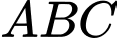 là tam giác vuông tại
là tam giác vuông tại 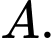
d) Đúng.
Theo tính chất của đường phân giác trong tam giác vuông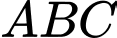 với
với 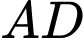 là đường phân giác của góc vuông nên suy ra
là đường phân giác của góc vuông nên suy ra 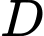 là trung điểm của cạnh
là trung điểm của cạnh 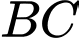 suy ra
suy ra 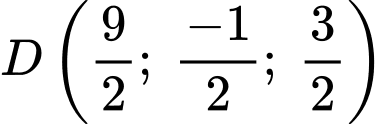
Suy ra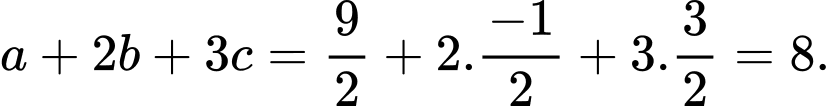 Vậy giá trị
Vậy giá trị 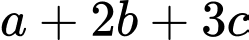 là một số nguyên.
là một số nguyên.
Áp dụng công thức tính toạ độ trọng tâm tam giác, ta suy ra
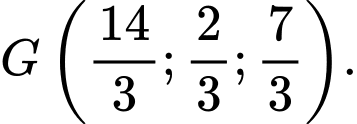
b) Sai.
Ta có
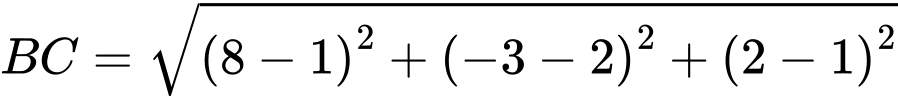
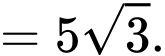
c) Đúng.
Ta có
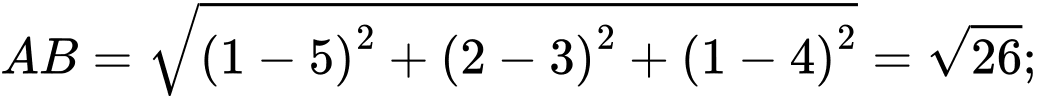
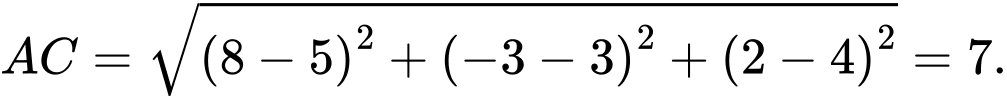
Nhận thấy
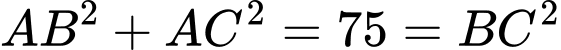 nên tam giác
nên tam giác 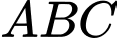 là tam giác vuông tại
là tam giác vuông tại 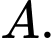
d) Đúng.
Theo tính chất của đường phân giác trong tam giác vuông
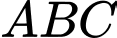 với
với 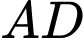 là đường phân giác của góc vuông nên suy ra
là đường phân giác của góc vuông nên suy ra 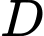 là trung điểm của cạnh
là trung điểm của cạnh 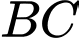 suy ra
suy ra 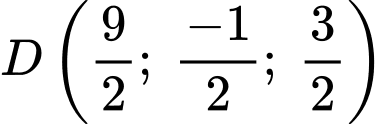
Suy ra
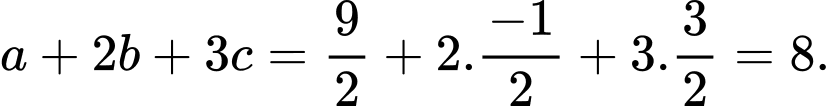 Vậy giá trị
Vậy giá trị 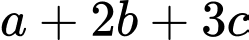 là một số nguyên.
là một số nguyên.
Câu 15 [775017]: Một chiếc máy được đặt trên một giá đỡ ba chân với điểm đặt 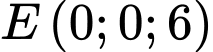 và các điếm tiếp xúc với mặt đất của ba chân lần lượt là
và các điếm tiếp xúc với mặt đất của ba chân lần lượt là 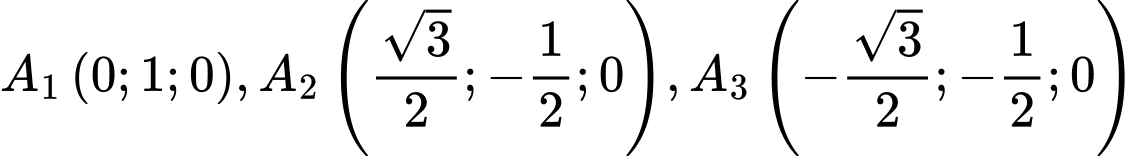 (xem hình vẽ).
(xem hình vẽ).
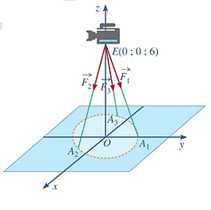 Biết rằng trọng lượng của chiếc máy là
Biết rằng trọng lượng của chiếc máy là 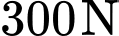 và ba lực tác dụng lên giá đỡ được phân bố như hình vẽ là ba lực
và ba lực tác dụng lên giá đỡ được phân bố như hình vẽ là ba lực 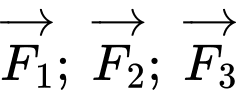 có độ lớn đo bằng đơn vị N. Khi đó
có độ lớn đo bằng đơn vị N. Khi đó
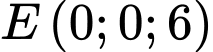 và các điếm tiếp xúc với mặt đất của ba chân lần lượt là
và các điếm tiếp xúc với mặt đất của ba chân lần lượt là 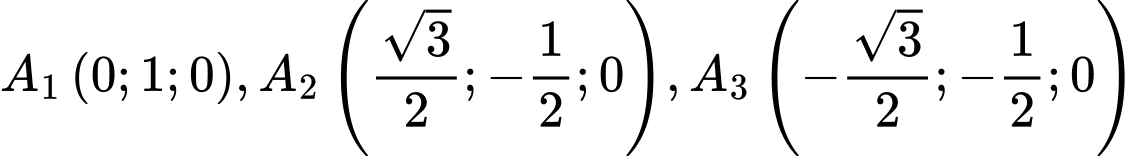 (xem hình vẽ).
(xem hình vẽ).
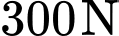 và ba lực tác dụng lên giá đỡ được phân bố như hình vẽ là ba lực
và ba lực tác dụng lên giá đỡ được phân bố như hình vẽ là ba lực 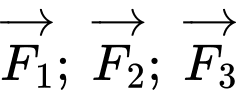 có độ lớn đo bằng đơn vị N. Khi đó
có độ lớn đo bằng đơn vị N. Khi đó
Theo giả thiết, ta có các điểm 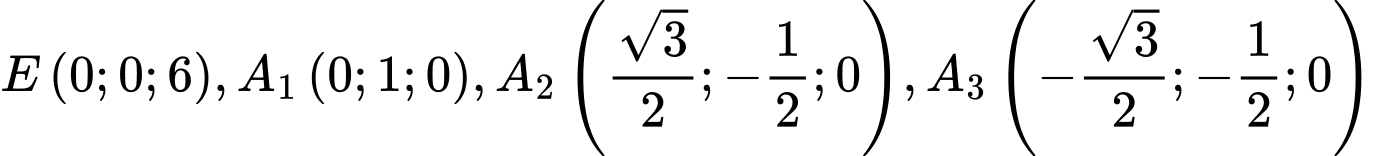 .
.
a) Đúng.
Suy ra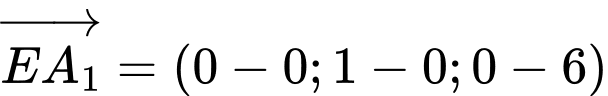 hay
hay 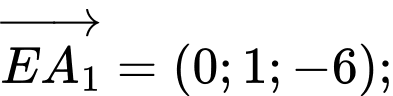
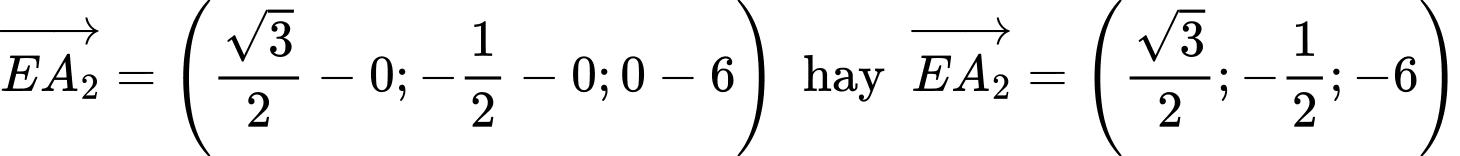
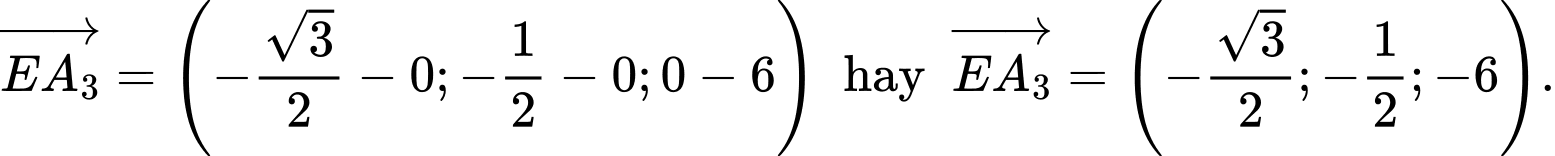
b) Sai.
Vì chiếc máy đứng yên nên tổng của các lực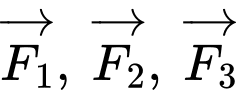 sẽ bằng với trọng lượng của chiếc máy nên suy ra
sẽ bằng với trọng lượng của chiếc máy nên suy ra 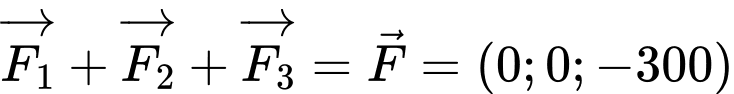
c) Đúng.
Tồn tại hằng số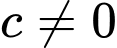 sao cho:
sao cho:
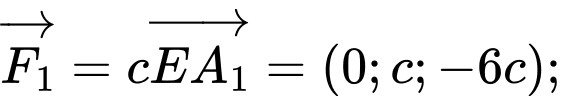
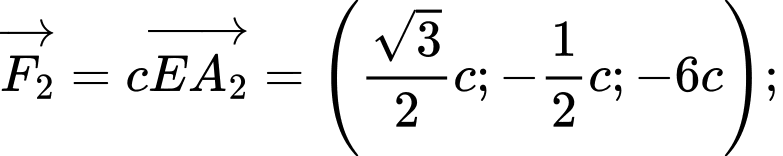
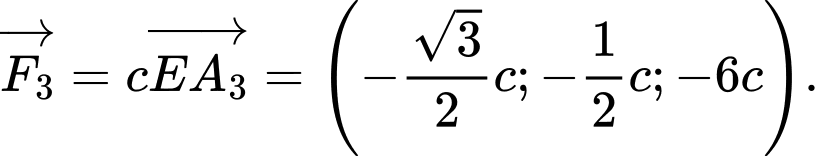
Suy ra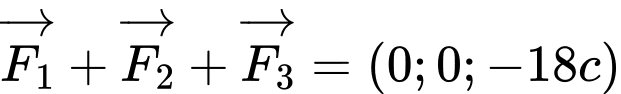 .
.
Mặt khác, ta có: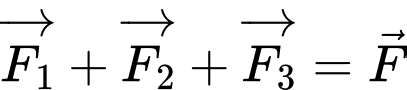 , trong đó
, trong đó 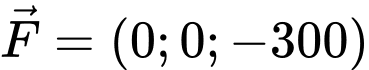 là trọng lực tác dụng lên máy quay. Suy ra
là trọng lực tác dụng lên máy quay. Suy ra 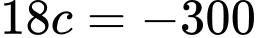
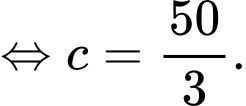
Suy ra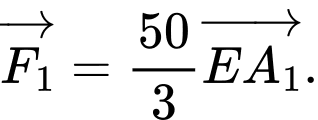
d) Đúng.
Từ phần c), ta suy ra được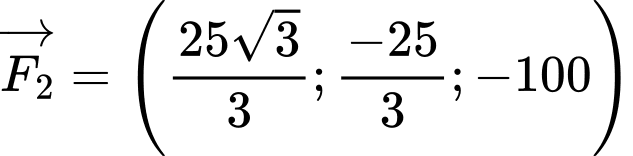
Suy ra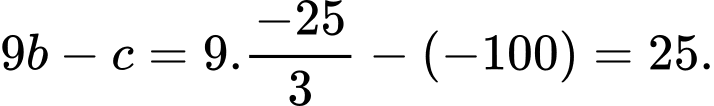
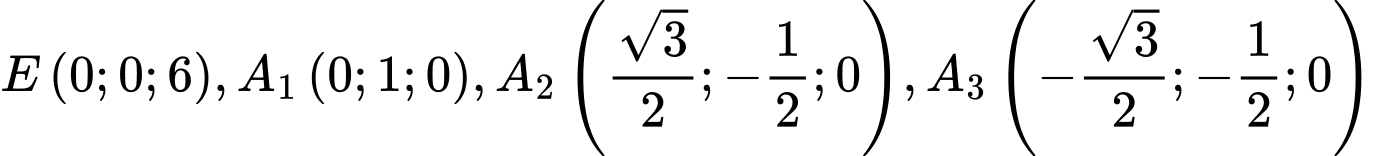 .
.
a) Đúng.
Suy ra
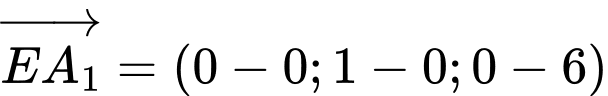 hay
hay 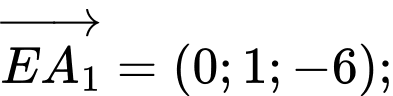
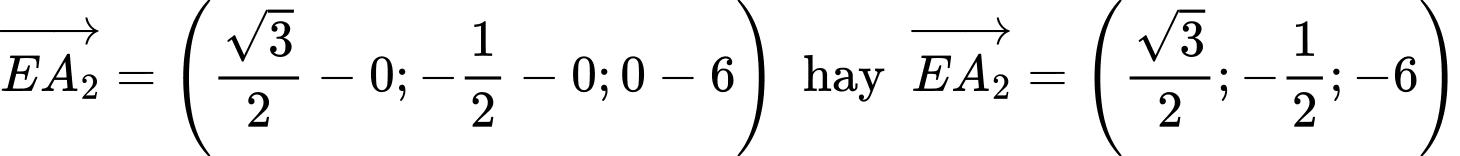
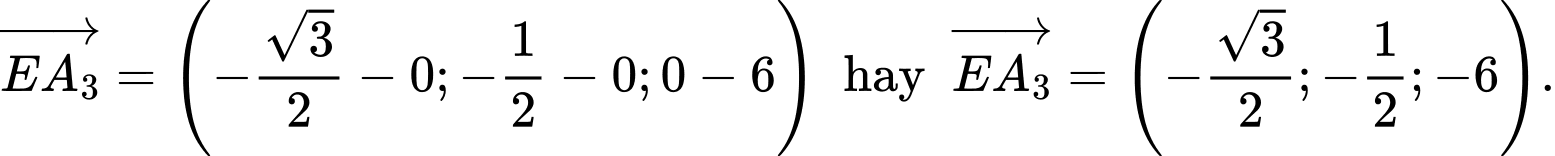
b) Sai.
Vì chiếc máy đứng yên nên tổng của các lực
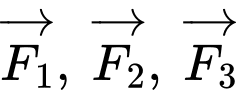 sẽ bằng với trọng lượng của chiếc máy nên suy ra
sẽ bằng với trọng lượng của chiếc máy nên suy ra 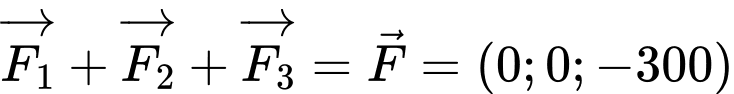
c) Đúng.
Tồn tại hằng số
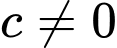 sao cho:
sao cho:
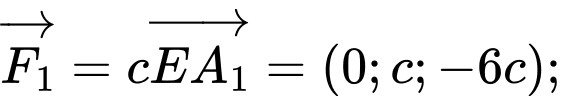
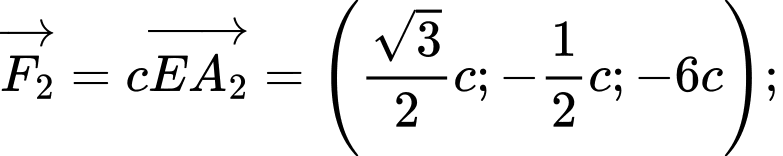
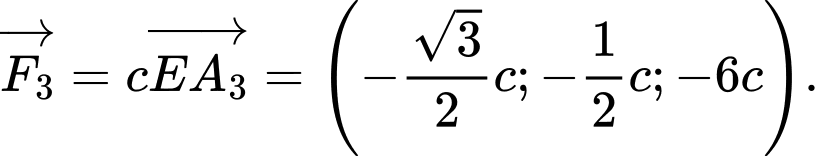
Suy ra
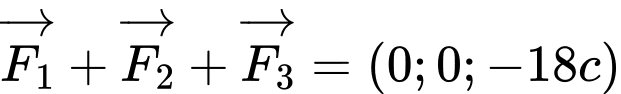 .
.
Mặt khác, ta có:
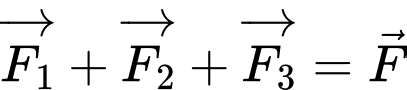 , trong đó
, trong đó 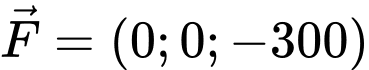 là trọng lực tác dụng lên máy quay. Suy ra
là trọng lực tác dụng lên máy quay. Suy ra 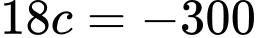
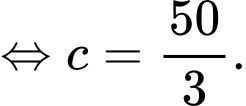
Suy ra
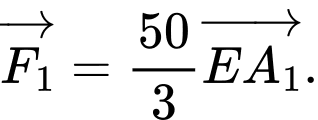
d) Đúng.
Từ phần c), ta suy ra được
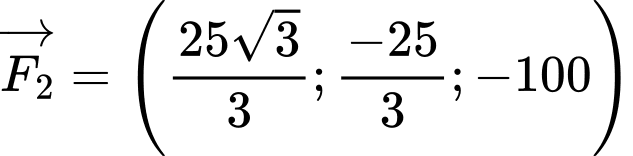
Suy ra
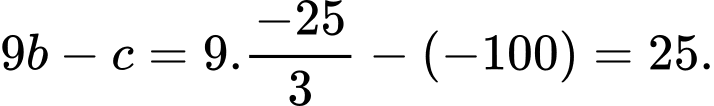
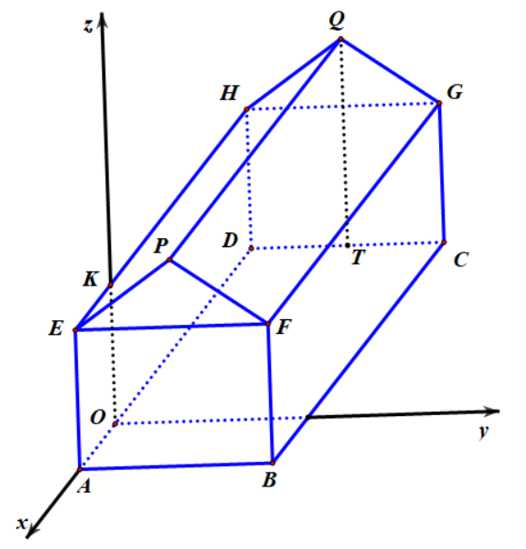
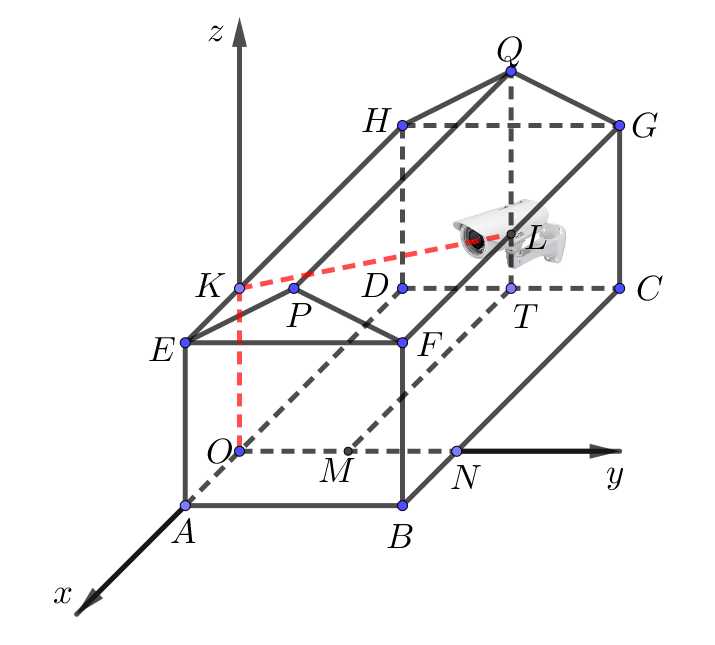
Câu 16 [775019]: Một kho chứa hàng có dạng hình lăng trụ đứng 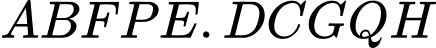 với
với 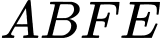 là hình chữ nhật và
là hình chữ nhật và 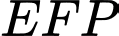 là tam giác cân tại
là tam giác cân tại 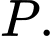 Gọi
Gọi 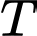 là trung điểm của
là trung điểm của 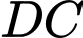 . Các kích thước của kho chứa lần lượt là
. Các kích thước của kho chứa lần lượt là 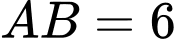 m;
m;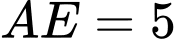 m;
m; 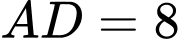 m;
m; 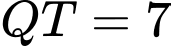 m. Người ta mô hình hoá nhà kho bằng cách chọn hệ trục toạ độ có gốc toạ độ là điểm
m. Người ta mô hình hoá nhà kho bằng cách chọn hệ trục toạ độ có gốc toạ độ là điểm  thuộc đoạn
thuộc đoạn 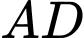 sao cho
sao cho  m và các trục toạ độ tương ứng như hình vẽ dưới đây. Khi đó:
m và các trục toạ độ tương ứng như hình vẽ dưới đây. Khi đó:
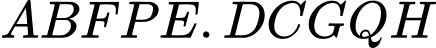 với
với 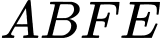 là hình chữ nhật và
là hình chữ nhật và 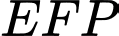 là tam giác cân tại
là tam giác cân tại 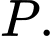 Gọi
Gọi 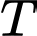 là trung điểm của
là trung điểm của 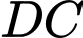 . Các kích thước của kho chứa lần lượt là
. Các kích thước của kho chứa lần lượt là 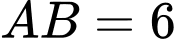 m;
m;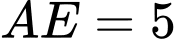 m;
m; 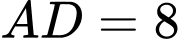 m;
m; 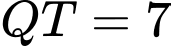 m. Người ta mô hình hoá nhà kho bằng cách chọn hệ trục toạ độ có gốc toạ độ là điểm
m. Người ta mô hình hoá nhà kho bằng cách chọn hệ trục toạ độ có gốc toạ độ là điểm  thuộc đoạn
thuộc đoạn 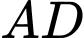 sao cho
sao cho  m và các trục toạ độ tương ứng như hình vẽ dưới đây. Khi đó:
m và các trục toạ độ tương ứng như hình vẽ dưới đây. Khi đó:
a) Sai.
Kẻ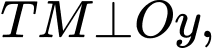
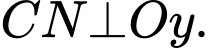
Vì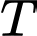 là hình chiếu của
là hình chiếu của  lên mặt phẳng
lên mặt phẳng 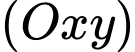 nên
nên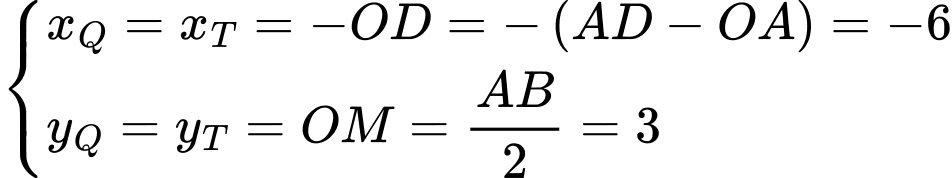
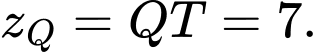
Suy ra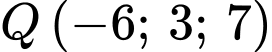 .
.
b) Đúng.
Vì nên
nên 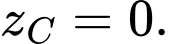
Ta có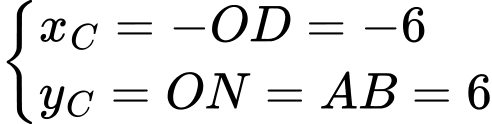 .
.
Suy ra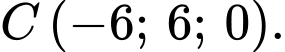
Vậy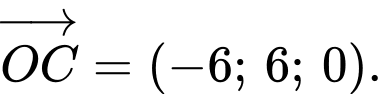
c) Đúng.
Gọi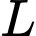 là trung điểm của
là trung điểm của 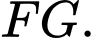
Ta có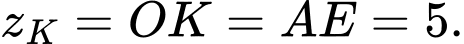
Suy ra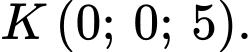
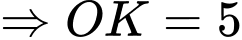
Lại có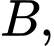
 lần lượt là hình chiếu của
lần lượt là hình chiếu của 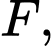
 lên mặt phẳng
lên mặt phẳng 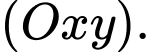
Suy ra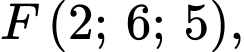
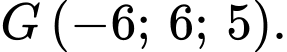 Mà
Mà 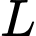 là trung điểm của
là trung điểm của 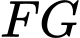 nên
nên 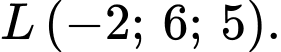
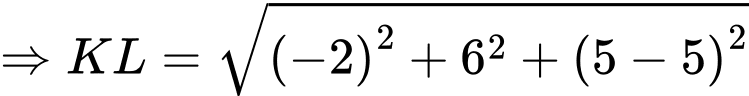
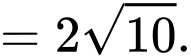
Vậy độ dài đoạn cáp tối thiểu từ đến
đến 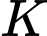 sau đó nối thẳng đến camera là
sau đó nối thẳng đến camera là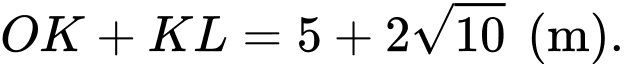
d) Sai.
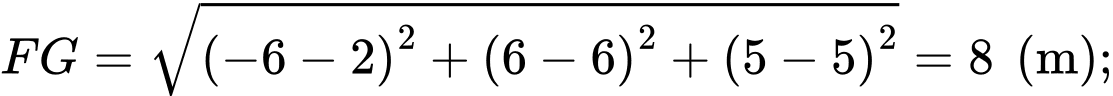
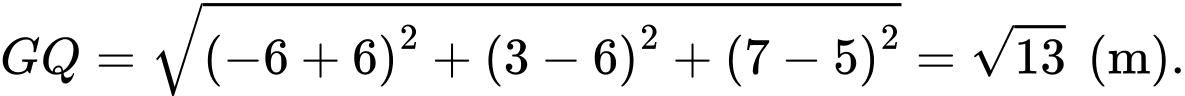
Suy ra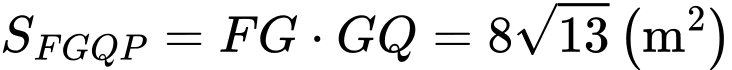
Diện tích lợp tôn mái nhà là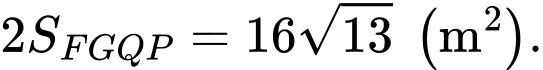
Vậy số tiền cần bỏ ra để mua tôn lợp mái nhà là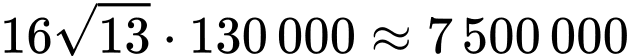 (đồng).
(đồng).

Kẻ
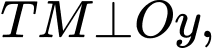
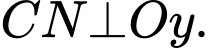
Vì
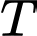 là hình chiếu của
là hình chiếu của  lên mặt phẳng
lên mặt phẳng 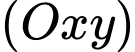 nên
nên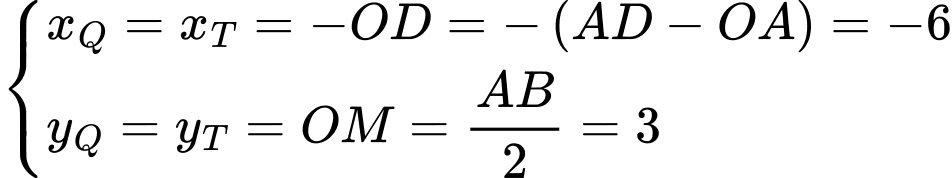
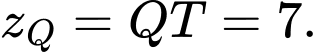
Suy ra
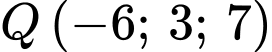 .
.b) Đúng.
Vì
 nên
nên 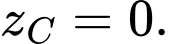
Ta có
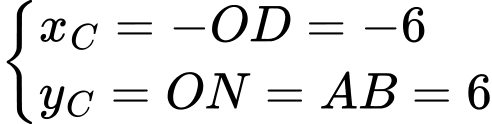 .
.Suy ra
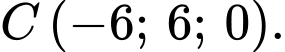
Vậy
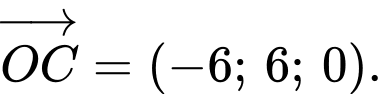
c) Đúng.
Gọi
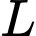 là trung điểm của
là trung điểm của 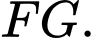
Ta có
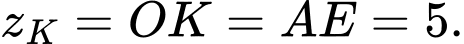
Suy ra
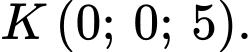
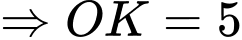
Lại có
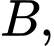
 lần lượt là hình chiếu của
lần lượt là hình chiếu của 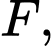
 lên mặt phẳng
lên mặt phẳng 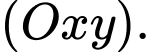
Suy ra
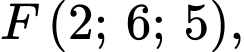
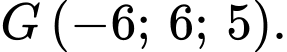 Mà
Mà 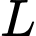 là trung điểm của
là trung điểm của 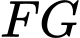 nên
nên 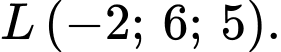
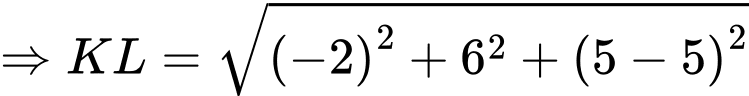
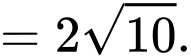
Vậy độ dài đoạn cáp tối thiểu từ
 đến
đến 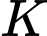 sau đó nối thẳng đến camera là
sau đó nối thẳng đến camera là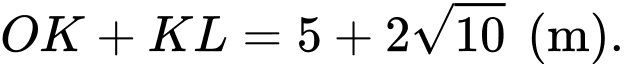
d) Sai.
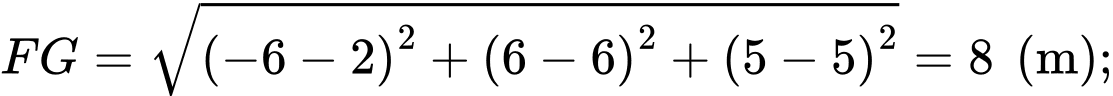
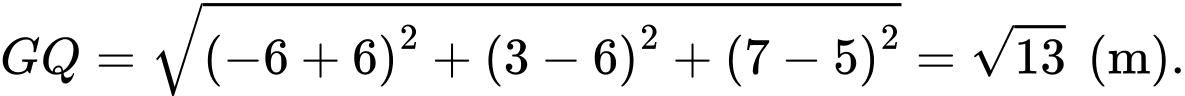
Suy ra
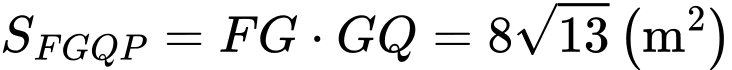
Diện tích lợp tôn mái nhà là
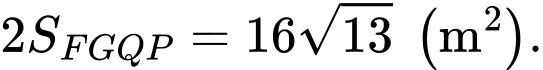
Vậy số tiền cần bỏ ra để mua tôn lợp mái nhà là
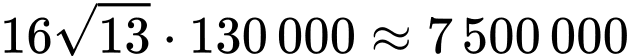 (đồng).
(đồng). PHẦN III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 17 đến câu 22.
Câu 17 [708369]: Trong không gian với một hệ trục tọa độ cho trước (đơn vị đo lấy theo kilômét), ra đa phát hiện một chiếc máy bay di chuyển với vận tốc và hướng không đổi từ điểm 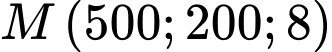 đến điểm
đến điểm 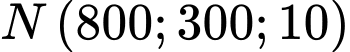 trong 20 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì sau 5 phút tiếp theo máy bay ở vị trí có tọa độ là
trong 20 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì sau 5 phút tiếp theo máy bay ở vị trí có tọa độ là 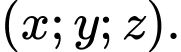 Tính tổng
Tính tổng 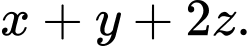

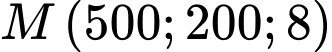 đến điểm
đến điểm 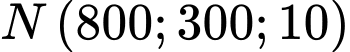 trong 20 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì sau 5 phút tiếp theo máy bay ở vị trí có tọa độ là
trong 20 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì sau 5 phút tiếp theo máy bay ở vị trí có tọa độ là 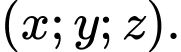 Tính tổng
Tính tổng 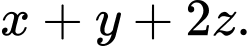

Điền đáp án: 1221
Gọi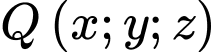 là vị trí của máy bay sau 5 phút tiếp theo.
là vị trí của máy bay sau 5 phút tiếp theo.

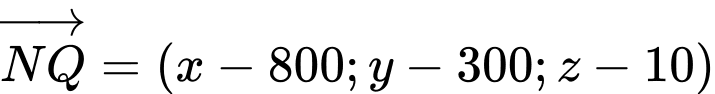
Vì máy bay giữ nguyên hướng bay nên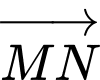 và
và 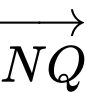 cùng hướng.
cùng hướng.
Do máy bay tiếp tục giữ nguyên vận tốc và thời gian bay từ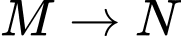 gấp 4 lần thời gian bay từ
gấp 4 lần thời gian bay từ  nên
nên 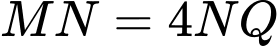
Suy ra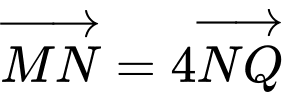
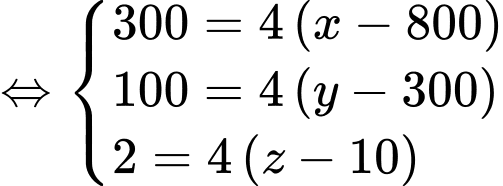
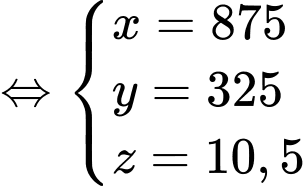
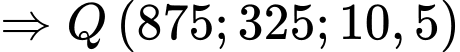
Vậy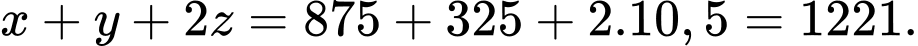
Gọi
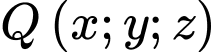 là vị trí của máy bay sau 5 phút tiếp theo.
là vị trí của máy bay sau 5 phút tiếp theo.
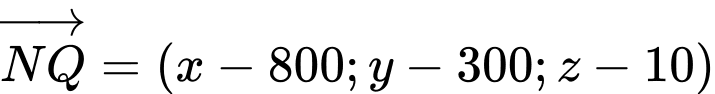
Vì máy bay giữ nguyên hướng bay nên
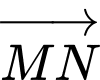 và
và 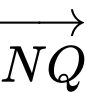 cùng hướng.
cùng hướng.Do máy bay tiếp tục giữ nguyên vận tốc và thời gian bay từ
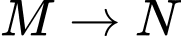 gấp 4 lần thời gian bay từ
gấp 4 lần thời gian bay từ  nên
nên 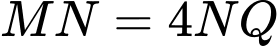
Suy ra
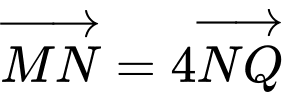
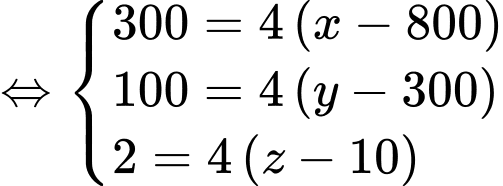
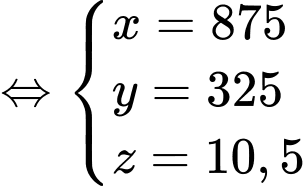
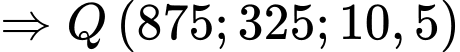
Vậy
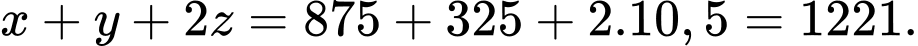
Câu 18 [715977]: Trong không gian 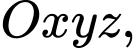 cho hai điểm
cho hai điểm 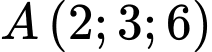 và
và 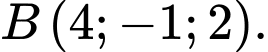 Điểm
Điểm 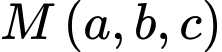 thuộc mặt phẳng
thuộc mặt phẳng 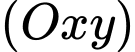 sao cho
sao cho  đạt giá trị nhỏ nhất. Khi đó giá trị của
đạt giá trị nhỏ nhất. Khi đó giá trị của 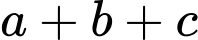 bằng bao nhiêu?
bằng bao nhiêu?
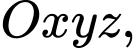 cho hai điểm
cho hai điểm 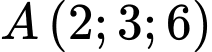 và
và 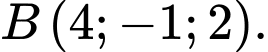 Điểm
Điểm 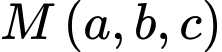 thuộc mặt phẳng
thuộc mặt phẳng 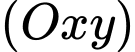 sao cho
sao cho  đạt giá trị nhỏ nhất. Khi đó giá trị của
đạt giá trị nhỏ nhất. Khi đó giá trị của 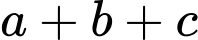 bằng bao nhiêu?
bằng bao nhiêu?
Điền đáp án: 4.
Gọi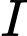 là trung điểm
là trung điểm 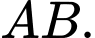 Suy ra
Suy ra 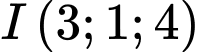 và
và 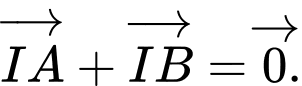
Có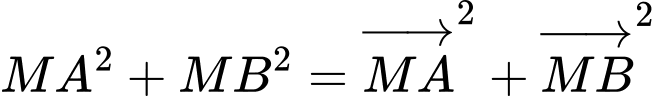
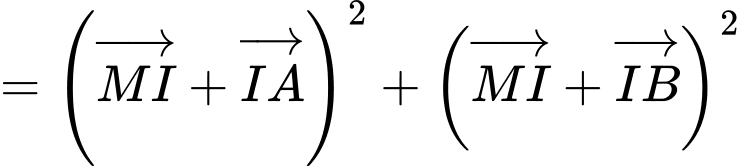
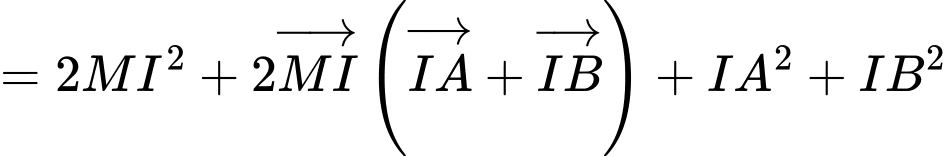
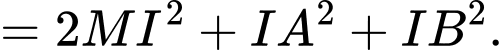
 đạt giá trị nhỏ nhất khi
đạt giá trị nhỏ nhất khi 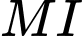 đạt giá trị nhỏ nhất. Khi đó,
đạt giá trị nhỏ nhất. Khi đó, 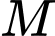 là hình chiếu vuông góc của
là hình chiếu vuông góc của 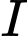 lên mặt phẳng
lên mặt phẳng 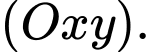 Nên
Nên 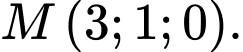
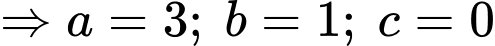
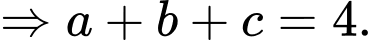
Gọi
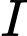 là trung điểm
là trung điểm 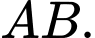 Suy ra
Suy ra 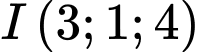 và
và 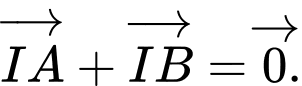
Có
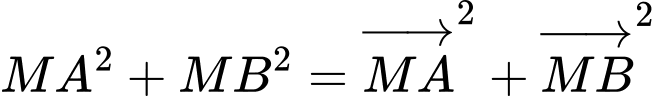
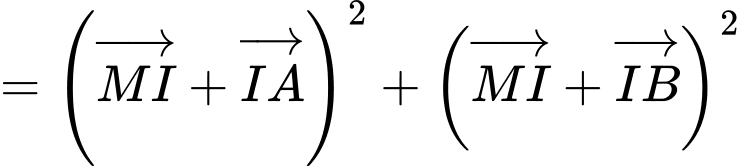
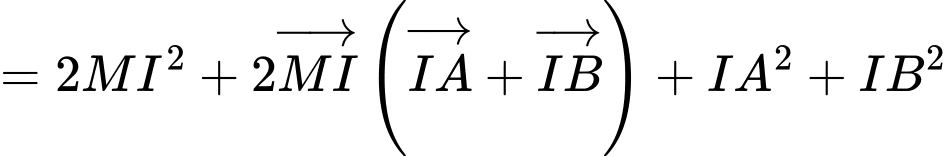
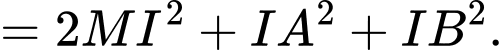
 đạt giá trị nhỏ nhất khi
đạt giá trị nhỏ nhất khi 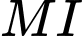 đạt giá trị nhỏ nhất. Khi đó,
đạt giá trị nhỏ nhất. Khi đó, 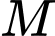 là hình chiếu vuông góc của
là hình chiếu vuông góc của 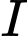 lên mặt phẳng
lên mặt phẳng 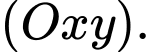 Nên
Nên 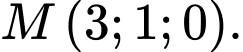
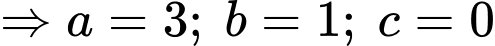
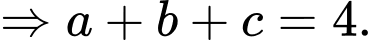
Câu 19 [716847]: Trong không gian 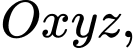 cho
cho 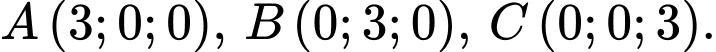 Điểm
Điểm 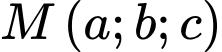 trong không gian thỏa mãn
trong không gian thỏa mãn 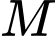 không trùng với các điểm
không trùng với các điểm 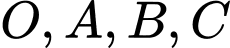 và
và 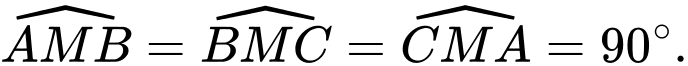 Khi đó tổng
Khi đó tổng 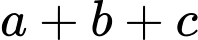 bằng
bằng
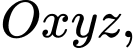 cho
cho 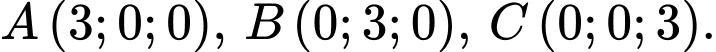 Điểm
Điểm 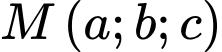 trong không gian thỏa mãn
trong không gian thỏa mãn 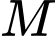 không trùng với các điểm
không trùng với các điểm 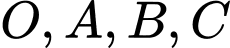 và
và 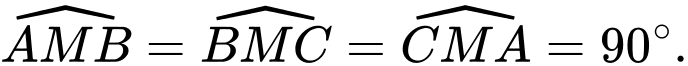 Khi đó tổng
Khi đó tổng 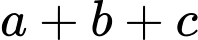 bằng
bằng
Điền đáp án: 6.
Gọi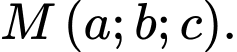
Vì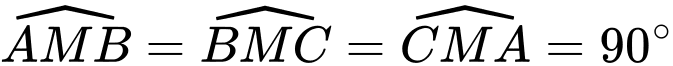 nên
nên 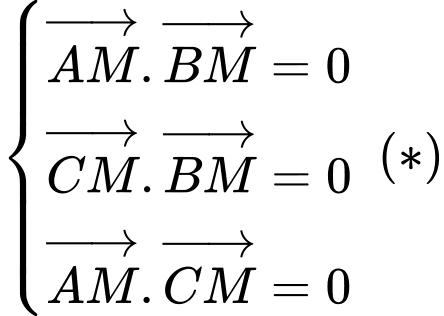
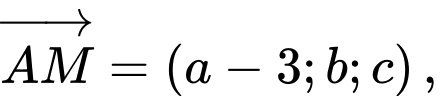
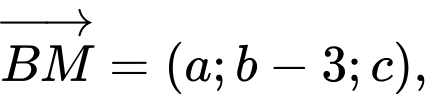
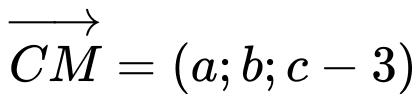
Từ biểu thức ta có biểu thức tọa độ
ta có biểu thức tọa độ
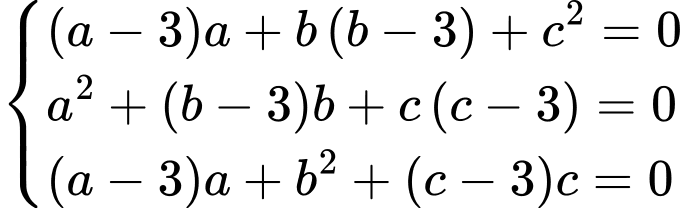
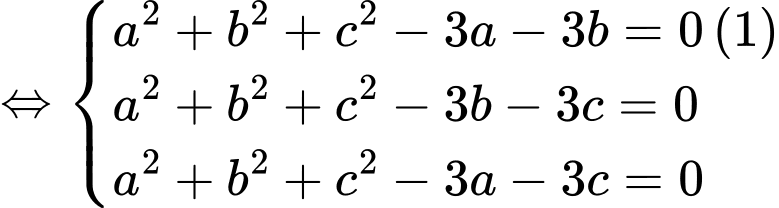
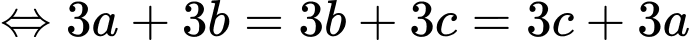
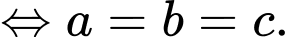
Thay vào biểu thức ta có
ta có 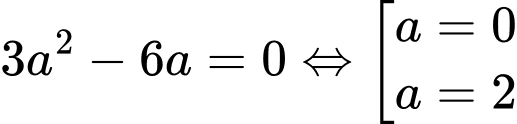
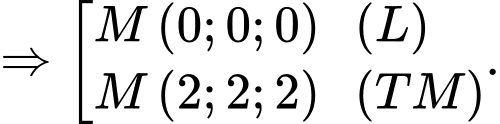
Vậy
Gọi
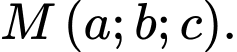
Vì
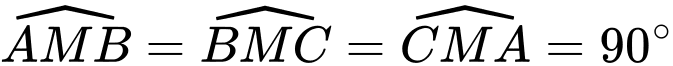 nên
nên 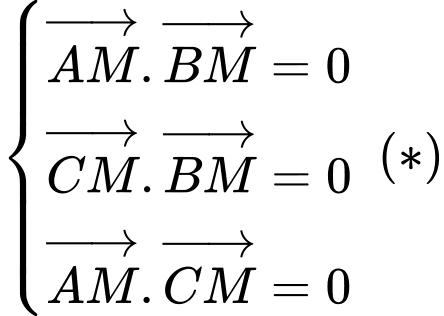
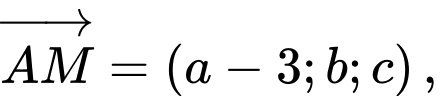
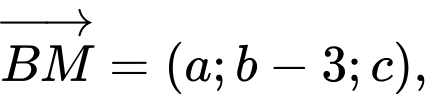
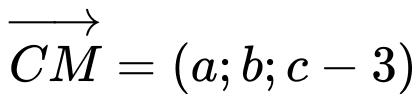
Từ biểu thức
 ta có biểu thức tọa độ
ta có biểu thức tọa độ
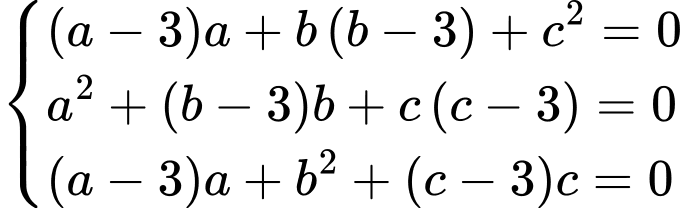
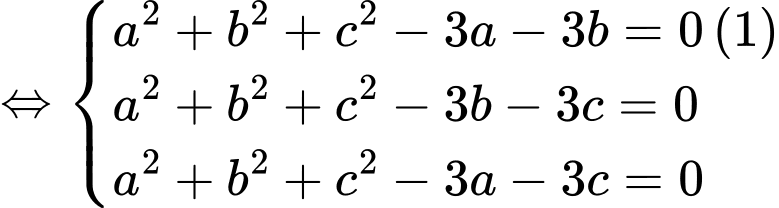
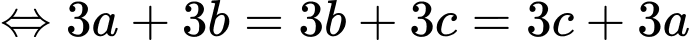
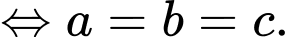
Thay vào biểu thức
 ta có
ta có 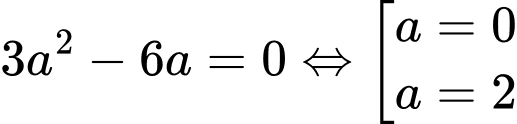
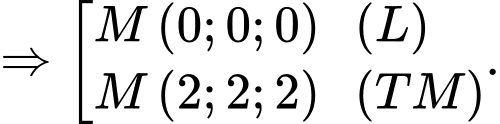
Vậy

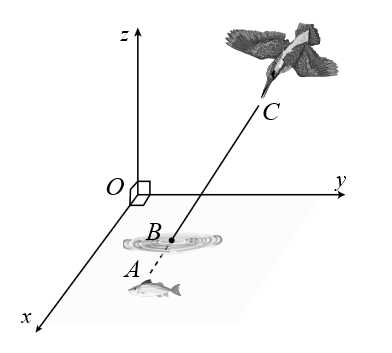
Câu 20 [717151]: Với hệ trục tọa độ 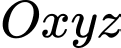 sao cho
sao cho  nằm trên mặt nước, mặt phẳng
nằm trên mặt nước, mặt phẳng 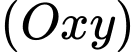 là mặt nước, trục
là mặt nước, trục  hướng lên trên (đơn vị đo: mét), một con chim bói cá đang ở vị trí cách mặt nước
hướng lên trên (đơn vị đo: mét), một con chim bói cá đang ở vị trí cách mặt nước 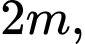 cách mặt phẳng
cách mặt phẳng 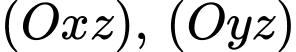 lần lượt là
lần lượt là 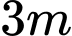 và
và  phóng thẳng xuống vị trí con cá, biết con cá cách mặt nước
phóng thẳng xuống vị trí con cá, biết con cá cách mặt nước 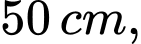 cách mặt phẳng
cách mặt phẳng 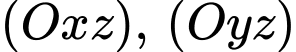 lần lượt là
lần lượt là 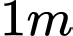 và
và 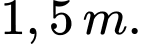 Tọa độ điểm
Tọa độ điểm 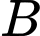 lúc chim bói cá vừa tiếp xúc với mặt nước là
lúc chim bói cá vừa tiếp xúc với mặt nước là 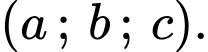 Tính
Tính 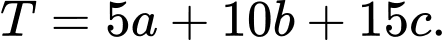
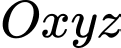 sao cho
sao cho  nằm trên mặt nước, mặt phẳng
nằm trên mặt nước, mặt phẳng 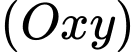 là mặt nước, trục
là mặt nước, trục  hướng lên trên (đơn vị đo: mét), một con chim bói cá đang ở vị trí cách mặt nước
hướng lên trên (đơn vị đo: mét), một con chim bói cá đang ở vị trí cách mặt nước 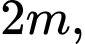 cách mặt phẳng
cách mặt phẳng 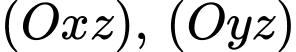 lần lượt là
lần lượt là 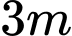 và
và  phóng thẳng xuống vị trí con cá, biết con cá cách mặt nước
phóng thẳng xuống vị trí con cá, biết con cá cách mặt nước 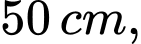 cách mặt phẳng
cách mặt phẳng 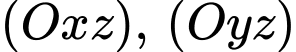 lần lượt là
lần lượt là 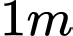 và
và 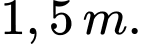 Tọa độ điểm
Tọa độ điểm 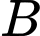 lúc chim bói cá vừa tiếp xúc với mặt nước là
lúc chim bói cá vừa tiếp xúc với mặt nước là 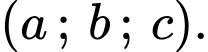 Tính
Tính 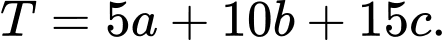

Điền đáp án: 21.
Từ giả thiết và hình vẽ ta suy ra:
+) Vị trí của con chim bói cá là điểm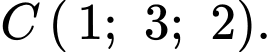
+) Vị trí của con cá là điểm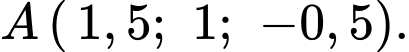
Điểm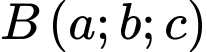 là vị trí lúc chim bói cá vừa tiếp xúc với mặt nước. Vì điểm
là vị trí lúc chim bói cá vừa tiếp xúc với mặt nước. Vì điểm  nên
nên 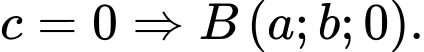
Ta có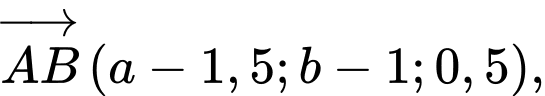
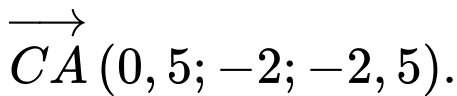
Để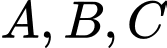 thẳng hàng thì
thẳng hàng thì 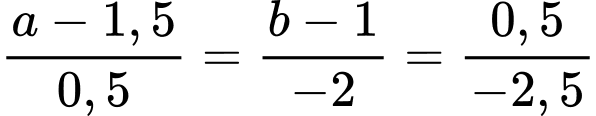
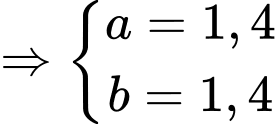
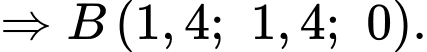
Vậy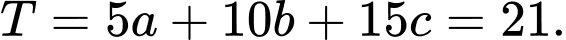
Từ giả thiết và hình vẽ ta suy ra:
+) Vị trí của con chim bói cá là điểm
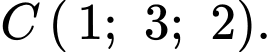
+) Vị trí của con cá là điểm
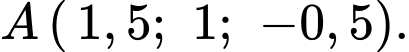
Điểm
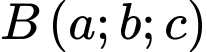 là vị trí lúc chim bói cá vừa tiếp xúc với mặt nước. Vì điểm
là vị trí lúc chim bói cá vừa tiếp xúc với mặt nước. Vì điểm  nên
nên 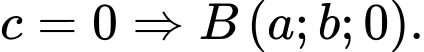
Ta có
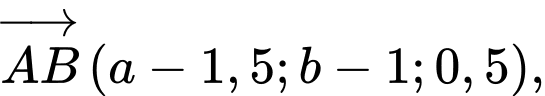
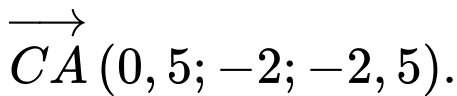
Để
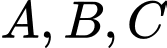 thẳng hàng thì
thẳng hàng thì 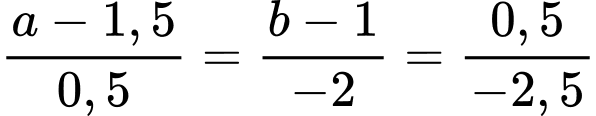
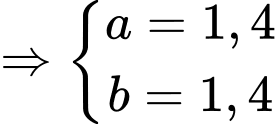
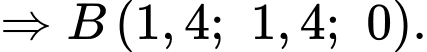
Vậy
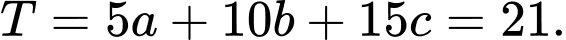
Câu 21 [775023]: Trong không gian 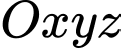 , cho ba điểm
, cho ba điểm 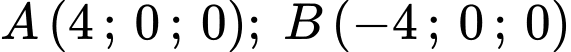 và
và 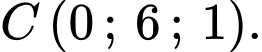 Gọi
Gọi 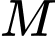 là một điểm nằm trên mặt phẳng
là một điểm nằm trên mặt phẳng 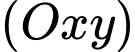 sao cho
sao cho 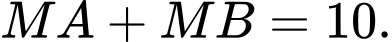 Tìm giá trị nhỏ nhất của
Tìm giá trị nhỏ nhất của 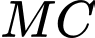 ? (kết quả làm tròn đến hàng phần trăm).
? (kết quả làm tròn đến hàng phần trăm).
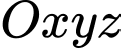 , cho ba điểm
, cho ba điểm 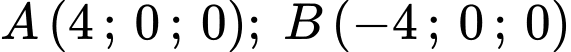 và
và 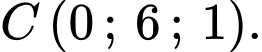 Gọi
Gọi 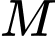 là một điểm nằm trên mặt phẳng
là một điểm nằm trên mặt phẳng 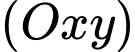 sao cho
sao cho 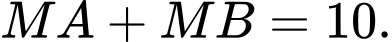 Tìm giá trị nhỏ nhất của
Tìm giá trị nhỏ nhất của 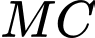 ? (kết quả làm tròn đến hàng phần trăm).
? (kết quả làm tròn đến hàng phần trăm).
Điền đáp án: 3,16.
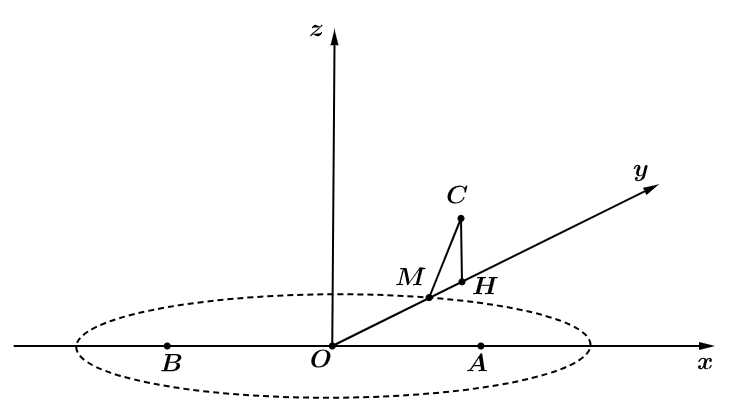
Vì và
và 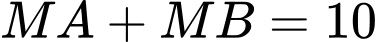 nên
nên 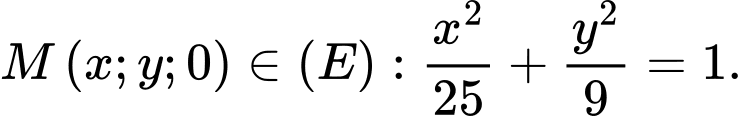
Gọi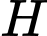 là hình chiếu vuông góc của
là hình chiếu vuông góc của  lên mặt phẳng
lên mặt phẳng 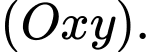 Suy ra
Suy ra 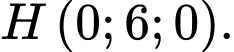
Áp dụng định lý Pytago vào tam giác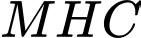 vuông tại
vuông tại 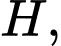 ta có
ta có
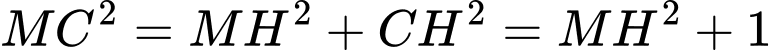
Do đó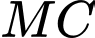 đạt giá trị nhỏ nhất khi và chỉ khi
đạt giá trị nhỏ nhất khi và chỉ khi 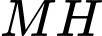 đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất.
Ta có suy ra
suy ra 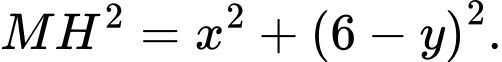
Mặc khác, vì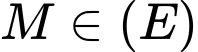 nên
nên 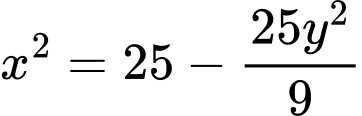 .
.
Do đó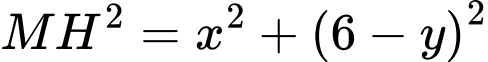
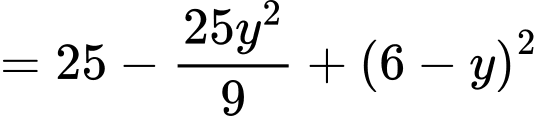
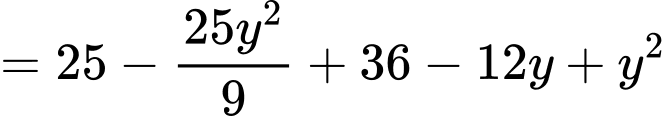
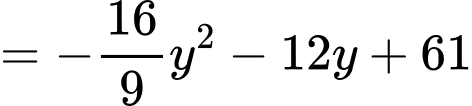 với
với 
Xét hàm số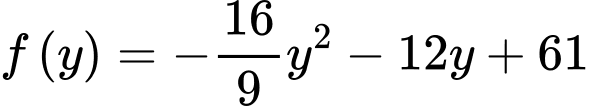 với
với  .
.
Ta có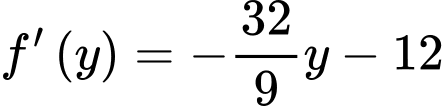
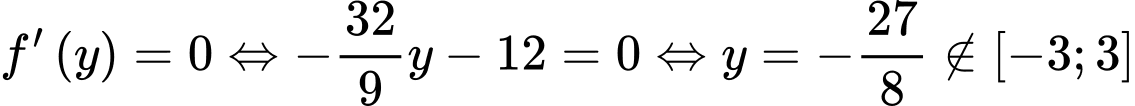
Ta có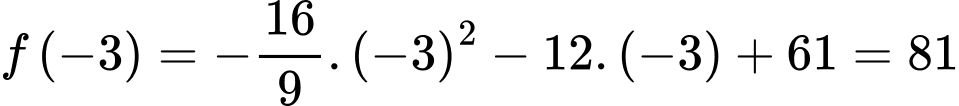 và
và 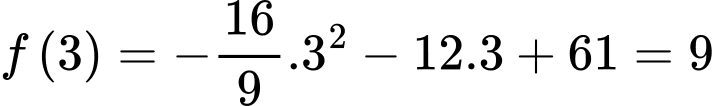
Do đó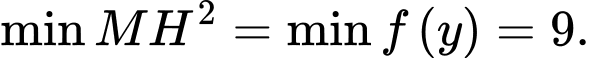 Suy ra
Suy ra 
Vậy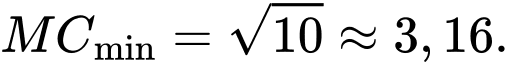

Vì
 và
và 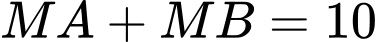 nên
nên 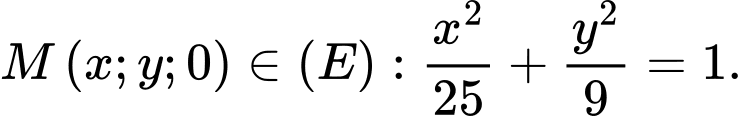
Gọi
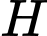 là hình chiếu vuông góc của
là hình chiếu vuông góc của  lên mặt phẳng
lên mặt phẳng 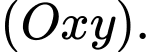 Suy ra
Suy ra 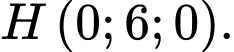
Áp dụng định lý Pytago vào tam giác
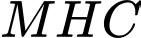 vuông tại
vuông tại 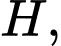 ta có
ta có
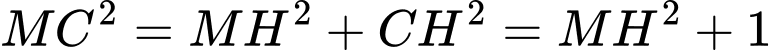
Do đó
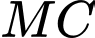 đạt giá trị nhỏ nhất khi và chỉ khi
đạt giá trị nhỏ nhất khi và chỉ khi 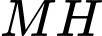 đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất.
Ta có
 suy ra
suy ra 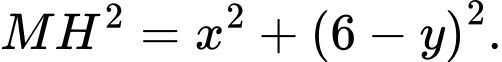
Mặc khác, vì
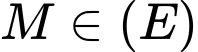 nên
nên 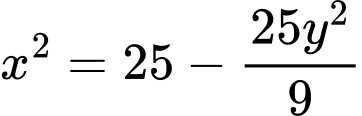 .
.
Do đó
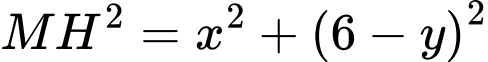
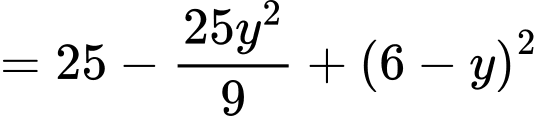
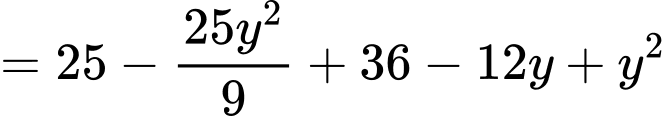
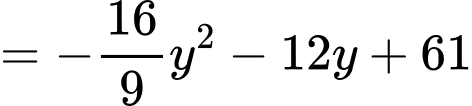 với
với 
Xét hàm số
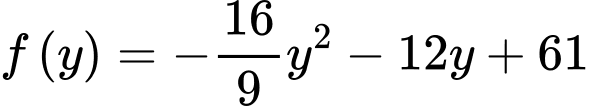 với
với  .
.
Ta có
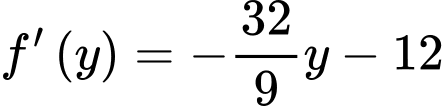
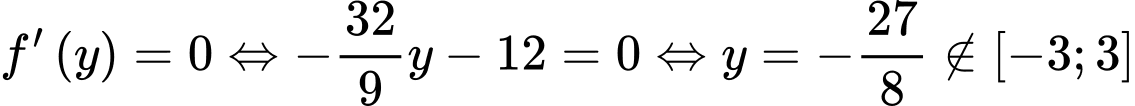
Ta có
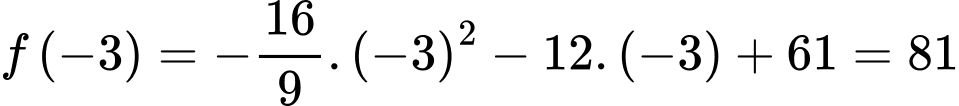 và
và 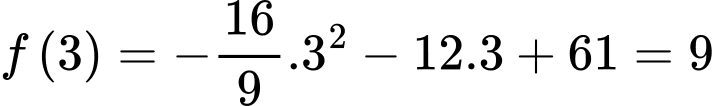
Do đó
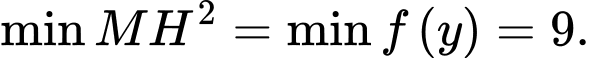 Suy ra
Suy ra 
Vậy
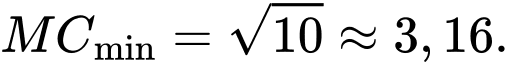
Câu 22 [775024]: Trong không gian với hệ tọa độ 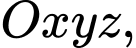 cho hai điểm
cho hai điểm 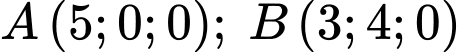 và điểm
và điểm  nằm trên trục
nằm trên trục 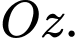 Gọi
Gọi 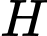 là trực tâm tam giác
là trực tâm tam giác 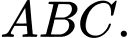 Khi
Khi  di chuyển trên trục
di chuyển trên trục  thì
thì 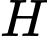 luôn thuộc một đường tròn cố định. Tính bán kính của đường tròn đó (kết quả làm tròn đến hàng phần trăm).
luôn thuộc một đường tròn cố định. Tính bán kính của đường tròn đó (kết quả làm tròn đến hàng phần trăm).
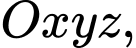 cho hai điểm
cho hai điểm 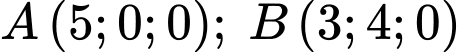 và điểm
và điểm  nằm trên trục
nằm trên trục 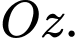 Gọi
Gọi 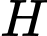 là trực tâm tam giác
là trực tâm tam giác 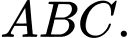 Khi
Khi  di chuyển trên trục
di chuyển trên trục  thì
thì 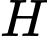 luôn thuộc một đường tròn cố định. Tính bán kính của đường tròn đó (kết quả làm tròn đến hàng phần trăm).
luôn thuộc một đường tròn cố định. Tính bán kính của đường tròn đó (kết quả làm tròn đến hàng phần trăm).
Điền đáp án: 0,56.
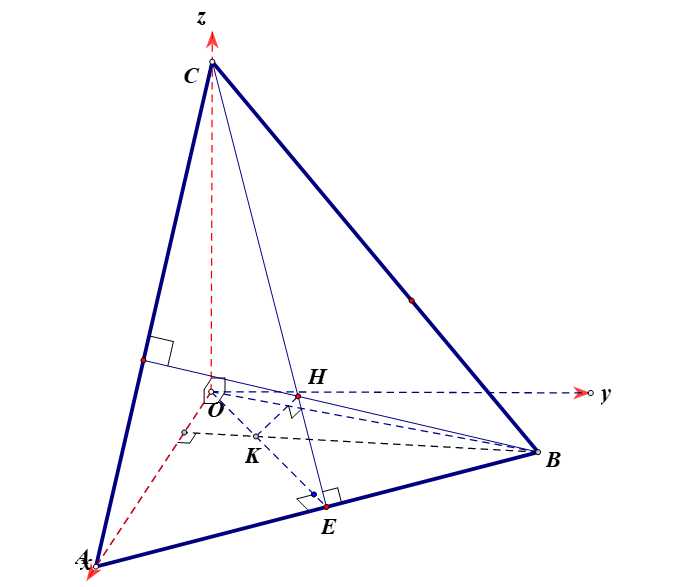 Ta có
Ta có  nên tam giác
nên tam giác 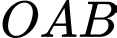 cân tại
cân tại  .
.
Ta có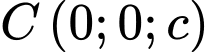 .
.
Gọi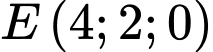 là trung điểm của
là trung điểm của  .
.
Do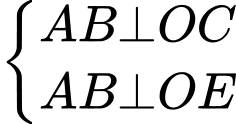 , suy ra mặt phẳng
, suy ra mặt phẳng  cố định vuông góc với
cố định vuông góc với  và tam giác
và tam giác 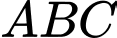 cân tại
cân tại  . Khi đó
. Khi đó  .
.
Gọi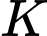 là trực tâm tam giác
là trực tâm tam giác 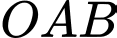 , do
, do 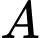 ,
, 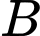 và
và 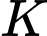 cùng nằm trong mặt phẳng
cùng nằm trong mặt phẳng 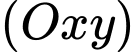 nên
nên 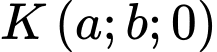 .
.
Ta có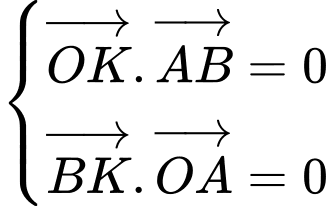
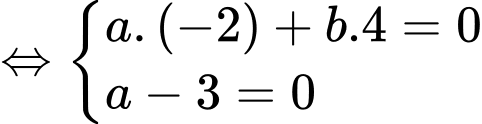
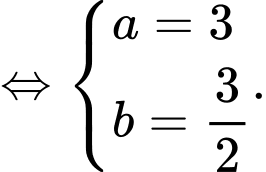 Tìm được
Tìm được 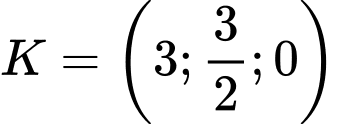 .
.
Ta chứng minh được (do
(do 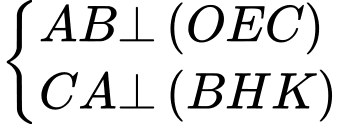
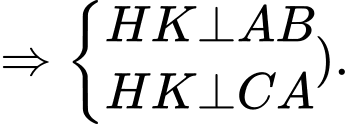
Suy ra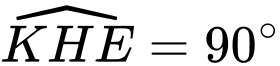 .
.
Suy ra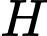 thuộc mặt cầu đường kính
thuộc mặt cầu đường kính 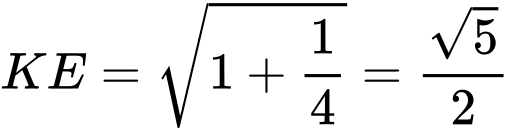 và thuộc mặt phẳng
và thuộc mặt phẳng  cố định.
cố định.
Vậy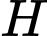 luôn thuộc một đường tròn cố định có bán kính
luôn thuộc một đường tròn cố định có bán kính 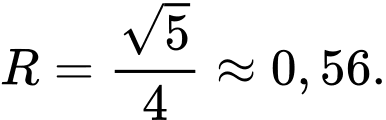

 nên tam giác
nên tam giác 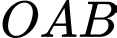 cân tại
cân tại  .
.Ta có
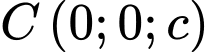 .
.Gọi
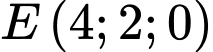 là trung điểm của
là trung điểm của  .
.Do
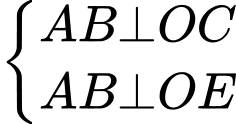 , suy ra mặt phẳng
, suy ra mặt phẳng  cố định vuông góc với
cố định vuông góc với  và tam giác
và tam giác 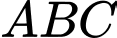 cân tại
cân tại  . Khi đó
. Khi đó  .
.Gọi
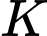 là trực tâm tam giác
là trực tâm tam giác 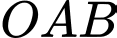 , do
, do 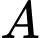 ,
, 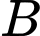 và
và 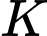 cùng nằm trong mặt phẳng
cùng nằm trong mặt phẳng 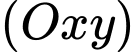 nên
nên 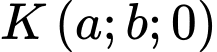 .
.Ta có
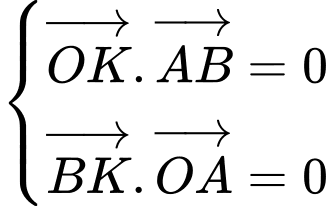
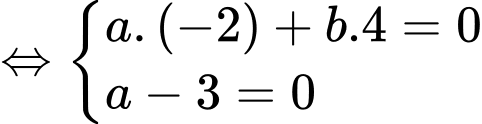
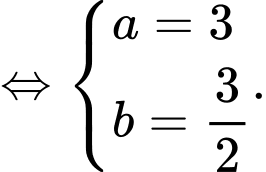 Tìm được
Tìm được 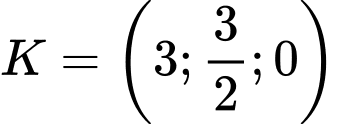 .
.Ta chứng minh được
 (do
(do 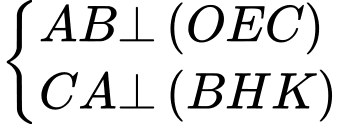
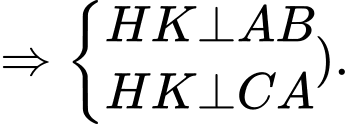
Suy ra
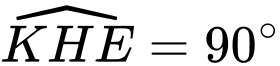 .
.Suy ra
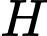 thuộc mặt cầu đường kính
thuộc mặt cầu đường kính 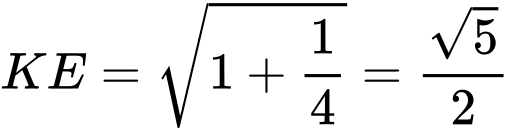 và thuộc mặt phẳng
và thuộc mặt phẳng  cố định.
cố định. Vậy
 luôn thuộc một đường tròn cố định có bán kính
luôn thuộc một đường tròn cố định có bán kính