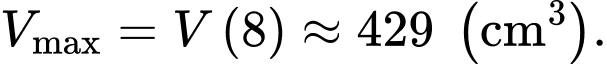PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1 [377915]: Cho hàm số 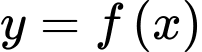 có bảng biến thiên như sau:
có bảng biến thiên như sau:
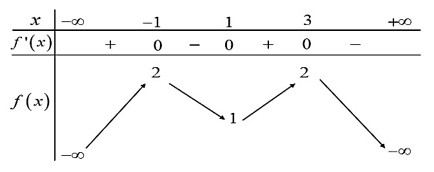
Hỏi hàm số đã cho đồng biến trên khoảng nào dưới đây?
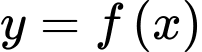 có bảng biến thiên như sau:
có bảng biến thiên như sau:
Hỏi hàm số đã cho đồng biến trên khoảng nào dưới đây?
A, 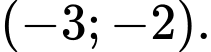
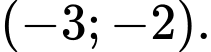
B, 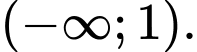
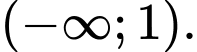
C, 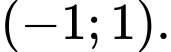
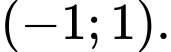
D, 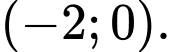
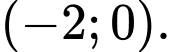
Phương pháp:
Quan sát bbt và nhận xét khoảng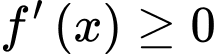
Cách giải:
Từ bbt ta thấy hàm số đồng biến trên khoảng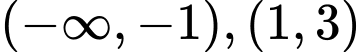
Chọn A. Đáp án: A
Quan sát bbt và nhận xét khoảng
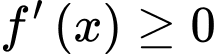
Cách giải:
Từ bbt ta thấy hàm số đồng biến trên khoảng
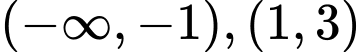
Chọn A. Đáp án: A
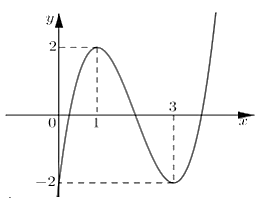
Câu 2 [377937]: Cho hàm số bậc ba 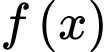 có đồ thị như hình vẽ bên. Giá trị cực tiểu của hàm số đã cho bằng
có đồ thị như hình vẽ bên. Giá trị cực tiểu của hàm số đã cho bằng
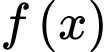 có đồ thị như hình vẽ bên. Giá trị cực tiểu của hàm số đã cho bằng
có đồ thị như hình vẽ bên. Giá trị cực tiểu của hàm số đã cho bằng
A, 3.
B, -2.
C, 1.
D, 2.
Phương pháp:
Quan sát đồ thị và tọa độ điểm cực tiểu
Cách giải:
Từ đồ thị ta thấy hàm số đạt cực tiểu tại điểm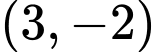 và giá trị cực tiểu bằng -2
và giá trị cực tiểu bằng -2
Chọn B. Đáp án: B
Quan sát đồ thị và tọa độ điểm cực tiểu
Cách giải:
Từ đồ thị ta thấy hàm số đạt cực tiểu tại điểm
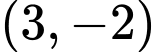 và giá trị cực tiểu bằng -2
và giá trị cực tiểu bằng -2Chọn B. Đáp án: B
Câu 3 [377740]: Cho hàm số 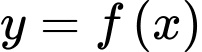 liên tục trên đoạn
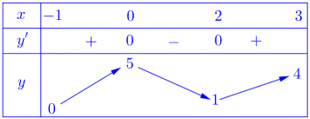
liên tục trên đoạn 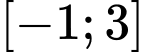 và có bảng biến thiên như hình vẽ bên. Giá trị lớn nhất của hàm số
và có bảng biến thiên như hình vẽ bên. Giá trị lớn nhất của hàm số 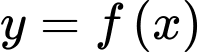 trên đoạn
trên đoạn 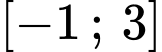 bằng
bằng
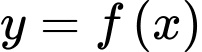 liên tục trên đoạn
liên tục trên đoạn 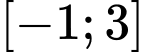 và có bảng biến thiên như hình vẽ bên. Giá trị lớn nhất của hàm số
và có bảng biến thiên như hình vẽ bên. Giá trị lớn nhất của hàm số 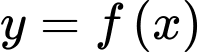 trên đoạn
trên đoạn 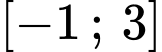 bằng
bằng
A, 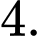
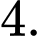
B, 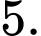
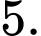
C, 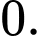
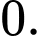
D, 
Phương pháp:
Dựa vào bảng biến thiên
Cách giải:
Dựa vào bảng biến thiên ta thấy hàm số có giá trị lớn nhất trên [-1;3] là 5
Chọn B. Đáp án: B
Dựa vào bảng biến thiên
Cách giải:
Dựa vào bảng biến thiên ta thấy hàm số có giá trị lớn nhất trên [-1;3] là 5
Chọn B. Đáp án: B
Câu 4 [554561]: Cho hàm số 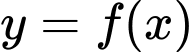 có đạo hàm
có đạo hàm 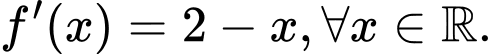 Hàm số đã cho đồng bié́n trên khoảng nào dưới đây?
Hàm số đã cho đồng bié́n trên khoảng nào dưới đây?
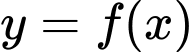 có đạo hàm
có đạo hàm 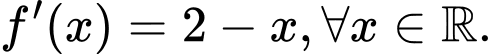 Hàm số đã cho đồng bié́n trên khoảng nào dưới đây?
Hàm số đã cho đồng bié́n trên khoảng nào dưới đây? A, 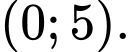
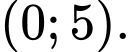
B, 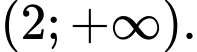
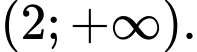
C, 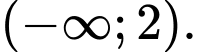
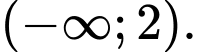
D, 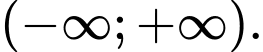
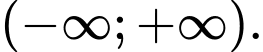
Hàm số đã cho đồng bié́n khi 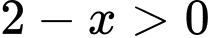 hay
hay  . Chọn C. Đáp án: C
. Chọn C. Đáp án: C
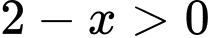 hay
hay  . Chọn C. Đáp án: C
. Chọn C. Đáp án: C
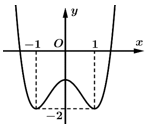
Câu 5 [520156]: Cho hàm số bậc bốn 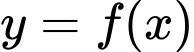 có đồ thị trong hình vẽ bên.Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
có đồ thị trong hình vẽ bên.Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
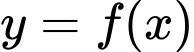 có đồ thị trong hình vẽ bên.Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
có đồ thị trong hình vẽ bên.Hàm số đã cho nghịch biến trên khoảng nào dưới đây? 
A, 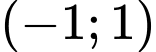 .
.
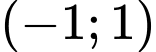 .
.B, 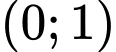 .
.
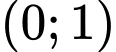 .
.C, 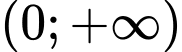 .
.
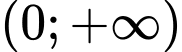 .
.D, 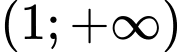 .
.
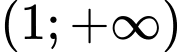 .
.
Chọn B
Từ đồ thị ta thấy hàm số nghịch biến trên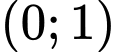 . Đáp án: B
. Đáp án: B
Từ đồ thị ta thấy hàm số nghịch biến trên
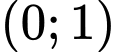 . Đáp án: B
. Đáp án: B
Câu 6 [377817]: Gọi 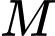 và
và 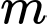 lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 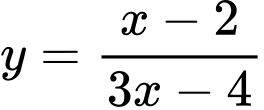 trên đoạn
trên đoạn 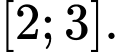 Khi đó tổng
Khi đó tổng  bằng
bằng
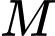 và
và 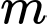 lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 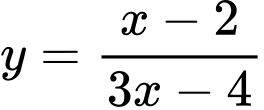 trên đoạn
trên đoạn 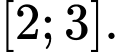 Khi đó tổng
Khi đó tổng  bằng
bằng A, 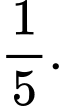
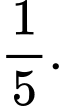
B, 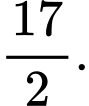
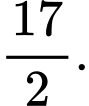
C, 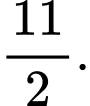
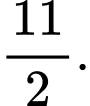
D, 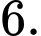
Chọn A
Hàm số đồng biến, do đó giá trị lớn nhất trên đoạn bằng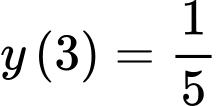 , giá trị nhỏ nhất trên đoạn bằng
, giá trị nhỏ nhất trên đoạn bằng 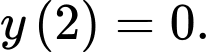 Tổng
Tổng 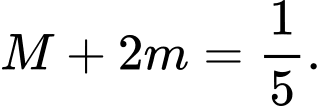 Đáp án: A
Đáp án: A
Hàm số đồng biến, do đó giá trị lớn nhất trên đoạn bằng
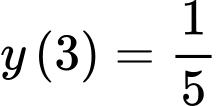 , giá trị nhỏ nhất trên đoạn bằng
, giá trị nhỏ nhất trên đoạn bằng 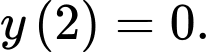 Tổng
Tổng 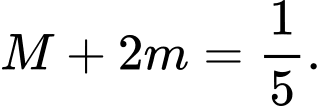 Đáp án: A
Đáp án: A
Câu 7 [538524]: Giá trị cực tiểu của hàm số 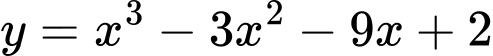 là
là
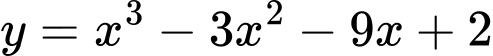 là
là A, 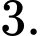
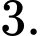
B, 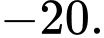
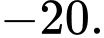
C, 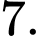
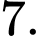
D, 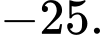
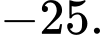
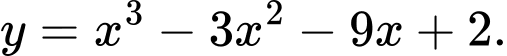 Casio ta có
Casio ta cóGiá trị cực tiểu là
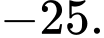 Đáp án: D
Đáp án: D
Câu 8 [545814]: Cho hàm số 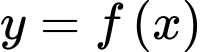 liên tục trên
liên tục trên  và có đạo hàm
và có đạo hàm 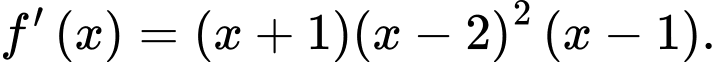 Điểm cực đại của hàm số đã cho là
Điểm cực đại của hàm số đã cho là
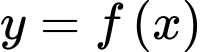 liên tục trên
liên tục trên  và có đạo hàm
và có đạo hàm 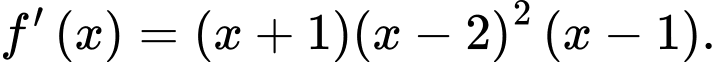 Điểm cực đại của hàm số đã cho là
Điểm cực đại của hàm số đã cho là A, 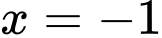 .
.
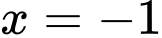 .
.B, 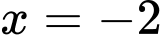 .
.
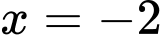 .
.C, 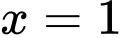 .
.
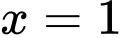 .
.D, 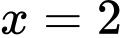 .
.
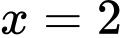 .
.
Ta có: 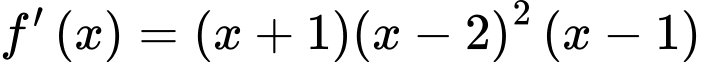 , suy ra
, suy ra 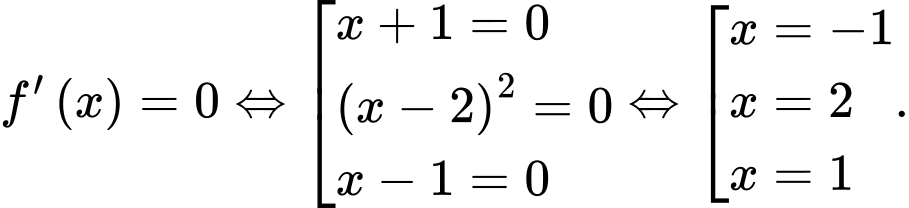
Bảng biến thiên:
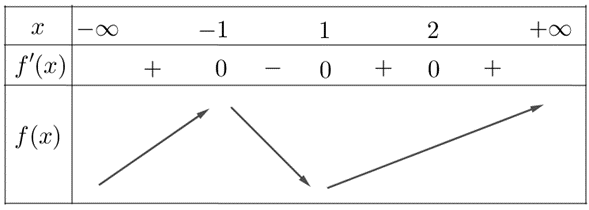
Từ bảng biến thiên, suy ra điểm cực đại của hàm số đã cho là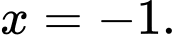 Đáp án: A
Đáp án: A
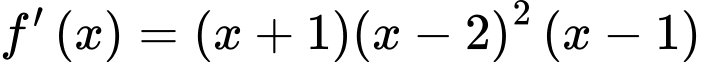 , suy ra
, suy ra 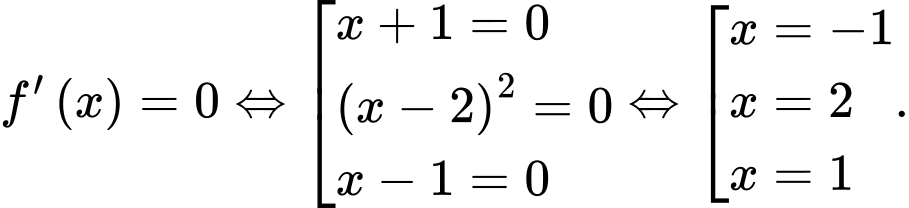
Bảng biến thiên:

Từ bảng biến thiên, suy ra điểm cực đại của hàm số đã cho là
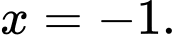 Đáp án: A
Đáp án: A
Câu 9 [391011]: Giá trị lớn nhất của hàm số  trên đoạn
trên đoạn 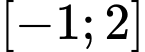 bằng:
bằng:
 trên đoạn
trên đoạn 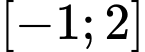 bằng:
bằng: A, 37.
B, 1.
C, 12.
D, 33.
Phương pháp:
- Tính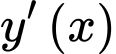 , xác định các nghiệm
, xác định các nghiệm  của phương trình
của phương trình 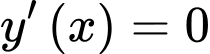
- Tính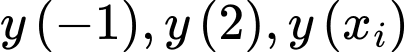
- KL: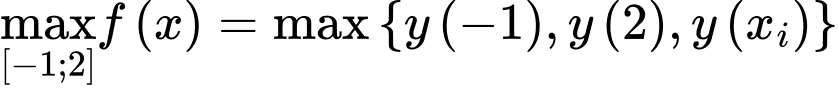
Cách giải:
Ta có: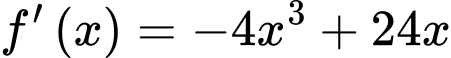
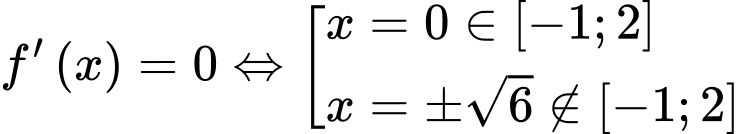
Ta có: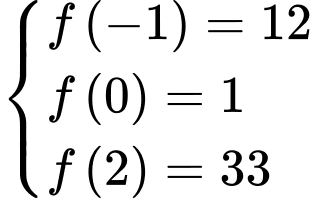
Vậy giá trị lớn nhất của hàm số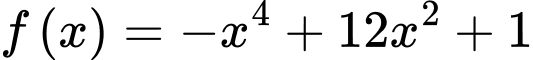 trên đoạn
trên đoạn 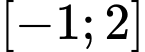 bằng 33
bằng 33
Chọn D. Đáp án: D
- Tính
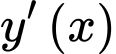 , xác định các nghiệm
, xác định các nghiệm  của phương trình
của phương trình 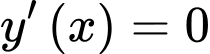
- Tính
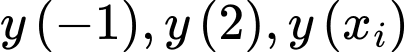
- KL:
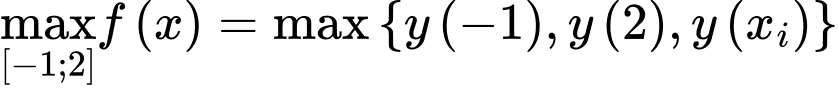
Cách giải:
Ta có:
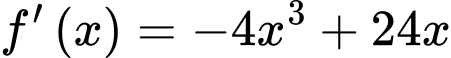
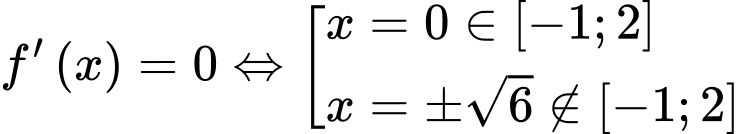
Ta có:
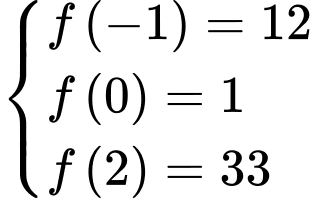
Vậy giá trị lớn nhất của hàm số
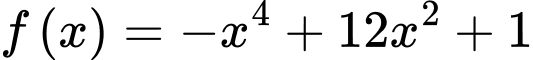 trên đoạn
trên đoạn 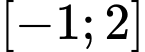 bằng 33
bằng 33
Chọn D. Đáp án: D
Câu 10 [538882]: Cho hàm số 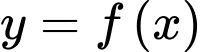 có đồ thị hàm số
có đồ thị hàm số 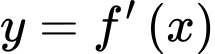 như hình vẽ bên. Hàm số
như hình vẽ bên. Hàm số 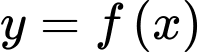 đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây?
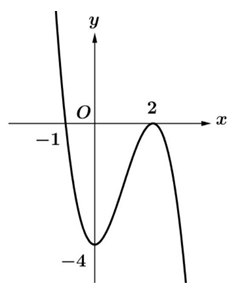
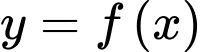 có đồ thị hàm số
có đồ thị hàm số 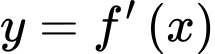 như hình vẽ bên. Hàm số
như hình vẽ bên. Hàm số 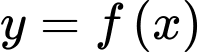 đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây?
A, 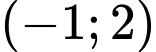 .
.
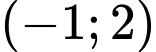 .
.B, 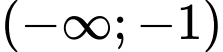 .
.
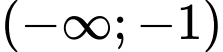 .
.C, 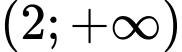 .
.
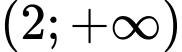 .
.D, 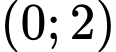 .
.
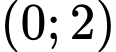 .
.
Phương pháp:
Dựa vào đồ thị hàm số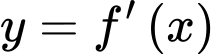 xác định các khoảng
xác định các khoảng 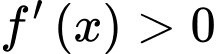 - tương ứng với phần đồ thị hàm số
- tương ứng với phần đồ thị hàm số 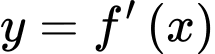 nằm phía trên trục hoành.
nằm phía trên trục hoành.
Cách giải:
Dựa vào đồ thị hàm số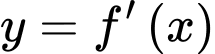 ta thấy
ta thấy 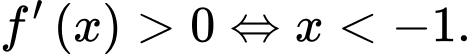
Vậy hàm số đồng biến trên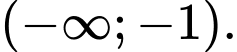
Chọn B Đáp án: B
Dựa vào đồ thị hàm số
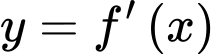 xác định các khoảng
xác định các khoảng 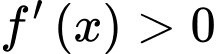 - tương ứng với phần đồ thị hàm số
- tương ứng với phần đồ thị hàm số 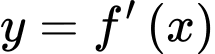 nằm phía trên trục hoành.
nằm phía trên trục hoành.Cách giải:
Dựa vào đồ thị hàm số
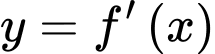 ta thấy
ta thấy 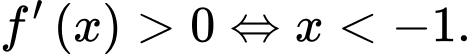
Vậy hàm số đồng biến trên
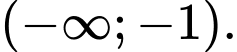
Chọn B Đáp án: B
Câu 11 [377811]: Trong các hàm số dưới đây, hàm số nào đồng biến trên 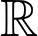 ?
?
 ?
? A,  .
.
 .
.B, 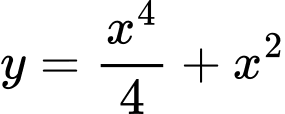 .
.
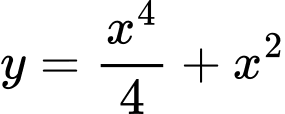 .
.C, 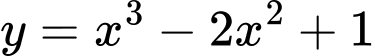 .
.
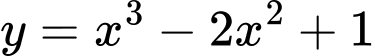 .
.D, 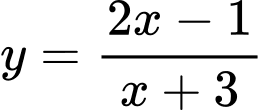
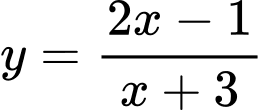
Chọn A.
Trong các đáp án, chỉ có hàm số có đạo hàm luôn dương với mọi
có đạo hàm luôn dương với mọi 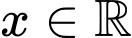 . Do đó chỉ có
. Do đó chỉ có  đồng biến trên
đồng biến trên 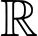 Đáp án: A
Đáp án: A
Trong các đáp án, chỉ có hàm số
 có đạo hàm luôn dương với mọi
có đạo hàm luôn dương với mọi 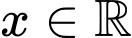 . Do đó chỉ có
. Do đó chỉ có  đồng biến trên
đồng biến trên 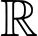 Đáp án: A
Đáp án: A
Câu 12 [554581]: Hàm số  đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây?
 đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây? A, 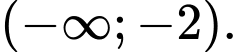
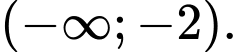
B, 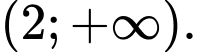
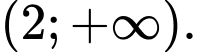
C, 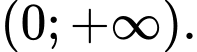
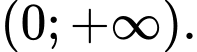
D, 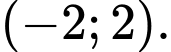
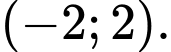
Chọn đáp án B.
Điều kiện xác định: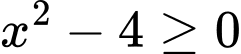
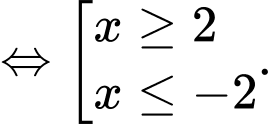
Áp dụng công thức đạo hàm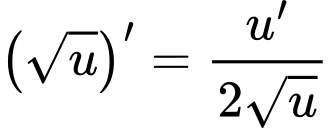 với
với 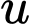 là hàm hợp, ta có
là hàm hợp, ta có
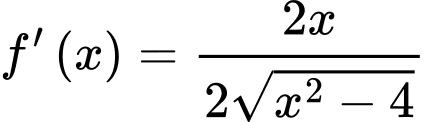
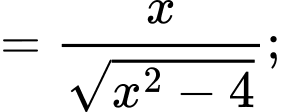
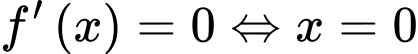 (loại, vì
(loại, vì 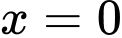 không thuộc vào khoảng xác định)
không thuộc vào khoảng xác định)
Bảng biến thiên
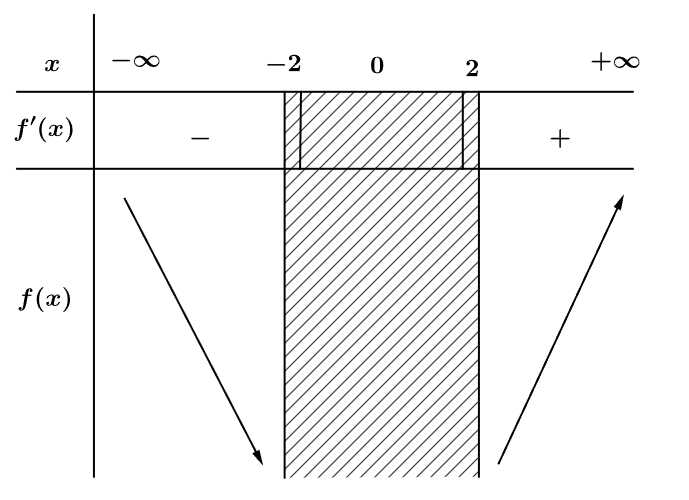
Vậy hàm số đồng biến trên khoảng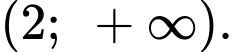 Đáp án: B
Đáp án: B
Điều kiện xác định:
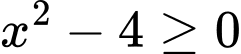
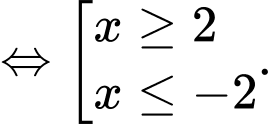
Áp dụng công thức đạo hàm
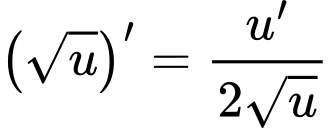 với
với 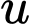 là hàm hợp, ta có
là hàm hợp, ta có 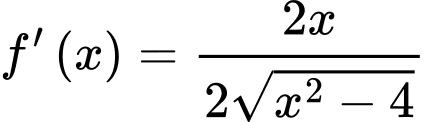
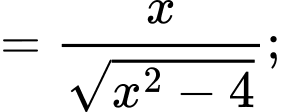
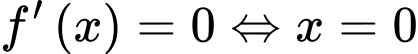 (loại, vì
(loại, vì 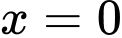 không thuộc vào khoảng xác định)
không thuộc vào khoảng xác định)Bảng biến thiên

Vậy hàm số đồng biến trên khoảng
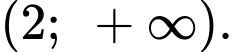 Đáp án: B
Đáp án: B PHẦN II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a),b),c),d) ở mỗi câu học sinh chọn đúng hoặc sai.
Câu 13 [716840]: Cho hàm số 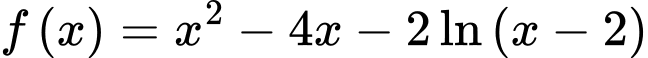 có tập xác định là
có tập xác định là 
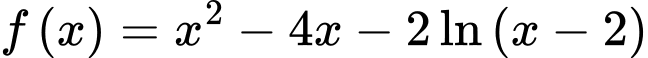 có tập xác định là
có tập xác định là 
a) Đúng.
Điều kiện xác định của hàm số là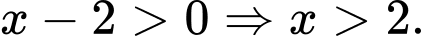 Suy ra tập xác định
Suy ra tập xác định 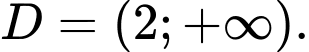
b) Sai.
Đạo hàm của hàm số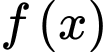 trên
trên 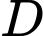 là
là 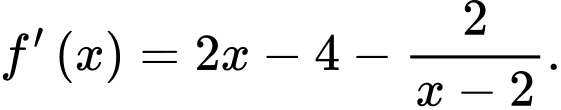
c) Sai.
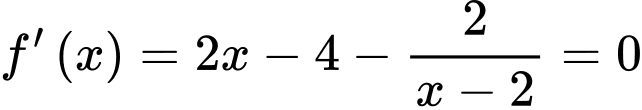
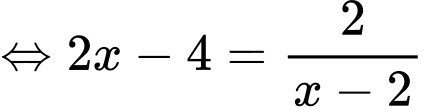
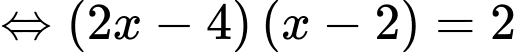
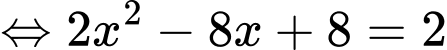
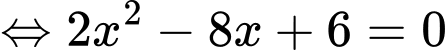
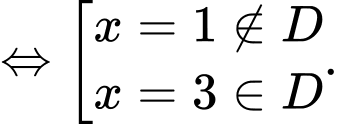 Vậy phương trình
Vậy phương trình 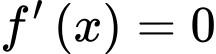 có 1 nghiệm
có 1 nghiệm 
d) Sai
Lập BBT suy ra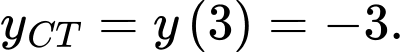
Điều kiện xác định của hàm số là
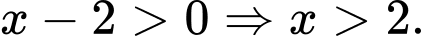 Suy ra tập xác định
Suy ra tập xác định 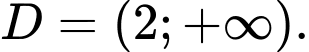
b) Sai.
Đạo hàm của hàm số
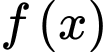 trên
trên 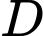 là
là 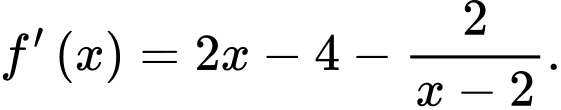
c) Sai.
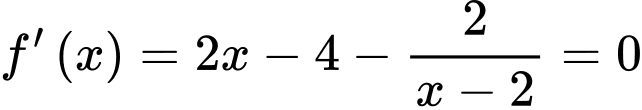
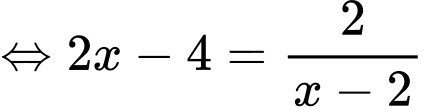
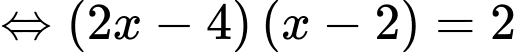
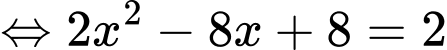
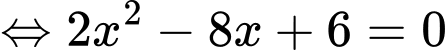
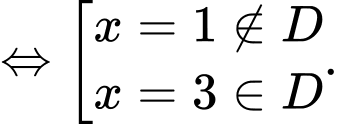 Vậy phương trình
Vậy phương trình 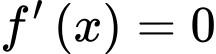 có 1 nghiệm
có 1 nghiệm 
d) Sai
Lập BBT suy ra
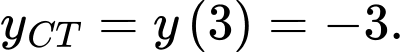
Câu 14 [680680]: Cho hàm số 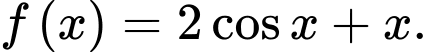
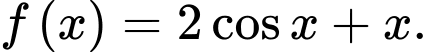
a) Đúng.
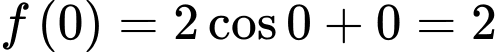 và
và 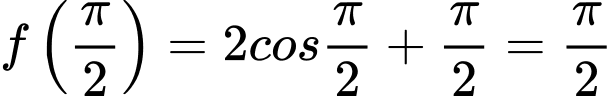 .
.
b) Sai.
Đạo hàm của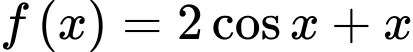 là
là 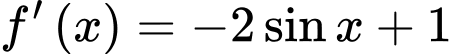 .
.
c) Đúng.
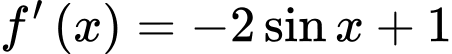 khi đó
khi đó 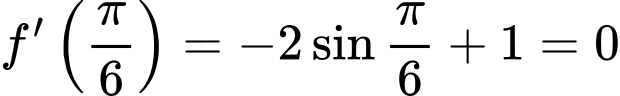 , suy ra
, suy ra 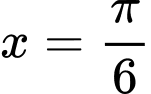 là nghiệm của phương trình
là nghiệm của phương trình 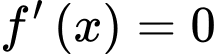 trên đoạn
trên đoạn 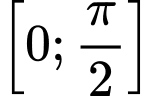 .
.
d) Đúng.
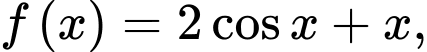
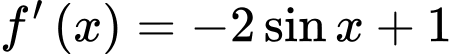 có nghiệm
có nghiệm  ,
,
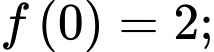
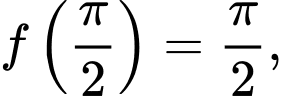
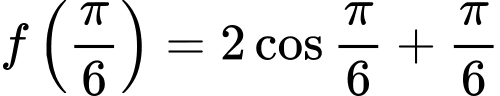
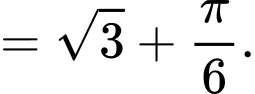
Do đó, giá trị lớn nhất của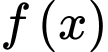 trên đoạn
trên đoạn 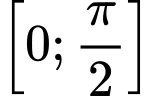 là
là 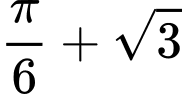 .
.
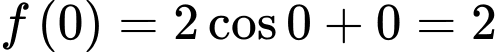 và
và 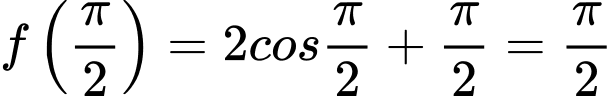 .
. b) Sai.
Đạo hàm của
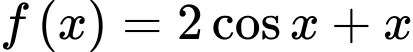 là
là 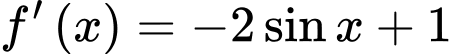 .
. c) Đúng.
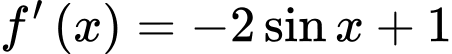 khi đó
khi đó 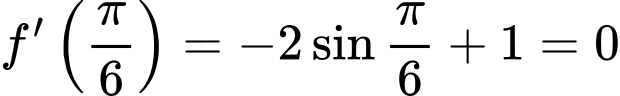 , suy ra
, suy ra 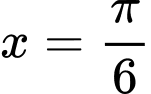 là nghiệm của phương trình
là nghiệm của phương trình 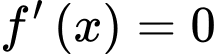 trên đoạn
trên đoạn 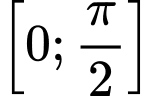 .
. d) Đúng.
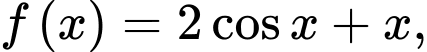
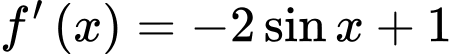 có nghiệm
có nghiệm  ,
,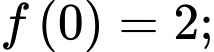
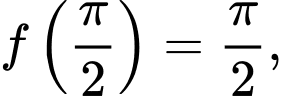
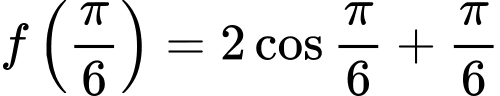
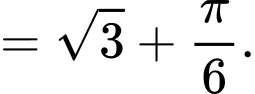
Do đó, giá trị lớn nhất của
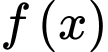 trên đoạn
trên đoạn 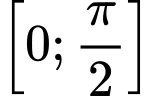 là
là 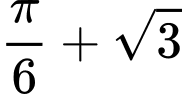 .
.
Câu 15 [599931]: Một công ty sản xuất một sản phẩm. Bộ phận tài chính của công ty đưa ra hàm giá bán một sản phẩm là 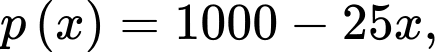 trong đó
trong đó 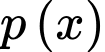 (đơn vị: triệu đồng) là giá bán của mỗi sản phẩm mà tại giá bán này có
(đơn vị: triệu đồng) là giá bán của mỗi sản phẩm mà tại giá bán này có 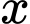 sản phẩm được bán ra.
sản phẩm được bán ra.
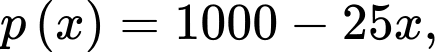 trong đó
trong đó 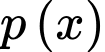 (đơn vị: triệu đồng) là giá bán của mỗi sản phẩm mà tại giá bán này có
(đơn vị: triệu đồng) là giá bán của mỗi sản phẩm mà tại giá bán này có 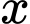 sản phẩm được bán ra.
sản phẩm được bán ra.
a) Mỗi sản phẩm có giá bán là 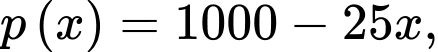 nên doanh thu của công ty là
nên doanh thu của công ty là 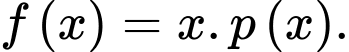
Chọn ĐÚNG.
b)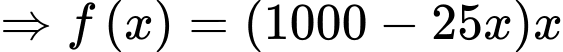
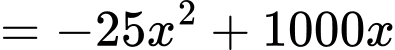
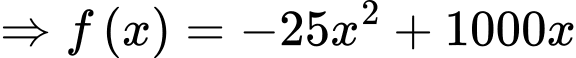
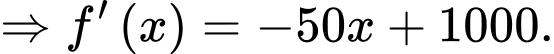
Chọn ĐÚNG.
c) Xét bất phương trình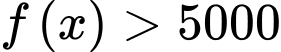
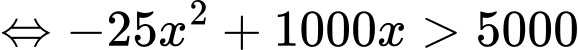
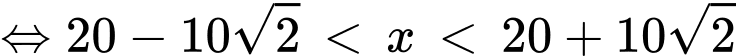
Vậy để doanh thu lớn hơn 5 tỉ đồng thì cần bán được ít nhất 6 sản phẩm.
Chọn SAI.
d)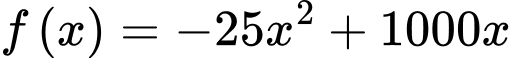
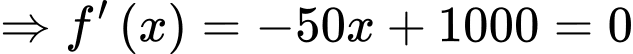
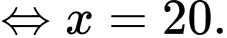
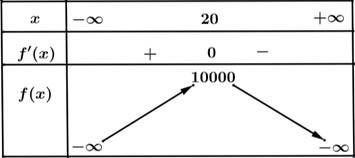
Vậy doanh thu lớn nhất bằng 10000 triệu đồng khi bán được 20 sản phẩm.
Chọn ĐÚNG.
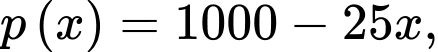 nên doanh thu của công ty là
nên doanh thu của công ty là 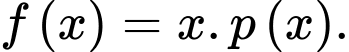
Chọn ĐÚNG.
b)
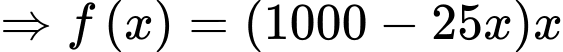
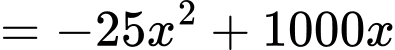
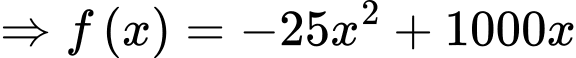
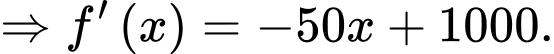
Chọn ĐÚNG.
c) Xét bất phương trình
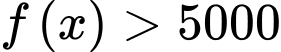
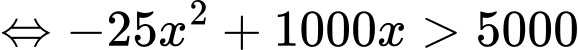
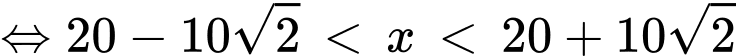
Vậy để doanh thu lớn hơn 5 tỉ đồng thì cần bán được ít nhất 6 sản phẩm.
Chọn SAI.
d)
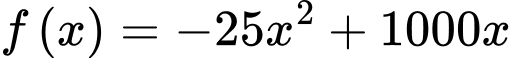
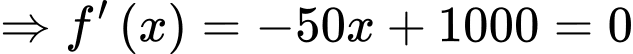
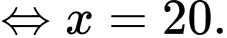

Vậy doanh thu lớn nhất bằng 10000 triệu đồng khi bán được 20 sản phẩm.
Chọn ĐÚNG.
Câu 16 [716843]: Giả sử doanh số bán hàng (tính bằng số sản phẩm) của một sản phẩm mới được mô hình hoá bằng hàm số 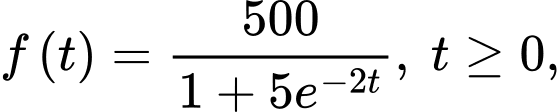 trong đó thời gian
trong đó thời gian 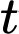 được tính bằng năm kể từ khi phát hành sản phẩm mới. Khi đó hàm số
được tính bằng năm kể từ khi phát hành sản phẩm mới. Khi đó hàm số 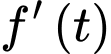 sẽ biểu thị tốc độ bán hàng.
sẽ biểu thị tốc độ bán hàng.
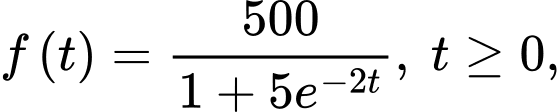 trong đó thời gian
trong đó thời gian 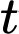 được tính bằng năm kể từ khi phát hành sản phẩm mới. Khi đó hàm số
được tính bằng năm kể từ khi phát hành sản phẩm mới. Khi đó hàm số 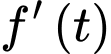 sẽ biểu thị tốc độ bán hàng.
sẽ biểu thị tốc độ bán hàng.
a) Sai.
Do nên chỉ có giới hạn dần về
nên chỉ có giới hạn dần về 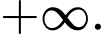
Xét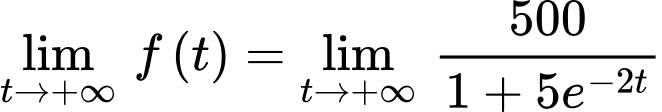
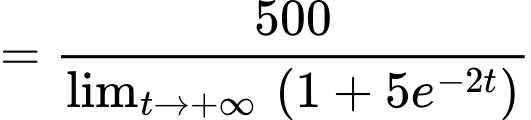
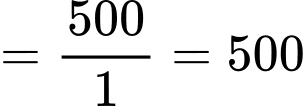
Do đó hàm số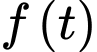 có tiệm cận ngang
có tiệm cận ngang 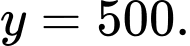
b) Đúng.
Ta có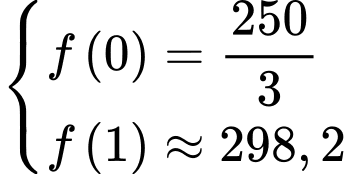 nên
nên 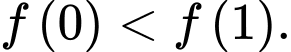
c) Sai.
Ta có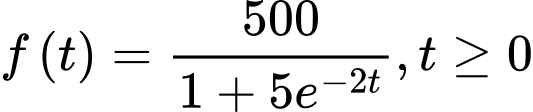 nên
nên 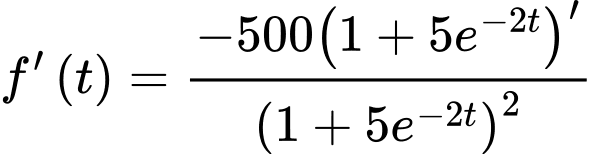
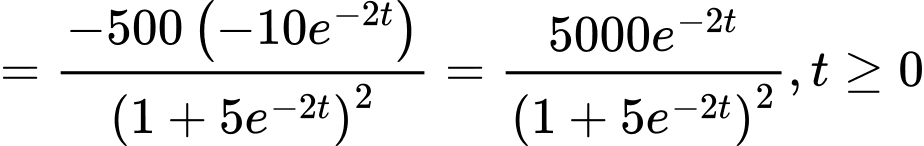
d) Sai.
Cách 1:
Đặt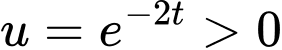
Ta có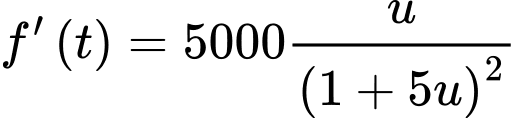
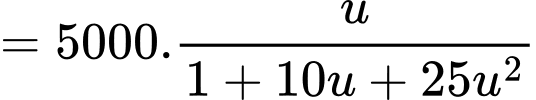
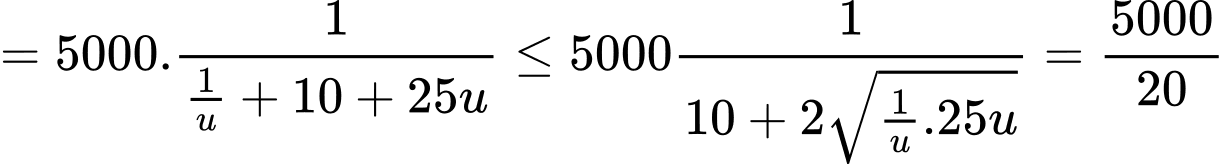
Dấu “=” xảy ra khi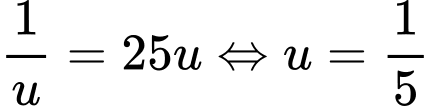
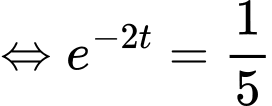
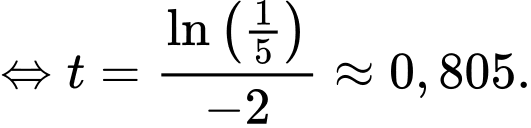
Cách 2:
Ta có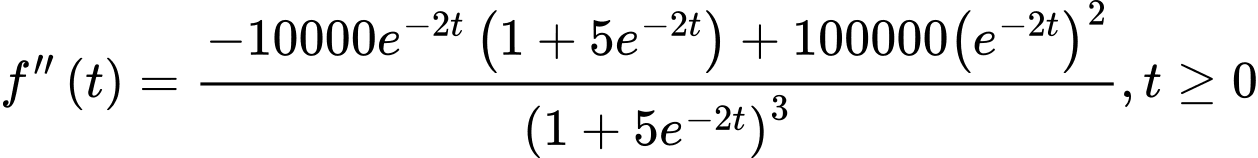
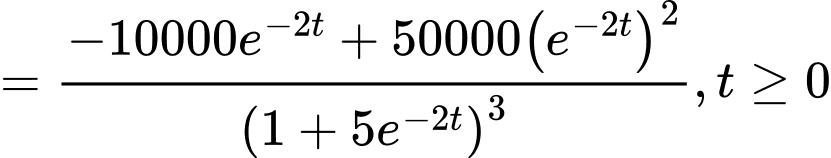
Khi đó,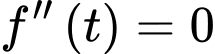
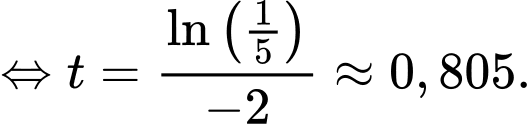 Nên tốc độ bán hàng của sản phẩm đạt cực đại sau khoảng
Nên tốc độ bán hàng của sản phẩm đạt cực đại sau khoảng 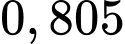 năm.
năm.
Do
 nên chỉ có giới hạn dần về
nên chỉ có giới hạn dần về 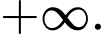
Xét
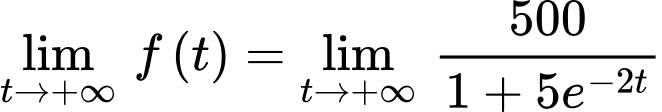
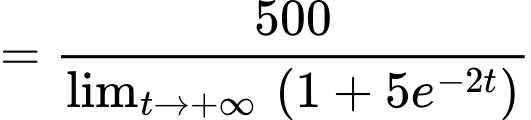
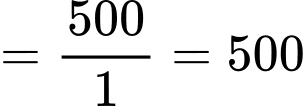
Do đó hàm số
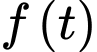 có tiệm cận ngang
có tiệm cận ngang 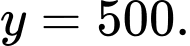
b) Đúng.
Ta có
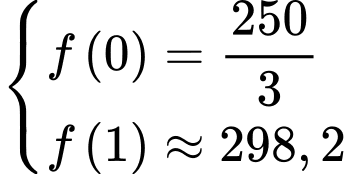 nên
nên 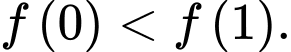
c) Sai.
Ta có
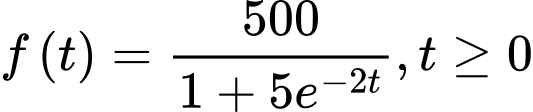 nên
nên 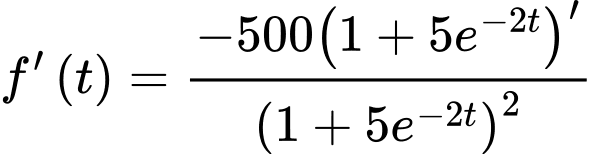
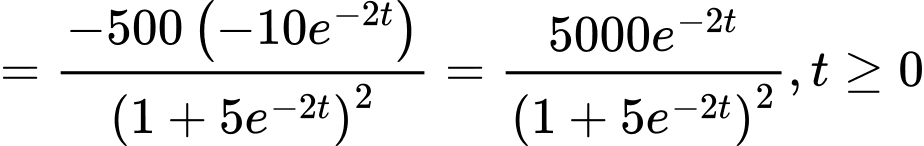
d) Sai.
Cách 1:
Đặt
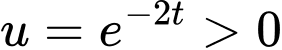
Ta có
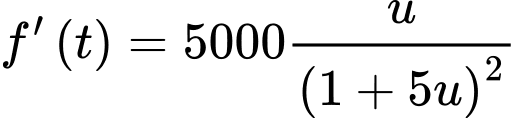
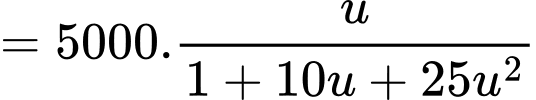
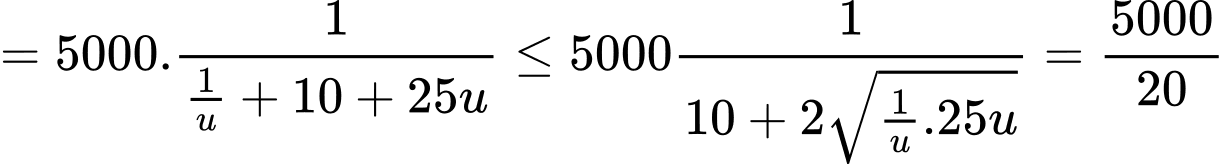
Dấu “=” xảy ra khi
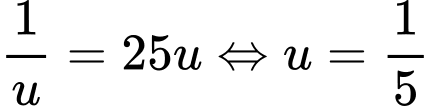
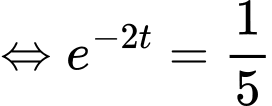
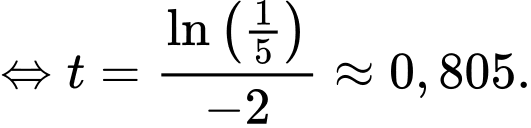
Cách 2:
Ta có
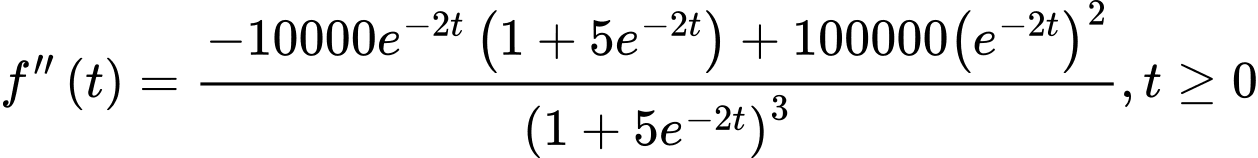
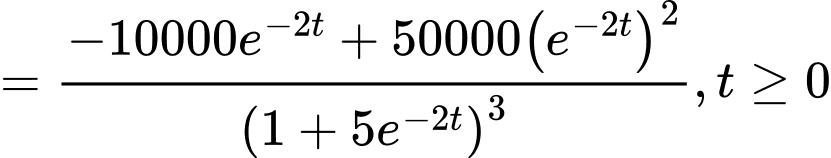
Khi đó,
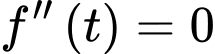
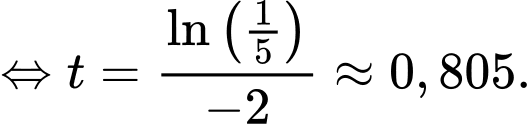 Nên tốc độ bán hàng của sản phẩm đạt cực đại sau khoảng
Nên tốc độ bán hàng của sản phẩm đạt cực đại sau khoảng 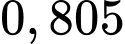 năm.
năm. PHẦN III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 17 đến câu 22.
Câu 17 [716846]: Gọi 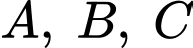 là ba điểm cực trị của đồ thị hàm số
là ba điểm cực trị của đồ thị hàm số 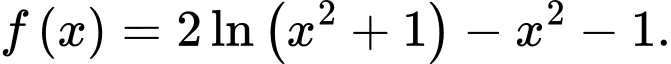 Tính chu vi tam giác
Tính chu vi tam giác 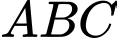 (làm tròn kết quả đến hàng phần trăm).
(làm tròn kết quả đến hàng phần trăm).
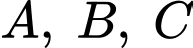 là ba điểm cực trị của đồ thị hàm số
là ba điểm cực trị của đồ thị hàm số 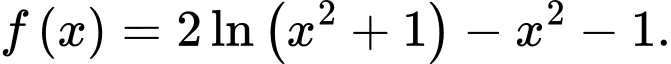 Tính chu vi tam giác
Tính chu vi tam giác 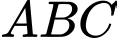 (làm tròn kết quả đến hàng phần trăm).
(làm tròn kết quả đến hàng phần trăm).
Điền đáp án: 4,14.
Tập xác định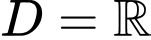 .
.
Đạo hàm: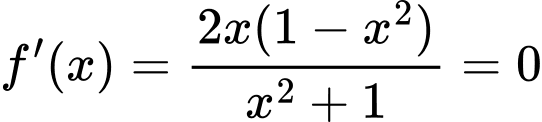 , suy ra nghiệm như sau:
, suy ra nghiệm như sau:
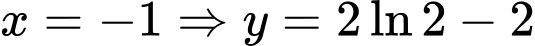
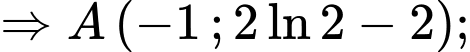
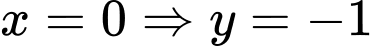
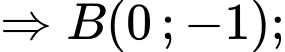
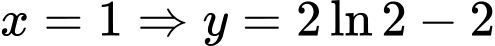
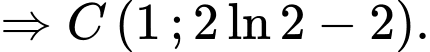 .
.
Ta được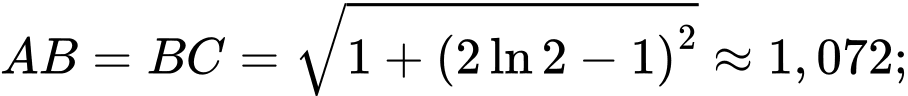
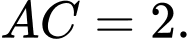
Vậy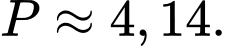
Tập xác định
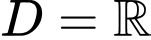 .
.Đạo hàm:
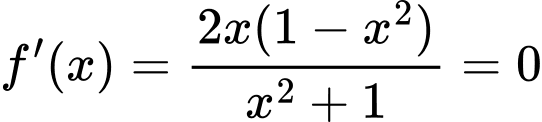 , suy ra nghiệm như sau:
, suy ra nghiệm như sau: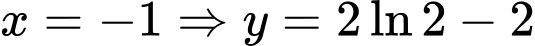
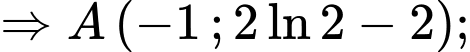
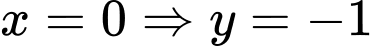
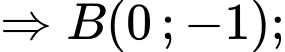
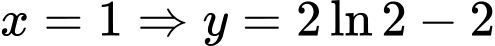
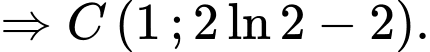 .
.Ta được
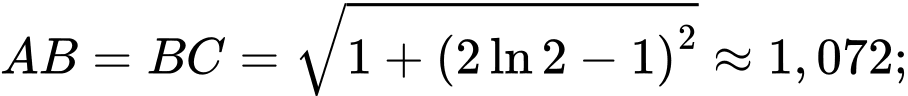
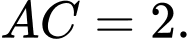
Vậy
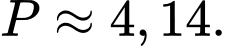
Câu 18 [774125]: Một đợt dịch cúm xảy ra tại một trường học có 763 học sinh. Số em nhiễm bệnh 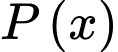 được mô phỏng bởi hàm số
được mô phỏng bởi hàm số 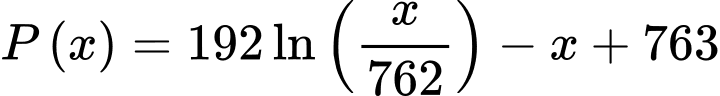 với
với 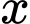 là số em có nguy cơ nhiễm bệnh nhưng hiện tại vẫn đang khoẻ (
là số em có nguy cơ nhiễm bệnh nhưng hiện tại vẫn đang khoẻ (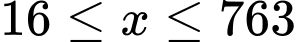 ). Hỏi số học sinh bị nhiễm bệnh tối đa là bao nhiêu em? (kết quả làm tròn đến hàng đơn vị).
). Hỏi số học sinh bị nhiễm bệnh tối đa là bao nhiêu em? (kết quả làm tròn đến hàng đơn vị).
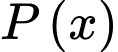 được mô phỏng bởi hàm số
được mô phỏng bởi hàm số 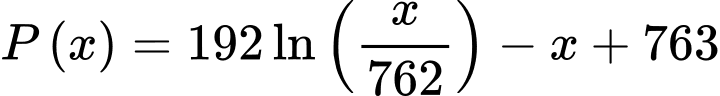 với
với 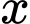 là số em có nguy cơ nhiễm bệnh nhưng hiện tại vẫn đang khoẻ (
là số em có nguy cơ nhiễm bệnh nhưng hiện tại vẫn đang khoẻ (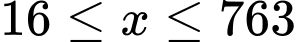 ). Hỏi số học sinh bị nhiễm bệnh tối đa là bao nhiêu em? (kết quả làm tròn đến hàng đơn vị).
). Hỏi số học sinh bị nhiễm bệnh tối đa là bao nhiêu em? (kết quả làm tròn đến hàng đơn vị).
Điền đáp án: 306.
|Ta có: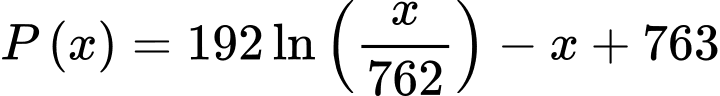
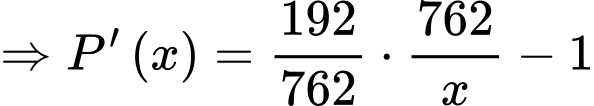
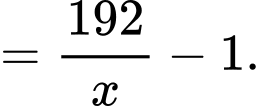
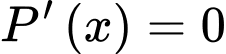
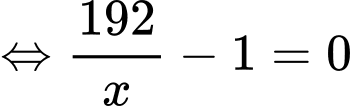
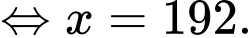
Mặt khác ta có: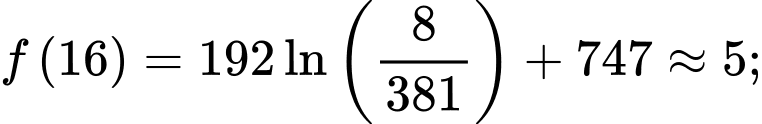
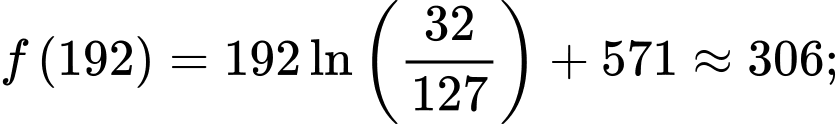
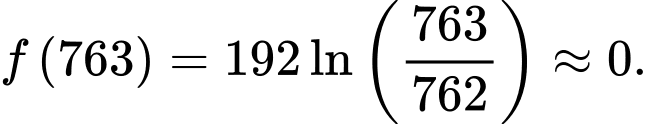
Vậy số học sinh bị nhiễm bệnh tối đa là 306.
|Ta có:
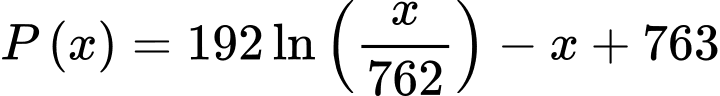
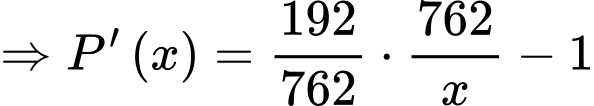
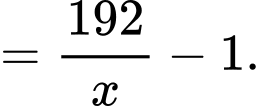
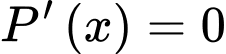
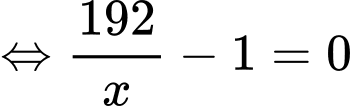
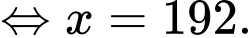
Mặt khác ta có:
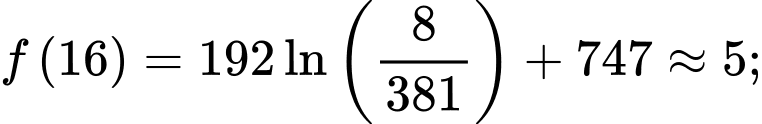
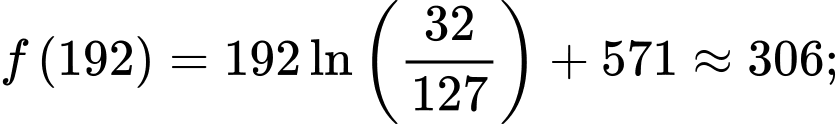
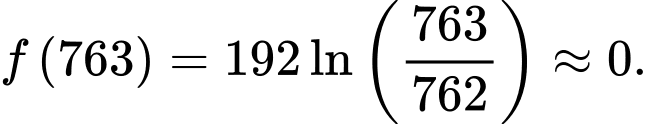
Vậy số học sinh bị nhiễm bệnh tối đa là 306.
Câu 19 [774126]: Để tạo một kiện hàng dạng hình lăng trụ đứng với đáy là hình chữ nhật có chiều dài gấp đôi chiều rộng, người ta dùng các thanh gỗ ghép khít đóng lại với nhau. Biết rằng, dung tích kiện hàng bằng  và giá thành
và giá thành  gỗ sử dụng là
gỗ sử dụng là 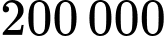 đồng. Hỏi sau khi hoàn thành kiện hàng đó, người ta cần bỏ ra ít nhất bao nhiêu triệu đồng? (diện tích các mép giữa hai mặt kề nhau không đáng kể).
đồng. Hỏi sau khi hoàn thành kiện hàng đó, người ta cần bỏ ra ít nhất bao nhiêu triệu đồng? (diện tích các mép giữa hai mặt kề nhau không đáng kể).

 và giá thành
và giá thành  gỗ sử dụng là
gỗ sử dụng là 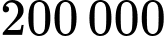 đồng. Hỏi sau khi hoàn thành kiện hàng đó, người ta cần bỏ ra ít nhất bao nhiêu triệu đồng? (diện tích các mép giữa hai mặt kề nhau không đáng kể).
đồng. Hỏi sau khi hoàn thành kiện hàng đó, người ta cần bỏ ra ít nhất bao nhiêu triệu đồng? (diện tích các mép giữa hai mặt kề nhau không đáng kể).
Điền đáp án: 5,4.
Gọi chiều dài đáy hình chữ nhật của hình lăng trụ là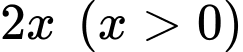 khi đó chiều rộng của đáy hình chữ nhật hình lăng trụ là
khi đó chiều rộng của đáy hình chữ nhật hình lăng trụ là 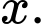
Chiều cao lăng trụ là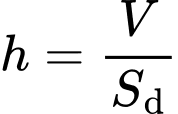
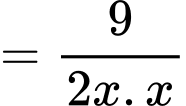
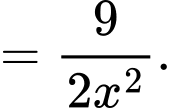
Diện tích toàn phần của hình lăng trụ là:
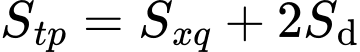
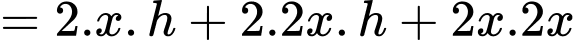
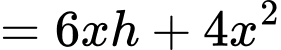
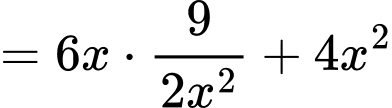
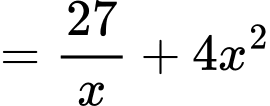
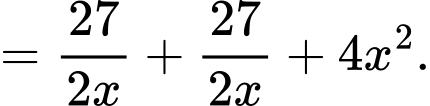
Áp dụng bất đẳng thức Cô- si cho 3 số không âm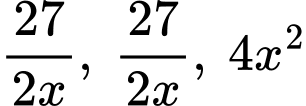 ta có:
ta có:
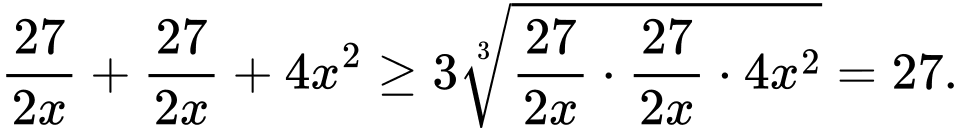
Do đó: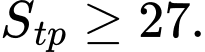
Dấu bằng xảy ra khi: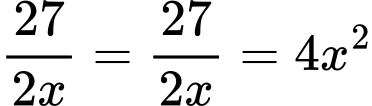
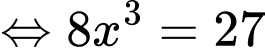
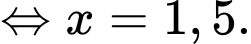
Vậy sau khi hoàn thành kiện hàng đó, người ta cần bỏ ra ít nhất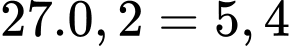 (triệu đồng).
(triệu đồng).
Gọi chiều dài đáy hình chữ nhật của hình lăng trụ là
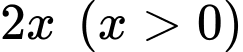 khi đó chiều rộng của đáy hình chữ nhật hình lăng trụ là
khi đó chiều rộng của đáy hình chữ nhật hình lăng trụ là 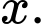
Chiều cao lăng trụ là
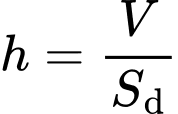
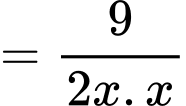
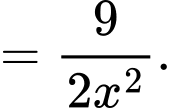
Diện tích toàn phần của hình lăng trụ là:
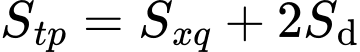
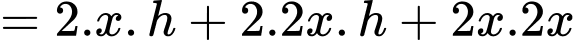
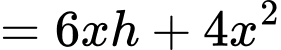
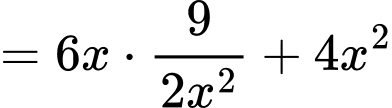
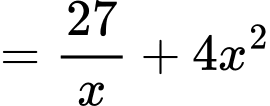
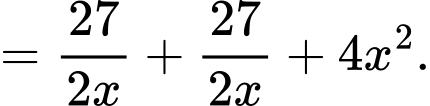
Áp dụng bất đẳng thức Cô- si cho 3 số không âm
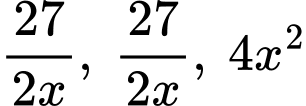 ta có:
ta có: 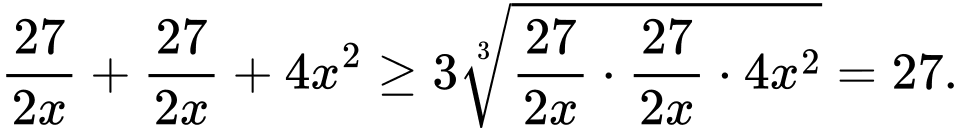
Do đó:
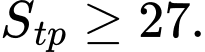
Dấu bằng xảy ra khi:
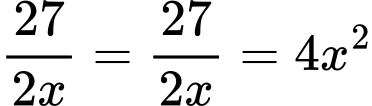
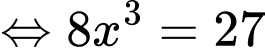
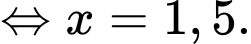
Vậy sau khi hoàn thành kiện hàng đó, người ta cần bỏ ra ít nhất
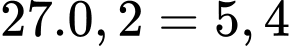 (triệu đồng).
(triệu đồng).
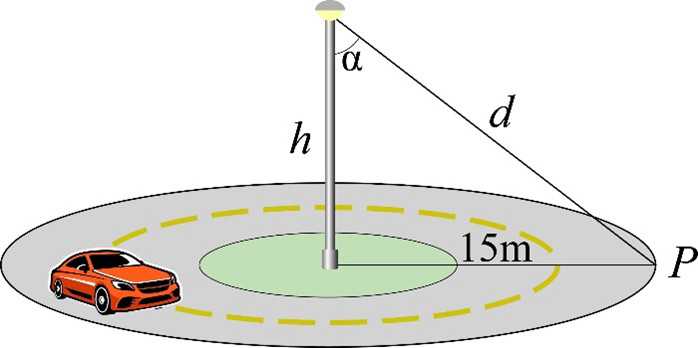
Câu 20 [715980]: Người ta đặt một ngọn đèn trên đỉnh một cột cao 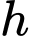 (mét) để chiếu sáng một vòng tròn giao thông đông đúc có bán kính
(mét) để chiếu sáng một vòng tròn giao thông đông đúc có bán kính  (mét). Cường độ chiếu sáng
(mét). Cường độ chiếu sáng 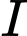 tại bất kỳ điểm
tại bất kỳ điểm 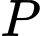 nào nằm trên vòng tròn đều tỉ lệ thuận với côsin của góc
nào nằm trên vòng tròn đều tỉ lệ thuận với côsin của góc 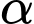 (xem hình vẽ) và tỉ lệ nghịch với bình phương khoảng cách
(xem hình vẽ) và tỉ lệ nghịch với bình phương khoảng cách 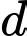 từ nguồn sáng. Cột đèn phải cao bao nhiêu mét để
từ nguồn sáng. Cột đèn phải cao bao nhiêu mét để 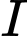 đạt giá trị lớn nhất? (kết quả làm tròn đến hàng phần chục).
đạt giá trị lớn nhất? (kết quả làm tròn đến hàng phần chục).
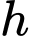 (mét) để chiếu sáng một vòng tròn giao thông đông đúc có bán kính
(mét) để chiếu sáng một vòng tròn giao thông đông đúc có bán kính  (mét). Cường độ chiếu sáng
(mét). Cường độ chiếu sáng 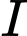 tại bất kỳ điểm
tại bất kỳ điểm 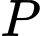 nào nằm trên vòng tròn đều tỉ lệ thuận với côsin của góc
nào nằm trên vòng tròn đều tỉ lệ thuận với côsin của góc 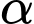 (xem hình vẽ) và tỉ lệ nghịch với bình phương khoảng cách
(xem hình vẽ) và tỉ lệ nghịch với bình phương khoảng cách 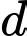 từ nguồn sáng. Cột đèn phải cao bao nhiêu mét để
từ nguồn sáng. Cột đèn phải cao bao nhiêu mét để 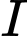 đạt giá trị lớn nhất? (kết quả làm tròn đến hàng phần chục).
đạt giá trị lớn nhất? (kết quả làm tròn đến hàng phần chục).
Điền đáp án: 10,6.
Trong hình vẽ ta có: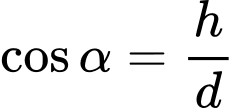 và
và 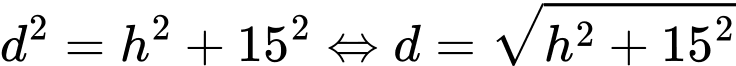 (theo định lí Pythagore).
(theo định lí Pythagore).
Ta có: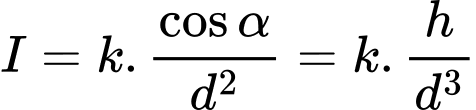
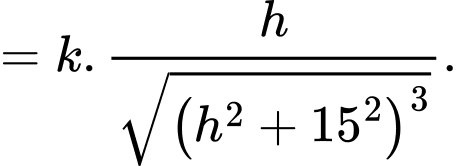
Cách 1: Xét hàm số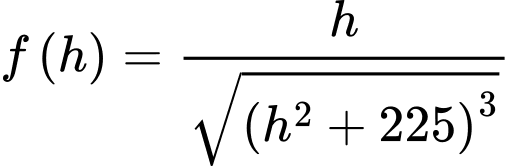 ta dùng máy tính Casio ta có
ta dùng máy tính Casio ta có 
Cách 2: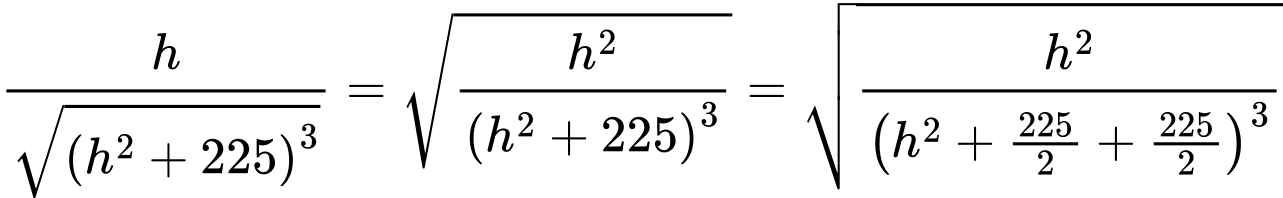
Áp dụng BĐT: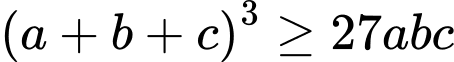
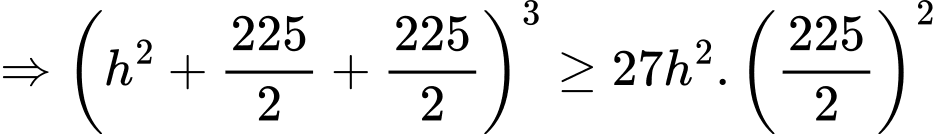
Suy ra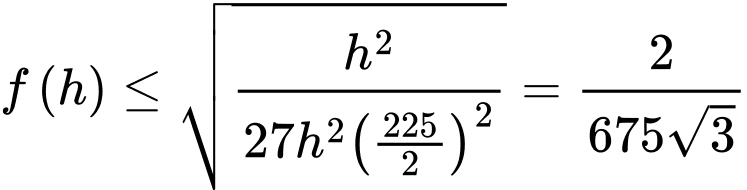 đạt được khi
đạt được khi 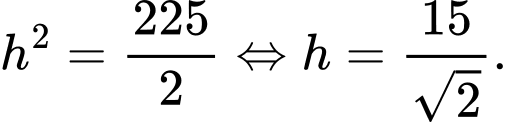
Và giá trị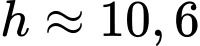 là giá trị làm cho
là giá trị làm cho 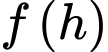 lớn nhất.
lớn nhất.
Trong hình vẽ ta có:
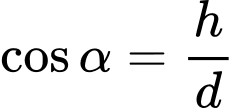 và
và 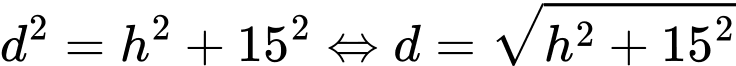 (theo định lí Pythagore).
(theo định lí Pythagore). Ta có:
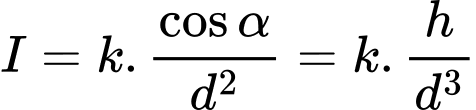
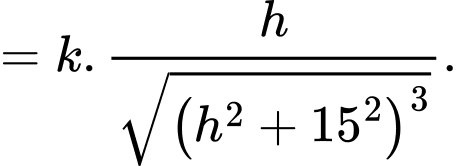
Cách 1: Xét hàm số
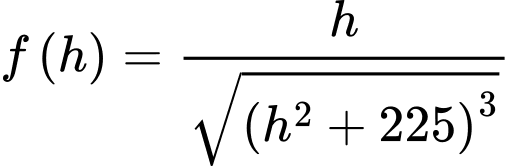 ta dùng máy tính Casio ta có
ta dùng máy tính Casio ta có 
Cách 2:
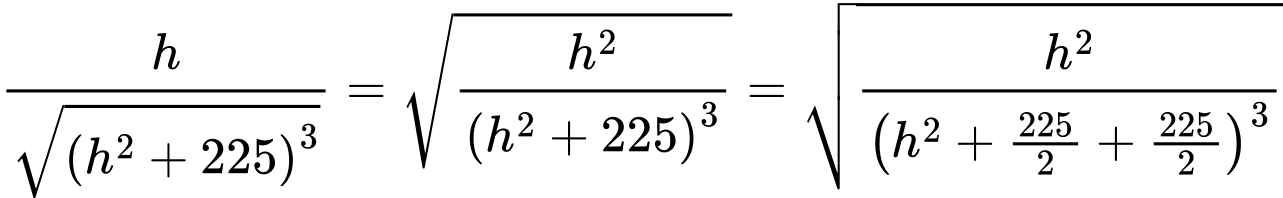
Áp dụng BĐT:
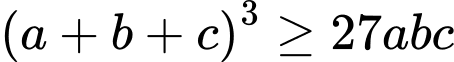
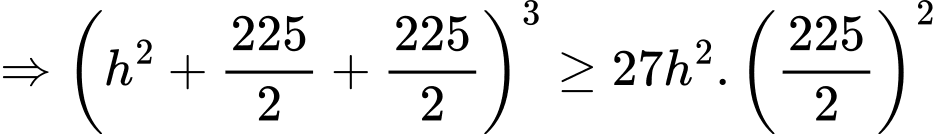
Suy ra
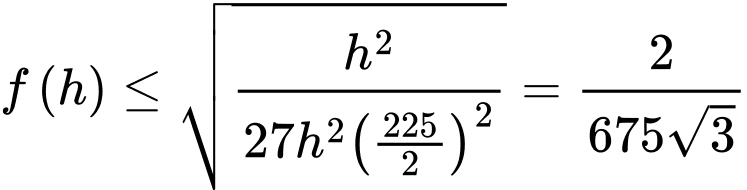 đạt được khi
đạt được khi 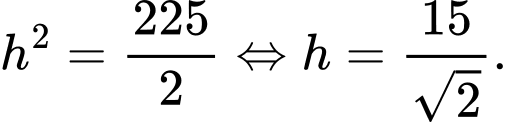
Và giá trị
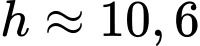 là giá trị làm cho
là giá trị làm cho 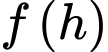 lớn nhất.
lớn nhất.
Câu 21 [713220]: Một cửa hàng nhận làm những chiếc xô bằng nhôm hình trụ có dung tích  (lít), không có nắp để chứa nước. Gọi
(lít), không có nắp để chứa nước. Gọi  là bán kính đáy của chiếc xô và
là bán kính đáy của chiếc xô và 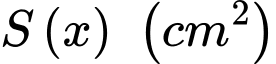 là diện tích nhôm cần dùng để làm một cái xô như vậy, giả sử diện tích các mối hàn không đáng kể, hỏi công ty cần ít nhất bao nhiêu
là diện tích nhôm cần dùng để làm một cái xô như vậy, giả sử diện tích các mối hàn không đáng kể, hỏi công ty cần ít nhất bao nhiêu 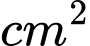 nhôm để làm một chiếc xô như vậy (làm tròn kết quả đến hàng đơn vị).
nhôm để làm một chiếc xô như vậy (làm tròn kết quả đến hàng đơn vị).

 (lít), không có nắp để chứa nước. Gọi
(lít), không có nắp để chứa nước. Gọi  là bán kính đáy của chiếc xô và
là bán kính đáy của chiếc xô và 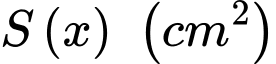 là diện tích nhôm cần dùng để làm một cái xô như vậy, giả sử diện tích các mối hàn không đáng kể, hỏi công ty cần ít nhất bao nhiêu
là diện tích nhôm cần dùng để làm một cái xô như vậy, giả sử diện tích các mối hàn không đáng kể, hỏi công ty cần ít nhất bao nhiêu 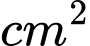 nhôm để làm một chiếc xô như vậy (làm tròn kết quả đến hàng đơn vị).
nhôm để làm một chiếc xô như vậy (làm tròn kết quả đến hàng đơn vị).
Điền đáp án: 2303.
Chiều cao khối trụ là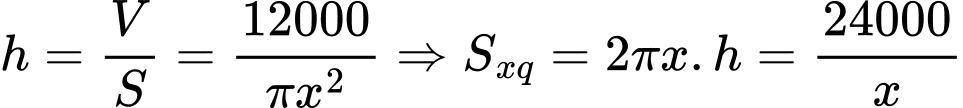
Ta có: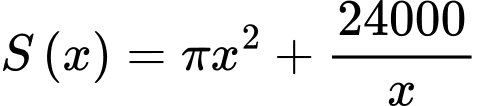
Cách 1: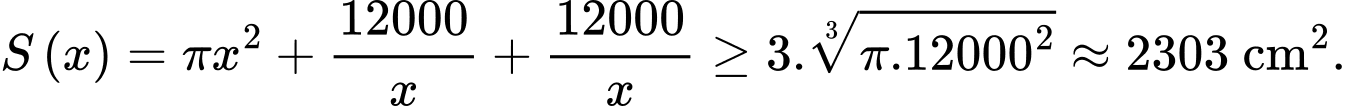
Cách 2: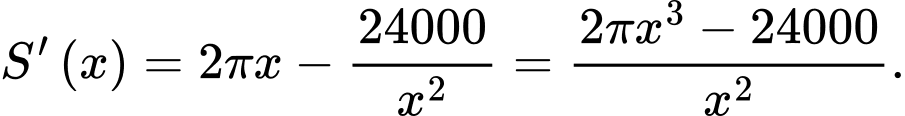
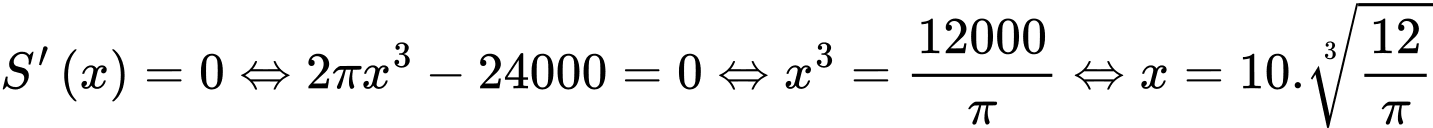
Suy ra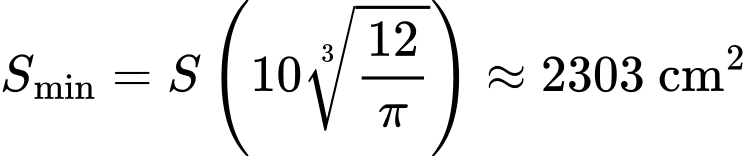
Chiều cao khối trụ là
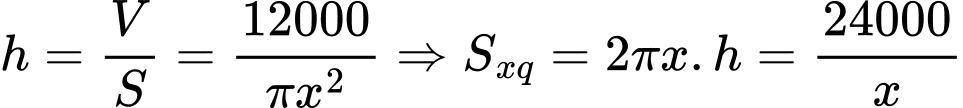
Ta có:
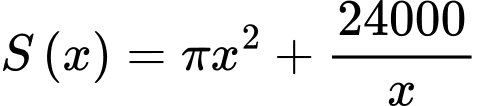
Cách 1:
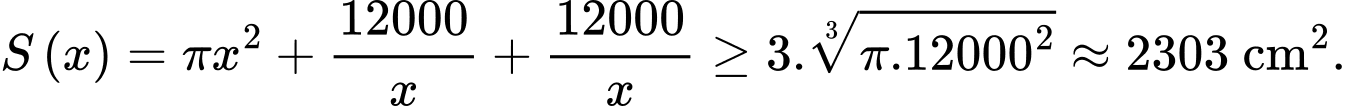
Cách 2:
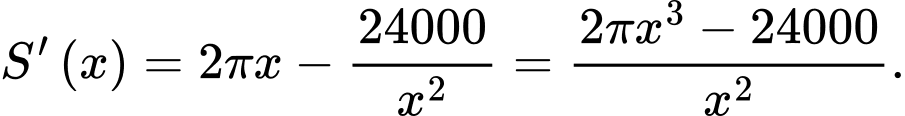
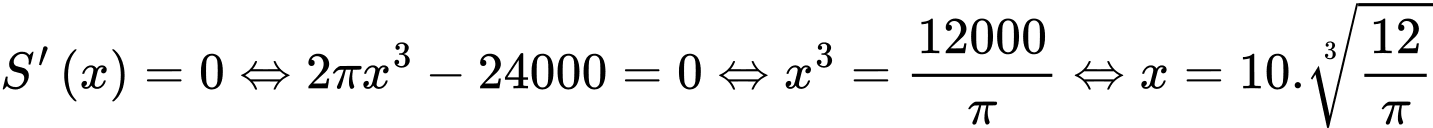
Suy ra
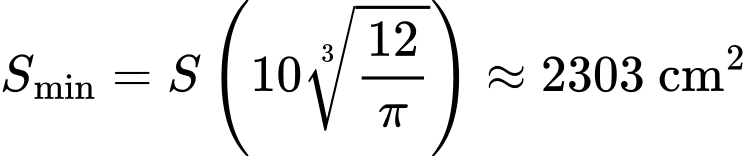
Câu 22 [715757]: Từ một tấm bìa lục giác đều cạnh 20 cm, bạn Tuấn muốn làm một hình chóp lục giác đều bằng cách cắt bỏ phần tô đậm và dán các mép lại với nhau (các mối ghép nổi có kích thước không đăng kể, tham khảo hình vẽ). Thể tích hình chóp lục giác đều tạo thành lớn nhất là bao nhiêu  (làm tròn kết quả đến hàng đơn vị)
(làm tròn kết quả đến hàng đơn vị)
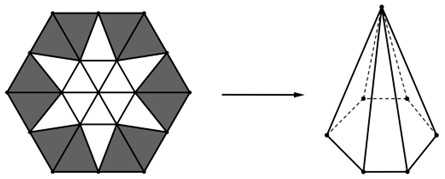
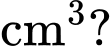 (làm tròn kết quả đến hàng đơn vị)
(làm tròn kết quả đến hàng đơn vị)
Điền đáp án: 429.
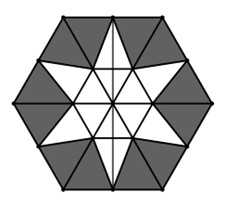
Đặt cạnh đáy của chóp lục giác đều là thì
thì 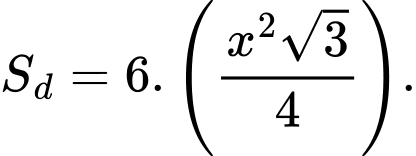
Độ dài đường cao của mặt bên chóp lục giác đều là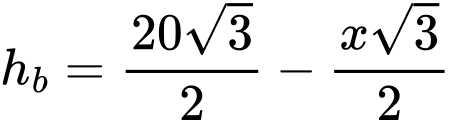
Chiều cao của lục giác đều là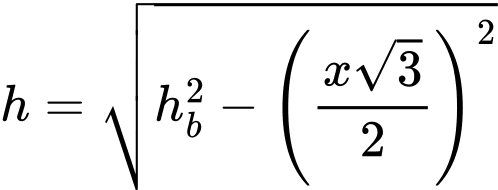
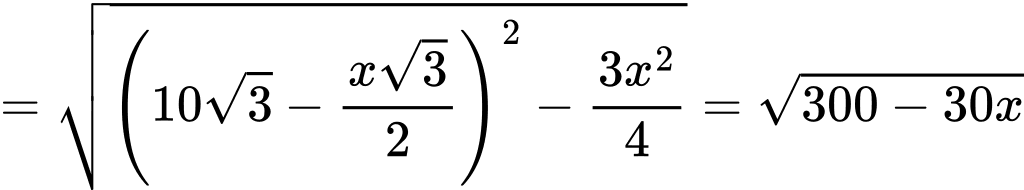
Thể tích khối chóp thu được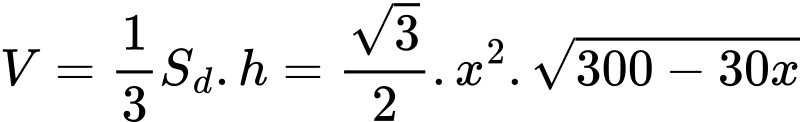
Ta có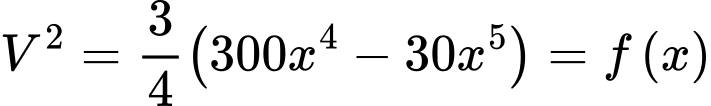
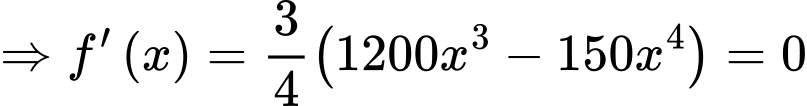
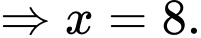
Suy ra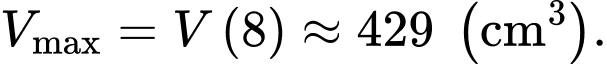

Đặt cạnh đáy của chóp lục giác đều là
 thì
thì 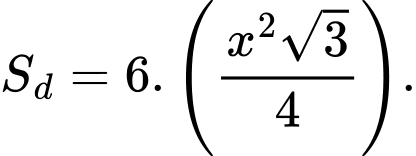
Độ dài đường cao của mặt bên chóp lục giác đều là
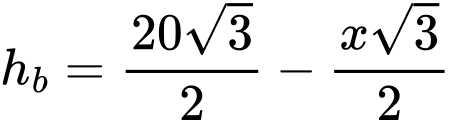
Chiều cao của lục giác đều là
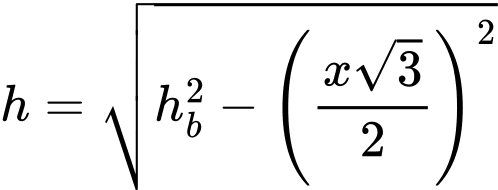
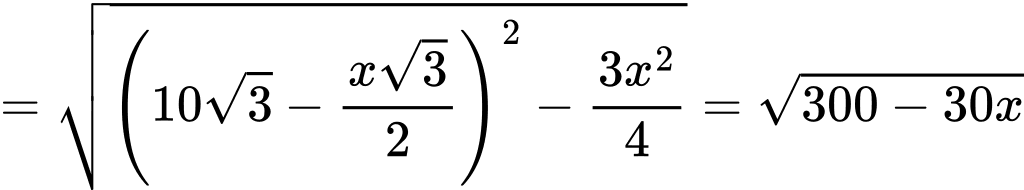
Thể tích khối chóp thu được
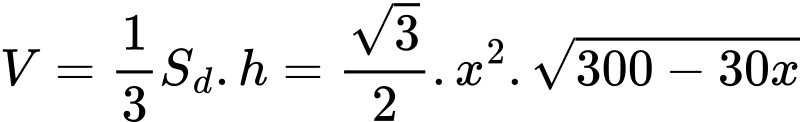
Ta có
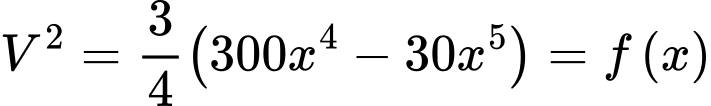
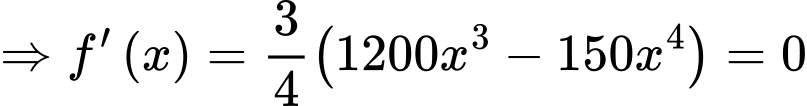
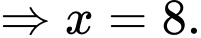
Suy ra