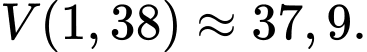PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1 [713206]: Cho hàm số 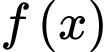 đồng biến trên tập số thực
đồng biến trên tập số thực 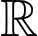 , mệnh đề nào sau đây là đúng?
, mệnh đề nào sau đây là đúng?
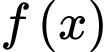 đồng biến trên tập số thực
đồng biến trên tập số thực  , mệnh đề nào sau đây là đúng?
, mệnh đề nào sau đây là đúng? A, Với mọi 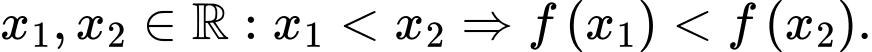
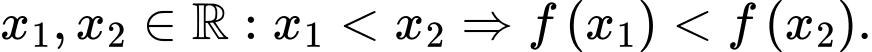
B, Với mọi 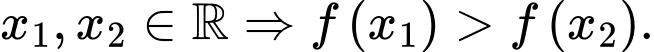
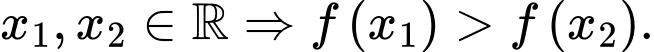
C, Với mọi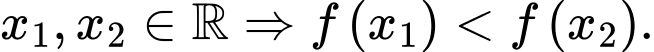
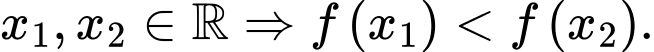
D, Với mọi 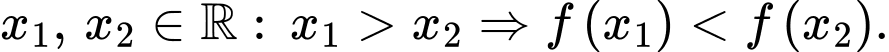
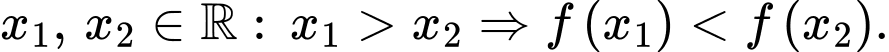
Chọn đáp án A.
Theo định nghĩa về tính đơn điệu của hàm số suy ra A đúng. Đáp án: A
Theo định nghĩa về tính đơn điệu của hàm số suy ra A đúng. Đáp án: A
Câu 2 [6335]: Cho hàm số 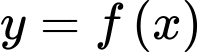 có bảng biến thiên như sau:
có bảng biến thiên như sau:
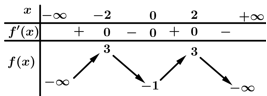
Hàm số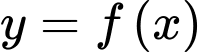 nghịch biến trên khoảng nào dưới đây?
nghịch biến trên khoảng nào dưới đây?
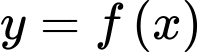 có bảng biến thiên như sau:
có bảng biến thiên như sau:
Hàm số
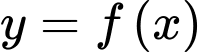 nghịch biến trên khoảng nào dưới đây?
nghịch biến trên khoảng nào dưới đây? A, 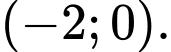
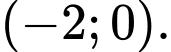
B, 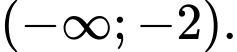
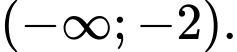
C, 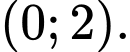
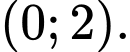
D, 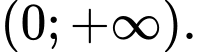
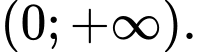
Hàm số 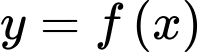 nghịch biến trên mỗi khoảng
nghịch biến trên mỗi khoảng 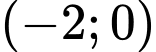 và
và 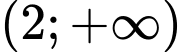 . Đáp án: A
. Đáp án: A
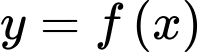 nghịch biến trên mỗi khoảng
nghịch biến trên mỗi khoảng 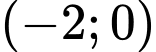 và
và 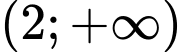 . Đáp án: A
. Đáp án: A
Câu 3 [545825]: Cho hàm số 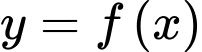 có bảng biến thiên như hình vẽ sau:
có bảng biến thiên như hình vẽ sau:
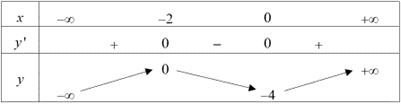
Giá trị cực tiểu của hàm số đã cho là
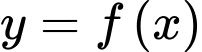 có bảng biến thiên như hình vẽ sau:
có bảng biến thiên như hình vẽ sau:
Giá trị cực tiểu của hàm số đã cho là
A,  .
.
 .
.B, 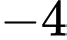 .
.
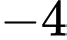 .
.C, 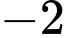 .
.
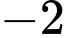 .
.D, 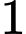 .
.
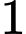 .
.
Quan sát BBT của hàm số 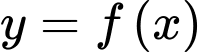 suy ra giá trị cực tiểu của
suy ra giá trị cực tiểu của 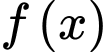 là
là 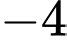 . Đáp án: B
. Đáp án: B
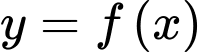 suy ra giá trị cực tiểu của
suy ra giá trị cực tiểu của 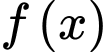 là
là 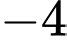 . Đáp án: B
. Đáp án: B
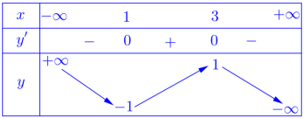
Câu 4 [377720]: Cho hàm số 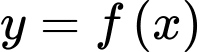 có bảng biến thiên như hình vẽ bên. Khẳng định nào dưới đây đúng?
có bảng biến thiên như hình vẽ bên. Khẳng định nào dưới đây đúng?
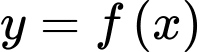 có bảng biến thiên như hình vẽ bên. Khẳng định nào dưới đây đúng?
có bảng biến thiên như hình vẽ bên. Khẳng định nào dưới đây đúng?
A, Hàm số đã cho đồng biến trên khoảng 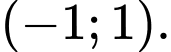
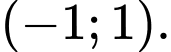
B, Hàm số đã cho đồng biến trên khoảng 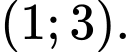
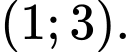
C, Hàm số đã cho có một điểm cực trị.
D, Hàm số đã cho đạt cực đại tại 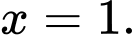
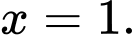
Phương pháp:
Dựa vào bảng biến thiên.
Cách giải:
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng (1;3).
Chọn B. Đáp án: B
Dựa vào bảng biến thiên.
Cách giải:
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng (1;3).
Chọn B. Đáp án: B
Câu 5 [399672]: Hàm số 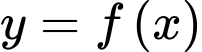 liên tục trên
liên tục trên 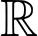 và có bảng biến thiên như hình bên dưới
và có bảng biến thiên như hình bên dưới
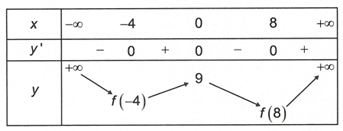
Biết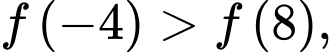 khi đó giá trị nhỏ nhất của hàm số đã cho trên
khi đó giá trị nhỏ nhất của hàm số đã cho trên 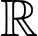 bằng
bằng
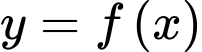 liên tục trên
liên tục trên 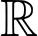 và có bảng biến thiên như hình bên dưới
và có bảng biến thiên như hình bên dưới

Biết
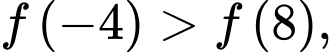 khi đó giá trị nhỏ nhất của hàm số đã cho trên
khi đó giá trị nhỏ nhất của hàm số đã cho trên 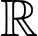 bằng
bằng A, 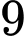
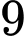
B, 

C, 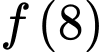
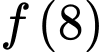
D, 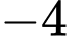
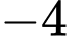
Từ bảng biến thiên ta có 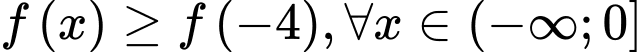 và
và 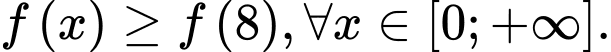
Mặt khác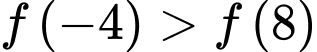 suy ra
suy ra 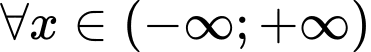 thì
thì 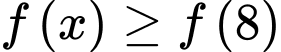
Vậy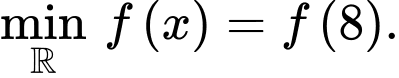 Đáp án: C
Đáp án: C
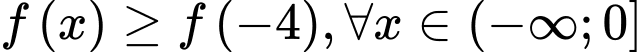 và
và 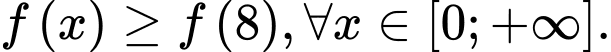
Mặt khác
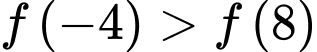 suy ra
suy ra 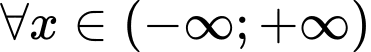 thì
thì 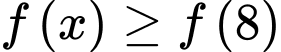
Vậy
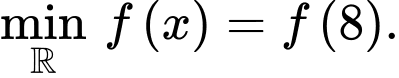 Đáp án: C
Đáp án: C
Câu 6 [909045]: Cho hàm số 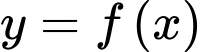 có bảng xét dấu đạo hàm như hình vẽ.
có bảng xét dấu đạo hàm như hình vẽ.
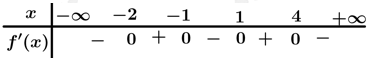
Số điểm cực trị của hàm số đã cho là
 có bảng xét dấu đạo hàm như hình vẽ.
có bảng xét dấu đạo hàm như hình vẽ.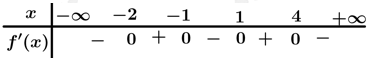
Số điểm cực trị của hàm số đã cho là
A, 
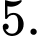
B, 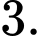
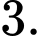
C, 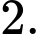
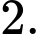
D, 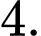
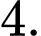
Chọn D
Dựa vào bảng xét dấu,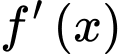 đổi dấu khi qua các điểm
đổi dấu khi qua các điểm 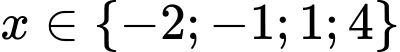 .
.
Vậy số điểm cực trị của hàm số đã cho là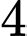 .
Đáp án: D
.
Đáp án: D
Dựa vào bảng xét dấu,
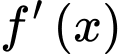 đổi dấu khi qua các điểm
đổi dấu khi qua các điểm 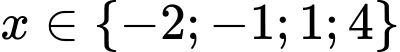 .
.Vậy số điểm cực trị của hàm số đã cho là
 .
Đáp án: D
.
Đáp án: D
Câu 7 [545842]: Giá trị nhỏ nhất của hàm số 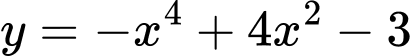 trên đoạn
trên đoạn 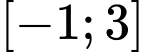 bằng
bằng
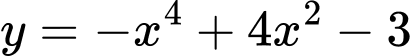 trên đoạn
trên đoạn 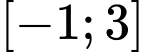 bằng
bằng A, 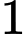 .
.
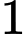 .
.B, 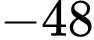 .
.
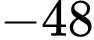 .
.C,  .
.
 .
.D, 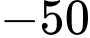 .
.
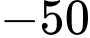 .
.
Xét 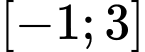
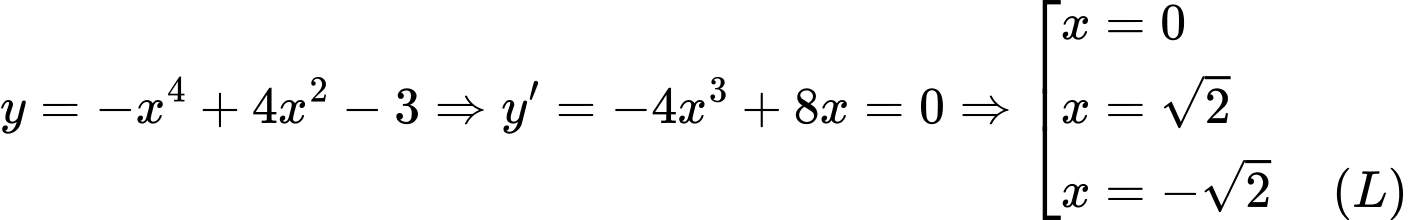
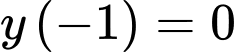
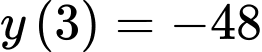
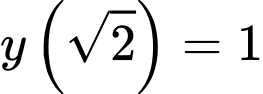 Đáp án: B
Đáp án: B
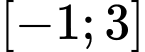
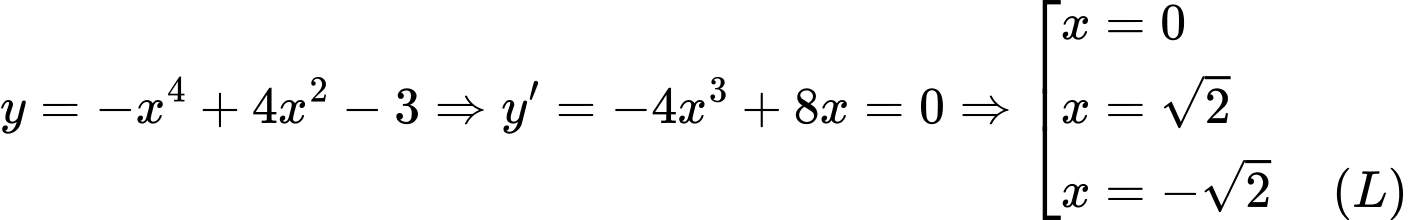
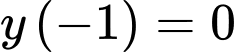
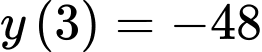
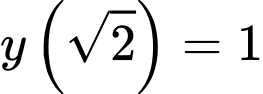 Đáp án: B
Đáp án: B
Câu 8 [378327]: Giá trị cực đại của hàm số 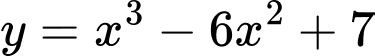 là
là
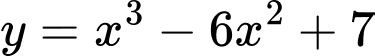 là
là A, 7.
B, -25.
C, -9.
D, 2.
Phương pháp:
Tính đạo hàm và lập bảng biến thiên
Cách giải:
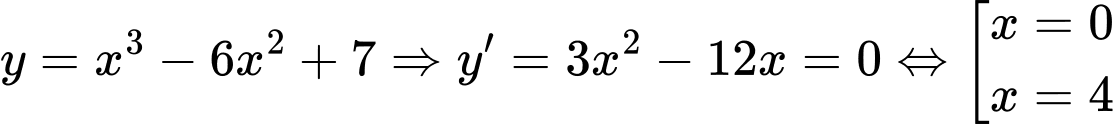
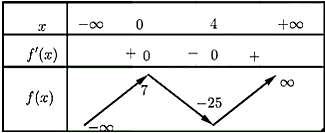
Từ bbt suy ra hàm số có giá trị cực đại bằng 7 Đáp án: A
Tính đạo hàm và lập bảng biến thiên
Cách giải:
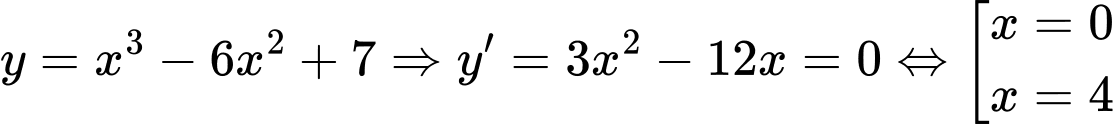

Từ bbt suy ra hàm số có giá trị cực đại bằng 7 Đáp án: A
Câu 9 [306987]: Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số 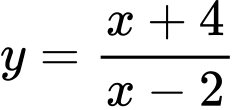 trên đoạn
trên đoạn 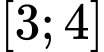 là
là 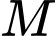 và
và 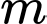 , khi đó
, khi đó 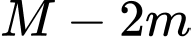 bằng
bằng
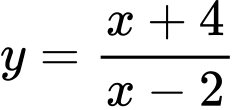 trên đoạn
trên đoạn 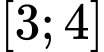 là
là 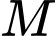 và
và 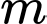 , khi đó
, khi đó 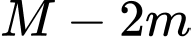 bằng
bằng A, 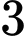 .
.
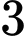 .
.B, 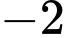 .
.
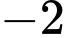 .
.C, 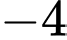 .
.
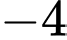 .
.D, 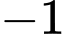 .
.
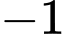 .
.
Chọn D
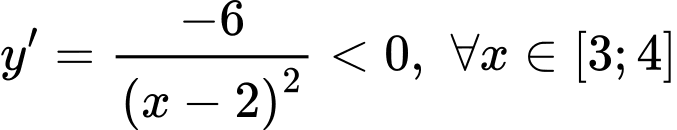
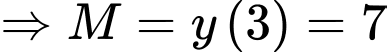 và
và 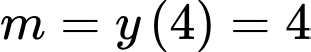 .
.
Vậy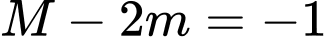 . Đáp án: D
. Đáp án: D
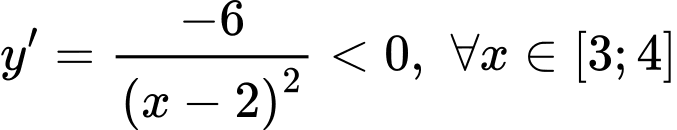
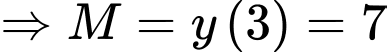 và
và 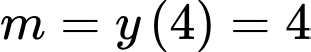 .
.
Vậy
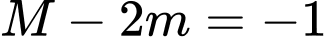 . Đáp án: D
. Đáp án: D
Câu 10 [391029]: Cho hàm số 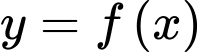 có đạo hàm là
có đạo hàm là 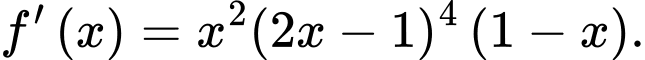 Số điểm cực trị của hàm số đã cho là
Số điểm cực trị của hàm số đã cho là
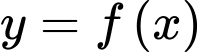 có đạo hàm là
có đạo hàm là 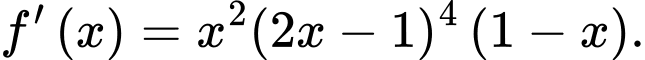 Số điểm cực trị của hàm số đã cho là
Số điểm cực trị của hàm số đã cho là A, 4.
B, 0.
C, 2.
D, 1.
Phương pháp:
Điểm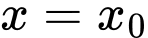 là điểm cực trị của hàm số
là điểm cực trị của hàm số 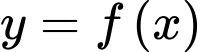 nếu
nếu 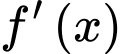 đổi dấu qua
đổi dấu qua 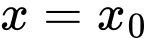
Cách giải:
Ta có: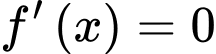

Do đó hàm số đã cho có 1 điểm cực trị
Chọn D. Đáp án: D
Điểm
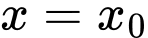 là điểm cực trị của hàm số
là điểm cực trị của hàm số 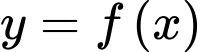 nếu
nếu 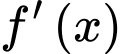 đổi dấu qua
đổi dấu qua 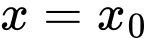
Cách giải:
Ta có:
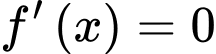

Do đó hàm số đã cho có 1 điểm cực trị
Chọn D. Đáp án: D
Câu 11 [538497]: Hàm số nào sau đây không đồng biến trên khoảng 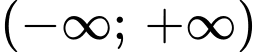 ?
?
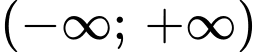 ?
? A, 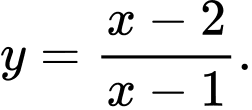
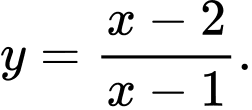
B, 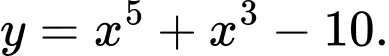
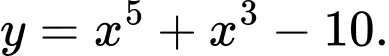
C, 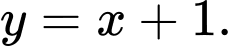
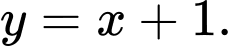
D, 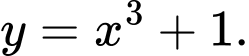
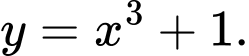
Chọn đáp án A.
Vì tính đơn điệu sẽ được xét trên tập xác định của hàm số, nên ta dễ dàng thấy được đáp án A sai. Vì tập xác định của đáp án A là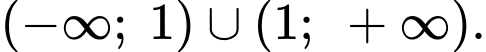
Các đáp án còn lại các em tự kiểm tra nhé! Đáp án: A
Vì tính đơn điệu sẽ được xét trên tập xác định của hàm số, nên ta dễ dàng thấy được đáp án A sai. Vì tập xác định của đáp án A là
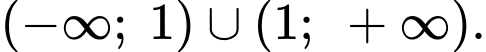
Các đáp án còn lại các em tự kiểm tra nhé! Đáp án: A
Câu 12 [546639]: Cho hàm số 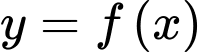 có đạo hàm
có đạo hàm 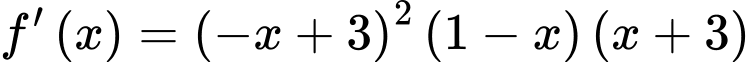 với mọi
với mọi 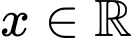 . Hàm số đã cho đồng biến trên khoảng nào dưới đây?
. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
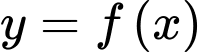 có đạo hàm
có đạo hàm 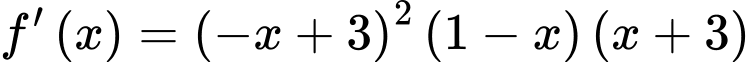 với mọi
với mọi 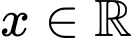 . Hàm số đã cho đồng biến trên khoảng nào dưới đây?
. Hàm số đã cho đồng biến trên khoảng nào dưới đây? A, 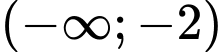 .
.
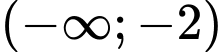 .
.B, 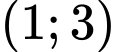 .
.
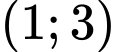 .
.C, 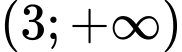 .
.
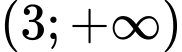 .
.D, 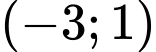 .
.
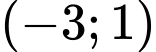 .
.
Chọn D 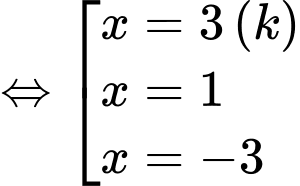
Cho 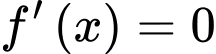
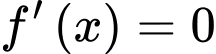
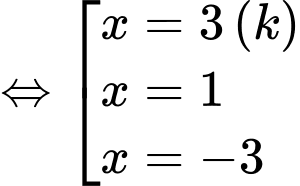
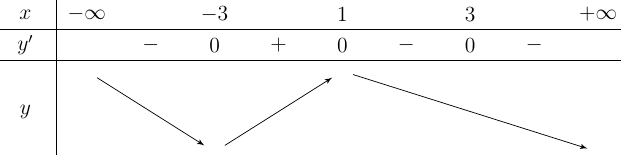
Bảng biến thiên:

Dựa vào bảng biến thiên hàm số đồng biến trên khoảng 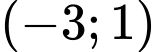
Đáp án: D 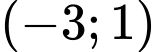
PHẦN II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a),b),c),d) ở mỗi câu học sinh chọn đúng hoặc sai.
Câu 13 [599928]: Cho hàm số 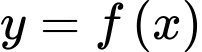 có đạo hàm
có đạo hàm 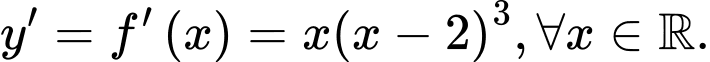 Các mệnh đề sau đúng hay sai?
Các mệnh đề sau đúng hay sai?
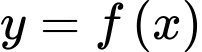 có đạo hàm
có đạo hàm 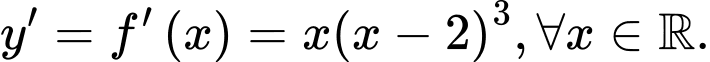 Các mệnh đề sau đúng hay sai?
Các mệnh đề sau đúng hay sai?
a) Đúng; b) Sai; c) Sai; d) Sai
Ta có: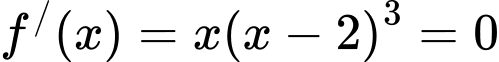

Bảng biến thiên:
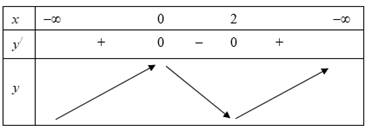
Từ bảng biến thiên ta có:
Hàm số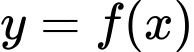 có hai điểm cực trị (1 điểm cực đại và 1 điểm cực tiểu) do vậy mệnh đề a) đúng và mệnh đề b) sai
có hai điểm cực trị (1 điểm cực đại và 1 điểm cực tiểu) do vậy mệnh đề a) đúng và mệnh đề b) sai
Trên khoảng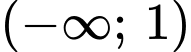 hàm
hàm 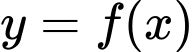 vừa tăng vừa giảm nên mệnh đề c) sai
vừa tăng vừa giảm nên mệnh đề c) sai
Hàm số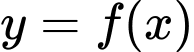 đồng biến trên khoảng
đồng biến trên khoảng 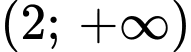 suy ra
suy ra 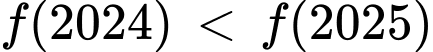 nên mệnh đề d) sai.
nên mệnh đề d) sai.
Ta có:
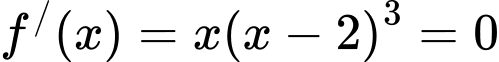

Bảng biến thiên:

Từ bảng biến thiên ta có:
Hàm số
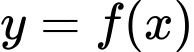 có hai điểm cực trị (1 điểm cực đại và 1 điểm cực tiểu) do vậy mệnh đề a) đúng và mệnh đề b) sai
có hai điểm cực trị (1 điểm cực đại và 1 điểm cực tiểu) do vậy mệnh đề a) đúng và mệnh đề b) saiTrên khoảng
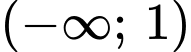 hàm
hàm 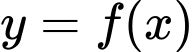 vừa tăng vừa giảm nên mệnh đề c) sai
vừa tăng vừa giảm nên mệnh đề c) saiHàm số
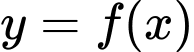 đồng biến trên khoảng
đồng biến trên khoảng 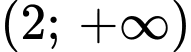 suy ra
suy ra 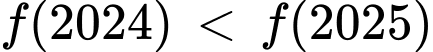 nên mệnh đề d) sai.
nên mệnh đề d) sai.
Câu 14 [774132]: Cho hàm số 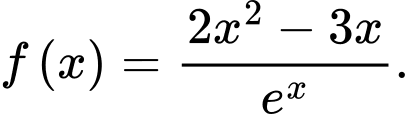
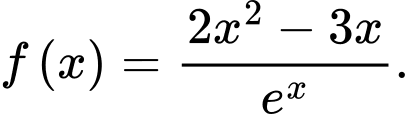
a) Sai.
Điều kiện xác định: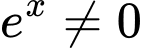 thỏa mãn với mọi giá trị của
thỏa mãn với mọi giá trị của 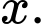 Nên tập xác định của hàm số đã cho là
Nên tập xác định của hàm số đã cho là 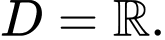
b) Sai.
Áp dụng công thức đạo hàm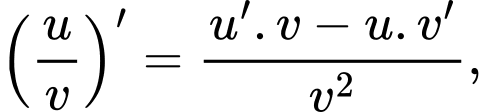 ta có
ta có
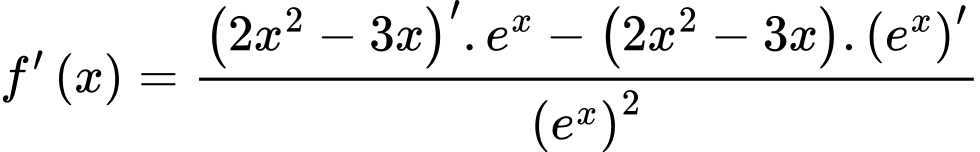
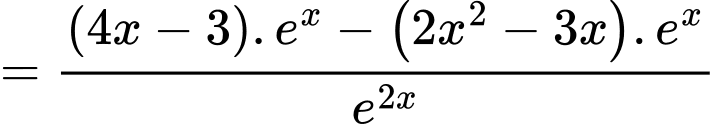
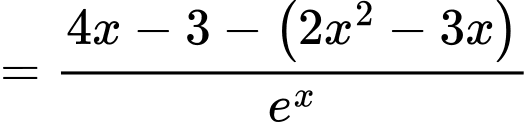
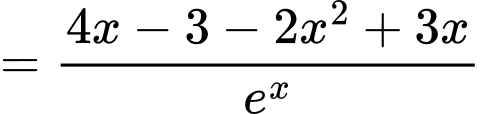
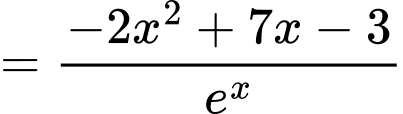
c) Đúng.
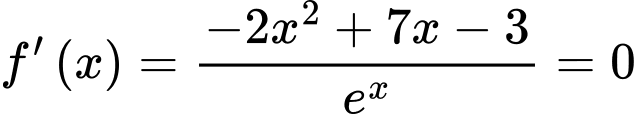
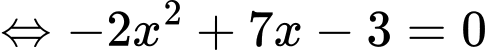
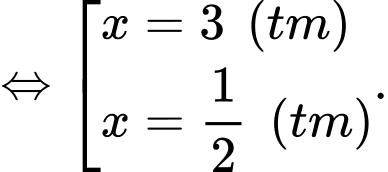
Vậy phương trình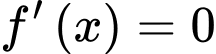 có hai nghiệm phân biệt trong khoảng
có hai nghiệm phân biệt trong khoảng 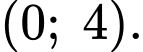
d) Đúng.
Xét hàm số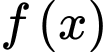 trong khoảng
trong khoảng 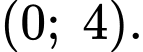
Dựa vào kết quả phần c) ta có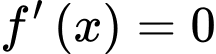
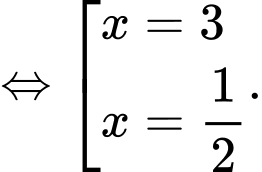
Bảng biến thiên
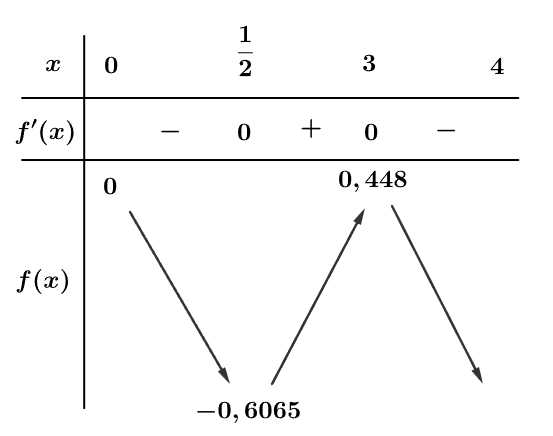
Vậy giá trị lớn nhất của hàm số là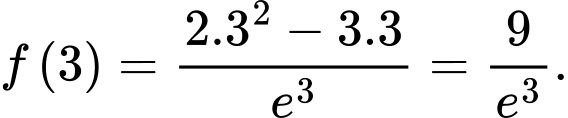
Điều kiện xác định:
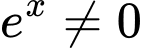 thỏa mãn với mọi giá trị của
thỏa mãn với mọi giá trị của 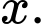 Nên tập xác định của hàm số đã cho là
Nên tập xác định của hàm số đã cho là 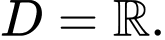
b) Sai.
Áp dụng công thức đạo hàm
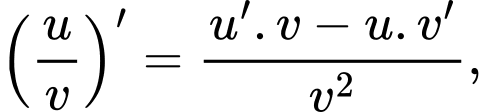 ta có
ta có
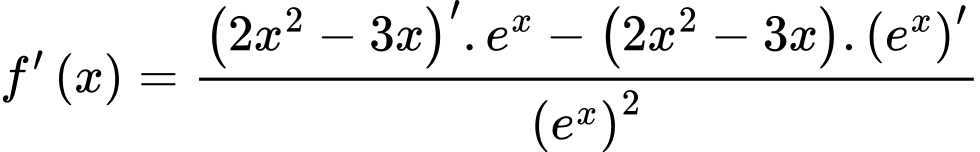
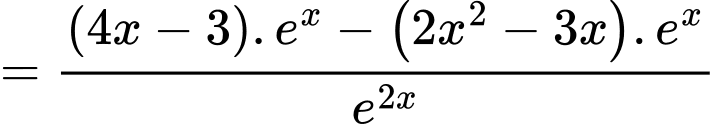
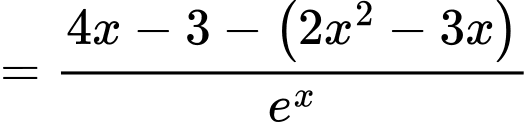
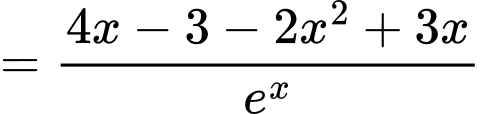
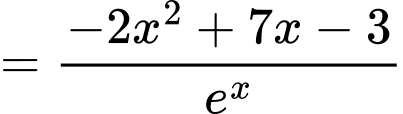
c) Đúng.
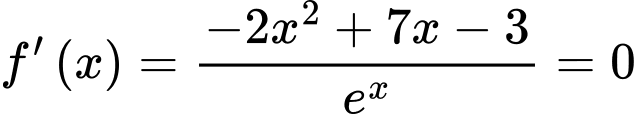
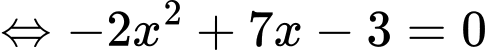
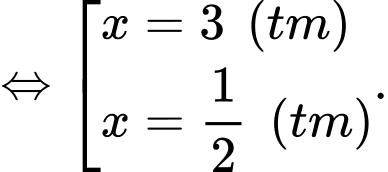
Vậy phương trình
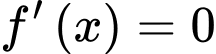 có hai nghiệm phân biệt trong khoảng
có hai nghiệm phân biệt trong khoảng 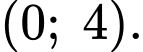
d) Đúng.
Xét hàm số
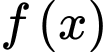 trong khoảng
trong khoảng 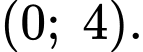
Dựa vào kết quả phần c) ta có
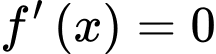
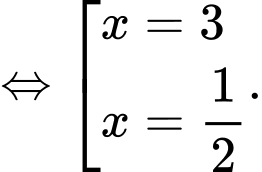
Bảng biến thiên

Vậy giá trị lớn nhất của hàm số là
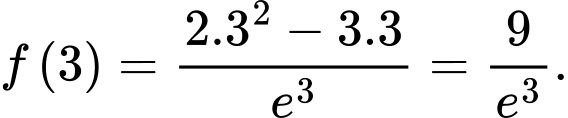
Câu 15 [717145]: Một chất điểm chuyển động trong  giây đầu tiên theo phương trình
giây đầu tiên theo phương trình 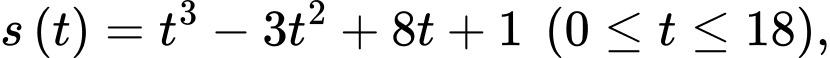 trong đó
trong đó 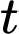 tính bằng giây và
tính bằng giây và 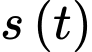 tính bằng mét.
tính bằng mét.
 giây đầu tiên theo phương trình
giây đầu tiên theo phương trình 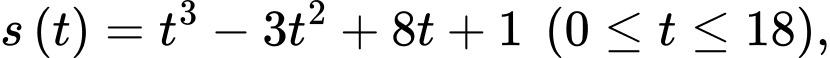 trong đó
trong đó 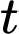 tính bằng giây và
tính bằng giây và 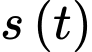 tính bằng mét.
tính bằng mét.
a) Đúng.
Vận tốc của chất điểm tại thời điểm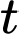 là:
là: 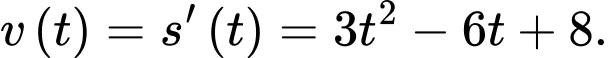
Suy ra vận tốc của chất điểm tại thời điểm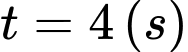 bằng
bằng 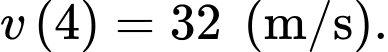
b) Đúng.
Tại thời điểm mà chất điểm di chuyển được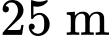 ta có:
ta có: 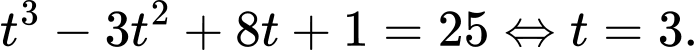
Vận tốc khi đó bằng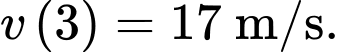
c) Sai.
Vì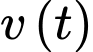 là hàm số bậc hai với hệ số của
là hàm số bậc hai với hệ số của 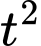 là:
là: 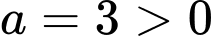 , đồ thị của
, đồ thị của 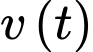 có dạng parabol bề lõm hướng lên.
có dạng parabol bề lõm hướng lên.
Do đó hàm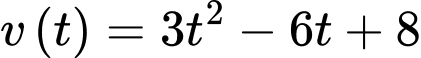 đạt giá trị nhỏ nhất trên
đạt giá trị nhỏ nhất trên 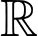 khi
khi 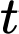 là hoành độ của đỉnh parabol
là hoành độ của đỉnh parabol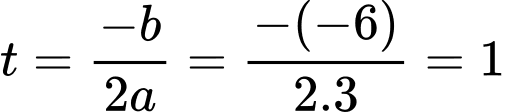 (
(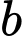 là hệ số của
là hệ số của 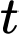 trong hàm
trong hàm 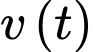 )
)
Khi đó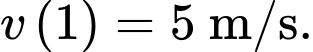
d) Sai.
Gia tốc tức thời tại thời điểm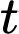 là:
là: 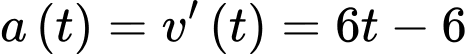 .
.
Gia tốc tại thời điểm chất điểm đạt vận tốc nhỏ nhất bằng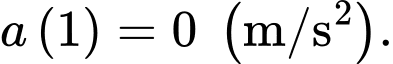
Vận tốc của chất điểm tại thời điểm
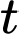 là:
là: 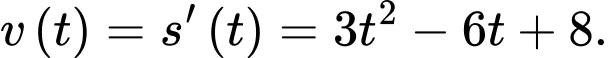
Suy ra vận tốc của chất điểm tại thời điểm
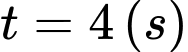 bằng
bằng 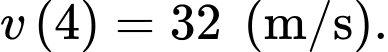
b) Đúng.
Tại thời điểm mà chất điểm di chuyển được
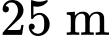 ta có:
ta có: 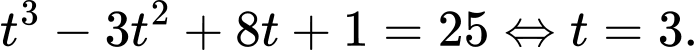
Vận tốc khi đó bằng
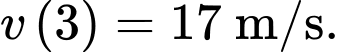
c) Sai.
Vì
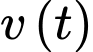 là hàm số bậc hai với hệ số của
là hàm số bậc hai với hệ số của 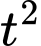 là:
là: 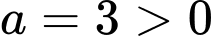 , đồ thị của
, đồ thị của 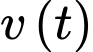 có dạng parabol bề lõm hướng lên.
có dạng parabol bề lõm hướng lên.Do đó hàm
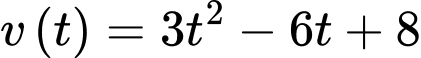 đạt giá trị nhỏ nhất trên
đạt giá trị nhỏ nhất trên 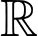 khi
khi 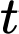 là hoành độ của đỉnh parabol
là hoành độ của đỉnh parabol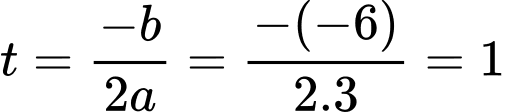 (
(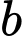 là hệ số của
là hệ số của 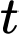 trong hàm
trong hàm 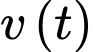 )
)Khi đó
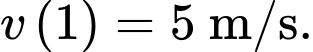
d) Sai.
Gia tốc tức thời tại thời điểm
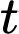 là:
là: 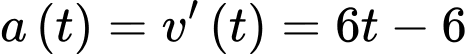 .
.Gia tốc tại thời điểm chất điểm đạt vận tốc nhỏ nhất bằng
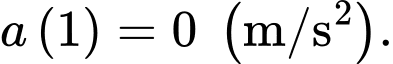
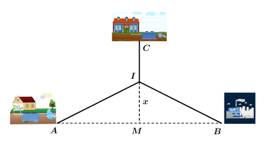
Câu 16 [695538]: Hai nhà máy được đặt tại các vị trí 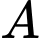 và
và 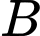 cách nhau 8 km. Nhà máy xử lí nước thải được đặt ở vị trí
cách nhau 8 km. Nhà máy xử lí nước thải được đặt ở vị trí  trên đường trung trực của đoạn thăng
trên đường trung trực của đoạn thăng  cách trung điểm
cách trung điểm 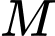 của đoạn thẳng
của đoạn thẳng  một khoảng là 3 km. Người ta muốn làm đường ống dẫn nước thải từ hai nhà máy
một khoảng là 3 km. Người ta muốn làm đường ống dẫn nước thải từ hai nhà máy 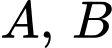 đến nhà máy xử lí nước thái
đến nhà máy xử lí nước thái  gồm các đoạn thẳng
gồm các đoạn thẳng 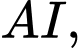
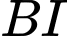 và
và 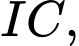 với
với 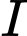 là vị trí nằm giữa
là vị trí nằm giữa 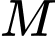 và
và 
Đặt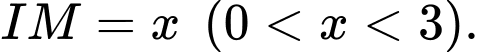
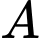 và
và 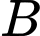 cách nhau 8 km. Nhà máy xử lí nước thải được đặt ở vị trí
cách nhau 8 km. Nhà máy xử lí nước thải được đặt ở vị trí  trên đường trung trực của đoạn thăng
trên đường trung trực của đoạn thăng  cách trung điểm
cách trung điểm 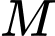 của đoạn thẳng
của đoạn thẳng  một khoảng là 3 km. Người ta muốn làm đường ống dẫn nước thải từ hai nhà máy
một khoảng là 3 km. Người ta muốn làm đường ống dẫn nước thải từ hai nhà máy 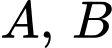 đến nhà máy xử lí nước thái
đến nhà máy xử lí nước thái  gồm các đoạn thẳng
gồm các đoạn thẳng 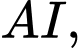
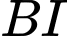 và
và 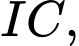 với
với 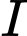 là vị trí nằm giữa
là vị trí nằm giữa 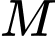 và
và 
Đặt
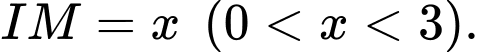

a) Sai.
Ta có: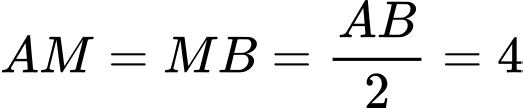
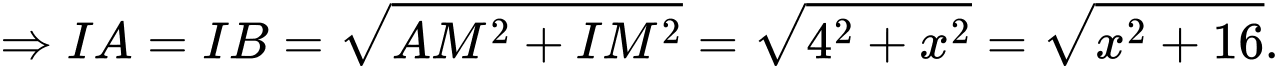
b) Sai.
Tổng độ dài đường ống được biểu diễn qua hàm số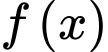 là:
là:
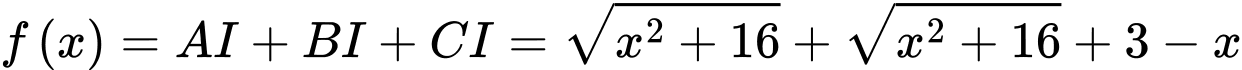
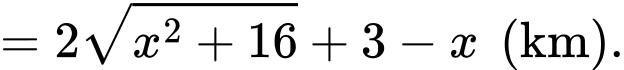
c) Đúng.
Ta có: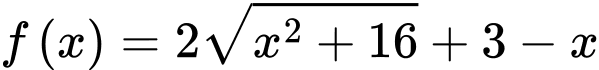
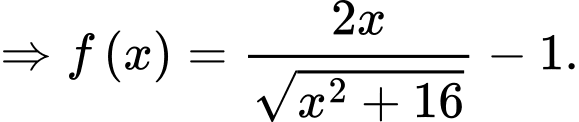
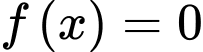
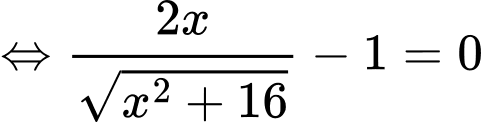

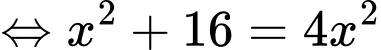
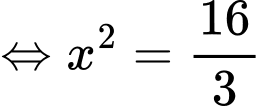
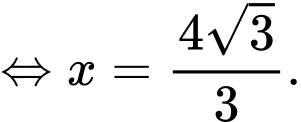
Bảng biến thiên hàm số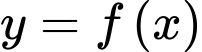 với
với 
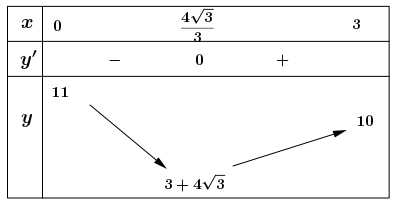
Dựa vào BBT ta có: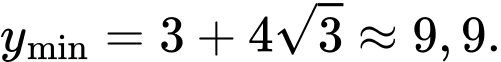
Vậy tổng độ dài đường ống nhỏ nhất bằng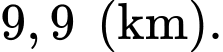
d) Đúng.
Khi tổng độ dài đường ống nhỏ nhất thì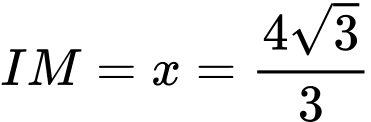
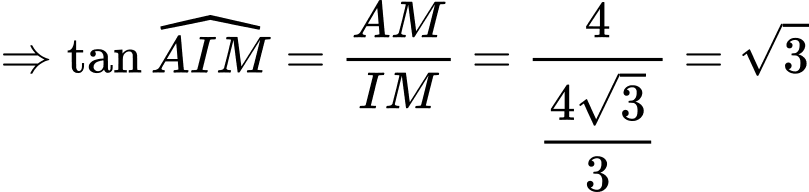
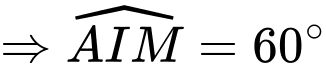
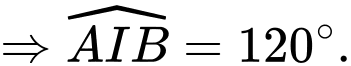
Ta có:
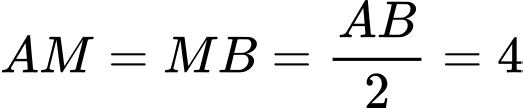
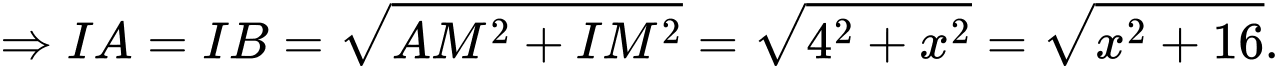
b) Sai.
Tổng độ dài đường ống được biểu diễn qua hàm số
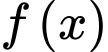 là:
là: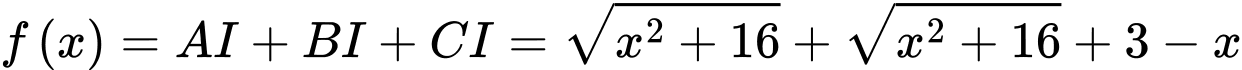
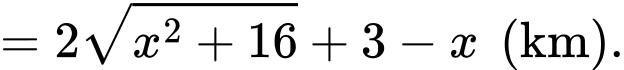
c) Đúng.
Ta có:
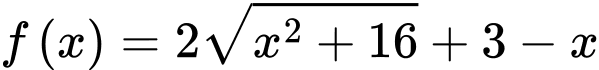
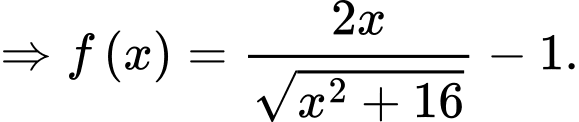
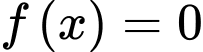
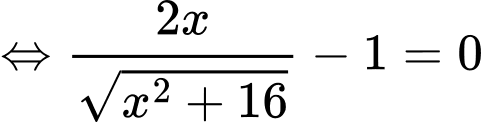

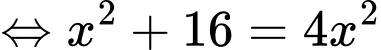
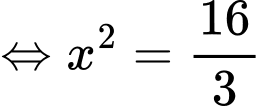
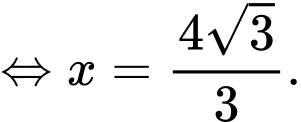
Bảng biến thiên hàm số
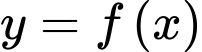 với
với 

Dựa vào BBT ta có:
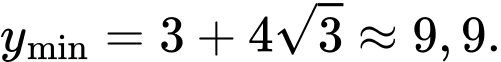
Vậy tổng độ dài đường ống nhỏ nhất bằng
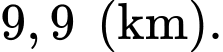
d) Đúng.
Khi tổng độ dài đường ống nhỏ nhất thì
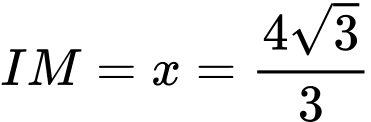
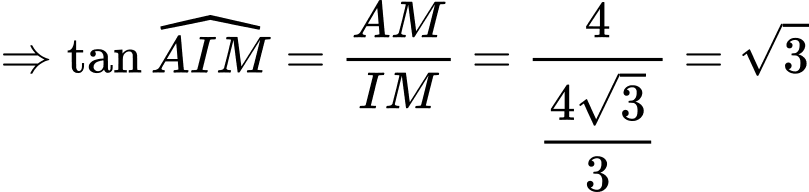
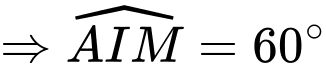
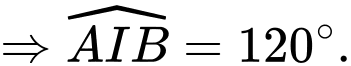
PHẦN III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 17 đến câu 22.
Câu 17 [774133]: Giả sử mức tiêu thụ xăng 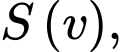 tính theo lít/km của một chiếc xe hơi phụ thuộc vào vận tốc
tính theo lít/km của một chiếc xe hơi phụ thuộc vào vận tốc 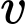 (km/h) của nó. Tốc độ biến thiên của hàm số
(km/h) của nó. Tốc độ biến thiên của hàm số 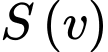 được mô phỏng bởi hàm số
được mô phỏng bởi hàm số 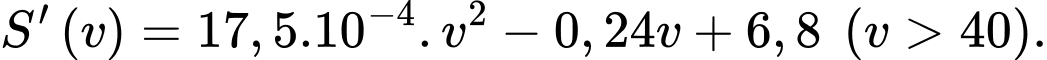 Biết xe đi với vận tốc đủ lớn (tối thiểu là 40 km/h), hỏi xe nên đi với tốc độ bao nhiêu km/h thì mức tiêu thụ xăng là ít nhất (viết kết quả làm tròn đến hàng đơn vị).
Biết xe đi với vận tốc đủ lớn (tối thiểu là 40 km/h), hỏi xe nên đi với tốc độ bao nhiêu km/h thì mức tiêu thụ xăng là ít nhất (viết kết quả làm tròn đến hàng đơn vị).
Đính chính: Bài này cần thêm dữ kiện "Biết xe đi với vận tốc đủ lớn (tối thiểu là 40 km/h)" để biết chính xác vận tốc cần đi các em nhé!
Tác giả xin đính chính và sửa lại ở lần tái bản tiếp theo
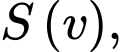 tính theo lít/km của một chiếc xe hơi phụ thuộc vào vận tốc
tính theo lít/km của một chiếc xe hơi phụ thuộc vào vận tốc 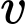 (km/h) của nó. Tốc độ biến thiên của hàm số
(km/h) của nó. Tốc độ biến thiên của hàm số 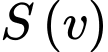 được mô phỏng bởi hàm số
được mô phỏng bởi hàm số 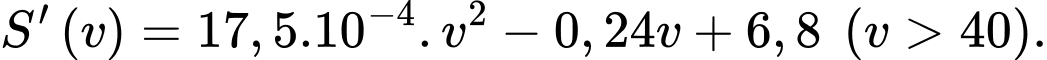 Biết xe đi với vận tốc đủ lớn (tối thiểu là 40 km/h), hỏi xe nên đi với tốc độ bao nhiêu km/h thì mức tiêu thụ xăng là ít nhất (viết kết quả làm tròn đến hàng đơn vị).
Biết xe đi với vận tốc đủ lớn (tối thiểu là 40 km/h), hỏi xe nên đi với tốc độ bao nhiêu km/h thì mức tiêu thụ xăng là ít nhất (viết kết quả làm tròn đến hàng đơn vị).Đính chính: Bài này cần thêm dữ kiện "Biết xe đi với vận tốc đủ lớn (tối thiểu là 40 km/h)" để biết chính xác vận tốc cần đi các em nhé!
Tác giả xin đính chính và sửa lại ở lần tái bản tiếp theo
Điền đáp án: 97
Ta có: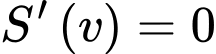

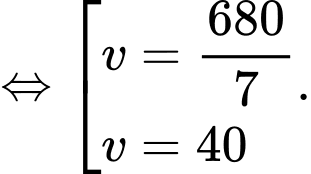
Bảng biến thiên:

Dựa vào bảng biên thiên ta có: Xe nên đi với tốc độ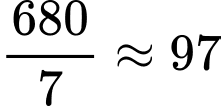 km/h thì mức tiêu thụ xăng là ít nhất.
km/h thì mức tiêu thụ xăng là ít nhất.
Ta có:
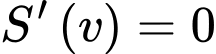

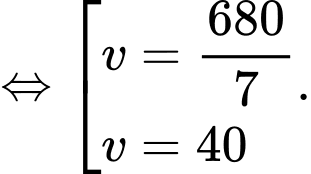
Bảng biến thiên:

Dựa vào bảng biên thiên ta có: Xe nên đi với tốc độ
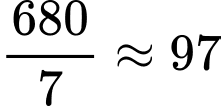 km/h thì mức tiêu thụ xăng là ít nhất.
km/h thì mức tiêu thụ xăng là ít nhất.
Câu 18 [774134]: Một chuyến xe buýt có sức chứa tối đa 60 hành khách. Giả định một chuyến xe chở 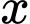 hành khách thì giá cho mỗi hành khách là
hành khách thì giá cho mỗi hành khách là 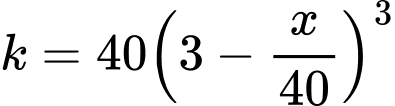 , đơn vị nghìn đồng. Xác định số khách đi xe buýt sao cho doanh thu một chuyến xe buýt đạt giá trị lớn nhất.
, đơn vị nghìn đồng. Xác định số khách đi xe buýt sao cho doanh thu một chuyến xe buýt đạt giá trị lớn nhất.
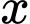 hành khách thì giá cho mỗi hành khách là
hành khách thì giá cho mỗi hành khách là 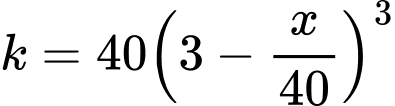 , đơn vị nghìn đồng. Xác định số khách đi xe buýt sao cho doanh thu một chuyến xe buýt đạt giá trị lớn nhất.
, đơn vị nghìn đồng. Xác định số khách đi xe buýt sao cho doanh thu một chuyến xe buýt đạt giá trị lớn nhất.
Điền đáp án: 30
Doanh thu chuyến xe buýt chở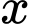 hành khách là:
hành khách là:
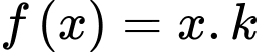
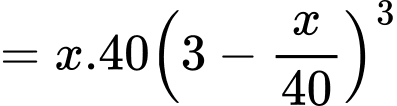
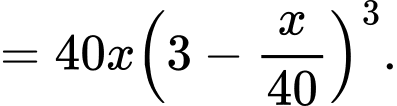
Ta có: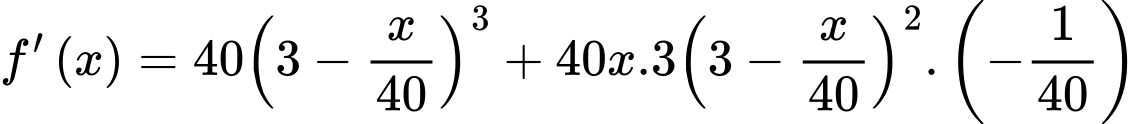
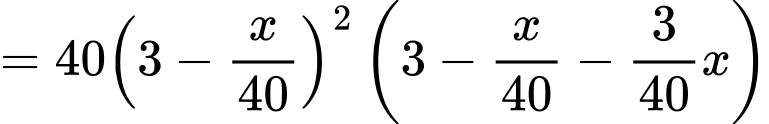
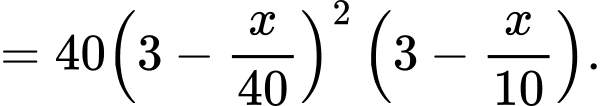
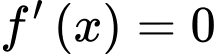
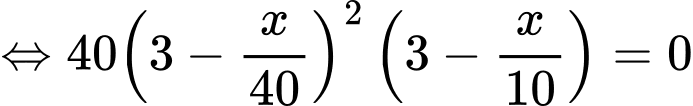
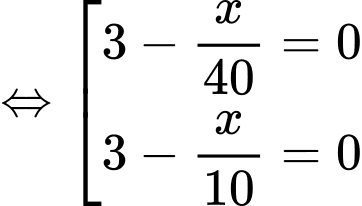
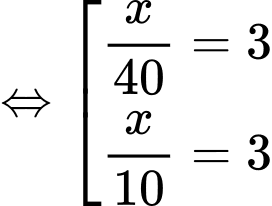
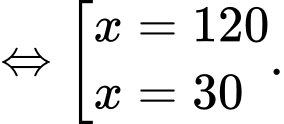
Bảng biến thiên:
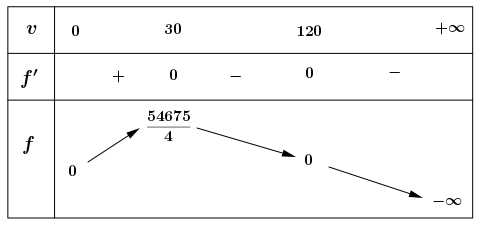
Dựa vào bảng biến thiên ta có: Với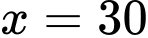 thì doanh thu chuyến xe buýt là lớn nhất.
thì doanh thu chuyến xe buýt là lớn nhất.
Doanh thu chuyến xe buýt chở
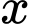 hành khách là:
hành khách là: 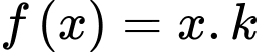
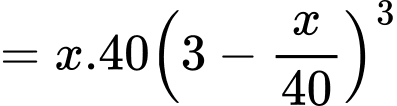
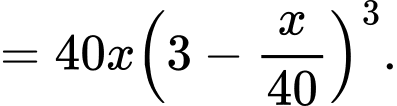
Ta có:
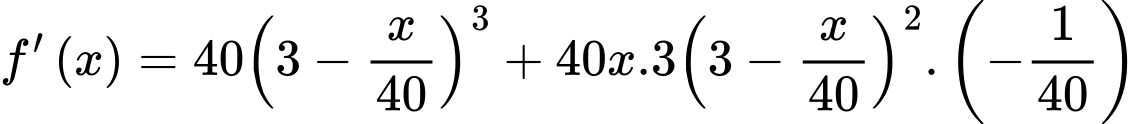
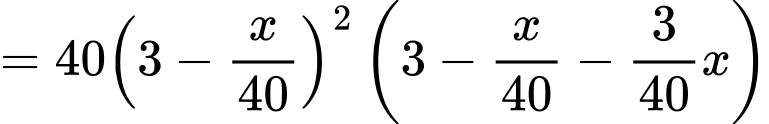
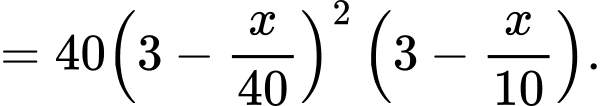
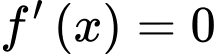
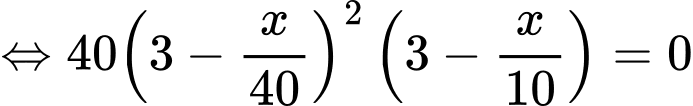
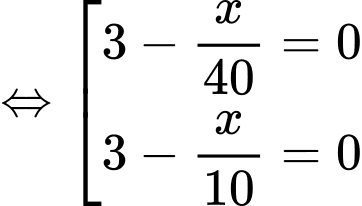
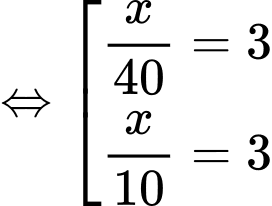
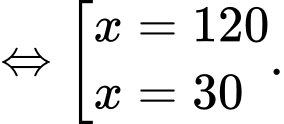
Bảng biến thiên:

Dựa vào bảng biến thiên ta có: Với
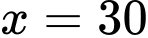 thì doanh thu chuyến xe buýt là lớn nhất.
thì doanh thu chuyến xe buýt là lớn nhất.
Câu 19 [774135]: Một hộ sản xuất kinh doanh hạt điều sấy mỗi ngày sản xuất được 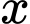 kg
kg 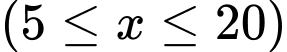 . Tổng chi phí sản xuất
. Tổng chi phí sản xuất 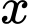 kg được cho bởi hàm chi phí
kg được cho bởi hàm chi phí 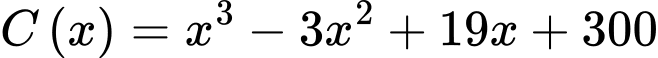 (đơn vị: nghìn đồng). Giả sử hộ sản xuất này bán hết sản phẩm mỗi ngày với giá
(đơn vị: nghìn đồng). Giả sử hộ sản xuất này bán hết sản phẩm mỗi ngày với giá 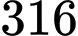 nghìn đồng/kg. Hỏi hộ sản xuất này cần sản xuất và bán ra mỗi ngày bao nhiêu kilôgam hạt điều để thu được lợi nhuận lớn nhất?
nghìn đồng/kg. Hỏi hộ sản xuất này cần sản xuất và bán ra mỗi ngày bao nhiêu kilôgam hạt điều để thu được lợi nhuận lớn nhất?
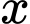 kg
kg 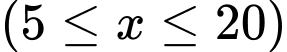 . Tổng chi phí sản xuất
. Tổng chi phí sản xuất 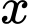 kg được cho bởi hàm chi phí
kg được cho bởi hàm chi phí 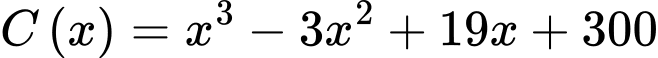 (đơn vị: nghìn đồng). Giả sử hộ sản xuất này bán hết sản phẩm mỗi ngày với giá
(đơn vị: nghìn đồng). Giả sử hộ sản xuất này bán hết sản phẩm mỗi ngày với giá 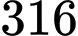 nghìn đồng/kg. Hỏi hộ sản xuất này cần sản xuất và bán ra mỗi ngày bao nhiêu kilôgam hạt điều để thu được lợi nhuận lớn nhất?
nghìn đồng/kg. Hỏi hộ sản xuất này cần sản xuất và bán ra mỗi ngày bao nhiêu kilôgam hạt điều để thu được lợi nhuận lớn nhất?
Điền đáp án: 11
Lợi nhuận bán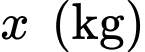 hạt điều mỗi ngày là:
hạt điều mỗi ngày là:
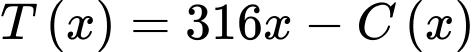
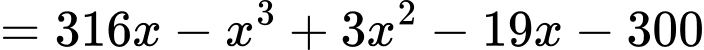
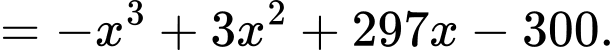
Ta có: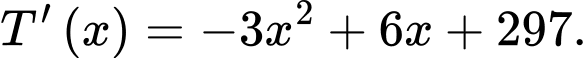
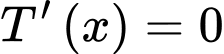
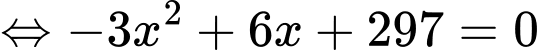
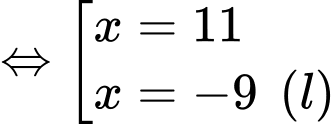
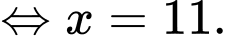
Mặt khác ta có: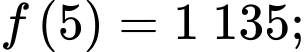
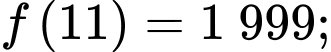
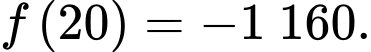
Vậy hộ sản xuất này cần sản xuất và bán ra mỗi ngày 11 kilôgam hạt điều để thu được lợi nhuận lớn nhất.
Lợi nhuận bán
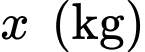 hạt điều mỗi ngày là:
hạt điều mỗi ngày là: 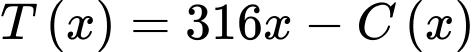
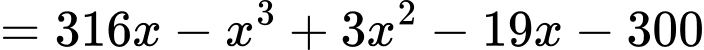
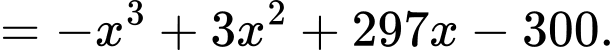
Ta có:
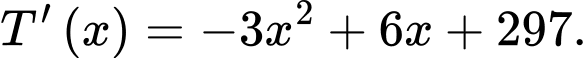
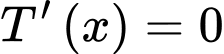
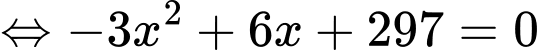
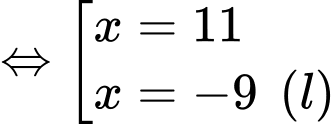
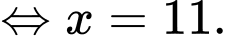
Mặt khác ta có:
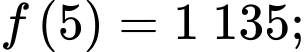
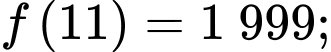
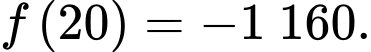
Vậy hộ sản xuất này cần sản xuất và bán ra mỗi ngày 11 kilôgam hạt điều để thu được lợi nhuận lớn nhất.
Câu 20 [774136]: Một doanh nghiệp dự định sản xuất không quá  sản phẩm. Nếu doanh nghiệp sản xuất
sản phẩm. Nếu doanh nghiệp sản xuất 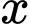 sản phẩm (
sản phẩm (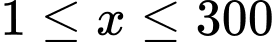 ) thì doanh thu nhận được khi bán hết số sản phẩm đó là
) thì doanh thu nhận được khi bán hết số sản phẩm đó là 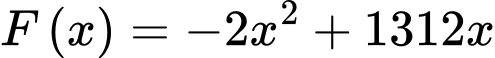 (nghìn đồng), trong khi chi phí sản xuất bình quân cho một sản phẩm là
(nghìn đồng), trong khi chi phí sản xuất bình quân cho một sản phẩm là 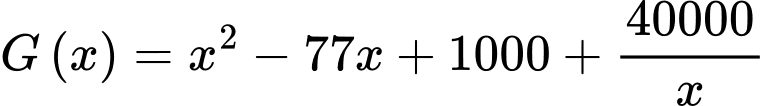 (nghìn đồng). Lợi nhuận thu được của doanh nghiệp (tính theo đơn vị triệu đồng) đạt giá trị lớn nhất bằng bao nhiêu (làm tròn kết quả đến hàng đơn vị)?
(nghìn đồng). Lợi nhuận thu được của doanh nghiệp (tính theo đơn vị triệu đồng) đạt giá trị lớn nhất bằng bao nhiêu (làm tròn kết quả đến hàng đơn vị)?
 sản phẩm. Nếu doanh nghiệp sản xuất
sản phẩm. Nếu doanh nghiệp sản xuất 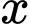 sản phẩm (
sản phẩm (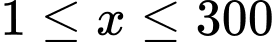 ) thì doanh thu nhận được khi bán hết số sản phẩm đó là
) thì doanh thu nhận được khi bán hết số sản phẩm đó là 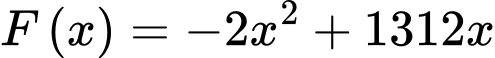 (nghìn đồng), trong khi chi phí sản xuất bình quân cho một sản phẩm là
(nghìn đồng), trong khi chi phí sản xuất bình quân cho một sản phẩm là 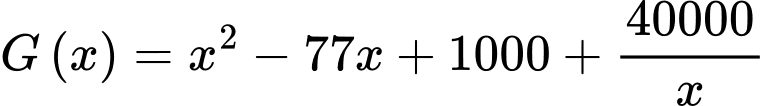 (nghìn đồng). Lợi nhuận thu được của doanh nghiệp (tính theo đơn vị triệu đồng) đạt giá trị lớn nhất bằng bao nhiêu (làm tròn kết quả đến hàng đơn vị)?
(nghìn đồng). Lợi nhuận thu được của doanh nghiệp (tính theo đơn vị triệu đồng) đạt giá trị lớn nhất bằng bao nhiêu (làm tròn kết quả đến hàng đơn vị)?
Điền đáp án: 
Lợi nhuận = doanh thu – chi phí sản xuất bình quân

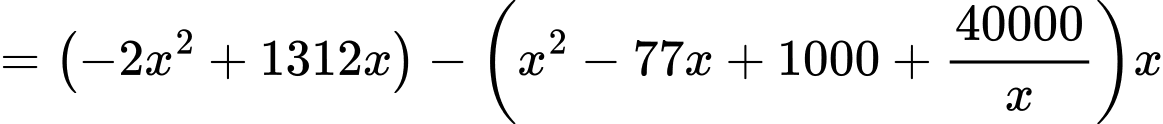

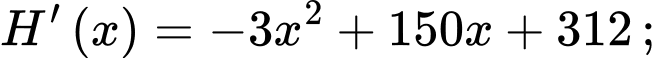

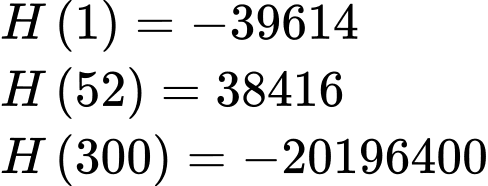
Vậy lợi nhuận lớn nhất đạt được là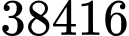 nghìn đồng
nghìn đồng 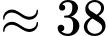 triệu đồng.
triệu đồng.
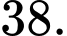
Lợi nhuận = doanh thu – chi phí sản xuất bình quân

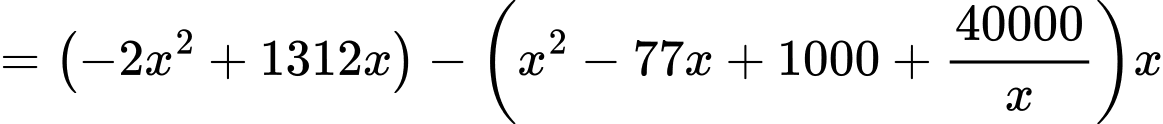

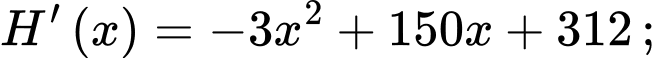

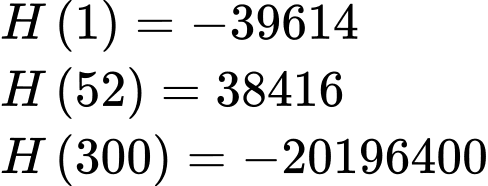
Vậy lợi nhuận lớn nhất đạt được là
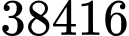 nghìn đồng
nghìn đồng 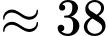 triệu đồng.
triệu đồng.
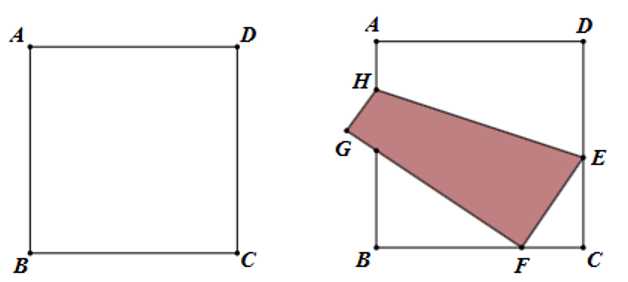
Câu 21 [774139]: Một tờ giấy hình vuông 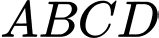 cạnh 3 dm. Tờ giấy được gấp lại sao cho đỉnh
cạnh 3 dm. Tờ giấy được gấp lại sao cho đỉnh 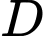 chạm vào điểm
chạm vào điểm 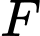 trên cạnh
trên cạnh 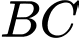 (như hình vẽ). Diện tích tam giác
(như hình vẽ). Diện tích tam giác 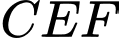 có giá trị lớn nhất là bao nhiêu decimét vuông (kết quả làm tròn đến hàng phần trăm).
có giá trị lớn nhất là bao nhiêu decimét vuông (kết quả làm tròn đến hàng phần trăm).
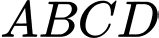 cạnh 3 dm. Tờ giấy được gấp lại sao cho đỉnh
cạnh 3 dm. Tờ giấy được gấp lại sao cho đỉnh 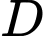 chạm vào điểm
chạm vào điểm 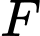 trên cạnh
trên cạnh 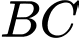 (như hình vẽ). Diện tích tam giác
(như hình vẽ). Diện tích tam giác 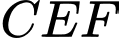 có giá trị lớn nhất là bao nhiêu decimét vuông (kết quả làm tròn đến hàng phần trăm).
có giá trị lớn nhất là bao nhiêu decimét vuông (kết quả làm tròn đến hàng phần trăm).
Điền đáp án: 0,87
Đặt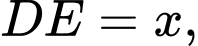 khi đó:
khi đó: 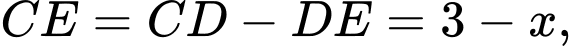
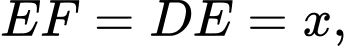
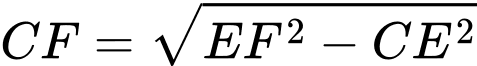
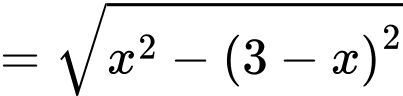
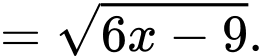
Diện tích tam giác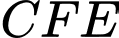 là:
là: 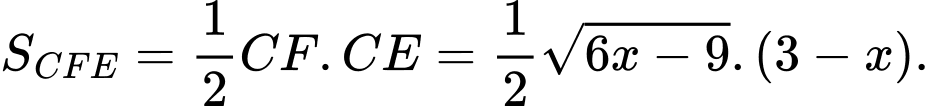
Xét hàm số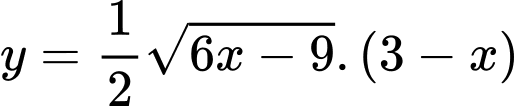 với
với 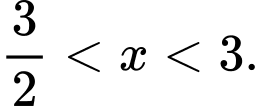
Ta có: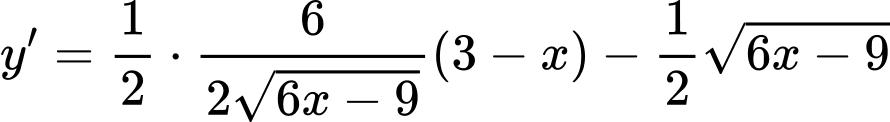
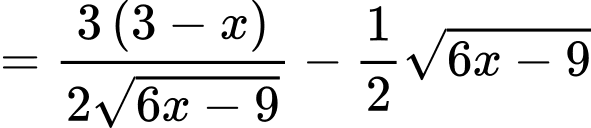
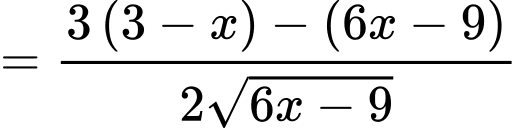
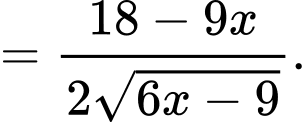
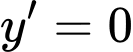
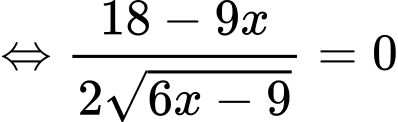
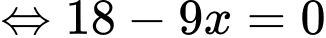
Bảng biến thiên:
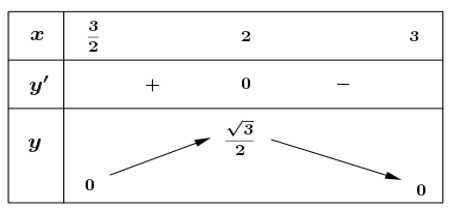
Dựa vào bảng biến thiên ta có: Với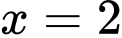 thì diện tích tam giác
thì diện tích tam giác  có giá trị lớn nhất là
có giá trị lớn nhất là 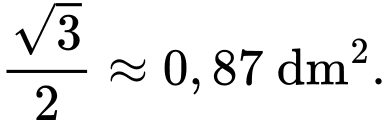
Đặt
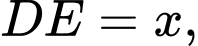 khi đó:
khi đó: 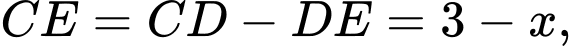
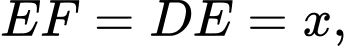
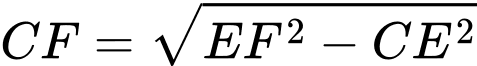
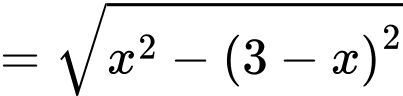
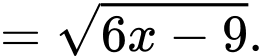
Diện tích tam giác
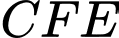 là:
là: 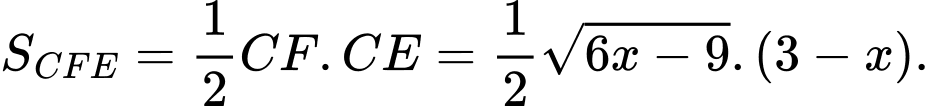
Xét hàm số
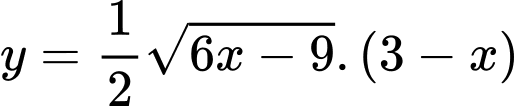 với
với 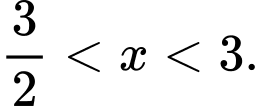
Ta có:
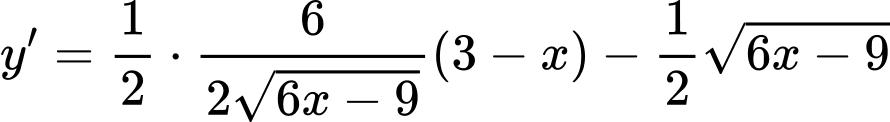
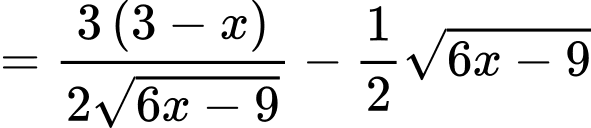
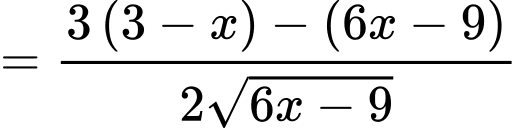
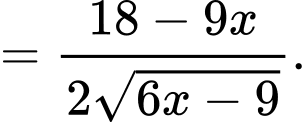
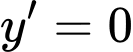
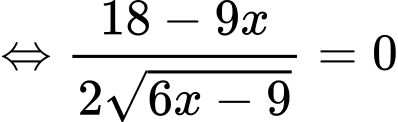
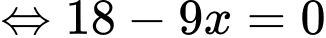
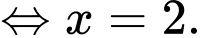
Bảng biến thiên:

Dựa vào bảng biến thiên ta có: Với
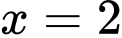 thì diện tích tam giác
thì diện tích tam giác 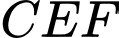 có giá trị lớn nhất là
có giá trị lớn nhất là 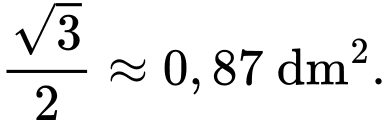
Câu 22 [774140]: Cho một tấm tôn hình một ngũ giác đều có cạnh bằng 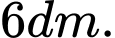 Người ta thực hiện các bước sau:
Người ta thực hiện các bước sau:
Bước 1: Cắt ở mỗi đỉnh của ngũ giác đều đó hai tam giác vuông bằng nhau.
Bước 2: Cắt theo nét đứt đoạn để thu được hình hợp bởi một ngũ giác đều và năm hình chữ nhật.
Bước 3: Gấp các hình chữ nhật để tạo thành khối lăng trụ ngũ giác đều (tham khảo hình vẽ).
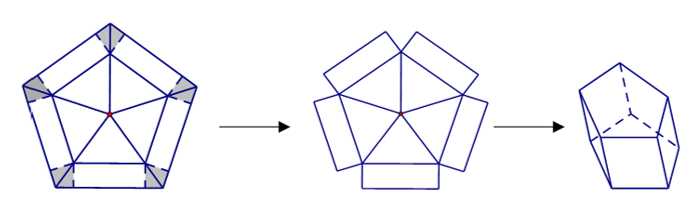
Thể tích của khối lăng trụ lớn nhất bằng bao nhiêu đề-xi-mét khối? (làm tròn kết quả đến hàng chục).
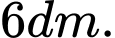 Người ta thực hiện các bước sau:
Người ta thực hiện các bước sau:Bước 1: Cắt ở mỗi đỉnh của ngũ giác đều đó hai tam giác vuông bằng nhau.
Bước 2: Cắt theo nét đứt đoạn để thu được hình hợp bởi một ngũ giác đều và năm hình chữ nhật.
Bước 3: Gấp các hình chữ nhật để tạo thành khối lăng trụ ngũ giác đều (tham khảo hình vẽ).

Thể tích của khối lăng trụ lớn nhất bằng bao nhiêu đề-xi-mét khối? (làm tròn kết quả đến hàng chục).
Điền đáp án: 37,9
Ngũ giác được chia thành 5 tam giác.
Xét tam giác ABC cân tại C có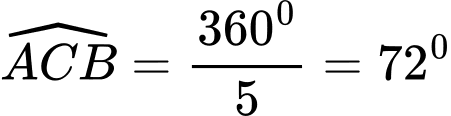 .
.
Gọi H là chân đường cao kẻ từ C xuống AB, có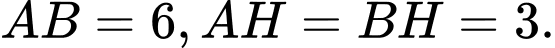
Mặt khác CH là đường phân giác góc C, có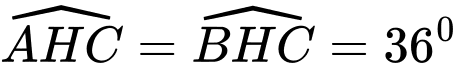
Suy ra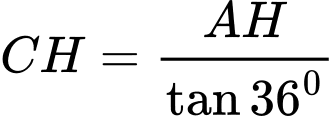
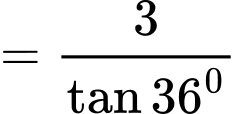
Đặt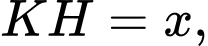 khi đó
khi đó 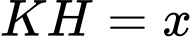 là đường cao của khối lăng trụ và
là đường cao của khối lăng trụ và
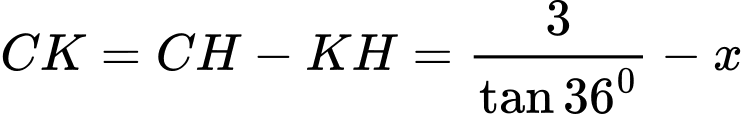
Xét tam giác vuông CEK, có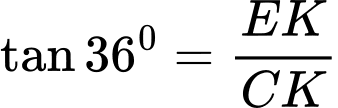
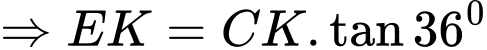
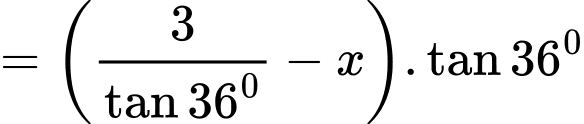
Suy ra
Diện tích tam giác CEF:
Diện tích đáy khối lăng trụ là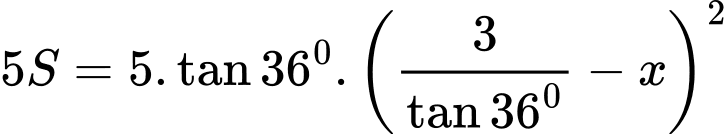
Thể tích khối lăng trụ là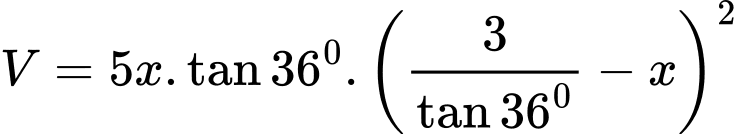

Xét hàm số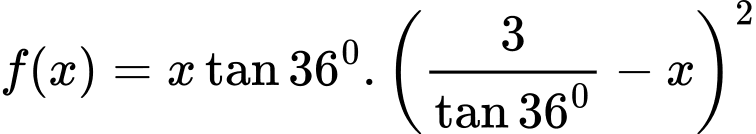
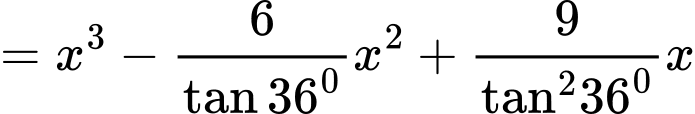
Có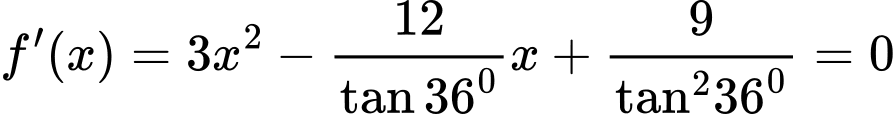
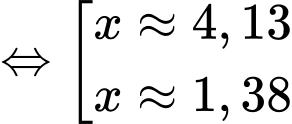
Thay hai giá trị của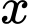 vào
vào  , ta được thể tích lớn nhất của khối lăng trụ là:
, ta được thể tích lớn nhất của khối lăng trụ là:
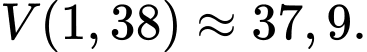
Ngũ giác được chia thành 5 tam giác.
Xét tam giác ABC cân tại C có
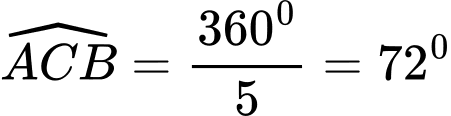 .
.
Gọi H là chân đường cao kẻ từ C xuống AB, có
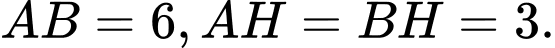
Mặt khác CH là đường phân giác góc C, có
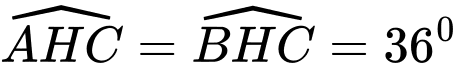
Suy ra
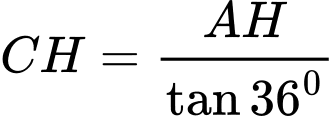
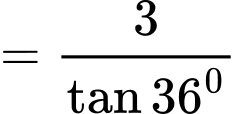
Đặt
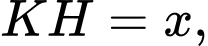 khi đó
khi đó 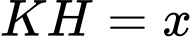 là đường cao của khối lăng trụ và
là đường cao của khối lăng trụ và
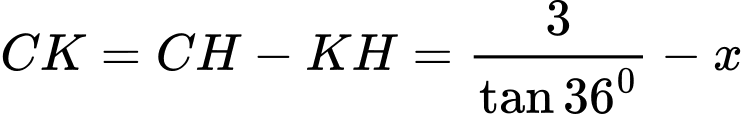
Xét tam giác vuông CEK, có
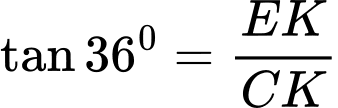
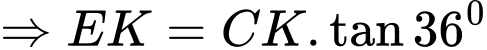
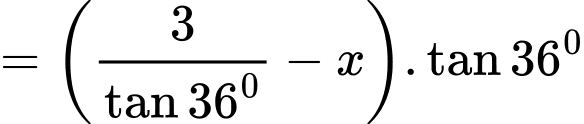
Suy ra

Diện tích tam giác CEF:

Diện tích đáy khối lăng trụ là
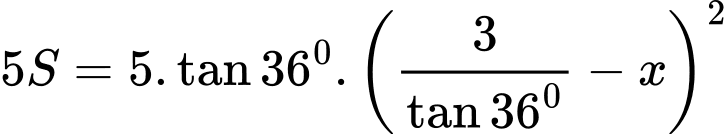
Thể tích khối lăng trụ là
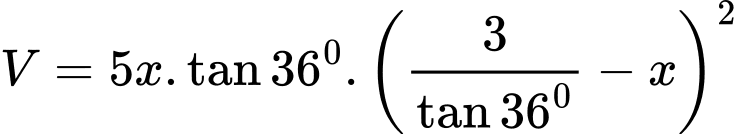

Xét hàm số
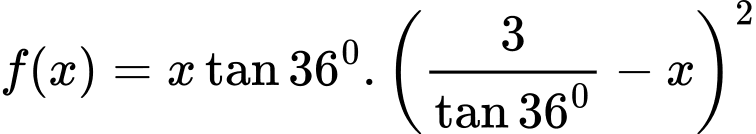
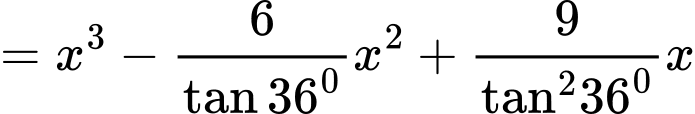
Có
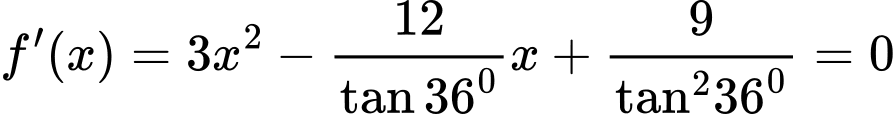
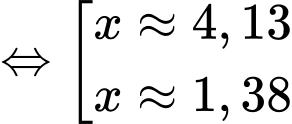
Thay hai giá trị của
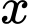 vào
vào  , ta được thể tích lớn nhất của khối lăng trụ là:
, ta được thể tích lớn nhất của khối lăng trụ là: