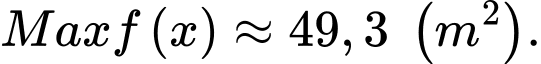PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1 [318836]: Cho hàm số 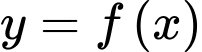 có bảng biến thiên như sau:
có bảng biến thiên như sau:
=kphan2de1/3.kslan6.png)
Hàm số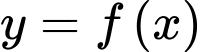 đồng biến trên các khoảng nào sau đây?
đồng biến trên các khoảng nào sau đây?
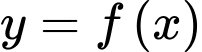 có bảng biến thiên như sau:
có bảng biến thiên như sau:=kphan2de1/3.kslan6.png)
Hàm số
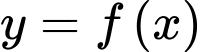 đồng biến trên các khoảng nào sau đây?
đồng biến trên các khoảng nào sau đây? A, 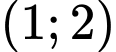 .
.
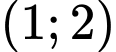 .
.B, 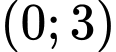 .
.
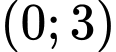 .
.C, 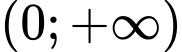 .
.
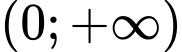 .
.D, 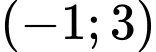 .
.
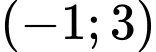 .
.
Chọn A
Hàm số đồng biến trên khoảng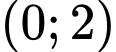 nên đồng biến trên khoảng
nên đồng biến trên khoảng 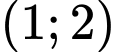 . Đáp án: A
. Đáp án: A
Hàm số đồng biến trên khoảng
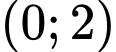 nên đồng biến trên khoảng
nên đồng biến trên khoảng  . Đáp án: A
. Đáp án: A
Câu 2 [306979]: Cho hàm số 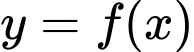 có bảng biến thiên như sau
có bảng biến thiên như sau
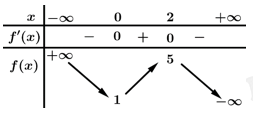
Hàm số đạt cực tiểu tại điểm
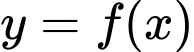 có bảng biến thiên như sau
có bảng biến thiên như sau
Hàm số đạt cực tiểu tại điểm
A, 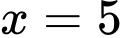 .
.
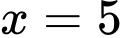 .
.B, 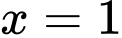 .
.
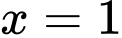 .
.C, 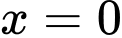 .
.
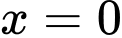 .
.D, 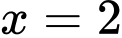 .
.
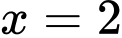 .
.
Chọn C
Từ bảng biến thiên nhận thấy hàm số đạt cực tiểu tại điểm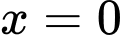 . Đáp án: C
. Đáp án: C
Từ bảng biến thiên nhận thấy hàm số đạt cực tiểu tại điểm
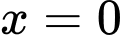 . Đáp án: C
. Đáp án: C
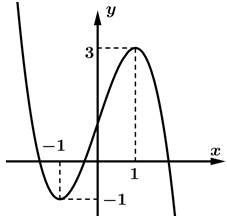
Câu 3 [185179]: Cho hàm số 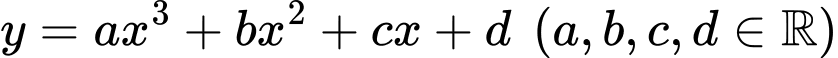 có đồ thị là đường cong trong hình bên. Giá trị cực đại của hàm số đã cho bằng
có đồ thị là đường cong trong hình bên. Giá trị cực đại của hàm số đã cho bằng
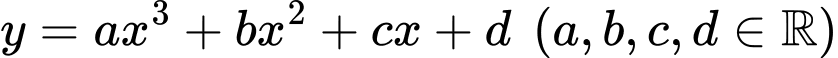 có đồ thị là đường cong trong hình bên. Giá trị cực đại của hàm số đã cho bằng
có đồ thị là đường cong trong hình bên. Giá trị cực đại của hàm số đã cho bằng
A, 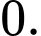
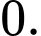
B, 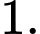
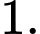
C, 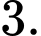
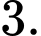
D, 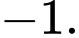
Giá trị cực đại của hàm số là 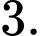 Đáp án: C
Đáp án: C
 Đáp án: C
Đáp án: C
Câu 4 [520624]: Cho hàm số 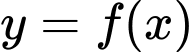 liên tục trên
liên tục trên 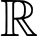 và có bảng xét dấu của đạo hàm như hình vẽ. Hàm số đã cho có bao nhiêu điểm cực trị?
và có bảng xét dấu của đạo hàm như hình vẽ. Hàm số đã cho có bao nhiêu điểm cực trị?
=kphan2de1/2.ksl;an6.png)
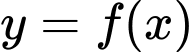 liên tục trên
liên tục trên 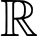 và có bảng xét dấu của đạo hàm như hình vẽ. Hàm số đã cho có bao nhiêu điểm cực trị?
và có bảng xét dấu của đạo hàm như hình vẽ. Hàm số đã cho có bao nhiêu điểm cực trị? =kphan2de1/2.ksl;an6.png)
A, 1.
B, 3.
C, 2.
D, 4.
Chọn D
Hàm số đạt cực trị tại bốn điểm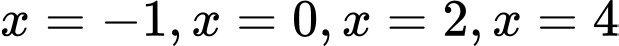 Đáp án: D
Đáp án: D
Hàm số đạt cực trị tại bốn điểm
 Đáp án: D
Đáp án: D
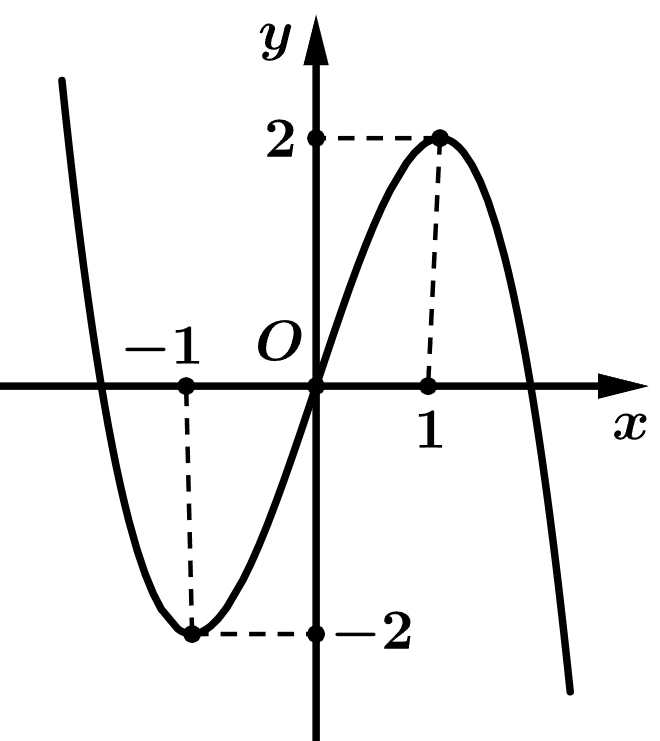
Câu 5 [680679]: Cho hàm số có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào sau đây?

A, 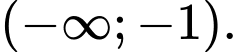
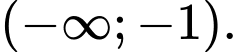
B, 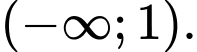
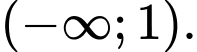
C, 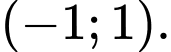
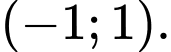
D, 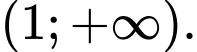
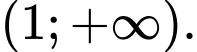
Chọn đáp án C.
Từ đồ thị hàm số, ta thấy hàm số đồng biến trên khoảng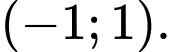 Đáp án: C
Đáp án: C
Từ đồ thị hàm số, ta thấy hàm số đồng biến trên khoảng
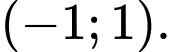 Đáp án: C
Đáp án: C
Câu 6 [33133]: Cho hàm số 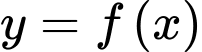 liên tục trên đoạn
liên tục trên đoạn 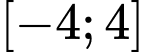 và có đồ thị như hình vẽ bên dưới. Gọi
và có đồ thị như hình vẽ bên dưới. Gọi 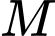 và
và 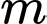 lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn 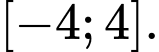 Giá trị của
Giá trị của 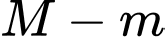 bằng
bằng
=kphan2de1/7.kslan6.png)
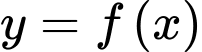 liên tục trên đoạn
liên tục trên đoạn 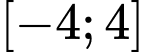 và có đồ thị như hình vẽ bên dưới. Gọi
và có đồ thị như hình vẽ bên dưới. Gọi 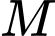 và
và 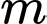 lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn 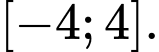 Giá trị của
Giá trị của 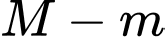 bằng
bằng=kphan2de1/7.kslan6.png)
A, 4.
B, 6.
C, 8
D, 1.
Đáp án B. 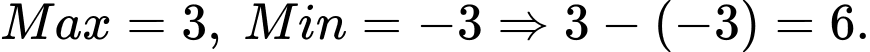 Đáp án: B
Đáp án: B
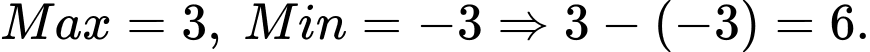 Đáp án: B
Đáp án: B
Câu 7 [547071]: Giá trị nhỏ nhất của hàm số 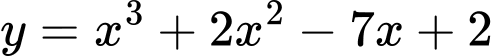 trên đoạn
trên đoạn 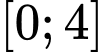 bằng
bằng
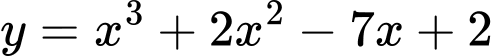 trên đoạn
trên đoạn 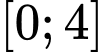 bằng
bằng A, 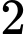 .
.
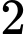 .
.B, 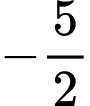 .
.
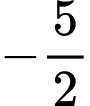 .
.C, 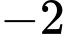 .
.
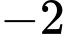 .
.D,  .
.
 .
.
Chọn C. 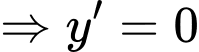
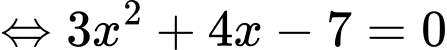
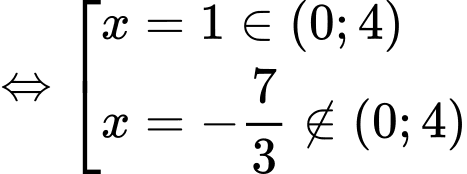 .
.
Hàm số 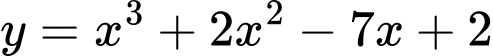 liên tục trên đoạn
liên tục trên đoạn 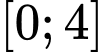 .
.
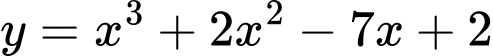 liên tục trên đoạn
liên tục trên đoạn 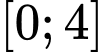 .
. Ta có 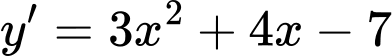
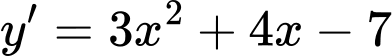
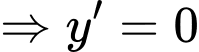
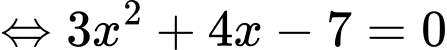
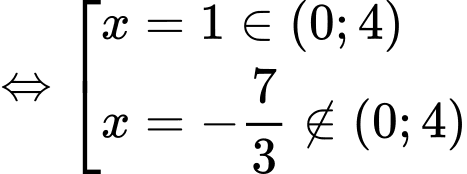 .
. Do 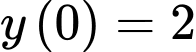 ,
, 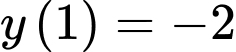 ,
, 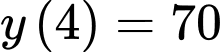 nên giá trị nhỏ nhất của hàm số
nên giá trị nhỏ nhất của hàm số 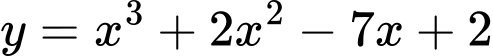 trên đoạn
trên đoạn 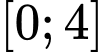 bằng
bằng 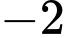 .
.
Đáp án: C 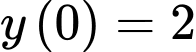 ,
, 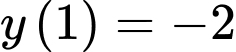 ,
, 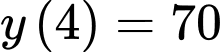 nên giá trị nhỏ nhất của hàm số
nên giá trị nhỏ nhất của hàm số 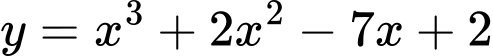 trên đoạn
trên đoạn 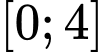 bằng
bằng 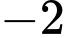 .
.
Câu 8 [146534]: Hàm số nào sau đây không có điểm cực trị?
A, 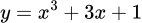 .
.
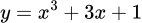 .
.B, 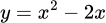 .
.
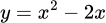 .
.C, 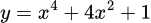 .
.
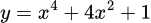 .
.D,  .
.
 .
. Đáp án: A
Đáp án: A
Câu 9 [543267]: Cho hàm số 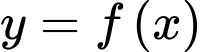 có đạo hàm
có đạo hàm 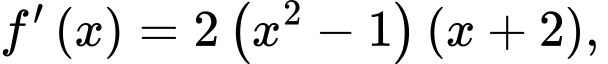
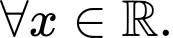 Hàm số đã cho có bao nhiêu điểm cực tiểu?
Hàm số đã cho có bao nhiêu điểm cực tiểu?
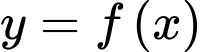 có đạo hàm
có đạo hàm 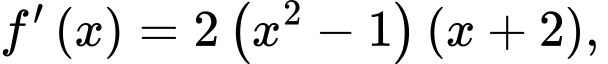
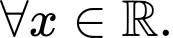 Hàm số đã cho có bao nhiêu điểm cực tiểu?
Hàm số đã cho có bao nhiêu điểm cực tiểu? A, 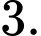
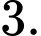
B, 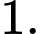
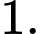
C, 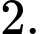
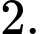
D, 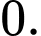
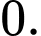
Chọn C
Ta có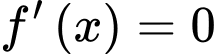
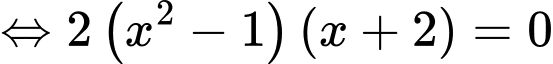
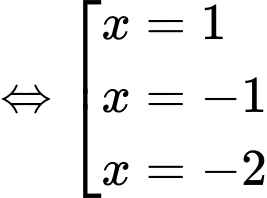
BBT:
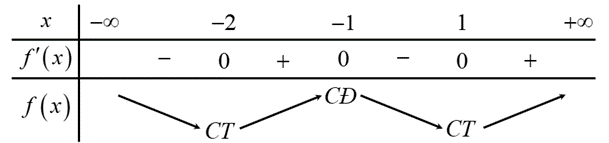
Vậy hàm số đã cho có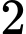 điểm cực tiểu. Đáp án: C
điểm cực tiểu. Đáp án: C
Ta có
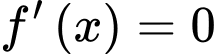
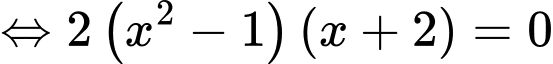
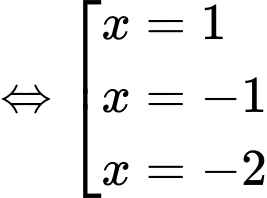
BBT:
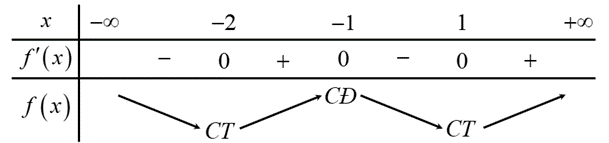
Vậy hàm số đã cho có
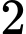 điểm cực tiểu. Đáp án: C
điểm cực tiểu. Đáp án: C
Câu 10 [538694]: Trong các hàm số dưới đây, hàm số nào đồng biến trên 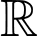 ?
?
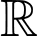 ?
? A, 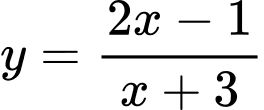 .
.
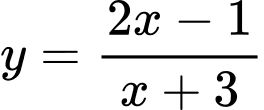 .
.B, 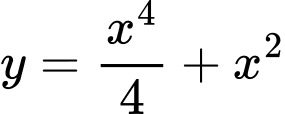 .
.
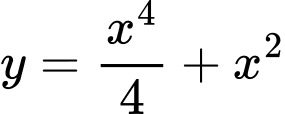 .
.C, 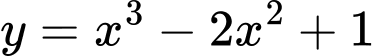 .
.
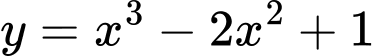 .
.D,  .
.
 .
.
Phương pháp:
Hàm số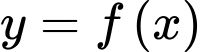 đồng biến trên
đồng biến trên 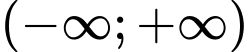 thoả mãn
thoả mãn 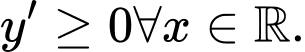
Cách giải:
Trong các đáp án, chỉ có hàm số có đạo hàm
có đạo hàm
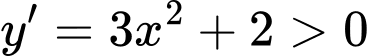 với mọi
với mọi 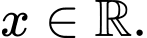 Do đó chỉ có
Do đó chỉ có  đồng biến trên
đồng biến trên 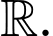 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
Hàm số
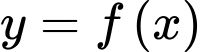 đồng biến trên
đồng biến trên 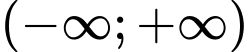 thoả mãn
thoả mãn 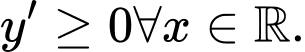
Cách giải:
Trong các đáp án, chỉ có hàm số
 có đạo hàm
có đạo hàm 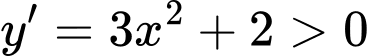 với mọi
với mọi 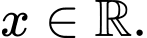 Do đó chỉ có
Do đó chỉ có  đồng biến trên
đồng biến trên 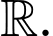 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
Câu 11 [185186]: Cho hàm số 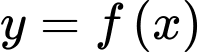 có đạo hàm
có đạo hàm 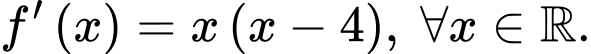 Khẳng định nào dưới đây đúng?
Khẳng định nào dưới đây đúng?
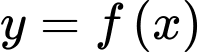 có đạo hàm
có đạo hàm 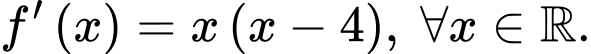 Khẳng định nào dưới đây đúng?
Khẳng định nào dưới đây đúng? A, 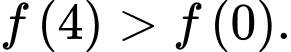
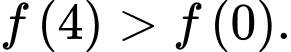
B, 

C, 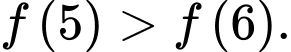
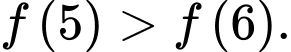
D, 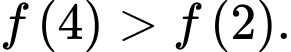
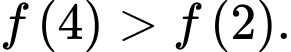
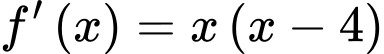 nên
nên 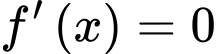

Khi đó lập bảng biến thiên, dựa vào bảng biến thiên ta được

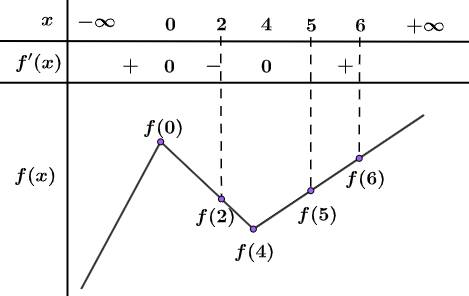 Đáp án: B
Đáp án: B
Câu 12 [628956]: Cho hàm số 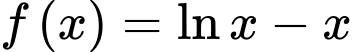 . Khẳng định nào dưới đây đúng?
. Khẳng định nào dưới đây đúng?
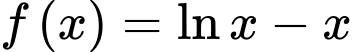 . Khẳng định nào dưới đây đúng?
. Khẳng định nào dưới đây đúng? A, Hàm số đồng biến trên khoảng 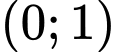 .
.
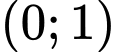 .
.B, Hàm số đồng biến trên khoảng 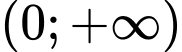 .
.
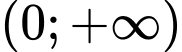 .
.C, Hàm số đồng biến trên các khoảng  và
và 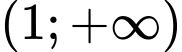 .
.
 và
và 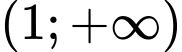 .
.D, Hàm số đồng biến trên khoảng 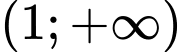 .
.
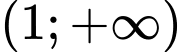 .
.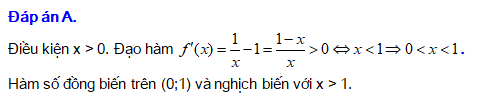 Đáp án: A
Đáp án: A PHẦN II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a),b),c),d) ở mỗi câu học sinh chọn đúng hoặc sai.
Câu 13 [696328]: Cho hàm số 

a) Đúng.
b) Sai.
Ta có: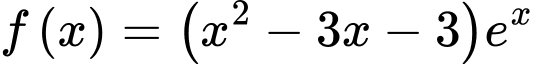
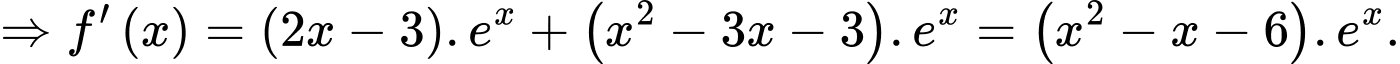
c) Đúng.
Ta có: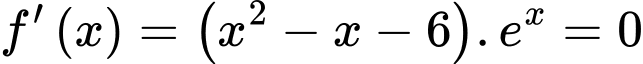
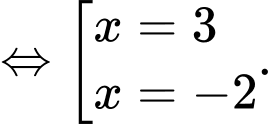
Vậy phương trình có hai nghiệm thực phân biệt.
d) Đúng.
Ta có: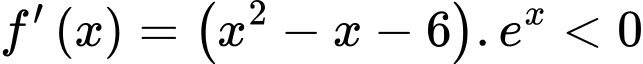

Vậy hàm số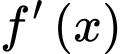 nghịch biến trên
nghịch biến trên 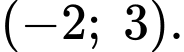
b) Sai.
Ta có:
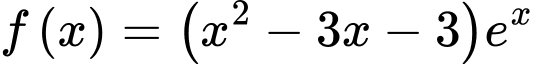
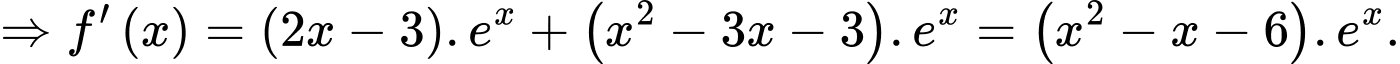
c) Đúng.
Ta có:
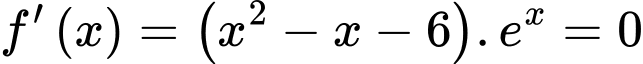
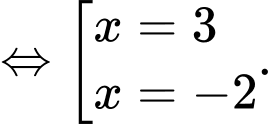
Vậy phương trình có hai nghiệm thực phân biệt.
d) Đúng.
Ta có:
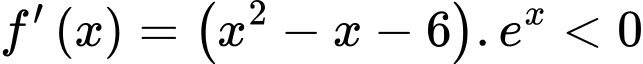

Vậy hàm số
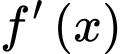 nghịch biến trên
nghịch biến trên 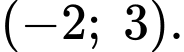
Câu 14 [687395]: Cho hàm số 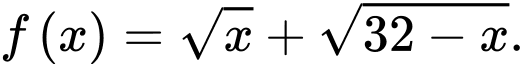 Các mệnh đề sau đúng hay sai?
Các mệnh đề sau đúng hay sai?
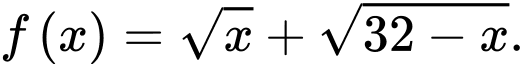 Các mệnh đề sau đúng hay sai?
Các mệnh đề sau đúng hay sai?
a) Đúng.
Điều kiện: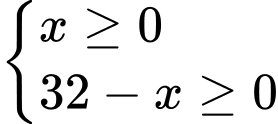
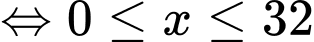

b) Đúng.
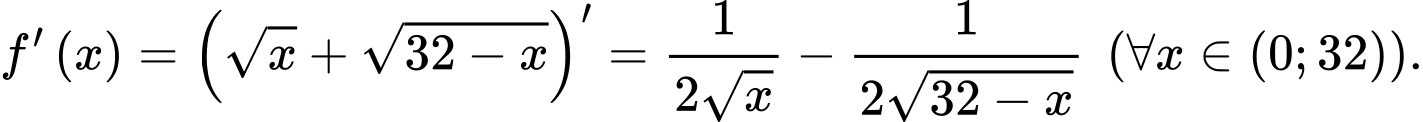
c) Sai
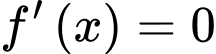
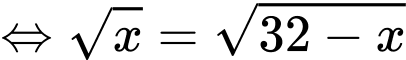
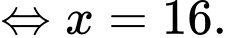
Vậy phương trình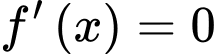 có 1 nghiệm.
có 1 nghiệm.
d) Đúng
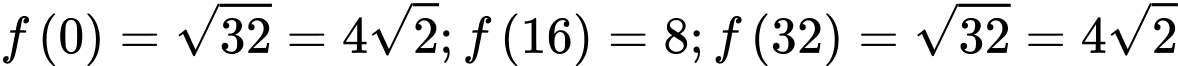 ;
;
Vậy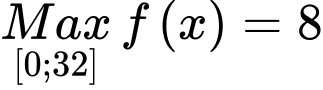
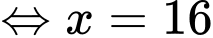 và
và 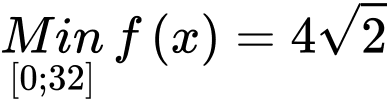
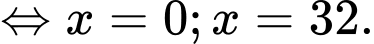
Điều kiện:
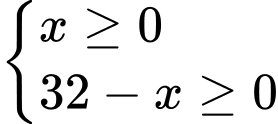
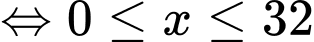

b) Đúng.
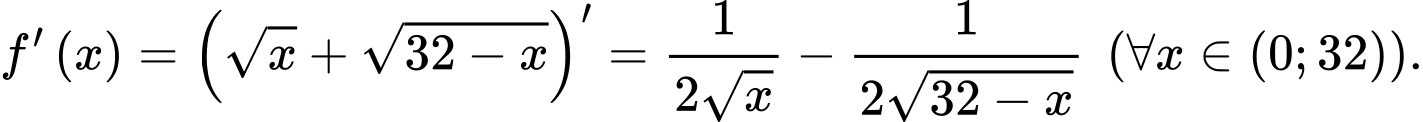
c) Sai
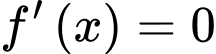
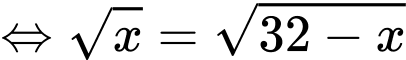
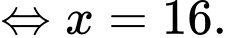
Vậy phương trình
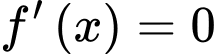 có 1 nghiệm.
có 1 nghiệm.d) Đúng
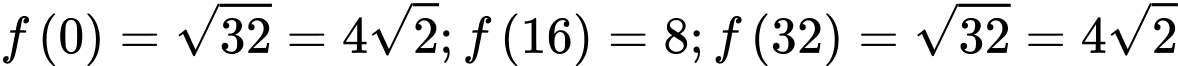 ;
;Vậy
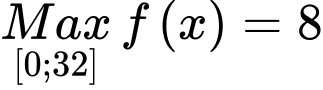
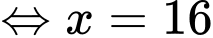 và
và 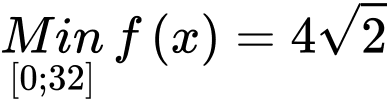
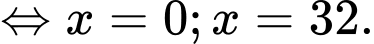
Câu 15 [774142]: Hằng ngày mực nước của một con kênh lên xuống theo thủy triều. Độ sâu  của mực nước trong kênh tại thời điểm
của mực nước trong kênh tại thời điểm 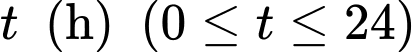 trong ngày được xác định bởi công thức
trong ngày được xác định bởi công thức 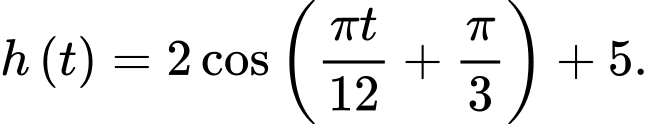
 của mực nước trong kênh tại thời điểm
của mực nước trong kênh tại thời điểm 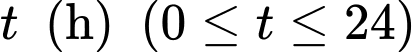 trong ngày được xác định bởi công thức
trong ngày được xác định bởi công thức 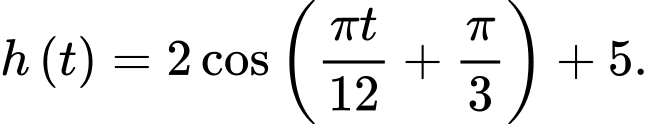
a) Sai.
Áp dụng công thức đạo hàm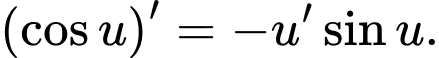 ta có
ta có 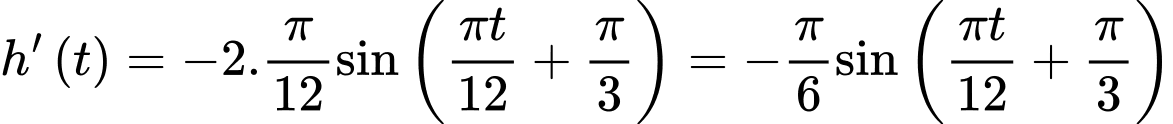
b) Đúng.
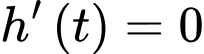
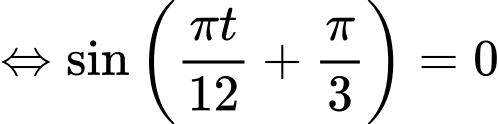
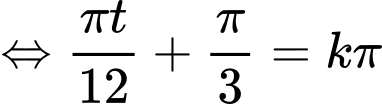
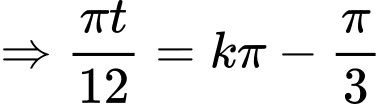
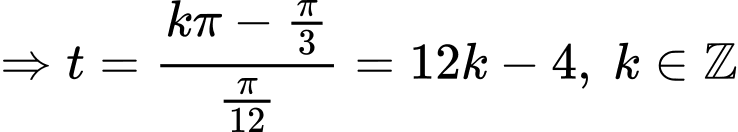
Suy ra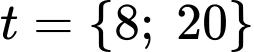 là các nghiệm của phương trình trong khoảng
là các nghiệm của phương trình trong khoảng 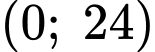
c) Sai.
Xét hàm số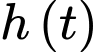 trong đoạn
trong đoạn 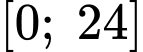
Từ kết quả phần b), ta có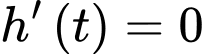
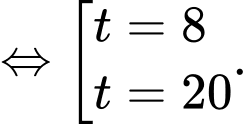
Bảng biến thiên
Dựa vào bảng biến thiên, ta thấy mệnh đề sai.
d) Sai.
Vì dựa vào bảng biến thiên của phần c), ta thấy rằng chỉ có 2 thời điểm trong ngày mực nước trong kênh đạt 4 m.
Áp dụng công thức đạo hàm
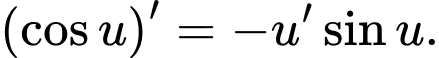 ta có
ta có 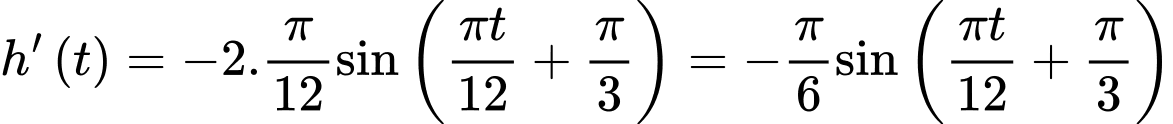
b) Đúng.
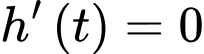
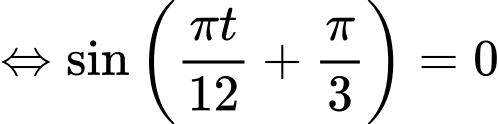
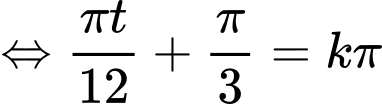
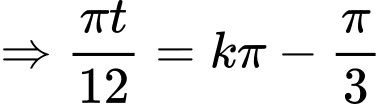
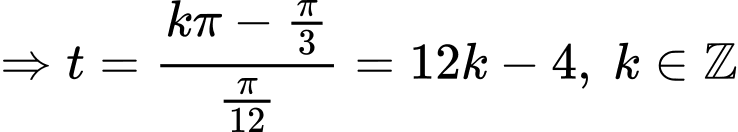
Suy ra
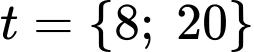 là các nghiệm của phương trình trong khoảng
là các nghiệm của phương trình trong khoảng 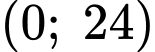
c) Sai.
Xét hàm số
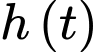 trong đoạn
trong đoạn 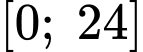
Từ kết quả phần b), ta có
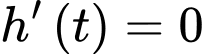
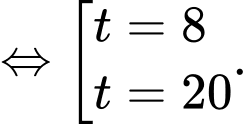
Bảng biến thiên

Dựa vào bảng biến thiên, ta thấy mệnh đề sai.
d) Sai.
Vì dựa vào bảng biến thiên của phần c), ta thấy rằng chỉ có 2 thời điểm trong ngày mực nước trong kênh đạt 4 m.
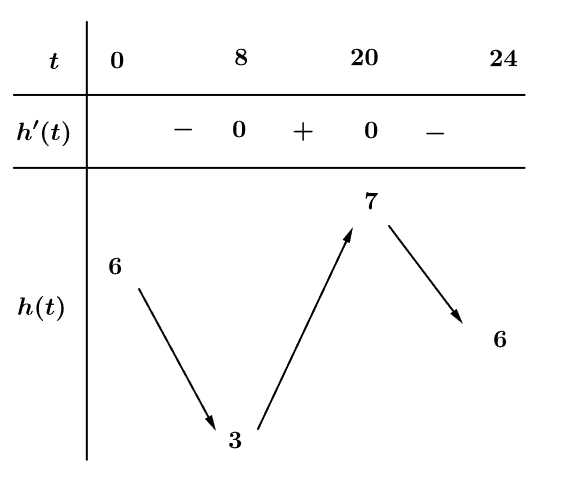
Câu 16 [700496]: Khi thả một quả bóng từ đỉnh một toà tháp xuống, nó chạm đất sau 3 giây. Sau đó, quả bóng nảy lên trước khi chạm đất lần nữa 4 giây sau đó. Chiều cao tính bằng mét của quả bóng so với mặt đất sau 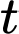 giây tuân theo một hàm số liên tục trên
giây tuân theo một hàm số liên tục trên 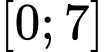 như sau:
như sau: 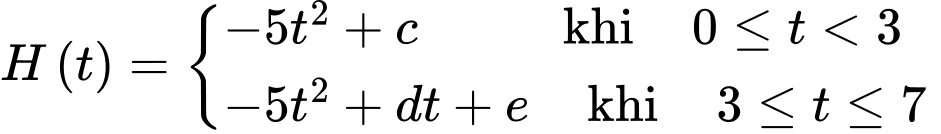
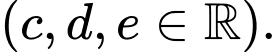
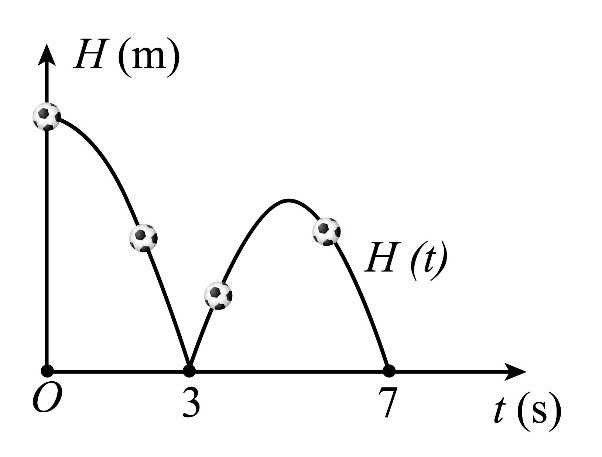
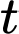 giây tuân theo một hàm số liên tục trên
giây tuân theo một hàm số liên tục trên 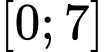 như sau:
như sau: 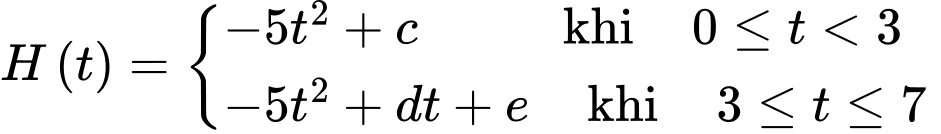
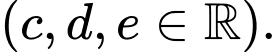

a) Đúng.
Dựa vào hình vẽ ta thấy
b) Sai.
Quả bóng được thả tại thời điểm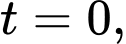 nên để tìm độ cao quả bóng ta cần đi tìm
nên để tìm độ cao quả bóng ta cần đi tìm 
Vì hàm số liên tục tại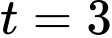 nên
nên 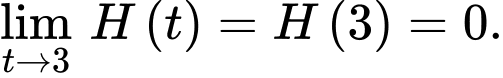
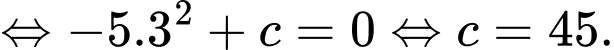
Vậy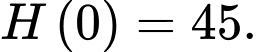 Do đó, quả bóng được thả từ độ cao 45 m.
Do đó, quả bóng được thả từ độ cao 45 m.
c) Sai.
Ta có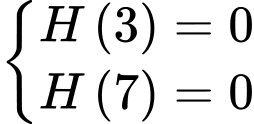
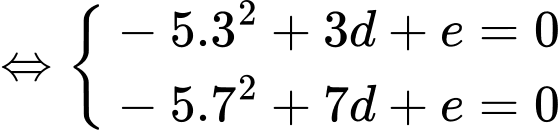
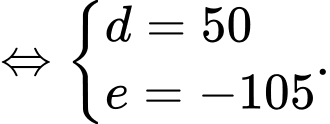
Vậy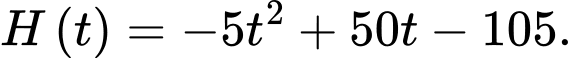
d) Đúng.
Độ cao của quả bóng sau lần nảy đầu tiên trong khoảng thời gian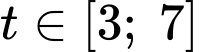 nên sẽ được mô tả bởi
nên sẽ được mô tả bởi 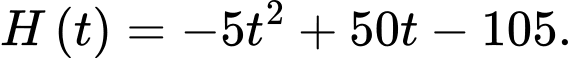
Khảo sát hàm số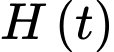 trên đoạn
trên đoạn 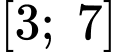
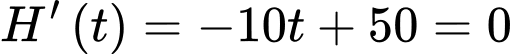
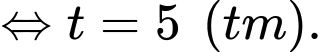
Ta có
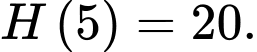
Vậy độ cao lớn nhất mà quả bóng đạt được sau lần nảy đầu tiên là 20 m.
Dựa vào hình vẽ ta thấy

b) Sai.
Quả bóng được thả tại thời điểm
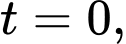 nên để tìm độ cao quả bóng ta cần đi tìm
nên để tìm độ cao quả bóng ta cần đi tìm 
Vì hàm số liên tục tại
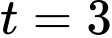 nên
nên 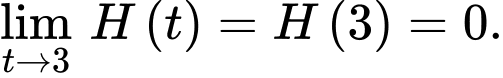
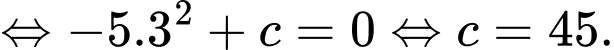
Vậy
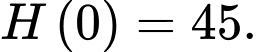 Do đó, quả bóng được thả từ độ cao 45 m.
Do đó, quả bóng được thả từ độ cao 45 m.
c) Sai.
Ta có
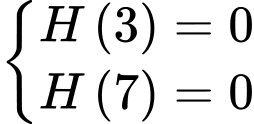
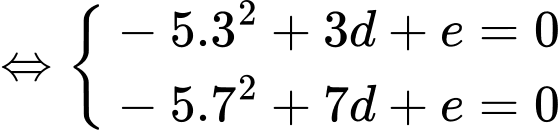
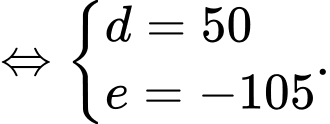
Vậy
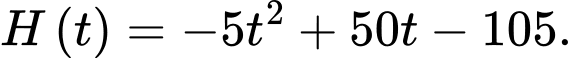
d) Đúng.
Độ cao của quả bóng sau lần nảy đầu tiên trong khoảng thời gian
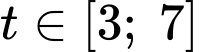 nên sẽ được mô tả bởi
nên sẽ được mô tả bởi 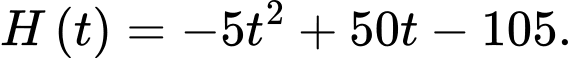
Khảo sát hàm số
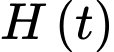 trên đoạn
trên đoạn 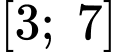
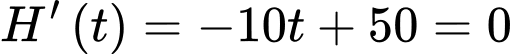
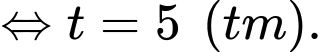
Ta có

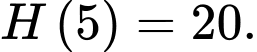
Vậy độ cao lớn nhất mà quả bóng đạt được sau lần nảy đầu tiên là 20 m.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 17 đến câu 22.
Câu 17 [774143]: Nghiên cứu về độ dày của vỏ não, phần tạo ra khả năng tư duy, các nhà nghiên cứu đo độ dày vỏ não của một số trẻ từ thuở ấu thơ đến tuổi khi 25 tuổi. Họ nhận thấy, số trẻ có chỉ số IQ cao (chỉ số IQ từ 121 dến 149), thì ở 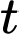 (tuổi), độ dày vỏ não được mô hình hoá bằng hàm số
(tuổi), độ dày vỏ não được mô hình hoá bằng hàm số 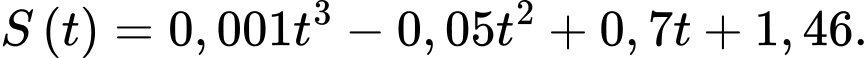 Dựa vào hàm số đã cho, hãy cho biết độ dày vỏ não của những đứa trẻ có chỉ số IQ cao đạt tối đa ở độ tuổi nào?
Dựa vào hàm số đã cho, hãy cho biết độ dày vỏ não của những đứa trẻ có chỉ số IQ cao đạt tối đa ở độ tuổi nào?
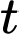 (tuổi), độ dày vỏ não được mô hình hoá bằng hàm số
(tuổi), độ dày vỏ não được mô hình hoá bằng hàm số 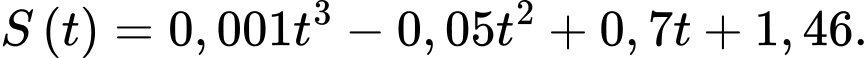 Dựa vào hàm số đã cho, hãy cho biết độ dày vỏ não của những đứa trẻ có chỉ số IQ cao đạt tối đa ở độ tuổi nào?
Dựa vào hàm số đã cho, hãy cho biết độ dày vỏ não của những đứa trẻ có chỉ số IQ cao đạt tối đa ở độ tuổi nào?
Điền đáp án: 10
Ta có: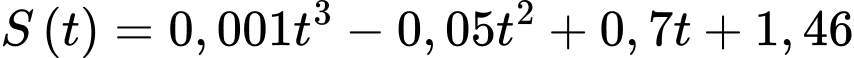
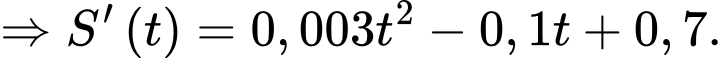
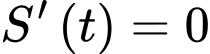
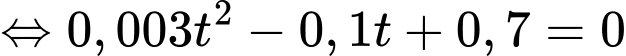
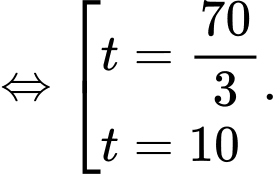
Bảng biến thiên:
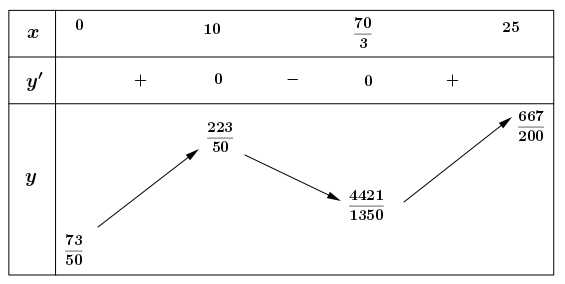
Dựa vào bảng biến thiên ta có: Độ dày vỏ não của những đứa trẻ có chỉ số IQ cao đạt tối đa ở độ tuổi 10 tuổi.
Ta có:
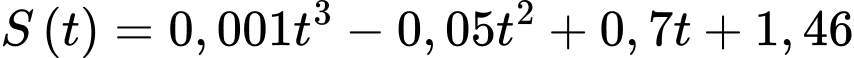
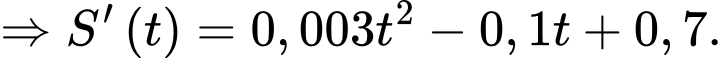
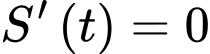
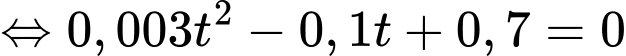
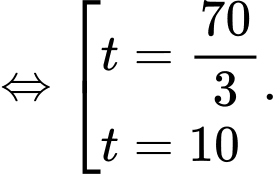
Bảng biến thiên:

Dựa vào bảng biến thiên ta có: Độ dày vỏ não của những đứa trẻ có chỉ số IQ cao đạt tối đa ở độ tuổi 10 tuổi.
Câu 18 [680756]: Một doanh nghiệp dự định sản xuất không quá 500 sản phẩm. Nếu doanh nghiệp sản xuất 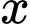 sản phẩm
sản phẩm 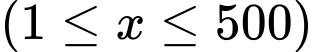 thì doanh thu nhận được khi bán hết số sản phẩm đó là
thì doanh thu nhận được khi bán hết số sản phẩm đó là 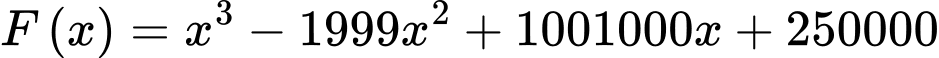 (đồng), trong khi chi phí sản xuất bình quân cho một sản phẩm là
(đồng), trong khi chi phí sản xuất bình quân cho một sản phẩm là 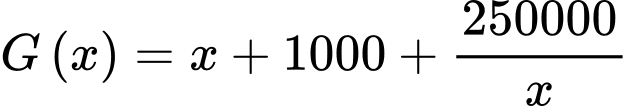 (đồng). Doanh nghiệp cần sản xuất bao nhiêu sản phẩm để lợi nhuận thu được là lớn nhất?
(đồng). Doanh nghiệp cần sản xuất bao nhiêu sản phẩm để lợi nhuận thu được là lớn nhất?
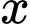 sản phẩm
sản phẩm 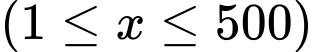 thì doanh thu nhận được khi bán hết số sản phẩm đó là
thì doanh thu nhận được khi bán hết số sản phẩm đó là 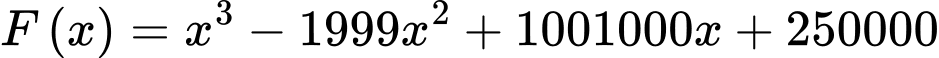 (đồng), trong khi chi phí sản xuất bình quân cho một sản phẩm là
(đồng), trong khi chi phí sản xuất bình quân cho một sản phẩm là 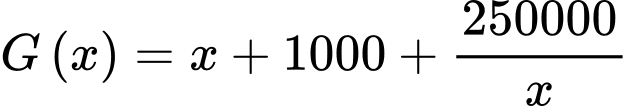 (đồng). Doanh nghiệp cần sản xuất bao nhiêu sản phẩm để lợi nhuận thu được là lớn nhất?
(đồng). Doanh nghiệp cần sản xuất bao nhiêu sản phẩm để lợi nhuận thu được là lớn nhất?
Điền đáp án: 333.
Lợi nhuận của doanh nghiệp khi sản xuất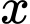 sản phẩm là:
sản phẩm là:
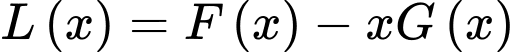
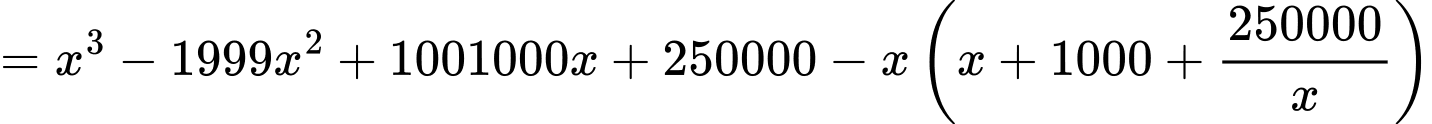 .
.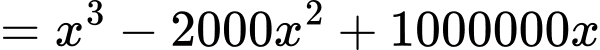 .
.
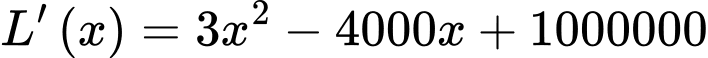

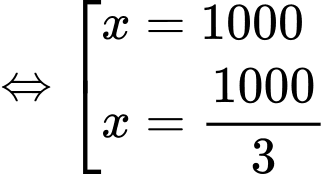 (Vì
(Vì 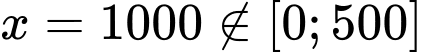 suy ra loại)
suy ra loại)
Lập BBT của hàm số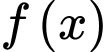 trên đoạn
trên đoạn 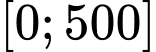
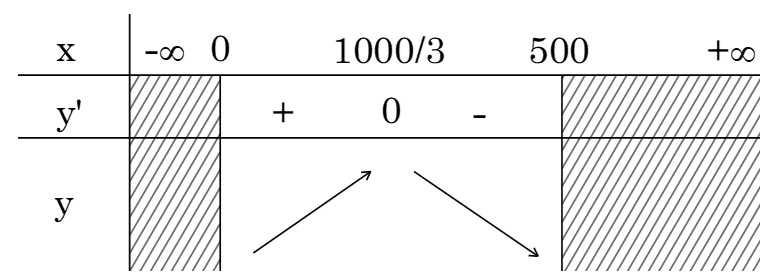
Do số sản phẩm là số nguyên, nên ta xét giá trị của hàm số tại hai điểm nguyên trước và sau giá trị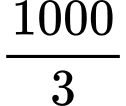 là 333 và 334.
là 333 và 334.
Ta có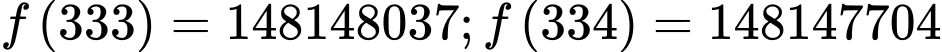
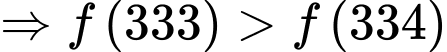
Do đó, doanh nghiệp nên sản xuất 333 sản phẩm để lợi nhuận thu được là lớn nhất.
Lợi nhuận của doanh nghiệp khi sản xuất
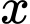 sản phẩm là:
sản phẩm là: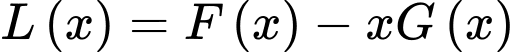
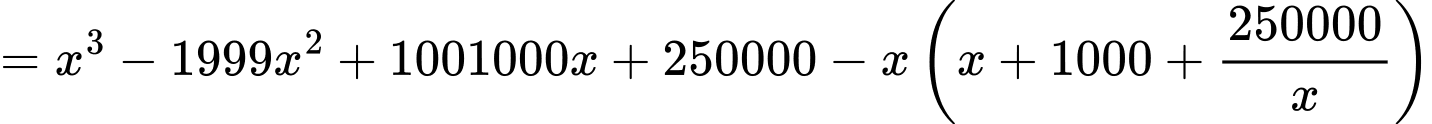 .
.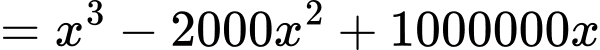 .
.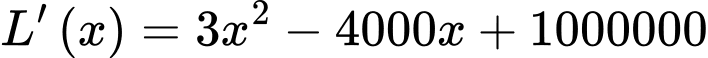

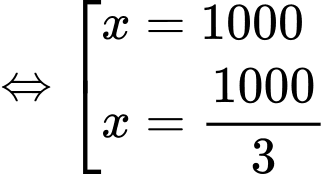 (Vì
(Vì 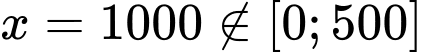 suy ra loại)
suy ra loại)Lập BBT của hàm số
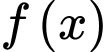 trên đoạn
trên đoạn 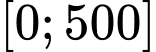

Do số sản phẩm là số nguyên, nên ta xét giá trị của hàm số tại hai điểm nguyên trước và sau giá trị
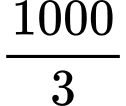 là 333 và 334.
là 333 và 334. Ta có
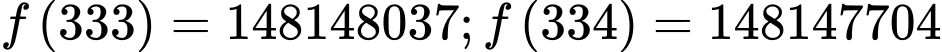
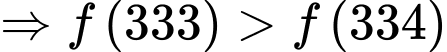
Do đó, doanh nghiệp nên sản xuất 333 sản phẩm để lợi nhuận thu được là lớn nhất.
Câu 19 [774144]: Ông An muốn xây 1 bể chứa nước hình hộp chữ nhật với thể tích 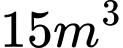 , chiều dài bằng
, chiều dài bằng 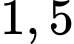 lần chiều rộng. Chi phí làm đáy và nắp bể là 1,2 triệu/
lần chiều rộng. Chi phí làm đáy và nắp bể là 1,2 triệu/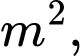 chi phí làm mặt xung quanh bể là 1 triệu/
chi phí làm mặt xung quanh bể là 1 triệu/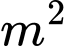 . Tính chiều cao của bể để chi phí làm bể là thấp nhất (đơn vị tính là
. Tính chiều cao của bể để chi phí làm bể là thấp nhất (đơn vị tính là 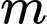 và làm tròn đến hàng phần trăm)
và làm tròn đến hàng phần trăm)
Đính chính: Các em thêm dữ kiện bể nước hình hộp chữ nhật cho đầy đủ nhé
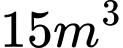 , chiều dài bằng
, chiều dài bằng 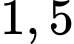 lần chiều rộng. Chi phí làm đáy và nắp bể là 1,2 triệu/
lần chiều rộng. Chi phí làm đáy và nắp bể là 1,2 triệu/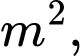 chi phí làm mặt xung quanh bể là 1 triệu/
chi phí làm mặt xung quanh bể là 1 triệu/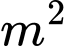 . Tính chiều cao của bể để chi phí làm bể là thấp nhất (đơn vị tính là
. Tính chiều cao của bể để chi phí làm bể là thấp nhất (đơn vị tính là 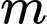 và làm tròn đến hàng phần trăm)
và làm tròn đến hàng phần trăm)Đính chính: Các em thêm dữ kiện bể nước hình hộp chữ nhật cho đầy đủ nhé
Điền đáp án: 2,75.
Gọi chiều rộng của bể là: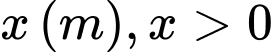 .
.
Khi đó chiều dài của bể là: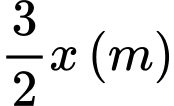 .
.
Ta có thể tích bể là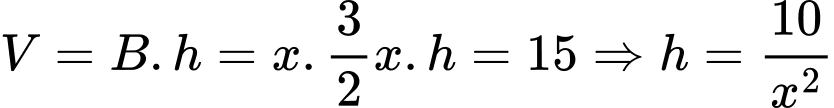 .
.
Khi đó tổng chi phí để làm bể là: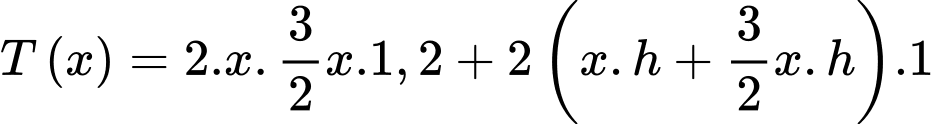
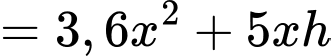
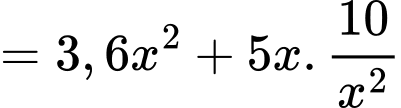
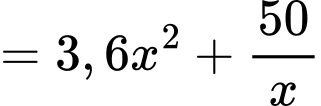
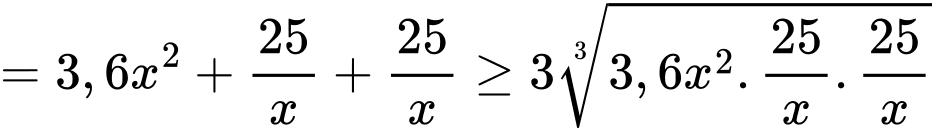
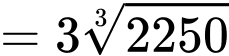 (theo bất đẳng thức Cauchy)
(theo bất đẳng thức Cauchy)
Dấu “=” xảy ra khi và khỉ chi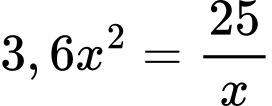
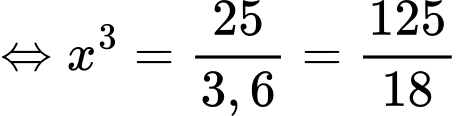
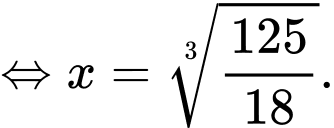
Khi đó chiều cao của bể là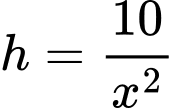
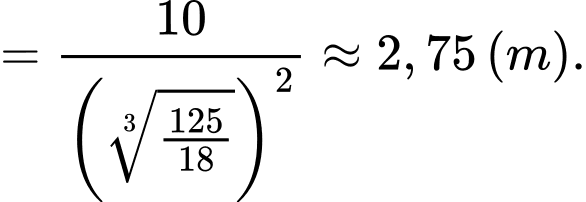
Gọi chiều rộng của bể là:
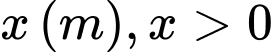 .
.Khi đó chiều dài của bể là:
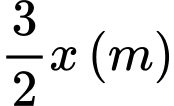 .
.Ta có thể tích bể là
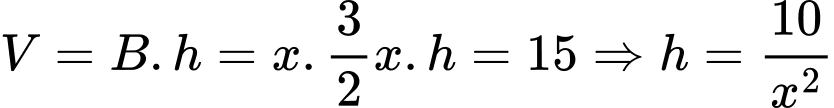 .
.Khi đó tổng chi phí để làm bể là:
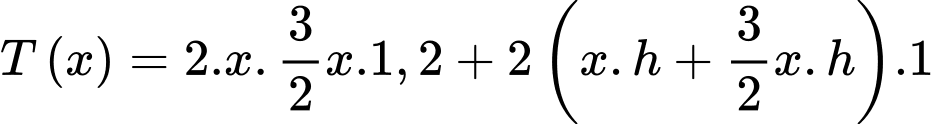
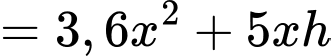
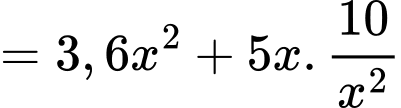
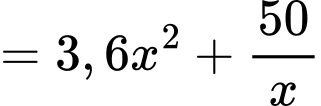
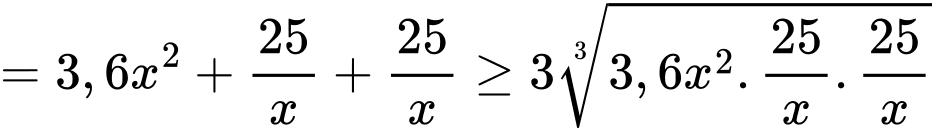
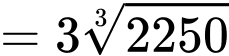 (theo bất đẳng thức Cauchy)
(theo bất đẳng thức Cauchy)Dấu “=” xảy ra khi và khỉ chi
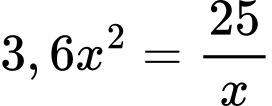
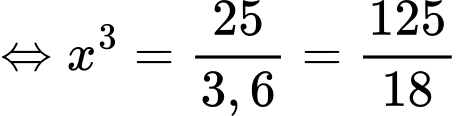
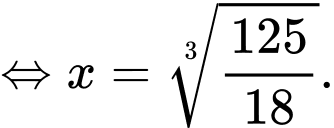
Khi đó chiều cao của bể là
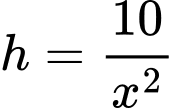
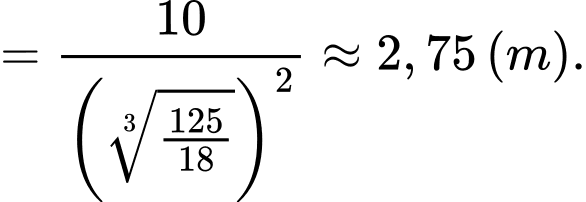
Câu 20 [774146]: Một công ty sản xuất dụng cụ thể thao nhận được một đơn đặt hàng sản xuất 8000 quả bóng tennis. Biết công ty này có 38 máy và mỗi máy có thể sản xuất 30 quả bóng trong một giờ. Chi phí thiết lập các máy này là 200 nghìn đồng cho mỗi máy. Khi được thiết lập, hoạt động sản xuất sẽ hoàn toàn diễn ra tự động dưới sự giám sát. Số tiền phải trả cho người giám sát là 192 nghìn đồng một giờ. Số máy công ty nên sử dụng để sản xuất đơn hàng trên là bao nhiêu để chi phí hoạt động là thấp nhất?
Điền đáp án: 16.
Gọi x là số máy công ty sử dụng để sản xuất đơn hàng 8000 quả bóng tennis.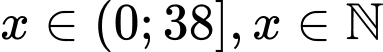 .
.
Số bóng mỗi máy cần sản xuất: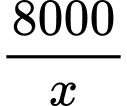
Số giờ cần thiết để hoàn thành đơn hàng: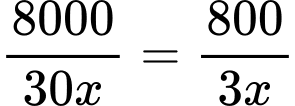
Chi phí hoạt động: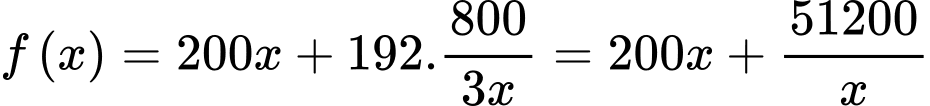 (nghìn đồng)
(nghìn đồng)
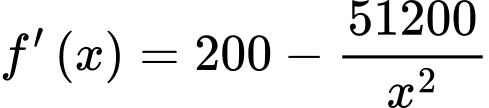
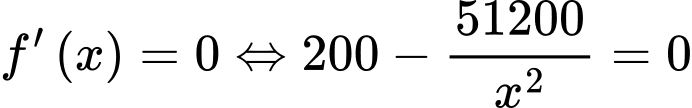
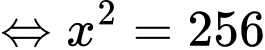
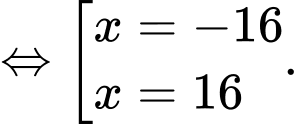
BBT:
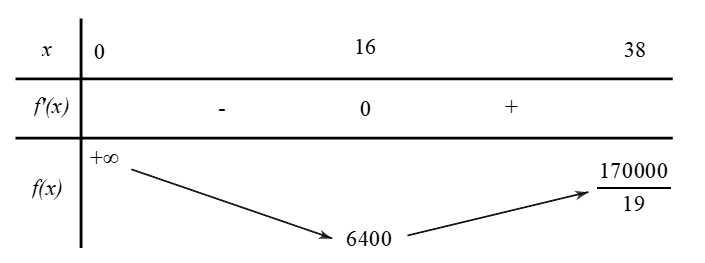
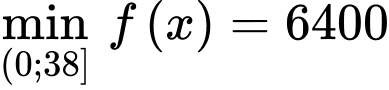 khi x = 16
Vậy công ty nên sử dụng 16 máy để sản xuất đơn hàng 8000 quả bóng tennis cho chi phí hoạt.
khi x = 16
Vậy công ty nên sử dụng 16 máy để sản xuất đơn hàng 8000 quả bóng tennis cho chi phí hoạt.
Gọi x là số máy công ty sử dụng để sản xuất đơn hàng 8000 quả bóng tennis.
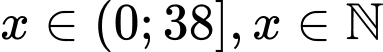 .
.
Số bóng mỗi máy cần sản xuất:
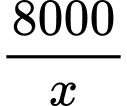
Số giờ cần thiết để hoàn thành đơn hàng:
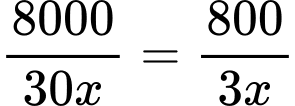
Chi phí hoạt động:
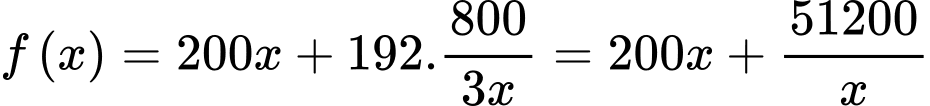 (nghìn đồng)
(nghìn đồng)
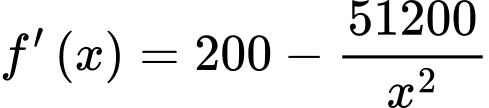
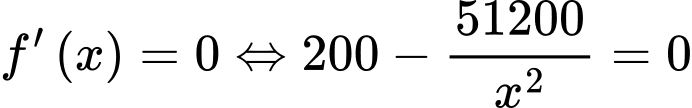
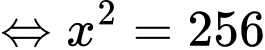
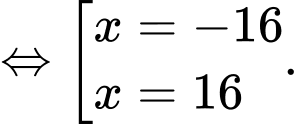
BBT:

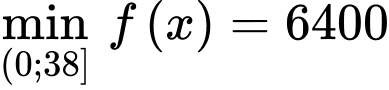 khi x = 16
Vậy công ty nên sử dụng 16 máy để sản xuất đơn hàng 8000 quả bóng tennis cho chi phí hoạt.
khi x = 16
Vậy công ty nên sử dụng 16 máy để sản xuất đơn hàng 8000 quả bóng tennis cho chi phí hoạt.
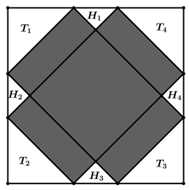
Câu 21 [717152]: Từ hình vuông có cạnh bằng 8 cm người ta cắt bỏ các tam giác vuông cân và giữ lại phần tô đậm như hình vẽ bên, biết bốn tam giác 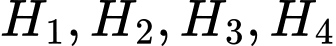 bằng nhau và bốn tam giác
bằng nhau và bốn tam giác 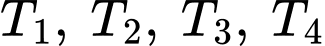 bằng nhau. Sau đó gập phần còn lại thành hình hộp chữ nhật không nắp. Thể tích lớn nhất của khối hộp chữ nhật đó là bao nhiêu cen-ti-mét khối? (kết quả làm tròn hết hàng phần mười).
bằng nhau. Sau đó gập phần còn lại thành hình hộp chữ nhật không nắp. Thể tích lớn nhất của khối hộp chữ nhật đó là bao nhiêu cen-ti-mét khối? (kết quả làm tròn hết hàng phần mười).
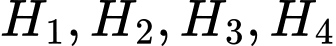 bằng nhau và bốn tam giác
bằng nhau và bốn tam giác 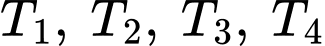 bằng nhau. Sau đó gập phần còn lại thành hình hộp chữ nhật không nắp. Thể tích lớn nhất của khối hộp chữ nhật đó là bao nhiêu cen-ti-mét khối? (kết quả làm tròn hết hàng phần mười).
bằng nhau. Sau đó gập phần còn lại thành hình hộp chữ nhật không nắp. Thể tích lớn nhất của khối hộp chữ nhật đó là bao nhiêu cen-ti-mét khối? (kết quả làm tròn hết hàng phần mười).
Điền đáp án: 26,8.
Gọi cạnh góc vuông của tam giác vuông cân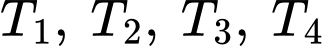 bị cắt bỏ là
bị cắt bỏ là 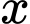 , (đk:
, (đk: 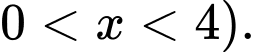
Suy ra cạnh đáy của khối hộp là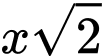 nên diện tích mặt đáy khối hộp
nên diện tích mặt đáy khối hộp 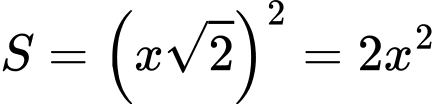
Chiều cao của khối hộp là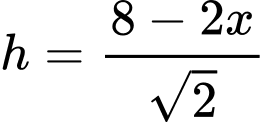
Thể tích khối hộp chữ nhật là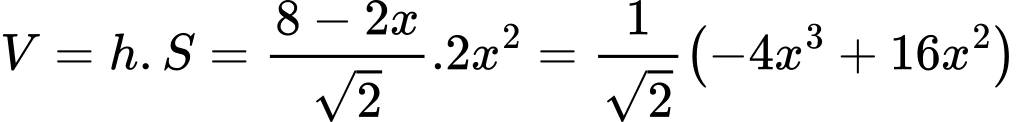
Xét hàm số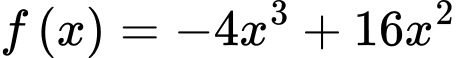 với
với 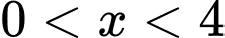
Ta có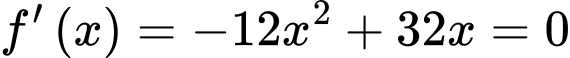
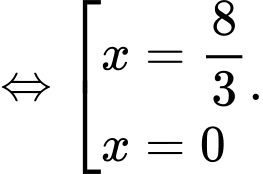
Bảng biến thiên:
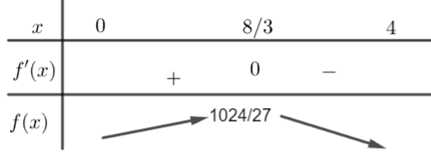
Suy ra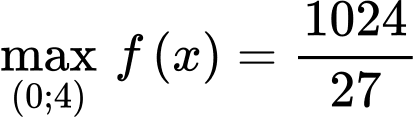 khi
khi 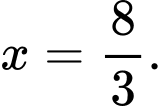
Vậy thể tích lớn nhất của khối hộp chữ nhật là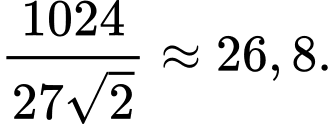
Gọi cạnh góc vuông của tam giác vuông cân
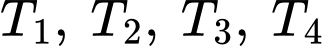 bị cắt bỏ là
bị cắt bỏ là 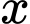 , (đk:
, (đk: 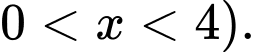
Suy ra cạnh đáy của khối hộp là
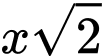 nên diện tích mặt đáy khối hộp
nên diện tích mặt đáy khối hộp 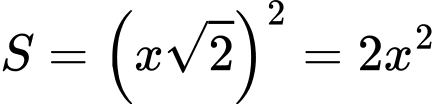
Chiều cao của khối hộp là
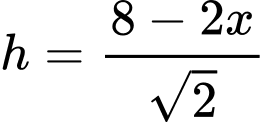
Thể tích khối hộp chữ nhật là
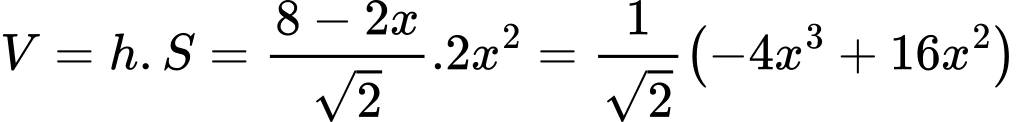
Xét hàm số
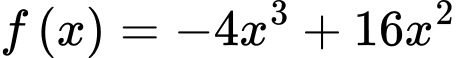 với
với 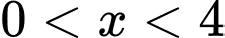
Ta có
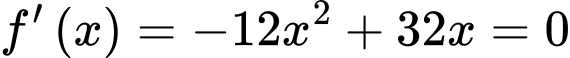
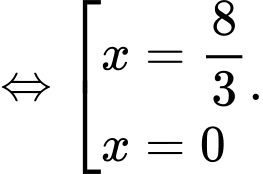
Bảng biến thiên:

Suy ra
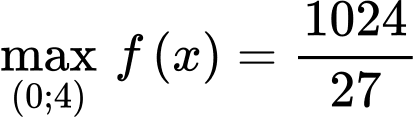 khi
khi 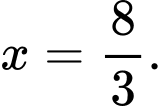
Vậy thể tích lớn nhất của khối hộp chữ nhật là
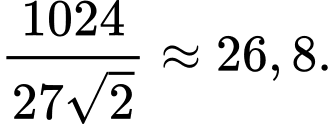
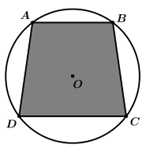
Câu 22 [774148]: Trong khu vườn có dạng hình tròn tâm  bán kính 5 m, ông Tuấn muốn rào một phần đất hình thang cân
bán kính 5 m, ông Tuấn muốn rào một phần đất hình thang cân 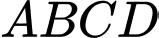 nội tiếp đường tròn trên có hai đáy
nội tiếp đường tròn trên có hai đáy  và
và 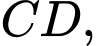 trong đó đáy lớn
trong đó đáy lớn 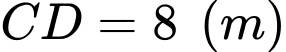 dùng để trồng hoa (tham khảo hình vẽ). Diện tích lớn nhất của hình thang
dùng để trồng hoa (tham khảo hình vẽ). Diện tích lớn nhất của hình thang 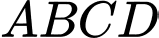 ông Tuấn có thể rào lại là bao nhiêu
ông Tuấn có thể rào lại là bao nhiêu 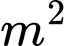 (kết quả làm tròn đến hàng phần mười).
(kết quả làm tròn đến hàng phần mười).
 bán kính 5 m, ông Tuấn muốn rào một phần đất hình thang cân
bán kính 5 m, ông Tuấn muốn rào một phần đất hình thang cân 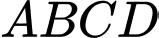 nội tiếp đường tròn trên có hai đáy
nội tiếp đường tròn trên có hai đáy  và
và 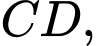 trong đó đáy lớn
trong đó đáy lớn 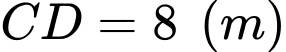 dùng để trồng hoa (tham khảo hình vẽ). Diện tích lớn nhất của hình thang
dùng để trồng hoa (tham khảo hình vẽ). Diện tích lớn nhất của hình thang 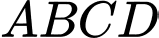 ông Tuấn có thể rào lại là bao nhiêu
ông Tuấn có thể rào lại là bao nhiêu 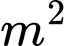 (kết quả làm tròn đến hàng phần mười).
(kết quả làm tròn đến hàng phần mười).
Điền đáp án: 49,3.
Đặt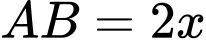 thì
thì 
Chiều cao hình thang là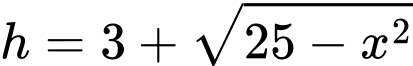
Diện tích hình thang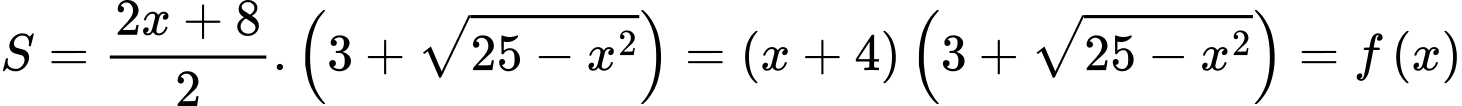
Suy ra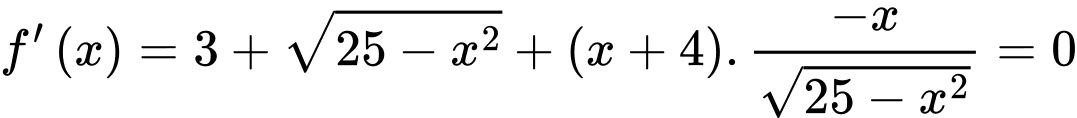
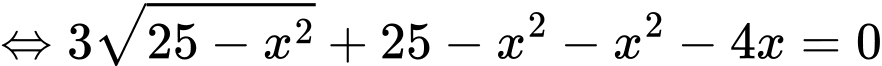
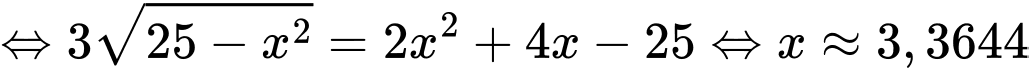 (sử dụng máy tính Casio nhẩm nghiệm).
(sử dụng máy tính Casio nhẩm nghiệm).
Suy ra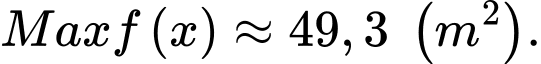
Đặt
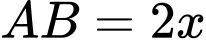 thì
thì 
Chiều cao hình thang là
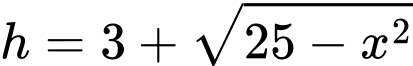
Diện tích hình thang
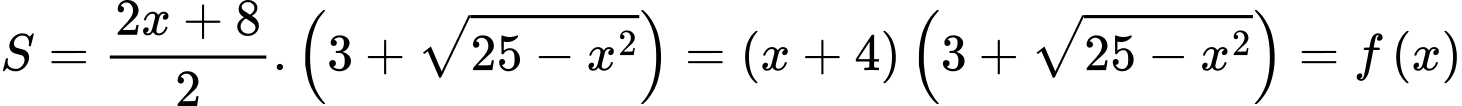
Suy ra
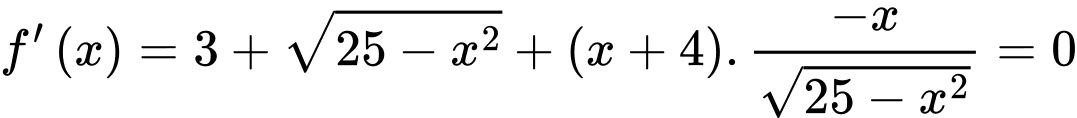
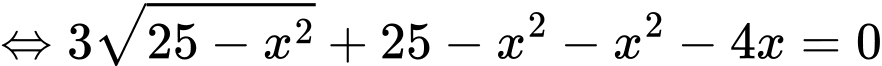
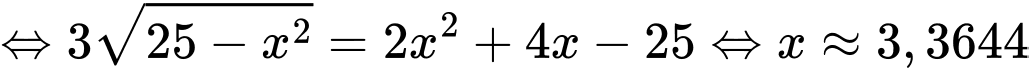 (sử dụng máy tính Casio nhẩm nghiệm).
(sử dụng máy tính Casio nhẩm nghiệm).
Suy ra