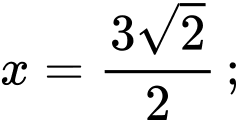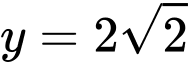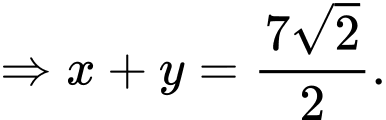PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1 [135936]: Cho hàm số 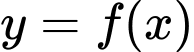 có bảng biến thiên như sau
có bảng biến thiên như sau
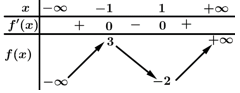
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
 có bảng biến thiên như sau
có bảng biến thiên như sau
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A, 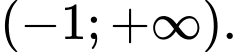
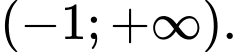
B, 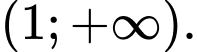
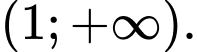
C, 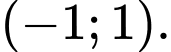
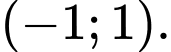
D, 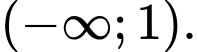
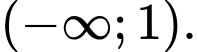
Chọn đáp án B.
Dựa vào bảng biến thiên, ta có hàm số đã cho đồng biến trên các khoảng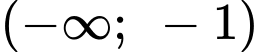 và
và 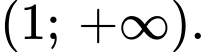 So với các đáp án, ta thấy đáp án B thỏa mãn.
Đáp án: B
So với các đáp án, ta thấy đáp án B thỏa mãn.
Đáp án: B
Dựa vào bảng biến thiên, ta có hàm số đã cho đồng biến trên các khoảng
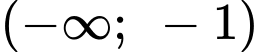 và
và 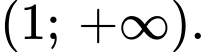 So với các đáp án, ta thấy đáp án B thỏa mãn.
Đáp án: B
So với các đáp án, ta thấy đáp án B thỏa mãn.
Đáp án: B
Câu 2 [801372]: Cho hàm số 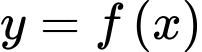 xác định trên
xác định trên 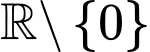 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
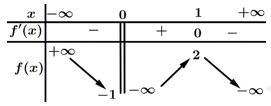
Hàm số đã cho có bao nhiêu điểm cực trị?
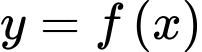 xác định trên
xác định trên 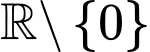 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
Hàm số đã cho có bao nhiêu điểm cực trị?
A, 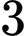 .
.
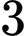 .
.B,  .
.
 .
.C, 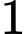 .
.
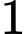 .
.D, 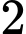 .
.
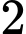 .
.
Chọn đáp án C.
Từ bảng biến thiên ta thấy hàm số đã cho xác định và có đạo hàm đổi dấu qua điểm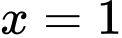 nên hàm số chỉ có 1 điểm cực trị là điểm
nên hàm số chỉ có 1 điểm cực trị là điểm 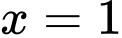 . Đáp án: C
. Đáp án: C
Từ bảng biến thiên ta thấy hàm số đã cho xác định và có đạo hàm đổi dấu qua điểm
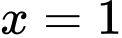 nên hàm số chỉ có 1 điểm cực trị là điểm
nên hàm số chỉ có 1 điểm cực trị là điểm 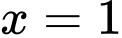 . Đáp án: C
. Đáp án: C
Câu 3 [808933]: Cho hàm số 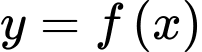 xác định trên tập
xác định trên tập 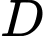 . Số
. Số 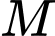 được gọi là giá trị lớn nhất của hàm số
được gọi là giá trị lớn nhất của hàm số 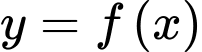 trên
trên 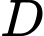 nếu
nếu
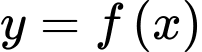 xác định trên tập
xác định trên tập 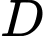 . Số
. Số 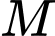 được gọi là giá trị lớn nhất của hàm số
được gọi là giá trị lớn nhất của hàm số 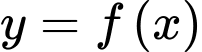 trên
trên 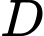 nếu
nếu A, 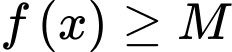 với mọi
với mọi 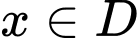 .
.
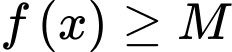 với mọi
với mọi 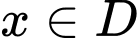 .
.B, 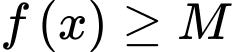 với mọi
với mọi 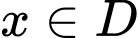 và tồn tại
và tồn tại  sao cho
sao cho 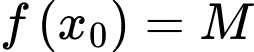 .
.
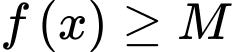 với mọi
với mọi 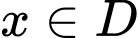 và tồn tại
và tồn tại  sao cho
sao cho 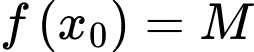 .
.C, 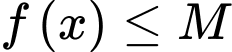 với mọi
với mọi 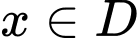 .
.
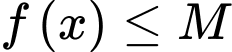 với mọi
với mọi 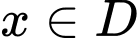 .
.D, 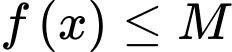 với mọi
với mọi 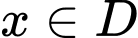 và tồn tại
và tồn tại  sao cho
sao cho 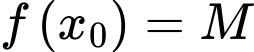 .
.
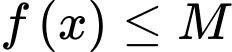 với mọi
với mọi 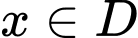 và tồn tại
và tồn tại  sao cho
sao cho 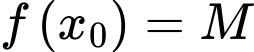 .
.
Chọn D
Theo định nghĩa giá trị lớn nhất của hàm số trên một khoảng. Đáp án: D
Theo định nghĩa giá trị lớn nhất của hàm số trên một khoảng. Đáp án: D
Câu 4 [677108]: Cho hàm số bậc bốn 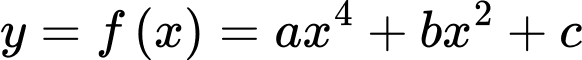 có đồ thị sau
có đồ thị sau
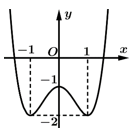
Giá trị cực đại của hàm số là
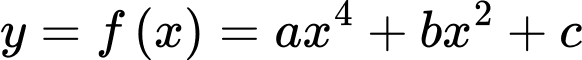 có đồ thị sau
có đồ thị sau
Giá trị cực đại của hàm số là
A, 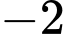 .
.
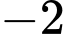 .
.B, 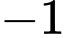 .
.
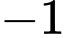 .
.C,  .
.
 .
.D, 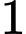 .
.
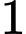 .
.
Chọn B
Dựa vào đồ thị, nhận thấy hàm số đạt cực đại tại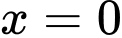 và
và 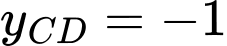 . Đáp án: B
. Đáp án: B
Dựa vào đồ thị, nhận thấy hàm số đạt cực đại tại
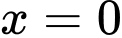 và
và 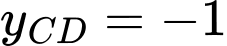 . Đáp án: B
. Đáp án: B
Câu 5 [315724]: Cho hàm số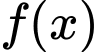 có bảng biến thiên như sau:
có bảng biến thiên như sau:
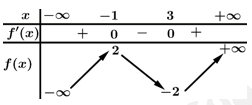
Giá trị cực tiểu của hàm số là
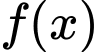 có bảng biến thiên như sau:
có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số là
A, 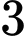 .
.
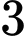 .
.B, 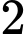 .
.
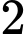 .
.C, 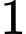 .
.
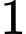 .
.D, 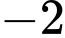 .
.
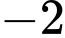 .
.
Chọn đáp án D.
Dựa vào bảng biến thiên, ta có hàm số đã cho đạt cực tiểu tại điểm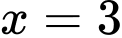 nên suy ra giá trị cực tiểu của hàm số là
nên suy ra giá trị cực tiểu của hàm số là 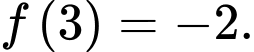 Đáp án: D
Đáp án: D
Dựa vào bảng biến thiên, ta có hàm số đã cho đạt cực tiểu tại điểm
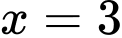 nên suy ra giá trị cực tiểu của hàm số là
nên suy ra giá trị cực tiểu của hàm số là 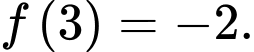 Đáp án: D
Đáp án: D
Câu 6 [9143]: Cho hàm số 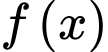 có đồ thị như hình vẽ bên. Hàm số đồng biến trên khoảng nào sau đây?
có đồ thị như hình vẽ bên. Hàm số đồng biến trên khoảng nào sau đây?
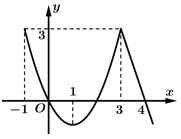
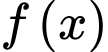 có đồ thị như hình vẽ bên. Hàm số đồng biến trên khoảng nào sau đây?
có đồ thị như hình vẽ bên. Hàm số đồng biến trên khoảng nào sau đây?
A, 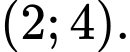
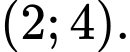
B, 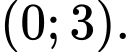
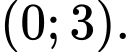
C, 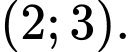
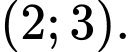
D, 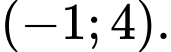
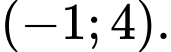
 Đáp án: C
Đáp án: C
Câu 7 [539115]: Hàm số 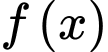 có đạo hàm
có đạo hàm 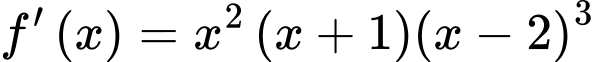 ,
, 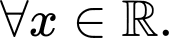 Hỏi
Hỏi 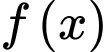 có bao nhiêu điểm cực đại?
có bao nhiêu điểm cực đại?
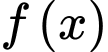 có đạo hàm
có đạo hàm 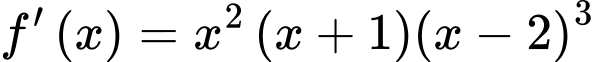 ,
, 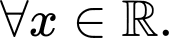 Hỏi
Hỏi 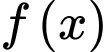 có bao nhiêu điểm cực đại?
có bao nhiêu điểm cực đại? A, 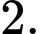
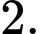
B, 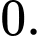
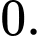
C, 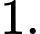
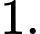
D, 
Chọn C
Ta có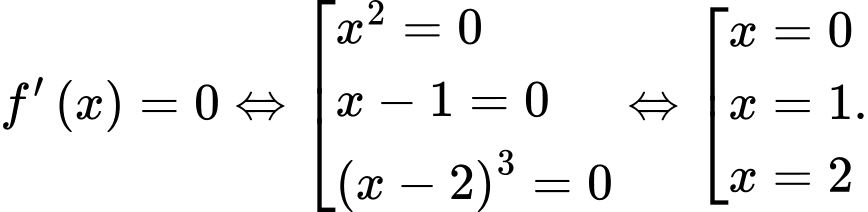
Bảng biến thiên
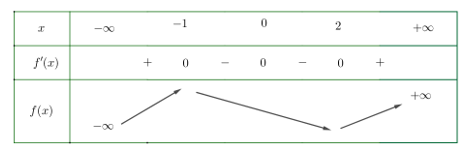
Dựa vào bảng biến thiên suy ra hàm số có điểm cực đại Đáp án: C
điểm cực đại Đáp án: C
Ta có
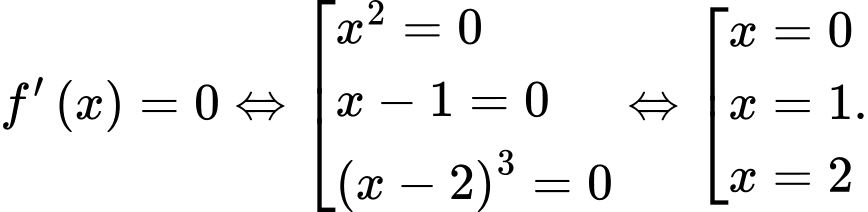
Bảng biến thiên

Dựa vào bảng biến thiên suy ra hàm số có
 điểm cực đại Đáp án: C
điểm cực đại Đáp án: C
Câu 8 [380966]: Hàm số 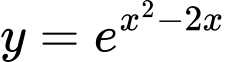 nghịch biến trên khoảng nào dưới đây?
nghịch biến trên khoảng nào dưới đây?
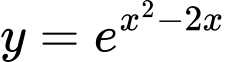 nghịch biến trên khoảng nào dưới đây?
nghịch biến trên khoảng nào dưới đây? A, 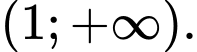
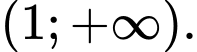
B, 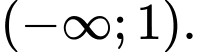
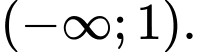
C, 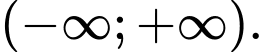
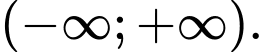
D, 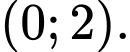
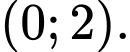
Ta có: 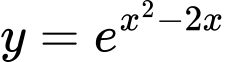
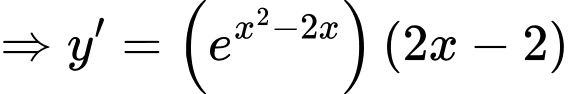
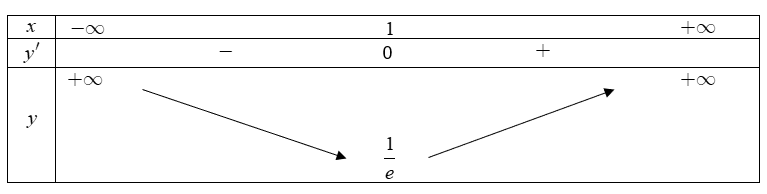
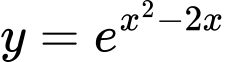
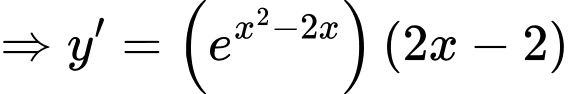
Khi đó 

Ta có bảng biến thiên

Hàm số đã cho nghịch biến trên khoảng  ..
..
Đáp án: B  ..
..
Câu 9 [378821]: Giá trị nhỏ nhất của hàm số 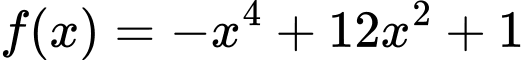 trên đoạn
trên đoạn 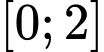 bằng
bằng
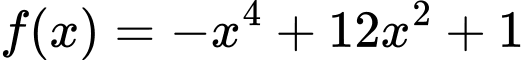 trên đoạn
trên đoạn 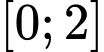 bằng
bằng A, 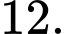
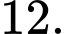
B, 
C, 
D, 
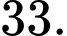
Phương pháp:
Tính đạo hàm và lập BBT trên đoạn [0,2]
Cách giải:
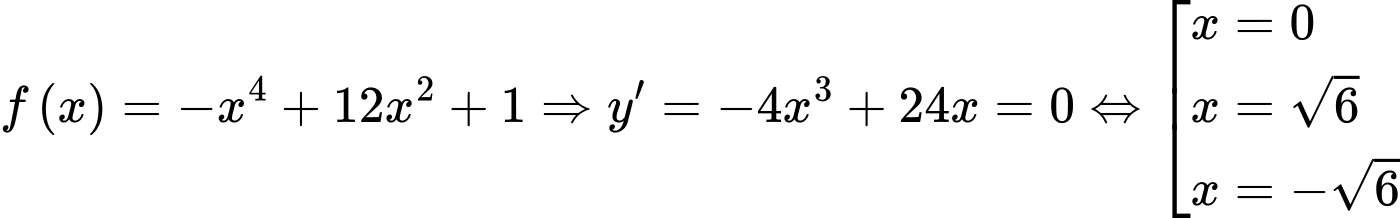
Ta có BBT
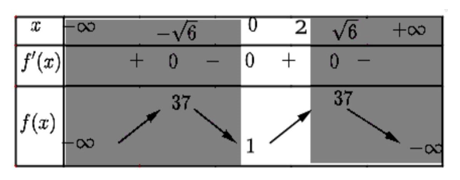
Hàm số đạt GTNN bằng 1 với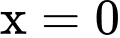 trên đoạn [0,2]
trên đoạn [0,2]
Chọn B. Đáp án: B
Tính đạo hàm và lập BBT trên đoạn [0,2]
Cách giải:
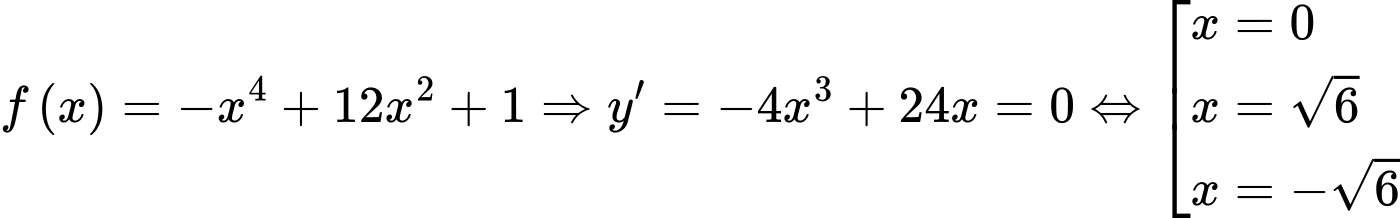
Ta có BBT

Hàm số đạt GTNN bằng 1 với
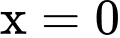 trên đoạn [0,2]
trên đoạn [0,2] Chọn B. Đáp án: B
Câu 10 [628239]: Giá trị cực tiểu của hàm số 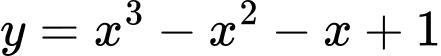 là
là
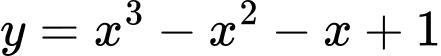 là
là A, 1.
B, 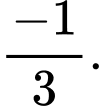
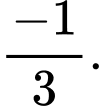
C, 0.
D, 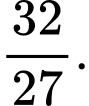
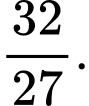
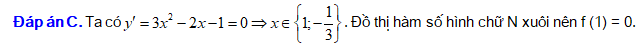 Đáp án: C
Đáp án: C
Câu 11 [378791]: Hàm số nào sau đây nghịch biến trên 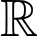 ?
?
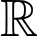 ?
? A, 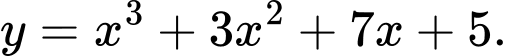
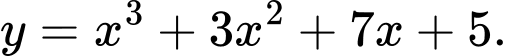
B, 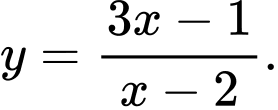
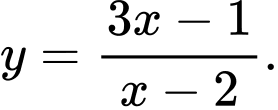
C, 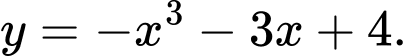
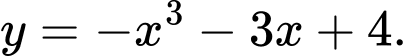
D, 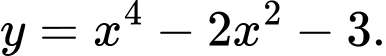
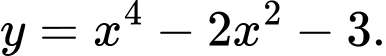
Phương pháp:
Hàm số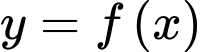 nghịch biến trên
nghịch biến trên 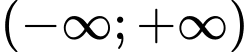 thoả mãn
thoả mãn 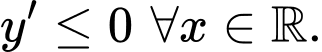
Cách giải:
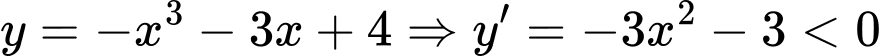 nên hàm số
nên hàm số 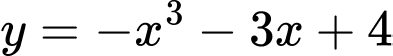 luôn nghịch biến trên
luôn nghịch biến trên 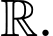
Chọn C Đáp án: C
Hàm số
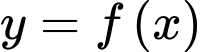 nghịch biến trên
nghịch biến trên 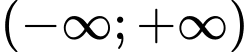 thoả mãn
thoả mãn 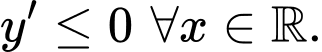
Cách giải:
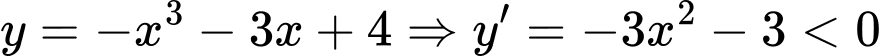 nên hàm số
nên hàm số 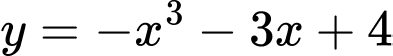 luôn nghịch biến trên
luôn nghịch biến trên 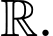
Chọn C Đáp án: C
Câu 12 [538492]: Cho hàm số 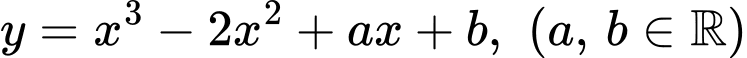 có đồ thị
có đồ thị  Biết đồ thị
Biết đồ thị  có điểm cực trị là
có điểm cực trị là 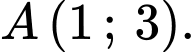 Tính giá trị của
Tính giá trị của 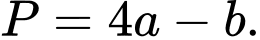
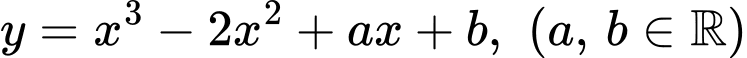 có đồ thị
có đồ thị  Biết đồ thị
Biết đồ thị  có điểm cực trị là
có điểm cực trị là 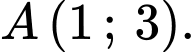 Tính giá trị của
Tính giá trị của 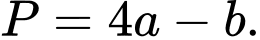
A, 

B, 

C, 

D, 

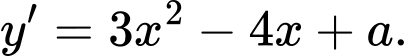
 có điểm cực trị là
có điểm cực trị là 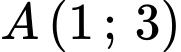 khi:
khi: 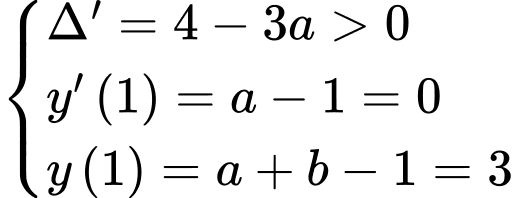
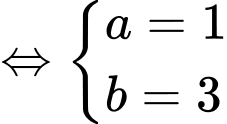 Đáp án: A
Đáp án: A PHẦN II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a),b),c),d) ở mỗi câu học sinh chọn đúng hoặc sai.
Câu 13 [693123]: Cho hàm số 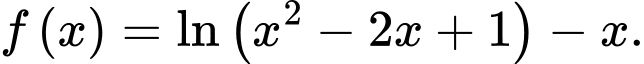
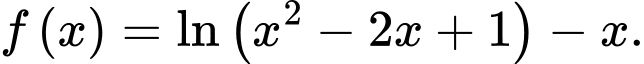
a) Sai.
Điều kiện: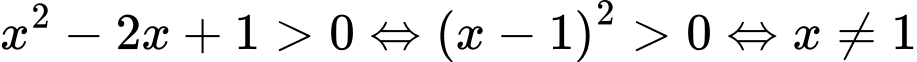
Suy ra tập xác định của hàm số là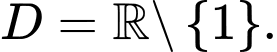
b) Đúng.
Áp dụng công thức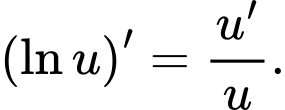
Ta có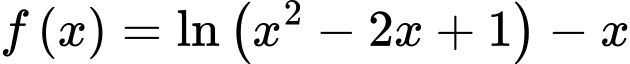
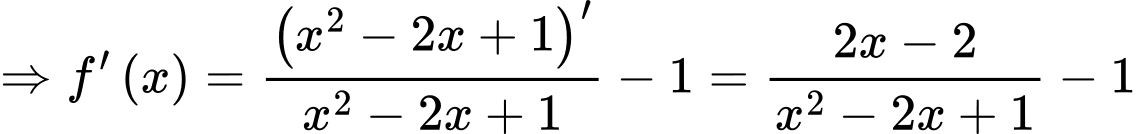
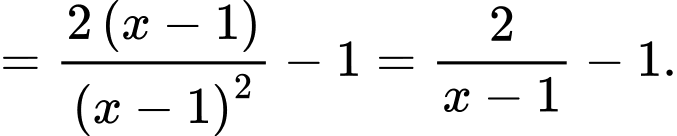
c) Đúng.
Ta có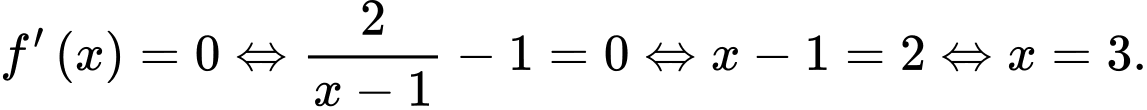
Suy ra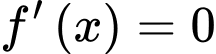 có nghiệm duy nhất.
có nghiệm duy nhất.
d) Sai.
Lập bảng biến thiên
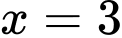 là điểm cực đại của hàm số
là điểm cực đại của hàm số
Do đó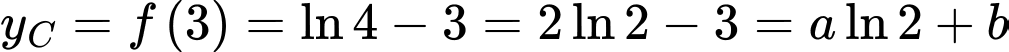
Suy ra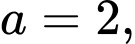
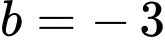 nên
nên 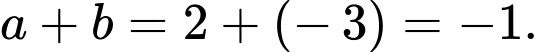
Điều kiện:
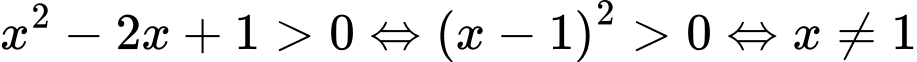
Suy ra tập xác định của hàm số là
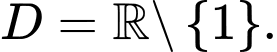
b) Đúng.
Áp dụng công thức
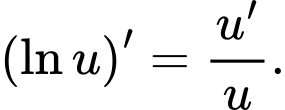
Ta có
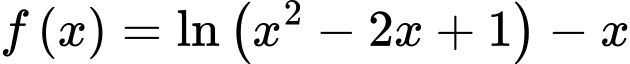
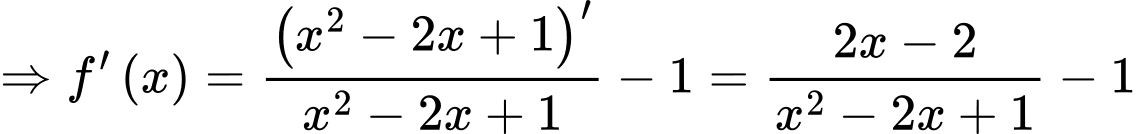
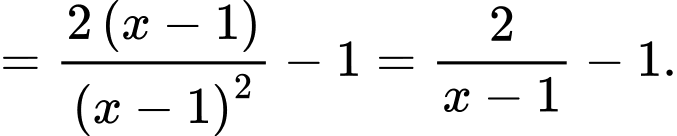
c) Đúng.
Ta có
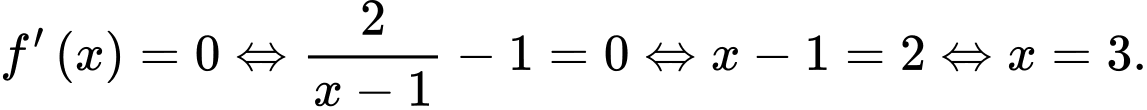
Suy ra
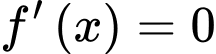 có nghiệm duy nhất.
có nghiệm duy nhất.
d) Sai.
Lập bảng biến thiên
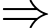
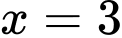 là điểm cực đại của hàm số
là điểm cực đại của hàm số
Do đó
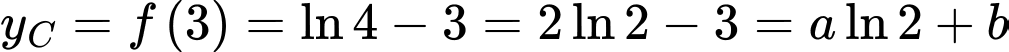
Suy ra
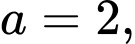
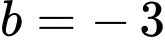 nên
nên 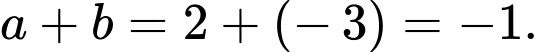
Câu 14 [717143]: Cho hàm số 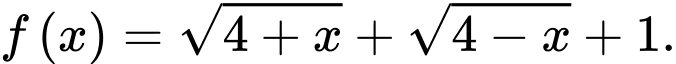
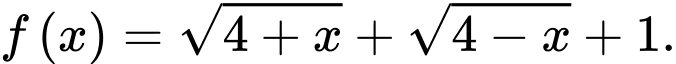
a) Đúng.
Điều kiện xác định của hàm số là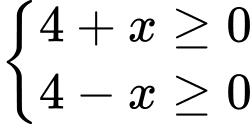
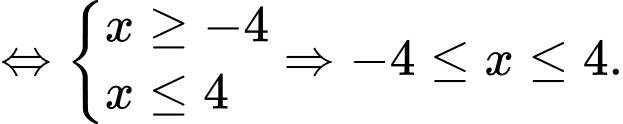 Vậy tập xác định của hàm số là
Vậy tập xác định của hàm số là 
b) Sai.
Ta có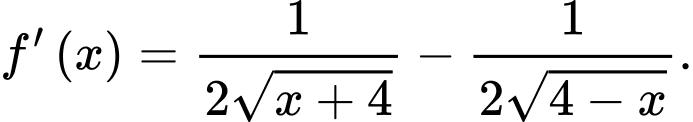
c) Đúng.
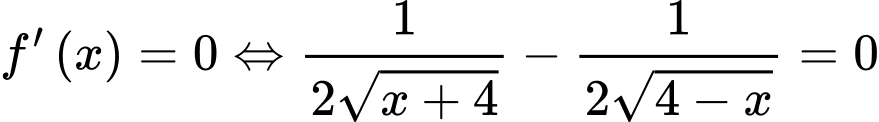
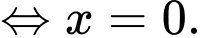
d) Sai.
Hàm số không tồn tại đạo hàm tại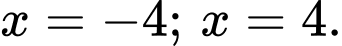
Bảng biến thiên
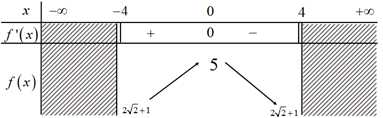
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên tập xác định của nó bằng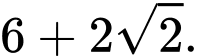
Điều kiện xác định của hàm số là
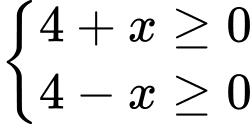
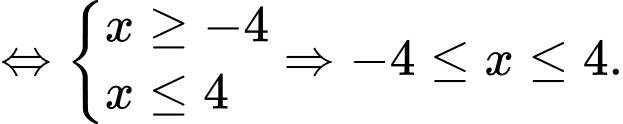 Vậy tập xác định của hàm số là
Vậy tập xác định của hàm số là 
b) Sai.
Ta có
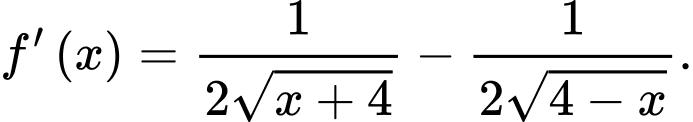
c) Đúng.
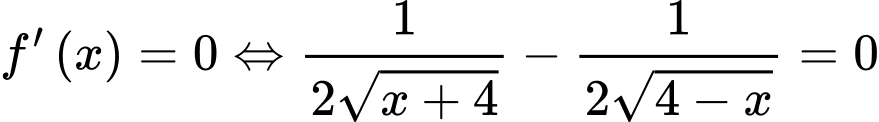
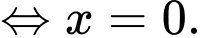
d) Sai.
Hàm số không tồn tại đạo hàm tại
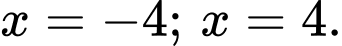
Bảng biến thiên

Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên tập xác định của nó bằng
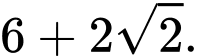
Câu 15 [774149]: Một cửa hàng bán đồ thủ công với giá bán là 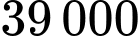 đồng/sản phẩm. Giá nhập vào của sản phẩm đó là
đồng/sản phẩm. Giá nhập vào của sản phẩm đó là 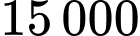 đồng/sản phẩm. Với giá này cửa hàng ước chừng bán được
đồng/sản phẩm. Với giá này cửa hàng ước chừng bán được 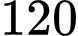 sản phẩm/ngày. Cửa hàng dự định giảm giá bán, ước tính cứ giảm
sản phẩm/ngày. Cửa hàng dự định giảm giá bán, ước tính cứ giảm 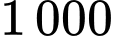 đồng/sản phẩm thì số sản phẩm bán được sẽ tăng thêm là 15 sản phẩm.
đồng/sản phẩm thì số sản phẩm bán được sẽ tăng thêm là 15 sản phẩm.
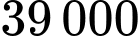 đồng/sản phẩm. Giá nhập vào của sản phẩm đó là
đồng/sản phẩm. Giá nhập vào của sản phẩm đó là 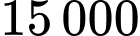 đồng/sản phẩm. Với giá này cửa hàng ước chừng bán được
đồng/sản phẩm. Với giá này cửa hàng ước chừng bán được 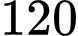 sản phẩm/ngày. Cửa hàng dự định giảm giá bán, ước tính cứ giảm
sản phẩm/ngày. Cửa hàng dự định giảm giá bán, ước tính cứ giảm 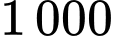 đồng/sản phẩm thì số sản phẩm bán được sẽ tăng thêm là 15 sản phẩm.
đồng/sản phẩm thì số sản phẩm bán được sẽ tăng thêm là 15 sản phẩm.
a) Sai.
Nếu giảm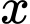 nghìn đồng/ sản phẩm thì cửa hàng bán được số sản phẩm là
nghìn đồng/ sản phẩm thì cửa hàng bán được số sản phẩm là 
Nếu giá bán là 25 nghìn đồng nghĩa là giảm 14 nghìn đồng/ sản phẩm thì cửa hàng bán được số sản phẩm là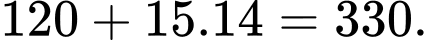
b) Đúng.
Lợi nhuận tối đa theo ngày của cửa hàng khi chưa giảm giá sản phẩm là
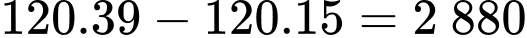 (nghìn đồng).
(nghìn đồng).
c) Đúng.
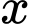 (nghìn đồng) là giá tiền mà cửa hàng dự định bán sản phẩm đó nghĩa là giảm
(nghìn đồng) là giá tiền mà cửa hàng dự định bán sản phẩm đó nghĩa là giảm 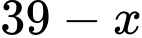 (nghìn đồng)/ sản phẩm thì cửa hàng bán được số sản phẩm là:
(nghìn đồng)/ sản phẩm thì cửa hàng bán được số sản phẩm là:
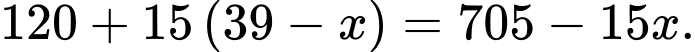
Lợi nhuận bán mỗi sản phẩm là: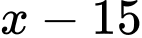 (nghìn đồng).
(nghìn đồng).
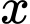 (nghìn đồng) là giá tiền mà cửa hàng dự định bán sản phẩm đó
(nghìn đồng) là giá tiền mà cửa hàng dự định bán sản phẩm đó 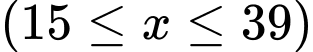 , khi đó lợi nhuận theo ngày của cửa hàng được xác định bởi hàm số
, khi đó lợi nhuận theo ngày của cửa hàng được xác định bởi hàm số 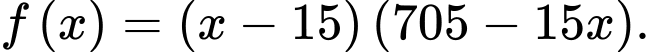
d) Đúng.
Xét hàm số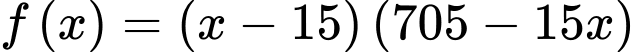 với
với 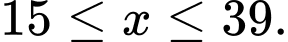
Ta có:
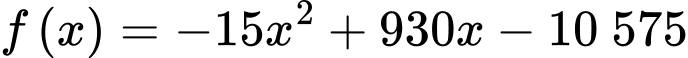
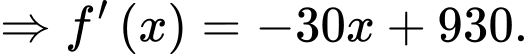
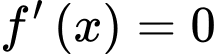

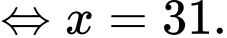

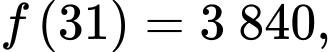
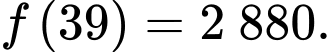
Vậy lợi nhuận tối đa theo ngày mà cửa hàng thu được là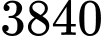 (nghìn đồng).
(nghìn đồng).
Nếu giảm
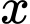 nghìn đồng/ sản phẩm thì cửa hàng bán được số sản phẩm là
nghìn đồng/ sản phẩm thì cửa hàng bán được số sản phẩm là 
Nếu giá bán là 25 nghìn đồng nghĩa là giảm 14 nghìn đồng/ sản phẩm thì cửa hàng bán được số sản phẩm là
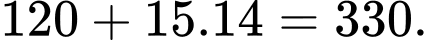
b) Đúng.
Lợi nhuận tối đa theo ngày của cửa hàng khi chưa giảm giá sản phẩm là
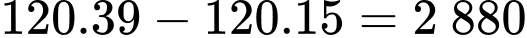 (nghìn đồng).
(nghìn đồng).
c) Đúng.
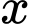 (nghìn đồng) là giá tiền mà cửa hàng dự định bán sản phẩm đó nghĩa là giảm
(nghìn đồng) là giá tiền mà cửa hàng dự định bán sản phẩm đó nghĩa là giảm 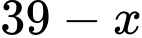 (nghìn đồng)/ sản phẩm thì cửa hàng bán được số sản phẩm là:
(nghìn đồng)/ sản phẩm thì cửa hàng bán được số sản phẩm là: 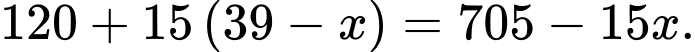
Lợi nhuận bán mỗi sản phẩm là:
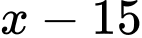 (nghìn đồng).
(nghìn đồng).
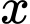 (nghìn đồng) là giá tiền mà cửa hàng dự định bán sản phẩm đó
(nghìn đồng) là giá tiền mà cửa hàng dự định bán sản phẩm đó 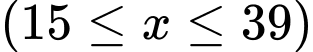 , khi đó lợi nhuận theo ngày của cửa hàng được xác định bởi hàm số
, khi đó lợi nhuận theo ngày của cửa hàng được xác định bởi hàm số 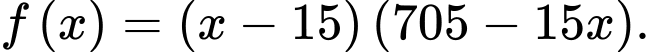
d) Đúng.
Xét hàm số
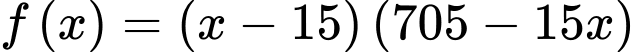 với
với 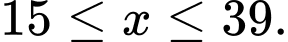
Ta có:
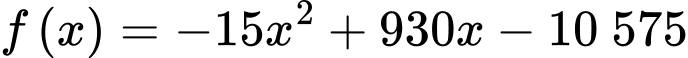
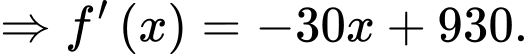
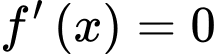

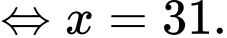

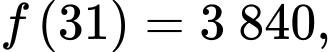
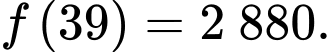
Vậy lợi nhuận tối đa theo ngày mà cửa hàng thu được là
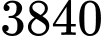 (nghìn đồng).
(nghìn đồng).
Câu 16 [774150]: Trong một trò chơi thử thách, bạn Giáp đang ở trên thuyền (vị trí 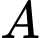 ) cách bờ hồ (vị trí C)
) cách bờ hồ (vị trí C) 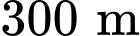 và cần đi đến vị trí
và cần đi đến vị trí 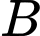 trên bờ hồ như hình vẽ, khoảng cách từ
trên bờ hồ như hình vẽ, khoảng cách từ  đến
đến 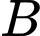 là
là 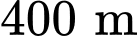 , lưu ý là Giáp có thể chèo thuyền thẳng từ
, lưu ý là Giáp có thể chèo thuyền thẳng từ 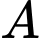 đến
đến 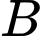 hoặc chèo thuyền từ
hoặc chèo thuyền từ 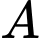 đến một điểm nằm giữa
đến một điểm nằm giữa  và
và 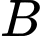 rồi chạy bộ đến
rồi chạy bộ đến 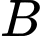 .
.
Biết rằng Giáp chèo thuyền với tốc độ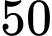 m/phút và chạy bộ với tốc độ
m/phút và chạy bộ với tốc độ 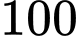 m/phút.
m/phút.
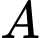 ) cách bờ hồ (vị trí C)
) cách bờ hồ (vị trí C) 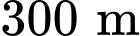 và cần đi đến vị trí
và cần đi đến vị trí 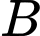 trên bờ hồ như hình vẽ, khoảng cách từ
trên bờ hồ như hình vẽ, khoảng cách từ  đến
đến 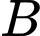 là
là 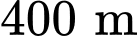 , lưu ý là Giáp có thể chèo thuyền thẳng từ
, lưu ý là Giáp có thể chèo thuyền thẳng từ 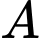 đến
đến 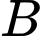 hoặc chèo thuyền từ
hoặc chèo thuyền từ 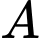 đến một điểm nằm giữa
đến một điểm nằm giữa  và
và 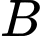 rồi chạy bộ đến
rồi chạy bộ đến 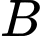 .
.
Biết rằng Giáp chèo thuyền với tốc độ
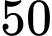 m/phút và chạy bộ với tốc độ
m/phút và chạy bộ với tốc độ 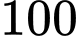 m/phút.
m/phút. 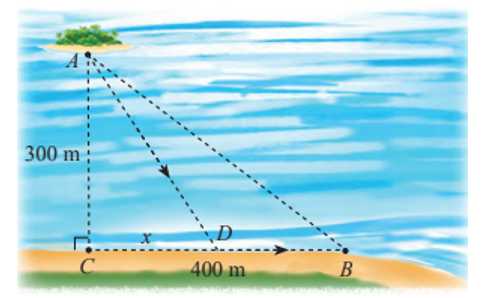
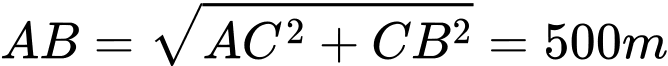 . Suy ra thời gian đi thẳng từ
. Suy ra thời gian đi thẳng từ 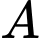 đến
đến 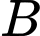 là
là  phút.
phút.Suy ra a) đúng.
b) Thời gian đi từ 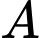 đến
đến  rồi chạy bộ từ
rồi chạy bộ từ  đến
đến 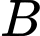
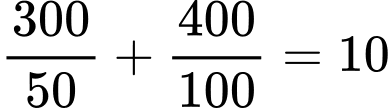 phút.
phút.
Suy ra b) đúng.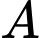 đến
đến  rồi chạy bộ từ
rồi chạy bộ từ  đến
đến 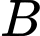
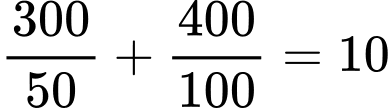 phút.
phút.c) Ta có
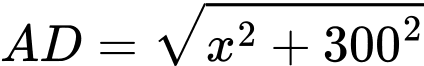 (m),
(m), 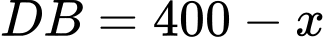 (m) với
(m) với 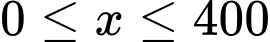 ).
).Thời gian đi từ
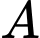 đến
đến 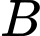 là
là 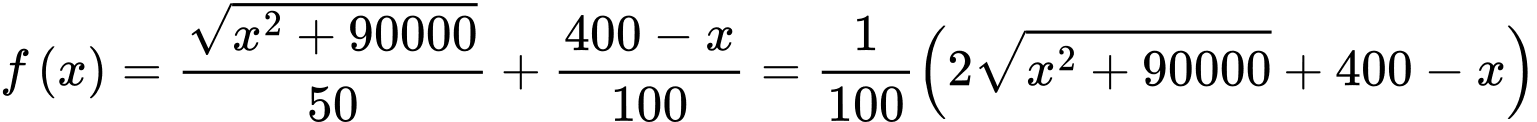 (phút).
(phút).Suy ra c) sai.
d) Ta có
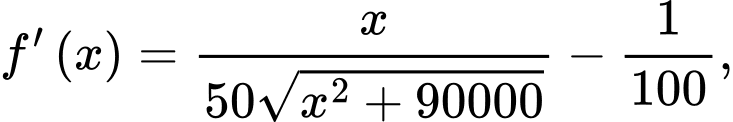
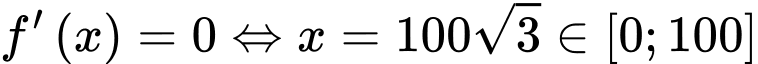 .
.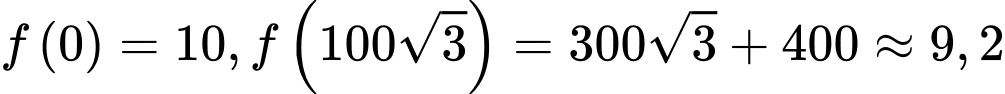 ,
, 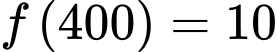 .
.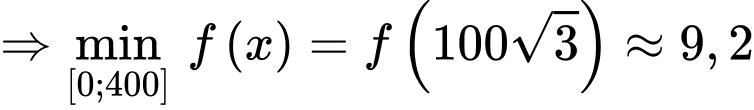 (phút).
(phút).Suy ra d) đúng.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 17 đến câu 22.
Câu 17 [684128]: Đồ thị hàm số 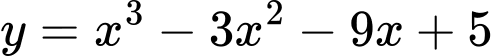 có điểm cực đại và điểm cực tiểu lần lượt là
có điểm cực đại và điểm cực tiểu lần lượt là 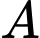 và
và 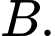 Gọi
Gọi 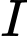 là giao điểm của
là giao điểm của  với trục
với trục 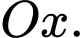 Khi đó tỷ số
Khi đó tỷ số 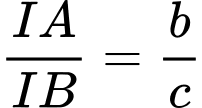 (với
(với 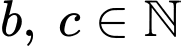 và phân số
và phân số 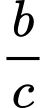 tối giản). tính
tối giản). tính 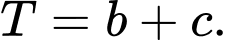
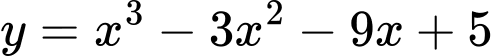 có điểm cực đại và điểm cực tiểu lần lượt là
có điểm cực đại và điểm cực tiểu lần lượt là 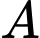 và
và 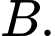 Gọi
Gọi 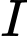 là giao điểm của
là giao điểm của  với trục
với trục 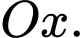 Khi đó tỷ số
Khi đó tỷ số 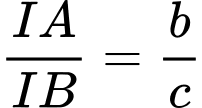 (với
(với 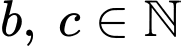 và phân số
và phân số 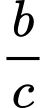 tối giản). tính
tối giản). tính 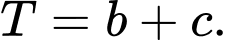
Ta có: 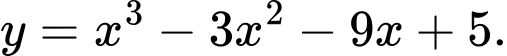
Tập xác định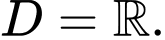
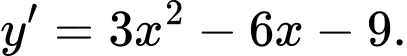
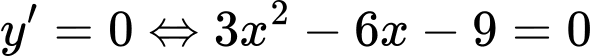
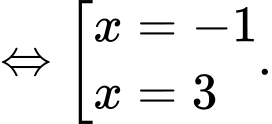
Với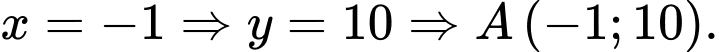
Với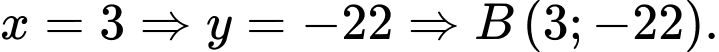
Ta có phương trình đường thẳng là:
là: 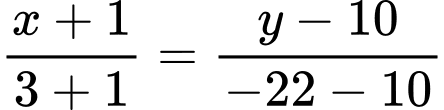
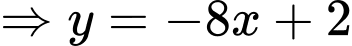
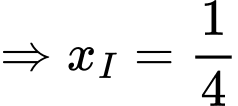
Vậy suy ra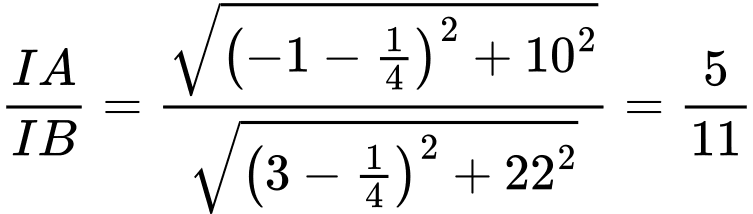
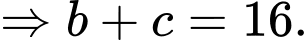
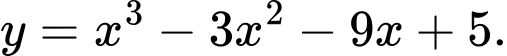
Tập xác định
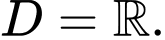
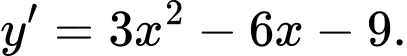
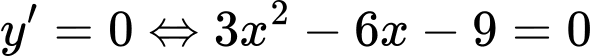
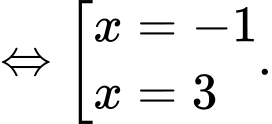
Với
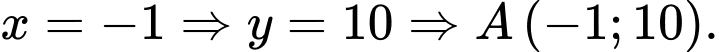
Với
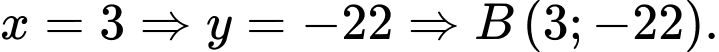
Ta có phương trình đường thẳng
 là:
là: 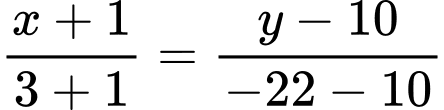
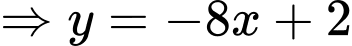
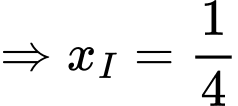
Vậy suy ra
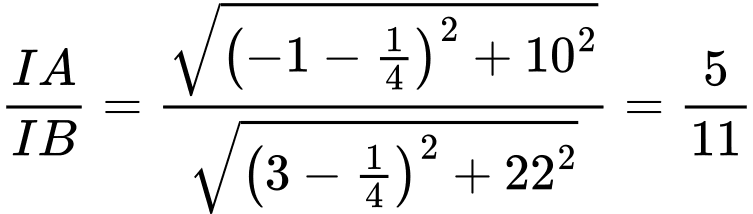
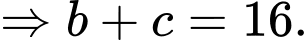
Câu 18 [687398]: Một hộ làm nghề dệt vải lụa tơ tằm sản suất mỗi ngày được 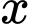 mét vải lụa
mét vải lụa 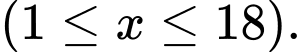 Tổng chi phí sản xuất
Tổng chi phí sản xuất 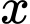 mét vải lụa, tính bằng nghìn đồng, cho bởi hàm chi phí:
mét vải lụa, tính bằng nghìn đồng, cho bởi hàm chi phí:
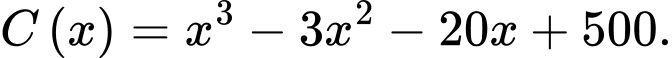
Giả sử hộ làm nghề dệt này bán hết sản phẩm mỗi ngày với giá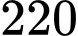 nghìn đồng/mét. Gọi
nghìn đồng/mét. Gọi 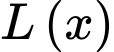 là lợi nhuận thu được khi bán
là lợi nhuận thu được khi bán 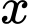 mét vải lụa. Hỏi lợi nhuận tối đa của hộ làm nghề dệt vải lụa tơ tằm trong một ngày? (đơn vị triệu đồng).
mét vải lụa. Hỏi lợi nhuận tối đa của hộ làm nghề dệt vải lụa tơ tằm trong một ngày? (đơn vị triệu đồng).
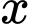 mét vải lụa
mét vải lụa 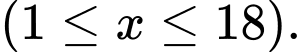 Tổng chi phí sản xuất
Tổng chi phí sản xuất 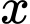 mét vải lụa, tính bằng nghìn đồng, cho bởi hàm chi phí:
mét vải lụa, tính bằng nghìn đồng, cho bởi hàm chi phí:
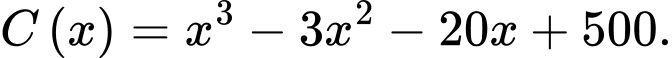
Giả sử hộ làm nghề dệt này bán hết sản phẩm mỗi ngày với giá
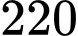 nghìn đồng/mét. Gọi
nghìn đồng/mét. Gọi 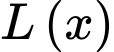 là lợi nhuận thu được khi bán
là lợi nhuận thu được khi bán 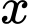 mét vải lụa. Hỏi lợi nhuận tối đa của hộ làm nghề dệt vải lụa tơ tằm trong một ngày? (đơn vị triệu đồng).
mét vải lụa. Hỏi lợi nhuận tối đa của hộ làm nghề dệt vải lụa tơ tằm trong một ngày? (đơn vị triệu đồng).
Trả lời: 1,2
Số tiền thu về khi bán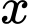 mét vải lụa là:
mét vải lụa là: 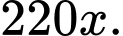
Lợi nhuận thu được khi bán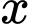 mét vải lụa là:
mét vải lụa là:
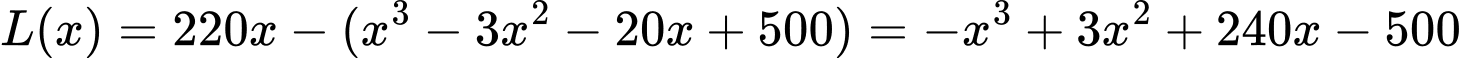
Xét hàm số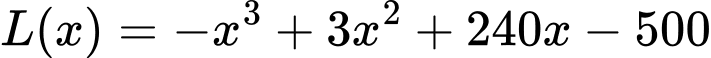 với
với 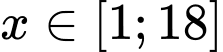
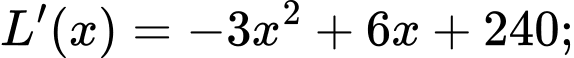

Bảng biến thiên
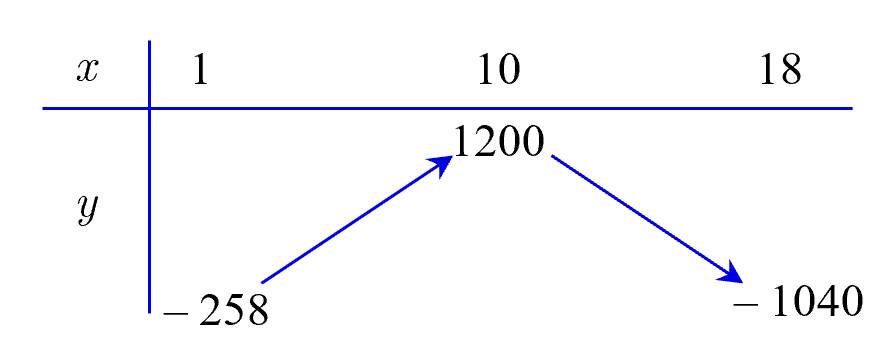
Vậy hộ làm nghề dệt này thu được lợi nhuận tối đa trong một ngày là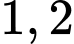 triệu đồng khi sản xuất
triệu đồng khi sản xuất  mét vải lụa trong một ngày.
mét vải lụa trong một ngày.
Số tiền thu về khi bán
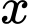 mét vải lụa là:
mét vải lụa là: 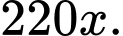
Lợi nhuận thu được khi bán
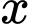 mét vải lụa là:
mét vải lụa là:
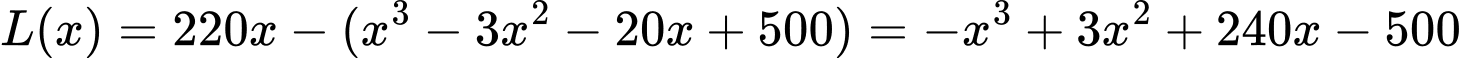
Xét hàm số
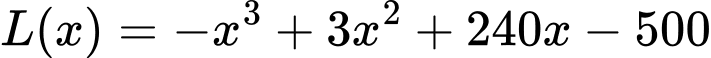 với
với 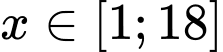
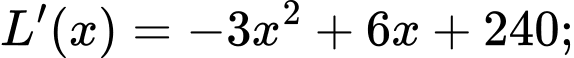

Bảng biến thiên

Vậy hộ làm nghề dệt này thu được lợi nhuận tối đa trong một ngày là
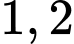 triệu đồng khi sản xuất
triệu đồng khi sản xuất  mét vải lụa trong một ngày.
mét vải lụa trong một ngày.
Câu 19 [715978]: Cho một tấm gỗ hình vuông cạnh 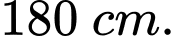 Người ta cắt một tẩm gỗ có hình tam giác vuông
Người ta cắt một tẩm gỗ có hình tam giác vuông 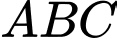 từ tẩm gố hình vuông đã cho như hình vẽ. Biết
từ tẩm gố hình vuông đã cho như hình vẽ. Biết 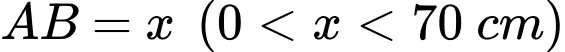 là một cạnh góc vuông của tam giác
là một cạnh góc vuông của tam giác 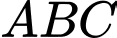 và tổng độ dài cạnh góc vuông
và tổng độ dài cạnh góc vuông  với canh huyền
với canh huyền 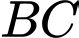 bằng
bằng 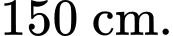 Diện tích lớn nhất của tam giác
Diện tích lớn nhất của tam giác 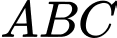 là bao nhiêu
là bao nhiêu 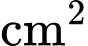 (làm tròn kết quả đến hàng đơn vị).
(làm tròn kết quả đến hàng đơn vị).
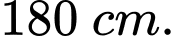 Người ta cắt một tẩm gỗ có hình tam giác vuông
Người ta cắt một tẩm gỗ có hình tam giác vuông 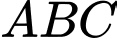 từ tẩm gố hình vuông đã cho như hình vẽ. Biết
từ tẩm gố hình vuông đã cho như hình vẽ. Biết 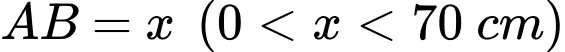 là một cạnh góc vuông của tam giác
là một cạnh góc vuông của tam giác 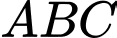 và tổng độ dài cạnh góc vuông
và tổng độ dài cạnh góc vuông  với canh huyền
với canh huyền 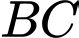 bằng
bằng 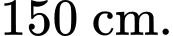 Diện tích lớn nhất của tam giác
Diện tích lớn nhất của tam giác 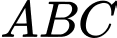 là bao nhiêu
là bao nhiêu 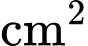 (làm tròn kết quả đến hàng đơn vị).
(làm tròn kết quả đến hàng đơn vị).
Điền đáp án: 2165.
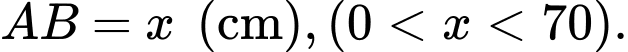
Ta có: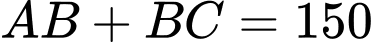
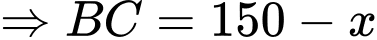
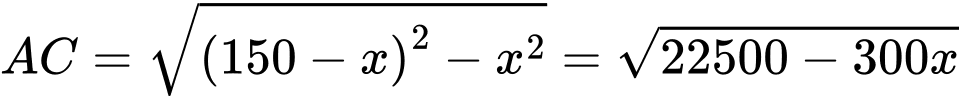
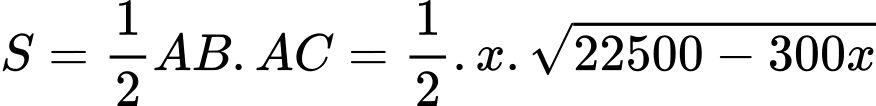
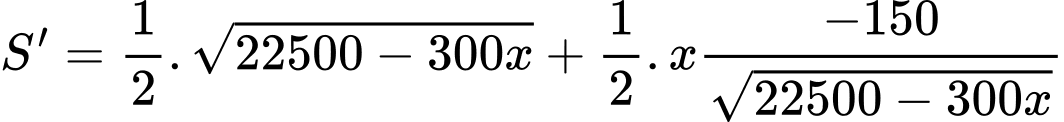
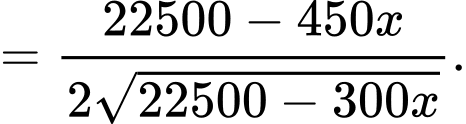
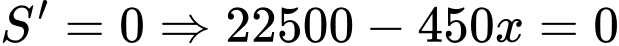
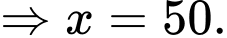
Lập bảng biến thiên
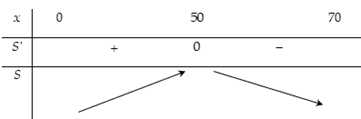
Vậy
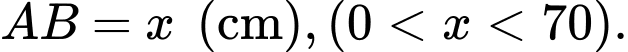
Ta có:
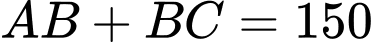
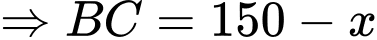
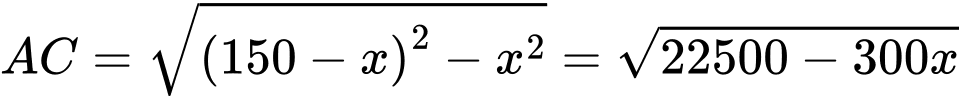
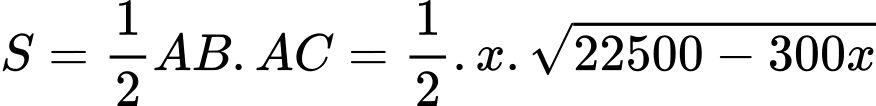
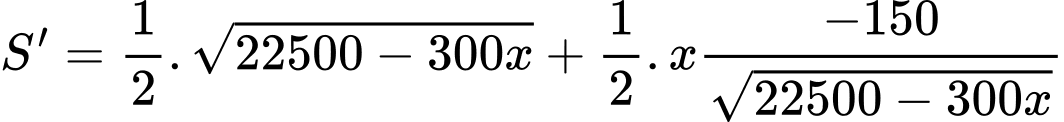
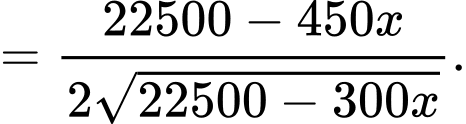
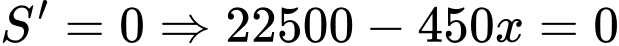
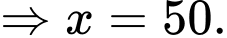
Lập bảng biến thiên

Vậy

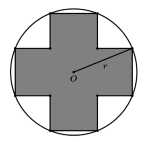
Câu 20 [703025]: Hai hình chữ nhật bằng nhau, nội tiếp trong đường tròn tâm  bán kính
bán kính 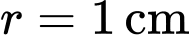 tạo thành một hình chữ thập đối xứng (như hình vẽ bên). Diện tích lớn nhất của hình chữ thập là bao nhiêu
tạo thành một hình chữ thập đối xứng (như hình vẽ bên). Diện tích lớn nhất của hình chữ thập là bao nhiêu 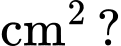 (kết quả làm tròn đến hàng phần trăm).
(kết quả làm tròn đến hàng phần trăm).
 bán kính
bán kính 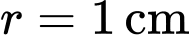 tạo thành một hình chữ thập đối xứng (như hình vẽ bên). Diện tích lớn nhất của hình chữ thập là bao nhiêu
tạo thành một hình chữ thập đối xứng (như hình vẽ bên). Diện tích lớn nhất của hình chữ thập là bao nhiêu 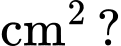 (kết quả làm tròn đến hàng phần trăm).
(kết quả làm tròn đến hàng phần trăm).
Điền đáp án: 2,47.
Ta kí hiệu các điểm trên hình như sau:
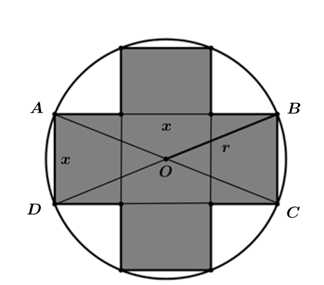
(Nhận xét: các đường chéo của 2 hình chữ nhật sẽ trùng với đường kính của đường tròn tâm .)
.)
Đặt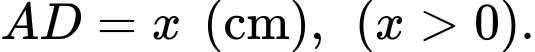
Trong tam giác vuông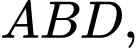 ta có
ta có 
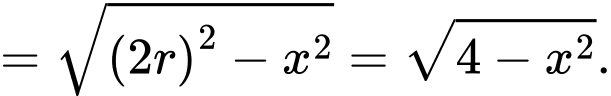
Diện tích của hình chữ thập Diện tích hình vuông (là giao của 2 hình chữ nhật)
Diện tích hình vuông (là giao của 2 hình chữ nhật)
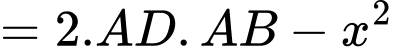
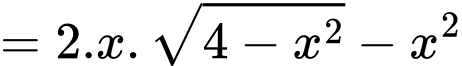
Xét hàm số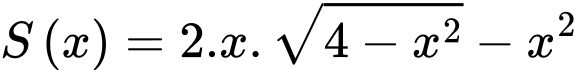 trên khoảng
trên khoảng 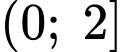
Ta có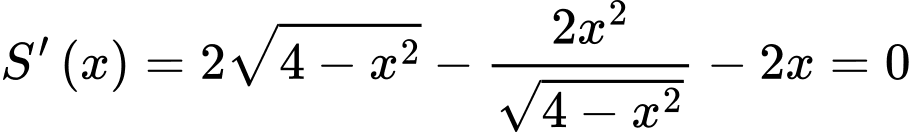
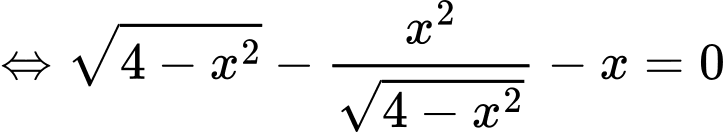
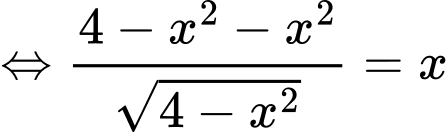
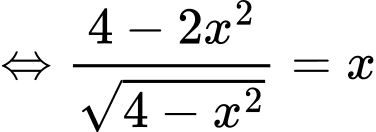

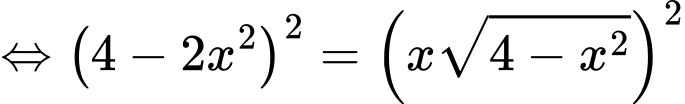
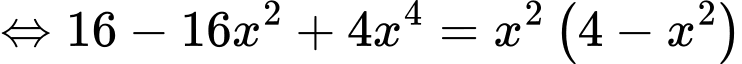
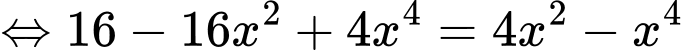

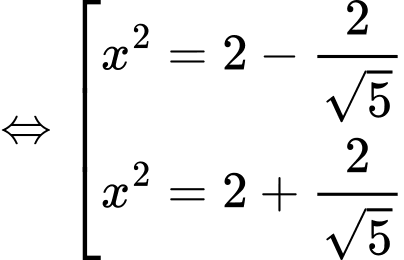
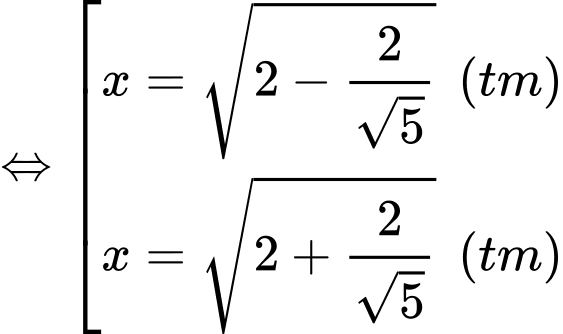
Ta có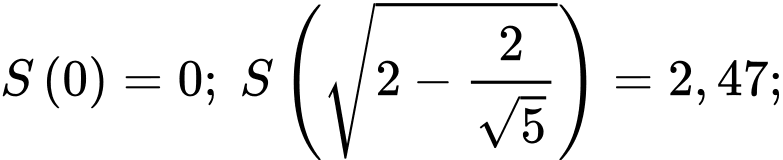
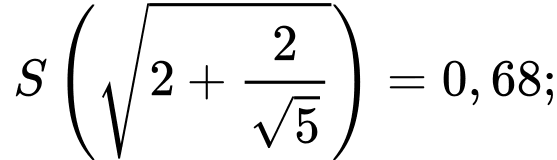
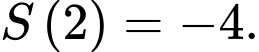
Vậy diện tích lớn nhất của hình chữ thập là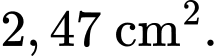
Ta kí hiệu các điểm trên hình như sau:

(Nhận xét: các đường chéo của 2 hình chữ nhật sẽ trùng với đường kính của đường tròn tâm
 .)
.)
Đặt
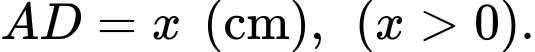
Trong tam giác vuông
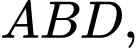 ta có
ta có 
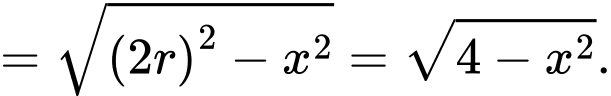
Diện tích của hình chữ thập
 Diện tích hình vuông (là giao của 2 hình chữ nhật)
Diện tích hình vuông (là giao của 2 hình chữ nhật)
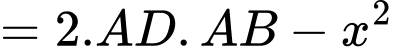
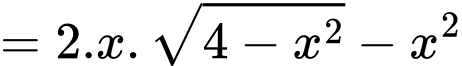
Xét hàm số
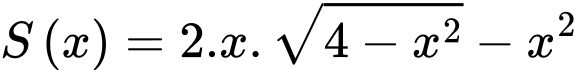 trên khoảng
trên khoảng 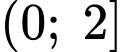
Ta có
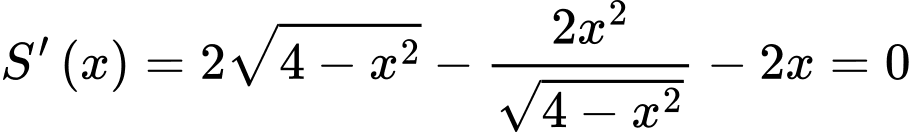
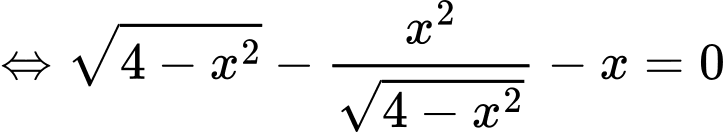
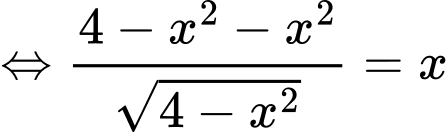
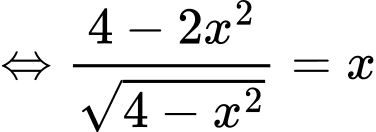

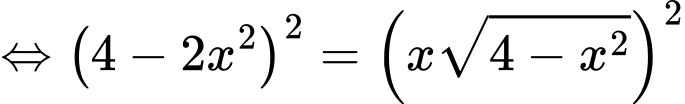
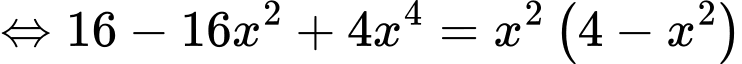
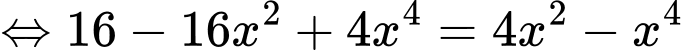

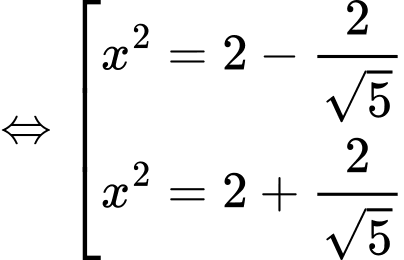
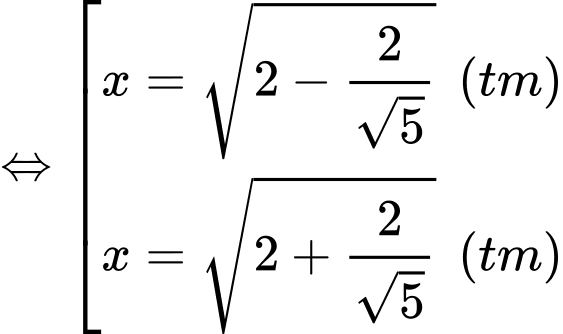
Ta có
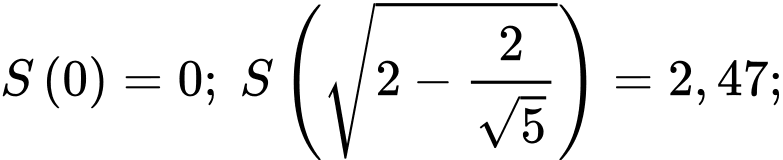
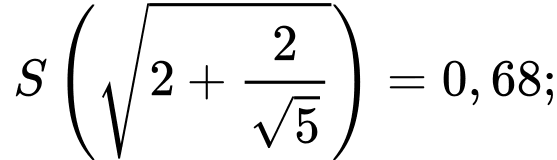
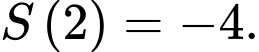
Vậy diện tích lớn nhất của hình chữ thập là
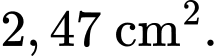
Câu 21 [774153]: Trong một cửa hàng, nhà quản lý dự định treo một đồ trang trí trên cao. Vật trang trí được đặt trên giá đỡ nằm dưới thanh treo 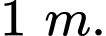 Biết khoảng cách giữa hai thanh treo là
Biết khoảng cách giữa hai thanh treo là 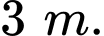 Khi tổng độ dài của tất cả các đoạn dây xích là nhỏ nhất hãy tính độ dài của đoạn dây xích
Khi tổng độ dài của tất cả các đoạn dây xích là nhỏ nhất hãy tính độ dài của đoạn dây xích 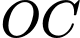 (làm tròn đến hàng phần chục).
(làm tròn đến hàng phần chục).
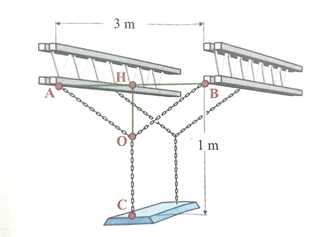
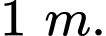 Biết khoảng cách giữa hai thanh treo là
Biết khoảng cách giữa hai thanh treo là 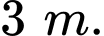 Khi tổng độ dài của tất cả các đoạn dây xích là nhỏ nhất hãy tính độ dài của đoạn dây xích
Khi tổng độ dài của tất cả các đoạn dây xích là nhỏ nhất hãy tính độ dài của đoạn dây xích 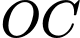 (làm tròn đến hàng phần chục).
(làm tròn đến hàng phần chục).
Điền đáp án: 0,1.
Đặt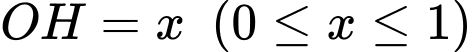 thì
thì 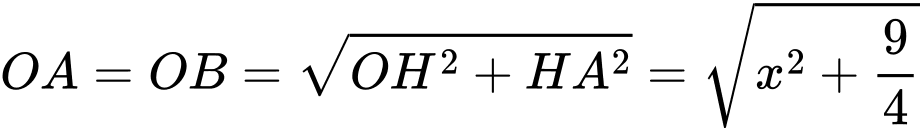
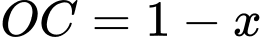 .
.
Tổng chiều dài của các đoạn dây xích là
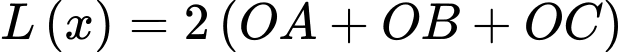
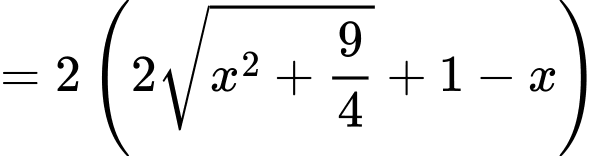
Suy ra: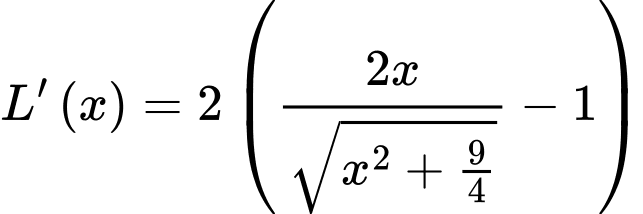
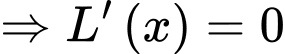
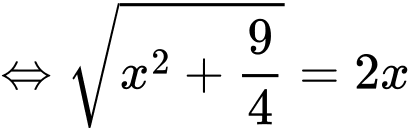
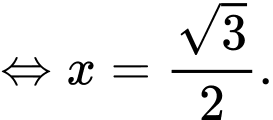
Do đó chiều dài tối thiểu của các đoạn dây xích là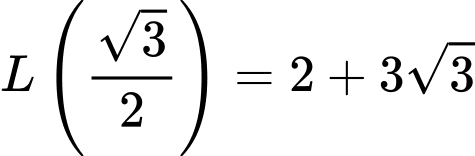
Khi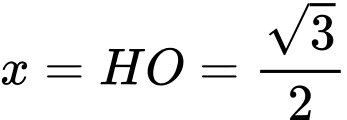
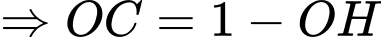
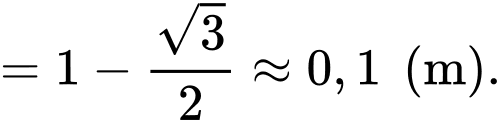
Đặt
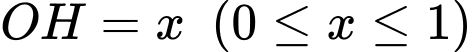 thì
thì 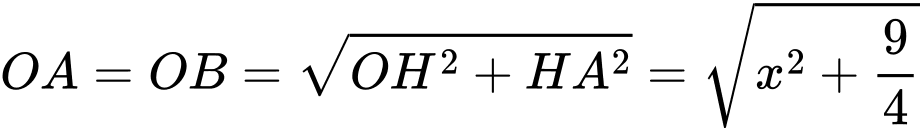
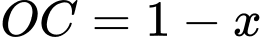 .
.Tổng chiều dài của các đoạn dây xích là
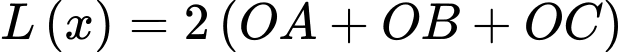
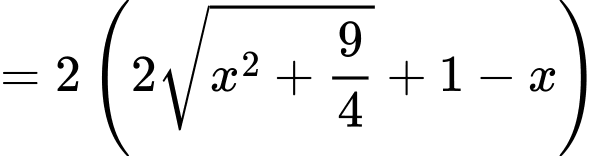
Suy ra:
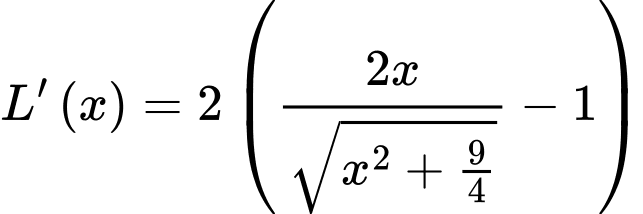
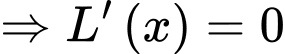
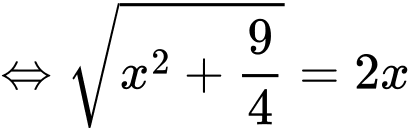
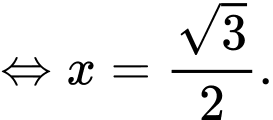
Do đó chiều dài tối thiểu của các đoạn dây xích là
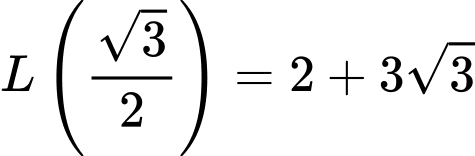
Khi
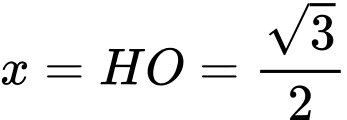
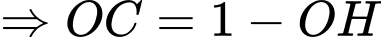
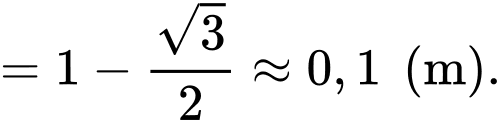
Câu 22 [31077]: Cho một tấm nhôm hình vuông cạnh 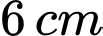 . Người ta muốn cắt một hình thang như hình vẽ. Tìm tổng
. Người ta muốn cắt một hình thang như hình vẽ. Tìm tổng  để diện tích hình thang
để diện tích hình thang 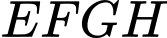 đạt giá trị nhỏ nhất (làm tròn kết quả đến hàng phần trăm).
đạt giá trị nhỏ nhất (làm tròn kết quả đến hàng phần trăm).
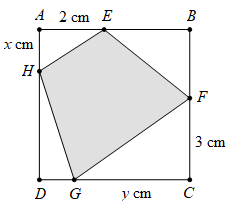
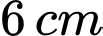 . Người ta muốn cắt một hình thang như hình vẽ. Tìm tổng
. Người ta muốn cắt một hình thang như hình vẽ. Tìm tổng  để diện tích hình thang
để diện tích hình thang 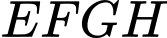 đạt giá trị nhỏ nhất (làm tròn kết quả đến hàng phần trăm).
đạt giá trị nhỏ nhất (làm tròn kết quả đến hàng phần trăm).
Điền đáp án: 4,95.
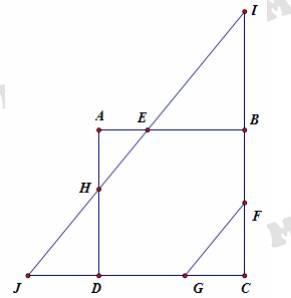
Đường thẳng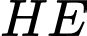 cắt
cắt 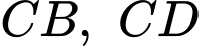 lần lượt tại
lần lượt tại 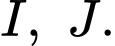
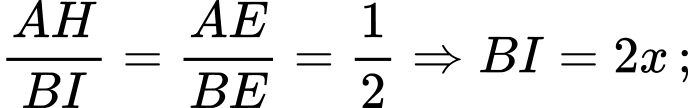
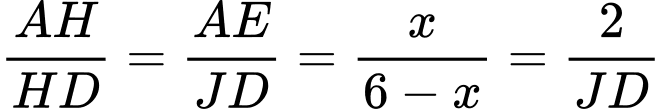
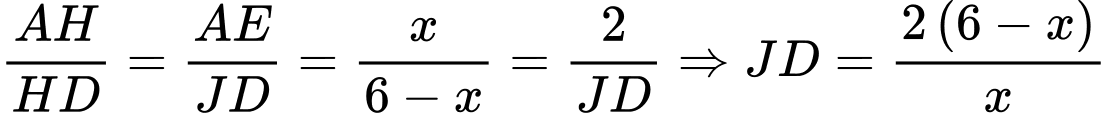
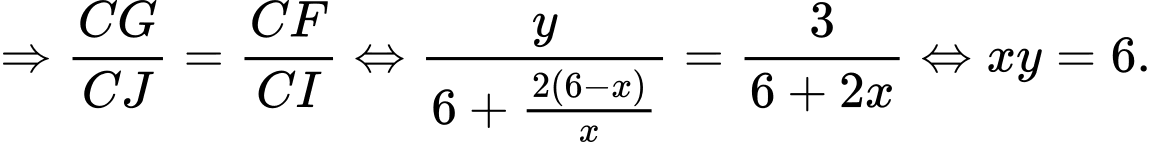
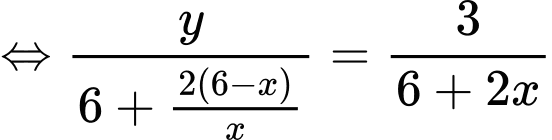
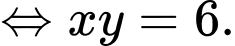

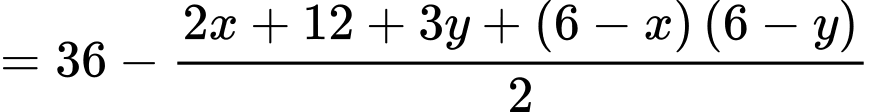
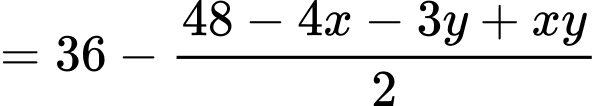
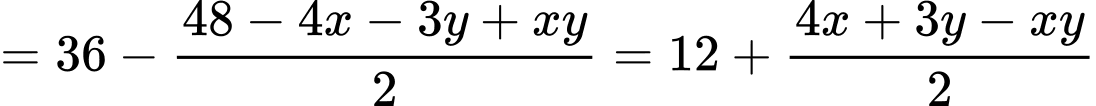
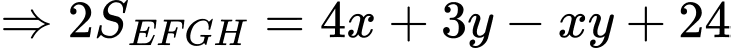
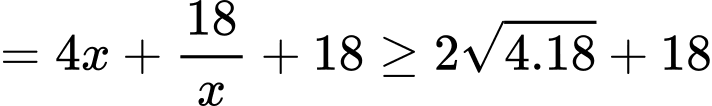
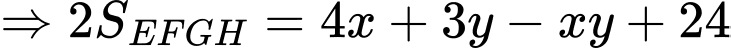
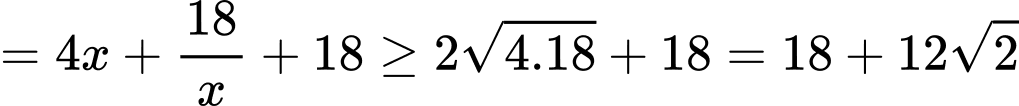
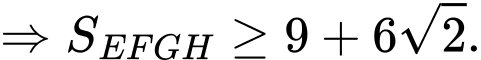
Dấu “=” xảy ra khi và chỉ khi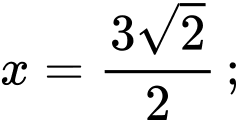
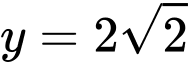
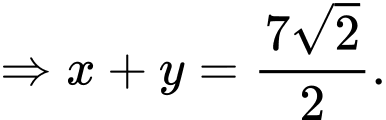

Đường thẳng
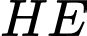 cắt
cắt 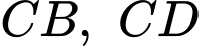 lần lượt tại
lần lượt tại 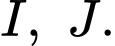
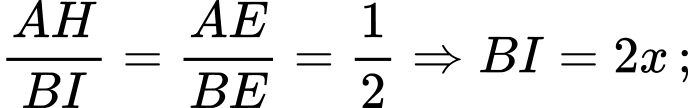
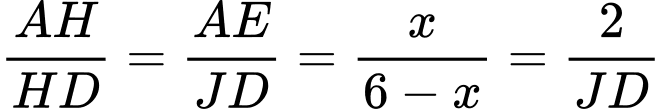
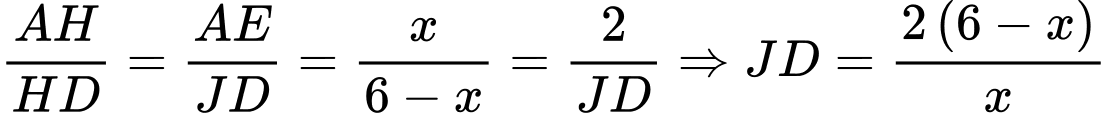
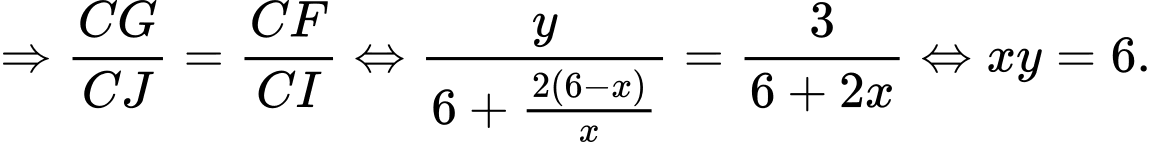
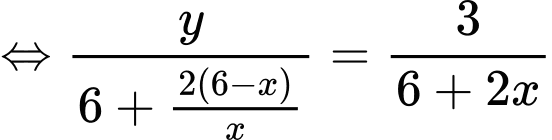
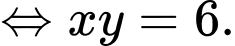

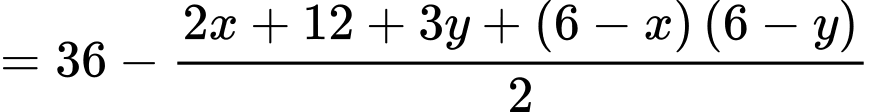
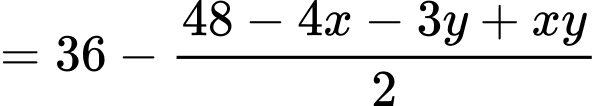
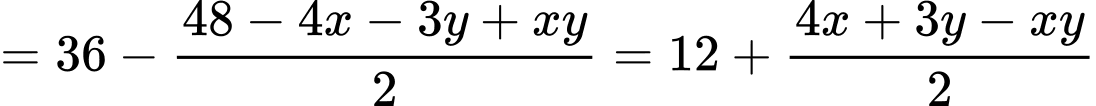
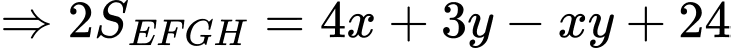
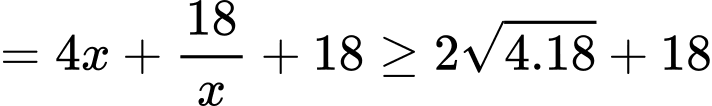
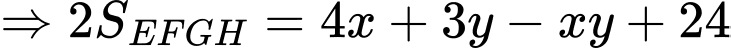
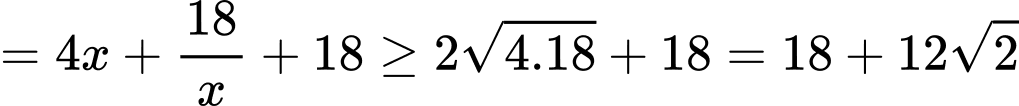
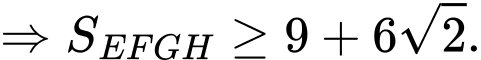
Dấu “=” xảy ra khi và chỉ khi