PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1 [512897]: Phương trình đường tiệm cận ngang của đồ thị hàm số 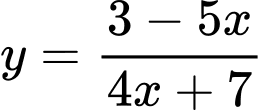 là
là
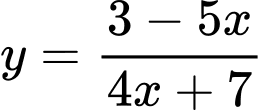 là
là A, 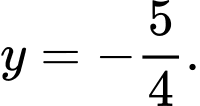
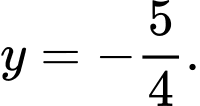
B, 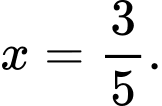
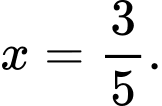
C, 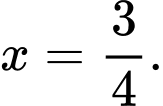
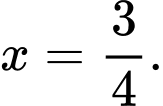
D, 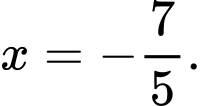
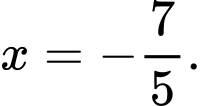
Chọn A
Ta có: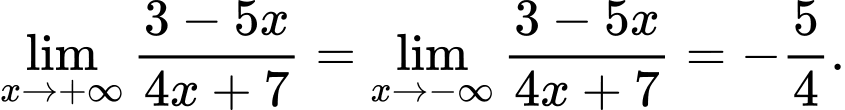
Đường tiệm cận ngang của đồ thị hàm số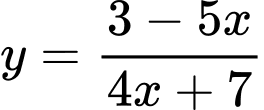 là
là 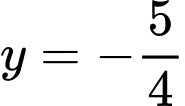 Đáp án: A
Đáp án: A
Ta có:
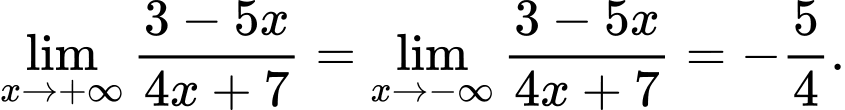
Đường tiệm cận ngang của đồ thị hàm số
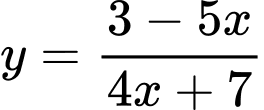 là
là 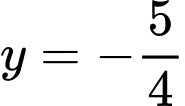 Đáp án: A
Đáp án: A
Câu 2 [328883]: Cho hàm số 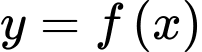 có đồ thị như hình bên:
có đồ thị như hình bên:
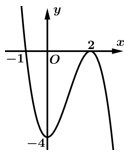
Hàm số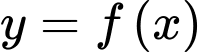 đồng biến trên khoảng nào?
đồng biến trên khoảng nào?
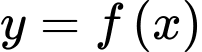 có đồ thị như hình bên:
có đồ thị như hình bên:
Hàm số
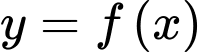 đồng biến trên khoảng nào?
đồng biến trên khoảng nào? A, 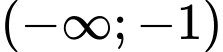
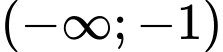
B, 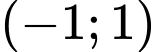
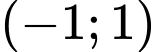
C, 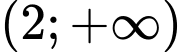
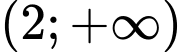
D, 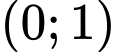
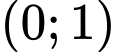
Chọn đáp án D.
Dựa vào hình vẽ, ta thấy trong khoảng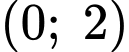 đồ thị hàm số có hướng đi lên từ trái qua phải nên hàm số đồng biến trong khoảng
đồ thị hàm số có hướng đi lên từ trái qua phải nên hàm số đồng biến trong khoảng 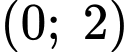 mà
mà  do đó đáp án D thỏa mãn.
Đáp án: D
do đó đáp án D thỏa mãn.
Đáp án: D
Dựa vào hình vẽ, ta thấy trong khoảng
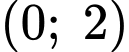 đồ thị hàm số có hướng đi lên từ trái qua phải nên hàm số đồng biến trong khoảng
đồ thị hàm số có hướng đi lên từ trái qua phải nên hàm số đồng biến trong khoảng 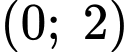 mà
mà  do đó đáp án D thỏa mãn.
Đáp án: D
do đó đáp án D thỏa mãn.
Đáp án: D
Câu 3 [680672]: Cho hàm số 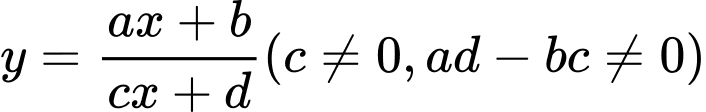 có đồ thị như hình vẽ bên.
có đồ thị như hình vẽ bên.
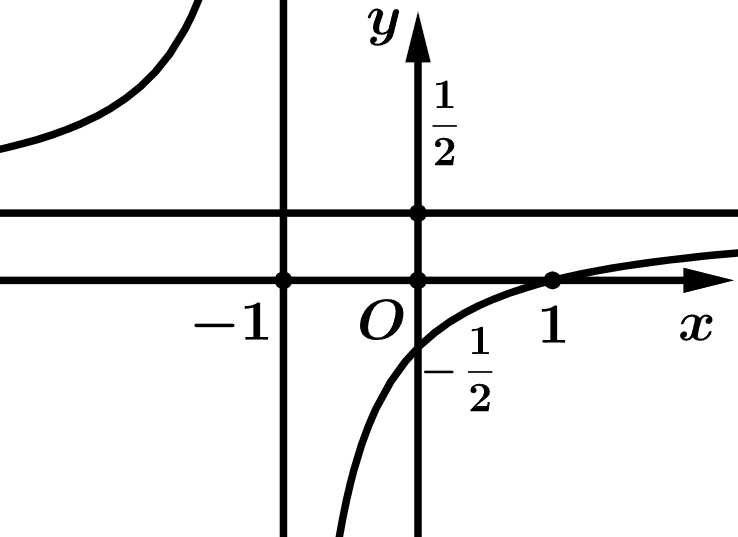
Tiệm cận ngang của đồ thị hàm số là:
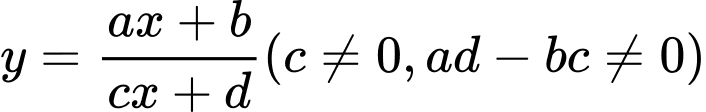 có đồ thị như hình vẽ bên.
có đồ thị như hình vẽ bên.
Tiệm cận ngang của đồ thị hàm số là:
A, 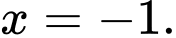
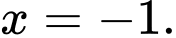
B, 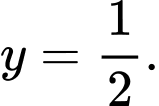
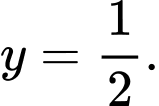
C, 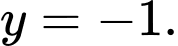
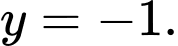
D, 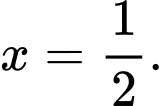
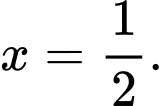
Chọn đáp án B.
Từ đồ thị hàm số, ta thấy tiệm cận ngang của đồ thị hàm số là đường thẳng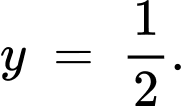 Đáp án: B
Đáp án: B
Từ đồ thị hàm số, ta thấy tiệm cận ngang của đồ thị hàm số là đường thẳng
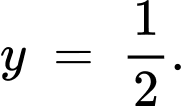 Đáp án: B
Đáp án: B
Câu 4 [378807]: Đường cong ở hình bên là đồ thị của hàm số nào dưới đây?
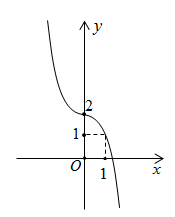
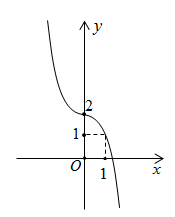
A, 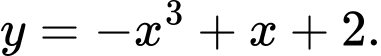
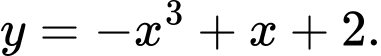
B, 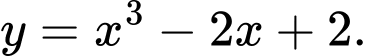
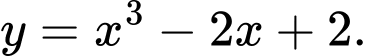
C, 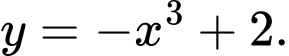
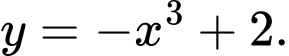
D, 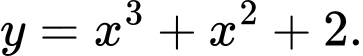
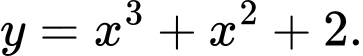
Phương pháp:
Dựa vào hình dáng đồ thị, tính đối xứng, các giao điểm với trục tung, trục hoành và các điểm cực trị để xác định hàm số.
Cách giải:
Ta thấy hàm số luôn nghịch biến trên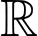 nên
nên 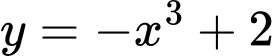 có
có 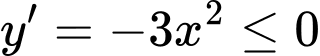 thỏa mãn
thỏa mãn
Chọn C. Đáp án: C
Dựa vào hình dáng đồ thị, tính đối xứng, các giao điểm với trục tung, trục hoành và các điểm cực trị để xác định hàm số.
Cách giải:
Ta thấy hàm số luôn nghịch biến trên
 nên
nên 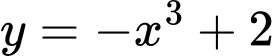 có
có 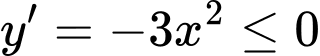 thỏa mãn
thỏa mãnChọn C. Đáp án: C
Câu 5 [803994]: Cho hàm số 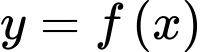 xác định trên
xác định trên  . Biết
. Biết 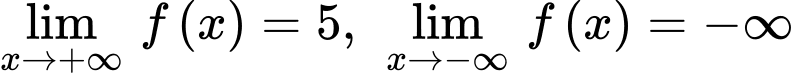 ,
, 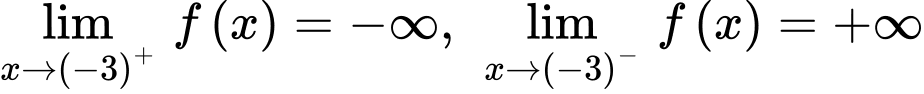 . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
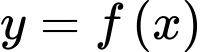 xác định trên
xác định trên  . Biết
. Biết 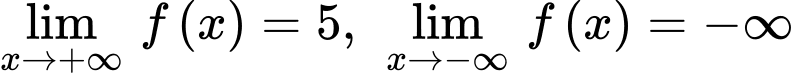 ,
, 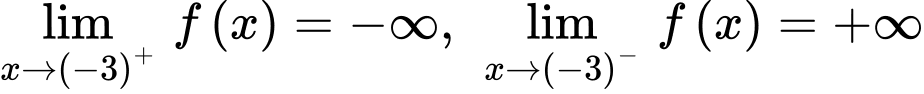 . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng? A, Đồ thị hàm số có 1 tiệm cận ngang và không có tiệm cận đứng.
B, Đồ thị hàm số có 1 tiệm cận ngang và 2 tiệm cận đứng.
C, Đồ thị hàm số không có tiệm cận ngang và có 1 tiệm cận đứng.
D, Đồ thị hàm số có 1 tiệm cận ngang và 1 tiệm cận đứng.
Chọn D
Ta có: đường thẳng
đường thẳng 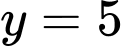 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
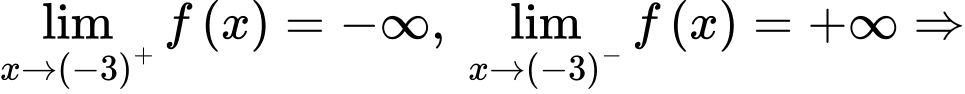 đường thẳng
đường thẳng 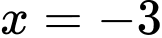 là tiệm cận đứng của đồ thị hàm số. Đáp án: D
là tiệm cận đứng của đồ thị hàm số. Đáp án: D
Ta có:
 đường thẳng
đường thẳng 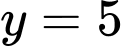 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số. 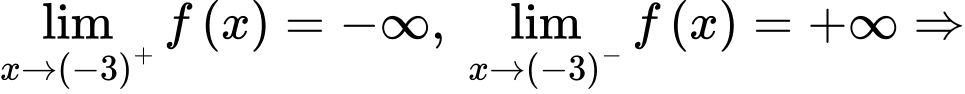 đường thẳng
đường thẳng 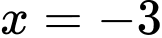 là tiệm cận đứng của đồ thị hàm số. Đáp án: D
là tiệm cận đứng của đồ thị hàm số. Đáp án: D
Câu 6 [599332]: Cho các hằng số 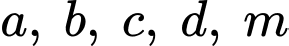 khác 0. Đồ thị của hàm số
khác 0. Đồ thị của hàm số 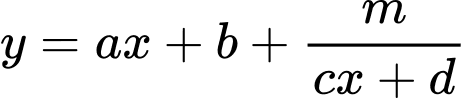 có đường tiệm cận xiên là:
có đường tiệm cận xiên là:
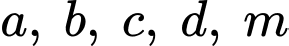 khác 0. Đồ thị của hàm số
khác 0. Đồ thị của hàm số 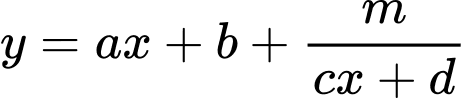 có đường tiệm cận xiên là:
có đường tiệm cận xiên là:
A, 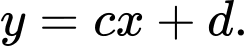
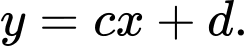
B, 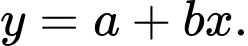
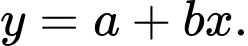
C, 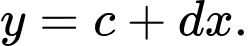
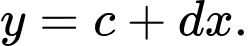
D, 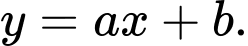
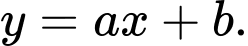
Tập xác định: 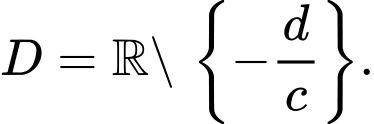
Ta có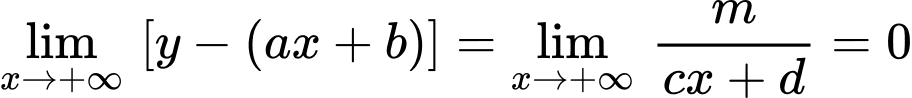 và
và 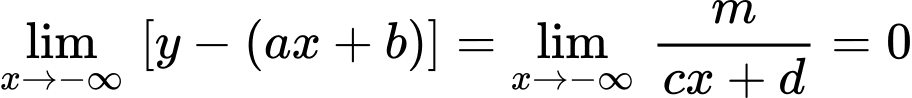 nên đồ thị hàm số đã cho có đường tiệm cận xiên là
nên đồ thị hàm số đã cho có đường tiệm cận xiên là 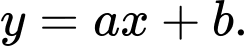 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
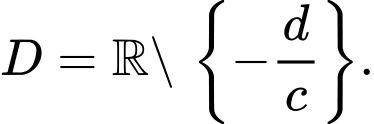
Ta có
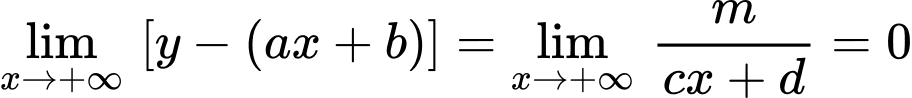 và
và 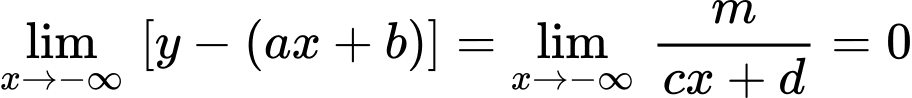 nên đồ thị hàm số đã cho có đường tiệm cận xiên là
nên đồ thị hàm số đã cho có đường tiệm cận xiên là 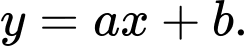 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
Câu 7 [546625]: Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây? 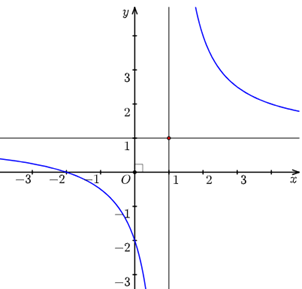

A, 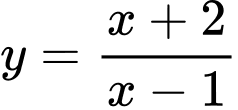 .
.
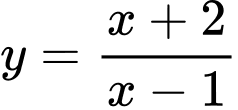 .
.B, 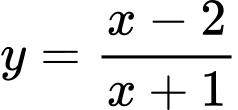 .
.
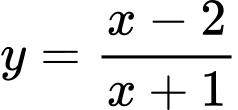 .
. C, 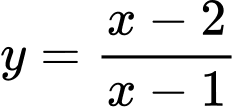 .
.
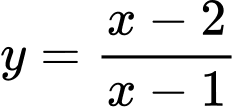 .
.D, 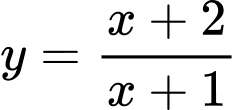 .
.
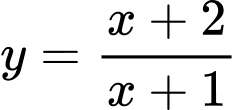 .
.
Chọn A
Ta có
+ Đồ thị hàm số có hướng đi xuống nên hàm số nghịch biến trên từng khoảng xác định.
+ Đồ thị hàm số có hai đường tiệm cận: TCĐ: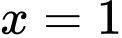 và TCN:
và TCN: 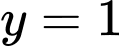 .
.
+ Đồ thị hàm số cắt các trục tọa độ lần lượt tại các điểm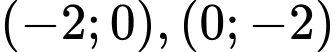 .
.
Suy ra hàm số cần tìm là: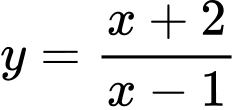 . Đáp án: A
. Đáp án: A
Ta có
+ Đồ thị hàm số có hướng đi xuống nên hàm số nghịch biến trên từng khoảng xác định.
+ Đồ thị hàm số có hai đường tiệm cận: TCĐ:
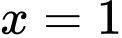 và TCN:
và TCN: 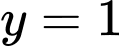 .
.
+ Đồ thị hàm số cắt các trục tọa độ lần lượt tại các điểm
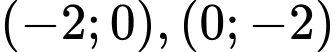 .
.
Suy ra hàm số cần tìm là:
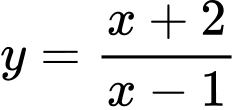 . Đáp án: A
. Đáp án: A
Câu 8 [801781]: Tọa độ giao điểm 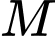 của đồ thị hàm số
của đồ thị hàm số 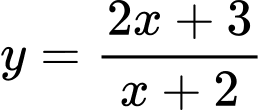 với trục hoành là
với trục hoành là
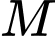 của đồ thị hàm số
của đồ thị hàm số 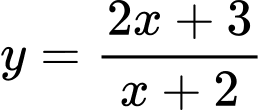 với trục hoành là
với trục hoành là A, 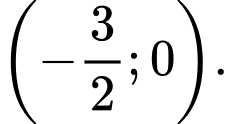
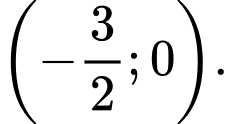
B, 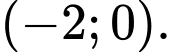
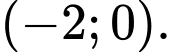
C, 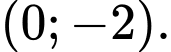
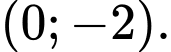
D, 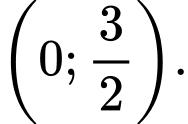
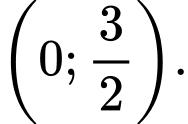
Chọn A.
Cho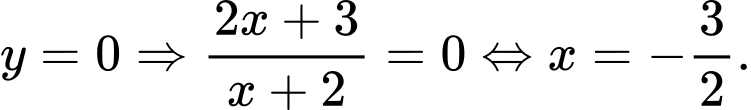
Vậy đồ thị hàm số cắt trục hoành tại điểm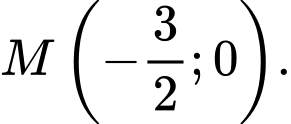 Đáp án: A
Đáp án: A
Cho
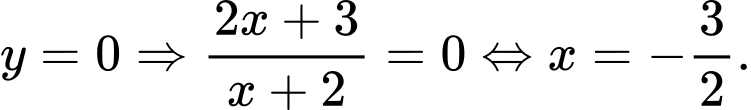
Vậy đồ thị hàm số cắt trục hoành tại điểm
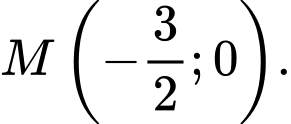 Đáp án: A
Đáp án: A
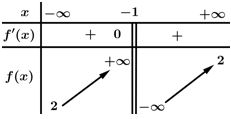
Câu 9 [600465]: Bảng biến thiên sau đây của hàm số nào?

A, 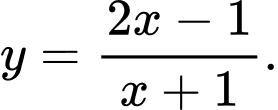
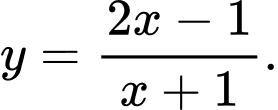
B, 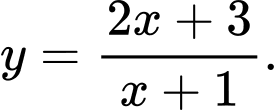
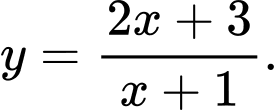
C, 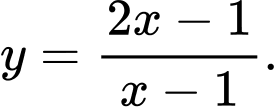
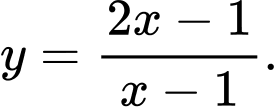
D, 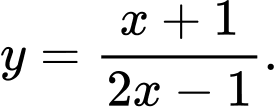
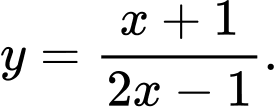
Chọn A
Nhận xét đồ thị hàm số có tiệm cận đứng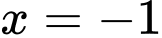 và tiệm cận ngang
và tiệm cận ngang 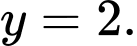 Loại đáp án C, D.
Loại đáp án C, D.
Xét hàm số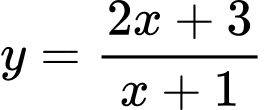
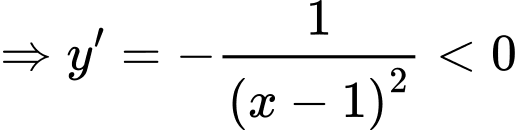 với
với 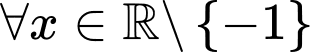 . Loại đáp án B.
. Loại đáp án B.
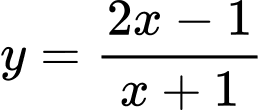
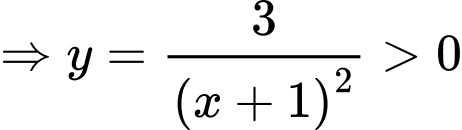 với
với 
Chọn đáp án A. Đáp án: A
Nhận xét đồ thị hàm số có tiệm cận đứng
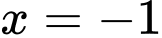 và tiệm cận ngang
và tiệm cận ngang 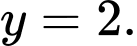 Loại đáp án C, D.
Loại đáp án C, D. Xét hàm số
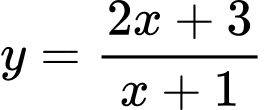
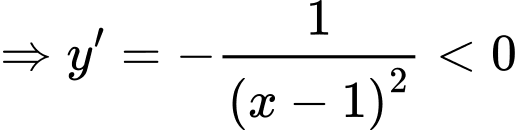 với
với 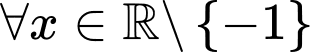 . Loại đáp án B.
. Loại đáp án B. 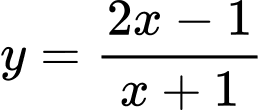
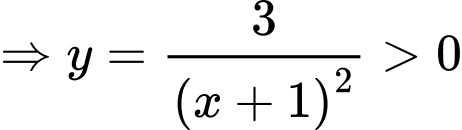 với
với 
Chọn đáp án A. Đáp án: A
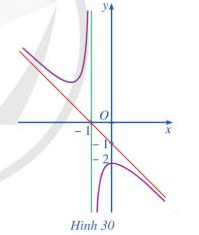
Câu 10 [360115]: Đường cong ở Hình 30 là đồ thị của hàm số:

A, 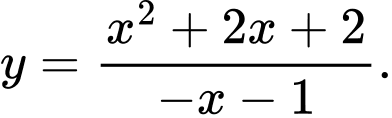
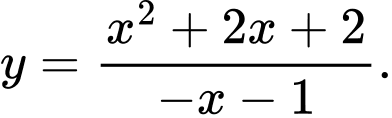
B, 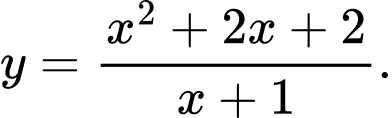
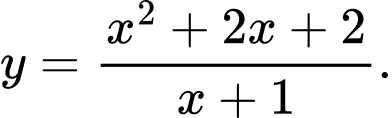
C, 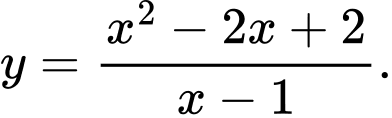
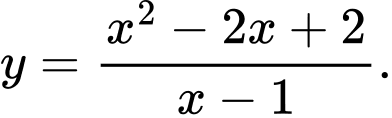
D, 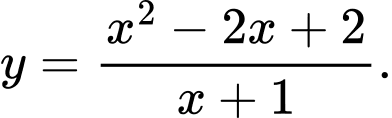
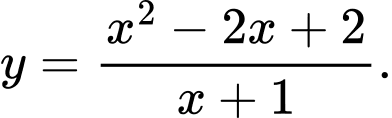
Dựa vào hình dạng đồ thị ta thấy hàm số đã có có 2 cực trị và 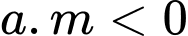 .
.
Chọn đáp án A. Đáp án: A
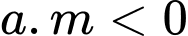 .
.
Chọn đáp án A. Đáp án: A
Câu 11 [613511]: Cho hàm số 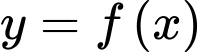 có bảng biến thiên như sau
có bảng biến thiên như sau
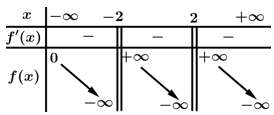
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
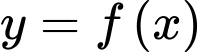 có bảng biến thiên như sau
có bảng biến thiên như sau 
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A, 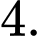
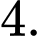
B, 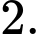
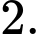
C, 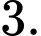
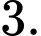
D, 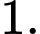
 Đáp án: C
Đáp án: C
Câu 12 [522609]: Tổng số tiệm cận đứng và ngang của đồ thị hàm số 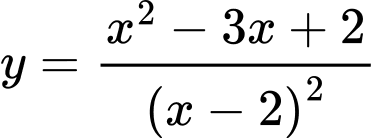 là
là
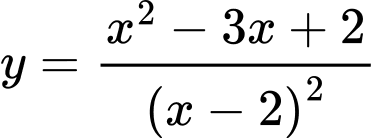 là
là A, 1.
B, 2.
C, 3.
D, 4.
Chọn B
Khi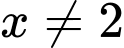 thì
thì 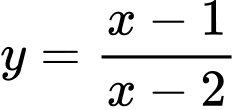
Do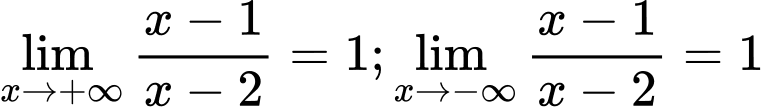
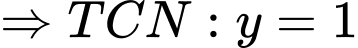
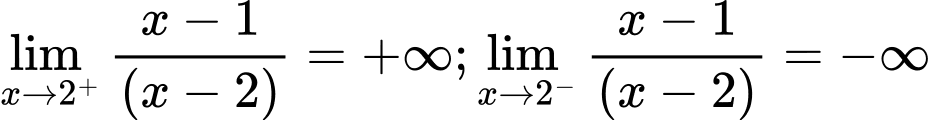
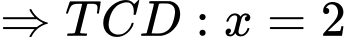
Từ đây ta suy ra tổng số TCN và TCĐ là 2. Đáp án: B
Khi
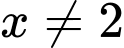 thì
thì 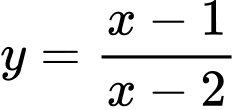
Do
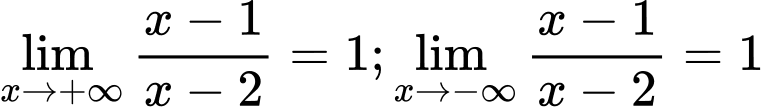
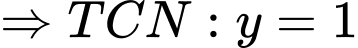
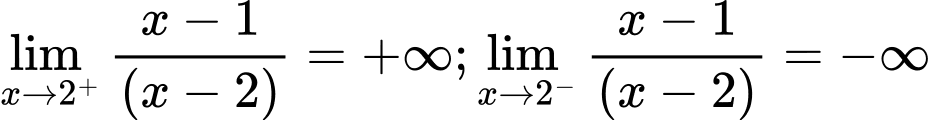
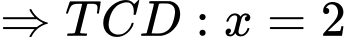
Từ đây ta suy ra tổng số TCN và TCĐ là 2. Đáp án: B
PHẦN II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a),b),c),d) ở mỗi câu học sinh chọn đúng hoặc sai.
Câu 13 [774154]: Cho hàm số 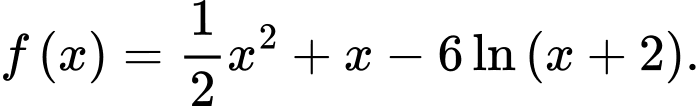
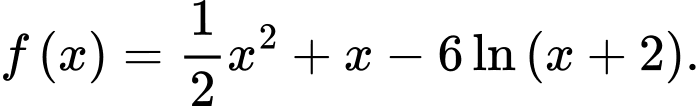
a) Đúng.
Điều kiện: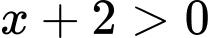

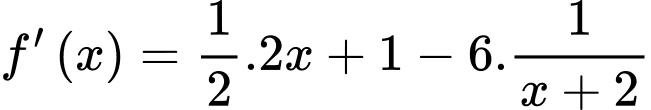
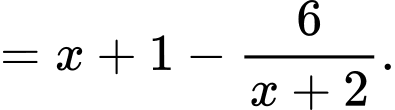
b) Sai.
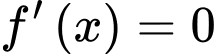
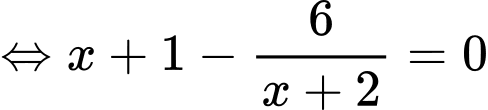
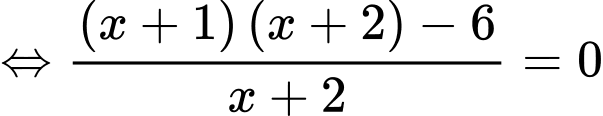
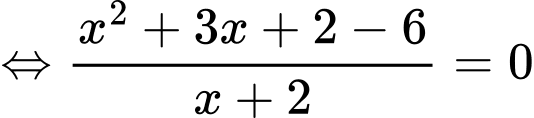
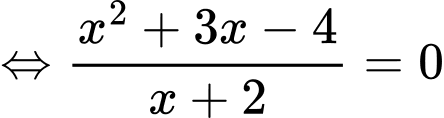
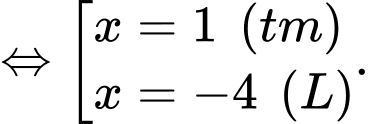
Vậy phương trình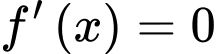 có duy nhất 1 nghiệm thuộc đoạn
có duy nhất 1 nghiệm thuộc đoạn 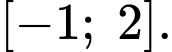
c) Đúng.
Thay lần lượt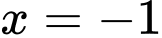 và
và 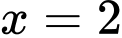 vào hàm số
vào hàm số 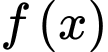 ta được
ta được 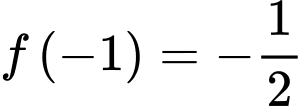 và
và 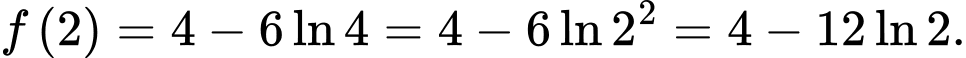
d) Sai.
Xét hàm số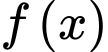 trên đoạn
trên đoạn 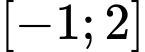
Dựa vào kết quả phần b) ta có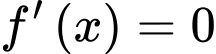
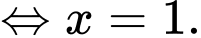
Ta có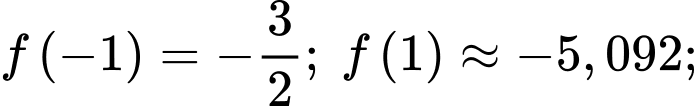
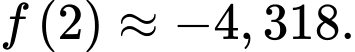
Vậy giá trị nhỏ nhất của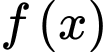 trên đoạn
trên đoạn 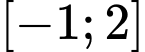 bằng -5,092 và nhỏ hơn
bằng -5,092 và nhỏ hơn 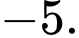
Điều kiện:
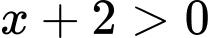

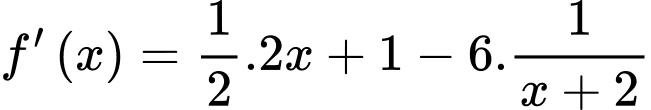
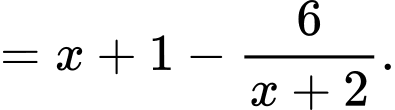
b) Sai.
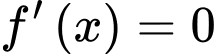
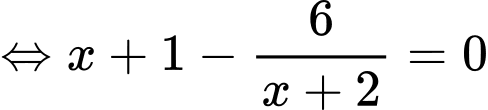
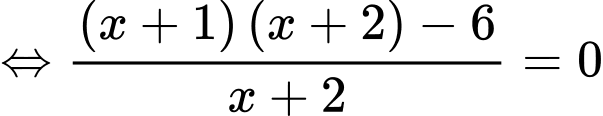
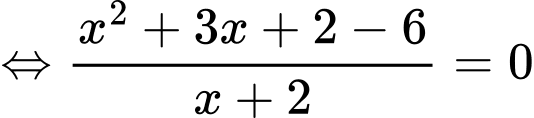
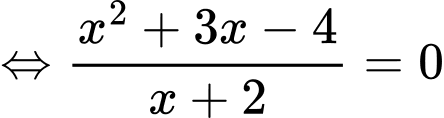
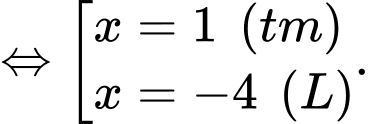
Vậy phương trình
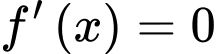 có duy nhất 1 nghiệm thuộc đoạn
có duy nhất 1 nghiệm thuộc đoạn 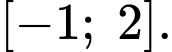
c) Đúng.
Thay lần lượt
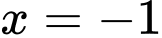 và
và 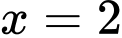 vào hàm số
vào hàm số 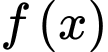 ta được
ta được 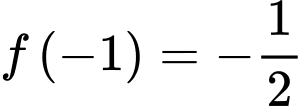 và
và 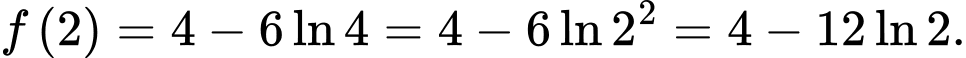
d) Sai.
Xét hàm số
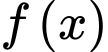 trên đoạn
trên đoạn 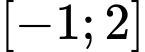
Dựa vào kết quả phần b) ta có
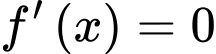
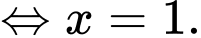
Ta có
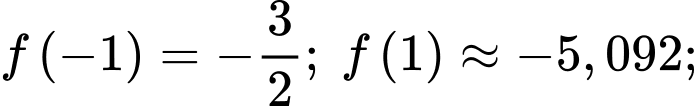
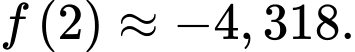
Vậy giá trị nhỏ nhất của
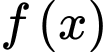 trên đoạn
trên đoạn 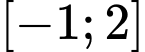 bằng -5,092 và nhỏ hơn
bằng -5,092 và nhỏ hơn 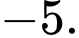
Câu 14 [715749]: Cho hàm số 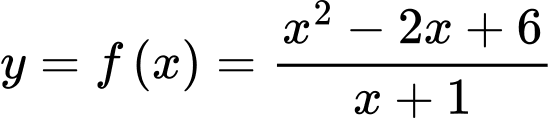 có đồ thị
có đồ thị 
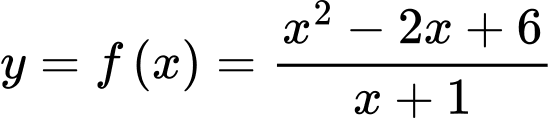 có đồ thị
có đồ thị 
a) Đúng.
b) Đúng.
Ta có: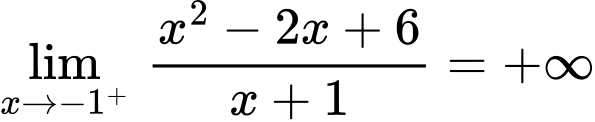
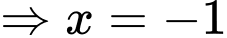 là đường tiệm cận đứng.
là đường tiệm cận đứng.
c) Sai.
Ta có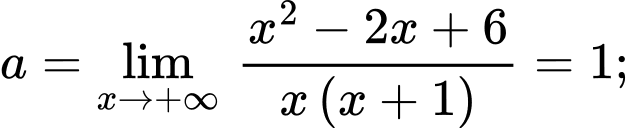
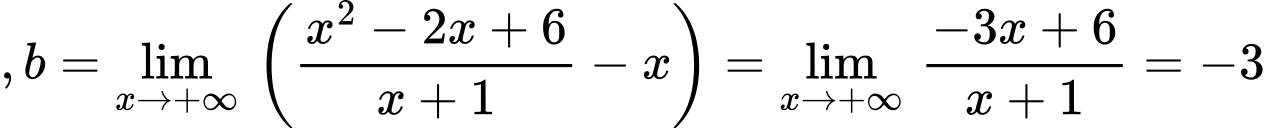
Tiệm cận xiên của đồ thị hàm số là đường thẳng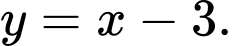
Đồ thị hàm số có tiệm cận đứng là đường thẳng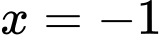 và tiệm cận xiên là đường thẳng
và tiệm cận xiên là đường thẳng 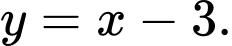
Tâm đối xứng của đồ thị là giao điểm của hai đường tiệm cận là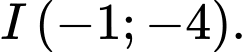
d) Đúng.
Ta có: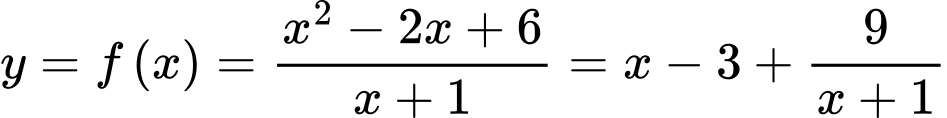
Điểm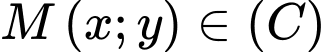 có tọa độ nguyên thì
có tọa độ nguyên thì 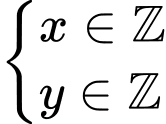
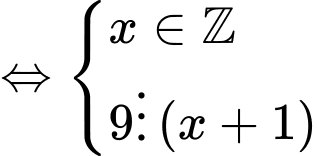
Mà 9 có 6 ước số nên có 6 điểm có tọa độ nguyên.
b) Đúng.
Ta có:
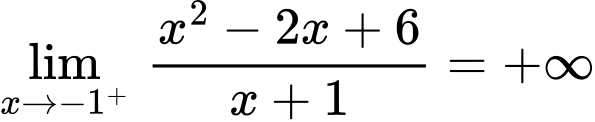
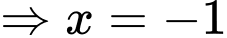 là đường tiệm cận đứng.
là đường tiệm cận đứng.c) Sai.
Ta có
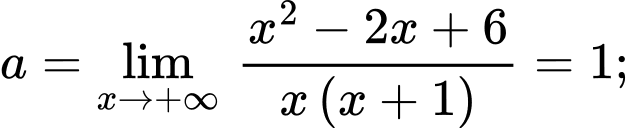
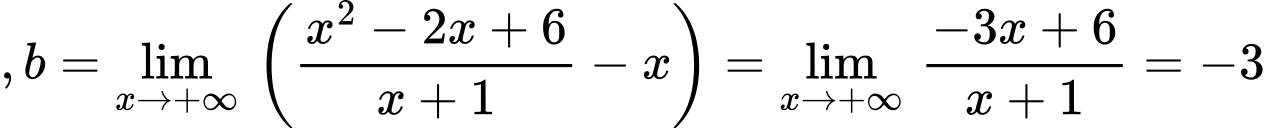
Tiệm cận xiên của đồ thị hàm số là đường thẳng
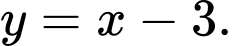
Đồ thị hàm số có tiệm cận đứng là đường thẳng
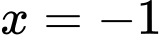 và tiệm cận xiên là đường thẳng
và tiệm cận xiên là đường thẳng 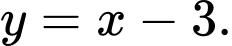
Tâm đối xứng của đồ thị là giao điểm của hai đường tiệm cận là
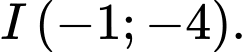
d) Đúng.
Ta có:
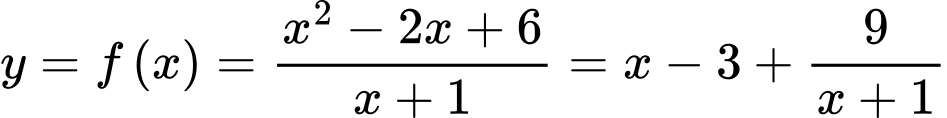
Điểm
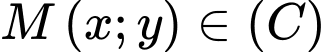 có tọa độ nguyên thì
có tọa độ nguyên thì 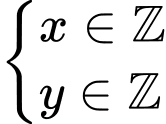
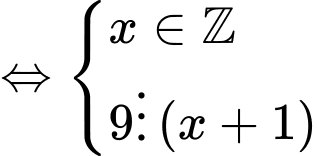
Mà 9 có 6 ước số nên có 6 điểm có tọa độ nguyên.
Câu 15 [715752]: Sau khi tiêm thuốc cho bệnh nhân thì nồng độ thuốc trong máu của bệnh nhân theo thời gian được thống kê theo công thức 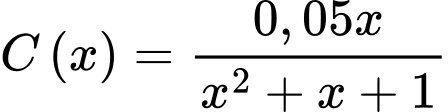 tính theo
tính theo 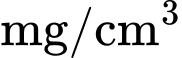 (thời gian tính theo giờ).
(thời gian tính theo giờ).
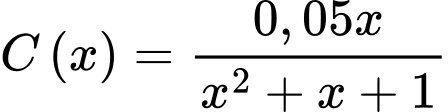 tính theo
tính theo 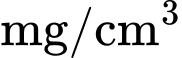 (thời gian tính theo giờ).
(thời gian tính theo giờ).
a) Đúng.
Ta có: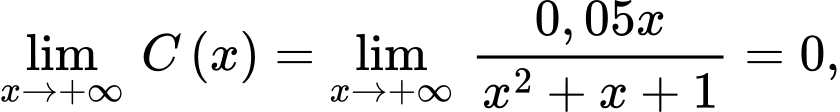 đồ thị hàm số có tiệm cận ngang
đồ thị hàm số có tiệm cận ngang 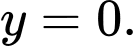
b) Sai.
Ta có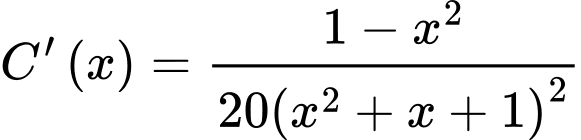
Hàm số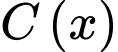 đồng biến trên khoảng
đồng biến trên khoảng 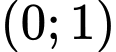 và nghịch biến trên
và nghịch biến trên
khoảng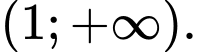
c) Đúng.
Hàm số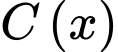 đạt giá trị lớn nhất tại
đạt giá trị lớn nhất tại 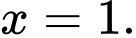
d) Sai.
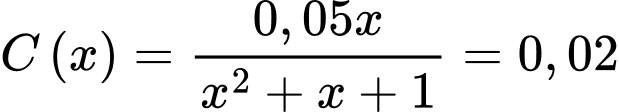
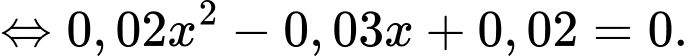 Phương trình vô nghiệm.
Phương trình vô nghiệm.
Ta có:
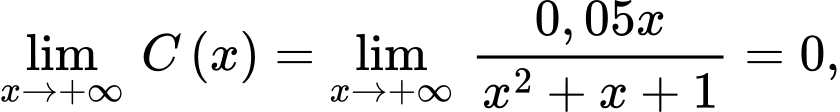 đồ thị hàm số có tiệm cận ngang
đồ thị hàm số có tiệm cận ngang 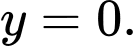
b) Sai.
Ta có
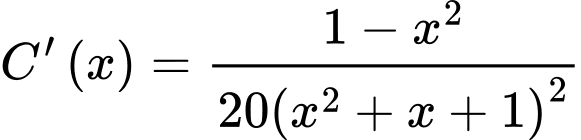
Hàm số
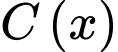 đồng biến trên khoảng
đồng biến trên khoảng 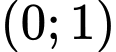 và nghịch biến trên
và nghịch biến trên khoảng
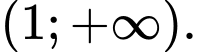
c) Đúng.
Hàm số
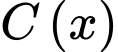 đạt giá trị lớn nhất tại
đạt giá trị lớn nhất tại 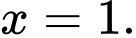
d) Sai.
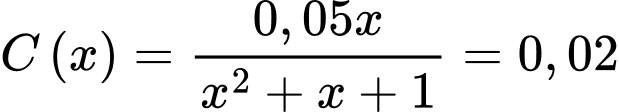
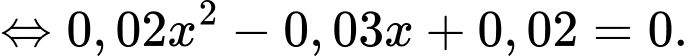 Phương trình vô nghiệm.
Phương trình vô nghiệm.
Câu 16 [702939]: Trong một số trường hợp, tin đồn lan truyền và được mô hình hoá bằng hàm số: 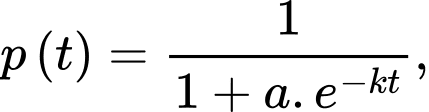 trong đó
trong đó 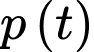 là tỉ lệ dân số biết tin đồn tại thời điểm t (giờ) và a và k là hằng số dương.
là tỉ lệ dân số biết tin đồn tại thời điểm t (giờ) và a và k là hằng số dương.
Giả sử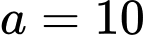 và
và 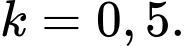 Khi đó:
Khi đó:
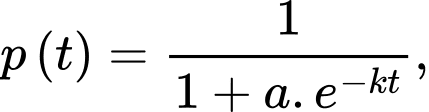 trong đó
trong đó 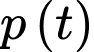 là tỉ lệ dân số biết tin đồn tại thời điểm t (giờ) và a và k là hằng số dương.
là tỉ lệ dân số biết tin đồn tại thời điểm t (giờ) và a và k là hằng số dương.Giả sử
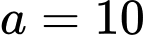 và
và 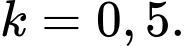 Khi đó:
Khi đó:
a) Đúng.
Ta có: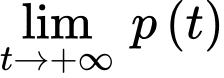
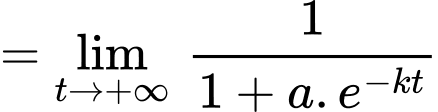
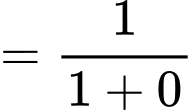
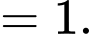
b) Sai.
Tốc độ lan truyền tin đồn là:
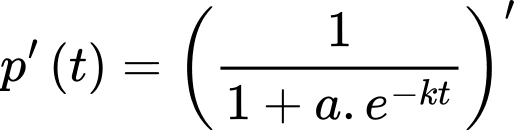
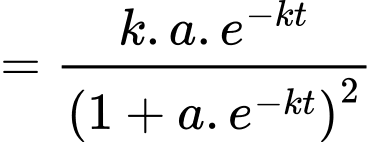
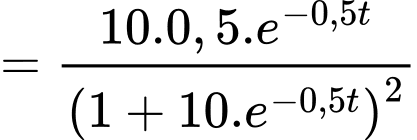
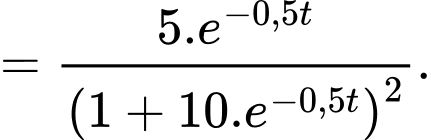
c) Sai.
Đặt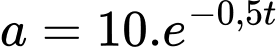 khi đó:
khi đó:
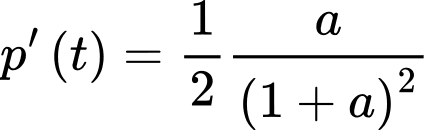
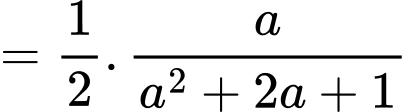
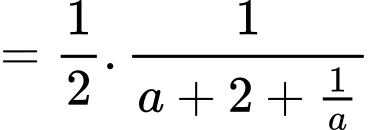
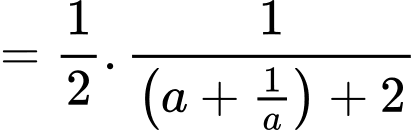
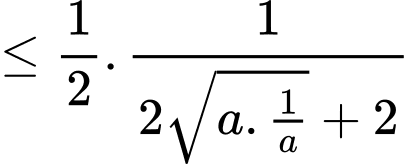 (BĐT Cô-si)
(BĐT Cô-si) 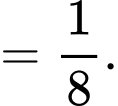
Dấu bằng xảy ra khi: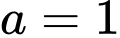
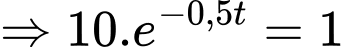
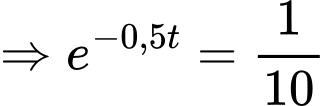
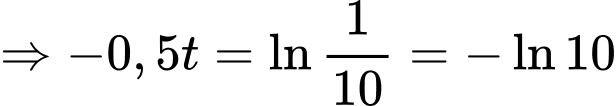
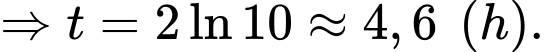
d) Đúng.
Tại thời điểm tin đồn lan truyền với tốc độ lớn nhất thì tỉ lệ dân số biết tin đồn là
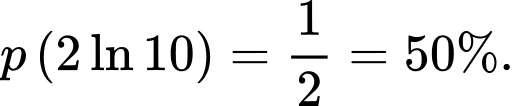
Ta có:
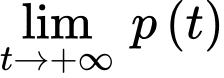
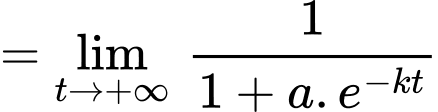
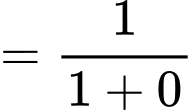
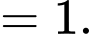
b) Sai.
Tốc độ lan truyền tin đồn là:
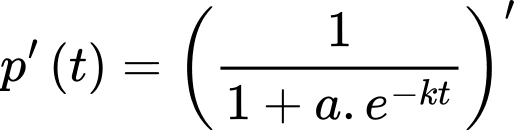
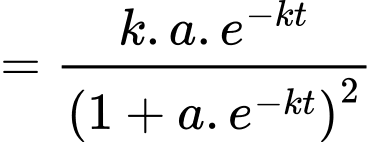
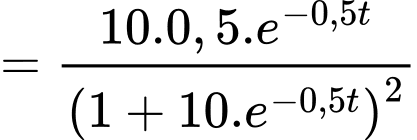
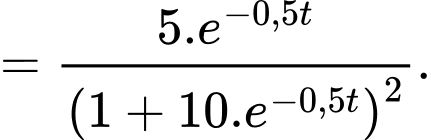
c) Sai.
Đặt
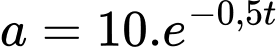 khi đó:
khi đó: 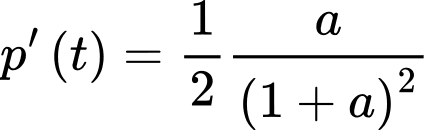
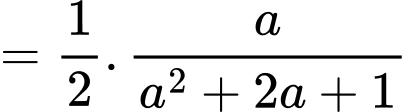
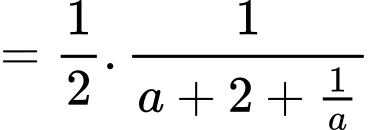
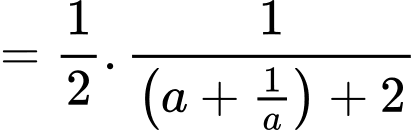
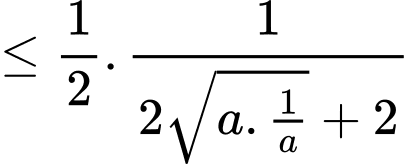 (BĐT Cô-si)
(BĐT Cô-si) 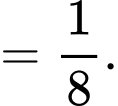
Dấu bằng xảy ra khi:
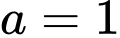
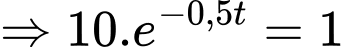
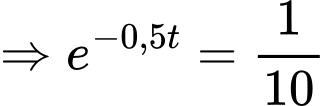
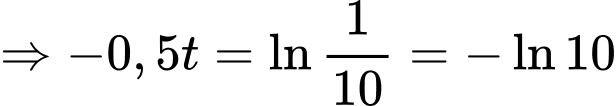
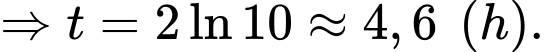
d) Đúng.
Tại thời điểm tin đồn lan truyền với tốc độ lớn nhất thì tỉ lệ dân số biết tin đồn là
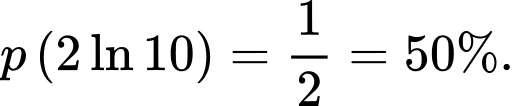
PHẦN III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 17 đến câu 22.
Câu 17 [382495]: Đồ thị của hàm số 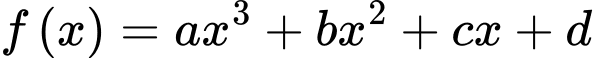 có hai điểm cực trị là
có hai điểm cực trị là 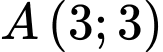 và
và 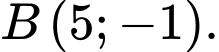 Tính giá trị của
Tính giá trị của 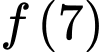 .
.
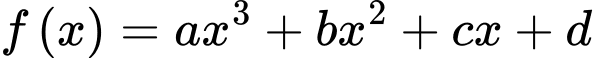 có hai điểm cực trị là
có hai điểm cực trị là 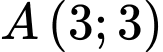 và
và 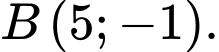 Tính giá trị của
Tính giá trị của 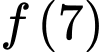 .
.
Ta có 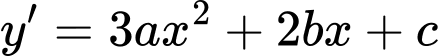
Theo đề bài ta có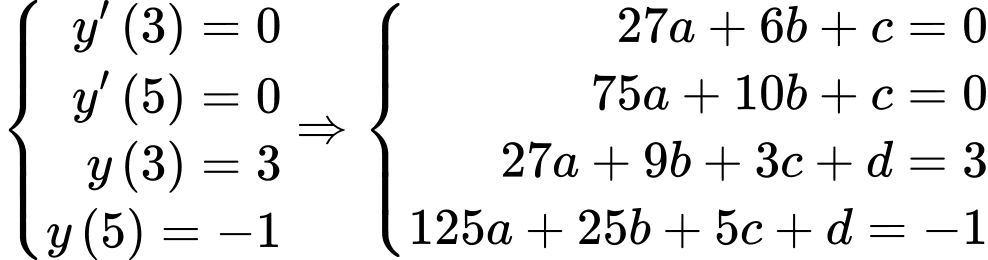
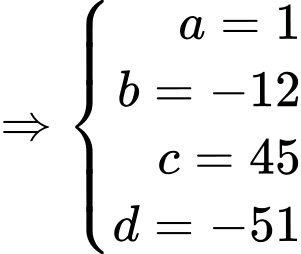
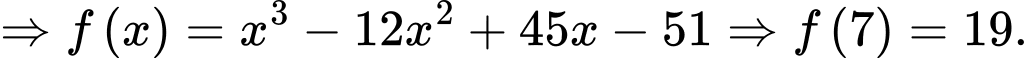
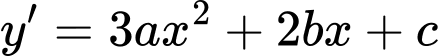
Theo đề bài ta có
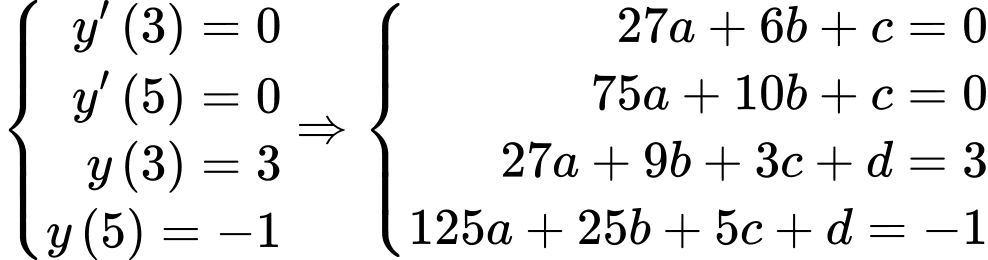
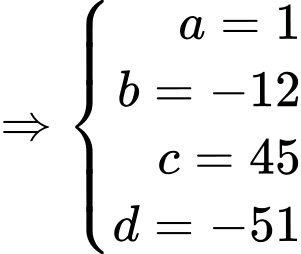
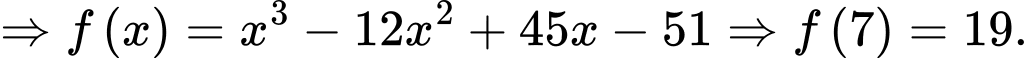
Câu 18 [774159]: Số lượng sản phẩm bán được của một cửa hàng quần áo trong 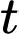 (tháng) được cho bởi công thức:
(tháng) được cho bởi công thức: 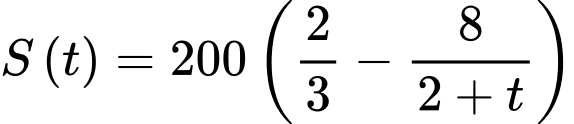 với
với  . Xem
. Xem 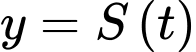 là một hàm số xác định trên nửa khoảng
là một hàm số xác định trên nửa khoảng 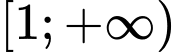 , biết rằng tiệm cận ngang của đồ thị hàm số có dạng
, biết rằng tiệm cận ngang của đồ thị hàm số có dạng 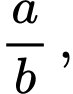 trong đó
trong đó 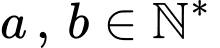 và phân số
và phân số 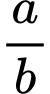 tối giản. Tính
tối giản. Tính 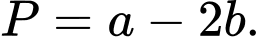
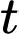 (tháng) được cho bởi công thức:
(tháng) được cho bởi công thức: 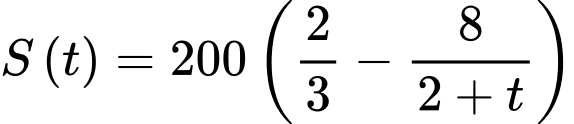 với
với  . Xem
. Xem 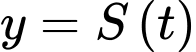 là một hàm số xác định trên nửa khoảng
là một hàm số xác định trên nửa khoảng 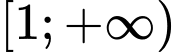 , biết rằng tiệm cận ngang của đồ thị hàm số có dạng
, biết rằng tiệm cận ngang của đồ thị hàm số có dạng 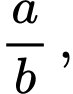 trong đó
trong đó 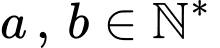 và phân số
và phân số 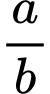 tối giản. Tính
tối giản. Tính 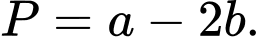
Điền đáp án: 394.
Ta có: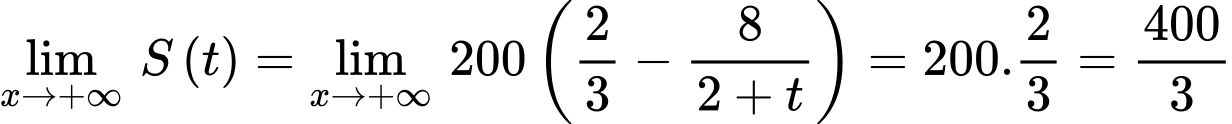
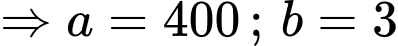
Vậy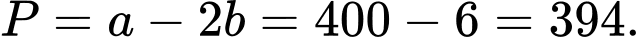
Ta có:
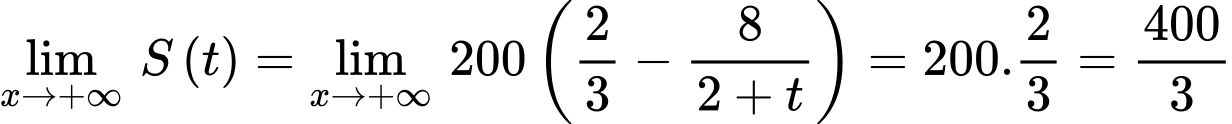
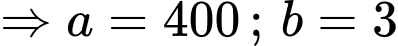
Vậy
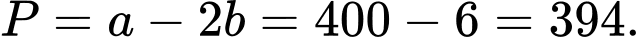
Câu 19 [681577]: Lát cắt ngang của một vùng đất ven biển được mô hình hoá thành một hàm số bậc ba 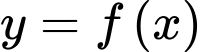 có đồ thị như hình vẽ (đơn vị độ dài trên các trục là km).
có đồ thị như hình vẽ (đơn vị độ dài trên các trục là km).
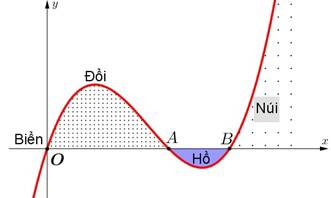
Biết khoảng cách hai bên chân đồi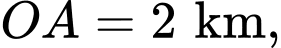 độ rộng của hồ
độ rộng của hồ 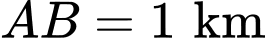 và ngọn đồi cao
và ngọn đồi cao 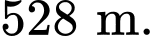 Tìm độ sâu của hồ (tính bằng mét) tại điểm sâu nhất? (làm tròn đến hàng đơn vị).
Tìm độ sâu của hồ (tính bằng mét) tại điểm sâu nhất? (làm tròn đến hàng đơn vị).
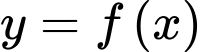 có đồ thị như hình vẽ (đơn vị độ dài trên các trục là km).
có đồ thị như hình vẽ (đơn vị độ dài trên các trục là km).
Biết khoảng cách hai bên chân đồi
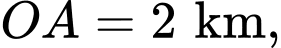 độ rộng của hồ
độ rộng của hồ 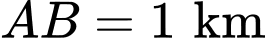 và ngọn đồi cao
và ngọn đồi cao 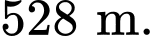 Tìm độ sâu của hồ (tính bằng mét) tại điểm sâu nhất? (làm tròn đến hàng đơn vị).
Tìm độ sâu của hồ (tính bằng mét) tại điểm sâu nhất? (làm tròn đến hàng đơn vị).
Theo đề bài ta có : 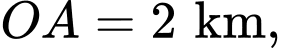
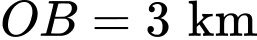 và
và 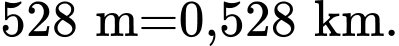
Đồ thị hàm số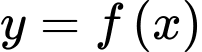 đi qua các điểm
đi qua các điểm 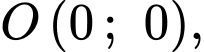
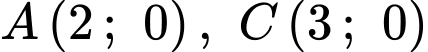 suy ra
suy ra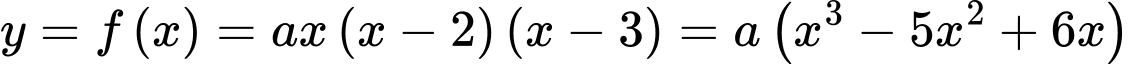 với
với 
Ta có :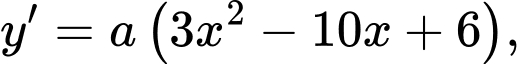
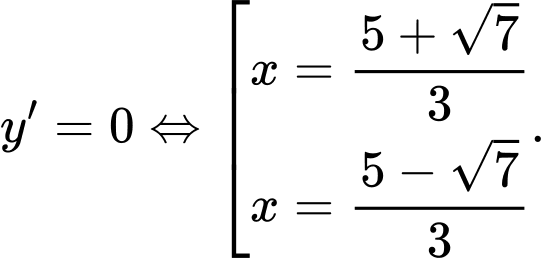
Từ độ cao của đồi ta có tại vị trí điểm cực đại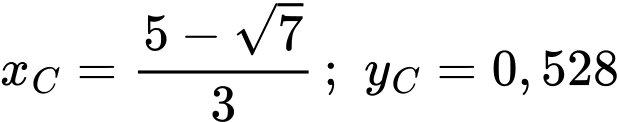 suy ra
suy ra 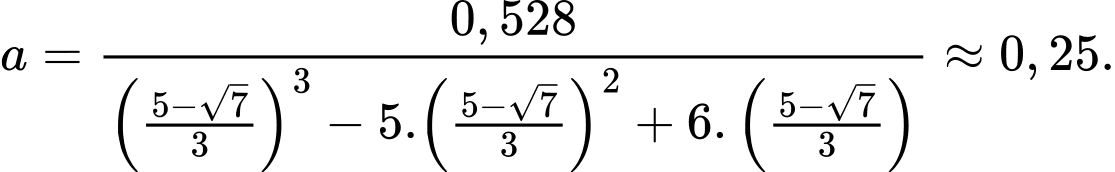
Điểm sâu nhất của hồ ứng với vị trí của điểm cực tiểu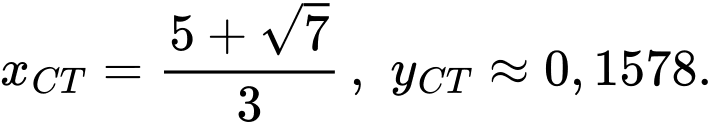
Vậy độ sâu của hồ tại điểm sâu nhất xấp xỉ hay xấp xỉ
hay xấp xỉ 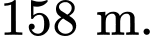
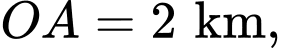
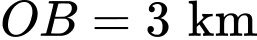 và
và 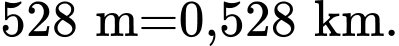
Đồ thị hàm số
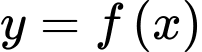 đi qua các điểm
đi qua các điểm 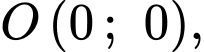
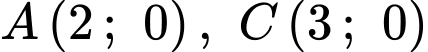 suy ra
suy ra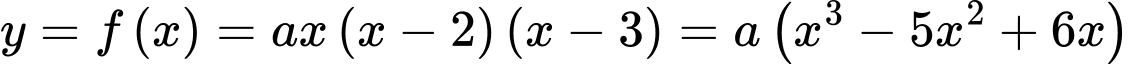 với
với 
Ta có :
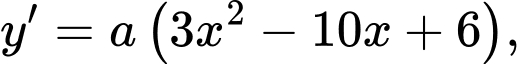
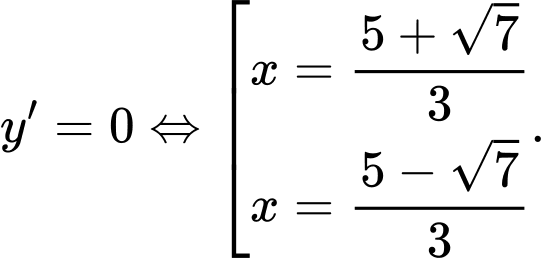
Từ độ cao của đồi ta có tại vị trí điểm cực đại
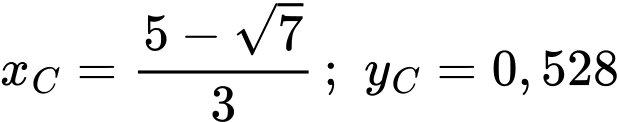 suy ra
suy ra 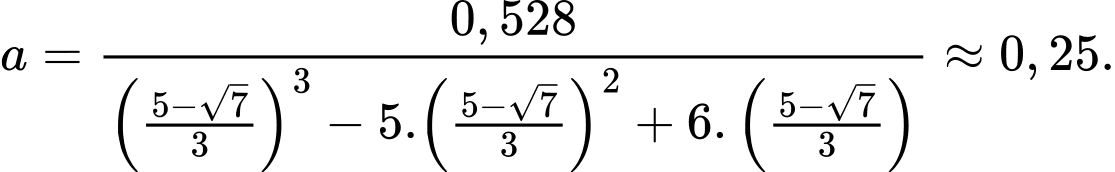
Điểm sâu nhất của hồ ứng với vị trí của điểm cực tiểu
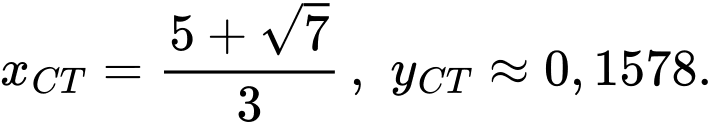
Vậy độ sâu của hồ tại điểm sâu nhất xấp xỉ
 hay xấp xỉ
hay xấp xỉ 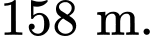
Câu 20 [708374]: Một người nông dân có 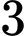 tấm lưới thép
tấm lưới thép 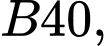 mỗi tấm dài
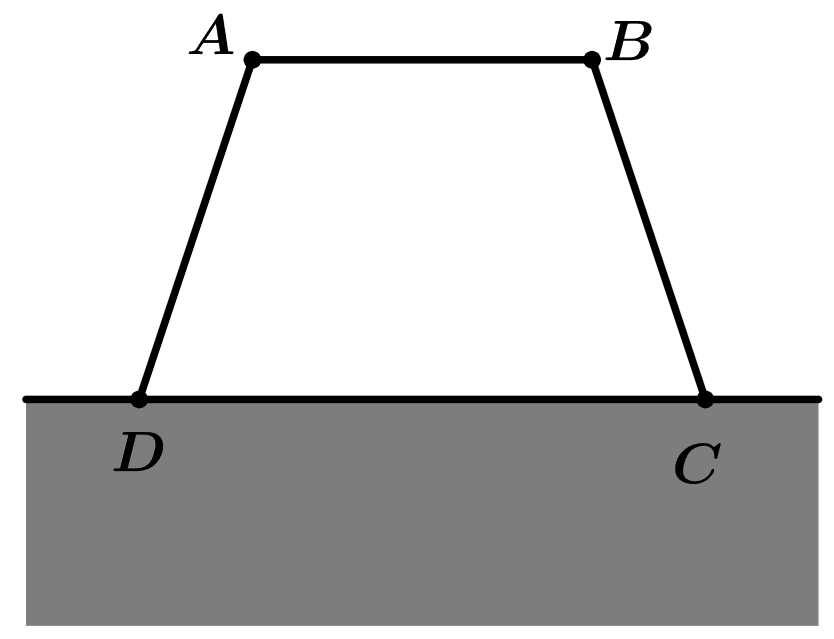
mỗi tấm dài 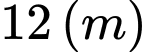 và muốn rào một mảnh vườn dọc bờ sông có dạng hình thang cân
và muốn rào một mảnh vườn dọc bờ sông có dạng hình thang cân 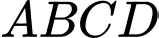 như hình vẽ (bờ sông là đường thẳng
như hình vẽ (bờ sông là đường thẳng 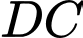 không phải rào, mỗi tấm là một cạnh của hình thang). Ông ta có thể rào được mảnh vườn có diện tích lớn nhất là
không phải rào, mỗi tấm là một cạnh của hình thang). Ông ta có thể rào được mảnh vườn có diện tích lớn nhất là 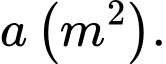 Tính
Tính 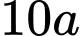 ( kết quả làm tròn đến hàng đơn vị)?
( kết quả làm tròn đến hàng đơn vị)?
 tấm lưới thép
tấm lưới thép 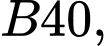 mỗi tấm dài
mỗi tấm dài 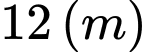 và muốn rào một mảnh vườn dọc bờ sông có dạng hình thang cân
và muốn rào một mảnh vườn dọc bờ sông có dạng hình thang cân 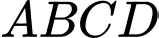 như hình vẽ (bờ sông là đường thẳng
như hình vẽ (bờ sông là đường thẳng 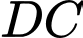 không phải rào, mỗi tấm là một cạnh của hình thang). Ông ta có thể rào được mảnh vườn có diện tích lớn nhất là
không phải rào, mỗi tấm là một cạnh của hình thang). Ông ta có thể rào được mảnh vườn có diện tích lớn nhất là 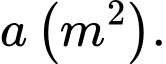 Tính
Tính 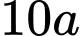 ( kết quả làm tròn đến hàng đơn vị)?
( kết quả làm tròn đến hàng đơn vị)?
Điền đáp án: 1871.
Kẻ đường cao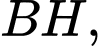 gọi số đo 2 góc ở đáy
gọi số đo 2 góc ở đáy 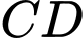 của hình thang là
của hình thang là 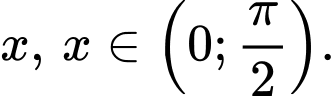
Diện tích mảnh vườn là:
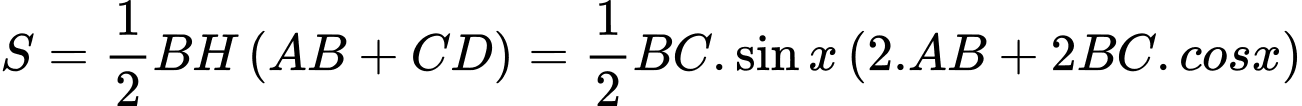
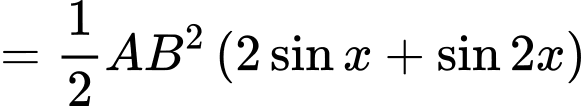
Xét hàm số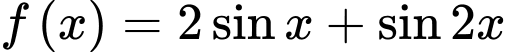 với
với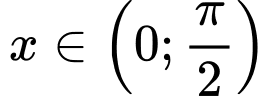 có
có 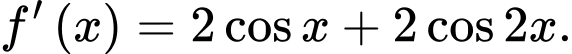
Ta có:
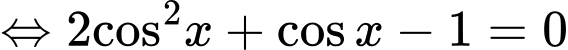
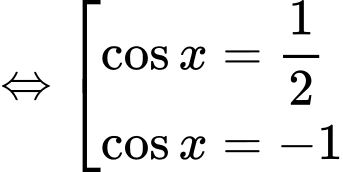
Do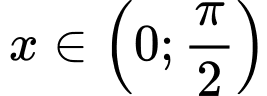 nên ta nhận
nên ta nhận 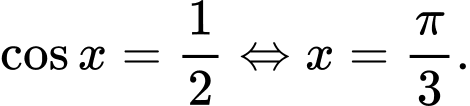 Ta có bảng biến thiên:
Ta có bảng biến thiên:
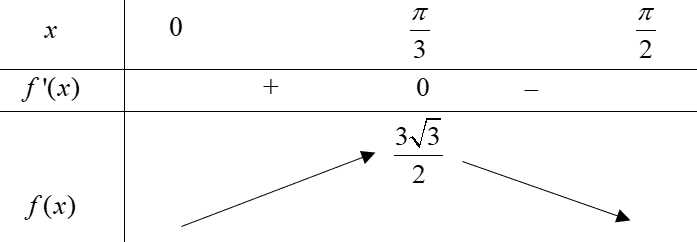
Từ bảng biến thiên ta thấy: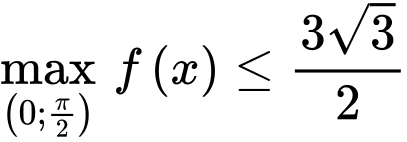 đạt được tại
đạt được tại 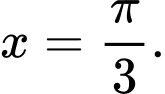
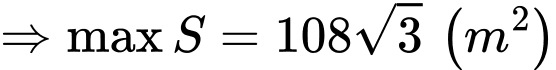 khi góc ở đáy
khi góc ở đáy 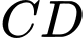 của hình thang bằng
của hình thang bằng 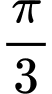
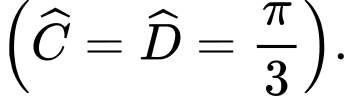
Khi đó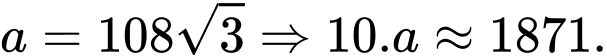
Kẻ đường cao
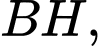 gọi số đo 2 góc ở đáy
gọi số đo 2 góc ở đáy 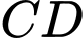 của hình thang là
của hình thang là 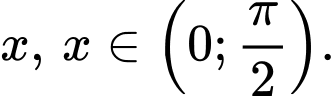
Diện tích mảnh vườn là:
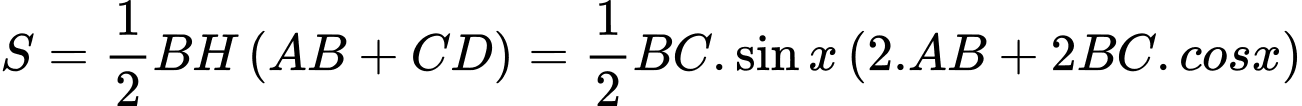
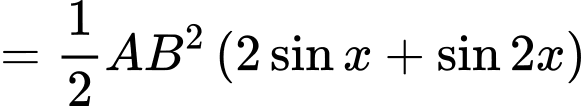
Xét hàm số
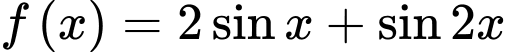 với
với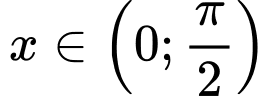 có
có 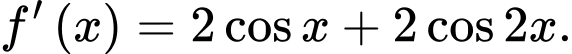
Ta có:

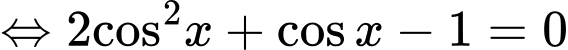
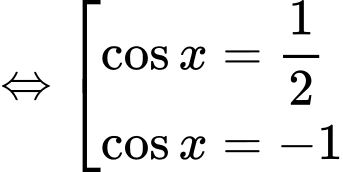
Do
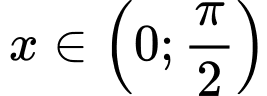 nên ta nhận
nên ta nhận 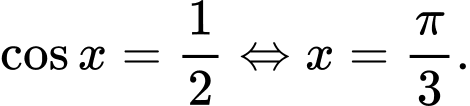 Ta có bảng biến thiên:
Ta có bảng biến thiên:
Từ bảng biến thiên ta thấy:
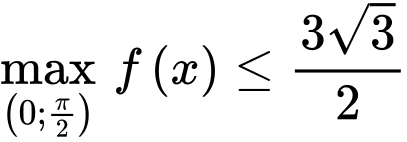 đạt được tại
đạt được tại 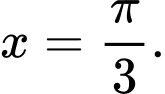
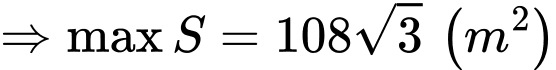 khi góc ở đáy
khi góc ở đáy 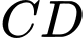 của hình thang bằng
của hình thang bằng 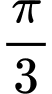
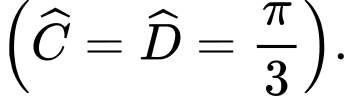
Khi đó
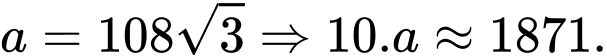
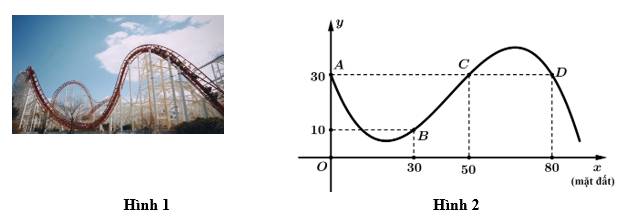
Câu 21 [696310]: Một phần của đường chạy của tàu lượn siêu tốc khi gắn hệ trục tọa độ 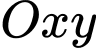 được mô phỏng ở hình 2. Biết đường chạy của nó có dạng đồ thị hàm số bậc ba
được mô phỏng ở hình 2. Biết đường chạy của nó có dạng đồ thị hàm số bậc ba 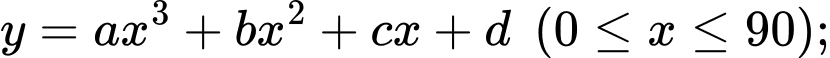 tàu lượn xuất phát từ điểm
tàu lượn xuất phát từ điểm 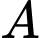 đồng thời đi qua các điểm
đồng thời đi qua các điểm 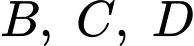 (như hình vẽ). Đơn vị mỗi trục là mét, dựa vào đồ thị hình 2, em hay tính độ cao lớn nhất (theo đơn vị mét) mà tàu lượn siêu tốc đạt được so với mặt đất (xem
(như hình vẽ). Đơn vị mỗi trục là mét, dựa vào đồ thị hình 2, em hay tính độ cao lớn nhất (theo đơn vị mét) mà tàu lượn siêu tốc đạt được so với mặt đất (xem 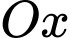 là mặt đất). Kết quả làm tròn đến hàng phần mười.
là mặt đất). Kết quả làm tròn đến hàng phần mười.
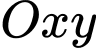 được mô phỏng ở hình 2. Biết đường chạy của nó có dạng đồ thị hàm số bậc ba
được mô phỏng ở hình 2. Biết đường chạy của nó có dạng đồ thị hàm số bậc ba 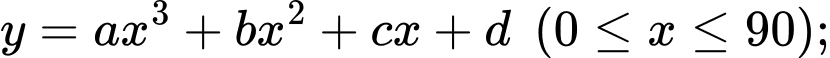 tàu lượn xuất phát từ điểm
tàu lượn xuất phát từ điểm 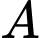 đồng thời đi qua các điểm
đồng thời đi qua các điểm 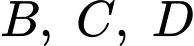 (như hình vẽ). Đơn vị mỗi trục là mét, dựa vào đồ thị hình 2, em hay tính độ cao lớn nhất (theo đơn vị mét) mà tàu lượn siêu tốc đạt được so với mặt đất (xem
(như hình vẽ). Đơn vị mỗi trục là mét, dựa vào đồ thị hình 2, em hay tính độ cao lớn nhất (theo đơn vị mét) mà tàu lượn siêu tốc đạt được so với mặt đất (xem 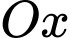 là mặt đất). Kết quả làm tròn đến hàng phần mười.
là mặt đất). Kết quả làm tròn đến hàng phần mười.
Điền đáp án: 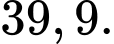
Ta có:
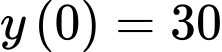
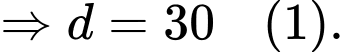
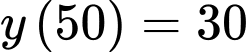
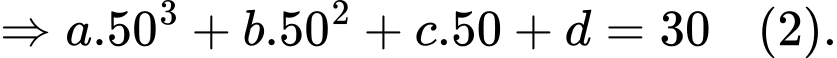
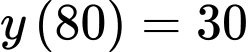
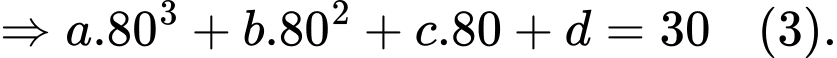
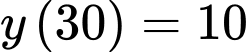
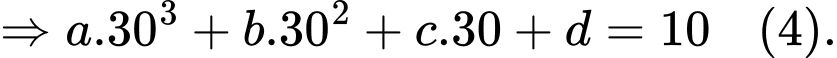
Từ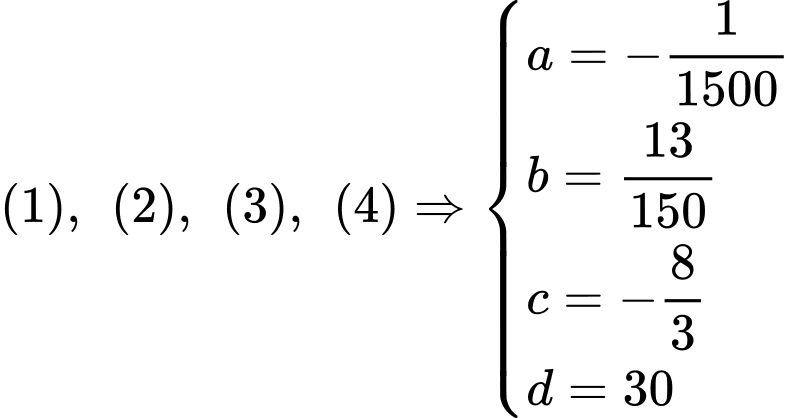
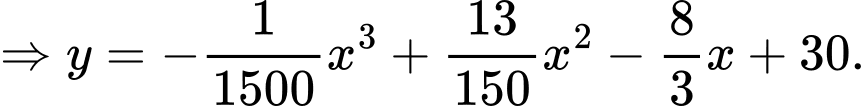
Khi đó: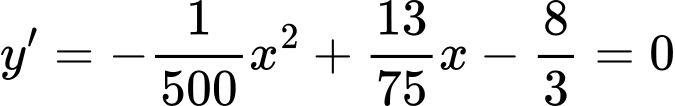
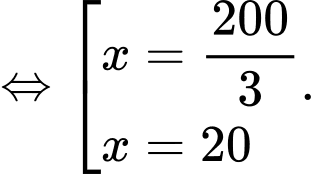
Nhìn vào đồ thị hàm số ta có: Độ cao lớn nhất mà tàu lượn siêu tốc đạt được so với mặt đất là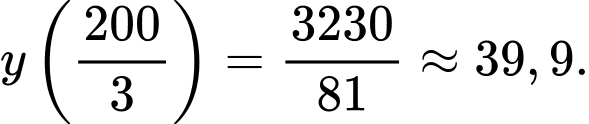
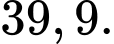
Ta có:
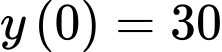
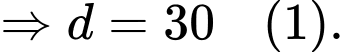
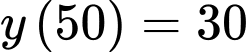
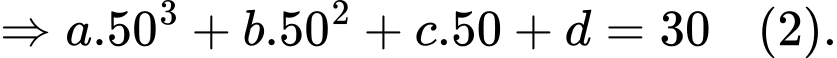
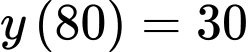
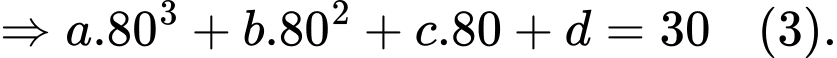
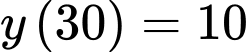
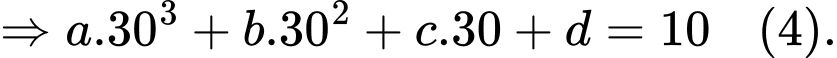
Từ
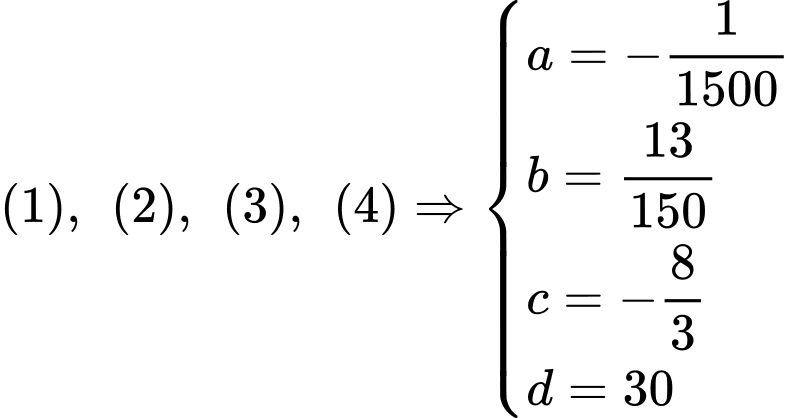
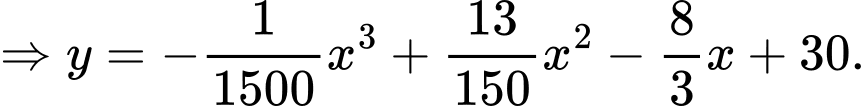
Khi đó:
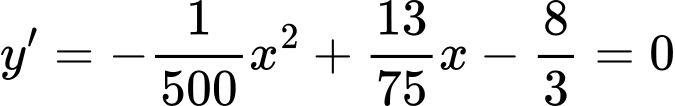
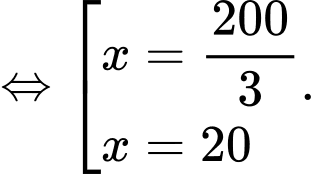
Nhìn vào đồ thị hàm số ta có: Độ cao lớn nhất mà tàu lượn siêu tốc đạt được so với mặt đất là
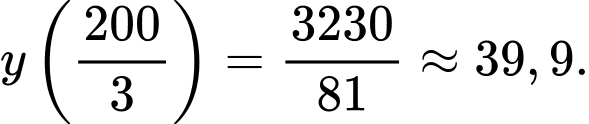
Câu 22 [390554]: Một người quan sát đang đứng ở điểm 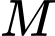 cách con đường một khoảng
cách con đường một khoảng 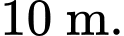 Tại một thời điểm nào đó, có một chiếc xe đạp và xe máy cùng xuất phát tại điểm A và chạy về cùng một hướng (xem hình vẽ bên), biết rằng vận tốc của xe máy gấp bốn lần vận tốc xe đạp. Tìm giá trị lớn nhất của góc nhìn
Tại một thời điểm nào đó, có một chiếc xe đạp và xe máy cùng xuất phát tại điểm A và chạy về cùng một hướng (xem hình vẽ bên), biết rằng vận tốc của xe máy gấp bốn lần vận tốc xe đạp. Tìm giá trị lớn nhất của góc nhìn 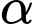 của người quan sát với hai chiếc xe đó. Viết kết quả làm tròn đến hàng đơn vị theo đơn vị độ.
của người quan sát với hai chiếc xe đó. Viết kết quả làm tròn đến hàng đơn vị theo đơn vị độ. 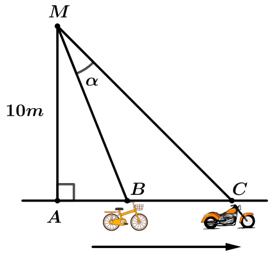
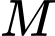 cách con đường một khoảng
cách con đường một khoảng 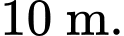 Tại một thời điểm nào đó, có một chiếc xe đạp và xe máy cùng xuất phát tại điểm A và chạy về cùng một hướng (xem hình vẽ bên), biết rằng vận tốc của xe máy gấp bốn lần vận tốc xe đạp. Tìm giá trị lớn nhất của góc nhìn
Tại một thời điểm nào đó, có một chiếc xe đạp và xe máy cùng xuất phát tại điểm A và chạy về cùng một hướng (xem hình vẽ bên), biết rằng vận tốc của xe máy gấp bốn lần vận tốc xe đạp. Tìm giá trị lớn nhất của góc nhìn 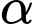 của người quan sát với hai chiếc xe đó. Viết kết quả làm tròn đến hàng đơn vị theo đơn vị độ.
của người quan sát với hai chiếc xe đó. Viết kết quả làm tròn đến hàng đơn vị theo đơn vị độ. 
Đáp số:……………………..
Đặt 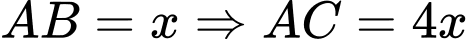 (vì vận tốc của xe máy gấp 4 lần vân tốc xe đạp)
(vì vận tốc của xe máy gấp 4 lần vân tốc xe đạp)
Ta có: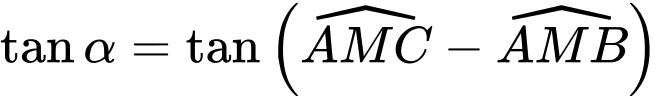
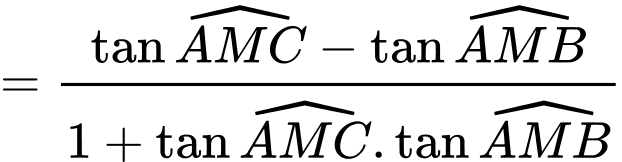
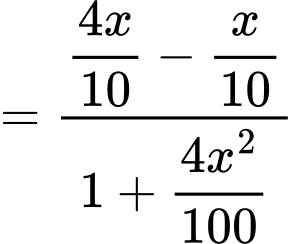
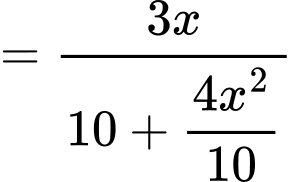
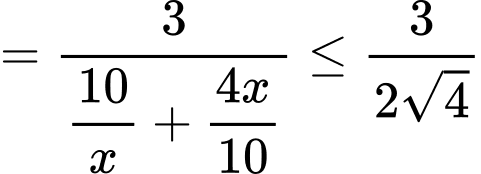
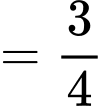
Do đó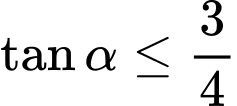

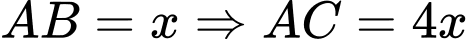 (vì vận tốc của xe máy gấp 4 lần vân tốc xe đạp)
(vì vận tốc của xe máy gấp 4 lần vân tốc xe đạp)Ta có:
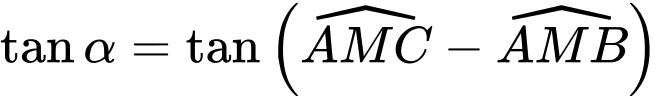
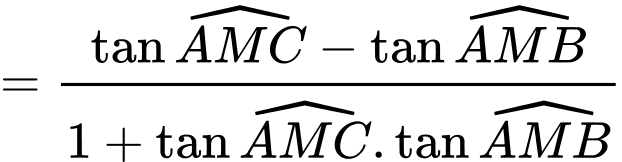
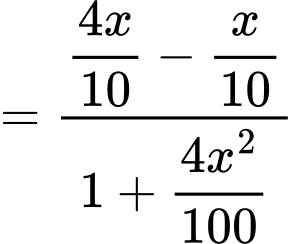
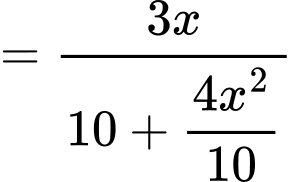
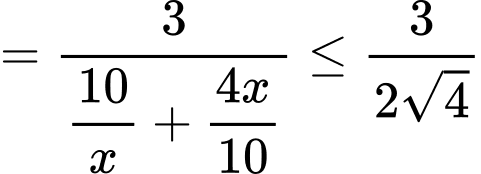
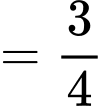
Do đó