PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1 [151227]: Cho hàm số 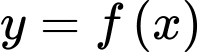 liên tục trên khoảng
liên tục trên khoảng 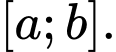 Diện tích hình phẳng giới hạn bởi đồ thị hàm số
Diện tích hình phẳng giới hạn bởi đồ thị hàm số 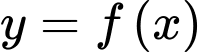 , đường thẳng
, đường thẳng 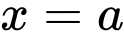 , đường thẳng
, đường thẳng 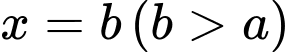 và trục hoành là
và trục hoành là
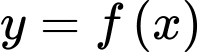 liên tục trên khoảng
liên tục trên khoảng 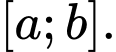 Diện tích hình phẳng giới hạn bởi đồ thị hàm số
Diện tích hình phẳng giới hạn bởi đồ thị hàm số 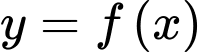 , đường thẳng
, đường thẳng 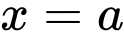 , đường thẳng
, đường thẳng 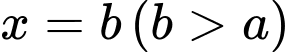 và trục hoành là
và trục hoành là A, 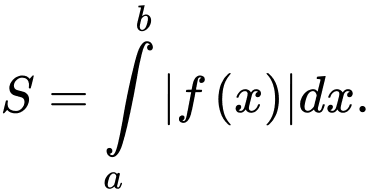
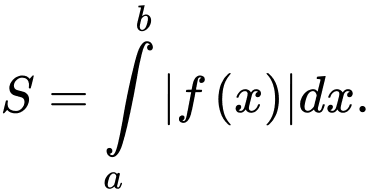
B, 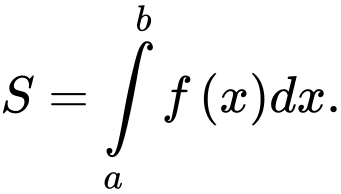
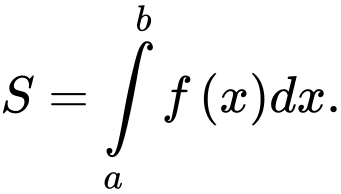
C, 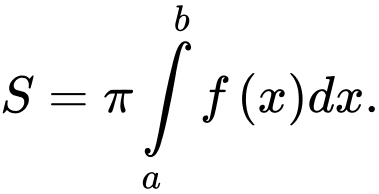
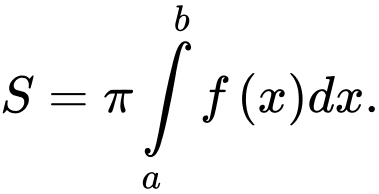
D, 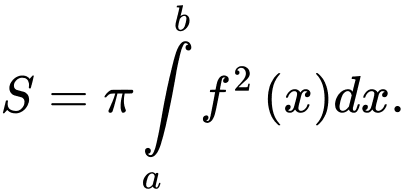
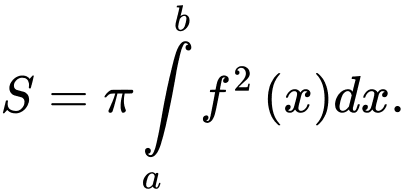
Chọn đáp án A. Đáp án: A
Câu 2 [151426]: Trong không gian với hệ tọa độ 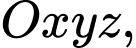 cho vật thể
cho vật thể  được giới hạn bởi hai mặt phẳng có phương trình
được giới hạn bởi hai mặt phẳng có phương trình 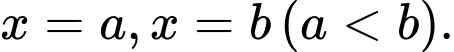 Gọi
Gọi 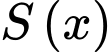 là diện tích thiết diện của
là diện tích thiết diện của  bị cắt bởi mặt phẳng vuông góc với trục
bị cắt bởi mặt phẳng vuông góc với trục 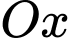 tại điểm có hoành độ là
tại điểm có hoành độ là 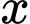
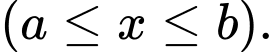 Giả sử hàm số
Giả sử hàm số 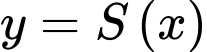 liên tục trên đoạn
liên tục trên đoạn 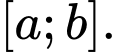 Khi đó thể tích
Khi đó thể tích  của vật thể được cho bởi công thức
của vật thể được cho bởi công thức
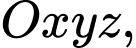 cho vật thể
cho vật thể  được giới hạn bởi hai mặt phẳng có phương trình
được giới hạn bởi hai mặt phẳng có phương trình 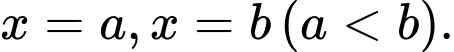 Gọi
Gọi 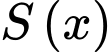 là diện tích thiết diện của
là diện tích thiết diện của  bị cắt bởi mặt phẳng vuông góc với trục
bị cắt bởi mặt phẳng vuông góc với trục 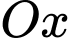 tại điểm có hoành độ là
tại điểm có hoành độ là 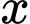
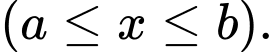 Giả sử hàm số
Giả sử hàm số 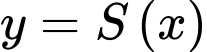 liên tục trên đoạn
liên tục trên đoạn 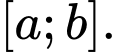 Khi đó thể tích
Khi đó thể tích  của vật thể được cho bởi công thức
của vật thể được cho bởi công thức A, 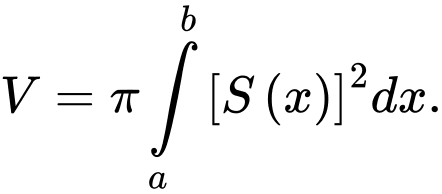
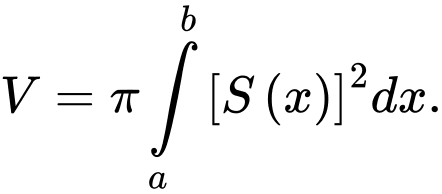
B, 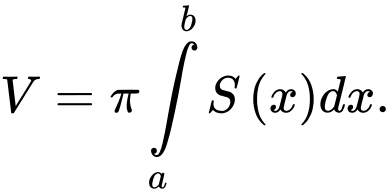
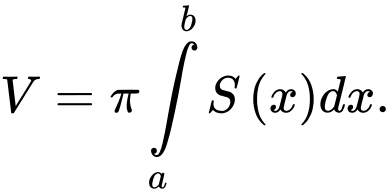
C, 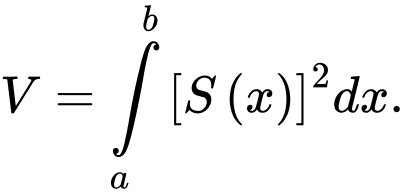
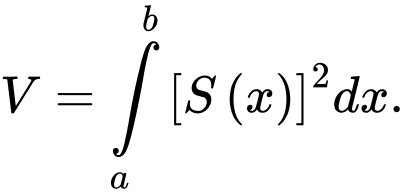
D, 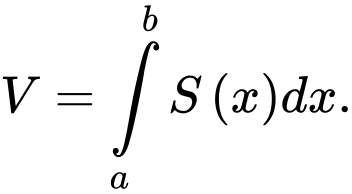
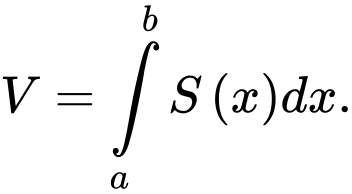
Chọn đáp án D. Đáp án: D
Câu 3 [542971]: Cho hàm số 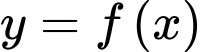 liên tục trên
liên tục trên 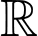 và có đồ thị như hình vẽ. Gọi
và có đồ thị như hình vẽ. Gọi 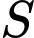 là diện tích hình phẳng giới hạn bởi các đường cong
là diện tích hình phẳng giới hạn bởi các đường cong 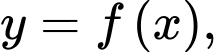
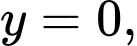
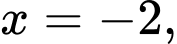
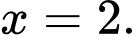
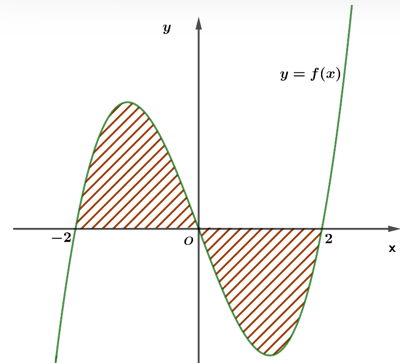
Mệnh đề nào sau đây đúng?
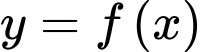 liên tục trên
liên tục trên 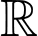 và có đồ thị như hình vẽ. Gọi
và có đồ thị như hình vẽ. Gọi 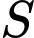 là diện tích hình phẳng giới hạn bởi các đường cong
là diện tích hình phẳng giới hạn bởi các đường cong 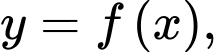
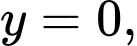
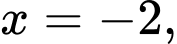
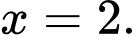

Mệnh đề nào sau đây đúng?
A, 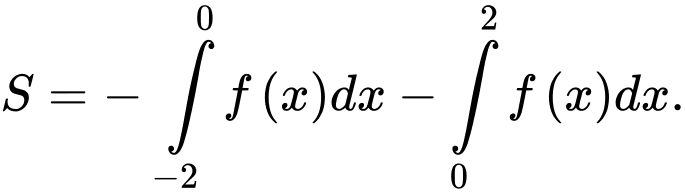
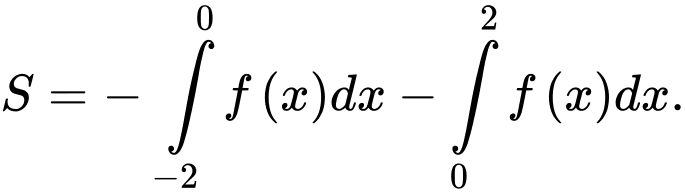
B, 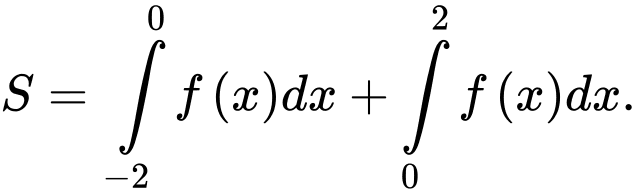
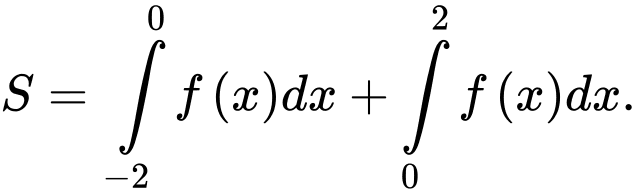
C, 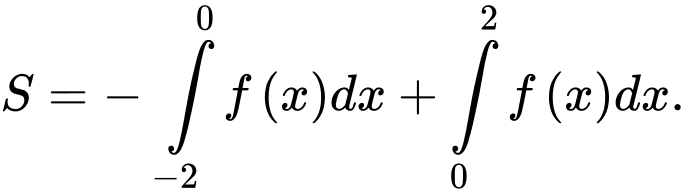
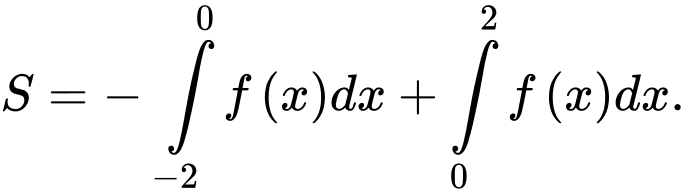
D, 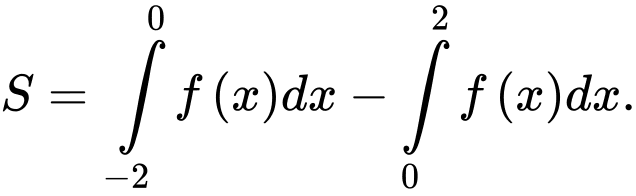
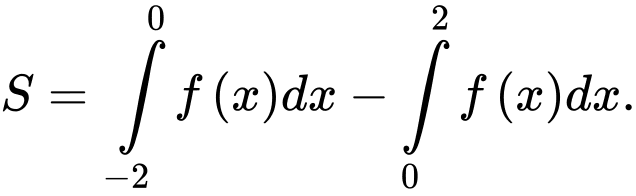
Chọn đáp án D.
Ta có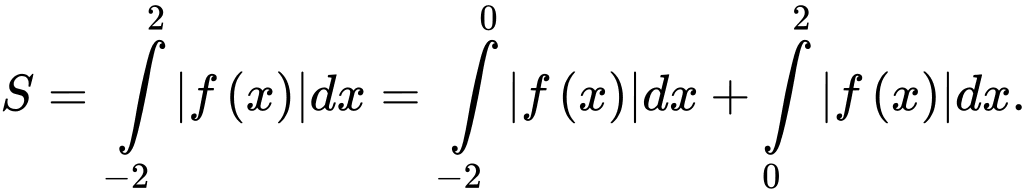
Do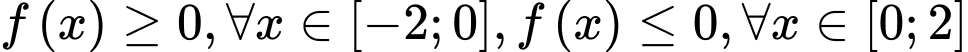 nên
nên 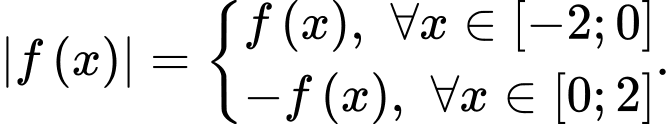
Khi đó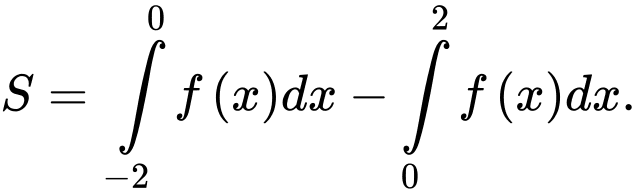 Đáp án: D
Đáp án: D
Ta có
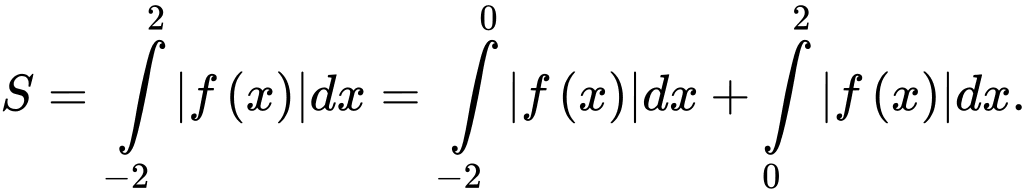
Do
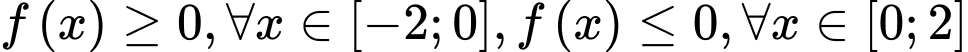 nên
nên 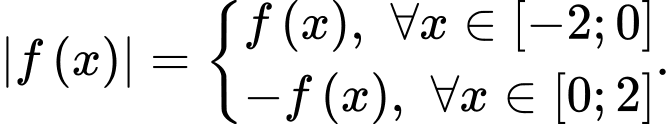
Khi đó
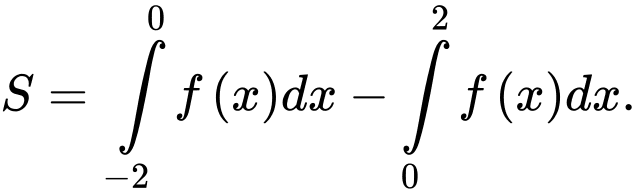 Đáp án: D
Đáp án: D
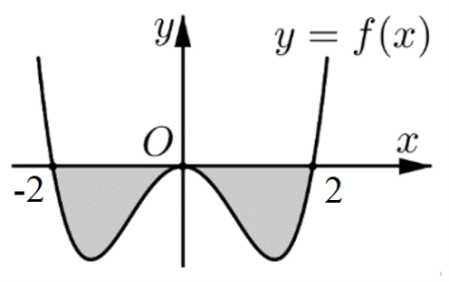
Câu 4 [778740]: Hình vẽ bên dưới biểu diễn trục hoành cắt đồ thị hàm số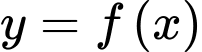 tại ba điểm có hoành độ
tại ba điểm có hoành độ 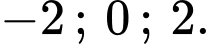 Gọi
Gọi 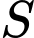 là hình phẳng giới hạn bởi đồ thị
là hình phẳng giới hạn bởi đồ thị 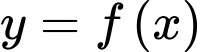 và trục hoành. Khẳng định nào sau đây sai?
và trục hoành. Khẳng định nào sau đây sai?
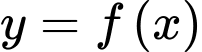 tại ba điểm có hoành độ
tại ba điểm có hoành độ 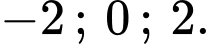 Gọi
Gọi 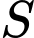 là hình phẳng giới hạn bởi đồ thị
là hình phẳng giới hạn bởi đồ thị 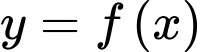 và trục hoành. Khẳng định nào sau đây sai?
và trục hoành. Khẳng định nào sau đây sai?
A, 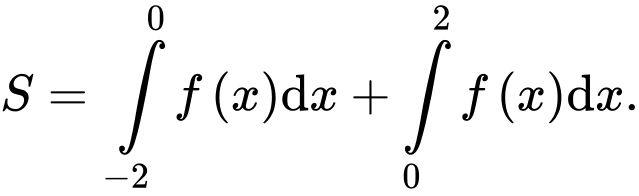
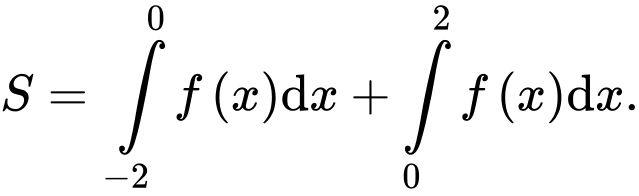
B, 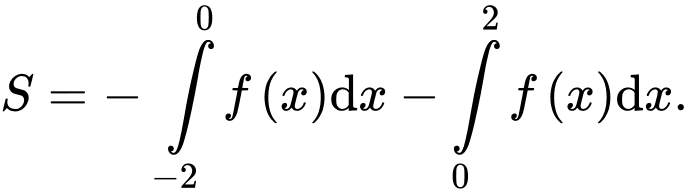
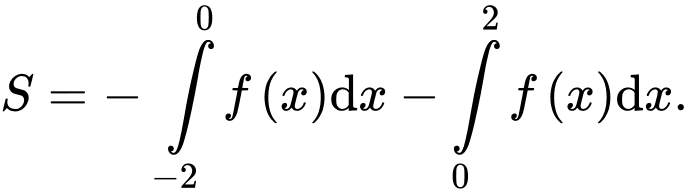
C, 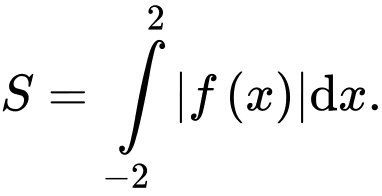
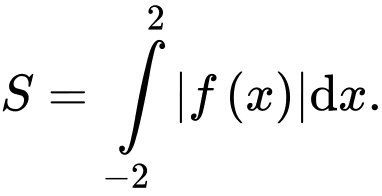
D, 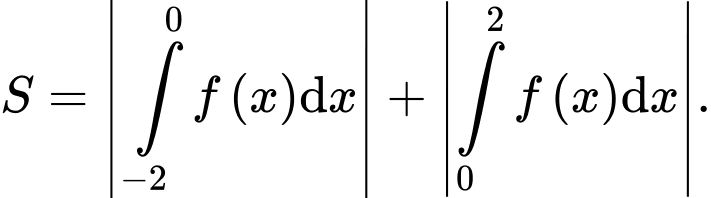
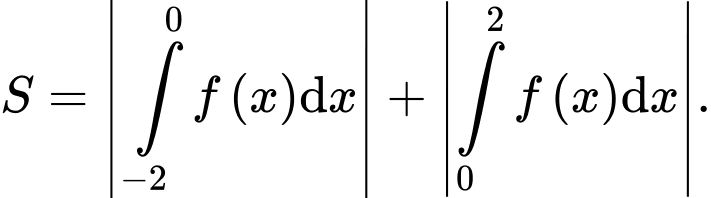
Chọn đáp án A. Đáp án: A
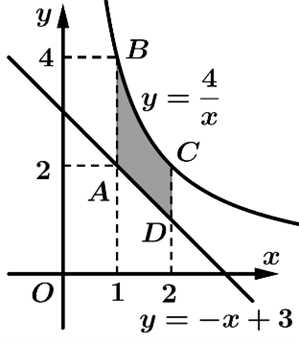
Câu 5 [360292]: Hình thang cong 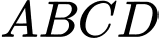 ở hình vẽ có diện tích bằng:
ở hình vẽ có diện tích bằng:
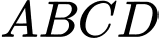 ở hình vẽ có diện tích bằng:
ở hình vẽ có diện tích bằng:
A, 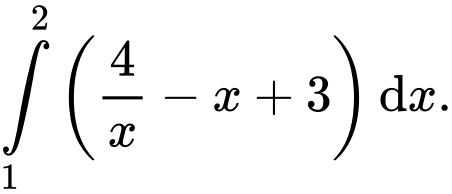
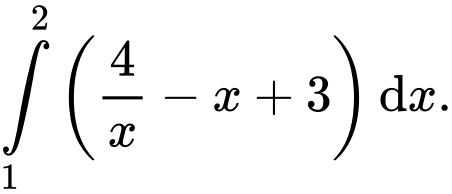
B, 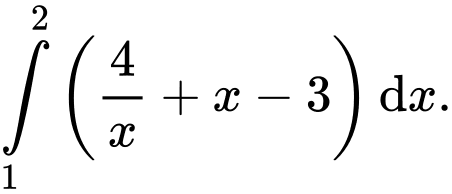
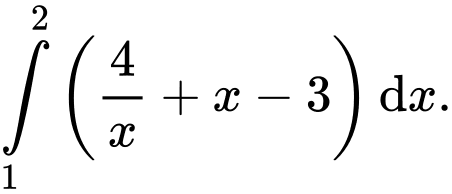
C, 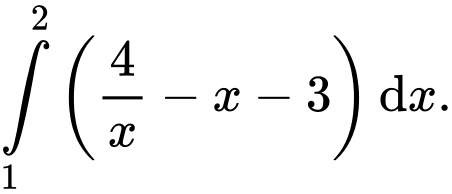
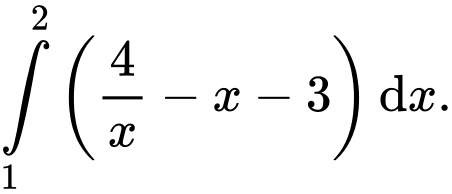
D, 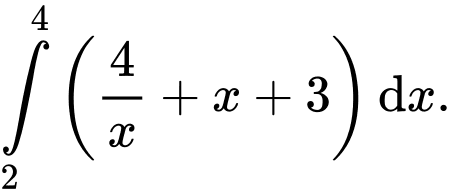
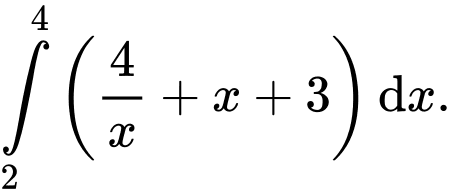
Chọn đáp án B.
Dựa vào hình vẽ ta có diện tích hình thang cong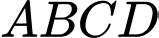 là
là
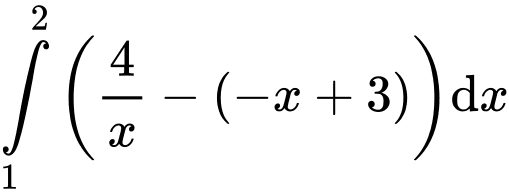
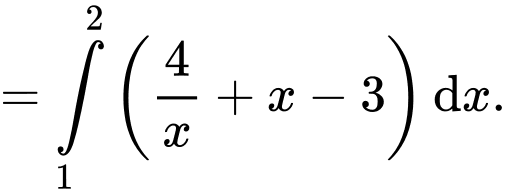 Đáp án: B
Đáp án: B
Dựa vào hình vẽ ta có diện tích hình thang cong
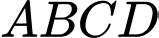 là
là 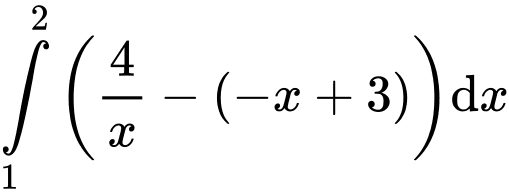
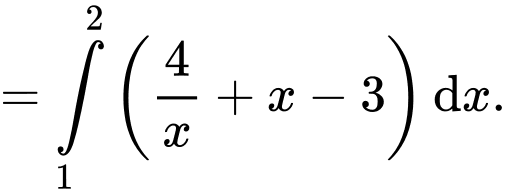 Đáp án: B
Đáp án: B
Câu 6 [146623]: Gọi 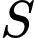 là diện tích hình phẳng giới hạn bởi các đường
là diện tích hình phẳng giới hạn bởi các đường 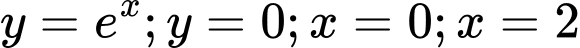 . Mệnh đề nào dưới đây đúng?
. Mệnh đề nào dưới đây đúng?
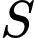 là diện tích hình phẳng giới hạn bởi các đường
là diện tích hình phẳng giới hạn bởi các đường 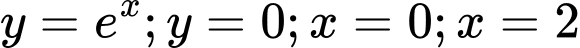 . Mệnh đề nào dưới đây đúng?
. Mệnh đề nào dưới đây đúng? A, 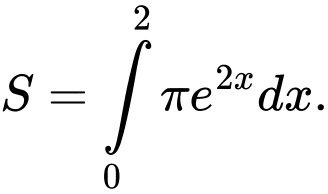
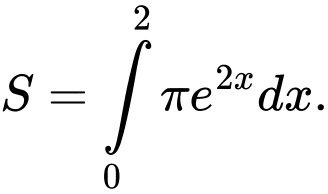
B, 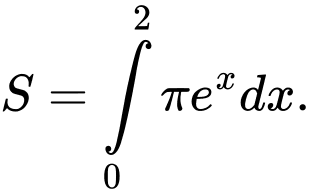
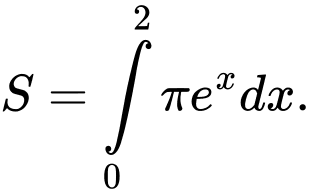
C, 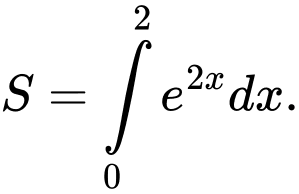
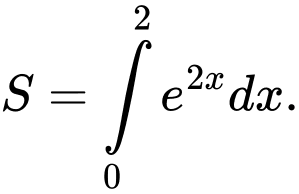
D, 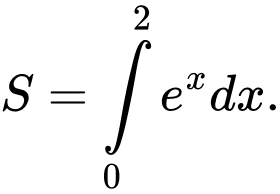
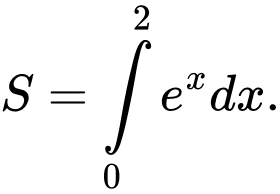
Chọn đáp án D. Đáp án: D
Câu 7 [543566]: Diện tích hình phẳng được giới hạn bởi đồ thị hàm số 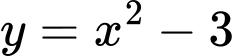 và đường thẳng
và đường thẳng 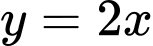 bằng
bằng
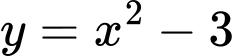 và đường thẳng
và đường thẳng 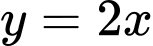 bằng
bằng A, 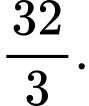
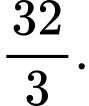
B, 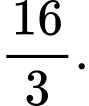
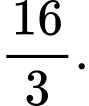
C, 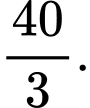
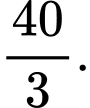
D, 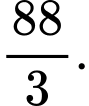
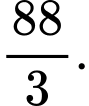
Chọn đáp án A.
Phương trình hoành độ giao điểm: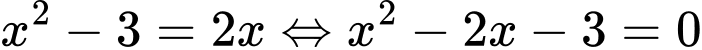
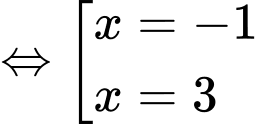
Vậy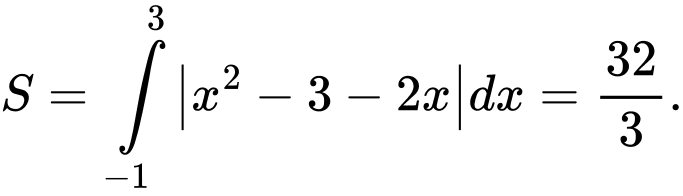 Đáp án: A
Đáp án: A
Phương trình hoành độ giao điểm:
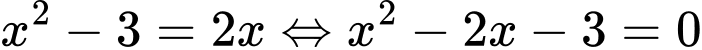
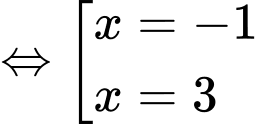
Vậy
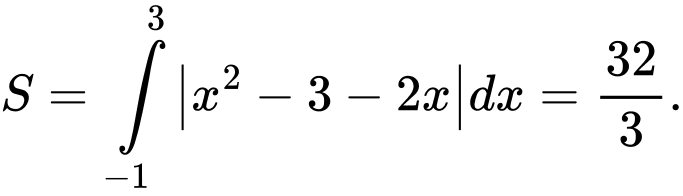 Đáp án: A
Đáp án: A
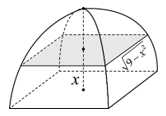
Câu 8 [778741]: Một chiếc lều mái vòm có hình dạng như hình. Nếu cắt lều bằng mặt phẳng song song với mặt đáy và cách mặt đáy một khoảng 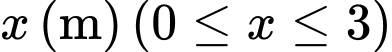 thì được hình vuông có cạnh
thì được hình vuông có cạnh 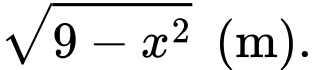 Thể tích của lều theo đơn vị
Thể tích của lều theo đơn vị 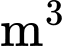 là
là
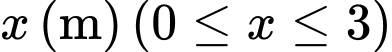 thì được hình vuông có cạnh
thì được hình vuông có cạnh 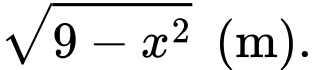 Thể tích của lều theo đơn vị
Thể tích của lều theo đơn vị 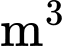 là
là
A, 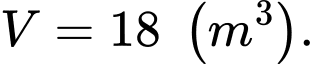
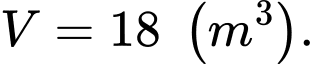
B, 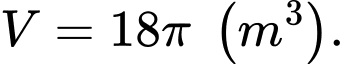
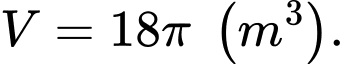
C, 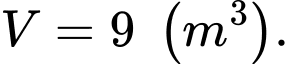
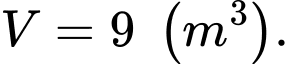
D, 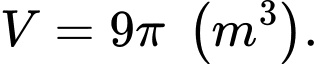
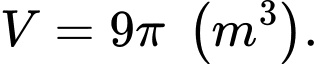
Chọn đáp án A.
Diện tích mặt cắt là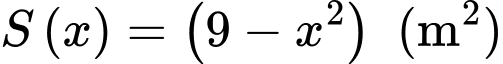
Thể tích của lều là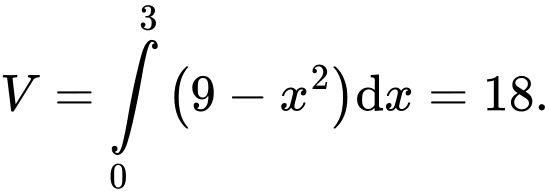 Đáp án: A
Đáp án: A
Diện tích mặt cắt là
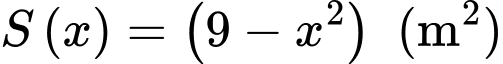
Thể tích của lều là
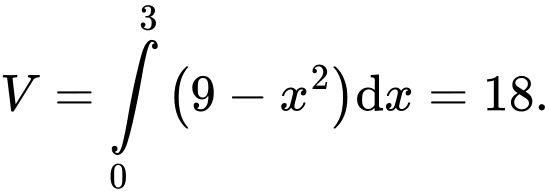 Đáp án: A
Đáp án: A
Câu 9 [151633]: Thể tích của khối tròn xoay khi quay quanh trục hoành hình  được giới hạn bởi các đường
được giới hạn bởi các đường 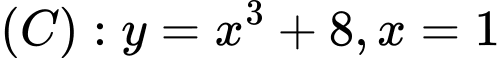 , trục hoành, trục tung là
, trục hoành, trục tung là
 được giới hạn bởi các đường
được giới hạn bởi các đường 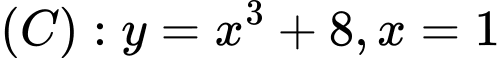 , trục hoành, trục tung là
, trục hoành, trục tung là A, 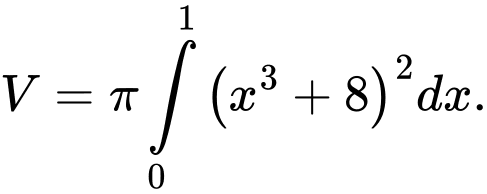
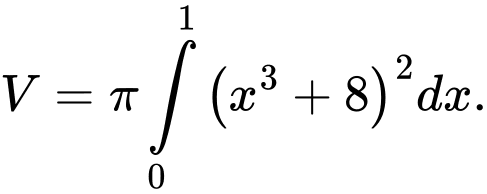
B, 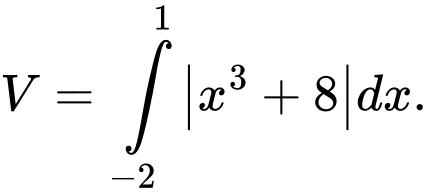
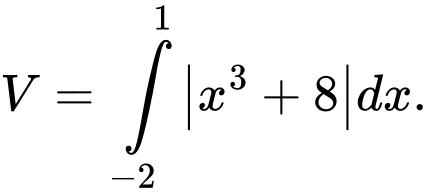
C, 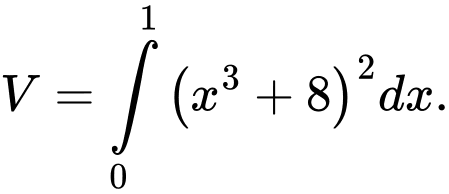
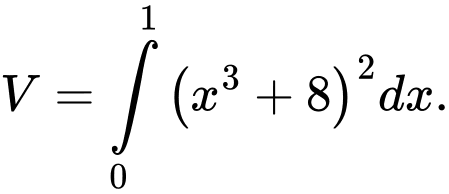
D, 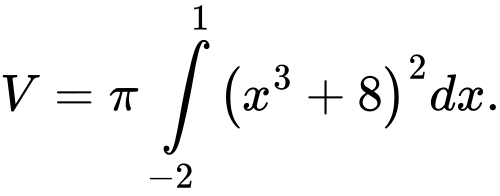
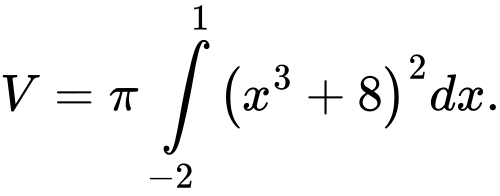
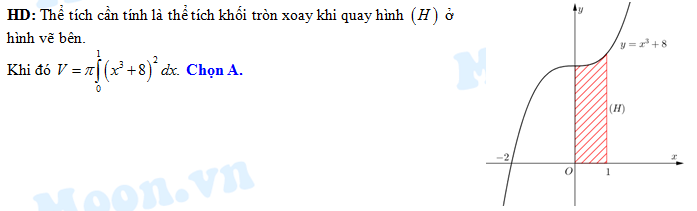 Đáp án: A
Đáp án: A
Câu 10 [151640]: Gọi  là hình phẳng giới hạn bởi các đường
là hình phẳng giới hạn bởi các đường 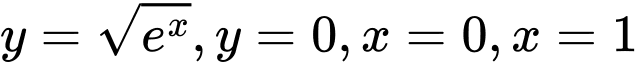 . Tính thể tích
. Tính thể tích  của vật thể tròn xoay được sinh ra khi ta quay hình
của vật thể tròn xoay được sinh ra khi ta quay hình  quanh trục
quanh trục 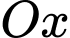 .
.
 là hình phẳng giới hạn bởi các đường
là hình phẳng giới hạn bởi các đường 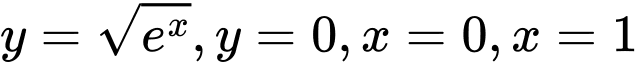 . Tính thể tích
. Tính thể tích  của vật thể tròn xoay được sinh ra khi ta quay hình
của vật thể tròn xoay được sinh ra khi ta quay hình  quanh trục
quanh trục 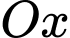 .
. A, 

B, 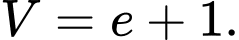
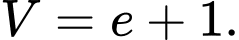
C, 

D, 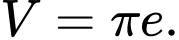
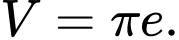
Chọn đáp án A.
Thể tích cần tính là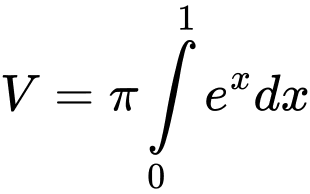
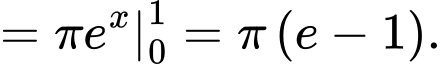 Đáp án: A
Đáp án: A
Thể tích cần tính là
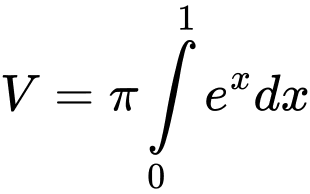
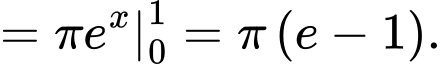 Đáp án: A
Đáp án: A
Câu 11 [151239]: Tính diện tích hình phẳng được giới hạn bới các đường 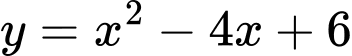 và
và 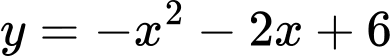 .
.
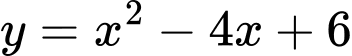 và
và 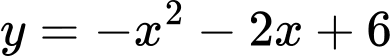 .
. A, 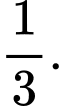
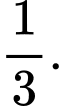
B, 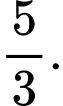
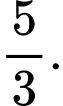
C, 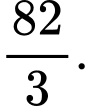
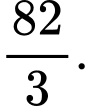
D, 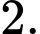
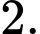
Chọn đáp án A.
Phương trình hoành độ giao điểm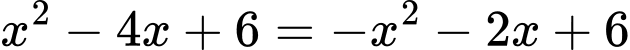

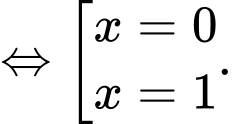
Khi đó diện tích cần tìm là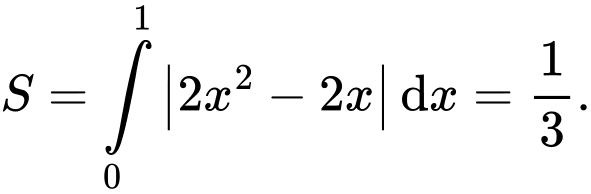 Đáp án: A
Đáp án: A
Phương trình hoành độ giao điểm
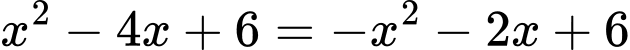

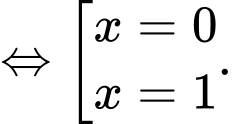
Khi đó diện tích cần tìm là
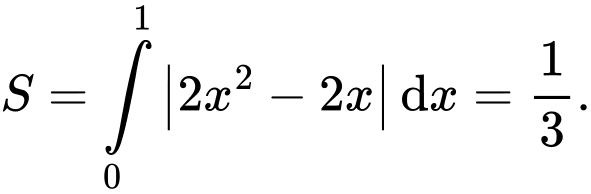 Đáp án: A
Đáp án: A
Câu 12 [151658]: Cho hình phẳng 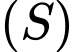 giới hạn bởi đường cong có phương trình
giới hạn bởi đường cong có phương trình 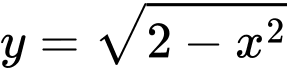 và trục
và trục 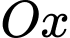 , quay
, quay 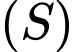 xung quanh
xung quanh 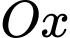 . Thể tích của khối tròn xoay được tạo thành bằng
. Thể tích của khối tròn xoay được tạo thành bằng
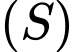 giới hạn bởi đường cong có phương trình
giới hạn bởi đường cong có phương trình 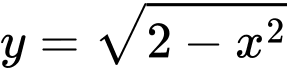 và trục
và trục 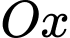 , quay
, quay 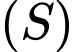 xung quanh
xung quanh 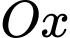 . Thể tích của khối tròn xoay được tạo thành bằng
. Thể tích của khối tròn xoay được tạo thành bằng A, 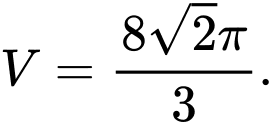
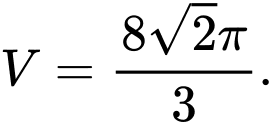
B, 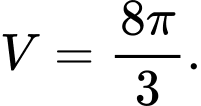
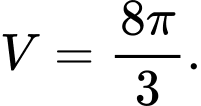
C, 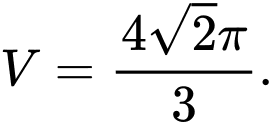
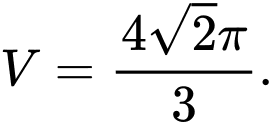
D, 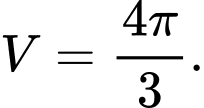
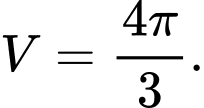
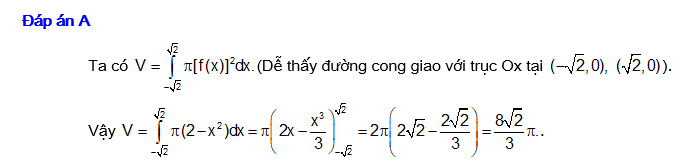 Đáp án: A
Đáp án: A PHẦN II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a),b),c),d) ở mỗi câu học sinh chọn đúng hoặc sai.
Câu 13 [778743]: Cho hình phẳng  giới hạn bởi các đồ thị hàm số
giới hạn bởi các đồ thị hàm số 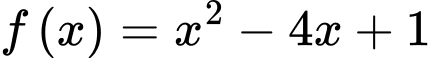 và
và 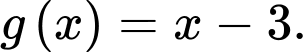 Xét hàm số
Xét hàm số 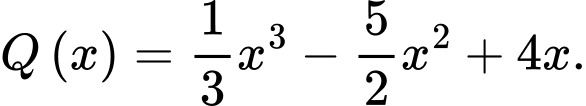
 giới hạn bởi các đồ thị hàm số
giới hạn bởi các đồ thị hàm số 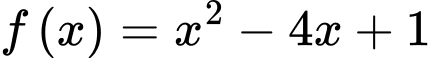 và
và 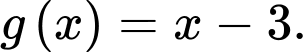 Xét hàm số
Xét hàm số 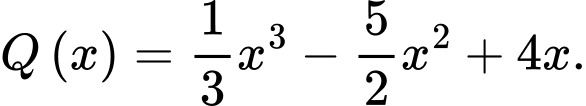
a) Đúng.
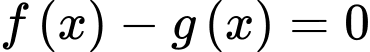
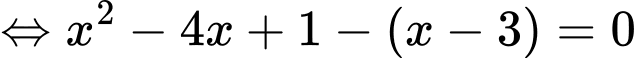
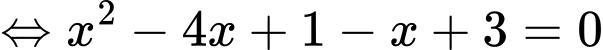
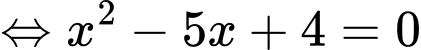
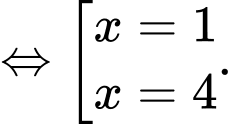
b) Sai.
Phát biểu đúng phải là: “Hiệu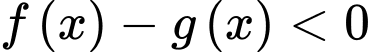 với mọi
với mọi 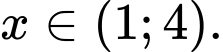 ”
”
c) Đúng.
Hàm số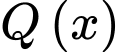 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số  khi và chỉ khi
khi và chỉ khi 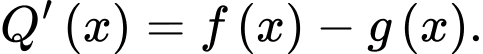
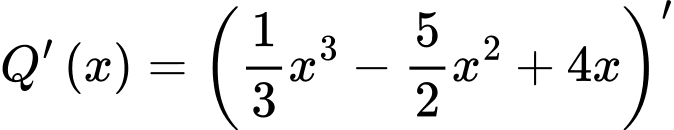
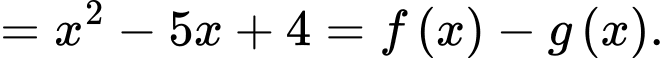
Vậy mệnh đề đúng.
d) Sai.
Diện tích hình phẳng bằng
bằng 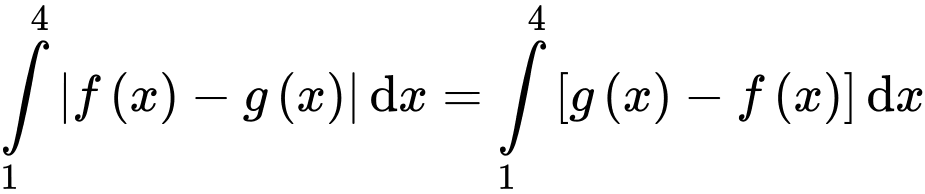 (vì đồ thị hàm số
(vì đồ thị hàm số 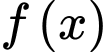 nằm dưới đồ thị hàm số
nằm dưới đồ thị hàm số 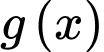 trong khoảng
trong khoảng 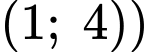
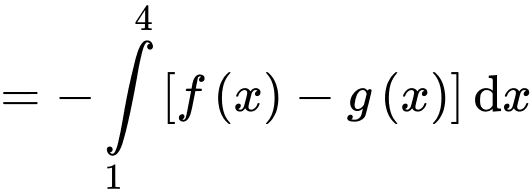
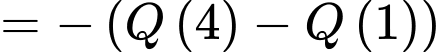

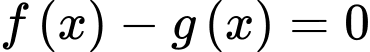
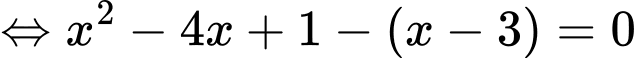
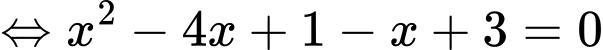
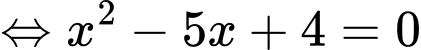
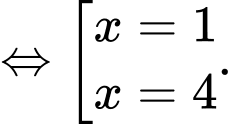
b) Sai.
Phát biểu đúng phải là: “Hiệu
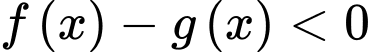 với mọi
với mọi 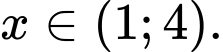 ”
”
c) Đúng.
Hàm số
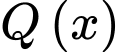 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số  khi và chỉ khi
khi và chỉ khi 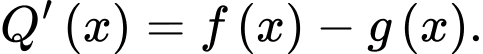
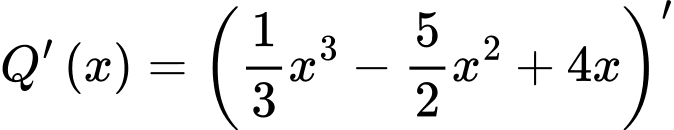
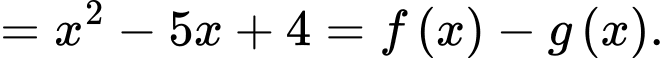
Vậy mệnh đề đúng.
d) Sai.
Diện tích hình phẳng
 bằng
bằng 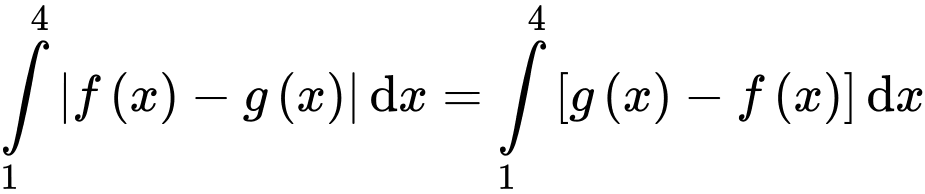 (vì đồ thị hàm số
(vì đồ thị hàm số 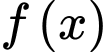 nằm dưới đồ thị hàm số
nằm dưới đồ thị hàm số 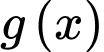 trong khoảng
trong khoảng 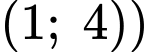
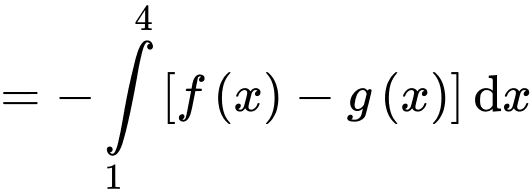
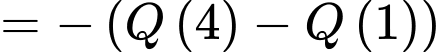

Câu 14 [779600]: Cho hàm số 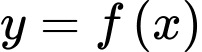 có đạo hàm trên
có đạo hàm trên 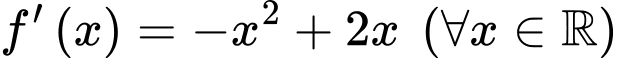 và thoả mãn
và thoả mãn 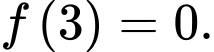 Gọi
Gọi  là hình phẳng xác định bởi các đường
là hình phẳng xác định bởi các đường 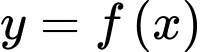 và trục
và trục 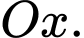
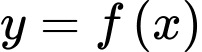 có đạo hàm trên
có đạo hàm trên 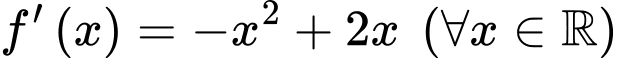 và thoả mãn
và thoả mãn 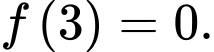 Gọi
Gọi  là hình phẳng xác định bởi các đường
là hình phẳng xác định bởi các đường 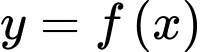 và trục
và trục 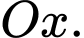
a) Đúng.
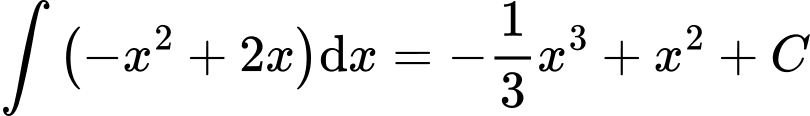
b) Sai.
Ta có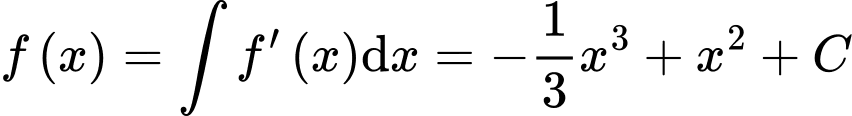
Mà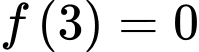
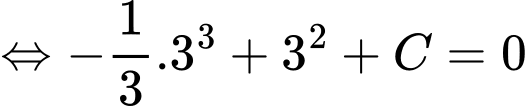
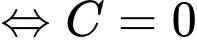
Suy ra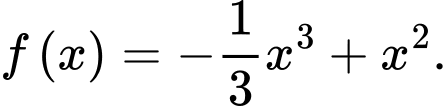
c) Đúng.
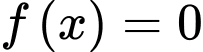
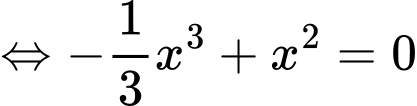
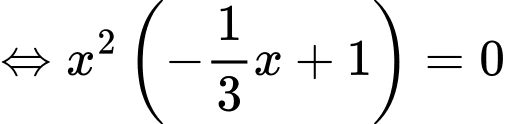
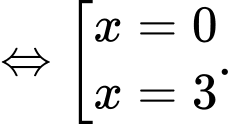
Vậy phương trình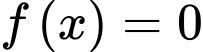 có hai nghiệm phân biệt trên tập
có hai nghiệm phân biệt trên tập 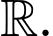
d) Sai.
Áp dụng công thức thể tích khối tròn xoay, ta có thể tích vật tròn xoay khi quay hình phẳng xung quanh trục
xung quanh trục 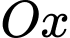 bằng
bằng 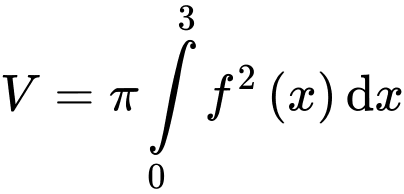
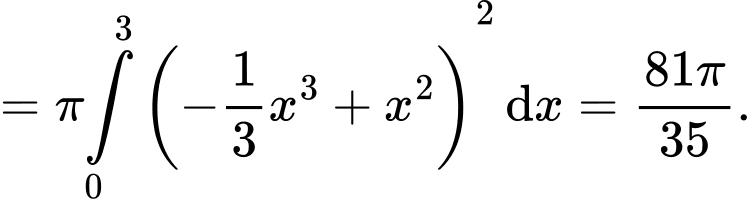
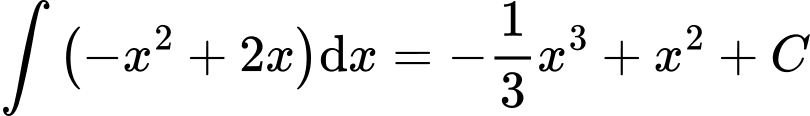
b) Sai.
Ta có
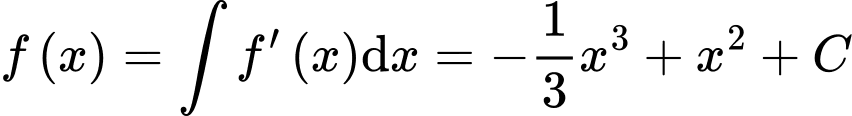
Mà
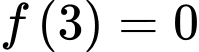
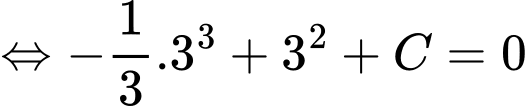
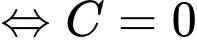
Suy ra
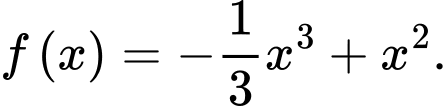
c) Đúng.
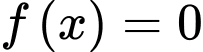
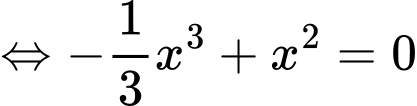
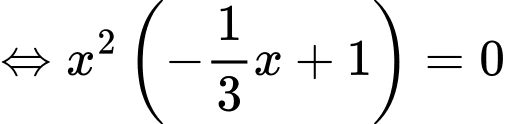
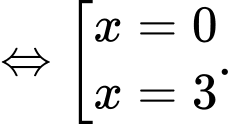
Vậy phương trình
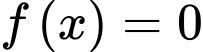 có hai nghiệm phân biệt trên tập
có hai nghiệm phân biệt trên tập 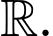
d) Sai.
Áp dụng công thức thể tích khối tròn xoay, ta có thể tích vật tròn xoay khi quay hình phẳng
 xung quanh trục
xung quanh trục 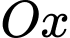 bằng
bằng 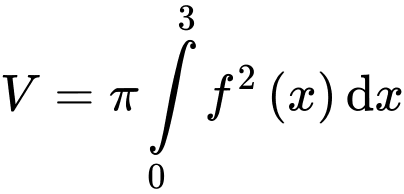
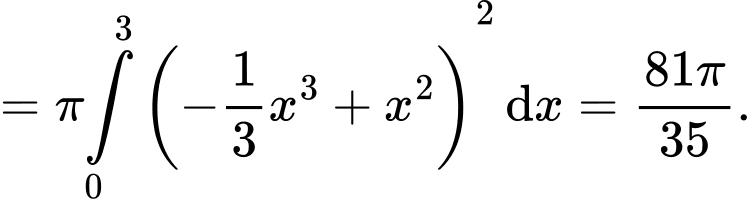
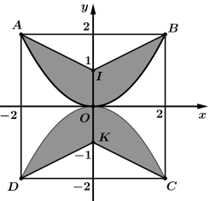
Câu 15 [778745]: Để trang trí cho một hình vuông 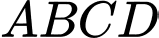 cạnh
cạnh 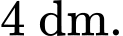 Bạn Tuấn chọn một hệ toạ độ
Bạn Tuấn chọn một hệ toạ độ 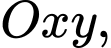 sau đó vẽ các Parabol có đỉnh là gốc toạ độ
sau đó vẽ các Parabol có đỉnh là gốc toạ độ  và lần lượt đi qua các điểm
và lần lượt đi qua các điểm 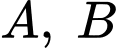 và
và 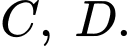 Nối điểm
Nối điểm 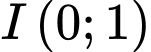 với điểm
với điểm 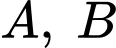 , nối điểm
, nối điểm 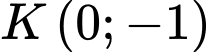 với điểm
với điểm  và tô đậm một phần như hình vẽ. Biết đơn vị mỗi trục toạ độ là
và tô đậm một phần như hình vẽ. Biết đơn vị mỗi trục toạ độ là 
 cạnh
cạnh 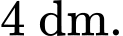 Bạn Tuấn chọn một hệ toạ độ
Bạn Tuấn chọn một hệ toạ độ 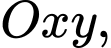 sau đó vẽ các Parabol có đỉnh là gốc toạ độ
sau đó vẽ các Parabol có đỉnh là gốc toạ độ  và lần lượt đi qua các điểm
và lần lượt đi qua các điểm 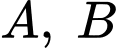 và
và 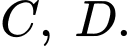 Nối điểm
Nối điểm 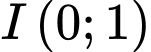 với điểm
với điểm 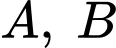 , nối điểm
, nối điểm 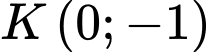 với điểm
với điểm 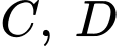 và tô đậm một phần như hình vẽ. Biết đơn vị mỗi trục toạ độ là
và tô đậm một phần như hình vẽ. Biết đơn vị mỗi trục toạ độ là 

a) Đúng.
b) Sai.
Đường cong là 1 phần của parabol nên giả sử phương trình có dạng:
là 1 phần của parabol nên giả sử phương trình có dạng: 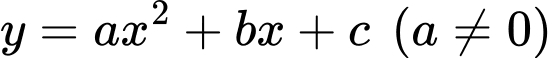
Biết Đường cong đi qua các điểm
đi qua các điểm 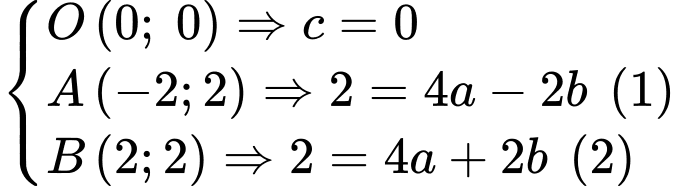
Từ (1) và (2) ta suy ra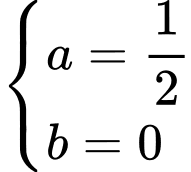
Vậy phương trình đường cong là
là 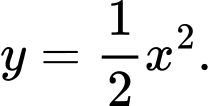
c) Đúng.
Giả sử phương trình đường thẳng đi qua hai điểm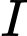 và
và 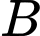 có dạng
có dạng 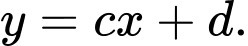
Biết đường thẳng đi qua hai điểm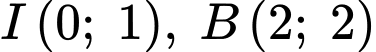 nên ta được hệ phương trình
nên ta được hệ phương trình 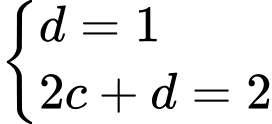
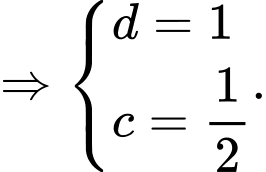
Vậy phương trình đường thẳng đi qua hai điểm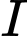 và
và 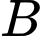 là
là 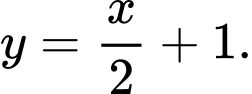
d) Đúng.
Diện tích hình phẳng bạn Tuấn tô đậm bằng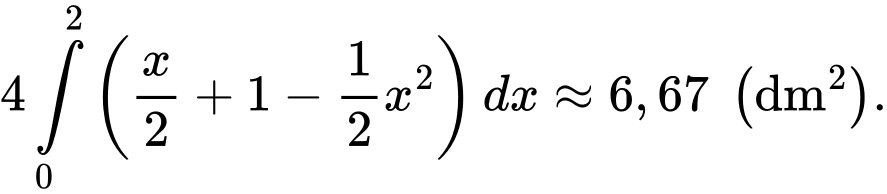
b) Sai.
Đường cong
 là 1 phần của parabol nên giả sử phương trình có dạng:
là 1 phần của parabol nên giả sử phương trình có dạng: 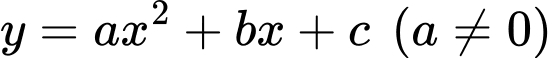
Biết Đường cong
 đi qua các điểm
đi qua các điểm 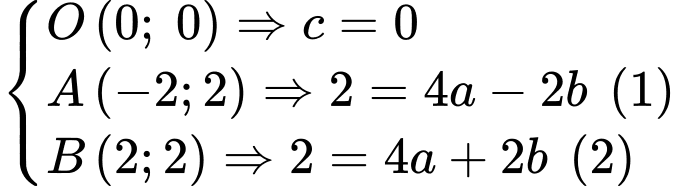
Từ (1) và (2) ta suy ra
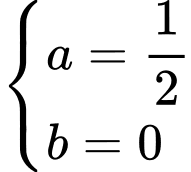
Vậy phương trình đường cong
 là
là 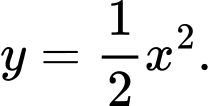
c) Đúng.
Giả sử phương trình đường thẳng đi qua hai điểm
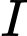 và
và 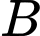 có dạng
có dạng 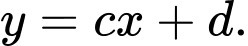
Biết đường thẳng đi qua hai điểm
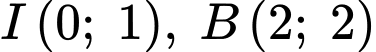 nên ta được hệ phương trình
nên ta được hệ phương trình 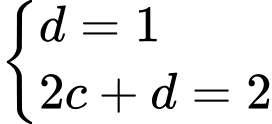
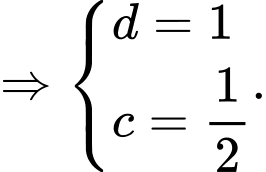
Vậy phương trình đường thẳng đi qua hai điểm
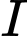 và
và 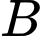 là
là 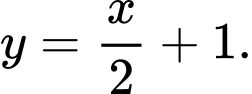
d) Đúng.
Diện tích hình phẳng bạn Tuấn tô đậm bằng
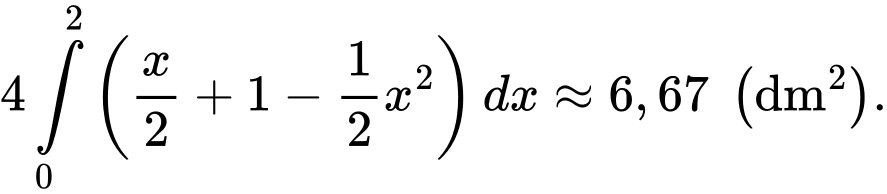
Câu 16 [695649]: Hình 1 sau thể hiện một vật rắn  có đáy là hình tròn bán kính bằng 1. Các mặt cắt song song, vuông góc với đáy là các tam giác đều. Trên mặt phẳng đáy của vật rắn, chọn hệ trục toạ độ
có đáy là hình tròn bán kính bằng 1. Các mặt cắt song song, vuông góc với đáy là các tam giác đều. Trên mặt phẳng đáy của vật rắn, chọn hệ trục toạ độ 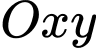 sao cho
sao cho  là tâm đường tròn đáy. Một mặt phăng tuỳ ý vuông góc với
là tâm đường tròn đáy. Một mặt phăng tuỳ ý vuông góc với 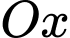 tại
tại 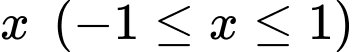 cắt vật thể đó theo hình phẳng là tam giác đều
cắt vật thể đó theo hình phẳng là tam giác đều 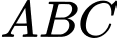 (Hình 2) có diện tích là
(Hình 2) có diện tích là 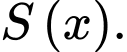
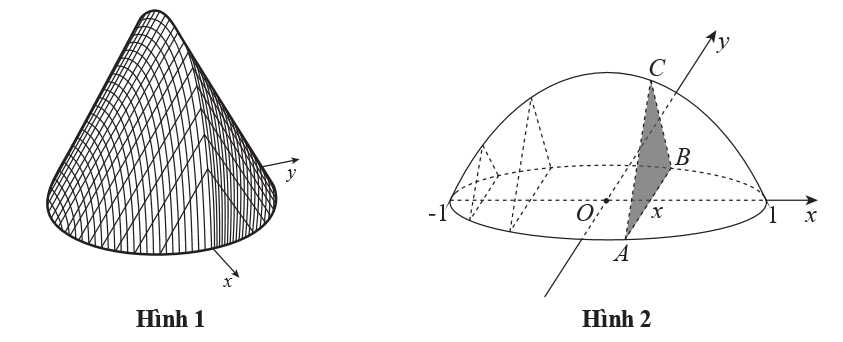
 có đáy là hình tròn bán kính bằng 1. Các mặt cắt song song, vuông góc với đáy là các tam giác đều. Trên mặt phẳng đáy của vật rắn, chọn hệ trục toạ độ
có đáy là hình tròn bán kính bằng 1. Các mặt cắt song song, vuông góc với đáy là các tam giác đều. Trên mặt phẳng đáy của vật rắn, chọn hệ trục toạ độ 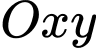 sao cho
sao cho  là tâm đường tròn đáy. Một mặt phăng tuỳ ý vuông góc với
là tâm đường tròn đáy. Một mặt phăng tuỳ ý vuông góc với 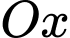 tại
tại 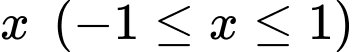 cắt vật thể đó theo hình phẳng là tam giác đều
cắt vật thể đó theo hình phẳng là tam giác đều 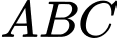 (Hình 2) có diện tích là
(Hình 2) có diện tích là 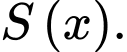

a) Đúng.
Vì đáy là hình tròn tâm bán kính bằng 1.
bán kính bằng 1.
b) Sai.
Ta có: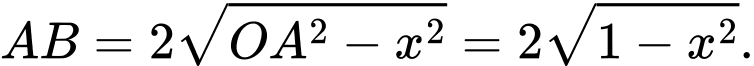
c) Sai.
Ta có: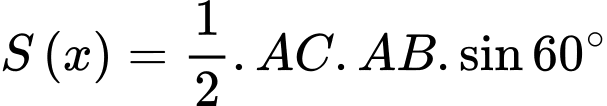
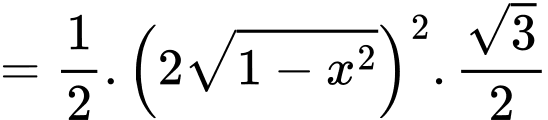
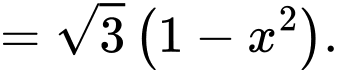
d) Đúng.
Ta có :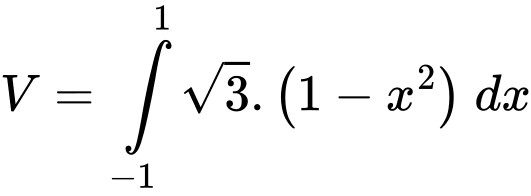
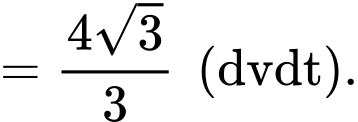
Vì đáy là hình tròn tâm
 bán kính bằng 1.
bán kính bằng 1.b) Sai.
Ta có:
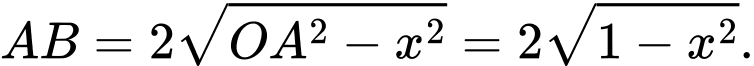
c) Sai.
Ta có:
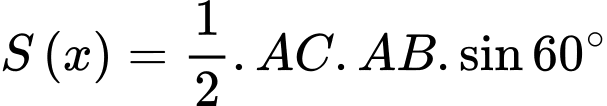
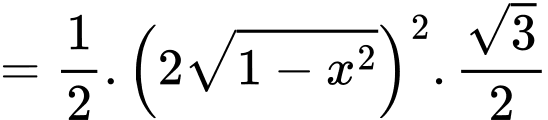
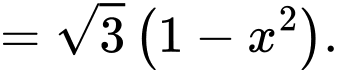
d) Đúng.
Ta có :
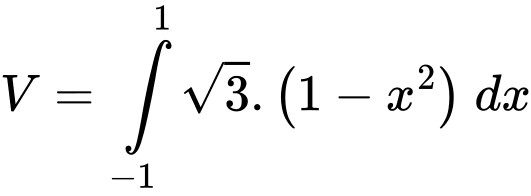
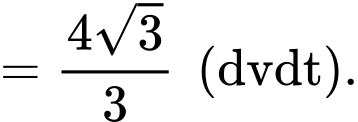
PHẦN III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 17 đến câu 22.
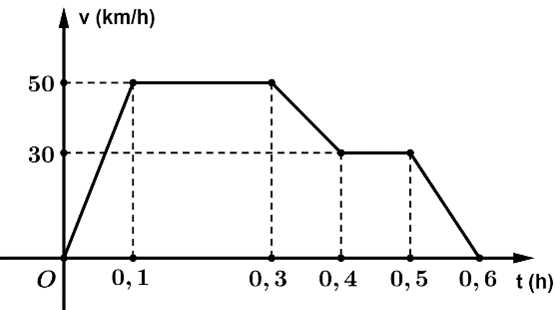
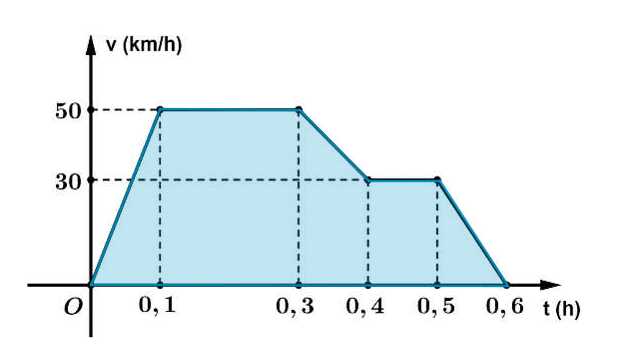
Câu 17 [778747]: Biểu đồ vận tốc 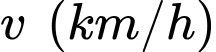 -thời gian
-thời gian 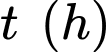 của một chuyến tàu từ lúc khởi hành đến khi dừng lại được minh họa là một đường gấp khúc trong biểu đồ bên cạnh. Tốc độ trung bình của tàu tính từ lúc khởi hành đến khi dừng lại là bao nhiêu km/h.
của một chuyến tàu từ lúc khởi hành đến khi dừng lại được minh họa là một đường gấp khúc trong biểu đồ bên cạnh. Tốc độ trung bình của tàu tính từ lúc khởi hành đến khi dừng lại là bao nhiêu km/h.
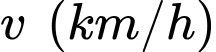 -thời gian
-thời gian 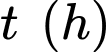 của một chuyến tàu từ lúc khởi hành đến khi dừng lại được minh họa là một đường gấp khúc trong biểu đồ bên cạnh. Tốc độ trung bình của tàu tính từ lúc khởi hành đến khi dừng lại là bao nhiêu km/h.
của một chuyến tàu từ lúc khởi hành đến khi dừng lại được minh họa là một đường gấp khúc trong biểu đồ bên cạnh. Tốc độ trung bình của tàu tính từ lúc khởi hành đến khi dừng lại là bao nhiêu km/h.
Điền đáp án: 35.
Tốc độ trung bình của tàu được tính bằng tổng quãng đường chia cho tổng thời gian.
Vì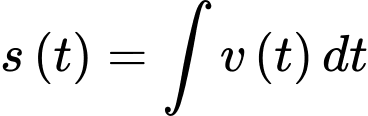 nên tổng quãng đường từ 0 giờ đến 0,6 giờ sẽ là
nên tổng quãng đường từ 0 giờ đến 0,6 giờ sẽ là 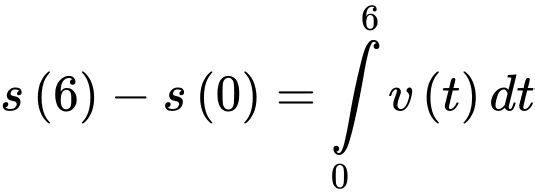
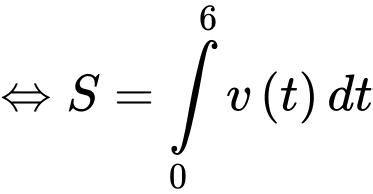 và tích phân này bằng với diện tích phần tô màu như hình.
và tích phân này bằng với diện tích phần tô màu như hình.
Suy ra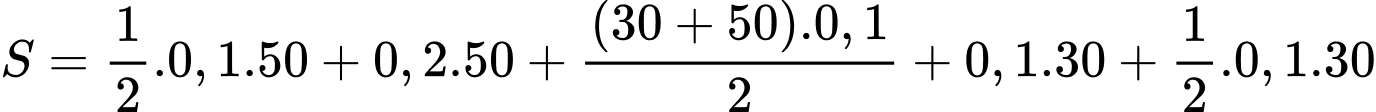
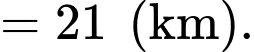
Vậy tốc độ trung bình của tàu tính từ lúc khởi hành đến khi dừng lại là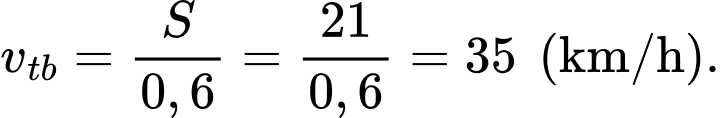
Tốc độ trung bình của tàu được tính bằng tổng quãng đường chia cho tổng thời gian.
Vì
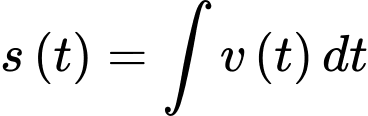 nên tổng quãng đường từ 0 giờ đến 0,6 giờ sẽ là
nên tổng quãng đường từ 0 giờ đến 0,6 giờ sẽ là 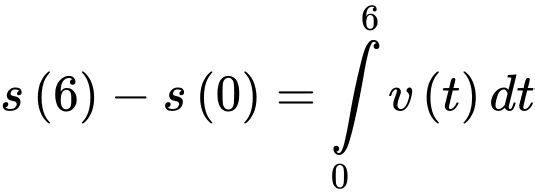
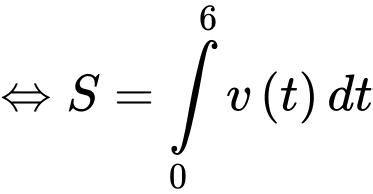 và tích phân này bằng với diện tích phần tô màu như hình.
và tích phân này bằng với diện tích phần tô màu như hình.
Suy ra
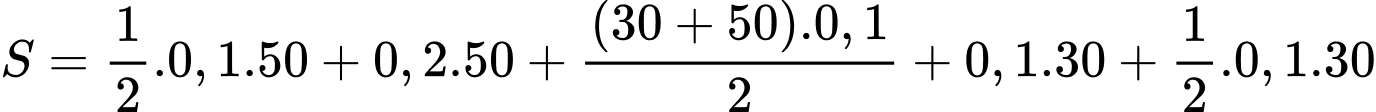
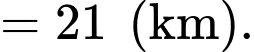
Vậy tốc độ trung bình của tàu tính từ lúc khởi hành đến khi dừng lại là
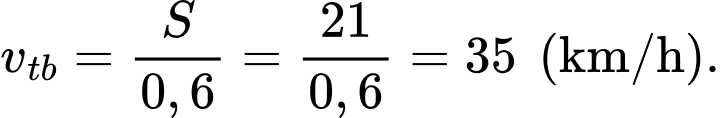
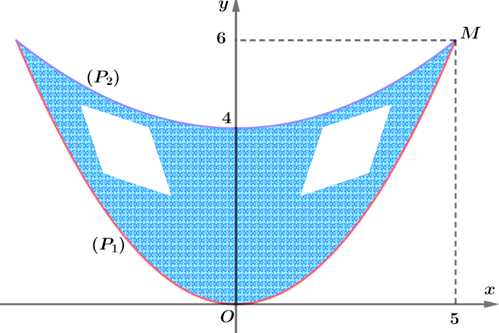
Câu 18 [778748]: Để tham gia lễ hội hóa trang, bạn An dự định làm một chiếc mặt nạ nửa mặt bằng chất liệu giấy cứng. Hình dạng của chiếc mặt nạ được bạn thiết kế trên mặt phẳng tọa độ 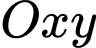 , là phần hình phẳng giới hạn bởi hai đường parabol
, là phần hình phẳng giới hạn bởi hai đường parabol 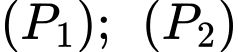 lần lượt có đỉnh là gốc tọa độ
lần lượt có đỉnh là gốc tọa độ  và điểm có tọa độ
và điểm có tọa độ 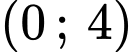 , cùng nhận trục
, cùng nhận trục 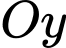 làm trục đối xứng và cùng đi qua điểm
làm trục đối xứng và cùng đi qua điểm 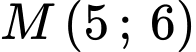 . Mỗi đơn vị trên các trục tọa độ có độ dài
. Mỗi đơn vị trên các trục tọa độ có độ dài 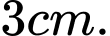 Sau đó, bạn vẽ hai hình thoi bằng nhau có độ dài các đường chéo là
Sau đó, bạn vẽ hai hình thoi bằng nhau có độ dài các đường chéo là 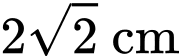 và
và 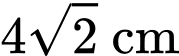 để khoét làm mắt. Diện tích giấy được bạn An sử dụng để làm chiếc mặt nạ này là bao nhiêu
để khoét làm mắt. Diện tích giấy được bạn An sử dụng để làm chiếc mặt nạ này là bao nhiêu 
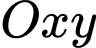 , là phần hình phẳng giới hạn bởi hai đường parabol
, là phần hình phẳng giới hạn bởi hai đường parabol 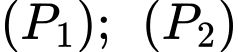 lần lượt có đỉnh là gốc tọa độ
lần lượt có đỉnh là gốc tọa độ  và điểm có tọa độ
và điểm có tọa độ 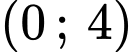 , cùng nhận trục
, cùng nhận trục 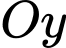 làm trục đối xứng và cùng đi qua điểm
làm trục đối xứng và cùng đi qua điểm 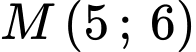 . Mỗi đơn vị trên các trục tọa độ có độ dài
. Mỗi đơn vị trên các trục tọa độ có độ dài 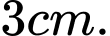 Sau đó, bạn vẽ hai hình thoi bằng nhau có độ dài các đường chéo là
Sau đó, bạn vẽ hai hình thoi bằng nhau có độ dài các đường chéo là 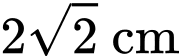 và
và 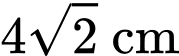 để khoét làm mắt. Diện tích giấy được bạn An sử dụng để làm chiếc mặt nạ này là bao nhiêu
để khoét làm mắt. Diện tích giấy được bạn An sử dụng để làm chiếc mặt nạ này là bao nhiêu 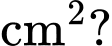

Điền đáp án: 224.
Diện tích giấy làm mặt nạ sẽ bằng diện tích giới hạn bởi 2 đường Parabol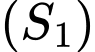 trừ đi diện tích 2 hình thoi
trừ đi diện tích 2 hình thoi 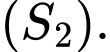
Đầu tiên, ta sẽ đi tính diện tích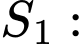
(Note: Parabol đối xứng qua trục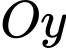 thì có dạng
thì có dạng 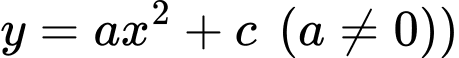
Giả sử parabol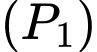 có dạng
có dạng 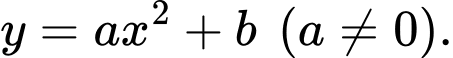 Parabol
Parabol 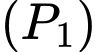 đi qua các điểm
đi qua các điểm 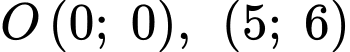 nên suy ra
nên suy ra 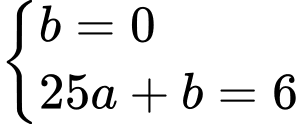
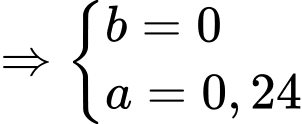
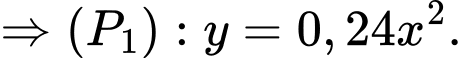
Giả sử parabol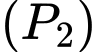 có dạng
có dạng 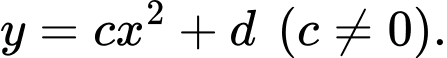 Parabol
Parabol 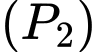 đi qua các điểm
đi qua các điểm 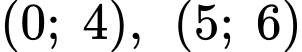 nên ta có hệ
nên ta có hệ 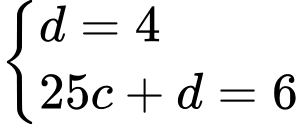
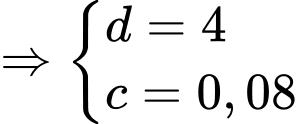
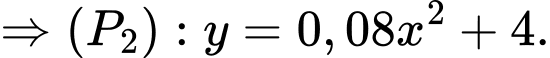
Suy ra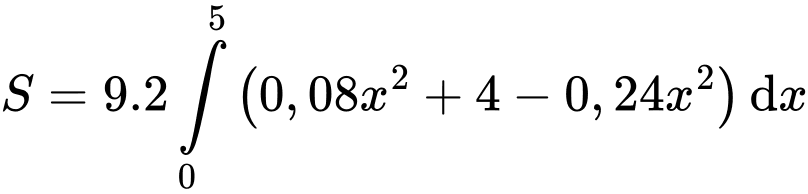
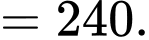 (nhân với 9 vì mỗi đơn vị trên các trục tọa độ có độ dài 3 cm)
(nhân với 9 vì mỗi đơn vị trên các trục tọa độ có độ dài 3 cm)
Tiếp đến, ta sẽ đi tính diện tích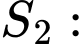
Áp dụng công thức tính diện tích hình thoi, ta có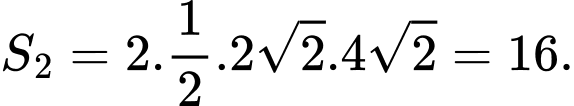
Vậy diện tích giấy cần dùng để làm mặt nạ là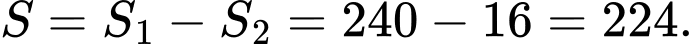 .
.
Diện tích giấy làm mặt nạ sẽ bằng diện tích giới hạn bởi 2 đường Parabol
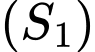 trừ đi diện tích 2 hình thoi
trừ đi diện tích 2 hình thoi 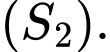
Đầu tiên, ta sẽ đi tính diện tích
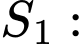
(Note: Parabol đối xứng qua trục
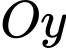 thì có dạng
thì có dạng 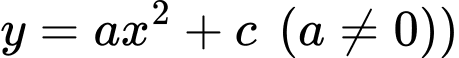
Giả sử parabol
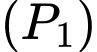 có dạng
có dạng 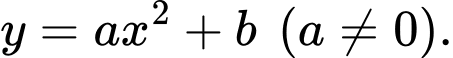 Parabol
Parabol 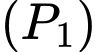 đi qua các điểm
đi qua các điểm 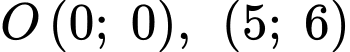 nên suy ra
nên suy ra 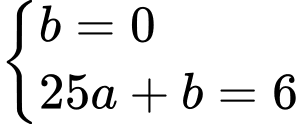
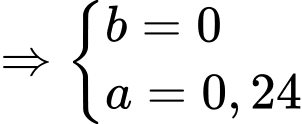
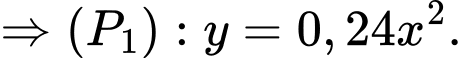
Giả sử parabol
 có dạng
có dạng 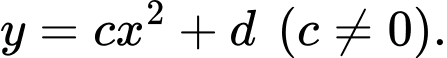 Parabol
Parabol 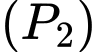 đi qua các điểm
đi qua các điểm 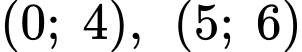 nên ta có hệ
nên ta có hệ 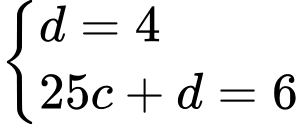
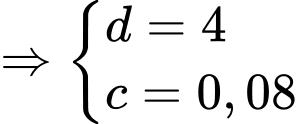
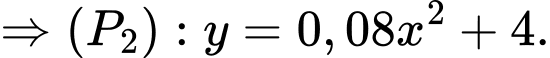
Suy ra
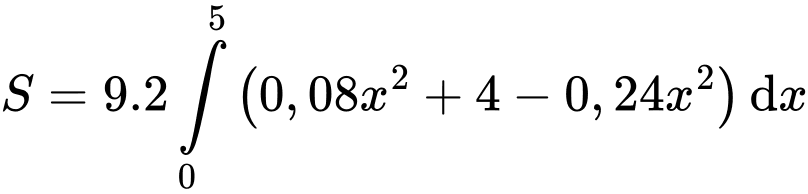
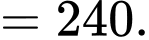 (nhân với 9 vì mỗi đơn vị trên các trục tọa độ có độ dài 3 cm)
(nhân với 9 vì mỗi đơn vị trên các trục tọa độ có độ dài 3 cm)Tiếp đến, ta sẽ đi tính diện tích
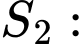
Áp dụng công thức tính diện tích hình thoi, ta có
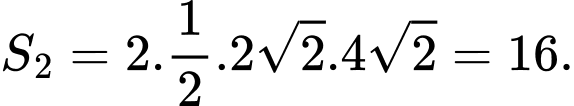
Vậy diện tích giấy cần dùng để làm mặt nạ là
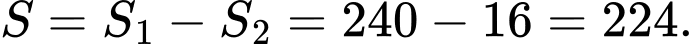 .
.
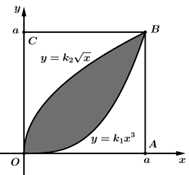
Câu 19 [778750]: Trong hệ toạ độ 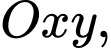 xét hình vuông
xét hình vuông 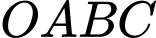 có cạnh bằng
có cạnh bằng 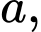 ta vẽ các đường cong
ta vẽ các đường cong 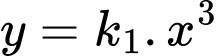 và
và  Biết diện tích phần tô đậm bằng
Biết diện tích phần tô đậm bằng 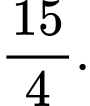 Tính diện tích miền không tô đậm nằm bên trong hình vuông.
Tính diện tích miền không tô đậm nằm bên trong hình vuông.
 xét hình vuông
xét hình vuông  có cạnh bằng
có cạnh bằng  ta vẽ các đường cong
ta vẽ các đường cong 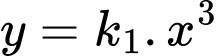 và
và  Biết diện tích phần tô đậm bằng
Biết diện tích phần tô đậm bằng 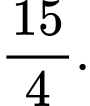 Tính diện tích miền không tô đậm nằm bên trong hình vuông.
Tính diện tích miền không tô đậm nằm bên trong hình vuông.
Điền đáp án: 5,25.
Diện tích miền không tô đậm nằm bên trong hình vuông = Diện tích hình vuông – Diện tích miền tô đậm.
Do đó, để tính được diện tích miền không tô đậm nằm bên trong hình vuông, ta cần đi tìm cạnh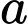 của hình vuông.
của hình vuông.
Đường cong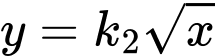 đi qua điểm
đi qua điểm 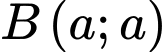
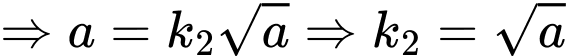
Khi đó đường cong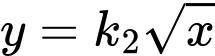 trở thành
trở thành 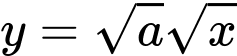
Tương tự, ta có đường cong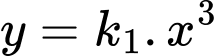 đi qua điểm
đi qua điểm 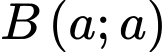
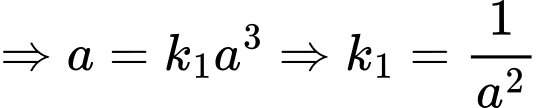
Khi đó đường cong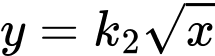 trở thành
trở thành 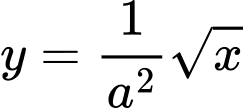
Ta có diện tích phần tô đậm là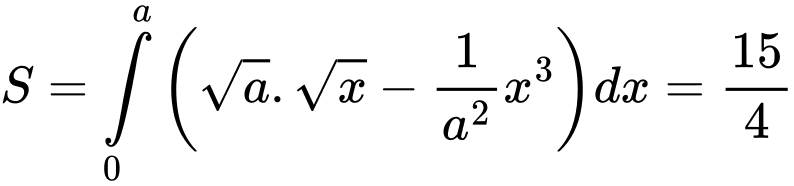
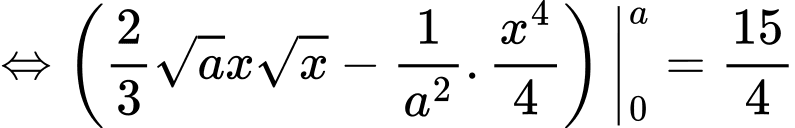
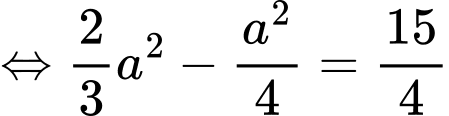
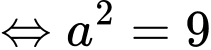
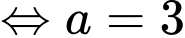
Suy ra diện tích cần tính bằng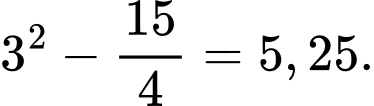
Diện tích miền không tô đậm nằm bên trong hình vuông = Diện tích hình vuông – Diện tích miền tô đậm.
Do đó, để tính được diện tích miền không tô đậm nằm bên trong hình vuông, ta cần đi tìm cạnh
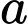 của hình vuông.
của hình vuông.Đường cong
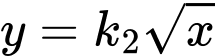 đi qua điểm
đi qua điểm 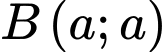
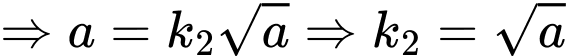
Khi đó đường cong
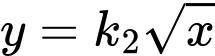 trở thành
trở thành 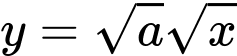
Tương tự, ta có đường cong
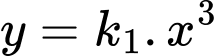 đi qua điểm
đi qua điểm 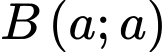
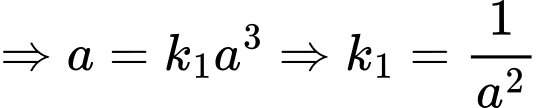
Khi đó đường cong
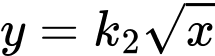 trở thành
trở thành 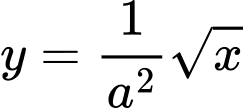
Ta có diện tích phần tô đậm là
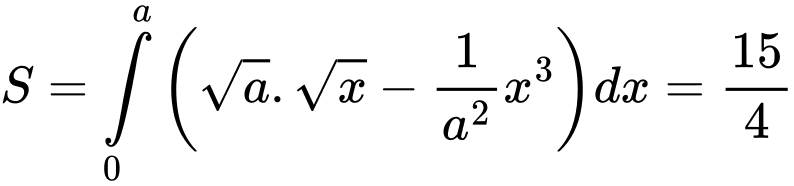
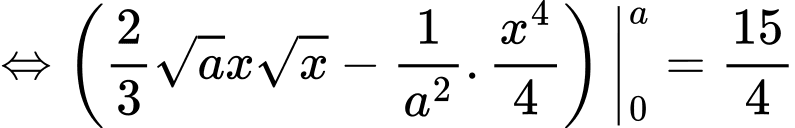
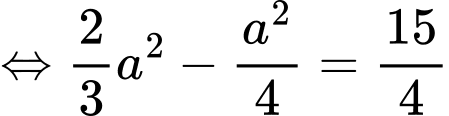
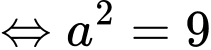
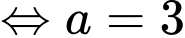
Suy ra diện tích cần tính bằng
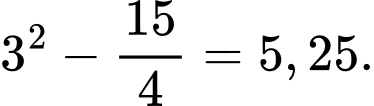
Câu 20 [151409]: Để trang trí tòa nhà người ta vẽ lên tường một hình như sau: trên mỗi cạnh hình lục giác đều có cạnh là 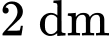 là một cánh hoa hình parabol mà đỉnh parabol
là một cánh hoa hình parabol mà đỉnh parabol 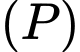 cách cạnh lục giác là
cách cạnh lục giác là 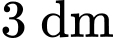 và nằm phía ngoài lục giác, 2 đầu mút của cạnh cũng là 2 điểm giới hạn của đường
và nằm phía ngoài lục giác, 2 đầu mút của cạnh cũng là 2 điểm giới hạn của đường 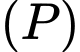 đó. Hãy tính diện tích hình trên (kể cả lục giác) (đơn vị
đó. Hãy tính diện tích hình trên (kể cả lục giác) (đơn vị 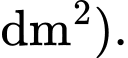 Viết kết quả làm tròn đến hàng đơn vị.
Viết kết quả làm tròn đến hàng đơn vị.

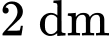 là một cánh hoa hình parabol mà đỉnh parabol
là một cánh hoa hình parabol mà đỉnh parabol 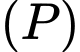 cách cạnh lục giác là
cách cạnh lục giác là 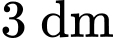 và nằm phía ngoài lục giác, 2 đầu mút của cạnh cũng là 2 điểm giới hạn của đường
và nằm phía ngoài lục giác, 2 đầu mút của cạnh cũng là 2 điểm giới hạn của đường 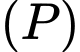 đó. Hãy tính diện tích hình trên (kể cả lục giác) (đơn vị
đó. Hãy tính diện tích hình trên (kể cả lục giác) (đơn vị 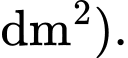 Viết kết quả làm tròn đến hàng đơn vị.
Viết kết quả làm tròn đến hàng đơn vị. 
Điền đáp án: 34.
Xét cánh hoa hình parabol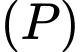 đi qua các điểm
đi qua các điểm 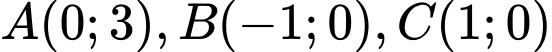 với
với 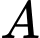 là đỉnh của
là đỉnh của 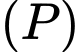 và
và 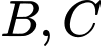 là hai đầu mút thỏa mãn
là hai đầu mút thỏa mãn 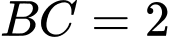 là độ dài cạnh của hình lục giác đều.
là độ dài cạnh của hình lục giác đều.
Gọi phương trình parabol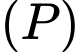 là
là 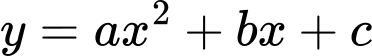 , điểm
, điểm 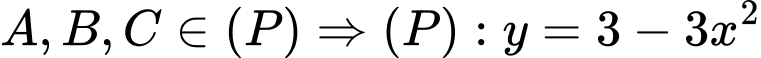 .
.
Diện tích hình cánh hoa được giới hạn bởi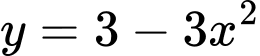 , trục hoành và hai đường thẳng
, trục hoành và hai đường thẳng 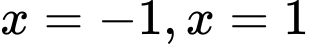 là
là
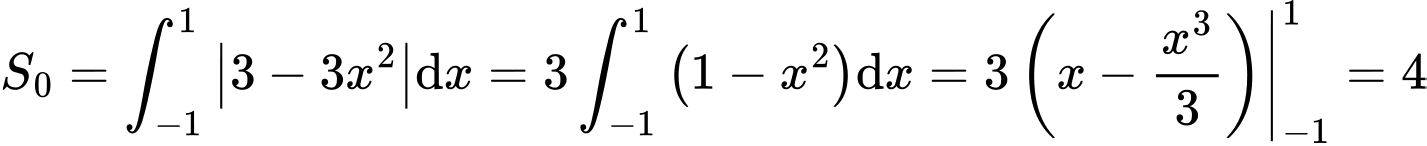
Vậy diện tích cần tính là tổng diện tích của sáu cánh hoa ứng với sáu cạnh của lục giác cộng với diện tích của lục giác đều và bằng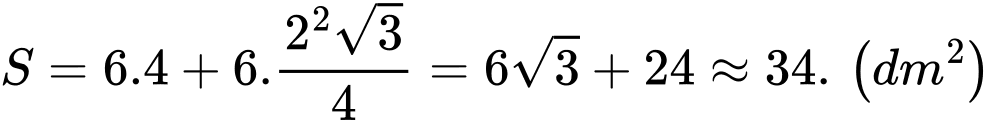
Xét cánh hoa hình parabol
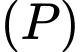 đi qua các điểm
đi qua các điểm 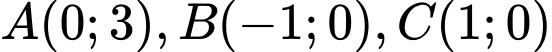 với
với 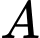 là đỉnh của
là đỉnh của 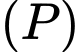 và
và 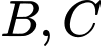 là hai đầu mút thỏa mãn
là hai đầu mút thỏa mãn 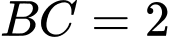 là độ dài cạnh của hình lục giác đều.
là độ dài cạnh của hình lục giác đều.Gọi phương trình parabol
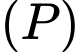 là
là 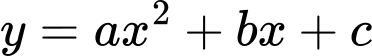 , điểm
, điểm 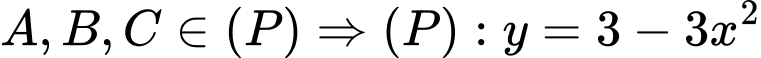 .
.Diện tích hình cánh hoa được giới hạn bởi
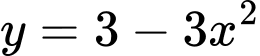 , trục hoành và hai đường thẳng
, trục hoành và hai đường thẳng 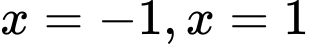 là
là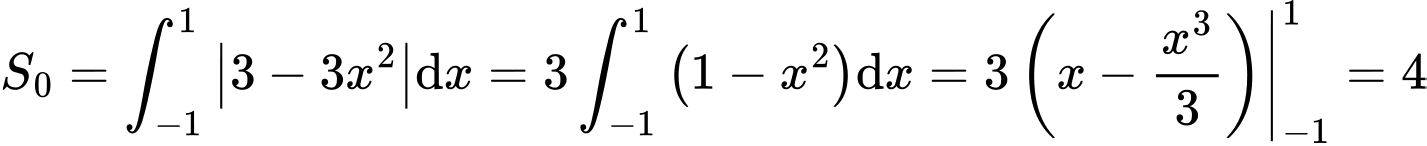
Vậy diện tích cần tính là tổng diện tích của sáu cánh hoa ứng với sáu cạnh của lục giác cộng với diện tích của lục giác đều và bằng
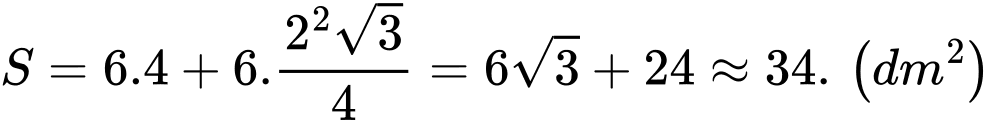
Câu 21 [779024]: Phần tô đậm trong hình vẽ bên cho biết một miền D nằm trong hình vuông có cạnh bằng 4. Miền D này gồm các điểm có khoảng cách tới tâm hình vuông nhỏ hơn hoặc bằng khoảng cách tới cạnh gần nhất của hình vuông. Tính diện tích của miền D (kết quả làm tròn đến hàng phần chục).
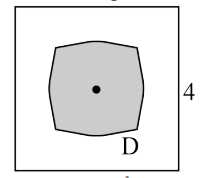

Đáp án: 
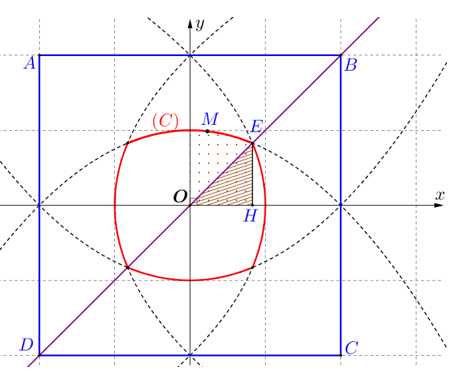
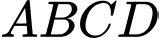 và gắn hệ trục tọa độ
và gắn hệ trục tọa độ 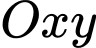 như hình vẽ.
như hình vẽ.Do vai trò của các đường cong như nhau, giả sử
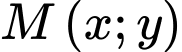 là một điểm thuộc đường cong
là một điểm thuộc đường cong  của miền D như hình vẽ.
của miền D như hình vẽ.Ta có khoảng cách từ
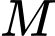 tới
tới  là
là 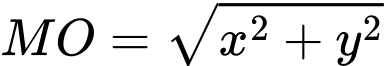 .
.Khoảng cách từ
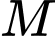 tới cạnh
tới cạnh  của hình vuông là
của hình vuông là 
Khoảng cách từ
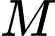 tới
tới  bằng khoảng cách từ
bằng khoảng cách từ 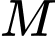 tới
tới  nên
nên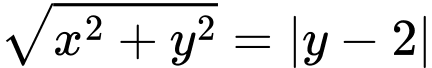
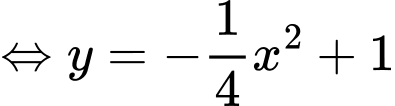
Hoành độ giao điểm của Parabol
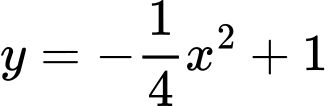 và đường thẳng
và đường thẳng 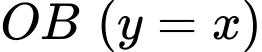 (thuộc góc phần tư thứ nhất) là nghiệm của phương trình
(thuộc góc phần tư thứ nhất) là nghiệm của phương trình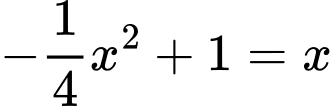
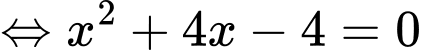
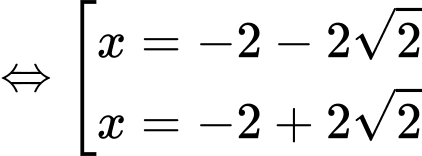
Parabol
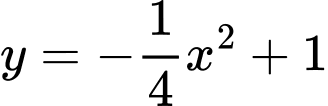 cắt đường thẳng
cắt đường thẳng 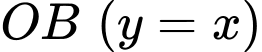 tại điểm
tại điểm 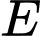 thuộc góc phần tư thứ nhất nên
thuộc góc phần tư thứ nhất nên 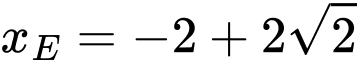
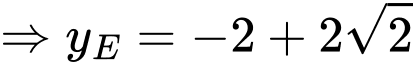 .
.Diện tích hình phẳng giới hạn bởi Parabol, trục
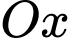 , trục
, trục 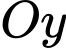 và đường thẳng
và đường thẳng 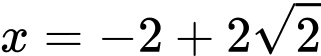 là:
là: 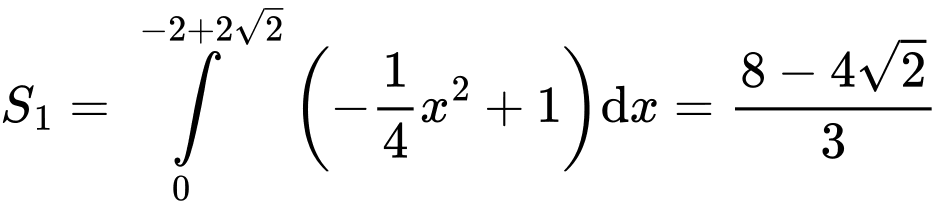 .
.Diện tích tam giác
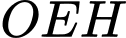 là
là 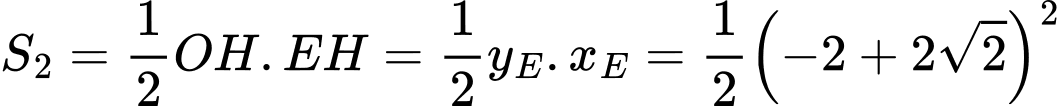 .
.Diện tích của
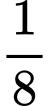 miền
miền 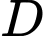 là
là 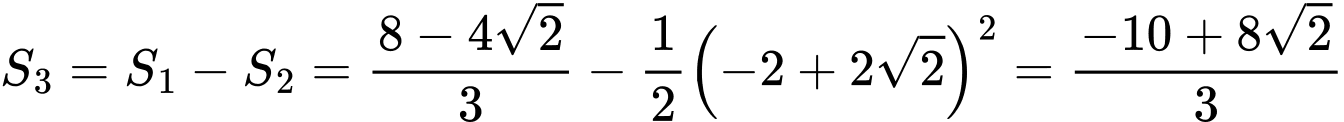 .
.Diện tích miền D là
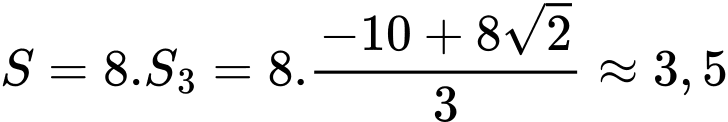 .
.
Câu 22 [702800]: Một con quạ khát nước, nó tìm thấy một cái lọ có nước nhưng cổ lọ lại cao nó không thò mỏ uống được nên đã gắp từng viên bi (hình cầu) bỏ vào trong lọ để nước dâng lên. Hỏi con quạ cần bỏ vào lọ ít nhất bao nhiêu viên bi để có thể uống nước? Biết rằng viên bi có bán kính là  và không thấm nước, khi đặt nằm ngang cái lọ có hình dáng là một khối tròn xoay với đường sinh là đồ thị của một hàm bậc 3 (hình 2), mực nước trong lọ ban đầu ở vị trí mà hình tròn có bán kính lớn nhất
và không thấm nước, khi đặt nằm ngang cái lọ có hình dáng là một khối tròn xoay với đường sinh là đồ thị của một hàm bậc 3 (hình 2), mực nước trong lọ ban đầu ở vị trí mà hình tròn có bán kính lớn nhất 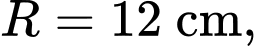 mực nước mà quạ có thể uống được là vị trí mà hình tròn có bán kính nhỏ nhất
mực nước mà quạ có thể uống được là vị trí mà hình tròn có bán kính nhỏ nhất 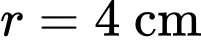 và khoảng cách giữa hai mặt này bằng
và khoảng cách giữa hai mặt này bằng  được minh họa ở hình vẽ bên dưới.
được minh họa ở hình vẽ bên dưới.
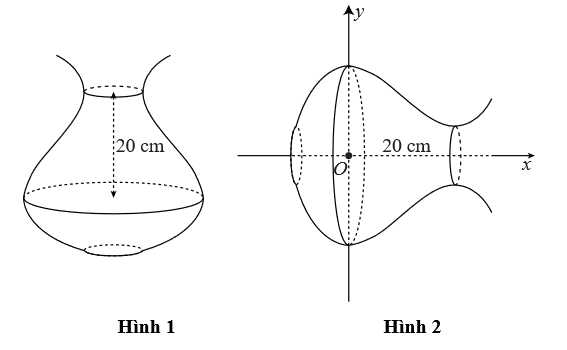
 và không thấm nước, khi đặt nằm ngang cái lọ có hình dáng là một khối tròn xoay với đường sinh là đồ thị của một hàm bậc 3 (hình 2), mực nước trong lọ ban đầu ở vị trí mà hình tròn có bán kính lớn nhất
và không thấm nước, khi đặt nằm ngang cái lọ có hình dáng là một khối tròn xoay với đường sinh là đồ thị của một hàm bậc 3 (hình 2), mực nước trong lọ ban đầu ở vị trí mà hình tròn có bán kính lớn nhất 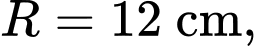 mực nước mà quạ có thể uống được là vị trí mà hình tròn có bán kính nhỏ nhất
mực nước mà quạ có thể uống được là vị trí mà hình tròn có bán kính nhỏ nhất 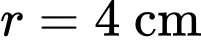 và khoảng cách giữa hai mặt này bằng
và khoảng cách giữa hai mặt này bằng  được minh họa ở hình vẽ bên dưới.
được minh họa ở hình vẽ bên dưới.
Gọi phương trình của đường sinh là 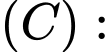
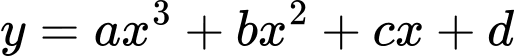
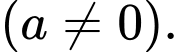
Theo đề bài, ta có: có điểm cực đại
có điểm cực đại 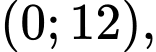 điểm cực tiểu là
điểm cực tiểu là 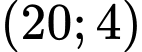
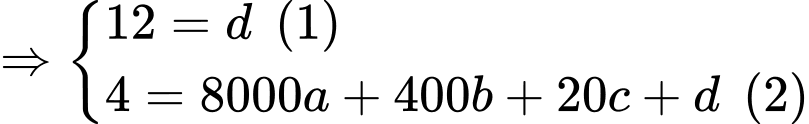
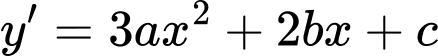
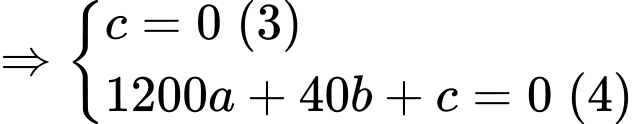
Từ (1), (2), (3) và (4)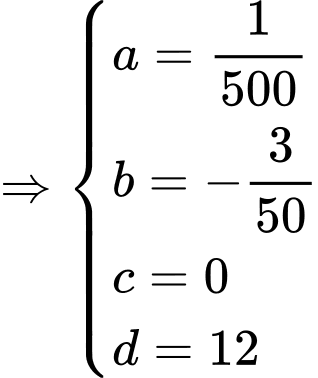

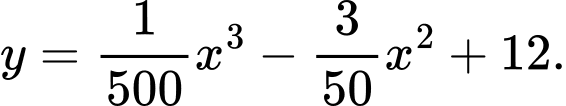
Thể tích đã cho vào:
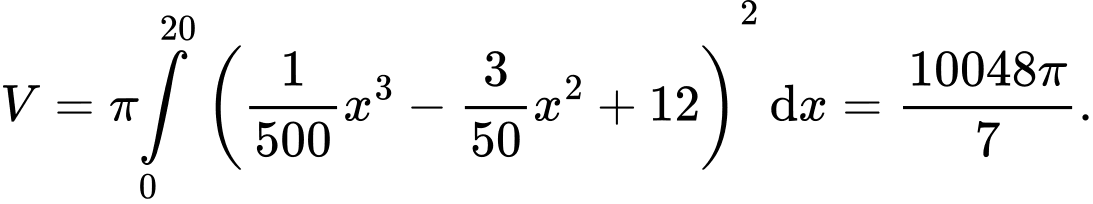
Thể tích 1 viên bi là
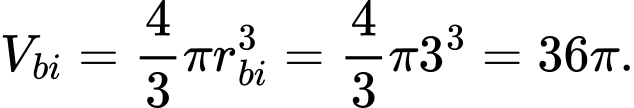
Cần số viên bi: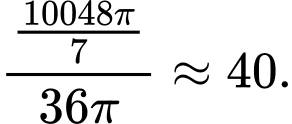 (viên).
(viên).
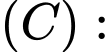
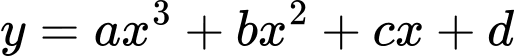
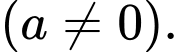
Theo đề bài, ta có:
 có điểm cực đại
có điểm cực đại 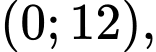 điểm cực tiểu là
điểm cực tiểu là 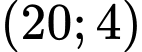
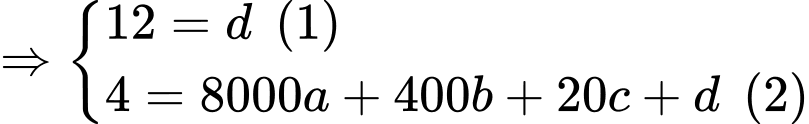
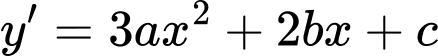
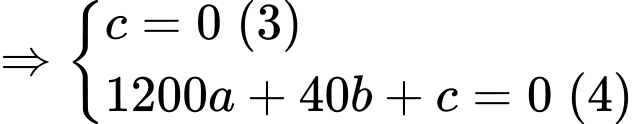
Từ (1), (2), (3) và (4)
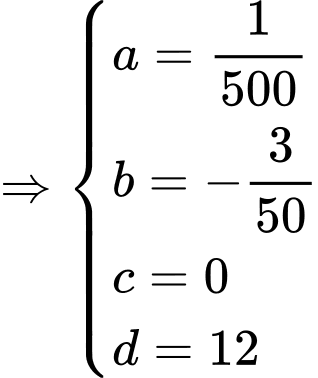

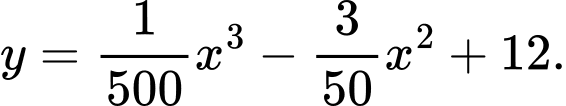
Thể tích đã cho vào:
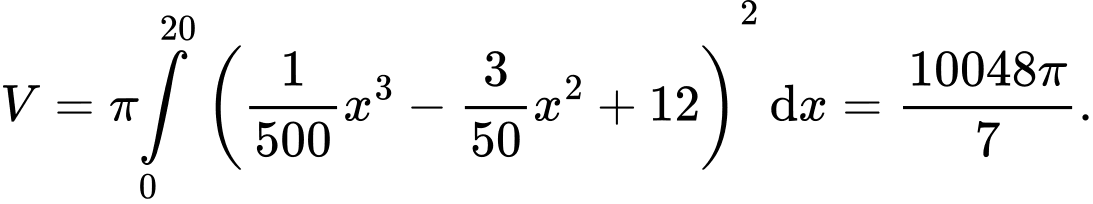
Thể tích 1 viên bi là
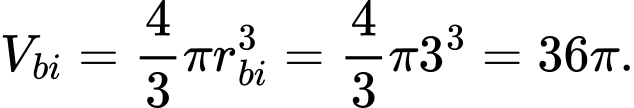
Cần số viên bi:
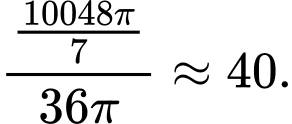 (viên).
(viên).