PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1 [680669]: Cho hàm số 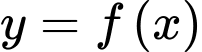 liên tục, nhận giá trị dương trên đoạn
liên tục, nhận giá trị dương trên đoạn 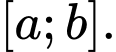 Xét hình phẳng
Xét hình phẳng  giới hạn bởi đồ thị hàm số
giới hạn bởi đồ thị hàm số 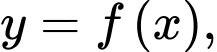 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 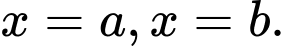 Khối tròn xoay được tạo thành khi quay hình phẳng
Khối tròn xoay được tạo thành khi quay hình phẳng  quanh trục
quanh trục 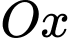 có thể tích là:
có thể tích là:
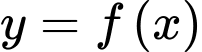 liên tục, nhận giá trị dương trên đoạn
liên tục, nhận giá trị dương trên đoạn 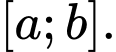 Xét hình phẳng
Xét hình phẳng  giới hạn bởi đồ thị hàm số
giới hạn bởi đồ thị hàm số 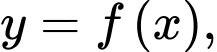 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 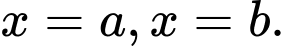 Khối tròn xoay được tạo thành khi quay hình phẳng
Khối tròn xoay được tạo thành khi quay hình phẳng  quanh trục
quanh trục 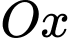 có thể tích là:
có thể tích là: A, 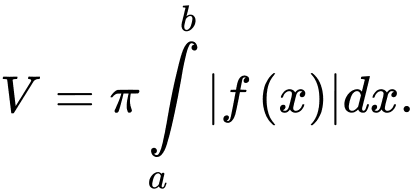
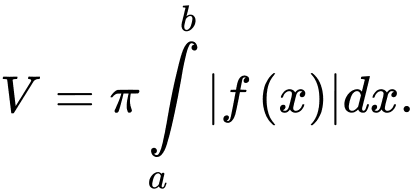
B, 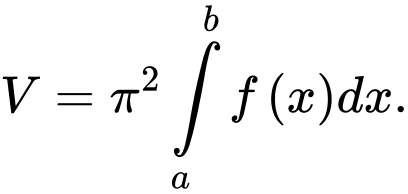
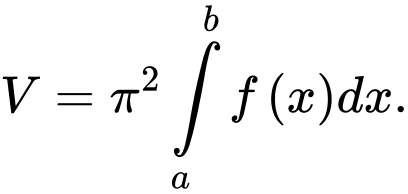
C, 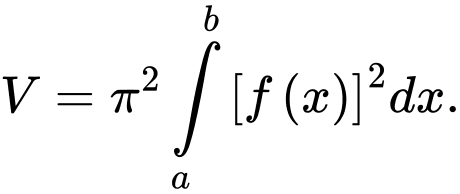
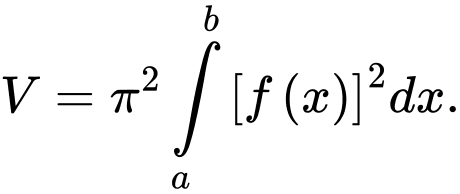
D, 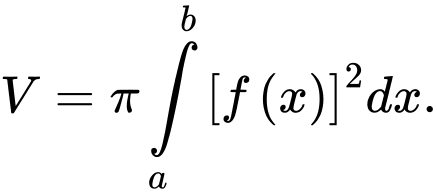
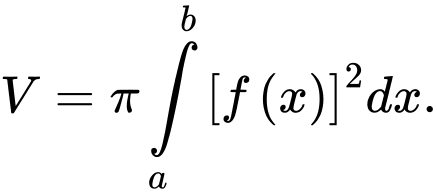
Chọn đáp án D.
Thể tích khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số
giới hạn bởi đồ thị hàm số 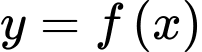 , trục hoành và hai đường thẳng
, trục hoành và hai đường thẳng 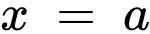 ,
, 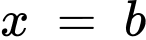 quanh trục
quanh trục 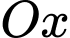 được tính theo công thức:
được tính theo công thức: 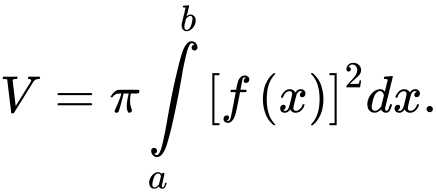 Đáp án: D
Đáp án: D
Thể tích khối tròn xoay được tạo thành khi quay hình phẳng
 giới hạn bởi đồ thị hàm số
giới hạn bởi đồ thị hàm số 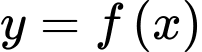 , trục hoành và hai đường thẳng
, trục hoành và hai đường thẳng 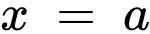 ,
, 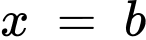 quanh trục
quanh trục 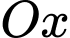 được tính theo công thức:
được tính theo công thức: 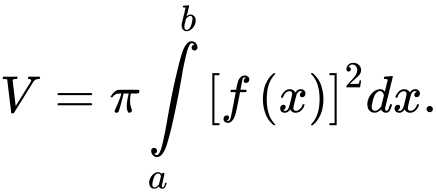 Đáp án: D
Đáp án: D
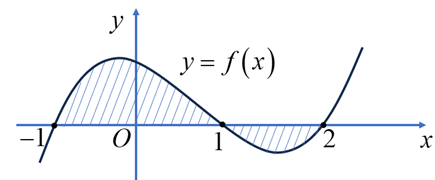
Câu 2 [544302]: Gọi 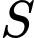 là diện tích hình phẳng được gạch chéo theo hình dưới đây, với
là diện tích hình phẳng được gạch chéo theo hình dưới đây, với 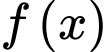 là hàm số liên tục trên
là hàm số liên tục trên 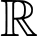 .
. 
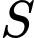 là diện tích hình phẳng được gạch chéo theo hình dưới đây, với
là diện tích hình phẳng được gạch chéo theo hình dưới đây, với 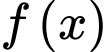 là hàm số liên tục trên
là hàm số liên tục trên 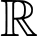 .
. 
Công thức tính  là
là
 là
làA, 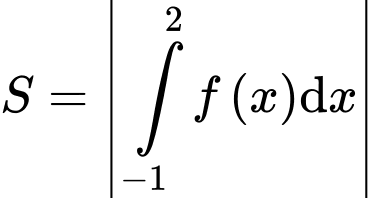 .
.
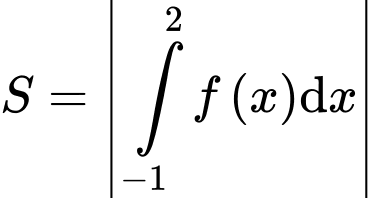 .
.B, 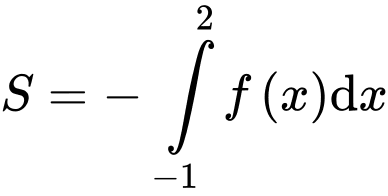 .
.
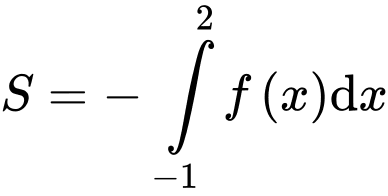 .
.C, 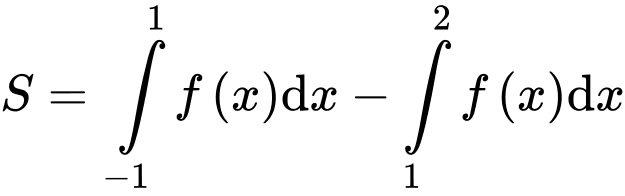 .
.
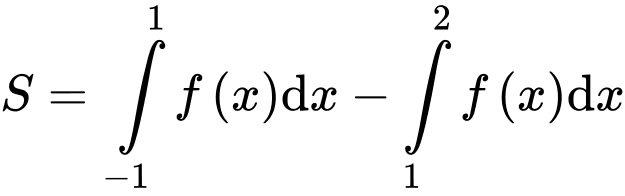 .
.D, 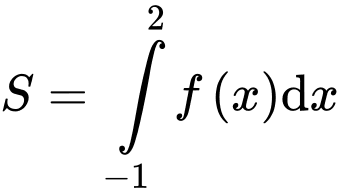 .
.
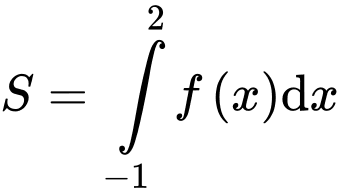 .
.
Chọn đáp án C. Đáp án: C
Câu 3 [151630]: Cho hình phẳng 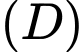 được giới hạn bởi các đường
được giới hạn bởi các đường 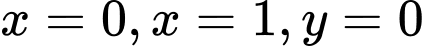 và
và 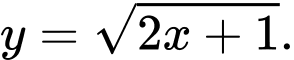 Thể tích
Thể tích  của khối tròn xoay tạo thành khi quay
của khối tròn xoay tạo thành khi quay 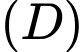 xung quanh trục
xung quanh trục 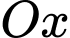 được tính theo công thức
được tính theo công thức
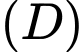 được giới hạn bởi các đường
được giới hạn bởi các đường 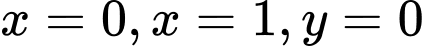 và
và 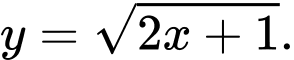 Thể tích
Thể tích  của khối tròn xoay tạo thành khi quay
của khối tròn xoay tạo thành khi quay 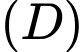 xung quanh trục
xung quanh trục 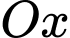 được tính theo công thức
được tính theo công thức A, 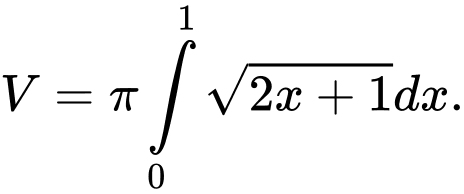
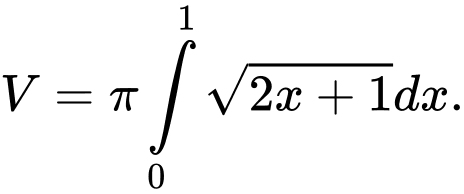
B, 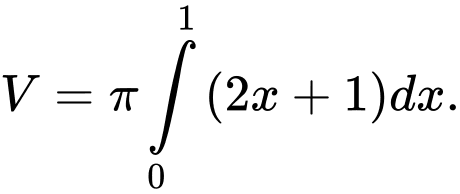
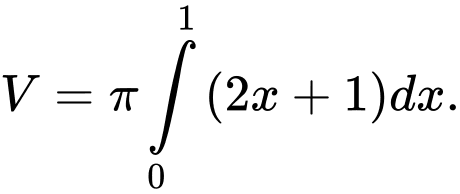
C, 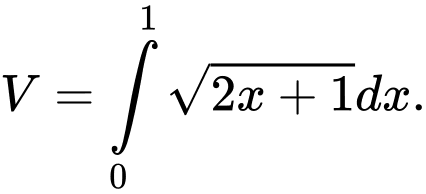
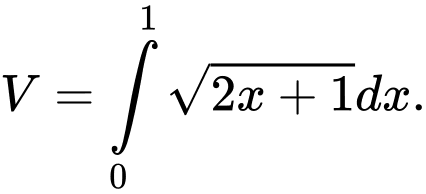
D, 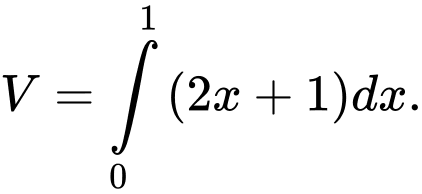
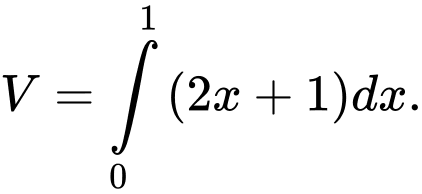
Chọn đáp án B.
Theo công thức tính thể tích khối tròn xoay, ta có thể tích của khối tròn xoay tạo thành là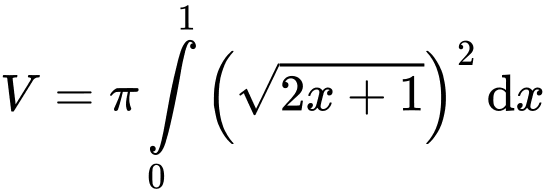
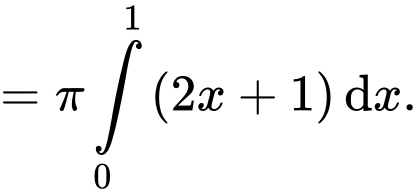 Đáp án: B
Đáp án: B
Theo công thức tính thể tích khối tròn xoay, ta có thể tích của khối tròn xoay tạo thành là
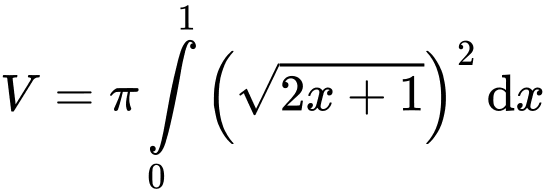
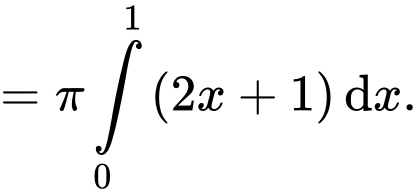 Đáp án: B
Đáp án: B
Câu 4 [693778]: Tính thể tích khối tròn xoay sinh ra khi quay quanh trục 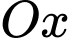 hình phẳng giới hạn bởiđồ thị hàm số
hình phẳng giới hạn bởiđồ thị hàm số 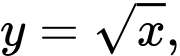 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 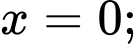
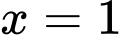 (hình vẽ)
(hình vẽ)
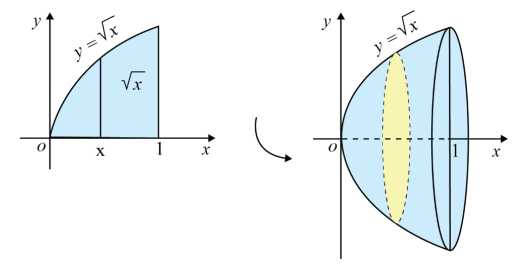
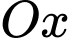 hình phẳng giới hạn bởiđồ thị hàm số
hình phẳng giới hạn bởiđồ thị hàm số 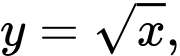 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 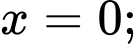
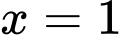 (hình vẽ)
(hình vẽ)
A, 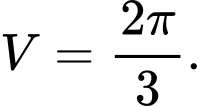
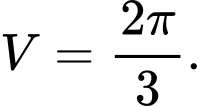
B, 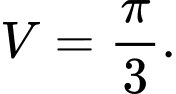
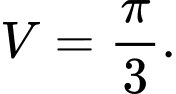
C, 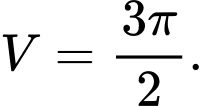
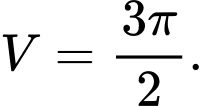
D, 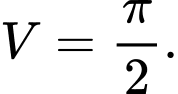
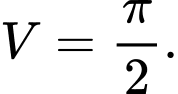
Chọn đáp án D.
Thể tích khối tròn xoay sinh ra khi quay quanh trục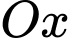 hình phẳng giới hạn bởi đồ thị hàm số
hình phẳng giới hạn bởi đồ thị hàm số 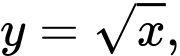 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 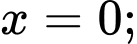
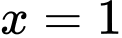 là
là
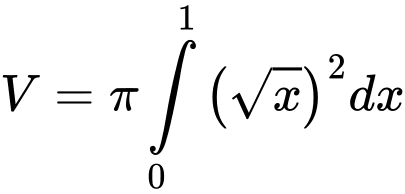
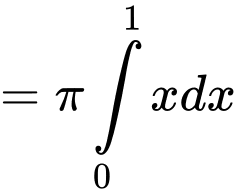
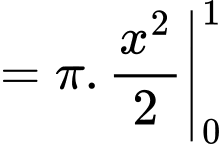
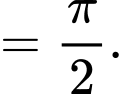 Đáp án: D
Đáp án: D
Thể tích khối tròn xoay sinh ra khi quay quanh trục
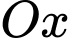 hình phẳng giới hạn bởi đồ thị hàm số
hình phẳng giới hạn bởi đồ thị hàm số 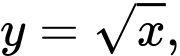 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 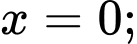
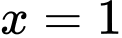 là
là 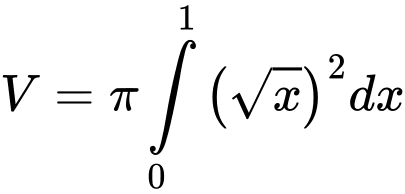
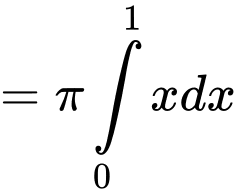
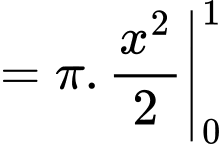
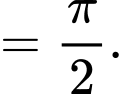 Đáp án: D
Đáp án: D
Câu 5 [151258]: Gọi S là diện tích hình phẳng  giới hạn bởi các đường
giới hạn bởi các đường 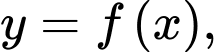 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 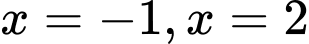 (như hình vẽ bên).
(như hình vẽ bên).

Đặt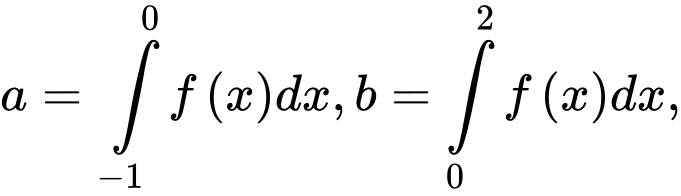 mệnh đề nào sau đây đúng?
mệnh đề nào sau đây đúng?
 giới hạn bởi các đường
giới hạn bởi các đường 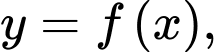 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 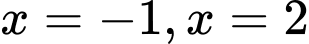 (như hình vẽ bên).
(như hình vẽ bên).
Đặt
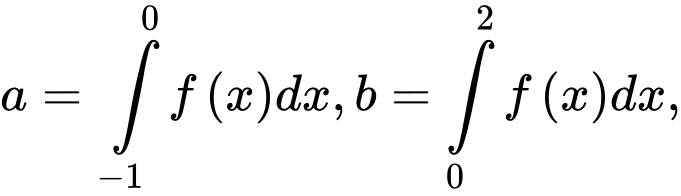 mệnh đề nào sau đây đúng?
mệnh đề nào sau đây đúng? A, 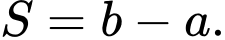
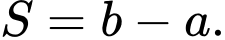
B, 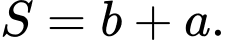
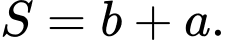
C, 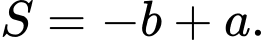
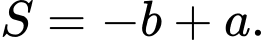
D, 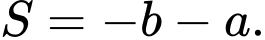
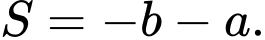
Chọn đáp án A.
Diện tích hình phẳng là
là 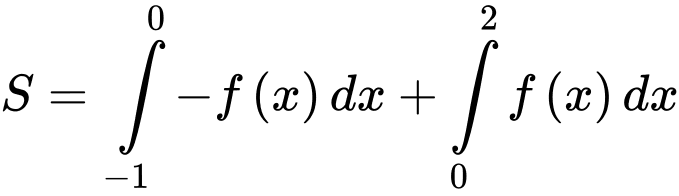
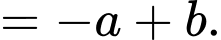 Đáp án: A
Đáp án: A
Diện tích hình phẳng
 là
là 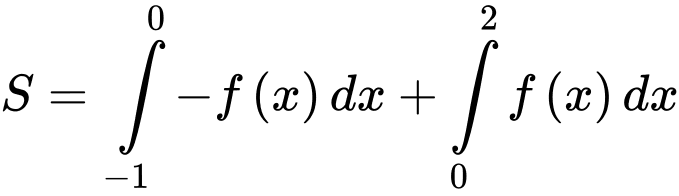
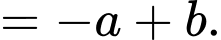 Đáp án: A
Đáp án: A
Câu 6 [151233]: Diện tích 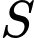 của hình phẳng giới hạn bởi đồ thị các hàm số
của hình phẳng giới hạn bởi đồ thị các hàm số 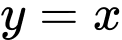 và
và 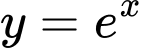 , trục tung và đường thẳng
, trục tung và đường thẳng 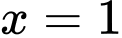 được tính theo công thức
được tính theo công thức
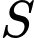 của hình phẳng giới hạn bởi đồ thị các hàm số
của hình phẳng giới hạn bởi đồ thị các hàm số 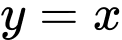 và
và 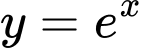 , trục tung và đường thẳng
, trục tung và đường thẳng 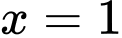 được tính theo công thức
được tính theo công thức A, 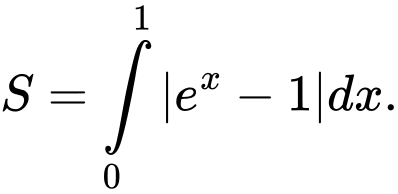
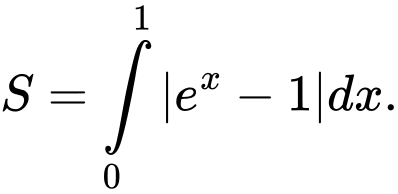
B, 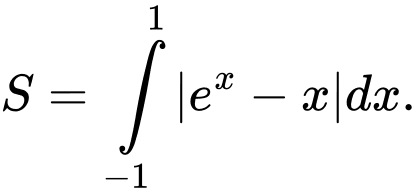
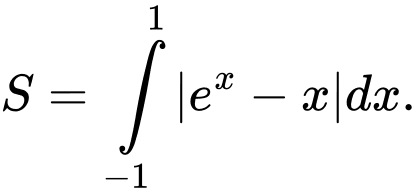
C, 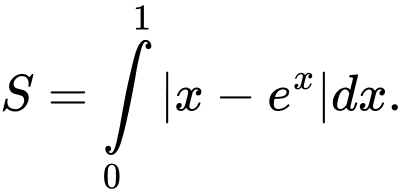
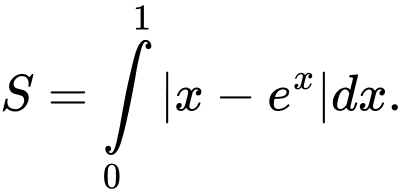
D, 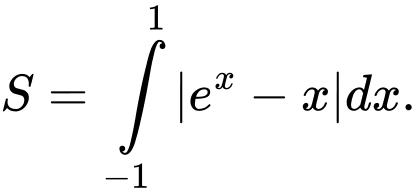
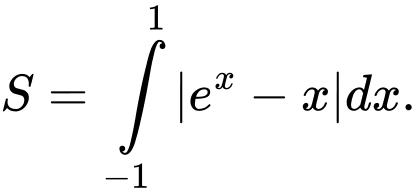
Chọn đáp án C. Đáp án: C
Câu 7 [151232]: Diện tích hình phẳng giới hạn bởi các đường 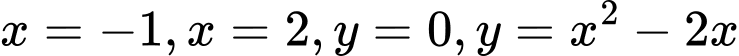 là
là
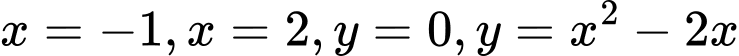 là
là A, 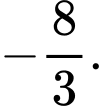
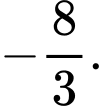
B, 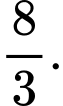
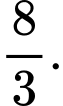
C, 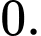
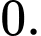
D, 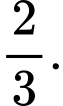
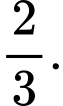
Chọn đáp án B.
Diện tích hình phẳng cần tính là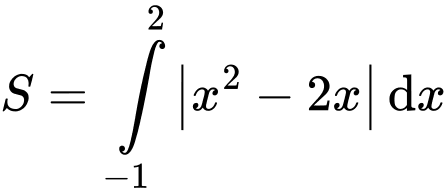
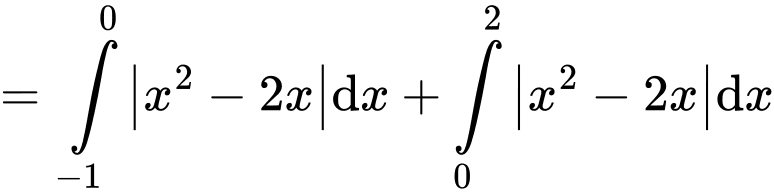
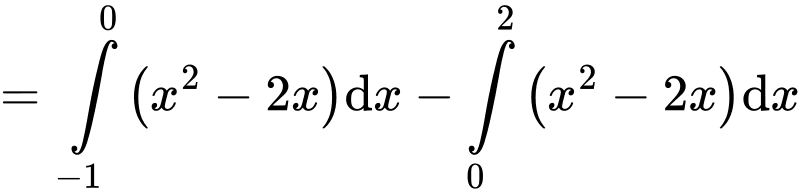
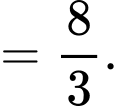 Đáp án: B
Đáp án: B
Diện tích hình phẳng cần tính là
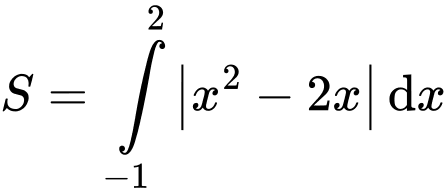
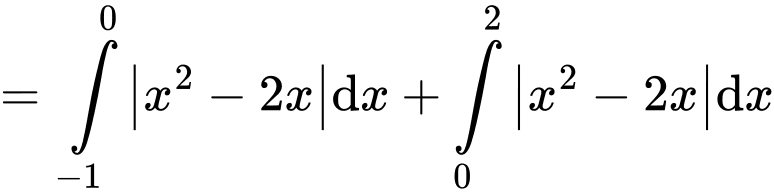
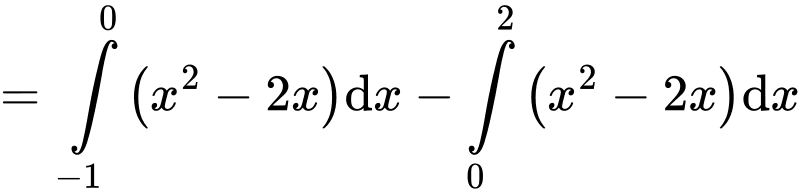
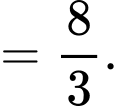 Đáp án: B
Đáp án: B
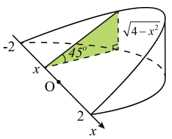
Câu 8 [778751]: Khi cắt một vật thể hình chiếc nêm bởi mặt phẳng vuông góc với trục 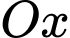 tại điểm có hoành độ
tại điểm có hoành độ 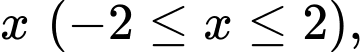 mặt cắt là tam giác vuông có một góc
mặt cắt là tam giác vuông có một góc 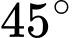 và độ dài một cạnh góc vuông là
và độ dài một cạnh góc vuông là 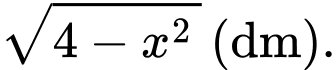 Tính thể tích của vật thể theo đơn vị
Tính thể tích của vật thể theo đơn vị 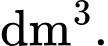
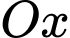 tại điểm có hoành độ
tại điểm có hoành độ 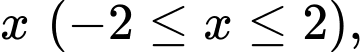 mặt cắt là tam giác vuông có một góc
mặt cắt là tam giác vuông có một góc 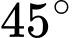 và độ dài một cạnh góc vuông là
và độ dài một cạnh góc vuông là 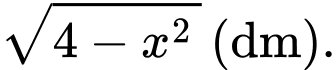 Tính thể tích của vật thể theo đơn vị
Tính thể tích của vật thể theo đơn vị 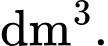

A, 

B, 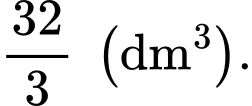
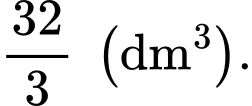
C, 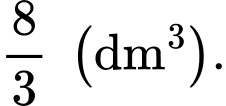
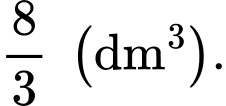
D, 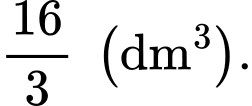
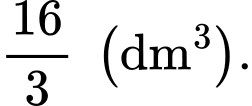
Chọn đáp án D.
Diện tích của thiết diện hình tam giác vuông là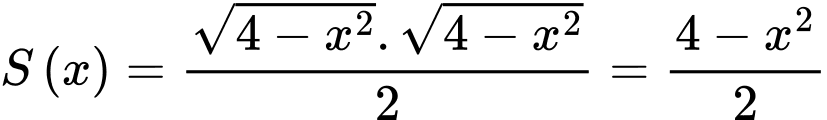
(vì tam giác vuông có thêm 1 góc bằng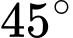 thì sẽ là tam giác vuông cân nên hai cạnh góc vuông sẽ đều bằng
thì sẽ là tam giác vuông cân nên hai cạnh góc vuông sẽ đều bằng 
Suy ra thể tích vật thể là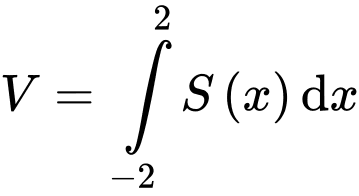
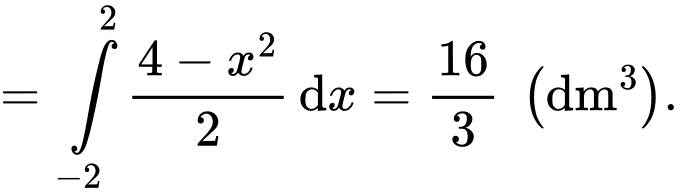 Đáp án: D
Đáp án: D
Diện tích của thiết diện hình tam giác vuông là
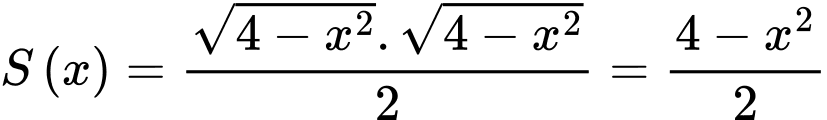
(vì tam giác vuông có thêm 1 góc bằng
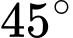 thì sẽ là tam giác vuông cân nên hai cạnh góc vuông sẽ đều bằng
thì sẽ là tam giác vuông cân nên hai cạnh góc vuông sẽ đều bằng 
Suy ra thể tích vật thể là
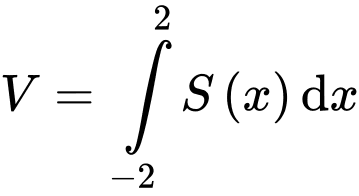
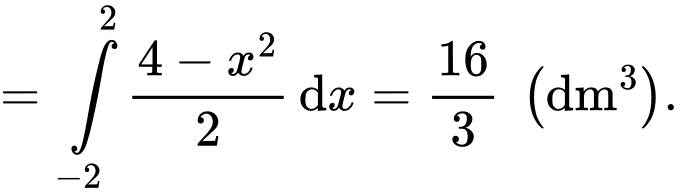 Đáp án: D
Đáp án: D
Câu 9 [392134]: Diện tích phần tô đậm trong hình vẽ bên, bằng tích phân nào dưới đây?
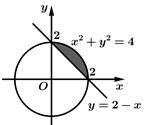

A, 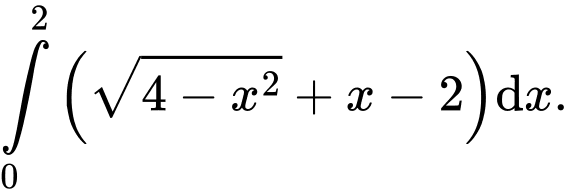
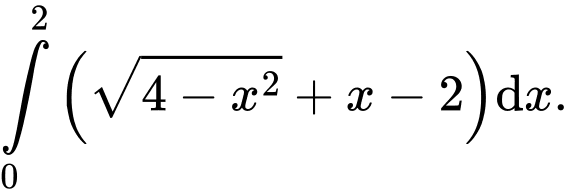
B, 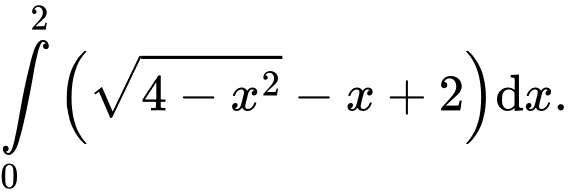
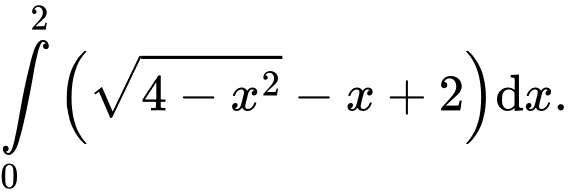
C, 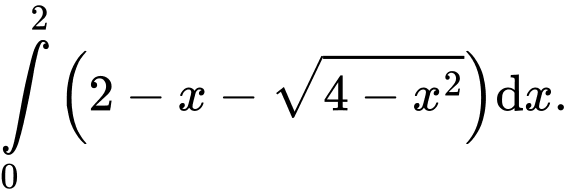
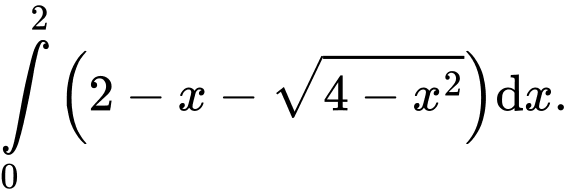
D, 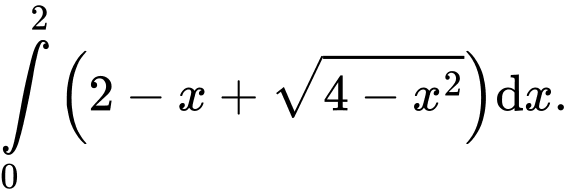
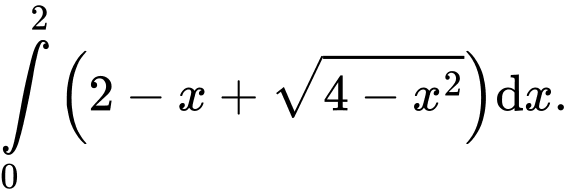
Chọn đáp án A.
Ta có:
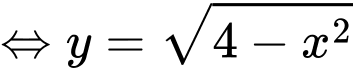
Và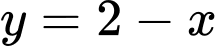
Theo hình vẽ ta có:
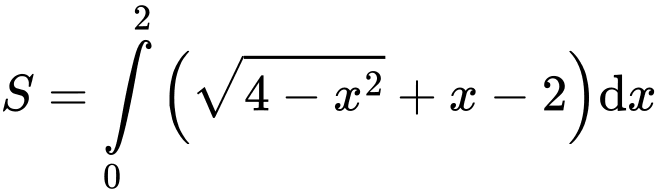
Đáp án: A
Ta có:

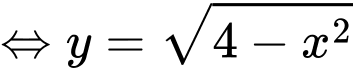
Và
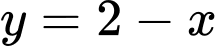
Theo hình vẽ ta có:
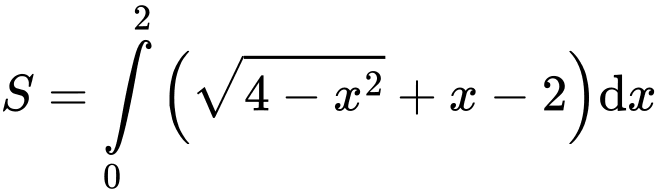
Đáp án: A
Câu 10 [539486]: Diện tích hình phẳng giới hạn bởi các đường  là
là
 là
là A, 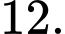
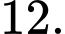
B, 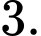
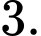
C, 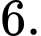
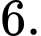
D, 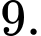
Chọn đáp án D.
Hoành độ giao điểm là nghiệm pt: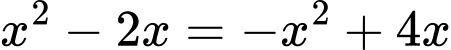

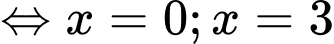
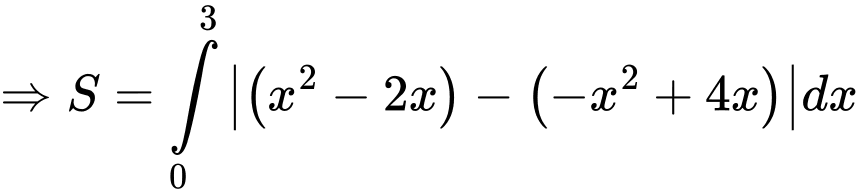
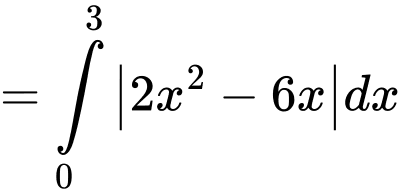
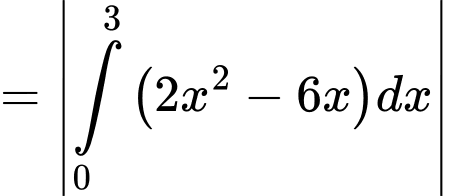
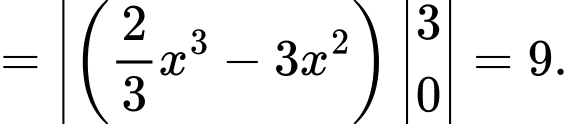 Đáp án: D
Đáp án: D
Hoành độ giao điểm là nghiệm pt:
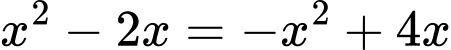

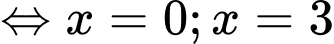
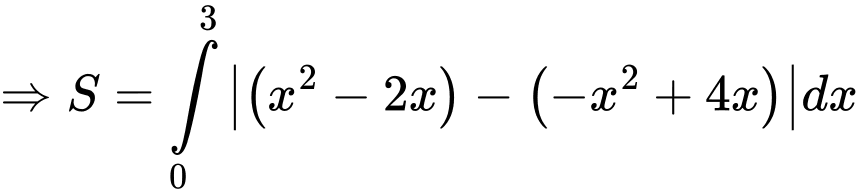
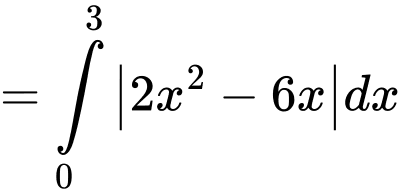
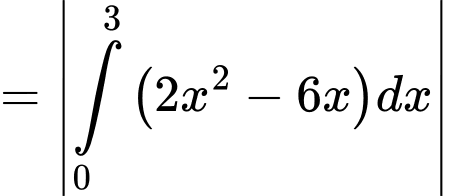
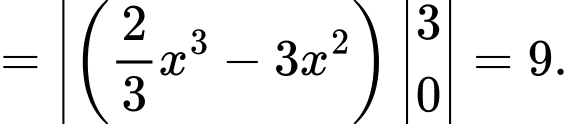 Đáp án: D
Đáp án: D
Câu 11 [543471]: Thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường 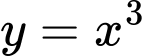 ,
, 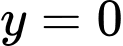 ,
, 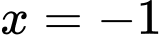 và
và 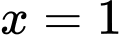 quanh trục
quanh trục 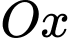 bằng
bằng
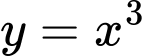 ,
, 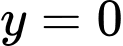 ,
, 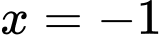 và
và 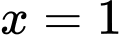 quanh trục
quanh trục 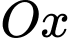 bằng
bằng A, 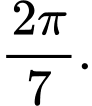
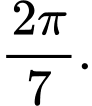
B, 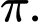
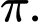
C, 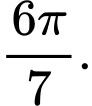
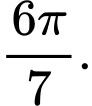
D, 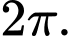
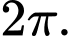
Chọn đáp án A.
Thể tích khối tròn xoay là: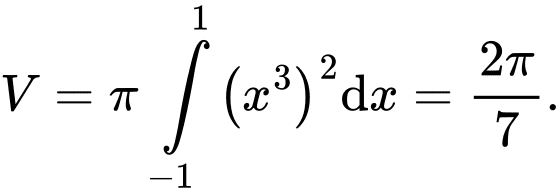 Đáp án: A
Đáp án: A
Thể tích khối tròn xoay là:
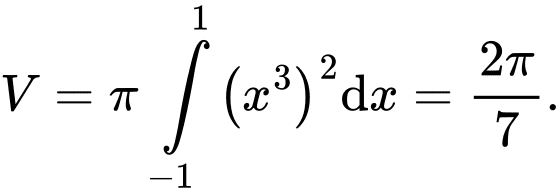 Đáp án: A
Đáp án: A
Câu 12 [147229]: Tính thể tích  của phần vật thể giới hạn bởi hai mặt phẳng
của phần vật thể giới hạn bởi hai mặt phẳng 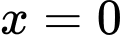 và
và 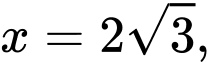 biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục
biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục 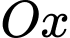 tại điểm có hoành độ
tại điểm có hoành độ 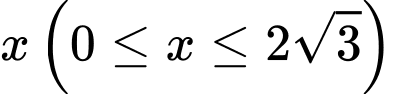 thì thiết diện là một hình tam giác đều có cạnh là
thì thiết diện là một hình tam giác đều có cạnh là 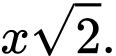
 của phần vật thể giới hạn bởi hai mặt phẳng
của phần vật thể giới hạn bởi hai mặt phẳng 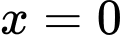 và
và 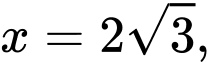 biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục
biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục 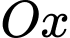 tại điểm có hoành độ
tại điểm có hoành độ 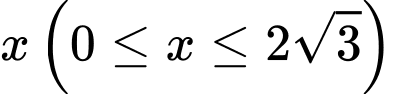 thì thiết diện là một hình tam giác đều có cạnh là
thì thiết diện là một hình tam giác đều có cạnh là 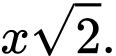
A, 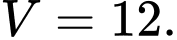
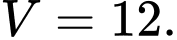
B, 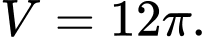
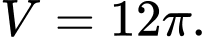
C, 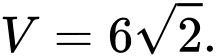
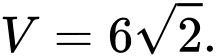
D, 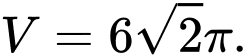
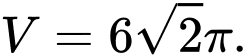
Chọn đáp án A.
Diện tích của thiết diện hình tam giác đều là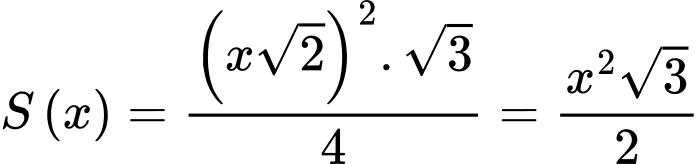
Suy ra thể tích vật thể cần tìm là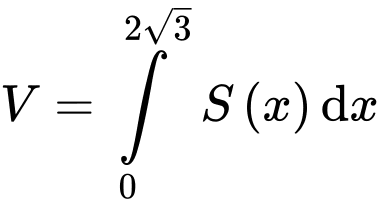
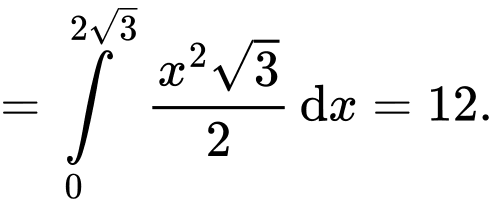
Note kiến thức sử dụng trong bài:
+) Công thức tính nhanh diện tích tam giác đều cạnh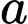 là
là 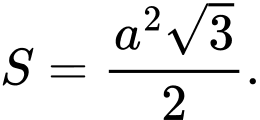
+) Công thức tính thể tích vật thể. Đáp án: A
Diện tích của thiết diện hình tam giác đều là
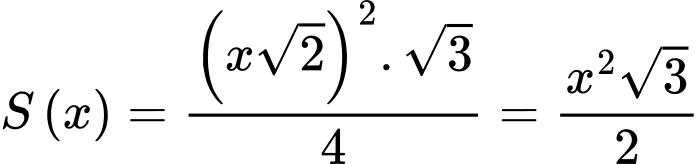
Suy ra thể tích vật thể cần tìm là
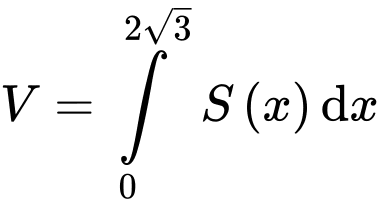
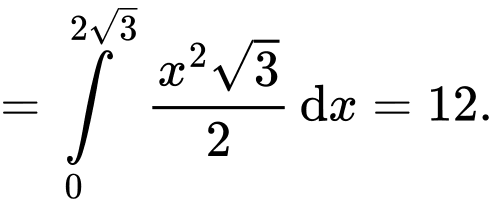
Note kiến thức sử dụng trong bài:
+) Công thức tính nhanh diện tích tam giác đều cạnh
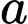 là
là 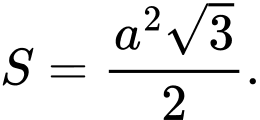
+) Công thức tính thể tích vật thể. Đáp án: A
PHẦN II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a),b),c),d) ở mỗi câu học sinh chọn đúng hoặc sai.
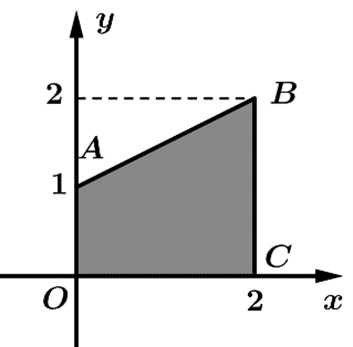
Câu 13 [779603]: Trong mặt phẳng toạ độ 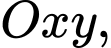 cho hình thang
cho hình thang 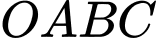 có
có 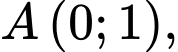
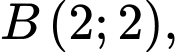 và
và 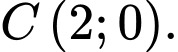 Đường thẳng
Đường thẳng 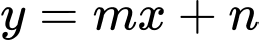 đi qua hai điểm
đi qua hai điểm 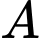 và
và 
 cho hình thang
cho hình thang 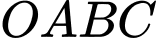 có
có 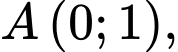
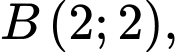 và
và 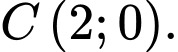 Đường thẳng
Đường thẳng 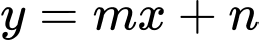 đi qua hai điểm
đi qua hai điểm 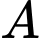 và
và 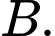

a) Đúng.
Đường thẳng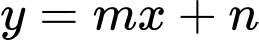 đi qua điểm
đi qua điểm 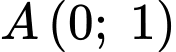 nên suy ra
nên suy ra 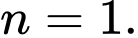
Suy ra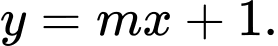
b) Sai.
Đường thẳng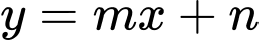 đi qua điểm
đi qua điểm 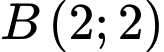 nên suy ra
nên suy ra 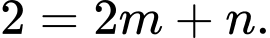
Suy ra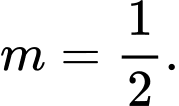
c) Đúng.
Diện tích hình thang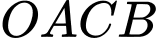 bằng
bằng 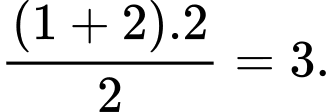
d) Sai.
Cách 1: Áp dụng ứng dụng tích phân để tính thể tích khối tròn xoay:
Từ kết quả tính được từ phần a) và b) ta suy ra phương trình đường thẳng đi qua 2 điểm là
là 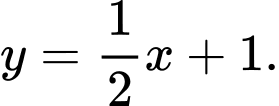 Khối tròn xoay tạo thành khi quay mặt phẳng giới hạn bởi đồ thị hàm số
Khối tròn xoay tạo thành khi quay mặt phẳng giới hạn bởi đồ thị hàm số 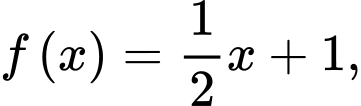 trục
trục 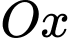 và hai đường thẳng
và hai đường thẳng 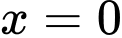 và
và 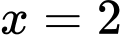 quanh trục
quanh trục 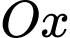 nên có thể tích là
nên có thể tích là 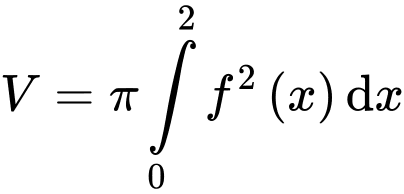
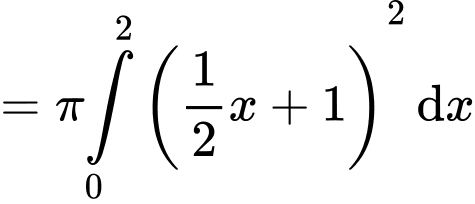
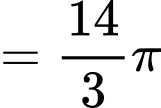
Cách 2: Sử dụng công thức tính thể tích khối nón cụt. (vì khi quay hình thang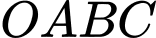 quanh trục
quanh trục 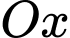 ta sẽ được 1 khối nón cụt với bán kính đáy bé bằng 1, bán kính đáy lớn bằng 2 và chiều cao bằng 2)
ta sẽ được 1 khối nón cụt với bán kính đáy bé bằng 1, bán kính đáy lớn bằng 2 và chiều cao bằng 2)
Đường thẳng
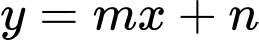 đi qua điểm
đi qua điểm 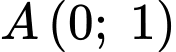 nên suy ra
nên suy ra 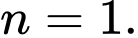
Suy ra
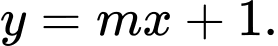
b) Sai.
Đường thẳng
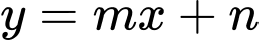 đi qua điểm
đi qua điểm 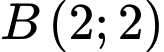 nên suy ra
nên suy ra 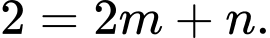
Suy ra
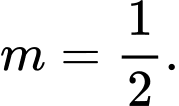
c) Đúng.
Diện tích hình thang
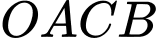 bằng
bằng 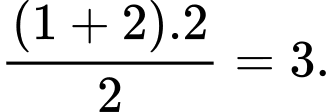
d) Sai.
Cách 1: Áp dụng ứng dụng tích phân để tính thể tích khối tròn xoay:
Từ kết quả tính được từ phần a) và b) ta suy ra phương trình đường thẳng đi qua 2 điểm
 là
là 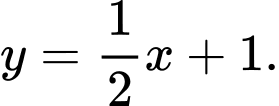 Khối tròn xoay tạo thành khi quay mặt phẳng giới hạn bởi đồ thị hàm số
Khối tròn xoay tạo thành khi quay mặt phẳng giới hạn bởi đồ thị hàm số 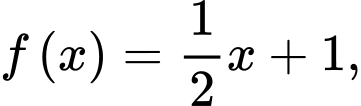 trục
trục 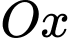 và hai đường thẳng
và hai đường thẳng 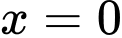 và
và 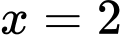 quanh trục
quanh trục 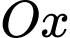 nên có thể tích là
nên có thể tích là 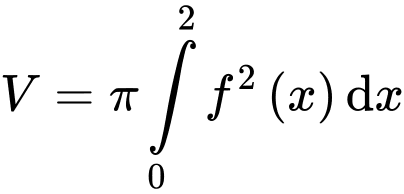
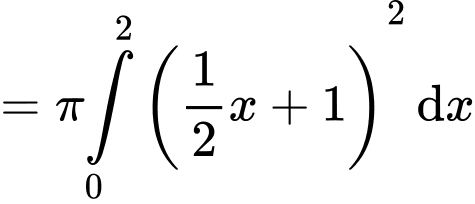
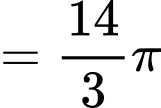
Cách 2: Sử dụng công thức tính thể tích khối nón cụt. (vì khi quay hình thang
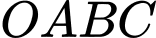 quanh trục
quanh trục 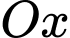 ta sẽ được 1 khối nón cụt với bán kính đáy bé bằng 1, bán kính đáy lớn bằng 2 và chiều cao bằng 2)
ta sẽ được 1 khối nón cụt với bán kính đáy bé bằng 1, bán kính đáy lớn bằng 2 và chiều cao bằng 2)
Câu 14 [778754]: Cho hình  giới hạn bởi các đường
giới hạn bởi các đường 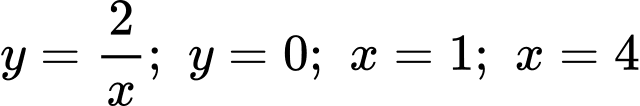 (xem hình vẽ).
(xem hình vẽ).
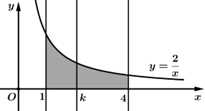
 giới hạn bởi các đường
giới hạn bởi các đường 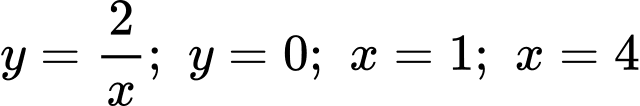 (xem hình vẽ).
(xem hình vẽ).
a) Đúng.
b) Sai.
Vì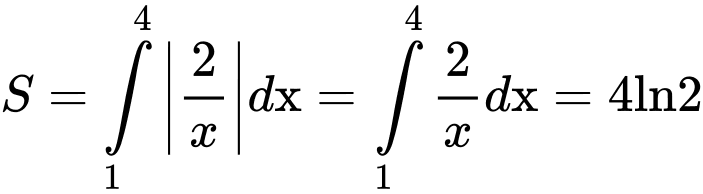
c) Sai.
Vì thể tích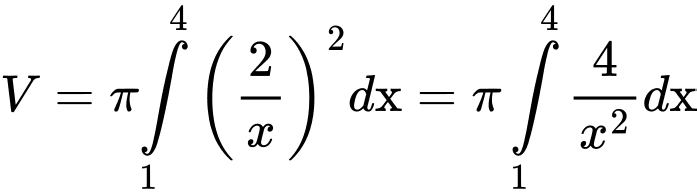
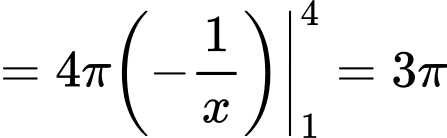
d) Sai.
Đường thẳng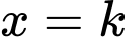 là đường thẳng chia hình (H) thành 2 phần có diện tích bằng nhau, nên
là đường thẳng chia hình (H) thành 2 phần có diện tích bằng nhau, nên 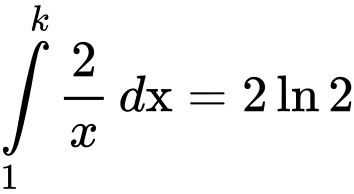
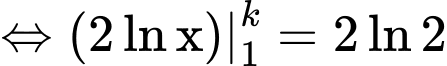
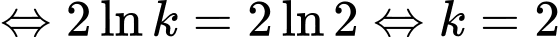
b) Sai.
Vì
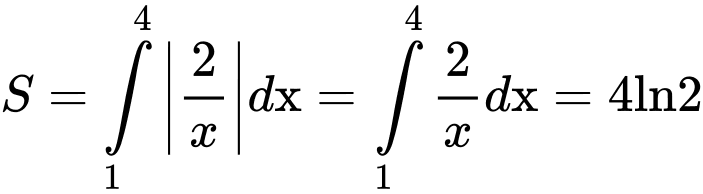
c) Sai.
Vì thể tích
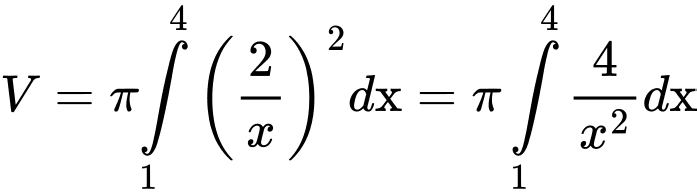
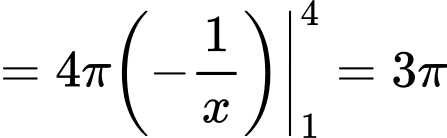
d) Sai.
Đường thẳng
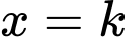 là đường thẳng chia hình (H) thành 2 phần có diện tích bằng nhau, nên
là đường thẳng chia hình (H) thành 2 phần có diện tích bằng nhau, nên 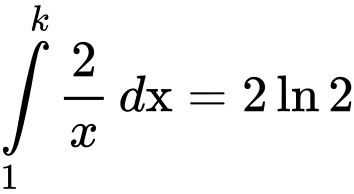
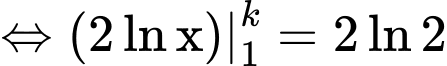
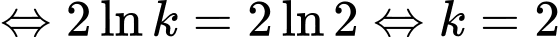
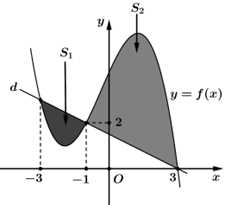
Câu 15 [778744]: Cho hàm số đa thức bậc ba 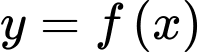 và đường thẳng
và đường thẳng 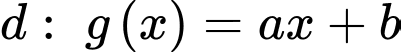 cắt nhau tại ba điểm phân biệt có hoành độ
cắt nhau tại ba điểm phân biệt có hoành độ 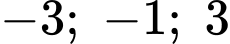 như hình vẽ. Biết rằng diện tích hình phẳng
như hình vẽ. Biết rằng diện tích hình phẳng 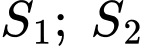 giới hạn bởi đồ thị hàm số
giới hạn bởi đồ thị hàm số 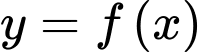 và đường thẳng
và đường thẳng  lần lượt bằng
lần lượt bằng 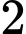 và
và 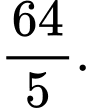
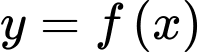 và đường thẳng
và đường thẳng 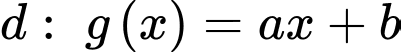 cắt nhau tại ba điểm phân biệt có hoành độ
cắt nhau tại ba điểm phân biệt có hoành độ 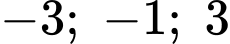 như hình vẽ. Biết rằng diện tích hình phẳng
như hình vẽ. Biết rằng diện tích hình phẳng 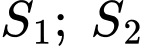 giới hạn bởi đồ thị hàm số
giới hạn bởi đồ thị hàm số 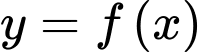 và đường thẳng
và đường thẳng  lần lượt bằng
lần lượt bằng 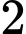 và
và 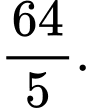

a) Đúng.
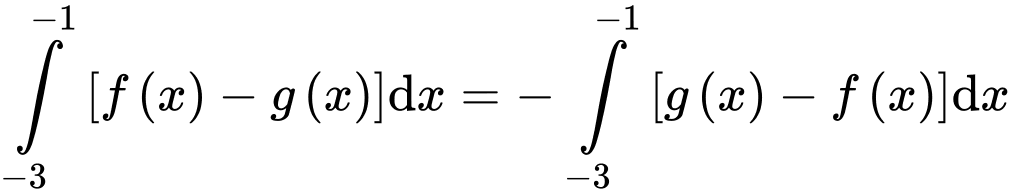
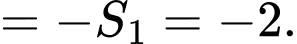
b) Đúng.
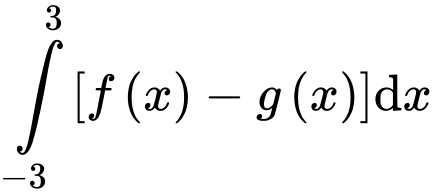
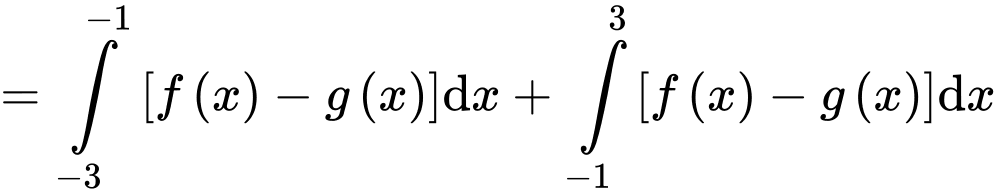
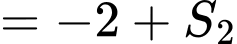
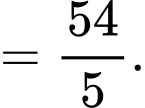
c) Đúng.
Đường thẳng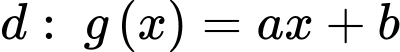 đi qua các điểm có tọa độ
đi qua các điểm có tọa độ 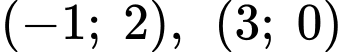 nên ta được hệ
nên ta được hệ 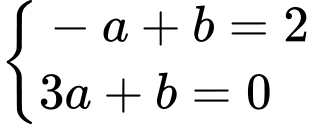
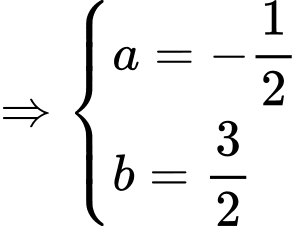
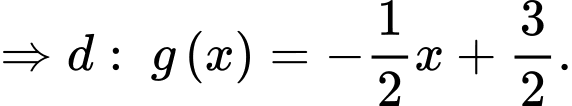
Ta có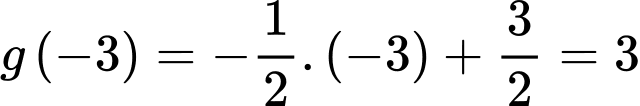
Hình phẳng giới hạn bởi đồ thị hàm số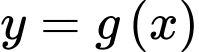 với trục hoành là một tam giác vuông có hai cạnh góc vuông bằng 3 và 6. Vậy diện tích cần tìm bằng
với trục hoành là một tam giác vuông có hai cạnh góc vuông bằng 3 và 6. Vậy diện tích cần tìm bằng 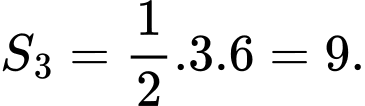
d) Đúng.
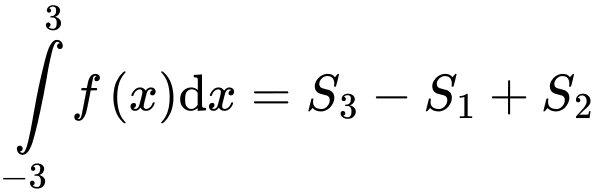
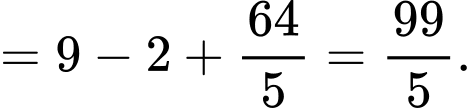
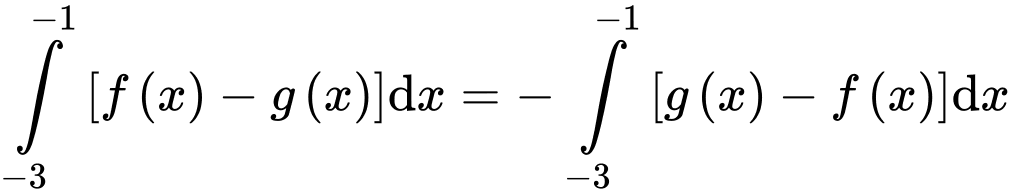
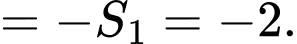
b) Đúng.
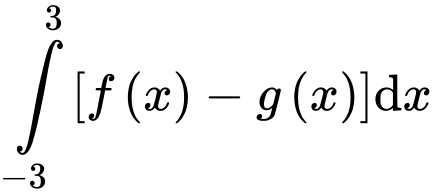
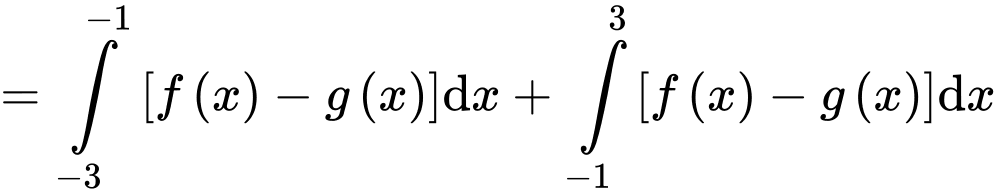
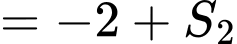
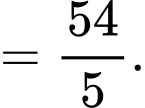
c) Đúng.
Đường thẳng
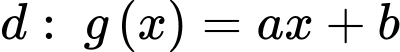 đi qua các điểm có tọa độ
đi qua các điểm có tọa độ 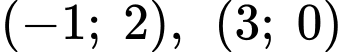 nên ta được hệ
nên ta được hệ 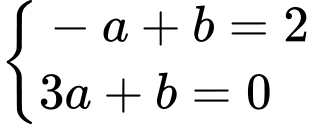
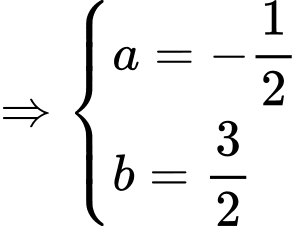
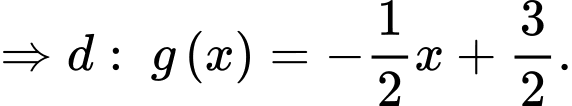
Ta có
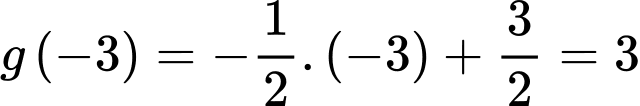
Hình phẳng giới hạn bởi đồ thị hàm số
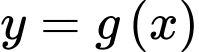 với trục hoành là một tam giác vuông có hai cạnh góc vuông bằng 3 và 6. Vậy diện tích cần tìm bằng
với trục hoành là một tam giác vuông có hai cạnh góc vuông bằng 3 và 6. Vậy diện tích cần tìm bằng 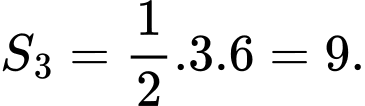
d) Đúng.
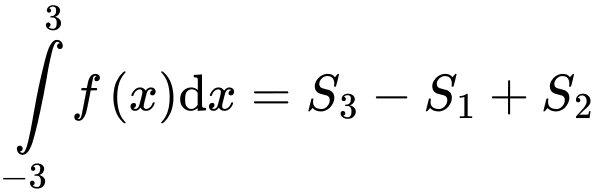
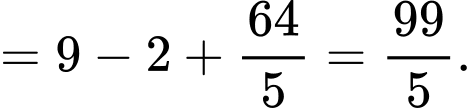
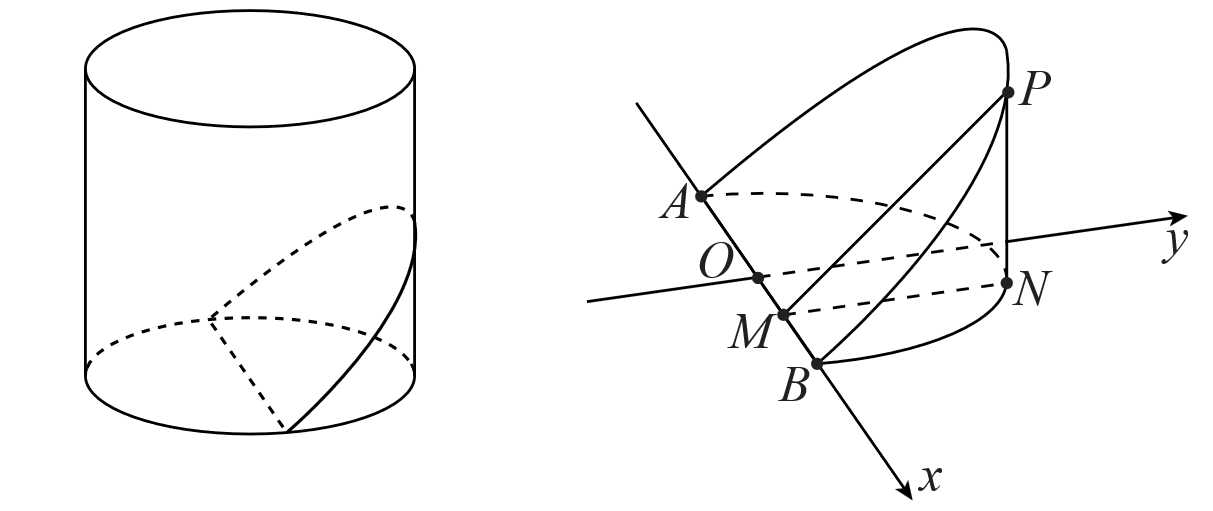
Câu 16 [696404]: Cho một vật thể bằng gỗ có dạng hình trụ với chiều cao và bán kính đáy cùng bằng 1. Cắt khối gỗ đó bởi một mặt phẳng đi qua đường kính của một mặt đáy của khối gỗ và tạo với mặt phẳng đáy của khối gỗ một góc 30o ta thu được khối gỗ hình nêm  và đặt khối
và đặt khối  vào hệ trục tọa độ như hình vẽ.
vào hệ trục tọa độ như hình vẽ.
 và đặt khối
và đặt khối  vào hệ trục tọa độ như hình vẽ.
vào hệ trục tọa độ như hình vẽ.
a) Sai.
Nửa đường tròn đáy của khối gỗ hình trụ (đường kính ) có phương trình là
) có phương trình là 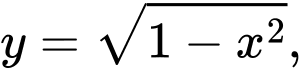

b) Đúng.
Một mặt phẳng vuông góc với trục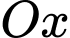 tại điểm
tại điểm 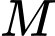 có hoành độ
có hoành độ 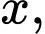 cắt hình nêm theo thiết diện là
cắt hình nêm theo thiết diện là 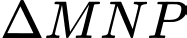 vuông tại
vuông tại 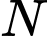 và độ dài
và độ dài 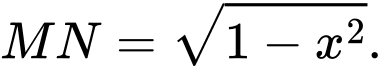
c) Sai.
Một mặt phẳng vuông góc với trục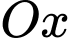 tại điểm
tại điểm 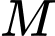 có hoành độ
có hoành độ 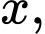 cắt hình nêm theo thiết diện là
cắt hình nêm theo thiết diện là 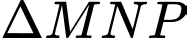 vuông tại
vuông tại 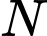 và
và 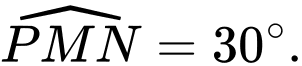
Ta có: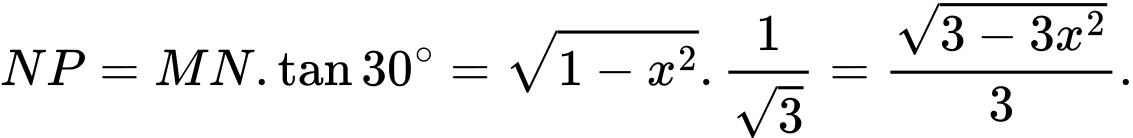
Diện tích tam giác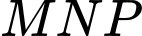 bằng
bằng
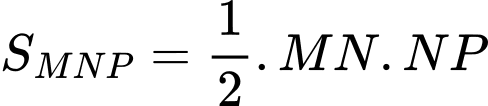
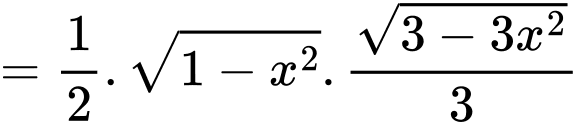
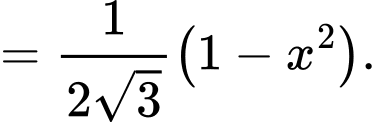
d) Đúng.
Thể tích hình nêm là:
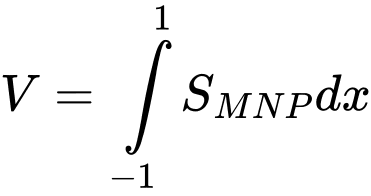
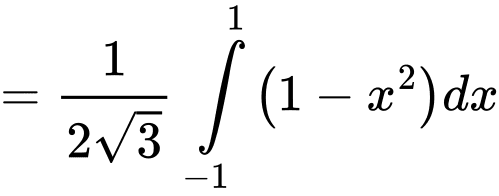
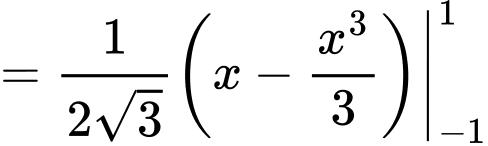
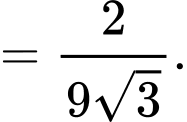
Nửa đường tròn đáy của khối gỗ hình trụ (đường kính
 ) có phương trình là
) có phương trình là 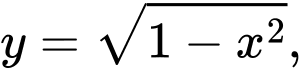

b) Đúng.
Một mặt phẳng vuông góc với trục
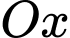 tại điểm
tại điểm 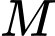 có hoành độ
có hoành độ 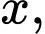 cắt hình nêm theo thiết diện là
cắt hình nêm theo thiết diện là 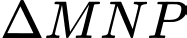 vuông tại
vuông tại 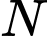 và độ dài
và độ dài 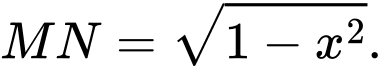
c) Sai.
Một mặt phẳng vuông góc với trục
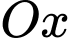 tại điểm
tại điểm 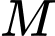 có hoành độ
có hoành độ 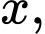 cắt hình nêm theo thiết diện là
cắt hình nêm theo thiết diện là 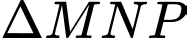 vuông tại
vuông tại 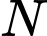 và
và 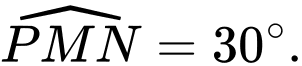
Ta có:
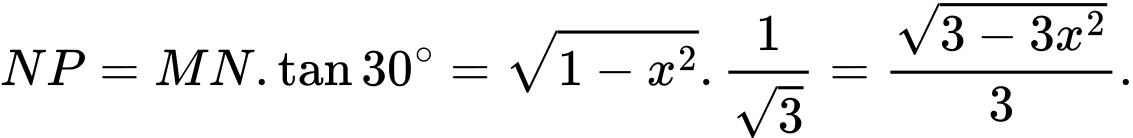
Diện tích tam giác
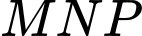 bằng
bằng 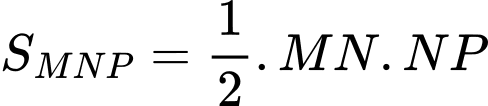
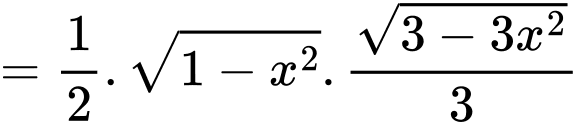
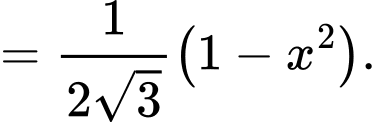
d) Đúng.
Thể tích hình nêm là:
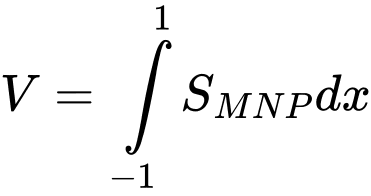
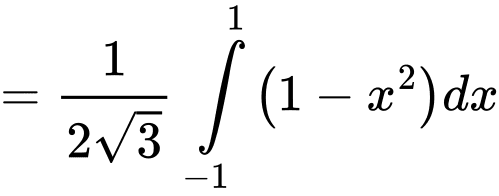
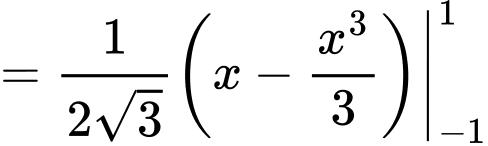
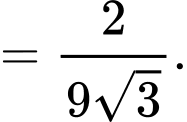
PHẦN III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 17 đến câu 22.
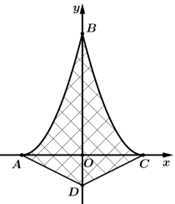
Câu 17 [778758]: Một nhà thiết kế dự định thiết kế logo cho một công ty (xem hình minh họa bên). Đường viền của logo bao gồm các đoạn thẳng  hai cung
hai cung  và
và 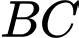 lần lượt là một phần của các parabol đỉnh
lần lượt là một phần của các parabol đỉnh 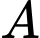 và đỉnh
và đỉnh 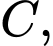 trục đối xứng của mỗi parabol vuông góc với đường thẳng
trục đối xứng của mỗi parabol vuông góc với đường thẳng 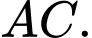 Chọn hệ trục toạ độ
Chọn hệ trục toạ độ 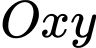 như hình vẽ (đơn vị mỗi trục là dm) thì
như hình vẽ (đơn vị mỗi trục là dm) thì 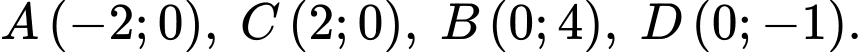 Diện tích logo là bao nhiêu
Diện tích logo là bao nhiêu  (kết quả làm tròn đến hàng phần trăm).
(kết quả làm tròn đến hàng phần trăm).
 hai cung
hai cung  và
và 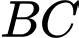 lần lượt là một phần của các parabol đỉnh
lần lượt là một phần của các parabol đỉnh 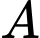 và đỉnh
và đỉnh 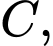 trục đối xứng của mỗi parabol vuông góc với đường thẳng
trục đối xứng của mỗi parabol vuông góc với đường thẳng 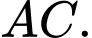 Chọn hệ trục toạ độ
Chọn hệ trục toạ độ 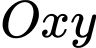 như hình vẽ (đơn vị mỗi trục là dm) thì
như hình vẽ (đơn vị mỗi trục là dm) thì 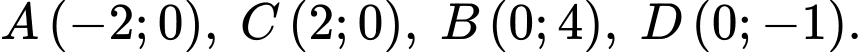 Diện tích logo là bao nhiêu
Diện tích logo là bao nhiêu  (kết quả làm tròn đến hàng phần trăm).
(kết quả làm tròn đến hàng phần trăm).
Điền đáp án: 7,33.
Vì logo đối xứng qua trục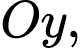 nên diện tích của logo sẽ bằng 2 lần diện tích logo nằm bên phải trục
nên diện tích của logo sẽ bằng 2 lần diện tích logo nằm bên phải trục 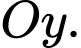 Và phần diện tích này bằng tổng diện tích tam giác vuông
Và phần diện tích này bằng tổng diện tích tam giác vuông  và diện tích miền
và diện tích miền 
Gọi phương trình parabol có đỉnh là
là 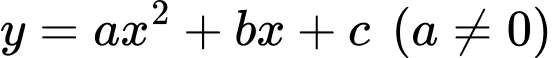
Dựa vào giả thiết, ta có hệ phương trình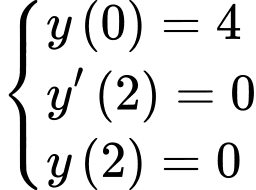
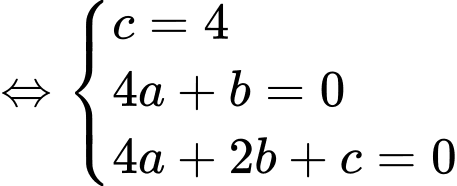
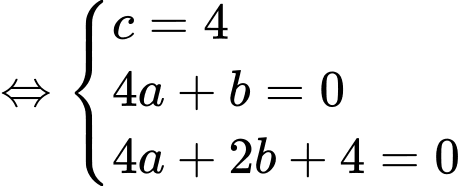
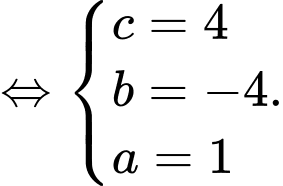
Suy ra phương trình parabol là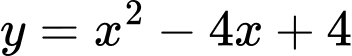
Suy ra diện tích logo bằng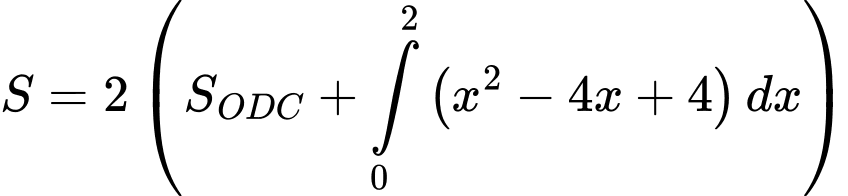
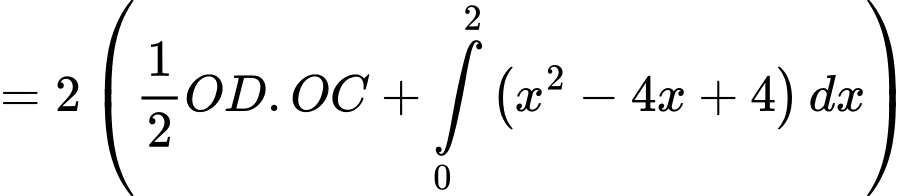
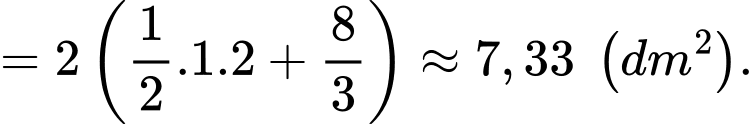
Vì logo đối xứng qua trục
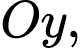 nên diện tích của logo sẽ bằng 2 lần diện tích logo nằm bên phải trục
nên diện tích của logo sẽ bằng 2 lần diện tích logo nằm bên phải trục 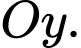 Và phần diện tích này bằng tổng diện tích tam giác vuông
Và phần diện tích này bằng tổng diện tích tam giác vuông  và diện tích miền
và diện tích miền 
Gọi phương trình parabol có đỉnh
 là
là 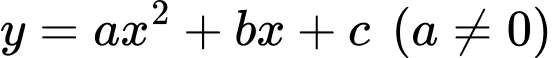
Dựa vào giả thiết, ta có hệ phương trình
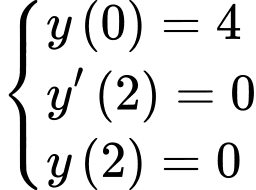
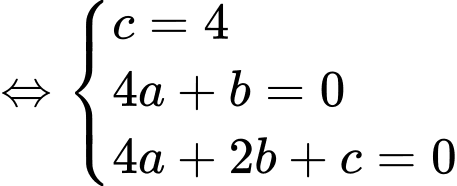
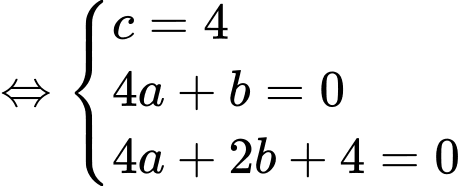
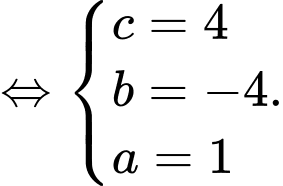
Suy ra phương trình parabol là
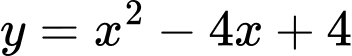
Suy ra diện tích logo bằng
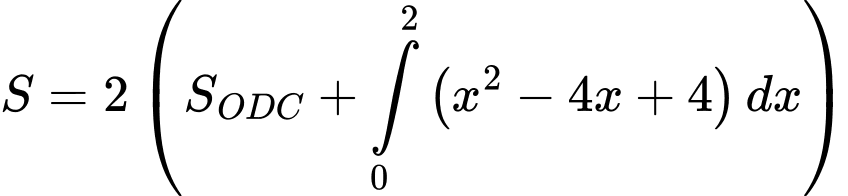
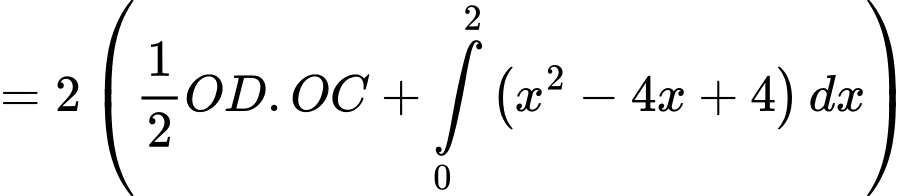
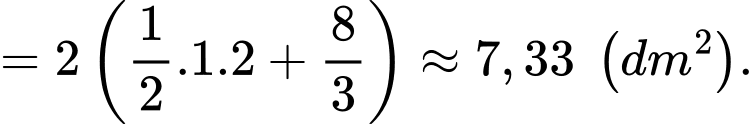
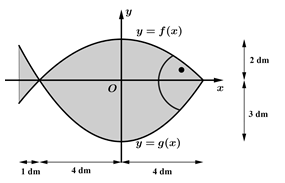
Câu 18 [392145]: Hoạ sĩ thiết kế logo hình con cá cho một doanh nghiệp kinh doanh hải sản. Logo là hình phẳng giới hạn bởi hai parabol với các kích thước được cho trong Hình vẽ bên (đơn vị trên mỗi trục toạ độ là decimét). Diện tích logo là bao nhiêu  Kết quả làm tròn đến hàng đơn vị.
Kết quả làm tròn đến hàng đơn vị.
 Kết quả làm tròn đến hàng đơn vị.
Kết quả làm tròn đến hàng đơn vị.
Dựa vào đồ thị, ta có diện tích logo là diện tích được giới hạn bởi hai đường parabol 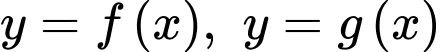 và hai đường thẳng
và hai đường thẳng 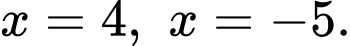 Quan sát đồ thị, ta thấy +) Parabol
Quan sát đồ thị, ta thấy +) Parabol 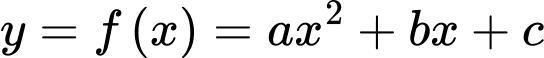 đi qua 3 điểm
đi qua 3 điểm 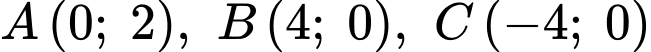
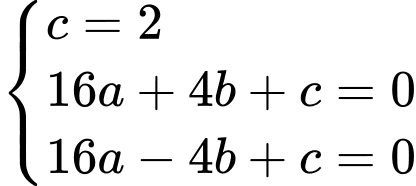
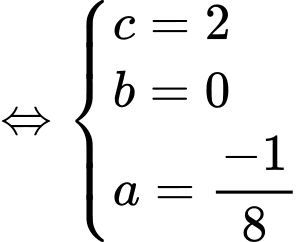
+) Parabol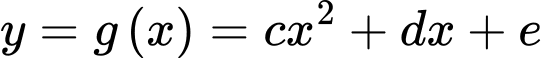 đi qua 3 điểm
đi qua 3 điểm 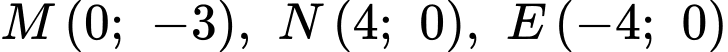
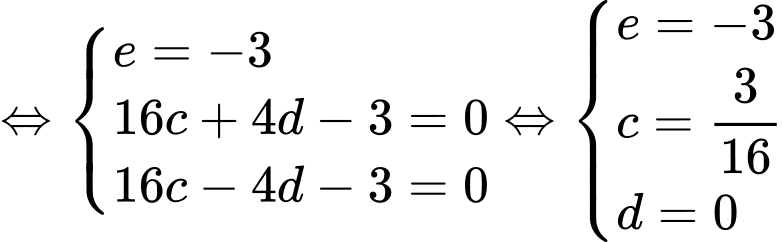
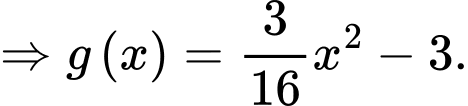
Vậy diện tích logo bằng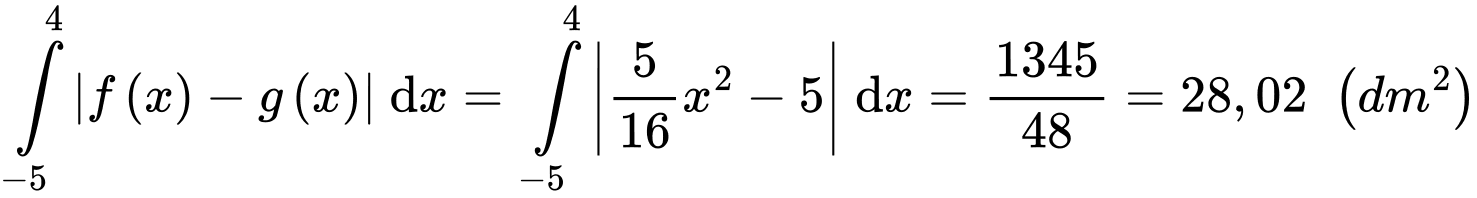
Điền đáp án: 28
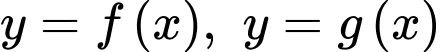 và hai đường thẳng
và hai đường thẳng 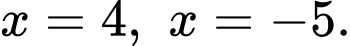 Quan sát đồ thị, ta thấy +) Parabol
Quan sát đồ thị, ta thấy +) Parabol 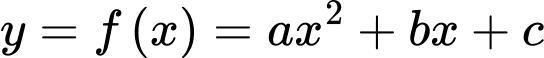 đi qua 3 điểm
đi qua 3 điểm 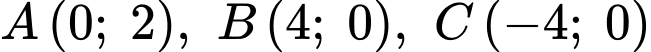
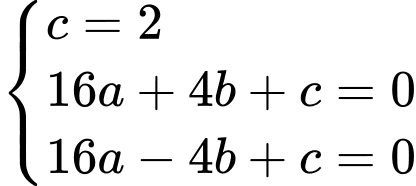
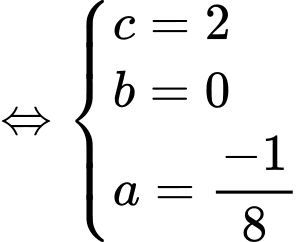
+) Parabol
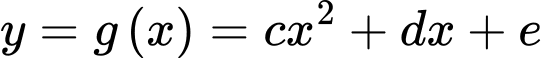 đi qua 3 điểm
đi qua 3 điểm 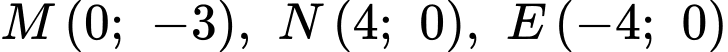
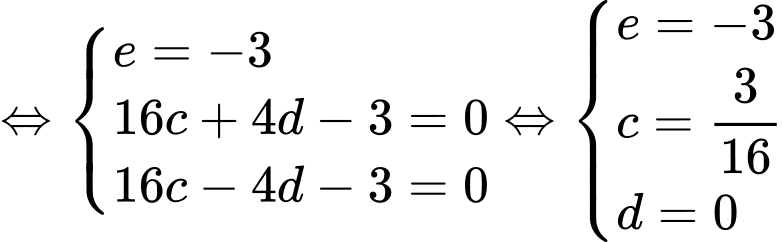
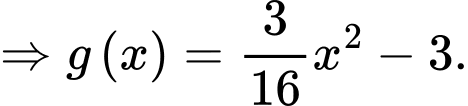
Vậy diện tích logo bằng
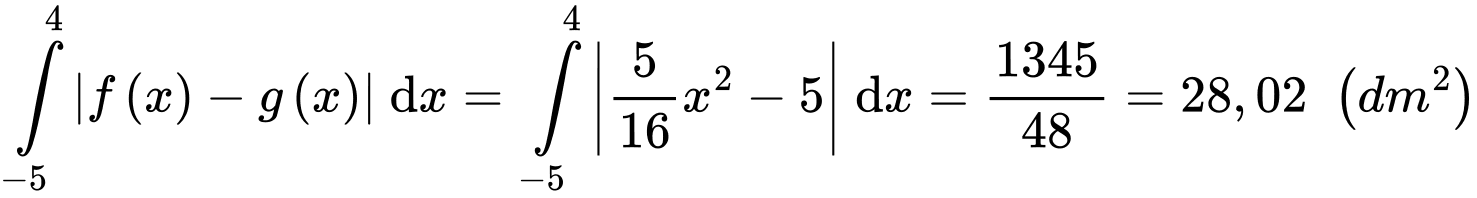
Điền đáp án: 28
Câu 19 [778759]: Một tấm kính làm mặt bàn (hình 1) có hình dáng tam giác đều với 3 đỉnh được làm cong đẹp mắt như hình 2. Biết cạnh tấm kính tam giác ban đầu bằng 12 (dm). Một góc bàn được cắt theo đường cong là đường Parabol (P): 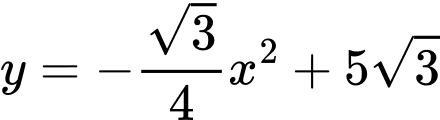 (như hình 3) có hai nhánh tiếp xúc với hai cạnh của tam giác (hình 4). Hai góc còn lại được cắt sao cho mặt bàn có tính đối xứng.
(như hình 3) có hai nhánh tiếp xúc với hai cạnh của tam giác (hình 4). Hai góc còn lại được cắt sao cho mặt bàn có tính đối xứng.
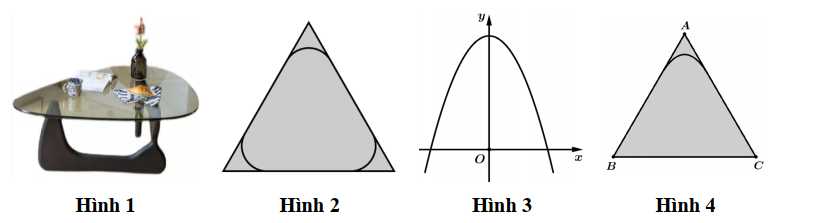
Diện tích mặt kính làm mặt bàn (hình 1) bằng Tính
Tính 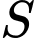 (kết quả làm tròn đến hàng phần chục).
(kết quả làm tròn đến hàng phần chục).
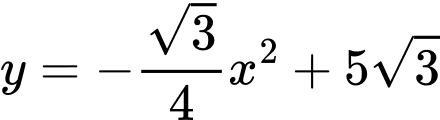 (như hình 3) có hai nhánh tiếp xúc với hai cạnh của tam giác (hình 4). Hai góc còn lại được cắt sao cho mặt bàn có tính đối xứng.
(như hình 3) có hai nhánh tiếp xúc với hai cạnh của tam giác (hình 4). Hai góc còn lại được cắt sao cho mặt bàn có tính đối xứng.
Diện tích mặt kính làm mặt bàn (hình 1) bằng
 Tính
Tính 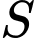 (kết quả làm tròn đến hàng phần chục).
(kết quả làm tròn đến hàng phần chục).
Đáp số: 55,4
Diện tích tam giác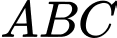 bằng
bằng 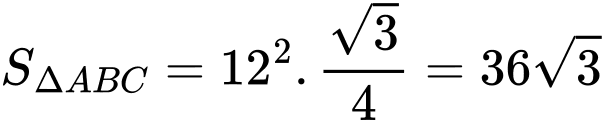
Dựng hệ trục như hình vẽ
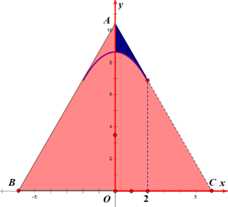
Vì tam giác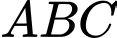 đều cạnh bằng 12 nên
đều cạnh bằng 12 nên 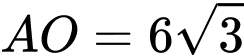 .
.
Phương trình đường thẳng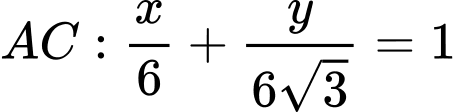
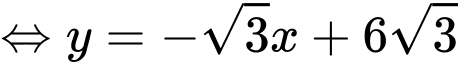
Ta có phương trình hoành độ giao điểm của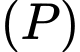 và đường thẳng
và đường thẳng 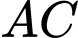
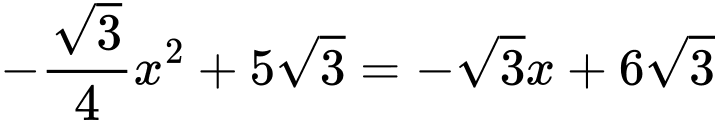
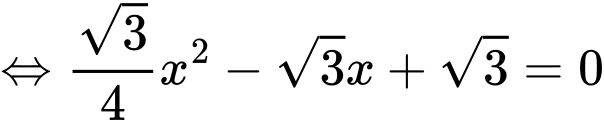
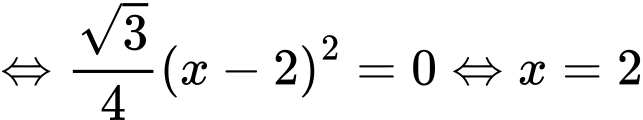
Diện tích phần tô đậm giới hạn bởi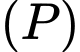 ,
, 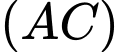 và trục
và trục 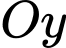 trong hình bằng
trong hình bằng
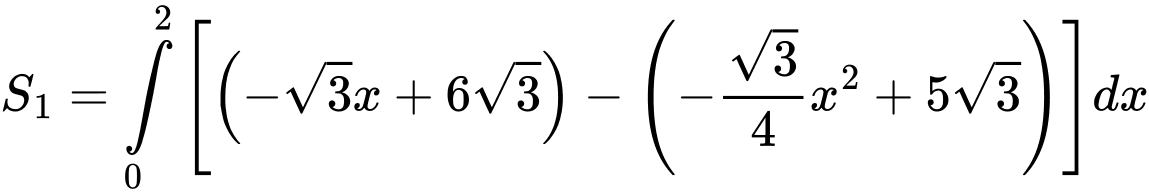
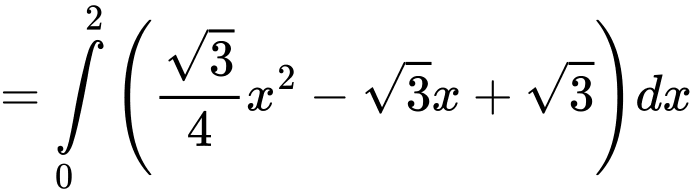
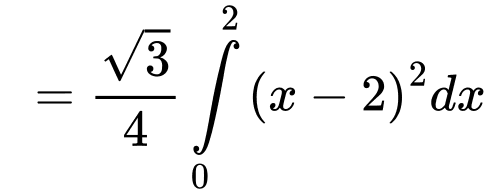
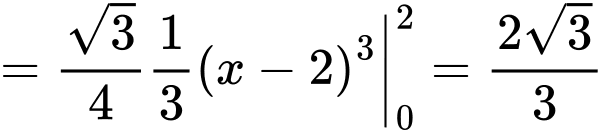
Vì mặt bàn đối xứng nên diện tích kính cần tính bằng
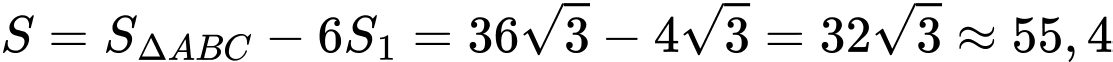
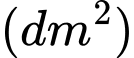 .
.
Diện tích tam giác
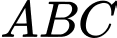 bằng
bằng 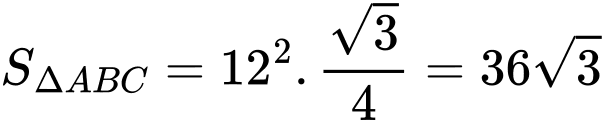
Dựng hệ trục như hình vẽ

Vì tam giác
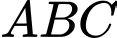 đều cạnh bằng 12 nên
đều cạnh bằng 12 nên 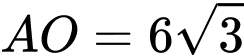 .
.Phương trình đường thẳng
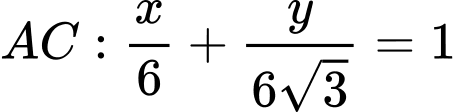
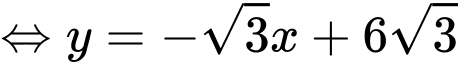
Ta có phương trình hoành độ giao điểm của
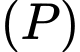 và đường thẳng
và đường thẳng 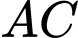
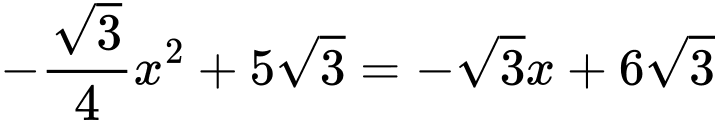
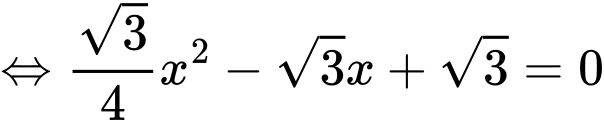
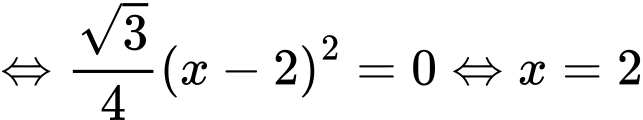
Diện tích phần tô đậm giới hạn bởi
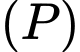 ,
, 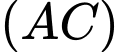 và trục
và trục 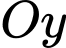 trong hình bằng
trong hình bằng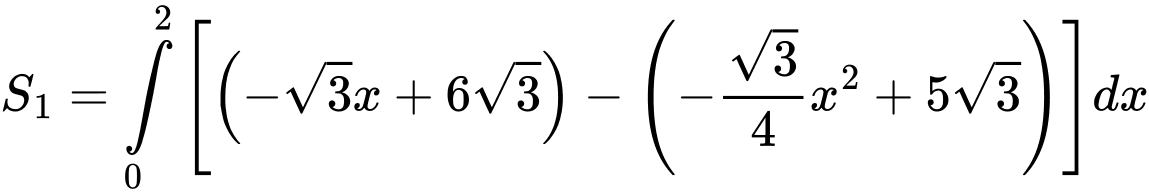
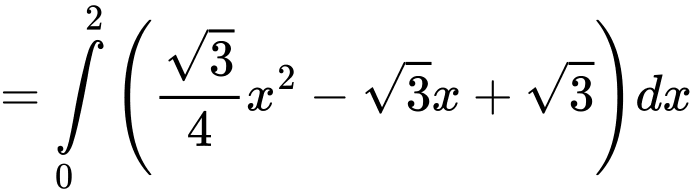
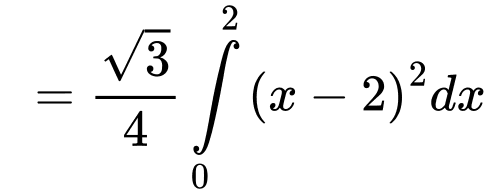
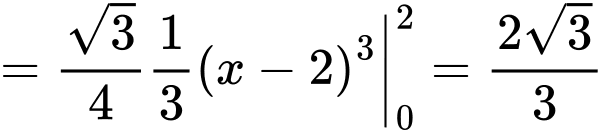
Vì mặt bàn đối xứng nên diện tích kính cần tính bằng
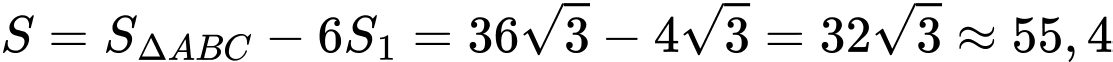
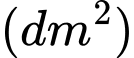 .
.
Câu 20 [778760]: Hình elip được ứng dụng nhiều trong thực tiễn, đặc biệt là kiến trúc xây dựng như đấu trường La Mã, tòa nhà Ellipse Tower Hà Nội, sử dụng trong thiết kế logo quảng cáo, thiết bị nội thất. Xét một Lavabo (bồn rửa) làm bằng sứ đặc hình dạng là một nửa khối elip tròn xoay có thông số kĩ thuật mặt trên của Lavabo là: dài rộng:
rộng: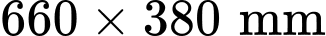 (tham khảo hình vẽ bên dưới), Lavabo có độ dày đều là
(tham khảo hình vẽ bên dưới), Lavabo có độ dày đều là 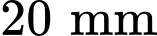 . Thể tích chứa nước của Lavabo bằng bao nhiêu
. Thể tích chứa nước của Lavabo bằng bao nhiêu  (kết quả làm tròn đến hàng phần chục)?
(kết quả làm tròn đến hàng phần chục)?

 rộng:
rộng: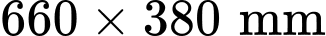 (tham khảo hình vẽ bên dưới), Lavabo có độ dày đều là
(tham khảo hình vẽ bên dưới), Lavabo có độ dày đều là 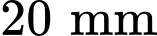 . Thể tích chứa nước của Lavabo bằng bao nhiêu
. Thể tích chứa nước của Lavabo bằng bao nhiêu  (kết quả làm tròn đến hàng phần chục)?
(kết quả làm tròn đến hàng phần chục)?
Trả lời: 18,8
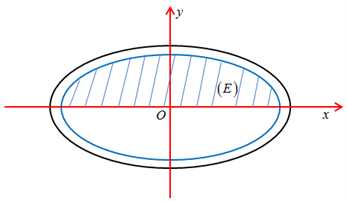
Giả sử mặt trên của Lavabo được biểu diễn như hình vẽ bên dưới. Gọi hệ trục tọa độ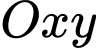 như hình vẽ. Gọi
như hình vẽ. Gọi  là elip nhỏ bên trong.
là elip nhỏ bên trong.
Độ dài trục lớn của là
là 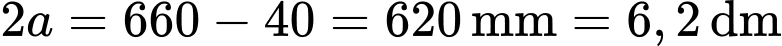
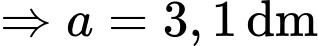 .
.
Độ dài trục bé của là
là 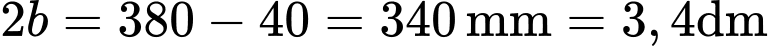
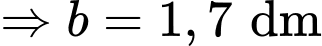 .
.
Vậy phương trình của là:
là: 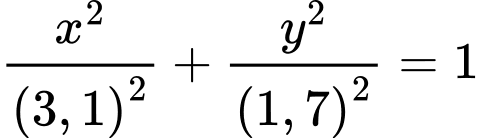
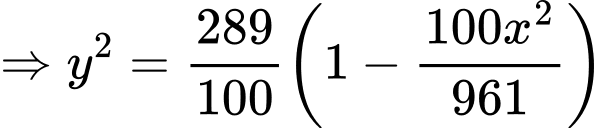 .
.
Thể tích khối tròn xoay khi quay miền giới hạn bởi , trục
, trục 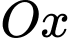 và
và 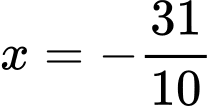 ,
, 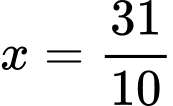 (Phần gạch chéo trong hình) quanh trục
(Phần gạch chéo trong hình) quanh trục 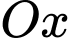 là:
là:
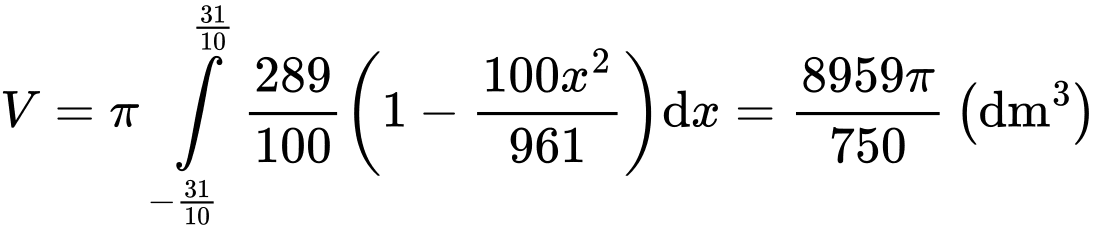
Vậy thể tích chứa nước của Lavabo là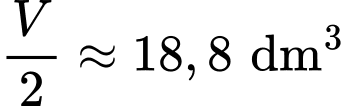 .
.
Giả sử mặt trên của Lavabo được biểu diễn như hình vẽ bên dưới. Gọi hệ trục tọa độ
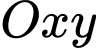 như hình vẽ. Gọi
như hình vẽ. Gọi  là elip nhỏ bên trong.
là elip nhỏ bên trong.
Độ dài trục lớn của
 là
là 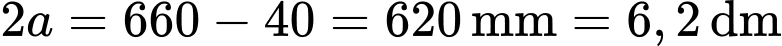
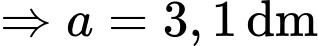 .
.Độ dài trục bé của
 là
là 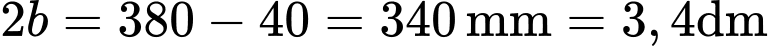
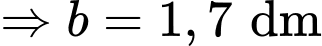 .
.Vậy phương trình của
 là:
là: 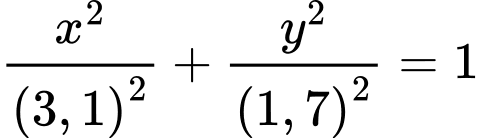
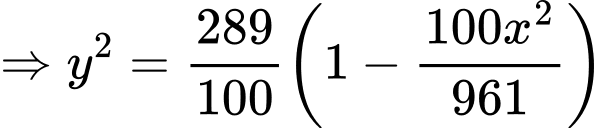 .
.Thể tích khối tròn xoay khi quay miền giới hạn bởi
 , trục
, trục 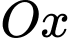 và
và 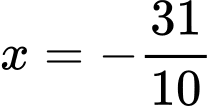 ,
, 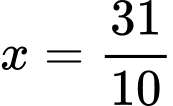 (Phần gạch chéo trong hình) quanh trục
(Phần gạch chéo trong hình) quanh trục 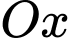 là:
là: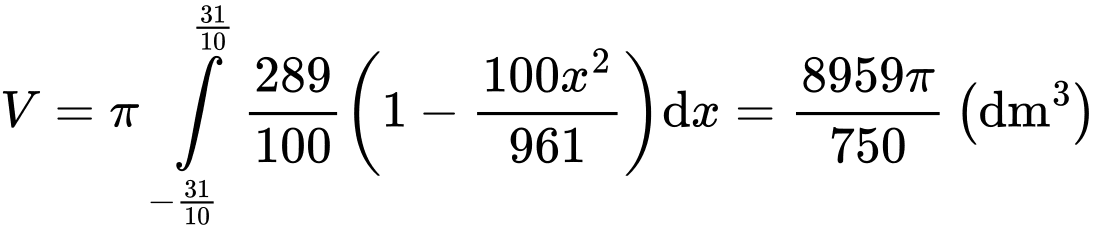
Vậy thể tích chứa nước của Lavabo là
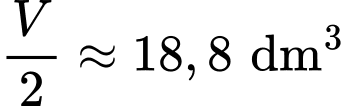 .
.
Câu 21 [779017]: Người nghệ sĩ vẽ một bông hoa không màu trên một miếng bìa hình vuông 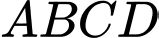 tâm
tâm  bằng một đường cong kính
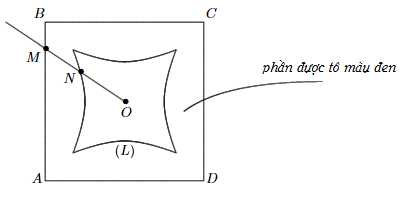
bằng một đường cong kính 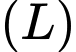 rồi tô màu đen phần bên ngoài đường cong này của hình vuông (tham khảo hình vẽ). Nếu điểm
rồi tô màu đen phần bên ngoài đường cong này của hình vuông (tham khảo hình vẽ). Nếu điểm 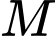 thuộc cạnh của hình vuông
thuộc cạnh của hình vuông 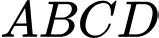 và tia
và tia 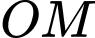 cắt
cắt 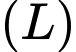 tại điểm
tại điểm 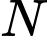 thì
thì 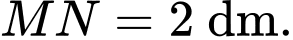 Biết rằng
Biết rằng 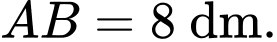 Phần được nghệ sĩ tô màu đen có diện tích bằng bao nhiêu centimet vuông? (làm tròn kết quả đến hàng đơn vị).
Phần được nghệ sĩ tô màu đen có diện tích bằng bao nhiêu centimet vuông? (làm tròn kết quả đến hàng đơn vị).
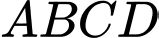 tâm
tâm  bằng một đường cong kính
bằng một đường cong kính 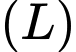 rồi tô màu đen phần bên ngoài đường cong này của hình vuông (tham khảo hình vẽ). Nếu điểm
rồi tô màu đen phần bên ngoài đường cong này của hình vuông (tham khảo hình vẽ). Nếu điểm 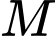 thuộc cạnh của hình vuông
thuộc cạnh của hình vuông 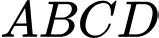 và tia
và tia 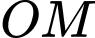 cắt
cắt 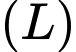 tại điểm
tại điểm 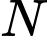 thì
thì 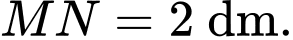 Biết rằng
Biết rằng 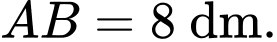 Phần được nghệ sĩ tô màu đen có diện tích bằng bao nhiêu centimet vuông? (làm tròn kết quả đến hàng đơn vị).
Phần được nghệ sĩ tô màu đen có diện tích bằng bao nhiêu centimet vuông? (làm tròn kết quả đến hàng đơn vị).
Điền đáp án: 4384.
Diện tích của cả hình vuông là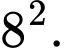 Gắn hệ trục tọa độ
Gắn hệ trục tọa độ 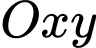 như hình vẽ sau (đơn vị trên mỗi trục tọa độ là decimét).
như hình vẽ sau (đơn vị trên mỗi trục tọa độ là decimét).
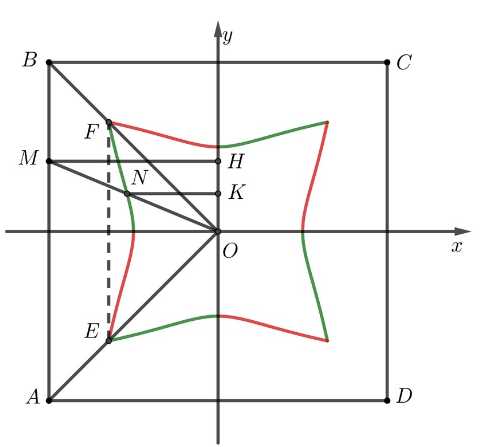
Khi đó ta suy ra toạ độ các đỉnh và tâm là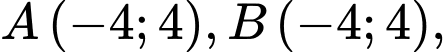
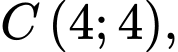
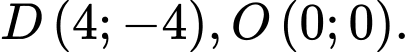 Và phương trình các cạnh là
Và phương trình các cạnh là 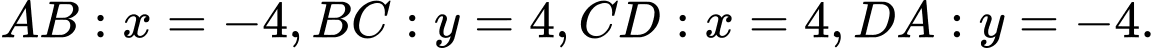
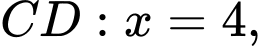
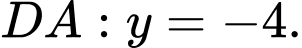
Vì tính đối xứng của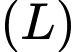 ta chỉ cần xét phần của
ta chỉ cần xét phần của 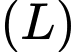 nằm trong góc phần tư thứ hai và thứ ba của hệ trục tọa độ (kết quả sẽ bằng bốn phần diện tích này).
nằm trong góc phần tư thứ hai và thứ ba của hệ trục tọa độ (kết quả sẽ bằng bốn phần diện tích này).
Gọi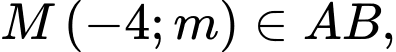
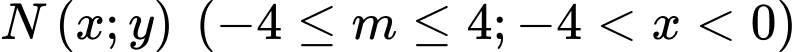
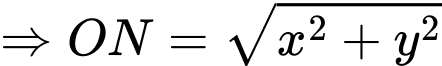 và
và 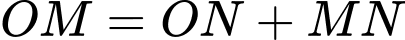

Gọi lần lượt là hình chiếu vuông góc của
lần lượt là hình chiếu vuông góc của 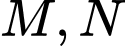 lên trục tung.
lên trục tung.
Áp dụng định lý Thalès trong tam giác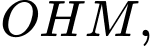 ta có:
ta có:
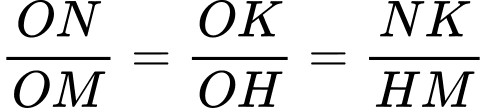
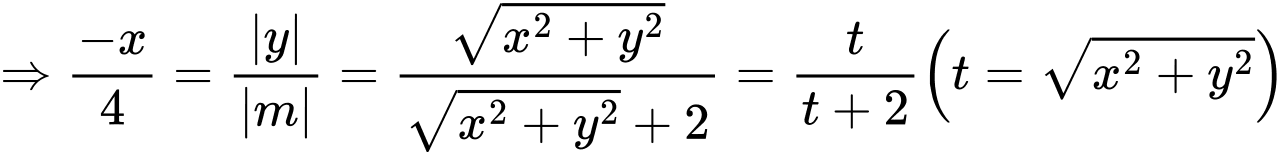
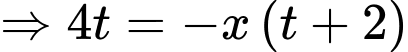
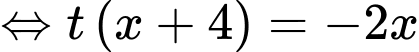
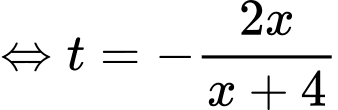
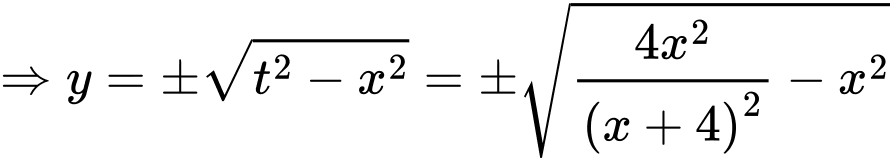 (dấu +, - tương ứng với nửa trên trục hoành và nửa dưới trục hoành)
(dấu +, - tương ứng với nửa trên trục hoành và nửa dưới trục hoành)
Xét một phần tư bông hoa giới hạn bởi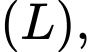 đoạn thẳng
đoạn thẳng 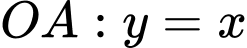 và đoạn thẳng
và đoạn thẳng 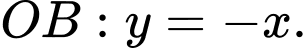
Giả sử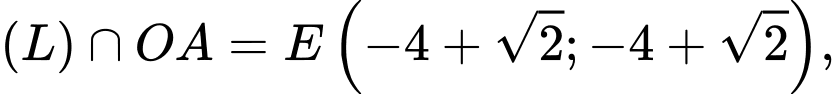
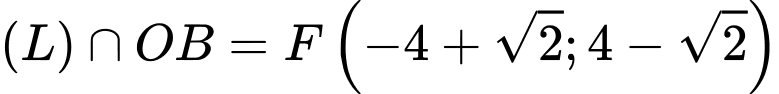

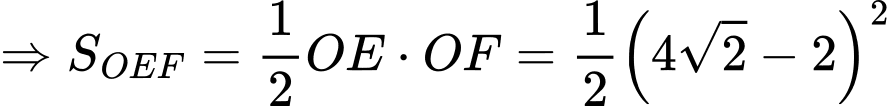
Xét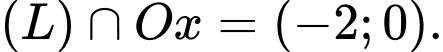
Vậy diện tích cả công hoa là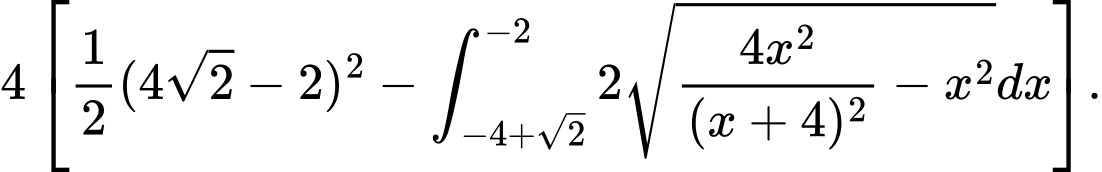
Vậy diện tích phần tô màu đen là bên ngoài bông hoa bằng
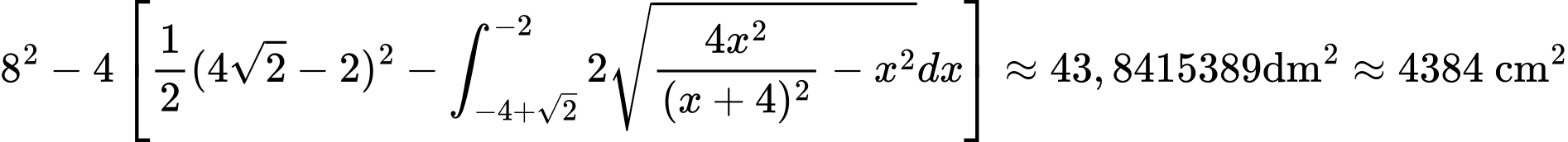
Diện tích của cả hình vuông là
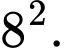 Gắn hệ trục tọa độ
Gắn hệ trục tọa độ 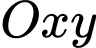 như hình vẽ sau (đơn vị trên mỗi trục tọa độ là decimét).
như hình vẽ sau (đơn vị trên mỗi trục tọa độ là decimét).
Khi đó ta suy ra toạ độ các đỉnh và tâm là
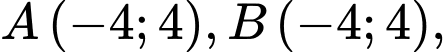
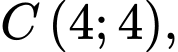
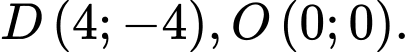 Và phương trình các cạnh là
Và phương trình các cạnh là 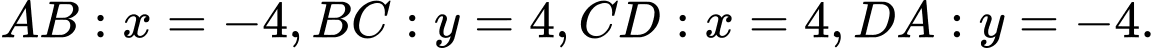
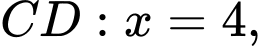
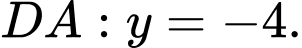
Vì tính đối xứng của
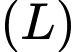 ta chỉ cần xét phần của
ta chỉ cần xét phần của 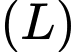 nằm trong góc phần tư thứ hai và thứ ba của hệ trục tọa độ (kết quả sẽ bằng bốn phần diện tích này).
nằm trong góc phần tư thứ hai và thứ ba của hệ trục tọa độ (kết quả sẽ bằng bốn phần diện tích này).Gọi
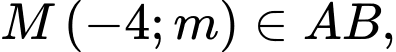
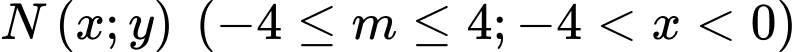
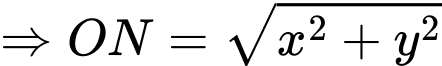 và
và 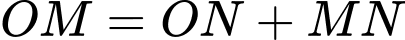

Gọi
 lần lượt là hình chiếu vuông góc của
lần lượt là hình chiếu vuông góc của 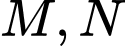 lên trục tung.
lên trục tung.Áp dụng định lý Thalès trong tam giác
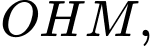 ta có:
ta có: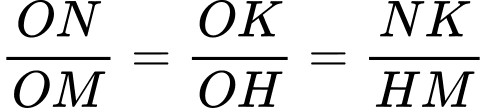
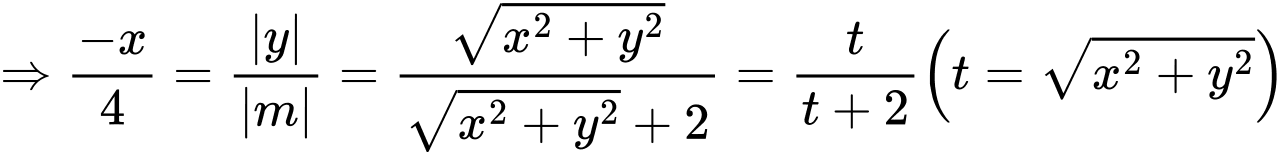
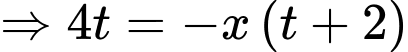
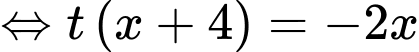
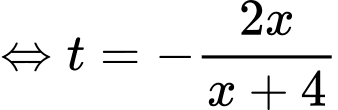
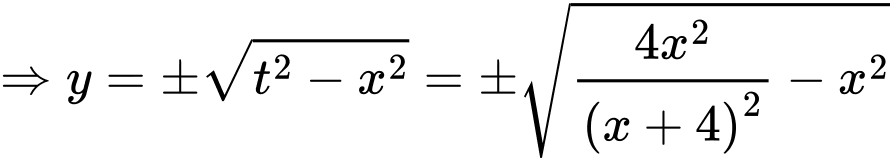 (dấu +, - tương ứng với nửa trên trục hoành và nửa dưới trục hoành)
(dấu +, - tương ứng với nửa trên trục hoành và nửa dưới trục hoành)Xét một phần tư bông hoa giới hạn bởi
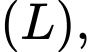 đoạn thẳng
đoạn thẳng 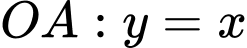 và đoạn thẳng
và đoạn thẳng 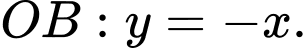
Giả sử
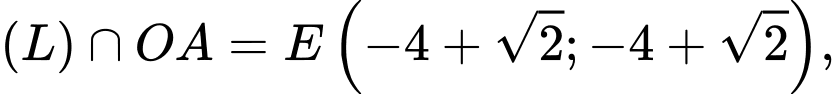
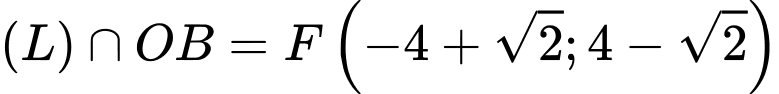

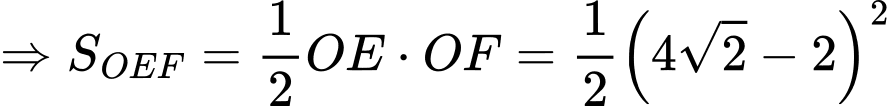
Xét
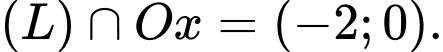
Vậy diện tích cả công hoa là
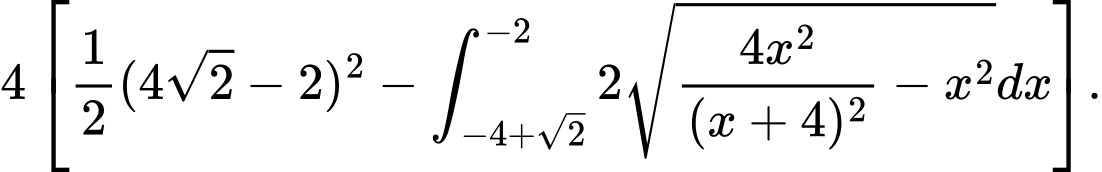
Vậy diện tích phần tô màu đen là bên ngoài bông hoa bằng
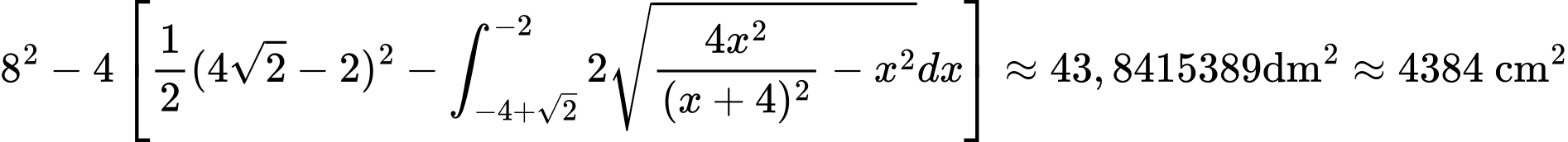
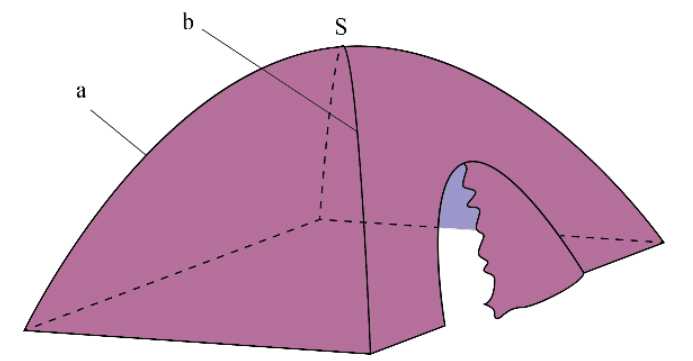
Câu 22 [204876]: Một chiếc lều vải du lịch dạng hình cong như hình vẽ. Khung chính bao gồm đáy là hình vuông cạnh 2 m và hai xương dây 𝑎, 𝑏 nằm trên các đường parabol đỉnh 𝑆. Biết chiều cao của lều là 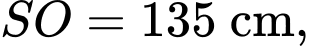 𝑂 là tâm của đáy. Tính thể tích chiếc lều theo đơn vị
𝑂 là tâm của đáy. Tính thể tích chiếc lều theo đơn vị 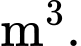 Viết kết quả dưới dạng số thập phân.
Viết kết quả dưới dạng số thập phân.
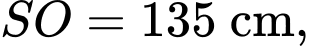 𝑂 là tâm của đáy. Tính thể tích chiếc lều theo đơn vị
𝑂 là tâm của đáy. Tính thể tích chiếc lều theo đơn vị 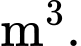 Viết kết quả dưới dạng số thập phân.
Viết kết quả dưới dạng số thập phân.
Điền đáp án: 2,7.
Gắn hệ trục như hình vẽ.
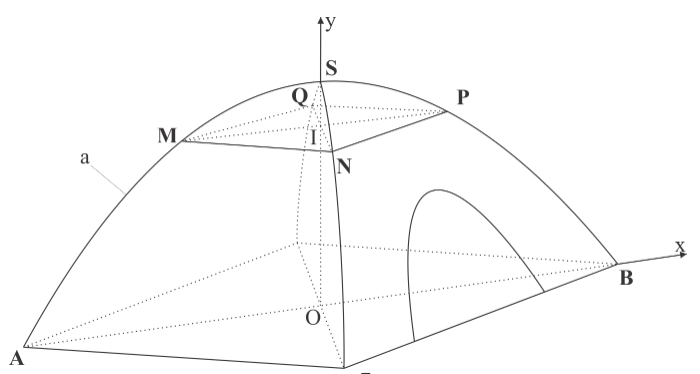
Ta tính được
Gọi phương trình của đường thẳng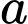 là
là 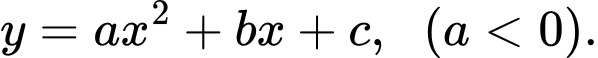
Ta có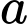 đi qua các điểm
đi qua các điểm
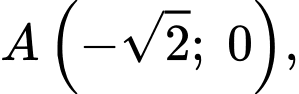
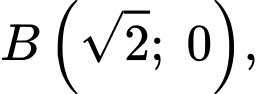
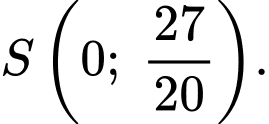
Suy ra ta có hệ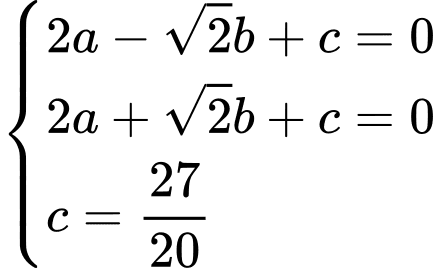
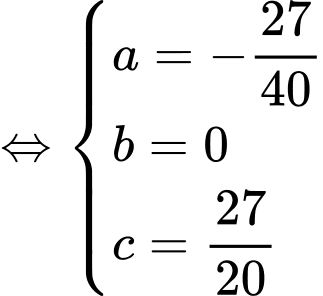
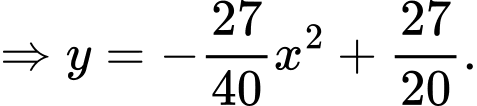
Gọi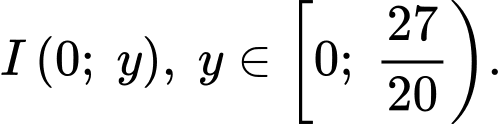
Mặt phẳng vuông góc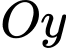 tại
tại 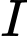 cắt hình đa cho theo 1 thiết diện là hình vuông
cắt hình đa cho theo 1 thiết diện là hình vuông 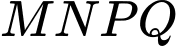 có diện tích
có diện tích 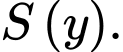
Theo giả thiết trên các điểm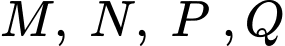 cùng có tung độ bằng
cùng có tung độ bằng 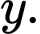 Mà hai điểm
Mà hai điểm  thuộc đường
thuộc đường 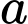 có phương trình
có phương trình 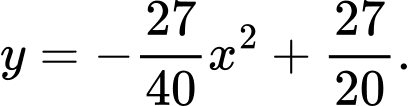
Suy ra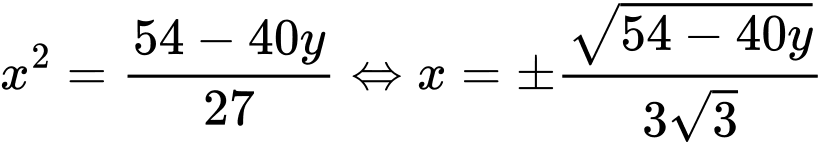
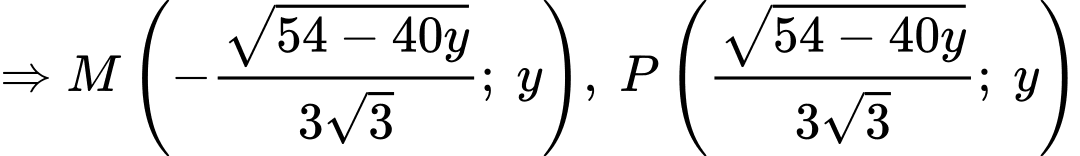
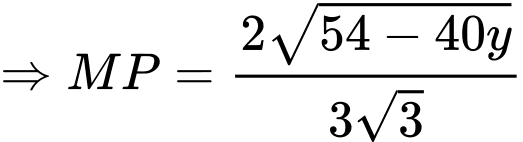
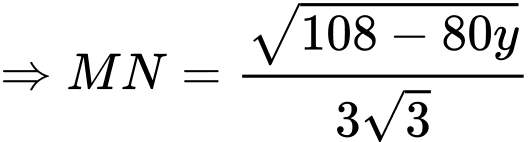
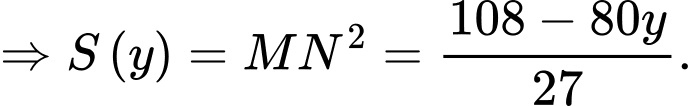
Suy ra thể tích chiếc lều là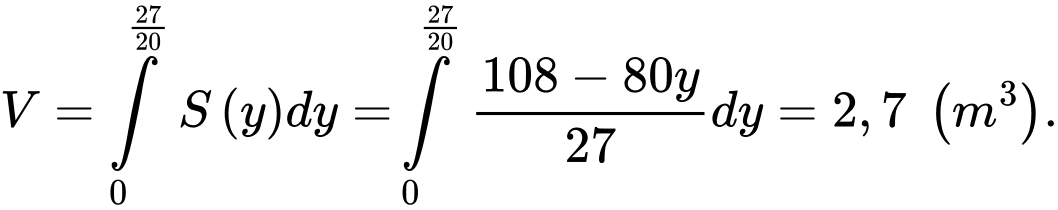
Gắn hệ trục như hình vẽ.

Ta tính được

Gọi phương trình của đường thẳng
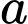 là
là 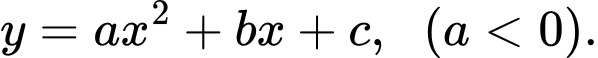
Ta có
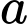 đi qua các điểm
đi qua các điểm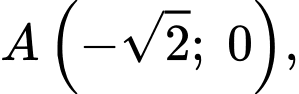
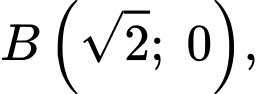
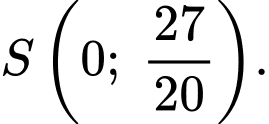
Suy ra ta có hệ
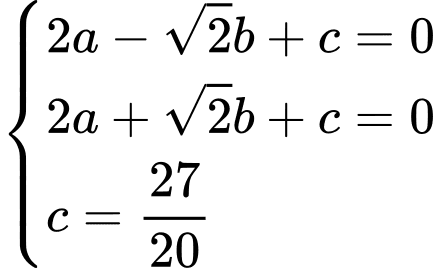
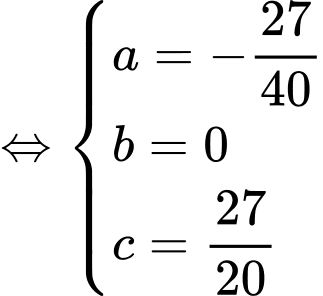
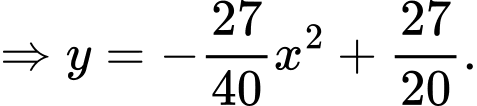
Gọi
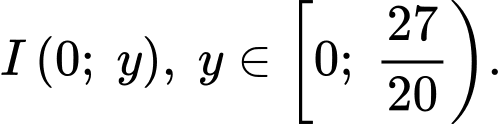
Mặt phẳng vuông góc
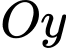 tại
tại 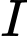 cắt hình đa cho theo 1 thiết diện là hình vuông
cắt hình đa cho theo 1 thiết diện là hình vuông 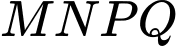 có diện tích
có diện tích 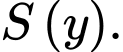
Theo giả thiết trên các điểm
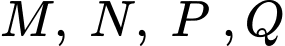 cùng có tung độ bằng
cùng có tung độ bằng 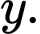 Mà hai điểm
Mà hai điểm  thuộc đường
thuộc đường 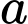 có phương trình
có phương trình 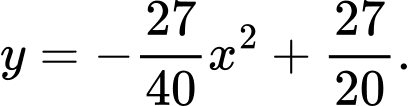
Suy ra
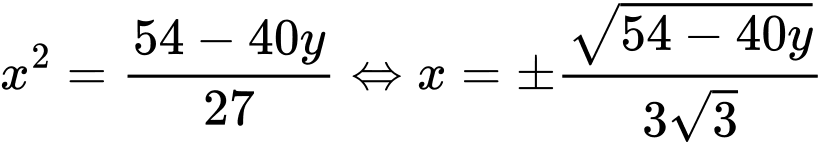
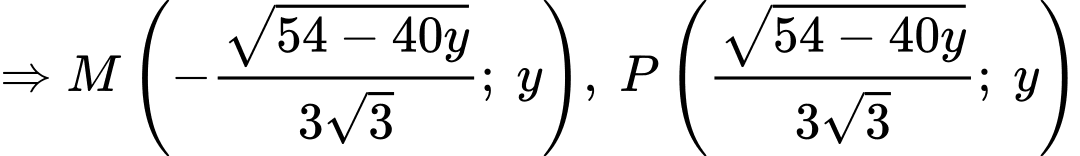
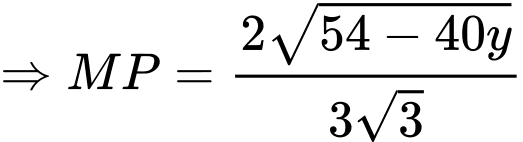
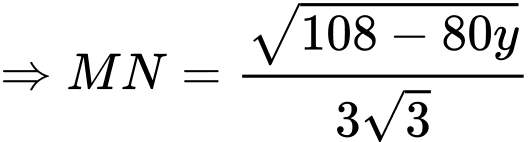
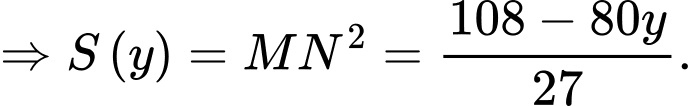
Suy ra thể tích chiếc lều là