PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1 [543785]: Cho hàm số 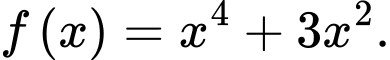 Khẳng định nào dưới đây đúng?
Khẳng định nào dưới đây đúng?
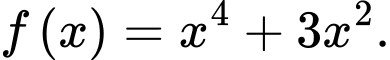 Khẳng định nào dưới đây đúng?
Khẳng định nào dưới đây đúng? A, 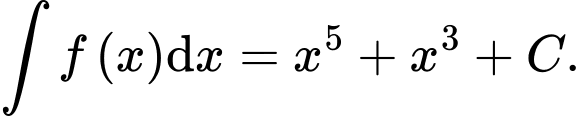
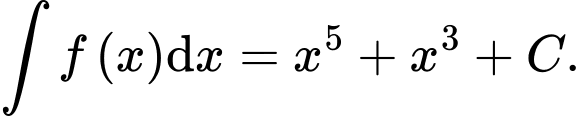
B, 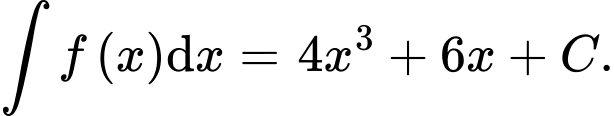
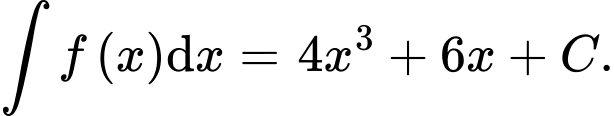
C, 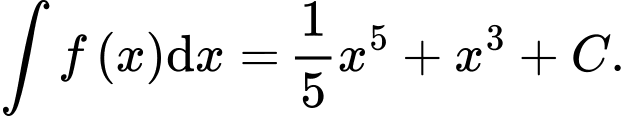
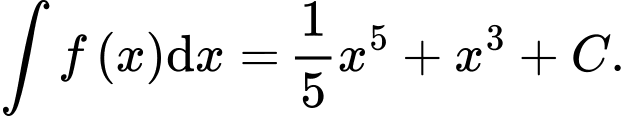
D, 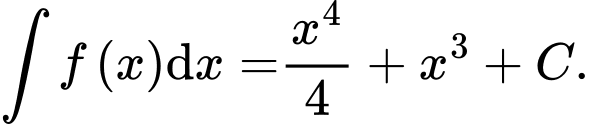
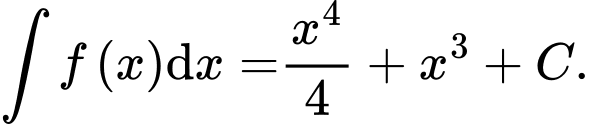
Chọn đáp án C.
Ta có: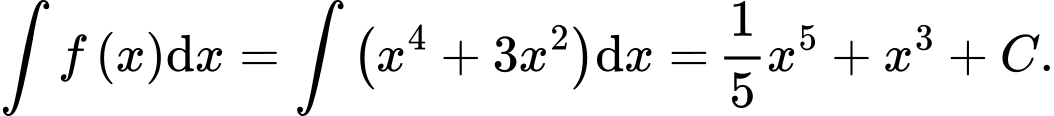 Đáp án: C
Đáp án: C
Ta có:
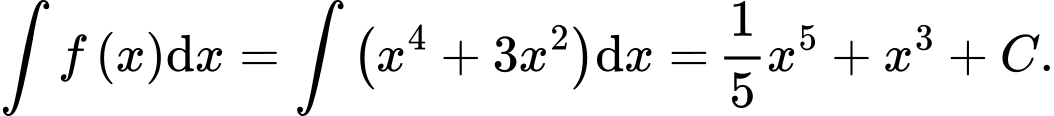 Đáp án: C
Đáp án: C
Câu 2 [754786]: Nếu 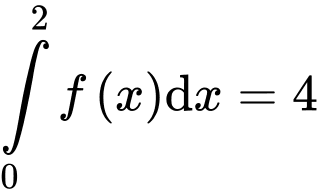 thì
thì 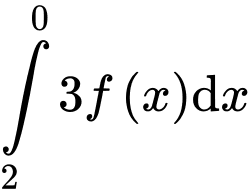 bằng
bằng
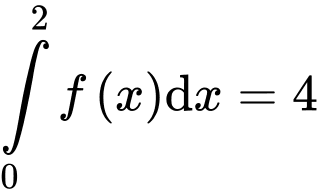 thì
thì 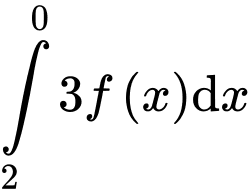 bằng
bằng A,
 .
.
B,
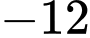 .
.
C,
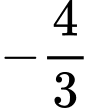 .
.
D,
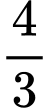 .
.
Chọn đáp án B.
Ta có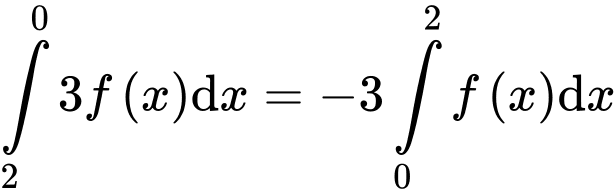
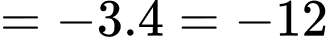 Đáp án: B
Đáp án: B
Ta có
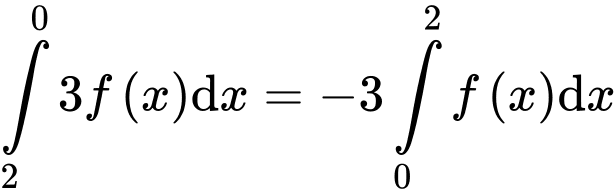
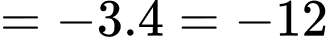 Đáp án: B
Đáp án: B
Câu 3 [393599]: Gọi 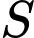 là diện tích của hình phẳng giới hạn bởi các đường
là diện tích của hình phẳng giới hạn bởi các đường 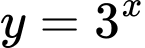 ,
, 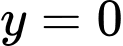 ,
, 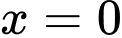 ,
, 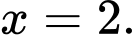 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng?
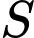 là diện tích của hình phẳng giới hạn bởi các đường
là diện tích của hình phẳng giới hạn bởi các đường 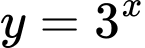 ,
, 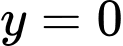 ,
, 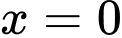 ,
, 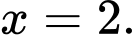 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng? A, 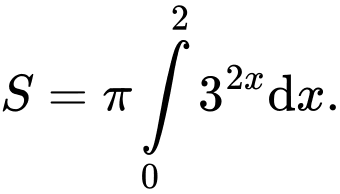
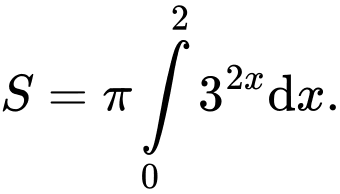
B, 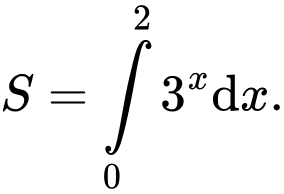
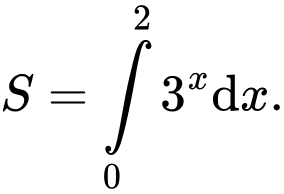
C, 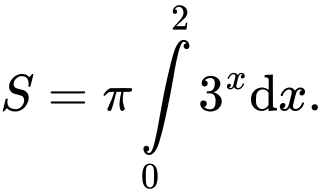
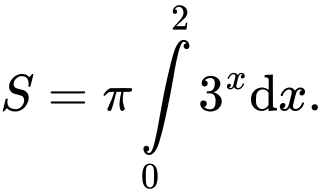
D, 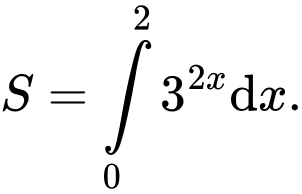
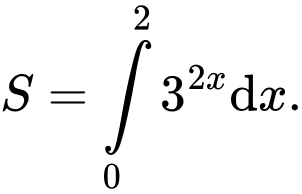
Chọn đáp án B.
Diện tích của hình phẳng giới hạn bởi các đường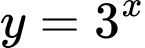 ,
, 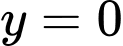 ,
, 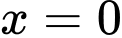 ,
, 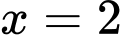 là
là
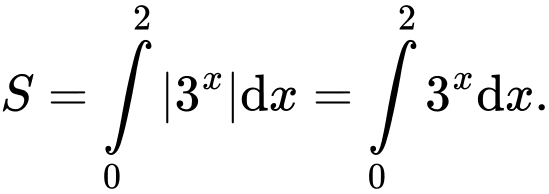 Đáp án: B
Đáp án: B
Diện tích của hình phẳng giới hạn bởi các đường
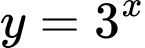 ,
, 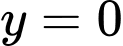 ,
, 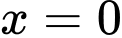 ,
, 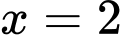 là
là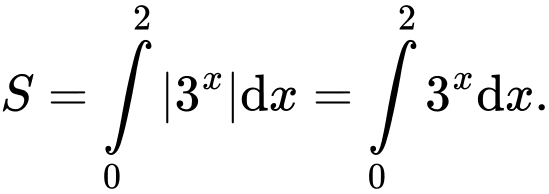 Đáp án: B
Đáp án: B
Câu 4 [151429]: Tính thể tích  của phần vật thế giới hạn bởi hai mặt phẳng
của phần vật thế giới hạn bởi hai mặt phẳng 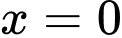 và
và 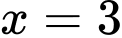 , biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục
, biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục 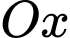 tại điểm có hoành độ
tại điểm có hoành độ 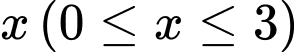 là một hình chữ nhật có hai kích thước là
là một hình chữ nhật có hai kích thước là 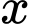 và
và  .
.
 của phần vật thế giới hạn bởi hai mặt phẳng
của phần vật thế giới hạn bởi hai mặt phẳng 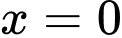 và
và 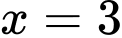 , biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục
, biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục 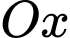 tại điểm có hoành độ
tại điểm có hoành độ 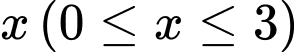 là một hình chữ nhật có hai kích thước là
là một hình chữ nhật có hai kích thước là 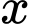 và
và  .
. A, 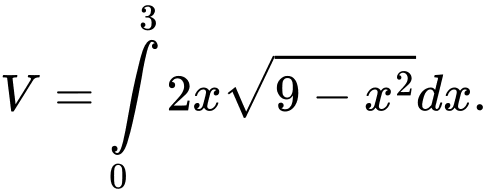
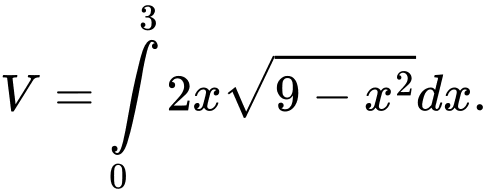
B, 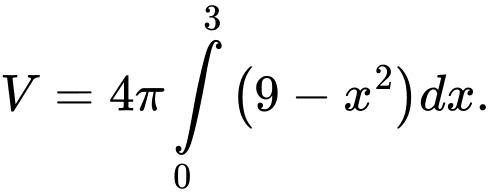
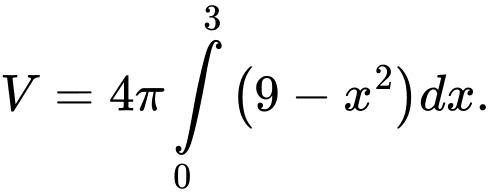
C, 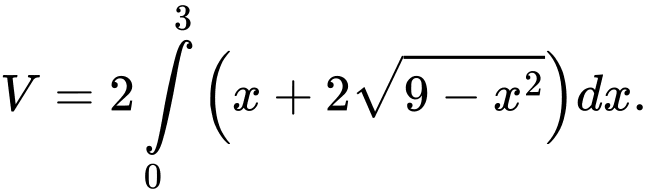
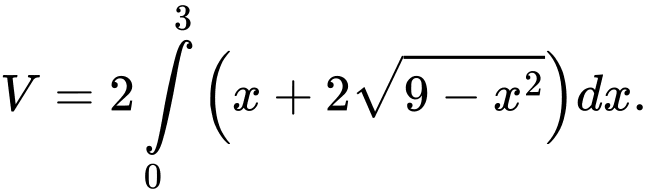
D, 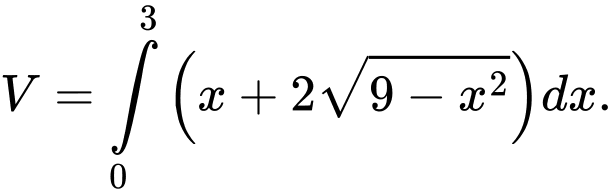
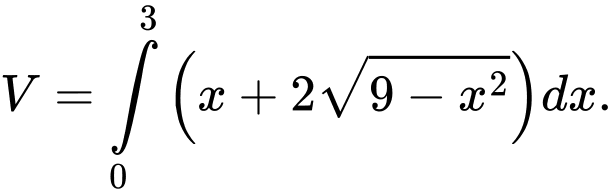
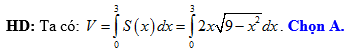 Đáp án: A
Đáp án: A
Câu 5 [543562]: Khẳng định nào sau đây đúng?
A, 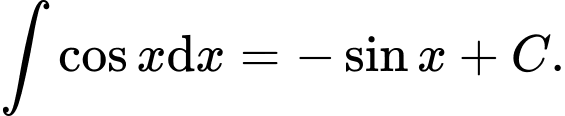
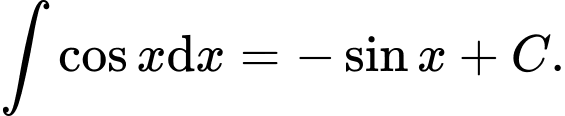
B, 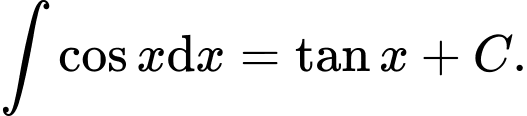
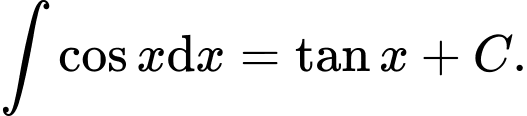
C, 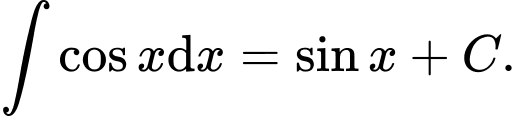
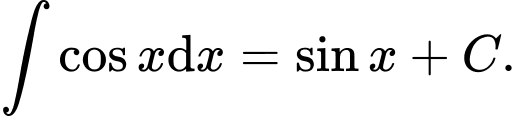
D, 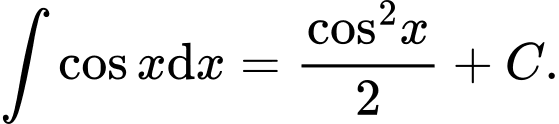
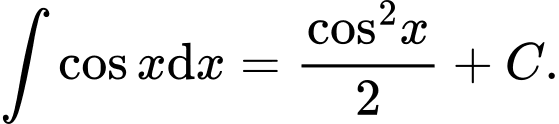
Chọn C
Theo công thức nguyên hàm của các hàm số sơ cấp ta có: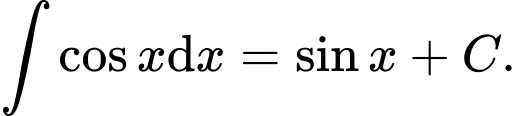 Đáp án: C
Đáp án: C
Theo công thức nguyên hàm của các hàm số sơ cấp ta có:
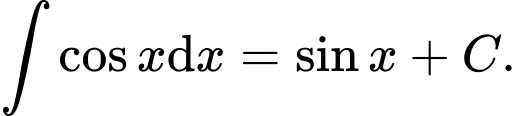 Đáp án: C
Đáp án: C
Câu 6 [151266]: Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?
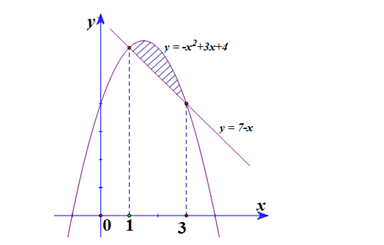

A, 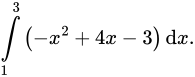
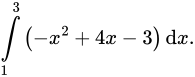
B, 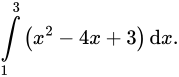
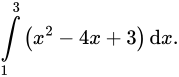
C, 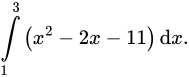
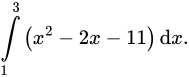
D, 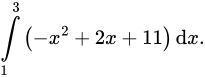
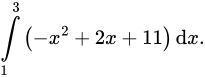
 Đáp án: A
Đáp án: A
Câu 7 [116482]: Cho hình phẳng 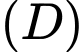 được giới hạn bởi các đường
được giới hạn bởi các đường 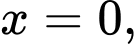
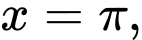
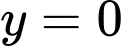 và
và 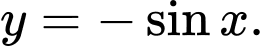 Thể tích
Thể tích  của khối tròn xoay tạo thành khi quay
của khối tròn xoay tạo thành khi quay 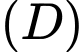 xung quanh trục
xung quanh trục 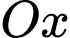 được tính theo công thức:
được tính theo công thức:
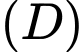 được giới hạn bởi các đường
được giới hạn bởi các đường 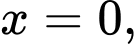
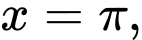
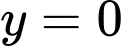 và
và 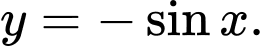 Thể tích
Thể tích  của khối tròn xoay tạo thành khi quay
của khối tròn xoay tạo thành khi quay 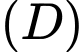 xung quanh trục
xung quanh trục 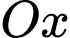 được tính theo công thức:
được tính theo công thức: A, 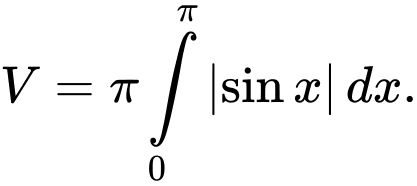
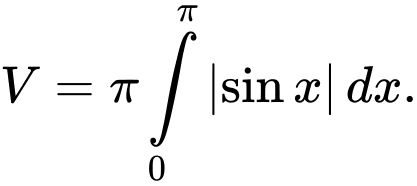
B, 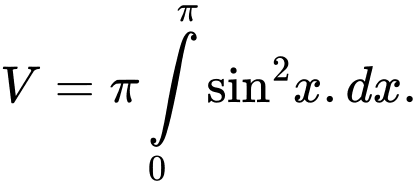
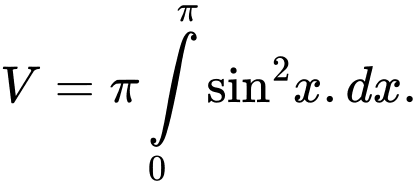
C, 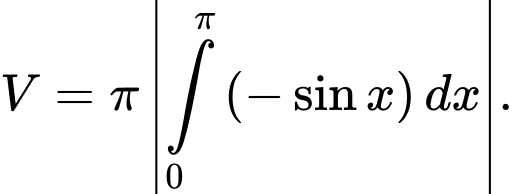
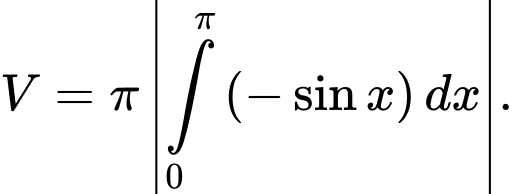
D, 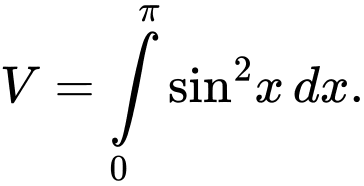
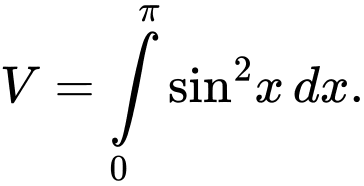
HD: Ta có 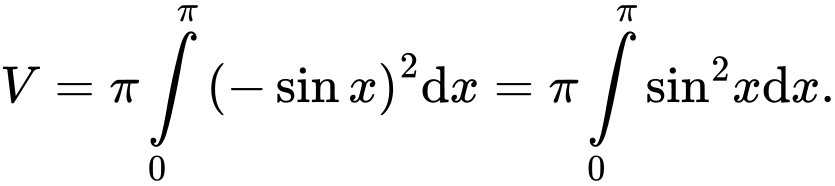 Chọn B. Đáp án: B
Chọn B. Đáp án: B
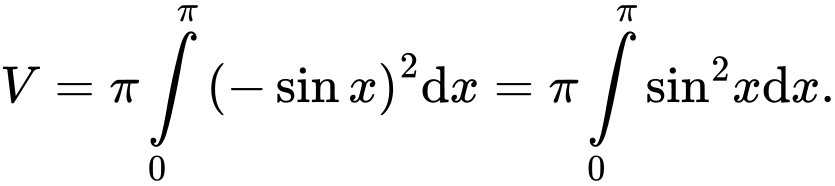 Chọn B. Đáp án: B
Chọn B. Đáp án: B
Câu 8 [732028]: [MĐ1] Diện tích hình phẳng giới hạn bởi các đường 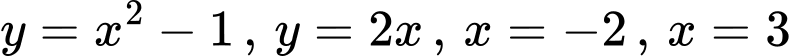 được tính bằng
được tính bằng
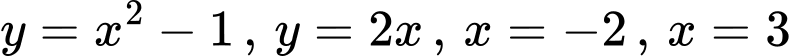 được tính bằng
được tính bằng A, 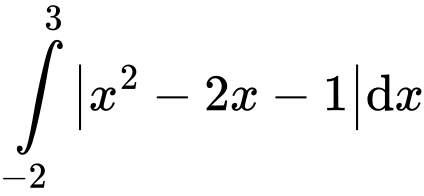 .
.
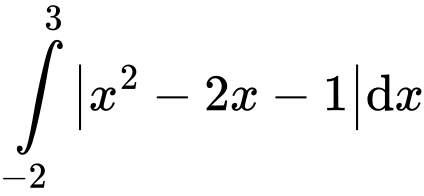 .
.B, 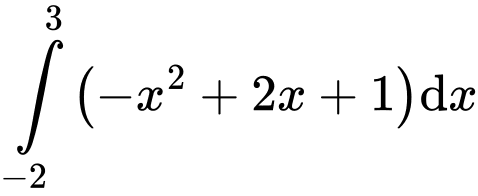 .
.
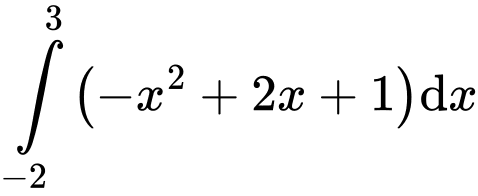 .
.C, 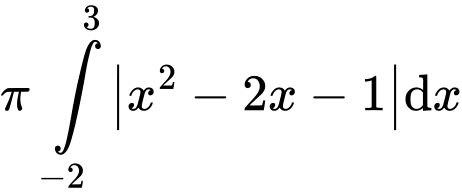 .
.
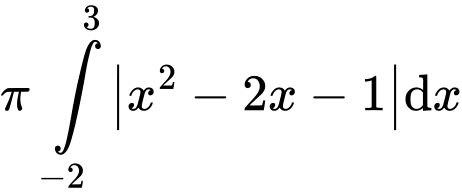 .
.D, 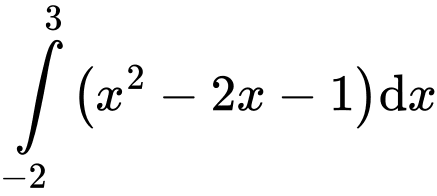 .
.
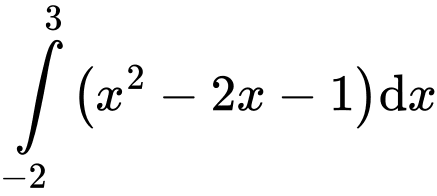 .
.
Diện tích hình phẳng giới hạn bởi các đường 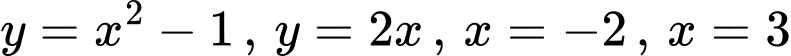 được tính bởi công thức
được tính bởi công thức 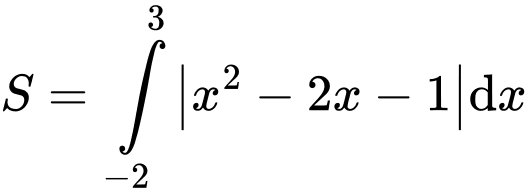 . Đáp án: A
. Đáp án: A
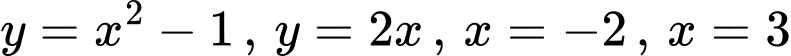 được tính bởi công thức
được tính bởi công thức 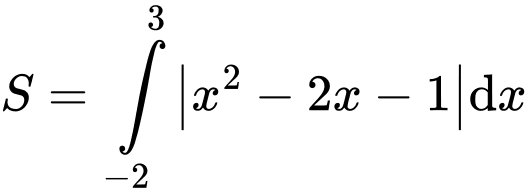 . Đáp án: A
. Đáp án: A
Câu 9 [547052]: Nếu 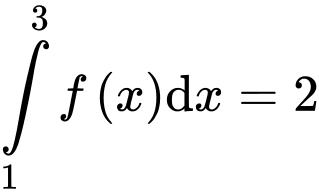 và
và 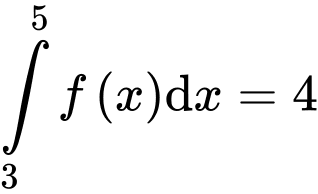 thì
thì 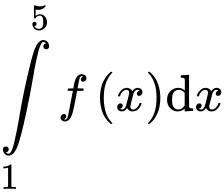 bằng
bằng
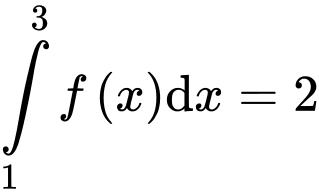 và
và 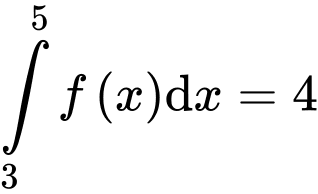 thì
thì 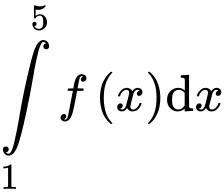 bằng
bằng A, 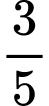 .
.
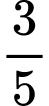 .
.B, 12.
C, 6.
D, 3.
Chọn C.
Ta có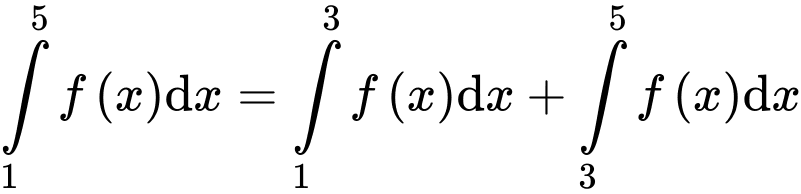
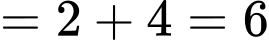 . Đáp án: C
. Đáp án: C
Ta có
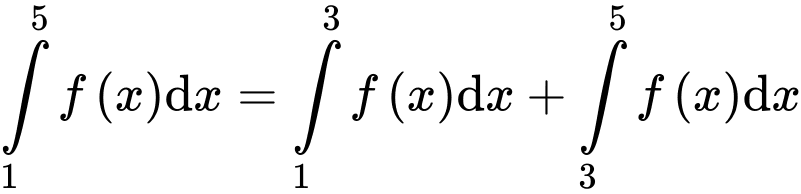
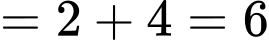 . Đáp án: C
. Đáp án: C
Câu 10 [80737]: Cho đồ thị hàm số 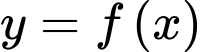 như hình vẽ. Diện tích
như hình vẽ. Diện tích 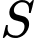 của hình phẳng được giới hạn bởi đồ thị hàm số
của hình phẳng được giới hạn bởi đồ thị hàm số 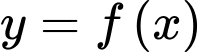 và trục
và trục 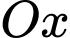 (phần gạch sọc) được tính bởi công thức
(phần gạch sọc) được tính bởi công thức
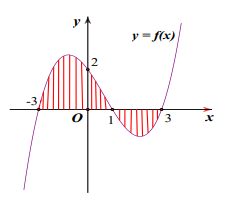
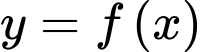 như hình vẽ. Diện tích
như hình vẽ. Diện tích 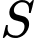 của hình phẳng được giới hạn bởi đồ thị hàm số
của hình phẳng được giới hạn bởi đồ thị hàm số 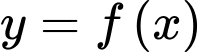 và trục
và trục 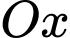 (phần gạch sọc) được tính bởi công thức
(phần gạch sọc) được tính bởi công thức
A, 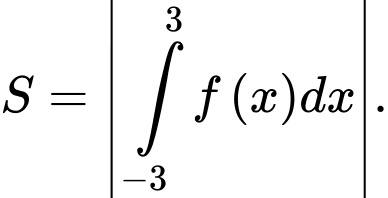
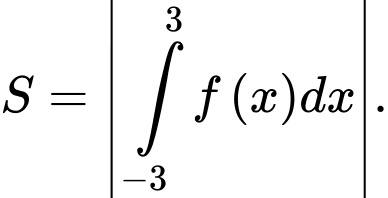
B, 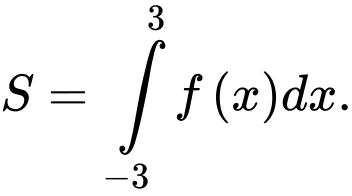
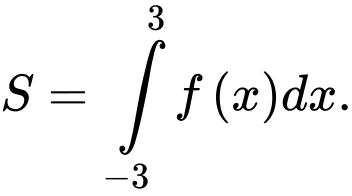
C, 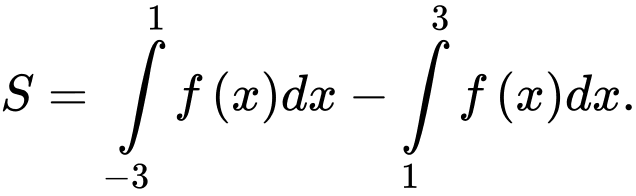
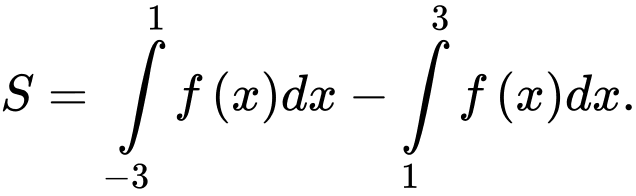
D, 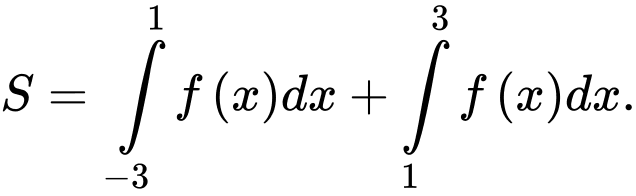
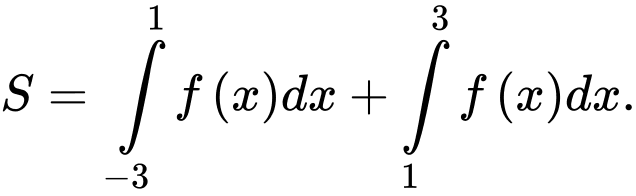
 Đáp án: C
Đáp án: C
Câu 11 [151240]: Diện tích của hình phẳng được giới hạn bởi miền 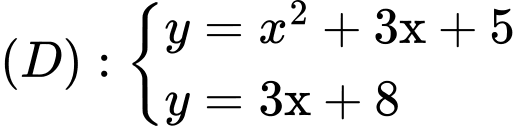 bằng
bằng
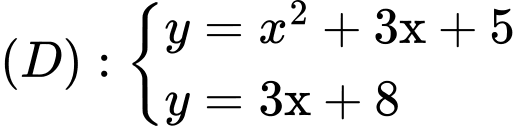 bằng
bằng A, 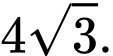
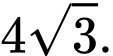
B, 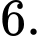
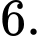
C, 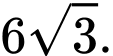
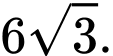
D, 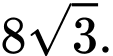
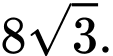
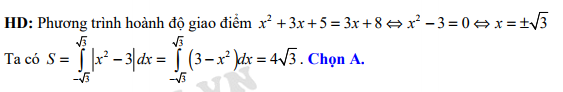 Đáp án: A
Đáp án: A
Câu 12 [151634]: Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường 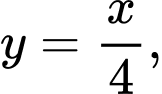
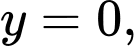
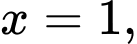
 khi quay quanh trục
khi quay quanh trục 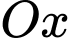 bằng
bằng
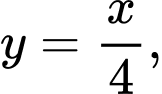
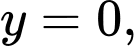
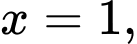
 khi quay quanh trục
khi quay quanh trục 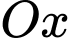 bằng
bằng A, 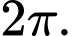
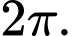
B, 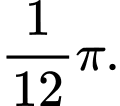
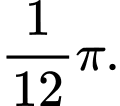
C, 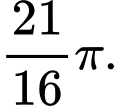
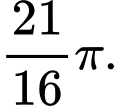
D, 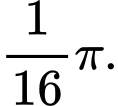
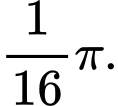
Đáp án C
Thể tích khối tròn xoay cần tìm là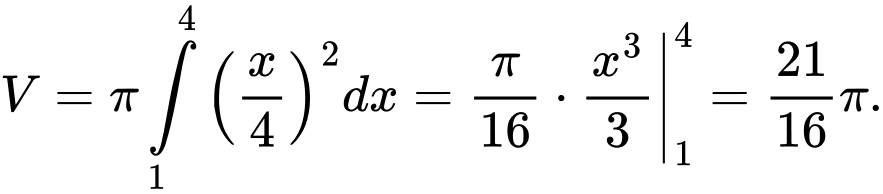 Đáp án: C
Đáp án: C
Thể tích khối tròn xoay cần tìm là
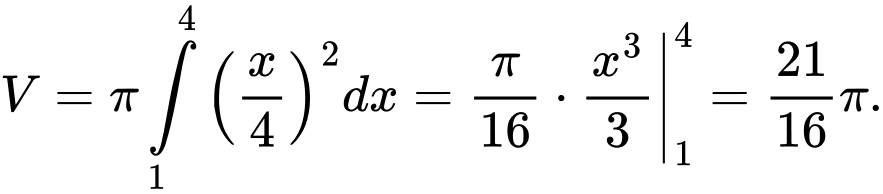 Đáp án: C
Đáp án: C PHẦN II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a), b), c), d) ở mỗi câu học sinh chọn đúng hoặc sai.
Câu 13 [779605]: Cho hàm số 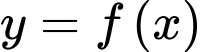 có đạo hàm
có đạo hàm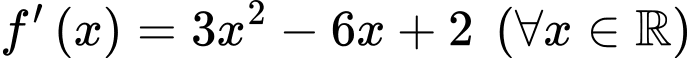 và thoả mãn
và thoả mãn 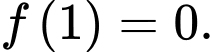
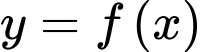 có đạo hàm
có đạo hàm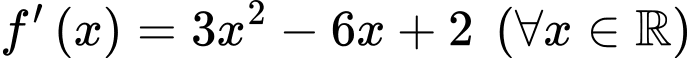 và thoả mãn
và thoả mãn 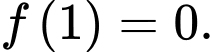
a) Sai.
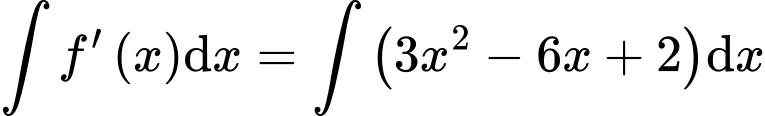
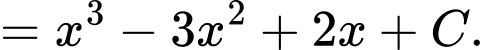
b) Đúng.
Ta có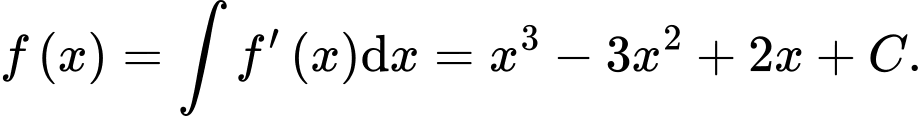
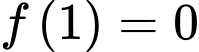

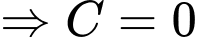
Suy ra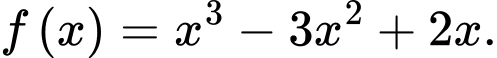
Vậy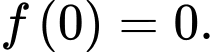
c) Đúng.
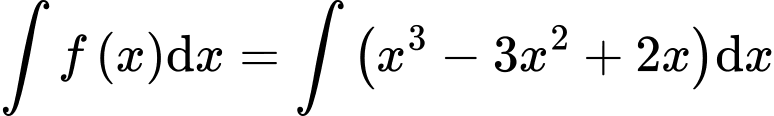
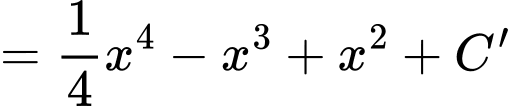
d) Sai.
Phương trình hoành độ giao điểm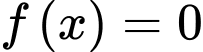
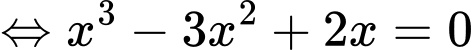
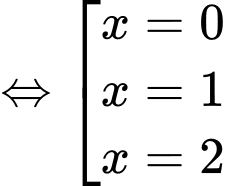
Diện tích hình phẳng giới hạn bởi đồ thị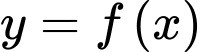 trục hoành, trục tung và đường thẳng
trục hoành, trục tung và đường thẳng 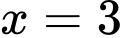 bằng
bằng 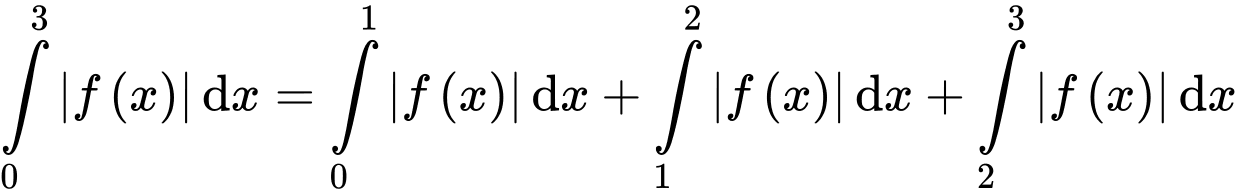
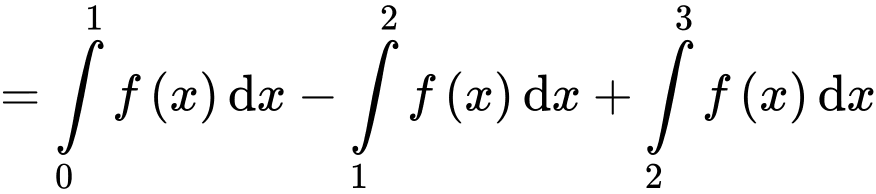
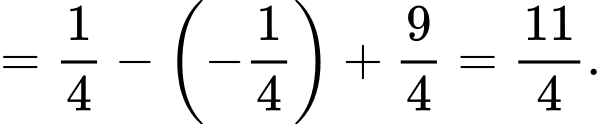
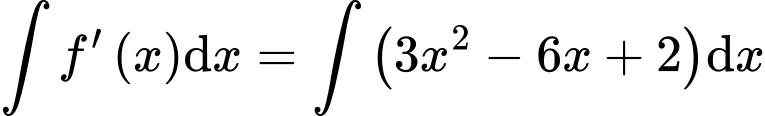
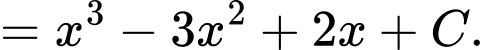
b) Đúng.
Ta có
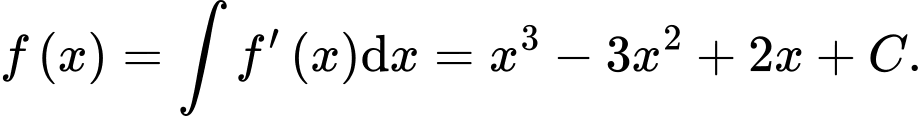
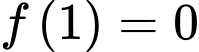

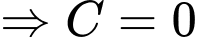
Suy ra
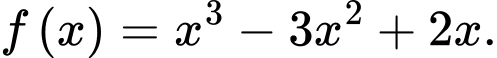
Vậy
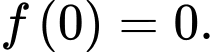
c) Đúng.
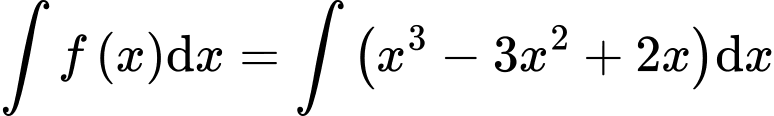
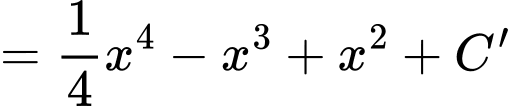
d) Sai.
Phương trình hoành độ giao điểm
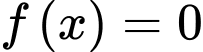
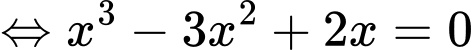
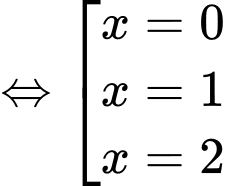
Diện tích hình phẳng giới hạn bởi đồ thị
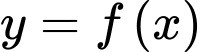 trục hoành, trục tung và đường thẳng
trục hoành, trục tung và đường thẳng 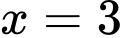 bằng
bằng 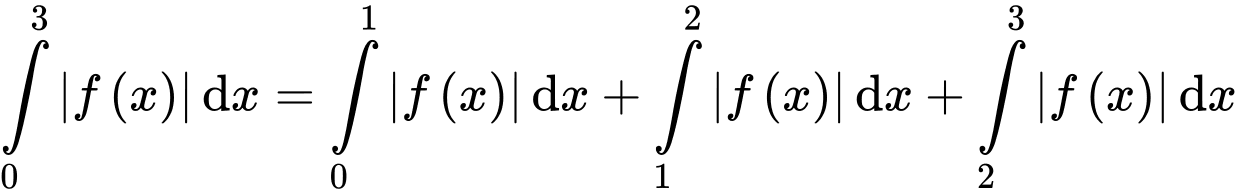
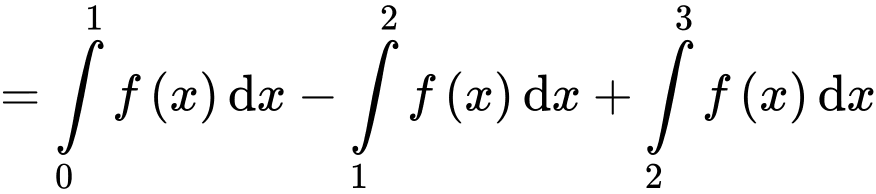
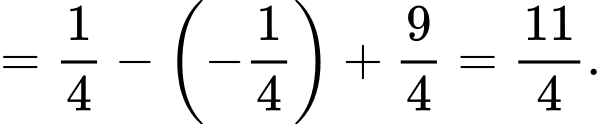
Câu 14 [779607]: Một công ty thiết kế mẫu huy hiệu để tặng cho khách hàng thân thiết của mình (xem hình bên). Trong đó 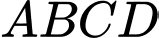 là hình vuông có cạnh bằng 4 cm, các đường cong
là hình vuông có cạnh bằng 4 cm, các đường cong  và
và  là một phần của các parabol đỉnh
là một phần của các parabol đỉnh  Với hệ trục tọa độ
Với hệ trục tọa độ 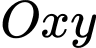 (đơn vị trên mỗi trục tọa độ là centimét) thì điểm
(đơn vị trên mỗi trục tọa độ là centimét) thì điểm 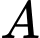 có tung độ bằng 1. Biết phần tô đậm trong hình vẽ được phủ vàng với chi phí 1 triệu đồng/
có tung độ bằng 1. Biết phần tô đậm trong hình vẽ được phủ vàng với chi phí 1 triệu đồng/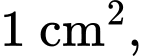 phần còn lại được phủ bạc với chi phí 300 nghìn đồng/
phần còn lại được phủ bạc với chi phí 300 nghìn đồng/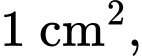 các chi phí còn lại là 500 nghìn đồng.
các chi phí còn lại là 500 nghìn đồng.
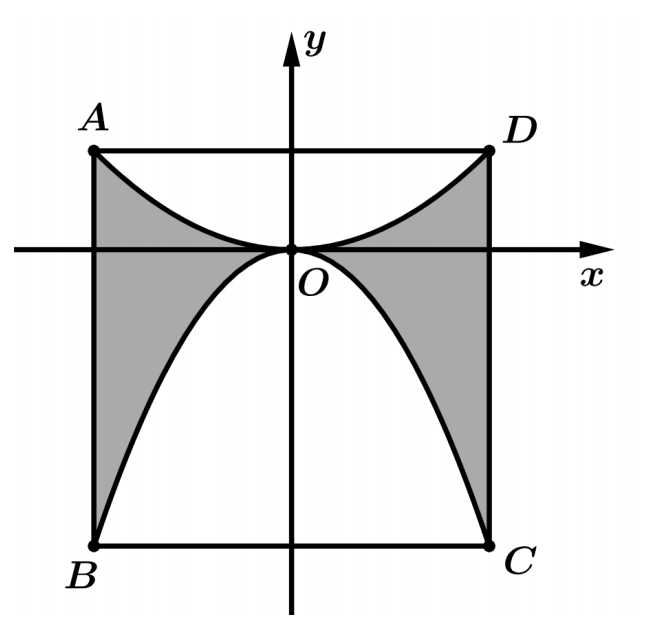
 là hình vuông có cạnh bằng 4 cm, các đường cong
là hình vuông có cạnh bằng 4 cm, các đường cong  và
và  là một phần của các parabol đỉnh
là một phần của các parabol đỉnh  Với hệ trục tọa độ
Với hệ trục tọa độ 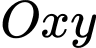 (đơn vị trên mỗi trục tọa độ là centimét) thì điểm
(đơn vị trên mỗi trục tọa độ là centimét) thì điểm 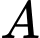 có tung độ bằng 1. Biết phần tô đậm trong hình vẽ được phủ vàng với chi phí 1 triệu đồng/
có tung độ bằng 1. Biết phần tô đậm trong hình vẽ được phủ vàng với chi phí 1 triệu đồng/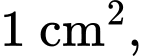 phần còn lại được phủ bạc với chi phí 300 nghìn đồng/
phần còn lại được phủ bạc với chi phí 300 nghìn đồng/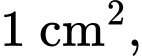 các chi phí còn lại là 500 nghìn đồng.
các chi phí còn lại là 500 nghìn đồng.
Ta có 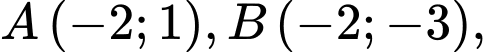
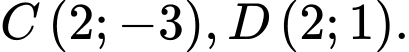
a) Sai.
Gọi phương trình parabol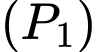 chứa đường cong
chứa đường cong  có dạng:
có dạng: 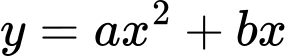
Ta có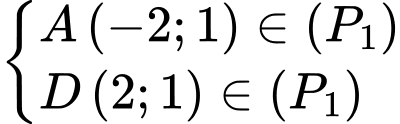
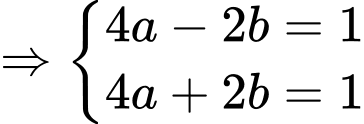
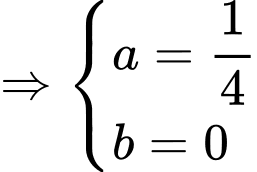
Vậy parabol chứa đường cong có phương trình là
có phương trình là 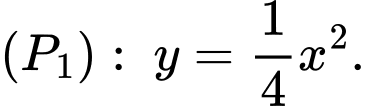
b) Đúng.
Gọi phương trình parabol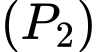 chứa đường cong
chứa đường cong  có dạng:
có dạng: 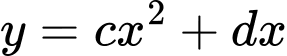
Ta có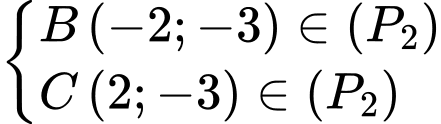
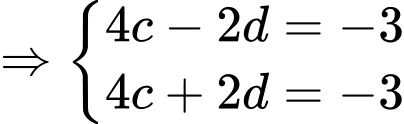
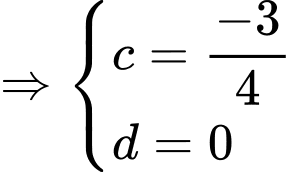
Vậy parabol chứa đường cong có phương trình là
có phương trình là 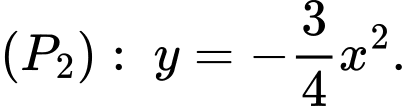
c) Sai.
Vì diện tích của huy hiệu đối xứng qua trục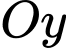 nên diện tích của phần tô đậm sẽ bằng 2 lần diện tích miền giới hạn bởi đường cong
nên diện tích của phần tô đậm sẽ bằng 2 lần diện tích miền giới hạn bởi đường cong 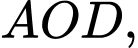
 và các đường thẳng
và các đường thẳng 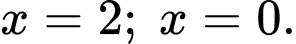 Áp dụng công thức ứng dụng tích phân vào tính diện tích, ta được:
Áp dụng công thức ứng dụng tích phân vào tính diện tích, ta được:
Diện tích phần tô đậm trong hình vẽ bằng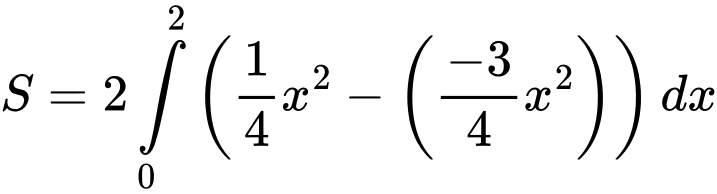
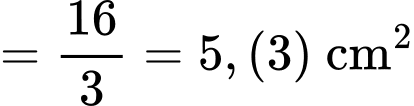
d) Sai.
Diện tích phần không tô đậm bằng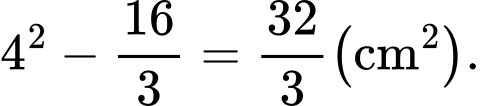
Chi phí sản xuất 1 chiếc huy hiệu là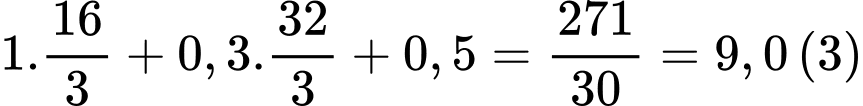 triệu đồng.
triệu đồng.
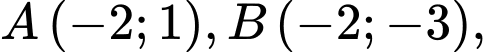
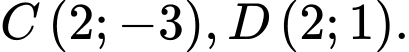
a) Sai.
Gọi phương trình parabol
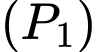 chứa đường cong
chứa đường cong  có dạng:
có dạng: 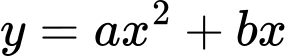
Ta có
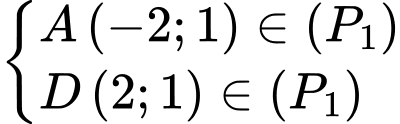
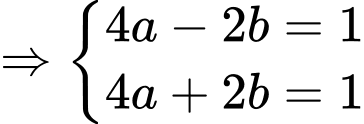
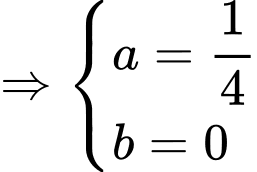
Vậy parabol chứa đường cong
 có phương trình là
có phương trình là 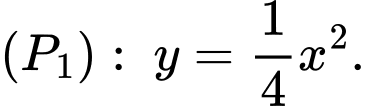
b) Đúng.
Gọi phương trình parabol
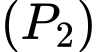 chứa đường cong
chứa đường cong  có dạng:
có dạng: 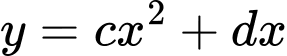
Ta có
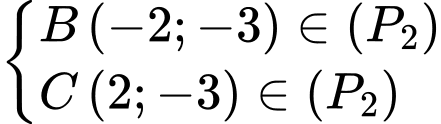
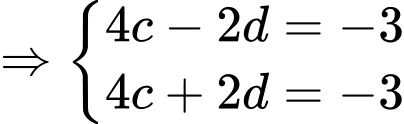
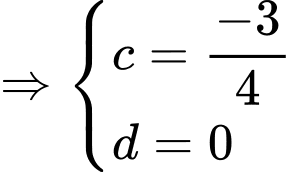
Vậy parabol chứa đường cong
 có phương trình là
có phương trình là 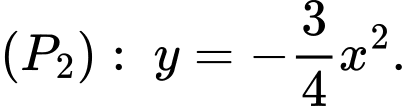
c) Sai.
Vì diện tích của huy hiệu đối xứng qua trục
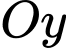 nên diện tích của phần tô đậm sẽ bằng 2 lần diện tích miền giới hạn bởi đường cong
nên diện tích của phần tô đậm sẽ bằng 2 lần diện tích miền giới hạn bởi đường cong 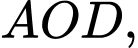
 và các đường thẳng
và các đường thẳng 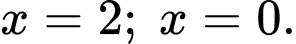 Áp dụng công thức ứng dụng tích phân vào tính diện tích, ta được:
Áp dụng công thức ứng dụng tích phân vào tính diện tích, ta được:Diện tích phần tô đậm trong hình vẽ bằng
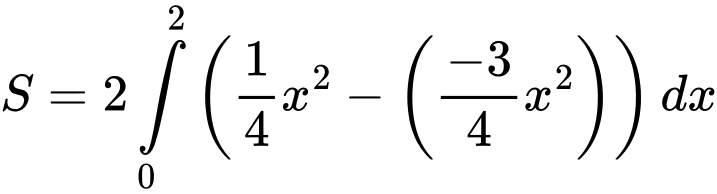
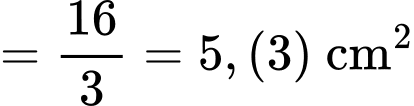
d) Sai.
Diện tích phần không tô đậm bằng
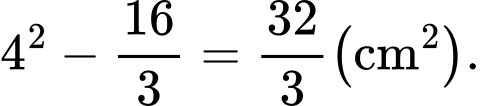
Chi phí sản xuất 1 chiếc huy hiệu là
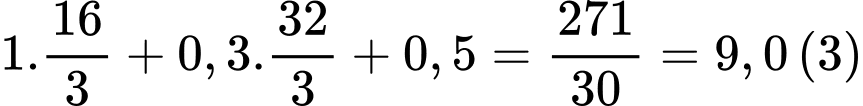 triệu đồng.
triệu đồng.
Câu 15 [778756]: Biết 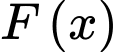 và
và 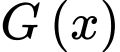 là hai nguyên hàm của hàm số
là hai nguyên hàm của hàm số 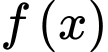 trên
trên 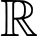 và
và 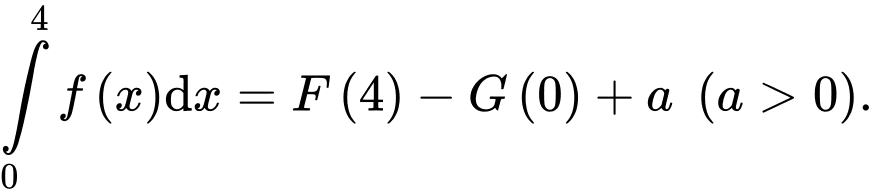 Gọi
Gọi 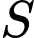 là diện tích hình phẳng giới hạn bởi các đường
là diện tích hình phẳng giới hạn bởi các đường 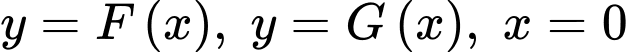 và
và 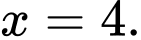
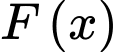 và
và 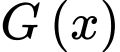 là hai nguyên hàm của hàm số
là hai nguyên hàm của hàm số 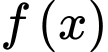 trên
trên 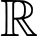 và
và 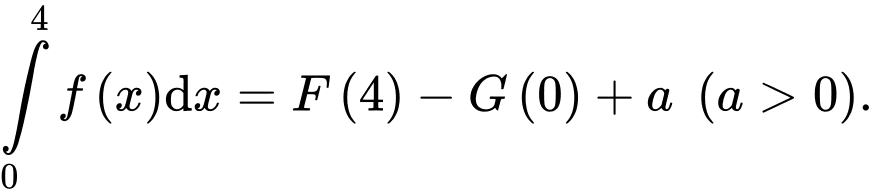 Gọi
Gọi 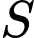 là diện tích hình phẳng giới hạn bởi các đường
là diện tích hình phẳng giới hạn bởi các đường 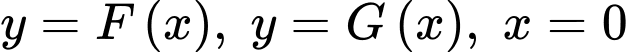 và
và 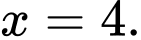
a) Sai.
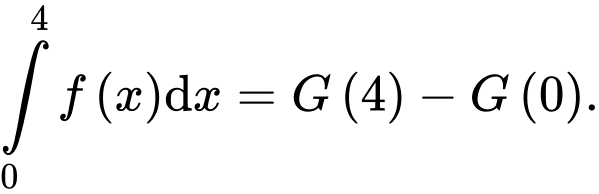
b) Đúng.
c) Đúng.
Khi thì
thì 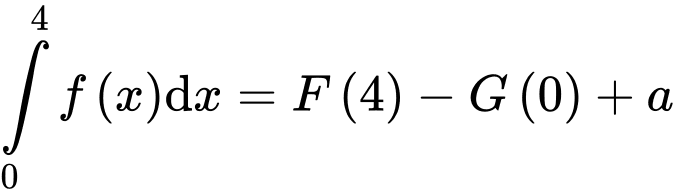
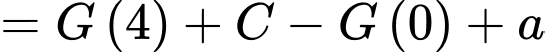
Mặt khác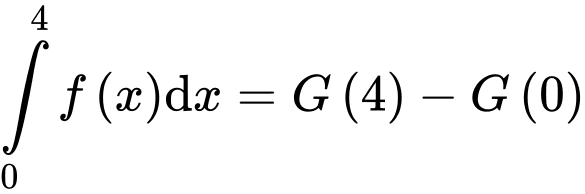 nên
nên 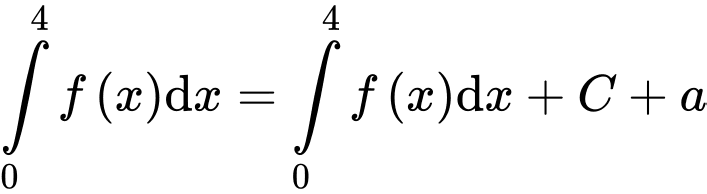
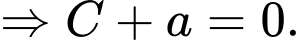
d) Sai.
Lại có: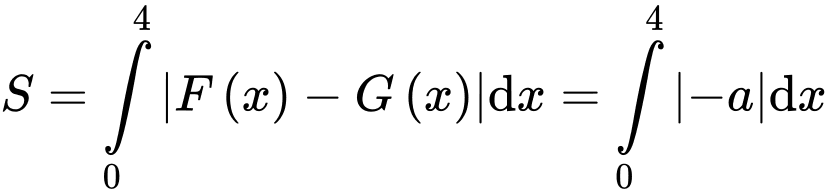
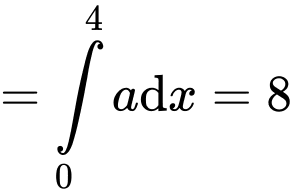
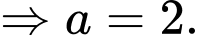
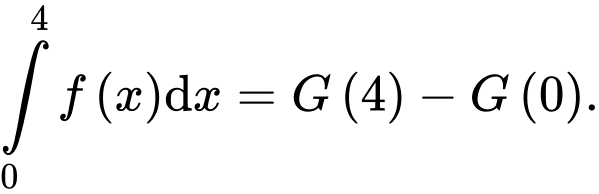
b) Đúng.
c) Đúng.
Khi
 thì
thì 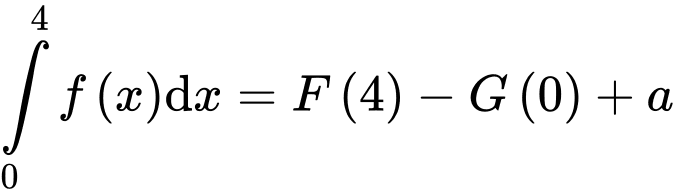
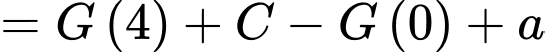
Mặt khác
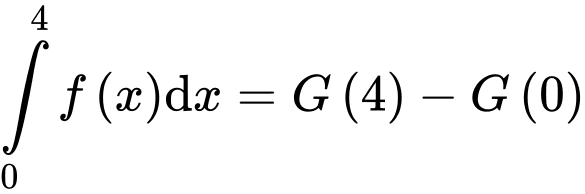 nên
nên 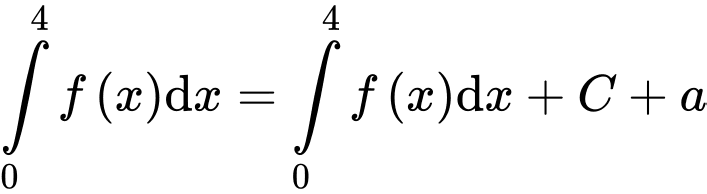
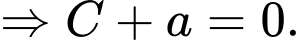
d) Sai.
Lại có:
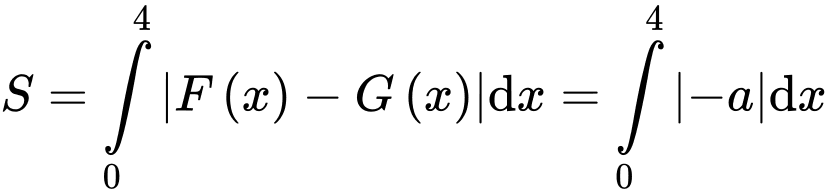
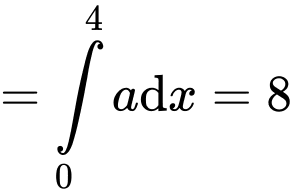
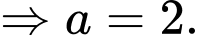
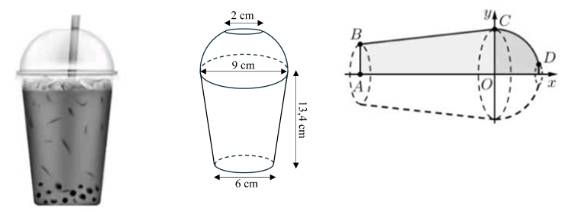
Câu 16 [693783]: Một ly trà sữa dạng hình nón cụt, có đường kính đáy ly là 6 cm, đường kính miệng ly là 9cm, chiều cao 13, 4 cm, ở miệng ly có sử dụng một nắp đậy có hình dạng nửa mặt cầu và ở đỉnh của nửa mặt cầu này có một hình tròn có đường kính 2cm để cắm ống hút, mặt phẳng chứa hình tròn này song song với mặt phẳng chứa miệng ly (tham khảo hình vẽ)
Chọn hệ trục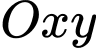 (đơn vị trên trục là centimet) với trục
(đơn vị trên trục là centimet) với trục 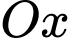 đi qua tâm của 2 đáy hình nón cụt và gốc toạ độ
đi qua tâm của 2 đáy hình nón cụt và gốc toạ độ  trùng với tâm của đáy lớn như hình vẽ.
trùng với tâm của đáy lớn như hình vẽ.

Chọn hệ trục
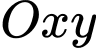 (đơn vị trên trục là centimet) với trục
(đơn vị trên trục là centimet) với trục 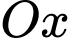 đi qua tâm của 2 đáy hình nón cụt và gốc toạ độ
đi qua tâm của 2 đáy hình nón cụt và gốc toạ độ  trùng với tâm của đáy lớn như hình vẽ.
trùng với tâm của đáy lớn như hình vẽ.
a) Đúng.
Phương trình đường thẳng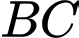 có dạng
có dạng 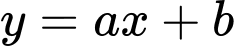 đi qua 2 điểm
đi qua 2 điểm 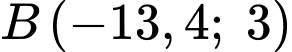 và
và 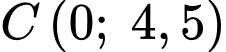 nên
nên
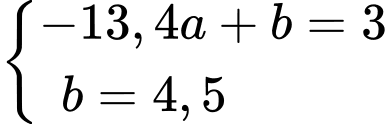
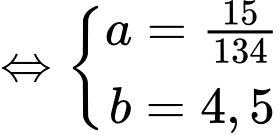
Vậy phương trình đường thẳng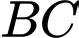 là
là 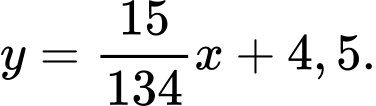
b) Đúng.
Phương trình đường tròn tâm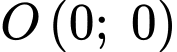 bán kính
bán kính 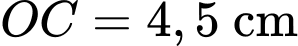 là
là 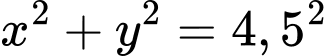 .
.
Do đường tròn đi qua điểm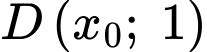 nên
nên 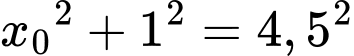
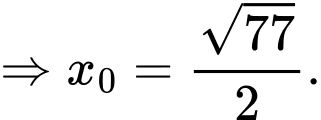
Vậy toạ độ điểm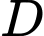 là
là 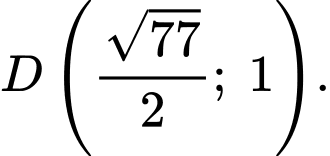
c) Đúng.
Thể tích bên trong ly không bao gồm nắp là
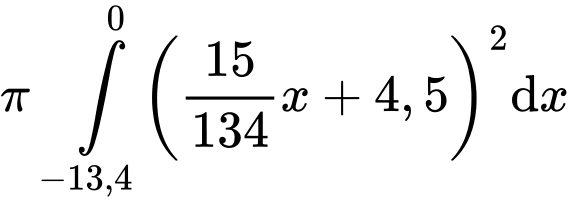
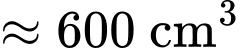
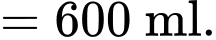
d) Đúng.
Đường tròn nắp ly có phương trình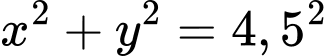
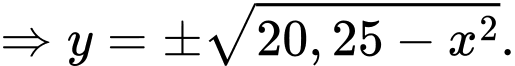
Ta xét phần dương của nắp ly, ta có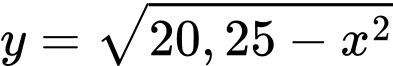 .
.
Thế tích nắp ly là: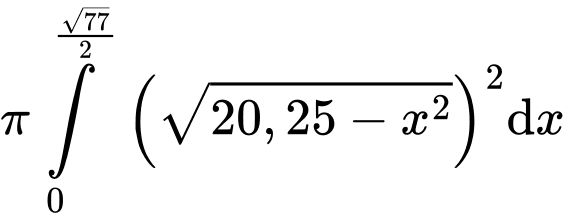
Vậy thể tích bên trong ly bao gồm cả thể tích nắp là:
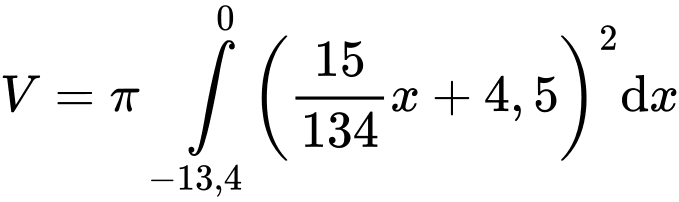
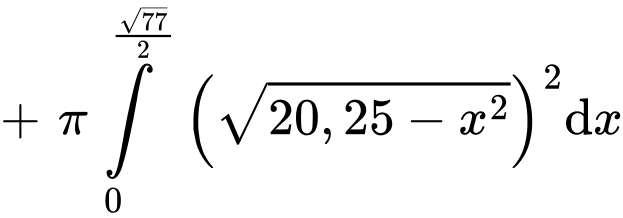
Phương trình đường thẳng
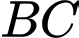 có dạng
có dạng 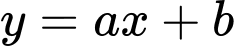 đi qua 2 điểm
đi qua 2 điểm 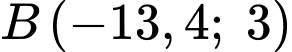 và
và 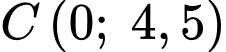 nên
nên
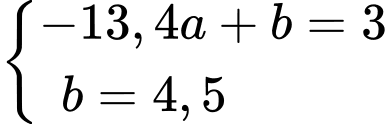
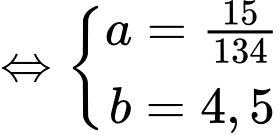
Vậy phương trình đường thẳng
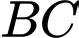 là
là 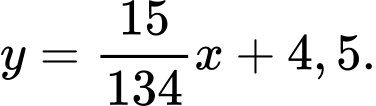
b) Đúng.
Phương trình đường tròn tâm
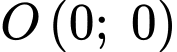 bán kính
bán kính 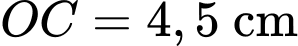 là
là 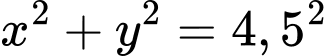 .
.
Do đường tròn đi qua điểm
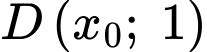 nên
nên 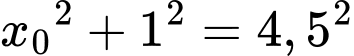
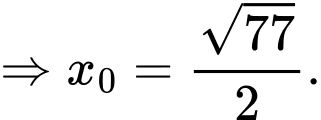
Vậy toạ độ điểm
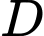 là
là 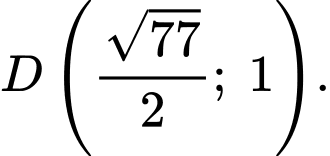
c) Đúng.
Thể tích bên trong ly không bao gồm nắp là
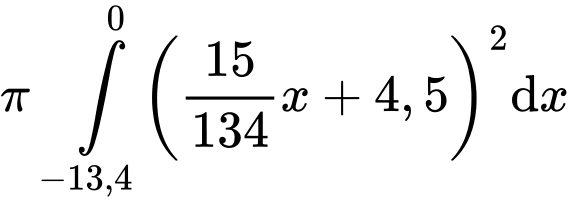
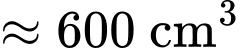
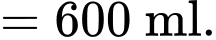
d) Đúng.
Đường tròn nắp ly có phương trình
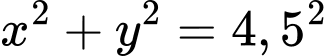
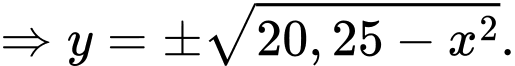
Ta xét phần dương của nắp ly, ta có
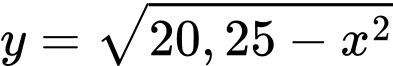 .
.
Thế tích nắp ly là:
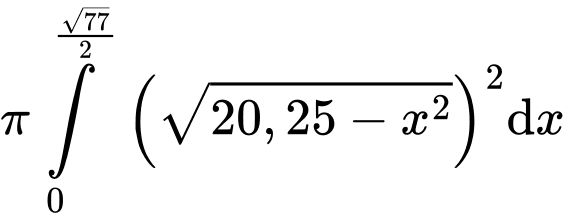
Vậy thể tích bên trong ly bao gồm cả thể tích nắp là:
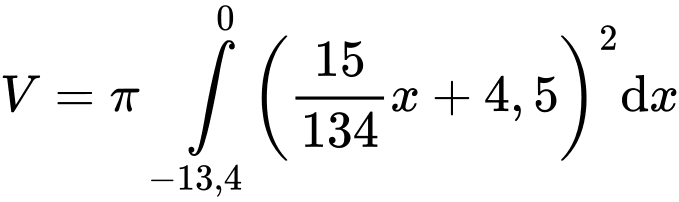
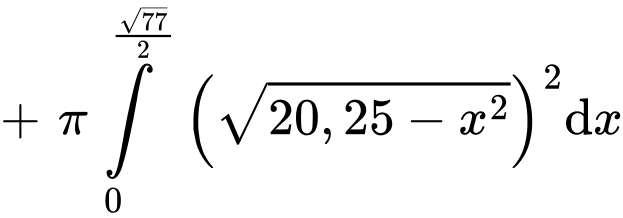
PHẦN III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 17 đến câu 22.
Câu 17 [779022]: Người ta cho một chiếc xe điện mô hình chạy thử nghiệm trên một đường thẳng trong 24 giây với vận tốc 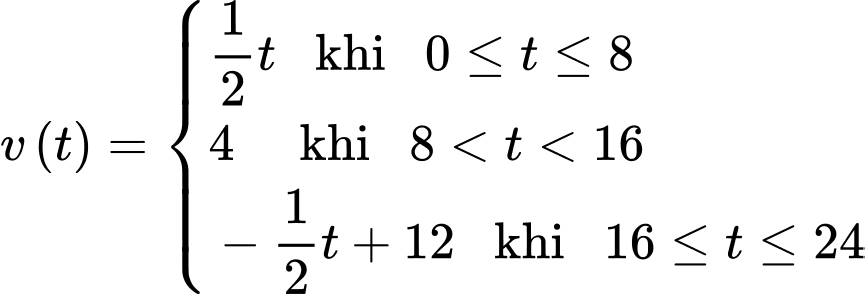 (decimet/giây), trong đó
(decimet/giây), trong đó 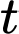 là khoảng thời gian tính bằng giây kể từ lúc xe bắt đầu chuyển động. Trong 24 giây chạy thử nghiệm đó, chiếc xe mô hình đi được quãng đường bao nhiêu decimet?
là khoảng thời gian tính bằng giây kể từ lúc xe bắt đầu chuyển động. Trong 24 giây chạy thử nghiệm đó, chiếc xe mô hình đi được quãng đường bao nhiêu decimet?
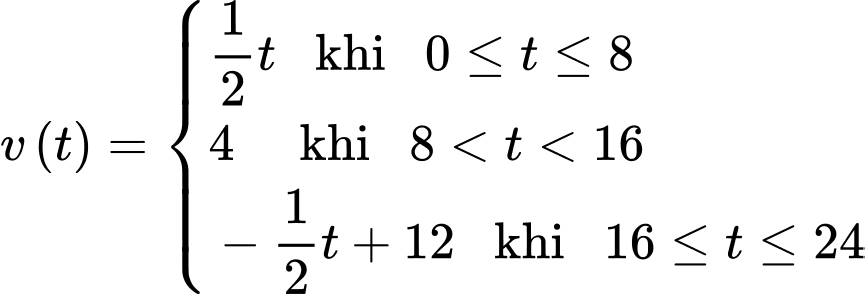 (decimet/giây), trong đó
(decimet/giây), trong đó 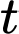 là khoảng thời gian tính bằng giây kể từ lúc xe bắt đầu chuyển động. Trong 24 giây chạy thử nghiệm đó, chiếc xe mô hình đi được quãng đường bao nhiêu decimet?
là khoảng thời gian tính bằng giây kể từ lúc xe bắt đầu chuyển động. Trong 24 giây chạy thử nghiệm đó, chiếc xe mô hình đi được quãng đường bao nhiêu decimet?
Điền đáp án: 64.
Gọi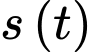 là hàm quãng đường.
là hàm quãng đường.
Ta có công thức là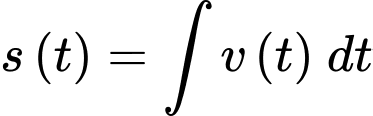
Suy ra trong 24 giây chạy thử nghiệm đó, chiếc xe mô hình đi được quãng đường
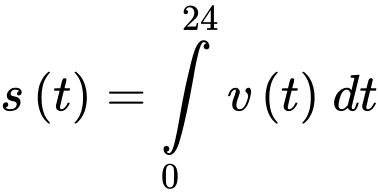
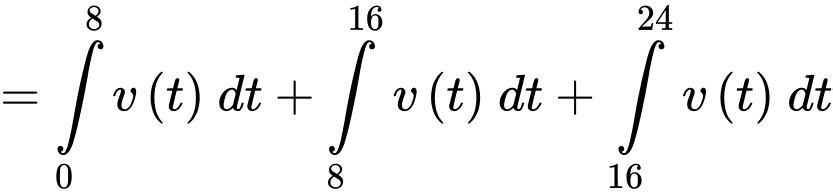
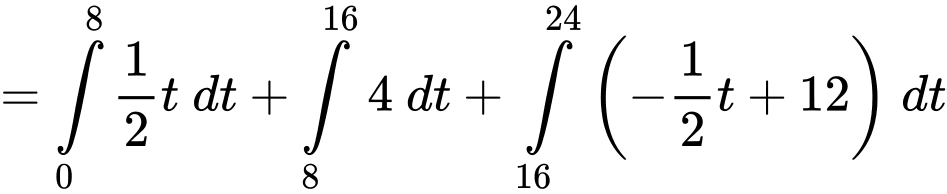
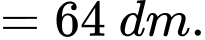
Vậy trong 24 giây chạy thử nghiệm đó, chiếc xe mô hình đi được quãng đường 64 dm.
Gọi
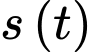 là hàm quãng đường.
là hàm quãng đường.Ta có công thức là
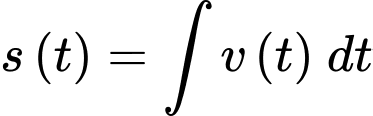
Suy ra trong 24 giây chạy thử nghiệm đó, chiếc xe mô hình đi được quãng đường
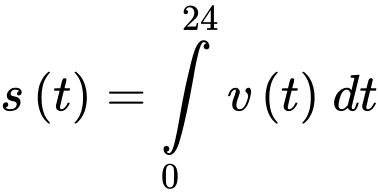
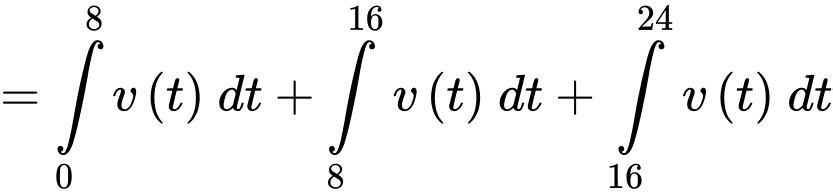
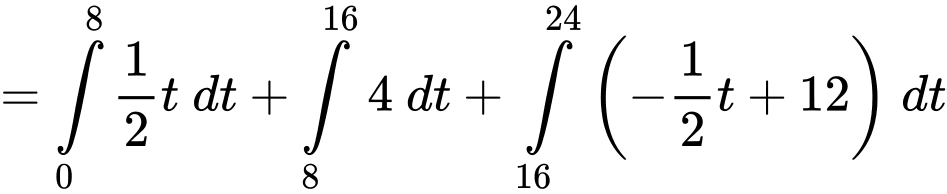
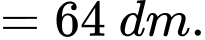
Vậy trong 24 giây chạy thử nghiệm đó, chiếc xe mô hình đi được quãng đường 64 dm.
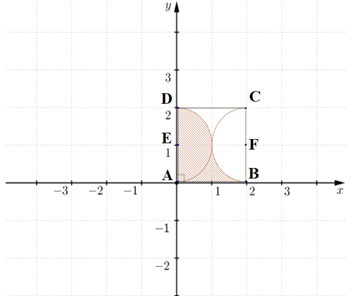
Câu 18 [395596]: Một vật trang trí có dạng một khối tròn xoay được tạo thành khi quay miền  (phần gạch chéo trong hình vẽ bên) quanh trục
(phần gạch chéo trong hình vẽ bên) quanh trục 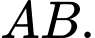 Miền
Miền  được giới hạn bởi các cạnh
được giới hạn bởi các cạnh  ,
, 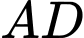 của hình vuông
của hình vuông 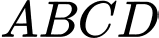 và các cung phần tư của các đường tròn bán kính bằng
và các cung phần tư của các đường tròn bán kính bằng 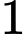 cm với tâm lần lượt là trung điểm của các cạnh
cm với tâm lần lượt là trung điểm của các cạnh 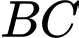 ,
, 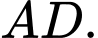
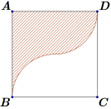
Tính thể tích của vật trang trí đó, làm tròn kết quả đến hàng phần mười
 (phần gạch chéo trong hình vẽ bên) quanh trục
(phần gạch chéo trong hình vẽ bên) quanh trục 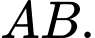 Miền
Miền  được giới hạn bởi các cạnh
được giới hạn bởi các cạnh  ,
, 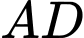 của hình vuông
của hình vuông 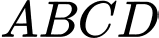 và các cung phần tư của các đường tròn bán kính bằng
và các cung phần tư của các đường tròn bán kính bằng 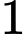 cm với tâm lần lượt là trung điểm của các cạnh
cm với tâm lần lượt là trung điểm của các cạnh 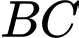 ,
, 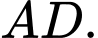

Tính thể tích của vật trang trí đó, làm tròn kết quả đến hàng phần mười
Điền đáp án: 10,5.
Chọn hệ trục tọa độ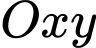 sao cho trục
sao cho trục 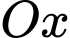 chứa cạnh
chứa cạnh  và
và 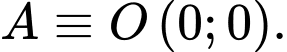
Khi đó và
và 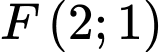 với
với 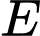 ,
, 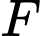 lần lượt là trung điểm của
lần lượt là trung điểm của 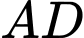 ,
, 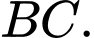
Khi đó đường tròn tâm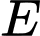 chứa cung tròn
chứa cung tròn 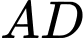 là
là 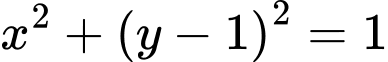 và đường tròn tâm
và đường tròn tâm 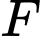 chứa cung tròn
chứa cung tròn 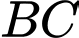 là
là 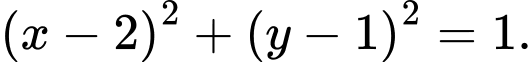
Suy ra phương trình cung trên của đường tròn tâm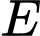 là
là 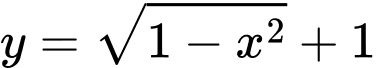 và phương trình cung dưới của của đường tròn tâm
và phương trình cung dưới của của đường tròn tâm 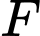 là
là 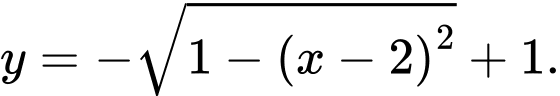
Khi đó, thể tích vật thể trang trí là
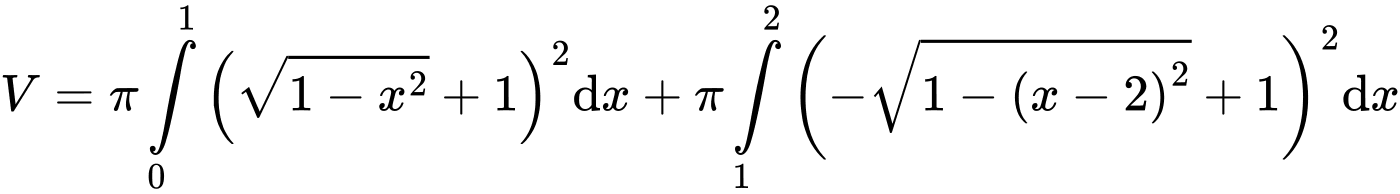
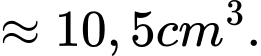

Chọn hệ trục tọa độ
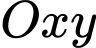 sao cho trục
sao cho trục 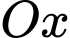 chứa cạnh
chứa cạnh  và
và 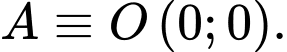
Khi đó
 và
và 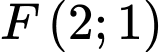 với
với 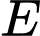 ,
, 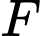 lần lượt là trung điểm của
lần lượt là trung điểm của 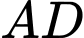 ,
, 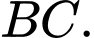
Khi đó đường tròn tâm
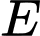 chứa cung tròn
chứa cung tròn 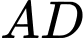 là
là 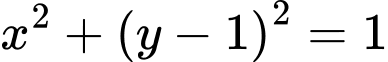 và đường tròn tâm
và đường tròn tâm 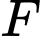 chứa cung tròn
chứa cung tròn 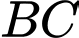 là
là 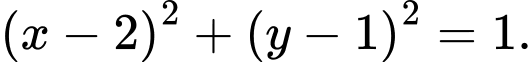
Suy ra phương trình cung trên của đường tròn tâm
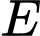 là
là 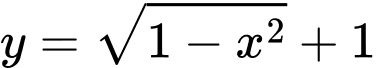 và phương trình cung dưới của của đường tròn tâm
và phương trình cung dưới của của đường tròn tâm 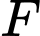 là
là 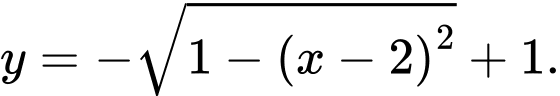
Khi đó, thể tích vật thể trang trí là
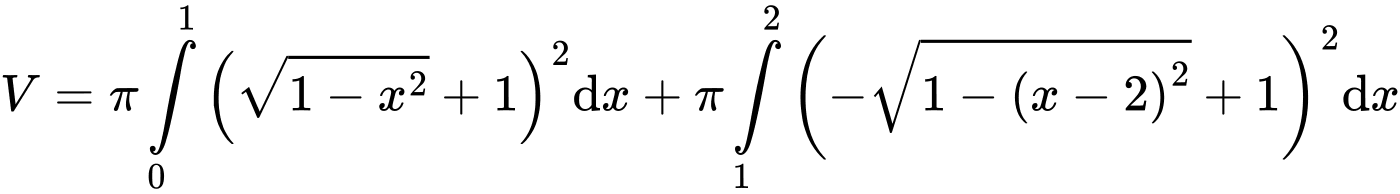
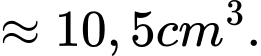
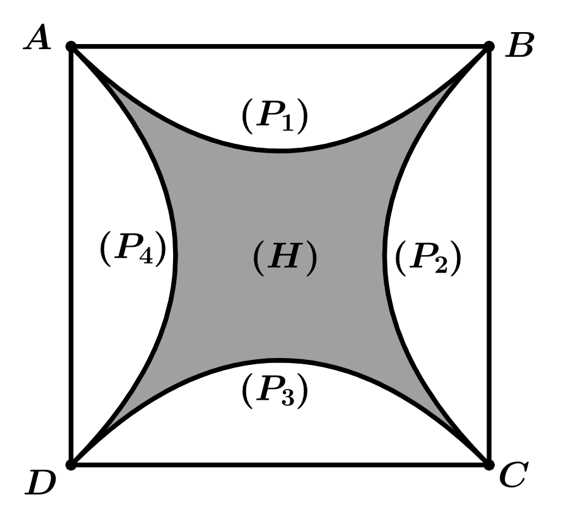
Câu 19 [785634]: Từ hình vuông 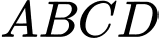 có cạnh bằng
có cạnh bằng 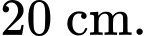 Ta vẽ bốn Parabol
Ta vẽ bốn Parabol 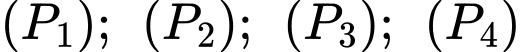 có đỉnh thuộc một trục đối xứng của hình vuông, đồng thời mỗi Parabol này tiếp xúc với các hai đường chéo của hình vuông
có đỉnh thuộc một trục đối xứng của hình vuông, đồng thời mỗi Parabol này tiếp xúc với các hai đường chéo của hình vuông 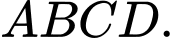 Bốn Parabol này tạo thành miền
Bốn Parabol này tạo thành miền  như hình vẽ. Diện tích miền
như hình vẽ. Diện tích miền  bằng bao nhiêu
bằng bao nhiêu 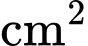 (kết quả làm tròn đến hàng đơn vị).
(kết quả làm tròn đến hàng đơn vị).
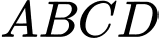 có cạnh bằng
có cạnh bằng 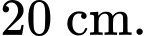 Ta vẽ bốn Parabol
Ta vẽ bốn Parabol 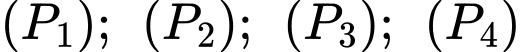 có đỉnh thuộc một trục đối xứng của hình vuông, đồng thời mỗi Parabol này tiếp xúc với các hai đường chéo của hình vuông
có đỉnh thuộc một trục đối xứng của hình vuông, đồng thời mỗi Parabol này tiếp xúc với các hai đường chéo của hình vuông 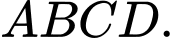 Bốn Parabol này tạo thành miền
Bốn Parabol này tạo thành miền  như hình vẽ. Diện tích miền
như hình vẽ. Diện tích miền  bằng bao nhiêu
bằng bao nhiêu 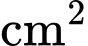 (kết quả làm tròn đến hàng đơn vị).
(kết quả làm tròn đến hàng đơn vị).
Điền đáp án: 133.
Gắn hệ trục tọa độ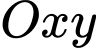 như hình vẽ, với gốc toạ độ
như hình vẽ, với gốc toạ độ  trùng với tâm của hình vuông
trùng với tâm của hình vuông
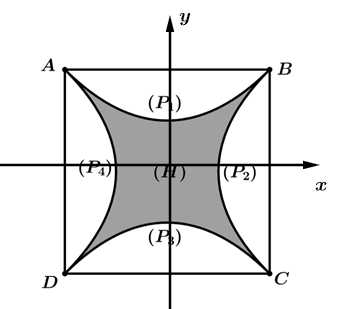
Ta có dạng tổng quát của Parabol: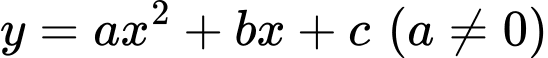
Xét đường cong phía dưới thuộc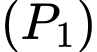 ta có:
ta có: 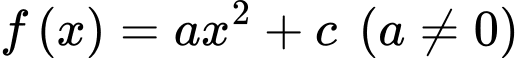 đi qua điểm
đi qua điểm 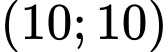
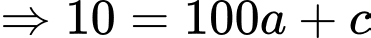
Đường chéo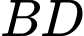 có phương trình
có phương trình 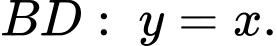
Mặt khác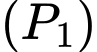 tiếp xúc với đường thẳng
tiếp xúc với đường thẳng 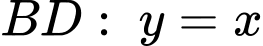 nên phương trình
nên phương trình
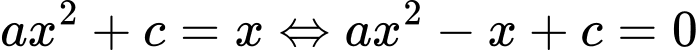 có nghiệm kép
có nghiệm kép
Suy ra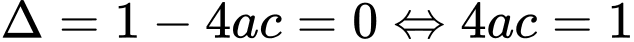
Ta thế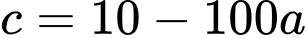 vào
vào 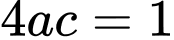
ta có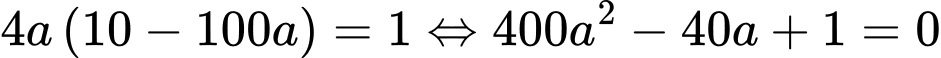
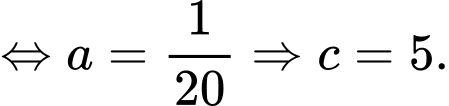
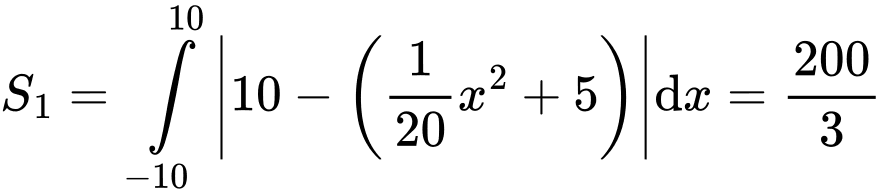
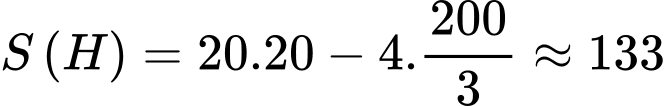
Gắn hệ trục tọa độ
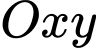 như hình vẽ, với gốc toạ độ
như hình vẽ, với gốc toạ độ  trùng với tâm của hình vuông
trùng với tâm của hình vuông
Ta có dạng tổng quát của Parabol:
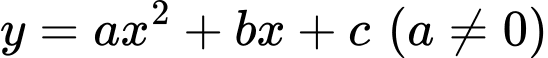
Xét đường cong phía dưới thuộc
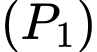 ta có:
ta có: 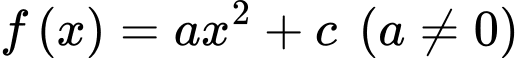 đi qua điểm
đi qua điểm 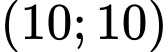
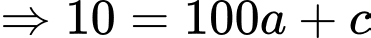
Đường chéo
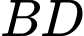 có phương trình
có phương trình 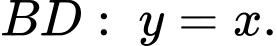
Mặt khác
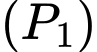 tiếp xúc với đường thẳng
tiếp xúc với đường thẳng 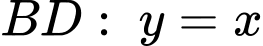 nên phương trình
nên phương trình 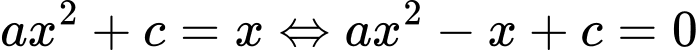 có nghiệm kép
có nghiệm kép
Suy ra
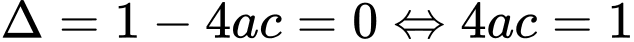
Ta thế
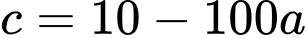 vào
vào 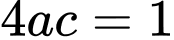
ta có
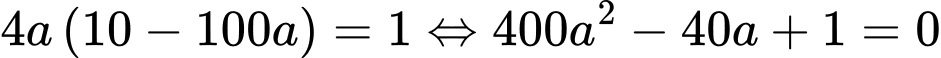
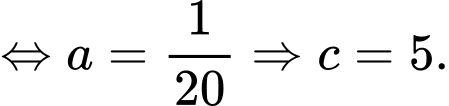
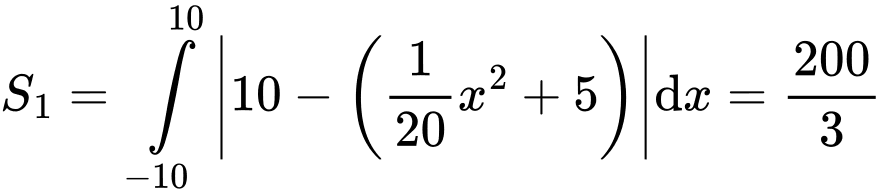
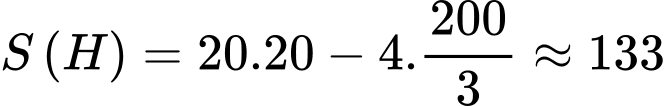
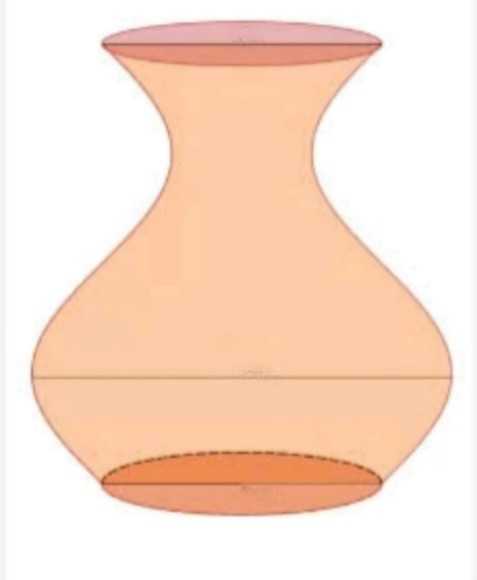
Câu 20 [779611]: Một bình hoa có dạng khối tròn xoay với chiều cao là 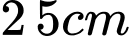 (tham khảo hình vẽ). Khi cắt bình hoa theo một mặt phẳng vuông góc với trục của nó thì ta luôn được thiết diện là một hình tròn có bán kính
(tham khảo hình vẽ). Khi cắt bình hoa theo một mặt phẳng vuông góc với trục của nó thì ta luôn được thiết diện là một hình tròn có bán kính 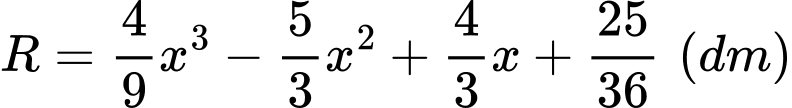 với
với 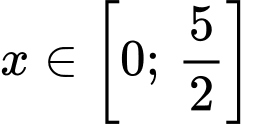 là khoảng cách từ mặt cắt tới mặt đáy của bình hoa ( tính theo đơn vị
là khoảng cách từ mặt cắt tới mặt đáy của bình hoa ( tính theo đơn vị 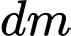 ). Lượng nước cần đổ vào bình để mức nước trong bình cao bằng
). Lượng nước cần đổ vào bình để mức nước trong bình cao bằng 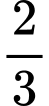 chiều cao của bình chiếm tỉ lệ bao nhiêu phần trăm so với thể tích của bình hoa? (Kết quả làm tròn đến hàng đơn vị).
chiều cao của bình chiếm tỉ lệ bao nhiêu phần trăm so với thể tích của bình hoa? (Kết quả làm tròn đến hàng đơn vị).
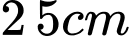 (tham khảo hình vẽ). Khi cắt bình hoa theo một mặt phẳng vuông góc với trục của nó thì ta luôn được thiết diện là một hình tròn có bán kính
(tham khảo hình vẽ). Khi cắt bình hoa theo một mặt phẳng vuông góc với trục của nó thì ta luôn được thiết diện là một hình tròn có bán kính 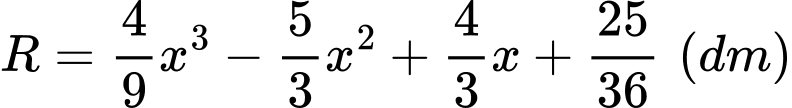 với
với 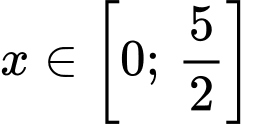 là khoảng cách từ mặt cắt tới mặt đáy của bình hoa ( tính theo đơn vị
là khoảng cách từ mặt cắt tới mặt đáy của bình hoa ( tính theo đơn vị 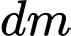 ). Lượng nước cần đổ vào bình để mức nước trong bình cao bằng
). Lượng nước cần đổ vào bình để mức nước trong bình cao bằng 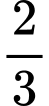 chiều cao của bình chiếm tỉ lệ bao nhiêu phần trăm so với thể tích của bình hoa? (Kết quả làm tròn đến hàng đơn vị).
chiều cao của bình chiếm tỉ lệ bao nhiêu phần trăm so với thể tích của bình hoa? (Kết quả làm tròn đến hàng đơn vị).
Trả lời: 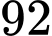
Diện tích của mặt cắt vuông góc với trục tại vị trí cách mặt đáy của bình hoa một khoảng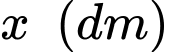 là:
là: 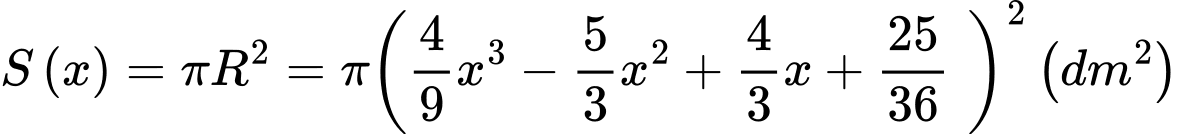
Lượng nước đổ đầy bình hoa là: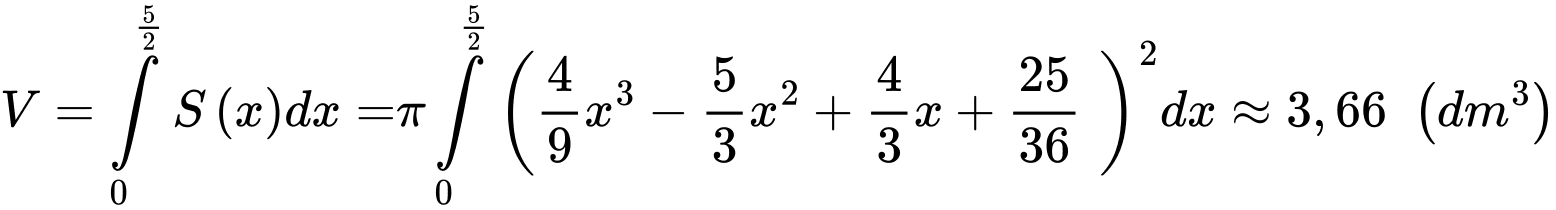
Lượng nước đổ vào bình cao bằng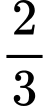 chiều cao của bình là:
chiều cao của bình là: 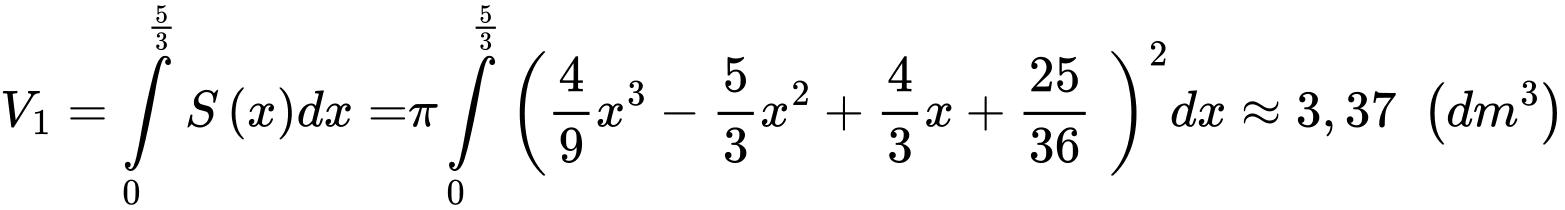
Vậy tỉ lệ phần trăm lượng nước cần đổ vào bình để mức nước trong bình cao bằng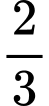 chiều cao của bình so với thể tích của bình hoa là
chiều cao của bình so với thể tích của bình hoa là 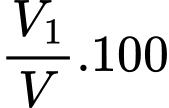 .
.
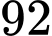
Diện tích của mặt cắt vuông góc với trục tại vị trí cách mặt đáy của bình hoa một khoảng
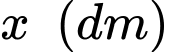 là:
là: 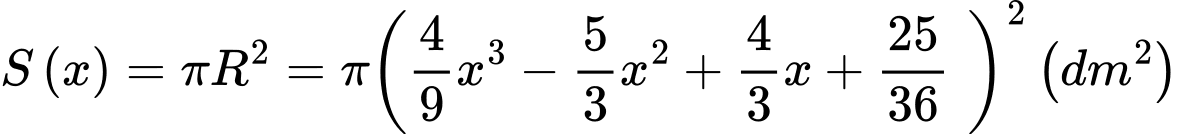
Lượng nước đổ đầy bình hoa là:
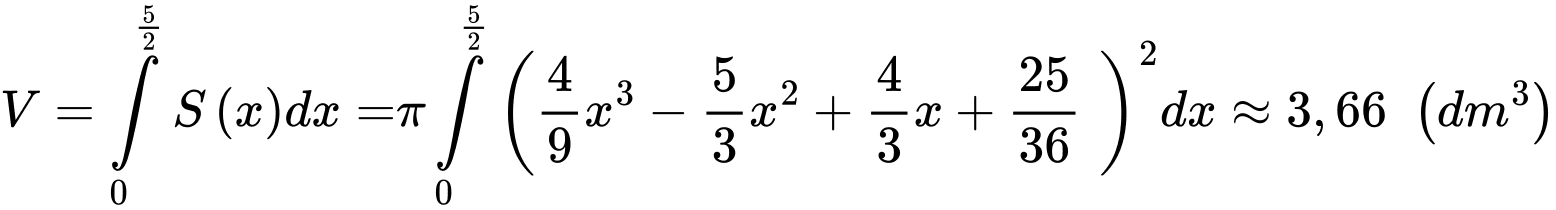
Lượng nước đổ vào bình cao bằng
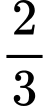 chiều cao của bình là:
chiều cao của bình là: 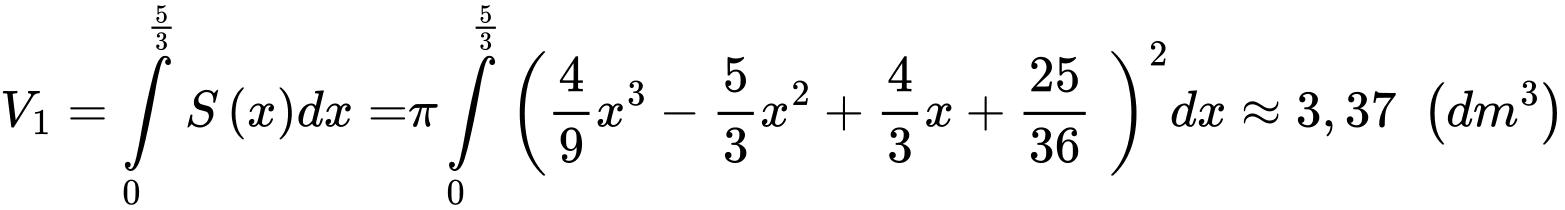
Vậy tỉ lệ phần trăm lượng nước cần đổ vào bình để mức nước trong bình cao bằng
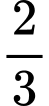 chiều cao của bình so với thể tích của bình hoa là
chiều cao của bình so với thể tích của bình hoa là 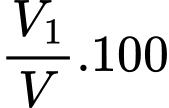 .
.
Câu 21 [779593]: Một công ty thiết kế tròng kính sao cho mỗi phần đường viền của tròng kính là một phần đồ thị của hàm số bậc hai hoặc một phần đồ thị của hàm số bậc bốn rồi ghép chúng lại với nhau như hình vẽ bên dưới (sau đó họ sẽ điều chỉnh theo tỳ lệ phù hợp). Xét hệ trục toạ độ 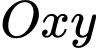 như hình vẽ, biết rằng
như hình vẽ, biết rằng  và
và 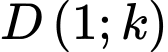 với
với  Cho biết đường cong
Cho biết đường cong 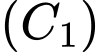 đi qua các điểm
đi qua các điểm 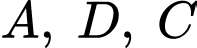 là một phần của đồ thị hàm số bậc hai nào đó, đường cong
là một phần của đồ thị hàm số bậc hai nào đó, đường cong 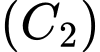 ứng với đường viền nối
ứng với đường viền nối 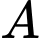 với
với 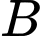 là một phần của đồ thị hàm số
là một phần của đồ thị hàm số 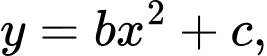 còn đường cong
còn đường cong 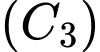 ứng với đường viền nối
ứng với đường viền nối 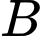 với
với  là một phần của đồ thị hàm số
là một phần của đồ thị hàm số 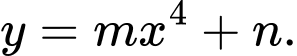 Tìm
Tìm 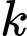 (làm tròn đến hàng phần trăm) biết diện tích tròng kính đó bằng
(làm tròn đến hàng phần trăm) biết diện tích tròng kính đó bằng 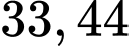 (đơn vị diện tích).
(đơn vị diện tích).
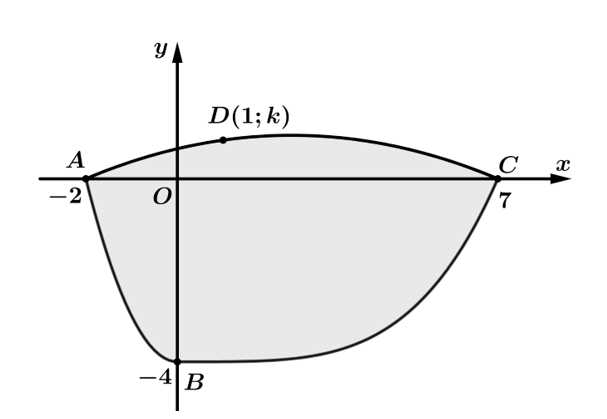
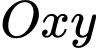 như hình vẽ, biết rằng
như hình vẽ, biết rằng  và
và 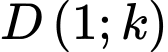 với
với  Cho biết đường cong
Cho biết đường cong 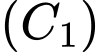 đi qua các điểm
đi qua các điểm 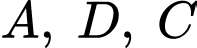 là một phần của đồ thị hàm số bậc hai nào đó, đường cong
là một phần của đồ thị hàm số bậc hai nào đó, đường cong 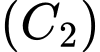 ứng với đường viền nối
ứng với đường viền nối 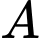 với
với 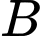 là một phần của đồ thị hàm số
là một phần của đồ thị hàm số 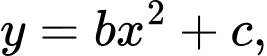 còn đường cong
còn đường cong 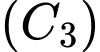 ứng với đường viền nối
ứng với đường viền nối 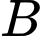 với
với  là một phần của đồ thị hàm số
là một phần của đồ thị hàm số 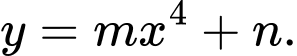 Tìm
Tìm 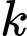 (làm tròn đến hàng phần trăm) biết diện tích tròng kính đó bằng
(làm tròn đến hàng phần trăm) biết diện tích tròng kính đó bằng 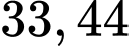 (đơn vị diện tích).
(đơn vị diện tích).
Điền đáp án: 0,85.
Chia diện tích tròng kính thành 3 phần có diện tích như hình vẽ.
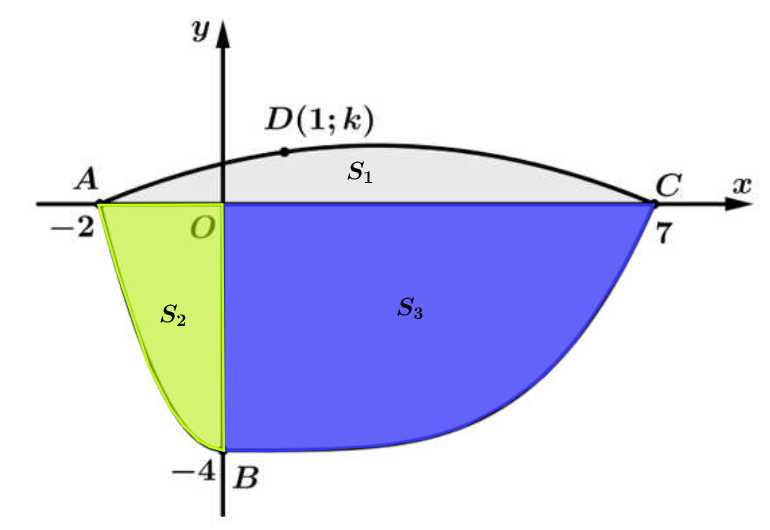
+) Diện tích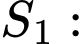 là hình phẳng giới hạn bởi đường cong
là hình phẳng giới hạn bởi đường cong 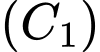 , trục hoành và các đường thẳng
, trục hoành và các đường thẳng 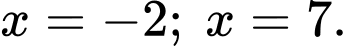
Vì đường cong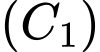 là một phần của đồ thị hàm số bậc hai nên ta đặt
là một phần của đồ thị hàm số bậc hai nên ta đặt 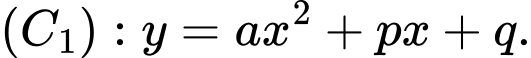 Do
Do 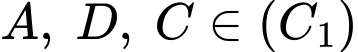 nên ta có hệ phương trình
nên ta có hệ phương trình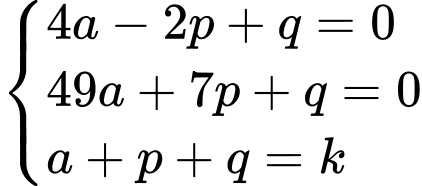
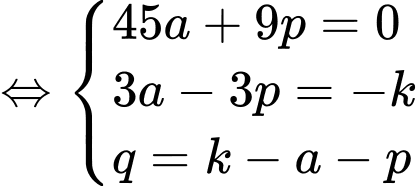 (lấy phương trình 2 trừ đi phương trình 1 và lấy PT 1 trừ đi PT 3)
(lấy phương trình 2 trừ đi phương trình 1 và lấy PT 1 trừ đi PT 3)
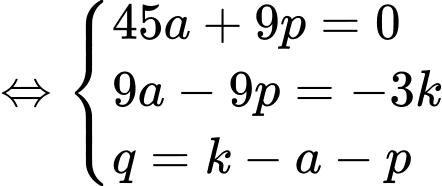 (nhân 2 vế của PT 2 với 3)
(nhân 2 vế của PT 2 với 3)
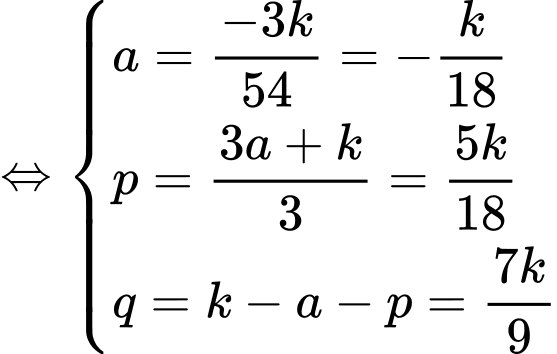
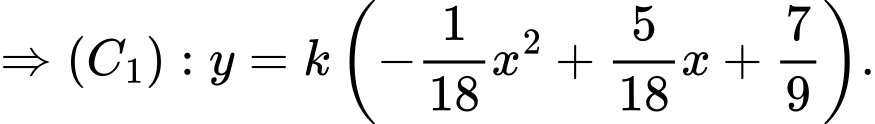
Suy ra diện tích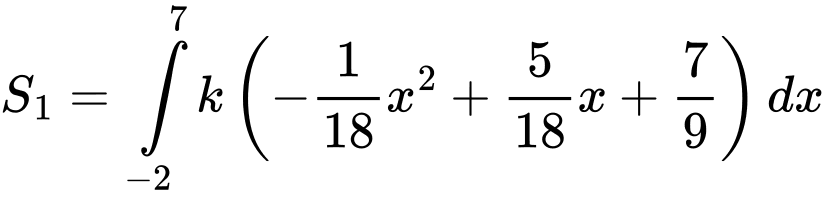
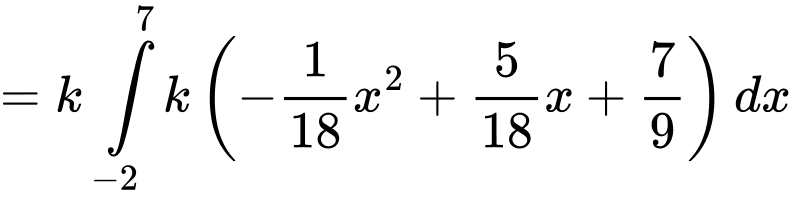
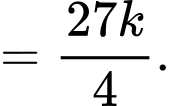
+) Diện tích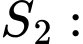 là hình phẳng giới hạn bởi đường cong
là hình phẳng giới hạn bởi đường cong 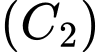 , trục hoành và các đường thẳng
, trục hoành và các đường thẳng 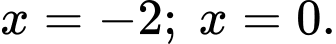
Biết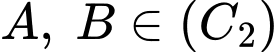 nên ta có hệ phương trình
nên ta có hệ phương trình 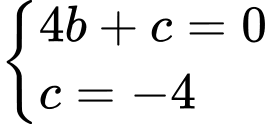
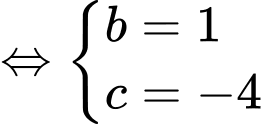
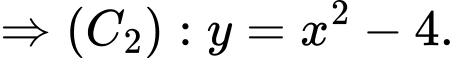
Suy ra diện tích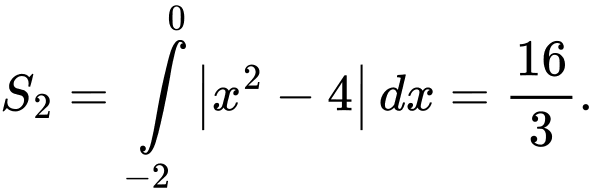
+) Diện tích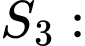 là hình phẳng giới hạn bởi đường cong
là hình phẳng giới hạn bởi đường cong 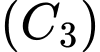 , trục hoành và các đường thẳng
, trục hoành và các đường thẳng 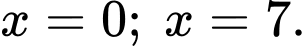
Biết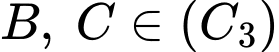 nên ta có hệ
nên ta có hệ 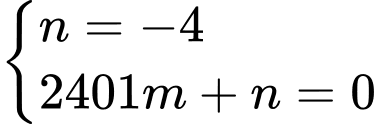
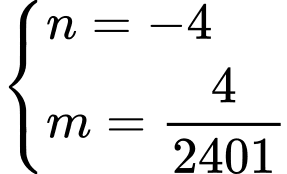
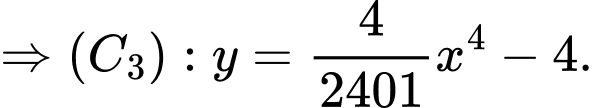
Suy ra diện tích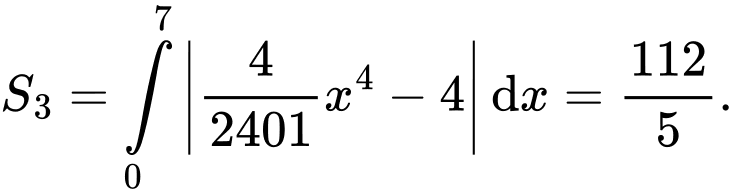
Biết diện tích tròng kính bằng 33,44 hay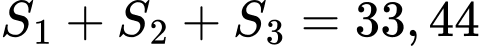
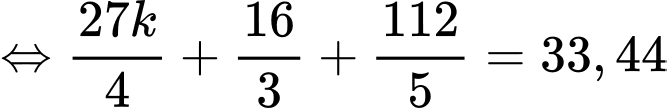
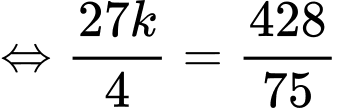
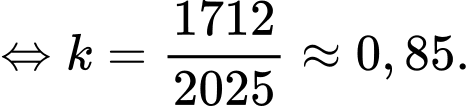
Chia diện tích tròng kính thành 3 phần có diện tích như hình vẽ.

+) Diện tích
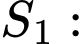 là hình phẳng giới hạn bởi đường cong
là hình phẳng giới hạn bởi đường cong 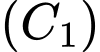 , trục hoành và các đường thẳng
, trục hoành và các đường thẳng 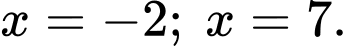
Vì đường cong
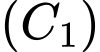 là một phần của đồ thị hàm số bậc hai nên ta đặt
là một phần của đồ thị hàm số bậc hai nên ta đặt 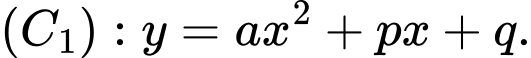 Do
Do 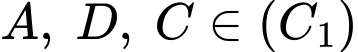 nên ta có hệ phương trình
nên ta có hệ phương trình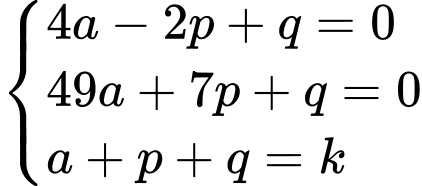
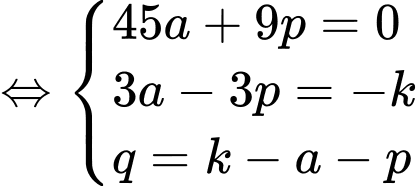 (lấy phương trình 2 trừ đi phương trình 1 và lấy PT 1 trừ đi PT 3)
(lấy phương trình 2 trừ đi phương trình 1 và lấy PT 1 trừ đi PT 3) 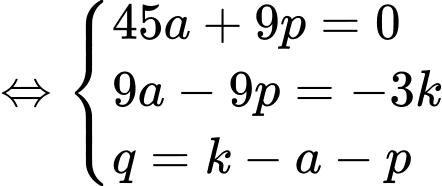 (nhân 2 vế của PT 2 với 3)
(nhân 2 vế của PT 2 với 3)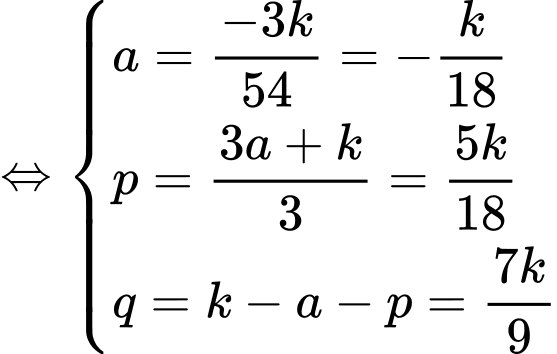
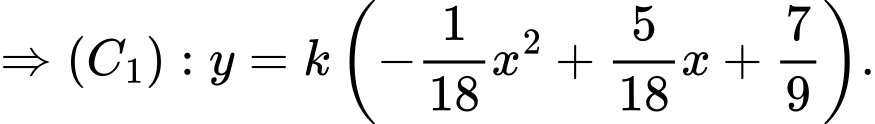
Suy ra diện tích
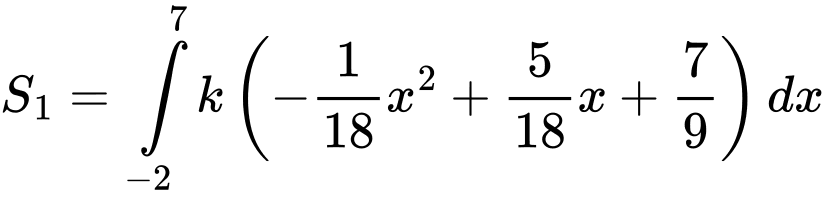
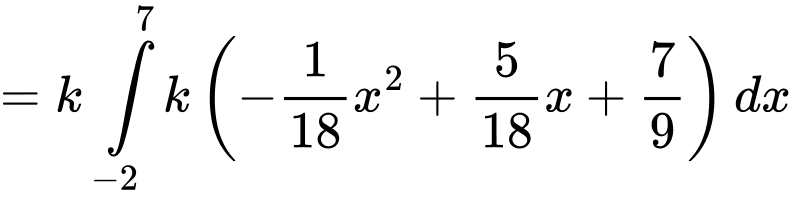
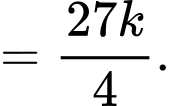
+) Diện tích
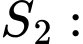 là hình phẳng giới hạn bởi đường cong
là hình phẳng giới hạn bởi đường cong 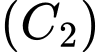 , trục hoành và các đường thẳng
, trục hoành và các đường thẳng 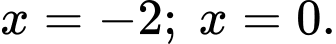
Biết
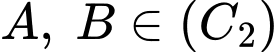 nên ta có hệ phương trình
nên ta có hệ phương trình 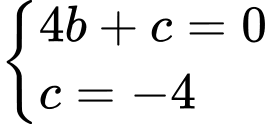
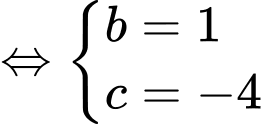
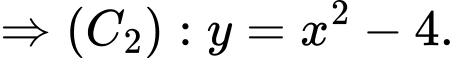
Suy ra diện tích
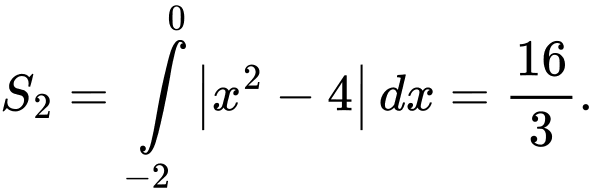
+) Diện tích
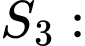 là hình phẳng giới hạn bởi đường cong
là hình phẳng giới hạn bởi đường cong 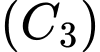 , trục hoành và các đường thẳng
, trục hoành và các đường thẳng 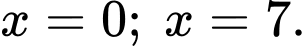
Biết
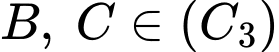 nên ta có hệ
nên ta có hệ 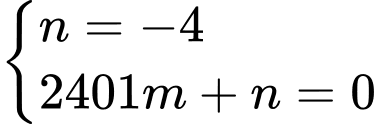
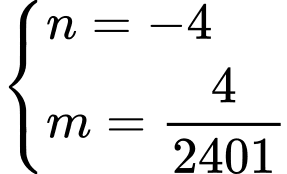
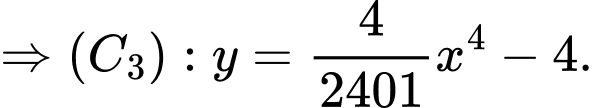
Suy ra diện tích
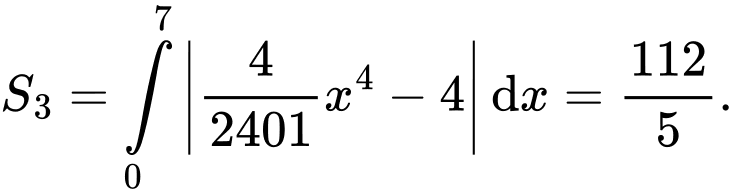
Biết diện tích tròng kính bằng 33,44 hay
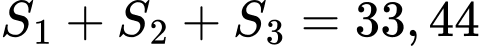
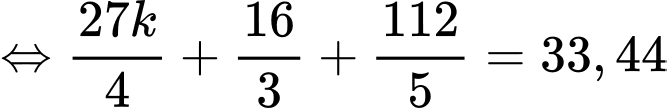
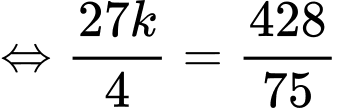
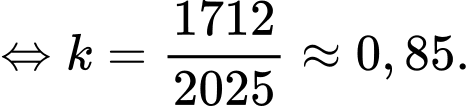
Câu 22 [785638]: Tại một công viên người ta làm một cái cổng chào hình Parabol với chiều cao 12 m và chiều rộng giữa hai chân cổng là 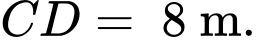
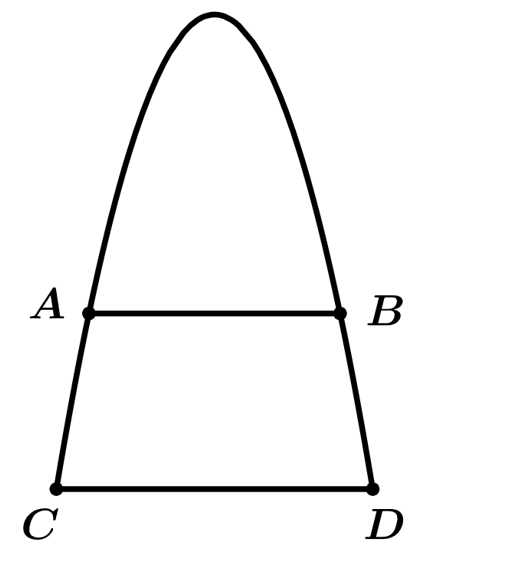
Người ta muốn trang trí cổng bằng cách chia cổng thành hai phần có diện tích bằng nhau bằng đoạn song song với
song song với 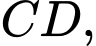 phần phía trên làm màn hình Led. Khoảng cách giữa hai đường thẳng
phần phía trên làm màn hình Led. Khoảng cách giữa hai đường thẳng  và
và 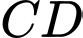 bằng bao nhiêu mét (kết quả làm tròn đến hàng phần mười).
bằng bao nhiêu mét (kết quả làm tròn đến hàng phần mười).
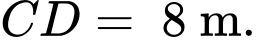

Người ta muốn trang trí cổng bằng cách chia cổng thành hai phần có diện tích bằng nhau bằng đoạn
 song song với
song song với 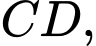 phần phía trên làm màn hình Led. Khoảng cách giữa hai đường thẳng
phần phía trên làm màn hình Led. Khoảng cách giữa hai đường thẳng  và
và 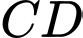 bằng bao nhiêu mét (kết quả làm tròn đến hàng phần mười).
bằng bao nhiêu mét (kết quả làm tròn đến hàng phần mười).
Điền đáp án: 4,4.
Đặt hệ trục tọa độ như hình vẽ.
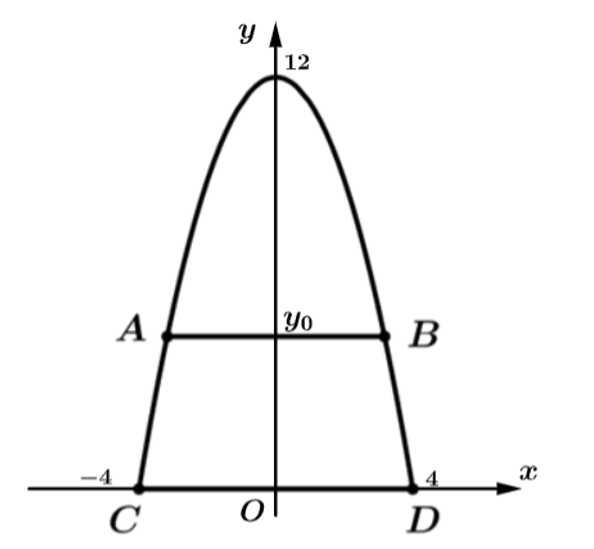
Giả sử cổng chào có dạng parabol với đỉnh tại gốc tọa độ (hệ trục đối xứng theo trục Oy)
Ta có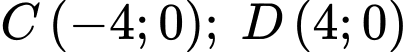
Dạng phương trình parabol sẽ là: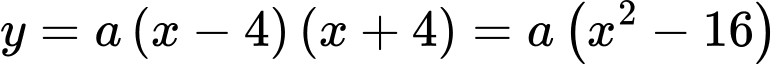
Thay điểm đỉnh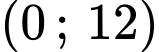 vào phương trình:
vào phương trình: 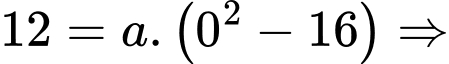
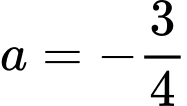
Vậy phương trình parabol là: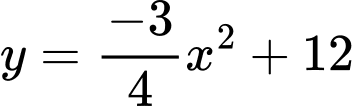
Diện tích parabol là: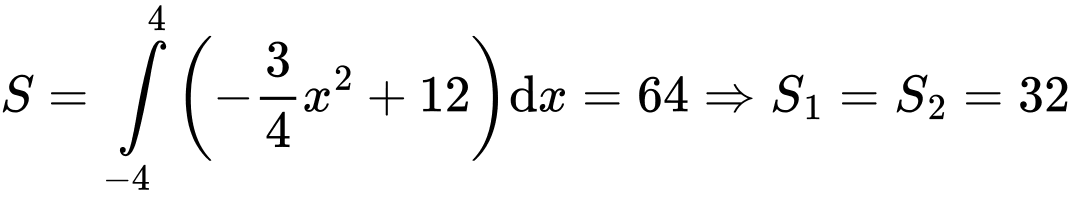
Gọi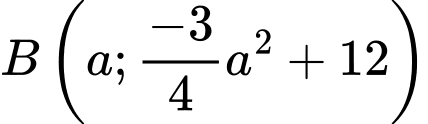 suy ra
suy ra 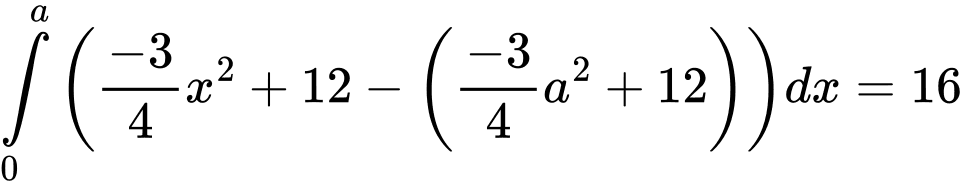
Do đó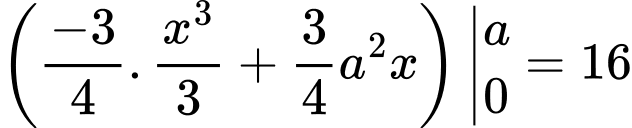
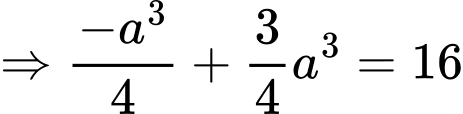

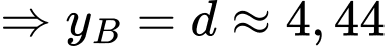
Đặt hệ trục tọa độ như hình vẽ.

Giả sử cổng chào có dạng parabol với đỉnh tại gốc tọa độ (hệ trục đối xứng theo trục Oy)
Ta có
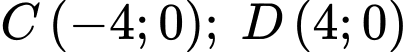
Dạng phương trình parabol sẽ là:
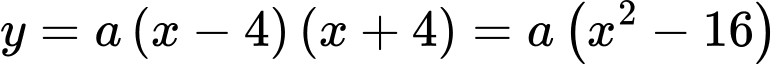
Thay điểm đỉnh
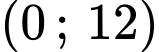 vào phương trình:
vào phương trình: 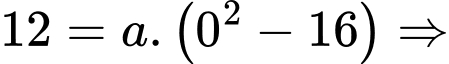
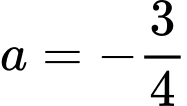
Vậy phương trình parabol là:
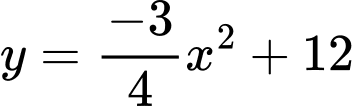
Diện tích parabol là:
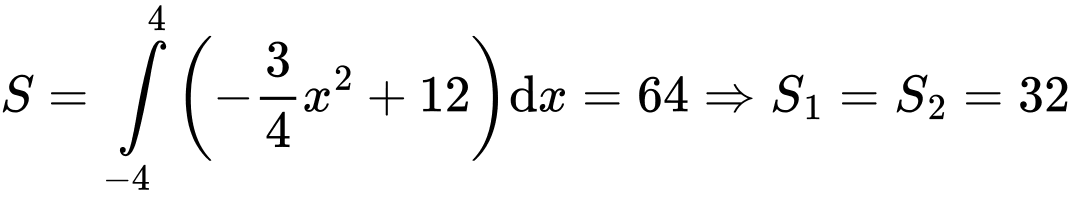
Gọi
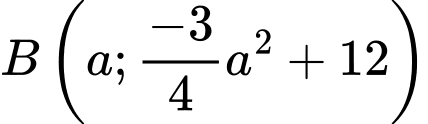 suy ra
suy ra 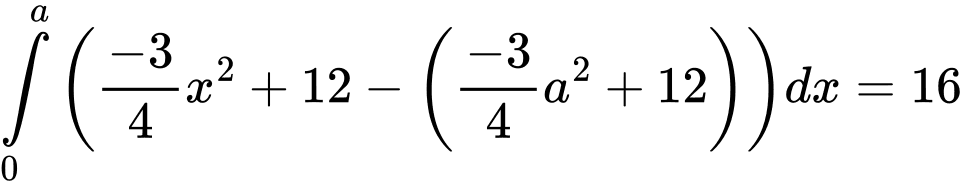
Do đó