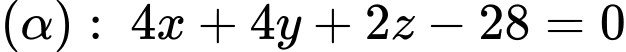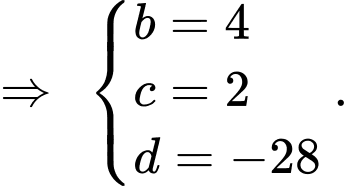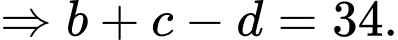PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1 [393582]: Trong không gian 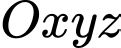 , cho mặt phẳng
, cho mặt phẳng 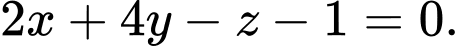 Véc tơ nào dưới đây là vectơ pháp tuyến của mặt phẳng
Véc tơ nào dưới đây là vectơ pháp tuyến của mặt phẳng 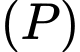 ?
?
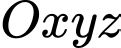 , cho mặt phẳng
, cho mặt phẳng 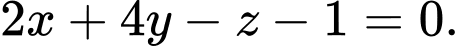 Véc tơ nào dưới đây là vectơ pháp tuyến của mặt phẳng
Véc tơ nào dưới đây là vectơ pháp tuyến của mặt phẳng 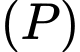 ?
? A, 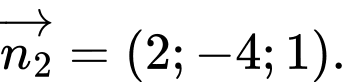
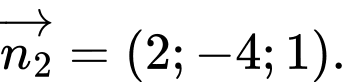
B, 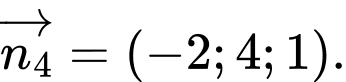
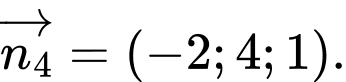
C, 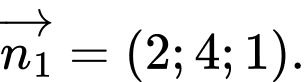
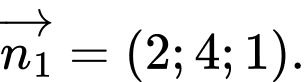
D, 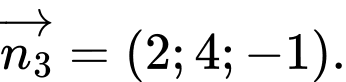
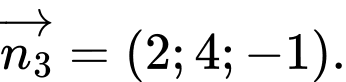
Chọn D
Véc tơ nào dưới đây là véc tơ pháp tuyến của mặt phẳng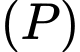 là
là 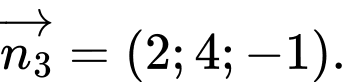 Đáp án: D
Đáp án: D
Véc tơ nào dưới đây là véc tơ pháp tuyến của mặt phẳng
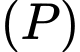 là
là 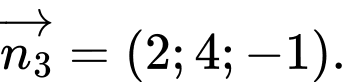 Đáp án: D
Đáp án: D
Câu 2 [360328]: Phương trình nào sau đây là phương trình tổng quát của mặt phẳng?
A, 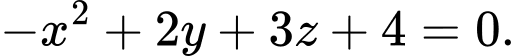
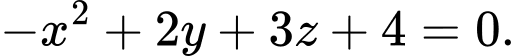
B, 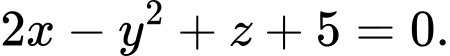
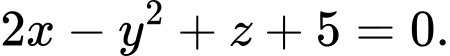
C, 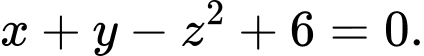
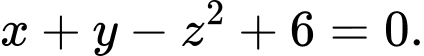
D, 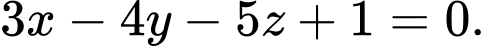
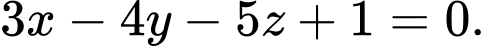
Phương trình mặt phẳng có dạng: 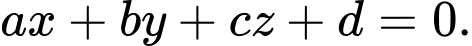 Chọn D. Đáp án: D
Chọn D. Đáp án: D
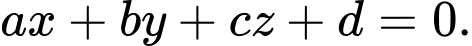 Chọn D. Đáp án: D
Chọn D. Đáp án: D
Câu 3 [543208]: Trong không gian 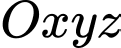 , điểm nào sau đây thuộc mặt phẳng
, điểm nào sau đây thuộc mặt phẳng 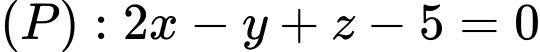 ?
?
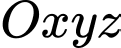 , điểm nào sau đây thuộc mặt phẳng
, điểm nào sau đây thuộc mặt phẳng 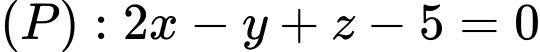 ?
? A, 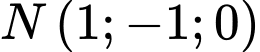 .
.
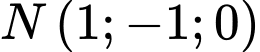 .
.B, 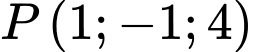 .
.
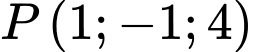 .
.C, 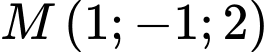 .
.
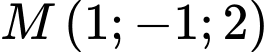 .
.D, 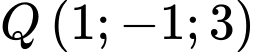 .
.
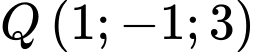 .
.
Thay tọa độ của các điểm vào phương trình mặt phẳng 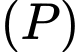 ta được:
ta được:
+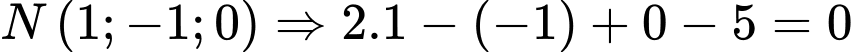 (vô lí).
(vô lí).
+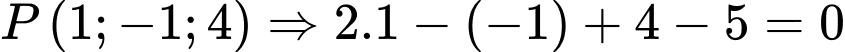 (vô lí).
(vô lí).
+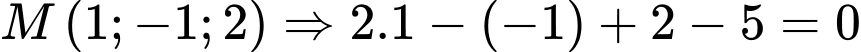 (thỏa mãn).
(thỏa mãn).
+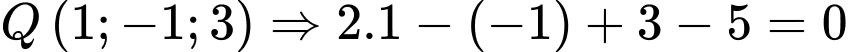 (vô lí). Đáp án: C
(vô lí). Đáp án: C
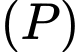 ta được:
ta được: +
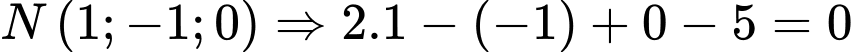 (vô lí).
(vô lí). +
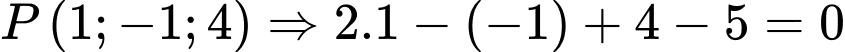 (vô lí).
(vô lí). +
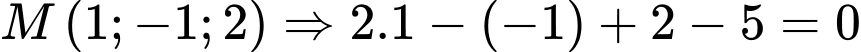 (thỏa mãn).
(thỏa mãn). +
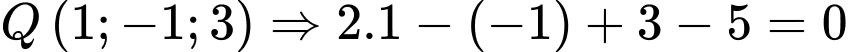 (vô lí). Đáp án: C
(vô lí). Đáp án: C
Câu 4 [543194]: Trong không gian 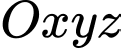 , phương trình mặt phẳng qua
, phương trình mặt phẳng qua 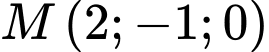 và có một véctơ pháp tuyến
và có một véctơ pháp tuyến 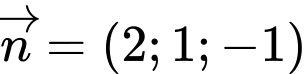 là
là
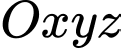 , phương trình mặt phẳng qua
, phương trình mặt phẳng qua 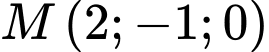 và có một véctơ pháp tuyến
và có một véctơ pháp tuyến 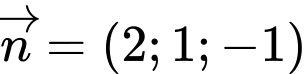 là
là A, 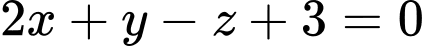 .
.
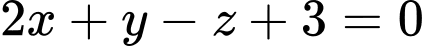 .
.B, 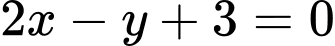 .
.
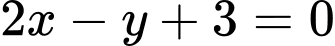 .
.C, 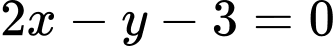 .
.
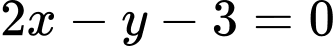 .
.D, 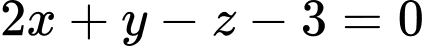 .
.
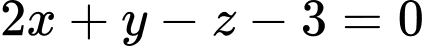 .
.
Ta có mặt phẳng có VTPT 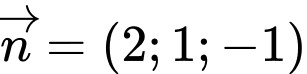 và đi qua
và đi qua 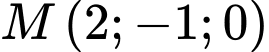 nên
nên
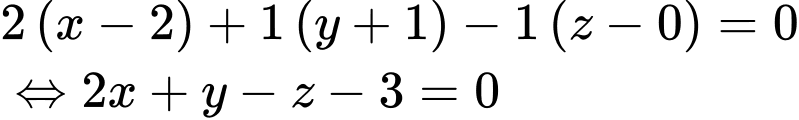 Đáp án: D
Đáp án: D
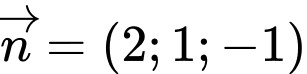 và đi qua
và đi qua 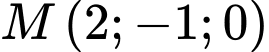 nên
nên
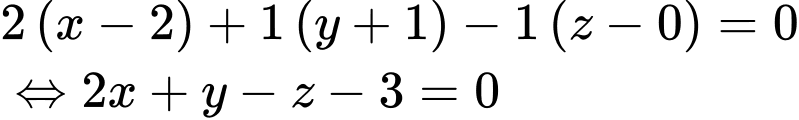 Đáp án: D
Đáp án: D
Câu 5 [393604]: Trong không gian 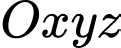 , cho điểm
, cho điểm 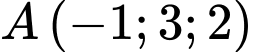 và mặt phẳng
và mặt phẳng  Mặt phẳng đi qua
Mặt phẳng đi qua 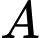 và song song với
và song song với 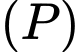 có phương trình là:
có phương trình là:
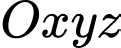 , cho điểm
, cho điểm 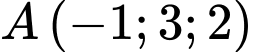 và mặt phẳng
và mặt phẳng  Mặt phẳng đi qua
Mặt phẳng đi qua 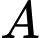 và song song với
và song song với 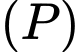 có phương trình là:
có phương trình là: A, 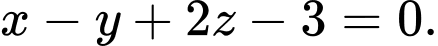
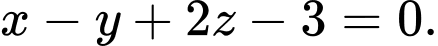
B, 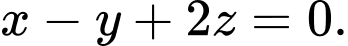
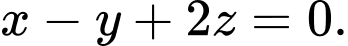
C, 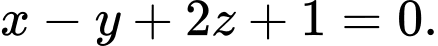
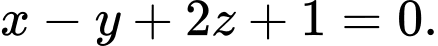
D, 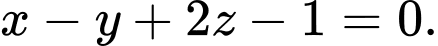
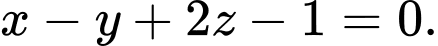
Chọn B
Mặt phẳng đi qua
đi qua 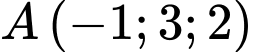 và có vectơ pháp tuyến
và có vectơ pháp tuyến 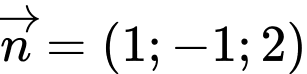 có phương trình là:
có phương trình là:
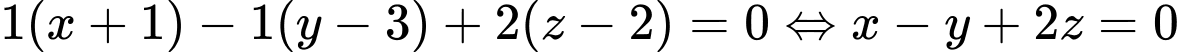 Đáp án: B
Đáp án: B
Mặt phẳng
 đi qua
đi qua 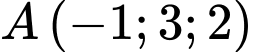 và có vectơ pháp tuyến
và có vectơ pháp tuyến 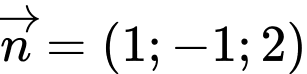 có phương trình là:
có phương trình là: 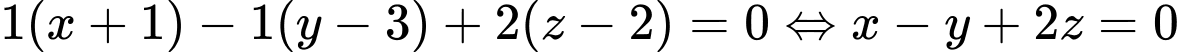 Đáp án: B
Đáp án: B
Câu 6 [393611]: Trong không gian 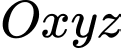 , mặt phẳng đi qua điểm
, mặt phẳng đi qua điểm 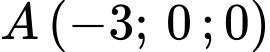 ,
, 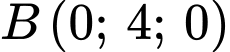 ,
, 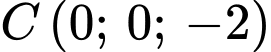 có phương trình là
có phương trình là
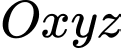 , mặt phẳng đi qua điểm
, mặt phẳng đi qua điểm 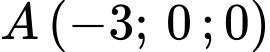 ,
, 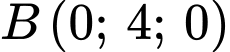 ,
, 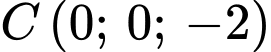 có phương trình là
có phương trình là A, 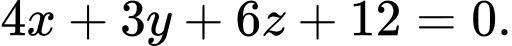
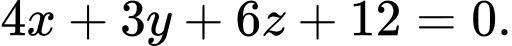
B, 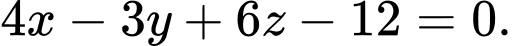
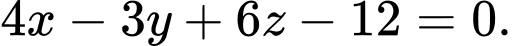
C, 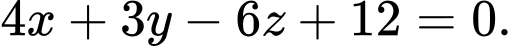
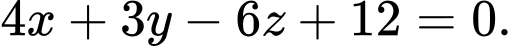
D, 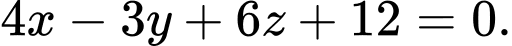
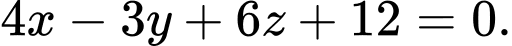
Chọn D
Mặt phẳng đi qua điểm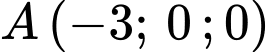 ,
, 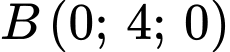 ,
, 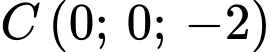 có phương trình là:
có phương trình là:
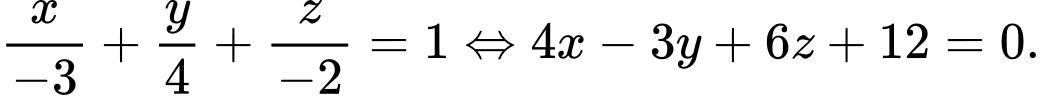 Đáp án: D
Đáp án: D
Mặt phẳng đi qua điểm
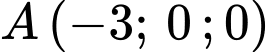 ,
, 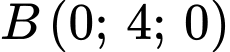 ,
, 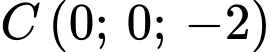 có phương trình là:
có phương trình là: 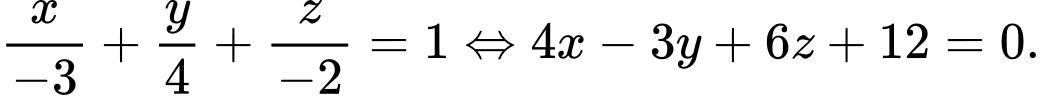 Đáp án: D
Đáp án: D
Câu 7 [544292]: Trong không gian 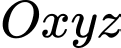 , phương trình nào dưới đây là phương trình của mặt phẳng
, phương trình nào dưới đây là phương trình của mặt phẳng 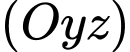 ?
?
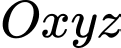 , phương trình nào dưới đây là phương trình của mặt phẳng
, phương trình nào dưới đây là phương trình của mặt phẳng 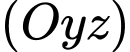 ?
? A, 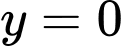 .
.
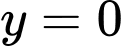 .
.B,  .
.
 .
.C, 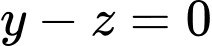
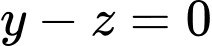
D, 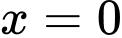 .
.
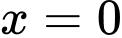 .
.
Chọn D.
Mặt phẳng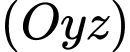 qua điểm
qua điểm 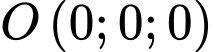 nhận
nhận 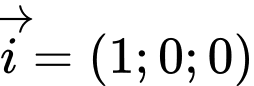 làm vectơ pháp tuyến nên phương trình là
làm vectơ pháp tuyến nên phương trình là 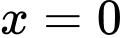 Đáp án: D
Đáp án: D
Mặt phẳng
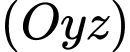 qua điểm
qua điểm 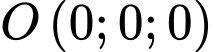 nhận
nhận 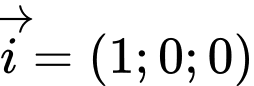 làm vectơ pháp tuyến nên phương trình là
làm vectơ pháp tuyến nên phương trình là 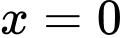 Đáp án: D
Đáp án: D
Câu 8 [899186]: Trong không gian tọa độ 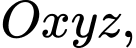 cho hai điểm
cho hai điểm 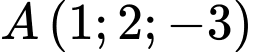 và
và 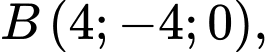 phương trình mặt phẳng qua điểm
phương trình mặt phẳng qua điểm 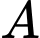 và vuông góc với
và vuông góc với  là
là
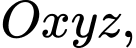 cho hai điểm
cho hai điểm 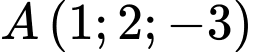 và
và 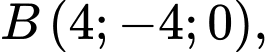 phương trình mặt phẳng qua điểm
phương trình mặt phẳng qua điểm  và vuông góc với
và vuông góc với  là
là A, 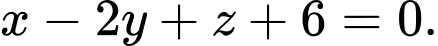
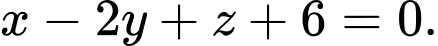
B, 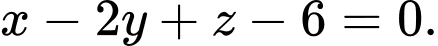
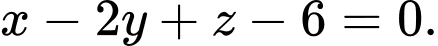
C, 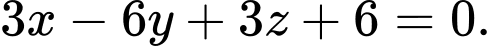
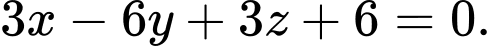
D, 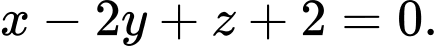
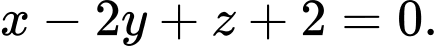
Chọn đáp án A.
Gọi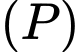 là mặt phẳng cần tìm, mặt phẳng
là mặt phẳng cần tìm, mặt phẳng 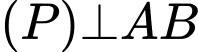 nên
nên 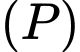 có vectơ pháp tuyến là
có vectơ pháp tuyến là 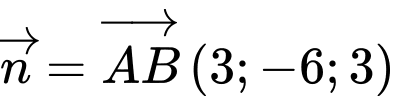
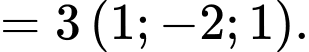
Mặt phẳng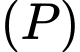 qua
qua 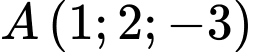 và có 1 vectơ pháp tuyến là
và có 1 vectơ pháp tuyến là 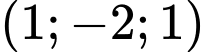 suy ra
suy ra 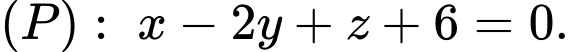 Đáp án: A
Đáp án: A
Gọi
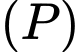 là mặt phẳng cần tìm, mặt phẳng
là mặt phẳng cần tìm, mặt phẳng 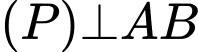 nên
nên 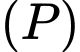 có vectơ pháp tuyến là
có vectơ pháp tuyến là 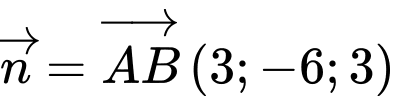
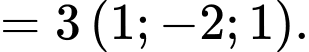
Mặt phẳng
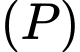 qua
qua 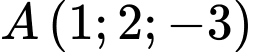 và có 1 vectơ pháp tuyến là
và có 1 vectơ pháp tuyến là 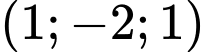 suy ra
suy ra 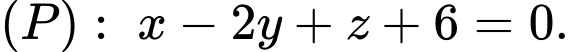 Đáp án: A
Đáp án: A
Câu 9 [543228]: Trong không gian 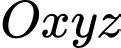 , cho hai điểm
, cho hai điểm 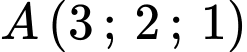 và
và 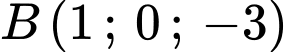 . Mặt phẳng trung trực của đoạn
. Mặt phẳng trung trực của đoạn  có phương trình là
có phương trình là
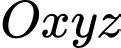 , cho hai điểm
, cho hai điểm 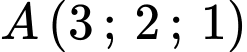 và
và 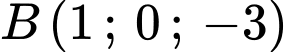 . Mặt phẳng trung trực của đoạn
. Mặt phẳng trung trực của đoạn  có phương trình là
có phương trình là A, 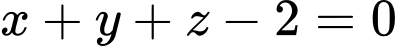 .
.
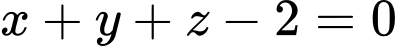 .
.B, 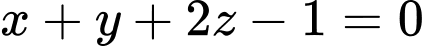 .
.
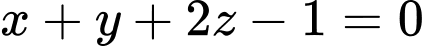 .
.C, 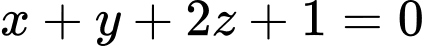 .
.
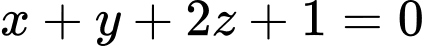 .
.D, 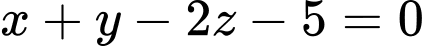 .
.
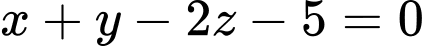 .
.
Gọi 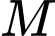 là trung điểm của
là trung điểm của 
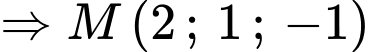 .
Gọi
.
Gọi  là mặt phẳng trung trực của đoạn thẳng
là mặt phẳng trung trực của đoạn thẳng  .
Khi đó
.
Khi đó  qua điểm
qua điểm 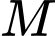 và có vectơ pháp tuyến là
và có vectơ pháp tuyến là 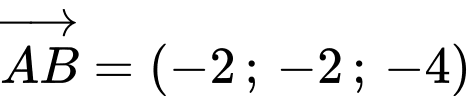
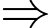 Phương trình
Phương trình 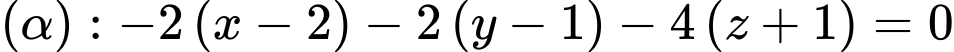
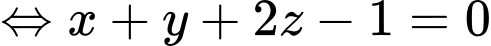 . Đáp án: B
. Đáp án: B
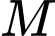 là trung điểm của
là trung điểm của 
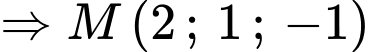 .
Gọi
.
Gọi  là mặt phẳng trung trực của đoạn thẳng
là mặt phẳng trung trực của đoạn thẳng  .
Khi đó
.
Khi đó  qua điểm
qua điểm 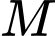 và có vectơ pháp tuyến là
và có vectơ pháp tuyến là 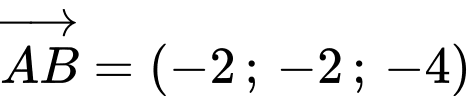
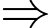 Phương trình
Phương trình 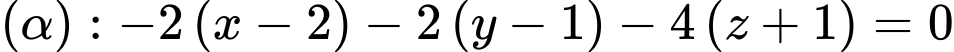
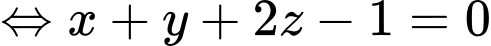 . Đáp án: B
. Đáp án: B
Câu 10 [544657]: Trong không gian với hệ tọa độ 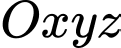 , khoảng cách từ điểm
, khoảng cách từ điểm 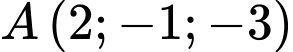 đến mặt phẳng
đến mặt phẳng 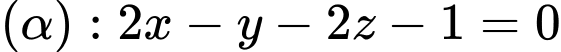 là
là
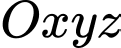 , khoảng cách từ điểm
, khoảng cách từ điểm 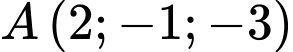 đến mặt phẳng
đến mặt phẳng 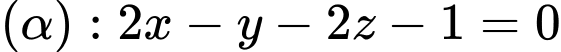 là
là A, 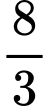 .
.
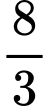 .
.B,  .
.
 .
.C, 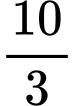 .
.
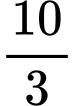 .
.D, 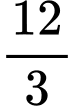 .
.
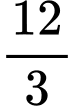 .
.
Chọn đáp án C.
Khoảng cách từ điểm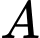 đến mặt phẳng
đến mặt phẳng  là:
là: 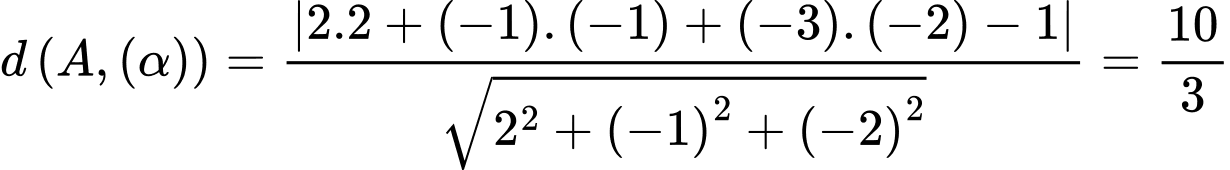 . Đáp án: C
. Đáp án: C
Khoảng cách từ điểm
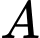 đến mặt phẳng
đến mặt phẳng  là:
là: 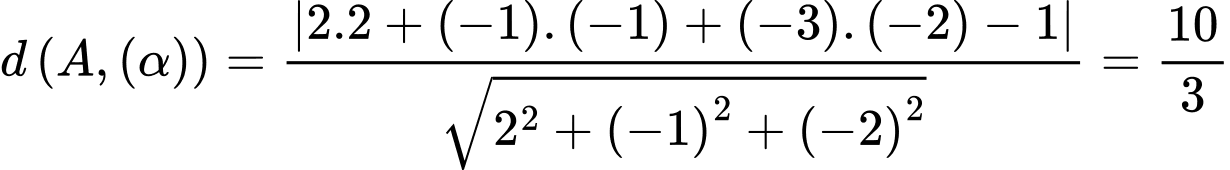 . Đáp án: C
. Đáp án: C
Câu 11 [57135]: Trong không gian với hệ toạ độ 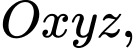 cho mặt phẳng
cho mặt phẳng 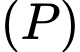 có phương trình là
có phương trình là  . Tính góc giữa
. Tính góc giữa 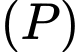 và mặt phẳng
và mặt phẳng 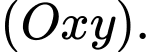
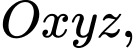 cho mặt phẳng
cho mặt phẳng 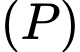 có phương trình là
có phương trình là  . Tính góc giữa
. Tính góc giữa 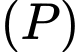 và mặt phẳng
và mặt phẳng 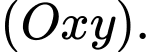
A, 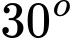 .
.
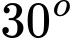 .
.B, 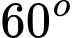 .
.
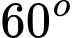 .
.C, 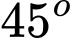 .
.
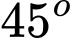 .
.D, 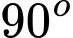 .
.
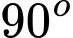 .
.
Chọn đáp án C.
Vectơ pháp tuyến của mặt phẳng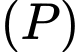 là
là 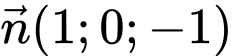
Vectơ pháp tuyến của mặt phẳng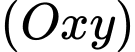 là
là 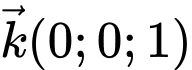
Gọi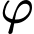 là góc hợp bởi mặt phẳng
là góc hợp bởi mặt phẳng 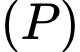 và mặt phảng
và mặt phảng 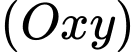
Ta có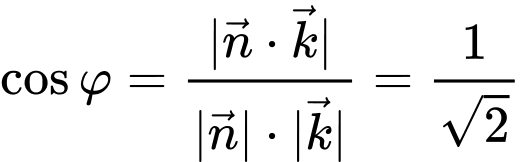
Vậy góc hợp bời mặt phẳng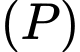 mặt phả̉ng
mặt phả̉ng 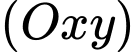 là
là 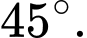 Đáp án: C
Đáp án: C
Vectơ pháp tuyến của mặt phẳng
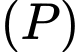 là
là 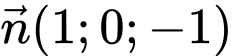
Vectơ pháp tuyến của mặt phẳng
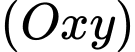 là
là 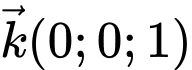
Gọi
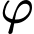 là góc hợp bởi mặt phẳng
là góc hợp bởi mặt phẳng 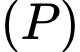 và mặt phảng
và mặt phảng 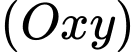
Ta có
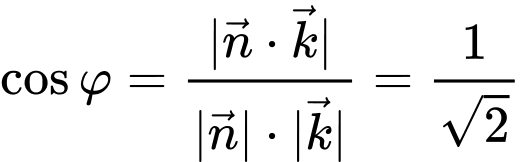
Vậy góc hợp bời mặt phẳng
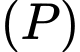 mặt phả̉ng
mặt phả̉ng 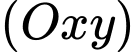 là
là 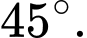 Đáp án: C
Đáp án: C
Câu 12 [899205]: Phương trình mặt phẳng qua 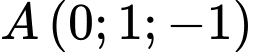 và vuông góc đồng thời với cả hai mặt phẳng
và vuông góc đồng thời với cả hai mặt phẳng 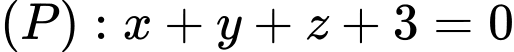 và
và 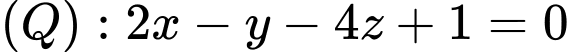 là
là
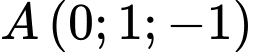 và vuông góc đồng thời với cả hai mặt phẳng
và vuông góc đồng thời với cả hai mặt phẳng 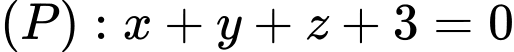 và
và 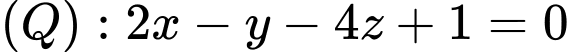 là
là A, 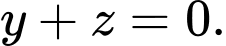
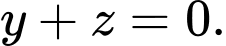
B, 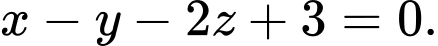
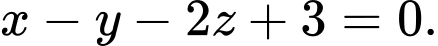
C, 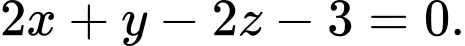
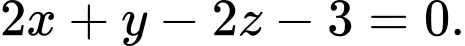
D, 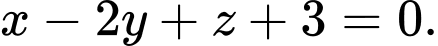
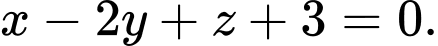
Gọi  là mặt phẳng cần tìm và vectơ pháp tuyến của
là mặt phẳng cần tìm và vectơ pháp tuyến của  là
là 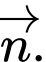
Vectơ pháp tuyến của hai mặt phẳng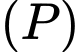 và
và  lần lượt là
lần lượt là 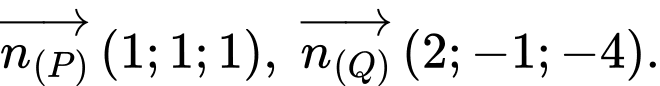
Do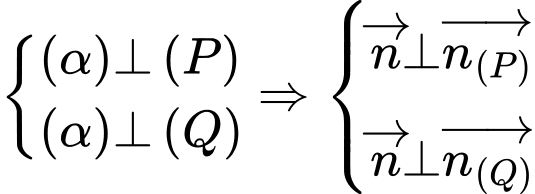
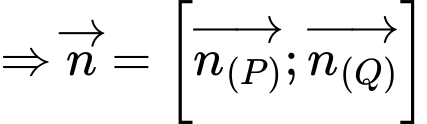
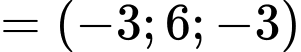
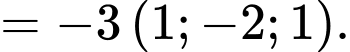
Suy ra qua
qua 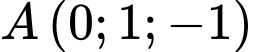 và có 1 vectơ pháp tuyến là
và có 1 vectơ pháp tuyến là 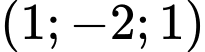 nên
nên 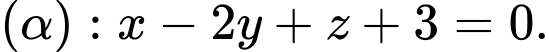 Chọn D. Đáp án: D
Chọn D. Đáp án: D
 là mặt phẳng cần tìm và vectơ pháp tuyến của
là mặt phẳng cần tìm và vectơ pháp tuyến của  là
là 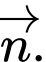
Vectơ pháp tuyến của hai mặt phẳng
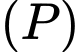 và
và  lần lượt là
lần lượt là 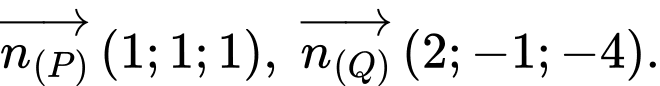
Do
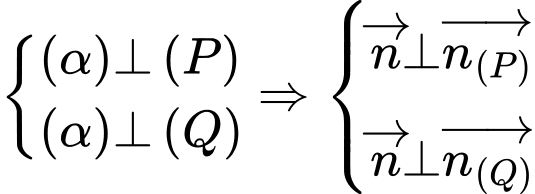
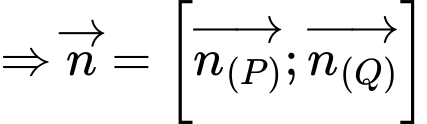
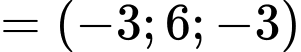
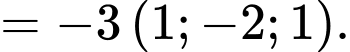
Suy ra
 qua
qua 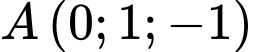 và có 1 vectơ pháp tuyến là
và có 1 vectơ pháp tuyến là 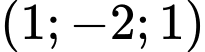 nên
nên 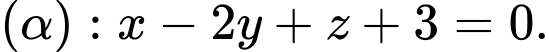 Chọn D. Đáp án: D
Chọn D. Đáp án: D PHẦN II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a),b),c),d) ở mỗi câu học sinh chọn đúng hoặc sai.
Câu 13 [778763]: Trong không gian với hệ tọa độ 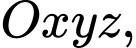 cho các điểm
cho các điểm 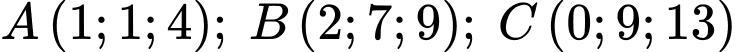 và
và 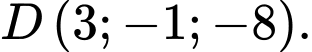
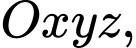 cho các điểm
cho các điểm 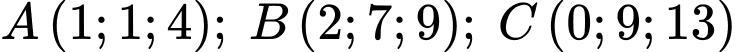 và
và 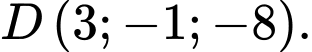
a) 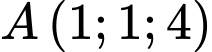 ,
, 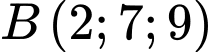
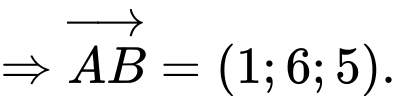
Chọn ĐÚNG.
b)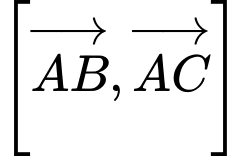

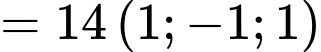 nên Mặt phẳng
nên Mặt phẳng 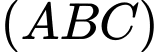 có 1 vectơ pháp tuyến là
có 1 vectơ pháp tuyến là 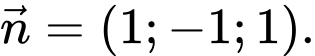
Chọn SAI.
c)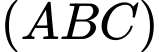 đi qua
đi qua 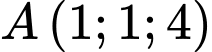 có vtpt
có vtpt 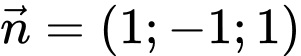 nên có phương trình
nên có phương trình 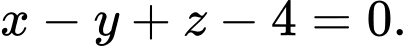
Chọn ĐÚNG.
d) Tọa độ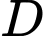 không thỏa phương trình
không thỏa phương trình 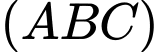 nên
nên 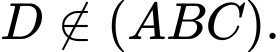
Chọn SAI.
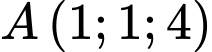 ,
, 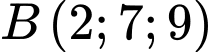
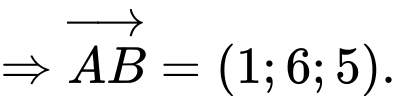
Chọn ĐÚNG.
b)
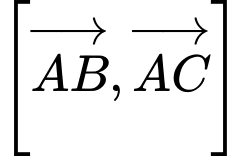

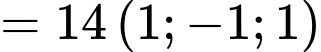 nên Mặt phẳng
nên Mặt phẳng 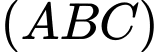 có 1 vectơ pháp tuyến là
có 1 vectơ pháp tuyến là 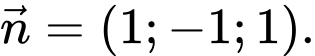
Chọn SAI.
c)
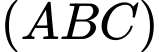 đi qua
đi qua 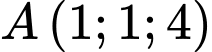 có vtpt
có vtpt 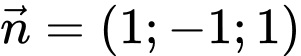 nên có phương trình
nên có phương trình 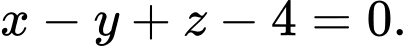
Chọn ĐÚNG.
d) Tọa độ
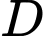 không thỏa phương trình
không thỏa phương trình 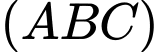 nên
nên 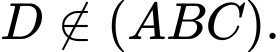
Chọn SAI.
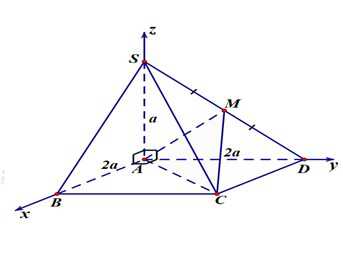
Câu 14 [778764]: Cho hình chóp 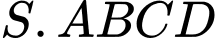 có đáy
có đáy 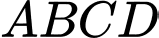 là hình vuông cạnh
là hình vuông cạnh 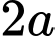 , cạnh bên
, cạnh bên  và vuông góc với mặt phẳng đáy. Gọi
và vuông góc với mặt phẳng đáy. Gọi 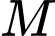 là trung điểm cạnh
là trung điểm cạnh 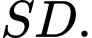 Chọn hệ trục toạ độ
Chọn hệ trục toạ độ 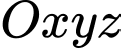 như hình vẽ, với
như hình vẽ, với 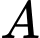 trùng với gốc toạ độ
trùng với gốc toạ độ  điểm
điểm 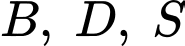 lần lượt thuộc các tia
lần lượt thuộc các tia 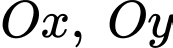 và
và 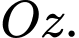
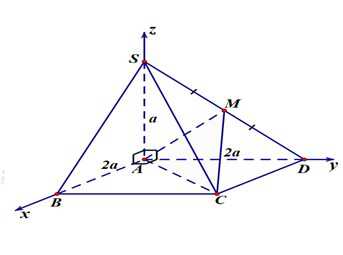
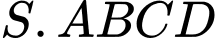 có đáy
có đáy 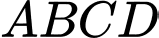 là hình vuông cạnh
là hình vuông cạnh 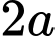 , cạnh bên
, cạnh bên  và vuông góc với mặt phẳng đáy. Gọi
và vuông góc với mặt phẳng đáy. Gọi 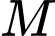 là trung điểm cạnh
là trung điểm cạnh 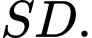 Chọn hệ trục toạ độ
Chọn hệ trục toạ độ 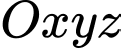 như hình vẽ, với
như hình vẽ, với 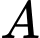 trùng với gốc toạ độ
trùng với gốc toạ độ  điểm
điểm 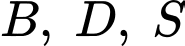 lần lượt thuộc các tia
lần lượt thuộc các tia 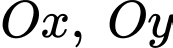 và
và 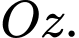

a) Sai.
Vì
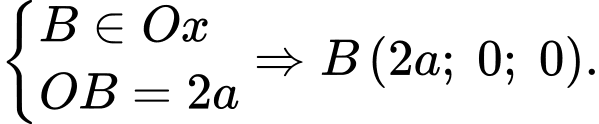
Và ta tìm được tọa độ
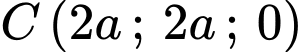 và
và 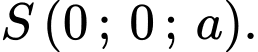
b) Đúng.
Ta có mặt phẳng
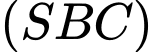 có 2 vectơ chỉ phương là
có 2 vectơ chỉ phương là 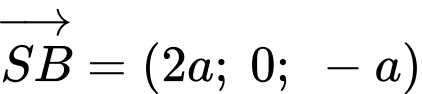 và
và 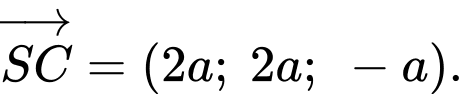
Suy ra một vectơ pháp tuyến của mặt phẳng
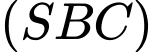 là
là 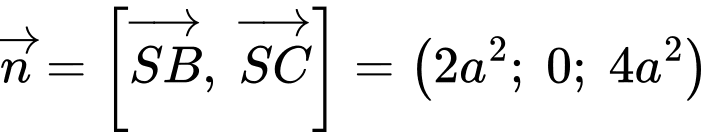 cùng phương với
cùng phương với 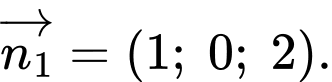
Vậy vectơ
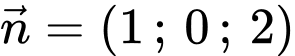 là một vectơ pháp tuyến của mặt phẳng
là một vectơ pháp tuyến của mặt phẳng 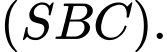
c) Đúng.
Dựa vào kết quả phần b) ta có mặt phẳng
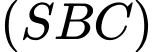 có một vectơ pháp tuyến
có một vectơ pháp tuyến 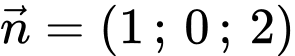 và đi qua điểm
và đi qua điểm 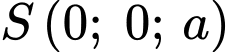 có phương trình là
có phương trình là 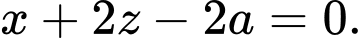
Vì
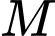 là trung điểm của
là trung điểm của 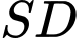 (với điểm
(với điểm 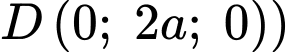 có tọa độ là
có tọa độ là 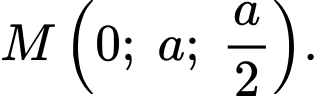
Khi đó khoảng cách từ điểm
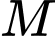 đến mặt phẳng
đến mặt phẳng 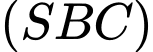 bằng
bằng 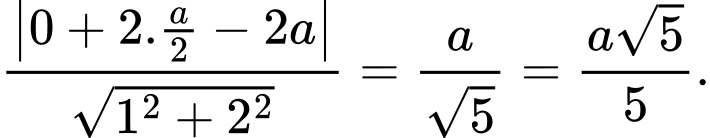
d) Sai.
Thể tích tứ diện
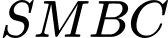 bằng
bằng 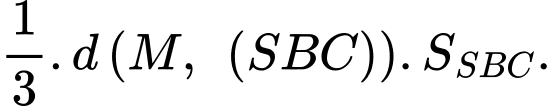
Ta có
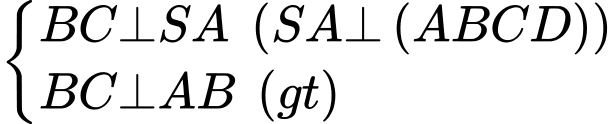
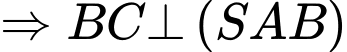

Nên tam giác
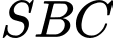 vuông tại
vuông tại 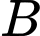 và có diện tích bằng
và có diện tích bằng 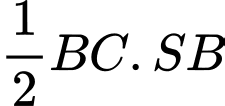

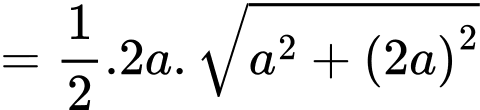
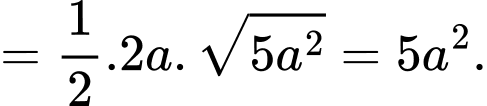
Suy ra thể tích tứ diện
 bằng
bằng 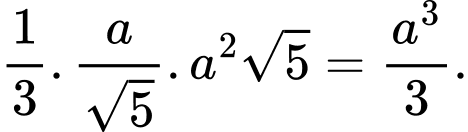
Câu 15 [778766]: Một căn phòng có dạng là một hình hộp chữ nhật, được mô hình hóa và gắn hệ trục tọa độ 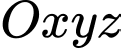 như hình vẽ sau:
như hình vẽ sau:
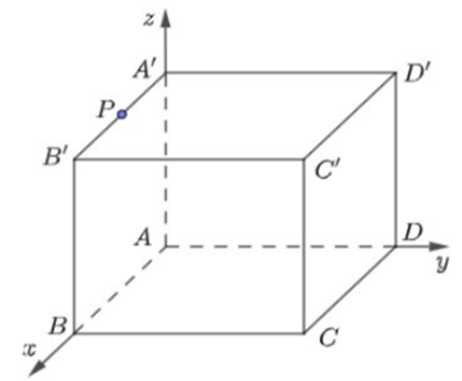
Người ta thiết kế một công tắc điện tại điểm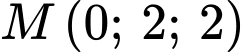 và một bóng đèn để chiếu sáng căn phòng tại điểm
và một bóng đèn để chiếu sáng căn phòng tại điểm 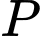 là trung điểm của
là trung điểm của 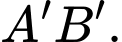 Biết
Biết 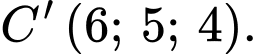 Khi đó:
Khi đó:
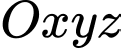 như hình vẽ sau:
như hình vẽ sau:
Người ta thiết kế một công tắc điện tại điểm
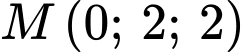 và một bóng đèn để chiếu sáng căn phòng tại điểm
và một bóng đèn để chiếu sáng căn phòng tại điểm 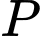 là trung điểm của
là trung điểm của 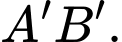 Biết
Biết 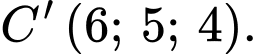 Khi đó:
Khi đó:
a) Đúng.
Vì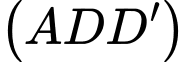 là mặt phẳng
là mặt phẳng 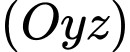 nên
nên 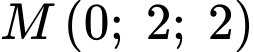 thuộc mặt phẳng
thuộc mặt phẳng 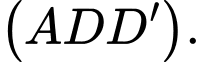
b) Sai.
Ta có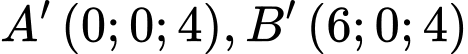 nên toạ độ trung điểm của
nên toạ độ trung điểm của 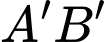 là
là 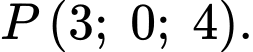
c) Sai.
Ta có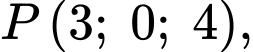
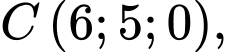
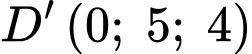
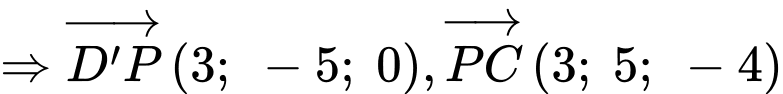 và
và 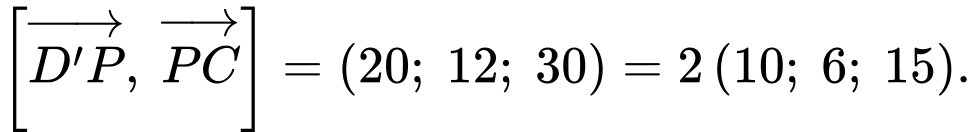 nên mặt phẳng
nên mặt phẳng 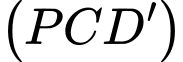 có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 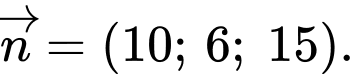
d) Đúng.
Yêu cầu bài toán là tìm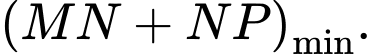
Thực hiện trải các điểm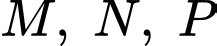 trên mặt phẳng
trên mặt phẳng 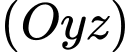 ta được các tọa độ mới như sau:
ta được các tọa độ mới như sau: 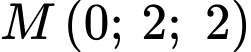 sẽ có tọa độ mới là
sẽ có tọa độ mới là 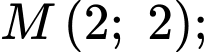
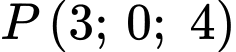 sẽ có tọa độ mới là
sẽ có tọa độ mới là 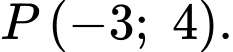 Tham khảo hình vẽ sau:
Tham khảo hình vẽ sau:
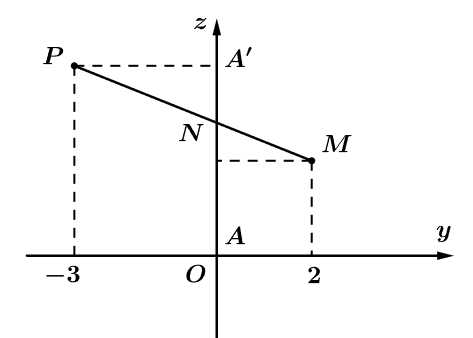
Từ hình vẽ, ta suy ra độ dài dây cáp điện nhỏ nhất khi và chỉ khi
nhỏ nhất khi và chỉ khi 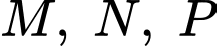 thẳng hàng. Khi đó
thẳng hàng. Khi đó 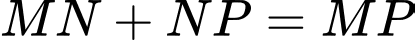
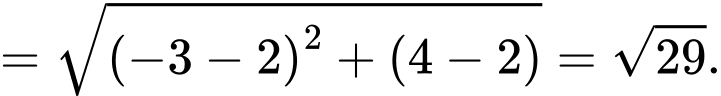
Vậy độ dài dây cáp tối thiểu bằng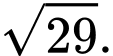
Vì
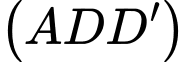 là mặt phẳng
là mặt phẳng 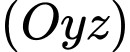 nên
nên 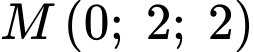 thuộc mặt phẳng
thuộc mặt phẳng 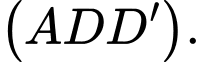
b) Sai.
Ta có
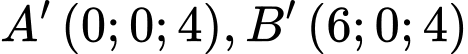 nên toạ độ trung điểm của
nên toạ độ trung điểm của 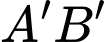 là
là 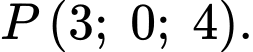
c) Sai.
Ta có
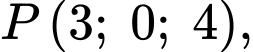
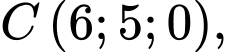
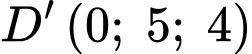
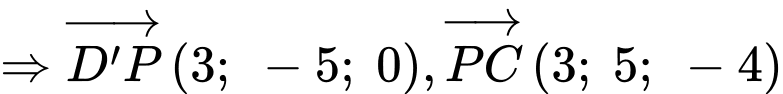 và
và 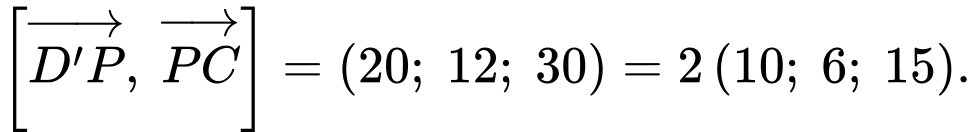 nên mặt phẳng
nên mặt phẳng 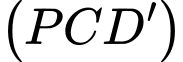 có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 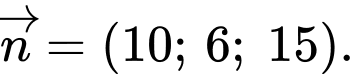
d) Đúng.
Yêu cầu bài toán là tìm
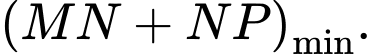
Thực hiện trải các điểm
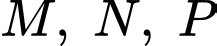 trên mặt phẳng
trên mặt phẳng 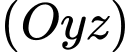 ta được các tọa độ mới như sau:
ta được các tọa độ mới như sau: 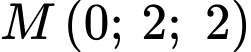 sẽ có tọa độ mới là
sẽ có tọa độ mới là 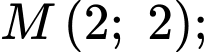
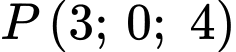 sẽ có tọa độ mới là
sẽ có tọa độ mới là 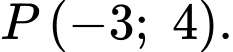 Tham khảo hình vẽ sau:
Tham khảo hình vẽ sau:
Từ hình vẽ, ta suy ra độ dài dây cáp điện
 nhỏ nhất khi và chỉ khi
nhỏ nhất khi và chỉ khi 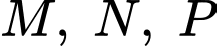 thẳng hàng. Khi đó
thẳng hàng. Khi đó 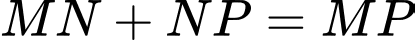
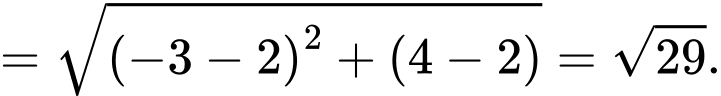
Vậy độ dài dây cáp tối thiểu bằng
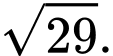
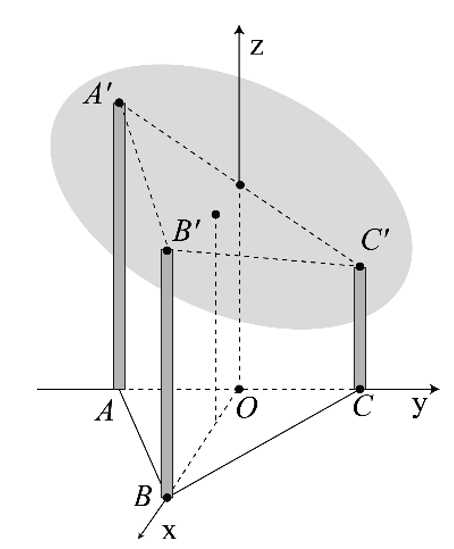
Câu 16 [694447]: Một mái nhà hình tròn được đặt trên ba cây cột trụ. Các cây cộc trụ vuông góc với mặt sàn nhà phẳng và có độ cao lần lượt là 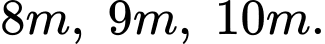 Ba chân cột là ba đỉnh của một tam giác đều trên mặt sàn nhà với cạnh dài
Ba chân cột là ba đỉnh của một tam giác đều trên mặt sàn nhà với cạnh dài 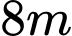 . Chọn hệ trục toạ độ như hình vẽ, với
. Chọn hệ trục toạ độ như hình vẽ, với 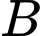 thuộc tia
thuộc tia 
 thuộc tia
thuộc tia 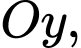 tia
tia  cùng hướng với vectơ
cùng hướng với vectơ 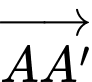 gốc toạ độ
gốc toạ độ  trùng với trung điểm của
trùng với trung điểm của 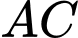 và mỗi đơn vị trên trục có độ dài 1 mét (xem hình vẽ).
và mỗi đơn vị trên trục có độ dài 1 mét (xem hình vẽ).
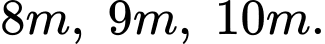 Ba chân cột là ba đỉnh của một tam giác đều trên mặt sàn nhà với cạnh dài
Ba chân cột là ba đỉnh của một tam giác đều trên mặt sàn nhà với cạnh dài 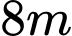 . Chọn hệ trục toạ độ như hình vẽ, với
. Chọn hệ trục toạ độ như hình vẽ, với 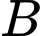 thuộc tia
thuộc tia 
 thuộc tia
thuộc tia 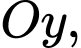 tia
tia  cùng hướng với vectơ
cùng hướng với vectơ 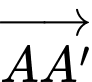 gốc toạ độ
gốc toạ độ  trùng với trung điểm của
trùng với trung điểm của 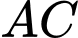 và mỗi đơn vị trên trục có độ dài 1 mét (xem hình vẽ).
và mỗi đơn vị trên trục có độ dài 1 mét (xem hình vẽ).
a) Đúng.
Ta có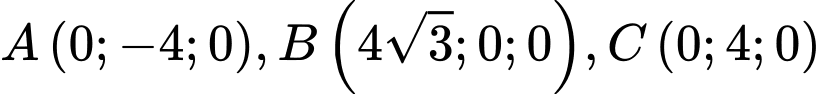 .
. 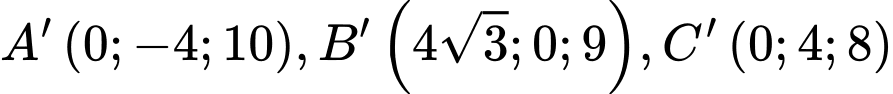 .
.
b) Đúng.
Ta có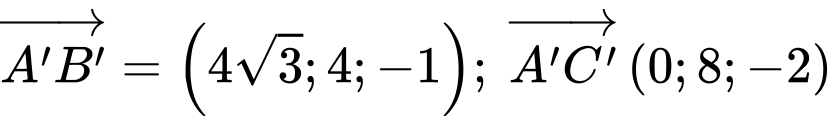 <.
<.
Vectơ pháp tuyến của mặt phẳng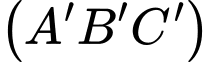 là:
là: 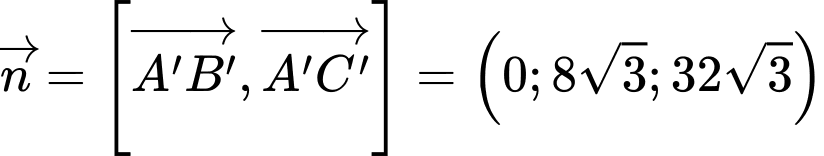
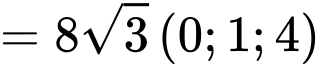 suy ra phương trình mặt phẳng
suy ra phương trình mặt phẳng 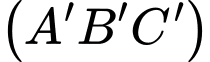 là:
là: 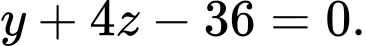
c) Sai.
Vectơ pháp tuyến của mặt phẳng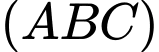 là
là 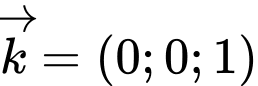
Khi đó: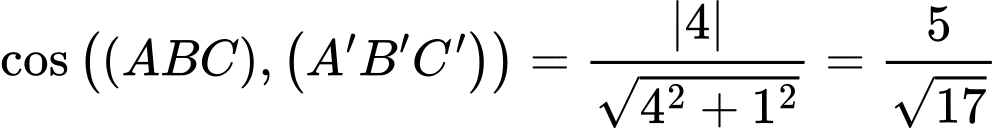
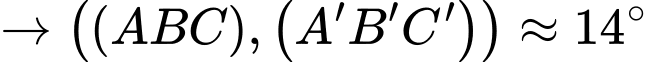
Vậy độ dốc của mái khoảng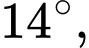 mái nhà trên không ở mức tiêu chuẩn
mái nhà trên không ở mức tiêu chuẩn
d) Đúng.
Gọi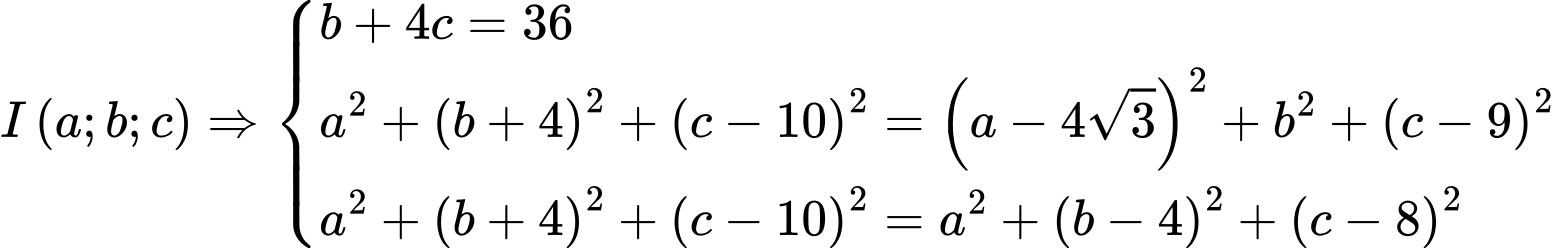
Suy ra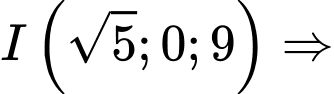 điểm I cách mặt sàn một khoảng là 9 mét.
điểm I cách mặt sàn một khoảng là 9 mét.
Ta có
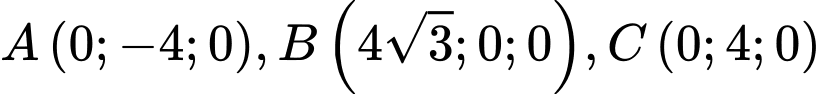 .
. 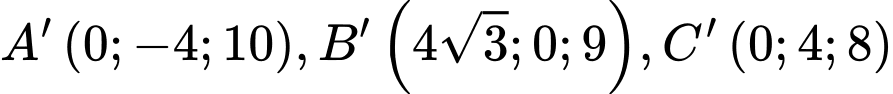 .
.b) Đúng.
Ta có
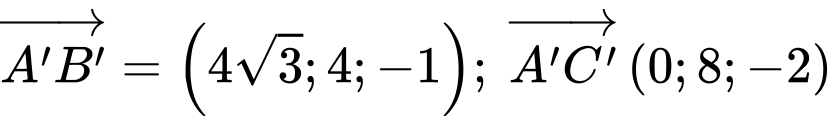 <.
<.Vectơ pháp tuyến của mặt phẳng
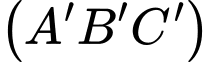 là:
là: 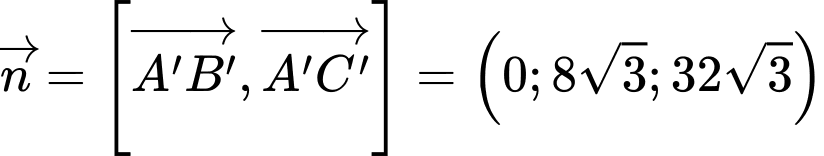
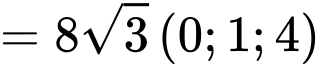 suy ra phương trình mặt phẳng
suy ra phương trình mặt phẳng 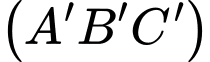 là:
là: 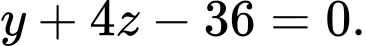
c) Sai.
Vectơ pháp tuyến của mặt phẳng
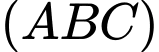 là
là 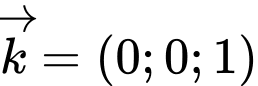
Khi đó:
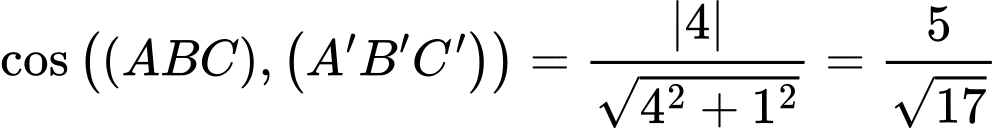
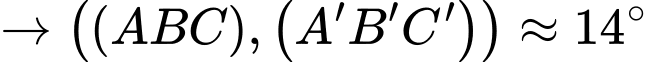
Vậy độ dốc của mái khoảng
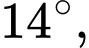 mái nhà trên không ở mức tiêu chuẩn
mái nhà trên không ở mức tiêu chuẩnd) Đúng.
Gọi
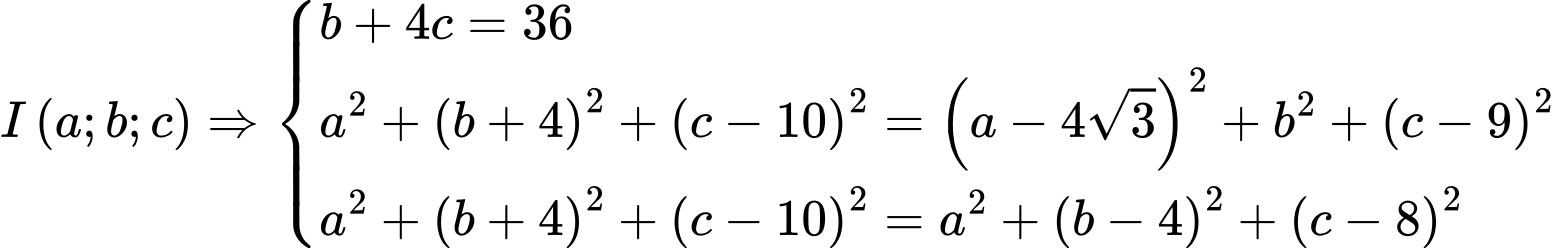
Suy ra
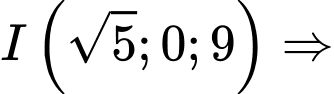 điểm I cách mặt sàn một khoảng là 9 mét.
điểm I cách mặt sàn một khoảng là 9 mét. PHẦN III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 17 đến câu 22.
Câu 17 [778770]: Trong không gian với hệ trục tọa độ 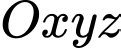 , cho hai điểm
, cho hai điểm 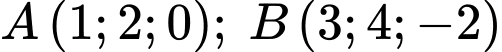 và mặt phẳng
và mặt phẳng 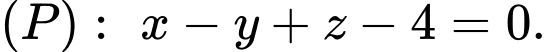 Phương trình mặt phẳng
Phương trình mặt phẳng  đi qua hai điểm
đi qua hai điểm 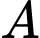 ,
, 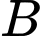 và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 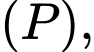 có dạng
có dạng 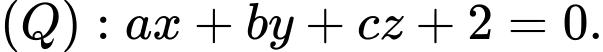 Tính
Tính 
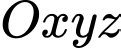 , cho hai điểm
, cho hai điểm 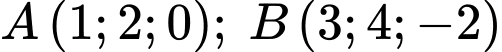 và mặt phẳng
và mặt phẳng 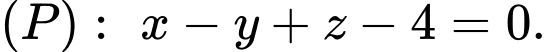 Phương trình mặt phẳng
Phương trình mặt phẳng  đi qua hai điểm
đi qua hai điểm 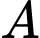 ,
, 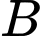 và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 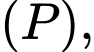 có dạng
có dạng 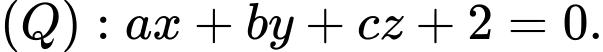 Tính
Tính 
Trả lời: 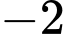
Ta có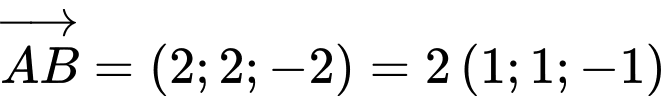 .
.
Mặt phẳng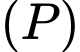 có một vectơ pháp tuyến
có một vectơ pháp tuyến 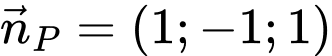 .
.
Mặt phẳng có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 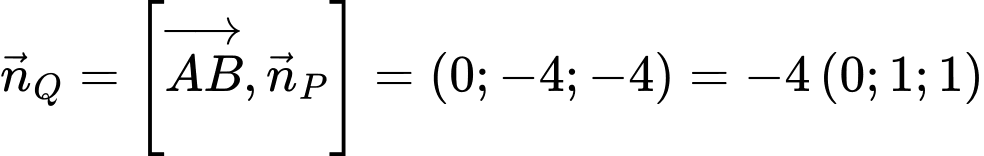 .
.
Vậy phương trình mặt phẳng :
: 
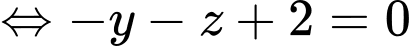
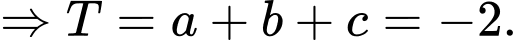
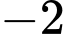
Ta có
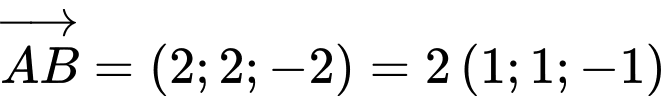 .
. Mặt phẳng
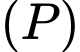 có một vectơ pháp tuyến
có một vectơ pháp tuyến 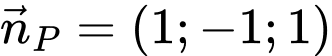 .
. Mặt phẳng
 có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 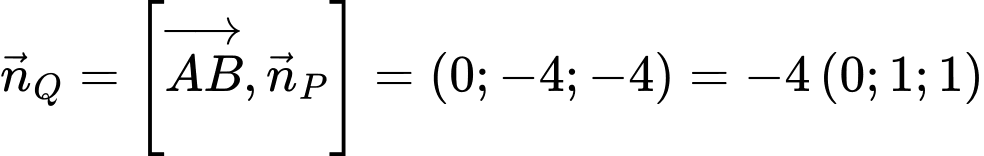 .
.Vậy phương trình mặt phẳng
 :
: 
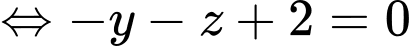
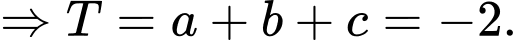
Câu 18 [778771]: Hình vẽ minh họa một khu nhà đang xây dựng được gắn hệ trục tọa độ 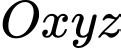 (đơn vị trên các trục là mét). Mỗi cột bê tông có dạng hình lăng trụ tứ giác đều và tâm của mặt đáy trên lần lượt là các điểm
(đơn vị trên các trục là mét). Mỗi cột bê tông có dạng hình lăng trụ tứ giác đều và tâm của mặt đáy trên lần lượt là các điểm 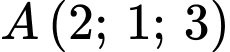 ,
, 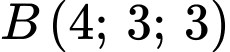 ,
, 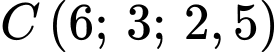 ,
, 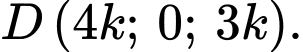 Biết rằng 4 điểm
Biết rằng 4 điểm 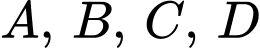 đồng phẳng, tính giá trị của
đồng phẳng, tính giá trị của 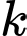 (viết kết quả làm tròn đến hàng phần mười).
(viết kết quả làm tròn đến hàng phần mười).

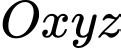 (đơn vị trên các trục là mét). Mỗi cột bê tông có dạng hình lăng trụ tứ giác đều và tâm của mặt đáy trên lần lượt là các điểm
(đơn vị trên các trục là mét). Mỗi cột bê tông có dạng hình lăng trụ tứ giác đều và tâm của mặt đáy trên lần lượt là các điểm 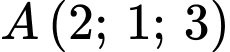 ,
, 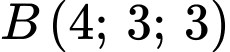 ,
, 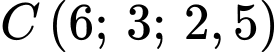 ,
, 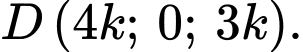 Biết rằng 4 điểm
Biết rằng 4 điểm 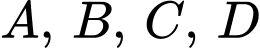 đồng phẳng, tính giá trị của
đồng phẳng, tính giá trị của 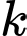 (viết kết quả làm tròn đến hàng phần mười).
(viết kết quả làm tròn đến hàng phần mười).
Điền đáp án: 0,8.
Ta có: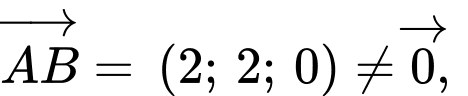
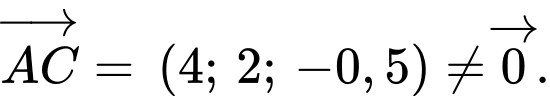
Xét: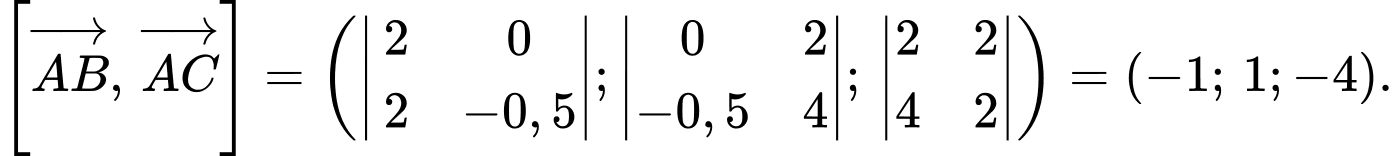
Hay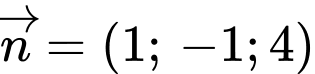 là một vectơ pháp tuyến của mặt phẳng
là một vectơ pháp tuyến của mặt phẳng 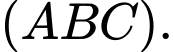
Phương trình mặt phẳng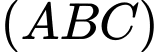 là:
là: 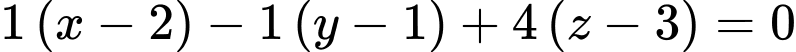
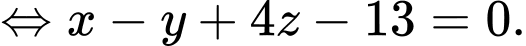
Vì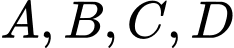 đồng phẳng nên
đồng phẳng nên  thay tọa độ điểm
thay tọa độ điểm 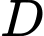 vào phương trình mặt phẳng
vào phương trình mặt phẳng 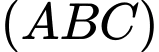 ta được
ta được 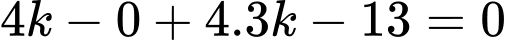
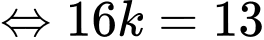
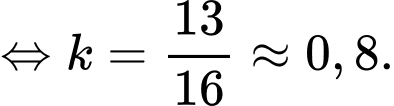
Ta có:
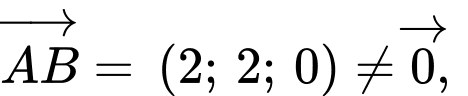
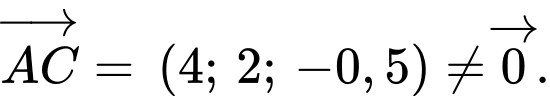
Xét:
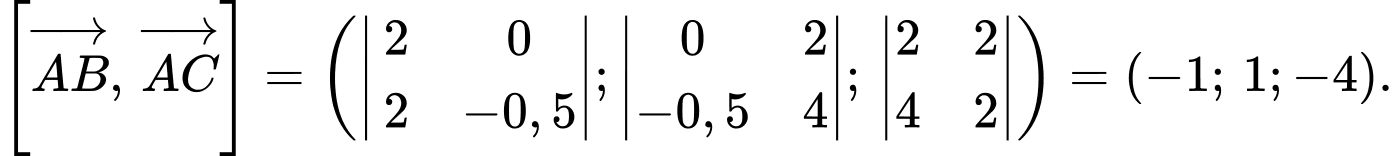
Hay
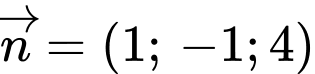 là một vectơ pháp tuyến của mặt phẳng
là một vectơ pháp tuyến của mặt phẳng 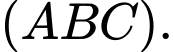
Phương trình mặt phẳng
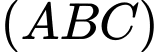 là:
là: 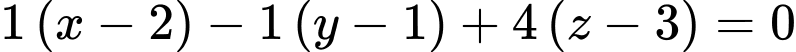
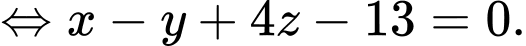
Vì
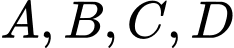 đồng phẳng nên
đồng phẳng nên  thay tọa độ điểm
thay tọa độ điểm 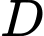 vào phương trình mặt phẳng
vào phương trình mặt phẳng 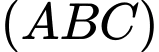 ta được
ta được 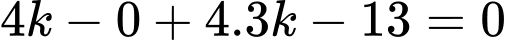
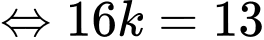
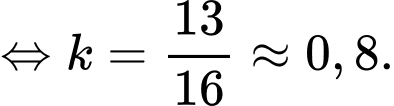
Câu 19 [778772]: Trong không gian với hệ tọa độ 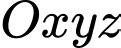 , cho điểm
, cho điểm 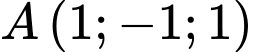 ,
, 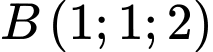 và mặt phẳng
và mặt phẳng 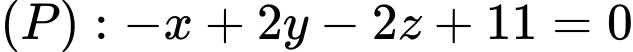 . Phương trình mặt phẳng
. Phương trình mặt phẳng  song song với mặt phẳng
song song với mặt phẳng 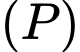 và cách đều hai điểm
và cách đều hai điểm 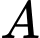 ,
, 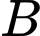 là
là 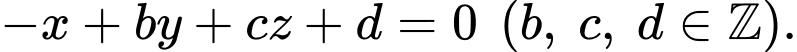 Tính
Tính 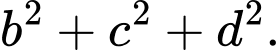
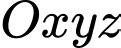 , cho điểm
, cho điểm 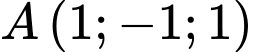 ,
, 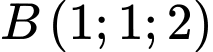 và mặt phẳng
và mặt phẳng 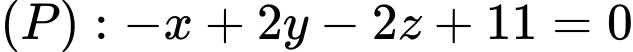 . Phương trình mặt phẳng
. Phương trình mặt phẳng  song song với mặt phẳng
song song với mặt phẳng 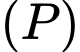 và cách đều hai điểm
và cách đều hai điểm 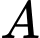 ,
, 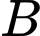 là
là 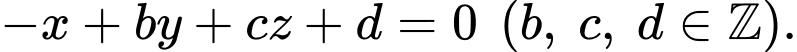 Tính
Tính 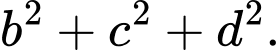
Điền đáp án: 24.
Do là mặt phẳng song song
là mặt phẳng song song 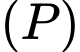 nên ptmp
nên ptmp 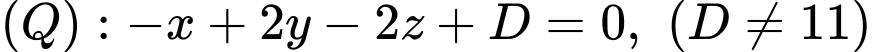
Ta có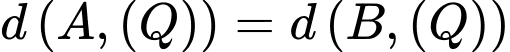
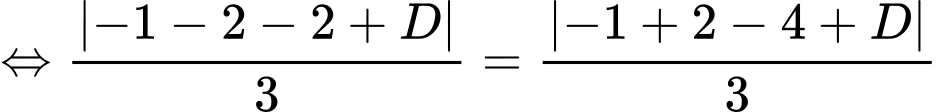
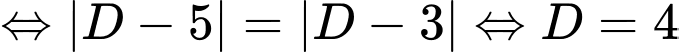 (Nhận)
(Nhận)
Vậy phương trình mặt phẳng là
là 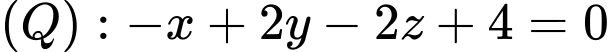
Suy ra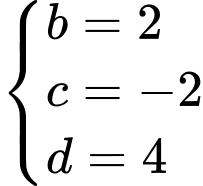
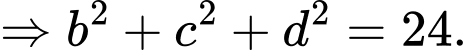
Do
 là mặt phẳng song song
là mặt phẳng song song 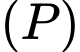 nên ptmp
nên ptmp 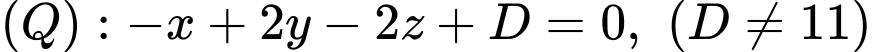
Ta có
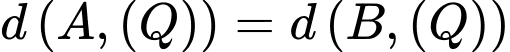
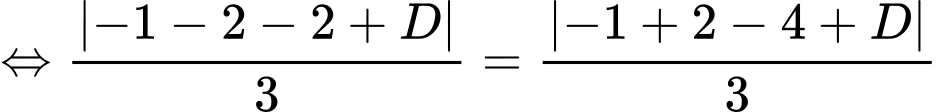
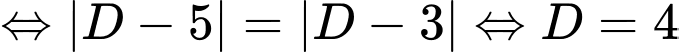 (Nhận)
(Nhận) Vậy phương trình mặt phẳng
 là
là 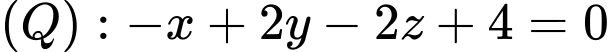
Suy ra
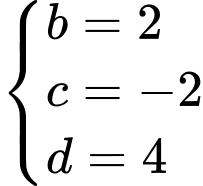
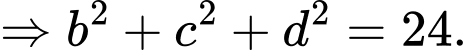
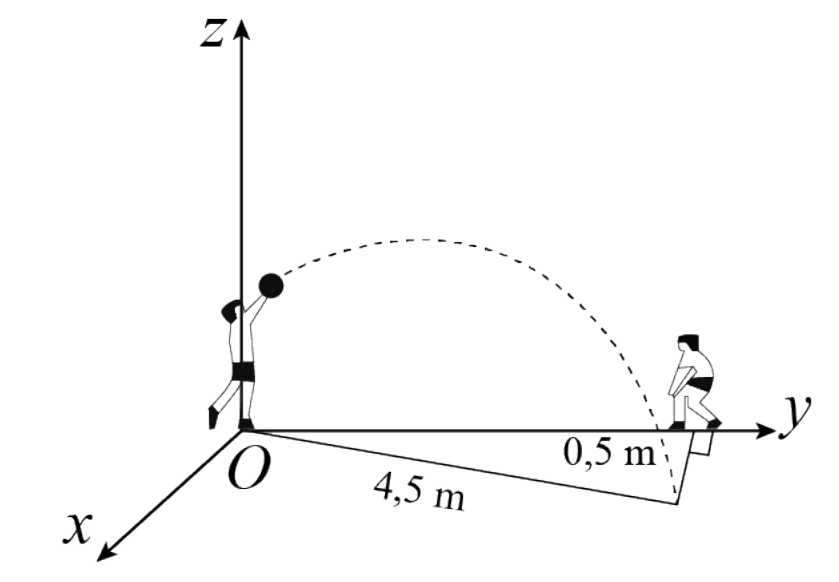
Câu 20 [778774]: Trong tiết thể dục học về kĩ thuật chuyền bóng hơi, Nam và An đang tập chuyền bóng cho nhau, Nam ném bóng cho An đỡ, quả bóng bay lên cao nhưng lại lệch sang phải của Nam và rơi xuống vị trí cách An 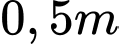 và cách Nam
và cách Nam 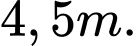 Chọn hệ trục như hình vẽ, gốc toạ độ trùng với vị trí đứng của Nam. Biết rằng quỹ đạo của quả bóng nằm trong mặt phẳng
Chọn hệ trục như hình vẽ, gốc toạ độ trùng với vị trí đứng của Nam. Biết rằng quỹ đạo của quả bóng nằm trong mặt phẳng 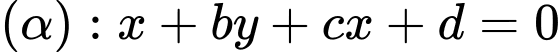 và vuông góc với mặt đất. Khi đó giá trị của
và vuông góc với mặt đất. Khi đó giá trị của 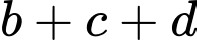 bằng bao nhiêu (kết quả làm tròn đến hàng phần mười).
bằng bao nhiêu (kết quả làm tròn đến hàng phần mười).
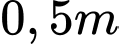 và cách Nam
và cách Nam 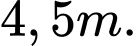 Chọn hệ trục như hình vẽ, gốc toạ độ trùng với vị trí đứng của Nam. Biết rằng quỹ đạo của quả bóng nằm trong mặt phẳng
Chọn hệ trục như hình vẽ, gốc toạ độ trùng với vị trí đứng của Nam. Biết rằng quỹ đạo của quả bóng nằm trong mặt phẳng 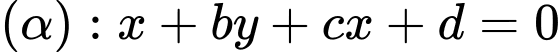 và vuông góc với mặt đất. Khi đó giá trị của
và vuông góc với mặt đất. Khi đó giá trị của 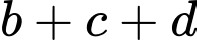 bằng bao nhiêu (kết quả làm tròn đến hàng phần mười).
bằng bao nhiêu (kết quả làm tròn đến hàng phần mười).
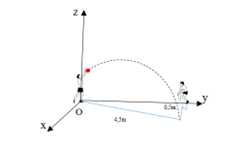
Gọi
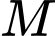 là điểm mà quả bóng chạm đất.
là điểm mà quả bóng chạm đất.Khi đó
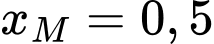 ,
, 
Vì
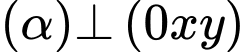 nên
nên  có véc tơ chỉ phương
có véc tơ chỉ phương 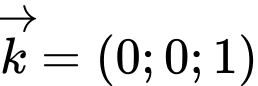 .
.Mà
 có véc tơ chỉ phương
có véc tơ chỉ phương 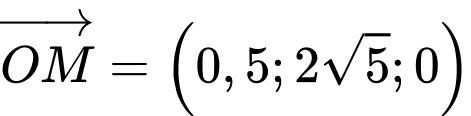
Khi đó véc tơ pháp tuyến của
 là
là 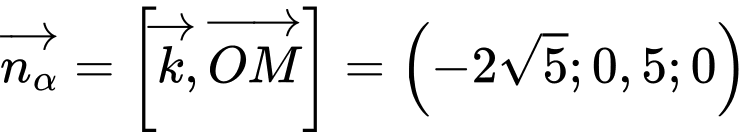 .
.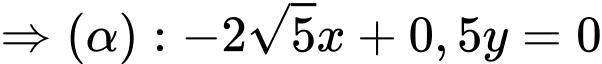
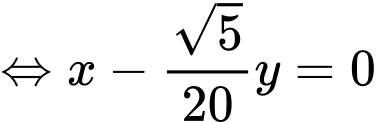
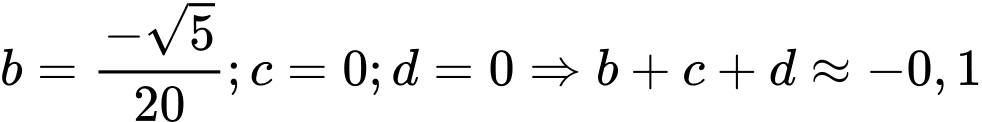 .
.
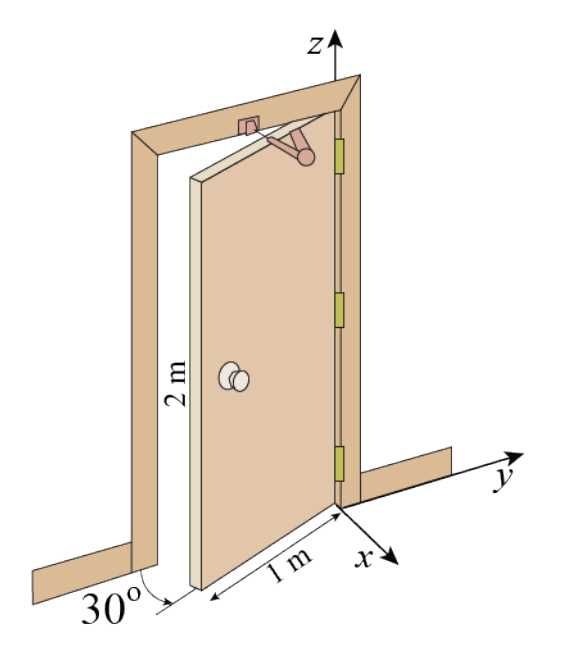
Câu 21 [778782]: Hình ảnh bên minh hoạ một cánh cửa hình chữ nhật có chiều rộng  và chiều cao
và chiều cao  khi đang mở. Chọn hệ toạ độ như hình vẽ, biết cánh cửa tạo với bức tường một góc
khi đang mở. Chọn hệ toạ độ như hình vẽ, biết cánh cửa tạo với bức tường một góc 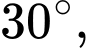 bờ tường vuông góc với mặt sàn. Bỏ qua bề dày của cánh cửa thì phương trình mặt phẳng chứa cánh cửa là
bờ tường vuông góc với mặt sàn. Bỏ qua bề dày của cánh cửa thì phương trình mặt phẳng chứa cánh cửa là 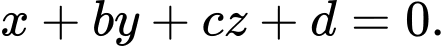 Tính giá trị
Tính giá trị 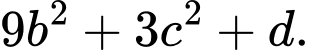
 và chiều cao
và chiều cao  khi đang mở. Chọn hệ toạ độ như hình vẽ, biết cánh cửa tạo với bức tường một góc
khi đang mở. Chọn hệ toạ độ như hình vẽ, biết cánh cửa tạo với bức tường một góc 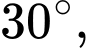 bờ tường vuông góc với mặt sàn. Bỏ qua bề dày của cánh cửa thì phương trình mặt phẳng chứa cánh cửa là
bờ tường vuông góc với mặt sàn. Bỏ qua bề dày của cánh cửa thì phương trình mặt phẳng chứa cánh cửa là 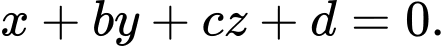 Tính giá trị
Tính giá trị 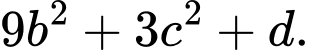

Điền đáp án: 3.
Giả sử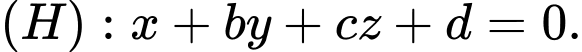
Vì ta đã có dạng của phương trình mặt phẳng chứa cánh cửa (chứa 3 ẩn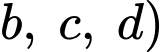 nên để viết được phương trình mặt phẳng
nên để viết được phương trình mặt phẳng 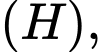 ta cần đi tìm được 3 điểm thuộc mặt phẳng đó.
ta cần đi tìm được 3 điểm thuộc mặt phẳng đó.
Ta vẽ lại hình như và kí hiệu các điểm như hình sau:
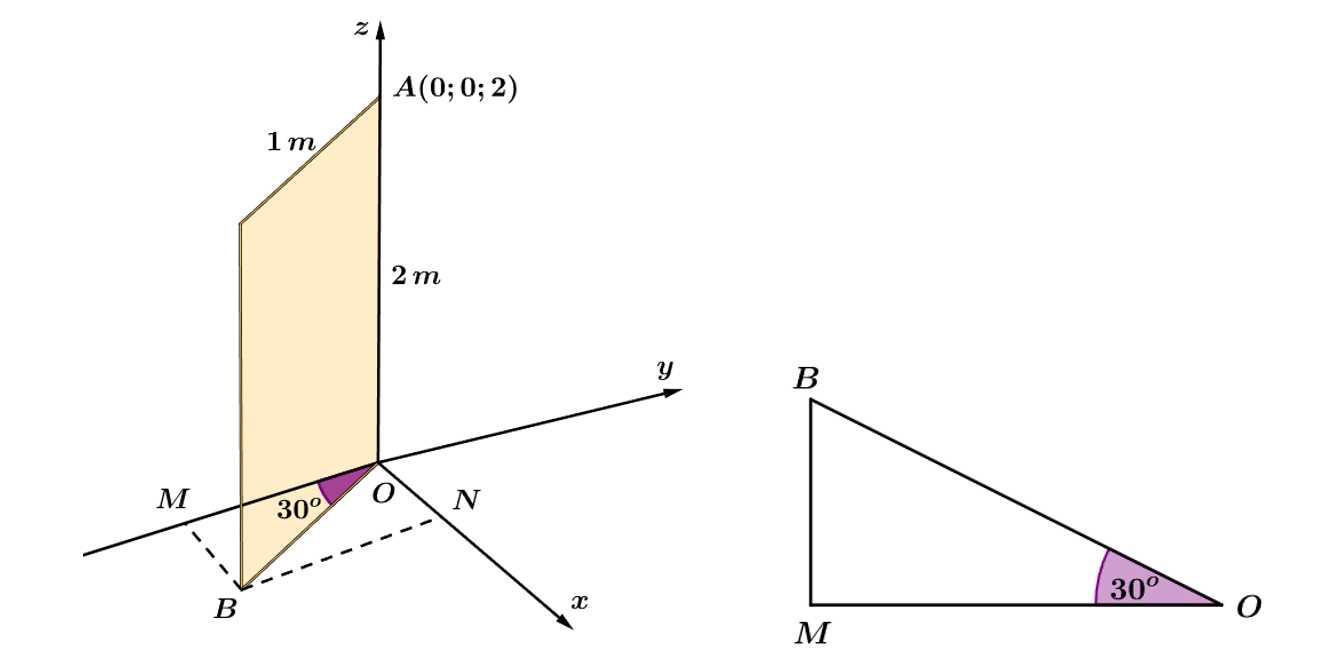
Với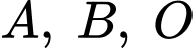 là các điểm thuộc mặt phẳng
là các điểm thuộc mặt phẳng  Kẻ
Kẻ 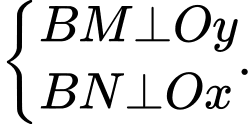 Dựa vào hình vẽ, ta thấy mặt phẳng cần tìm đi qua các điểm
Dựa vào hình vẽ, ta thấy mặt phẳng cần tìm đi qua các điểm 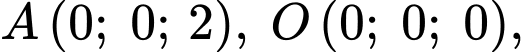
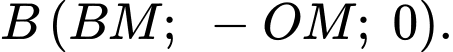
Trong tam giác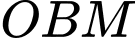 vuông tại
vuông tại 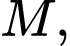 ta có
ta có
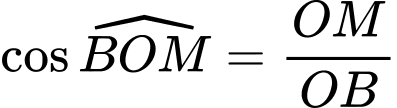
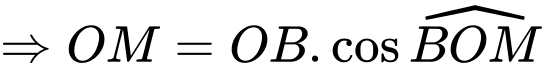

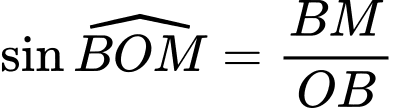

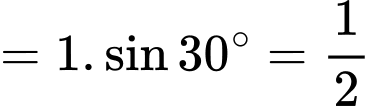
Suy ra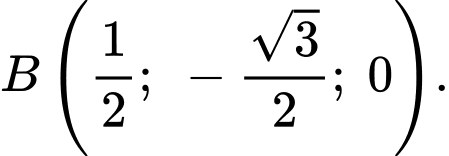
Vì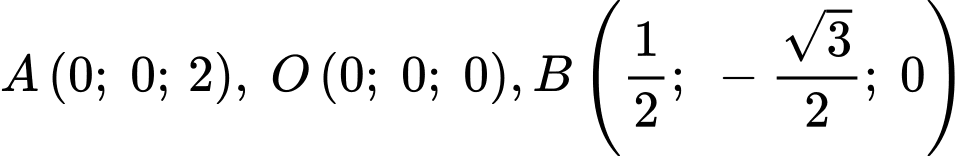 đều thuộc mặt phẳng
đều thuộc mặt phẳng  nên ta có hệ phương trình
nên ta có hệ phương trình 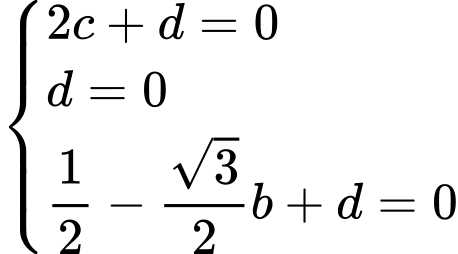
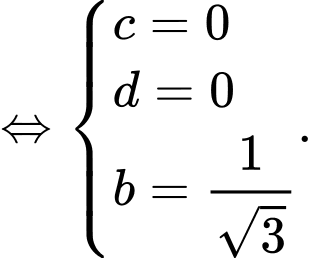 Vậy
Vậy 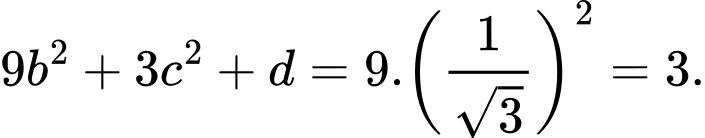
Giả sử
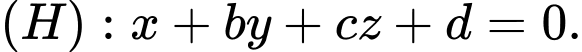
Vì ta đã có dạng của phương trình mặt phẳng chứa cánh cửa (chứa 3 ẩn
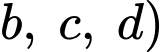 nên để viết được phương trình mặt phẳng
nên để viết được phương trình mặt phẳng 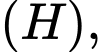 ta cần đi tìm được 3 điểm thuộc mặt phẳng đó.
ta cần đi tìm được 3 điểm thuộc mặt phẳng đó.
Ta vẽ lại hình như và kí hiệu các điểm như hình sau:

Với
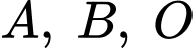 là các điểm thuộc mặt phẳng
là các điểm thuộc mặt phẳng  Kẻ
Kẻ 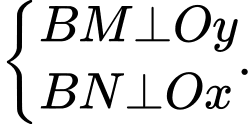 Dựa vào hình vẽ, ta thấy mặt phẳng cần tìm đi qua các điểm
Dựa vào hình vẽ, ta thấy mặt phẳng cần tìm đi qua các điểm 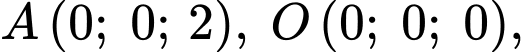
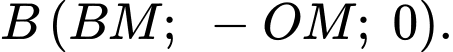
Trong tam giác
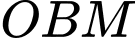 vuông tại
vuông tại 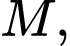 ta có
ta có
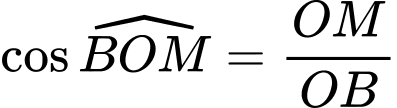
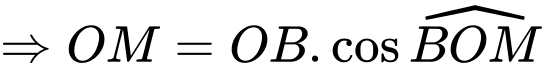

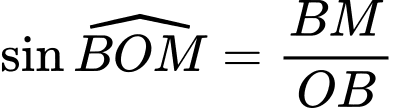

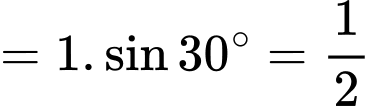
Suy ra
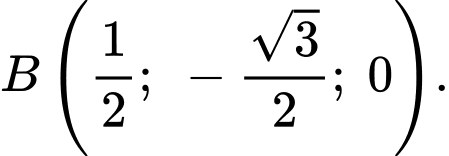
Vì
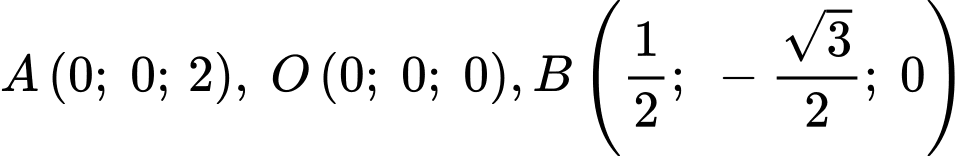 đều thuộc mặt phẳng
đều thuộc mặt phẳng  nên ta có hệ phương trình
nên ta có hệ phương trình 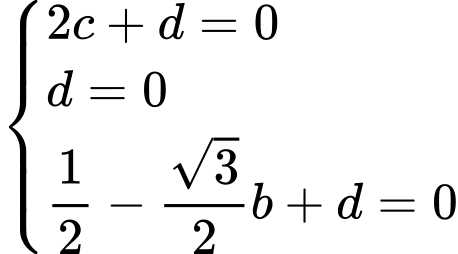
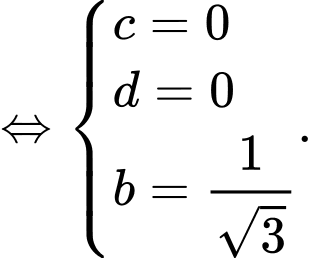 Vậy
Vậy 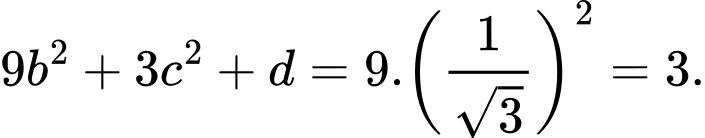
Câu 22 [398970]: Trong không gian với hệ tọa độ 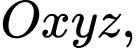 mặt phẳng
mặt phẳng  đi qua điểm
đi qua điểm  và chắn trên tia
và chắn trên tia  một đoạn dài gấp đôi các đoạn chắn trên các tia
một đoạn dài gấp đôi các đoạn chắn trên các tia 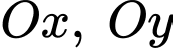 có phương trình là
có phương trình là 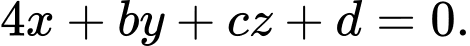 Tính
Tính 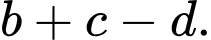
Đáp án:……………………………….
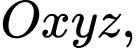 mặt phẳng
mặt phẳng  đi qua điểm
đi qua điểm  và chắn trên tia
và chắn trên tia  một đoạn dài gấp đôi các đoạn chắn trên các tia
một đoạn dài gấp đôi các đoạn chắn trên các tia 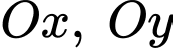 có phương trình là
có phương trình là 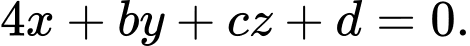 Tính
Tính 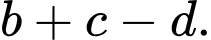
Đáp án:……………………………….
HD: Giả sử mặt phẳng  cắt các tia
cắt các tia 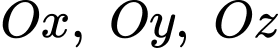 lần lượt tại các điểm
lần lượt tại các điểm 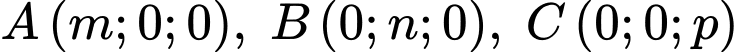 thì phương trình mặt phẳng
thì phương trình mặt phẳng  là:
là: 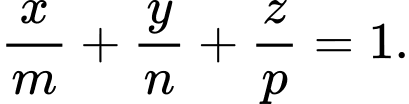
Chú ý rằng cắt các tia
cắt các tia 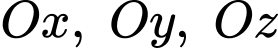 nên ta có điều kiện
nên ta có điều kiện 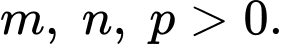
Theo bài ra ta có: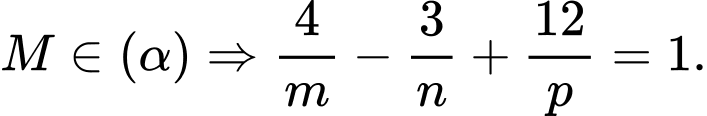
Mặt khác theo giả thiết ta suy ra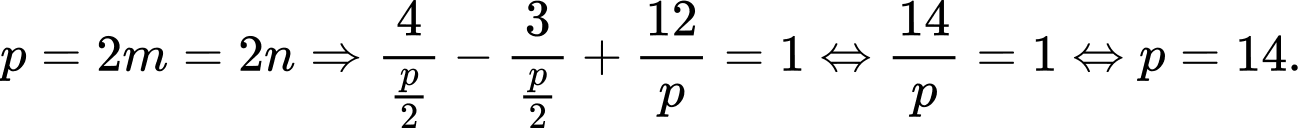
Do đó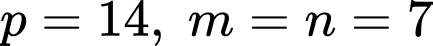
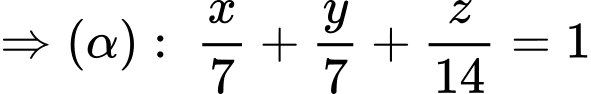
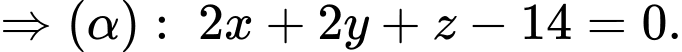
Hay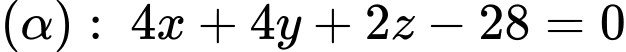
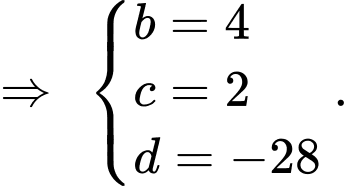
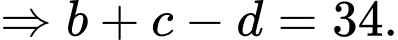
 cắt các tia
cắt các tia 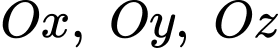 lần lượt tại các điểm
lần lượt tại các điểm 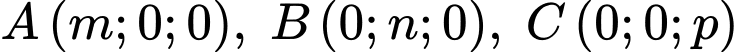 thì phương trình mặt phẳng
thì phương trình mặt phẳng  là:
là: 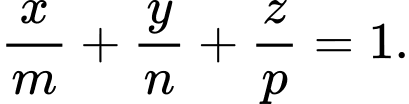
Chú ý rằng
 cắt các tia
cắt các tia 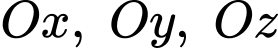 nên ta có điều kiện
nên ta có điều kiện 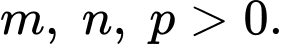
Theo bài ra ta có:
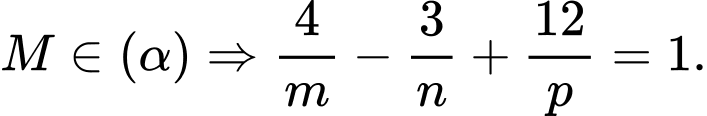
Mặt khác theo giả thiết ta suy ra
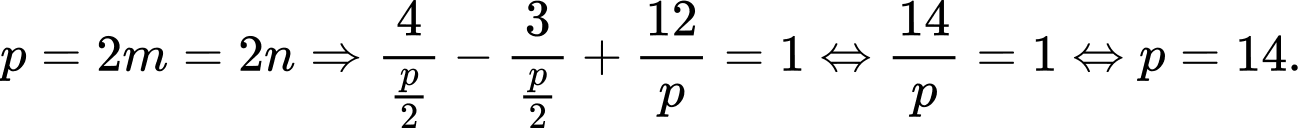
Do đó
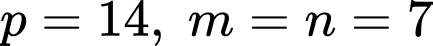
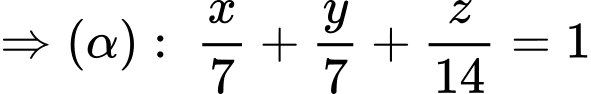
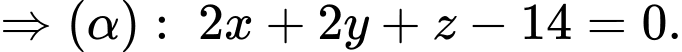
Hay