PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1 [546606]: Trong không gian , cho đường thẳng
, cho đường thẳng 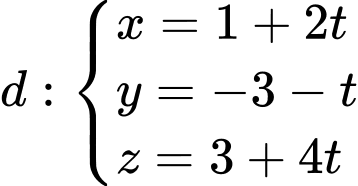 . Véc tơ nào sau đây là một véctơ chỉ phương của
. Véc tơ nào sau đây là một véctơ chỉ phương của  ?
?
 , cho đường thẳng
, cho đường thẳng 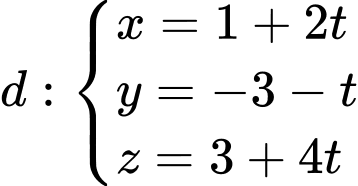 . Véc tơ nào sau đây là một véctơ chỉ phương của
. Véc tơ nào sau đây là một véctơ chỉ phương của 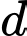 ?
? A, 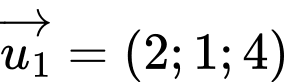 .
.
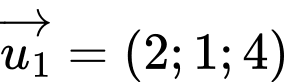 .
.B, 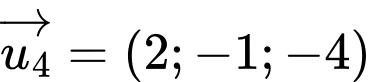 .
.
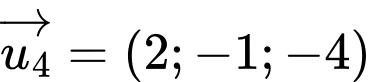 .
.C, 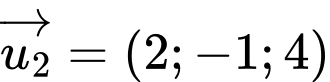 .
.
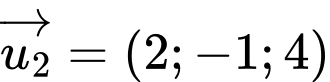 .
.D, 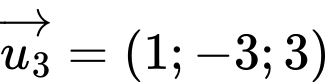 .
.
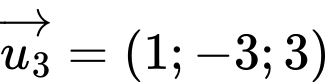 .
.
Chọn C.
Véctơ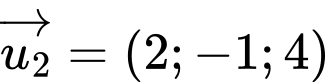 là một véctơ chỉ phương của
là một véctơ chỉ phương của  . Đáp án: C
. Đáp án: C
Véctơ
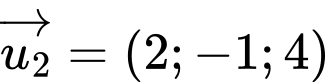 là một véctơ chỉ phương của
là một véctơ chỉ phương của 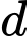 . Đáp án: C
. Đáp án: C
Câu 2 [395556]: Trong không gian 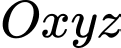 , cho đường thẳng
, cho đường thẳng 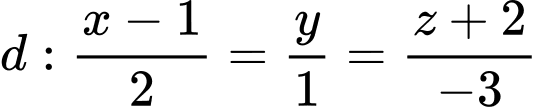 . Vectơ nào dưới đây là một vectơ chỉ phương của
. Vectơ nào dưới đây là một vectơ chỉ phương của 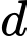 ?
?
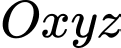 , cho đường thẳng
, cho đường thẳng 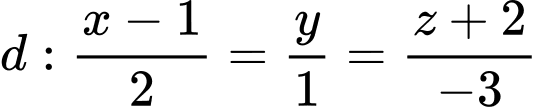 . Vectơ nào dưới đây là một vectơ chỉ phương của
. Vectơ nào dưới đây là một vectơ chỉ phương của 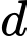 ?
? A, 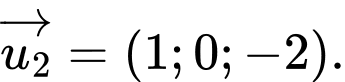
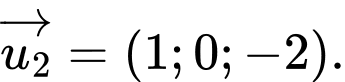
B, 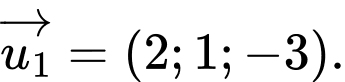
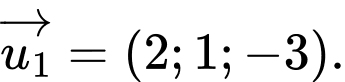
C, 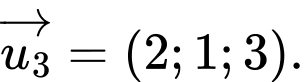
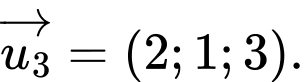
D, 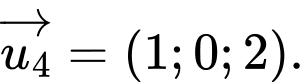
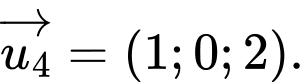
Chọn B
Đường thẳng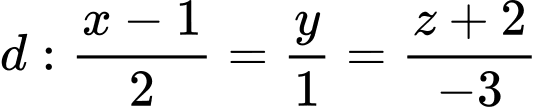 có vtcp là:
có vtcp là: 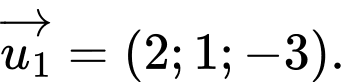 Đáp án: B
Đáp án: B
Đường thẳng
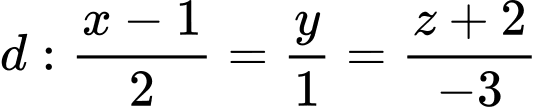 có vtcp là:
có vtcp là: 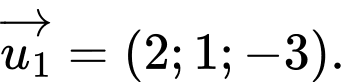 Đáp án: B
Đáp án: B
Câu 3 [755181]: Trong không gian 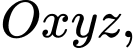 đường thẳng nào có phương trình được cho dưới đây đi qua điểm
đường thẳng nào có phương trình được cho dưới đây đi qua điểm 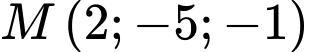 ?
?
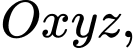 đường thẳng nào có phương trình được cho dưới đây đi qua điểm
đường thẳng nào có phương trình được cho dưới đây đi qua điểm 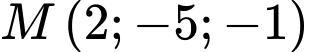 ?
? A, 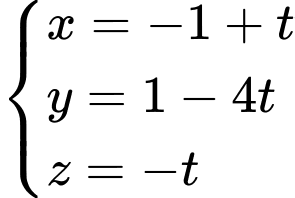 .
.
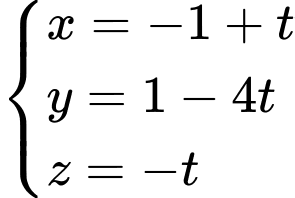 .
.B, 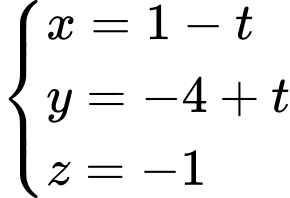 .
.
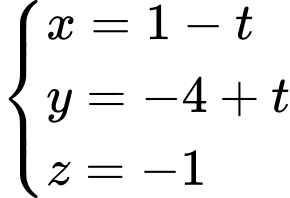 .
.C, 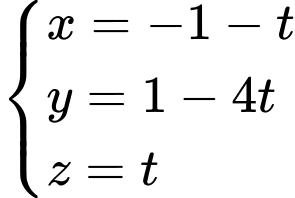 .
.
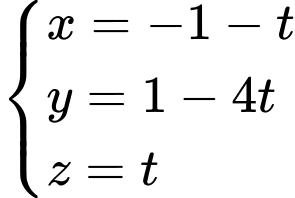 .
.D, 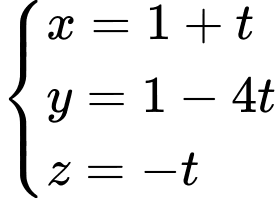 .
.
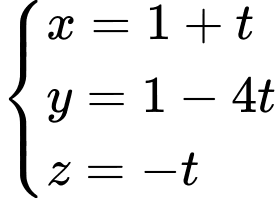 .
.
Chọn B.
Với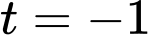 thay vào phương trình
thay vào phương trình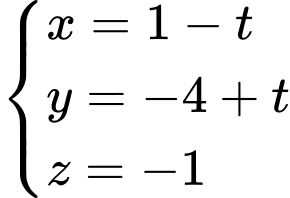 ta được
ta được
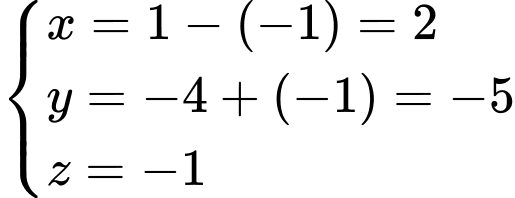
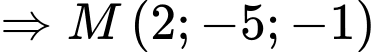 . Đáp án: B
. Đáp án: B
Với
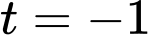 thay vào phương trình
thay vào phương trình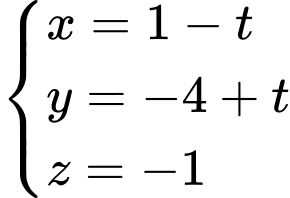 ta được
ta được
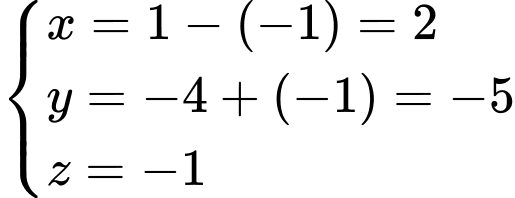
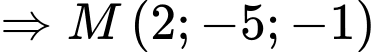 . Đáp án: B
. Đáp án: B
Câu 4 [360349]: Đường thẳng đi qua điểm 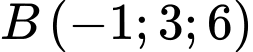 nhận
nhận 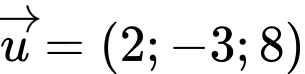 làm vectơ chỉ phương có phương trình chính tắc là:
làm vectơ chỉ phương có phương trình chính tắc là:
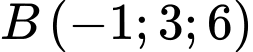 nhận
nhận 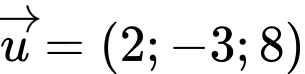 làm vectơ chỉ phương có phương trình chính tắc là:
làm vectơ chỉ phương có phương trình chính tắc là: A, 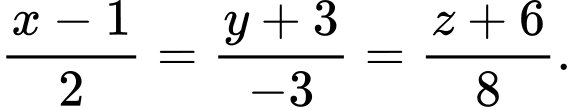
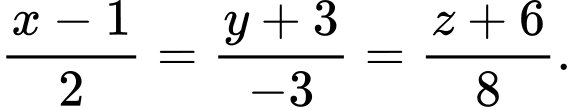
B, 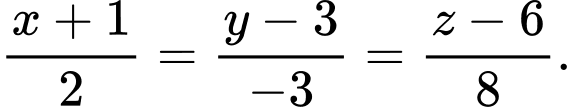
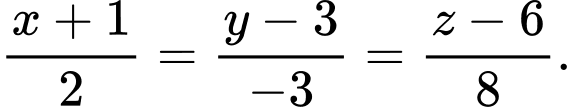
C, 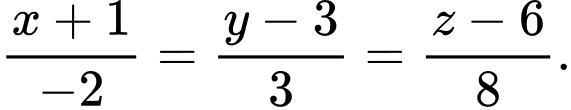
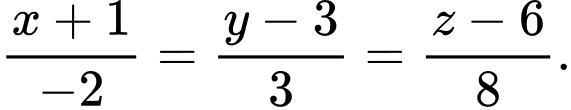
D, 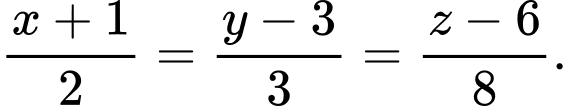
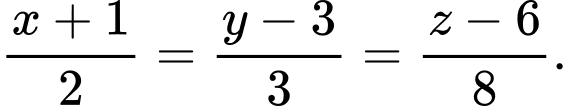
Chọn đáp án B. Đáp án: B
Câu 5 [53288]: Trong không gian 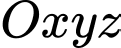 , cho đường thẳng
, cho đường thẳng  có phương trình chính tắc
có phương trình chính tắc 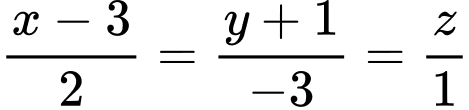 . Phương trình tham số của đường thẳng
. Phương trình tham số của đường thẳng  là
là
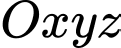 , cho đường thẳng
, cho đường thẳng  có phương trình chính tắc
có phương trình chính tắc 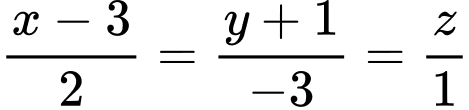 . Phương trình tham số của đường thẳng
. Phương trình tham số của đường thẳng  là
là A, 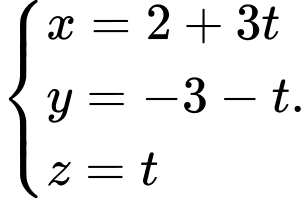
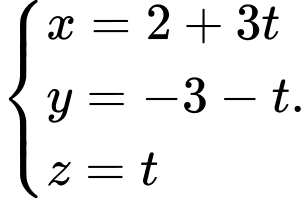
B, 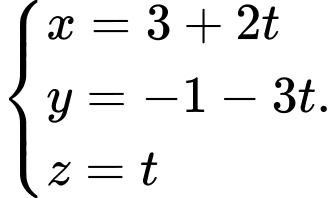
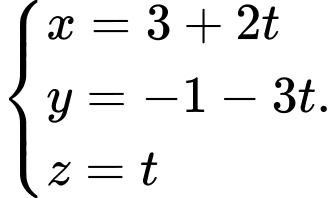
C, 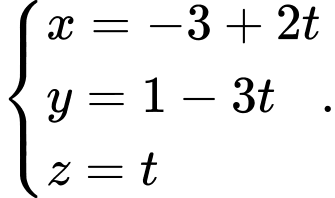
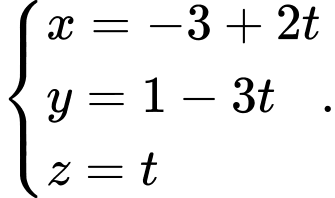
D, 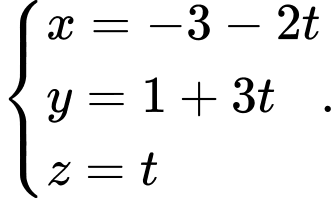
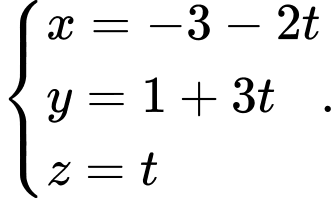
Chọn đáp án B. Đáp án: B
Câu 6 [543261]: Trong không gian 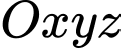 , cho điểm
, cho điểm 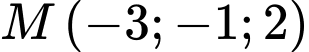 và đường thẳng
và đường thẳng 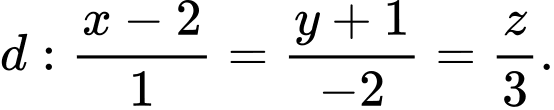 Mặt phẳng
Mặt phẳng 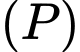 đi qua
đi qua 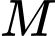 và vuông góc với
và vuông góc với 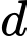 có phương trình là
có phương trình là
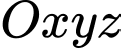 , cho điểm
, cho điểm 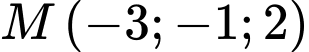 và đường thẳng
và đường thẳng 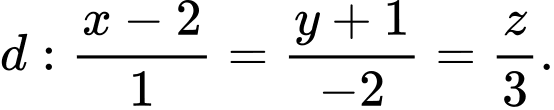 Mặt phẳng
Mặt phẳng 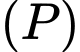 đi qua
đi qua 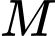 và vuông góc với
và vuông góc với 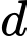 có phương trình là
có phương trình là A, 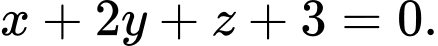
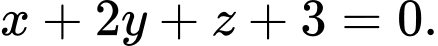
B, 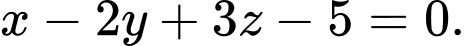
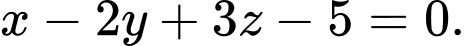
C, 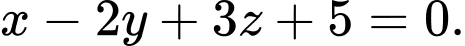
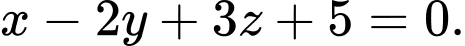
D, 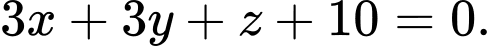
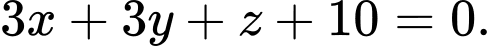
Chọn B
Vì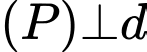 nên
nên 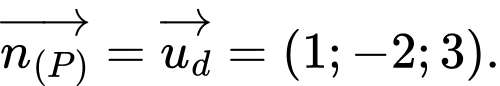
Mặt phẳng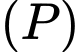 đi qua
đi qua 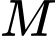 và nhận
và nhận 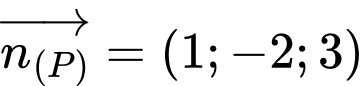 làm véc-tơ pháp tuyến có phương trình
làm véc-tơ pháp tuyến có phương trình 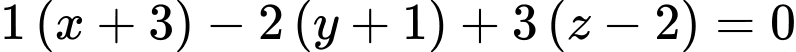
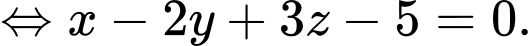 Đáp án: B
Đáp án: B
Vì
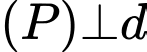 nên
nên 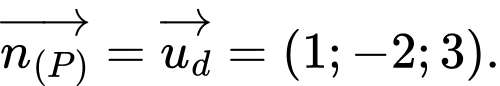
Mặt phẳng
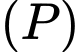 đi qua
đi qua 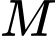 và nhận
và nhận 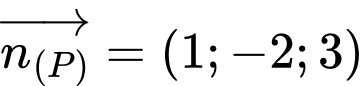 làm véc-tơ pháp tuyến có phương trình
làm véc-tơ pháp tuyến có phương trình 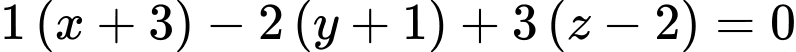
 Đáp án: B
Đáp án: B
Câu 7 [395586]: Trong không gian 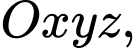 cho ba điểm
cho ba điểm 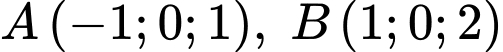 và
và 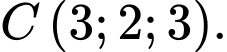 Đường thẳng đi qua
Đường thẳng đi qua 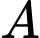 và song song với
và song song với 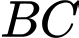 có phương trình là
có phương trình là
 cho ba điểm
cho ba điểm 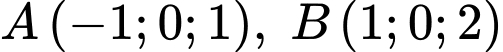 và
và 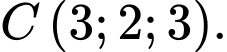 Đường thẳng đi qua
Đường thẳng đi qua 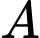 và song song với
và song song với 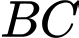 có phương trình là
có phương trình là A, 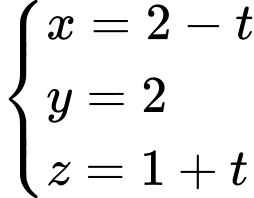
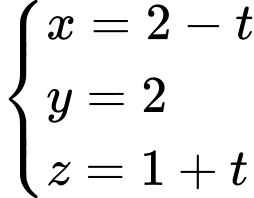
B, 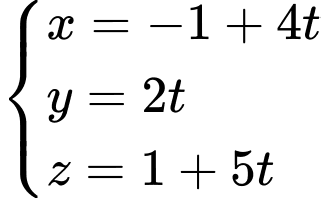
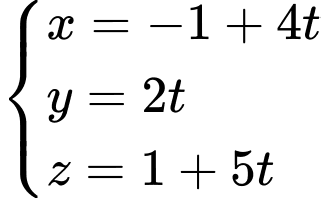
C, 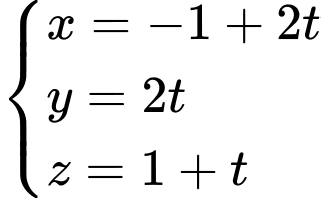
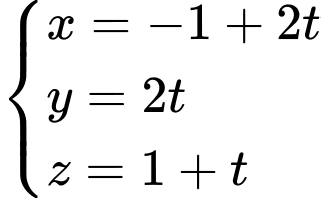
D, 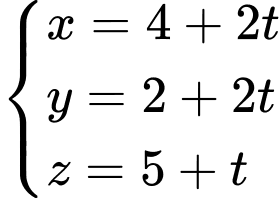
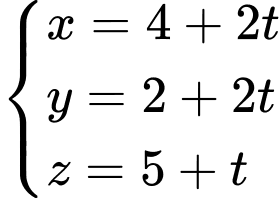
Gọi 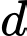 là đường thẳng cần tìm.
là đường thẳng cần tìm.
Ta có: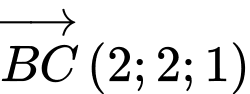 suy ra vectơ chỉ phương của đường thẳng cần tìm là
suy ra vectơ chỉ phương của đường thẳng cần tìm là 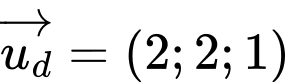
Phương trình đường thẳng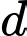 là
là 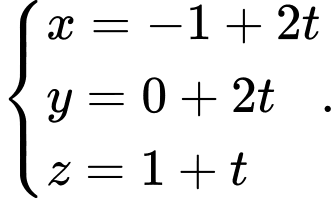 Đáp án C. Đáp án: C
Đáp án C. Đáp án: C
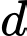 là đường thẳng cần tìm.
là đường thẳng cần tìm. Ta có:
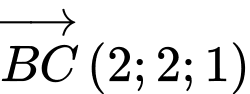 suy ra vectơ chỉ phương của đường thẳng cần tìm là
suy ra vectơ chỉ phương của đường thẳng cần tìm là 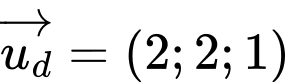
Phương trình đường thẳng
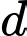 là
là 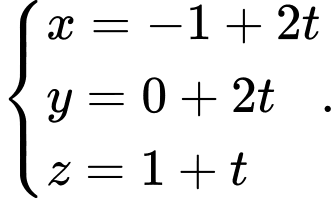 Đáp án C. Đáp án: C
Đáp án C. Đáp án: C
Câu 8 [546635]: Trong không gian 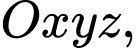 cho điểm
cho điểm 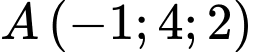 và mặt phẳng
và mặt phẳng 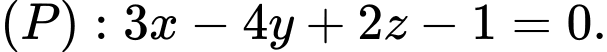 Đường thẳng đi qua
Đường thẳng đi qua 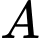 và vuông góc với mp
và vuông góc với mp 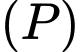 có phương trình là
có phương trình là
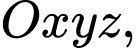 cho điểm
cho điểm 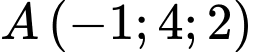 và mặt phẳng
và mặt phẳng 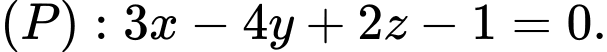 Đường thẳng đi qua
Đường thẳng đi qua  và vuông góc với mp
và vuông góc với mp  có phương trình là
có phương trình là A, 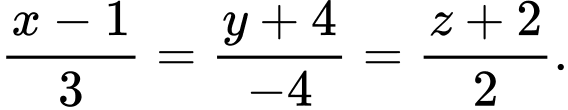
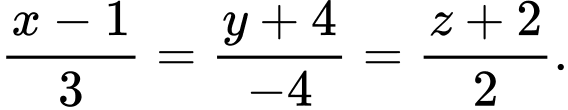
B, 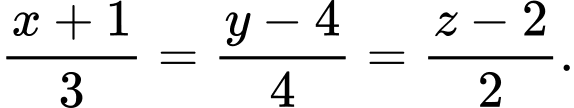
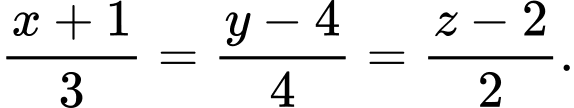
C, 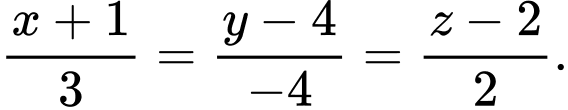
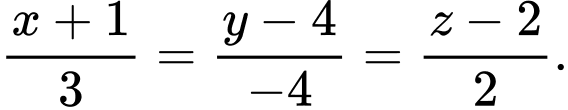
D, 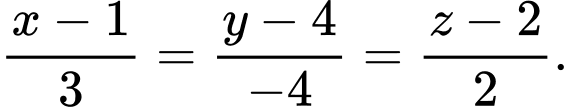
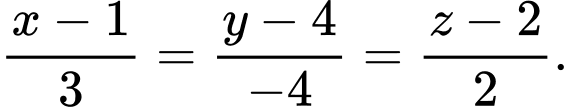
Chọn C.
Gọi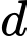 là đường thẳng đi qua
là đường thẳng đi qua 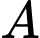 và vuông góc với mp
và vuông góc với mp 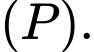
Vì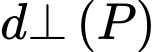 nên đường thẳng
nên đường thẳng 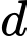 nhận vectơ pháp tuyến của
nhận vectơ pháp tuyến của 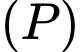 là
là 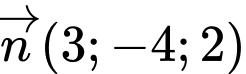 làm vectơ chỉ phương.
làm vectơ chỉ phương.
Vậy phương trình đường thẳng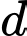 là
là 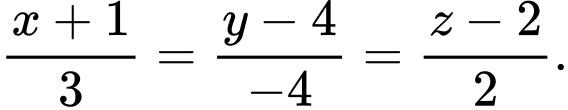 Đáp án: C
Đáp án: C
Gọi
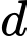 là đường thẳng đi qua
là đường thẳng đi qua 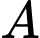 và vuông góc với mp
và vuông góc với mp 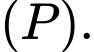
Vì
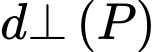 nên đường thẳng
nên đường thẳng 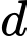 nhận vectơ pháp tuyến của
nhận vectơ pháp tuyến của 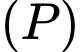 là
là 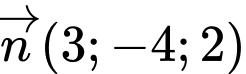 làm vectơ chỉ phương.
làm vectơ chỉ phương.
Vậy phương trình đường thẳng
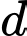 là
là 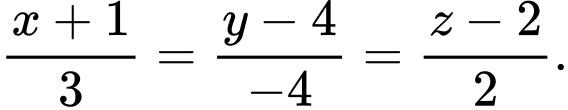 Đáp án: C
Đáp án: C
Câu 9 [543821]: Trong không gian 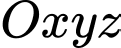 phương trình đường thẳng
phương trình đường thẳng 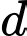 đi qua điểm
đi qua điểm 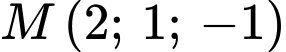 và song song với đường thẳng
và song song với đường thẳng 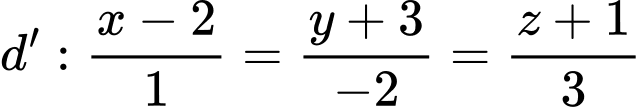 là
là
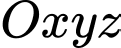 phương trình đường thẳng
phương trình đường thẳng 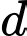 đi qua điểm
đi qua điểm 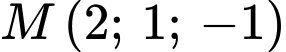 và song song với đường thẳng
và song song với đường thẳng 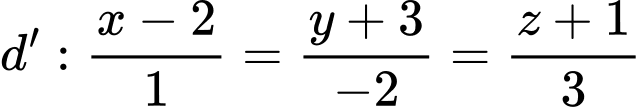 là
là A, 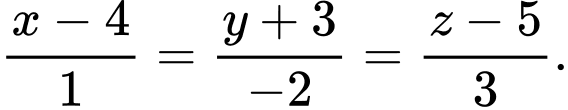
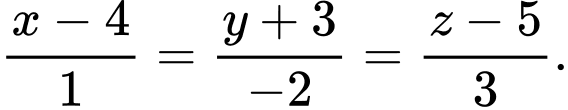
B, 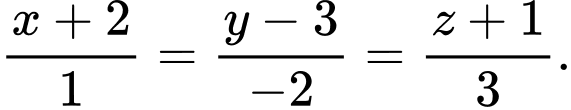
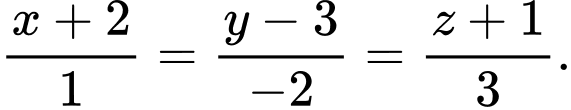
C, 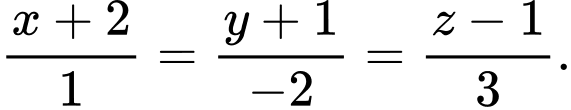
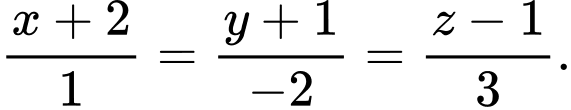
D, 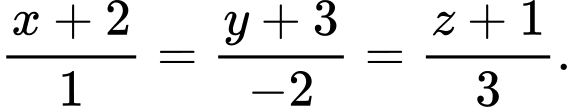
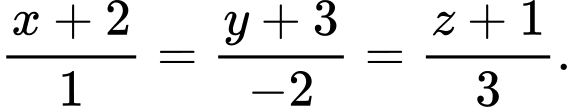
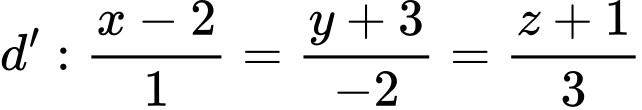 có VTCP
có VTCP 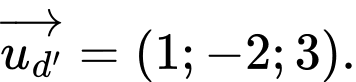
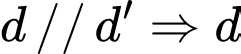 có VTCP
có VTCP 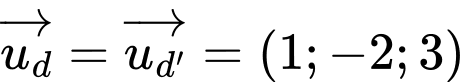
Phương án
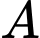 : Thay tọa độ điểm
: Thay tọa độ điểm 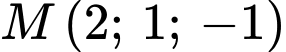 vào phương trình đường thẳng ở phương án
vào phương trình đường thẳng ở phương án 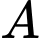 ta được
ta được 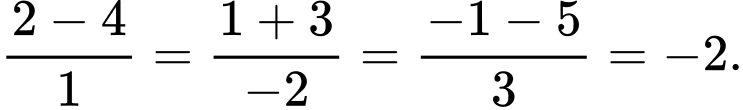
Suy ra phương trình đường thẳng
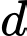 là
là 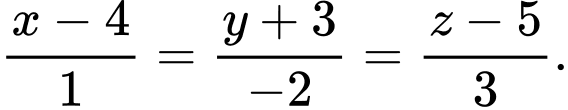
Phương án
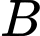 : Thay tọa độ điểm
: Thay tọa độ điểm 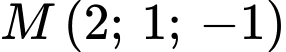 vào phương trình đường thẳng ở phương án
vào phương trình đường thẳng ở phương án 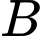 ta được
ta được 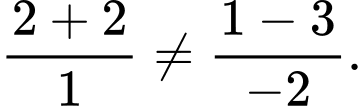
Phương án
 : Thay tọa độ điểm
: Thay tọa độ điểm 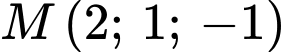 vào phương trình đường thẳng ở phương án
vào phương trình đường thẳng ở phương án  ta được
ta được 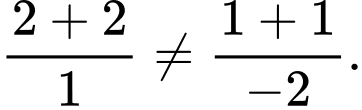
Phương án
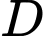 : Thay tọa độ điểm
: Thay tọa độ điểm 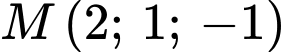 vào phương trình đường thẳng ở phương án
vào phương trình đường thẳng ở phương án 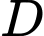 ta được
ta được  Đáp án: A
Đáp án: A
Câu 10 [57271]: Trong không gian 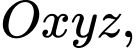 cho đường thẳng
cho đường thẳng 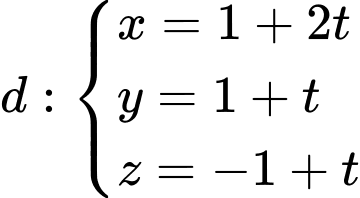 và mặt phẳng
và mặt phẳng 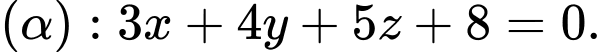 Góc giữa
Góc giữa  và
và  là
là
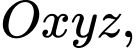 cho đường thẳng
cho đường thẳng 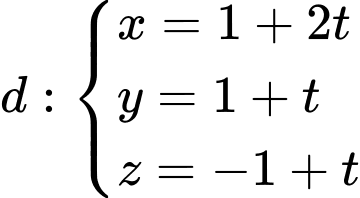 và mặt phẳng
và mặt phẳng 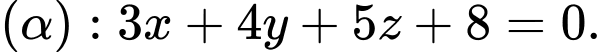 Góc giữa
Góc giữa  và
và  là
là A, 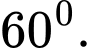
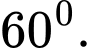
B, 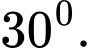
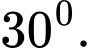
C, 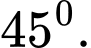
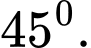
D, 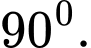
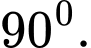
Xét 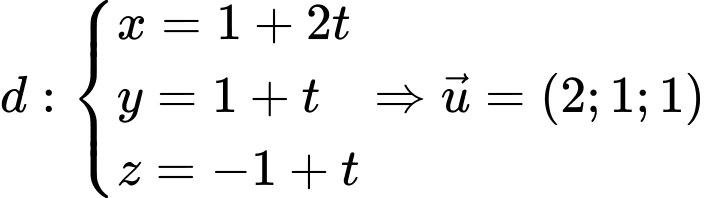 và
và 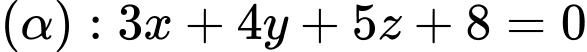
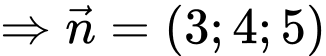
Áp dụng công thức tính góc giữa đường thẳng và mặt phẳng, ta có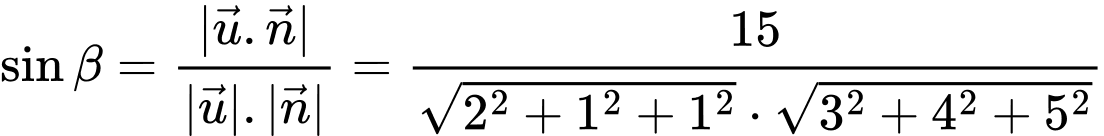
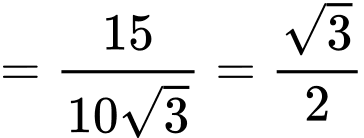
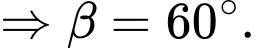
Chọn đáp án A. Đáp án: A
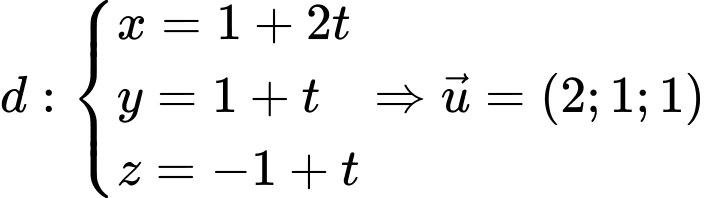 và
và 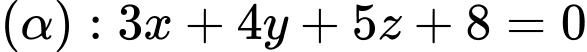
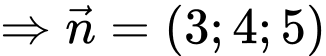
Áp dụng công thức tính góc giữa đường thẳng và mặt phẳng, ta có
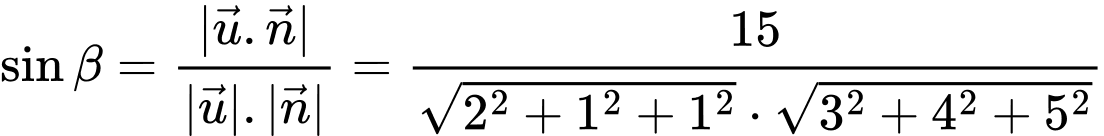
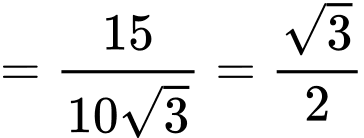
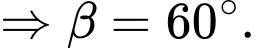
Chọn đáp án A. Đáp án: A
Câu 11 [544673]: Trong không gian 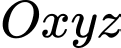 , cho hai đường thẳng
, cho hai đường thẳng 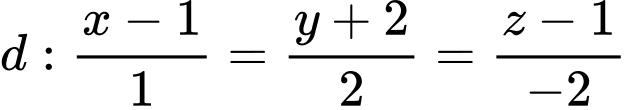 và
và 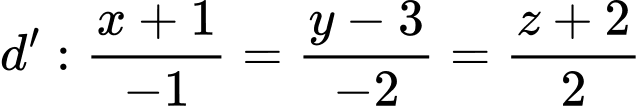 . Vị trí tương đối của
. Vị trí tương đối của 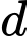 và
và 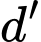 là
là
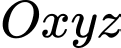 , cho hai đường thẳng
, cho hai đường thẳng 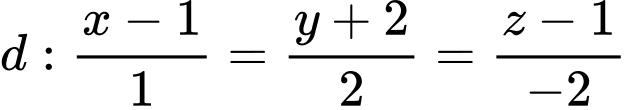 và
và 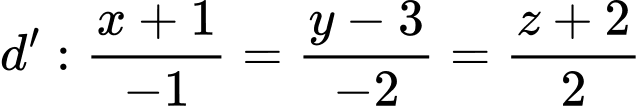 . Vị trí tương đối của
. Vị trí tương đối của 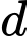 và
và 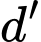 là
là A, chéo nhau.
B, cắt nhau.
C, trùng nhau.
D, song song.
Chọn D.
Ta có vectơ chỉ phương của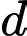 và
và 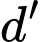 lần lượt là
lần lượt là 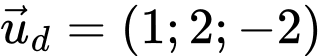 ;
; 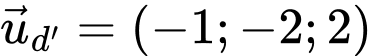 .
.
Ta thấy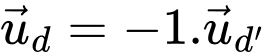 và
và 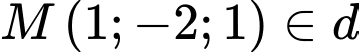 nhưng
nhưng 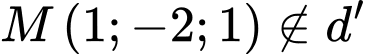 .
.
Vậy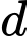 và
và 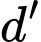 song song nhau. Đáp án: D
song song nhau. Đáp án: D
Ta có vectơ chỉ phương của
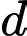 và
và 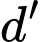 lần lượt là
lần lượt là 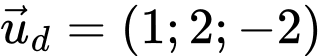 ;
; 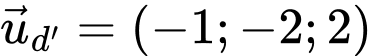 .
.
Ta thấy
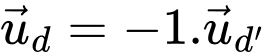 và
và 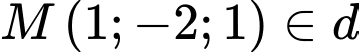 nhưng
nhưng 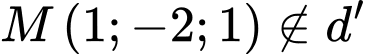 .
.
Vậy
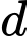 và
và 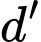 song song nhau. Đáp án: D
song song nhau. Đáp án: D
Câu 12 [544670]: Trong không gian với hệ toạ độ 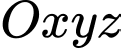 , mặt phẳng chứa điểm
, mặt phẳng chứa điểm 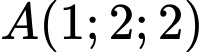 và đường thẳng
và đường thẳng 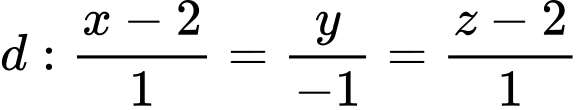 có phương trình là
có phương trình là
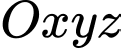 , mặt phẳng chứa điểm
, mặt phẳng chứa điểm 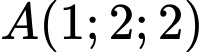 và đường thẳng
và đường thẳng 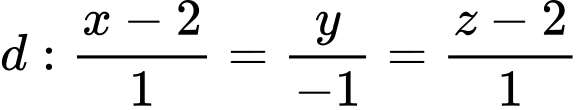 có phương trình là
có phương trình là A, 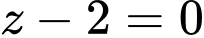 .
.
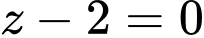 .
.B, 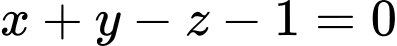 .
.
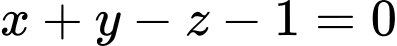 .
.C, 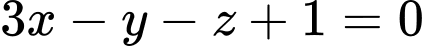 .
.
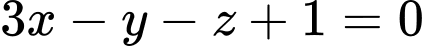 .
. D, 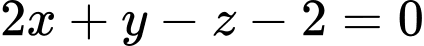 .
.
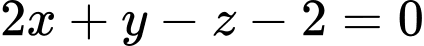 .
.
Chọn D.
Đường thẳng d đi qua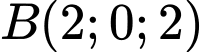 và có vtcp
và có vtcp 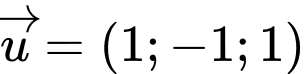 .
.
Gọi mặt phẳng cần tìm là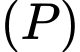 và có vtpt là
và có vtpt là 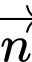 .
.
Từ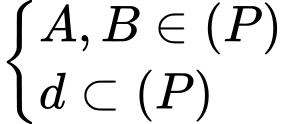
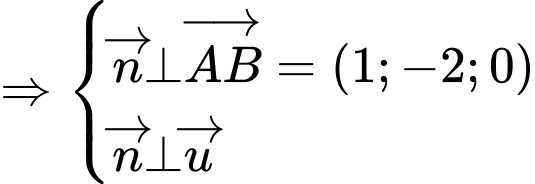
Do đó mặt phẳng đi qua
đi qua 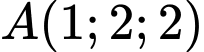 , nhận
, nhận 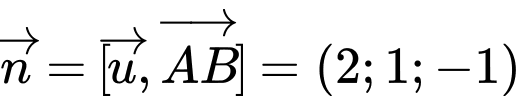
Vậy mặt phẳng có phương trình
có phương trình 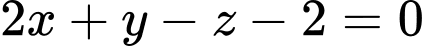 . Đáp án: D
. Đáp án: D
Đường thẳng d đi qua
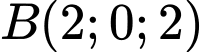 và có vtcp
và có vtcp 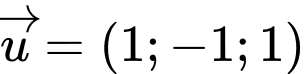 .
.
Gọi mặt phẳng cần tìm là
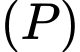 và có vtpt là
và có vtpt là 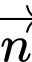 .
.
Từ
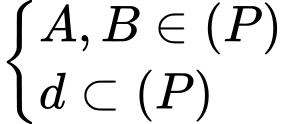
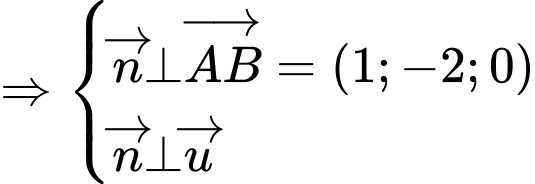
Do đó mặt phẳng
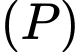 đi qua
đi qua 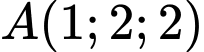 , nhận
, nhận 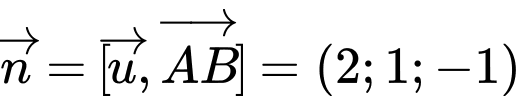
Vậy mặt phẳng
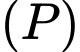 có phương trình
có phương trình 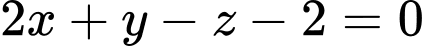 . Đáp án: D
. Đáp án: D PHẦN II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a),b),c),d) ở mỗi câu học sinh chọn đúng hoặc sai.
Câu 13 [696283]: Trong không gian 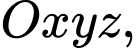 cho hai điểm
cho hai điểm 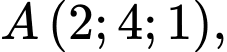
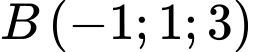 và mặt phẳng
và mặt phẳng 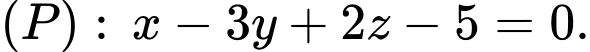 Mặt phẳng
Mặt phẳng  đi qua hai điểm
đi qua hai điểm 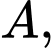
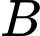 và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 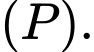
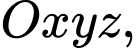 cho hai điểm
cho hai điểm 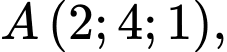
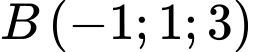 và mặt phẳng
và mặt phẳng 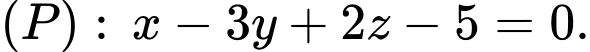 Mặt phẳng
Mặt phẳng  đi qua hai điểm
đi qua hai điểm 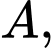
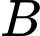 và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 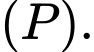
a) Đúng
Sử dụng công thức phương trình tổng quát của mặt phẳng, do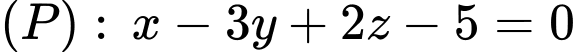 nên VTPT là
nên VTPT là 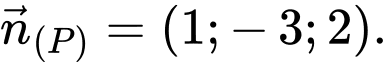
b) Sai
Áp dụng công thức tính tọa độ vecto khi biết hai điểm đầu cuối, ta có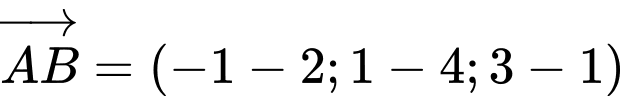
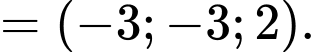
c) Sai
Vì mặt phẳng đi qua hai điểm
đi qua hai điểm 
 và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 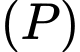 nên
nên 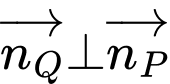 và
và 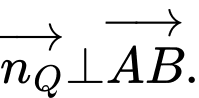
Do đó,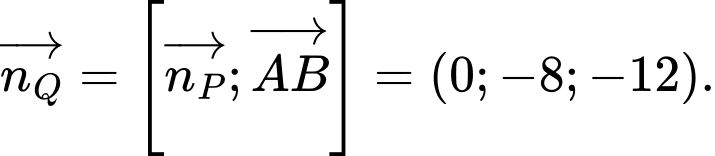
Ta có thể chọn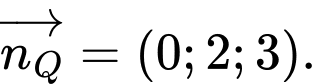
Vậy mặt phẳng đi qua điểm
đi qua điểm  và có
và có 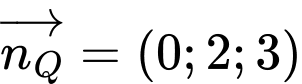 có phương trình là:
có phương trình là:
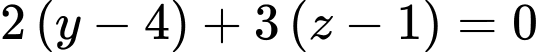
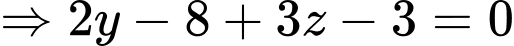
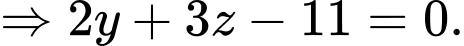
d) Sai
Vì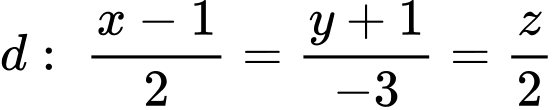 nên
nên 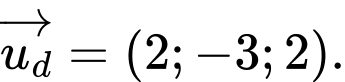
Ta thấy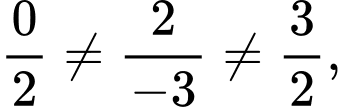 do đó
do đó 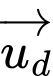 không cùng phương với
không cùng phương với 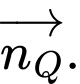
Do đó, đường thẳng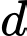 không vuông góc với mặt phẳng
không vuông góc với mặt phẳng 
Sử dụng công thức phương trình tổng quát của mặt phẳng, do
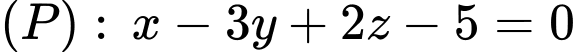 nên VTPT là
nên VTPT là 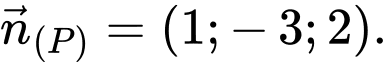
b) Sai
Áp dụng công thức tính tọa độ vecto khi biết hai điểm đầu cuối, ta có
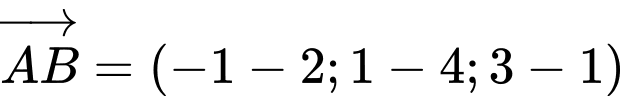
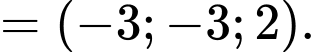
c) Sai
Vì mặt phẳng
 đi qua hai điểm
đi qua hai điểm 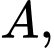
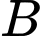 và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 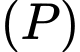 nên
nên 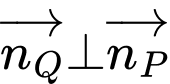 và
và 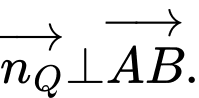
Do đó,
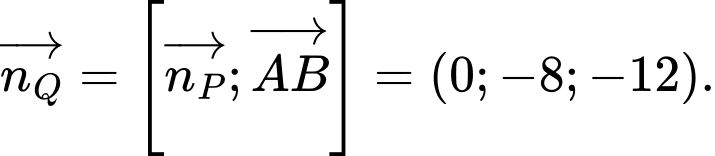
Ta có thể chọn
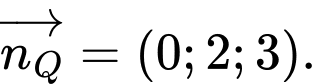
Vậy mặt phẳng
 đi qua điểm
đi qua điểm 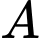 và có
và có 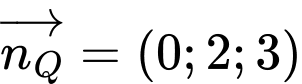 có phương trình là:
có phương trình là: 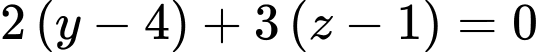
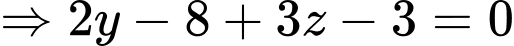
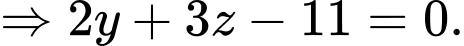
d) Sai
Vì
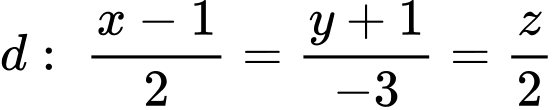 nên
nên 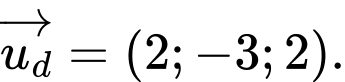
Ta thấy
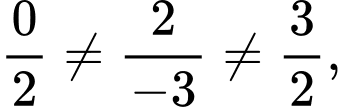 do đó
do đó 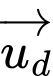 không cùng phương với
không cùng phương với 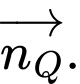
Do đó, đường thẳng
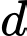 không vuông góc với mặt phẳng
không vuông góc với mặt phẳng 
Câu 14 [778813]: Trong không gian với hệ tọa độ 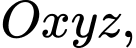 cho điểm
cho điểm 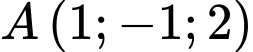 và mặt phẳng
và mặt phẳng 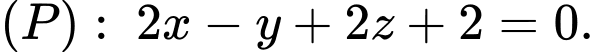
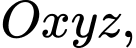 cho điểm
cho điểm 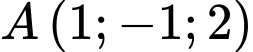 và mặt phẳng
và mặt phẳng 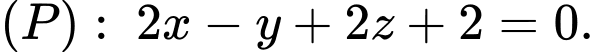
a) Đúng.
b) Sai.
Gọi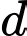 là đường thẳng cần tìm. Vì
là đường thẳng cần tìm. Vì 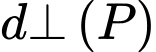 nên sẽ nhận vectơ pháp tuyến của mặt phẳng
nên sẽ nhận vectơ pháp tuyến của mặt phẳng 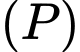 là
là 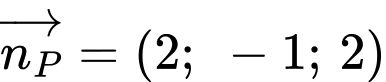 làm vectơ chỉ phương. Khi đó phương trình chính tắc của đường thẳng
làm vectơ chỉ phương. Khi đó phương trình chính tắc của đường thẳng 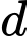 là
là 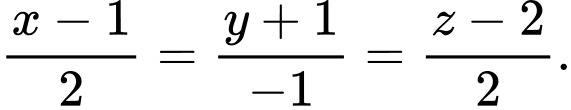
c) Sai.
Vì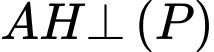 nên đường thẳng
nên đường thẳng 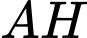 sẽ nhận vectơ pháp tuyến của mặt phẳng
sẽ nhận vectơ pháp tuyến của mặt phẳng 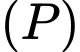 là
là 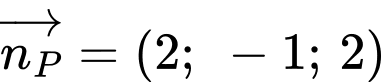 làm vectơ chỉ phương. Suy ra phương trình tham số của đường thẳng
làm vectơ chỉ phương. Suy ra phương trình tham số của đường thẳng 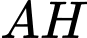 là
là 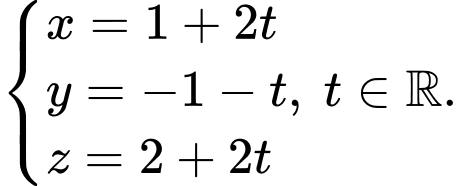
Vì

Hơn nữa,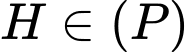 nên ta có
nên ta có 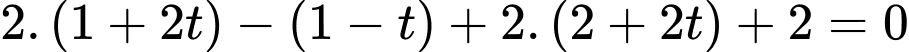
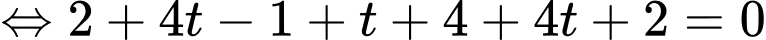

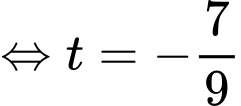
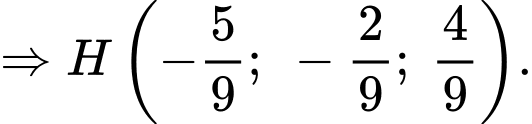
Vậy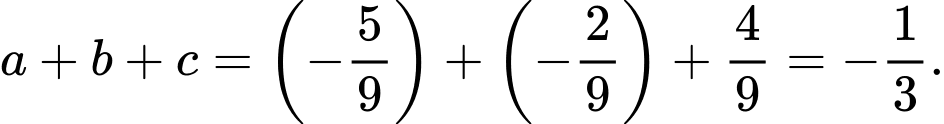
d) Đúng.
Vì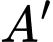 là điểm đối xứng của điểm
là điểm đối xứng của điểm 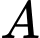 qua mặt phẳng
qua mặt phẳng 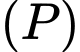 nên suy ra
nên suy ra 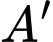 sẽ thuộc vào đường thẳng
sẽ thuộc vào đường thẳng 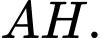 Và
Và 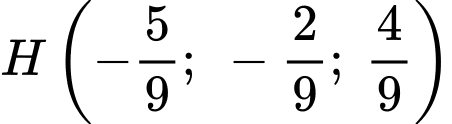 là trung điểm của đoạn
là trung điểm của đoạn 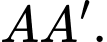
Suy ra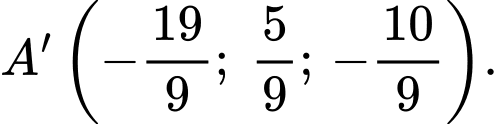
Vậy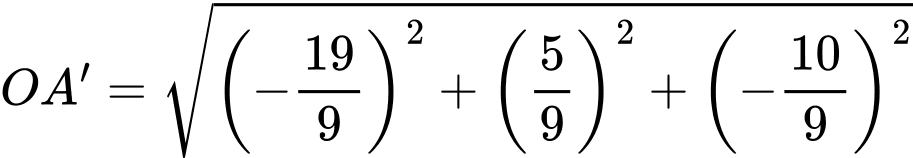

b) Sai.
Gọi
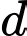 là đường thẳng cần tìm. Vì
là đường thẳng cần tìm. Vì 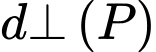 nên sẽ nhận vectơ pháp tuyến của mặt phẳng
nên sẽ nhận vectơ pháp tuyến của mặt phẳng 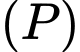 là
là 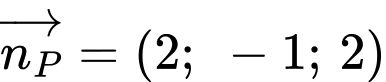 làm vectơ chỉ phương. Khi đó phương trình chính tắc của đường thẳng
làm vectơ chỉ phương. Khi đó phương trình chính tắc của đường thẳng 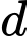 là
là 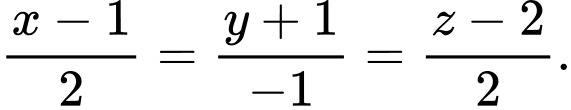
c) Sai.
Vì
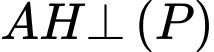 nên đường thẳng
nên đường thẳng 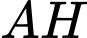 sẽ nhận vectơ pháp tuyến của mặt phẳng
sẽ nhận vectơ pháp tuyến của mặt phẳng 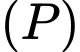 là
là 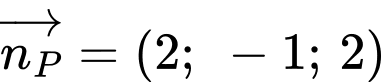 làm vectơ chỉ phương. Suy ra phương trình tham số của đường thẳng
làm vectơ chỉ phương. Suy ra phương trình tham số của đường thẳng 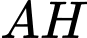 là
là 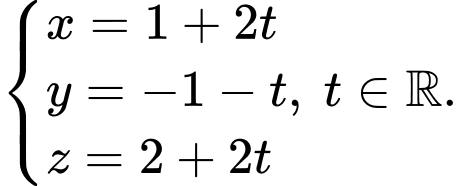
Vì


Hơn nữa,
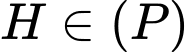 nên ta có
nên ta có 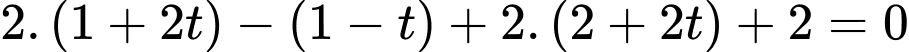
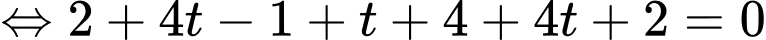

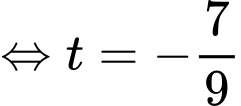
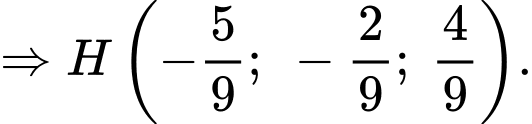
Vậy
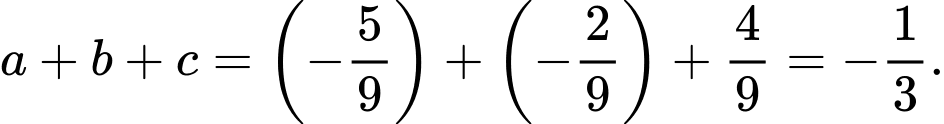
d) Đúng.
Vì
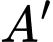 là điểm đối xứng của điểm
là điểm đối xứng của điểm 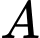 qua mặt phẳng
qua mặt phẳng 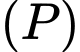 nên suy ra
nên suy ra 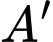 sẽ thuộc vào đường thẳng
sẽ thuộc vào đường thẳng 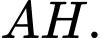 Và
Và 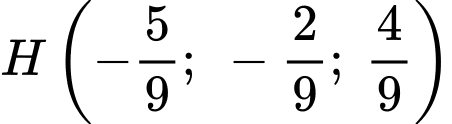 là trung điểm của đoạn
là trung điểm của đoạn 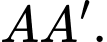
Suy ra
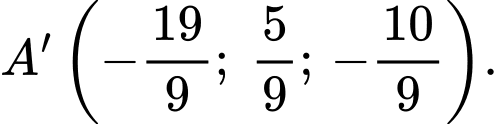
Vậy
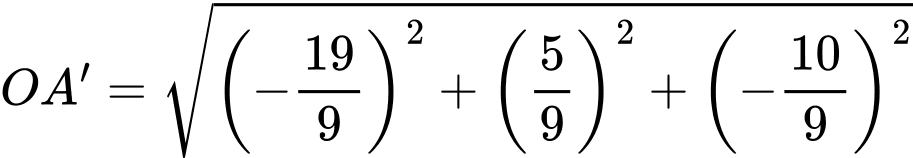

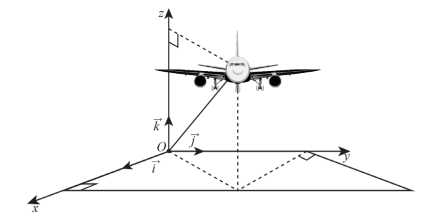
Câu 15 [695035]: Hình vẽ sau mô tả vị trí của máy bay vào thời điểm 9h30 phút. Biết các đơn vị trên hình tính theo đơn vị km. Trong các khẳng định sau đây, khẳng định nào đúng, khẳng định nào sai?
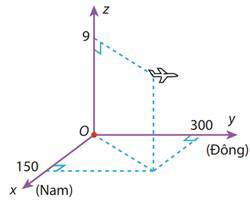

a) Đúng.
Dựa vào hình vẽ ta thấy máy bay đang ở độ cao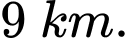
b) Sai.
Máy bay ở tọa độ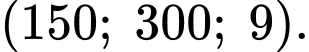
c) Đúng.
Vận tốc gió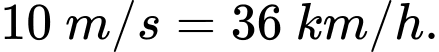
Từ 9h30 phút đến 10h30 phút, máy bay bay tự động được 1 giờ với quãng đường: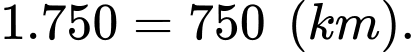
Quãng đường máy bay bay được là: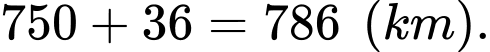
Do đó tọa độ của máy bay là: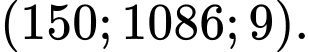
d) Sai.
Quãng đường máy bay bay được là: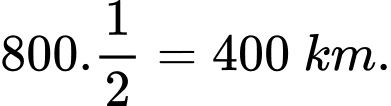 .
.
Do đó tọa độ máy bay là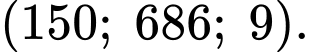
Dựa vào hình vẽ ta thấy máy bay đang ở độ cao
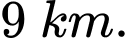
b) Sai.
Máy bay ở tọa độ
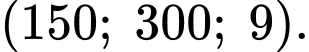
c) Đúng.
Vận tốc gió
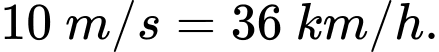
Từ 9h30 phút đến 10h30 phút, máy bay bay tự động được 1 giờ với quãng đường:
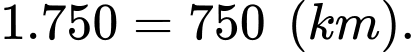
Quãng đường máy bay bay được là:
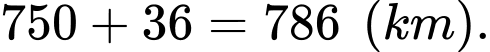
Do đó tọa độ của máy bay là:
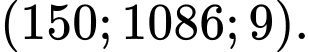
d) Sai.
Quãng đường máy bay bay được là:
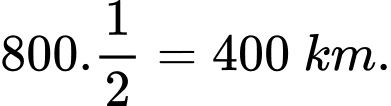 .
. Do đó tọa độ máy bay là
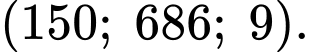
Câu 16 [695252]: Một chiếc máy bay đang bay trên không trung (coi vận tốc gió không đáng kể). Xét hệ trục tọa độ  được gắn như hình vẽ, trong đó gốc
được gắn như hình vẽ, trong đó gốc  là vị trí của trạm kiểm soát không lưu, mặt đất trùng với mặt phẳng
là vị trí của trạm kiểm soát không lưu, mặt đất trùng với mặt phẳng 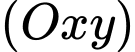 và
và 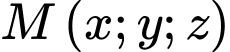 (km) biểu thị vị trí máy bay trên không trung. Tại thời điểm 8h máy bay đang ở vị trí
(km) biểu thị vị trí máy bay trên không trung. Tại thời điểm 8h máy bay đang ở vị trí 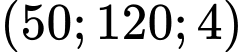 và chuyển động với vận tốc
và chuyển động với vận tốc 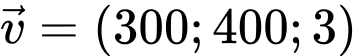 (km/h).
(km/h).
 được gắn như hình vẽ, trong đó gốc
được gắn như hình vẽ, trong đó gốc  là vị trí của trạm kiểm soát không lưu, mặt đất trùng với mặt phẳng
là vị trí của trạm kiểm soát không lưu, mặt đất trùng với mặt phẳng  và
và  (km) biểu thị vị trí máy bay trên không trung. Tại thời điểm 8h máy bay đang ở vị trí
(km) biểu thị vị trí máy bay trên không trung. Tại thời điểm 8h máy bay đang ở vị trí 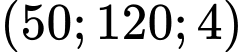 và chuyển động với vận tốc
và chuyển động với vận tốc 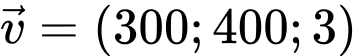 (km/h).
(km/h).
a) Đúng.
Khoảng cách giữa máy bay và trạm kiểm soát không lưu là
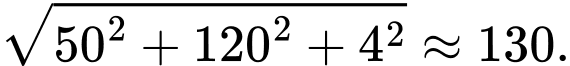
b) Sai.
Ta có phương trình chuyển động của máy bay bắt đầu ở thời điểm 8h là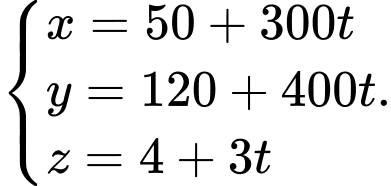
Độ cao của máy bay so vối mặt đất tại thời điểm 9h là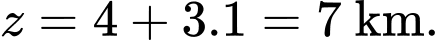
c) Sai.
Tọa độ của máy bay tại thời điểm 10h là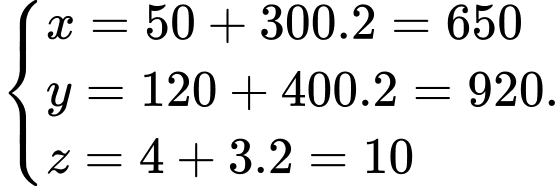
Khoảng cách giữa máy bay và tháp truyền hình là
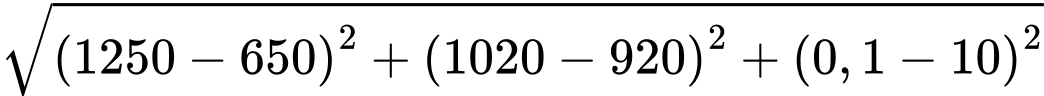
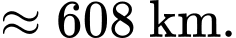
d) Đúng.
Phương trình chuyển động của máy bay ở thời điểm 10h là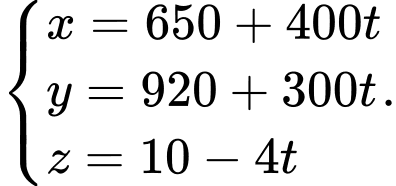
Để máy bay hạ cánh thì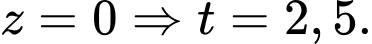
Khoảng cách giữa máy bay và trạm kiểm soát không lưu là
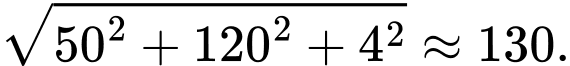
b) Sai.
Ta có phương trình chuyển động của máy bay bắt đầu ở thời điểm 8h là
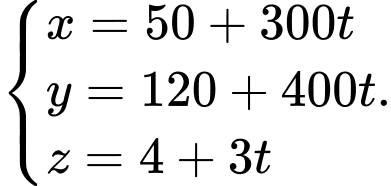
Độ cao của máy bay so vối mặt đất tại thời điểm 9h là
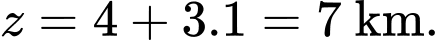
c) Sai.
Tọa độ của máy bay tại thời điểm 10h là
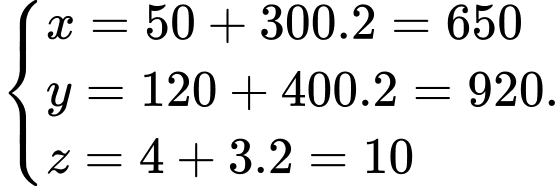
Khoảng cách giữa máy bay và tháp truyền hình là
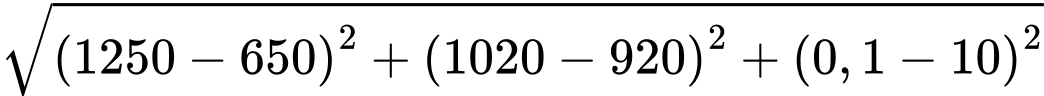
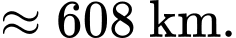
d) Đúng.
Phương trình chuyển động của máy bay ở thời điểm 10h là
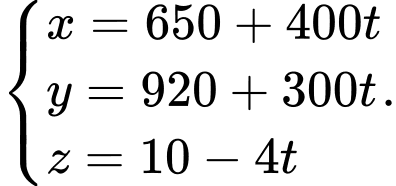
Để máy bay hạ cánh thì
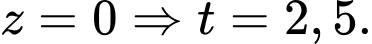
PHẦN III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 17 đến câu 22.
Câu 17 [778815]: Trong không gian  cho trước (1 đơn vị =
cho trước (1 đơn vị =  ), có một chú kiến vàng và một chú kiến đen bò trên hai sợi dây thẳng khác nhau. Giả sử sau
), có một chú kiến vàng và một chú kiến đen bò trên hai sợi dây thẳng khác nhau. Giả sử sau  (phút), kiến vàng ở vị trí
(phút), kiến vàng ở vị trí 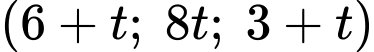 trên đường thẳng
trên đường thẳng 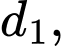 còn kiến đen ở vị trí
còn kiến đen ở vị trí 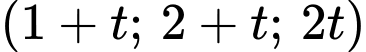 trên đường thẳng
trên đường thẳng 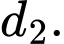 Khoảng cách giữa hai chú kiến sau 4 phút là bao nhiêu
Khoảng cách giữa hai chú kiến sau 4 phút là bao nhiêu  (viết kết quả làm tròn đến hàng phần mười).
(viết kết quả làm tròn đến hàng phần mười).
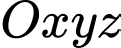 cho trước (1 đơn vị =
cho trước (1 đơn vị =  ), có một chú kiến vàng và một chú kiến đen bò trên hai sợi dây thẳng khác nhau. Giả sử sau
), có một chú kiến vàng và một chú kiến đen bò trên hai sợi dây thẳng khác nhau. Giả sử sau 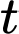 (phút), kiến vàng ở vị trí
(phút), kiến vàng ở vị trí 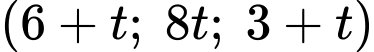 trên đường thẳng
trên đường thẳng 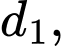 còn kiến đen ở vị trí
còn kiến đen ở vị trí 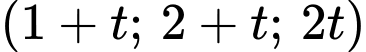 trên đường thẳng
trên đường thẳng 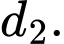 Khoảng cách giữa hai chú kiến sau 4 phút là bao nhiêu
Khoảng cách giữa hai chú kiến sau 4 phút là bao nhiêu  (viết kết quả làm tròn đến hàng phần mười).
(viết kết quả làm tròn đến hàng phần mười).
Điền đáp án: 26,5.
Sau 4 phút thì vị trí của chú kiến vàng và kiến đen lần lượt là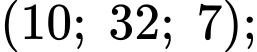
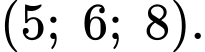
Suy ra khoảng cách giữa hai chú kiến bằng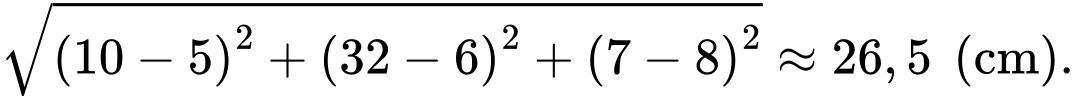
Sau 4 phút thì vị trí của chú kiến vàng và kiến đen lần lượt là
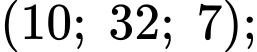
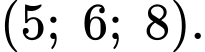
Suy ra khoảng cách giữa hai chú kiến bằng
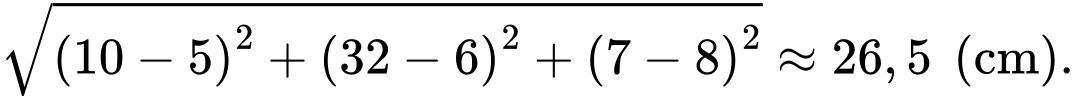
Câu 18 [755217]: Trong không gian 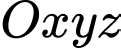 , cho điểm
, cho điểm 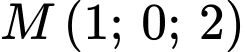 và đường thẳng
và đường thẳng 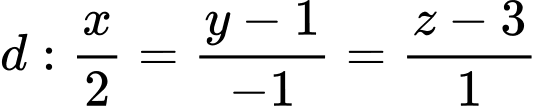 . Đường thẳng
. Đường thẳng  đi qua
đi qua 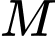 cắt và vuông góc với
cắt và vuông góc với 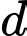 , biết
, biết 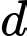 có một véctơ chỉ phương là
có một véctơ chỉ phương là 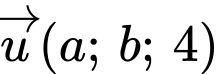 . Giá trị biểu thức
. Giá trị biểu thức 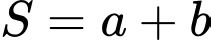 bằng
bằng
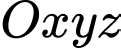 , cho điểm
, cho điểm 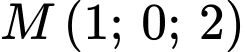 và đường thẳng
và đường thẳng 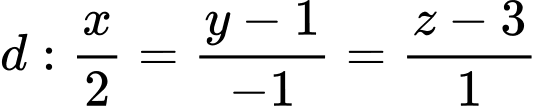 . Đường thẳng
. Đường thẳng  đi qua
đi qua 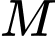 cắt và vuông góc với
cắt và vuông góc với 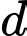 , biết
, biết 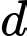 có một véctơ chỉ phương là
có một véctơ chỉ phương là 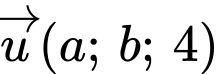 . Giá trị biểu thức
. Giá trị biểu thức 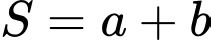 bằng
bằng
Điền đáp án: 1.
Phương trình tham số của đường thẳng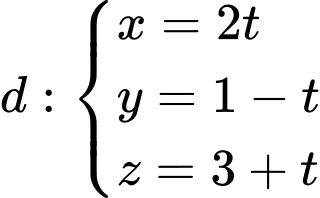 và VTCP
và VTCP 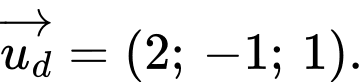
Gọi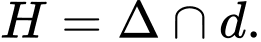 Suy ra tọa độ
Suy ra tọa độ 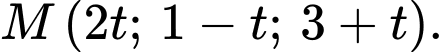
Khi đó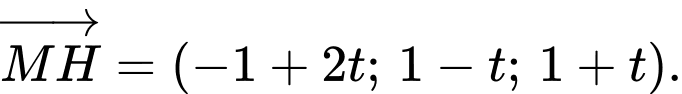
Do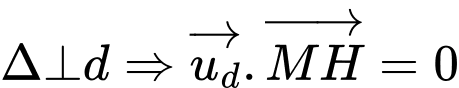
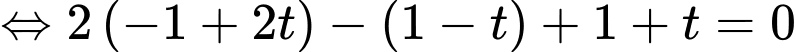
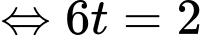
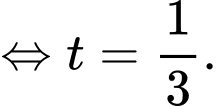
Suy ra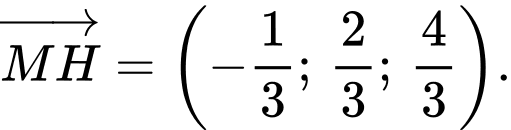
Khi đó VCTP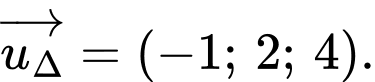
Vậy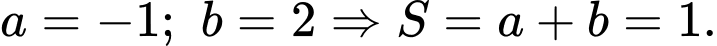
Phương trình tham số của đường thẳng
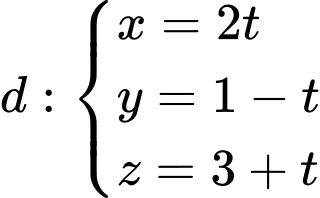 và VTCP
và VTCP 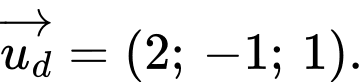
Gọi
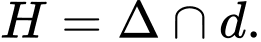 Suy ra tọa độ
Suy ra tọa độ 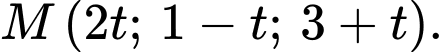
Khi đó
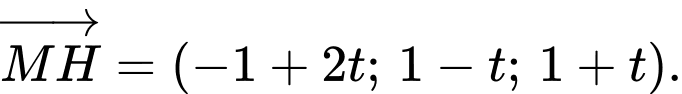
Do
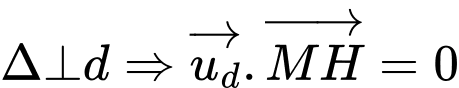
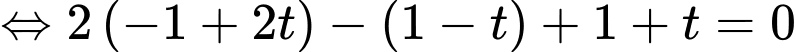
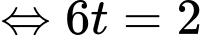
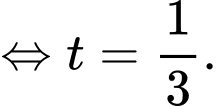
Suy ra
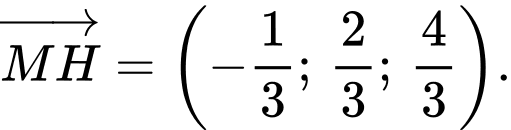
Khi đó VCTP
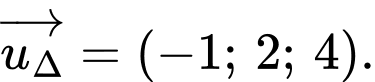
Vậy
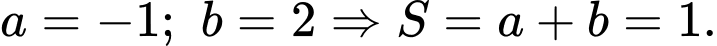
Câu 19 [778816]: Trong không gian với hệ tọa độ 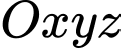 (đơn vị trên mỗi trục tọa độ là kilômét), một máy bay đang ở vị trị trí
(đơn vị trên mỗi trục tọa độ là kilômét), một máy bay đang ở vị trị trí 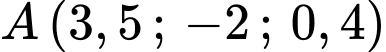 và sẽ hạ cánh ở vị trí
và sẽ hạ cánh ở vị trí 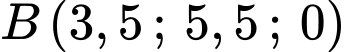 trên đường băng
trên đường băng 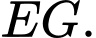 Có một lớp mây được mô phỏng bởi một mặt phẳng
Có một lớp mây được mô phỏng bởi một mặt phẳng  đi qua ba điểm
đi qua ba điểm 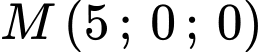 ,
, 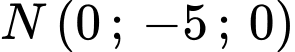 ,
, 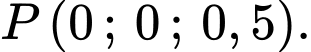 Điểm
Điểm  là vị trí mà máy bay xuyên qua đám mây để hạ cánh thì
là vị trí mà máy bay xuyên qua đám mây để hạ cánh thì  cách mặt đất một khoảng là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị của mét).
cách mặt đất một khoảng là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị của mét).
 (đơn vị trên mỗi trục tọa độ là kilômét), một máy bay đang ở vị trị trí
(đơn vị trên mỗi trục tọa độ là kilômét), một máy bay đang ở vị trị trí 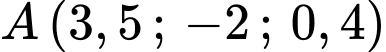 và sẽ hạ cánh ở vị trí
và sẽ hạ cánh ở vị trí 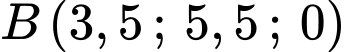 trên đường băng
trên đường băng 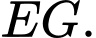 Có một lớp mây được mô phỏng bởi một mặt phẳng
Có một lớp mây được mô phỏng bởi một mặt phẳng  đi qua ba điểm
đi qua ba điểm 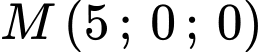 ,
, 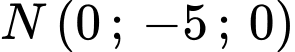 ,
, 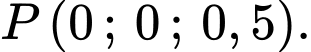 Điểm
Điểm  là vị trí mà máy bay xuyên qua đám mây để hạ cánh thì
là vị trí mà máy bay xuyên qua đám mây để hạ cánh thì  cách mặt đất một khoảng là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị của mét).
cách mặt đất một khoảng là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị của mét).
Điền đáp án: 200.
Yêu cầu bài toán là xác định cao độ của điểm
Từ giữ kiện bài toán, ta có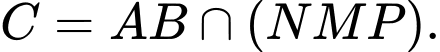
Giả sử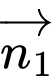 là một vectơ pháp tuyến của mặt phẳng
là một vectơ pháp tuyến của mặt phẳng 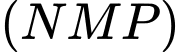
Ta có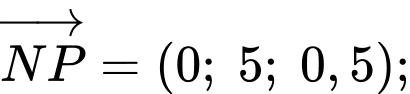
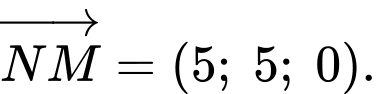 Lại có
Lại có 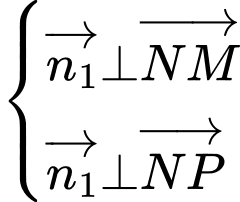
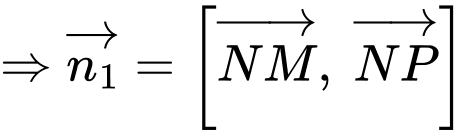
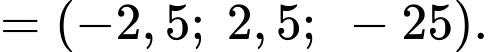
Suy ra phương trình mặt phẳng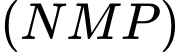 là
là 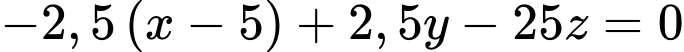
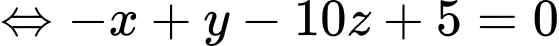
Đường thẳng đi qua điểm
đi qua điểm 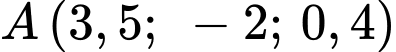 và có vectơ chỉ phương
và có vectơ chỉ phương 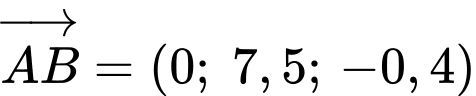 có phương trình tham số là
có phương trình tham số là 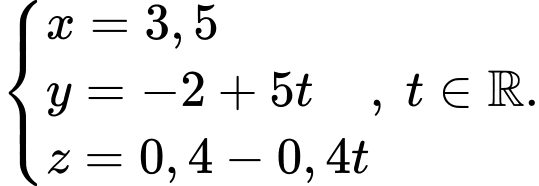
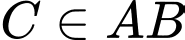

Vì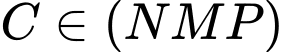 nên ta có
nên ta có 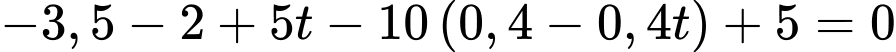
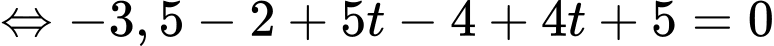
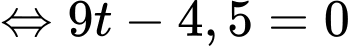
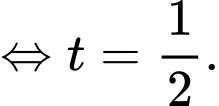
Suy ra cao độ của điểm bằng
bằng 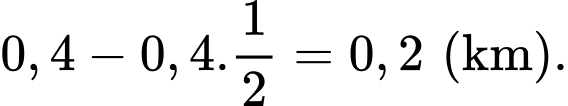 Vậy
Vậy  cách mặt đất một khoảng 200 m.
cách mặt đất một khoảng 200 m.
Yêu cầu bài toán là xác định cao độ của điểm

Từ giữ kiện bài toán, ta có
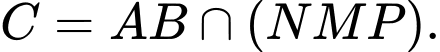
Giả sử
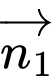 là một vectơ pháp tuyến của mặt phẳng
là một vectơ pháp tuyến của mặt phẳng 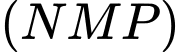
Ta có
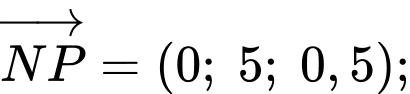
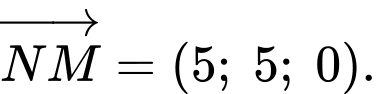 Lại có
Lại có 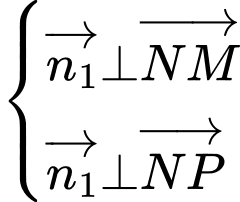
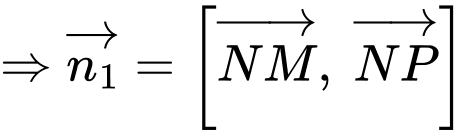
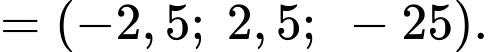
Suy ra phương trình mặt phẳng
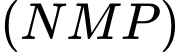 là
là 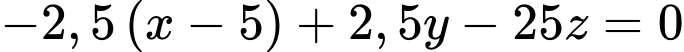
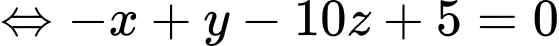
Đường thẳng
 đi qua điểm
đi qua điểm 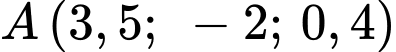 và có vectơ chỉ phương
và có vectơ chỉ phương 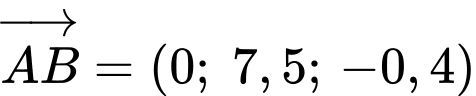 có phương trình tham số là
có phương trình tham số là 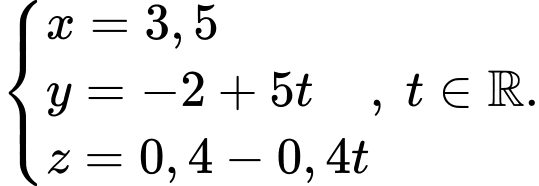
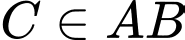

Vì
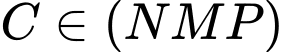 nên ta có
nên ta có 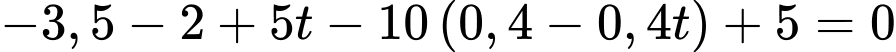
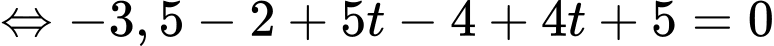
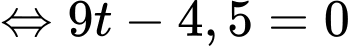
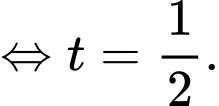
Suy ra cao độ của điểm
 bằng
bằng 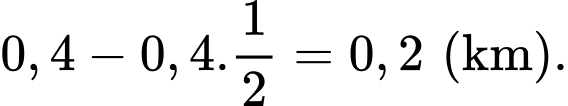 Vậy
Vậy  cách mặt đất một khoảng 200 m.
cách mặt đất một khoảng 200 m.
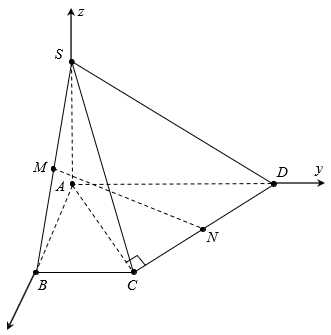
Câu 20 [778825]: Cho hình chóp 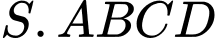 có đáy là hình thang vuông tại
có đáy là hình thang vuông tại 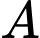 và
và 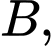 thỏa mãn điều kiện,
thỏa mãn điều kiện, 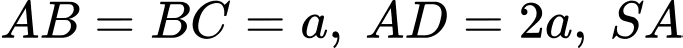 vuông góc với mặt đáy
vuông góc với mặt đáy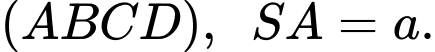 Gọi
Gọi 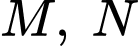 lần lượt là trung điểm của
lần lượt là trung điểm của 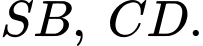 Bằng cách chọn hệ trục toạ độ
Bằng cách chọn hệ trục toạ độ 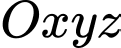 như hình vẽ, tính cosin của góc giữa
như hình vẽ, tính cosin của góc giữa 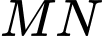 và
và 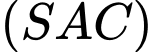 (làm tròn kết quả đến hàng phần trăm).
(làm tròn kết quả đến hàng phần trăm).
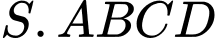 có đáy là hình thang vuông tại
có đáy là hình thang vuông tại 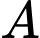 và
và 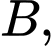 thỏa mãn điều kiện,
thỏa mãn điều kiện, 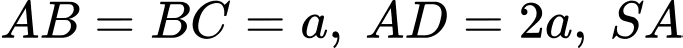 vuông góc với mặt đáy
vuông góc với mặt đáy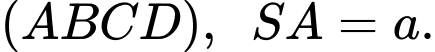 Gọi
Gọi 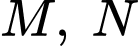 lần lượt là trung điểm của
lần lượt là trung điểm của 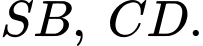 Bằng cách chọn hệ trục toạ độ
Bằng cách chọn hệ trục toạ độ 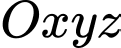 như hình vẽ, tính cosin của góc giữa
như hình vẽ, tính cosin của góc giữa 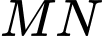 và
và 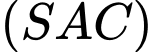 (làm tròn kết quả đến hàng phần trăm).
(làm tròn kết quả đến hàng phần trăm).
Trả lời: 0,74
Chọn hệ trục tọa độ như hình vẽ
Chọn đơn vị là a
Có
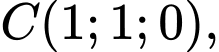
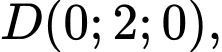
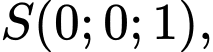
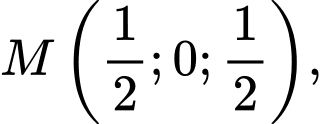
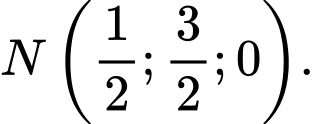
Vecto chỉ phương của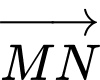 là
là 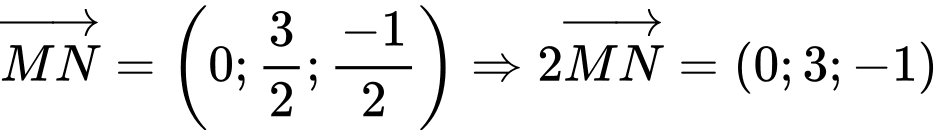
Vecto pháp tuyến của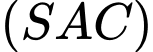 là
là 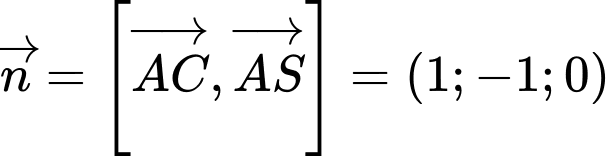
Vậy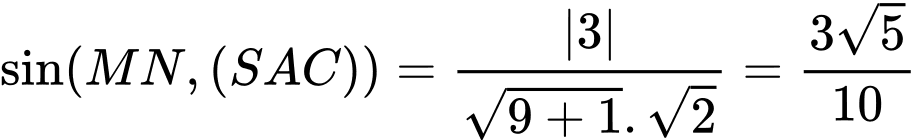
Suy ra: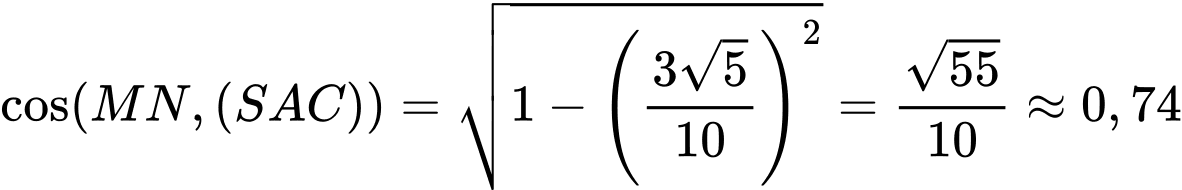
Chọn hệ trục tọa độ như hình vẽ

Chọn đơn vị là a
Có
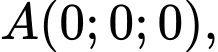
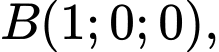
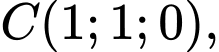
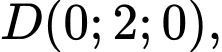
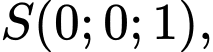
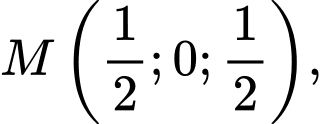
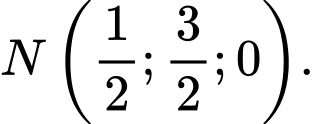
Vecto chỉ phương của
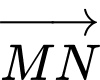 là
là 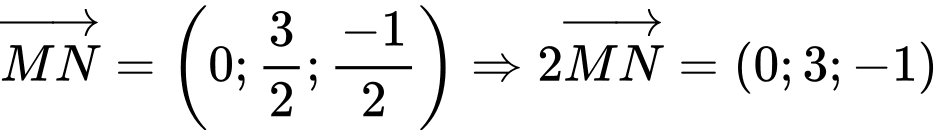
Vecto pháp tuyến của
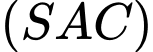 là
là 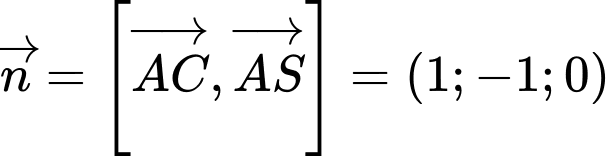
Vậy
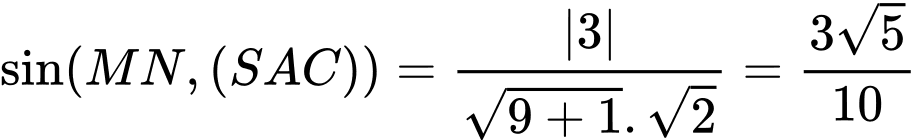
Suy ra:
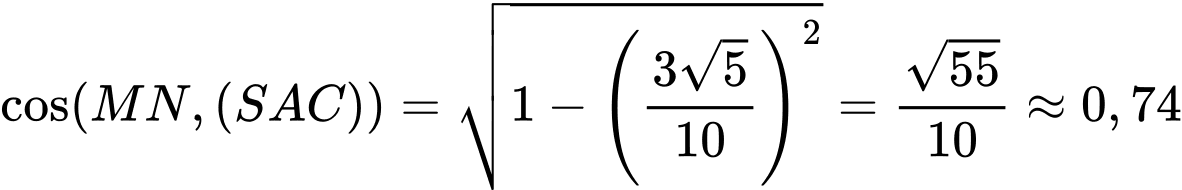
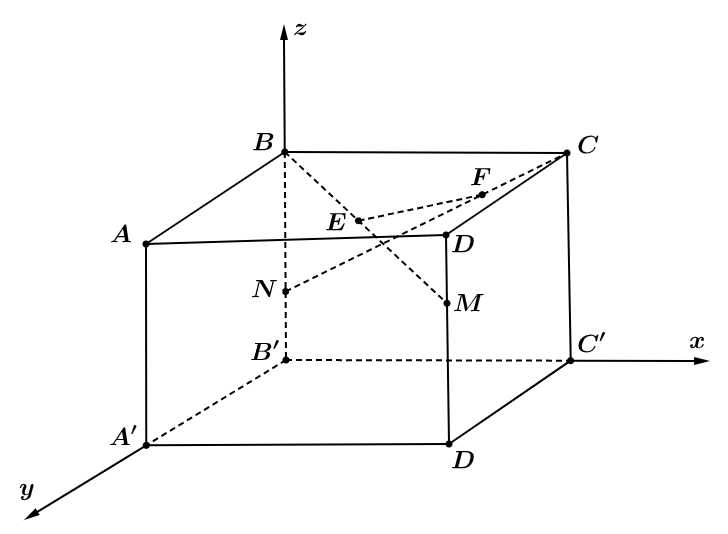
Câu 21 [778828]: Phòng khách nhà bác An có dạng là một hình hộp chữ nhật  với
với 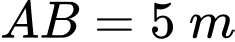 ,
, ,
, 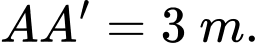 Để chuẩn bị đón Tết Nguyên Đán bác lên kế hoạch trang trí cho phần không gian của phòng khách bằng các dây đèn trang trí
Để chuẩn bị đón Tết Nguyên Đán bác lên kế hoạch trang trí cho phần không gian của phòng khách bằng các dây đèn trang trí  được mắc như hình vẽ sau:
được mắc như hình vẽ sau:
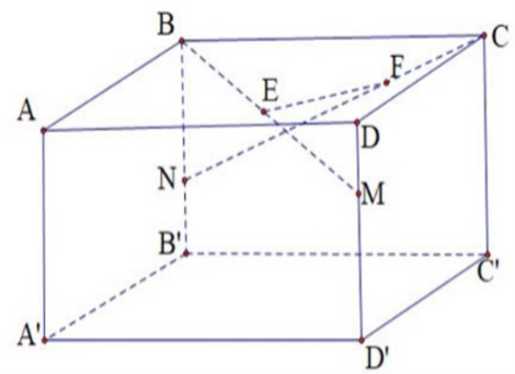
Biết rằng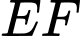 song song với
song song với 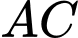 và
và 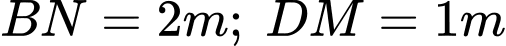 . Giá mỗi mét dây đèn trang trí là 120000 đồng. Hỏi số tiền bác An cần dùng để mua dây đèn trang trí là bao nhiêu triệu đồng? (viết kết quả làm tròn đến hàng phần trăm).
. Giá mỗi mét dây đèn trang trí là 120000 đồng. Hỏi số tiền bác An cần dùng để mua dây đèn trang trí là bao nhiêu triệu đồng? (viết kết quả làm tròn đến hàng phần trăm).
 với
với 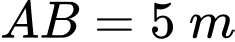 ,
, ,
, 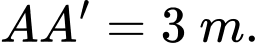 Để chuẩn bị đón Tết Nguyên Đán bác lên kế hoạch trang trí cho phần không gian của phòng khách bằng các dây đèn trang trí
Để chuẩn bị đón Tết Nguyên Đán bác lên kế hoạch trang trí cho phần không gian của phòng khách bằng các dây đèn trang trí 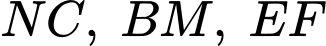 được mắc như hình vẽ sau:
được mắc như hình vẽ sau:
Biết rằng
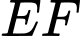 song song với
song song với 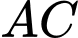 và
và 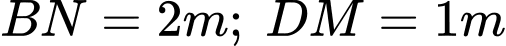 . Giá mỗi mét dây đèn trang trí là 120000 đồng. Hỏi số tiền bác An cần dùng để mua dây đèn trang trí là bao nhiêu triệu đồng? (viết kết quả làm tròn đến hàng phần trăm).
. Giá mỗi mét dây đèn trang trí là 120000 đồng. Hỏi số tiền bác An cần dùng để mua dây đèn trang trí là bao nhiêu triệu đồng? (viết kết quả làm tròn đến hàng phần trăm).
Điền đáp án: 2,08.
Ta có: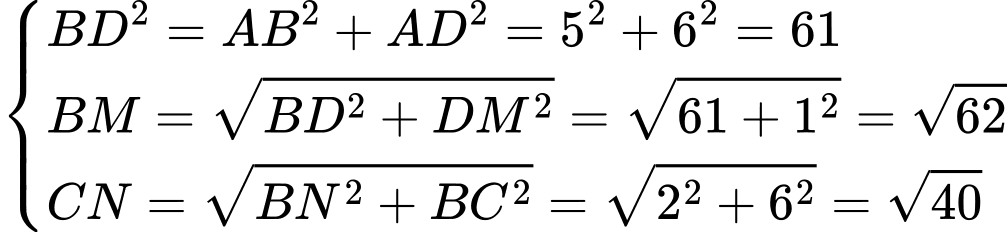
Gắn hệ trục tọa độ như hình vẽ trên, với
như hình vẽ trên, với 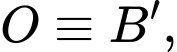
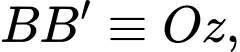
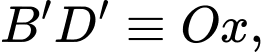
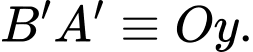
Ta có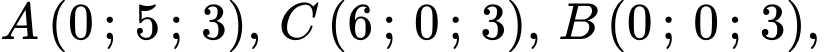
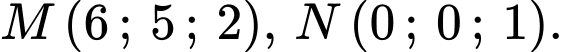
Ta đã tính được độ dài của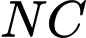 và
và 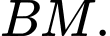 Việc còn lại là ta cần phải đi tìm độ dài đoạn thẳng
Việc còn lại là ta cần phải đi tìm độ dài đoạn thẳng 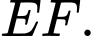 Ta sẽ toạ độ hoá điểm
Ta sẽ toạ độ hoá điểm 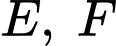 và dựa vào dữ kiện
và dựa vào dữ kiện 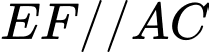 để tìm được toạ độ của chúng.
để tìm được toạ độ của chúng.
Phương trình đường thẳng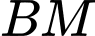 qua
qua 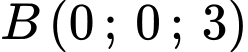 và có VTCP
và có VTCP 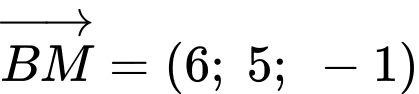 là
là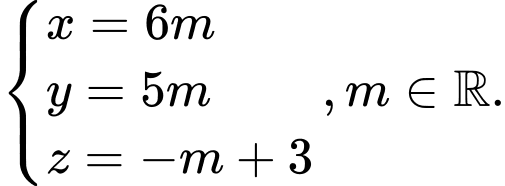
Phương trình đường thẳng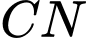 qua
qua 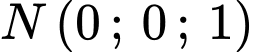 và có VTCP
và có VTCP 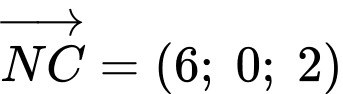 là
là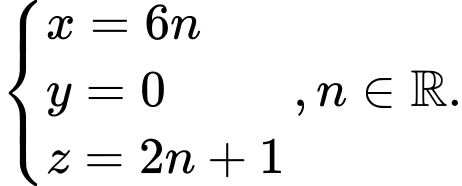
Ta có: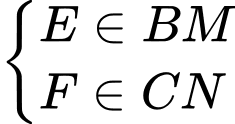
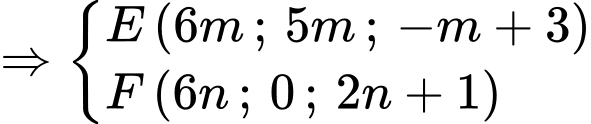
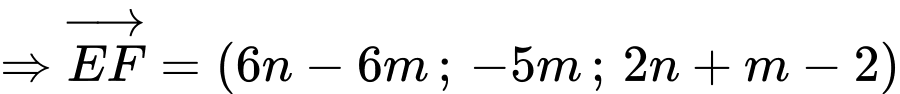 .
.
Vì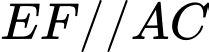 nên
nên 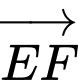 và
và 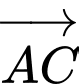 cùng phương.
cùng phương.
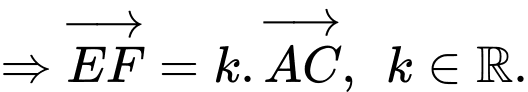
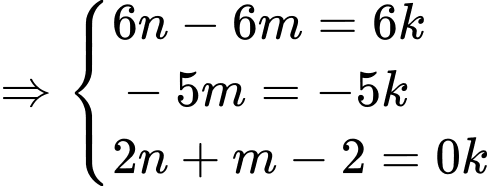
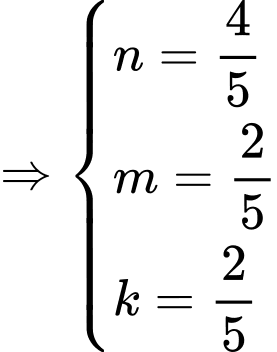
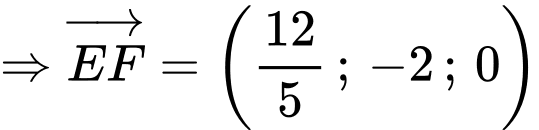
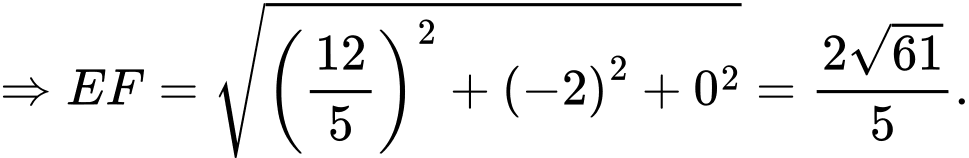
Vậy số tiền (triệu đồng) bác Nam cần dùng để mua dây đèn trang trí là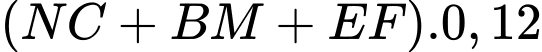
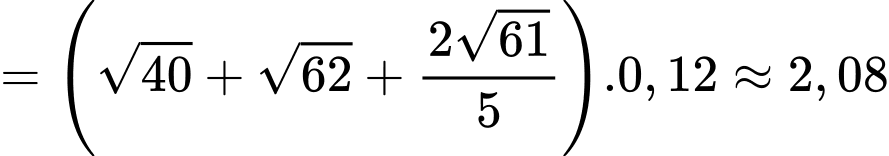 (triệu đồng).
(triệu đồng).

Ta có:
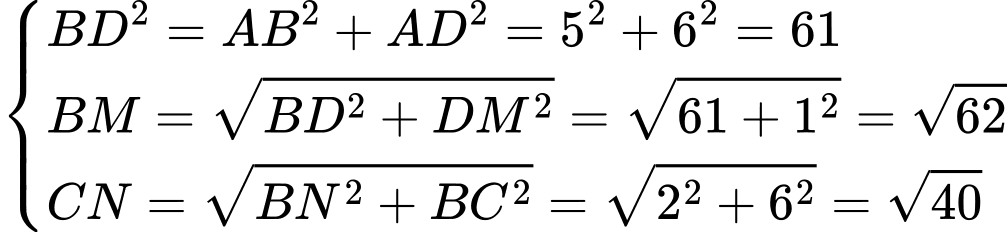
Gắn hệ trục tọa độ
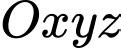 như hình vẽ trên, với
như hình vẽ trên, với 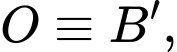
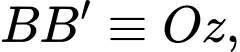
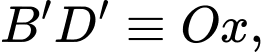
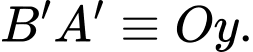
Ta có
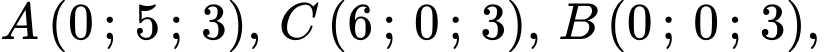
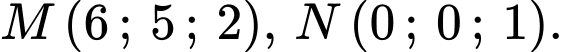
Ta đã tính được độ dài của
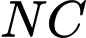 và
và 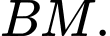 Việc còn lại là ta cần phải đi tìm độ dài đoạn thẳng
Việc còn lại là ta cần phải đi tìm độ dài đoạn thẳng 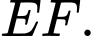 Ta sẽ toạ độ hoá điểm
Ta sẽ toạ độ hoá điểm 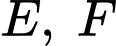 và dựa vào dữ kiện
và dựa vào dữ kiện 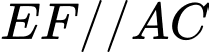 để tìm được toạ độ của chúng.
để tìm được toạ độ của chúng.Phương trình đường thẳng
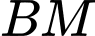 qua
qua 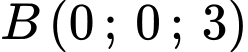 và có VTCP
và có VTCP 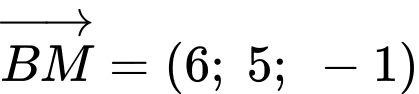 là
là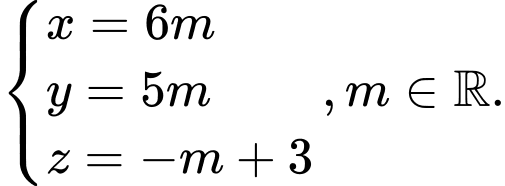
Phương trình đường thẳng
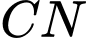 qua
qua 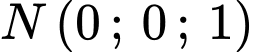 và có VTCP
và có VTCP 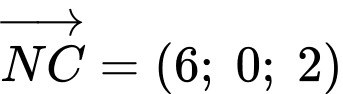 là
là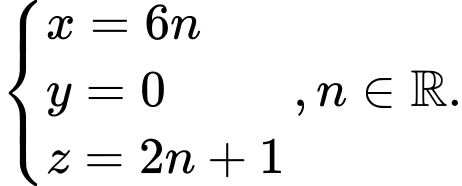
Ta có:
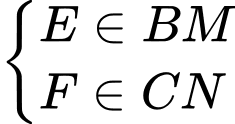
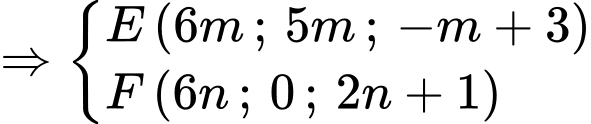
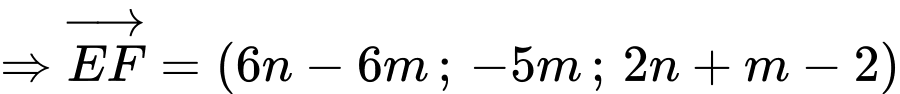 .
. Vì
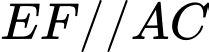 nên
nên  và
và  cùng phương.
cùng phương.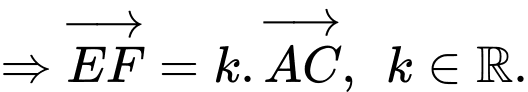
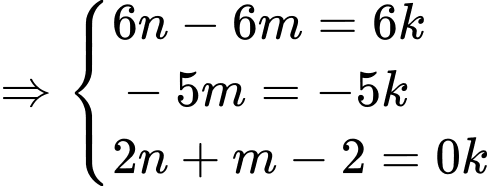
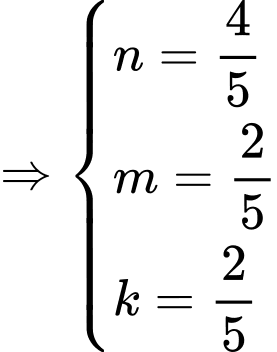
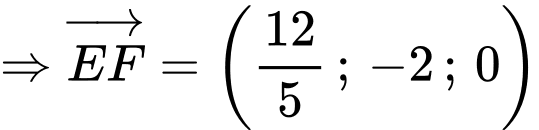
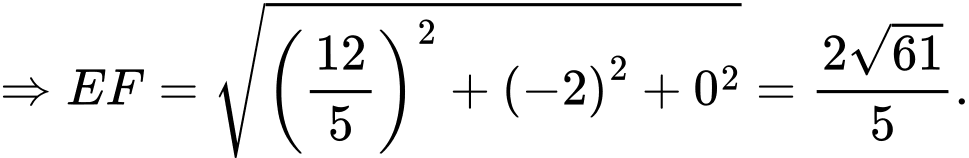
Vậy số tiền (triệu đồng) bác Nam cần dùng để mua dây đèn trang trí là
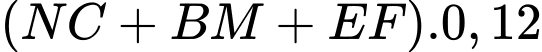
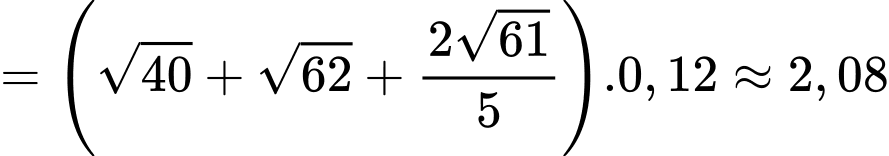 (triệu đồng).
(triệu đồng).
Câu 22 [779035]: Khi khắc phục hậu quả của thiên tai, bão lũ, một trong những giải pháp nhằm tiếp tế hàng cứu trợ đến những nơi khó tiếp cận là sử dụng flycam để xác định vị trí chính xác của người cần cứu trợ, sau đó sử dụng drone để vận chuyển các vật dụng thiết yếu thả xuống cho người này, giúp họ có thể cầm cự trong khi chờ đợi lực lượng cứu hộ đến nơi. Hai chiếc drone làm nhiệm vụ chuyển hàng cứu trợ bay lên từ cùng một địa điểm. Chiếc thứ nhất bay đến điểm cách điểm xuất phát 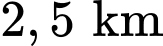 về phía nam và
về phía nam và 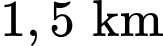 về phía đông, đồng thời cách mặt đất
về phía đông, đồng thời cách mặt đất 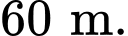 Chiếc thứ hai bay đến điểm cách điểm xuất phát
Chiếc thứ hai bay đến điểm cách điểm xuất phát 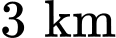 về phía bắc và
về phía bắc và 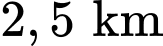 về phía tây, đồng thời cách mặt đất
về phía tây, đồng thời cách mặt đất 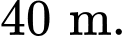 Trong không gian, xét hệ tọa độ
Trong không gian, xét hệ tọa độ 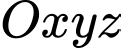 với gốc toạ độ
với gốc toạ độ  đặt tại điểm xuất phát của hai drone, mặt phẳng
đặt tại điểm xuất phát của hai drone, mặt phẳng 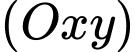 trùng với mặt đất (được coi là mặt phẳng). Giả sử trong trường hợp khẩn cấp, cần tìm một vị trí trên mặt đất để tiếp nhiên liệu và các vật dụng cứu trợ cho hai drone sao cho tổng khoảng cách từ vị trí tiếp nhiên liệu đó tới hai drone nhỏ nhất. Vị trí cần tìm cách gốc tọa độ
trùng với mặt đất (được coi là mặt phẳng). Giả sử trong trường hợp khẩn cấp, cần tìm một vị trí trên mặt đất để tiếp nhiên liệu và các vật dụng cứu trợ cho hai drone sao cho tổng khoảng cách từ vị trí tiếp nhiên liệu đó tới hai drone nhỏ nhất. Vị trí cần tìm cách gốc tọa độ 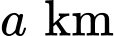 theo hướng bắc và
theo hướng bắc và 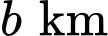 theo hướng tây. Khi đó
theo hướng tây. Khi đó  bằng bao nhiêu?
bằng bao nhiêu?

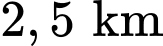 về phía nam và
về phía nam và 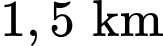 về phía đông, đồng thời cách mặt đất
về phía đông, đồng thời cách mặt đất 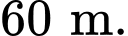 Chiếc thứ hai bay đến điểm cách điểm xuất phát
Chiếc thứ hai bay đến điểm cách điểm xuất phát 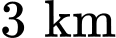 về phía bắc và
về phía bắc và 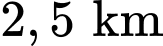 về phía tây, đồng thời cách mặt đất
về phía tây, đồng thời cách mặt đất 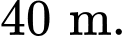 Trong không gian, xét hệ tọa độ
Trong không gian, xét hệ tọa độ 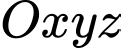 với gốc toạ độ
với gốc toạ độ  đặt tại điểm xuất phát của hai drone, mặt phẳng
đặt tại điểm xuất phát của hai drone, mặt phẳng 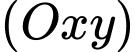 trùng với mặt đất (được coi là mặt phẳng). Giả sử trong trường hợp khẩn cấp, cần tìm một vị trí trên mặt đất để tiếp nhiên liệu và các vật dụng cứu trợ cho hai drone sao cho tổng khoảng cách từ vị trí tiếp nhiên liệu đó tới hai drone nhỏ nhất. Vị trí cần tìm cách gốc tọa độ
trùng với mặt đất (được coi là mặt phẳng). Giả sử trong trường hợp khẩn cấp, cần tìm một vị trí trên mặt đất để tiếp nhiên liệu và các vật dụng cứu trợ cho hai drone sao cho tổng khoảng cách từ vị trí tiếp nhiên liệu đó tới hai drone nhỏ nhất. Vị trí cần tìm cách gốc tọa độ 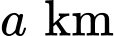 theo hướng bắc và
theo hướng bắc và 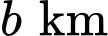 theo hướng tây. Khi đó
theo hướng tây. Khi đó  bằng bao nhiêu?
bằng bao nhiêu?
Đáp số: 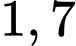 .
.
Giả sử tia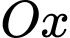 chỉ về hường nam, tia
chỉ về hường nam, tia 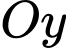 chỉ về hướng đông và tia
chỉ về hướng đông và tia  hướng lên trời. Khi đó chiếc drone thứ nhất ở vị trí
hướng lên trời. Khi đó chiếc drone thứ nhất ở vị trí 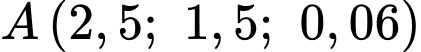 , chiếc drone thứ hai ở vị trí
, chiếc drone thứ hai ở vị trí 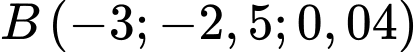
Gọi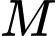 là vị trí trên mặt đất để tiếp nhiên liệu và các vật dụng cứu trợ,
là vị trí trên mặt đất để tiếp nhiên liệu và các vật dụng cứu trợ,  . Ta phải tìm tọa độ của
. Ta phải tìm tọa độ của 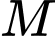 sao cho
sao cho  nhỏ nhất.
nhỏ nhất.
Nhận xét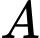 và
và 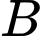 nằm cùng phía đối với mặt phẳng
nằm cùng phía đối với mặt phẳng 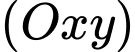 .
.
Gọi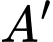 là điểm đối xứng với
là điểm đối xứng với 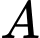 qua mặt phẳng
qua mặt phẳng 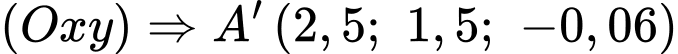
Khi đó: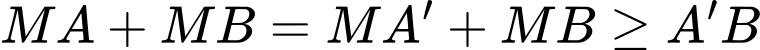 . Đẳng thức xảy ra (tức là
. Đẳng thức xảy ra (tức là  nhỏ nhất) khi
nhỏ nhất) khi 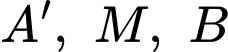 thẳng hàng.
thẳng hàng.
Gọi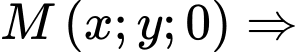
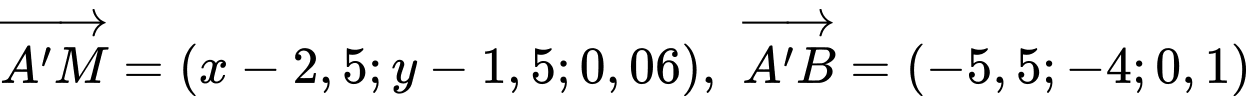
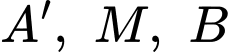 thẳng hàng
thẳng hàng  .
.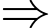 Vị trí cần tìm cách gốc tọa độ
Vị trí cần tìm cách gốc tọa độ 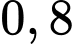 km theo hướng bắc và
km theo hướng bắc và 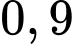 km theo hướng tây
km theo hướng tây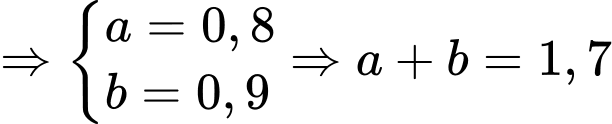 .
.
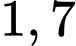 .
.Giả sử tia
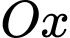 chỉ về hường nam, tia
chỉ về hường nam, tia 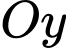 chỉ về hướng đông và tia
chỉ về hướng đông và tia  hướng lên trời. Khi đó chiếc drone thứ nhất ở vị trí
hướng lên trời. Khi đó chiếc drone thứ nhất ở vị trí 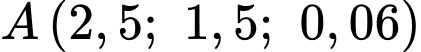 , chiếc drone thứ hai ở vị trí
, chiếc drone thứ hai ở vị trí 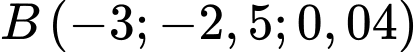
Gọi
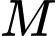 là vị trí trên mặt đất để tiếp nhiên liệu và các vật dụng cứu trợ,
là vị trí trên mặt đất để tiếp nhiên liệu và các vật dụng cứu trợ,  . Ta phải tìm tọa độ của
. Ta phải tìm tọa độ của 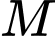 sao cho
sao cho  nhỏ nhất.
nhỏ nhất.Nhận xét
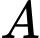 và
và 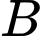 nằm cùng phía đối với mặt phẳng
nằm cùng phía đối với mặt phẳng 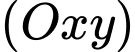 .
.Gọi
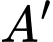 là điểm đối xứng với
là điểm đối xứng với 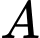 qua mặt phẳng
qua mặt phẳng 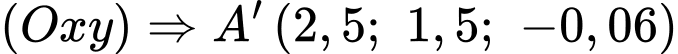
Khi đó:
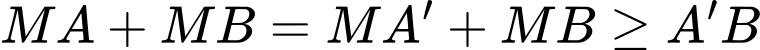 . Đẳng thức xảy ra (tức là
. Đẳng thức xảy ra (tức là  nhỏ nhất) khi
nhỏ nhất) khi 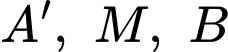 thẳng hàng.
thẳng hàng.Gọi
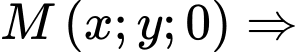
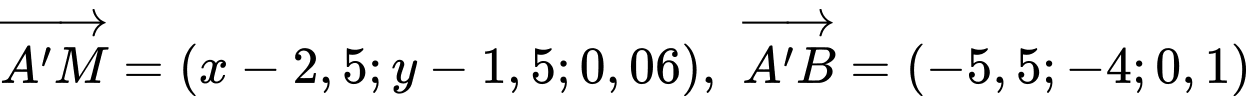
 thẳng hàng
thẳng hàng  .
. Vị trí cần tìm cách gốc tọa độ
Vị trí cần tìm cách gốc tọa độ 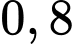 km theo hướng bắc và
km theo hướng bắc và 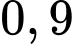 km theo hướng tây
km theo hướng tây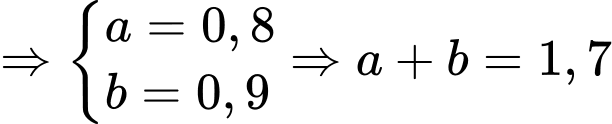 .
.