PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1 [543452]: 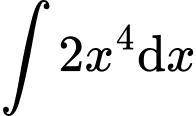 bằng
bằng
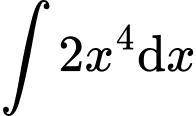 bằng
bằng A, 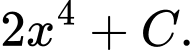
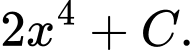
B, 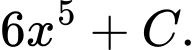
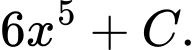
C, 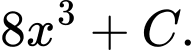
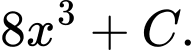
D, 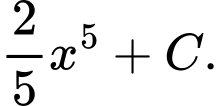
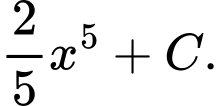
Chọn D
Ta có: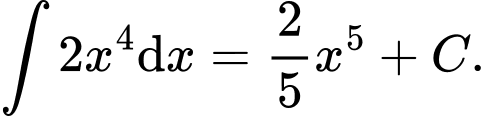 Đáp án: D
Đáp án: D
Ta có:
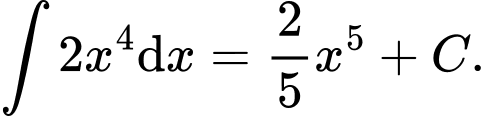 Đáp án: D
Đáp án: D
Câu 2 [680668]: Nguyên hàm của hàm số 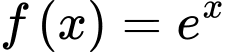 là:
là:
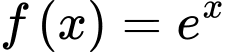 là:
là: A, 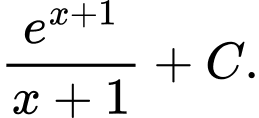
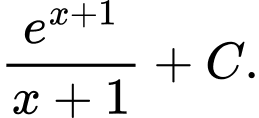
B, 

C, 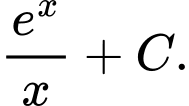
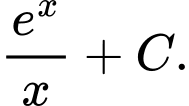
D, 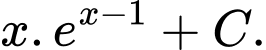
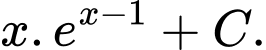
Chọn đáp án B.
Ta có: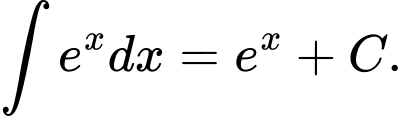 Đáp án: B
Đáp án: B
Ta có:
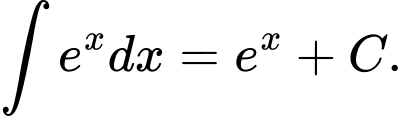 Đáp án: B
Đáp án: B
Câu 3 [810769]: Cho hàm số 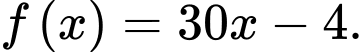 Trong các khẳng định sau khẳng định nào đúng?
Trong các khẳng định sau khẳng định nào đúng?
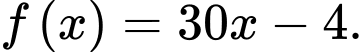 Trong các khẳng định sau khẳng định nào đúng?
Trong các khẳng định sau khẳng định nào đúng? A, 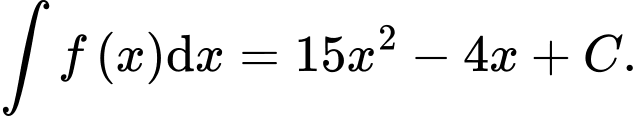
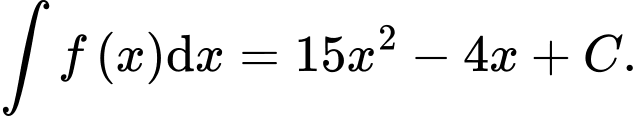
B, 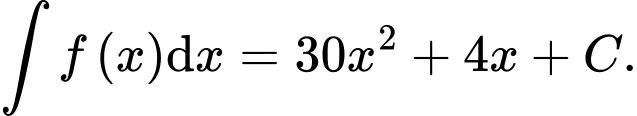
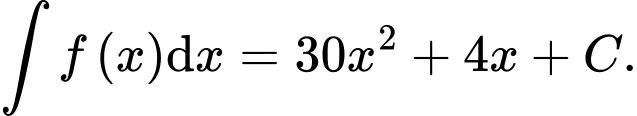
C, 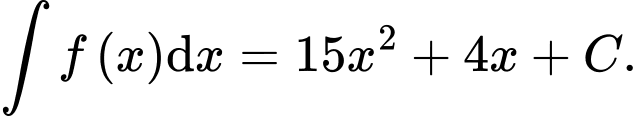
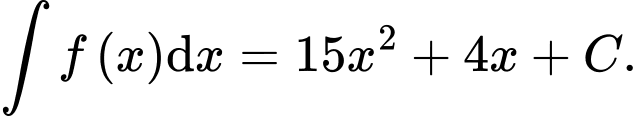
D, 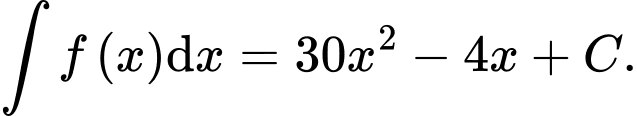
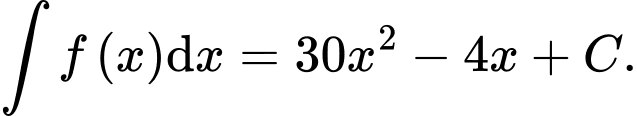
Chọn đáp án A.
Ta có: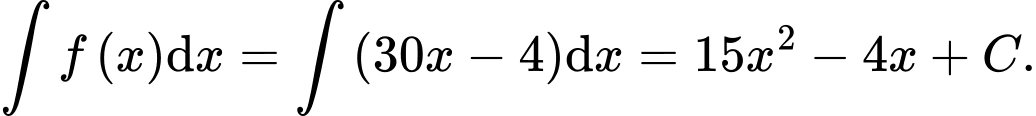 Đáp án: A
Đáp án: A
Ta có:
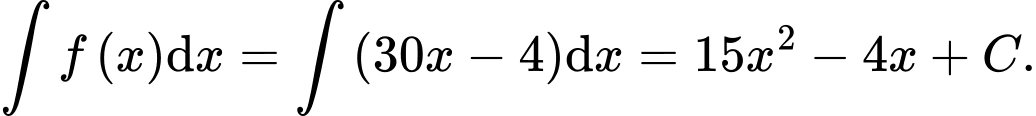 Đáp án: A
Đáp án: A
Câu 4 [801230]: 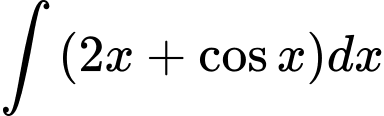 bằng
bằng
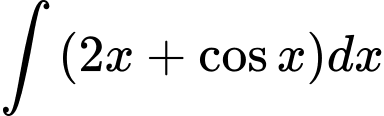 bằng
bằng A, 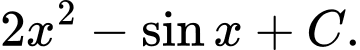
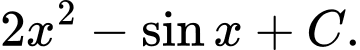
B, 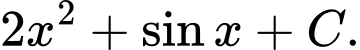
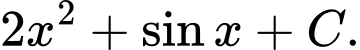
C, 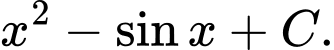
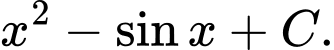
D, 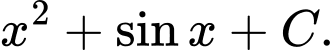
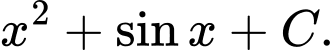
Chọn đáp án D.
Ta có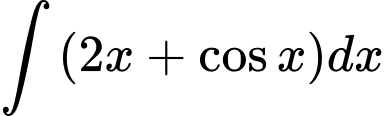
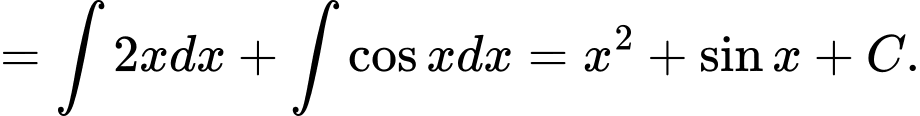 Đáp án: D
Đáp án: D
Ta có
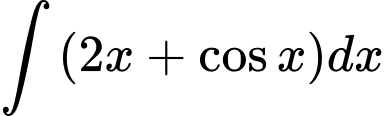
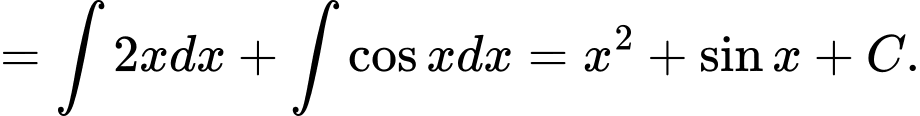 Đáp án: D
Đáp án: D
Câu 5 [732029]: [MĐ1] Nếu 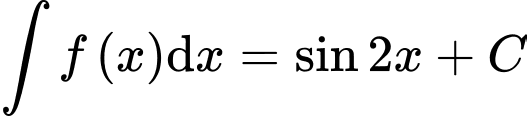 thì
thì 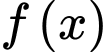 bằng
bằng
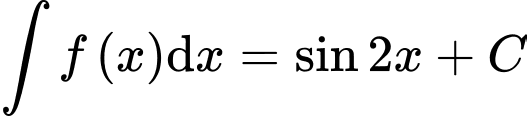 thì
thì 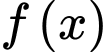 bằng
bằng A, 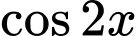 .
.
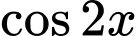 .
.B, 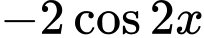 .
.
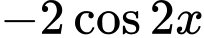 .
.C, 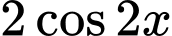 .
.
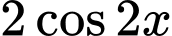 .
.D, 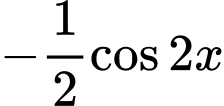 .
.
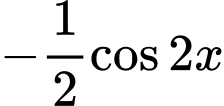 .
.
Ta có 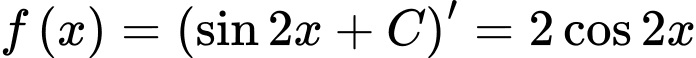 Đáp án: C
Đáp án: C
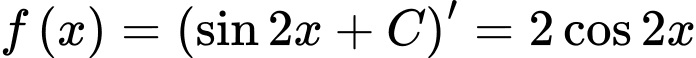 Đáp án: C
Đáp án: C
Câu 6 [297510]: Mệnh đề nào sau đây đúng?
A, 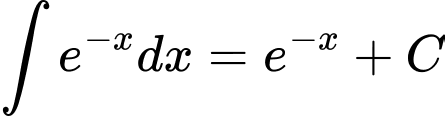 .
.
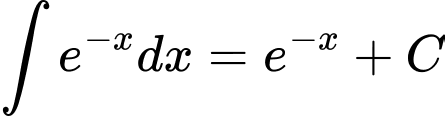 .
.B, 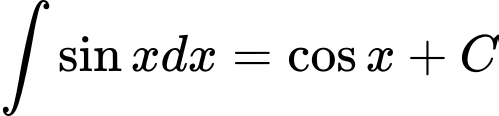 .
.
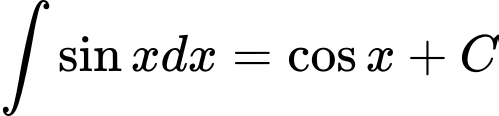 .
.C, 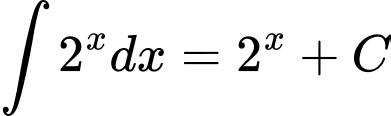 .
.
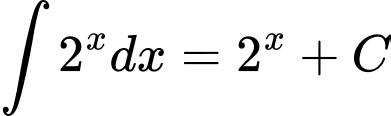 .
.D, 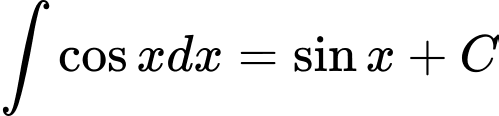 .
.
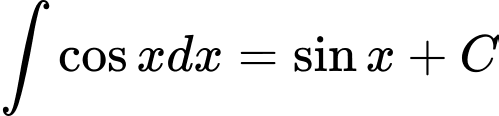 .
.
Chọn D
Mệnh đề đúng là: 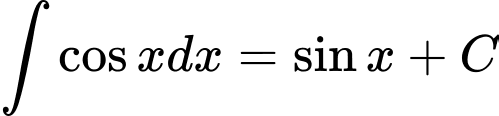 . Đáp án: D
. Đáp án: D
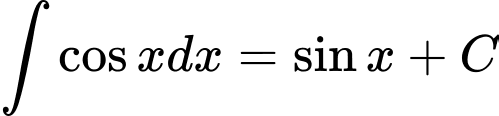 . Đáp án: D
. Đáp án: D
Câu 7 [399920]: Hàm số 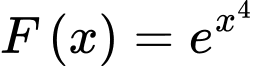 là nguyên hàm của hàm số nào dưới đây?
là nguyên hàm của hàm số nào dưới đây?
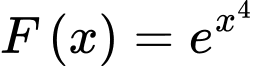 là nguyên hàm của hàm số nào dưới đây?
là nguyên hàm của hàm số nào dưới đây? A, 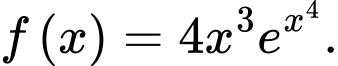
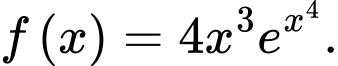
B, 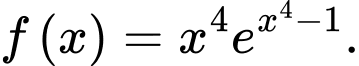
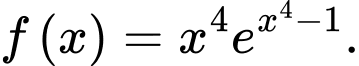
C, 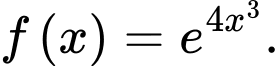
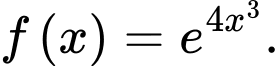
D, 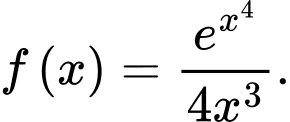
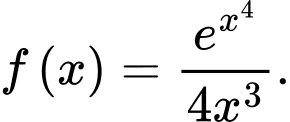
Chọn A
Ta có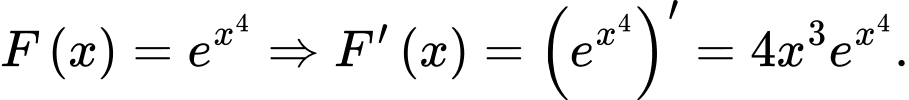
Suy ra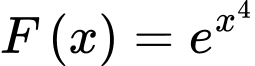 là nguyên hàm của hàm số
là nguyên hàm của hàm số 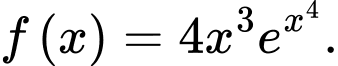 Đáp án: A
Đáp án: A
Ta có
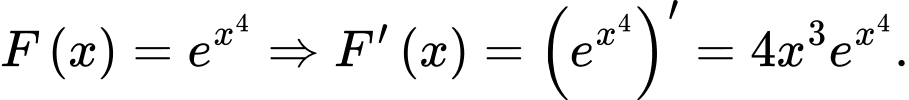
Suy ra
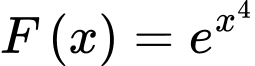 là nguyên hàm của hàm số
là nguyên hàm của hàm số 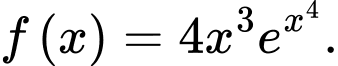 Đáp án: A
Đáp án: A
Câu 8 [543246]: Cho hàm số 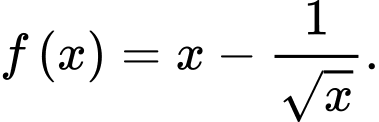 Khẳng định nào dưới đây đúng?
Khẳng định nào dưới đây đúng?
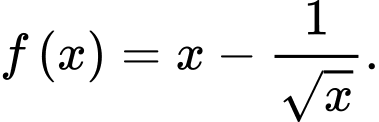 Khẳng định nào dưới đây đúng?
Khẳng định nào dưới đây đúng? A, 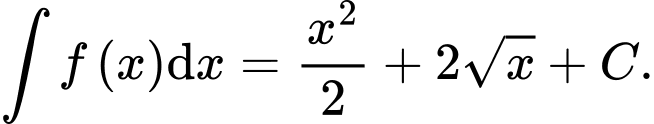
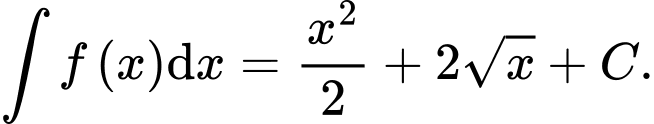
B, 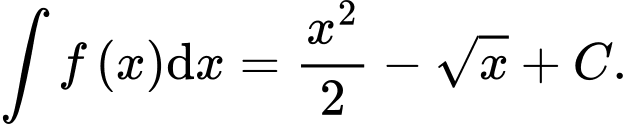
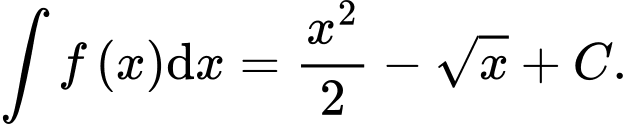
C, 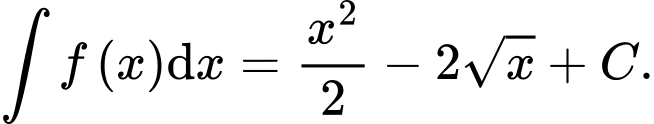
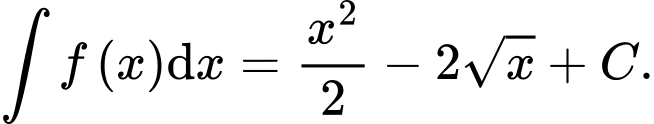
D, 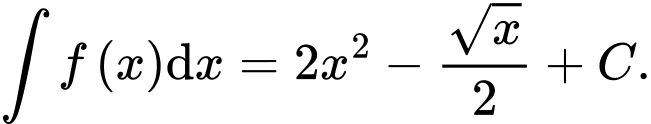
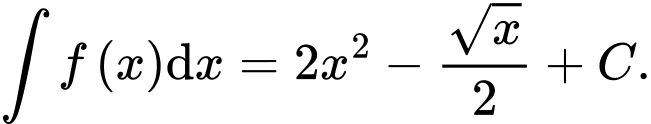
Chọn C
Ta có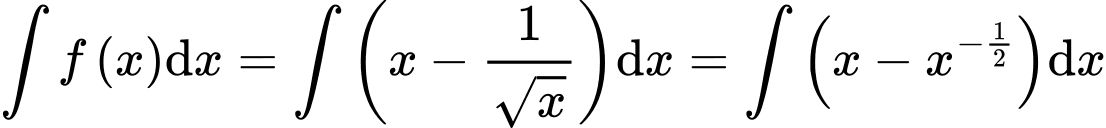
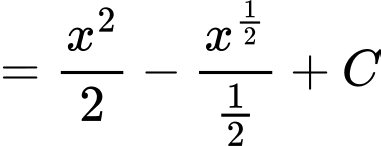
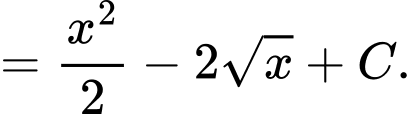 Đáp án: C
Đáp án: C
Ta có
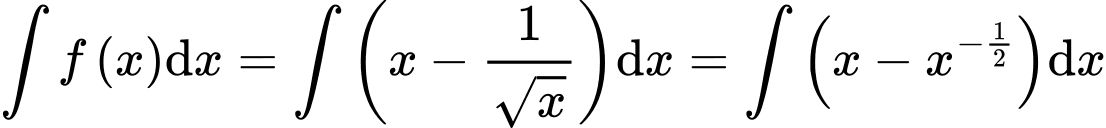
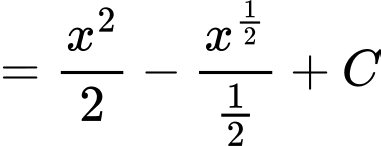
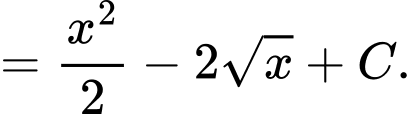 Đáp án: C
Đáp án: C
Câu 9 [297964]: [MĐ1] Cho 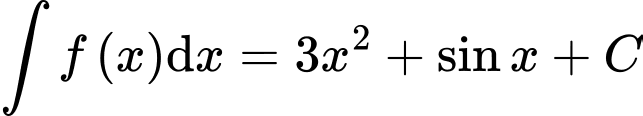 . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
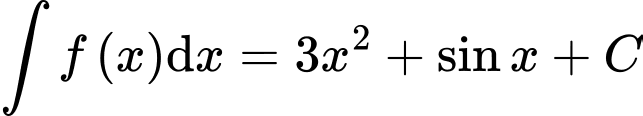 . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng? A, 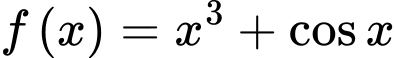 .
.
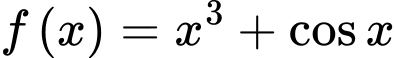 .
.B, 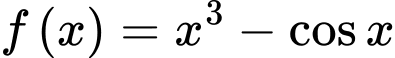 .
.
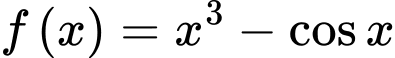 .
.C, 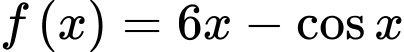 .
.
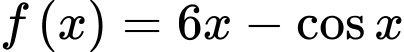 .
.D, 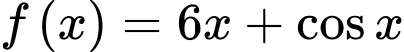 .
.
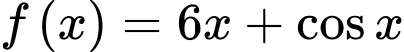 .
.
Ta có 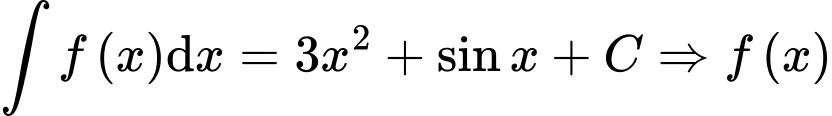
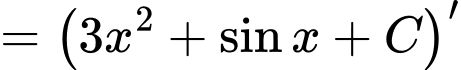
 Đáp án: D
Đáp án: D
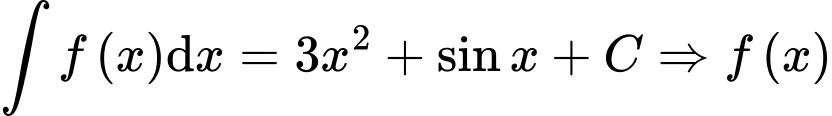
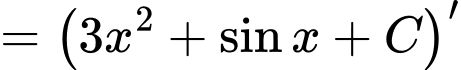
 Đáp án: D
Đáp án: D
Câu 10 [360263]: 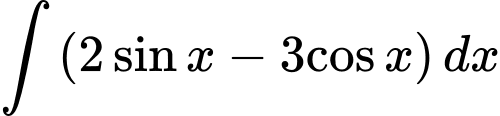 bằng:
bằng:
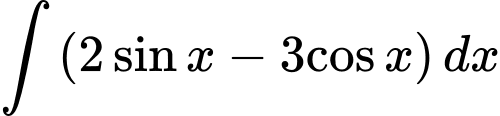 bằng:
bằng: A, 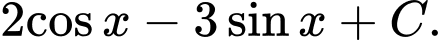
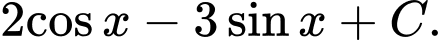
B, 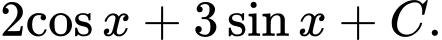
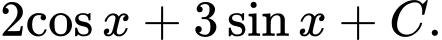
C, 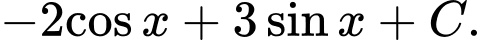
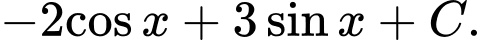
D, 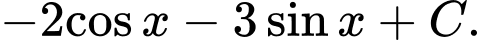
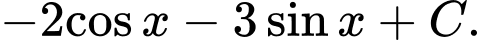
Áp dụng công thức nguyên hàm: 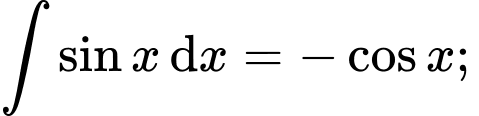
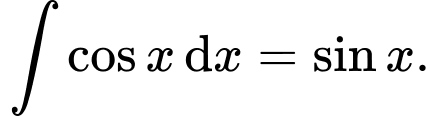
Ta được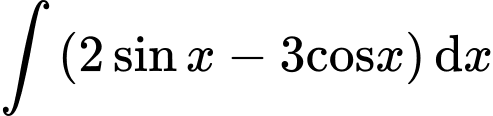
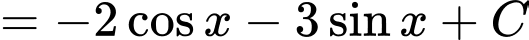
Chọn D. Đáp án: D
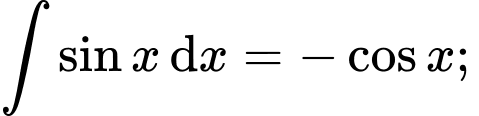
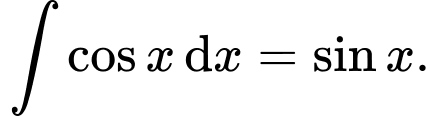
Ta được
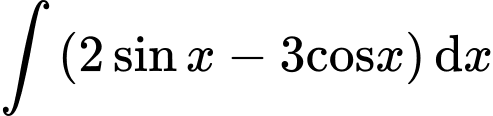
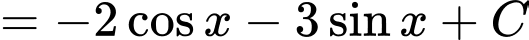
Chọn D. Đáp án: D
Câu 11 [148014]: Tìm nguyên hàm của hàm số 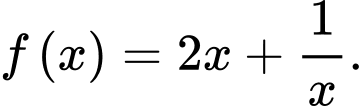
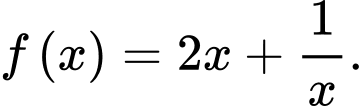
A, 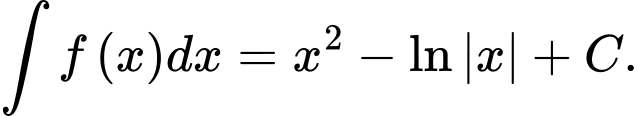
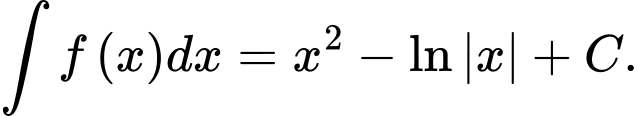
B, 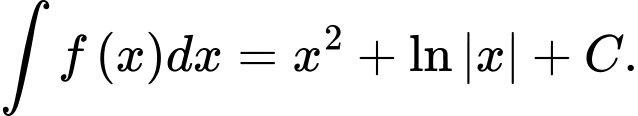
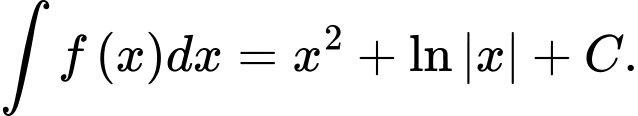
C, 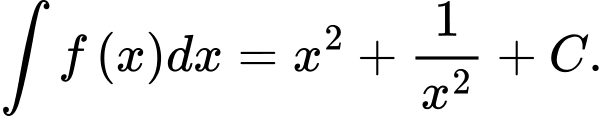
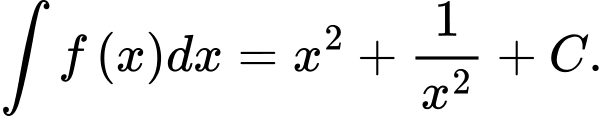
D, 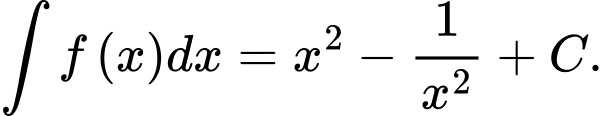
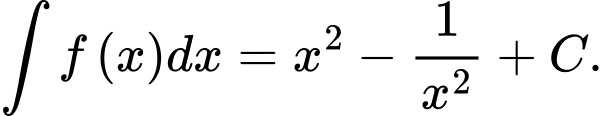
Chọn đáp án B. Đáp án: B
Câu 12 [148223]: Cho hàm số 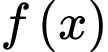 thỏa mãn
thỏa mãn 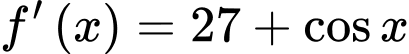 và
và 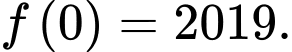 Mệnh đề nào dưới đây đúng?
Mệnh đề nào dưới đây đúng?
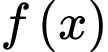 thỏa mãn
thỏa mãn 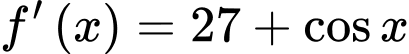 và
và 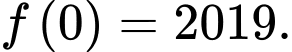 Mệnh đề nào dưới đây đúng?
Mệnh đề nào dưới đây đúng? A, 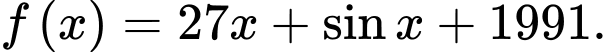
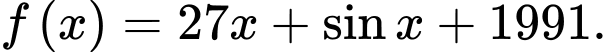
B, 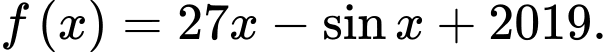
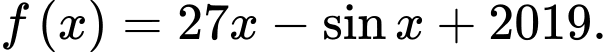
C, 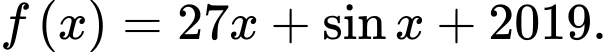
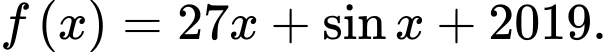
D, 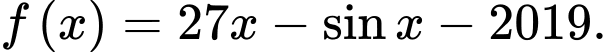
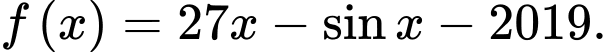
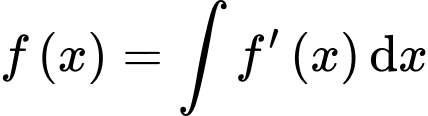
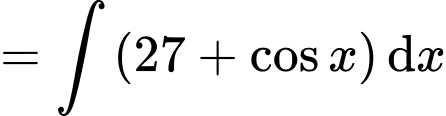
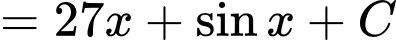
Mà
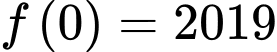
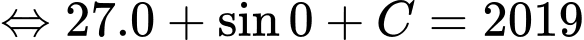

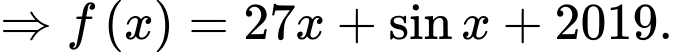
Chọn đáp án C. Đáp án: C
PHẦN II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a),b),c),d) ở mỗi câu học sinh chọn đúng hoặc sai.
Câu 13 [775025]: Cho hàm số 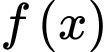 liên tục trên
liên tục trên 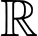 thoả mãn
thoả mãn 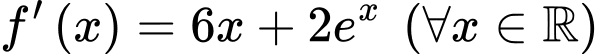 và
và 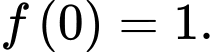 Biết hàm số
Biết hàm số 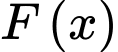 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 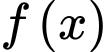 và
và 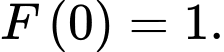
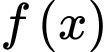 liên tục trên
liên tục trên 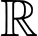 thoả mãn
thoả mãn 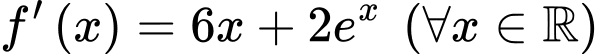 và
và 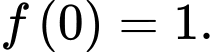 Biết hàm số
Biết hàm số 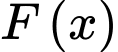 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 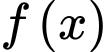 và
và 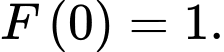
a) Đúng.
b) Đúng.
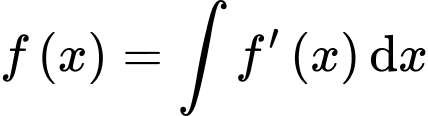
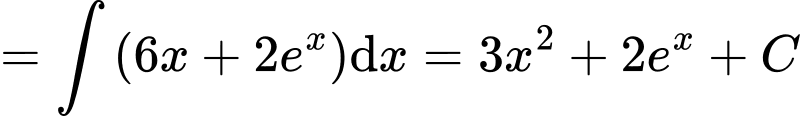
Mặt khác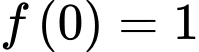
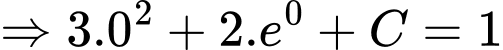
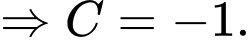
Vậy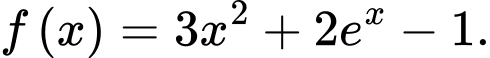
c) Sai.
Vì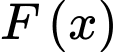 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 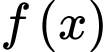 nên
nên 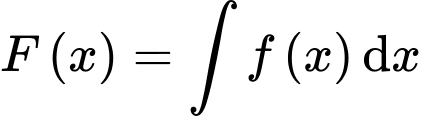
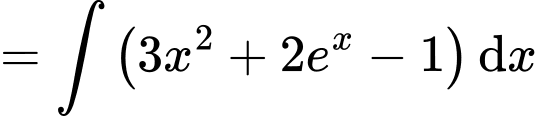
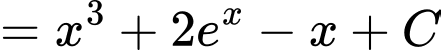
Ta có nên
nên 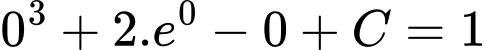
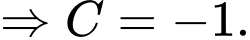
Suy ra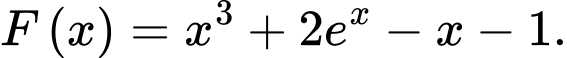
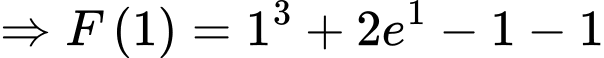
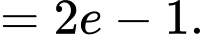
d) Đúng.
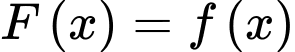
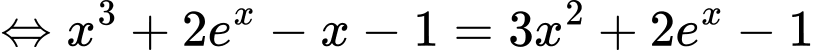
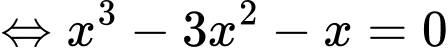 (bấm máy tính, ta thấy phương trình có 3 nghiệm phân biệt)
(bấm máy tính, ta thấy phương trình có 3 nghiệm phân biệt)
b) Đúng.
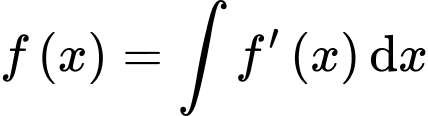
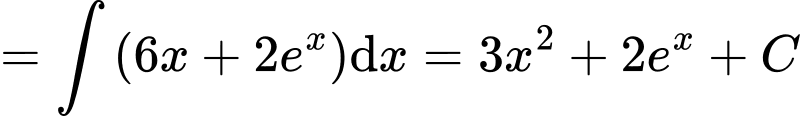
Mặt khác
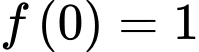
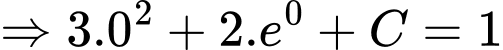
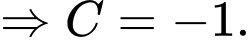
Vậy
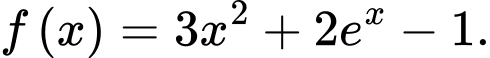
c) Sai.
Vì
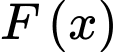 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 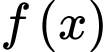 nên
nên 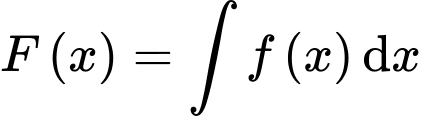
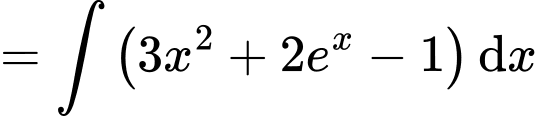
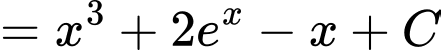
Ta có
 nên
nên 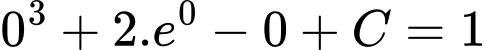
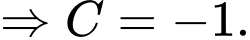
Suy ra
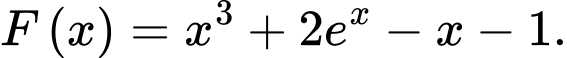
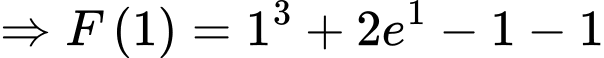
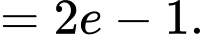
d) Đúng.
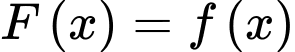
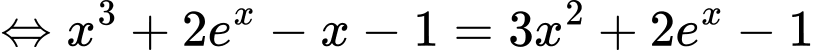
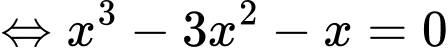 (bấm máy tính, ta thấy phương trình có 3 nghiệm phân biệt)
(bấm máy tính, ta thấy phương trình có 3 nghiệm phân biệt)
Câu 14 [775026]: Một viên đạn được bắn thẳng đứng lên trên từ mặt đất. Giả sử tại thời điểm t giây (coi 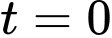 là thời điểm viên đạn được bắn lên), vận tốc của viên đạn tuân theo quy luật là
là thời điểm viên đạn được bắn lên), vận tốc của viên đạn tuân theo quy luật là 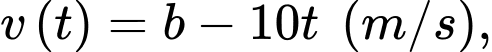 trong đó
trong đó 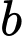 là hằng số. Biết rằng sau khi bay lên 32 giây thì viên đạn rơi lại mặt đất.
là hằng số. Biết rằng sau khi bay lên 32 giây thì viên đạn rơi lại mặt đất.
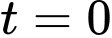 là thời điểm viên đạn được bắn lên), vận tốc của viên đạn tuân theo quy luật là
là thời điểm viên đạn được bắn lên), vận tốc của viên đạn tuân theo quy luật là 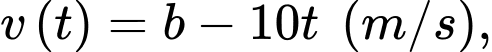 trong đó
trong đó 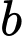 là hằng số. Biết rằng sau khi bay lên 32 giây thì viên đạn rơi lại mặt đất.
là hằng số. Biết rằng sau khi bay lên 32 giây thì viên đạn rơi lại mặt đất.
a) Đúng.
Gọi x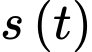 là hàm số biểu thị độ cao của viên đạn so với mặt đất tại thời điểm
là hàm số biểu thị độ cao của viên đạn so với mặt đất tại thời điểm 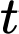 giây.
giây.
Ta có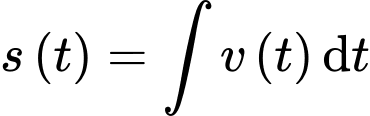
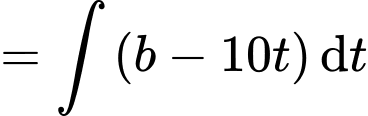
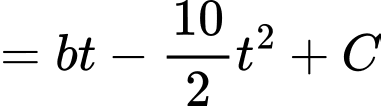
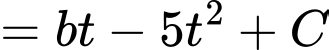
Biết tại thời điểm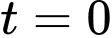 thì
thì 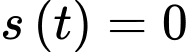
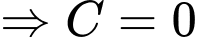
Khi đó,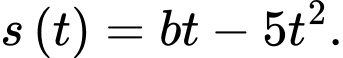
b) Đúng.
Biết sau khi bay lên 32 giây thì viên đạn rơi lại chạm mặt đất tức tại thời điểm 32 giây thì viên đạn nằm trên mặt đất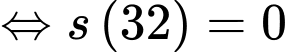
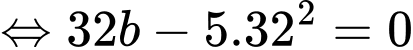

Suy ra Vậy vận tốc ban đầu của viên đạn là
Vậy vận tốc ban đầu của viên đạn là 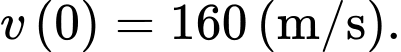
c) Đúng.
Khảo sát hàm số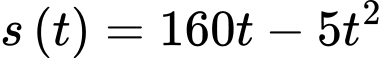 trong đoạn
trong đoạn 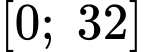
Ta có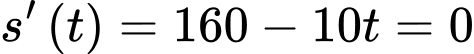
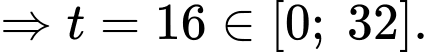
Khi đó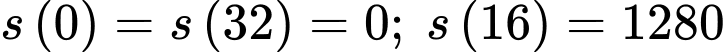
Vậy độ cao lớn nhất mà viên đạn đạt được là 1280 mét.
d) Đúng.
Vì viên đạn sẽ bay lên từ mặt đất tới độ cao cao nhất là 1280 mét rồi quay trở lại mặt đất, nên quãng đường viên đạn đi được bằng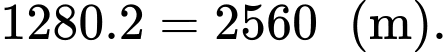
Tốc độ trung bình của viên đạn = Tổng quãng đường đi được/Tổng thời gian
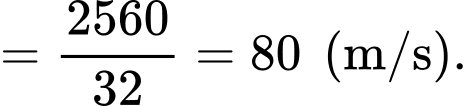 .
.
Gọi x
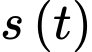 là hàm số biểu thị độ cao của viên đạn so với mặt đất tại thời điểm
là hàm số biểu thị độ cao của viên đạn so với mặt đất tại thời điểm 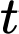 giây.
giây.
Ta có
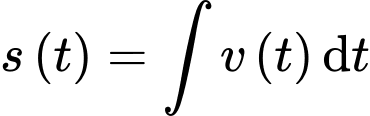
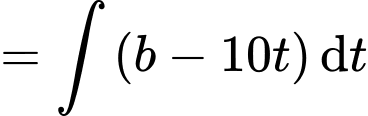
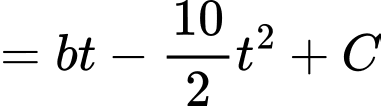
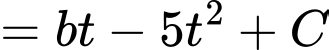
Biết tại thời điểm
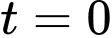 thì
thì 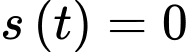
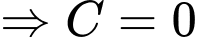
Khi đó,
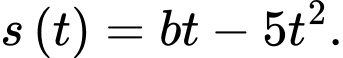
b) Đúng.
Biết sau khi bay lên 32 giây thì viên đạn rơi lại chạm mặt đất tức tại thời điểm 32 giây thì viên đạn nằm trên mặt đất
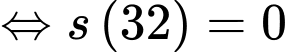
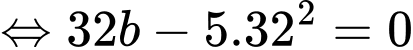

Suy ra
 Vậy vận tốc ban đầu của viên đạn là
Vậy vận tốc ban đầu của viên đạn là 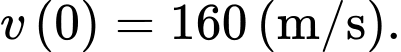
c) Đúng.
Khảo sát hàm số
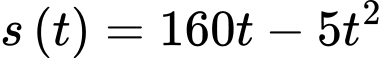 trong đoạn
trong đoạn 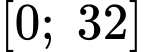
Ta có
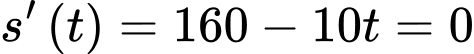
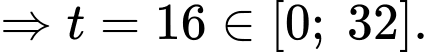
Khi đó
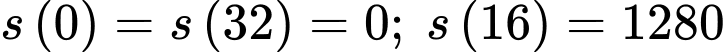
Vậy độ cao lớn nhất mà viên đạn đạt được là 1280 mét.
d) Đúng.
Vì viên đạn sẽ bay lên từ mặt đất tới độ cao cao nhất là 1280 mét rồi quay trở lại mặt đất, nên quãng đường viên đạn đi được bằng
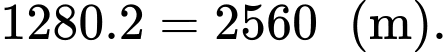
Tốc độ trung bình của viên đạn = Tổng quãng đường đi được/Tổng thời gian
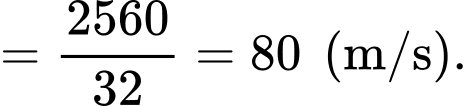 .
.
Câu 15 [775028]: Những ngày giáp Tết Nguyên Đán cũng là dịp bước vào vụ Đông Xuân, bà con nông dân tích cực xuống đồng cấy lúa. Cây lúa sau khi được cấy trải qua quá trình tăng trưởng đẻ nhánh và phát triển chiều cao trước khi làm đòng, trổ bông. Qua nghiên cứu một giống lúa mới, các nhà khoa học nhận thấy một cây lúa tính từ lúc được cấy bằng một cây mạ với chiều cao 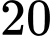 cm có tốc độ tăng trưởng chiều cao cho bởi hàm số
cm có tốc độ tăng trưởng chiều cao cho bởi hàm số 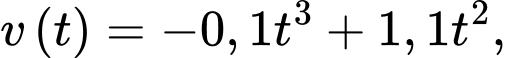 trong đó
trong đó 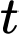 tính theo tuần,
tính theo tuần, 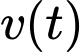 tính bằng cm/tuần. Gọi
tính bằng cm/tuần. Gọi 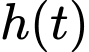 là chiều cao của cây lúa ở tuần thứ
là chiều cao của cây lúa ở tuần thứ 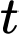 (
( ).
).
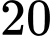 cm có tốc độ tăng trưởng chiều cao cho bởi hàm số
cm có tốc độ tăng trưởng chiều cao cho bởi hàm số 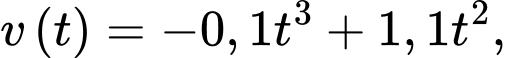 trong đó
trong đó 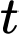 tính theo tuần,
tính theo tuần, 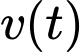 tính bằng cm/tuần. Gọi
tính bằng cm/tuần. Gọi 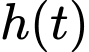 là chiều cao của cây lúa ở tuần thứ
là chiều cao của cây lúa ở tuần thứ 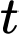 (
( ).
).
a) Đúng.
Vì tốc độ tăng trưởng chiều cao được tính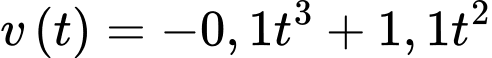
Nên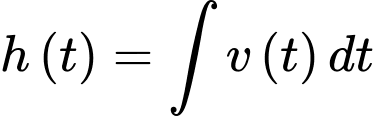
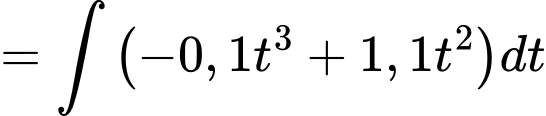
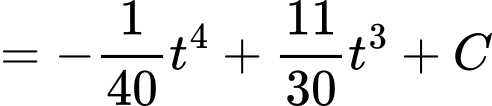
Do chiều cao ban đầu của cây lúa là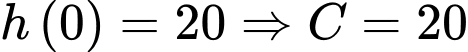
Vậy chiều cao của cây lúa ở tuần thứ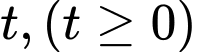 là
là 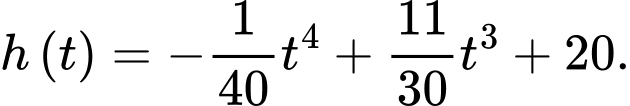
b) Sai.
Giai đoạn tăng trưởng chiều cao của cây lúa sẽ dừng lại khi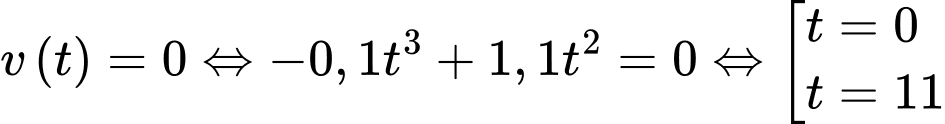
Nên cây lúa sẽ chỉ tăng trưởng trong 11 tuần.
c) Sai.
Kẻ bảng biến thiên, ta sẽ thấy cây lúa cao nhất vào tuần thứ 11 nên chiều cao tối đa của cây lúa là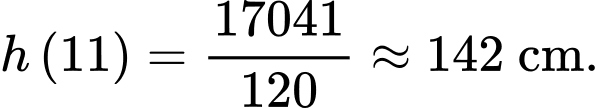
d) Đúng.
Thời điểm cây phát triển nhanh nhất, tức tốc độ phát triển lớn nhất hay tìm thời điểm mà hàm số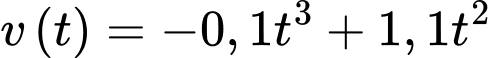 với
với 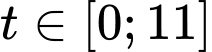 đạt giá trị lớn nhất.
đạt giá trị lớn nhất.
Ta có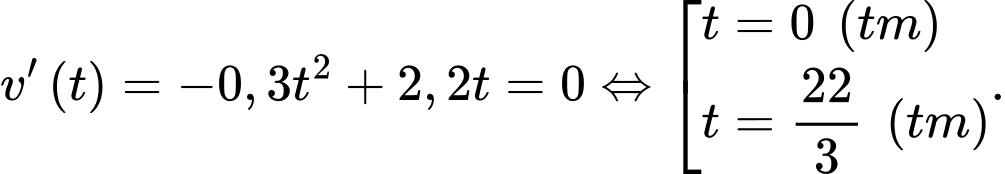
Bảng biến thiên
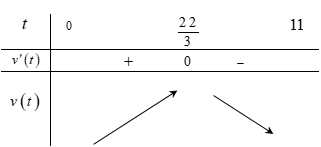
Vậy cây lúa phát triển nhanh nhất tại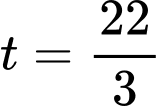 suy ra chiều cao của cây lúa tại thời điểm này là
suy ra chiều cao của cây lúa tại thời điểm này là 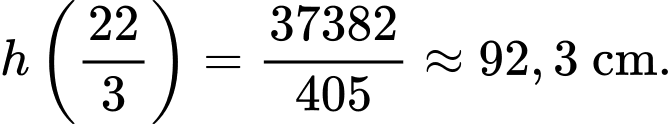
Vì tốc độ tăng trưởng chiều cao được tính
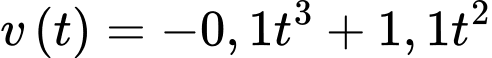
Nên
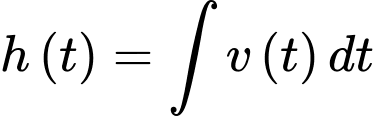
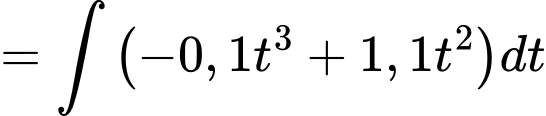
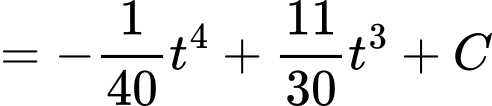
Do chiều cao ban đầu của cây lúa là
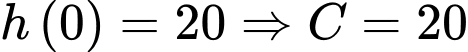
Vậy chiều cao của cây lúa ở tuần thứ
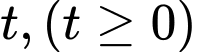 là
là 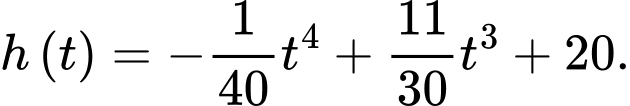
b) Sai.
Giai đoạn tăng trưởng chiều cao của cây lúa sẽ dừng lại khi
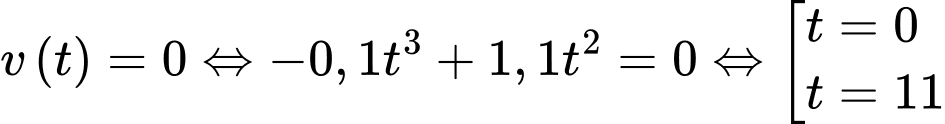
Nên cây lúa sẽ chỉ tăng trưởng trong 11 tuần.
c) Sai.
Kẻ bảng biến thiên, ta sẽ thấy cây lúa cao nhất vào tuần thứ 11 nên chiều cao tối đa của cây lúa là
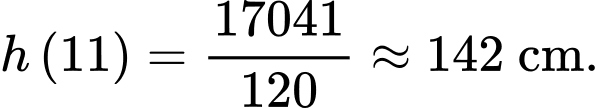
d) Đúng.
Thời điểm cây phát triển nhanh nhất, tức tốc độ phát triển lớn nhất hay tìm thời điểm mà hàm số
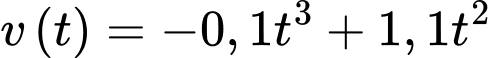 với
với 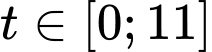 đạt giá trị lớn nhất.
đạt giá trị lớn nhất.
Ta có
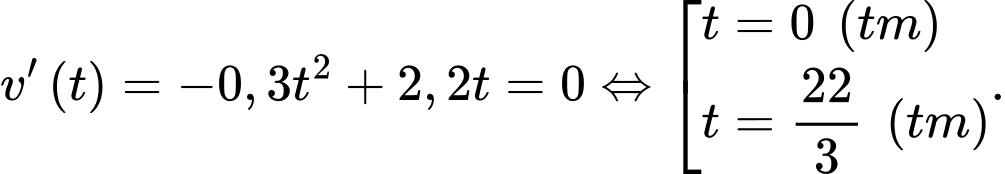
Bảng biến thiên

Vậy cây lúa phát triển nhanh nhất tại
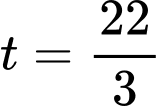 suy ra chiều cao của cây lúa tại thời điểm này là
suy ra chiều cao của cây lúa tại thời điểm này là 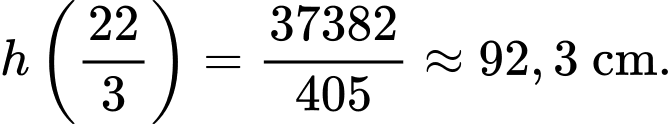
Câu 16 [695527]: Khi đun nước, nhiệt độ ban đầu của nước trong ấm là 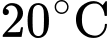 và tăng dần với tốc độ
và tăng dần với tốc độ 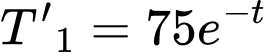 (
( phút)
phút) 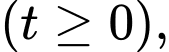 trong đó
trong đó 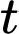 (phút) là thời gian tính từ lúc bếp được bật lên. Khi nước trong ấm đạt
(phút) là thời gian tính từ lúc bếp được bật lên. Khi nước trong ấm đạt 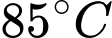 thì bếp được tắt đi và nhiệt độ
thì bếp được tắt đi và nhiệt độ  của nước trong ấm khi này xác định theo công thức
của nước trong ấm khi này xác định theo công thức 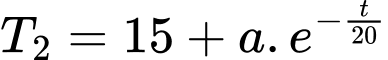
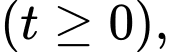 trong đó
trong đó 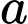 là hằng số và
là hằng số và 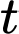 (phút) là thời gian tính từ lúc tắt bếp.
(phút) là thời gian tính từ lúc tắt bếp.
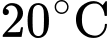 và tăng dần với tốc độ
và tăng dần với tốc độ 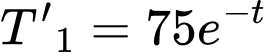 (
( phút)
phút) 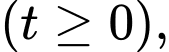 trong đó
trong đó 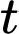 (phút) là thời gian tính từ lúc bếp được bật lên. Khi nước trong ấm đạt
(phút) là thời gian tính từ lúc bếp được bật lên. Khi nước trong ấm đạt 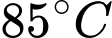 thì bếp được tắt đi và nhiệt độ
thì bếp được tắt đi và nhiệt độ  của nước trong ấm khi này xác định theo công thức
của nước trong ấm khi này xác định theo công thức 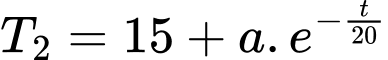
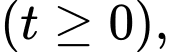 trong đó
trong đó 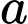 là hằng số và
là hằng số và 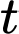 (phút) là thời gian tính từ lúc tắt bếp.
(phút) là thời gian tính từ lúc tắt bếp.
a) Đúng.
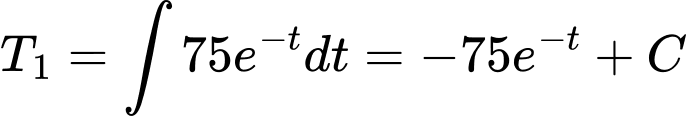 với
với  là hằng số.
là hằng số.
Vì nhiệt độ ban đầu là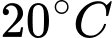 nên
nên 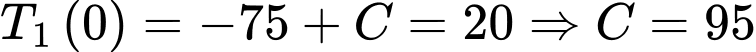
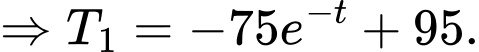
b) Sai.
Vì khi nước trong ấm đạt 85°C thì bếp được tắt đi nên ta có: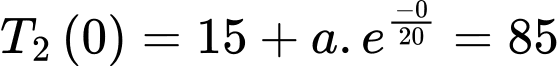
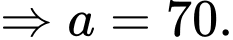
c) Sai.
Ta có: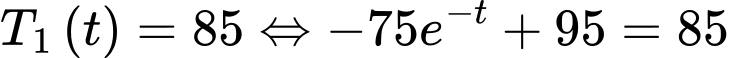
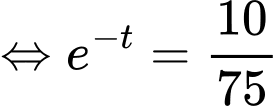
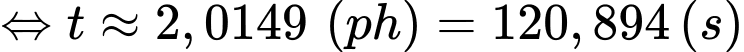
d) Sai.
Theo câu c) ta có sau 2 phút kể từ khi mở bếp thì nước trong ấm đạt nhiệt độ
Sau đó thì nhiệt độ của nước trong ấm sẽ tính theo công thức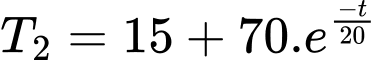
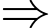 Sau 21 phút kể từ khi bật bếp thì nhiệt độ của ấm là
Sau 21 phút kể từ khi bật bếp thì nhiệt độ của ấm là 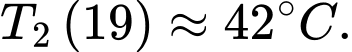
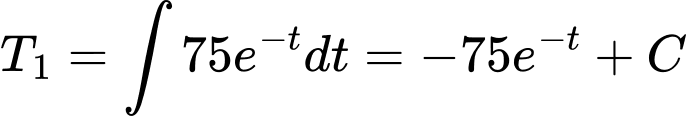 với
với  là hằng số.
là hằng số.Vì nhiệt độ ban đầu là
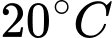 nên
nên 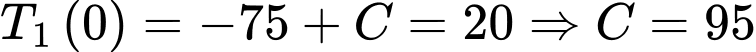
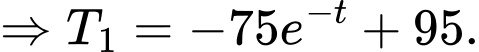
b) Sai.
Vì khi nước trong ấm đạt 85°C thì bếp được tắt đi nên ta có:
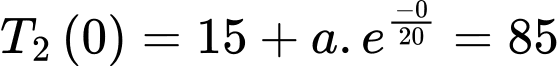
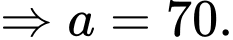
c) Sai.
Ta có:
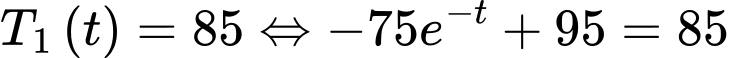
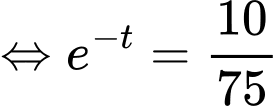
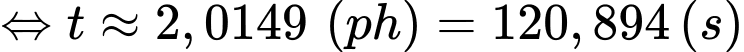
d) Sai.
Theo câu c) ta có sau 2 phút kể từ khi mở bếp thì nước trong ấm đạt nhiệt độ

Sau đó thì nhiệt độ của nước trong ấm sẽ tính theo công thức
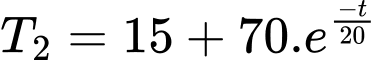
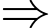 Sau 21 phút kể từ khi bật bếp thì nhiệt độ của ấm là
Sau 21 phút kể từ khi bật bếp thì nhiệt độ của ấm là 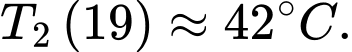
PHẦN III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 17 đến câu 22.
Câu 17 [775033]: Cho hàm số 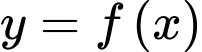 có đạo hàm cấp hai trên
có đạo hàm cấp hai trên 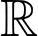 thoả mãn
thoả mãn 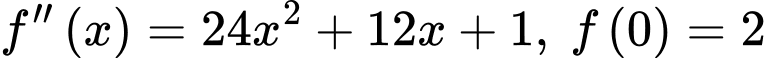 và
và 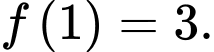 Tính giá trị của
Tính giá trị của 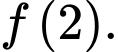
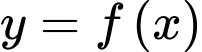 có đạo hàm cấp hai trên
có đạo hàm cấp hai trên 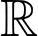 thoả mãn
thoả mãn 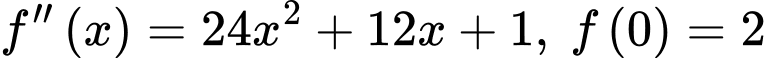 và
và 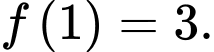 Tính giá trị của
Tính giá trị của 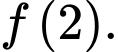
Điền đáp án: 45.
Ta có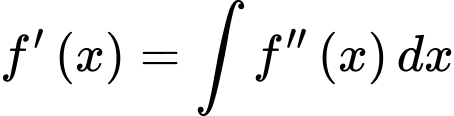
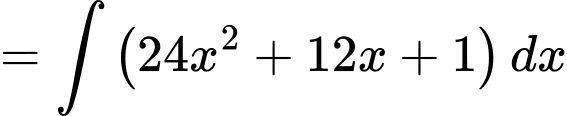
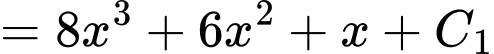
Suy ra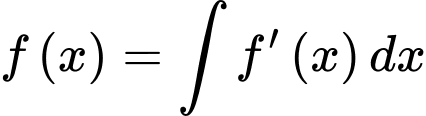
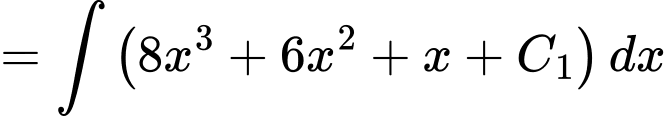
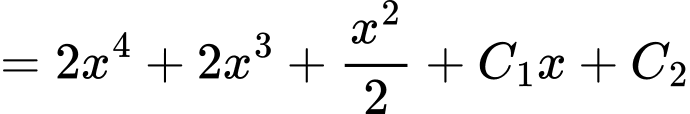
Theo giả thiết, ta có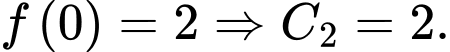
Suy ra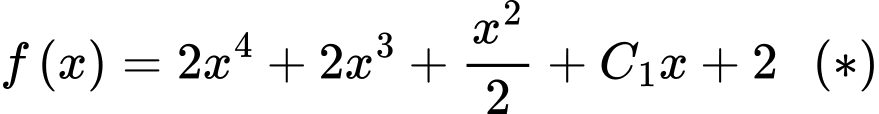
Lại có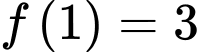 khi đó
khi đó 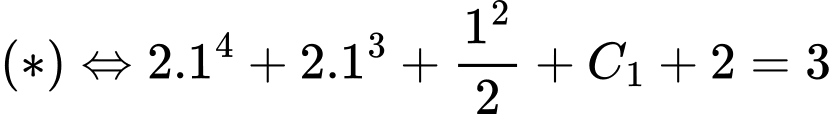
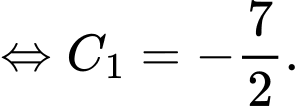
Vậy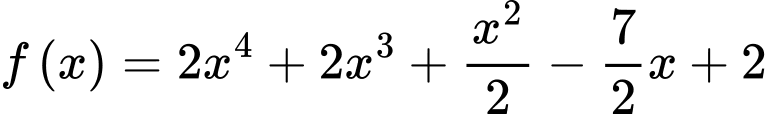
Suy ra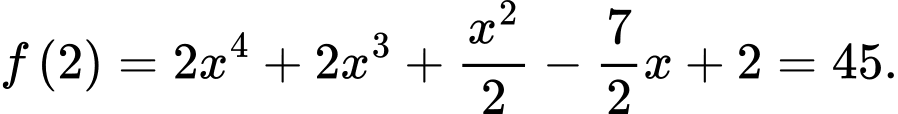
Ta có
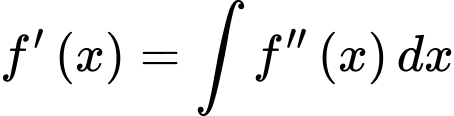
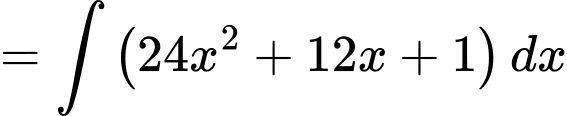
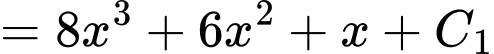
Suy ra
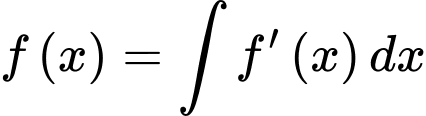
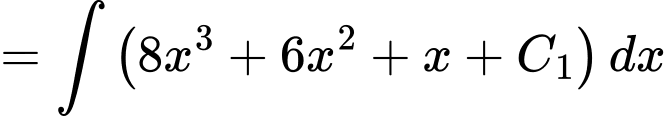
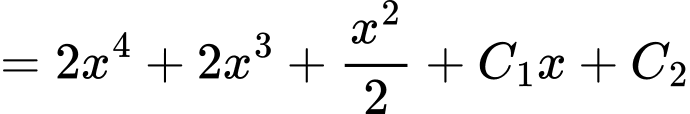
Theo giả thiết, ta có
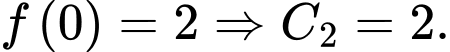
Suy ra
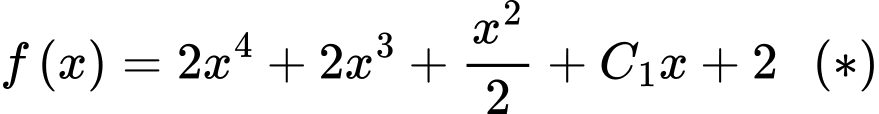
Lại có
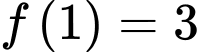 khi đó
khi đó 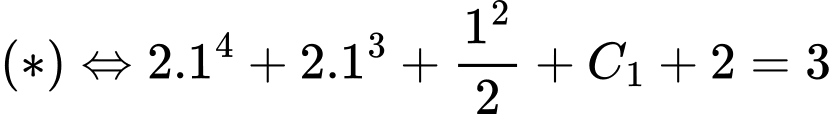
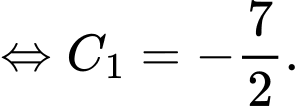
Vậy
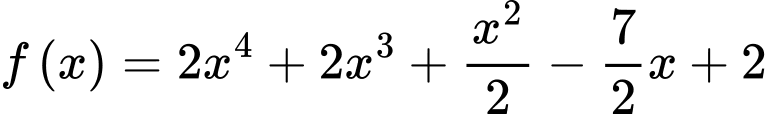
Suy ra
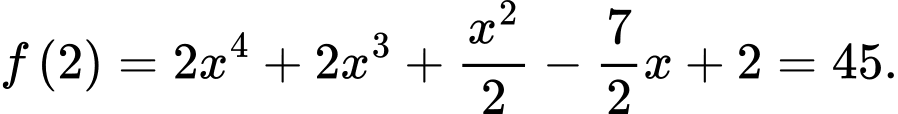
Câu 18 [775035]: Một đoàn tàu ban đầu đứng yên tại một nhà ga, sau đó nó bắt đầu tăng tốc với gia tốc 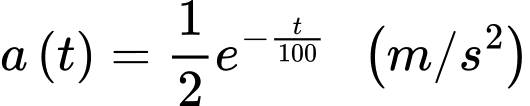 (trong đó
(trong đó 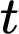 tính bằng giây, tính từ lúc tàu bắt đầu chuyển động). Hỏi sau 54 phút, tàu đi được bao nhiêu km (viết kết quả làm tròn đến hàng phần mười).
tính bằng giây, tính từ lúc tàu bắt đầu chuyển động). Hỏi sau 54 phút, tàu đi được bao nhiêu km (viết kết quả làm tròn đến hàng phần mười).

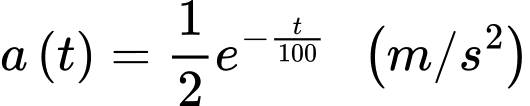 (trong đó
(trong đó 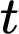 tính bằng giây, tính từ lúc tàu bắt đầu chuyển động). Hỏi sau 54 phút, tàu đi được bao nhiêu km (viết kết quả làm tròn đến hàng phần mười).
tính bằng giây, tính từ lúc tàu bắt đầu chuyển động). Hỏi sau 54 phút, tàu đi được bao nhiêu km (viết kết quả làm tròn đến hàng phần mười).
Điền đáp án: 157.
Kiến thức cần nhớ: Với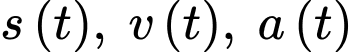 lần lượt là các hàm biểu thị quãng đường, vận tốc và gia tốc tại thời điểm
lần lượt là các hàm biểu thị quãng đường, vận tốc và gia tốc tại thời điểm 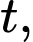 thì ta có
thì ta có 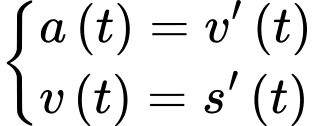
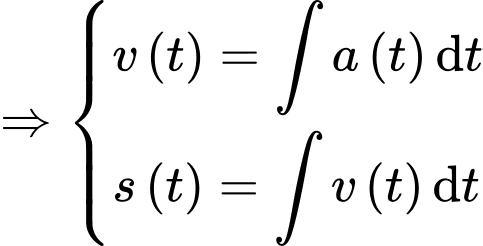
Dựa vào công thức trên, ta sẽ đi tính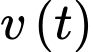 và từ đó ta sẽ tìm được
và từ đó ta sẽ tìm được 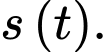
Ta có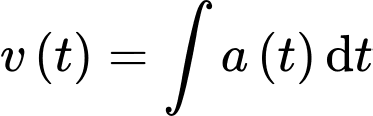
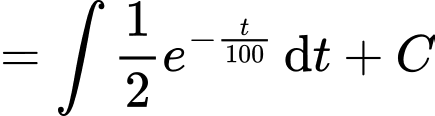
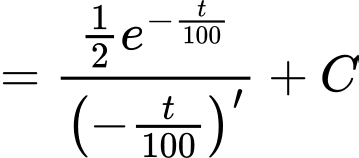
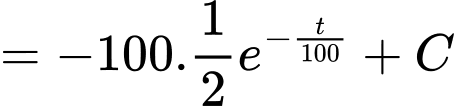
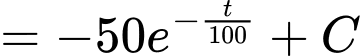
Vì đoàn tàu ban đầu là đứng yên, nên ta có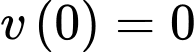
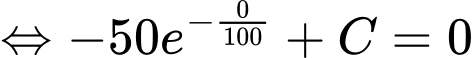

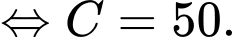
Suy ra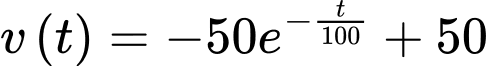
Quãng đường tàu đi được sau 54 phút (hay 3240 giây) bằng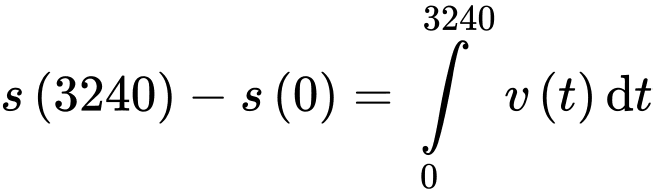
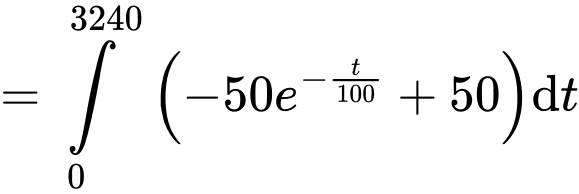
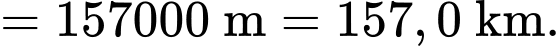
Kiến thức cần nhớ: Với
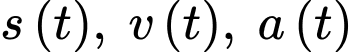 lần lượt là các hàm biểu thị quãng đường, vận tốc và gia tốc tại thời điểm
lần lượt là các hàm biểu thị quãng đường, vận tốc và gia tốc tại thời điểm 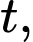 thì ta có
thì ta có 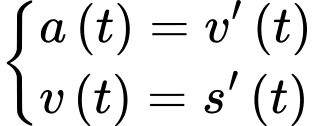
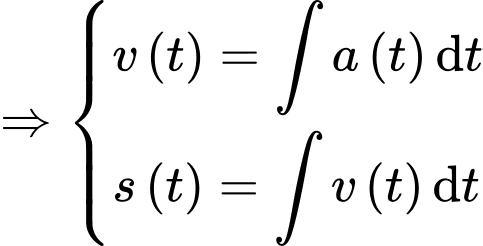
Dựa vào công thức trên, ta sẽ đi tính
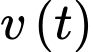 và từ đó ta sẽ tìm được
và từ đó ta sẽ tìm được 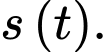
Ta có
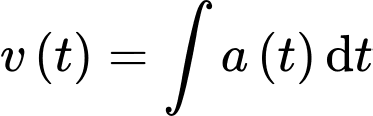
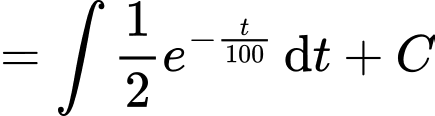
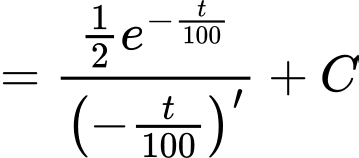
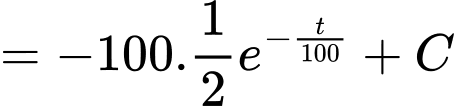
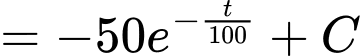
Vì đoàn tàu ban đầu là đứng yên, nên ta có
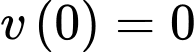
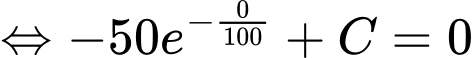

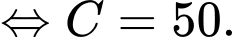
Suy ra
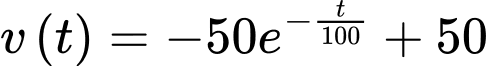
Quãng đường tàu đi được sau 54 phút (hay 3240 giây) bằng
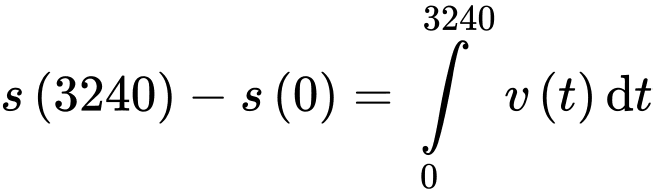
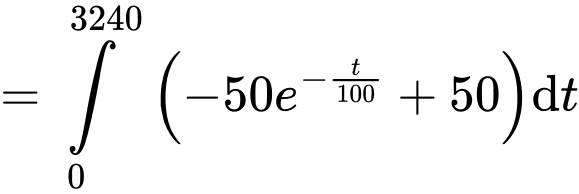
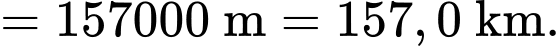
Câu 19 [779011]: Tốc độ giải ngân 2 tỷ tiền trợ cấp 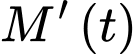 dành cho một vùng A bị thiệt hại về lũ lụt tỉ lệ thuận với bình phương của
dành cho một vùng A bị thiệt hại về lũ lụt tỉ lệ thuận với bình phương của 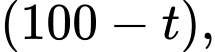 trong đó
trong đó 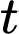 là thời gian tính bằng ngày
là thời gian tính bằng ngày 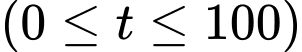 và
và 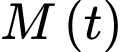 là số tiền còn lại chưa giải ngân. Tìm số tiền còn lại chưa giải ngân sau 40 ngày, biết rằng toàn bộ số tiền sẽ được giải ngân trong 100 ngày (đơn vị triệu đồng).
là số tiền còn lại chưa giải ngân. Tìm số tiền còn lại chưa giải ngân sau 40 ngày, biết rằng toàn bộ số tiền sẽ được giải ngân trong 100 ngày (đơn vị triệu đồng).
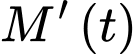 dành cho một vùng A bị thiệt hại về lũ lụt tỉ lệ thuận với bình phương của
dành cho một vùng A bị thiệt hại về lũ lụt tỉ lệ thuận với bình phương của 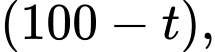 trong đó
trong đó 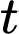 là thời gian tính bằng ngày
là thời gian tính bằng ngày 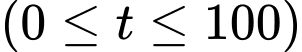 và
và 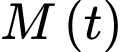 là số tiền còn lại chưa giải ngân. Tìm số tiền còn lại chưa giải ngân sau 40 ngày, biết rằng toàn bộ số tiền sẽ được giải ngân trong 100 ngày (đơn vị triệu đồng).
là số tiền còn lại chưa giải ngân. Tìm số tiền còn lại chưa giải ngân sau 40 ngày, biết rằng toàn bộ số tiền sẽ được giải ngân trong 100 ngày (đơn vị triệu đồng).
Điền đáp án 432.
Vì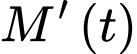 tỉ lệ thuận với bình phương của
tỉ lệ thuận với bình phương của 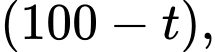 nên ta có
nên ta có 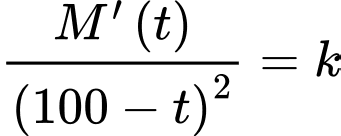
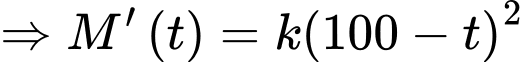
Theo công thức nguyên hàm, ta có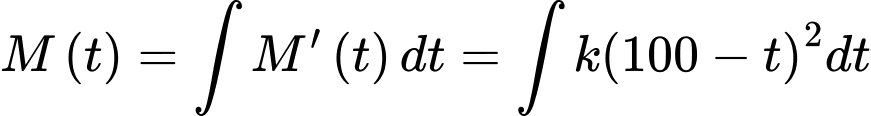
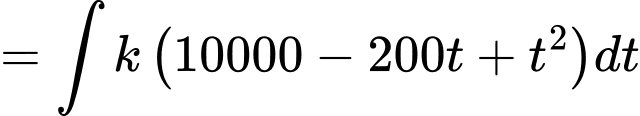
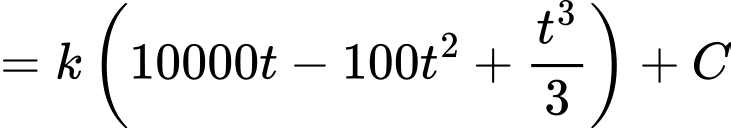
Từ giả thiết, ta có số tiền còn lại chưa giải ngân tại thời điểm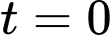 là bằng 2000 triệu đồng
là bằng 2000 triệu đồng 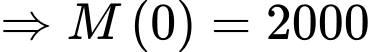
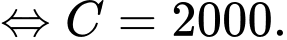
Khi đó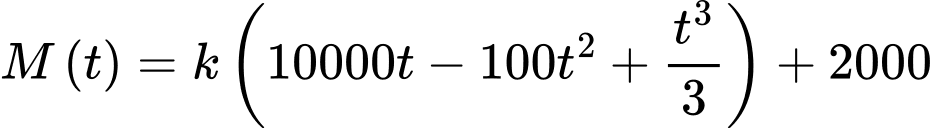
Vì toàn bộ số tiền sẽ được giải ngân trong 100 ngày nên ta có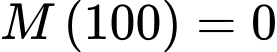
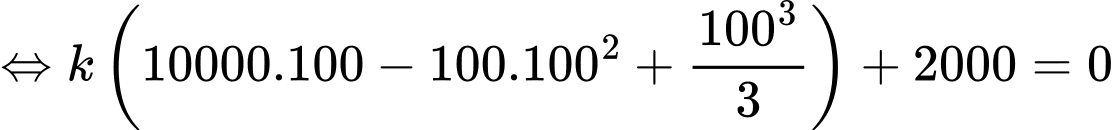
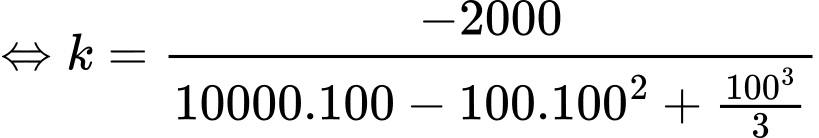
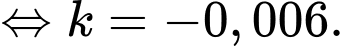
Suy ra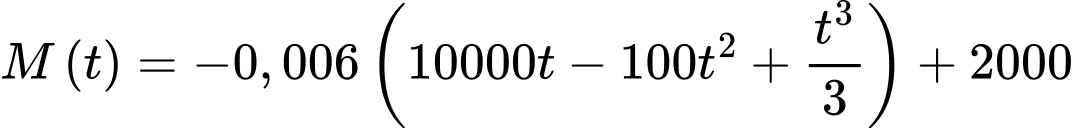
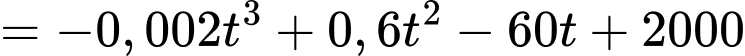
Vậy số tiền còn lại chưa giải ngân sau 40 ngày là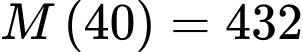 (triệu đồng)
(triệu đồng)
Vì
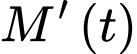 tỉ lệ thuận với bình phương của
tỉ lệ thuận với bình phương của 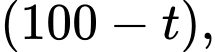 nên ta có
nên ta có 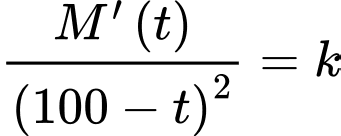
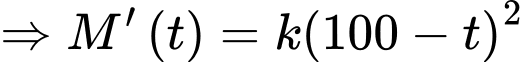
Theo công thức nguyên hàm, ta có
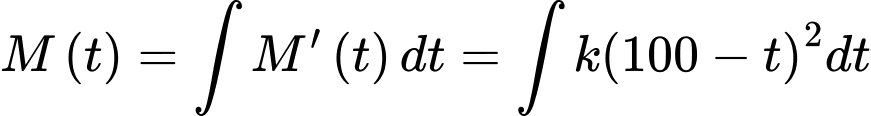
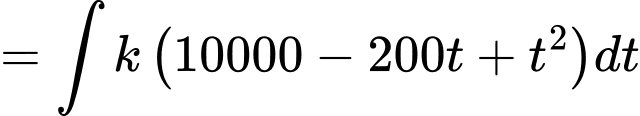
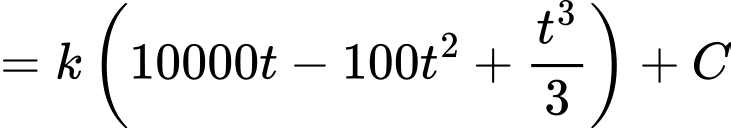
Từ giả thiết, ta có số tiền còn lại chưa giải ngân tại thời điểm
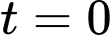 là bằng 2000 triệu đồng
là bằng 2000 triệu đồng 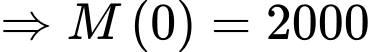
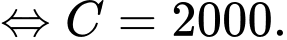
Khi đó
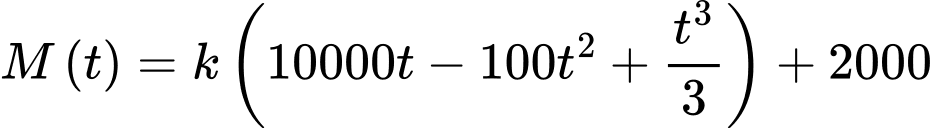
Vì toàn bộ số tiền sẽ được giải ngân trong 100 ngày nên ta có
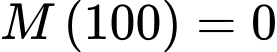
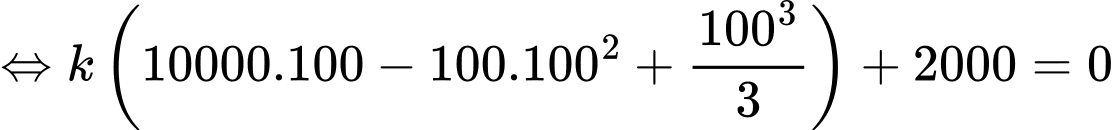
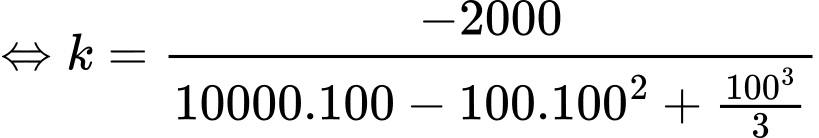
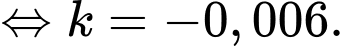
Suy ra
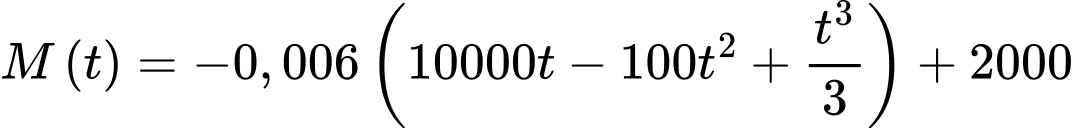
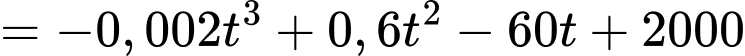
Vậy số tiền còn lại chưa giải ngân sau 40 ngày là
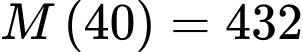 (triệu đồng)
(triệu đồng)
Câu 20 [775037]: Mặt cắt ngang của một ống dẫn nước nóng là hình vành khuyên như hình vẽ. Nước bên trong ống được duy trì ở 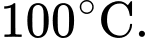 Biết rằng nhiệt độ
Biết rằng nhiệt độ 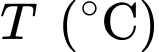 tại điểm
tại điểm 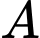 trên thành ống là hàm số của khoảng cách
trên thành ống là hàm số của khoảng cách  từ
từ 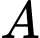 đến tâm của mặt cắt và
đến tâm của mặt cắt và 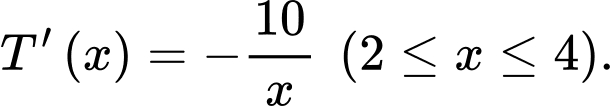 Tìm nhiệt độ mặt ngoài của ống. Viết kết quả làm tròn đến hàng phần chục của
Tìm nhiệt độ mặt ngoài của ống. Viết kết quả làm tròn đến hàng phần chục của 
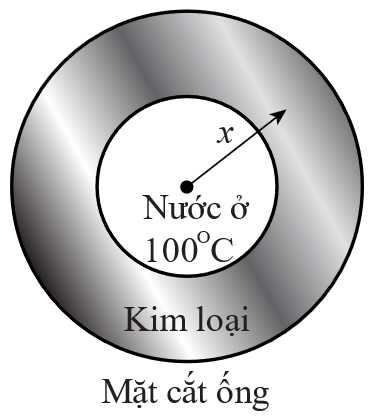
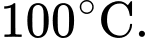 Biết rằng nhiệt độ
Biết rằng nhiệt độ 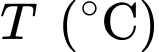 tại điểm
tại điểm 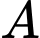 trên thành ống là hàm số của khoảng cách
trên thành ống là hàm số của khoảng cách  từ
từ 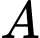 đến tâm của mặt cắt và
đến tâm của mặt cắt và 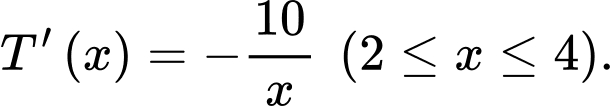 Tìm nhiệt độ mặt ngoài của ống. Viết kết quả làm tròn đến hàng phần chục của
Tìm nhiệt độ mặt ngoài của ống. Viết kết quả làm tròn đến hàng phần chục của 

Điền đáp án: 93,1.
Theo định nghĩa nguyên hàm, ta có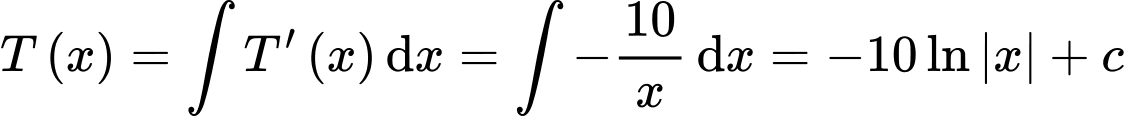
Vì ống có độ dày 2 cm, nên tại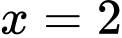 là phần thành ống bên trong (tiếp xúc trực tiếp với nước nóng) nên sẽ có nhiệt độ là
là phần thành ống bên trong (tiếp xúc trực tiếp với nước nóng) nên sẽ có nhiệt độ là 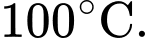 Còn tại
Còn tại  là mặt ngoài của ống. Do đó, yêu cầu bài toán
là mặt ngoài của ống. Do đó, yêu cầu bài toán  Tính
Tính 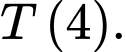

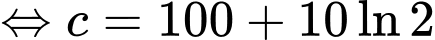
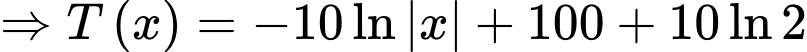
Vậy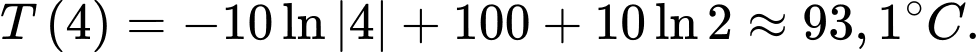
Theo định nghĩa nguyên hàm, ta có
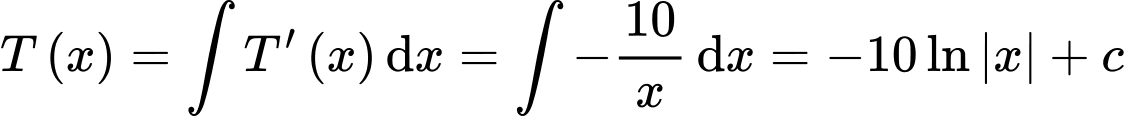
Vì ống có độ dày 2 cm, nên tại
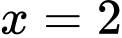 là phần thành ống bên trong (tiếp xúc trực tiếp với nước nóng) nên sẽ có nhiệt độ là
là phần thành ống bên trong (tiếp xúc trực tiếp với nước nóng) nên sẽ có nhiệt độ là 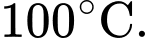 Còn tại
Còn tại  là mặt ngoài của ống. Do đó, yêu cầu bài toán
là mặt ngoài của ống. Do đó, yêu cầu bài toán  Tính
Tính 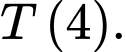

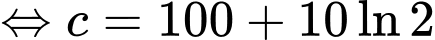
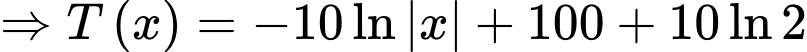
Vậy
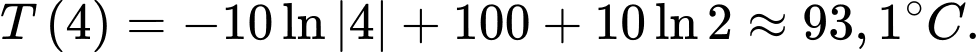
Câu 21 [775045]: Một trang trại nuôi cá hồi có số lượng cá ban đầu là 100 con. Sau 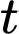 (năm) số lượng cá là
(năm) số lượng cá là 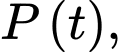 số lượng cá tăng theo tốc độ
số lượng cá tăng theo tốc độ 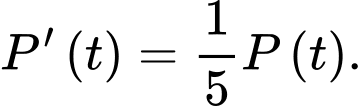 Dựa vào mô hình trên, hay tính số lượng cá hồi sau 10 năm (viết kết quả làm tròn đến hàng đơn vị).
Dựa vào mô hình trên, hay tính số lượng cá hồi sau 10 năm (viết kết quả làm tròn đến hàng đơn vị).
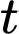 (năm) số lượng cá là
(năm) số lượng cá là 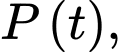 số lượng cá tăng theo tốc độ
số lượng cá tăng theo tốc độ 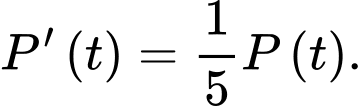 Dựa vào mô hình trên, hay tính số lượng cá hồi sau 10 năm (viết kết quả làm tròn đến hàng đơn vị).
Dựa vào mô hình trên, hay tính số lượng cá hồi sau 10 năm (viết kết quả làm tròn đến hàng đơn vị).
Điền đáp án: 739.
Ta có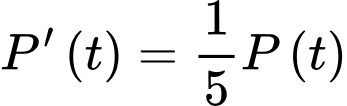
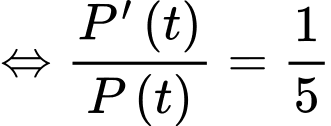 (chia cả hai vế cho
(chia cả hai vế cho 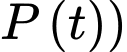
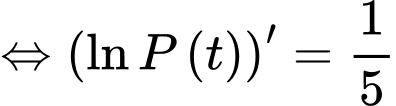
Nguyên hàm 2 vế, ta được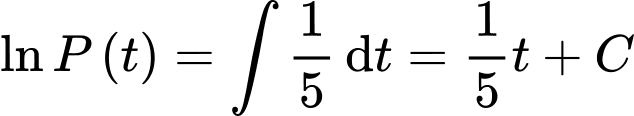
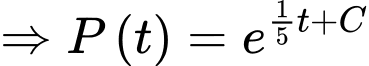
Ta có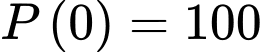
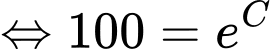
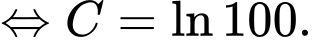
Suy ra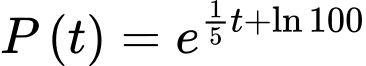
Vậy số lượng cá hồi sau 10 năm là x con. .
Ta có
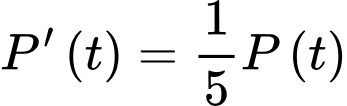
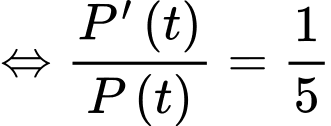 (chia cả hai vế cho
(chia cả hai vế cho 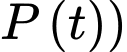
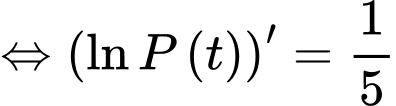
Nguyên hàm 2 vế, ta được
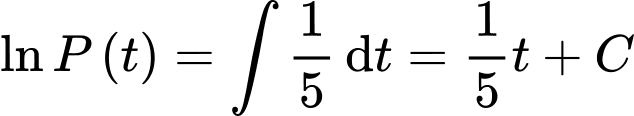
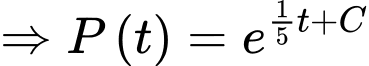
Ta có
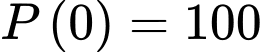
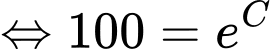
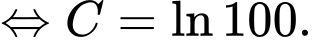
Suy ra
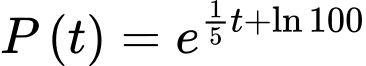
Vậy số lượng cá hồi sau 10 năm là x con. .
Câu 22 [775047]: Etylen oxit phản ứng với nước dư khi có mặt chất xúc tác là axit sunfuric để tạo thành etylen glycol. Giả sử 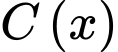 là nồng độ chất etylen oxit còn lại (đơn vị mol/lít) tại thời điểm
là nồng độ chất etylen oxit còn lại (đơn vị mol/lít) tại thời điểm 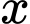 (phút),
(phút), 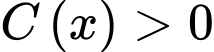 với
với 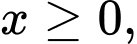 thỏa mãn hệ thức
thỏa mãn hệ thức 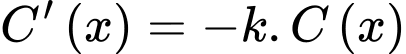 , trong đó
, trong đó 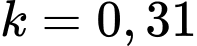 là hằng số chỉ tốc độ phản ứng. Biết nồng độ ban đầu của etilen oxit là 1 mol/lít. Hỏi cần bao nhiêu phút để phản ứng hết 80% etilen oxit (viết kết quả làm tròn đến hàng phần trăm).
là hằng số chỉ tốc độ phản ứng. Biết nồng độ ban đầu của etilen oxit là 1 mol/lít. Hỏi cần bao nhiêu phút để phản ứng hết 80% etilen oxit (viết kết quả làm tròn đến hàng phần trăm).
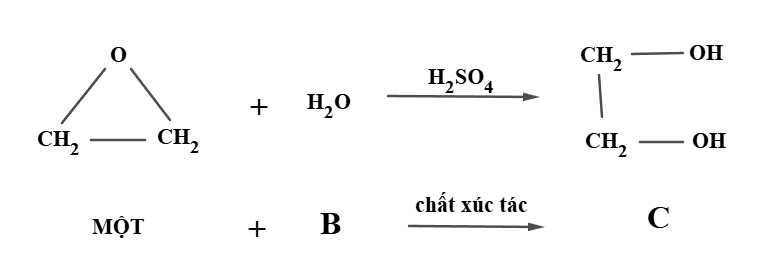
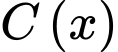 là nồng độ chất etylen oxit còn lại (đơn vị mol/lít) tại thời điểm
là nồng độ chất etylen oxit còn lại (đơn vị mol/lít) tại thời điểm 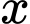 (phút),
(phút), 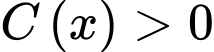 với
với 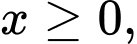 thỏa mãn hệ thức
thỏa mãn hệ thức 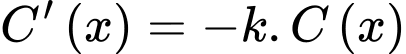 , trong đó
, trong đó 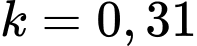 là hằng số chỉ tốc độ phản ứng. Biết nồng độ ban đầu của etilen oxit là 1 mol/lít. Hỏi cần bao nhiêu phút để phản ứng hết 80% etilen oxit (viết kết quả làm tròn đến hàng phần trăm).
là hằng số chỉ tốc độ phản ứng. Biết nồng độ ban đầu của etilen oxit là 1 mol/lít. Hỏi cần bao nhiêu phút để phản ứng hết 80% etilen oxit (viết kết quả làm tròn đến hàng phần trăm).
Điền đáp án: 5,19.
Do nồng độ ban đầu của etilen oxit là 1 mol/lít nên khi phản ứng hết 80% etilen oxit thì nồng độ còn lại sẽ bằng 0,2 mol/lít. Do đó, yêu cầu bài toán là tìm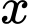 (phút) để
(phút) để 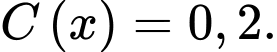
Ta có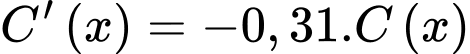
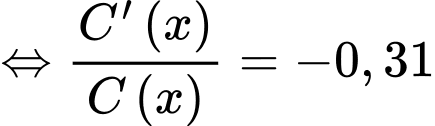 (chia cả hai vế cho
(chia cả hai vế cho 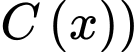
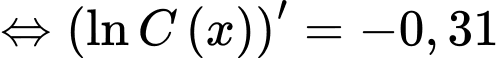
Nguyên hàm 2 vế, ta được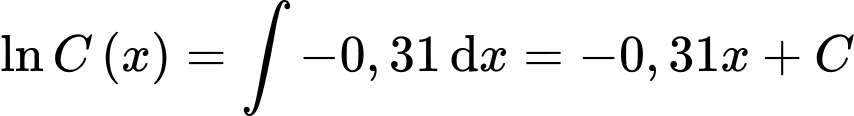
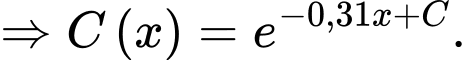
Vì nồng độ ban đầu của etilen oxit là 1 mol/lít nên ta có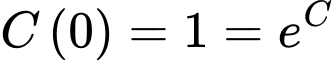
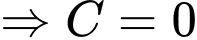
Suy ra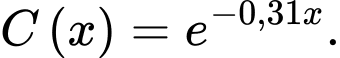
Suy ra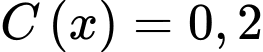
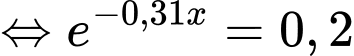
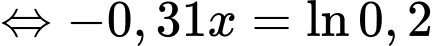
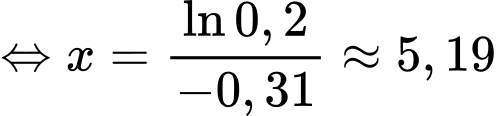
Vậy cần 5,19 phút để phản ứng hết 80% etilen oxit.
Do nồng độ ban đầu của etilen oxit là 1 mol/lít nên khi phản ứng hết 80% etilen oxit thì nồng độ còn lại sẽ bằng 0,2 mol/lít. Do đó, yêu cầu bài toán là tìm
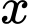 (phút) để
(phút) để 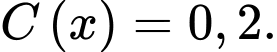
Ta có
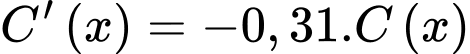
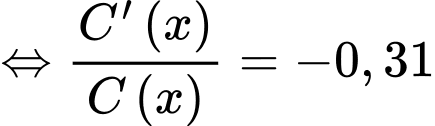 (chia cả hai vế cho
(chia cả hai vế cho 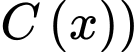
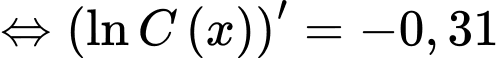
Nguyên hàm 2 vế, ta được
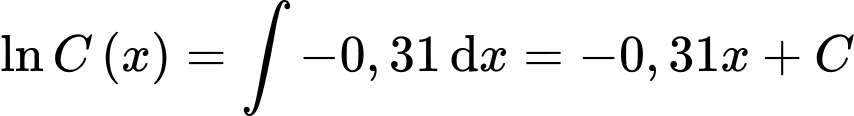
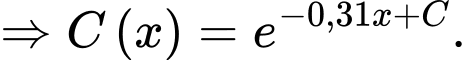
Vì nồng độ ban đầu của etilen oxit là 1 mol/lít nên ta có
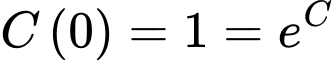
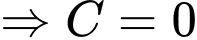
Suy ra
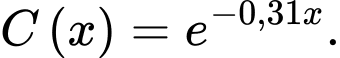
Suy ra
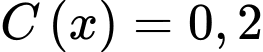
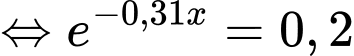
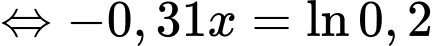
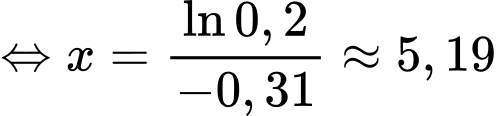
Vậy cần 5,19 phút để phản ứng hết 80% etilen oxit.