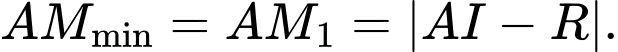PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1 [755166]: Trong không gian  , tâm của mặt cầu
, tâm của mặt cầu 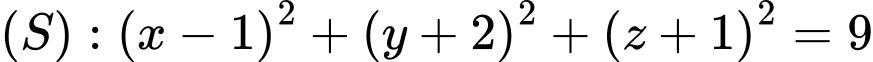 có tọa độ là
có tọa độ là
 , tâm của mặt cầu
, tâm của mặt cầu 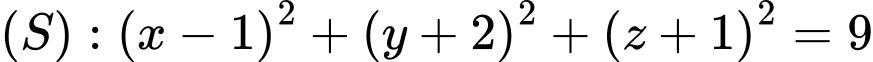 có tọa độ là
có tọa độ là A,
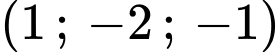 .
.
B,
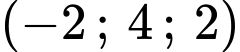 .
.
C,
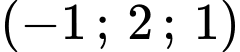 .
.
D,
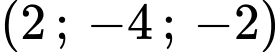 .
.
Chọn A .
Tâm của mặt cầu 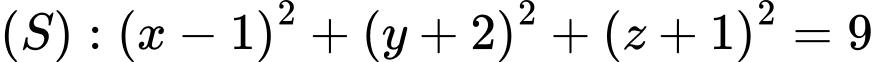 có tọa độ là
có tọa độ là 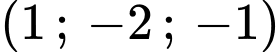 .
.
Câu 2 [755443]: Trong không gian với hệ tọa độ 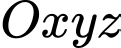 cho mặt cầu
cho mặt cầu 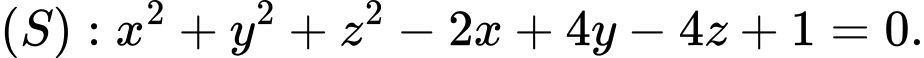 Bán kính của mặt cầu
Bán kính của mặt cầu 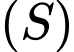 bằng:
bằng:
 cho mặt cầu
cho mặt cầu 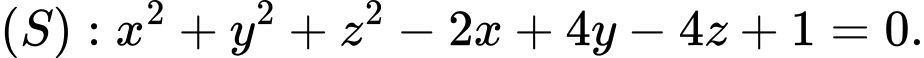 Bán kính của mặt cầu
Bán kính của mặt cầu 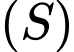 bằng:
bằng: A, 
B, 
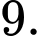
C, 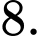
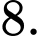
D, 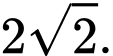
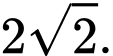
Ta viết lại phương trình mặt cầu dưới dạng 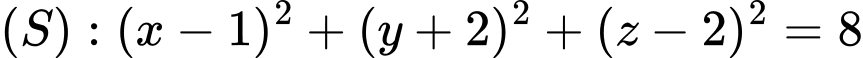
Do đó bán kính mặt cầu là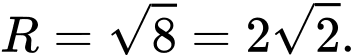 Đáp án: D
Đáp án: D
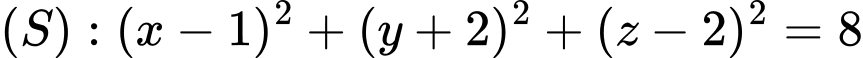
Do đó bán kính mặt cầu là
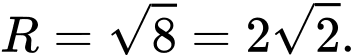 Đáp án: D
Đáp án: D
Câu 3 [395558]: Trong không gian 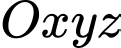 , cho mặt cầu
, cho mặt cầu 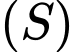 có tâm
có tâm 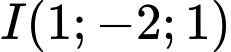 và bán kính
và bán kính  Phương trình của
Phương trình của 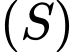 là
là
 , cho mặt cầu
, cho mặt cầu 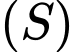 có tâm
có tâm 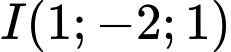 và bán kính
và bán kính  Phương trình của
Phương trình của  là
là A, 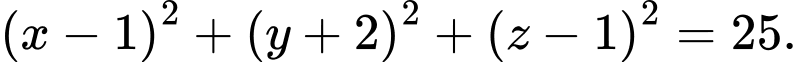
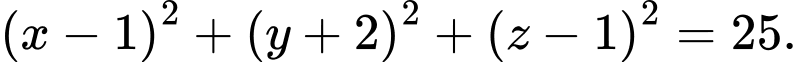
B, 
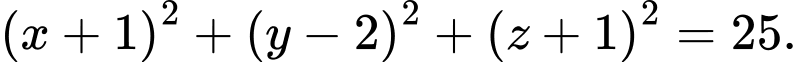
C, 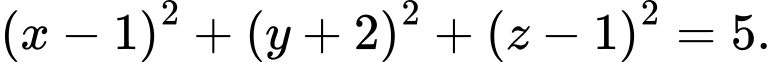
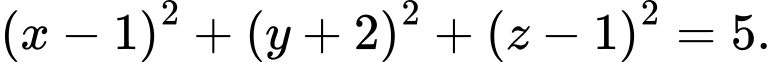
D, 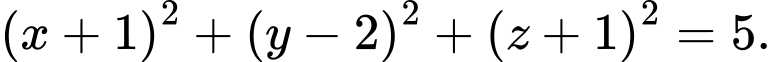
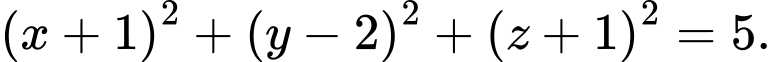
Chọn A
Phương trình mặt cầu tâm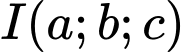 và bán kính
và bán kính  là:
là:
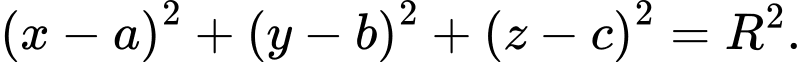
Do đó phương trình mặt cầu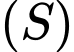 là:
là: 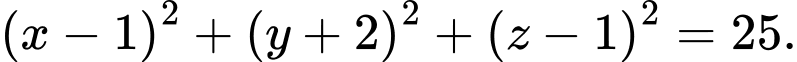 Đáp án: A
Đáp án: A
Phương trình mặt cầu tâm
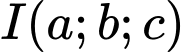 và bán kính
và bán kính  là:
là: 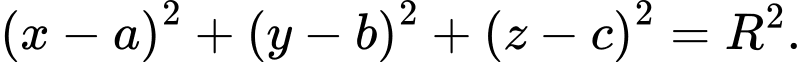
Do đó phương trình mặt cầu
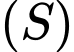 là:
là: 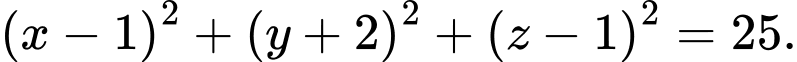 Đáp án: A
Đáp án: A
Câu 4 [543814]: Trong không gian  , mặt cầu có tâm
, mặt cầu có tâm  và đi qua điểm
và đi qua điểm 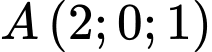 có phương trình là
có phương trình là
 , mặt cầu có tâm
, mặt cầu có tâm  và đi qua điểm
và đi qua điểm 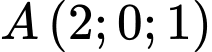 có phương trình là
có phương trình là A, 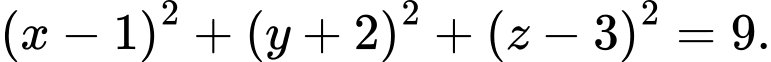
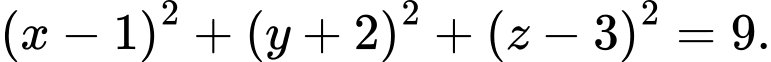
B, 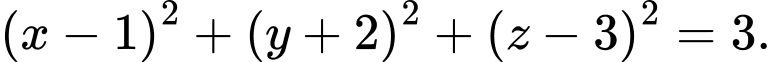
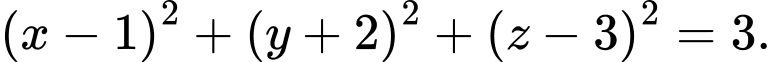
C, 

D, 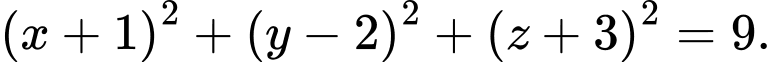
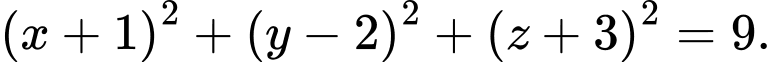
Mặt cầu có tâm  và đi qua điểm
và đi qua điểm 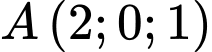 .
.
 Bán kính
Bán kính 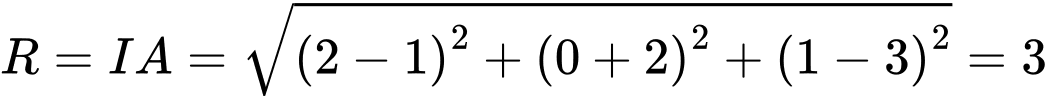 .
.
 Phương trình mặt cầu là:
Phương trình mặt cầu là: 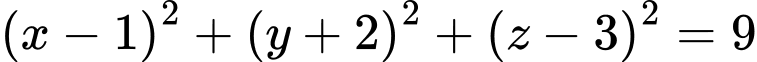 .
Đáp án: A
.
Đáp án: A
 và đi qua điểm
và đi qua điểm 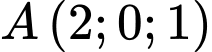 .
.
 Bán kính
Bán kính 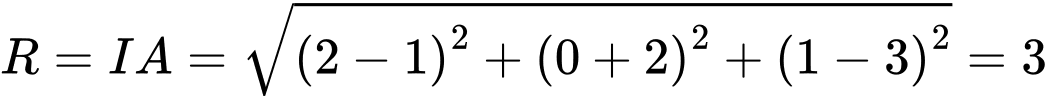 .
.
 Phương trình mặt cầu là:
Phương trình mặt cầu là: 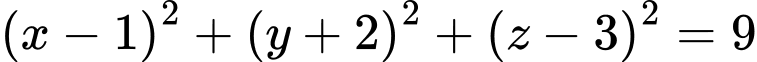 .
Đáp án: A
.
Đáp án: A
Câu 5 [543229]: Trong không gian 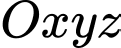 , phương trình mặt cầu tâm
, phương trình mặt cầu tâm 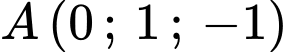 và đi qua điểm
và đi qua điểm 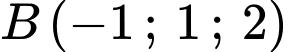 là
là
 , phương trình mặt cầu tâm
, phương trình mặt cầu tâm 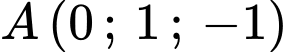 và đi qua điểm
và đi qua điểm 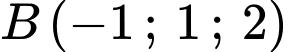 là
là A, 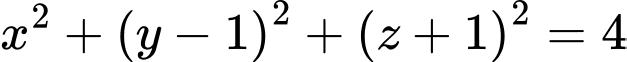 .
.
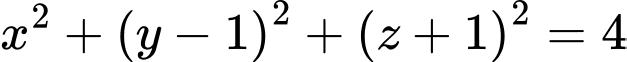 .
. B,  .
.
 .
. C, 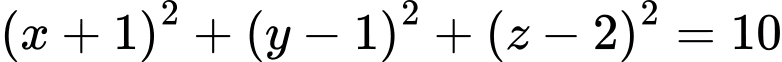 .
.
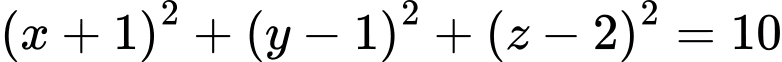 .
.D,  .
.
 .
.
Ta có 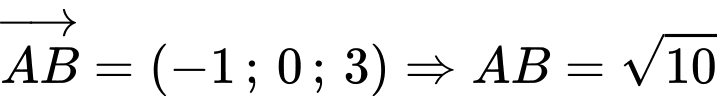 .
Gọi
.
Gọi 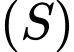 là mặt cầu tâm
là mặt cầu tâm 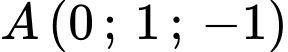 và có bán kính
và có bán kính 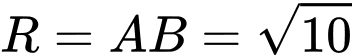
 Phương trình
Phương trình 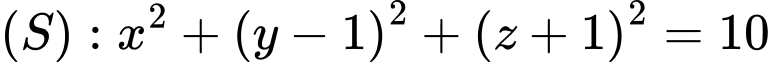 . Đáp án: D
. Đáp án: D
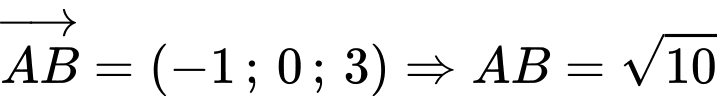 .
Gọi
.
Gọi 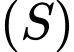 là mặt cầu tâm
là mặt cầu tâm 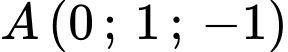 và có bán kính
và có bán kính 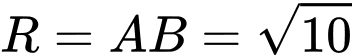
 Phương trình
Phương trình 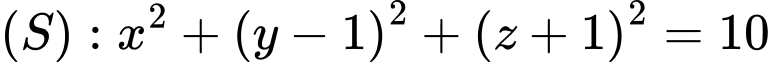 . Đáp án: D
. Đáp án: D
Câu 6 [544720]: Trong không gian 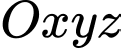 , cho mặt cầu
, cho mặt cầu 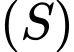 có phương trình
có phương trình 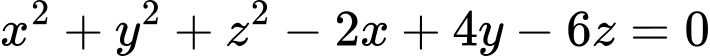 . Tìm tọa độ tâm
. Tìm tọa độ tâm 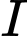 và bán kính
và bán kính 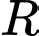 .
.
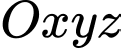 , cho mặt cầu
, cho mặt cầu 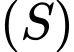 có phương trình
có phương trình 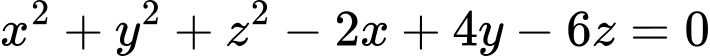 . Tìm tọa độ tâm
. Tìm tọa độ tâm 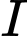 và bán kính
và bán kính 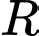 .
. A, 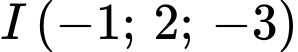 và
và 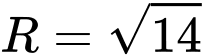 .
.
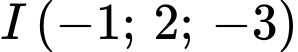 và
và 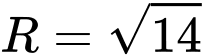 .
. B, 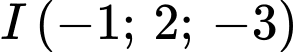 và
và 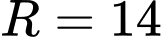 .
.
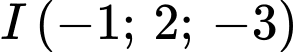 và
và 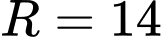 .
.C, 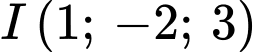 và
và 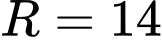 .
.
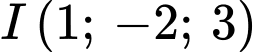 và
và 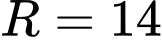 .
.D, 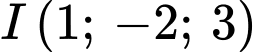 và
và 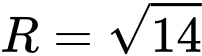 .
.
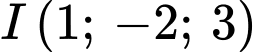 và
và 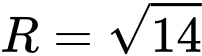 .
.
Chọn D.
Mặt cầu có phương trình
có phương trình 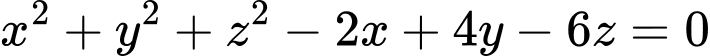 .
.
Tìm tọa độ tâm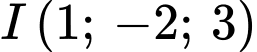 và
và 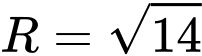 . Đáp án: D
. Đáp án: D
Mặt cầu
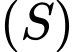 có phương trình
có phương trình 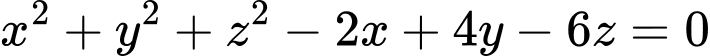 .
.
Tìm tọa độ tâm
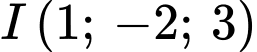 và
và 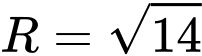 . Đáp án: D
. Đáp án: D
Câu 7 [542960]: Trong mặt phẳng 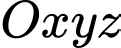 , phương trình nào sau đây không phải là phương trình của một mặt cầu ?
, phương trình nào sau đây không phải là phương trình của một mặt cầu ?
 , phương trình nào sau đây không phải là phương trình của một mặt cầu ?
, phương trình nào sau đây không phải là phương trình của một mặt cầu ? A, 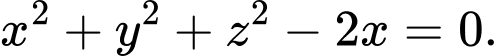
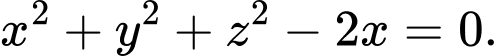
B, 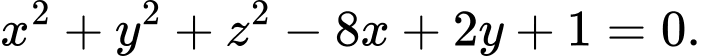
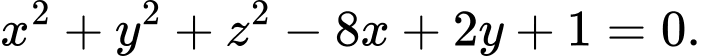
C, 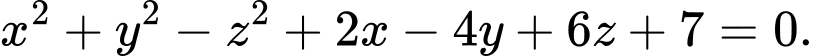
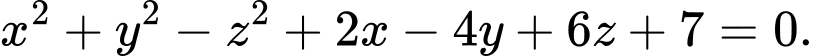
D, 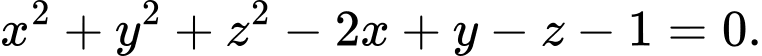
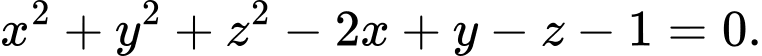
Chọn C
Ta có phương trình mặt cầu có dạng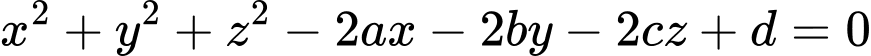 , với điều kiện
, với điều kiện 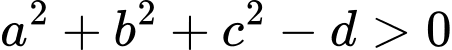 nên chọn đáp án C Đáp án: C
nên chọn đáp án C Đáp án: C
Ta có phương trình mặt cầu có dạng
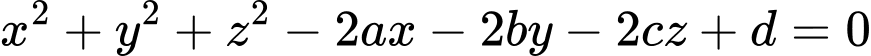 , với điều kiện
, với điều kiện 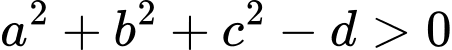 nên chọn đáp án C Đáp án: C
nên chọn đáp án C Đáp án: C
Câu 8 [755199]: Trong không gian 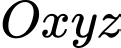 , cho hai điểm
, cho hai điểm 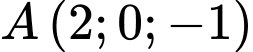 và
và 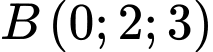 . Mặt cầu
. Mặt cầu 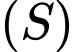 đường kính
đường kính  có phương trình là
có phương trình là
 , cho hai điểm
, cho hai điểm 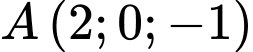 và
và 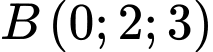 . Mặt cầu
. Mặt cầu 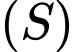 đường kính
đường kính  có phương trình là
có phương trình là A, 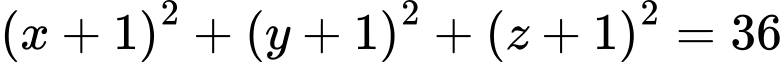 .
.
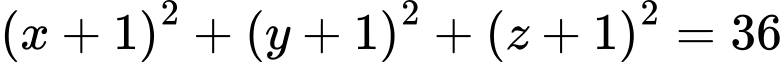 .
.B, 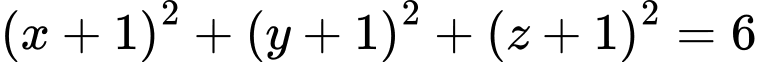
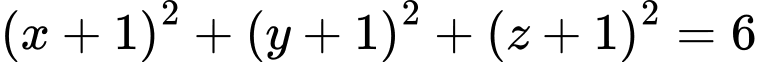
C, 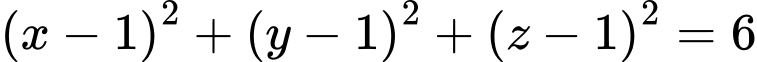 .
.
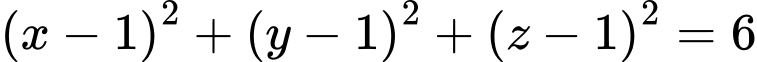 .
.D, 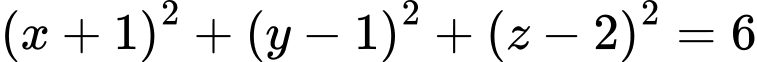 .
.
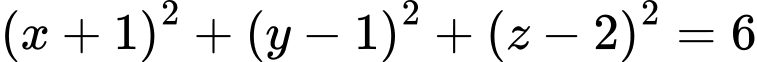 .
.
Chọn C.
Tâm mặt cầu là trung điểm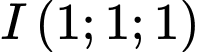 của đoạn
của đoạn  .
.
Bán kính mặt cầu là .
.
Vậy phương trình mặt cầu là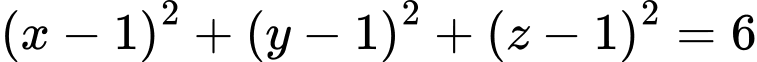 . Đáp án: C
. Đáp án: C
Tâm mặt cầu là trung điểm
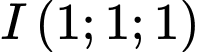 của đoạn
của đoạn  .
.
Bán kính mặt cầu là
 .
.
Vậy phương trình mặt cầu là
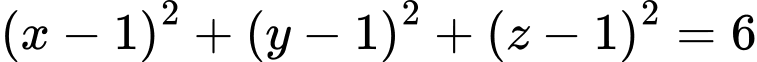 . Đáp án: C
. Đáp án: C
Câu 9 [399917]: Trong không gian 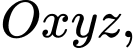 mặt cầu có tâm
mặt cầu có tâm 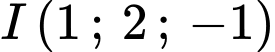 và tiếp xúc với mặt phẳng
và tiếp xúc với mặt phẳng 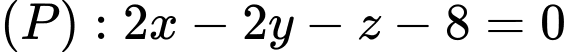 có phương trình là
có phương trình là
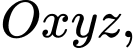 mặt cầu có tâm
mặt cầu có tâm 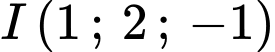 và tiếp xúc với mặt phẳng
và tiếp xúc với mặt phẳng 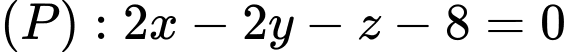 có phương trình là
có phương trình là A, 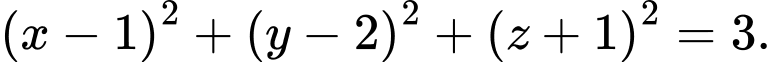
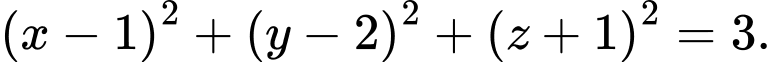
B, 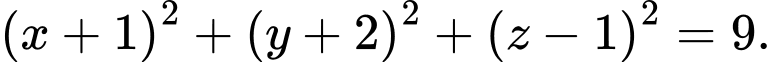
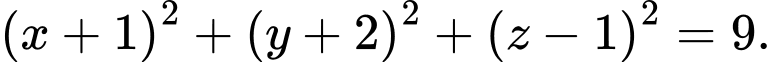
C, 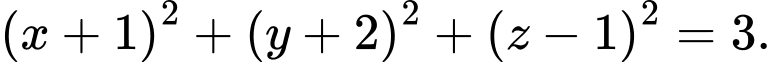
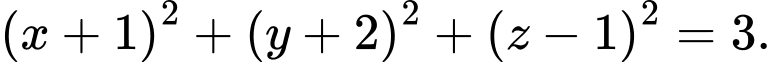
D, 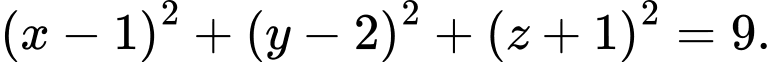
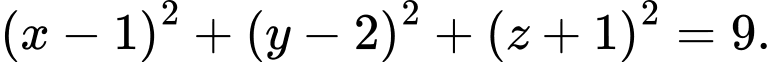
Chọn D.
Có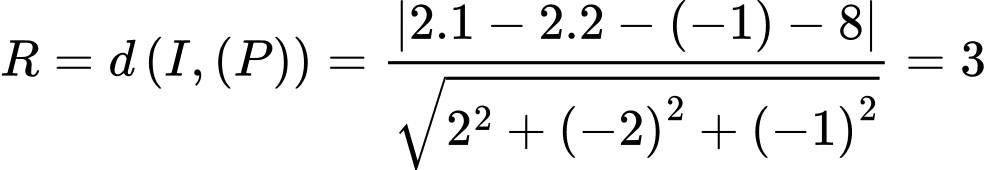
suy ra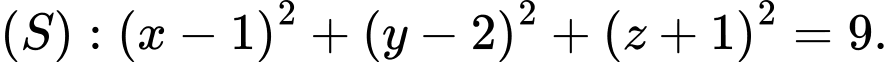 Đáp án: D
Đáp án: D
Có
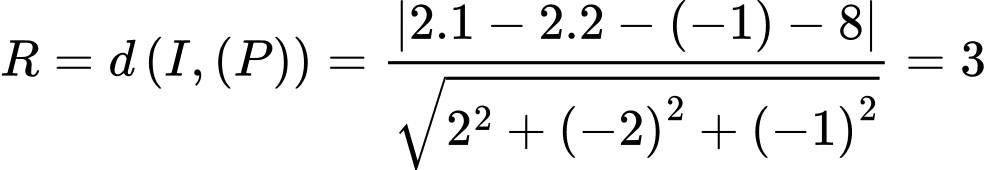
suy ra
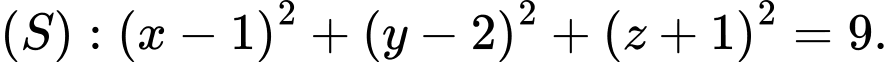 Đáp án: D
Đáp án: D
Câu 10 [57455]: Trong không gian với hệ tọa độ  mặt cầu
mặt cầu 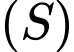 đi qua hai điểm
đi qua hai điểm 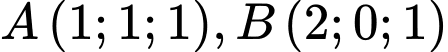 và có tâm
và có tâm 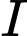 thuộc trục
thuộc trục 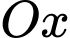 . phương trình mặt cầu
. phương trình mặt cầu 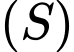 là
là
 mặt cầu
mặt cầu 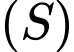 đi qua hai điểm
đi qua hai điểm 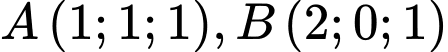 và có tâm
và có tâm 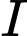 thuộc trục
thuộc trục 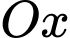 . phương trình mặt cầu
. phương trình mặt cầu 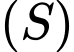 là
là A, 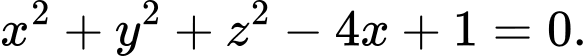
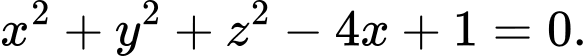
B, 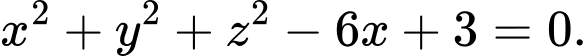
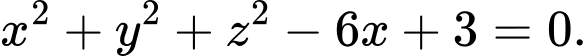
C, 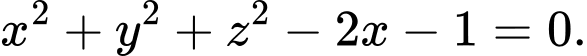
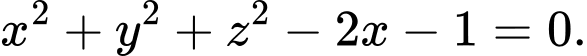
D, 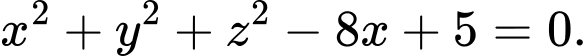
Chọn đáp án C.

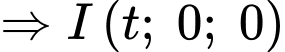
Suy ra phương trình mặt cầu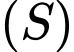 có dạng
có dạng 
Vì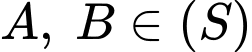 nên ta có hệ phương trình
nên ta có hệ phương trình 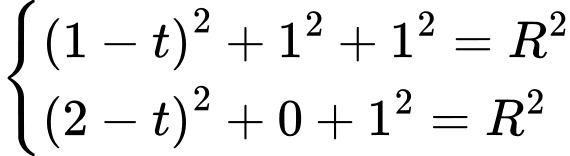
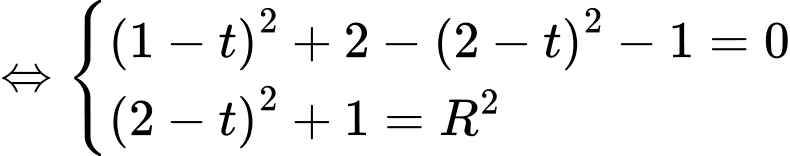
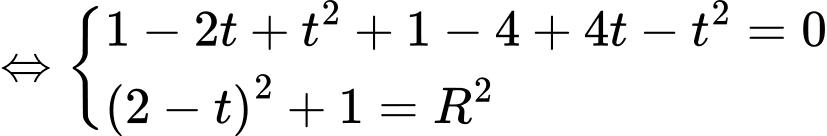
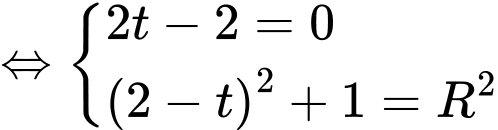
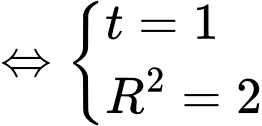
Vậy phương trình mặt cầu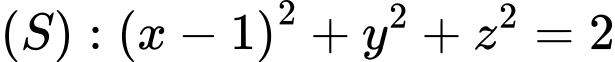
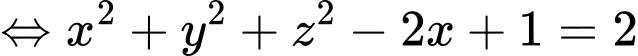
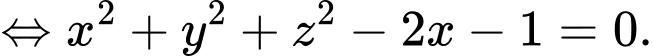 Đáp án: C
Đáp án: C

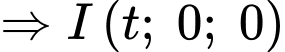
Suy ra phương trình mặt cầu
 có dạng
có dạng 
Vì
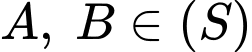 nên ta có hệ phương trình
nên ta có hệ phương trình 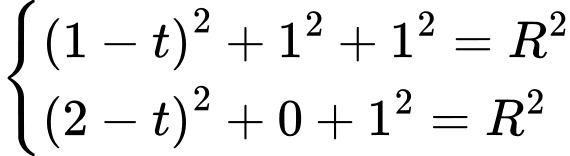
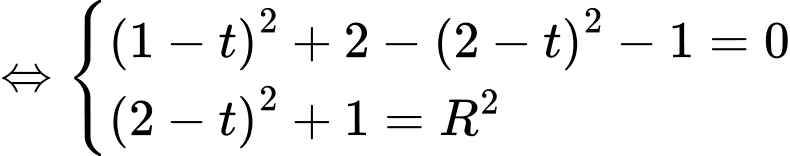
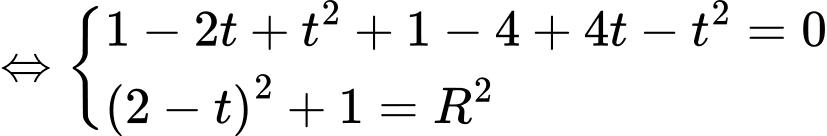
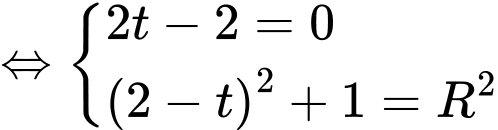
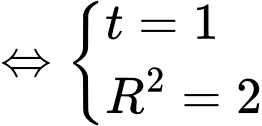
Vậy phương trình mặt cầu
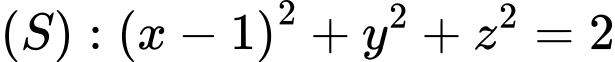
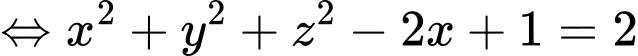
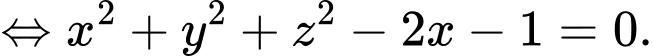 Đáp án: C
Đáp án: C
Câu 11 [544704]: Cho mặt phẳng 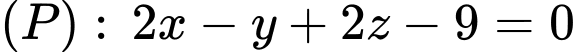 . Viết phương trình mặt cầu
. Viết phương trình mặt cầu 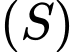 tâm
tâm  cắt
cắt 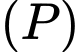 theo giao tuyến là đường tròn có bán kính bằng
theo giao tuyến là đường tròn có bán kính bằng 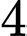 .
.
 . Viết phương trình mặt cầu
. Viết phương trình mặt cầu 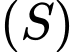 tâm
tâm  cắt
cắt 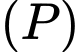 theo giao tuyến là đường tròn có bán kính bằng
theo giao tuyến là đường tròn có bán kính bằng 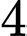 .
. A, 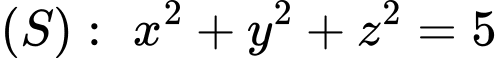 .
.
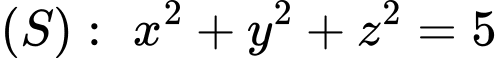 .
.B, 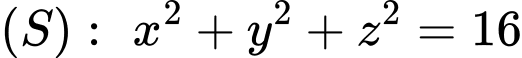 .
.
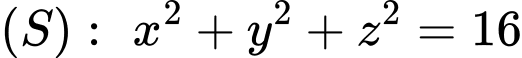 .
.C, 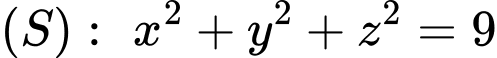 .
.
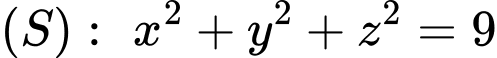 .
.D, 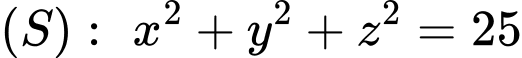 .
.
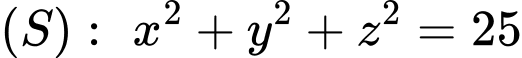 .
.
Chọn D.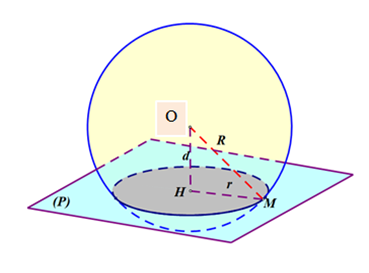
Ta có: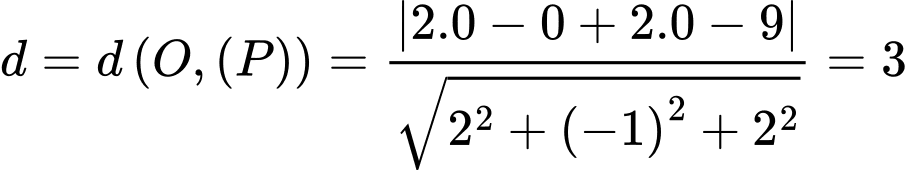 .
.
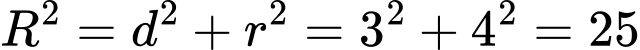 .
.
Vậy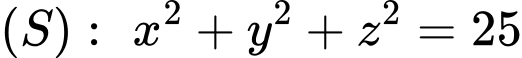 . Đáp án: D
. Đáp án: D

Ta có:
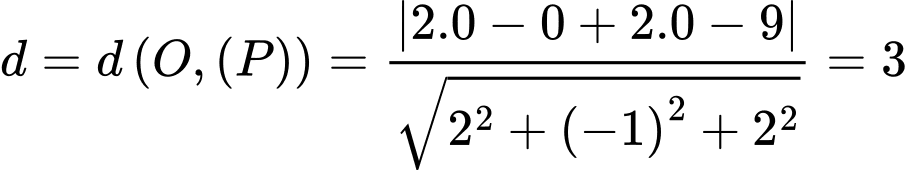 .
.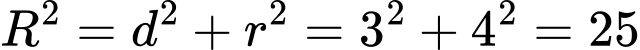 .
. Vậy
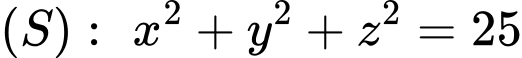 . Đáp án: D
. Đáp án: D
Câu 12 [399929]: Trong không gian 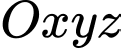 , cho điểm
, cho điểm 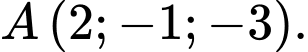 Mặt cầu có tâm thuộc trục
Mặt cầu có tâm thuộc trục 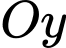 , đi qua
, đi qua 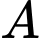 đồng thời tiếp xúc với mặt phẳng
đồng thời tiếp xúc với mặt phẳng 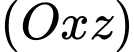 có bán kính là
có bán kính là
 , cho điểm
, cho điểm 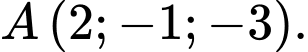 Mặt cầu có tâm thuộc trục
Mặt cầu có tâm thuộc trục 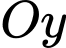 , đi qua
, đi qua 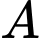 đồng thời tiếp xúc với mặt phẳng
đồng thời tiếp xúc với mặt phẳng 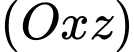 có bán kính là
có bán kính là A, 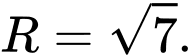
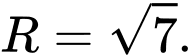
B, 

C, 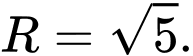
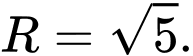
D, 

Chọn B
Gọi tâm của mặt cầu là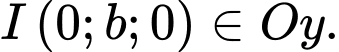
Vì mặt cầu đi qua điểm nên
nên 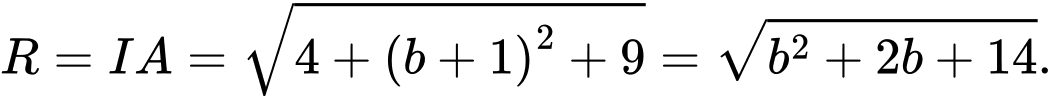
Vì mặt cầu tiếp xúc với mặt phẳng nên
nên 
Do đó,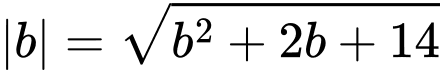
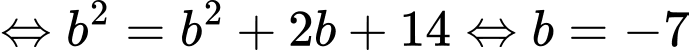
Vậy bán kính của mặt cầu là Đáp án: B
Đáp án: B
Gọi tâm của mặt cầu là
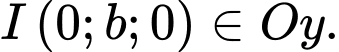
Vì mặt cầu đi qua điểm
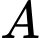 nên
nên 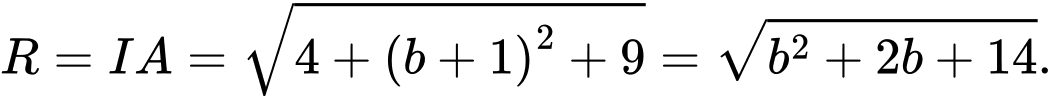
Vì mặt cầu tiếp xúc với mặt phẳng
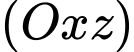 nên
nên 
Do đó,
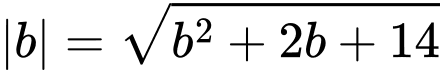
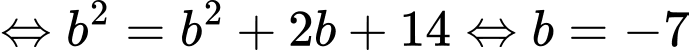
Vậy bán kính của mặt cầu là
 Đáp án: B
Đáp án: B PHẦN II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a),b),c),d) ở mỗi câu học sinh chọn đúng hoặc sai.
Câu 13 [778846]: Trong không gian với hệ tọa độ 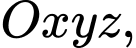 cho mặt phẳng
cho mặt phẳng 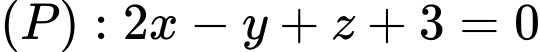 và điểm
và điểm 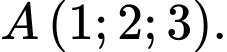 Gọi
Gọi 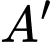 là điểm đối xứng của
là điểm đối xứng của 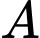 qua mặt phẳng
qua mặt phẳng 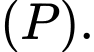
 cho mặt phẳng
cho mặt phẳng 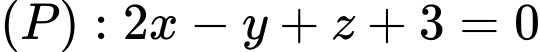 và điểm
và điểm 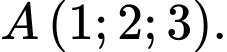 Gọi
Gọi  là điểm đối xứng của
là điểm đối xứng của 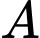 qua mặt phẳng
qua mặt phẳng 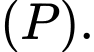
a) Sai.
Một vectơ pháp tuyến của mặt phẳng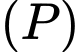 là
là 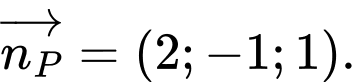
b) Đúng.
Vì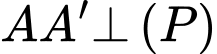 nên sẽ nhận vectơ pháp tuyến của mặt phẳng
nên sẽ nhận vectơ pháp tuyến của mặt phẳng 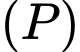 làm một vectơ chỉ phương.
làm một vectơ chỉ phương.
Suy ra phương trình chính tắc của đường thẳng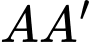 là
là 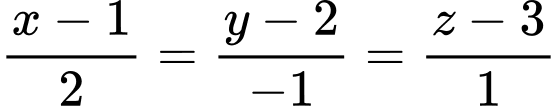
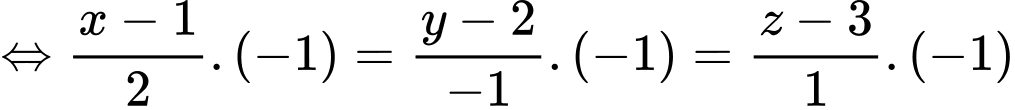
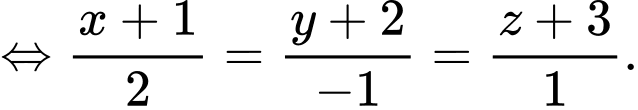
c) Sai.
Phương trình tham số của đường thẳng là
là 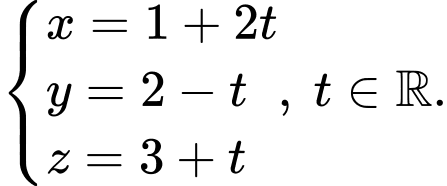
Vì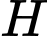 là hình chiếu của điểm
là hình chiếu của điểm 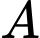 trên mặt phẳng
trên mặt phẳng 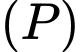 nên
nên 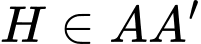
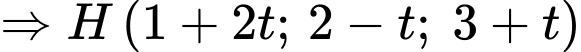
Vì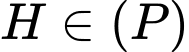 nên tọa độ điểm
nên tọa độ điểm 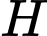 thỏa mãn phương trình mặt phẳng
thỏa mãn phương trình mặt phẳng 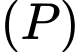 nên
nên 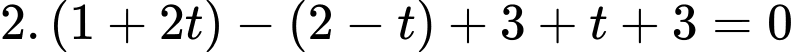


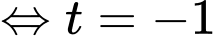
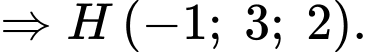
Vậy tung độ của điểm bằng 3.
bằng 3.
d) Đúng.
Mặt cầu đường kính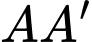 có tâm là trung điểm
có tâm là trung điểm 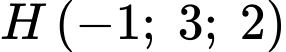 và có bán kính
và có bán kính 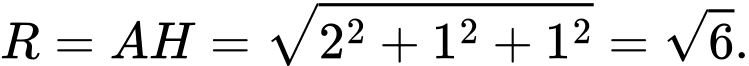 Suy ra phương trình mặt cầu cần tính là
Suy ra phương trình mặt cầu cần tính là 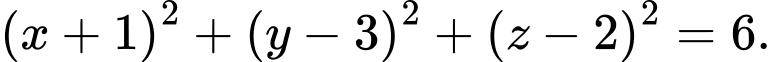
Một vectơ pháp tuyến của mặt phẳng
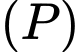 là
là 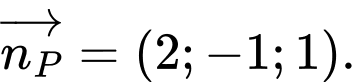
b) Đúng.
Vì
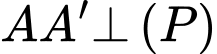 nên sẽ nhận vectơ pháp tuyến của mặt phẳng
nên sẽ nhận vectơ pháp tuyến của mặt phẳng 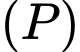 làm một vectơ chỉ phương.
làm một vectơ chỉ phương.
Suy ra phương trình chính tắc của đường thẳng
 là
là 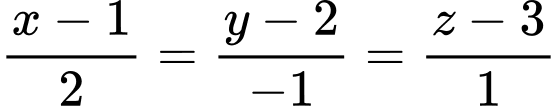
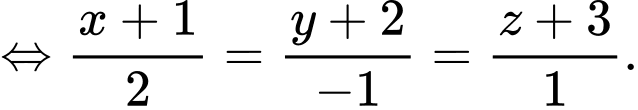
c) Sai.
Phương trình tham số của đường thẳng
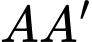 là
là 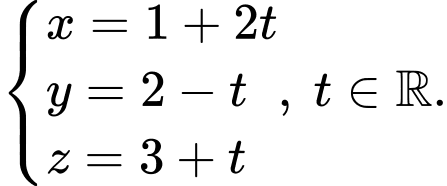
Vì
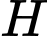 là hình chiếu của điểm
là hình chiếu của điểm 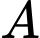 trên mặt phẳng
trên mặt phẳng 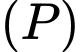 nên
nên 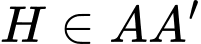
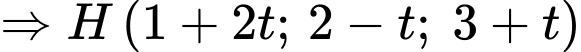
Vì
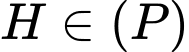 nên tọa độ điểm
nên tọa độ điểm 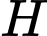 thỏa mãn phương trình mặt phẳng
thỏa mãn phương trình mặt phẳng 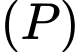 nên
nên 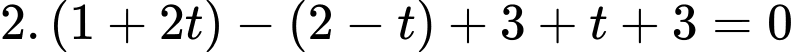


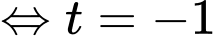
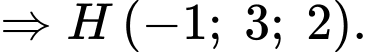
Vậy tung độ của điểm
 bằng 3.
bằng 3.
d) Đúng.
Mặt cầu đường kính
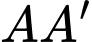 có tâm là trung điểm
có tâm là trung điểm 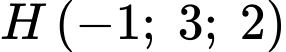 và có bán kính
và có bán kính 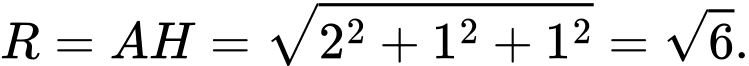 Suy ra phương trình mặt cầu cần tính là
Suy ra phương trình mặt cầu cần tính là 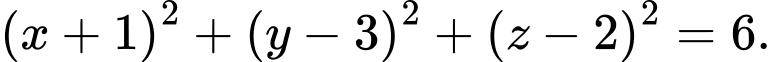
Câu 14 [778847]: Trong không gian toạ độ 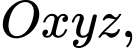 với
với  là tâm trái đất, bề mặt trái đất có phương trình là
là tâm trái đất, bề mặt trái đất có phương trình là  Giả sử một thiết bị GPS được đặt trên mặt đất và ta xác định được khoảng cách từ nó đến ba vệ tinh
Giả sử một thiết bị GPS được đặt trên mặt đất và ta xác định được khoảng cách từ nó đến ba vệ tinh 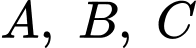 tương ứng là
tương ứng là 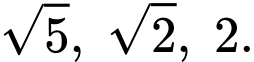 Tại thời điểm đó, các vệ tinh trên ở vị trí có toạ độ
Tại thời điểm đó, các vệ tinh trên ở vị trí có toạ độ 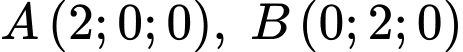 và
và 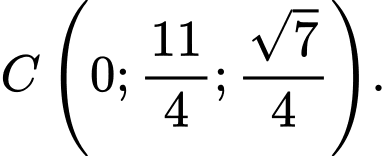 Giả sử tại thời điểm đã cho, thiết bị GPS ở vị trí
Giả sử tại thời điểm đã cho, thiết bị GPS ở vị trí 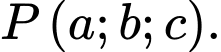
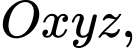 với
với  là tâm trái đất, bề mặt trái đất có phương trình là
là tâm trái đất, bề mặt trái đất có phương trình là  Giả sử một thiết bị GPS được đặt trên mặt đất và ta xác định được khoảng cách từ nó đến ba vệ tinh
Giả sử một thiết bị GPS được đặt trên mặt đất và ta xác định được khoảng cách từ nó đến ba vệ tinh 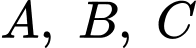 tương ứng là
tương ứng là 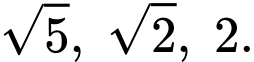 Tại thời điểm đó, các vệ tinh trên ở vị trí có toạ độ
Tại thời điểm đó, các vệ tinh trên ở vị trí có toạ độ 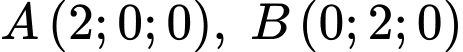 và
và 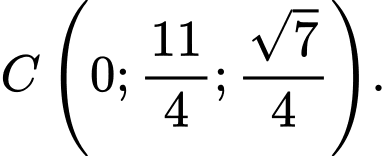 Giả sử tại thời điểm đã cho, thiết bị GPS ở vị trí
Giả sử tại thời điểm đã cho, thiết bị GPS ở vị trí 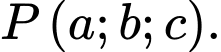
a) Sai.
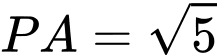
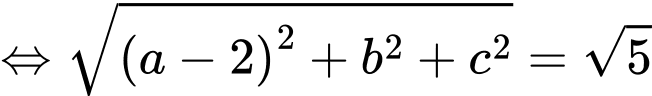
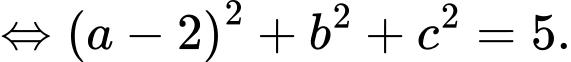
b) Đúng.
Vì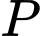 thuộc bề mặt trái đất nên ta có
thuộc bề mặt trái đất nên ta có 
Từ giả thiết, ta có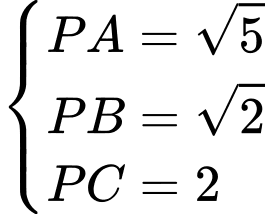
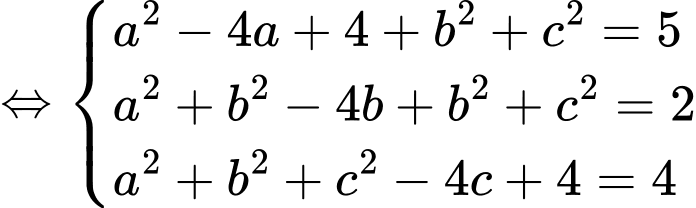
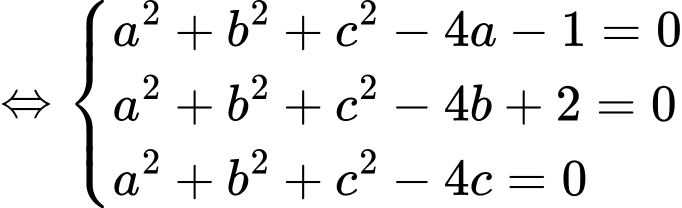
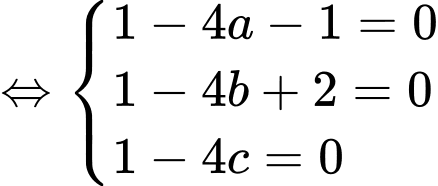
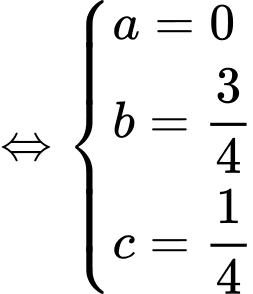
c) Đúng.
d) Sai.
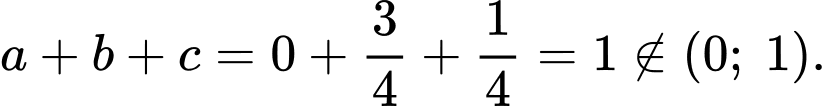
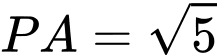
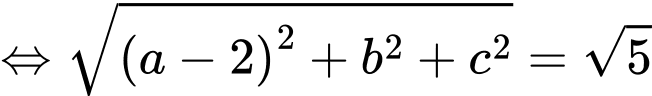
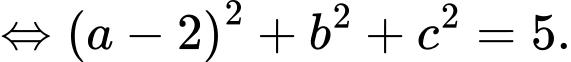
b) Đúng.
Vì
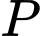 thuộc bề mặt trái đất nên ta có
thuộc bề mặt trái đất nên ta có 
Từ giả thiết, ta có
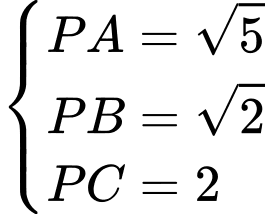
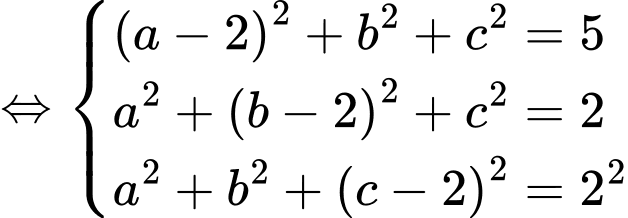
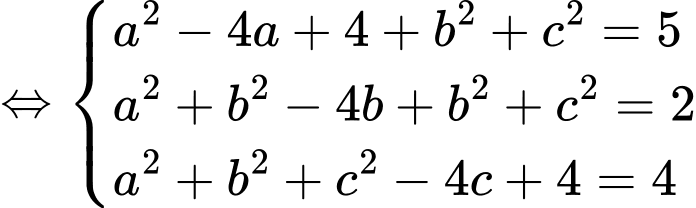
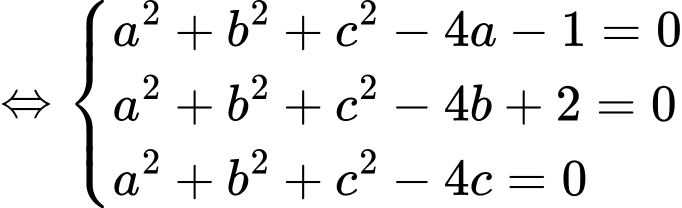
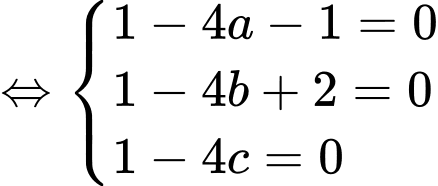
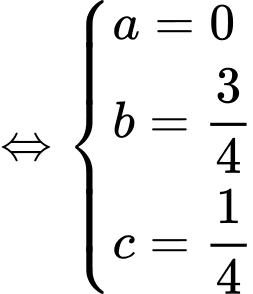
c) Đúng.
d) Sai.
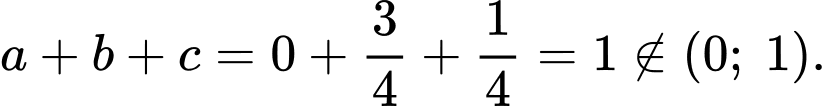
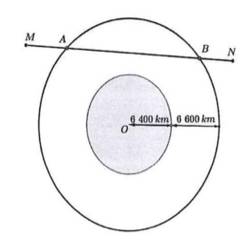
Câu 15 [680751]: Các thiên thạch có đường kính lớn hơn 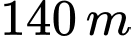 và có thể lại gần Trái Đất ở khoảng cách nhỏ hơn 7 500 000 km được coi là những vật thể có khả năng va chạm gây nguy hiểm cho Trái Đất. Để theo dõi những thiên thạch này, người ta đã thiết lập các trạm quan sát các vật thể bay gần Trái Đất. Giả sử có một hệ thống quan sát có khả năng theo dõi các vật thể ở độ cao không vượt quá 6 600 km so với mực nước biển. Coi Trái Đất là khối cầu có bán kính 6 400 km. Chọn hệ trục tọa độ
và có thể lại gần Trái Đất ở khoảng cách nhỏ hơn 7 500 000 km được coi là những vật thể có khả năng va chạm gây nguy hiểm cho Trái Đất. Để theo dõi những thiên thạch này, người ta đã thiết lập các trạm quan sát các vật thể bay gần Trái Đất. Giả sử có một hệ thống quan sát có khả năng theo dõi các vật thể ở độ cao không vượt quá 6 600 km so với mực nước biển. Coi Trái Đất là khối cầu có bán kính 6 400 km. Chọn hệ trục tọa độ 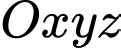 trong không gian có gốc
trong không gian có gốc  tại tâm Trái Đất và đơn vị độ dài trên mỗi trục tọa độ là 1 000 km . Một thiên thạch (coi như một hạt) chuyển động với tốc độ không đổi theo một đường thẳng từ điểm
tại tâm Trái Đất và đơn vị độ dài trên mỗi trục tọa độ là 1 000 km . Một thiên thạch (coi như một hạt) chuyển động với tốc độ không đổi theo một đường thẳng từ điểm 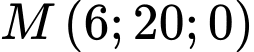 đến điểm
đến điểm 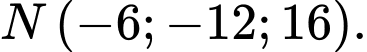
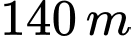 và có thể lại gần Trái Đất ở khoảng cách nhỏ hơn 7 500 000 km được coi là những vật thể có khả năng va chạm gây nguy hiểm cho Trái Đất. Để theo dõi những thiên thạch này, người ta đã thiết lập các trạm quan sát các vật thể bay gần Trái Đất. Giả sử có một hệ thống quan sát có khả năng theo dõi các vật thể ở độ cao không vượt quá 6 600 km so với mực nước biển. Coi Trái Đất là khối cầu có bán kính 6 400 km. Chọn hệ trục tọa độ
và có thể lại gần Trái Đất ở khoảng cách nhỏ hơn 7 500 000 km được coi là những vật thể có khả năng va chạm gây nguy hiểm cho Trái Đất. Để theo dõi những thiên thạch này, người ta đã thiết lập các trạm quan sát các vật thể bay gần Trái Đất. Giả sử có một hệ thống quan sát có khả năng theo dõi các vật thể ở độ cao không vượt quá 6 600 km so với mực nước biển. Coi Trái Đất là khối cầu có bán kính 6 400 km. Chọn hệ trục tọa độ  trong không gian có gốc
trong không gian có gốc  tại tâm Trái Đất và đơn vị độ dài trên mỗi trục tọa độ là 1 000 km . Một thiên thạch (coi như một hạt) chuyển động với tốc độ không đổi theo một đường thẳng từ điểm
tại tâm Trái Đất và đơn vị độ dài trên mỗi trục tọa độ là 1 000 km . Một thiên thạch (coi như một hạt) chuyển động với tốc độ không đổi theo một đường thẳng từ điểm 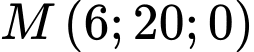 đến điểm
đến điểm 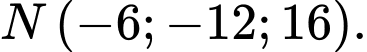

a) Đúng.
Ta có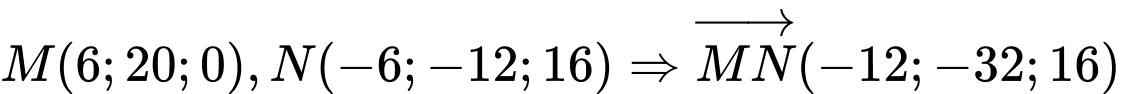 . Chọn
. Chọn 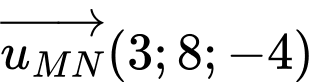 .
.
Khi đó, phương trình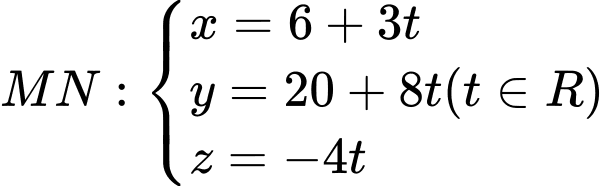 .
.
b) Sai.
Phạm vi theo dõi của hệ thống ra đa là mặt cầu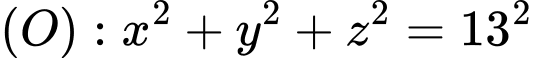 .
.
Tọa độ giao điểm của và
và  là nghiệm của phương trình
là nghiệm của phương trình
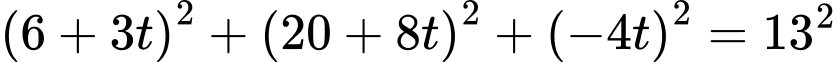
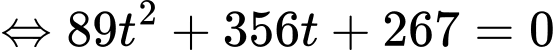
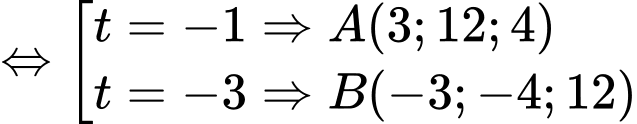
Ta có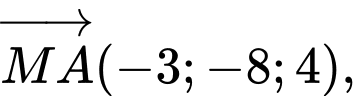
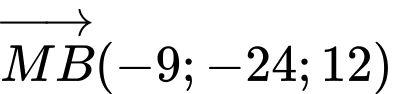
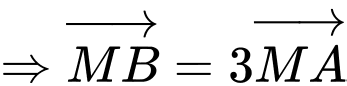
Suy ra: Điểm gặp đầu tiên là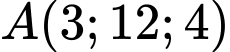 .
.
c) Đúng.
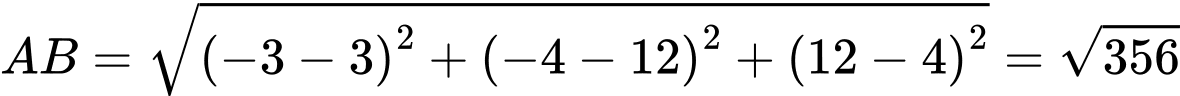
Đơn vị độ dài trên mỗi trục là 1 000 km nên khoảng cách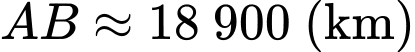
d) Đúng.
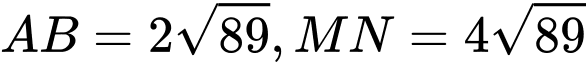
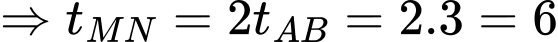 (phút)
(phút)
Ta có
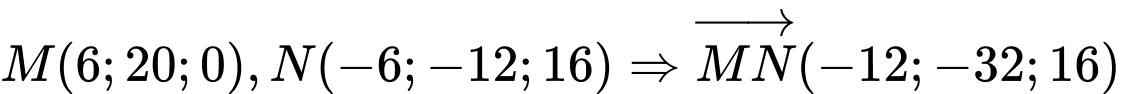 . Chọn
. Chọn 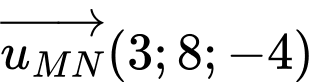 .
.Khi đó, phương trình
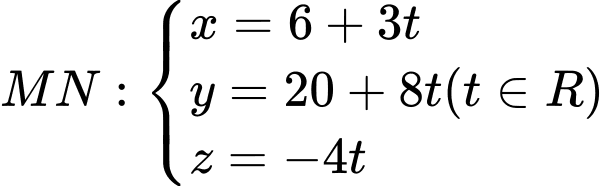 .
.b) Sai.
Phạm vi theo dõi của hệ thống ra đa là mặt cầu
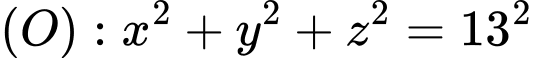 .
.Tọa độ giao điểm của
 và
và  là nghiệm của phương trình
là nghiệm của phương trình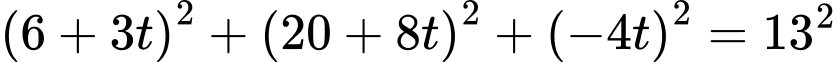
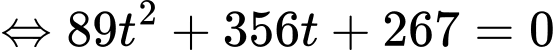
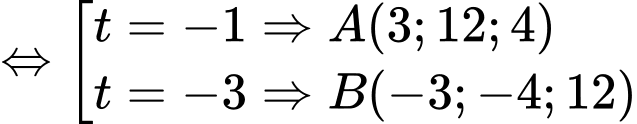
Ta có
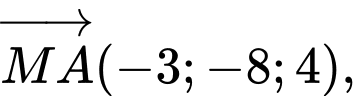
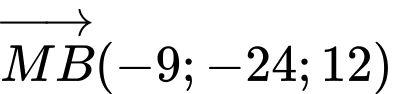
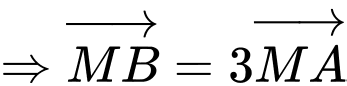
Suy ra: Điểm gặp đầu tiên là
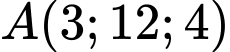 .
.c) Đúng.
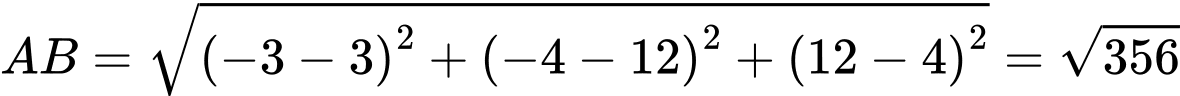
Đơn vị độ dài trên mỗi trục là 1 000 km nên khoảng cách
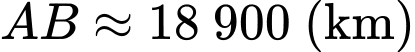
d) Đúng.
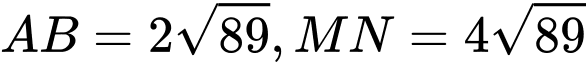
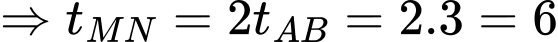 (phút)
(phút)
Câu 16 [696431]: Hải đăng là một ngọn tháp (nhà hoặc khung) được thiết kế để chiếu sáng từ một hệ thống đèn và thấu kính, hoặc thời xưa là chiếu sáng bằng lửa, với mục đích hỗ trợ cho các hoa tiêu trên biển định hướng và tìm đường. Vào năm 293 trước Công nguyên, ngọn hải đăng đầu tiên đã được người Phoenicia xây dựng trên hòn đảo Pharos tại Alexandria. Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục là một mét), coi một phần mặt biển được khảo sát là mặt phẳng 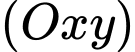 , trục
, trục  hướng lên trên vuông góc với mặt biển; một ngọn hải đăng đỉnh cao
hướng lên trên vuông góc với mặt biển; một ngọn hải đăng đỉnh cao 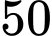 mét so với mực nước biển (hình vẽ bên dưới) biết đỉnh ở vị trí
mét so với mực nước biển (hình vẽ bên dưới) biết đỉnh ở vị trí 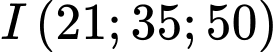 , biết rằng ngọn hải đăng này được thiết kế với bán kính phủ sáng là 4 km.
, biết rằng ngọn hải đăng này được thiết kế với bán kính phủ sáng là 4 km.

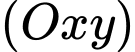 , trục
, trục  hướng lên trên vuông góc với mặt biển; một ngọn hải đăng đỉnh cao
hướng lên trên vuông góc với mặt biển; một ngọn hải đăng đỉnh cao 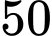 mét so với mực nước biển (hình vẽ bên dưới) biết đỉnh ở vị trí
mét so với mực nước biển (hình vẽ bên dưới) biết đỉnh ở vị trí 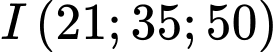 , biết rằng ngọn hải đăng này được thiết kế với bán kính phủ sáng là 4 km.
, biết rằng ngọn hải đăng này được thiết kế với bán kính phủ sáng là 4 km. 
a) Sai.
Vì đỉnh là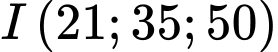 và có bán kính phủ sóng
và có bán kính phủ sóng 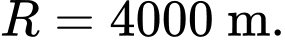
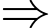 Phương trình mặt cầu tâm
Phương trình mặt cầu tâm 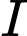 bán kính
bán kính 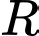 là
là 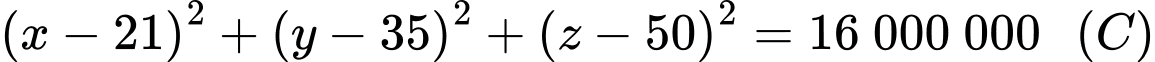 .
.
b) Sai.
Thay tọa độ điểm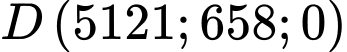 vào phương trình mặt cầu
vào phương trình mặt cầu  ta được:
ta được: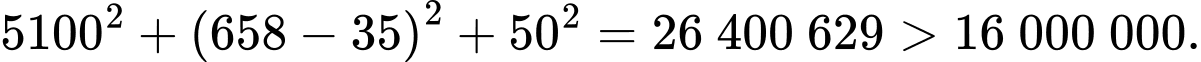
c) Đúng.
Bán kính vùng sáng này là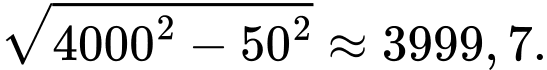
d) Đúng.
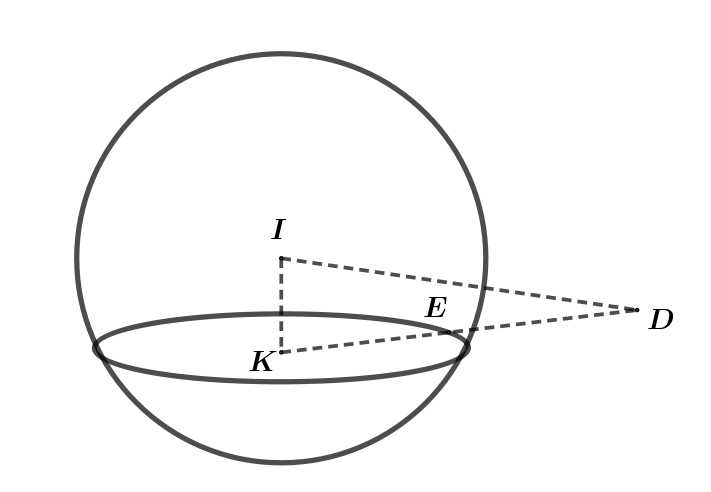
Chân ngọn hải đăng là hình chiếu của điểm lên mặt phẳng
lên mặt phẳng 
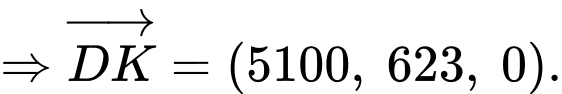
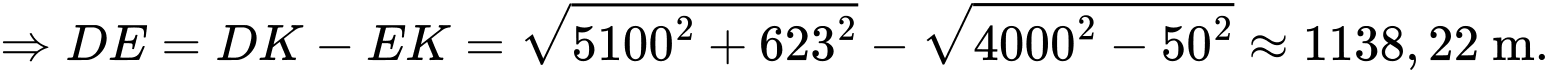
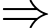 Thời gian để đến điểm đầu tiên nhìn thấy được ánh sáng ngọn hải đăng trên là
Thời gian để đến điểm đầu tiên nhìn thấy được ánh sáng ngọn hải đăng trên là 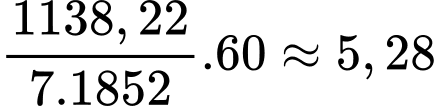 phút.
phút.
Vì đỉnh là
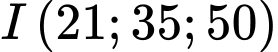 và có bán kính phủ sóng
và có bán kính phủ sóng 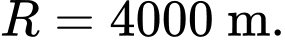
 Phương trình mặt cầu tâm
Phương trình mặt cầu tâm 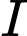 bán kính
bán kính 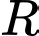 là
là 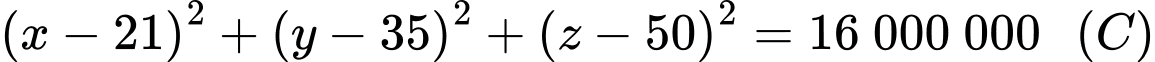 .
.b) Sai.
Thay tọa độ điểm
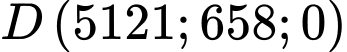 vào phương trình mặt cầu
vào phương trình mặt cầu  ta được:
ta được: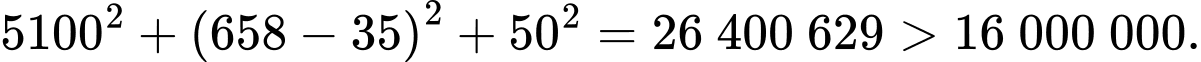
c) Đúng.
Bán kính vùng sáng này là
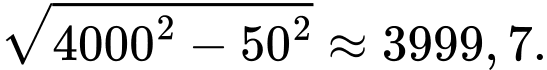
d) Đúng.

Chân ngọn hải đăng là hình chiếu của điểm
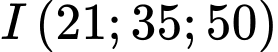 lên mặt phẳng
lên mặt phẳng 
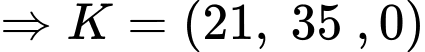
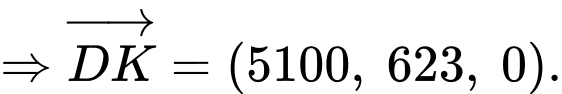
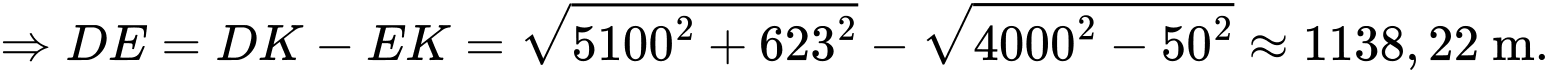
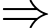 Thời gian để đến điểm đầu tiên nhìn thấy được ánh sáng ngọn hải đăng trên là
Thời gian để đến điểm đầu tiên nhìn thấy được ánh sáng ngọn hải đăng trên là 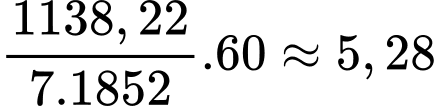 phút.
phút. PHẦN III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 17 đến câu 22.
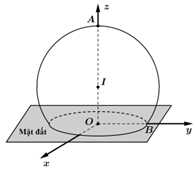
Câu 17 [778849]: Ericsson Globe (Thuỵ Điển) là toà nhà bán cầu lớn nhất trên thế giới (năm 2020),với hình dạng một quả cầu màu trắng. Giả sử người ta biểu diễn mô phỏng của toà nhà Ericsson Globe trong hệ trục toạ độ 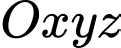 bởi một mặt cầu có tâm
bởi một mặt cầu có tâm 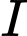 và đo được chiều cao toà nhà
và đo được chiều cao toà nhà 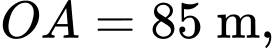 đáy toà nhà là đường tròn có bán kính
đáy toà nhà là đường tròn có bán kính 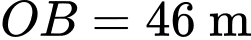 (xem hình vẽ). Biết đơn vị trục là mét, tính đường kính mặt cầu này bằng bao nhiêu mét (viết kết quả làm tròn đến hàng đơn vị).
(xem hình vẽ). Biết đơn vị trục là mét, tính đường kính mặt cầu này bằng bao nhiêu mét (viết kết quả làm tròn đến hàng đơn vị).

 bởi một mặt cầu có tâm
bởi một mặt cầu có tâm  và đo được chiều cao toà nhà
và đo được chiều cao toà nhà 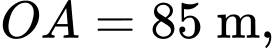 đáy toà nhà là đường tròn có bán kính
đáy toà nhà là đường tròn có bán kính 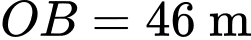 (xem hình vẽ). Biết đơn vị trục là mét, tính đường kính mặt cầu này bằng bao nhiêu mét (viết kết quả làm tròn đến hàng đơn vị).
(xem hình vẽ). Biết đơn vị trục là mét, tính đường kính mặt cầu này bằng bao nhiêu mét (viết kết quả làm tròn đến hàng đơn vị).

Điền đáp án: 110.
Giả sử bán kính của mặt cầu là Khi đó,
Khi đó, 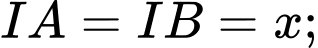
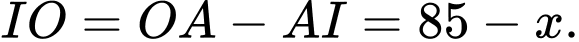
Áp dụng định lý Pythagore trong tam giác vuông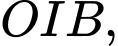 ta có
ta có 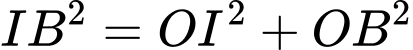
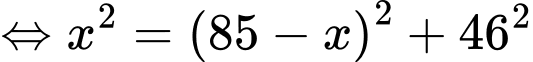
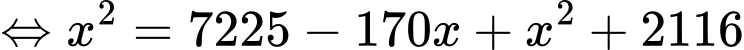
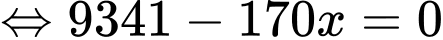
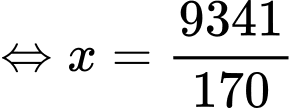
Suy ra đường kính của mặt cầu bằng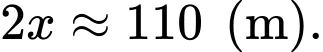
Giả sử bán kính của mặt cầu là
 Khi đó,
Khi đó, 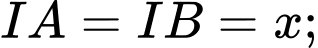
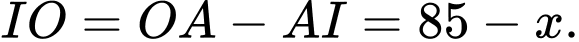
Áp dụng định lý Pythagore trong tam giác vuông
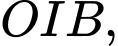 ta có
ta có 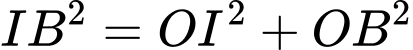
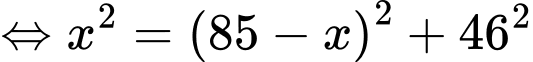
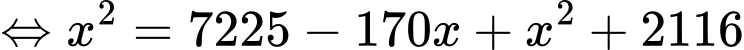
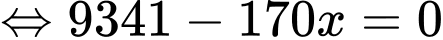
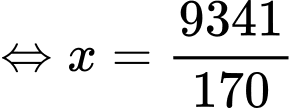
Suy ra đường kính của mặt cầu bằng
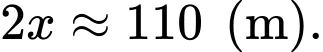
Câu 18 [778850]: Trong không gian  cho đường thẳng
cho đường thẳng 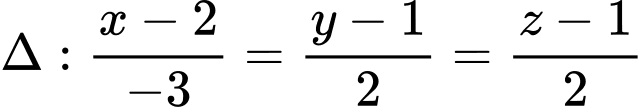 ,
, 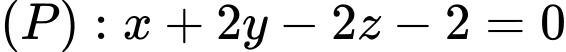 ,
,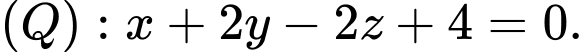 Gọi mặt cầu
Gọi mặt cầu 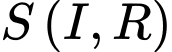 có tâm
có tâm 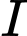 thuộc
thuộc  và tiếp xúc với
và tiếp xúc với 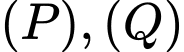 . Biết toạ độ điểm
. Biết toạ độ điểm 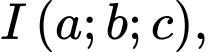 tính tổng
tính tổng 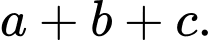
 cho đường thẳng
cho đường thẳng 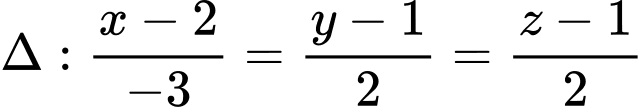 ,
, 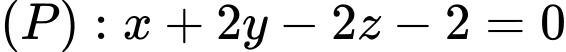 ,
,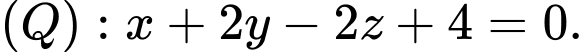 Gọi mặt cầu
Gọi mặt cầu 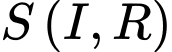 có tâm
có tâm 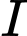 thuộc
thuộc  và tiếp xúc với
và tiếp xúc với 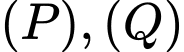 . Biết toạ độ điểm
. Biết toạ độ điểm 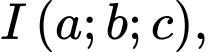 tính tổng
tính tổng 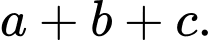
Trả lời: 5
Ta có: phương trình tham số của là
là 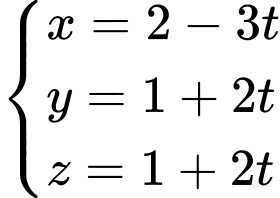 . Vì
. Vì  .
.
Mặt cầu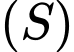 có tâm
có tâm  thuộc
thuộc  và tiếp xúc với
và tiếp xúc với 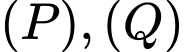 nên ta có:
nên ta có:
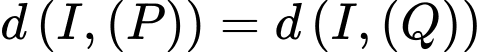
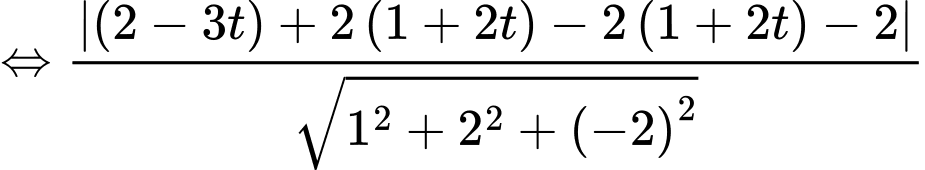
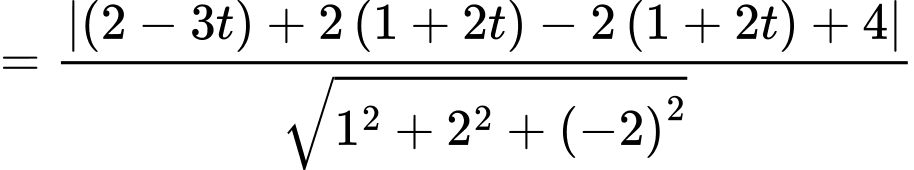
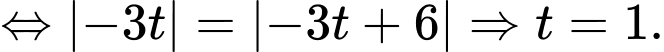
Suy ra mặt cầu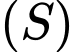 có tâm
có tâm 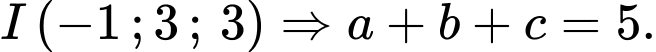
Ta có: phương trình tham số của
 là
là 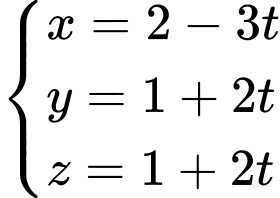 . Vì
. Vì  .
.Mặt cầu
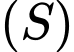 có tâm
có tâm  thuộc
thuộc  và tiếp xúc với
và tiếp xúc với 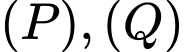 nên ta có:
nên ta có: 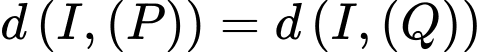
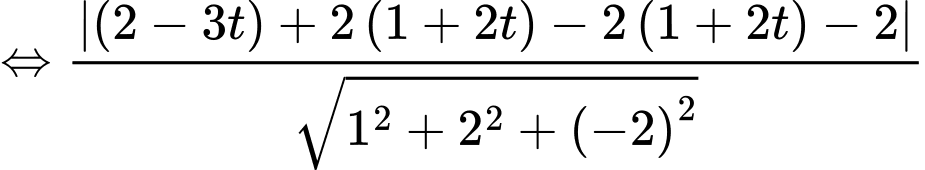
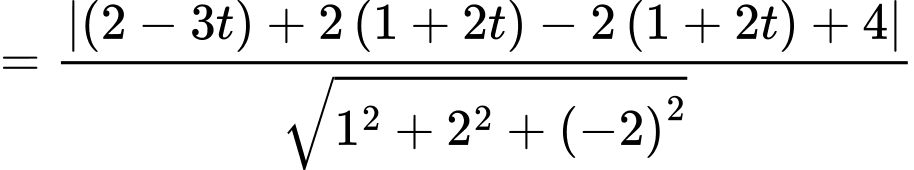
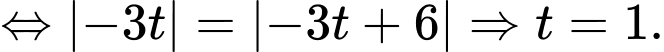
Suy ra mặt cầu
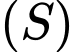 có tâm
có tâm 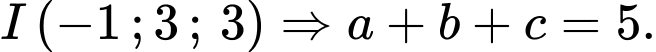
Câu 19 [713221]: Mỗi cạnh của một hộp lập phương có chiều dài 1 m. Hộp chứa chín quả cầu hình cầu có cùng bán kính  Tâm của một quả cầu nằm ở tâm của khối lập phương và nó tiếp xúc với tám quả cầu còn lại. Mỗi quả cầu trong tám quả cầu còn lại tiếp xúc với ba cạnh của hộp. Do đó, các quả cầu được xếp chặt trong hộp (xem hình vẽ). Tìm
Tâm của một quả cầu nằm ở tâm của khối lập phương và nó tiếp xúc với tám quả cầu còn lại. Mỗi quả cầu trong tám quả cầu còn lại tiếp xúc với ba cạnh của hộp. Do đó, các quả cầu được xếp chặt trong hộp (xem hình vẽ). Tìm 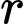 (kết quả làm tròn đến hàng phần trăm theo đơn vị mét)
(kết quả làm tròn đến hàng phần trăm theo đơn vị mét)
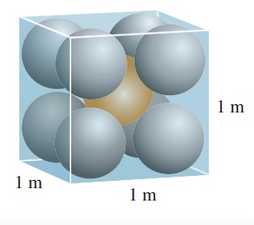
 Tâm của một quả cầu nằm ở tâm của khối lập phương và nó tiếp xúc với tám quả cầu còn lại. Mỗi quả cầu trong tám quả cầu còn lại tiếp xúc với ba cạnh của hộp. Do đó, các quả cầu được xếp chặt trong hộp (xem hình vẽ). Tìm
Tâm của một quả cầu nằm ở tâm của khối lập phương và nó tiếp xúc với tám quả cầu còn lại. Mỗi quả cầu trong tám quả cầu còn lại tiếp xúc với ba cạnh của hộp. Do đó, các quả cầu được xếp chặt trong hộp (xem hình vẽ). Tìm  (kết quả làm tròn đến hàng phần trăm theo đơn vị mét)
(kết quả làm tròn đến hàng phần trăm theo đơn vị mét)
Điền đáp án: 0,23.
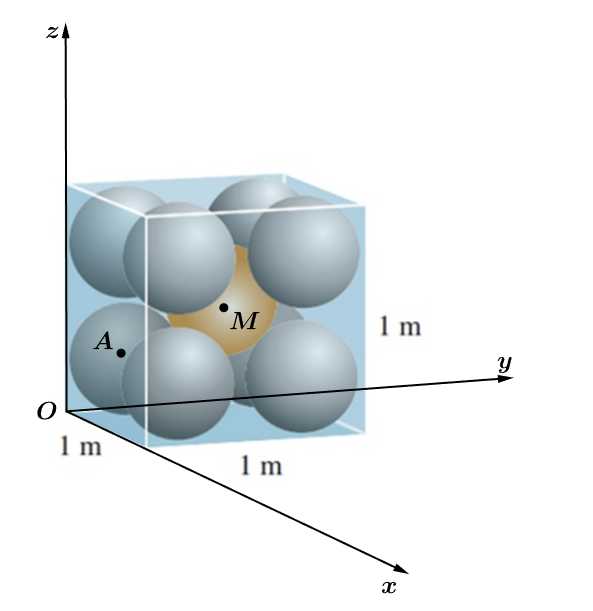
Ghép khối hộp vào hệ trục toạ độ như hình vẽ trên. Gọi
như hình vẽ trên. Gọi 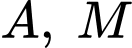 là tâm của các quả cầu. Với
là tâm của các quả cầu. Với 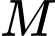 là tâm của quả cầu nằm ở tâm của khối lập phương.
là tâm của quả cầu nằm ở tâm của khối lập phương.
Khi đó, ta có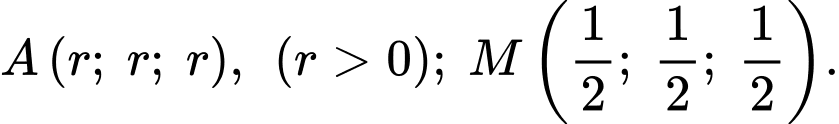
Vì quả cầu tâm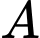 tiếp xúc với quả cầu trung tâm nên ta có
tiếp xúc với quả cầu trung tâm nên ta có 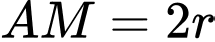
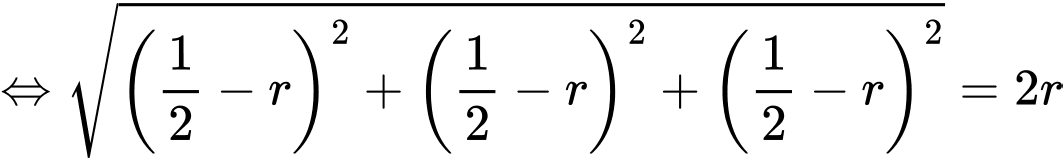
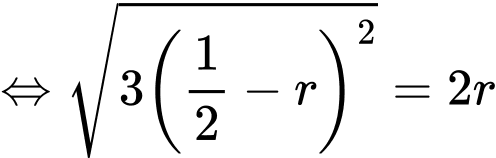
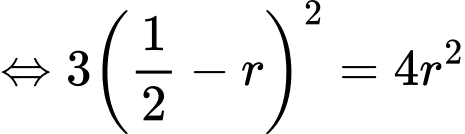
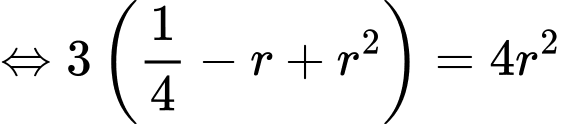
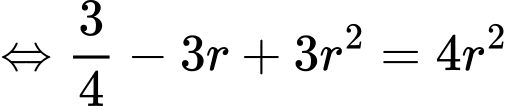
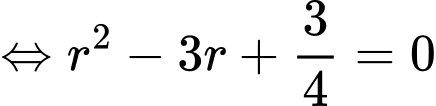
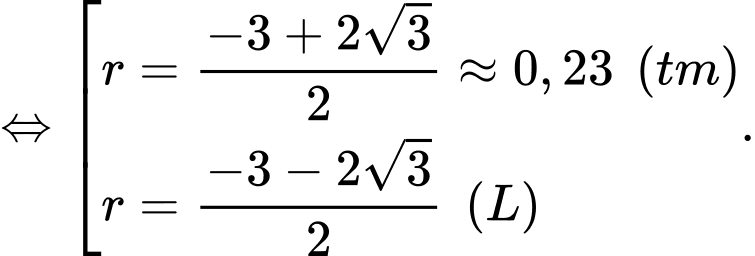
Vậy bán kính của các quả cầu là 0,23 m.

Ghép khối hộp vào hệ trục toạ độ
 như hình vẽ trên. Gọi
như hình vẽ trên. Gọi 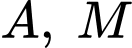 là tâm của các quả cầu. Với
là tâm của các quả cầu. Với  là tâm của quả cầu nằm ở tâm của khối lập phương.
là tâm của quả cầu nằm ở tâm của khối lập phương.Khi đó, ta có
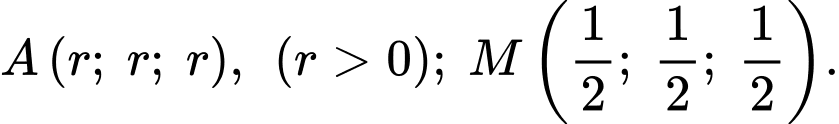
Vì quả cầu tâm
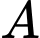 tiếp xúc với quả cầu trung tâm nên ta có
tiếp xúc với quả cầu trung tâm nên ta có 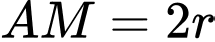
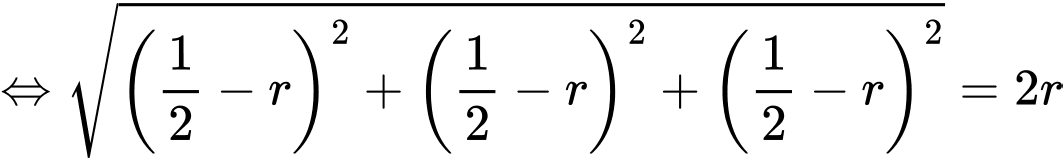
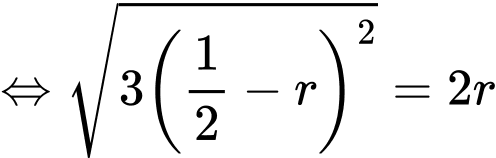
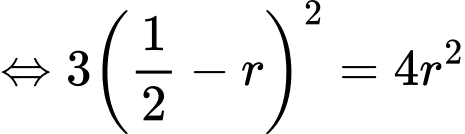
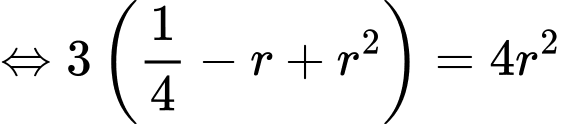
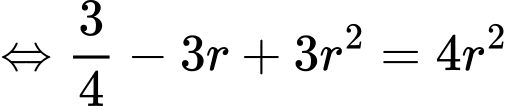
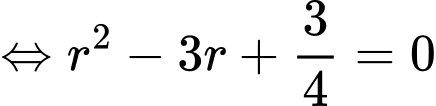
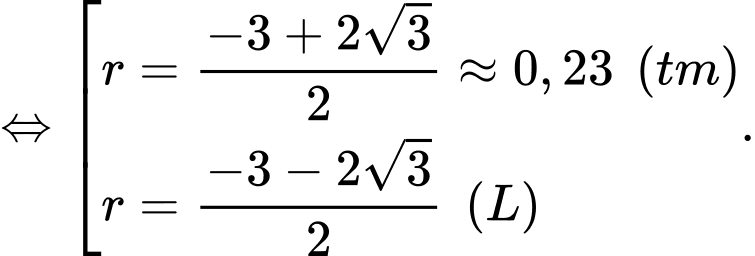
Vậy bán kính của các quả cầu là 0,23 m.
Câu 20 [778851]: Trong không gian với hệ trục tọa độ 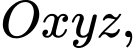 cho ba điểm
cho ba điểm 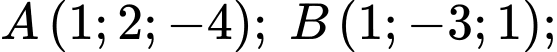
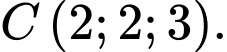 Tính đường kính của mặt cầu
Tính đường kính của mặt cầu 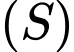 đi qua ba điểm trên và có tâm nằm trên mặt phẳng
đi qua ba điểm trên và có tâm nằm trên mặt phẳng 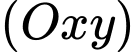 (làm tròn kết quả đến hàng phần chục).
(làm tròn kết quả đến hàng phần chục).
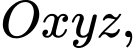 cho ba điểm
cho ba điểm 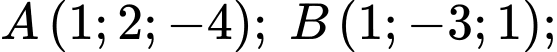
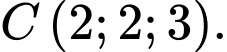 Tính đường kính của mặt cầu
Tính đường kính của mặt cầu 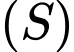 đi qua ba điểm trên và có tâm nằm trên mặt phẳng
đi qua ba điểm trên và có tâm nằm trên mặt phẳng 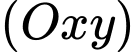 (làm tròn kết quả đến hàng phần chục).
(làm tròn kết quả đến hàng phần chục).
Trả lời: 10,2
Gọi tâm mặt cầu là: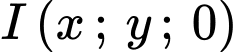 .
.
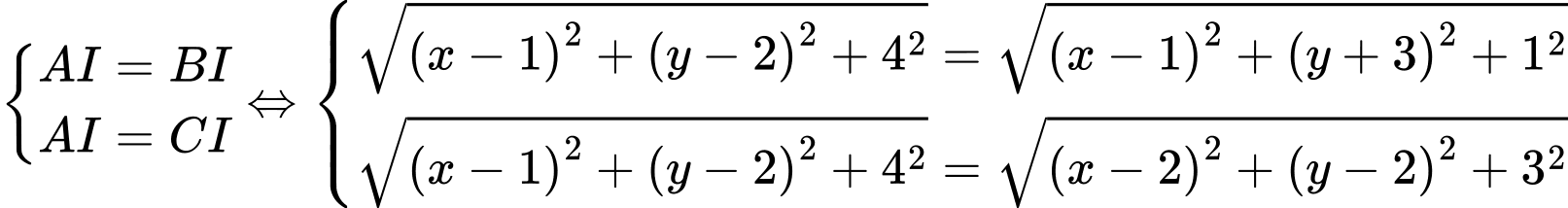
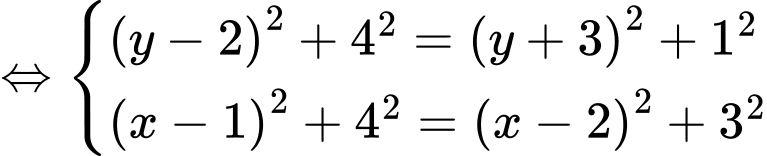
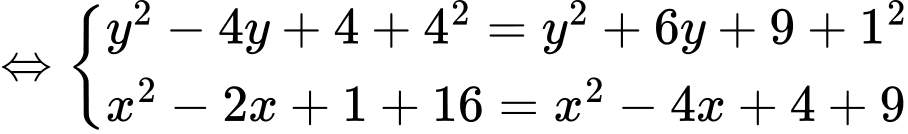
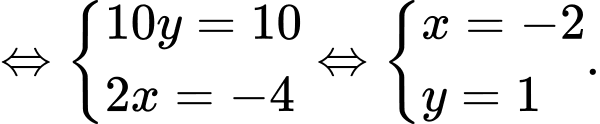 Suy ra
Suy ra 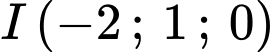
Vậy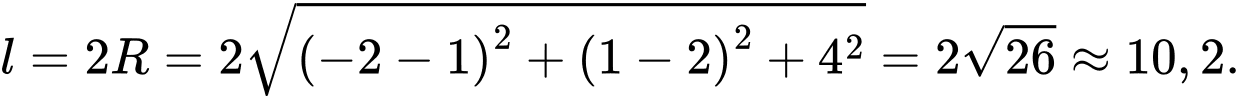
Gọi tâm mặt cầu là:
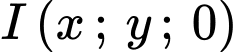 .
.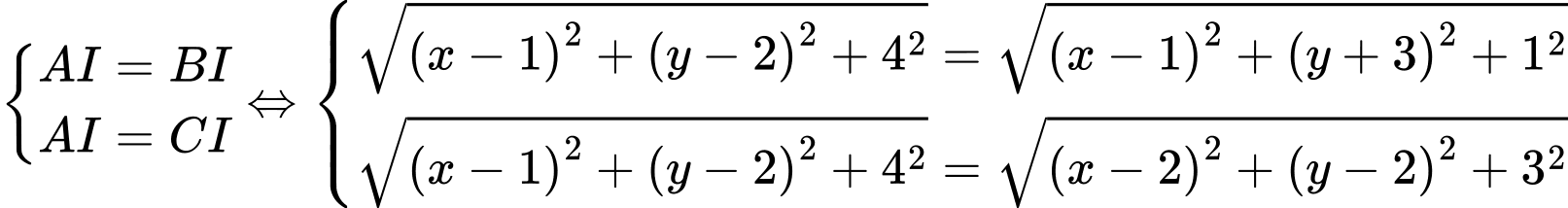
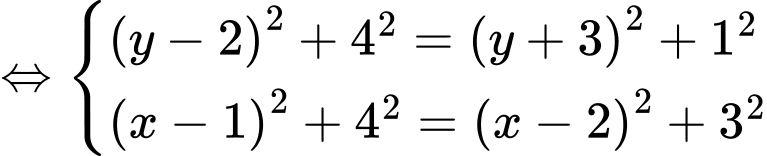
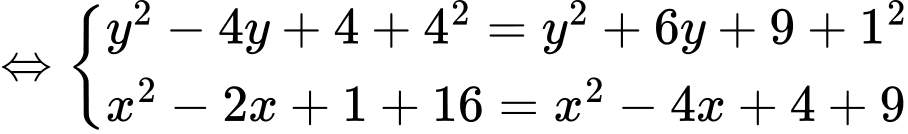
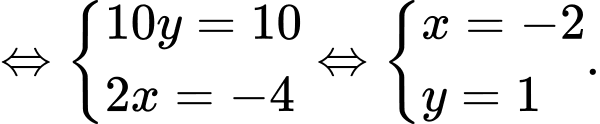 Suy ra
Suy ra 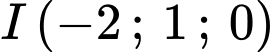
Vậy
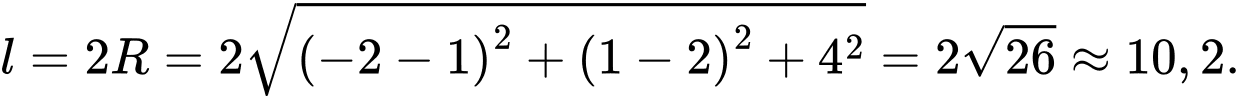
Câu 21 [778852]: Hệ thống định vị toàn cầu (tên tiếng Anh là: Global Positioning System, viết tắt là GPS) là một hệ thống cho phép xác định chính xác vị trí của một vật thể trong không gian. Ta có thể mô phỏng cơ chế hoạt động của hệ thống GPS trong không gian như sau: Trong cùng một thời điểm, toạ độ của một điểm  trong không gian sẽ được xác định bởi bốn vệ tinh cho trước, trên mỗi vệ tinh có một máy thu tín hiệu. Bằng cách so sánh sự sai lệch về thời gian từ lúc tín hiệu được phát đi với thời gian nhận phản hồi tín hiệu đó, mỗi máy thu tín hiệu xác định được khoảng cách từ vệ tinh đến vị trí
trong không gian sẽ được xác định bởi bốn vệ tinh cho trước, trên mỗi vệ tinh có một máy thu tín hiệu. Bằng cách so sánh sự sai lệch về thời gian từ lúc tín hiệu được phát đi với thời gian nhận phản hồi tín hiệu đó, mỗi máy thu tín hiệu xác định được khoảng cách từ vệ tinh đến vị trí  cần tìm toạ độ. Trong không gian với hệ toạ độ
cần tìm toạ độ. Trong không gian với hệ toạ độ  cho bốn vệ tinh
cho bốn vệ tinh  Tính khoảng cách từ gốc toạ độ
Tính khoảng cách từ gốc toạ độ  đến điểm
đến điểm 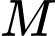 biết rằng khoảng cách từ các vệ tinh đến điểm
biết rằng khoảng cách từ các vệ tinh đến điểm 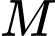 lần lượt là
lần lượt là 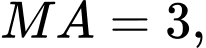
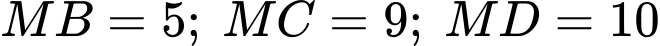 (kết quả làm tròn đến hàng phần trăm).
(kết quả làm tròn đến hàng phần trăm).
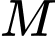 trong không gian sẽ được xác định bởi bốn vệ tinh cho trước, trên mỗi vệ tinh có một máy thu tín hiệu. Bằng cách so sánh sự sai lệch về thời gian từ lúc tín hiệu được phát đi với thời gian nhận phản hồi tín hiệu đó, mỗi máy thu tín hiệu xác định được khoảng cách từ vệ tinh đến vị trí
trong không gian sẽ được xác định bởi bốn vệ tinh cho trước, trên mỗi vệ tinh có một máy thu tín hiệu. Bằng cách so sánh sự sai lệch về thời gian từ lúc tín hiệu được phát đi với thời gian nhận phản hồi tín hiệu đó, mỗi máy thu tín hiệu xác định được khoảng cách từ vệ tinh đến vị trí 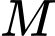 cần tìm toạ độ. Trong không gian với hệ toạ độ
cần tìm toạ độ. Trong không gian với hệ toạ độ 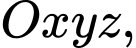 cho bốn vệ tinh
cho bốn vệ tinh  Tính khoảng cách từ gốc toạ độ
Tính khoảng cách từ gốc toạ độ  đến điểm
đến điểm 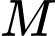 biết rằng khoảng cách từ các vệ tinh đến điểm
biết rằng khoảng cách từ các vệ tinh đến điểm 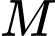 lần lượt là
lần lượt là 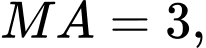
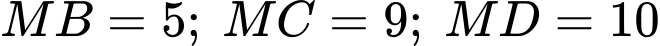 (kết quả làm tròn đến hàng phần trăm).
(kết quả làm tròn đến hàng phần trăm). 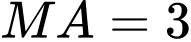
 Điểm
Điểm 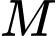 thuộc mặt cầu tâm
thuộc mặt cầu tâm 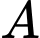 , bán kính
, bán kính 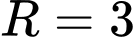 có phương trình
có phương trình 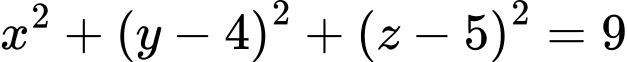 .
. 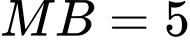
 Điểm
Điểm 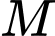 thuộc mặt cầu tâm
thuộc mặt cầu tâm 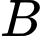 , bán kính
, bán kính 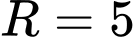 có phương trình
có phương trình 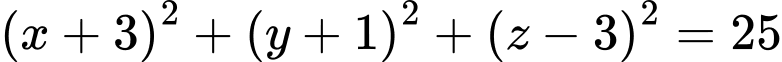 .
.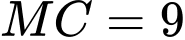
 Điểm
Điểm 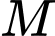 thuộc mặt cầu tâm
thuộc mặt cầu tâm  , bán kính
, bán kính 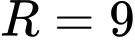 có phương trình
có phương trình 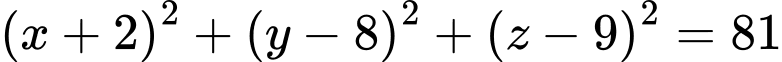 .
.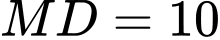
 Điểm
Điểm 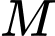 thuộc mặt cầu tâm
thuộc mặt cầu tâm 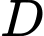 , bán kính
, bán kính 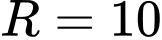 có phương trình
có phương trình 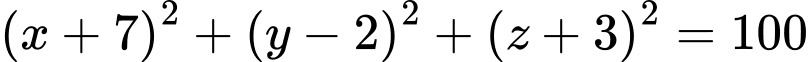 .
.Ta có
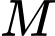 là giao điểm của bốn mặt cầu với tâm lần lượt là bốn vệ tinh
là giao điểm của bốn mặt cầu với tâm lần lượt là bốn vệ tinh 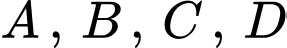 .
.Toạ độ
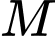 là nghiệm của hệ phương trình:
là nghiệm của hệ phương trình: 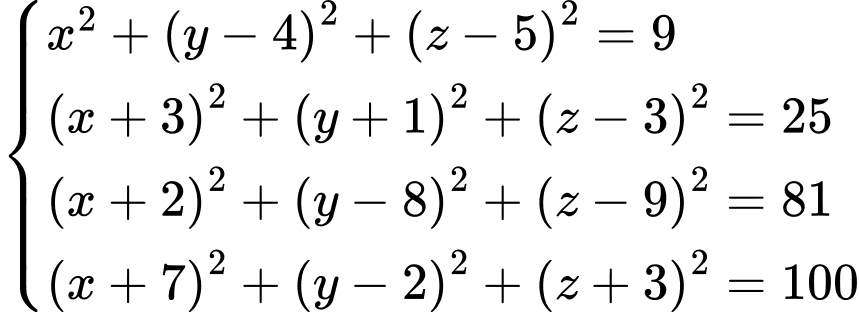
Giải hệ phương trình ta được
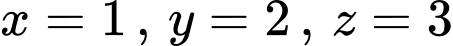
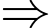
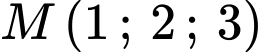 .
.Khoảng cách từ gốc toạ độ
 đến điểm
đến điểm 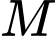 là
là 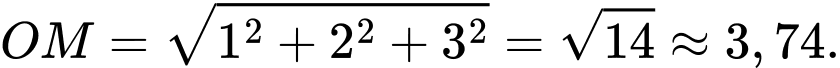
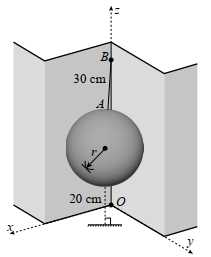
Câu 22 [693130]: Một quả bóng hình cầu có bán kính 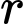 đang được treo trong một góc của tường nhà (hai bờ tường vuông góc), một điểm
đang được treo trong một góc của tường nhà (hai bờ tường vuông góc), một điểm 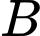 cố định nằm trên mép của hai bờ tường và cách mặt đất
cố định nằm trên mép của hai bờ tường và cách mặt đất 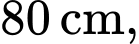 sợi dây treo bóng có độ dài
sợi dây treo bóng có độ dài 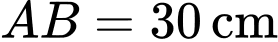 và đây cũng là độ dài ngắn nhất nối điểm
và đây cũng là độ dài ngắn nhất nối điểm 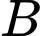 với mặt xung quanh của quả bóng. Biết rằng quả bóng tiếp xúc với hai bên bờ tường và điểm thấp nhất của quả bóng cách mặt đất
với mặt xung quanh của quả bóng. Biết rằng quả bóng tiếp xúc với hai bên bờ tường và điểm thấp nhất của quả bóng cách mặt đất  Hỏi đường kính của quả bóng là bao nhiêu centimet (làm tròn kết quả đến hàng đơn vị).
Hỏi đường kính của quả bóng là bao nhiêu centimet (làm tròn kết quả đến hàng đơn vị).
 đang được treo trong một góc của tường nhà (hai bờ tường vuông góc), một điểm
đang được treo trong một góc của tường nhà (hai bờ tường vuông góc), một điểm  cố định nằm trên mép của hai bờ tường và cách mặt đất
cố định nằm trên mép của hai bờ tường và cách mặt đất 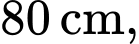 sợi dây treo bóng có độ dài
sợi dây treo bóng có độ dài 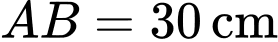 và đây cũng là độ dài ngắn nhất nối điểm
và đây cũng là độ dài ngắn nhất nối điểm 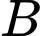 với mặt xung quanh của quả bóng. Biết rằng quả bóng tiếp xúc với hai bên bờ tường và điểm thấp nhất của quả bóng cách mặt đất
với mặt xung quanh của quả bóng. Biết rằng quả bóng tiếp xúc với hai bên bờ tường và điểm thấp nhất của quả bóng cách mặt đất  Hỏi đường kính của quả bóng là bao nhiêu centimet (làm tròn kết quả đến hàng đơn vị).
Hỏi đường kính của quả bóng là bao nhiêu centimet (làm tròn kết quả đến hàng đơn vị).
Điền đáp án: 38.
Giả sử mặt cầu có toạ độ tâm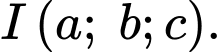 Từ giả thiết, ta thấy rằng
Từ giả thiết, ta thấy rằng 
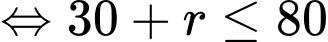

Ta khai thác dữ kiện đề bài:
Vì điểm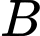 nằm trên trục
nằm trên trục  và cách mặt đất 80 cm nên
và cách mặt đất 80 cm nên 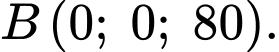
Lại có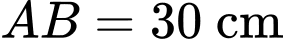 và là độ dài ngắn nhất nối điểm
và là độ dài ngắn nhất nối điểm 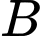 với mặt xung quanh của quả bóng, nên ta có
với mặt xung quanh của quả bóng, nên ta có 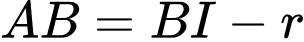
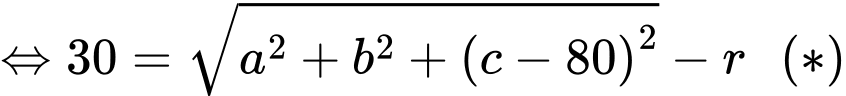
Vì quả bóng tiếp xúc với hai bên bờ tường (tức hai mặt phẳng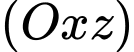 và
và 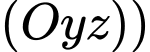 nên ta có
nên ta có 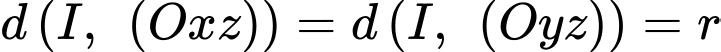 mà
mà 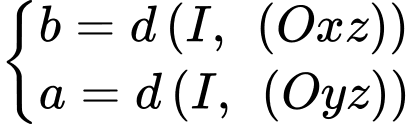
Suy ra toạ độ điểm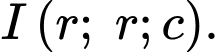
Từ giả thiết: vị trí thấp nhất của quả bóng cách mặt đất 20 cm nên ta có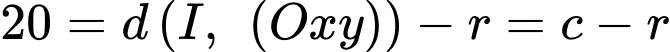
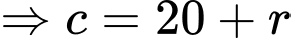
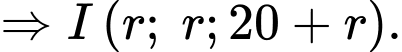
Khi đó, phương trình (*) tương đương với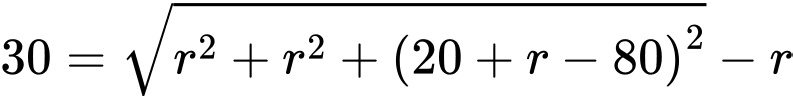
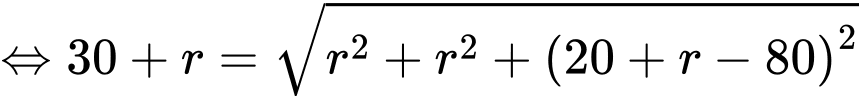
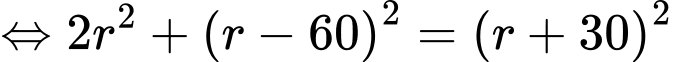
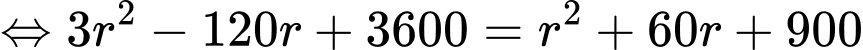
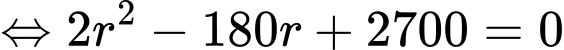
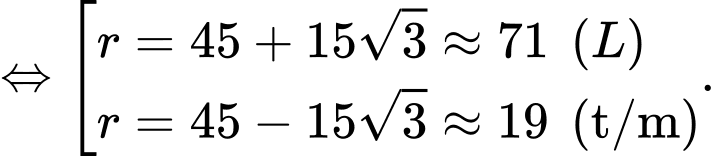
Vậy đường kính của quả bóng là 38 cm.
Note: Để chứng minh bài trên, ta sử dụng bổ đề sau:
Cho một điểm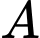 bất kì; mặt cầu
bất kì; mặt cầu 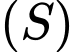 có tâm
có tâm 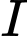 và bán kính
và bán kính 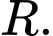 Gọi
Gọi 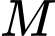 là một điểm di động trên mặt cầu
là một điểm di động trên mặt cầu 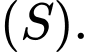 Minh hoạ như hình vẽ.
Minh hoạ như hình vẽ.
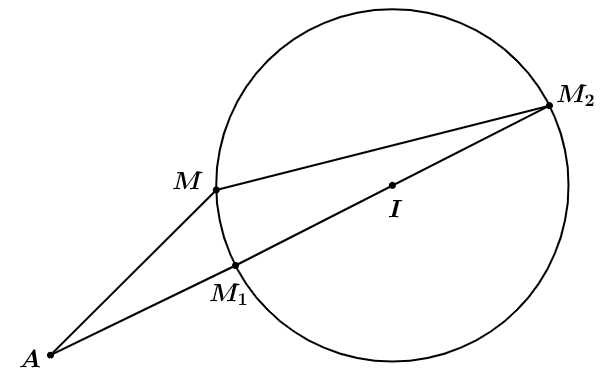
Khi đó:
+)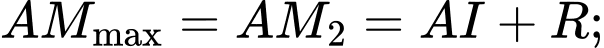
+)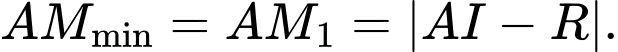
Giả sử mặt cầu có toạ độ tâm
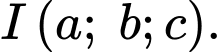 Từ giả thiết, ta thấy rằng
Từ giả thiết, ta thấy rằng 
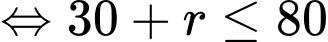

Ta khai thác dữ kiện đề bài:
Vì điểm
 nằm trên trục
nằm trên trục  và cách mặt đất 80 cm nên
và cách mặt đất 80 cm nên 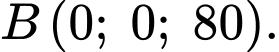
Lại có
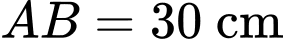 và là độ dài ngắn nhất nối điểm
và là độ dài ngắn nhất nối điểm 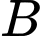 với mặt xung quanh của quả bóng, nên ta có
với mặt xung quanh của quả bóng, nên ta có 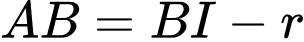
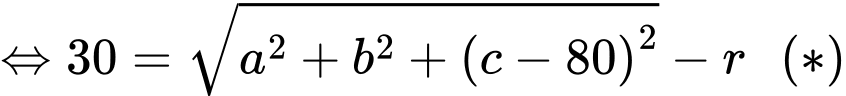
Vì quả bóng tiếp xúc với hai bên bờ tường (tức hai mặt phẳng
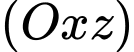 và
và 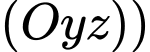 nên ta có
nên ta có 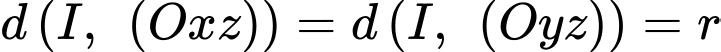 mà
mà 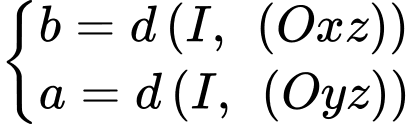
Suy ra toạ độ điểm
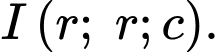
Từ giả thiết: vị trí thấp nhất của quả bóng cách mặt đất 20 cm nên ta có
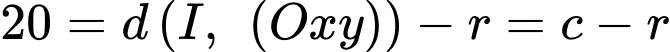
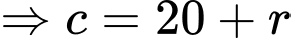
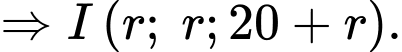
Khi đó, phương trình (*) tương đương với
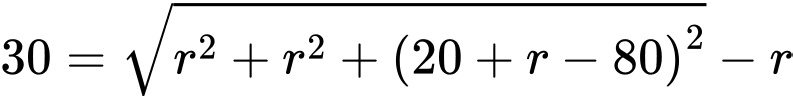
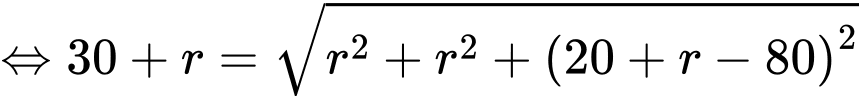
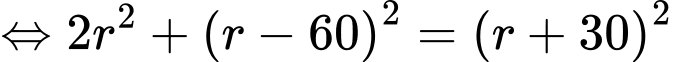
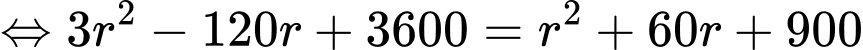
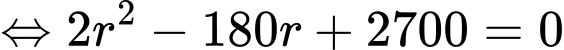
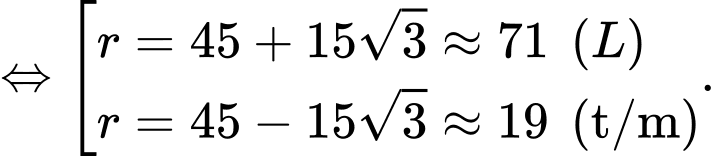
Vậy đường kính của quả bóng là 38 cm.
Note: Để chứng minh bài trên, ta sử dụng bổ đề sau:
Cho một điểm
 bất kì; mặt cầu
bất kì; mặt cầu 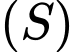 có tâm
có tâm 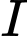 và bán kính
và bán kính 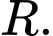 Gọi
Gọi 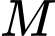 là một điểm di động trên mặt cầu
là một điểm di động trên mặt cầu  Minh hoạ như hình vẽ.
Minh hoạ như hình vẽ.
Khi đó:
+)
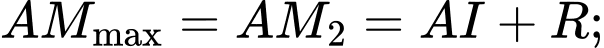
+)