PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1 [134706]: Cho hai biến cố 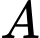 và
và 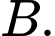 Công thức nào sau đây là công thức đúng tính xác suất của biến cố
Công thức nào sau đây là công thức đúng tính xác suất của biến cố 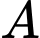 với điều kiện
với điều kiện 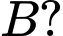
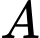 và
và 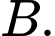 Công thức nào sau đây là công thức đúng tính xác suất của biến cố
Công thức nào sau đây là công thức đúng tính xác suất của biến cố 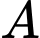 với điều kiện
với điều kiện 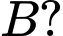
A, 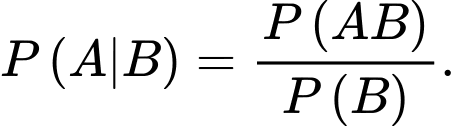
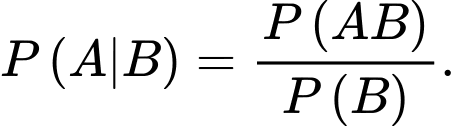
B, 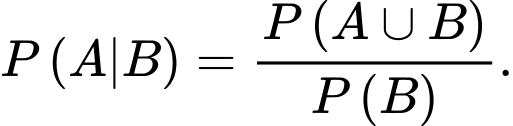
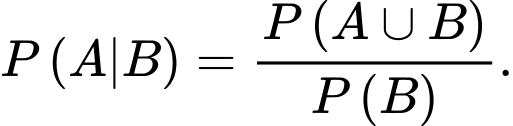
C, 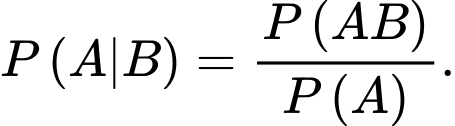
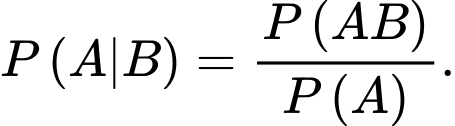
D, 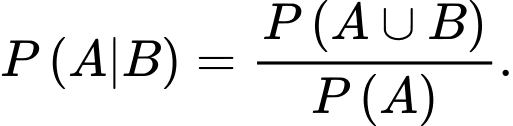
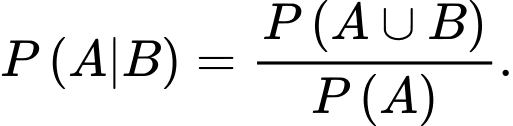
Theo công thức xác suất có điều kiện ta có: 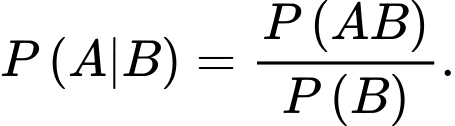
Chọn A. Đáp án: A
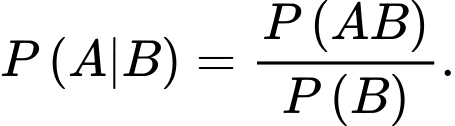
Chọn A. Đáp án: A
Câu 2 [778927]: Cho hai biến cố 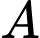 và
và  với
với 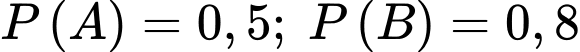 và
và  Tính xác suất của
Tính xác suất của 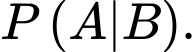
 và
và 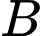 với
với 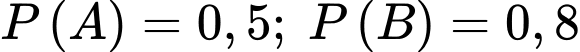 và
và  Tính xác suất của
Tính xác suất của 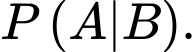
A, 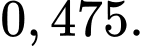
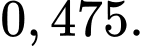
B, 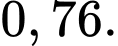
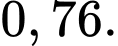
C, 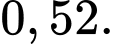
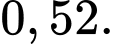
D, 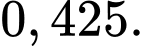
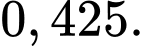
Ta có: 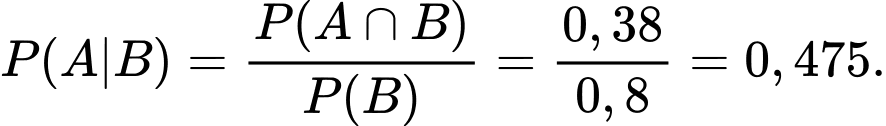 Đáp án: A
Đáp án: A
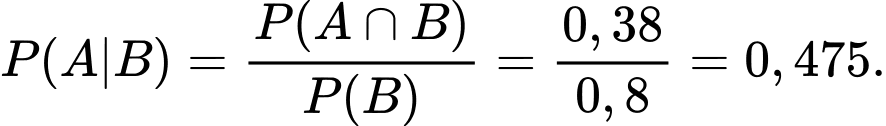 Đáp án: A
Đáp án: A
Câu 3 [134710]: Cho hai biến cố 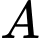 và
và 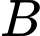 là hai biến cố độc lập. Khẳng định nào dưới đây là đúng.
là hai biến cố độc lập. Khẳng định nào dưới đây là đúng.
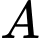 và
và 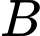 là hai biến cố độc lập. Khẳng định nào dưới đây là đúng.
là hai biến cố độc lập. Khẳng định nào dưới đây là đúng. A, 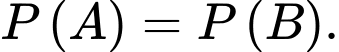
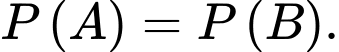
B, 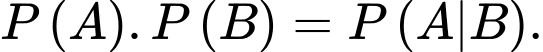
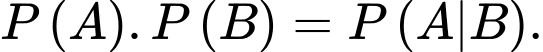
C, 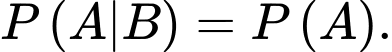
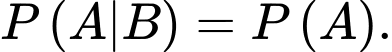
D, 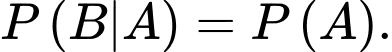
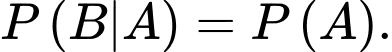
Theo công thức xác suất có điều kiện: 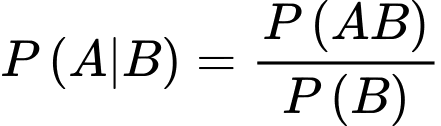
Nếu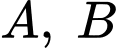 la hai biến cố độc lập ta có:
la hai biến cố độc lập ta có: 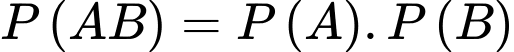
Suy ra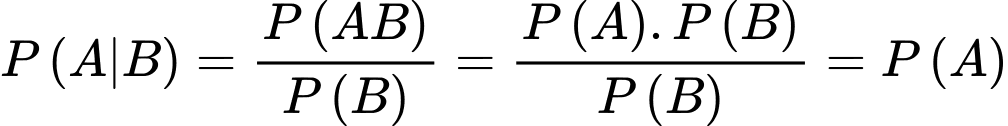 . Chọn C.
Đáp án: C
. Chọn C.
Đáp án: C
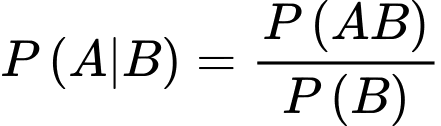
Nếu
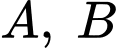 la hai biến cố độc lập ta có:
la hai biến cố độc lập ta có: 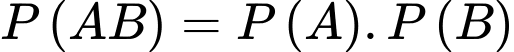
Suy ra
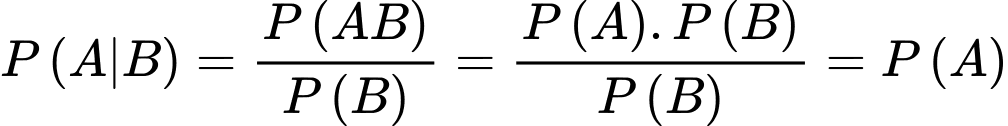 . Chọn C.
Đáp án: C
. Chọn C.
Đáp án: C
Câu 4 [360664]: Cho hai biến cố độc lập 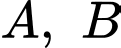 với
với 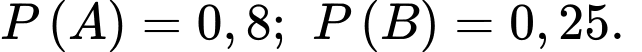 Khi đó,
Khi đó,  bằng:
bằng:
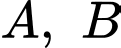 với
với 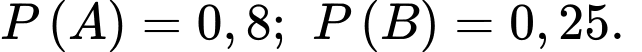 Khi đó,
Khi đó,  bằng:
bằng: A, 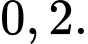
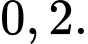
B, 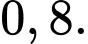
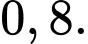
C, 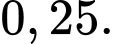
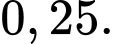
D, 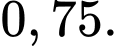
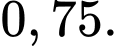
Chọn đáp án C.
Hai biến cố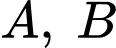 độc lập nên
độc lập nên 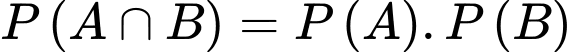
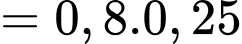
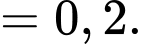
Hai biến cố
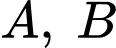 độc lập nên
độc lập nên 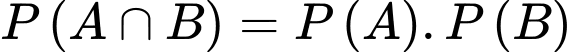
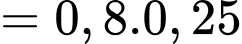
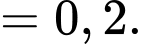
Khi đó, 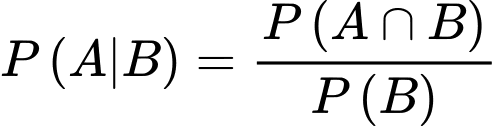
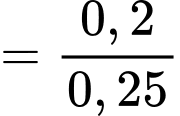
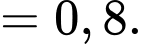
Đáp án: B 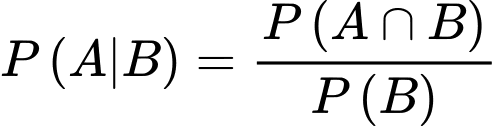
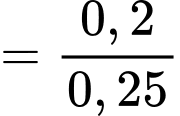
Câu 5 [778928]: Cho hai biến cố 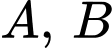 với
với 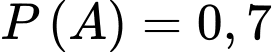 và
và 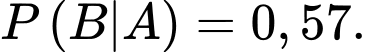 Khi đó,
Khi đó, 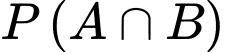 bằng bao nhiêu %?
bằng bao nhiêu %?
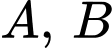 với
với 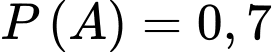 và
và 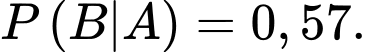 Khi đó,
Khi đó, 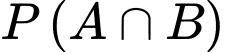 bằng bao nhiêu %?
bằng bao nhiêu %? A, 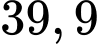
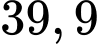
B, 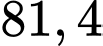
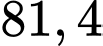
C, 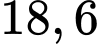
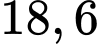
D, 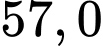
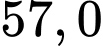
Chọn đáp án A.
Ta có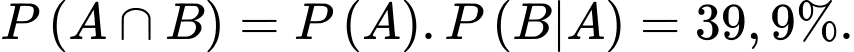 Đáp án: A
Đáp án: A
Ta có
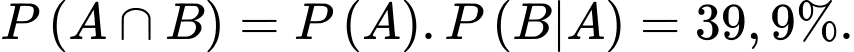 Đáp án: A
Đáp án: A
Câu 6 [360681]: Cho hai biến cố xung khắc 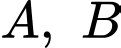 với
với 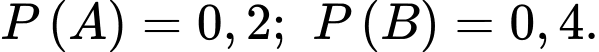 Khi đó,
Khi đó,  bằng:
bằng:
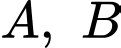 với
với 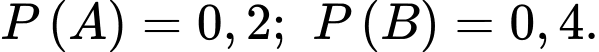 Khi đó,
Khi đó,  bằng:
bằng: A, 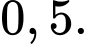
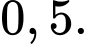
B, 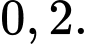
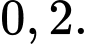
C, 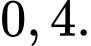
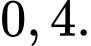
D, 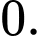
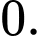
Chọn đáp án D.
Vì A và B là hai biến cố xung khắc nên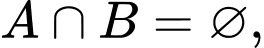 do đó
do đó 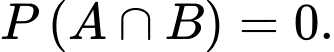
Khi đó,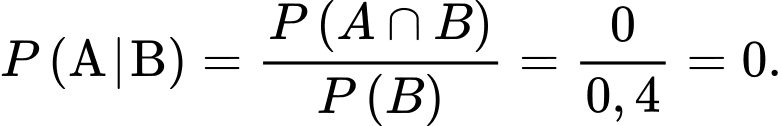 Đáp án: D
Đáp án: D
Vì A và B là hai biến cố xung khắc nên
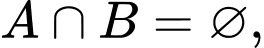 do đó
do đó 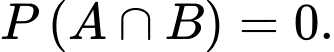
Khi đó,
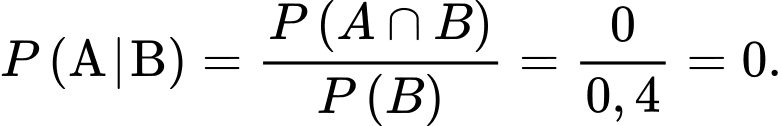 Đáp án: D
Đáp án: D
Câu 7 [778929]: Cho hai biến cố 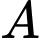 và
và 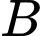 với
với 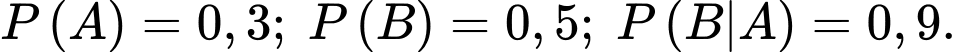 Khi đó xác suất của biến cố
Khi đó xác suất của biến cố  bằng
bằng
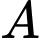 và
và 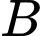 với
với 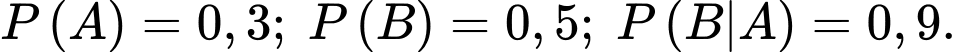 Khi đó xác suất của biến cố
Khi đó xác suất của biến cố  bằng
bằng A, 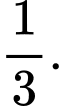
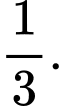
B, 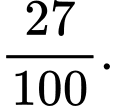
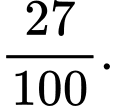
C, 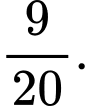
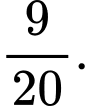
D, 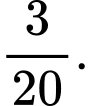
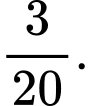
Ta có 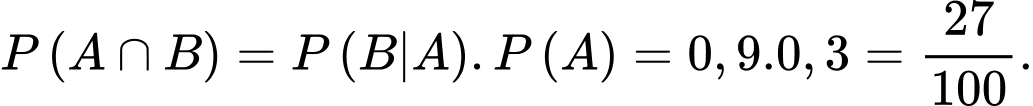 Chọn B. Đáp án: B
Chọn B. Đáp án: B
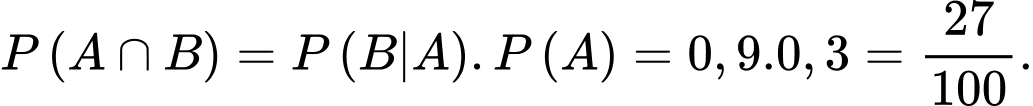 Chọn B. Đáp án: B
Chọn B. Đáp án: B
Câu 8 [778930]: Cho hai biến cố 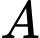 và
và 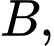 với
với 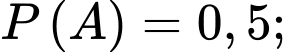
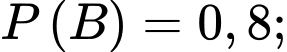
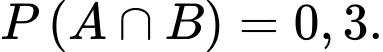 Tính
Tính 
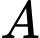 và
và 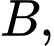 với
với 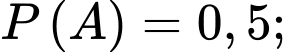
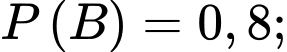
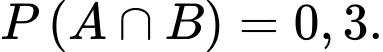 Tính
Tính 
A, 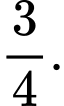
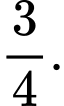
B, 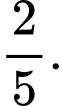
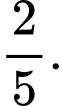
C, 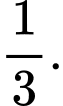
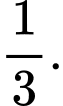
D, 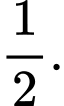
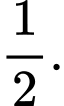
Ta có: 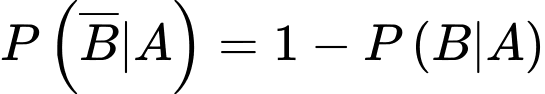
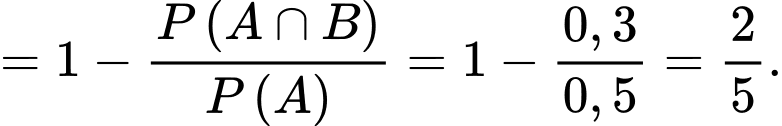 Đáp án: B
Đáp án: B
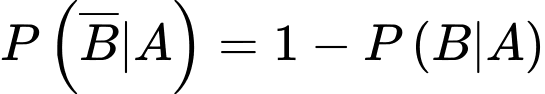
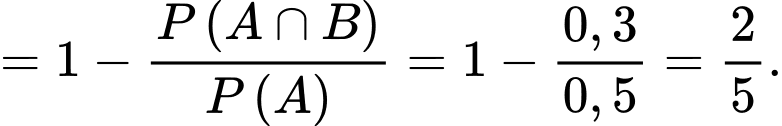 Đáp án: B
Đáp án: B
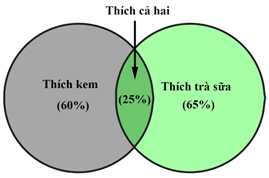
Câu 9 [778931]: Trong cuộc khảo sát trên một nhóm học sinh gồm các bạn thích trà sữa hoặc kem, người ta có được kết quả sau: Có 60% số học sinh thích kem, 65% số học sinh thích trà sữa, 25% số học sinh thích cả trà sữa và kem (xem hình vẽ). Chọn ngẫu nhiên một bạn học sinh trong nhóm được khảo sát này. Tính xác suất để chọn được học sinh thích kem, biết rằng học sinh đó thích trà sữa (kết quả làm tròn đến hàng phần trăm).

A, 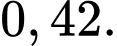
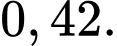
B, 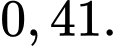
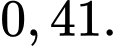
C, 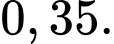
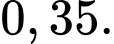
D, 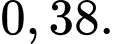
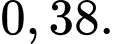
Chọn đáp án D.
Gọi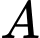 là biến cố “Học sinh đó thích kem”
là biến cố “Học sinh đó thích kem”
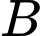 là biến cố “Học sinh đó thích trà sữa”
là biến cố “Học sinh đó thích trà sữa”
Từ giả thiết, ta có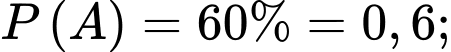
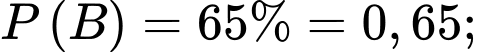
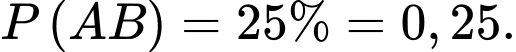
Yêu cầu bài toán là tính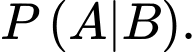
Áp dụng công thức tính xác suất có điều kiện, ta có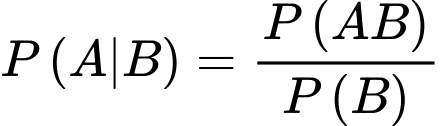
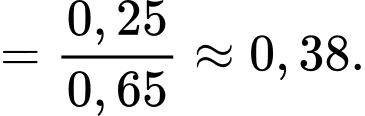 Đáp án: D
Đáp án: D
Gọi
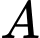 là biến cố “Học sinh đó thích kem”
là biến cố “Học sinh đó thích kem”
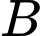 là biến cố “Học sinh đó thích trà sữa”
là biến cố “Học sinh đó thích trà sữa”
Từ giả thiết, ta có
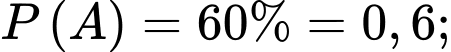
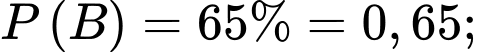
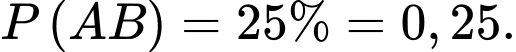
Yêu cầu bài toán là tính
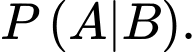
Áp dụng công thức tính xác suất có điều kiện, ta có
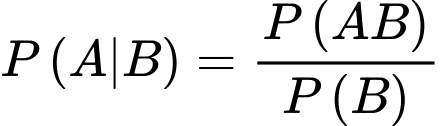
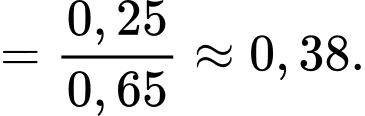 Đáp án: D
Đáp án: D
Câu 10 [778932]: Một nhóm học sinh có 30 học sinh, trong đó có 16 em học khá môn Toán, 25 em học khá môn Hóa học, 12 em học khá cả hai môn Toán và Hóa học. Chọn ngẫu nhiên một học sinh trong số đó. Tính xác suất để học sinh đó học khá môn Toán biết rằng học sinh đó học khá môn Hóa học.
A, 
B, 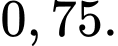
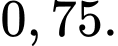
C, 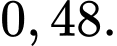
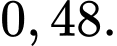
D, 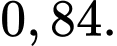
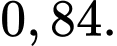
Chọn C
Gọi A là biến cố: “Học sinh đó học khá môn Toán”, B là biến cố: “Học sinh đó học khá môn Hóa học”.
Từ bài ra ta có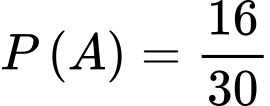 ,
, 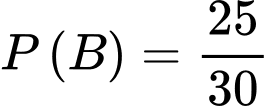 ;
; 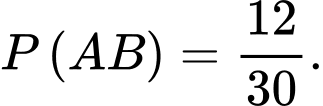
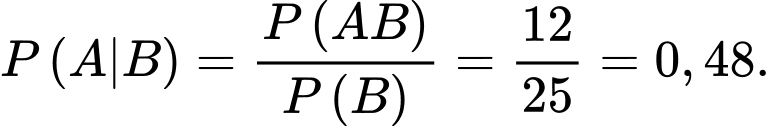 Đáp án: C
Đáp án: C
Gọi A là biến cố: “Học sinh đó học khá môn Toán”, B là biến cố: “Học sinh đó học khá môn Hóa học”.
Từ bài ra ta có
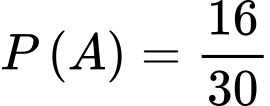 ,
, 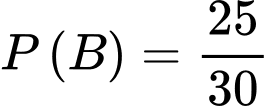 ;
; 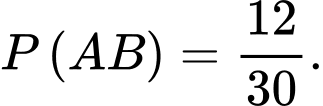
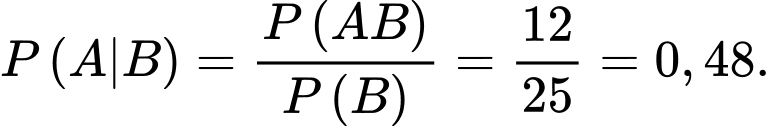 Đáp án: C
Đáp án: C
Câu 11 [778934]: Lớp 12A1 có 25 học sinh nam và 15 học sinh nữ. Trong số đó có 16 bạn nam và 6 bạn nữ thích chơi thể thao. Chọn một bạn bất kì của lớp 12A1, tính xác suất học sinh được chọn thích chơi thể thao, biết rằng học sinh đó là nữ.
A, 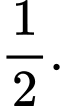
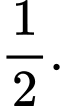
B, 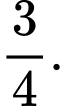
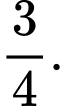
C, 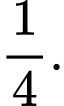
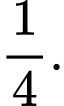
D, 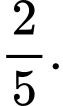
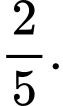
Số phần tử của không gian mẫu: 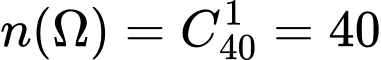 .
.
Gọi A là biến cố “học sinh được chọn là nữ” và B là biến cố “học sinh được chọn thích chơi thể thao”
Ta có: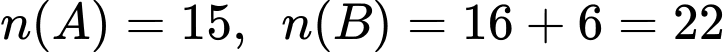 .
.
Ta có: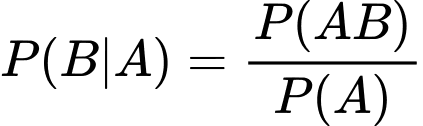
Trong đó:
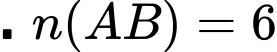 . Suy ra
. Suy ra 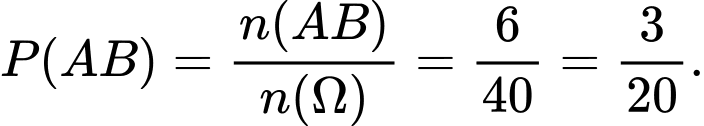
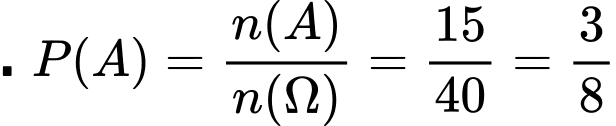 .
.
Vậy xác suất cần tìm là: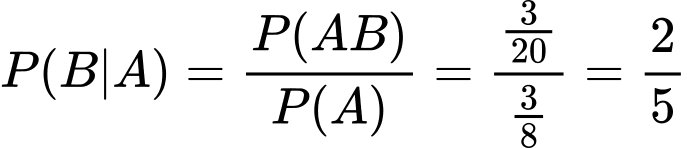 .
Đáp án: D
.
Đáp án: D
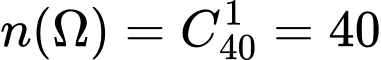 .
.Gọi A là biến cố “học sinh được chọn là nữ” và B là biến cố “học sinh được chọn thích chơi thể thao”
Ta có:
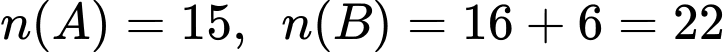 .
.Ta có:
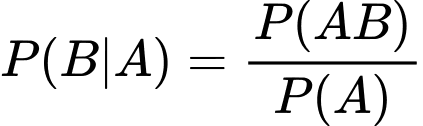
Trong đó:
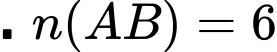 . Suy ra
. Suy ra 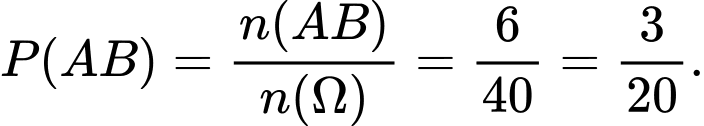
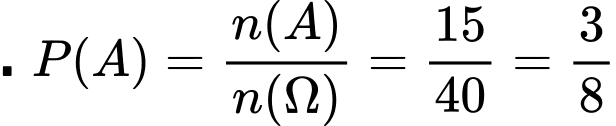 .
. Vậy xác suất cần tìm là:
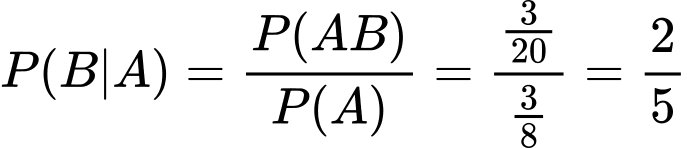 .
Đáp án: D
.
Đáp án: D
Câu 12 [778938]: Một bình đựng 5 viên bi kích thước và chất liệu giống nhau, chỉ khác nhau về màu sắc. Trong đó có 3 viên bi xanh và 2 viên bi đỏ. Lấy ngẫu nhiên từ bình ra một viên bi ta được viên bi màu xanh, rồi lại lấy ngẫu nhiên ra một viên bi nữa. Tính xác suất để lấy được viên bi đỏ ở lần thứ hai.
A, 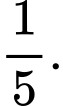
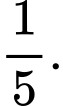
B, 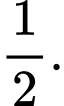
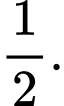
C, 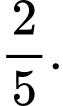
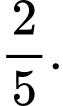
D, 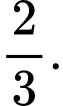
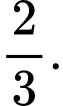
Chọn B
Gọi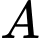 là biến cố “lấy viên bi thứ nhất là màu xanh”.
là biến cố “lấy viên bi thứ nhất là màu xanh”.
Gọi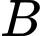 là biến cố “lấy viên bi thứ hai là màu đỏ”.
là biến cố “lấy viên bi thứ hai là màu đỏ”.
Ta đi tính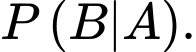
Ta có: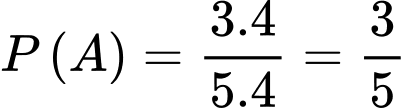 ;
; 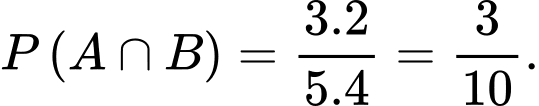 Do đó:
Do đó: 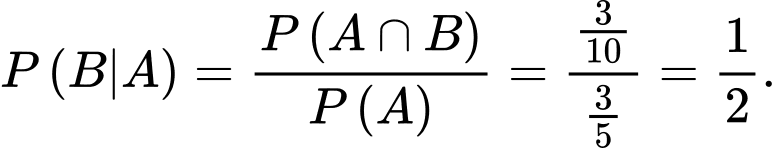 Đáp án: B
Đáp án: B
Gọi
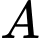 là biến cố “lấy viên bi thứ nhất là màu xanh”.
là biến cố “lấy viên bi thứ nhất là màu xanh”.Gọi
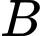 là biến cố “lấy viên bi thứ hai là màu đỏ”.
là biến cố “lấy viên bi thứ hai là màu đỏ”.Ta đi tính
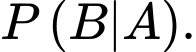
Ta có:
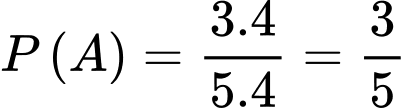 ;
; 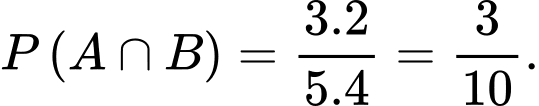 Do đó:
Do đó: 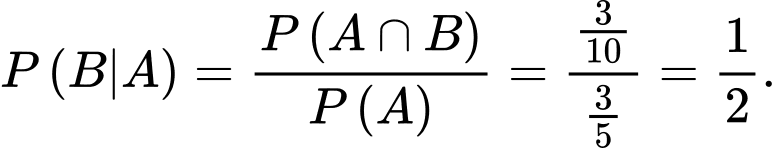 Đáp án: B
Đáp án: B PHẦN II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a),b),c),d) ở mỗi câu học sinh chọn đúng hoặc sai.
Câu 13 [778940]: Cho hai biến cố 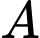 ,
,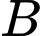 với
với 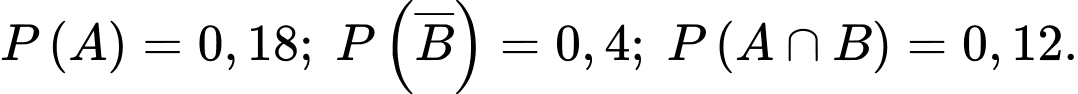
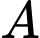 ,
,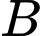 với
với 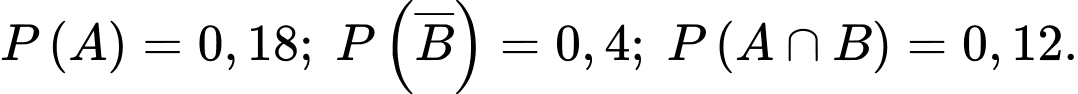
a) Đúng.
Ta có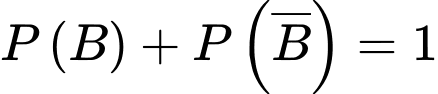
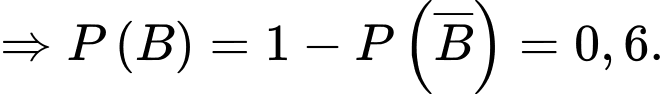
b) Đúng.
Áp dụng công thức xác suất có điều kiện, ta có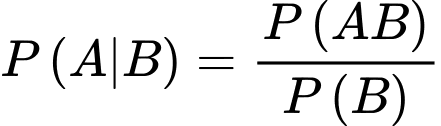
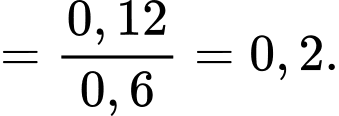
c) Sai.
Ta có hai biến cố và
và 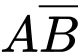 là xung khắc lẫn nhau nên ta có được
là xung khắc lẫn nhau nên ta có được 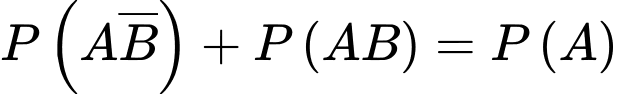
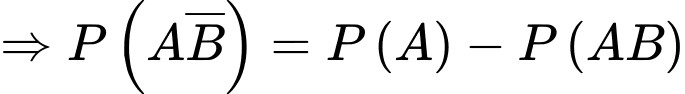
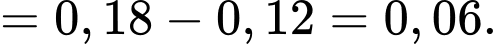
d) Sai.
Áp dụng công thức xác suất có điều kiện, ta có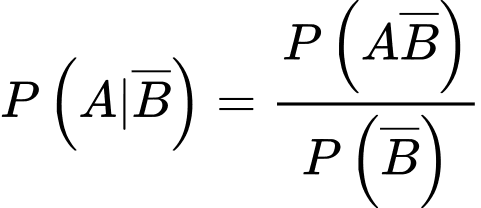
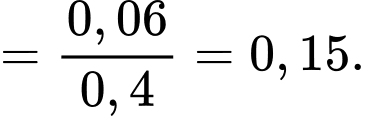
Ta có
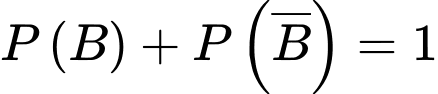
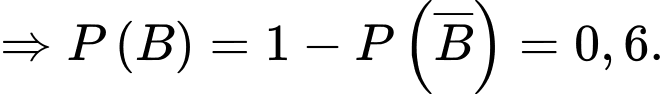
b) Đúng.
Áp dụng công thức xác suất có điều kiện, ta có
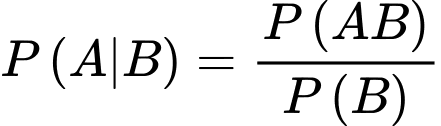
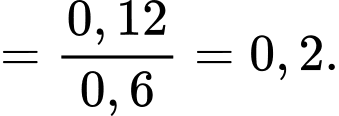
c) Sai.
Ta có hai biến cố
 và
và 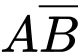 là xung khắc lẫn nhau nên ta có được
là xung khắc lẫn nhau nên ta có được 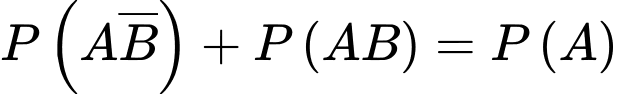
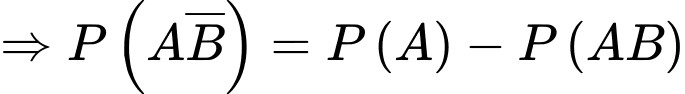
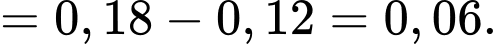
d) Sai.
Áp dụng công thức xác suất có điều kiện, ta có
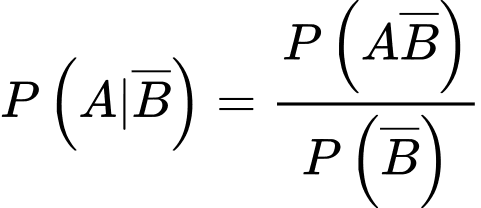
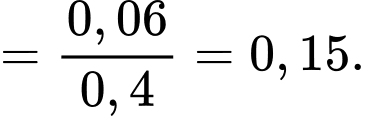
Câu 14 [778941]: Một phòng nghiên cứu dược học cho 500 người bị bệnh H dùng hai loại thuốc X, Y để
điều trị. Một số người được điều trị bằng thuốc X và số người còn lại được điều trị bằng thuốc Y. Kết quả nghiên cứu được trình bày ở bảng sau đây
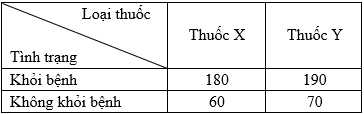
Chọn ngẫu nhiên một người trong số này. Gọi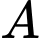 là biến cố "Người được chọn khỏi bệnh",
là biến cố "Người được chọn khỏi bệnh", 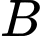 là biến cố "Người được chọn điều trị bằng thuốc X",
là biến cố "Người được chọn điều trị bằng thuốc X",  là biến cố "Người được chọn điều trị bằng thuốc Y".
là biến cố "Người được chọn điều trị bằng thuốc Y".
điều trị. Một số người được điều trị bằng thuốc X và số người còn lại được điều trị bằng thuốc Y. Kết quả nghiên cứu được trình bày ở bảng sau đây

Chọn ngẫu nhiên một người trong số này. Gọi
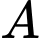 là biến cố "Người được chọn khỏi bệnh",
là biến cố "Người được chọn khỏi bệnh", 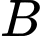 là biến cố "Người được chọn điều trị bằng thuốc X",
là biến cố "Người được chọn điều trị bằng thuốc X",  là biến cố "Người được chọn điều trị bằng thuốc Y".
là biến cố "Người được chọn điều trị bằng thuốc Y".
Từ dữ kiện đề bài, ta có 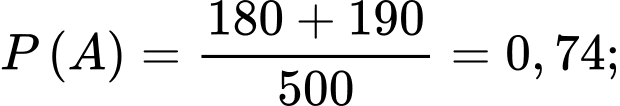
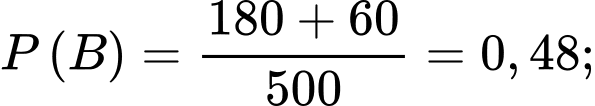
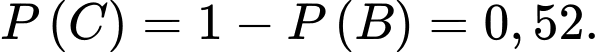
a) Đúng.
b) Đúng.
Xác suất chọn được người điều trị bằng thuốc X khỏi bệnh bằng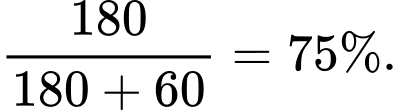
c) Sai.
 là xác suất người được chọn khỏi bệnh biết người đó điều trị bằng thuốc Y, nên ta có
là xác suất người được chọn khỏi bệnh biết người đó điều trị bằng thuốc Y, nên ta có 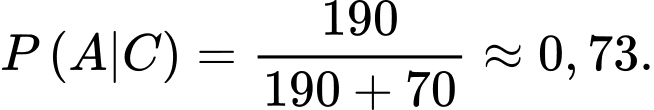
d) Sai.
Để xác định được thuốc nào có hiệu quả hơn thì ta so sánh xác suất khỏi bệnh khi dùng thuốc đó. Ta có tỉ lệ khỏi bệnh khi dùng thuốc X:Y là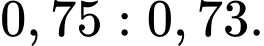 Từ đó ta thấy được thuốc X hiệu quả hơn thuốc Y.
Từ đó ta thấy được thuốc X hiệu quả hơn thuốc Y.
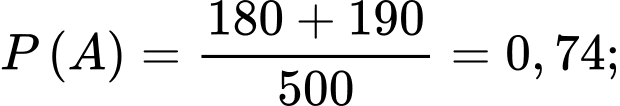
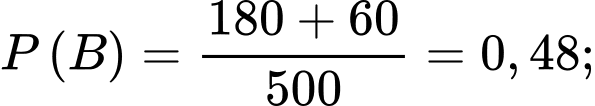
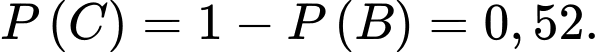
a) Đúng.
b) Đúng.
Xác suất chọn được người điều trị bằng thuốc X khỏi bệnh bằng
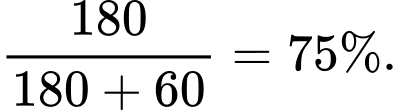
c) Sai.
 là xác suất người được chọn khỏi bệnh biết người đó điều trị bằng thuốc Y, nên ta có
là xác suất người được chọn khỏi bệnh biết người đó điều trị bằng thuốc Y, nên ta có 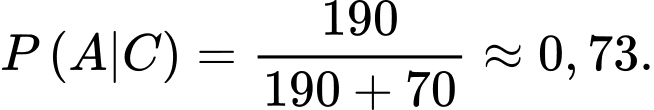
d) Sai.
Để xác định được thuốc nào có hiệu quả hơn thì ta so sánh xác suất khỏi bệnh khi dùng thuốc đó. Ta có tỉ lệ khỏi bệnh khi dùng thuốc X:Y là
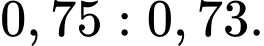 Từ đó ta thấy được thuốc X hiệu quả hơn thuốc Y.
Từ đó ta thấy được thuốc X hiệu quả hơn thuốc Y.
Câu 15 [778942]: Ba sinh viên A, B, C cùng làm bài thi một cách độc lập. Xác suất làm được bài thi của từng sinh viên A, B, C tương ứng là 0,6; 0,7 và 0,8.
Ta có xác suất làm được bài thi của từng sinh viên A, B, C tương ứng là 0,6; 0,7; 0,8 nên xác suất không làm được bài thi tương ứng là 0,4; 0,3; 0,2.
a) Đúng.
Vì 3 sinh viên A, B, C làm bài thi 1 cách độc lập nên xác suất để cả 3 sinh viên đều làm được bài là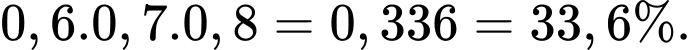
b) Sai.
Xác suất để chỉ sinh viên C làm được bài (tức A và B đều không làm được bài) là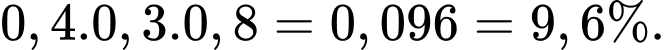
c) Đúng.
Gọi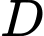 là biến cố “Có đúng 1 sinh viên làm được bài”.
là biến cố “Có đúng 1 sinh viên làm được bài”.
Có 3 TH xảy ra là
TH1: A làm được bài và B, C không làm được bài có xác suất bằng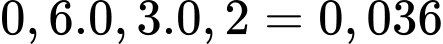
TH2: B làm được bài và A, C không làm được bài có xác suất bằng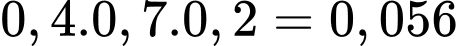
TH3: C làm được bài và A, B không làm được bài có xác suất bằng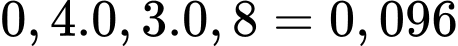
Khi đó, xác suất có đúng 1 sinh viên làm được bài bằng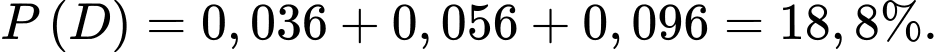
d) Sai.
Gọi là biến cố “Sinh viên C làm được bài”
là biến cố “Sinh viên C làm được bài”
Yêu cầu bài toán Tính
Tính 
(dựa vào kết quả tính toán từ phần c) , ta có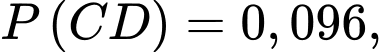
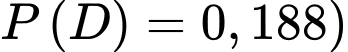
Áp dụng công thức xác suất có điều kiện, ta có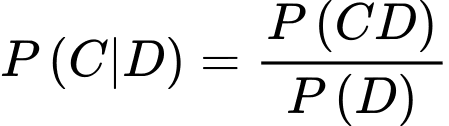
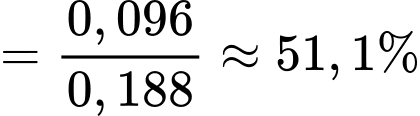
a) Đúng.
Vì 3 sinh viên A, B, C làm bài thi 1 cách độc lập nên xác suất để cả 3 sinh viên đều làm được bài là
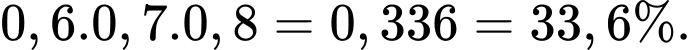
b) Sai.
Xác suất để chỉ sinh viên C làm được bài (tức A và B đều không làm được bài) là
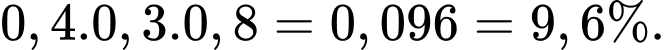
c) Đúng.
Gọi
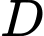 là biến cố “Có đúng 1 sinh viên làm được bài”.
là biến cố “Có đúng 1 sinh viên làm được bài”.Có 3 TH xảy ra là
TH1: A làm được bài và B, C không làm được bài có xác suất bằng
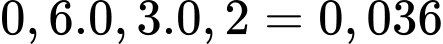
TH2: B làm được bài và A, C không làm được bài có xác suất bằng
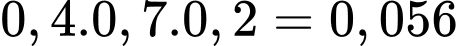
TH3: C làm được bài và A, B không làm được bài có xác suất bằng
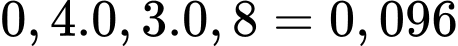
Khi đó, xác suất có đúng 1 sinh viên làm được bài bằng
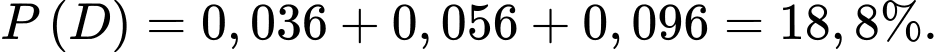
d) Sai.
Gọi
 là biến cố “Sinh viên C làm được bài”
là biến cố “Sinh viên C làm được bài”Yêu cầu bài toán
 Tính
Tính 
(dựa vào kết quả tính toán từ phần c) , ta có
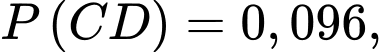
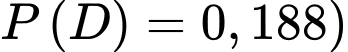
Áp dụng công thức xác suất có điều kiện, ta có
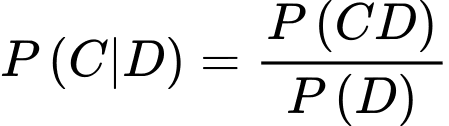
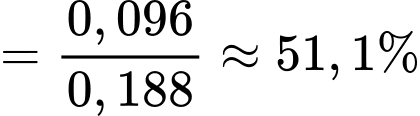
Câu 16 [702324]: Trong 1 lô hàng 10 sản phẩm có 2 sản phẩm xấu còn lại là các sản phẩm tốt, chọn ngẫu nhiên không hoàn lại mỗi lần một sản phẩm để phát hiện ra 2 sản phẩm xấu, khi nào chọn được sản phẩm xấu thứ 2 thì dừng lại.
a) Sai.
Xác suất lần thứ nhất chọn được một sản phẩm xấu là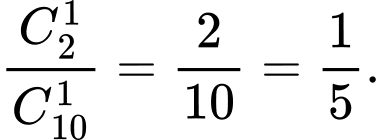
b) Sai.
Xác suất dừng lại ở lần chọn thứ hai (tức lần 1 và lần 2 đều chọn được sản phẩm xấu) là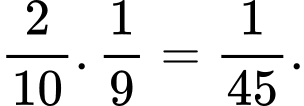
c) Sai.
Gọi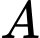 là biến cố “Dừng lại ở lần chọn thứ 3”.
là biến cố “Dừng lại ở lần chọn thứ 3”.
Để dừng lại ở lần thứ 3, có 2 trường hợp xảy ra:
+) Lần 1 lấy được sản phẩm xấu, lần 2 và lần 3 lấy được sản phẩm tốt;
+) Lần 2 lấy được sản phẩm xấu, lần 1 và lần 3 lấy được sản phẩm tốt;
Khi đó, xác suất dừng lại ở lần chọn thứ 3 là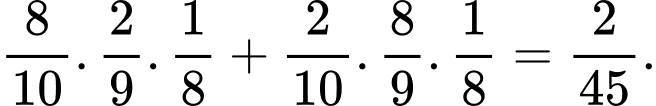
d) Đúng.
Gọi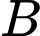 là biến cố “Lần đầu chọn được sản phẩm xấu”
là biến cố “Lần đầu chọn được sản phẩm xấu”
Ta có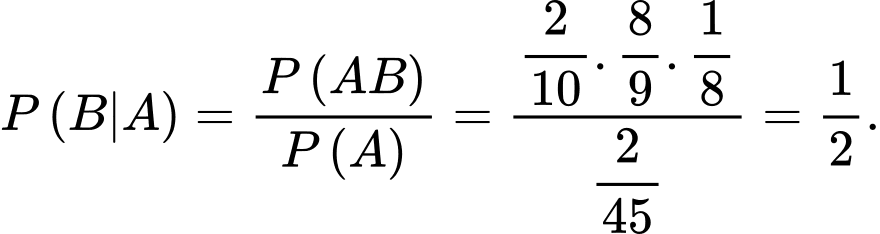
Xác suất lần thứ nhất chọn được một sản phẩm xấu là
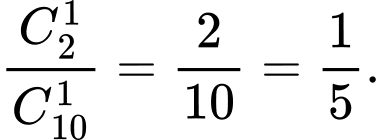
b) Sai.
Xác suất dừng lại ở lần chọn thứ hai (tức lần 1 và lần 2 đều chọn được sản phẩm xấu) là
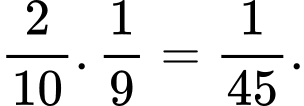
c) Sai.
Gọi
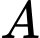 là biến cố “Dừng lại ở lần chọn thứ 3”.
là biến cố “Dừng lại ở lần chọn thứ 3”.Để dừng lại ở lần thứ 3, có 2 trường hợp xảy ra:
+) Lần 1 lấy được sản phẩm xấu, lần 2 và lần 3 lấy được sản phẩm tốt;
+) Lần 2 lấy được sản phẩm xấu, lần 1 và lần 3 lấy được sản phẩm tốt;
Khi đó, xác suất dừng lại ở lần chọn thứ 3 là
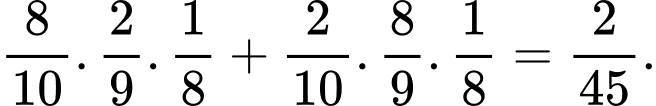
d) Đúng.
Gọi
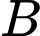 là biến cố “Lần đầu chọn được sản phẩm xấu”
là biến cố “Lần đầu chọn được sản phẩm xấu”Ta có
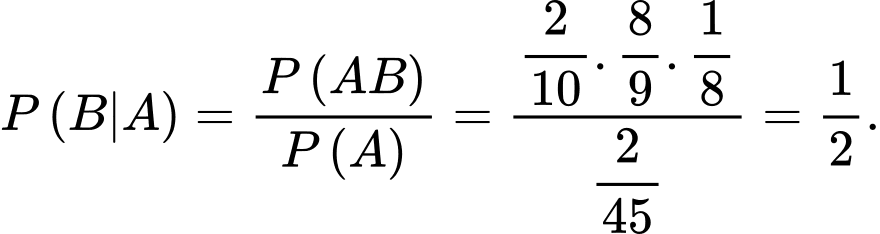
PHẦN III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 17 đến câu 22.
Câu 17 [778945]: Một chiếc máy có 3 động cơ 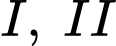 và
và 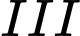 chạy độc lập nhau. Khả năng để động cơ
chạy độc lập nhau. Khả năng để động cơ 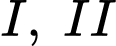 và
và 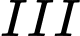 hoạt động tốt trong ngày lần lượt là
hoạt động tốt trong ngày lần lượt là 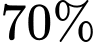 ,
, 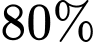 và
và 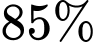 . Xác suất để có ít nhất 1 động cơ chạy tốt trong ngày là bao nhiêu phần trăm (kết quả viết dưới dạng số thập phân).
. Xác suất để có ít nhất 1 động cơ chạy tốt trong ngày là bao nhiêu phần trăm (kết quả viết dưới dạng số thập phân).
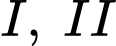 và
và 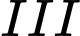 chạy độc lập nhau. Khả năng để động cơ
chạy độc lập nhau. Khả năng để động cơ 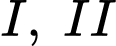 và
và 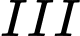 hoạt động tốt trong ngày lần lượt là
hoạt động tốt trong ngày lần lượt là 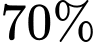 ,
, 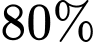 và
và 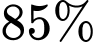 . Xác suất để có ít nhất 1 động cơ chạy tốt trong ngày là bao nhiêu phần trăm (kết quả viết dưới dạng số thập phân).
. Xác suất để có ít nhất 1 động cơ chạy tốt trong ngày là bao nhiêu phần trăm (kết quả viết dưới dạng số thập phân).
Điền đáp án: 99,1.
Từ giả thiết, ta có khả năng để động cơ I, II, III hoạt động không tốt trong ngày lần lượt là 30%, 20%, 15%.
Xác suất để không có động cơ nào chạy tốt trong ngày bằng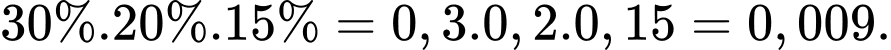
Suy ra xác suất để có ít nhất 1 động cơ chạy tốt bằng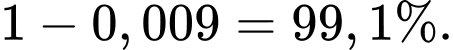
Từ giả thiết, ta có khả năng để động cơ I, II, III hoạt động không tốt trong ngày lần lượt là 30%, 20%, 15%.
Xác suất để không có động cơ nào chạy tốt trong ngày bằng
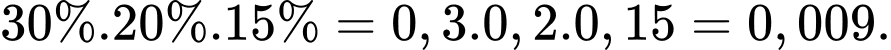
Suy ra xác suất để có ít nhất 1 động cơ chạy tốt bằng
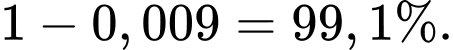
Câu 18 [778949]: Tại một trường học, tỷ lệ học sinh thích chơi cầu lông là 20%, tỷ lệ học sinh thích chơi bóng chuyền 14%, tỷ lệ học sinh vừa thích chơi cầu lông vừa thích chơi bóng chuyền là 9%. Chọn ngẫu nhiên một học sinh ở trường học này. Nếu biết học sinh đó thích chơi bóng chuyền thì xác suất học sinh đó không thích chơi cầu lông là bao nhiêu phần trăm? (viết kết quả làm tròn đến hàng phần chục).
Điền đáp án: 0,4.
Gọi là biến cố “Học sinh đó thích chơi cầu lông”;
là biến cố “Học sinh đó thích chơi cầu lông”;  là biến cố “Học sinh đó không thích chơi cầu lông”.
là biến cố “Học sinh đó không thích chơi cầu lông”.
Gọi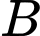 là biến cố “Học sinh đó thích chơi bóng chuyền”;
là biến cố “Học sinh đó thích chơi bóng chuyền”; 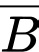 là biến cố “Học sinh đó không thích chơi bóng chuyền”.
là biến cố “Học sinh đó không thích chơi bóng chuyền”.
Từ giả thiết, ta có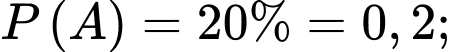
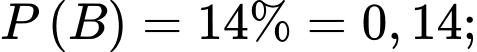
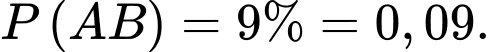
Vì hai biến cố và
và  là hai biến cố xung khắc lẫn nhau nên ta có
là hai biến cố xung khắc lẫn nhau nên ta có 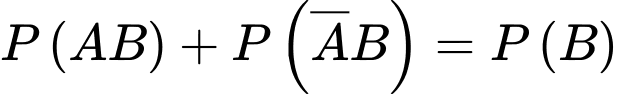
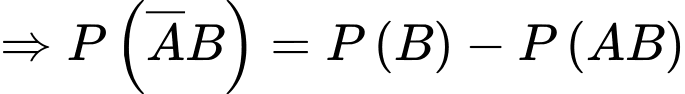
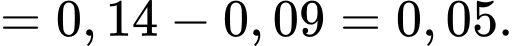
Yêu cầu bài toán Tính
Tính 
Áp dụng công thức tính xác suất có điều kiện, ta có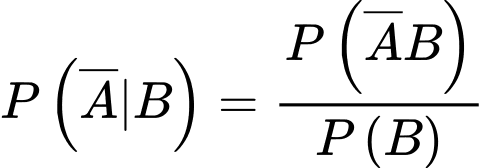
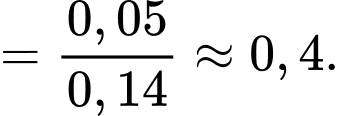
Gọi
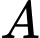 là biến cố “Học sinh đó thích chơi cầu lông”;
là biến cố “Học sinh đó thích chơi cầu lông”;  là biến cố “Học sinh đó không thích chơi cầu lông”.
là biến cố “Học sinh đó không thích chơi cầu lông”.
Gọi
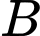 là biến cố “Học sinh đó thích chơi bóng chuyền”;
là biến cố “Học sinh đó thích chơi bóng chuyền”; 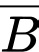 là biến cố “Học sinh đó không thích chơi bóng chuyền”.
là biến cố “Học sinh đó không thích chơi bóng chuyền”.
Từ giả thiết, ta có
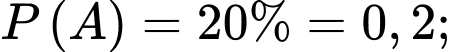
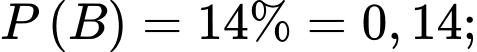
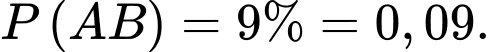
Vì hai biến cố
 và
và  là hai biến cố xung khắc lẫn nhau nên ta có
là hai biến cố xung khắc lẫn nhau nên ta có 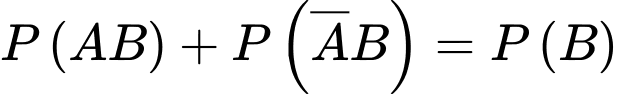
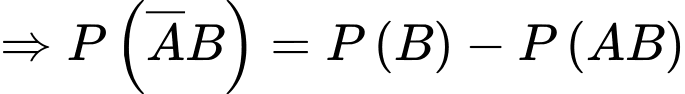
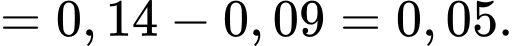
Yêu cầu bài toán
 Tính
Tính 
Áp dụng công thức tính xác suất có điều kiện, ta có
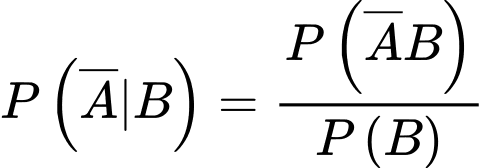
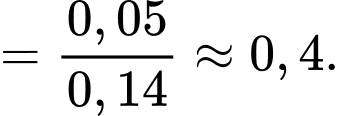
Câu 19 [778951]: Một cửa hàng sách ước lượng rằng: trong tổng số các khách hàng đến cửa hàng có 30% khách cần hỏi nhân viên bán hàng, 20% khách mua sách và 15% khách thực hiện cả hai điều trên. Gặp ngẫu nhiên một khách trong nhà sách. Tính xác suất để người này không mua sách, biết rằng người này đã hỏi nhân viên bán hàng.
Điền đáp án: 0,5.
Gọi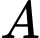 là biến cố “Khách hàng đó hỏi nhân viên bán hàng”;
là biến cố “Khách hàng đó hỏi nhân viên bán hàng”;  là biến cố “Khách hàng đó không hỏi nhân viên bán hàng”.
là biến cố “Khách hàng đó không hỏi nhân viên bán hàng”.
Gọi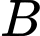 là biến cố “Khách hàng đó mua sách”;
là biến cố “Khách hàng đó mua sách”; 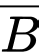 là biến cố “Khách hàng đó không mua sách”.
là biến cố “Khách hàng đó không mua sách”.
Từ giả thiết, ta có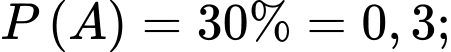
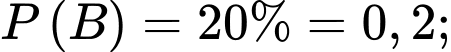
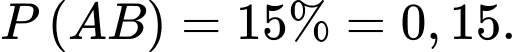
Vì hai biến cố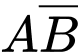 và
và  là hai biến cố xung khắc lẫn nhau nên ta có
là hai biến cố xung khắc lẫn nhau nên ta có 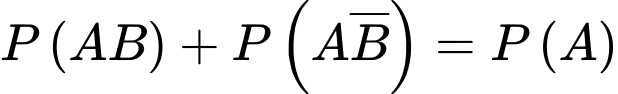
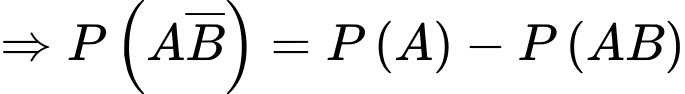
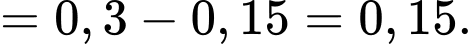
Yêu cầu bài toán Tính
Tính 
Áp dụng công thức tính xác suất có điều kiện, ta có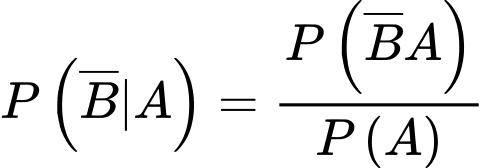
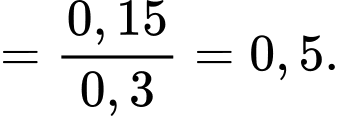
Gọi
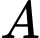 là biến cố “Khách hàng đó hỏi nhân viên bán hàng”;
là biến cố “Khách hàng đó hỏi nhân viên bán hàng”;  là biến cố “Khách hàng đó không hỏi nhân viên bán hàng”.
là biến cố “Khách hàng đó không hỏi nhân viên bán hàng”.
Gọi
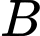 là biến cố “Khách hàng đó mua sách”;
là biến cố “Khách hàng đó mua sách”; 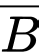 là biến cố “Khách hàng đó không mua sách”.
là biến cố “Khách hàng đó không mua sách”.
Từ giả thiết, ta có
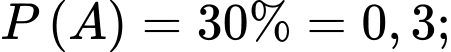
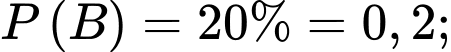
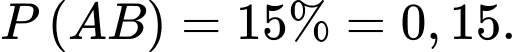
Vì hai biến cố
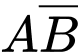 và
và  là hai biến cố xung khắc lẫn nhau nên ta có
là hai biến cố xung khắc lẫn nhau nên ta có 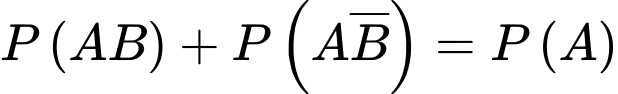
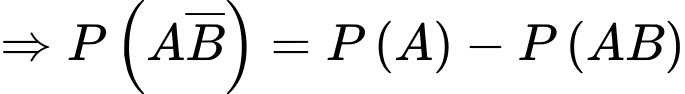
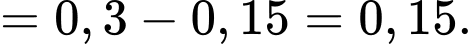
Yêu cầu bài toán
 Tính
Tính 
Áp dụng công thức tính xác suất có điều kiện, ta có
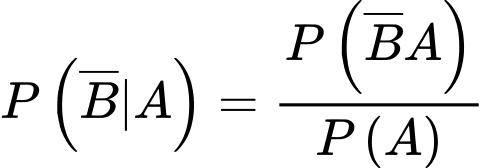
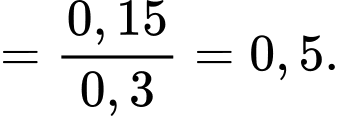
Câu 20 [778952]: Có ba người A, B và C cùng phỏng vấn xin việc ở một công ty. Xác suất trúng tuyển của mỗi người lần lượt là 0,8; 0,6 và 0,7. Việc trúng tuyển của mỗi người là độc lập. Biết rằng có đúng hai người trúng tuyển. Tính xác suất để hai người đó là A và B (viết kết quả làm tròn đến hàng phần trăm).
Điền đáp án: 0,32.
Từ giả thiết, ta có:
Xác suất trúng tuyển của A là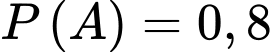 suy ra xác suất không trúng tuyển của A là
suy ra xác suất không trúng tuyển của A là 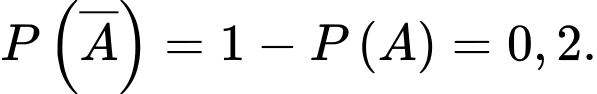
Xác suất trúng tuyển của B là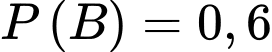 suy ra xác suất không trúng tuyển của B là
suy ra xác suất không trúng tuyển của B là 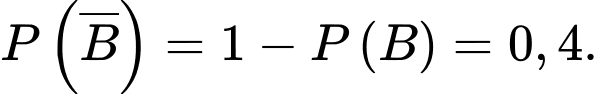
Xác suất trúng tuyển của C là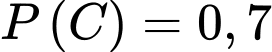 suy ra xác suất không trúng tuyển của C là
suy ra xác suất không trúng tuyển của C là 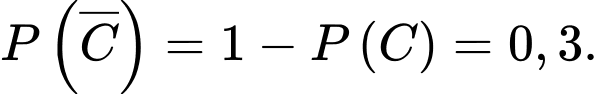
Từ giả thiết, ta suy ra xác suất không trúng tuyển của A, B, C lần lượt là 0,2; 0,4; 0,3.
Có đúng hai người trúng tuyển sẽ có 3 trường hợp xảy ra:
TH1: A và B trúng tuyển; C không trúng tuyển: có xác suất là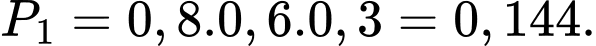
TH2: B và C trúng tuyển; A không trúng tuyển: có xác suất là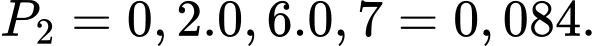
TH3: A và C trúng tuyển; B không trúng tuyển: có xác suất là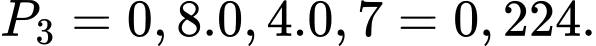
Suy ra xác suất có đúng 2 người trúng tuyển là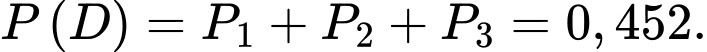
Khi đó, xác suất để hai người trúng tuyển là A và B khi biết rằng có đúng hai người trúng tuyển bằng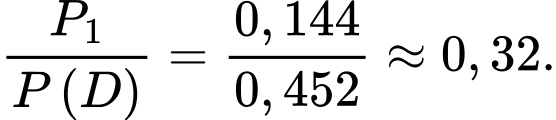
Từ giả thiết, ta có:
Xác suất trúng tuyển của A là
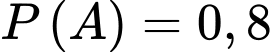 suy ra xác suất không trúng tuyển của A là
suy ra xác suất không trúng tuyển của A là 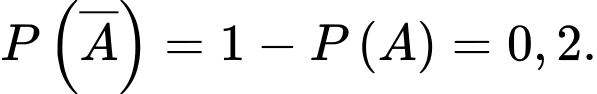
Xác suất trúng tuyển của B là
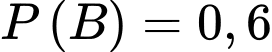 suy ra xác suất không trúng tuyển của B là
suy ra xác suất không trúng tuyển của B là 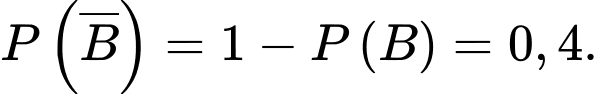
Xác suất trúng tuyển của C là
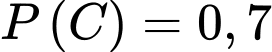 suy ra xác suất không trúng tuyển của C là
suy ra xác suất không trúng tuyển của C là 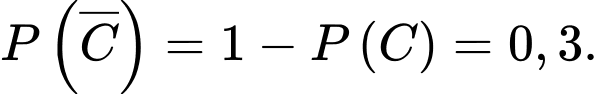
Từ giả thiết, ta suy ra xác suất không trúng tuyển của A, B, C lần lượt là 0,2; 0,4; 0,3.
Có đúng hai người trúng tuyển sẽ có 3 trường hợp xảy ra:
TH1: A và B trúng tuyển; C không trúng tuyển: có xác suất là
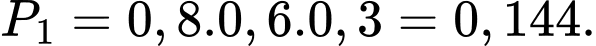
TH2: B và C trúng tuyển; A không trúng tuyển: có xác suất là
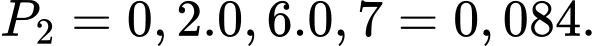
TH3: A và C trúng tuyển; B không trúng tuyển: có xác suất là
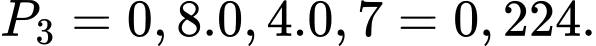
Suy ra xác suất có đúng 2 người trúng tuyển là
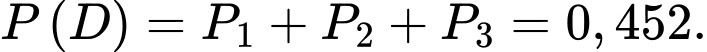
Khi đó, xác suất để hai người trúng tuyển là A và B khi biết rằng có đúng hai người trúng tuyển bằng
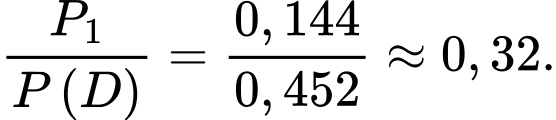
Câu 21 [778953]: Một thủ quỹ có một chùm chìa khóa gồm 12 chiếc bề ngoài giống hệt nhau, trong đó có 4 chìa mở được cửa chính của thư viện. Cô ta thử từng chìa một một cách ngẫu nhiên, chìa nào không trúng thì bỏ ra. Xác suất để cô ta mở được cửa chính của thư viện ở lần mở thứ 5 là bao nhiêu % (kết quả làm tròn đến hàng phần mười).
Điền đáp án: 70,1.
Không gian mẫu là số cách lấy chìa trong 5 lần và bằng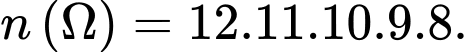
Số cách lấy để cô ấy mở được cửa chính ở lần mở thứ 5 là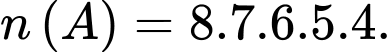
Xác suất cần tính bằng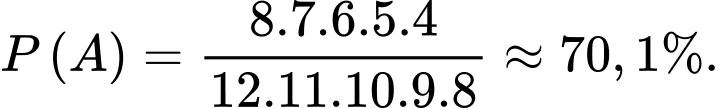
Không gian mẫu là số cách lấy chìa trong 5 lần và bằng
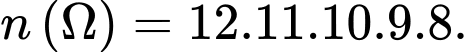
Số cách lấy để cô ấy mở được cửa chính ở lần mở thứ 5 là
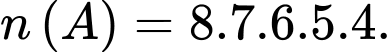
Xác suất cần tính bằng
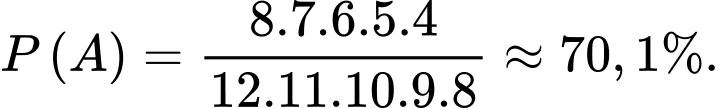
Câu 22 [778955]: Để thành lập đội tuyển quốc gia về một môn học, người ta tổ chức một cuộc thi tuyển gồm 3 vòng. Vòng thứ nhất lấy 80% thí sinh; vòng thứ hai lấy 70% thí sinh đã qua vòng thứ nhất và vòng thứ ba lấy 45% thí sinh đã qua vòng thứ hai. Để vào được đội tuyển, thí sinh phải vượt qua được cả 3 vòng thi. Tính xác suất để một thí sinh bất kỳ bị loại ở vòng thứ hai, biết rằng thí sinh này bị loại (viết kết quả làm tròn đến hàng phần trăm).
Điền đáp án: 0,32.
Gọi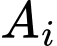 là biến cố “Thí sinh đó vượt qua được vòng thi thứ
là biến cố “Thí sinh đó vượt qua được vòng thi thứ 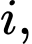 với
với 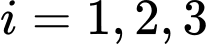 ”.
”.
Gọi là biến cố “Thí sinh đó bị loại”
là biến cố “Thí sinh đó bị loại”
Yêu cầu bài toán: tính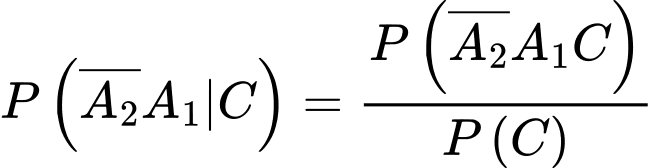
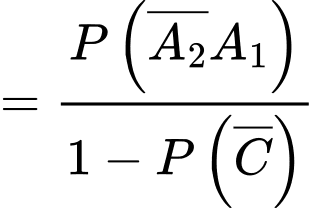 (với
(với  là xác suất thí sinh đó vượt qua được cả 3 vòng)
là xác suất thí sinh đó vượt qua được cả 3 vòng)
Từ giả thiết, ta có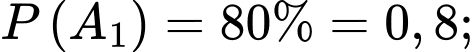
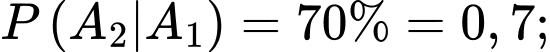
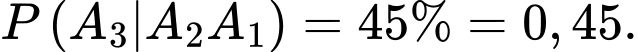
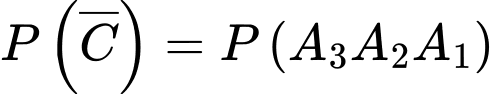
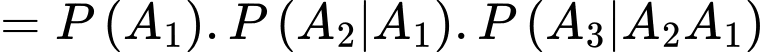
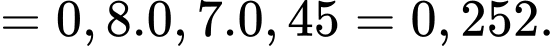
Ta có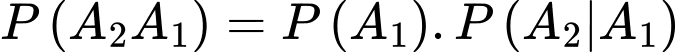
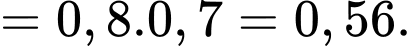
Vì hai biến cố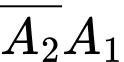 và
và 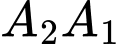 là hai biến cố xung khắc lẫn nhau, nên ta có
là hai biến cố xung khắc lẫn nhau, nên ta có 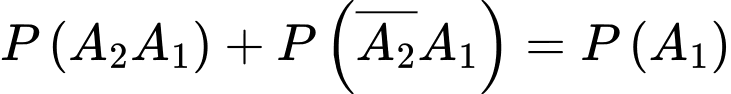
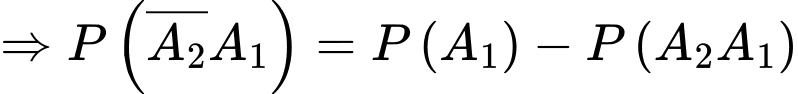
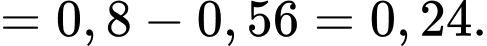
Vậy xác suất cần tìm là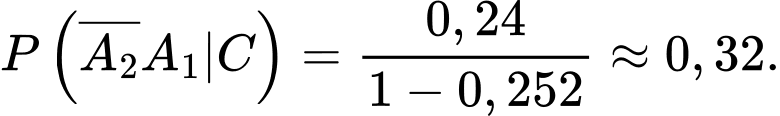
Gọi
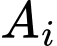 là biến cố “Thí sinh đó vượt qua được vòng thi thứ
là biến cố “Thí sinh đó vượt qua được vòng thi thứ 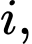 với
với 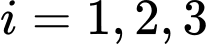 ”.
”.
Gọi
 là biến cố “Thí sinh đó bị loại”
là biến cố “Thí sinh đó bị loại”
Yêu cầu bài toán: tính
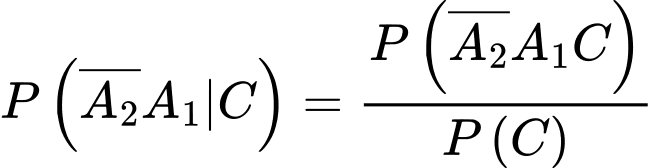
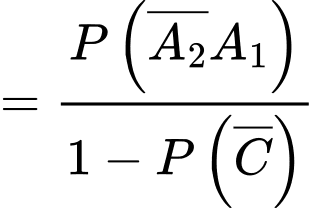 (với
(với  là xác suất thí sinh đó vượt qua được cả 3 vòng)
là xác suất thí sinh đó vượt qua được cả 3 vòng)
Từ giả thiết, ta có
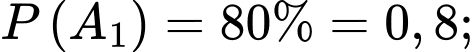
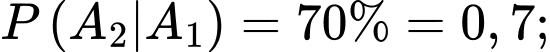
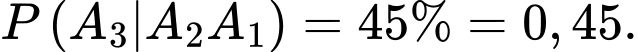
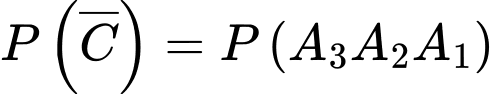
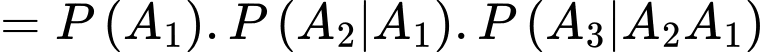
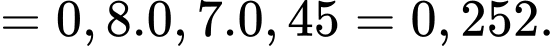
Ta có
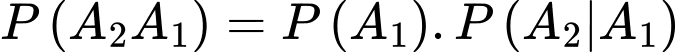
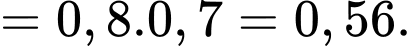
Vì hai biến cố
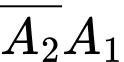 và
và 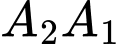 là hai biến cố xung khắc lẫn nhau, nên ta có
là hai biến cố xung khắc lẫn nhau, nên ta có 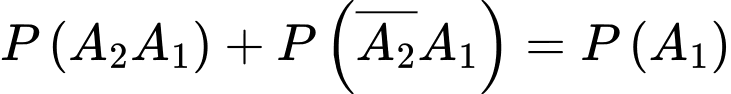
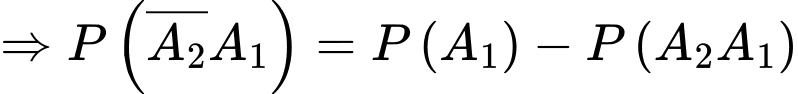
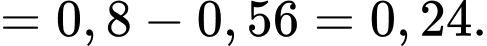
Vậy xác suất cần tìm là