PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1 [778956]: Nếu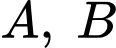 là hai biến cố bất kì với
là hai biến cố bất kì với 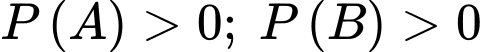 thì
thì
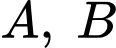 là hai biến cố bất kì với
là hai biến cố bất kì với 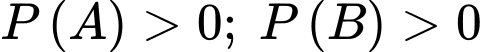 thì
thì A, 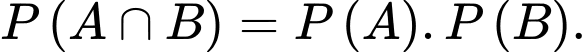
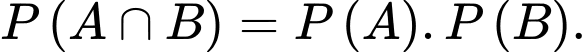
B, 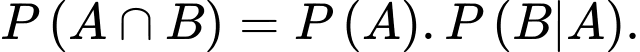
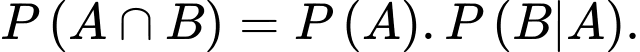
C, 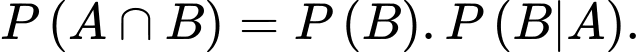
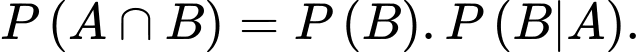
D, 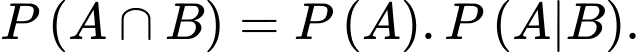
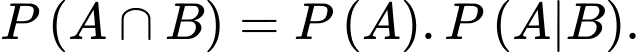
Chọn đáp án B. Đáp án: B
Câu 2 [778957]: Cho hai biến cố 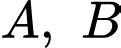 có
có 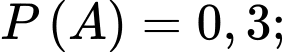
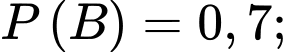
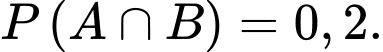 Xác suất
Xác suất  bằng
bằng
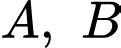 có
có 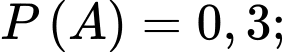
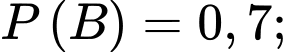
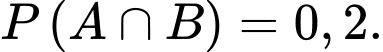 Xác suất
Xác suất  bằng
bằng A, 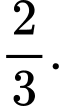
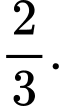
B, 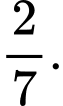
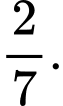
C, 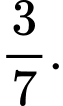
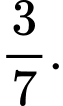
D, 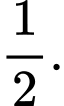
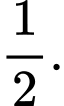
Ta có: 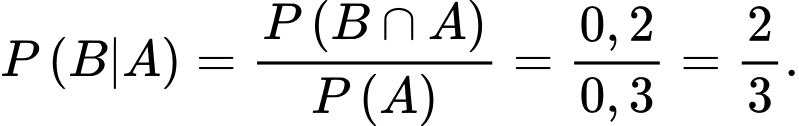 Chọn A. Đáp án: A
Chọn A. Đáp án: A
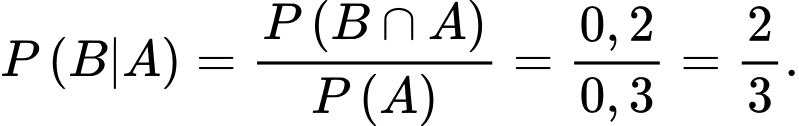 Chọn A. Đáp án: A
Chọn A. Đáp án: A
Câu 3 [778958]: Cho hai biến cố 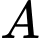 và
và 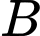 bất kì với
bất kì với 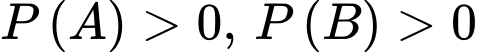 . Chọn khẳng định đúng trong các khẳng định sau là
. Chọn khẳng định đúng trong các khẳng định sau là
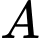 và
và 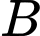 bất kì với
bất kì với 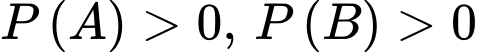 . Chọn khẳng định đúng trong các khẳng định sau là
. Chọn khẳng định đúng trong các khẳng định sau là A, 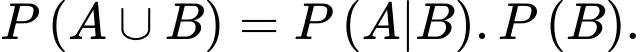
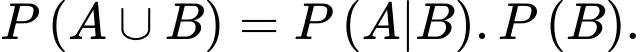
B, 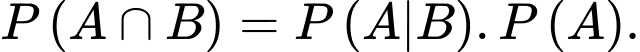
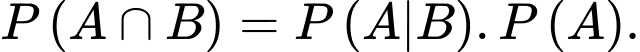
C, 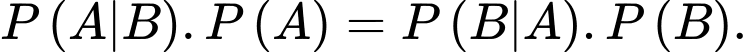
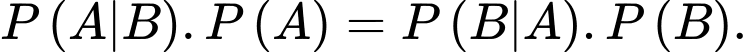
D, 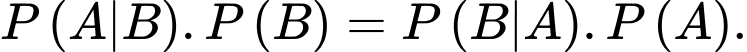
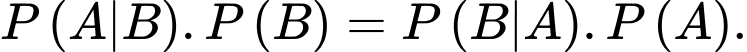
Nếu 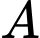 và
và 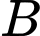 là hai biến cố bất kì thì
là hai biến cố bất kì thì 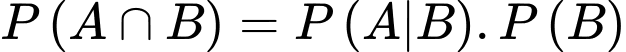
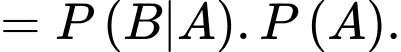
Chọn D. Đáp án: D
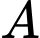 và
và 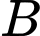 là hai biến cố bất kì thì
là hai biến cố bất kì thì 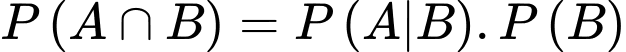
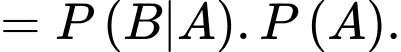
Chọn D. Đáp án: D
Câu 4 [778959]: Cho hai biến cố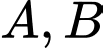 sao cho
sao cho 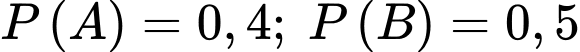 và
và 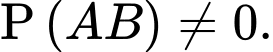 Tính
Tính 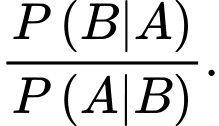
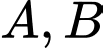 sao cho
sao cho 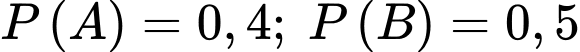 và
và 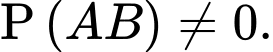 Tính
Tính 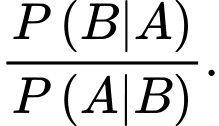
A, 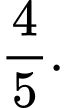
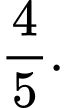
B, 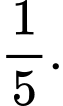
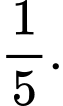
C, 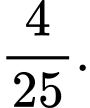
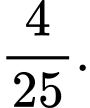
D, 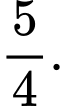
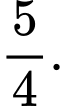
Ta có 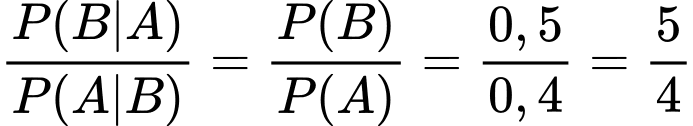 . Chọn D. Đáp án: D
. Chọn D. Đáp án: D
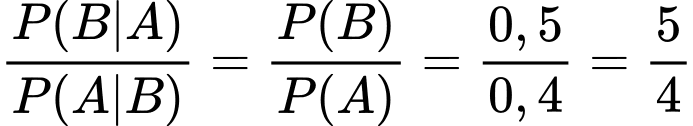 . Chọn D. Đáp án: D
. Chọn D. Đáp án: D
Câu 5 [778960]: Cho hai biến cố độc lập 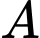 và
và 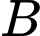 với
với 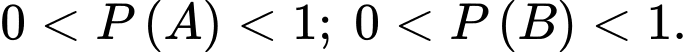 Chọn khẳng định đúng trong các khẳng định sau
Chọn khẳng định đúng trong các khẳng định sau
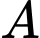 và
và 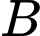 với
với 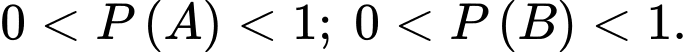 Chọn khẳng định đúng trong các khẳng định sau
Chọn khẳng định đúng trong các khẳng định sau A, 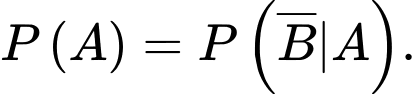
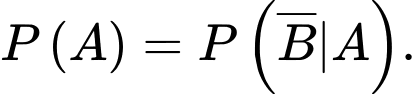
B, 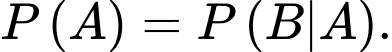
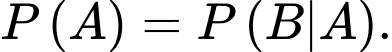
C, 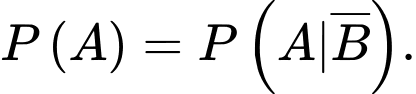
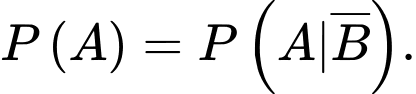
D, 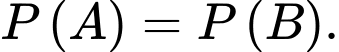
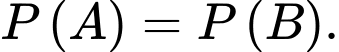
Cho hai biến cố độc lập 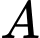 và
và 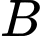 với
với 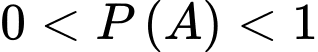 ,
, 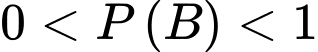 thì
thì 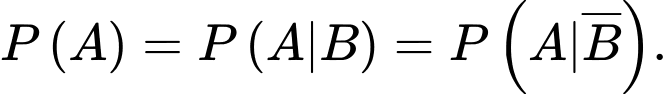 Chọn C. Đáp án: C
Chọn C. Đáp án: C
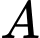 và
và 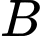 với
với 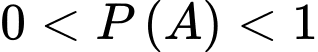 ,
, 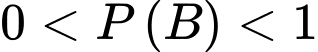 thì
thì 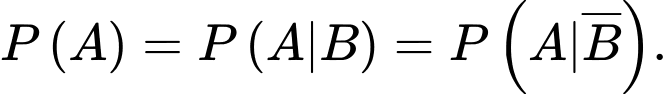 Chọn C. Đáp án: C
Chọn C. Đáp án: C
Câu 6 [134720]: Cho hai biến cố ngẫu nhiên 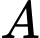 và
và 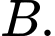 Biết rằng
Biết rằng 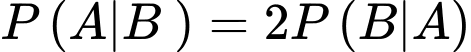 và
và 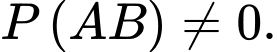 Tính tỉ số
Tính tỉ số 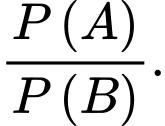
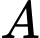 và
và 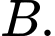 Biết rằng
Biết rằng 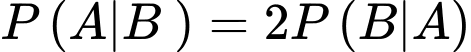 và
và 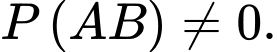 Tính tỉ số
Tính tỉ số 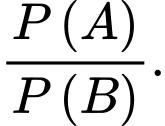
A, 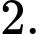
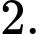
B, 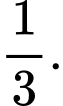
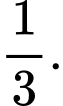
C, 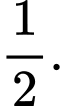
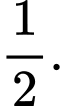
D, 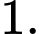
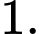
Nếu 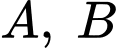 là hai biến cố bất kì thì
là hai biến cố bất kì thì 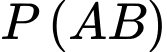
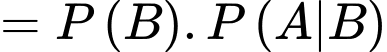
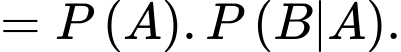
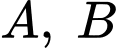 là hai biến cố bất kì thì
là hai biến cố bất kì thì 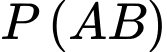
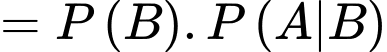
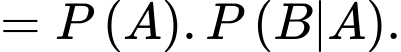
Suy ra 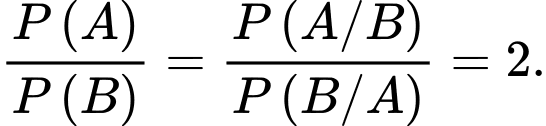
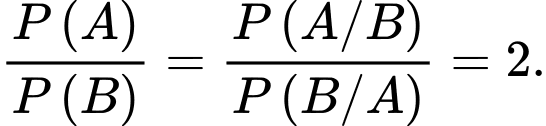
Chọn A.
Đáp án: A
Câu 7 [134807]: Cho hai biến cố 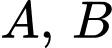 sao cho
sao cho 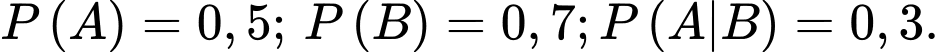 Tính
Tính 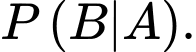
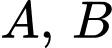 sao cho
sao cho 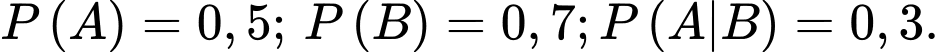 Tính
Tính 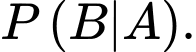
A, 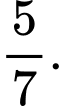
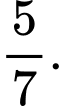
B, 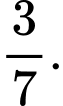
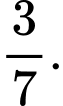
C, 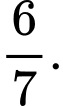
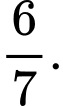
D, 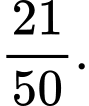
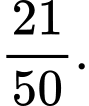
Chọn đáp án D.
Ta có: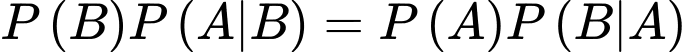
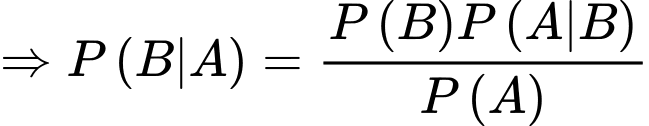
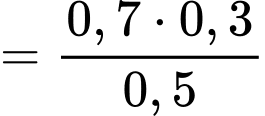
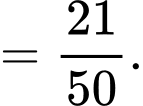 Đáp án: D
Đáp án: D
Ta có:
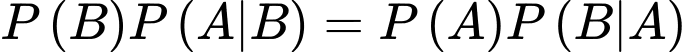
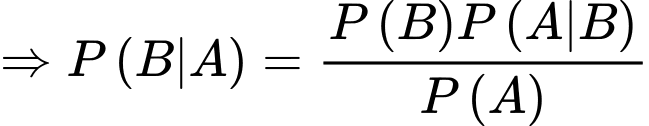
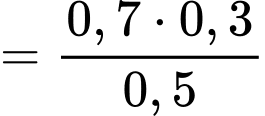
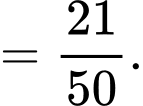 Đáp án: D
Đáp án: D
Câu 8 [145267]: Cho hai biến cố 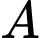 và
và 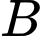 có
có 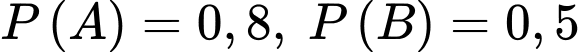 và
và 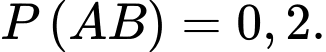 Xác suất của biến cố
Xác suất của biến cố 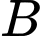 không xảy ra với điều kiện biến cố
không xảy ra với điều kiện biến cố 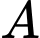 xảy ra là
xảy ra là
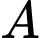 và
và 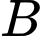 có
có 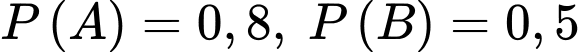 và
và 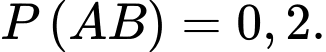 Xác suất của biến cố
Xác suất của biến cố 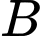 không xảy ra với điều kiện biến cố
không xảy ra với điều kiện biến cố 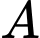 xảy ra là
xảy ra là A, 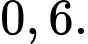
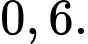
B, 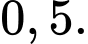
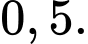
C, 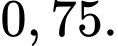
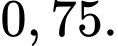
D, 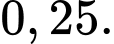
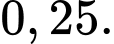
Ta có: 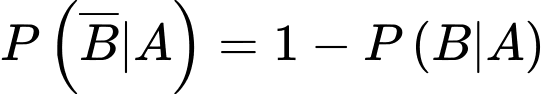
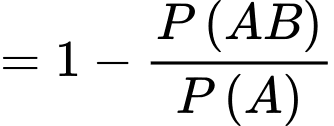
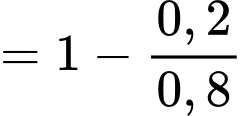
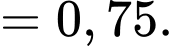
Chọn C. Đáp án: C
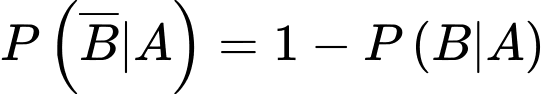
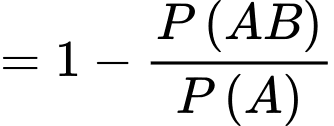
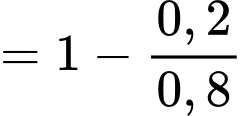
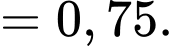
Chọn C. Đáp án: C
Câu 9 [778961]: Cho hai biến cố 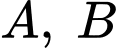 có
có 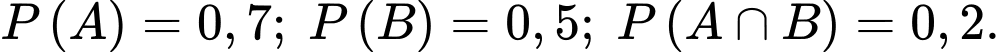 Khi đó xác suất
Khi đó xác suất  bằng:
bằng:
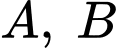 có
có 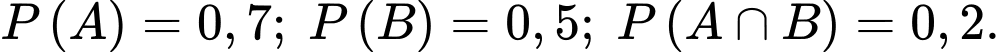 Khi đó xác suất
Khi đó xác suất  bằng:
bằng: A, 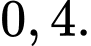
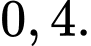
B, 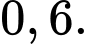
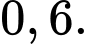
C, 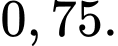
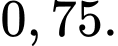
D, 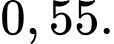
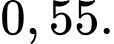
Chọn đáp án B.
Ta có: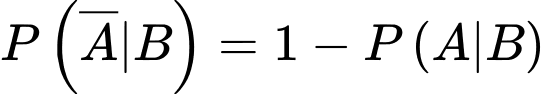
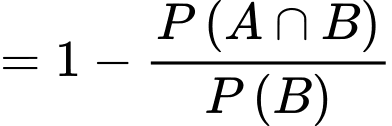
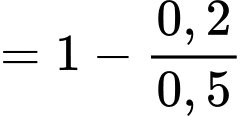
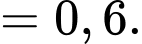 Đáp án: B
Đáp án: B
Ta có:
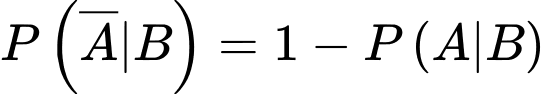
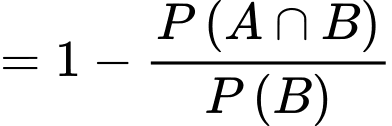
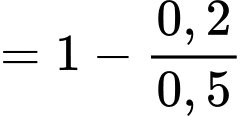
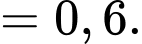 Đáp án: B
Đáp án: B
Câu 10 [778962]: Trong một kỳ thi, có 60% học sinh đã làm đúng bài toán đầu tiên và 40% học sinh đã làm đúng bài toán thứ hai. Biết rằng có 20% học sinh làm đúng cả hai bài toán. Xác suất để một học sinh làm đúng bài toán thứ hai biết rằng học sinh đó đã làm đúng bài toán đầu tiên là bao nhiêu?
A, 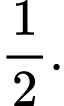
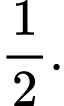
B, 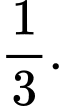
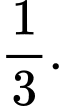
C, 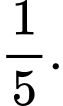
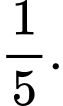
D, 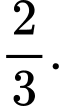
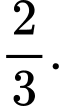
Chọn B
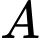 : "học sinh đã làm đúng bài toán đầu tiên" , thì
: "học sinh đã làm đúng bài toán đầu tiên" , thì 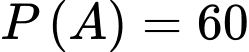
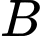 : "học sinh đã làm đúng bài toán thứ hai", thì
: "học sinh đã làm đúng bài toán thứ hai", thì 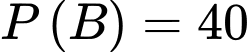
 : "học sinh làm đúng cả hai bài toán", thì
: "học sinh làm đúng cả hai bài toán", thì 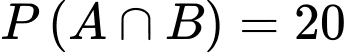 Xác suất để một học sinh làm đúng bài toán thứ hai biết rằng học sinh đó đã làm đúng bài toán đầu tiên là
Xác suất để một học sinh làm đúng bài toán thứ hai biết rằng học sinh đó đã làm đúng bài toán đầu tiên là 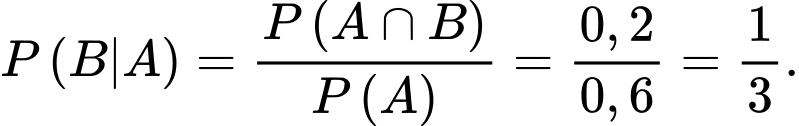 Đáp án: B
Đáp án: B
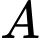 : "học sinh đã làm đúng bài toán đầu tiên" , thì
: "học sinh đã làm đúng bài toán đầu tiên" , thì 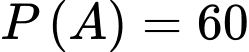
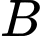 : "học sinh đã làm đúng bài toán thứ hai", thì
: "học sinh đã làm đúng bài toán thứ hai", thì 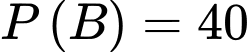
 : "học sinh làm đúng cả hai bài toán", thì
: "học sinh làm đúng cả hai bài toán", thì 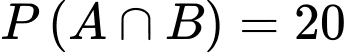 Xác suất để một học sinh làm đúng bài toán thứ hai biết rằng học sinh đó đã làm đúng bài toán đầu tiên là
Xác suất để một học sinh làm đúng bài toán thứ hai biết rằng học sinh đó đã làm đúng bài toán đầu tiên là 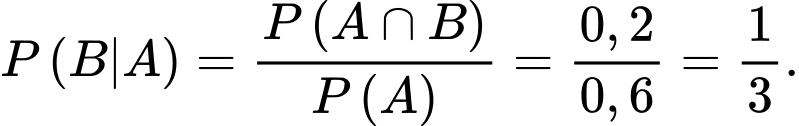 Đáp án: B
Đáp án: B
Câu 11 [134813]: Cho hai biến cố A và B có 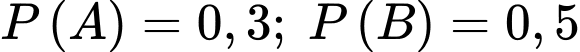 và
và  Tính
Tính 
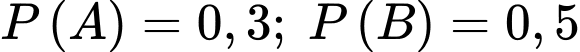 và
và  Tính
Tính 
A, 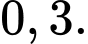
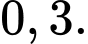
B, 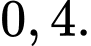
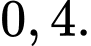
C, 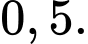
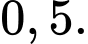
D, 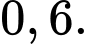
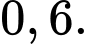
Chọn đáp án A.
Ta có: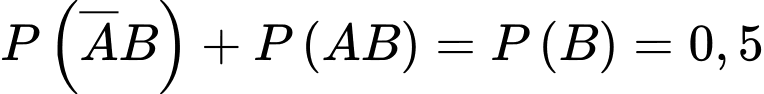
Mặt khác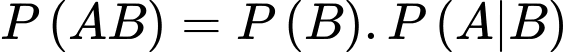
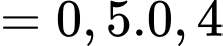
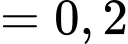
Suy ra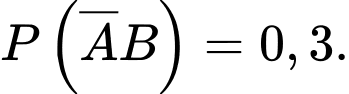 Đáp án: A
Đáp án: A
Ta có:
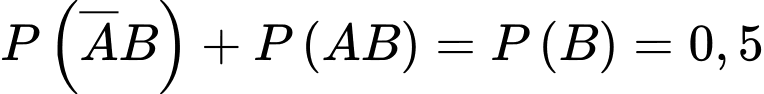
Mặt khác
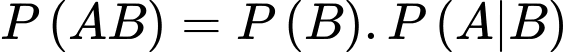
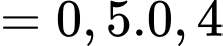
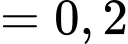
Suy ra
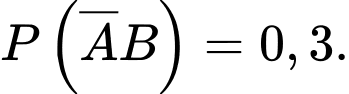 Đáp án: A
Đáp án: A
Câu 12 [778963]: Lớp 12A1 có 48 bạn đều giỏi ít nhất một trong hai môn Toán và Lý, trong đó có 36 bạn giỏi Toán, 24 bạn giỏi Lý. Chọn ngẫu nhiên 1 bạn. Xác suất chọn được bạn giỏi Toán, biết bạn đó giỏi Lý là bao nhiêu?
A, 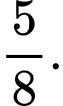
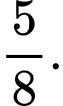
B, 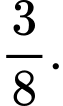
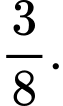
C, 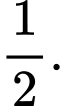
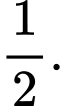
D, 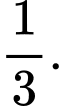
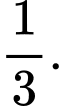
Chọn đáp án C.
Xét các biến cố: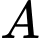 : "Chọn được bạn giỏi Toán";
: "Chọn được bạn giỏi Toán";
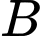 : "Chọn được bạn giỏi Lý".
: "Chọn được bạn giỏi Lý".
Khi đó,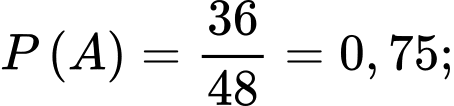
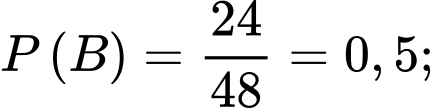
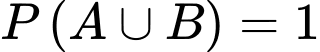 .
.
Suy ra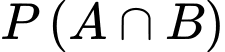


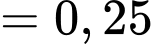 .
.
Vậy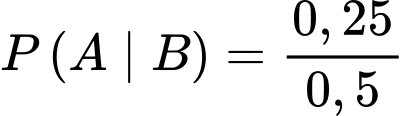
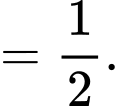 Đáp án: C
Đáp án: C
Xét các biến cố:
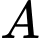 : "Chọn được bạn giỏi Toán";
: "Chọn được bạn giỏi Toán";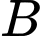 : "Chọn được bạn giỏi Lý".
: "Chọn được bạn giỏi Lý".Khi đó,
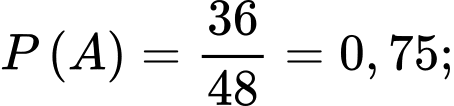
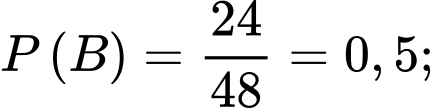
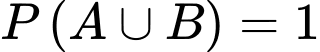 .
.Suy ra
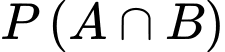


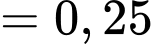 .
.Vậy
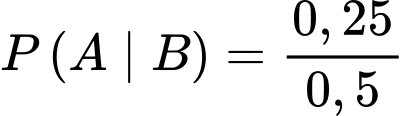
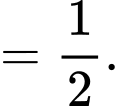 Đáp án: C
Đáp án: C PHẦN II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a),b),c),d) ở mỗi câu học sinh chọn đúng hoặc sai.
Câu 13 [778964]: Cho hai biến cố 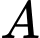 và
và 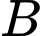 có
có 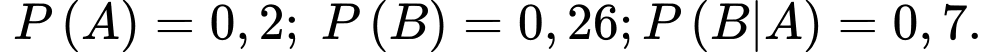
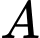 và
và 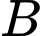 có
có 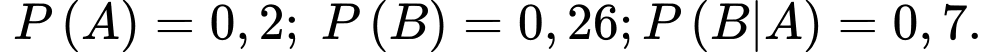
a) Sai.
Vì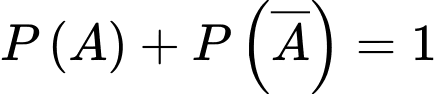 nên
nên 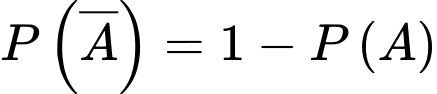
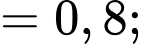
Tương tự,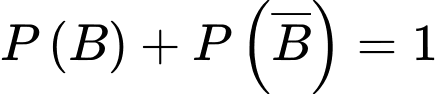 nên
nên 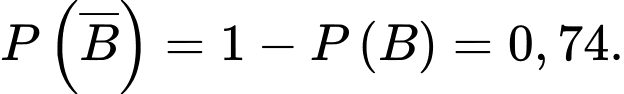
b) Sai.
Ta có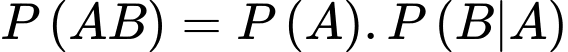
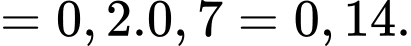
c) Sai.
Hai biến cố và
và  là hai biến cố xung khắc lẫn nhau nên ta có
là hai biến cố xung khắc lẫn nhau nên ta có 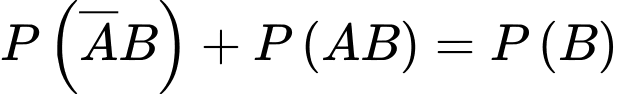
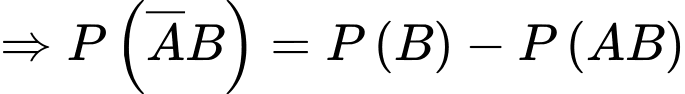
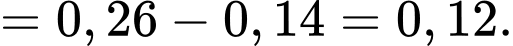
d) Đúng.
Xác suất có điều kiện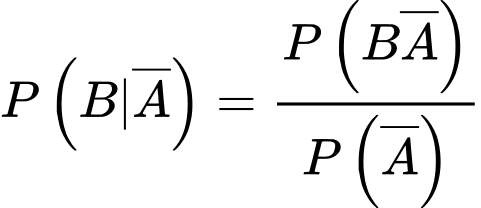
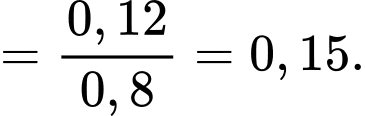
Vì
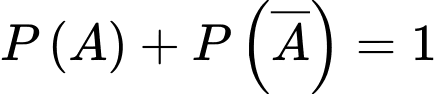 nên
nên 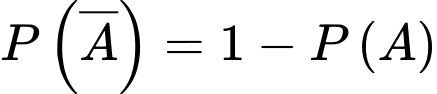
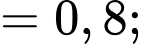
Tương tự,
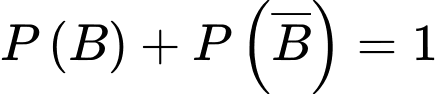 nên
nên 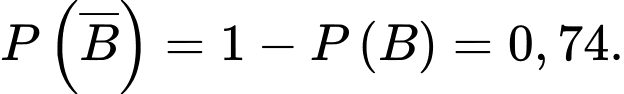
b) Sai.
Ta có
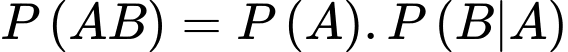
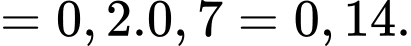
c) Sai.
Hai biến cố
 và
và  là hai biến cố xung khắc lẫn nhau nên ta có
là hai biến cố xung khắc lẫn nhau nên ta có 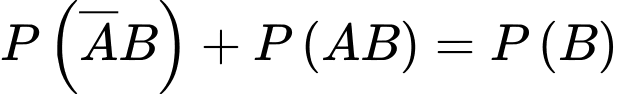
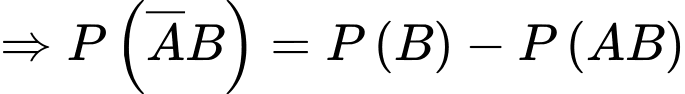
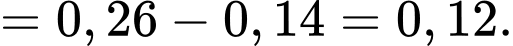
d) Đúng.
Xác suất có điều kiện
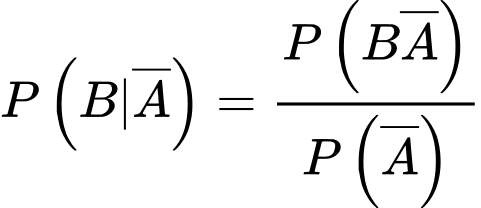
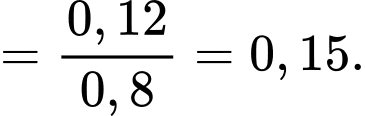
Câu 14 [778965]: Lớp 12A có 30 học sinh, trong đó có 17 bạn nữ còn lại là nam. Có 3 bạn tên Hiền, trong đó có 1 bạn nữ và 2 bạn nam. Thầy giáo gọi ngẫu nhiên 1 bạn lên bảng.
Gọi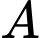 là biến cố "Học sinh được gọi lên bảng tên là Hiền"
là biến cố "Học sinh được gọi lên bảng tên là Hiền"
Gọi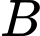 là biến cố "Học sinh được chọn mang giới tính nữ".
là biến cố "Học sinh được chọn mang giới tính nữ".
Gọi
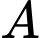 là biến cố "Học sinh được gọi lên bảng tên là Hiền"
là biến cố "Học sinh được gọi lên bảng tên là Hiền"Gọi
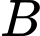 là biến cố "Học sinh được chọn mang giới tính nữ".
là biến cố "Học sinh được chọn mang giới tính nữ".
a) Xác suất để học sinh được gọi có tên là Hiền là: 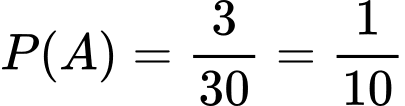 .
.
Chọn ĐÚNG.
b) Xác suất để thầy giáo gọi bạn đó lên bảng có tên Hiền, nhưng với điều kiện bạn đó nữ là
Ta có: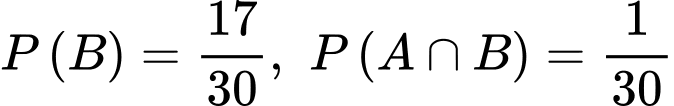
Do đó: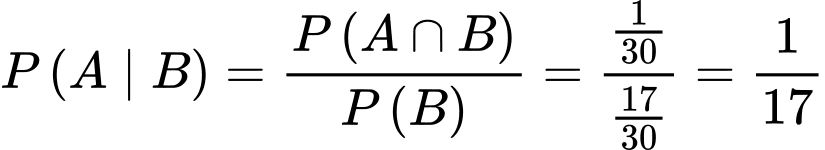
Chọn SAI.
c) Gọi là biến cố " Học sinh được chọn mang giới tính nam".
là biến cố " Học sinh được chọn mang giới tính nam".
Xác suất thầy giáo gọi bạn đó lên bảng có tên Hiền, với điều kiện bạn đó nam là .
.
Ta có: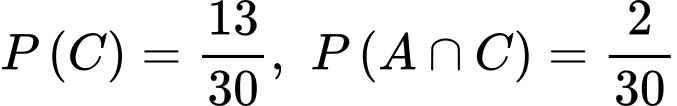 . Do đó:
. Do đó: 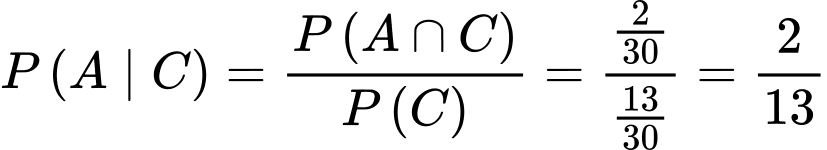
Chọn ĐÚNG.
d) Nếu thầy giáo gọi 1 bạn có tên là Hiền lên bảng thì xác xuất để bạn đó là bạn nữ là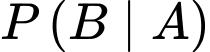
Ta có: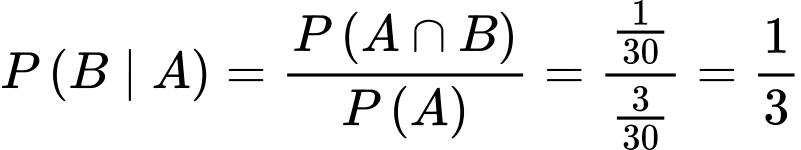
Chọn SAI.
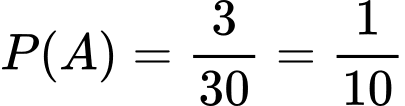 .
.Chọn ĐÚNG.
b) Xác suất để thầy giáo gọi bạn đó lên bảng có tên Hiền, nhưng với điều kiện bạn đó nữ là

Ta có:
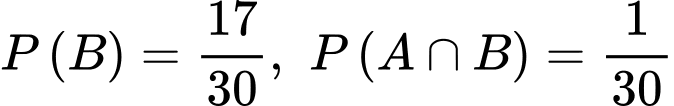
Do đó:
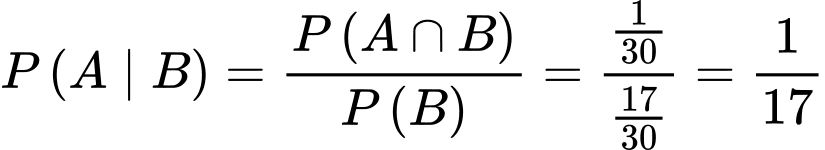
Chọn SAI.
c) Gọi
 là biến cố " Học sinh được chọn mang giới tính nam".
là biến cố " Học sinh được chọn mang giới tính nam".Xác suất thầy giáo gọi bạn đó lên bảng có tên Hiền, với điều kiện bạn đó nam là
 .
.Ta có:
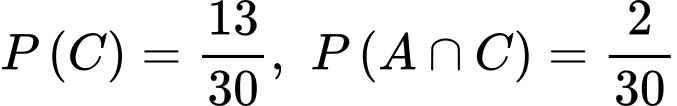 . Do đó:
. Do đó: 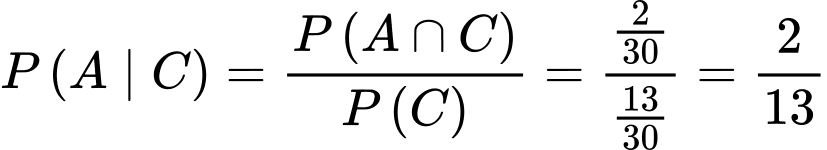
Chọn ĐÚNG.
d) Nếu thầy giáo gọi 1 bạn có tên là Hiền lên bảng thì xác xuất để bạn đó là bạn nữ là
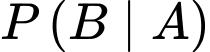
Ta có:
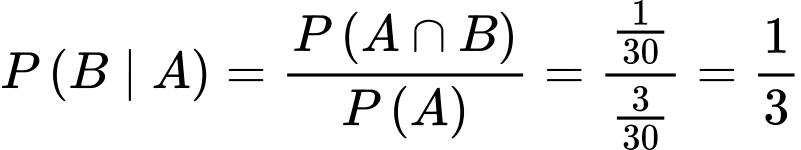
Chọn SAI.
Câu 15 [695536]: Bảng sau đây tóm tắt kết quả phân tích quá trình tự phân hủy (sự phá hủy tế bào sau khi tế bảo chết do hoạt động của các enzym của chính tế bào) và sự thối rữa (sự phân hủy chất hữu cơ, đặc biệt là protein, bởi vi sinh vật dẫn đến tạo ra mùi hôi thối) của các con bọ cánh cứng chết

Chọn ngẫu nhiên một con bọ cánh cứng trong các mẫu phân tích trên.

Chọn ngẫu nhiên một con bọ cánh cứng trong các mẫu phân tích trên.

a) Sai.
Xác suất để mẫu chọn ra có quá trình tự phân hủy cao là
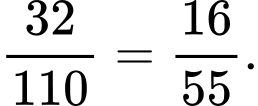
b) Sai.
Xác suất để mẫu chọn ra có quá trình tự phân hủy cao và độ thối rữa thấp là
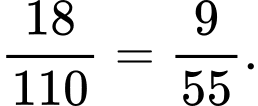
c) Đúng.
Nếu quá trình tự phân hủy của một mẫu chọn ra là cao thì xác suất để thối rữathấp là
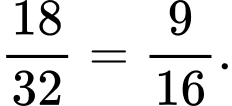
d) Đúng.
Nếu độ thối rữa một mẫu chọn ra là cao thì xác suất để quá trình tự phân hủy cao bằng
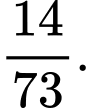
Câu 16 [702630]: Một công ty cần tuyển 2 nhân viên, có 6 người nộp đơn trong đó có 2 nam và 4 nữ. Biết rằng khả năng được tuyển của mỗi người là như nhau.
a) Sai.
Xác suất cả hai người được chọn đều là nữ là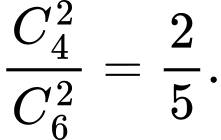
b) Đúng.
Xác suất cả hai người được chọn đều là nam là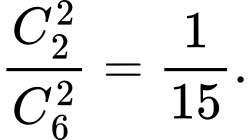
Do vậy xác suất để ít nhất một nữ được chọn là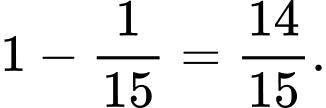
c) Sai.
Gọi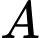 là biến cố “Cả hai nữ được chọn” và
là biến cố “Cả hai nữ được chọn” và 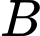 là biến cố ít nhất một nữ được chọn”
là biến cố ít nhất một nữ được chọn”
Ta có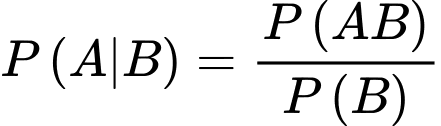
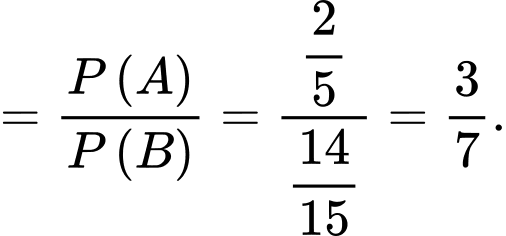 (vì
(vì 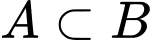 nên
nên 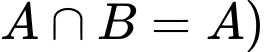
d) Đúng.
Gọi là biến cố “Hoa được chọn” thì
là biến cố “Hoa được chọn” thì 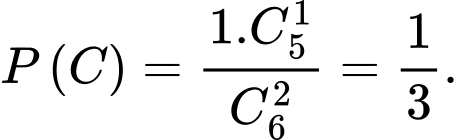
YCBT Tính
Tính 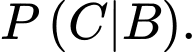
Ta có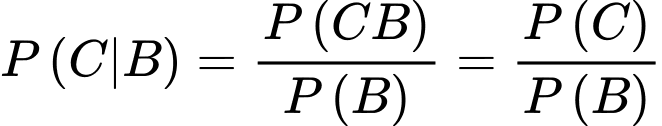
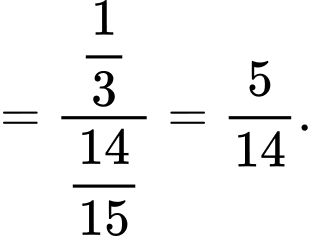 (vì
(vì 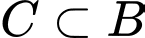 nên
nên 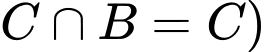
Xác suất cả hai người được chọn đều là nữ là
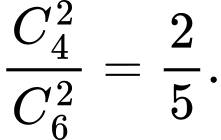
b) Đúng.
Xác suất cả hai người được chọn đều là nam là
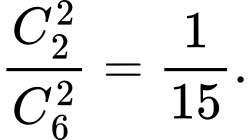
Do vậy xác suất để ít nhất một nữ được chọn là
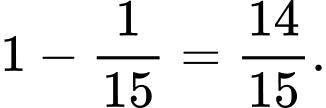
c) Sai.
Gọi
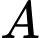 là biến cố “Cả hai nữ được chọn” và
là biến cố “Cả hai nữ được chọn” và 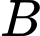 là biến cố ít nhất một nữ được chọn”
là biến cố ít nhất một nữ được chọn”Ta có
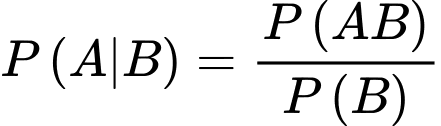
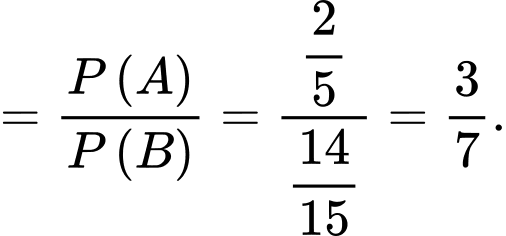 (vì
(vì 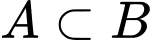 nên
nên 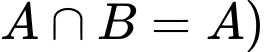
d) Đúng.
Gọi
 là biến cố “Hoa được chọn” thì
là biến cố “Hoa được chọn” thì 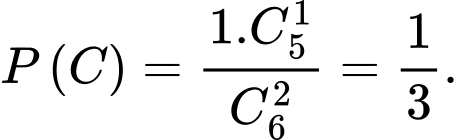
YCBT
 Tính
Tính 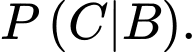
Ta có
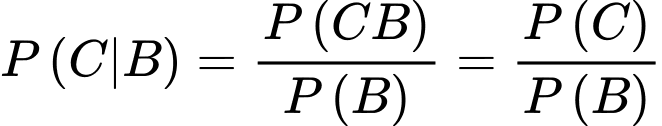
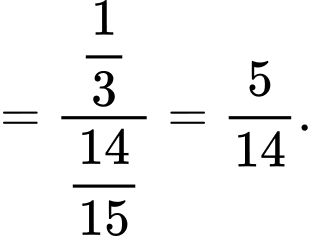 (vì
(vì 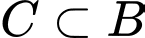 nên
nên 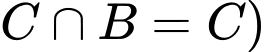
PHẦN III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 17 đến câu 22.
Câu 17 [778969]: Ba xạ thủ 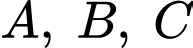 độc lập với nhau cùng bắn súng vào bia. Xác suất bắn trúng bia của 3 người
độc lập với nhau cùng bắn súng vào bia. Xác suất bắn trúng bia của 3 người 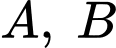 và
và  tương ứng là
tương ứng là 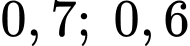 và
và 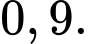 Tính xác suất để xạ thủ
Tính xác suất để xạ thủ 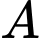 bắn trúng bia biết rằng có hai xạ thủ bắn trúng bia (viết kết quả làm tròn đến hàng phần trăm).
bắn trúng bia biết rằng có hai xạ thủ bắn trúng bia (viết kết quả làm tròn đến hàng phần trăm).
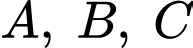 độc lập với nhau cùng bắn súng vào bia. Xác suất bắn trúng bia của 3 người
độc lập với nhau cùng bắn súng vào bia. Xác suất bắn trúng bia của 3 người 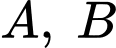 và
và  tương ứng là
tương ứng là 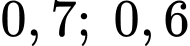 và
và 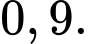 Tính xác suất để xạ thủ
Tính xác suất để xạ thủ 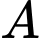 bắn trúng bia biết rằng có hai xạ thủ bắn trúng bia (viết kết quả làm tròn đến hàng phần trăm).
bắn trúng bia biết rằng có hai xạ thủ bắn trúng bia (viết kết quả làm tròn đến hàng phần trăm).
Điền đáp án: 0,64.
Gọi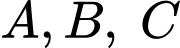 lần lượt là biến cố “Bắn trúng bia” của 3 xạ thủ A, B, C;
lần lượt là biến cố “Bắn trúng bia” của 3 xạ thủ A, B, C; 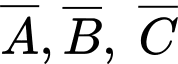 lần lượt là biến cố bắn không trúng của 3 xạ thủ A, B, C.
lần lượt là biến cố bắn không trúng của 3 xạ thủ A, B, C.
Từ giả thiết, ta có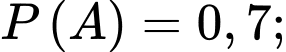
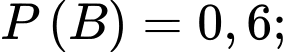
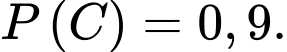 Suy ra
Suy ra 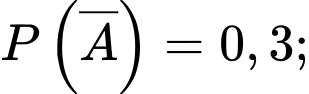
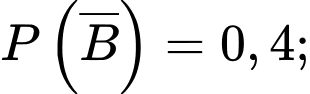
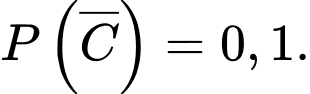
Gọi là biến cố “Có đúng hai xạ thủ bắn trúng bia”.
là biến cố “Có đúng hai xạ thủ bắn trúng bia”.
Yêu cầu bài toán Tính
Tính 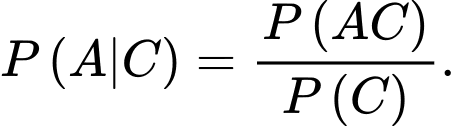
Để có đúng 2 xạ thủ bắn trúng bia, xảy ra 3 trường hợp sau (với các lần bắn của 3 xạ thủ là độc lập):
TH1: A, B bắn trúng bia và C bắn không trúng bia, có xác suất bằng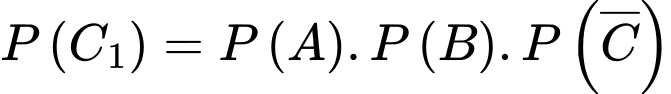
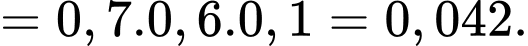
TH2: A, C bắn trúng bia và B bắn không trúng bia, có xác suất bằng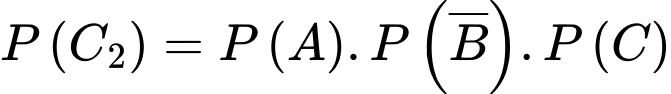
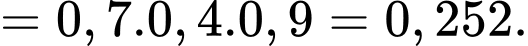
TH3: B, C bắn trúng bia và A bắn không trúng bia, có xác suất bằng
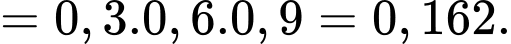
Suy ra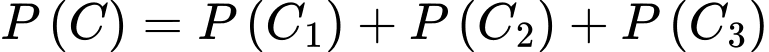
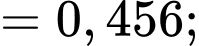
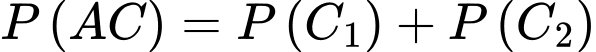
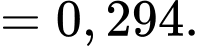
Vậy xác suất cần tính bằng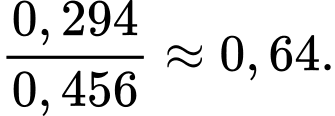
Gọi
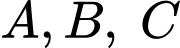 lần lượt là biến cố “Bắn trúng bia” của 3 xạ thủ A, B, C;
lần lượt là biến cố “Bắn trúng bia” của 3 xạ thủ A, B, C; 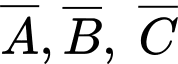 lần lượt là biến cố bắn không trúng của 3 xạ thủ A, B, C.
lần lượt là biến cố bắn không trúng của 3 xạ thủ A, B, C.
Từ giả thiết, ta có
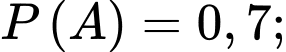
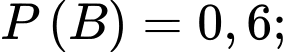
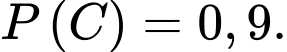 Suy ra
Suy ra 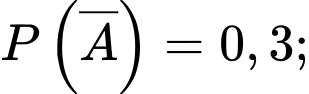
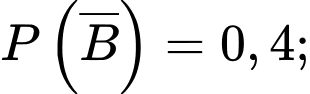
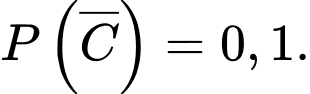
Gọi
 là biến cố “Có đúng hai xạ thủ bắn trúng bia”.
là biến cố “Có đúng hai xạ thủ bắn trúng bia”.
Yêu cầu bài toán
 Tính
Tính 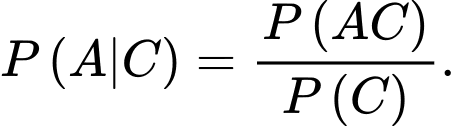
Để có đúng 2 xạ thủ bắn trúng bia, xảy ra 3 trường hợp sau (với các lần bắn của 3 xạ thủ là độc lập):
TH1: A, B bắn trúng bia và C bắn không trúng bia, có xác suất bằng
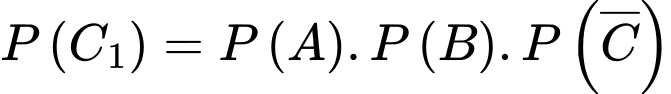
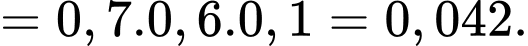
TH2: A, C bắn trúng bia và B bắn không trúng bia, có xác suất bằng
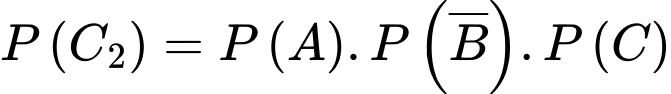
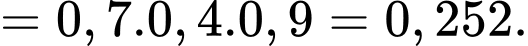
TH3: B, C bắn trúng bia và A bắn không trúng bia, có xác suất bằng

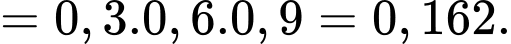
Suy ra
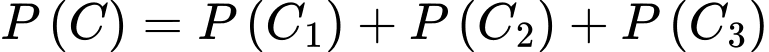
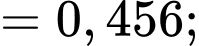
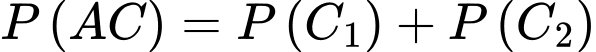
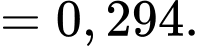
Vậy xác suất cần tính bằng
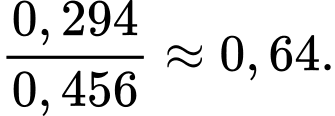
Câu 18 [778970]: Trong các cặp vợ chồng sống ở một vùng ngoại ô, xác suất người chồng tham gia bỏ phiếu trong một cuộc trưng cầu dân ý là 0,7; xác suất người vợ tham gia bỏ phiếu là 0,6 và xác suất cả hai cùng tham gia bỏ phiếu là 0,5. Tìm xác suất để người vợ tham gia bỏ phiếu, biết rằng chồng cô ta không tham gia bỏ phiếu (kết quả làm tròn đến hàng phần trăm).
Điền đáp án: 0,33.
Gọi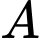 là biến cố “Người chồng tham gia bỏ phiếu”
là biến cố “Người chồng tham gia bỏ phiếu”
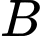 là biến cố “Người vợ tham gia bỏ phiếu”
là biến cố “Người vợ tham gia bỏ phiếu”
Từ giả thiết, ta có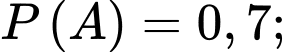
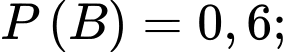
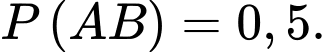
Yêu cầu bài toán Tính
Tính 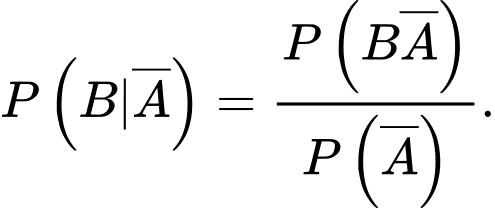
Vì và
và  là hai biến cố xung khắc, nên ta có
là hai biến cố xung khắc, nên ta có 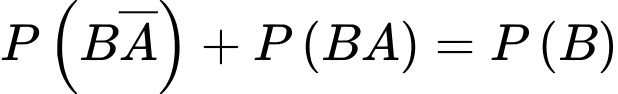
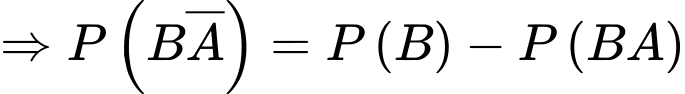
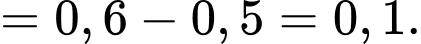
Vậy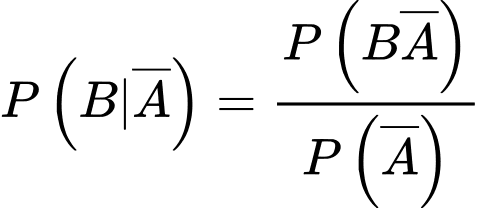
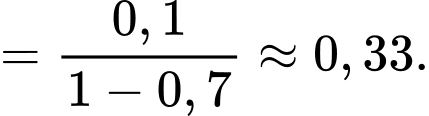
Gọi
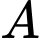 là biến cố “Người chồng tham gia bỏ phiếu”
là biến cố “Người chồng tham gia bỏ phiếu”
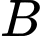 là biến cố “Người vợ tham gia bỏ phiếu”
là biến cố “Người vợ tham gia bỏ phiếu”
Từ giả thiết, ta có
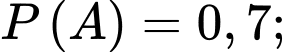
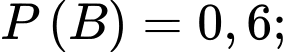
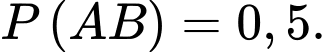
Yêu cầu bài toán
 Tính
Tính 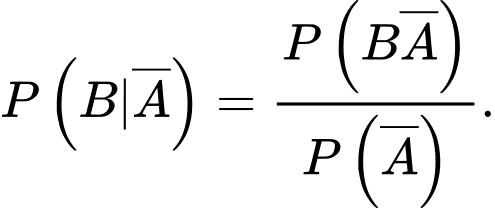
Vì
 và
và  là hai biến cố xung khắc, nên ta có
là hai biến cố xung khắc, nên ta có 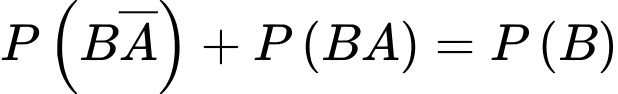
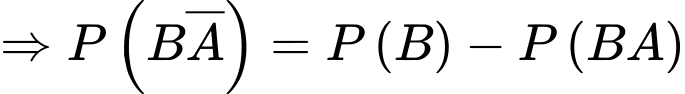
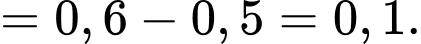
Vậy
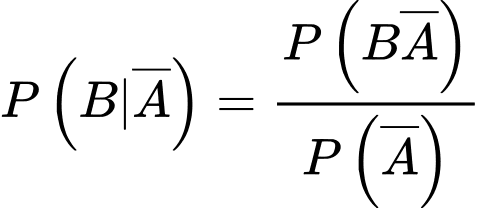
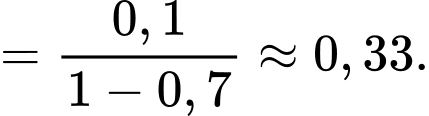
Câu 19 [778972]: Trong một kì thi. Thí sinh được phép thi tối đa 3 lần. Xác suất lần đầu vượt qua kì thi là 0,9. Nếu trượt lần đầu thì xác suất vượt qua kì thi lần hai là 0,7. Nếu trượt cả hai lần thì xác suất vượt qua kì thi ở lần thứ ba là 0,3. Biết rằng thí sinh thi đậu, xác suất thí sinh này thi đậu ở lần thứ hai là bao nhiêu phần trăm (kết quả làm tròn đến hàng phần trăm).
Điền đáp án: 7,15.
Gọi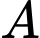 là biến cố “Thí sinh thi đậu ở lần thứ hai” và
là biến cố “Thí sinh thi đậu ở lần thứ hai” và 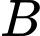 là biến cố “Thí sinh thi đậu”.
là biến cố “Thí sinh thi đậu”.
Yêu cầu bài toán: Tính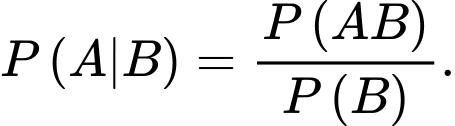
Từ dữ kiện đề bài, ta có sơ đồ cây sau:
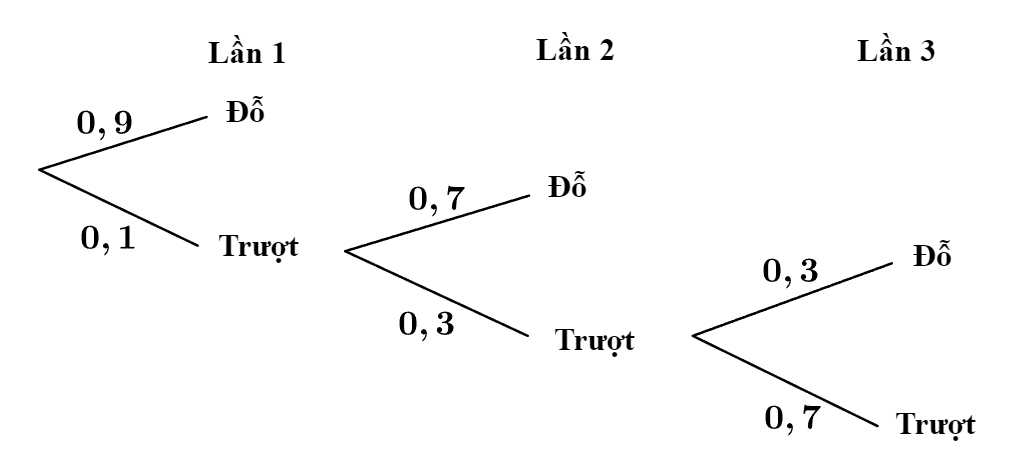
Áp dụng công thức xác suất toàn phần, ta có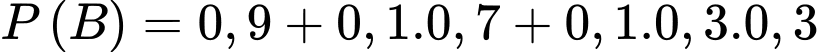
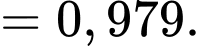
Vậy xác suất cần tính là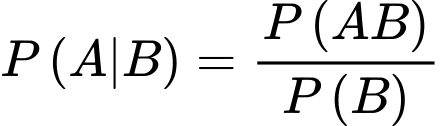
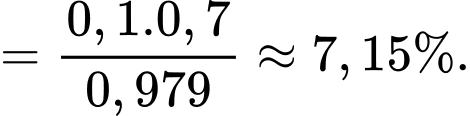
Gọi
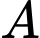 là biến cố “Thí sinh thi đậu ở lần thứ hai” và
là biến cố “Thí sinh thi đậu ở lần thứ hai” và 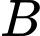 là biến cố “Thí sinh thi đậu”.
là biến cố “Thí sinh thi đậu”.
Yêu cầu bài toán: Tính
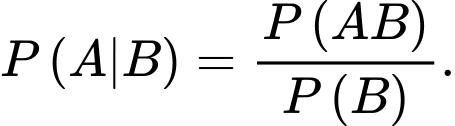
Từ dữ kiện đề bài, ta có sơ đồ cây sau:

Áp dụng công thức xác suất toàn phần, ta có
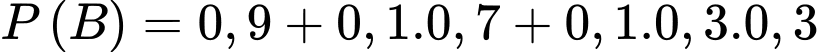
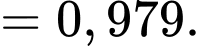
Vậy xác suất cần tính là
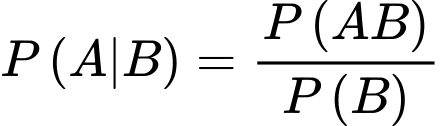
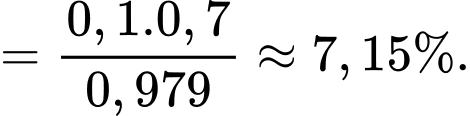
Câu 20 [143812]: Theo thống kê xác suất để hai ngày liên tiếp có mưa ở một thành phố vào mùa hè là0,5; còn không mưa là 0,3. Biết các sự kiện có một ngày mưa, một ngày không mưa là đồng khả năng. Tính xác suất để ngày thứ hai có mưa, biết ngày đầu không mưa.
Điền đáp án: 0,25.
Gọi A là “ngày đầu mưa" và B là “ngày thứ hai mưa" thì ta có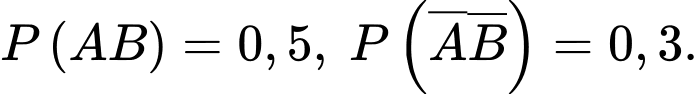
Vì các sự kiện có một ngày mưa, một ngày không mưa là đồng khả năng nên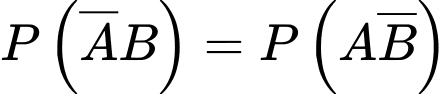
Lại có: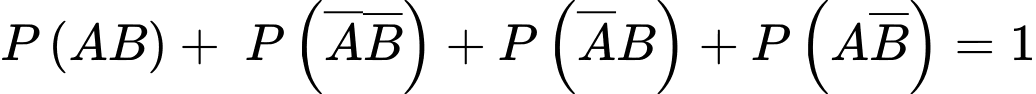 nên
nên 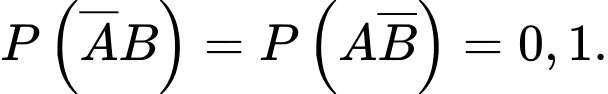
Xác suất cần tính là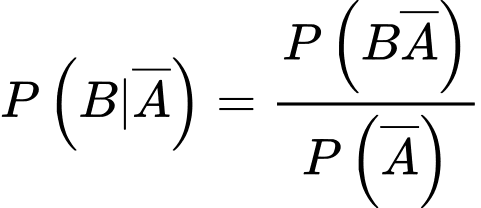
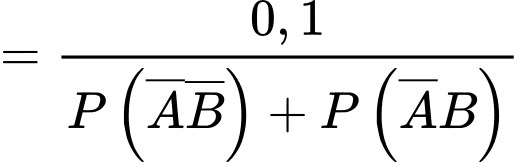
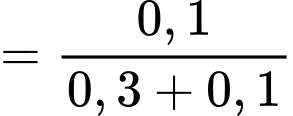
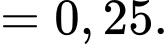
Gọi A là “ngày đầu mưa" và B là “ngày thứ hai mưa" thì ta có
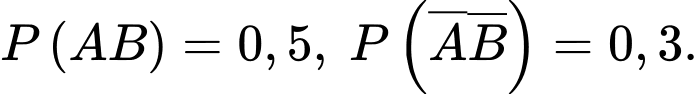
Vì các sự kiện có một ngày mưa, một ngày không mưa là đồng khả năng nên
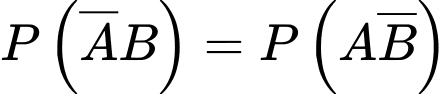
Lại có:
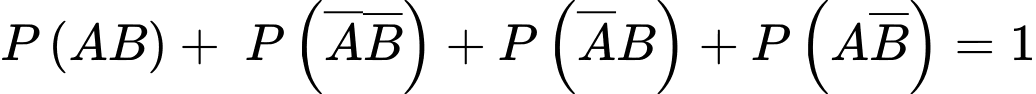 nên
nên 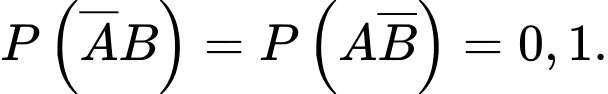
Xác suất cần tính là
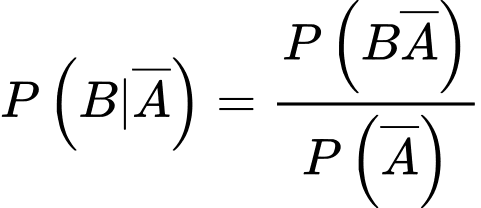
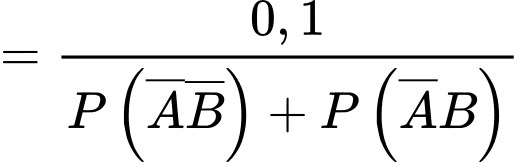
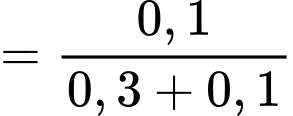
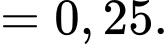
Câu 21 [146672]: Một lô hàng có 6 sản phẩm tốt, 4 sản phẩm xấu. Lấy ngẫu nhiên không hoàn lại từng sản phẩm cho đến khi lấy được 2 sản phẩm tốt thì ngừng, Biết đã ngừng lại ở lần lấy sản phẩm thứ 4. Tính xác suất để lần lấy thứ nhất lấy được sản phẩm tốt. Viết kết quả làm tròn đến hàng phần trăm.
Điền đáp án: 0,33.
Gọi A là biến cố: lần thứ nhất lấy được sản phẩm tốt
B là biến cố: Ngưng lại ở lần thứ 4
Ta có: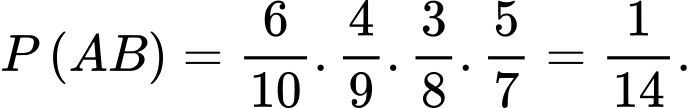
Mặt khác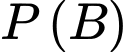
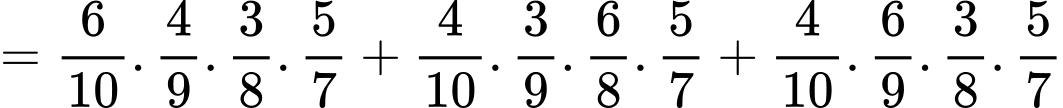
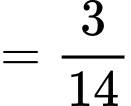
Do đó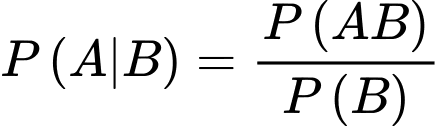
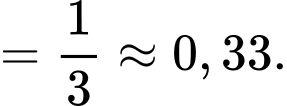
Gọi A là biến cố: lần thứ nhất lấy được sản phẩm tốt
B là biến cố: Ngưng lại ở lần thứ 4
Ta có:
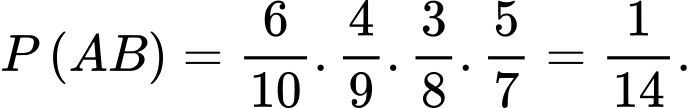
Mặt khác
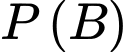
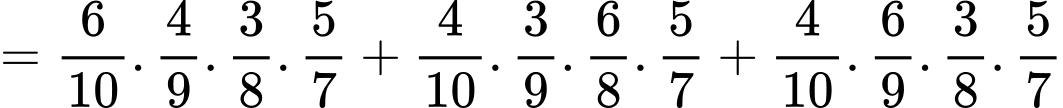
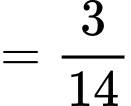
Do đó
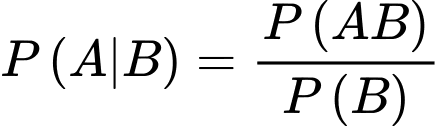
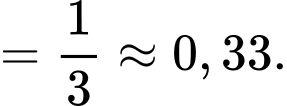
Câu 22 [135872]: Gieo đồng thời ba con xúc xắc cân đối đồng chất. Tính xác suất để tổng số chấm xuất hiện trên ba con bằng 8 biết rằng ít nhất có một con xuất hiện mặt 5 chấm. Viết kết quả làm tròn đến hàng phần trăm.
Không gian mẫu gồm các phần tử 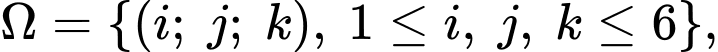 trong đó bộ số
trong đó bộ số 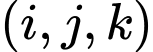 kí hiệu cho việc “con xúc xắc thứ nhất xuất hiện mặt
kí hiệu cho việc “con xúc xắc thứ nhất xuất hiện mặt 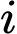 chấm, con xúc xắc thứ hai xuất hiện mặt
chấm, con xúc xắc thứ hai xuất hiện mặt 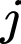 chấm và con xúc xắc thứ ba xuất hiện mặt
chấm và con xúc xắc thứ ba xuất hiện mặt 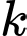 chấm”.
chấm”.
Gọi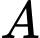 là biến cố: “Tổng số chấm xuất hiện trên ba con xúc xắc bằng 8”,
là biến cố: “Tổng số chấm xuất hiện trên ba con xúc xắc bằng 8”,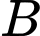 là biến cố: “Ít nhất một con xúc xắc ra 5 chấm”.
là biến cố: “Ít nhất một con xúc xắc ra 5 chấm”.
Ta có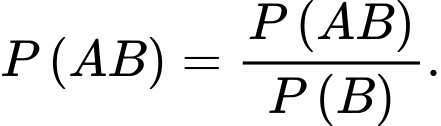
Vì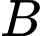 là biến cố: “Ít nhất một con xúc xắc xuất hiện mặt 5 chấm” nên
là biến cố: “Ít nhất một con xúc xắc xuất hiện mặt 5 chấm” nên 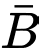 là biến cố: “Không có con xúc xắc nào xuất hiện mặt 5 chấm”, do đó
là biến cố: “Không có con xúc xắc nào xuất hiện mặt 5 chấm”, do đó 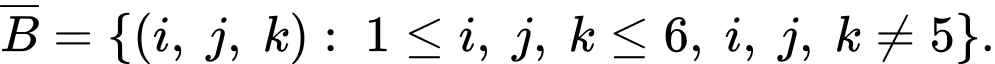
Suy ra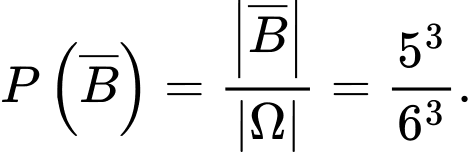
Do đó,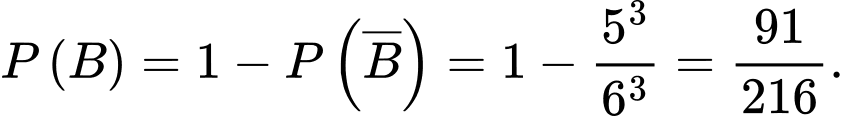
Ta thấy là biến cố: “ Tổng số chấm xuất hiện trên ba con xúc xắc bằng 8 và ít nhất một con xúc xắc ra 5 chấm”, do đó:
là biến cố: “ Tổng số chấm xuất hiện trên ba con xúc xắc bằng 8 và ít nhất một con xúc xắc ra 5 chấm”, do đó: 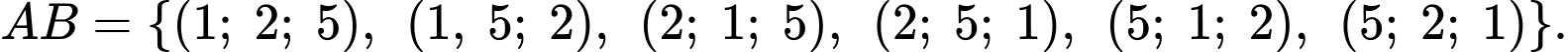
Suy ra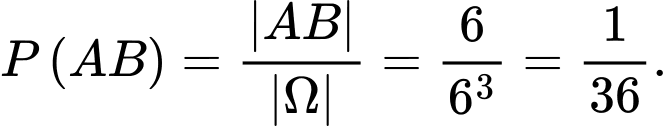
Vậy xác suất cần tìm là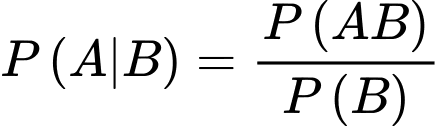
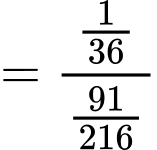
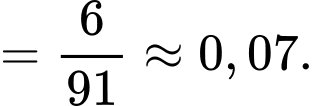
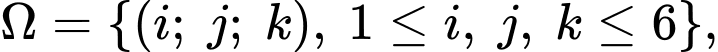 trong đó bộ số
trong đó bộ số 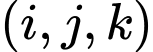 kí hiệu cho việc “con xúc xắc thứ nhất xuất hiện mặt
kí hiệu cho việc “con xúc xắc thứ nhất xuất hiện mặt 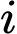 chấm, con xúc xắc thứ hai xuất hiện mặt
chấm, con xúc xắc thứ hai xuất hiện mặt 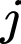 chấm và con xúc xắc thứ ba xuất hiện mặt
chấm và con xúc xắc thứ ba xuất hiện mặt 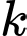 chấm”.
chấm”.
Gọi
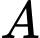 là biến cố: “Tổng số chấm xuất hiện trên ba con xúc xắc bằng 8”,
là biến cố: “Tổng số chấm xuất hiện trên ba con xúc xắc bằng 8”,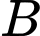 là biến cố: “Ít nhất một con xúc xắc ra 5 chấm”.
là biến cố: “Ít nhất một con xúc xắc ra 5 chấm”.
Ta có
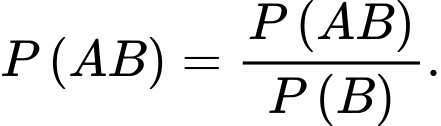
Vì
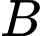 là biến cố: “Ít nhất một con xúc xắc xuất hiện mặt 5 chấm” nên
là biến cố: “Ít nhất một con xúc xắc xuất hiện mặt 5 chấm” nên 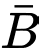 là biến cố: “Không có con xúc xắc nào xuất hiện mặt 5 chấm”, do đó
là biến cố: “Không có con xúc xắc nào xuất hiện mặt 5 chấm”, do đó 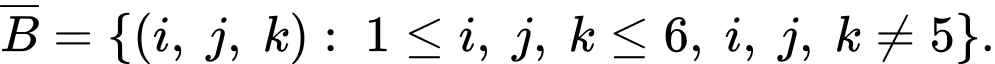
Suy ra
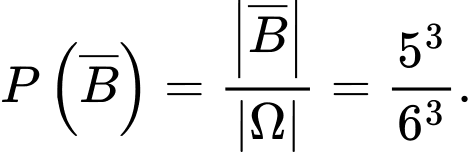
Do đó,
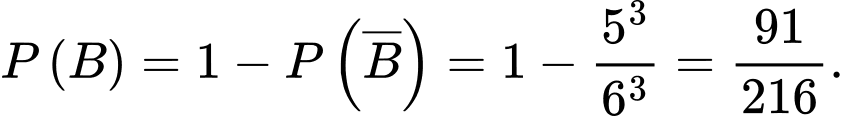
Ta thấy
 là biến cố: “ Tổng số chấm xuất hiện trên ba con xúc xắc bằng 8 và ít nhất một con xúc xắc ra 5 chấm”, do đó:
là biến cố: “ Tổng số chấm xuất hiện trên ba con xúc xắc bằng 8 và ít nhất một con xúc xắc ra 5 chấm”, do đó: 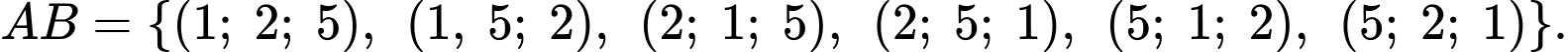
Suy ra
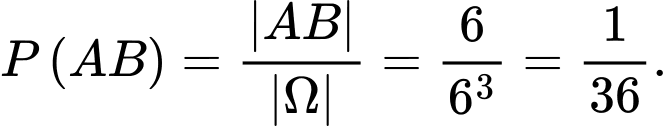
Vậy xác suất cần tìm là