PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1 [778853]: Cho 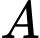 và
và  là hai biến cố bất kỳ. Khẳng định nào dưới đây là đúng?
là hai biến cố bất kỳ. Khẳng định nào dưới đây là đúng?
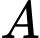 và
và  là hai biến cố bất kỳ. Khẳng định nào dưới đây là đúng?
là hai biến cố bất kỳ. Khẳng định nào dưới đây là đúng? A, 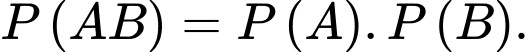
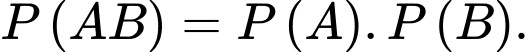
B, 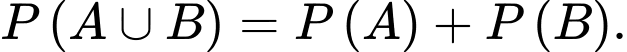
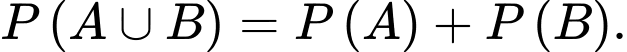
C, 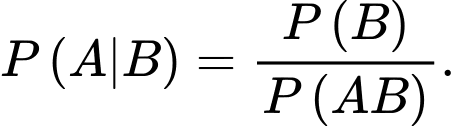
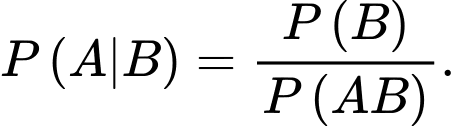
D, 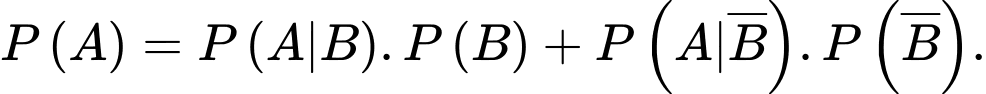
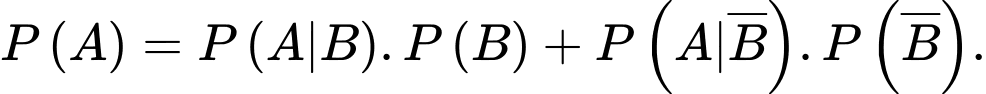
Chọn D
Theo công thức xác suất toàn phần, ta có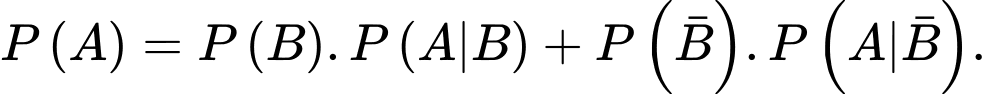 Đáp án: D
Đáp án: D
Theo công thức xác suất toàn phần, ta có
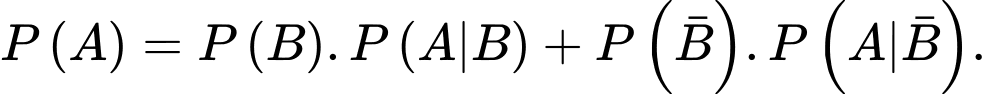 Đáp án: D
Đáp án: D
Câu 2 [778854]: Cho 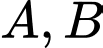 là các biến cố của một phép thử
là các biến cố của một phép thử 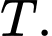 Biết rằng
Biết rằng  xác suất của biến cố
xác suất của biến cố 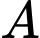 với điều kiện biến cố
với điều kiện biến cố 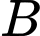 đã xảy ra được tính theo công thức nào sau đây?
đã xảy ra được tính theo công thức nào sau đây?
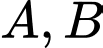 là các biến cố của một phép thử
là các biến cố của một phép thử 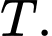 Biết rằng
Biết rằng  xác suất của biến cố
xác suất của biến cố 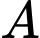 với điều kiện biến cố
với điều kiện biến cố 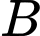 đã xảy ra được tính theo công thức nào sau đây?
đã xảy ra được tính theo công thức nào sau đây? A, 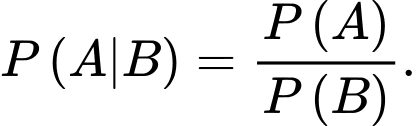
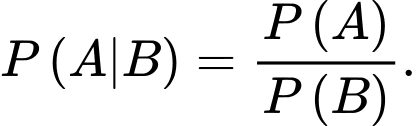
B, 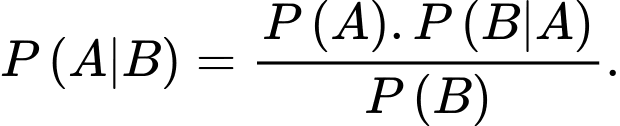
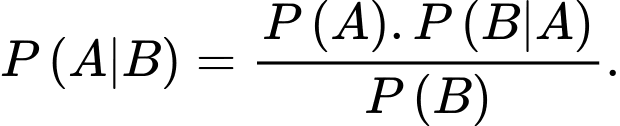
C, 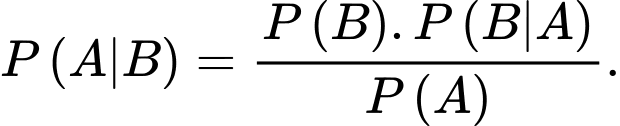
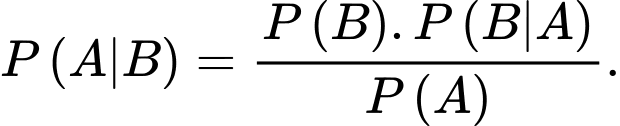
D, 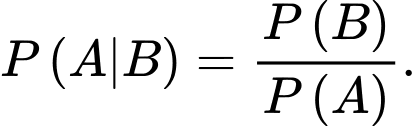
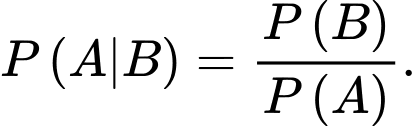
Chọn B
Theo công thức Bayes, ta có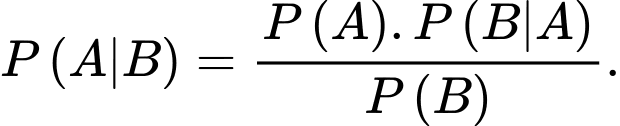 Đáp án: B
Đáp án: B
Theo công thức Bayes, ta có
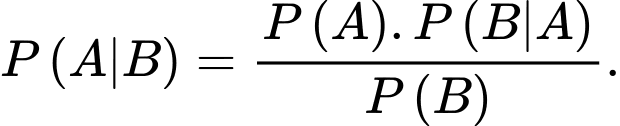 Đáp án: B
Đáp án: B
Câu 3 [778855]: Cho 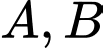 là các biến cố của một phép thử
là các biến cố của một phép thử 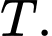 Biết rằng
Biết rằng 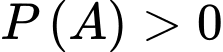 và
và  Xác suất của biến cố
Xác suất của biến cố 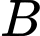 với điều kiện biến cố
với điều kiện biến cố 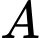 đã xảy ra được tính theo công thức nào sau đây?
đã xảy ra được tính theo công thức nào sau đây?
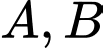 là các biến cố của một phép thử
là các biến cố của một phép thử 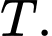 Biết rằng
Biết rằng 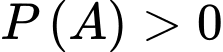 và
và  Xác suất của biến cố
Xác suất của biến cố 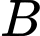 với điều kiện biến cố
với điều kiện biến cố 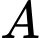 đã xảy ra được tính theo công thức nào sau đây?
đã xảy ra được tính theo công thức nào sau đây? A, 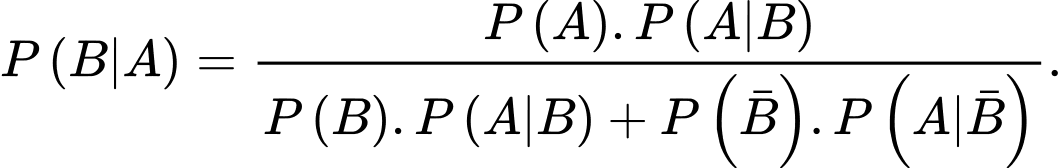
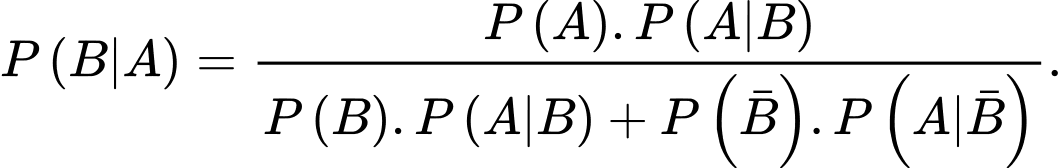
B, 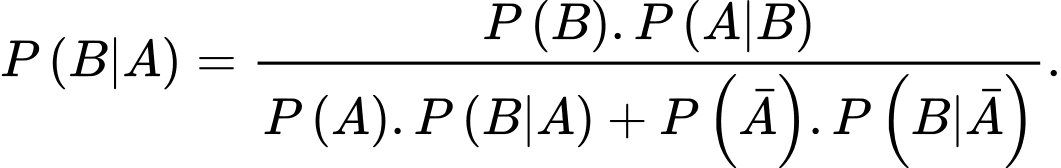
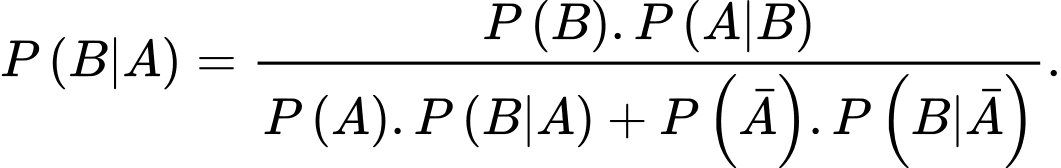
C, 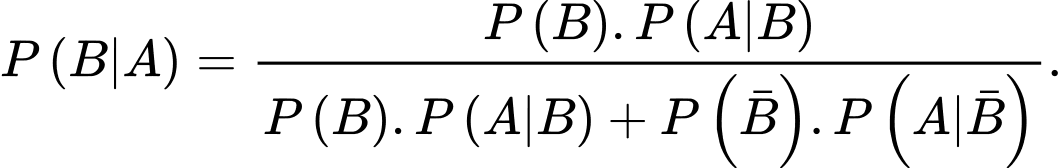
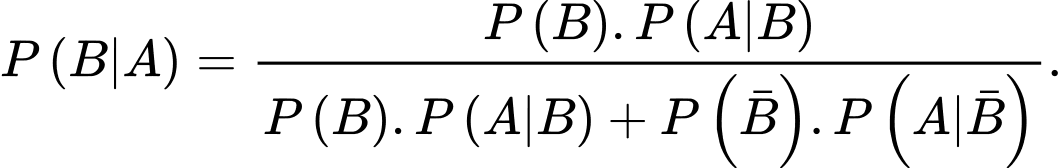
D, 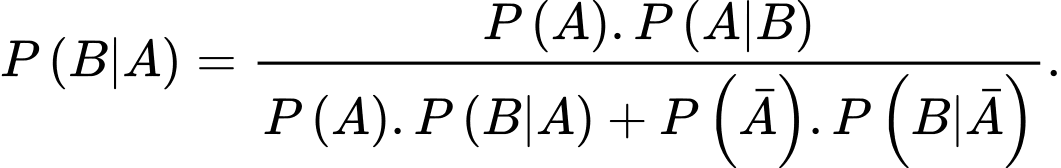
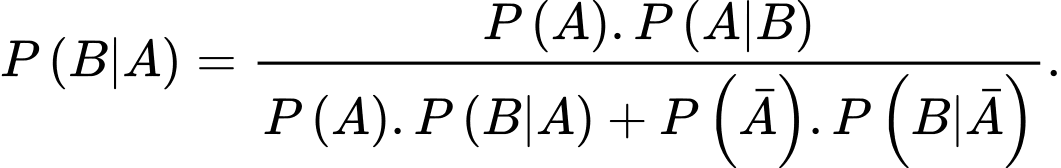
Chọn C.
Theo công thức Bayes, ta có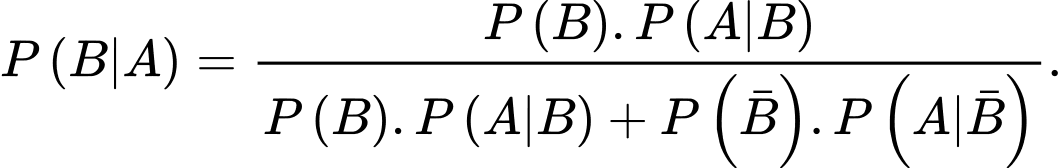 Đáp án: C
Đáp án: C
Theo công thức Bayes, ta có
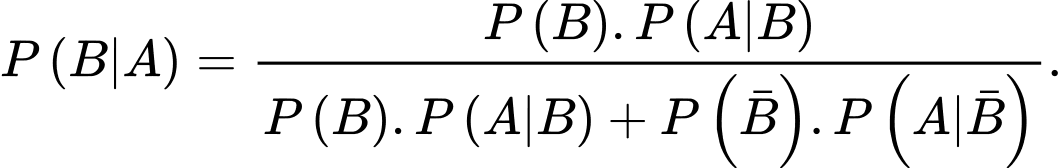 Đáp án: C
Đáp án: C
Câu 4 [778861]: Cho 2 biến cố 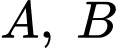 sao cho
sao cho 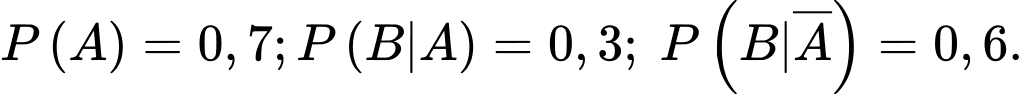 Tính
Tính 
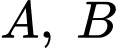 sao cho
sao cho 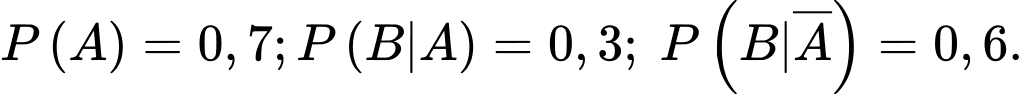 Tính
Tính 
A, 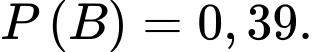
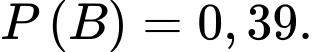
B, 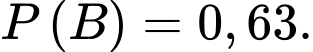
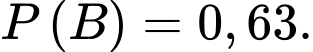
C, 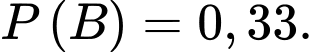
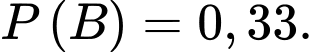
D, 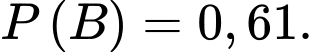
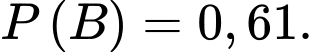
Ta có: 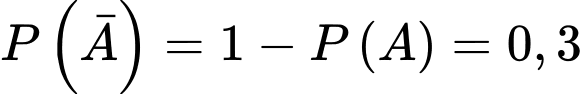
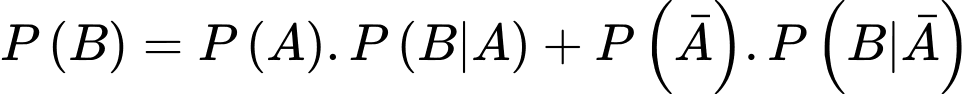
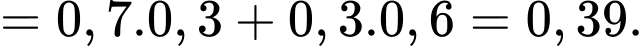 Chọn A.
Đáp án: A
Chọn A.
Đáp án: A
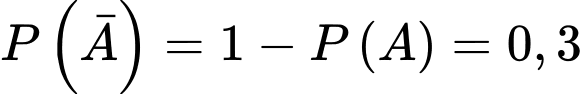
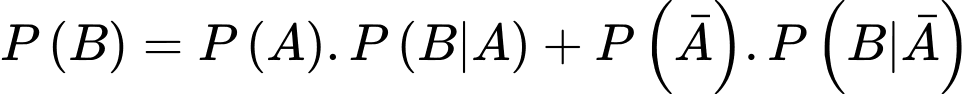
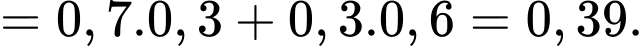 Chọn A.
Đáp án: A
Chọn A.
Đáp án: A
Câu 5 [778862]: Nếu hai biến cố 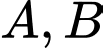 thỏa mãn
thỏa mãn 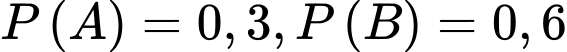 và
và 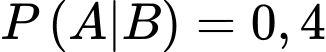 thì
thì  bằng
bằng
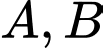 thỏa mãn
thỏa mãn 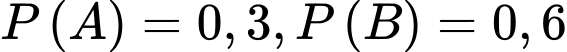 và
và 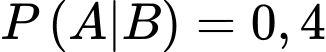 thì
thì  bằng
bằng A, 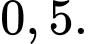
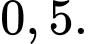
B, 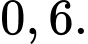
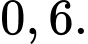
C, 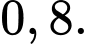
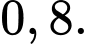
D, 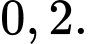
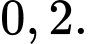
Theo công thức Bayes, ta có 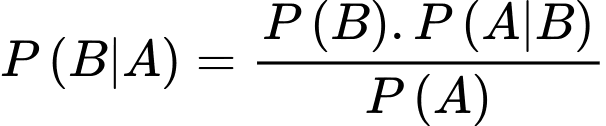
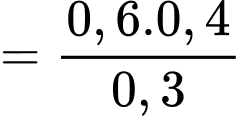
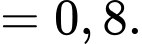
Chọn đáp án C. Đáp án: C
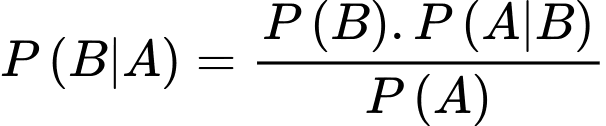
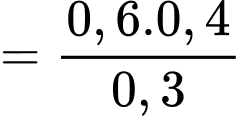
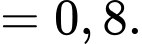
Chọn đáp án C. Đáp án: C
Câu 6 [778863]: Cho hai biến cố  thoả mãn
thoả mãn 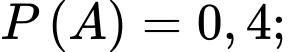
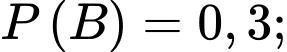
 . Khi đó,
. Khi đó, 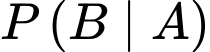 bằng
bằng
 thoả mãn
thoả mãn 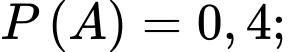
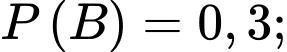
 . Khi đó,
. Khi đó, 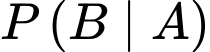 bằng
bằng A, 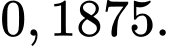
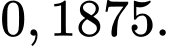
B, 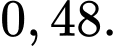
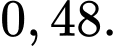
C, 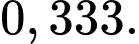
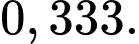
D, 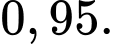
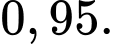
Chọn A
Theo công thức Bayes, ta có: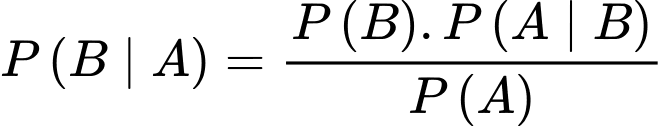
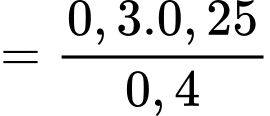
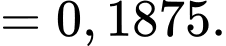 Đáp án: A
Đáp án: A
Theo công thức Bayes, ta có:
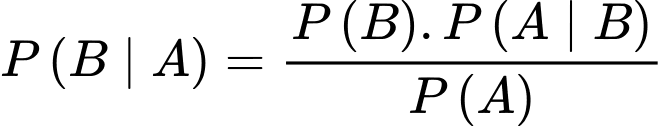
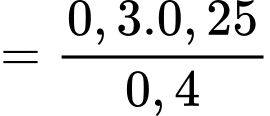
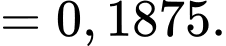 Đáp án: A
Đáp án: A
Câu 7 [360676]: Cho hai biến cố 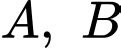 với
với 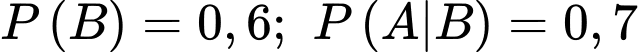 và
và 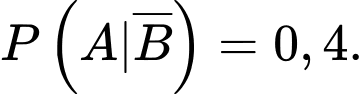 Khi đó,
Khi đó, 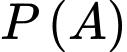 bằng:
bằng:
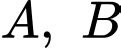 với
với 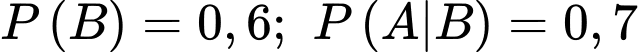 và
và 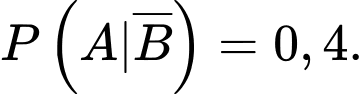 Khi đó,
Khi đó, 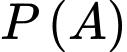 bằng:
bằng: A, 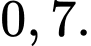
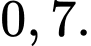
B, 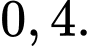
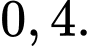
C, 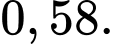
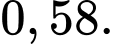
D, 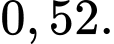
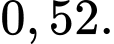
Ta có: 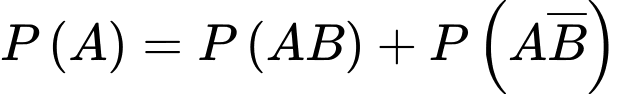
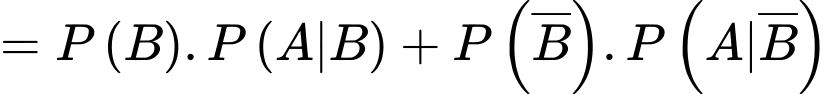
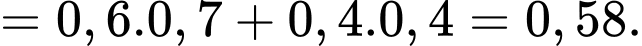
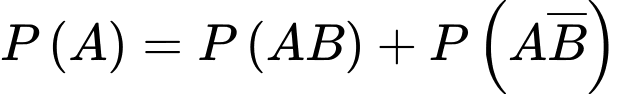
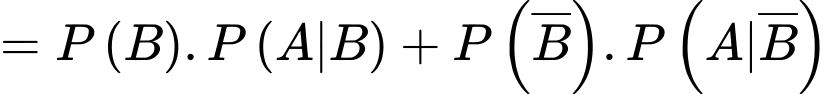
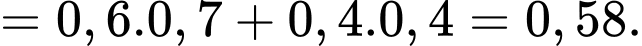
Chọn C.
Đáp án: C
Câu 8 [143807]: Một học sinh đi học muộn với xác suất là 0,3. Nếu người đó đi học muộn thì xác suất để người đó ăn sáng là 0,2. Nếu người đó không đi học muộn thì xác suất để người đó ăn sáng là 0,6. Ta có sơ đồ hình cây như sau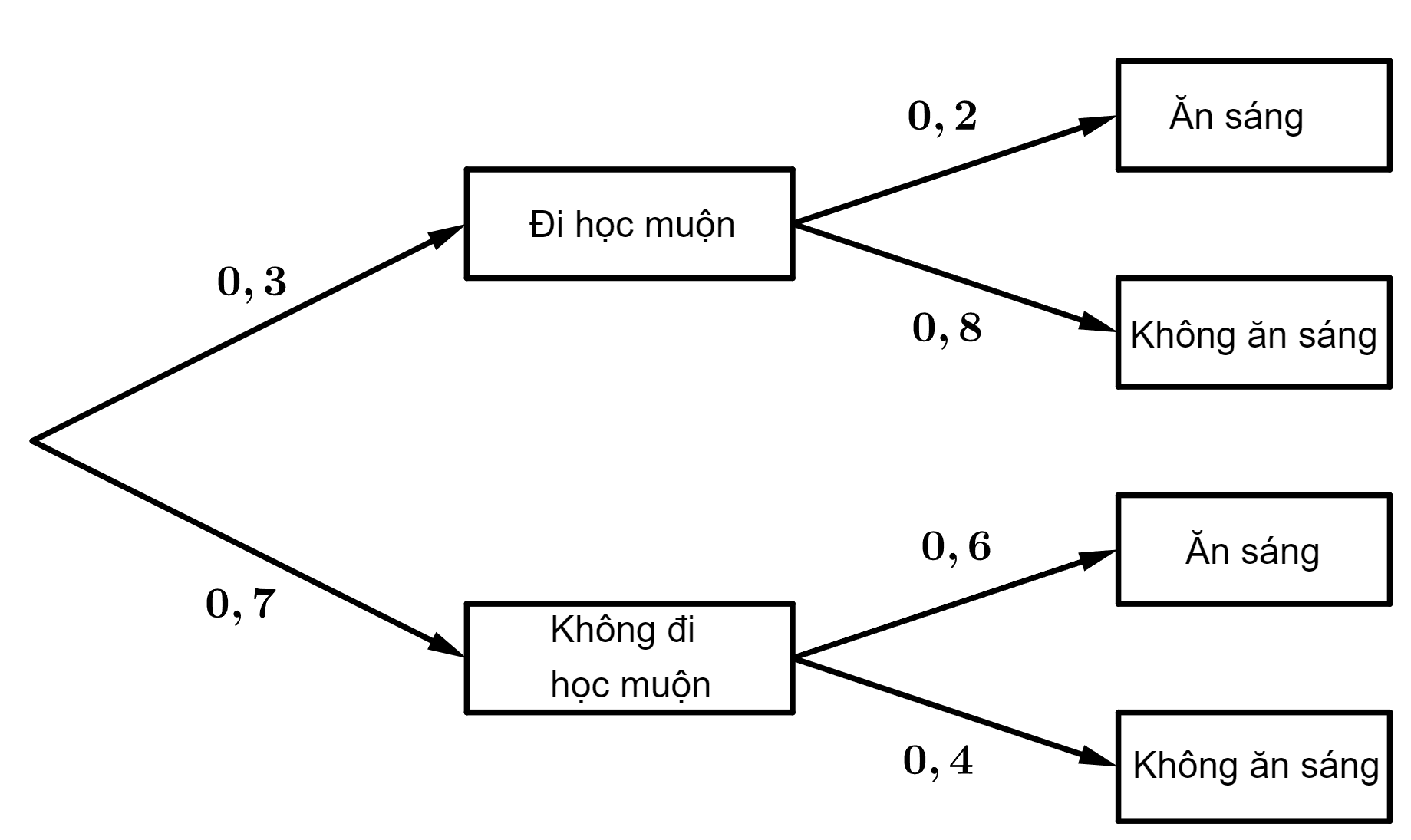

Xác suất của biến cố người đó ăn sáng là
A, 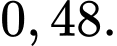
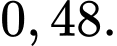
B, 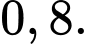
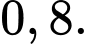
C, 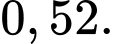
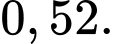
D, 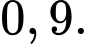
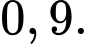
Xác suất của biến cố người đó ăn sáng là: 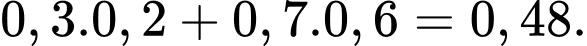
Chọn A. Đáp án: A
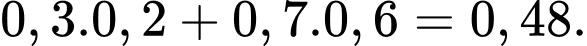
Chọn A. Đáp án: A
Câu 9 [143810]: Hai nhà máy cùng sản xuất 1 loại linh kiện điện tử. Năng suất nhà máy hai
gấp 3 lần năng suất nhà máy một. Tỷ lệ hỏng của nhà máy một và hai lần lượt là 0,1% và
0,2%. Giả sử linh kiện bán ở Trung tâm chỉ do hai nhà máy này sản xuất. Mua 1 linh
kiện ở Trung tâm. Tính xác suất để linh kiện ấy hỏng
gấp 3 lần năng suất nhà máy một. Tỷ lệ hỏng của nhà máy một và hai lần lượt là 0,1% và
0,2%. Giả sử linh kiện bán ở Trung tâm chỉ do hai nhà máy này sản xuất. Mua 1 linh
kiện ở Trung tâm. Tính xác suất để linh kiện ấy hỏng
A, 0,175%.
B, 0,125%.
C, 0,225%.
D, 0,233%.
Gọi 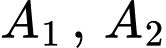 lần lượt là biến cố linh kiện điện tử do nhà máy I và nhà máy II sản xuất.
lần lượt là biến cố linh kiện điện tử do nhà máy I và nhà máy II sản xuất.
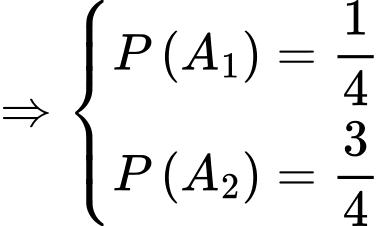
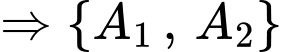 là một hệ đầy đủ.
là một hệ đầy đủ.
Gọi B là biến cố linh kiện điện tử bị hỏng
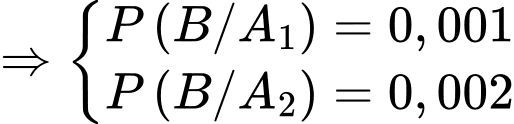
Xác suất linh kiện bán ra là một linh kiện bị hỏng là:
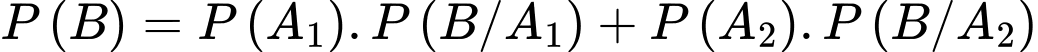
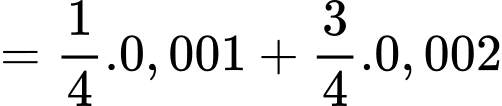
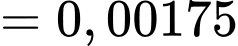
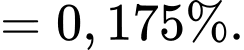
Đáp án: A. Đáp án: A
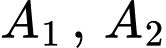 lần lượt là biến cố linh kiện điện tử do nhà máy I và nhà máy II sản xuất.
lần lượt là biến cố linh kiện điện tử do nhà máy I và nhà máy II sản xuất.
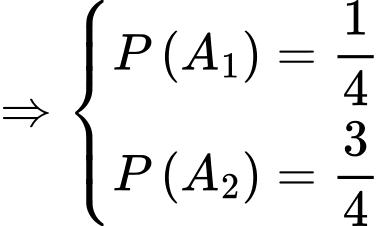
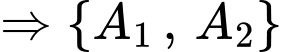 là một hệ đầy đủ.
là một hệ đầy đủ.
Gọi B là biến cố linh kiện điện tử bị hỏng
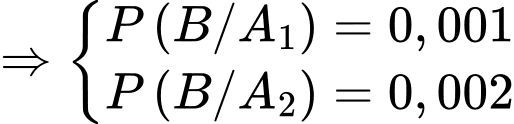
Xác suất linh kiện bán ra là một linh kiện bị hỏng là:
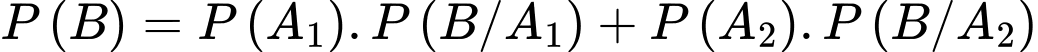
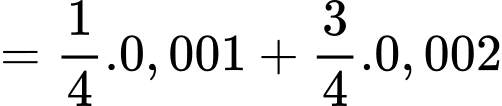
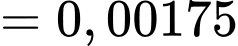
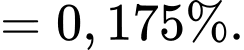
Đáp án: A. Đáp án: A
Câu 10 [778864]: Tỉ lệ người dân của tỉnh A có thu nhập cao là 20%; tỉ lệ người gửi tiết kiệm trong số người có thu nhập cao là 75%, còn tỉ lệ người gửi tiết kiệm trong số người không có thu nhập cao là 15%. Hỏi khi gặp ngẫu nhiên một người dân tỉnh A thì khả năng người đó bị gửi tiết kiệm là bao nhiêu phần trăm?
A, 
B, 
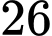
C, 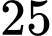
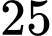
D, 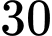
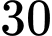
Gọi 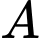 là biến cố “Người nghiện thuốc lá”, suy ra:
là biến cố “Người nghiện thuốc lá”, suy ra:  là biến cố “Người không nghiện thuốc lá”
là biến cố “Người không nghiện thuốc lá”
Gọi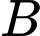 là biến cố “ Gặp người bị bệnh phổi”
là biến cố “ Gặp người bị bệnh phổi”
Để người mà ta gặp bị bệnh phổi thì người đó nghiện thuốc lá hoặc không nghiện thuốc lá
Ta cần tính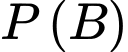
Với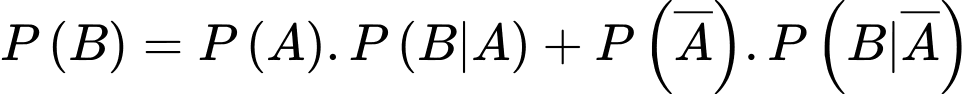
Ta có: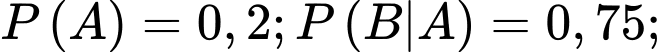
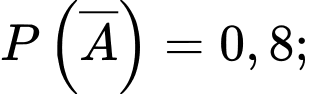
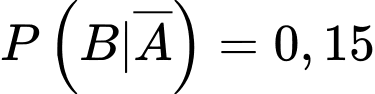
Vậy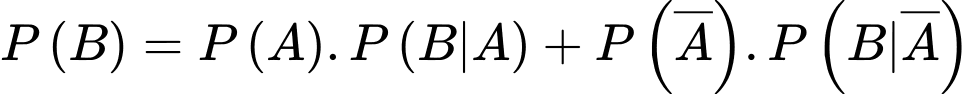
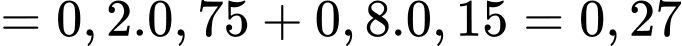 Đáp án: A
Đáp án: A
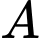 là biến cố “Người nghiện thuốc lá”, suy ra:
là biến cố “Người nghiện thuốc lá”, suy ra:  là biến cố “Người không nghiện thuốc lá”
là biến cố “Người không nghiện thuốc lá” Gọi
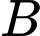 là biến cố “ Gặp người bị bệnh phổi”
là biến cố “ Gặp người bị bệnh phổi” Để người mà ta gặp bị bệnh phổi thì người đó nghiện thuốc lá hoặc không nghiện thuốc lá
Ta cần tính
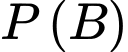
Với
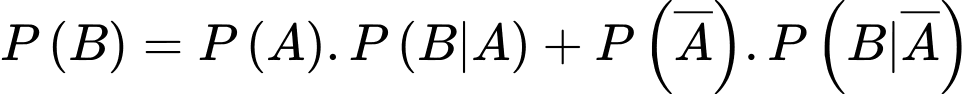
Ta có:
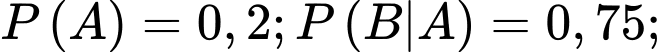
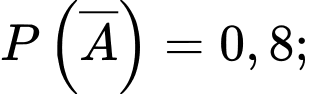
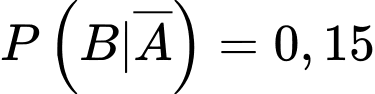
Vậy
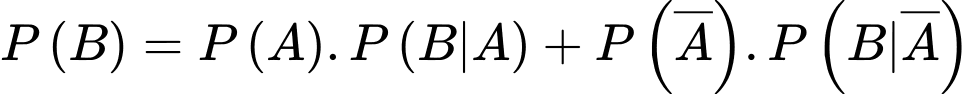
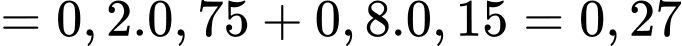 Đáp án: A
Đáp án: A
Câu 11 [378717]: Số khán giả đến xem buổi biểu diễn ca nhạc ngoài trời phụ thuộc vào thời tiết. Giả sử, nếu trời không mưa thì xác suất để bán hết vé là 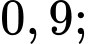 còn nếu trời mưa thì xác suất để bán hết vé chỉ là
còn nếu trời mưa thì xác suất để bán hết vé chỉ là 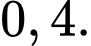 Dự báo thời tiết cho thấy xác suất để trời mưa vào buổi biểu diễn là
Dự báo thời tiết cho thấy xác suất để trời mưa vào buổi biểu diễn là 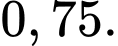 Tính xác suất để nhà tổ chức sự kiện bán hết vé.
Tính xác suất để nhà tổ chức sự kiện bán hết vé.
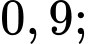 còn nếu trời mưa thì xác suất để bán hết vé chỉ là
còn nếu trời mưa thì xác suất để bán hết vé chỉ là 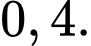 Dự báo thời tiết cho thấy xác suất để trời mưa vào buổi biểu diễn là
Dự báo thời tiết cho thấy xác suất để trời mưa vào buổi biểu diễn là 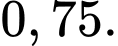 Tính xác suất để nhà tổ chức sự kiện bán hết vé.
Tính xác suất để nhà tổ chức sự kiện bán hết vé. A, 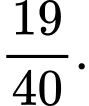
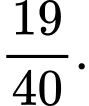
B, 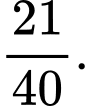
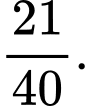
C, 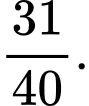
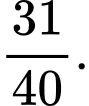
D, 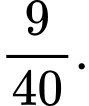
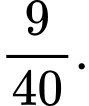
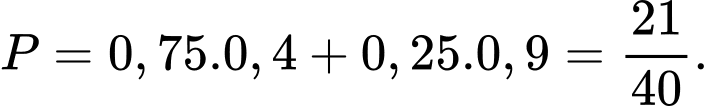 Đáp án: B
Đáp án: B
Câu 12 [778865]: Một dây chuyền may sản xuất ra hai sản phẩm: áo thun và áo sơ mi. Theo thống kê, trong một ngày dây chuyền này có 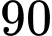 áo thun sản xuất đạt chất lượng và
áo thun sản xuất đạt chất lượng và 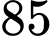 áo sơ mi sản xuất đạt chất lượng. Áo thun chiếm
áo sơ mi sản xuất đạt chất lượng. Áo thun chiếm 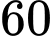 sản lượng sản xuất trong một ngày. Chọn ngẫu nhiên một sản phẩm trong số sản phẩm dây chuyền này sản xuất trong một ngày. Xác suất để sản phẩm được chọn đạt chất lượng là
sản lượng sản xuất trong một ngày. Chọn ngẫu nhiên một sản phẩm trong số sản phẩm dây chuyền này sản xuất trong một ngày. Xác suất để sản phẩm được chọn đạt chất lượng là
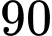 áo thun sản xuất đạt chất lượng và
áo thun sản xuất đạt chất lượng và 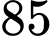 áo sơ mi sản xuất đạt chất lượng. Áo thun chiếm
áo sơ mi sản xuất đạt chất lượng. Áo thun chiếm 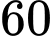 sản lượng sản xuất trong một ngày. Chọn ngẫu nhiên một sản phẩm trong số sản phẩm dây chuyền này sản xuất trong một ngày. Xác suất để sản phẩm được chọn đạt chất lượng là
sản lượng sản xuất trong một ngày. Chọn ngẫu nhiên một sản phẩm trong số sản phẩm dây chuyền này sản xuất trong một ngày. Xác suất để sản phẩm được chọn đạt chất lượng là A, 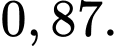
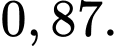
B, 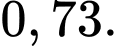
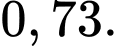
C, 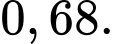
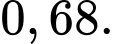
D, 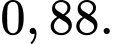
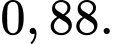
Xét hai biến cố:
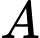 : “Sản phẩm được chọn là đạt chất lượng”;
: “Sản phẩm được chọn là đạt chất lượng”;
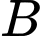 : “Sản phẩm được chọn là áo thun”.
: “Sản phẩm được chọn là áo thun”.
Từ giả thiết ta có:
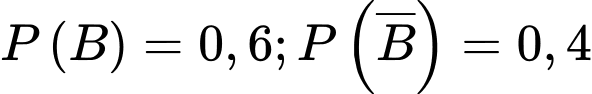 ;
;
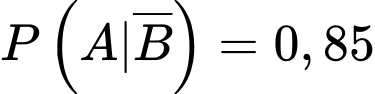 .
.
Áp dụng công thức xác suất toàn phần, ta có:
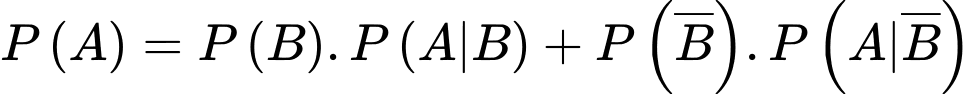
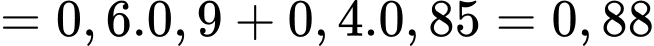 .
.
Vậy xác suất để để sản phẩm được chọn đạt chất lượng là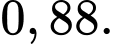
Chọn đáp án D. Đáp án: D
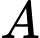 : “Sản phẩm được chọn là đạt chất lượng”;
: “Sản phẩm được chọn là đạt chất lượng”;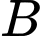 : “Sản phẩm được chọn là áo thun”.
: “Sản phẩm được chọn là áo thun”.Từ giả thiết ta có:
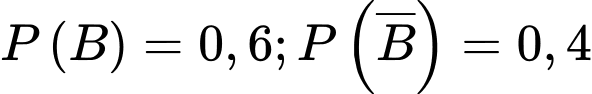 ;
;
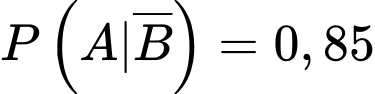 .
.Áp dụng công thức xác suất toàn phần, ta có:
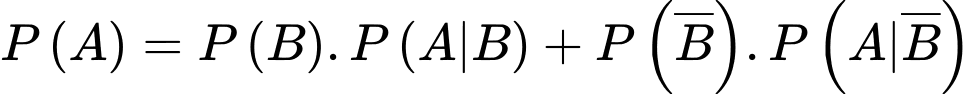
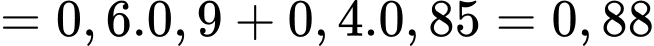 .
.Vậy xác suất để để sản phẩm được chọn đạt chất lượng là
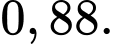
Chọn đáp án D. Đáp án: D
PHẦN II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a),b),c),d) ở mỗi câu học sinh chọn đúng hoặc sai.
Câu 13 [778866]: Dây chuyền lắp ráp nhận được các chi tiết do hai máy sản xuất. Trung bình máy thứ nhất cung cấp 60% chi tiết, còn lại là của máy thứ hai. Khoảng 90% chi tiết do máy thứ nhất sản xuất đạt tiêu chuẩn, còn 85% chi tiết do máy thứ 2 sản xuất là đạt tiêu chuẩn. Lấy ngẫu nhiên từ dây chuyền một sản phẩm.
Gọi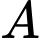 là biến cố: “Chi tiết lấy từ dây chuyền đạt tiêu chuẩn”
là biến cố: “Chi tiết lấy từ dây chuyền đạt tiêu chuẩn”
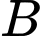 là biến cố: “Chi tiết do máy thứ nhất sản xuất”.
là biến cố: “Chi tiết do máy thứ nhất sản xuất”.
Gọi
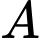 là biến cố: “Chi tiết lấy từ dây chuyền đạt tiêu chuẩn”
là biến cố: “Chi tiết lấy từ dây chuyền đạt tiêu chuẩn”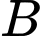 là biến cố: “Chi tiết do máy thứ nhất sản xuất”.
là biến cố: “Chi tiết do máy thứ nhất sản xuất”.
a) Sai.
Từ giả thiết: “Trung bình máy thứ nhất cung cấp 60% chi tiết, còn lại là của máy thứ hai” nên ta có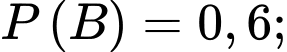
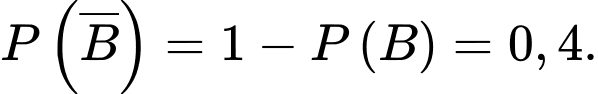
b) Sai.
 là xác suất chi tiết đạt tiêu chuẩn biết chi tiết đó do máy thứ hai sản xuất. Và giả thiết cho: “85% chi tiết do máy thứ hai sản xuất là đạt tiêu chuẩn” nên
là xác suất chi tiết đạt tiêu chuẩn biết chi tiết đó do máy thứ hai sản xuất. Và giả thiết cho: “85% chi tiết do máy thứ hai sản xuất là đạt tiêu chuẩn” nên 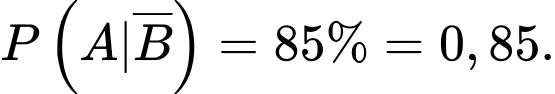
c) Sai.
Xác suất chi tiết lấy được do máy thứ nhất sản xuất bằng 60\% hay bằng 0,6.
d) Đúng.
Ta cần tính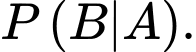
Ta có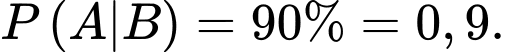
Theo công thức Bayes, ta có
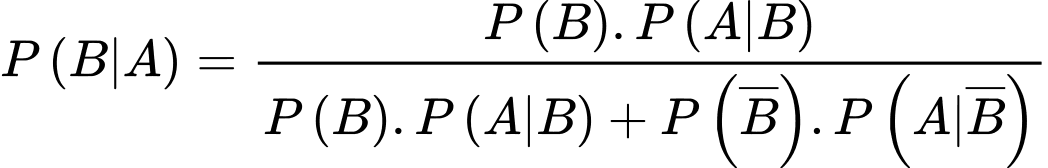
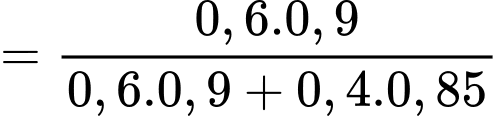
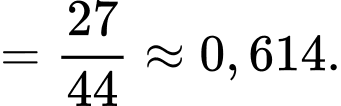
Từ giả thiết: “Trung bình máy thứ nhất cung cấp 60% chi tiết, còn lại là của máy thứ hai” nên ta có
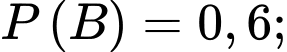
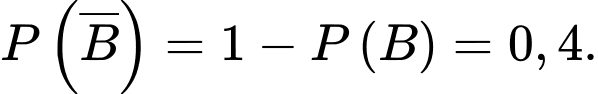
b) Sai.
 là xác suất chi tiết đạt tiêu chuẩn biết chi tiết đó do máy thứ hai sản xuất. Và giả thiết cho: “85% chi tiết do máy thứ hai sản xuất là đạt tiêu chuẩn” nên
là xác suất chi tiết đạt tiêu chuẩn biết chi tiết đó do máy thứ hai sản xuất. Và giả thiết cho: “85% chi tiết do máy thứ hai sản xuất là đạt tiêu chuẩn” nên 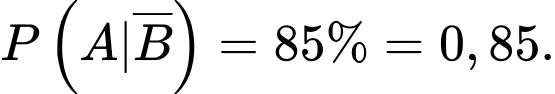
c) Sai.
Xác suất chi tiết lấy được do máy thứ nhất sản xuất bằng 60\% hay bằng 0,6.
d) Đúng.
Ta cần tính
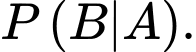
Ta có
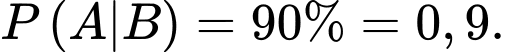
Theo công thức Bayes, ta có
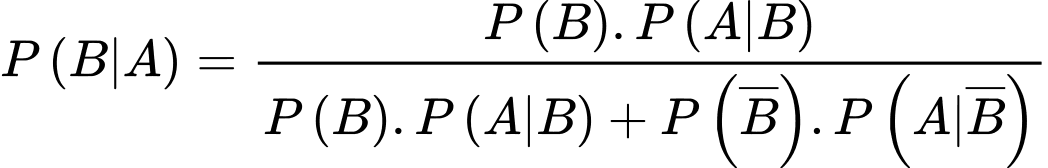
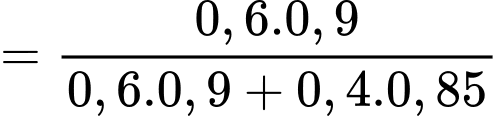
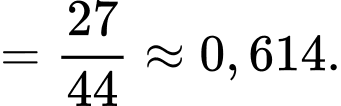
Câu 14 [778869]: Tại một trường THPT có 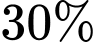 học sinh tham gia câu lạc bộ thể thao. Trong số những học sinh này, có
học sinh tham gia câu lạc bộ thể thao. Trong số những học sinh này, có 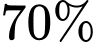 biết bơi. Ngoài ra, có
biết bơi. Ngoài ra, có 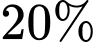 số học sinh không tham gia câu lạc bộ thể thao cũng biết bơi. Chọn ngẫu nhiên một học sinh của trường.
số học sinh không tham gia câu lạc bộ thể thao cũng biết bơi. Chọn ngẫu nhiên một học sinh của trường.
Gọi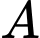 là biến cố: "Chọn được học sinh thuộc câu lạc bộ thể thao";
là biến cố: "Chọn được học sinh thuộc câu lạc bộ thể thao";
Gọi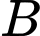 là biến cố: “Chọn được học sinh biết bơi”.
là biến cố: “Chọn được học sinh biết bơi”.
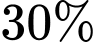 học sinh tham gia câu lạc bộ thể thao. Trong số những học sinh này, có
học sinh tham gia câu lạc bộ thể thao. Trong số những học sinh này, có 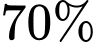 biết bơi. Ngoài ra, có
biết bơi. Ngoài ra, có 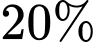 số học sinh không tham gia câu lạc bộ thể thao cũng biết bơi. Chọn ngẫu nhiên một học sinh của trường.
số học sinh không tham gia câu lạc bộ thể thao cũng biết bơi. Chọn ngẫu nhiên một học sinh của trường.Gọi
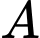 là biến cố: "Chọn được học sinh thuộc câu lạc bộ thể thao";
là biến cố: "Chọn được học sinh thuộc câu lạc bộ thể thao"; Gọi
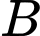 là biến cố: “Chọn được học sinh biết bơi”.
là biến cố: “Chọn được học sinh biết bơi”.
a) Đúng.
Từ giả thiết: “có 30% học sinh tham gia câu lạc bộ thể thao” nên ta được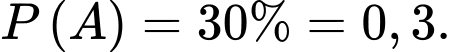 Suy ra
Suy ra 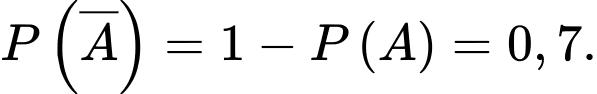
b) Đúng.
Từ giả thiết: “có 20% số học sinh không tham gia câu lạc bộ thể thao cũng biết bơi” nên ta được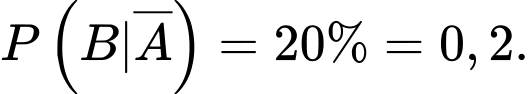
c) Sai.
Vẽ sơ đồ cây thì ta dễ tính được, thông qua áp dụng công thức xác suất toàn phần, ta có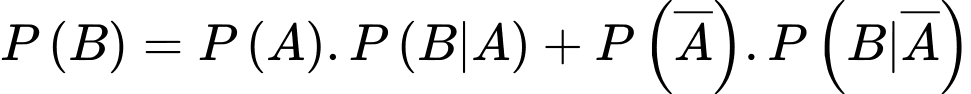
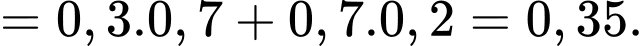
d) Đúng.
Ta cần tính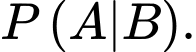
Ta có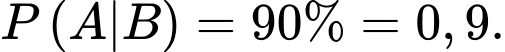
Theo công thức Bayes, ta có
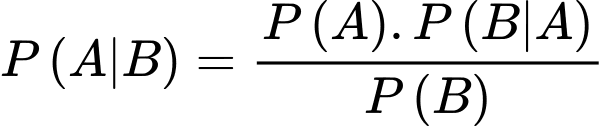
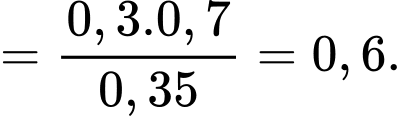
Từ giả thiết: “có 30% học sinh tham gia câu lạc bộ thể thao” nên ta được
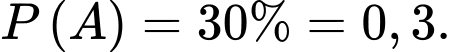 Suy ra
Suy ra 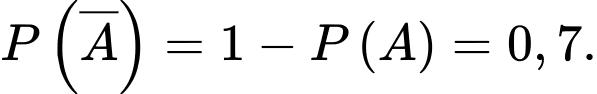
b) Đúng.
Từ giả thiết: “có 20% số học sinh không tham gia câu lạc bộ thể thao cũng biết bơi” nên ta được
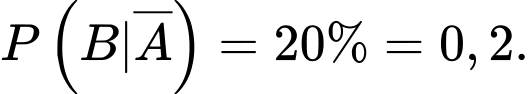
c) Sai.
Vẽ sơ đồ cây thì ta dễ tính được, thông qua áp dụng công thức xác suất toàn phần, ta có
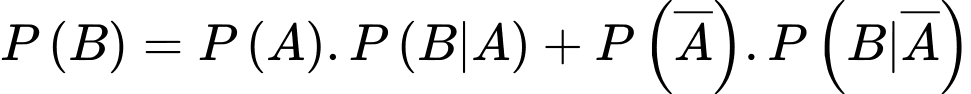
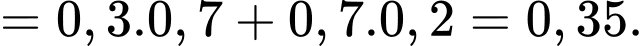
d) Đúng.
Ta cần tính
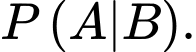
Ta có
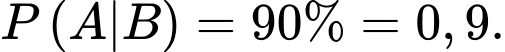
Theo công thức Bayes, ta có
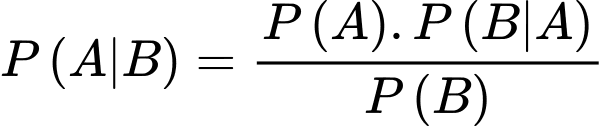
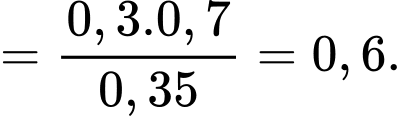
Câu 15 [680750]: Trước khi đưa một loại sản phẩm ra thị trường, người ta đã phỏng vấn ngẫu nhiên 200 khách hàng về sản phẩm đó. Kết quả thống kê như sau: có 105 người trả lời “sẽ mua”; có 95 người trả lời “không mua”. Kinh nghiệm cho thấy tỉ lệ khách hàng thực sự sẽ mua sản phẩm tương ứng với những cách trả lời “sẽ mua” và “không mua” lần lượt là 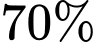 và
và 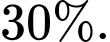
Gọi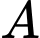 là biến cố “Người được phỏng vấn thực sự sẽ mua sản phẩm”.
là biến cố “Người được phỏng vấn thực sự sẽ mua sản phẩm”.
Gọi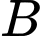 là biến cố “Người được phỏng vấn trả lời sẽ mua sản phẩm”.
là biến cố “Người được phỏng vấn trả lời sẽ mua sản phẩm”.
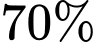 và
và 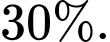
Gọi
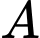 là biến cố “Người được phỏng vấn thực sự sẽ mua sản phẩm”.
là biến cố “Người được phỏng vấn thực sự sẽ mua sản phẩm”.Gọi
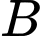 là biến cố “Người được phỏng vấn trả lời sẽ mua sản phẩm”.
là biến cố “Người được phỏng vấn trả lời sẽ mua sản phẩm”. a) Đúng.
Xác suất của biến cố 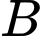 là
là 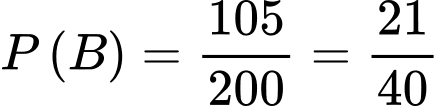 .
.Xác suất của biến cố
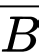 là
là 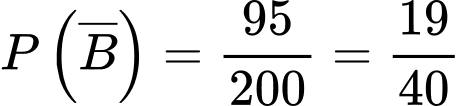 .
.b) Sai.
Biến cố
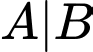 là biến cố: “Người được phỏng vấn thực sự sẽ mua sản phẩm nếu người đó được phỏng vấn trả lời sẽ mua sản phẩm”.
là biến cố: “Người được phỏng vấn thực sự sẽ mua sản phẩm nếu người đó được phỏng vấn trả lời sẽ mua sản phẩm”.Theo giả thiết: Tỉ lệ khách hàng thực sự sẽ mua sản phẩm tương ứng với những cách trả lời "sẽ mua" là
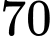 nên ta có
nên ta có 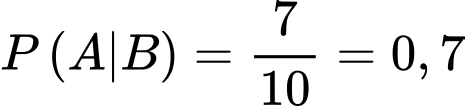 .
.c) Đúng.
Ta có
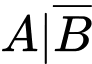 là biến cố: “Người được phỏng vấn thực sự sẽ mua sản phẩm nếu người đó được phỏng vấn trả lời không mua”.
là biến cố: “Người được phỏng vấn thực sự sẽ mua sản phẩm nếu người đó được phỏng vấn trả lời không mua”.Theo giả thiết ta có
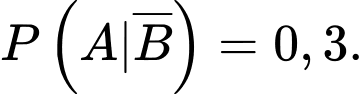 Ta có sơ đồ cây:
Ta có sơ đồ cây: 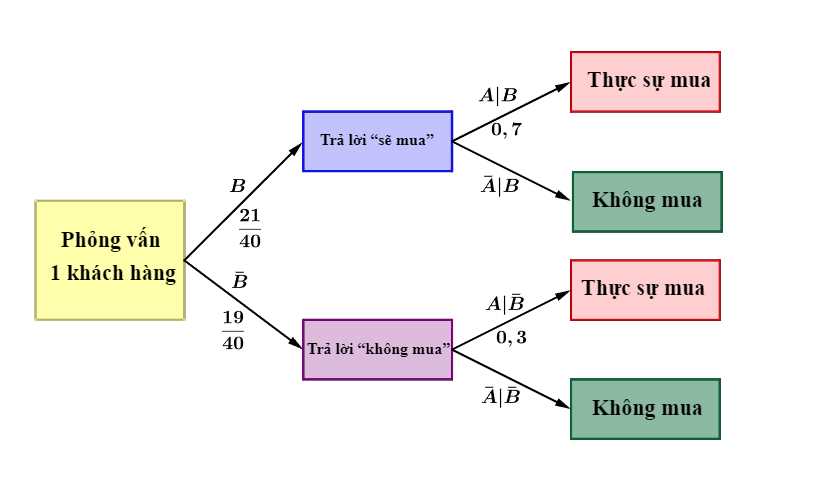
Theo công thức xác suất toàn phần:
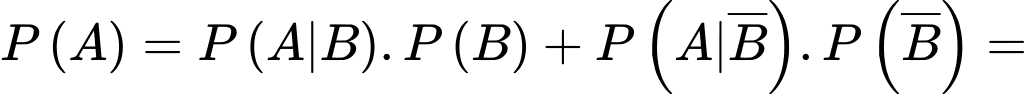
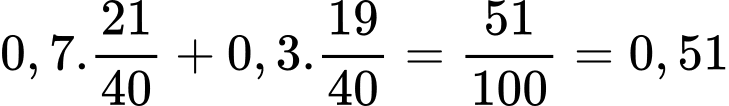 .
.d) Sai.
Ta có
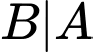 là biến cố: “Người đó đã trả lời sẽ mua sản phẩm khi được phỏng vấn và người được phỏng vấn thực sự sẽ mua sản phẩm ”.
là biến cố: “Người đó đã trả lời sẽ mua sản phẩm khi được phỏng vấn và người được phỏng vấn thực sự sẽ mua sản phẩm ”.Theo công thức BAYES ta có
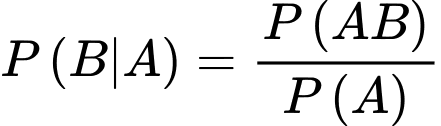
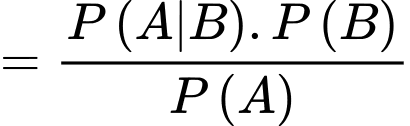
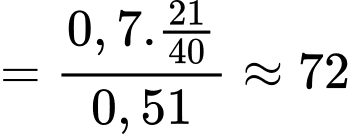
Câu 16 [693209]: Một tờ tiền giả lần lượt bị hai người A và B kiểm tra. Xác suất để người A phát hiện ra tờ này giả là 0,7. Nếu người A cho rằng tờ này tiền giả, thì xác suất để người B cũng nhận định như thể là 0,8. Ngược lại, nếu người A cho rằng tờ này là tiền thật thì xác suất để người B cũng nhận định như thể là 0,4.
Gọi 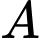 là biến cố: “Người A phát hiện ra tờ này là tiền giả”.
là biến cố: “Người A phát hiện ra tờ này là tiền giả”.
Gọi B là biến cố: “Người B phát hiện ra tờ tiền này là giả”.
Khi đó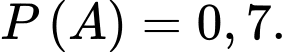
a) Sai.
Xác suất để A không phát hiện ra tờ tiền đó giả là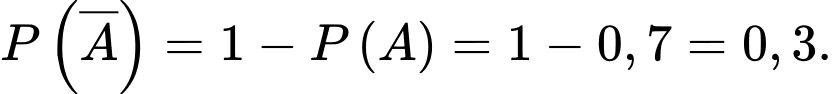
b) Đúng.
Xác suất để hai người này đều nhận định đây là tờ tiền thật là

c) Đúng.
Dựa vào ý b) ta có: Xác suất để ít nhất một trong hai người này phát hiện ra tờ tiền đó là giả là: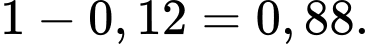
d) Đúng.
Biết tờ tiền đó đã bị ít nhất một trong hai người này phát hiện là giả, xác suất để A phát hiện ra nó giả là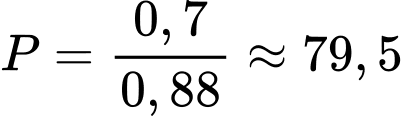
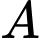 là biến cố: “Người A phát hiện ra tờ này là tiền giả”.
là biến cố: “Người A phát hiện ra tờ này là tiền giả”.Gọi B là biến cố: “Người B phát hiện ra tờ tiền này là giả”.
Khi đó
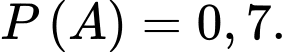
a) Sai.
Xác suất để A không phát hiện ra tờ tiền đó giả là
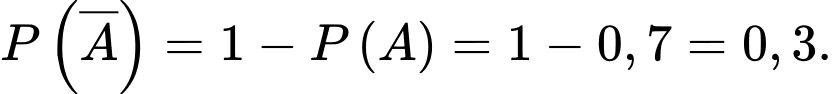
b) Đúng.
Xác suất để hai người này đều nhận định đây là tờ tiền thật là

c) Đúng.
Dựa vào ý b) ta có: Xác suất để ít nhất một trong hai người này phát hiện ra tờ tiền đó là giả là:
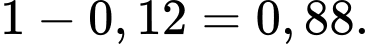
d) Đúng.
Biết tờ tiền đó đã bị ít nhất một trong hai người này phát hiện là giả, xác suất để A phát hiện ra nó giả là
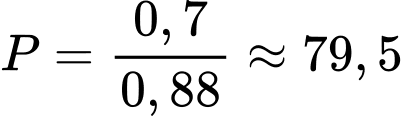
PHẦN III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 17 đến câu 22.
Câu 17 [778872]: Một nhà máy lắp ráp nhận được các chi tiết do hai máy sản xuất. Trung bình máy thứ nhất cung cấp 65% chi tiết, máy thứ hai cung cấp 35% chi tiết. Có 80% chi tiết do máy thứ nhất sản xuất đạt tiêu chuẩn, còn 85% chi tiết do máy thứ hai sản xuất là đạt tiêu chuẩn. Lấy ngẫu nhiên từ nhà máy một sản phẩm thì thấy nó đạt tiêu chuẩn. Tìm xác suất để sản phẩm đó do máy thứ nhất sản xuất. (kết quả làm tròn đến hàng phần trăm).
Điền đáp án: 0,64.
Gọi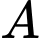 là biến cố “Chi tiết đó do nhà máy thứ nhất cung cấp” suy ra
là biến cố “Chi tiết đó do nhà máy thứ nhất cung cấp” suy ra  là biến cố “Chi tiết đó do nhà máy thứ hai cung cấp”.
là biến cố “Chi tiết đó do nhà máy thứ hai cung cấp”.
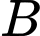 là biến cố “Chi tiết máy đó đạt tiêu chuẩn”;
là biến cố “Chi tiết máy đó đạt tiêu chuẩn”; 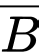 là biến cố “Chi tiết máy đó không đạt tiêu chuẩn”.
là biến cố “Chi tiết máy đó không đạt tiêu chuẩn”.
Từ giả thiết, ta có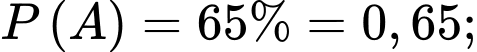
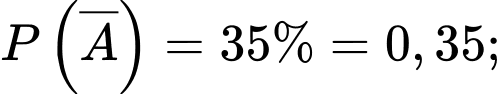
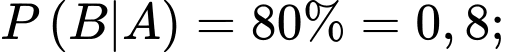
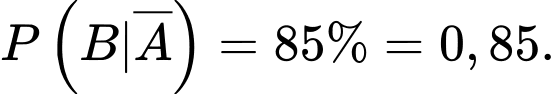
Yêu cầu bài toán Tính
Tính 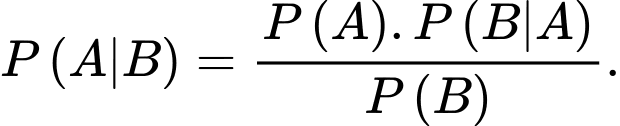
Vẽ sơ đồ cây ta dễ dạng tính được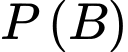 dựa vào công thức xác suất toàn phần, ta có
dựa vào công thức xác suất toàn phần, ta có 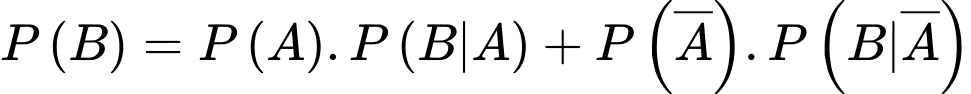
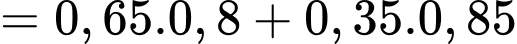
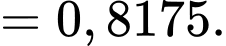
Áp dụng công thức Bayes, ta có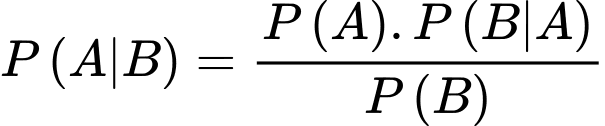
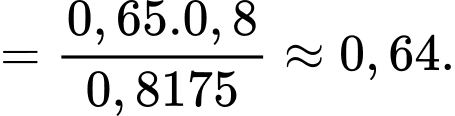
Gọi
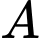 là biến cố “Chi tiết đó do nhà máy thứ nhất cung cấp” suy ra
là biến cố “Chi tiết đó do nhà máy thứ nhất cung cấp” suy ra  là biến cố “Chi tiết đó do nhà máy thứ hai cung cấp”.
là biến cố “Chi tiết đó do nhà máy thứ hai cung cấp”.
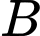 là biến cố “Chi tiết máy đó đạt tiêu chuẩn”;
là biến cố “Chi tiết máy đó đạt tiêu chuẩn”; 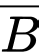 là biến cố “Chi tiết máy đó không đạt tiêu chuẩn”.
là biến cố “Chi tiết máy đó không đạt tiêu chuẩn”.
Từ giả thiết, ta có
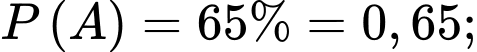
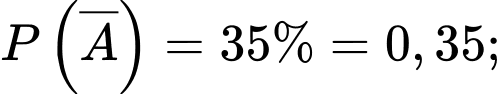
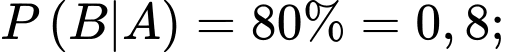
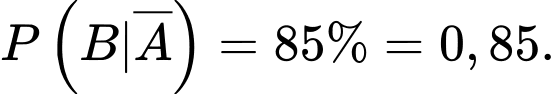
Yêu cầu bài toán
 Tính
Tính 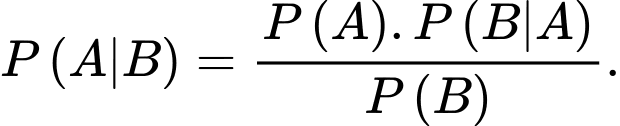
Vẽ sơ đồ cây ta dễ dạng tính được
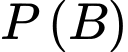 dựa vào công thức xác suất toàn phần, ta có
dựa vào công thức xác suất toàn phần, ta có 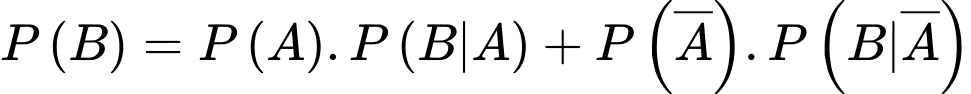
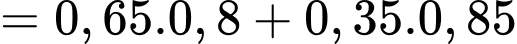
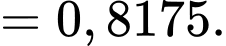
Áp dụng công thức Bayes, ta có
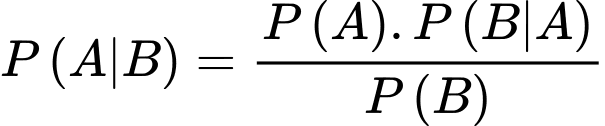
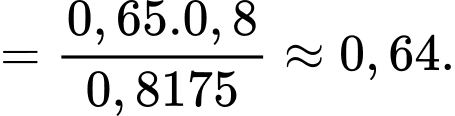
Câu 18 [778873]: Trong một đợt kiểm tra sức khoẻ, có một loại bệnh X mà tỉ lệ người mắc bệnh là 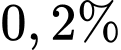 và một loại xét nghiệm Y mà ai mắc bệnh X khi xét nghiệm Y cũng có phản ứng dương tính. Tuy nhiên, có
và một loại xét nghiệm Y mà ai mắc bệnh X khi xét nghiệm Y cũng có phản ứng dương tính. Tuy nhiên, có 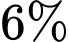 những người không bị bệnh X lại có phản ứng dương tính với xét nghiệm Y. Chọn ngẫu nhiên 1 người trong đợt kiểm tra sức khoẻ đó. Giả sử người đó có phản ứng dương tính với xét nghiệm Y. Xác suất người đó bị mắc bệnh X là bao nhiêu phần trăm (làm tròn kết quả đến hàng phần chục)?
những người không bị bệnh X lại có phản ứng dương tính với xét nghiệm Y. Chọn ngẫu nhiên 1 người trong đợt kiểm tra sức khoẻ đó. Giả sử người đó có phản ứng dương tính với xét nghiệm Y. Xác suất người đó bị mắc bệnh X là bao nhiêu phần trăm (làm tròn kết quả đến hàng phần chục)?
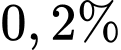 và một loại xét nghiệm Y mà ai mắc bệnh X khi xét nghiệm Y cũng có phản ứng dương tính. Tuy nhiên, có
và một loại xét nghiệm Y mà ai mắc bệnh X khi xét nghiệm Y cũng có phản ứng dương tính. Tuy nhiên, có 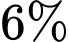 những người không bị bệnh X lại có phản ứng dương tính với xét nghiệm Y. Chọn ngẫu nhiên 1 người trong đợt kiểm tra sức khoẻ đó. Giả sử người đó có phản ứng dương tính với xét nghiệm Y. Xác suất người đó bị mắc bệnh X là bao nhiêu phần trăm (làm tròn kết quả đến hàng phần chục)?
những người không bị bệnh X lại có phản ứng dương tính với xét nghiệm Y. Chọn ngẫu nhiên 1 người trong đợt kiểm tra sức khoẻ đó. Giả sử người đó có phản ứng dương tính với xét nghiệm Y. Xác suất người đó bị mắc bệnh X là bao nhiêu phần trăm (làm tròn kết quả đến hàng phần chục)?
Xét các biến cố:
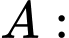 "Người được chọn mắc bệnh X";
"Người được chọn mắc bệnh X";
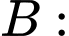 "Người được chọn có phản ứng dương tính với xét nghiệm Y".
"Người được chọn có phản ứng dương tính với xét nghiệm Y".
Theo giả thiết ta có: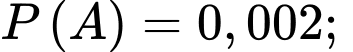
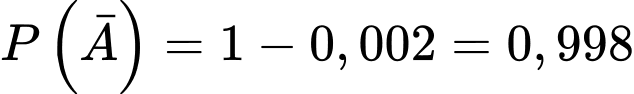 ;
;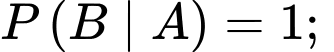
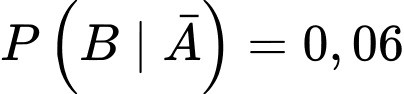 .
.
Theo công thức Bayes, ta có:
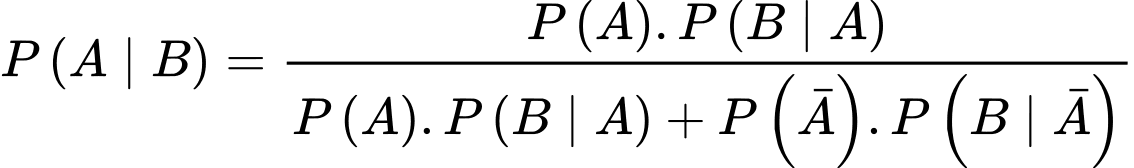
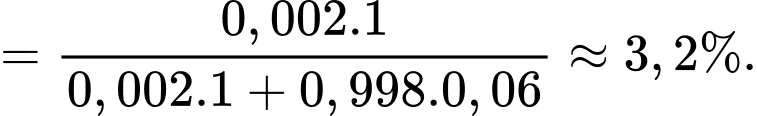
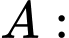 "Người được chọn mắc bệnh X";
"Người được chọn mắc bệnh X";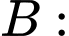 "Người được chọn có phản ứng dương tính với xét nghiệm Y".
"Người được chọn có phản ứng dương tính với xét nghiệm Y".Theo giả thiết ta có:
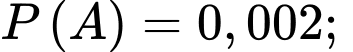
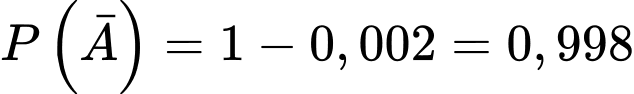 ;
;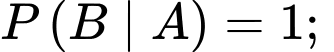
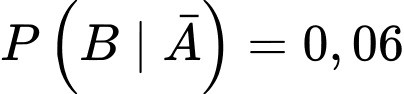 .
.Theo công thức Bayes, ta có:
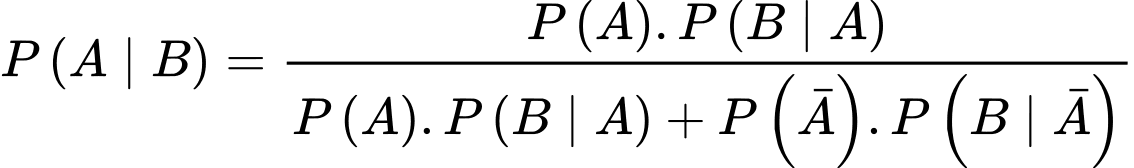
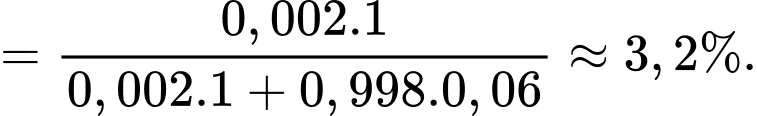
Câu 19 [696435]: Để nghiên cứu xác suất của một loại cây trồng mới phát triển bình thường, người ta trồng hạt giống của loại cây đó trên hai ô đất thí nghiệm 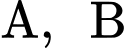 khác nhau. Xác suất phát triển bình thường của hạt giống đó trên các ô đất
khác nhau. Xác suất phát triển bình thường của hạt giống đó trên các ô đất 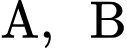 lần lượt là 0,61 và 0,7. Lặp lại thí nghiệm trên với đầy đủ các điều kiện tương đồng thì thấy hạt giống chỉ phát triển bình thường được trên duy nhất một ô đất. Tính xác suất hạt giống chỉ phát triển bình thường trên ô đất A. (làm tròn kết quả đến hàng phần trăm).
lần lượt là 0,61 và 0,7. Lặp lại thí nghiệm trên với đầy đủ các điều kiện tương đồng thì thấy hạt giống chỉ phát triển bình thường được trên duy nhất một ô đất. Tính xác suất hạt giống chỉ phát triển bình thường trên ô đất A. (làm tròn kết quả đến hàng phần trăm).
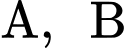 khác nhau. Xác suất phát triển bình thường của hạt giống đó trên các ô đất
khác nhau. Xác suất phát triển bình thường của hạt giống đó trên các ô đất 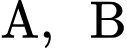 lần lượt là 0,61 và 0,7. Lặp lại thí nghiệm trên với đầy đủ các điều kiện tương đồng thì thấy hạt giống chỉ phát triển bình thường được trên duy nhất một ô đất. Tính xác suất hạt giống chỉ phát triển bình thường trên ô đất A. (làm tròn kết quả đến hàng phần trăm).
lần lượt là 0,61 và 0,7. Lặp lại thí nghiệm trên với đầy đủ các điều kiện tương đồng thì thấy hạt giống chỉ phát triển bình thường được trên duy nhất một ô đất. Tính xác suất hạt giống chỉ phát triển bình thường trên ô đất A. (làm tròn kết quả đến hàng phần trăm).
Điền đáp án: 0,18.
Gọi: A: Biến cố "Hạt giống phát triển bình thường trên ô đất A"
B: Biến cố "Hạt giống phát triển bình thường trên ô đất B"
Biết: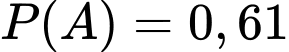 ,
,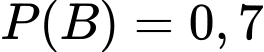
Ta cần tính xác suất để hạt giống chỉ phát triển bình thường trên ô đất A , tức là biến cố
Do các ô đất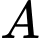 và
và 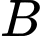 là độc lập, nên:
là độc lập, nên:
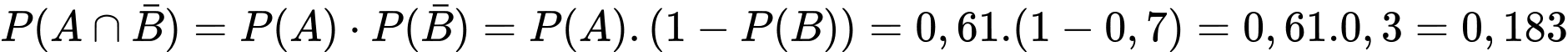
Vậy xác suất hạt giống chỉ phát triển bình thường trên ô đất A là: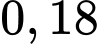
Gọi: A: Biến cố "Hạt giống phát triển bình thường trên ô đất A"
B: Biến cố "Hạt giống phát triển bình thường trên ô đất B"
Biết:
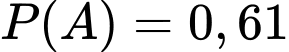 ,
,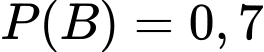
Ta cần tính xác suất để hạt giống chỉ phát triển bình thường trên ô đất A , tức là biến cố

Do các ô đất
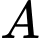 và
và 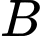 là độc lập, nên:
là độc lập, nên:
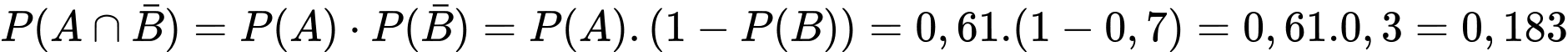
Vậy xác suất hạt giống chỉ phát triển bình thường trên ô đất A là:
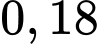
Câu 20 [694452]: Có một kho chứa bia kém chất lượng chứa các thùng giống nhau (24 lon/thùng) gồm 2 loại: loại I để lẫn mỗi thùng 5 lon quá hạn sử dụng, loại II để lẫn mỗi thùng 3 lon quá hạn. Biết số lượng thùng loại I gấp 2 lần số lượng thùng loại II. Chọn ngẫu nhiên 1 thùng từ trong kho, từ thùng đó chọn ngẫu nhiên 10 lon thì thấy trong 10 lon đó có hai lon quá hạn sử dụng. Tính xác suất 10 lon được lấy là bia loại I (làm tròn kết quả đến hàng phần trăm).
Điền đáp án: 0,71.
Gọi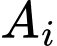 là biến cố chọn được thùng loại
là biến cố chọn được thùng loại 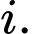
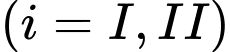
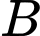 là biến cố chọn được 10 sản phẩm trong đó có 2 lon quá hạn từ thùng được chọn ra.
là biến cố chọn được 10 sản phẩm trong đó có 2 lon quá hạn từ thùng được chọn ra.
Từ đó, ta có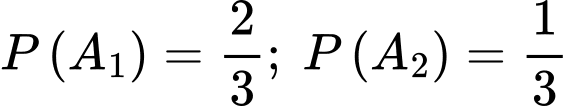
Áp dụng công thức xác suất có điều kiện, ta có: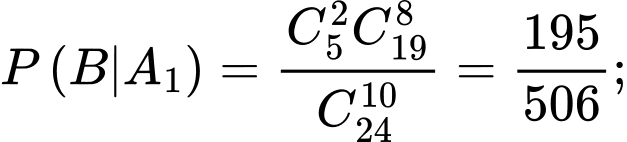
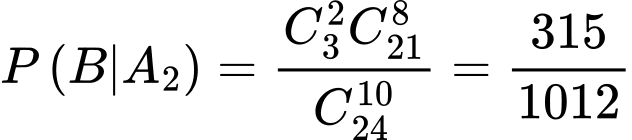
Ta có sơ đồ cây sau:
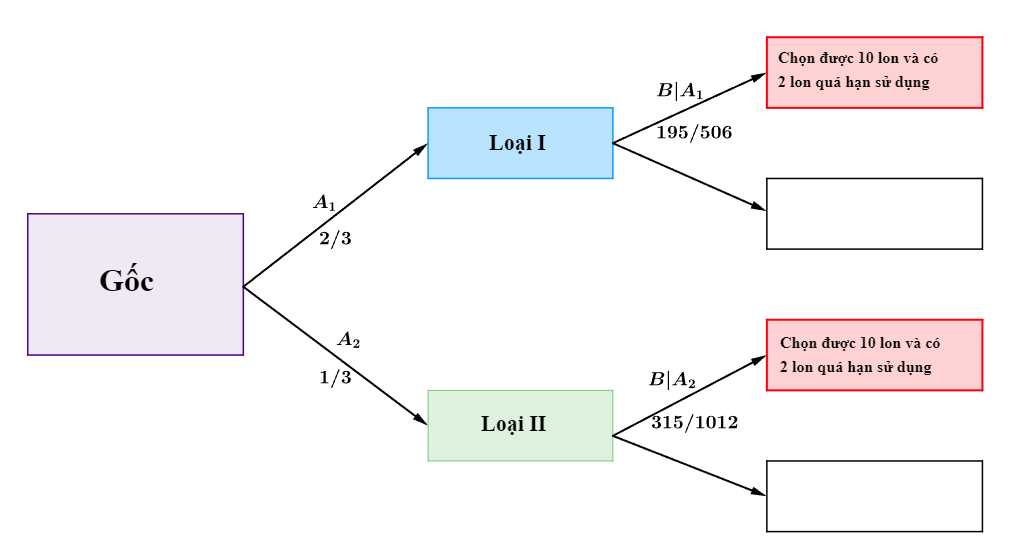
Xác suất để chọn được 2 lon quá hạn là:

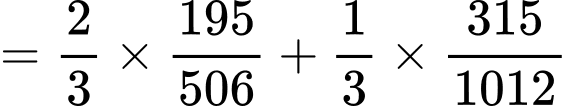
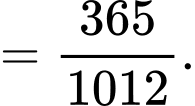
Suy ra xác suất bia được lấy thuộc loại I là: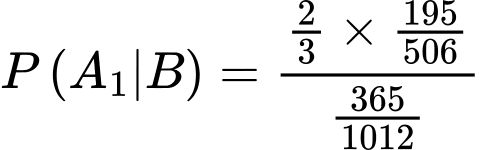
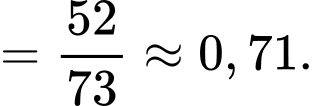
Gọi
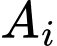 là biến cố chọn được thùng loại
là biến cố chọn được thùng loại 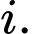
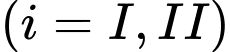
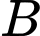 là biến cố chọn được 10 sản phẩm trong đó có 2 lon quá hạn từ thùng được chọn ra.
là biến cố chọn được 10 sản phẩm trong đó có 2 lon quá hạn từ thùng được chọn ra.Từ đó, ta có
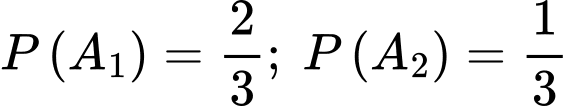
Áp dụng công thức xác suất có điều kiện, ta có:
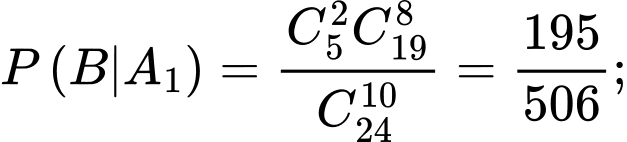
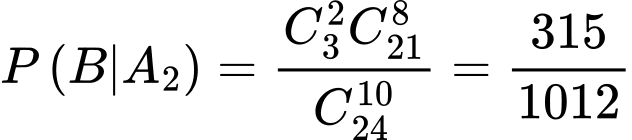
Ta có sơ đồ cây sau:

Xác suất để chọn được 2 lon quá hạn là:

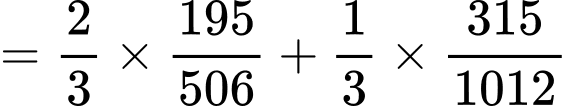
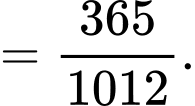
Suy ra xác suất bia được lấy thuộc loại I là:
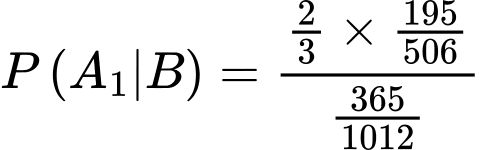
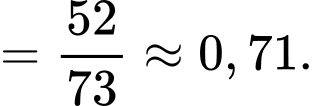
Câu 21 [680757]: Có hai chiếc hộp, hộp I có 6 quả bóng màu đỏ và 4 quả bóng màu vàng, hộp II có 7 quả bóng màu đỏ và 3 quả bóng màu vàng, các quả bóng có cùng kích thước và khối lượng. Lấy ngẫu nhiên một quả bóng từ hộp I bỏ vào hộp II. Sau đó, lấy ra ngẫu nhiên một quả bóng từ hộp II. Tính xác suất để quả bóng được lấy ra từ hộp II là quả bóng được chuyển từ hộp I sang, biết rằng quả bóng đó có màu đỏ (làm tròn kết quả đến hàng phần trăm).
Điền đáp án: 0,08.
Gọi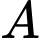 là biến cố “Quả bóng lấy ra từ hộp II là quả bóng đỏ được chuyển từ hộp I”.
là biến cố “Quả bóng lấy ra từ hộp II là quả bóng đỏ được chuyển từ hộp I”.
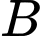 là biến cố “Quả bóng lấy ra từ hộp II có màu đỏ.”
là biến cố “Quả bóng lấy ra từ hộp II có màu đỏ.”
Theo công thức Bayes: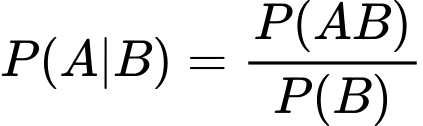
Với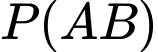 : Xác suất vừa chuyển bóng đỏ từ hộp I và lấy đúng quả bóng đỏ đó từ hộp II.
: Xác suất vừa chuyển bóng đỏ từ hộp I và lấy đúng quả bóng đỏ đó từ hộp II.
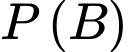 : Xác suất lấy được một quả bóng đỏ từ hộp II (bất kể là bóng nào).
: Xác suất lấy được một quả bóng đỏ từ hộp II (bất kể là bóng nào).
Gọi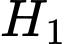 là biến cố “Chuyển một quả bóng đỏ từ hộp I sang hộp II.”
là biến cố “Chuyển một quả bóng đỏ từ hộp I sang hộp II.”
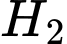 là biến cố “Chuyển một quả bóng vàng từ hộp I sang hộp II.”
là biến cố “Chuyển một quả bóng vàng từ hộp I sang hộp II.”
Ta có hệ biến cố đầy đủ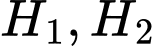 , với các xác suất:
, với các xác suất: 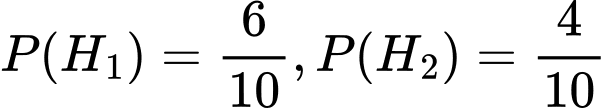
Trường hợp 1 (chuyển bóng đỏ từ hộp I):
- Khi chuyển một quả bóng đỏ từ hộp I sang, hộp II có 8 quả bóng đỏ và 3 quả bóng vàng.
- Xác suất lấy bóng đỏ trong trường hợp này là: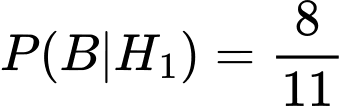
Trường hợp 2 (chuyển bóng vàng từ hộp I):
- Khi chuyển một quả bóng vàng từ hộp I sang, hộp II có 7 quả bóng đỏ và 4 quả bóng vàng.
- Xác suất lấy bóng đỏ trong trường hợp này là: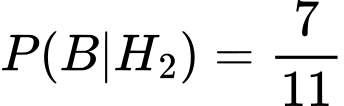
Ta có sơ đồ cây:
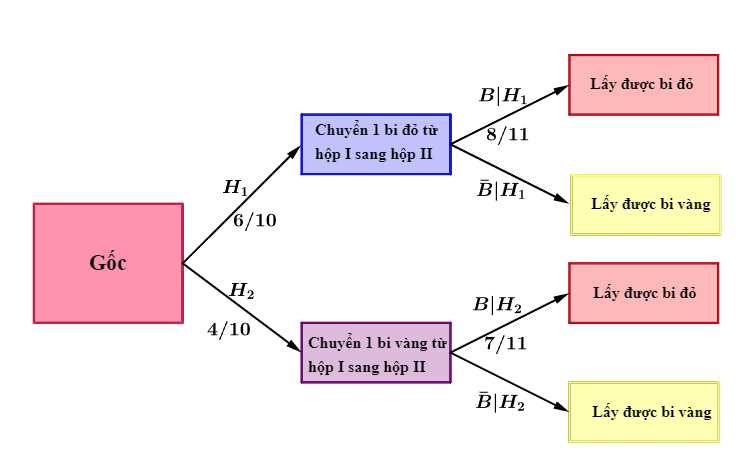
Vậy xác suất lấy được một quả bóng đỏ từ hộp II là:
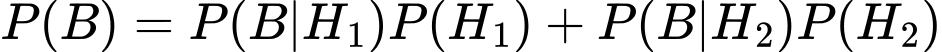
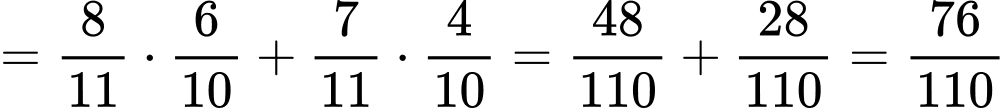
Xác suất vừa chuyển một quả bóng đỏ từ hộp I và lấy đúng quả đó từ hộp II là:
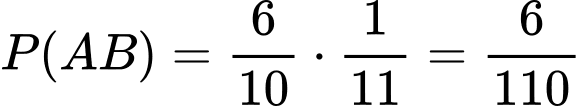
Áp dụng công thức Bayes: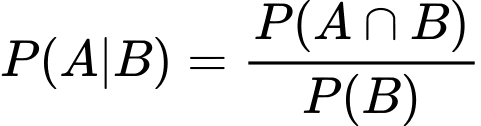
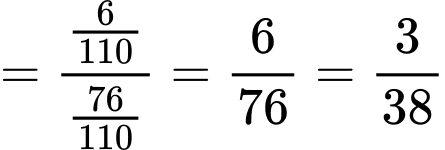
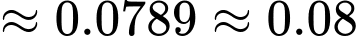
Xác suất để quả bóng lấy ra từ hộp II là quả bóng đỏ đã được chuyển từ hộp I là 0.08.
Gọi
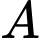 là biến cố “Quả bóng lấy ra từ hộp II là quả bóng đỏ được chuyển từ hộp I”.
là biến cố “Quả bóng lấy ra từ hộp II là quả bóng đỏ được chuyển từ hộp I”.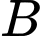 là biến cố “Quả bóng lấy ra từ hộp II có màu đỏ.”
là biến cố “Quả bóng lấy ra từ hộp II có màu đỏ.” Theo công thức Bayes:
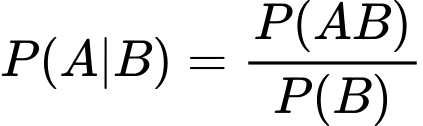
Với
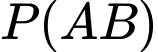 : Xác suất vừa chuyển bóng đỏ từ hộp I và lấy đúng quả bóng đỏ đó từ hộp II.
: Xác suất vừa chuyển bóng đỏ từ hộp I và lấy đúng quả bóng đỏ đó từ hộp II.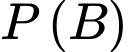 : Xác suất lấy được một quả bóng đỏ từ hộp II (bất kể là bóng nào).
: Xác suất lấy được một quả bóng đỏ từ hộp II (bất kể là bóng nào).Gọi
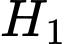 là biến cố “Chuyển một quả bóng đỏ từ hộp I sang hộp II.”
là biến cố “Chuyển một quả bóng đỏ từ hộp I sang hộp II.”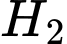 là biến cố “Chuyển một quả bóng vàng từ hộp I sang hộp II.”
là biến cố “Chuyển một quả bóng vàng từ hộp I sang hộp II.”Ta có hệ biến cố đầy đủ
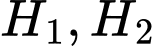 , với các xác suất:
, với các xác suất: 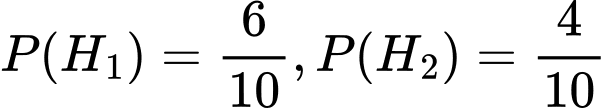
Trường hợp 1 (chuyển bóng đỏ từ hộp I):
- Khi chuyển một quả bóng đỏ từ hộp I sang, hộp II có 8 quả bóng đỏ và 3 quả bóng vàng.
- Xác suất lấy bóng đỏ trong trường hợp này là:
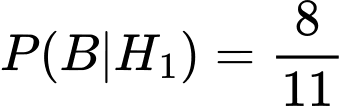
Trường hợp 2 (chuyển bóng vàng từ hộp I):
- Khi chuyển một quả bóng vàng từ hộp I sang, hộp II có 7 quả bóng đỏ và 4 quả bóng vàng.
- Xác suất lấy bóng đỏ trong trường hợp này là:
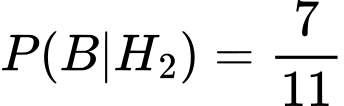
Ta có sơ đồ cây:

Vậy xác suất lấy được một quả bóng đỏ từ hộp II là:
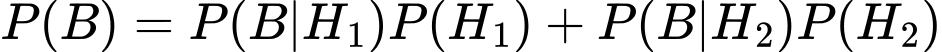
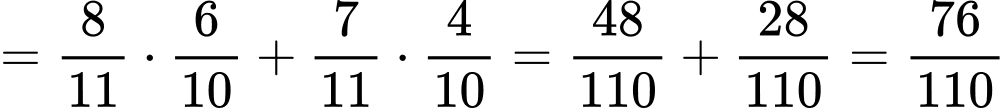
Xác suất vừa chuyển một quả bóng đỏ từ hộp I và lấy đúng quả đó từ hộp II là:
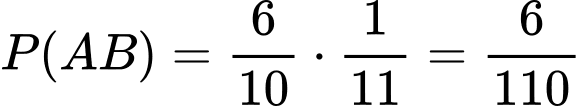
Áp dụng công thức Bayes:
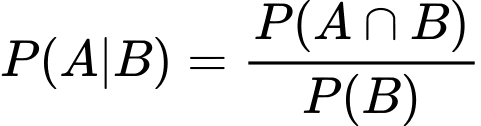
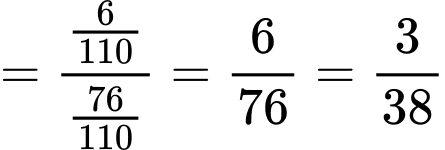
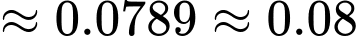
Xác suất để quả bóng lấy ra từ hộp II là quả bóng đỏ đã được chuyển từ hộp I là 0.08.
Câu 22 [145241]: Tại một phòng khám chuyên khoa tỷ lệ người đến khám có bệnh là 83%. Theo thống kê biết rằng nếu chẩn đoán có bệnh thì đúng tới 90%, còn nếu chẩn đoán không bệnh thì chỉ đúng 80%. Xác suất chẩn đoán đúng là bao nhiêu?
Gọi A là biến cố: “Người đến khám có bệnh” và B là biến cố: “Phòng khám chẩn đoán có bệnh”
Ta có:
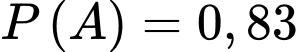 . Xác suất chuẩn đoán đúng khi có bệnh là
. Xác suất chuẩn đoán đúng khi có bệnh là 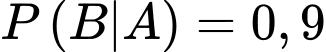
Xác suất chuẩn đoán đúng khi không có bệnh là:
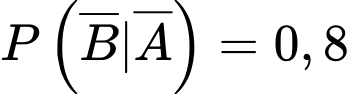
Suy ra: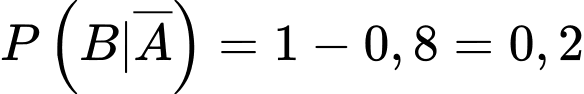
Xác suất không có bệnh là: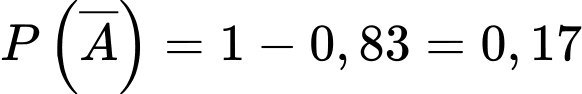
Áp dụng công thức có điều kiện ta tính xác suất chuẩn đoán có bệnh:
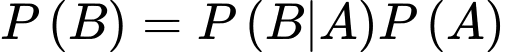
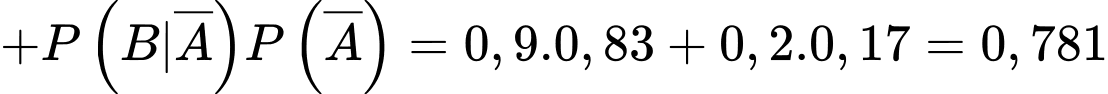
Xác suất chuẩn đoán đúng bao gồm cả trường hợp chuẩn đoán đúng có bệnh và chuẩn đoán đúng không bệnh là
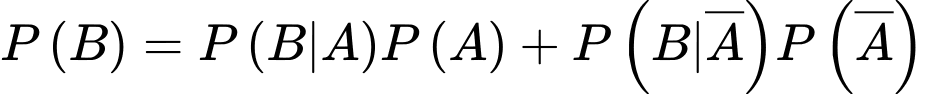
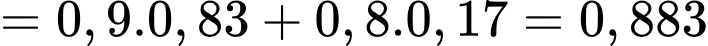
Đáp án: 0,883.
Ta có:
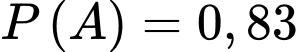 . Xác suất chuẩn đoán đúng khi có bệnh là
. Xác suất chuẩn đoán đúng khi có bệnh là 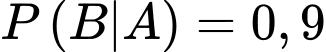
Xác suất chuẩn đoán đúng khi không có bệnh là:
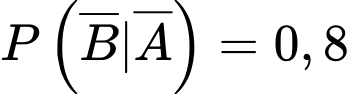
Suy ra:
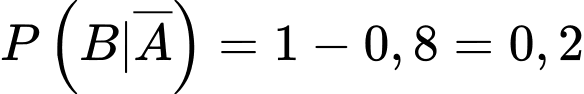
Xác suất không có bệnh là:
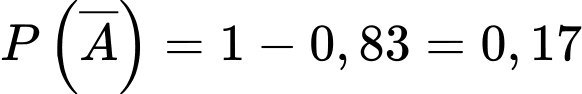
Áp dụng công thức có điều kiện ta tính xác suất chuẩn đoán có bệnh:
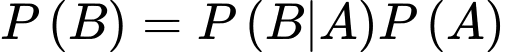
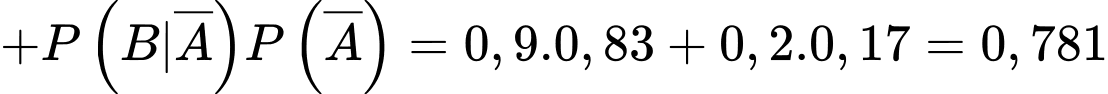
Xác suất chuẩn đoán đúng bao gồm cả trường hợp chuẩn đoán đúng có bệnh và chuẩn đoán đúng không bệnh là
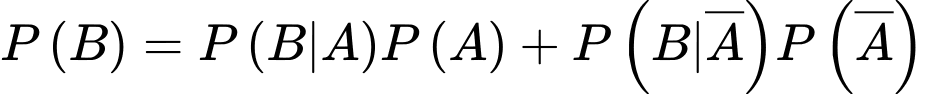
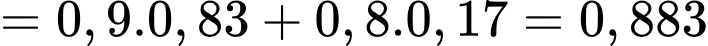
Đáp án: 0,883.