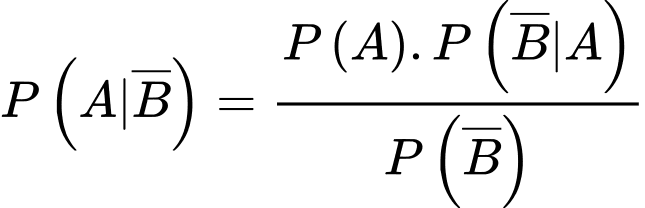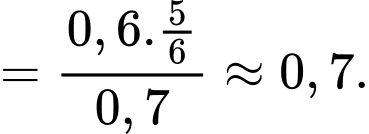PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1 [778973]: Cho 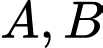 là các biến cố của một phép thử
là các biến cố của một phép thử 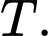 Biết rằng
Biết rằng  xác suất của biến cố
xác suất của biến cố 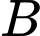 được tính theo công thức nào sau đây?
được tính theo công thức nào sau đây?
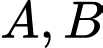 là các biến cố của một phép thử
là các biến cố của một phép thử 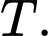 Biết rằng
Biết rằng  xác suất của biến cố
xác suất của biến cố 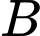 được tính theo công thức nào sau đây?
được tính theo công thức nào sau đây? A, 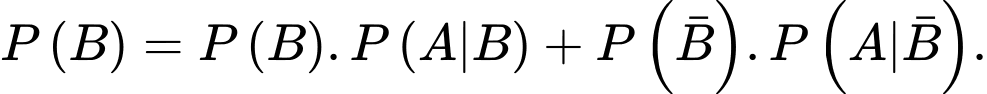
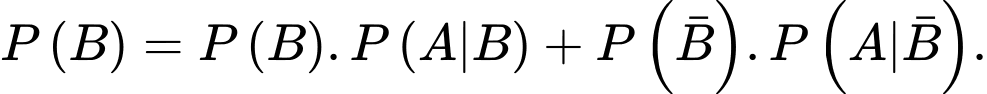
B, 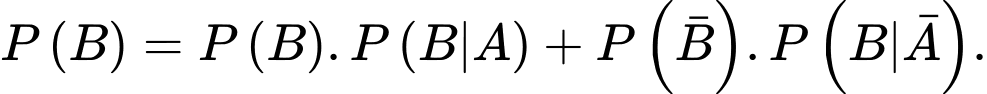
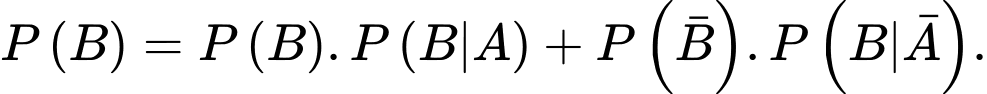
C, 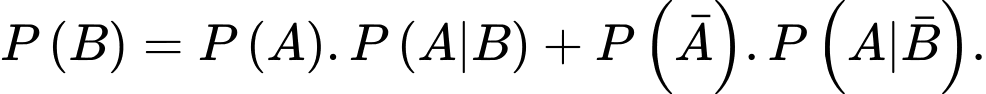
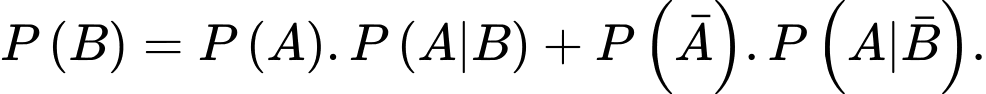
D, 

Chọn D.
Theo công thức xác suất toàn phần, ta có Đáp án: D
Đáp án: D
Theo công thức xác suất toàn phần, ta có
 Đáp án: D
Đáp án: D
Câu 2 [778975]: Với hai biến cố 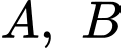 thỏa mãn
thỏa mãn 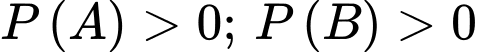 và
và 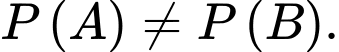 Khẳng định nào dưới đây đúng?
Khẳng định nào dưới đây đúng?
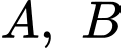 thỏa mãn
thỏa mãn 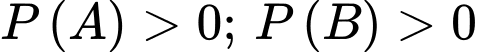 và
và 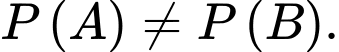 Khẳng định nào dưới đây đúng?
Khẳng định nào dưới đây đúng? A, 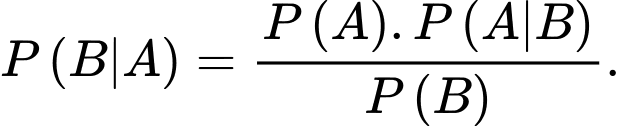
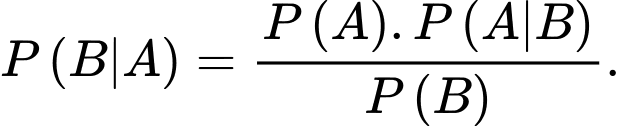
B, 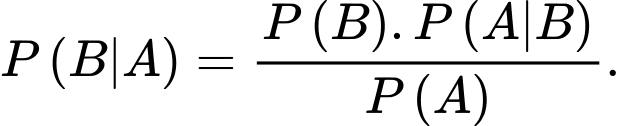
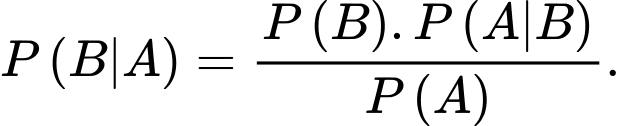
C, 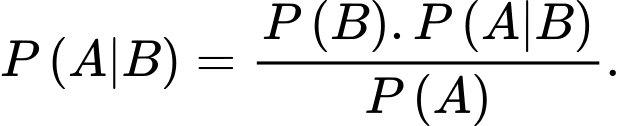
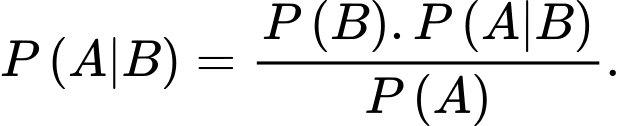
D, 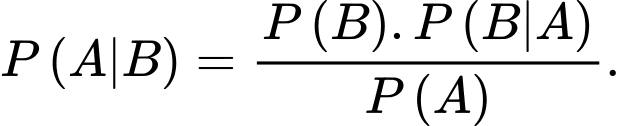
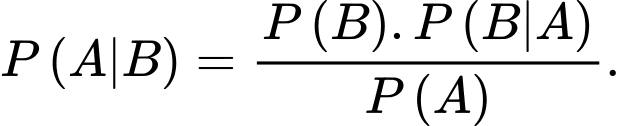
Với hai biến cố 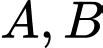 mà
mà 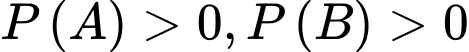 . Ta có:
. Ta có: 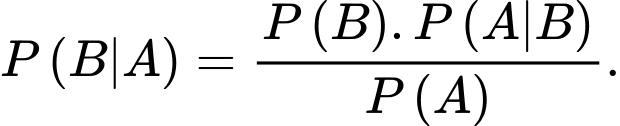 Chọn B. Đáp án: B
Chọn B. Đáp án: B
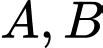 mà
mà 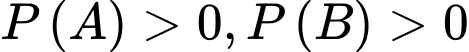 . Ta có:
. Ta có: 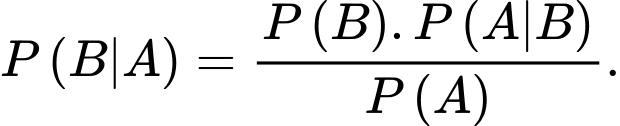 Chọn B. Đáp án: B
Chọn B. Đáp án: B
Câu 3 [778976]: Cho hai biến cố 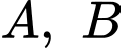 sao cho
sao cho 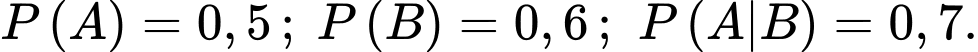 Tính
Tính 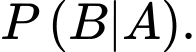
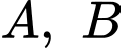 sao cho
sao cho 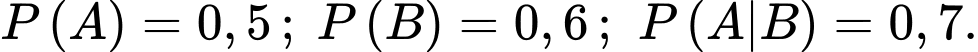 Tính
Tính 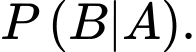
A, 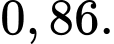
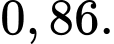
B, 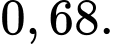
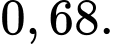
C, 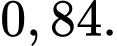
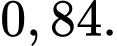
D, 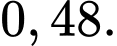
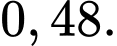
Áp dụng công thức Bayes, ta có:
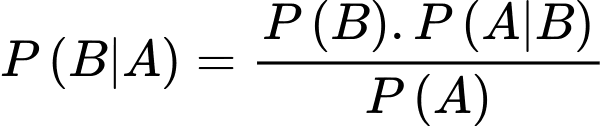
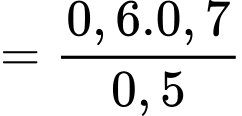
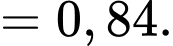
Chọn C. Đáp án: C
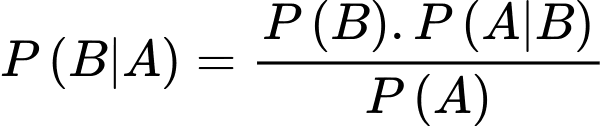
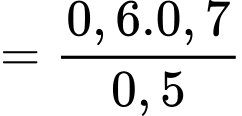
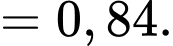
Chọn C. Đáp án: C
Câu 4 [778979]: Cho hai biến cố 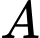 và
và 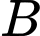 sao cho
sao cho 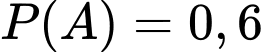 ;
; 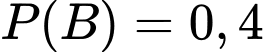 ;
; 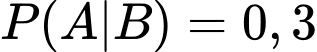 Khi đó
Khi đó 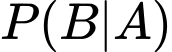 bằng:
bằng:
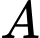 và
và 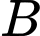 sao cho
sao cho 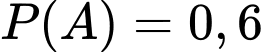 ;
; 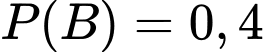 ;
; 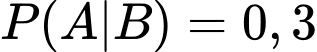 Khi đó
Khi đó 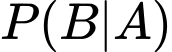 bằng:
bằng: A, 0,2.
B, 0,3.
C, 0,4.
D, 0,6.
Áp dụng công thức Bayes, ta có: 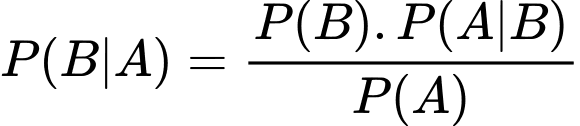
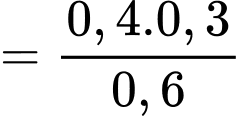
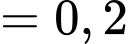 Đáp án: A
Đáp án: A
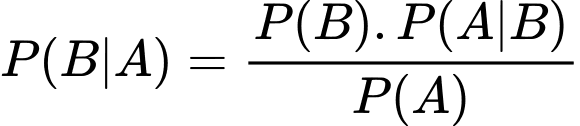
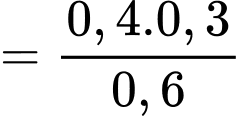
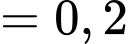 Đáp án: A
Đáp án: A
Câu 5 [778980]: Cho hai biến cố 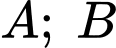 sao cho
sao cho 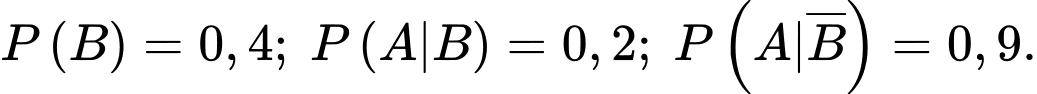 Tính
Tính 
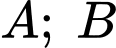 sao cho
sao cho 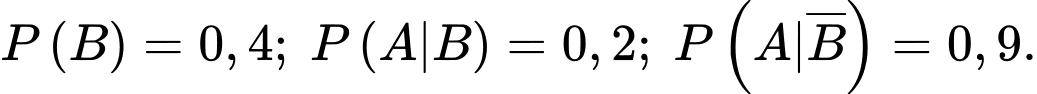 Tính
Tính 
A, 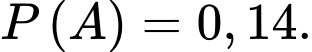
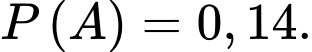
B, 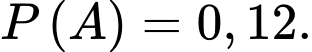
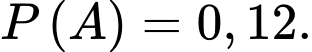
C, 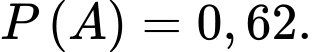
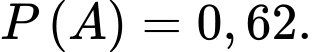
D, 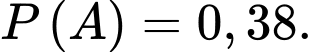
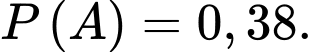
Ta có: 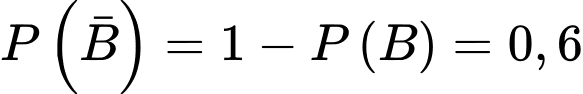
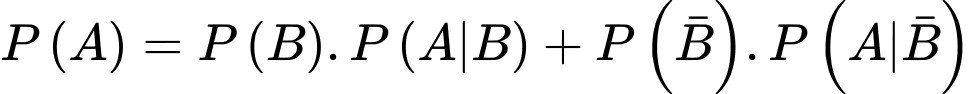
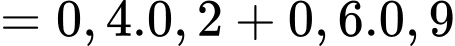
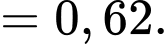 Chọn C. Đáp án: C
Chọn C. Đáp án: C
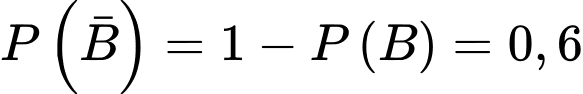
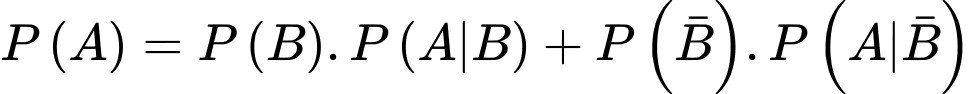
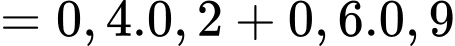
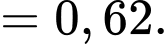 Chọn C. Đáp án: C
Chọn C. Đáp án: C
Câu 6 [778983]: Cho hai biến cố 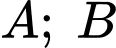 sao cho
sao cho 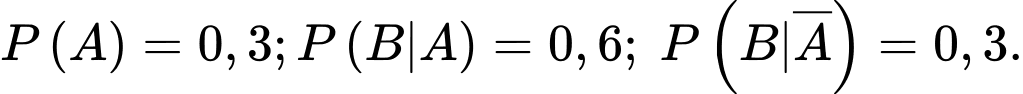 Tính
Tính 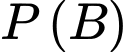
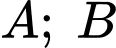 sao cho
sao cho 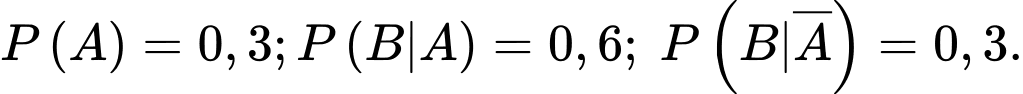 Tính
Tính 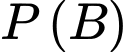
A, 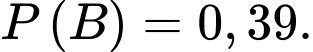
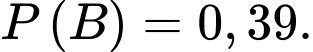
B, 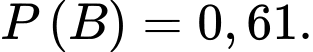
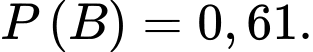
C, 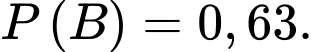
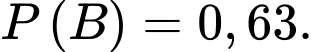
D, 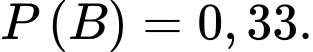
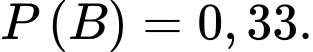
Ta có: 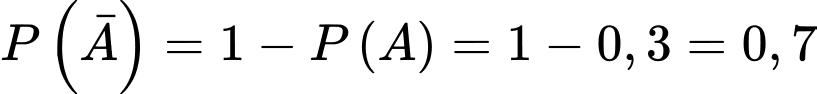
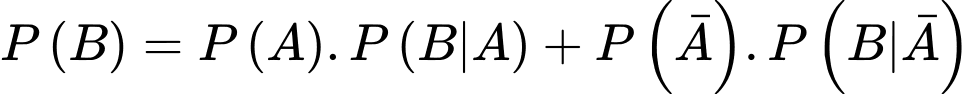
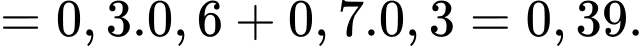 Chọn A.
Đáp án: A
Chọn A.
Đáp án: A
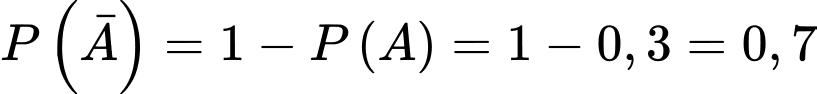
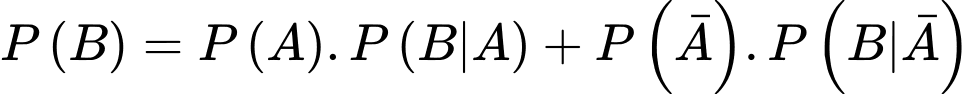
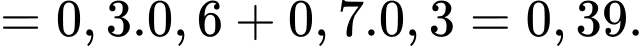 Chọn A.
Đáp án: A
Chọn A.
Đáp án: A
Câu 7 [778986]: Cho hai biến cố A và B khi đó 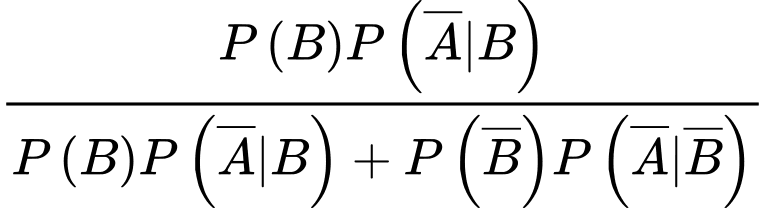 bằng
bằng
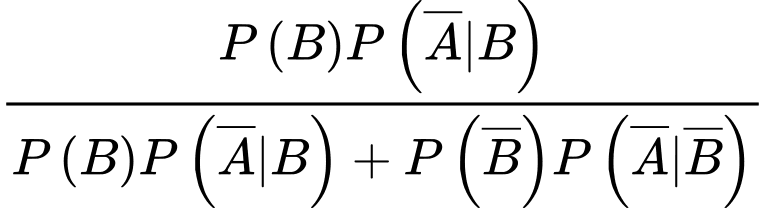 bằng
bằng A, 

B, 

C, 

D, 

Chọn C.
Theo công thức Bayes ta có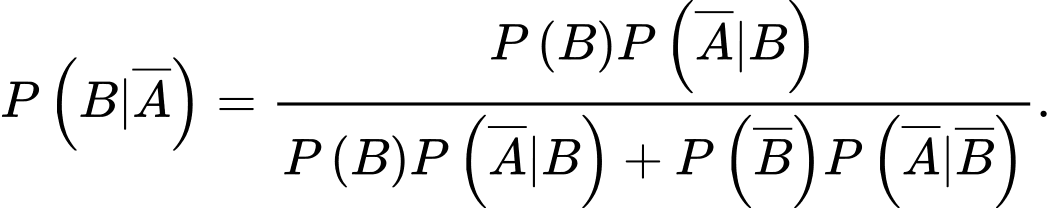 Đáp án: C
Đáp án: C
Theo công thức Bayes ta có
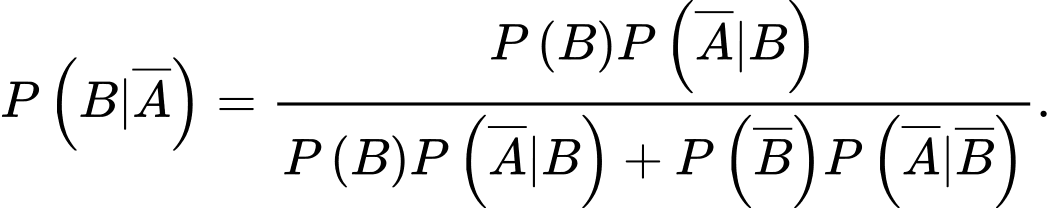 Đáp án: C
Đáp án: C
Câu 8 [778990]: Cho hai biến cố 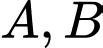 sao cho
sao cho 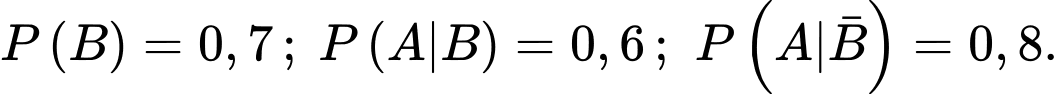 Tính
Tính 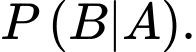
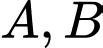 sao cho
sao cho 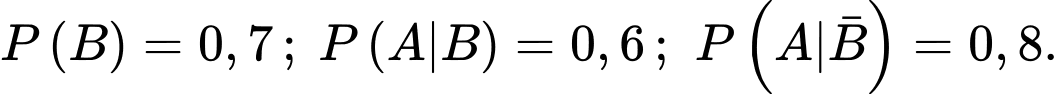 Tính
Tính 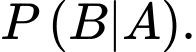
A, 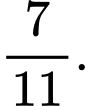
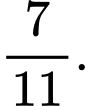
B, 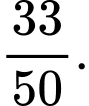
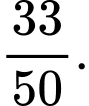
C, 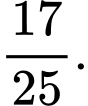
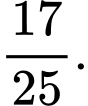
D, 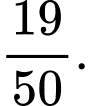
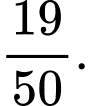
Ta có: 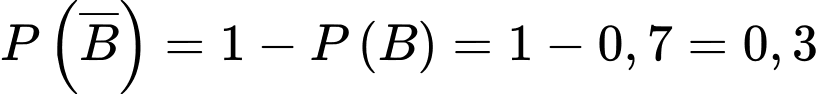 .
.
Áp dụng công thức xác suất toàn phần, ta có:
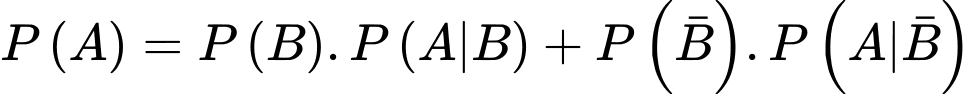
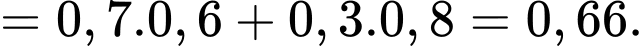
Áp dụng công thức Bayes, ta có: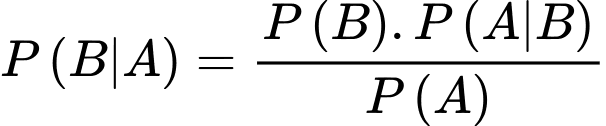
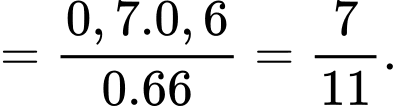
Chọn đáp án A. Đáp án: A
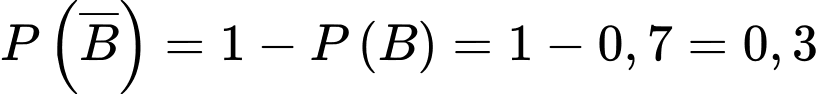 .
.Áp dụng công thức xác suất toàn phần, ta có:
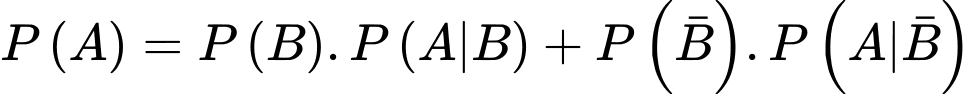
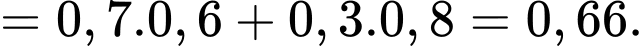
Áp dụng công thức Bayes, ta có:
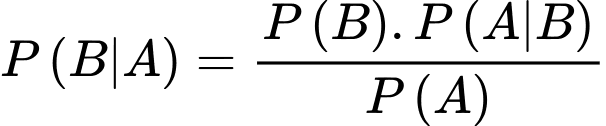
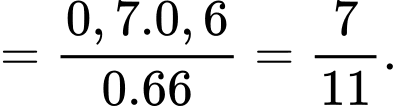
Chọn đáp án A. Đáp án: A
Câu 9 [778991]: Cho hai biến cố 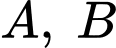 sao cho
sao cho 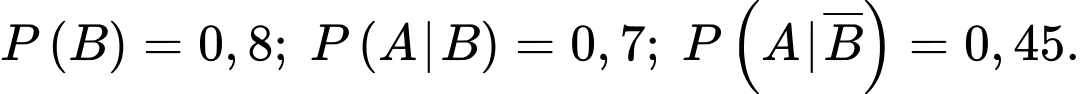 Tính
Tính 
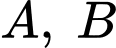 sao cho
sao cho 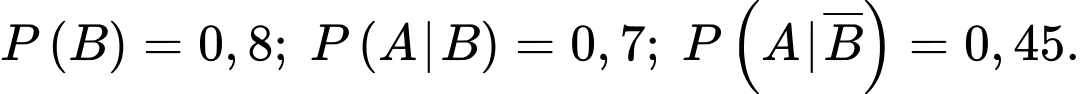 Tính
Tính 
A, 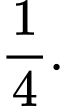
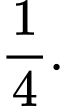
B, 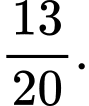
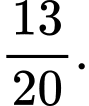
C, 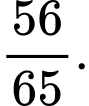
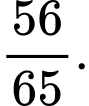
D, 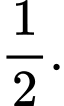
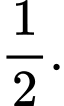
Áp dụng công thức Bayes, ta có: 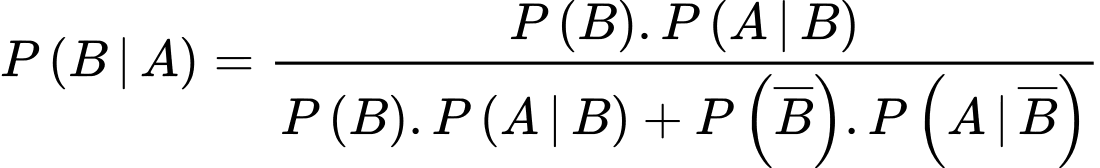
Suy ra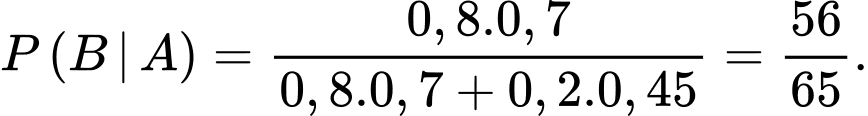 Chọn C.
Đáp án: C
Chọn C.
Đáp án: C
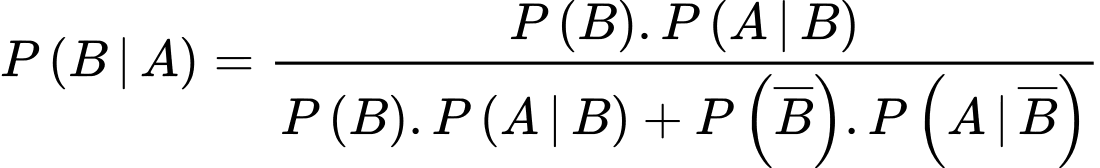
Suy ra
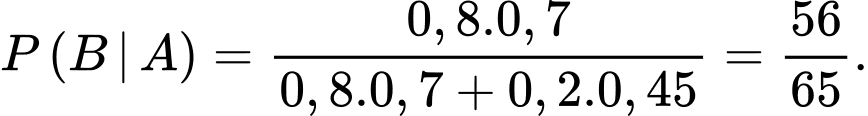 Chọn C.
Đáp án: C
Chọn C.
Đáp án: C
Câu 10 [778992]: Một doanh nghiệp có 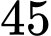 nhân viên nữ. Tỉ lệ nhân viên nữ và tỉ lệ nhân viên nam mua bảo hiểm nhân thọ lần lượt là
nhân viên nữ. Tỉ lệ nhân viên nữ và tỉ lệ nhân viên nam mua bảo hiểm nhân thọ lần lượt là 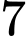 và
và 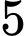 . Gặp ngẫu nhiên một nhân viên của doanh nghiệp. Tính xác suất nhân viên đó có mua bảo hiểm nhân thọ.
. Gặp ngẫu nhiên một nhân viên của doanh nghiệp. Tính xác suất nhân viên đó có mua bảo hiểm nhân thọ.
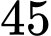 nhân viên nữ. Tỉ lệ nhân viên nữ và tỉ lệ nhân viên nam mua bảo hiểm nhân thọ lần lượt là
nhân viên nữ. Tỉ lệ nhân viên nữ và tỉ lệ nhân viên nam mua bảo hiểm nhân thọ lần lượt là 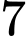 và
và 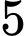 . Gặp ngẫu nhiên một nhân viên của doanh nghiệp. Tính xác suất nhân viên đó có mua bảo hiểm nhân thọ.
. Gặp ngẫu nhiên một nhân viên của doanh nghiệp. Tính xác suất nhân viên đó có mua bảo hiểm nhân thọ. A, 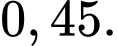
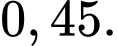
B, 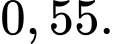
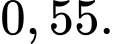
C, 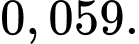
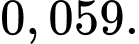
D, 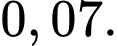
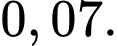
Gọi các biến cố:
A: “Nhân viên được chọn là nữ”.
B: “Nhân viên được chọn là nam”.
Ta có: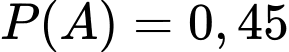 ;
; 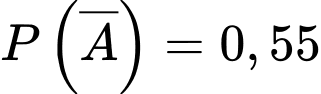 ;
; 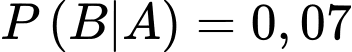 ;
; 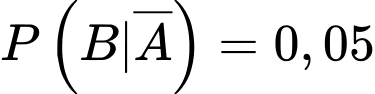 .
.
Áp dụng công thức xác suất toàn phần:
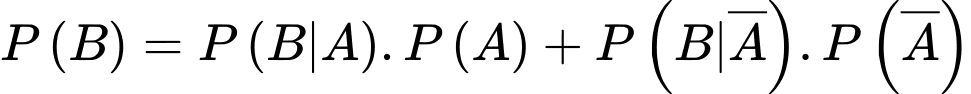
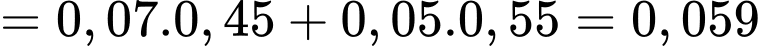 .
.
Vậy xác suất một nhân viên được chọn mua bảo hiểm nhân thọ là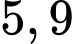 . Chọn C.
Đáp án: C
. Chọn C.
Đáp án: C
A: “Nhân viên được chọn là nữ”.
B: “Nhân viên được chọn là nam”.
Ta có:
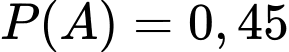 ;
; 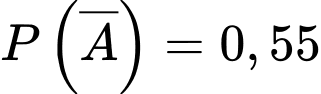 ;
; 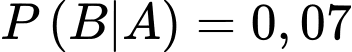 ;
; 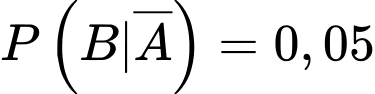 .
.Áp dụng công thức xác suất toàn phần:
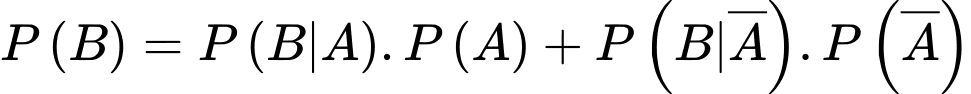
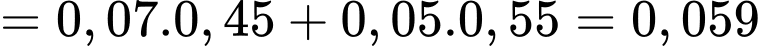 .
.Vậy xác suất một nhân viên được chọn mua bảo hiểm nhân thọ là
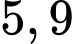 . Chọn C.
Đáp án: C
. Chọn C.
Đáp án: C
Câu 11 [778994]: Được biết có 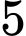 đàn ông bị mù màu và
đàn ông bị mù màu và 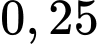 phụ nữ bị mù màu. Giả sử số đàn ông bằng số phụ nữ. Chọn ngẫu nhiên một người bị mù màu. Xác suất để người được chọn là đàn ông bằng bao nhiêu?
phụ nữ bị mù màu. Giả sử số đàn ông bằng số phụ nữ. Chọn ngẫu nhiên một người bị mù màu. Xác suất để người được chọn là đàn ông bằng bao nhiêu?
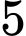 đàn ông bị mù màu và
đàn ông bị mù màu và 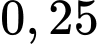 phụ nữ bị mù màu. Giả sử số đàn ông bằng số phụ nữ. Chọn ngẫu nhiên một người bị mù màu. Xác suất để người được chọn là đàn ông bằng bao nhiêu?
phụ nữ bị mù màu. Giả sử số đàn ông bằng số phụ nữ. Chọn ngẫu nhiên một người bị mù màu. Xác suất để người được chọn là đàn ông bằng bao nhiêu? A, 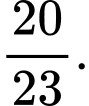
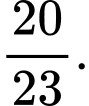
B, 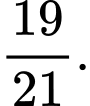
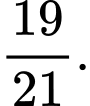
C, 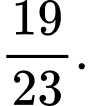
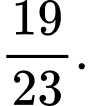
D, 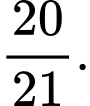
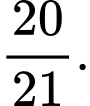
Gọi 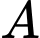 là biến cố : “người được chọn là đàn ông”
là biến cố : “người được chọn là đàn ông”
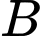 là biến cố : “người được chọn bị mù màu”
là biến cố : “người được chọn bị mù màu”
Theo bài ra ta có: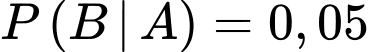 ;
; 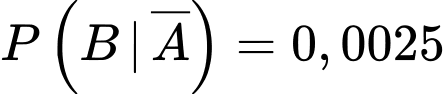 .
.
Vì số đàn ông bằng số phụ nữ nên ta có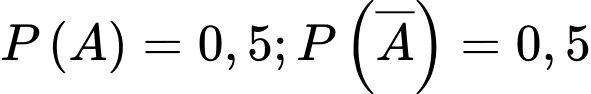 .
.
Áp dụng công thức Bayes, ta có: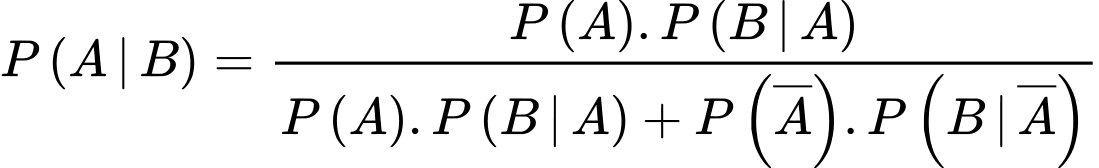
Suy ra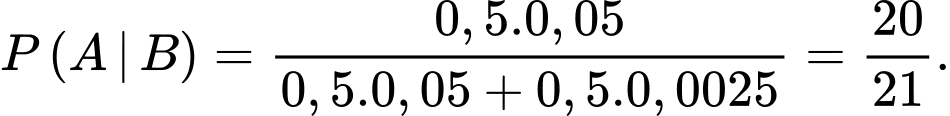 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
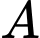 là biến cố : “người được chọn là đàn ông”
là biến cố : “người được chọn là đàn ông”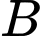 là biến cố : “người được chọn bị mù màu”
là biến cố : “người được chọn bị mù màu”Theo bài ra ta có:
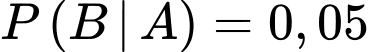 ;
; 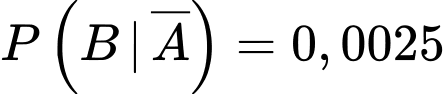 .
.Vì số đàn ông bằng số phụ nữ nên ta có
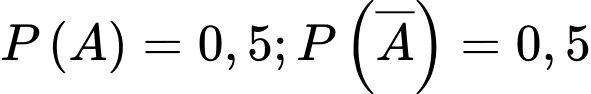 .
.Áp dụng công thức Bayes, ta có:
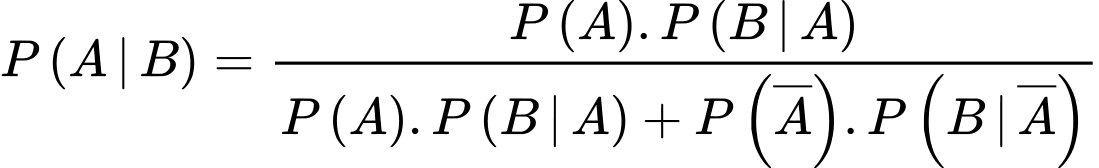
Suy ra
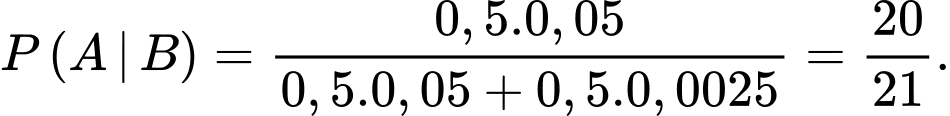 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
Câu 12 [145262]: [Trích SGK Cùng Khám Phá]: Một bệnh viện đang xét nghiệm cho một số bệnh nhân để xác định liệu họ có nhiễm virus X hay không. Xác suất để một bệnh nhân bị nhiễm virus X là 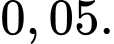 Khi xét nghiệm, nếu một bệnh nhân bị nhiễm thì xác suất để kết quả xét nghiệm dương tính là
Khi xét nghiệm, nếu một bệnh nhân bị nhiễm thì xác suất để kết quả xét nghiệm dương tính là 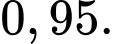 Nếu một bệnh nhân không bị nhiễm thì xác suất để kết quả xét nghiệm âm tính là
Nếu một bệnh nhân không bị nhiễm thì xác suất để kết quả xét nghiệm âm tính là 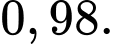 Một bệnh nhân được chọn ngẫu nhiên và có kết quả xét nghiệm dương tính. Xác suất để bệnh nhân đó thực sự bị nhiễm virus X là
Một bệnh nhân được chọn ngẫu nhiên và có kết quả xét nghiệm dương tính. Xác suất để bệnh nhân đó thực sự bị nhiễm virus X là
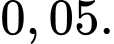 Khi xét nghiệm, nếu một bệnh nhân bị nhiễm thì xác suất để kết quả xét nghiệm dương tính là
Khi xét nghiệm, nếu một bệnh nhân bị nhiễm thì xác suất để kết quả xét nghiệm dương tính là 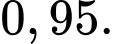 Nếu một bệnh nhân không bị nhiễm thì xác suất để kết quả xét nghiệm âm tính là
Nếu một bệnh nhân không bị nhiễm thì xác suất để kết quả xét nghiệm âm tính là 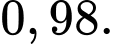 Một bệnh nhân được chọn ngẫu nhiên và có kết quả xét nghiệm dương tính. Xác suất để bệnh nhân đó thực sự bị nhiễm virus X là
Một bệnh nhân được chọn ngẫu nhiên và có kết quả xét nghiệm dương tính. Xác suất để bệnh nhân đó thực sự bị nhiễm virus X là A, 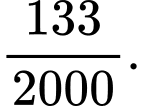
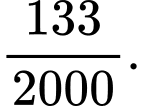
B, 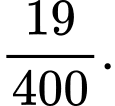
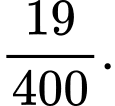
C, 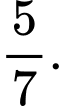
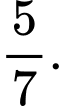
D, 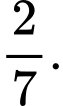
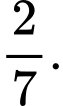
HD: 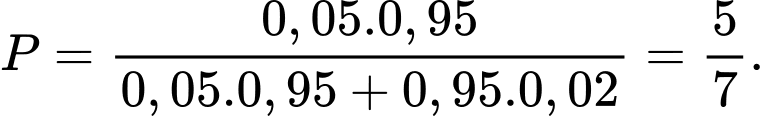 Chọn C. Đáp án: C
Chọn C. Đáp án: C
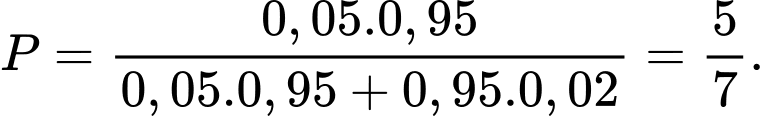 Chọn C. Đáp án: C
Chọn C. Đáp án: C PHẦN II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a),b),c),d) ở mỗi câu học sinh chọn đúng hoặc sai.
Câu 13 [778997]: Nghiên cứu số bệnh nhân trong một viện bỏng, thấy rằng có 2 nguyên nhân gây ra bỏng là bỏng nhiệt và bỏng do hóa chất. Bỏng nhiệt chiếm 70% số bệnh nhân và bỏng do hóa chất chiếm 30%. Trong những bệnh nhân bị bỏng nhiệt thì có 30% bị biến chứng, trong những bệnh nhân bị bỏng hóa chất thì có 50% bị biến chứng. Rút ngẫu nhiên một bệnh án
Gọi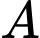 là biến cố “gặp bệnh án của bệnh nhân bị biến chứng”
là biến cố “gặp bệnh án của bệnh nhân bị biến chứng”
Gọi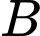 là biến cố “gặp bệnh án của bệnh nhân bị bỏng nhiệt”
là biến cố “gặp bệnh án của bệnh nhân bị bỏng nhiệt”
Gọi
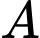 là biến cố “gặp bệnh án của bệnh nhân bị biến chứng”
là biến cố “gặp bệnh án của bệnh nhân bị biến chứng”Gọi
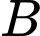 là biến cố “gặp bệnh án của bệnh nhân bị bỏng nhiệt”
là biến cố “gặp bệnh án của bệnh nhân bị bỏng nhiệt”
Từ giả thiết bài cho, ta có xác suất do bị bỏng nhiệt là 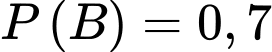
Suy ra xác suất do bị bỏng hóa chất là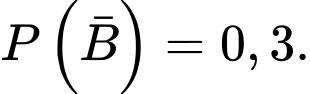
a) Đúng.
Xác suất bị biến chứng trong bỏng nhiệt là 30%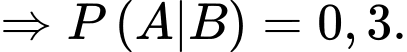
b) Đúng.
Xác suất bị biến chứng trong bỏng hóa chất là 50%
c) Sai.
Áp dụng công thức xác suất toàn phần, ta có xác suất biến bệnh án bị biến chứng là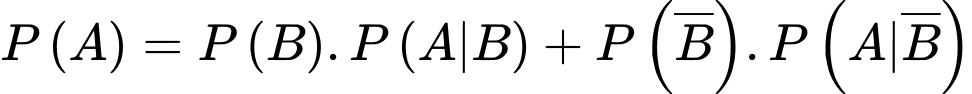
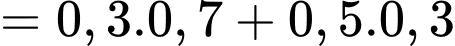
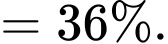
d) Đúng.
Áp dụng công thức Bayes, ta có xác suất của bệnh án bị biến chứng do bỏng nhiệt là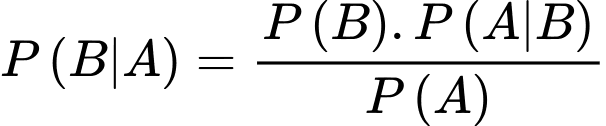
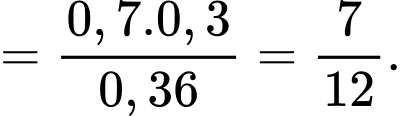
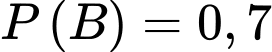
Suy ra xác suất do bị bỏng hóa chất là
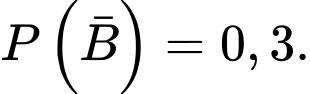
a) Đúng.
Xác suất bị biến chứng trong bỏng nhiệt là 30%
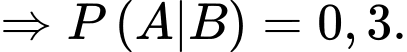
b) Đúng.
Xác suất bị biến chứng trong bỏng hóa chất là 50%

c) Sai.
Áp dụng công thức xác suất toàn phần, ta có xác suất biến bệnh án bị biến chứng là
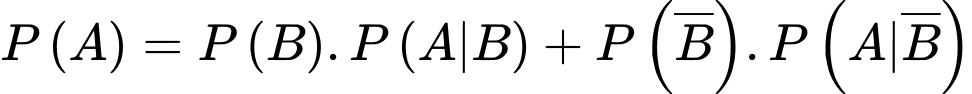
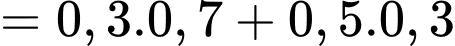
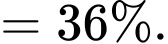
d) Đúng.
Áp dụng công thức Bayes, ta có xác suất của bệnh án bị biến chứng do bỏng nhiệt là
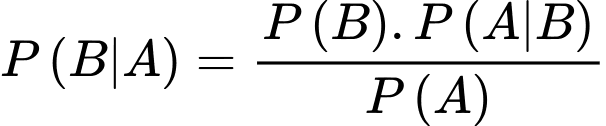
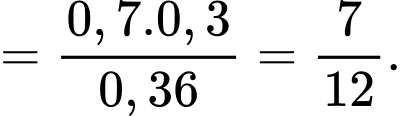
Câu 14 [693311]: Trong một ngôi làng có 500 người thì 240 người là nam. Thống kê cho thấy rằng, khả năng mắc bệnh hô hấp ở người nam trong làng là 0,6% và ở người nữ trong làng là 0,35%. Giả sử gặp một người trong làng.
Gọi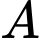 là biến cố “gặp người mắc bệnh trong làng”
là biến cố “gặp người mắc bệnh trong làng”
Gọi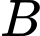 là biến cố “gặp được nam trong làng”
là biến cố “gặp được nam trong làng”
Gọi
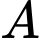 là biến cố “gặp người mắc bệnh trong làng”
là biến cố “gặp người mắc bệnh trong làng”Gọi
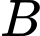 là biến cố “gặp được nam trong làng”
là biến cố “gặp được nam trong làng”
Tỉ lệ mắc bệnh chung trong làng chính là xác suất của 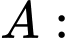 “gặp người mắc bệnh trong làng”
“gặp người mắc bệnh trong làng”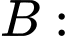 “gặp được nam trong làng”
“gặp được nam trong làng”
a) Đúng.
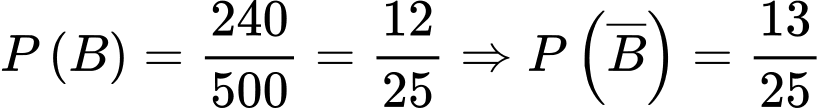
b) Sai.
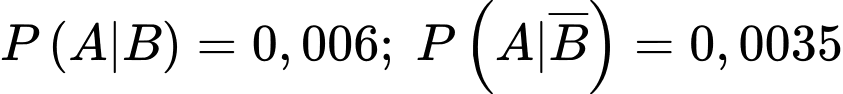
Ta có sơ đồ cây sau:
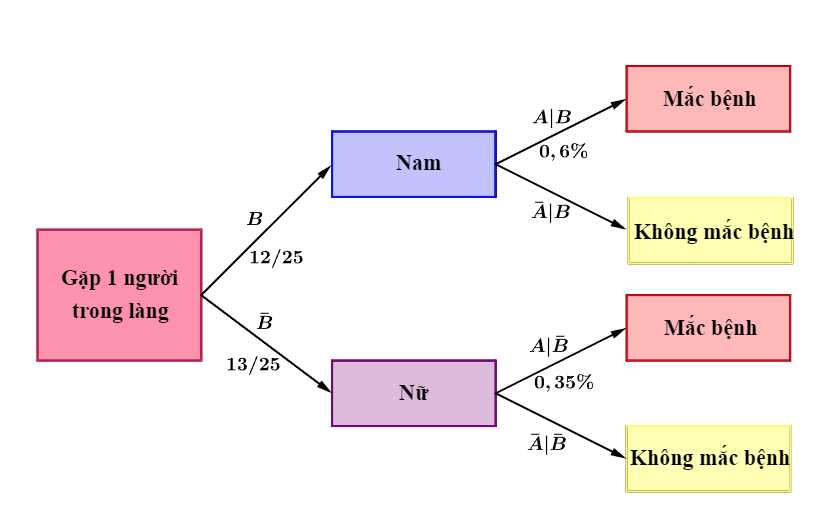
c) Sai.
Ta có: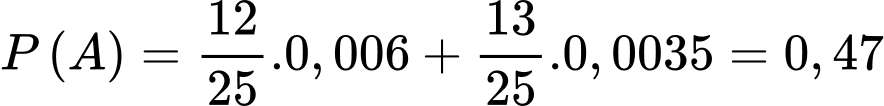
d) Sai.
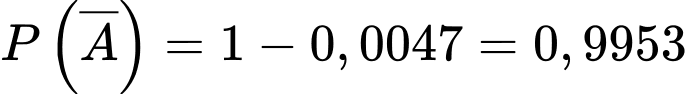
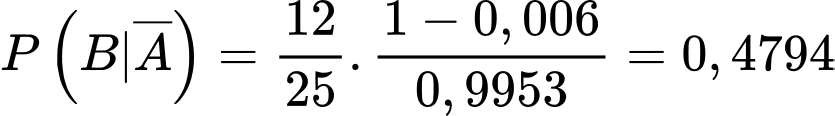
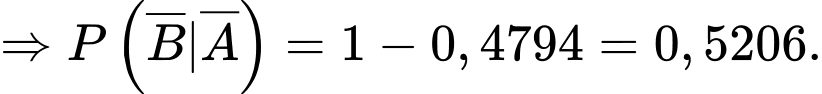
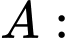 “gặp người mắc bệnh trong làng”
“gặp người mắc bệnh trong làng”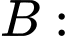 “gặp được nam trong làng”
“gặp được nam trong làng”a) Đúng.
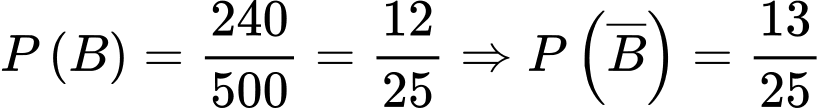
b) Sai.
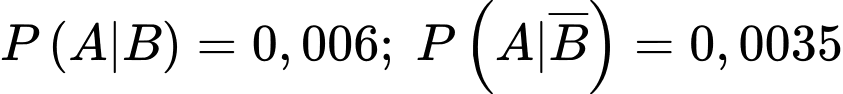
Ta có sơ đồ cây sau:

c) Sai.
Ta có:
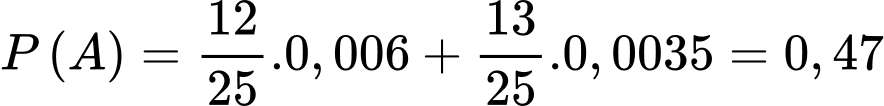
d) Sai.
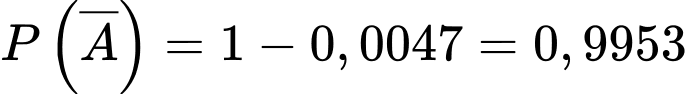
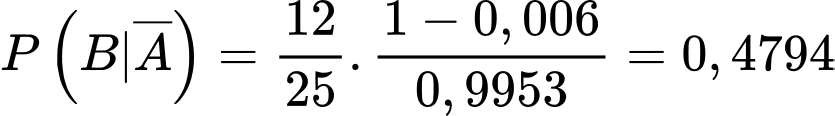
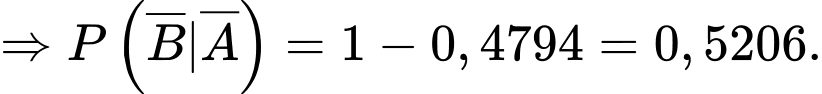
Câu 15 [779001]: Hộp thứ nhất có chứa 4 viên bi xanh và 3 viên bi đỏ, hộp thứ hai có chứa 5 bi xanh và 2 bi đỏ. Từ hộp thứ nhất lấy ra ngẫu nhiên 1 viên bi bỏ vào hộp thứ hai, sau đó từ hộp thứ hai lấy ra ngẫu nhiên 2 viên bi.
Gọi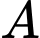 là biến cố “ở lần thứ nhất lấy được viên bi màu xanh”
là biến cố “ở lần thứ nhất lấy được viên bi màu xanh”
Gọi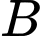 là biến cố “ở lần thứ hai lấy được hai viên bi màu xanh”
là biến cố “ở lần thứ hai lấy được hai viên bi màu xanh”
Gọi
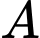 là biến cố “ở lần thứ nhất lấy được viên bi màu xanh”
là biến cố “ở lần thứ nhất lấy được viên bi màu xanh”Gọi
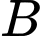 là biến cố “ở lần thứ hai lấy được hai viên bi màu xanh”
là biến cố “ở lần thứ hai lấy được hai viên bi màu xanh”
a) Đúng.
b) Sai.
 là xác suất lần thứ hai lấy được hai viên bi màu xanh khi biết lần thứ nhất lấy được viên bi màu xanh. Khi lần thứ nhất lấy được viên bi màu xanh, thì lúc này ở hộp 2 có tổng cộng 8 viên trong đó có 6 viên bi màu xanh, khi đó xác suất lấy được hai viên bi xanh ở hộp 2 là
là xác suất lần thứ hai lấy được hai viên bi màu xanh khi biết lần thứ nhất lấy được viên bi màu xanh. Khi lần thứ nhất lấy được viên bi màu xanh, thì lúc này ở hộp 2 có tổng cộng 8 viên trong đó có 6 viên bi màu xanh, khi đó xác suất lấy được hai viên bi xanh ở hộp 2 là 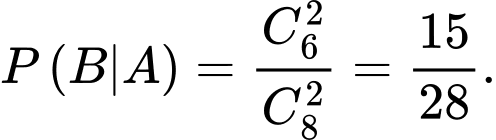
c) Đúng.
YCBT: Tính
Tương tự như phần b), ta cũng tính được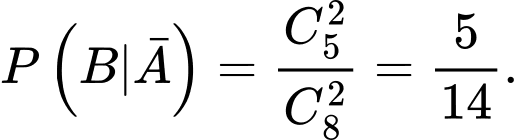
(các em hãy vẽ sơ đồ cây để dễ hình dung hơn nhé!)
Áp dụng công thức xác suất toàn phần, ta có
Ta cần tính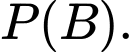 Theo công thức xác suất toàn phần, ta có
Theo công thức xác suất toàn phần, ta có
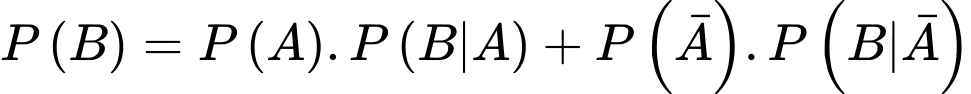
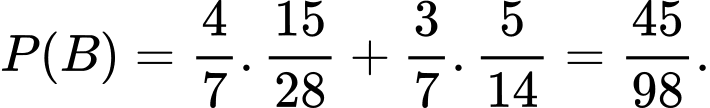
d) Sai.
Áp dụng công thức Bayes, xác suất lần thứ nhất lấy được bi màu đỏ khi biết lần thứ hai lấy ra được hai viên bi màu xanh là
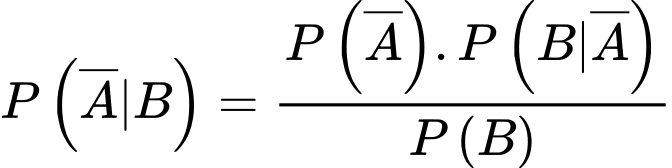
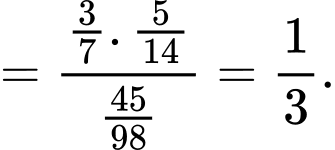
b) Sai.
 là xác suất lần thứ hai lấy được hai viên bi màu xanh khi biết lần thứ nhất lấy được viên bi màu xanh. Khi lần thứ nhất lấy được viên bi màu xanh, thì lúc này ở hộp 2 có tổng cộng 8 viên trong đó có 6 viên bi màu xanh, khi đó xác suất lấy được hai viên bi xanh ở hộp 2 là
là xác suất lần thứ hai lấy được hai viên bi màu xanh khi biết lần thứ nhất lấy được viên bi màu xanh. Khi lần thứ nhất lấy được viên bi màu xanh, thì lúc này ở hộp 2 có tổng cộng 8 viên trong đó có 6 viên bi màu xanh, khi đó xác suất lấy được hai viên bi xanh ở hộp 2 là 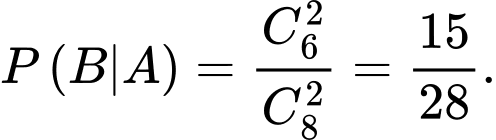
c) Đúng.
YCBT: Tính

Tương tự như phần b), ta cũng tính được
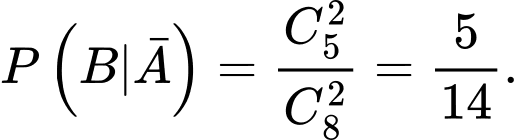
(các em hãy vẽ sơ đồ cây để dễ hình dung hơn nhé!)
Áp dụng công thức xác suất toàn phần, ta có
Ta cần tính
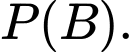 Theo công thức xác suất toàn phần, ta có
Theo công thức xác suất toàn phần, ta có
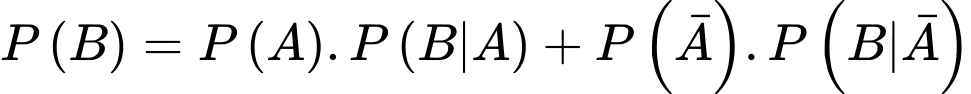
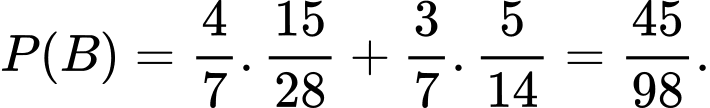
d) Sai.
Áp dụng công thức Bayes, xác suất lần thứ nhất lấy được bi màu đỏ khi biết lần thứ hai lấy ra được hai viên bi màu xanh là
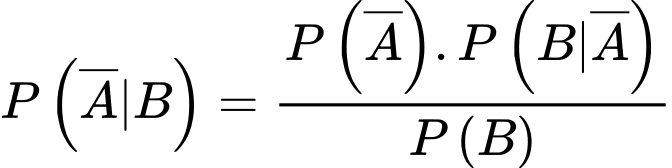
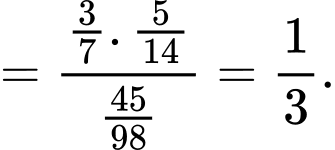
Câu 16 [697014]: Một nghiên cứu cho thấy có 5% các tin nhắn trên một mạng viễn thông X là tin nhắn quảng cáo. Trong các tin nhắn quảng cáo, 80% tin nhắn có chứa chữ “sale”. Trong các tin nhắn không quảng cáo, 2% tin nhắn có chữ “sale”. Chọn ngẫu nhiên 1 tin nhắn trên mạng viễn thông X.
Gọi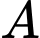 là biến cố: “tin nhắn là tin nhắn quảng cáo”.
là biến cố: “tin nhắn là tin nhắn quảng cáo”.
Gọi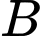 là biến cố: “tin nhắn chứa chữ “sale”.
là biến cố: “tin nhắn chứa chữ “sale”.
Gọi
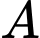 là biến cố: “tin nhắn là tin nhắn quảng cáo”.
là biến cố: “tin nhắn là tin nhắn quảng cáo”. Gọi
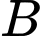 là biến cố: “tin nhắn chứa chữ “sale”.
là biến cố: “tin nhắn chứa chữ “sale”.
Gọi 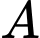 là biến cố “ Tin nhắn là tin nhắn quảng cáo”
là biến cố “ Tin nhắn là tin nhắn quảng cáo”
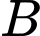 là biến cố “ Tin nhắn chứa chữ sale”
là biến cố “ Tin nhắn chứa chữ sale”
a) Đúng.
Theo đề bài ta có: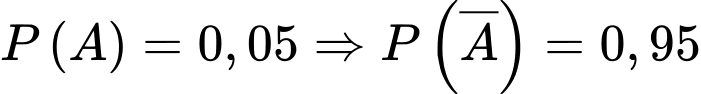
b) Sai.
Vì trong các tin nhắn quảng cáo, 80% tin nhắn có chứa chữ “sale”
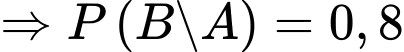 .
.
c) Sai.
Theo công thức xác suất toàn phần ta có:
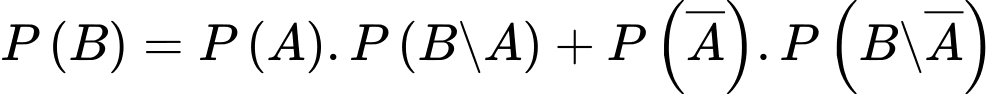
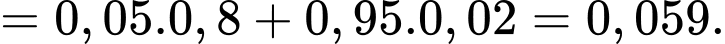
d) Đúng.
Theo công thức Bayes ta có: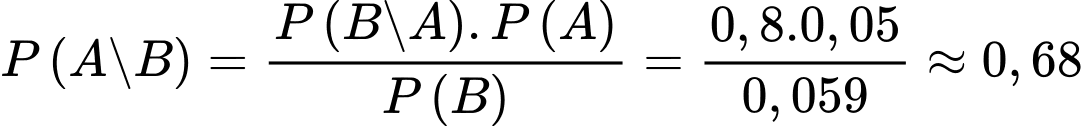
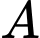 là biến cố “ Tin nhắn là tin nhắn quảng cáo”
là biến cố “ Tin nhắn là tin nhắn quảng cáo”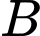 là biến cố “ Tin nhắn chứa chữ sale”
là biến cố “ Tin nhắn chứa chữ sale”a) Đúng.
Theo đề bài ta có:
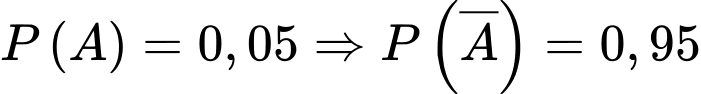
b) Sai.
Vì trong các tin nhắn quảng cáo, 80% tin nhắn có chứa chữ “sale”
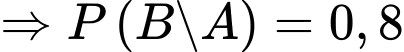 .
.c) Sai.
Theo công thức xác suất toàn phần ta có:
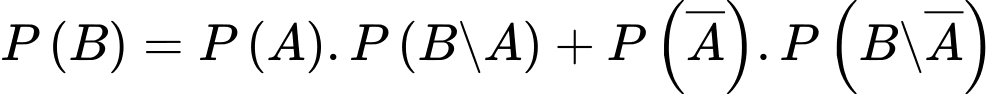
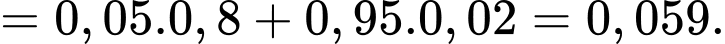
d) Đúng.
Theo công thức Bayes ta có:
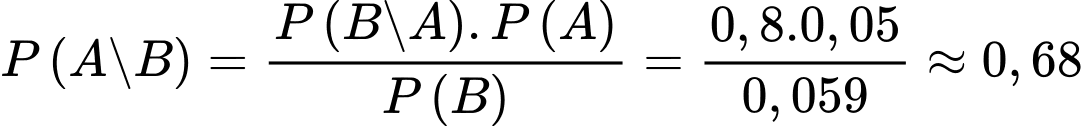
PHẦN III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 17 đến câu 22.
Câu 17 [779002]: Một cửa hàng có hai loại bóng đèn Led, trong đó có 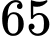 bóng đèn Led là màu trắng và
bóng đèn Led là màu trắng và 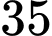 bóng đèn Led là màu xanh, các bóng đèn có kích thước như nhau. Các bóng đèn Led màu trắng có tỉ lệ hỏng là
bóng đèn Led là màu xanh, các bóng đèn có kích thước như nhau. Các bóng đèn Led màu trắng có tỉ lệ hỏng là 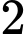 và các bóng đèn Led màu xanh có tỉ lệ hỏng là
và các bóng đèn Led màu xanh có tỉ lệ hỏng là 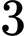 Một khách hàng chọn mua ngẫu nhiên 1 bóng đèn Led từ cửa hàng. Xác suất để khách hàng chọn được bóng đèn Led không hỏng bằng bao nhiêu (làm tròn kết quả đến hàng phần trăm).
Một khách hàng chọn mua ngẫu nhiên 1 bóng đèn Led từ cửa hàng. Xác suất để khách hàng chọn được bóng đèn Led không hỏng bằng bao nhiêu (làm tròn kết quả đến hàng phần trăm).
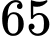 bóng đèn Led là màu trắng và
bóng đèn Led là màu trắng và 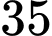 bóng đèn Led là màu xanh, các bóng đèn có kích thước như nhau. Các bóng đèn Led màu trắng có tỉ lệ hỏng là
bóng đèn Led là màu xanh, các bóng đèn có kích thước như nhau. Các bóng đèn Led màu trắng có tỉ lệ hỏng là 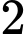 và các bóng đèn Led màu xanh có tỉ lệ hỏng là
và các bóng đèn Led màu xanh có tỉ lệ hỏng là 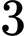 Một khách hàng chọn mua ngẫu nhiên 1 bóng đèn Led từ cửa hàng. Xác suất để khách hàng chọn được bóng đèn Led không hỏng bằng bao nhiêu (làm tròn kết quả đến hàng phần trăm).
Một khách hàng chọn mua ngẫu nhiên 1 bóng đèn Led từ cửa hàng. Xác suất để khách hàng chọn được bóng đèn Led không hỏng bằng bao nhiêu (làm tròn kết quả đến hàng phần trăm).
Xét các biến cố:
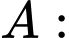 "Khách hàng chọn được bóng đèn Led màu trắng";
"Khách hàng chọn được bóng đèn Led màu trắng";
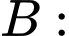 "Khách hàng chọn được bóng đèn Led không hỏng".
"Khách hàng chọn được bóng đèn Led không hỏng".
Ta có: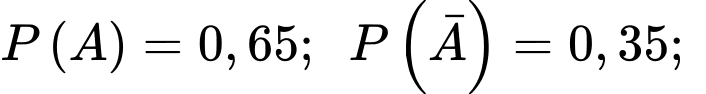
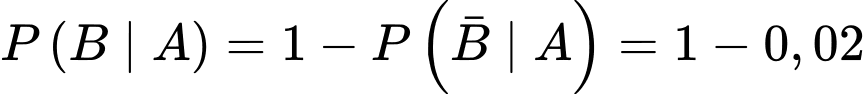
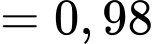 ;
;
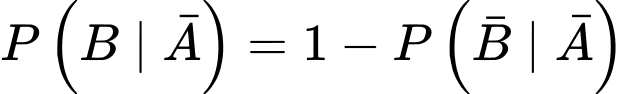
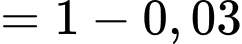
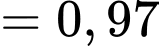 .
.
Theo công thức xác suất toàn phần, ta có:
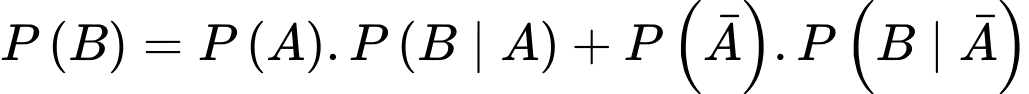
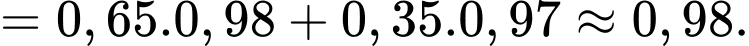
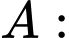 "Khách hàng chọn được bóng đèn Led màu trắng";
"Khách hàng chọn được bóng đèn Led màu trắng";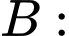 "Khách hàng chọn được bóng đèn Led không hỏng".
"Khách hàng chọn được bóng đèn Led không hỏng".Ta có:
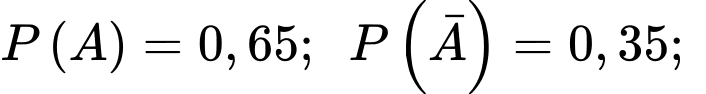
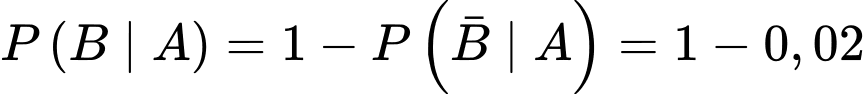
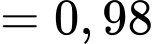 ;
;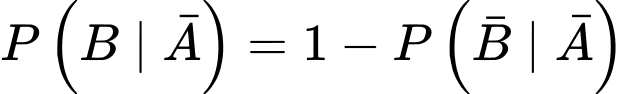
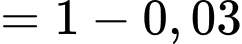
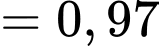 .
.Theo công thức xác suất toàn phần, ta có:
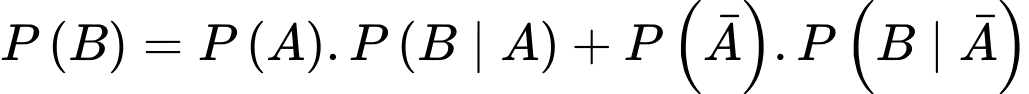
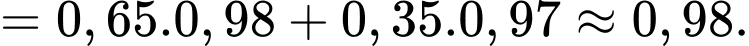
Câu 18 [779003]: Có 7 khẩu súng cũ và 5 khẩu súng mới, trong đó xác suất trúng khi bắn bằng súng cũ là 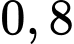 còn súng mới là
còn súng mới là 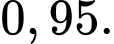 Một người lấy ngẫu nhiên một khẩu súng và bắn một mục tiêu. Giả sử người đó bắn trúng mục tiêu thì xác suất người đó dùng súng mới là bao nhiêu phần trăm (kết quả làm tròn đến hàng đơn vị).
Một người lấy ngẫu nhiên một khẩu súng và bắn một mục tiêu. Giả sử người đó bắn trúng mục tiêu thì xác suất người đó dùng súng mới là bao nhiêu phần trăm (kết quả làm tròn đến hàng đơn vị).
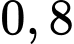 còn súng mới là
còn súng mới là 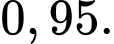 Một người lấy ngẫu nhiên một khẩu súng và bắn một mục tiêu. Giả sử người đó bắn trúng mục tiêu thì xác suất người đó dùng súng mới là bao nhiêu phần trăm (kết quả làm tròn đến hàng đơn vị).
Một người lấy ngẫu nhiên một khẩu súng và bắn một mục tiêu. Giả sử người đó bắn trúng mục tiêu thì xác suất người đó dùng súng mới là bao nhiêu phần trăm (kết quả làm tròn đến hàng đơn vị).
Điền đáp án: 46.
Gọi là biến cố “Khẩu súng đó là khẩu súng mới”;
là biến cố “Khẩu súng đó là khẩu súng mới”;  là biến cố “Khẩu súng đó là khẩu súng cũ”.
là biến cố “Khẩu súng đó là khẩu súng cũ”.
Gọi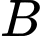 là biến cố “Người đó bắn trúng mục tiêu”;
là biến cố “Người đó bắn trúng mục tiêu”; 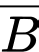 là biến cố “Người đó bắn trượt mục tiêu”.
là biến cố “Người đó bắn trượt mục tiêu”.
Yêu cầu bài toán: Tính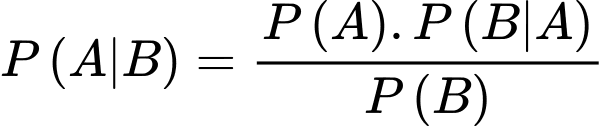
Từ giả thiết, ta có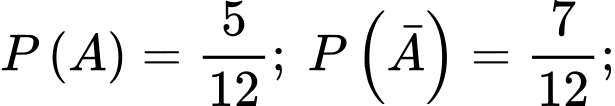
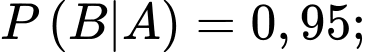
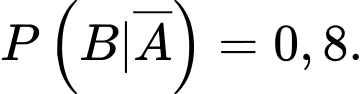
(Các em hãy vẽ sơ đồ cây để dễ dàng thấy được cách tính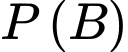 bằng công thức xác suất toàn phần nhé!)
bằng công thức xác suất toàn phần nhé!)
Áp dụng công thức xác suất toàn phần, ta có
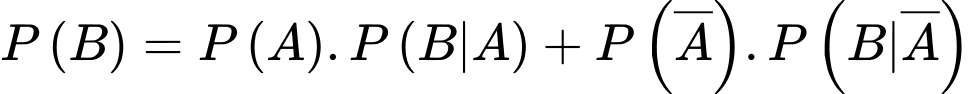
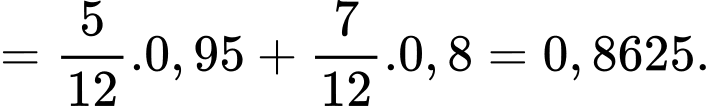
Áp dụng công thức Bayes, xác suất cần tìm là
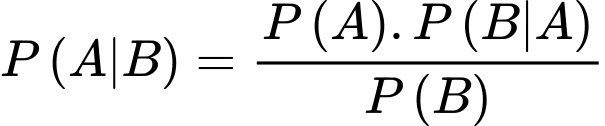
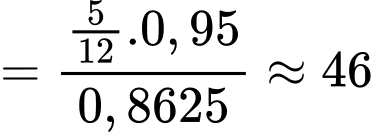
Gọi
 là biến cố “Khẩu súng đó là khẩu súng mới”;
là biến cố “Khẩu súng đó là khẩu súng mới”;  là biến cố “Khẩu súng đó là khẩu súng cũ”.
là biến cố “Khẩu súng đó là khẩu súng cũ”.Gọi
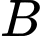 là biến cố “Người đó bắn trúng mục tiêu”;
là biến cố “Người đó bắn trúng mục tiêu”; 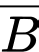 là biến cố “Người đó bắn trượt mục tiêu”.
là biến cố “Người đó bắn trượt mục tiêu”.Yêu cầu bài toán: Tính
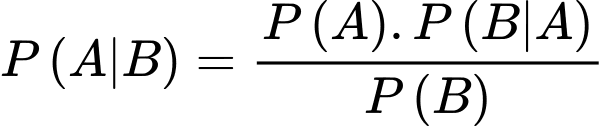
Từ giả thiết, ta có
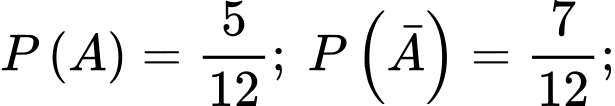
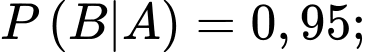
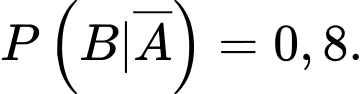
(Các em hãy vẽ sơ đồ cây để dễ dàng thấy được cách tính
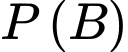 bằng công thức xác suất toàn phần nhé!)
bằng công thức xác suất toàn phần nhé!)Áp dụng công thức xác suất toàn phần, ta có
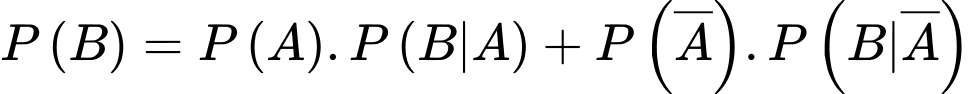
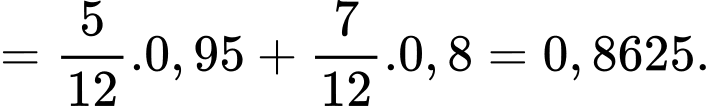
Áp dụng công thức Bayes, xác suất cần tìm là
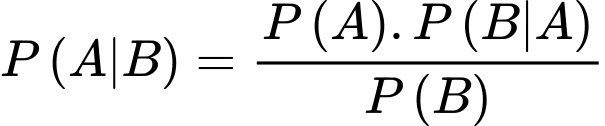
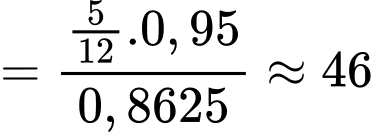
Câu 19 [695298]: Một chiếc máy bay có thể xuất hiện ở vị trí A với xác suất 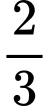 và ở vị trí B với xác suất
và ở vị trí B với xác suất 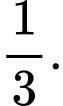 Người ta bố trí 1 khẩu đặt tại A, 3 khẩu đặt tại B. Biết rằng xác suất bắn trúng máy bay của mỗi khẩu pháo là 0,7 và các khẩu pháo hoạt động độc lập với nhau. Giả sử máy bay bị bắn trúng thì xác suất máy bay bị bắn trúng tại vị trí A là bao nhiêu? Kết quả làm tròn đến hàng phần trăm?
Người ta bố trí 1 khẩu đặt tại A, 3 khẩu đặt tại B. Biết rằng xác suất bắn trúng máy bay của mỗi khẩu pháo là 0,7 và các khẩu pháo hoạt động độc lập với nhau. Giả sử máy bay bị bắn trúng thì xác suất máy bay bị bắn trúng tại vị trí A là bao nhiêu? Kết quả làm tròn đến hàng phần trăm?
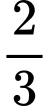 và ở vị trí B với xác suất
và ở vị trí B với xác suất 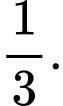 Người ta bố trí 1 khẩu đặt tại A, 3 khẩu đặt tại B. Biết rằng xác suất bắn trúng máy bay của mỗi khẩu pháo là 0,7 và các khẩu pháo hoạt động độc lập với nhau. Giả sử máy bay bị bắn trúng thì xác suất máy bay bị bắn trúng tại vị trí A là bao nhiêu? Kết quả làm tròn đến hàng phần trăm?
Người ta bố trí 1 khẩu đặt tại A, 3 khẩu đặt tại B. Biết rằng xác suất bắn trúng máy bay của mỗi khẩu pháo là 0,7 và các khẩu pháo hoạt động độc lập với nhau. Giả sử máy bay bị bắn trúng thì xác suất máy bay bị bắn trúng tại vị trí A là bao nhiêu? Kết quả làm tròn đến hàng phần trăm?
Điền đáp án: 0,59.
Gọi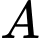 là biến cố “Máy bay xuất hiện ở vị trí A”
là biến cố “Máy bay xuất hiện ở vị trí A”
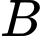 là biến cố “Máy bay bị bắn trúng”
là biến cố “Máy bay bị bắn trúng”
Khi đó là biến cố “Máy bay xuất hiện ở vị trí B” và
là biến cố “Máy bay xuất hiện ở vị trí B” và 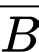 là biến cố “Máy bay không bị bắn trúng”
là biến cố “Máy bay không bị bắn trúng”
Yêu cầu bài toán Tính
Tính 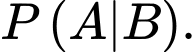
(Theo công thức xác suất có điều kiện, ta có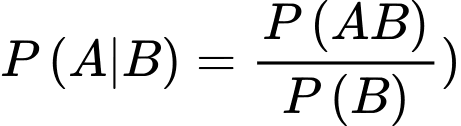
Vì có 3 khẩu đặt tại B nên để máy bay rơi cần ít nhất một khẩu bắn trúng. Xác suất để ít nhất một khẩu tại B bắn trúng máy bay là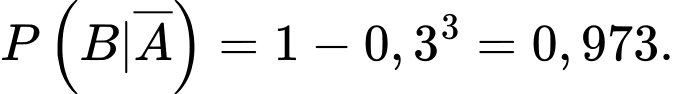
Ta có sơ đồ cây sau:
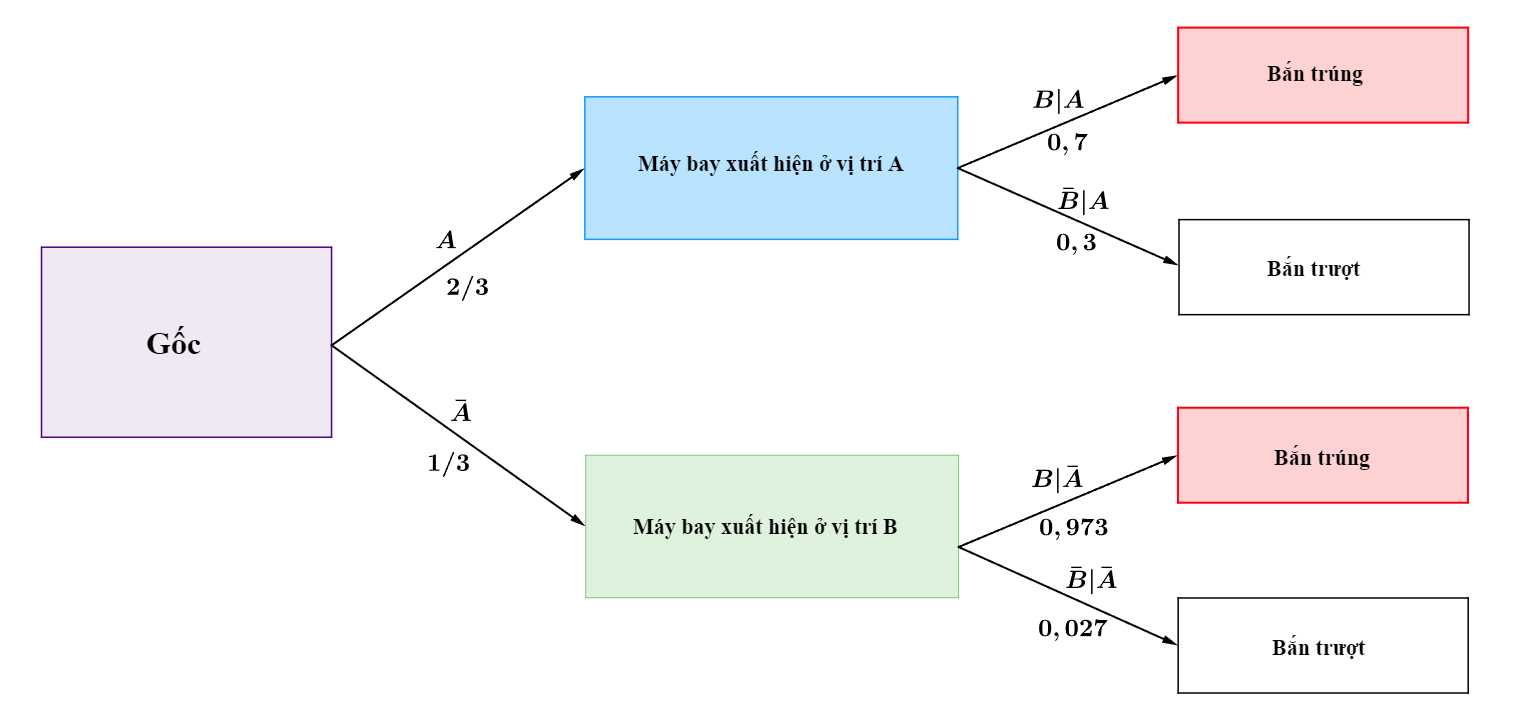
Suy ra xác suất để máy bay rơi (bị bắn trúng) là: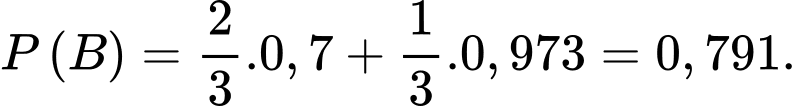
Xác suất cần tìm là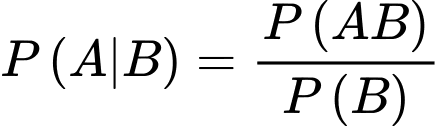
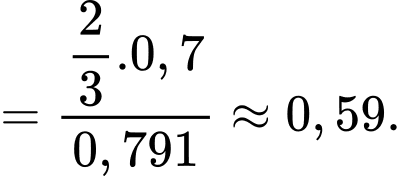
Gọi
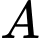 là biến cố “Máy bay xuất hiện ở vị trí A”
là biến cố “Máy bay xuất hiện ở vị trí A”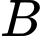 là biến cố “Máy bay bị bắn trúng”
là biến cố “Máy bay bị bắn trúng”Khi đó
 là biến cố “Máy bay xuất hiện ở vị trí B” và
là biến cố “Máy bay xuất hiện ở vị trí B” và 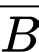 là biến cố “Máy bay không bị bắn trúng”
là biến cố “Máy bay không bị bắn trúng”Yêu cầu bài toán
 Tính
Tính 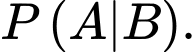
(Theo công thức xác suất có điều kiện, ta có
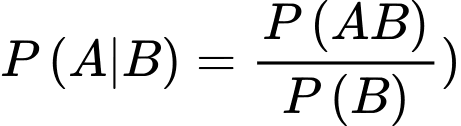
Vì có 3 khẩu đặt tại B nên để máy bay rơi cần ít nhất một khẩu bắn trúng. Xác suất để ít nhất một khẩu tại B bắn trúng máy bay là
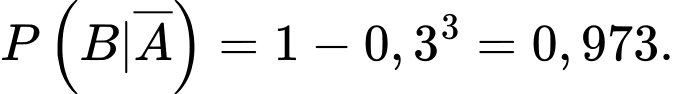
Ta có sơ đồ cây sau:

Suy ra xác suất để máy bay rơi (bị bắn trúng) là:
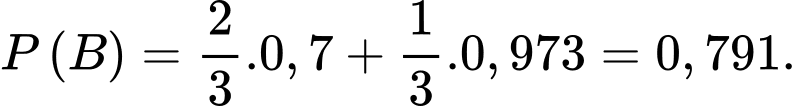
Xác suất cần tìm là
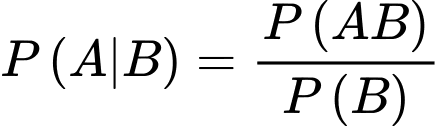
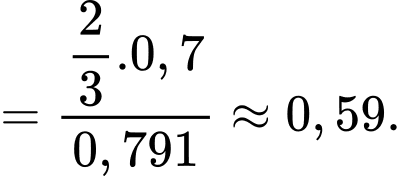
Câu 20 [693508]: Một người nghi ngờ bị bệnh B, với xác suất 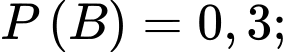 cho người này làm xét nghiệm A. Xét nghiệm A sẽ trả về hoặc dương tính, hoặc âm tính. Thống kê cho thấy, trong số những người có xét nghiệm dương tính chỉ có 80% là bị bệnh B, còn trong số những người âm tính thì có 90% không bị bệnh này. Trong y học, độ nhạy của một xét nghiệm là tỷ lệ những trường hợp thực sự có bệnh và có kết quả xét nghiệm dương tính trong toàn bộ các trường hợp có bệnh. Tính độ nhạy của xét nghiệm A. Kết quả làm tròn đến hàng phần trăm?
cho người này làm xét nghiệm A. Xét nghiệm A sẽ trả về hoặc dương tính, hoặc âm tính. Thống kê cho thấy, trong số những người có xét nghiệm dương tính chỉ có 80% là bị bệnh B, còn trong số những người âm tính thì có 90% không bị bệnh này. Trong y học, độ nhạy của một xét nghiệm là tỷ lệ những trường hợp thực sự có bệnh và có kết quả xét nghiệm dương tính trong toàn bộ các trường hợp có bệnh. Tính độ nhạy của xét nghiệm A. Kết quả làm tròn đến hàng phần trăm?
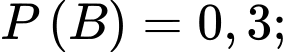 cho người này làm xét nghiệm A. Xét nghiệm A sẽ trả về hoặc dương tính, hoặc âm tính. Thống kê cho thấy, trong số những người có xét nghiệm dương tính chỉ có 80% là bị bệnh B, còn trong số những người âm tính thì có 90% không bị bệnh này. Trong y học, độ nhạy của một xét nghiệm là tỷ lệ những trường hợp thực sự có bệnh và có kết quả xét nghiệm dương tính trong toàn bộ các trường hợp có bệnh. Tính độ nhạy của xét nghiệm A. Kết quả làm tròn đến hàng phần trăm?
cho người này làm xét nghiệm A. Xét nghiệm A sẽ trả về hoặc dương tính, hoặc âm tính. Thống kê cho thấy, trong số những người có xét nghiệm dương tính chỉ có 80% là bị bệnh B, còn trong số những người âm tính thì có 90% không bị bệnh này. Trong y học, độ nhạy của một xét nghiệm là tỷ lệ những trường hợp thực sự có bệnh và có kết quả xét nghiệm dương tính trong toàn bộ các trường hợp có bệnh. Tính độ nhạy của xét nghiệm A. Kết quả làm tròn đến hàng phần trăm?
Điền đáp án: 0,76.
Gọi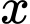 là tỷ lệ cho kết quả dương tính, khi đó
là tỷ lệ cho kết quả dương tính, khi đó 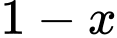 là tỷ lệ cho kết quả âm tính.
là tỷ lệ cho kết quả âm tính.
Gọi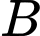 là biến cố “Người đó bị bệnh B”.
là biến cố “Người đó bị bệnh B”.
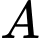 là biến cố “Xét nghiệm A trả về kết quả dương tính”
là biến cố “Xét nghiệm A trả về kết quả dương tính”
Yêu cầu bài toán tương đương với tìm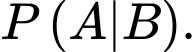
Dựa vào giả thiết, ta có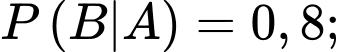
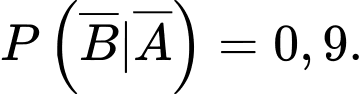
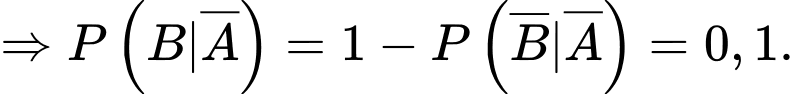
Từ đó, ta có sơ đồ cây như sau:
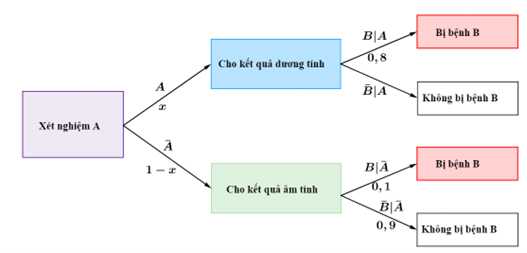
Ta có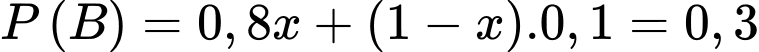
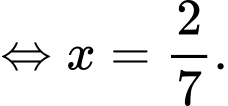
Suy ra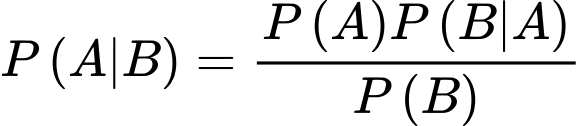
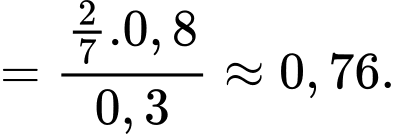
Gọi
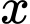 là tỷ lệ cho kết quả dương tính, khi đó
là tỷ lệ cho kết quả dương tính, khi đó 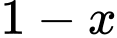 là tỷ lệ cho kết quả âm tính.
là tỷ lệ cho kết quả âm tính.Gọi
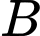 là biến cố “Người đó bị bệnh B”.
là biến cố “Người đó bị bệnh B”.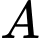 là biến cố “Xét nghiệm A trả về kết quả dương tính”
là biến cố “Xét nghiệm A trả về kết quả dương tính”Yêu cầu bài toán tương đương với tìm
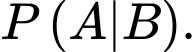
Dựa vào giả thiết, ta có
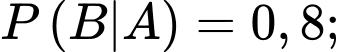
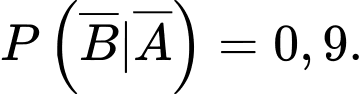
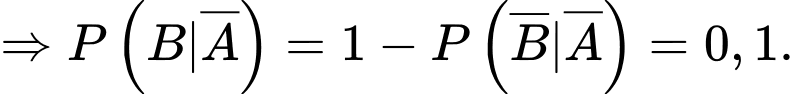
Từ đó, ta có sơ đồ cây như sau:

Ta có
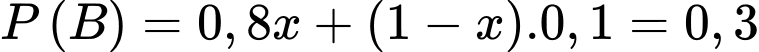
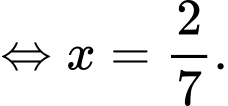
Suy ra
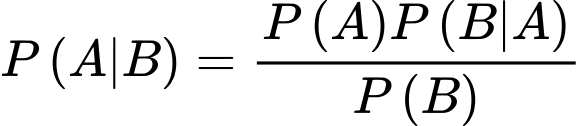
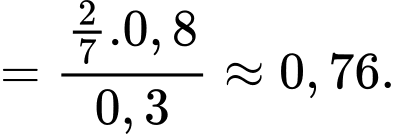
Câu 21 [696347]: Có 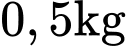 thóc giống ST24 bị trộn lẫn với
thóc giống ST24 bị trộn lẫn với 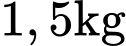 thóc giống ST25 và được gieo trên một thửa ruộng, xác suất hạt nảy mầm của thóc giống ST24 gấp 1,125 lần xác suất hạt nảy mầm của thóc giống ST25. Biết rằng, xác suất nảy mầm của các hạt thóc trên thửa ruộng này là
thóc giống ST25 và được gieo trên một thửa ruộng, xác suất hạt nảy mầm của thóc giống ST24 gấp 1,125 lần xác suất hạt nảy mầm của thóc giống ST25. Biết rằng, xác suất nảy mầm của các hạt thóc trên thửa ruộng này là 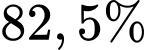 và số hạt thóc trên
và số hạt thóc trên 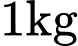 của các giống là bằng nhau. Chọn ngẫu nhiên một hạt nảy mầm, tính xác suất hạt này thuộc giống ST24. Kết quả làm tròn đến hàng phần trăm.
của các giống là bằng nhau. Chọn ngẫu nhiên một hạt nảy mầm, tính xác suất hạt này thuộc giống ST24. Kết quả làm tròn đến hàng phần trăm.
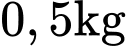 thóc giống ST24 bị trộn lẫn với
thóc giống ST24 bị trộn lẫn với 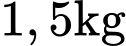 thóc giống ST25 và được gieo trên một thửa ruộng, xác suất hạt nảy mầm của thóc giống ST24 gấp 1,125 lần xác suất hạt nảy mầm của thóc giống ST25. Biết rằng, xác suất nảy mầm của các hạt thóc trên thửa ruộng này là
thóc giống ST25 và được gieo trên một thửa ruộng, xác suất hạt nảy mầm của thóc giống ST24 gấp 1,125 lần xác suất hạt nảy mầm của thóc giống ST25. Biết rằng, xác suất nảy mầm của các hạt thóc trên thửa ruộng này là 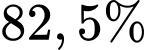 và số hạt thóc trên
và số hạt thóc trên  của các giống là bằng nhau. Chọn ngẫu nhiên một hạt nảy mầm, tính xác suất hạt này thuộc giống ST24. Kết quả làm tròn đến hàng phần trăm.
của các giống là bằng nhau. Chọn ngẫu nhiên một hạt nảy mầm, tính xác suất hạt này thuộc giống ST24. Kết quả làm tròn đến hàng phần trăm.
Điền đáp án: 0,27.
Gọi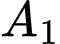 là biến cố “Lấy được một hạt thóc thuộc giống ST24”. Suy ra
là biến cố “Lấy được một hạt thóc thuộc giống ST24”. Suy ra 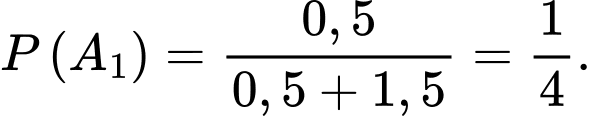
Gọi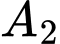 là biến cố “Lấy được một hạt thóc thuộc giống ST25”. Suy ra
là biến cố “Lấy được một hạt thóc thuộc giống ST25”. Suy ra 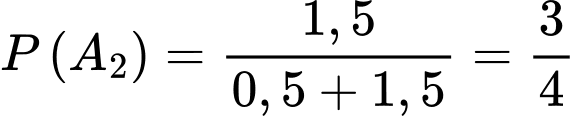 .
.
Gọi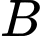 là biến cố “Lấy được một hạt nảy mầm”.
là biến cố “Lấy được một hạt nảy mầm”.
YCBT Tính
Tính 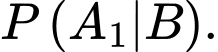
Giả sử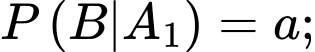
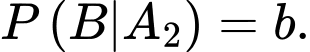
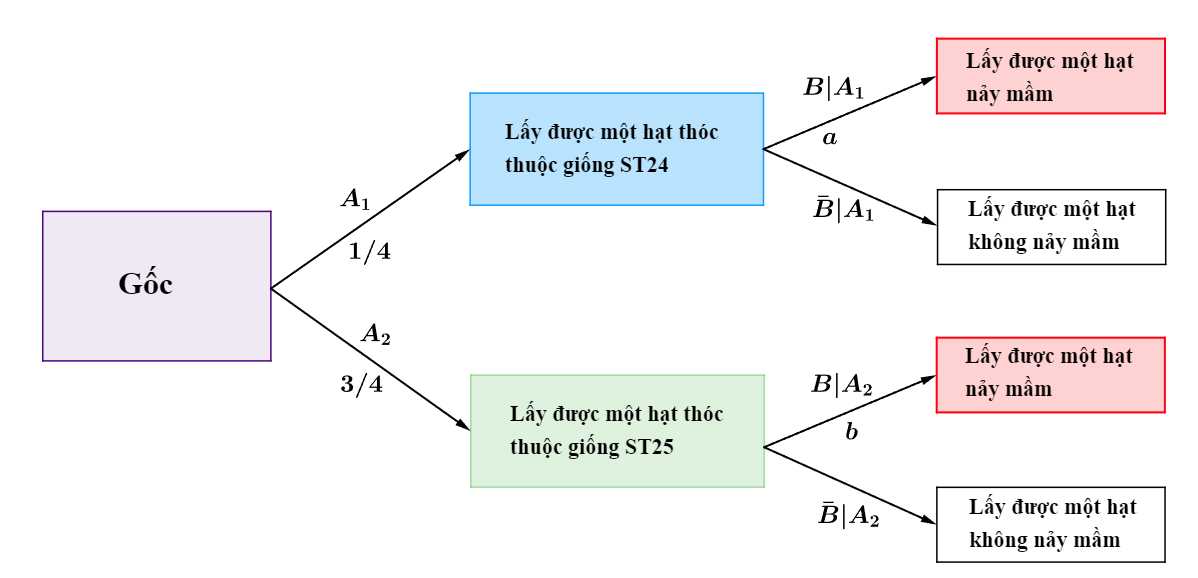
Ta có sơ đồ cây sau:
Áp dụng công thức xác suất toàn phần, ta có xác suất nảy mầm của các hạt thóc trên thửa ruộng là
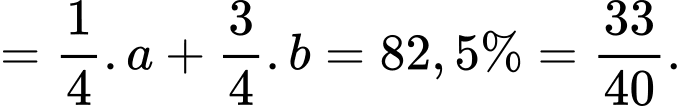
Lại có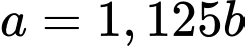 suy ra
suy ra 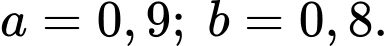
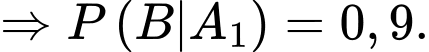
Khi đó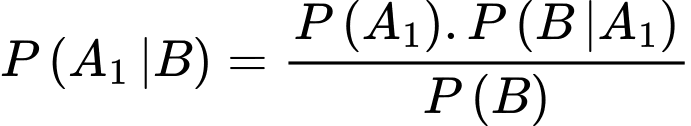
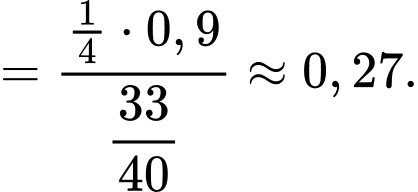
Gọi
 là biến cố “Lấy được một hạt thóc thuộc giống ST24”. Suy ra
là biến cố “Lấy được một hạt thóc thuộc giống ST24”. Suy ra 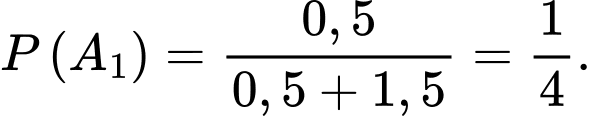
Gọi
 là biến cố “Lấy được một hạt thóc thuộc giống ST25”. Suy ra
là biến cố “Lấy được một hạt thóc thuộc giống ST25”. Suy ra 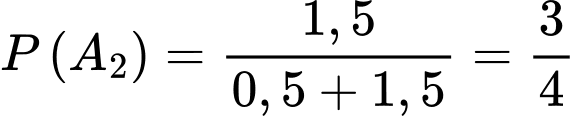 .
.Gọi
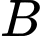 là biến cố “Lấy được một hạt nảy mầm”.
là biến cố “Lấy được một hạt nảy mầm”. YCBT
 Tính
Tính 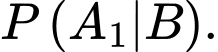
Giả sử
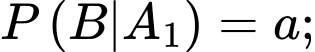
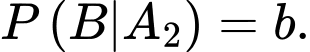
Ta có sơ đồ cây sau:

Áp dụng công thức xác suất toàn phần, ta có xác suất nảy mầm của các hạt thóc trên thửa ruộng là

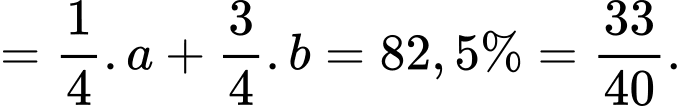
Lại có
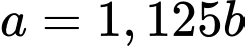 suy ra
suy ra 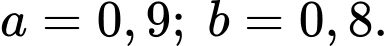
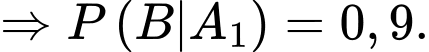
Khi đó
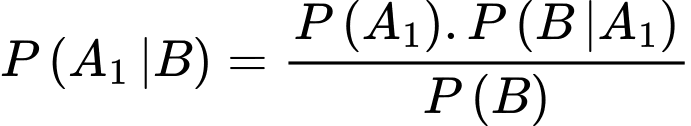
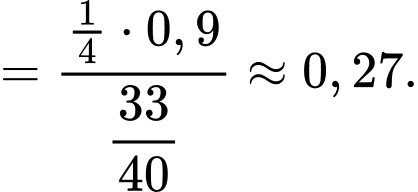
Câu 22 [779005]: Ở vùng A, tỷ lệ người có thu nhập tốt là 60%, tỷ lệ người gửi tiết kiệm là 30%. Biết rằng số người vừa có thu nhập tốt vừa gửi tiết kiệm bằng một nửa số người không có thu nhập tốt và cũng không gửi tiết kiệm. Gặp một người ở vùng A, biết người này không gửi tiết kiệm, tính xác suất có thu nhập tốt (viết kết quả làm tròn đến hàng phần chục).
Điền đáp án: 0,7.
Gọi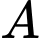 là biến cố “Người đó có thu nhập tốt”;
là biến cố “Người đó có thu nhập tốt”;  là biến cố “Người đó không có thu nhập tốt”
là biến cố “Người đó không có thu nhập tốt”
Gọi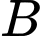 là biến cố “Người đó gửi tiết kiệm”;
là biến cố “Người đó gửi tiết kiệm”; 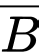 là biến cố “Người đó không gửi tiết kiệm”.
là biến cố “Người đó không gửi tiết kiệm”.
Yêu cầu bài toán: Tính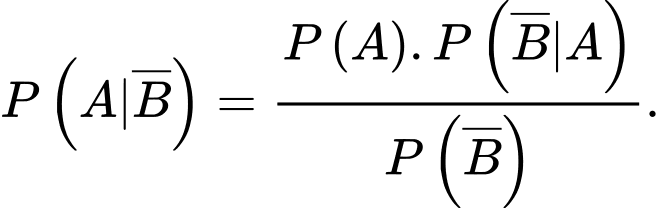
Từ giả thiết, ta có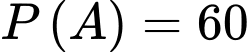
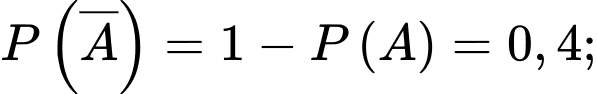
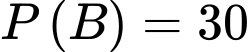
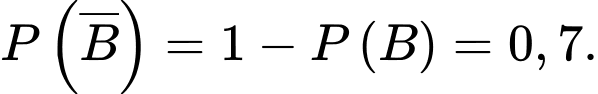
Giả sử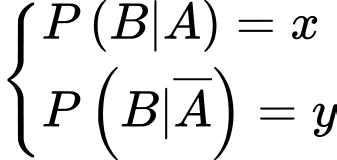
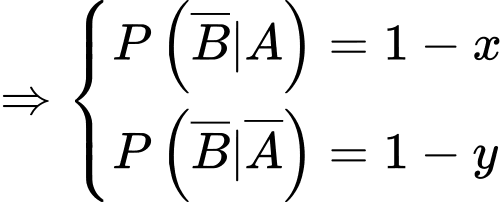
Từ các dữ kiện trên, ta có sơ đồ cây như sau:
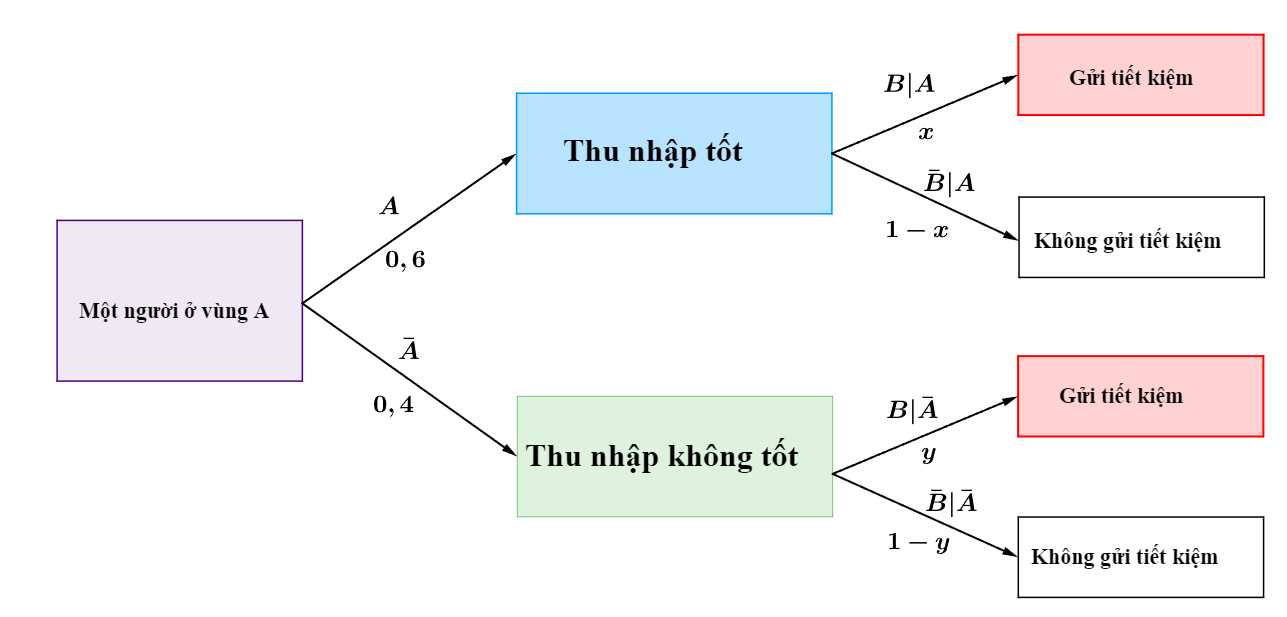
Từ giả thiết:
“Tỷ lệ người gửi tiết kiệm là 30%”, ta có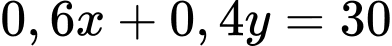
“Số người vừa có thu nhập tốt vừa gửi tiết kiệm bằng 1 nửa số người không có thu nhập tốt và không gửi tiết kiệm” nên ta có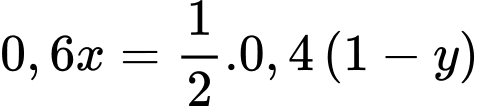
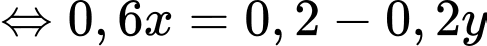
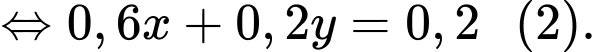
Từ (1) và (2) ta có hệ phương trình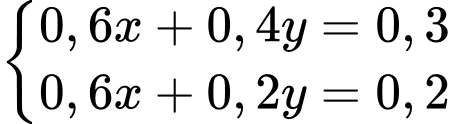
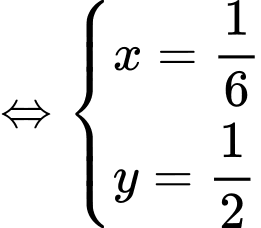
Suy ra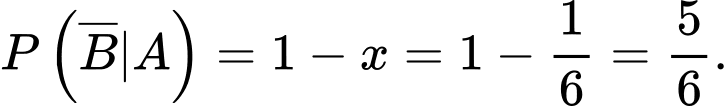
Vậy xác suất cần tính bằng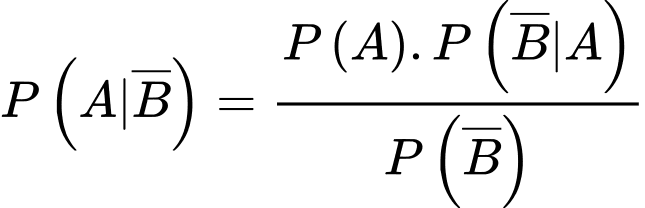
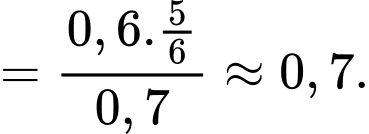
Gọi
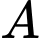 là biến cố “Người đó có thu nhập tốt”;
là biến cố “Người đó có thu nhập tốt”;  là biến cố “Người đó không có thu nhập tốt”
là biến cố “Người đó không có thu nhập tốt”
Gọi
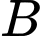 là biến cố “Người đó gửi tiết kiệm”;
là biến cố “Người đó gửi tiết kiệm”; 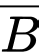 là biến cố “Người đó không gửi tiết kiệm”.
là biến cố “Người đó không gửi tiết kiệm”.
Yêu cầu bài toán: Tính
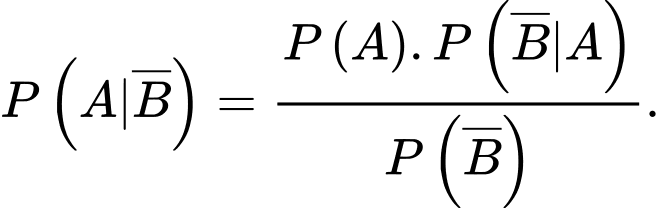
Từ giả thiết, ta có
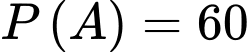
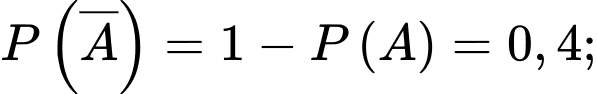
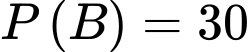
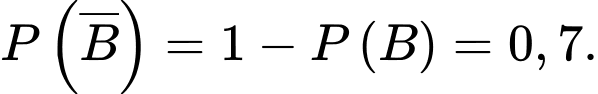
Giả sử
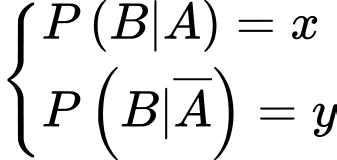
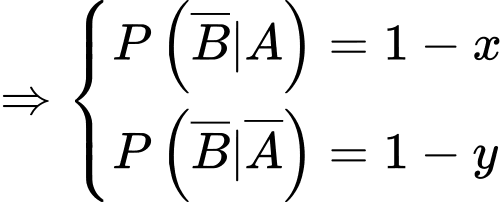
Từ các dữ kiện trên, ta có sơ đồ cây như sau:

Từ giả thiết:
“Tỷ lệ người gửi tiết kiệm là 30%”, ta có
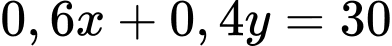
“Số người vừa có thu nhập tốt vừa gửi tiết kiệm bằng 1 nửa số người không có thu nhập tốt và không gửi tiết kiệm” nên ta có
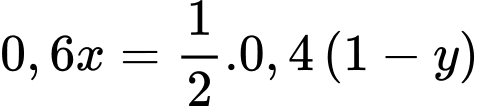
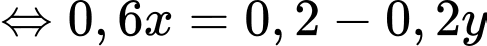
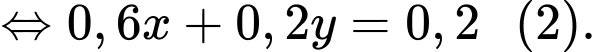
Từ (1) và (2) ta có hệ phương trình
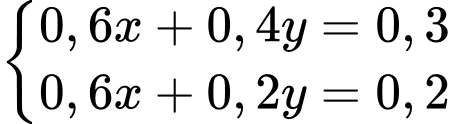
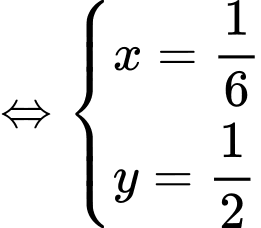
Suy ra
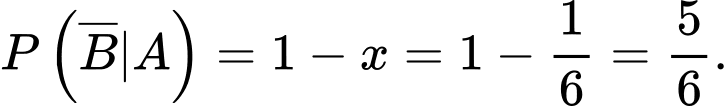
Vậy xác suất cần tính bằng