PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1 [541973]: Cho hàm số 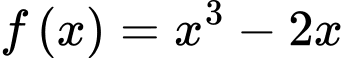 . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
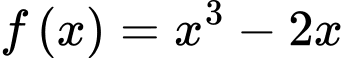 . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng? A, 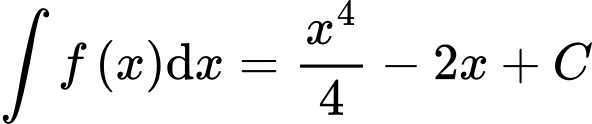 .
.
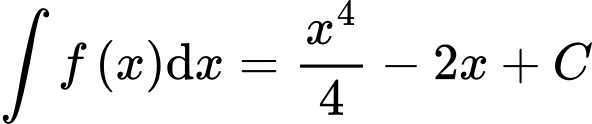 .
.B, 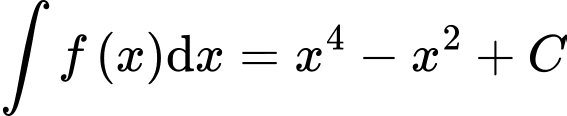 .
.
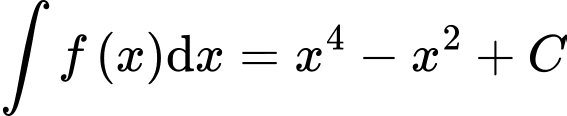 .
.C, 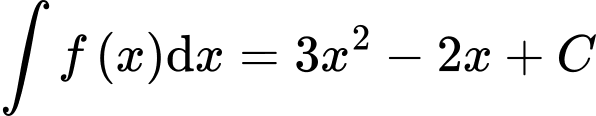 .
.
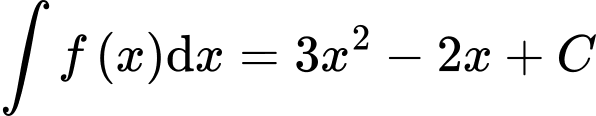 .
.D, 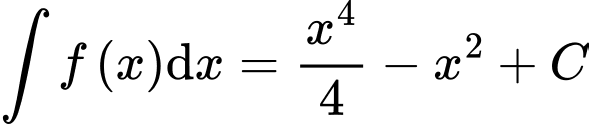 .
.
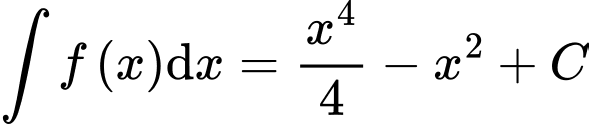 .
.
Ta có 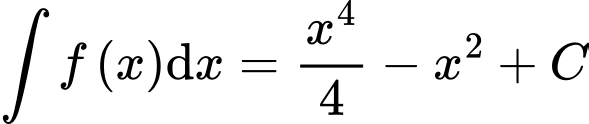 . Đáp án: D
. Đáp án: D
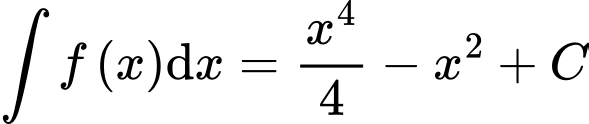 . Đáp án: D
. Đáp án: D
Câu 2 [391213]: Tìm họ nguyên hàm của hàm số 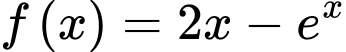
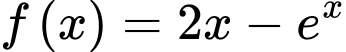
A, 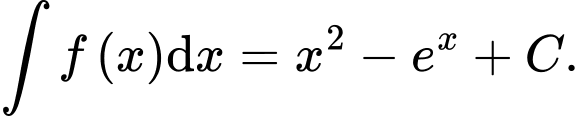
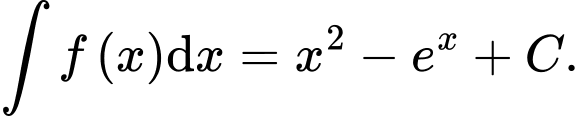
B, 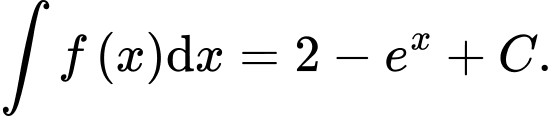
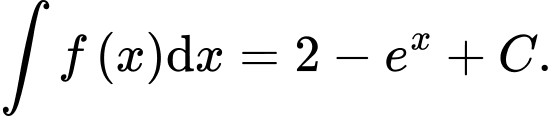
C, 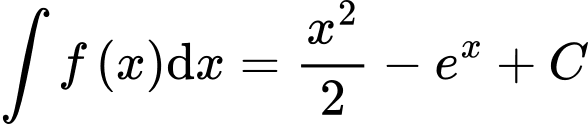
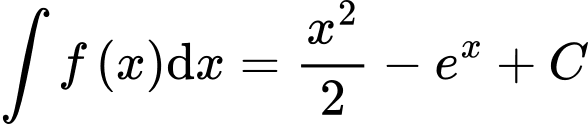
D, 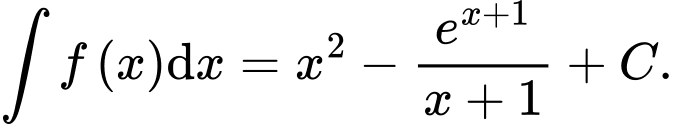
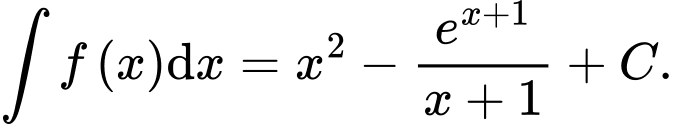
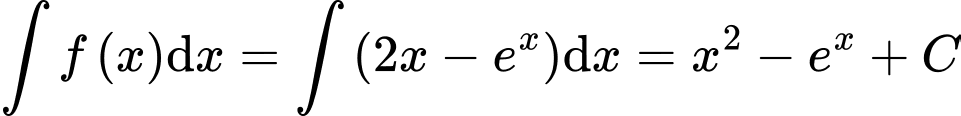 Đáp án: A
Đáp án: A
Câu 3 [395550]: Cho hàm số 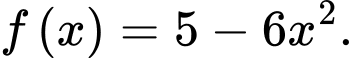 Khẳng định nào dưới đây đúng?
Khẳng định nào dưới đây đúng?
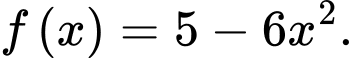 Khẳng định nào dưới đây đúng?
Khẳng định nào dưới đây đúng? A, 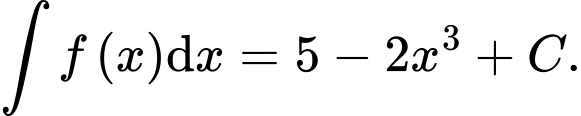
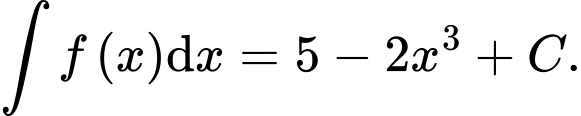
B, 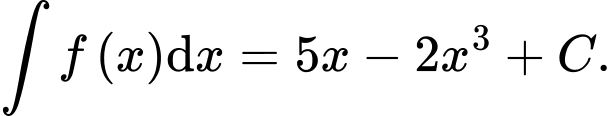
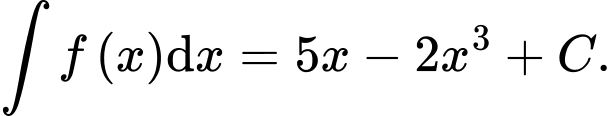
C, 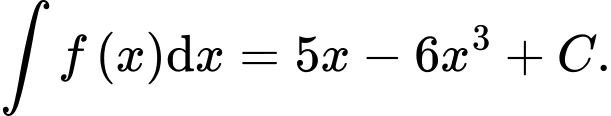
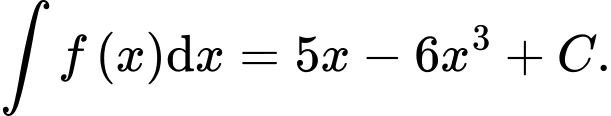
D, 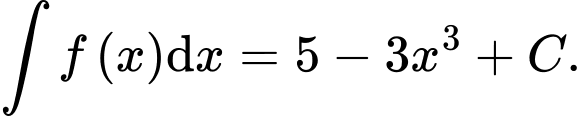
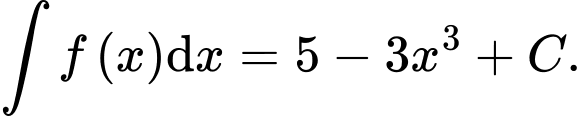
Chọn B
Ta có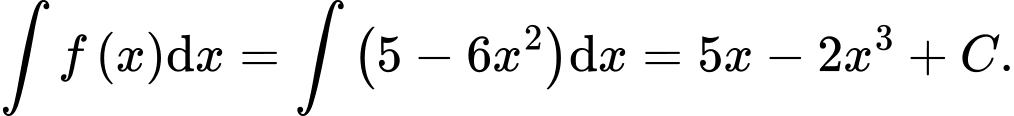 Đáp án: B
Đáp án: B
Ta có
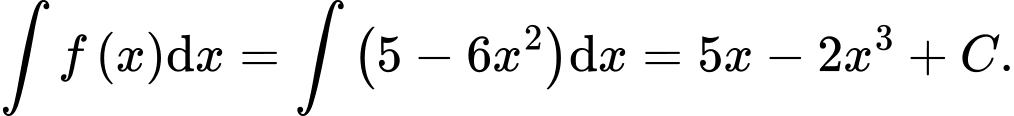 Đáp án: B
Đáp án: B
Câu 4 [543540]: Khẳng định nào sau đây đúng?
A, 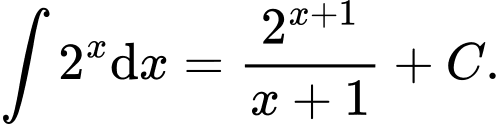
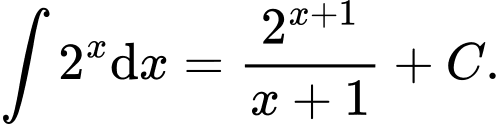
B, 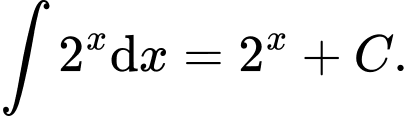
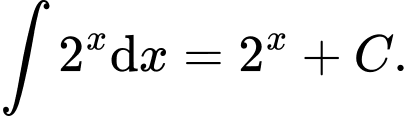
C, 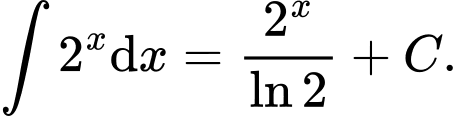
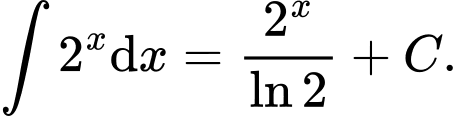
D, 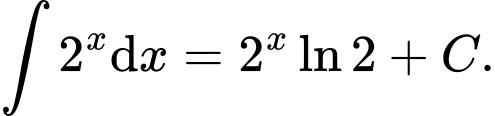
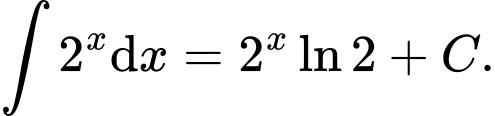
Chọn C
Áp dụng công thức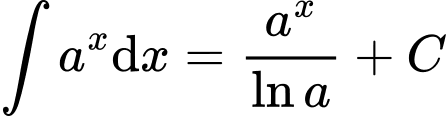 ta có
ta có 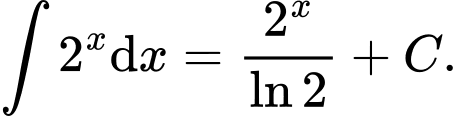 Đáp án: C
Đáp án: C
Áp dụng công thức
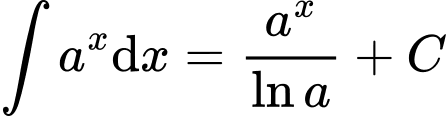 ta có
ta có 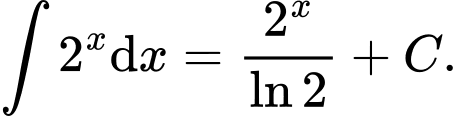 Đáp án: C
Đáp án: C
Câu 5 [147941]: Tìm nguyên hàm của hàm số 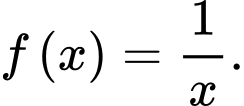
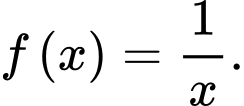
A, 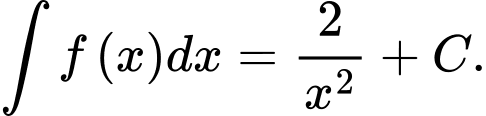
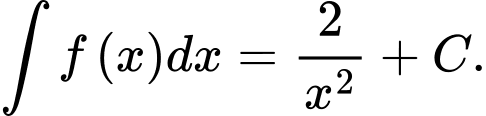
B, 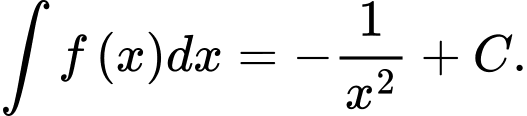
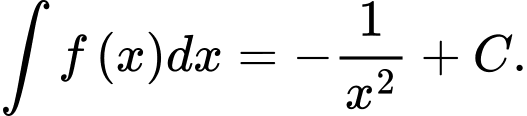
C, 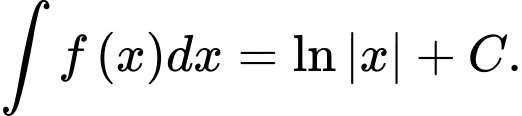
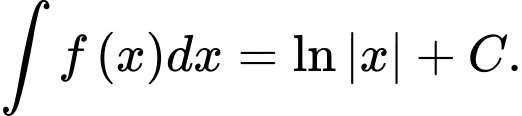
D, 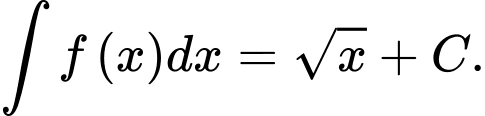
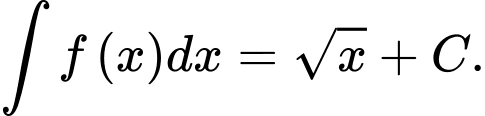
Chọn đáp án C. Đáp án: C
Câu 6 [148038]: Hàm số 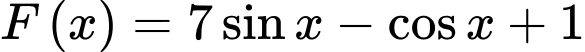 là một nguyên hàm của hàm số nào sau đây?
là một nguyên hàm của hàm số nào sau đây?
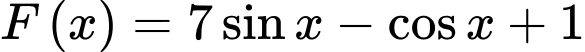 là một nguyên hàm của hàm số nào sau đây?
là một nguyên hàm của hàm số nào sau đây? A, 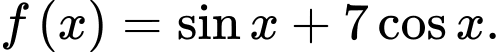
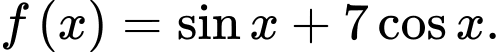
B, 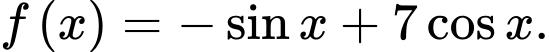
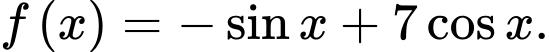
C, 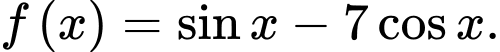
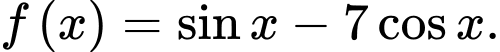
D, 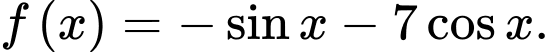
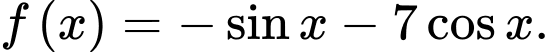
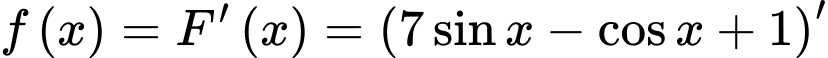
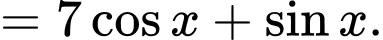
Chọn đáp án A. Đáp án: A
Câu 7 [511766]: Giả sử các biểu thức sau đây đều có nghĩa, khi đó công thức nào sau đây sai?
A, 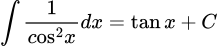 .
.
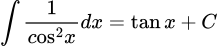 .
.B, 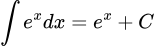 .
.
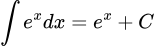 .
.C, 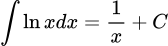 .
.
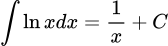 .
.D, 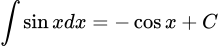 .
.
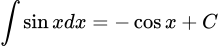 .
.
Chọn C
Theo bảng công thức nguyên hàm các đáp án A, B, D đúng. Đáp án C sai. Vì đúng là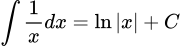 . Đáp án: C
. Đáp án: C
Theo bảng công thức nguyên hàm các đáp án A, B, D đúng. Đáp án C sai. Vì đúng là
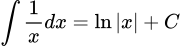 . Đáp án: C
. Đáp án: C
Câu 8 [148048]: Tìm nguyên hàm của hàm số 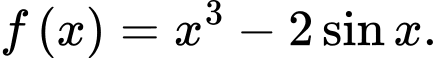
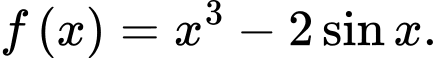
A, 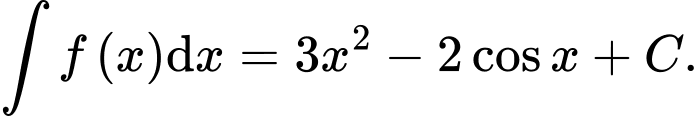
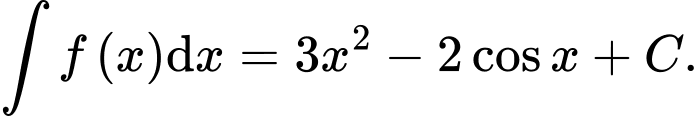
B, 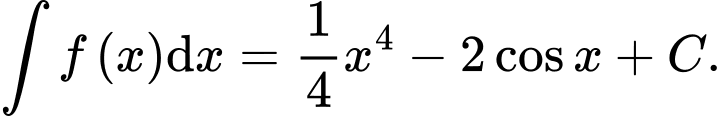
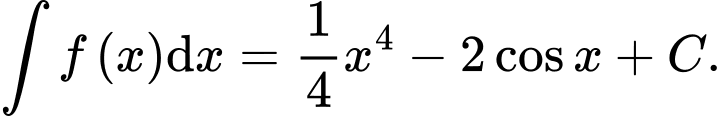
C, 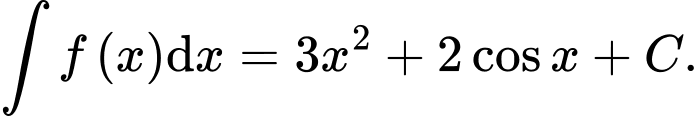
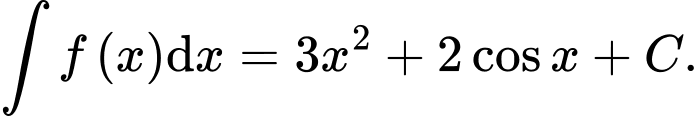
D, 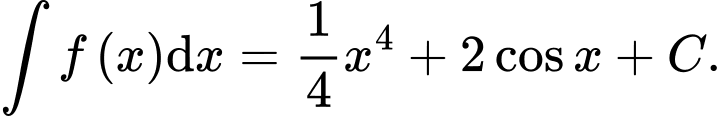
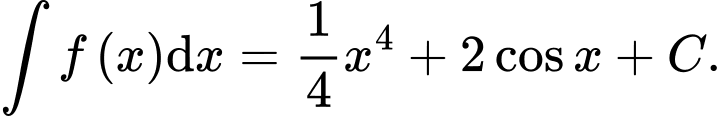
Ta có 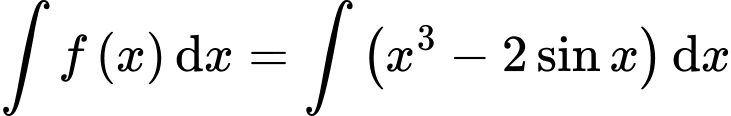
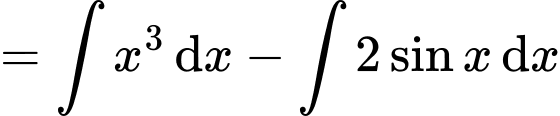
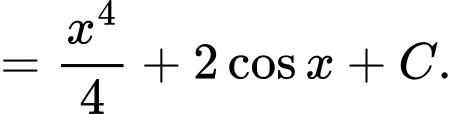
Chọn đáp án D. Đáp án: D
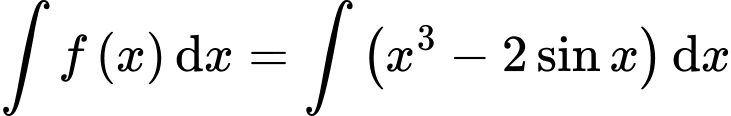
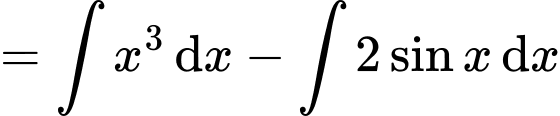
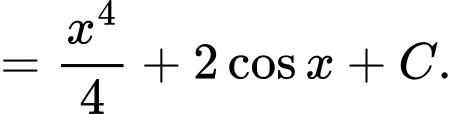
Chọn đáp án D. Đáp án: D
Câu 9 [389364]: Nếu 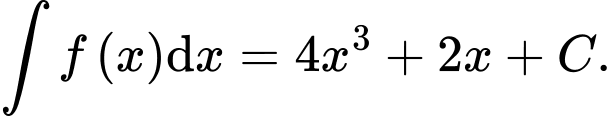 Khẳng định nào dưới đây là đúng?
Khẳng định nào dưới đây là đúng?
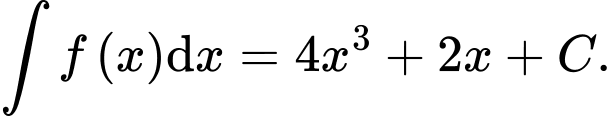 Khẳng định nào dưới đây là đúng?
Khẳng định nào dưới đây là đúng? A, 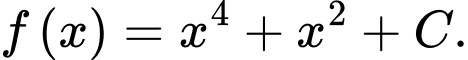
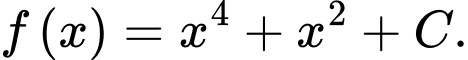
B, 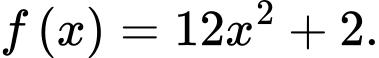
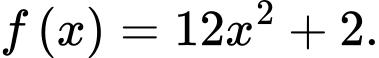
C, 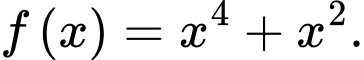
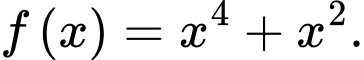
D, 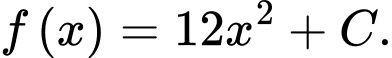
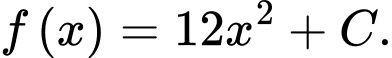
Ta có 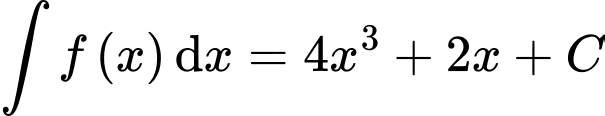
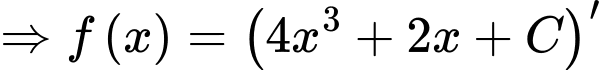
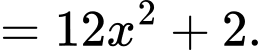
Chọn B. Đáp án: B
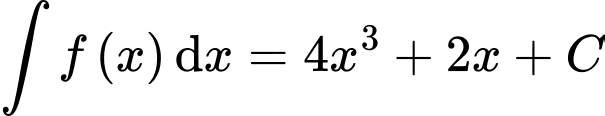
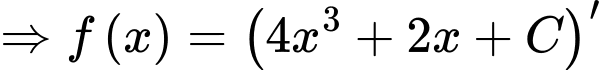
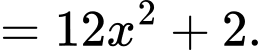
Chọn B. Đáp án: B
Câu 10 [539463]: Cho hàm số 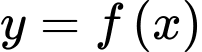 thỏa mãn
thỏa mãn 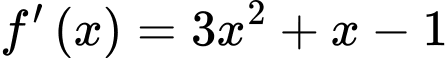 và
và 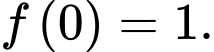 Hàm
Hàm 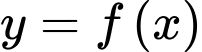 là
là
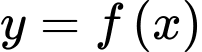 thỏa mãn
thỏa mãn 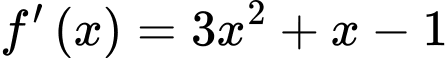 và
và 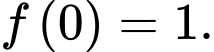 Hàm
Hàm 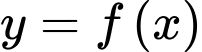 là
là A, 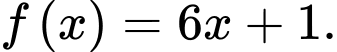
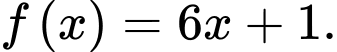
B, 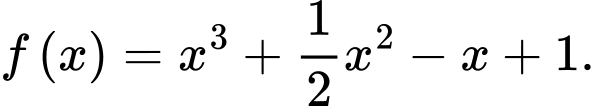
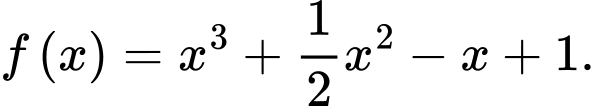
C, 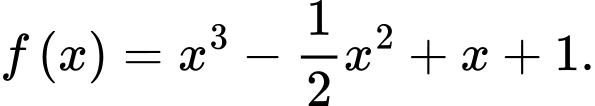
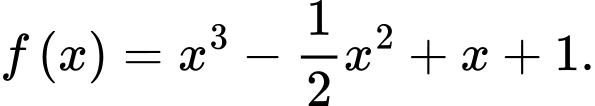
D, 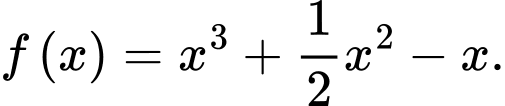
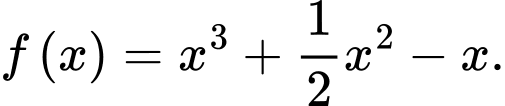
Chọn đáp án B.
Ta có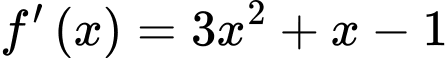
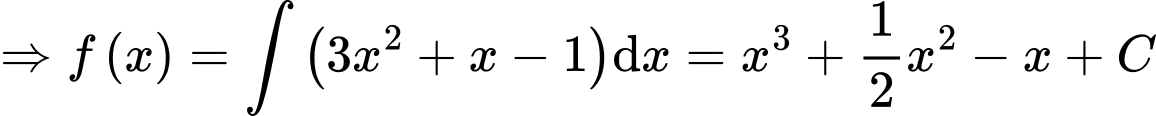 .
Mà
.
Mà 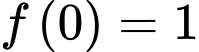
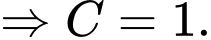
Vậy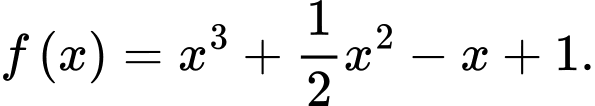 Đáp án: B
Đáp án: B
Ta có
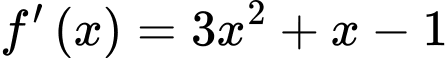
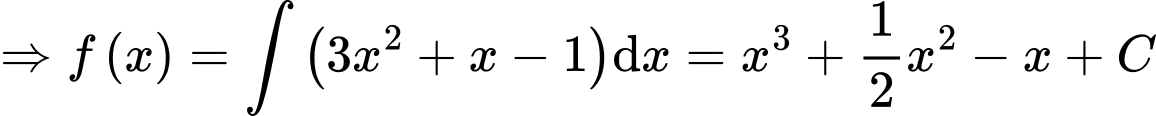 .
Mà
.
Mà 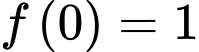
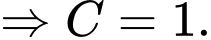
Vậy
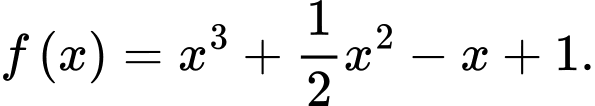 Đáp án: B
Đáp án: B
Câu 11 [396622]: 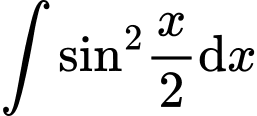 bằng
bằng
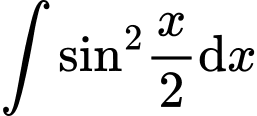 bằng
bằng A, 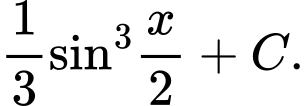
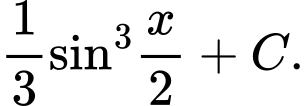
B, 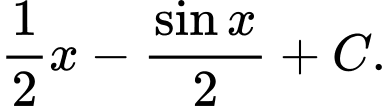
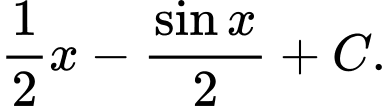
C, 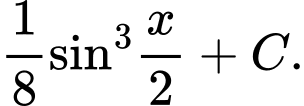
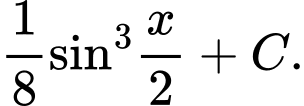
D, 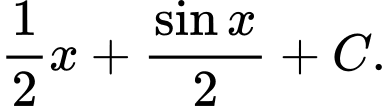
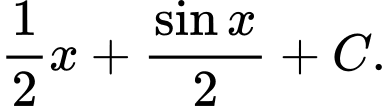
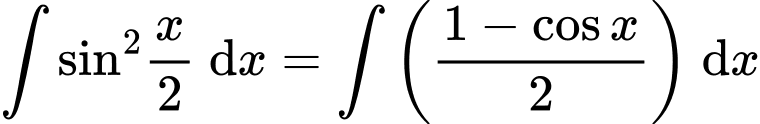
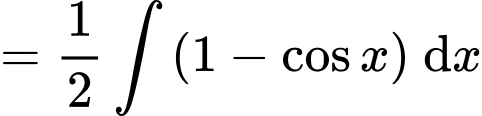
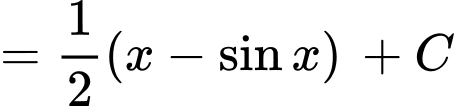
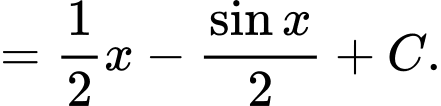
Chọn đáp án B. Đáp án: B
Câu 12 [148351]: Tìm 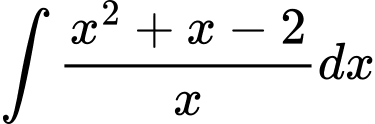 .
.
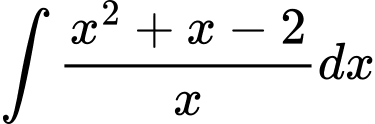 .
. A, 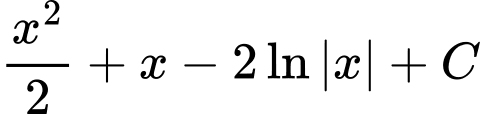 .
.
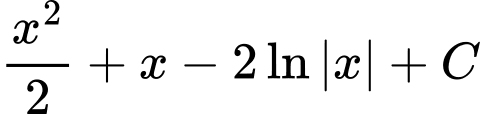 .
.B, 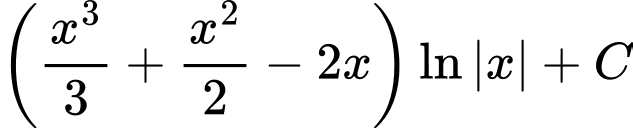 .
.
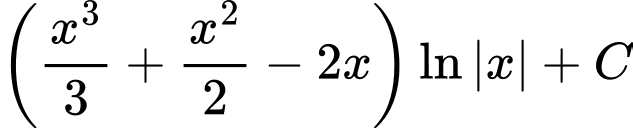 .
.C, 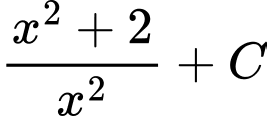 .
.
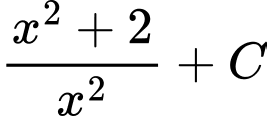 .
.D, 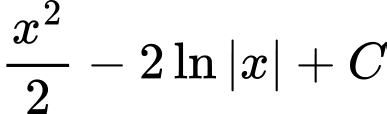 .
.
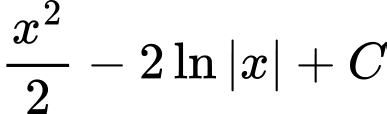 .
.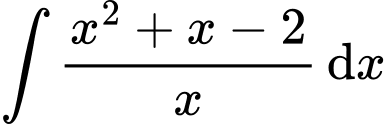
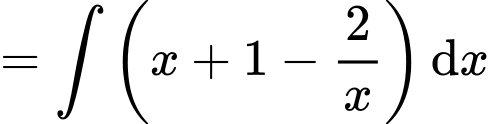
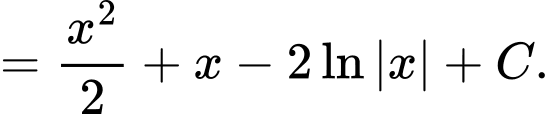
Chọn đáp án A. Đáp án: A
PHẦN II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a),b),c),d) ở mỗi câu học sinh chọn đúng hoặc sai.
Câu 13 [775050]: Cho hàm số 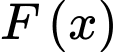 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 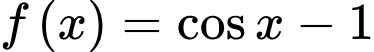 trên tập
trên tập 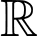 và thoả mãn
và thoả mãn 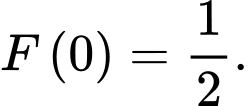
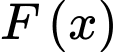 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 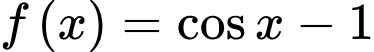 trên tập
trên tập 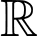 và thoả mãn
và thoả mãn 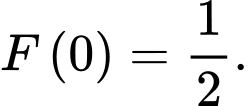
a) Sai.
Vì hàm số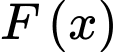 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 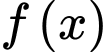 nên theo khái niệm nguyên hàm, ta có
nên theo khái niệm nguyên hàm, ta có 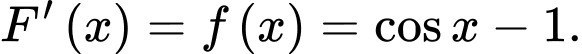
b) Sai.
Áp dụng công thức nguyên hàm, ta có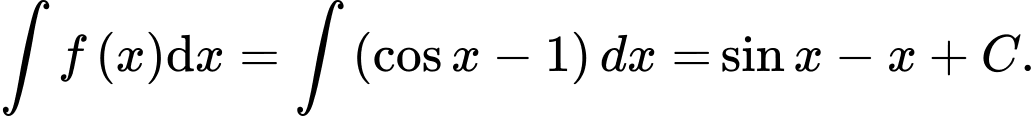
c) Đúng.
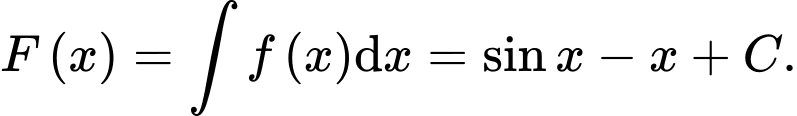
Mà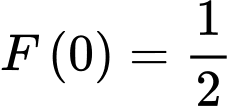 nên
nên 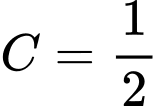 suy ra
suy ra 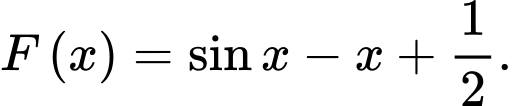
d) Sai.
Thay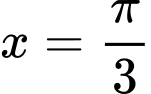 vào phương trình
vào phương trình 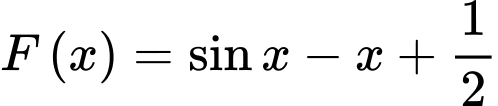 ta được
ta được
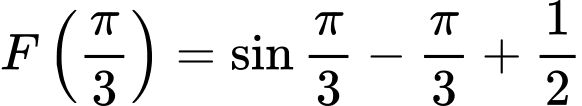
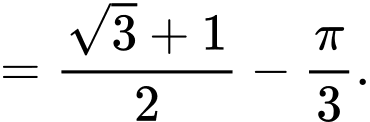
Vì hàm số
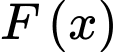 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 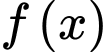 nên theo khái niệm nguyên hàm, ta có
nên theo khái niệm nguyên hàm, ta có 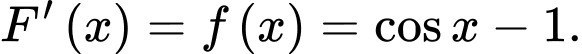
b) Sai.
Áp dụng công thức nguyên hàm, ta có
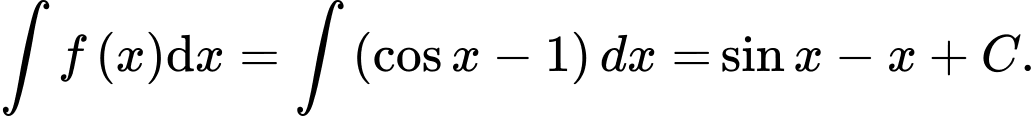
c) Đúng.
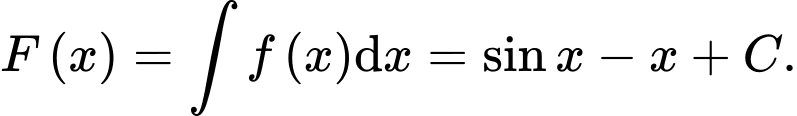
Mà
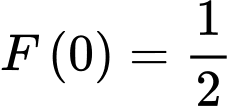 nên
nên 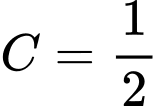 suy ra
suy ra 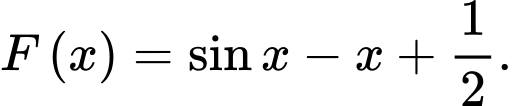
d) Sai.
Thay
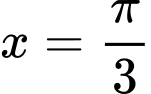 vào phương trình
vào phương trình 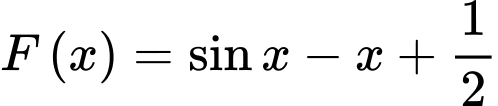 ta được
ta được 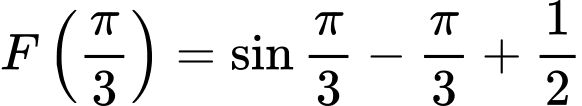
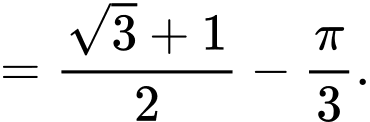
Câu 14 [775907]: Trên một mặt hồ phẳng rộng 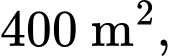 một đợt tảo lam độc hại đang phát triển, nếu ta gọi
một đợt tảo lam độc hại đang phát triển, nếu ta gọi 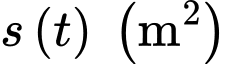 là diện tích của đợt tảo này sau
là diện tích của đợt tảo này sau 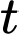 ngày tính từ lúc phát hiện thì tốc độ phát triển của nó là
ngày tính từ lúc phát hiện thì tốc độ phát triển của nó là 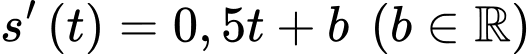 (
(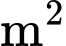 /ngày). Khi mới phát hiện, đợt tảo này bao phủ
/ngày). Khi mới phát hiện, đợt tảo này bao phủ 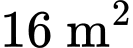 mặt hồ. Diện tích của nó tăng gấp bốn lần trong 8 ngày tiếp theo.
mặt hồ. Diện tích của nó tăng gấp bốn lần trong 8 ngày tiếp theo.

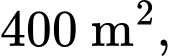 một đợt tảo lam độc hại đang phát triển, nếu ta gọi
một đợt tảo lam độc hại đang phát triển, nếu ta gọi 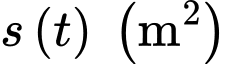 là diện tích của đợt tảo này sau
là diện tích của đợt tảo này sau 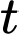 ngày tính từ lúc phát hiện thì tốc độ phát triển của nó là
ngày tính từ lúc phát hiện thì tốc độ phát triển của nó là 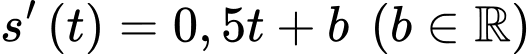 (
(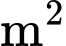 /ngày). Khi mới phát hiện, đợt tảo này bao phủ
/ngày). Khi mới phát hiện, đợt tảo này bao phủ 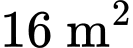 mặt hồ. Diện tích của nó tăng gấp bốn lần trong 8 ngày tiếp theo.
mặt hồ. Diện tích của nó tăng gấp bốn lần trong 8 ngày tiếp theo.
a) Sai.
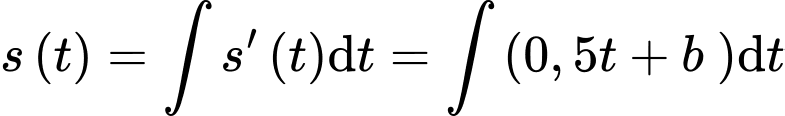
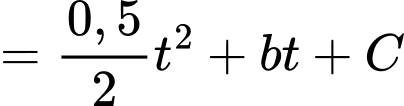
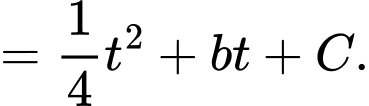
b) Đúng.
Theo giả thiết: Khi mới phát hiện, đợt tảo này bao phủ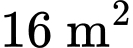 mặt hồ, tức tại thời điểm
mặt hồ, tức tại thời điểm 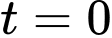 thì diện tích tảo là
thì diện tích tảo là 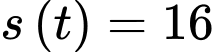
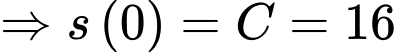
Suy ra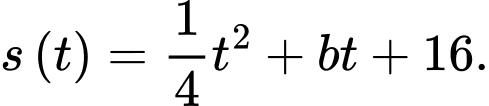
Lại có: Diện tích của nó tăng gấp bốn lần trong 8 ngày tiếp theo, tức khi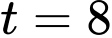 thì diện tích tảo bao phủ là
thì diện tích tảo bao phủ là 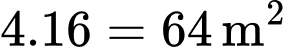 nên ta có phương trình
nên ta có phương trình 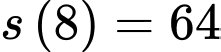
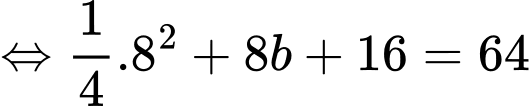
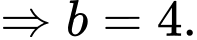
Suy ra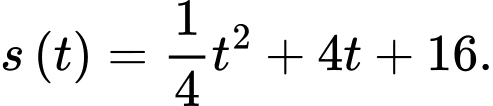
c) Đúng.
Thay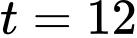 vào hàm số
vào hàm số 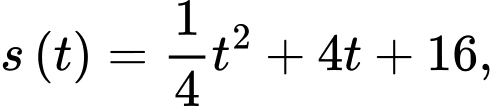 ta được
ta được 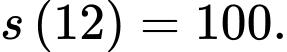
d) Đúng.
Diện tích tảo phủ được sau 32 ngày kể từ lúc phát hiện bằng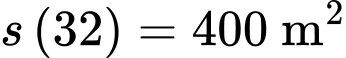 và diện tích này bằng đúng diện tích mặt hồ. Nên mệnh đề đúng.
và diện tích này bằng đúng diện tích mặt hồ. Nên mệnh đề đúng.
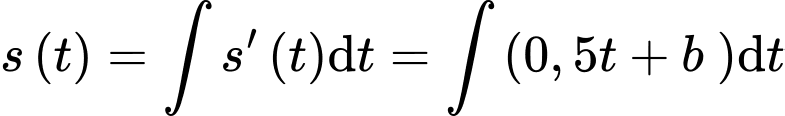
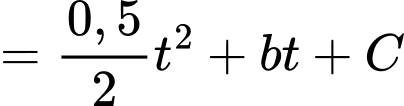
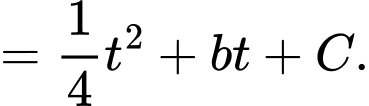
b) Đúng.
Theo giả thiết: Khi mới phát hiện, đợt tảo này bao phủ
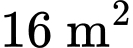 mặt hồ, tức tại thời điểm
mặt hồ, tức tại thời điểm 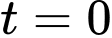 thì diện tích tảo là
thì diện tích tảo là 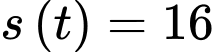
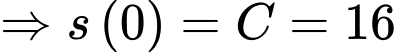
Suy ra
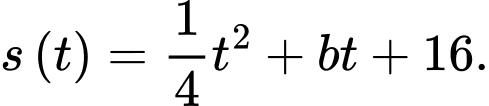
Lại có: Diện tích của nó tăng gấp bốn lần trong 8 ngày tiếp theo, tức khi
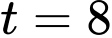 thì diện tích tảo bao phủ là
thì diện tích tảo bao phủ là 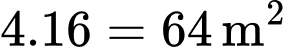 nên ta có phương trình
nên ta có phương trình 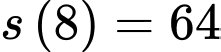
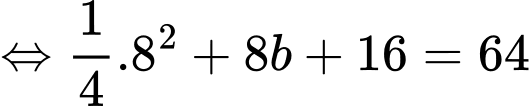
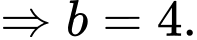
Suy ra
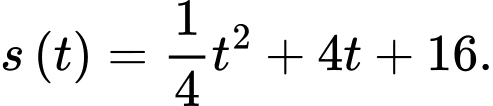
c) Đúng.
Thay
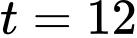 vào hàm số
vào hàm số 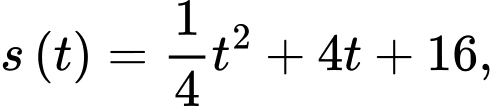 ta được
ta được 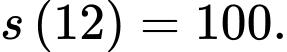
d) Đúng.
Diện tích tảo phủ được sau 32 ngày kể từ lúc phát hiện bằng
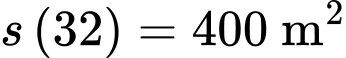 và diện tích này bằng đúng diện tích mặt hồ. Nên mệnh đề đúng.
và diện tích này bằng đúng diện tích mặt hồ. Nên mệnh đề đúng.
Câu 15 [775908]: Một chiếc xe đang chuyển động thẳng đều trên đường thẳng với tốc độ 54 km/giờ thì người lái phải phanh gấp để tránh chướng ngại vật ở phía trước. Lực hãm tạo giúp xe chuyển động chậm dần đều với tốc độ 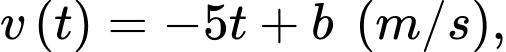 trong đó
trong đó 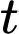 là thời gian tính bằng giây kể từ khi phanh. Gọi
là thời gian tính bằng giây kể từ khi phanh. Gọi 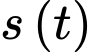 (đơn vị mét) là quãng đường mà xe đi được và vận tốc của xe sau
(đơn vị mét) là quãng đường mà xe đi được và vận tốc của xe sau 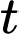 giây kể từ khi bắt đầu phanh.
giây kể từ khi bắt đầu phanh.
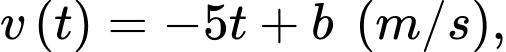 trong đó
trong đó 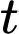 là thời gian tính bằng giây kể từ khi phanh. Gọi
là thời gian tính bằng giây kể từ khi phanh. Gọi 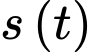 (đơn vị mét) là quãng đường mà xe đi được và vận tốc của xe sau
(đơn vị mét) là quãng đường mà xe đi được và vận tốc của xe sau 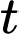 giây kể từ khi bắt đầu phanh.
giây kể từ khi bắt đầu phanh.
a) Sai.
Đúng phải là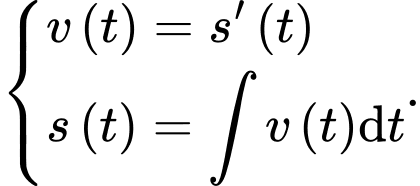
b) Đúng.
Đổi 54 km/giờ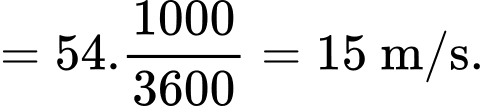
Vì trước khi phanh gấp thì người lái đi với vận tốc 15 m/s nên ta có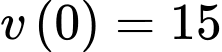
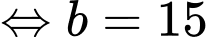
Suy ra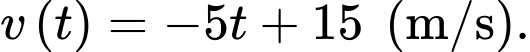
c) Sai.
Áp dụng công thức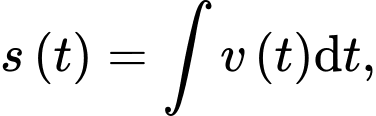 ta có
ta có 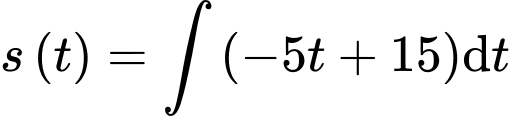
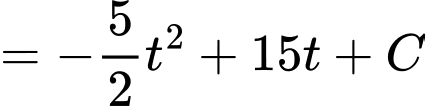
Vì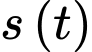 (đơn vị mét) là quãng đường mà xe đi được kể từ khi bắt đầu phanh nên
(đơn vị mét) là quãng đường mà xe đi được kể từ khi bắt đầu phanh nên 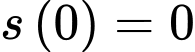
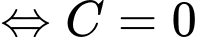
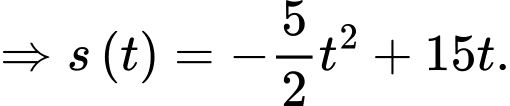
d) Đúng.
Khi xe dừng hẳn thì vận tốc bằng 0 hay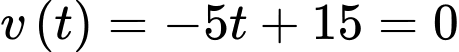
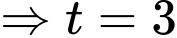
Vậy tại thời điểm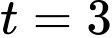 giây thì xe đi được quãng đường là
giây thì xe đi được quãng đường là 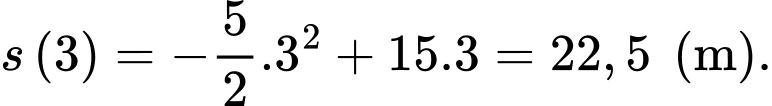
Đúng phải là
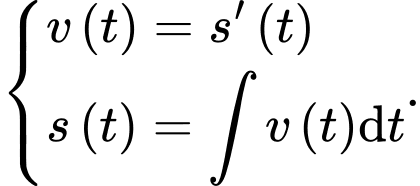
b) Đúng.
Đổi 54 km/giờ
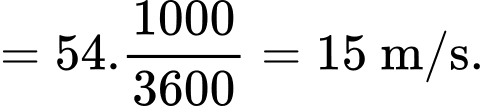
Vì trước khi phanh gấp thì người lái đi với vận tốc 15 m/s nên ta có
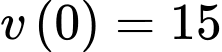
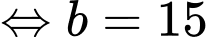
Suy ra
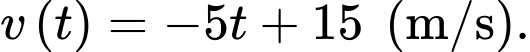
c) Sai.
Áp dụng công thức
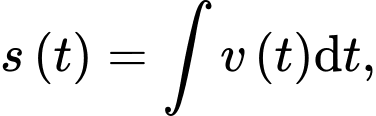 ta có
ta có 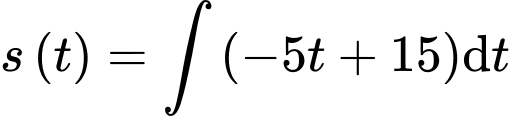
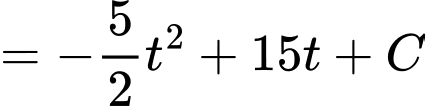
Vì
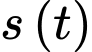 (đơn vị mét) là quãng đường mà xe đi được kể từ khi bắt đầu phanh nên
(đơn vị mét) là quãng đường mà xe đi được kể từ khi bắt đầu phanh nên 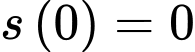
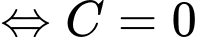
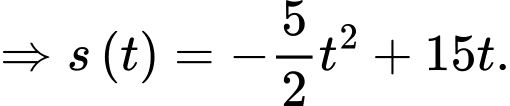
d) Đúng.
Khi xe dừng hẳn thì vận tốc bằng 0 hay
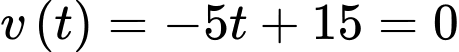
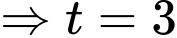
Vậy tại thời điểm
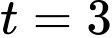 giây thì xe đi được quãng đường là
giây thì xe đi được quãng đường là 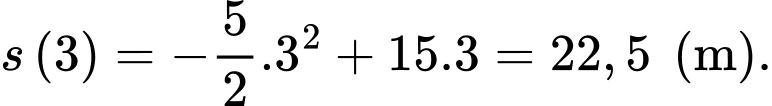
Câu 16 [775910]: Nhiệt độ bên trong tủ lạnh được duy trì ổn định ở mức 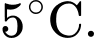 Một cốc nước có nhiệt độ
Một cốc nước có nhiệt độ 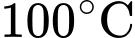 được cho vào tủ lạnh để làm mát. Nhiệt độ của cốc nước là
được cho vào tủ lạnh để làm mát. Nhiệt độ của cốc nước là 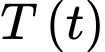 (độ C) và giảm dần với tốc độ
(độ C) và giảm dần với tốc độ 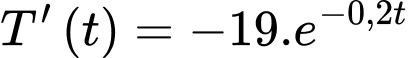 °C/phút.
°C/phút.
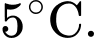 Một cốc nước có nhiệt độ
Một cốc nước có nhiệt độ 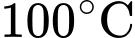 được cho vào tủ lạnh để làm mát. Nhiệt độ của cốc nước là
được cho vào tủ lạnh để làm mát. Nhiệt độ của cốc nước là 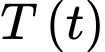 (độ C) và giảm dần với tốc độ
(độ C) và giảm dần với tốc độ 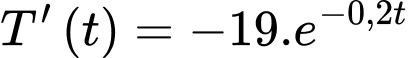 °C/phút.
°C/phút.
a) Đúng.
Theo định nghĩa nguyên hàm,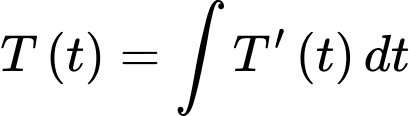 nên mệnh đề đúng.
nên mệnh đề đúng.
b) Sai.
Ta có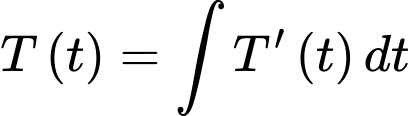
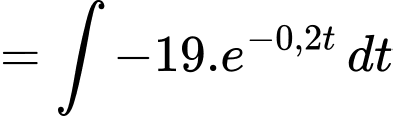
Áp dụng công thức nguyên hàm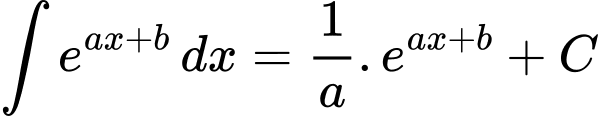 ta có
ta có 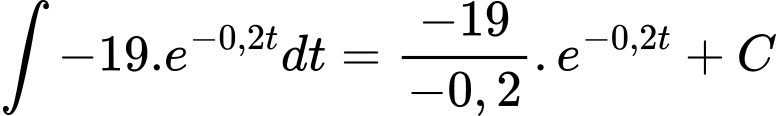
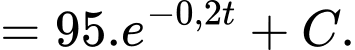
c) Sai.
Dựa vào kết quả tính được ở phần b) ta có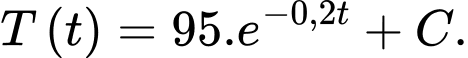
Ta có nhiệt độ của cốc nước tại thời điểm ban đầu tức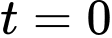 là
là 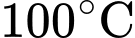 nên ta có
nên ta có 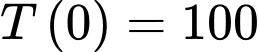
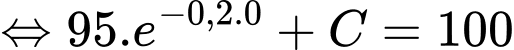
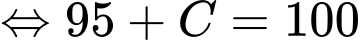
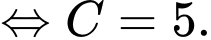
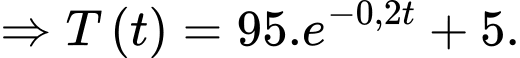
Vậy sau 1 phút, nhiệt độ của cốc nước là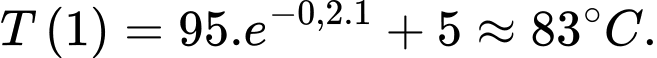
d) Sai.
Để cốc nước có nhiệt độ dưới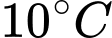 thì
thì 
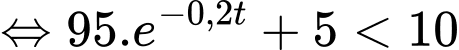
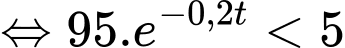
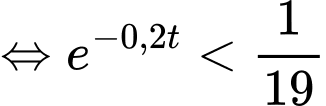
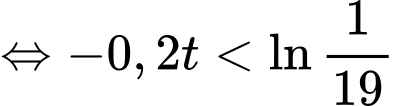
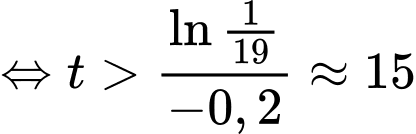 (phút).
(phút).
Vậy ít nhất 15 phút bạn Tuấn có thể lấy cốc nước ra ngoài.
Theo định nghĩa nguyên hàm,
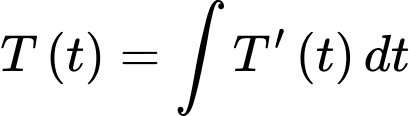 nên mệnh đề đúng.
nên mệnh đề đúng.b) Sai.
Ta có
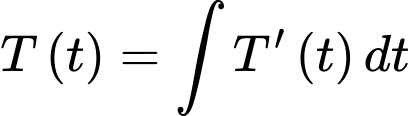
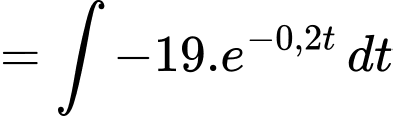
Áp dụng công thức nguyên hàm
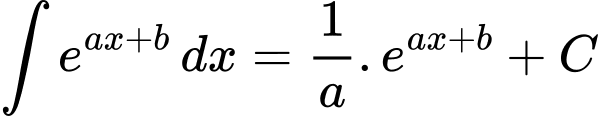 ta có
ta có 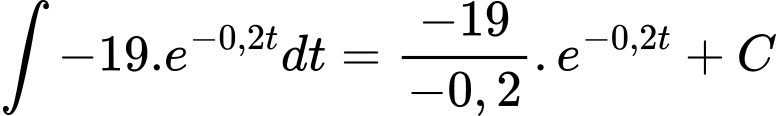
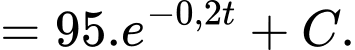
c) Sai.
Dựa vào kết quả tính được ở phần b) ta có
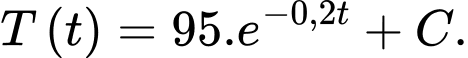
Ta có nhiệt độ của cốc nước tại thời điểm ban đầu tức
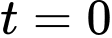 là
là 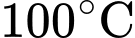 nên ta có
nên ta có 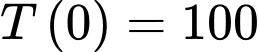
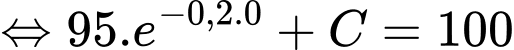
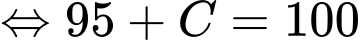
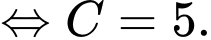
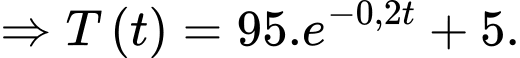
Vậy sau 1 phút, nhiệt độ của cốc nước là
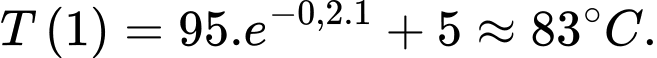
d) Sai.
Để cốc nước có nhiệt độ dưới
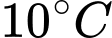 thì
thì 
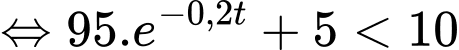
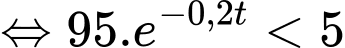
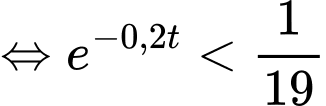
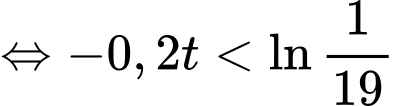
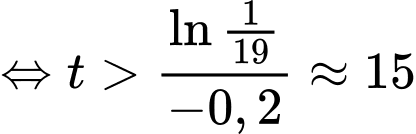 (phút).
(phút).Vậy ít nhất 15 phút bạn Tuấn có thể lấy cốc nước ra ngoài.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 17 đến câu 22.
Câu 17 [775911]: Một nhà bảo tồn sinh vật học phát hiện ra rằng số lượng cá thể 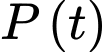 của một loài đang phát triển với tốc độ được mô phỏng bởi hàm số
của một loài đang phát triển với tốc độ được mô phỏng bởi hàm số 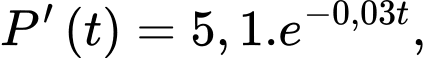 trong đó
trong đó 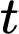 là số năm kể từ khi bắt đầu ghi chép. Biết số lượng cá thể hiện tại (thời điểm
là số năm kể từ khi bắt đầu ghi chép. Biết số lượng cá thể hiện tại (thời điểm 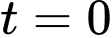 ) là
) là 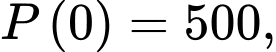 hỏi số lượng cá thể sẽ là bao nhiêu con sau 10 năm (làm tròn kết quả đến hàng đơn vị).
hỏi số lượng cá thể sẽ là bao nhiêu con sau 10 năm (làm tròn kết quả đến hàng đơn vị).
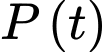 của một loài đang phát triển với tốc độ được mô phỏng bởi hàm số
của một loài đang phát triển với tốc độ được mô phỏng bởi hàm số 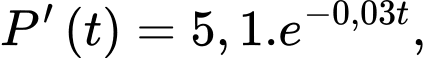 trong đó
trong đó 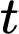 là số năm kể từ khi bắt đầu ghi chép. Biết số lượng cá thể hiện tại (thời điểm
là số năm kể từ khi bắt đầu ghi chép. Biết số lượng cá thể hiện tại (thời điểm 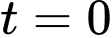 ) là
) là 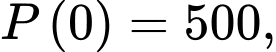 hỏi số lượng cá thể sẽ là bao nhiêu con sau 10 năm (làm tròn kết quả đến hàng đơn vị).
hỏi số lượng cá thể sẽ là bao nhiêu con sau 10 năm (làm tròn kết quả đến hàng đơn vị).
Điền đáp án: 544.
YCBT là tính
Vì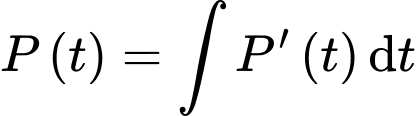 nên theo công thức nguyên hàm, ta có
nên theo công thức nguyên hàm, ta có 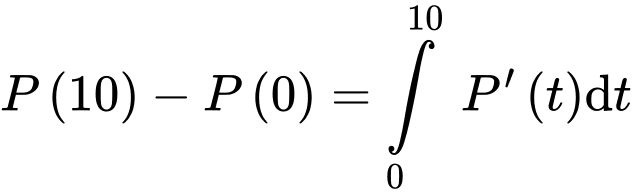
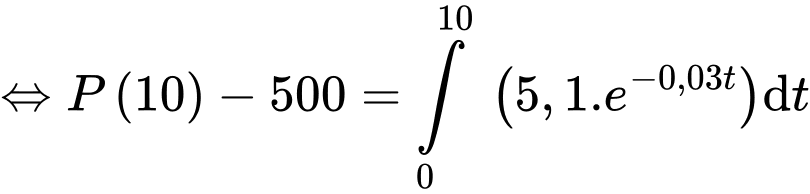
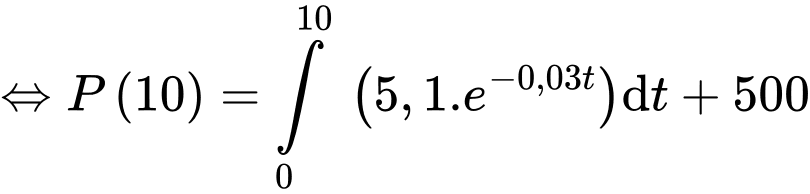
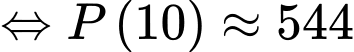 con.
con.
YCBT là tính

Vì
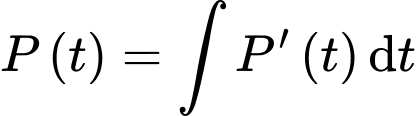 nên theo công thức nguyên hàm, ta có
nên theo công thức nguyên hàm, ta có 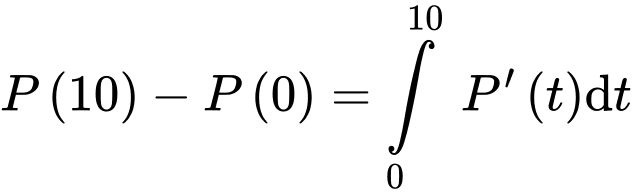
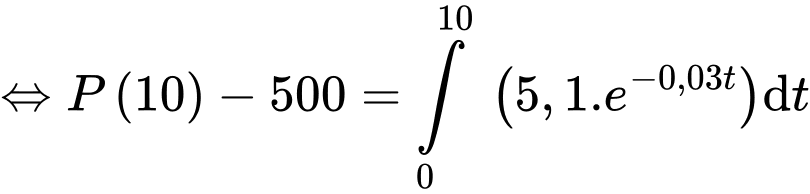
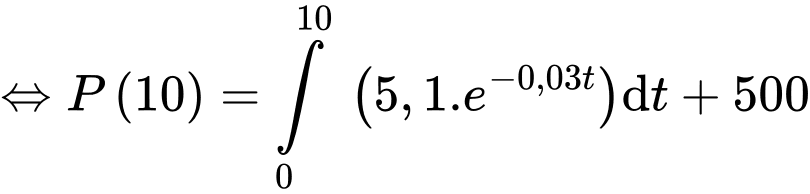
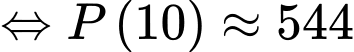 con.
con.
Câu 18 [775912]: Nước chảy ra từ một vòi ở đáy một bể nước hình trụ lớn có bán kính đáy 2m và chiều cao là 9m. Ban đầu bể đầy nước và độ cao nước trong bể giảm dần với tốc độ 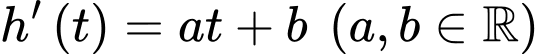 (mét/phút). Biết rằng chiều cao của cột nước sau 15 phút và 30 phút lần lượt là 4 mét và 1 mét. Hỏi sau bao nhiêu phút thì bể cạn nước.
(mét/phút). Biết rằng chiều cao của cột nước sau 15 phút và 30 phút lần lượt là 4 mét và 1 mét. Hỏi sau bao nhiêu phút thì bể cạn nước.
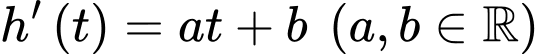 (mét/phút). Biết rằng chiều cao của cột nước sau 15 phút và 30 phút lần lượt là 4 mét và 1 mét. Hỏi sau bao nhiêu phút thì bể cạn nước.
(mét/phút). Biết rằng chiều cao của cột nước sau 15 phút và 30 phút lần lượt là 4 mét và 1 mét. Hỏi sau bao nhiêu phút thì bể cạn nước.
Điền đáp án: 45.
Ta sẽ dựa vào tốc độ giảm độ cao của nước trong bể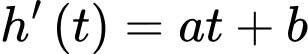 để tìm ra hàm biểu diễn
để tìm ra hàm biểu diễn 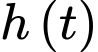 (là chiều cao của cột nước trong bể còn lại sau
(là chiều cao của cột nước trong bể còn lại sau 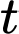 phút) và từ đó ta có thể tính được bể cạn nước khi nào bằng cách giải phương trình
phút) và từ đó ta có thể tính được bể cạn nước khi nào bằng cách giải phương trình 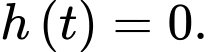
Ta có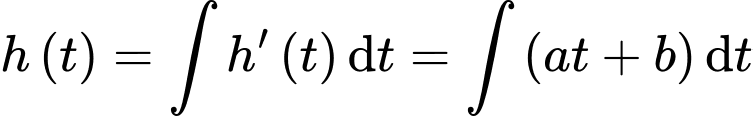
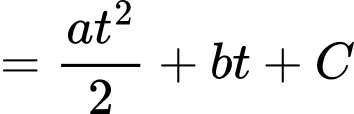
Từ các dữ kiện đề bài, ta có hệ phương trình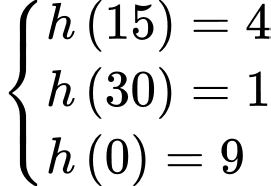
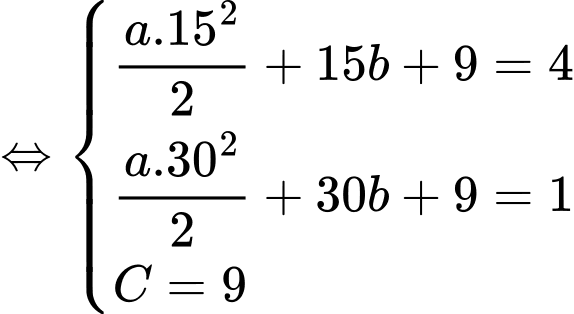
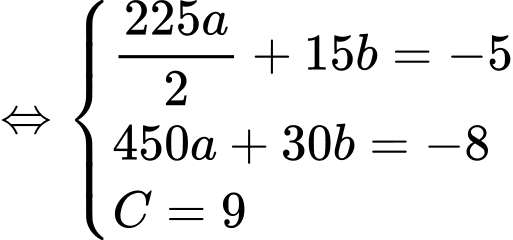
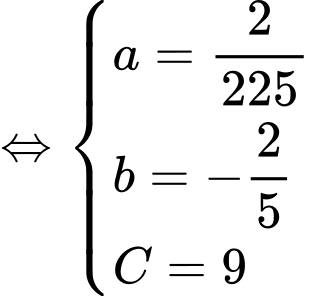
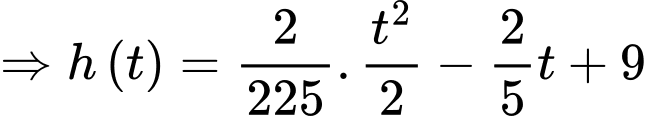
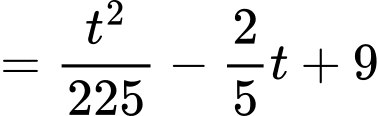
Bể cạn nước khi và chỉ khi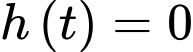
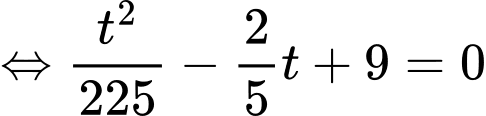
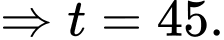
Vậy sau 45 phút thì bể cạn nước.
Ta sẽ dựa vào tốc độ giảm độ cao của nước trong bể
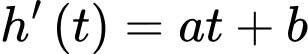 để tìm ra hàm biểu diễn
để tìm ra hàm biểu diễn 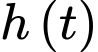 (là chiều cao của cột nước trong bể còn lại sau
(là chiều cao của cột nước trong bể còn lại sau 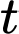 phút) và từ đó ta có thể tính được bể cạn nước khi nào bằng cách giải phương trình
phút) và từ đó ta có thể tính được bể cạn nước khi nào bằng cách giải phương trình 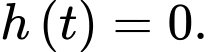
Ta có
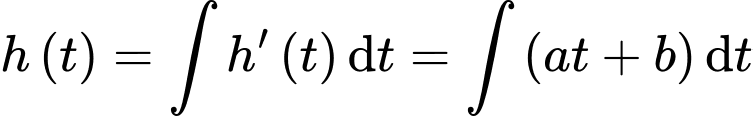
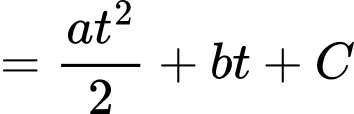
Từ các dữ kiện đề bài, ta có hệ phương trình
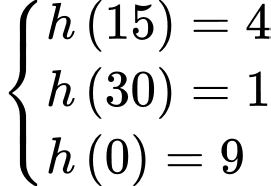
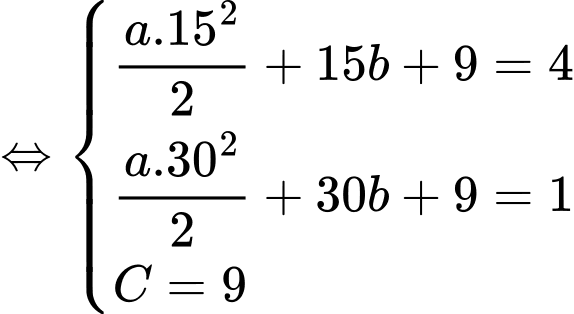
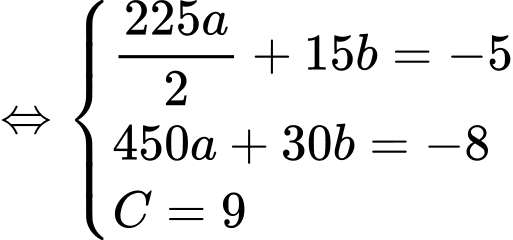
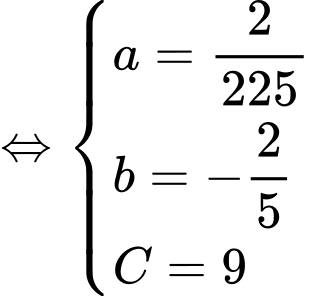
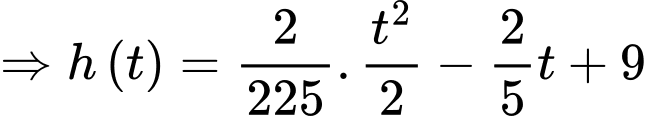
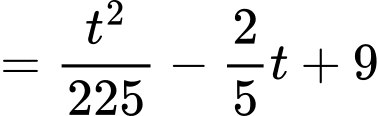
Bể cạn nước khi và chỉ khi
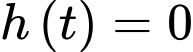
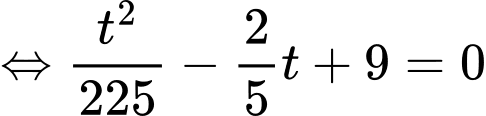
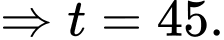
Vậy sau 45 phút thì bể cạn nước.
Câu 19 [775913]: Một tấm ván gỗ chỉ được hỗ trợ ở hai đầu  và
và 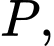 cách nhau 4 m. Tấm ván võng xuống dưới do trọng lượng của nó tạo thành một đường cong. Xét trên hệ trục
cách nhau 4 m. Tấm ván võng xuống dưới do trọng lượng của nó tạo thành một đường cong. Xét trên hệ trục 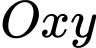 như hình vẽ dưới, đơn vị mỗi trục là mét, đường cong trong hình vẽ có phương trình
như hình vẽ dưới, đơn vị mỗi trục là mét, đường cong trong hình vẽ có phương trình 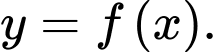
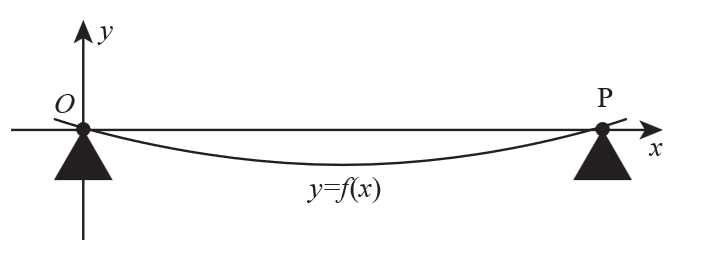
Khi đó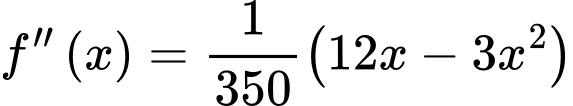 với
với 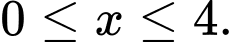 Hỏi tấm ván bị võng xuống so với phương ngang một khoảng lớn nhất bao nhiêu cm (kết quả làm tròn đến hàng phần mười).
Hỏi tấm ván bị võng xuống so với phương ngang một khoảng lớn nhất bao nhiêu cm (kết quả làm tròn đến hàng phần mười).
 và
và 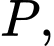 cách nhau 4 m. Tấm ván võng xuống dưới do trọng lượng của nó tạo thành một đường cong. Xét trên hệ trục
cách nhau 4 m. Tấm ván võng xuống dưới do trọng lượng của nó tạo thành một đường cong. Xét trên hệ trục 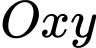 như hình vẽ dưới, đơn vị mỗi trục là mét, đường cong trong hình vẽ có phương trình
như hình vẽ dưới, đơn vị mỗi trục là mét, đường cong trong hình vẽ có phương trình 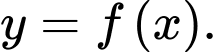

Khi đó
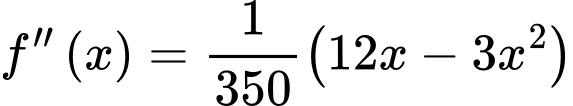 với
với 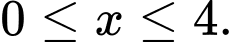 Hỏi tấm ván bị võng xuống so với phương ngang một khoảng lớn nhất bao nhiêu cm (kết quả làm tròn đến hàng phần mười).
Hỏi tấm ván bị võng xuống so với phương ngang một khoảng lớn nhất bao nhiêu cm (kết quả làm tròn đến hàng phần mười).
Điền đáp án: 5,7.
Khoảng võng xuống lớn nhất so với phương ngang của tấm ván là bằng với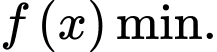 Do đó, ta cần đi tìm hàm
Do đó, ta cần đi tìm hàm 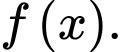 Và ta sẽ sử dụng các công thức
Và ta sẽ sử dụng các công thức 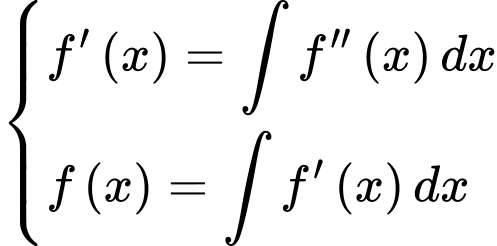 để tìm được hàm
để tìm được hàm 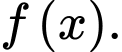 Thực hiện như sau:
Thực hiện như sau:
Ta có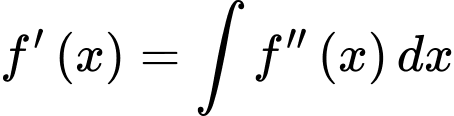
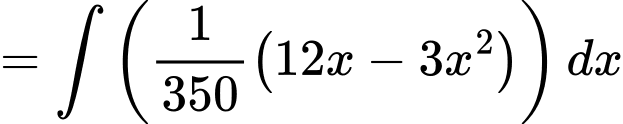
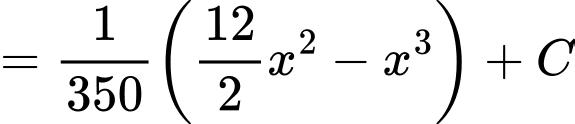
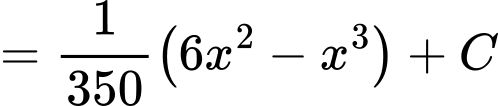
Tiếp đến, ta có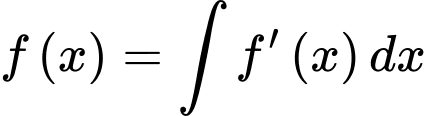
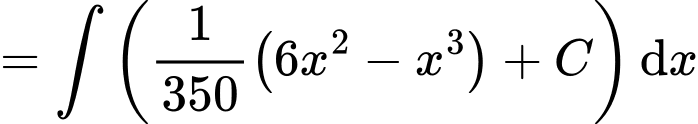
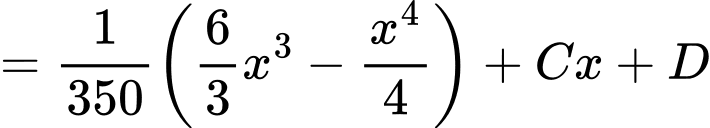
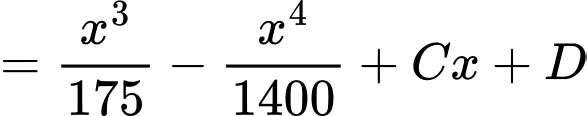
Dựa vào hình vẽ, ta có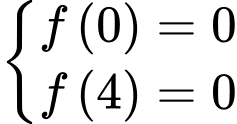
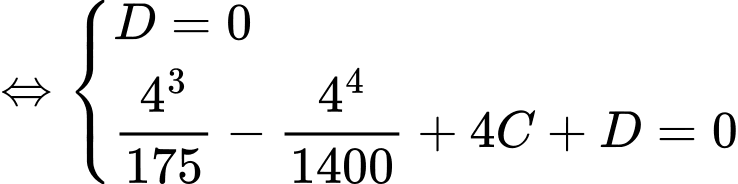
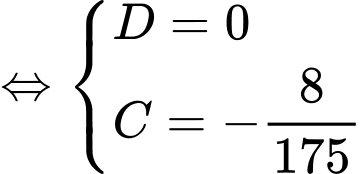
Suy ra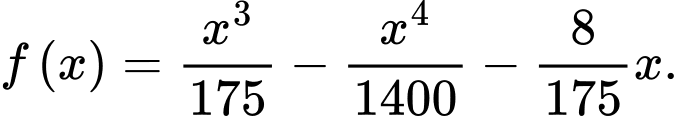
Xét hàm số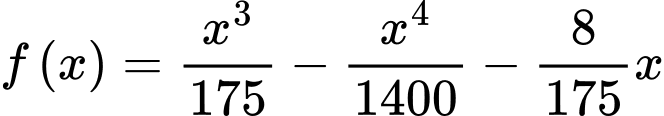 trên đoạn
trên đoạn 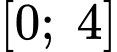
Ta có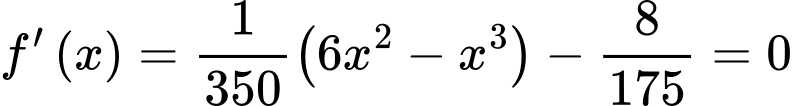
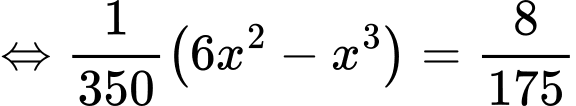
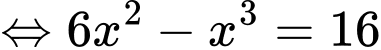
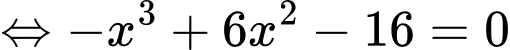
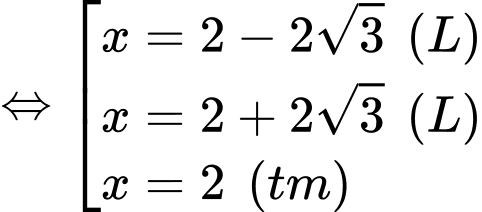
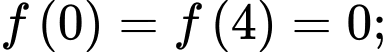
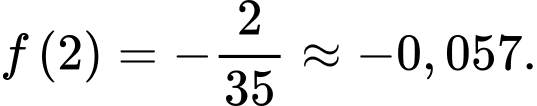
Vậy tấm ván bị võng xuống so với phương ngang một khoảng lớn nhất là 0,057 m hay 5,7 cm.
Khoảng võng xuống lớn nhất so với phương ngang của tấm ván là bằng với
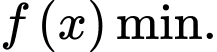 Do đó, ta cần đi tìm hàm
Do đó, ta cần đi tìm hàm 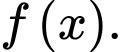 Và ta sẽ sử dụng các công thức
Và ta sẽ sử dụng các công thức 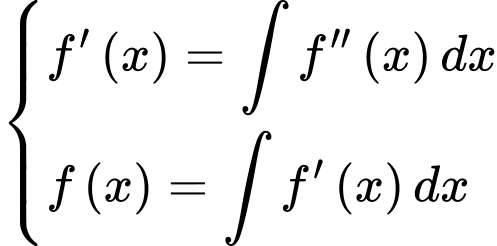 để tìm được hàm
để tìm được hàm 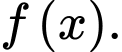 Thực hiện như sau:
Thực hiện như sau:Ta có
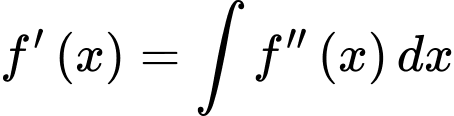
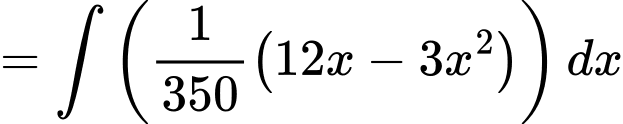
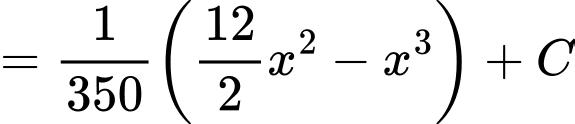
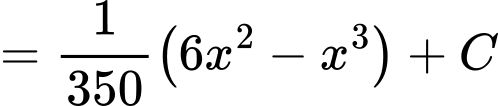
Tiếp đến, ta có
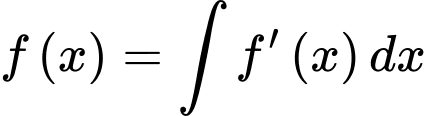
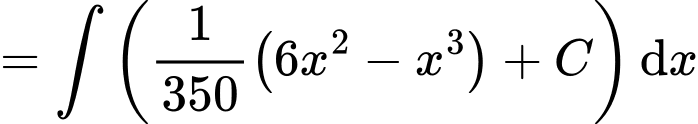
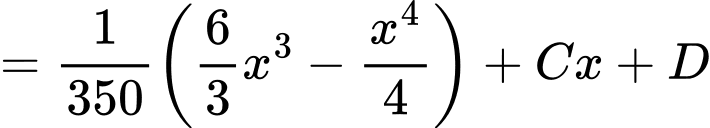
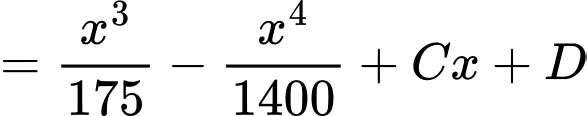
Dựa vào hình vẽ, ta có
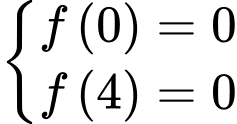
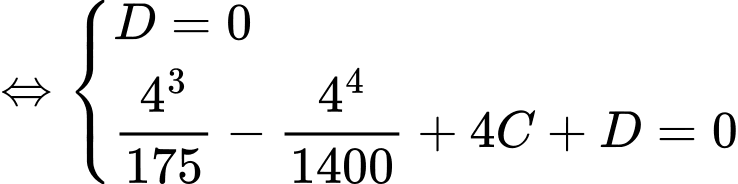
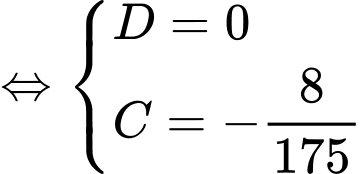
Suy ra
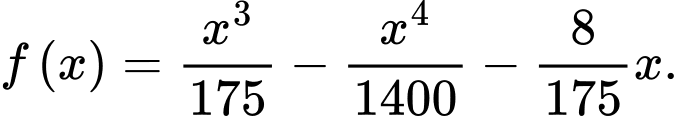
Xét hàm số
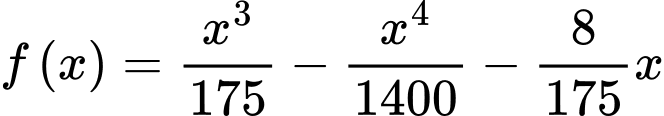 trên đoạn
trên đoạn 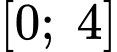
Ta có
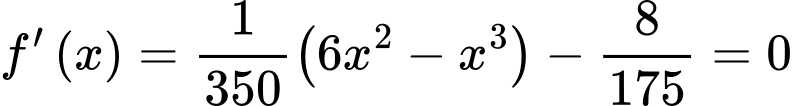
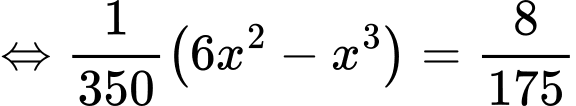
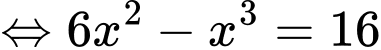
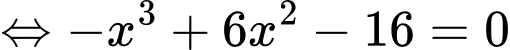
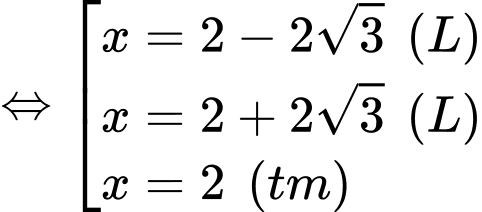
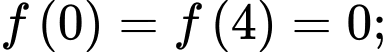
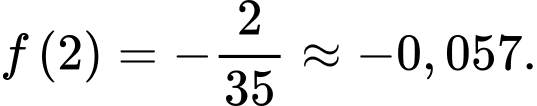
Vậy tấm ván bị võng xuống so với phương ngang một khoảng lớn nhất là 0,057 m hay 5,7 cm.
Câu 20 [775914]: Ông Tuấn đang đổ đầy nước từ vòi vào bình tưới nước. Nước chảy vào bình với tốc độ 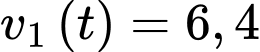 lít mỗi phút. Bình tưới nước của ông ta ban đầu đầu rỗng và có thể chứa được 16 lít nước. Thật không may, bình có một lỗ ở đáy nên nước bị rò rỉ với tốc độ
lít mỗi phút. Bình tưới nước của ông ta ban đầu đầu rỗng và có thể chứa được 16 lít nước. Thật không may, bình có một lỗ ở đáy nên nước bị rò rỉ với tốc độ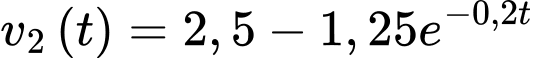 lít mỗi phút, trong đó
lít mỗi phút, trong đó 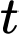 là thời gian tính bằng phút. Mất bao lâu bình tưới nước mới đầy (làm tròn đến hàng đơn vị của giây)?
là thời gian tính bằng phút. Mất bao lâu bình tưới nước mới đầy (làm tròn đến hàng đơn vị của giây)?
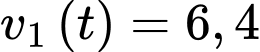 lít mỗi phút. Bình tưới nước của ông ta ban đầu đầu rỗng và có thể chứa được 16 lít nước. Thật không may, bình có một lỗ ở đáy nên nước bị rò rỉ với tốc độ
lít mỗi phút. Bình tưới nước của ông ta ban đầu đầu rỗng và có thể chứa được 16 lít nước. Thật không may, bình có một lỗ ở đáy nên nước bị rò rỉ với tốc độ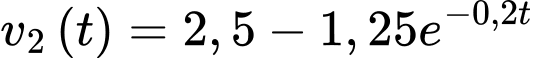 lít mỗi phút, trong đó
lít mỗi phút, trong đó 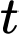 là thời gian tính bằng phút. Mất bao lâu bình tưới nước mới đầy (làm tròn đến hàng đơn vị của giây)?
là thời gian tính bằng phút. Mất bao lâu bình tưới nước mới đầy (làm tròn đến hàng đơn vị của giây)?
Điền đáp án: 199.
Để bình tưới nước đầy thì sự chênh lệch giữa nước chảy vào bình và nước bị rò rỉ phải bằng thể tích bình hay bằng 16 lít. Ở bài này ta áp dụng công thức: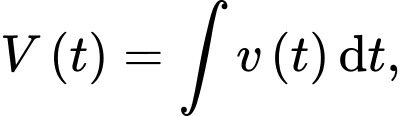 với
với 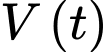 là lượng nước có trong bình tại thời điểm
là lượng nước có trong bình tại thời điểm 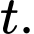
Giả sử tại thời điểm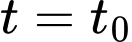 (phút) thì bình đầy nước.
(phút) thì bình đầy nước.
Vì nước chảy vào bình với tốc độ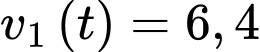 lít mỗi phút nên lượng nước chảy vào bình trong
lít mỗi phút nên lượng nước chảy vào bình trong 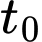 phút là
phút là 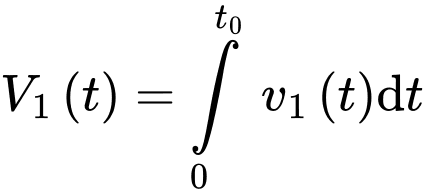
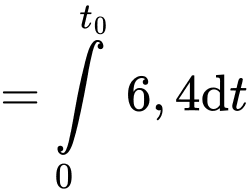
Tương tự, ta có lượng nước rò rỉ ra ngoài trong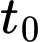 phút là
phút là 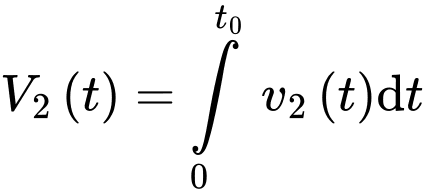
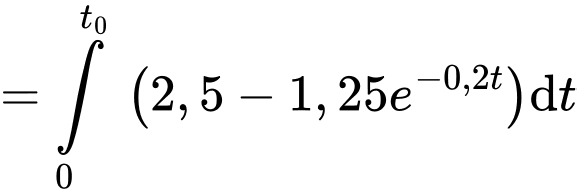
Bình tưới nước đầy khi và chỉ khi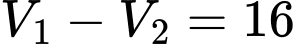
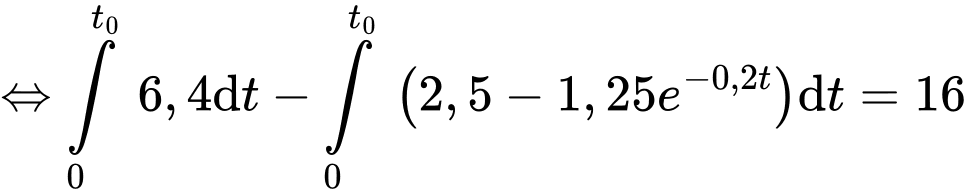
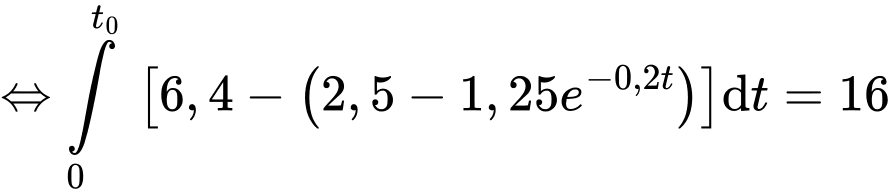
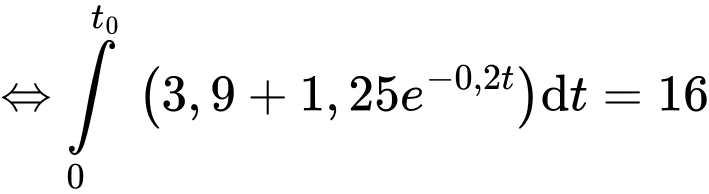
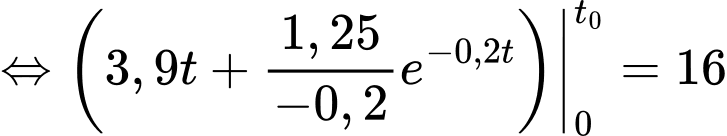
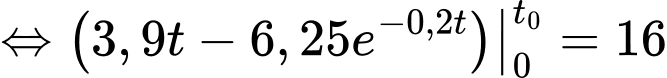
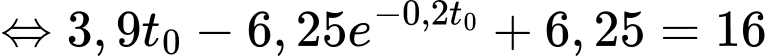

Bấm phương trình vào máy tính casio sau đó ấn SHIFT -> SOLVE, ta thu được nghiệm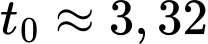 phút hay 199 giây. Vậy sau 199 giây thì bình tưới nước mới đầy.
phút hay 199 giây. Vậy sau 199 giây thì bình tưới nước mới đầy.
Để bình tưới nước đầy thì sự chênh lệch giữa nước chảy vào bình và nước bị rò rỉ phải bằng thể tích bình hay bằng 16 lít. Ở bài này ta áp dụng công thức:
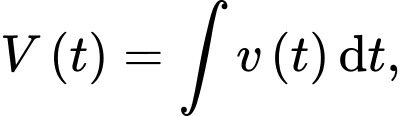 với
với 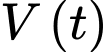 là lượng nước có trong bình tại thời điểm
là lượng nước có trong bình tại thời điểm 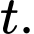
Giả sử tại thời điểm
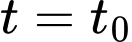 (phút) thì bình đầy nước.
(phút) thì bình đầy nước.
Vì nước chảy vào bình với tốc độ
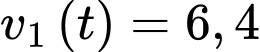 lít mỗi phút nên lượng nước chảy vào bình trong
lít mỗi phút nên lượng nước chảy vào bình trong 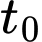 phút là
phút là 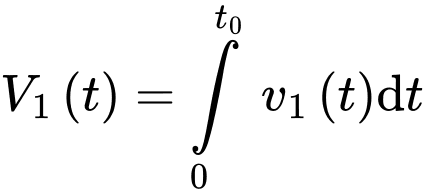
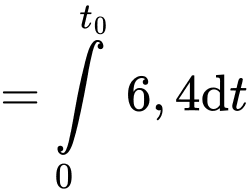
Tương tự, ta có lượng nước rò rỉ ra ngoài trong
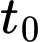 phút là
phút là 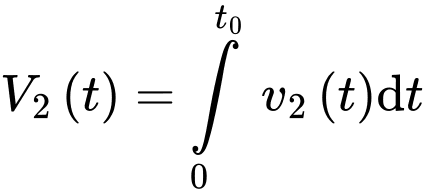
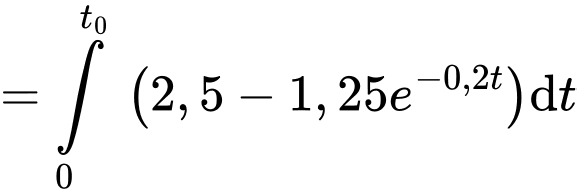
Bình tưới nước đầy khi và chỉ khi
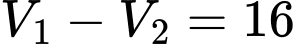
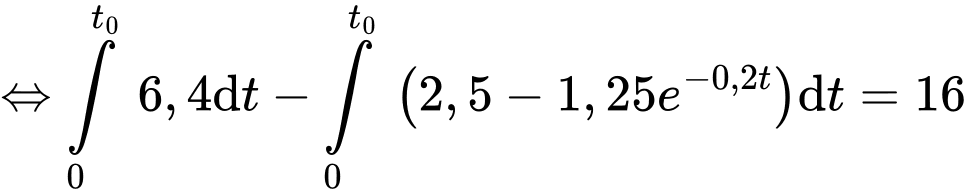
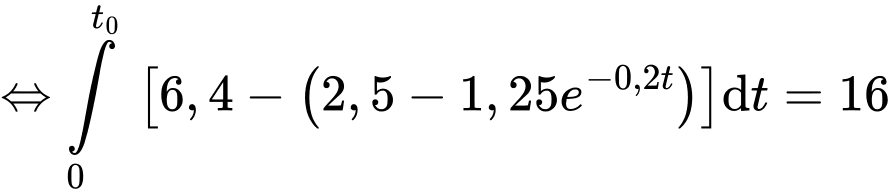
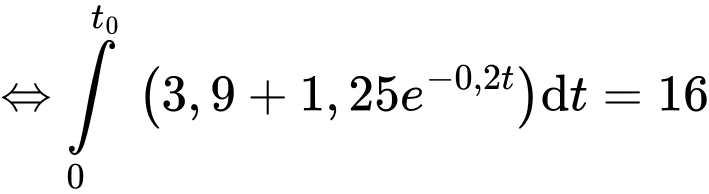
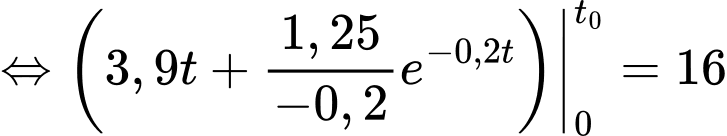
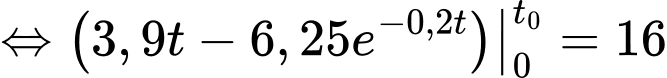
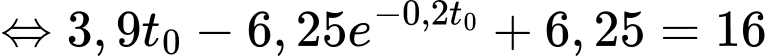

Bấm phương trình vào máy tính casio sau đó ấn SHIFT -> SOLVE, ta thu được nghiệm
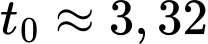 phút hay 199 giây. Vậy sau 199 giây thì bình tưới nước mới đầy.
phút hay 199 giây. Vậy sau 199 giây thì bình tưới nước mới đầy.
Câu 21 [775916]: Một khu vực dân cư có 10000 người nghe tin tức qua các kênh thông tin khác nhau khi bạn Tuấn trúng sổ xổ jackpot trị giá 108 tỷ đồng. Ban đầu, không một ai biết tin này, nhưng sau đó 5 phút thì 3000 người đã nhận được thông tin. Gọi 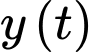 là số người nhận được thông tin sau
là số người nhận được thông tin sau 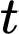 (phút). Vì tốc độ lan truyền thông tin trong số 10000 người này tỷ lệ thuận với số người nhận được thông tin nên
(phút). Vì tốc độ lan truyền thông tin trong số 10000 người này tỷ lệ thuận với số người nhận được thông tin nên 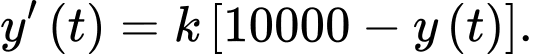 Hỏi sau bao nhiêu phút thì có 90% số người ở khu vực này nhận được thông tin (kết quả làm tròn đến hàng đơn vị).
Hỏi sau bao nhiêu phút thì có 90% số người ở khu vực này nhận được thông tin (kết quả làm tròn đến hàng đơn vị).
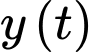 là số người nhận được thông tin sau
là số người nhận được thông tin sau 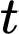 (phút). Vì tốc độ lan truyền thông tin trong số 10000 người này tỷ lệ thuận với số người nhận được thông tin nên
(phút). Vì tốc độ lan truyền thông tin trong số 10000 người này tỷ lệ thuận với số người nhận được thông tin nên 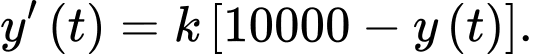 Hỏi sau bao nhiêu phút thì có 90% số người ở khu vực này nhận được thông tin (kết quả làm tròn đến hàng đơn vị).
Hỏi sau bao nhiêu phút thì có 90% số người ở khu vực này nhận được thông tin (kết quả làm tròn đến hàng đơn vị).
Điền đáp án: 32.
Để 90% số người ở khu vực này nhận được thông tin, tức có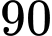 người nhận được thông tin. YCBT tương đương với tìm
người nhận được thông tin. YCBT tương đương với tìm 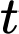 để
để 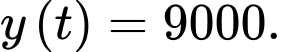
Ta có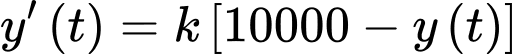
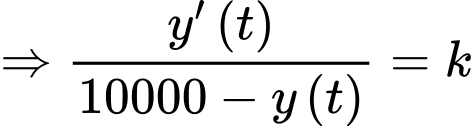
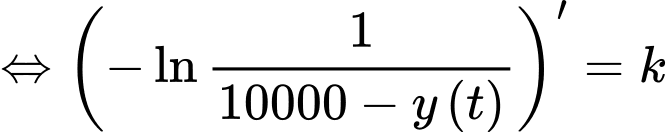
Nguyên hàm 2 vế, ta được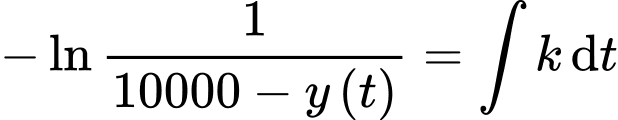
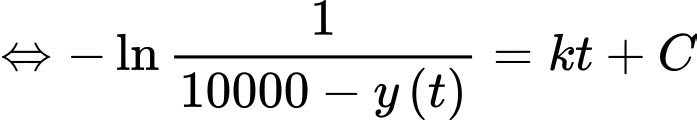
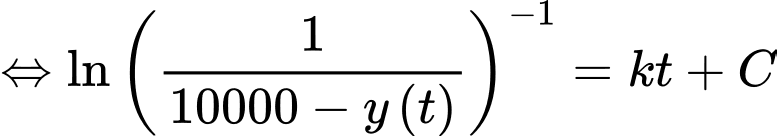
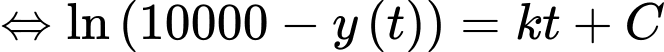
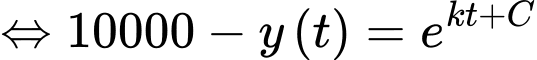
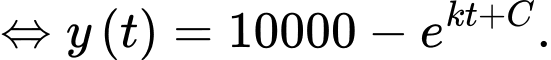
Từ giả thiết: “Ngay sau khi toà nhà bị tấn công, không một ai biết tin này, nhưng sau đó 5 phút thì 3000 người đã nhận được thông tin” ta thu được hệ phương trình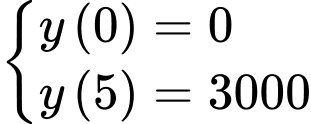
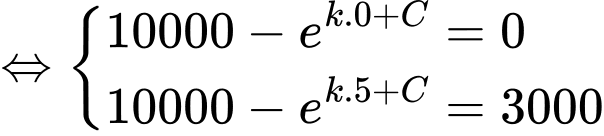
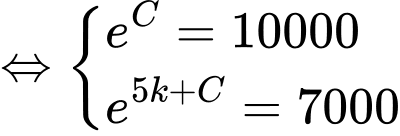
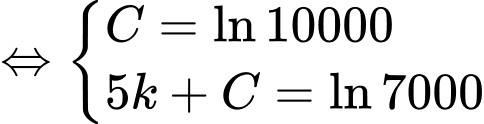
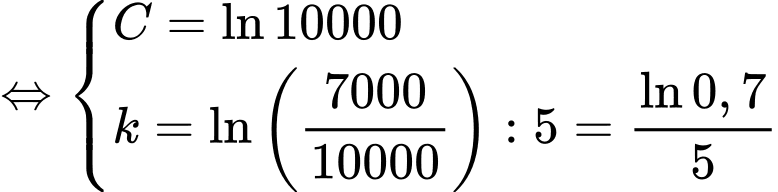
Suy ra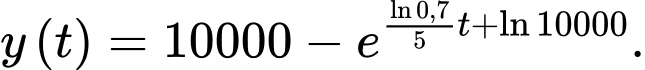
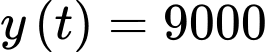
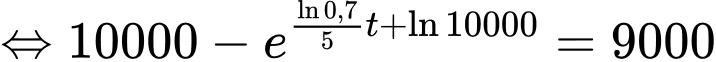

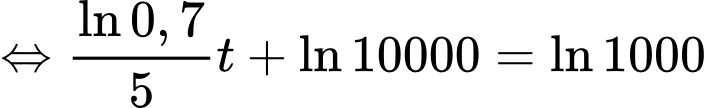
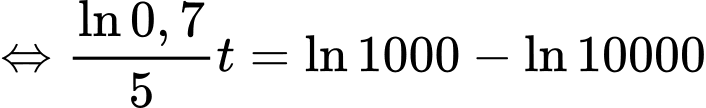
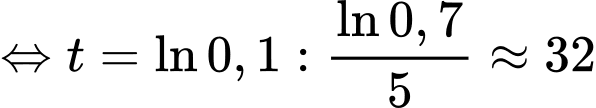
Vậy sau 32 phút thì có 90% số người ở khu vực này nhận được thông tin.
Để 90% số người ở khu vực này nhận được thông tin, tức có
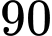 người nhận được thông tin. YCBT tương đương với tìm
người nhận được thông tin. YCBT tương đương với tìm 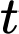 để
để 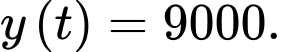
Ta có
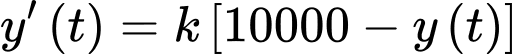
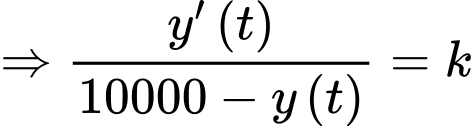
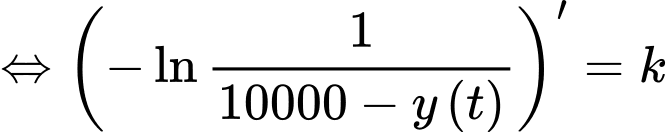
Nguyên hàm 2 vế, ta được
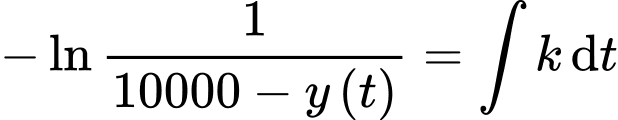
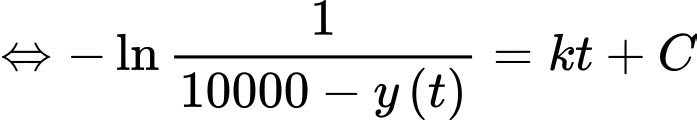
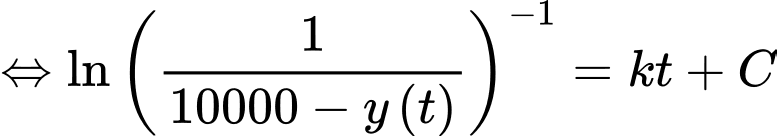
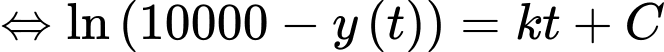
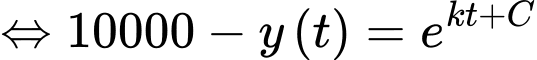
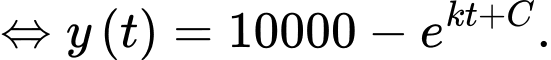
Từ giả thiết: “Ngay sau khi toà nhà bị tấn công, không một ai biết tin này, nhưng sau đó 5 phút thì 3000 người đã nhận được thông tin” ta thu được hệ phương trình
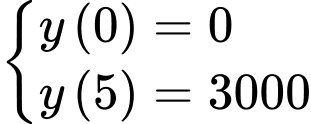
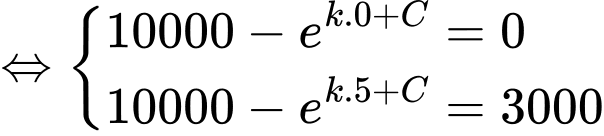
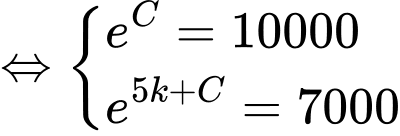
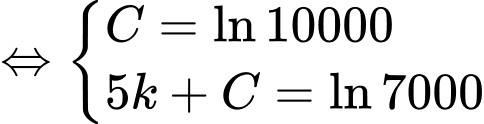
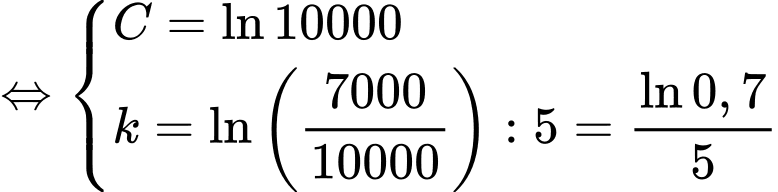
Suy ra
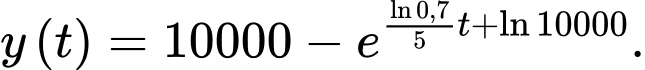
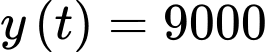
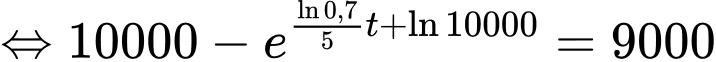

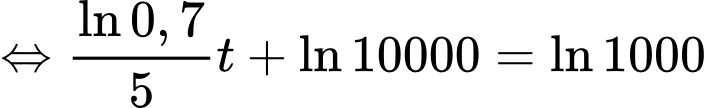
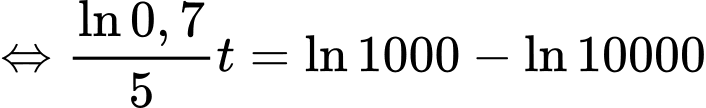
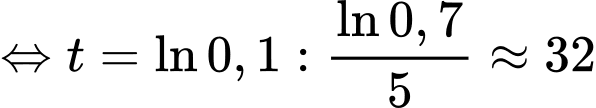
Vậy sau 32 phút thì có 90% số người ở khu vực này nhận được thông tin.
Câu 22 [779013]: Vì nước và dầu không hoà tan vào nhau nên nếu dầu đổ vào nước sẽ tạo thành một mảng hình trụ trên bề mặt nước. Bán kính 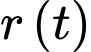 của mảng này lan ra với tốc độ tỉ lệ thuận với chiều cao
của mảng này lan ra với tốc độ tỉ lệ thuận với chiều cao 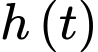 của mảng dầu. Giả sử một lít dầu bị đổ trên mặt hồ tĩnh lặng. Bán kính ban đầu của vết tràn là 20 cm và sau 2 giây nó tăng lên 50 cm. Hỏi sau bao nhiêu phút (làm tròn đến hàng đơn vị) thì bán kính vết tràn đạt 4 mét?
của mảng dầu. Giả sử một lít dầu bị đổ trên mặt hồ tĩnh lặng. Bán kính ban đầu của vết tràn là 20 cm và sau 2 giây nó tăng lên 50 cm. Hỏi sau bao nhiêu phút (làm tròn đến hàng đơn vị) thì bán kính vết tràn đạt 4 mét?
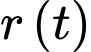 của mảng này lan ra với tốc độ tỉ lệ thuận với chiều cao
của mảng này lan ra với tốc độ tỉ lệ thuận với chiều cao 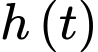 của mảng dầu. Giả sử một lít dầu bị đổ trên mặt hồ tĩnh lặng. Bán kính ban đầu của vết tràn là 20 cm và sau 2 giây nó tăng lên 50 cm. Hỏi sau bao nhiêu phút (làm tròn đến hàng đơn vị) thì bán kính vết tràn đạt 4 mét?
của mảng dầu. Giả sử một lít dầu bị đổ trên mặt hồ tĩnh lặng. Bán kính ban đầu của vết tràn là 20 cm và sau 2 giây nó tăng lên 50 cm. Hỏi sau bao nhiêu phút (làm tròn đến hàng đơn vị) thì bán kính vết tràn đạt 4 mét?
Điền đáp án: 18.
Vì mảng dầu này lan có dạng hình trụ, nên ta có thể tích khối dầu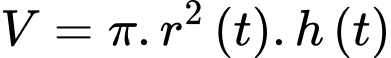 (thể tích này là không đổi)
(thể tích này là không đổi)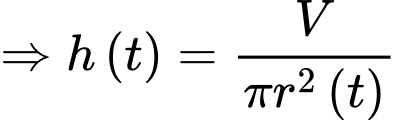
Bán kính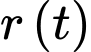 của mảng dầu lan ra với tốc độ
của mảng dầu lan ra với tốc độ 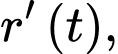 mà tốc độ lan ra
mà tốc độ lan ra 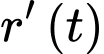 tỉ lệ thuận với chiều cao
tỉ lệ thuận với chiều cao 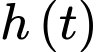 của mảng dầu nên theo tính chất của hai đại lượng tỉ lệ thuận, ta có
của mảng dầu nên theo tính chất của hai đại lượng tỉ lệ thuận, ta có 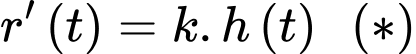
Thay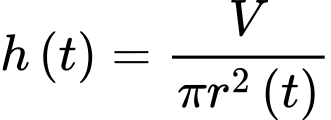 vào biểu thức (*) ta được
vào biểu thức (*) ta được 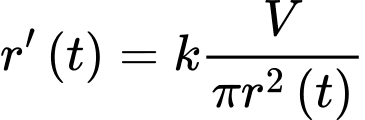
Vì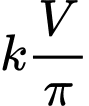 là 1 đại lượng không đổi nên đặt
là 1 đại lượng không đổi nên đặt 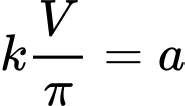
Khi đó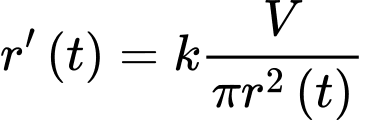
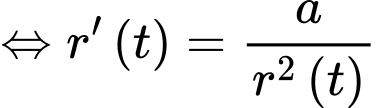
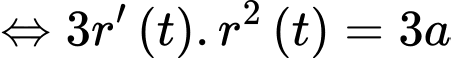
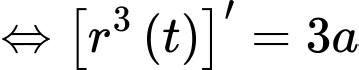
Nguyên hàm 2 vế, ta được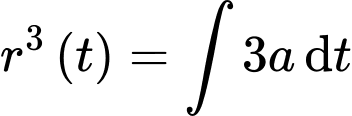
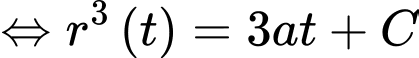
Từ giả thiết: bán kính ban đầu của vết tràn là 20 cm và sau 2 giây nó tăng lên 50 cm, ta có hệ phương trình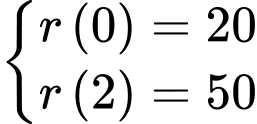
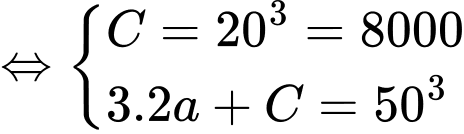
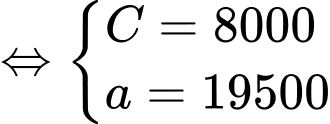
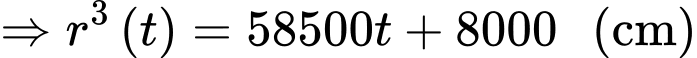
Đổi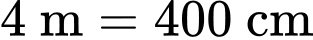
Bán kính vết tràn đạt 4 m tương đương với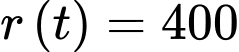
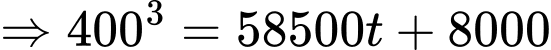
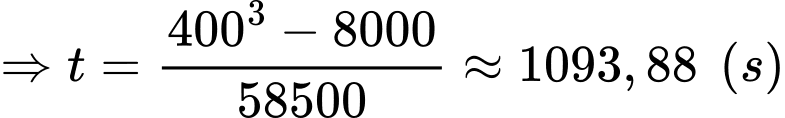
Vậy sau 1093,88 giây hay 18 phút thì bán kính vết tràn đạt 4 mét.
Vì mảng dầu này lan có dạng hình trụ, nên ta có thể tích khối dầu
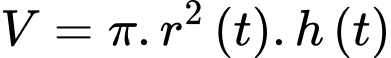 (thể tích này là không đổi)
(thể tích này là không đổi)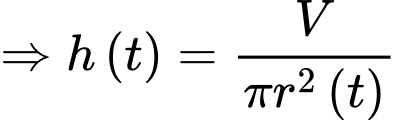
Bán kính
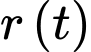 của mảng dầu lan ra với tốc độ
của mảng dầu lan ra với tốc độ 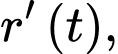 mà tốc độ lan ra
mà tốc độ lan ra 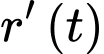 tỉ lệ thuận với chiều cao
tỉ lệ thuận với chiều cao 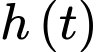 của mảng dầu nên theo tính chất của hai đại lượng tỉ lệ thuận, ta có
của mảng dầu nên theo tính chất của hai đại lượng tỉ lệ thuận, ta có 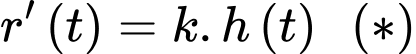
Thay
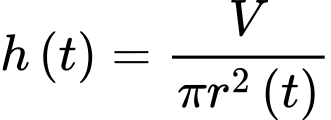 vào biểu thức (*) ta được
vào biểu thức (*) ta được 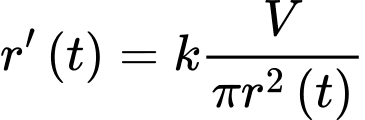
Vì
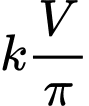 là 1 đại lượng không đổi nên đặt
là 1 đại lượng không đổi nên đặt 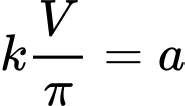
Khi đó
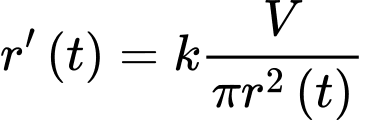
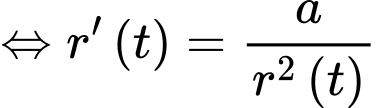
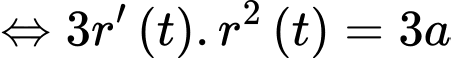
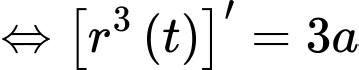
Nguyên hàm 2 vế, ta được
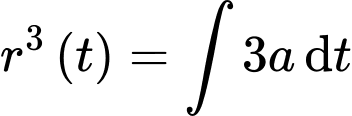
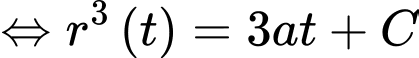
Từ giả thiết: bán kính ban đầu của vết tràn là 20 cm và sau 2 giây nó tăng lên 50 cm, ta có hệ phương trình
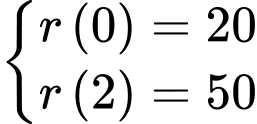
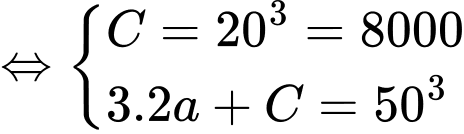
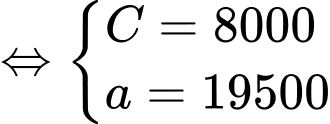
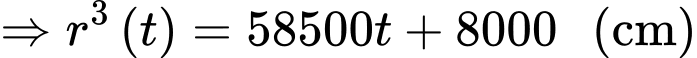
Đổi
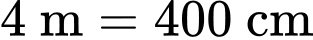
Bán kính vết tràn đạt 4 m tương đương với
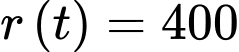
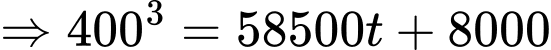
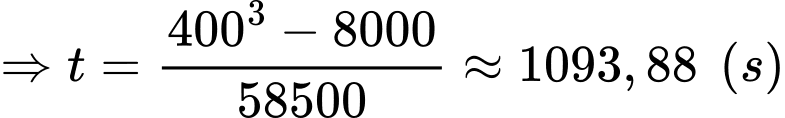
Vậy sau 1093,88 giây hay 18 phút thì bán kính vết tràn đạt 4 mét.