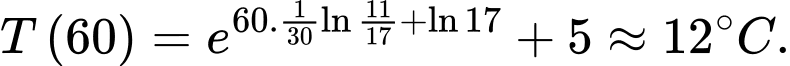PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1 [298815]: [MĐ1] Tìm nguyên hàm của hàm số 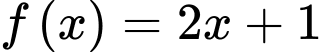
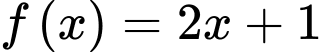
A, 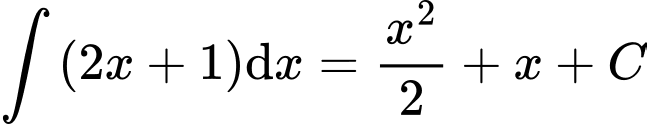 .
.
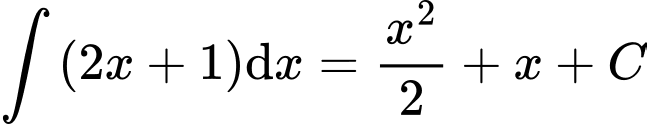 .
.B, 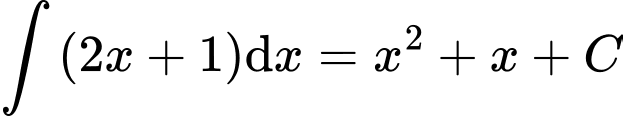 .
.
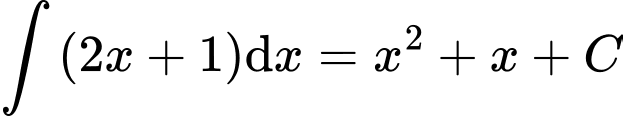 .
.C, 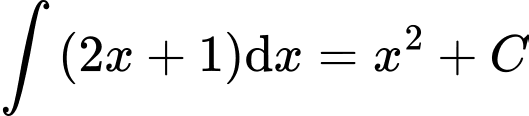 .
.
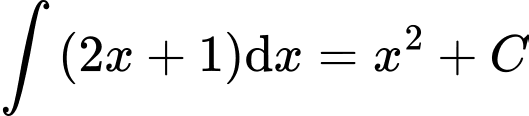 .
.D, 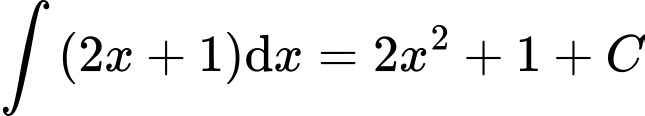 .
.
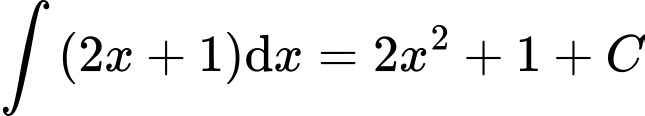 .
.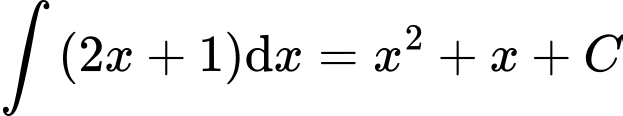 . Đáp án: B
. Đáp án: B
Câu 2 [732031]: [MĐ2] Nguyên hàm của hàm số 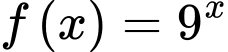 là
là
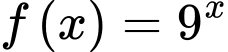 là
là A,  .
.
 .
.B, 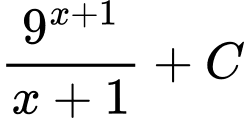 .
.
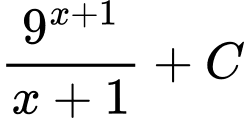 .
.C, 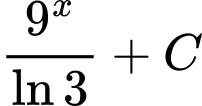 .
.
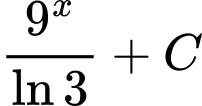 .
.D, 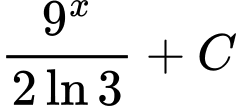 .
.
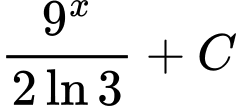 .
.
Ta có 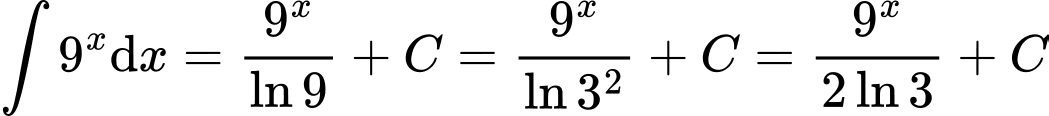 . Đáp án: D
. Đáp án: D
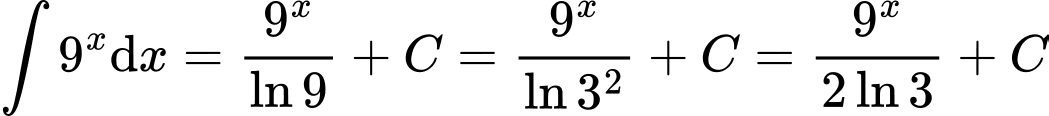 . Đáp án: D
. Đáp án: D
Câu 3 [544645]: Khẳng định nào sau đây sai?
A, 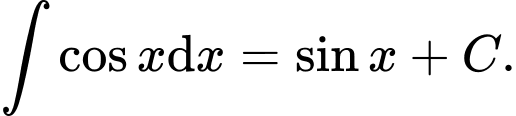
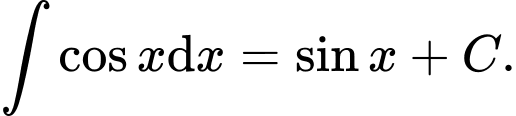
B, 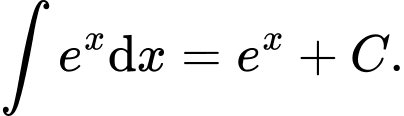
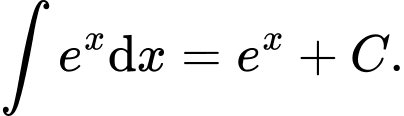
C, 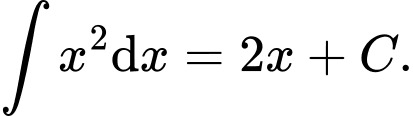
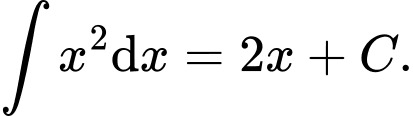
D, 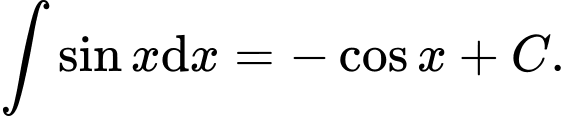
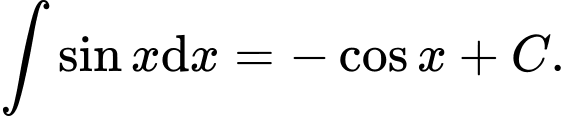
Chọn C.
Ta có: 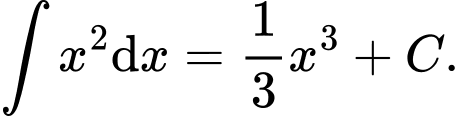
Đáp án: C 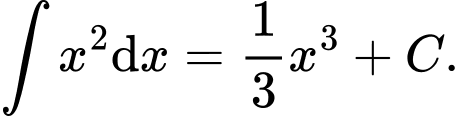
Câu 4 [147993]: Tìm nguyên hàm của hàm số 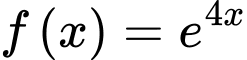
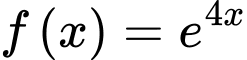
A, 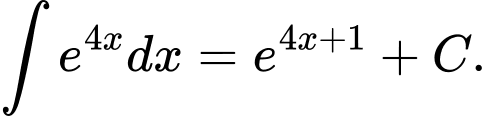
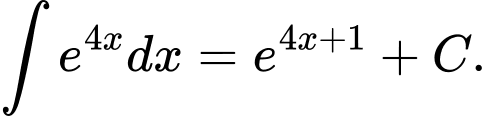
B, 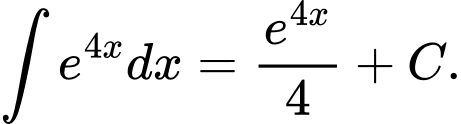
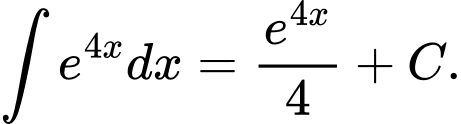
C, 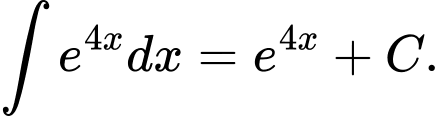
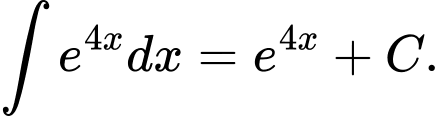
D, 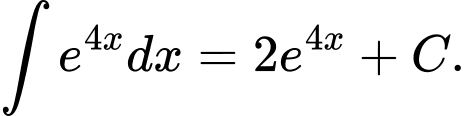
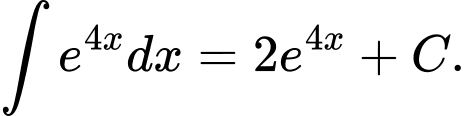
HD: Ta có: 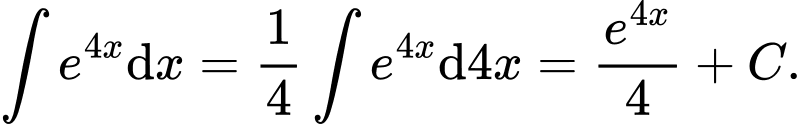 Chọn B. Đáp án: B
Chọn B. Đáp án: B
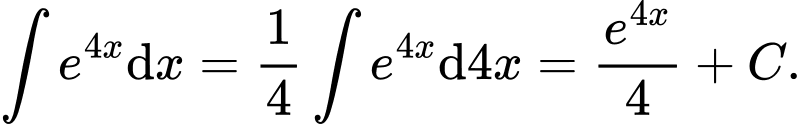 Chọn B. Đáp án: B
Chọn B. Đáp án: B
Câu 5 [543643]: Cho hàm số 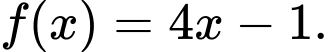 Khẳng định nào dưới đây đúng?
Khẳng định nào dưới đây đúng?
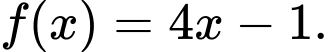 Khẳng định nào dưới đây đúng?
Khẳng định nào dưới đây đúng? A, 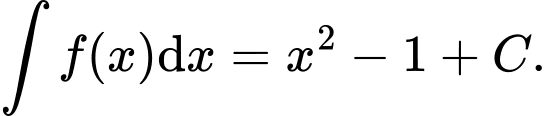
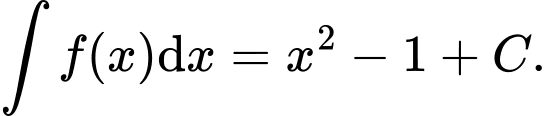
B, 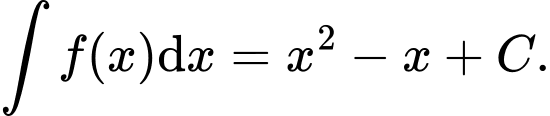
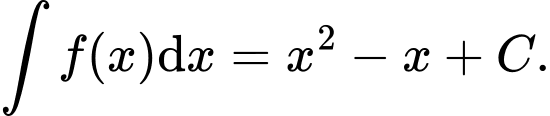
C, 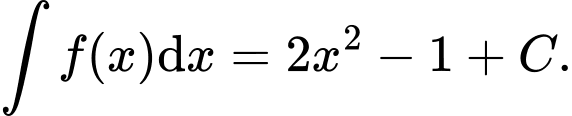
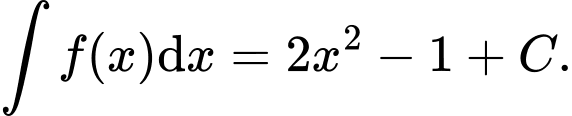
D, 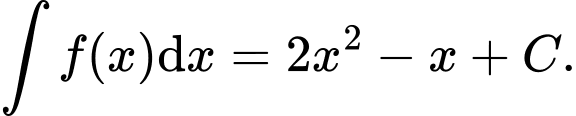
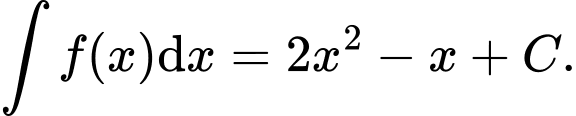
Ta có 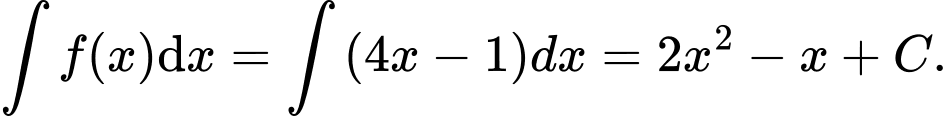 Đáp án: D
Đáp án: D
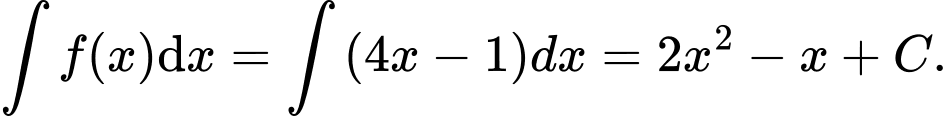 Đáp án: D
Đáp án: D
Câu 6 [297970]: [MĐ2] Cho hàm số 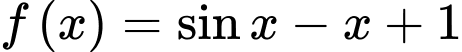 . Khẳng định nào dưới đây đúng?
. Khẳng định nào dưới đây đúng?
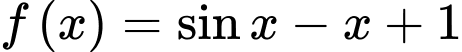 . Khẳng định nào dưới đây đúng?
. Khẳng định nào dưới đây đúng? A, 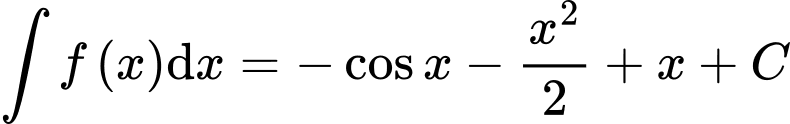 .
.
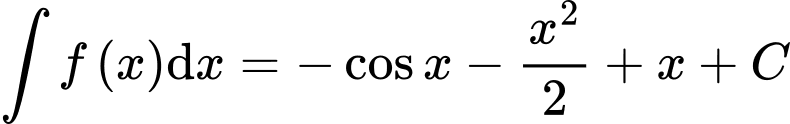 .
.B, 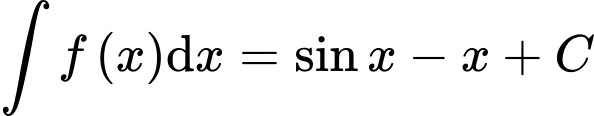 .
.
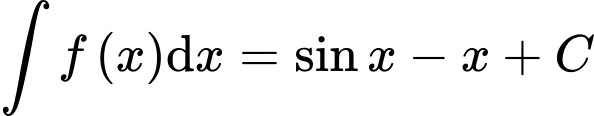 .
.C, 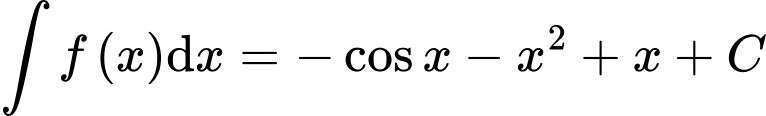 .
.
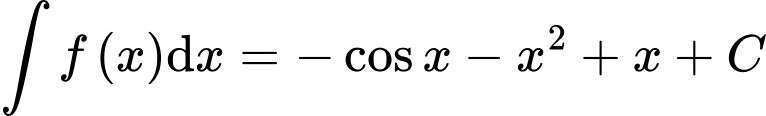 .
.D, 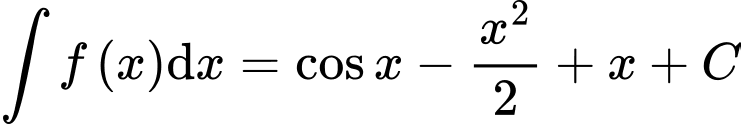 .
.
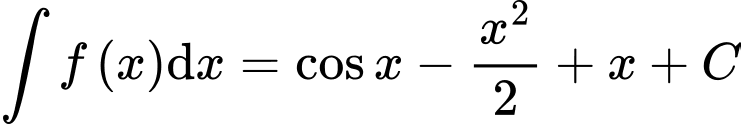 .
.
Ta có:  . Đáp án: A
. Đáp án: A
 . Đáp án: A
. Đáp án: A
Câu 7 [755180]: Trên khoảng 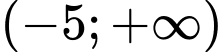 , hàm số
, hàm số 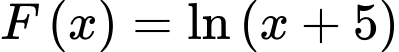 là một nguyên hàm của hàm số nào dưới đây?
là một nguyên hàm của hàm số nào dưới đây?
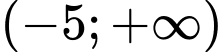 , hàm số
, hàm số 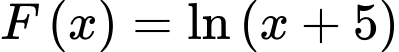 là một nguyên hàm của hàm số nào dưới đây?
là một nguyên hàm của hàm số nào dưới đây? A,
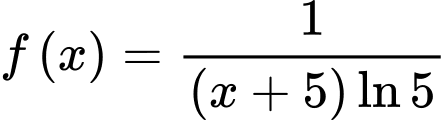 .
.
B,
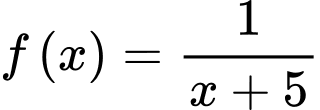 .
.
C,
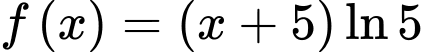 .
.
D,
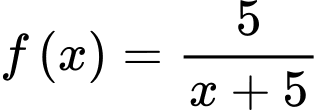 .
.
Chọn B.
Ta có
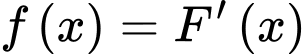
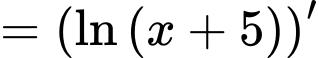
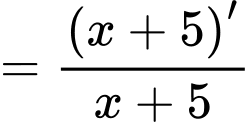
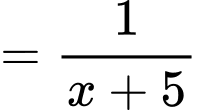 .
.
Câu 8 [732230]: [MĐ1] Cho hàm số 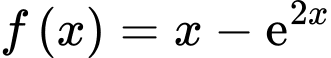 . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
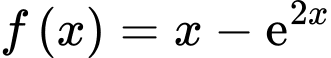 . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng? A, 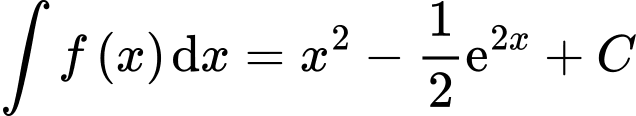 .
.
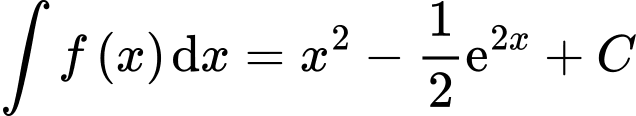 .
.B, 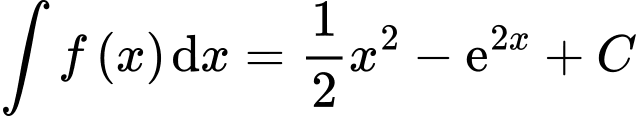 .
.
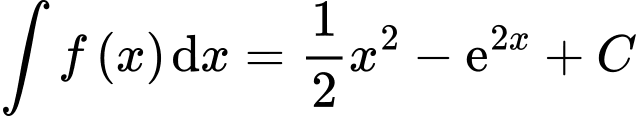 .
.C, 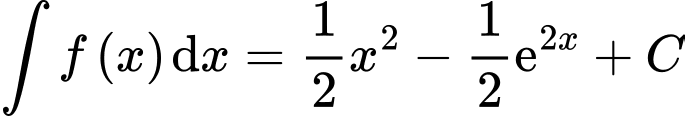 .
.
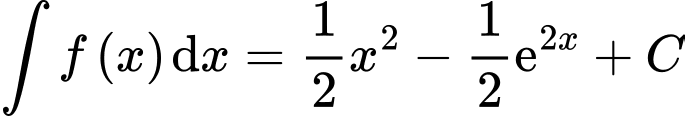 .
.D, 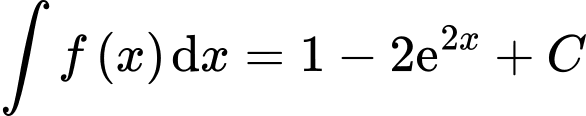 .
.
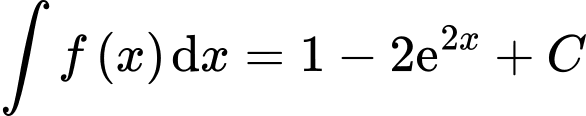 .
.
Ta có 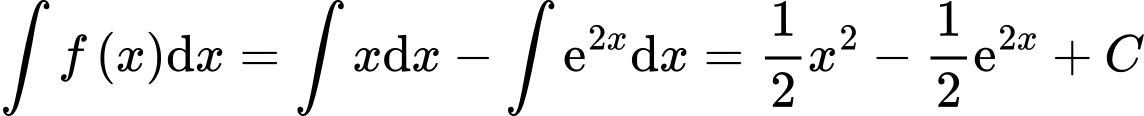 . Đáp án: C
. Đáp án: C
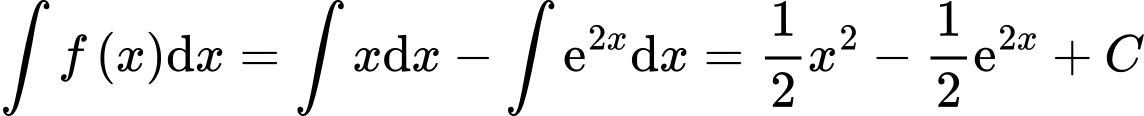 . Đáp án: C
. Đáp án: C
Câu 9 [541800]: Cho hàm số 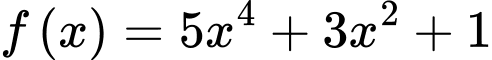 . Khẳng định nào dưới đây đúng?
. Khẳng định nào dưới đây đúng?
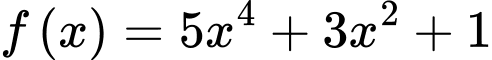 . Khẳng định nào dưới đây đúng?
. Khẳng định nào dưới đây đúng? A, 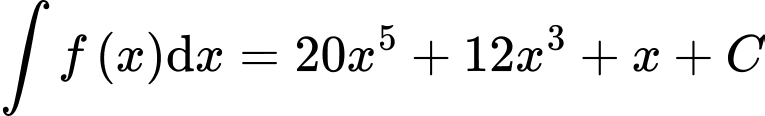 .
.
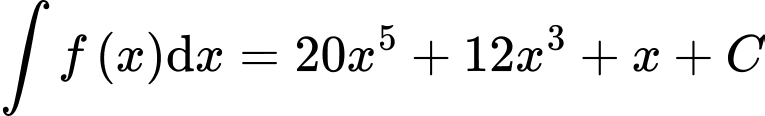 .
.B, 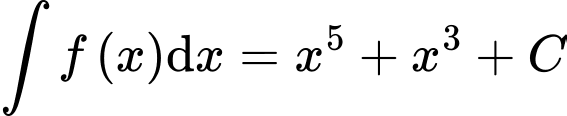 .
.
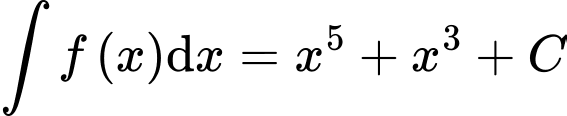 .
.C, 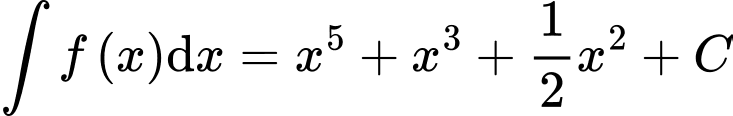 .
.
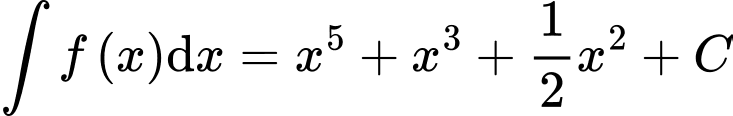 .
.D, 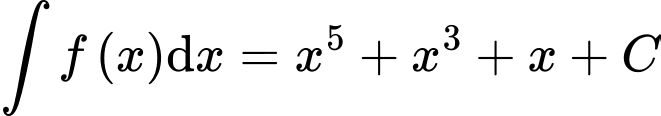 .
.
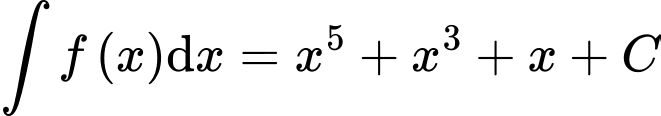 .
.
Dựa vào công thức 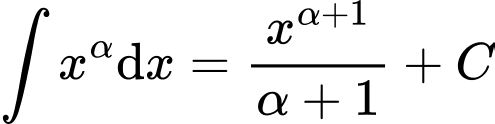 nên ta có
nên ta có 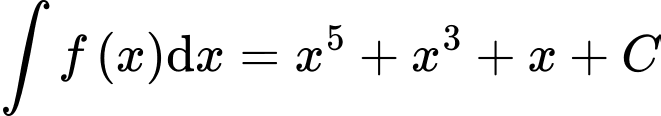 . Đáp án: D
. Đáp án: D
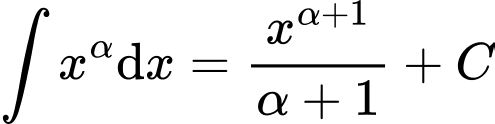 nên ta có
nên ta có 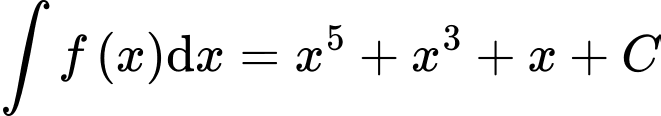 . Đáp án: D
. Đáp án: D
Câu 10 [298003]: [MĐ1] Biết  . Mệnh đề nào sau đây là mệnh đề đúng?
. Mệnh đề nào sau đây là mệnh đề đúng?
 . Mệnh đề nào sau đây là mệnh đề đúng?
. Mệnh đề nào sau đây là mệnh đề đúng? A, 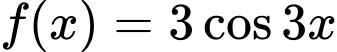 .
.
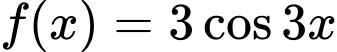 .
.B, 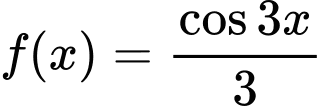 .
.
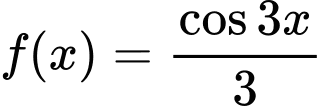 .
.C, 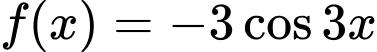 .
.
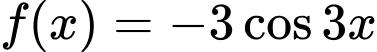 .
.D, 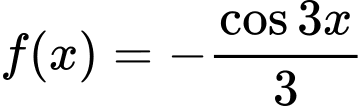 .
.
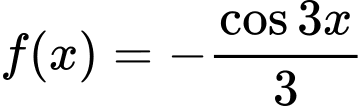 .
.
Ta có 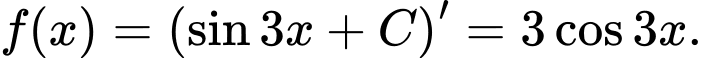 Đáp án: A
Đáp án: A
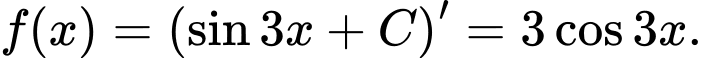 Đáp án: A
Đáp án: A
Câu 11 [396623]: 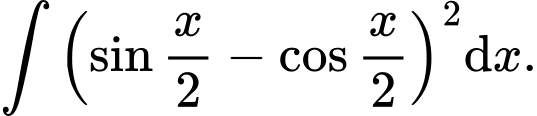
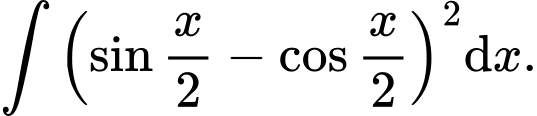
A, 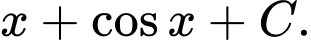
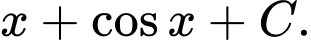
B, 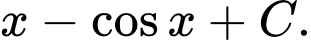
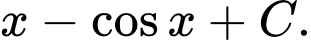
C, 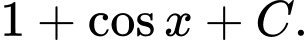
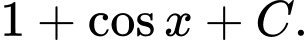
D, 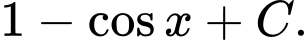
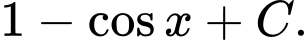
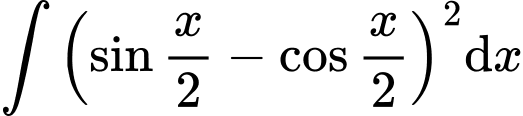
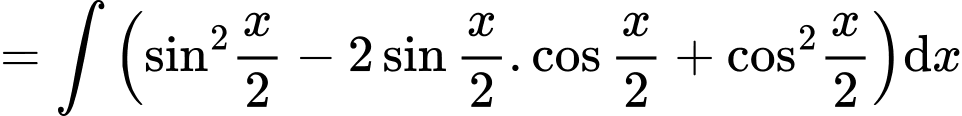
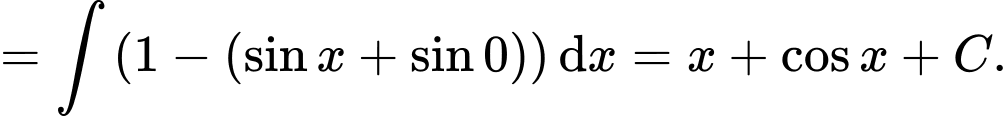
Chọn đáp án A.
Câu 12 [542669]: Khẳng định nào dưới đây đúng?
A, 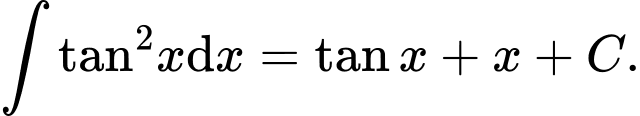
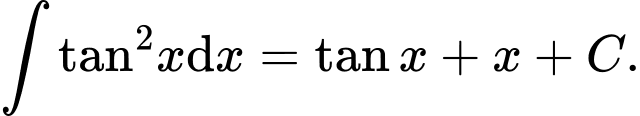
B, 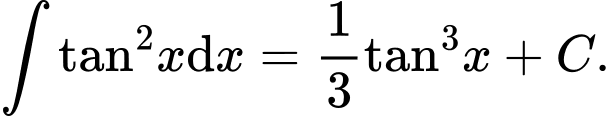
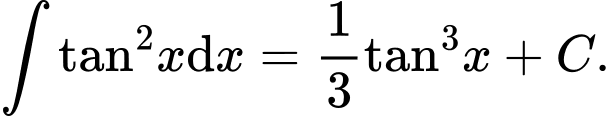
C, 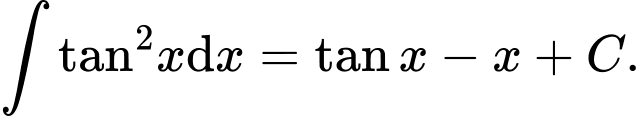
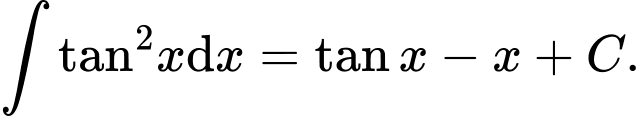
D, 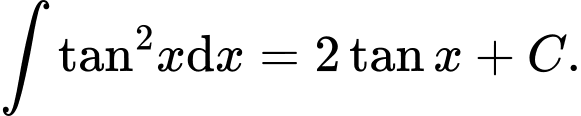
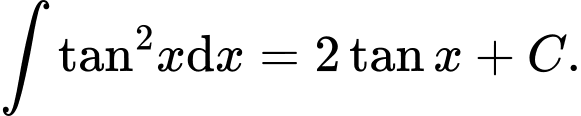
Chọn C
Ta có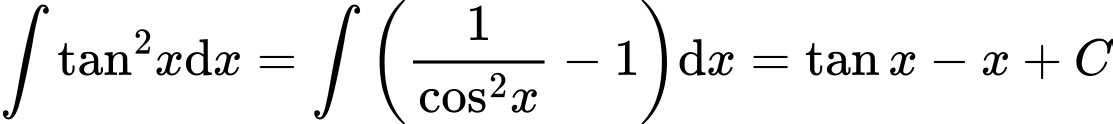 Đáp án: C
Đáp án: C
Ta có
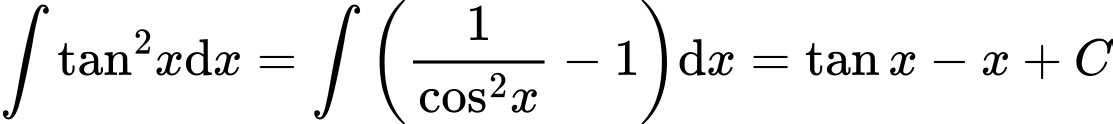 Đáp án: C
Đáp án: C PHẦN II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a),b),c),d) ở mỗi câu học sinh chọn đúng hoặc sai.
Câu 13 [779045]: Cho hàm số 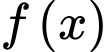 liên tục trên
liên tục trên 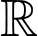 thoả mãn
thoả mãn 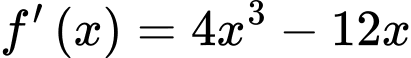 và
và 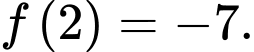
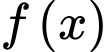 liên tục trên
liên tục trên 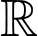 thoả mãn
thoả mãn 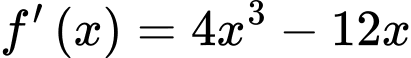 và
và 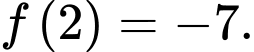
a) Đúng.
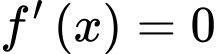
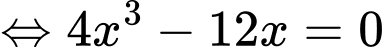
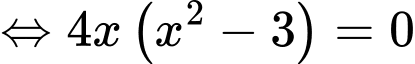
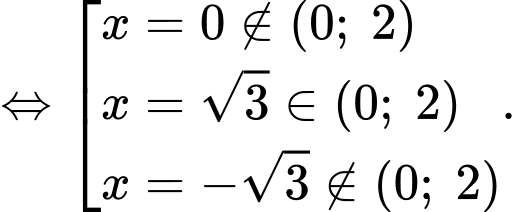
Vậy phương trình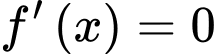 có duy nhất một nghiệm trên khoảng
có duy nhất một nghiệm trên khoảng 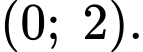
b) Sai.
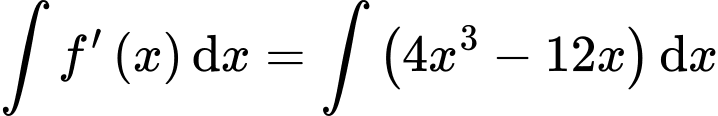
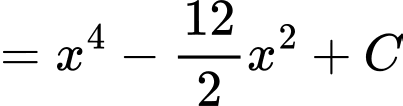
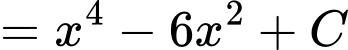
c) Đúng.
Ta có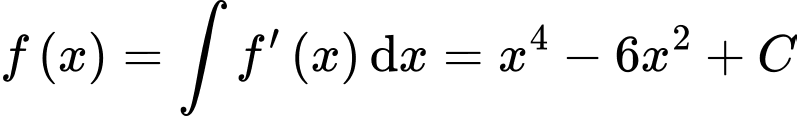
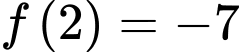
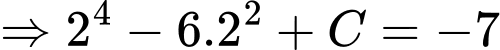
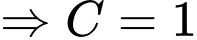
Suy ra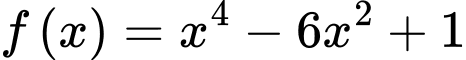
Vậy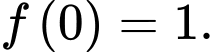
d) Đúng.
Xét hàm số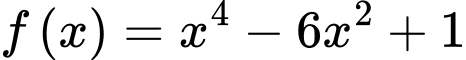 trên đoạn
trên đoạn 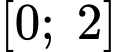
Ta có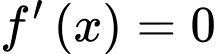
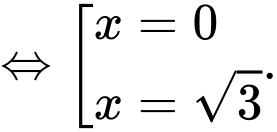
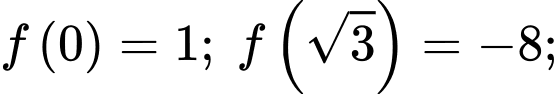
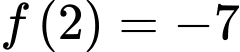
Vậy giá trị nhỏ nhất của hàm số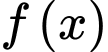 trên đoạn
trên đoạn 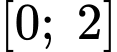 bằng -8.
bằng -8.
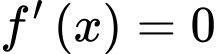
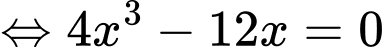
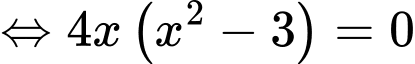
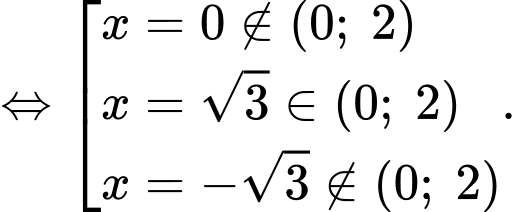
Vậy phương trình
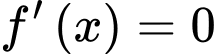 có duy nhất một nghiệm trên khoảng
có duy nhất một nghiệm trên khoảng 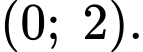
b) Sai.
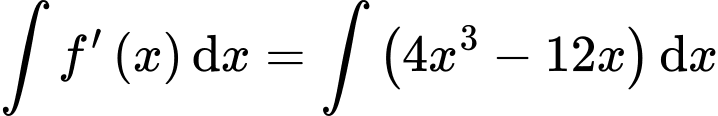
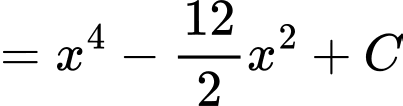
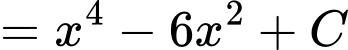
c) Đúng.
Ta có
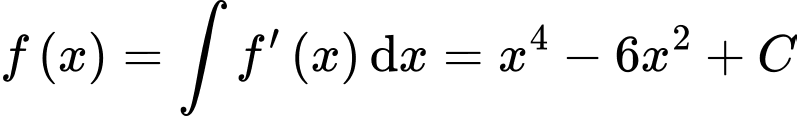
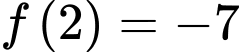
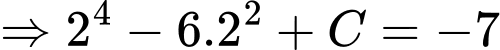
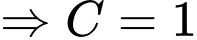
Suy ra
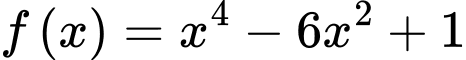
Vậy
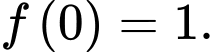
d) Đúng.
Xét hàm số
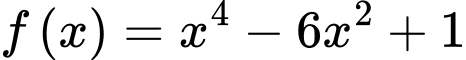 trên đoạn
trên đoạn 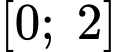
Ta có
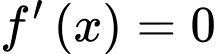
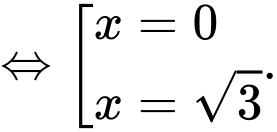
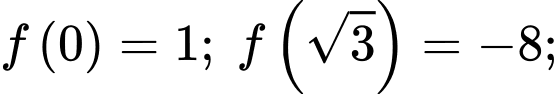
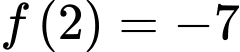
Vậy giá trị nhỏ nhất của hàm số
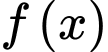 trên đoạn
trên đoạn 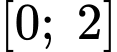 bằng -8.
bằng -8.
Câu 14 [779046]: Tại một khu di tích vào ngày lễ hội, người ta tính được tốc độ thay đổi lượng khách tham quan được biểu diễn bằng hàm số 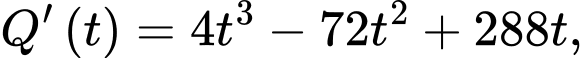 trong đó
trong đó 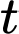 tính bằng giờ
tính bằng giờ 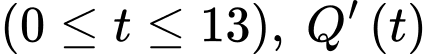 tính bằng khách/giờ. Biết rằng sau 2 giờ đã có 500 người có mặt. Dựa vào mô hình trên ta có:
tính bằng khách/giờ. Biết rằng sau 2 giờ đã có 500 người có mặt. Dựa vào mô hình trên ta có:
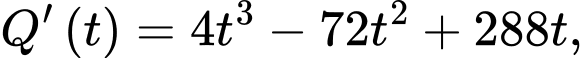 trong đó
trong đó 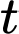 tính bằng giờ
tính bằng giờ 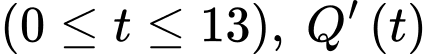 tính bằng khách/giờ. Biết rằng sau 2 giờ đã có 500 người có mặt. Dựa vào mô hình trên ta có:
tính bằng khách/giờ. Biết rằng sau 2 giờ đã có 500 người có mặt. Dựa vào mô hình trên ta có:
a) Đúng.
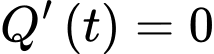
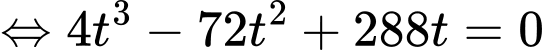
Bấm máy tính ta được kết quả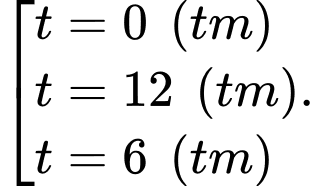
b) Sai.
Ta có: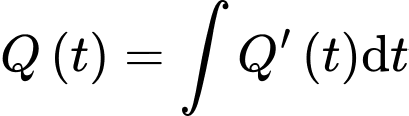
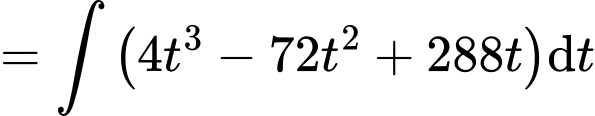
 .
.
Mà sau 2 giờ đã có 500 người nên ta có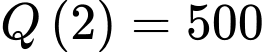 suy ra
suy ra 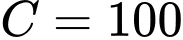 .
.
Vậy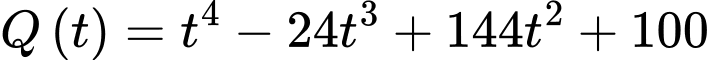 .
.
c) Đúng.
Dựa vào kết quả phần c), ta suy ra tại thời điểm ban đầu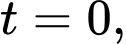 có
có 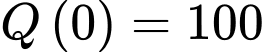 khách du lịch.
khách du lịch.
d) Đúng.
Ta tìm GTLN của hàm số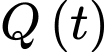 trên đoạn
trên đoạn 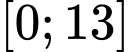 .
.
Dựa vào phần a) ta có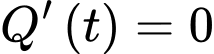 khi
khi 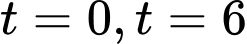 và
và 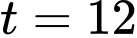 .
.
Mà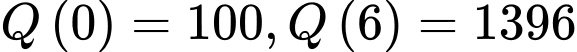 ,
, 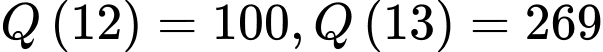 .
.
Nên lượng khách tham quan lớn nhất là sau 6 giờ, có 1396 người.
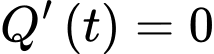
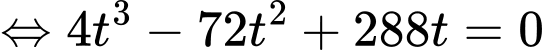
Bấm máy tính ta được kết quả
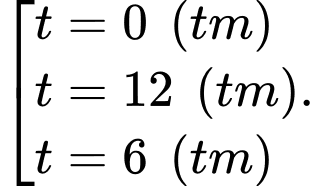
b) Sai.
Ta có:
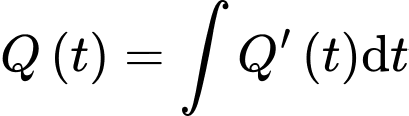
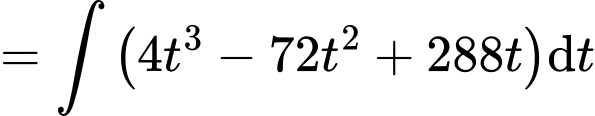
 .
.Mà sau 2 giờ đã có 500 người nên ta có
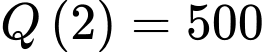 suy ra
suy ra 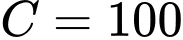 .
.Vậy
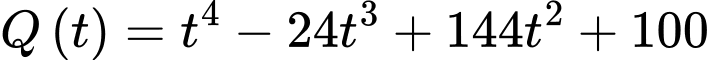 .
.c) Đúng.
Dựa vào kết quả phần c), ta suy ra tại thời điểm ban đầu
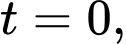 có
có 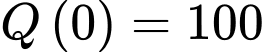 khách du lịch.
khách du lịch.d) Đúng.
Ta tìm GTLN của hàm số
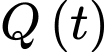 trên đoạn
trên đoạn 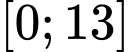 .
.Dựa vào phần a) ta có
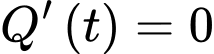 khi
khi 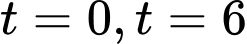 và
và 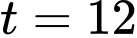 .
.Mà
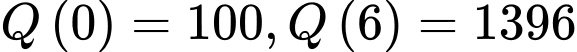 ,
, 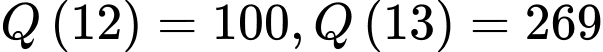 .
.Nên lượng khách tham quan lớn nhất là sau 6 giờ, có 1396 người.
Câu 15 [695514]: Một khinh khí cầu bay với độ cao (so với mặt đất) tại thời điểm 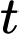 là
là 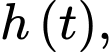 trong đó
trong đó 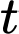 tính bằng phút,
tính bằng phút, 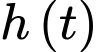 tính bằng mét. Vận tốc bay của khinh khí cầu được cho bởi hàm số
tính bằng mét. Vận tốc bay của khinh khí cầu được cho bởi hàm số 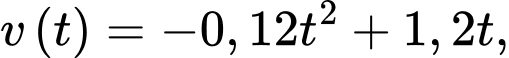 với
với 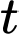 tính bằng phút,
tính bằng phút, 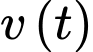 tính bằng mét/phút. Từ thời điểm xuất phát
tính bằng mét/phút. Từ thời điểm xuất phát 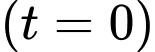 thì
thì 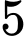 phút sau khi xuất phát, khinh khí cầu đã ở độ cao
phút sau khi xuất phát, khinh khí cầu đã ở độ cao 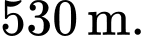
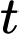 là
là 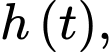 trong đó
trong đó 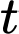 tính bằng phút,
tính bằng phút, 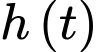 tính bằng mét. Vận tốc bay của khinh khí cầu được cho bởi hàm số
tính bằng mét. Vận tốc bay của khinh khí cầu được cho bởi hàm số 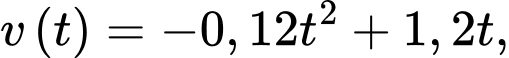 với
với 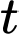 tính bằng phút,
tính bằng phút, 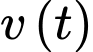 tính bằng mét/phút. Từ thời điểm xuất phát
tính bằng mét/phút. Từ thời điểm xuất phát 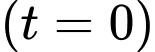 thì
thì 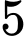 phút sau khi xuất phát, khinh khí cầu đã ở độ cao
phút sau khi xuất phát, khinh khí cầu đã ở độ cao 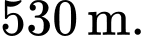
(Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma – 1, Cornelsen 2016).
a) Đúng.
Ta có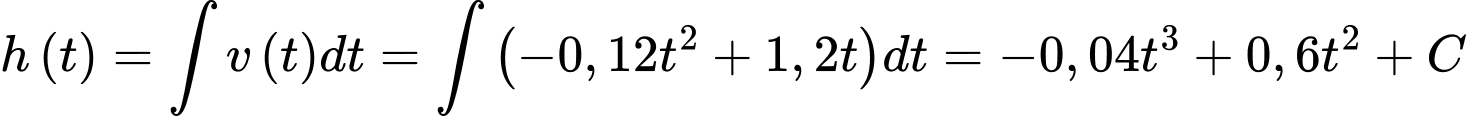 .
.
Khi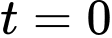 thì
thì 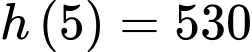 suy ra
suy ra 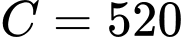 .
.
Vậy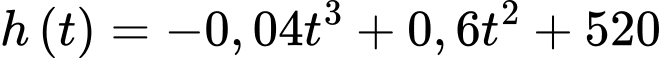
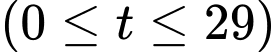
b) Đúng.
Độ cao tối đa của khinh khí cầu khi bay chính là giá trị lớn nhất của hàm số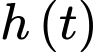 trên đoạn
trên đoạn 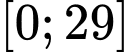 .
.
Ta có: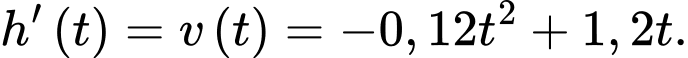
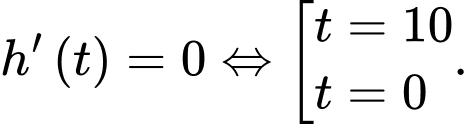
Có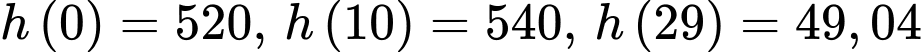 nên
nên 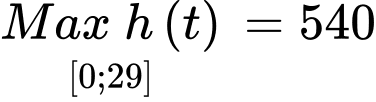 khi
khi 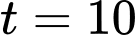 .
.
Độ cao tối đa của khinh khí cầu khi bay là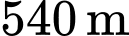 .
.
c) Đúng.
Khinh khí cầu trở lại độ cao khi xuất phát tức có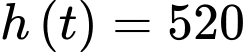 với
với 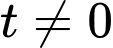 .
.
Ta có phương trình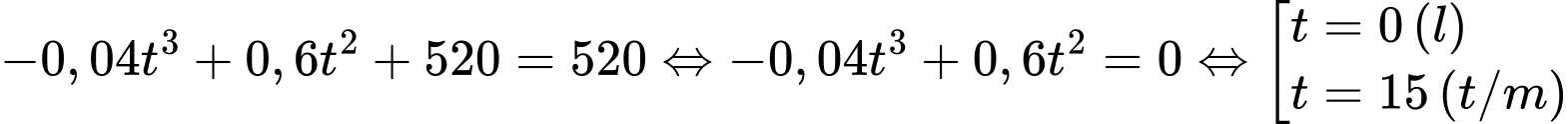
Vậy sau phút từ khi xuất phát thì khinh khí cầu trở lại độ cao khi bắt đầu xuất phát.
phút từ khi xuất phát thì khinh khí cầu trở lại độ cao khi bắt đầu xuất phát.
d) Đúng.
Khinh khí cầu tiếp đất khi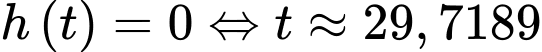
Vận tốc của khinh khí cầu khi đó là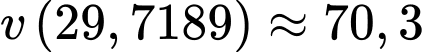 mét/phút.
mét/phút.
Ta có
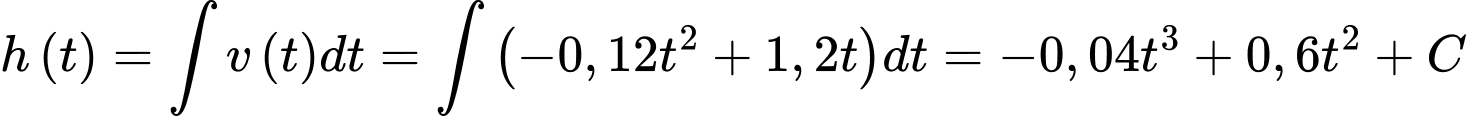 .
.
Khi
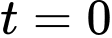 thì
thì 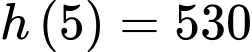 suy ra
suy ra 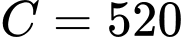 .
.
Vậy
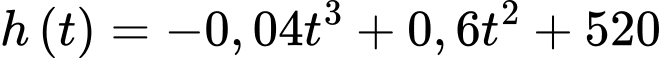
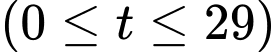
b) Đúng.
Độ cao tối đa của khinh khí cầu khi bay chính là giá trị lớn nhất của hàm số
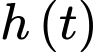 trên đoạn
trên đoạn 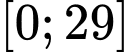 .
.
Ta có:
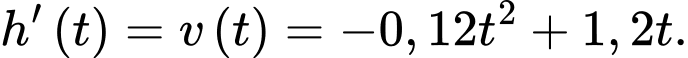
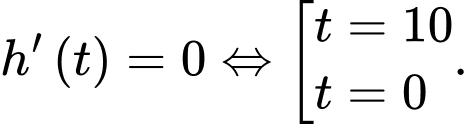
Có
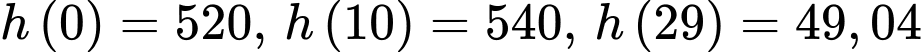 nên
nên 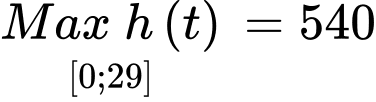 khi
khi 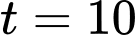 .
.
Độ cao tối đa của khinh khí cầu khi bay là
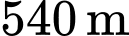 .
.
c) Đúng.
Khinh khí cầu trở lại độ cao khi xuất phát tức có
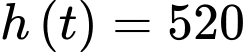 với
với 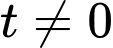 .
.
Ta có phương trình
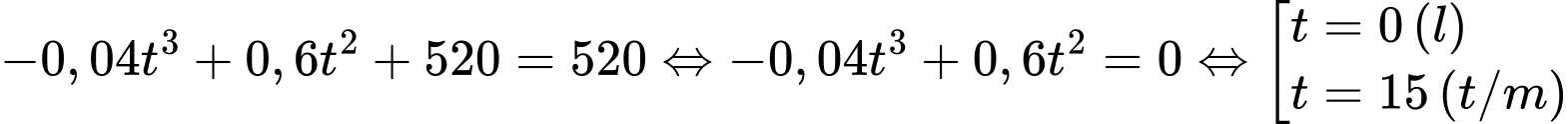
Vậy sau
 phút từ khi xuất phát thì khinh khí cầu trở lại độ cao khi bắt đầu xuất phát.
phút từ khi xuất phát thì khinh khí cầu trở lại độ cao khi bắt đầu xuất phát.
d) Đúng.
Khinh khí cầu tiếp đất khi
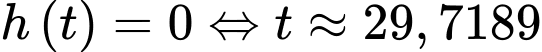
Vận tốc của khinh khí cầu khi đó là
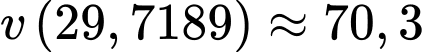 mét/phút.
mét/phút.
Câu 16 [779047]: Một quần thể vi khuẩn ban đầu gồm 500 con vi khuẩn, sau đó bắt đầu tăng trưởng. Gọi 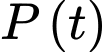 (con) là số lượng vi khuẩn của quần thể đó tại thời điểm
(con) là số lượng vi khuẩn của quần thể đó tại thời điểm 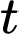 , trong đó
, trong đó 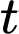 tính theo ngày (
tính theo ngày (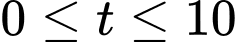 ). Tốc độ tăng trưởng của quần thể vi khuẩn đó cho bởi hàm số
). Tốc độ tăng trưởng của quần thể vi khuẩn đó cho bởi hàm số 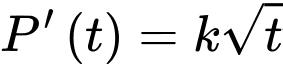 , trong đó k là hằng số. Sau 1 ngày, số lượng vi khuẩn của quần thể đó đã tăng lên thành 600 con vi khuẩn. Khi đó
, trong đó k là hằng số. Sau 1 ngày, số lượng vi khuẩn của quần thể đó đã tăng lên thành 600 con vi khuẩn. Khi đó
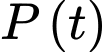 (con) là số lượng vi khuẩn của quần thể đó tại thời điểm
(con) là số lượng vi khuẩn của quần thể đó tại thời điểm 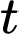 , trong đó
, trong đó 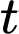 tính theo ngày (
tính theo ngày (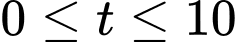 ). Tốc độ tăng trưởng của quần thể vi khuẩn đó cho bởi hàm số
). Tốc độ tăng trưởng của quần thể vi khuẩn đó cho bởi hàm số 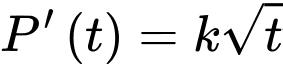 , trong đó k là hằng số. Sau 1 ngày, số lượng vi khuẩn của quần thể đó đã tăng lên thành 600 con vi khuẩn. Khi đó
, trong đó k là hằng số. Sau 1 ngày, số lượng vi khuẩn của quần thể đó đã tăng lên thành 600 con vi khuẩn. Khi đó
a) Sai.
Từ giả thiết: “Một quần thể vi khuẩn ban đầu gồm 500 con vi khuẩn” suy ra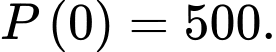
Lại biết: “Sau 1 ngày, số lượng vi khuẩn của quần thể đó đã tăng lên thành 600 con vi khuẩn” suy ra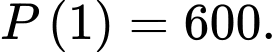
Nên mệnh đề sai.
b) Đúng.
Từ định nghĩa nguyên hàm, ta có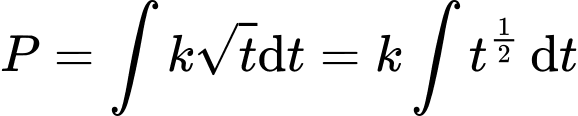
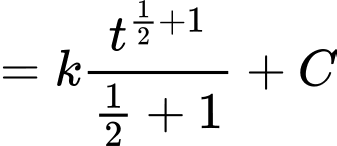
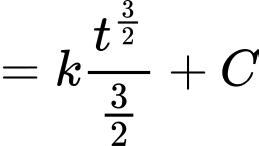
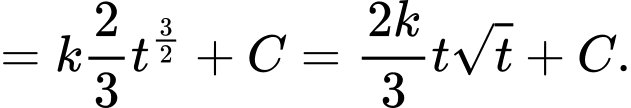
Nên mệnh đề đúng.
c) Sai.
Dựa vào kết quả của phần a) ta có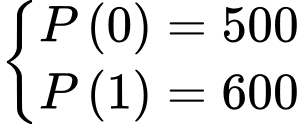
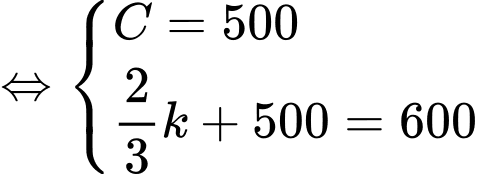
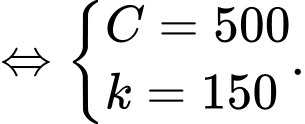
Suy ra mệnh đề sai.
d) Đúng.
Từ kết quả phần c) ta suy ra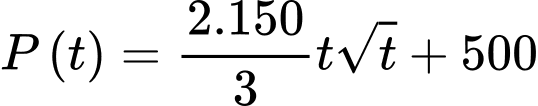
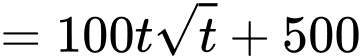
Khi đó số lượng vi khuẩn của quần thể đó sau 9 ngày là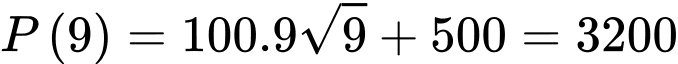 (con).
(con).
Vậy mệnh đề đúng.
Từ giả thiết: “Một quần thể vi khuẩn ban đầu gồm 500 con vi khuẩn” suy ra
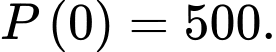
Lại biết: “Sau 1 ngày, số lượng vi khuẩn của quần thể đó đã tăng lên thành 600 con vi khuẩn” suy ra
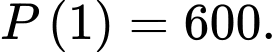
Nên mệnh đề sai.
b) Đúng.
Từ định nghĩa nguyên hàm, ta có
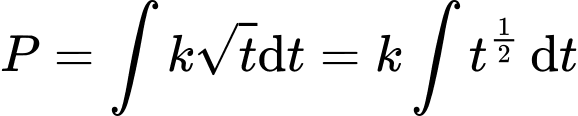
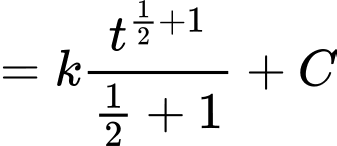
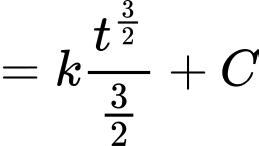
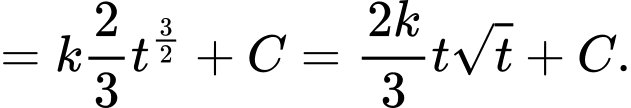
Nên mệnh đề đúng.
c) Sai.
Dựa vào kết quả của phần a) ta có
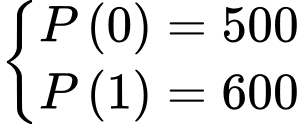
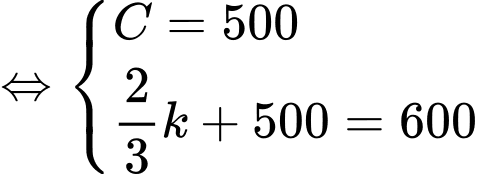
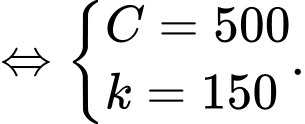
Suy ra mệnh đề sai.
d) Đúng.
Từ kết quả phần c) ta suy ra
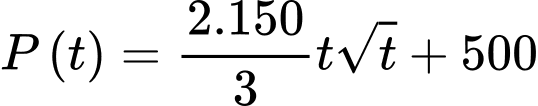
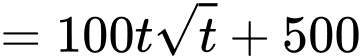
Khi đó số lượng vi khuẩn của quần thể đó sau 9 ngày là
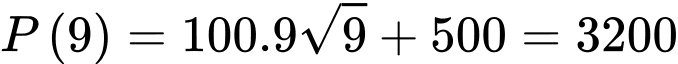 (con).
(con).Vậy mệnh đề đúng.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 17 đến câu 22.
Câu 17 [775936]: Chủ một trung tâm thương mại muốn cho thuê một số gian hàng như nhau. Người đó muốn cho thuê mỗi gian hàng với giá là 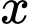 triệu đồng
triệu đồng 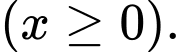 Khi đó doanh thu của cửa hàng được biểu diễn theo hàm số
Khi đó doanh thu của cửa hàng được biểu diễn theo hàm số 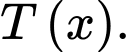 Tốc độ thay đổi doanh thu từ các gian hàng đó được biểu diễn bởi hàm số
Tốc độ thay đổi doanh thu từ các gian hàng đó được biểu diễn bởi hàm số 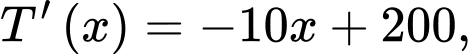 trong đó
trong đó 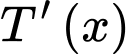 tính bằng triệu đồng. Biết rằng nếu giá thuê cho mỗi gian hàng là 10 triệu đồng thì doanh thu là
tính bằng triệu đồng. Biết rằng nếu giá thuê cho mỗi gian hàng là 10 triệu đồng thì doanh thu là 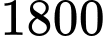 triệu đồng. Doanh thu cao nhất mà chủ trung tâm thương mại có thể thu về là bao nhiêu triệu đồng?
triệu đồng. Doanh thu cao nhất mà chủ trung tâm thương mại có thể thu về là bao nhiêu triệu đồng?
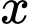 triệu đồng
triệu đồng  Khi đó doanh thu của cửa hàng được biểu diễn theo hàm số
Khi đó doanh thu của cửa hàng được biểu diễn theo hàm số 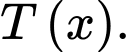 Tốc độ thay đổi doanh thu từ các gian hàng đó được biểu diễn bởi hàm số
Tốc độ thay đổi doanh thu từ các gian hàng đó được biểu diễn bởi hàm số 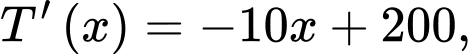 trong đó
trong đó 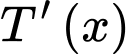 tính bằng triệu đồng. Biết rằng nếu giá thuê cho mỗi gian hàng là 10 triệu đồng thì doanh thu là
tính bằng triệu đồng. Biết rằng nếu giá thuê cho mỗi gian hàng là 10 triệu đồng thì doanh thu là 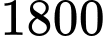 triệu đồng. Doanh thu cao nhất mà chủ trung tâm thương mại có thể thu về là bao nhiêu triệu đồng?
triệu đồng. Doanh thu cao nhất mà chủ trung tâm thương mại có thể thu về là bao nhiêu triệu đồng?
Điền đáp án: 2300.
Ta có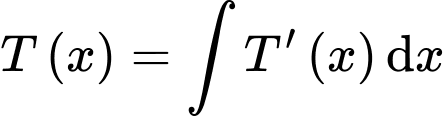
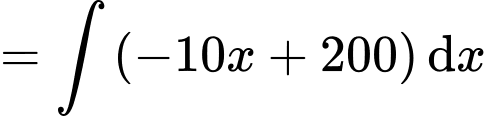
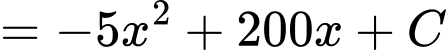
Biết giá thuê cho mỗi gian hàng là 10 triệu đồng thì doanh thu là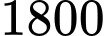 triệu đồng nên ta có
triệu đồng nên ta có 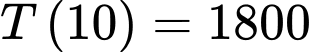
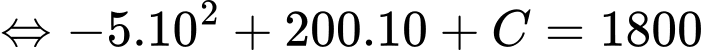
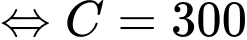
Suy ra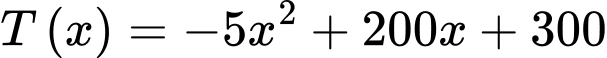
Để tìm được doanh thu cao nhất của chủ trung tâm thương mại thì ta cần tìm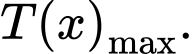
Ta có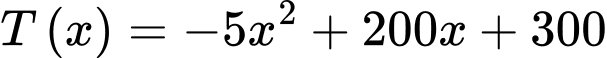
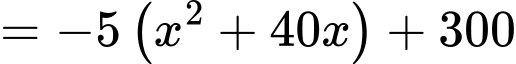
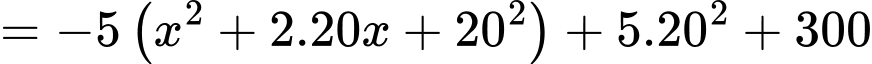
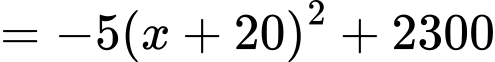
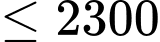
Vậy doanh thu cao nhất mà chủ trung tâm thương mại có thể thu về là 2300 triệu đồng. .
Ta có
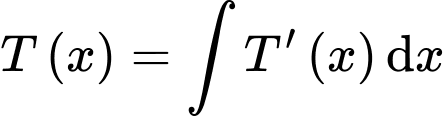
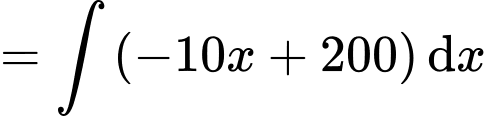
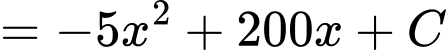
Biết giá thuê cho mỗi gian hàng là 10 triệu đồng thì doanh thu là
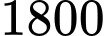 triệu đồng nên ta có
triệu đồng nên ta có 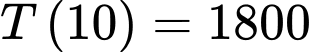
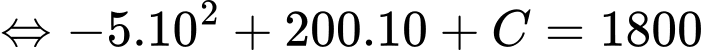
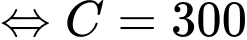
Suy ra
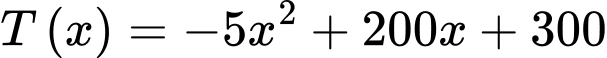
Để tìm được doanh thu cao nhất của chủ trung tâm thương mại thì ta cần tìm
Ta có
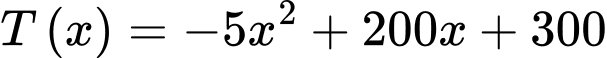
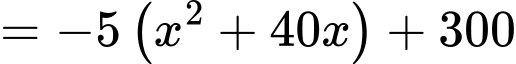
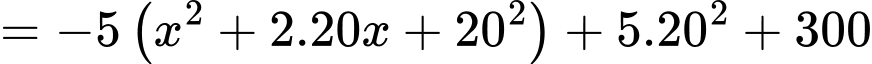
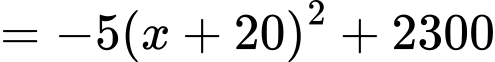
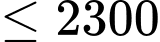
Vậy doanh thu cao nhất mà chủ trung tâm thương mại có thể thu về là 2300 triệu đồng. .
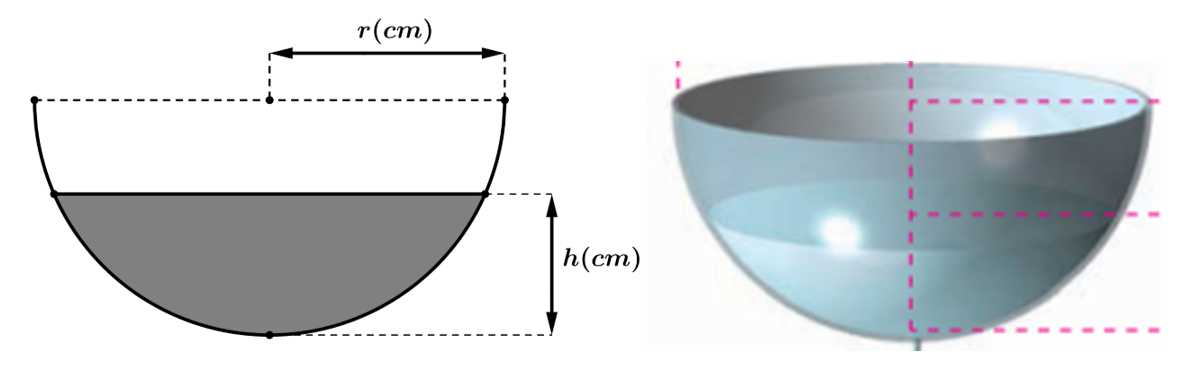
Câu 18 [779014]: Nước bốc hơi từ một bát hình bán cầu có bán kính  (cm) với tốc độ
(cm) với tốc độ 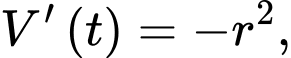 trong đó
trong đó 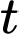 là thời gian tính bằng giờ. Giả sử bán kính của bát là
là thời gian tính bằng giờ. Giả sử bán kính của bát là 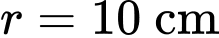 và ban đầu (lúc
và ban đầu (lúc 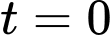 ) bát chứa đầy nước. Hỏi sau bao nhiêu giờ (làm tròn kết quả đến hàng phần chục) thì bát cạn nước.
) bát chứa đầy nước. Hỏi sau bao nhiêu giờ (làm tròn kết quả đến hàng phần chục) thì bát cạn nước.
 (cm) với tốc độ
(cm) với tốc độ 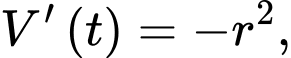 trong đó
trong đó  là thời gian tính bằng giờ. Giả sử bán kính của bát là
là thời gian tính bằng giờ. Giả sử bán kính của bát là 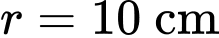 và ban đầu (lúc
và ban đầu (lúc 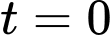 ) bát chứa đầy nước. Hỏi sau bao nhiêu giờ (làm tròn kết quả đến hàng phần chục) thì bát cạn nước.
) bát chứa đầy nước. Hỏi sau bao nhiêu giờ (làm tròn kết quả đến hàng phần chục) thì bát cạn nước.
Điền đáp án: 20,9.
Vì bát có dạng là 1 nửa hình cầu với bán kính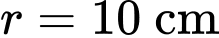 nên ta có thể tích của bát khi chứa đầy nước là
nên ta có thể tích của bát khi chứa đầy nước là 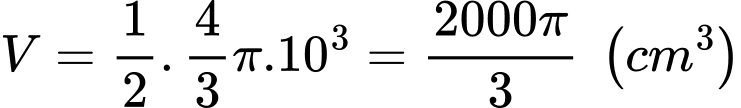
Theo định nghĩa nguyên hàm, ta có lượng nước trong bát là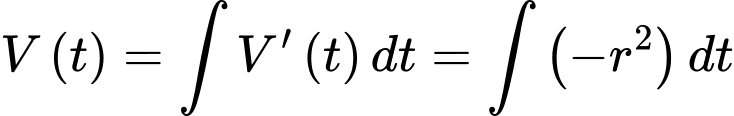
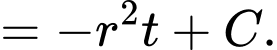
Biết tại thời điểm ban đầu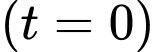 thì bát đầy nước nên ta có
thì bát đầy nước nên ta có 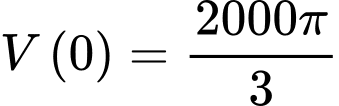
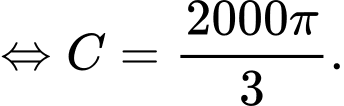
Suy ra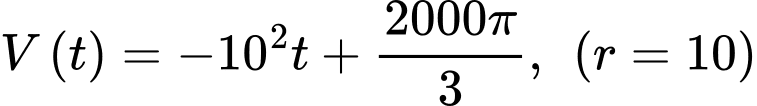
Bát cạn nước khi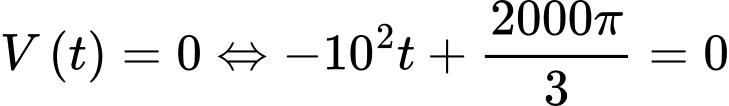
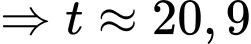 giờ.
giờ.
Vì bát có dạng là 1 nửa hình cầu với bán kính
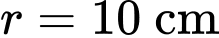 nên ta có thể tích của bát khi chứa đầy nước là
nên ta có thể tích của bát khi chứa đầy nước là 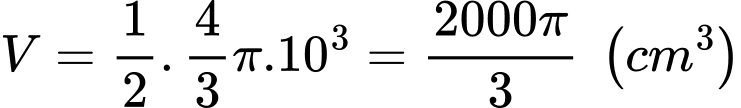
Theo định nghĩa nguyên hàm, ta có lượng nước trong bát là
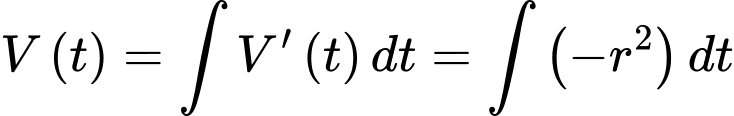
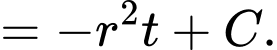
Biết tại thời điểm ban đầu
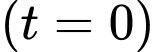 thì bát đầy nước nên ta có
thì bát đầy nước nên ta có 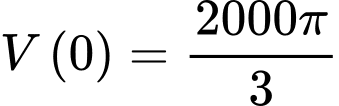
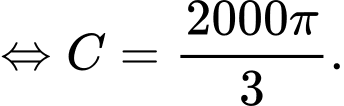
Suy ra
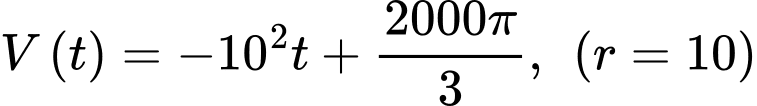
Bát cạn nước khi
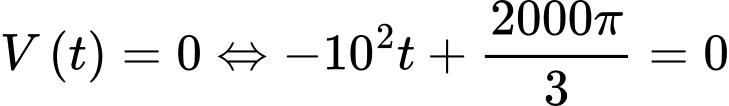
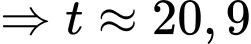 giờ.
giờ.
Câu 19 [775036]: Tại một nhà máy, gọi 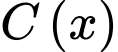 là tổng chi phí (tính theo triệu đồng) để sản xuất
là tổng chi phí (tính theo triệu đồng) để sản xuất 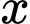 tấn sản phẩm A trong một tháng. Khi đó, đạo hàm
tấn sản phẩm A trong một tháng. Khi đó, đạo hàm 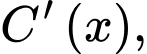 gọi là chi phí cận biên, cho biết tốc độ gia tăng tổng chi phí theo lượng gia tăng sản phẩm được sản xuất. Giả sử chi phí cận biên (tính theo triệu đồng trên tấn) của nhà máy được ước lượng bởi công thức
gọi là chi phí cận biên, cho biết tốc độ gia tăng tổng chi phí theo lượng gia tăng sản phẩm được sản xuất. Giả sử chi phí cận biên (tính theo triệu đồng trên tấn) của nhà máy được ước lượng bởi công thức 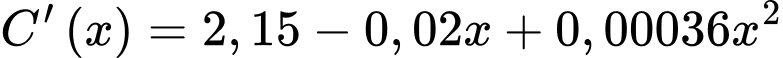 với
với  Biết rằng
Biết rằng 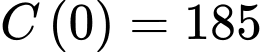 triệu đồng, gọi là chi phí cố định. Tổng chi phí khi nhà máy sản xuất 100 tấn sản phẩm A trong tháng là bao nhiêu triệu đồng?
triệu đồng, gọi là chi phí cố định. Tổng chi phí khi nhà máy sản xuất 100 tấn sản phẩm A trong tháng là bao nhiêu triệu đồng?
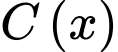 là tổng chi phí (tính theo triệu đồng) để sản xuất
là tổng chi phí (tính theo triệu đồng) để sản xuất 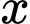 tấn sản phẩm A trong một tháng. Khi đó, đạo hàm
tấn sản phẩm A trong một tháng. Khi đó, đạo hàm 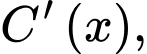 gọi là chi phí cận biên, cho biết tốc độ gia tăng tổng chi phí theo lượng gia tăng sản phẩm được sản xuất. Giả sử chi phí cận biên (tính theo triệu đồng trên tấn) của nhà máy được ước lượng bởi công thức
gọi là chi phí cận biên, cho biết tốc độ gia tăng tổng chi phí theo lượng gia tăng sản phẩm được sản xuất. Giả sử chi phí cận biên (tính theo triệu đồng trên tấn) của nhà máy được ước lượng bởi công thức 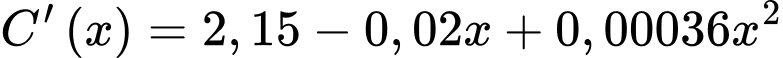 với
với  Biết rằng
Biết rằng 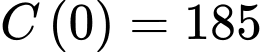 triệu đồng, gọi là chi phí cố định. Tổng chi phí khi nhà máy sản xuất 100 tấn sản phẩm A trong tháng là bao nhiêu triệu đồng?
triệu đồng, gọi là chi phí cố định. Tổng chi phí khi nhà máy sản xuất 100 tấn sản phẩm A trong tháng là bao nhiêu triệu đồng?
Điền đáp án: 420.
Ta có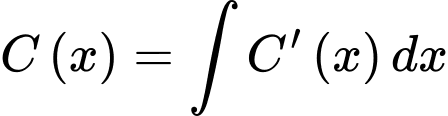
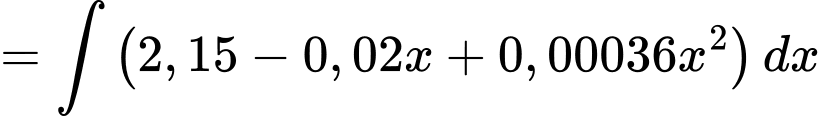
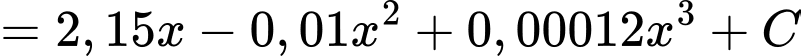
Biết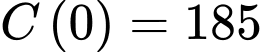
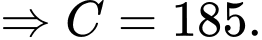
Suy ra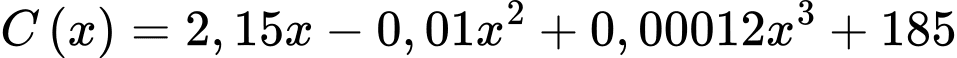
Vậy tổng chi phí khi nhà máy sản xuất 100 tấn sản phẩm A trong tháng là triệu đồng.
triệu đồng.
Ta có
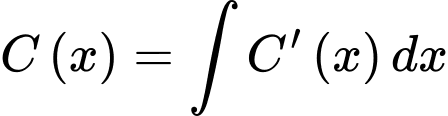
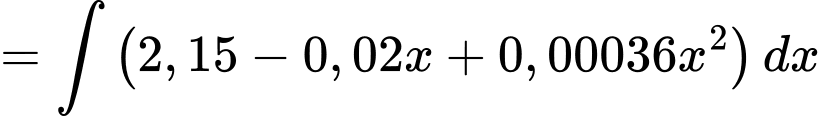
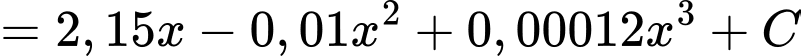
Biết
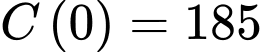
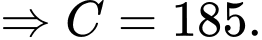
Suy ra
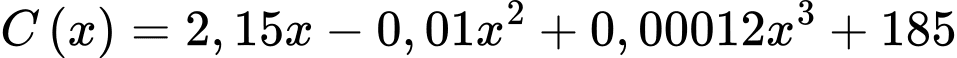
Vậy tổng chi phí khi nhà máy sản xuất 100 tấn sản phẩm A trong tháng là
 triệu đồng.
triệu đồng.
Câu 20 [779048]: Cây cà chua khi trồng có chiều cao 5 cm. Tốc độ tăng chiều cao của cây cà chua sau khi trồng được cho bởi hàm số 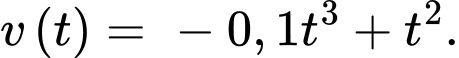 Trong đó
Trong đó 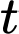 tính theo tuần,
tính theo tuần, 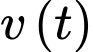 tính bằng centimet. Gọi
tính bằng centimet. Gọi 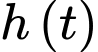 (tính bằng cm) là độ cao của cây cà chua ở tuần thứ
(tính bằng cm) là độ cao của cây cà chua ở tuần thứ 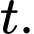 Vào thời điểm cây cà chua đó phát triển nhanh nhất thì cây cà chua sẽ cao bao nhiêu cm (kết quả làm tròn đến hàng phần mười)?
Vào thời điểm cây cà chua đó phát triển nhanh nhất thì cây cà chua sẽ cao bao nhiêu cm (kết quả làm tròn đến hàng phần mười)?
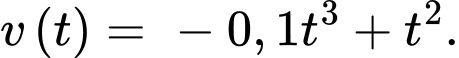 Trong đó
Trong đó 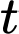 tính theo tuần,
tính theo tuần, 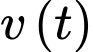 tính bằng centimet. Gọi
tính bằng centimet. Gọi 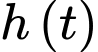 (tính bằng cm) là độ cao của cây cà chua ở tuần thứ
(tính bằng cm) là độ cao của cây cà chua ở tuần thứ 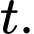 Vào thời điểm cây cà chua đó phát triển nhanh nhất thì cây cà chua sẽ cao bao nhiêu cm (kết quả làm tròn đến hàng phần mười)?
Vào thời điểm cây cà chua đó phát triển nhanh nhất thì cây cà chua sẽ cao bao nhiêu cm (kết quả làm tròn đến hàng phần mười)?
Điền đáp án: 54,4.
Ta có: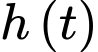 là nguyên hàm của
là nguyên hàm của 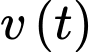
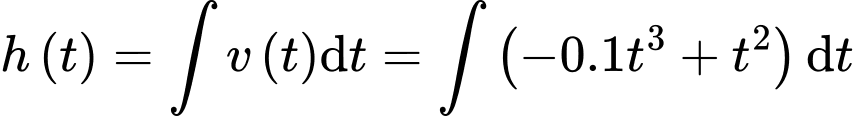
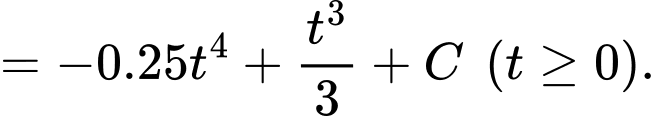
Vì cây cà chua khi trồng có chiều cao 5 cm nên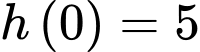 .
.
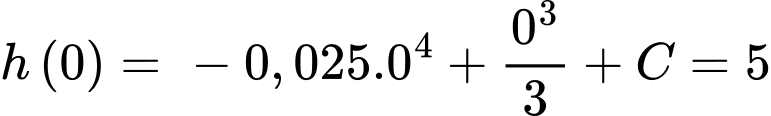
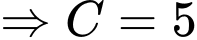
Vậy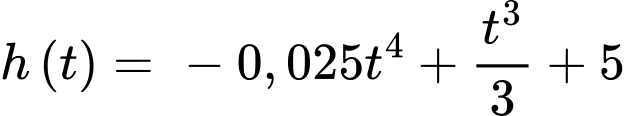
Xét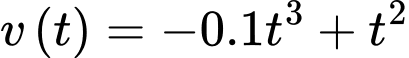
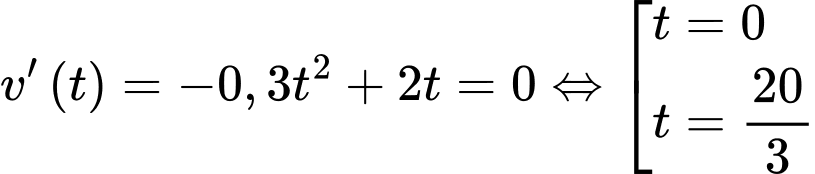 .
.
Bảng biến thiên
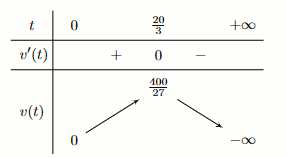 Từ bảng biến thiên ta thấy, vào thời điểm cây cà chua đó phát triển nhanh nhất thì cây cà chua sẽ cao
Từ bảng biến thiên ta thấy, vào thời điểm cây cà chua đó phát triển nhanh nhất thì cây cà chua sẽ cao 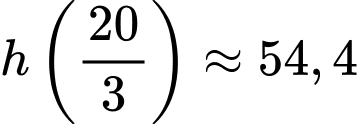 cm.
cm.
Ta có:
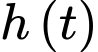 là nguyên hàm của
là nguyên hàm của 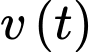
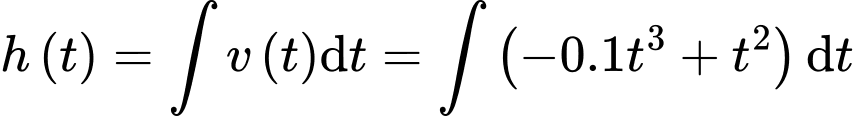
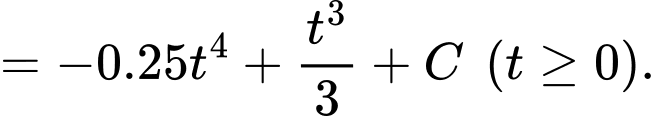
Vì cây cà chua khi trồng có chiều cao 5 cm nên
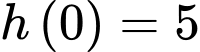 .
.
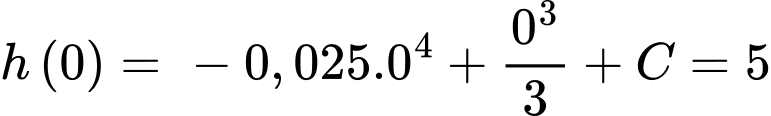
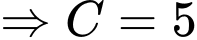
Vậy
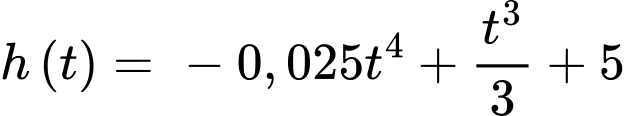
Xét
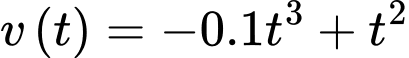
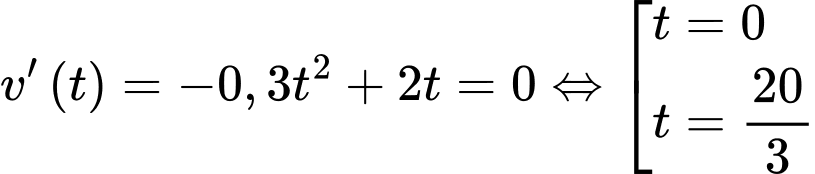 .
.
Bảng biến thiên

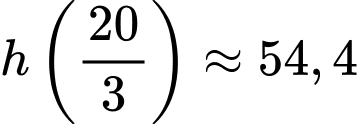 cm.
cm.
Câu 21 [701398]: Nước bốc hơi khỏi hồ với tốc độ tỷ lệ thuận với thể tích nước còn lại. Giả sử 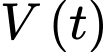 là tổng lượng nước bốc hơi sau
là tổng lượng nước bốc hơi sau 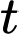 ngày và
ngày và 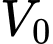 là thể tích nước ban đầu trong hồ thì ta có:
là thể tích nước ban đầu trong hồ thì ta có:  Nếu 50% lượng nước bốc hơi trong 20 ngày, hãy tìm phần trăm lượng nước còn lại sau 50 ngày không mưa (kết quả làm tròn đến hàng phần chục).
Nếu 50% lượng nước bốc hơi trong 20 ngày, hãy tìm phần trăm lượng nước còn lại sau 50 ngày không mưa (kết quả làm tròn đến hàng phần chục).

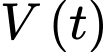 là tổng lượng nước bốc hơi sau
là tổng lượng nước bốc hơi sau 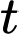 ngày và
ngày và 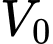 là thể tích nước ban đầu trong hồ thì ta có:
là thể tích nước ban đầu trong hồ thì ta có:  Nếu 50% lượng nước bốc hơi trong 20 ngày, hãy tìm phần trăm lượng nước còn lại sau 50 ngày không mưa (kết quả làm tròn đến hàng phần chục).
Nếu 50% lượng nước bốc hơi trong 20 ngày, hãy tìm phần trăm lượng nước còn lại sau 50 ngày không mưa (kết quả làm tròn đến hàng phần chục).
Điền đáp án: 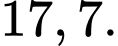
Ta có:
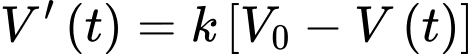
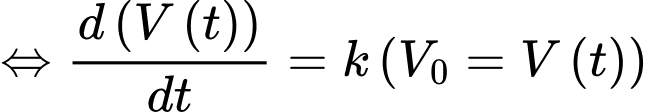
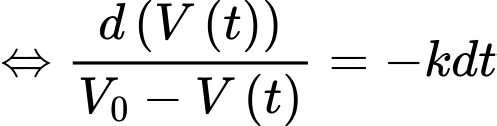
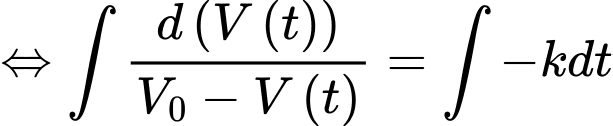

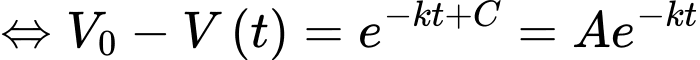
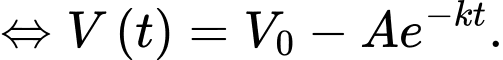
 nên
nên 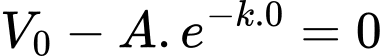
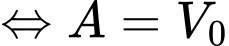

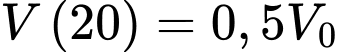
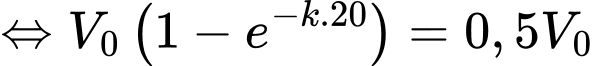
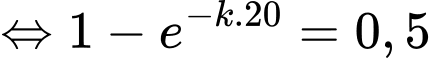
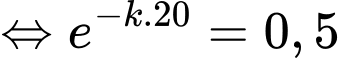
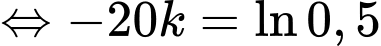
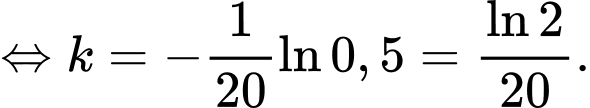
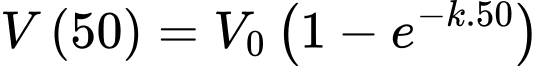
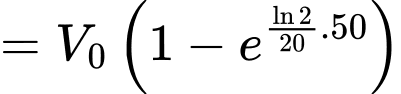
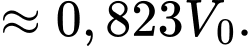
Vậy sau 50 ngày không có mưa, khoảng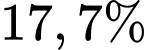 lượng nước ban đầu vẫn còn trong hồ.
lượng nước ban đầu vẫn còn trong hồ.
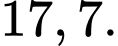
Ta có:
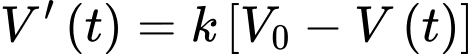
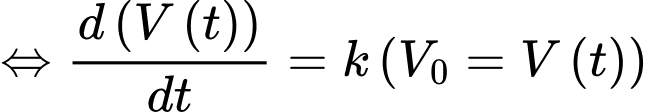
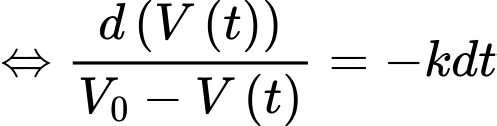
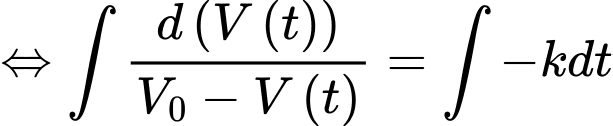

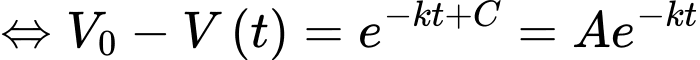
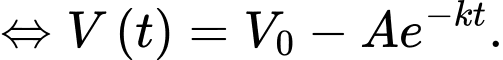
 nên
nên 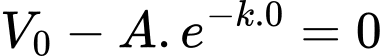
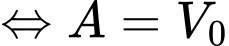

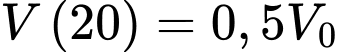
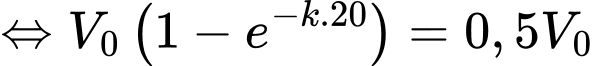
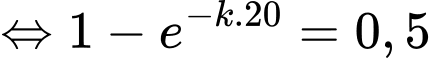
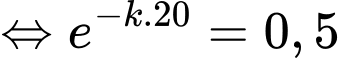
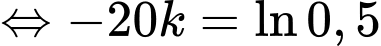
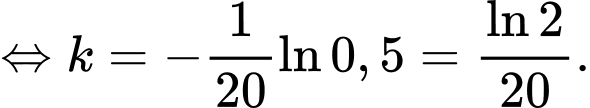
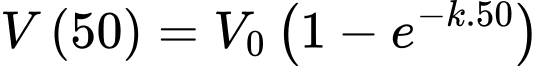
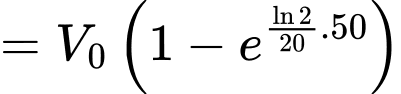
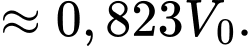
Vậy sau 50 ngày không có mưa, khoảng
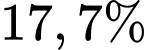 lượng nước ban đầu vẫn còn trong hồ.
lượng nước ban đầu vẫn còn trong hồ.
Câu 22 [775941]: Theo định luật làm mát của Newton thì tốc độ làm mát của một vật tỉ lệ thuận với chênh lệch nhiệt độ giữa vật đó và môi trường xung quanh, với điều kiện là chênh lệch này không quá lớn. Giả sử 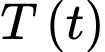 là nhiệt độ của vật thể (đơn vị: độ C) tại thời điểm
là nhiệt độ của vật thể (đơn vị: độ C) tại thời điểm 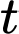 (đơn vị: phút) và
(đơn vị: phút) và 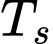 là nhiệt độ của môi trường xung quanh, chênh lệch giữa nhiệt độ của vật thể và môi trường xung quanh là
là nhiệt độ của môi trường xung quanh, chênh lệch giữa nhiệt độ của vật thể và môi trường xung quanh là 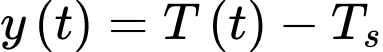 thì
thì 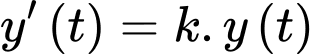 với
với 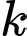 là hằng số. Một cốc nước đang ở nhiệt độ phòng là 22°C được đưa vào ngăn mát tủ lạnh có nhiệt độ là 5°C. Sau 30 phút, nhiệt độ của cốc nước được đo lại là 16°C. Hỏi sau một tiếng trong tủ lạnh, nhiệt độ cốc nước là bao nhiêu độ C (kết quả làm tròn đến hàng đơn vị).
là hằng số. Một cốc nước đang ở nhiệt độ phòng là 22°C được đưa vào ngăn mát tủ lạnh có nhiệt độ là 5°C. Sau 30 phút, nhiệt độ của cốc nước được đo lại là 16°C. Hỏi sau một tiếng trong tủ lạnh, nhiệt độ cốc nước là bao nhiêu độ C (kết quả làm tròn đến hàng đơn vị).
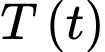 là nhiệt độ của vật thể (đơn vị: độ C) tại thời điểm
là nhiệt độ của vật thể (đơn vị: độ C) tại thời điểm 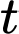 (đơn vị: phút) và
(đơn vị: phút) và 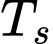 là nhiệt độ của môi trường xung quanh, chênh lệch giữa nhiệt độ của vật thể và môi trường xung quanh là
là nhiệt độ của môi trường xung quanh, chênh lệch giữa nhiệt độ của vật thể và môi trường xung quanh là 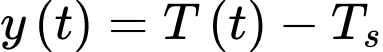 thì
thì 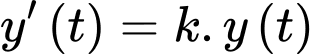 với
với 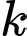 là hằng số. Một cốc nước đang ở nhiệt độ phòng là 22°C được đưa vào ngăn mát tủ lạnh có nhiệt độ là 5°C. Sau 30 phút, nhiệt độ của cốc nước được đo lại là 16°C. Hỏi sau một tiếng trong tủ lạnh, nhiệt độ cốc nước là bao nhiêu độ C (kết quả làm tròn đến hàng đơn vị).
là hằng số. Một cốc nước đang ở nhiệt độ phòng là 22°C được đưa vào ngăn mát tủ lạnh có nhiệt độ là 5°C. Sau 30 phút, nhiệt độ của cốc nước được đo lại là 16°C. Hỏi sau một tiếng trong tủ lạnh, nhiệt độ cốc nước là bao nhiêu độ C (kết quả làm tròn đến hàng đơn vị).
Điền đáp án: 12.
Đổi 1 giờ = 60 phút;
YCBT là xác định nhiệt độ của cốc nước sau 1 giờ hay
Ta có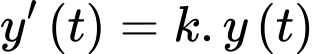
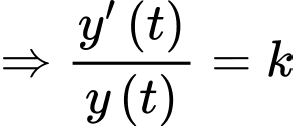
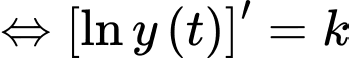
Nguyên hàm 2 vế, ta được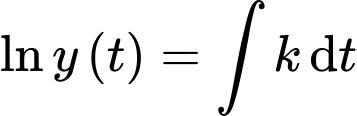
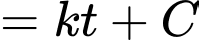
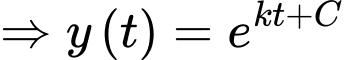
(Khi đặt cốc nước vào tủ lạnh thì khi đó nhiệt độ môi trường xung quanh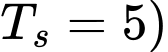
Khi đó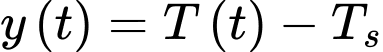 tương đương với
tương đương với 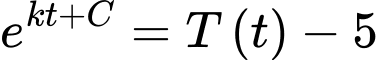
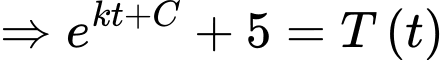
Ta có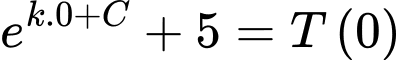
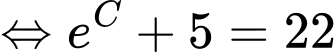
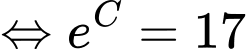

Suy ra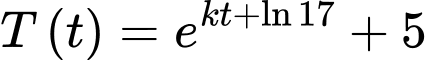
Biết: sau 30 phút, nhiệt độ của cốc nước là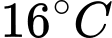 nên ta có
nên ta có 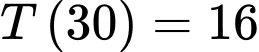
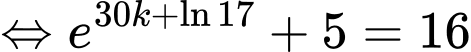
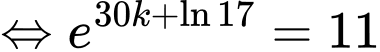
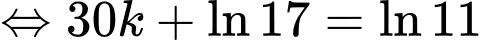
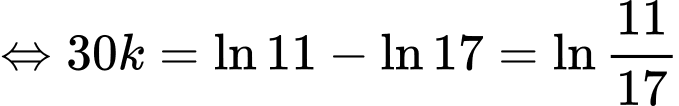
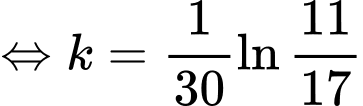
Suy ra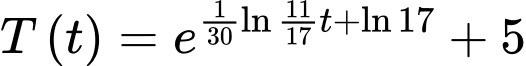
Vậy nhiệt độ của cốc nước sau 1 giờ trong tủ lạnh là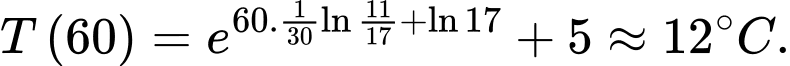
Đổi 1 giờ = 60 phút;
YCBT là xác định nhiệt độ của cốc nước sau 1 giờ hay

Ta có
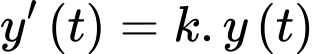
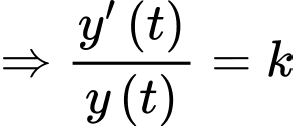
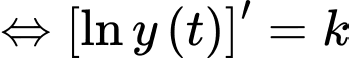
Nguyên hàm 2 vế, ta được
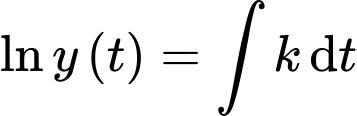
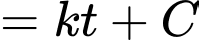
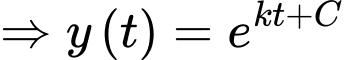
(Khi đặt cốc nước vào tủ lạnh thì khi đó nhiệt độ môi trường xung quanh
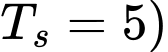
Khi đó
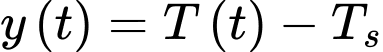 tương đương với
tương đương với 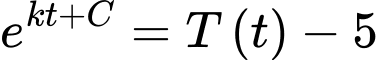
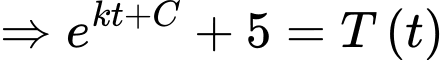
Ta có
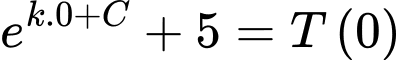
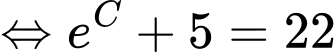
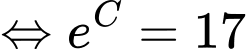

Suy ra
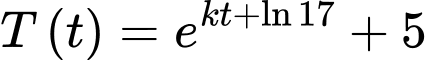
Biết: sau 30 phút, nhiệt độ của cốc nước là
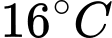 nên ta có
nên ta có 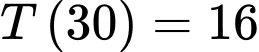
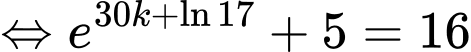
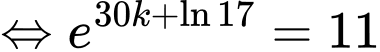
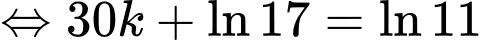
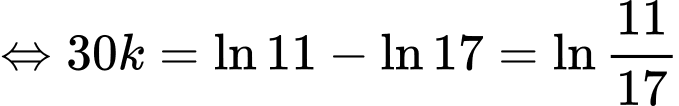
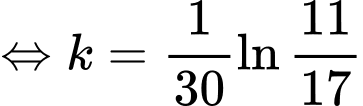
Suy ra
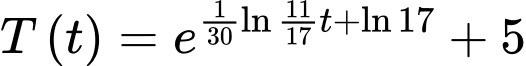
Vậy nhiệt độ của cốc nước sau 1 giờ trong tủ lạnh là