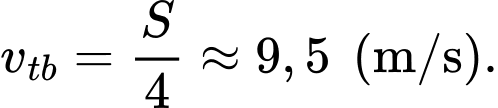PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1 [80815]: Cho hai số thực 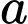 ,
, 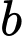 tùy ý,
tùy ý, 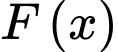 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 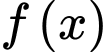 trên tập
trên tập 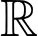 . Mệnh đề nào dưới đây là đúng?
. Mệnh đề nào dưới đây là đúng?
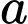 ,
, 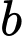 tùy ý,
tùy ý, 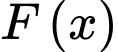 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 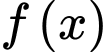 trên tập
trên tập 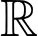 . Mệnh đề nào dưới đây là đúng?
. Mệnh đề nào dưới đây là đúng? A, 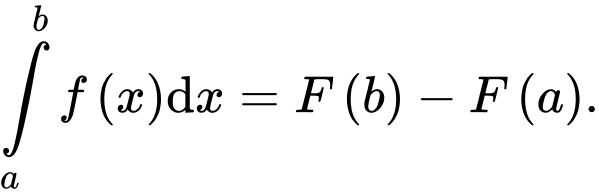
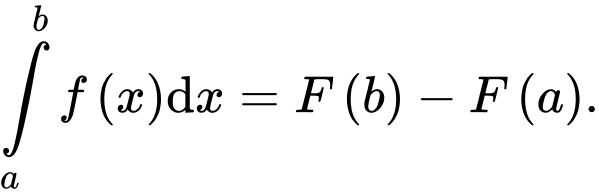
B, 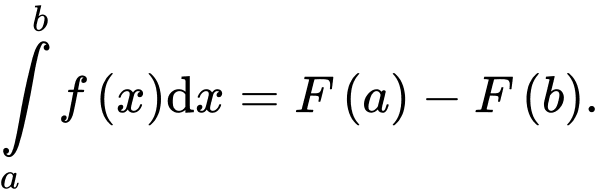
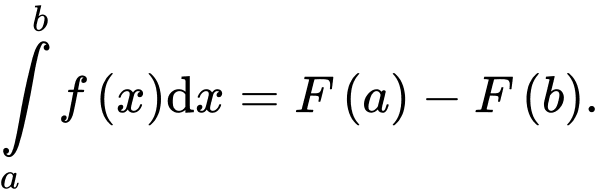
C, 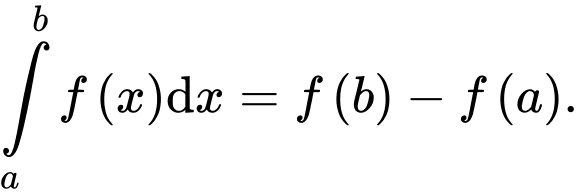
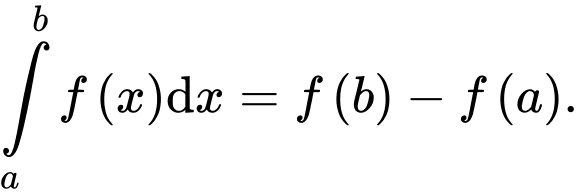
D, 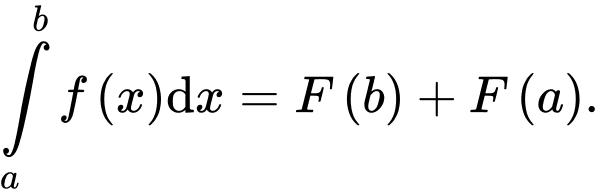
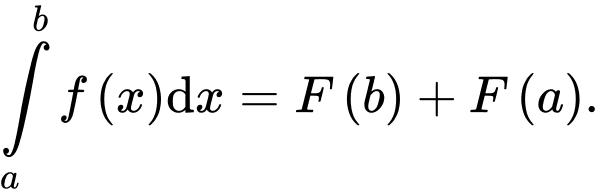
Chọn đáp án A.
Theo định nghĩa tích phân, ta có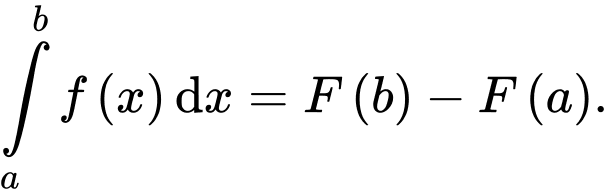 Đáp án: A
Đáp án: A
Theo định nghĩa tích phân, ta có
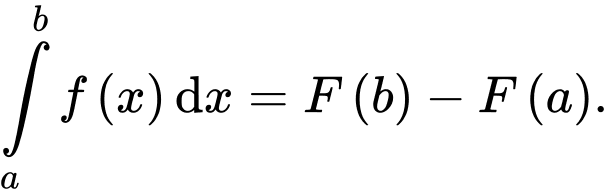 Đáp án: A
Đáp án: A
Câu 2 [395567]: Nếu 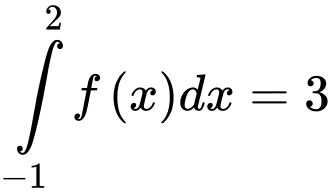 thì
thì 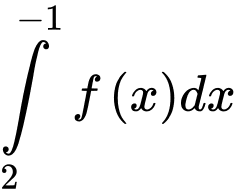 bằng
bằng
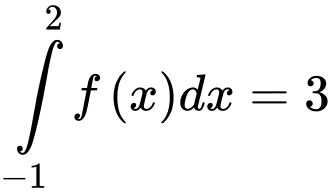 thì
thì 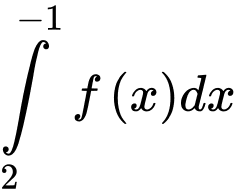 bằng
bằng A, 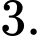
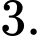
B, 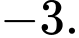
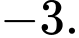
C, 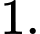
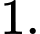
D, 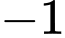
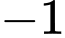
Chọn đáp án B
Ta có: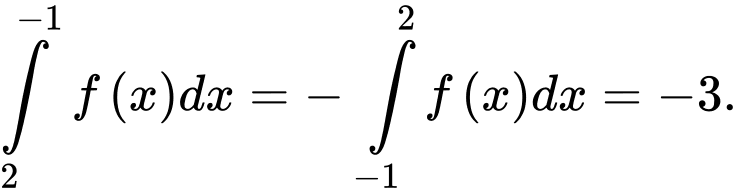 Đáp án: B
Đáp án: B
Ta có:
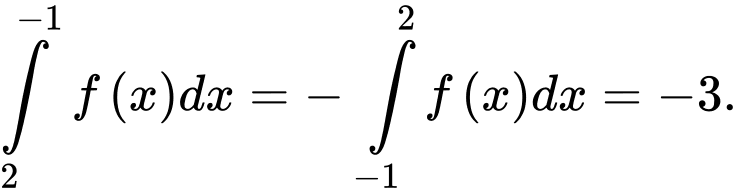 Đáp án: B
Đáp án: B
Câu 3 [542412]: Giá trị của 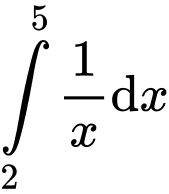 bằng
bằng
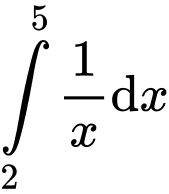 bằng
bằng A, 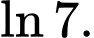
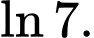
B, 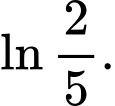
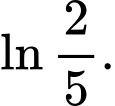
C, 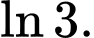
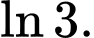
D, 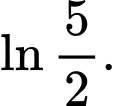
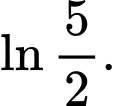
Chọn đáp án D
Ta có: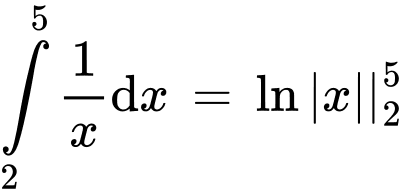
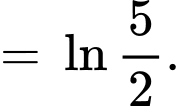 Đáp án: D
Đáp án: D
Ta có:
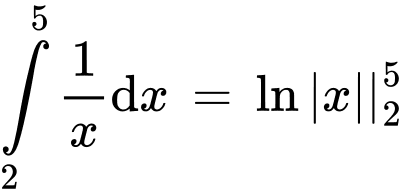
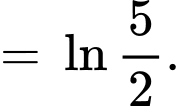 Đáp án: D
Đáp án: D
Câu 4 [547049]: Biết 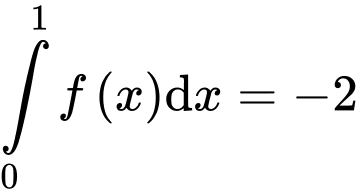 và
và 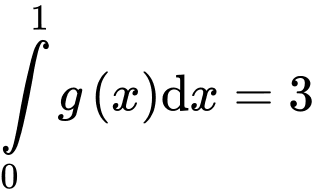 . Khi đó
. Khi đó 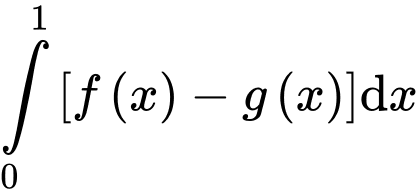 bằng
bằng
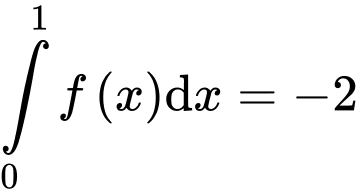 và
và 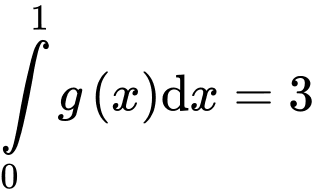 . Khi đó
. Khi đó 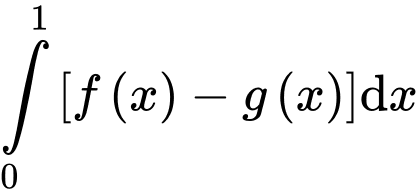 bằng
bằng A, 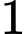 .
.
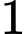 .
.B, 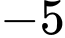 .
.
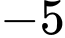 .
.C, 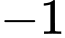 .
.
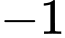 .
.D, 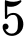 .
.
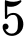 .
.
Chọn đáp án B.
Ta có:
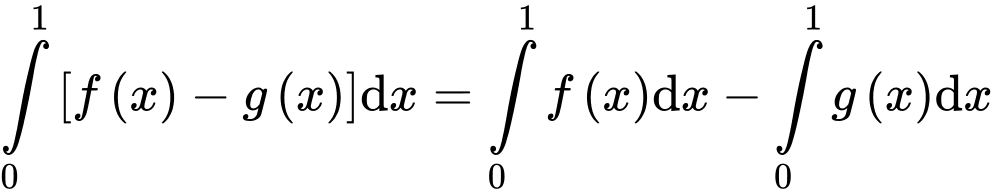
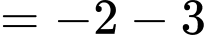
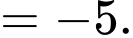 Đáp án: B
Đáp án: B
Ta có:
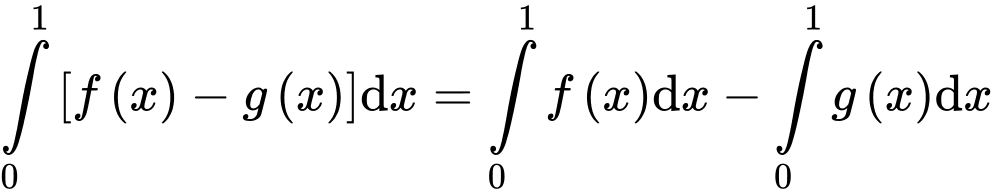
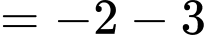
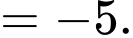 Đáp án: B
Đáp án: B
Câu 5 [149140]: Cho hàm số 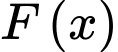 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 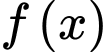 trên đoạn
trên đoạn 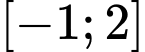 . Biết
. Biết 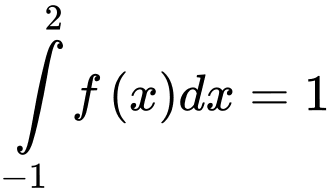 và
và 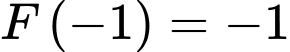 . Tính
. Tính 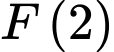 .
.
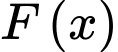 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 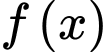 trên đoạn
trên đoạn 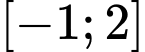 . Biết
. Biết 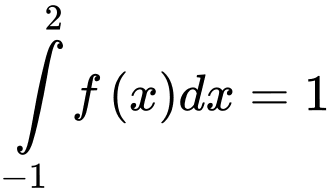 và
và 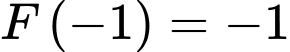 . Tính
. Tính 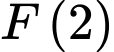 .
. A, 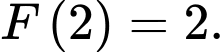
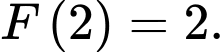
B, 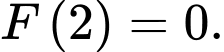
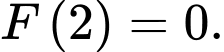
C, 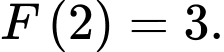
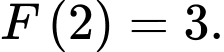
D, 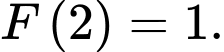
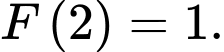
Chọn đáp án B.
Theo định nghĩa tích phân: Nếu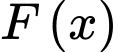 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 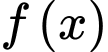 trên đoạn
trên đoạn 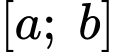 thì
thì 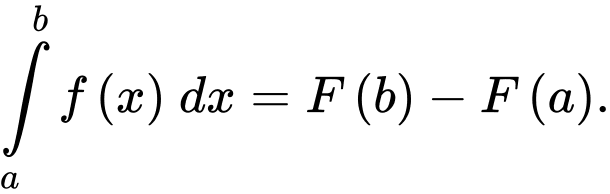
Áp dụng định nghĩa trên, ta có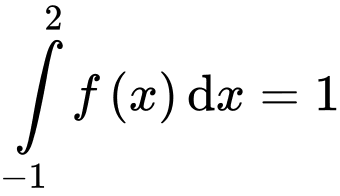
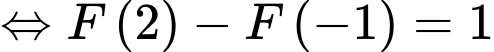
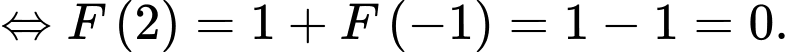
Đáp án: B
Theo định nghĩa tích phân: Nếu
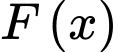 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 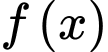 trên đoạn
trên đoạn 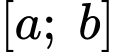 thì
thì 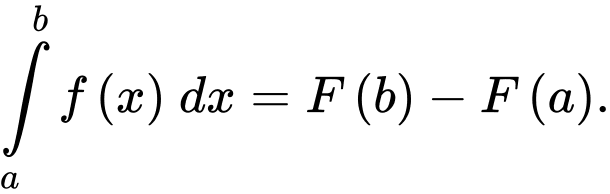
Áp dụng định nghĩa trên, ta có
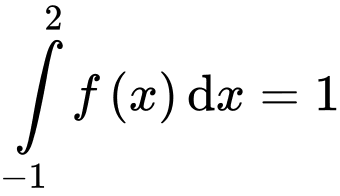
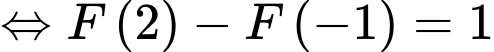
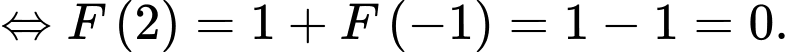
Đáp án: B
Câu 6 [360303]: Biết 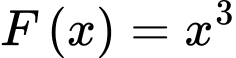 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 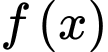 trên
trên 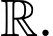 Giá trị của
Giá trị của 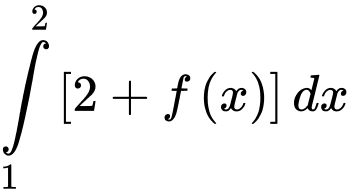 bằng:
bằng:
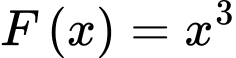 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 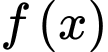 trên
trên 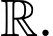 Giá trị của
Giá trị của 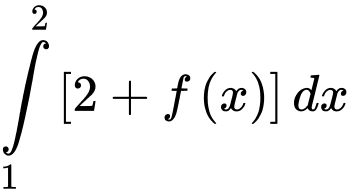 bằng:
bằng: A, 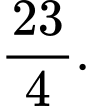
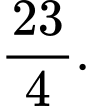
B, 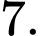
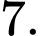
C, 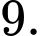
D, 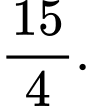
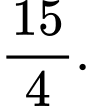
Chọn đáp án C.
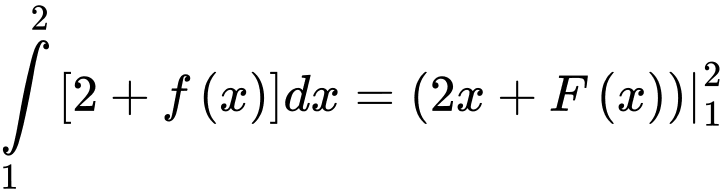
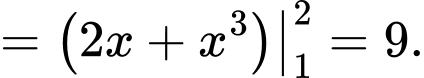
Đáp án: C
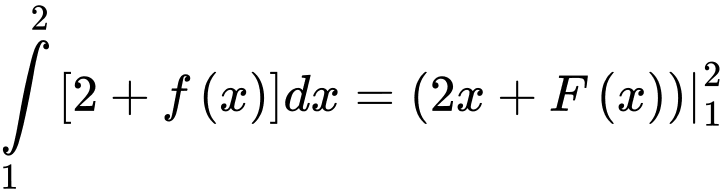
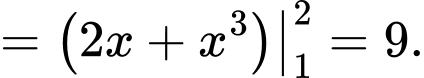
Đáp án: C
Câu 7 [543454]: Biết 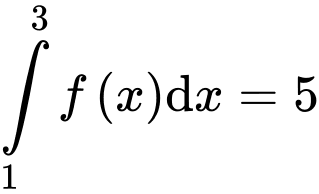 và
và 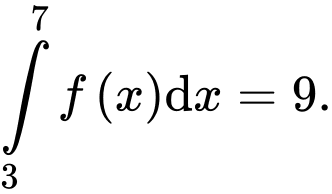 Giá trị của
Giá trị của 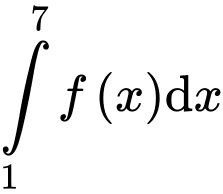 bằng
bằng
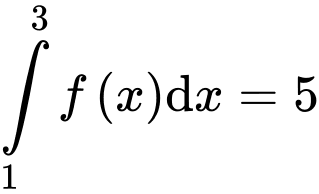 và
và 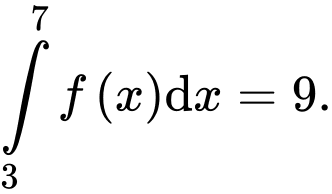 Giá trị của
Giá trị của 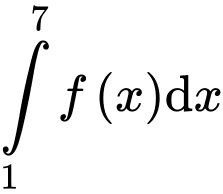 bằng
bằng A, 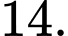
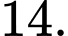
B, 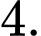
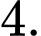
C, 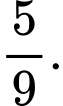
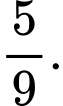
D, 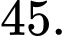
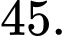
Chọn đáp án A.
Ta có: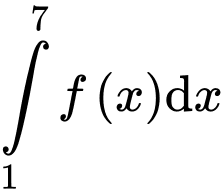
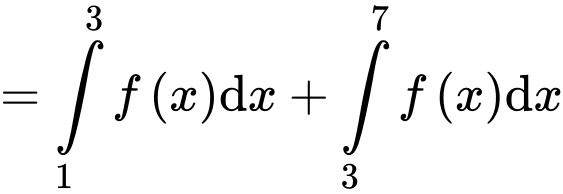
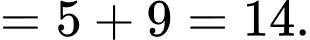 Đáp án: A
Đáp án: A
Ta có:
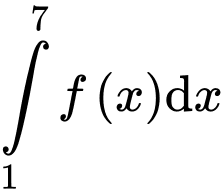
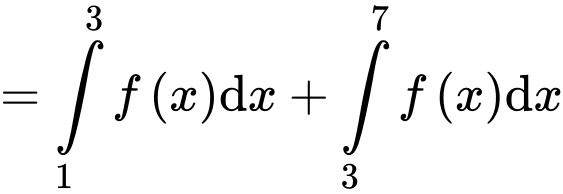
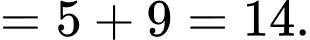 Đáp án: A
Đáp án: A
Câu 8 [543262]: Nếu 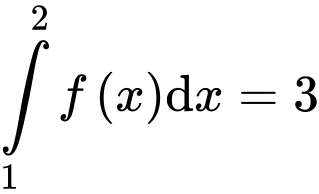 và
và 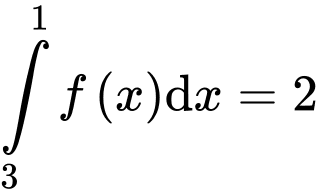 thì
thì 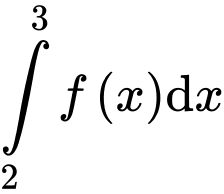 bằng
bằng
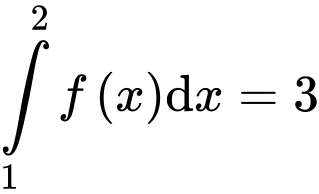 và
và 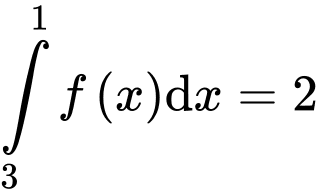 thì
thì 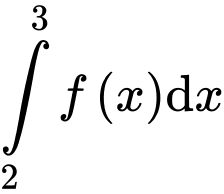 bằng
bằng A, 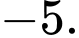
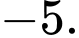
B, 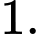
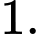
C, 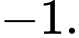
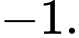
D, 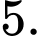
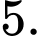
Chọn đáp án A.
Ta có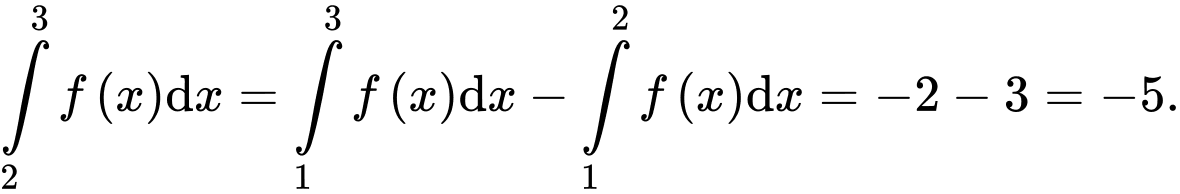 Đáp án: A
Đáp án: A
Ta có
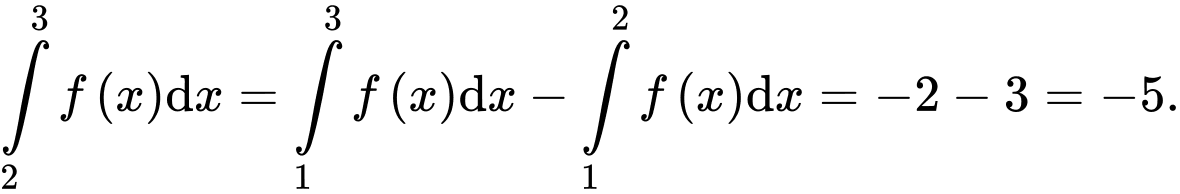 Đáp án: A
Đáp án: A
Câu 9 [146606]: Cho 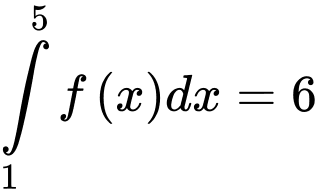 và
và 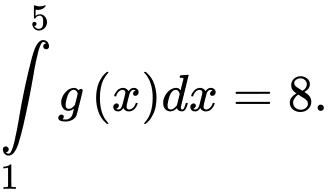 Giá trị của
Giá trị của 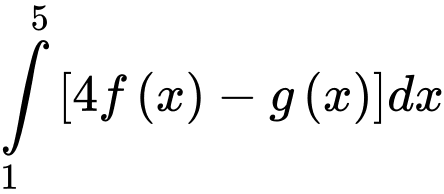 bằng
bằng
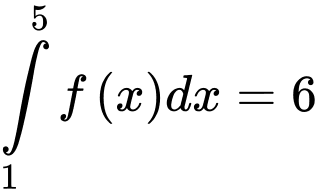 và
và 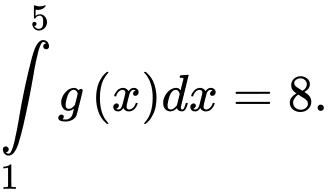 Giá trị của
Giá trị của 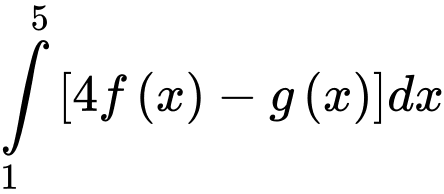 bằng
bằng A, 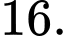
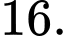
B, 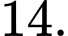
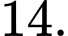
C, 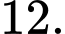
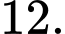
D, 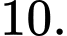
Chọn đáp án A.
Ta có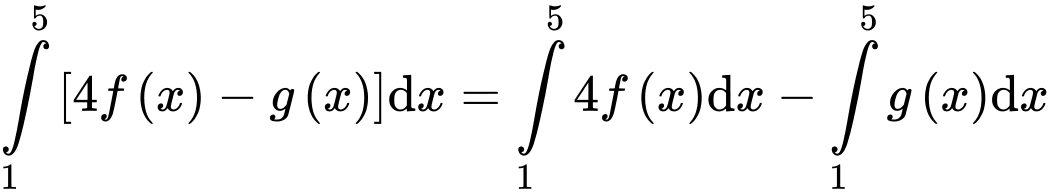 (tính chất của tích phân)
(tính chất của tích phân)
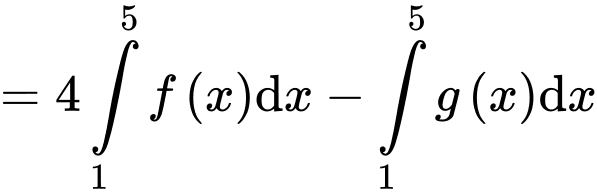
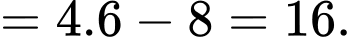 Đáp án: A
Đáp án: A
Ta có
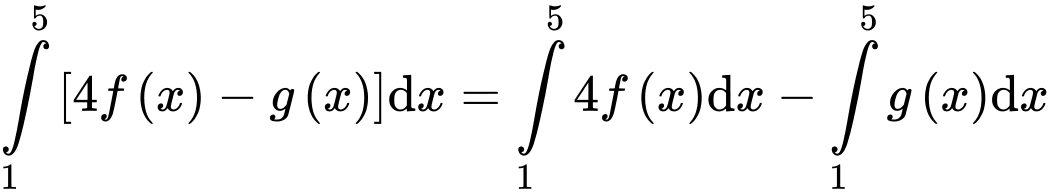 (tính chất của tích phân)
(tính chất của tích phân)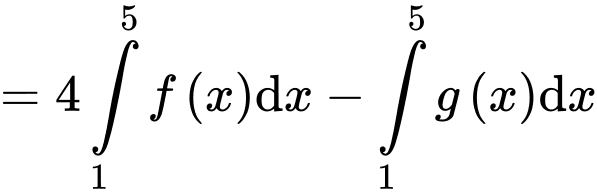
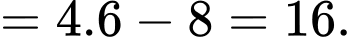 Đáp án: A
Đáp án: A
Câu 10 [149139]: Tính 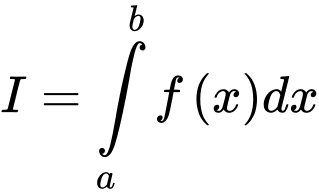 , biết
, biết 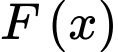 là một nguyên hàm của
là một nguyên hàm của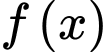 và
và 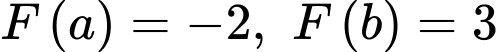 .
.
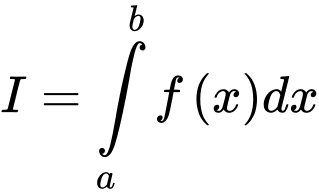 , biết
, biết 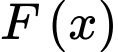 là một nguyên hàm của
là một nguyên hàm của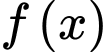 và
và 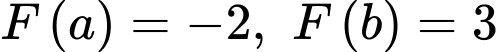 .
. A,  .
.
 .
.B, 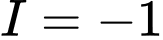 .
.
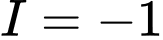 .
.C, 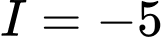 .
.
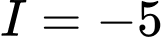 .
.D,  .
.
 .
.
Chọn đáp án D.
Theo định nghĩa tích phân, ta có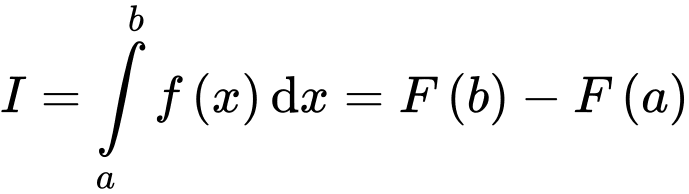
 Đáp án: D
Đáp án: D
Theo định nghĩa tích phân, ta có
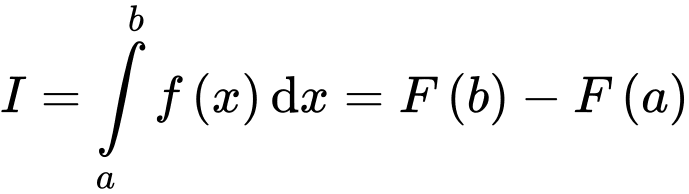
 Đáp án: D
Đáp án: D
Câu 11 [389954]: Diện tích hình thang cong được tô đậm trong hình vẽ bên bằng: 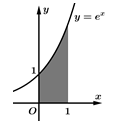

A, 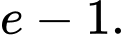
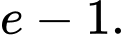
B, 

C, 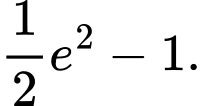
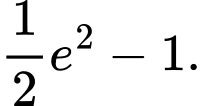
D, 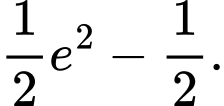
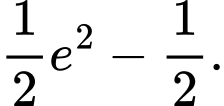
Chọn đáp án A.
Diện tích hình tô đậm là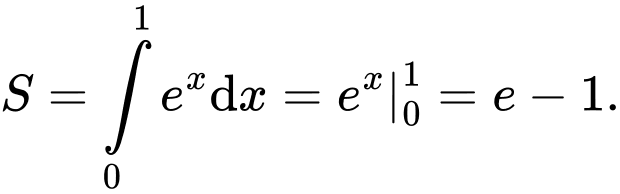
Đáp án: A
Diện tích hình tô đậm là
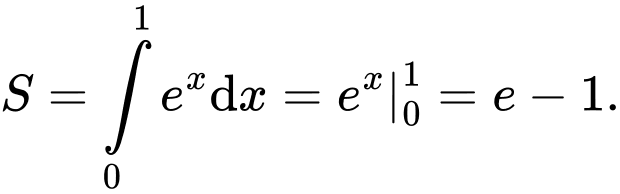
Đáp án: A
Câu 12 [543820]: Cho hàm số 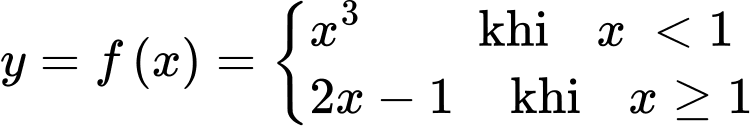 Khi đó
Khi đó 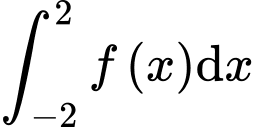 bằng
bằng
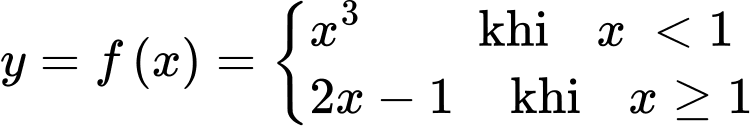 Khi đó
Khi đó 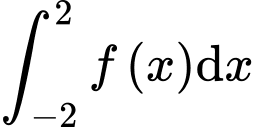 bằng
bằng A, 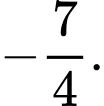
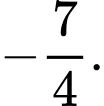
B, 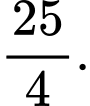
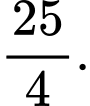
C, 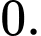
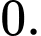
D, 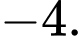
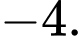
Chọn đáp án A.
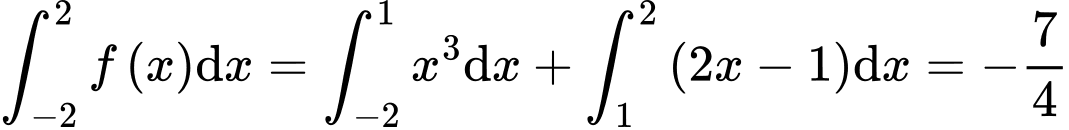 . Đáp án: A
. Đáp án: A
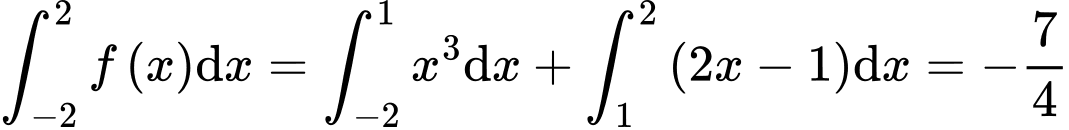 . Đáp án: A
. Đáp án: A PHẦN II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a),b),c),d) ở mỗi câu học sinh chọn đúng hoặc sai.
Câu 13 [775963]: Cho hàm số 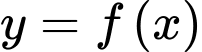 liên tục trên
liên tục trên 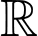 thoả mãn
thoả mãn 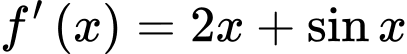 và
và 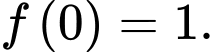
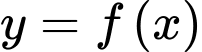 liên tục trên
liên tục trên 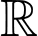 thoả mãn
thoả mãn 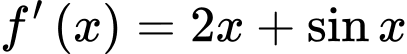 và
và 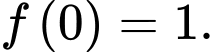
a) Sai.
Ta có: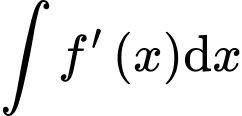
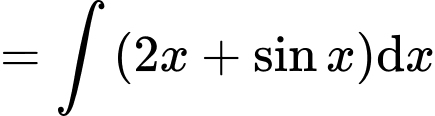
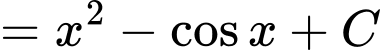 với
với  là hằng số.
là hằng số.
b) Sai.
Ta có: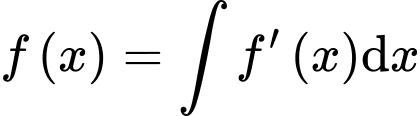
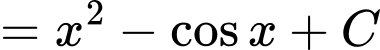
Biết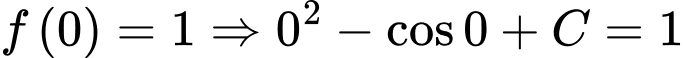
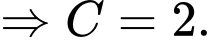
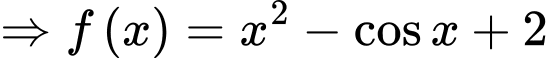
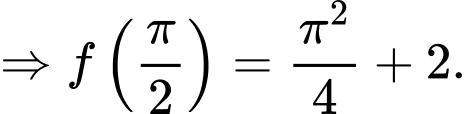
c) Sai.
Vì nếu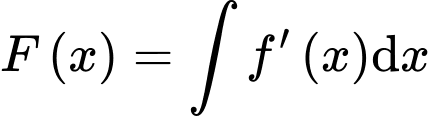 là một nguyên hàm của
là một nguyên hàm của 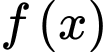 thì ta có
thì ta có 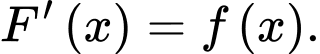 Và ta sẽ áp dụng tính chất này để xác định xem
Và ta sẽ áp dụng tính chất này để xác định xem 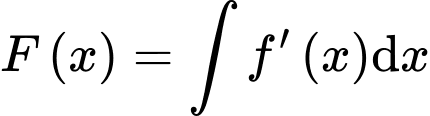 có là một nguyên hàm của
có là một nguyên hàm của 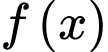 hay không.
hay không.
Ta có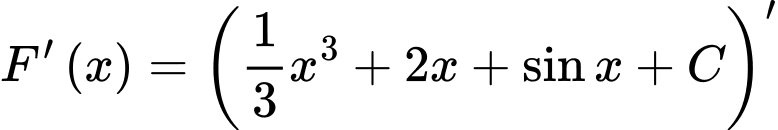
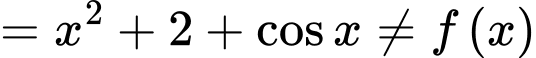
Nên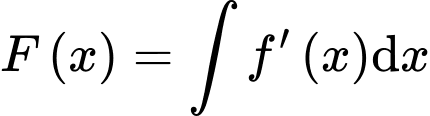 không là nguyên hàm của
không là nguyên hàm của 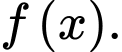
d) Đúng.
Ta có: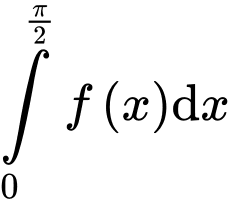
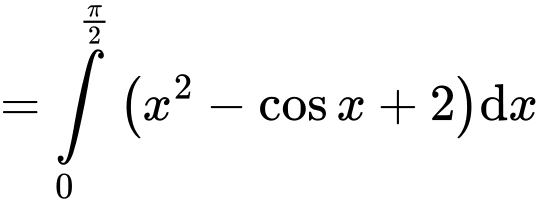
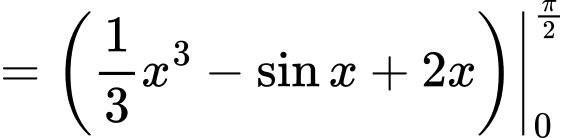
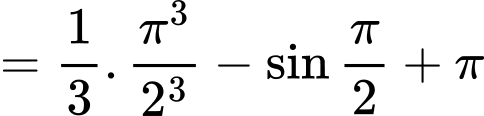
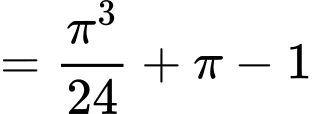
Do đó,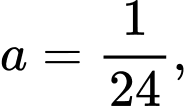
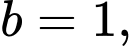
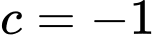
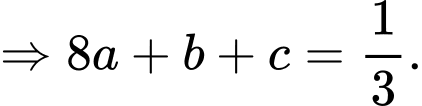
Ta có:
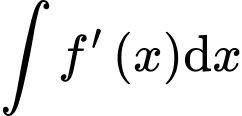
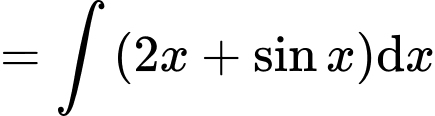
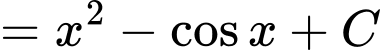 với
với  là hằng số.
là hằng số.
b) Sai.
Ta có:
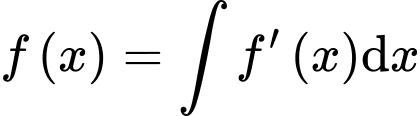
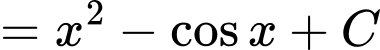
Biết
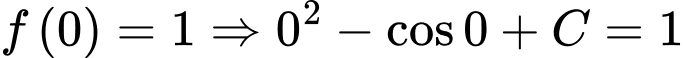
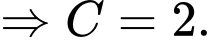
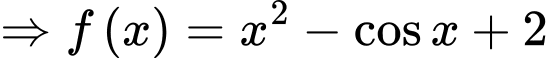
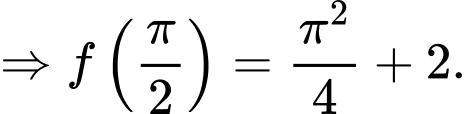
c) Sai.
Vì nếu
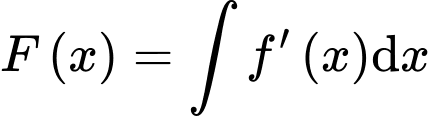 là một nguyên hàm của
là một nguyên hàm của 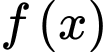 thì ta có
thì ta có 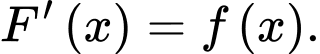 Và ta sẽ áp dụng tính chất này để xác định xem
Và ta sẽ áp dụng tính chất này để xác định xem 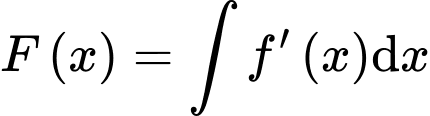 có là một nguyên hàm của
có là một nguyên hàm của 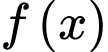 hay không.
hay không.
Ta có
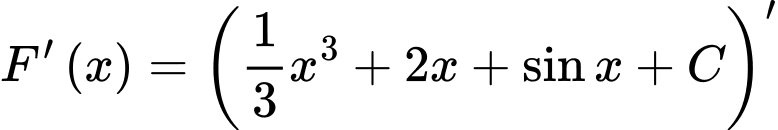
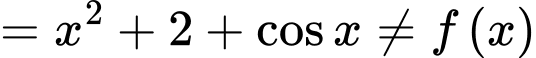
Nên
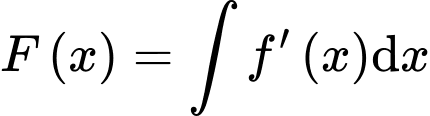 không là nguyên hàm của
không là nguyên hàm của 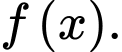
d) Đúng.
Ta có:
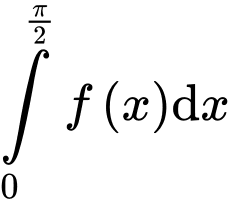
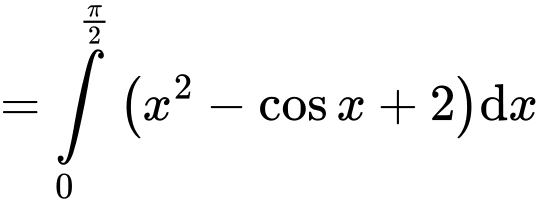
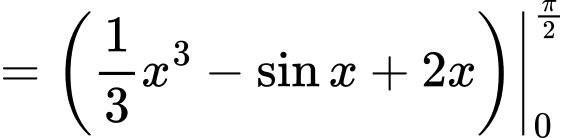
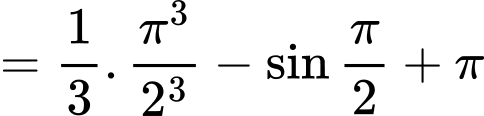
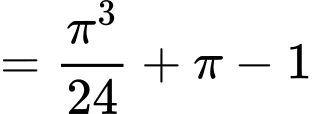
Do đó,
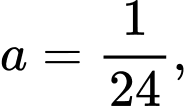
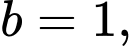
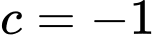
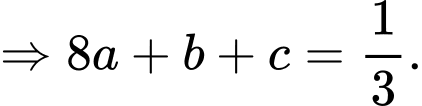
Câu 14 [775964]: Sau khi xuất phát, một vật chuyển động trong 10 giây đầu tiên với tốc độ 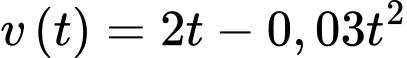
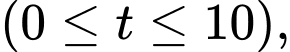 trong đó
trong đó 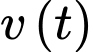 tính bằng
tính bằng 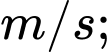 thời gian
thời gian 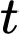 tính bằng giây với
tính bằng giây với 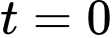 là thời điểm xe xuất phát.
là thời điểm xe xuất phát.
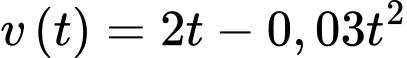
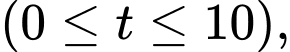 trong đó
trong đó 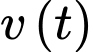 tính bằng
tính bằng 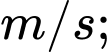 thời gian
thời gian 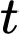 tính bằng giây với
tính bằng giây với 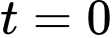 là thời điểm xe xuất phát.
là thời điểm xe xuất phát.
a) Đúng.
Vận tốc của vật tại thời điểm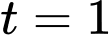 giây là
giây là 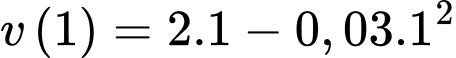
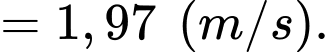
b) Sai.
Quãng đường vật di chuyển được theo thời gian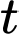 là
là
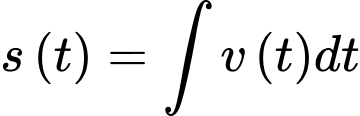
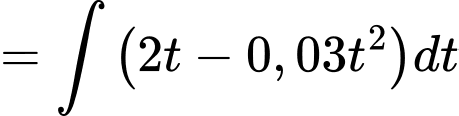
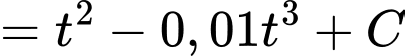 với
với  là hằng số.
là hằng số.
c) Đúng.
Quãng đường vật đi được từ thời điểm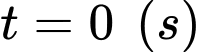 đến thời điểm
đến thời điểm 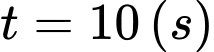 là
là
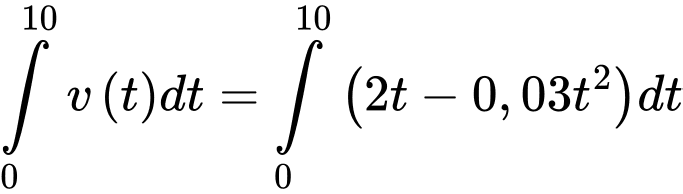
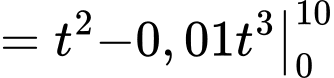
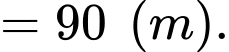
d) Đúng.
Tốc độ trung bình của vật trong khoảng 10 giây đầu tiên bằng
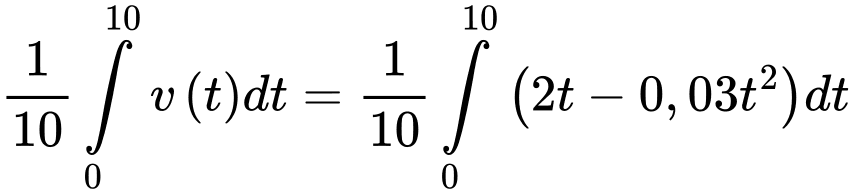
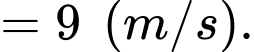
Vận tốc của vật tại thời điểm
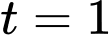 giây là
giây là 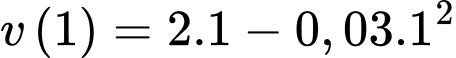
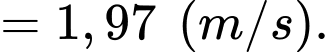
b) Sai.
Quãng đường vật di chuyển được theo thời gian
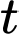 là
là
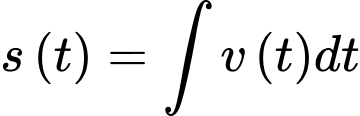
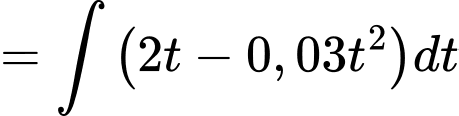
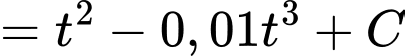 với
với  là hằng số.
là hằng số.
c) Đúng.
Quãng đường vật đi được từ thời điểm
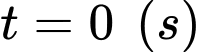 đến thời điểm
đến thời điểm 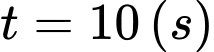 là
là
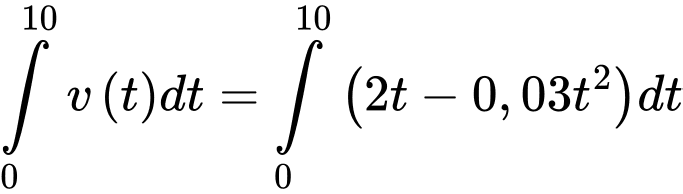
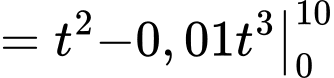
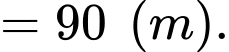
d) Đúng.
Tốc độ trung bình của vật trong khoảng 10 giây đầu tiên bằng
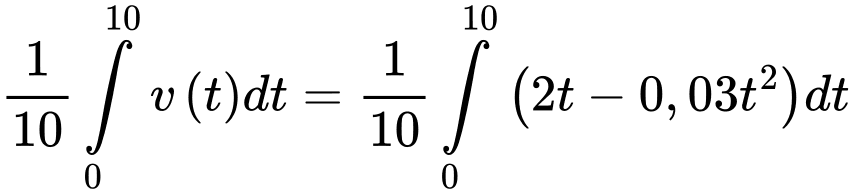
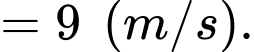
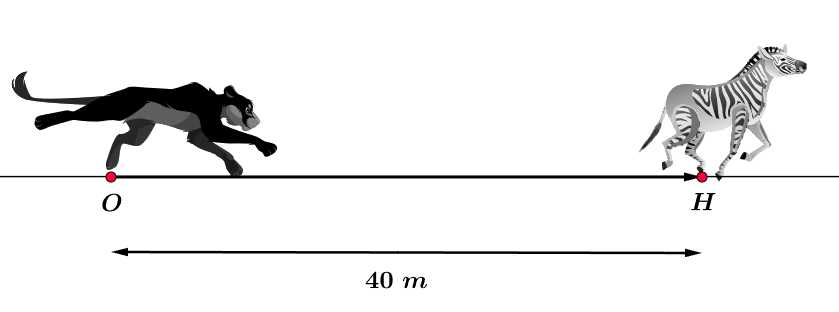
Câu 15 [702909]: Một con sư tử đang đuổi theo một con ngựa vằn. Con ngựa vằn nhận ra con sư tử khi con sư tử cách xa nó 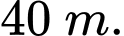 Từ thời điểm này, con sư tử đuổi con ngựa vằn với tốc độ
Từ thời điểm này, con sư tử đuổi con ngựa vằn với tốc độ 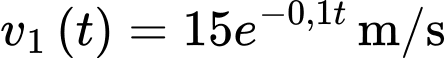 và con ngựa vằn chạy trốn với tốc độ
và con ngựa vằn chạy trốn với tốc độ 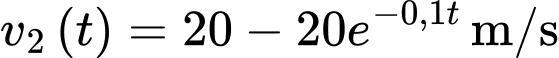 trên cùng một đường thẳng (với
trên cùng một đường thẳng (với 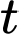 tính theo giây và
tính theo giây và 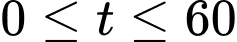 ).
).

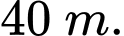 Từ thời điểm này, con sư tử đuổi con ngựa vằn với tốc độ
Từ thời điểm này, con sư tử đuổi con ngựa vằn với tốc độ 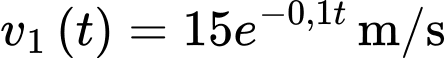 và con ngựa vằn chạy trốn với tốc độ
và con ngựa vằn chạy trốn với tốc độ 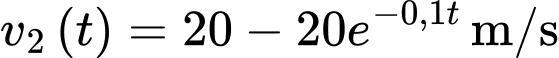 trên cùng một đường thẳng (với
trên cùng một đường thẳng (với 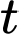 tính theo giây và
tính theo giây và 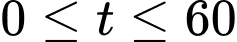 ).
).
a) Sai.
Tại thời điểm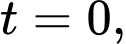 vận tốc của con ngựa vằn là
vận tốc của con ngựa vằn là 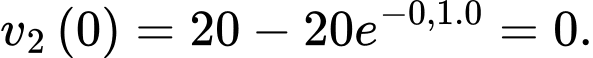
b) Đúng.
+) Ta có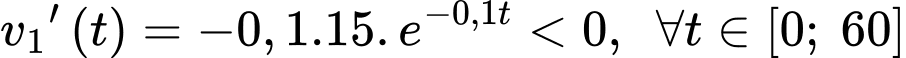
Suy ra tốc độ của sư tử giảm dần theo thời gian.
+) Ta có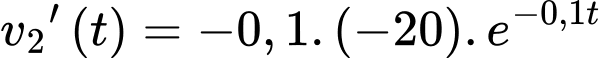
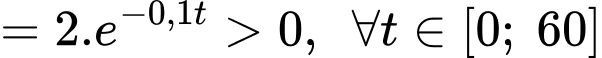
Suy ra tốc độ của ngựa vằn tăng dần theo thời gian.
Vậy tốc độ của sư tử giảm dần theo thời gian, trong khi tốc độ của ngựa vằn tăng dần theo thời gian.
c) Sai.
Vì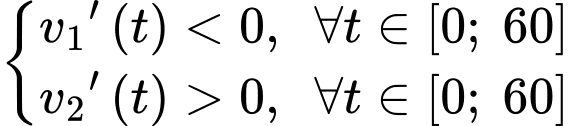
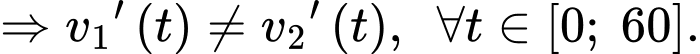
d) Sai.
Gọi quãng đường chạy được của sư tử và ngựa vằn lần lượt là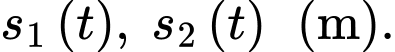
+) Ta có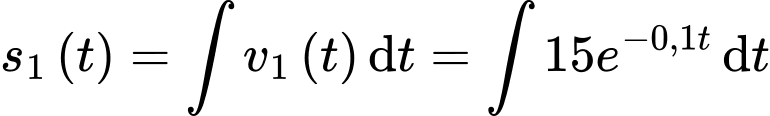
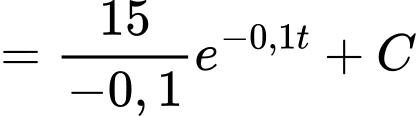
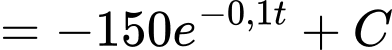
Coi điểm là vị trí xuất phát ban đầu, ta có tại thời điểm xuất phát
là vị trí xuất phát ban đầu, ta có tại thời điểm xuất phát 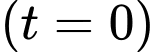 quãng đường mà sư tử chạy được bằng 0
quãng đường mà sư tử chạy được bằng 0
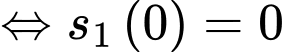
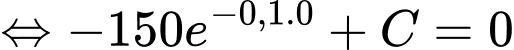
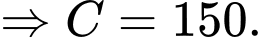
Vậy
+) Ta có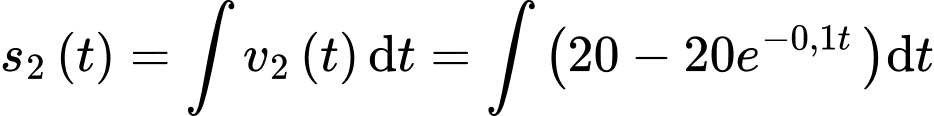
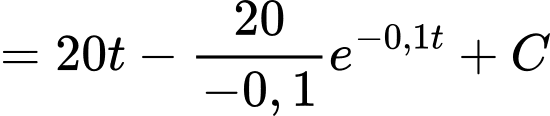
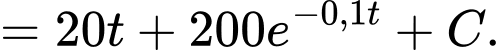
So với vị trí xuất phát ban đầu tại thời điểm
tại thời điểm 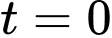 ngựa vằn chạy được quãng đường là
ngựa vằn chạy được quãng đường là 

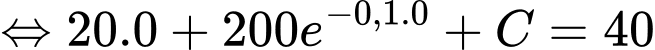
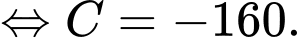
Vậy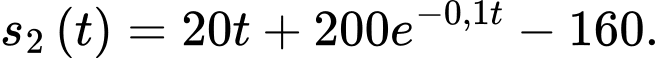
Suy ra khoảng cách giữa sư tử và ngựa vằn là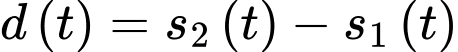
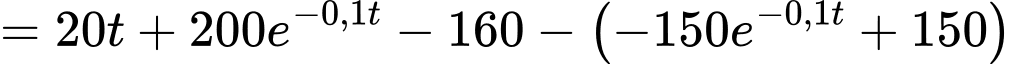
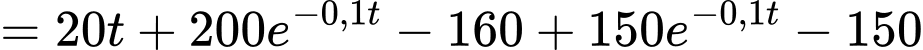

*) Xét hàm số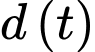 trên đoạn
trên đoạn 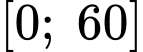
Ta có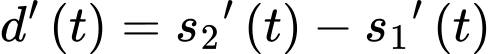
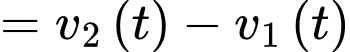
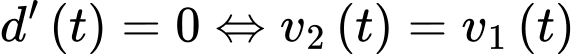
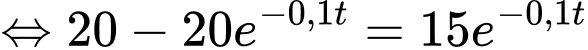
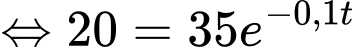
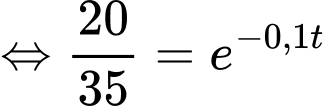
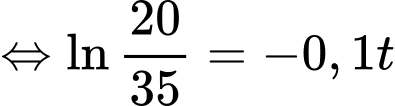
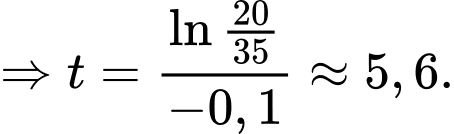
Bảng biến thiên
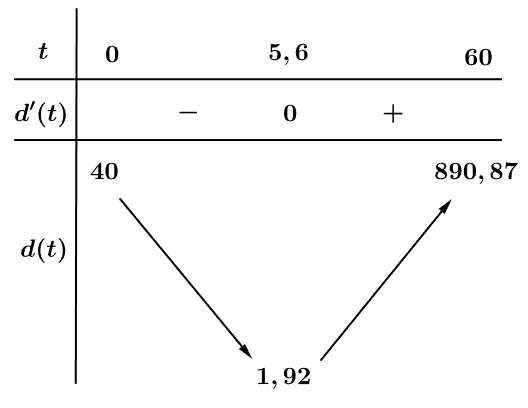
Vậy sư tử ở gần ngữa vằn nhất khi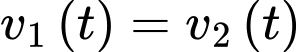 và khoảng cách ngắn nhất giữa chúng là 1,92 mét.
và khoảng cách ngắn nhất giữa chúng là 1,92 mét.
Tại thời điểm
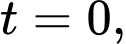 vận tốc của con ngựa vằn là
vận tốc của con ngựa vằn là 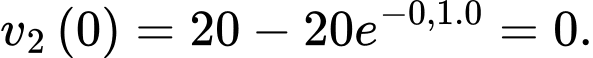
b) Đúng.
+) Ta có
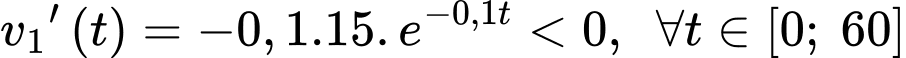
Suy ra tốc độ của sư tử giảm dần theo thời gian.
+) Ta có
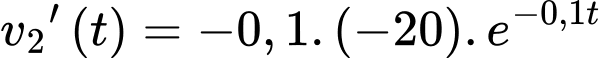
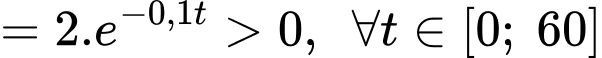
Suy ra tốc độ của ngựa vằn tăng dần theo thời gian.
Vậy tốc độ của sư tử giảm dần theo thời gian, trong khi tốc độ của ngựa vằn tăng dần theo thời gian.
c) Sai.
Vì
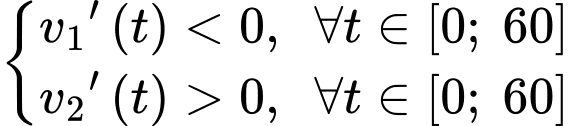
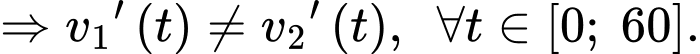
d) Sai.
Gọi quãng đường chạy được của sư tử và ngựa vằn lần lượt là
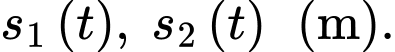

+) Ta có
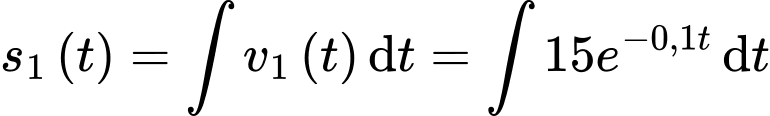
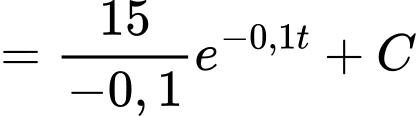
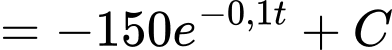
Coi điểm
 là vị trí xuất phát ban đầu, ta có tại thời điểm xuất phát
là vị trí xuất phát ban đầu, ta có tại thời điểm xuất phát 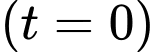 quãng đường mà sư tử chạy được bằng 0
quãng đường mà sư tử chạy được bằng 0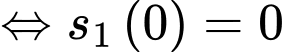
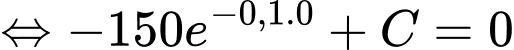
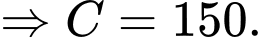
Vậy

+) Ta có
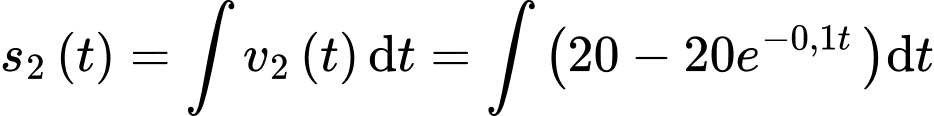
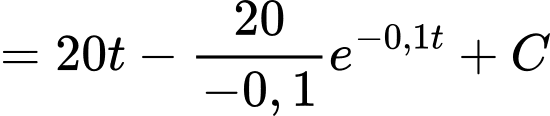
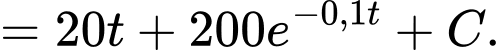
So với vị trí xuất phát ban đầu
 tại thời điểm
tại thời điểm 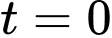 ngựa vằn chạy được quãng đường là
ngựa vằn chạy được quãng đường là 

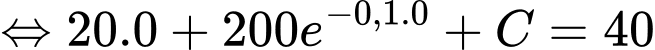
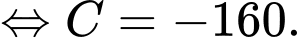
Vậy
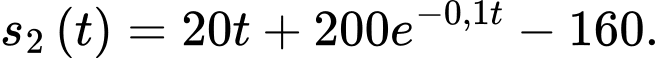
Suy ra khoảng cách giữa sư tử và ngựa vằn là
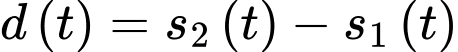
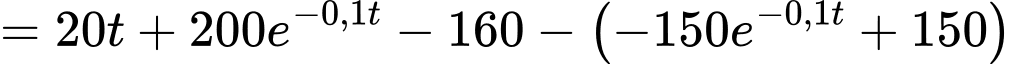
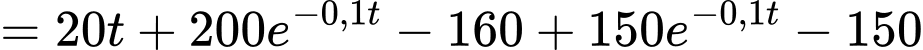

*) Xét hàm số
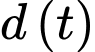 trên đoạn
trên đoạn 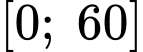
Ta có
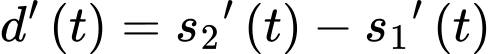
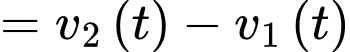
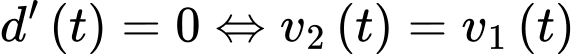
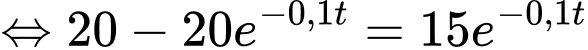
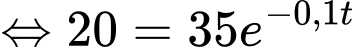
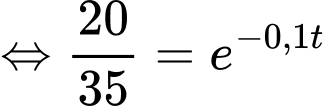
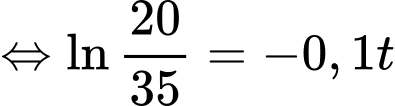
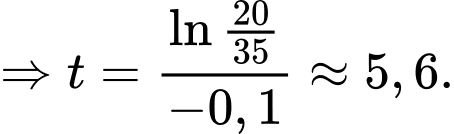
Bảng biến thiên

Vậy sư tử ở gần ngữa vằn nhất khi
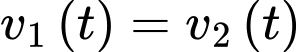 và khoảng cách ngắn nhất giữa chúng là 1,92 mét.
và khoảng cách ngắn nhất giữa chúng là 1,92 mét.
Câu 16 [703158]: Hệ thống lọc nước bể bơi vô cùng quan trọng để nguồn nước được làm sạch thường xuyên và giữ vệ sinh cho người bơi. Trong quá trình vận hành lọc nước thì lượng nước trong bể sẽ thay đổi theo thời gian. Lượng nước trong bể giảm nếu hệ thống đang xả nước bẩn ra khỏi bể và tăng nếu hệ thống đang cấp thêm nước sạch cho bể. Biết rằng 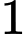 gallon gần bằng
gallon gần bằng 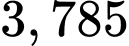 lít, dung tích của bể là
lít, dung tích của bể là 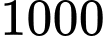 gallon và thời điểm
gallon và thời điểm 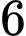 giờ sáng bể chứa
giờ sáng bể chứa 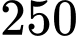 gallon nước. Hàm số
gallon nước. Hàm số 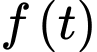 liên tục trên đoạn
liên tục trên đoạn 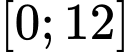 biểu thị cho tốc độ thay đổi lượng nước trong bể theo thời gian
biểu thị cho tốc độ thay đổi lượng nước trong bể theo thời gian 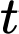 giờ, từ thời điểm
giờ, từ thời điểm 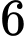 giờ sáng đến
giờ sáng đến 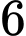 giờ chiều được cho bởi hàm số
giờ chiều được cho bởi hàm số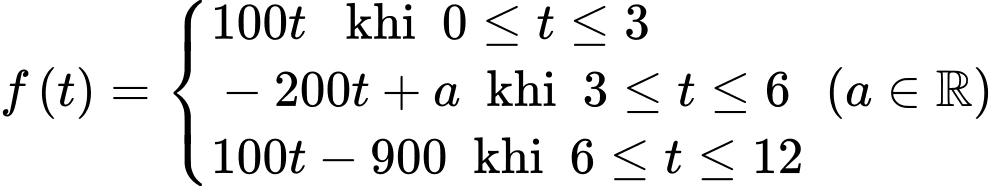 với mốc thời gian
với mốc thời gian 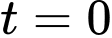 tại thời điểm
tại thời điểm 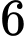 giờ sáng.
giờ sáng.
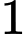 gallon gần bằng
gallon gần bằng 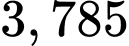 lít, dung tích của bể là
lít, dung tích của bể là 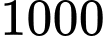 gallon và thời điểm
gallon và thời điểm 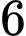 giờ sáng bể chứa
giờ sáng bể chứa 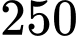 gallon nước. Hàm số
gallon nước. Hàm số 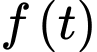 liên tục trên đoạn
liên tục trên đoạn 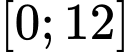 biểu thị cho tốc độ thay đổi lượng nước trong bể theo thời gian
biểu thị cho tốc độ thay đổi lượng nước trong bể theo thời gian 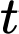 giờ, từ thời điểm
giờ, từ thời điểm  giờ sáng đến
giờ sáng đến  giờ chiều được cho bởi hàm số
giờ chiều được cho bởi hàm số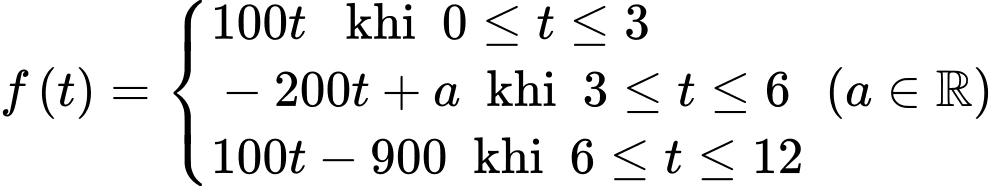 với mốc thời gian
với mốc thời gian 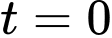 tại thời điểm
tại thời điểm 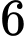 giờ sáng.
giờ sáng.
a) Sai.
Do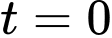 tại thời điểm
tại thời điểm 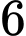 giờ sáng nên tại thời điểm
giờ sáng nên tại thời điểm 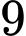 giờ sáng thì
giờ sáng thì 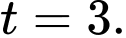
Ta có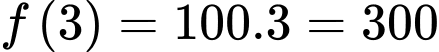 gallon/giờ.
gallon/giờ.
b) Đúng.
Với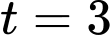 ,
, 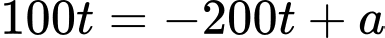

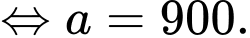
c) Sai.
Tại giờ trưa (tương đương
giờ trưa (tương đương 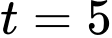 ), tốc độ thay đổi lượng nước trong bể là
), tốc độ thay đổi lượng nước trong bể là
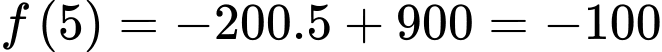 gallon/giờ.
gallon/giờ.
Tại giờ chiều (tương đương
giờ chiều (tương đương 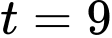 ), tốc độ thay đổi lượng nước trong bể là
), tốc độ thay đổi lượng nước trong bể là
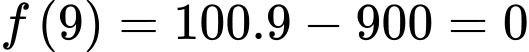 gallon/giờ.
gallon/giờ.
d) Sai.
Từ giờ sáng đến giờ chiều tức là
giờ chiều tức là 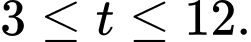
Từ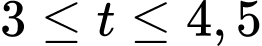 lượng nước đang tăng
lượng nước đang tăng
Lượng nước trong bể bắt đầu giảm từ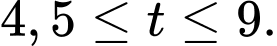
Lượng nước trong bể bắt đầu tăng trở lại từ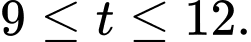
Lượng nước trong bể từ giờ chiều đến
giờ chiều đến  giờ chiều là
giờ chiều là
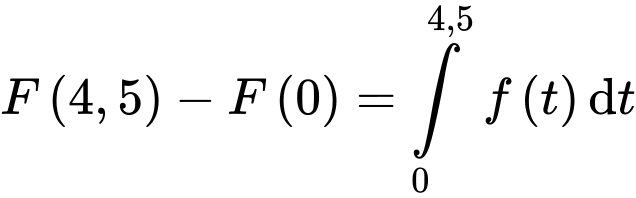
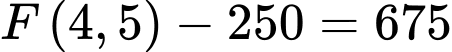
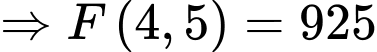 (gallon).
(gallon).
Lại có: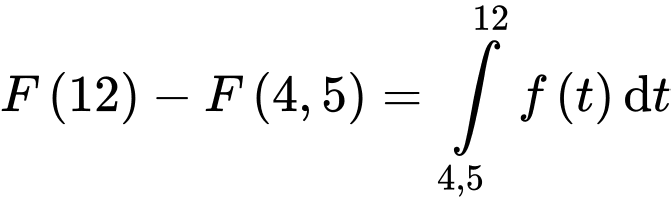
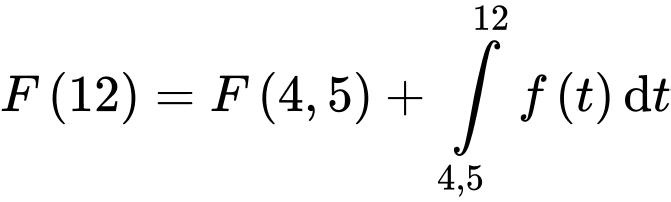
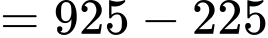
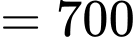 (gallon).
(gallon).
Do
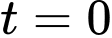 tại thời điểm
tại thời điểm 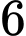 giờ sáng nên tại thời điểm
giờ sáng nên tại thời điểm 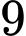 giờ sáng thì
giờ sáng thì 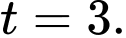
Ta có
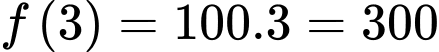 gallon/giờ.
gallon/giờ.b) Đúng.
Với
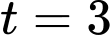 ,
, 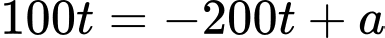

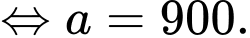
c) Sai.
Tại
 giờ trưa (tương đương
giờ trưa (tương đương 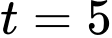 ), tốc độ thay đổi lượng nước trong bể là
), tốc độ thay đổi lượng nước trong bể là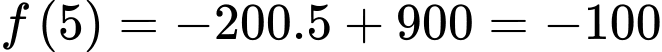 gallon/giờ.
gallon/giờ.Tại
 giờ chiều (tương đương
giờ chiều (tương đương 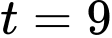 ), tốc độ thay đổi lượng nước trong bể là
), tốc độ thay đổi lượng nước trong bể là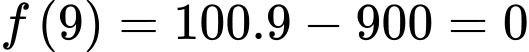 gallon/giờ.
gallon/giờ.d) Sai.
Từ giờ sáng đến
 giờ chiều tức là
giờ chiều tức là 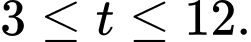
Từ
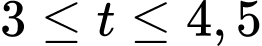 lượng nước đang tăng
lượng nước đang tăng Lượng nước trong bể bắt đầu giảm từ
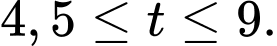
Lượng nước trong bể bắt đầu tăng trở lại từ
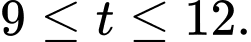
Lượng nước trong bể từ
 giờ chiều đến
giờ chiều đến  giờ chiều là
giờ chiều là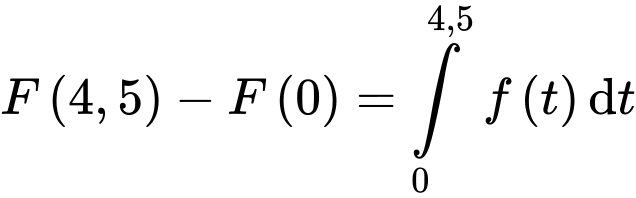
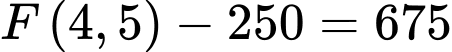
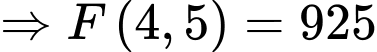 (gallon).
(gallon).Lại có:
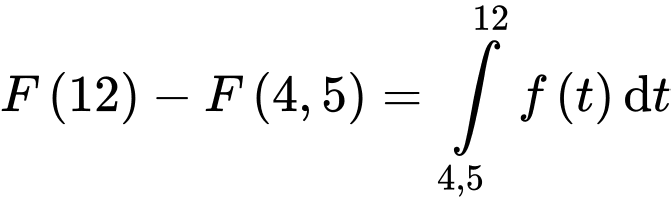
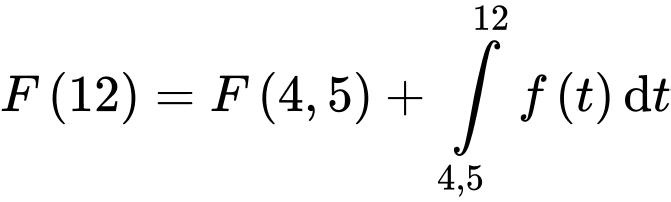
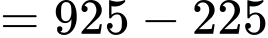
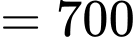 (gallon).
(gallon). PHẦN III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 17 đến câu 22.
Câu 17 [775968]: Cho hàm số 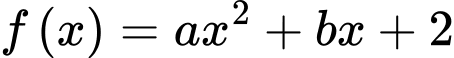 thoả mãn
thoả mãn 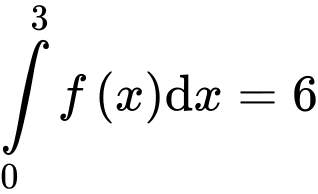 và
và 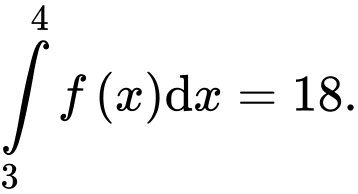 Tính giá trị của biểu thức
Tính giá trị của biểu thức 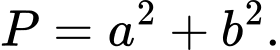
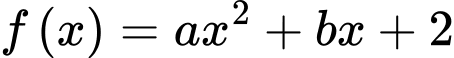 thoả mãn
thoả mãn 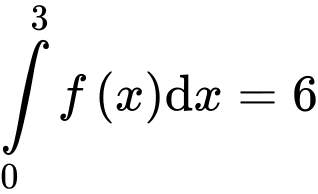 và
và 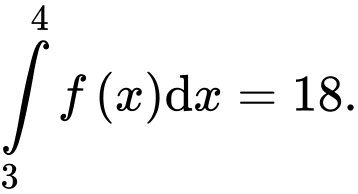 Tính giá trị của biểu thức
Tính giá trị của biểu thức 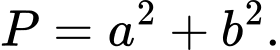
Điền đáp án: 45.
Ta có:
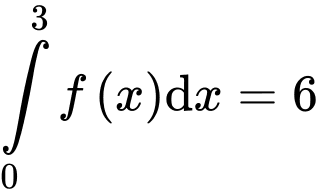
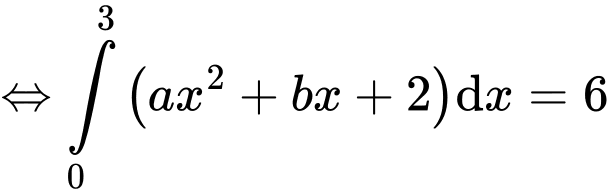
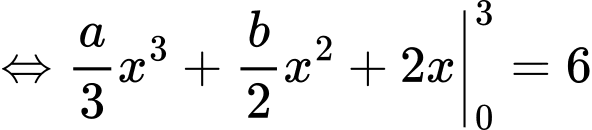
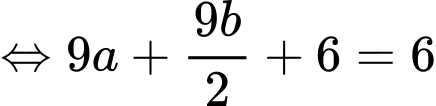
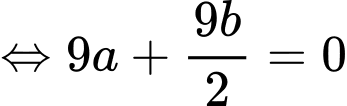
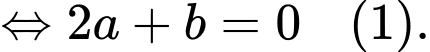
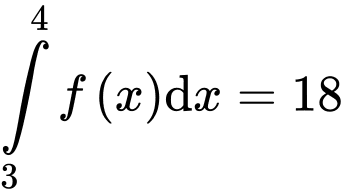
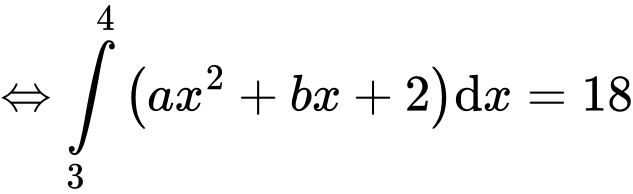
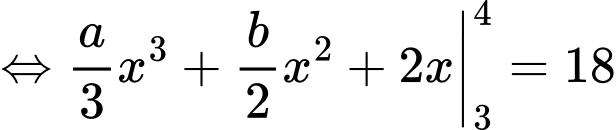
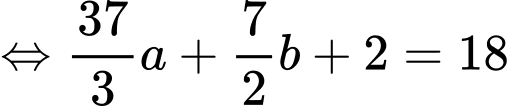
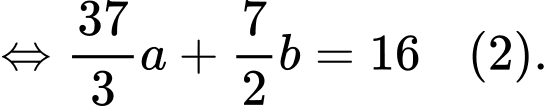
Từ (1) và (2) ta có: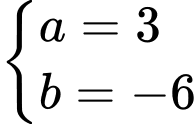
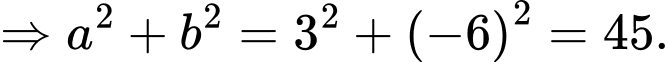
Ta có:
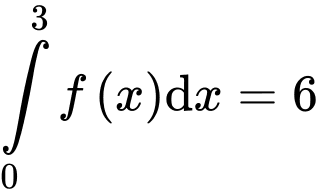
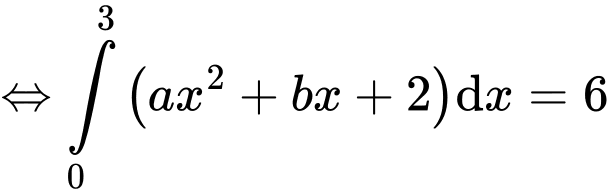
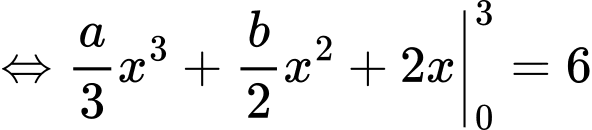
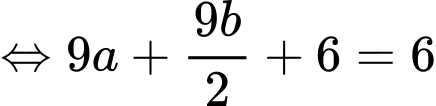
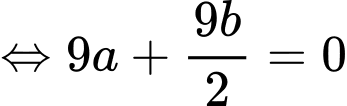
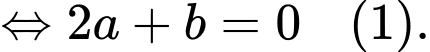
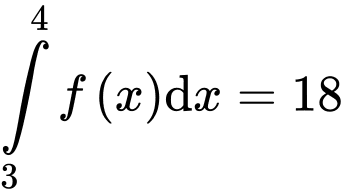
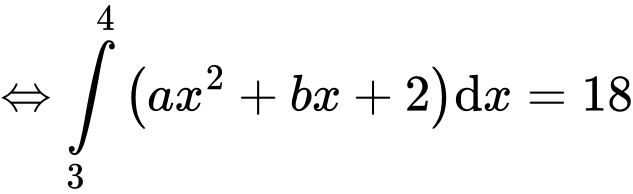
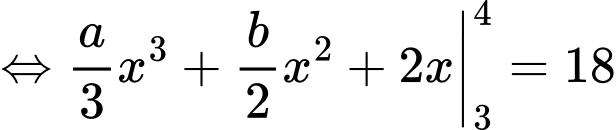
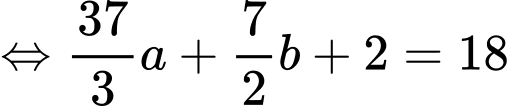
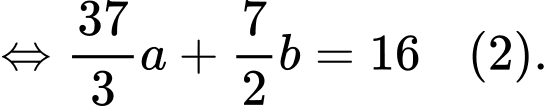
Từ (1) và (2) ta có:
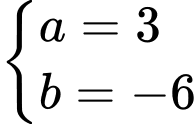
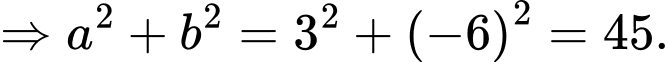
Câu 18 [775970]: Cho hàm số 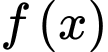 liên tục trên đoạn
liên tục trên đoạn 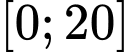 thoả mãn
thoả mãn 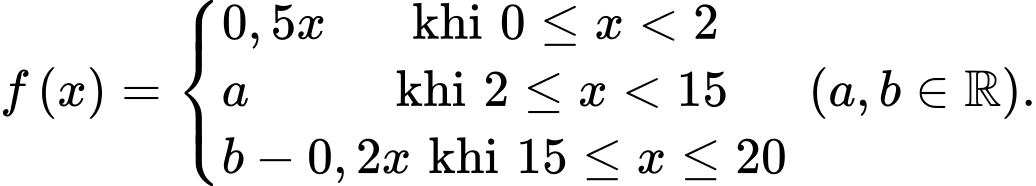 Tính tích phân
Tính tích phân 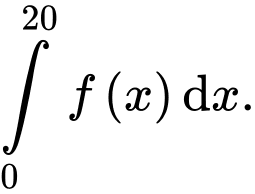
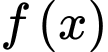 liên tục trên đoạn
liên tục trên đoạn 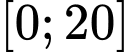 thoả mãn
thoả mãn 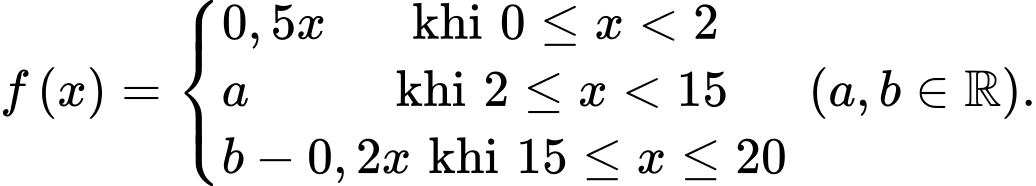 Tính tích phân
Tính tích phân 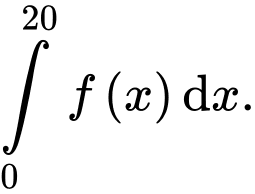
Điền đáp án: 16,5.
Ta có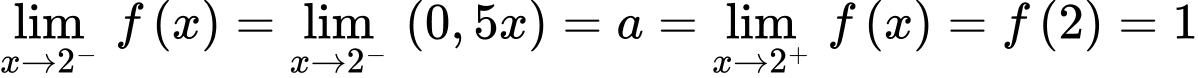 và
và
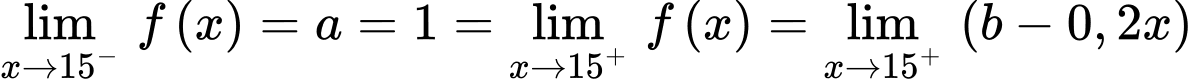
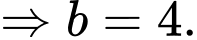
Do đó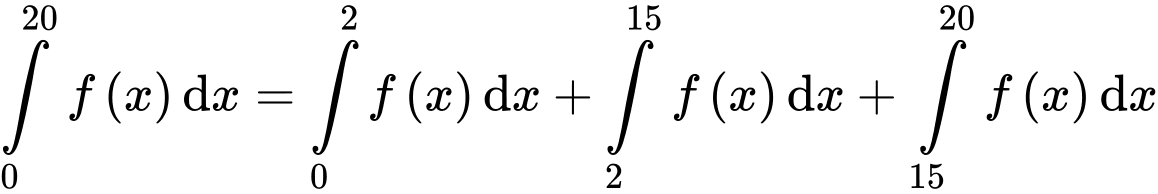
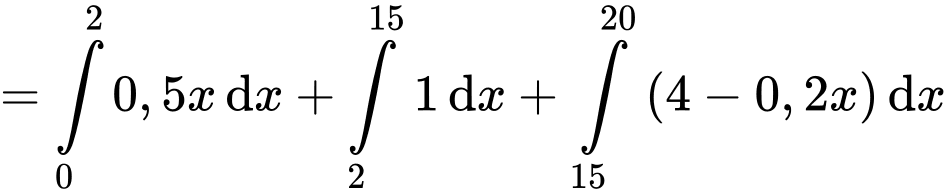
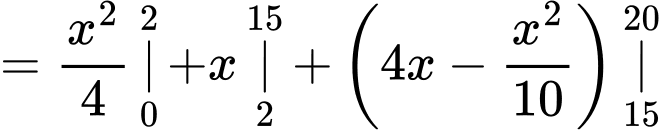
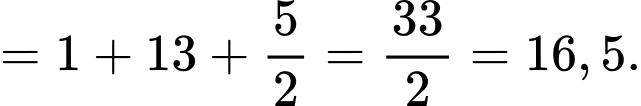
Ta có
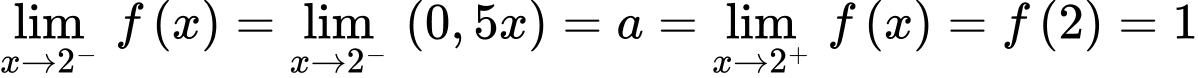 và
và
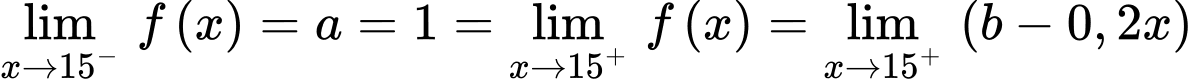
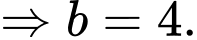
Do đó
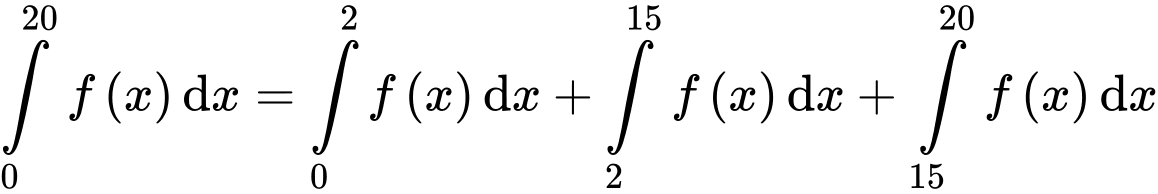
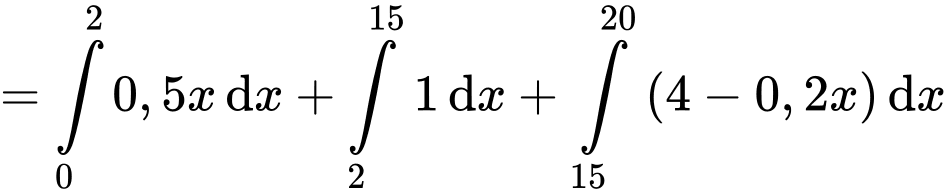
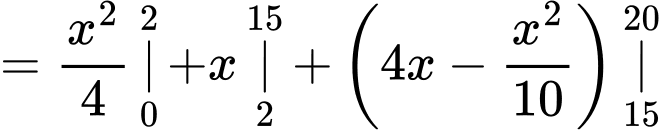
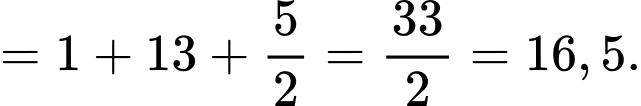
Câu 19 [782436]: Giả sử anh Nam nhảy dù từ một chiếc trực thăng. Vào thời điểm 19 giây sau khi rời khỏi trựcthăng, anh Nam mở chiếc dù của mình trong 2 giây, anh Nam chạm đất sau 19 giây kể từ lúc bung dù. Tại thời điểm 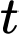 (giây), vị trí của anh Nam cách mặt đất một khoảng
(giây), vị trí của anh Nam cách mặt đất một khoảng 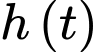 mét và vận tốc rơi của anh Nam (tính bằng m/s) là một hàm số được cho bởi công thức:
mét và vận tốc rơi của anh Nam (tính bằng m/s) là một hàm số được cho bởi công thức: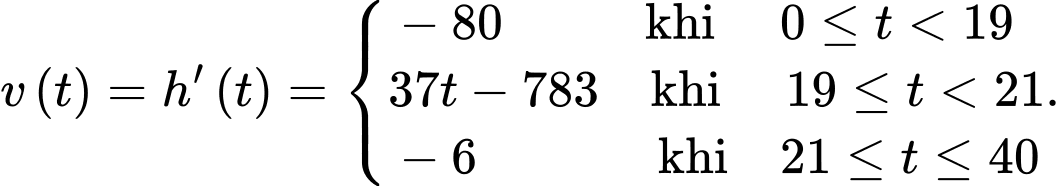
Độ cao vị trí của anh Nam khi bắt đầu nhảy ra khỏi trực thăng bằng bao nhiêu mét?
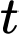 (giây), vị trí của anh Nam cách mặt đất một khoảng
(giây), vị trí của anh Nam cách mặt đất một khoảng 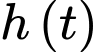 mét và vận tốc rơi của anh Nam (tính bằng m/s) là một hàm số được cho bởi công thức:
mét và vận tốc rơi của anh Nam (tính bằng m/s) là một hàm số được cho bởi công thức: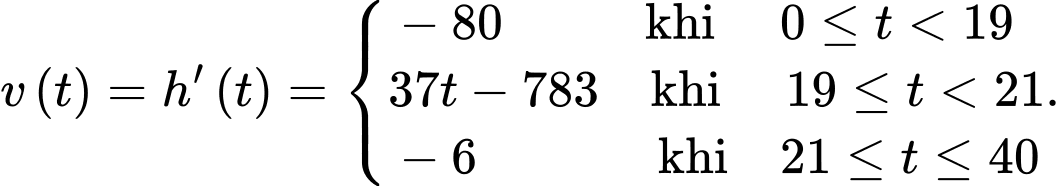
Độ cao vị trí của anh Nam khi bắt đầu nhảy ra khỏi trực thăng bằng bao nhiêu mét?
Điền đáp án: 1720.
Khi bắt đầu nhảy dù độ cao vị trí của anh Nam là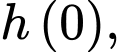 khi tiếp đất độ cao so với mặt đất là
khi tiếp đất độ cao so với mặt đất là 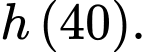 Khi đó độ cao vị trí của anh Nam khi bắt đầu nhảy ra khỏi trực thăng bằng
Khi đó độ cao vị trí của anh Nam khi bắt đầu nhảy ra khỏi trực thăng bằng 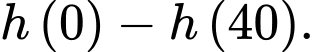
Ta có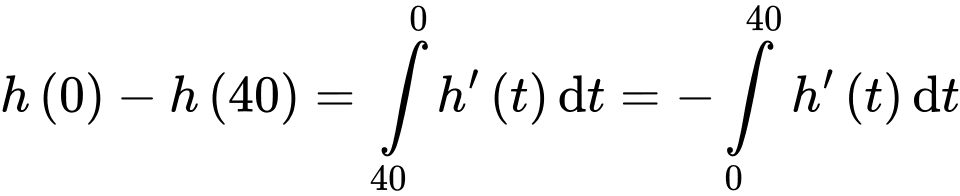
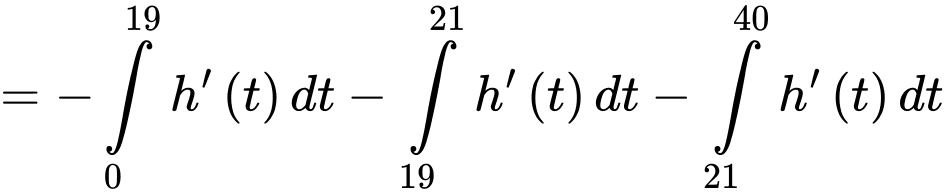
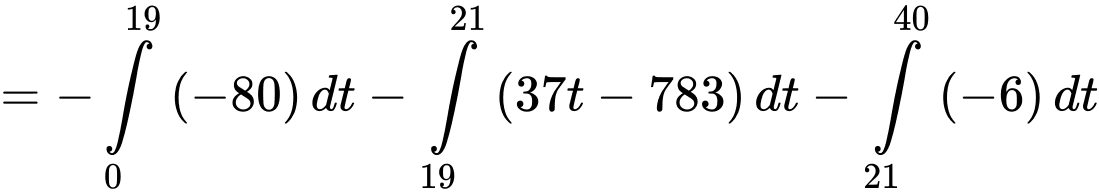
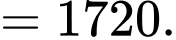
Khi bắt đầu nhảy dù độ cao vị trí của anh Nam là
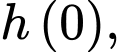 khi tiếp đất độ cao so với mặt đất là
khi tiếp đất độ cao so với mặt đất là 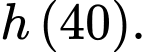 Khi đó độ cao vị trí của anh Nam khi bắt đầu nhảy ra khỏi trực thăng bằng
Khi đó độ cao vị trí của anh Nam khi bắt đầu nhảy ra khỏi trực thăng bằng 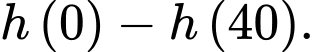
Ta có
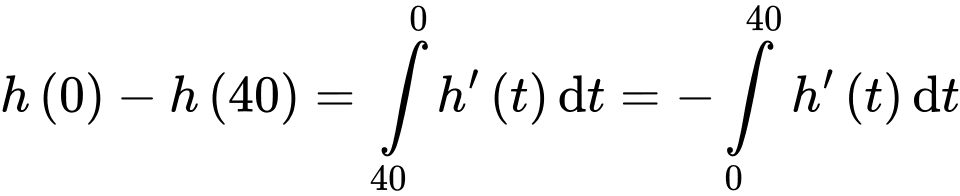
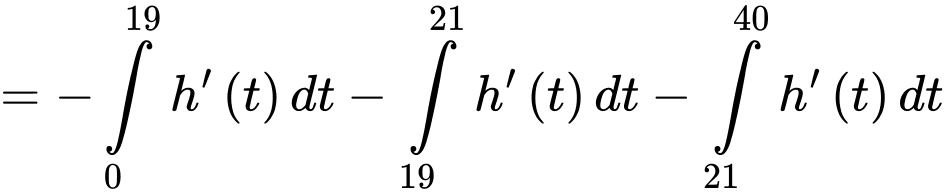
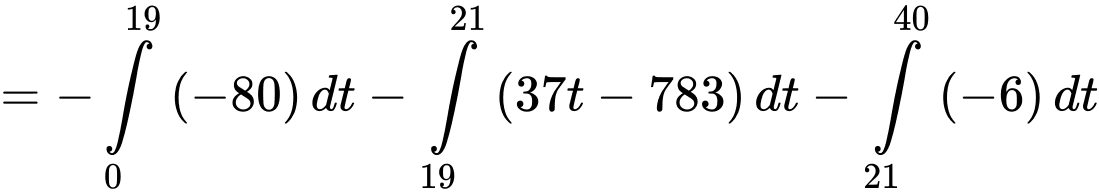
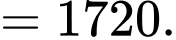
Câu 20 [775972]: Giá trị trung bình của hàm số liên tục 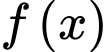 trên đoạn
trên đoạn 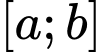 được định nghĩa là
được định nghĩa là 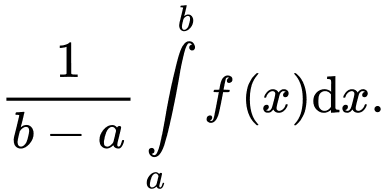 Một nhà nghiên cứu mô hình hóa nhiệt độ T (° C) trong khoảng thời gian từ 6 giờ sáng đến 6 giờ chiều trong một thành phố phía Bắc nhất định bằng hàm số
Một nhà nghiên cứu mô hình hóa nhiệt độ T (° C) trong khoảng thời gian từ 6 giờ sáng đến 6 giờ chiều trong một thành phố phía Bắc nhất định bằng hàm số 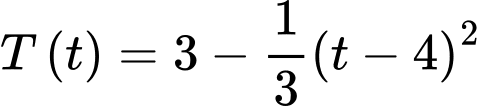 với
với 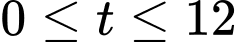 trong đó
trong đó 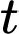 là số giờ sau 6 giờ sáng. Hỏi khi
là số giờ sau 6 giờ sáng. Hỏi khi 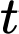 bằng bao nhiêu thì nhiệt độ trong thành phố bằng với nhiệt độ trung bình từ 8 giờ sáng đến 5 giờ chiều (làm tròn đến hàng phần chục).
bằng bao nhiêu thì nhiệt độ trong thành phố bằng với nhiệt độ trung bình từ 8 giờ sáng đến 5 giờ chiều (làm tròn đến hàng phần chục).
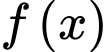 trên đoạn
trên đoạn 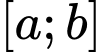 được định nghĩa là
được định nghĩa là 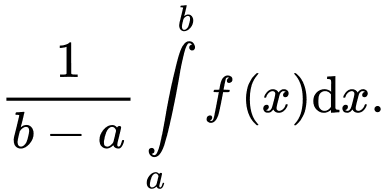 Một nhà nghiên cứu mô hình hóa nhiệt độ T (° C) trong khoảng thời gian từ 6 giờ sáng đến 6 giờ chiều trong một thành phố phía Bắc nhất định bằng hàm số
Một nhà nghiên cứu mô hình hóa nhiệt độ T (° C) trong khoảng thời gian từ 6 giờ sáng đến 6 giờ chiều trong một thành phố phía Bắc nhất định bằng hàm số 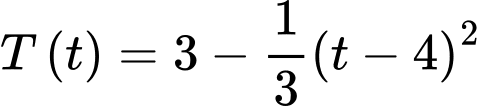 với
với 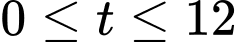 trong đó
trong đó 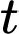 là số giờ sau 6 giờ sáng. Hỏi khi
là số giờ sau 6 giờ sáng. Hỏi khi 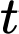 bằng bao nhiêu thì nhiệt độ trong thành phố bằng với nhiệt độ trung bình từ 8 giờ sáng đến 5 giờ chiều (làm tròn đến hàng phần chục).
bằng bao nhiêu thì nhiệt độ trong thành phố bằng với nhiệt độ trung bình từ 8 giờ sáng đến 5 giờ chiều (làm tròn đến hàng phần chục).
Điền đáp án: 7,6.
Vì 8 giờ sáng và 5 giờ chiều lần lượt là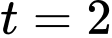 và
và 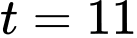 giờ sau 6 giờ sáng, nên chúng ta muốn tính nhiệt độ trung bình
giờ sau 6 giờ sáng, nên chúng ta muốn tính nhiệt độ trung bình 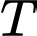 với
với 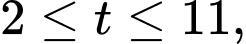 được cho bởi tích phân xác định
được cho bởi tích phân xác định
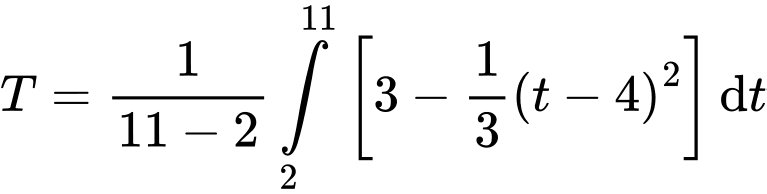
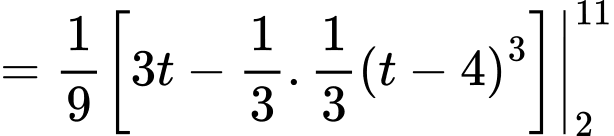
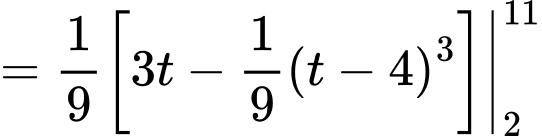
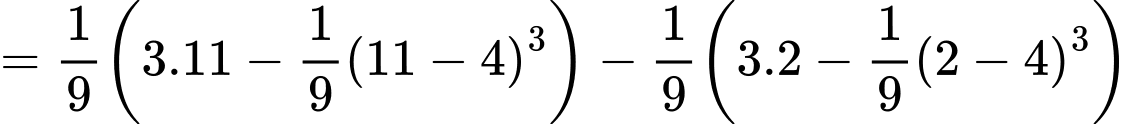
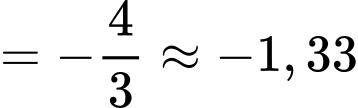
Do đó nhiệt độ trung bình trong thành phố trong giờ làm việc xấp xỉ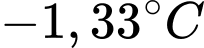 (hoặc
(hoặc 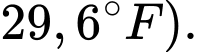
Chúng ta muốn tìm thời điểm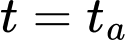 với
với 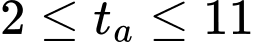 sao cho
sao cho 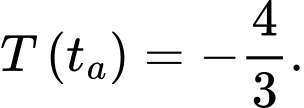
Giải phương trình này, chúng ta tìm được
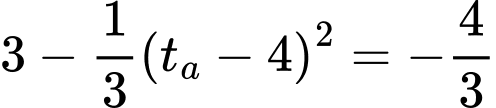
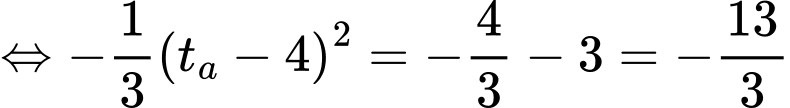
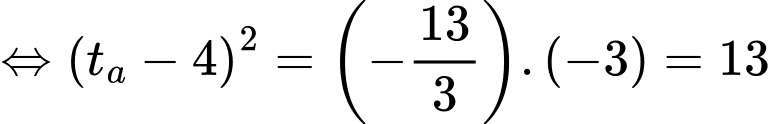
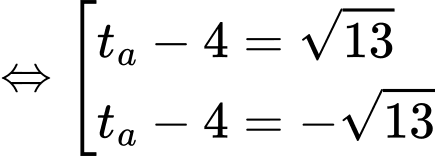
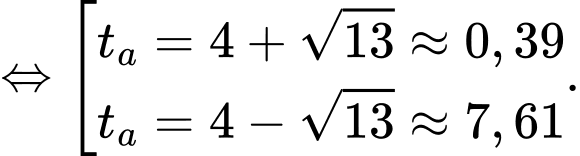
Vì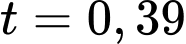 nằm ngoài khoảng thời gian
nằm ngoài khoảng thời gian 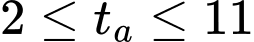 (8 giờ sáng đến 5 giờ chiều), suy ra nhiệt độ trong thành phố bằng với nhiệt độ trung bình chỉ khi
(8 giờ sáng đến 5 giờ chiều), suy ra nhiệt độ trong thành phố bằng với nhiệt độ trung bình chỉ khi 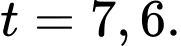
Vì 8 giờ sáng và 5 giờ chiều lần lượt là
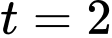 và
và 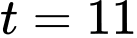 giờ sau 6 giờ sáng, nên chúng ta muốn tính nhiệt độ trung bình
giờ sau 6 giờ sáng, nên chúng ta muốn tính nhiệt độ trung bình 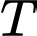 với
với 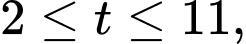 được cho bởi tích phân xác định
được cho bởi tích phân xác định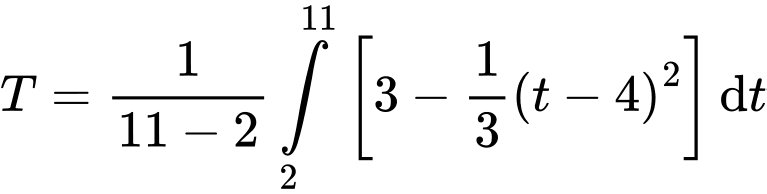
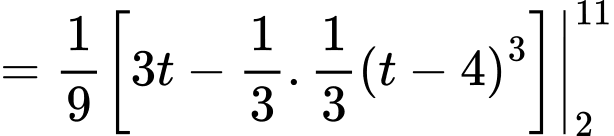
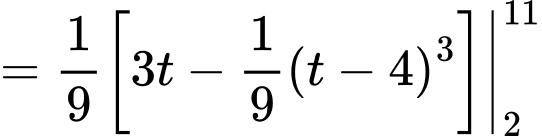
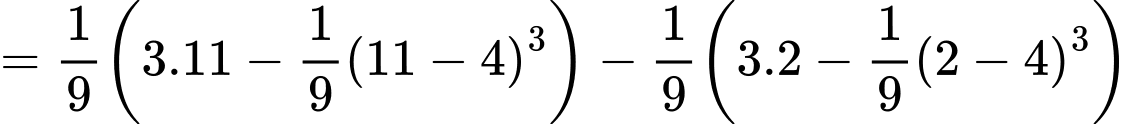
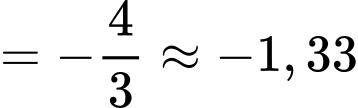
Do đó nhiệt độ trung bình trong thành phố trong giờ làm việc xấp xỉ
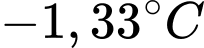 (hoặc
(hoặc 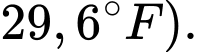
Chúng ta muốn tìm thời điểm
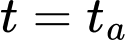 với
với 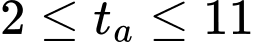 sao cho
sao cho 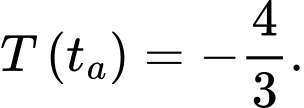
Giải phương trình này, chúng ta tìm được
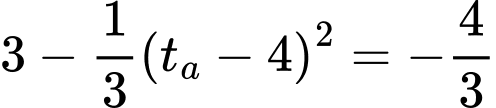
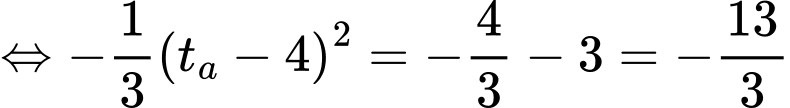
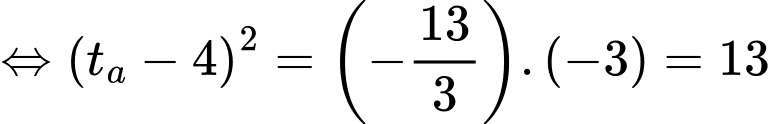
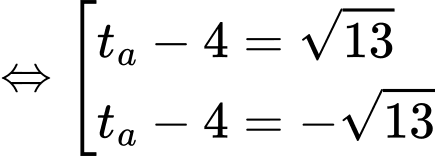
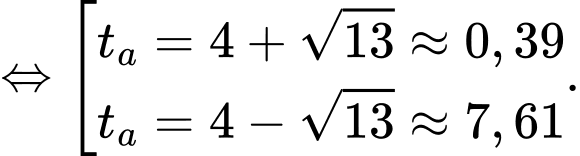
Vì
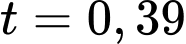 nằm ngoài khoảng thời gian
nằm ngoài khoảng thời gian 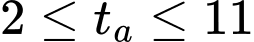 (8 giờ sáng đến 5 giờ chiều), suy ra nhiệt độ trong thành phố bằng với nhiệt độ trung bình chỉ khi
(8 giờ sáng đến 5 giờ chiều), suy ra nhiệt độ trong thành phố bằng với nhiệt độ trung bình chỉ khi 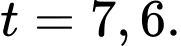
Câu 21 [396716]: Năng lượng gió trên đất liền là một trong những công nghệ năng lượng tái tạo đang được phát triển ở quy mô toàn cầu. Các turbine gió thường có ba cánh quay trên một trục ngang, lấy động năng từ quá trình di chuyển dòng không khí (gió) để chuyển đổi thành điện năng thông qua một máy phát điện được kết nối với lưới điện. Hình thang cong (tô màu đậm) trong hình dưới mô tả một phần mặt cắt đứng của cánh turbine, được giới hạn bởi các đường thẳng 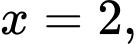
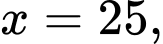 trục
trục 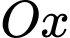 và đồ thị hàm số
và đồ thị hàm số 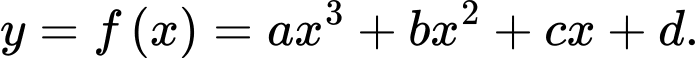 Biết rằng đồ thị hàm số
Biết rằng đồ thị hàm số 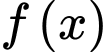 đi qua điểm
đi qua điểm 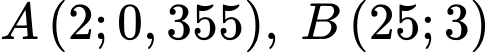 và đạt cực trị tại điểm
và đạt cực trị tại điểm 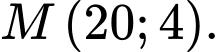 Diện tích hình thang cong đó là bao nhiêu
Diện tích hình thang cong đó là bao nhiêu 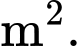 Viết kết quả làm tròn đến hàng phần mười.
Viết kết quả làm tròn đến hàng phần mười.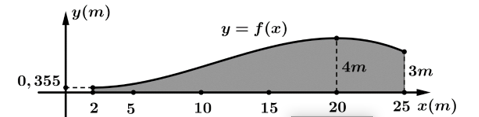
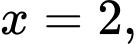
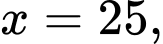 trục
trục 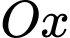 và đồ thị hàm số
và đồ thị hàm số 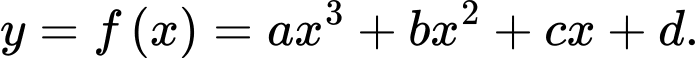 Biết rằng đồ thị hàm số
Biết rằng đồ thị hàm số 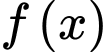 đi qua điểm
đi qua điểm 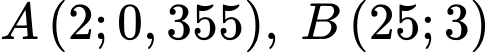 và đạt cực trị tại điểm
và đạt cực trị tại điểm 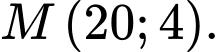 Diện tích hình thang cong đó là bao nhiêu
Diện tích hình thang cong đó là bao nhiêu 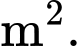 Viết kết quả làm tròn đến hàng phần mười.
Viết kết quả làm tròn đến hàng phần mười.
Xét hàm số 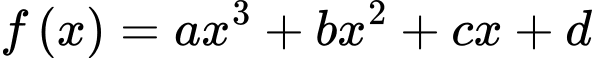
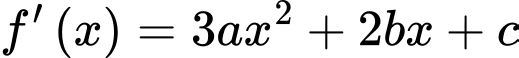
Vì hàm số đạt cực trị tại điểm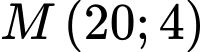 nên
nên 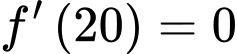
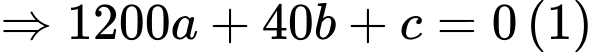
Vì đồ thị hàm số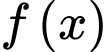 đi qua 2 điểm
đi qua 2 điểm 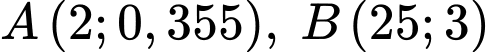 và đạt cực trị tại điểm
và đạt cực trị tại điểm 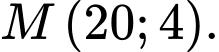
Nên thay tọa độ điểm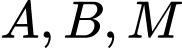 vào phương trình
vào phương trình 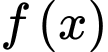 ta được
ta được
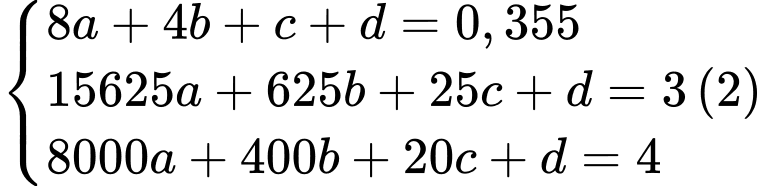
Từ (1)(2) suy ra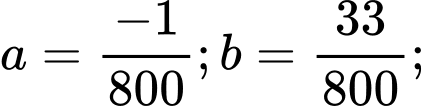
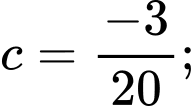
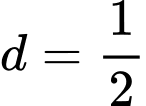
Diện tích của hình thang cong là:
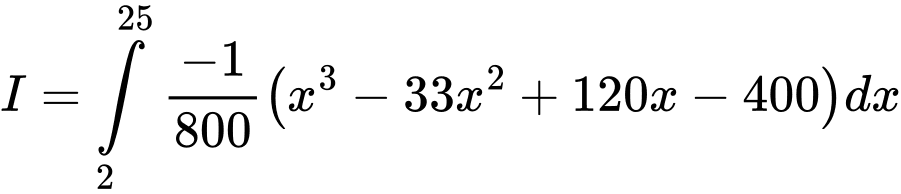
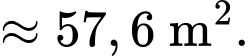
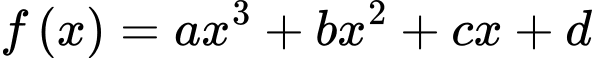
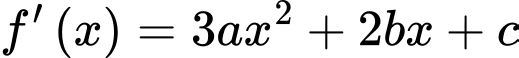
Vì hàm số đạt cực trị tại điểm
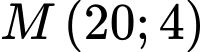 nên
nên 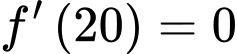
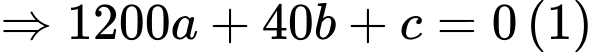
Vì đồ thị hàm số
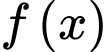 đi qua 2 điểm
đi qua 2 điểm 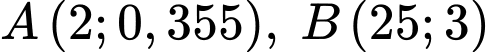 và đạt cực trị tại điểm
và đạt cực trị tại điểm 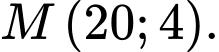
Nên thay tọa độ điểm
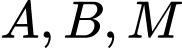 vào phương trình
vào phương trình 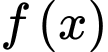 ta được
ta được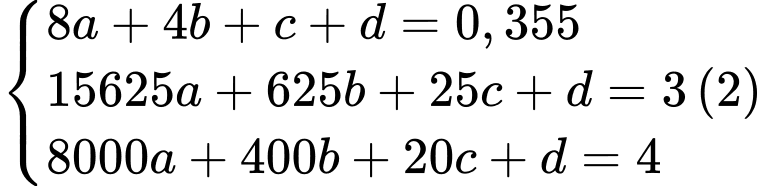
Từ (1)(2) suy ra
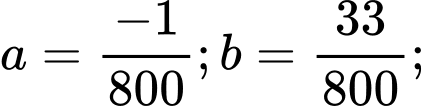
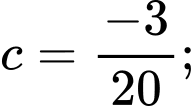
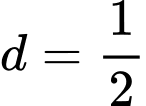
Diện tích của hình thang cong là:
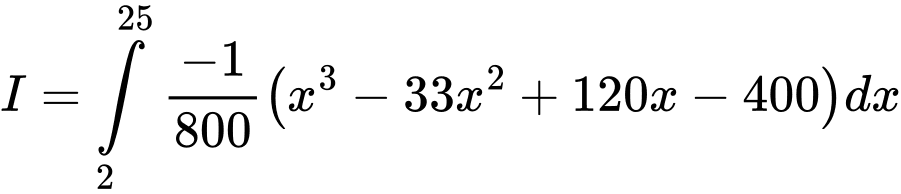
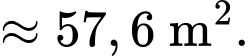
Câu 22 [775973]: Từ thời điểm 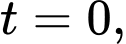 một chất điểm bắt đầu chuyển động thẳng đều với vận tốc
một chất điểm bắt đầu chuyển động thẳng đều với vận tốc 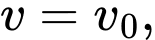 sau
sau 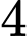 giây chuyển động thì chất điểm gặp chướng ngại vật nên bắt đầu giảm tốc độ với vận tốc chuyển động
giây chuyển động thì chất điểm gặp chướng ngại vật nên bắt đầu giảm tốc độ với vận tốc chuyển động 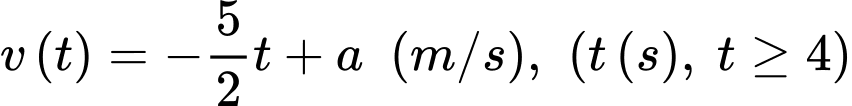 cho đến khi dừng hẳn. Quãng đường chất điểm đi được kể từ lúc chuyển động đến khi dừng hẳn là
cho đến khi dừng hẳn. Quãng đường chất điểm đi được kể từ lúc chuyển động đến khi dừng hẳn là 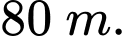 Vận tốc trung bình
Vận tốc trung bình 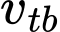 của chất điểm trong khoảng thời gian từ
của chất điểm trong khoảng thời gian từ 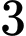 giây đến
giây đến 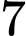 giây kể từ lúc bắt đầu bằng bao nhiêu m/s (kết quả làm tròn đến hàng phần mười).
giây kể từ lúc bắt đầu bằng bao nhiêu m/s (kết quả làm tròn đến hàng phần mười).
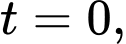 một chất điểm bắt đầu chuyển động thẳng đều với vận tốc
một chất điểm bắt đầu chuyển động thẳng đều với vận tốc 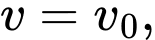 sau
sau 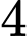 giây chuyển động thì chất điểm gặp chướng ngại vật nên bắt đầu giảm tốc độ với vận tốc chuyển động
giây chuyển động thì chất điểm gặp chướng ngại vật nên bắt đầu giảm tốc độ với vận tốc chuyển động 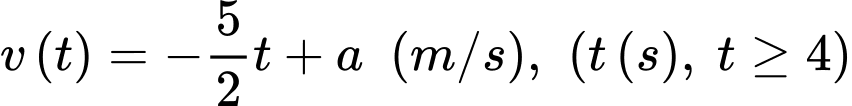 cho đến khi dừng hẳn. Quãng đường chất điểm đi được kể từ lúc chuyển động đến khi dừng hẳn là
cho đến khi dừng hẳn. Quãng đường chất điểm đi được kể từ lúc chuyển động đến khi dừng hẳn là 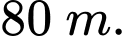 Vận tốc trung bình
Vận tốc trung bình 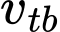 của chất điểm trong khoảng thời gian từ
của chất điểm trong khoảng thời gian từ 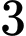 giây đến
giây đến 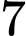 giây kể từ lúc bắt đầu bằng bao nhiêu m/s (kết quả làm tròn đến hàng phần mười).
giây kể từ lúc bắt đầu bằng bao nhiêu m/s (kết quả làm tròn đến hàng phần mười).
Điền đáp án: 9,5.
Vì trong 4 giây đầu chất điểm chuyển động đều với vận tốc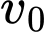 nên quãng đường di chuyển được tại bất kì thời điểm nào trong 4 giây đầu là:
nên quãng đường di chuyển được tại bất kì thời điểm nào trong 4 giây đầu là: 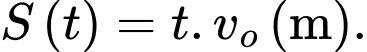 (với
(với 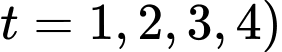
Tại thời điểm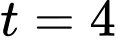 vật đang chuyển động với vận tốc
vật đang chuyển động với vận tốc 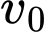 nên có
nên có 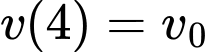
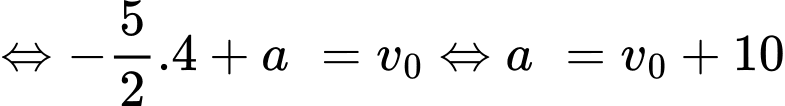 suy ra
suy ra 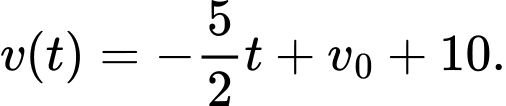
Gọi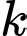 (giây) là thời điểm vật dừng hẳn, ta có:
(giây) là thời điểm vật dừng hẳn, ta có:
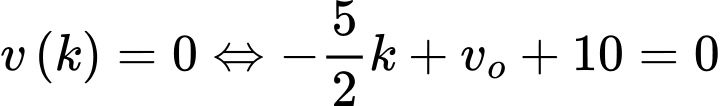
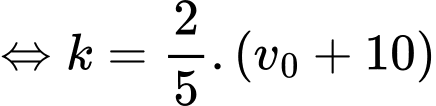
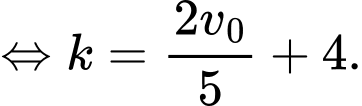
Tổng quãng đường vật đi được là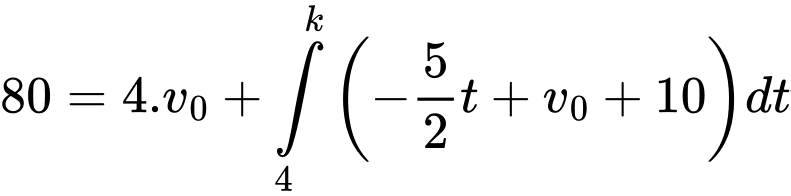
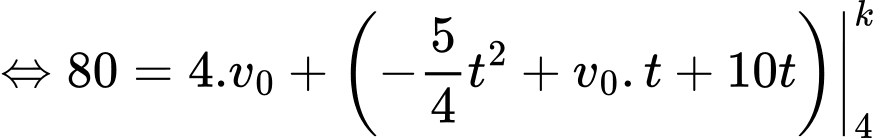
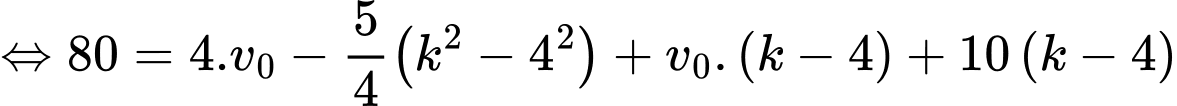
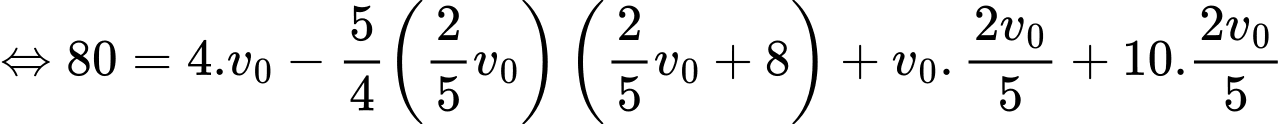
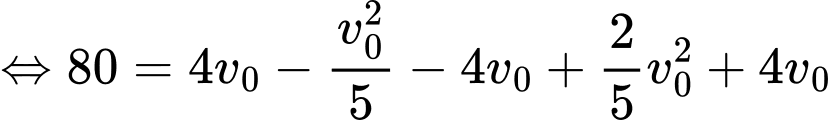
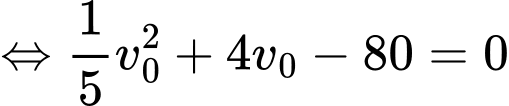
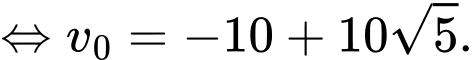
Quãng đường chất điểm đi được trong khoảng thời gian từ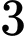 đến
đến 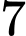 giây là
giây là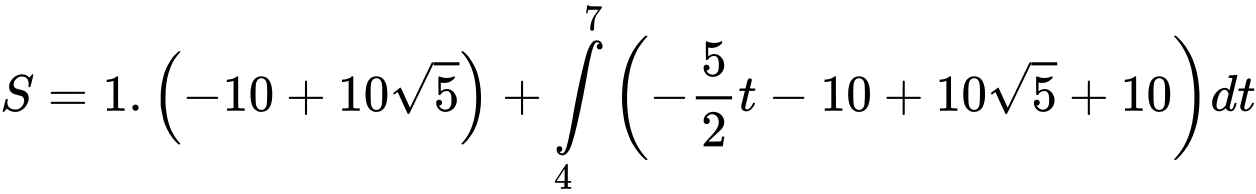
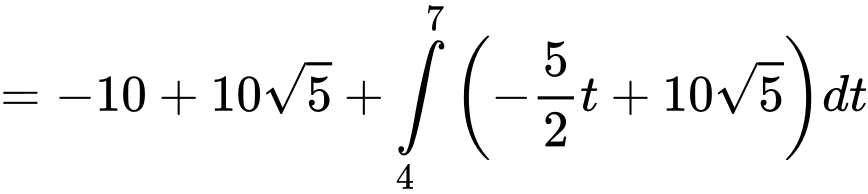
Vận tốc trung bình là :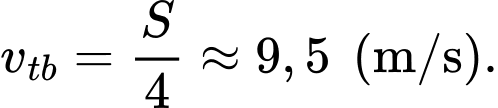
Vì trong 4 giây đầu chất điểm chuyển động đều với vận tốc
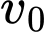 nên quãng đường di chuyển được tại bất kì thời điểm nào trong 4 giây đầu là:
nên quãng đường di chuyển được tại bất kì thời điểm nào trong 4 giây đầu là: 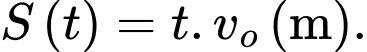 (với
(với 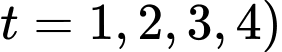
Tại thời điểm
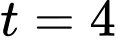 vật đang chuyển động với vận tốc
vật đang chuyển động với vận tốc 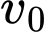 nên có
nên có 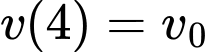
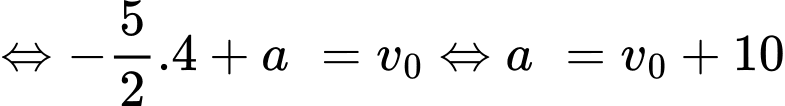 suy ra
suy ra 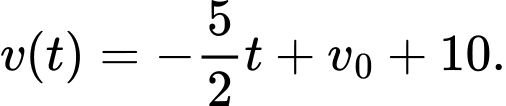
Gọi
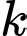 (giây) là thời điểm vật dừng hẳn, ta có:
(giây) là thời điểm vật dừng hẳn, ta có:
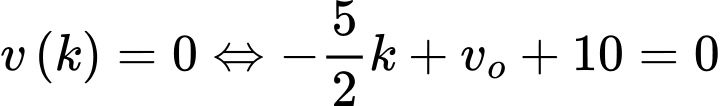
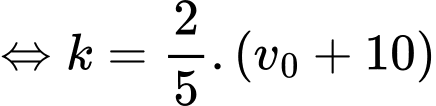
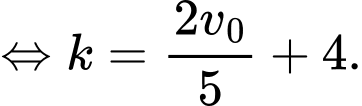
Tổng quãng đường vật đi được là
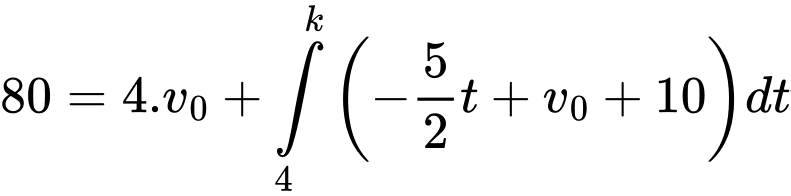
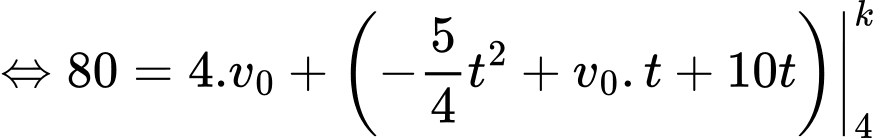
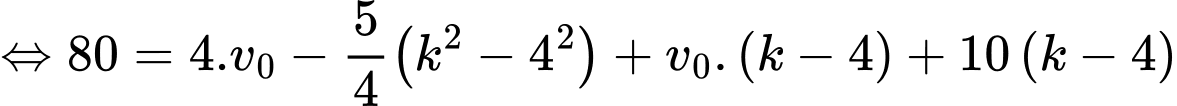
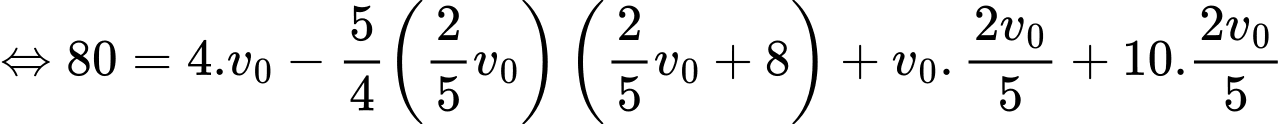
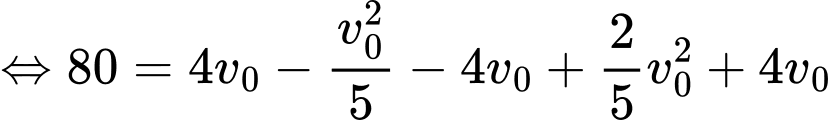
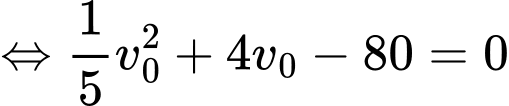
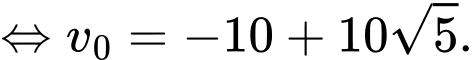
Quãng đường chất điểm đi được trong khoảng thời gian từ
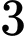 đến
đến 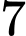 giây là
giây là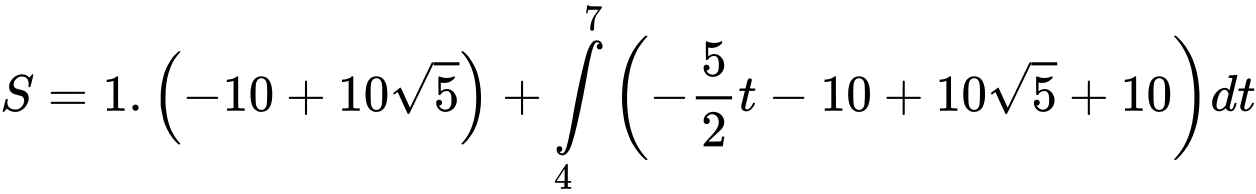
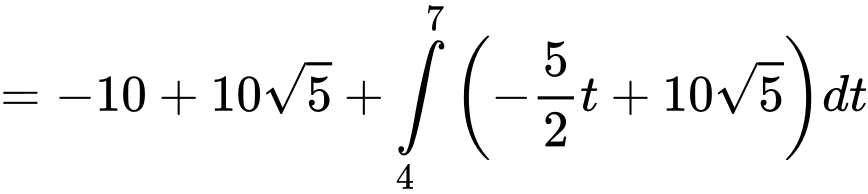
Vận tốc trung bình là :