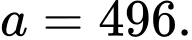PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1 [80724]: Biết 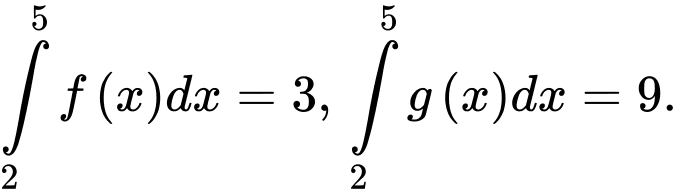 Tích phân
Tích phân 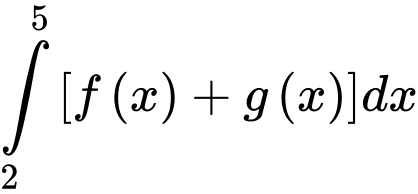 bằng
bằng
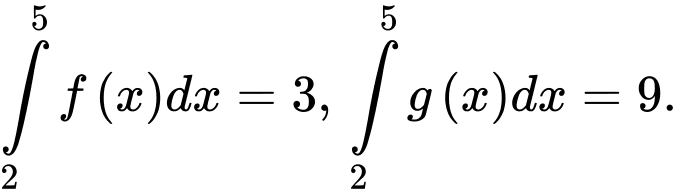 Tích phân
Tích phân 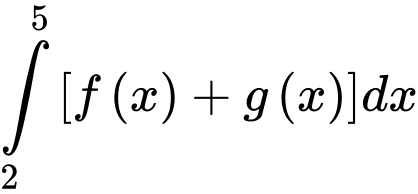 bằng
bằng A, 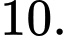
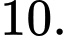
B, 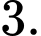
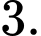
C, 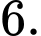
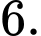
D, 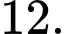
Chọn đáp án D.
Áp dụng tính chất của tích phân, ta có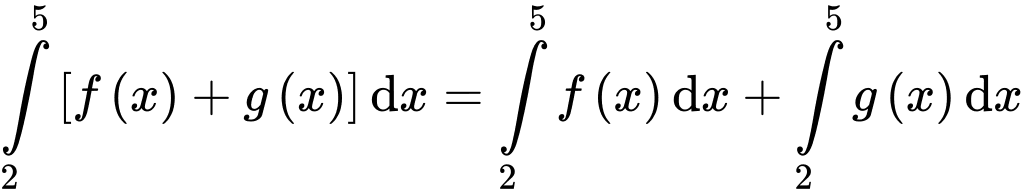
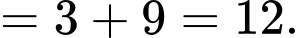 Đáp án: D
Đáp án: D
Áp dụng tính chất của tích phân, ta có
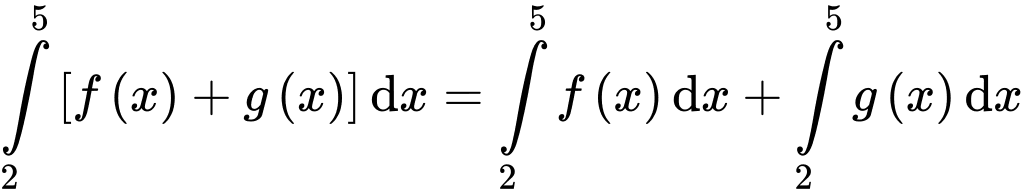
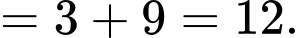 Đáp án: D
Đáp án: D
Câu 2 [149133]: Với 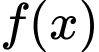 là hàm số tùy ý và liên tục trên
là hàm số tùy ý và liên tục trên 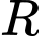 , chọn mệnh đề sai trong các mệnh đề sau:
, chọn mệnh đề sai trong các mệnh đề sau:
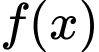 là hàm số tùy ý và liên tục trên
là hàm số tùy ý và liên tục trên 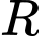 , chọn mệnh đề sai trong các mệnh đề sau:
, chọn mệnh đề sai trong các mệnh đề sau: A, 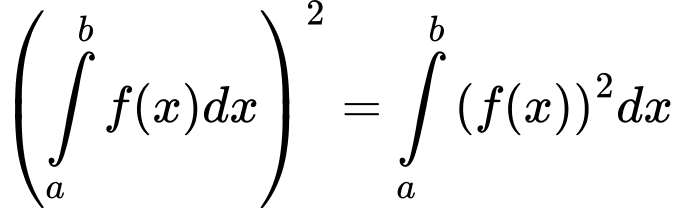 .
.
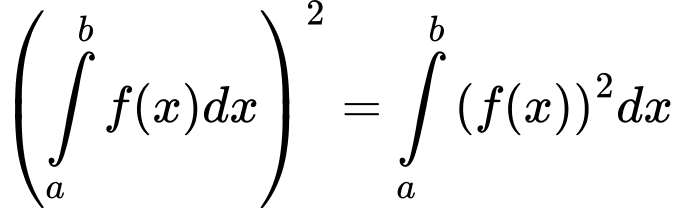 .
.B, 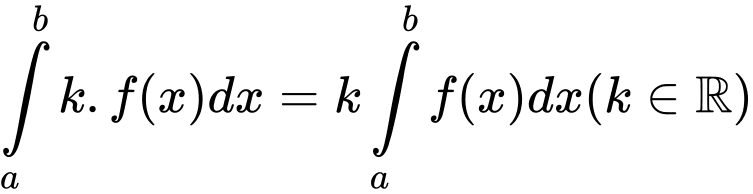 .
.
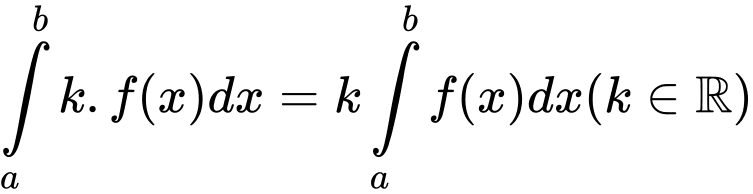 .
.C, 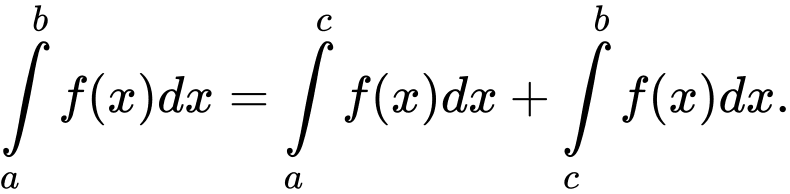 .
.
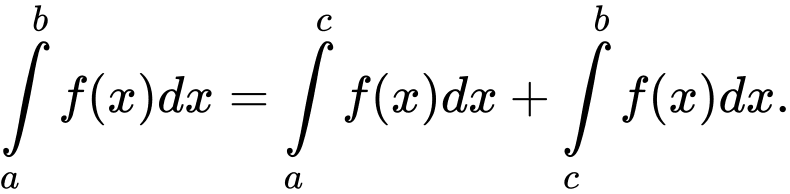 .
.D, 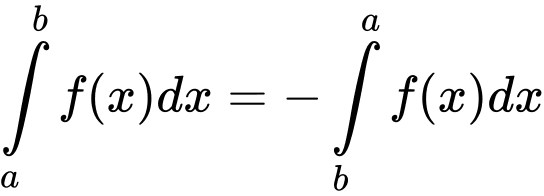 .
.
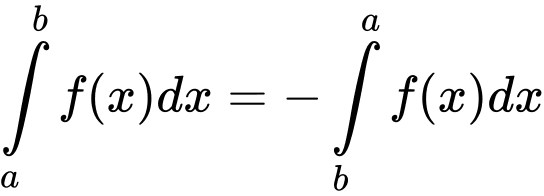 .
.
Chọn đáp án A.
Từ các tính chất của tích phân, ta thấy đáp án A sai. Ta có thể dễ dàng kiểm chứng từ ví dụ sau: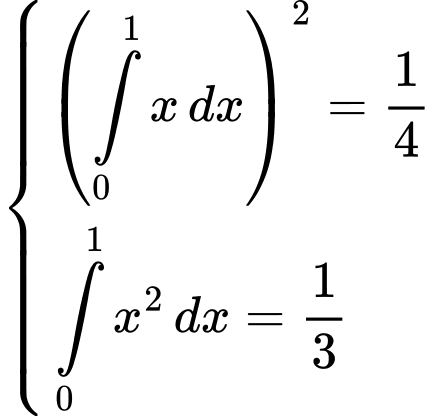
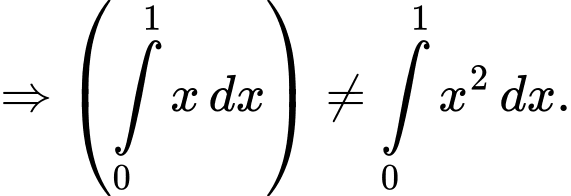 Đáp án: A
Đáp án: A
Từ các tính chất của tích phân, ta thấy đáp án A sai. Ta có thể dễ dàng kiểm chứng từ ví dụ sau:
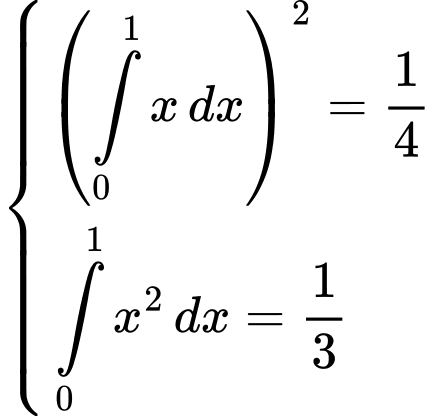
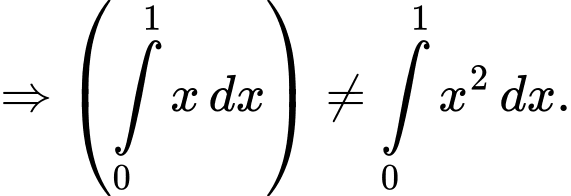 Đáp án: A
Đáp án: A
Câu 3 [775664]: Tích phân 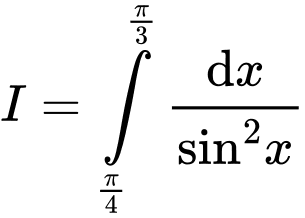 bằng
bằng
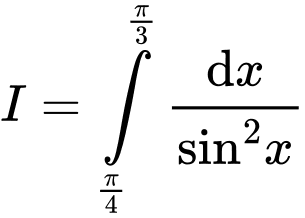 bằng
bằng A, 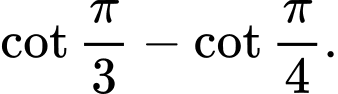
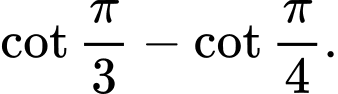
B, 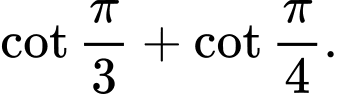
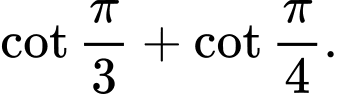
C, 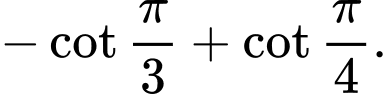
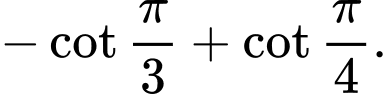
D, 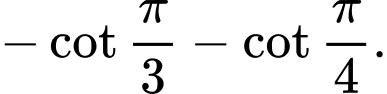
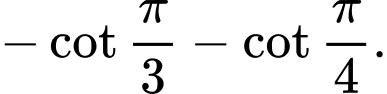
Chọn đáp án C.
Áp dụng công thức nguyên hàm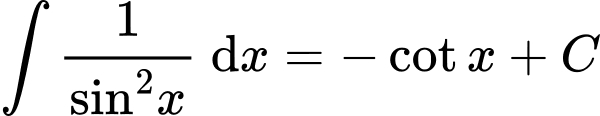
Ta có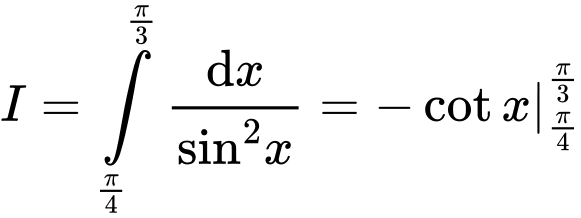
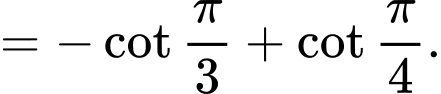 Đáp án: C
Đáp án: C
Áp dụng công thức nguyên hàm
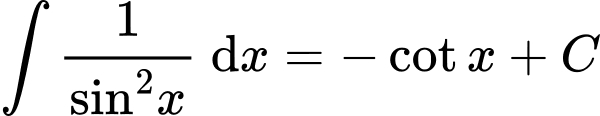
Ta có
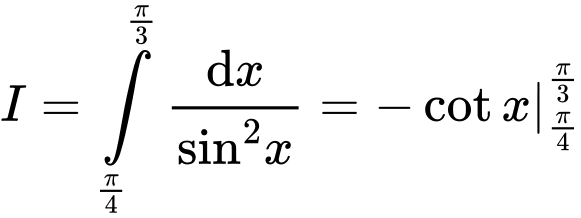
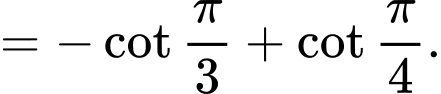 Đáp án: C
Đáp án: C
Câu 4 [775666]: Cho một vật chuyển động với tốc độ  Biết
Biết 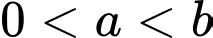 và
và 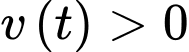 với mọi
với mọi 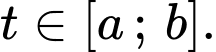 Khi đó quãng đường mà vật đó đi được trong khoảng thời gian từ
Khi đó quãng đường mà vật đó đi được trong khoảng thời gian từ 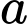 đến
đến 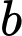 (
(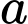 và
và 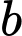 tính theo giây) bằng
tính theo giây) bằng
 Biết
Biết 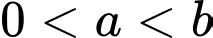 và
và 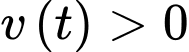 với mọi
với mọi 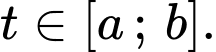 Khi đó quãng đường mà vật đó đi được trong khoảng thời gian từ
Khi đó quãng đường mà vật đó đi được trong khoảng thời gian từ 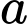 đến
đến 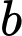 (
(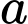 và
và 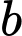 tính theo giây) bằng
tính theo giây) bằng A, 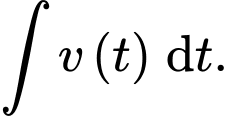
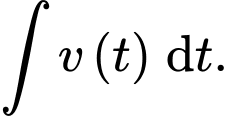
B, 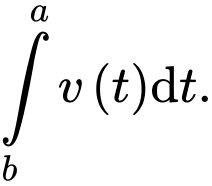
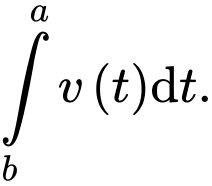
C, 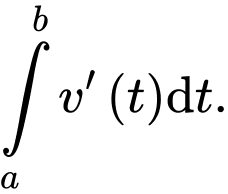
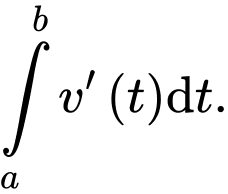
D, 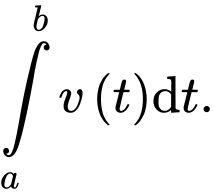
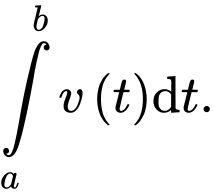
Chọn đáp án D. Đáp án: D
Câu 5 [149143]: Cho 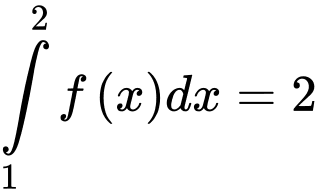 và
và 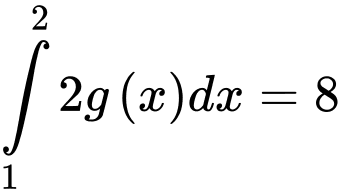 . Khi đó
. Khi đó 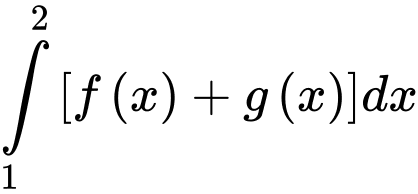 bằng
bằng
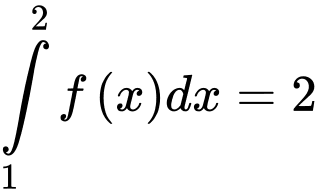 và
và 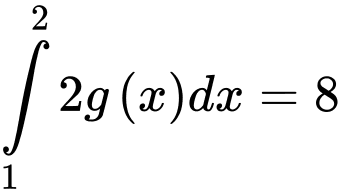 . Khi đó
. Khi đó 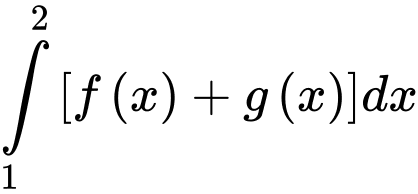 bằng
bằng A, 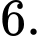
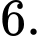
B, 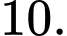
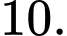
C, 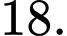
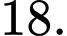
D, 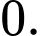
Chọn đáp án A.
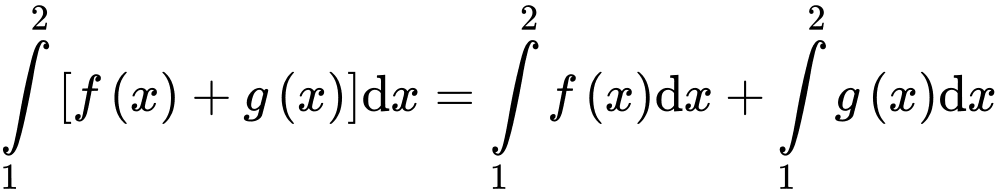
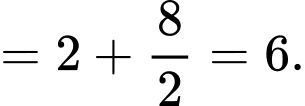 Đáp án: A
Đáp án: A
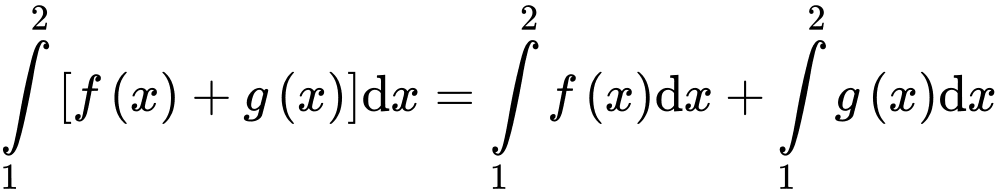
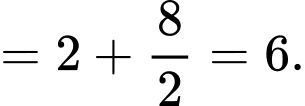 Đáp án: A
Đáp án: A
Câu 6 [149159]: Cho hàm số 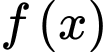 liên tục trên
liên tục trên 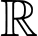 và
và 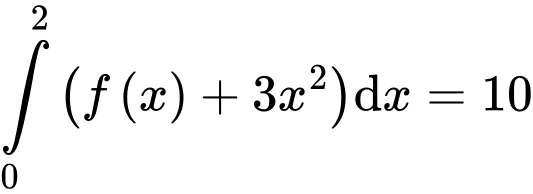 . Tính
. Tính 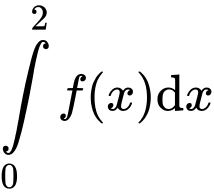 .
.
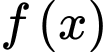 liên tục trên
liên tục trên 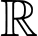 và
và 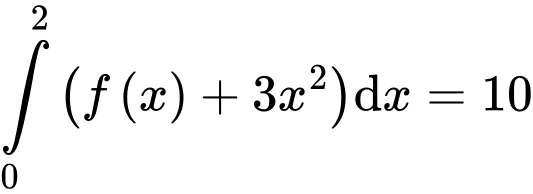 . Tính
. Tính 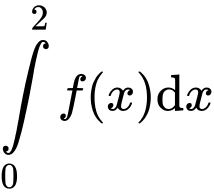 .
. A, 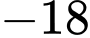 .
.
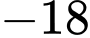 .
.B, 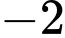 .
.
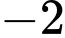 .
.C,  .
.
 .
.D, 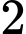 .
.
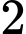 .
.
Chọn đáp án D.
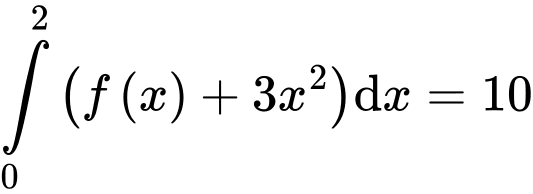
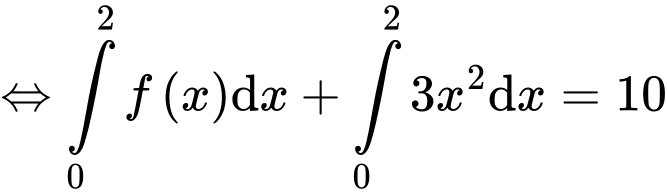
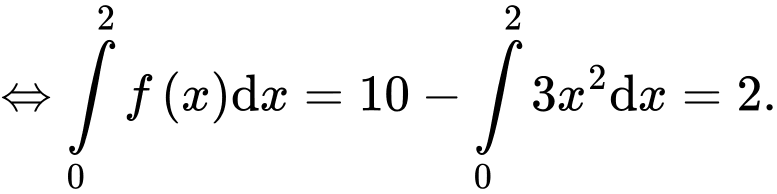 Đáp án: D
Đáp án: D
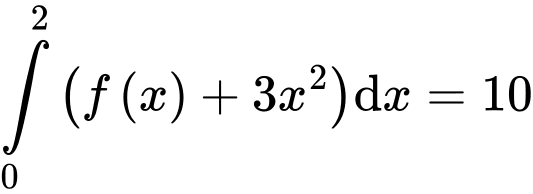
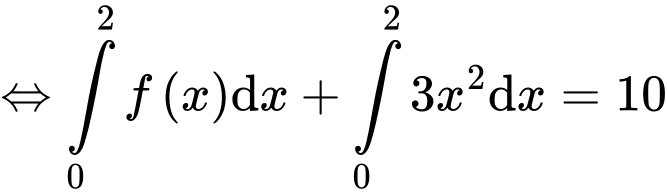
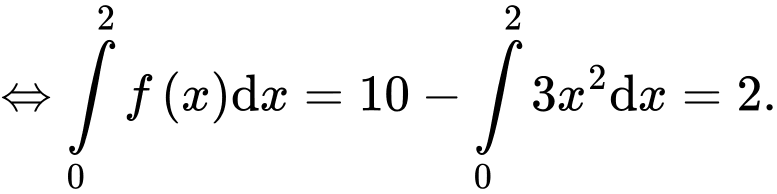 Đáp án: D
Đáp án: D
Câu 7 [149177]: Cho hàm số 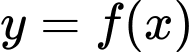 thoả mãn
thoả mãn 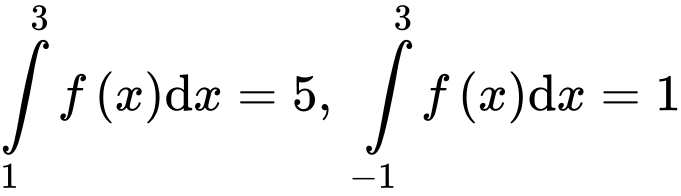 . Tính tích phân
. Tính tích phân 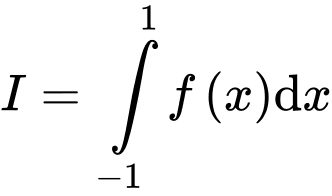 .
.
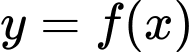 thoả mãn
thoả mãn 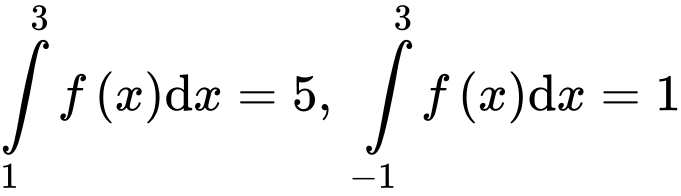 . Tính tích phân
. Tính tích phân 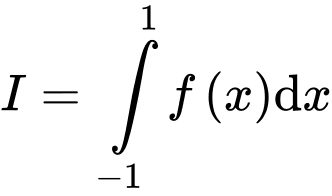 .
. A, 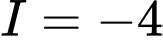 .
.
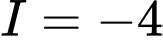 .
.B, 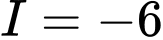 .
.
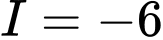 .
.C,  .
.
 .
.D,  .
.
 .
.
Chọn đáp án A.
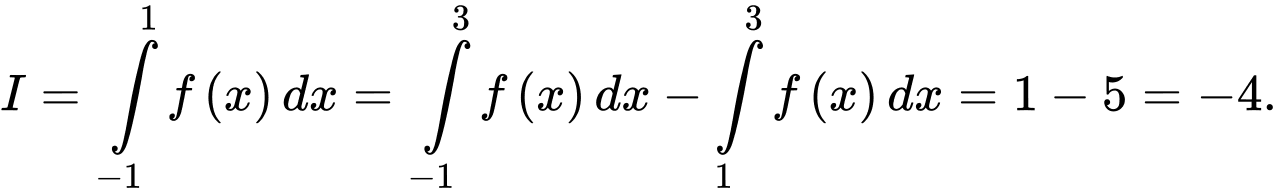 Đáp án: A
Đáp án: A
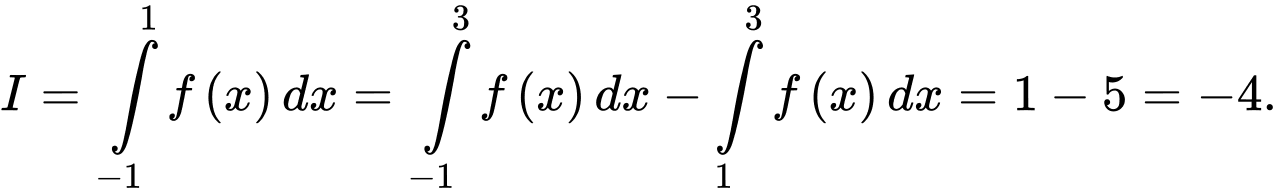 Đáp án: A
Đáp án: A
Câu 8 [775670]: Tích phân 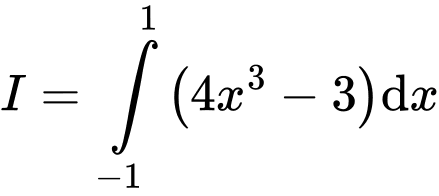 bằng
bằng
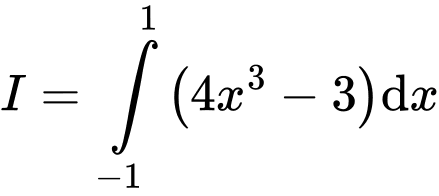 bằng
bằng A, 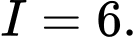
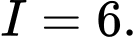
B, 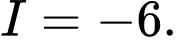
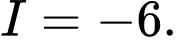
C, 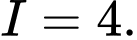
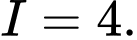
D, 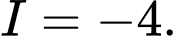
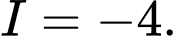
Chọn đáp án B.
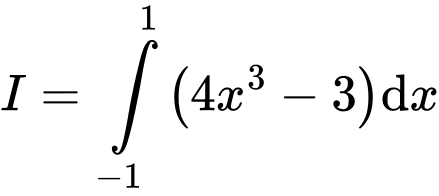
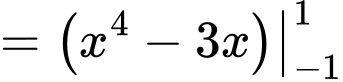
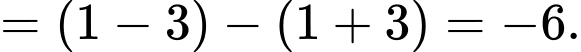 Đáp án: B
Đáp án: B
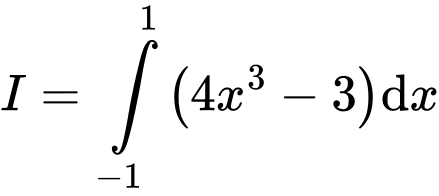
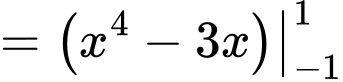
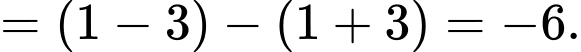 Đáp án: B
Đáp án: B
Câu 9 [149165]: Cho hàm số 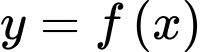 có đạo hàm liên tục trên đoạn
có đạo hàm liên tục trên đoạn 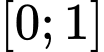 và
và 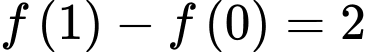 . Tính
. Tính 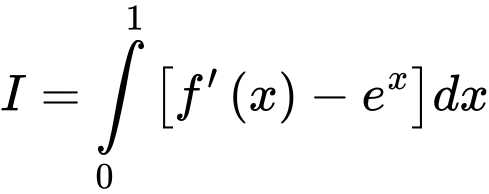 .
.
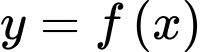 có đạo hàm liên tục trên đoạn
có đạo hàm liên tục trên đoạn 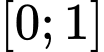 và
và 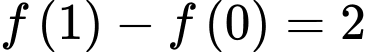 . Tính
. Tính 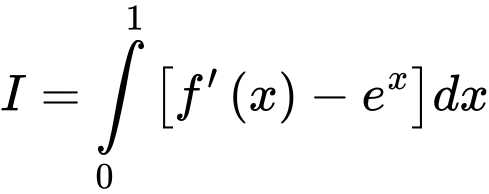 .
. A, 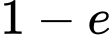 .
.
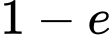 .
.B,  .
.
 .
.C, 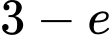 .
.
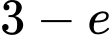 .
.D,  .
.
 .
.
Chọn đáp án C.
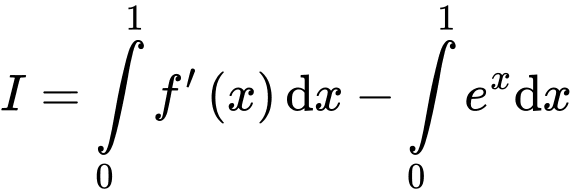
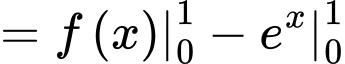
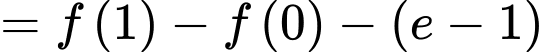

Đáp án: C
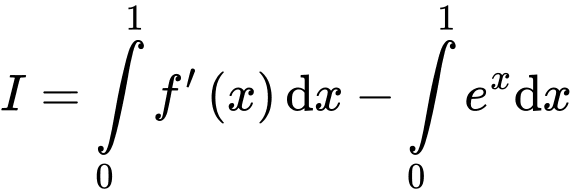
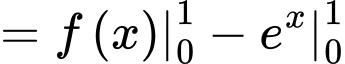
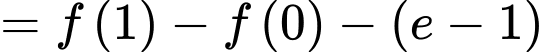

Đáp án: C
Câu 10 [149208]: Tính tích phân 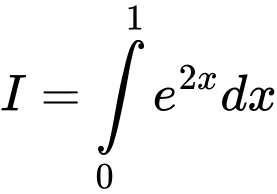 .
.
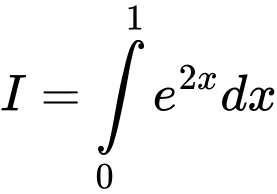 .
. A, 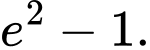
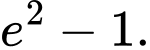
B, 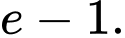
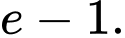
C, 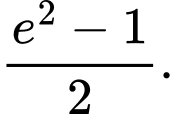
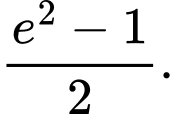
D, 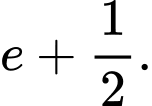
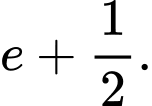
Chọn đáp án C.
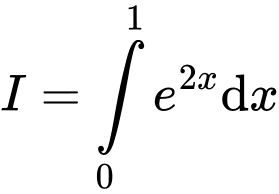
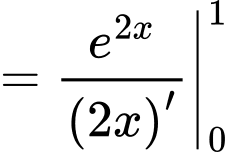
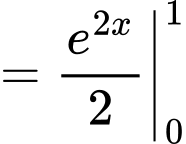
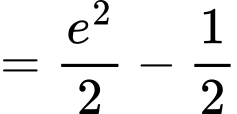 Đáp án: C
Đáp án: C
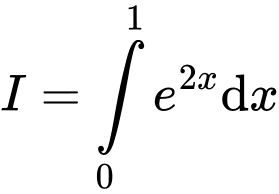
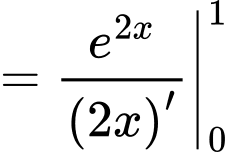
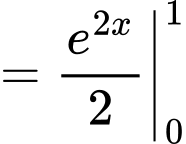
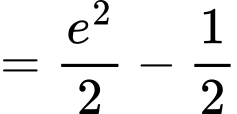 Đáp án: C
Đáp án: C
Câu 11 [149164]: Cho 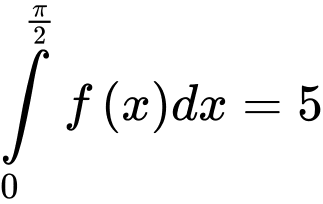 . Khi đó
. Khi đó 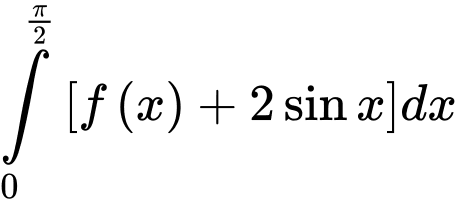 bằng
bằng
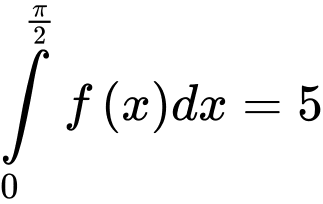 . Khi đó
. Khi đó 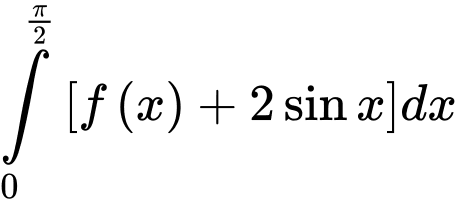 bằng
bằng A, 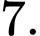
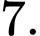
B, 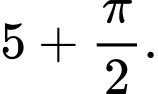
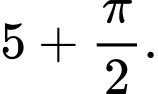
C, 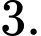
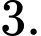
D, 

Chọn đáp án A.
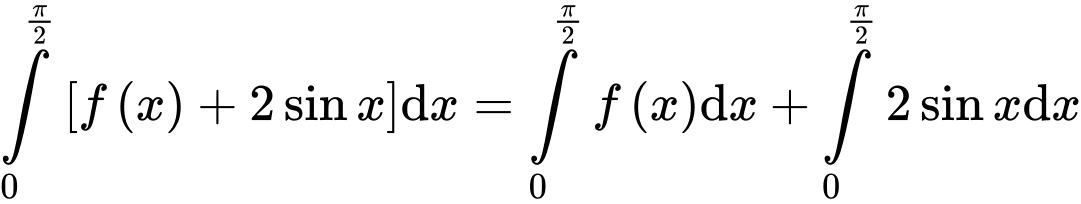
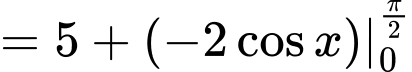
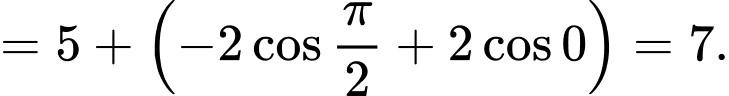 Đáp án: A
Đáp án: A
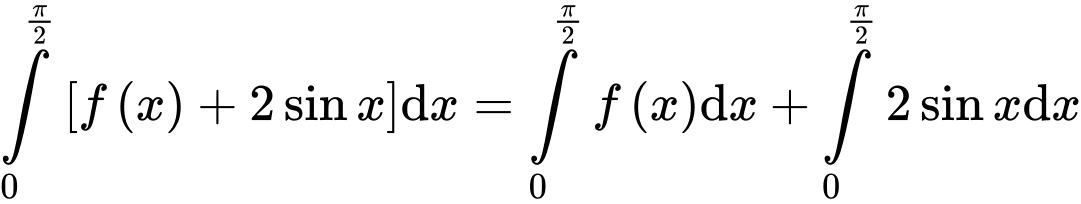
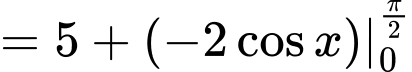
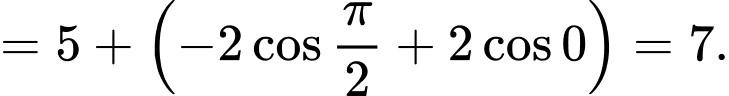 Đáp án: A
Đáp án: A
Câu 12 [396701]: Biết rằng 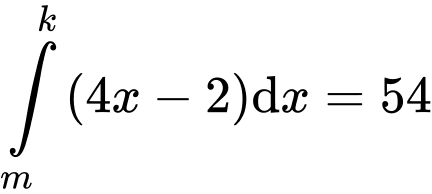 và
và 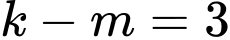 với
với 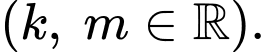 Tính
Tính 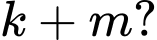
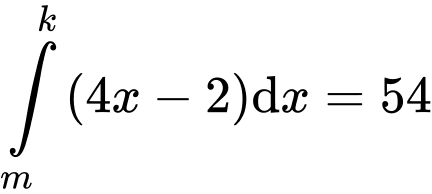 và
và 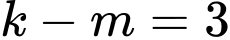 với
với 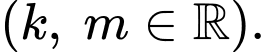 Tính
Tính 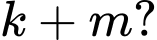
A, 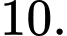
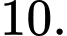
B, 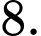
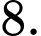
C, 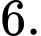
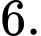
D, 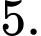
Chọn đáp án A.
Ta có: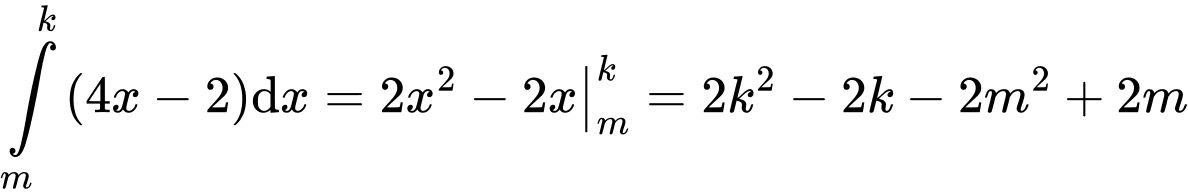
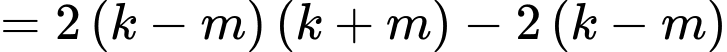
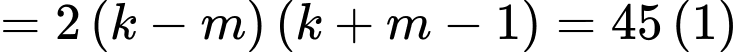
Mà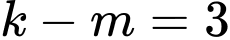 .
.
Thay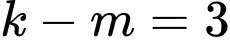 vào (1) có:
vào (1) có: 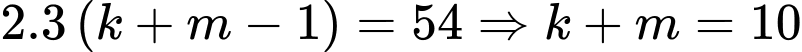 .
.
Đáp án: A
Ta có:
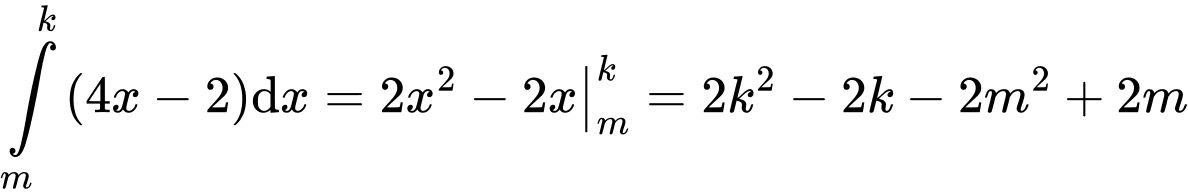
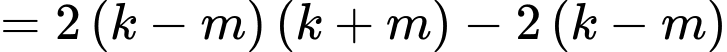
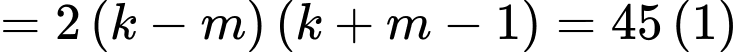
Mà
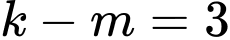 .
.Thay
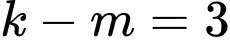 vào (1) có:
vào (1) có: 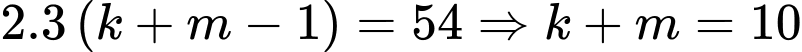 .
.Đáp án: A
PHẦN II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a),b),c),d) ở mỗi câu học sinh chọn đúng hoặc sai.
Câu 13 [775974]: Cho hàm số 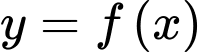 liên tục trên khoảng
liên tục trên khoảng 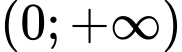 thoả mãn
thoả mãn 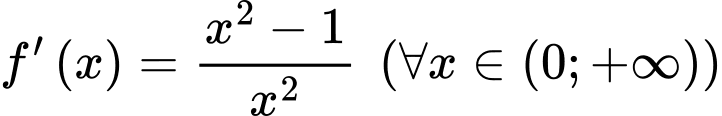 và
và 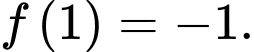
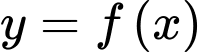 liên tục trên khoảng
liên tục trên khoảng 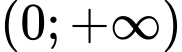 thoả mãn
thoả mãn 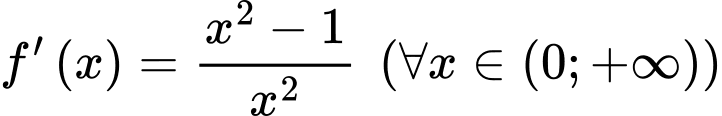 và
và 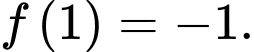
a) Đúng.
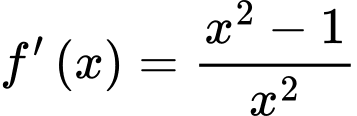
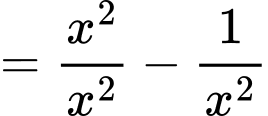
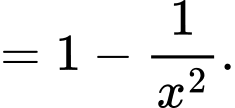
b) Sai.
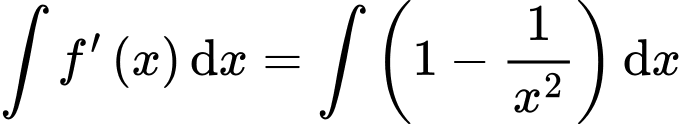
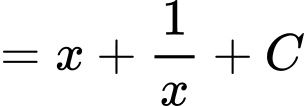
c) Đúng.
Ta có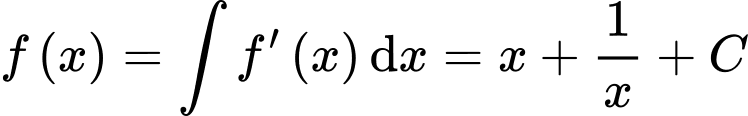
Mà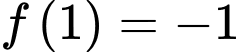 nên
nên 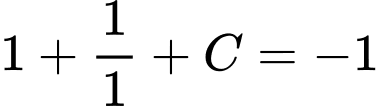
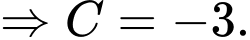
Suy ra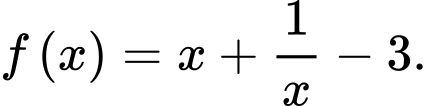
Note: Nếu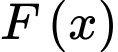 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 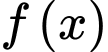 khi và chỉ khi
khi và chỉ khi 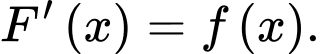
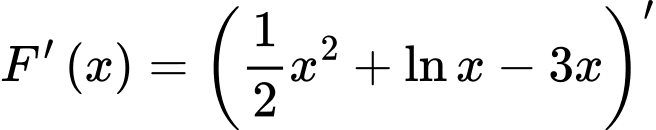
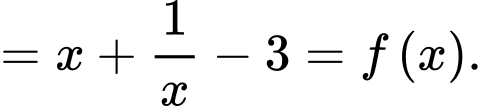
Vậy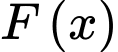 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 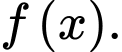
d) Đúng.
Vì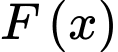 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 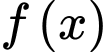 nên theo khái niệm nguyên hàm, ta có
nên theo khái niệm nguyên hàm, ta có
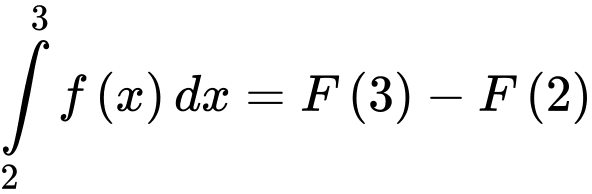
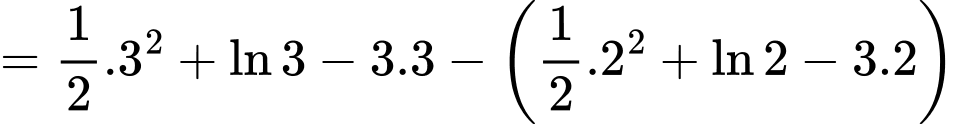
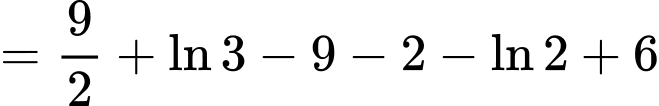
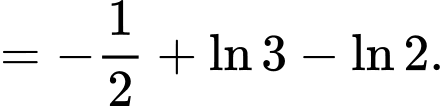
Suy ra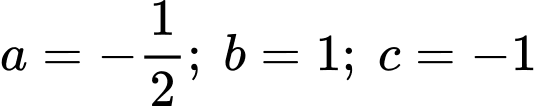
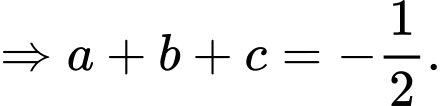
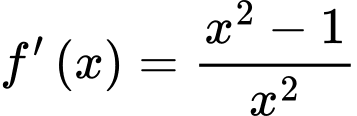
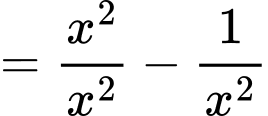
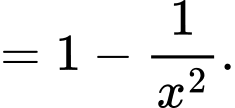
b) Sai.
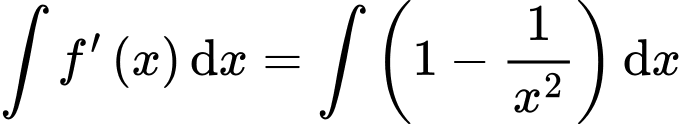
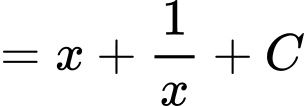
c) Đúng.
Ta có
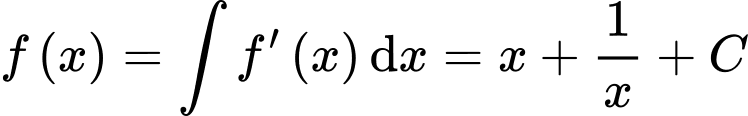
Mà
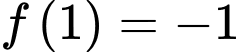 nên
nên 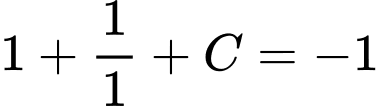
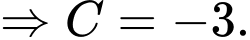
Suy ra
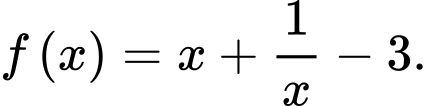
Note: Nếu
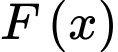 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 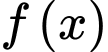 khi và chỉ khi
khi và chỉ khi 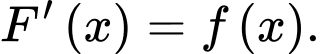
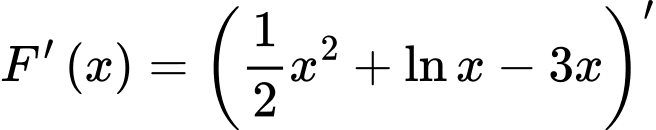
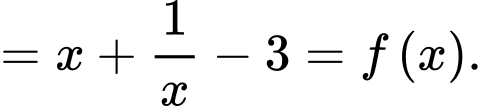
Vậy
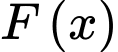 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 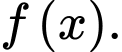
d) Đúng.
Vì
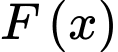 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 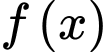 nên theo khái niệm nguyên hàm, ta có
nên theo khái niệm nguyên hàm, ta có
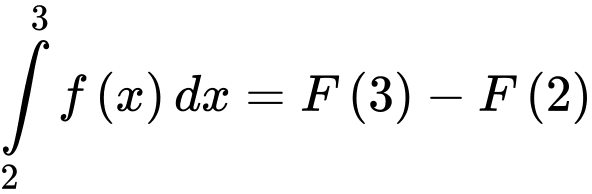
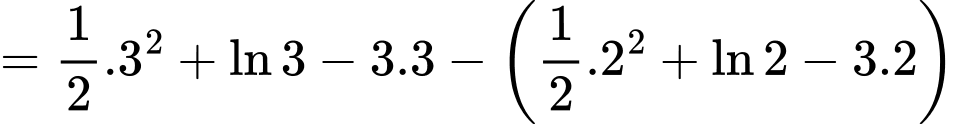
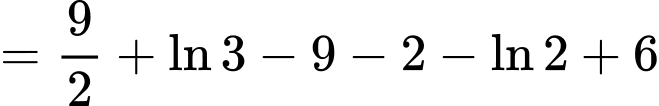
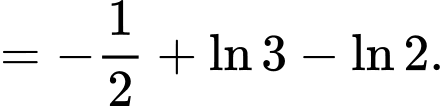
Suy ra
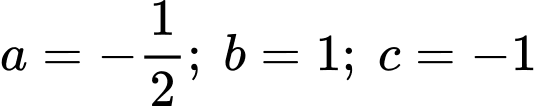
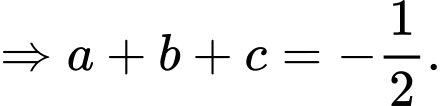
Câu 14 [775977]: Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc 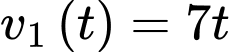 (m/s), trong đó
(m/s), trong đó 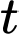 (giây) là khoảng thời gian tính từ lúc ô tô bắt đầu chuyển động. Đi được 5 (s), người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc
(giây) là khoảng thời gian tính từ lúc ô tô bắt đầu chuyển động. Đi được 5 (s), người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc 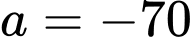 (m/s2).
(m/s2).
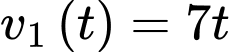 (m/s), trong đó
(m/s), trong đó 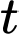 (giây) là khoảng thời gian tính từ lúc ô tô bắt đầu chuyển động. Đi được 5 (s), người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc
(giây) là khoảng thời gian tính từ lúc ô tô bắt đầu chuyển động. Đi được 5 (s), người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc 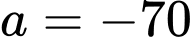 (m/s2).
(m/s2).
a) Đúng.
Vì cho đến khi xe phanh gấp (hay từ 0 giây đến 5 giây) thì xe ô tô chuyển động nhanh dần đều với vận tốc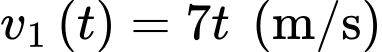 nên ta có quãng đường ô tô đi được từ lúc xe lăn bánh đến khi được phanh là
nên ta có quãng đường ô tô đi được từ lúc xe lăn bánh đến khi được phanh là 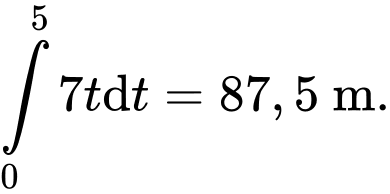
b) Sai.
Ta có từ khi phanh gấp ô tô tiếp tục chuyển động chậm dần đều với gia tốc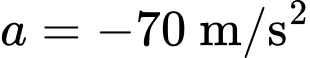 và
và 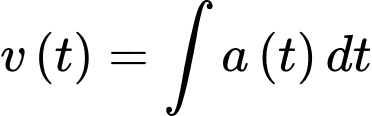 nên
nên 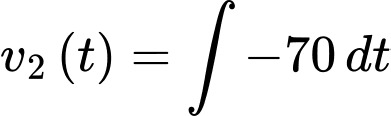
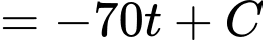
Biết vào lúc bắt đầu phanh (tức tại thời điểm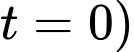 thì xe có vận tốc
thì xe có vận tốc 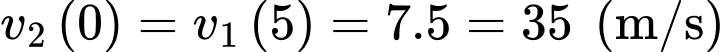
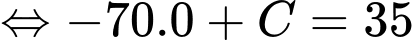

Vậy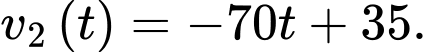
c) Sai.
Vì trong khoảng thời gian từ lúc đạp phanh đến khi xe ô tô dừng hẳn, xe đi với vận tốc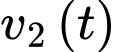 và ô tô dừng hẳn khi vận tốc bằng 0 nên
và ô tô dừng hẳn khi vận tốc bằng 0 nên 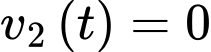
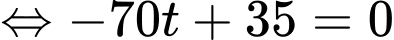
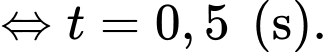
Vậy thời gian kể từ lúc đạp phanh đến khi xe ô tô dừng hẳn là 0,5 giây.
d) Đúng.
Dựa vào kết quả phần a, ta có quãng đường đi được từ 0 s đến 5 s bằng 87,5 m.
Quãng đường ô tô đi được từ 0 s đến 0,5 s là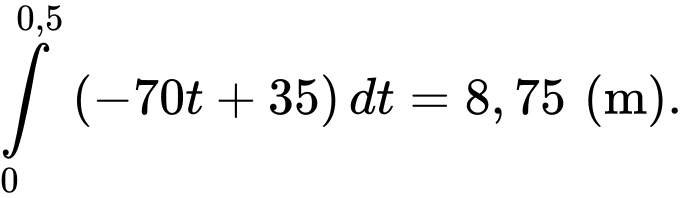
Vậy quãng đường của ô tô đi được bằng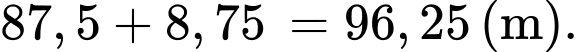
Vì cho đến khi xe phanh gấp (hay từ 0 giây đến 5 giây) thì xe ô tô chuyển động nhanh dần đều với vận tốc
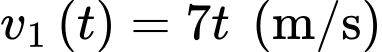 nên ta có quãng đường ô tô đi được từ lúc xe lăn bánh đến khi được phanh là
nên ta có quãng đường ô tô đi được từ lúc xe lăn bánh đến khi được phanh là 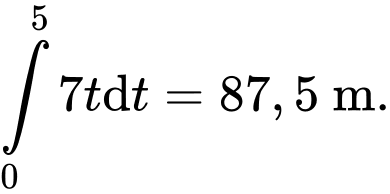
b) Sai.
Ta có từ khi phanh gấp ô tô tiếp tục chuyển động chậm dần đều với gia tốc
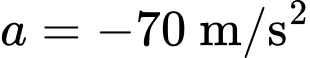 và
và 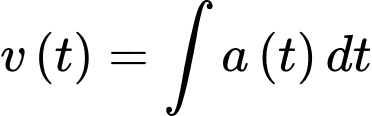 nên
nên 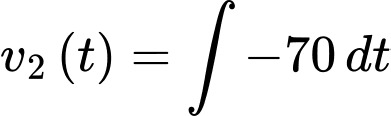
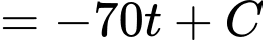
Biết vào lúc bắt đầu phanh (tức tại thời điểm
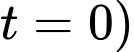 thì xe có vận tốc
thì xe có vận tốc 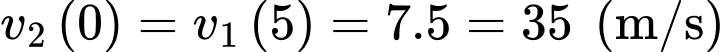
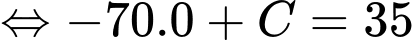

Vậy
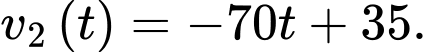
c) Sai.
Vì trong khoảng thời gian từ lúc đạp phanh đến khi xe ô tô dừng hẳn, xe đi với vận tốc
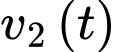 và ô tô dừng hẳn khi vận tốc bằng 0 nên
và ô tô dừng hẳn khi vận tốc bằng 0 nên 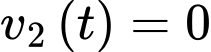
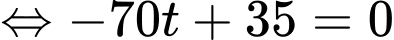
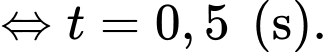
Vậy thời gian kể từ lúc đạp phanh đến khi xe ô tô dừng hẳn là 0,5 giây.
d) Đúng.
Dựa vào kết quả phần a, ta có quãng đường đi được từ 0 s đến 5 s bằng 87,5 m.
Quãng đường ô tô đi được từ 0 s đến 0,5 s là
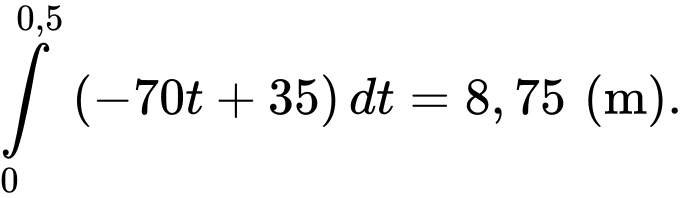
Vậy quãng đường của ô tô đi được bằng
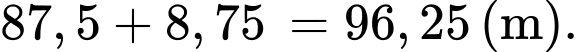
Câu 15 [775978]: Một bác thợ xây bơm nước vào bể chứa nước. Gọi 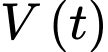 (đơn vị
(đơn vị 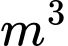 ) là thể tích nước bơm được sau
) là thể tích nước bơm được sau 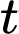 phút. Cho biết tốc độ nước được bơm vào bể bằng
phút. Cho biết tốc độ nước được bơm vào bể bằng 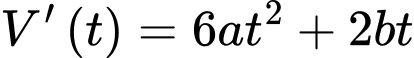 (
(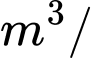 phút)
phút) 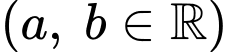 và ban đầu bể không có nước. Sau 3 phút thì thể tích nước trong bể là
và ban đầu bể không có nước. Sau 3 phút thì thể tích nước trong bể là 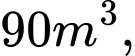 sau
sau 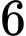 phút thì thể tích nước trong bể là
phút thì thể tích nước trong bể là 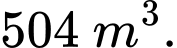
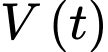 (đơn vị
(đơn vị 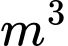 ) là thể tích nước bơm được sau
) là thể tích nước bơm được sau 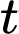 phút. Cho biết tốc độ nước được bơm vào bể bằng
phút. Cho biết tốc độ nước được bơm vào bể bằng 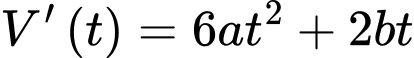 (
(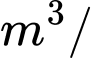 phút)
phút) 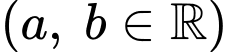 và ban đầu bể không có nước. Sau 3 phút thì thể tích nước trong bể là
và ban đầu bể không có nước. Sau 3 phút thì thể tích nước trong bể là 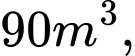 sau
sau 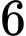 phút thì thể tích nước trong bể là
phút thì thể tích nước trong bể là 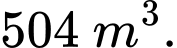
a) Đúng.
Vì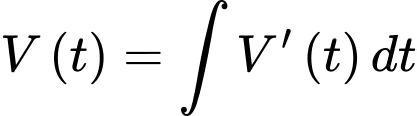 nên
nên 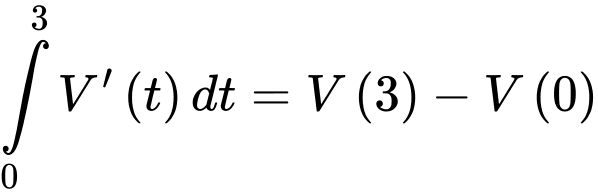
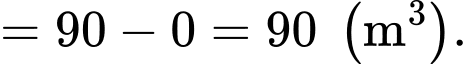
(vì ban đầu bể không có nước nên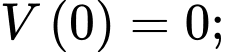 và sau 3 phút thì bể có 90 m3 nước nên
và sau 3 phút thì bể có 90 m3 nước nên 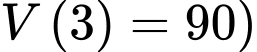
b) Sai.
Ta có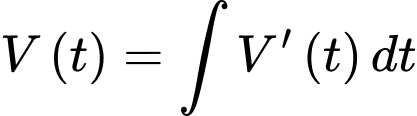
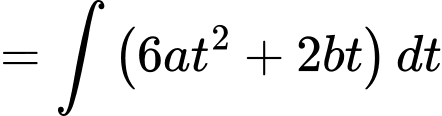
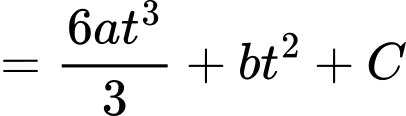
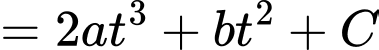
Biết
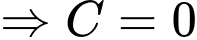
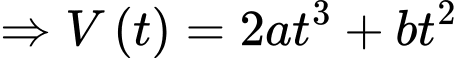
Lại có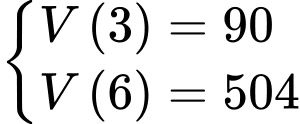
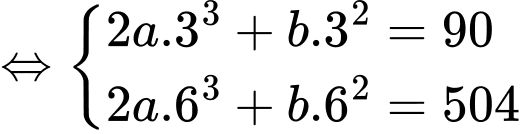
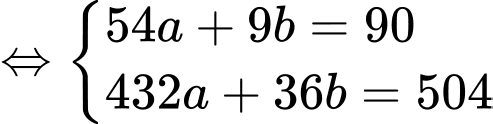
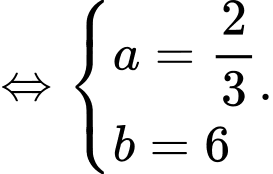
Suy ra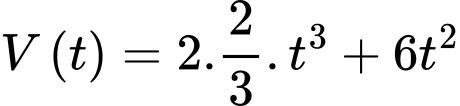
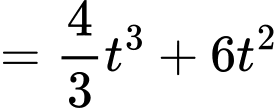
Vậy mệnh đề sai.
c) Đúng.
Từ kết quả tính toán được ở phần b) ta thấy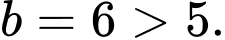
d) Sai.
Bể nước đầy khi thể tích của nước trong bể bằng 2000 m3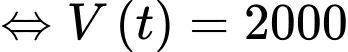
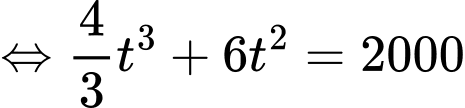
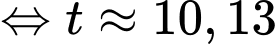 phút.
phút.
Vì
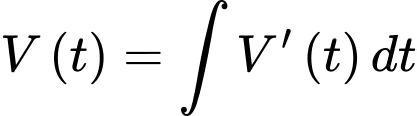 nên
nên 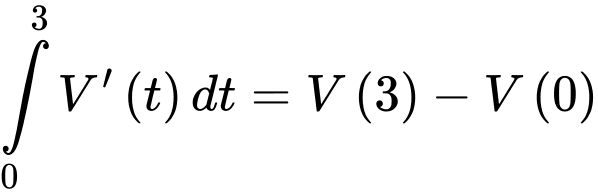
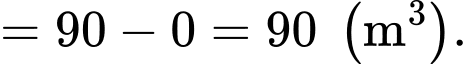
(vì ban đầu bể không có nước nên
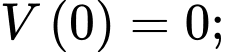 và sau 3 phút thì bể có 90 m3 nước nên
và sau 3 phút thì bể có 90 m3 nước nên 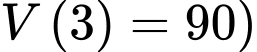
b) Sai.
Ta có
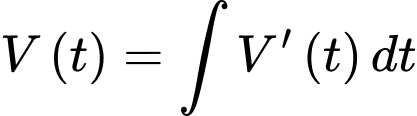
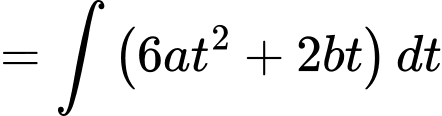
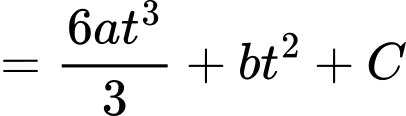
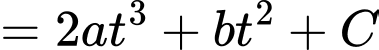
Biết

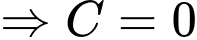
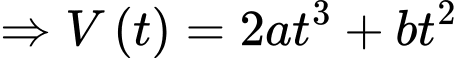
Lại có
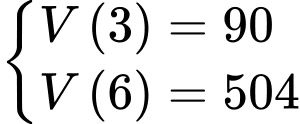
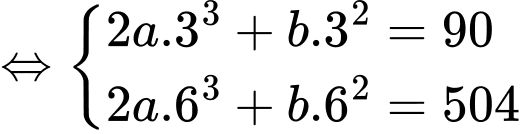
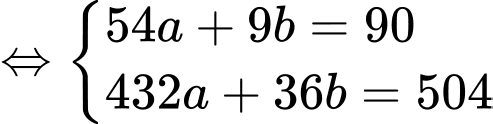
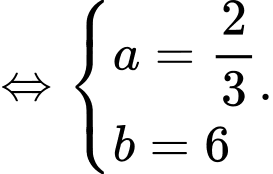
Suy ra
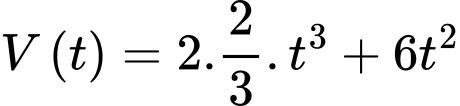
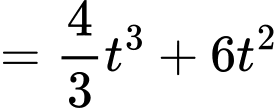
Vậy mệnh đề sai.
c) Đúng.
Từ kết quả tính toán được ở phần b) ta thấy
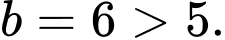
d) Sai.
Bể nước đầy khi thể tích của nước trong bể bằng 2000 m3
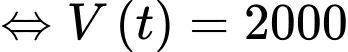
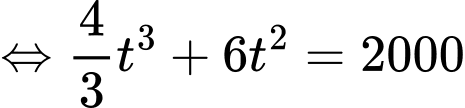
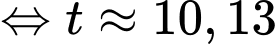 phút.
phút.
Câu 16 [775981]: Một chất điểm 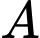 xuất phát từ
xuất phát từ  chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật
chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật 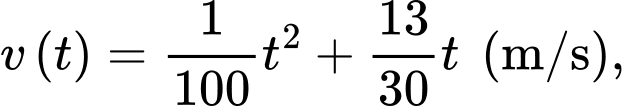 trong đó
trong đó 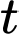 (giây) là khoảng thời gian tính từ lúc
(giây) là khoảng thời gian tính từ lúc 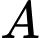 bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm
bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm 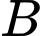 cũng xuất phát từ
cũng xuất phát từ  chuyển động thẳng cùng hướng với
chuyển động thẳng cùng hướng với 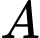 nhưng chậm hơn 10 giây so với
nhưng chậm hơn 10 giây so với 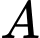 và có gia tốc bằng
và có gia tốc bằng 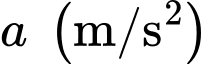 (
(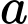 là hằng số). Sau khi
là hằng số). Sau khi 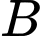 xuất phát được 15 giây thì đuổi kịp
xuất phát được 15 giây thì đuổi kịp 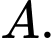
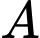 xuất phát từ
xuất phát từ  chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật
chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật 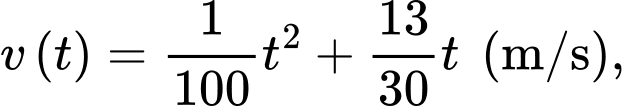 trong đó
trong đó 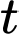 (giây) là khoảng thời gian tính từ lúc
(giây) là khoảng thời gian tính từ lúc 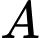 bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm
bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm 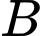 cũng xuất phát từ
cũng xuất phát từ  chuyển động thẳng cùng hướng với
chuyển động thẳng cùng hướng với 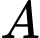 nhưng chậm hơn 10 giây so với
nhưng chậm hơn 10 giây so với 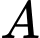 và có gia tốc bằng
và có gia tốc bằng 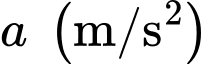 (
(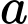 là hằng số). Sau khi
là hằng số). Sau khi 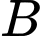 xuất phát được 15 giây thì đuổi kịp
xuất phát được 15 giây thì đuổi kịp 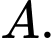
a) Đúng.
Vì sau 15 giây thì B đuổi kịp A nên A đi được 15 giây. Quãng đường A đi được trong 15 giây và 10 giây đầu là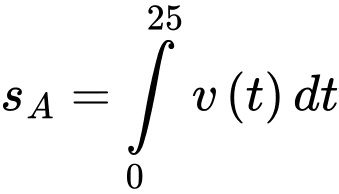
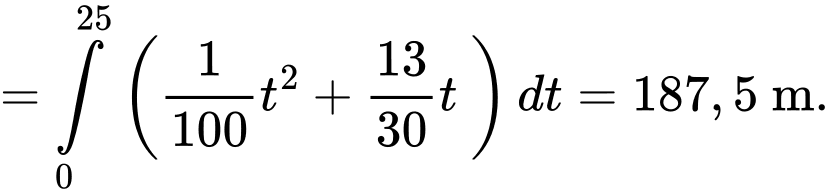
b) Đúng.
Vận tốc của chất điểm B tính từ lúc B xuất phát là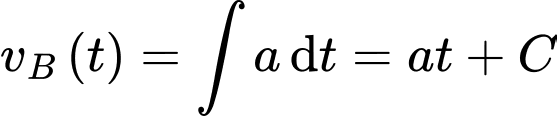
Biết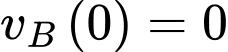
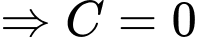
Suy ra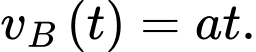
c) Sai.
Vì B xuất phát muộn hơn A 10 giây nên B đã đi được trong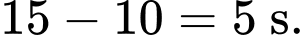 Khi đó, quãng đường mà B đi được trong 5 giây là
Khi đó, quãng đường mà B đi được trong 5 giây là 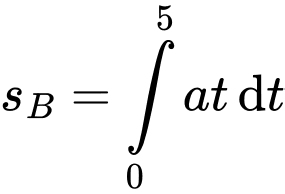
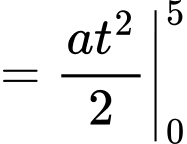
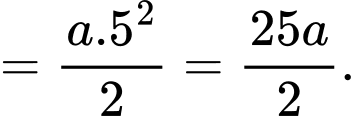
d) Sai.
Vì B đuổi kịp A nên quãng đường B đi được sẽ bằng với quãng đường mà A đi được, tương đương
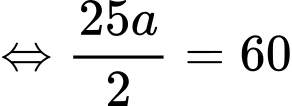
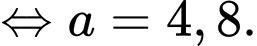
Suy ra vận tốc của B là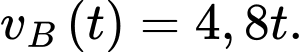
Vì sau 5 giây thì B đuổi kịp A nên vận tốc tại thời điểm B đuổi kịp A là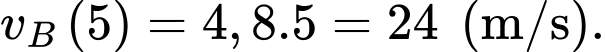
Vì sau 15 giây thì B đuổi kịp A nên A đi được 15 giây. Quãng đường A đi được trong 15 giây và 10 giây đầu là
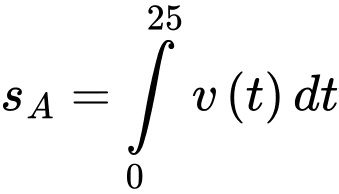
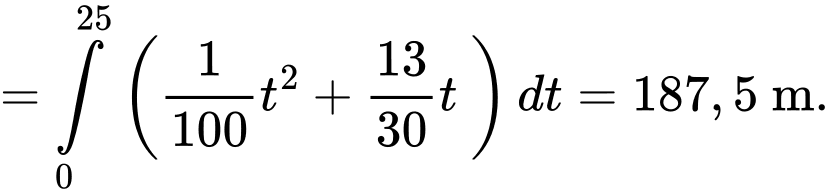
b) Đúng.
Vận tốc của chất điểm B tính từ lúc B xuất phát là
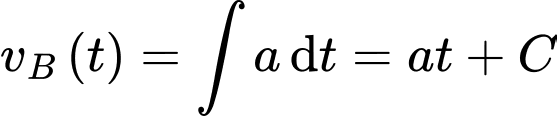
Biết
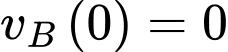
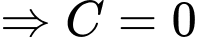
Suy ra
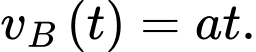
c) Sai.
Vì B xuất phát muộn hơn A 10 giây nên B đã đi được trong
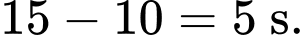 Khi đó, quãng đường mà B đi được trong 5 giây là
Khi đó, quãng đường mà B đi được trong 5 giây là 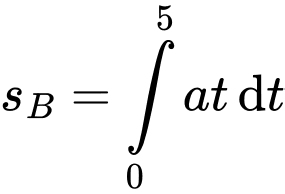
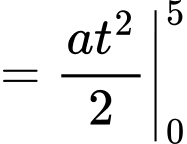
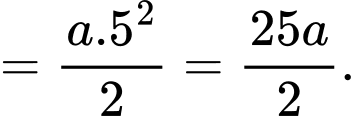
d) Sai.
Vì B đuổi kịp A nên quãng đường B đi được sẽ bằng với quãng đường mà A đi được, tương đương

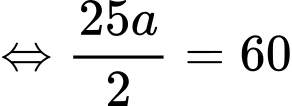
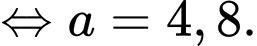
Suy ra vận tốc của B là
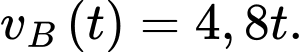
Vì sau 5 giây thì B đuổi kịp A nên vận tốc tại thời điểm B đuổi kịp A là
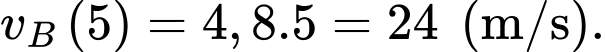
PHẦN III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 17 đến câu 22.
Câu 17 [775984]: Có bao nhiêu giá trị nguyên của 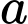 để
để 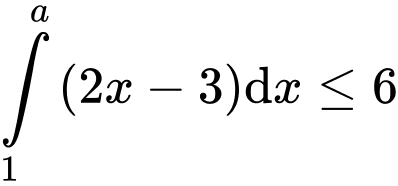 ?
?
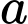 để
để 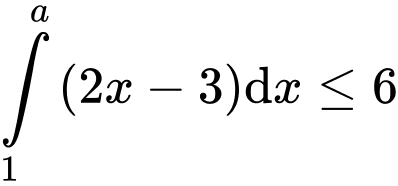 ?
?
Điền đáp án: 6.
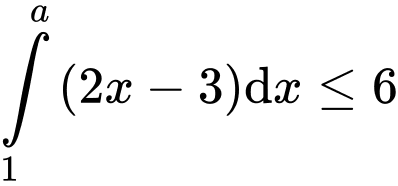
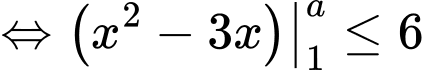
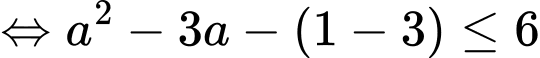
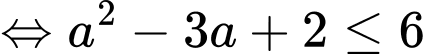
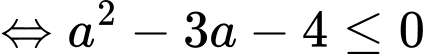

Kết hợp với điều kiện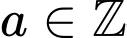
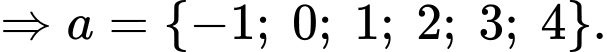 Vậy có 6 giá trị nguyên của
Vậy có 6 giá trị nguyên của 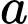 thoả mãn yêu cầu bài toán.
thoả mãn yêu cầu bài toán.
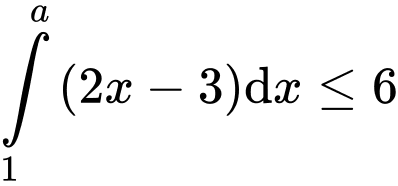
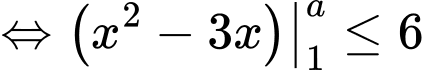
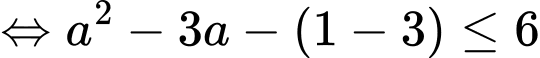
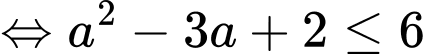
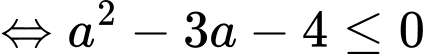

Kết hợp với điều kiện
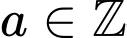
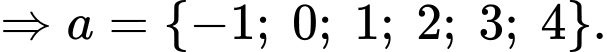 Vậy có 6 giá trị nguyên của
Vậy có 6 giá trị nguyên của 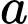 thoả mãn yêu cầu bài toán.
thoả mãn yêu cầu bài toán.
Câu 18 [584113]: Cho 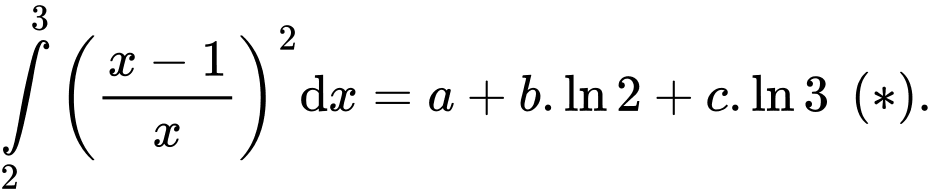 Biết rằng, tồn tại duy nhất bộ ba số hữu tỉ
Biết rằng, tồn tại duy nhất bộ ba số hữu tỉ 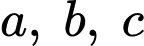 thỏa mãn
thỏa mãn  Tổng
Tổng 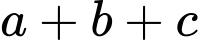 có giá trị bằng bao nhiêu (nhập đáp án vào ô trống)?
có giá trị bằng bao nhiêu (nhập đáp án vào ô trống)?
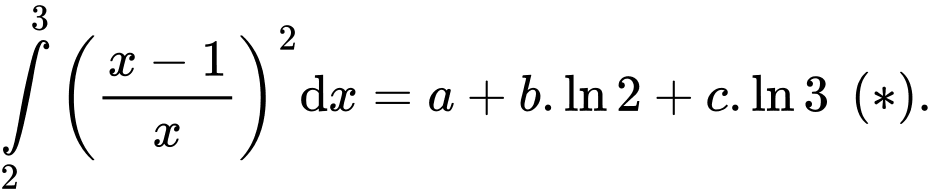 Biết rằng, tồn tại duy nhất bộ ba số hữu tỉ
Biết rằng, tồn tại duy nhất bộ ba số hữu tỉ 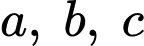 thỏa mãn
thỏa mãn  Tổng
Tổng 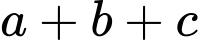 có giá trị bằng bao nhiêu (nhập đáp án vào ô trống)?
có giá trị bằng bao nhiêu (nhập đáp án vào ô trống)?
HD: 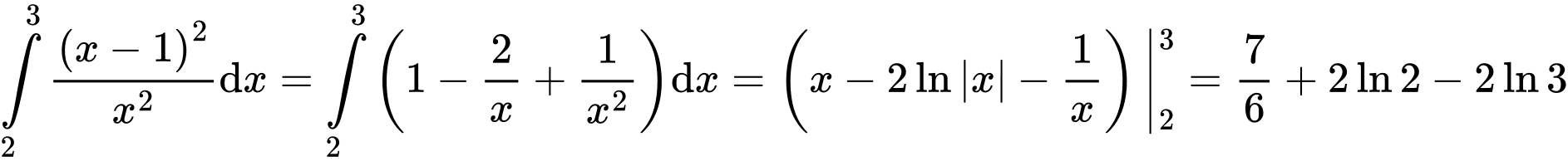 Vậy
Vậy 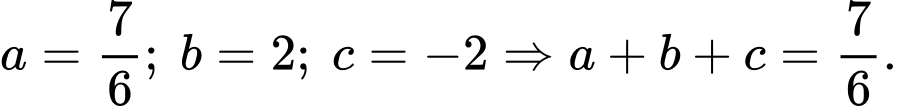
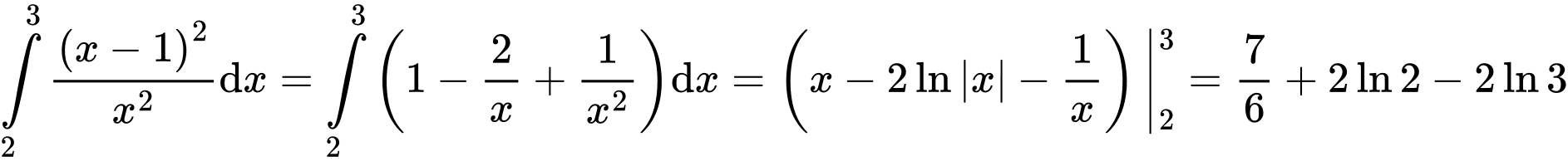 Vậy
Vậy 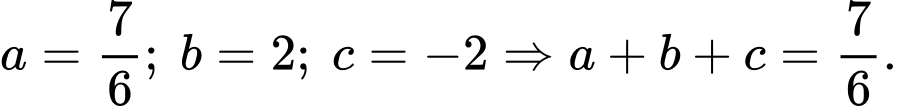
Câu 19 [775985]: Giả sử doanh số (tính bằng số sản phẩm) của một sản phẩm mới (trong vòng một số năm nhất định) tuân theo quy luật logistic được mô hình hoá bằng hàm số 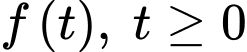 trong đó thời gian
trong đó thời gian 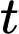 được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm
được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm 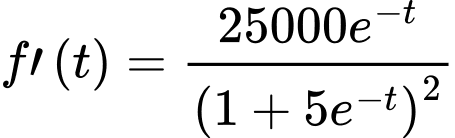 sẽ biểu thị tốc độ bán hàng. Biết rằng sau 2 năm đạt doanh số
sẽ biểu thị tốc độ bán hàng. Biết rằng sau 2 năm đạt doanh số 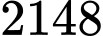 sản phẩm. Tính doanh số trong vòng 5 năm của sản phẩm (kết quả làm tròn đến hàng đơn vị).
sản phẩm. Tính doanh số trong vòng 5 năm của sản phẩm (kết quả làm tròn đến hàng đơn vị).
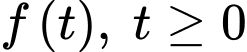 trong đó thời gian
trong đó thời gian 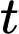 được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm
được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm 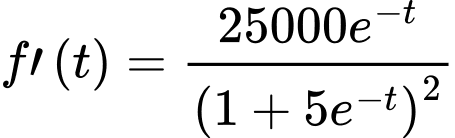 sẽ biểu thị tốc độ bán hàng. Biết rằng sau 2 năm đạt doanh số
sẽ biểu thị tốc độ bán hàng. Biết rằng sau 2 năm đạt doanh số 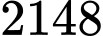 sản phẩm. Tính doanh số trong vòng 5 năm của sản phẩm (kết quả làm tròn đến hàng đơn vị).
sản phẩm. Tính doanh số trong vòng 5 năm của sản phẩm (kết quả làm tròn đến hàng đơn vị).
Điền đáp án: 4003.
YCBT là tính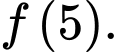
Ta có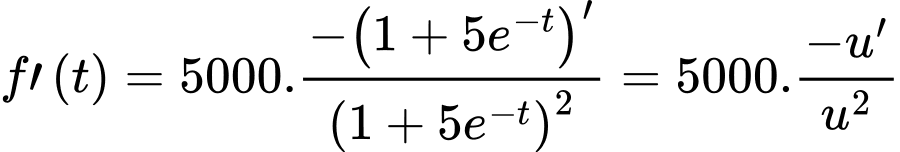 với
với 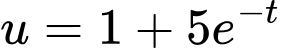
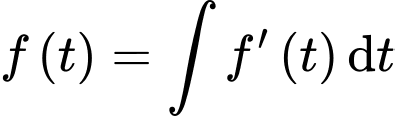
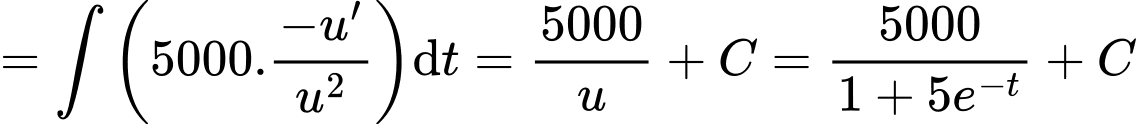
Từ giả thiết: “sau 2 năm đạt doanh số 2148 sản phẩm” nên ta có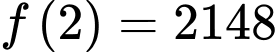
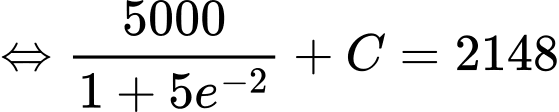
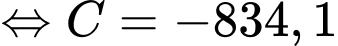
Suy ra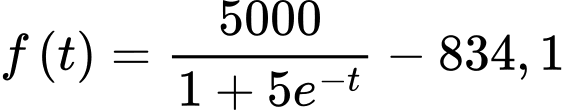
Vậy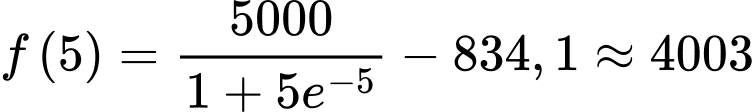 sản phẩm.
sản phẩm.
YCBT là tính
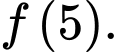
Ta có
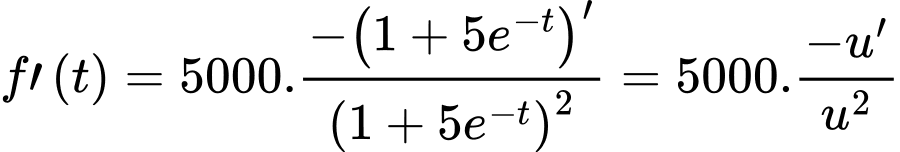 với
với 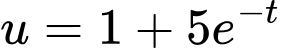
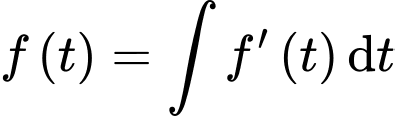
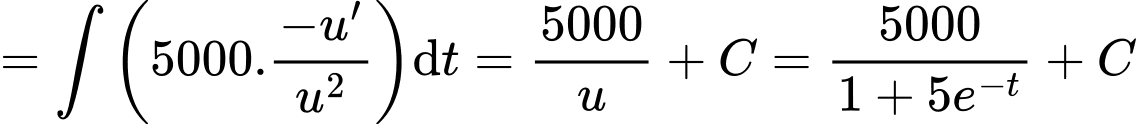
Từ giả thiết: “sau 2 năm đạt doanh số 2148 sản phẩm” nên ta có
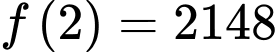
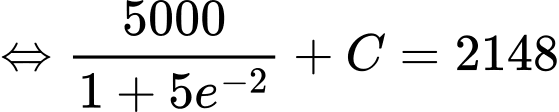
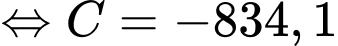
Suy ra
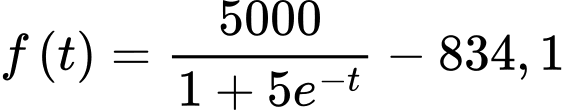
Vậy
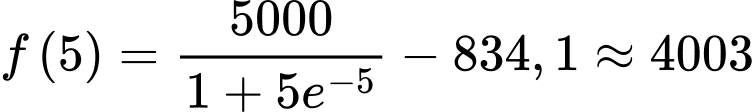 sản phẩm.
sản phẩm.
Câu 20 [779036]: Trong một trò chơi điện tử, hai bạn Tít và Mít thi xem ai chạy được quãng đường xa hơn. Tít chạy với vận tốc 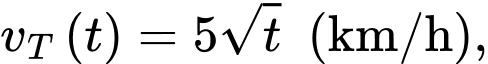 quãng đường Mít chạy được cho bởi phương trình
quãng đường Mít chạy được cho bởi phương trình 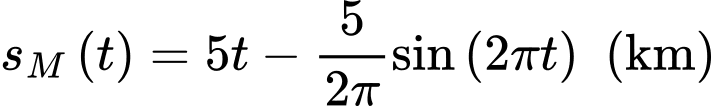 (với
(với 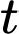 là thời gian tính theo giờ). Nếu cuộc đua kết thúc khi Tít hoặc Mít chạy được
là thời gian tính theo giờ). Nếu cuộc đua kết thúc khi Tít hoặc Mít chạy được 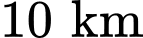 đầu tiên thì khoảng cách giữa hai bạn là bao nhiêu kilômét? (Kết quả làm tròn đến hàng phần trăm)
đầu tiên thì khoảng cách giữa hai bạn là bao nhiêu kilômét? (Kết quả làm tròn đến hàng phần trăm)
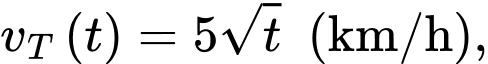 quãng đường Mít chạy được cho bởi phương trình
quãng đường Mít chạy được cho bởi phương trình 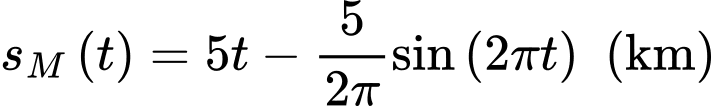 (với
(với 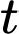 là thời gian tính theo giờ). Nếu cuộc đua kết thúc khi Tít hoặc Mít chạy được
là thời gian tính theo giờ). Nếu cuộc đua kết thúc khi Tít hoặc Mít chạy được 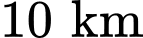 đầu tiên thì khoảng cách giữa hai bạn là bao nhiêu kilômét? (Kết quả làm tròn đến hàng phần trăm)
đầu tiên thì khoảng cách giữa hai bạn là bao nhiêu kilômét? (Kết quả làm tròn đến hàng phần trăm)
Đáp số: 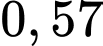 .
.
Chọn gốc thời gian là thời điểm xuất phát . Ta hiểu là hai bạn thi chạy nên xuất phát cùng vị trí, cùng thời điểm và chạy cùng hướng.
Quãng đường Tít chạy được là: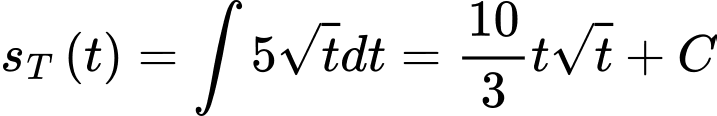 .
.
Do: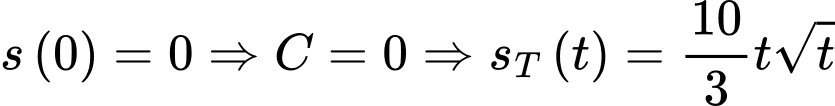 (km).
(km).
Tít chạy được 10 km khi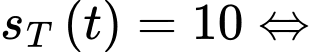
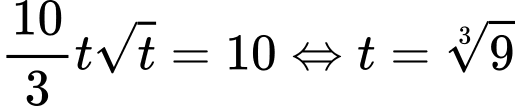 (h)
(h)
Mít chạy được 10 km khi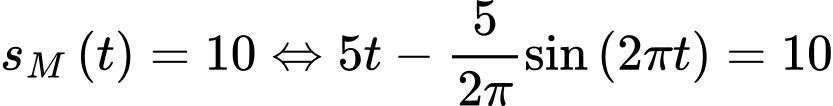
Nhận thấy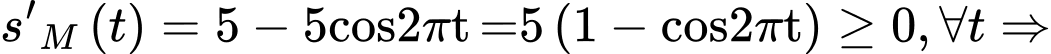 phương trình
phương trình 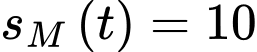 có nhiều
nhất một nghiệm, mà ta nhẩm được nghiệm
có nhiều
nhất một nghiệm, mà ta nhẩm được nghiệm 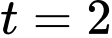 . Do đó:
. Do đó: 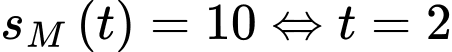 (h)
(h)
Do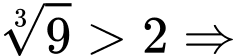 Mít là người thắng cuộc.
Mít là người thắng cuộc.
Khi đó khoảng cách giữa hai bạn là: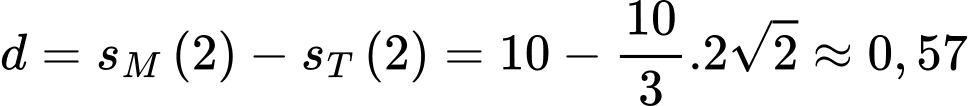 (km).
(km).
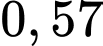 .
.
Chọn gốc thời gian là thời điểm xuất phát . Ta hiểu là hai bạn thi chạy nên xuất phát cùng vị trí, cùng thời điểm và chạy cùng hướng.
Quãng đường Tít chạy được là:
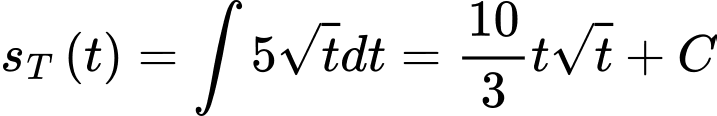 .
.
Do:
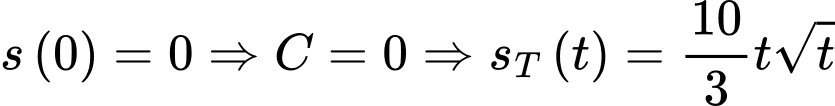 (km).
(km).
Tít chạy được 10 km khi
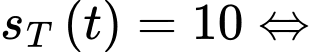
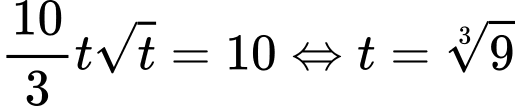 (h)
(h)
Mít chạy được 10 km khi
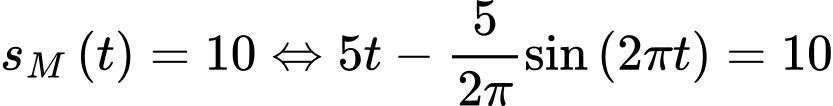
Nhận thấy
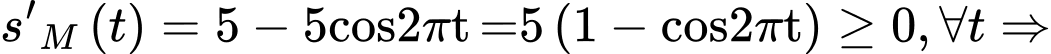 phương trình
phương trình 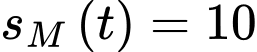 có nhiều
nhất một nghiệm, mà ta nhẩm được nghiệm
có nhiều
nhất một nghiệm, mà ta nhẩm được nghiệm 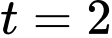 . Do đó:
. Do đó: 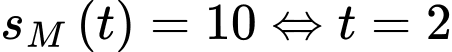 (h)
(h)
Do
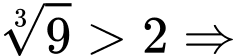 Mít là người thắng cuộc.
Mít là người thắng cuộc.
Khi đó khoảng cách giữa hai bạn là:
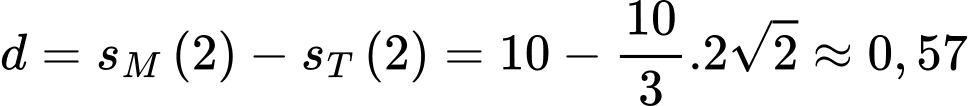 (km).
(km).
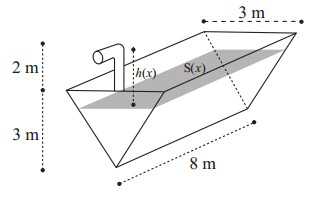
Câu 21 [775990]: Một bể nước hình lăng trụ với các kích thước như hình vẽ chứa đầy nước. Công để bơm hết nước trong bể trên ra từ một vòi cao 2 mét được tính theo công thức 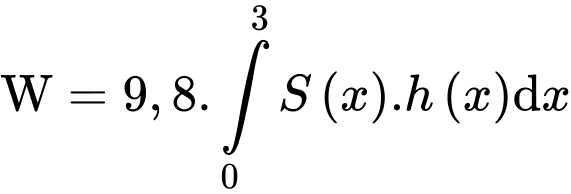 (đơn vị kilôJun), trong đó
(đơn vị kilôJun), trong đó 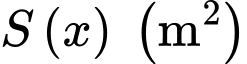 là diện tích của lớp nước cách mặt bể
là diện tích của lớp nước cách mặt bể 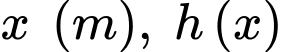 mét là khoảng cách từ vòi đến lớp nước đó. Tính
mét là khoảng cách từ vòi đến lớp nước đó. Tính 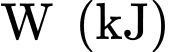 (kết quả làm tròn đến hàng đơn vị).
(kết quả làm tròn đến hàng đơn vị).
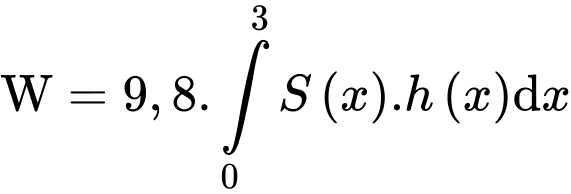 (đơn vị kilôJun), trong đó
(đơn vị kilôJun), trong đó 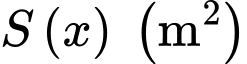 là diện tích của lớp nước cách mặt bể
là diện tích của lớp nước cách mặt bể 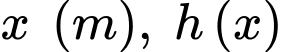 mét là khoảng cách từ vòi đến lớp nước đó. Tính
mét là khoảng cách từ vòi đến lớp nước đó. Tính 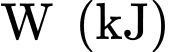 (kết quả làm tròn đến hàng đơn vị).
(kết quả làm tròn đến hàng đơn vị).
Điền đáp án: 1058.
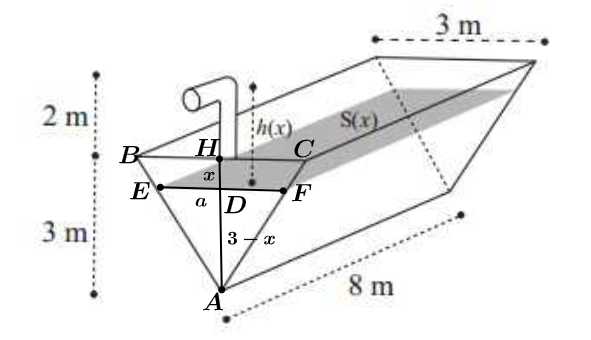
Kẻ và kí hiệu các điểm như hình vẽ.
và kí hiệu các điểm như hình vẽ.
Theo giả thiết, ta có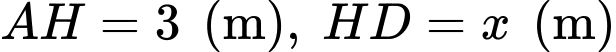 suy ra
suy ra 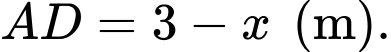 Giả sử
Giả sử 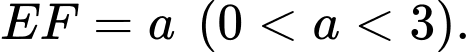
Lại có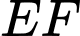 là chiều rộng của lớp nước cách mặt bể
là chiều rộng của lớp nước cách mặt bể  nên
nên 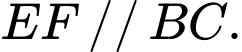
Xét tam giác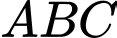 có
có  nên theo định lý Thalet, ta có
nên theo định lý Thalet, ta có 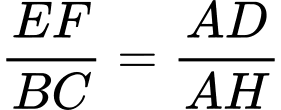
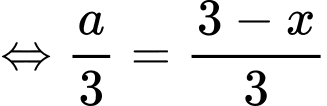
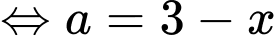
Khi đó, diện tích lớp nước (có dạng hình chữ nhật) là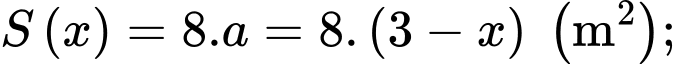 và khoảng cách từ vòi đến lớp nước là
và khoảng cách từ vòi đến lớp nước là 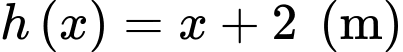
Suy ra công bơm nước là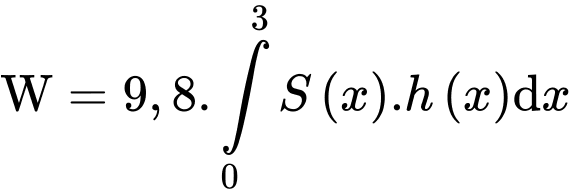
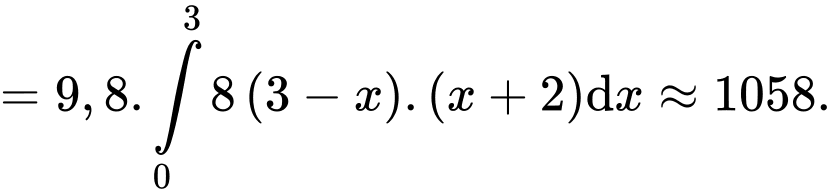

Kẻ
 và kí hiệu các điểm như hình vẽ.
và kí hiệu các điểm như hình vẽ.
Theo giả thiết, ta có
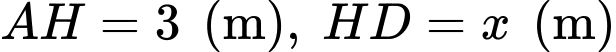 suy ra
suy ra 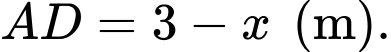 Giả sử
Giả sử 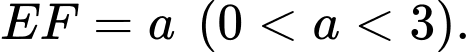
Lại có
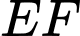 là chiều rộng của lớp nước cách mặt bể
là chiều rộng của lớp nước cách mặt bể  nên
nên 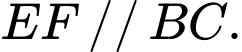
Xét tam giác
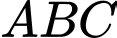 có
có  nên theo định lý Thalet, ta có
nên theo định lý Thalet, ta có 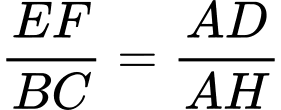
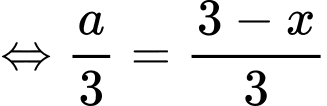
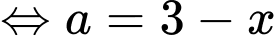
Khi đó, diện tích lớp nước (có dạng hình chữ nhật) là
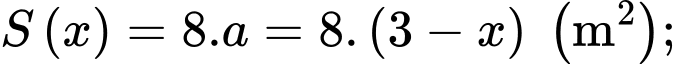 và khoảng cách từ vòi đến lớp nước là
và khoảng cách từ vòi đến lớp nước là 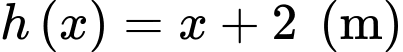
Suy ra công bơm nước là
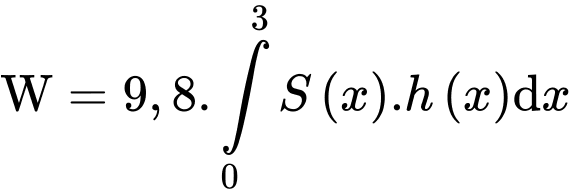
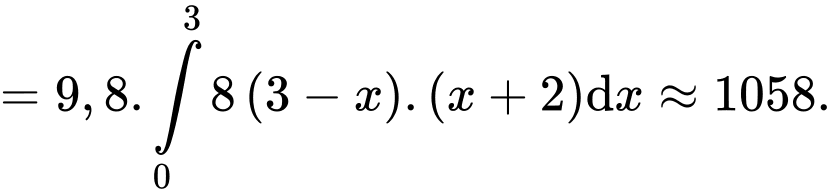
Câu 22 [779008]: Ở  phản ứng hoá học phân huỷ
phản ứng hoá học phân huỷ 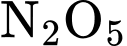 xảy ra theo phương trình
xảy ra theo phương trình  với nồng độ
với nồng độ 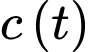 (mol/L) của
(mol/L) của 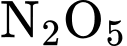
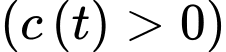 tại thời điểm
tại thời điểm 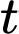 giây (
giây ( ) thoả mãn
) thoả mãn 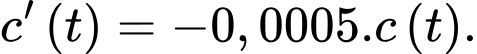 Biết khi
Biết khi 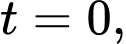 nồng độ ban đầu của
nồng độ ban đầu của 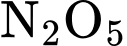 là
là 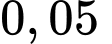 mol/L và nồng độ trung bình của
mol/L và nồng độ trung bình của 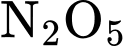 (mol/L) từ thời điểm
(mol/L) từ thời điểm 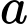 giây đến thời điểm
giây đến thời điểm 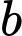 giây
giây 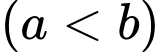 được cho bởi công thức
được cho bởi công thức 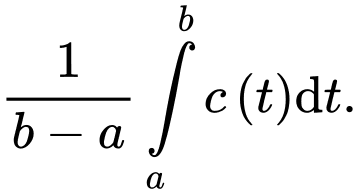 Nồng độ trung bình của
Nồng độ trung bình của 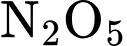 từ thời điểm 10 giây đến thời điểm 20 giây là
từ thời điểm 10 giây đến thời điểm 20 giây là 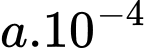 (moL/L). Tính
(moL/L). Tính 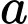 (làm tròn kết quả đến hàng đơn vị).
(làm tròn kết quả đến hàng đơn vị).
 phản ứng hoá học phân huỷ
phản ứng hoá học phân huỷ 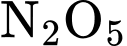 xảy ra theo phương trình
xảy ra theo phương trình  với nồng độ
với nồng độ 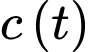 (mol/L) của
(mol/L) của 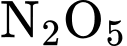
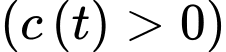 tại thời điểm
tại thời điểm 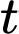 giây (
giây ( ) thoả mãn
) thoả mãn 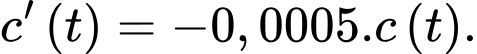 Biết khi
Biết khi 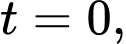 nồng độ ban đầu của
nồng độ ban đầu của 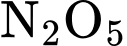 là
là 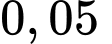 mol/L và nồng độ trung bình của
mol/L và nồng độ trung bình của 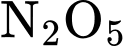 (mol/L) từ thời điểm
(mol/L) từ thời điểm 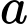 giây đến thời điểm
giây đến thời điểm 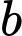 giây
giây 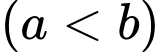 được cho bởi công thức
được cho bởi công thức 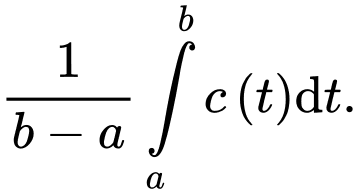 Nồng độ trung bình của
Nồng độ trung bình của 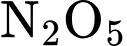 từ thời điểm 10 giây đến thời điểm 20 giây là
từ thời điểm 10 giây đến thời điểm 20 giây là 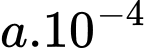 (moL/L). Tính
(moL/L). Tính 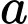 (làm tròn kết quả đến hàng đơn vị).
(làm tròn kết quả đến hàng đơn vị).
Điền đáp án: 496.
Để tính được nồng độ trung bình, ta cần đi tìm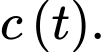
Theo giả thiết, ta có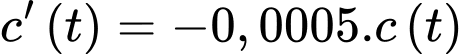
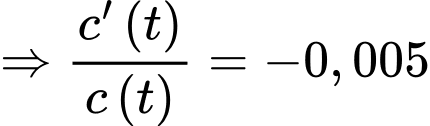
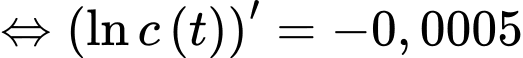
Nguyên hàm 2 vế, ta được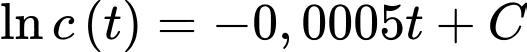
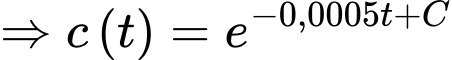
Biết tại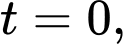 thì
thì 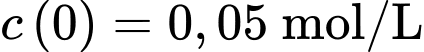
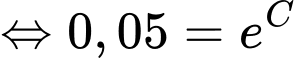
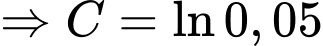
Suy ra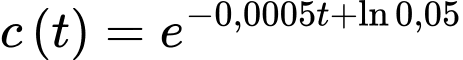
Có nồng độ trung bình từ thời điểm 10 giây đến thời điểm 20 giây bằng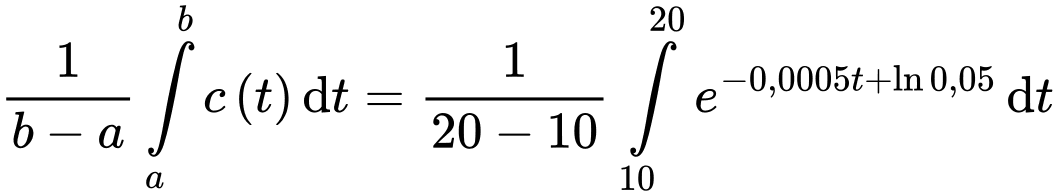
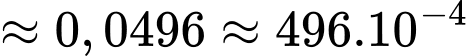
Vậy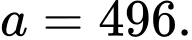
Để tính được nồng độ trung bình, ta cần đi tìm
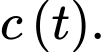
Theo giả thiết, ta có
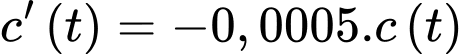
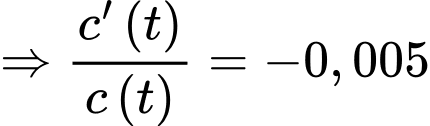
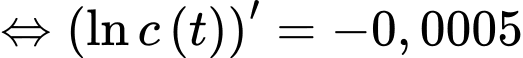
Nguyên hàm 2 vế, ta được
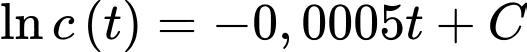
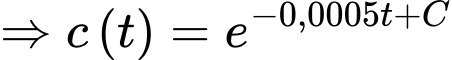
Biết tại
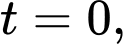 thì
thì 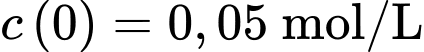
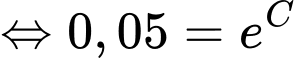
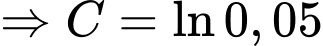
Suy ra
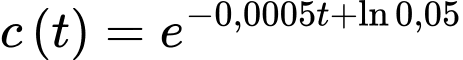
Có nồng độ trung bình từ thời điểm 10 giây đến thời điểm 20 giây bằng
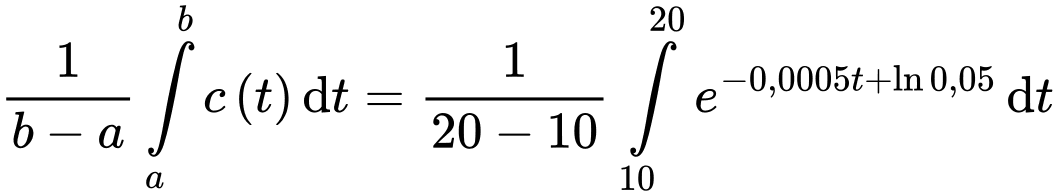
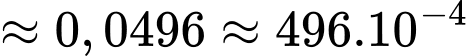
Vậy