PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 15. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1 [512833]: Thể tích của khối lập phương có cạnh bằng 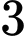 là
là
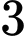 là
là A, 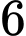 .
.
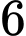 .
.B, 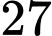 .
.
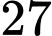 .
.C, 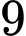 .
.
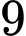 .
.D, 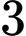 .
.
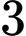 .
.
Chọn B
Thể tích khối lập phương có cạnh bằng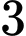 là:
là: 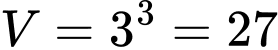 . Đáp án: B
. Đáp án: B
Thể tích khối lập phương có cạnh bằng
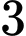 là:
là: 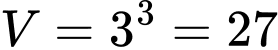 . Đáp án: B
. Đáp án: B
Câu 2 [509006]: Thể tích khối lăng trụ có diện tích đáy bằng 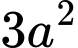 , chiều cao bằng
, chiều cao bằng 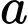 là
là
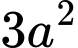 , chiều cao bằng
, chiều cao bằng 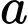 là
là A, 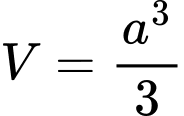 .
.
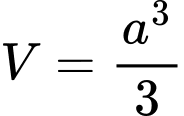 .
.B, 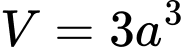 .
.
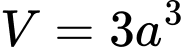 .
.C, 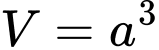 .
.
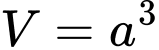 .
.D, 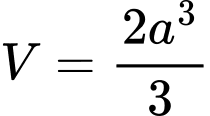 .
.
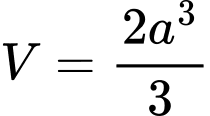 .
.
Chọn B
Thể tích khối lăng trụ có diện tích đáy bằng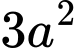 , chiều cao bằng
, chiều cao bằng 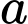 là:
là: 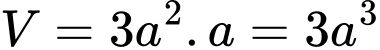 . Đáp án: B
. Đáp án: B
Thể tích khối lăng trụ có diện tích đáy bằng
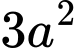 , chiều cao bằng
, chiều cao bằng 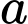 là:
là: 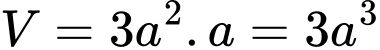 . Đáp án: B
. Đáp án: B
Câu 3 [325690]: Thể tích khối lập phương có độ dài đường chéo bằng 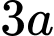 là:
là:
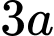 là:
là: A, 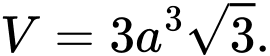
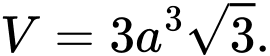
B, 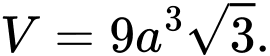
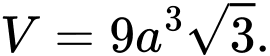
C, . 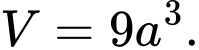
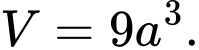
D, 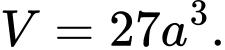
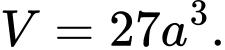
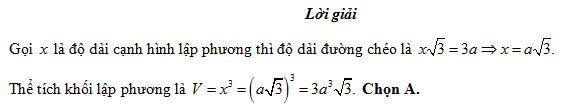 Đáp án: A
Đáp án: A
Câu 4 [520570]: Cho khối hộp chữ nhật  có
có 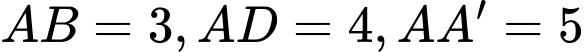 . Thể tích khối hộp chữ nhật đã cho bằng
. Thể tích khối hộp chữ nhật đã cho bằng
 có
có 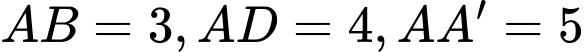 . Thể tích khối hộp chữ nhật đã cho bằng
. Thể tích khối hộp chữ nhật đã cho bằng A,  .
.
 .
.B,  .
.
 .
.C, 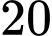 .
.
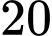 .
.D, 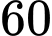 .
.
 .
.
Chọn D
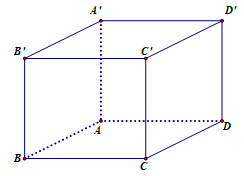
Thể tích khối hộp chữ nhật đã cho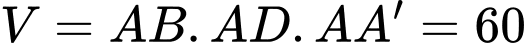 . Đáp án: D
. Đáp án: D

Thể tích khối hộp chữ nhật đã cho
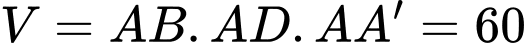 . Đáp án: D
. Đáp án: D
Câu 5 [506519]: Cho khối chóp 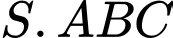 có đáy
có đáy 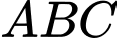 là tam giác đều cạnh
là tam giác đều cạnh 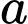 ,
, 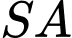 vuông góc với mặt phẳng đáy và
vuông góc với mặt phẳng đáy và 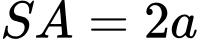 . Tính thể tích khối chóp
. Tính thể tích khối chóp 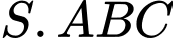 .
.
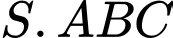 có đáy
có đáy 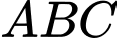 là tam giác đều cạnh
là tam giác đều cạnh 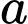 ,
, 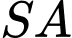 vuông góc với mặt phẳng đáy và
vuông góc với mặt phẳng đáy và 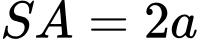 . Tính thể tích khối chóp
. Tính thể tích khối chóp 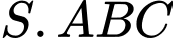 .
. A, 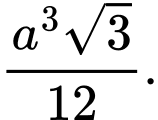
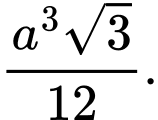
B, 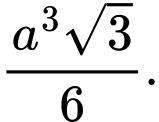
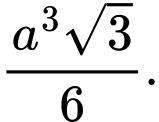
C, 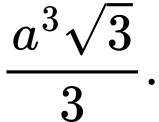
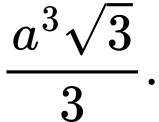
D, 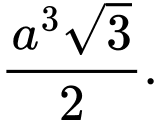
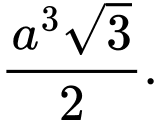
Đáp án B
Thể tích khối chóp là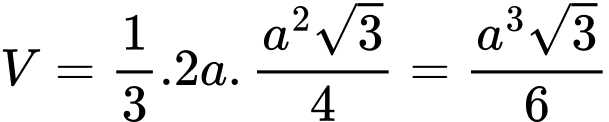 . Đáp án: B
. Đáp án: B
Thể tích khối chóp là
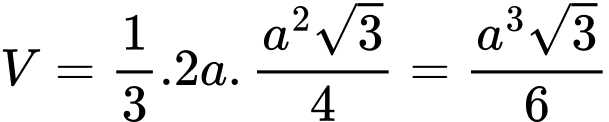 . Đáp án: B
. Đáp án: B
Câu 6 [275893]: Cho lăng trụ tam giác đều  có
có 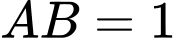 ,
, 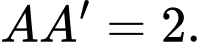 Thể tích của khối lăng trụ
Thể tích của khối lăng trụ  bằng
bằng
 có
có 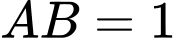 ,
, 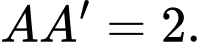 Thể tích của khối lăng trụ
Thể tích của khối lăng trụ  bằng
bằng A, 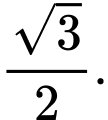
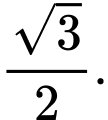
B, 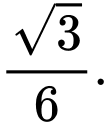
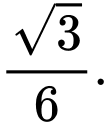
C, 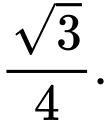
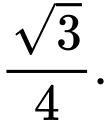
D, 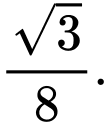
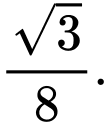
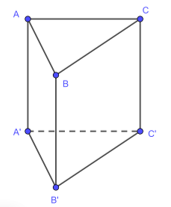
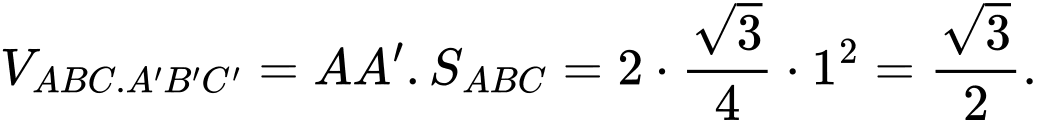
Chọn đáp án A.
Đáp án: A
Câu 7 [324930]: Cho hình chóp 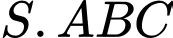 có đáy
có đáy 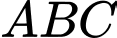 là tam giác đều cạnh a, cạnh bên
là tam giác đều cạnh a, cạnh bên 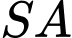 vuông góc với đáy, đường thẳng
vuông góc với đáy, đường thẳng 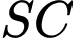 tạo với mặt đáy một góc
tạo với mặt đáy một góc 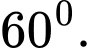 Thể tích khối chóp
Thể tích khối chóp 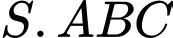 bằng ?
bằng ?
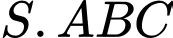 có đáy
có đáy 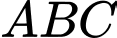 là tam giác đều cạnh a, cạnh bên
là tam giác đều cạnh a, cạnh bên 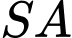 vuông góc với đáy, đường thẳng
vuông góc với đáy, đường thẳng 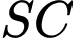 tạo với mặt đáy một góc
tạo với mặt đáy một góc 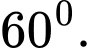 Thể tích khối chóp
Thể tích khối chóp 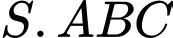 bằng ?
bằng ? A, 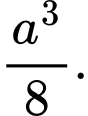
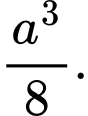
B, 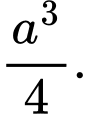
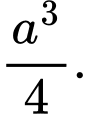
C, 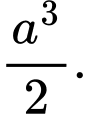
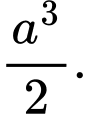
D, 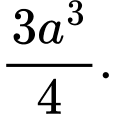
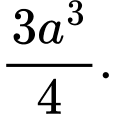
 Đáp án: B
Đáp án: B
Câu 8 [319354]: Cho khối hộp chữ nhật  có
có 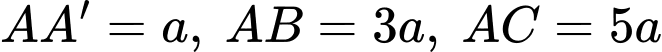 . Thể tích khối hộp là
. Thể tích khối hộp là
 có
có 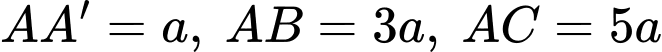 . Thể tích khối hộp là
. Thể tích khối hộp là A, 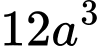 .
.
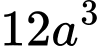 .
.B, 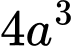 .
.
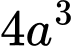 .
.C, 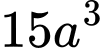 .
.
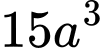 .
.D, 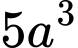 .
.
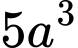 .
.
Chọn A
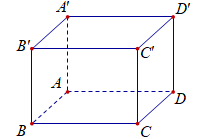
Ta có: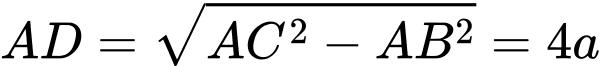 .
.
Thể tích khối hộp: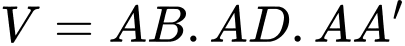
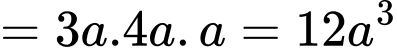 . Đáp án: A
. Đáp án: A

Ta có:
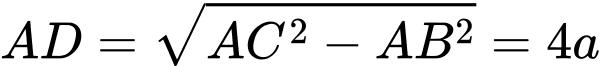 .
.Thể tích khối hộp:
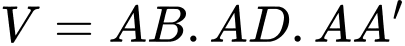
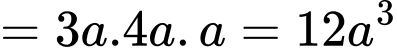 . Đáp án: A
. Đáp án: A
Câu 9 [339508]: Cho lăng trụ đứng  có đáy là tam giác đều cạnh
có đáy là tam giác đều cạnh 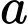 và
và 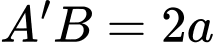 . Thể tích của khối lăng trụ đã cho bằng
. Thể tích của khối lăng trụ đã cho bằng
 có đáy là tam giác đều cạnh
có đáy là tam giác đều cạnh 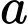 và
và 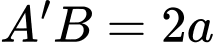 . Thể tích của khối lăng trụ đã cho bằng
. Thể tích của khối lăng trụ đã cho bằng A, 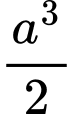 .
.
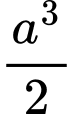 .
.B, 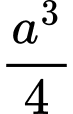 .
.
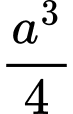 .
.C, 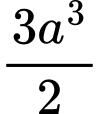 .
.
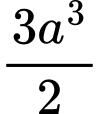 .
.D, 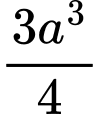 .
.
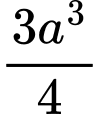 .
.
Chọn D
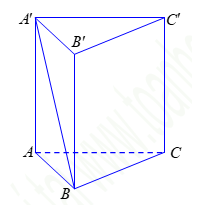
Diện tích đáy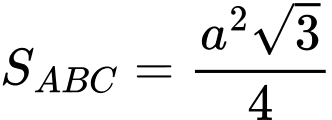
Tam giác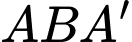 vuông tại
vuông tại 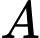 nên
nên 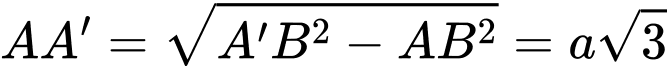 .
.
Thể tích khối lăng trụ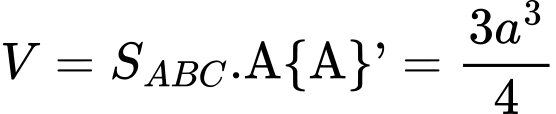 . Đáp án: D
. Đáp án: D

Diện tích đáy
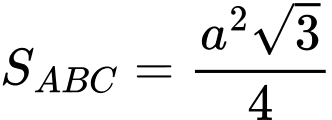
Tam giác
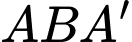 vuông tại
vuông tại 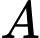 nên
nên 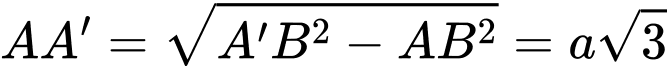 .
.Thể tích khối lăng trụ
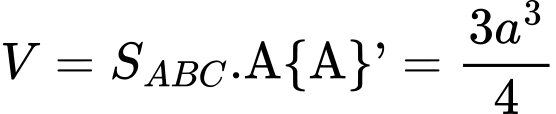 . Đáp án: D
. Đáp án: D
Câu 10 [8570]: Cho khối chóp đều 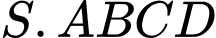 có cạnh đáy bằng
có cạnh đáy bằng 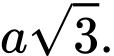 Tính thể tích khối chóp
Tính thể tích khối chóp 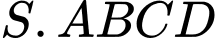 biết góc giữa cạnh bên và mặt đáy bằng
biết góc giữa cạnh bên và mặt đáy bằng 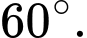
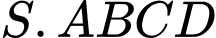 có cạnh đáy bằng
có cạnh đáy bằng 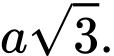 Tính thể tích khối chóp
Tính thể tích khối chóp 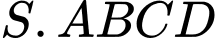 biết góc giữa cạnh bên và mặt đáy bằng
biết góc giữa cạnh bên và mặt đáy bằng 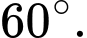
A, 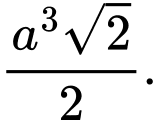
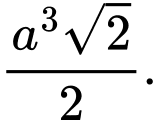
B, 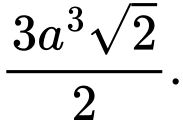
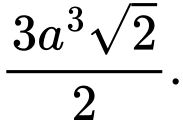
C, 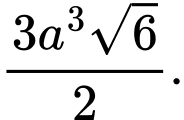
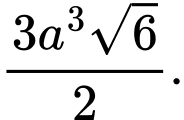
D, 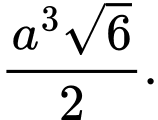
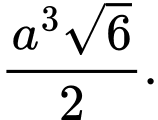
 Đáp án: B
Đáp án: B
Câu 11 [8531]: Cho hình chóp 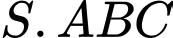 có đáy là tam giác
có đáy là tam giác 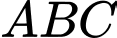 đều cạnh
đều cạnh 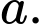 Hai mặt phẳng
Hai mặt phẳng 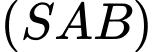 và
và 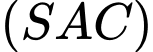 cùng vuông góc với mặt phẳng đáy. Tính thể tích khối chóp
cùng vuông góc với mặt phẳng đáy. Tính thể tích khối chóp 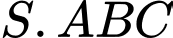 biết
biết 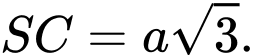
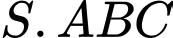 có đáy là tam giác
có đáy là tam giác 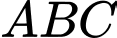 đều cạnh
đều cạnh 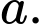 Hai mặt phẳng
Hai mặt phẳng 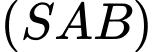 và
và 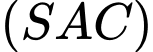 cùng vuông góc với mặt phẳng đáy. Tính thể tích khối chóp
cùng vuông góc với mặt phẳng đáy. Tính thể tích khối chóp 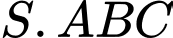 biết
biết 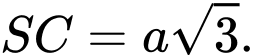
A, 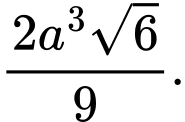
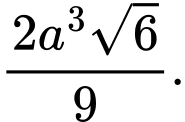
B, 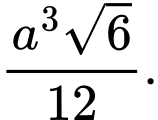
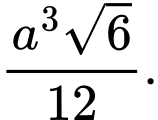
C, 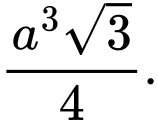
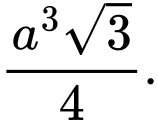
D, 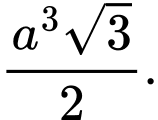
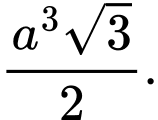
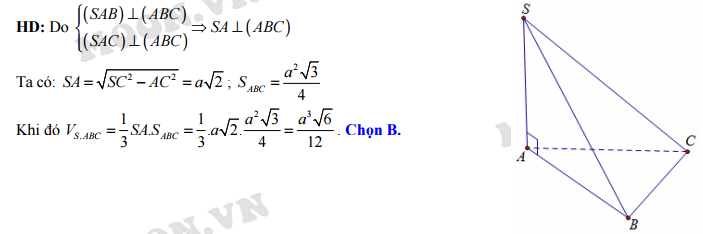 Đáp án: B
Đáp án: B
Câu 12 [8544]: Cho hình chóp 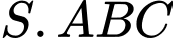 có đáy
có đáy 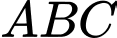 là tam giác vuông cân tại
là tam giác vuông cân tại 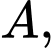 với cạnh
với cạnh 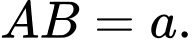 Tam giác
Tam giác 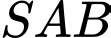 đều và nằm trong mặt phẳng vuông góc với mặt đáy. Thể tích khối chóp
đều và nằm trong mặt phẳng vuông góc với mặt đáy. Thể tích khối chóp 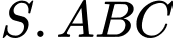 bằng
bằng
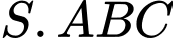 có đáy
có đáy 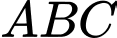 là tam giác vuông cân tại
là tam giác vuông cân tại 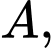 với cạnh
với cạnh 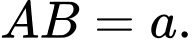 Tam giác
Tam giác 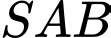 đều và nằm trong mặt phẳng vuông góc với mặt đáy. Thể tích khối chóp
đều và nằm trong mặt phẳng vuông góc với mặt đáy. Thể tích khối chóp 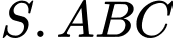 bằng
bằng A, 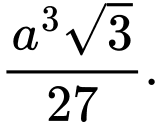
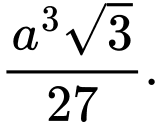
B, 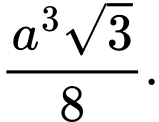
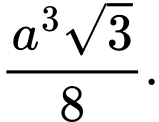
C, 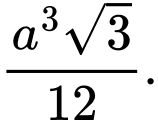
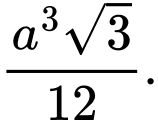
D, 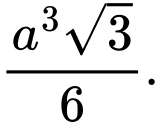
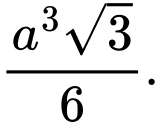
 Đáp án: C
Đáp án: C
Câu 13 [8565]: Cho hình chóp 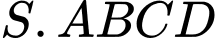 có đáy
có đáy 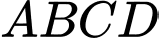 là hình vuông cạnh
là hình vuông cạnh 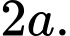 Tam giác
Tam giác 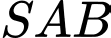 cân tại
cân tại 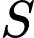 và nằm trong mặt phẳng vuông góc với mặt đáy. Đường thẳng
và nằm trong mặt phẳng vuông góc với mặt đáy. Đường thẳng 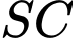 tạo với mặt đáy một góc
tạo với mặt đáy một góc 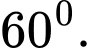 Thể tích khối chóp
Thể tích khối chóp 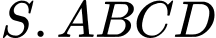 bằng
bằng
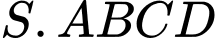 có đáy
có đáy 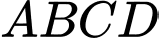 là hình vuông cạnh
là hình vuông cạnh 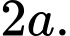 Tam giác
Tam giác 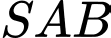 cân tại
cân tại 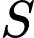 và nằm trong mặt phẳng vuông góc với mặt đáy. Đường thẳng
và nằm trong mặt phẳng vuông góc với mặt đáy. Đường thẳng 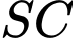 tạo với mặt đáy một góc
tạo với mặt đáy một góc 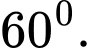 Thể tích khối chóp
Thể tích khối chóp 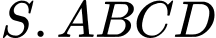 bằng
bằng A, . 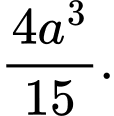
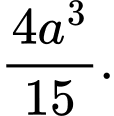
B, 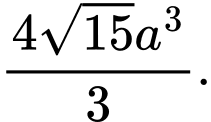
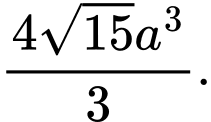
C, 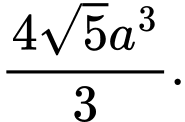
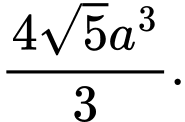
D, 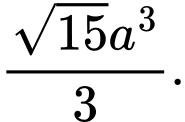
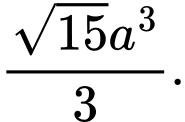
 Đáp án: B
Đáp án: B
Câu 14 [557132]: Cho lăng trụ đứng  có đáy
có đáy 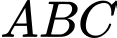 là tam giác vuông tại
là tam giác vuông tại 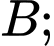
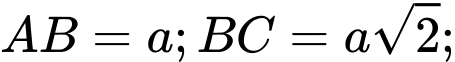 biết số đo góc nhị diện
biết số đo góc nhị diện 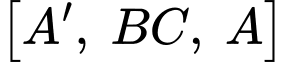 bằng
bằng 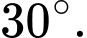 Thể tích của khối lăng trụ là
Thể tích của khối lăng trụ là
 có đáy
có đáy 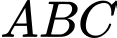 là tam giác vuông tại
là tam giác vuông tại 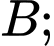
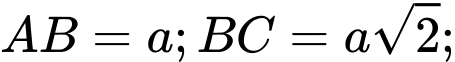 biết số đo góc nhị diện
biết số đo góc nhị diện 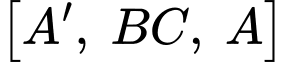 bằng
bằng 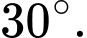 Thể tích của khối lăng trụ là
Thể tích của khối lăng trụ là A, 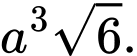
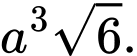
B, 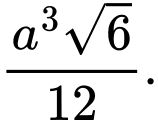
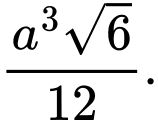
C, 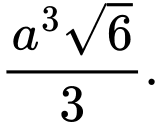
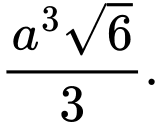
D, 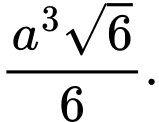
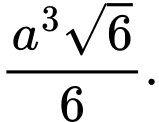

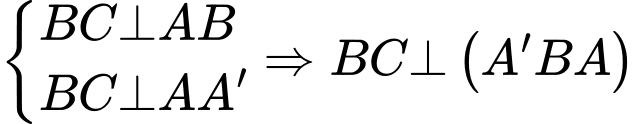 Do đó
Do đó 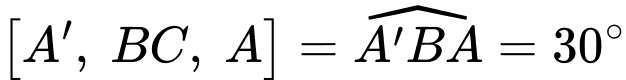 Suy ra
Suy ra 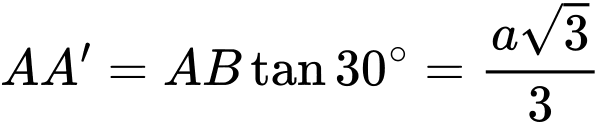 Thể tích của khối lăng trụ là:
Thể tích của khối lăng trụ là: 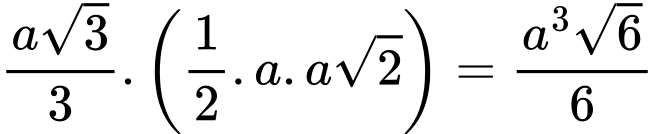 . Chọn D. Đáp án: D
. Chọn D. Đáp án: D
Câu 15 [280885]: Cho hình chóp cụt tứ giác đều  có cạnh đáy lớn và cạnh đáy nhỏ lần lượt là
có cạnh đáy lớn và cạnh đáy nhỏ lần lượt là 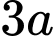 và
và 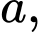 mặt bên tạo với đáy lớn một góc nhị diện có số đo bằng
mặt bên tạo với đáy lớn một góc nhị diện có số đo bằng 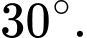 Thể tích khối chóp cụt đã cho là
Thể tích khối chóp cụt đã cho là
 có cạnh đáy lớn và cạnh đáy nhỏ lần lượt là
có cạnh đáy lớn và cạnh đáy nhỏ lần lượt là 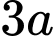 và
và 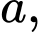 mặt bên tạo với đáy lớn một góc nhị diện có số đo bằng
mặt bên tạo với đáy lớn một góc nhị diện có số đo bằng 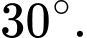 Thể tích khối chóp cụt đã cho là
Thể tích khối chóp cụt đã cho là A, 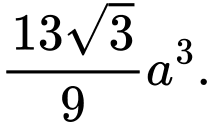
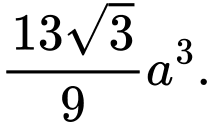
B, 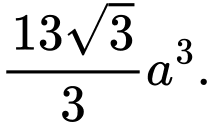
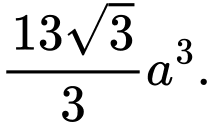
C, 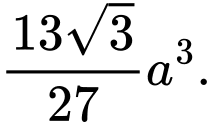
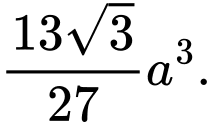
D, 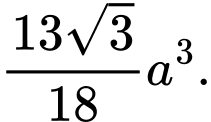
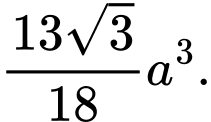
Chọn đáp án A.
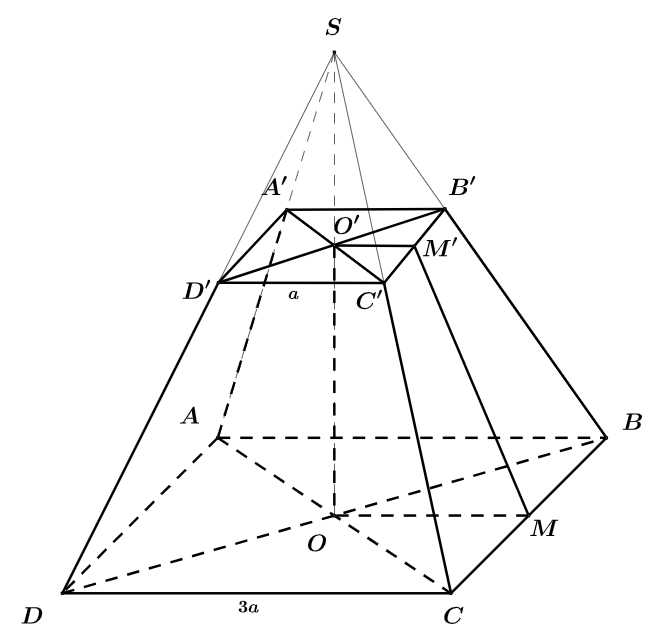
Ta áp dụng công thức tính thể tích chóp cụt: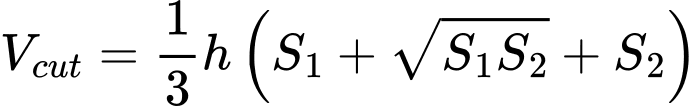
Ta có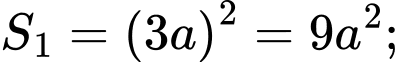
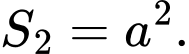
Gọi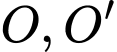 lần lượt là tâm của đáy lớn và đáy bé. Gọi
lần lượt là tâm của đáy lớn và đáy bé. Gọi 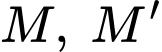 lần lượt là trung điểm của
lần lượt là trung điểm của 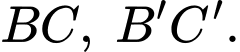 Kẻ
Kẻ 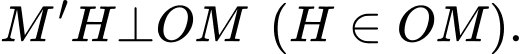 Khi đó,
Khi đó, 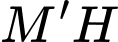 là chiều cao cần tìm và góc nhị diện tạo bởi mặt bên và đáy lớn là
là chiều cao cần tìm và góc nhị diện tạo bởi mặt bên và đáy lớn là 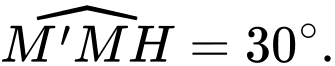
Dễ dàng chứng minh được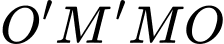 là hình chữ nhật.
là hình chữ nhật.
Ta có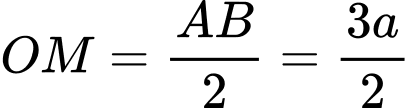 (do
(do 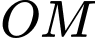 là đường trung bình của tam giác
là đường trung bình của tam giác 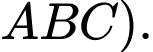 Và ta cũng có
Và ta cũng có 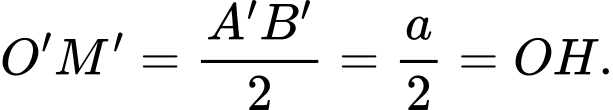 Suy ra
Suy ra 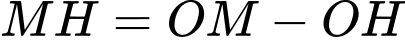
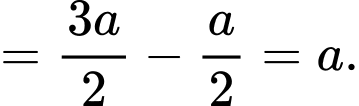
Xét tam giác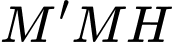 vuông tại
vuông tại 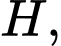 ta có
ta có 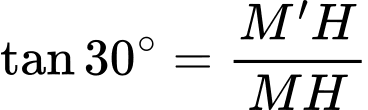
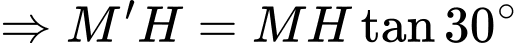
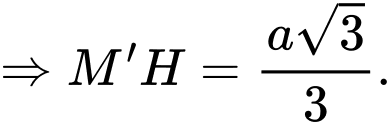
Vậy thể tích khối chóp cụt cần tính là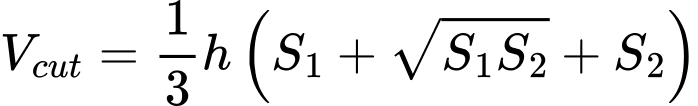
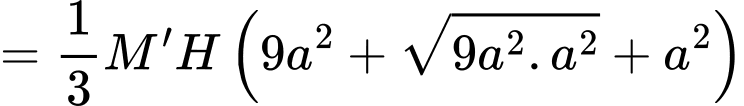
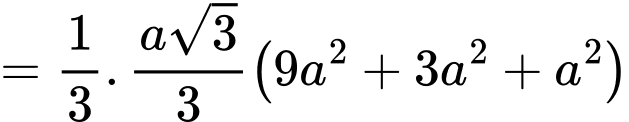
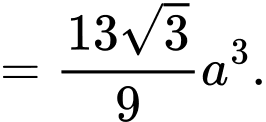 Đáp án: A
Đáp án: A

Ta áp dụng công thức tính thể tích chóp cụt:
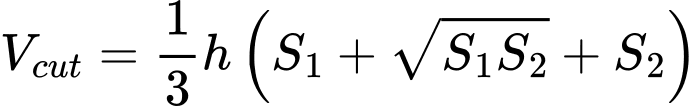
Ta có
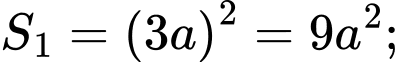
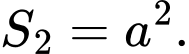
Gọi
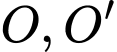 lần lượt là tâm của đáy lớn và đáy bé. Gọi
lần lượt là tâm của đáy lớn và đáy bé. Gọi 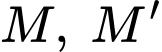 lần lượt là trung điểm của
lần lượt là trung điểm của 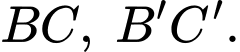 Kẻ
Kẻ 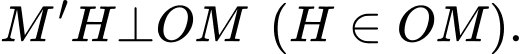 Khi đó,
Khi đó, 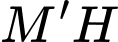 là chiều cao cần tìm và góc nhị diện tạo bởi mặt bên và đáy lớn là
là chiều cao cần tìm và góc nhị diện tạo bởi mặt bên và đáy lớn là 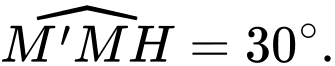
Dễ dàng chứng minh được
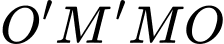 là hình chữ nhật.
là hình chữ nhật.
Ta có
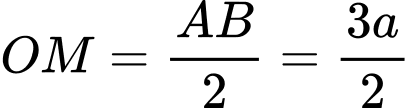 (do
(do 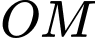 là đường trung bình của tam giác
là đường trung bình của tam giác 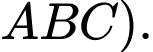 Và ta cũng có
Và ta cũng có 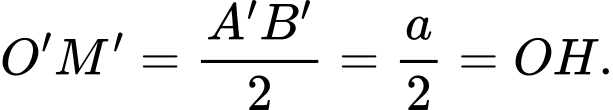 Suy ra
Suy ra 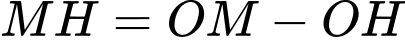
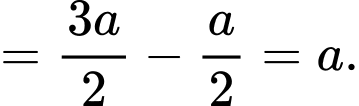
Xét tam giác
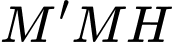 vuông tại
vuông tại 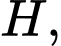 ta có
ta có 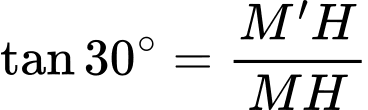
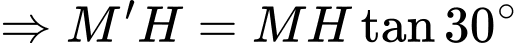
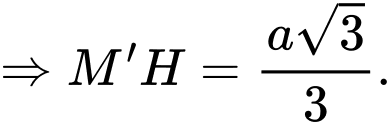
Vậy thể tích khối chóp cụt cần tính là
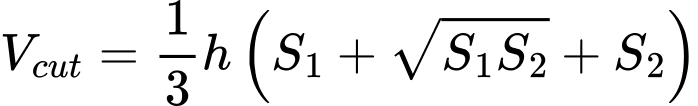
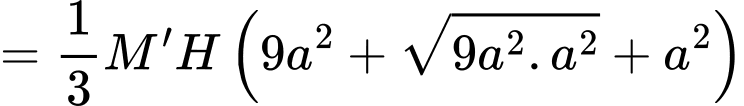
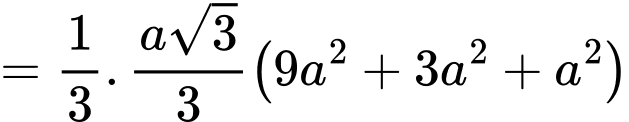
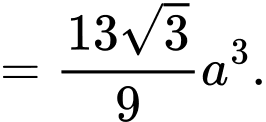 Đáp án: A
Đáp án: A PHẦN II. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 16 đến câu 20.
Câu 16 [275734]: Người ta định đào một cái hầm có dạng hình chóp cụt tứ giác đều có hai cạnh đáy là 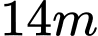 và
và 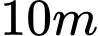 . Mặt bên tạo với đáy nhỏ thành một góc nhị diện có số đo bằng
. Mặt bên tạo với đáy nhỏ thành một góc nhị diện có số đo bằng 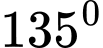 . Tính số mét khối đất cần phải di chuyển ra khỏi hầm.
. Tính số mét khối đất cần phải di chuyển ra khỏi hầm.
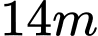 và
và 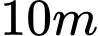 . Mặt bên tạo với đáy nhỏ thành một góc nhị diện có số đo bằng
. Mặt bên tạo với đáy nhỏ thành một góc nhị diện có số đo bằng 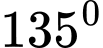 . Tính số mét khối đất cần phải di chuyển ra khỏi hầm.
. Tính số mét khối đất cần phải di chuyển ra khỏi hầm. 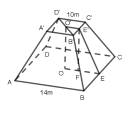
Diện tích đáy bé là:
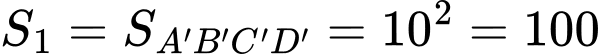
Diện tích đáy lớn là:
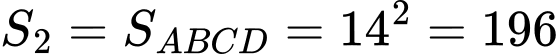
Ta có mặt bên và đáy nhỏ tạo với nhau một góc nhị diện có số đo
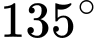
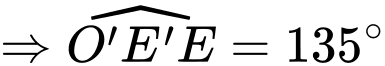
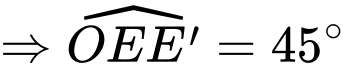 .
.Lấy
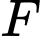 là trung điểm của
là trung điểm của 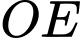
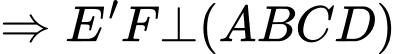
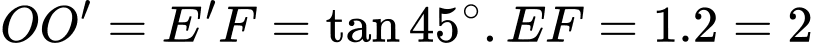
Số mét khối cần phải di chuyển ra khỏi hầm là:
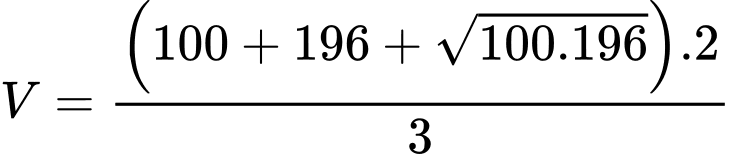
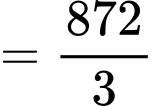 (
(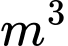 )
)
Câu 17 [582125]: Cho khối lăng trụ  có đáy là tam giác đều cạnh
có đáy là tam giác đều cạnh 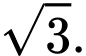 Hình chiếu vuông góc của
Hình chiếu vuông góc của 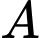 trên mặt phẳng
trên mặt phẳng 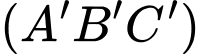 là trung điểm của cạnh
là trung điểm của cạnh 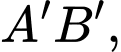 góc tạo bởi
góc tạo bởi 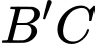 với mặt phẳng
với mặt phẳng 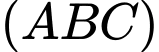 là
là 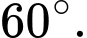 Thể tích khối lăng trụ
Thể tích khối lăng trụ  là
là
 có đáy là tam giác đều cạnh
có đáy là tam giác đều cạnh 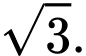 Hình chiếu vuông góc của
Hình chiếu vuông góc của 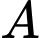 trên mặt phẳng
trên mặt phẳng 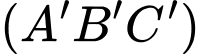 là trung điểm của cạnh
là trung điểm của cạnh 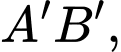 góc tạo bởi
góc tạo bởi 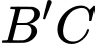 với mặt phẳng
với mặt phẳng 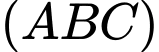 là
là 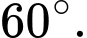 Thể tích khối lăng trụ
Thể tích khối lăng trụ  là
là 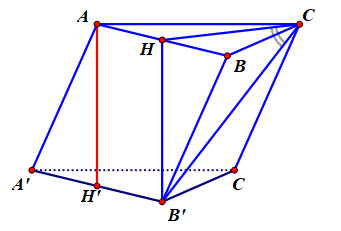
Gọi
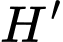 là trung điểm
là trung điểm 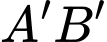 , suy ra
, suy ra 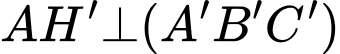 , gọi
, gọi 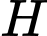 là trung điểm
là trung điểm  có
có 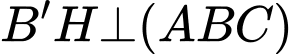 và
và 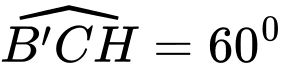
Có
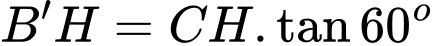
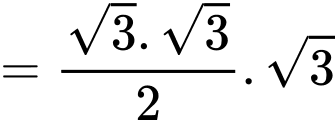
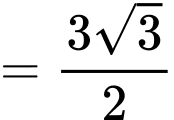 và
và 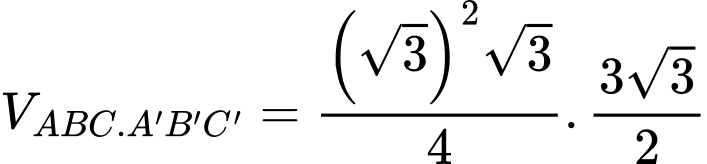
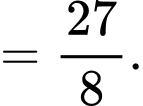
Câu 18 [582126]: Cho hình lăng trụ  có đáy
có đáy 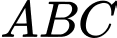 là tam giác vuông cân tại
là tam giác vuông cân tại 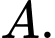 Hình chiếu vuông góc của
Hình chiếu vuông góc của 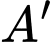 trên mặt phẳng
trên mặt phẳng 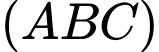 trùng với trung điểm của cạnh
trùng với trung điểm của cạnh 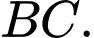 Cạnh bên
Cạnh bên 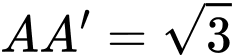 và tạo với mặt phẳng
và tạo với mặt phẳng 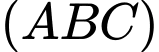 một góc bằng
một góc bằng 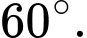 Tính thể tích
Tính thể tích  của khối lăng trụ
của khối lăng trụ 
 có đáy
có đáy 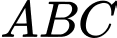 là tam giác vuông cân tại
là tam giác vuông cân tại 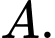 Hình chiếu vuông góc của
Hình chiếu vuông góc của 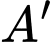 trên mặt phẳng
trên mặt phẳng 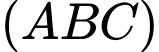 trùng với trung điểm của cạnh
trùng với trung điểm của cạnh 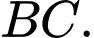 Cạnh bên
Cạnh bên 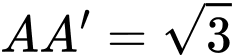 và tạo với mặt phẳng
và tạo với mặt phẳng 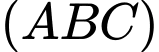 một góc bằng
một góc bằng 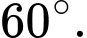 Tính thể tích
Tính thể tích  của khối lăng trụ
của khối lăng trụ 
Điền đáp án: 9/8.
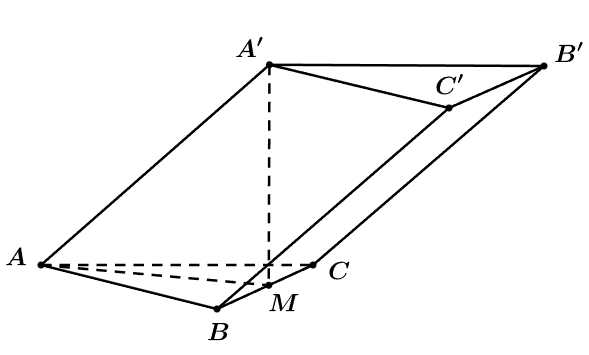
Gọi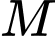 là trung điểm
là trung điểm 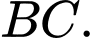 Vì
Vì 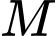 là hình chiếu vuông góc của
là hình chiếu vuông góc của 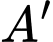 trên mặt phẳng
trên mặt phẳng 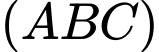 nên
nên 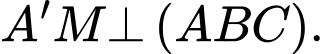 Suy ra góc tạo bởi cạnh bên
Suy ra góc tạo bởi cạnh bên 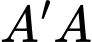 và mặt phẳng
và mặt phẳng 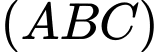 là góc
là góc 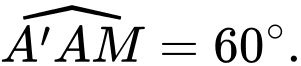
Trong tam giác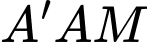 vuông tại
vuông tại 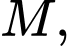 ta có
ta có
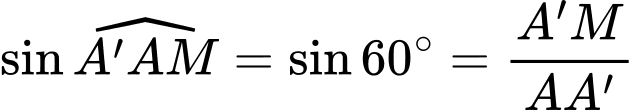
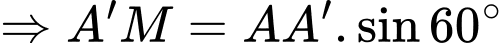
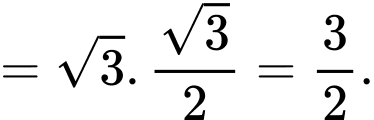
Suy ra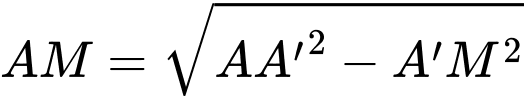
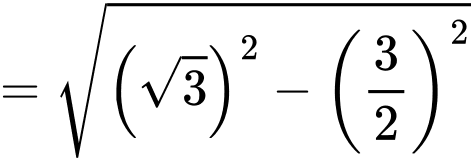
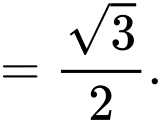
Vì là đường trung tuyến ứng với góc vuông của tam giác
là đường trung tuyến ứng với góc vuông của tam giác 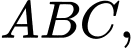 nên ta có
nên ta có 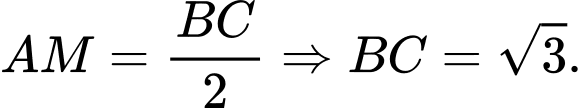
Xét tam giác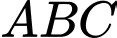 vuông cân tại
vuông cân tại 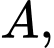 ta có
ta có 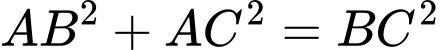
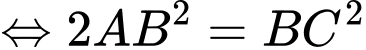
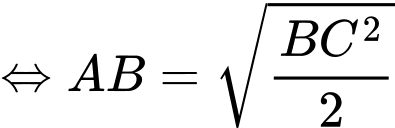
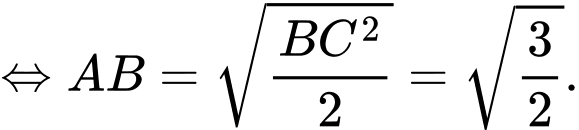
Vậy thể tích khối lăng trụ bằng
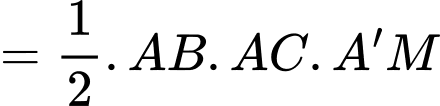
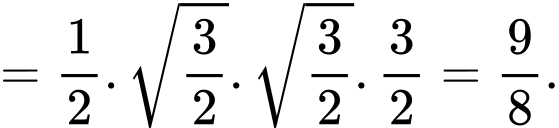

Gọi
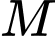 là trung điểm
là trung điểm 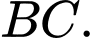 Vì
Vì 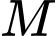 là hình chiếu vuông góc của
là hình chiếu vuông góc của 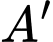 trên mặt phẳng
trên mặt phẳng 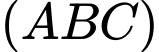 nên
nên 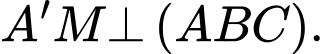 Suy ra góc tạo bởi cạnh bên
Suy ra góc tạo bởi cạnh bên 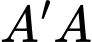 và mặt phẳng
và mặt phẳng 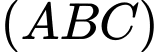 là góc
là góc 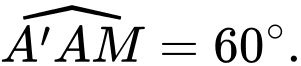
Trong tam giác
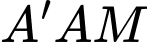 vuông tại
vuông tại 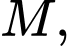 ta có
ta có
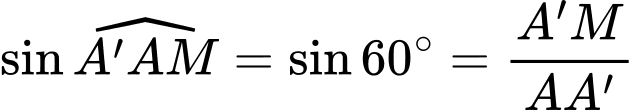
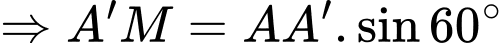
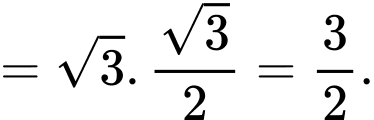
Suy ra
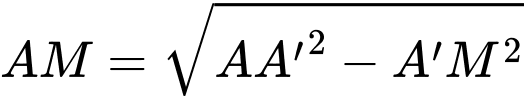
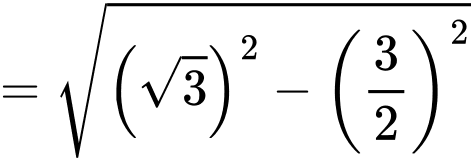
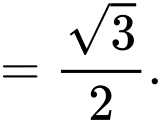
Vì
 là đường trung tuyến ứng với góc vuông của tam giác
là đường trung tuyến ứng với góc vuông của tam giác 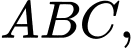 nên ta có
nên ta có 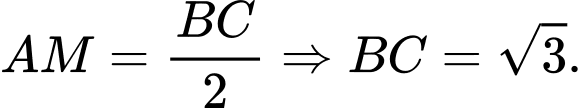
Xét tam giác
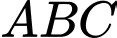 vuông cân tại
vuông cân tại 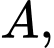 ta có
ta có 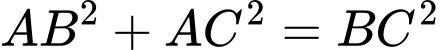
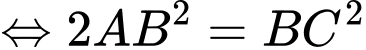
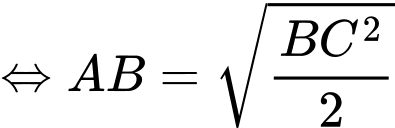
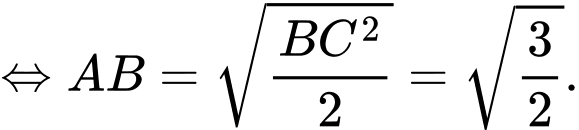
Vậy thể tích khối lăng trụ bằng

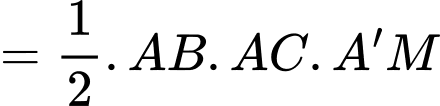
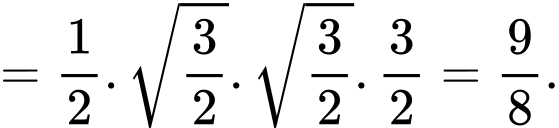
Câu 19 [582127]: Cho lăng trụ  có đáy ABCD là hình chữ nhật có
có đáy ABCD là hình chữ nhật có 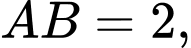
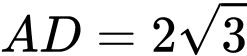 , hình chiếu vuông góc của
, hình chiếu vuông góc của 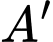 lên mặt phẳng
lên mặt phẳng 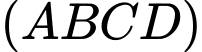 trùng với tâm O của hình chữ nhật ABCD, biết cạnh bên
trùng với tâm O của hình chữ nhật ABCD, biết cạnh bên 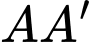 tạo với đáy một góc
tạo với đáy một góc 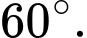 Thể tích lăng trụ
Thể tích lăng trụ  là
là
 có đáy ABCD là hình chữ nhật có
có đáy ABCD là hình chữ nhật có 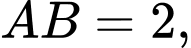
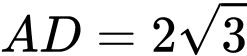 , hình chiếu vuông góc của
, hình chiếu vuông góc của 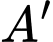 lên mặt phẳng
lên mặt phẳng 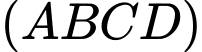 trùng với tâm O của hình chữ nhật ABCD, biết cạnh bên
trùng với tâm O của hình chữ nhật ABCD, biết cạnh bên 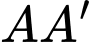 tạo với đáy một góc
tạo với đáy một góc 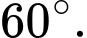 Thể tích lăng trụ
Thể tích lăng trụ  là
là
Điền đáp án: 24.
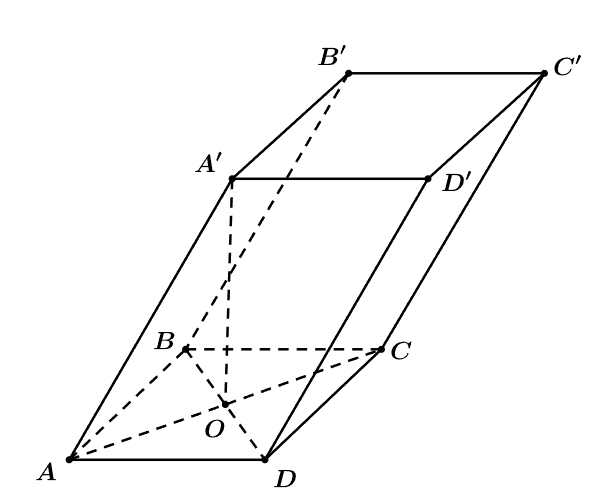
Ta có hình minh họa như trên. (Để tính được thể tích của lăng trụ, ta cần biết được diện tích đáy và chiều cao của lăng trụ).
Vì là hình chiếu vuông góc của
là hình chiếu vuông góc của 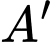 lên mặt phẳng
lên mặt phẳng 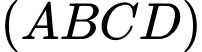 nên suy ra
nên suy ra 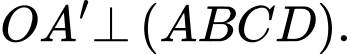 Vậy
Vậy  là chiều cao của lăng trụ
là chiều cao của lăng trụ 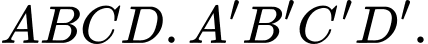
Khi đó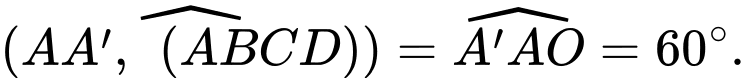
Ta có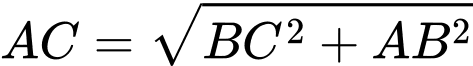
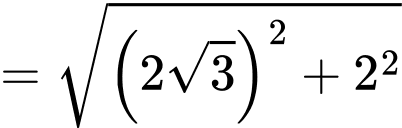
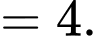
Suy ra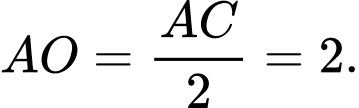
Trong tam giác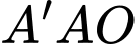 vuông tại
vuông tại  ta có
ta có 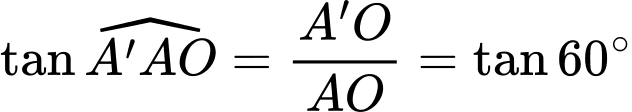
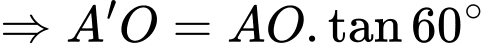
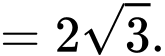
Vậy thể tích lăng trụ bằng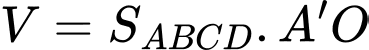
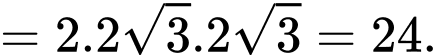

Ta có hình minh họa như trên. (Để tính được thể tích của lăng trụ, ta cần biết được diện tích đáy và chiều cao của lăng trụ).
Vì
 là hình chiếu vuông góc của
là hình chiếu vuông góc của 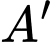 lên mặt phẳng
lên mặt phẳng 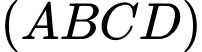 nên suy ra
nên suy ra 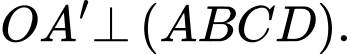 Vậy
Vậy  là chiều cao của lăng trụ
là chiều cao của lăng trụ 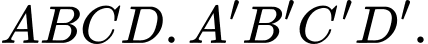
Khi đó
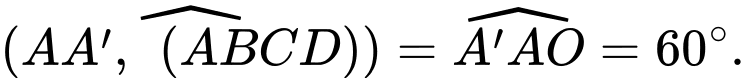
Ta có
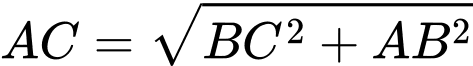
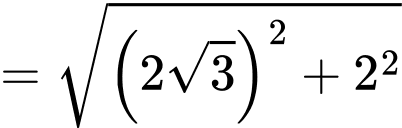
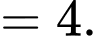
Suy ra
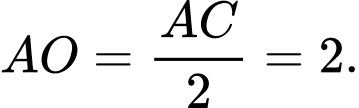
Trong tam giác
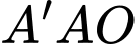 vuông tại
vuông tại  ta có
ta có 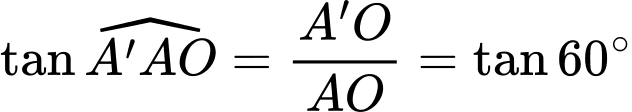
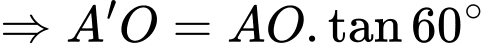
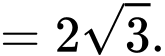
Vậy thể tích lăng trụ bằng
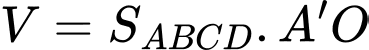
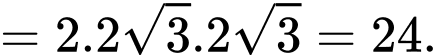
Câu 20 [779096]: Một chiếc khay đựng đầy nước có dạng hình hộp chữ nhật với kích thước: chiều dài 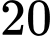
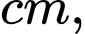 chiều rộng
chiều rộng 
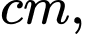 chiều cao
chiều cao 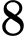
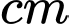 (hình
(hình 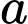 ). Để san bớt nước cho đỡ đầy, người ta đổ nước từ chiếc khay thứ nhất đó sang chiếc khay thứ hai có dạng hình chóp cụt tứ giác đều với đáy khay là hình vuông nhỏ có đường chéo dài
). Để san bớt nước cho đỡ đầy, người ta đổ nước từ chiếc khay thứ nhất đó sang chiếc khay thứ hai có dạng hình chóp cụt tứ giác đều với đáy khay là hình vuông nhỏ có đường chéo dài  , miệng khay là hình vuông lớn có đường chéo dài
, miệng khay là hình vuông lớn có đường chéo dài  (hình b). Sau khi đổ, mực nước ở khay thứ hai cao bằng
(hình b). Sau khi đổ, mực nước ở khay thứ hai cao bằng 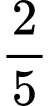 chiều cao của khay đó và lượng nước trong khay thứ nhất giảm đi
chiều cao của khay đó và lượng nước trong khay thứ nhất giảm đi 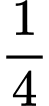 so với ban đầu. Thể tích của chiếc khay thứ hai theo đơn vị centimét khối có kết quả chính xác đến hàng đơn vị là
so với ban đầu. Thể tích của chiếc khay thứ hai theo đơn vị centimét khối có kết quả chính xác đến hàng đơn vị là 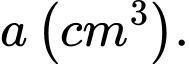 Tổng các chữ số của số
Tổng các chữ số của số 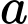 bằng bao nhiêu?
bằng bao nhiêu?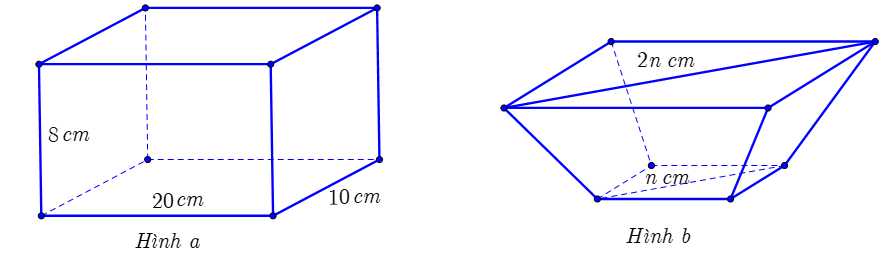
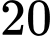
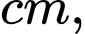 chiều rộng
chiều rộng 
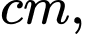 chiều cao
chiều cao 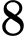
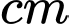 (hình
(hình 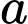 ). Để san bớt nước cho đỡ đầy, người ta đổ nước từ chiếc khay thứ nhất đó sang chiếc khay thứ hai có dạng hình chóp cụt tứ giác đều với đáy khay là hình vuông nhỏ có đường chéo dài
). Để san bớt nước cho đỡ đầy, người ta đổ nước từ chiếc khay thứ nhất đó sang chiếc khay thứ hai có dạng hình chóp cụt tứ giác đều với đáy khay là hình vuông nhỏ có đường chéo dài  , miệng khay là hình vuông lớn có đường chéo dài
, miệng khay là hình vuông lớn có đường chéo dài  (hình b). Sau khi đổ, mực nước ở khay thứ hai cao bằng
(hình b). Sau khi đổ, mực nước ở khay thứ hai cao bằng 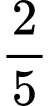 chiều cao của khay đó và lượng nước trong khay thứ nhất giảm đi
chiều cao của khay đó và lượng nước trong khay thứ nhất giảm đi 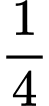 so với ban đầu. Thể tích của chiếc khay thứ hai theo đơn vị centimét khối có kết quả chính xác đến hàng đơn vị là
so với ban đầu. Thể tích của chiếc khay thứ hai theo đơn vị centimét khối có kết quả chính xác đến hàng đơn vị là 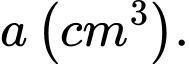 Tổng các chữ số của số
Tổng các chữ số của số 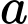 bằng bao nhiêu?
bằng bao nhiêu?
Điền đáp án: 13.
Vì khay đựng đầy nước có dạng hình hộp chữ nhật với kích thước: chiều dài 20 cm, chiều rộng 10 cm và chiều cao 8 cm, nên ta có thể tích nước trong khay thứ nhất trước khi đổ ra là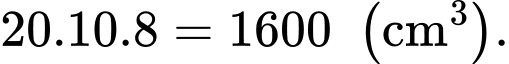
Sau khi đổ nước sang khay thứ hai, ta thấy rằng lượng nước trong khay thứ nhất giảm đi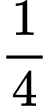 so với ban đầu, cho nên lượng nước có ở trong khay thứ 2 bằng
so với ban đầu, cho nên lượng nước có ở trong khay thứ 2 bằng 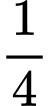 lượng nước ban đầu có ở trong khay thứ nhất.
lượng nước ban đầu có ở trong khay thứ nhất.
Như vậy, thể tích nước có trong khay thứ hai là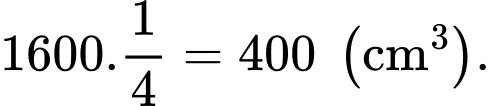
Gọi chiều cao của khay thứ hai là
Xét hình vẽ sau:
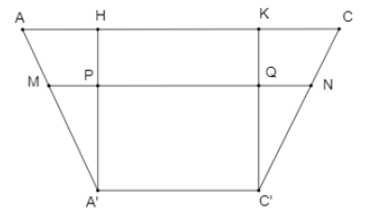
(Với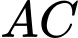 là đường chéo của đáy lớn và
là đường chéo của đáy lớn và 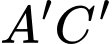 là đường chéo của đáy bé)
là đường chéo của đáy bé)
Dễ dàng chứng minh được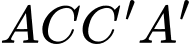 là hình thang cân. Kẻ
là hình thang cân. Kẻ 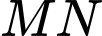 song song với
song song với 
 lần lượt là hình chiếu vuông góc của
lần lượt là hình chiếu vuông góc của  trên
trên 
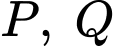 lần lượt là giao điểm của
lần lượt là giao điểm của  và
và 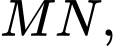
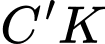 và
và 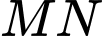 như hình trên.
như hình trên.
Ta có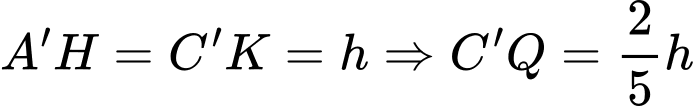
Do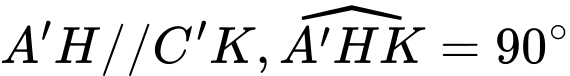 nên tứ giác
nên tứ giác 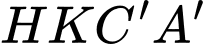 là hình chữ nhật suy ra
là hình chữ nhật suy ra 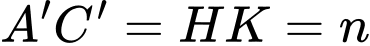
Ta có: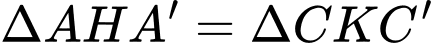
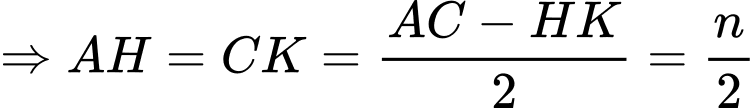
Áp dụng định lý talet cho tam giác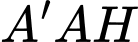 ta có:
ta có: 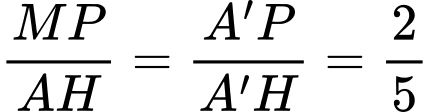
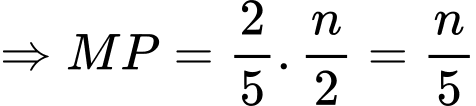
Tương tự có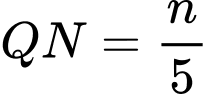
Do đó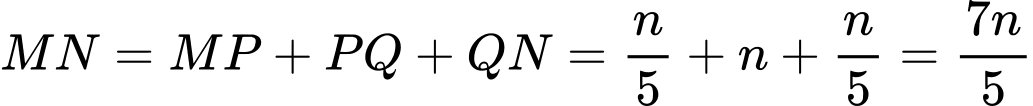
Theo giả thiết ta có thể tích nước trong khay thứ hai bằng thể tích khối chóp cụt đều với đáy lớn là hình vuông có đường chéo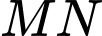 có diện tích
có diện tích 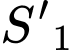 và đáy nhỏ là hình vuông nhận
và đáy nhỏ là hình vuông nhận 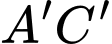 làm đường chéo có diện tích
làm đường chéo có diện tích 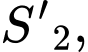 chiều cao bằng
chiều cao bằng 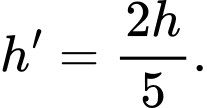
Ta có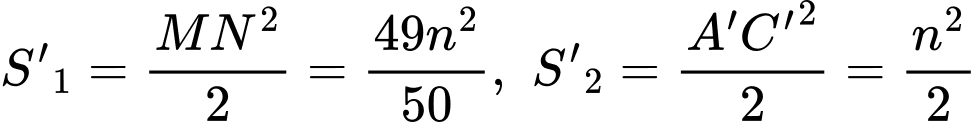
Áp dụng công thức tính thể tích hình chóp cụt đều, ta được thể tích khối chóp cụt đều là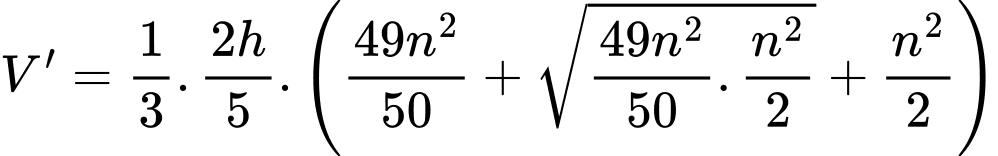
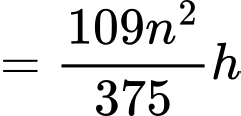
Mà thể tích nước trong khay thứ hai là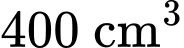 nên
nên 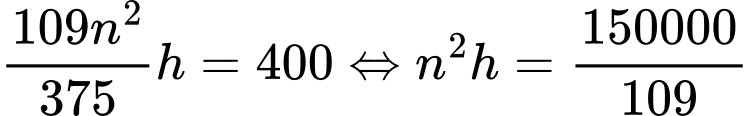
Mặt khác thể tích khay thứ hai bằng thể tích khối chóp cụt tứ giác đều với đáy lớn hình vuông nhận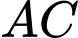 là đường chéo và có diện tích
là đường chéo và có diện tích 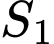 và đáy nhỏ hình vuông nhận
và đáy nhỏ hình vuông nhận 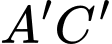 là đường chéo có diện tích
là đường chéo có diện tích 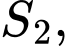 chiều cao bằng
chiều cao bằng 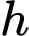
Ta có: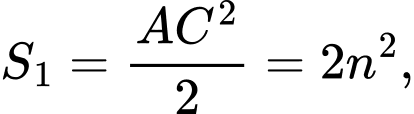
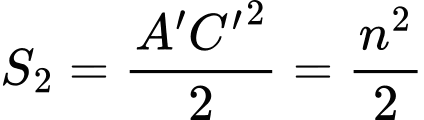
Khi đó: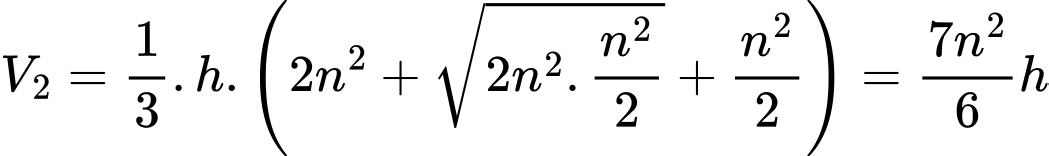
Mà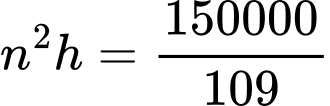
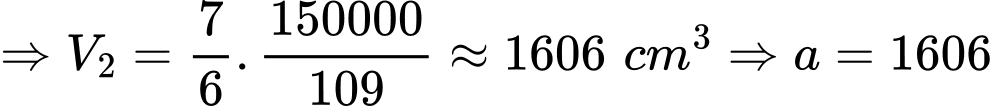
Vậy tổng các chữ số của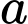 là 13.
là 13.
Vì khay đựng đầy nước có dạng hình hộp chữ nhật với kích thước: chiều dài 20 cm, chiều rộng 10 cm và chiều cao 8 cm, nên ta có thể tích nước trong khay thứ nhất trước khi đổ ra là
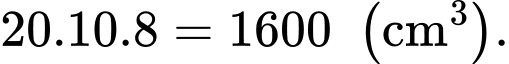
Sau khi đổ nước sang khay thứ hai, ta thấy rằng lượng nước trong khay thứ nhất giảm đi
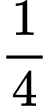 so với ban đầu, cho nên lượng nước có ở trong khay thứ 2 bằng
so với ban đầu, cho nên lượng nước có ở trong khay thứ 2 bằng 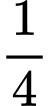 lượng nước ban đầu có ở trong khay thứ nhất.
lượng nước ban đầu có ở trong khay thứ nhất.
Như vậy, thể tích nước có trong khay thứ hai là
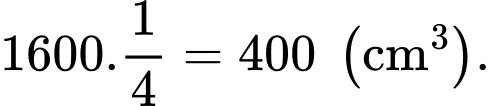
Gọi chiều cao của khay thứ hai là

Xét hình vẽ sau:

(Với
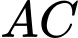 là đường chéo của đáy lớn và
là đường chéo của đáy lớn và 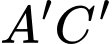 là đường chéo của đáy bé)
là đường chéo của đáy bé)Dễ dàng chứng minh được
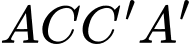 là hình thang cân. Kẻ
là hình thang cân. Kẻ 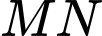 song song với
song song với 
 lần lượt là hình chiếu vuông góc của
lần lượt là hình chiếu vuông góc của  trên
trên 
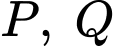 lần lượt là giao điểm của
lần lượt là giao điểm của  và
và 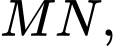
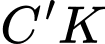 và
và 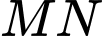 như hình trên.
như hình trên.
Ta có
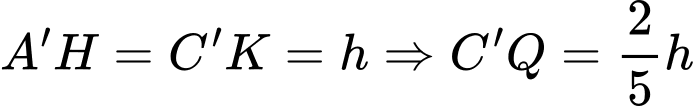
Do
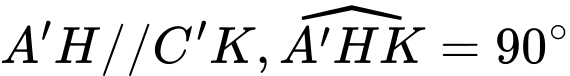 nên tứ giác
nên tứ giác 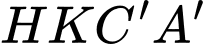 là hình chữ nhật suy ra
là hình chữ nhật suy ra 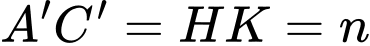
Ta có:
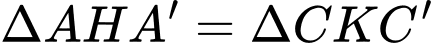
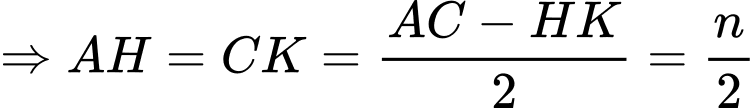
Áp dụng định lý talet cho tam giác
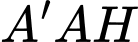 ta có:
ta có: 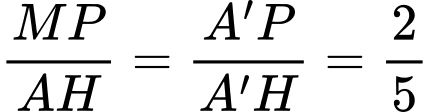
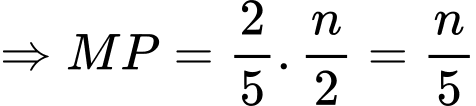
Tương tự có
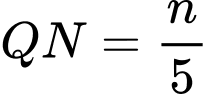
Do đó
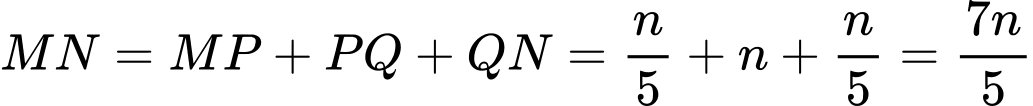
Theo giả thiết ta có thể tích nước trong khay thứ hai bằng thể tích khối chóp cụt đều với đáy lớn là hình vuông có đường chéo
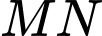 có diện tích
có diện tích 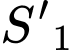 và đáy nhỏ là hình vuông nhận
và đáy nhỏ là hình vuông nhận 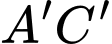 làm đường chéo có diện tích
làm đường chéo có diện tích 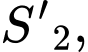 chiều cao bằng
chiều cao bằng 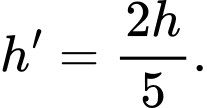
Ta có
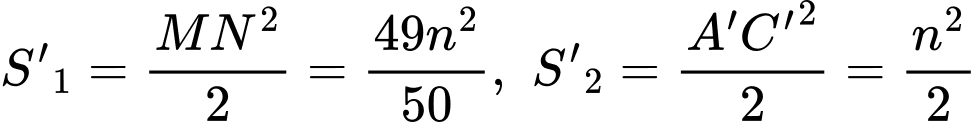
Áp dụng công thức tính thể tích hình chóp cụt đều, ta được thể tích khối chóp cụt đều là
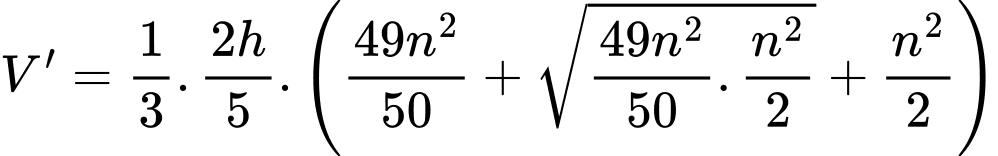
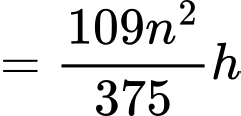
Mà thể tích nước trong khay thứ hai là
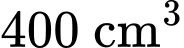 nên
nên 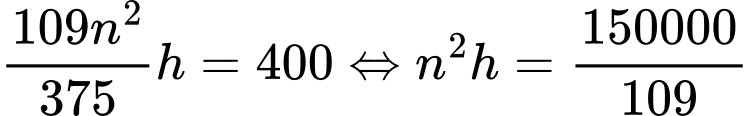
Mặt khác thể tích khay thứ hai bằng thể tích khối chóp cụt tứ giác đều với đáy lớn hình vuông nhận
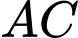 là đường chéo và có diện tích
là đường chéo và có diện tích 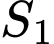 và đáy nhỏ hình vuông nhận
và đáy nhỏ hình vuông nhận 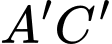 là đường chéo có diện tích
là đường chéo có diện tích 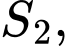 chiều cao bằng
chiều cao bằng 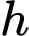
Ta có:
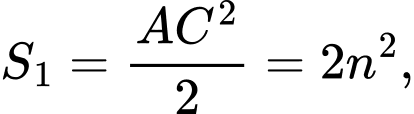
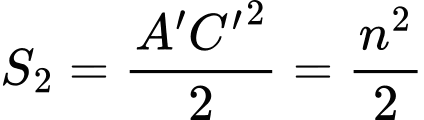
Khi đó:
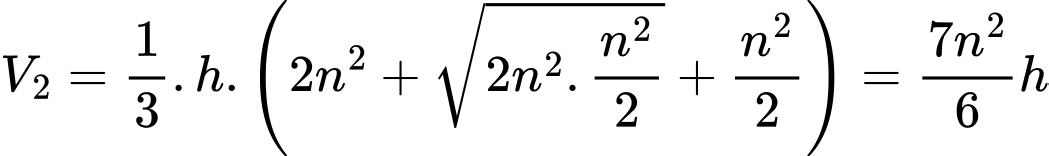
Mà
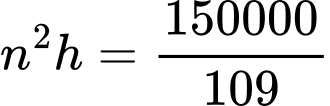
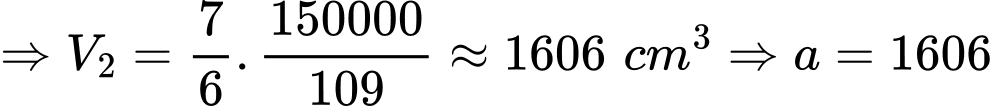
Vậy tổng các chữ số của
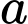 là 13.
là 13.