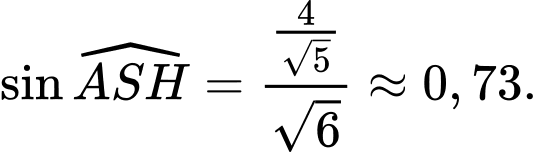PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 20. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1 [331151]: Cho hình chóp 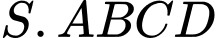 có đáy là hình chữ nhật tâm
có đáy là hình chữ nhật tâm  với
với  Biết
Biết 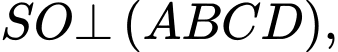 tính khoảng cách từ
tính khoảng cách từ  đến mặt phẳng
đến mặt phẳng 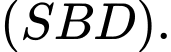
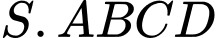 có đáy là hình chữ nhật tâm
có đáy là hình chữ nhật tâm  với
với  Biết
Biết 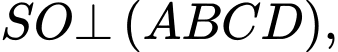 tính khoảng cách từ
tính khoảng cách từ  đến mặt phẳng
đến mặt phẳng 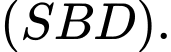
A, 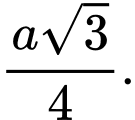
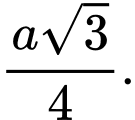
B, 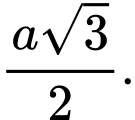
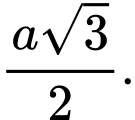
C, 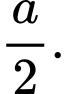
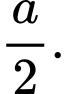
D, 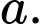
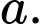
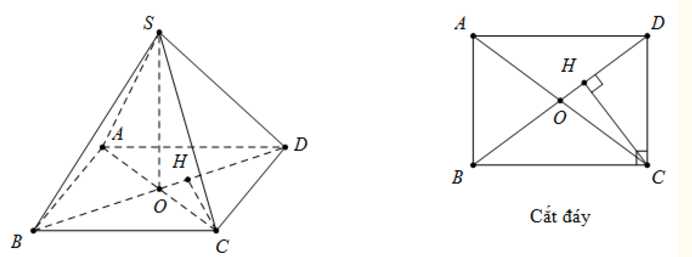
Dựng
 , ta có:
, ta có:  .
.Do đó
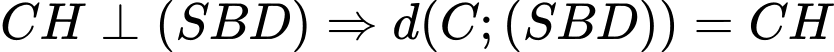 .
.Mặt khác
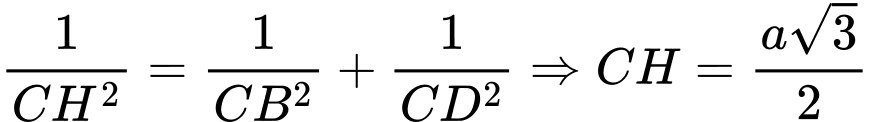 .
. Chọn đáp án B. Đáp án: B
Câu 2 [6492]: Cho hình chóp 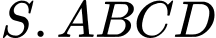 có đáy
có đáy 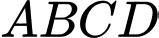 là hình chữ nhật,
là hình chữ nhật, 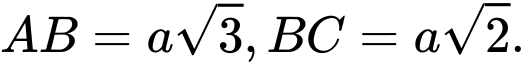 Cạnh bên
Cạnh bên  và
và 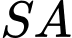 vuông góc với mặt phẳng đáy. Khoảng cách giữa
vuông góc với mặt phẳng đáy. Khoảng cách giữa 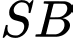 và
và 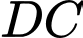 bằng
bằng
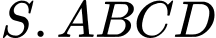 có đáy
có đáy 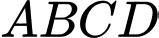 là hình chữ nhật,
là hình chữ nhật, 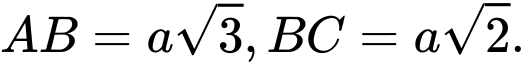 Cạnh bên
Cạnh bên  và
và 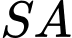 vuông góc với mặt phẳng đáy. Khoảng cách giữa
vuông góc với mặt phẳng đáy. Khoảng cách giữa 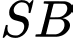 và
và 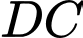 bằng
bằng A, 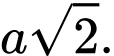
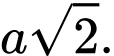
B, 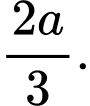
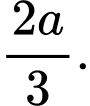
C, 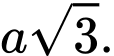
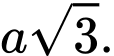
D, 
Ta có
 đồng thời vuông với
đồng thời vuông với 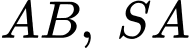 nên
nên 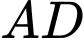 vuông với
vuông với 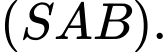
Khoảng cách giữa
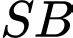 và
và 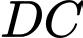 chính là khoảng cách giữa
chính là khoảng cách giữa 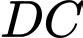 và
và 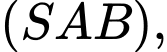 chính là
chính là 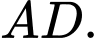 Đáp án: A
Đáp án: A
Câu 3 [6549]: Cho hình chóp 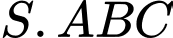 có đáy
có đáy 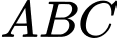 là tam giác đều cạnh
là tam giác đều cạnh 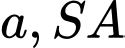 vuông góc với mặt phẳng đáy và
vuông góc với mặt phẳng đáy và 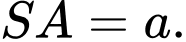 Tính khoảng cách giữa hai đường thẳng
Tính khoảng cách giữa hai đường thẳng 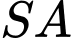 và
và 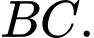
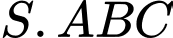 có đáy
có đáy 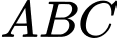 là tam giác đều cạnh
là tam giác đều cạnh 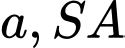 vuông góc với mặt phẳng đáy và
vuông góc với mặt phẳng đáy và 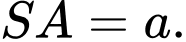 Tính khoảng cách giữa hai đường thẳng
Tính khoảng cách giữa hai đường thẳng 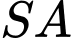 và
và 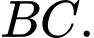
A, 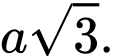
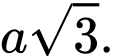
B, 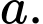
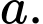
C, 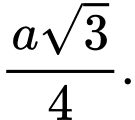
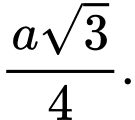
D, 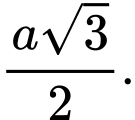
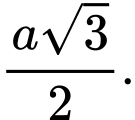
Gọi
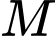 là trung điếm của
là trung điếm của 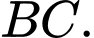 Ta có:
Ta có:  là đoạn vuông góc chung của
là đoạn vuông góc chung của 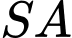 và
và 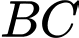
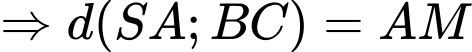
Ta có:
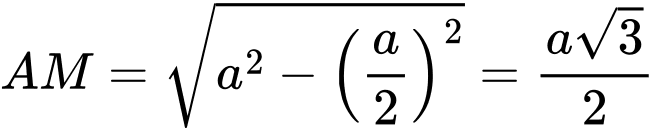 .
. Chọn đáp án D. Đáp án: D
Câu 4 [6470]: Cho hình chóp 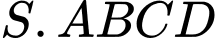 có đáy
có đáy 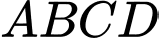 là hình chữ nhật với
là hình chữ nhật với 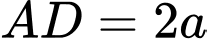 . Cạnh bên
. Cạnh bên 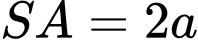 và vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng
và vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng  và
và 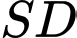 .
.
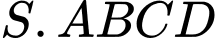 có đáy
có đáy 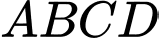 là hình chữ nhật với
là hình chữ nhật với 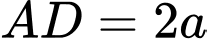 . Cạnh bên
. Cạnh bên 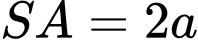 và vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng
và vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng  và
và 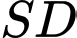 .
. A, 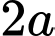 .
.
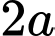 .
.B, 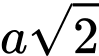 .
.
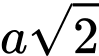 .
.C, 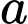 .
.
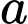 .
.D, 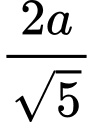 .
.
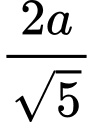 .
.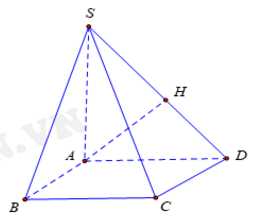
Ta có
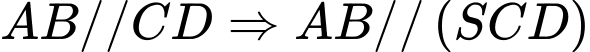
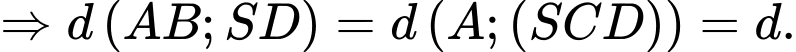
Kẻ

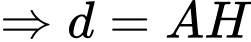
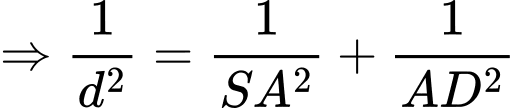
 .
.Chọn đáp án B. Đáp án: B
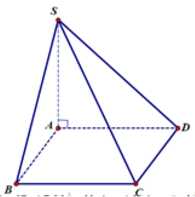
Câu 5 [325151]: Cho chóp S.ABC có đáy 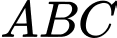 là tam giác vuông cân tại
là tam giác vuông cân tại 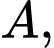 tam giác SBC là tam giác đều cạnh a và thuộc mặt phẳng vuông góc với đáy. Tính khoảng cách
tam giác SBC là tam giác đều cạnh a và thuộc mặt phẳng vuông góc với đáy. Tính khoảng cách 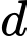 giữa 2 đường thẳng SA và
giữa 2 đường thẳng SA và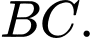
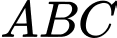 là tam giác vuông cân tại
là tam giác vuông cân tại 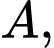 tam giác SBC là tam giác đều cạnh a và thuộc mặt phẳng vuông góc với đáy. Tính khoảng cách
tam giác SBC là tam giác đều cạnh a và thuộc mặt phẳng vuông góc với đáy. Tính khoảng cách 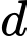 giữa 2 đường thẳng SA và
giữa 2 đường thẳng SA và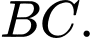
A, 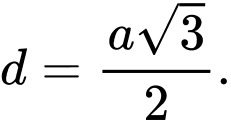
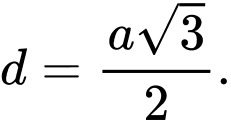
B, 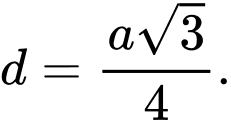
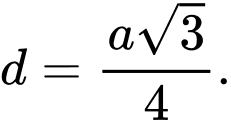
C, 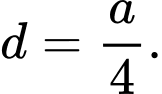
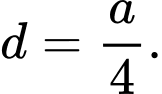
D, 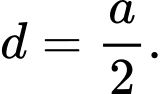
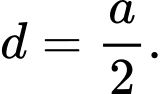
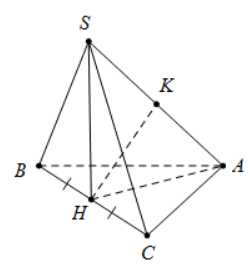
Gọi
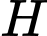 là trung điểm của
là trung điểm của 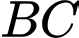 khi đó
khi đó 
Mặt khác
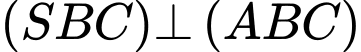 do đó
do đó 
Ta có:
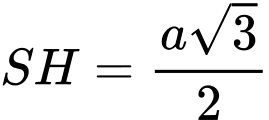 và
và 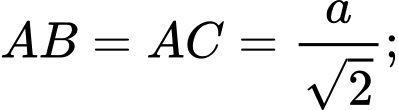
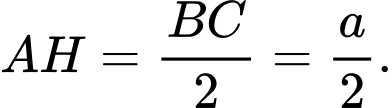
Do
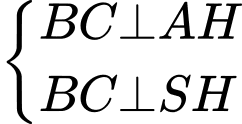
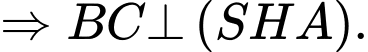
Dựng
 khi đó
khi đó 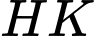 là đoạn vuông góc chung của
là đoạn vuông góc chung của 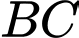 và
và 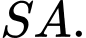
Lai có:
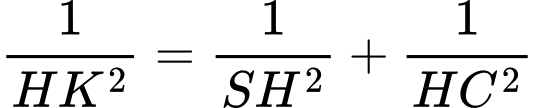
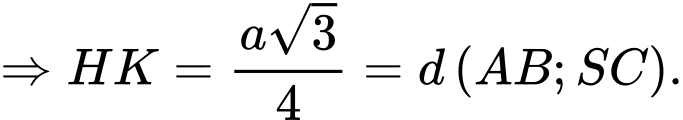
Cách 2: Ta có:
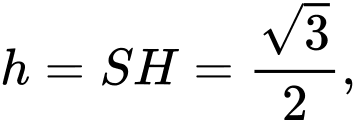
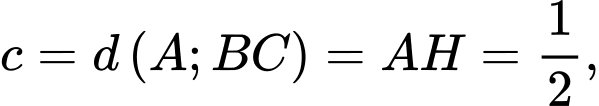
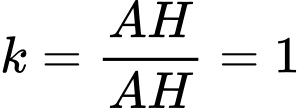
Suy ra
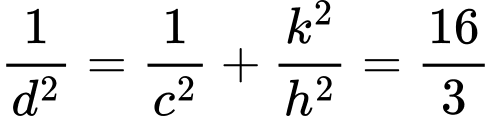
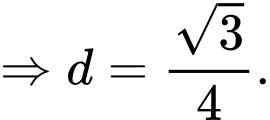
Chọn đáp án B. Đáp án: B
Câu 6 [6508]: Cho hình chóp 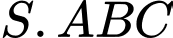 có đáy là tam giác đều cạnh
có đáy là tam giác đều cạnh 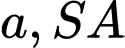 vuông góc với
vuông góc với 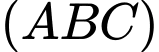 và
và  . Tính khoảng cách giữa
. Tính khoảng cách giữa 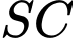 và
và  .
.
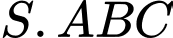 có đáy là tam giác đều cạnh
có đáy là tam giác đều cạnh 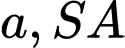 vuông góc với
vuông góc với 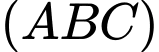 và
và  . Tính khoảng cách giữa
. Tính khoảng cách giữa  và
và  .
. A, 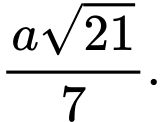
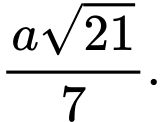
B, 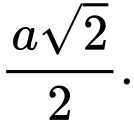
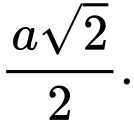
C, 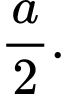
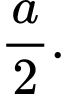
D, 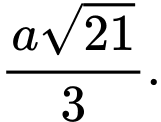
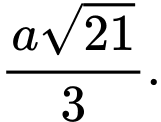
Gọi 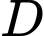 sao cho
sao cho 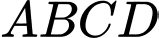 là hình bình hành và
là hình bình hành và 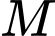 là trung điểm
là trung điểm 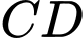 .
.
Ta có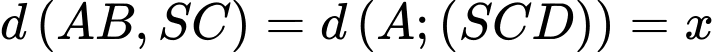 với
với 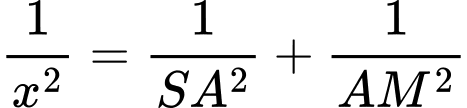
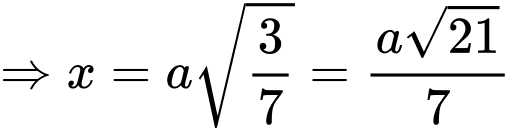 .
.
Chọn đáp án A. Đáp án: A
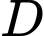 sao cho
sao cho 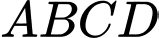 là hình bình hành và
là hình bình hành và 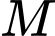 là trung điểm
là trung điểm 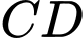 .
. Ta có
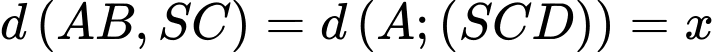 với
với 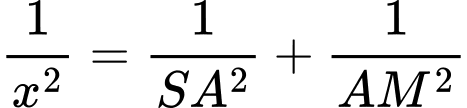
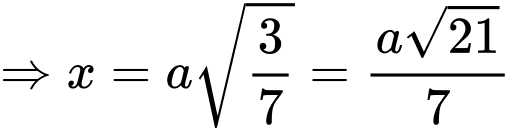 .
. Chọn đáp án A. Đáp án: A
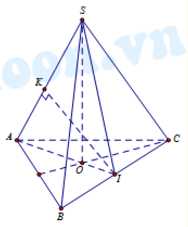
Câu 7 [6504]: Cho hình chóp đều 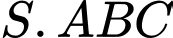 có cạnh đáy bằng
có cạnh đáy bằng 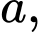 khoảng cách giữa cạnh bên
khoảng cách giữa cạnh bên 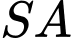 và cạnh đáy
và cạnh đáy 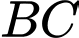 bằng
bằng 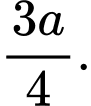 Thể tích khối chóp
Thể tích khối chóp 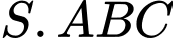 là
là
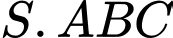 có cạnh đáy bằng
có cạnh đáy bằng 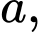 khoảng cách giữa cạnh bên
khoảng cách giữa cạnh bên 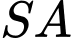 và cạnh đáy
và cạnh đáy 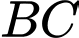 bằng
bằng 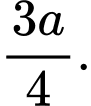 Thể tích khối chóp
Thể tích khối chóp 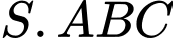 là
là A, 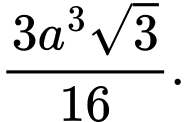
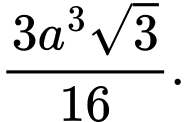
B, 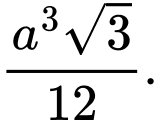
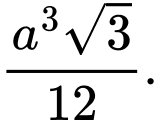
C, 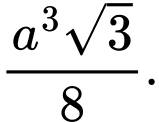
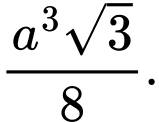
D, 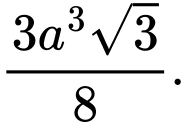
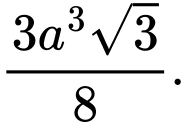
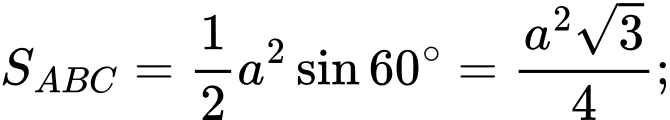
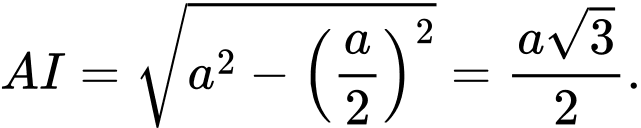
Đặt
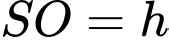 .
. Ta có

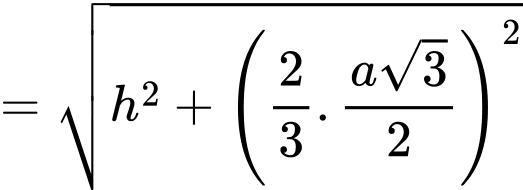
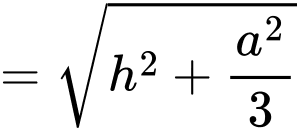
Lại có
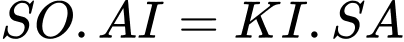
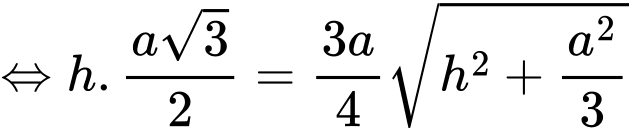
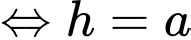
Thể tích khối chóp
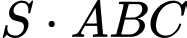 là
là 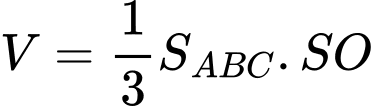
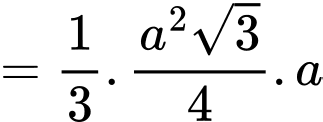
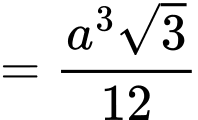
Chọn đáp án B. Đáp án: B
Câu 8 [6485]: Cho hình chóp đều 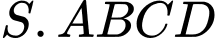 có đáy là hình vuông
có đáy là hình vuông 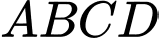 tâm
tâm  cạnh
cạnh 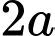 , cạnh bên
, cạnh bên 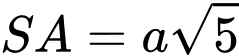 . Khoảng cách giữa
. Khoảng cách giữa 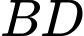 và
và 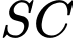 là
là
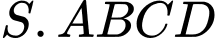 có đáy là hình vuông
có đáy là hình vuông 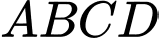 tâm
tâm  cạnh
cạnh 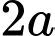 , cạnh bên
, cạnh bên 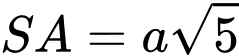 . Khoảng cách giữa
. Khoảng cách giữa 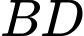 và
và 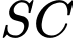 là
là A, 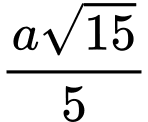 .
.
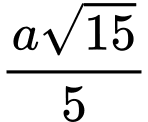 .
.B, 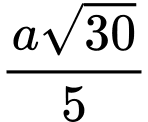 .
.
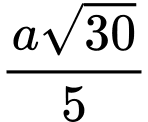 .
.C, 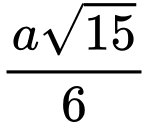 .
.
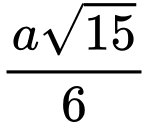 .
.D, 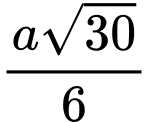 .
.
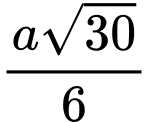 .
.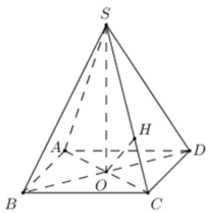
Vì chóp
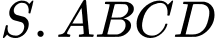 đều
đều 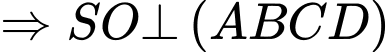 .
.Trong
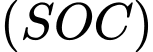 kẻ
kẻ 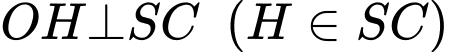 .
.Ta có:
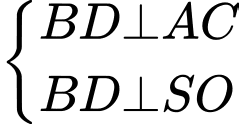
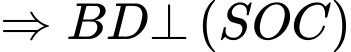
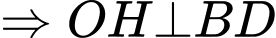
 là đoạn vuông góc chung của
là đoạn vuông góc chung của 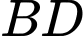 và
và 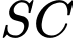
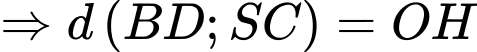
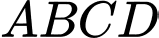 là hình vuông cạnh
là hình vuông cạnh 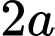
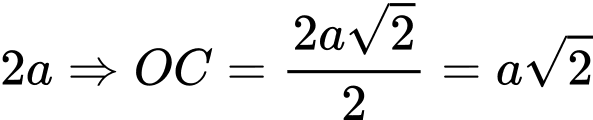
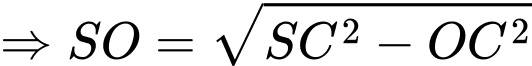
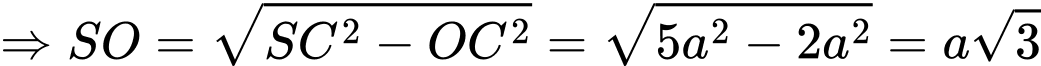
Áp dụng hệ thức lượng trong tam giác vuông
 :
: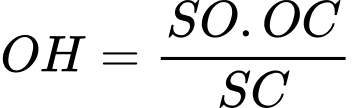
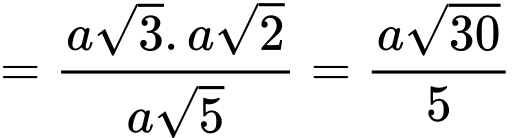 .
. Vậy
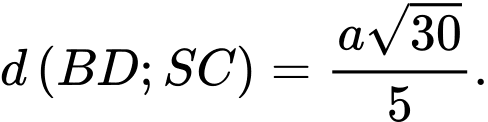
Chọn đáp án B. Đáp án: B
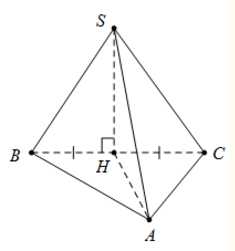
Câu 9 [325154]: Cho hình chóp 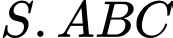 đáy
đáy 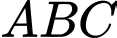 là tam giác có
là tam giác có 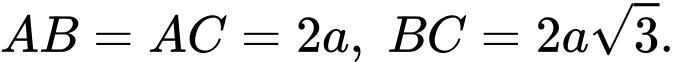 Tam giác
Tam giác 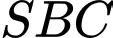 vuông cân tại
vuông cân tại 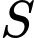 và thuộc mặt phẳng vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng
và thuộc mặt phẳng vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng 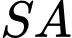 và
và 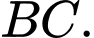
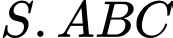 đáy
đáy 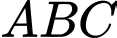 là tam giác có
là tam giác có 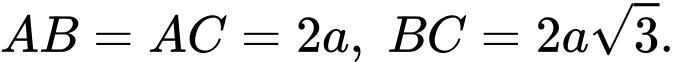 Tam giác
Tam giác 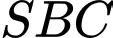 vuông cân tại
vuông cân tại 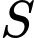 và thuộc mặt phẳng vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng
và thuộc mặt phẳng vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng 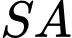 và
và 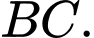
A, 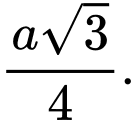
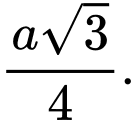
B, 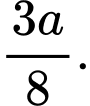
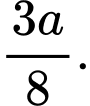
C, 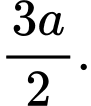
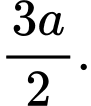
D, 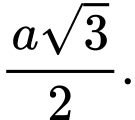
Gọi
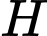 là trung điểm của
là trung điểm của 
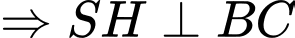
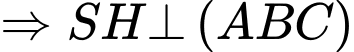
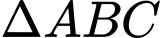 cân tại
cân tại 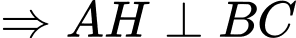
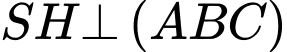
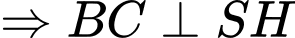
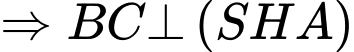
Ta có:
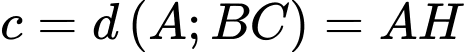
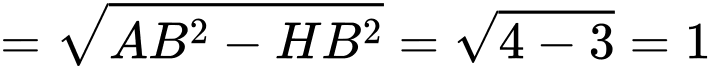
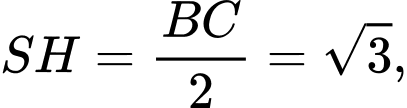
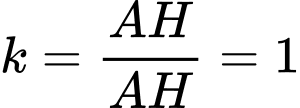
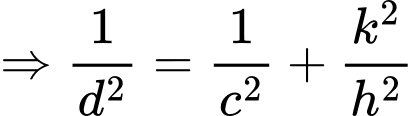
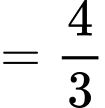
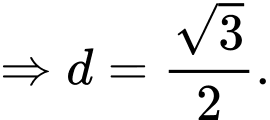
Chọn đáp án D. Đáp án: D
Câu 10 [325134]: [Đề thi thử chuyên ĐH Vinh lần 2 năm 2018] Cho hình chóp 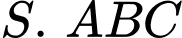 có đáy
có đáy 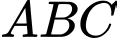 là tam giác vuông cân tại
là tam giác vuông cân tại 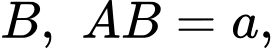 cạnh bên
cạnh bên 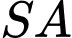 vuông góc với mặt phẳng đáy, góc tạo bởi hai mặt phẳng
vuông góc với mặt phẳng đáy, góc tạo bởi hai mặt phẳng 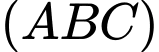 và
và 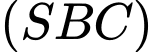 bằng
bằng 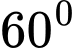 (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng
(tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng  và
và 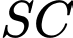 bằng
bằng=kphan2de1/2.kc2duong%20cheo%20nhaup2.png)
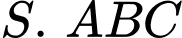 có đáy
có đáy 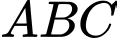 là tam giác vuông cân tại
là tam giác vuông cân tại 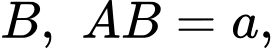 cạnh bên
cạnh bên 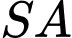 vuông góc với mặt phẳng đáy, góc tạo bởi hai mặt phẳng
vuông góc với mặt phẳng đáy, góc tạo bởi hai mặt phẳng 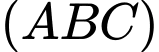 và
và 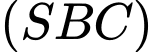 bằng
bằng 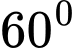 (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng
(tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng  và
và 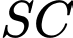 bằng
bằng=kphan2de1/2.kc2duong%20cheo%20nhaup2.png)
A, 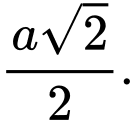
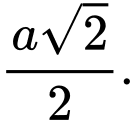
B, 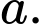
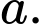
C, 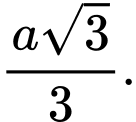
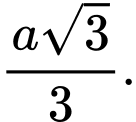
D, 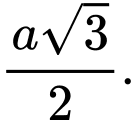
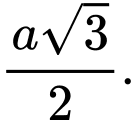
Ta có: 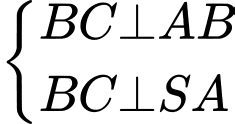
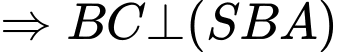 . Do đó
. Do đó 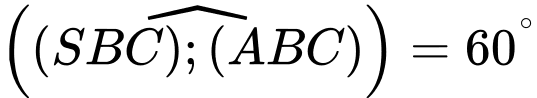
 .
.
Qua điểm dựng
dựng 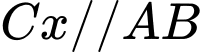
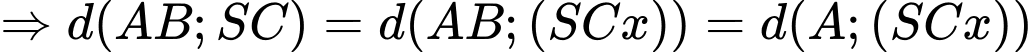 .
.
Dựng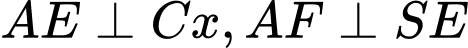
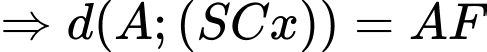 .
.
Lại có: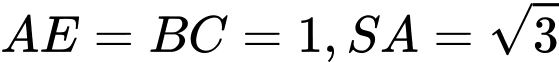
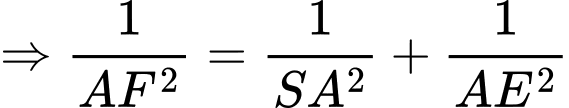
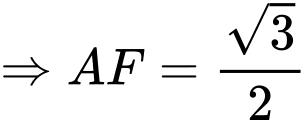 .
.
Cách 2: Áp dụng công thức nhanh: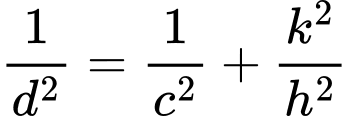 vói
vói 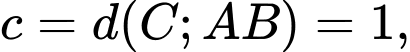

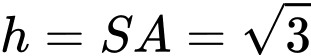
Suy ra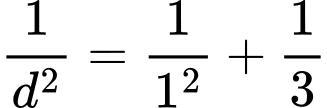
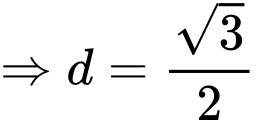 .
.
Chọn đáp án D. Đáp án: D
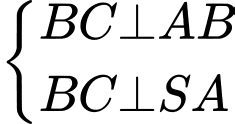
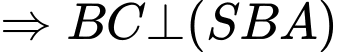 . Do đó
. Do đó 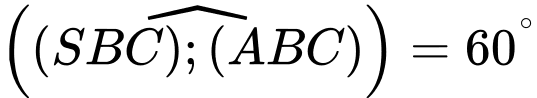
 .
.Qua điểm
 dựng
dựng 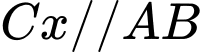
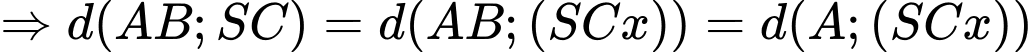 .
.Dựng
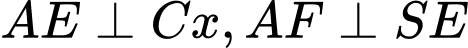
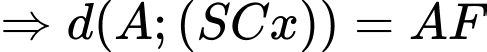 .
.Lại có:
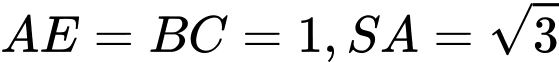
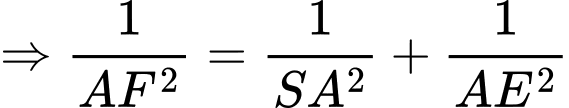
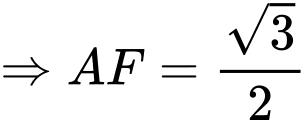 .
.Cách 2: Áp dụng công thức nhanh:
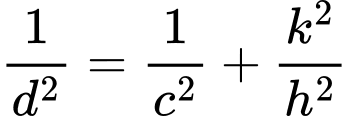 vói
vói 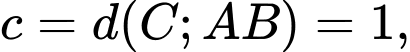

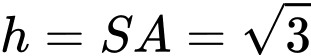
Suy ra
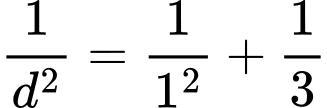
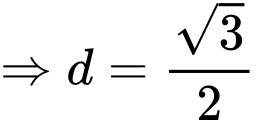 .
. Chọn đáp án D. Đáp án: D
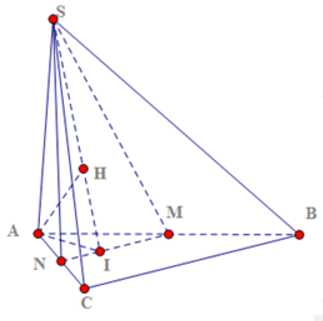
Câu 11 [677679]: Cho hình chóp 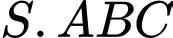 có đáy là tam giác vuông tại
có đáy là tam giác vuông tại 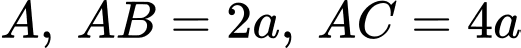 ,
, 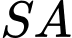 vuông góc với mặt phẳng đáy và
vuông góc với mặt phẳng đáy và  (minh họa như hình vẽ). Gọi
(minh họa như hình vẽ). Gọi 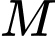 là trung điểm của
là trung điểm của 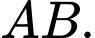 Khoảng cách giữa hai đường thẳng
Khoảng cách giữa hai đường thẳng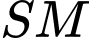 và
và 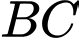 bằng
bằng
=kphan2de1/1.kc2uongcheonhaude1.png)
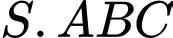 có đáy là tam giác vuông tại
có đáy là tam giác vuông tại 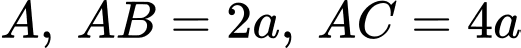 ,
, 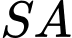 vuông góc với mặt phẳng đáy và
vuông góc với mặt phẳng đáy và  (minh họa như hình vẽ). Gọi
(minh họa như hình vẽ). Gọi 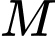 là trung điểm của
là trung điểm của 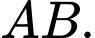 Khoảng cách giữa hai đường thẳng
Khoảng cách giữa hai đường thẳng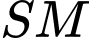 và
và 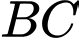 bằng
bằng =kphan2de1/1.kc2uongcheonhaude1.png)
A, 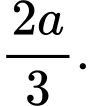
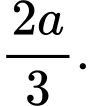
B, 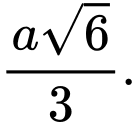
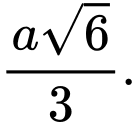
C, 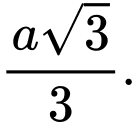
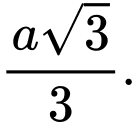
D, 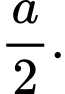
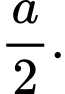
Gọi
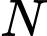 là trung điểm cạnh
là trung điểm cạnh 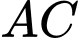 , khi đó mặt phẳng
, khi đó mặt phẳng 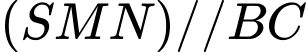 .
.Ta có
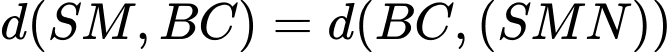
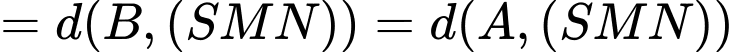 .
.Gọi
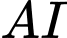 là đường cao trong tam giác vuông
là đường cao trong tam giác vuông 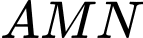 , ta có
, ta có 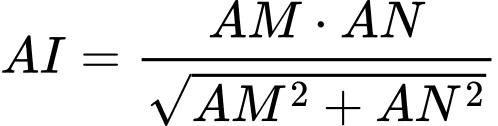
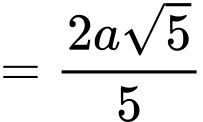
Lại có
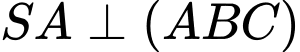
 , suy ra
, suy ra 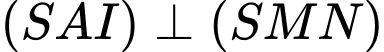 .
.Kẻ
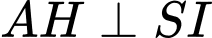
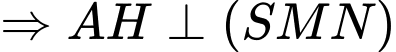
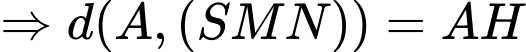
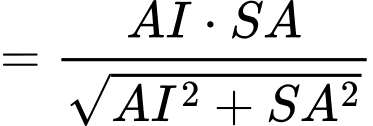
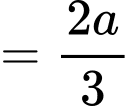 .
.Vậy
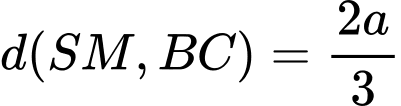 .
.Chọn đáp án A. Đáp án: A
Câu 12 [325153]: Cho hình chóp 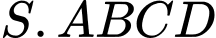 có đáy là hình vuông
có đáy là hình vuông 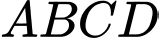 cạnh
cạnh 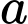 và
và 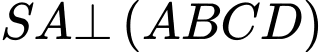 . Biết mặt phẳng
. Biết mặt phẳng 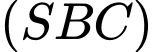 tạo với đáy một góc
tạo với đáy một góc 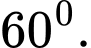 Tính khoảng cách giữa 2 đường thẳng
Tính khoảng cách giữa 2 đường thẳng 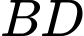 và
và 
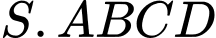 có đáy là hình vuông
có đáy là hình vuông 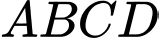 cạnh
cạnh 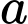 và
và 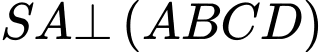 . Biết mặt phẳng
. Biết mặt phẳng 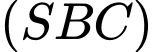 tạo với đáy một góc
tạo với đáy một góc 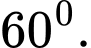 Tính khoảng cách giữa 2 đường thẳng
Tính khoảng cách giữa 2 đường thẳng 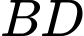 và
và 
A, 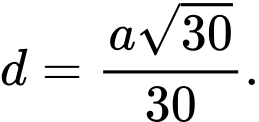
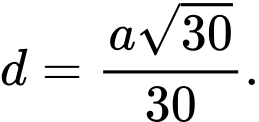
B, 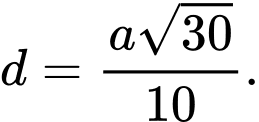
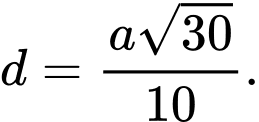
C, 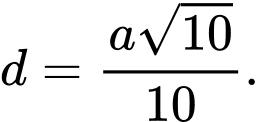
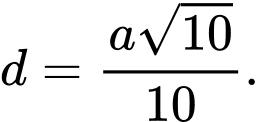
D, 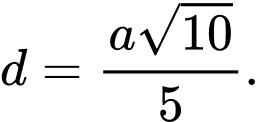
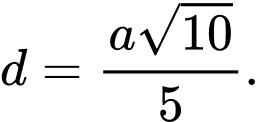
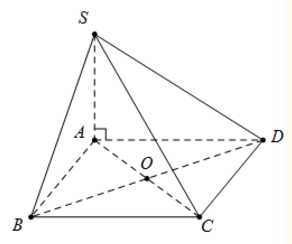
Do
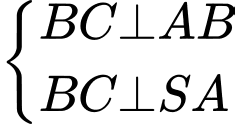
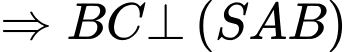
Suy ra
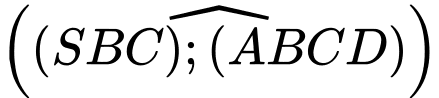
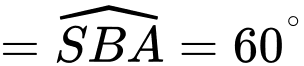
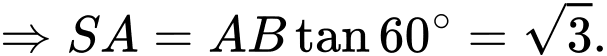
Ta có:

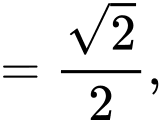
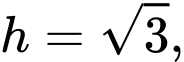
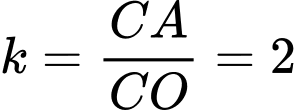
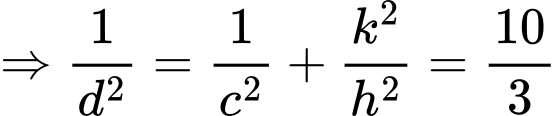
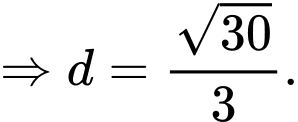
Chọn đáp án B. Đáp án: B
PHẦN II. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 13 đến câu 20.
Câu 13 [680752]: Cho hình lăng trụ đứng  có
có 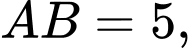
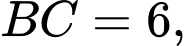
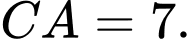 Khoảng cách giữa hai đường thẳng
Khoảng cách giữa hai đường thẳng 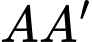 và
và 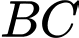 bằng bao nhiêu? (làm tròn kết quả đến hàng đơn vị).
bằng bao nhiêu? (làm tròn kết quả đến hàng đơn vị).
 có
có 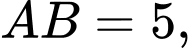
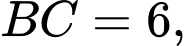
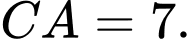 Khoảng cách giữa hai đường thẳng
Khoảng cách giữa hai đường thẳng 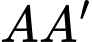 và
và 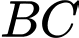 bằng bao nhiêu? (làm tròn kết quả đến hàng đơn vị).
bằng bao nhiêu? (làm tròn kết quả đến hàng đơn vị).
Điền đáp án: 4,9.
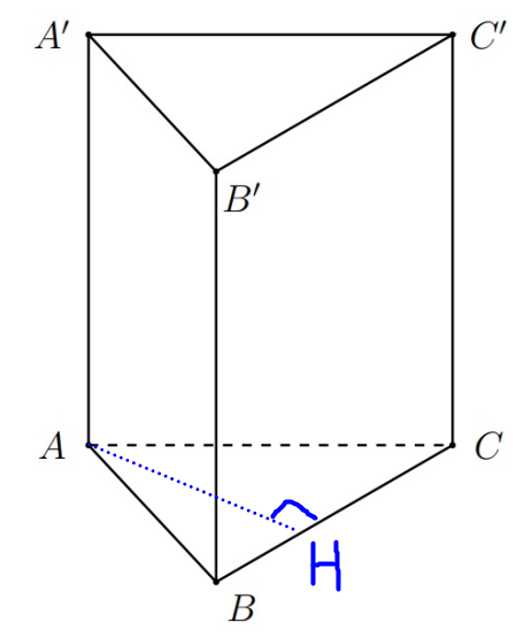
Dựng đường cao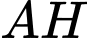 của
của 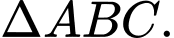 Lại có:
Lại có: 
Suy ra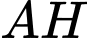 là đường vuông góc chung của hai đường thẳng
là đường vuông góc chung của hai đường thẳng 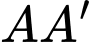 và
và 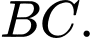 Suy ra:
Suy ra: 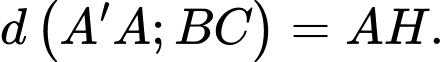
Ta có: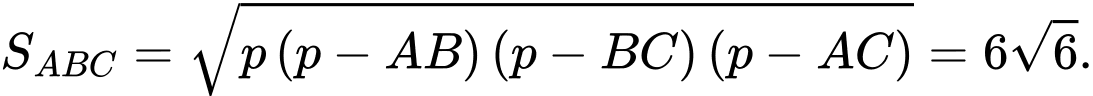
Vậy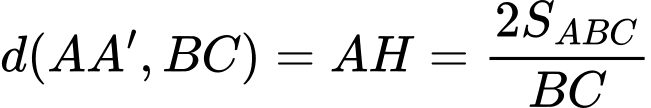
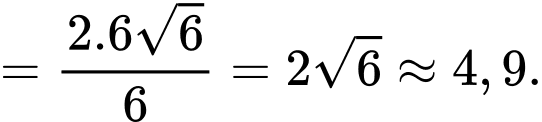

Dựng đường cao
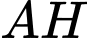 của
của 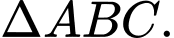 Lại có:
Lại có: 
Suy ra
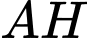 là đường vuông góc chung của hai đường thẳng
là đường vuông góc chung của hai đường thẳng 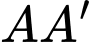 và
và 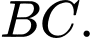 Suy ra:
Suy ra: 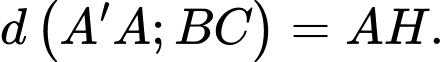
Ta có:
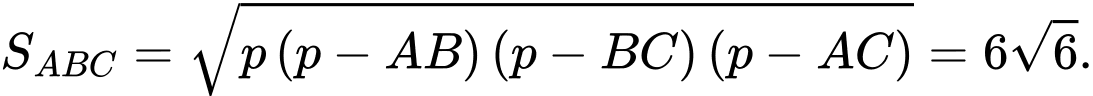
Vậy
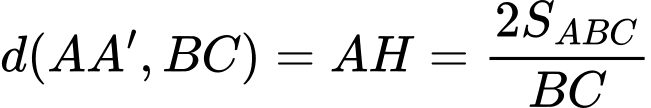
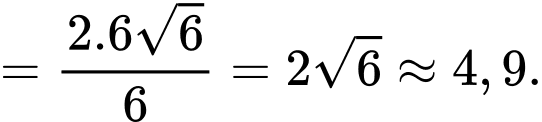
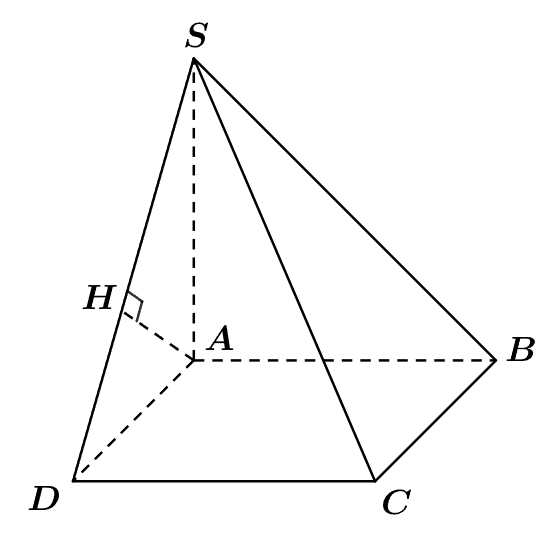
Câu 14 [779100]: Cho hình chóp 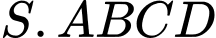 có đáy
có đáy 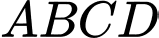 là hình vuông,
là hình vuông, 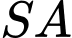 vuông góc với đáy và
vuông góc với đáy và 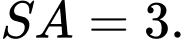 Biết rằng khoảng cách giữa giữa hai đường thẳng
Biết rằng khoảng cách giữa giữa hai đường thẳng  và
và 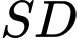 bằng
bằng 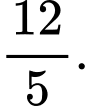 Thể tích của khối chóp đã cho bằng bao nhiêu?
Thể tích của khối chóp đã cho bằng bao nhiêu?
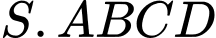 có đáy
có đáy 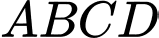 là hình vuông,
là hình vuông, 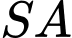 vuông góc với đáy và
vuông góc với đáy và 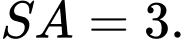 Biết rằng khoảng cách giữa giữa hai đường thẳng
Biết rằng khoảng cách giữa giữa hai đường thẳng  và
và 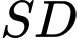 bằng
bằng 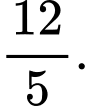 Thể tích của khối chóp đã cho bằng bao nhiêu?
Thể tích của khối chóp đã cho bằng bao nhiêu?
Điền đáp án: 16.
Để tính được thể tích của hình chóp đã cho, ta cần đi tìm độ dài cạnh đáy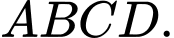
Giả sử độ dài cạnh đáy bằng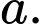
Kẻ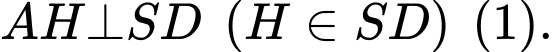
Ta có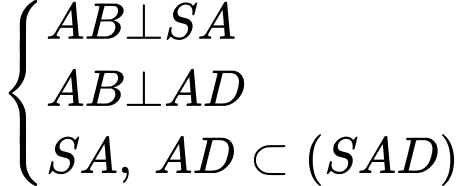
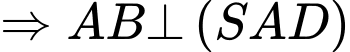
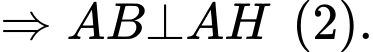
Từ (1) và (2) suy ra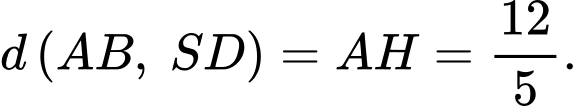
Xét tam giác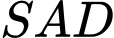 vuông tại
vuông tại 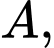 ta có
ta có 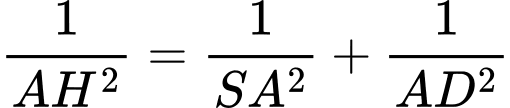
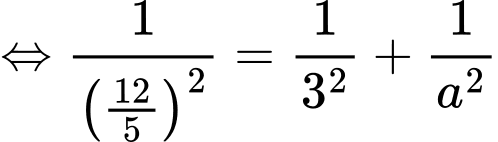
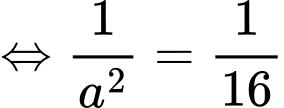
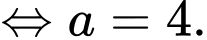
Vậy thể tích khối chóp là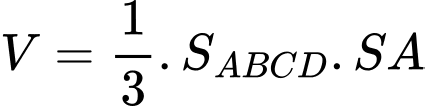
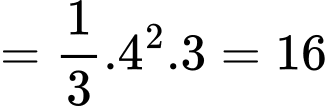
Để tính được thể tích của hình chóp đã cho, ta cần đi tìm độ dài cạnh đáy
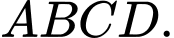
Giả sử độ dài cạnh đáy bằng
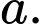
Kẻ
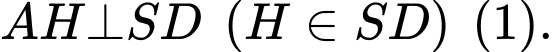

Ta có
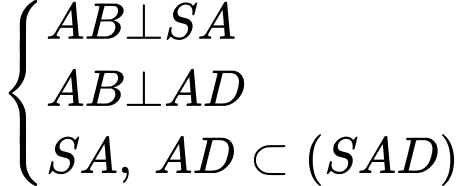
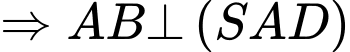
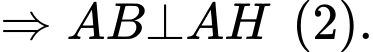
Từ (1) và (2) suy ra
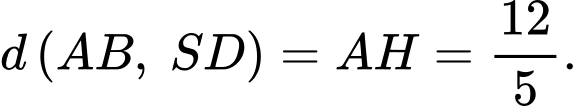
Xét tam giác
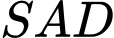 vuông tại
vuông tại 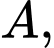 ta có
ta có 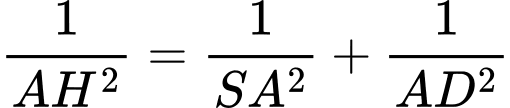
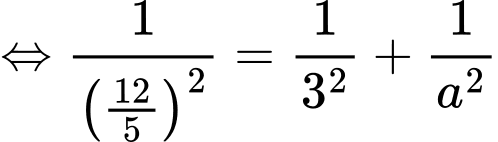
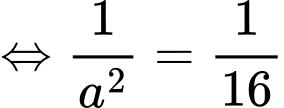
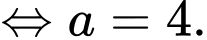
Vậy thể tích khối chóp là
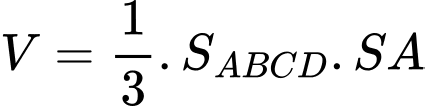
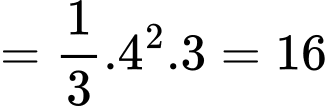
Câu 15 [308897]: Cho tứ diện đều 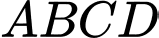 có cạnh
có cạnh 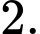 Tìm khoảng cách giữa hai đường thẳng chéo nhau
Tìm khoảng cách giữa hai đường thẳng chéo nhau 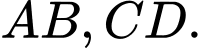 (Kết quả làm tròn đến hàng phần trăm)
(Kết quả làm tròn đến hàng phần trăm)
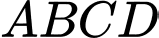 có cạnh
có cạnh 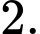 Tìm khoảng cách giữa hai đường thẳng chéo nhau
Tìm khoảng cách giữa hai đường thẳng chéo nhau 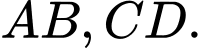 (Kết quả làm tròn đến hàng phần trăm)
(Kết quả làm tròn đến hàng phần trăm) 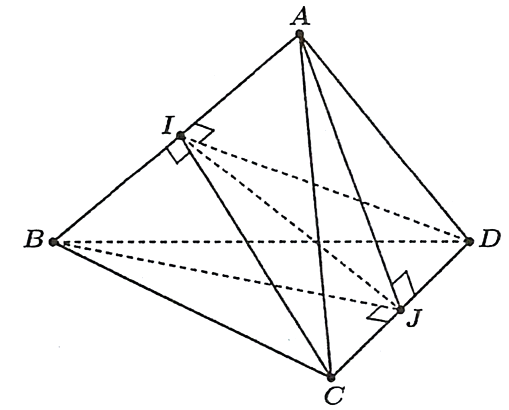
Gọi
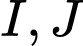 theo thứ tự là trung điểm của
theo thứ tự là trung điểm của 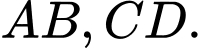
Các tam giác
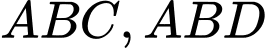 đều có
đều có 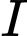 là trung điểm
là trung điểm  nên
nên 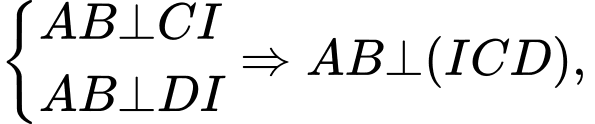 mà
mà 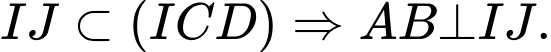 (1)
(1)Tương tự, các tam giác
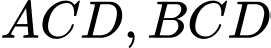 đều có
đều có 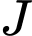 là trung điểm
là trung điểm 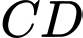 nên
nên 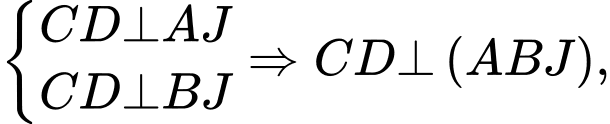 mà
mà 
Từ (1) và (2) suy ra
 là đoạn vuông góc chung của hai đường thẳng
là đoạn vuông góc chung của hai đường thẳng 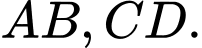
Ta có:
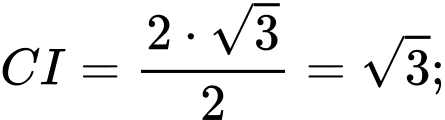
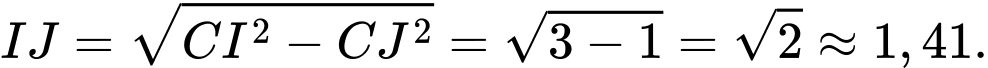
Đáp án: 1,41
Câu 16 [582235]: Cho hình chóp 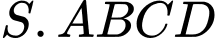 có đáy
có đáy 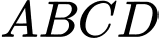 là hình vuông cạnh
là hình vuông cạnh 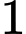 , tâm
, tâm  . Cạnh bên
. Cạnh bên 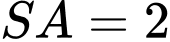 và
và 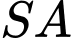 vuông góc với mặt đáy
vuông góc với mặt đáy 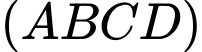 . Gọi
. Gọi 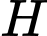 và
và 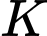 lần lượt là trung điểm của cạnh
lần lượt là trung điểm của cạnh 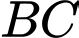 và
và 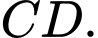 Tính khoảng cách giữa hai đường thẳng
Tính khoảng cách giữa hai đường thẳng 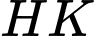 và
và 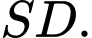
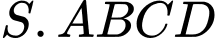 có đáy
có đáy 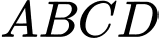 là hình vuông cạnh
là hình vuông cạnh 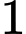 , tâm
, tâm  . Cạnh bên
. Cạnh bên 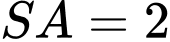 và
và 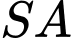 vuông góc với mặt đáy
vuông góc với mặt đáy 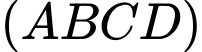 . Gọi
. Gọi 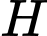 và
và 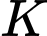 lần lượt là trung điểm của cạnh
lần lượt là trung điểm của cạnh 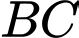 và
và 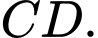 Tính khoảng cách giữa hai đường thẳng
Tính khoảng cách giữa hai đường thẳng 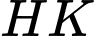 và
và 
Điền đáp án: 1/3.
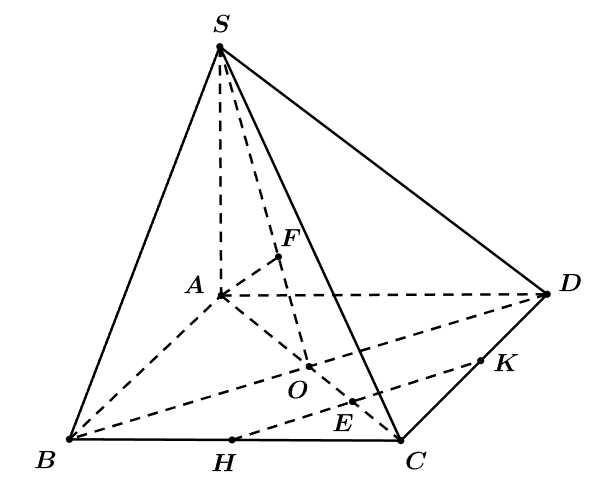
Gọi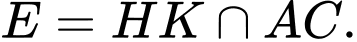 Do
Do  nên suy ra
nên suy ra
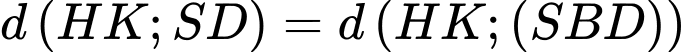
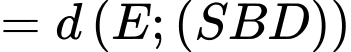
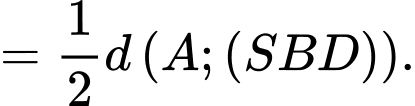
Kẻ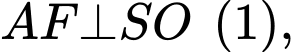 ta có
ta có 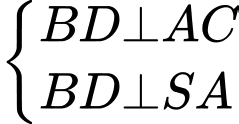
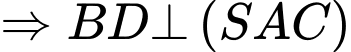
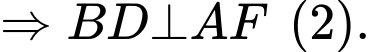
Từ (1) và (2)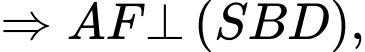 khi đó
khi đó
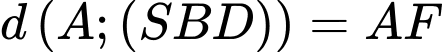
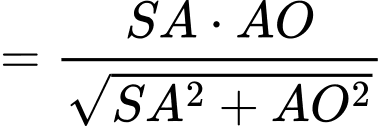
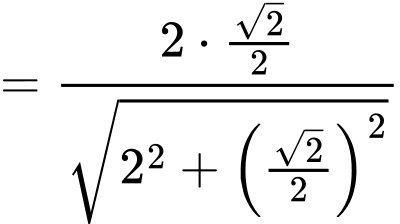
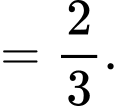
Vậy khoảng cách cần tìm là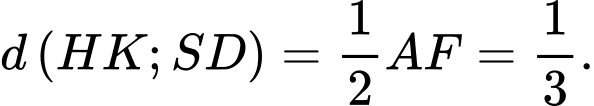

Gọi
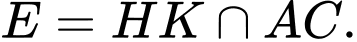 Do
Do  nên suy ra
nên suy ra
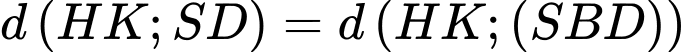
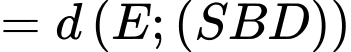
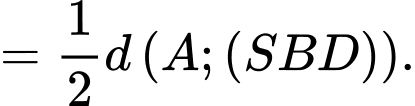
Kẻ
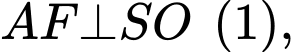 ta có
ta có 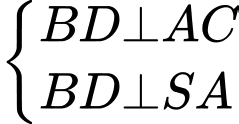
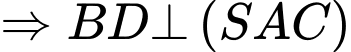
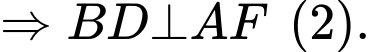
Từ (1) và (2)
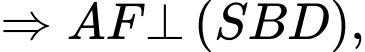 khi đó
khi đó
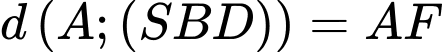
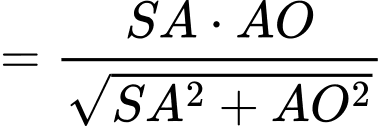
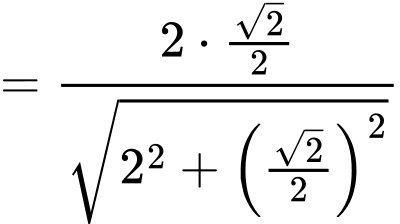
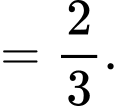
Vậy khoảng cách cần tìm là
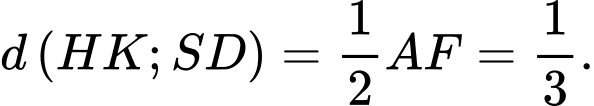
Câu 17 [779102]: Cho hình chóp 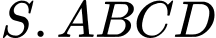 có đáy
có đáy 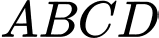 là hình chữ nhật;
là hình chữ nhật; 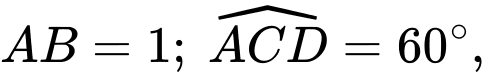
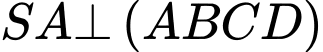 và số đo của góc nhị diện
và số đo của góc nhị diện 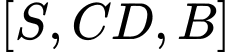 bằng
bằng 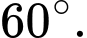 Tính khoảng cách giữa hai đường thẳng
Tính khoảng cách giữa hai đường thẳng 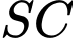 và
và 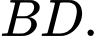
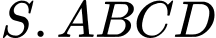 có đáy
có đáy 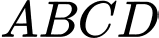 là hình chữ nhật;
là hình chữ nhật; 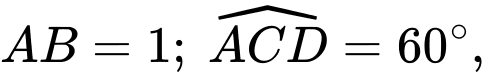
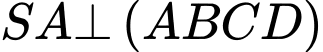 và số đo của góc nhị diện
và số đo của góc nhị diện 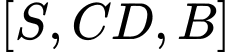 bằng
bằng 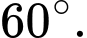 Tính khoảng cách giữa hai đường thẳng
Tính khoảng cách giữa hai đường thẳng 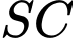 và
và 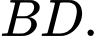
Điền đáp án: 0,75.
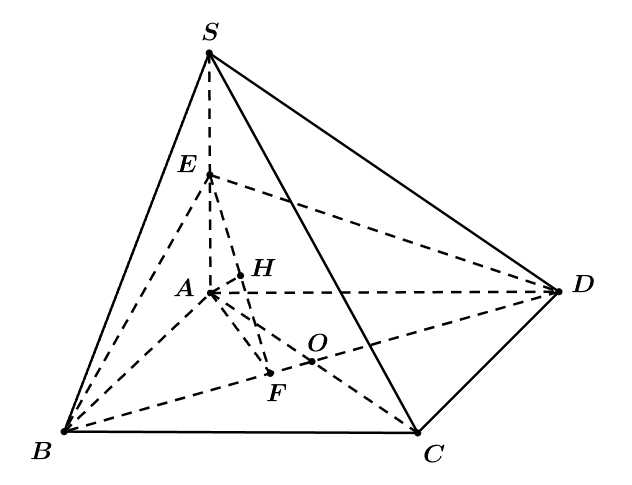
Xét tam giác vuông tại
vuông tại 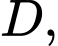 có
có 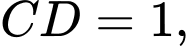

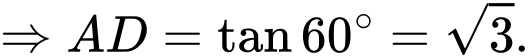
Có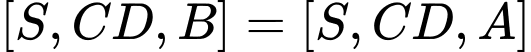
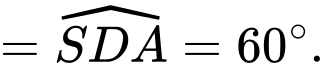
Xét tam giác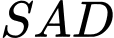 vuông tại
vuông tại 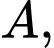 ta có
ta có 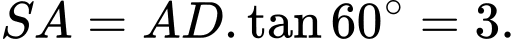
Gọi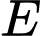 là trung điểm của
là trung điểm của 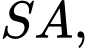 là giao điểm của
là giao điểm của 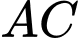 và
và 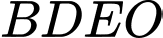 là đường trung bình của tam giác
là đường trung bình của tam giác 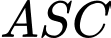
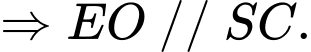
Khi đó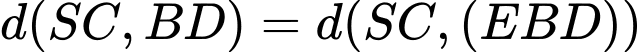
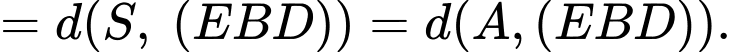
Kẻ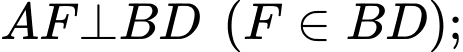
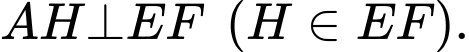
Khi đó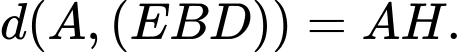
Xét tam giác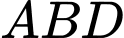 vuông tại A có đường cao
vuông tại A có đường cao 
Suy ra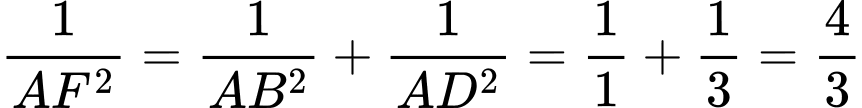
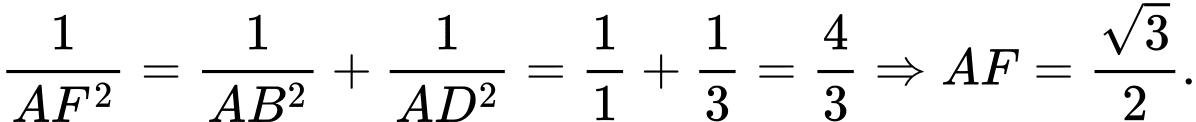
Xét tam giác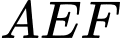 vuông tại
vuông tại 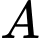 có đường cao
có đường cao 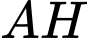
Suy ra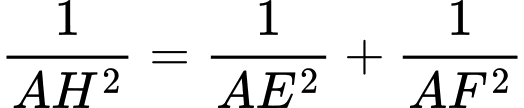
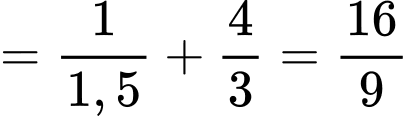
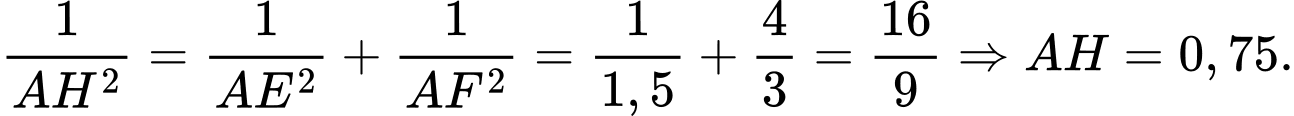

Xét tam giác
 vuông tại
vuông tại 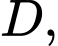 có
có 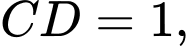

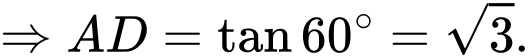
Có
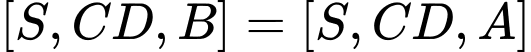
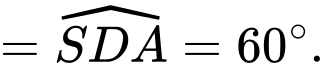
Xét tam giác
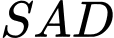 vuông tại
vuông tại 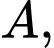 ta có
ta có 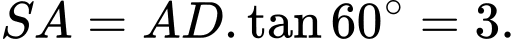
Gọi
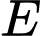 là trung điểm của
là trung điểm của 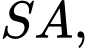 là giao điểm của
là giao điểm của 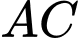 và
và 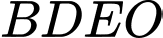 là đường trung bình của tam giác
là đường trung bình của tam giác 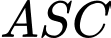
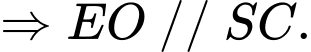
Khi đó
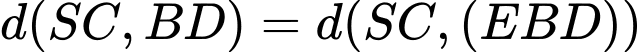
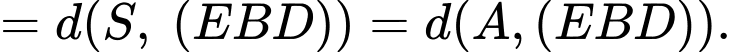
Kẻ
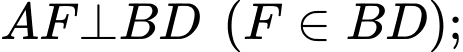
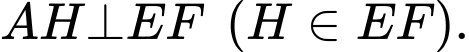
Khi đó
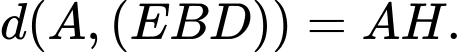
Xét tam giác
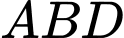 vuông tại A có đường cao
vuông tại A có đường cao 
Suy ra
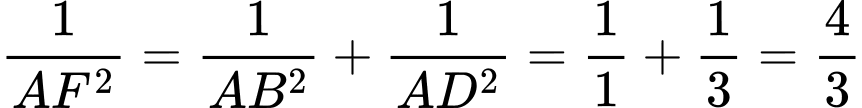
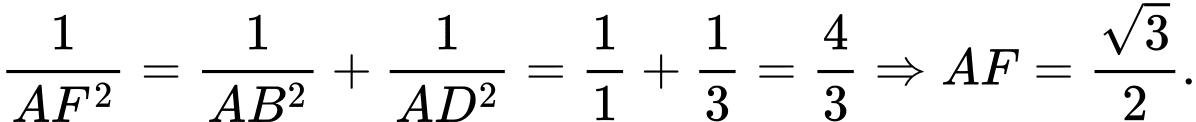
Xét tam giác
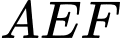 vuông tại
vuông tại 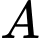 có đường cao
có đường cao 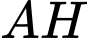
Suy ra
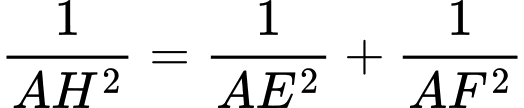
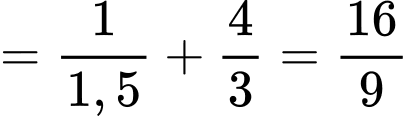
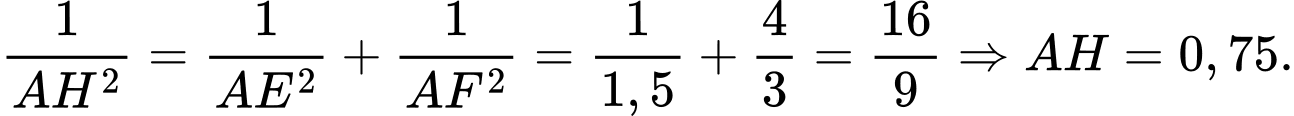
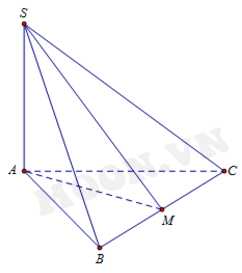
Câu 18 [582265]: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại 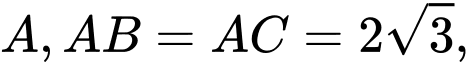 hình chiếu vuông góc của đỉnh S lên mặt phẳng
hình chiếu vuông góc của đỉnh S lên mặt phẳng 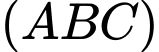 trùng với trung điểm của cạnh AB, biết
trùng với trung điểm của cạnh AB, biết  Tính khoảng cách
Tính khoảng cách 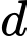 giữa hai đường thẳng SA và BC.
giữa hai đường thẳng SA và BC.
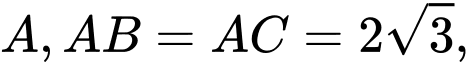 hình chiếu vuông góc của đỉnh S lên mặt phẳng
hình chiếu vuông góc của đỉnh S lên mặt phẳng 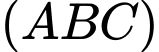 trùng với trung điểm của cạnh AB, biết
trùng với trung điểm của cạnh AB, biết  Tính khoảng cách
Tính khoảng cách 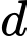 giữa hai đường thẳng SA và BC.
giữa hai đường thẳng SA và BC.
Điền đáp án: 2.
Vẽ hình bình hành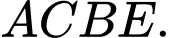
Ta có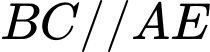
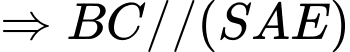

Gọi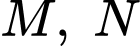 lần lượt là trung điểm của
lần lượt là trung điểm của 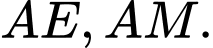 Kẻ
Kẻ 
Dựa vào cách dựng, ta có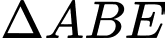 vuông cân tại
vuông cân tại 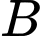 với
với 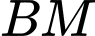 là đường trung tuyến nên
là đường trung tuyến nên 
Xét trong tam giác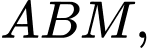 có
có 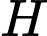 là trung điểm của
là trung điểm của  và
và 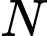 là trung điểm của
là trung điểm của  nên suy ra
nên suy ra
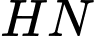 là đường trung bình của tam giác
là đường trung bình của tam giác 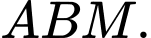 Suy ra
Suy ra 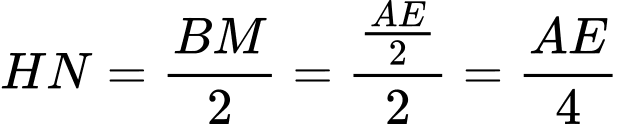
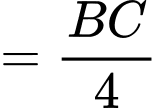
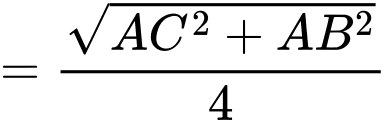
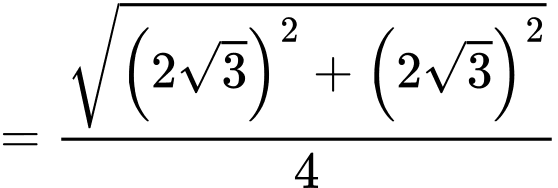
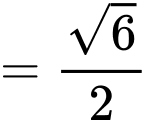
Ta có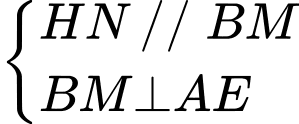
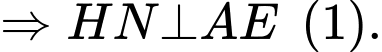
Vì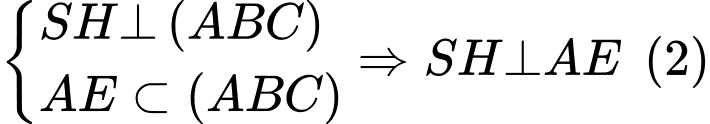
Từ (1) và (2) ta suy ra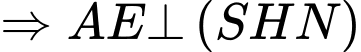
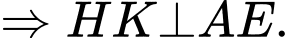
Mặt khác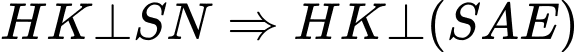
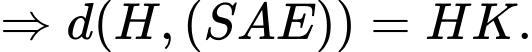
Trong tam giác vuông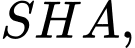 ta có
ta có 
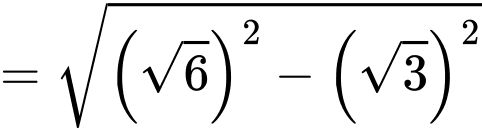
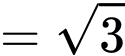
Xét tam giác vuông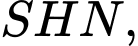 ta có
ta có 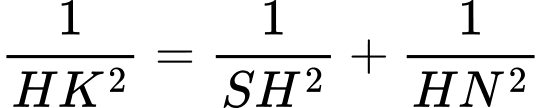
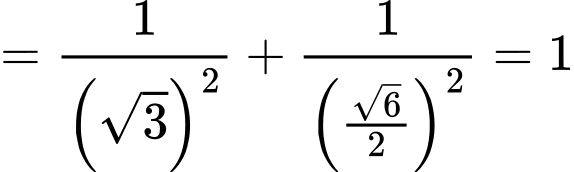
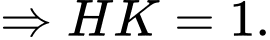
Vậy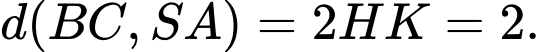

Vẽ hình bình hành
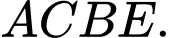
Ta có
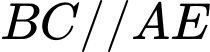
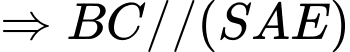

Gọi
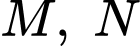 lần lượt là trung điểm của
lần lượt là trung điểm của 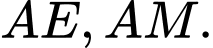 Kẻ
Kẻ 
Dựa vào cách dựng, ta có
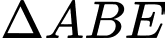 vuông cân tại
vuông cân tại 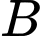 với
với 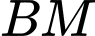 là đường trung tuyến nên
là đường trung tuyến nên 
Xét trong tam giác
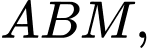 có
có 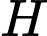 là trung điểm của
là trung điểm của  và
và 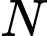 là trung điểm của
là trung điểm của  nên suy ra
nên suy ra 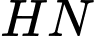 là đường trung bình của tam giác
là đường trung bình của tam giác 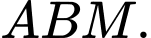 Suy ra
Suy ra 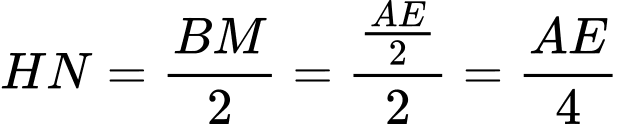
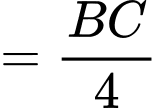
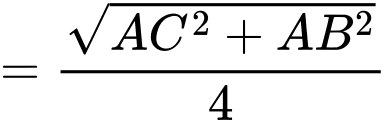
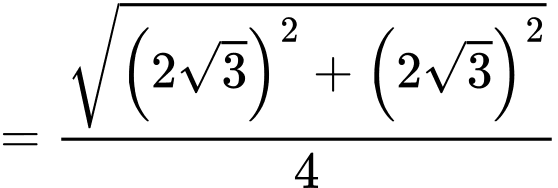
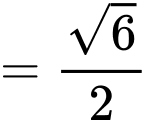
Ta có
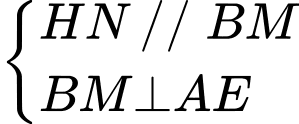
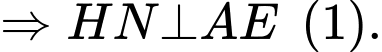
Vì
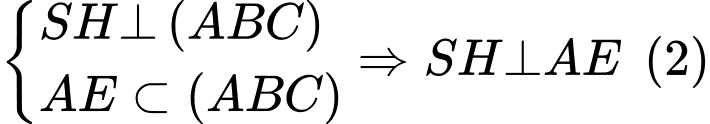
Từ (1) và (2) ta suy ra
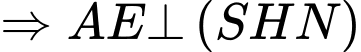
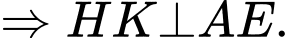
Mặt khác
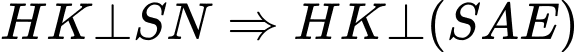
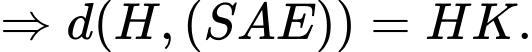
Trong tam giác vuông
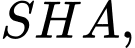 ta có
ta có 
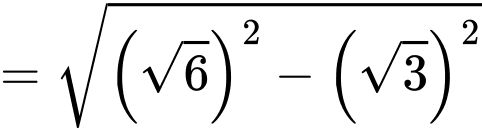
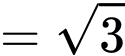
Xét tam giác vuông
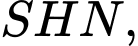 ta có
ta có 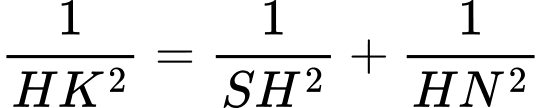
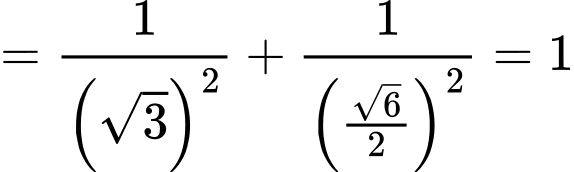
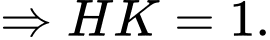
Vậy
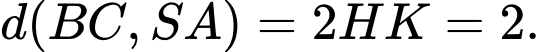
Câu 19 [582236]: Cho hình chóp 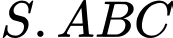 có đáy
có đáy 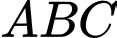 là tam giác đều cạnh
là tam giác đều cạnh 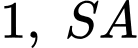 vuông góc với đáy. Gọi
vuông góc với đáy. Gọi 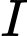 là trung điểm của
là trung điểm của 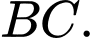 Biết góc giữa đường thẳng
Biết góc giữa đường thẳng 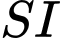 và mặt đáy bằng
và mặt đáy bằng 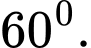 Khoảng cách giữa hai đường thẳng
Khoảng cách giữa hai đường thẳng 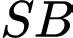 và
và 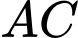 là
là
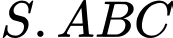 có đáy
có đáy 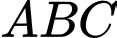 là tam giác đều cạnh
là tam giác đều cạnh 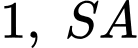 vuông góc với đáy. Gọi
vuông góc với đáy. Gọi 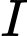 là trung điểm của
là trung điểm của 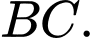 Biết góc giữa đường thẳng
Biết góc giữa đường thẳng 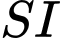 và mặt đáy bằng
và mặt đáy bằng 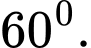 Khoảng cách giữa hai đường thẳng
Khoảng cách giữa hai đường thẳng 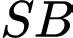 và
và 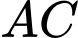 là
là
Điền đáp án: 3/4.
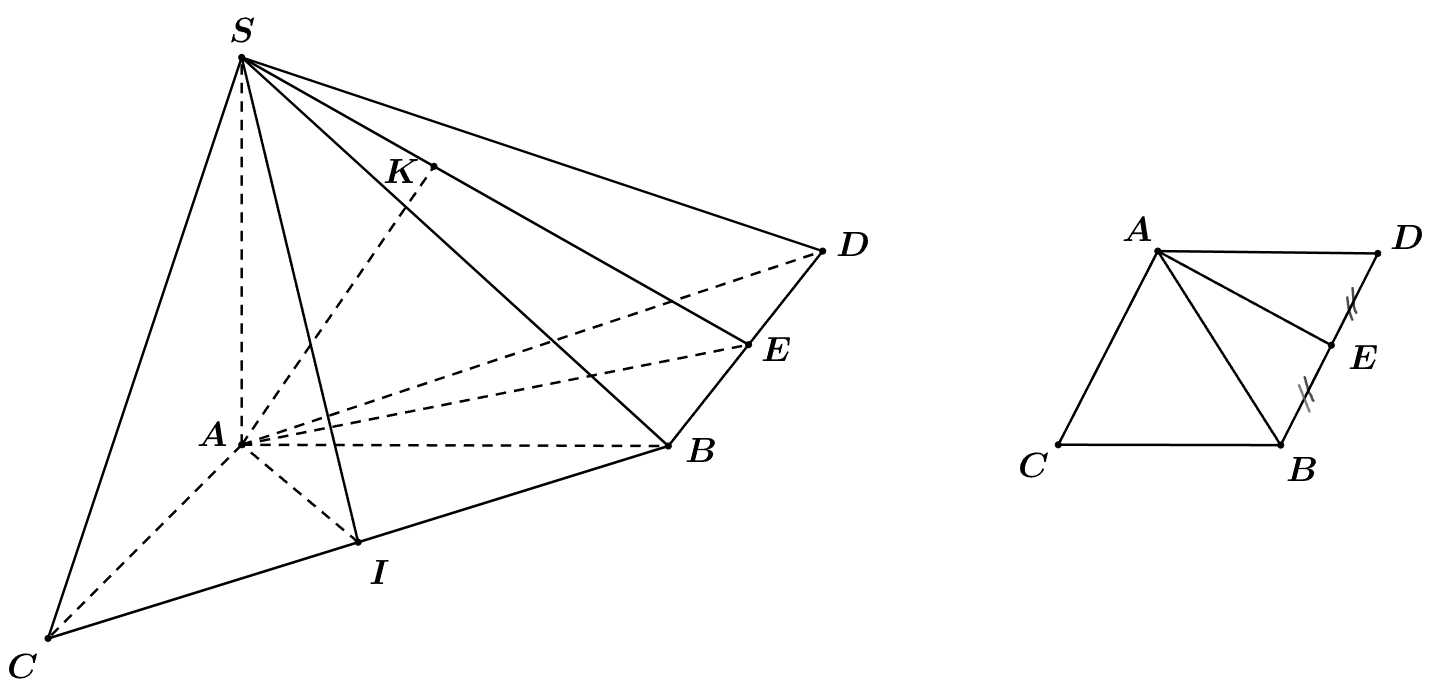
Kẻ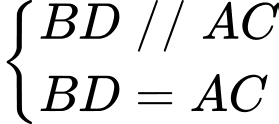 suy ra
suy ra 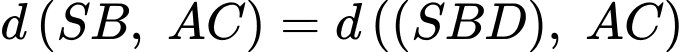
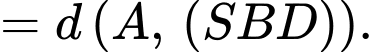
Từ cách dựng hình, ta có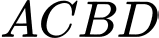 là hình thoi và
là hình thoi và 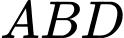 là tam giác đều cạnh bằng 1.
là tam giác đều cạnh bằng 1.
Gọi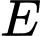 là trung điểm của
là trung điểm của 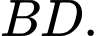 Kẻ
Kẻ  Ta có
Ta có 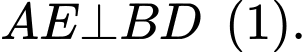
Lại có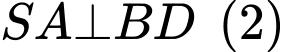 (vì
(vì 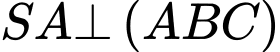 hay
hay 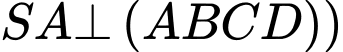
Từ (1) và (2) suy ra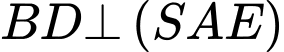
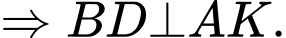 Mặt khác,
Mặt khác, 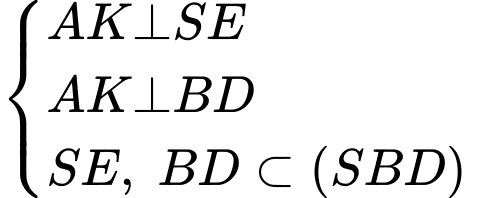
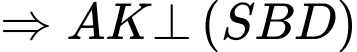
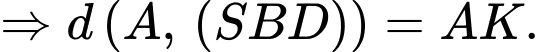
Xét tam giác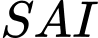 vuông tại
vuông tại 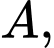 với
với 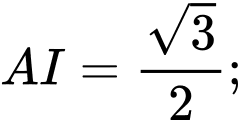
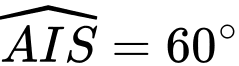 ta có
ta có 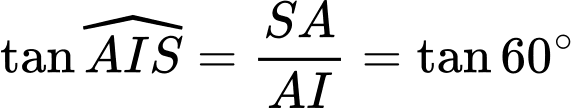
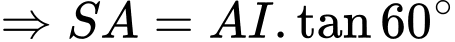
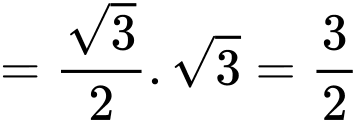
Vì tam giác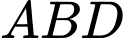 đều nên
đều nên 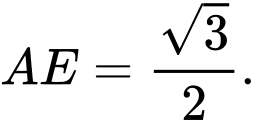
Xét tam giác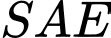 vuông tại
vuông tại 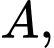 ta có
ta có 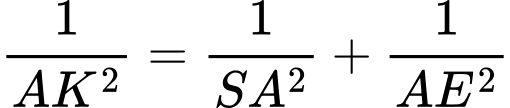
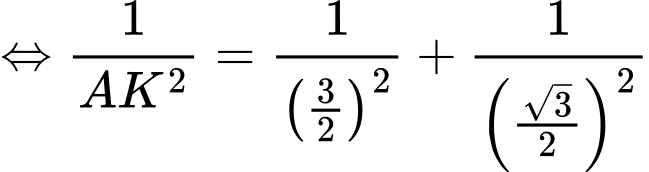
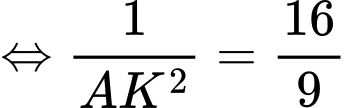
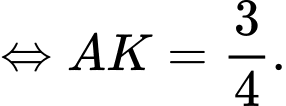

Kẻ
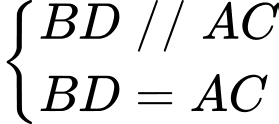 suy ra
suy ra 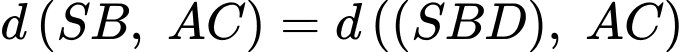
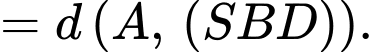
Từ cách dựng hình, ta có
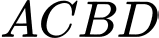 là hình thoi và
là hình thoi và 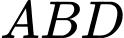 là tam giác đều cạnh bằng 1.
là tam giác đều cạnh bằng 1.
Gọi
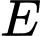 là trung điểm của
là trung điểm của 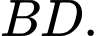 Kẻ
Kẻ  Ta có
Ta có 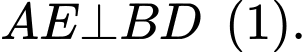
Lại có
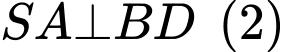 (vì
(vì 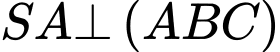 hay
hay 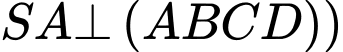
Từ (1) và (2) suy ra
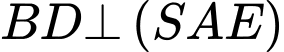
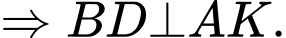 Mặt khác,
Mặt khác, 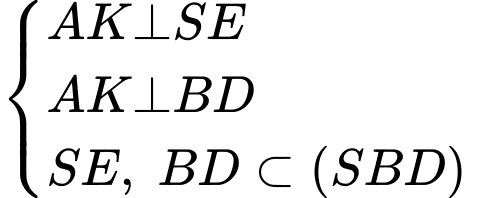
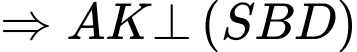
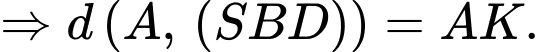
Xét tam giác
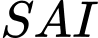 vuông tại
vuông tại 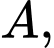 với
với 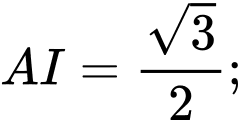
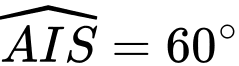 ta có
ta có 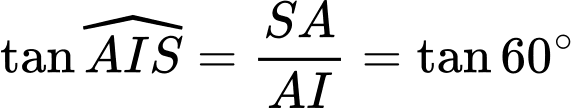
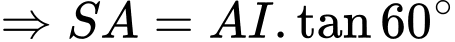
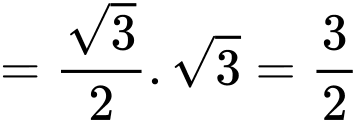
Vì tam giác
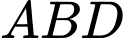 đều nên
đều nên 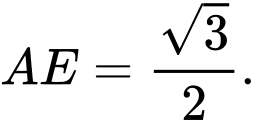
Xét tam giác
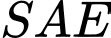 vuông tại
vuông tại 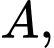 ta có
ta có 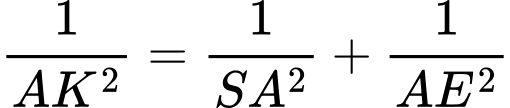
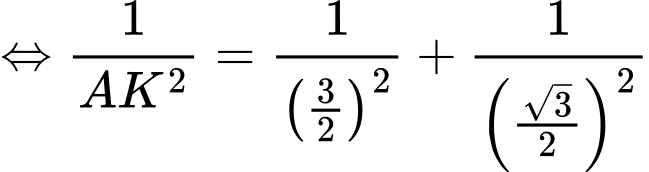
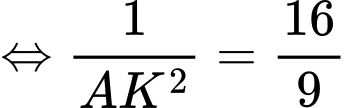
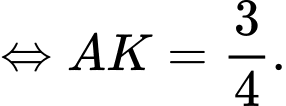
Câu 20 [582266]: Cho hình chóp 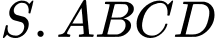 có đáy
có đáy 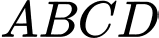 là hình chữ nhật
là hình chữ nhật 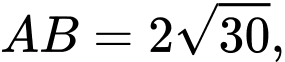
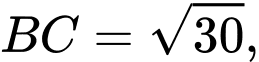 tam giác
tam giác 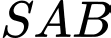 là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi
là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi 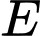 là trung điểm của
là trung điểm của 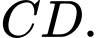 Tính khoảng cách giữa hai đường thẳng
Tính khoảng cách giữa hai đường thẳng 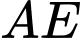 và
và 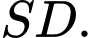
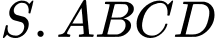 có đáy
có đáy 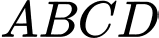 là hình chữ nhật
là hình chữ nhật 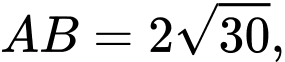
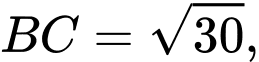 tam giác
tam giác 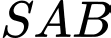 là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi
là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi 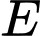 là trung điểm của
là trung điểm của 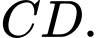 Tính khoảng cách giữa hai đường thẳng
Tính khoảng cách giữa hai đường thẳng 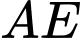 và
và 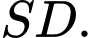
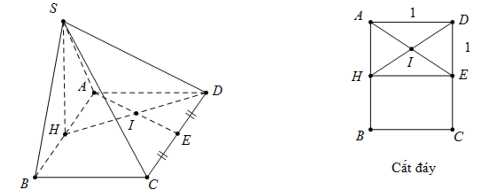
Gọi
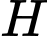 là trung điểm của
là trung điểm của  khi đó:
khi đó: 
Ta có:
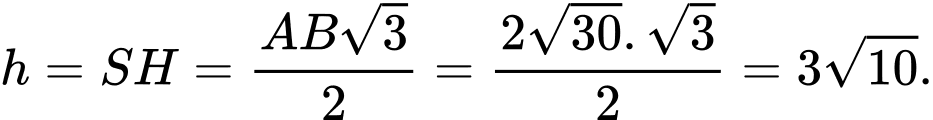
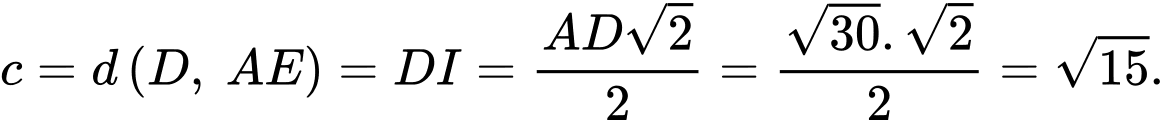
Tỷ số
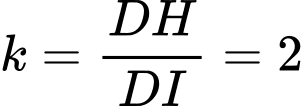
Do đó:
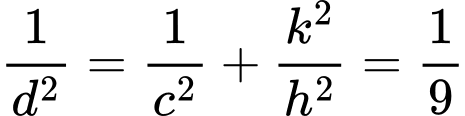
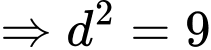
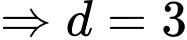
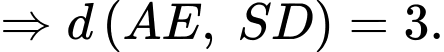
Câu 21 [696486]: Cho hình chóp 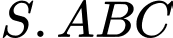 có đáy
có đáy 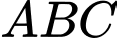 là tam giác đều, cạnh bên
là tam giác đều, cạnh bên 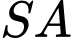 vuông góc với mặt phẳng đáy và
vuông góc với mặt phẳng đáy và 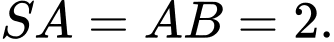 Góc giữa đường thẳng
Góc giữa đường thẳng 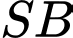 và mặt phẳng
và mặt phẳng 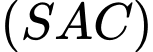 bằng bao nhiêu độ? (kết quả làm tròn đến độ).
bằng bao nhiêu độ? (kết quả làm tròn đến độ).
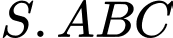 có đáy
có đáy 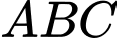 là tam giác đều, cạnh bên
là tam giác đều, cạnh bên 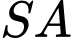 vuông góc với mặt phẳng đáy và
vuông góc với mặt phẳng đáy và 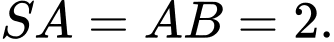 Góc giữa đường thẳng
Góc giữa đường thẳng 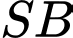 và mặt phẳng
và mặt phẳng 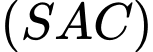 bằng bao nhiêu độ? (kết quả làm tròn đến độ).
bằng bao nhiêu độ? (kết quả làm tròn đến độ).
Điền đáp án: 38.
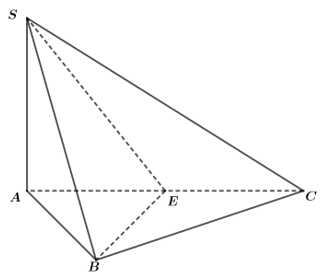
Gọi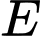 là trung điểm của
là trung điểm của 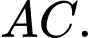
Do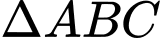 đều
đều 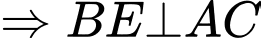
Mà
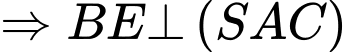
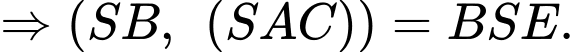
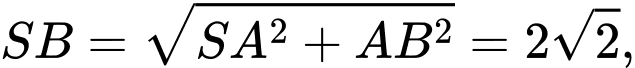
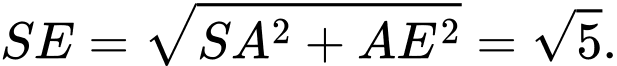
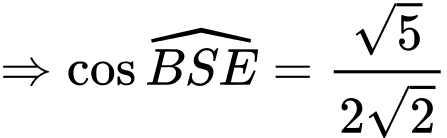
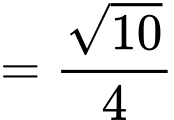
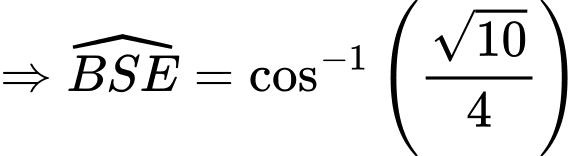
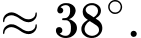

Gọi
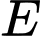 là trung điểm của
là trung điểm của 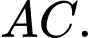
Do
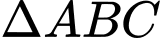 đều
đều 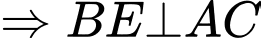
Mà

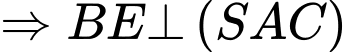
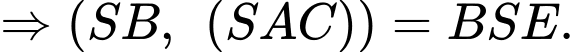
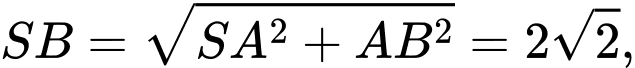
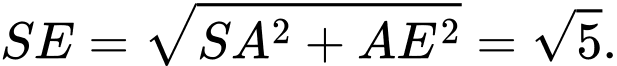
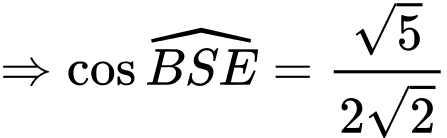
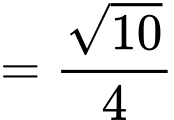
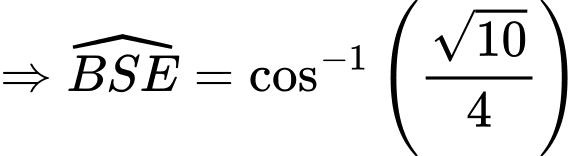
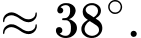
Câu 22 [779026]: Cho hình chóp tứ giác đều 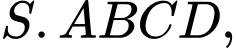 có
có  là giao điểm của
là giao điểm của 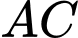 và
và 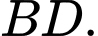 Biết
Biết 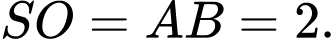 Giá trị sin của góc giữa đường thẳng
Giá trị sin của góc giữa đường thẳng 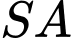 và mặt phẳng
và mặt phẳng 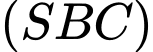 bằng bao nhiêu? (Kết quả làm tròn đến hàng phần trăm)
bằng bao nhiêu? (Kết quả làm tròn đến hàng phần trăm)
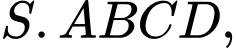 có
có  là giao điểm của
là giao điểm của 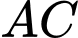 và
và 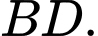 Biết
Biết 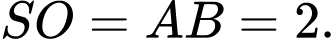 Giá trị sin của góc giữa đường thẳng
Giá trị sin của góc giữa đường thẳng 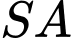 và mặt phẳng
và mặt phẳng 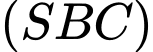 bằng bao nhiêu? (Kết quả làm tròn đến hàng phần trăm)
bằng bao nhiêu? (Kết quả làm tròn đến hàng phần trăm)
Điền đáp án: 0,73.
Gọi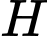 là hình chiếu của
là hình chiếu của 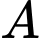 lên mặt phẳng
lên mặt phẳng 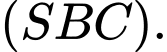
Ta có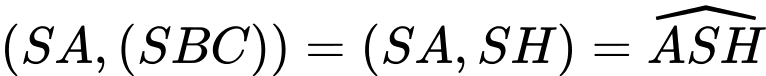
Suy ra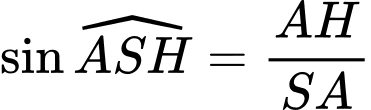
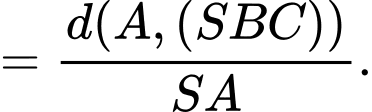
Vì là hình vuông và
là hình vuông và 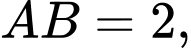 nên suy ra
nên suy ra 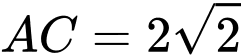
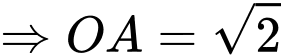
Xét tam giác vuông tại
vuông tại 

Mặt khác,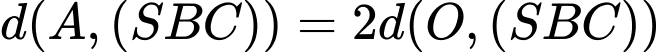
Gọi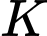 là hình chiếu vuông góc của
là hình chiếu vuông góc của  lên mặt phẳng
lên mặt phẳng 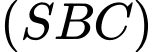
Từ kẻ đường thẳng vuông góc với
kẻ đường thẳng vuông góc với 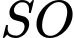 tại
tại 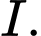
Ta có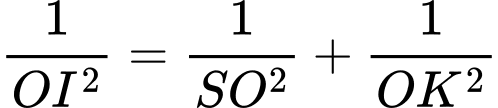
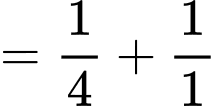
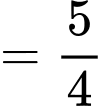
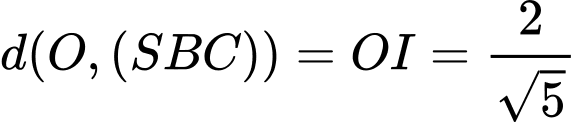
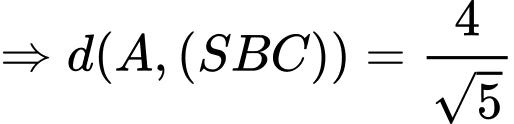
Vậy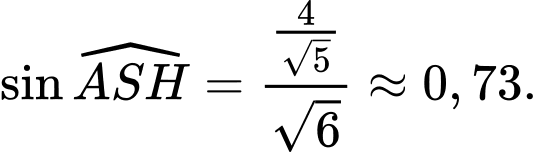
Gọi
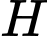 là hình chiếu của
là hình chiếu của 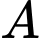 lên mặt phẳng
lên mặt phẳng 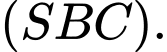
Ta có
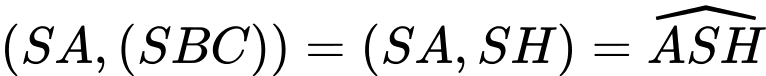
Suy ra
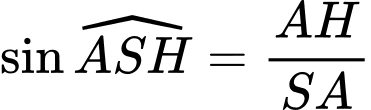
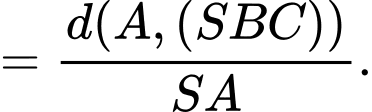
Vì
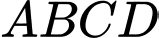 là hình vuông và
là hình vuông và 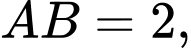 nên suy ra
nên suy ra 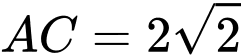
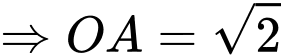
Xét tam giác
 vuông tại
vuông tại 

Mặt khác,
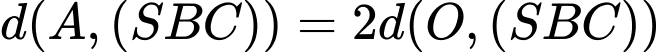
Gọi
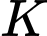 là hình chiếu vuông góc của
là hình chiếu vuông góc của  lên mặt phẳng
lên mặt phẳng 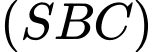
Từ
 kẻ đường thẳng vuông góc với
kẻ đường thẳng vuông góc với 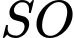 tại
tại 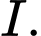
Ta có
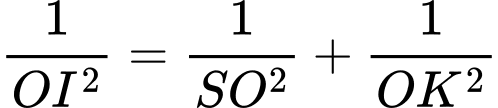
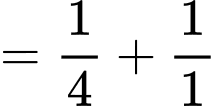
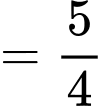
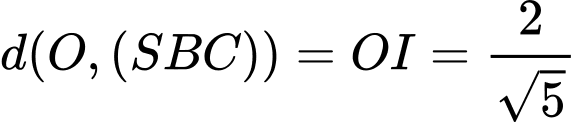
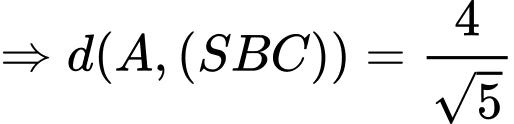
Vậy