Đáp án Bài tập tự luyện
Câu 1 [224447]: Cho dãy số 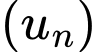 xác định bởi:
xác định bởi: 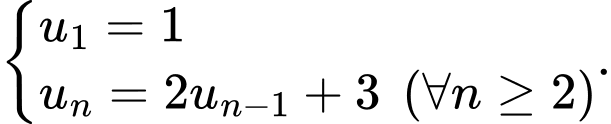 Viết năm số hạng đầu của dãy;
Viết năm số hạng đầu của dãy;
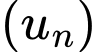 xác định bởi:
xác định bởi: 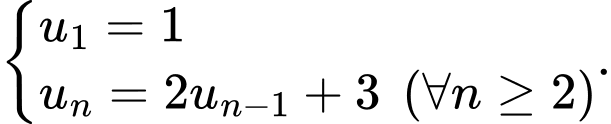 Viết năm số hạng đầu của dãy;
Viết năm số hạng đầu của dãy; A, 1; 5; 13; 28; 61.
B, 1; 5; 13; 29; 61.
C, 1; 5; 17; 29; 61.
D, 1; 5; 14; 29; 61.
Chọn B.
Ta có 5 số hạng đầu của dãy là: 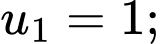
 ;
; 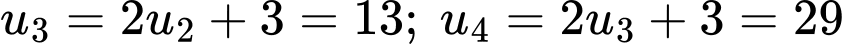
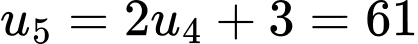 .
.
Đáp án: B 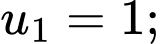
 ;
; 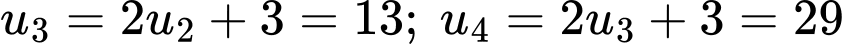
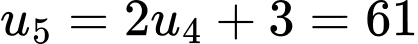 .
.
Câu 2 [805500]: Cho dãy số 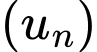 có số hạng tổng quát
có số hạng tổng quát 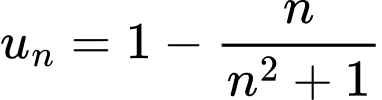 (với
(với  ). Số hạng đầu tiên của dãy là
). Số hạng đầu tiên của dãy là
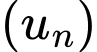 có số hạng tổng quát
có số hạng tổng quát 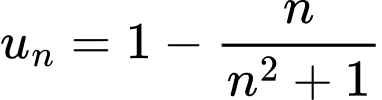 (với
(với  ). Số hạng đầu tiên của dãy là
). Số hạng đầu tiên của dãy là A, 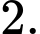
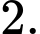
B, 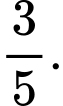
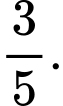
C, 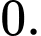
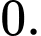
D, 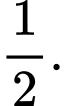
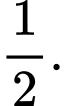
Chọn đáp án D.
Ta có: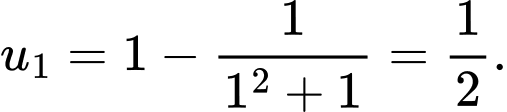 Đáp án: D
Đáp án: D
Ta có:
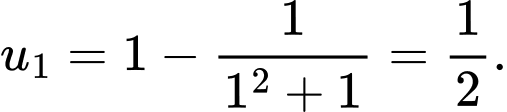 Đáp án: D
Đáp án: D
Câu 3 [805501]: Cho dãy số 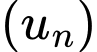 có
có 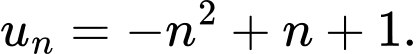 Số
Số 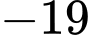 là số hạng thứ mấy của dãy?
là số hạng thứ mấy của dãy?
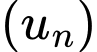 có
có 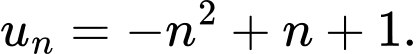 Số
Số 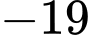 là số hạng thứ mấy của dãy?
là số hạng thứ mấy của dãy? A, 5.
B, 7.
C, 6.
D, 4.
Chọn A
Giả sử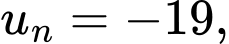
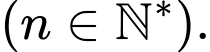
Suy ra
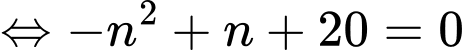
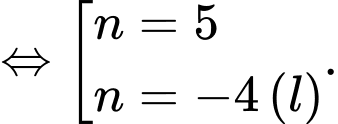
Vậy số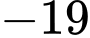 là số hạng thứ
là số hạng thứ 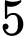 của dãy. Đáp án: A
của dãy. Đáp án: A
Giả sử
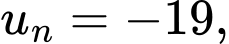
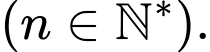
Suy ra

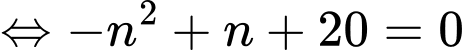
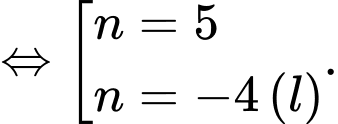
Vậy số
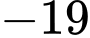 là số hạng thứ
là số hạng thứ 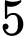 của dãy. Đáp án: A
của dãy. Đáp án: A
Câu 4 [805514]: Cho dãy số 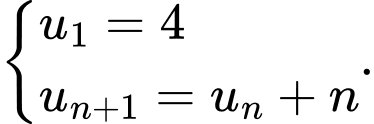 Tìm số hạng thứ 5 của dãy số.
Tìm số hạng thứ 5 của dãy số.
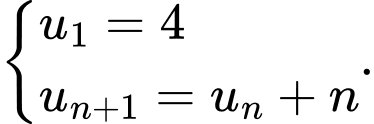 Tìm số hạng thứ 5 của dãy số.
Tìm số hạng thứ 5 của dãy số. A, 16.
B, 12.
C, 15.
D, 14.
Vì dãy số đã cho có số hạng tổng quát là 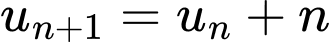
Với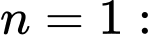

Với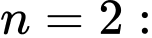

Tương tự ta có
Với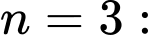

Với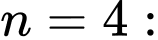
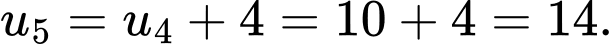
Vậy số hạng thứ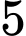 của dãy số là
của dãy số là 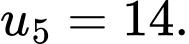
Chọn đáp án D. Đáp án: D
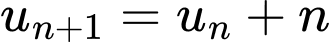
Với
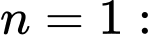

Với
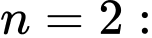

Tương tự ta có
Với
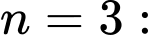

Với
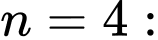
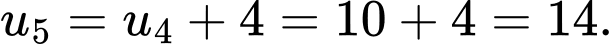
Vậy số hạng thứ
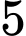 của dãy số là
của dãy số là 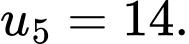
Chọn đáp án D. Đáp án: D
Câu 5 [805511]: Cho dãy số 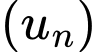 có
có 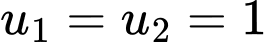 và
và  Tính
Tính 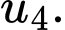
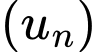 có
có 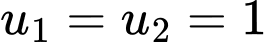 và
và  Tính
Tính 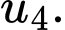
A, 5.
B, 3.
C, 2.
D, 4.
Chọn B
Ta có
 Đáp án: B
Đáp án: B
Ta có

 Đáp án: B
Đáp án: B
Câu 6 [805512]: Cho dãy số 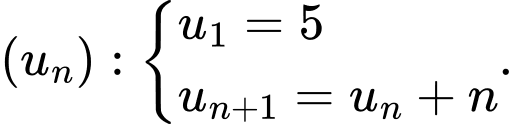 Số
Số 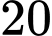 là số hạng thứ mấy trong dãy?
là số hạng thứ mấy trong dãy?
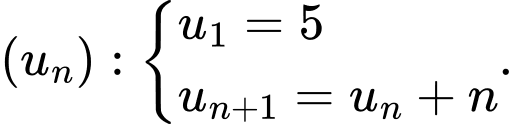 Số
Số 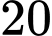 là số hạng thứ mấy trong dãy?
là số hạng thứ mấy trong dãy? A, 5.
B, 6.
C, 9.
D, 10.
Chọn B
Cách 1:
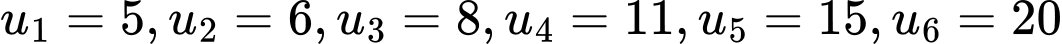
Vậy số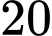 là số hạng thứ
là số hạng thứ 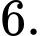
Cách 2:
Dựa vào công thức truy hồi ta có
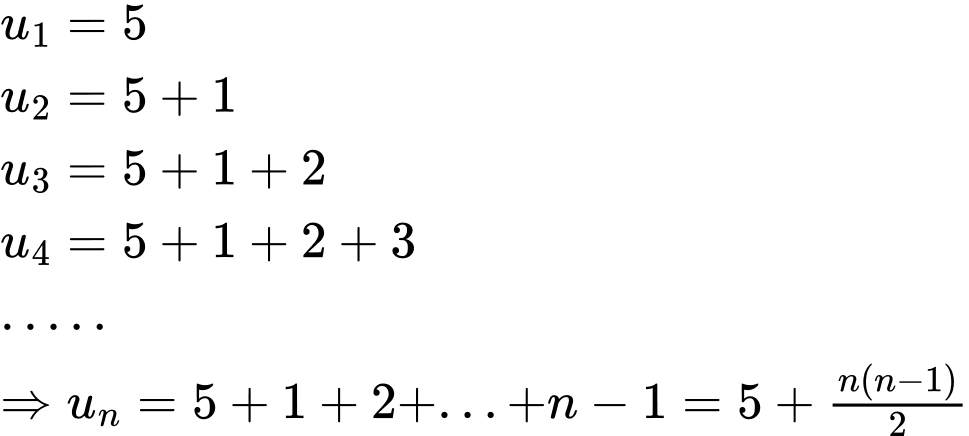
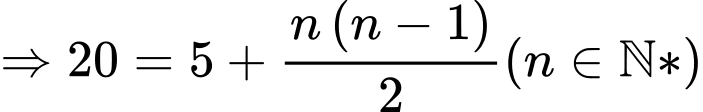
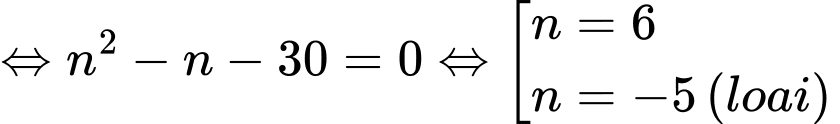
Vậy là số hạng thứ
là số hạng thứ 
Cách 3: Sử dụng máy tính CASIO fx – 570VN PLUS
1 SHIFT STO A
5 SHIFT STO B
Ghi vào màn hình C = B + A: A = A + 1: B = C
Ấn CALC và lặp lại phím =
Ta tìm được số 20 là số hạng thứ 6 Đáp án: B
Cách 1:
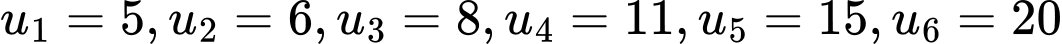
Vậy số
 là số hạng thứ
là số hạng thứ 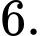
Cách 2:
Dựa vào công thức truy hồi ta có
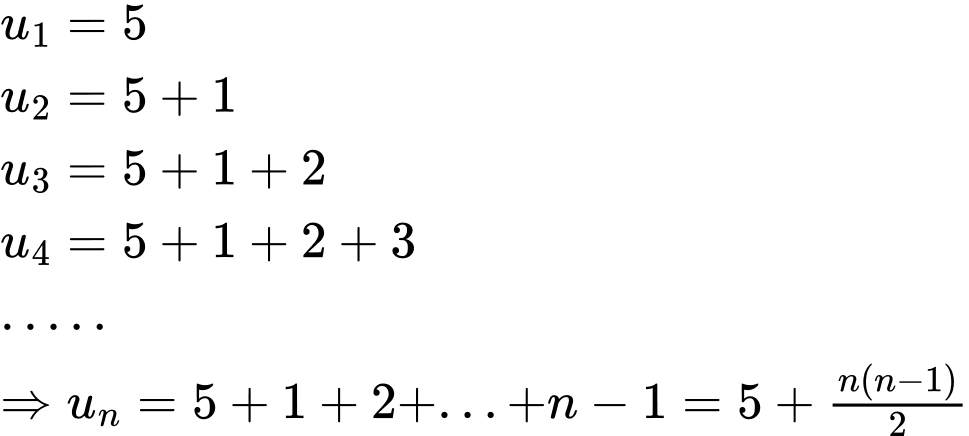
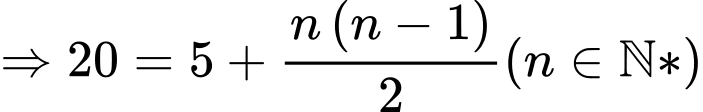
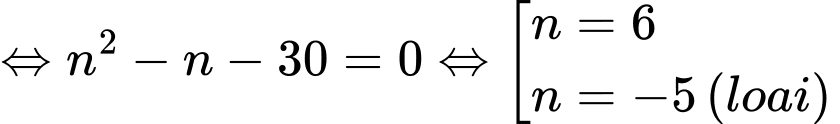
Vậy
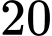 là số hạng thứ
là số hạng thứ 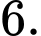
Cách 3: Sử dụng máy tính CASIO fx – 570VN PLUS
1 SHIFT STO A
5 SHIFT STO B
Ghi vào màn hình C = B + A: A = A + 1: B = C
Ấn CALC và lặp lại phím =
Ta tìm được số 20 là số hạng thứ 6 Đáp án: B
Câu 7 [805510]: Cho dãy số 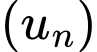 có số hạng tổng quát là
có số hạng tổng quát là 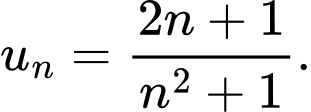 Khi đó
Khi đó 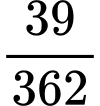 là số hạng thứ mấy của dãy số?
là số hạng thứ mấy của dãy số?
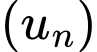 có số hạng tổng quát là
có số hạng tổng quát là 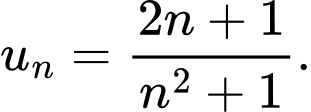 Khi đó
Khi đó 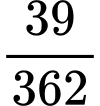 là số hạng thứ mấy của dãy số?
là số hạng thứ mấy của dãy số? A, 20.
B, 19.
C, 22.
D, 21.
Chọn B
Ta có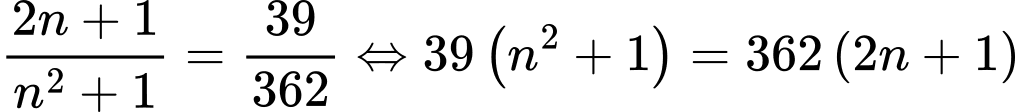
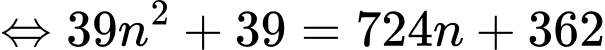
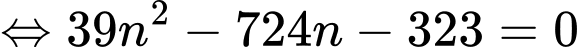
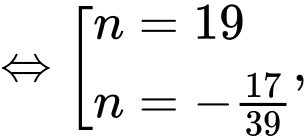 do
do  nên
nên 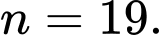 Đáp án: B
Đáp án: B
Ta có
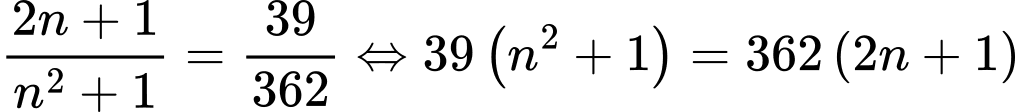
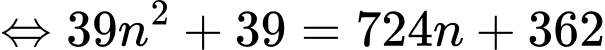
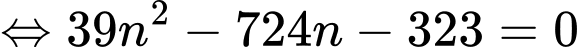
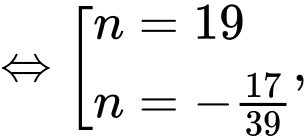 do
do  nên
nên 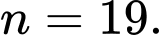 Đáp án: B
Đáp án: B
Câu 8 [805523]: Trong các dãy số 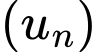 cho bởi số hạng tổng quát
cho bởi số hạng tổng quát 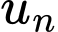 sau, dãy số nào là dãy số giảm?
sau, dãy số nào là dãy số giảm?
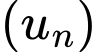 cho bởi số hạng tổng quát
cho bởi số hạng tổng quát 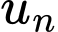 sau, dãy số nào là dãy số giảm?
sau, dãy số nào là dãy số giảm? A, 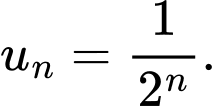
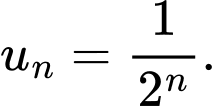
B, 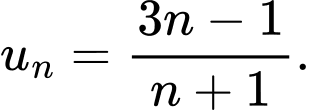
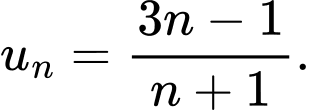
C, 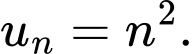
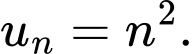
D, 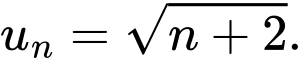
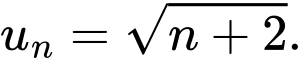
Ta có 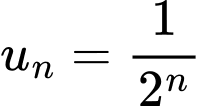
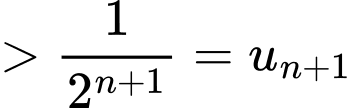
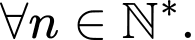 Đáp án: A
Đáp án: A
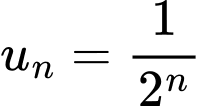
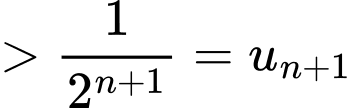
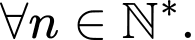 Đáp án: A
Đáp án: A
Câu 9 [805526]: Trong các dãy số sau, dãy số nào là dãy số giảm?
A, 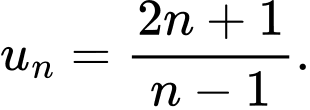
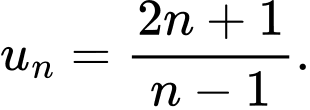
B, 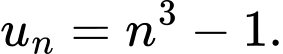
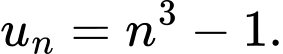
C, 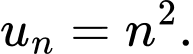
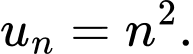
D, 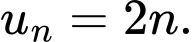
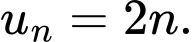
Với mọi 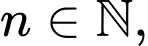
 Ta có
Ta có
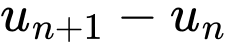
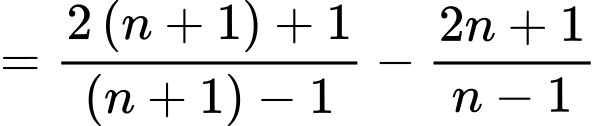
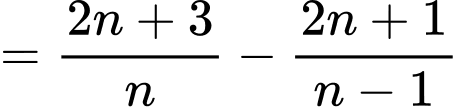
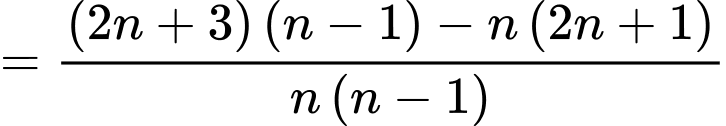
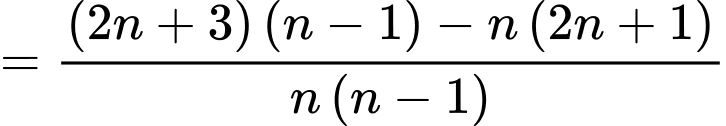
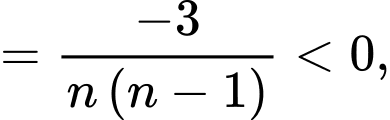 với mọi
với mọi 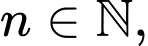

Suy ra dãy số giảm. Đáp án: A
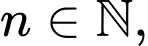
 Ta có
Ta có 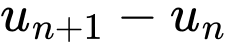
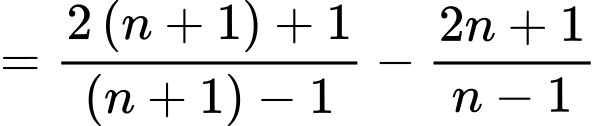
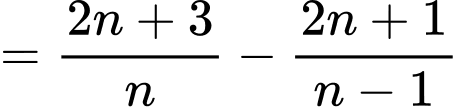
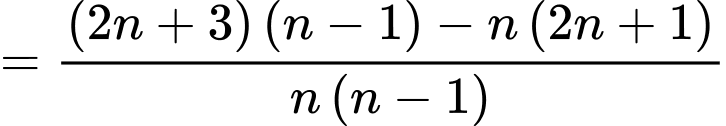
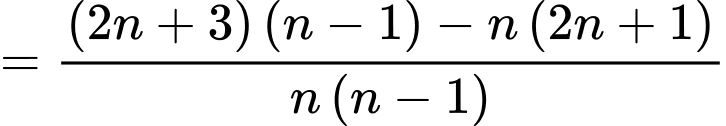
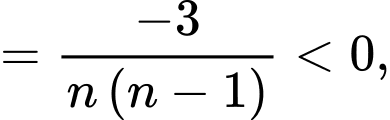 với mọi
với mọi 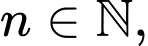

Suy ra dãy số giảm. Đáp án: A
Câu 10 [805537]: Trong các dãy số 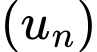 có số hạng tổng quát
có số hạng tổng quát 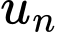 dưới đây, dãy số nào là dãy bị chặn?
dưới đây, dãy số nào là dãy bị chặn?
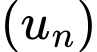 có số hạng tổng quát
có số hạng tổng quát 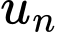 dưới đây, dãy số nào là dãy bị chặn?
dưới đây, dãy số nào là dãy bị chặn? A, 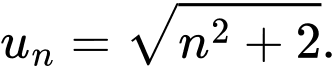
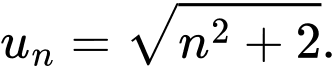
B, 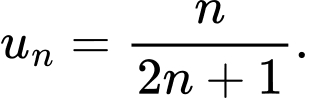
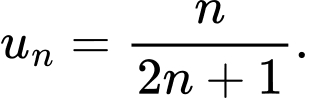
C, 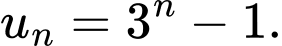
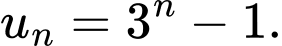
D, 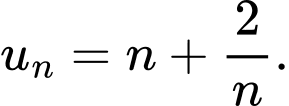
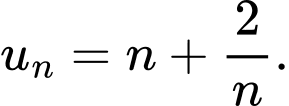
Chọn B
Ta thấy khi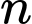 càng lớn thì
càng lớn thì 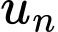 càng tiến đến
càng tiến đến 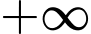
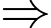 dãy số
dãy số 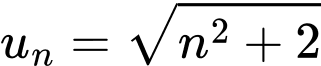 không bị chặn.
không bị chặn.
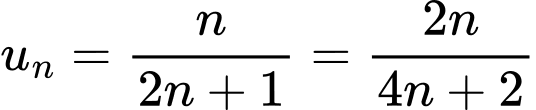
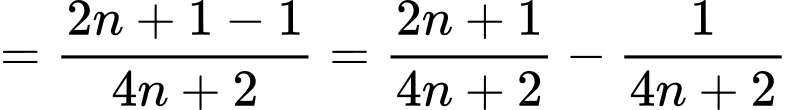
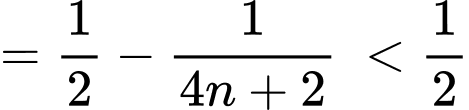
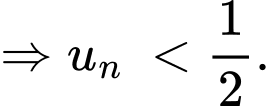
Mặt khác ta thấy ngay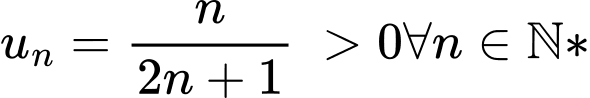
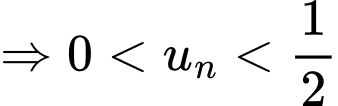
 dãy số
dãy số 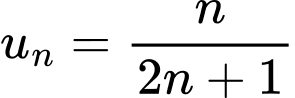 bị chặn. Đáp án: B
bị chặn. Đáp án: B
Ta thấy khi
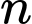 càng lớn thì
càng lớn thì 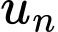 càng tiến đến
càng tiến đến 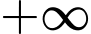
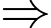 dãy số
dãy số 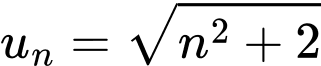 không bị chặn.
không bị chặn.
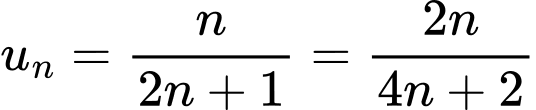
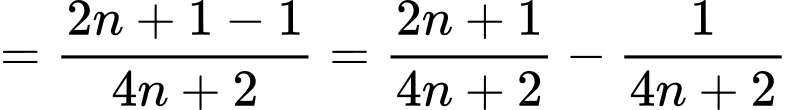
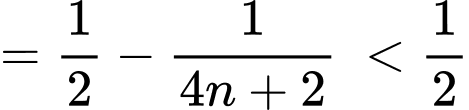
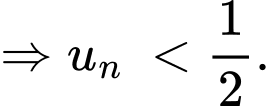
Mặt khác ta thấy ngay
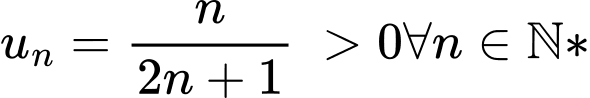
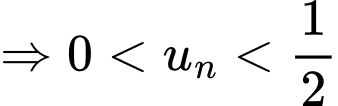
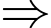 dãy số
dãy số 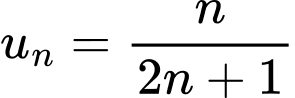 bị chặn. Đáp án: B
bị chặn. Đáp án: B
Câu 11 [805539]: Trong các dãy số sau, dãy nào là dãy số bị chặn?
A, 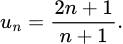
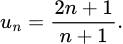
B, 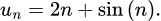
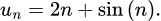
C, 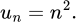
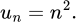
D, 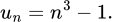
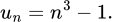
Xét dãy số 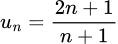 ta có:
ta có:
*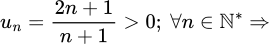 dãy
dãy 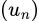 bị chặn dưới bởi giá trị
bị chặn dưới bởi giá trị 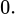
*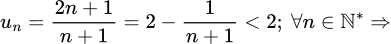 dãy
dãy 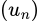 bị chặn trên bởi giá trị
bị chặn trên bởi giá trị 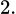
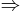 dãy
dãy 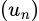 là dãy bị chặn. Đáp án: A
là dãy bị chặn. Đáp án: A
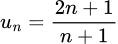 ta có:
ta có: *
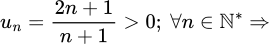 dãy
dãy 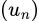 bị chặn dưới bởi giá trị
bị chặn dưới bởi giá trị 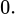
*
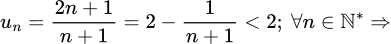 dãy
dãy 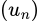 bị chặn trên bởi giá trị
bị chặn trên bởi giá trị 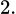
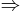 dãy
dãy 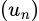 là dãy bị chặn. Đáp án: A
là dãy bị chặn. Đáp án: A
Câu 12 [805525]: Dãy số nào sau đây là dãy số giảm?
A, 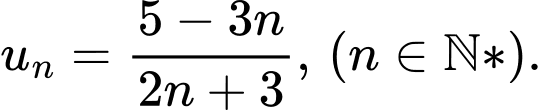
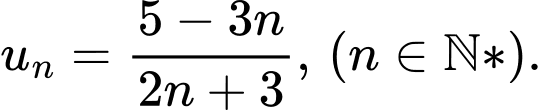
B, 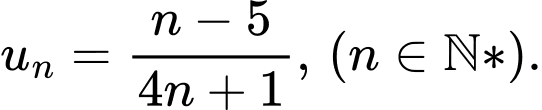
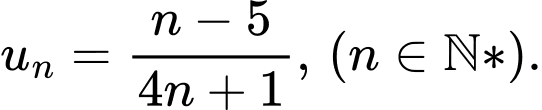
C, 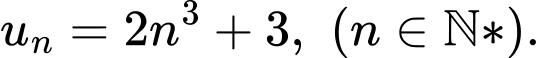
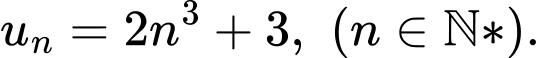
D, 

Xét 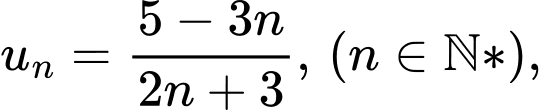 ta có
ta có 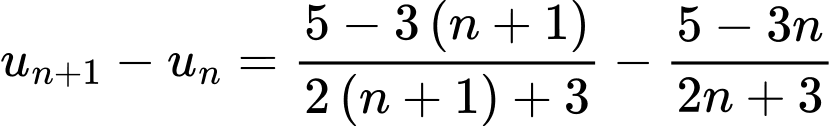
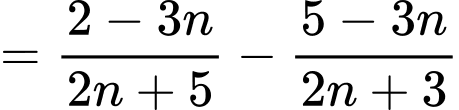
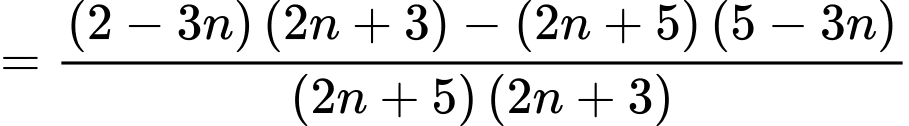
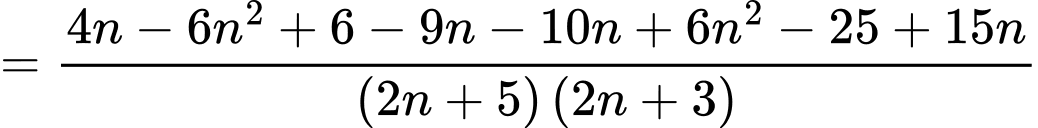
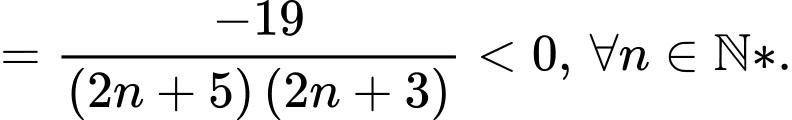
Vậy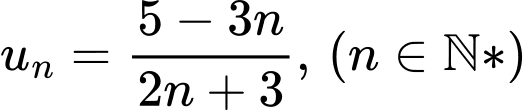 là dãy giảm. Đáp án: A
là dãy giảm. Đáp án: A
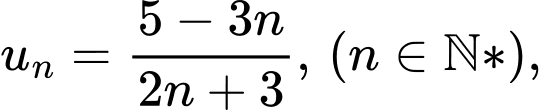 ta có
ta có 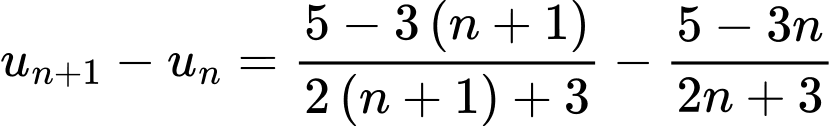
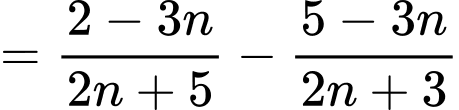
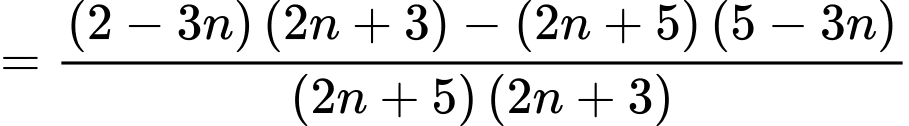
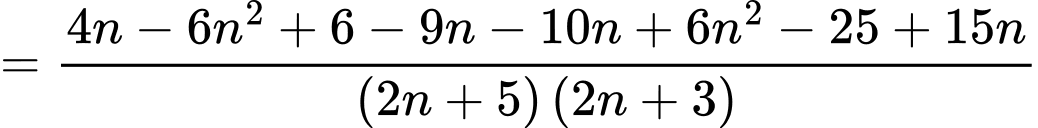
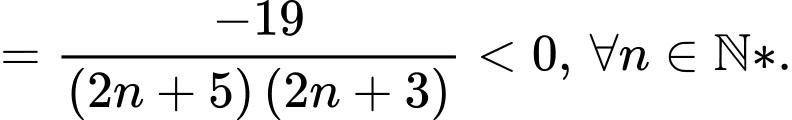
Vậy
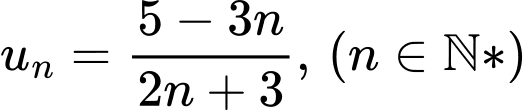 là dãy giảm. Đáp án: A
là dãy giảm. Đáp án: A
Câu 13 [805344]: Cho 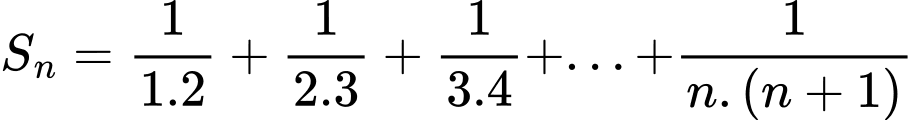 với
với 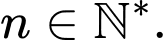 Mệnh đề nào sau đây đúng?
Mệnh đề nào sau đây đúng?
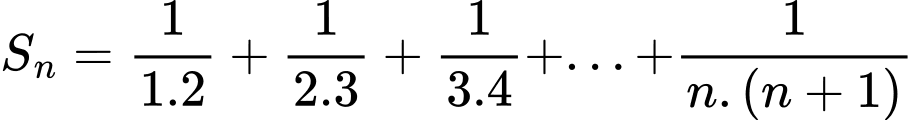 với
với 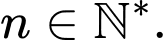 Mệnh đề nào sau đây đúng?
Mệnh đề nào sau đây đúng? A, 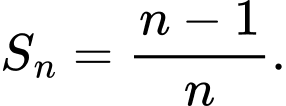
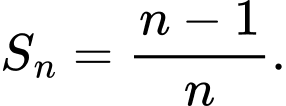
B, 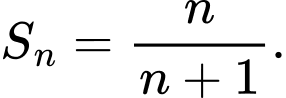
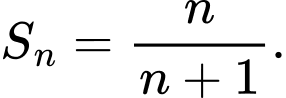
C, 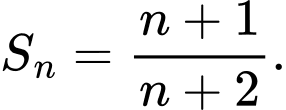
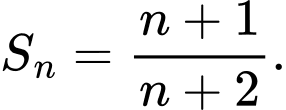
D, 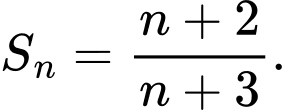
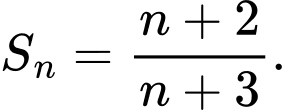
Cách trắc nghiệm: Ta tính được 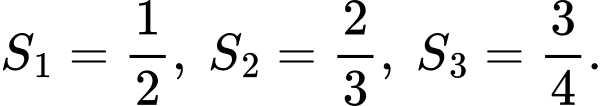 Từ đó ta thấy quy luật là từ nhỏ hơn mẫu đúng 1 đơn vị. Chọn B.
Từ đó ta thấy quy luật là từ nhỏ hơn mẫu đúng 1 đơn vị. Chọn B.
Cách tự luận. Ta có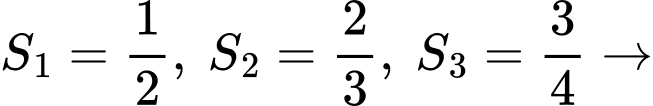 dự đoán
dự đoán 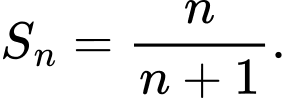
 Với
Với 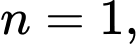 ta được
ta được 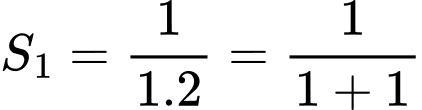 : đúng.
: đúng.
 Giả sử mệnh đề đúng khi
Giả sử mệnh đề đúng khi 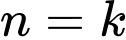
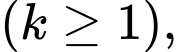 tức là
tức là 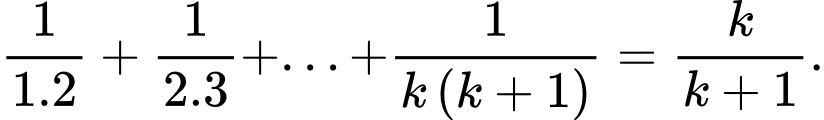
 Ta có
Ta có 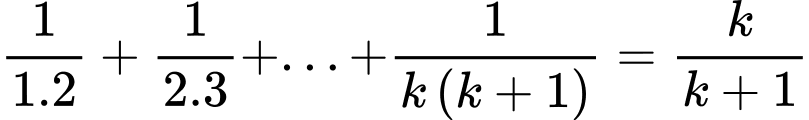
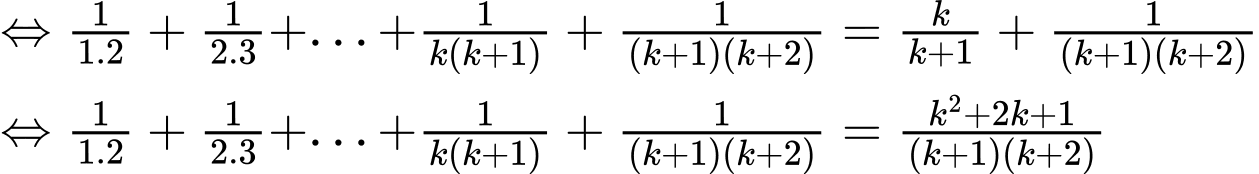
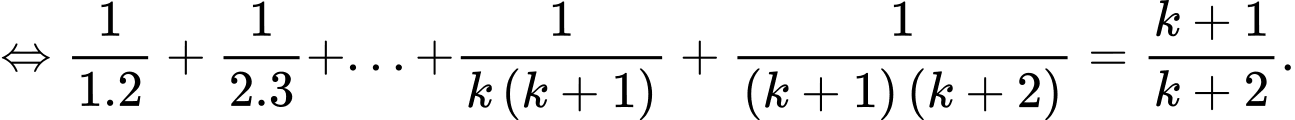 Suy ra mệnh đề đúng với
Suy ra mệnh đề đúng với 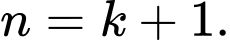 Đáp án: B
Đáp án: B
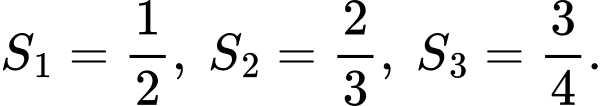 Từ đó ta thấy quy luật là từ nhỏ hơn mẫu đúng 1 đơn vị. Chọn B.
Từ đó ta thấy quy luật là từ nhỏ hơn mẫu đúng 1 đơn vị. Chọn B.Cách tự luận. Ta có
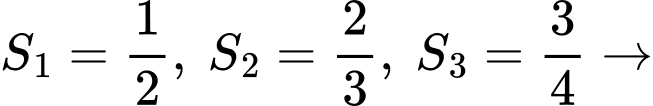 dự đoán
dự đoán 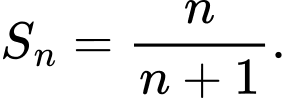
 Với
Với 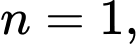 ta được
ta được 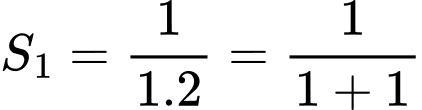 : đúng.
: đúng. Giả sử mệnh đề đúng khi
Giả sử mệnh đề đúng khi 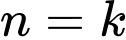
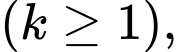 tức là
tức là 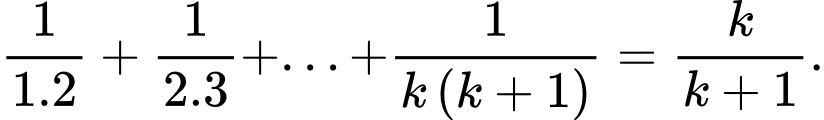
 Ta có
Ta có 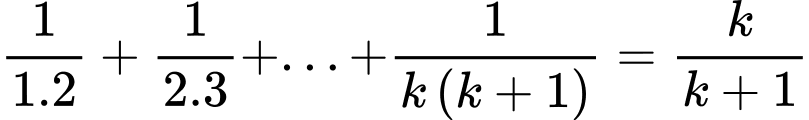
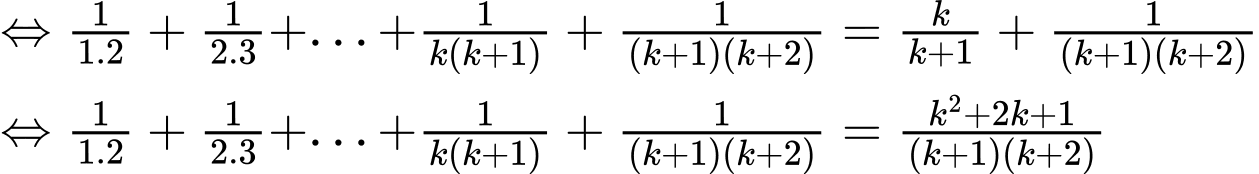
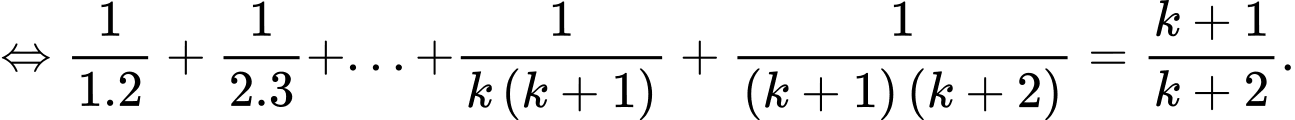 Suy ra mệnh đề đúng với
Suy ra mệnh đề đúng với 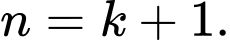 Đáp án: B
Đáp án: B
Câu 14 [805345]: Cho 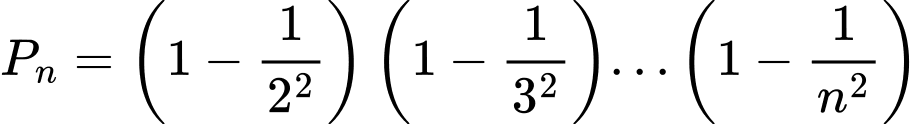 với
với  và
và 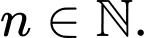 Mệnh đề nào sau đây đúng?
Mệnh đề nào sau đây đúng?
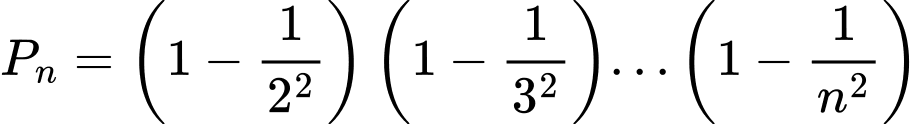 với
với  và
và 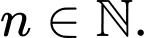 Mệnh đề nào sau đây đúng?
Mệnh đề nào sau đây đúng? A, 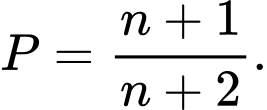
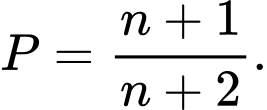
B, 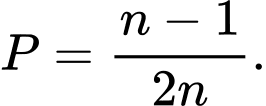
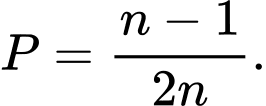
C, 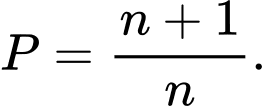
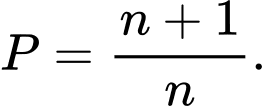
D, 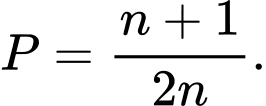
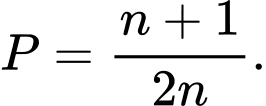
Vì  nên ta cho
nên ta cho 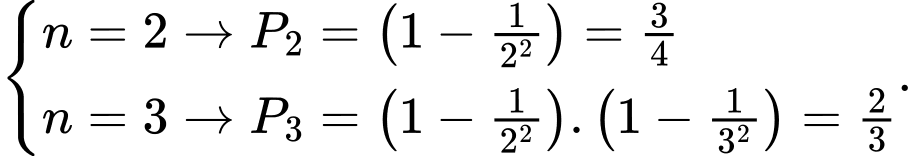
Kiểm tra các đáp án chỉ cho D thỏa. Chọn D. Đáp án: D
 nên ta cho
nên ta cho 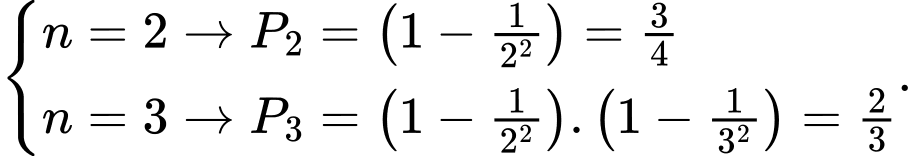
Kiểm tra các đáp án chỉ cho D thỏa. Chọn D. Đáp án: D
Câu 15 [398724]: Cho dãy số 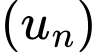 với
với 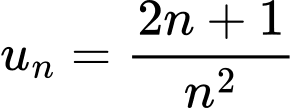 . Hãy tính số hạng thứ 6 của dãy số.
. Hãy tính số hạng thứ 6 của dãy số.
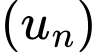 với
với 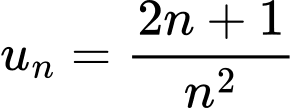 . Hãy tính số hạng thứ 6 của dãy số.
. Hãy tính số hạng thứ 6 của dãy số. 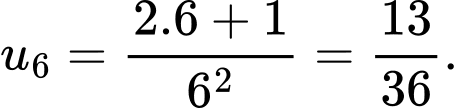
Câu 16 [398729]: Cho dãy số 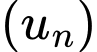 có số hạng tổng quát
có số hạng tổng quát 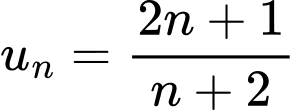 . Số
. Số 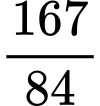 là số hạng thứ mấy của dãy?
là số hạng thứ mấy của dãy?
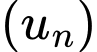 có số hạng tổng quát
có số hạng tổng quát 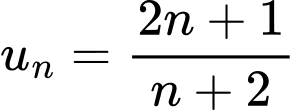 . Số
. Số 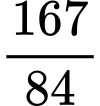 là số hạng thứ mấy của dãy?
là số hạng thứ mấy của dãy?
Ta có: 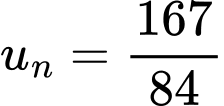
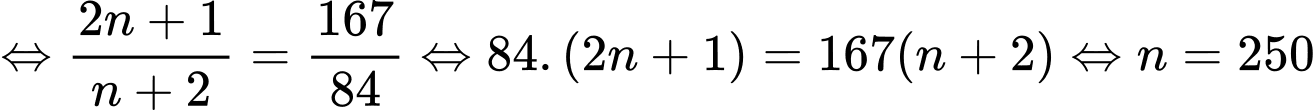
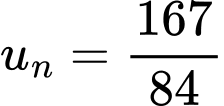
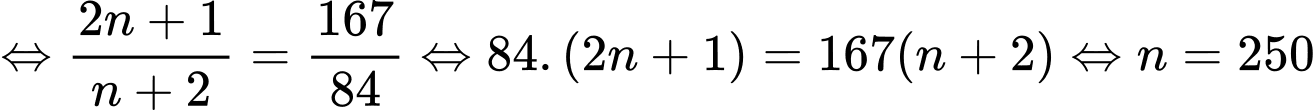
Vậy 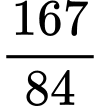 là số hạng thứ 250 của dãy số
là số hạng thứ 250 của dãy số 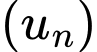 .
.
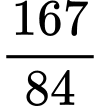 là số hạng thứ 250 của dãy số
là số hạng thứ 250 của dãy số 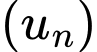 .
.
Câu 17 [805358]: Với mọi số nguyên dương 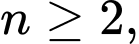 ta có:
ta có: 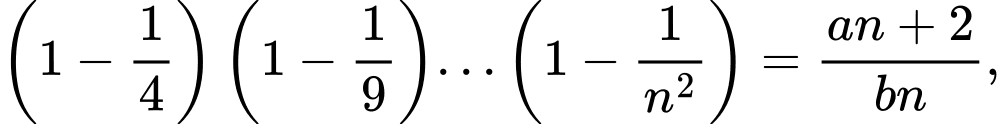 trong đó
trong đó 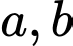 là các số nguyên. Tính các giá trị của biểu thức
là các số nguyên. Tính các giá trị của biểu thức 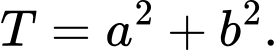
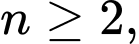 ta có:
ta có: 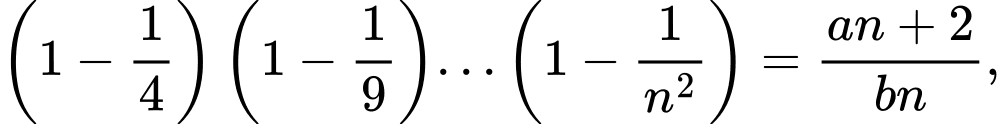 trong đó
trong đó 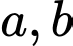 là các số nguyên. Tính các giá trị của biểu thức
là các số nguyên. Tính các giá trị của biểu thức 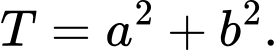
A, 

B, 

C, 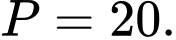
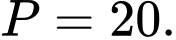
D, 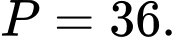
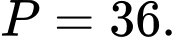
Đáp án C.
Cách 1: Bằng cách phân tích số hạng đại diện, ta có: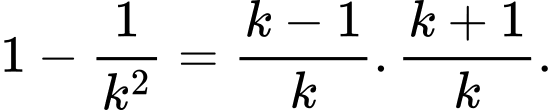 Suy ra
Suy ra
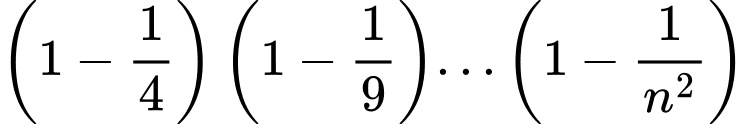
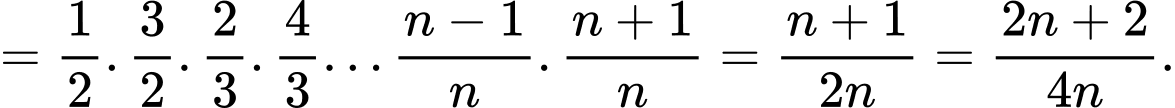
Đối chiếu với đẳng thức đã cho ta có: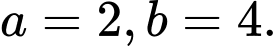 Suy ra
Suy ra 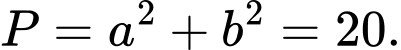
Cách 2: Cho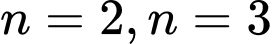 ta được
ta được 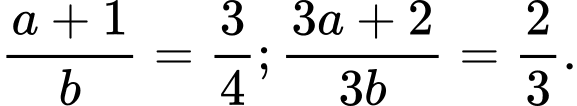
Giải hệ phương trình trên ta được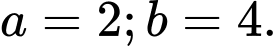 Suy ra
Suy ra 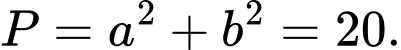 Đáp án: C
Đáp án: C
Cách 1: Bằng cách phân tích số hạng đại diện, ta có:
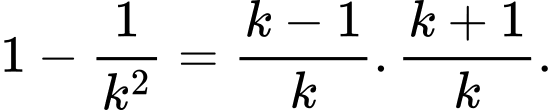 Suy ra
Suy ra 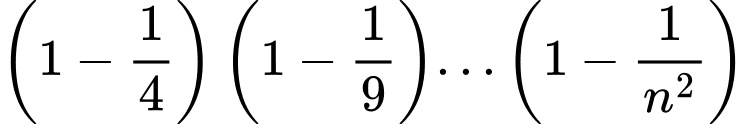
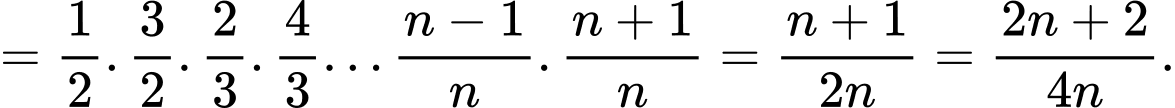
Đối chiếu với đẳng thức đã cho ta có:
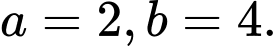 Suy ra
Suy ra 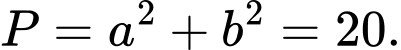
Cách 2: Cho
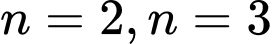 ta được
ta được 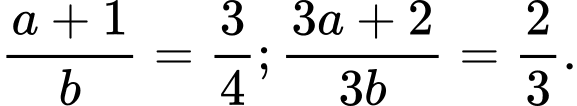
Giải hệ phương trình trên ta được
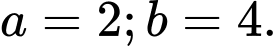 Suy ra
Suy ra 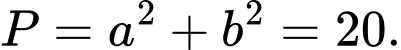 Đáp án: C
Đáp án: C
Câu 18 [398727]: Cho hình vuông 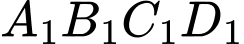 có cạnh bằng 4 . Với mọi số nguyên dương
có cạnh bằng 4 . Với mọi số nguyên dương  , gọi
, gọi 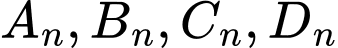 lần lượt là trung điểm của các cạnh
lần lượt là trung điểm của các cạnh 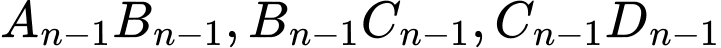 ,
, 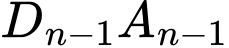 . Gọi
. Gọi 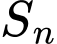 là diện tích của tứ giác
là diện tích của tứ giác 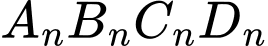 . Tính
. Tính 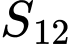 .
.
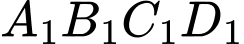 có cạnh bằng 4 . Với mọi số nguyên dương
có cạnh bằng 4 . Với mọi số nguyên dương  , gọi
, gọi 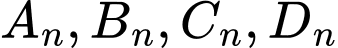 lần lượt là trung điểm của các cạnh
lần lượt là trung điểm của các cạnh 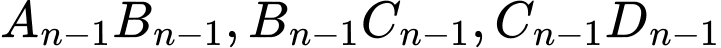 ,
, 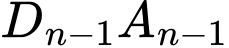 . Gọi
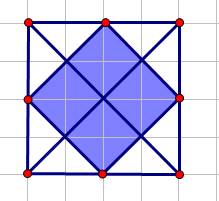
. Gọi 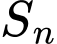 là diện tích của tứ giác
là diện tích của tứ giác 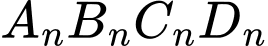 . Tính
. Tính 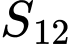 .
. 
Ta thấy mỗi tứ giác
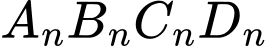 là một hình vuông có cạnh là
là một hình vuông có cạnh là 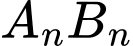 .
.
Ta có:
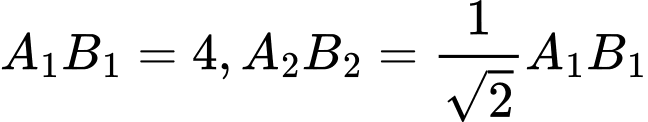
Suy ra
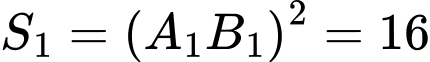 và
và 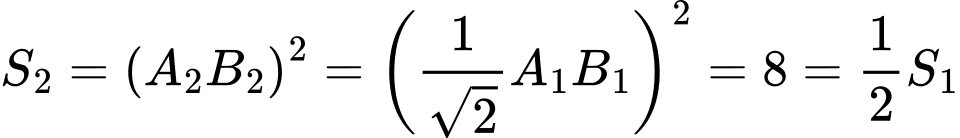
Gọi
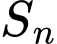 là diện tích hình vuông
là diện tích hình vuông 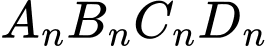 ta có:
ta có: 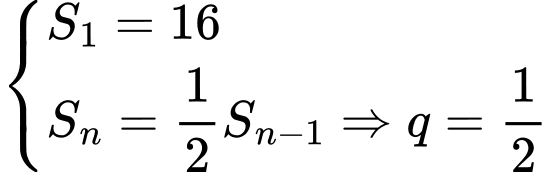
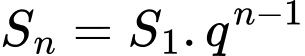 , với mọi
, với mọi 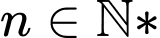
Áp dụng với
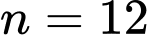 có:
có: 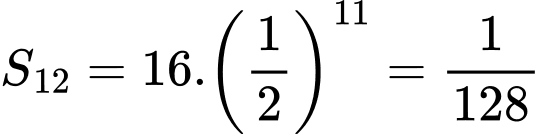 .
.
Câu 19 [805496]: Cho dãy số 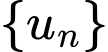 xác định bởi
xác định bởi 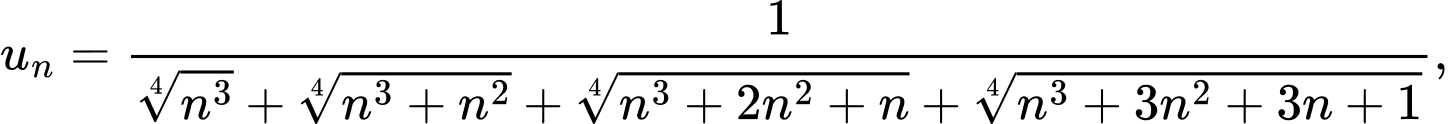
 Tính tổng
Tính tổng 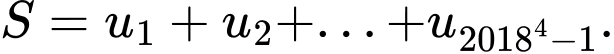
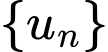 xác định bởi
xác định bởi 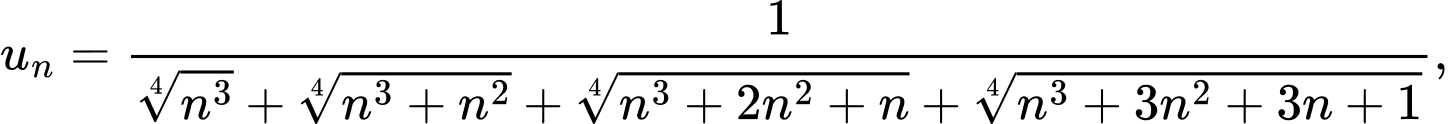
 Tính tổng
Tính tổng 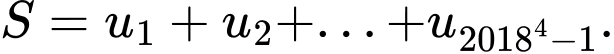
A, 2016.
B, 2017.
C, 2018.
D, 2019.
Ta có: 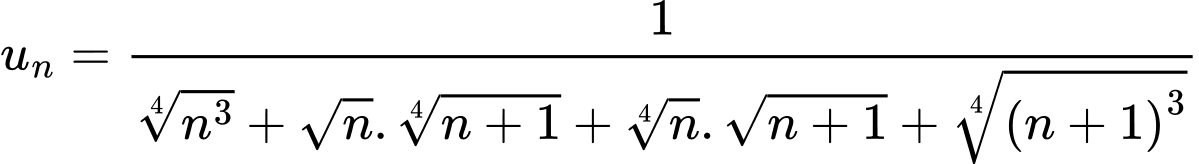
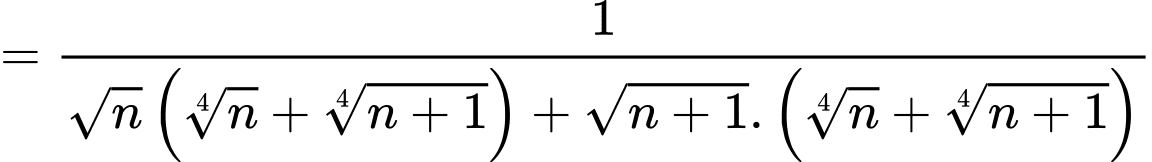
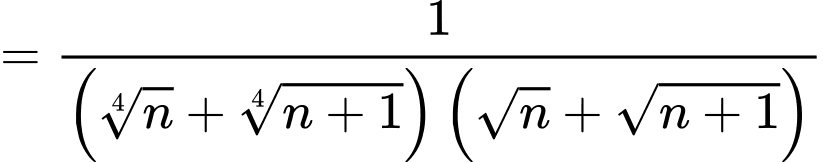
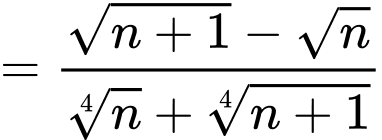
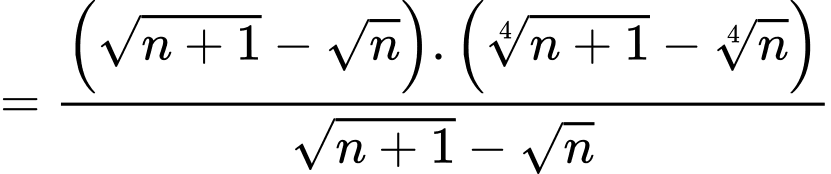
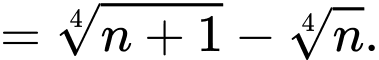
Do đó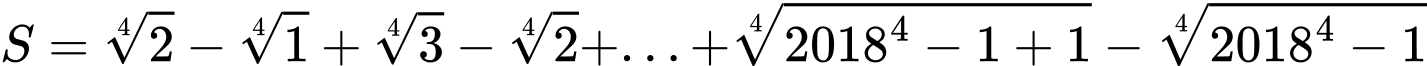
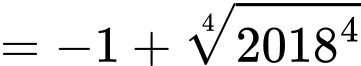

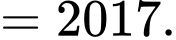 Đáp án: B
Đáp án: B
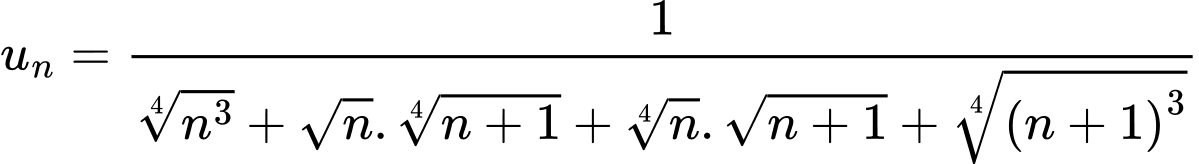
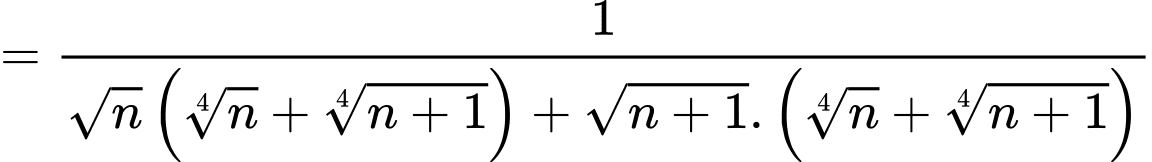
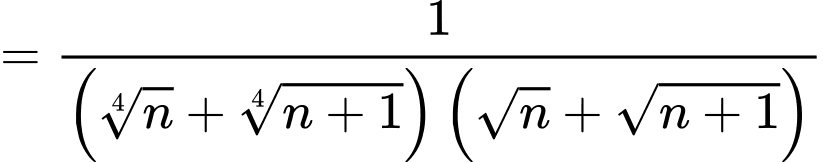
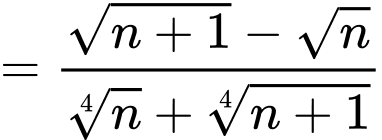
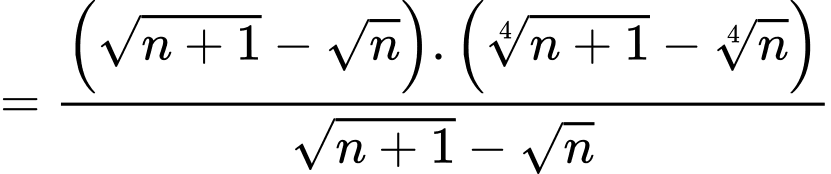
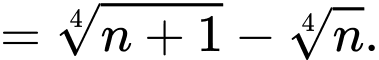
Do đó
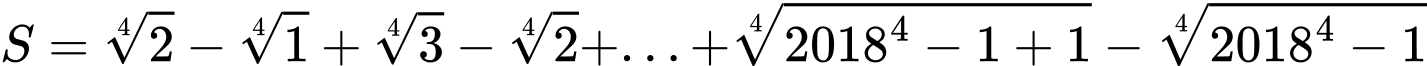
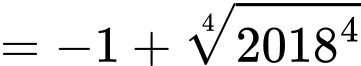

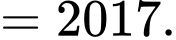 Đáp án: B
Đáp án: B
Câu 20 [398730]: Dãy số 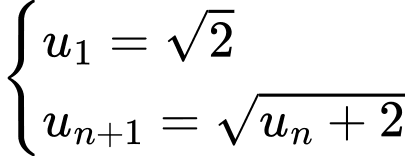 bị chặn trên bởi
bị chặn trên bởi 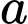 . Khi đó
. Khi đó 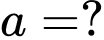
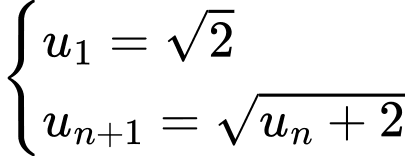 bị chặn trên bởi
bị chặn trên bởi 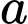 . Khi đó
. Khi đó 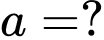
Ta có: 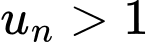 ,
Giả sử tồn tại
,
Giả sử tồn tại 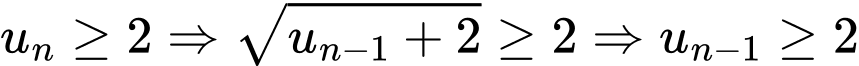 .
.
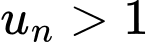 ,
Giả sử tồn tại
,
Giả sử tồn tại 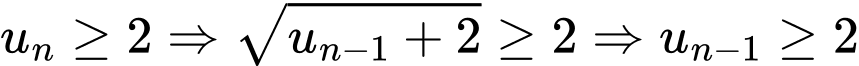 .
. Nếu tồn tại  thì suy ra
thì suy ra 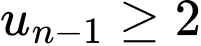 , từ đó suy ra được
, từ đó suy ra được 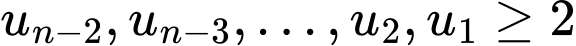 vô lý
Do
vô lý
Do 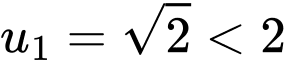 .
.
 thì suy ra
thì suy ra 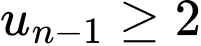 , từ đó suy ra được
, từ đó suy ra được 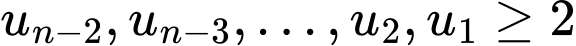 vô lý
Do
vô lý
Do 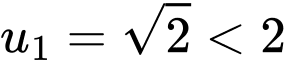 .
. Nên điều giả sử là sai. Suy ra: 

Xét 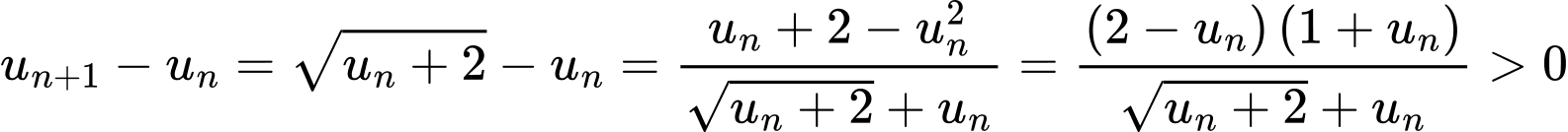 Suy ra:
Suy ra:  nên
nên 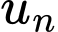 là dãy tăng.
là dãy tăng.
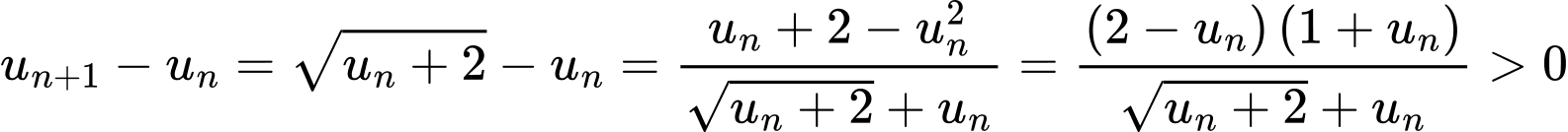 Suy ra:
Suy ra:  nên
nên 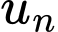 là dãy tăng.
là dãy tăng. Vậy dãy đã cho tăng và bị chặn trên bởi 2 .