Đáp án Bài tập tự luyện số 2
Câu 1 [806170]: Trong sân vận động có tất cả 30 dãy ghế, dãy đầu tiên có 15 ghế, các dãy liền sau nhiều hơn dãy trước 4 ghế, hỏi sân vận động đó có tất cả bao nhiêu ghế?
A, 2250.
B, 1740.
C, 4380.
D, 2190.
Gọi 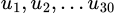 lần lượt là số ghế của dãy ghế thứ nhất, dãy ghế thứ hai,… và dãy ghế số ba mươi. Ta có công thức truy hồi ta có
lần lượt là số ghế của dãy ghế thứ nhất, dãy ghế thứ hai,… và dãy ghế số ba mươi. Ta có công thức truy hồi ta có 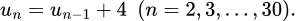
Ký hiệu: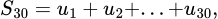 theo công thức tổng các số hạng của một cấp số cộng, ta được:
theo công thức tổng các số hạng của một cấp số cộng, ta được:
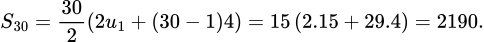 Đáp án: D
Đáp án: D
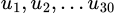 lần lượt là số ghế của dãy ghế thứ nhất, dãy ghế thứ hai,… và dãy ghế số ba mươi. Ta có công thức truy hồi ta có
lần lượt là số ghế của dãy ghế thứ nhất, dãy ghế thứ hai,… và dãy ghế số ba mươi. Ta có công thức truy hồi ta có 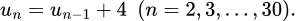
Ký hiệu:
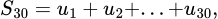 theo công thức tổng các số hạng của một cấp số cộng, ta được:
theo công thức tổng các số hạng của một cấp số cộng, ta được: 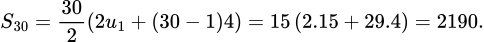 Đáp án: D
Đáp án: D
Câu 2 [224667]: Xác định số hạng đầu và công sai của cấp số cộng biết 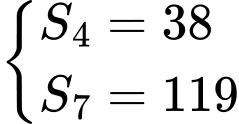 .
.
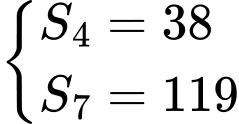 .
. A, 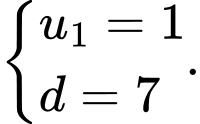
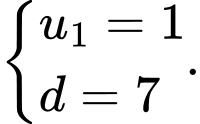
B, 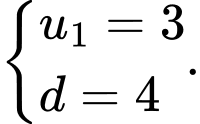
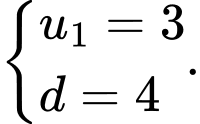
C, 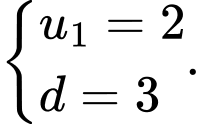
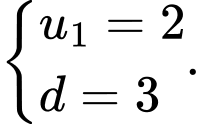
D, 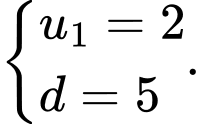
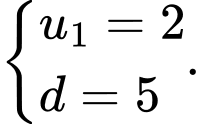
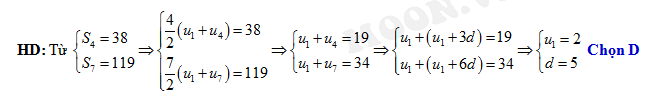 Đáp án: D
Đáp án: D
Câu 3 [224652]: Tìm công thức tổng quát của một cấp số cộng biết 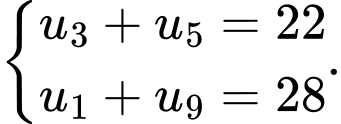
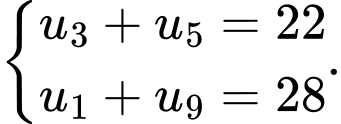
A, 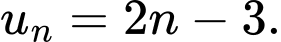
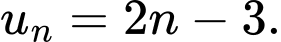
B, 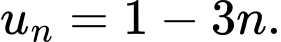
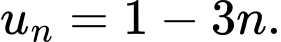
C, 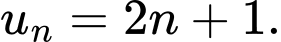
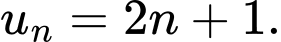
D, 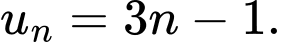
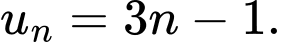
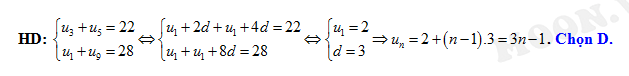 Đáp án: D
Đáp án: D
Câu 4 [805928]: Tìm công thức số hạng tổng quát của cấp số cộng 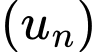 thỏa mãn:
thỏa mãn: 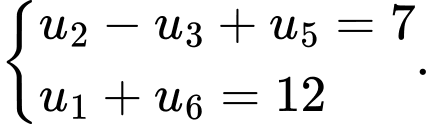
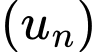 thỏa mãn:
thỏa mãn: 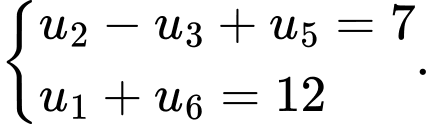
A, 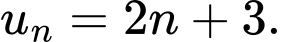
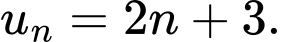
B, 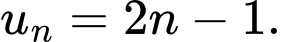
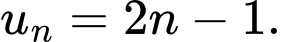
C, 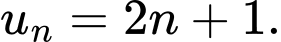
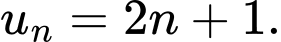
D, 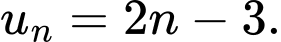
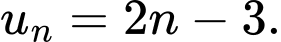
Chọn B
Giả sử dãy cấp số cộng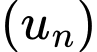 có công sai là
có công sai là 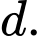 Khi đó,
Khi đó, 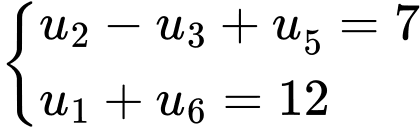 trở thành:
trở thành:
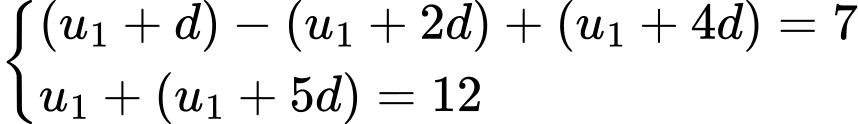
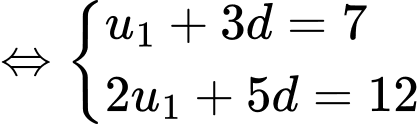
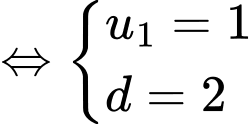
Số hạng tổng quát của cấp số cộng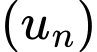 :
:

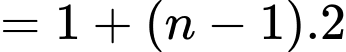
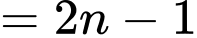
Vậy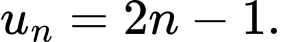 Đáp án: B
Đáp án: B
Giả sử dãy cấp số cộng
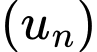 có công sai là
có công sai là 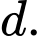 Khi đó,
Khi đó, 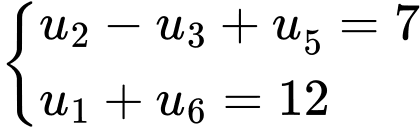 trở thành:
trở thành: 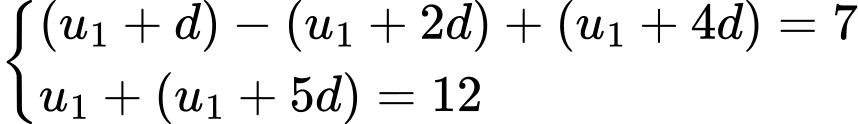
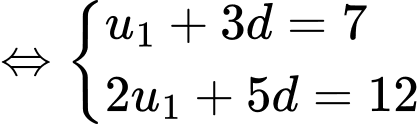
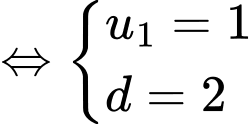
Số hạng tổng quát của cấp số cộng
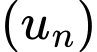 :
: 
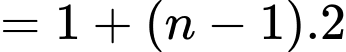
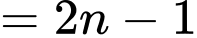
Vậy
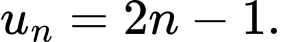 Đáp án: B
Đáp án: B
Câu 5 [224648]: Xác định 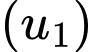 và
và 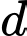 của cấp số cộng
của cấp số cộng 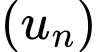 biết
biết 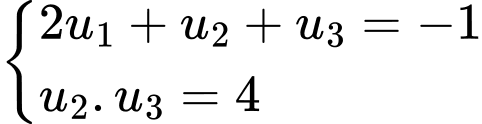 biết
biết 
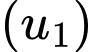 và
và 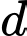 của cấp số cộng
của cấp số cộng 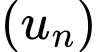 biết
biết 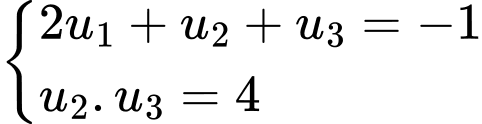 biết
biết 
A, 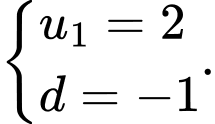
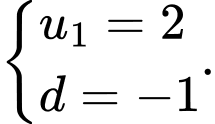
B, 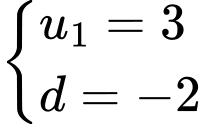
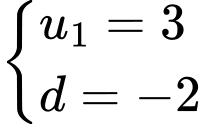
C, 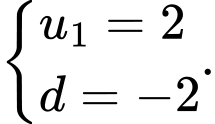
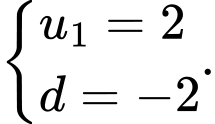
D, 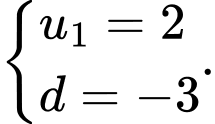
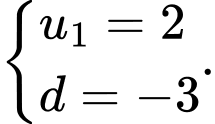
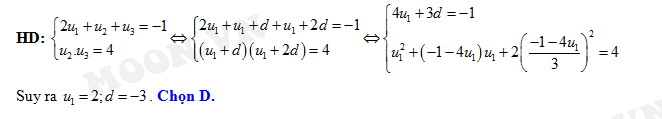 Đáp án: D
Đáp án: D
Câu 6 [806023]: Cho cấp số cộng  thỏa mãn
thỏa mãn 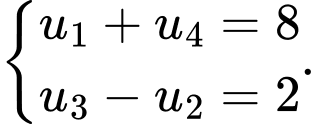 Tính tổng
Tính tổng  số hạng đầu của cấp số cộng trên.
số hạng đầu của cấp số cộng trên.
 thỏa mãn
thỏa mãn 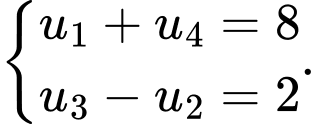 Tính tổng
Tính tổng  số hạng đầu của cấp số cộng trên.
số hạng đầu của cấp số cộng trên. A, 100.
B, 110.
C, 10.
D, 90.
Chọn A
Gọi cấp cố cộng có công sai là ta có
ta có 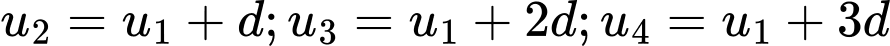
Khi đó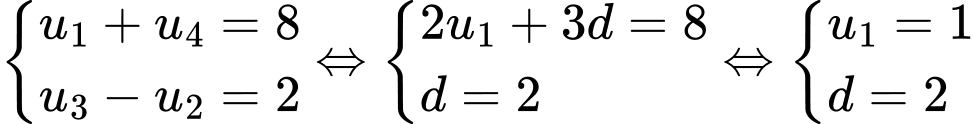
Áp dụng công thức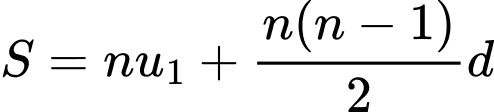
Vậy tổng của số hạng đầu của cấp số cộng là
số hạng đầu của cấp số cộng là 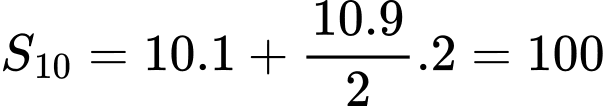 Đáp án: A
Đáp án: A
Gọi cấp cố cộng có công sai là
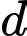 ta có
ta có 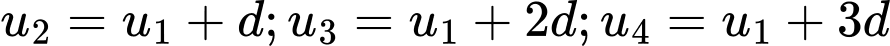
Khi đó
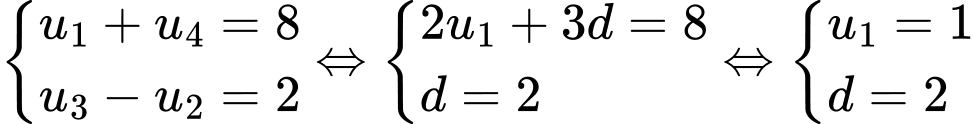
Áp dụng công thức
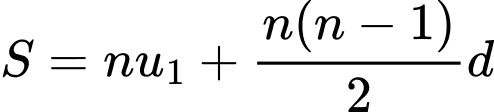
Vậy tổng của
 số hạng đầu của cấp số cộng là
số hạng đầu của cấp số cộng là 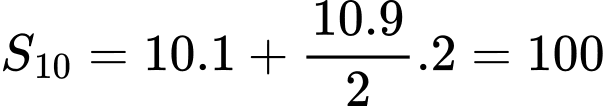 Đáp án: A
Đáp án: A
Câu 7 [805950]: Cho cấp số cộng 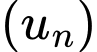 có
có 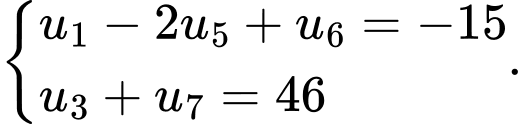 Số hạng đầu
Số hạng đầu  là
là
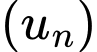 có
có 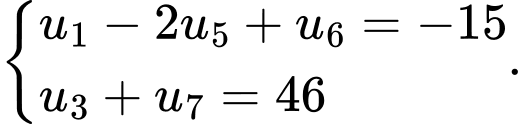 Số hạng đầu
Số hạng đầu 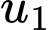 là
là A, 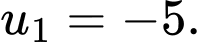
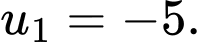
B, 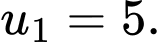
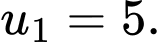
C, 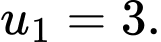
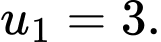
D, 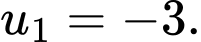
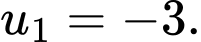
Chọn C.
Gọi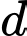 là công sai của CSC. Ta có
là công sai của CSC. Ta có 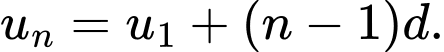
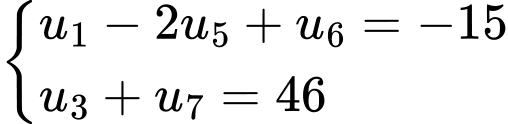
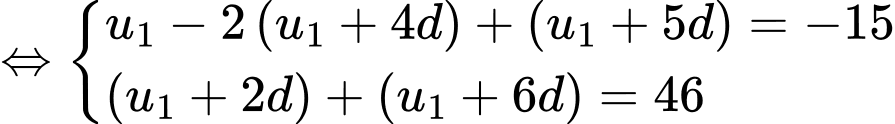
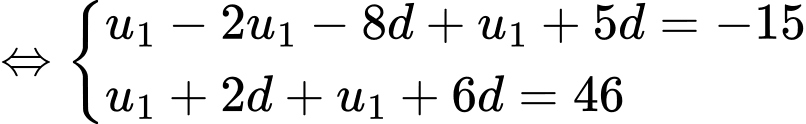
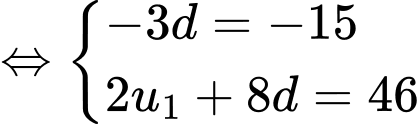
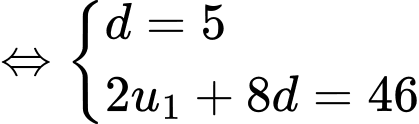
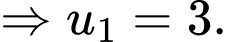 Đáp án: C
Đáp án: C
Gọi
 là công sai của CSC. Ta có
là công sai của CSC. Ta có 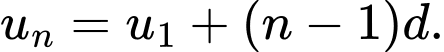
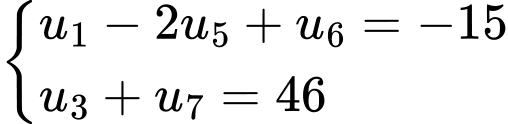
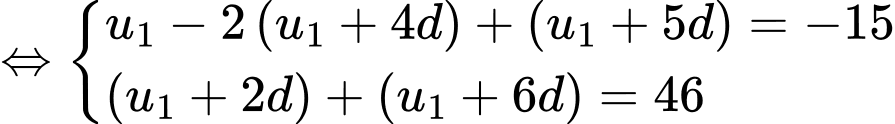
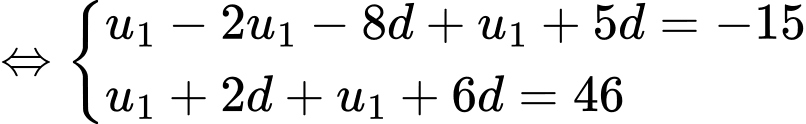
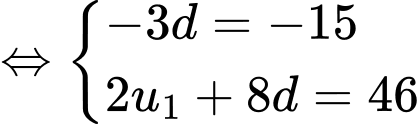
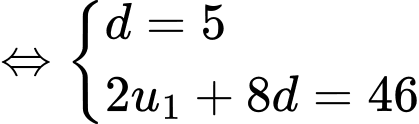
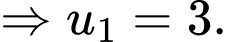 Đáp án: C
Đáp án: C
Câu 8 [224646]: Tỉnh tổng sau : 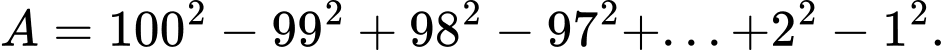
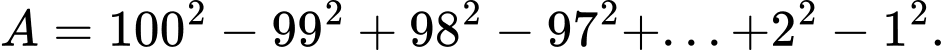
A, 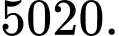
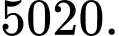
B, 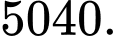
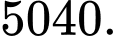
C, 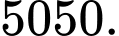
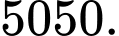
D, 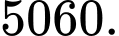
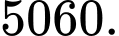
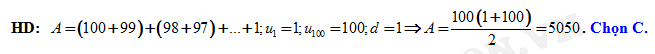 Đáp án: C
Đáp án: C
Câu 9 [398792]: Giải phương trình sau: 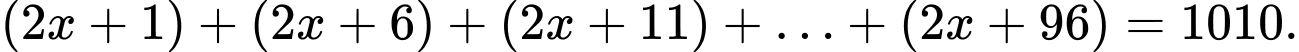
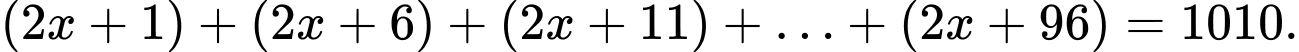
A, 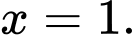
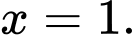
B, 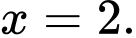
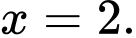
C, 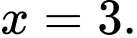
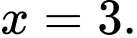
D, 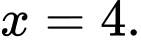
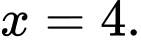
Ta có dãy số 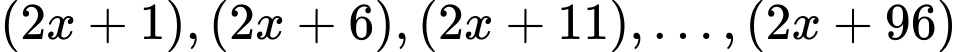 lập thành cấp số cộng có
lập thành cấp số cộng có 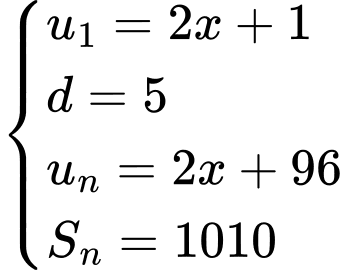
Suy ra: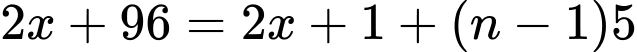
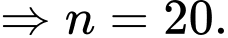
Vậy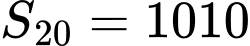
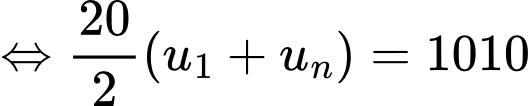
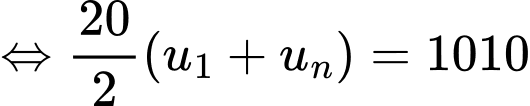
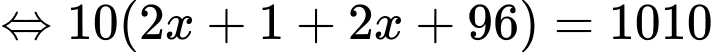
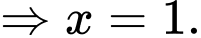 Đáp án: A
Đáp án: A
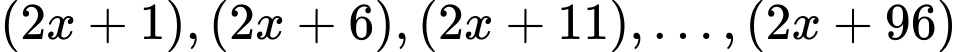 lập thành cấp số cộng có
lập thành cấp số cộng có 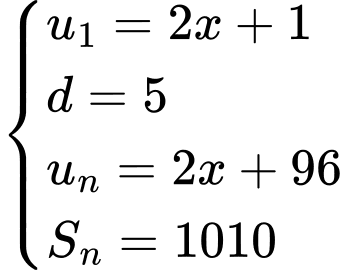
Suy ra:
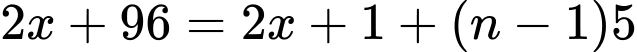
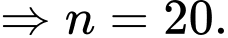
Vậy
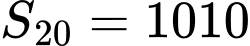
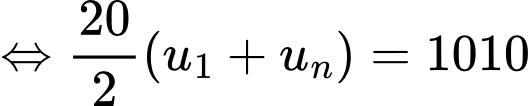
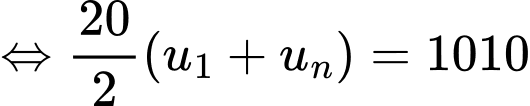
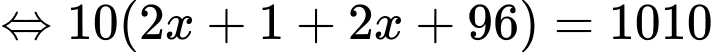
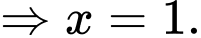 Đáp án: A
Đáp án: A
Câu 10 [806168]: Một công ti trách nhiệm hữu hạn thực hiện việc trả lương cho các kĩ sư theo phương thức sau: Mức lương của quý làm việc đầu tiên cho công ti là 4,5 triệu đồng/quý, và kể từ quý làm việc thứ hai, mức lương sẽ được tăng thêm 0,3 triệu đồng mỗi quý. Hãy tính tổng số tiền lương một kĩ sư nhận được sau 3 năm làm việc cho công ti.
A, 83,7 (triệu đồng).
B, 78,3 (triệu đồng).
C, 73,8 (triệu đồng).
D, 87,3 (triệu đồng).
Ta có 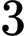 năm bằng
năm bằng  quý.
quý.
Gọi
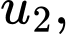 …,
…, 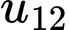 là tiền lương kĩ sư đó trong các quý (từ quý
là tiền lương kĩ sư đó trong các quý (từ quý 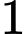 đến quý
đến quý  ).
).
Suy ra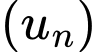 là cấp số cộng với công sai
là cấp số cộng với công sai 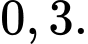
Vậy số tiền lương kĩ sư nhận được là
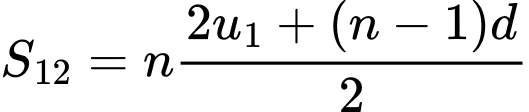
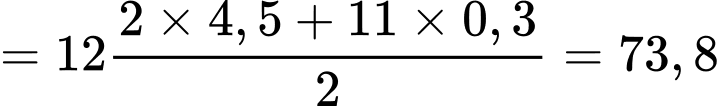 (triệu đồng). Đáp án: C
(triệu đồng). Đáp án: C
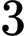 năm bằng
năm bằng  quý.
quý. Gọi
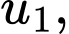
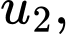 …,
…, 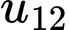 là tiền lương kĩ sư đó trong các quý (từ quý
là tiền lương kĩ sư đó trong các quý (từ quý 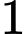 đến quý
đến quý  ).
). Suy ra
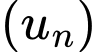 là cấp số cộng với công sai
là cấp số cộng với công sai 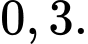
Vậy số tiền lương kĩ sư nhận được là
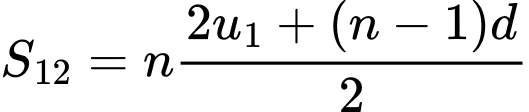
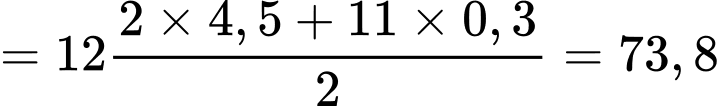 (triệu đồng). Đáp án: C
(triệu đồng). Đáp án: C
Câu 11 [159611]: Một cơ sở khoan giếng đưa ra định mức giá như sau: Giá của mét khoan đầu tiên là 100 nghìn đồng và kể từ mét khoan thứ hai, giá của mỗi mét sau tăng thêm 30 nghìn đồng so với giá của mét khoan ngay trước đó. Một người cần khoan một giếng sâu 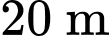 để lấy nước dùng cho sinh hoạt của gia đình. Hỏi sau khi hoàn thành việc khoan giếng, gia đình đó phải thanh toán cho cơ sở khoan giếng số tiền bao nhiêu nghìn đồng?
để lấy nước dùng cho sinh hoạt của gia đình. Hỏi sau khi hoàn thành việc khoan giếng, gia đình đó phải thanh toán cho cơ sở khoan giếng số tiền bao nhiêu nghìn đồng?
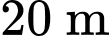 để lấy nước dùng cho sinh hoạt của gia đình. Hỏi sau khi hoàn thành việc khoan giếng, gia đình đó phải thanh toán cho cơ sở khoan giếng số tiền bao nhiêu nghìn đồng?
để lấy nước dùng cho sinh hoạt của gia đình. Hỏi sau khi hoàn thành việc khoan giếng, gia đình đó phải thanh toán cho cơ sở khoan giếng số tiền bao nhiêu nghìn đồng?
Gọi 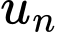 là giá của mét khoan thứ
là giá của mét khoan thứ 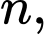 trong đó
trong đó 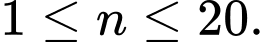
Khi đó,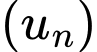 là cấp số cộng có số hạng đầu
là cấp số cộng có số hạng đầu 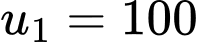 và công sai
và công sai 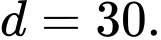
Số tiền mà gia đình phải thanh toán cho cơ sở khoan giếng là:
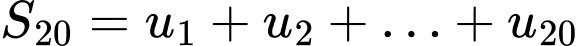
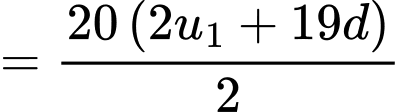
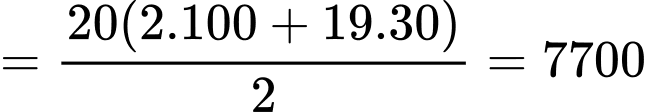 (nghìn đồng).
(nghìn đồng).
 là giá của mét khoan thứ
là giá của mét khoan thứ 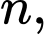 trong đó
trong đó 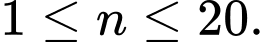
Khi đó,
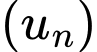 là cấp số cộng có số hạng đầu
là cấp số cộng có số hạng đầu 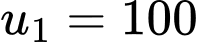 và công sai
và công sai 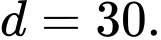
Số tiền mà gia đình phải thanh toán cho cơ sở khoan giếng là:
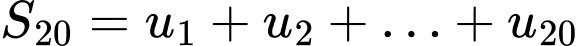
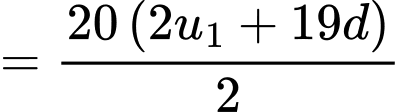
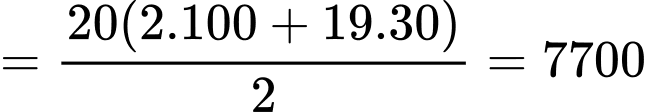 (nghìn đồng).
(nghìn đồng).
Câu 12 [159610]: Trên một bàn cờ có nhiều ô vuông, người ta đặt 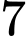 hạt dẻ vào ô đầu tiên, sau đó đặt tiếp vào ô thứ hai số hạt nhiều hơn ô thứ nhất là
hạt dẻ vào ô đầu tiên, sau đó đặt tiếp vào ô thứ hai số hạt nhiều hơn ô thứ nhất là 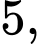 tiếp tục đặt vào ô thứ ba số hạt nhiều hơn ô thứ hai là
tiếp tục đặt vào ô thứ ba số hạt nhiều hơn ô thứ hai là 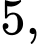 … và cứ thế tiếp tục đến ô thứ
… và cứ thế tiếp tục đến ô thứ 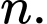 Biết rằng để đặt hết số ô trên bàn cờ người ta phải sử dụng
Biết rằng để đặt hết số ô trên bàn cờ người ta phải sử dụng 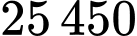 hạt. Hỏi bàn cờ đó có bao nhiêu ô vuông?
hạt. Hỏi bàn cờ đó có bao nhiêu ô vuông?
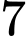 hạt dẻ vào ô đầu tiên, sau đó đặt tiếp vào ô thứ hai số hạt nhiều hơn ô thứ nhất là
hạt dẻ vào ô đầu tiên, sau đó đặt tiếp vào ô thứ hai số hạt nhiều hơn ô thứ nhất là 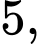 tiếp tục đặt vào ô thứ ba số hạt nhiều hơn ô thứ hai là
tiếp tục đặt vào ô thứ ba số hạt nhiều hơn ô thứ hai là 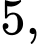 … và cứ thế tiếp tục đến ô thứ
… và cứ thế tiếp tục đến ô thứ 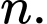 Biết rằng để đặt hết số ô trên bàn cờ người ta phải sử dụng
Biết rằng để đặt hết số ô trên bàn cờ người ta phải sử dụng 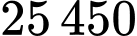 hạt. Hỏi bàn cờ đó có bao nhiêu ô vuông?
hạt. Hỏi bàn cờ đó có bao nhiêu ô vuông?
Số hạt dẻ trên mỗi ô (bắt đầu từ ô thứ nhất) theo thứ tự đó lập thành cấp số cộng 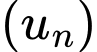 có
có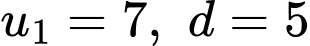
Gọi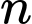 là số ô trên bàn cờ thì
là số ô trên bàn cờ thì 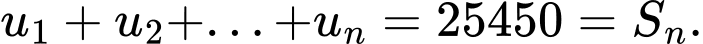
Ta có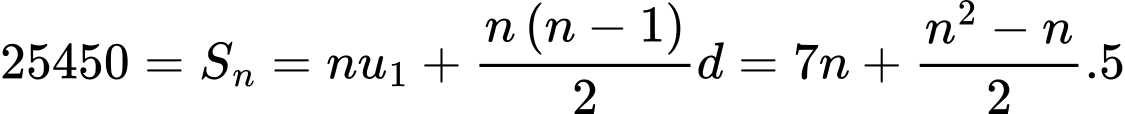
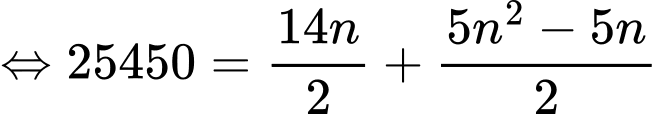
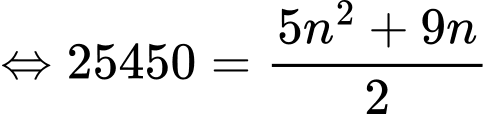
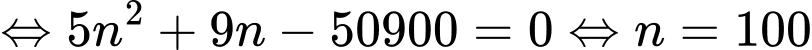
 có
có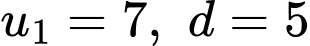
Gọi
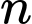 là số ô trên bàn cờ thì
là số ô trên bàn cờ thì 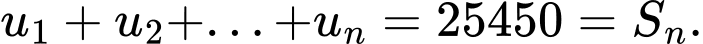
Ta có
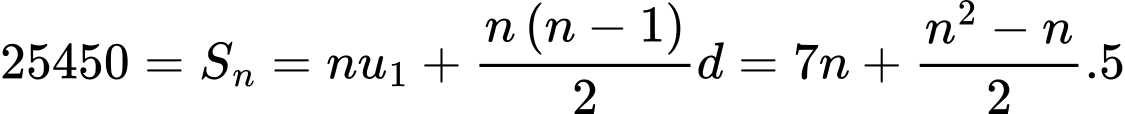
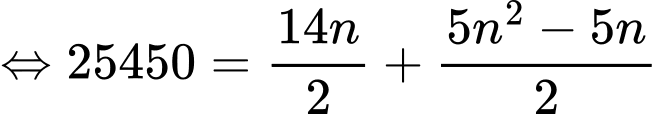
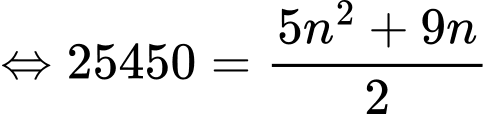
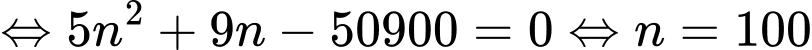
Câu 13 [274111]: Một kiến trúc sư thiết kế một hội trường với 15 ghế ngồi ở hàng thứ nhất, 18 ghế ngồi ở hàng thứ hai, 21 ghế ngồi ở hàng thứ ba và cứ như vậy (số ghế ở hàng sau nhiều hơn 3 ghế so với hàng liền trước nó). Nếu muốn hội trường đó có số sức chứa ít nhất 870 ghế ngồi thì kiến trúc sư phải thiết kế tối thiểu bao nhiêu hàng ghế?
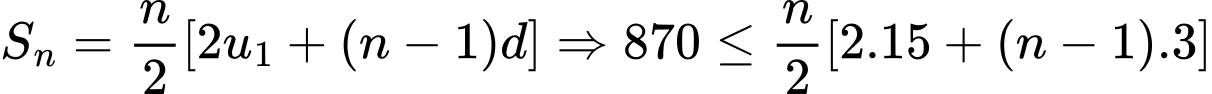
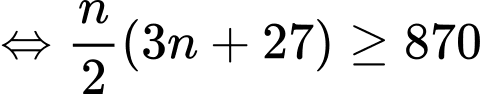
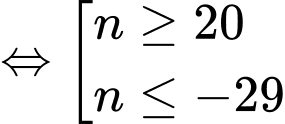
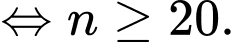
Vậy muốn hội trường đó có sức chứa ít nhất 870 ghế ngồi thì kiến trức sư phải thiết kế tối thiểu 20 hàng ghế.
Câu 14 [806033]: Cho cấp số cộng 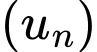 có số hạng đầu bằng 1 và tổng 100 số hạng đầu bằng 14950. Giá trị của tổng
có số hạng đầu bằng 1 và tổng 100 số hạng đầu bằng 14950. Giá trị của tổng 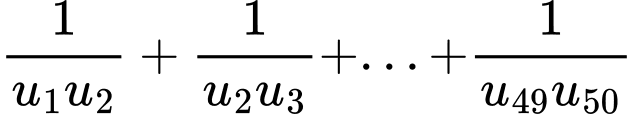 bằng
bằng
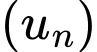 có số hạng đầu bằng 1 và tổng 100 số hạng đầu bằng 14950. Giá trị của tổng
có số hạng đầu bằng 1 và tổng 100 số hạng đầu bằng 14950. Giá trị của tổng 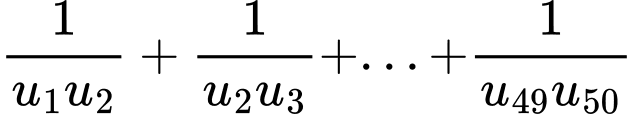 bằng
bằng A, 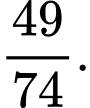
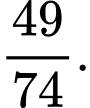
B, 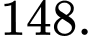
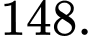
C, 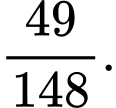
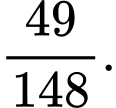
D, 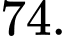
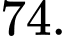
Gọi 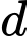 là công sai của cấp số cộng. Ta có
là công sai của cấp số cộng. Ta có 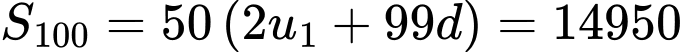 với
với 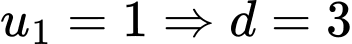
Đặt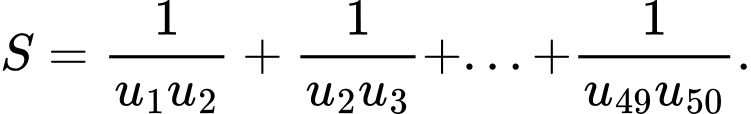
Ta có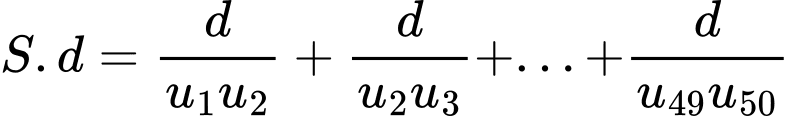
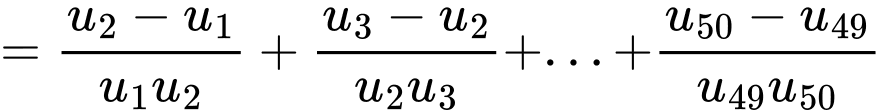
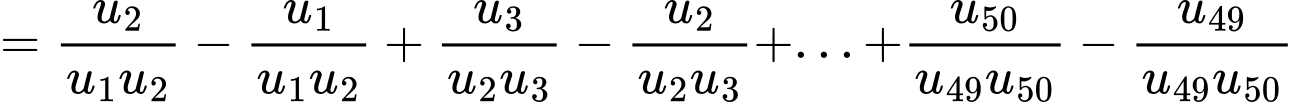
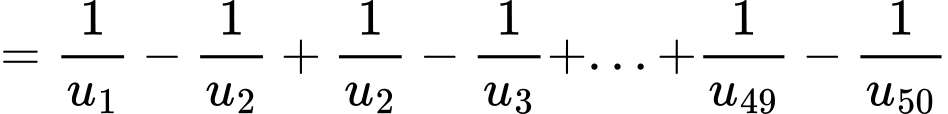
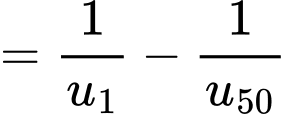
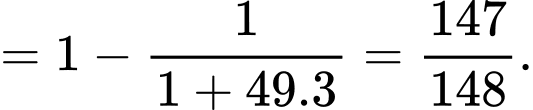
Với nên
nên 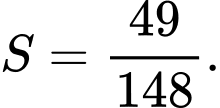 Đáp án: C
Đáp án: C
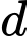 là công sai của cấp số cộng. Ta có
là công sai của cấp số cộng. Ta có 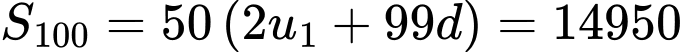 với
với 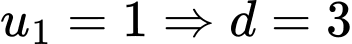
Đặt
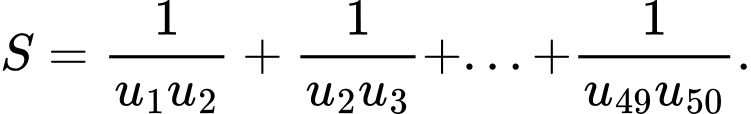
Ta có
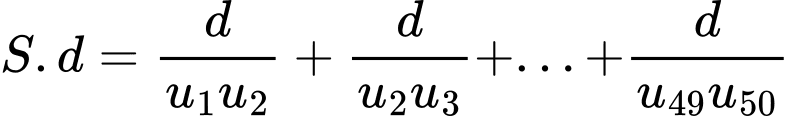
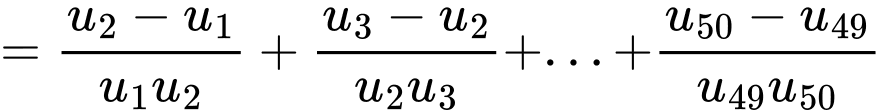
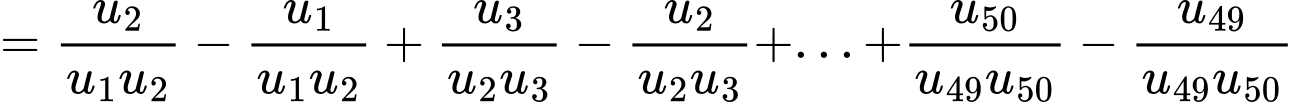
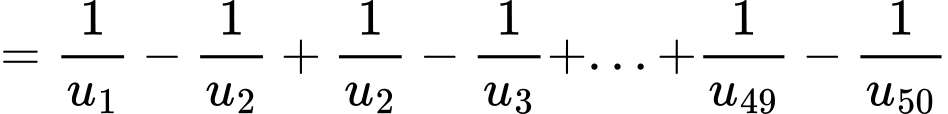
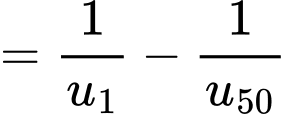
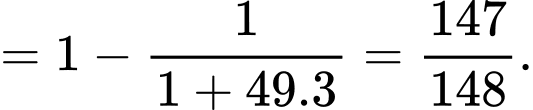
Với
 nên
nên 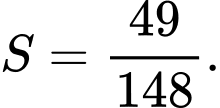 Đáp án: C
Đáp án: C
Câu 15 [806164]: Cho một cấp số cộng 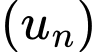 có
có 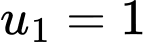 và tổng 100 số hạng đầu bằng 10000. Tính tổng
và tổng 100 số hạng đầu bằng 10000. Tính tổng 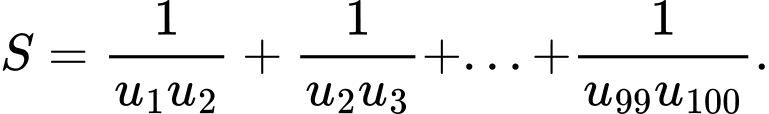
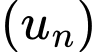 có
có 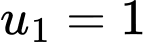 và tổng 100 số hạng đầu bằng 10000. Tính tổng
và tổng 100 số hạng đầu bằng 10000. Tính tổng 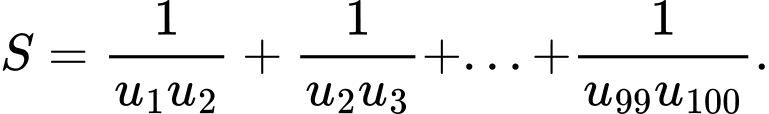
A, 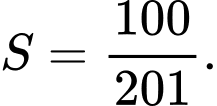
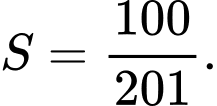
B, 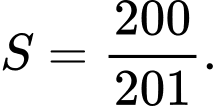
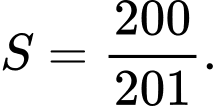
C, 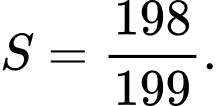
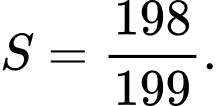
D, 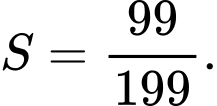
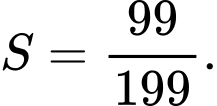
Chọn D
Gọi là công sai của cấp số cộng đã cho.
là công sai của cấp số cộng đã cho.
Ta có: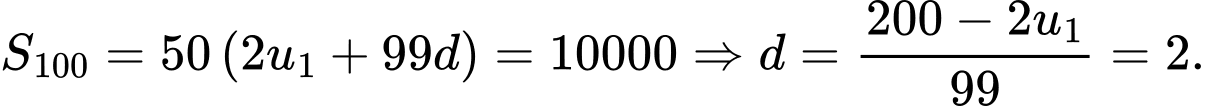
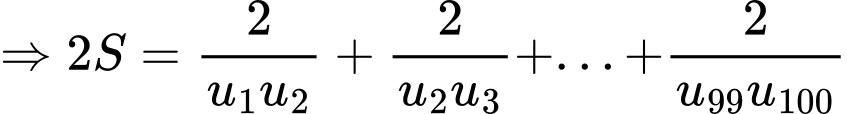
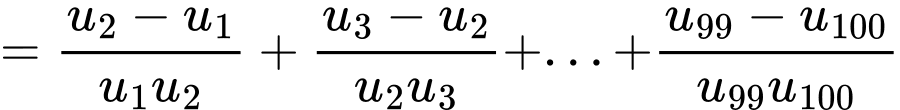
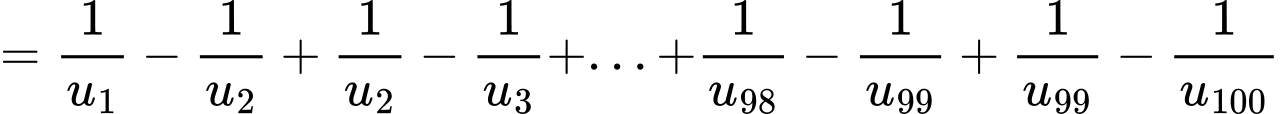
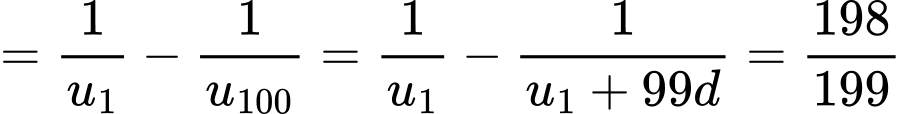
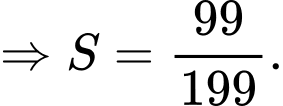 Đáp án: D
Đáp án: D
Gọi
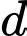 là công sai của cấp số cộng đã cho.
là công sai của cấp số cộng đã cho. Ta có:
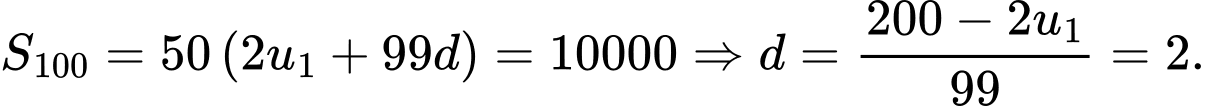
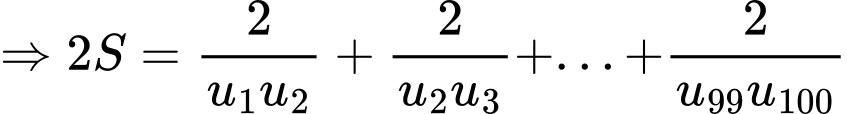
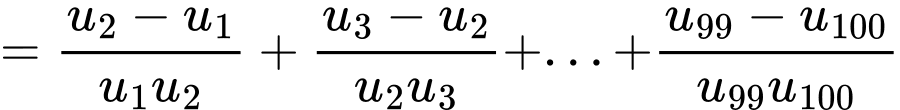
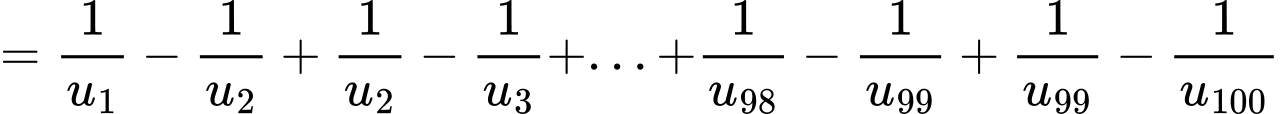
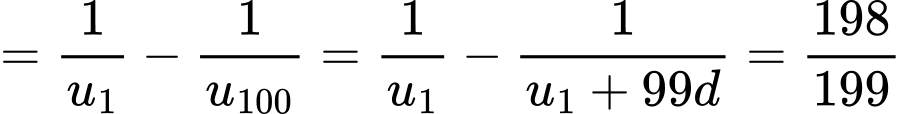
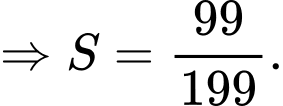 Đáp án: D
Đáp án: D
Câu 16 [806172]: Cho 4 số thực 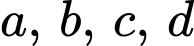 là 4 số hạng liên tiếp của một cấp số cộng. Biết tổng của chúng bằng 4 và tổng các bình phương của chúng bằng 24. Tính
là 4 số hạng liên tiếp của một cấp số cộng. Biết tổng của chúng bằng 4 và tổng các bình phương của chúng bằng 24. Tính 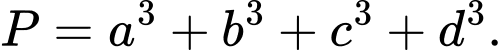
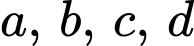 là 4 số hạng liên tiếp của một cấp số cộng. Biết tổng của chúng bằng 4 và tổng các bình phương của chúng bằng 24. Tính
là 4 số hạng liên tiếp của một cấp số cộng. Biết tổng của chúng bằng 4 và tổng các bình phương của chúng bằng 24. Tính 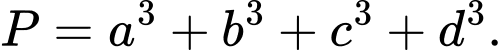
A, 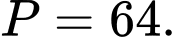
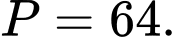
B, 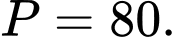
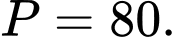
C, 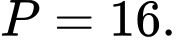
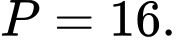
D, 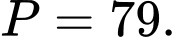
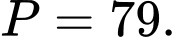
Theo giả thiết ta có: 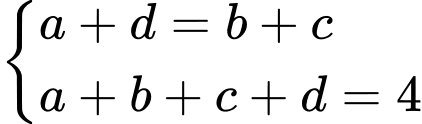
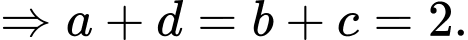

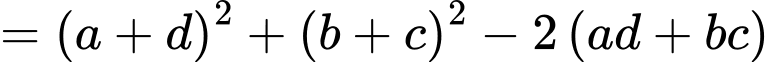
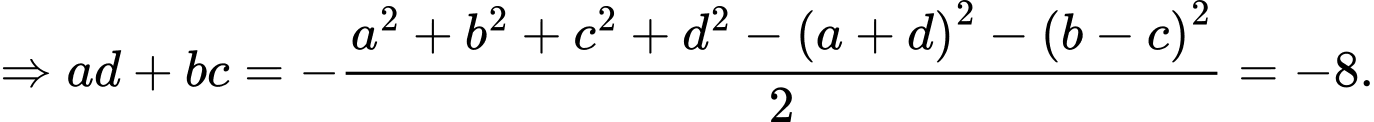
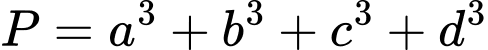
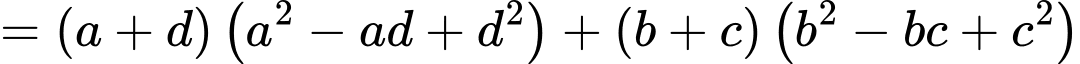
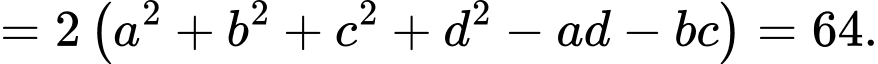 Đáp án: A
Đáp án: A
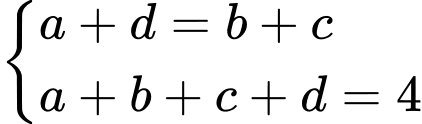
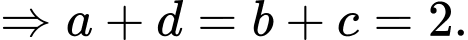

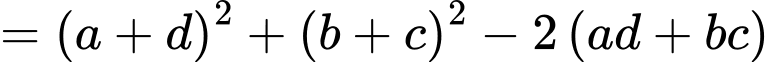
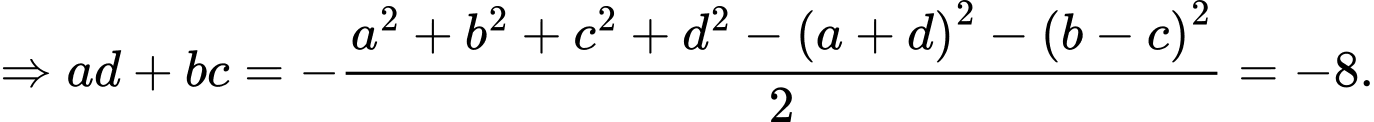
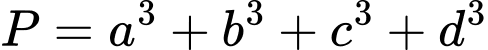
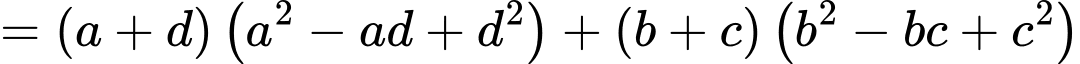
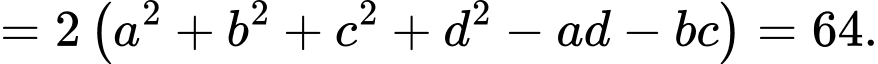 Đáp án: A
Đáp án: A
Câu 17 [805953]: Cho cấp số cộng  có công sai
có công sai  và biểu thức
và biểu thức 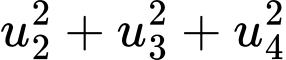 đạt giá trị nhỏ nhất. Số 2018 là số hạng thứ bao nhiêu của cấp số cộng
đạt giá trị nhỏ nhất. Số 2018 là số hạng thứ bao nhiêu của cấp số cộng 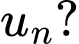
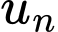 có công sai
có công sai  và biểu thức
và biểu thức 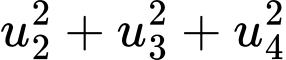 đạt giá trị nhỏ nhất. Số 2018 là số hạng thứ bao nhiêu của cấp số cộng
đạt giá trị nhỏ nhất. Số 2018 là số hạng thứ bao nhiêu của cấp số cộng 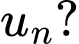
A, 1011.
B, 1014.
C, 1013.
D, 1012.
Chọn D
Ta có: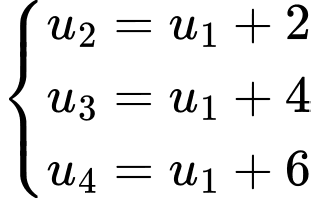
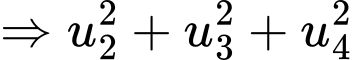
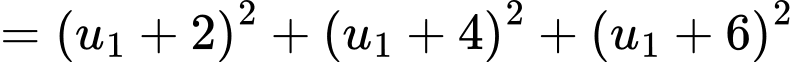
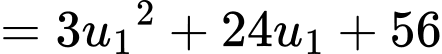
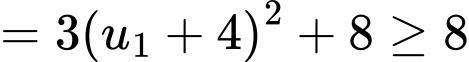
Vậy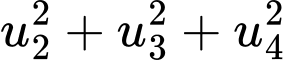 đạt giá trị nhỏ nhất khi
đạt giá trị nhỏ nhất khi 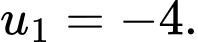
Từ đó suy ra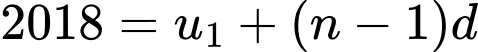
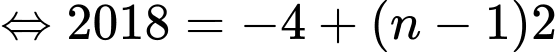
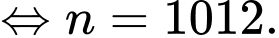 Đáp án: D
Đáp án: D
Ta có:
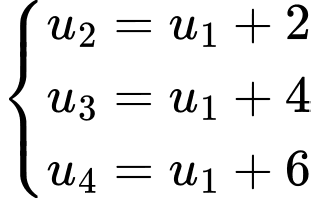
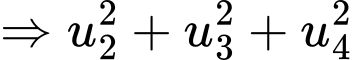
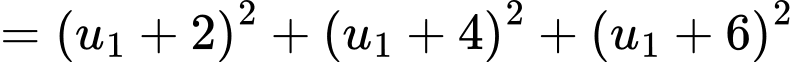
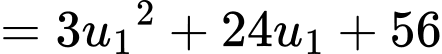
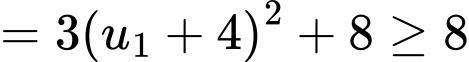
Vậy
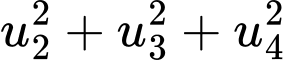 đạt giá trị nhỏ nhất khi
đạt giá trị nhỏ nhất khi 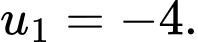
Từ đó suy ra
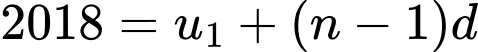
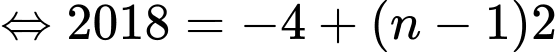
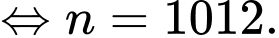 Đáp án: D
Đáp án: D
Câu 18 [806173]: Cho cấp số cộng 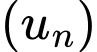 có
có 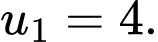 Tìm giá trị nhỏ nhất của
Tìm giá trị nhỏ nhất của 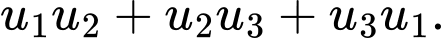
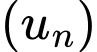 có
có 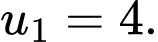 Tìm giá trị nhỏ nhất của
Tìm giá trị nhỏ nhất của 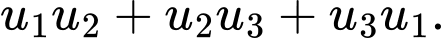
A, 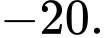
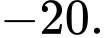
B, 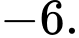
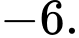
C, 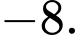
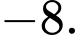
D, 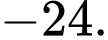
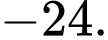
Ta gọi 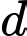 là công sai của cấp số cộng.
là công sai của cấp số cộng.
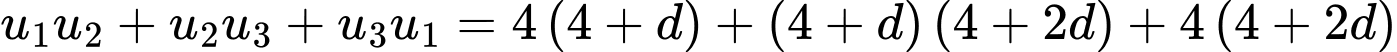
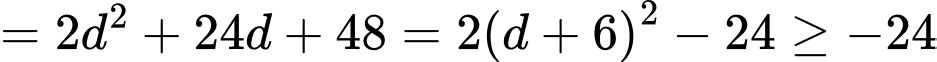
Dấu “=” xảy ra khi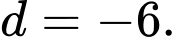
Vậy giá trị nhỏ nhất của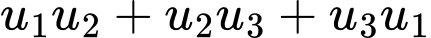 là
là 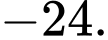 Đáp án: D
Đáp án: D
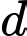 là công sai của cấp số cộng.
là công sai của cấp số cộng. 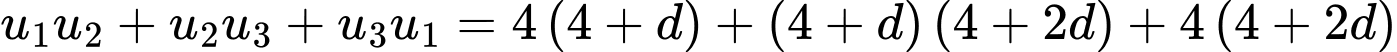
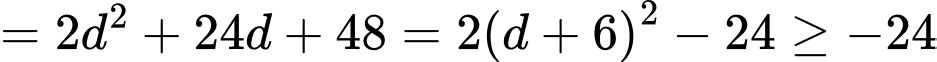
Dấu “=” xảy ra khi
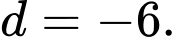
Vậy giá trị nhỏ nhất của
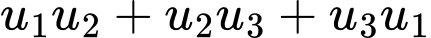 là
là 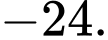 Đáp án: D
Đáp án: D
Câu 19 [805956]: Cho hai cấp số cộng 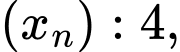
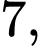
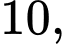 … và
… và 
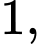
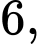
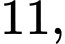 …. Hỏi trong
…. Hỏi trong  số hạng đầu tiên của mỗi cấp số có bao nhiêu số hạng chung?
số hạng đầu tiên của mỗi cấp số có bao nhiêu số hạng chung?
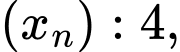
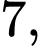
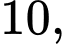 … và
… và 
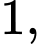
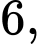
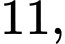 …. Hỏi trong
…. Hỏi trong  số hạng đầu tiên của mỗi cấp số có bao nhiêu số hạng chung?
số hạng đầu tiên của mỗi cấp số có bao nhiêu số hạng chung? A, 404.
B, 673.
C, 403.
D, 672.
Số hạng tổng quát của cấp số cộng 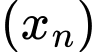 là:
là: 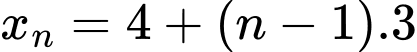
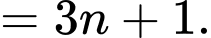
Số hạng tổng quát của cấp số cộng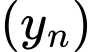 là:
là: 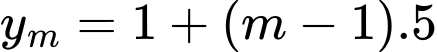
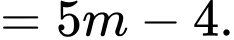
Giả sử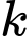 là
là 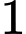 số hạng chung của hai cấp số cộng trong
số hạng chung của hai cấp số cộng trong  số hạng đầu tiên của mỗi cấp số.
số hạng đầu tiên của mỗi cấp số.
Vì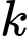 là
là 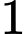 số hạng của cấp số cộng
số hạng của cấp số cộng 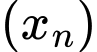 nên
nên 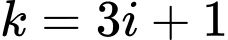 với
với  và
và 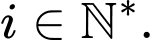
Vì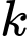 là
là 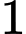 số hạng của cấp số cộng
số hạng của cấp số cộng 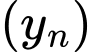 nên
nên 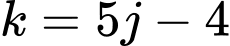 với
với 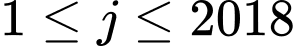 và
và 
Do đó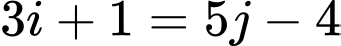
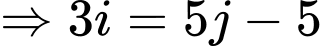

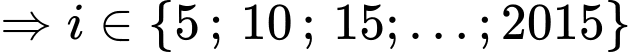
 có
có 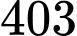 số hạng chung. Đáp án: C
số hạng chung. Đáp án: C
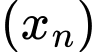 là:
là: 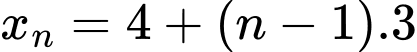
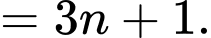
Số hạng tổng quát của cấp số cộng
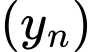 là:
là: 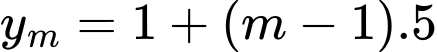
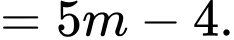
Giả sử
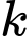 là
là 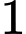 số hạng chung của hai cấp số cộng trong
số hạng chung của hai cấp số cộng trong  số hạng đầu tiên của mỗi cấp số.
số hạng đầu tiên của mỗi cấp số. Vì
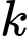 là
là 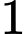 số hạng của cấp số cộng
số hạng của cấp số cộng 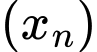 nên
nên 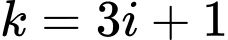 với
với  và
và 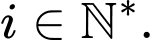
Vì
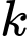 là
là 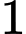 số hạng của cấp số cộng
số hạng của cấp số cộng 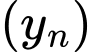 nên
nên 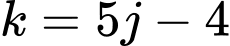 với
với 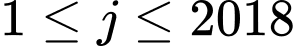 và
và 
Do đó
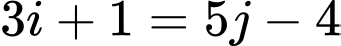
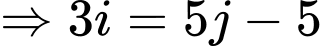

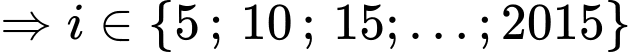
 có
có 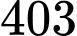 số hạng chung. Đáp án: C
số hạng chung. Đáp án: C
Câu 20 [579651]: [Đề mẫu HSA 2024]: Có bao nhiêu cấp số cộng có các số hạng là số tự nhiên, số hạng đầu là số chẵn, tổng các số hạng có giá trị lẻ bằng 33 và tổng các số hạng có giá trị chẵn bằng 44 (nhập đáp án vào ô trống)?
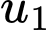 chẵn,
chẵn, 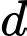 là số nguyên
là số nguyênNếu
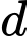 chẵn mọi số hạng đều chẵn
chẵn mọi số hạng đều chẵn 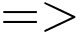 sai
saiVậy
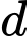 phải là số lẻ
phải là số lẻ 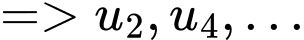 lẻ,
lẻ, 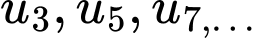 chẵn...
chẵn... Giả sử dãy số có
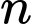 số hạng
số hạngNếu
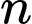 lẻ:
lẻ: 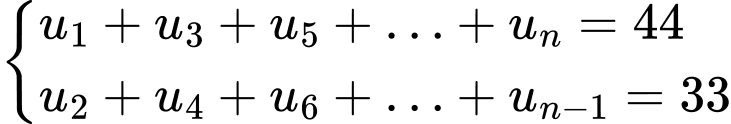
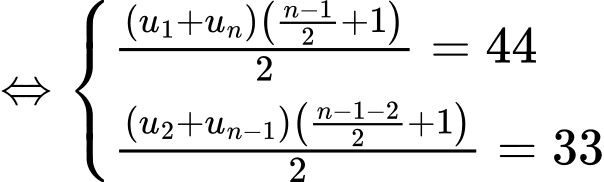
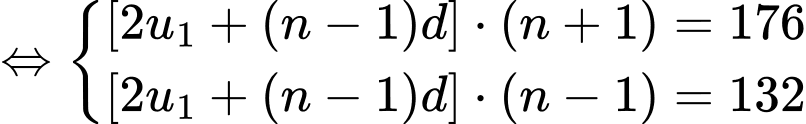
Chia vế cho vế có:
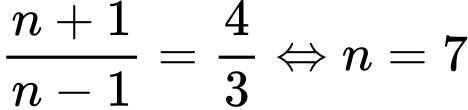 (thoả mãn)
(thoả mãn) Thay lại ta được
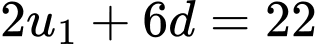
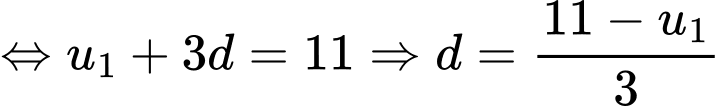
Do
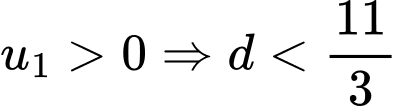
Do
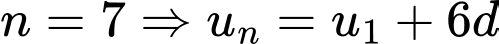
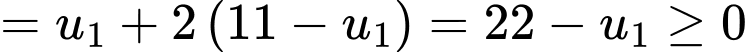
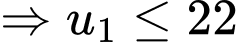
Vì
 nguyên nên
nguyên nên 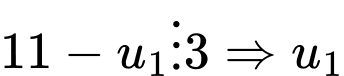 chia 3 dư 2
chia 3 dư 2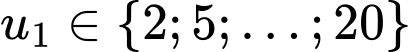
+)
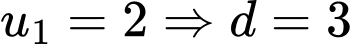 (thoả mãn)
(thoả mãn) +)
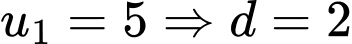 (loại vì
(loại vì 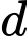 lẻ)
lẻ) +)
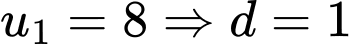 (thoả mãn)
(thoả mãn) +)
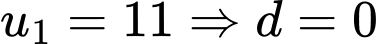 (loại vì
(loại vì 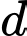 lẻ)
lẻ) +)
 (thoả mãn)
(thoả mãn) +)
 (loại vì
(loại vì 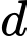 lẻ)
lẻ) +)
 (thoả mãn)
(thoả mãn)  Có 4 cấp số cộng
Có 4 cấp số cộngNếu n chã̃n
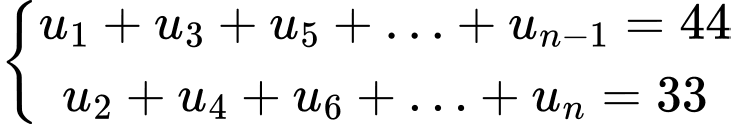
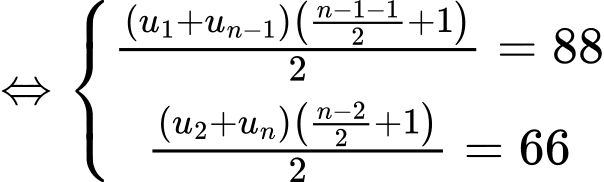
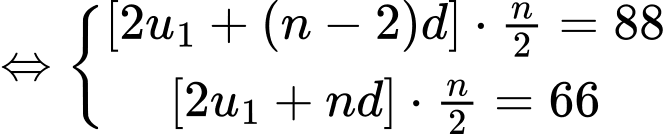
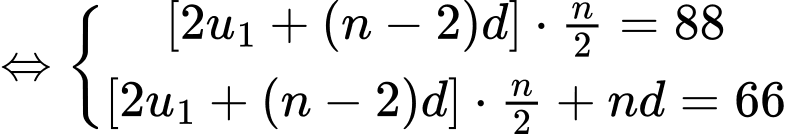
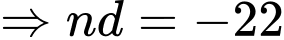
Do
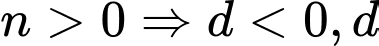 lẻ
lẻ 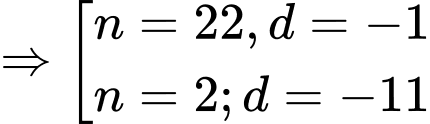
TH1:
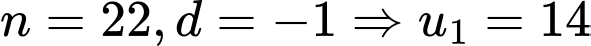 (thoả mãn)
(thoả mãn) Ta thấy
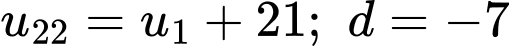 không là số tự nhiên nên loại
không là số tự nhiên nên loạiTH2:
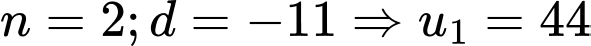 (thoả mãn)
(thoả mãn) Có 1 cấp số cộng
Kết hợp với TH 1 suy ra tổng cộng có 5 cấp số cộng.
Đáp số 5