Đáp án Bài tập tự luyện số 1
Câu 1 [57638]: Tập nghiệm  của bất phương trình
của bất phương trình 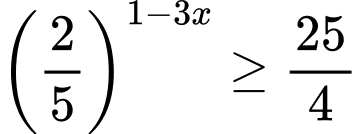 là
là
 của bất phương trình
của bất phương trình 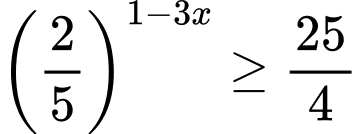 là
là A, 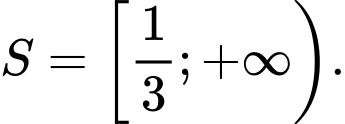
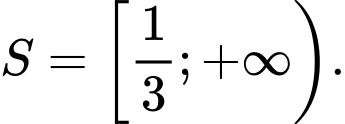
B, 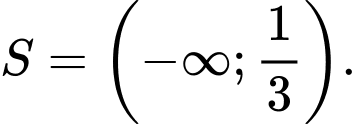
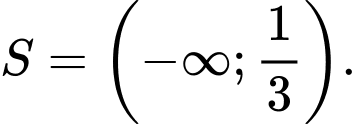
C, 

D, 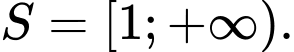
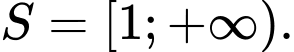
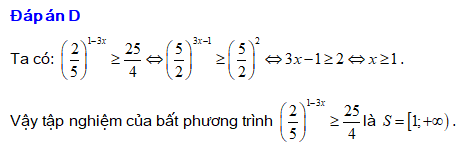 Đáp án: D
Đáp án: D
Câu 2 [529672]: Tập nghiệm 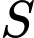 của bất phương trình
của bất phương trình 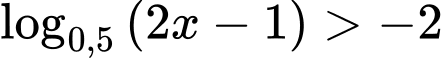 là
là
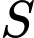 của bất phương trình
của bất phương trình 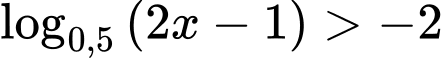 là
là A, 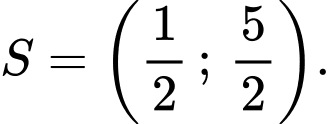
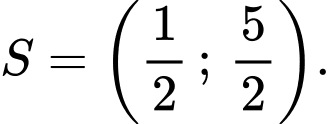
B, 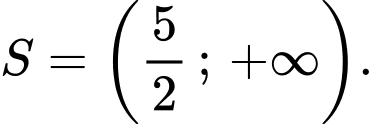
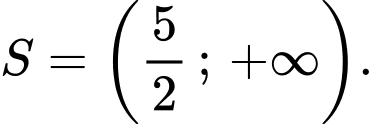
C, 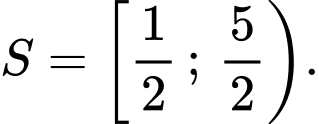
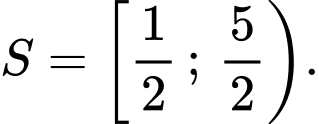
D, 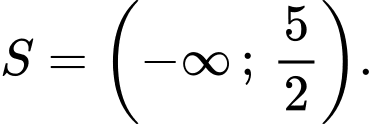
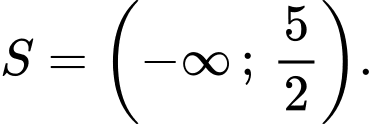
Chọn đáp án A.
Ta có:
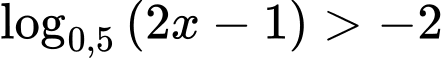
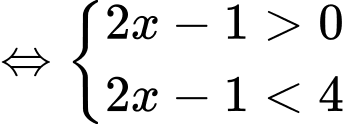
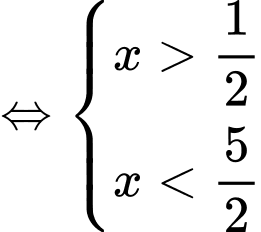
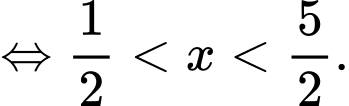
Vậy tập nghiệm của bất phương trình là: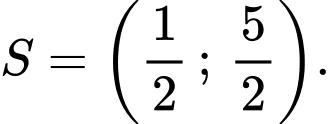 Đáp án: A
Đáp án: A
Ta có:
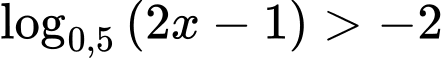
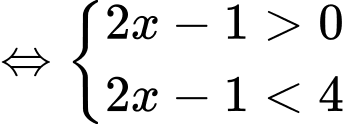
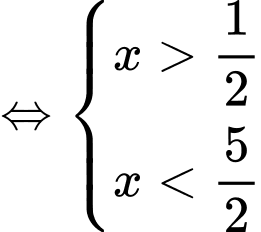
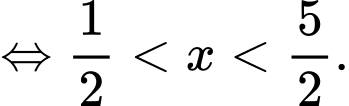
Vậy tập nghiệm của bất phương trình là:
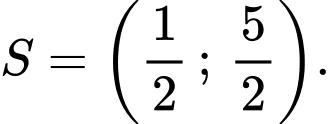 Đáp án: A
Đáp án: A
Câu 3 [581402]: Tập nghiệm của bất phương trình 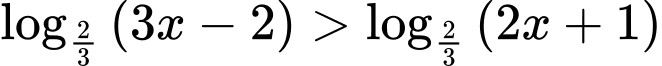 là
là
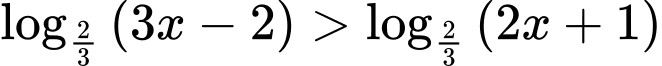 là
là A, 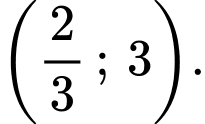
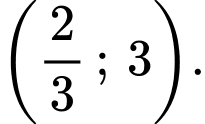
B, 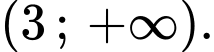
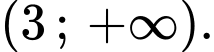
C, 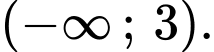
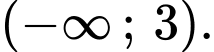
D, 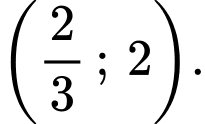
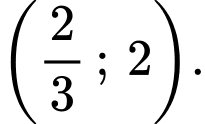
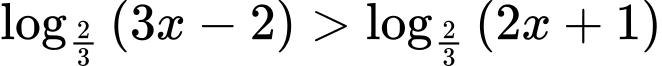
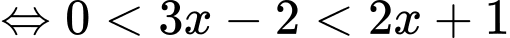
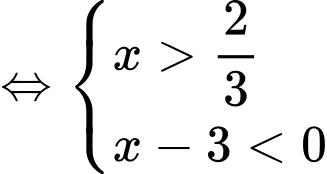
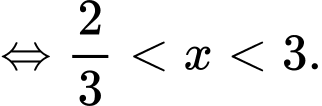
Vậy tập nghiệm của bất phương trình đã cho là
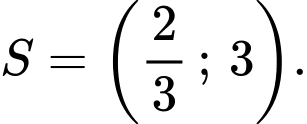
Chọn A. Đáp án: A
Câu 4 [27498]: Tìm tập nghiệm 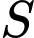 của bất phương trình
của bất phương trình 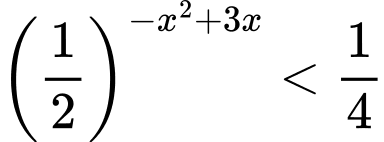
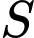 của bất phương trình
của bất phương trình 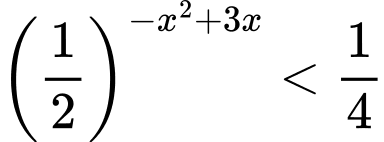
A, 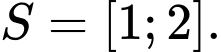
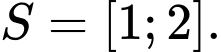
B, 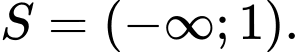
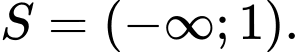
C, 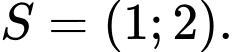
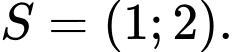
D, 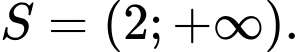
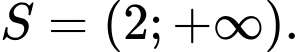
 Đáp án: C
Đáp án: C
Câu 5 [57676]: Bất phương trình: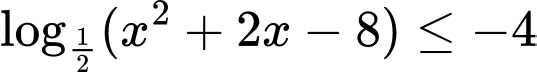 có tập nghiệm là
có tập nghiệm là
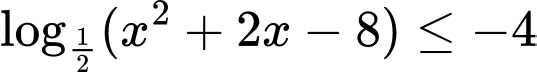 có tập nghiệm là
có tập nghiệm là A, 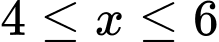 .
.
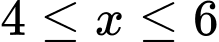 .
.B, 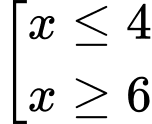 .
.
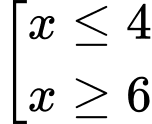 .
.C, 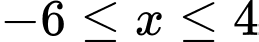 .
.
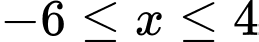 .
.D, 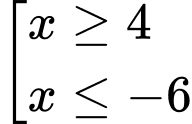 .
.
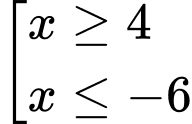 .
.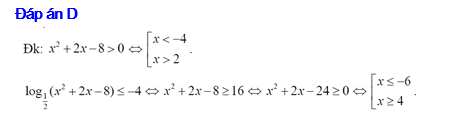 Đáp án: D
Đáp án: D
Câu 6 [57679]: Tập nghiệm của bất phương trình 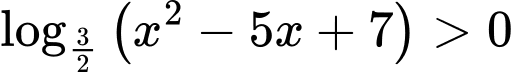 là
là
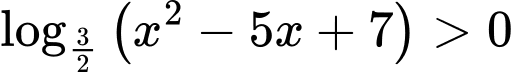 là
là A, 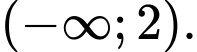
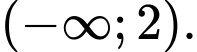
B, 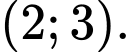
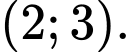
C, 

D, 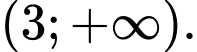
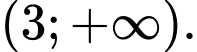
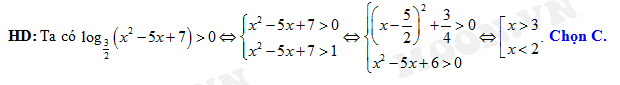 Đáp án: C
Đáp án: C
Câu 7 [662502]: Tìm tập nghiệm 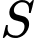 của bất phương trình
của bất phương trình 
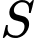 của bất phương trình
của bất phương trình 
A, 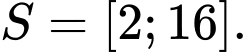
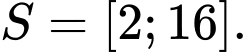
B, 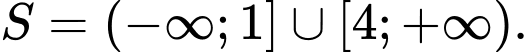
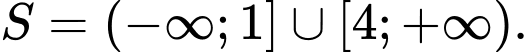
C, 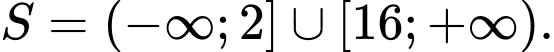
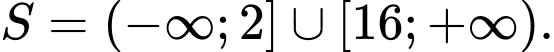
D, 

Điều kiện 
Đặt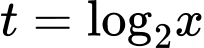 ta được
ta được 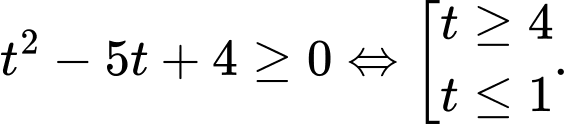 Suy ra
Suy ra 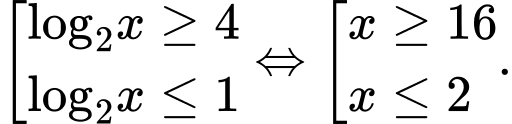
Kết hợp điều kiện suy ra nghiệm của bất phương trình là
suy ra nghiệm của bất phương trình là  Chọn D.
Đáp án: D
Chọn D.
Đáp án: D

Đặt
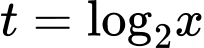 ta được
ta được 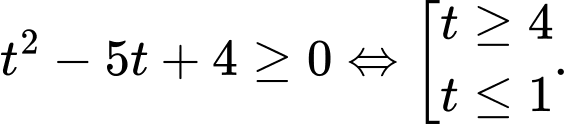 Suy ra
Suy ra 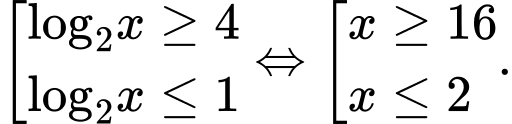
Kết hợp điều kiện
 suy ra nghiệm của bất phương trình là
suy ra nghiệm của bất phương trình là  Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
Câu 8 [27448]: Tập nghiệm 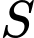 của bất phương trình
của bất phương trình 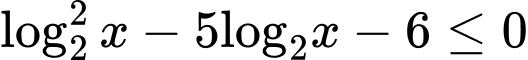
 của bất phương trình
của bất phương trình 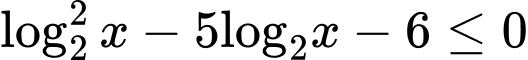
A, 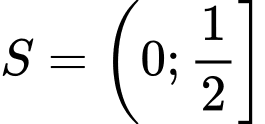 .
.
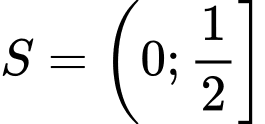 .
.B, 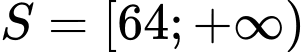 .
.
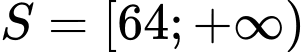 .
.C, 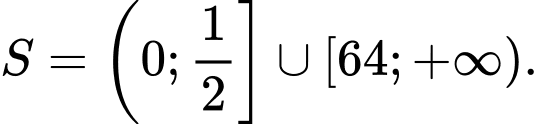
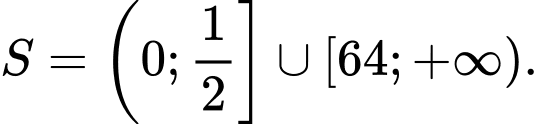
D, 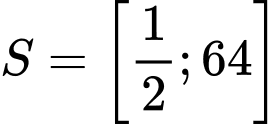 .
.
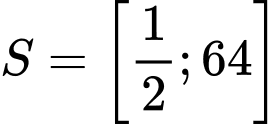 .
. Đáp án: D
Đáp án: D
Câu 9 [27472]: Khi đặt 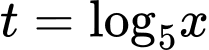 thì bất phương trình
thì bất phương trình  trở thành bất phương trình nào dưới đây?
trở thành bất phương trình nào dưới đây?
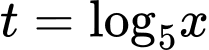 thì bất phương trình
thì bất phương trình  trở thành bất phương trình nào dưới đây?
trở thành bất phương trình nào dưới đây? A, 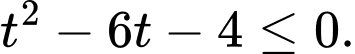
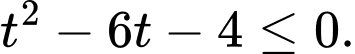
B, 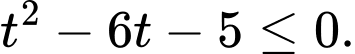
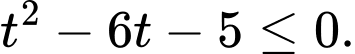
C, 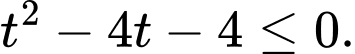
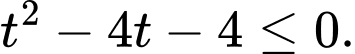
D, 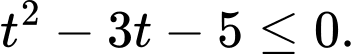
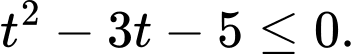
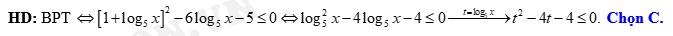 Đáp án: C
Đáp án: C
Câu 10 [27434]: Biết rằng bất phương trình 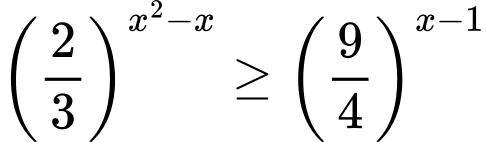 có tập nghiệm là đoạn
có tập nghiệm là đoạn 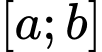 . Tính
. Tính 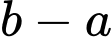 .
.
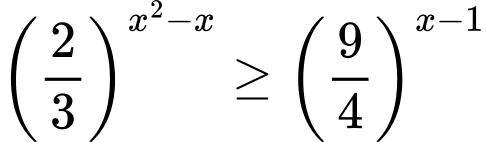 có tập nghiệm là đoạn
có tập nghiệm là đoạn 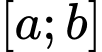 . Tính
. Tính 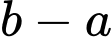 .
. A, 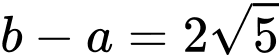 .
.
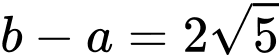 .
.B, 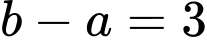 .
.
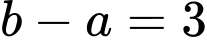 .
.C, 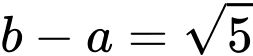 .
.
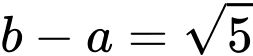 .
.D, 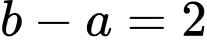 .
.
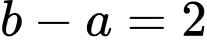 .
.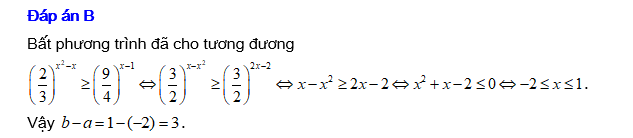 Đáp án: B
Đáp án: B
Câu 11 [27449]: Tập tập tất cả các số thực x thỏa mãn 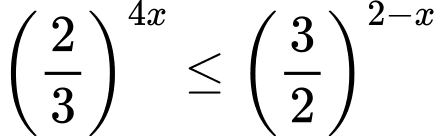 là:
là:
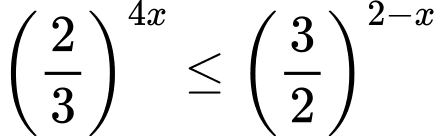 là:
là: A, 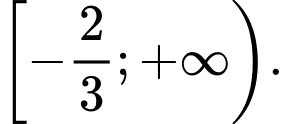
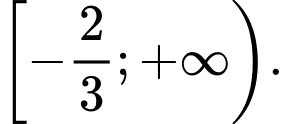
B, 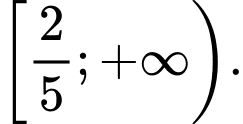
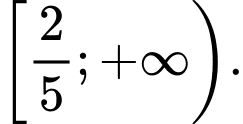
C, 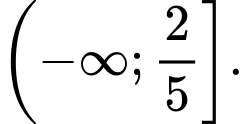
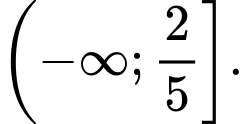
D, 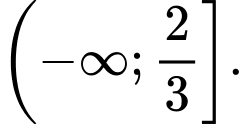
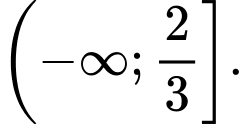
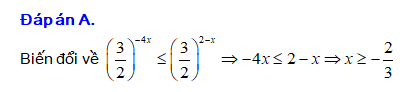 Đáp án: A
Đáp án: A
Câu 12 [27460]: Biết  là tập nghiệm của bất phương trình
là tập nghiệm của bất phương trình 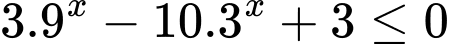 . Tìm
. Tìm 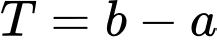 .
.
 là tập nghiệm của bất phương trình
là tập nghiệm của bất phương trình 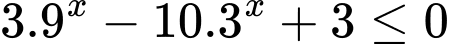 . Tìm
. Tìm 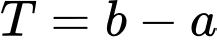 .
. A, 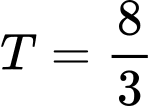 ..
..
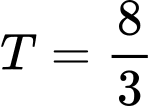 ..
..B, 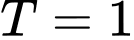 .
.
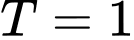 .
.C, 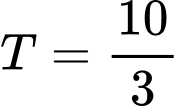 .
.
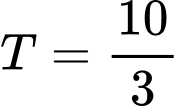 .
.D, 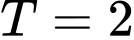 .
.
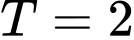 .
. Đáp án: D
Đáp án: D
Câu 13 [661657]: Biết tập hợp nghiệm của bất phương trình 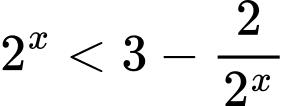 là khoảng
là khoảng 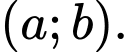 Giá trị
Giá trị  bằng
bằng
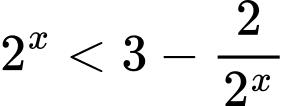 là khoảng
là khoảng 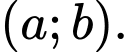 Giá trị
Giá trị  bằng
bằng A, 3.
B, 2.
C, 0.
D, 1.
Ta có: 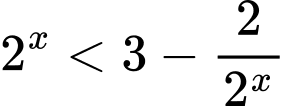
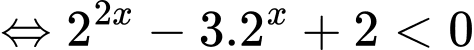
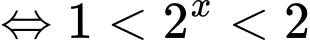

Vậy tập hợp nghiệm của bất phương trình đã cho là khoảng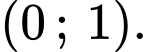
Từ đó ta có: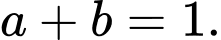 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
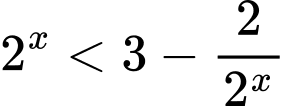
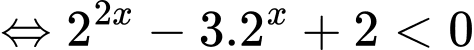
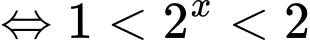

Vậy tập hợp nghiệm của bất phương trình đã cho là khoảng
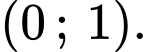
Từ đó ta có:
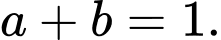 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
Câu 14 [27459]: Bất phương trình 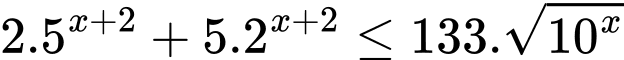 có tập nghiệm là
có tập nghiệm là  thì
thì 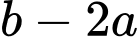 bằng
bằng
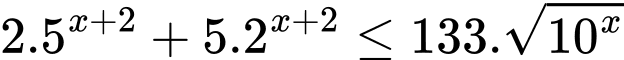 có tập nghiệm là
có tập nghiệm là  thì
thì 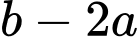 bằng
bằng A, 6.
B, 10.
C, 12.
D, 16.
 Đáp án: B
Đáp án: B
Câu 15 [27484]: Bất phương trình 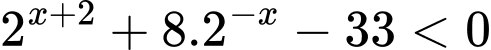 có bao nhiêu nghiệm nguyên?
có bao nhiêu nghiệm nguyên?
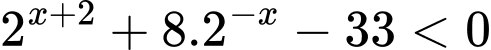 có bao nhiêu nghiệm nguyên?
có bao nhiêu nghiệm nguyên? A, Vô số.
B, 6.
C, 7.
D, 4.
 Đáp án: D
Đáp án: D
Câu 16 [661660]: Tìm tổng các nghiệm nguyên của bất phương trình 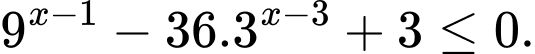
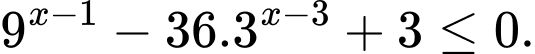
A, 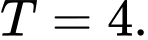
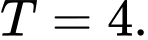
B, 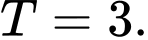
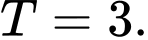
C, 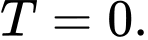
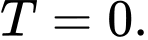
D, 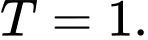
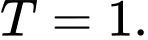
Ta có: BPT 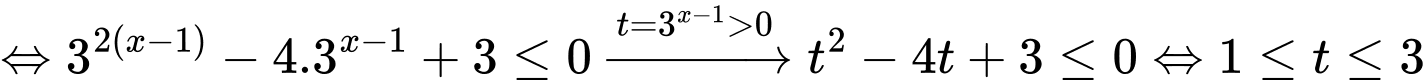
Khi đó: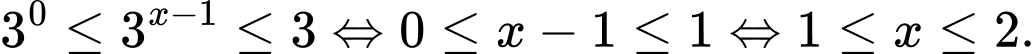
Kết hợp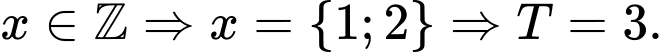 Chọn B.
Đáp án: B
Chọn B.
Đáp án: B
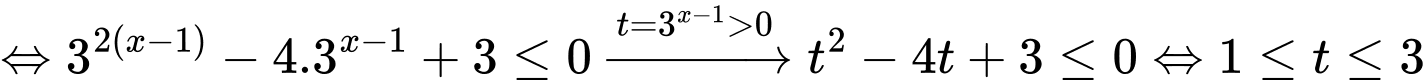
Khi đó:
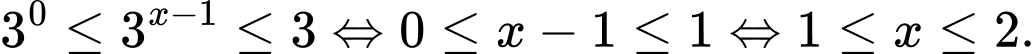
Kết hợp
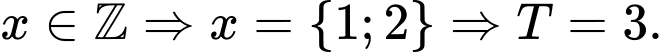 Chọn B.
Đáp án: B
Chọn B.
Đáp án: B
Câu 17 [661661]: Bất phương trình 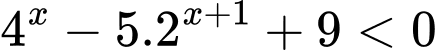 có số nghiệm nguyên là
có số nghiệm nguyên là
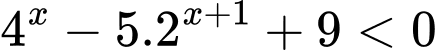 có số nghiệm nguyên là
có số nghiệm nguyên là A, 1.
B, 2.
C, 3.
D, 4.
Bất phương trình 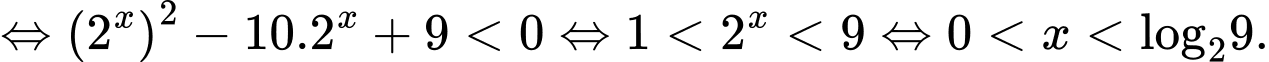
Kết hợp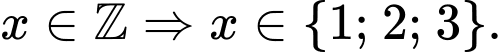 Chọn C
Đáp án: C
Chọn C
Đáp án: C
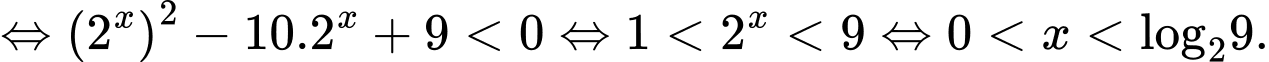
Kết hợp
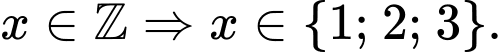 Chọn C
Đáp án: C
Chọn C
Đáp án: C
Câu 18 [661665]: Tập nghiệm 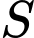 của bất phương trình
của bất phương trình  là
là
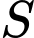 của bất phương trình
của bất phương trình  là
là A, 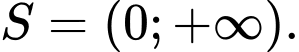
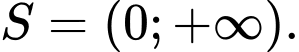
B, 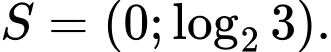
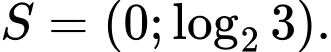
C, 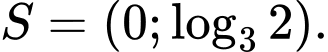
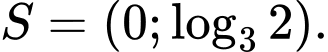
D, 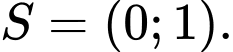
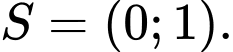
Lấy logarit cơ số 3 cả 2 vế ta có: 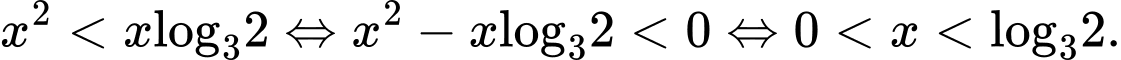 Chọn C. Đáp án: C
Chọn C. Đáp án: C
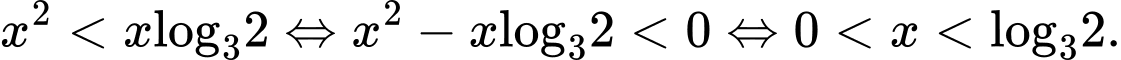 Chọn C. Đáp án: C
Chọn C. Đáp án: C
Câu 19 [661667]: Cho hàm số 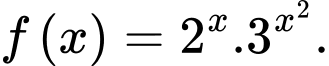 Khẳng định nào sau đây là sai?
Khẳng định nào sau đây là sai?
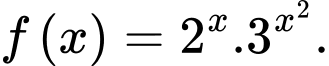 Khẳng định nào sau đây là sai?
Khẳng định nào sau đây là sai? A, 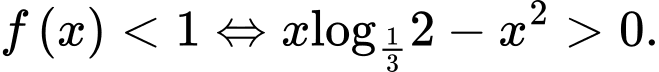
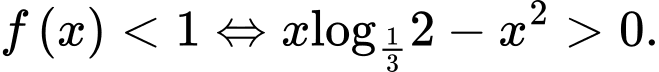
B, 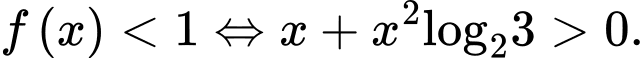
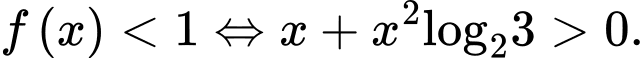
C, 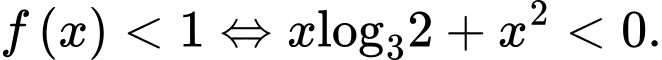
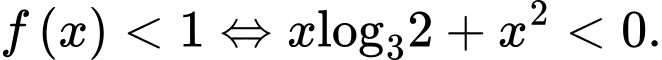
D, 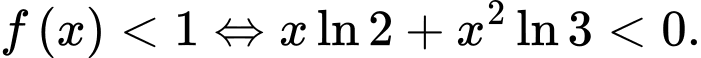
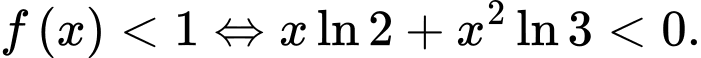
Ta có: 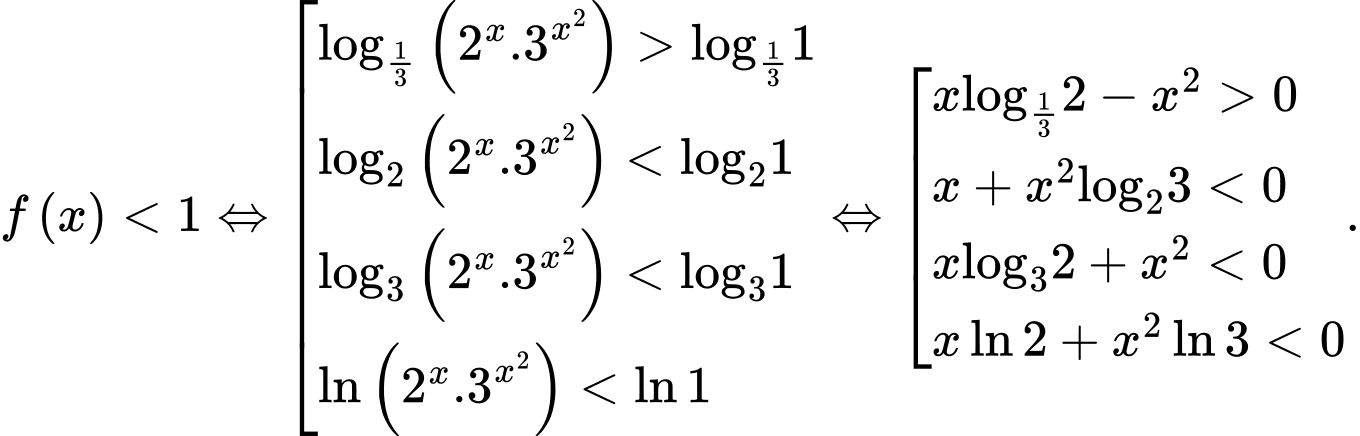
Đáp án sai là B. Chọn B. Đáp án: B
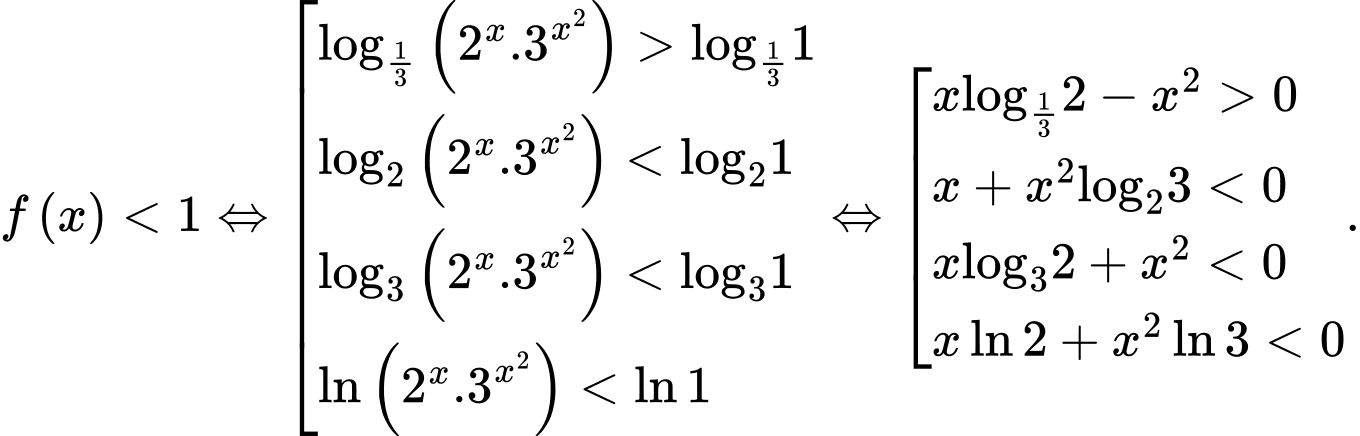
Đáp án sai là B. Chọn B. Đáp án: B
Câu 20 [27477]: Cho hàm số 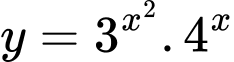 Khẳng định nào sau đây sai?
Khẳng định nào sau đây sai?
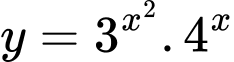 Khẳng định nào sau đây sai?
Khẳng định nào sau đây sai? A, 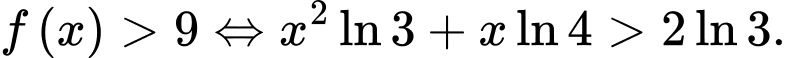
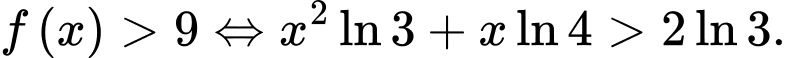
B, 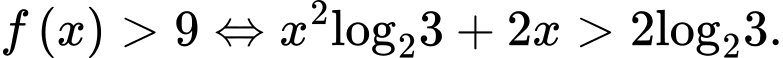
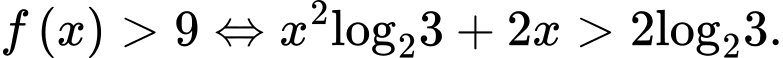
C, 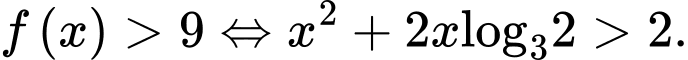
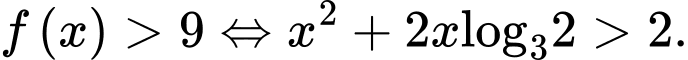
D, 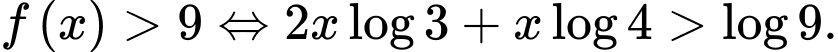
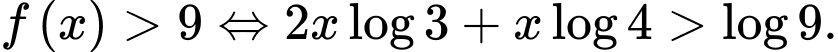
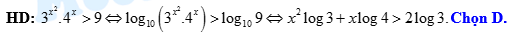 Đáp án: D
Đáp án: D
Câu 21 [661659]: Biết  là tập nghiệm của bất phương trình
là tập nghiệm của bất phương trình 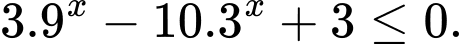 Tìm
Tìm 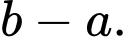
 là tập nghiệm của bất phương trình
là tập nghiệm của bất phương trình 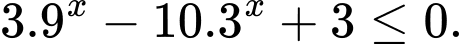 Tìm
Tìm 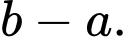
A, 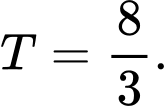
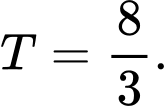
B, 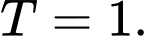
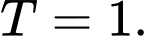
C, 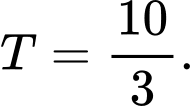
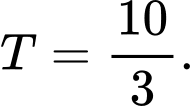
D, 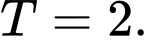
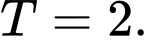
Đặt 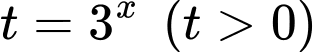 ta có:
ta có: 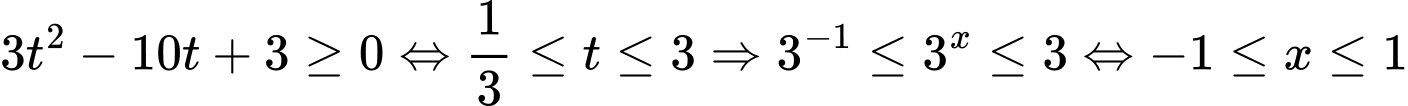
Suy ra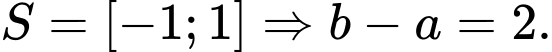 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
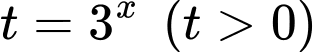 ta có:
ta có: 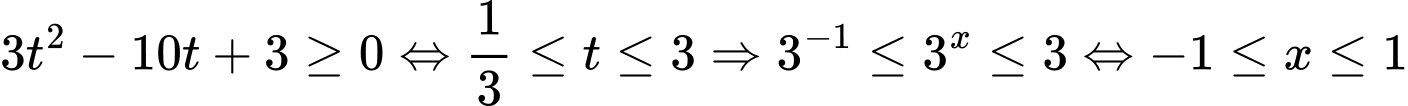
Suy ra
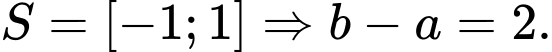 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
Câu 22 [662464]: Số nghiệm nguyên của bất phương trình 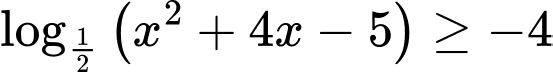 là
là
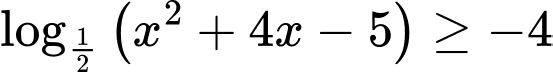 là
là A, 6.
B, 5.
C, 10.
D, 4.
Điều kiện 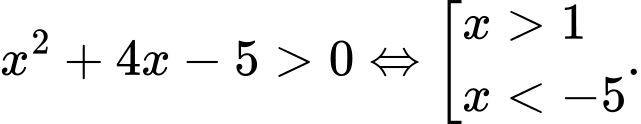
Với điều kiện trên bất phương trình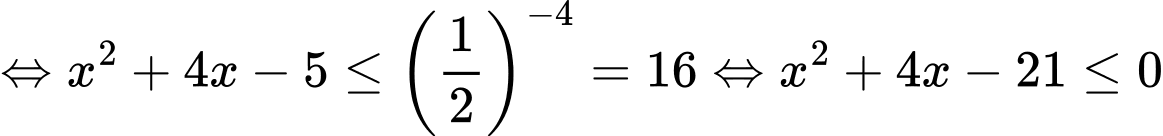
 Kết hợp điều kiện suy ra
Kết hợp điều kiện suy ra 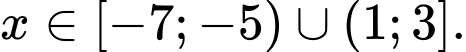
Kết hợp nên bất phương trình có 4 nghiệm nguyên. Chọn D.
Đáp án: D
nên bất phương trình có 4 nghiệm nguyên. Chọn D.
Đáp án: D
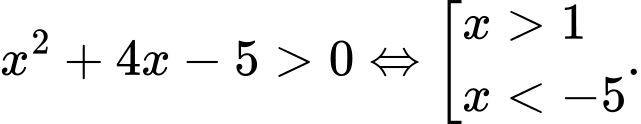
Với điều kiện trên bất phương trình
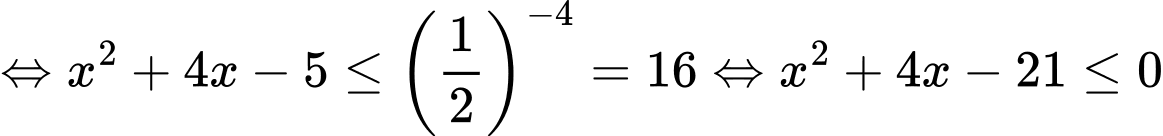
 Kết hợp điều kiện suy ra
Kết hợp điều kiện suy ra 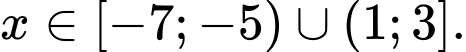
Kết hợp
 nên bất phương trình có 4 nghiệm nguyên. Chọn D.
Đáp án: D
nên bất phương trình có 4 nghiệm nguyên. Chọn D.
Đáp án: D
Câu 23 [661662]: Bất phương trình 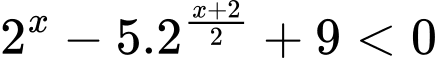 có số nghiệm nguyên là
có số nghiệm nguyên là
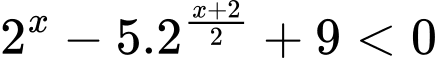 có số nghiệm nguyên là
có số nghiệm nguyên là A, 3.
B, 6.
C, 4.
D, 5.
Bất phương trình 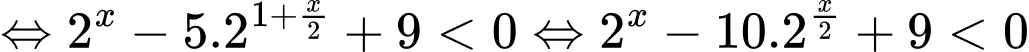
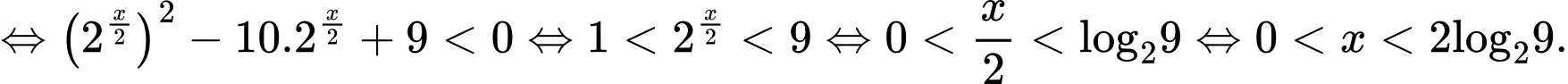
Mà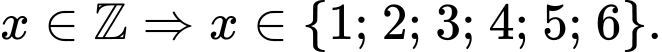 Chọn B.
Đáp án: B
Chọn B.
Đáp án: B
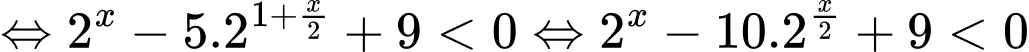
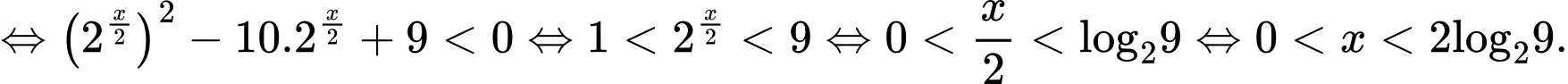
Mà
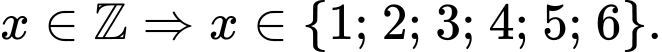 Chọn B.
Đáp án: B
Chọn B.
Đáp án: B
Câu 24 [662468]: Số nghiệm nguyên của bất phương trình 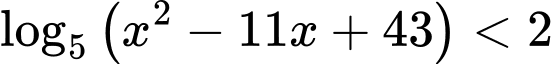 là
là
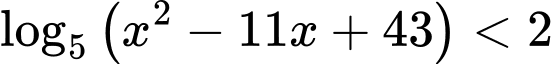 là
là A, 6.
B, 7.
C, 8.
D, 9.
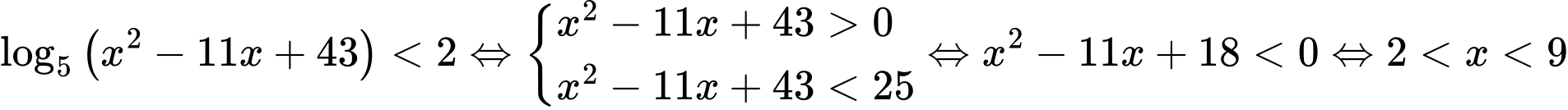
Vậy nghiệm của bất phương trình là:
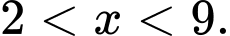
Kết hợp
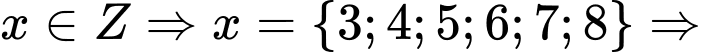 bất phương trình có 6 nghiệm nguyên. Chọn A.
Đáp án: A
bất phương trình có 6 nghiệm nguyên. Chọn A.
Đáp án: A
Câu 25 [662469]: Bất phương trình 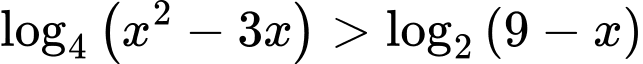 có bao nhiêu nghiệm nguyên?
có bao nhiêu nghiệm nguyên?
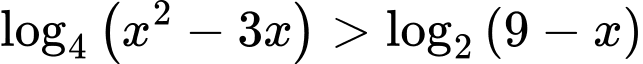 có bao nhiêu nghiệm nguyên?
có bao nhiêu nghiệm nguyên? A, Vô số.
B, 1.
C, 4.
D, 3.
Điều kiện: 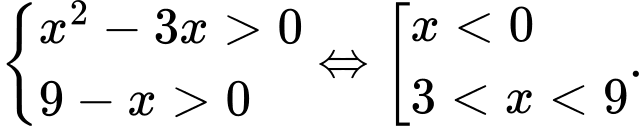
Ta có: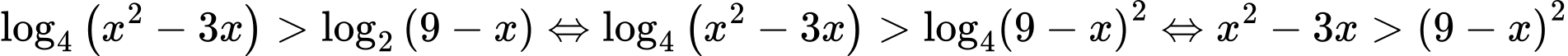
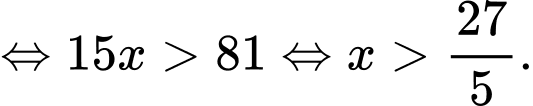 So sánh điều kiện, ta có:
So sánh điều kiện, ta có: 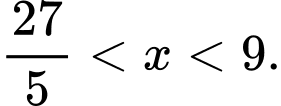
Vậy bất phương trình có 3 nghiệm nguyên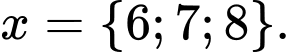 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
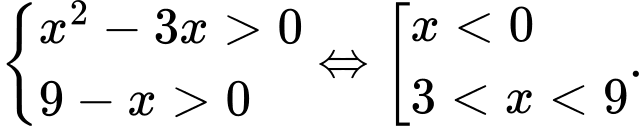
Ta có:
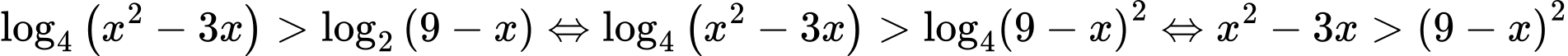
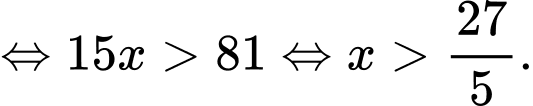 So sánh điều kiện, ta có:
So sánh điều kiện, ta có: 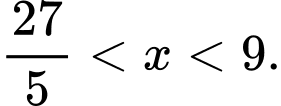
Vậy bất phương trình có 3 nghiệm nguyên
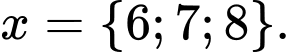 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
Câu 26 [662505]: Số nghiệm nguyên của bất phương trình  là
là
 là
là A, 5.
B, 6.
C, 7.
D, 8.
Điều kiện: 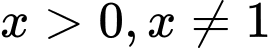
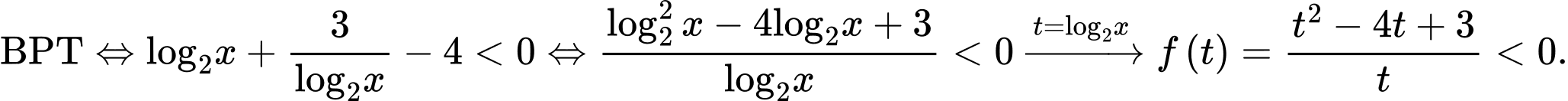
Lập bảng xét dấu cho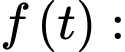
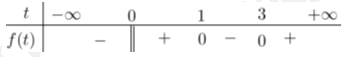
Từ bảng xét dấu ta có: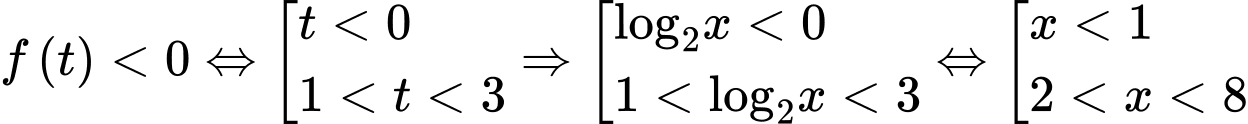
Vậy tập nghiệm của BPT là: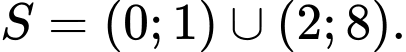
Kết hợp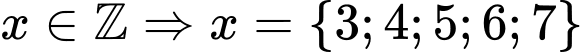 do đó bất phương trình có 5 nghiệm nguyên. Chọn A.
Đáp án: A
do đó bất phương trình có 5 nghiệm nguyên. Chọn A.
Đáp án: A
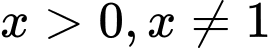
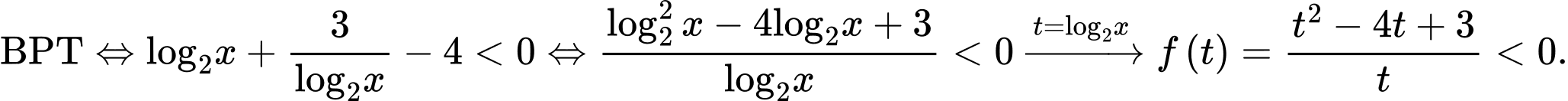
Lập bảng xét dấu cho
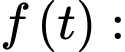
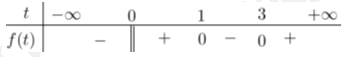
Từ bảng xét dấu ta có:
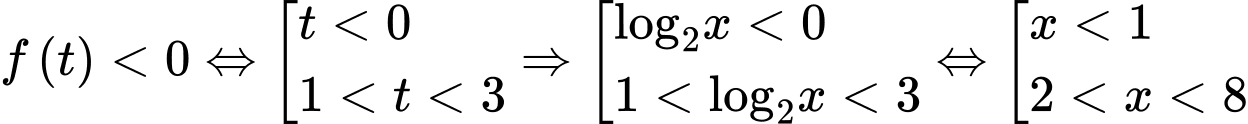
Vậy tập nghiệm của BPT là:
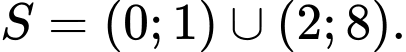
Kết hợp
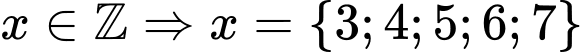 do đó bất phương trình có 5 nghiệm nguyên. Chọn A.
Đáp án: A
do đó bất phương trình có 5 nghiệm nguyên. Chọn A.
Đáp án: A
Câu 27 [662507]: Gọi 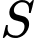 là tập hợp các số nguyên
là tập hợp các số nguyên 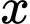 thỏa mãn
thỏa mãn 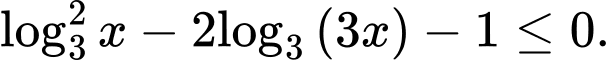 Tổng các phần tử của tập hợp
Tổng các phần tử của tập hợp 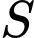 là
là
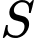 là tập hợp các số nguyên
là tập hợp các số nguyên 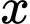 thỏa mãn
thỏa mãn 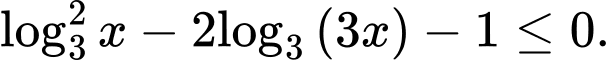 Tổng các phần tử của tập hợp
Tổng các phần tử của tập hợp 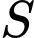 là
là A, 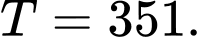
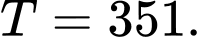
B, 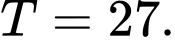
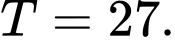
C, 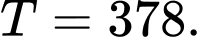
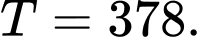
D, 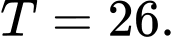
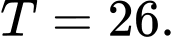
Điều kiện:  Bất phương trình
Bất phương trình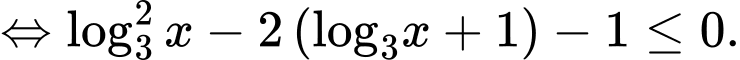
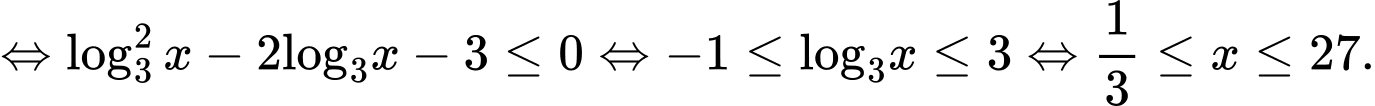 Kết hợp
Kết hợp 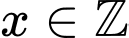
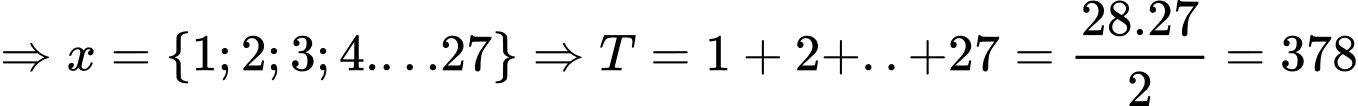 (cấp số cộng có
(cấp số cộng có 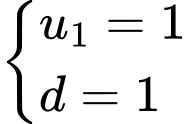 ). Chọn C.
Đáp án: C
). Chọn C.
Đáp án: C
 Bất phương trình
Bất phương trình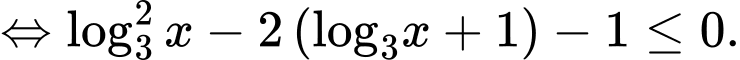
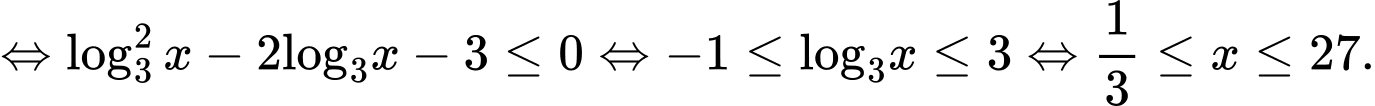 Kết hợp
Kết hợp 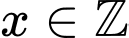
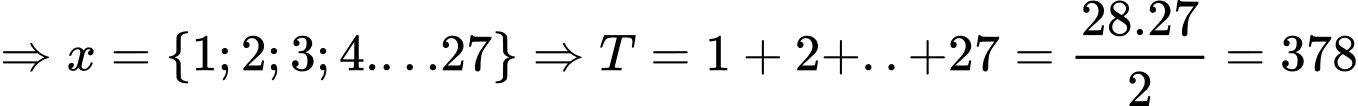 (cấp số cộng có
(cấp số cộng có 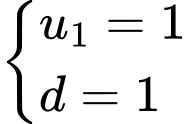 ). Chọn C.
Đáp án: C
). Chọn C.
Đáp án: C
Câu 28 [661664]: Số nghiệm nguyên của bất phương trình 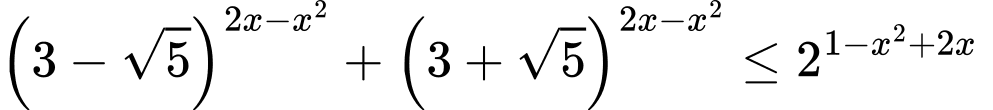 là
là
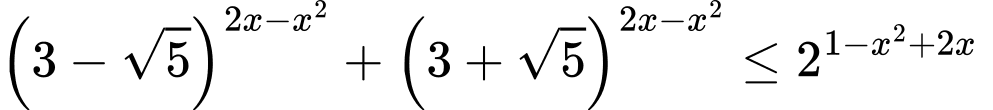 là
là A, 2.
B, 3.
C, 4.
D, 5.
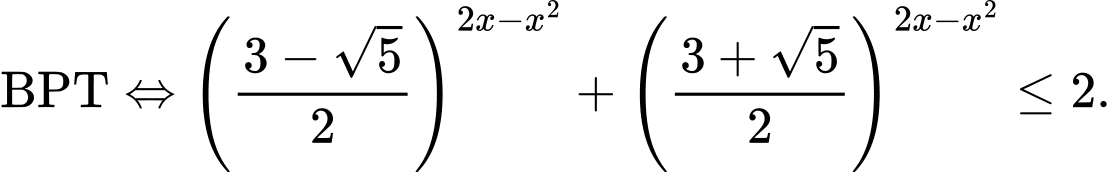 Nhận xét
Nhận xét 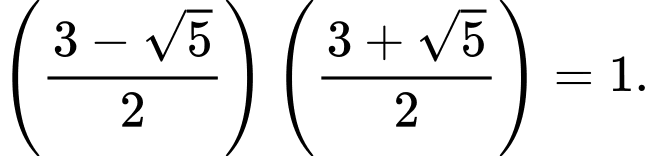
Đặt
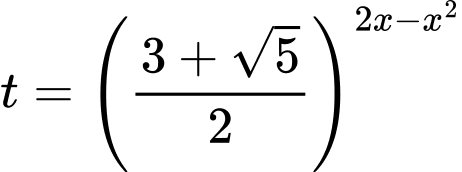 (với
(với  ) suy ra
) suy ra 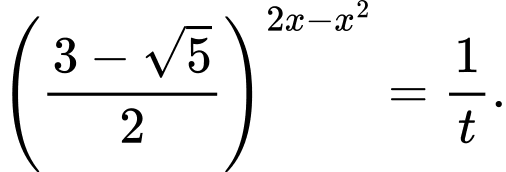
Ta có:
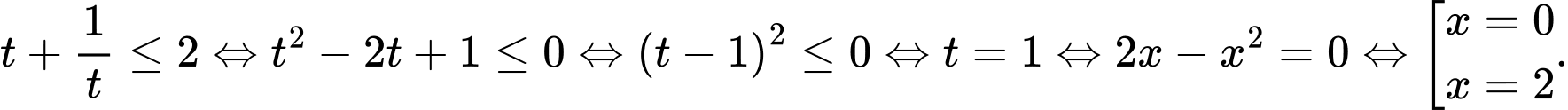
Vậy nghiệm của bất phương trình là:
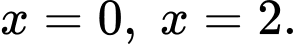 Chọn A.
Đáp án: A
Chọn A.
Đáp án: A
Câu 29 [280804]: Có bao nhiêu số nguyên 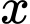 thỏa mãn
thỏa mãn 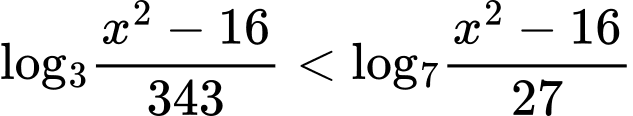 ?
?
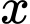 thỏa mãn
thỏa mãn 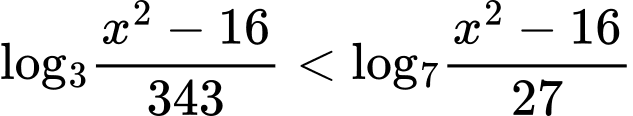 ?
? A, 193.
B, 92.
C, 186.
D, 184.
Chọn D
TXĐ: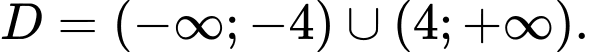
Ta có:
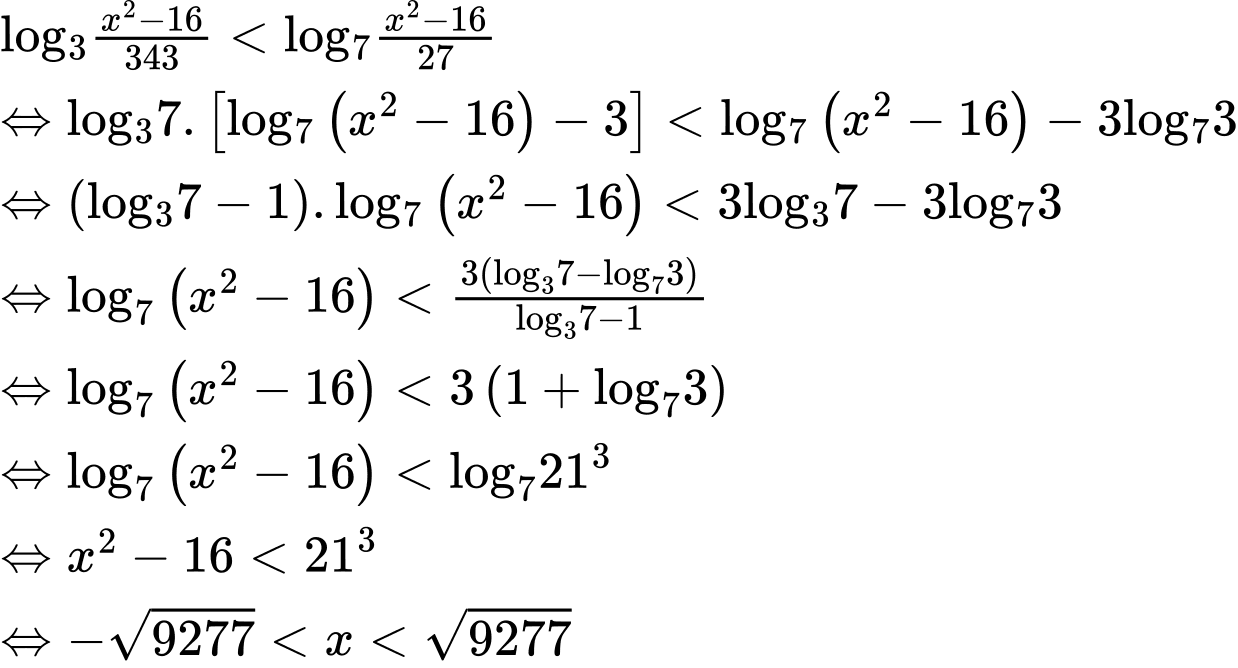
Kết hợp điều kiện ta có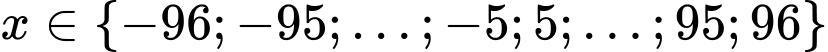 . Vậy có 184 số nguyên x thỏa mãn. Đáp án: D
. Vậy có 184 số nguyên x thỏa mãn. Đáp án: D
TXĐ:
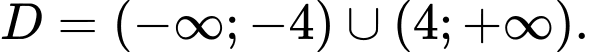
Ta có:
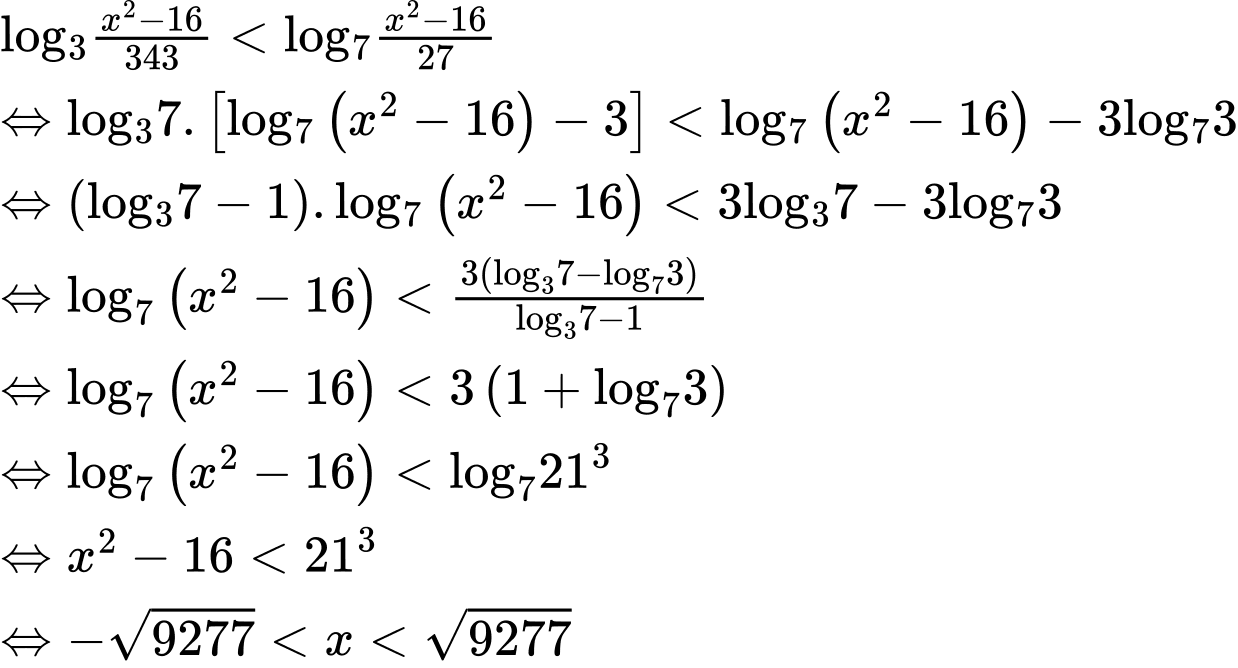
Kết hợp điều kiện ta có
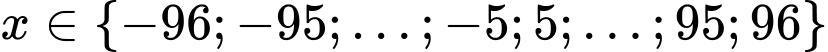 . Vậy có 184 số nguyên x thỏa mãn. Đáp án: D
. Vậy có 184 số nguyên x thỏa mãn. Đáp án: D
Câu 30 [769996]: [MĐ4] Có bao nhiêu số nguyên x thỏa mãn: 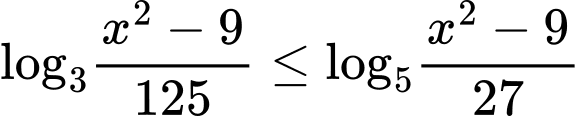 ?
?
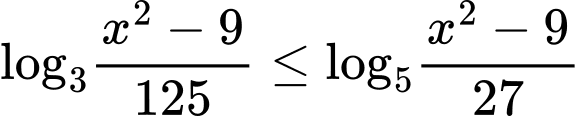 ?
? A, 58.
B, 112.
C, 110.
D, 117.
Chọn C
Điều kiện: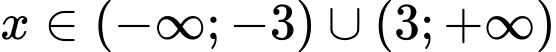 .
.
Ta có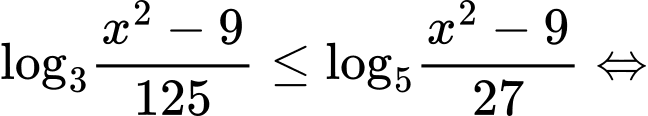
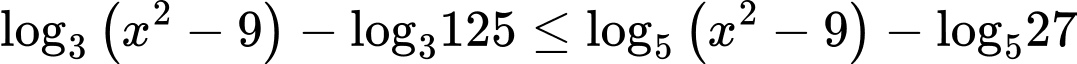
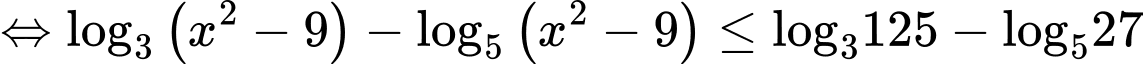
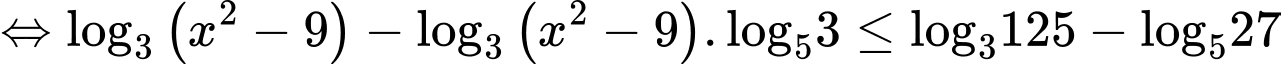
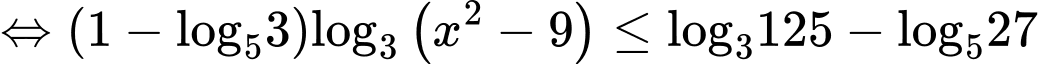
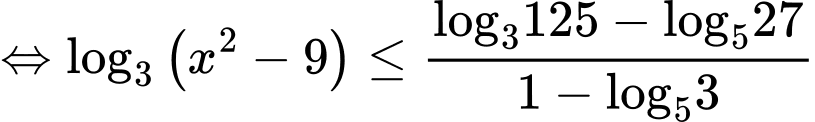
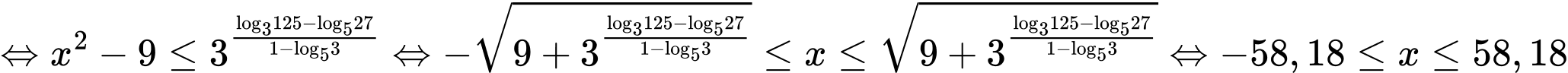
Vì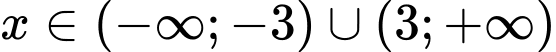 nên
nên 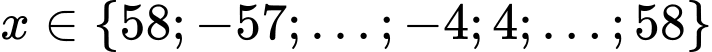 .
.
Có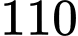 giá trị
giá trị 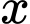 thỏa mãn đề bài. Đáp án: C
thỏa mãn đề bài. Đáp án: C
Điều kiện:
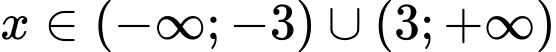 .
.
Ta có
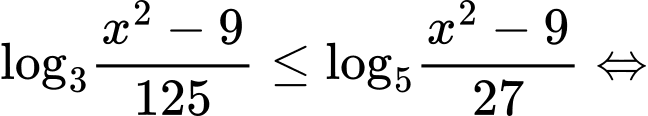
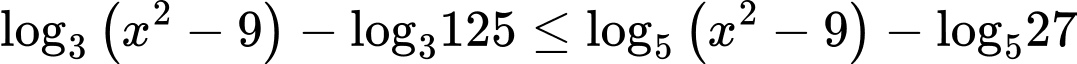
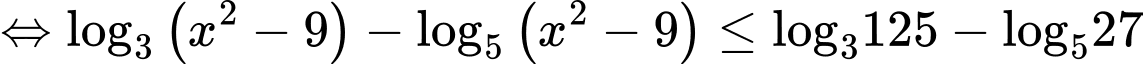
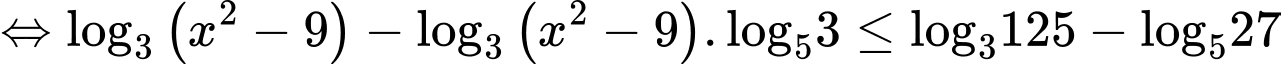
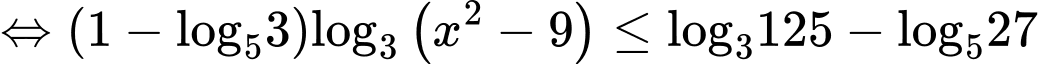
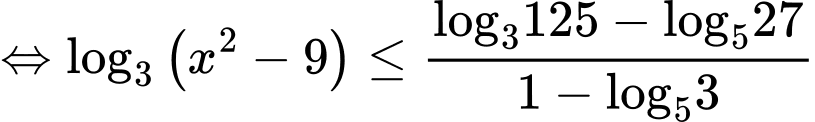
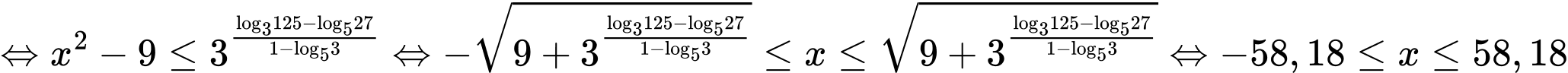
Vì
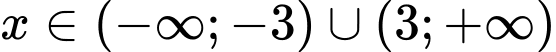 nên
nên 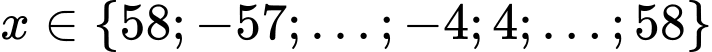 .
.
Có
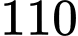 giá trị
giá trị 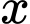 thỏa mãn đề bài. Đáp án: C
thỏa mãn đề bài. Đáp án: C