Đáp án Bài tập tự luyện số 2
Câu 1 [971671]: [Đề thi THPT QG 2021] Có bao nhiêu số nguyên 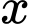 thỏa mãn
thỏa mãn
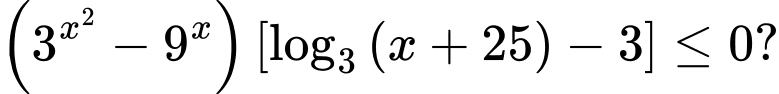
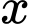 thỏa mãn
thỏa mãn
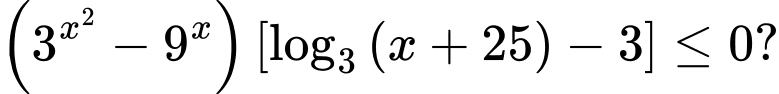
A, 24.
B, Vô số.
C, 26.
D, 25.
Chọn C
Điều kiện: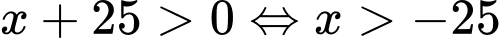 .
.
Ta giải các phương trình:
+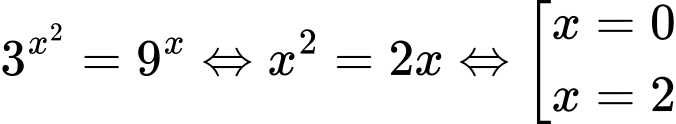 .
.
+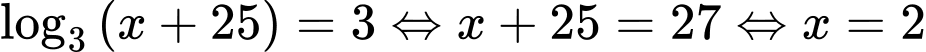 .
.
Ta có bảng xét dấu sau:
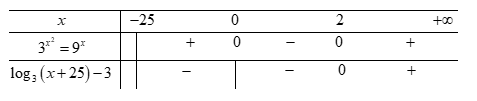
Dựa vào bẳng xét dấu, để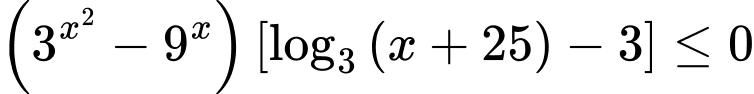 thì ta có
thì ta có
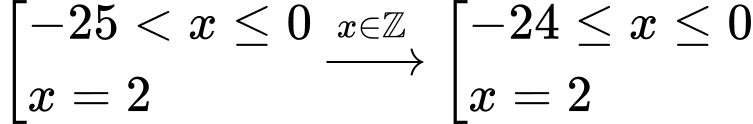 có 26 giá trị nguyên của
có 26 giá trị nguyên của 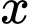 thỏa mãn.
Đáp án: C
thỏa mãn.
Đáp án: C
Điều kiện:
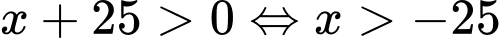 .
.Ta giải các phương trình:
+
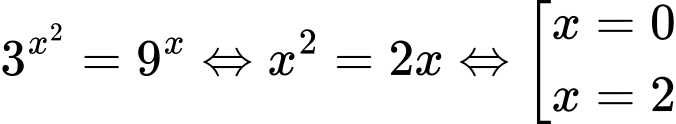 .
.+
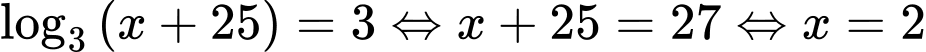 .
.Ta có bảng xét dấu sau:

Dựa vào bẳng xét dấu, để
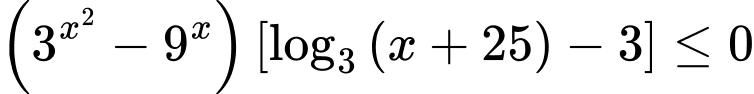 thì ta có
thì ta có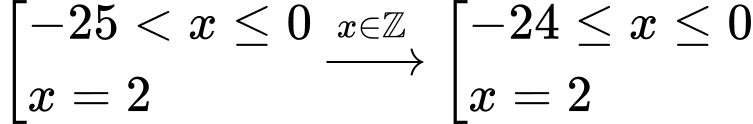 có 26 giá trị nguyên của
có 26 giá trị nguyên của 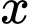 thỏa mãn.
Đáp án: C
thỏa mãn.
Đáp án: C
Câu 2 [971672]: Có bao nhiêu số nguyên 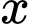 thỏa mãn
thỏa mãn
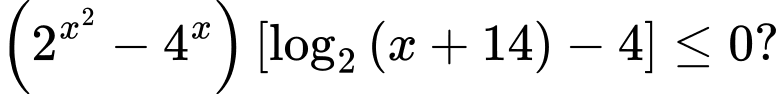
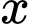 thỏa mãn
thỏa mãn
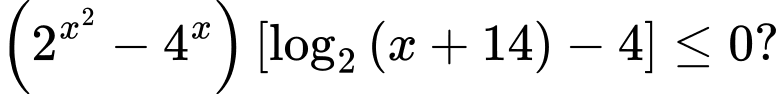
A, 14.
B, 13.
C, vô số.
D, 15.
Điều kiện:  .
.
 .
. Ta giải các phương trình:
+ 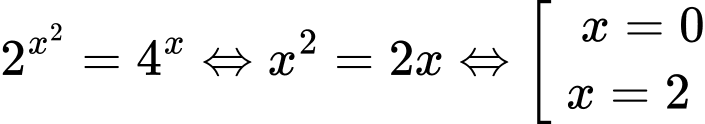 .
.
Đáp án: D 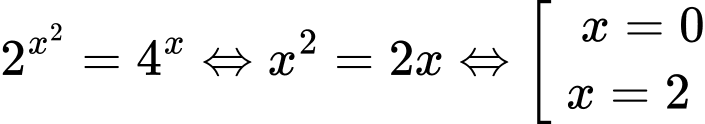 .
.+ 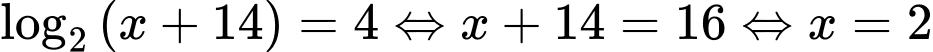 .
.
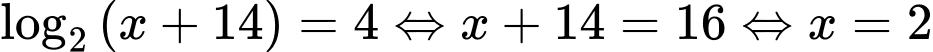 .
. Ta có bảng xét dấu sau:
Dựa vào bẳng xét dấu, để 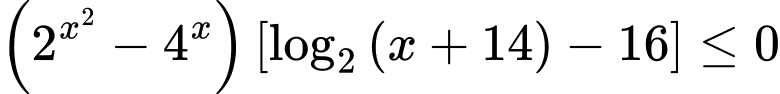 thì ta có
có 15 giá trị nguyên của
thì ta có
có 15 giá trị nguyên của 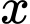 thỏa mãn.
thỏa mãn.
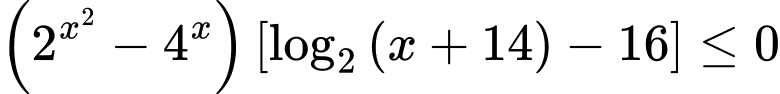 thì ta có
có 15 giá trị nguyên của
thì ta có
có 15 giá trị nguyên của 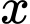 thỏa mãn.
thỏa mãn. Chọn đáp án D.
Câu 3 [971673]: Có bao nhiêu số nguyên  thỏa mãn
thỏa mãn
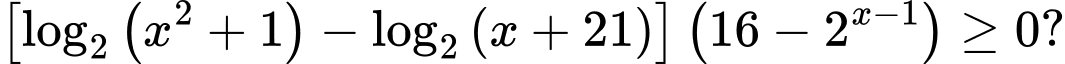
 thỏa mãn
thỏa mãn
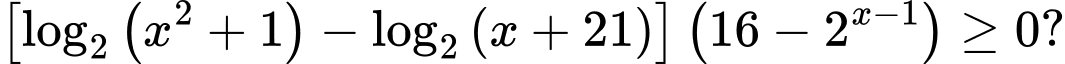
A, 17.
B, vô số.
C, 16.
D, 18.
Điều kiện: 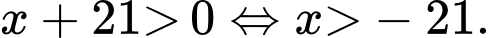
Ta giải các phương trình:
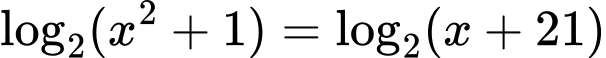
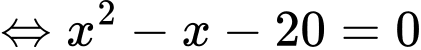
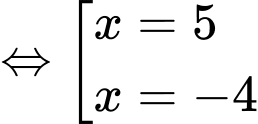
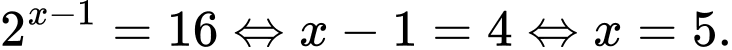
để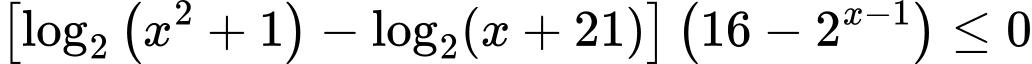 thì ta có có 18 giá trị nguyên của
thì ta có có 18 giá trị nguyên của 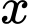 thỏa mãn
thỏa mãn
Chọn đáp án D. Đáp án: D
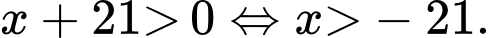
Ta giải các phương trình:
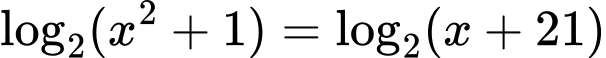
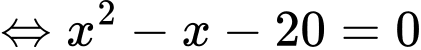
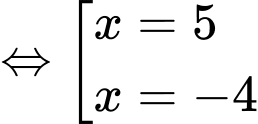
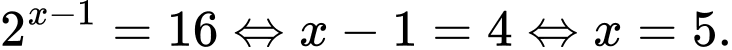
để
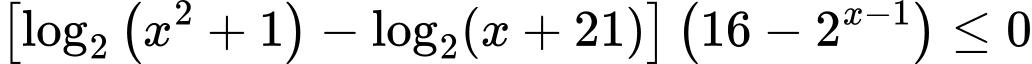 thì ta có có 18 giá trị nguyên của
thì ta có có 18 giá trị nguyên của 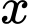 thỏa mãn
thỏa mãnChọn đáp án D. Đáp án: D
Câu 4 [230718]: Số nghiệm nguyên của bất phương trình 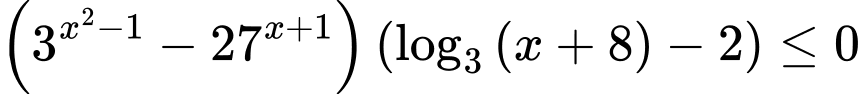 là
là
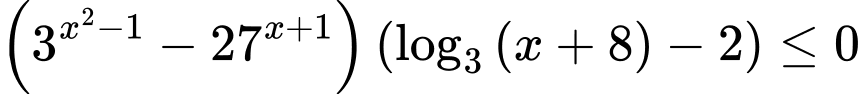 là
là A, 

B, Vô số.
C, 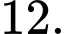
D, 
Chọn A 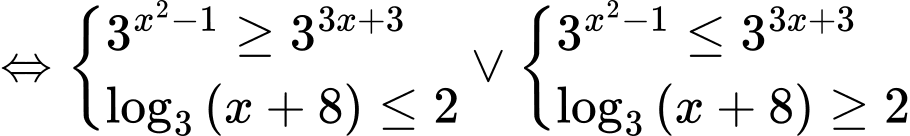
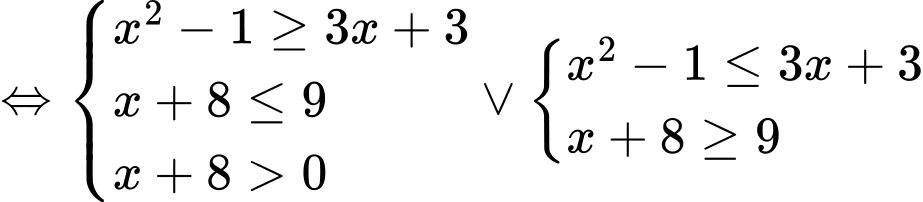
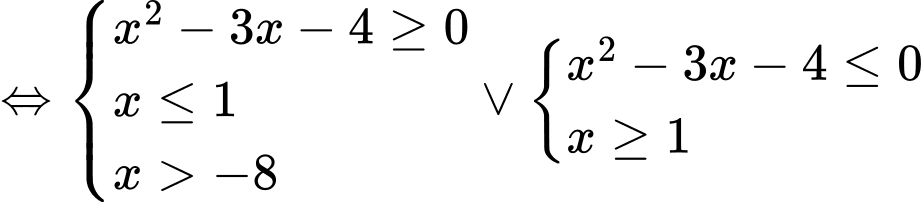
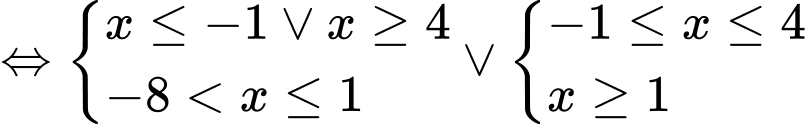
 Mà
Mà 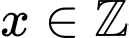 Nên
Nên 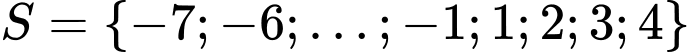
Ta có: 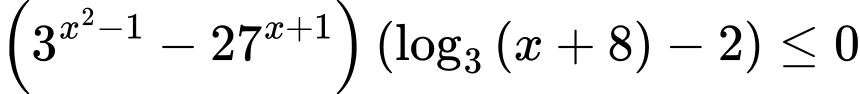
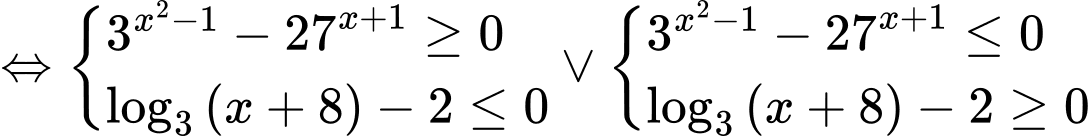
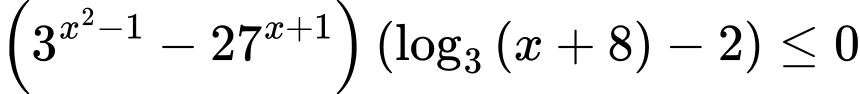
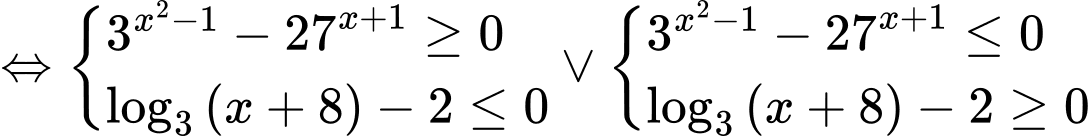
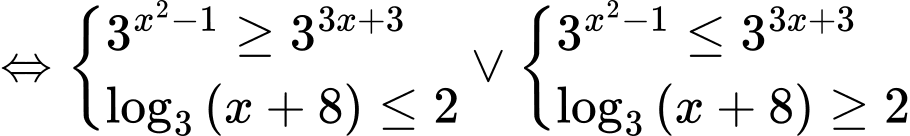
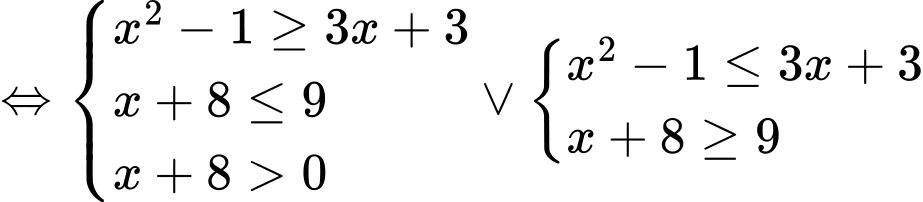
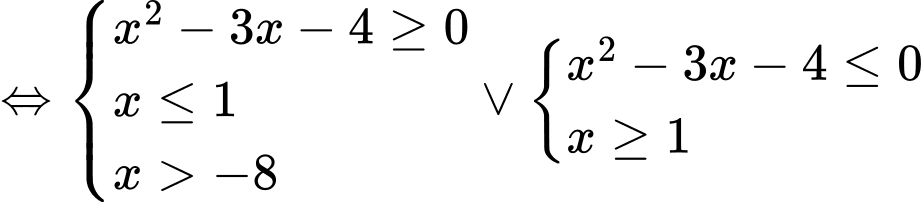
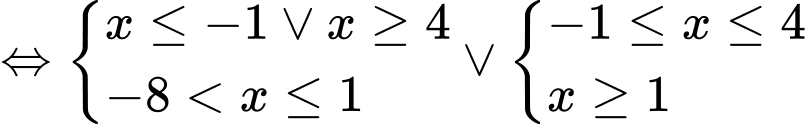
 Mà
Mà 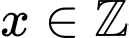 Nên
Nên 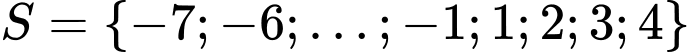
Bất phương trình có 11 nghiệm nguyên.
Đáp án: A
Câu 5 [222132]: Có bao nhiêu số nguyên 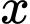 thỏa mãn bất phương trình
thỏa mãn bất phương trình 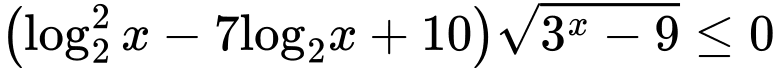 ?
?
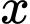 thỏa mãn bất phương trình
thỏa mãn bất phương trình 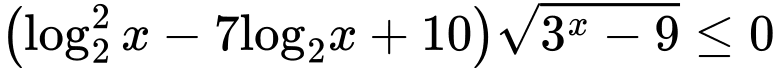 ?
? A, 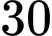 .
.
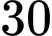 .
.B, 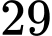 .
.
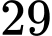 .
.C, 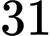 .
.
 .
.D,  .
.
 .
.
Chọn A
Điều kiện: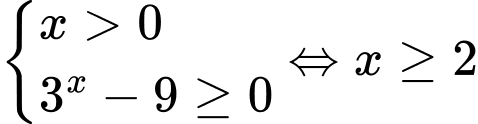 .
.
Ta có: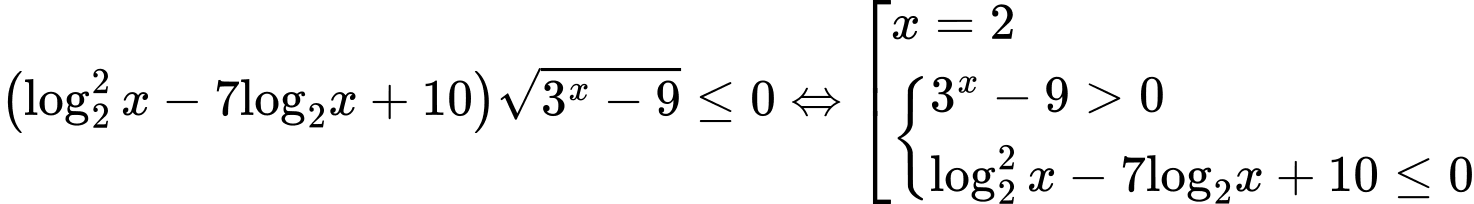
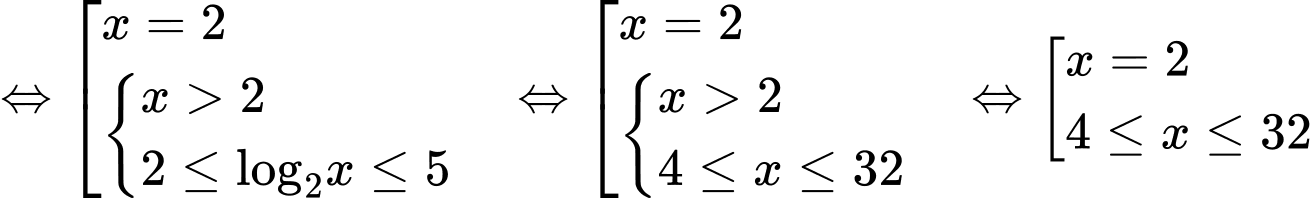
Vậy có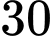 số nguyên
số nguyên 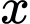 thỏa yêu cầu bài toán. Đáp án: A
thỏa yêu cầu bài toán. Đáp án: A
Điều kiện:
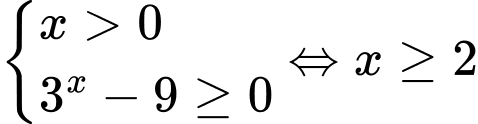 .
.Ta có:
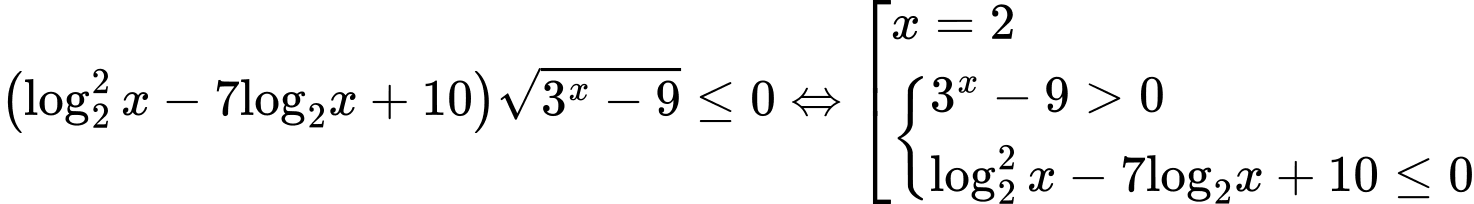
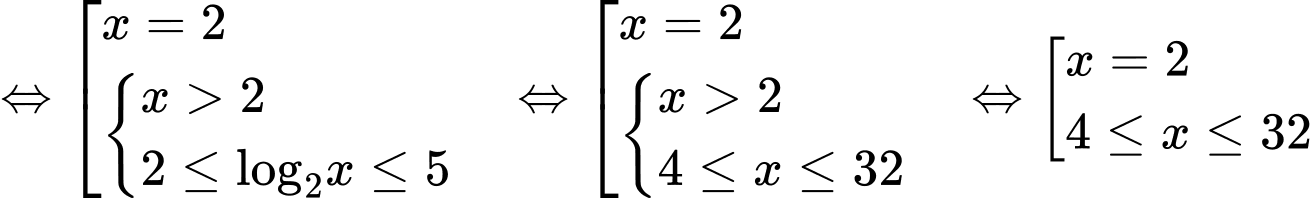
Vậy có
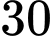 số nguyên
số nguyên 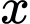 thỏa yêu cầu bài toán. Đáp án: A
thỏa yêu cầu bài toán. Đáp án: A
Câu 6 [184820]: [Câu 39 – Mã 104]: Có bao nhiêu số nguyên 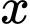 thỏa mãn
thỏa mãn 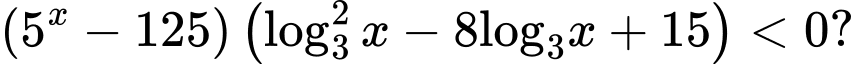
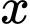 thỏa mãn
thỏa mãn 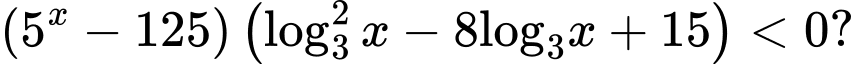
A, 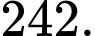
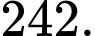
B, 

C, 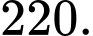
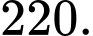
D, 

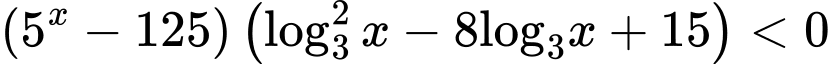
Điều kiện:

Xét:
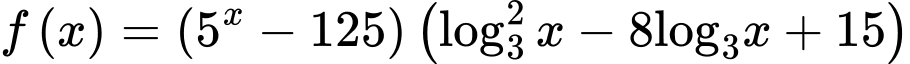
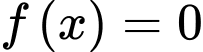
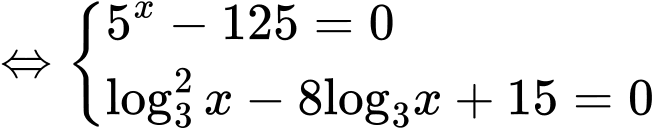
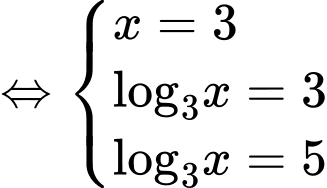
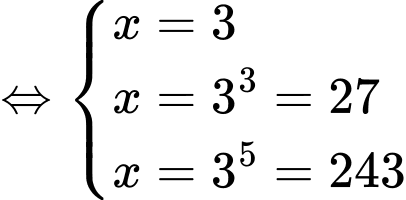

Từ trục số ta thấy,
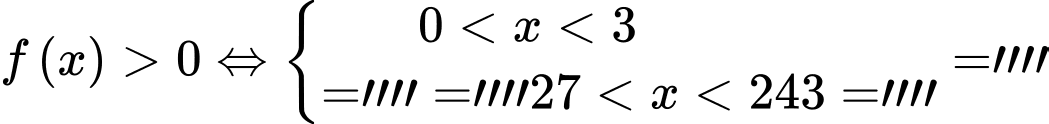 =""
="" 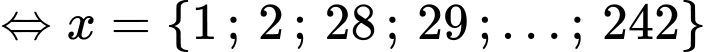
Có
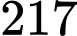 số nguyên
số nguyên 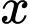 thỏa mãn điều kiện đề bài.
thỏa mãn điều kiện đề bài.
Đáp án: B.
Câu 7 [212390]: Có bao nhiêu số nguyên 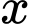 thỏa mãn
thỏa mãn 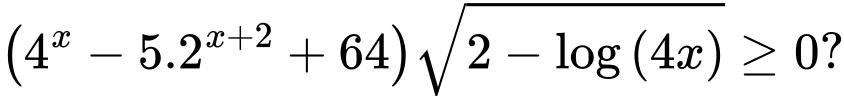
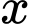 thỏa mãn
thỏa mãn 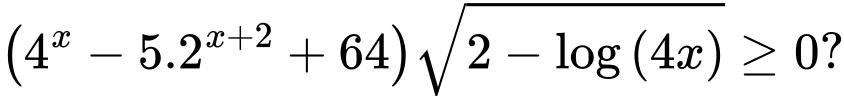
A, 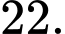
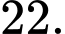
B, 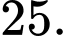
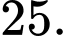
C, 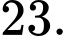
D, 
Chọn D
Điều kiện xác định: 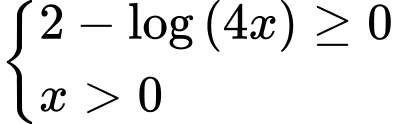
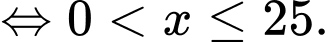
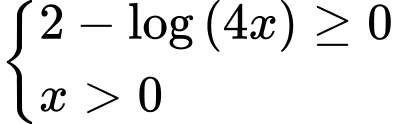
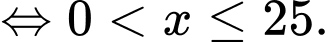
Bpt tương đương
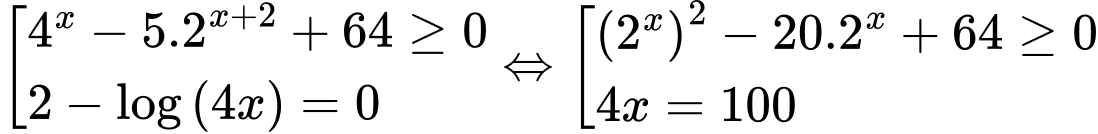
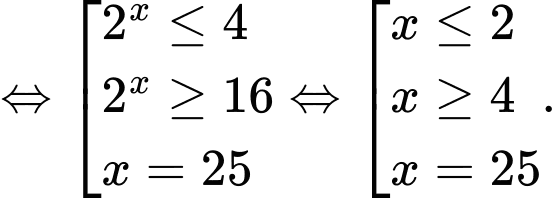
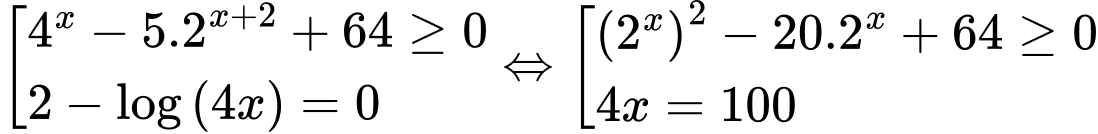
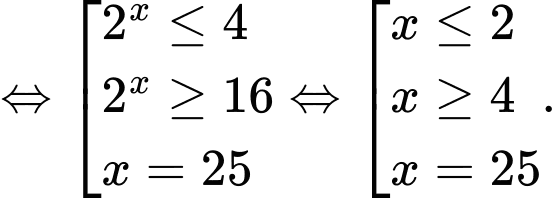
Kết hợp với điều kiện xác định ta được: 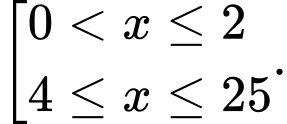
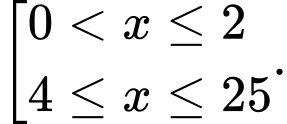
Vậy có 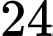 giá trị nguyên của
giá trị nguyên của 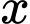 thoả mãn yêu cầu bài toán.
thoả mãn yêu cầu bài toán.
Đáp án: D 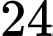 giá trị nguyên của
giá trị nguyên của 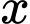 thoả mãn yêu cầu bài toán.
thoả mãn yêu cầu bài toán.
Câu 8 [222895]: Số nghiệm nguyên của bất phương trình 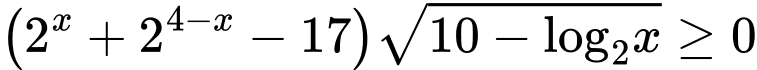 là
là
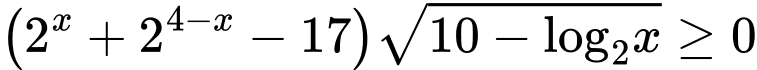 là
là A, 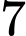 .
.
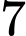 .
.B, 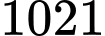 .
.
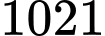 .
.C, 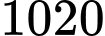 .
.
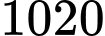 .
.D, 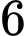 .
.
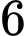 .
.
Chọn B
Điều kiện: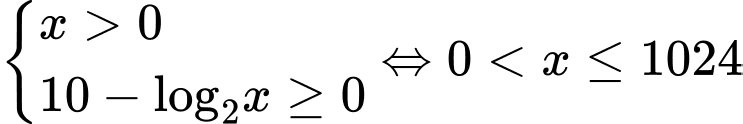 (*). Khi đó ta có 2 trường hợp xảy ra:
(*). Khi đó ta có 2 trường hợp xảy ra:
• TH 1: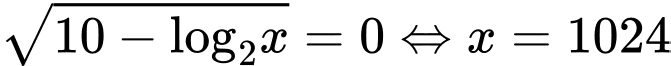 (thoả mãn)
(thoả mãn)
• TH 2: Bất phương trình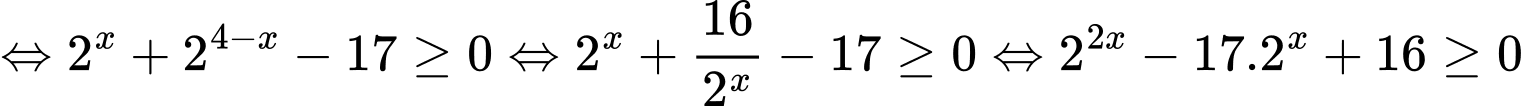
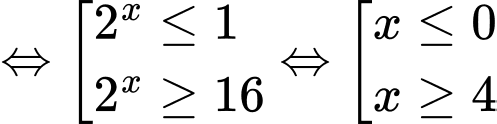 .
.
Kết hợp điều kiện (*) ta được nghiệm .
.
Kết hợp 2 trường hợp ta được tập nghiệm của bất phương trình là .
Vì
.
Vì 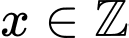 nên
nên 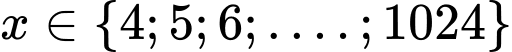 . Vậy có
. Vậy có 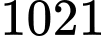 nghiệm nguyên
nghiệm nguyên 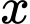 . Đáp án: B
. Đáp án: B
Điều kiện:
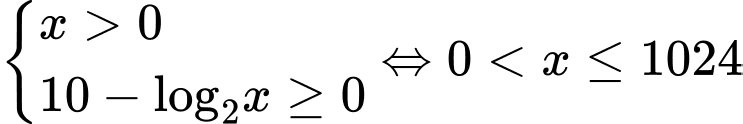 (*). Khi đó ta có 2 trường hợp xảy ra:
(*). Khi đó ta có 2 trường hợp xảy ra:
• TH 1:
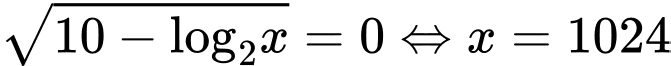 (thoả mãn)
(thoả mãn)
• TH 2: Bất phương trình
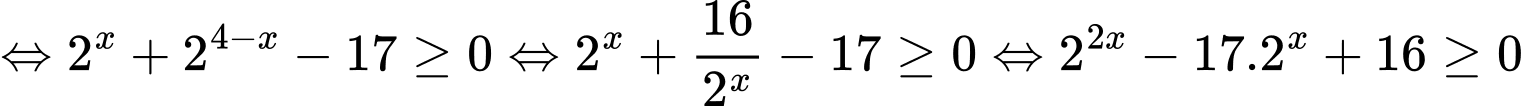
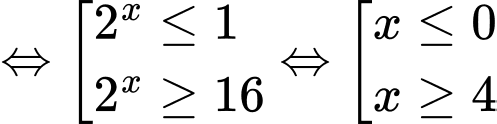 .
.
Kết hợp điều kiện (*) ta được nghiệm
 .
.
Kết hợp 2 trường hợp ta được tập nghiệm của bất phương trình là
 .
Vì
.
Vì 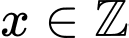 nên
nên 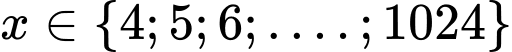 . Vậy có
. Vậy có 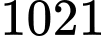 nghiệm nguyên
nghiệm nguyên 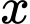 . Đáp án: B
. Đáp án: B
Câu 9 [662479]: Bất phương trình 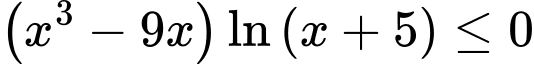 có bao nhiêu nghiệm nguyên?
có bao nhiêu nghiệm nguyên?
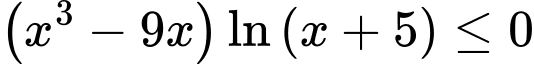 có bao nhiêu nghiệm nguyên?
có bao nhiêu nghiệm nguyên? A, 4.
B, 7.
C, 6.
D, Vô số.
Điều kiện 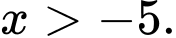 Vì
Vì 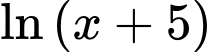 cùng dấu với
cùng dấu với 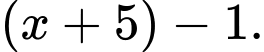
Nên bất phương trình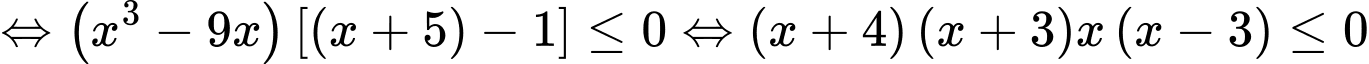
Lập bảng xét dấu cho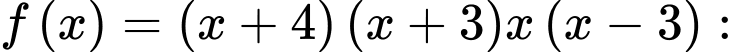
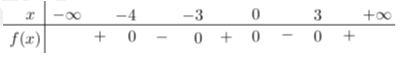
Suy ra
Kết hợp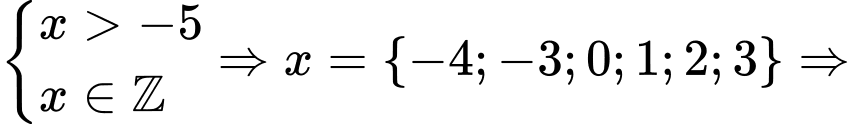 Phương trình có 6 nghiệm nguyên. Chọn C.
Đáp án: C
Phương trình có 6 nghiệm nguyên. Chọn C.
Đáp án: C
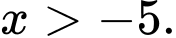 Vì
Vì 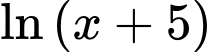 cùng dấu với
cùng dấu với 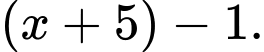
Nên bất phương trình
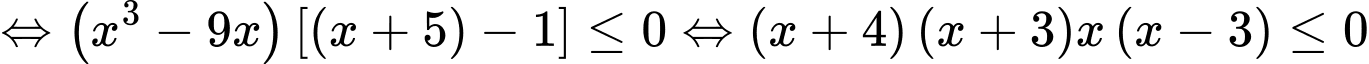
Lập bảng xét dấu cho
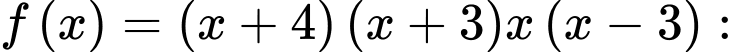
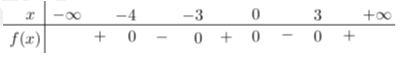
Suy ra

Kết hợp
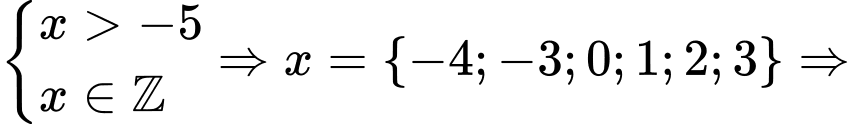 Phương trình có 6 nghiệm nguyên. Chọn C.
Đáp án: C
Phương trình có 6 nghiệm nguyên. Chọn C.
Đáp án: C
Câu 10 [224559]: Tập nghiệm của bất phương trình 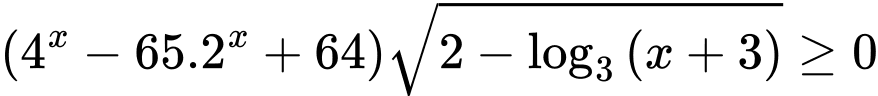 có tất cả bao nhiêu số nguyên?
có tất cả bao nhiêu số nguyên?
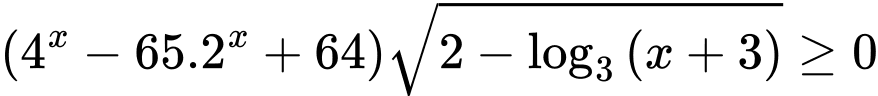 có tất cả bao nhiêu số nguyên?
có tất cả bao nhiêu số nguyên? A, 3.
B, Vô số.
C, 4.
D, 2.
Chọn C
Điều kiện: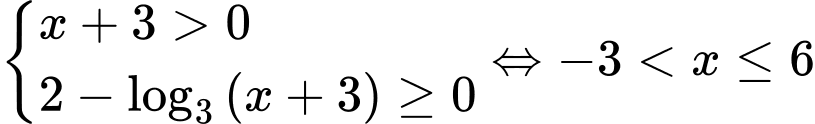 .
.
Ta có: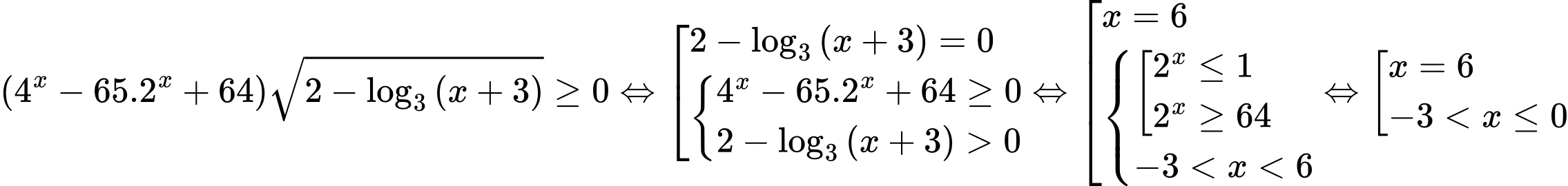 .
.
Tập nghiệm của bất phương trình là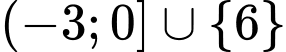 .
.
Có 4 số nguyên thỏa mãn là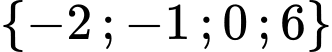 . Đáp án: C
. Đáp án: C
Điều kiện:
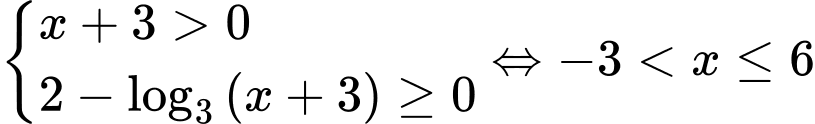 .
.Ta có:
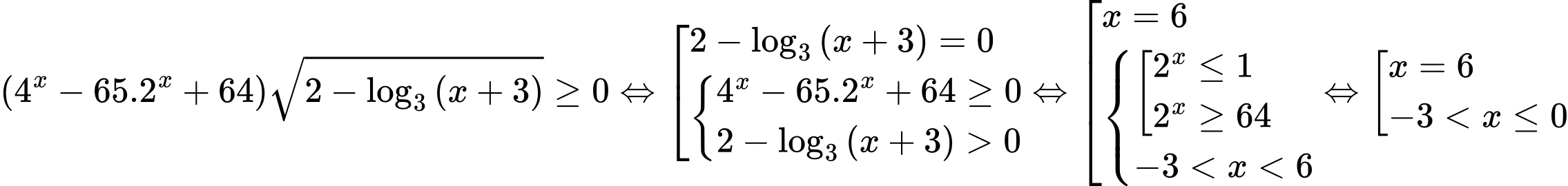 .
.Tập nghiệm của bất phương trình là
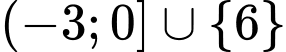 .
.Có 4 số nguyên thỏa mãn là
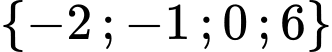 . Đáp án: C
. Đáp án: C
Câu 11 [226707]: Số nghiệm nguyên của bất phương trình 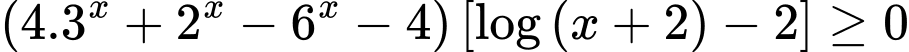 là
là
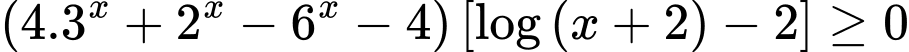 là
là A, 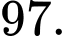
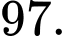
B, 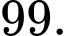
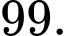
C, 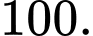
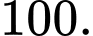
D, 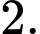
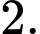
Chọn B
ĐKXĐ: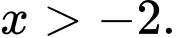
Ta có: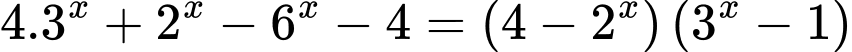 .
.
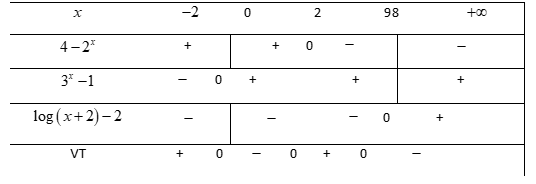
Tập nghiệm của bất phương trình là: ; nghiệm nguyên
; nghiệm nguyên 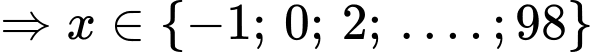 Vậy có 99 giá trị nguyên Đáp án: B
Vậy có 99 giá trị nguyên Đáp án: B
ĐKXĐ:
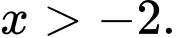
Ta có:
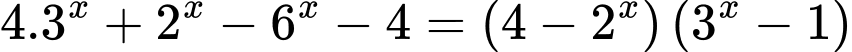 .
.
Tập nghiệm của bất phương trình là:
 ; nghiệm nguyên
; nghiệm nguyên 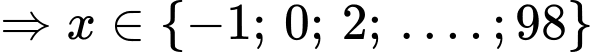 Vậy có 99 giá trị nguyên Đáp án: B
Vậy có 99 giá trị nguyên Đáp án: B
Câu 12 [225147]: Có bao nhiêu số nguyên x thỏa mãn 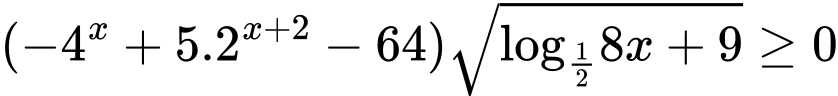 ?
?
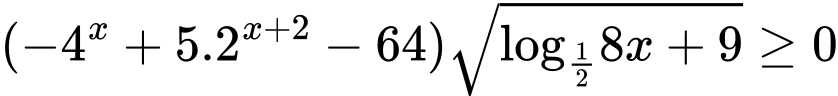 ?
? A,  .
.
 .
.B, 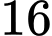 .
.
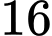 .
.C, 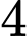 .
.
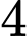 .
.D,  .
.
 .
.
Chọn C
Điều kiện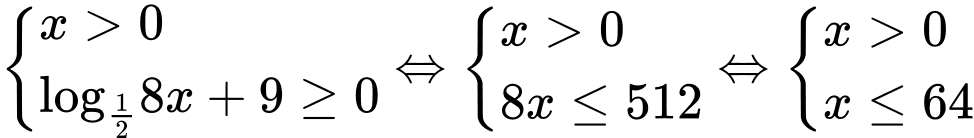 .
.
Ta có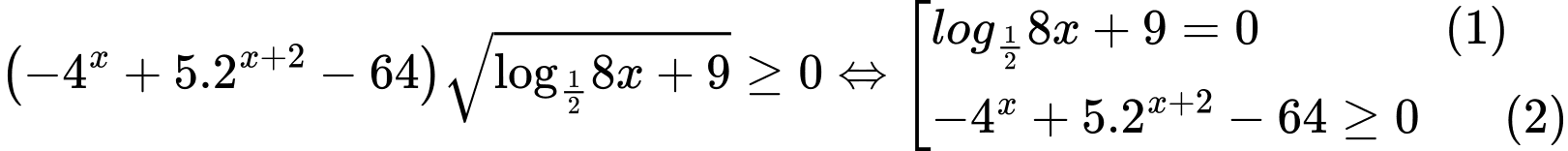
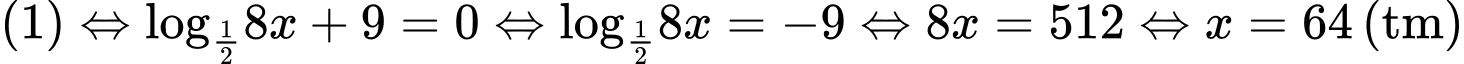 .
. 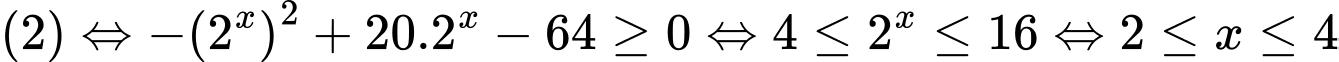 .
.
Kết hợp với điều kiện, ta có các giá trị nguyên thoả mãn là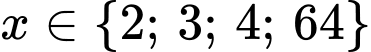 .
.
Vậy có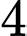 số nguyên
số nguyên 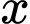 thoả mãn đề bài. Đáp án: C
thoả mãn đề bài. Đáp án: C
Điều kiện
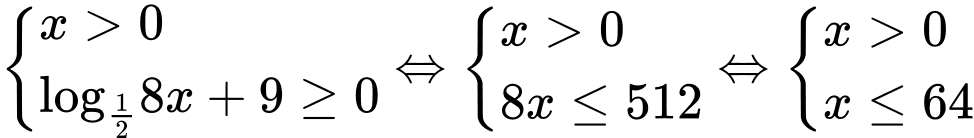 .
.
Ta có
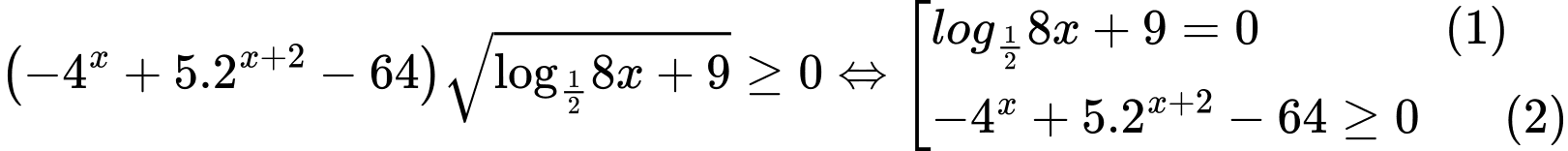
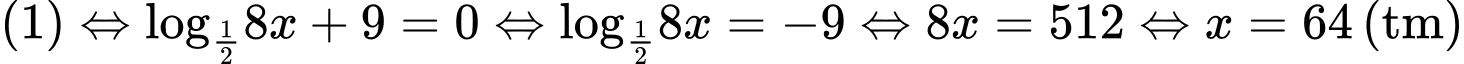 .
. 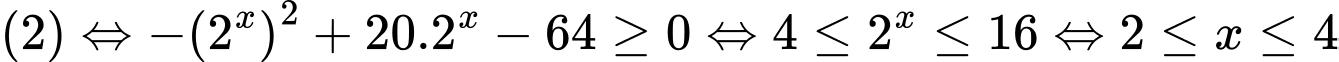 .
.
Kết hợp với điều kiện, ta có các giá trị nguyên thoả mãn là
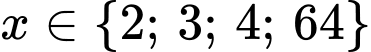 .
.
Vậy có
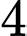 số nguyên
số nguyên 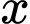 thoả mãn đề bài.
thoả mãn đề bài.
Câu 13 [999336]: Có bao nhiêu số nguyên 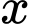 thỏa mãn bất phương trình
thỏa mãn bất phương trình
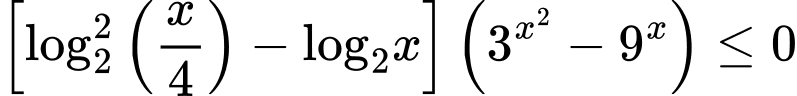
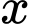 thỏa mãn bất phương trình
thỏa mãn bất phương trình
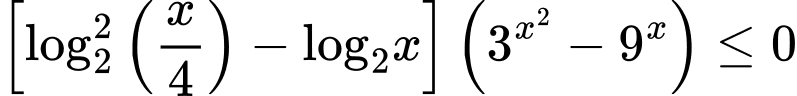
A, 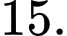
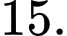
B, vô số.
C, 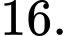
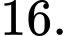
D, 
ĐKXĐ: 
Ta có: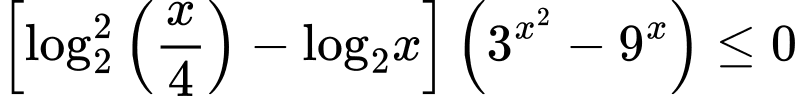
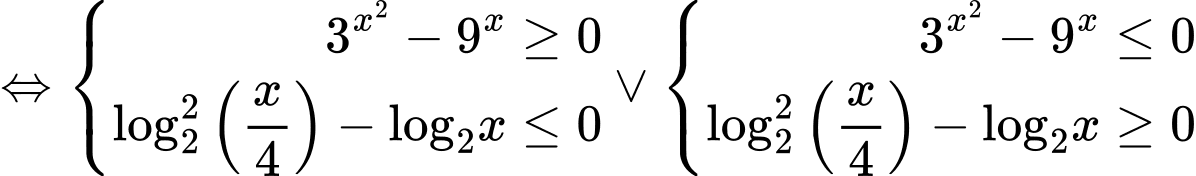
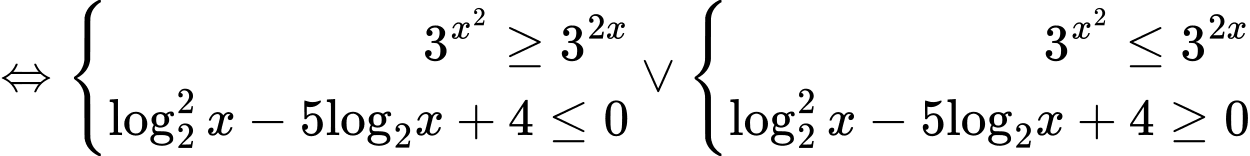
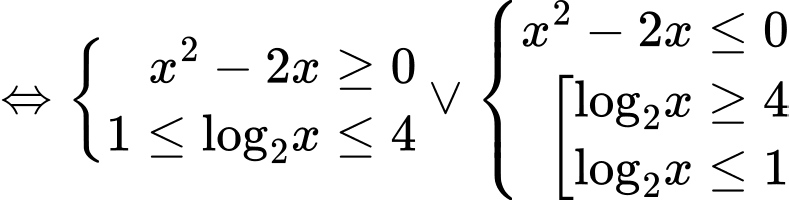
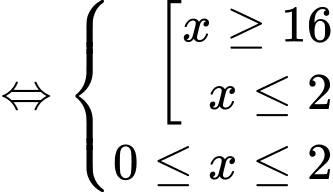
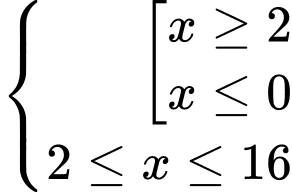
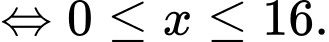
Kết hợp với ĐKXĐ ta có: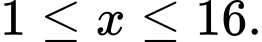
Mà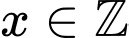 Nên
Nên 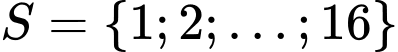
Bất phương trình có 16 nghiệm nguyên. Đáp án: C

Ta có:
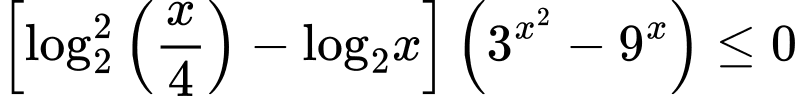
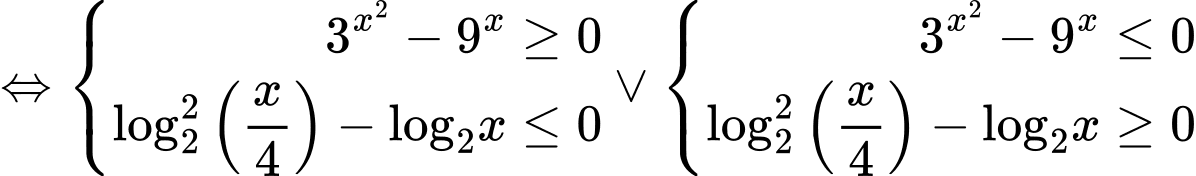
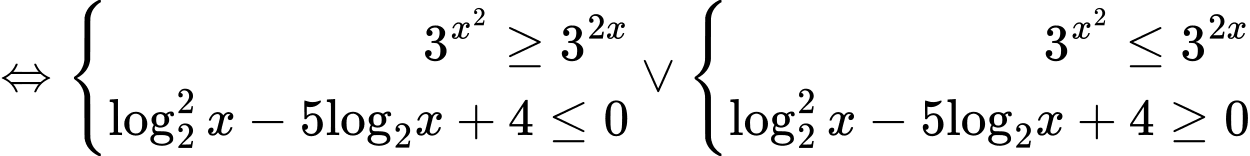
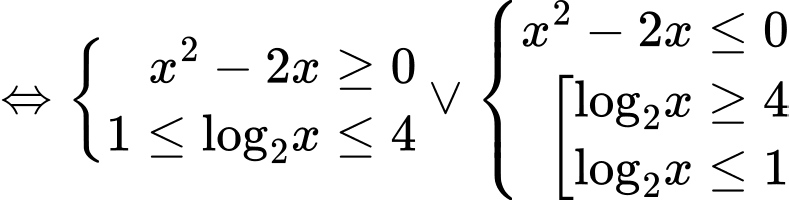
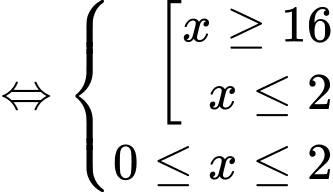
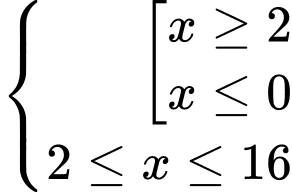
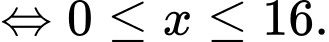
Kết hợp với ĐKXĐ ta có:
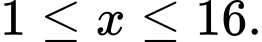
Mà
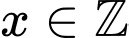 Nên
Nên 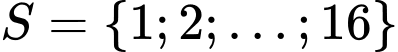
Bất phương trình có 16 nghiệm nguyên. Đáp án: C