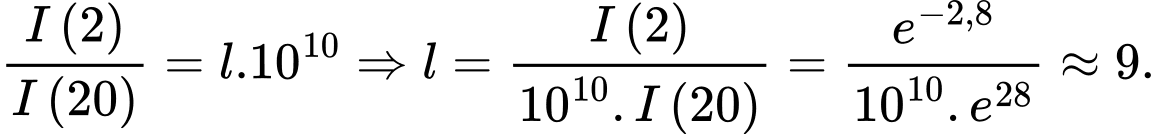Đáp án Bài tập tự luyện số 1
Câu 1 [27593]: Một người gửi 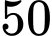 triệu đồng vào ngân hàng theo thể thức lãi kép với lãi suất
triệu đồng vào ngân hàng theo thể thức lãi kép với lãi suất 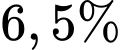 /năm, kì hạn một năm. Hỏi sau
/năm, kì hạn một năm. Hỏi sau  năm người đó rút cả vốn lẫn lãi được số tiền gần với số nào nhất trong các số tiền sau? (Biết lãi suất hàng năm không đổi).
năm người đó rút cả vốn lẫn lãi được số tiền gần với số nào nhất trong các số tiền sau? (Biết lãi suất hàng năm không đổi).
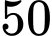 triệu đồng vào ngân hàng theo thể thức lãi kép với lãi suất
triệu đồng vào ngân hàng theo thể thức lãi kép với lãi suất 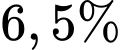 /năm, kì hạn một năm. Hỏi sau
/năm, kì hạn một năm. Hỏi sau 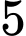 năm người đó rút cả vốn lẫn lãi được số tiền gần với số nào nhất trong các số tiền sau? (Biết lãi suất hàng năm không đổi).
năm người đó rút cả vốn lẫn lãi được số tiền gần với số nào nhất trong các số tiền sau? (Biết lãi suất hàng năm không đổi). A, 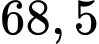 triệu đồng.
triệu đồng.
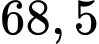 triệu đồng.
triệu đồng.B, 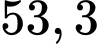 triệu đồng.
triệu đồng.
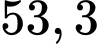 triệu đồng.
triệu đồng.C, 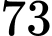 triệu đồng.
triệu đồng.
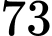 triệu đồng.
triệu đồng.D, 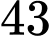 triệu đồng.
triệu đồng.
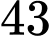 triệu đồng.
triệu đồng. Đáp án: A
Đáp án: A
Câu 2 [981664]: Một người gửi 50 triệu đồng vào một ngân hàng với lãi suất 6%/năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm người đó nhận được số tiền bao gồm cả gốc và lãi nhiều hơn 100 triệu đồng? Giả định trong suốt thời gian thì lãi suất không đổi và người đó không rút tiền ra.
A, 13 năm.
B, 12 năm.
C, 14 năm.
D, 11 năm.
Gọi  là số năm cần để có hơn 100 triệu đồng.
là số năm cần để có hơn 100 triệu đồng.
Suy ra năm.
năm.
Chọn B. Đáp án: B
 là số năm cần để có hơn 100 triệu đồng.
là số năm cần để có hơn 100 triệu đồng.
Suy ra
 năm.
năm.
Chọn B. Đáp án: B
Câu 3 [132929]: Một người gửi tiết kiệm vào một ngân hàng với lãi suất 7,5%/năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn để tính lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm người đó thu được (cả tiền gửi ban đầu và lãi) gấp đôi số tiền gửi ban đầu, giả định trong khoảng thời gian này lãi suất không thay đổi và người đó không rút tiền ra?
A,  năm.
năm.
 năm.
năm.B, 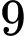 năm.
năm.
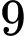 năm.
năm.C,  năm.
năm.
 năm.
năm.D,  năm.
năm.
 năm.
năm.
Áp dụng công thức 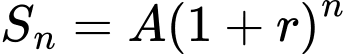
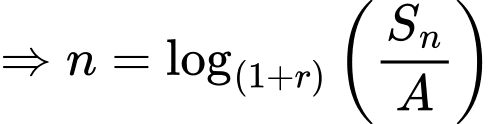
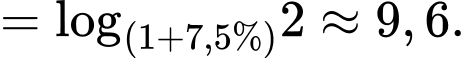 Chọn C. Đáp án: C
Chọn C. Đáp án: C
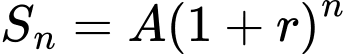
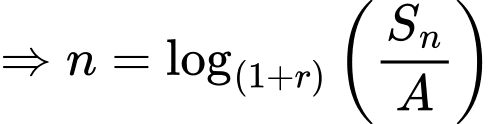
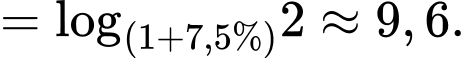 Chọn C. Đáp án: C
Chọn C. Đáp án: C
Câu 4 [27630]: Anh An gửi số tiền 58 triệu đồng vào một ngân hàng theo hình thức lãi kép và ổn định trong 9 tháng thì lĩnh về được 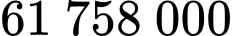 đồng. Hỏi lãi suất ngân hàng hàng tháng là bao nhiêu? Biết rằng lãi suất không thay đổi trong thời gian gửi.
đồng. Hỏi lãi suất ngân hàng hàng tháng là bao nhiêu? Biết rằng lãi suất không thay đổi trong thời gian gửi.
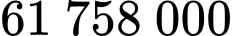 đồng. Hỏi lãi suất ngân hàng hàng tháng là bao nhiêu? Biết rằng lãi suất không thay đổi trong thời gian gửi.
đồng. Hỏi lãi suất ngân hàng hàng tháng là bao nhiêu? Biết rằng lãi suất không thay đổi trong thời gian gửi. A, 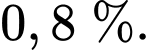
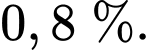
B, 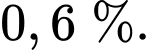
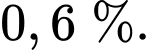
C, 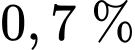 .
.
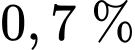 .
.D, 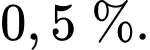
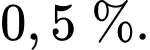
 Đáp án: C
Đáp án: C
Câu 5 [27617]: Ông A gửi vào ngân hàng 50 triệu đồng với lãi suất 0,5%/tháng. Hỏi sau ít nhất bao nhiêu tháng thì ông A có được số tiền cả gốc lẫn lãi nhiều hơn 60 triệu đồng? Biết rằng trong suốt thời gian gửi, lãi suất ngân hàng không đổi và ông A không rút tiền ra.
A, 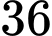 tháng.
tháng.
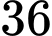 tháng.
tháng.B, 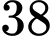 tháng.
tháng.
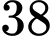 tháng.
tháng.C, 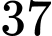 tháng.
tháng.
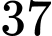 tháng.
tháng.D, 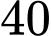 tháng.
tháng.
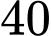 tháng.
tháng. Đáp án: C
Đáp án: C
Câu 6 [27679]: Bà X gửi 100 triệu vào ngân hàng theo hình thức lãi kép (đến kì hạn mà người gửi không rút lãi ra thì tiền lãi được tính vào vốn của kì kế tiếp) với lãi suất 7% một năm. Hỏi sau 2 năm bà X thu được lãi là bao nhiêu (Giả sử lãi suất không thay đổi)?
A, 14,50 triệu đồng.
B, 20 triệu đồng.
C, 15 triệu đồng.
D, 14,49 triệu đồng.
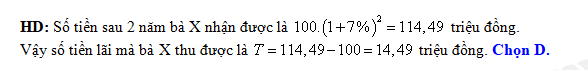 Đáp án: D
Đáp án: D
Câu 7 [27738]: Một người gửi vào ngân hàng theo hình thức lãi kép với lãi suất 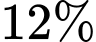 một năm, kỳ hạn
một năm, kỳ hạn 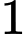 tháng. Hỏi sau bao nhiêu lâu, số tiền trong tài khoản của người đó gấp
tháng. Hỏi sau bao nhiêu lâu, số tiền trong tài khoản của người đó gấp 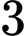 lần số tiền ban đầu?
lần số tiền ban đầu?
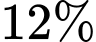 một năm, kỳ hạn
một năm, kỳ hạn 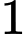 tháng. Hỏi sau bao nhiêu lâu, số tiền trong tài khoản của người đó gấp
tháng. Hỏi sau bao nhiêu lâu, số tiền trong tài khoản của người đó gấp 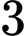 lần số tiền ban đầu?
lần số tiền ban đầu? A, 12 năm 5 tháng.
B, 9 năm 3 tháng.
C, 11 năm.
D, 10 năm 2 tháng.
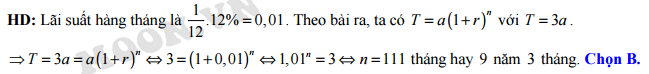 Đáp án: B
Đáp án: B
Câu 8 [27854]: Ông Việt dự định gửi vào ngân hàng một số tiền với lãi suất 6,5 % một năm. Biết rằng, cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn ban đầu. Tính số tiền tối thiểu 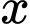 (triệu đồng
(triệu đồng 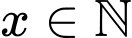 ) ông Việt gửi vào ngân hàng để sau 3 năm số tiền lãi đủ mua một chiếc xe gắn máy trị giá 30 triệu đồng.
) ông Việt gửi vào ngân hàng để sau 3 năm số tiền lãi đủ mua một chiếc xe gắn máy trị giá 30 triệu đồng.
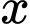 (triệu đồng
(triệu đồng 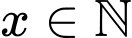 ) ông Việt gửi vào ngân hàng để sau 3 năm số tiền lãi đủ mua một chiếc xe gắn máy trị giá 30 triệu đồng.
) ông Việt gửi vào ngân hàng để sau 3 năm số tiền lãi đủ mua một chiếc xe gắn máy trị giá 30 triệu đồng. A, 150 triệu đồng.
B, 154 triệu đồng.
C, 145 triệu đồng.
D, 140 triệu đồng.
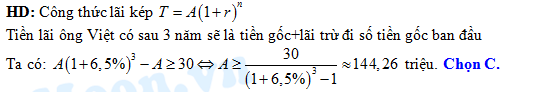 Đáp án: C
Đáp án: C
Câu 9 [27912]: Đầu năm 2016, ông A thành lập một công ty. Tổng số tiền ông A dùng để trả lương cho nhân viên trong năm 2016 là 1 tỷ đồng. Biết rằng biết sau mỗi năm thì số tiền dùng để trả cho nhân viên trong cả năm đó tăng thêm 15% so với năm trước. Hỏi năm nào dưới đây là năm đầu tiên mà tổng số tiền ông A dùng để trả lương cho nhân viên trong cả năm lớn hơn 2 tỷ đồng?
A, Năm 2022.
B, Năm 2021.
C, Năm 2020.
D, Năm 2023.
HD: Số tiền mà ông A phải trả cho nhân viên sau năm thứ n là 1.(1+15\%) tỷ đồng.
Theo bài ra, ta có
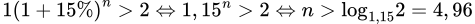
Vậy năm đầu tiên mà tổng số tiền ông A dùng để trả lớn hơn 2 tỷ đồng là 2016+5=2021. Chọn B.
Đáp án: B
Câu 10 [27920]: Số lượng của một số loài vi khuẩn sau 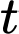 (giờ) được xấp xỉ bởi đẳng thức
(giờ) được xấp xỉ bởi đẳng thức 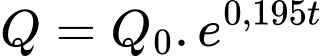 , trong đó
, trong đó 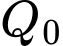 là số lượng vi khuẩn ban đầu. Nếu số lượng vi khuẩn đầu là 5000 con thì sau bao lâu có 100.000 con.
là số lượng vi khuẩn ban đầu. Nếu số lượng vi khuẩn đầu là 5000 con thì sau bao lâu có 100.000 con.
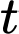 (giờ) được xấp xỉ bởi đẳng thức
(giờ) được xấp xỉ bởi đẳng thức 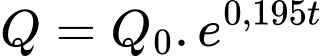 , trong đó
, trong đó 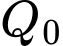 là số lượng vi khuẩn ban đầu. Nếu số lượng vi khuẩn đầu là 5000 con thì sau bao lâu có 100.000 con.
là số lượng vi khuẩn ban đầu. Nếu số lượng vi khuẩn đầu là 5000 con thì sau bao lâu có 100.000 con. A, 24 giờ.
B, 3,55 giờ.
C, 20 giờ.
D, 15,36 giờ.
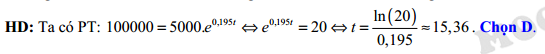 Đáp án: D
Đáp án: D
Câu 11 [27602]: Độ 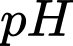 của một dung dịch được tính theo công thức
của một dung dịch được tính theo công thức 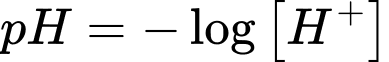 , với
, với 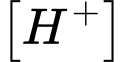 là nồng độ ion
là nồng độ ion 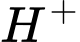 trong dung dịch đó. Cho dung dịch
trong dung dịch đó. Cho dung dịch 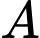 có độ
có độ 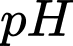 ban đầu bằng 6. Nếu nồng độ ion
ban đầu bằng 6. Nếu nồng độ ion 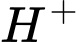 trong dung dịch
trong dung dịch 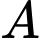 tăng lên 4 lần thì độ
tăng lên 4 lần thì độ 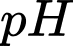 trong dung dịch mới gần bằng giá trị nào dưới đây?
trong dung dịch mới gần bằng giá trị nào dưới đây?
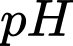 của một dung dịch được tính theo công thức
của một dung dịch được tính theo công thức 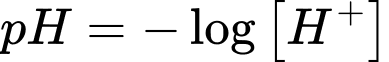 , với
, với 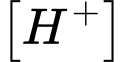 là nồng độ ion
là nồng độ ion 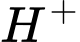 trong dung dịch đó. Cho dung dịch
trong dung dịch đó. Cho dung dịch  có độ
có độ 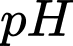 ban đầu bằng 6. Nếu nồng độ ion
ban đầu bằng 6. Nếu nồng độ ion 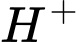 trong dung dịch
trong dung dịch 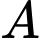 tăng lên 4 lần thì độ
tăng lên 4 lần thì độ 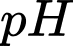 trong dung dịch mới gần bằng giá trị nào dưới đây?
trong dung dịch mới gần bằng giá trị nào dưới đây? A, 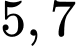 .
.
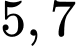 .
.B, 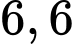 .
.
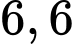 .
.C, 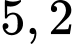 .
.
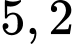 .
.D, 5,4
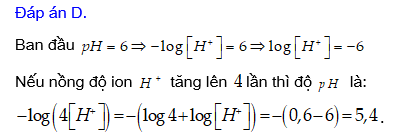 Đáp án: D
Đáp án: D
Câu 12 [29285]: Một trận động đất có cường độ 8,5 richter có biên độ mạnh gấp mấy lần biên độ của một trận động đất có cường độ 6,5 richter? Biết rằng cường độ một trận động đất  được cho bởi công thức
được cho bởi công thức 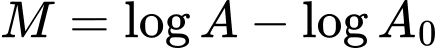 , đơn vị richter với
, đơn vị richter với 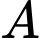 là biên độ rung chấn tối đa và
là biên độ rung chấn tối đa và 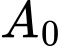 là biên độ chuẩn (hằng số).
là biên độ chuẩn (hằng số).
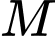 được cho bởi công thức
được cho bởi công thức 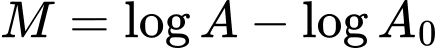 , đơn vị richter với
, đơn vị richter với 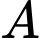 là biên độ rung chấn tối đa và
là biên độ rung chấn tối đa và 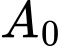 là biên độ chuẩn (hằng số).
là biên độ chuẩn (hằng số). A, 1000 lần.
B, 100 lần.
C, 2 lần.
D, 1024 lần.
Ta có: 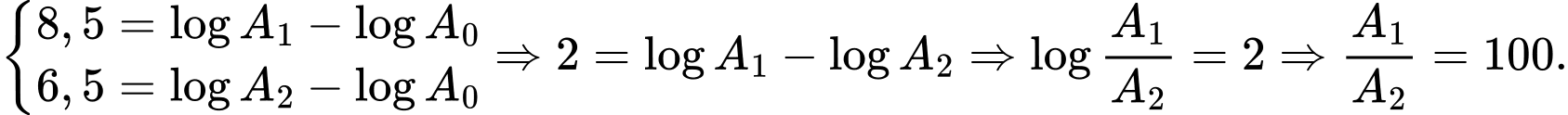
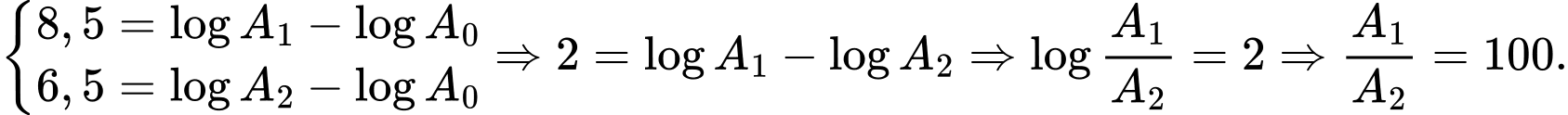
Chọn đáp án B.
Đáp án: B
Câu 13 [29277]: Cường độ một trận động đất M được cho bởi công thức 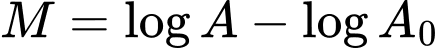 , đơn vị richter với
, đơn vị richter với 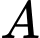 là biên độ rung chấn tối đa và
là biên độ rung chấn tối đa và 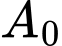 là biên độ chuẩn (hằng số). Vào tháng 2 năm 2010, một trận động đất ở Chile có cường độ 8,8 độ rrichter. Biết rằng trận động đất năm 2004 gây ra sóng thần tại Bắc Sumatra, Indonexia ngày 26.12.2004 có biên độ rung chấn manh gấp 3,26 lần so với biên độ rung chấn tối đa của trận động đất Chile. Tính cường độ trận động đất ở Bắc Sumatra.
là biên độ chuẩn (hằng số). Vào tháng 2 năm 2010, một trận động đất ở Chile có cường độ 8,8 độ rrichter. Biết rằng trận động đất năm 2004 gây ra sóng thần tại Bắc Sumatra, Indonexia ngày 26.12.2004 có biên độ rung chấn manh gấp 3,26 lần so với biên độ rung chấn tối đa của trận động đất Chile. Tính cường độ trận động đất ở Bắc Sumatra.
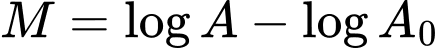 , đơn vị richter với
, đơn vị richter với 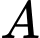 là biên độ rung chấn tối đa và
là biên độ rung chấn tối đa và 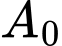 là biên độ chuẩn (hằng số). Vào tháng 2 năm 2010, một trận động đất ở Chile có cường độ 8,8 độ rrichter. Biết rằng trận động đất năm 2004 gây ra sóng thần tại Bắc Sumatra, Indonexia ngày 26.12.2004 có biên độ rung chấn manh gấp 3,26 lần so với biên độ rung chấn tối đa của trận động đất Chile. Tính cường độ trận động đất ở Bắc Sumatra.
là biên độ chuẩn (hằng số). Vào tháng 2 năm 2010, một trận động đất ở Chile có cường độ 8,8 độ rrichter. Biết rằng trận động đất năm 2004 gây ra sóng thần tại Bắc Sumatra, Indonexia ngày 26.12.2004 có biên độ rung chấn manh gấp 3,26 lần so với biên độ rung chấn tối đa của trận động đất Chile. Tính cường độ trận động đất ở Bắc Sumatra. A, 9,3 độ richter.
B, 9,2 độ richter.
C, 9,1 độ richter.
D, 9,4 độ richter.
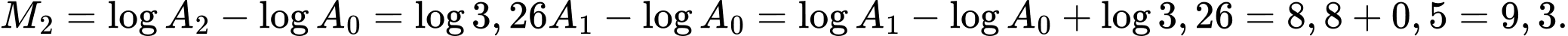
Chọn đáp án A.
Đáp án: A
Câu 14 [27836]: Một điện thoại đang nạp pin, dung lượng nạp được tính theo công thức 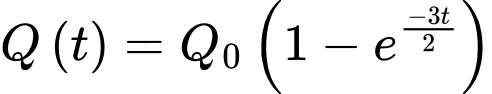 , với
, với 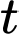 là khoảng thời gian tính bằng giờ và
là khoảng thời gian tính bằng giờ và 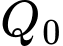 là dung lượng nạp tối đa (pin đầy). Nếu điện thoại nạp pin từ lúc cạn pin (tức là dung lượng pin lúc bắt đầu nạp là
là dung lượng nạp tối đa (pin đầy). Nếu điện thoại nạp pin từ lúc cạn pin (tức là dung lượng pin lúc bắt đầu nạp là  ) thì bao lâu sau sẽ nạp được
) thì bao lâu sau sẽ nạp được 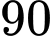 (kết quả làm tròn đến hàng phần trăm)?
(kết quả làm tròn đến hàng phần trăm)?
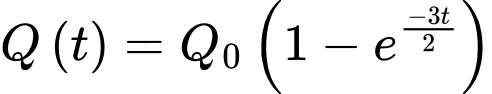 , với
, với  là khoảng thời gian tính bằng giờ và
là khoảng thời gian tính bằng giờ và  là dung lượng nạp tối đa (pin đầy). Nếu điện thoại nạp pin từ lúc cạn pin (tức là dung lượng pin lúc bắt đầu nạp là
là dung lượng nạp tối đa (pin đầy). Nếu điện thoại nạp pin từ lúc cạn pin (tức là dung lượng pin lúc bắt đầu nạp là  ) thì bao lâu sau sẽ nạp được
) thì bao lâu sau sẽ nạp được  (kết quả làm tròn đến hàng phần trăm)?
(kết quả làm tròn đến hàng phần trăm)? A, 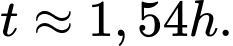
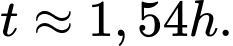
B, 
C, 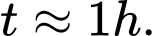
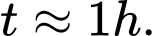
D, 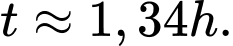
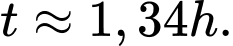
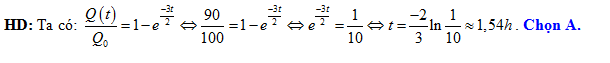 Đáp án: A
Đáp án: A
Câu 15 [28922]: Một sóng âm truyền trong không khí với mức cường độ âm được tính theo công thức 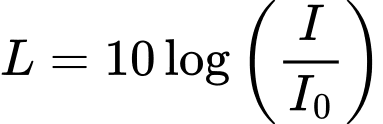 , đợi vị đề xi ben
, đợi vị đề xi ben 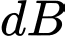 , trong đó
, trong đó 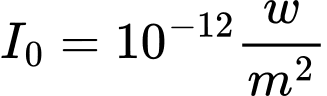 là cường độ ẩm chuẩn. Mức cường độ âm tại điểm
là cường độ ẩm chuẩn. Mức cường độ âm tại điểm 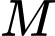 và tại điểm
và tại điểm 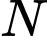 lần lượt là
lần lượt là 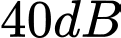 và
và 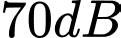 . Cường độ âm tại
. Cường độ âm tại 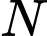 lớn hơn cường độ âm tại
lớn hơn cường độ âm tại 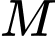 bao nhiêu lần?
bao nhiêu lần?
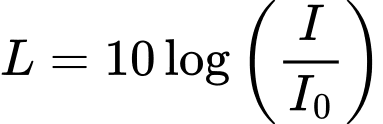 , đợi vị đề xi ben
, đợi vị đề xi ben 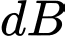 , trong đó
, trong đó 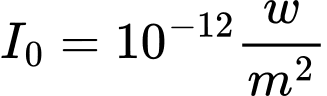 là cường độ ẩm chuẩn. Mức cường độ âm tại điểm
là cường độ ẩm chuẩn. Mức cường độ âm tại điểm 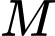 và tại điểm
và tại điểm 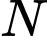 lần lượt là
lần lượt là 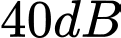 và
và 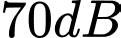 . Cường độ âm tại
. Cường độ âm tại 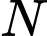 lớn hơn cường độ âm tại
lớn hơn cường độ âm tại 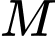 bao nhiêu lần?
bao nhiêu lần? A, 10000 lần.
B, 1000 lần.
C, 40 lần.
D, 20 lần.
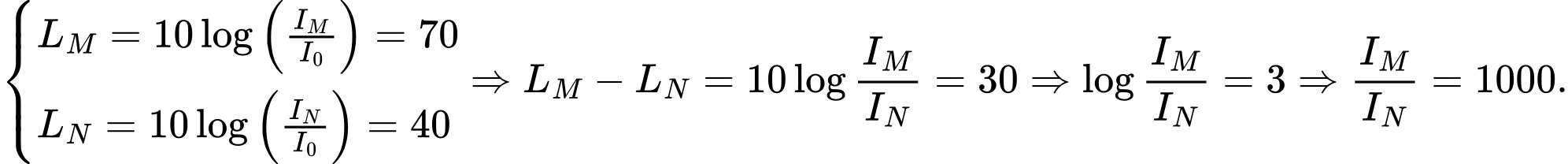 Chọn đáp án B.
Đáp án: B
Chọn đáp án B.
Đáp án: B
Câu 16 [27780]: Theo số liệu của Tổng cục thống kế, năm 2016 dân số Việt Nam ước tính khoảng 94.444.200 người. Tỉ lệ tăng dân số hàng năm ở Việt Nam được duy trì ở mức 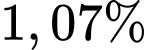 . Cho biết sự tăng dân số được tính theo công thức
. Cho biết sự tăng dân số được tính theo công thức 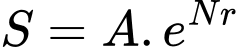 (trong đó
(trong đó 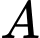 là dân số của năm lấy làm mốc tính,
là dân số của năm lấy làm mốc tính, 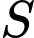 là dân số sau
là dân số sau 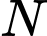 năm,
năm, 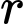 là tỉ lệ tăng dân số hàng năm). Cứ tăng dân số với tỉ lệ như vậy thì đến năm nào dân số nước ta ở mức 120 triệu người
là tỉ lệ tăng dân số hàng năm). Cứ tăng dân số với tỉ lệ như vậy thì đến năm nào dân số nước ta ở mức 120 triệu người
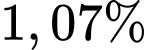 . Cho biết sự tăng dân số được tính theo công thức
. Cho biết sự tăng dân số được tính theo công thức 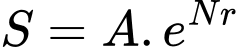 (trong đó
(trong đó 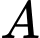 là dân số của năm lấy làm mốc tính,
là dân số của năm lấy làm mốc tính, 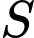 là dân số sau
là dân số sau 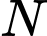 năm,
năm, 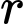 là tỉ lệ tăng dân số hàng năm). Cứ tăng dân số với tỉ lệ như vậy thì đến năm nào dân số nước ta ở mức 120 triệu người
là tỉ lệ tăng dân số hàng năm). Cứ tăng dân số với tỉ lệ như vậy thì đến năm nào dân số nước ta ở mức 120 triệu người A, 2040.
B, 2037.
C, 2038.
D, 2039.
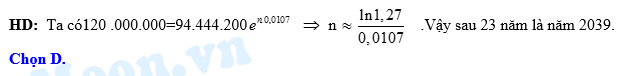 Đáp án: D
Đáp án: D
Câu 17 [27814]: Một người thả một lá bèo vào một cái ao, sau 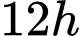 thì bèo sinh sôi phủ kín mặt ao. Hỏi sau mấy giờ thì bèo phủ kín
thì bèo sinh sôi phủ kín mặt ao. Hỏi sau mấy giờ thì bèo phủ kín 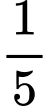 mặt ao, biết rằng sau mỗi giờ thì lượng bèo tăng gấp 10 lần lượng bèo trước đó và tốc độ tăng không đổi.
mặt ao, biết rằng sau mỗi giờ thì lượng bèo tăng gấp 10 lần lượng bèo trước đó và tốc độ tăng không đổi.
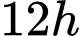 thì bèo sinh sôi phủ kín mặt ao. Hỏi sau mấy giờ thì bèo phủ kín
thì bèo sinh sôi phủ kín mặt ao. Hỏi sau mấy giờ thì bèo phủ kín 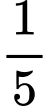 mặt ao, biết rằng sau mỗi giờ thì lượng bèo tăng gấp 10 lần lượng bèo trước đó và tốc độ tăng không đổi.
mặt ao, biết rằng sau mỗi giờ thì lượng bèo tăng gấp 10 lần lượng bèo trước đó và tốc độ tăng không đổi. A, 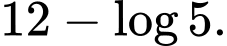
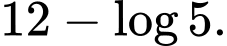
B, 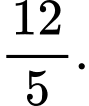
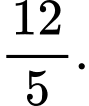
C, 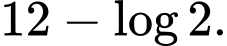
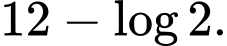
D, 

Ta có: 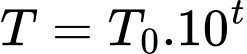 , khi đó sau 12 giờ lượng bèo sẽ là
, khi đó sau 12 giờ lượng bèo sẽ là 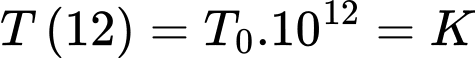
(trong đó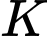 là lượng bèo phủ kín mặt hồ).
là lượng bèo phủ kín mặt hồ).
Gọi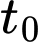 là thời gian bèo phủ
là thời gian bèo phủ 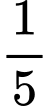 mặt hồ thì ta có:
mặt hồ thì ta có: 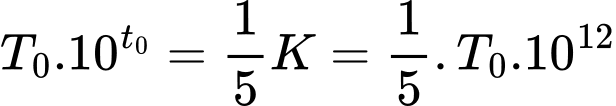
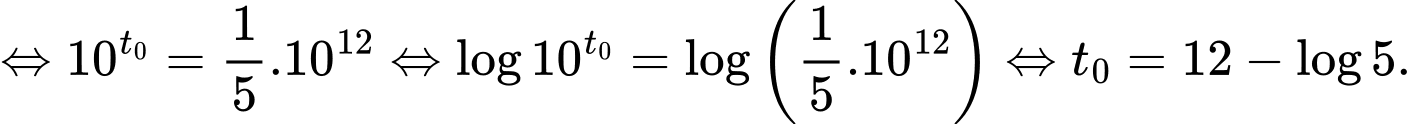 Chọn A. Đáp án: A
Chọn A. Đáp án: A
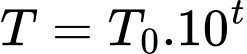 , khi đó sau 12 giờ lượng bèo sẽ là
, khi đó sau 12 giờ lượng bèo sẽ là 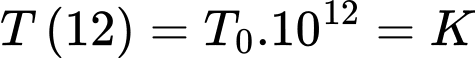
(trong đó
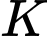 là lượng bèo phủ kín mặt hồ).
là lượng bèo phủ kín mặt hồ).
Gọi
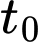 là thời gian bèo phủ
là thời gian bèo phủ 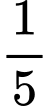 mặt hồ thì ta có:
mặt hồ thì ta có: 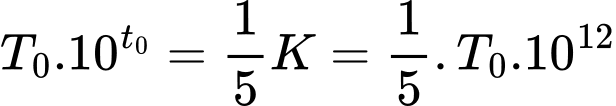
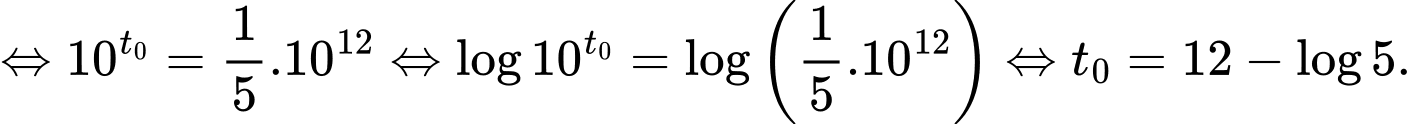 Chọn A. Đáp án: A
Chọn A. Đáp án: A
Câu 18 [27756]: Sự tăng trưởng của một loại vi khuẩn theo công thức 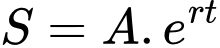 , trong đó
, trong đó 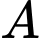 là số lượng vi khuẩn ban đầu,
là số lượng vi khuẩn ban đầu, 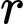 là tỉ lệ tăng trưởng
là tỉ lệ tăng trưởng 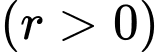 ,
, 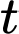 là thời gian tăng trưởng. Biết số lượng vi khuẩn ban đầu là 100 con và sau 5 giờ là 300 con. Khi đó sau thời gian bao lâu thì số lượng vi khuẩn tăng gấp 10 lần so với số lượng ban đầu
là thời gian tăng trưởng. Biết số lượng vi khuẩn ban đầu là 100 con và sau 5 giờ là 300 con. Khi đó sau thời gian bao lâu thì số lượng vi khuẩn tăng gấp 10 lần so với số lượng ban đầu
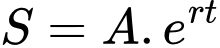 , trong đó
, trong đó 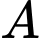 là số lượng vi khuẩn ban đầu,
là số lượng vi khuẩn ban đầu, 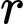 là tỉ lệ tăng trưởng
là tỉ lệ tăng trưởng 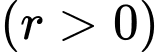 ,
, 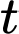 là thời gian tăng trưởng. Biết số lượng vi khuẩn ban đầu là 100 con và sau 5 giờ là 300 con. Khi đó sau thời gian bao lâu thì số lượng vi khuẩn tăng gấp 10 lần so với số lượng ban đầu
là thời gian tăng trưởng. Biết số lượng vi khuẩn ban đầu là 100 con và sau 5 giờ là 300 con. Khi đó sau thời gian bao lâu thì số lượng vi khuẩn tăng gấp 10 lần so với số lượng ban đầu A, 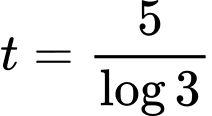 (giờ).
(giờ).
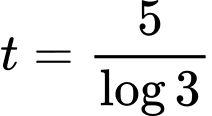 (giờ).
(giờ).B, 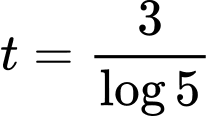 (giờ).
(giờ).
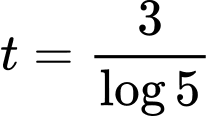 (giờ).
(giờ).C, 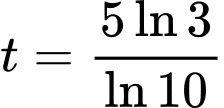 (giờ).
(giờ).
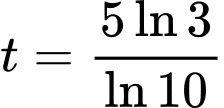 (giờ).
(giờ).D, 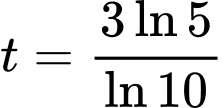 (giờ).
(giờ).
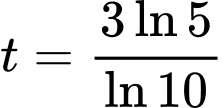 (giờ).
(giờ).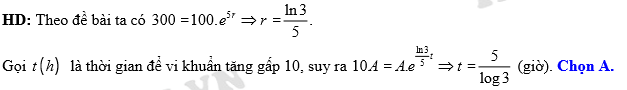 Đáp án: A
Đáp án: A
Câu 19 [579695]: [Đề mẫu HSA 2024]: Số chuột túi xám trên đảo năm 2025 là
A, 735.
B, 800.
C, 813.
D, 900.
Số chuột túi xám trên đảo năm 2022 là 600 con
Ta có: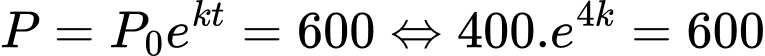
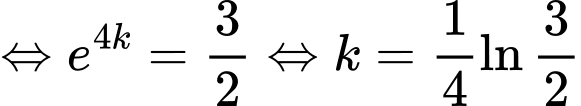
Số chuột túi xám trên đảo năm 2025 là: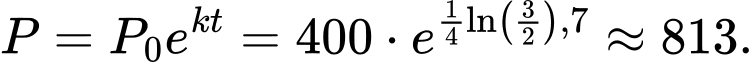
Chọn C. Đáp án: C
Ta có:
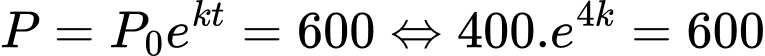
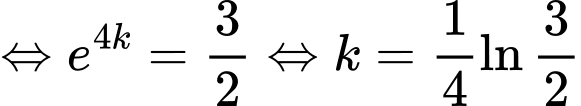
Số chuột túi xám trên đảo năm 2025 là:
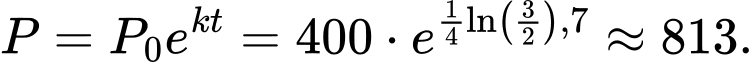
Chọn C. Đáp án: C
Câu 20 [579696]: [Đề mẫu HSA 2024]: Vào năm nào số chuột túi xám ở trên đảo tăng gấp đôi so với năm 2022?
A, 2028.
B, 2029.
C, 2034.
D, 2033.
Số chuột túi xám ở trên đảo tăng gấp đôi so với năm 2022 là 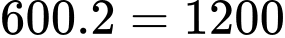 con
con
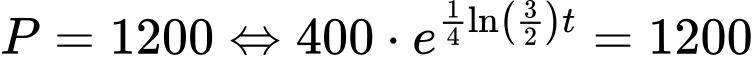
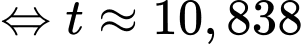
Vậy vào năm 2029 thì số chuột túi xám ở trên đảo tăng gấp đôi so với năm 2022.
Chọn B. Đáp án: B
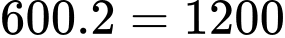 con
con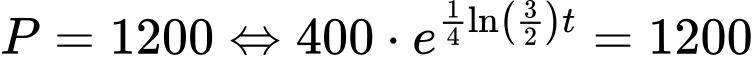
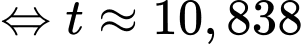
Vậy vào năm 2029 thì số chuột túi xám ở trên đảo tăng gấp đôi so với năm 2022.
Chọn B. Đáp án: B
Câu 21 [579697]: [Đề mẫu HSA 2024]: Trên đảo, ngoài loài chuột túi xám còn có loài chuột túi đỏ sinh sống, theo thống kê ở thời điểm 31 tháng 12 năm 2018 số lượng chuột túi đỏ là 1200 con. Biết số lượng chuột túi đỏ giảm 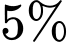 mỗi năm. Vào năm nào thì số chuột túi xám sẽ gấp đôi số chuột túi đỏ?
mỗi năm. Vào năm nào thì số chuột túi xám sẽ gấp đôi số chuột túi đỏ?
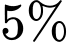 mỗi năm. Vào năm nào thì số chuột túi xám sẽ gấp đôi số chuột túi đỏ?
mỗi năm. Vào năm nào thì số chuột túi xám sẽ gấp đôi số chuột túi đỏ? A, 2028.
B, 2030.
C, 2031.
D, 2032.
Số lượng chuột túi đỏ sau t năm là 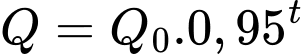 với
với 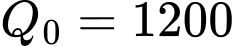 , t tính từ thời điểm
, t tính từ thời điểm 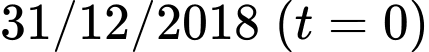
Số chuột túi xám gấp đôi số chuột túi đỏ ta có:
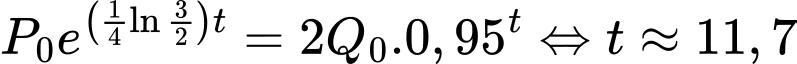
Vậy năm 2030 số chuột túi xám gấp đôi số chuột túi đỏ.
Chọn B. Đáp án: B
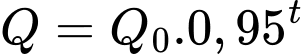 với
với 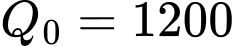 , t tính từ thời điểm
, t tính từ thời điểm 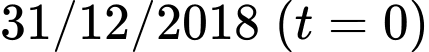
Số chuột túi xám gấp đôi số chuột túi đỏ ta có:
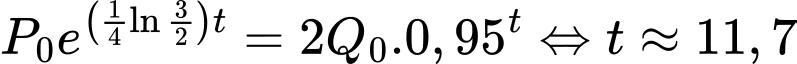
Vậy năm 2030 số chuột túi xám gấp đôi số chuột túi đỏ.
Chọn B. Đáp án: B
Câu 22 [27708]: Số lượng của loại vi khuẩn X trong một phòng thí nghiệm được tính theo công thức 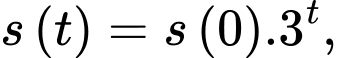 trong đó
trong đó  là số lượng vi khuẩn lúc ban đầu,
là số lượng vi khuẩn lúc ban đầu,  là số lượng vi khuẩn
là số lượng vi khuẩn 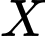 có sau
có sau 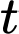 phút. Biết rằng sau 3 phút thì số lượng vi khuẩn X là 20 nghìn con. Hỏi sau bao lâu, kể từ lúc ban đầu, số lượng vi khuẩn X là 540 nghìn con?
phút. Biết rằng sau 3 phút thì số lượng vi khuẩn X là 20 nghìn con. Hỏi sau bao lâu, kể từ lúc ban đầu, số lượng vi khuẩn X là 540 nghìn con?
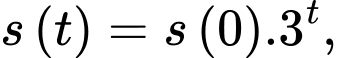 trong đó
trong đó  là số lượng vi khuẩn lúc ban đầu,
là số lượng vi khuẩn lúc ban đầu, 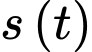 là số lượng vi khuẩn
là số lượng vi khuẩn 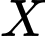 có sau
có sau 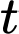 phút. Biết rằng sau 3 phút thì số lượng vi khuẩn X là 20 nghìn con. Hỏi sau bao lâu, kể từ lúc ban đầu, số lượng vi khuẩn X là 540 nghìn con?
phút. Biết rằng sau 3 phút thì số lượng vi khuẩn X là 20 nghìn con. Hỏi sau bao lâu, kể từ lúc ban đầu, số lượng vi khuẩn X là 540 nghìn con? A, 81 phút.
B, 6 phút.
C, 12 phút.
D, 9 phút.
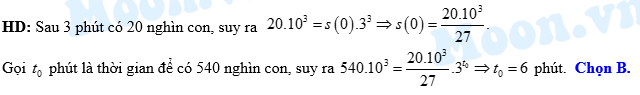 Đáp án: B
Đáp án: B
Câu 23 [271391]: Một vi khuẩn có khối lượng khoảng 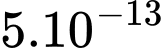 gam và cứ 20 phút vi khuẩn đó tự nhân đôi một lần (Nguồn: Câu hỏi và bài tập vi sinh học, NXB ĐHSP, 2008). Giả sử các vi khuẩn được nuôi trong các điều kiện sinh trưởng tối ưu và mỗi con vi khuẩn đều tồn tại trong ít nhất 60 giờ. Hỏi sau bao nhiêu giờ khối lượng do tế bào vi khuẩn này sinh ra đạt tới khối lượng của Trái Đất (lấy khối lượng của Trái Đất là
gam và cứ 20 phút vi khuẩn đó tự nhân đôi một lần (Nguồn: Câu hỏi và bài tập vi sinh học, NXB ĐHSP, 2008). Giả sử các vi khuẩn được nuôi trong các điều kiện sinh trưởng tối ưu và mỗi con vi khuẩn đều tồn tại trong ít nhất 60 giờ. Hỏi sau bao nhiêu giờ khối lượng do tế bào vi khuẩn này sinh ra đạt tới khối lượng của Trái Đất (lấy khối lượng của Trái Đất là 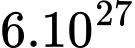 gam (làm tròn kết quả đến hàng đơn vị)?
gam (làm tròn kết quả đến hàng đơn vị)?
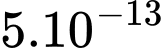 gam và cứ 20 phút vi khuẩn đó tự nhân đôi một lần (Nguồn: Câu hỏi và bài tập vi sinh học, NXB ĐHSP, 2008). Giả sử các vi khuẩn được nuôi trong các điều kiện sinh trưởng tối ưu và mỗi con vi khuẩn đều tồn tại trong ít nhất 60 giờ. Hỏi sau bao nhiêu giờ khối lượng do tế bào vi khuẩn này sinh ra đạt tới khối lượng của Trái Đất (lấy khối lượng của Trái Đất là
gam và cứ 20 phút vi khuẩn đó tự nhân đôi một lần (Nguồn: Câu hỏi và bài tập vi sinh học, NXB ĐHSP, 2008). Giả sử các vi khuẩn được nuôi trong các điều kiện sinh trưởng tối ưu và mỗi con vi khuẩn đều tồn tại trong ít nhất 60 giờ. Hỏi sau bao nhiêu giờ khối lượng do tế bào vi khuẩn này sinh ra đạt tới khối lượng của Trái Đất (lấy khối lượng của Trái Đất là 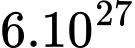 gam (làm tròn kết quả đến hàng đơn vị)?
gam (làm tròn kết quả đến hàng đơn vị)?
Số lần phân chia là 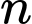 , khối lượng trái đất là
, khối lượng trái đất là 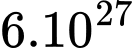 gam và khối lượng vi khuẩn là
gam và khối lượng vi khuẩn là 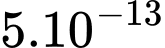 gam.
gam.
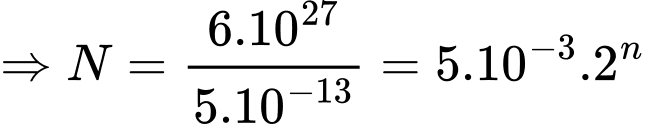
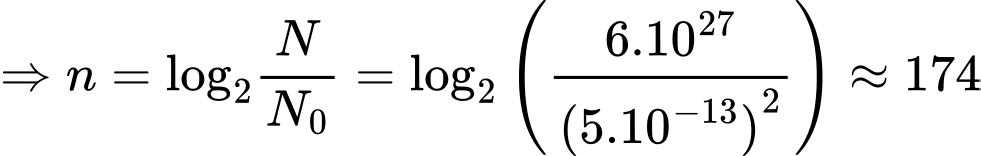
Thời gian cần thiết là: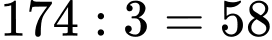 (giờ)
(giờ)
Đáp án: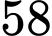 giờ.
giờ.
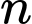 , khối lượng trái đất là
, khối lượng trái đất là 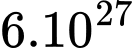 gam và khối lượng vi khuẩn là
gam và khối lượng vi khuẩn là 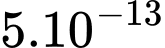 gam.
gam.
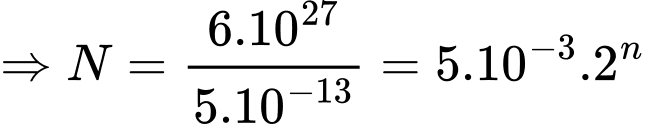
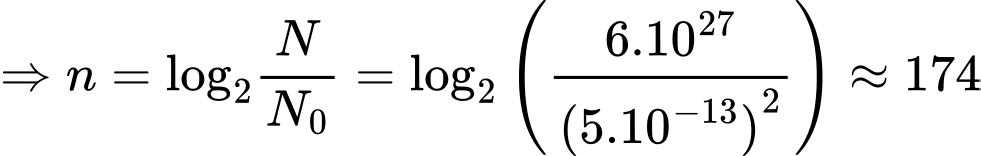
Thời gian cần thiết là:
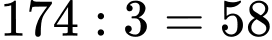 (giờ)
(giờ)Đáp án:
 giờ.
giờ.
Câu 24 [275792]: Biết rằng khi độ cao tăng lên, áp suất không khí sẽ giảm và công thức tính áp suất dựa trên độ cao là:
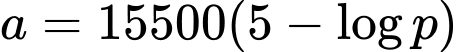 ,
,
Trong đó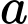 là độ cao so với mực nước biển (tính bằng mét) và
là độ cao so với mực nước biển (tính bằng mét) và 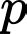 là áp suất không khí (tính bằng pascal). Tính áp suất không khí ở đỉnh Everest có độ cao 8850 m so với mực nước biển.
là áp suất không khí (tính bằng pascal). Tính áp suất không khí ở đỉnh Everest có độ cao 8850 m so với mực nước biển.
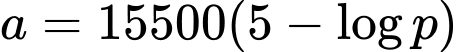 ,
,Trong đó
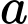 là độ cao so với mực nước biển (tính bằng mét) và
là độ cao so với mực nước biển (tính bằng mét) và 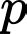 là áp suất không khí (tính bằng pascal). Tính áp suất không khí ở đỉnh Everest có độ cao 8850 m so với mực nước biển.
là áp suất không khí (tính bằng pascal). Tính áp suất không khí ở đỉnh Everest có độ cao 8850 m so với mực nước biển.
Áp suất không khí ở đỉnh Everest ở độ cao 8850 m so với mực nước biển là:
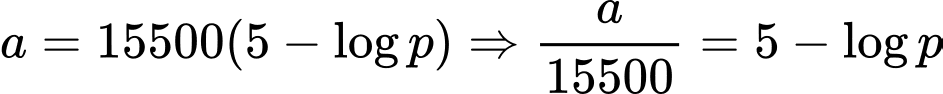
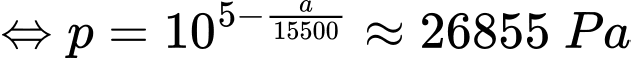
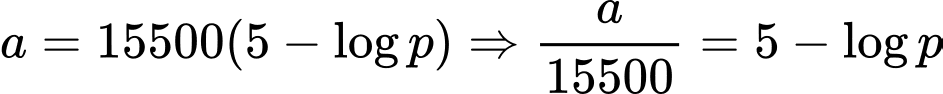
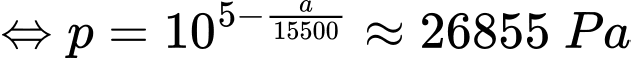
Câu 25 [27790]: Khi ánh sáng đi qua môi trường (chẳng hạn như không khí, nước, sương mù...), cường độ sẽ giảm dần theo quãng đường truyền 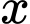 , theo công thức
, theo công thức 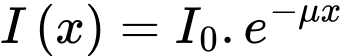 , trong đó
, trong đó 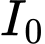 là cường độ của ánh sáng khi bắt đầu truyền vào môi trường và
là cường độ của ánh sáng khi bắt đầu truyền vào môi trường và 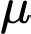 là hệ số hấp thụ của môi trường đó. Biết rằng nước biển có hệ số hấp thụ
là hệ số hấp thụ của môi trường đó. Biết rằng nước biển có hệ số hấp thụ 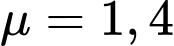 và người ta tính được rằng khi đi từ độ sâu
và người ta tính được rằng khi đi từ độ sâu 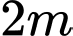 xuống đến độ sâu
xuống đến độ sâu 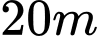 thì cường độ ánh sáng giảm
thì cường độ ánh sáng giảm 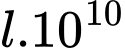 lần. Số nguyên nào sau đây gần với
lần. Số nguyên nào sau đây gần với 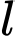 nhất?
nhất?
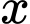 , theo công thức
, theo công thức 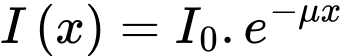 , trong đó
, trong đó 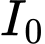 là cường độ của ánh sáng khi bắt đầu truyền vào môi trường và
là cường độ của ánh sáng khi bắt đầu truyền vào môi trường và 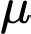 là hệ số hấp thụ của môi trường đó. Biết rằng nước biển có hệ số hấp thụ
là hệ số hấp thụ của môi trường đó. Biết rằng nước biển có hệ số hấp thụ 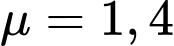 và người ta tính được rằng khi đi từ độ sâu
và người ta tính được rằng khi đi từ độ sâu 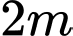 xuống đến độ sâu
xuống đến độ sâu 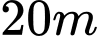 thì cường độ ánh sáng giảm
thì cường độ ánh sáng giảm 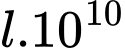 lần. Số nguyên nào sau đây gần với
lần. Số nguyên nào sau đây gần với 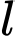 nhất?
nhất?
Ta có: Ở độ sâu 2m: 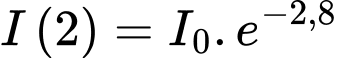
Ở độ sâu 20 m: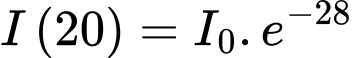
Theo giả thiết ta có: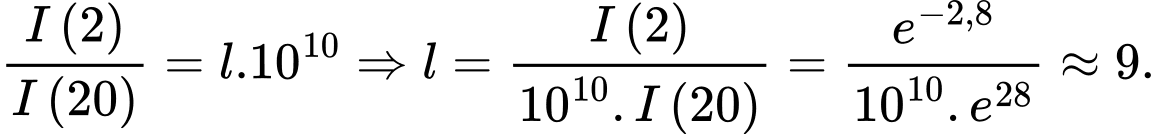
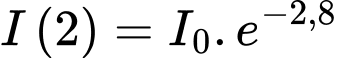
Ở độ sâu 20 m:
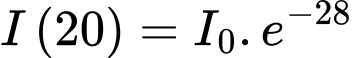
Theo giả thiết ta có: