Đáp án Bài tập tự luyện
Câu 1 [10479]: Với giá trị thực nào của 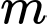 thì phương trình
thì phương trình 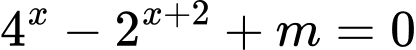 có hai nghiệm thực phân biệt?
có hai nghiệm thực phân biệt?
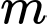 thì phương trình
thì phương trình 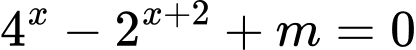 có hai nghiệm thực phân biệt?
có hai nghiệm thực phân biệt? A, 

B, 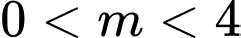
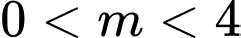
C, 

D, 

 Đáp án: B
Đáp án: B
Câu 2 [10473]: Tổng tất cả các giá trị nguyêm của tham số 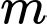 để phương trình
để phương trình 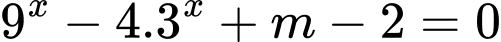 có hai nghiệm thực phân biệt.
có hai nghiệm thực phân biệt.
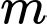 để phương trình
để phương trình 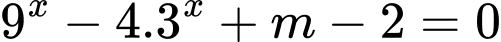 có hai nghiệm thực phân biệt.
có hai nghiệm thực phân biệt. A, 2019.
B, 15.
C, 12.
D, 2018.
Đặt 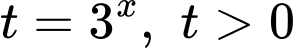
PT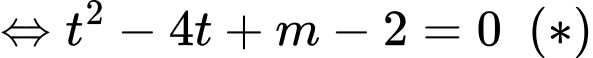
Để phương trình đã cho có 2 nghiệm thực phân biệt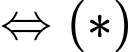 có 2 nghiệm dương phân biệt
có 2 nghiệm dương phân biệt
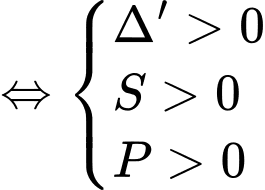
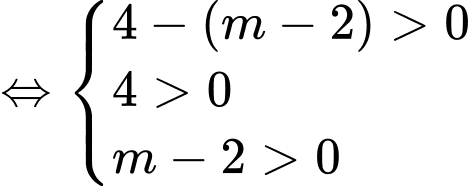
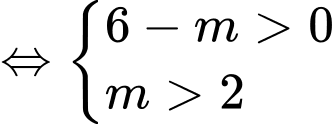
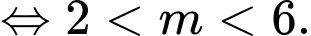
Suy ra 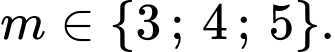
Vậy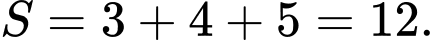 Chọn C. Đáp án: C
Chọn C. Đáp án: C
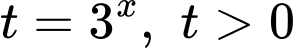
PT
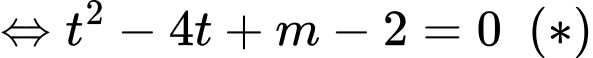
Để phương trình đã cho có 2 nghiệm thực phân biệt
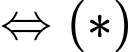 có 2 nghiệm dương phân biệt
có 2 nghiệm dương phân biệt
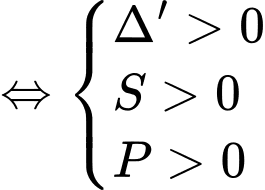
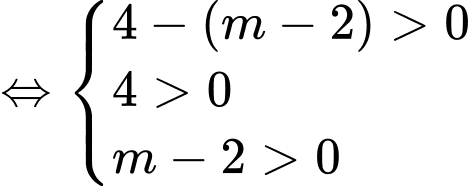
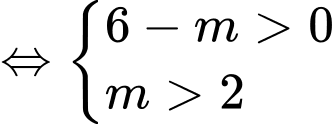
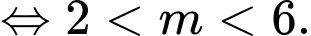
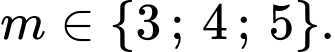
Vậy
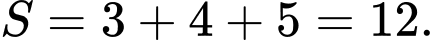 Chọn C. Đáp án: C
Chọn C. Đáp án: C
Câu 3 [10419]: Tìm giá trị thực của tham số 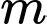 để phương trình
để phương trình 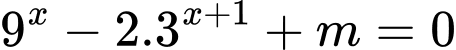 có hai nghiệm thực
có hai nghiệm thực 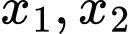 thỏa mãn
thỏa mãn 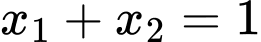
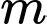 để phương trình
để phương trình 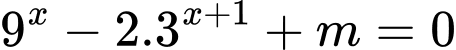 có hai nghiệm thực
có hai nghiệm thực 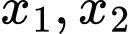 thỏa mãn
thỏa mãn 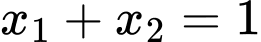
A, 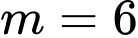
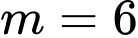
B, 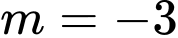
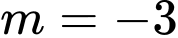
C, 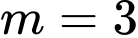
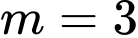
D, 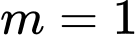
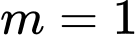
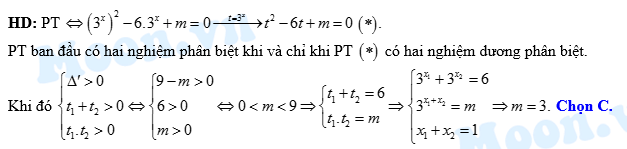 Đáp án: C
Đáp án: C
Câu 4 [79137]: [Đề thi THPT QG năm 2018] Gọi 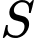 là tập hợp tất cả các giá trị nguyên của tham số
là tập hợp tất cả các giá trị nguyên của tham số 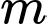 sao cho phương trình
sao cho phương trình  có 2 nghiệm phân biệt. Hỏi
có 2 nghiệm phân biệt. Hỏi 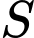 có bao nhiêu phần tử ?
có bao nhiêu phần tử ?
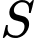 là tập hợp tất cả các giá trị nguyên của tham số
là tập hợp tất cả các giá trị nguyên của tham số 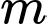 sao cho phương trình
sao cho phương trình  có 2 nghiệm phân biệt. Hỏi
có 2 nghiệm phân biệt. Hỏi 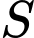 có bao nhiêu phần tử ?
có bao nhiêu phần tử ? A, 13.
B, 3.
C, 6.
D, 4.
 Đáp án: B
Đáp án: B
Câu 5 [79309]: [Đề thi THPT QG năm 2017] Tìm giá trị thực của tham số 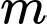 để phương trình
để phương trình 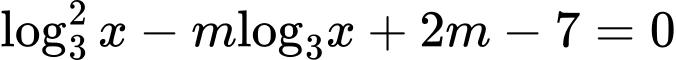 có hai nghiêệm thực
có hai nghiêệm thực 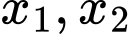 thỏa mãn
thỏa mãn 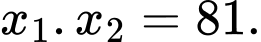
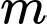 để phương trình
để phương trình 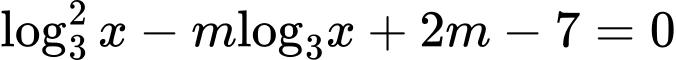 có hai nghiêệm thực
có hai nghiêệm thực 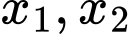 thỏa mãn
thỏa mãn 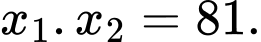
A, 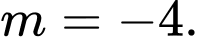
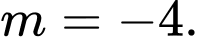
B, 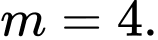
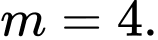
C, 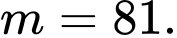
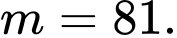
D, 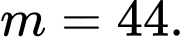
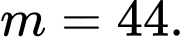
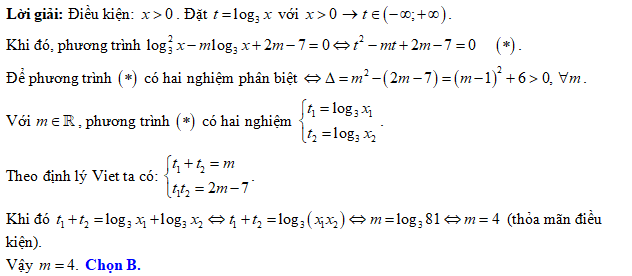 Đáp án: B
Đáp án: B
Câu 6 [508859]: Cho phương trình 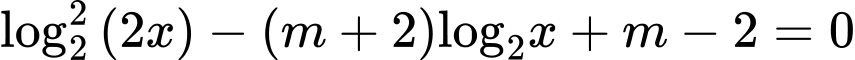 (với
(với 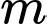 là tham số thực). Tập hợp các giá trị của tham số
là tham số thực). Tập hợp các giá trị của tham số 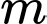 để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn
để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn 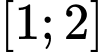 là
là
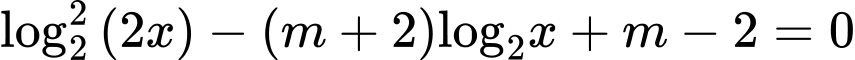 (với
(với 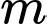 là tham số thực). Tập hợp các giá trị của tham số
là tham số thực). Tập hợp các giá trị của tham số 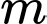 để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn
để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn 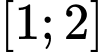 là
là A, 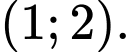
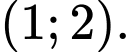
B, 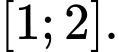
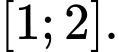
C, 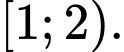
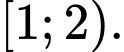
D, 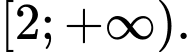
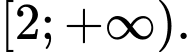
Ta có:
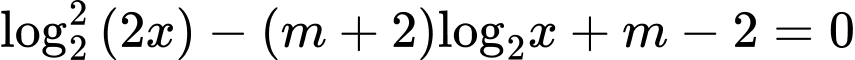
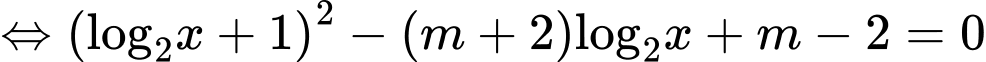

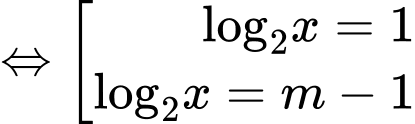
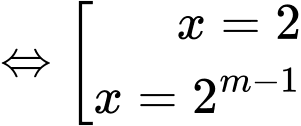
Để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn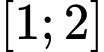 thì:
thì:

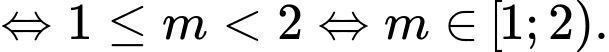
Chọn đáp án C. Đáp án: C
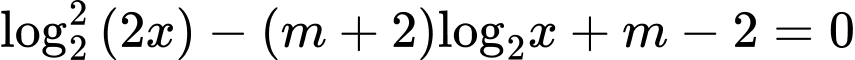
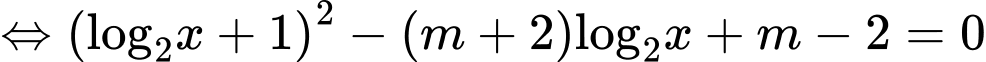

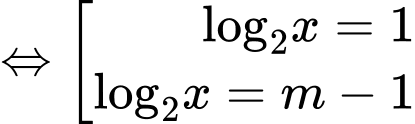
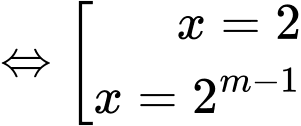
Để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn
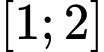 thì:
thì:
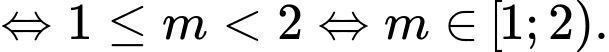
Chọn đáp án C. Đáp án: C
Câu 7 [508861]: Cho phương trình 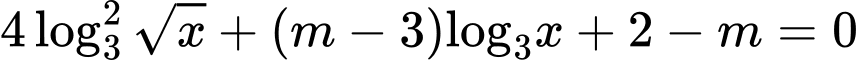 (với
(với 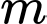 là tham số thực). Số giá trị nguyên của tham số
là tham số thực). Số giá trị nguyên của tham số 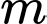 để phương trình đã cho có hai nghiệm phân biệt thuộc
để phương trình đã cho có hai nghiệm phân biệt thuộc 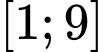 là
là
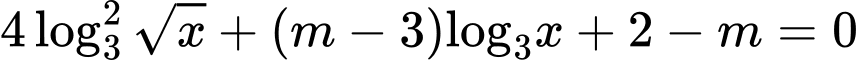 (với
(với 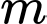 là tham số thực). Số giá trị nguyên của tham số
là tham số thực). Số giá trị nguyên của tham số 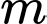 để phương trình đã cho có hai nghiệm phân biệt thuộc
để phương trình đã cho có hai nghiệm phân biệt thuộc 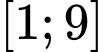 là
là A, 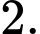
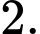
B, 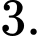
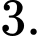
C, 
D, 
Xét 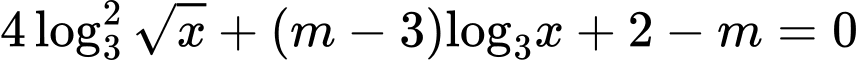
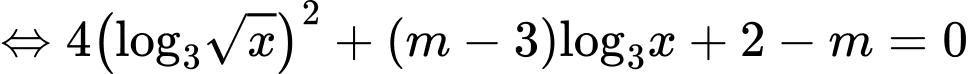
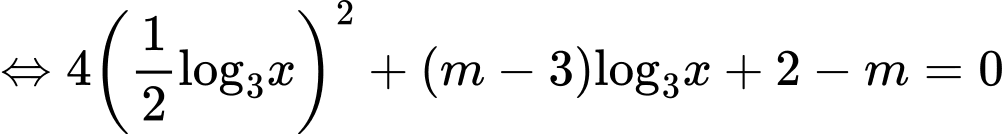
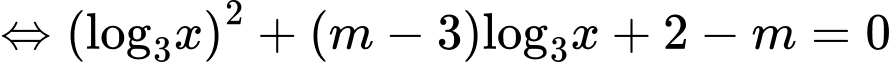
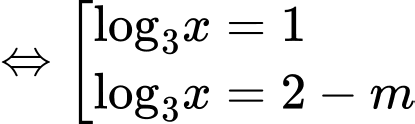
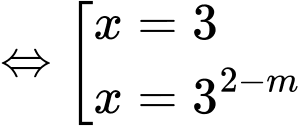
Để phương trình đã cho có hai nghiệm nguyên phân biệt thuộc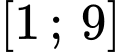
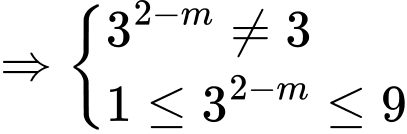
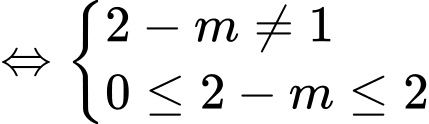
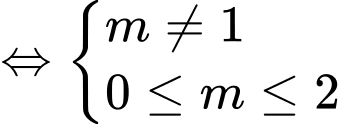
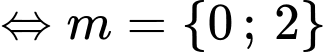
Đáp án: A Đáp án: A
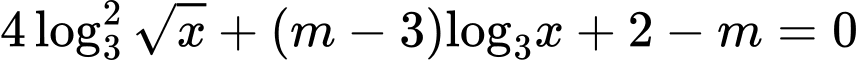
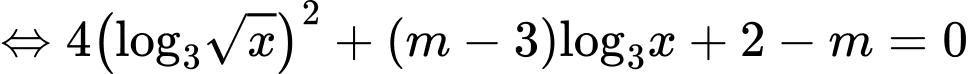
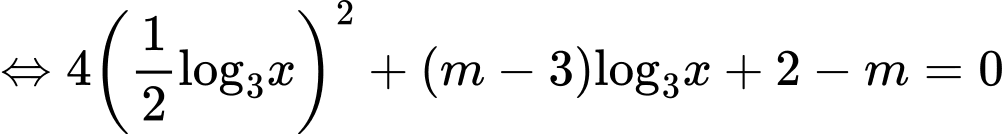
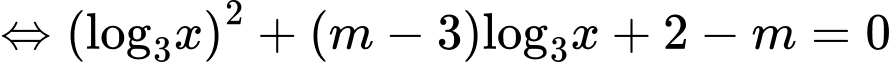
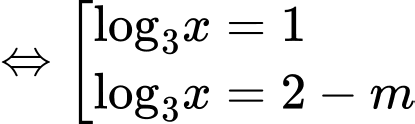
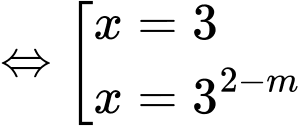
Để phương trình đã cho có hai nghiệm nguyên phân biệt thuộc
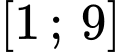
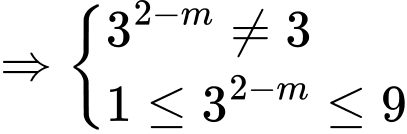
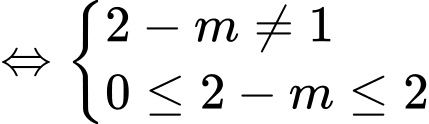
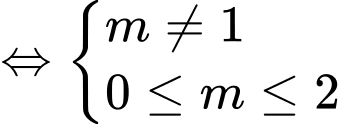
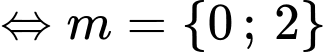
Đáp án: A Đáp án: A
Câu 8 [581590]: Có bao nhiêu giá trị nguyên âm của tham số 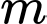 để bất phương trình
để bất phương trình 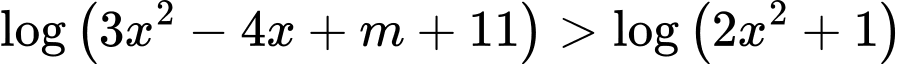 có tập nghiệm là
có tập nghiệm là 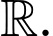
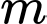 để bất phương trình
để bất phương trình 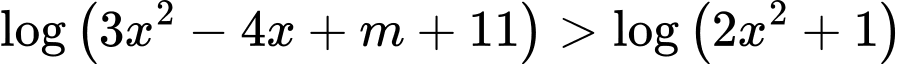 có tập nghiệm là
có tập nghiệm là 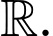
A, 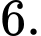
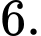
B, 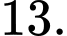
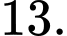
C, 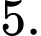
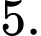
D, 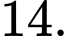
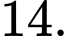
Lời giải:
Bất phương trình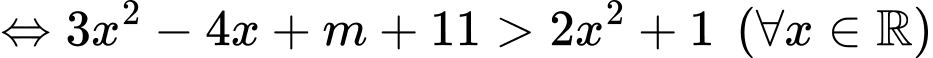
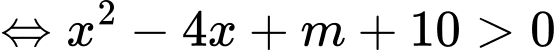
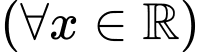
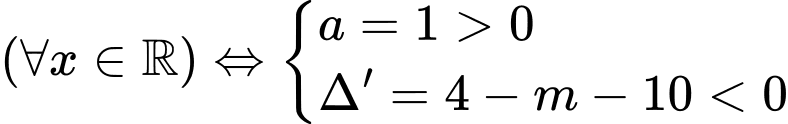
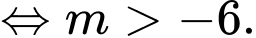
Do đó có 5 giá trị nguyên âm của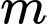 thoả mãn yêu cầu là
thoả mãn yêu cầu là 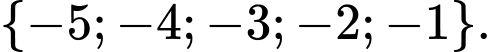
Bất phương trình
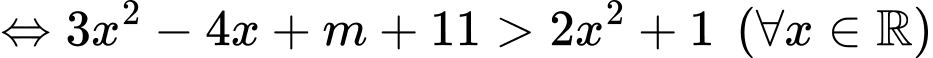
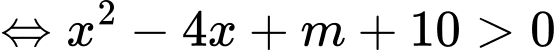
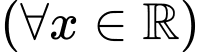
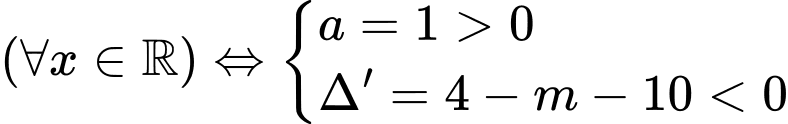
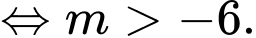
Do đó có 5 giá trị nguyên âm của
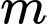 thoả mãn yêu cầu là
thoả mãn yêu cầu là 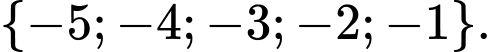
Câu 9 [10467]: Có bao nhiêu giá trị nguyên của tham số 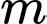 để bất phương trình
để bất phương trình 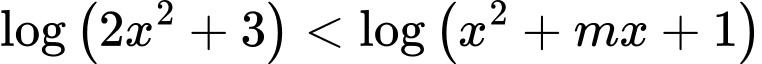 có tập nghiệm là
có tập nghiệm là 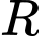 .
.
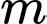 để bất phương trình
để bất phương trình 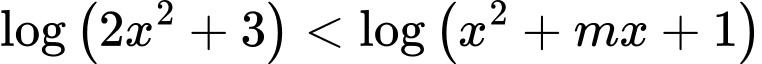 có tập nghiệm là
có tập nghiệm là 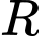 .
. A, Vô số.
B, 2.
C, 5.
D, 0.
 Đáp án: D
Đáp án: D
Câu 10 [79312]: Gọi 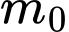 là giá trị của tham số
là giá trị của tham số 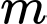 để phương trình
để phương trình 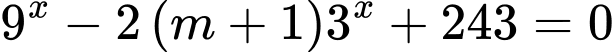 có hai nghiệm thực
có hai nghiệm thực 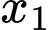 ;
;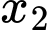 thỏa mãn
thỏa mãn 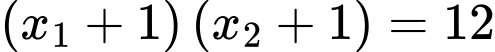 . Giá trị
. Giá trị 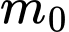 thuộc khoảng nào dưới đây ?
thuộc khoảng nào dưới đây ?
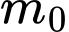 là giá trị của tham số
là giá trị của tham số 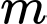 để phương trình
để phương trình 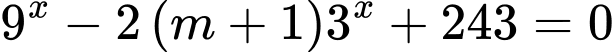 có hai nghiệm thực
có hai nghiệm thực 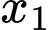 ;
;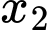 thỏa mãn
thỏa mãn 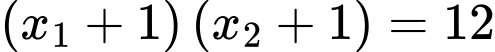 . Giá trị
. Giá trị 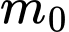 thuộc khoảng nào dưới đây ?
thuộc khoảng nào dưới đây ? A, 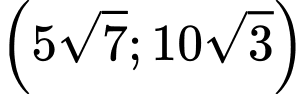
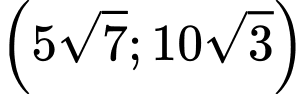
B, 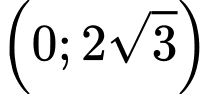
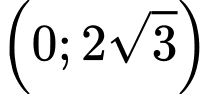
C, 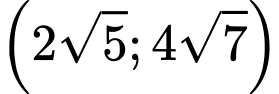
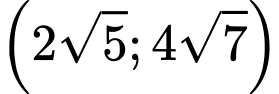
D, 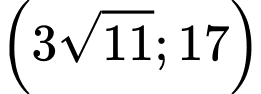
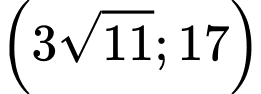
 Đáp án: A
Đáp án: A
Câu 11 [10345]: Tìm giá trị thực của 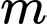 để phương trình
để phương trình 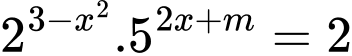 có hai nghiệm phân biệt
có hai nghiệm phân biệt 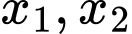 thoả mãn
thoả mãn 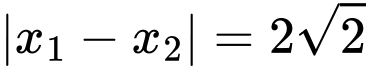
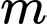 để phương trình
để phương trình 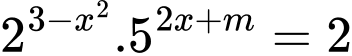 có hai nghiệm phân biệt
có hai nghiệm phân biệt 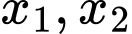 thoả mãn
thoả mãn 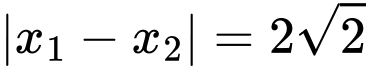
A, 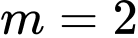
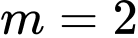
B, 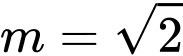
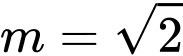
C, 

D, 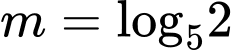
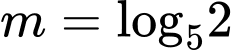
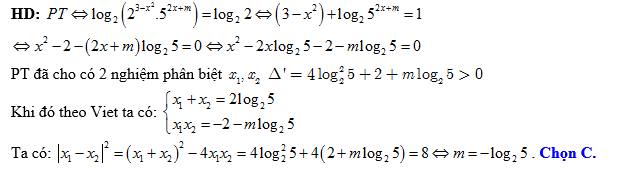 Đáp án: C
Đáp án: C
Câu 12 [79313]: Cho phương trình 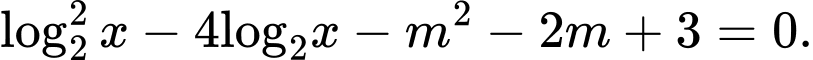 Biết rằng
Biết rằng 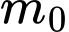 là giá trị thực lớn nhất của tham số
là giá trị thực lớn nhất của tham số 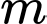 để phương trình trên có hai nghiệm thực phân biệt
để phương trình trên có hai nghiệm thực phân biệt 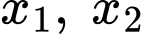 thỏa
thỏa 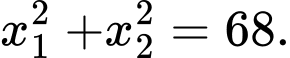 Giá trị của
Giá trị của 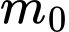 thuộc khoảng nào sau đây?
thuộc khoảng nào sau đây?
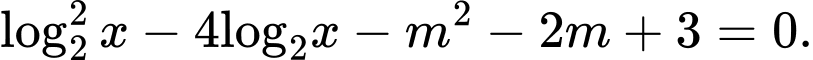 Biết rằng
Biết rằng 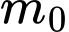 là giá trị thực lớn nhất của tham số
là giá trị thực lớn nhất của tham số 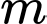 để phương trình trên có hai nghiệm thực phân biệt
để phương trình trên có hai nghiệm thực phân biệt 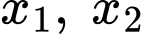 thỏa
thỏa 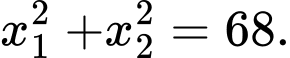 Giá trị của
Giá trị của 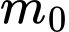 thuộc khoảng nào sau đây?
thuộc khoảng nào sau đây? A, 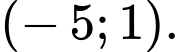
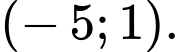
B, 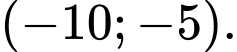
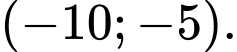
C, 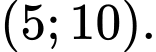
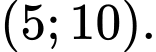
D, 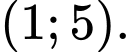
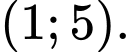
 Đáp án: A
Đáp án: A
Câu 13 [554591]: Có bao nhiêu số nguyên 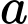 lớn hơn 1 sao cho ứng với mỗi
lớn hơn 1 sao cho ứng với mỗi 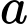 tồn tại không quá 7 số nguyên
tồn tại không quá 7 số nguyên 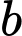 thỏa mãn
thỏa mãn 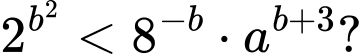
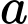 lớn hơn 1 sao cho ứng với mỗi
lớn hơn 1 sao cho ứng với mỗi 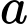 tồn tại không quá 7 số nguyên
tồn tại không quá 7 số nguyên 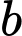 thỏa mãn
thỏa mãn 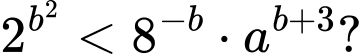
A, 32.
B, 16.
C, 15.
D, 31.
Chọn đáp án: D.
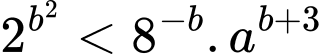
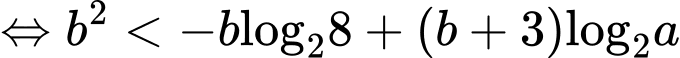
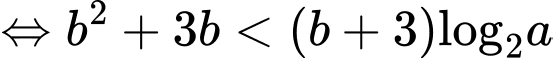
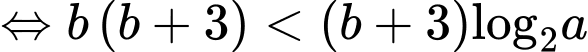
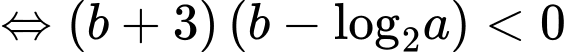
TH1: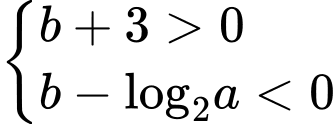
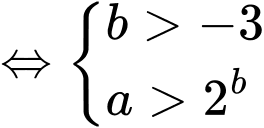
TH2: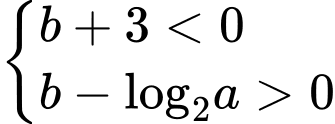
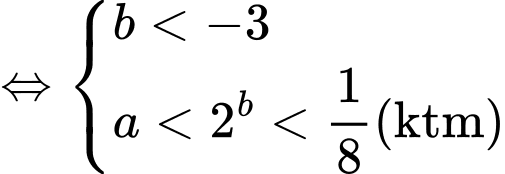
Do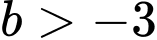 và có không quá 7 số nguyên b thỏa mãn nên
và có không quá 7 số nguyên b thỏa mãn nên 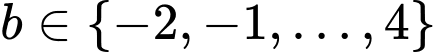
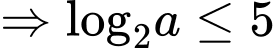
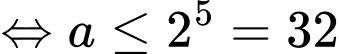
Mà a nguyên và nên
nên 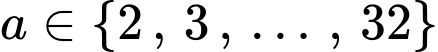
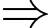 Có 31 giá trị nguyên a thỏa mãn. Đáp án: D
Có 31 giá trị nguyên a thỏa mãn. Đáp án: D
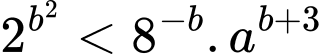
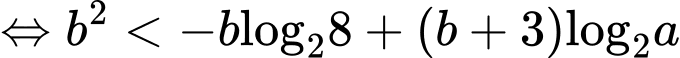
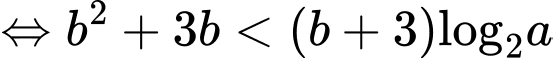
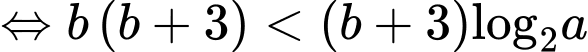
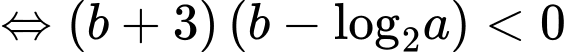
TH1:
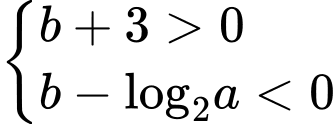
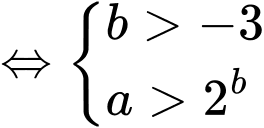
TH2:
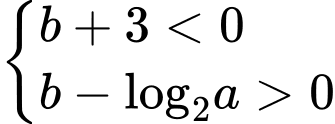
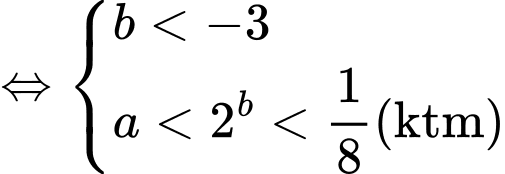
Do
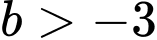 và có không quá 7 số nguyên b thỏa mãn nên
và có không quá 7 số nguyên b thỏa mãn nên 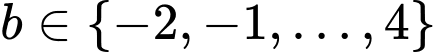
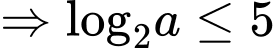
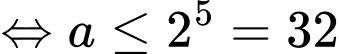
Mà a nguyên và
 nên
nên 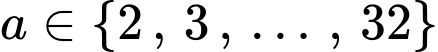
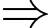 Có 31 giá trị nguyên a thỏa mãn. Đáp án: D
Có 31 giá trị nguyên a thỏa mãn. Đáp án: D
Câu 14 [804689]: Có bao nhiêu số nguyên dương 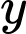 sao cho ứng với mỗi
sao cho ứng với mỗi 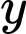 có không quá 10 số nguyên
có không quá 10 số nguyên 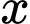 thỏa mãn
thỏa mãn 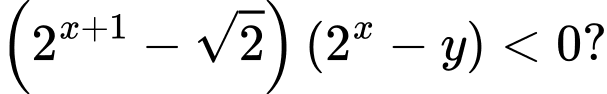
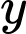 sao cho ứng với mỗi
sao cho ứng với mỗi 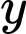 có không quá 10 số nguyên
có không quá 10 số nguyên 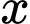 thỏa mãn
thỏa mãn 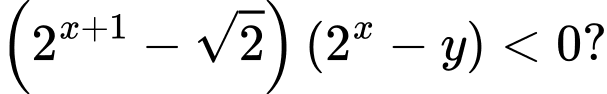
A, 1024.
B, 2047.
C, 1022.
D, 1023.
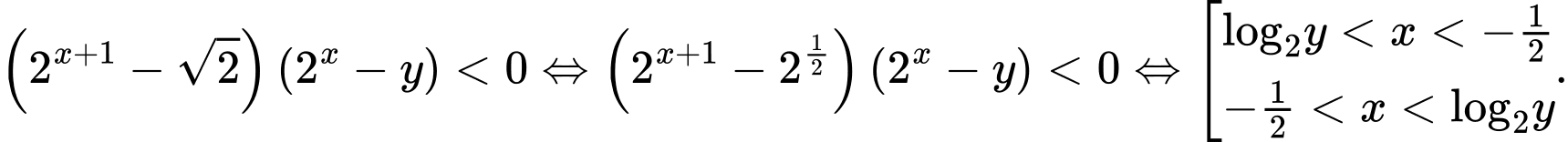
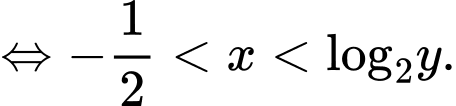
Theo bài ra, ứng với mỗi giá trị y có không quá 10 số nguyên x thỏa mãn nên: 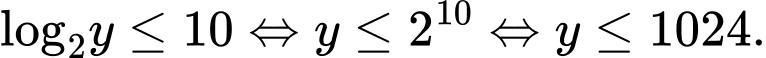
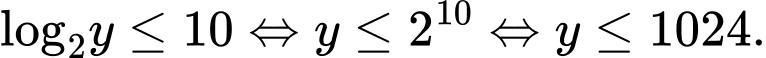
Vậy có 1024 số thỏa mãn.
Đáp án: A Chọn đáp án A.
Câu 15 [900246]: Gọi 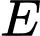 là tập hợp tất cả các số nguyên dương
là tập hợp tất cả các số nguyên dương 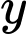 sao cho ứng với mỗi số
sao cho ứng với mỗi số 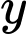 có không quá
có không quá 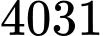 số nguyên
số nguyên 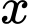 thỏa mãn
thỏa mãn 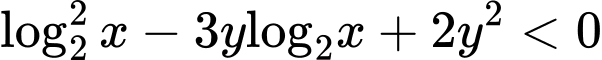 . Tập
. Tập 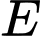 có bao nhiêu phần tử?
có bao nhiêu phần tử?
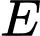 là tập hợp tất cả các số nguyên dương
là tập hợp tất cả các số nguyên dương 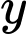 sao cho ứng với mỗi số
sao cho ứng với mỗi số 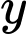 có không quá
có không quá 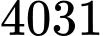 số nguyên
số nguyên 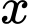 thỏa mãn
thỏa mãn 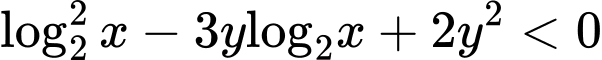 . Tập
. Tập 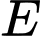 có bao nhiêu phần tử?
có bao nhiêu phần tử? A, 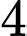 .
.
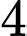 .
.B, 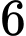 .
.
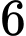 .
.C, 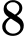 .
.
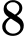 .
.D, 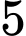 .
.
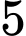 .
.
Chọn B
Điều kiện . Ta có
. Ta có
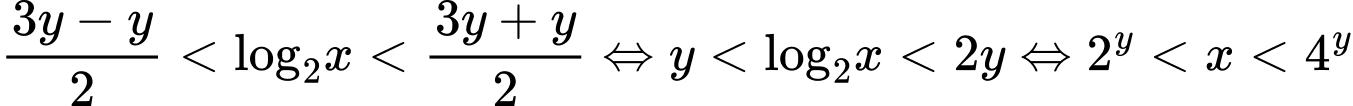 .
.
Do đó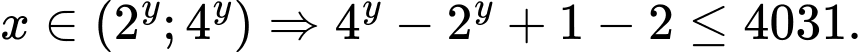 Yêu cầu đề bài trở thành
Yêu cầu đề bài trở thành
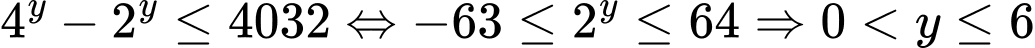 .
.
Vậy có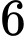 số nguyên dương
số nguyên dương 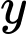 thỏa mãn. Đáp án: B
thỏa mãn. Đáp án: B
Điều kiện
 . Ta có
. Ta có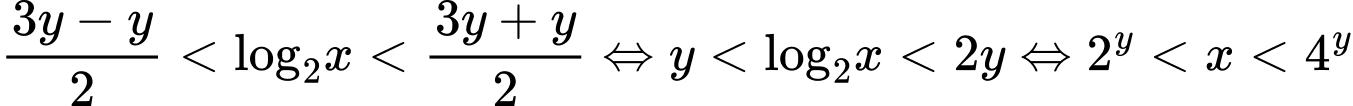 .
.Do đó
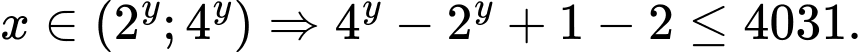 Yêu cầu đề bài trở thành
Yêu cầu đề bài trở thành 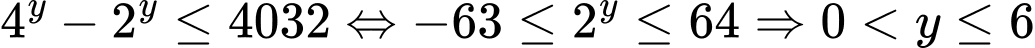 .
.Vậy có
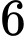 số nguyên dương
số nguyên dương 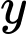 thỏa mãn. Đáp án: B
thỏa mãn. Đáp án: B
Câu 16 [581457]: Tìm giá trị của tham số 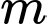 để phương trình
để phương trình 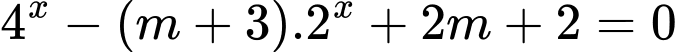 có hai nghiệm phân biệt
có hai nghiệm phân biệt 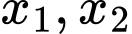 thỏa mãn
thỏa mãn 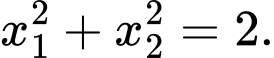
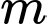 để phương trình
để phương trình 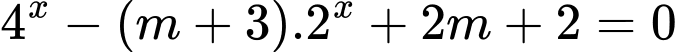 có hai nghiệm phân biệt
có hai nghiệm phân biệt 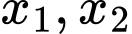 thỏa mãn
thỏa mãn 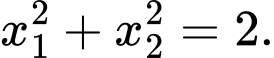
Đặt 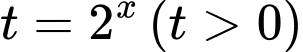 , phương trình đã cho trở thành:
, phương trình đã cho trở thành: 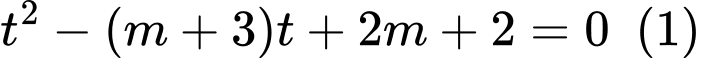 .
.
Phương trình đã cho có hai nghiệm phân biệt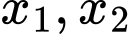
 Phương trình
Phương trình  có hai nghiệm dương phân biệt
có hai nghiệm dương phân biệt
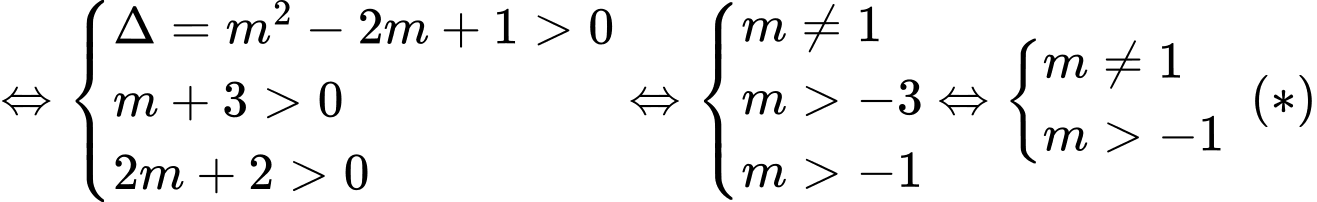 .
.
Với điều kiện thì phương trình
thì phương trình  có hai nghiệm phân biệt là:
có hai nghiệm phân biệt là: 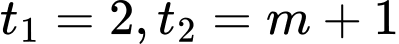 .
.
Suy ra: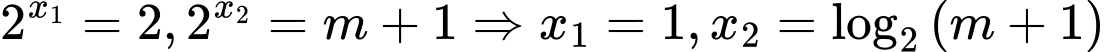 .
.
Theo đề bài:
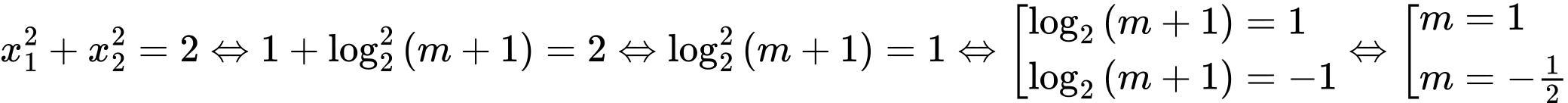
So với điều kiện ta có:
ta có: 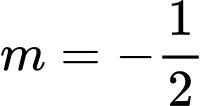 .
.
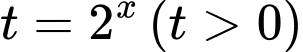 , phương trình đã cho trở thành:
, phương trình đã cho trở thành: 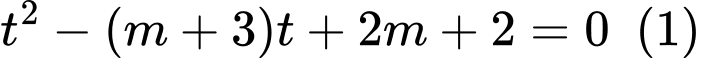 .
.Phương trình đã cho có hai nghiệm phân biệt
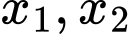
 Phương trình
Phương trình  có hai nghiệm dương phân biệt
có hai nghiệm dương phân biệt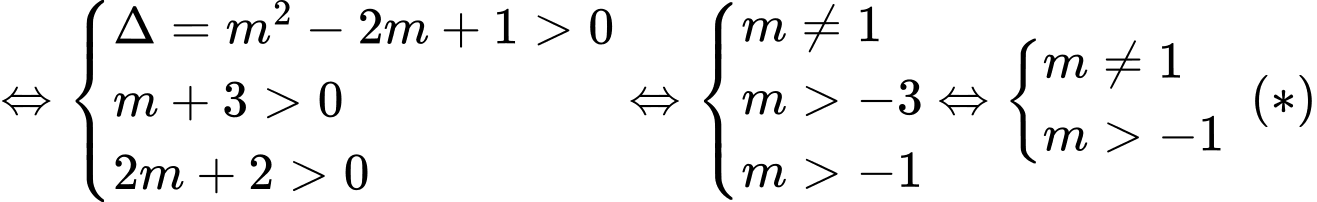 .
.Với điều kiện
 thì phương trình
thì phương trình  có hai nghiệm phân biệt là:
có hai nghiệm phân biệt là: 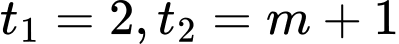 .
.Suy ra:
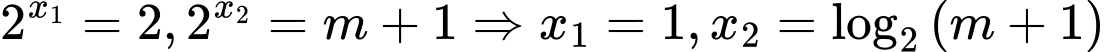 .
.Theo đề bài:
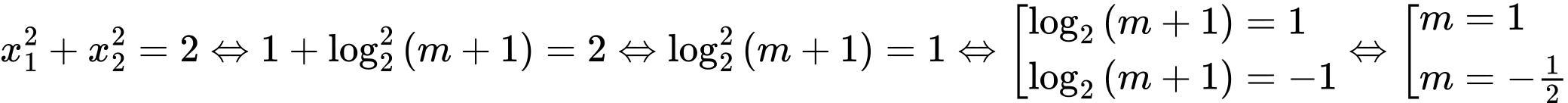
So với điều kiện
 ta có:
ta có: 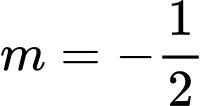 .
.
Câu 17 [511934]: Cho phương trình 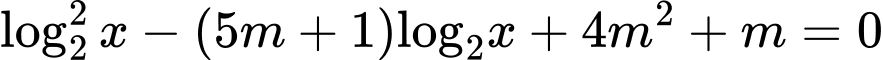 , biết phương trình có hai nghiệm phân biệt
, biết phương trình có hai nghiệm phân biệt 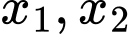 thỏa mãn
thỏa mãn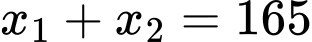 . Giá trị
. Giá trị  bằng
bằng
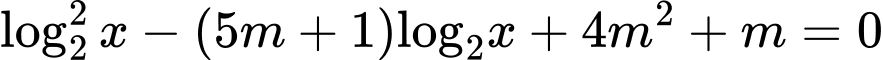 , biết phương trình có hai nghiệm phân biệt
, biết phương trình có hai nghiệm phân biệt 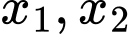 thỏa mãn
thỏa mãn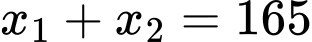 . Giá trị
. Giá trị  bằng
bằng A, 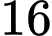 .
.
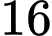 .
.B, 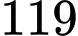 .
.
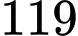 .
.C, 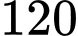 .
.
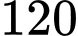 .
.D, 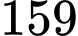 .
.
 .
.
Chọn D
Ta có: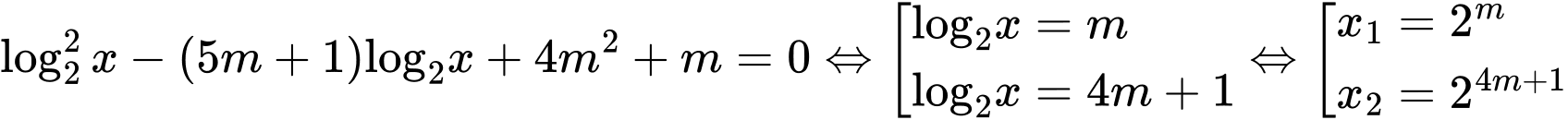
Mà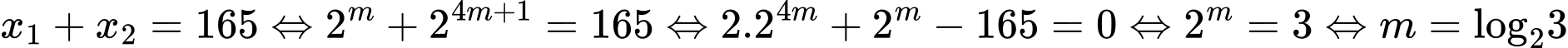
Từ đây ta suy ra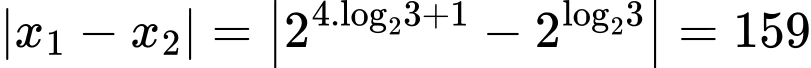 Đáp án: D
Đáp án: D
Ta có:
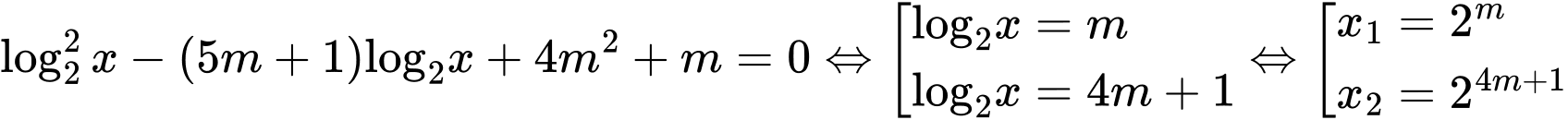
Mà
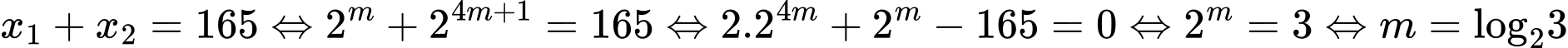
Từ đây ta suy ra
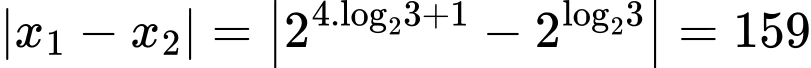 Đáp án: D
Đáp án: D
Câu 18 [581456]: Giá trị thực của tham số 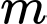 để phương trình
để phương trình 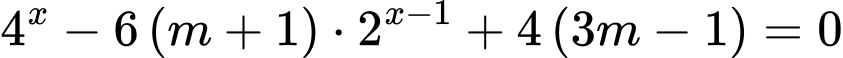 có hai nghiệm thực
có hai nghiệm thực 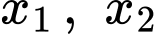 thỏa mãn
thỏa mãn 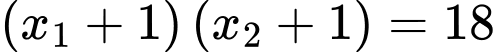 là bao nhiêu?
là bao nhiêu?
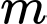 để phương trình
để phương trình 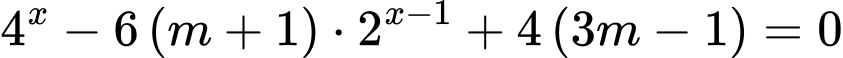 có hai nghiệm thực
có hai nghiệm thực 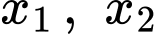 thỏa mãn
thỏa mãn 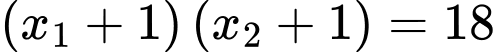 là bao nhiêu?
là bao nhiêu? 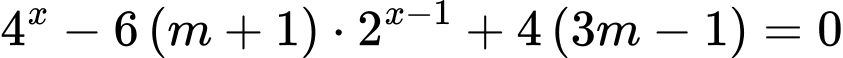
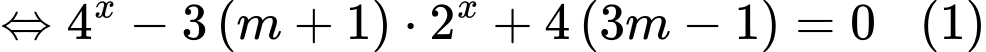 .
.Đặt
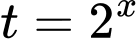 (
( ) thì phương trình
) thì phương trình  trở thành
trở thành 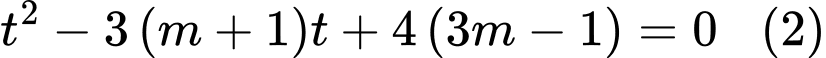
Ptr
 có hai nghiệm dương phân biệt khi
có hai nghiệm dương phân biệt khi 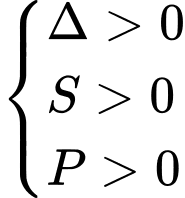
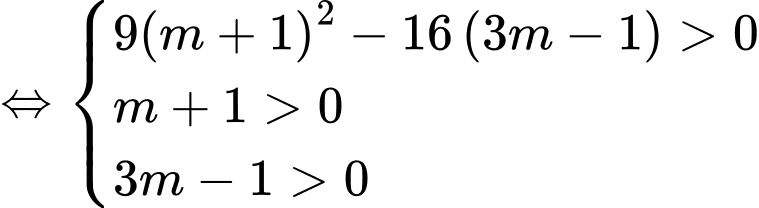
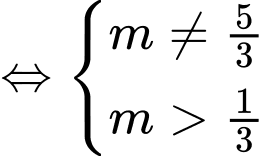
.
Suy ra pt
 có hai nghiệm:
có hai nghiệm: 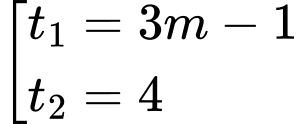
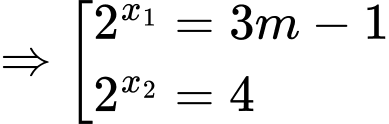
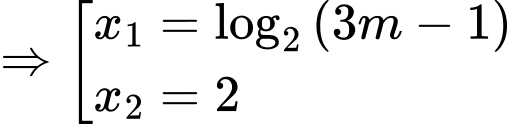
Ta có:
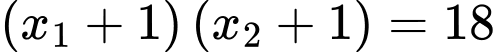
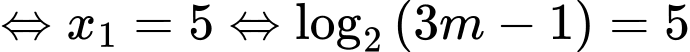
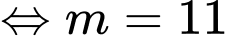 (thỏa mãn).
(thỏa mãn).
Câu 19 [579654]: [Đề mẫu HSA 2024]: Có bao nhiêu giá trị nguyên của tham số 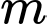 để bất phương trình
để bất phương trình 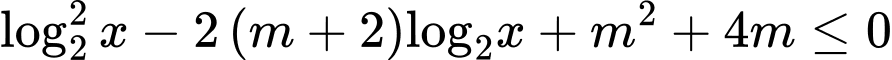 đúng với mọi
đúng với mọi 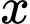 thuộc
thuộc 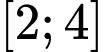 (nhập đáp án vào ô trống)?
(nhập đáp án vào ô trống)?
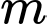 để bất phương trình
để bất phương trình 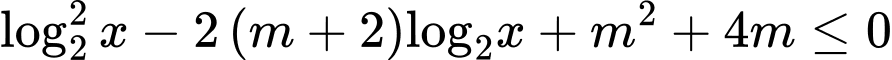 đúng với mọi
đúng với mọi 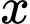 thuộc
thuộc 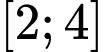 (nhập đáp án vào ô trống)?
(nhập đáp án vào ô trống)?
Đặt 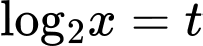 vì
vì 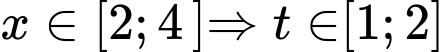
Ta có bất phương trình: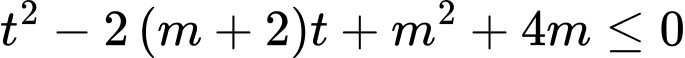 (1)
(1)
Dễ thấy phương trình bằng 0 luôn có 2 nghiệm phân biệt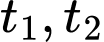
Để (1) đúng với mọi t thuộc [1;2] thì
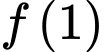 và
và 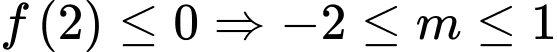
Vậy có 4 giá trị nguyên của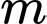 thỏa mãn yêu cầu bài toán.
thỏa mãn yêu cầu bài toán.
Đáp số 4
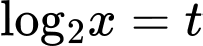 vì
vì 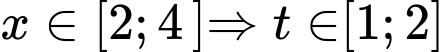
Ta có bất phương trình:
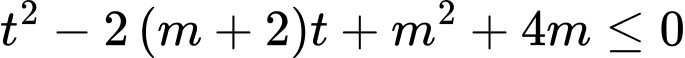 (1)
(1) Dễ thấy phương trình bằng 0 luôn có 2 nghiệm phân biệt
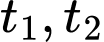
Để (1) đúng với mọi t thuộc [1;2] thì

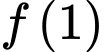 và
và 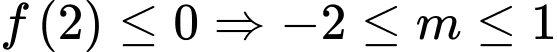
Vậy có 4 giá trị nguyên của
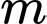 thỏa mãn yêu cầu bài toán.
thỏa mãn yêu cầu bài toán. Đáp số 4
Câu 20 [10367]: Cho bất phương trình 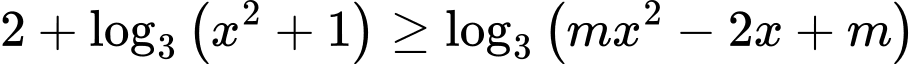 . Có bao nhiêu giá trị nguyên của tham số
. Có bao nhiêu giá trị nguyên của tham số 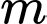 để bất phương trình trên nghiệm đúng với mọi
để bất phương trình trên nghiệm đúng với mọi 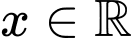
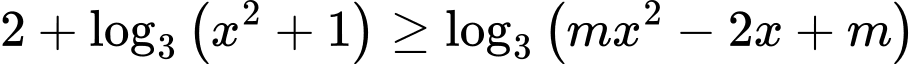 . Có bao nhiêu giá trị nguyên của tham số
. Có bao nhiêu giá trị nguyên của tham số 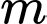 để bất phương trình trên nghiệm đúng với mọi
để bất phương trình trên nghiệm đúng với mọi 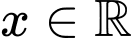
A, 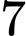 .
.
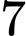 .
.B, 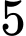 .
.
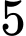 .
.C, 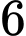 .
.
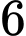 .
.D, 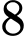 .
.
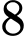 .
.
 Đáp án: A
Đáp án: A
Câu 21 [901201]: Có bao nhiêu số nguyên dương 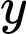 sao cho ứng với mỗi
sao cho ứng với mỗi 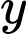 có không quá 50 số nguyên
có không quá 50 số nguyên 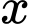 thỏa mãn
thỏa mãn 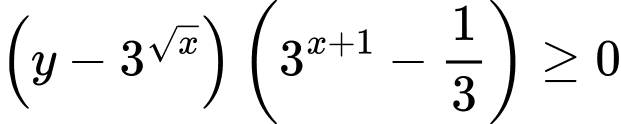 .
.
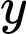 sao cho ứng với mỗi
sao cho ứng với mỗi 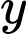 có không quá 50 số nguyên
có không quá 50 số nguyên 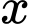 thỏa mãn
thỏa mãn 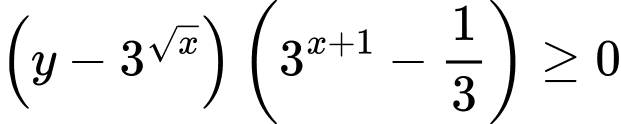 .
. A,  .
.
 .
.B, 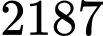 .
.
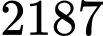 .
.C, 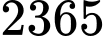 .
.
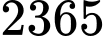 .
.D, 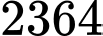 .
.
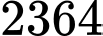 .
.
Chọn D
Bất phương trình đưa về
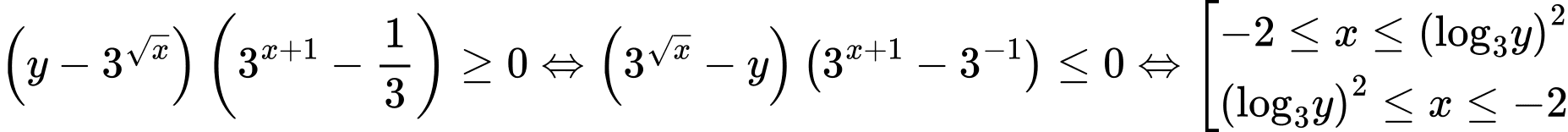
Chú ý nên ta chọn
nên ta chọn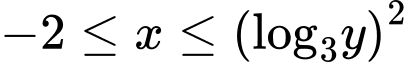 suy ra
suy ra 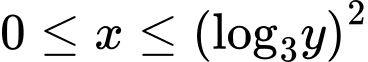 .
.
Theo bài ra, ứng với mỗi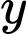 có không quá 50 số nguyên
có không quá 50 số nguyên 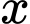 thỏa mãn thì
thỏa mãn thì
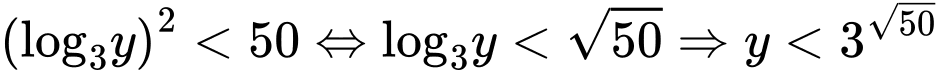 .
.
Từ đây ta có 2364 số nguyên dương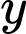 . Đáp án: D
. Đáp án: D
Bất phương trình đưa về
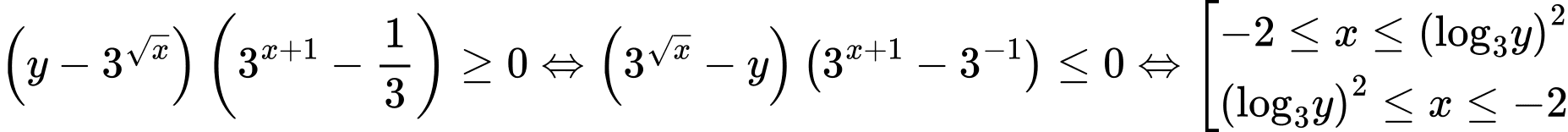
Chú ý
 nên ta chọn
nên ta chọn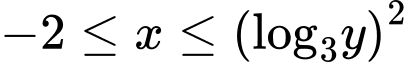 suy ra
suy ra 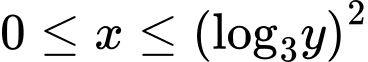 .
.Theo bài ra, ứng với mỗi
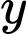 có không quá 50 số nguyên
có không quá 50 số nguyên 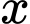 thỏa mãn thì
thỏa mãn thì
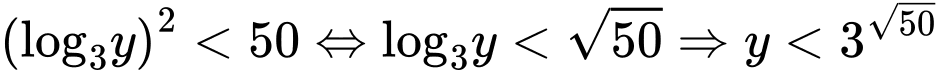 .
.Từ đây ta có 2364 số nguyên dương
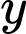 . Đáp án: D
. Đáp án: D
Câu 22 [679668]: Có bao nhiêu 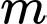 nguyên dương để tập nghiệm của bất phương trình
nguyên dương để tập nghiệm của bất phương trình 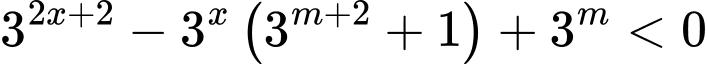 có không quá
có không quá 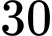 nghiệm nguyên?
nghiệm nguyên?
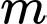 nguyên dương để tập nghiệm của bất phương trình
nguyên dương để tập nghiệm của bất phương trình 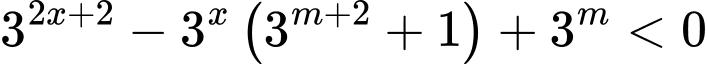 có không quá
có không quá 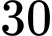 nghiệm nguyên?
nghiệm nguyên? A, 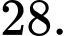
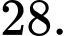
B, 
C, 
D, 
* Lời giải: Đặt 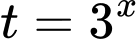 , điều kiện:
, điều kiện:  .
.
Khi đó bất phương trình trở thành: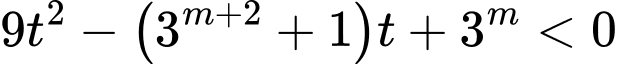
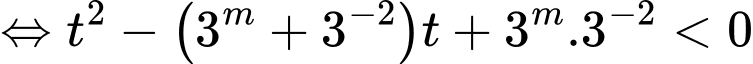
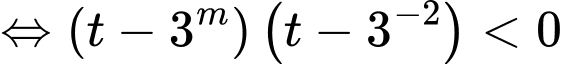 suy ra
suy ra 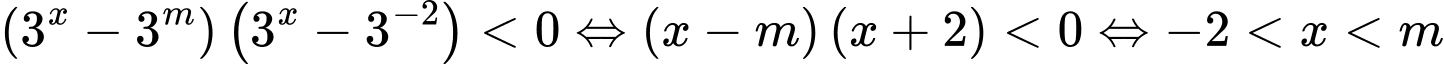
(vì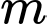 là số nguyên dương)
là số nguyên dương)
Để tập nghiệm của bất phương trình có không quá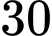 số nguyên thì
số nguyên thì  .
.
Vậy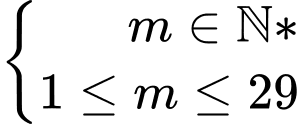 .
.
Do đó có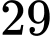 số nguyên dương
số nguyên dương 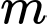 thỏa mãn yêu cầu bài toán. Chọn B.
Đáp án: B
thỏa mãn yêu cầu bài toán. Chọn B.
Đáp án: B
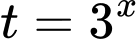 , điều kiện:
, điều kiện:  .
.Khi đó bất phương trình trở thành:
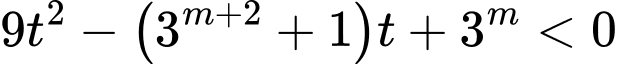
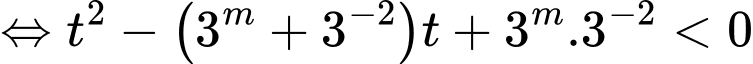
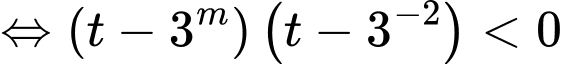 suy ra
suy ra 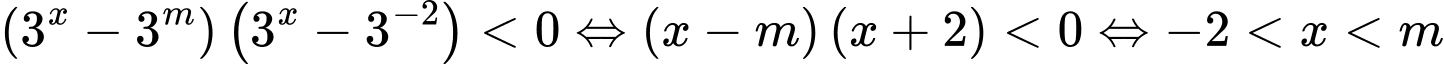
(vì
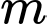 là số nguyên dương)
là số nguyên dương) Để tập nghiệm của bất phương trình có không quá
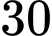 số nguyên thì
số nguyên thì  .
.Vậy
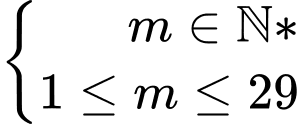 .
.Do đó có
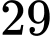 số nguyên dương
số nguyên dương 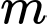 thỏa mãn yêu cầu bài toán. Chọn B.
Đáp án: B
thỏa mãn yêu cầu bài toán. Chọn B.
Đáp án: B
Câu 23 [234123]: [Đề thi TN THPT 2022]: Có bao nhiêu số nguyên dương 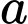 sao cho ứng với mỗi
sao cho ứng với mỗi 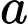 có đúng ba số nguyên
có đúng ba số nguyên 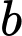 thỏa mãn
thỏa mãn 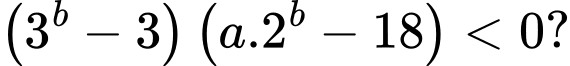
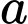 sao cho ứng với mỗi
sao cho ứng với mỗi 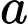 có đúng ba số nguyên
có đúng ba số nguyên 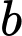 thỏa mãn
thỏa mãn 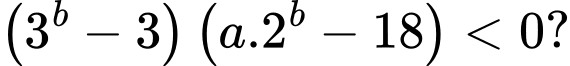
A, 72.
B, 73.
C, 71.
D, 74.
Chọn đáp án: B
+) TH1: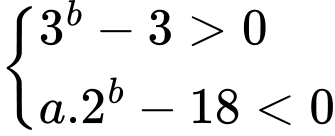
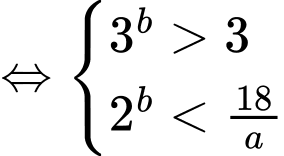
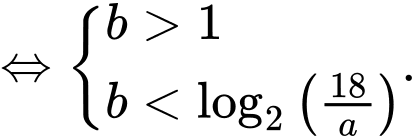
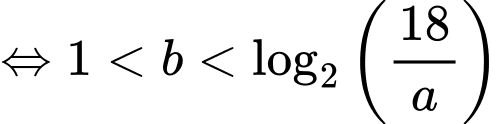
Để có đúng ba số nguyên b thì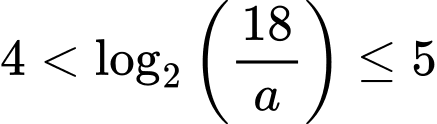
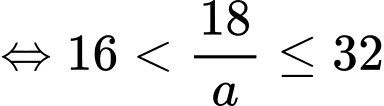
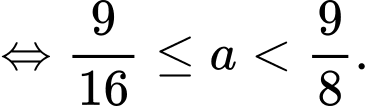
Trường hợp này có 1 giá trị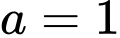 nguyên thỏa mãn.
nguyên thỏa mãn.
+) TH2: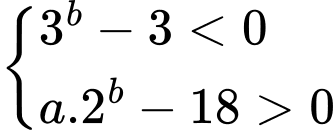
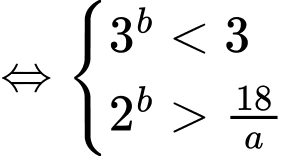
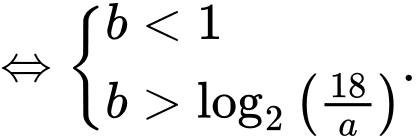
Để có đúng ba số nguyên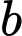 thì
thì
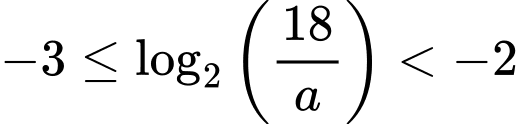
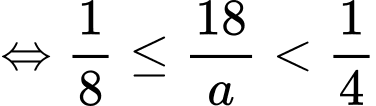
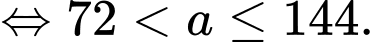
Trường hợp này có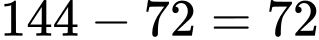 giá trị a nguyên thỏa mãn.
giá trị a nguyên thỏa mãn.
Vậy số giá trị nguyên của a là: Đáp án: B
Đáp án: B
+) TH1:
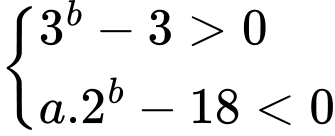
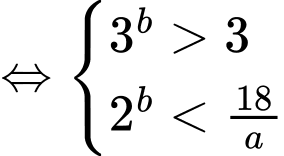
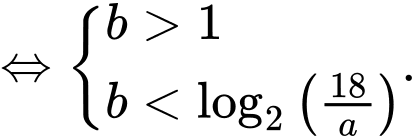
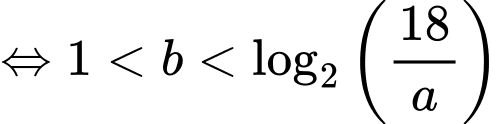
Để có đúng ba số nguyên b thì
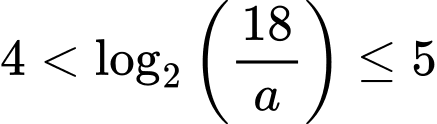
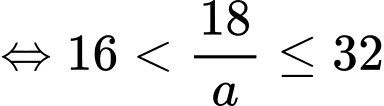
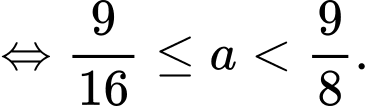
Trường hợp này có 1 giá trị
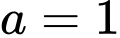 nguyên thỏa mãn.
nguyên thỏa mãn.
+) TH2:
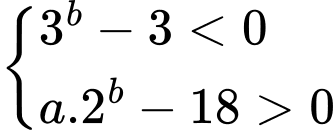
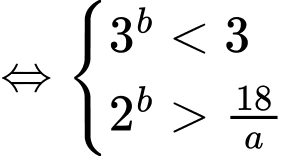
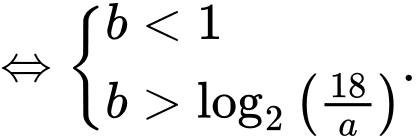
Để có đúng ba số nguyên
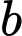 thì
thì
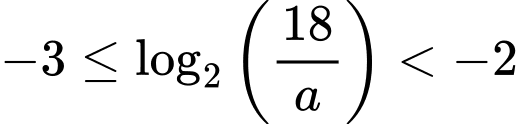
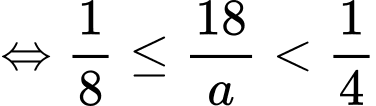
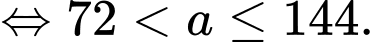
Trường hợp này có
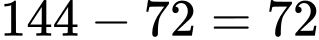 giá trị a nguyên thỏa mãn.
giá trị a nguyên thỏa mãn.
Vậy số giá trị nguyên của a là:
 Đáp án: B
Đáp án: B
Câu 24 [904818]: Cho các số nguyên dương 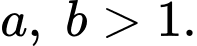 Biết phương trình
Biết phương trình 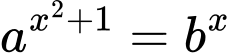 có hai nghiệm phân biệt
có hai nghiệm phân biệt 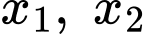 và phương trình
và phương trình 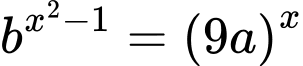 có hai nghiệm phân biệt
có hai nghiệm phân biệt 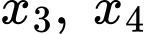 thỏa mãn
thỏa mãn 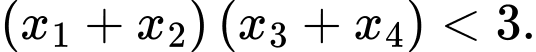 Tìm giá trị nhỏ nhất của biểu thức
Tìm giá trị nhỏ nhất của biểu thức 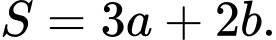
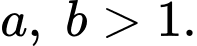 Biết phương trình
Biết phương trình 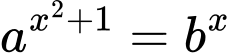 có hai nghiệm phân biệt
có hai nghiệm phân biệt 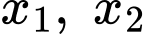 và phương trình
và phương trình 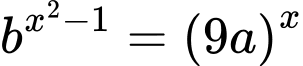 có hai nghiệm phân biệt
có hai nghiệm phân biệt 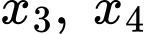 thỏa mãn
thỏa mãn 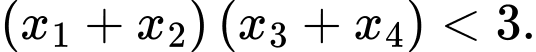 Tìm giá trị nhỏ nhất của biểu thức
Tìm giá trị nhỏ nhất của biểu thức 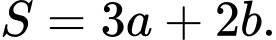
A, 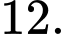
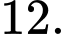
B, 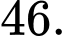
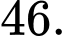
C, 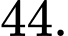
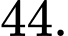
D, 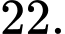
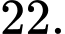
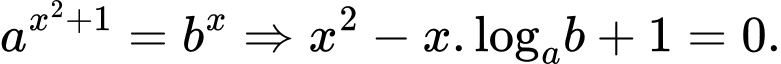
Phương trình có hai nghiệm
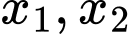 khi:
khi: 
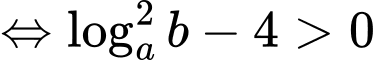
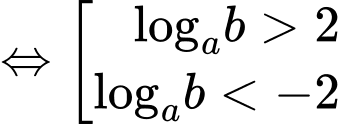
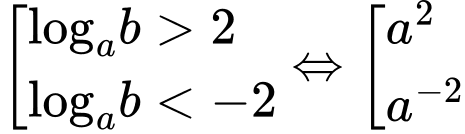
Khi đó:
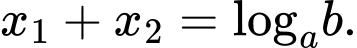
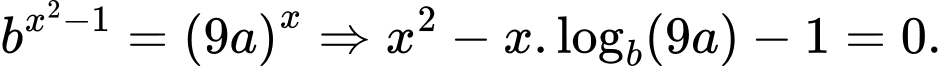
Phương trình có hai nghiệm
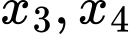 khi:
khi: 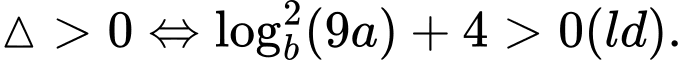
Khi đó:
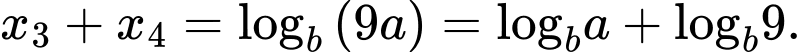
Do đó, 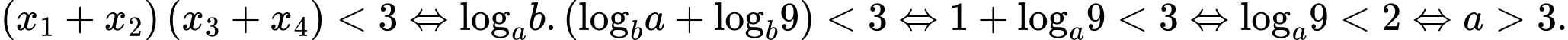
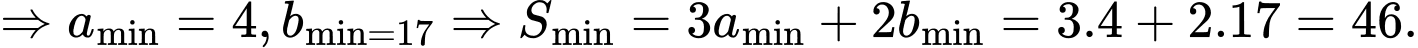
Chọn đáp án B.
Đáp án: B 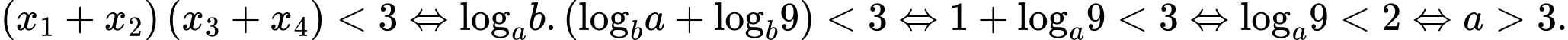
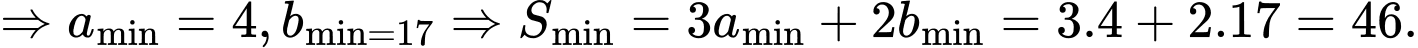
Chọn đáp án B.
Câu 25 [29492]: Xét các số nguyên dương 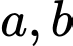 sao cho phương trình
sao cho phương trình 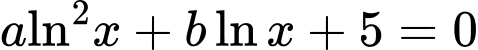 có hai nghiệm phân biệt
có hai nghiệm phân biệt 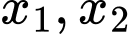 và phương trình
và phương trình 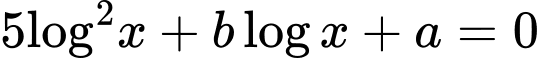 có hai nghiệm phân biệt
có hai nghiệm phân biệt 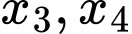 thỏa mãn
thỏa mãn  Tìm giá trị nhỏ nhất
Tìm giá trị nhỏ nhất  của
của 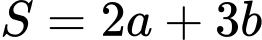
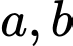 sao cho phương trình
sao cho phương trình 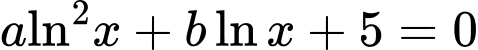 có hai nghiệm phân biệt
có hai nghiệm phân biệt 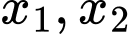 và phương trình
và phương trình 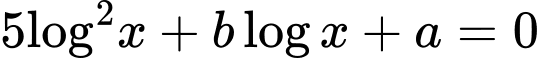 có hai nghiệm phân biệt
có hai nghiệm phân biệt 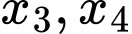 thỏa mãn
thỏa mãn  Tìm giá trị nhỏ nhất
Tìm giá trị nhỏ nhất  của
của 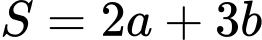
A, 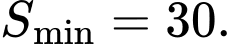
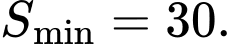
B, 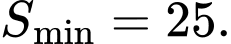
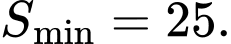
C, 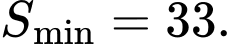
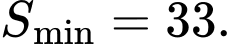
D, 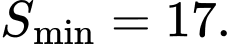
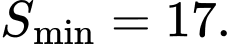
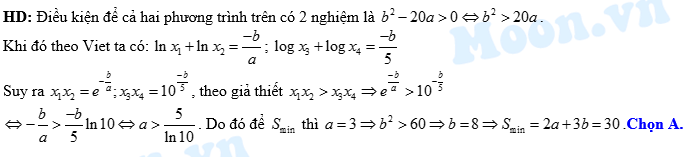 Đáp án: A
Đáp án: A