Đáp án Bài tập tự luyện số 1
Câu 1 [657021]: Hàm số nào sau đây đồng biến trên 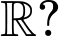
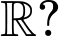
A, 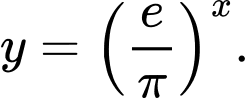
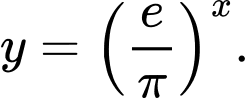
B, 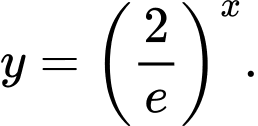
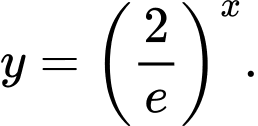
C, 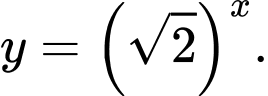
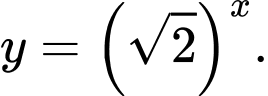
D, 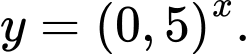
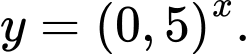
Hàm số có dạng 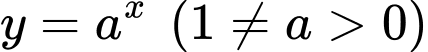 đồng biến trên
đồng biến trên 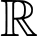 khi và chỉ khi
khi và chỉ khi 
Trong 4 hàm số đã cho thì hàm số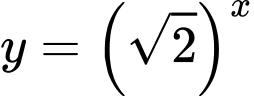 đồng biến trên
đồng biến trên 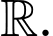 Chọn C.
Đáp án: C
Chọn C.
Đáp án: C
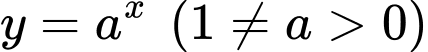 đồng biến trên
đồng biến trên 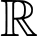 khi và chỉ khi
khi và chỉ khi 
Trong 4 hàm số đã cho thì hàm số
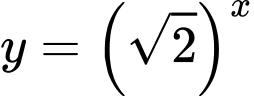 đồng biến trên
đồng biến trên 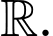 Chọn C.
Đáp án: C
Chọn C.
Đáp án: C
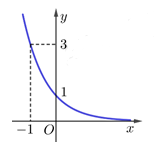
Câu 2 [657035]: Đồ thị hình bên là của hàm số nào?

A, 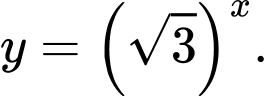
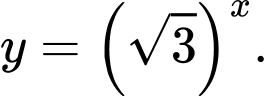
B, 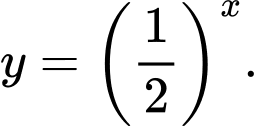
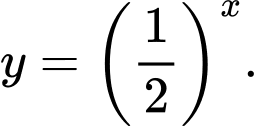
C, 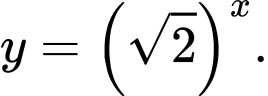
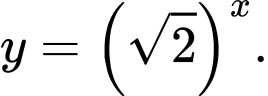
D, 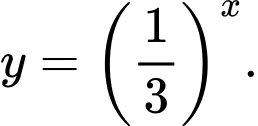
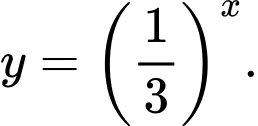
Dựa vào đồ thị hàm số suy ra hàm số đã cho có dạng 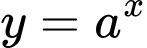 và là hàm nghịch biến (vì có đồ thị đi xuống) nên
và là hàm nghịch biến (vì có đồ thị đi xuống) nên 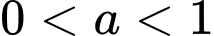 ta loại 2 phương án A và C.
ta loại 2 phương án A và C.
Đồ thị hàm số đi qua điểm điểm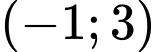 nên
nên 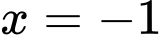 thì
thì 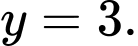
Do vậy đồ thị trên là đồ thị hàm số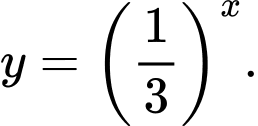
Chọn D. Đáp án: D
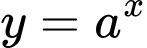 và là hàm nghịch biến (vì có đồ thị đi xuống) nên
và là hàm nghịch biến (vì có đồ thị đi xuống) nên 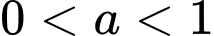 ta loại 2 phương án A và C.
ta loại 2 phương án A và C. Đồ thị hàm số đi qua điểm điểm
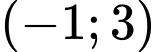 nên
nên 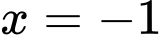 thì
thì 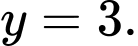
Do vậy đồ thị trên là đồ thị hàm số
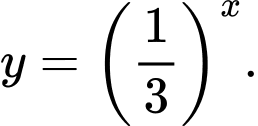
Chọn D. Đáp án: D
Câu 3 [277180]: Đồ thị hình vẽ bên là của hàm số nào trong bốn hàm số dưới đây?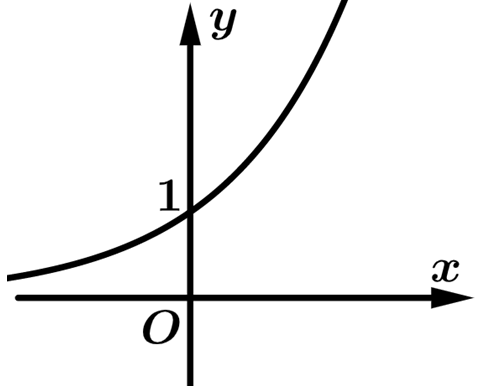

A, 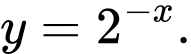
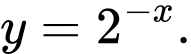
B, 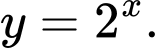
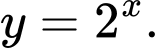
C, 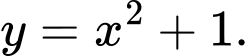
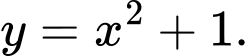
D, 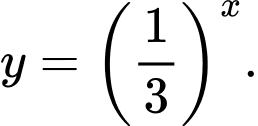
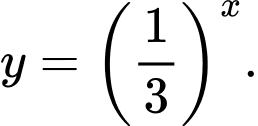
HD: Dựa vào đồ thị hàm số suy ra hàm số có đồ thị như hình vẽ là hàm số đồng biến nên chỉ đáp án B thoả mãn yêu cầu. Chọn B Đáp án: B
Câu 4 [501561]: Tìm 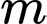 để hàm số
để hàm số 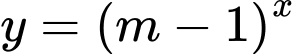 nghịch biến trên
nghịch biến trên 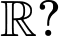
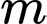 để hàm số
để hàm số 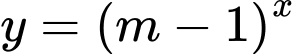 nghịch biến trên
nghịch biến trên 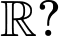
A, 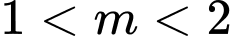 .
.
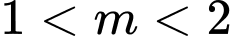 .
.B,  .
.
 .
.C, 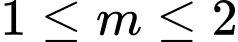 .
.
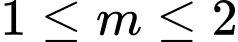 .
.D,  .
.
 .
.
Đáp án A
Điều kiện hàm số nghịch biến trên R là . Đáp án: A
. Đáp án: A
Điều kiện hàm số nghịch biến trên R là
 . Đáp án: A
. Đáp án: A
Câu 5 [657026]: Cho hàm số 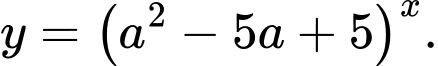 Tìm
Tìm 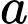 để hàm số đã cho đồng biến trên
để hàm số đã cho đồng biến trên 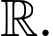
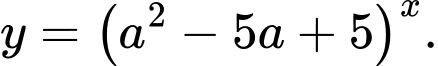 Tìm
Tìm 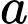 để hàm số đã cho đồng biến trên
để hàm số đã cho đồng biến trên 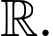
A, 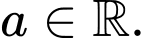
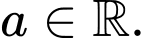
B, 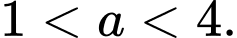
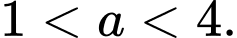
C, 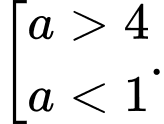
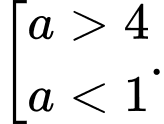
D, 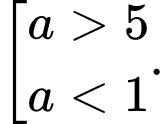
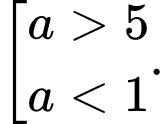
Hàm số 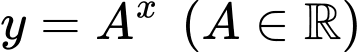 đồng biến trên
đồng biến trên 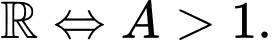
Do đó hàm số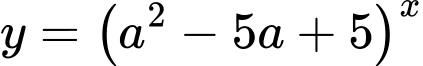 đồng biến trên
đồng biến trên 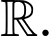
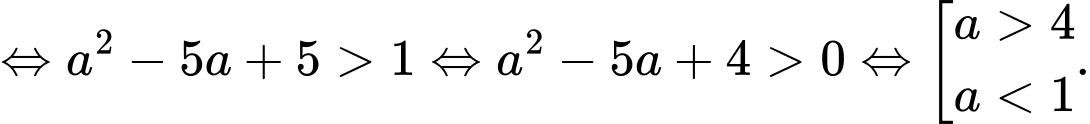 Chọn C.
Đáp án: C
Chọn C.
Đáp án: C
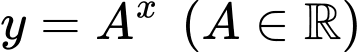 đồng biến trên
đồng biến trên 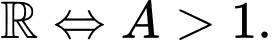
Do đó hàm số
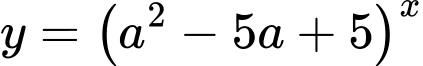 đồng biến trên
đồng biến trên 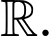
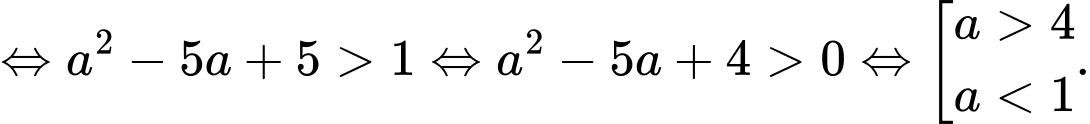 Chọn C.
Đáp án: C
Chọn C.
Đáp án: C
Câu 6 [50465]: Cho 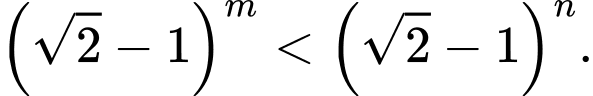 Khi đó
Khi đó
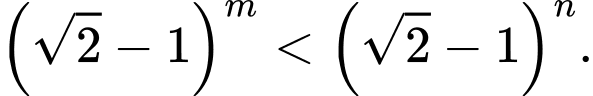 Khi đó
Khi đó A, 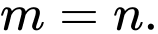
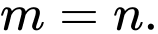
B, 

C, 

D, 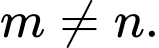
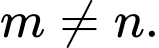
Đáp án C
Do Đáp án: C
Đáp án: C
Do
 Đáp án: C
Đáp án: C
Câu 7 [50489]: Khẳng định nào sau đây sai?
A, 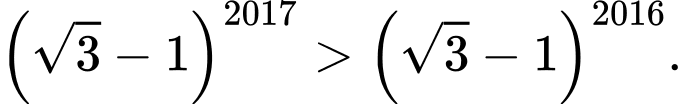
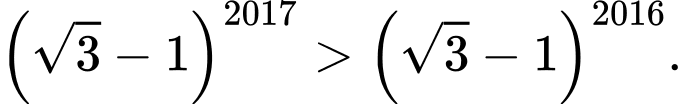
B, 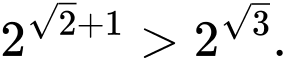
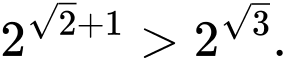
C, 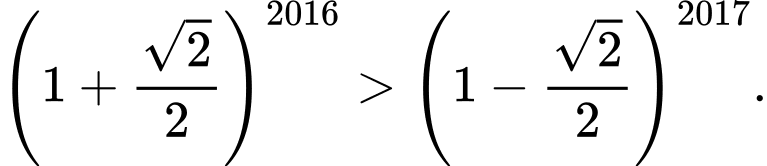
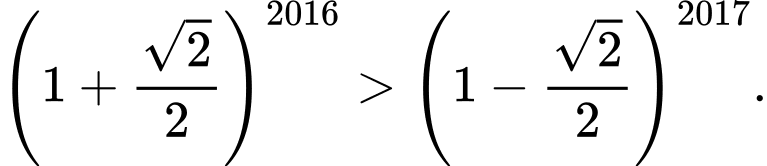
D, 

Hàm số 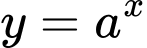 là hàm số đồng biến trên
là hàm số đồng biến trên 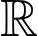 khi
khi  và là hàm số nghịch biến trên
và là hàm số nghịch biến trên 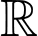 khi
khi 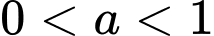 . Khi đó, xét với
. Khi đó, xét với  thì
thì  khi
khi  và
và  khi
khi 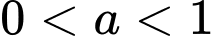 .
.
Dựa vào các đáp án, ta thấy rằng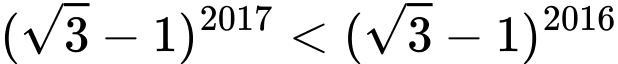 vì
vì 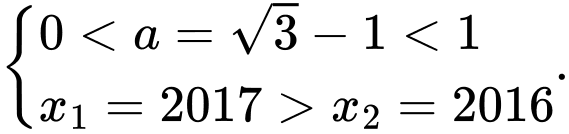 Chọn A. Đáp án: A
Chọn A. Đáp án: A
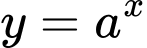 là hàm số đồng biến trên
là hàm số đồng biến trên 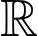 khi
khi  và là hàm số nghịch biến trên
và là hàm số nghịch biến trên 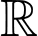 khi
khi 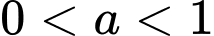 . Khi đó, xét với
. Khi đó, xét với  thì
thì  khi
khi  và
và  khi
khi 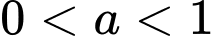 .
.
Dựa vào các đáp án, ta thấy rằng
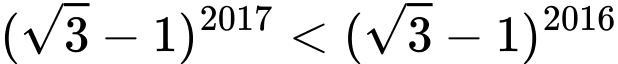 vì
vì 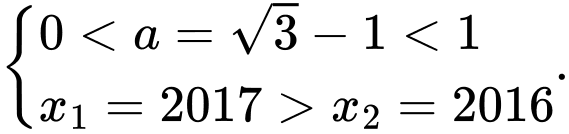 Chọn A. Đáp án: A
Chọn A. Đáp án: A
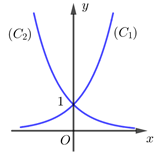
Câu 8 [657036]: Cho hai hàm số 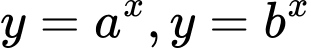 với
với 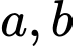 là hai số thực dương khác 1, lần lượt có đồ thị là
là hai số thực dương khác 1, lần lượt có đồ thị là 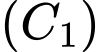 và
và 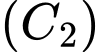 như hình bên dưới. Mệnh đề nào dưới đây đúng?
như hình bên dưới. Mệnh đề nào dưới đây đúng?
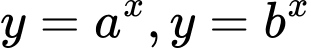 với
với 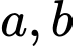 là hai số thực dương khác 1, lần lượt có đồ thị là
là hai số thực dương khác 1, lần lượt có đồ thị là 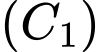 và
và 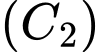 như hình bên dưới. Mệnh đề nào dưới đây đúng?
như hình bên dưới. Mệnh đề nào dưới đây đúng?
A, 

B, 

C, 

D, 

Dựa vào đồ thị suy ra hàm số 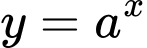 là hàm đồng biến (vì có đồ thị đi lên).
là hàm đồng biến (vì có đồ thị đi lên).
Hàm số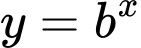 là hàm nghịch biến (vì có đồ thị đi xuống).
là hàm nghịch biến (vì có đồ thị đi xuống).
Suy ra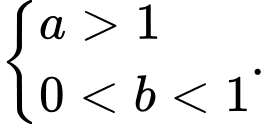 Chọn B.
Đáp án: B
Chọn B.
Đáp án: B
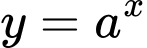 là hàm đồng biến (vì có đồ thị đi lên).
là hàm đồng biến (vì có đồ thị đi lên). Hàm số
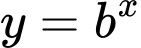 là hàm nghịch biến (vì có đồ thị đi xuống).
là hàm nghịch biến (vì có đồ thị đi xuống). Suy ra
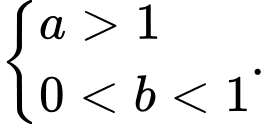 Chọn B.
Đáp án: B
Chọn B.
Đáp án: B
Câu 9 [657038]: Cho 3 số 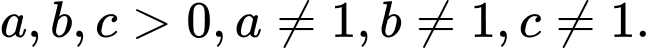 Đồ thị các hàm số
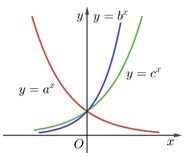
Đồ thị các hàm số 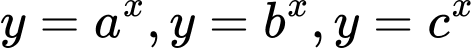 được cho trong hình vẽ dưới. Mệnh đề nào sau đây đúng?
được cho trong hình vẽ dưới. Mệnh đề nào sau đây đúng?
 Đồ thị các hàm số
Đồ thị các hàm số 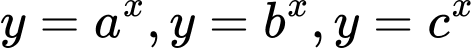 được cho trong hình vẽ dưới. Mệnh đề nào sau đây đúng?
được cho trong hình vẽ dưới. Mệnh đề nào sau đây đúng? 
A, 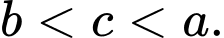
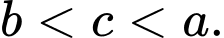
B, 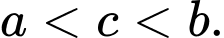
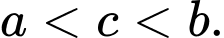
C, 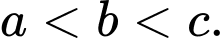
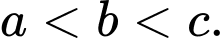
D, 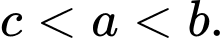
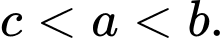
Dựa vào đồ thị hàm số ta thấy hàm số 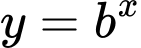 và
và 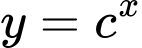 là các hàm số đồng biến nên
là các hàm số đồng biến nên 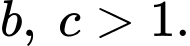 Hàm số
Hàm số 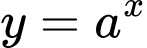 là hàm nghịch biến nên
là hàm nghịch biến nên 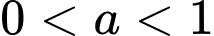
Với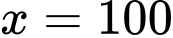 ta thấy
ta thấy  Chọn B.
Đáp án: B
Chọn B.
Đáp án: B
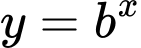 và
và 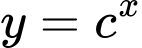 là các hàm số đồng biến nên
là các hàm số đồng biến nên 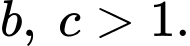 Hàm số
Hàm số 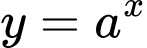 là hàm nghịch biến nên
là hàm nghịch biến nên 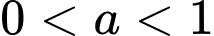
Với
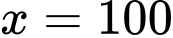 ta thấy
ta thấy  Chọn B.
Đáp án: B
Chọn B.
Đáp án: B
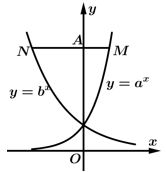
Câu 10 [657039]: Cho các số thực dương 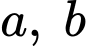 khác 1. Biết rằng bất kì đường thẳng nào song song với
khác 1. Biết rằng bất kì đường thẳng nào song song với 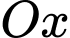 mà cắt các đường
mà cắt các đường 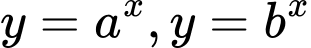 trục tung lần lượt tại
trục tung lần lượt tại 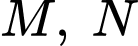 và
và 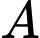 thì
thì 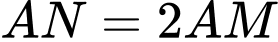 (hình vẽ bên). Mệnh đề nào sau đây đúng?
(hình vẽ bên). Mệnh đề nào sau đây đúng?
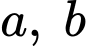 khác 1. Biết rằng bất kì đường thẳng nào song song với
khác 1. Biết rằng bất kì đường thẳng nào song song với 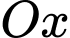 mà cắt các đường
mà cắt các đường 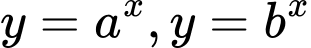 trục tung lần lượt tại
trục tung lần lượt tại 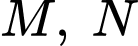 và
và 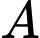 thì
thì 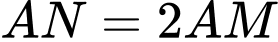 (hình vẽ bên). Mệnh đề nào sau đây đúng?
(hình vẽ bên). Mệnh đề nào sau đây đúng? 
A, 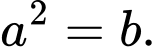
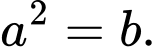
B, 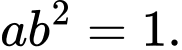
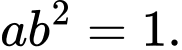
C, 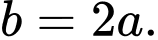
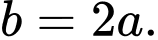
D, 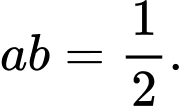
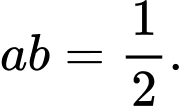
Với 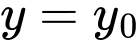 ta có:
ta có: 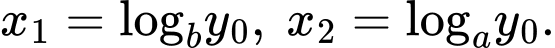
Theo giả thiết ta có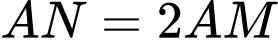 nên
nên 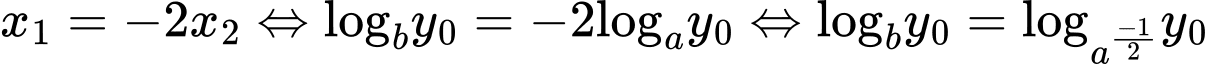
Khi đó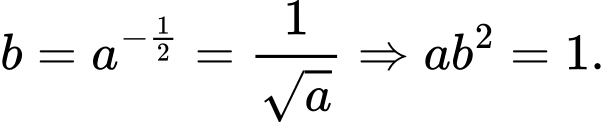 Chọn B. Đáp án: B
Chọn B. Đáp án: B
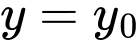 ta có:
ta có: 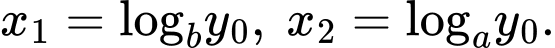
Theo giả thiết ta có
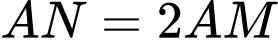 nên
nên 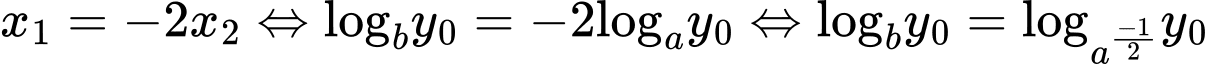
Khi đó
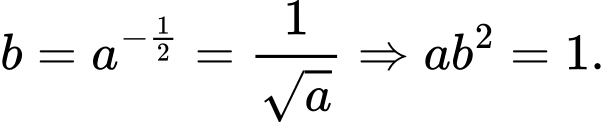 Chọn B. Đáp án: B
Chọn B. Đáp án: B
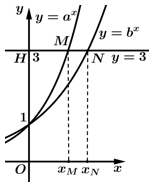
Câu 11 [27384]: Cho 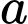 và
và 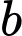 là hai số thực dương khác 1 và các hàm số
là hai số thực dương khác 1 và các hàm số 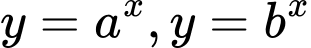 có đồ thị như hình bên. Đường thẳng
có đồ thị như hình bên. Đường thẳng 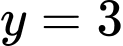 cắt trục tung, đồ thị hàm số
cắt trục tung, đồ thị hàm số 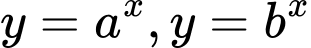 lần lượt tại
lần lượt tại 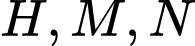 . Biết rằng
. Biết rằng 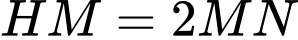 . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng?
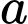 và
và 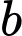 là hai số thực dương khác 1 và các hàm số
là hai số thực dương khác 1 và các hàm số 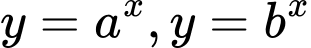 có đồ thị như hình bên. Đường thẳng
có đồ thị như hình bên. Đường thẳng 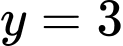 cắt trục tung, đồ thị hàm số
cắt trục tung, đồ thị hàm số 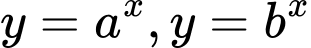 lần lượt tại
lần lượt tại 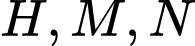 . Biết rằng
. Biết rằng 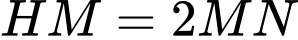 . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng?
A, 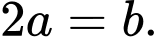
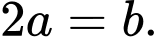
B, 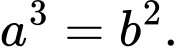
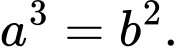
C, 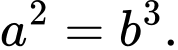
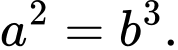
D, 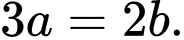
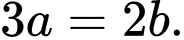
 Đáp án: C
Đáp án: C
Câu 12 [635774]: Cho 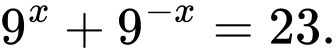 Tính giá trị biểu thức
Tính giá trị biểu thức 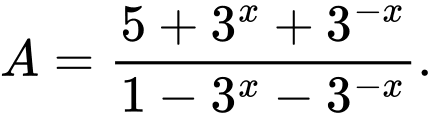
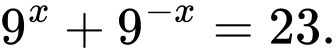 Tính giá trị biểu thức
Tính giá trị biểu thức 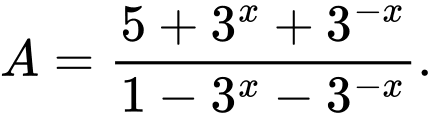
A, 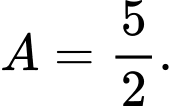
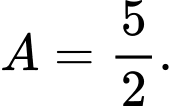
B, 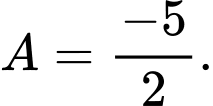
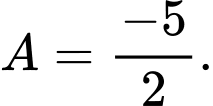
C, 

D, 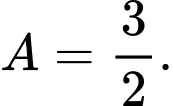
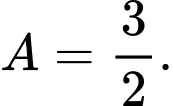
Viết lại biểu thức 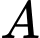 ta có:
ta có: 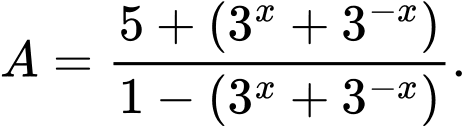
Như vậy dựa vào giả thiết đề bài cho ta cần tính giá trị của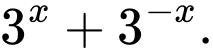
Ta có: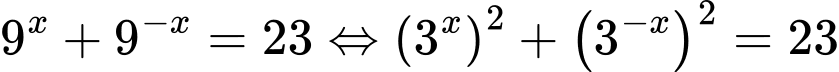
Chú ý rằng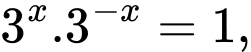 cộng hai vế với
cộng hai vế với 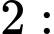
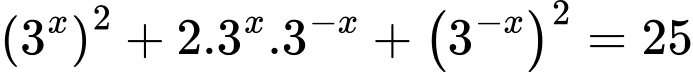
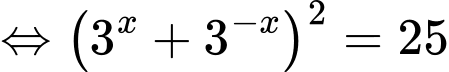
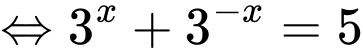 (vì
(vì 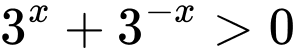 với mọi
với mọi 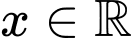 ). Khi đó
). Khi đó 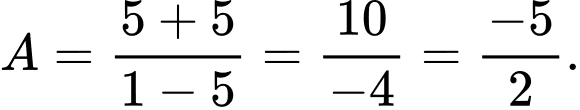 Chọn B.
Đáp án: B
Chọn B.
Đáp án: B
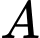 ta có:
ta có: 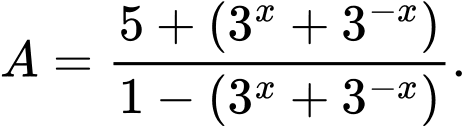
Như vậy dựa vào giả thiết đề bài cho ta cần tính giá trị của
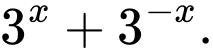
Ta có:
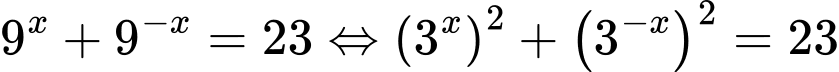
Chú ý rằng
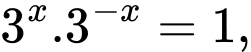 cộng hai vế với
cộng hai vế với 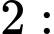
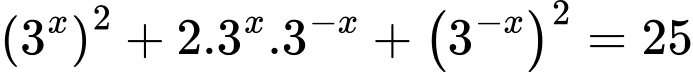
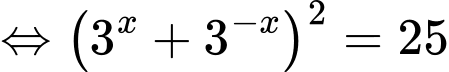
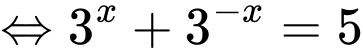 (vì
(vì 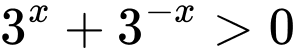 với mọi
với mọi 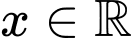 ). Khi đó
). Khi đó 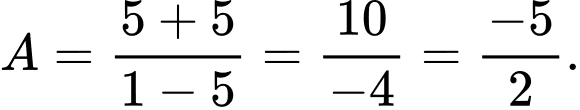 Chọn B.
Đáp án: B
Chọn B.
Đáp án: B
Câu 13 [635775]: Cho 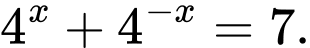 Tính giá trị của biểu thức
Tính giá trị của biểu thức 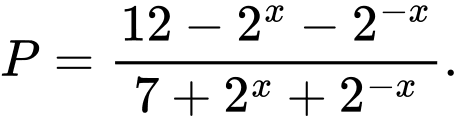
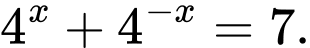 Tính giá trị của biểu thức
Tính giá trị của biểu thức 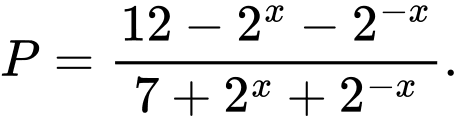
A, 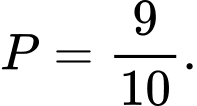
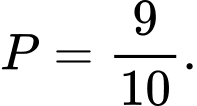
B, 

C, 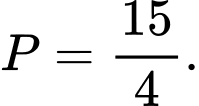
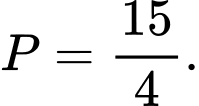
D, 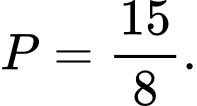
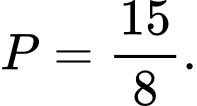
Tương tự Câu trên ta có:
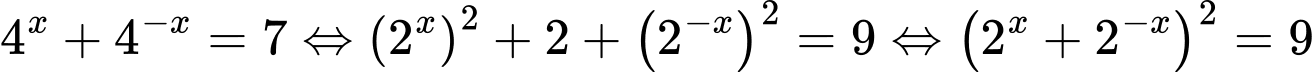
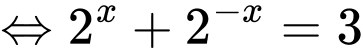 .
.
Thế vào biểu thức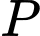 ta được:
ta được: 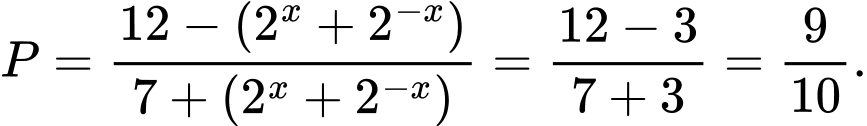 Chọn A.
Đáp án: A
Chọn A.
Đáp án: A
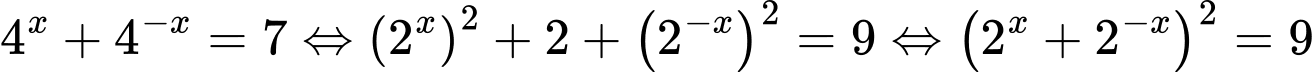
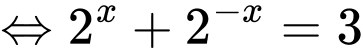 .
. Thế vào biểu thức
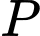 ta được:
ta được: 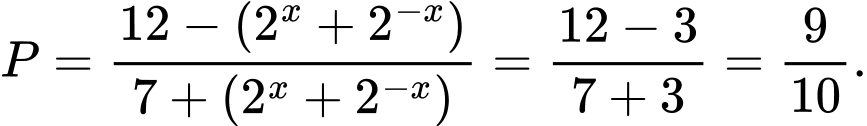 Chọn A.
Đáp án: A
Chọn A.
Đáp án: A
Câu 14 [28218]: Cho hàm số 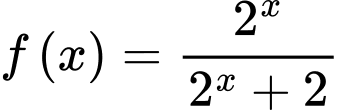 . Khi đó tổng
. Khi đó tổng 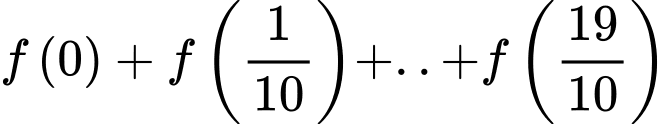 bằng
bằng
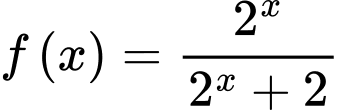 . Khi đó tổng
. Khi đó tổng 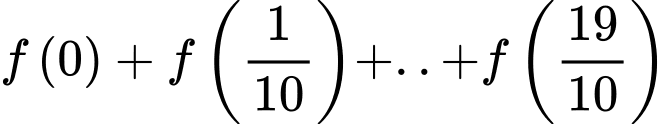 bằng
bằng A, 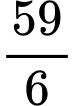 .
.
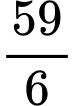 .
.B, 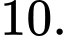
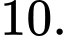
C, 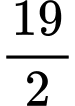 .
.
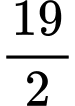 .
.D, 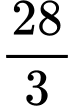 .
.
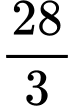 .
.
Ta có 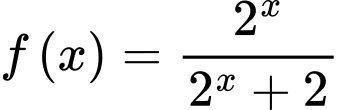
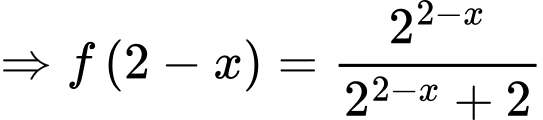
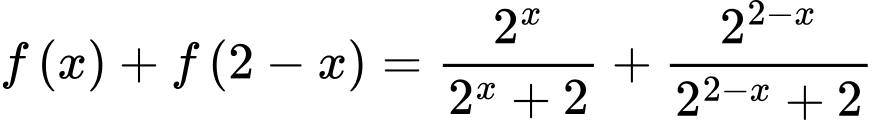
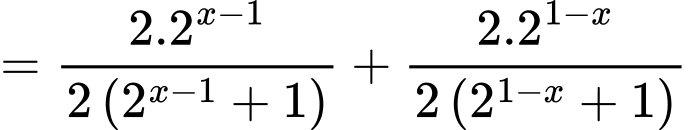
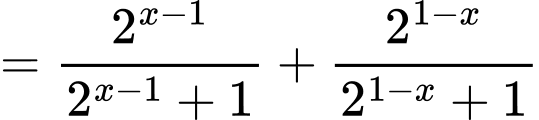
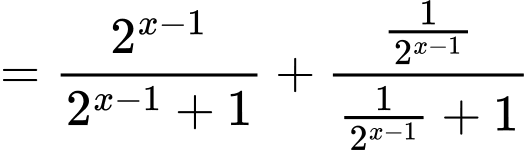
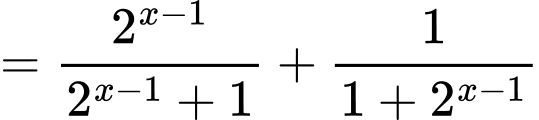
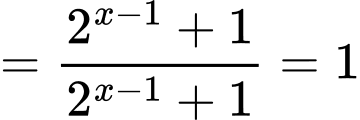
Vậy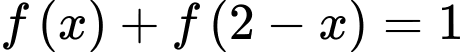
Suy ra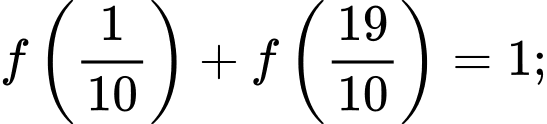
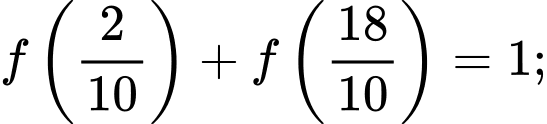
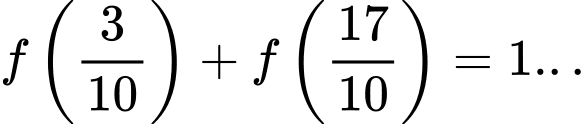 ta được 9 cặp như vậy trong tổng đã cho.
ta được 9 cặp như vậy trong tổng đã cho.
Ta có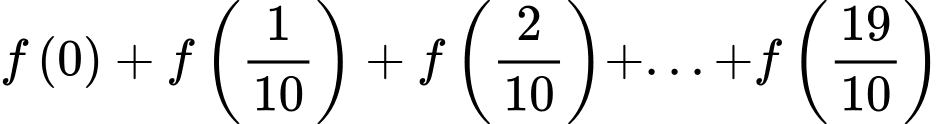
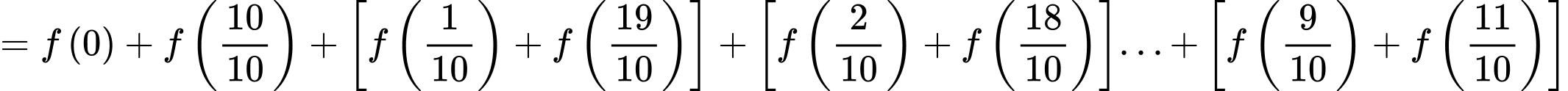
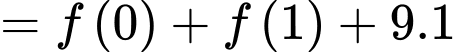
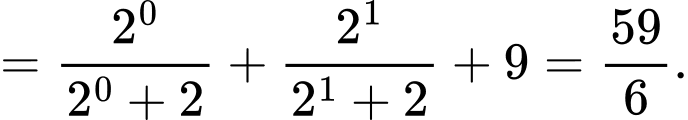
Chọn A. Đáp án: A
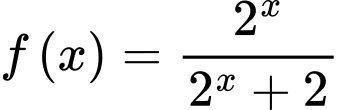
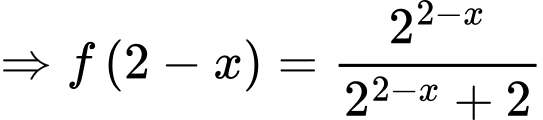
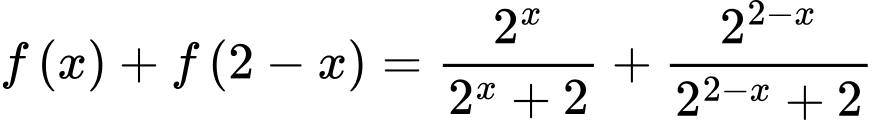
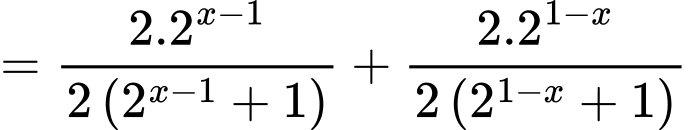
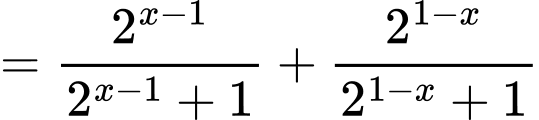
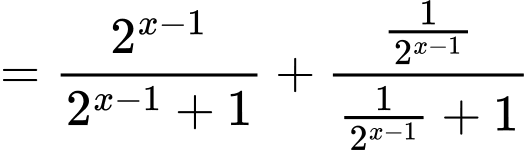
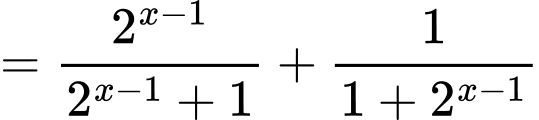
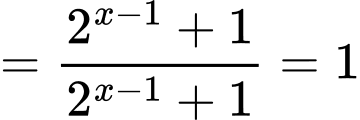
Vậy
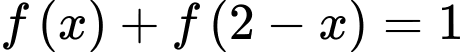
Suy ra
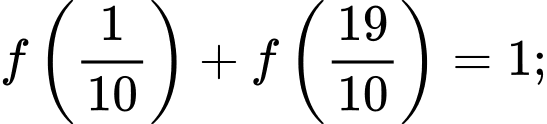
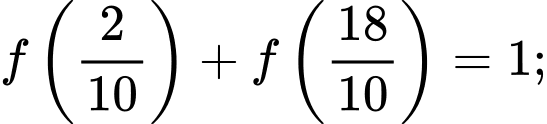
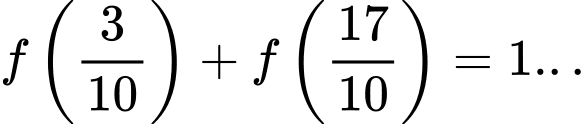 ta được 9 cặp như vậy trong tổng đã cho.
ta được 9 cặp như vậy trong tổng đã cho.Ta có
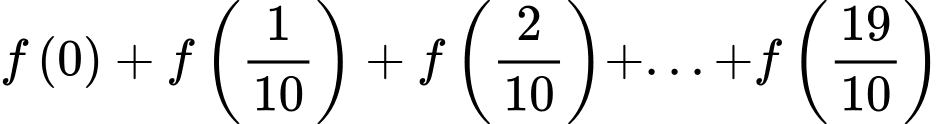
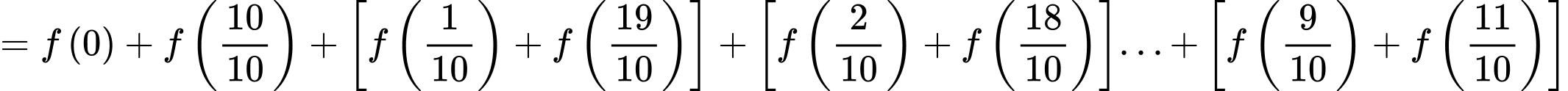
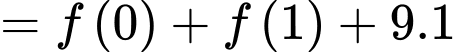
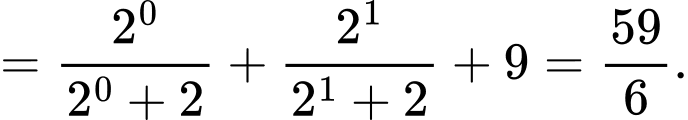
Chọn A. Đáp án: A
Câu 15 [28202]: Cho hàm số 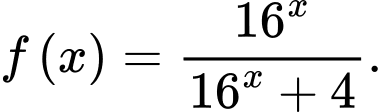 Tính
Tính 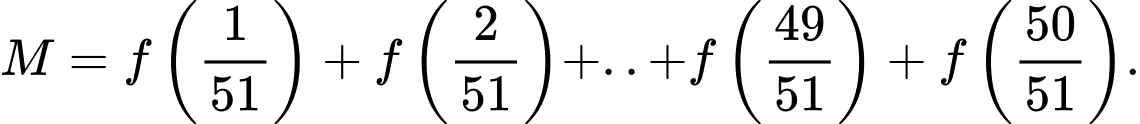
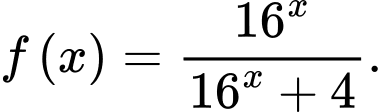 Tính
Tính 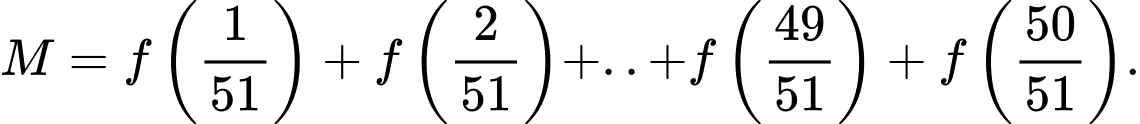
A, 10.
B, 25.
C, 40.
D, 18.
Ta có 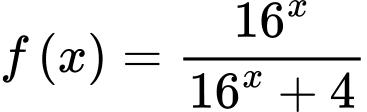
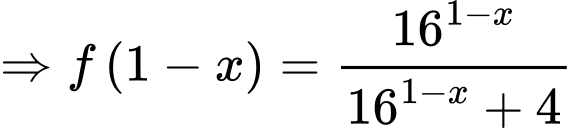
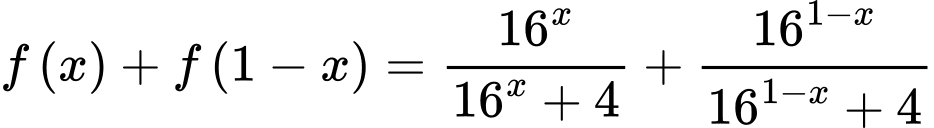
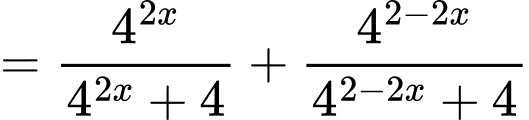
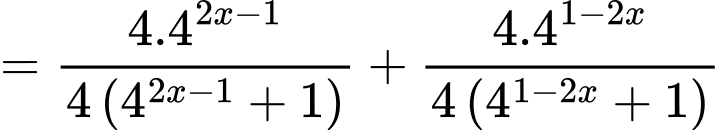
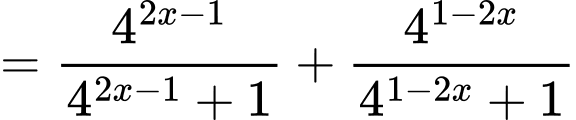
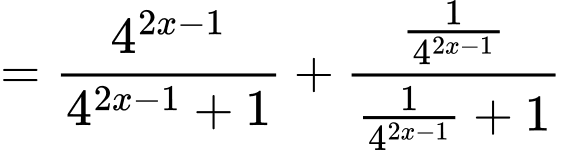
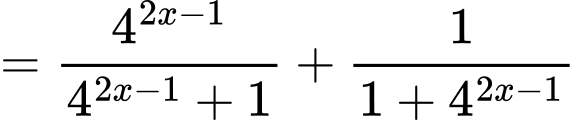
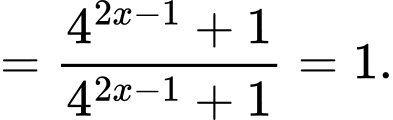
Vậy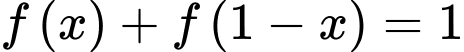
Suy ra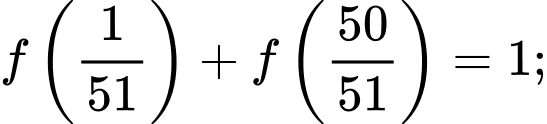
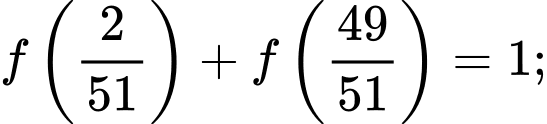
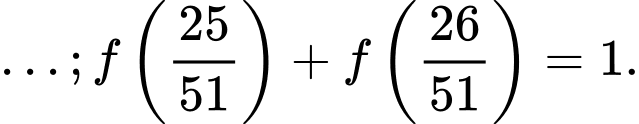 Ta được
Ta được 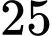 cặp như vậy trong tổng đã cho .
cặp như vậy trong tổng đã cho .
Ta có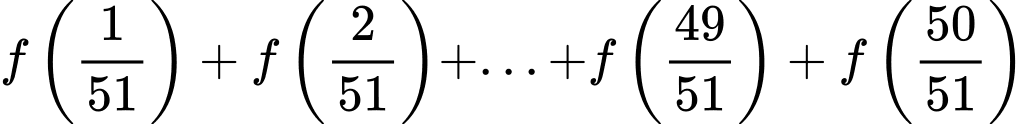
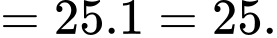
Chọn B. Đáp án: B
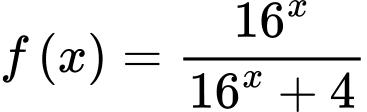
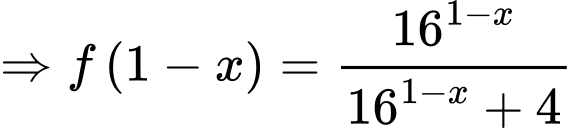
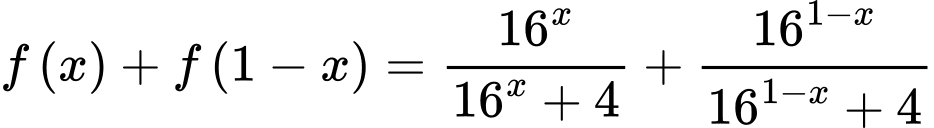
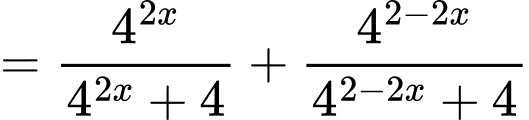
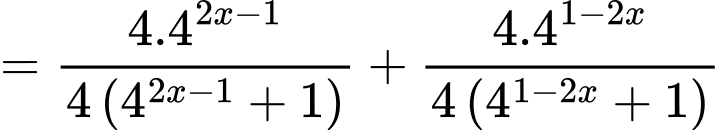
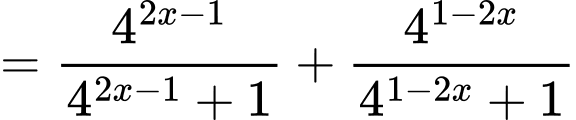
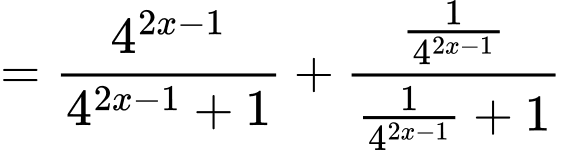
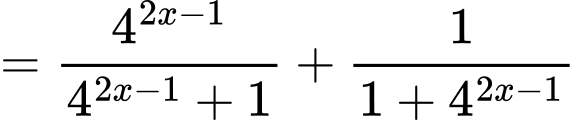
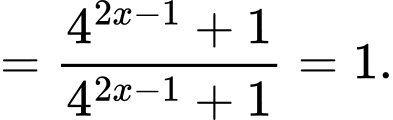
Vậy
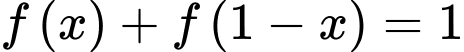
Suy ra
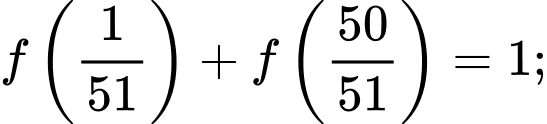
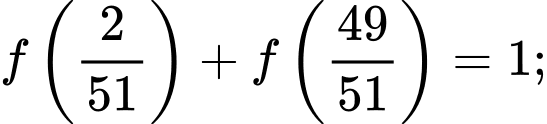
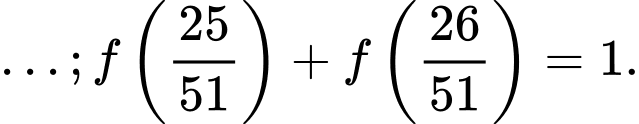 Ta được
Ta được 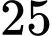 cặp như vậy trong tổng đã cho .
cặp như vậy trong tổng đã cho .Ta có
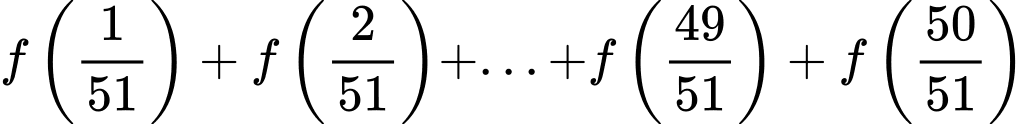
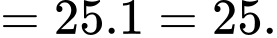
Chọn B. Đáp án: B
Câu 16 [552972]: Trong các hàm số 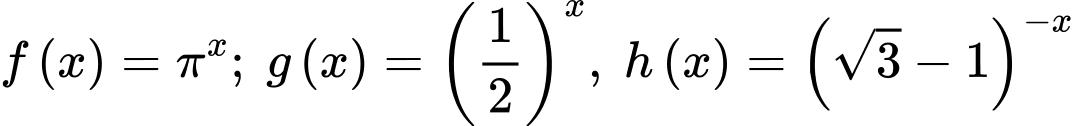 và
và  có bao nhiêu hàm số nghịch biến trên tập
có bao nhiêu hàm số nghịch biến trên tập 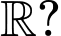
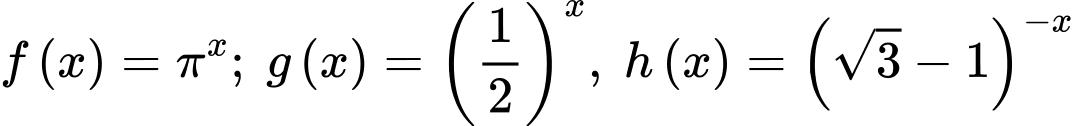 và
và  có bao nhiêu hàm số nghịch biến trên tập
có bao nhiêu hàm số nghịch biến trên tập 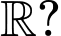
Trong các hàm số 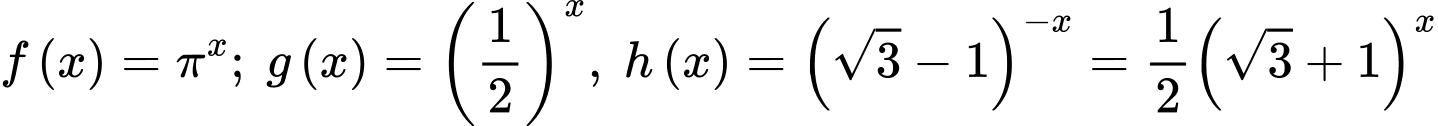 và
và  có 2 hàm số nghịch biến trên tập
có 2 hàm số nghịch biến trên tập 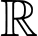 là:
là: 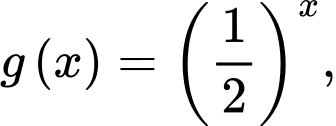

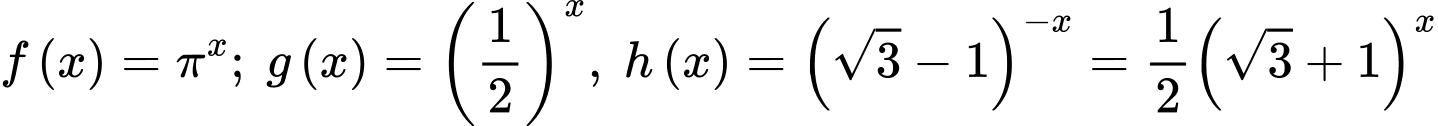 và
và  có 2 hàm số nghịch biến trên tập
có 2 hàm số nghịch biến trên tập 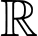 là:
là: 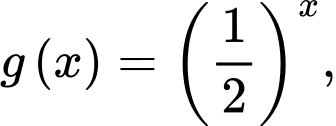

Câu 17 [550668]: Cho các hàm số 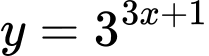 và
và 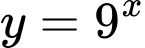 có đồ thị lần lượt là
có đồ thị lần lượt là 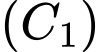 và
và 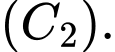 Gọi
Gọi 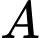 là giao điểm của
là giao điểm của 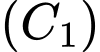 và
và 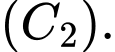 Gọi
Gọi 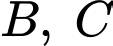 lần lượt là giao điểm của trục
lần lượt là giao điểm của trục 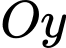 với
với 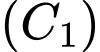 và
và 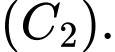 Diện tích của tam giác
Diện tích của tam giác 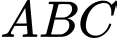 bằng bao nhiêu?
bằng bao nhiêu?
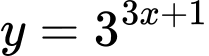 và
và 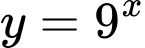 có đồ thị lần lượt là
có đồ thị lần lượt là 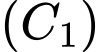 và
và 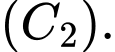 Gọi
Gọi 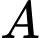 là giao điểm của
là giao điểm của 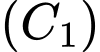 và
và 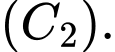 Gọi
Gọi 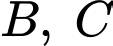 lần lượt là giao điểm của trục
lần lượt là giao điểm của trục 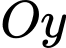 với
với 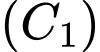 và
và 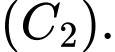 Diện tích của tam giác
Diện tích của tam giác 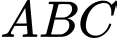 bằng bao nhiêu?
bằng bao nhiêu?
Phương trình hoành độ giao điểm là 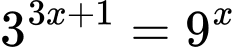
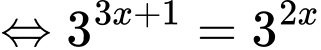

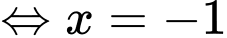
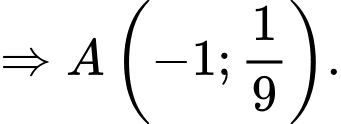
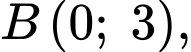
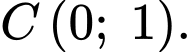
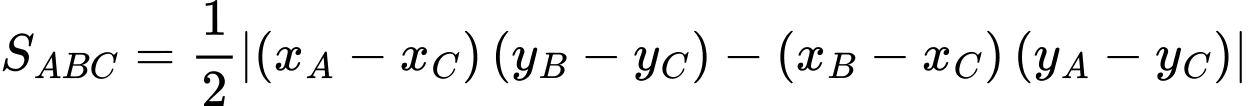
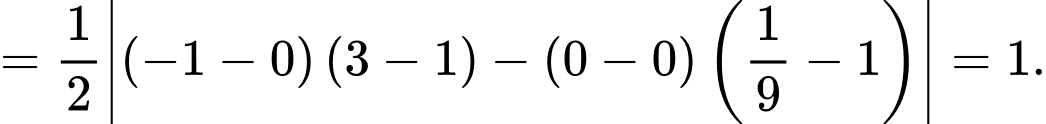
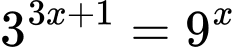
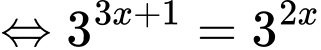

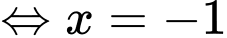
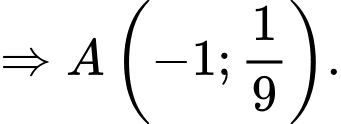
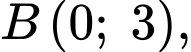
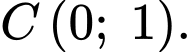
Diện tích tam giác 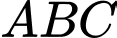 là
là
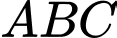 là
là 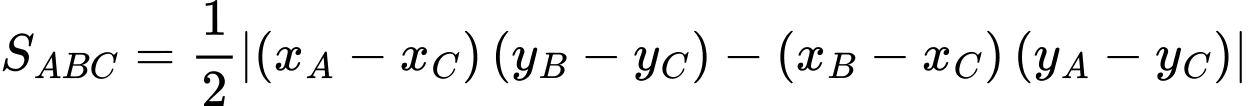
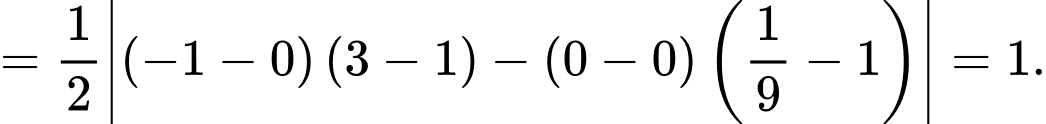
Điền đáp án: 1.
Câu 18 [28208]: Cho hàm số 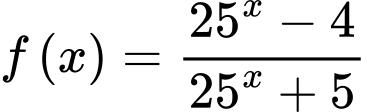 . Ký hiệu
. Ký hiệu 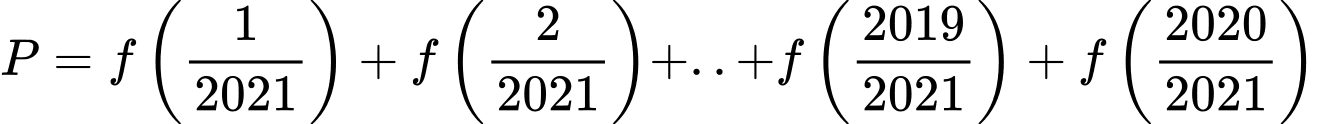 , hỏi
, hỏi 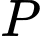 có bao nhiêu ước nguyên dương?
có bao nhiêu ước nguyên dương?
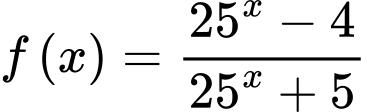 . Ký hiệu
. Ký hiệu 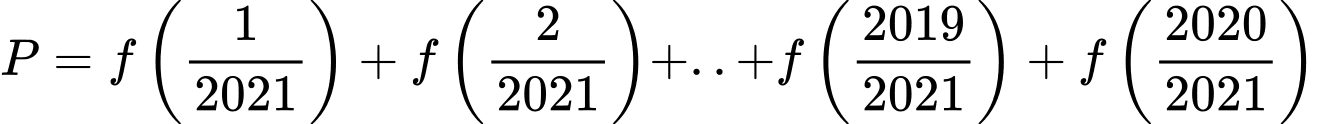 , hỏi
, hỏi 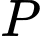 có bao nhiêu ước nguyên dương?
có bao nhiêu ước nguyên dương? A, 5.
B, 6.
C, 4.
D, 8.
Đáp án: C