Đáp án Bài tập tự luyện số 1
Câu 1 [802405]: Phương trình tiếp tuyến của đồ thị 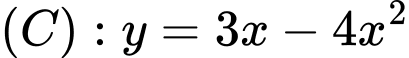 tại điểm có hoành độ
tại điểm có hoành độ 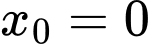 là
là
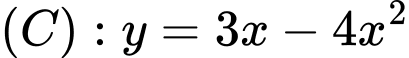 tại điểm có hoành độ
tại điểm có hoành độ 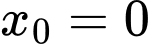 là
là A, 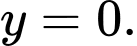
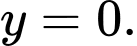
B, 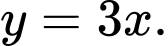
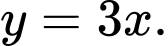
C, 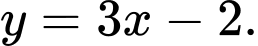
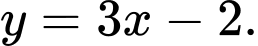
D, 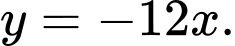
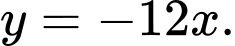
Chọn B
Tập xác định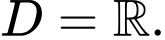
Đạo hàm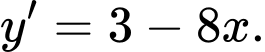
Phương trình tiếp tuyến: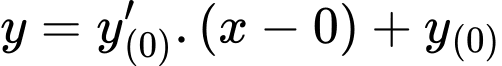
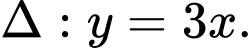 Đáp án: B
Đáp án: B
Tập xác định
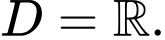
Đạo hàm
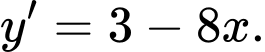
Phương trình tiếp tuyến:
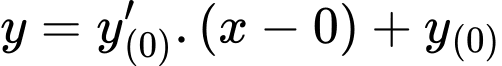
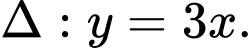 Đáp án: B
Đáp án: B
Câu 2 [802402]: Tiếp tuyến của đồ thị hàm số 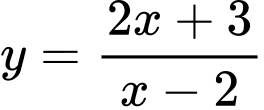 tại điểm có hoành độ bằng
tại điểm có hoành độ bằng 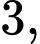 tương ứng là
tương ứng là
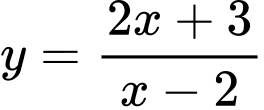 tại điểm có hoành độ bằng
tại điểm có hoành độ bằng 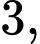 tương ứng là
tương ứng là A, 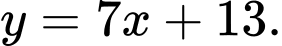
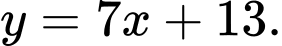
B, 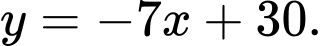
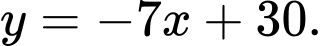
C, 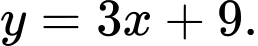
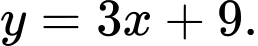
D, 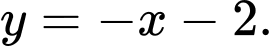
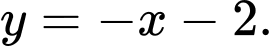
Chọn B
 ;
;
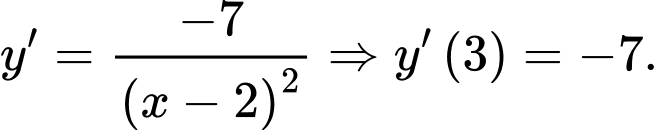
Phương trình tiếp tuyến tương ứng là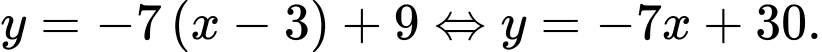 Đáp án: B
Đáp án: B
 ;
; 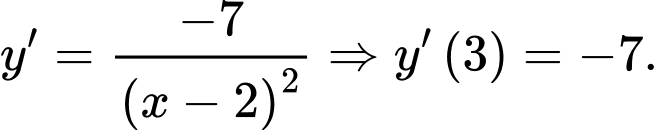
Phương trình tiếp tuyến tương ứng là
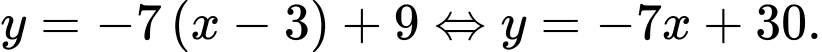 Đáp án: B
Đáp án: B
Câu 3 [30864]: Cho hàm số 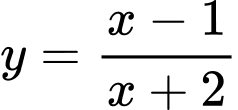 có đồ thị
có đồ thị  Tiếp tuyến của
Tiếp tuyến của  tại giao điểm của
tại giao điểm của  và trục hoành có phương trình là
và trục hoành có phương trình là
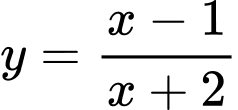 có đồ thị
có đồ thị  Tiếp tuyến của
Tiếp tuyến của  tại giao điểm của
tại giao điểm của  và trục hoành có phương trình là
và trục hoành có phương trình là A, 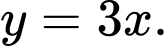
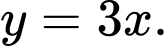
B, 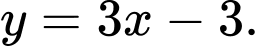
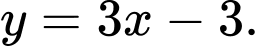
C, 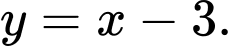
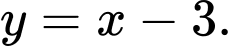
D, 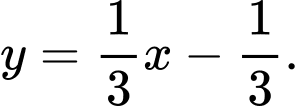
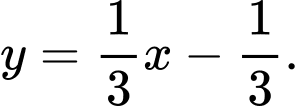
 Đáp án: D
Đáp án: D
Câu 4 [30852]: Cho hàm số 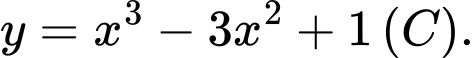 Ba tiếp tuyến của
Ba tiếp tuyến của  tại giao điểm của
tại giao điểm của  và đường thẳng
và đường thẳng 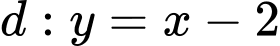 có tổng hệ số góc bằng
có tổng hệ số góc bằng
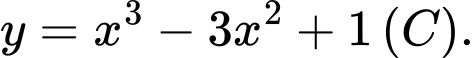 Ba tiếp tuyến của
Ba tiếp tuyến của  tại giao điểm của
tại giao điểm của  và đường thẳng
và đường thẳng 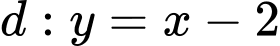 có tổng hệ số góc bằng
có tổng hệ số góc bằng A, 12.
B, 13.
C, 14.
D, 15.
 Đáp án: D
Đáp án: D
Câu 5 [528548]: Gọi 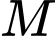 là giao điểm của trục tung với đồ thị hàm số
là giao điểm của trục tung với đồ thị hàm số 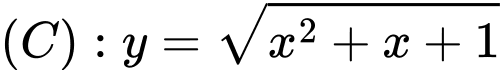 . Tiếp tuyến của
. Tiếp tuyến của  tại
tại 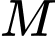 có phương trình là
có phương trình là
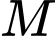 là giao điểm của trục tung với đồ thị hàm số
là giao điểm của trục tung với đồ thị hàm số 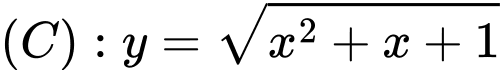 . Tiếp tuyến của
. Tiếp tuyến của  tại
tại 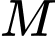 có phương trình là
có phương trình là A, 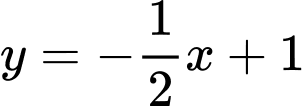 .
.
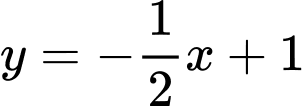 .
.B, 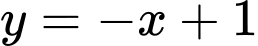 .
.
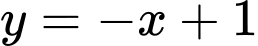 .
.C, 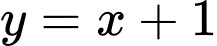 .
.
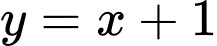 .
.D, 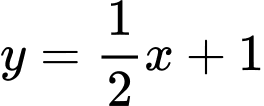 .
.
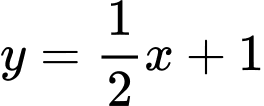 .
.
Chọn D
Do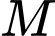 là giao điểm của trục tung với đồ thị hàm số
là giao điểm của trục tung với đồ thị hàm số 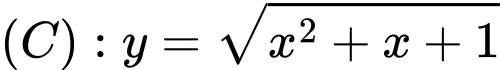 nên
nên  .
.
Ta có: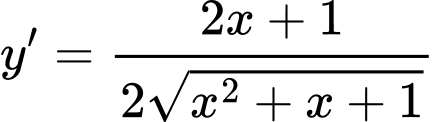 .
.
Hệ số góc tiếp tuyến của đồ thị tại
tại 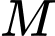 là
là 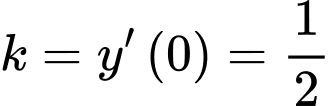 .
.
Vậy phương trình tiếp tuyến cần tìm là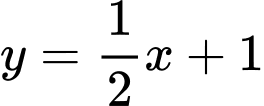 . Đáp án: D
. Đáp án: D
Do
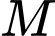 là giao điểm của trục tung với đồ thị hàm số
là giao điểm của trục tung với đồ thị hàm số 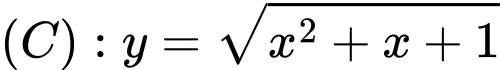 nên
nên  .
. Ta có:
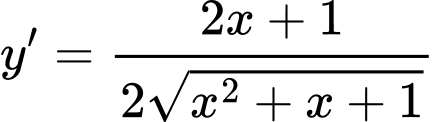 .
. Hệ số góc tiếp tuyến của đồ thị
 tại
tại 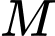 là
là 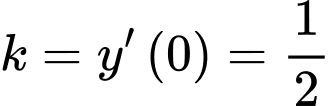 .
. Vậy phương trình tiếp tuyến cần tìm là
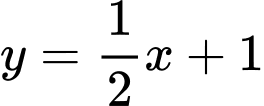 . Đáp án: D
. Đáp án: D
Câu 6 [25600]: Tiếp tuyến với đồ thị 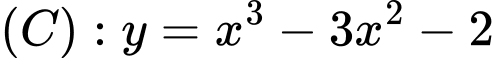 song song với đường thẳng
song song với đường thẳng 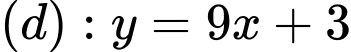 có phương trình là
có phương trình là
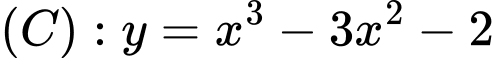 song song với đường thẳng
song song với đường thẳng 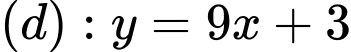 có phương trình là
có phương trình là A, 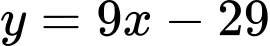 và
và 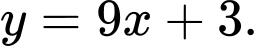
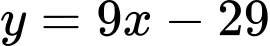 và
và 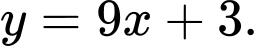
B, 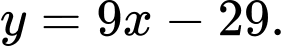
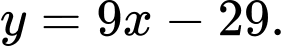
C, 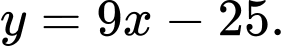
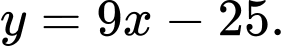
D, 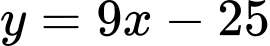 và
và 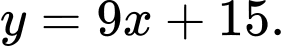
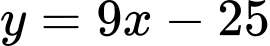 và
và 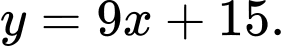
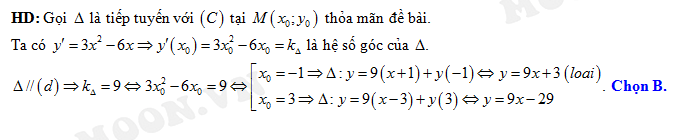 Đáp án: B
Đáp án: B
Câu 7 [25663]: Số tiếp tuyến của 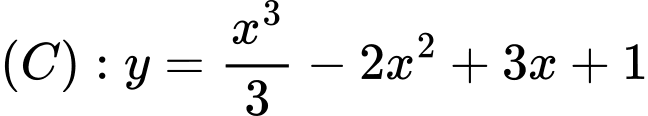 song song với
song song với 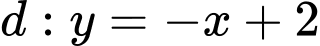 ?
?
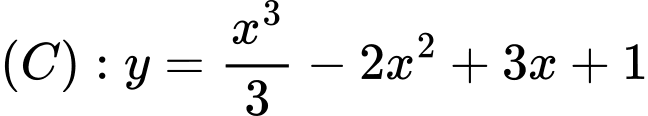 song song với
song song với 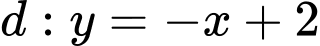 ?
? A, 3.
B, 2.
C, 0.
D, 1.
Gọi 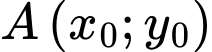 là tiếp điểm.
là tiếp điểm.
Do tiếp tuyến song song với đường thẳng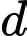
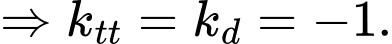
Khi đó,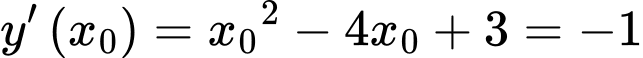
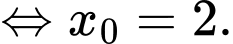
Suy ra phương trình tiếp tuyến là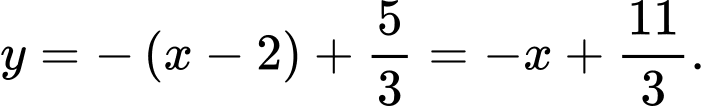
Vậy số tiếp tuyến thoả mãn YCBT là 1. Đáp án: D
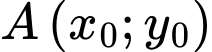 là tiếp điểm.
là tiếp điểm.Do tiếp tuyến song song với đường thẳng
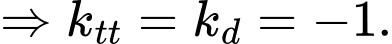
Khi đó,
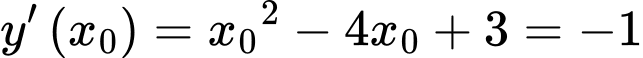
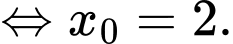
Suy ra phương trình tiếp tuyến là
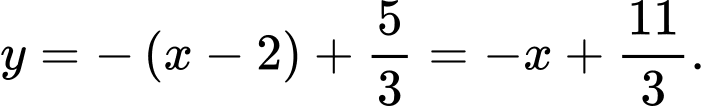
Vậy số tiếp tuyến thoả mãn YCBT là 1. Đáp án: D
Câu 8 [503021]: Có bao nhiêu tiếp tuyến của đồ thị hàm số 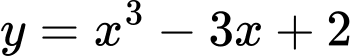 song song với đường thẳng
song song với đường thẳng  ?
?
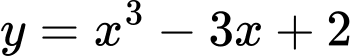 song song với đường thẳng
song song với đường thẳng  ?
? A, 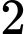 .
.
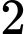 .
.B, 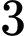 .
.
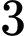 .
.C, 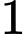 .
.
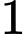 .
.D,  .
.
 .
.
Chọn C
+)Ta gọi là phương trình đường thẳng đã cho,
là phương trình đường thẳng đã cho,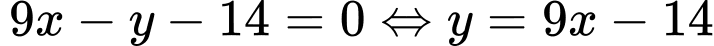 ,suy ra
,suy ra  có hệ số góc bằng
có hệ số góc bằng 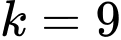 .Mà
.Mà 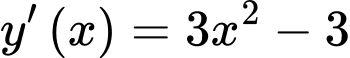 .Để tiếp tuyến của đồ thị hàm số
.Để tiếp tuyến của đồ thị hàm số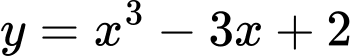 song song với
song song với  thì
thì 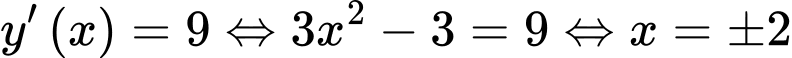 .
.
+)Với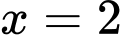 phương trình tiếp tuyến là
phương trình tiếp tuyến là 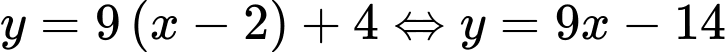 (Loại vì trùng với
(Loại vì trùng với  ).
).
+)Với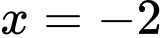 phương trình tiếp tuyến là
phương trình tiếp tuyến là  (Thỏa mãn). Đáp án: C
(Thỏa mãn). Đáp án: C
+)Ta gọi
 là phương trình đường thẳng đã cho,
là phương trình đường thẳng đã cho,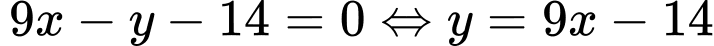 ,suy ra
,suy ra  có hệ số góc bằng
có hệ số góc bằng 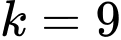 .Mà
.Mà 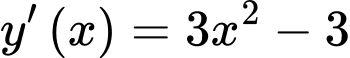 .Để tiếp tuyến của đồ thị hàm số
.Để tiếp tuyến của đồ thị hàm số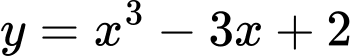 song song với
song song với  thì
thì 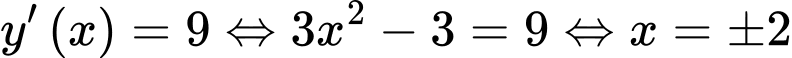 .
.+)Với
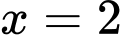 phương trình tiếp tuyến là
phương trình tiếp tuyến là 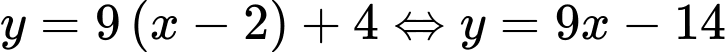 (Loại vì trùng với
(Loại vì trùng với  ).
).+)Với
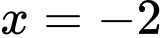 phương trình tiếp tuyến là
phương trình tiếp tuyến là  (Thỏa mãn). Đáp án: C
(Thỏa mãn). Đáp án: C
Câu 9 [25617]: Đồ thị hàm số 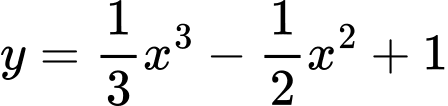 có bao nhiêu tiếp tuyến biết vuông góc với đường thẳng
có bao nhiêu tiếp tuyến biết vuông góc với đường thẳng 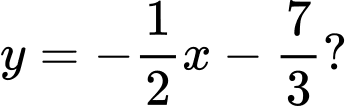
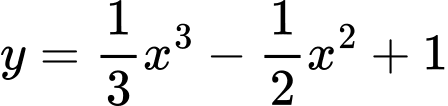 có bao nhiêu tiếp tuyến biết vuông góc với đường thẳng
có bao nhiêu tiếp tuyến biết vuông góc với đường thẳng 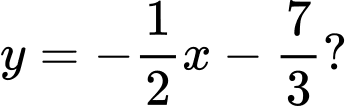
A, 2.
B, 0.
C, 3.
D, 1.
 Đáp án: A
Đáp án: A
Câu 10 [25584]: Có bao nhiêu phương trình tiếp tuyến của đồ thị hàm số 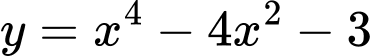 biết tiếp tuyến vuông góc với đường thẳng
biết tiếp tuyến vuông góc với đường thẳng 
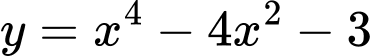 biết tiếp tuyến vuông góc với đường thẳng
biết tiếp tuyến vuông góc với đường thẳng 
A, 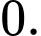
B, 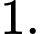
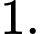
C, 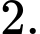
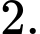
D, 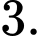
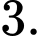
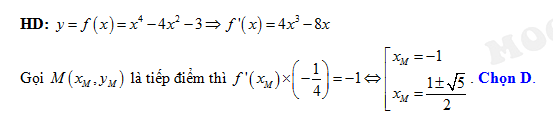 Đáp án: D
Đáp án: D
Câu 11 [25605]: Tìm 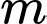 để mỗi tiếp tuyến của đồ thị hàm số
để mỗi tiếp tuyến của đồ thị hàm số 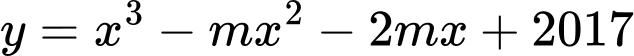 đều là đồ thị của hàm số bậc nhất đồng biến.
đều là đồ thị của hàm số bậc nhất đồng biến.
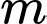 để mỗi tiếp tuyến của đồ thị hàm số
để mỗi tiếp tuyến của đồ thị hàm số 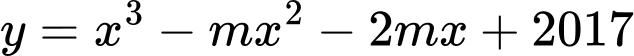 đều là đồ thị của hàm số bậc nhất đồng biến.
đều là đồ thị của hàm số bậc nhất đồng biến. A, 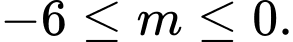
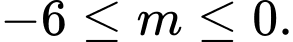
B, 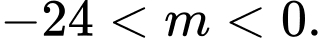
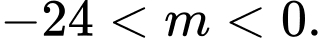
C, 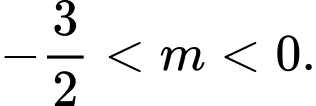
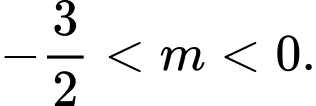
D, 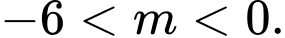
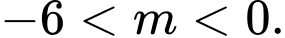
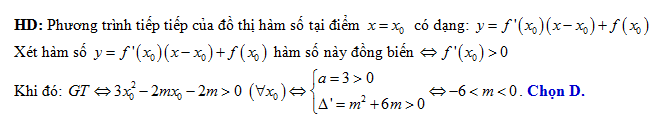 Đáp án: D
Đáp án: D
Câu 12 [25630]: Cho hàm số 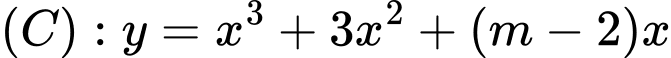 . Với giá trị nào của
. Với giá trị nào của 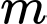 thì tiếp tuyến với đồ thị
thì tiếp tuyến với đồ thị  tại điểm có hệ số góc nhỏ nhất vuông góc với đường thẳng
tại điểm có hệ số góc nhỏ nhất vuông góc với đường thẳng 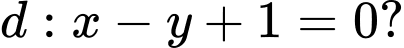
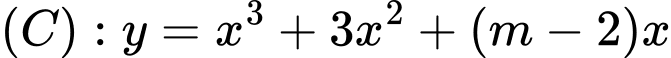 . Với giá trị nào của
. Với giá trị nào của 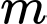 thì tiếp tuyến với đồ thị
thì tiếp tuyến với đồ thị  tại điểm có hệ số góc nhỏ nhất vuông góc với đường thẳng
tại điểm có hệ số góc nhỏ nhất vuông góc với đường thẳng 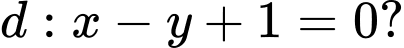
A, 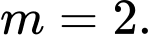
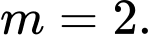
B, 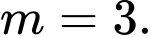
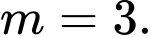
C, 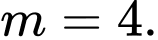
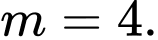
D, 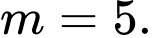
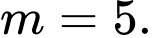
Chọn đáp án C
Hàm số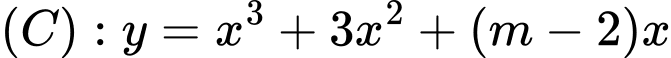

Hệ số góc của PTTT là: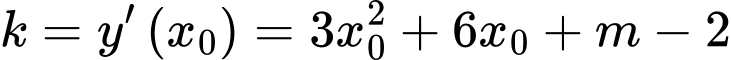
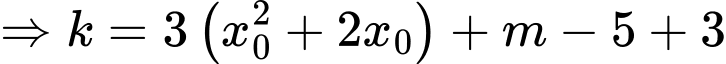
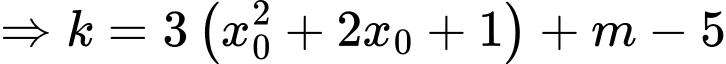
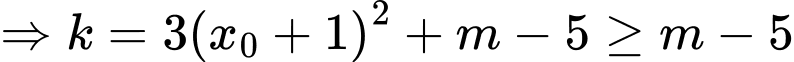
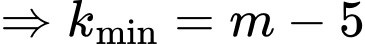
Ta có: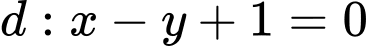
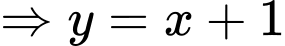 vuông góc với tiếp tuyến, suy ra
vuông góc với tiếp tuyến, suy ra 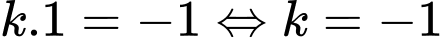

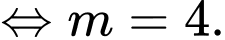 Đáp án: C
Đáp án: C
Hàm số
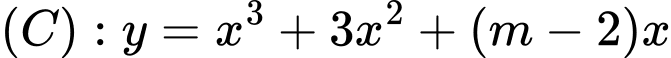

Hệ số góc của PTTT là:
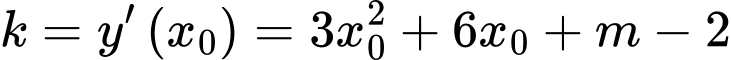
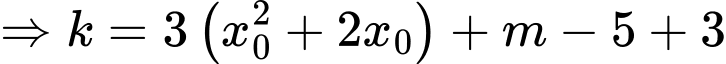
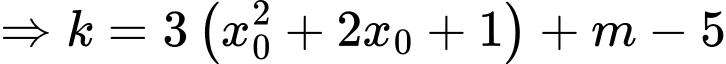
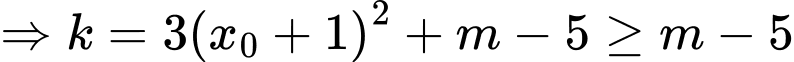
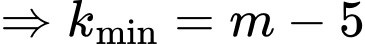
Ta có:
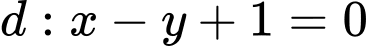
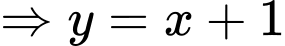 vuông góc với tiếp tuyến, suy ra
vuông góc với tiếp tuyến, suy ra 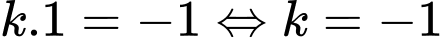

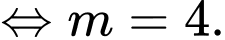 Đáp án: C
Đáp án: C
Câu 13 [30841]: Cho hàm số 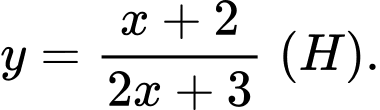 Viết phương trình tiếp tuyến của đồ thị hàm số
Viết phương trình tiếp tuyến của đồ thị hàm số 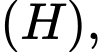 biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt
biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt 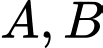 và tam giác
và tam giác  cân tại gốc tọa độ
cân tại gốc tọa độ  .
.
 Viết phương trình tiếp tuyến của đồ thị hàm số
Viết phương trình tiếp tuyến của đồ thị hàm số 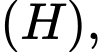 biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt
biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt  và tam giác
và tam giác  cân tại gốc tọa độ
cân tại gốc tọa độ  .
. A, 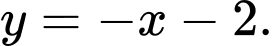
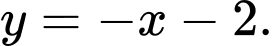
B, 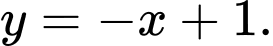
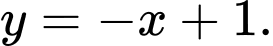
C, 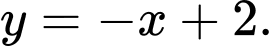
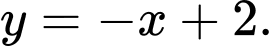
D, 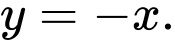 và
và 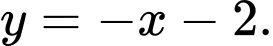
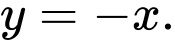 và
và 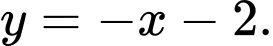
Tam giác 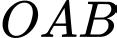 cân tại gốc tọa độ
cân tại gốc tọa độ  nên tiếp tuyến tạo với
nên tiếp tuyến tạo với 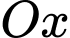 một góc
một góc 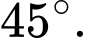
Do đó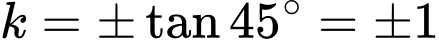
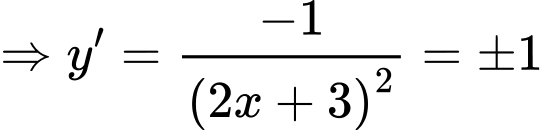
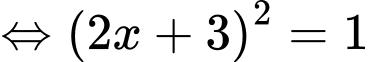
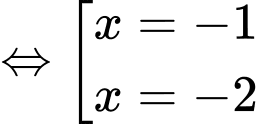
Với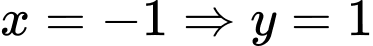
 PTTT:
PTTT: 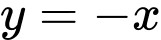
 (loai)
(loai)
Với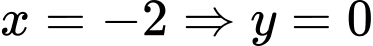
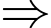 PTTT:
PTTT: 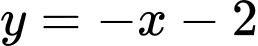
Chọn đáp án A. Đáp án: A
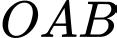 cân tại gốc tọa độ
cân tại gốc tọa độ  nên tiếp tuyến tạo với
nên tiếp tuyến tạo với 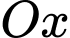 một góc
một góc 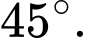
Do đó
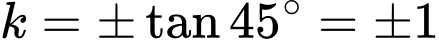
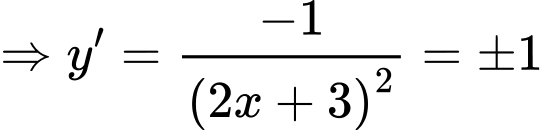
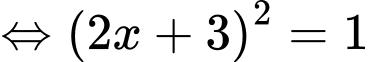
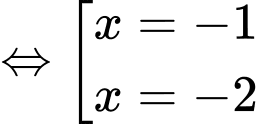
Với
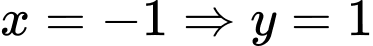
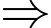 PTTT:
PTTT: 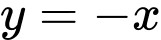
 (loai)
(loai)Với
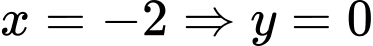
 PTTT:
PTTT: 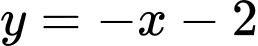
Chọn đáp án A. Đáp án: A
Câu 14 [802699]: Cho hàm số 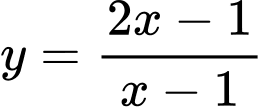 có đồ thị
có đồ thị  Có bao nhiêu tiếp tuyến của
Có bao nhiêu tiếp tuyến của  cắt trục
cắt trục 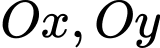 lần lượt tại tại hai điểm
lần lượt tại tại hai điểm 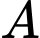 và
và 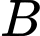 thỏa mãn điều kiện
thỏa mãn điều kiện 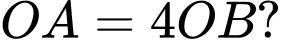
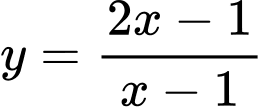 có đồ thị
có đồ thị  Có bao nhiêu tiếp tuyến của
Có bao nhiêu tiếp tuyến của  cắt trục
cắt trục 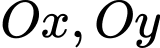 lần lượt tại tại hai điểm
lần lượt tại tại hai điểm 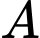 và
và 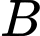 thỏa mãn điều kiện
thỏa mãn điều kiện 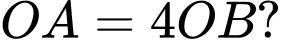
A, 2.
B, 3.
C, 1.
D, 4.
Chọn A
Giả sử tiếp tuyến của tại
tại 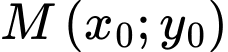 cắt
cắt 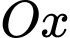 tại
tại 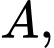
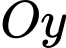 tại B sao cho
tại B sao cho 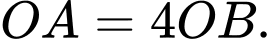
Do tam giác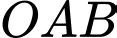 vuông tại
vuông tại  nên
nên 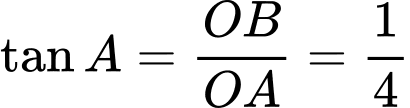
 Hệ số góc tiếp tuyến bằng
Hệ số góc tiếp tuyến bằng 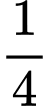 hoặc
hoặc 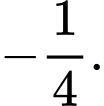
Hệ số góc tiếp tuyến là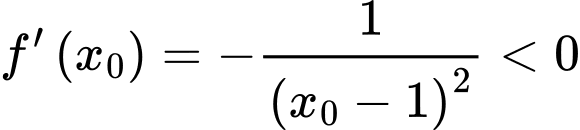
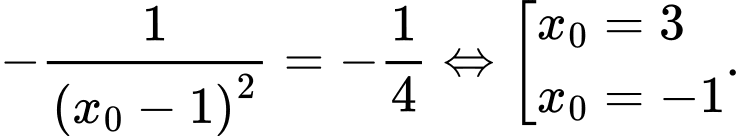
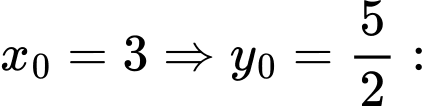
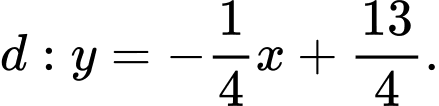
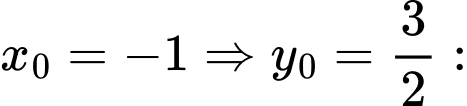
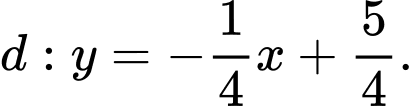 Đáp án: A
Đáp án: A
Giả sử tiếp tuyến của
 tại
tại 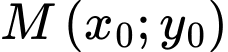 cắt
cắt 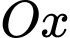 tại
tại 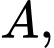
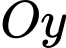 tại B sao cho
tại B sao cho 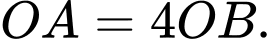
Do tam giác
 vuông tại
vuông tại  nên
nên 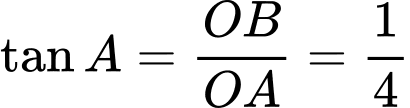
 Hệ số góc tiếp tuyến bằng
Hệ số góc tiếp tuyến bằng 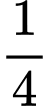 hoặc
hoặc 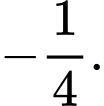
Hệ số góc tiếp tuyến là
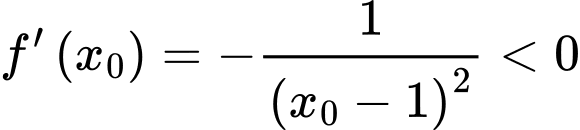
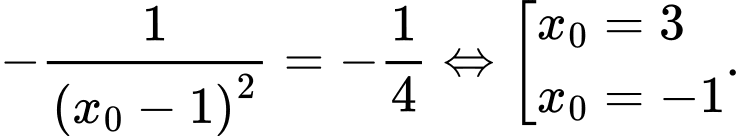
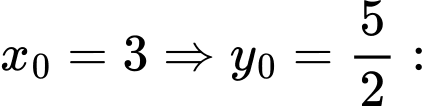
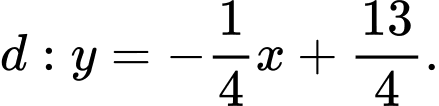
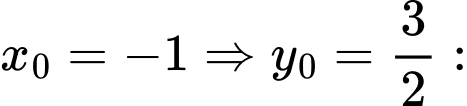
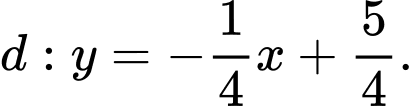 Đáp án: A
Đáp án: A
Câu 15 [25588]: Gọi 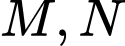 là hai điểm di động trên đồ thị
là hai điểm di động trên đồ thị  của hàm số
của hàm số 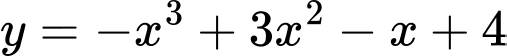 sao cho tiếp tuyến của
sao cho tiếp tuyến của  tại
tại 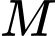 và
và 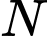 luôn song song với nhau. Hỏi khi
luôn song song với nhau. Hỏi khi 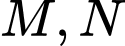 thay đổi, đường thẳng
thay đổi, đường thẳng 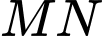 luôn đi qua nào trong các điểm dưới đây?
luôn đi qua nào trong các điểm dưới đây?
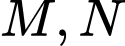 là hai điểm di động trên đồ thị
là hai điểm di động trên đồ thị  của hàm số
của hàm số 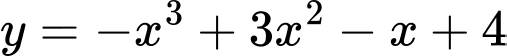 sao cho tiếp tuyến của
sao cho tiếp tuyến của  tại
tại 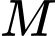 và
và 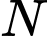 luôn song song với nhau. Hỏi khi
luôn song song với nhau. Hỏi khi 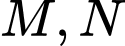 thay đổi, đường thẳng
thay đổi, đường thẳng 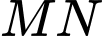 luôn đi qua nào trong các điểm dưới đây?
luôn đi qua nào trong các điểm dưới đây? A, Điểm 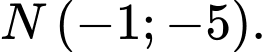
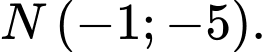
B, Điểm 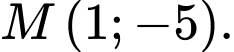
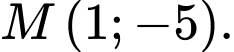
C, Điểm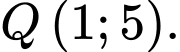
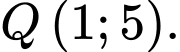
D, Điểm 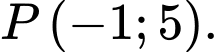
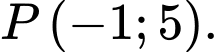
 Đáp án: C
Đáp án: C
Câu 16 [553945]: Cho hàm số 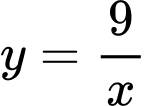 có đồ thị là
có đồ thị là  Biết tiếp tuyến của đồ thị
Biết tiếp tuyến của đồ thị  tại điểm
tại điểm 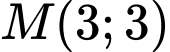 tạo với hai trục toạ độ một tam giác. Tính diện tích tam giác đó?
tạo với hai trục toạ độ một tam giác. Tính diện tích tam giác đó?
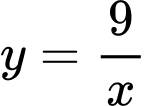 có đồ thị là
có đồ thị là  Biết tiếp tuyến của đồ thị
Biết tiếp tuyến của đồ thị  tại điểm
tại điểm 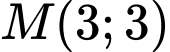 tạo với hai trục toạ độ một tam giác. Tính diện tích tam giác đó?
tạo với hai trục toạ độ một tam giác. Tính diện tích tam giác đó? 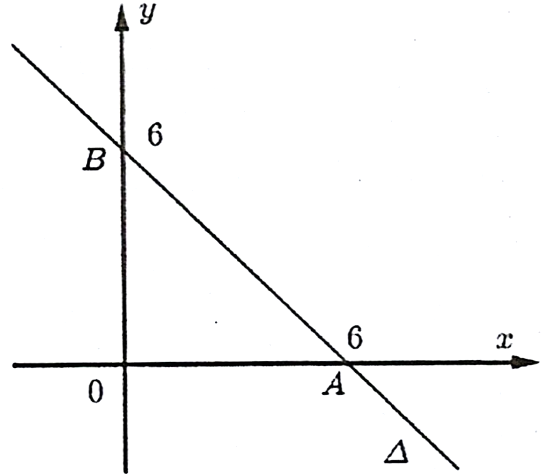
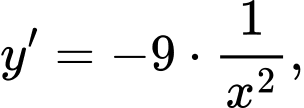 hệ số góc của tiếp tuyến tại điểm
hệ số góc của tiếp tuyến tại điểm 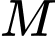 là
là 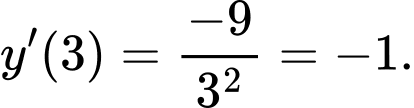
Phương trình tiếp tuyến  với
với  tại tiếp điểm
tại tiếp điểm  là
là
 với
với  tại tiếp điểm
tại tiếp điểm  là
là 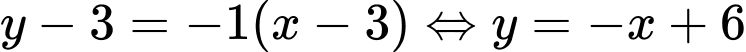
Biết  cắt trục hoành và trục tung lần lượt tại hai điểm
cắt trục hoành và trục tung lần lượt tại hai điểm 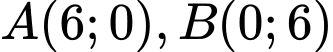 nên diện tích tam giác
nên diện tích tam giác  vuông tại
vuông tại  bằng
bằng 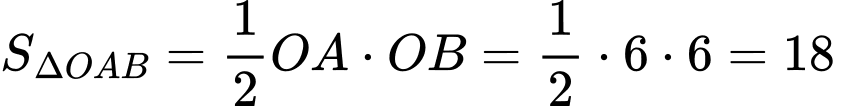 (đơn vị diện tích).
(đơn vị diện tích).
 cắt trục hoành và trục tung lần lượt tại hai điểm
cắt trục hoành và trục tung lần lượt tại hai điểm 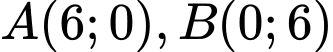 nên diện tích tam giác
nên diện tích tam giác 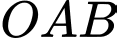 vuông tại
vuông tại  bằng
bằng 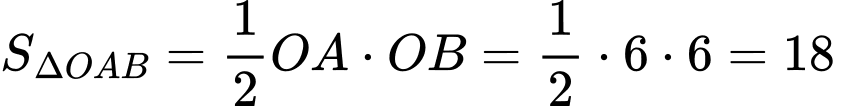 (đơn vị diện tích).
(đơn vị diện tích). Đáp án : 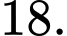
Câu 17 [579656]: [Đề mẫu HSA 2024]: Trên mặt phẳng tọa độ 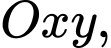 tiếp tuyến của đồ thị hàm số
tiếp tuyến của đồ thị hàm số 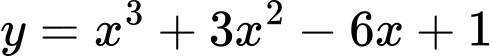 tại điểm có hoành độ bằng 1 và cắt hai trục tọa độ tại
tại điểm có hoành độ bằng 1 và cắt hai trục tọa độ tại 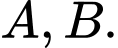 Tính diện tích tam giác
Tính diện tích tam giác 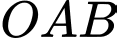 (nhập đáp án vào ô trống).
(nhập đáp án vào ô trống).
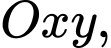 tiếp tuyến của đồ thị hàm số
tiếp tuyến của đồ thị hàm số 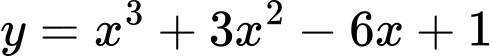 tại điểm có hoành độ bằng 1 và cắt hai trục tọa độ tại
tại điểm có hoành độ bằng 1 và cắt hai trục tọa độ tại 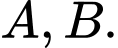 Tính diện tích tam giác
Tính diện tích tam giác 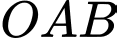 (nhập đáp án vào ô trống).
(nhập đáp án vào ô trống).
Ta có: 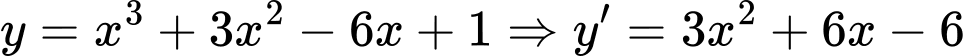
Phương trình tiếp tuyến tại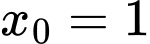 :
: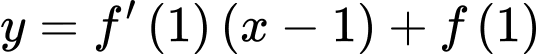
Hay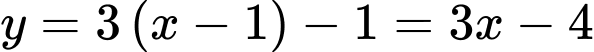
Phương trình tiếp tuyến cắt hai trục tọa độ tại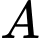 và
và 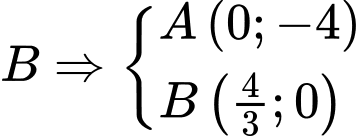
Diện tích tam giác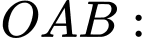
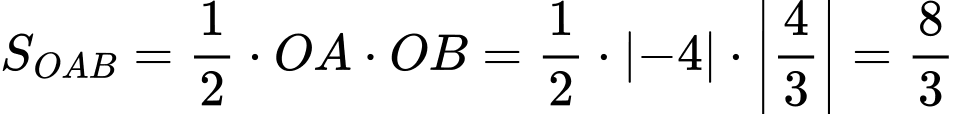
Đáp số: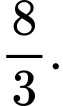
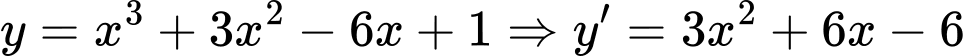
Phương trình tiếp tuyến tại
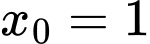 :
: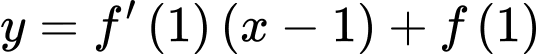
Hay
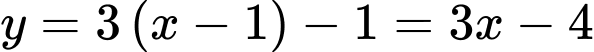
Phương trình tiếp tuyến cắt hai trục tọa độ tại
 và
và 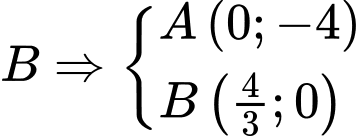
Diện tích tam giác
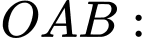
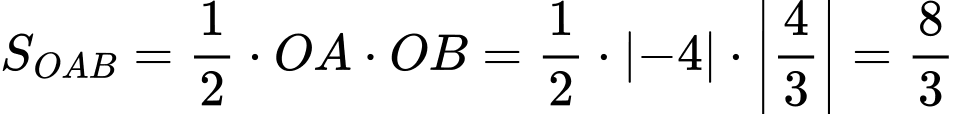
Đáp số:
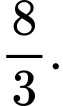
Câu 18 [301725]: Cho hàm số 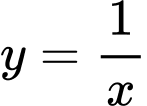 có đồ thị là
có đồ thị là  Cho điểm
Cho điểm 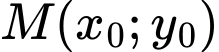 thuộc
thuộc  Tiếp tuyến của
Tiếp tuyến của  tại
tại 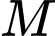 cắt các trục
cắt các trục 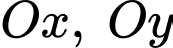 lần lượt tại điểm
lần lượt tại điểm 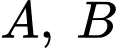 (
( là gốc tọa độ). Khi đó tam giác
là gốc tọa độ). Khi đó tam giác 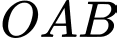 có diện tích bằng bao nhiêu?
có diện tích bằng bao nhiêu?
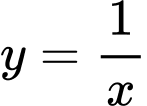 có đồ thị là
có đồ thị là  Cho điểm
Cho điểm 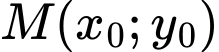 thuộc
thuộc  Tiếp tuyến của
Tiếp tuyến của  tại
tại 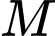 cắt các trục
cắt các trục 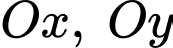 lần lượt tại điểm
lần lượt tại điểm 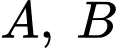 (
( là gốc tọa độ). Khi đó tam giác
là gốc tọa độ). Khi đó tam giác 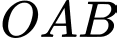 có diện tích bằng bao nhiêu?
có diện tích bằng bao nhiêu?
Điều kiện: 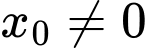
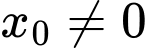
Ta có: 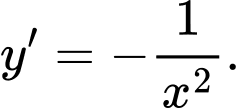
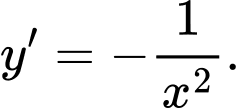
Vậy phương trình tiếp tuyến tại điểm 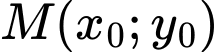 có dạng:
có dạng:
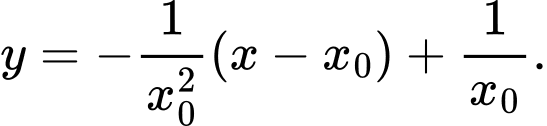
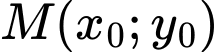 có dạng:
có dạng:
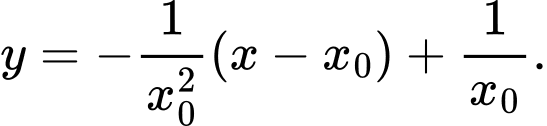
Ta có: 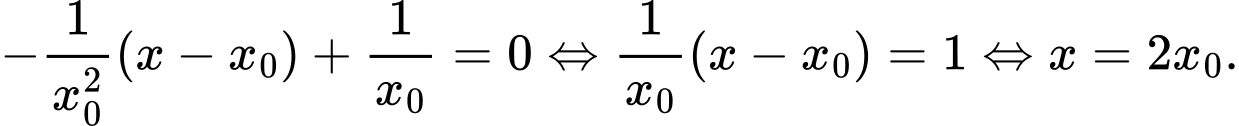
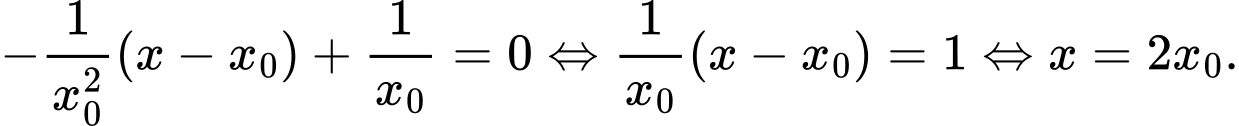
Vậy tọa độ điểm  là
là 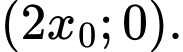
 là
là 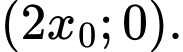
Ta có: 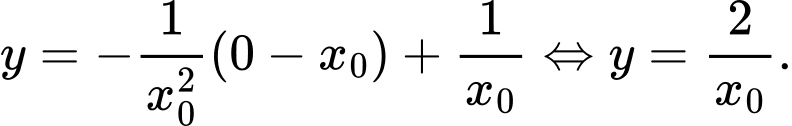
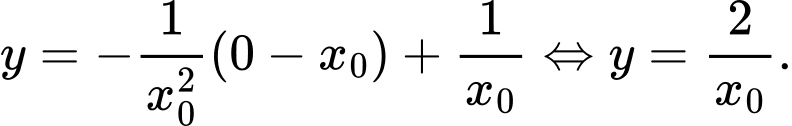
Vậy tọa độ điểm  là
là 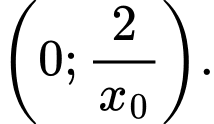
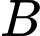 là
là 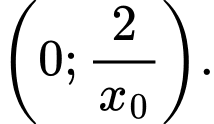
Vậy tam giác 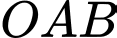 có diện tích bằng:
có diện tích bằng: 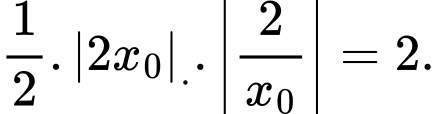
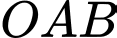 có diện tích bằng:
có diện tích bằng: 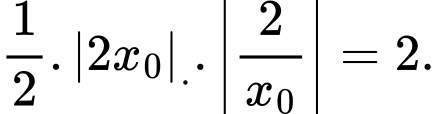
Câu 19 [581345]: Tiếp tuyến tại điểm  thuộc đồ thị
thuộc đồ thị 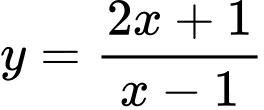 cắt
cắt 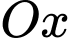 và
và 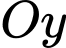 lần lượt tại hai điểm
lần lượt tại hai điểm 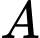 và
và 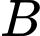 thỏa mãn
thỏa mãn 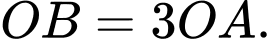 Biết điểm
Biết điểm 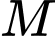 có tung độ dương, khi đó điểm
có tung độ dương, khi đó điểm 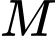 có tung độ là bao nhiêu?
có tung độ là bao nhiêu?
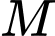 thuộc đồ thị
thuộc đồ thị 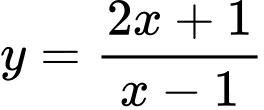 cắt
cắt 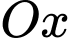 và
và 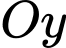 lần lượt tại hai điểm
lần lượt tại hai điểm 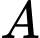 và
và 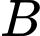 thỏa mãn
thỏa mãn 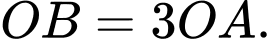 Biết điểm
Biết điểm 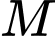 có tung độ dương, khi đó điểm
có tung độ dương, khi đó điểm 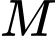 có tung độ là bao nhiêu?
có tung độ là bao nhiêu? 
Câu 20 [25590]: Cho đồ thị 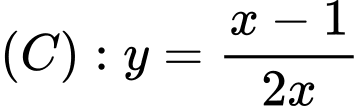 và
và 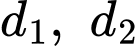 là hai tiếp tuyến của
là hai tiếp tuyến của  song song với nhau. Khoảng cách lớn nhất giữa
song song với nhau. Khoảng cách lớn nhất giữa 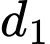 và
và 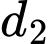 là
là
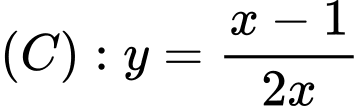 và
và 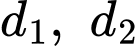 là hai tiếp tuyến của
là hai tiếp tuyến của  song song với nhau. Khoảng cách lớn nhất giữa
song song với nhau. Khoảng cách lớn nhất giữa 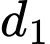 và
và 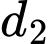 là
là A, 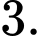
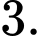
B, 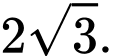
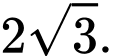
C, 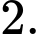
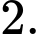
D, 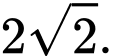
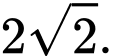
 Đáp án: C
Đáp án: C