Đáp án Bài tập tự luyện số 2
Câu 1 [802689]: Cho hàm số 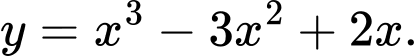 Có tất cả bao nhiêu tiếp tuyến của đồ thị hàm số đi qua điểm
Có tất cả bao nhiêu tiếp tuyến của đồ thị hàm số đi qua điểm 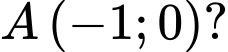
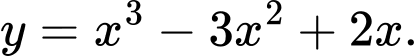 Có tất cả bao nhiêu tiếp tuyến của đồ thị hàm số đi qua điểm
Có tất cả bao nhiêu tiếp tuyến của đồ thị hàm số đi qua điểm 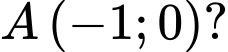
A, 1.
B, 2.
C, 3.
D, 4.
Phương trình đường thẳng qua điểm 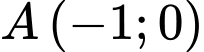 có dạng:
có dạng: 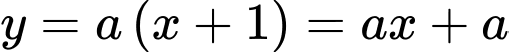

Đường thẳng là tiếp tuyến khi hệ
là tiếp tuyến khi hệ 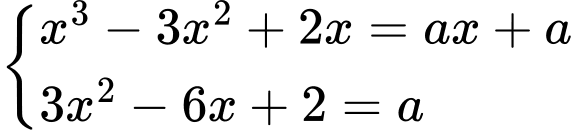 có nghiệm. Dễ thấy hệ có ba nghiệm
có nghiệm. Dễ thấy hệ có ba nghiệm 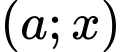 phân biệt nên có ba tiếp tuyến. Đáp án: C
phân biệt nên có ba tiếp tuyến. Đáp án: C
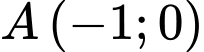 có dạng:
có dạng: 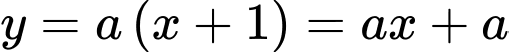

Đường thẳng
 là tiếp tuyến khi hệ
là tiếp tuyến khi hệ 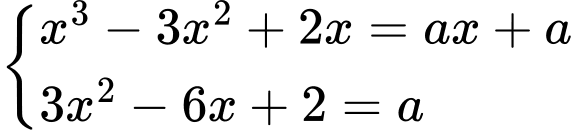 có nghiệm. Dễ thấy hệ có ba nghiệm
có nghiệm. Dễ thấy hệ có ba nghiệm 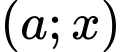 phân biệt nên có ba tiếp tuyến. Đáp án: C
phân biệt nên có ba tiếp tuyến. Đáp án: C
Câu 2 [802695]: Có bao nhiêu tiếp tuyến của đồ thị hàm số 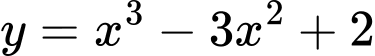 đi qua
đi qua 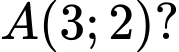
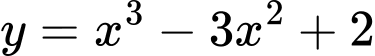 đi qua
đi qua 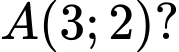
A, 3.
B, 0.
C, 1.
D, 2.
Chọn D
Ta có: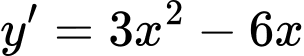
Phương trình tiếp tuyến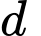 với đồ thị hàm số tại
với đồ thị hàm số tại 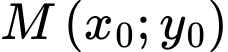 có dạng
có dạng
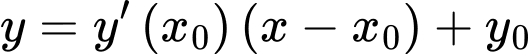

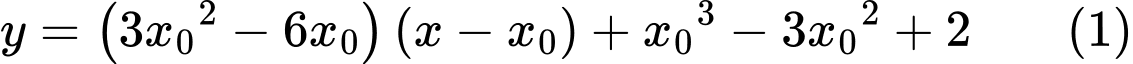
đi qua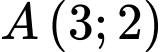 nên ta được phương trình
nên ta được phương trình
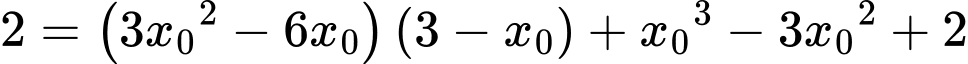
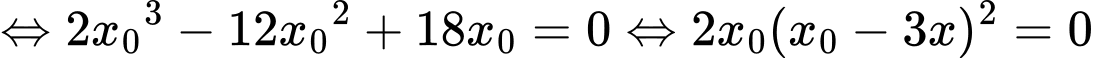
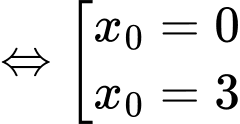
+)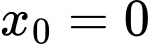 thay vào (1) ta được phương trình tiếp tuyến
thay vào (1) ta được phương trình tiếp tuyến 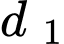 là
là 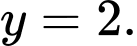
+)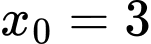 thay vào (1) ta được phương trình tiếp tuyến
thay vào (1) ta được phương trình tiếp tuyến 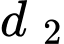 là
là 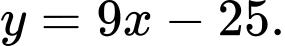
Vậy có 2 tiếp tuyến của đồ thị hàm số đi qua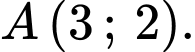
Ta cũng có thể sử dụng đồ thị của hàm số để suy ra đáp án Đáp án: D
Ta có:
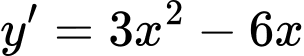
Phương trình tiếp tuyến
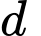 với đồ thị hàm số tại
với đồ thị hàm số tại 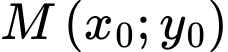 có dạng
có dạng 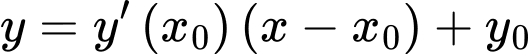

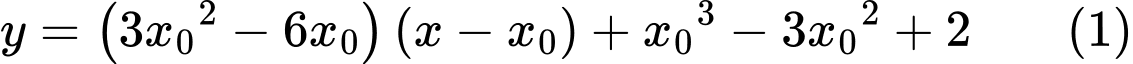
đi qua
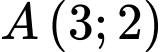 nên ta được phương trình
nên ta được phương trình 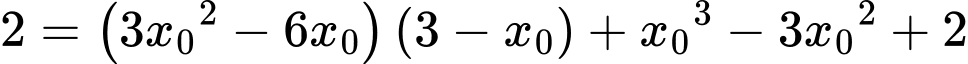
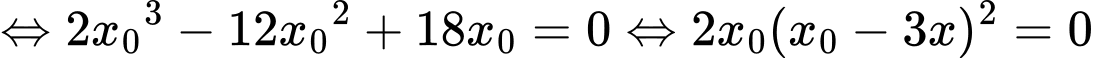
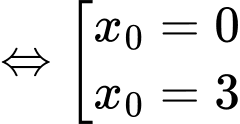
+)
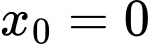 thay vào (1) ta được phương trình tiếp tuyến
thay vào (1) ta được phương trình tiếp tuyến 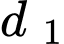 là
là 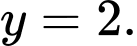
+)
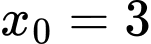 thay vào (1) ta được phương trình tiếp tuyến
thay vào (1) ta được phương trình tiếp tuyến 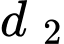 là
là 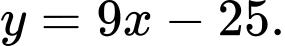
Vậy có 2 tiếp tuyến của đồ thị hàm số đi qua
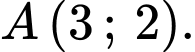
Ta cũng có thể sử dụng đồ thị của hàm số để suy ra đáp án Đáp án: D
Câu 3 [30789]: Phương trình tiếp tuyến của đồ thị hàm số 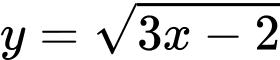 biết tiếp tuyến đi qua điểm
biết tiếp tuyến đi qua điểm 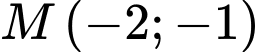 là
là
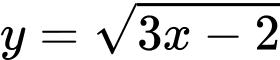 biết tiếp tuyến đi qua điểm
biết tiếp tuyến đi qua điểm 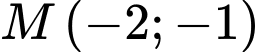 là
là A, 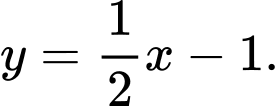
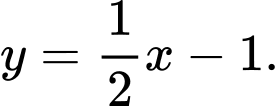
B, 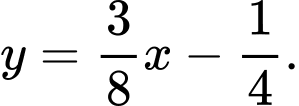
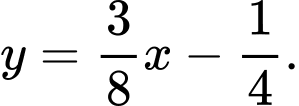
C, 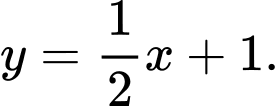
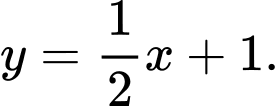
D, 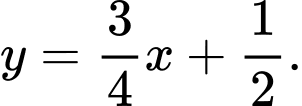
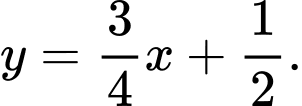
 Đáp án: D
Đáp án: D
Câu 4 [30802]: Số tiếp tuyến đi qua điểm  của đồ thị hàm số
của đồ thị hàm số 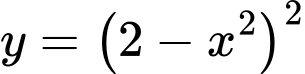 là
là
 của đồ thị hàm số
của đồ thị hàm số 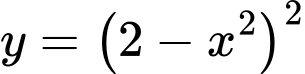 là
là A, 3.
B, 2.
C, 0.
D, 1.
 Đáp án: A
Đáp án: A
Câu 5 [802692]: Cho hàm số 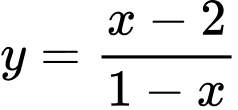 có đồ thị
có đồ thị  và điểm
và điểm 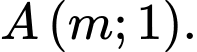 Gọi
Gọi 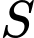 là tập tất cả các giá trị của
là tập tất cả các giá trị của 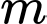 để có đúng một tiếp tuyến của
để có đúng một tiếp tuyến của  đi qua
đi qua 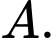 Tính tổng bình phương các phần tử của tập
Tính tổng bình phương các phần tử của tập 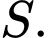
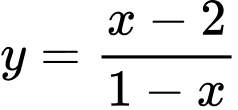 có đồ thị
có đồ thị  và điểm
và điểm 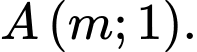 Gọi
Gọi 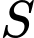 là tập tất cả các giá trị của
là tập tất cả các giá trị của 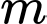 để có đúng một tiếp tuyến của
để có đúng một tiếp tuyến của  đi qua
đi qua 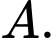 Tính tổng bình phương các phần tử của tập
Tính tổng bình phương các phần tử của tập 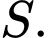
A, 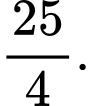
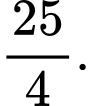
B, 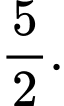
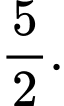
C, 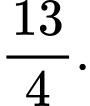
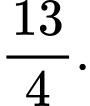
D, 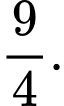
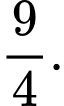
Chọn C
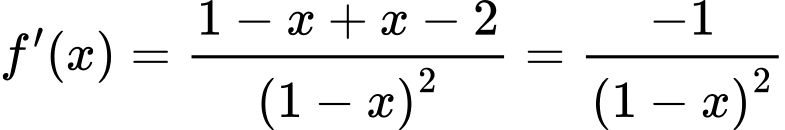
Phương trình tiếp tuyến của tại
tại 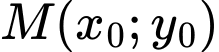 :
: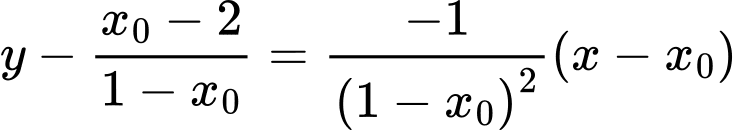
Tiếp tuyến đi qua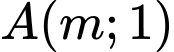
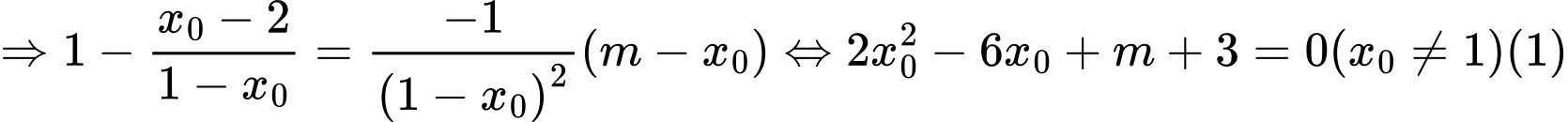
Để có 1 tiếp tuyến qua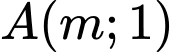
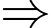 phương trình
phương trình  có 1 nghiệm
có 1 nghiệm 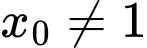
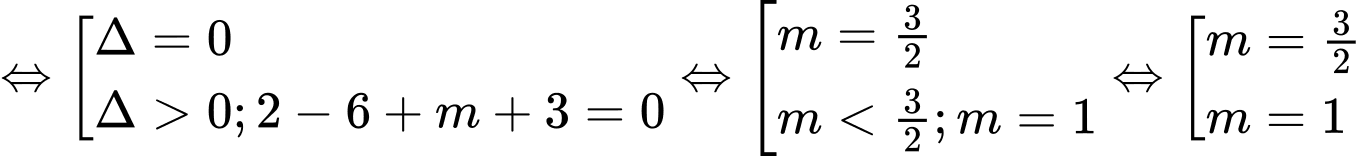
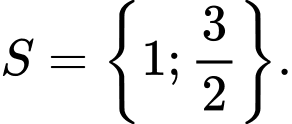 Ta có
Ta có 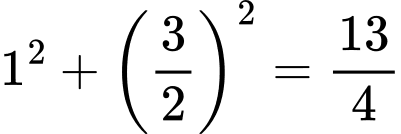 Đáp án: C
Đáp án: C
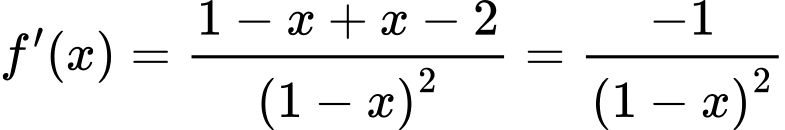
Phương trình tiếp tuyến của
 tại
tại 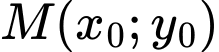 :
: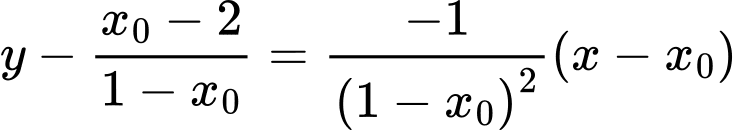
Tiếp tuyến đi qua
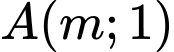
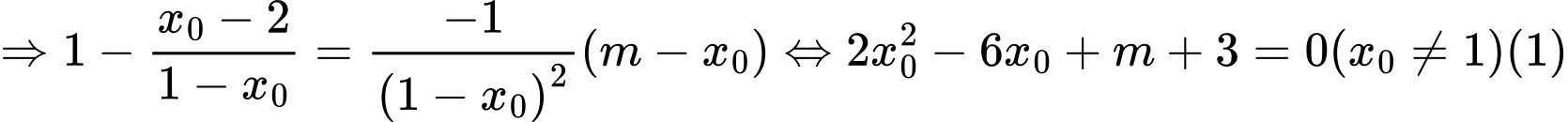
Để có 1 tiếp tuyến qua
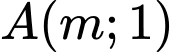
 phương trình
phương trình  có 1 nghiệm
có 1 nghiệm 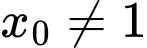
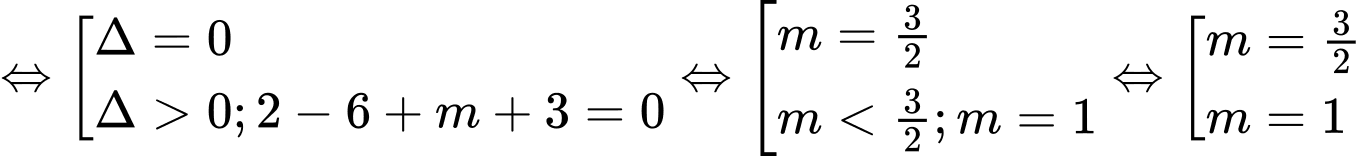
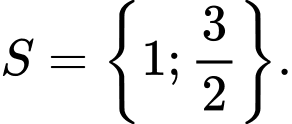 Ta có
Ta có 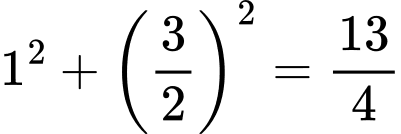 Đáp án: C
Đáp án: C
Câu 6 [30786]: Cho hàm số 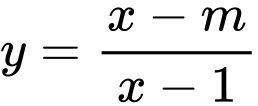 có đồ thị là
có đồ thị là 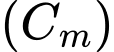 và điểm
và điểm 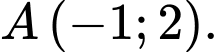 Gọi
Gọi 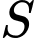 là tập hợp tất cả các giá trị thực của
là tập hợp tất cả các giá trị thực của 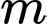 để có đúng một tiếp tuyến của
để có đúng một tiếp tuyến của 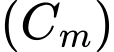 đi qua
đi qua 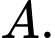 Tổng tất cả các phần tử của
Tổng tất cả các phần tử của 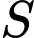 bằng
bằng
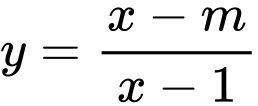 có đồ thị là
có đồ thị là 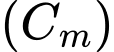 và điểm
và điểm 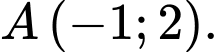 Gọi
Gọi 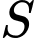 là tập hợp tất cả các giá trị thực của
là tập hợp tất cả các giá trị thực của 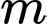 để có đúng một tiếp tuyến của
để có đúng một tiếp tuyến của 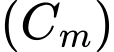 đi qua
đi qua 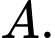 Tổng tất cả các phần tử của
Tổng tất cả các phần tử của 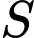 bằng
bằng A, 1.
B, 2.
C, 3.
D, 4.
 Đáp án: C
Đáp án: C
Câu 7 [30793]: Cho hàm số 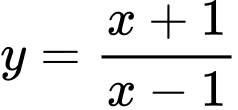 có đồ thị
có đồ thị  và điểm
và điểm 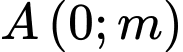 . Gọi
. Gọi 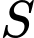 là tập hợp tất cả các giá trị thực của
là tập hợp tất cả các giá trị thực của 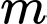 để có đúng một tiếp tuyến từ
để có đúng một tiếp tuyến từ  đi qua
đi qua 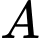 . Tổng tất cả giá trị của phần tử
. Tổng tất cả giá trị của phần tử 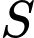 bằng
bằng
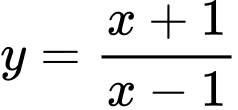 có đồ thị
có đồ thị  và điểm
và điểm 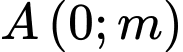 . Gọi
. Gọi 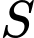 là tập hợp tất cả các giá trị thực của
là tập hợp tất cả các giá trị thực của 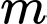 để có đúng một tiếp tuyến từ
để có đúng một tiếp tuyến từ  đi qua
đi qua 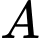 . Tổng tất cả giá trị của phần tử
. Tổng tất cả giá trị của phần tử 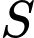 bằng
bằng A, 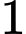 .
.
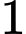 .
.B, 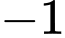 .
.
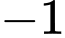 .
.C,  .
.
 .
.D, 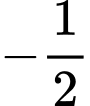 .
.
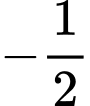 .
. Đáp án: C
Đáp án: C
Câu 8 [23769]: Cho hàm số 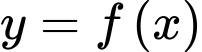 có đạo hàm, liên tục trên
có đạo hàm, liên tục trên 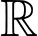 , gọi
, gọi 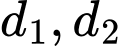 lần lượt là tiếp tuyến của đồ thị hàm số
lần lượt là tiếp tuyến của đồ thị hàm số 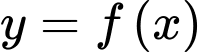 và
và 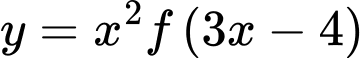 tại điểm có hoành độ bằng 2. Biết rằng hai đường thẳng
tại điểm có hoành độ bằng 2. Biết rằng hai đường thẳng 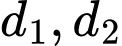 vuông góc nhau, khẳng định nào sau đây đúng?
vuông góc nhau, khẳng định nào sau đây đúng?
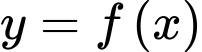 có đạo hàm, liên tục trên
có đạo hàm, liên tục trên 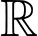 , gọi
, gọi 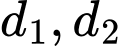 lần lượt là tiếp tuyến của đồ thị hàm số
lần lượt là tiếp tuyến của đồ thị hàm số 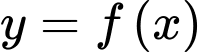 và
và 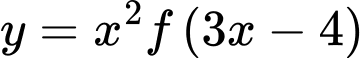 tại điểm có hoành độ bằng 2. Biết rằng hai đường thẳng
tại điểm có hoành độ bằng 2. Biết rằng hai đường thẳng 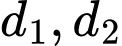 vuông góc nhau, khẳng định nào sau đây đúng?
vuông góc nhau, khẳng định nào sau đây đúng? A, 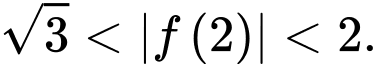
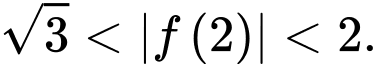
B, 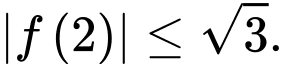
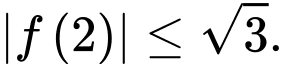
C, 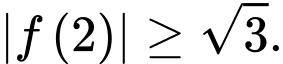
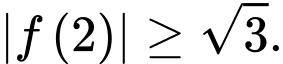
D, 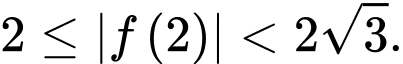
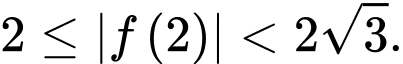
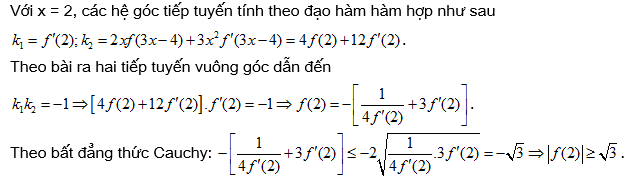 Đáp án: C
Đáp án: C
Câu 9 [23290]: Cho hàm số 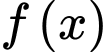 xác định, có đạo hàm trên
xác định, có đạo hàm trên  thỏa mãn
thỏa mãn 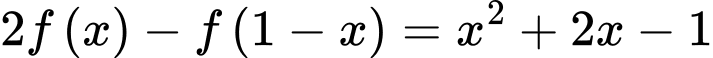 . Viết phương trình tiếp tuyến của đồ thị hàm số
. Viết phương trình tiếp tuyến của đồ thị hàm số 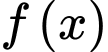 tại điểm có hoành độ bằng 1.
tại điểm có hoành độ bằng 1.
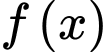 xác định, có đạo hàm trên
xác định, có đạo hàm trên 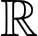 thỏa mãn
thỏa mãn 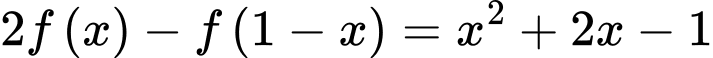 . Viết phương trình tiếp tuyến của đồ thị hàm số
. Viết phương trình tiếp tuyến của đồ thị hàm số 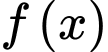 tại điểm có hoành độ bằng 1.
tại điểm có hoành độ bằng 1. A, 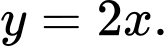
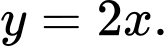
B, 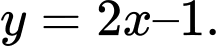
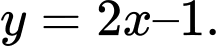
C, 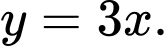
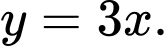
D, 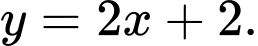
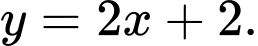
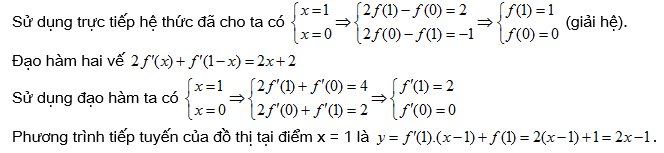 Đáp án: B
Đáp án: B
Câu 10 [512269]: Cho các hàm số 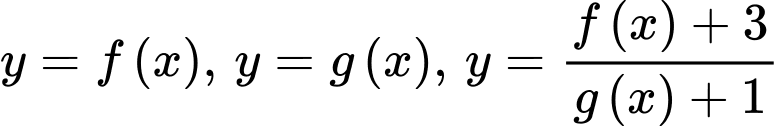 . Hệ số góc của các tiếp tuyến của các đồ thị hàm số đã cho tại điểm có hoành độ
. Hệ số góc của các tiếp tuyến của các đồ thị hàm số đã cho tại điểm có hoành độ 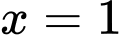 bằng nhau và khác
bằng nhau và khác  . Khẳng định nào dưới đây là đúng?
. Khẳng định nào dưới đây là đúng?
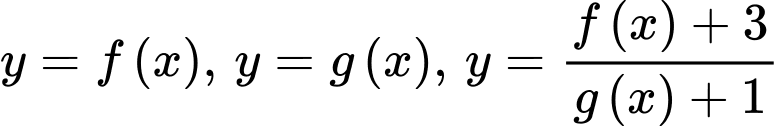 . Hệ số góc của các tiếp tuyến của các đồ thị hàm số đã cho tại điểm có hoành độ
. Hệ số góc của các tiếp tuyến của các đồ thị hàm số đã cho tại điểm có hoành độ 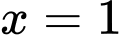 bằng nhau và khác
bằng nhau và khác  . Khẳng định nào dưới đây là đúng?
. Khẳng định nào dưới đây là đúng? A, 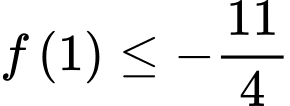 .
.
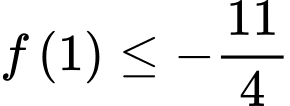 .
.B, 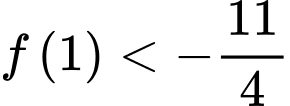 .
.
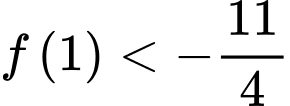 .
.C, 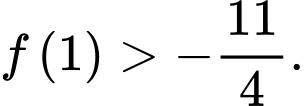
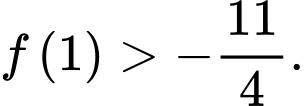
D, 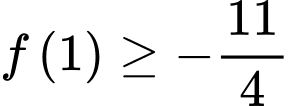 .
.
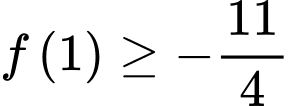 .
.
Chọn A
Đặt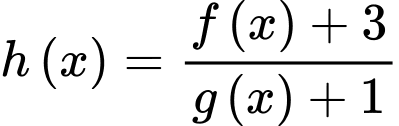 , ta có
, ta có 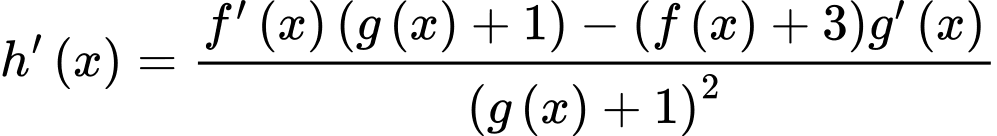 .
.
Theo giả thiết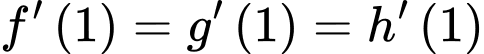 nên
nên
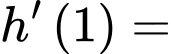
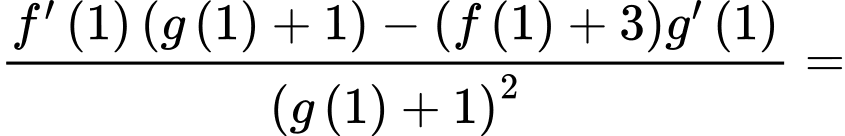
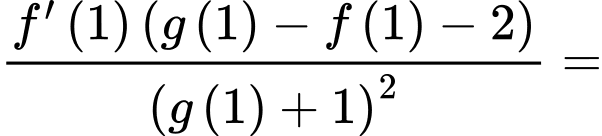
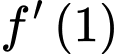
Suy ra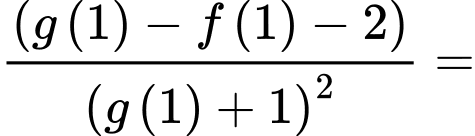
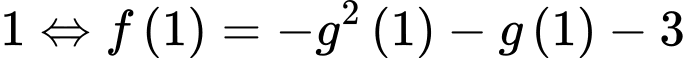 .
.
Xét hàm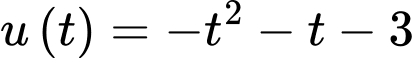 đạt max tại
đạt max tại 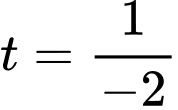 nên
nên 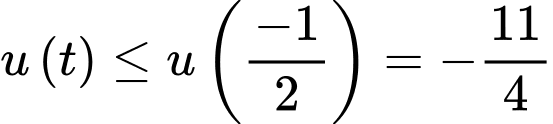 .
.
Từ đó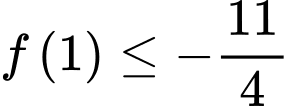 . Đáp án: A
. Đáp án: A
Đặt
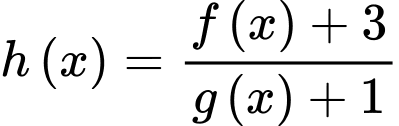 , ta có
, ta có 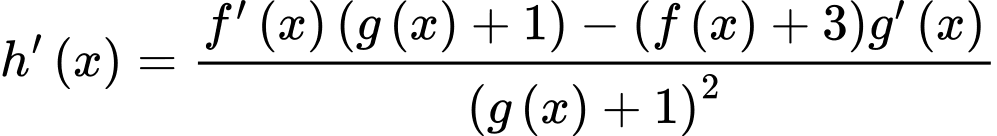 .
.Theo giả thiết
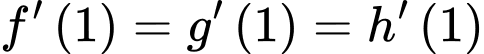 nên
nên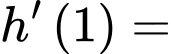
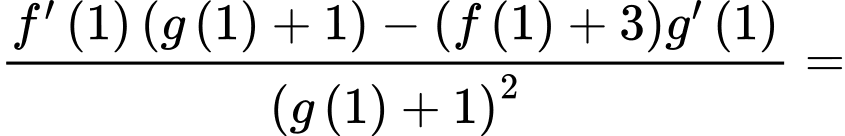
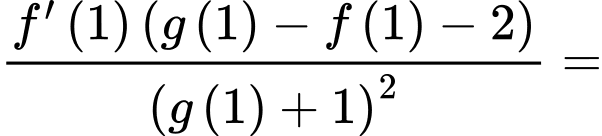
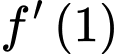
Suy ra
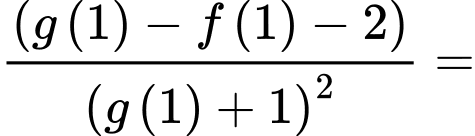
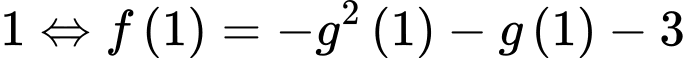 .
.Xét hàm
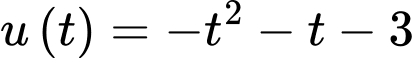 đạt max tại
đạt max tại 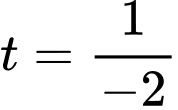 nên
nên 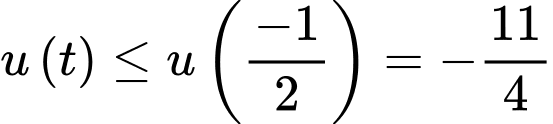 .
.Từ đó
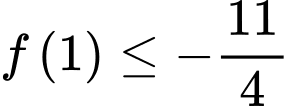 . Đáp án: A
. Đáp án: A
Câu 11 [30804]: Cho hàm số 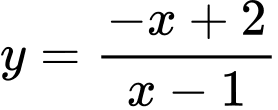 có đồ thị
có đồ thị  và điểm
và điểm 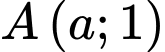 . Gọi
. Gọi 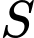 là tập hợp các giá trị của
là tập hợp các giá trị của 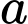 để có đúng một tiếp tuyến của
để có đúng một tiếp tuyến của  kẻ qua
kẻ qua 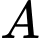 . Tổng giá trị các phần tử
. Tổng giá trị các phần tử 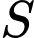 là
là
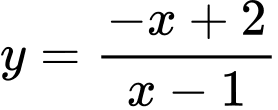 có đồ thị
có đồ thị  và điểm
và điểm 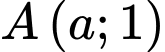 . Gọi
. Gọi 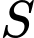 là tập hợp các giá trị của
là tập hợp các giá trị của 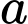 để có đúng một tiếp tuyến của
để có đúng một tiếp tuyến của  kẻ qua
kẻ qua 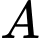 . Tổng giá trị các phần tử
. Tổng giá trị các phần tử 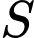 là
là A, 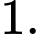
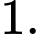
B, 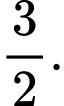
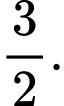
C, 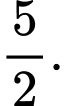
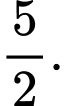
D, 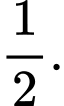
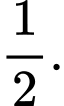
 Đáp án: C
Đáp án: C
Câu 12 [30812]: Cho hàm số 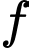 xác định và có đạo hàm trên
xác định và có đạo hàm trên 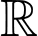 thỏa mãn
thỏa mãn 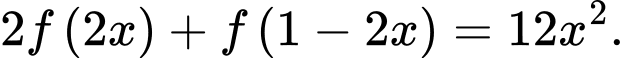 Phương trình tiếp tuyến của đồ thị hàm số
Phương trình tiếp tuyến của đồ thị hàm số 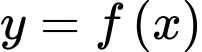 tại điểm có hoành độ bằng
tại điểm có hoành độ bằng 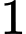 tạo với hai trục
tạo với hai trục 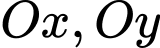 một tam giác có diện tích bằng
một tam giác có diện tích bằng
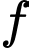 xác định và có đạo hàm trên
xác định và có đạo hàm trên 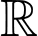 thỏa mãn
thỏa mãn 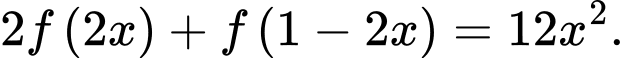 Phương trình tiếp tuyến của đồ thị hàm số
Phương trình tiếp tuyến của đồ thị hàm số 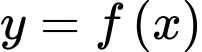 tại điểm có hoành độ bằng
tại điểm có hoành độ bằng 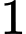 tạo với hai trục
tạo với hai trục 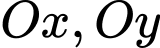 một tam giác có diện tích bằng
một tam giác có diện tích bằng A, 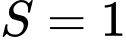 (đvdt).
(đvdt).
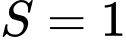 (đvdt).
(đvdt).B, 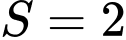 (đvdt).
(đvdt).
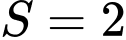 (đvdt).
(đvdt).C, 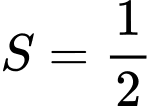 (đvdt).
(đvdt).
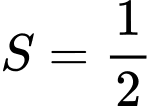 (đvdt).
(đvdt).D, 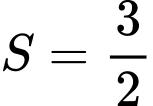 (đvdt).
(đvdt).
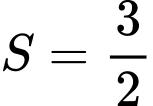 (đvdt).
(đvdt).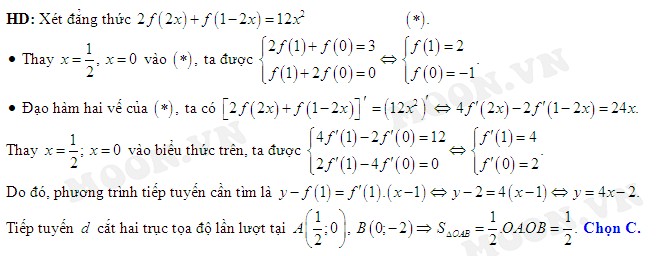 Đáp án: C
Đáp án: C
Câu 13 [23764]: Cho hàm số 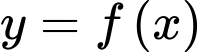 có đạo hàm, liên tục trên
có đạo hàm, liên tục trên 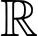 , gọi
, gọi 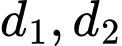 lần lượt là tiếp tuyến của đồ thị hàm số
lần lượt là tiếp tuyến của đồ thị hàm số 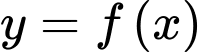 và
và 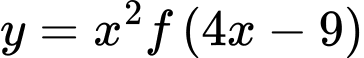 tại điểm có hoành độ bằng 3. Biết rằng hai đường thẳng
tại điểm có hoành độ bằng 3. Biết rằng hai đường thẳng 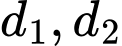 có tích hệ số góc bằng
có tích hệ số góc bằng 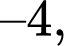 tìm giá trị nhỏ nhất của
tìm giá trị nhỏ nhất của 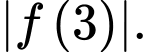
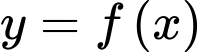 có đạo hàm, liên tục trên
có đạo hàm, liên tục trên 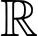 , gọi
, gọi 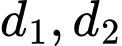 lần lượt là tiếp tuyến của đồ thị hàm số
lần lượt là tiếp tuyến của đồ thị hàm số 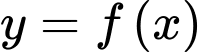 và
và 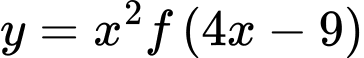 tại điểm có hoành độ bằng 3. Biết rằng hai đường thẳng
tại điểm có hoành độ bằng 3. Biết rằng hai đường thẳng 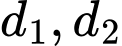 có tích hệ số góc bằng
có tích hệ số góc bằng 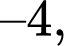 tìm giá trị nhỏ nhất của
tìm giá trị nhỏ nhất của 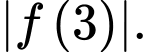
A, 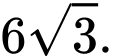
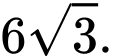
B, 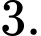
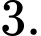
C, 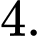
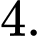
D, 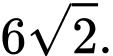
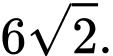
 Đáp án: C
Đáp án: C
Câu 14 [23040]: Cho hàm số 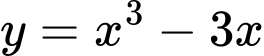 có đồ thị
có đồ thị  .
. 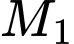 là một điểm thuộc
là một điểm thuộc  có hoành độ bằng 3. Tiếp tuyến tại điểm
có hoành độ bằng 3. Tiếp tuyến tại điểm 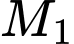 cắt
cắt  tại điểm thứ hai
tại điểm thứ hai 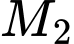 . Tiếp tuyến tại điểm
. Tiếp tuyến tại điểm 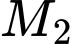 cắt
cắt  tại điểm
tại điểm 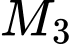 khác
khác 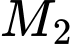 . Cứ như thế tiếp tuyến tại điểm
. Cứ như thế tiếp tuyến tại điểm 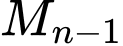 cắt
cắt  tại điểm thứ hai
tại điểm thứ hai 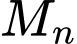 khác
khác 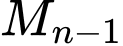 ,
, 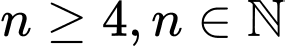 . Tìm số tự nhiên
. Tìm số tự nhiên 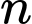 thỏa mãn điều kiện
thỏa mãn điều kiện 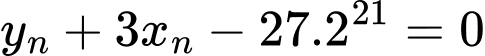 .
.
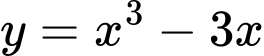 có đồ thị
có đồ thị  .
. 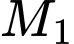 là một điểm thuộc
là một điểm thuộc  có hoành độ bằng 3. Tiếp tuyến tại điểm
có hoành độ bằng 3. Tiếp tuyến tại điểm 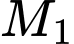 cắt
cắt  tại điểm thứ hai
tại điểm thứ hai 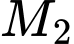 . Tiếp tuyến tại điểm
. Tiếp tuyến tại điểm 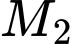 cắt
cắt  tại điểm
tại điểm 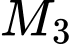 khác
khác 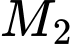 . Cứ như thế tiếp tuyến tại điểm
. Cứ như thế tiếp tuyến tại điểm 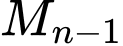 cắt
cắt  tại điểm thứ hai
tại điểm thứ hai 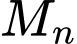 khác
khác 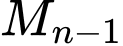 ,
, 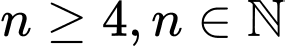 . Tìm số tự nhiên
. Tìm số tự nhiên 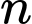 thỏa mãn điều kiện
thỏa mãn điều kiện 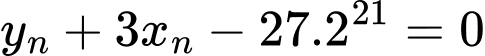 .
. A, 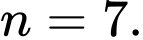
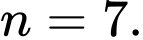
B, 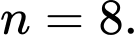
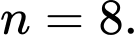
C, 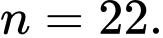
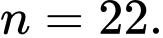
D, 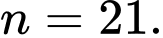
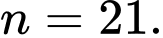
Đáp án: C