Đáp án Bài tập tự luyện
Câu 1 [803531]: Trong các giới hạn sau giới hạn nào bằng 0?
A, 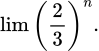
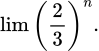
B, 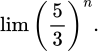
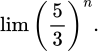
C, 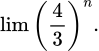
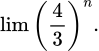
D, 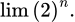
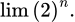
Chọn A
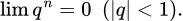 Đáp án: A
Đáp án: A
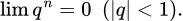 Đáp án: A
Đáp án: A
Câu 2 [803278]: Tính giới hạn 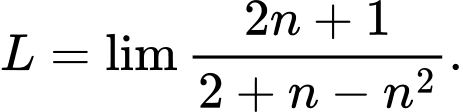
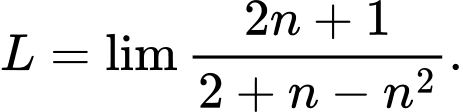
A, 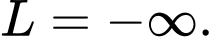
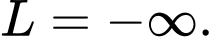
B, 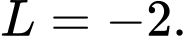
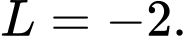
C, 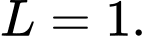
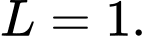
D, 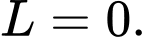
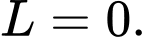
Chọn D
Ta có: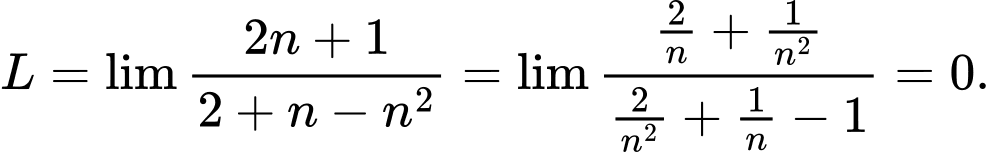 Đáp án: D
Đáp án: D
Ta có:
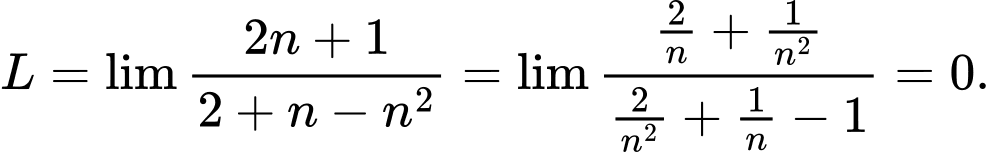 Đáp án: D
Đáp án: D
Câu 3 [519247]: 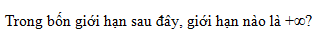
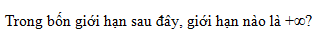
A, 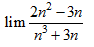
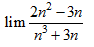
B, 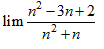
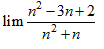
C, 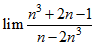
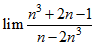
D, 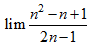
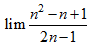
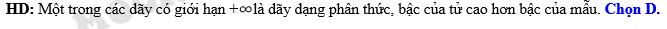 Đáp án: D
Đáp án: D
Câu 4 [519212]: 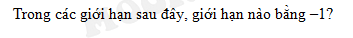
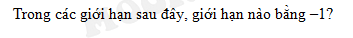
A, 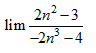
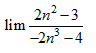
B, 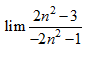
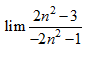
C, 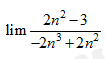
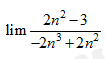
D, 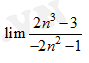
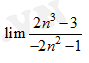
 Đáp án: B
Đáp án: B
Câu 5 [803295]: Tìm 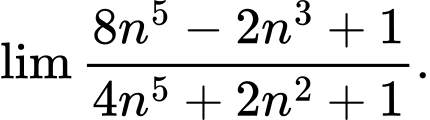
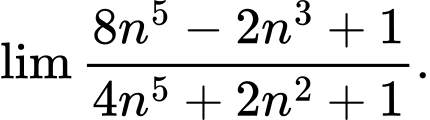
A, 2.
B, 8.
C, 1.
D, 4.
Chọn A
Ta có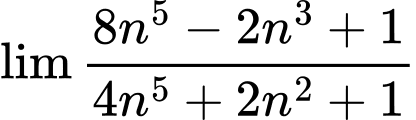
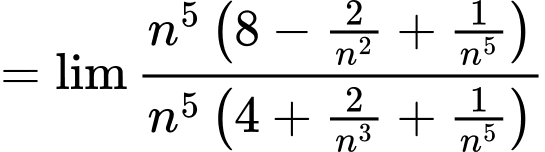 =
=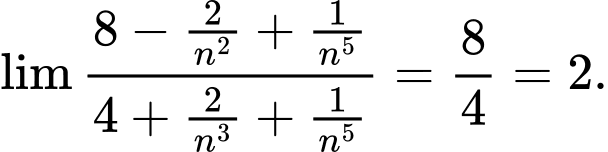 Đáp án: A
Đáp án: A
Ta có
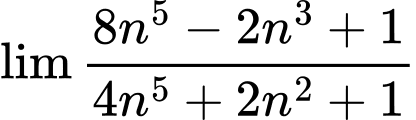
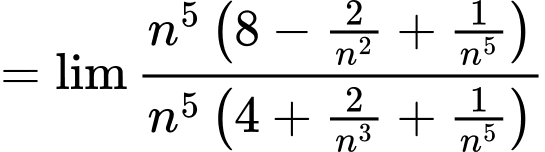 =
=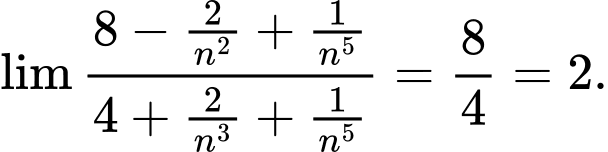 Đáp án: A
Đáp án: A
Câu 6 [519113]: 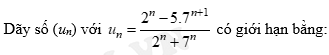
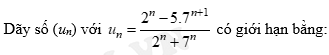
A, _35.
B, _25.
C, _5.
D, 15.
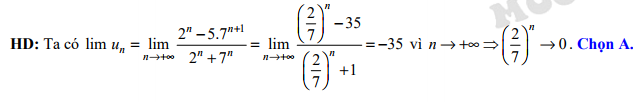 Đáp án: A
Đáp án: A
Câu 7 [677736]: 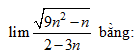
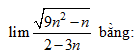
A, 0.
B, 3.
C, -1.
D, -3.
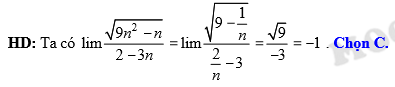 Đáp án: C
Đáp án: C
Câu 8 [803413]: Tính giới hạn 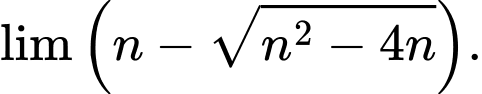
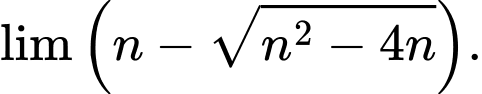
A, 3.
B, 1.
C, 2.
D, 4.
Chọn C
Ta có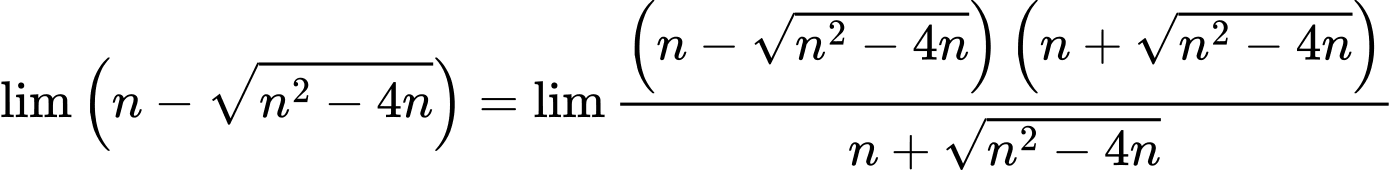
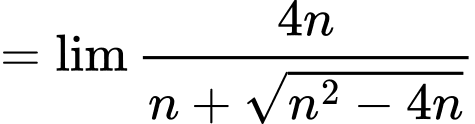
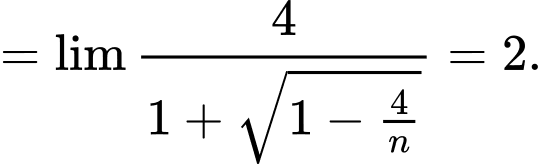 Đáp án: C
Đáp án: C
Ta có
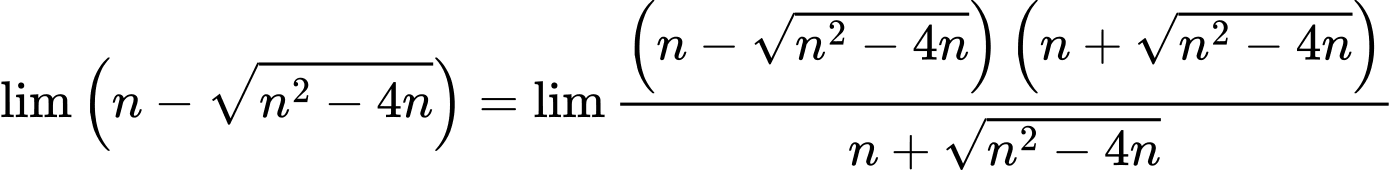
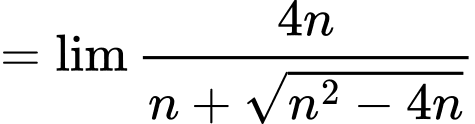
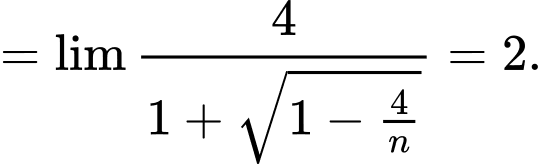 Đáp án: C
Đáp án: C
Câu 9 [803268]: Cho dãy số 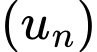 thỏa
thỏa 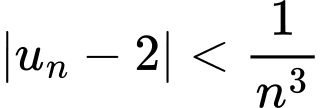 với mọi
với mọi  Khi đó
Khi đó
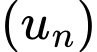 thỏa
thỏa 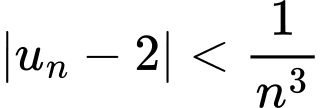 với mọi
với mọi  Khi đó
Khi đó A, 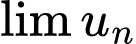 không tồn tại.
không tồn tại.
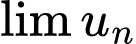 không tồn tại.
không tồn tại.B, 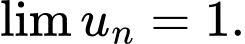
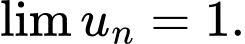
C, 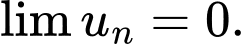
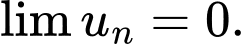
D, 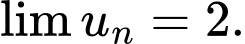
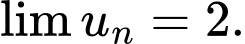
Chọn D
Ta có: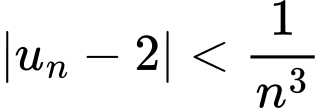
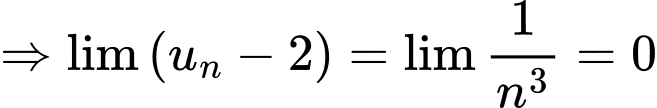
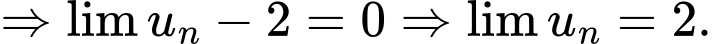 Đáp án: D
Đáp án: D
Ta có:
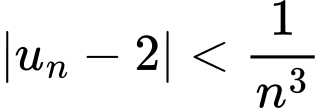
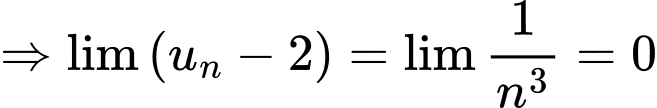
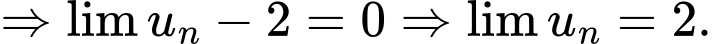 Đáp án: D
Đáp án: D
Câu 10 [677738]: 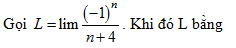
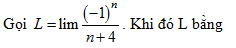
A, 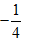
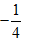
B, 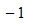
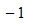
C, 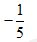
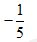
D, 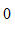
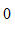
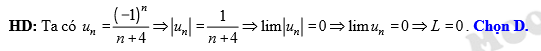 Đáp án: D
Đáp án: D
Câu 11 [803544]: Tổng 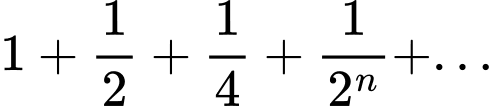 bằng
bằng
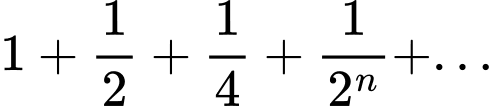 bằng
bằng A, 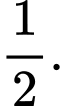
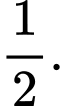
B, 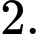
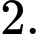
C, 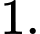
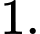
D, 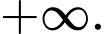
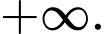
Chọn B
Ta có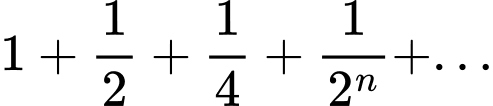 là tổng của một cấp số nhân lùi vô hạn với
là tổng của một cấp số nhân lùi vô hạn với 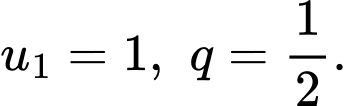
Áp dụng công thức được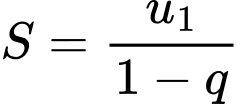 kết quả
kết quả 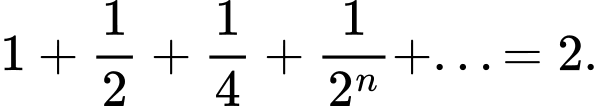 Đáp án: B
Đáp án: B
Ta có
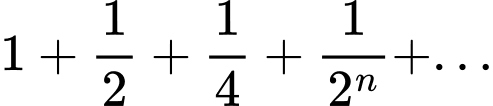 là tổng của một cấp số nhân lùi vô hạn với
là tổng của một cấp số nhân lùi vô hạn với 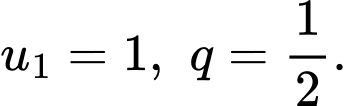
Áp dụng công thức được
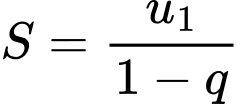 kết quả
kết quả 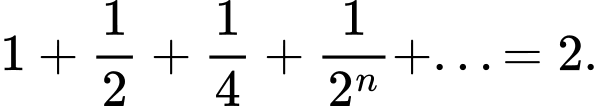 Đáp án: B
Đáp án: B
Câu 12 [803545]: Cho dãy số 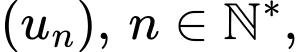 thỏa mãn điều kiện
thỏa mãn điều kiện 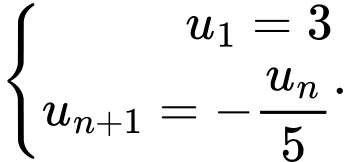 Gọi
Gọi  là tổng
là tổng 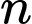 số hạng đầu tiên của dãy số đã cho. Khi đó
số hạng đầu tiên của dãy số đã cho. Khi đó 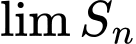 bằng
bằng
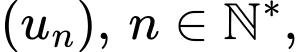 thỏa mãn điều kiện
thỏa mãn điều kiện 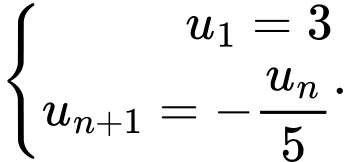 Gọi
Gọi  là tổng
là tổng 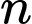 số hạng đầu tiên của dãy số đã cho. Khi đó
số hạng đầu tiên của dãy số đã cho. Khi đó 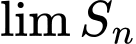 bằng
bằng A, 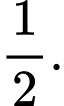
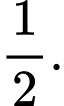
B, 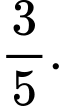
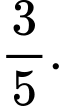
C, 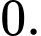
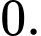
D, 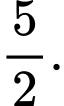
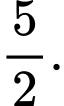
Chọn D
Ta có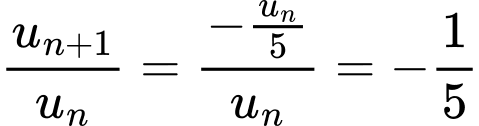 do đó dãy
do đó dãy 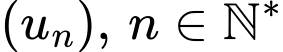 là một cấp số nhân lùi vô hạn có
là một cấp số nhân lùi vô hạn có 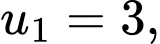
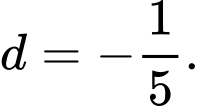
Suy ra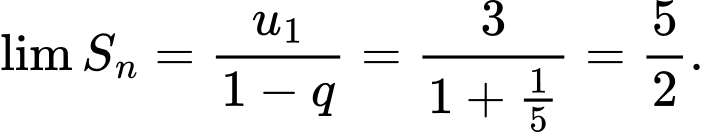 Đáp án: D
Đáp án: D
Ta có
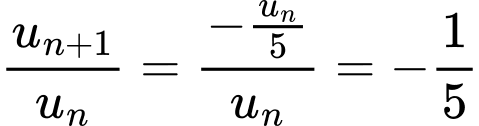 do đó dãy
do đó dãy 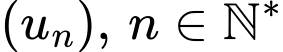 là một cấp số nhân lùi vô hạn có
là một cấp số nhân lùi vô hạn có 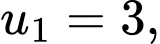
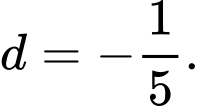
Suy ra
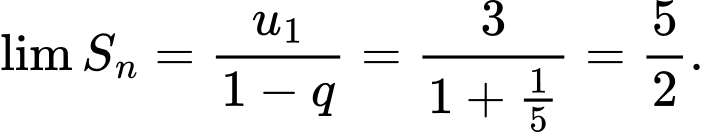 Đáp án: D
Đáp án: D
Câu 13 [519123]: 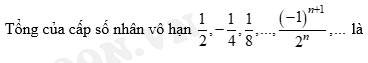
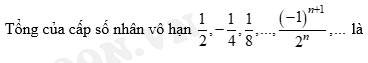
A, 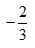
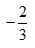
B, 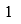
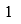
C, 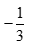
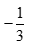
D, 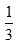
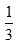
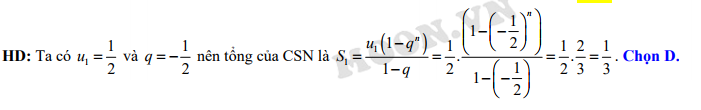 Đáp án: D
Đáp án: D
Câu 14 [803319]: 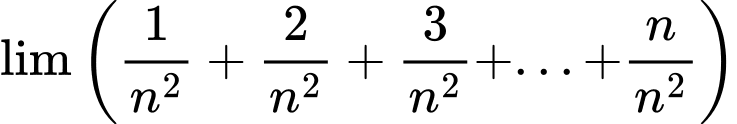
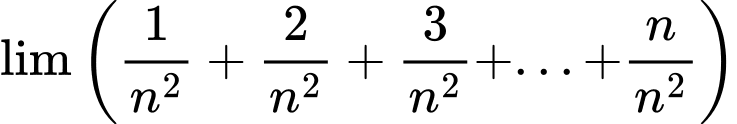
A, 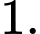
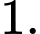
B, 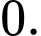
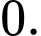
C, 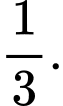
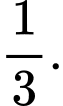
D, 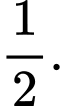
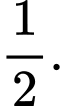
Chọn D
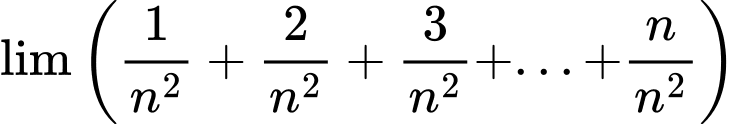
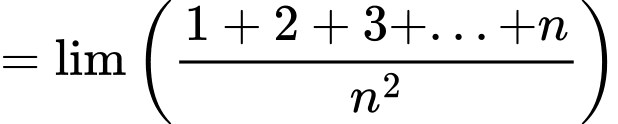
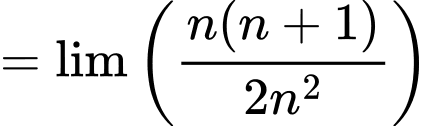
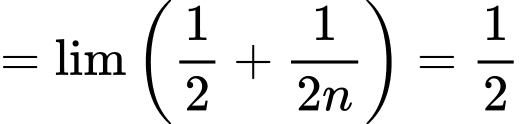 Đáp án: D
Đáp án: D
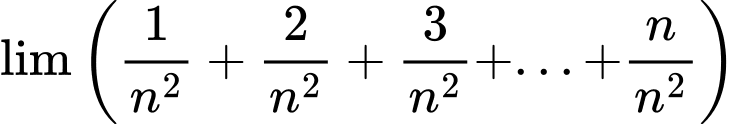
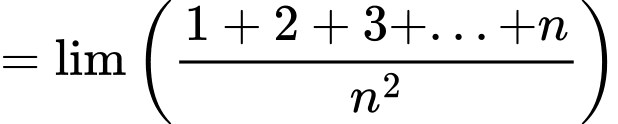
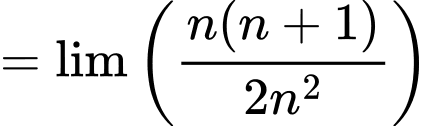
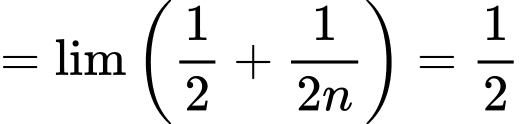 Đáp án: D
Đáp án: D
Câu 15 [803318]: 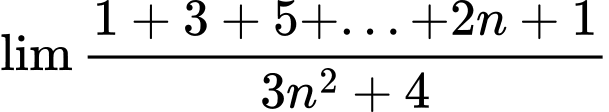 bằng
bằng
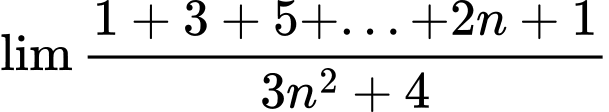 bằng
bằng A, 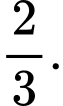
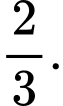
B, 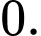
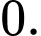
C, 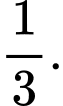
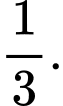
D, 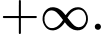
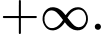
Chọn C.
Ta có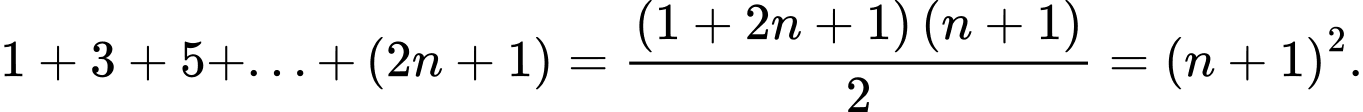
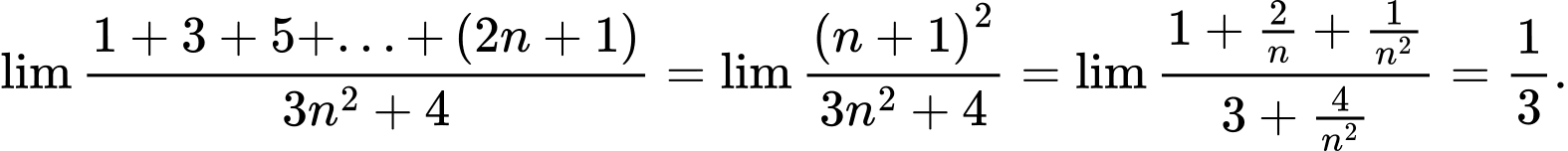 Đáp án: C
Đáp án: C
Ta có
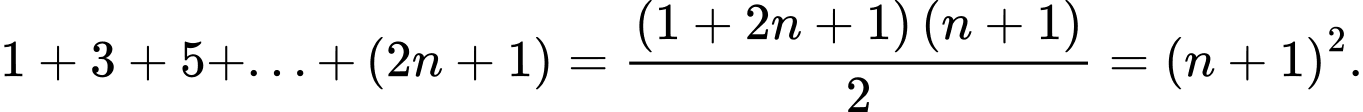
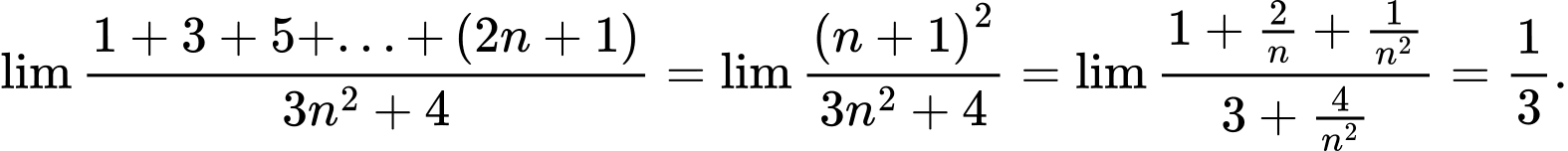 Đáp án: C
Đáp án: C
Câu 16 [806441]: Bạn A thả quả bóng cao su từ độ cao 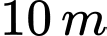 theo phương thẳng đứng. Mỗi khi chạm đất nó lại nảy lên theo phương thẳng đứng có độ cao bằng
theo phương thẳng đứng. Mỗi khi chạm đất nó lại nảy lên theo phương thẳng đứng có độ cao bằng 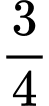 độ cao trước đó. Tính tổng quãng đường bóng đi được đến khi bóng dừng hẳn.
độ cao trước đó. Tính tổng quãng đường bóng đi được đến khi bóng dừng hẳn.
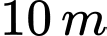 theo phương thẳng đứng. Mỗi khi chạm đất nó lại nảy lên theo phương thẳng đứng có độ cao bằng
theo phương thẳng đứng. Mỗi khi chạm đất nó lại nảy lên theo phương thẳng đứng có độ cao bằng 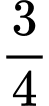 độ cao trước đó. Tính tổng quãng đường bóng đi được đến khi bóng dừng hẳn.
độ cao trước đó. Tính tổng quãng đường bóng đi được đến khi bóng dừng hẳn. A, 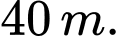
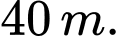
B, 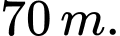
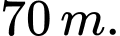
C, 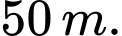
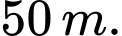
D, 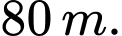
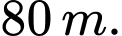
Các quãng đường khi bóng đi xuống tạo thành một cấp số nhân lùi vô hạn có 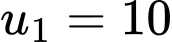 và
và 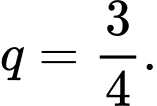
Tổng các quãng đường khi bóng đi xuống là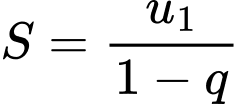
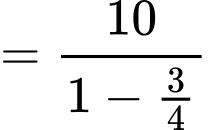
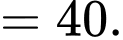
Tổng quãng đường bóng đi được đến khi bóng dừng hẳn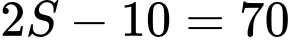 (m). Đáp án: B
(m). Đáp án: B
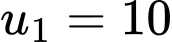 và
và 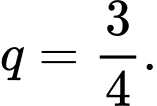
Tổng các quãng đường khi bóng đi xuống là
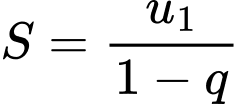
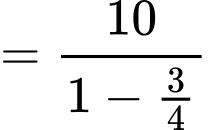
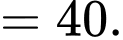
Tổng quãng đường bóng đi được đến khi bóng dừng hẳn
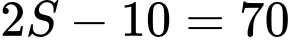 (m). Đáp án: B
(m). Đáp án: B
Câu 17 [803564]: Trong một lần Đoàn trường Lê Văn Hưu tổ chức chơi bóng chuyền hơi, bạn Nam thả một quả bóng chuyền hơi từ tầng ba, độ cao 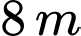 so với mặt đất và thấy rằng mỗi lần chạm đất thì quả bóng lại nảy lên một độ cao bằng ba phần tư độ cao lần rơi trước. Biết quả bóng chuyển động vuông góc với mặt đất. Khi đó tổng quảng đường quả bóng đã bay từ lúc thả bóng đến khi quả bóng không máy nữa gần bằng số nào dưới đây nhất?
so với mặt đất và thấy rằng mỗi lần chạm đất thì quả bóng lại nảy lên một độ cao bằng ba phần tư độ cao lần rơi trước. Biết quả bóng chuyển động vuông góc với mặt đất. Khi đó tổng quảng đường quả bóng đã bay từ lúc thả bóng đến khi quả bóng không máy nữa gần bằng số nào dưới đây nhất?
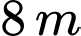 so với mặt đất và thấy rằng mỗi lần chạm đất thì quả bóng lại nảy lên một độ cao bằng ba phần tư độ cao lần rơi trước. Biết quả bóng chuyển động vuông góc với mặt đất. Khi đó tổng quảng đường quả bóng đã bay từ lúc thả bóng đến khi quả bóng không máy nữa gần bằng số nào dưới đây nhất?
so với mặt đất và thấy rằng mỗi lần chạm đất thì quả bóng lại nảy lên một độ cao bằng ba phần tư độ cao lần rơi trước. Biết quả bóng chuyển động vuông góc với mặt đất. Khi đó tổng quảng đường quả bóng đã bay từ lúc thả bóng đến khi quả bóng không máy nữa gần bằng số nào dưới đây nhất? A, 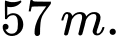
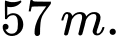
B, 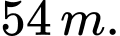
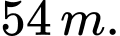
C, 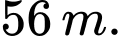
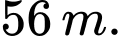
D, 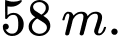
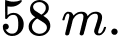
Chọn C
Lần đầu rơi xuống, quảng đường quả bóng đã bay đến lúc chạm đất là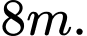
Sau đó quả bóng nảy lên và rơi xuống chạm đất lần thứ 2 thì quảng đường quả bóng đã bay là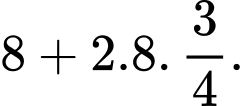
Tương tự, khi quả bóng nảy lên và rơi xuống chạm đất lần thứ n thì quảng đường quả bóng đã bay là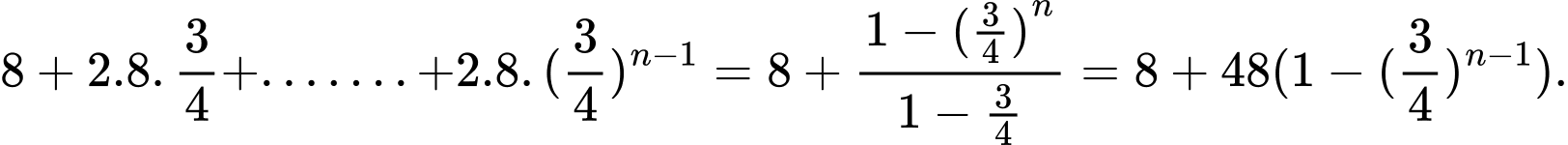
Quảng đường quả bóng đã bay từ lúc thả đến lúc không máy nữa bằng:
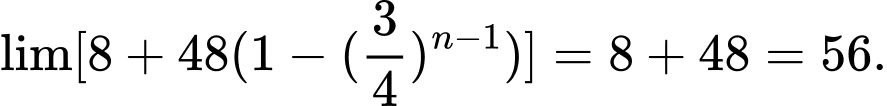 Đáp án: C
Đáp án: C
Lần đầu rơi xuống, quảng đường quả bóng đã bay đến lúc chạm đất là
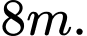
Sau đó quả bóng nảy lên và rơi xuống chạm đất lần thứ 2 thì quảng đường quả bóng đã bay là
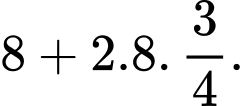
Tương tự, khi quả bóng nảy lên và rơi xuống chạm đất lần thứ n thì quảng đường quả bóng đã bay là
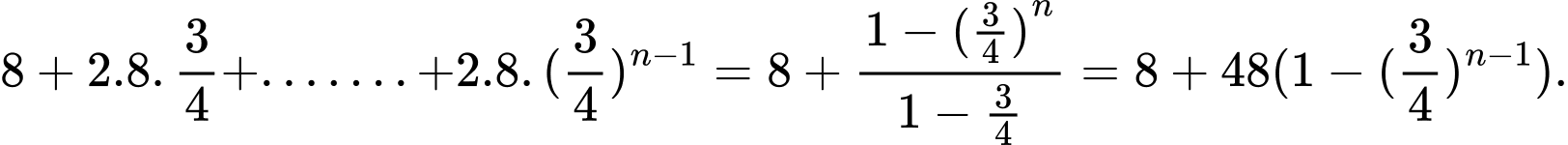
Quảng đường quả bóng đã bay từ lúc thả đến lúc không máy nữa bằng:
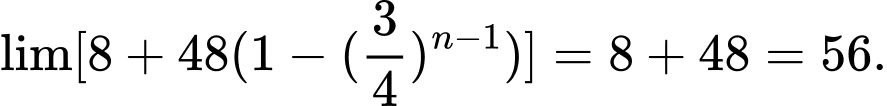 Đáp án: C
Đáp án: C
Câu 18 [806447]: Từ độ cao 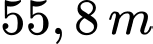 của tháp nghiêng Pisa nước Italia người ta thả một quả bóng cao su chạm xuống đất. Giả sử mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng
của tháp nghiêng Pisa nước Italia người ta thả một quả bóng cao su chạm xuống đất. Giả sử mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng 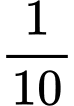 độ cao mà quả bóng đạt trước đó. Tổng độ dài hành trình của quả bóng được thả từ lúc ban đầu cho đến khi nó nằm yên trên mặt đất thuộc khoảng nào trong các khoảng sau đây?
độ cao mà quả bóng đạt trước đó. Tổng độ dài hành trình của quả bóng được thả từ lúc ban đầu cho đến khi nó nằm yên trên mặt đất thuộc khoảng nào trong các khoảng sau đây?

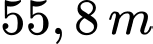 của tháp nghiêng Pisa nước Italia người ta thả một quả bóng cao su chạm xuống đất. Giả sử mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng
của tháp nghiêng Pisa nước Italia người ta thả một quả bóng cao su chạm xuống đất. Giả sử mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng 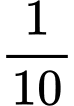 độ cao mà quả bóng đạt trước đó. Tổng độ dài hành trình của quả bóng được thả từ lúc ban đầu cho đến khi nó nằm yên trên mặt đất thuộc khoảng nào trong các khoảng sau đây?
độ cao mà quả bóng đạt trước đó. Tổng độ dài hành trình của quả bóng được thả từ lúc ban đầu cho đến khi nó nằm yên trên mặt đất thuộc khoảng nào trong các khoảng sau đây? 
A, 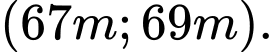
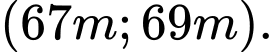
B, 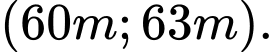
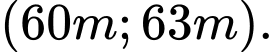
C, 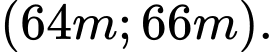
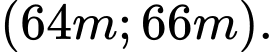
D, 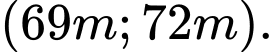
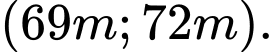
Chọn A
Gọi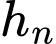 là độ dài đường đi của quả bóng ở lần rơi xuống thứ
là độ dài đường đi của quả bóng ở lần rơi xuống thứ 
Gọi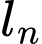 là độ dài đường đi của quả bóng ở lần nảy lên thứ
là độ dài đường đi của quả bóng ở lần nảy lên thứ 
Theo bài ra ta có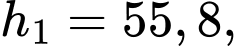
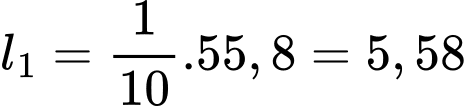 và các dãy số
và các dãy số 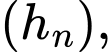
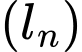 là các cấp số nhân lùi vô hạn với công bội
là các cấp số nhân lùi vô hạn với công bội 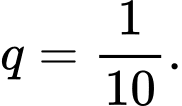
Từ đó ta suy ra tổng độ dài đường đi của quả bóng là:
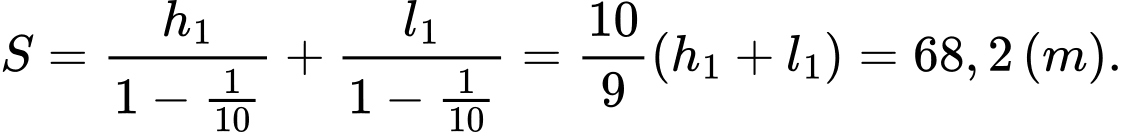 Đáp án: A
Đáp án: A
Gọi
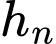 là độ dài đường đi của quả bóng ở lần rơi xuống thứ
là độ dài đường đi của quả bóng ở lần rơi xuống thứ 
Gọi
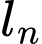 là độ dài đường đi của quả bóng ở lần nảy lên thứ
là độ dài đường đi của quả bóng ở lần nảy lên thứ 
Theo bài ra ta có
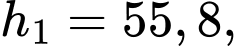
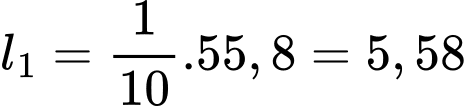 và các dãy số
và các dãy số 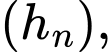
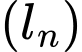 là các cấp số nhân lùi vô hạn với công bội
là các cấp số nhân lùi vô hạn với công bội 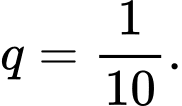
Từ đó ta suy ra tổng độ dài đường đi của quả bóng là:
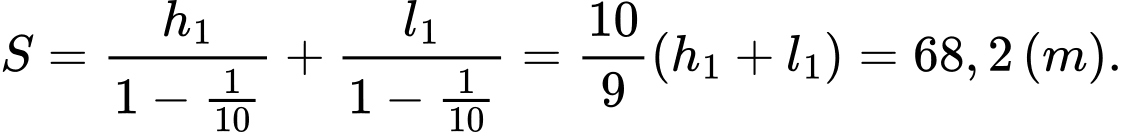 Đáp án: A
Đáp án: A
Câu 19 [803563]: Một mô hình gồm các khối cầu xếp chồng lên nhau tạo thành một cột thẳng đứng. Biết rằng mỗi khối cầu có bán kính gấp đôi khối cầu nằm ngay trên nó và bán kính khối cầu dưới cùng là 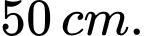 Hỏi mệnh đề nào sau đây là đúng?
Hỏi mệnh đề nào sau đây là đúng?
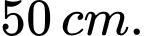 Hỏi mệnh đề nào sau đây là đúng?
Hỏi mệnh đề nào sau đây là đúng? A, Chiều cao mô hình không quá 1,5 mét.
B, Chiều cao mô hình tối đa là 2 mét.
C, Chiều cao mô hình dưới 2 mét.
D, Mô hình có thể đạt được chiều cao tùy ý.
Chọn C
Gọi bán kính khối cầu dưới cùng là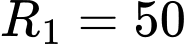 cm.
cm.
Gọi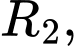
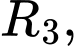 …,
…,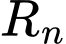 lần lượt là bán kính của các khối cầu
lần lượt là bán kính của các khối cầu 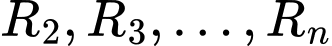 nằm nằm ngay trên khối cầu dưới cùng.
nằm nằm ngay trên khối cầu dưới cùng.
Ta có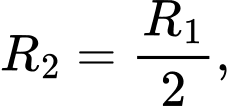
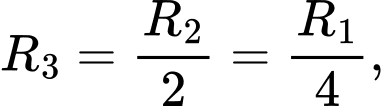 ….,
…., 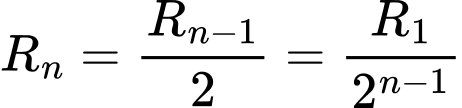
Gọi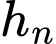 là chiều cao của mô hình gồm có
là chiều cao của mô hình gồm có 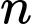 khối cầu chồng lên nhau.
khối cầu chồng lên nhau.
Ta có:
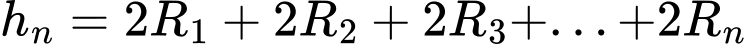
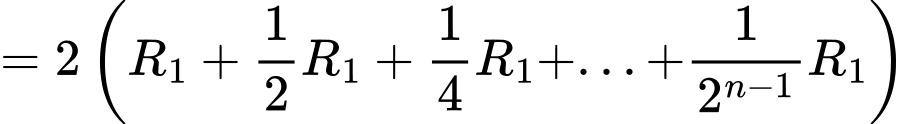
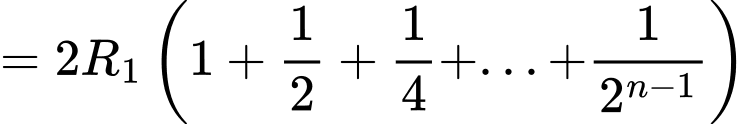
Suy ra chiều cao mô hình là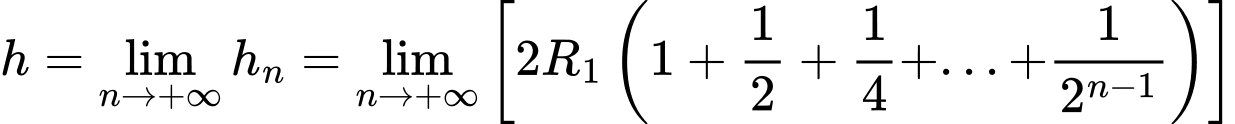
Xét dãy số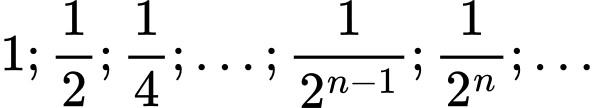 là một cấp số nhân có
là một cấp số nhân có 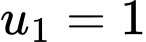 và công bội
và công bội 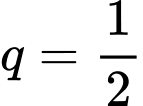 nên là dãy cấp số nhân lùi vô hạn. Do đó
nên là dãy cấp số nhân lùi vô hạn. Do đó 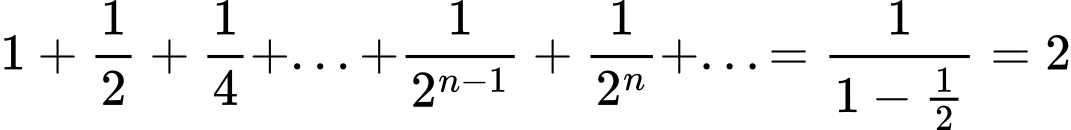
Suy ra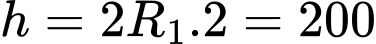 cm. Vậy chiều cao mô hình nhỏ hơn
cm. Vậy chiều cao mô hình nhỏ hơn 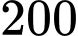 cm. Đáp án: C
cm. Đáp án: C
Gọi bán kính khối cầu dưới cùng là
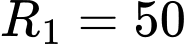 cm.
cm. Gọi
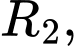
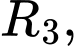 …,
…,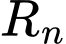 lần lượt là bán kính của các khối cầu
lần lượt là bán kính của các khối cầu 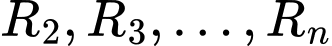 nằm nằm ngay trên khối cầu dưới cùng.
nằm nằm ngay trên khối cầu dưới cùng. Ta có
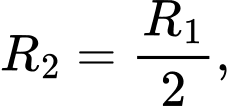
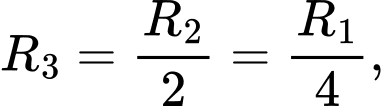 ….,
…., 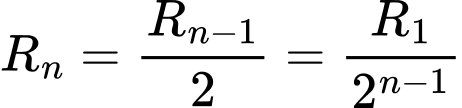
Gọi
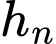 là chiều cao của mô hình gồm có
là chiều cao của mô hình gồm có 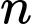 khối cầu chồng lên nhau.
khối cầu chồng lên nhau. Ta có:
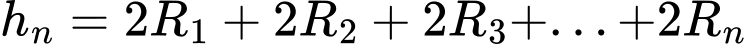
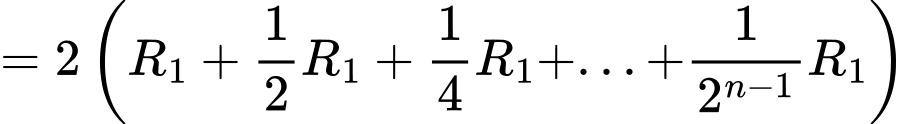
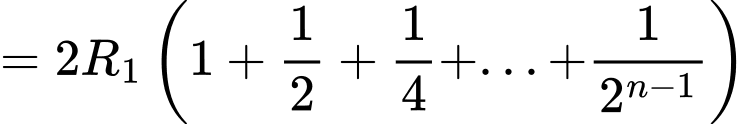
Suy ra chiều cao mô hình là
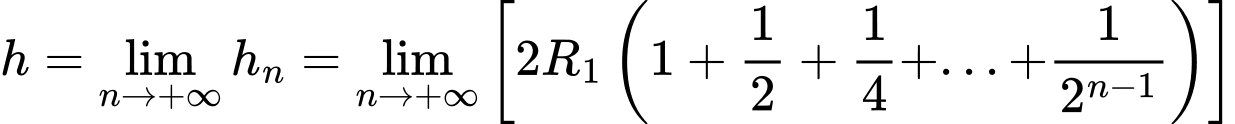
Xét dãy số
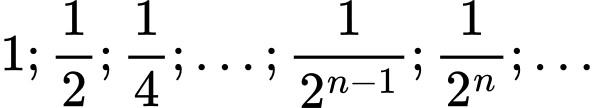 là một cấp số nhân có
là một cấp số nhân có 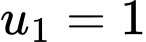 và công bội
và công bội 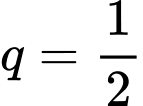 nên là dãy cấp số nhân lùi vô hạn. Do đó
nên là dãy cấp số nhân lùi vô hạn. Do đó 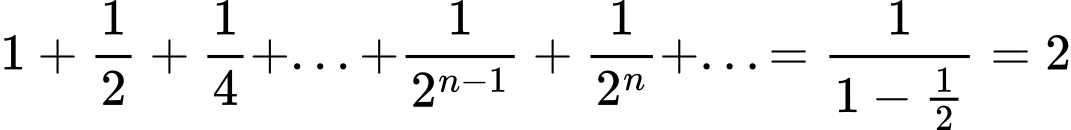
Suy ra
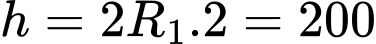 cm. Vậy chiều cao mô hình nhỏ hơn
cm. Vậy chiều cao mô hình nhỏ hơn 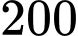 cm. Đáp án: C
cm. Đáp án: C
Câu 20 [579652]: [Đề mẫu HSA 2024]: Nghiên cứu về quá trình tăng trưởng của một quần thể sinh vật trong điều kiện môi trường sống hạn chế cho thấy: ban đầu số lượng cá thể tăng trưởng chậm, sau đó nhanh và cuối cùng khi thời gian đủ dài, số lượng cá thể của quần thể đạt đến trạng thái cân bằng, khi đó số lượng cá thể sinh ra xấp xỉ bằng số lượng chết đi. Số lượng cá thể 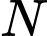 trong quần thể theo thời gian
trong quần thể theo thời gian 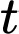 (ngày) được mô hình hóa và xấp xỉ theo hàm số:
(ngày) được mô hình hóa và xấp xỉ theo hàm số: 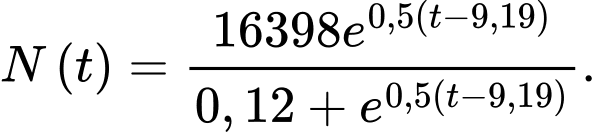 Khi quần thể sinh vật trên đạt trạng thái cân bằng, số cá thể của quần thể gần nhất với giá trị nào sau đây?
Khi quần thể sinh vật trên đạt trạng thái cân bằng, số cá thể của quần thể gần nhất với giá trị nào sau đây?
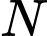 trong quần thể theo thời gian
trong quần thể theo thời gian 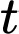 (ngày) được mô hình hóa và xấp xỉ theo hàm số:
(ngày) được mô hình hóa và xấp xỉ theo hàm số: 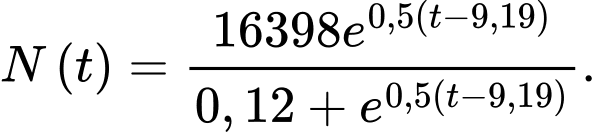 Khi quần thể sinh vật trên đạt trạng thái cân bằng, số cá thể của quần thể gần nhất với giá trị nào sau đây?
Khi quần thể sinh vật trên đạt trạng thái cân bằng, số cá thể của quần thể gần nhất với giá trị nào sau đây? A, 9264.
B, 136650.
C, 16398.
D, 224630.
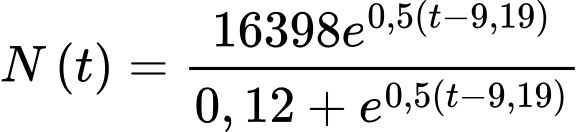
Khi quần thể sinh vật trên đạt trạng thái cân bằng thì
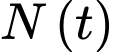 không đổi
không đổi
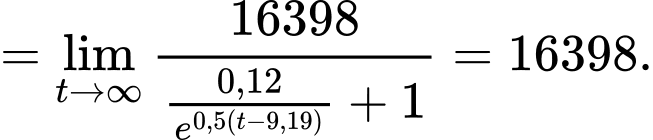
Chọn C Đáp án: C
Câu 21 [803315]: Biết 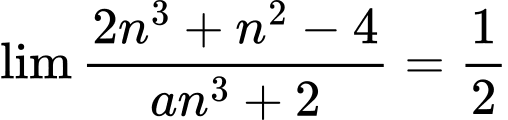 với
với 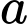 là tham số. Khi đó
là tham số. Khi đó 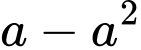 bằng
bằng
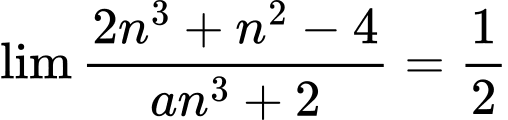 với
với 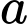 là tham số. Khi đó
là tham số. Khi đó 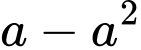 bằng
bằng A, 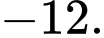
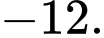
B, 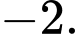
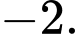
C, 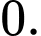
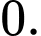
D, 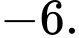
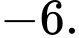
Chọn A
Ta có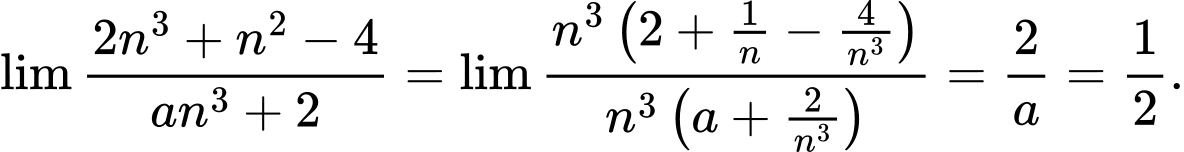
Suy ra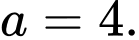 Khi đó
Khi đó  Đáp án: A
Đáp án: A
Ta có
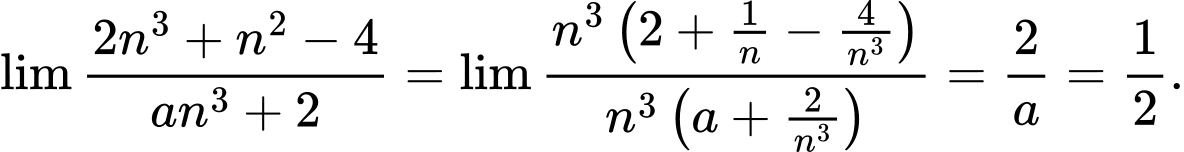
Suy ra
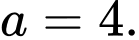 Khi đó
Khi đó  Đáp án: A
Đáp án: A
Câu 22 [677737]: Cho dãy số 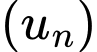 với
với 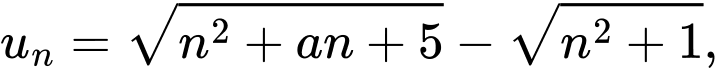 trong đó
trong đó 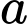 là một hằng số. Để
là một hằng số. Để 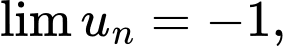 giá trị của
giá trị của 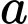 là:
là:
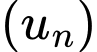 với
với 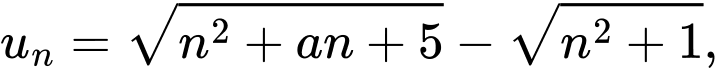 trong đó
trong đó 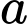 là một hằng số. Để
là một hằng số. Để 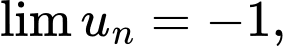 giá trị của
giá trị của 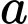 là:
là: A, 3.
B, 2.
C, -3.
D, -2.
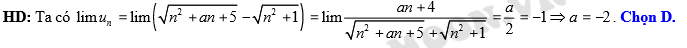 Đáp án: D
Đáp án: D
Câu 23 [160919]: Có bao nhiêu giá trị nguyên của tham số 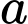 thuộc khoảng
thuộc khoảng 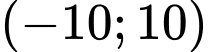 để
để
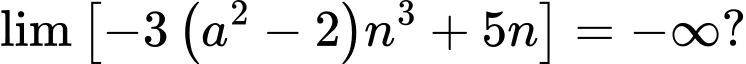
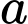 thuộc khoảng
thuộc khoảng 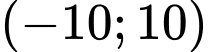 để
để
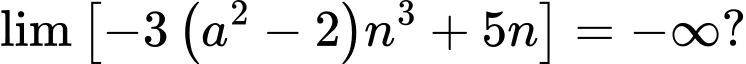
Ta có 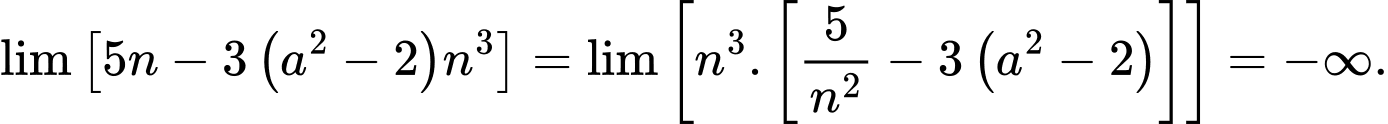
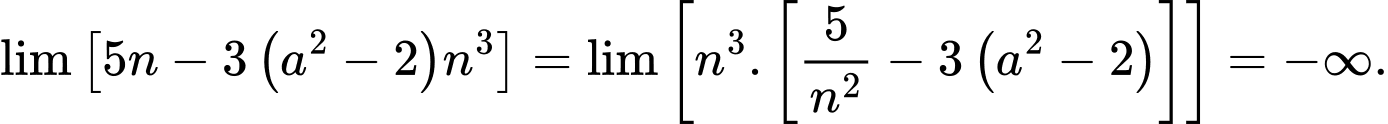
Suy ra 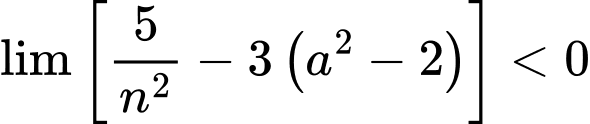 hay
hay 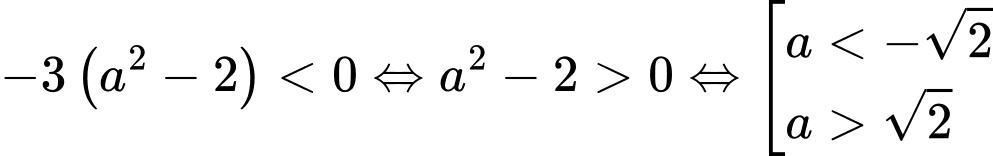
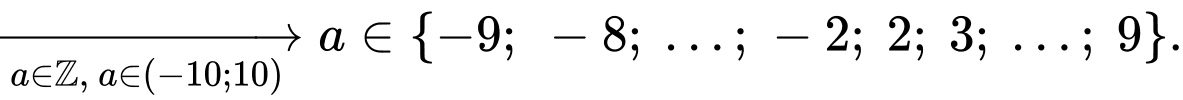 Đáp án :
Đáp án :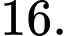
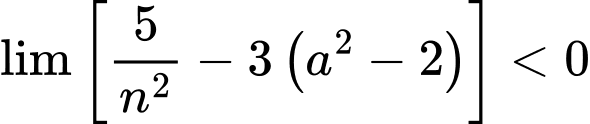 hay
hay 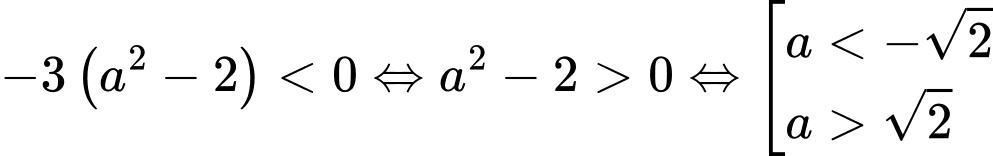
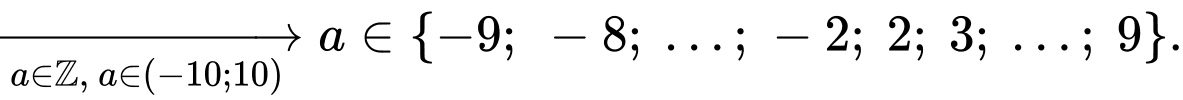 Đáp án :
Đáp án :
Câu 24 [803312]: Gọi 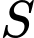 là tập hợp các tham số nguyên
là tập hợp các tham số nguyên 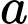 thỏa mãn
thỏa mãn 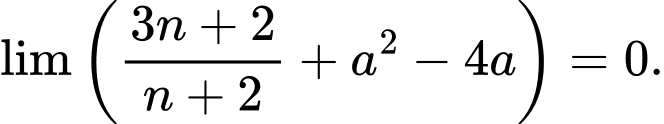 Tổng các phần tử của
Tổng các phần tử của 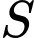 bằng
bằng
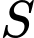 là tập hợp các tham số nguyên
là tập hợp các tham số nguyên 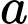 thỏa mãn
thỏa mãn 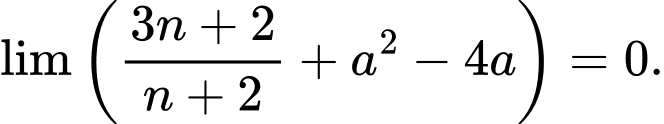 Tổng các phần tử của
Tổng các phần tử của 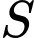 bằng
bằng A, 4.
B, 3.
C, 5.
D, 2.
Chọn A
Ta có: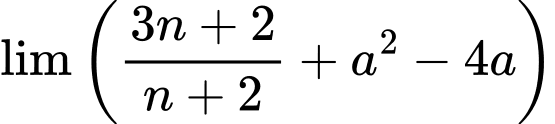
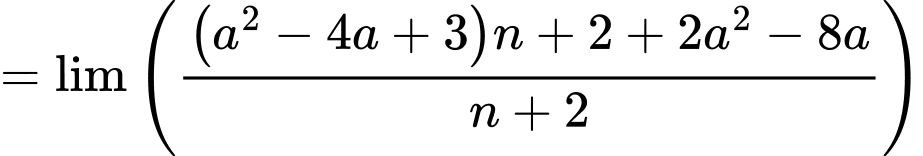
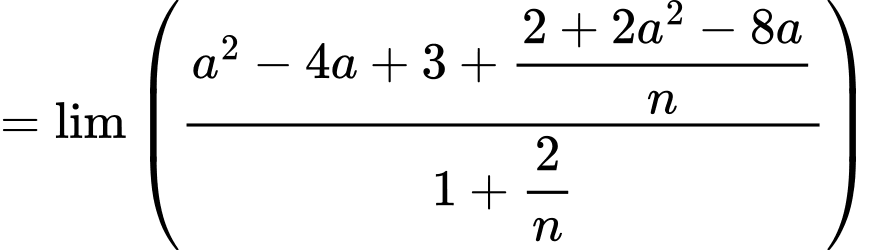
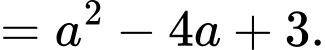
Theo giả thiết: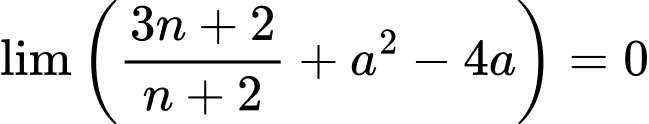
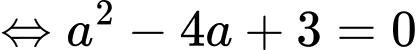
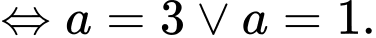
Vậy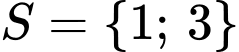
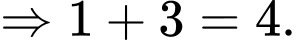 Đáp án: A
Đáp án: A
Ta có:
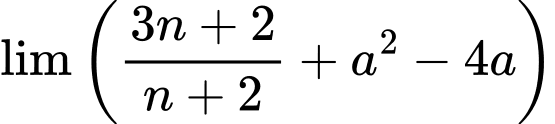
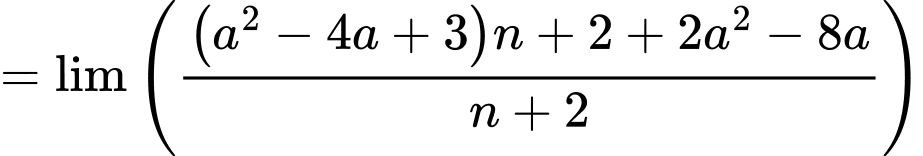
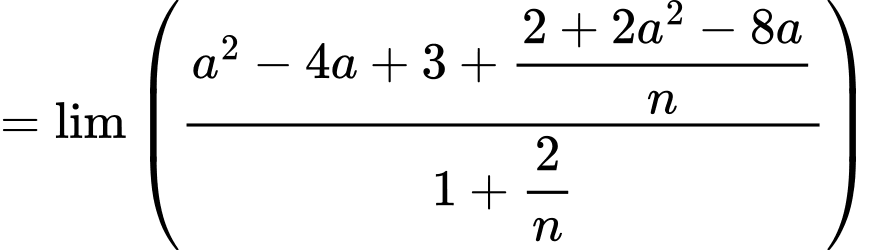
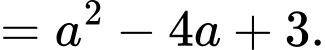
Theo giả thiết:
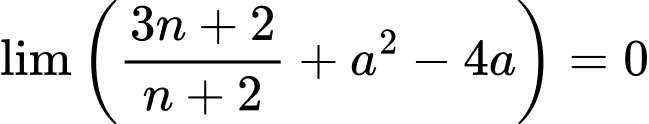
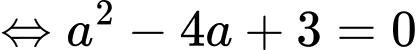
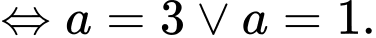
Vậy
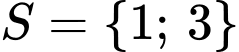
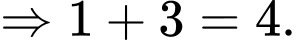 Đáp án: A
Đáp án: A
Câu 25 [803539]: Có tất cả bao nhiêu giá trị nguyên của tham số 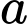 thuộc khoảng
thuộc khoảng 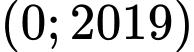 để
để 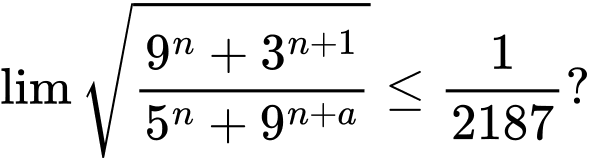
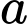 thuộc khoảng
thuộc khoảng 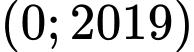 để
để 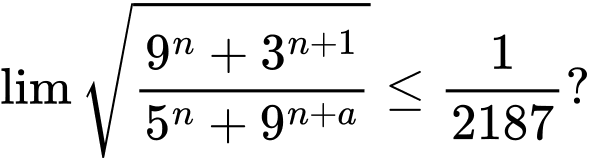
A, 2018.
B, 2012.
C, 2019.
D, 2011.
Chọn B
Ta có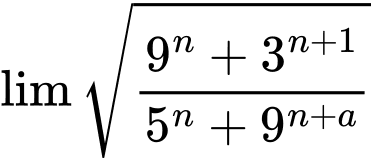
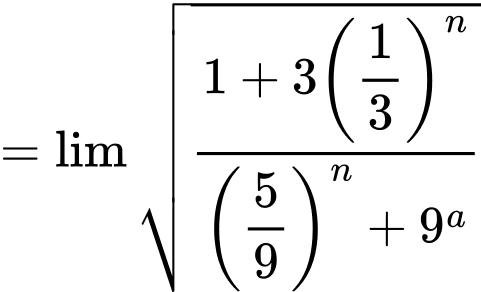
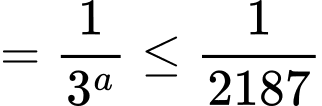
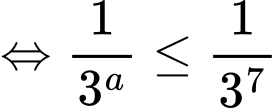
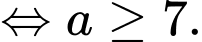
Do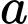 nguyên thuộc khoảng
nguyên thuộc khoảng 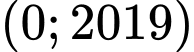 nên
nên 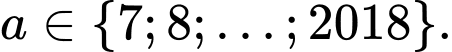 Đáp án: B
Đáp án: B
Ta có
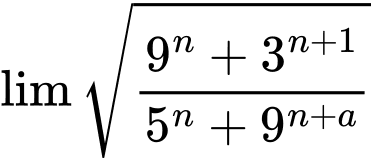
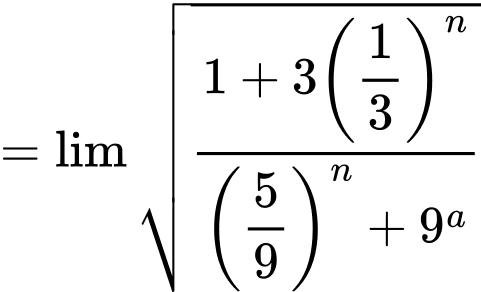
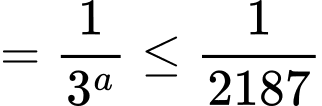
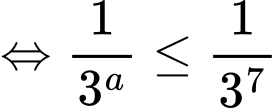
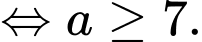
Do
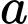 nguyên thuộc khoảng
nguyên thuộc khoảng 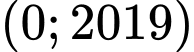 nên
nên 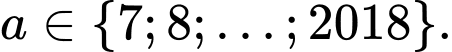 Đáp án: B
Đáp án: B
Câu 26 [398911]: Tính giới hạn sau: 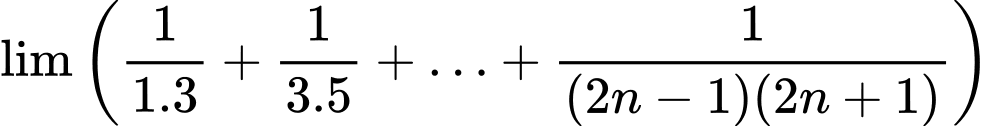
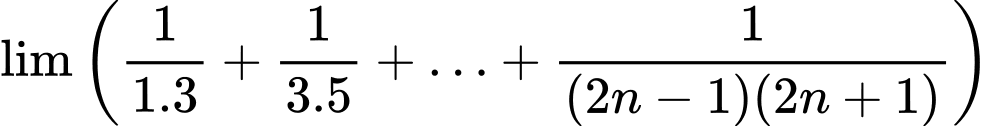
Xét 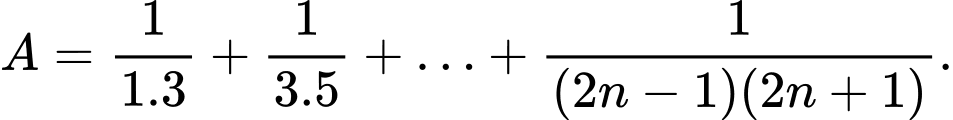
Ta có: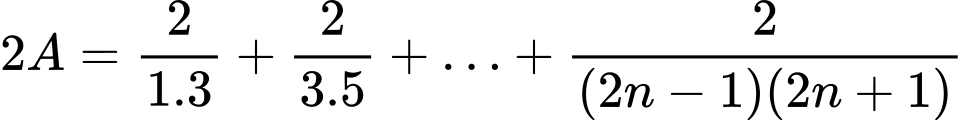
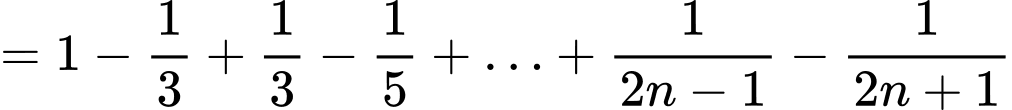
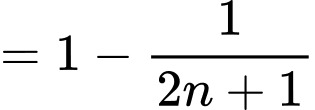
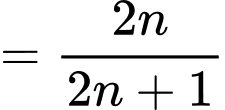
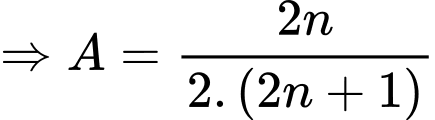
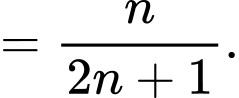
Suy ra
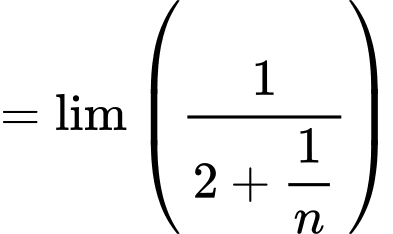
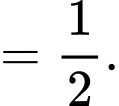
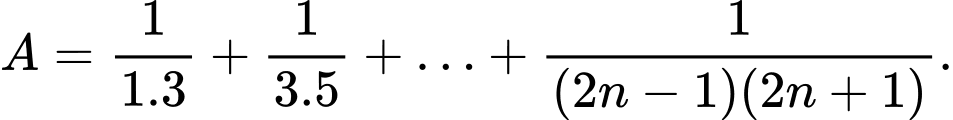
Ta có:
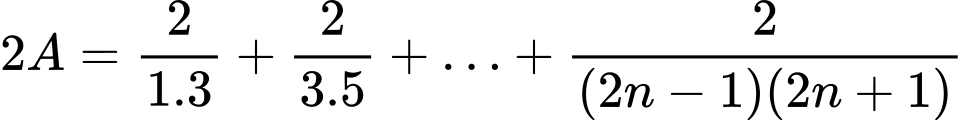
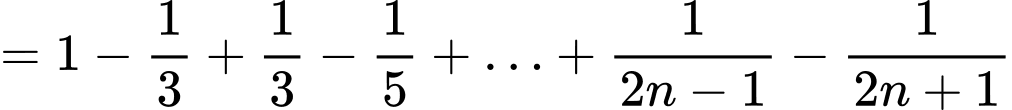
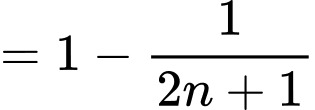
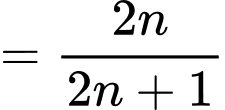
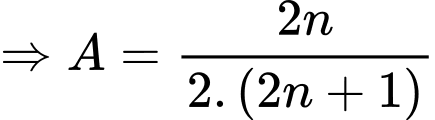
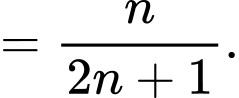
Suy ra

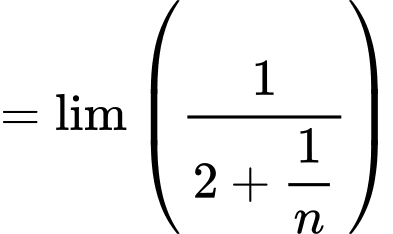
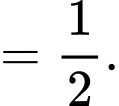
Câu 27 [806165]: Cho tam giác đều 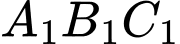 có độ dài cạnh bằng 4. Trung điểm của các cạnh tam giác
có độ dài cạnh bằng 4. Trung điểm của các cạnh tam giác 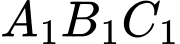 tạo thành tam giác
tạo thành tam giác 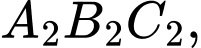 trung điểm của các cạnh tam giác
trung điểm của các cạnh tam giác 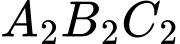 tạo thành tam giác
tạo thành tam giác 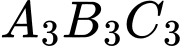 … Gọi
… Gọi 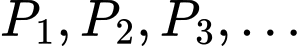 lần lượt là chu vi của tam giác
lần lượt là chu vi của tam giác 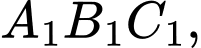
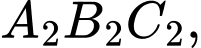
 …Tính tổng chu vi
…Tính tổng chu vi 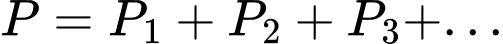
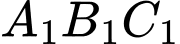 có độ dài cạnh bằng 4. Trung điểm của các cạnh tam giác
có độ dài cạnh bằng 4. Trung điểm của các cạnh tam giác 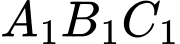 tạo thành tam giác
tạo thành tam giác 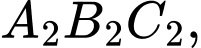 trung điểm của các cạnh tam giác
trung điểm của các cạnh tam giác 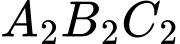 tạo thành tam giác
tạo thành tam giác 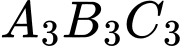 … Gọi
… Gọi 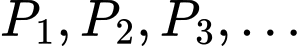 lần lượt là chu vi của tam giác
lần lượt là chu vi của tam giác 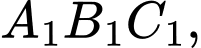
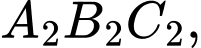
 …Tính tổng chu vi
…Tính tổng chu vi 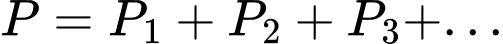
A, 

B, 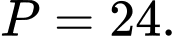
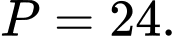
C, 

D, 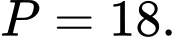
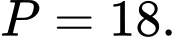
Chọn B
Ta có:
 ;
; 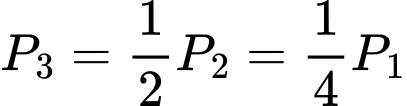 ;
; 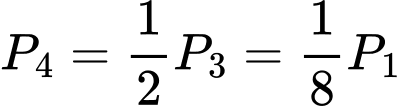 …;
…; 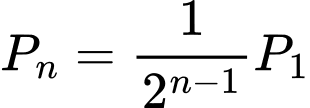
…
Vậy
Đáp án: B

Ta có:
 ;
; 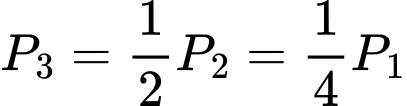 ;
; 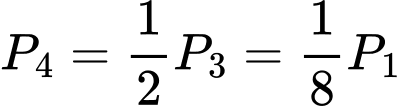 …;
…; 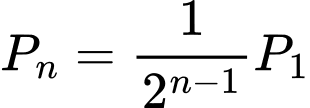
…
Vậy

Đáp án: B
Câu 28 [271655]: Một bệnh nhân hàng ngày phải uống một viên thuốc 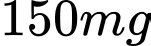 . Sau ngày đầu, trước mỗi lần uống , hàm lượng thuốc cũ trong cơ thể vẫn còn 5%. Tính lượng thuốc có trong cơ thể sau khi uống viên thuốc của ngày thứ 5. Ước tính lượng thuốc trong cơ thể nếu bệnh nhân sử dụng thuốc trong một thời gian dài.
. Sau ngày đầu, trước mỗi lần uống , hàm lượng thuốc cũ trong cơ thể vẫn còn 5%. Tính lượng thuốc có trong cơ thể sau khi uống viên thuốc của ngày thứ 5. Ước tính lượng thuốc trong cơ thể nếu bệnh nhân sử dụng thuốc trong một thời gian dài.
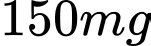 . Sau ngày đầu, trước mỗi lần uống , hàm lượng thuốc cũ trong cơ thể vẫn còn 5%. Tính lượng thuốc có trong cơ thể sau khi uống viên thuốc của ngày thứ 5. Ước tính lượng thuốc trong cơ thể nếu bệnh nhân sử dụng thuốc trong một thời gian dài.
. Sau ngày đầu, trước mỗi lần uống , hàm lượng thuốc cũ trong cơ thể vẫn còn 5%. Tính lượng thuốc có trong cơ thể sau khi uống viên thuốc của ngày thứ 5. Ước tính lượng thuốc trong cơ thể nếu bệnh nhân sử dụng thuốc trong một thời gian dài.
Lượng thuốc có trong cơ thể sau khi uống viên thuốc của ngày thứ hai là: 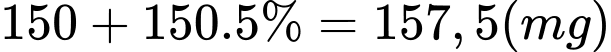 .
. 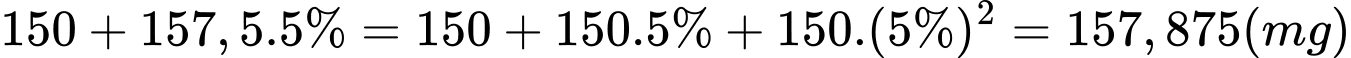 .
. 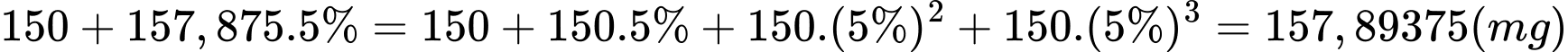 .
. 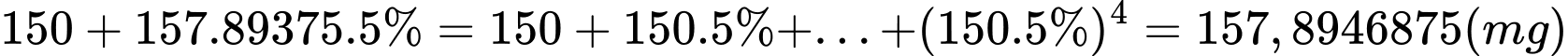 .
. 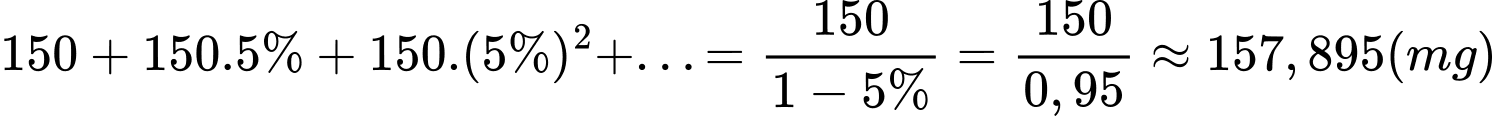 .
.
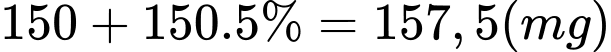 .
. Lượng thuốc có trong cơ thể sau khi uống viên thuốc của ngày thứ ba là:
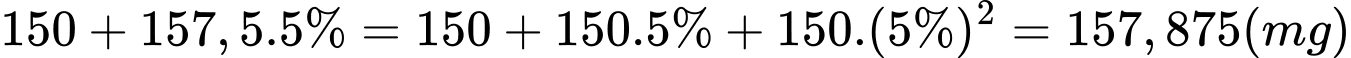 .
. Lượng thuốc có trong cơ thể sau khi uống viên thuốc của ngày thứ tư là:
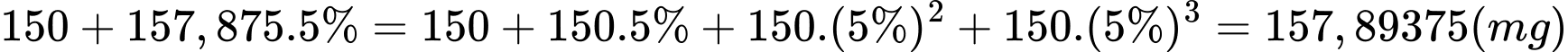 .
. Lượng thuốc có trong cơ thể sau khi uống viên thuốc của ngày thứ năm là:
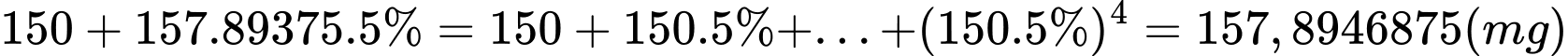 .
. Lượng thuốc có trong cơ thể sau khi uống thuốc một thời gian dài là:
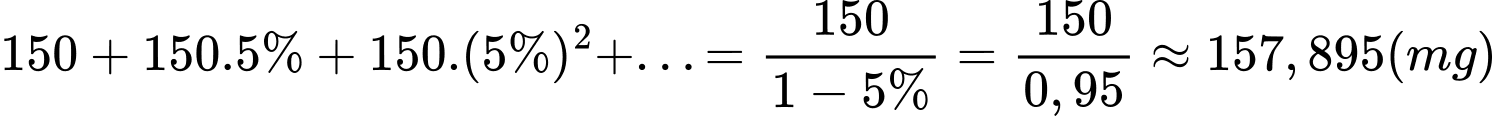 .
.
Câu 29 [806453]: Cho hình vuông 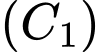 có cạnh bằng
có cạnh bằng 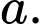 Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông
Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông  (Hình vẽ).
(Hình vẽ).
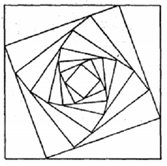
Từ hình vuông lại tiếp tục làm như trên ta nhận được dãy các hình vuông
lại tiếp tục làm như trên ta nhận được dãy các hình vuông 
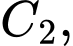
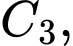 .,
., 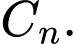 Gọi
Gọi 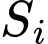 là diện tích của hình vuông
là diện tích của hình vuông 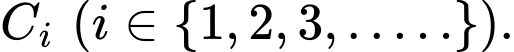 Đặt
Đặt 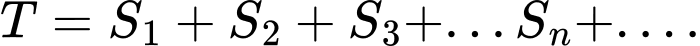 Biết
Biết 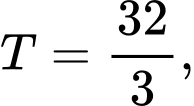 tính
tính 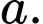
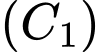 có cạnh bằng
có cạnh bằng 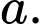 Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông
Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông 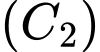 (Hình vẽ).
(Hình vẽ). 
Từ hình vuông
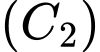 lại tiếp tục làm như trên ta nhận được dãy các hình vuông
lại tiếp tục làm như trên ta nhận được dãy các hình vuông 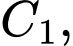
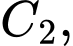
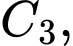 .,
., 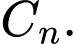 Gọi
Gọi 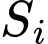 là diện tích của hình vuông
là diện tích của hình vuông 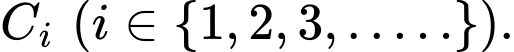 Đặt
Đặt 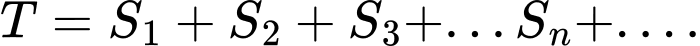 Biết
Biết 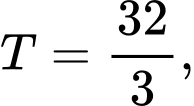 tính
tính 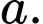
Cạnh của hình vuông 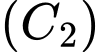 là:
là: 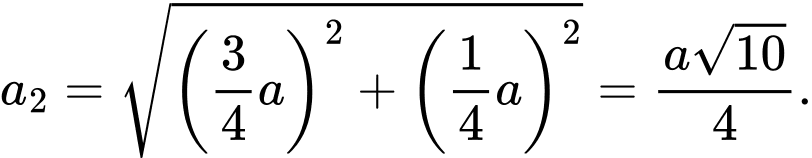
Do đó diện tích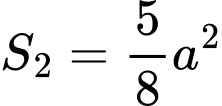
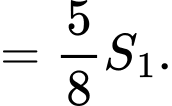
Cạnh của hình vuông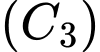 là:
là: 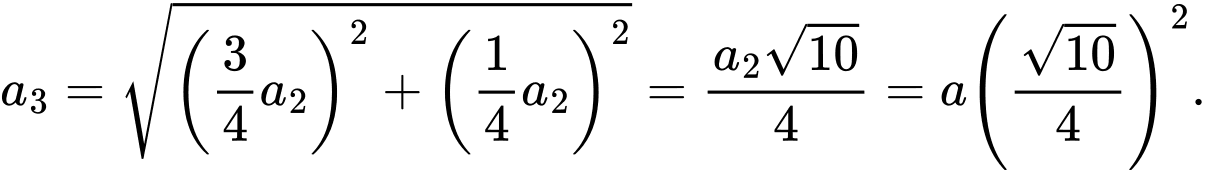
Do đó diện tích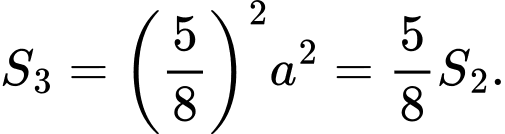
Lý luận tương tự ta có các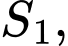
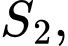
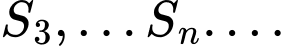 tạo thành một dãy cấp số nhân lùi vô hạn có
tạo thành một dãy cấp số nhân lùi vô hạn có 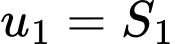 và công bội
và công bội 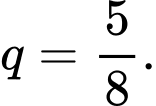
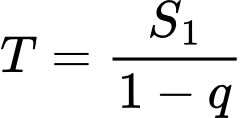
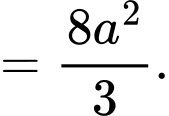
Với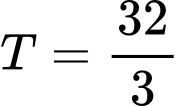 ta có
ta có 
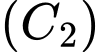 là:
là: 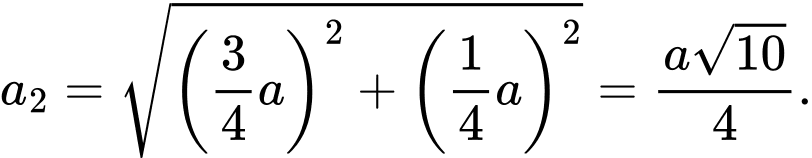
Do đó diện tích
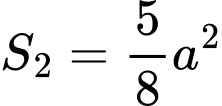
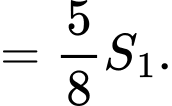
Cạnh của hình vuông
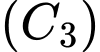 là:
là: 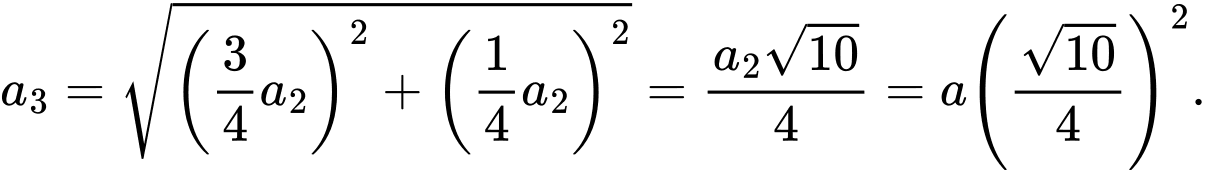
Do đó diện tích
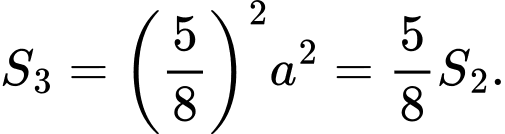
Lý luận tương tự ta có các
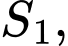
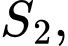
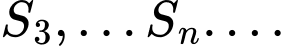 tạo thành một dãy cấp số nhân lùi vô hạn có
tạo thành một dãy cấp số nhân lùi vô hạn có 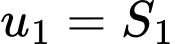 và công bội
và công bội 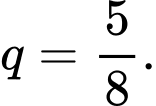
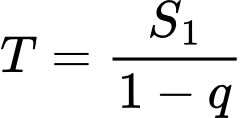
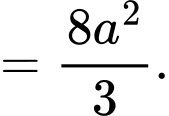
Với
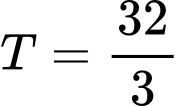 ta có
ta có 
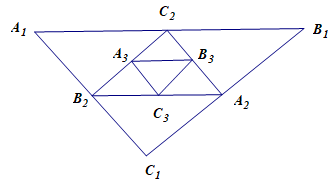
Câu 30 [581294]: Tam giác mà ba đỉnh của nó là ba trung điểm ba cạnh của tam giác 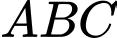 được gọi là tam giác trung bình của tam giác
được gọi là tam giác trung bình của tam giác 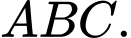 Ta xây dựng dãy các tam giác
Ta xây dựng dãy các tam giác 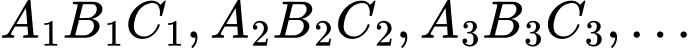 sao cho
sao cho 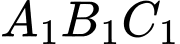 là một tam giác đều cạnh bằng 3 và với mỗi số nguyên dương
là một tam giác đều cạnh bằng 3 và với mỗi số nguyên dương 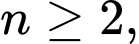 tam giác
tam giác 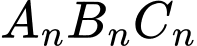 là tam giác trung bình của tam giác
là tam giác trung bình của tam giác 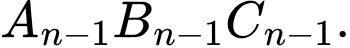 Với mỗi số nguyên dương
Với mỗi số nguyên dương 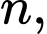 kí hiệu
kí hiệu 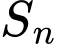 tương ứng là diện tích hình tròn ngoại tiếp tam giác
tương ứng là diện tích hình tròn ngoại tiếp tam giác 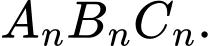 Tính tổng
Tính tổng 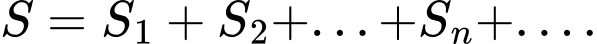
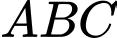 được gọi là tam giác trung bình của tam giác
được gọi là tam giác trung bình của tam giác 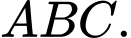 Ta xây dựng dãy các tam giác
Ta xây dựng dãy các tam giác 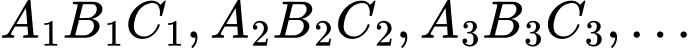 sao cho
sao cho 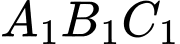 là một tam giác đều cạnh bằng 3 và với mỗi số nguyên dương
là một tam giác đều cạnh bằng 3 và với mỗi số nguyên dương 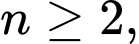 tam giác
tam giác 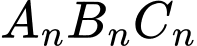 là tam giác trung bình của tam giác
là tam giác trung bình của tam giác 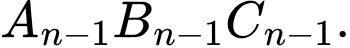 Với mỗi số nguyên dương
Với mỗi số nguyên dương 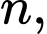 kí hiệu
kí hiệu 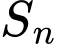 tương ứng là diện tích hình tròn ngoại tiếp tam giác
tương ứng là diện tích hình tròn ngoại tiếp tam giác 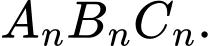 Tính tổng
Tính tổng 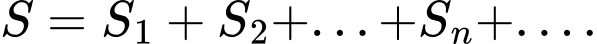
Vì dãy các tam giác 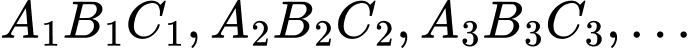 là các tam giác đều nên bán kính đường tròn ngoại tiếp các tam giác bằng cạnh
là các tam giác đều nên bán kính đường tròn ngoại tiếp các tam giác bằng cạnh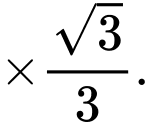
Với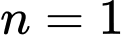 thì tam giác đều
thì tam giác đều 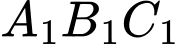 có cạnh bằng
có cạnh bằng 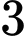 nên đường tròn ngoại tiếp tam giác
nên đường tròn ngoại tiếp tam giác 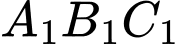 có bán kính
có bán kính 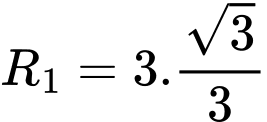
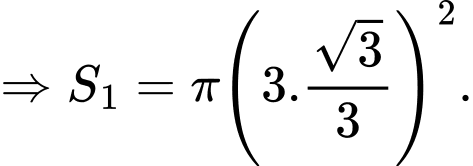
Với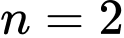 thì tam giác đều
thì tam giác đều 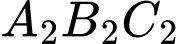 có cạnh bằng
có cạnh bằng 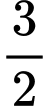 nên đường tròn ngoại tiếp tam giác
nên đường tròn ngoại tiếp tam giác 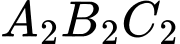 có bán kính
có bán kính 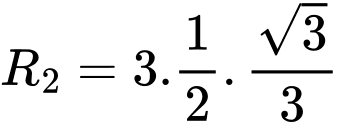
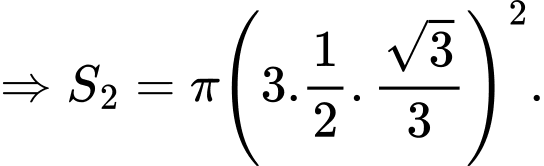
Với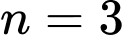 thì tam giác đều
thì tam giác đều 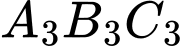 có cạnh bằng
có cạnh bằng 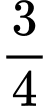 nên đường tròn ngoại tiếp tam giác
nên đường tròn ngoại tiếp tam giác 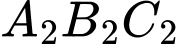 có bán kính
có bán kính 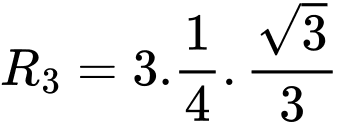
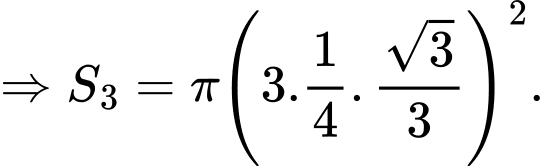
Như vậy tam giác đều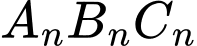 có cạnh bằng
có cạnh bằng 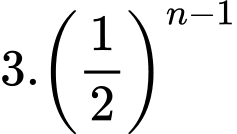 nên đường tròn ngoại tiếp tam giác
nên đường tròn ngoại tiếp tam giác 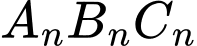 có bán kính
có bán kính 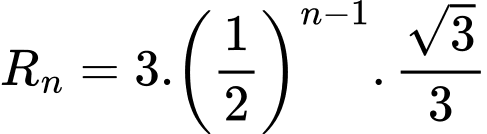
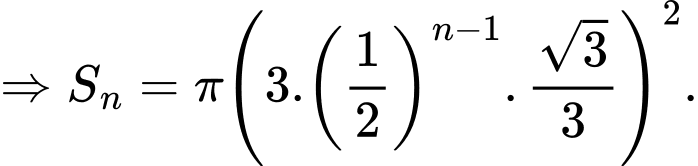
Khi đó ta được dãy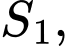
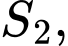 .
.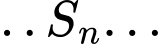 là một cấp số nhân lùi vô hạn với số hạng đầu
là một cấp số nhân lùi vô hạn với số hạng đầu 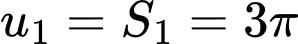 và công bội
và công bội 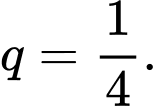
Do đó tổng
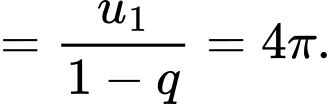
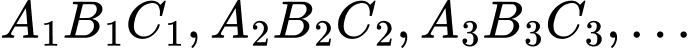 là các tam giác đều nên bán kính đường tròn ngoại tiếp các tam giác bằng cạnh
là các tam giác đều nên bán kính đường tròn ngoại tiếp các tam giác bằng cạnh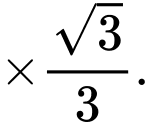
Với
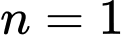 thì tam giác đều
thì tam giác đều 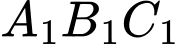 có cạnh bằng
có cạnh bằng 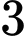 nên đường tròn ngoại tiếp tam giác
nên đường tròn ngoại tiếp tam giác 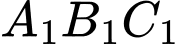 có bán kính
có bán kính 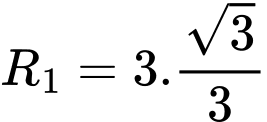
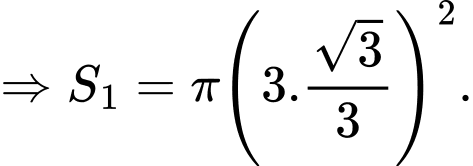
Với
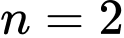 thì tam giác đều
thì tam giác đều 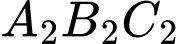 có cạnh bằng
có cạnh bằng 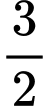 nên đường tròn ngoại tiếp tam giác
nên đường tròn ngoại tiếp tam giác 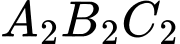 có bán kính
có bán kính 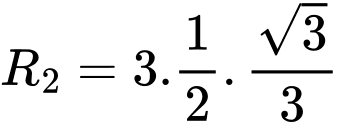
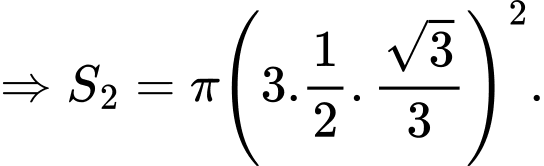
Với
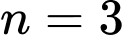 thì tam giác đều
thì tam giác đều 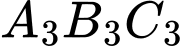 có cạnh bằng
có cạnh bằng 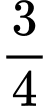 nên đường tròn ngoại tiếp tam giác
nên đường tròn ngoại tiếp tam giác 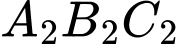 có bán kính
có bán kính 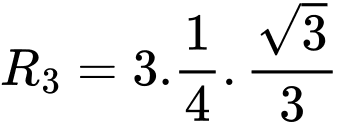
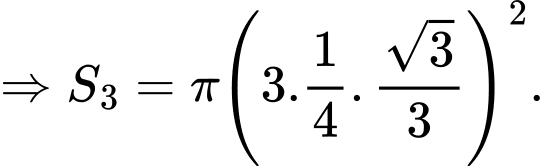
Như vậy tam giác đều
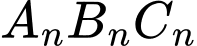 có cạnh bằng
có cạnh bằng 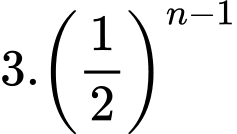 nên đường tròn ngoại tiếp tam giác
nên đường tròn ngoại tiếp tam giác 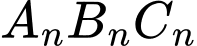 có bán kính
có bán kính 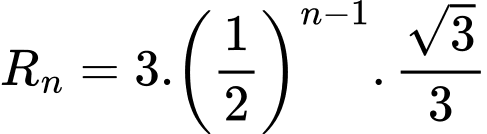
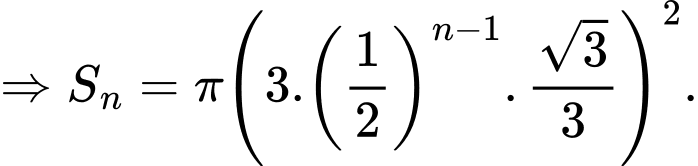
Khi đó ta được dãy
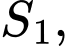
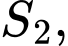 .
.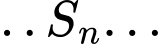 là một cấp số nhân lùi vô hạn với số hạng đầu
là một cấp số nhân lùi vô hạn với số hạng đầu 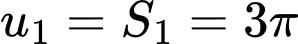 và công bội
và công bội 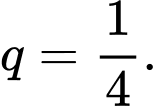
Do đó tổng

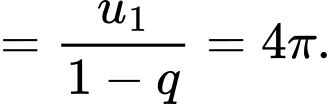
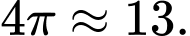
Câu 31 [398868]: Tìm giới hạn sau: 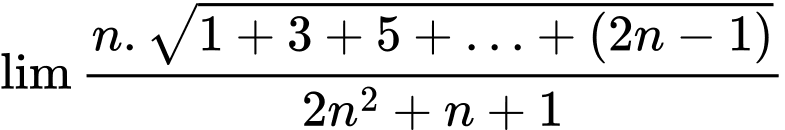
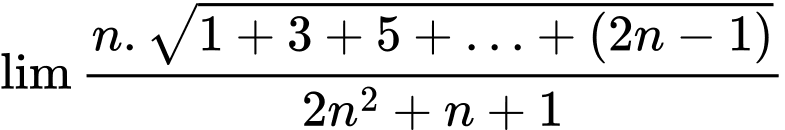
Nhận xét: 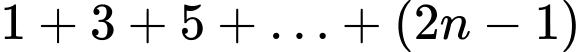 là tổng của
là tổng của 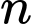 số hạng đầu tiên của một cấp số cộng có số hạng đầu là
số hạng đầu tiên của một cấp số cộng có số hạng đầu là 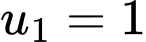 và công sai là
và công sai là 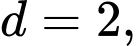 vì vậy, ta có:
vì vậy, ta có:
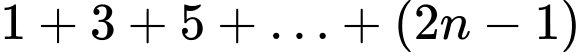
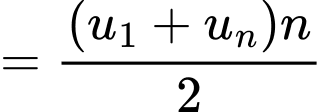
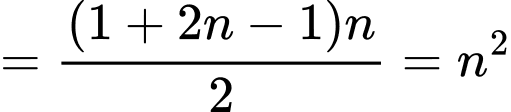
Vì vậy: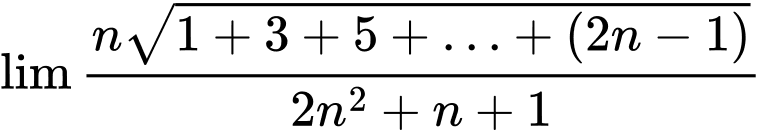
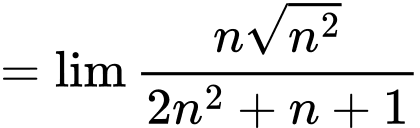
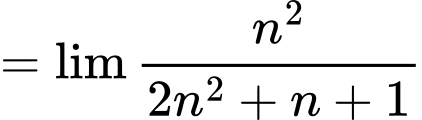
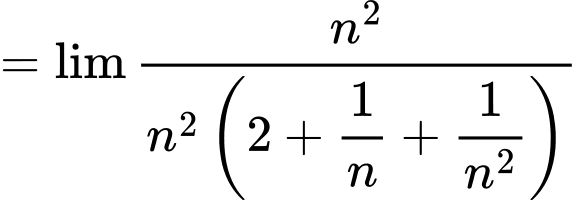
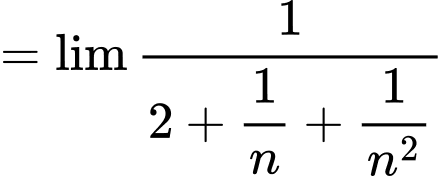
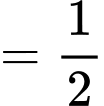
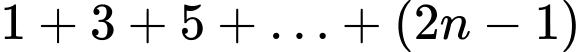 là tổng của
là tổng của 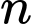 số hạng đầu tiên của một cấp số cộng có số hạng đầu là
số hạng đầu tiên của một cấp số cộng có số hạng đầu là 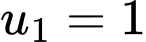 và công sai là
và công sai là 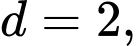 vì vậy, ta có:
vì vậy, ta có: 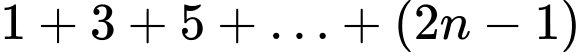
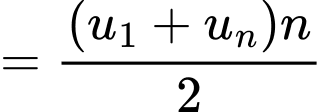
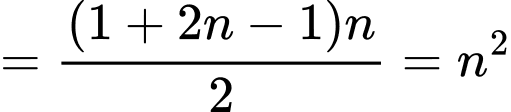
Vì vậy:
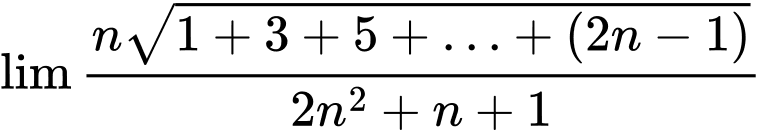
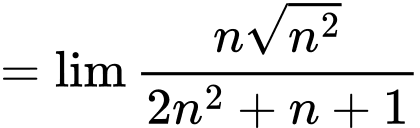
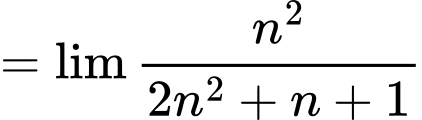
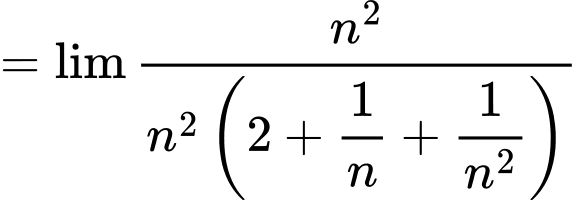
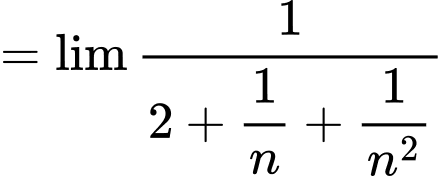
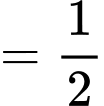
Câu 32 [803283]: Tìm 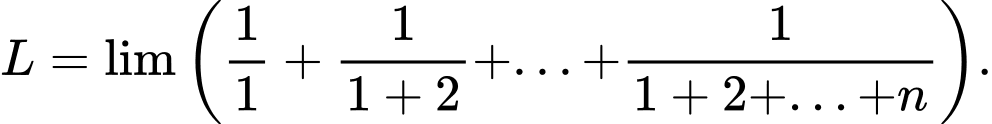
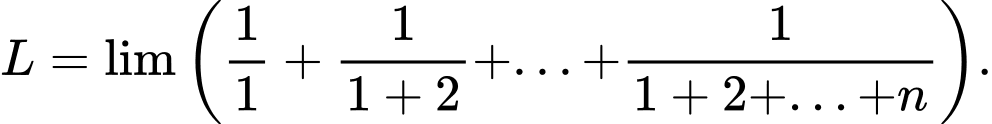
A, 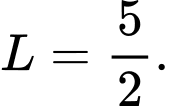
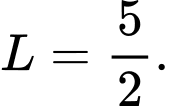
B, 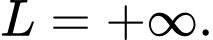
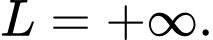
C, 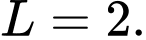
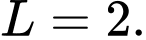
D, 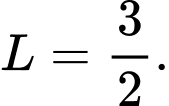
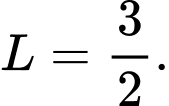
Ta có 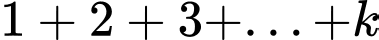 là tổng của cấp số cộng có
là tổng của cấp số cộng có 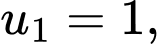
 nên
nên 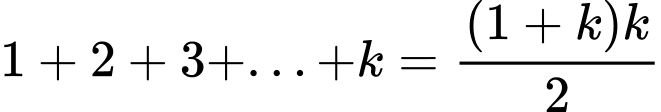
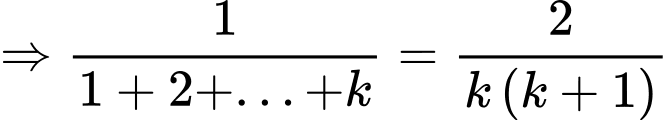
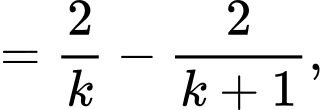
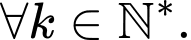
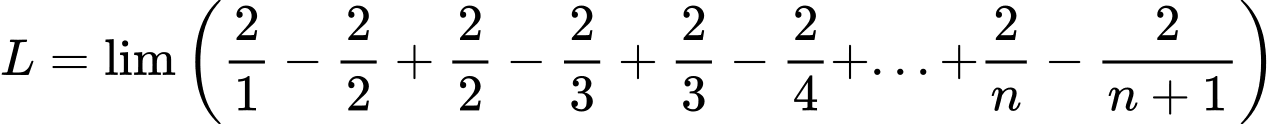
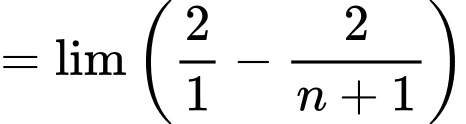
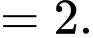 Đáp án: C
Đáp án: C
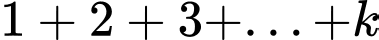 là tổng của cấp số cộng có
là tổng của cấp số cộng có 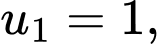
 nên
nên 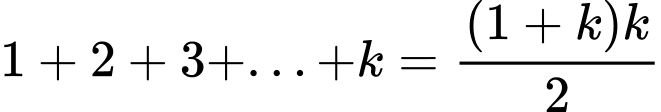
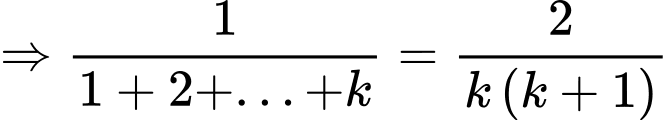
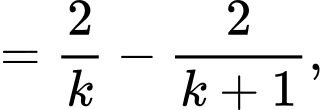
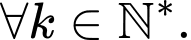
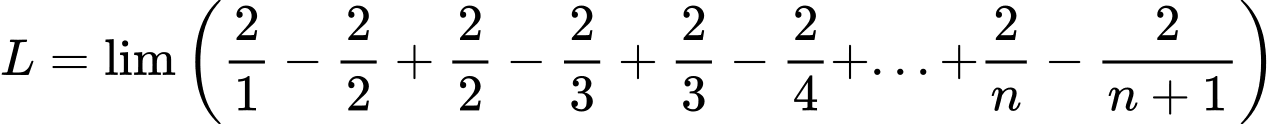
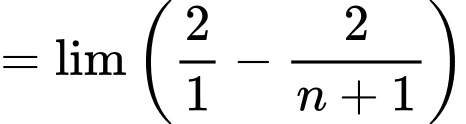
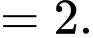 Đáp án: C
Đáp án: C
Câu 33 [398867]: Tìm giới hạn sau: 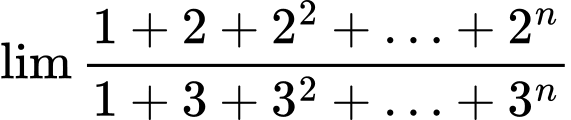
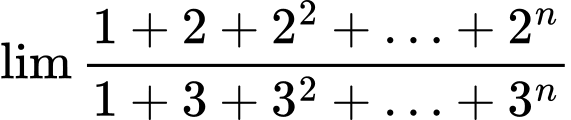
Nhận xét: Xét 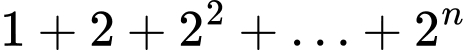 là tổng của
là tổng của  số hạng đầu của một cấp số nhân có số hạng đầu
số hạng đầu của một cấp số nhân có số hạng đầu 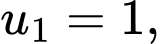 công bội bằng
công bội bằng 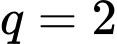 nên
nên
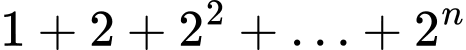
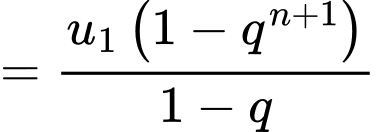
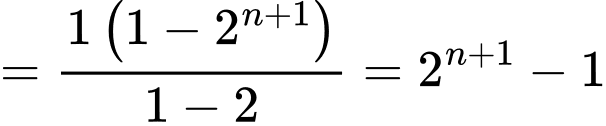
Hoàn toàn tương tự, ta có: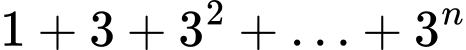
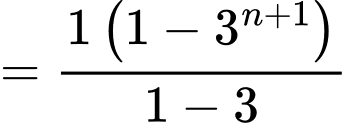
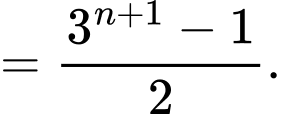
Khi đó: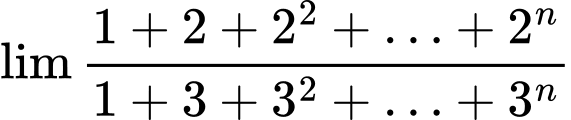
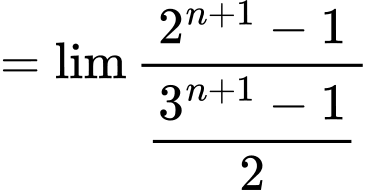
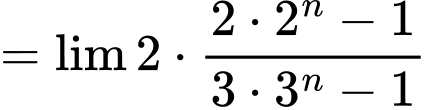
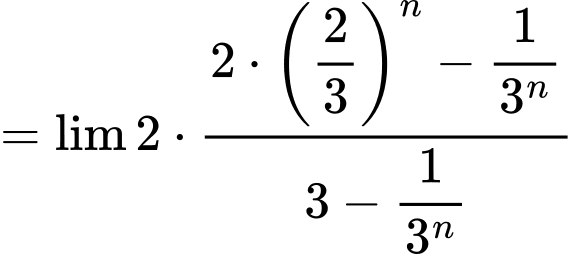
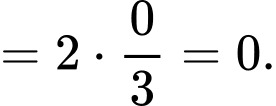
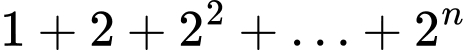 là tổng của
là tổng của  số hạng đầu của một cấp số nhân có số hạng đầu
số hạng đầu của một cấp số nhân có số hạng đầu 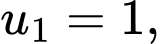 công bội bằng
công bội bằng 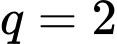 nên
nên 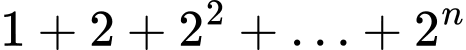
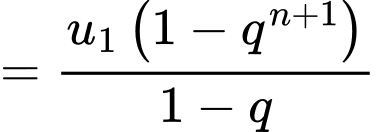
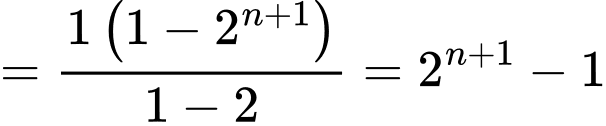
Hoàn toàn tương tự, ta có:
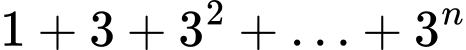
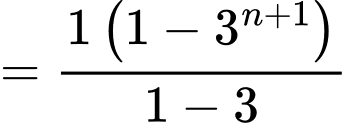
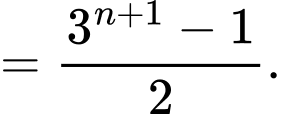
Khi đó:
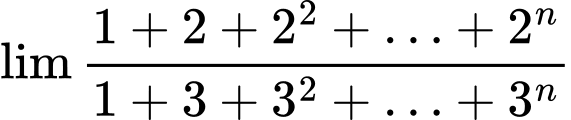
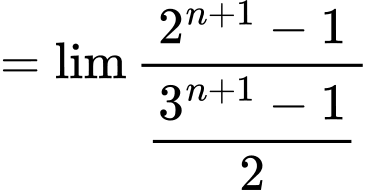
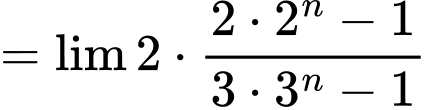
Câu 34 [398887]: Tìm giới hạn sau: