Đáp án Bài tập tự luyện số 2
Câu 1 [803890]: Kết quả của giới hạn 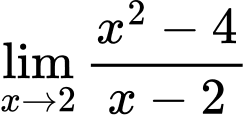 bằng
bằng
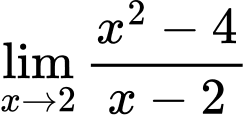 bằng
bằng A, 
B, 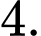
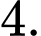
C, 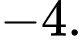
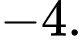
D, 
Chọn B
Ta có: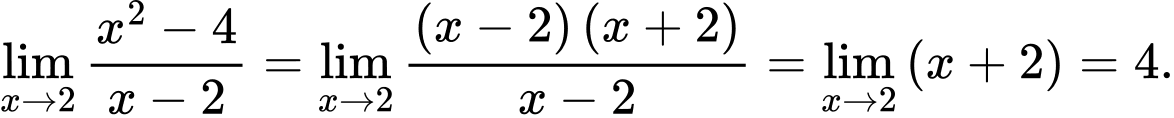 Đáp án: B
Đáp án: B
Ta có:
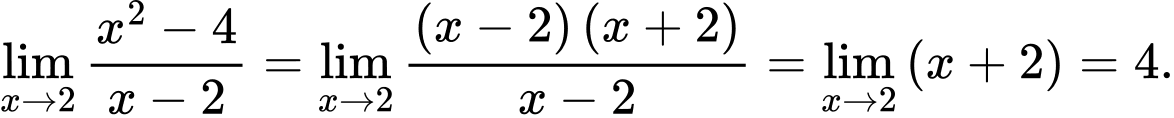 Đáp án: B
Đáp án: B
Câu 2 [803905]: Tính 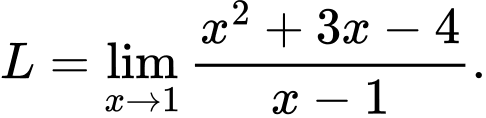
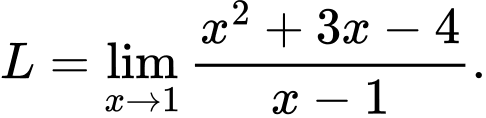
A, 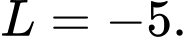
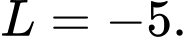
B, 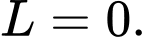
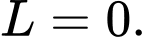
C, 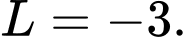
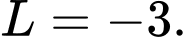
D, 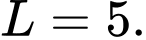
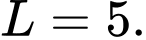
Ta có: 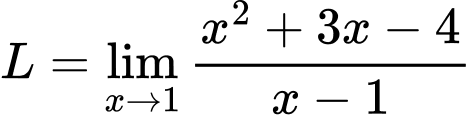
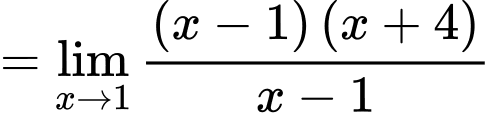
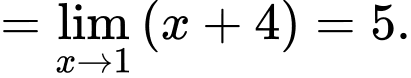 Đáp án: D
Đáp án: D
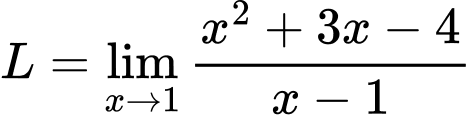
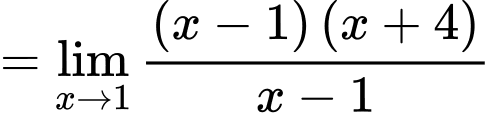
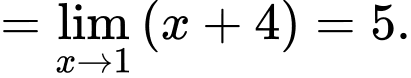 Đáp án: D
Đáp án: D
Câu 3 [803701]: Tìm tất cả các giá trị thực của tham số 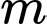 thỏa mãn
thỏa mãn 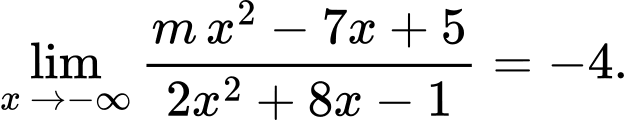
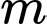 thỏa mãn
thỏa mãn 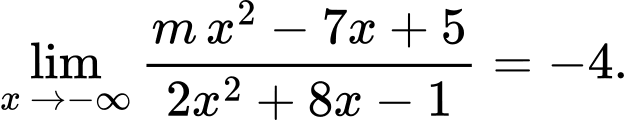
A, 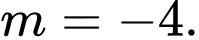
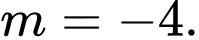
B, 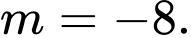
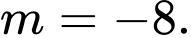
C, 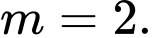
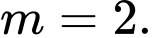
D, 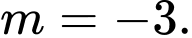
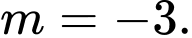
Chọn B
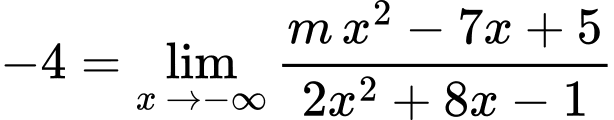
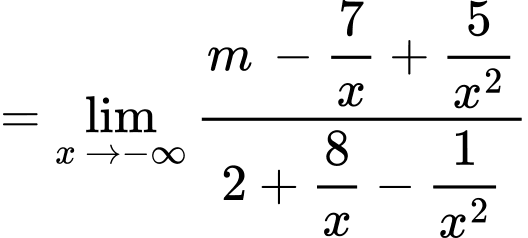
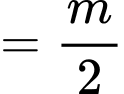
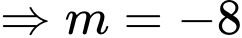 Đáp án: B
Đáp án: B
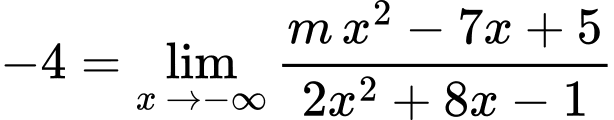
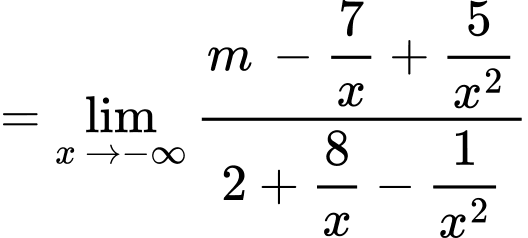
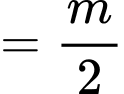
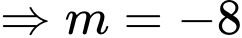 Đáp án: B
Đáp án: B
Câu 4 [803900]: Cho 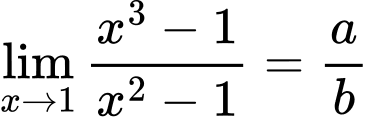 với
với 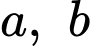 là các số nguyên dương và
là các số nguyên dương và 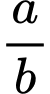 là phân số tối giản. Tính tổng
là phân số tối giản. Tính tổng 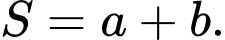
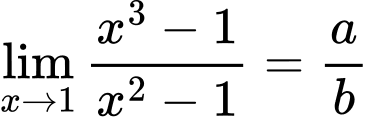 với
với 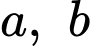 là các số nguyên dương và
là các số nguyên dương và 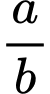 là phân số tối giản. Tính tổng
là phân số tối giản. Tính tổng 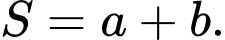
A, 5.
B, 10.
C, 3.
D, 4.
Chọn A
Ta có: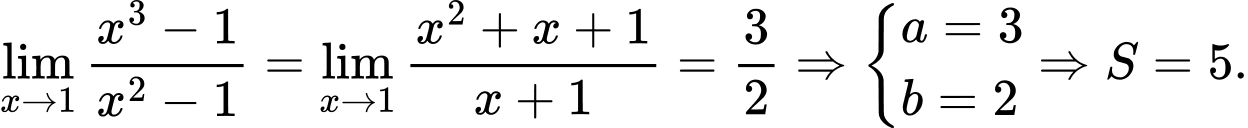 Đáp án: A
Đáp án: A
Ta có:
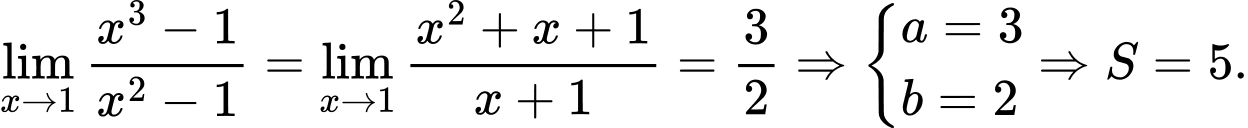 Đáp án: A
Đáp án: A
Câu 5 [803894]: Cho giới hạn 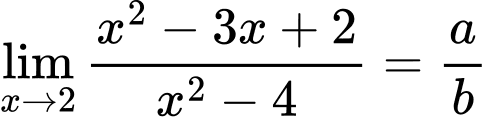 trong đó
trong đó 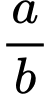 là phân số tối giản. Tính
là phân số tối giản. Tính 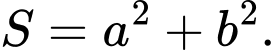
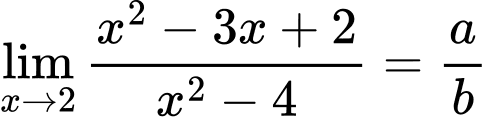 trong đó
trong đó 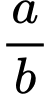 là phân số tối giản. Tính
là phân số tối giản. Tính 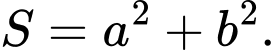
A, 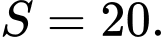
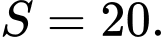
B, 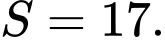
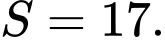
C, 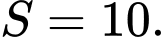
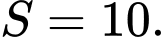
D, 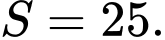
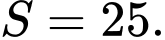
Chọn B
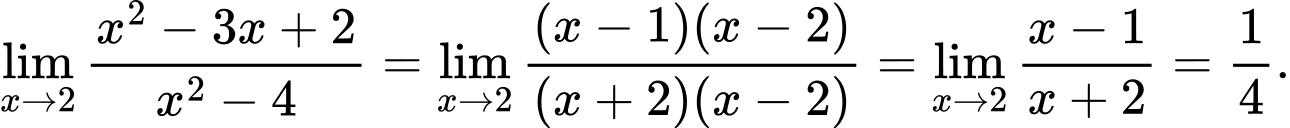
Do đó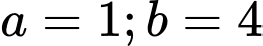 suy ra
suy ra 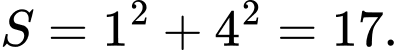 Đáp án: B
Đáp án: B
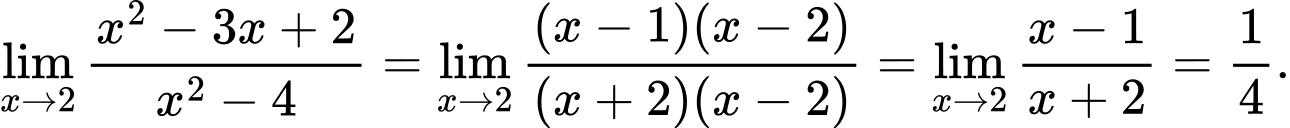
Do đó
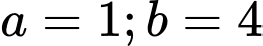 suy ra
suy ra 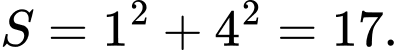 Đáp án: B
Đáp án: B
Câu 6 [519157]: 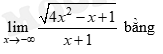
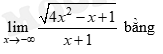
A, –2
B, 1
C, 2
D, –1
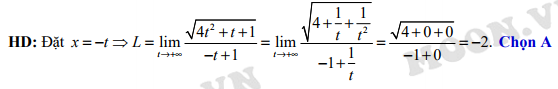 Đáp án: A
Đáp án: A
Câu 7 [519171]: 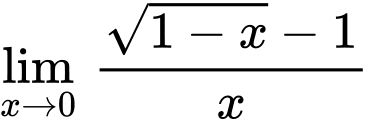 là
là
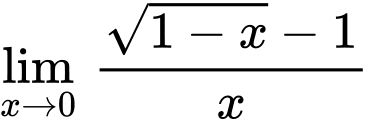 là
là A, 

B, 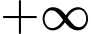
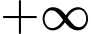
C, 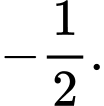
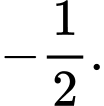
D, 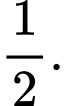
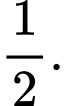
Ta có: 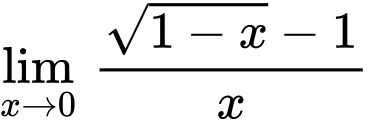
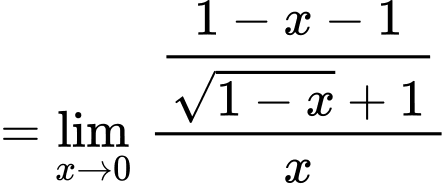
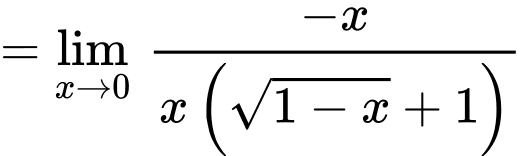
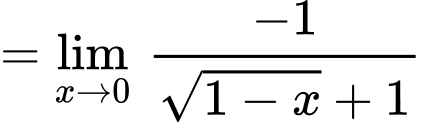
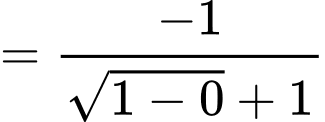
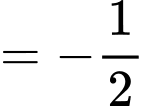 .
.
Chọn D. Đáp án: D
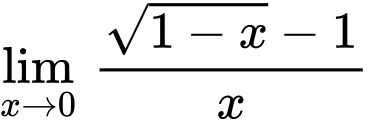
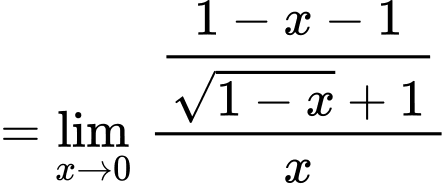
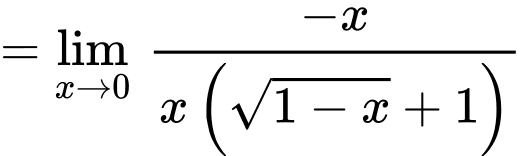
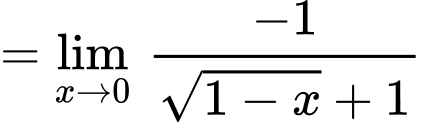
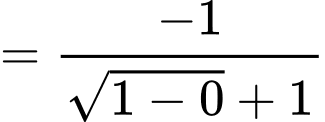
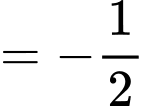 .
. Chọn D. Đáp án: D
Câu 8 [803933]: Tính gới hạn 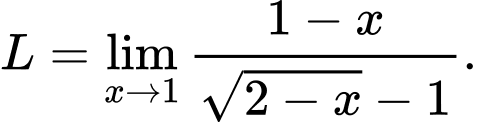
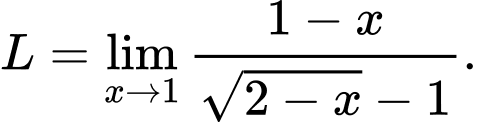
A, 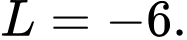
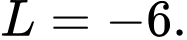
B, 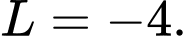
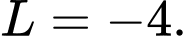
C, 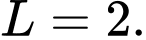
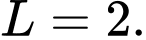
D, 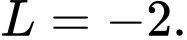
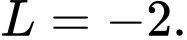
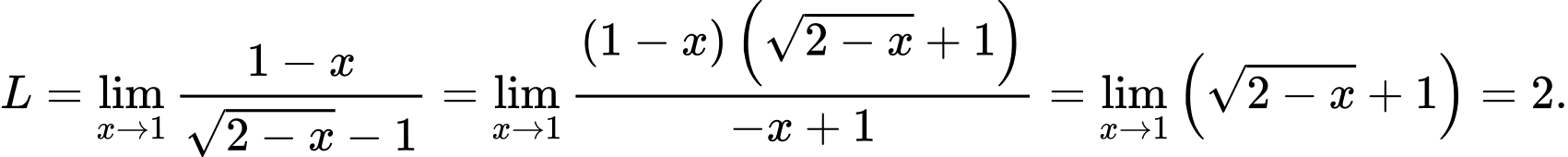 Đáp án: C
Đáp án: C
Câu 9 [804152]: Tìm tất cả các giá trị của tham số 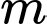 để hàm số
để hàm số 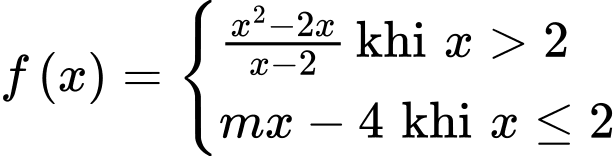 liên tục tại
liên tục tại 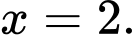
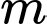 để hàm số
để hàm số 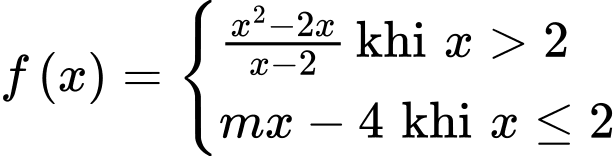 liên tục tại
liên tục tại 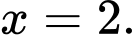
A, 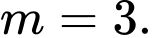
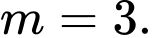
B, 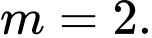
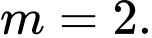
C, 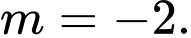
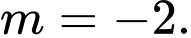
D, Không tồn tại 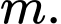
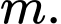
Chọn A
Ta có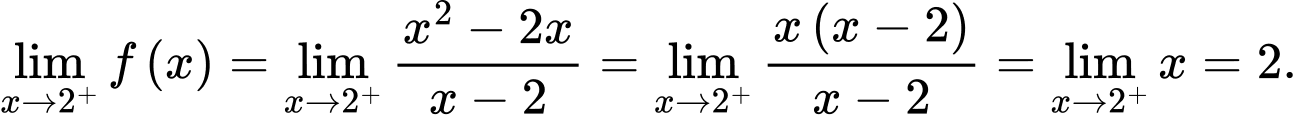
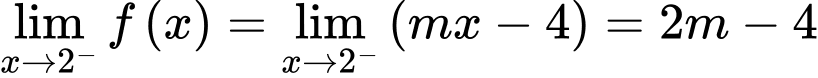
Hàm số liên tục tại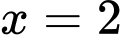 khi
khi  Đáp án: A
Đáp án: A
Ta có
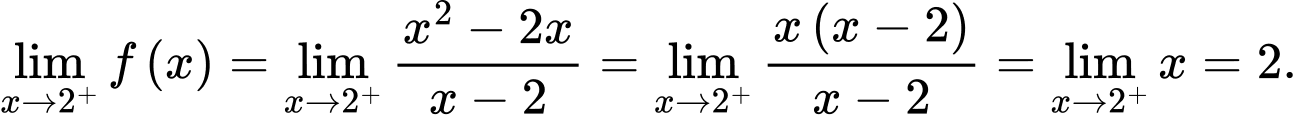
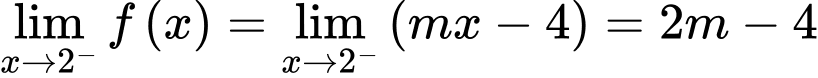
Hàm số liên tục tại
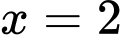 khi
khi  Đáp án: A
Đáp án: A
Câu 10 [804140]: Biết hàm số 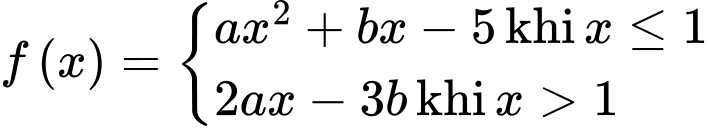 liên tục tại
liên tục tại 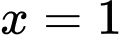 Tính giá trị của biểu thức
Tính giá trị của biểu thức 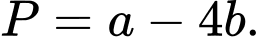
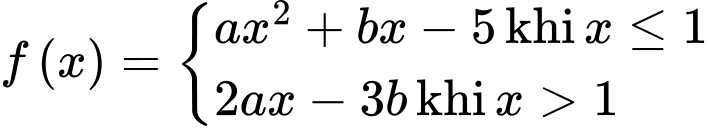 liên tục tại
liên tục tại 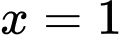 Tính giá trị của biểu thức
Tính giá trị của biểu thức 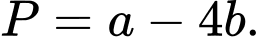
A, 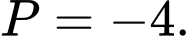
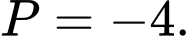
B, 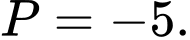
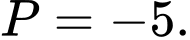
C, 

D, 

Chọn B
Ta có: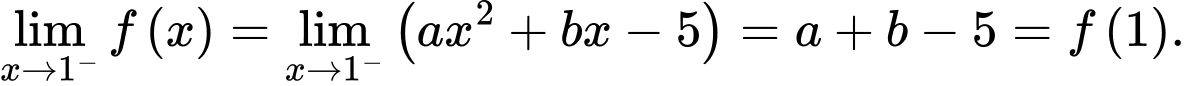
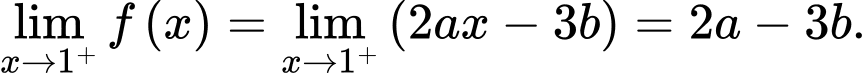
Do hàm số liên tục tại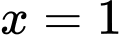 nên
nên 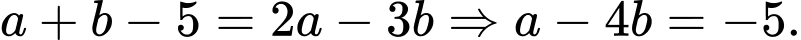 Đáp án: B
Đáp án: B
Ta có:
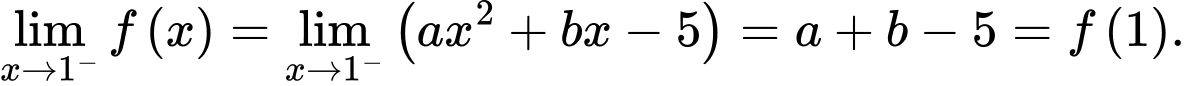
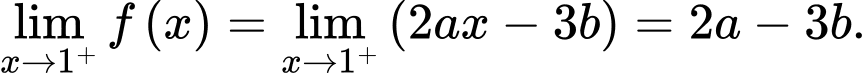
Do hàm số liên tục tại
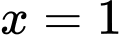 nên
nên 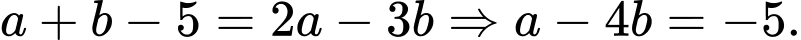 Đáp án: B
Đáp án: B
Câu 11 [803923]: Cho 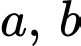 là hai số nguyên thỏa mãn
là hai số nguyên thỏa mãn 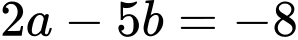 và
và 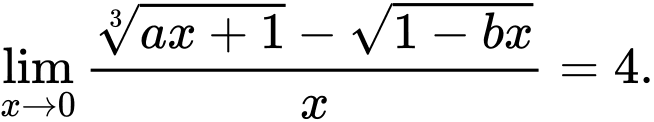 Mệnh đề nào dưới đây sai?
Mệnh đề nào dưới đây sai?
 là hai số nguyên thỏa mãn
là hai số nguyên thỏa mãn  và
và 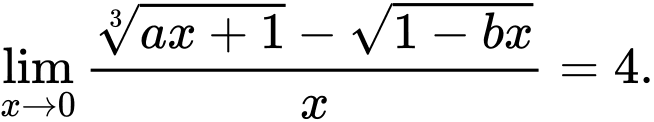 Mệnh đề nào dưới đây sai?
Mệnh đề nào dưới đây sai? A, 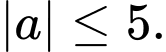
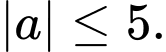
B, 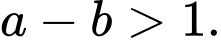
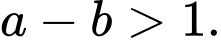
C, 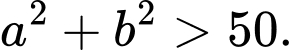
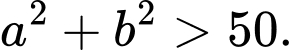
D, 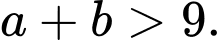
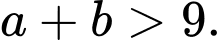
Chọn A
+)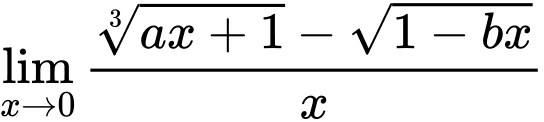
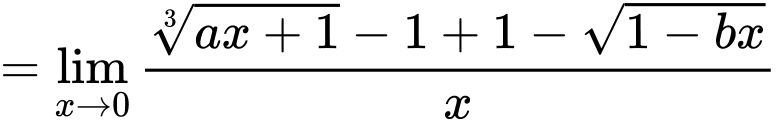
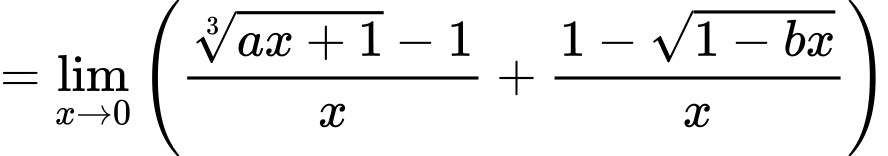
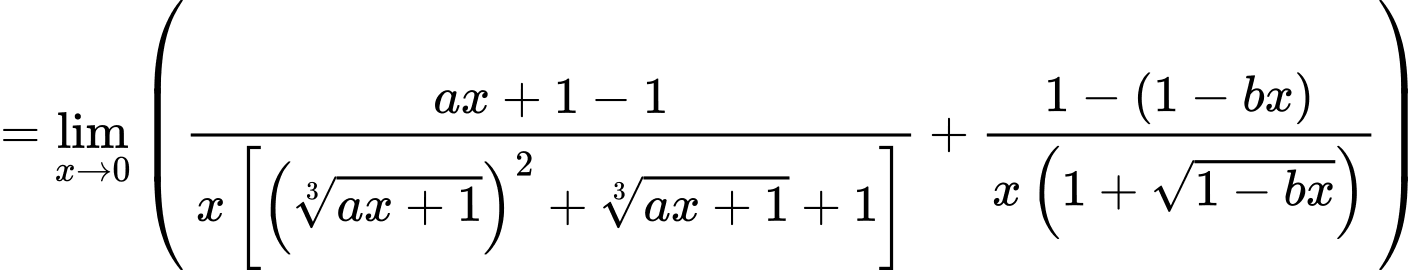
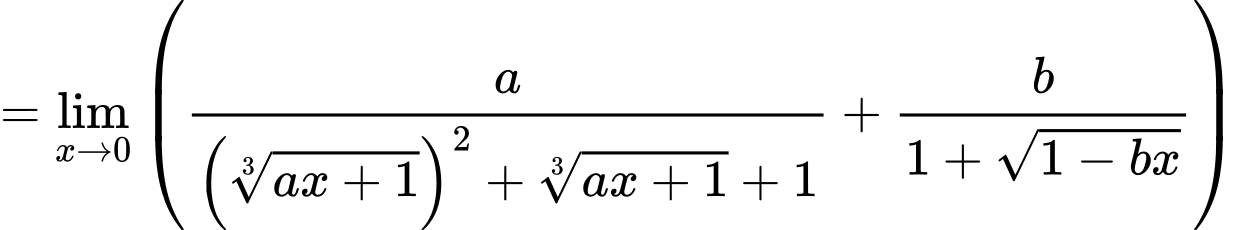
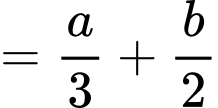
Theo giả thiết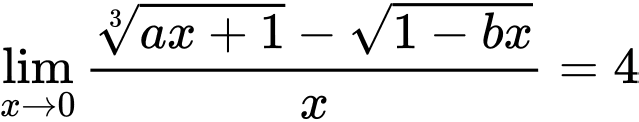
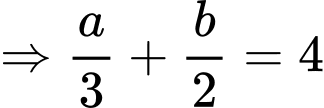
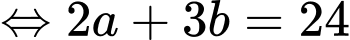
+) Ta có hệ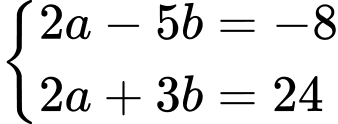
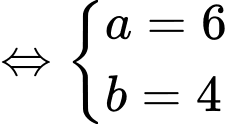 nên
nên  là sai. Đáp án: A
là sai. Đáp án: A
+)
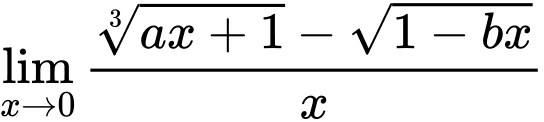
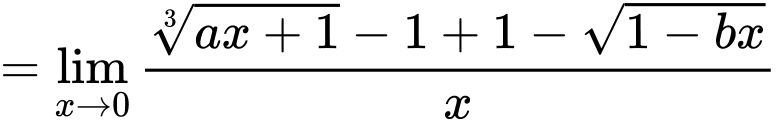
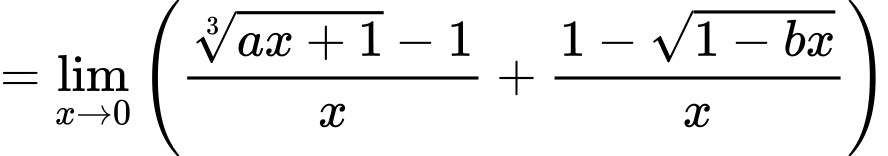
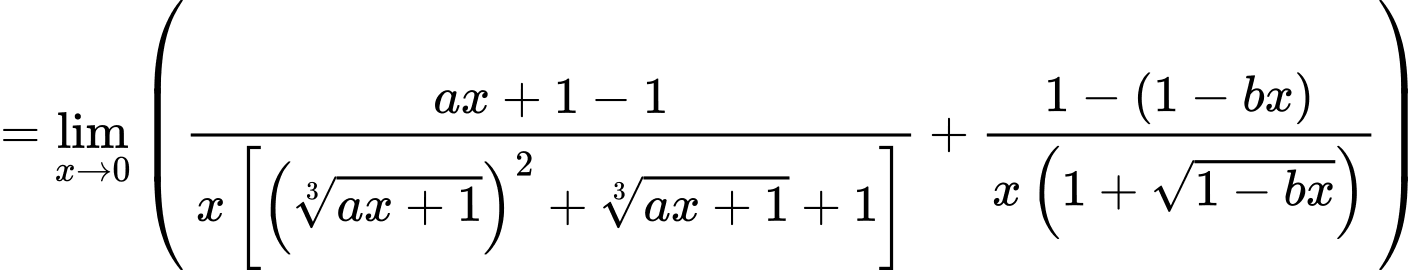
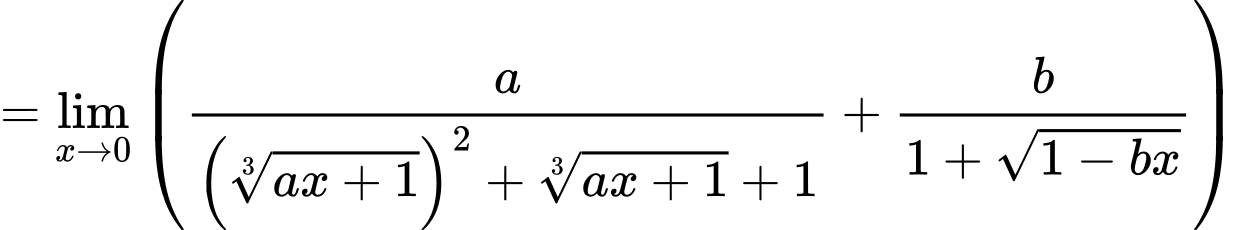
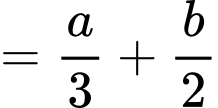
Theo giả thiết
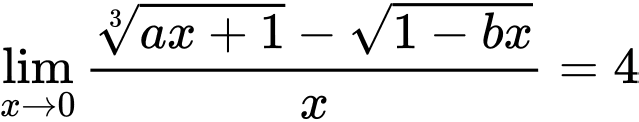
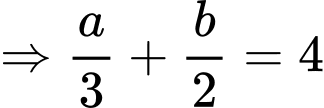
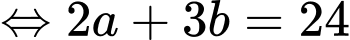
+) Ta có hệ
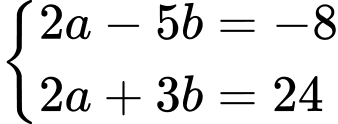
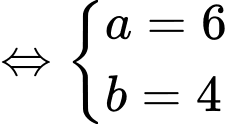 nên
nên  là sai. Đáp án: A
là sai. Đáp án: A
Câu 12 [204848]: Một cái hồ chứa 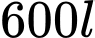 nước ngọt. Người ta bơm nước biển có nồng độ muối
nước ngọt. Người ta bơm nước biển có nồng độ muối 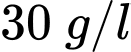 vào hồ với tốc độ
vào hồ với tốc độ 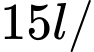 phút. Nồng độ muối trong hồ khi
phút. Nồng độ muối trong hồ khi 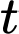 dần về dương vô cùng (đơn vị g/l) là ………
dần về dương vô cùng (đơn vị g/l) là ………
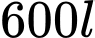 nước ngọt. Người ta bơm nước biển có nồng độ muối
nước ngọt. Người ta bơm nước biển có nồng độ muối 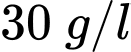 vào hồ với tốc độ
vào hồ với tốc độ 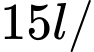 phút. Nồng độ muối trong hồ khi
phút. Nồng độ muối trong hồ khi 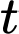 dần về dương vô cùng (đơn vị g/l) là ………
dần về dương vô cùng (đơn vị g/l) là ………
Sau 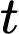 phút bơm nước vào hồ thì lượng nước là
phút bơm nước vào hồ thì lượng nước là  (
(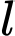 ) và lượng muối có được là
) và lượng muối có được là 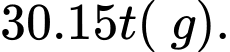
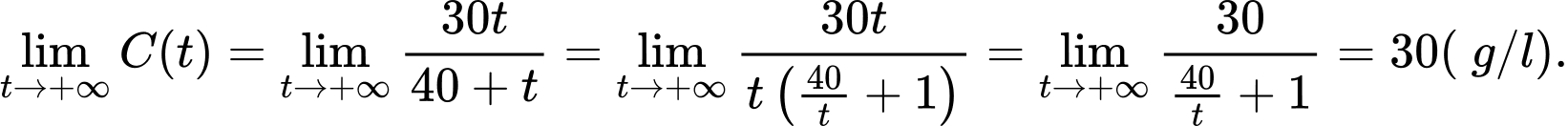
 phút bơm nước vào hồ thì lượng nước là
phút bơm nước vào hồ thì lượng nước là  (
( ) và lượng muối có được là
) và lượng muối có được là 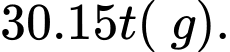
Nồng độ muối của nước là: 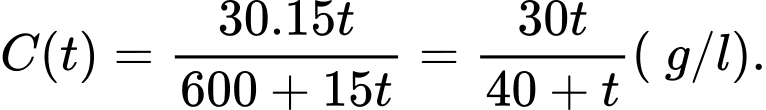
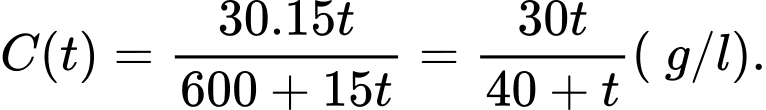
Khi 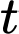 dần về dương vô cùng, ta có:
dần về dương vô cùng, ta có:
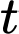 dần về dương vô cùng, ta có:
dần về dương vô cùng, ta có: 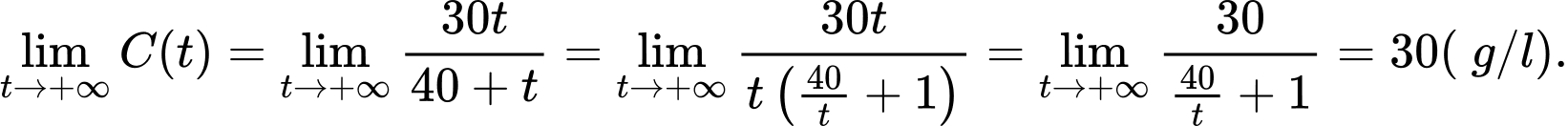
Vậy đáp án: 30.
Câu 13 [803962]: Cho 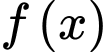 là một đa thức thỏa mãn
là một đa thức thỏa mãn 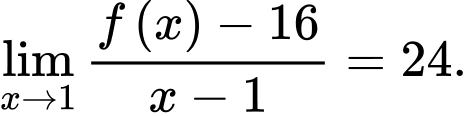 Tính
Tính 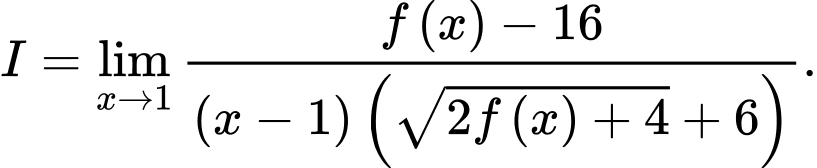
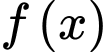 là một đa thức thỏa mãn
là một đa thức thỏa mãn 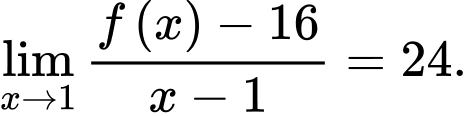 Tính
Tính 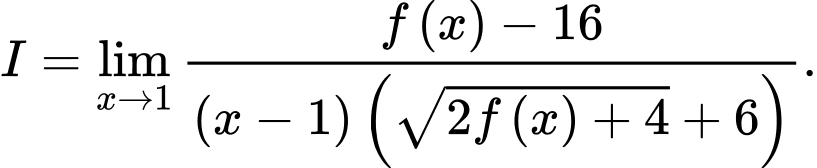
A, 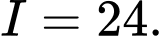
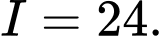
B, 

C, 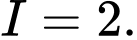
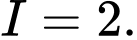
D, 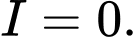
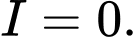
Chọn C
Vì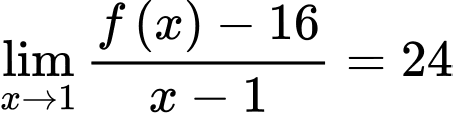
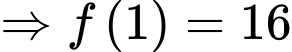 vì nếu
vì nếu 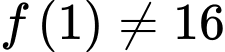 thì
thì 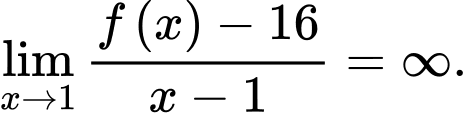
Ta có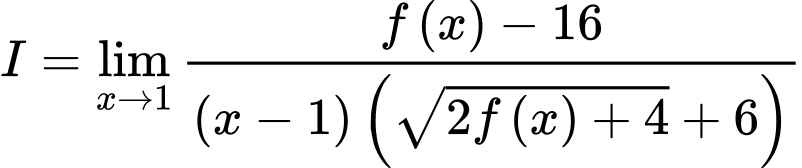
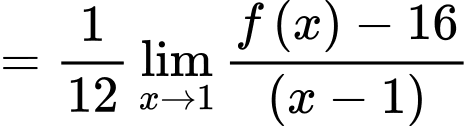
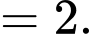 Đáp án: C
Đáp án: C
Vì
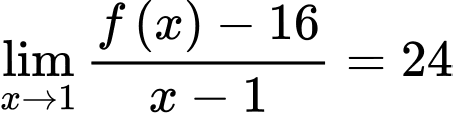
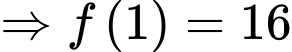 vì nếu
vì nếu 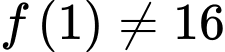 thì
thì 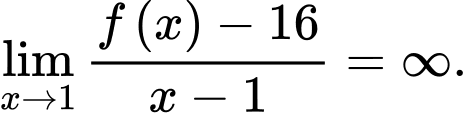
Ta có
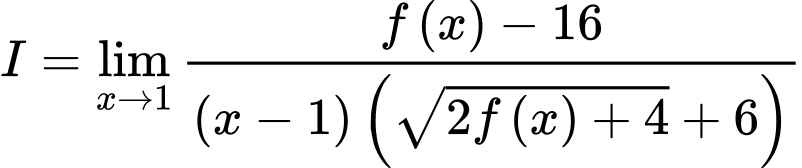
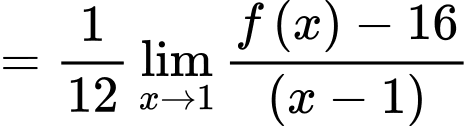
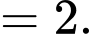 Đáp án: C
Đáp án: C
Câu 14 [803929]: Cho hàm số 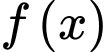 xác định trên
xác định trên 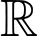 thỏa mãn
thỏa mãn 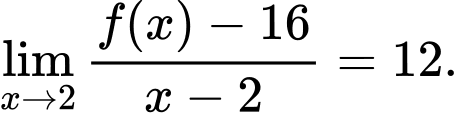 Tính giới hạn
Tính giới hạn 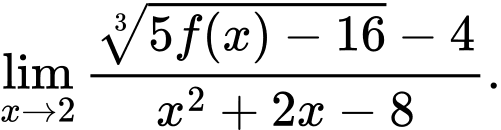
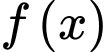 xác định trên
xác định trên 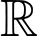 thỏa mãn
thỏa mãn 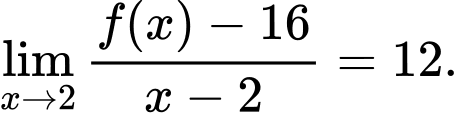 Tính giới hạn
Tính giới hạn 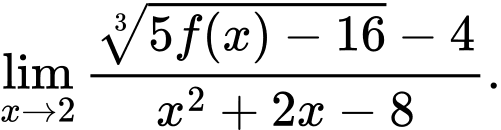
A, 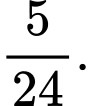
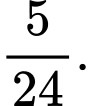
B, 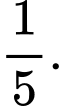
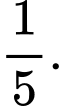
C, 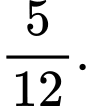
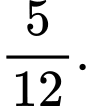
D, 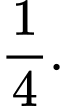
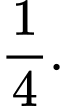
Chọn A
Do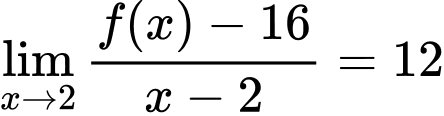 nên ta có
nên ta có 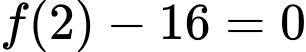 hay
hay 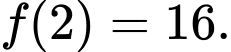
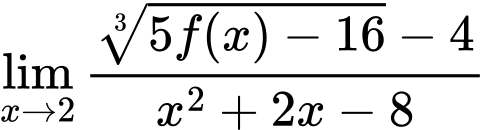
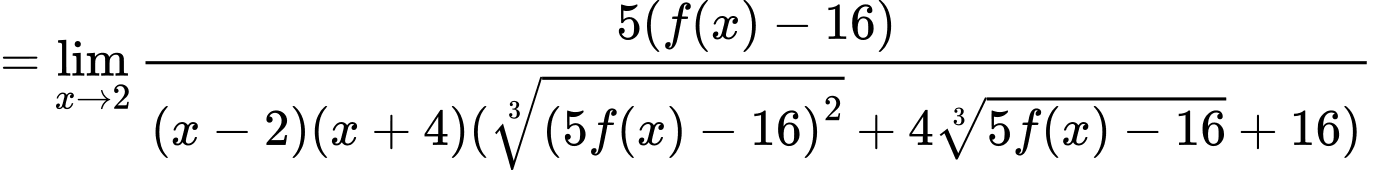
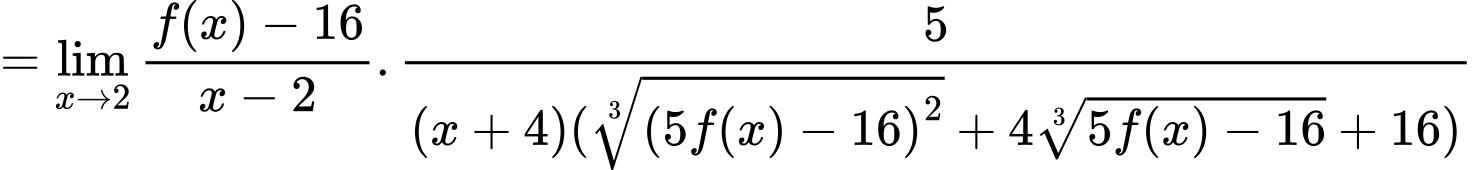
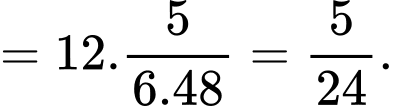 Đáp án: A
Đáp án: A
Do
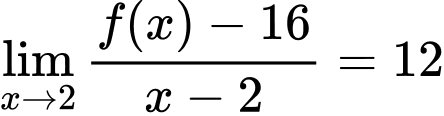 nên ta có
nên ta có 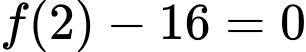 hay
hay 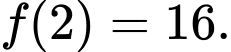
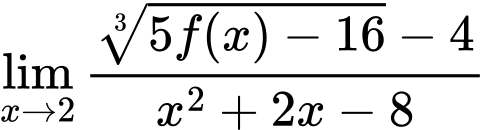
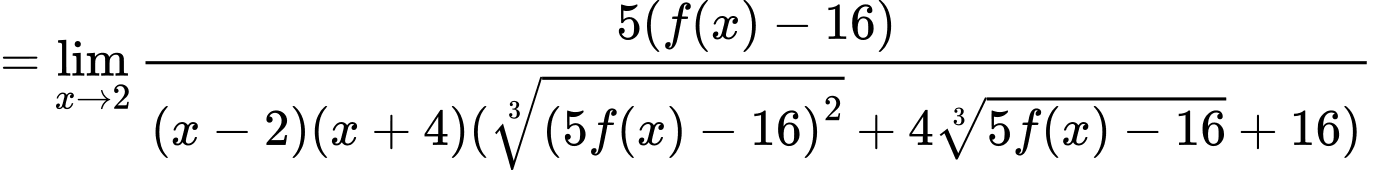
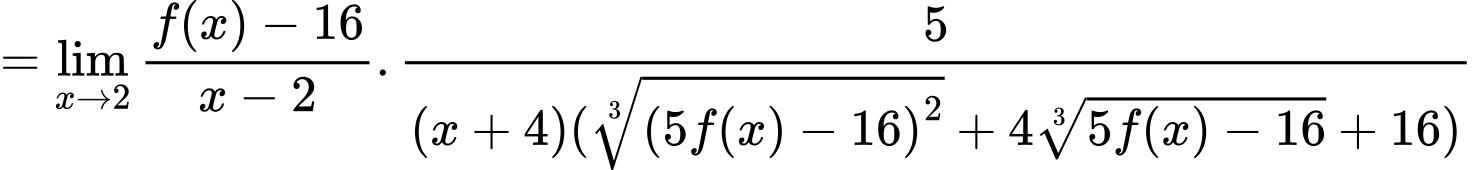
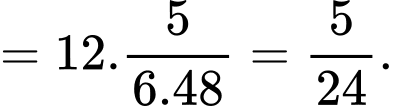 Đáp án: A
Đáp án: A
Câu 15 [803657]: Gọi 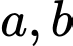 là các giá trị để hàm số
là các giá trị để hàm số 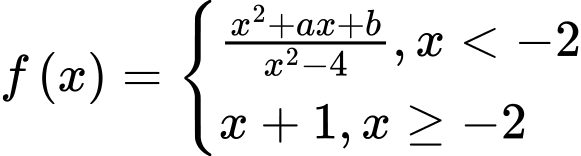 có giới hạn hữu hạn khi
có giới hạn hữu hạn khi 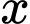 dần tới
dần tới 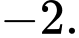 Tính
Tính 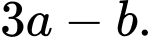
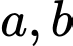 là các giá trị để hàm số
là các giá trị để hàm số 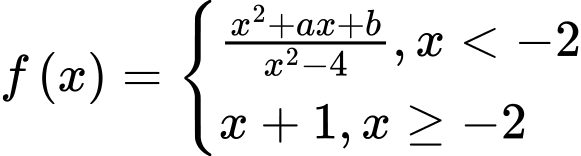 có giới hạn hữu hạn khi
có giới hạn hữu hạn khi 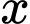 dần tới
dần tới 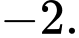 Tính
Tính 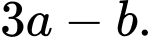
A, 8.
B, 4.
C, 24.
D, 12.
Chọn D
Do hàm số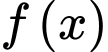 có giới hạn hữu hạn khi
có giới hạn hữu hạn khi 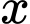 dần tới
dần tới 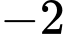 nên
nên 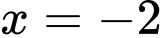 là nghiệm của phương trình
là nghiệm của phương trình 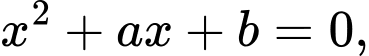 do đó ta
do đó ta 
Ta viết lại hàm số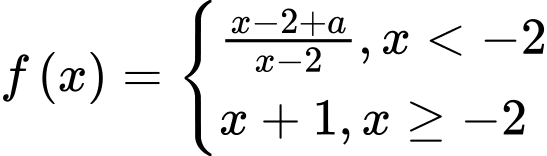
Mặt khác hàm số tồn tại giới hạn
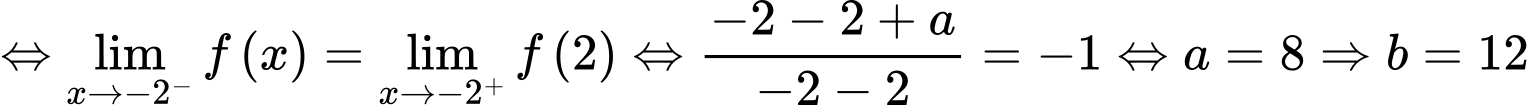
Do đó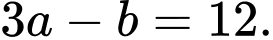 Đáp án: D
Đáp án: D
Do hàm số
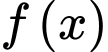 có giới hạn hữu hạn khi
có giới hạn hữu hạn khi 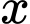 dần tới
dần tới 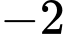 nên
nên 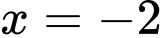 là nghiệm của phương trình
là nghiệm của phương trình 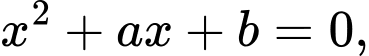 do đó ta
do đó ta 
Ta viết lại hàm số
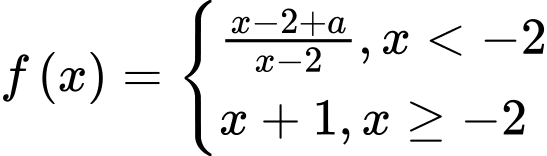
Mặt khác hàm số tồn tại giới hạn
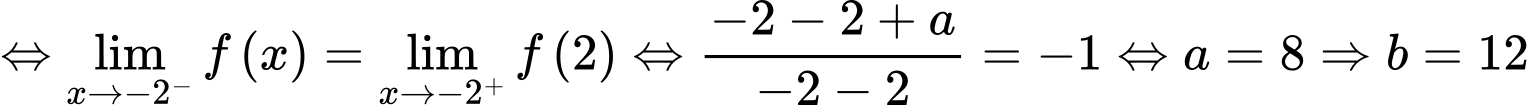
Do đó
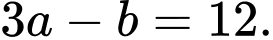 Đáp án: D
Đáp án: D
Câu 16 [804309]: Tìm 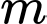 để hàm số
để hàm số 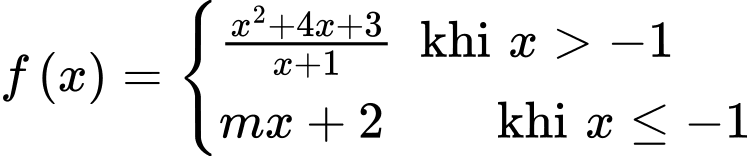 liên tục tại điểm
liên tục tại điểm 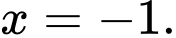
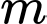 để hàm số
để hàm số 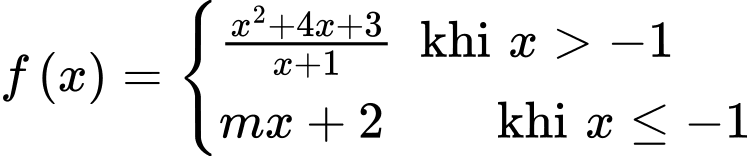 liên tục tại điểm
liên tục tại điểm 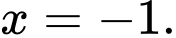
A, 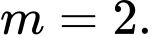
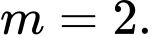
B, 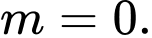
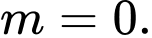
C, 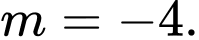
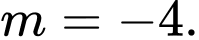
D, 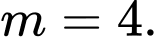
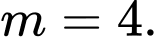
Ta có: 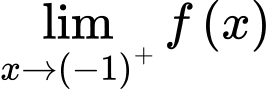
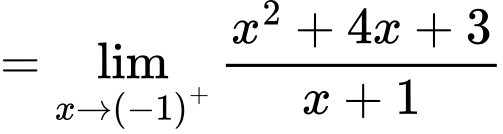
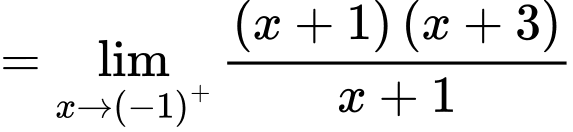
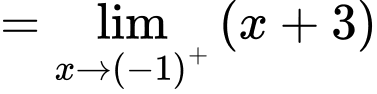
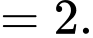
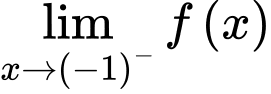
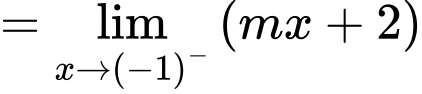
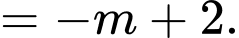
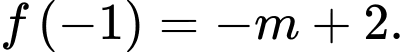
Để hàm số đã cho liên tục tại điểm thì
thì 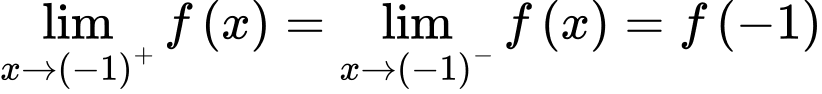
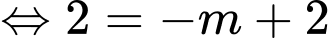
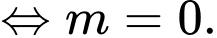 Đáp án: B
Đáp án: B
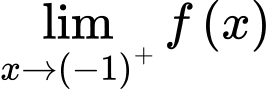
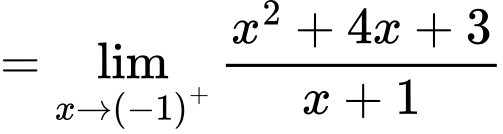
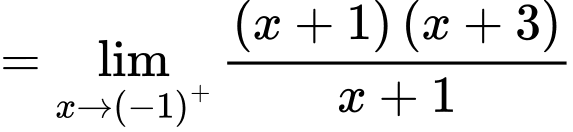
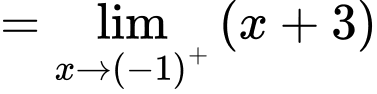
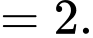
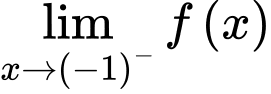
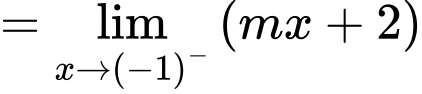
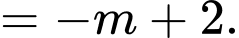
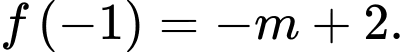
Để hàm số đã cho liên tục tại điểm
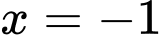 thì
thì 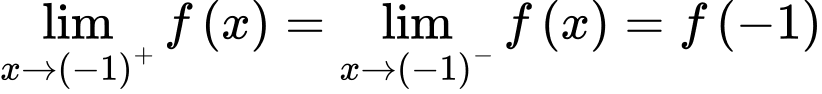
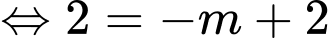
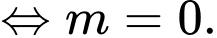 Đáp án: B
Đáp án: B
Câu 17 [804336]: Nếu hàm số 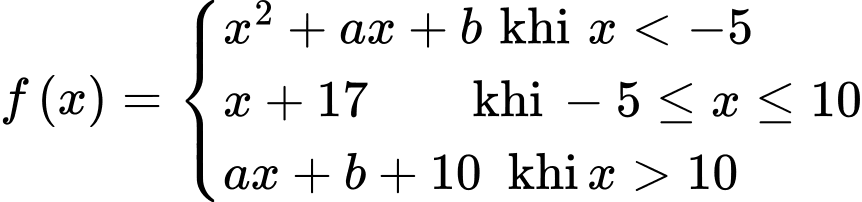 liên tục trên
liên tục trên 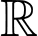 thì
thì  bằng
bằng
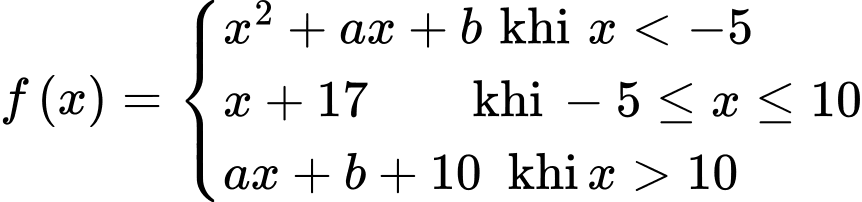 liên tục trên
liên tục trên 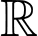 thì
thì  bằng
bằng A, 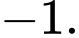
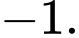
B, 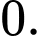
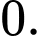
C, 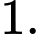
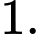
D, 
Với  ta có
ta có 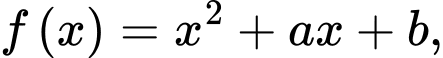 là hàm đa thức nên liên tục trên
là hàm đa thức nên liên tục trên 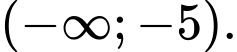
Với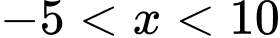 ta có
ta có 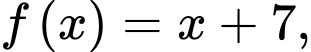 là hàm đa thức nên liên tục trên
là hàm đa thức nên liên tục trên 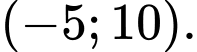
Với ta có
ta có 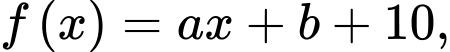 là hàm đa thức nên liên tục trên
là hàm đa thức nên liên tục trên 
Để hàm số liên tục trên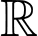 thì hàm số phải liên tục tại
thì hàm số phải liên tục tại 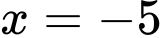 và
và 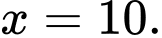
Ta có: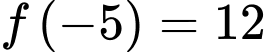 ;
; 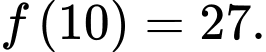
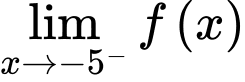
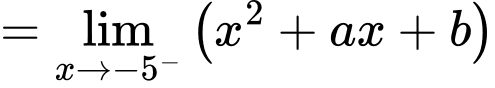

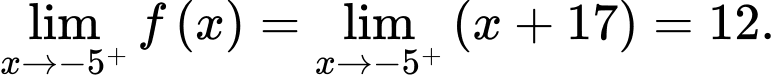
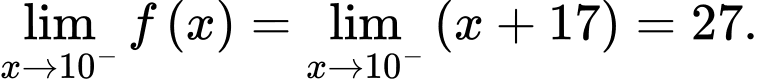
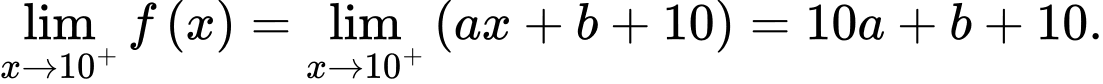
Hàm số liên tục tại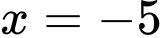 và
và 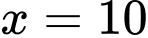 khi
khi
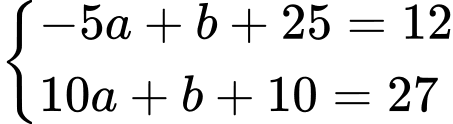
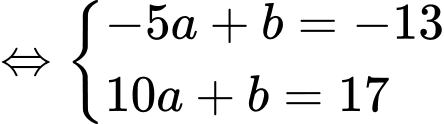
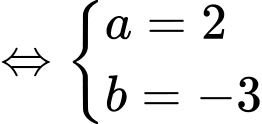
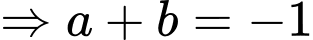 Đáp án: A
Đáp án: A
 ta có
ta có 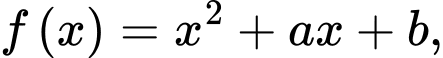 là hàm đa thức nên liên tục trên
là hàm đa thức nên liên tục trên 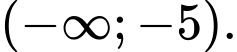
Với
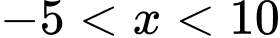 ta có
ta có 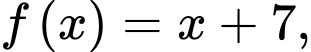 là hàm đa thức nên liên tục trên
là hàm đa thức nên liên tục trên 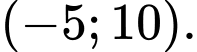
Với
 ta có
ta có 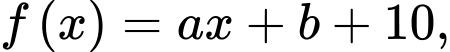 là hàm đa thức nên liên tục trên
là hàm đa thức nên liên tục trên 
Để hàm số liên tục trên
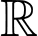 thì hàm số phải liên tục tại
thì hàm số phải liên tục tại 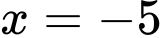 và
và 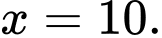
Ta có:
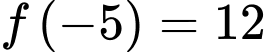 ;
; 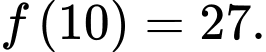
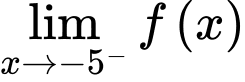
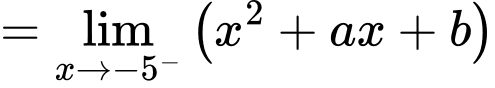

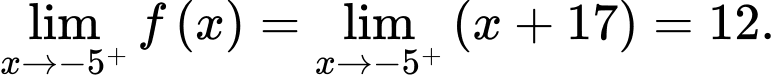
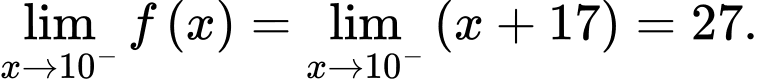
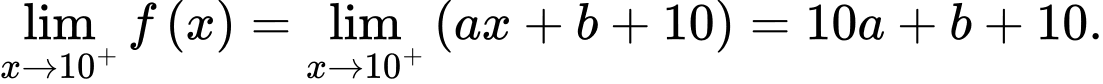
Hàm số liên tục tại
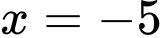 và
và 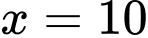 khi
khi 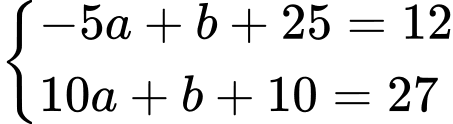
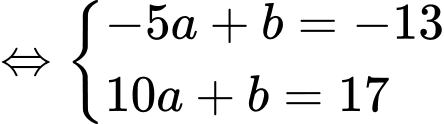
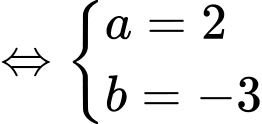
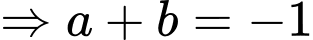 Đáp án: A
Đáp án: A
Câu 18 [804153]: Cho hàm số 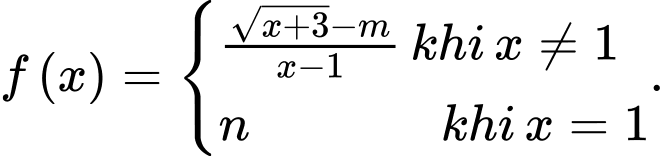 Để hàm số liên tục tại
Để hàm số liên tục tại 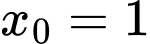 thì giá trị của biểu thức
thì giá trị của biểu thức  tương ứng bằng bao nhiêu?
tương ứng bằng bao nhiêu?
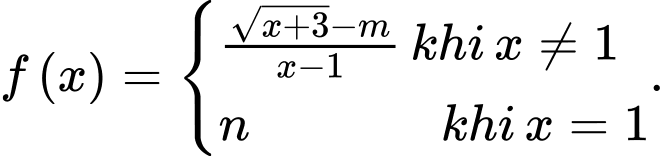 Để hàm số liên tục tại
Để hàm số liên tục tại 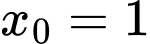 thì giá trị của biểu thức
thì giá trị của biểu thức  tương ứng bằng bao nhiêu?
tương ứng bằng bao nhiêu?
Chọn D
Ta có: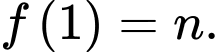
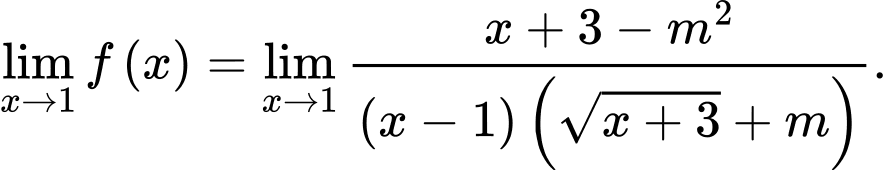
Hàm số liên tục tại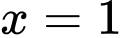
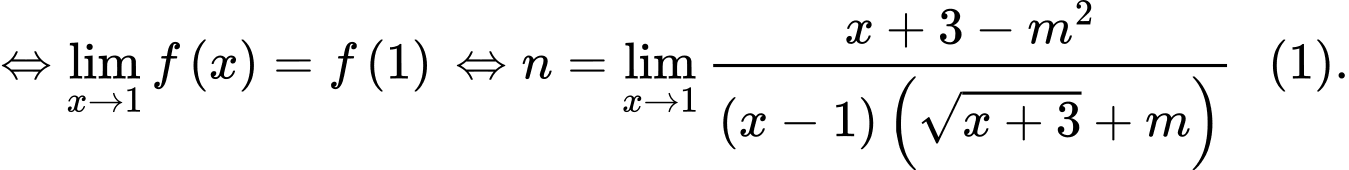
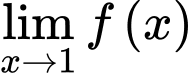 tồn tại khi
tồn tại khi 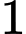 là nghiệm của phương trình:
là nghiệm của phương trình: 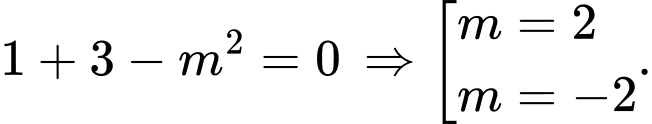
+ Khi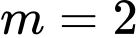 thì
thì 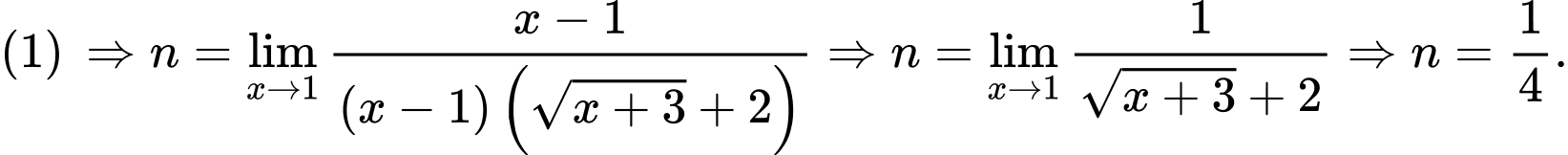
+ Khi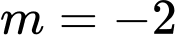 thì
thì 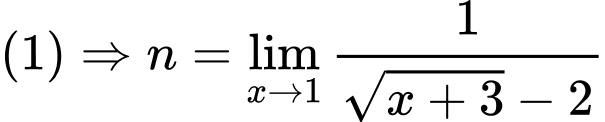 suy ra không tồn tại
suy ra không tồn tại 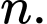
Vậy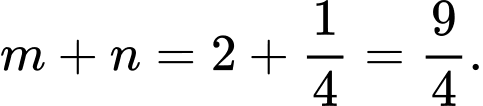 Đáp án: D
Đáp án: D
Ta có:
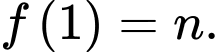
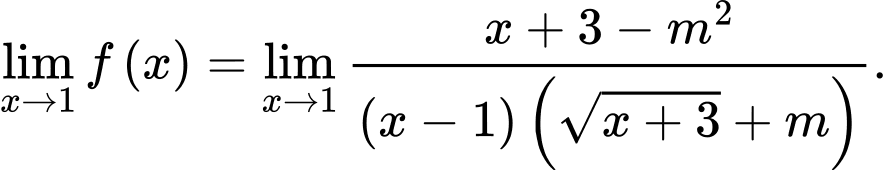
Hàm số liên tục tại
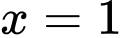
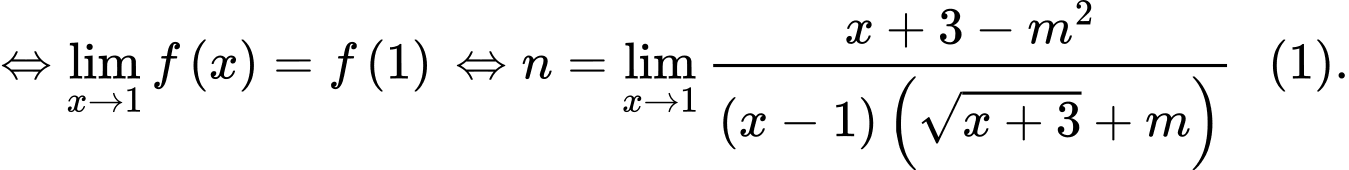
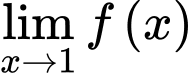 tồn tại khi
tồn tại khi 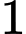 là nghiệm của phương trình:
là nghiệm của phương trình: 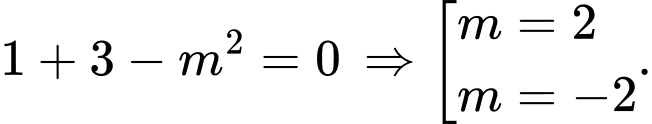
+ Khi
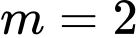 thì
thì 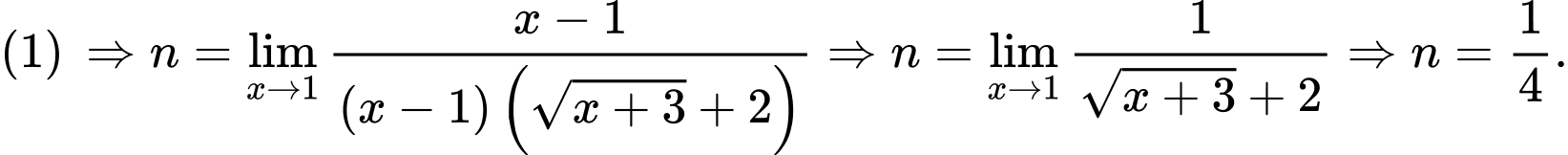
+ Khi
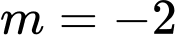 thì
thì 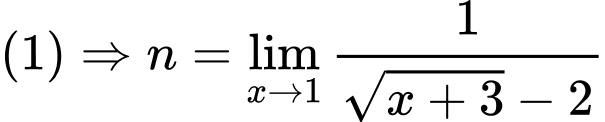 suy ra không tồn tại
suy ra không tồn tại 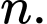
Vậy
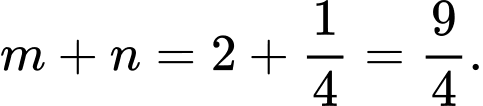 Đáp án: D
Đáp án: D
Câu 19 [204843]: Cho 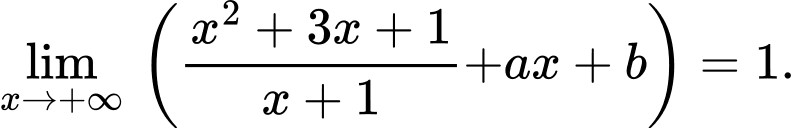 Giá trị của biểu thức
Giá trị của biểu thức 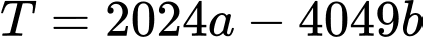 là ……..
là ……..
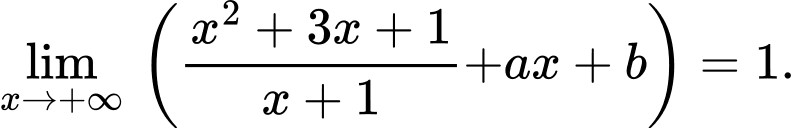 Giá trị của biểu thức
Giá trị của biểu thức 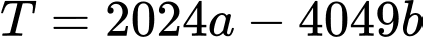 là ……..
là ……..
Ta có: 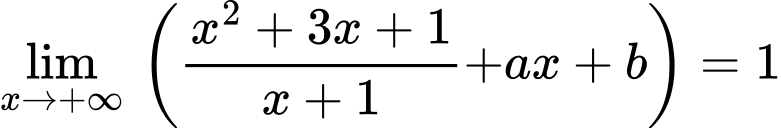
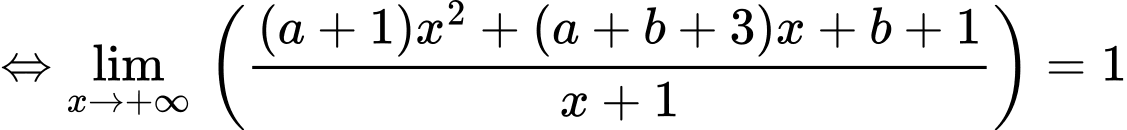
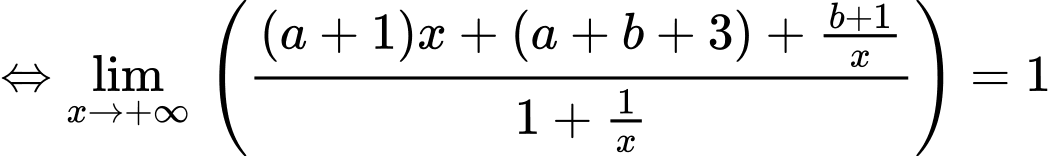
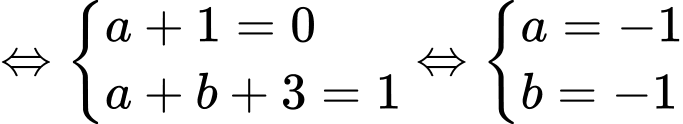
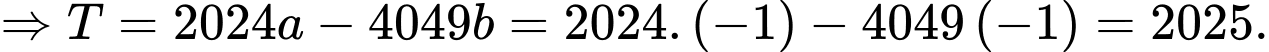
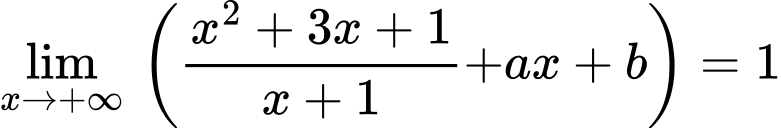
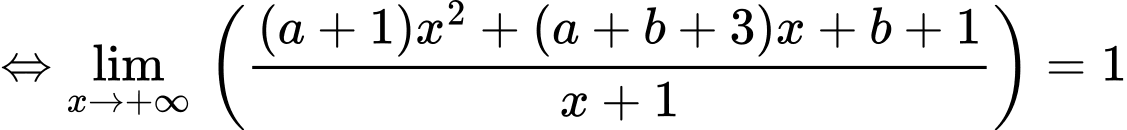
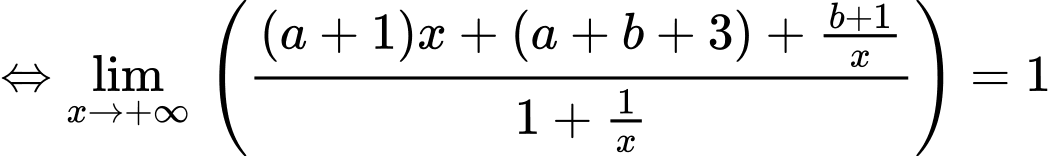
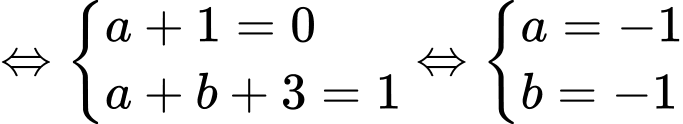
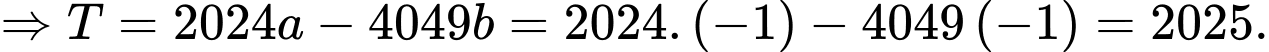
Câu 20 [204845]: Biết 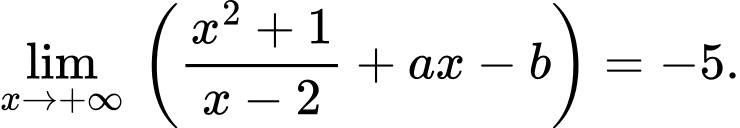 Giá trị biểu thức
Giá trị biểu thức 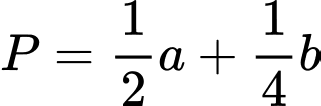 là ………
là ………
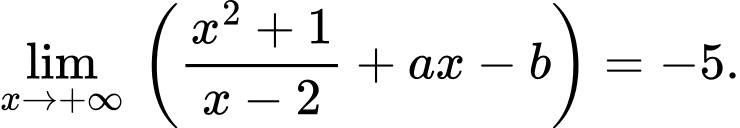 Giá trị biểu thức
Giá trị biểu thức 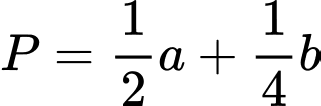 là ………
là ………
Ta có 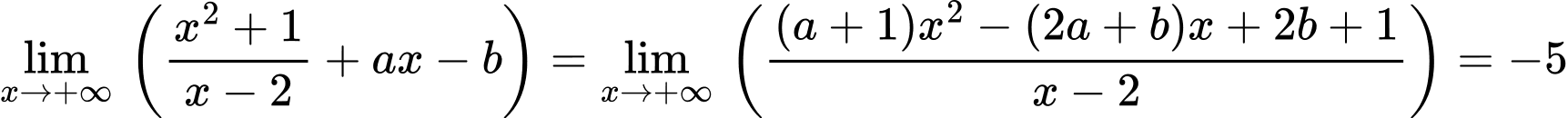
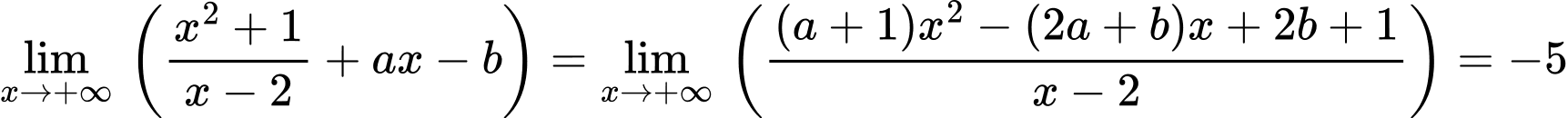
Vì giới hạn là hữu hạn và bằng 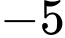 nên
nên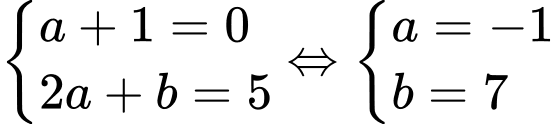
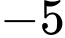 nên
nên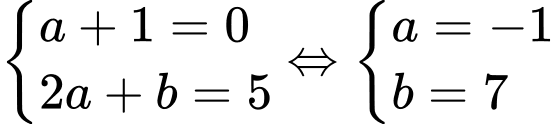
Vậy 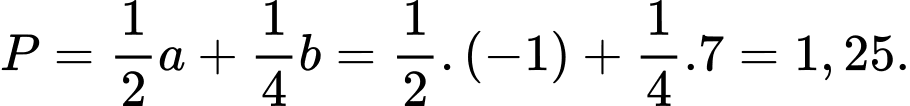
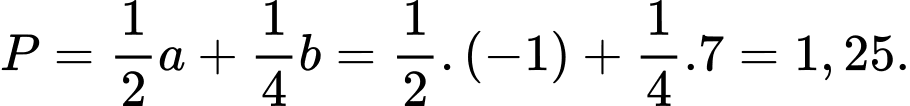
Câu 21 [803986]: Cho 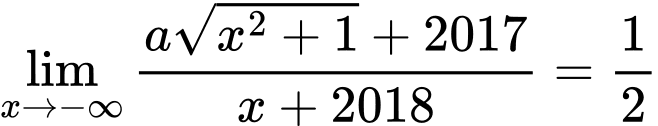 ;
; 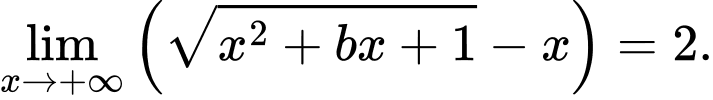 Tính
Tính 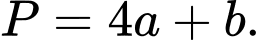
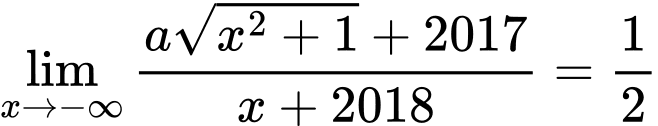 ;
; 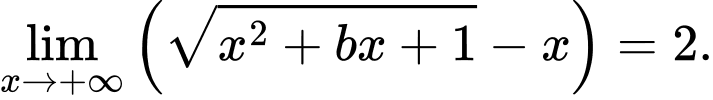 Tính
Tính 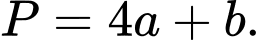
A, 

B, 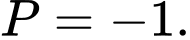
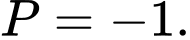
C, 

D, 

Chọn C
Ta có: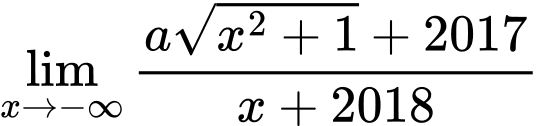
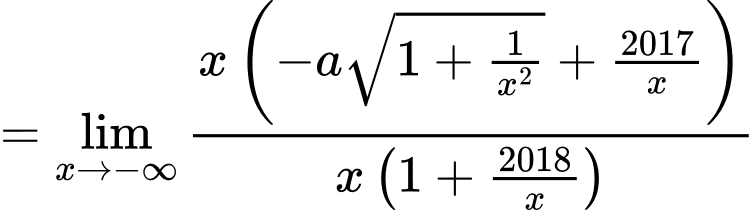
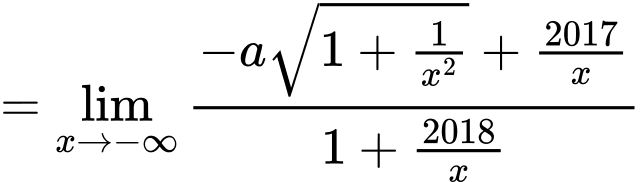
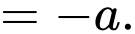
Nên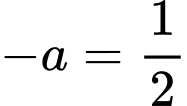
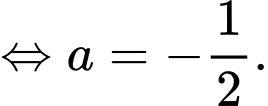
Ta có: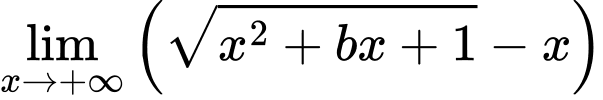
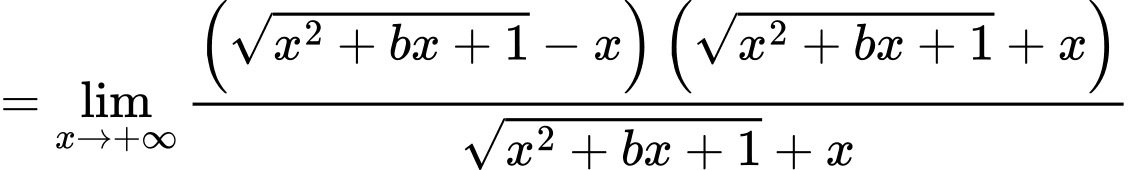
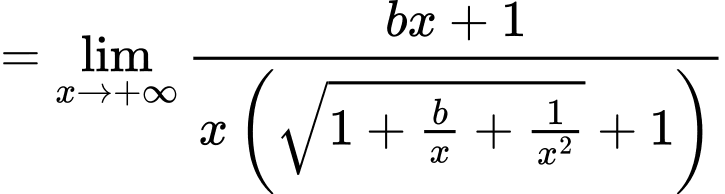
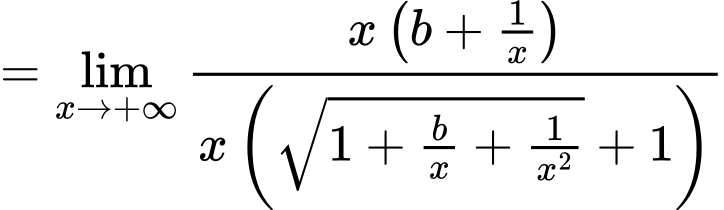
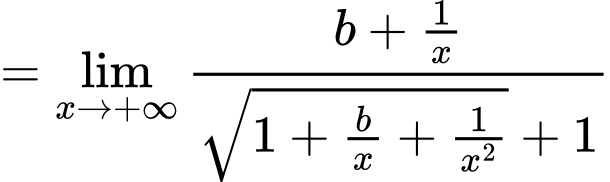
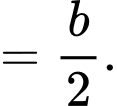
Nên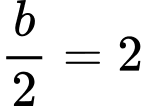
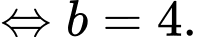
Vậy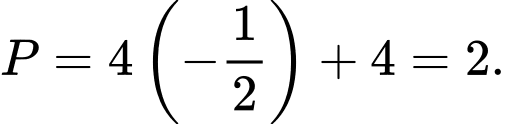 Đáp án: C
Đáp án: C
Ta có:
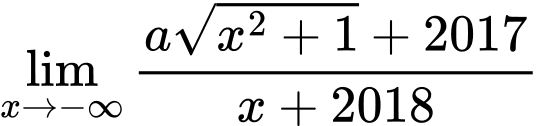
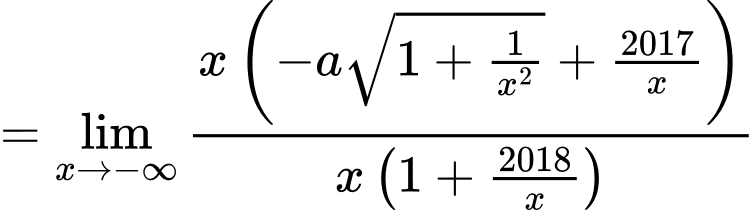
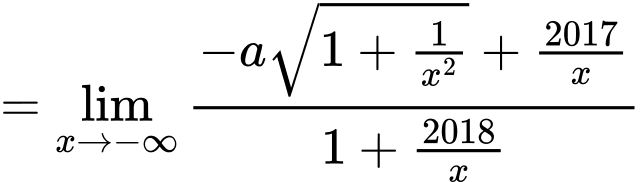
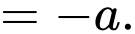
Nên
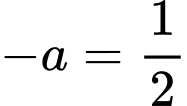
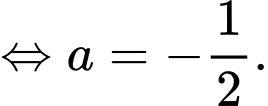
Ta có:
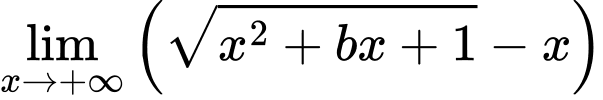
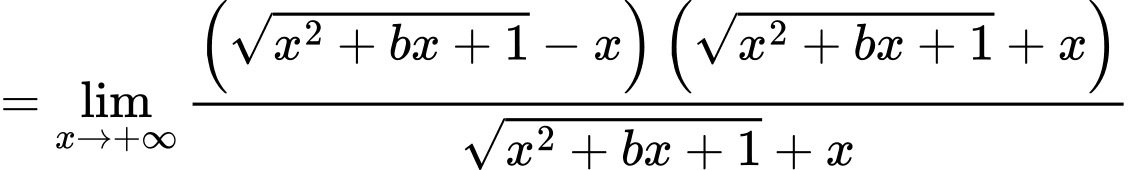
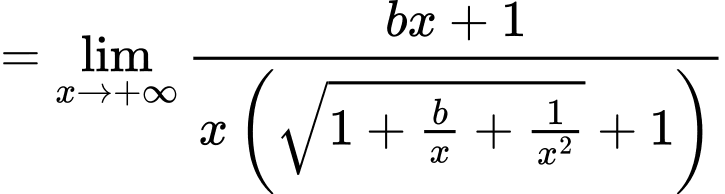
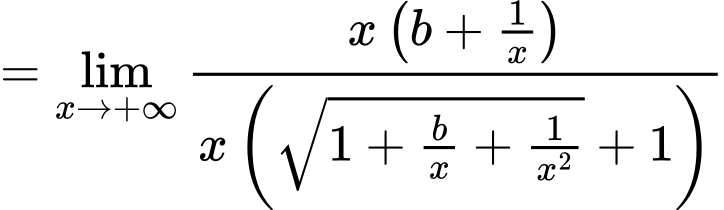
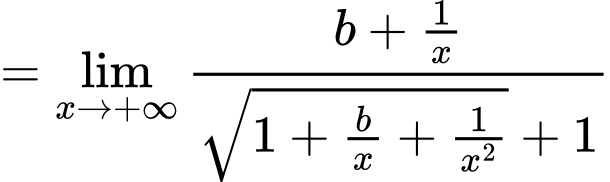
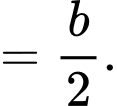
Nên
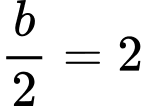
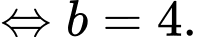
Vậy
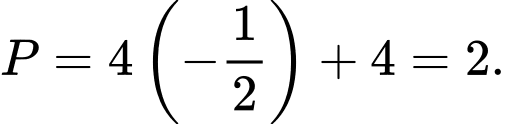 Đáp án: C
Đáp án: C
Câu 22 [803983]: Biết 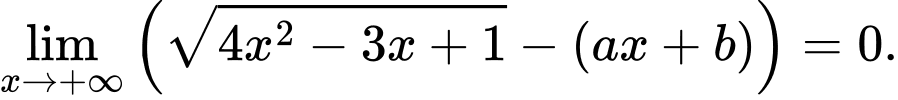 Tính
Tính 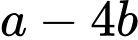 ta được
ta được
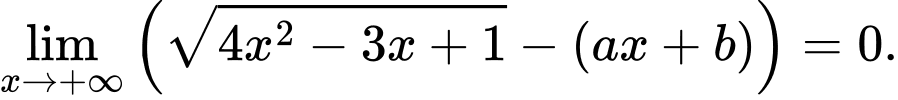 Tính
Tính 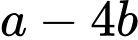 ta được
ta được A, 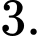
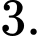
B, 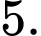
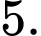
C, 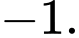
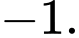
D, 
Ta có
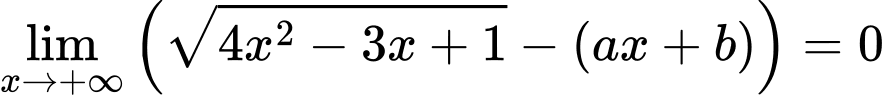
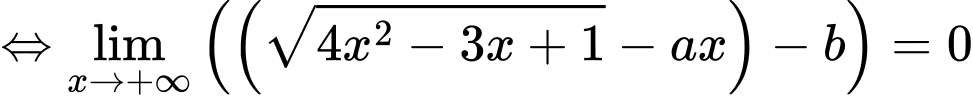
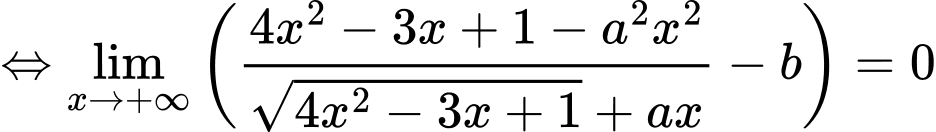
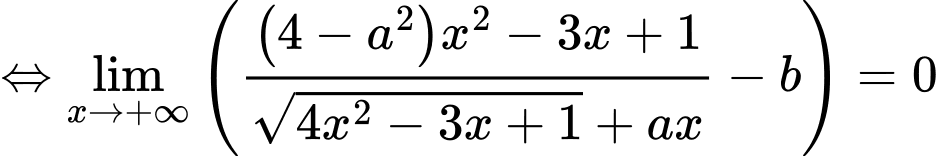
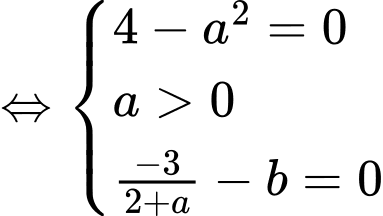
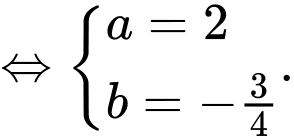
Vậy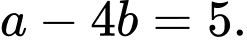 Đáp án: B
Đáp án: B
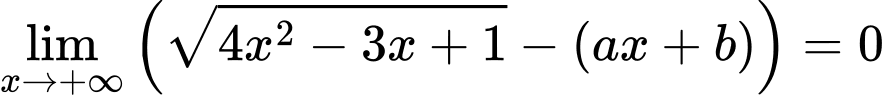
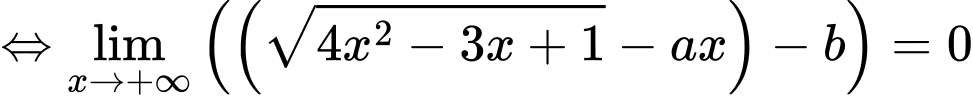
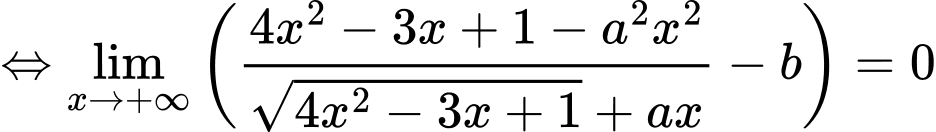
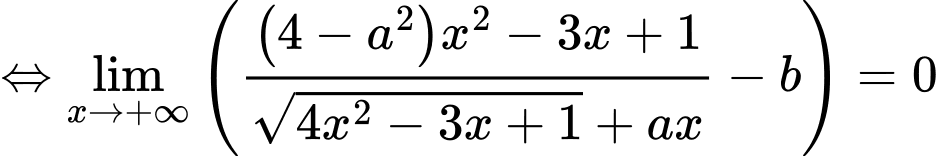
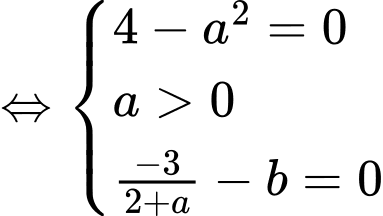
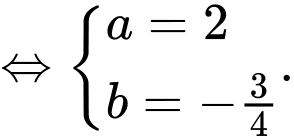
Vậy
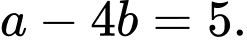 Đáp án: B
Đáp án: B
Câu 23 [803972]: Biết 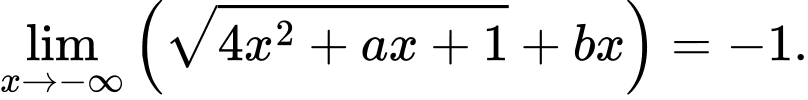 Tính giá của biểu thức
Tính giá của biểu thức 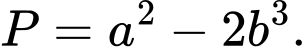
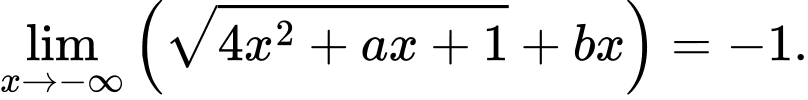 Tính giá của biểu thức
Tính giá của biểu thức 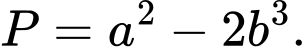
A, 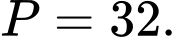
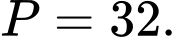
B, 

C, 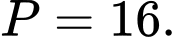
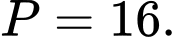
D, 

Chọn B
TH1: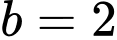
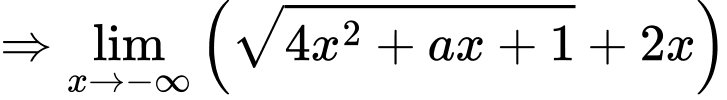
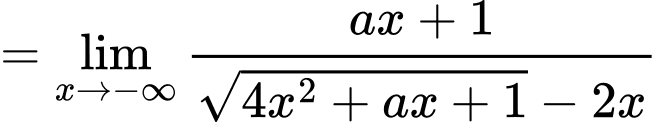
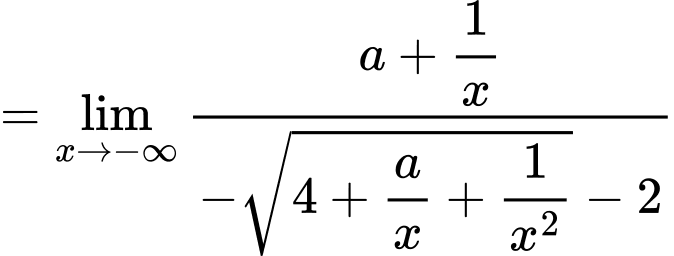
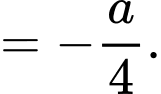
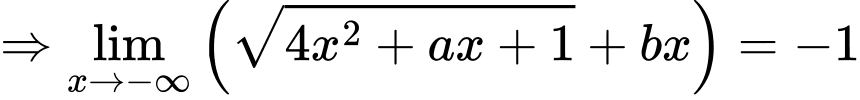
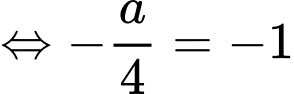
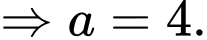
TH2: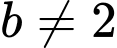
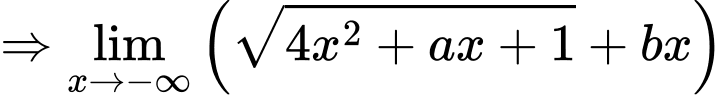
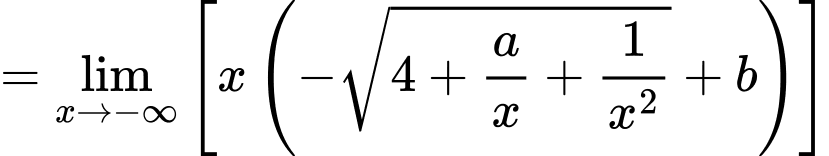

Vậy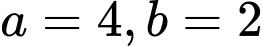
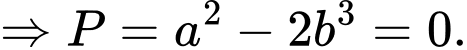 Đáp án: B
Đáp án: B
TH1:
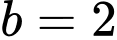
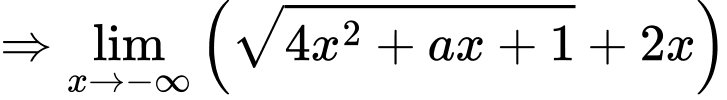
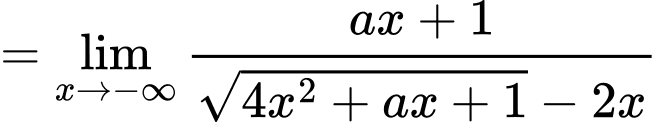
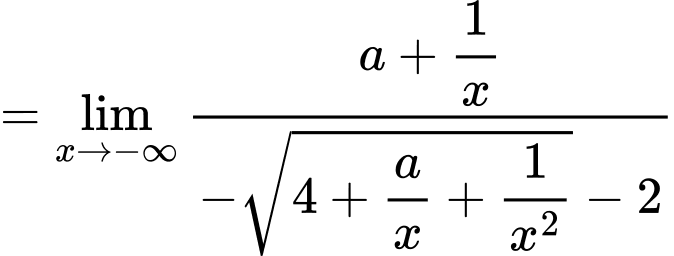
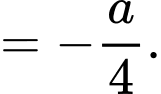
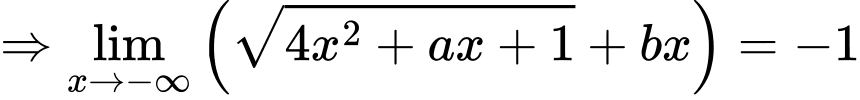
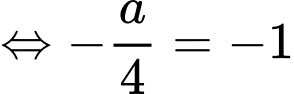
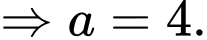
TH2:
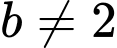
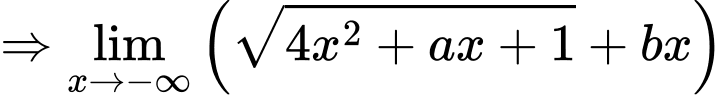
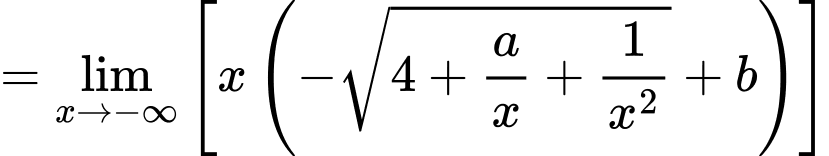

Vậy
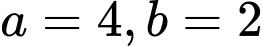
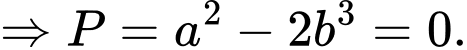 Đáp án: B
Đáp án: B
Câu 24 [804159]: Cho hàm số 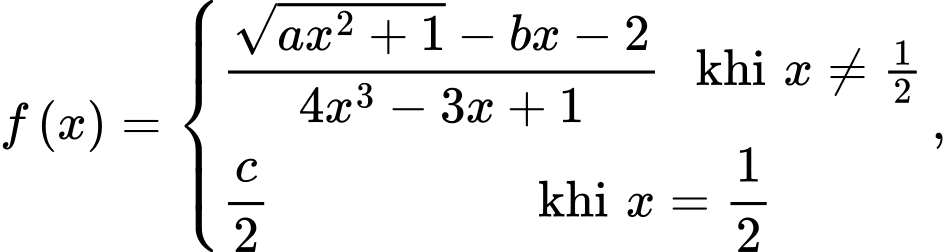
 Biết hàm số liên tục tại
Biết hàm số liên tục tại 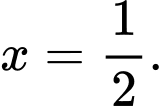 Tính
Tính 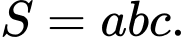
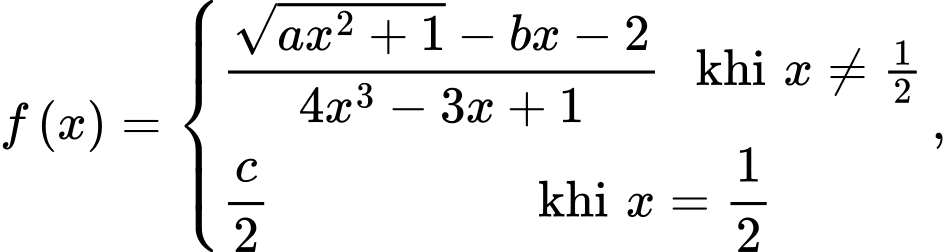
 Biết hàm số liên tục tại
Biết hàm số liên tục tại 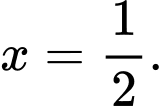 Tính
Tính 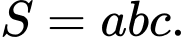
A, 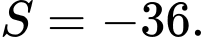
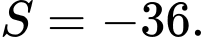
B, 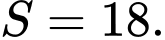
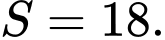
C, 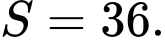
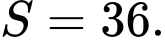
D, 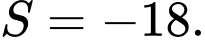
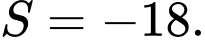
Chọn A
Ta có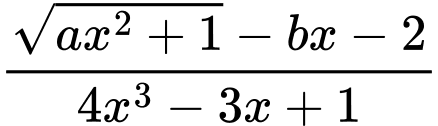
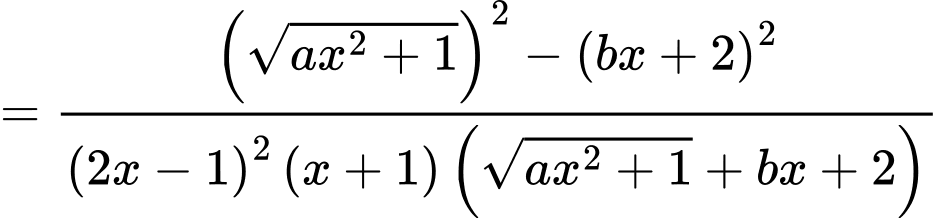
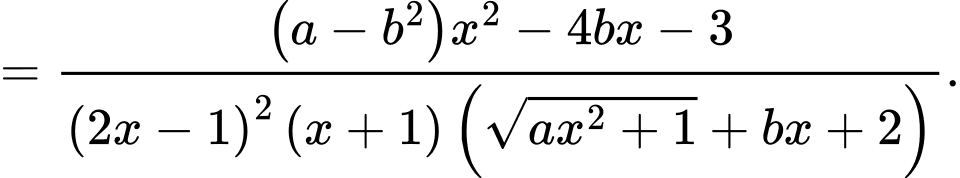
Để hàm số liên tục tại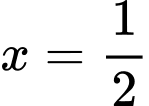
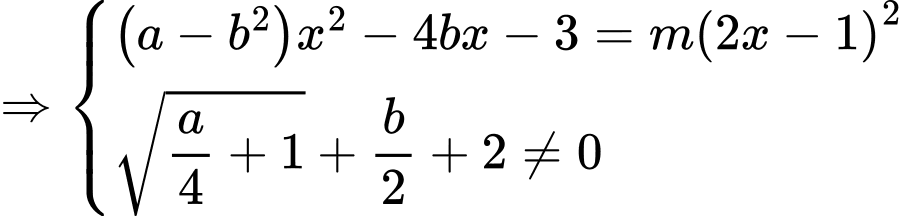
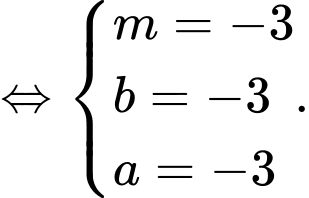
Khi đó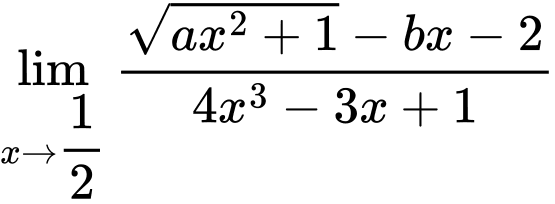
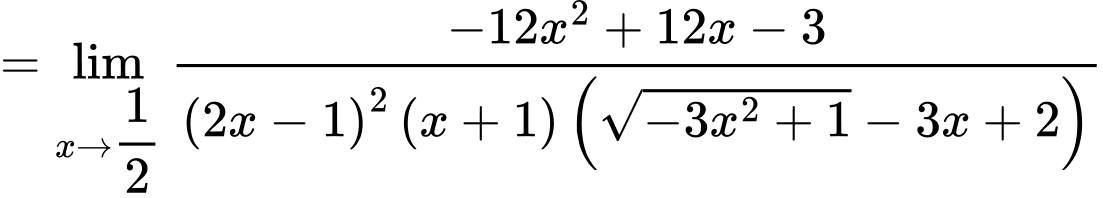
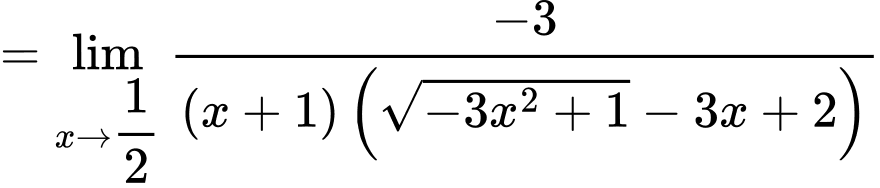
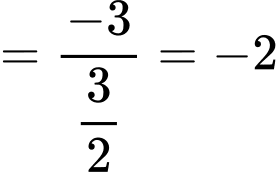
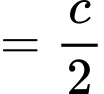
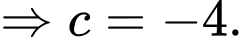
Vậy Đáp án: A
Đáp án: A
Ta có
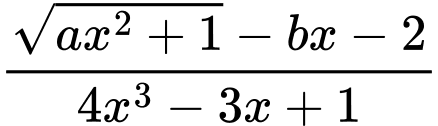
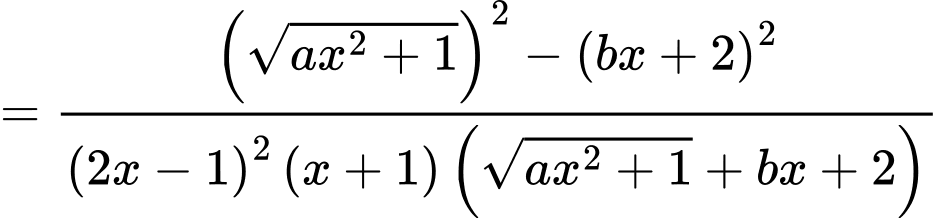
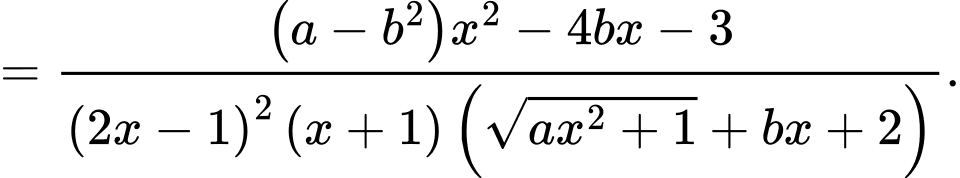
Để hàm số liên tục tại
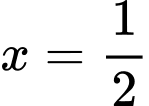
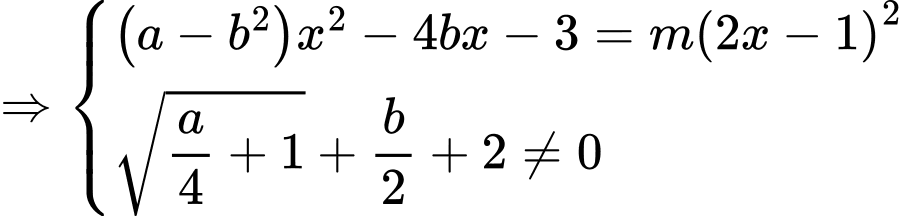
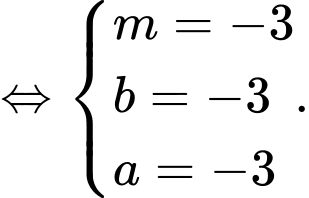
Khi đó
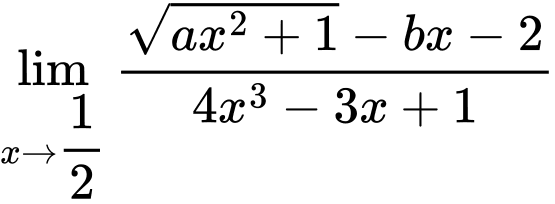
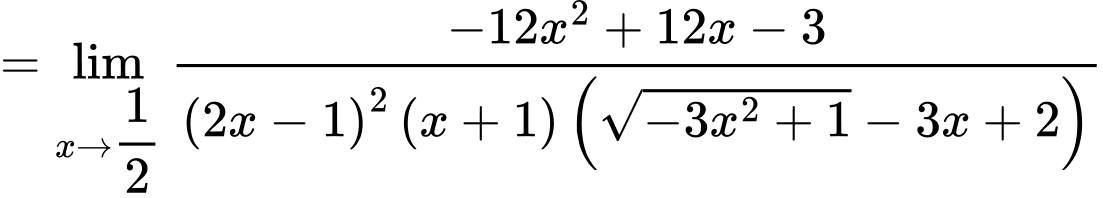
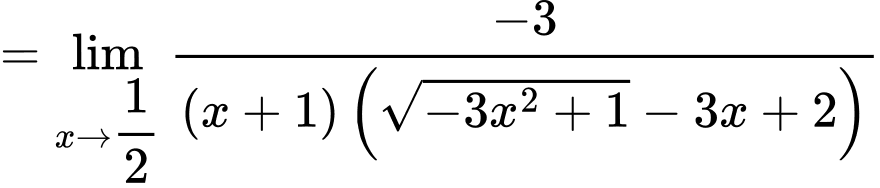
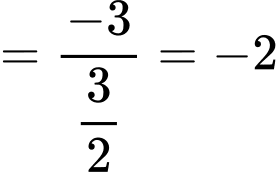
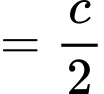
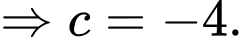
Vậy
 Đáp án: A
Đáp án: A
Câu 25 [803976]: Cho giới hạn 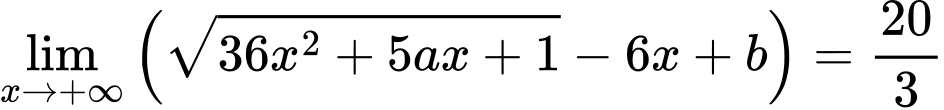 và đường thẳng
và đường thẳng 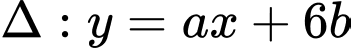 đi qua điểm
đi qua điểm 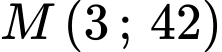 với
với 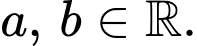 Giá trị của biểu thức
Giá trị của biểu thức 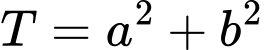 là
là
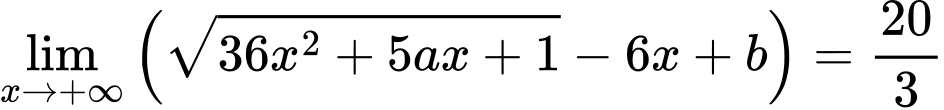 và đường thẳng
và đường thẳng 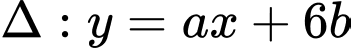 đi qua điểm
đi qua điểm 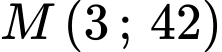 với
với 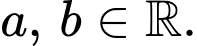 Giá trị của biểu thức
Giá trị của biểu thức 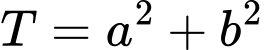 là
là A, 104.
B, 100.
C, 41.
D, 169.
Chọn C
Đường thẳng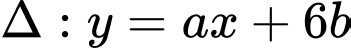 đi qua điểm
đi qua điểm 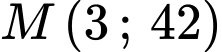 nên
nên 
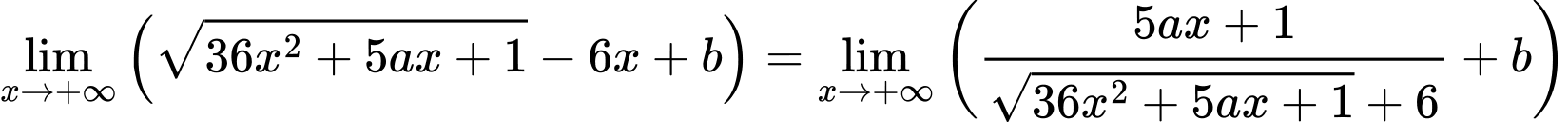
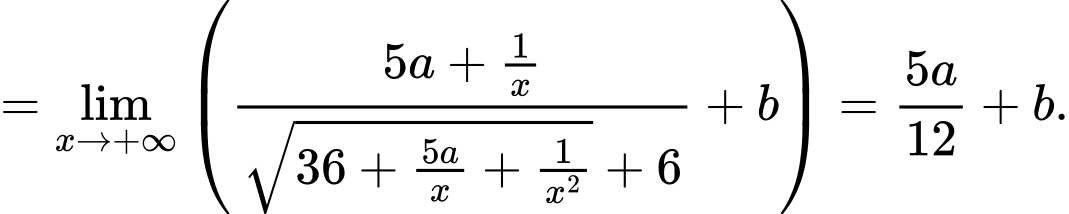
Do đó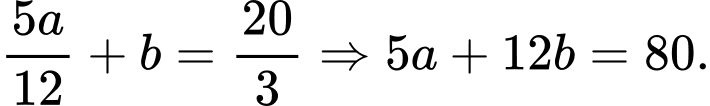 Ta có hệ:
Ta có hệ: 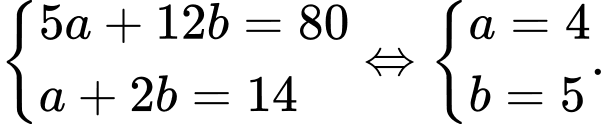
Vậy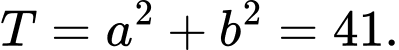 Đáp án: C
Đáp án: C
Đường thẳng
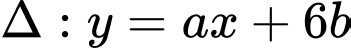 đi qua điểm
đi qua điểm 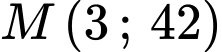 nên
nên 
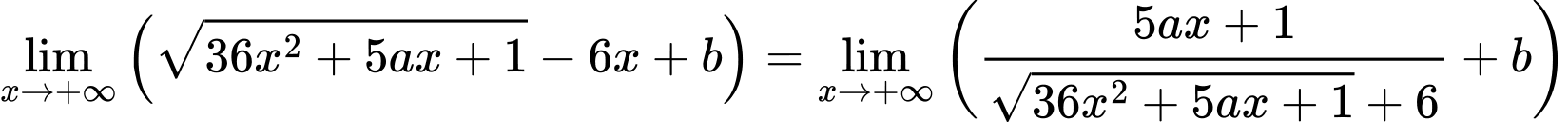
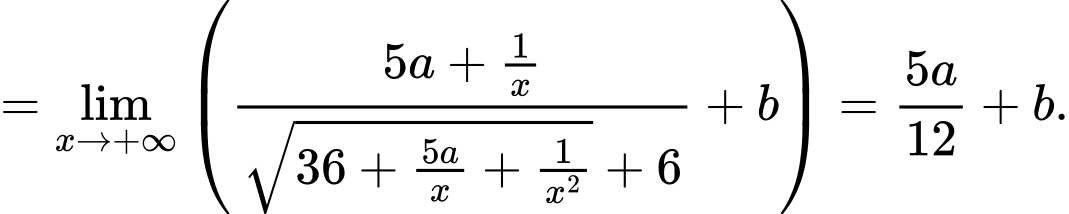
Do đó
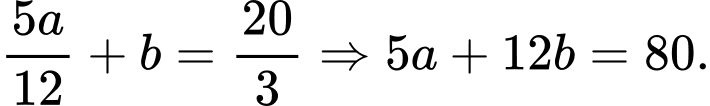 Ta có hệ:
Ta có hệ: 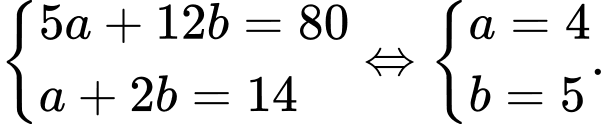
Vậy
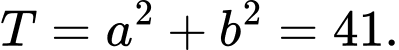 Đáp án: C
Đáp án: C