Đáp án Bài tập tự luyện
Câu 1 [971684]: (HKI_L11-NGUYỄN GIA THIỀU - HÀ NỘI 1718) Cho hình chóp 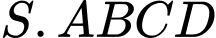 có đáy
có đáy 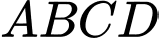 là hình thang với đáy lớn
là hình thang với đáy lớn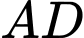 ,
, 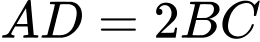 . Gọi
. Gọi  là giao điểm của
là giao điểm của 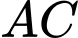 và
và 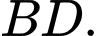 Tìm giao tuyến của hai mặt phẳng
Tìm giao tuyến của hai mặt phẳng 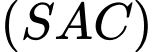 và
và 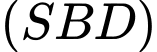 .
.
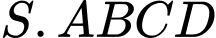 có đáy
có đáy 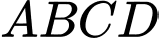 là hình thang với đáy lớn
là hình thang với đáy lớn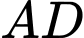 ,
, 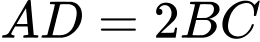 . Gọi
. Gọi  là giao điểm của
là giao điểm của 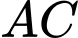 và
và 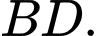 Tìm giao tuyến của hai mặt phẳng
Tìm giao tuyến của hai mặt phẳng 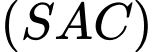 và
và 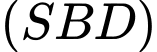 .
. A, 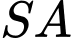 .
.
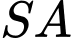 .
.B, 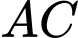 .
.
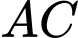 .
.C, 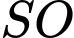 .
.
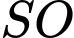 .
.D, 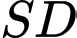 .
.
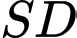 .
.
Chọn C
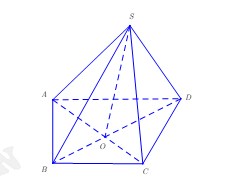
Có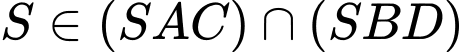 .
.
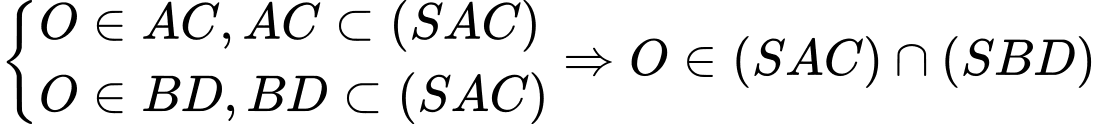 .
.
Nên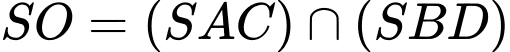 . Đáp án: C
. Đáp án: C

Có
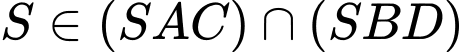 .
.
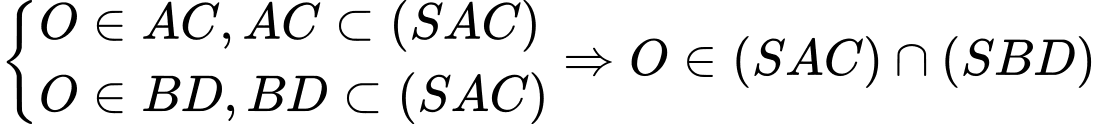 .
.Nên
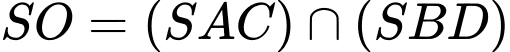 . Đáp án: C
. Đáp án: C
Câu 2 [971687]: Cho hình chóp 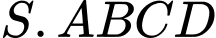 , biết
, biết 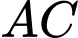 cắt
cắt 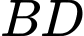 tại
tại 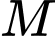 ,
,  cắt
cắt 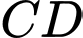 tại
tại  . Tìm giao tuyến của hai mặt phẳng
. Tìm giao tuyến của hai mặt phẳng 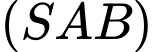 và
và  .
.
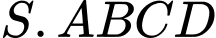 , biết
, biết 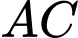 cắt
cắt 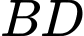 tại
tại 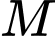 ,
,  cắt
cắt 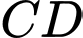 tại
tại  . Tìm giao tuyến của hai mặt phẳng
. Tìm giao tuyến của hai mặt phẳng 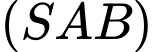 và
và  .
. A, 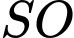 .
.
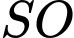 .
.B, 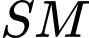 .
.
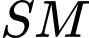 .
.C, 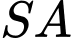 .
.
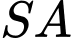 .
.D, 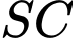 .
.
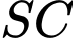 .
.
Chọn A
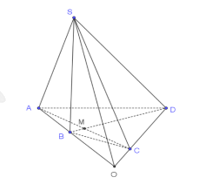
Ta có: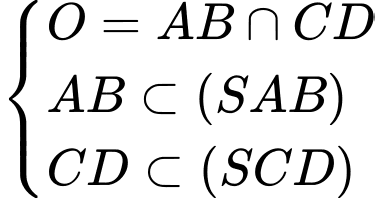
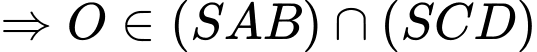 .
.
Lại có: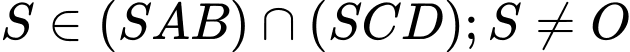 . Khi đó
. Khi đó 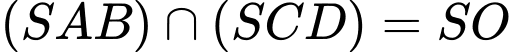 . Đáp án: A
. Đáp án: A

Ta có:
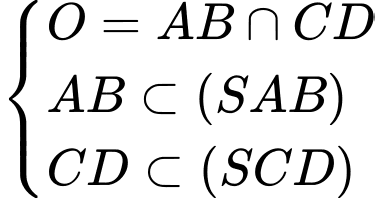
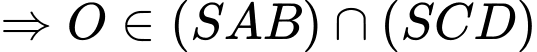 .
.Lại có:
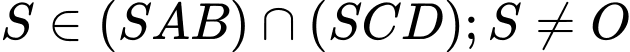 . Khi đó
. Khi đó 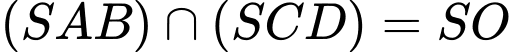 . Đáp án: A
. Đáp án: A
Câu 3 [971692]: Cho bốn điểm 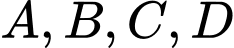 không cùng nằm trong một mặt phẳng. Trên
không cùng nằm trong một mặt phẳng. Trên 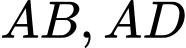 lần lượt lấy các điểm
lần lượt lấy các điểm 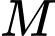 và
và 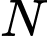 sao cho
sao cho 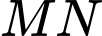 cắt
cắt 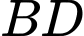 tại
tại 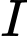 . Điểm
. Điểm 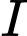 không thuộc mặt phẳng nào sao đây:
không thuộc mặt phẳng nào sao đây:
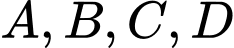 không cùng nằm trong một mặt phẳng. Trên
không cùng nằm trong một mặt phẳng. Trên 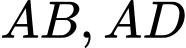 lần lượt lấy các điểm
lần lượt lấy các điểm 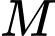 và
và 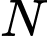 sao cho
sao cho 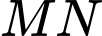 cắt
cắt 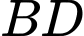 tại
tại 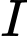 . Điểm
. Điểm 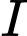 không thuộc mặt phẳng nào sao đây:
không thuộc mặt phẳng nào sao đây: A, 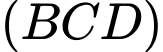 .
.
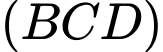 .
.B, 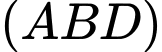 .
.
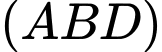 .
.C, 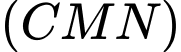 .
.
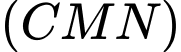 .
.D, 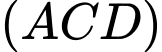 .
.
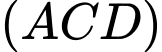 .
.
Chọn D
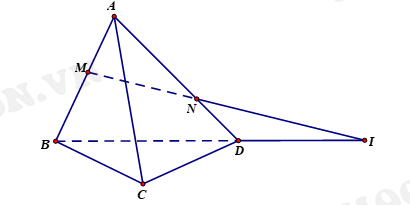
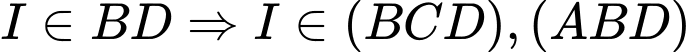
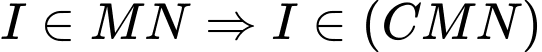 Đáp án: D
Đáp án: D

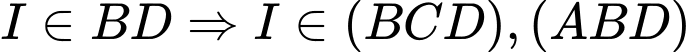
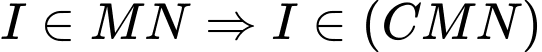 Đáp án: D
Đáp án: D
Câu 4 [971691]: Cho bốn điểm 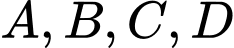 không đồng phẳng. Gọi
không đồng phẳng. Gọi 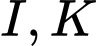 lần lượt là trung điểm hai đoạn thẳng
lần lượt là trung điểm hai đoạn thẳng 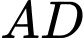 và
và 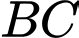 . Hỏi
. Hỏi 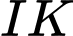 là giao tuyến của cặp mặt phẳng nào sau đây ?
là giao tuyến của cặp mặt phẳng nào sau đây ?
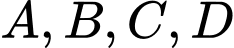 không đồng phẳng. Gọi
không đồng phẳng. Gọi 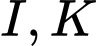 lần lượt là trung điểm hai đoạn thẳng
lần lượt là trung điểm hai đoạn thẳng 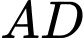 và
và 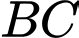 . Hỏi
. Hỏi 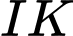 là giao tuyến của cặp mặt phẳng nào sau đây ?
là giao tuyến của cặp mặt phẳng nào sau đây ? A, 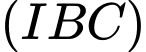 và
và 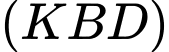 .
.
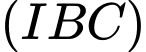 và
và 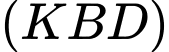 .
.B, 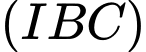 và
và  .
.
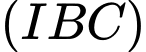 và
và  .
.C, 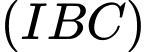 và
và 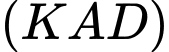 .
.
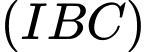 và
và 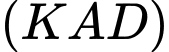 .
.D, 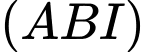 và
và 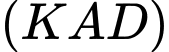 .
.
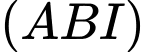 và
và 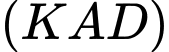 .
.
Chọn C.
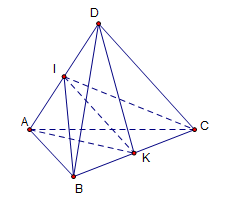
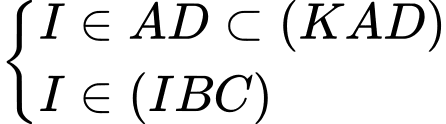
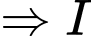 là điểm chung thứ nhất của hai mặt phẳng
là điểm chung thứ nhất của hai mặt phẳng 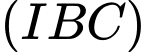 và
và 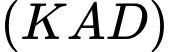 .
.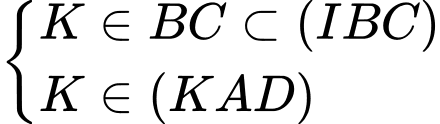
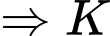 là điểm chung thứ hai của hai mặt phẳng
là điểm chung thứ hai của hai mặt phẳng 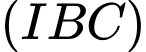 và
và 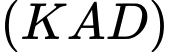 .
.
Vậy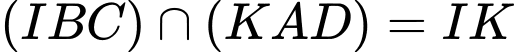 . Đáp án: C
. Đáp án: C

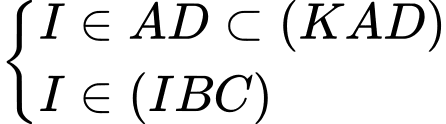
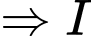 là điểm chung thứ nhất của hai mặt phẳng
là điểm chung thứ nhất của hai mặt phẳng 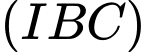 và
và 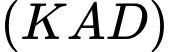 .
.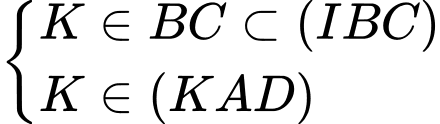
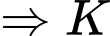 là điểm chung thứ hai của hai mặt phẳng
là điểm chung thứ hai của hai mặt phẳng 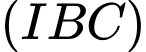 và
và 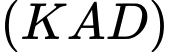 .
. Vậy
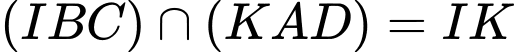 . Đáp án: C
. Đáp án: C
Câu 5 [971702]: Cho 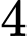 điểm không đồng phẳng
điểm không đồng phẳng 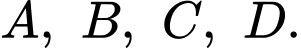 Gọi
Gọi 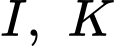 lần lượt là trung điểm của
lần lượt là trung điểm của 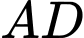 và
và 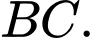 Giao tuyến của
Giao tuyến của 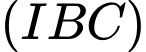 và
và 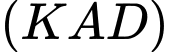 là
là
 điểm không đồng phẳng
điểm không đồng phẳng 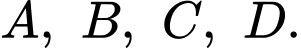 Gọi
Gọi 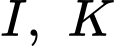 lần lượt là trung điểm của
lần lượt là trung điểm của 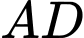 và
và 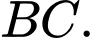 Giao tuyến của
Giao tuyến của 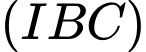 và
và 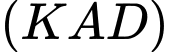 là
là A, 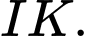
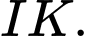
B, 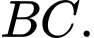
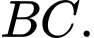
C, 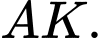
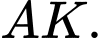
D, 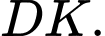
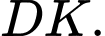
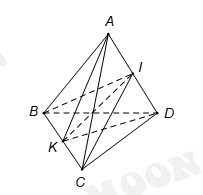
Điểm
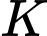 là trung điểm của
là trung điểm của 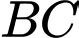 suy ra
suy ra 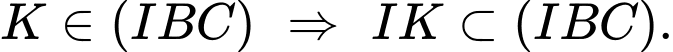 Điểm
Điểm 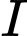 là trung điểm của
là trung điểm của 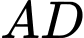 suy ra
suy ra 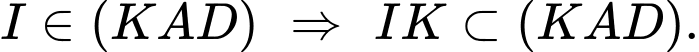 Vậy giao tuyến của hai mặt phẳng
Vậy giao tuyến của hai mặt phẳng 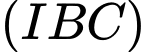 và
và 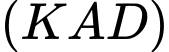 là IK Đáp án: A
là IK Đáp án: A
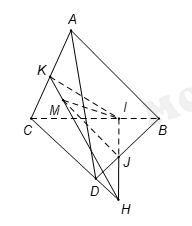
Câu 6 [971704]: Cho tứ diện 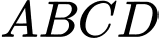 và điểm
và điểm 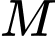 thuộc miền trong của tam giác
thuộc miền trong của tam giác  . Gọi
. Gọi 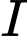 và
và 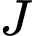 lần lượt là hai điểm trên cạnh
lần lượt là hai điểm trên cạnh 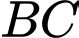 và
và 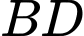 sao cho
sao cho  không song song với
không song song với 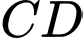 . Gọi
. Gọi  lần lượt là giao điểm của
lần lượt là giao điểm của  với
với 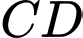 của
của 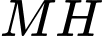 và
và 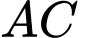 . Giao tuyến của hai mặt phẳng
. Giao tuyến của hai mặt phẳng 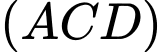 và
và 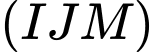 là
là
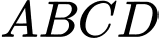 và điểm
và điểm 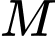 thuộc miền trong của tam giác
thuộc miền trong của tam giác  . Gọi
. Gọi 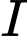 và
và 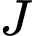 lần lượt là hai điểm trên cạnh
lần lượt là hai điểm trên cạnh 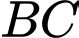 và
và 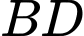 sao cho
sao cho  không song song với
không song song với 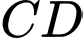 . Gọi
. Gọi  lần lượt là giao điểm của
lần lượt là giao điểm của  với
với 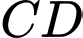 của
của 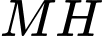 và
và 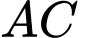 . Giao tuyến của hai mặt phẳng
. Giao tuyến của hai mặt phẳng 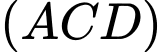 và
và 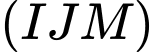 là
là A,  .
.
 .
.B,  .
.
 .
.C, 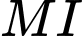 .
.
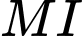 .
.D, 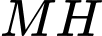 .
.
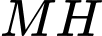 .
.
Trong mặt phẳng

 cắt
cắt 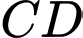 tại
tại 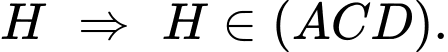
Điểm
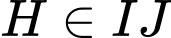 suy ra bốn điểm
suy ra bốn điểm 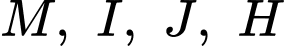 đồng phẳng.
đồng phẳng.Nên trong mặt phẳng
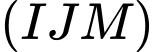 ,
, 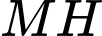 cắt
cắt  tại
tại 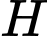 và
và 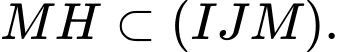
Mặt khác
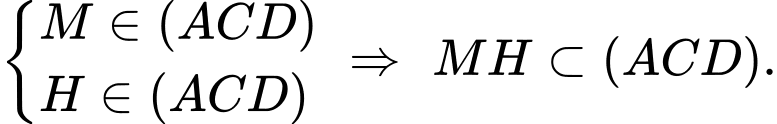 Vậy
Vậy 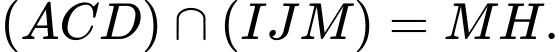 Đáp án: D
Đáp án: D
Câu 7 [632969]: Cho hình chóp 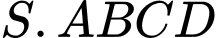 có đáy
có đáy 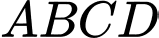 là hình bình hành. Gọi
là hình bình hành. Gọi 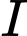 và
và 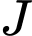 lần lượt là trung điểm của
lần lượt là trung điểm của 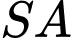 và
và 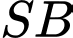 . Khẳng định nào sau đây sai?
. Khẳng định nào sau đây sai?
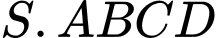 có đáy
có đáy 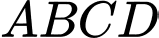 là hình bình hành. Gọi
là hình bình hành. Gọi 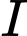 và
và 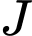 lần lượt là trung điểm của
lần lượt là trung điểm của 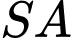 và
và 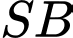 . Khẳng định nào sau đây sai?
. Khẳng định nào sau đây sai? A,  là hình thang
là hình thang
 là hình thang
là hình thangB, 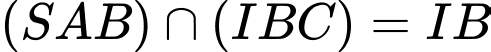
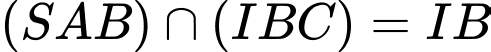
C, 

D, 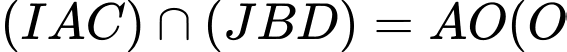 là tâm
là tâm 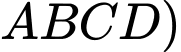
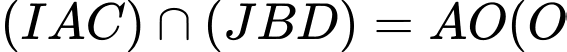 là tâm
là tâm 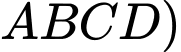

Ta có


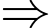 Loại A.
Loại A.+)
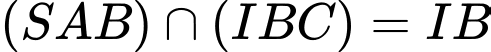
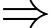 Loại B.
Loại B.+)

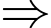 Loại C.
Loại C.+)
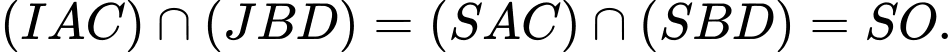
Chọn D. Đáp án: D
Câu 8 [632973]: Cho hình tứ diện  , trên các cạnh
, trên các cạnh  và
và  lần lượt lấy các điểm
lần lượt lấy các điểm  và
và  . Đường thẳng
. Đường thẳng  và
và  cắt nhau tại
cắt nhau tại  , đường thẳng
, đường thẳng  và
và  cắt nhau tại
cắt nhau tại  Khẳng định nào sau đây là sai.
Khẳng định nào sau đây là sai.
 , trên các cạnh
, trên các cạnh  và
và  lần lượt lấy các điểm
lần lượt lấy các điểm  và
và  . Đường thẳng
. Đường thẳng  và
và  cắt nhau tại
cắt nhau tại  , đường thẳng
, đường thẳng  và
và  cắt nhau tại
cắt nhau tại  Khẳng định nào sau đây là sai.
Khẳng định nào sau đây là sai. A, 

B, 

C, 

D, 


Điểm
 cùng thuộc 2 mặt phẳng
cùng thuộc 2 mặt phẳng  và
và  do đó
do đó 
Tương tự

+)

+)

Khẳng định sai là C. Chọn C. Đáp án: C
Câu 9 [518909]: Cho hình chóp 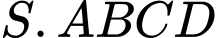 có đáy là hình bình hành tâm
có đáy là hình bình hành tâm  . Gọi
. Gọi 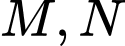 lần lượt là các điểm nằm trên cạnh
lần lượt là các điểm nằm trên cạnh 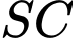 và
và 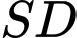 . Đường thẳng
. Đường thẳng 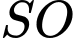 cắt đường thẳng
cắt đường thẳng  và
và 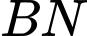 lần lượt tại
lần lượt tại 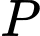 và
và  . Giao điểm của đường thẳng
. Giao điểm của đường thẳng  với mặt phẳng
với mặt phẳng 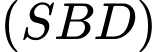 là điểm nào sau đây?
là điểm nào sau đây?
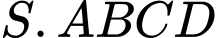 có đáy là hình bình hành tâm
có đáy là hình bình hành tâm  . Gọi
. Gọi 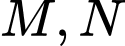 lần lượt là các điểm nằm trên cạnh
lần lượt là các điểm nằm trên cạnh 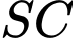 và
và 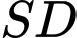 . Đường thẳng
. Đường thẳng 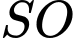 cắt đường thẳng
cắt đường thẳng  và
và 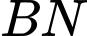 lần lượt tại
lần lượt tại 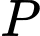 và
và  . Giao điểm của đường thẳng
. Giao điểm của đường thẳng  với mặt phẳng
với mặt phẳng 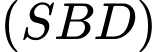 là điểm nào sau đây?
là điểm nào sau đây? A, Điểm 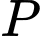
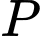
B, Điểm 

C, Điểm 

D, Điểm 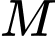
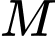

Xét
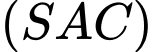 có:
có: 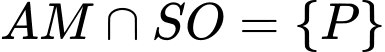
Mà
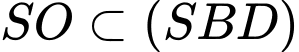

Chọn A. Đáp án: A
Câu 10 [518910]: Cho hình chóp 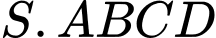 có đáy là hình bình hành tâm
có đáy là hình bình hành tâm  . Gọi
. Gọi 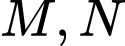 lần lượt là các điểm nằm trên cạnh
lần lượt là các điểm nằm trên cạnh 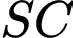 và
và 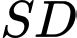 . Đường thẳng
. Đường thẳng 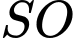 cắt đường thẳng
cắt đường thẳng  và
và 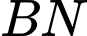 lần lượt tại
lần lượt tại 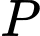 và
và  . Giao điểm của đường thẳng
. Giao điểm của đường thẳng 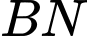 với mặt phẳng
với mặt phẳng 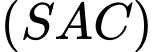 là điểm nào sau đây?
là điểm nào sau đây?
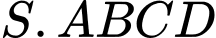 có đáy là hình bình hành tâm
có đáy là hình bình hành tâm  . Gọi
. Gọi 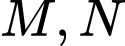 lần lượt là các điểm nằm trên cạnh
lần lượt là các điểm nằm trên cạnh 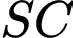 và
và 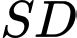 . Đường thẳng
. Đường thẳng 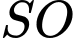 cắt đường thẳng
cắt đường thẳng  và
và 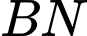 lần lượt tại
lần lượt tại 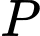 và
và  . Giao điểm của đường thẳng
. Giao điểm của đường thẳng 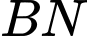 với mặt phẳng
với mặt phẳng 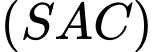 là điểm nào sau đây?
là điểm nào sau đây? A, Điểm 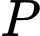
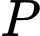
B, Điểm 

C, Điểm 

D, Điểm 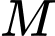
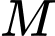

Ta có 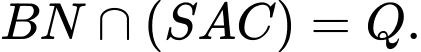 Chọn B.
Chọn B.
Câu 11 [518906]: Cho hình chóp 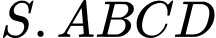 có đáy
có đáy 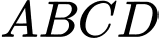 là hình bình hành. Gọi
là hình bình hành. Gọi 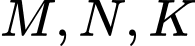 lần lượt là trung điểm của
lần lượt là trung điểm của 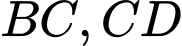 và
và 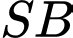 . Tìm giao điểm
. Tìm giao điểm 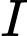 của đường thẳng
của đường thẳng 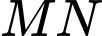 và mặt phẳng
và mặt phẳng 
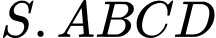 có đáy
có đáy 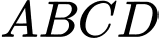 là hình bình hành. Gọi
là hình bình hành. Gọi 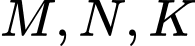 lần lượt là trung điểm của
lần lượt là trung điểm của 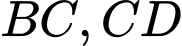 và
và 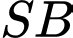 . Tìm giao điểm
. Tìm giao điểm 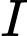 của đường thẳng
của đường thẳng 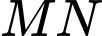 và mặt phẳng
và mặt phẳng 
A, 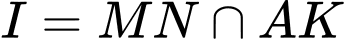
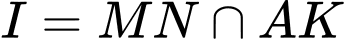
B, 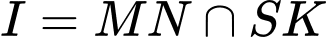
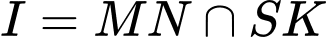
C, 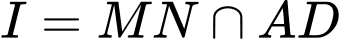
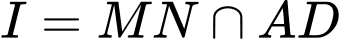
D, 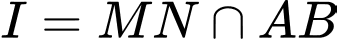
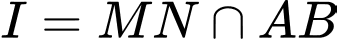

Gọi
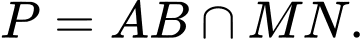
Suy ra
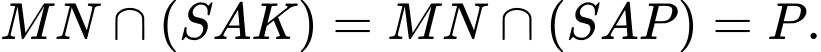
Chọn D. Đáp án: D
Câu 12 [972988]: Cho hình chóp 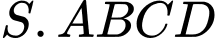 ,
,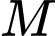 là một điểm trên cạnh
là một điểm trên cạnh 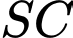 ,
, 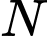 là một điểm trên cạnh
là một điểm trên cạnh 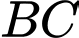 ,
,  ,
,  ,
, 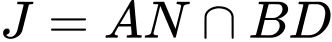 . Khi đó giao điểm của đường thẳng
. Khi đó giao điểm của đường thẳng 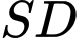 với mặt phẳng
với mặt phẳng 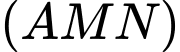 là
là
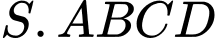 ,
,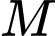 là một điểm trên cạnh
là một điểm trên cạnh 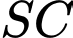 ,
, 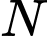 là một điểm trên cạnh
là một điểm trên cạnh 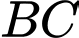 ,
,  ,
,  ,
, 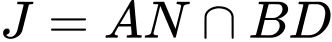 . Khi đó giao điểm của đường thẳng
. Khi đó giao điểm của đường thẳng 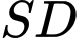 với mặt phẳng
với mặt phẳng 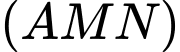 là
là A, Giao điểm của 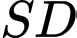 và
và 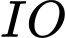 .
.
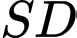 và
và 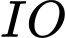 .
.B, Giao điểm của 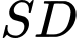 và
và 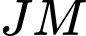 .
.
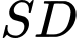 và
và 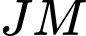 .
.C, Giao điểm của 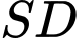 và
và  .
.
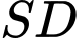 và
và  .
.D, Giao điểm của 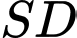 và
và 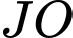 .
.
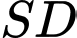 và
và 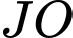 .
.
Chọn C
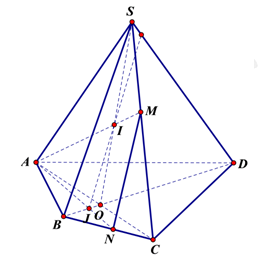
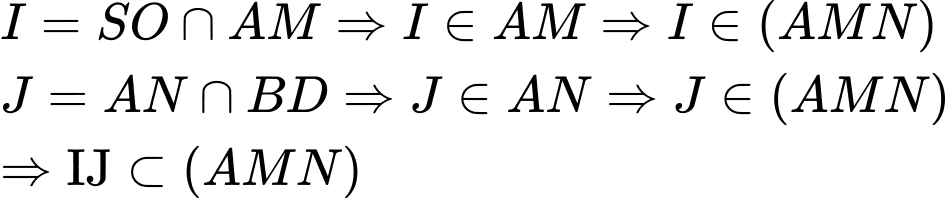
Khi đó giao điểm của đường thẳng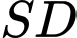 với mặt phẳng
với mặt phẳng 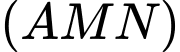 là giao điểm của
là giao điểm của 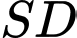 và
và  Đáp án: C
Đáp án: C

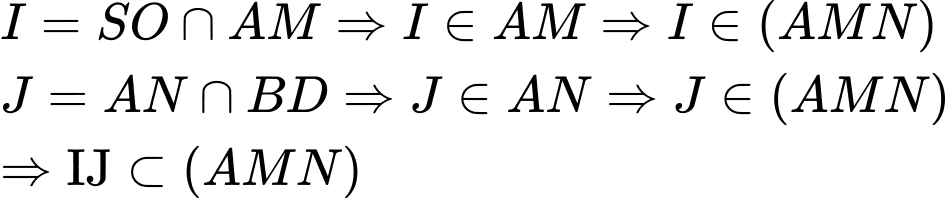
Khi đó giao điểm của đường thẳng
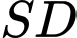 với mặt phẳng
với mặt phẳng 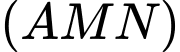 là giao điểm của
là giao điểm của 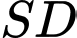 và
và  Đáp án: C
Đáp án: C
Câu 13 [972982]: Cho hình chóp 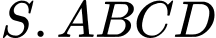 có đáy là hình bình hành.
có đáy là hình bình hành. 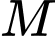 là trung điểm của
là trung điểm của 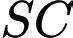 . Gọi
. Gọi 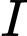 là giao điểm của đường thẳng
là giao điểm của đường thẳng  với mặt phẳng
với mặt phẳng 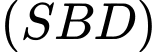 . Chọn khẳng định đúng trong các khẳng định sau đây
. Chọn khẳng định đúng trong các khẳng định sau đây
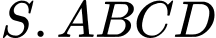 có đáy là hình bình hành.
có đáy là hình bình hành. 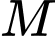 là trung điểm của
là trung điểm của 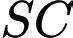 . Gọi
. Gọi 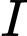 là giao điểm của đường thẳng
là giao điểm của đường thẳng  với mặt phẳng
với mặt phẳng 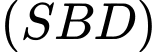 . Chọn khẳng định đúng trong các khẳng định sau đây
. Chọn khẳng định đúng trong các khẳng định sau đây A, 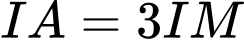 .
.
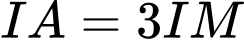 .
.B, 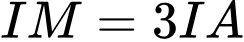 .
.
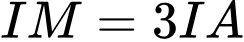 .
.C, 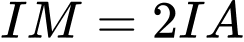 .
.
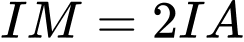 .
.D, 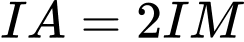 .
.
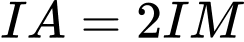 .
.
Chọn D.
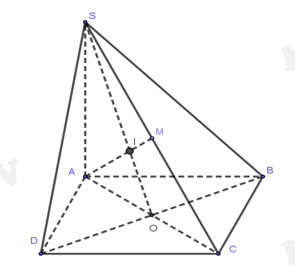
Gọi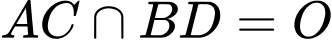 thì
thì 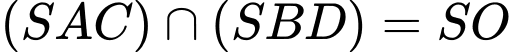 .
.
Trong mặt phẳng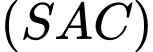 , lấy
, lấy 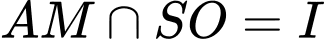
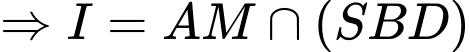 .
.
Do trong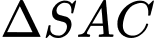 ,
,  và
và 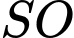 là hai đường trung tuyến, nên
là hai đường trung tuyến, nên 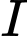 là trọng tâm
là trọng tâm 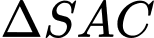 .
.
Vậy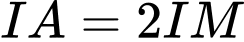 . Đáp án: D
. Đáp án: D

Gọi
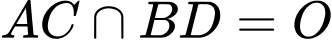 thì
thì 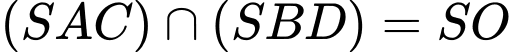 .
.Trong mặt phẳng
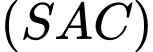 , lấy
, lấy 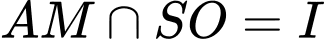
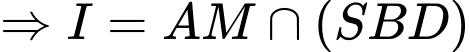 .
.Do trong
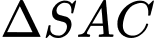 ,
,  và
và 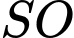 là hai đường trung tuyến, nên
là hai đường trung tuyến, nên 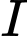 là trọng tâm
là trọng tâm 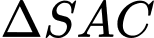 .
.Vậy
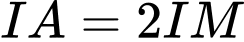 . Đáp án: D
. Đáp án: D
Câu 14 [229857]: (THPT XUÂN HÒA - VP - LẦN 1 - 2018) Cho hình tứ diện 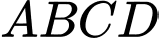 có
có 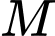 ,
, 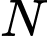 lần lượt là trung điểm của
lần lượt là trung điểm của  ,
, 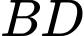 . Các điểm
. Các điểm  ,
, 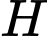 lần lượt trên cạnh
lần lượt trên cạnh 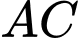 ,
, 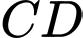 sao cho
sao cho 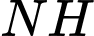 cắt
cắt 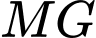 tại
tại 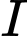 . Khẳng định nào sau đây là khẳng định đúng?
. Khẳng định nào sau đây là khẳng định đúng?
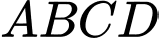 có
có 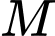 ,
, 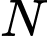 lần lượt là trung điểm của
lần lượt là trung điểm của  ,
, 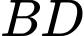 . Các điểm
. Các điểm  ,
, 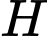 lần lượt trên cạnh
lần lượt trên cạnh 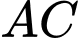 ,
, 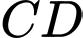 sao cho
sao cho 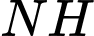 cắt
cắt 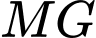 tại
tại 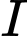 . Khẳng định nào sau đây là khẳng định đúng?
. Khẳng định nào sau đây là khẳng định đúng? A, 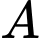 ,
,  ,
, 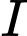 thẳng hàng
thẳng hàng
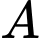 ,
,  ,
, 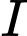 thẳng hàng
thẳng hàngB, 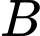 ,
,  ,
, 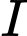 thẳng hàng.
thẳng hàng.
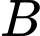 ,
,  ,
, 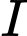 thẳng hàng.
thẳng hàng.C, 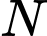 ,
,  ,
, 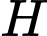 thẳng hàng
thẳng hàng
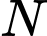 ,
,  ,
, 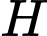 thẳng hàng
thẳng hàngD, 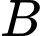 ,
,  ,
, 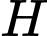 thẳng hàng.
thẳng hàng.
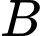 ,
,  ,
, 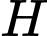 thẳng hàng.
thẳng hàng.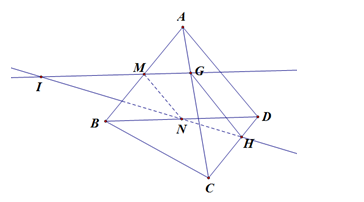
Do
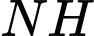 cắt
cắt 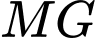 tại
tại 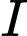 nên bốn điểm
nên bốn điểm 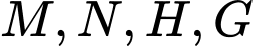 cùng thuộc mặt phẳng
cùng thuộc mặt phẳng  . Xét ba mặt phẳng
. Xét ba mặt phẳng 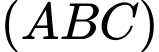 ,
, 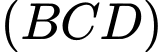 ,
,  phân biệt, đồng thời
phân biệt, đồng thời 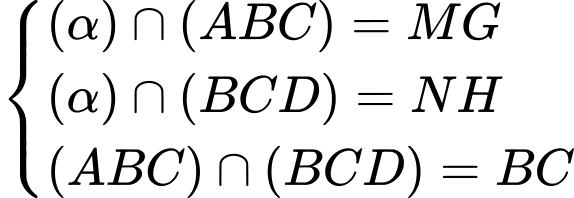 mà
mà 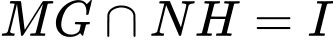
Suy ra
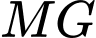 ,
, 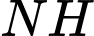 ,
, 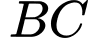 đồng quy tại
đồng quy tại 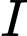 nên
nên 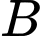 ,
,  ,
, 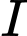 thẳng hàng. Đáp án: B
thẳng hàng. Đáp án: B
Câu 15 [229861]: Cho tứ diện 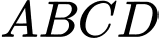 . Gọi
. Gọi 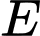 ,
, 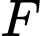 lần lượt là trung điểm của cạnh
lần lượt là trung điểm của cạnh  ,
, 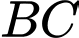 . Mặt phẳng
. Mặt phẳng 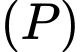 đi qua
đi qua 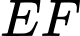 cắt
cắt 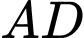 ,
, 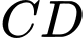 lần lượt tại
lần lượt tại 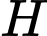 và
và  . Biết
. Biết 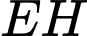 cắt
cắt 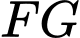 tại
tại 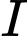 . Ba điểm nào sau đây thẳng hàng?
. Ba điểm nào sau đây thẳng hàng?
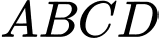 . Gọi
. Gọi 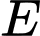 ,
, 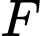 lần lượt là trung điểm của cạnh
lần lượt là trung điểm của cạnh  ,
, 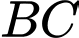 . Mặt phẳng
. Mặt phẳng 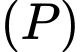 đi qua
đi qua 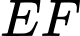 cắt
cắt 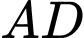 ,
, 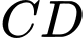 lần lượt tại
lần lượt tại 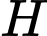 và
và  . Biết
. Biết 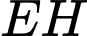 cắt
cắt 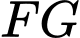 tại
tại 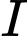 . Ba điểm nào sau đây thẳng hàng?
. Ba điểm nào sau đây thẳng hàng? A, 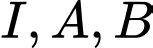 .
.
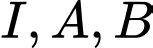 .
.B,  .
.
 .
.C, 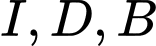 .
.
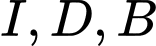 .
.D, 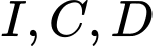 .
.
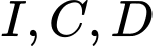 .
.
Chọn C
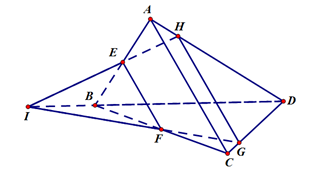
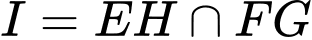
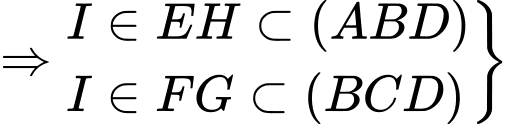
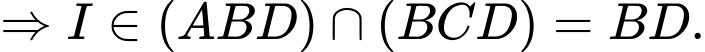
Vậy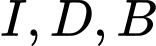 thẳng hàng. Đáp án: C
thẳng hàng. Đáp án: C

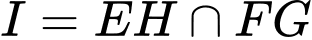
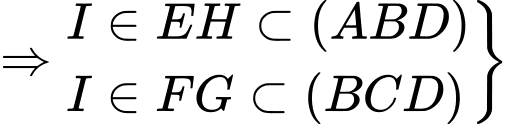
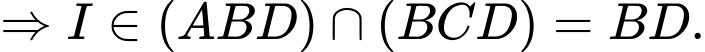
Vậy
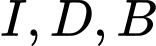 thẳng hàng. Đáp án: C
thẳng hàng. Đáp án: C
Câu 16 [295663]: Cho tứ diện 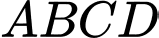 . Các điểm
. Các điểm 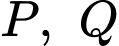 lần lượt là trung điểm của
lần lượt là trung điểm của  và
và 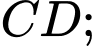 điểm
điểm 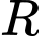 nằm trên cạnh
nằm trên cạnh 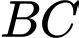 sao cho
sao cho 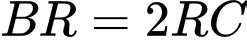 . Gọi
. Gọi 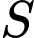 là giao điểm của mặt phẳng
là giao điểm của mặt phẳng 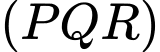 và cạnh
và cạnh 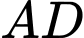 . Tính tỉ số
. Tính tỉ số  .
.
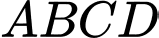 . Các điểm
. Các điểm 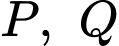 lần lượt là trung điểm của
lần lượt là trung điểm của  và
và 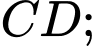 điểm
điểm 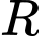 nằm trên cạnh
nằm trên cạnh 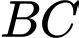 sao cho
sao cho 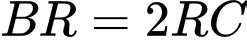 . Gọi
. Gọi 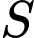 là giao điểm của mặt phẳng
là giao điểm của mặt phẳng 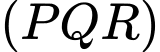 và cạnh
và cạnh 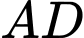 . Tính tỉ số
. Tính tỉ số  .
. A, 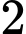 .
.
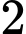 .
.B, 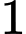 .
.
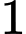 .
.C, 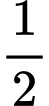 .
.
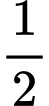 .
.D, 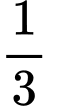 .
.
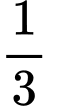 .
.
Gọi 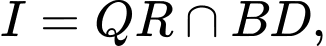 nối
nối 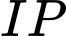 cắt
cắt 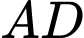 tại
tại 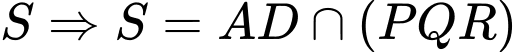 Dựng
Dựng 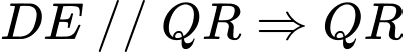 là đường trung bình của tam giác
là đường trung bình của tam giác 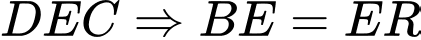
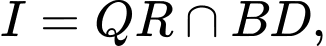 nối
nối 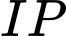 cắt
cắt 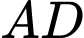 tại
tại 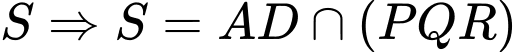 Dựng
Dựng 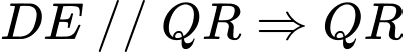 là đường trung bình của tam giác
là đường trung bình của tam giác 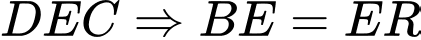
Khi đó 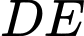 là đường trung bình của tam giác
là đường trung bình của tam giác 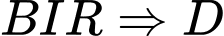 là trung điểm của
là trung điểm của 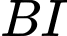 nên
nên 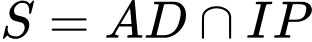 là trọng tâm tam giác
là trọng tâm tam giác 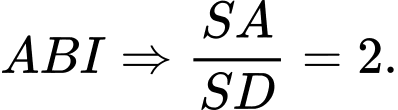
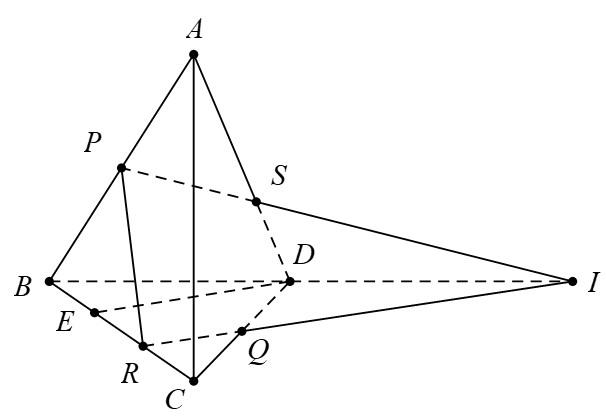
Đáp án: A 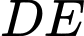 là đường trung bình của tam giác
là đường trung bình của tam giác 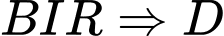 là trung điểm của
là trung điểm của 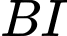 nên
nên 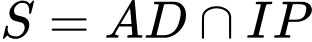 là trọng tâm tam giác
là trọng tâm tam giác 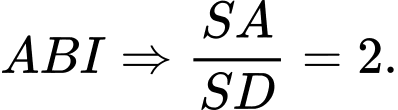

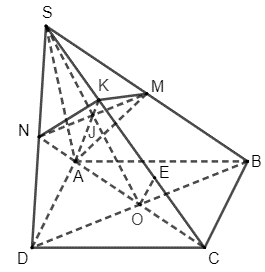
Câu 17 [274191]: Cho hình chóp 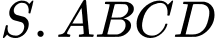 có đáy
có đáy 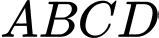 là hình bình hành. Gọi
là hình bình hành. Gọi 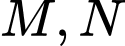 lần lượt là trung điểm của các cạnh
lần lượt là trung điểm của các cạnh 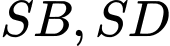 ;
; 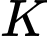 là giao điểm của mặt phẳng
là giao điểm của mặt phẳng 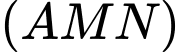 và đường thẳng
và đường thẳng 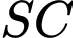 . Tỉ số
. Tỉ số 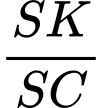 là:
là:
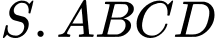 có đáy
có đáy 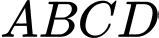 là hình bình hành. Gọi
là hình bình hành. Gọi 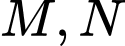 lần lượt là trung điểm của các cạnh
lần lượt là trung điểm của các cạnh 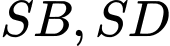 ;
; 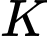 là giao điểm của mặt phẳng
là giao điểm của mặt phẳng 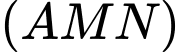 và đường thẳng
và đường thẳng 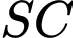 . Tỉ số
. Tỉ số 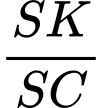 là:
là: A, 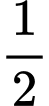 .
.
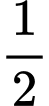 .
.B, 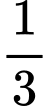 .
.
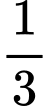 .
.C, 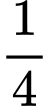 .
.
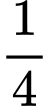 .
.D, 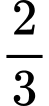 .
.
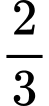 .
.
Ta có:
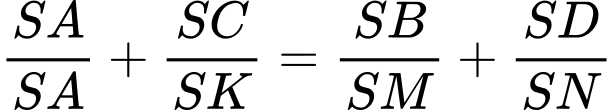
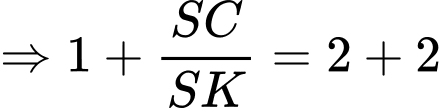
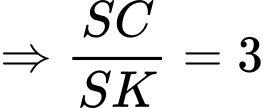
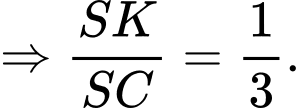
Chọn đáp án B. Đáp án: B
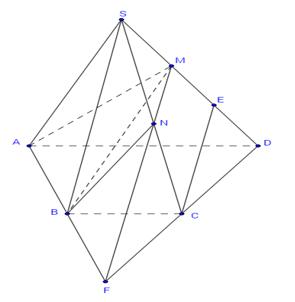
Câu 18 [296122]: Cho hình chóp 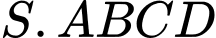 có đáy là hình thang
có đáy là hình thang 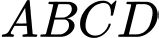 với
với 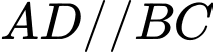 và
và 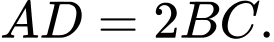 Gọi
Gọi 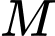 là điểm trên cạnh
là điểm trên cạnh 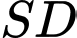 thỏa mãn
thỏa mãn 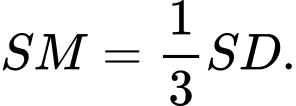 Mặt phẳng
Mặt phẳng 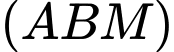 cắt cạnh bên
cắt cạnh bên 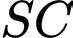 tại điểm
tại điểm 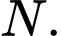 Tính tỉ số
Tính tỉ số 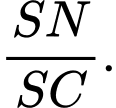
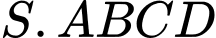 có đáy là hình thang
có đáy là hình thang 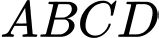 với
với 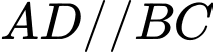 và
và 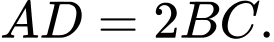 Gọi
Gọi 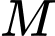 là điểm trên cạnh
là điểm trên cạnh 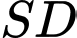 thỏa mãn
thỏa mãn 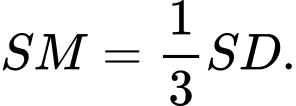 Mặt phẳng
Mặt phẳng 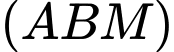 cắt cạnh bên
cắt cạnh bên 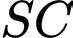 tại điểm
tại điểm 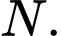 Tính tỉ số
Tính tỉ số 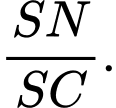
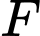 là giao điểm của
là giao điểm của  và
và 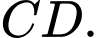 Nối
Nối 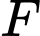 với
với 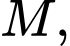
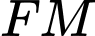 cắt
cắt 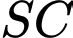 tại điểm
tại điểm 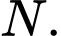 Khi đó
Khi đó 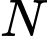 là giao điểm của
là giao điểm của 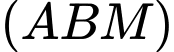 và
và 
Theo giả thiết, ta chứng minh được  là trung điểm
là trung điểm 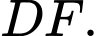
 là trung điểm
là trung điểm 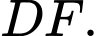
Trong mặt phẳng  kẻ
kẻ 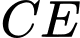 song song
song song 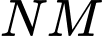 (
(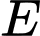 thuộc
thuộc 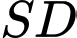 ).
).
 kẻ
kẻ 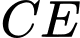 song song
song song 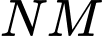 (
(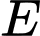 thuộc
thuộc 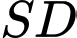 ).
). Do  là trung điểm
là trung điểm 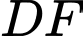 nên suy ra
nên suy ra 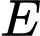 là trung điểm
là trung điểm 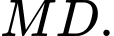
 là trung điểm
là trung điểm 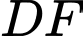 nên suy ra
nên suy ra 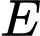 là trung điểm
là trung điểm 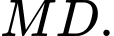
Khi đó, ta có 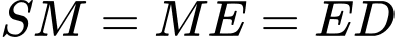 và
và 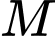 là trung điểm
là trung điểm 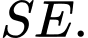
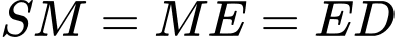 và
và 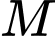 là trung điểm
là trung điểm 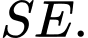
Do 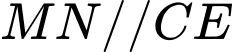 và
và 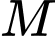 là trung điểm
là trung điểm 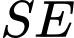 nên
nên 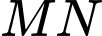 là đường trung bình của tam giác
là đường trung bình của tam giác  Từ đó suy ra
Từ đó suy ra 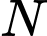 là trung điểm
là trung điểm 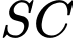 và
và 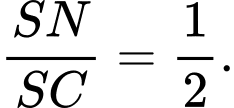
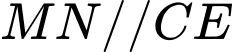 và
và 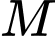 là trung điểm
là trung điểm 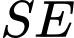 nên
nên 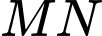 là đường trung bình của tam giác
là đường trung bình của tam giác  Từ đó suy ra
Từ đó suy ra 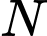 là trung điểm
là trung điểm 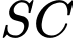 và
và 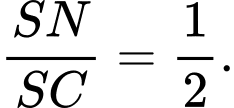
Câu 19 [229239]: (DHSP HÀ NỘI HKI 2017-2018) Cho hình chóp 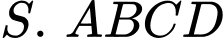 có đáy là hình bình hành. Gọi
có đáy là hình bình hành. Gọi 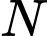 là trung điểm của cạnh
là trung điểm của cạnh 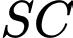 . Lấy điểm
. Lấy điểm 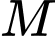 đối xứng với
đối xứng với 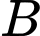 qua
qua 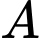 . Gọi giao điểm
. Gọi giao điểm  của đường thẳng
của đường thẳng 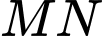 với mặt phẳng
với mặt phẳng 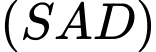 . Tính tỉ số
. Tính tỉ số 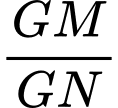 .
.
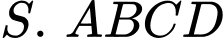 có đáy là hình bình hành. Gọi
có đáy là hình bình hành. Gọi 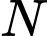 là trung điểm của cạnh
là trung điểm của cạnh 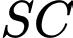 . Lấy điểm
. Lấy điểm 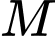 đối xứng với
đối xứng với 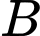 qua
qua 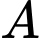 . Gọi giao điểm
. Gọi giao điểm  của đường thẳng
của đường thẳng 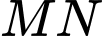 với mặt phẳng
với mặt phẳng 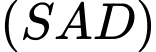 . Tính tỉ số
. Tính tỉ số 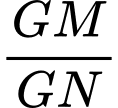 .
. A, 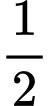 .
.
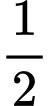 .
.B, 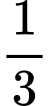 .
.
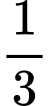 .
.C, 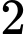 .
.
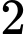 .
.D, 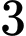 .
.
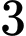 .
.
Chọn C
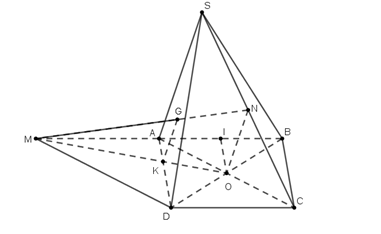
Gọi giao điểm của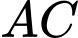 và
và 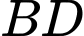 là
là  và kẻ
và kẻ 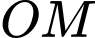 cắt
cắt 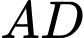 tại
tại 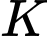 . Vì
. Vì  là trung điểm
là trung điểm 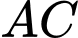 ,
,
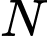 là trung điểm
là trung điểm 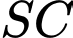 nên
nên  (tính chất đường trung bình). Vậy hai mặt phẳng
(tính chất đường trung bình). Vậy hai mặt phẳng  và
và 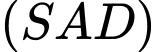 cắt nhau tại giao tuyến
cắt nhau tại giao tuyến 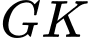 song song với
song song với 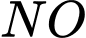 . Áp dụng định lí Talet cho
. Áp dụng định lí Talet cho
 , ta có:
, ta có:
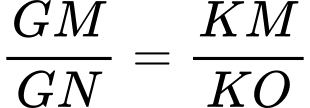 (1)
(1)
Gọi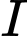 là trung điểm của
là trung điểm của  , vì
, vì  là trung điểm của
là trung điểm của 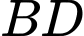 nên theo tính chất đường trung
bình,
nên theo tính chất đường trung
bình, 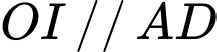 , vậy theo định lí Talet:
, vậy theo định lí Talet:
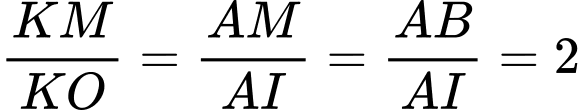 . (2)
. (2)
Từ (1) và (2), ta có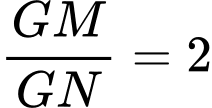 . Đáp án: C
. Đáp án: C

Gọi giao điểm của
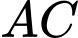 và
và 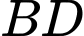 là
là  và kẻ
và kẻ 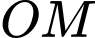 cắt
cắt 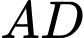 tại
tại 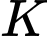 . Vì
. Vì  là trung điểm
là trung điểm 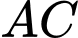 ,
,
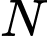 là trung điểm
là trung điểm 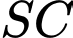 nên
nên  (tính chất đường trung bình). Vậy hai mặt phẳng
(tính chất đường trung bình). Vậy hai mặt phẳng  và
và 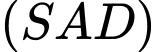 cắt nhau tại giao tuyến
cắt nhau tại giao tuyến 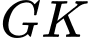 song song với
song song với 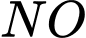 . Áp dụng định lí Talet cho
. Áp dụng định lí Talet cho
 , ta có:
, ta có: 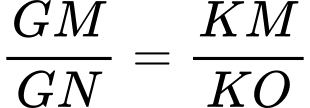 (1)
(1) Gọi
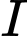 là trung điểm của
là trung điểm của  , vì
, vì  là trung điểm của
là trung điểm của 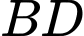 nên theo tính chất đường trung
bình,
nên theo tính chất đường trung
bình, 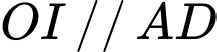 , vậy theo định lí Talet:
, vậy theo định lí Talet: 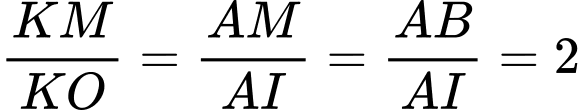 . (2)
. (2) Từ (1) và (2), ta có
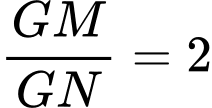 . Đáp án: C
. Đáp án: C
Câu 20 [402978]: Cho lăng trụ tam giác 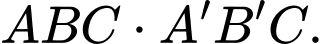 Trên đường thẳng
Trên đường thẳng 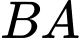 lấy điểm
lấy điểm 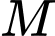 sao cho
sao cho 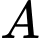 nằm giữa
nằm giữa 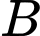 và
và 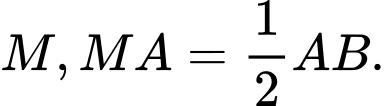 Gọi
Gọi 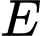 là trung điểm của
là trung điểm của 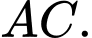 Gọi
Gọi 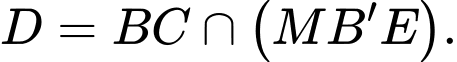 Tính tỉ số
Tính tỉ số 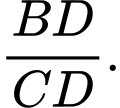
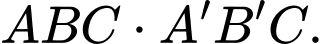 Trên đường thẳng
Trên đường thẳng 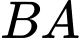 lấy điểm
lấy điểm 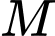 sao cho
sao cho 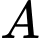 nằm giữa
nằm giữa 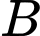 và
và 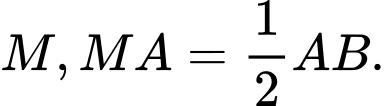 Gọi
Gọi 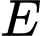 là trung điểm của
là trung điểm của 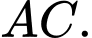 Gọi
Gọi 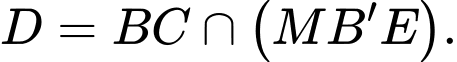 Tính tỉ số
Tính tỉ số 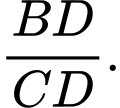
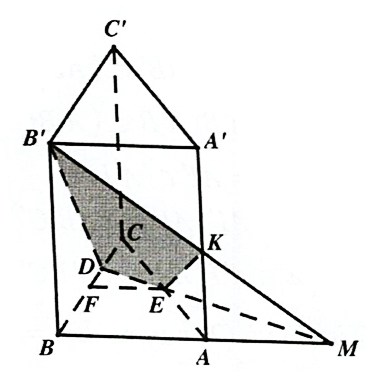
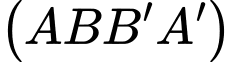 gọi
gọi 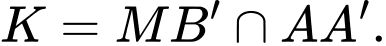 Trong
Trong 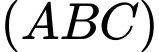 gọi
gọi 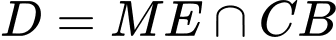 Thiết diện là tứ giác
Thiết diện là tứ giác 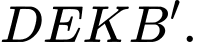
- Kẻ 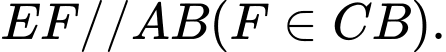 Khi đó
Khi đó 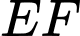 là đường trung bình của tam giác
là đường trung bình của tam giác 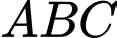 và
và 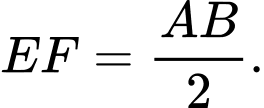
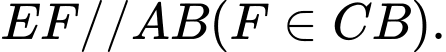 Khi đó
Khi đó 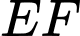 là đường trung bình của tam giác
là đường trung bình của tam giác 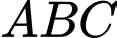 và
và 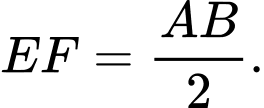
Xét tam giác 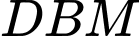 ta có:
ta có: 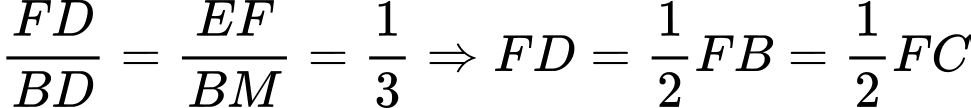 tức
tức 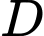 là trung điểm của
là trung điểm của 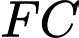 do đó
do đó 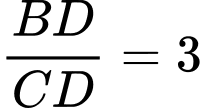
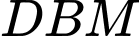 ta có:
ta có: 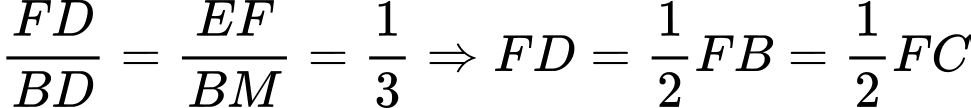 tức
tức 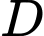 là trung điểm của
là trung điểm của 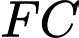 do đó
do đó 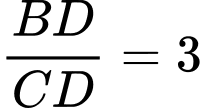
Câu 21 [582121]: Cho hình lăng trụ tam giác  Gọi
Gọi 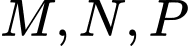 lần lượt là trung điểm của các cạnh
lần lượt là trung điểm của các cạnh 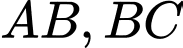 và
và 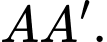 Gọi
Gọi 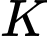 là giao điểm của mặt phẳng
là giao điểm của mặt phẳng 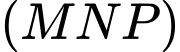 với đường thẳng
với đường thẳng 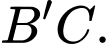 Tính tỉ số
Tính tỉ số 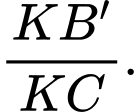
 Gọi
Gọi 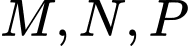 lần lượt là trung điểm của các cạnh
lần lượt là trung điểm của các cạnh 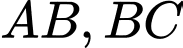 và
và 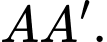 Gọi
Gọi 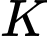 là giao điểm của mặt phẳng
là giao điểm của mặt phẳng 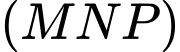 với đường thẳng
với đường thẳng 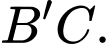 Tính tỉ số
Tính tỉ số 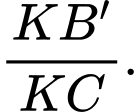
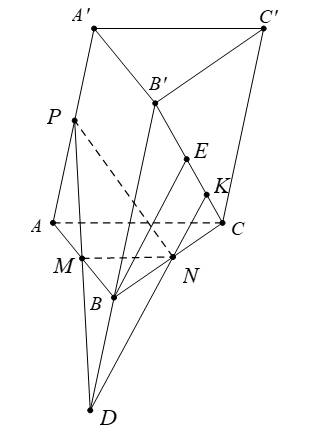
Trong mặt phẳng 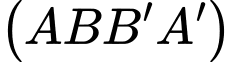 gọi
gọi 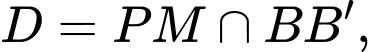
Trong mặt phẳng 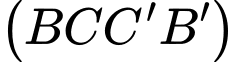 gọi
gọi 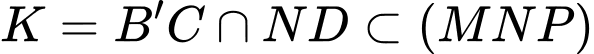
Suy ra 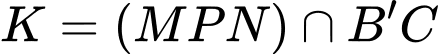
Dựng 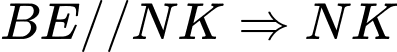 là đường trung bình của
là đường trung bình của 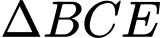 nên
nên  (1)
(1)
Lại có 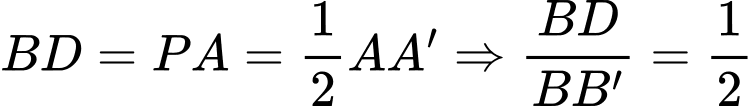
Suy ra 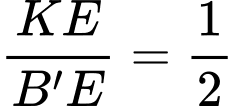 (2)
(2)
Từ (1) và (2) suy ra 
Câu 22 [402979]: Cho tứ diện 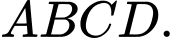 Gọi
Gọi 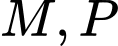 lần lượt là trung điểm các cạnh
lần lượt là trung điểm các cạnh 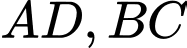 còn
còn 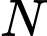 là điểm trên cạnh
là điểm trên cạnh  sao cho
sao cho 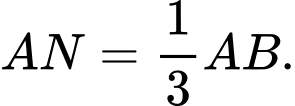 Gọi
Gọi  là giao điểm của
là giao điểm của 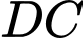 với
với 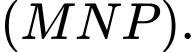
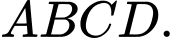 Gọi
Gọi 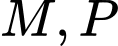 lần lượt là trung điểm các cạnh
lần lượt là trung điểm các cạnh 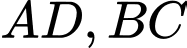 còn
còn 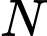 là điểm trên cạnh
là điểm trên cạnh  sao cho
sao cho 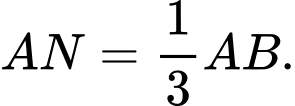 Gọi
Gọi  là giao điểm của
là giao điểm của 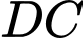 với
với 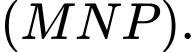
Tính tỉ số 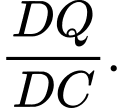
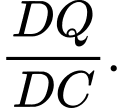
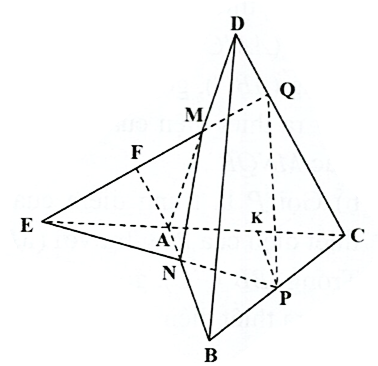
- Trong
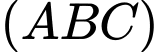 gọi
gọi  Trong
Trong 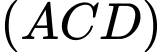 gọi
gọi 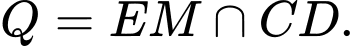
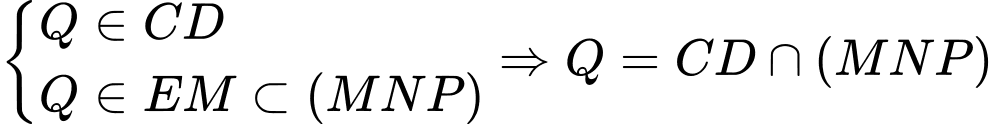
- Kẻ
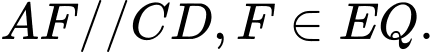 Kẻ
Kẻ 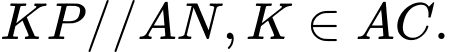
Ta có:
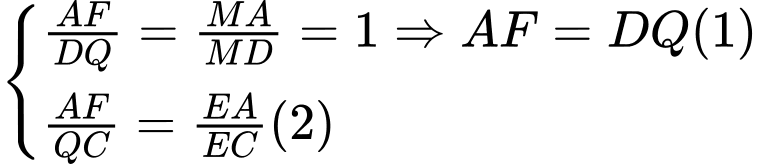
Do
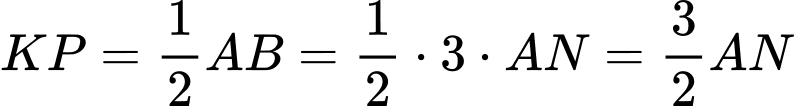 nên
nên 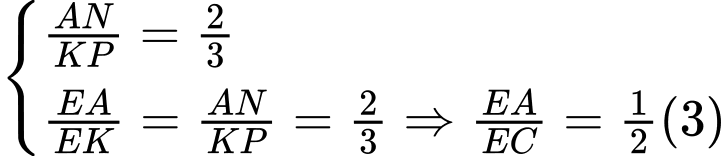
Từ (1), (2), (3) suy ra
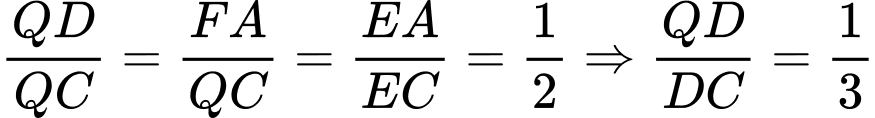
Câu 23 [229244]: (CHUYÊN LONG AN - LẦN 1 - 2018) Cho hình chóp 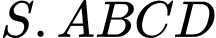 có đáy là hình bình hành. Gọi
có đáy là hình bình hành. Gọi 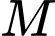 ,
, 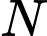 lần lượt là trung điểm của
lần lượt là trung điểm của  ,
, 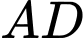 và
và  là trọng tâm tam giác
là trọng tâm tam giác 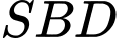 . Mặt phẳng
. Mặt phẳng 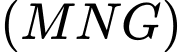 cắt
cắt 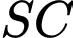 tại điểm
tại điểm 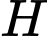 . Tính
. Tính 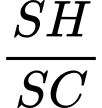
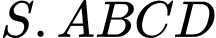 có đáy là hình bình hành. Gọi
có đáy là hình bình hành. Gọi 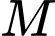 ,
, 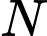 lần lượt là trung điểm của
lần lượt là trung điểm của  ,
, 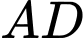 và
và  là trọng tâm tam giác
là trọng tâm tam giác 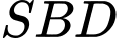 . Mặt phẳng
. Mặt phẳng 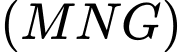 cắt
cắt 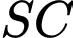 tại điểm
tại điểm 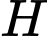 . Tính
. Tính 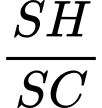
A, 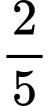 .
.
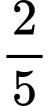 .
.B, 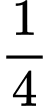 .
.
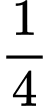 .
.C, 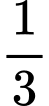 .
.
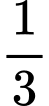 .
.D, 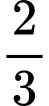 .
.
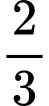 .
.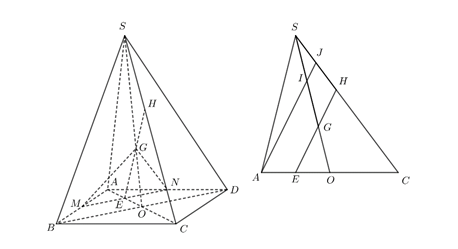
Trong mặt phẳng
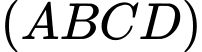 , gọi
, gọi 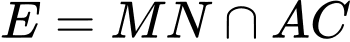 .
.Trong mặt phẳng
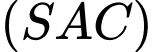 , gọi
, gọi 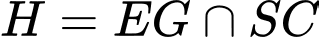 .
.Ta có:
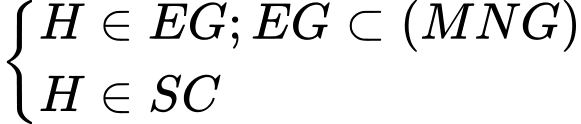
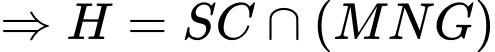 .
.Gọi
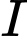 ,
, 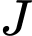 lần lượt là trung điểm của
lần lượt là trung điểm của 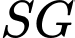 và
và 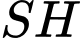 .
.Ta có
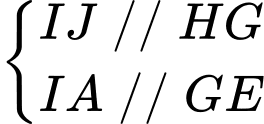
 ,
,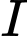 ,
,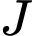 thẳng hàng
thẳng hàngXét
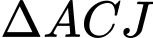 có
có 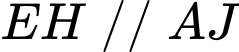
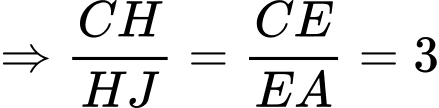
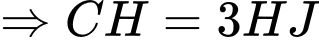 .
.Lại có
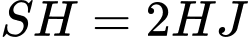 nên
nên 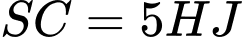 .
.Vậy
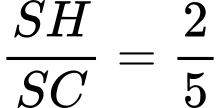 . Đáp án: A
. Đáp án: A