Đáp án Bài tập tự luyện
Câu 1 [229233]: (HKI_L11-NGUYỄN GIA THIỀU - HÀ NỘI 1718) Cho hình chóp 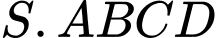 có đáy
có đáy 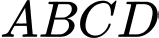 là hình thang với đáy lớn
là hình thang với đáy lớn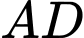 ,
, 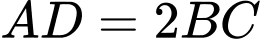 . Gọi
. Gọi  và
và 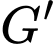 lần lượt là trọng tâm tam giác
lần lượt là trọng tâm tam giác 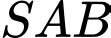 và
và 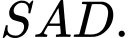
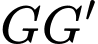 song song với đường thẳng
song song với đường thẳng
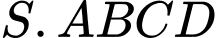 có đáy
có đáy 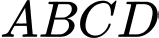 là hình thang với đáy lớn
là hình thang với đáy lớn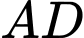 ,
, 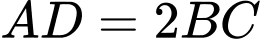 . Gọi
. Gọi  và
và 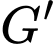 lần lượt là trọng tâm tam giác
lần lượt là trọng tâm tam giác 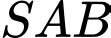 và
và 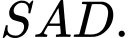
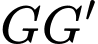 song song với đường thẳng
song song với đường thẳng A,  .
.
 .
.B, 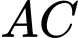 .
.
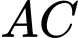 .
.C, 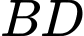 .
.
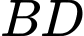 .
.D,  .
.
 .
.
Chọn C
Gọi và
và 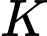 lần lượt là trung điểm cạnh
lần lượt là trung điểm cạnh 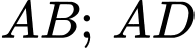 . Với
. Với  và
và 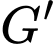 lần lượt là trọng tâm tam giác
lần lượt là trọng tâm tam giác 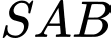 và
và 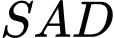 ta có:
ta có: 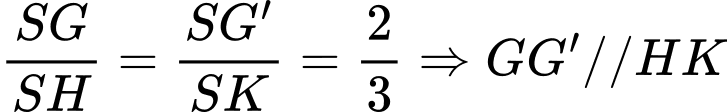 (1).
(1).
Mà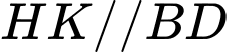 (
(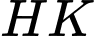 là đường trung bình tam giác
là đường trung bình tam giác 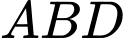 (2).
(2).
Từ (1) và (2) suy ra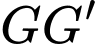 song song với
song song với 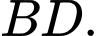 Đáp án: C
Đáp án: C

Gọi
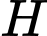 và
và 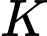 lần lượt là trung điểm cạnh
lần lượt là trung điểm cạnh 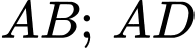 . Với
. Với  và
và 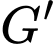 lần lượt là trọng tâm tam giác
lần lượt là trọng tâm tam giác 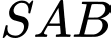 và
và 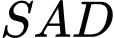 ta có:
ta có: 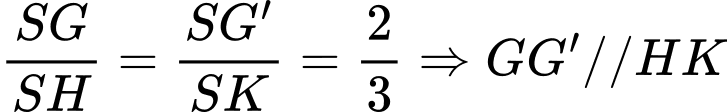 (1).
(1). Mà
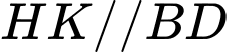 (
(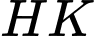 là đường trung bình tam giác
là đường trung bình tam giác 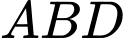 (2).
(2). Từ (1) và (2) suy ra
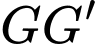 song song với
song song với 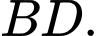 Đáp án: C
Đáp án: C
Câu 2 [229236]: Cho tứ diện 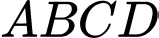 . Gọi
. Gọi 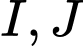 lần lượt là trọng tâm của các tam giác
lần lượt là trọng tâm của các tam giác 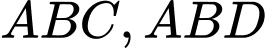 . Đường thẳng
. Đường thẳng  song song với đường thẳng:
song song với đường thẳng:
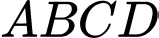 . Gọi
. Gọi 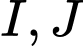 lần lượt là trọng tâm của các tam giác
lần lượt là trọng tâm của các tam giác 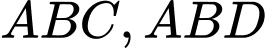 . Đường thẳng
. Đường thẳng  song song với đường thẳng:
song song với đường thẳng: A, 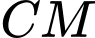 trong đó
trong đó 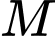 là trung điểm
là trung điểm 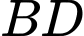 .
.
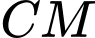 trong đó
trong đó 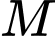 là trung điểm
là trung điểm 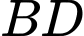 .
.B, 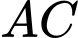 .
.
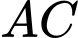 .
.C, 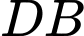 .
.
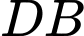 .
.D, 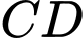 .
.
 .
.Đáp án D.
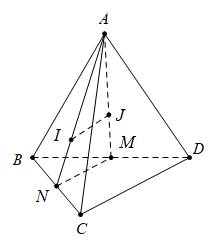
Cách 1: ( Đưa về cùng mặt phẳng và vận dụng kiến thức hình học phẳng)
Gọi  là trung điểm của
là trung điểm của  . Ta có
. Ta có  nên suy ra
nên suy ra  và
và 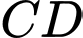 đồng phẳng.
đồng phẳng.
Do 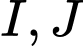 lần lượt là trọng tâm của các tam giác
lần lượt là trọng tâm của các tam giác 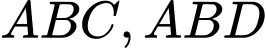 nên ta có:
nên ta có: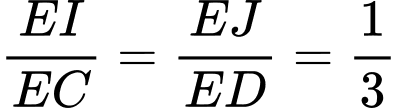 . Suy ra
. Suy ra  .
.
Cách 2: ( Sử dụng tính chất bắc cầu)
Gọi 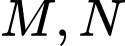 lần lượt là trung điểm của
lần lượt là trung điểm của 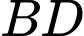 và
và 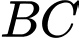 . Suy ra
. Suy ra  (1).
(1).
Do 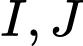 lần lượt là trọng tâm của các tam giác
lần lượt là trọng tâm của các tam giác 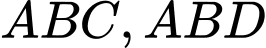 nên ta có:
nên ta có: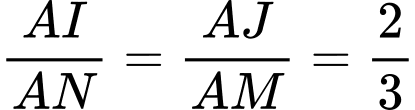 . Suy ra
. Suy ra 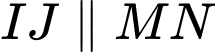 (2).
(2).
Từ (1) và (2) suy ra  .
.
Cách 3: (Sử dụng định lí giao tuyến của 3 mặt phẳng).
Có lẽ trong ví dụ này cách này hơi dài, song chúng tôi vẫn sẽ trình bày ở đây, để các bạn có thể hiểu và vận dụng cách 3 hợp lí trong các ví dụ khác.
Dễ thấy, bốn điểm 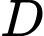 ,
,  ,
, 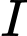 ,
, 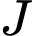 đồng phẳng.
đồng phẳng.
Ta có: 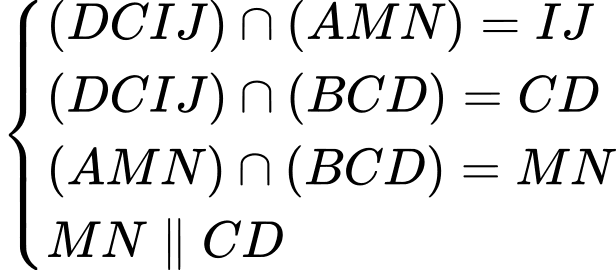

Câu 3 [229252]: Cho tứ diện 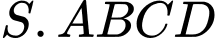 có đáy
có đáy 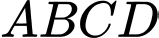 là hình thang
là hình thang  . Gọi
. Gọi 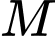 ,
,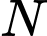 và
và 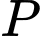 lần lượt là trung điểm của
lần lượt là trung điểm của 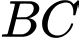 ,
, 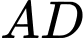 và
và 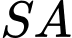 . Giao tuyến của hai mặt phẳng
. Giao tuyến của hai mặt phẳng 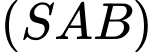 và
và 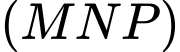 là
là
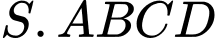 có đáy
có đáy 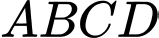 là hình thang
là hình thang  . Gọi
. Gọi 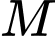 ,
,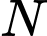 và
và 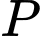 lần lượt là trung điểm của
lần lượt là trung điểm của 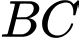 ,
, 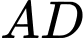 và
và 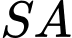 . Giao tuyến của hai mặt phẳng
. Giao tuyến của hai mặt phẳng 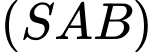 và
và 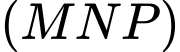 là
là A, đường thẳng qua 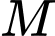 và song song với
và song song với 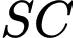 .
.
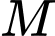 và song song với
và song song với 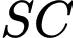 .
.B, đường thẳng qua 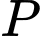 và song song với
và song song với  .
.
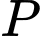 và song song với
và song song với  .
.C, đường thẳng 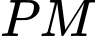 .
.
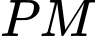 .
.D, đường thẳng qua 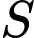 và song song với
và song song với  .
.
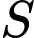 và song song với
và song song với  .
.
Chọn B
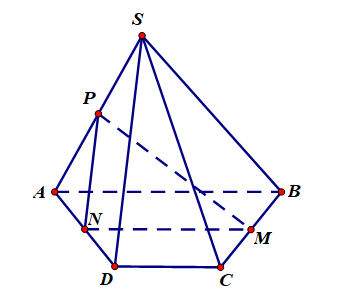
Ta có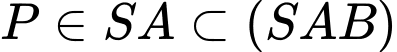 ;
; 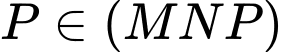 nên
nên 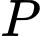 là điểm chung thứ nhất của mặt phẳng
là điểm chung thứ nhất của mặt phẳng 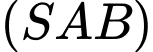 và
và
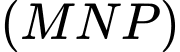 .
.
Mặt khác: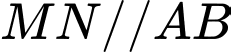 ( do
( do 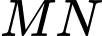 là đường trung bình của hình thang
là đường trung bình của hình thang 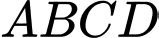 ).
).
Vậy giao tuyến của hai mặt phẳng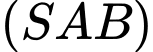 và
và 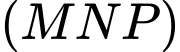 là đường thẳng qua
là đường thẳng qua 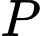 và song song
với
và song song
với  ,
, 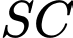 . Đáp án: B
. Đáp án: B

Ta có
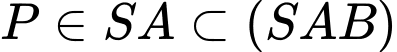 ;
; 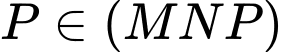 nên
nên 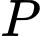 là điểm chung thứ nhất của mặt phẳng
là điểm chung thứ nhất của mặt phẳng 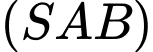 và
và
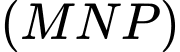 .
.Mặt khác:
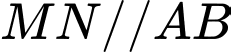 ( do
( do 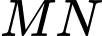 là đường trung bình của hình thang
là đường trung bình của hình thang 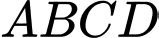 ).
).Vậy giao tuyến của hai mặt phẳng
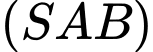 và
và 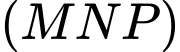 là đường thẳng qua
là đường thẳng qua 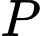 và song song
với
và song song
với  ,
, 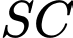 . Đáp án: B
. Đáp án: B
Câu 4 [229253]: Cho hình chóp 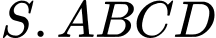 có đáy
có đáy 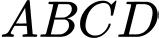 là hình thang
là hình thang  . Gọi
. Gọi 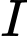 ,
, 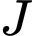 lần lượt là trung điểm của
lần lượt là trung điểm của 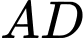 và
và 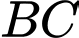 ,
,  là trọng tâm
là trọng tâm 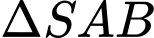 . Giao tuyến của hai mặt phẳng
. Giao tuyến của hai mặt phẳng 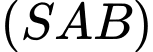 và
và  là
là
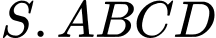 có đáy
có đáy 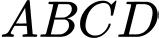 là hình thang
là hình thang  . Gọi
. Gọi 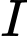 ,
, 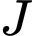 lần lượt là trung điểm của
lần lượt là trung điểm của 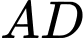 và
và 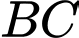 ,
,  là trọng tâm
là trọng tâm 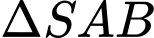 . Giao tuyến của hai mặt phẳng
. Giao tuyến của hai mặt phẳng 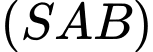 và
và  là
là A, đường thẳng qua 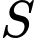 và song song với
và song song với  .
.
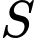 và song song với
và song song với  .
.B, đường thẳng qua  và song song với
và song song với  .
.
 và song song với
và song song với  .
.C, 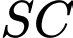 .
.
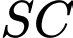 .
.D, đường thẳng qua  và cắt
và cắt 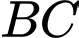 .
.
 và cắt
và cắt 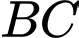 .
.
Chọn B.
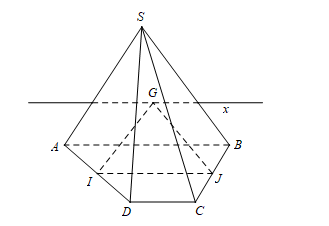
Ta có (đường trung bình hình thang ).
(đường trung bình hình thang ).
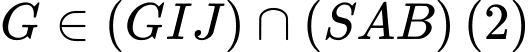 .
.
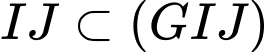 ,
,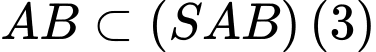
Từ ,
,  ,
, ,
,  ,
,  .
.
Đáp án: B

Ta có
 (đường trung bình hình thang ).
(đường trung bình hình thang ). 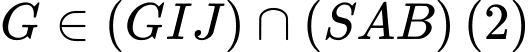 .
.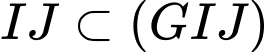 ,
,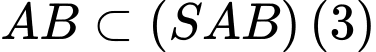
Từ
 ,
,  ,
, ,
,  ,
,  .
.Đáp án: B
Câu 5 [229617]: Cho tứ diện 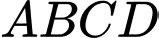 . Gọi
. Gọi 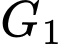 và
và 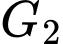 lần lượt là trọng tâm các tam giác
lần lượt là trọng tâm các tam giác  và
và  . Khẳng định nào sau đây SAI?
. Khẳng định nào sau đây SAI?
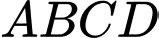 . Gọi
. Gọi 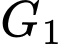 và
và 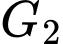 lần lượt là trọng tâm các tam giác
lần lượt là trọng tâm các tam giác  và
và  . Khẳng định nào sau đây SAI?
. Khẳng định nào sau đây SAI? A, 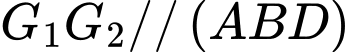 .
.
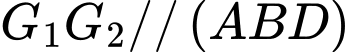 .
.B, 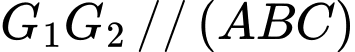 .
.
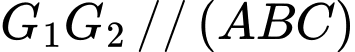 .
.C, 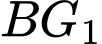 ,
, 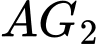 và
và 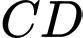 đồng quy.
đồng quy.
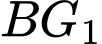 ,
, 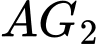 và
và 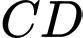 đồng quy.
đồng quy.D, 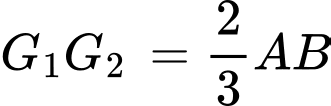 .
.
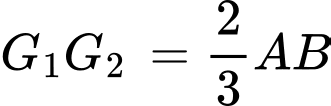 .
.
Chọn D
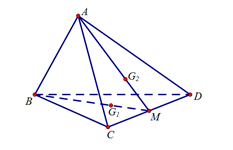
Gọi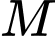 là trung điểm
là trung điểm 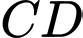
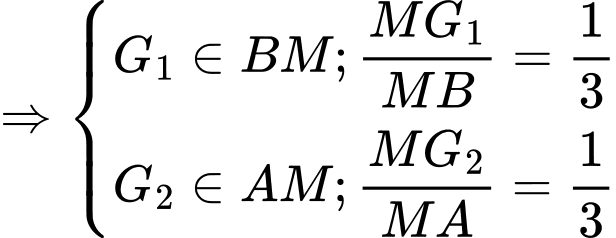
Xét tam giác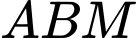 , ta có
, ta có 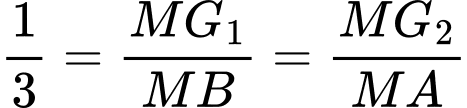
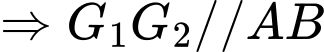 (định lí Thales đảo)
(định lí Thales đảo)
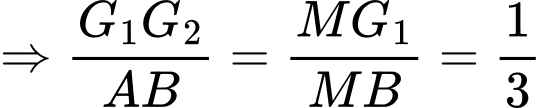
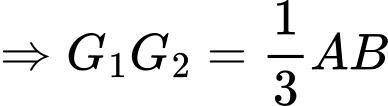 . Đáp án: D
. Đáp án: D

Gọi
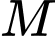 là trung điểm
là trung điểm 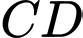
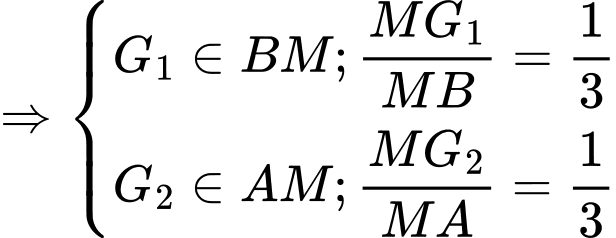
Xét tam giác
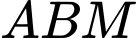 , ta có
, ta có 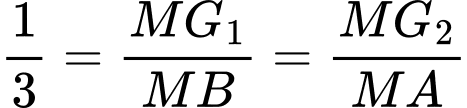
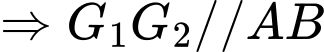 (định lí Thales đảo)
(định lí Thales đảo) 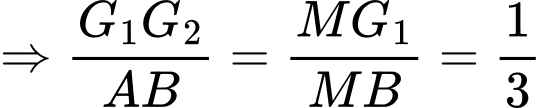
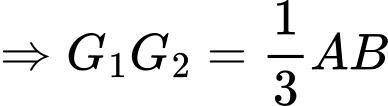 . Đáp án: D
. Đáp án: D
Câu 6 [229622]: Cho hình chóp 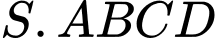 có đáy là hình bình hành. Các điểm
có đáy là hình bình hành. Các điểm 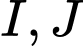 lần lượt là trọng tâm các tam giác
lần lượt là trọng tâm các tam giác 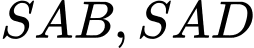 .
. 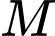 là trung điểm
là trung điểm 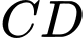 . Chọn mệnh đề đúng trong các mệnh đề sau:
. Chọn mệnh đề đúng trong các mệnh đề sau:
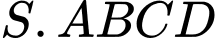 có đáy là hình bình hành. Các điểm
có đáy là hình bình hành. Các điểm 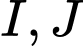 lần lượt là trọng tâm các tam giác
lần lượt là trọng tâm các tam giác 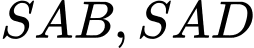 .
. 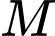 là trung điểm
là trung điểm 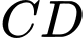 . Chọn mệnh đề đúng trong các mệnh đề sau:
. Chọn mệnh đề đúng trong các mệnh đề sau: A, 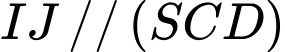 .
.
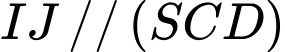 .
.B,  .
.
 .
.C, 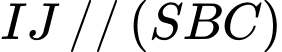 .
.
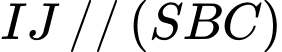 .
.D,  .
.
 .
.
Chọn D
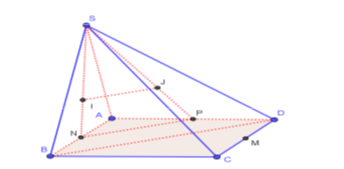
Gọi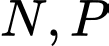 lần lượt là trung điểm của cạnh
lần lượt là trung điểm của cạnh 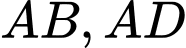 .
.
Xét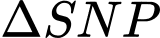 có
có 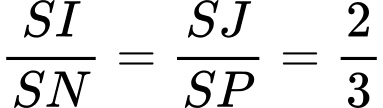
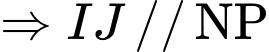 .
.
Xét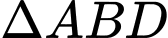 có
có 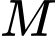 là đường trung bình trong tam giác
là đường trung bình trong tam giác 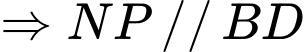 .
.
Suy ra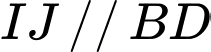 .
.
Ta có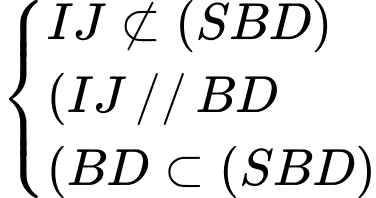
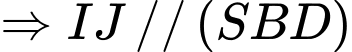 . Đáp án: D
. Đáp án: D

Gọi
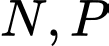 lần lượt là trung điểm của cạnh
lần lượt là trung điểm của cạnh 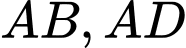 .
.Xét
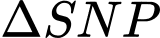 có
có 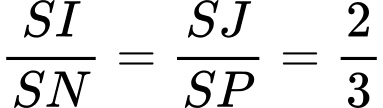
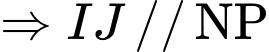 .
.Xét
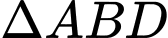 có
có 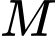 là đường trung bình trong tam giác
là đường trung bình trong tam giác 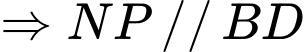 .
.Suy ra
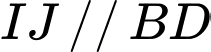 .
.Ta có
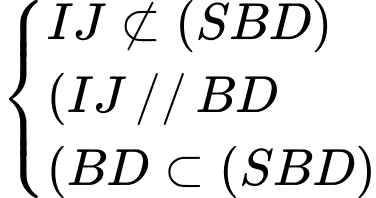
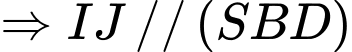 . Đáp án: D
. Đáp án: D
Câu 7 [229726]: (THPT Yên Định - Thanh Hóa - Lần 1 - 2017 - 2018 - BTN) Cho hình chóp 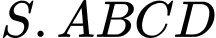 có đáy
có đáy 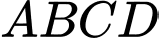 là hình bình hành tâm
là hình bình hành tâm  . Gọi
. Gọi 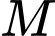 ,
, 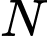 ,
, 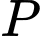 theo thứ tự là trung điểm của
theo thứ tự là trung điểm của 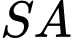 ,
, 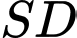 và
và  . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
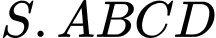 có đáy
có đáy 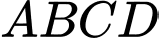 là hình bình hành tâm
là hình bình hành tâm  . Gọi
. Gọi 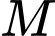 ,
, 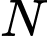 ,
, 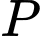 theo thứ tự là trung điểm của
theo thứ tự là trung điểm của 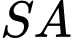 ,
, 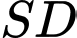 và
và  . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng? A, 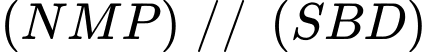 .
.
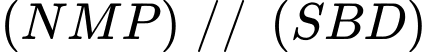 .
.B,  cắt
cắt 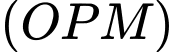 .
.
 cắt
cắt 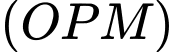 .
.C,  .
.
 .
.D, 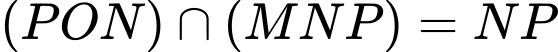 .
.
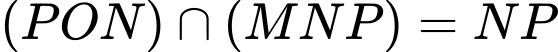 .
.
Chọn C
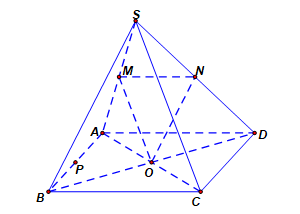
Xét hai mặt phẳng và
và 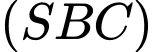 .
.
Ta có: và
và  .
.
Mà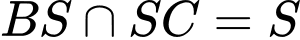 và
và  .
.
Do đó . Đáp án: C
. Đáp án: C

Xét hai mặt phẳng
 và
và 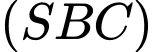 .
.Ta có:
 và
và  .
.Mà
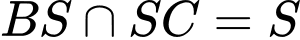 và
và  .
.Do đó
 . Đáp án: C
. Đáp án: C
Câu 8 [229722]: Cho hình hộp  . Mặt phẳng
. Mặt phẳng 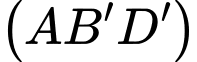 song song với mặt phẳng nào trong các mặt phẳng sau đây?
song song với mặt phẳng nào trong các mặt phẳng sau đây?
 . Mặt phẳng
. Mặt phẳng 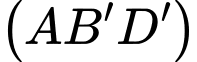 song song với mặt phẳng nào trong các mặt phẳng sau đây?
song song với mặt phẳng nào trong các mặt phẳng sau đây? A, 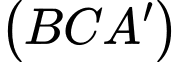 .
.
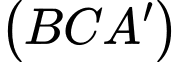 .
.B, 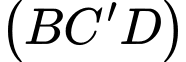 .
.
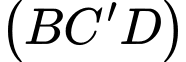 .
.C,  .
.
 .
.D, 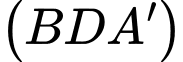 .
.
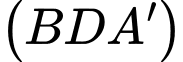 .
.
Chọn B
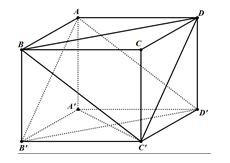
Do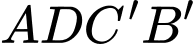 là hình bình hành nên
là hình bình hành nên 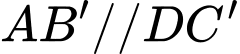 , và
, và 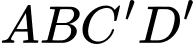 là hình bình hành nên
là hình bình hành nên 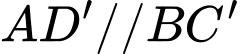 nên
nên 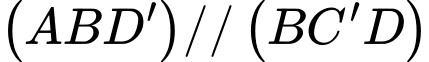 . Đáp án: B
. Đáp án: B

Do
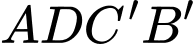 là hình bình hành nên
là hình bình hành nên 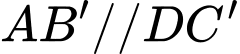 , và
, và 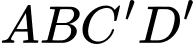 là hình bình hành nên
là hình bình hành nên 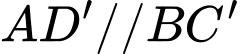 nên
nên 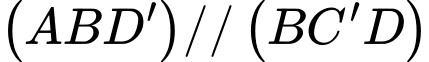 . Đáp án: B
. Đáp án: B
Câu 9 [272846]: Cho hình chóp tứ giác đều 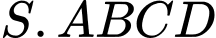 có cạnh đáy bằng
có cạnh đáy bằng 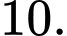
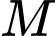 là điểm trên
là điểm trên 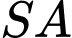 sao cho
sao cho 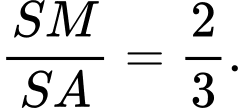 Một mặt phẳng
Một mặt phẳng  đi qua
đi qua 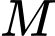 song song với
song song với  và
và 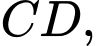 cắt hình chóp theo một tứ giác có diện tích là
cắt hình chóp theo một tứ giác có diện tích là
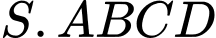 có cạnh đáy bằng
có cạnh đáy bằng 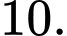
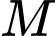 là điểm trên
là điểm trên 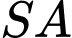 sao cho
sao cho 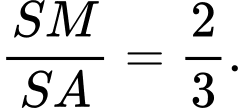 Một mặt phẳng
Một mặt phẳng  đi qua
đi qua 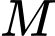 song song với
song song với  và
và 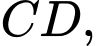 cắt hình chóp theo một tứ giác có diện tích là
cắt hình chóp theo một tứ giác có diện tích là A, 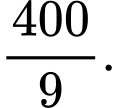
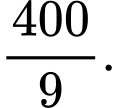
B, 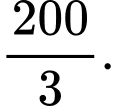
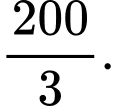
C, 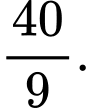
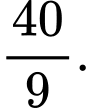
D, 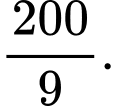
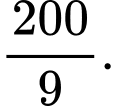
Chọn đáp án A.
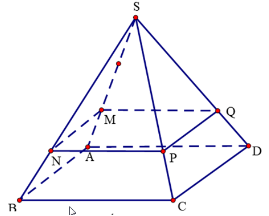
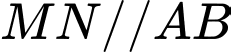
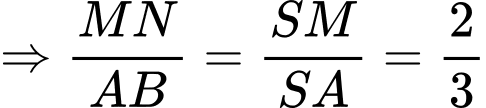
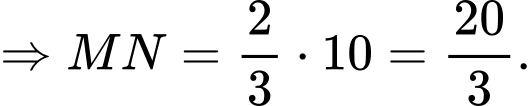
Dễ dàng chứng minh được: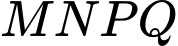 là hình vuông.
là hình vuông.
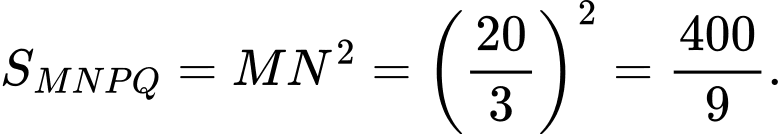 Đáp án: A
Đáp án: A

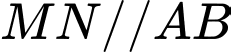
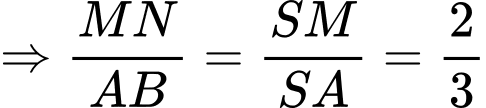
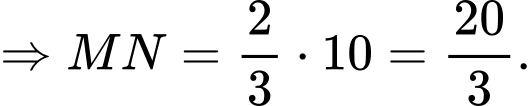
Dễ dàng chứng minh được:
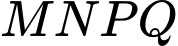 là hình vuông.
là hình vuông. 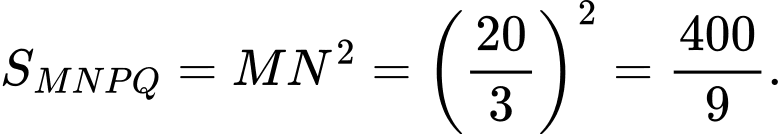 Đáp án: A
Đáp án: A
Câu 10 [295555]: Cho hình chóp 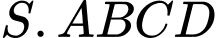 có đáy
có đáy 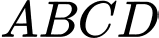 là hình bình hành. Gọi
là hình bình hành. Gọi 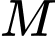 là điểm thuộc cạnh
là điểm thuộc cạnh 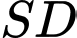 sao cho
sao cho 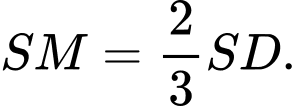 Mặt phẳng chứa
Mặt phẳng chứa  và song song với
và song song với 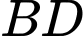 cắt cạnh
cắt cạnh 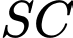 tại
tại 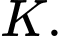 Tỷ số
Tỷ số 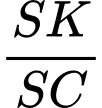 bằng
bằng
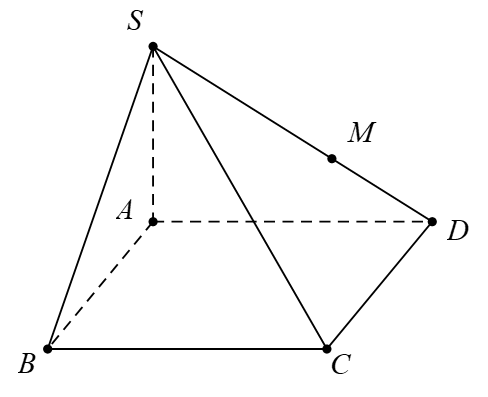
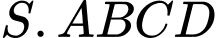 có đáy
có đáy 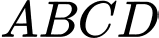 là hình bình hành. Gọi
là hình bình hành. Gọi 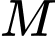 là điểm thuộc cạnh
là điểm thuộc cạnh 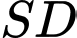 sao cho
sao cho 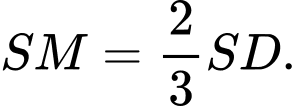 Mặt phẳng chứa
Mặt phẳng chứa  và song song với
và song song với 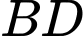 cắt cạnh
cắt cạnh 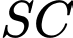 tại
tại 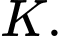 Tỷ số
Tỷ số 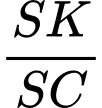 bằng
bằng

A, 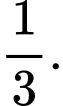
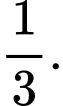
B, 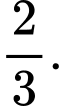
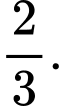
C, 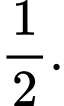
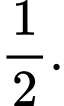
D, 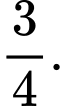
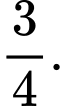
a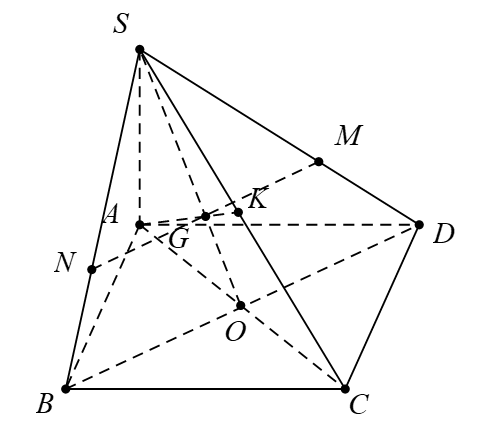
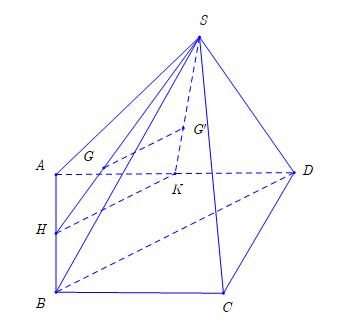
Trong mặt phẳng 
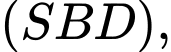 từ
từ 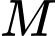 dựng đường thẳng song song với
dựng đường thẳng song song với 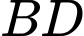 cắt
cắt 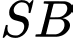 tại
tại 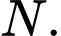 Gọi
Gọi  là tâm hình bình hành
là tâm hình bình hành 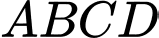 , trong mặt phẳng
, trong mặt phẳng 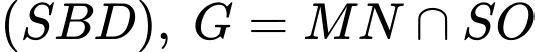 thì
thì 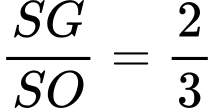 suy ra
suy ra  là trọng tâm tam giác SAC nên AG là đường trung tuyến suy ra K là trung điểm của SC Đáp án: C
là trọng tâm tam giác SAC nên AG là đường trung tuyến suy ra K là trung điểm của SC Đáp án: C
Câu 11 [295922]: Cho tứ diện 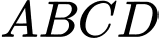 ,
,  là trọng tâm của tam giác
là trọng tâm của tam giác 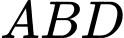 ,
, 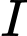 nằm trên cạnh
nằm trên cạnh 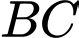 sao cho
sao cho 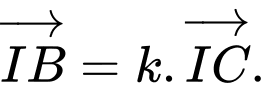 Biết đường thẳng
Biết đường thẳng 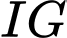 song song với mặt phẳng
song song với mặt phẳng 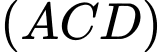 . Khẳng định nào dưới đây là đúng về số thực
. Khẳng định nào dưới đây là đúng về số thực 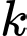 ?
?
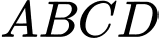 ,
,  là trọng tâm của tam giác
là trọng tâm của tam giác 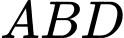 ,
, 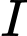 nằm trên cạnh
nằm trên cạnh 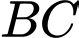 sao cho
sao cho 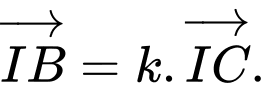 Biết đường thẳng
Biết đường thẳng 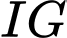 song song với mặt phẳng
song song với mặt phẳng 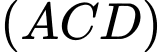 . Khẳng định nào dưới đây là đúng về số thực
. Khẳng định nào dưới đây là đúng về số thực 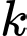 ?
? A,  .
.
 .
.B, 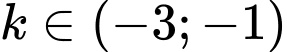 .
.
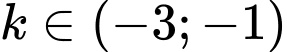 .
.C,  .
.
 .
.D, 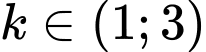 .
.
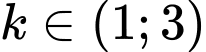 .
.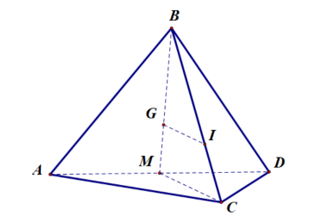
Gọi
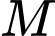 là trung điểm của
là trung điểm của 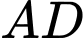 khi đó ta có
khi đó ta có 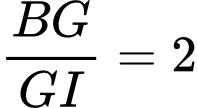 .
.
Theo giả thiết
 song song với mặt phẳng
song song với mặt phẳng 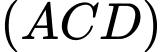 nên
nên  song song với
song song với 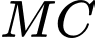 .
.
Trong mặt phẳng
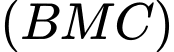 có
có 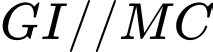 và
và 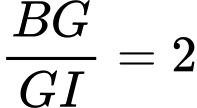 nên suy ra
nên suy ra 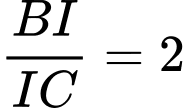 hay
hay 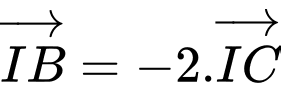 .
.
Vậy
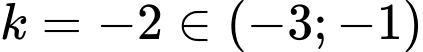 .
Đáp án: B
.
Đáp án: B
Câu 12 [579675]: [Đề mẫu HSA 2024]: Cho hình chóp 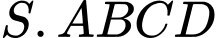 có đáy
có đáy 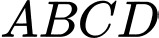 là hình bình hành tâm
là hình bình hành tâm  Gọi
Gọi 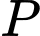 là trung điểm của
là trung điểm của 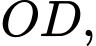 điểm
điểm 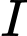 thuộc cạnh
thuộc cạnh 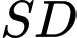 sao cho đường thẳng
sao cho đường thẳng 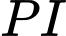 song song mặt phẳng
song song mặt phẳng 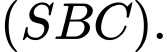 Tính tỉ số
Tính tỉ số 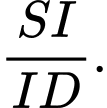
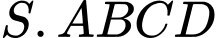 có đáy
có đáy 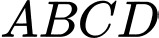 là hình bình hành tâm
là hình bình hành tâm  Gọi
Gọi 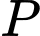 là trung điểm của
là trung điểm của 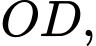 điểm
điểm 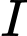 thuộc cạnh
thuộc cạnh 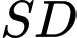 sao cho đường thẳng
sao cho đường thẳng 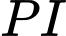 song song mặt phẳng
song song mặt phẳng 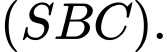 Tính tỉ số
Tính tỉ số 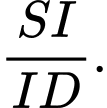
A, 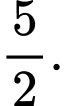
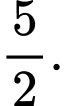
B, 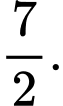
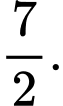
C, 3.
D, 4.
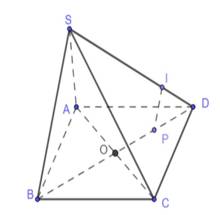
Vẽ
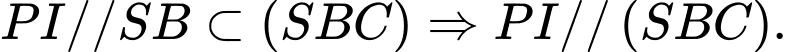
Có
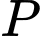 là trung điểm của
là trung điểm của 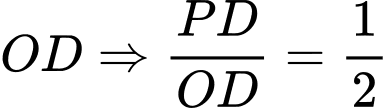 và
và  là trung điểm
là trung điểm 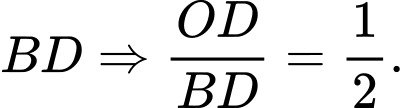
Suy ra
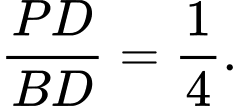
Có
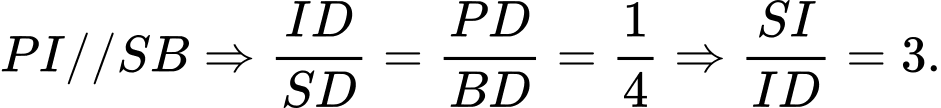
Chọn C. Đáp án: C
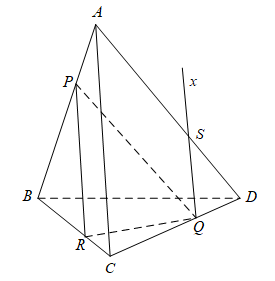
Câu 13 [229241]: Cho tứ diện 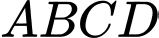 . Lấy ba điểm
. Lấy ba điểm  lần lượt trên ba cạnh
lần lượt trên ba cạnh  ,
, 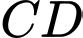 ,
, 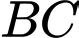 sao cho
sao cho 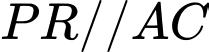 và
và 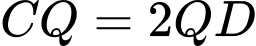 . Gọi giao điểm của đường thẳng
. Gọi giao điểm của đường thẳng 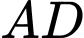 và mặt phẳng
và mặt phẳng 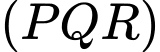 là
là 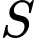 . Khẳng định nào dưới đây là đúng?
. Khẳng định nào dưới đây là đúng?
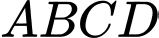 . Lấy ba điểm
. Lấy ba điểm  lần lượt trên ba cạnh
lần lượt trên ba cạnh  ,
, 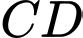 ,
, 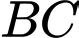 sao cho
sao cho 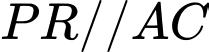 và
và 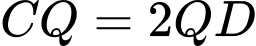 . Gọi giao điểm của đường thẳng
. Gọi giao điểm của đường thẳng 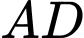 và mặt phẳng
và mặt phẳng 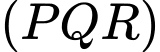 là
là 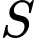 . Khẳng định nào dưới đây là đúng?
. Khẳng định nào dưới đây là đúng? A, 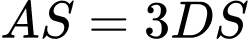 .
.
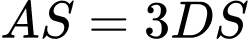 .
.B, 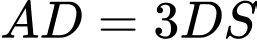 .
.
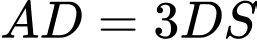 .
.C, 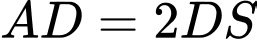 .
.
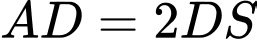 .
.D,  .
.
 .
.
Ta có:
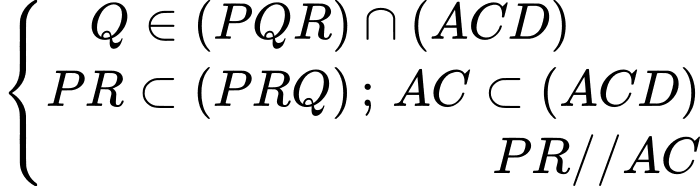
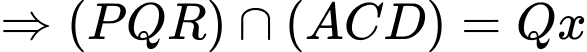 với
với 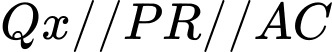
Gọi
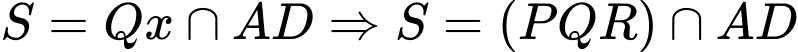
Xét tam giác
 có
có 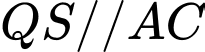
Ta có:
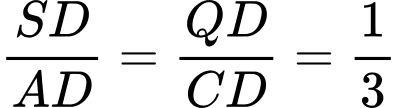
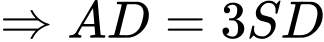 .
.Đáp án: B
Câu 14 [229237]: (HKI-Chuyên Hà Nội - Amsterdam 2017-2018) Cho hình chóp 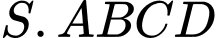 có đáy
có đáy 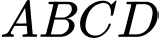 là hình chữ nhật. Gọi
là hình chữ nhật. Gọi 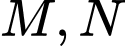 theo thứ tự là trọng tâm
theo thứ tự là trọng tâm 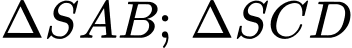 . Gọi I là giao điểm của các đường thẳng
. Gọi I là giao điểm của các đường thẳng 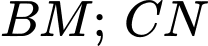 . Khi đó tỉ số
. Khi đó tỉ số 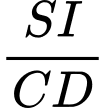 bằng
bằng
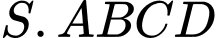 có đáy
có đáy 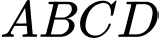 là hình chữ nhật. Gọi
là hình chữ nhật. Gọi 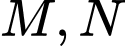 theo thứ tự là trọng tâm
theo thứ tự là trọng tâm 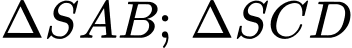 . Gọi I là giao điểm của các đường thẳng
. Gọi I là giao điểm của các đường thẳng 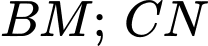 . Khi đó tỉ số
. Khi đó tỉ số 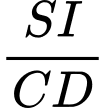 bằng
bằng A, 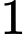
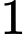
B, 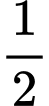 .
.
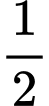 .
.C, 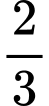
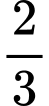
D, 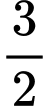 .
.
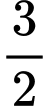 .
.
Chọn A
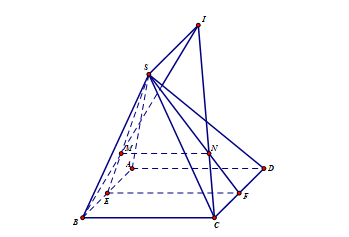
Gọi E và F lần lượt là trung điểm AB và CD.
Ta có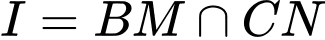
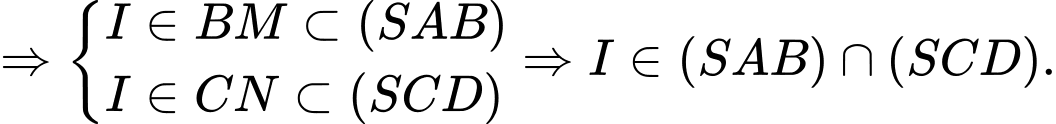
Mà . Do đó
. Do đó 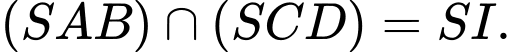
Ta có: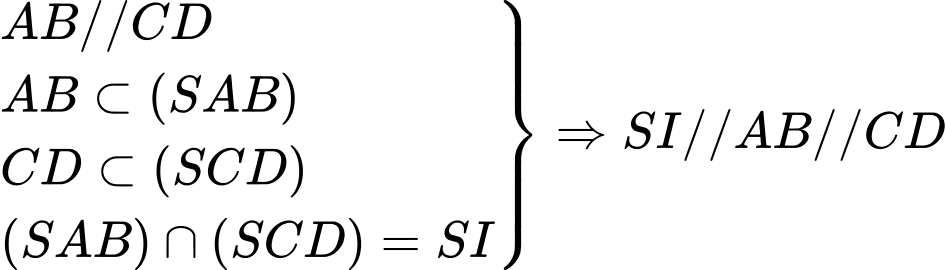 .Vì
.Vì 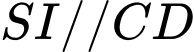 nên
nên 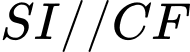 .
.
Theo định lý Ta – let ta có: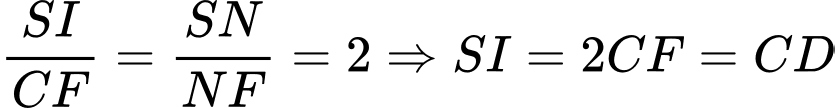
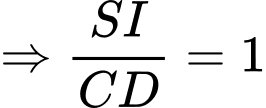 . Đáp án: A
. Đáp án: A

Gọi E và F lần lượt là trung điểm AB và CD.
Ta có
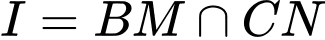
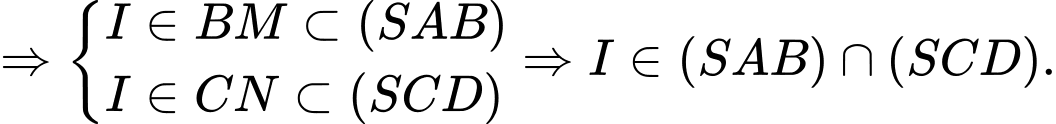
Mà
 . Do đó
. Do đó 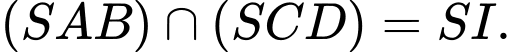
Ta có:
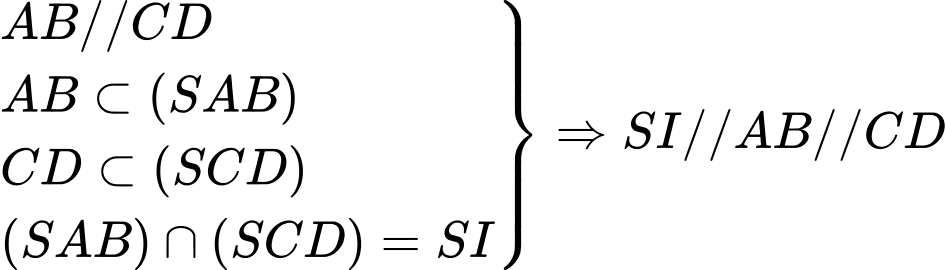 .Vì
.Vì 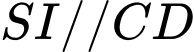 nên
nên 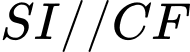 .
.Theo định lý Ta – let ta có:
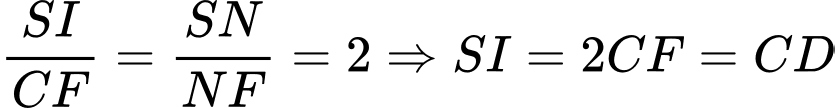
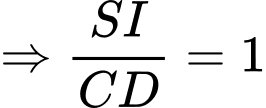 . Đáp án: A
. Đáp án: A
Câu 15 [229243]: (THPT NGHEN - HÀ TĨNH - LẦN 1 - 2018) Cho tứ diện 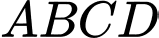 ,
, 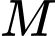 là điểm thuộc
là điểm thuộc 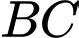 sao cho
sao cho 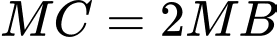 . Gọi
. Gọi 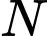 ,
, 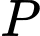 lần lượt là trung điểm của
lần lượt là trung điểm của 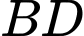 và
và 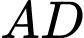 . Điểm
. Điểm  là giao điểm của
là giao điểm của 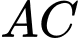 với
với 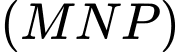 . Tính
. Tính 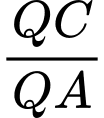 .
.
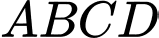 ,
, 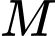 là điểm thuộc
là điểm thuộc 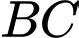 sao cho
sao cho 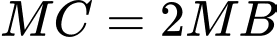 . Gọi
. Gọi 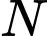 ,
, 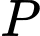 lần lượt là trung điểm của
lần lượt là trung điểm của 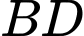 và
và 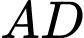 . Điểm
. Điểm  là giao điểm của
là giao điểm của 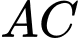 với
với 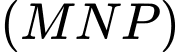 . Tính
. Tính 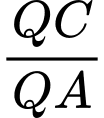 .
. A, 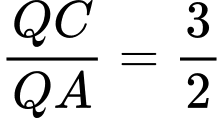 .
.
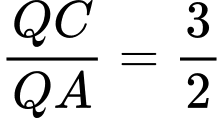 .
.B, 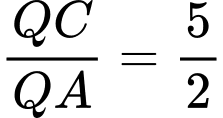 .
.
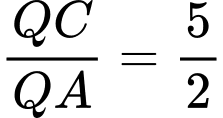 .
.C, 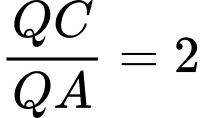 .
.
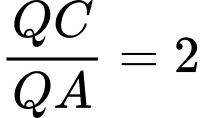 .
.D, 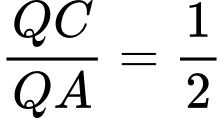 .
.
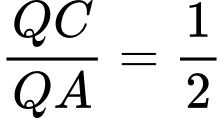 .
.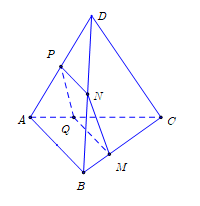
Ta có
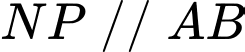
 .
.Mặt khác
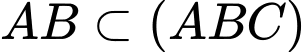 ,
, 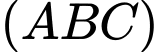 và
và 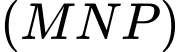 có điểm
có điểm 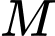 chung nên giao tuyến của
chung nên giao tuyến của 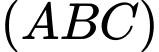 và
và 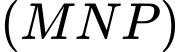 là đường thẳng
là đường thẳng 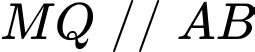
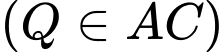 .
.Ta có:
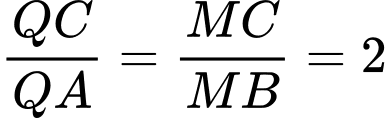 . Đáp án: C
. Đáp án: C
Câu 16 [582122]: Cho tứ diện 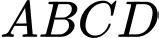 . Trên cạnh
. Trên cạnh  lấy điểm
lấy điểm 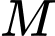 sao cho
sao cho 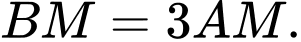 Mặt phẳng
Mặt phẳng 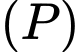 đi qua
đi qua 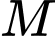 song song với hai đường thẳng
song song với hai đường thẳng 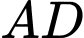 và
và 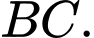 Gọi
Gọi 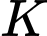 là giao điểm của mặt phẳng
là giao điểm của mặt phẳng 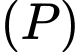 với đường thẳng
với đường thẳng 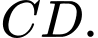 Tính tỉ số
Tính tỉ số 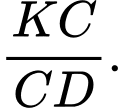
 . Trên cạnh
. Trên cạnh  lấy điểm
lấy điểm 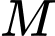 sao cho
sao cho 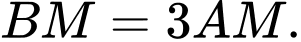 Mặt phẳng
Mặt phẳng 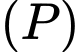 đi qua
đi qua 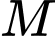 song song với hai đường thẳng
song song với hai đường thẳng 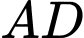 và
và 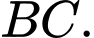 Gọi
Gọi 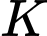 là giao điểm của mặt phẳng
là giao điểm của mặt phẳng 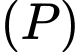 với đường thẳng
với đường thẳng 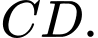 Tính tỉ số
Tính tỉ số 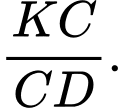
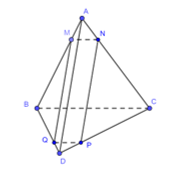
Ta có: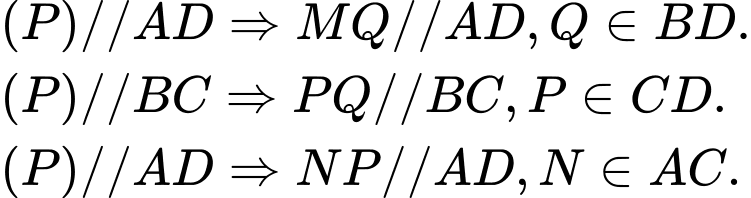
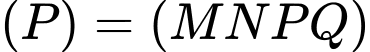
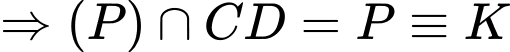 .
.
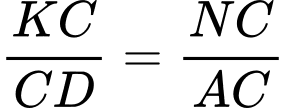
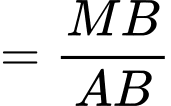
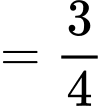
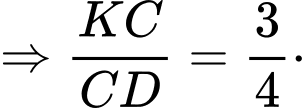
Câu 17 [582120]: Cho hai hình bình hành 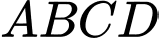 và
và 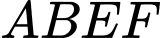 không cùng nằm trong một mặt phẳng. Gọi
không cùng nằm trong một mặt phẳng. Gọi 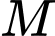 là trọng tâm của tam giác
là trọng tâm của tam giác 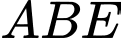 . Gọi
. Gọi 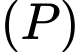 là mặt phẳng đi qua
là mặt phẳng đi qua 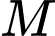 và song song với mặt phẳng
và song song với mặt phẳng 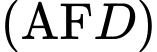 . Lấy
. Lấy 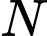 là giao điểm của
là giao điểm của 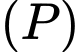 và
và 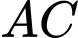 . Tính
. Tính 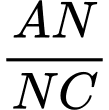 .
.
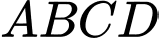 và
và 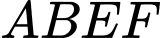 không cùng nằm trong một mặt phẳng. Gọi
không cùng nằm trong một mặt phẳng. Gọi 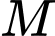 là trọng tâm của tam giác
là trọng tâm của tam giác 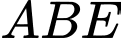 . Gọi
. Gọi 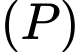 là mặt phẳng đi qua
là mặt phẳng đi qua 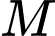 và song song với mặt phẳng
và song song với mặt phẳng 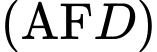 . Lấy
. Lấy 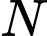 là giao điểm của
là giao điểm của 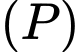 và
và 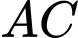 . Tính
. Tính 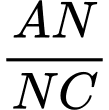 .
. 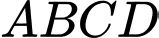 là hình bình hành
là hình bình hành 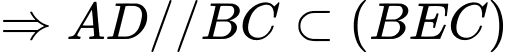
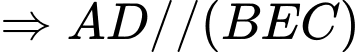 .
.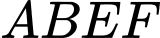 là hình bình hành
là hình bình hành 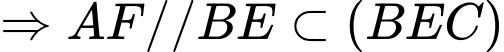
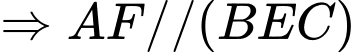 .
.Mà:
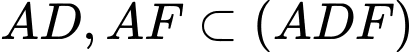
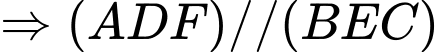 .
.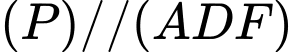
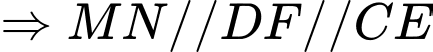
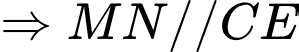 .
. 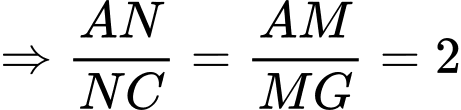 .
. 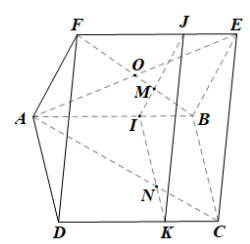
Câu 18 [229733]: Cho hình chóp 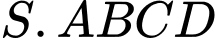 có đáy là hình thang,
có đáy là hình thang,  //
//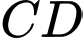 và
và 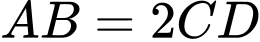 . Gọi
. Gọi  là giao điểm của
là giao điểm của 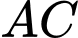 và
và 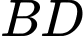 . Lấy
. Lấy 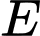 thuộc cạnh
thuộc cạnh 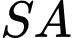 ,
, 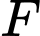 thuộc cạnh
thuộc cạnh 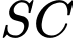 sao cho
sao cho 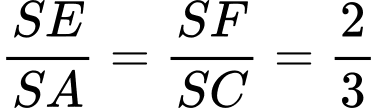 (tham khảo hình vẽ dưới đây).
(tham khảo hình vẽ dưới đây).
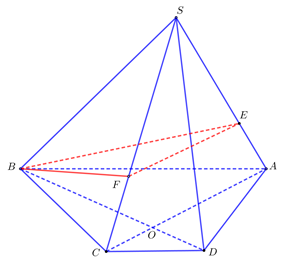
Gọi là mặt phẳng qua
là mặt phẳng qua  và song song với mặt phẳng
và song song với mặt phẳng 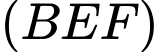 . Gọi
. Gọi 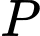 là giao điểm của
là giao điểm của 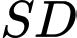 với
với  . Tính tỉ số
. Tính tỉ số 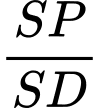 .
.
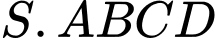 có đáy là hình thang,
có đáy là hình thang,  //
//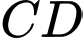 và
và 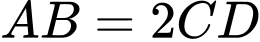 . Gọi
. Gọi  là giao điểm của
là giao điểm của 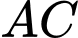 và
và 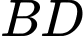 . Lấy
. Lấy 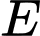 thuộc cạnh
thuộc cạnh 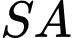 ,
, 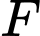 thuộc cạnh
thuộc cạnh 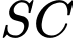 sao cho
sao cho 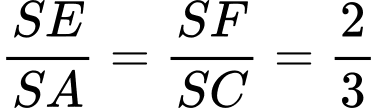 (tham khảo hình vẽ dưới đây).
(tham khảo hình vẽ dưới đây). 
Gọi
 là mặt phẳng qua
là mặt phẳng qua  và song song với mặt phẳng
và song song với mặt phẳng 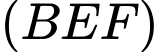 . Gọi
. Gọi 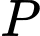 là giao điểm của
là giao điểm của 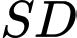 với
với  . Tính tỉ số
. Tính tỉ số 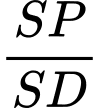 .
. A, 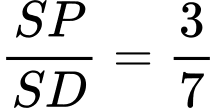 .
.
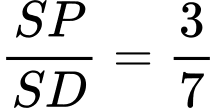 .
.B, 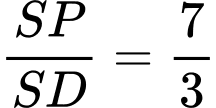 .
.
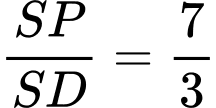 .
.C, 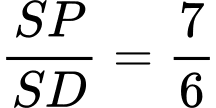 .
.
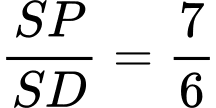 .
.D, 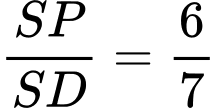 .
.
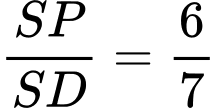 .
.
Chọn D
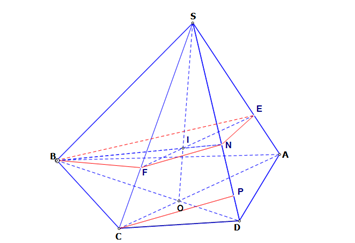
Vì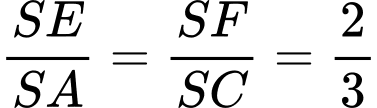 nên đường thẳng
nên đường thẳng 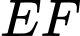 //
// 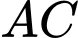 . Mà
. Mà 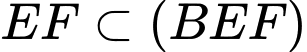 ,
, 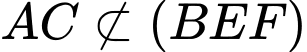 nên
nên 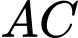 song song với mặt phẳng
song song với mặt phẳng 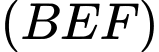 .
.
Vì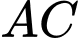 qua
qua  và song song với mặt phẳng
và song song với mặt phẳng 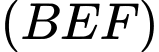 nên
nên  .
.
Trong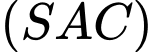 , gọi
, gọi  , trong
, trong 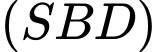 , gọi
, gọi 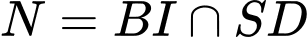 . Suy ra
. Suy ra 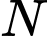 là giao điểm của đường thẳng
là giao điểm của đường thẳng 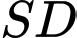 với mặt phẳng
với mặt phẳng 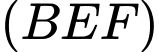 .
.
Hai mặt phẳng song song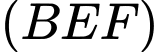 và
và  bị cắt bởi mặt phẳng thứ ba là
bị cắt bởi mặt phẳng thứ ba là  theo hai giao tuyến lần lượt là
theo hai giao tuyến lần lượt là 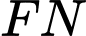 và
và  nên hai giao tuyến đó song song nhau, tức là
nên hai giao tuyến đó song song nhau, tức là  //
// 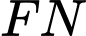 .
.
Trong ,
,  cắt
cắt 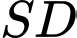 tại
tại 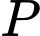 . Khi đó
. Khi đó 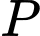 là giao điểm của
là giao điểm của 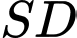 với
với  .
.
Trong hình thang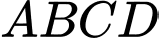 , do
, do  //
//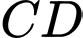 và
và 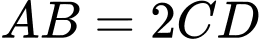 nên
nên 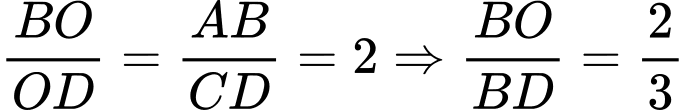 .
.
Trong tam giác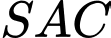 , có
, có 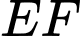 //
// 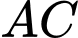 nên
nên 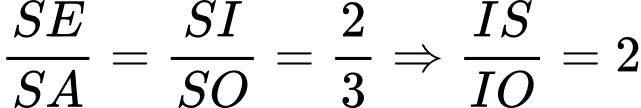 .
.
Xét tam giác với cát tuyến
với cát tuyến 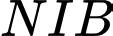 , ta có:
, ta có:  .
.
Suy ra: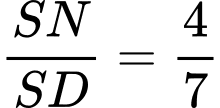 (1).
(1).
Lại có: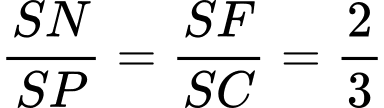 (Do
(Do 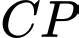 //
// 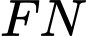 ) (2).
) (2).
Từ (1) và (2) suy ra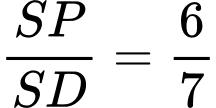 . Đáp án: D
. Đáp án: D

Vì
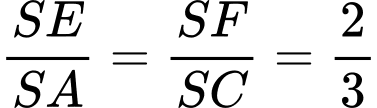 nên đường thẳng
nên đường thẳng 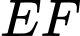 //
// 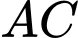 . Mà
. Mà 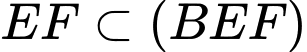 ,
, 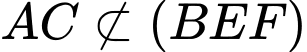 nên
nên 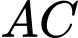 song song với mặt phẳng
song song với mặt phẳng 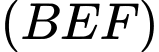 .
.Vì
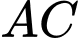 qua
qua  và song song với mặt phẳng
và song song với mặt phẳng 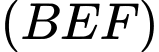 nên
nên  .
.Trong
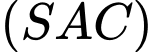 , gọi
, gọi  , trong
, trong 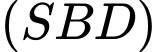 , gọi
, gọi 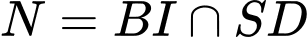 . Suy ra
. Suy ra 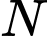 là giao điểm của đường thẳng
là giao điểm của đường thẳng 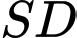 với mặt phẳng
với mặt phẳng 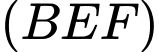 .
.Hai mặt phẳng song song
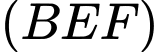 và
và  bị cắt bởi mặt phẳng thứ ba là
bị cắt bởi mặt phẳng thứ ba là  theo hai giao tuyến lần lượt là
theo hai giao tuyến lần lượt là 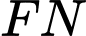 và
và  nên hai giao tuyến đó song song nhau, tức là
nên hai giao tuyến đó song song nhau, tức là  //
// 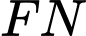 .
.Trong
 ,
,  cắt
cắt 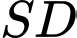 tại
tại 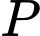 . Khi đó
. Khi đó 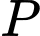 là giao điểm của
là giao điểm của 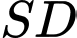 với
với  .
.Trong hình thang
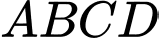 , do
, do  //
//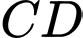 và
và 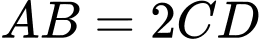 nên
nên 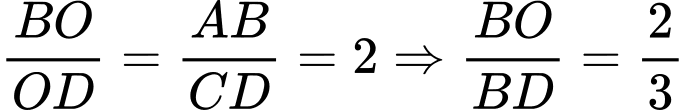 .
.Trong tam giác
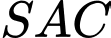 , có
, có 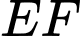 //
// 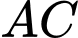 nên
nên 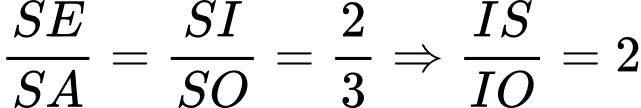 .
.Xét tam giác
 với cát tuyến
với cát tuyến 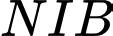 , ta có:
, ta có:  .
.Suy ra:
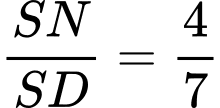 (1).
(1). Lại có:
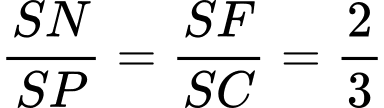 (Do
(Do 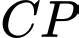 //
// 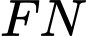 ) (2).
) (2). Từ (1) và (2) suy ra
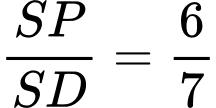 . Đáp án: D
. Đáp án: D
Câu 19 [229632]: (THPT CHUYÊN HÙNG VƯƠNG - BÌNH DƯƠNG - 2018) Cho hình hộp ABCD.A’B’C’D’. Trên các cạnh 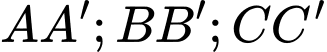 lần lượt lấy ba điểm
lần lượt lấy ba điểm 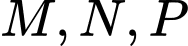 sao cho
sao cho 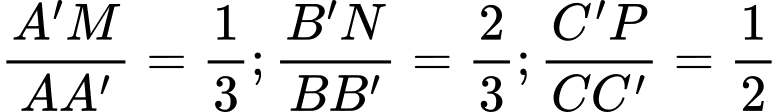 . Biết mặt phẳng
. Biết mặt phẳng 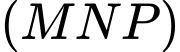 cắt cạnh
cắt cạnh 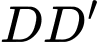 tại Q. Tính tỉ số
tại Q. Tính tỉ số 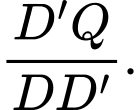
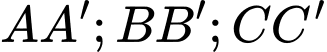 lần lượt lấy ba điểm
lần lượt lấy ba điểm 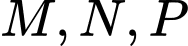 sao cho
sao cho 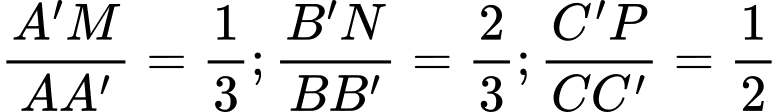 . Biết mặt phẳng
. Biết mặt phẳng 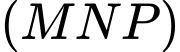 cắt cạnh
cắt cạnh 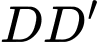 tại Q. Tính tỉ số
tại Q. Tính tỉ số 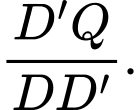
A, 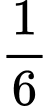 .
.
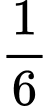 .
.B, 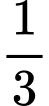 .
.
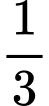 .
.C, 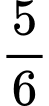 .
.
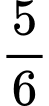 .
.D, 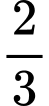 .
.
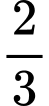 .
.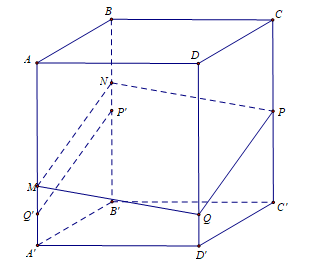
Gọi độ dài cạnh bên của hình hộp là
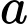 .
.Giao tuyến của mặt phẳng
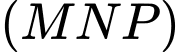 với
với 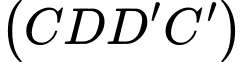 là đường thẳng đi qua
là đường thẳng đi qua 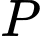 và song song với
và song song với 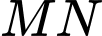 (do
(do  )
)Gọi
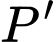 là trung điểm
là trung điểm 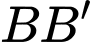 và
và 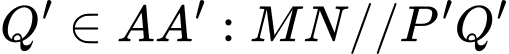 . Khi đó tứ giác
. Khi đó tứ giác 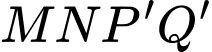 là hình bình hành và
là hình bình hành và 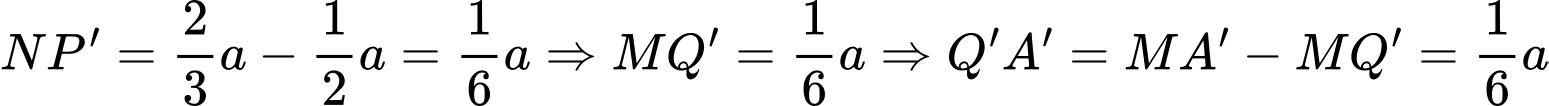 .
.Vậy
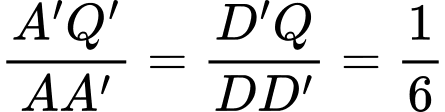 . Đáp án: A
. Đáp án: A
Câu 20 [229245]: (THPT CHUYÊN HÙNG VƯƠNG - BÌNH DƯƠNG - 2018) Cho hình chóp 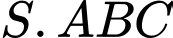 . Bên trong tam giác
. Bên trong tam giác 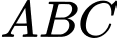 ta lấy một điểm
ta lấy một điểm  bất kỳ. Từ
bất kỳ. Từ  ta dựng các đường thẳng lần lượt song song với
ta dựng các đường thẳng lần lượt song song với  và cắt các mặt phẳng
và cắt các mặt phẳng 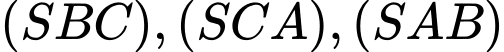 theo thứ tự tại
theo thứ tự tại 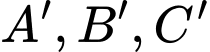 . Khi đó tổng tỉ số
. Khi đó tổng tỉ số 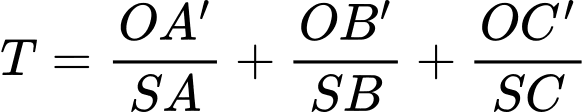 bằng bao nhiêu?
bằng bao nhiêu?
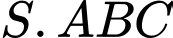 . Bên trong tam giác
. Bên trong tam giác 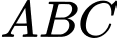 ta lấy một điểm
ta lấy một điểm  bất kỳ. Từ
bất kỳ. Từ  ta dựng các đường thẳng lần lượt song song với
ta dựng các đường thẳng lần lượt song song với  và cắt các mặt phẳng
và cắt các mặt phẳng 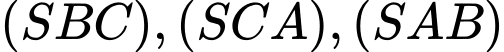 theo thứ tự tại
theo thứ tự tại 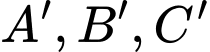 . Khi đó tổng tỉ số
. Khi đó tổng tỉ số 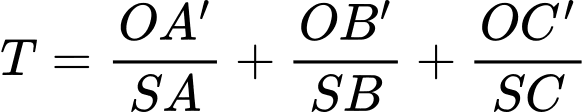 bằng bao nhiêu?
bằng bao nhiêu? A, 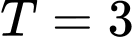 .
.
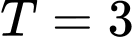 .
.B, 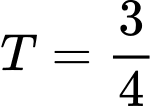 .
.
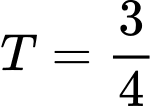 .
.C, 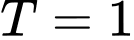 .
.
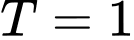 .
.D, 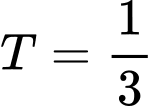 .
.
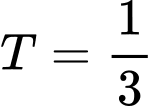 .
.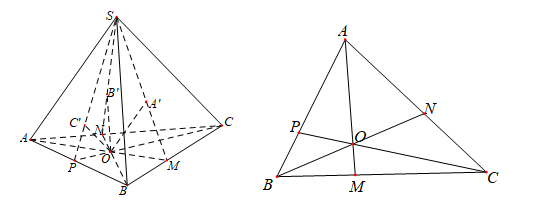
Gọi
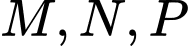 lần lượt là giao điểm của
lần lượt là giao điểm của 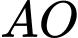 và
và 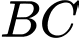 ,
, 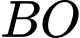 và
và 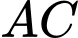 ,
, 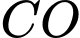 và
và  .
.Ta có
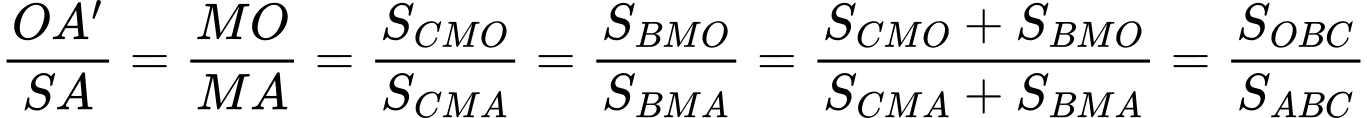
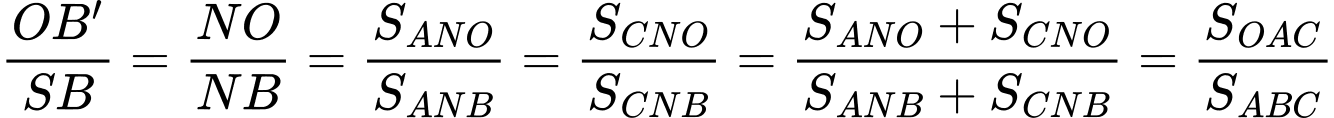 .
.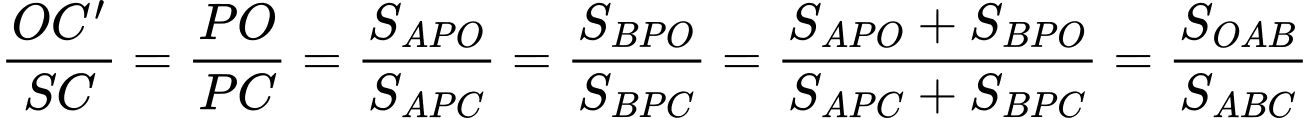
Từ đó
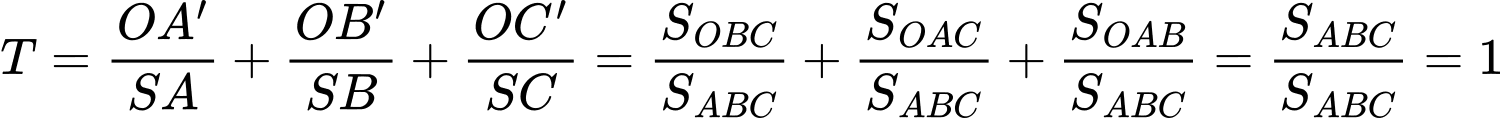 . Đáp án: C
. Đáp án: C