Đáp án Bài tập tự luyện
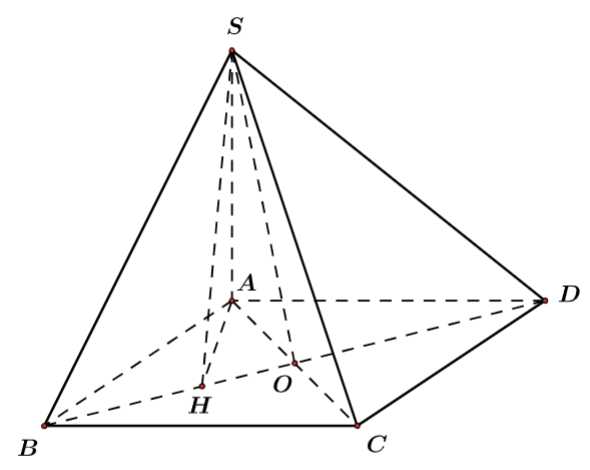
Câu 1 [502393]: [Đề tham khảo năm 2020]: Cho hình chóp 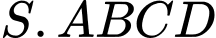 có đáy là hình vuông cạnh
có đáy là hình vuông cạnh 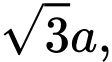
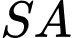 vuông góc với mặt phẳng đáy và
vuông góc với mặt phẳng đáy và 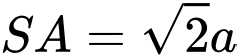 (minh họa như hình bên). Góc giữa
(minh họa như hình bên). Góc giữa 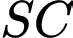 và mặt phẳng
và mặt phẳng 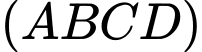 là
là 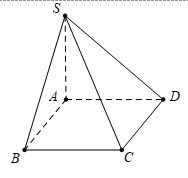
 có đáy là hình vuông cạnh
có đáy là hình vuông cạnh 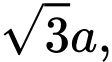
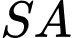 vuông góc với mặt phẳng đáy và
vuông góc với mặt phẳng đáy và 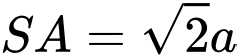 (minh họa như hình bên). Góc giữa
(minh họa như hình bên). Góc giữa 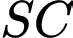 và mặt phẳng
và mặt phẳng 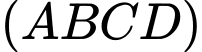 là
là 
A, 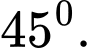
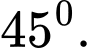
B, 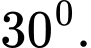
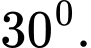
C, 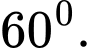
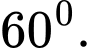
D, 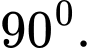
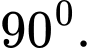
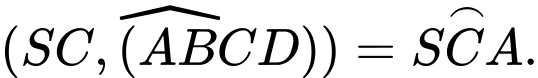
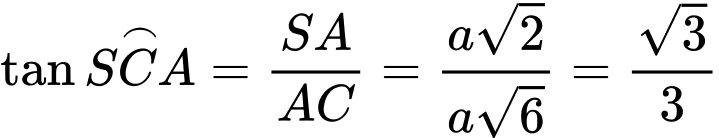
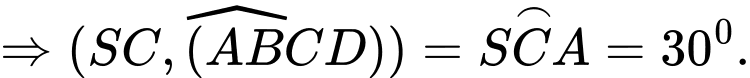
Chọn đáp án B. Đáp án: B
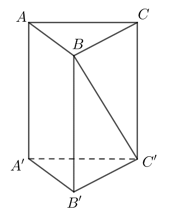
Câu 2 [983033]: Cho hình lăng trụ đứng  có tất cả các cạnh bằng nhau (tham khảo hình bên). Góc giữa đường thẳng
có tất cả các cạnh bằng nhau (tham khảo hình bên). Góc giữa đường thẳng 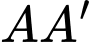 và
và 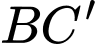 bằng
bằng
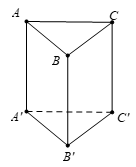
 có tất cả các cạnh bằng nhau (tham khảo hình bên). Góc giữa đường thẳng
có tất cả các cạnh bằng nhau (tham khảo hình bên). Góc giữa đường thẳng  và
và  bằng
bằng
A, 
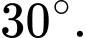
B, 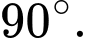
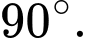
C, 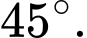
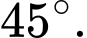
D, 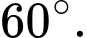
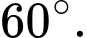
Chọn C
Vì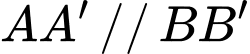 nên
nên 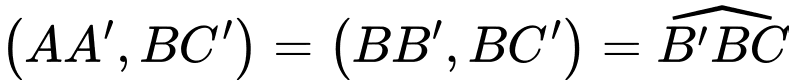
Ta có: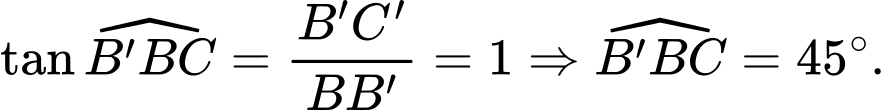 Đáp án: C
Đáp án: C

Vì
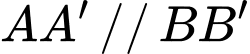 nên
nên 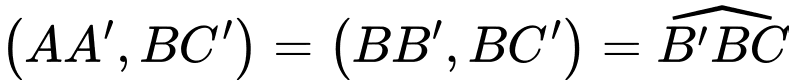
Ta có:
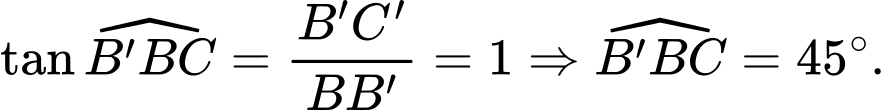 Đáp án: C
Đáp án: C
Câu 3 [324912]: Cho hình chóp  có đáy là hình chữ nhật
có đáy là hình chữ nhật  có
có 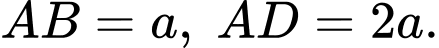 Cạnh
Cạnh 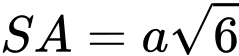 và vuông góc với mặt phẳng đáy. Gọi
và vuông góc với mặt phẳng đáy. Gọi 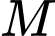 là trung điểm của
là trung điểm của 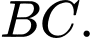 Tính góc giữa
Tính góc giữa 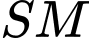 và
và 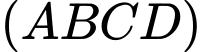
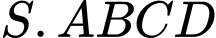 có đáy là hình chữ nhật
có đáy là hình chữ nhật 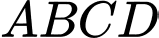 có
có 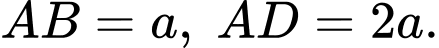 Cạnh
Cạnh 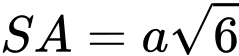 và vuông góc với mặt phẳng đáy. Gọi
và vuông góc với mặt phẳng đáy. Gọi 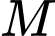 là trung điểm của
là trung điểm của 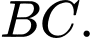 Tính góc giữa
Tính góc giữa 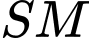 và
và 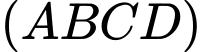
A, 
B, 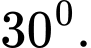
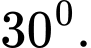
C, 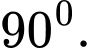
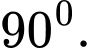
D, 
 Đáp án: A
Đáp án: A
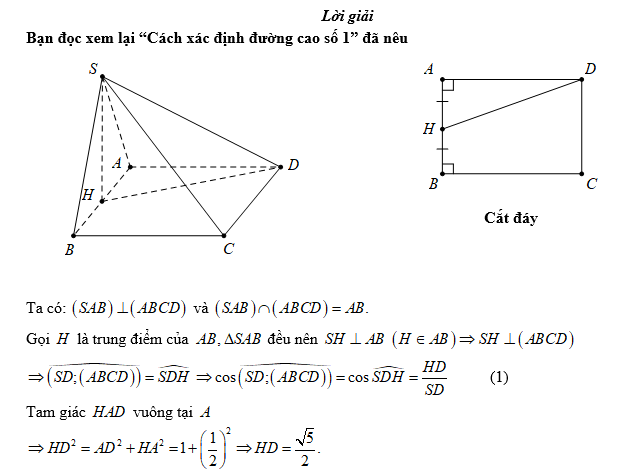
Câu 4 [324918]: Cho hình chóp  có đáy
có đáy 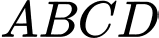 là hình vuông cạnh
là hình vuông cạnh  Tam giác
Tam giác  đều và nằm trong mặt phẳng vuông góc với mặt đáy. Côsin của góc giữa đường thẳng
đều và nằm trong mặt phẳng vuông góc với mặt đáy. Côsin của góc giữa đường thẳng  và mặt phẳng đáy bằng ?
và mặt phẳng đáy bằng ?
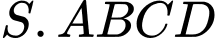 có đáy
có đáy 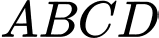 là hình vuông cạnh
là hình vuông cạnh 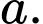 Tam giác
Tam giác 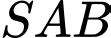 đều và nằm trong mặt phẳng vuông góc với mặt đáy. Côsin của góc giữa đường thẳng
đều và nằm trong mặt phẳng vuông góc với mặt đáy. Côsin của góc giữa đường thẳng  và mặt phẳng đáy bằng ?
và mặt phẳng đáy bằng ? A, 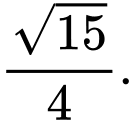
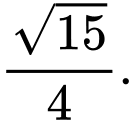
B, 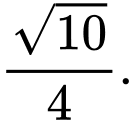
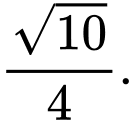
C, 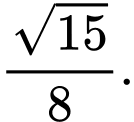
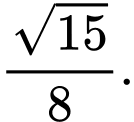
D, 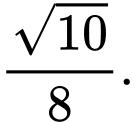
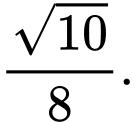
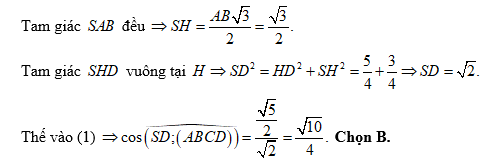 Đáp án: B
Đáp án: B
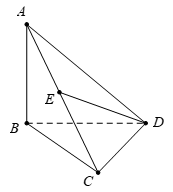
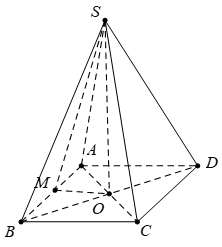
Câu 5 [319375]: Cho tứ diện 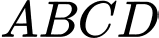 có
có  vuông góc với mặt phẳng
vuông góc với mặt phẳng 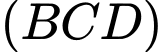 . Biết tam giác
. Biết tam giác  vuông góc tại
vuông góc tại  và
và 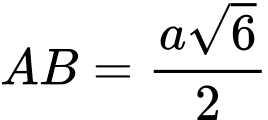 ,
, 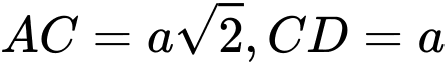 . Gọi
. Gọi 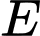 là trung điểm của
là trung điểm của 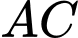 . Góc giữa hai đường thẳng
. Góc giữa hai đường thẳng  và
và 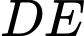 bằng :
bằng :
 có
có  vuông góc với mặt phẳng
vuông góc với mặt phẳng 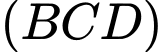 . Biết tam giác
. Biết tam giác  vuông góc tại
vuông góc tại  và
và 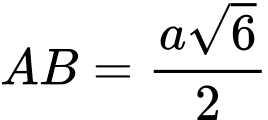 ,
, 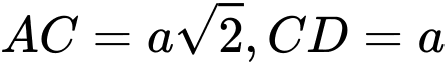 . Gọi
. Gọi 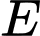 là trung điểm của
là trung điểm của 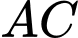 . Góc giữa hai đường thẳng
. Góc giữa hai đường thẳng  và
và 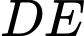 bằng :
bằng :
A, 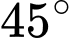 .
.
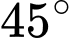 .
.B, 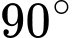 .
.
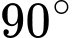 .
.C, 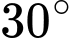 .
.
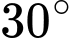 .
.D, 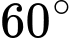 .
.
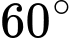 .
.
Chọn D
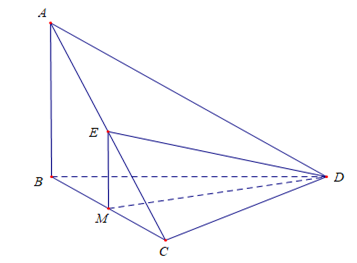
Gọi là trung điểm của
là trung điểm của 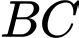 . Suy ra
. Suy ra 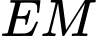 là đường trung bình của tam giác
là đường trung bình của tam giác 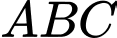 nên
nên 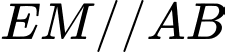
 góc giữa
góc giữa 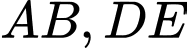 là góc giữa
là góc giữa 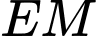 và
và 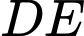 và
và 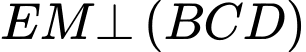 .
.
Ta có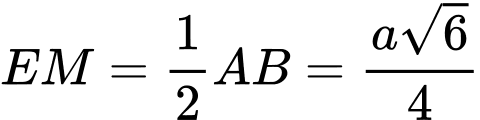 .
.
Ta có : tam giác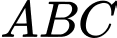 vuông tại
vuông tại 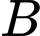 nên
nên 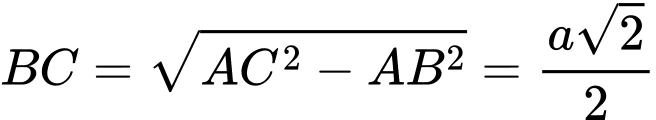 .
.
Tam giác vuông tại
vuông tại  nên
nên 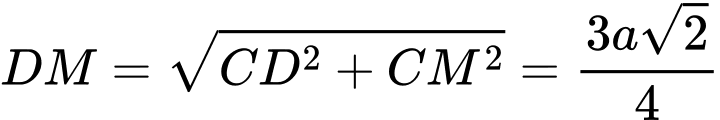 .
.
Tam giác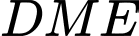 vuông tại
vuông tại 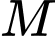 nên
nên 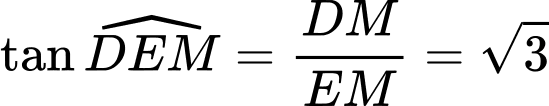
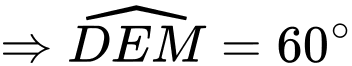 .
.
Vậy góc giữa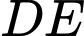 và
và 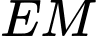 bằng
bằng 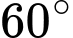 . Đáp án: D
. Đáp án: D

Gọi
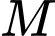 là trung điểm của
là trung điểm của 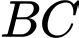 . Suy ra
. Suy ra 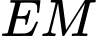 là đường trung bình của tam giác
là đường trung bình của tam giác  nên
nên 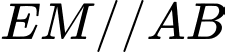
 góc giữa
góc giữa 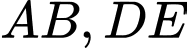 là góc giữa
là góc giữa 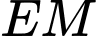 và
và 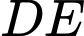 và
và 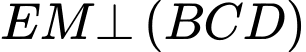 .
.Ta có
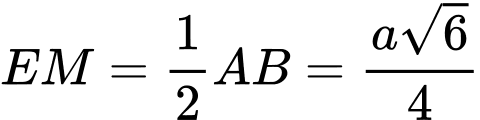 .
.Ta có : tam giác
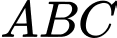 vuông tại
vuông tại 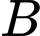 nên
nên 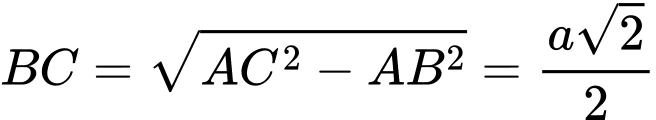 .
.Tam giác
 vuông tại
vuông tại  nên
nên 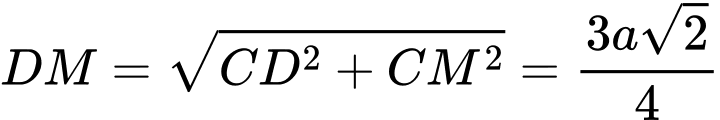 .
.Tam giác
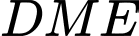 vuông tại
vuông tại 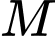 nên
nên 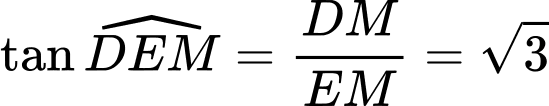
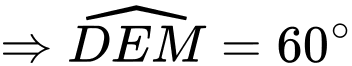 .
.Vậy góc giữa
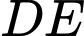 và
và 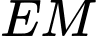 bằng
bằng 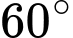 . Đáp án: D
. Đáp án: D
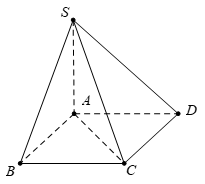
Câu 6 [280726]: Cho hình chóp  có đáy là hình vuông cạnh
có đáy là hình vuông cạnh 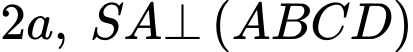 và
và 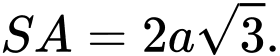 Tính số đo của góc nhị diện
Tính số đo của góc nhị diện 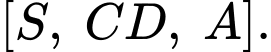
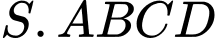 có đáy là hình vuông cạnh
có đáy là hình vuông cạnh 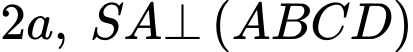 và
và 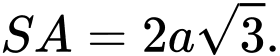 Tính số đo của góc nhị diện
Tính số đo của góc nhị diện 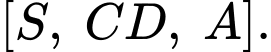
A, 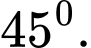
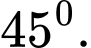
B, 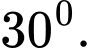
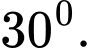
C, 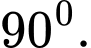
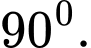
D, 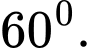
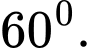
Ta có:

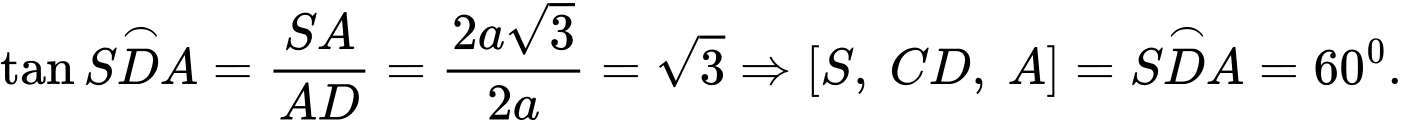
Chọn đáp án D. Đáp án: D
Câu 7 [280728]: Cho hình chóp 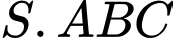 có đáy là tam giác đều cạnh bằng
có đáy là tam giác đều cạnh bằng 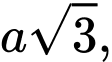
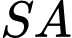 vuông góc với mặt phẳng đáy và
vuông góc với mặt phẳng đáy và 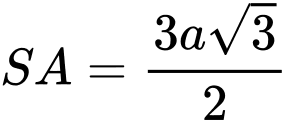 Tính số đo của góc nhị diện
Tính số đo của góc nhị diện 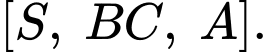
 có đáy là tam giác đều cạnh bằng
có đáy là tam giác đều cạnh bằng 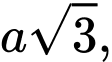
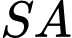 vuông góc với mặt phẳng đáy và
vuông góc với mặt phẳng đáy và 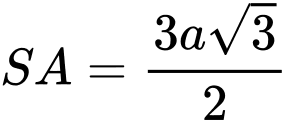 Tính số đo của góc nhị diện
Tính số đo của góc nhị diện 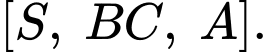
A, 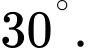
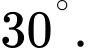
B, 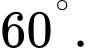
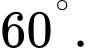
C, 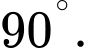
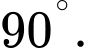
D, 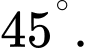
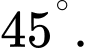
Lời giải: Kẻ 
Khi đó,
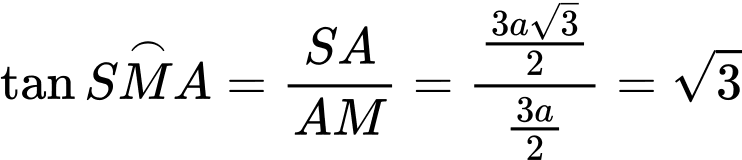
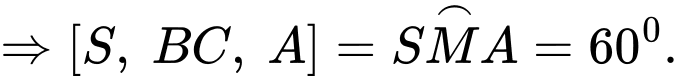
Chọn đáp án B.
 Đáp án: B
Đáp án: B

Khi đó,

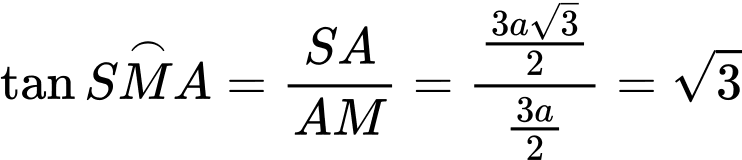
Chọn đáp án B.
 Đáp án: B
Đáp án: B
Câu 8 [280729]: Cho hình chóp 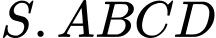 có
có  và
và 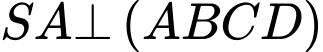 , đáy
, đáy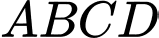 là hình chữ nhật có
là hình chữ nhật có 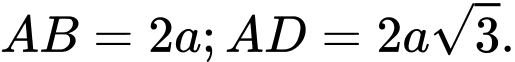 Tính số đo của góc nhị diện
Tính số đo của góc nhị diện 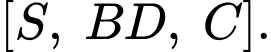
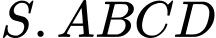 có
có  và
và 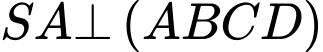 , đáy
, đáy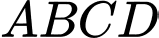 là hình chữ nhật có
là hình chữ nhật có 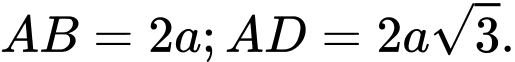 Tính số đo của góc nhị diện
Tính số đo của góc nhị diện 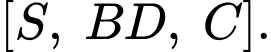
A, 
B, 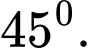
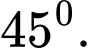
C, 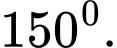
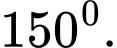
D, 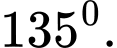
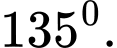
Gỉa sử  là hình chiếu của
là hình chiếu của  và
và 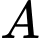 trên cạnh
trên cạnh 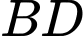
Ta có:

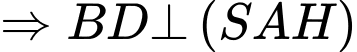
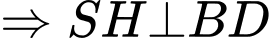
Mặt khác,
Do đó, là góc nhị diện của
là góc nhị diện của 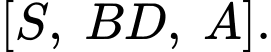
Ta có: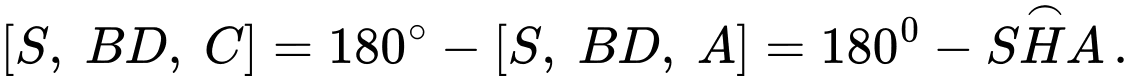
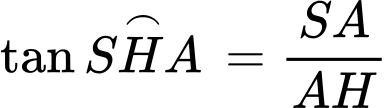
Có trong tam giác vuông tại
vuông tại  và
và 
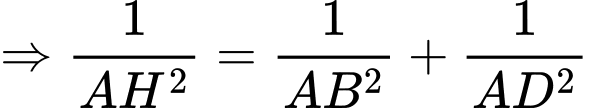
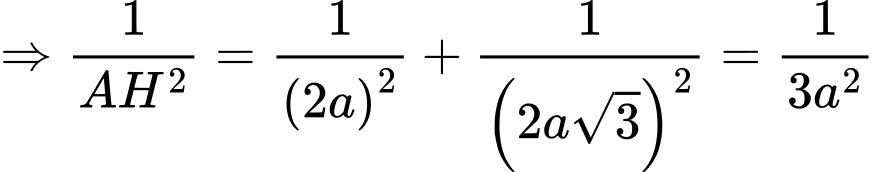
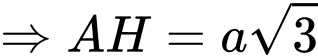


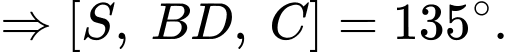
Chọn đáp án D. Đáp án: D
 là hình chiếu của
là hình chiếu của  và
và 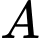 trên cạnh
trên cạnh 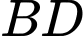

Ta có:

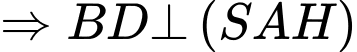
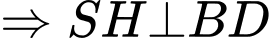
Mặt khác,

Do đó,
 là góc nhị diện của
là góc nhị diện của 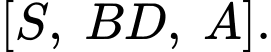
Ta có:
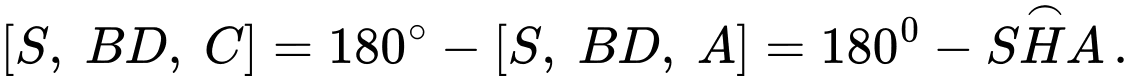
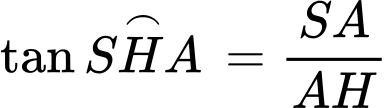
Có trong tam giác
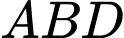 vuông tại
vuông tại 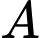 và
và 
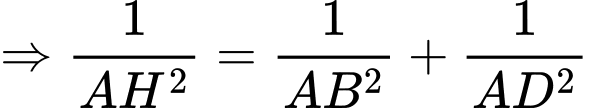
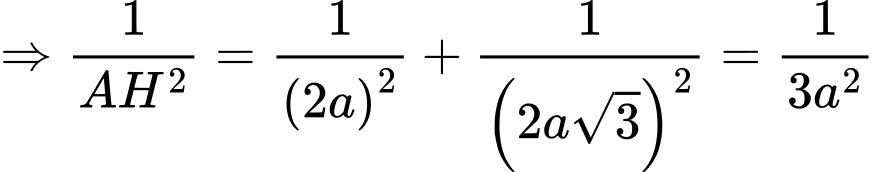
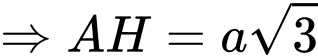


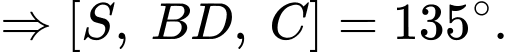
Chọn đáp án D. Đáp án: D
Câu 9 [329055]: Cho hình chóp 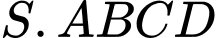 có đáy
có đáy 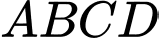 là hình vuông cạnh
là hình vuông cạnh 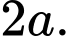 Cạnh
Cạnh  và vuông góc với mặt phẳng đáy. Gọi
và vuông góc với mặt phẳng đáy. Gọi 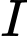 là trung điểm của cạnh
là trung điểm của cạnh 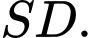 Đường thẳng
Đường thẳng 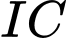 tạo với mặt phẳng đáy một góc
tạo với mặt phẳng đáy một góc 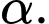 Tính
Tính 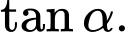
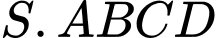 có đáy
có đáy 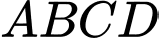 là hình vuông cạnh
là hình vuông cạnh 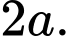 Cạnh
Cạnh  và vuông góc với mặt phẳng đáy. Gọi
và vuông góc với mặt phẳng đáy. Gọi 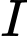 là trung điểm của cạnh
là trung điểm của cạnh 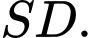 Đường thẳng
Đường thẳng 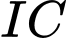 tạo với mặt phẳng đáy một góc
tạo với mặt phẳng đáy một góc 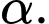 Tính
Tính 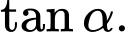
A, 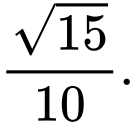
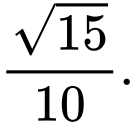
B, 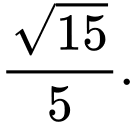
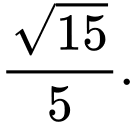
C, 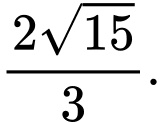
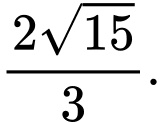
D, 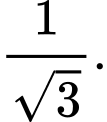
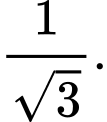
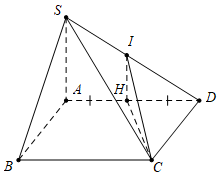
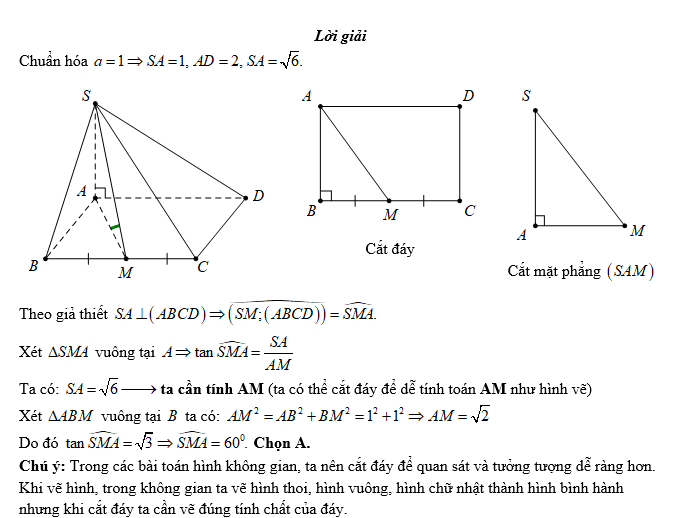
Chuẩn hóa
 Tìm hình chiếu của
Tìm hình chiếu của 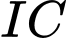 trên mặt đáy.
trên mặt đáy.Ta có :
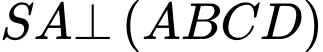 , từ điểm
, từ điểm 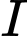 ta kẻ
ta kẻ 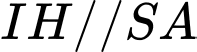
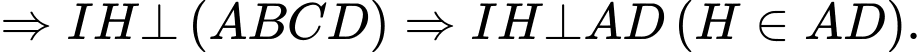
Do đó
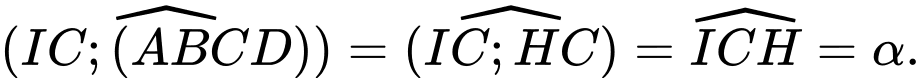
Cạnh
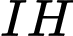 là đường trung bình của
là đường trung bình của 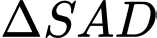
 Tam giác
Tam giác  vuông tại
vuông tại 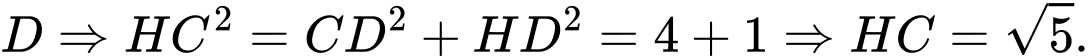
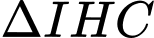 vuông tại
vuông tại 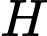
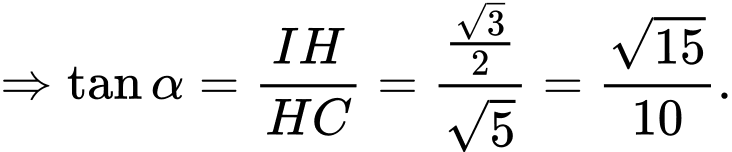 Chọn A.
Đáp án: A
Chọn A.
Đáp án: A
Câu 10 [280733]: Cho khối chóp  có đáy
có đáy 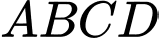 là hình thoi tâm
là hình thoi tâm  , cạnh
, cạnh 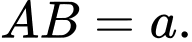 Cạnh
Cạnh 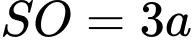 vuông góc với mặt phẳng đáy
vuông góc với mặt phẳng đáy 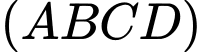 ,
, 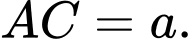 Gọi
Gọi 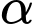 là số đo của góc nhị diện
là số đo của góc nhị diện 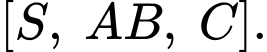 Tính
Tính 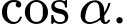
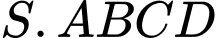 có đáy
có đáy 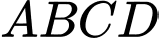 là hình thoi tâm
là hình thoi tâm  , cạnh
, cạnh 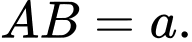 Cạnh
Cạnh 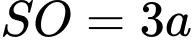 vuông góc với mặt phẳng đáy
vuông góc với mặt phẳng đáy 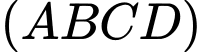 ,
, 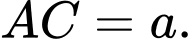 Gọi
Gọi 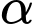 là số đo của góc nhị diện
là số đo của góc nhị diện 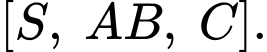 Tính
Tính 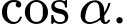
A, 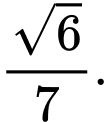
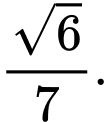
B, 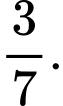
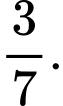
C, 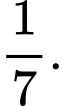
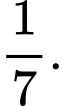
D, 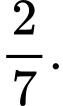
Kẻ 
Khi đó,
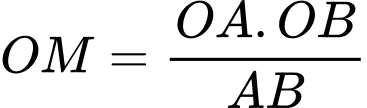
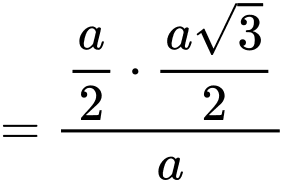
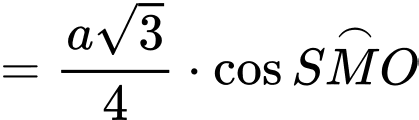

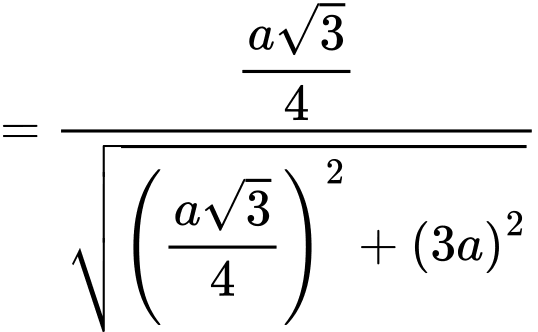
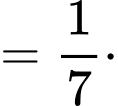
Chọn đáp án C. Đáp án: C


Khi đó,

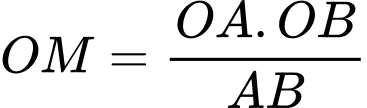
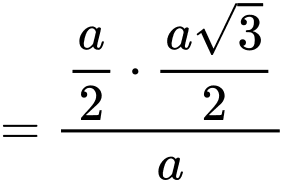
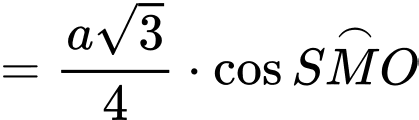

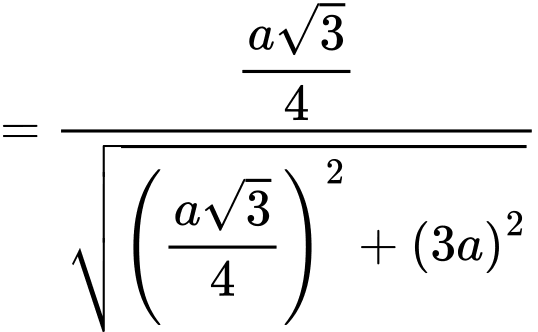
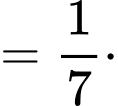
Chọn đáp án C. Đáp án: C
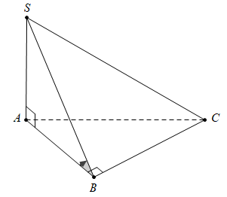
Câu 11 [280795]: Cho hình chóp 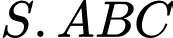 có đáy là tam giác vuông tại
có đáy là tam giác vuông tại 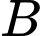 ,
, 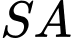 vuông góc với đáy và
vuông góc với đáy và  (tham khảo hình vẽ). Góc giữa hai mặt phẳng
(tham khảo hình vẽ). Góc giữa hai mặt phẳng 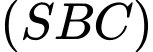 và
và  bằng
bằng
 có đáy là tam giác vuông tại
có đáy là tam giác vuông tại  ,
, 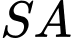 vuông góc với đáy và
vuông góc với đáy và  (tham khảo hình vẽ). Góc giữa hai mặt phẳng
(tham khảo hình vẽ). Góc giữa hai mặt phẳng 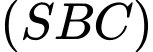 và
và 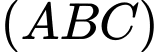 bằng
bằng
A, 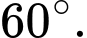
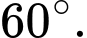
B, 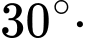
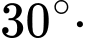
C, 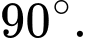
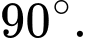
D, 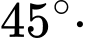
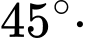
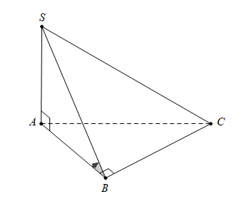
Ta có
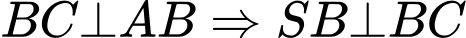 .
.
Suy ra góc giữa hai mặt phẳng
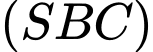 và
và 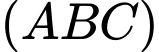 bằng
bằng 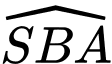 .
.
Do tam giác
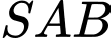 vuông cân tại
vuông cân tại  .
.
Vậy góc giữa hai mặt phẳng
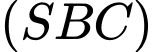 và
và 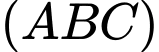 bằng
bằng 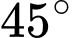 . Đáp án: D
. Đáp án: D
Câu 12 [8523]: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a. Đường thẳng SO vuông góc với mặt phẳng đáy 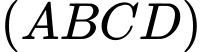 và
và 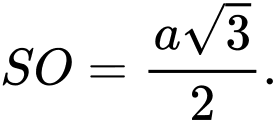 Tính góc giữa hai mặt phẳng
Tính góc giữa hai mặt phẳng 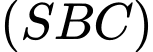 và
và 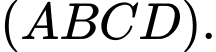
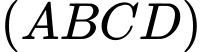 và
và 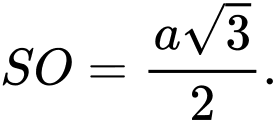 Tính góc giữa hai mặt phẳng
Tính góc giữa hai mặt phẳng 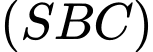 và
và 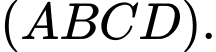
A, 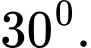
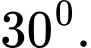
B, 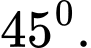
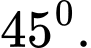
C, 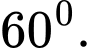
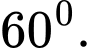
D, 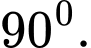
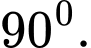
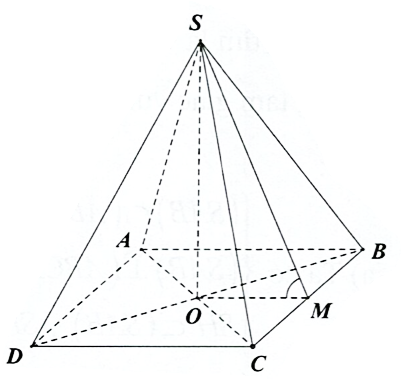
 nên
nên 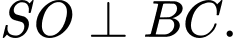
Gọi 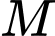 là trung điểm
là trung điểm 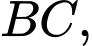 suy ra
suy ra 
Đáp án: C 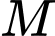 là trung điểm
là trung điểm 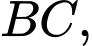 suy ra
suy ra 
Ta có 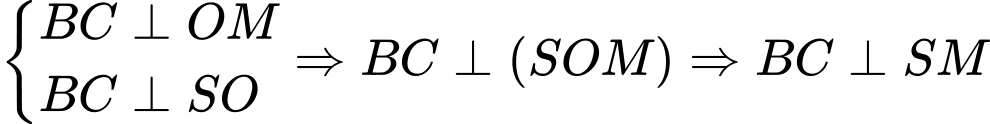
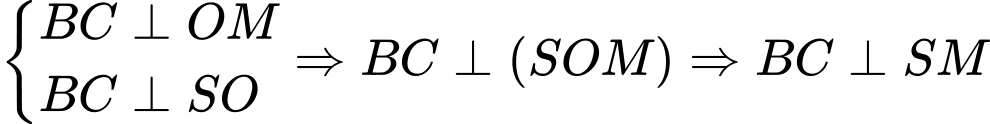
Do đó 

Xét tam giác vuông 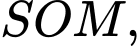 có
có 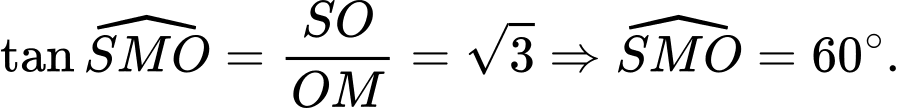
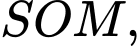 có
có 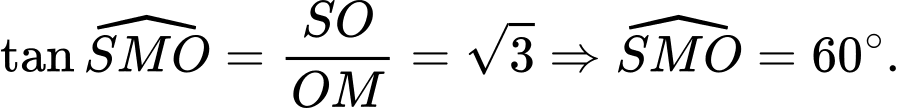
Vậy mặt phẳng 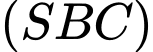 hợp với mặt đáy
hợp với mặt đáy 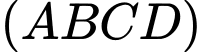 một góc
một góc 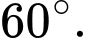
 hợp với mặt đáy
hợp với mặt đáy 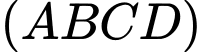 một góc
một góc 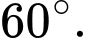
Câu 13 [280737]: Cho hình chóp 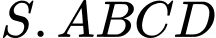 có đáy là hình vuông tâm
có đáy là hình vuông tâm  cạnh
cạnh 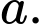 Biết
Biết 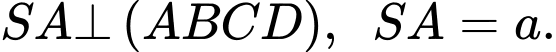 tính số đo góc nhị diện
tính số đo góc nhị diện 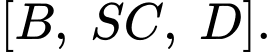
 có đáy là hình vuông tâm
có đáy là hình vuông tâm  cạnh
cạnh 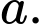 Biết
Biết 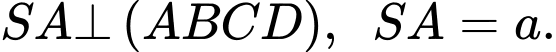 tính số đo góc nhị diện
tính số đo góc nhị diện 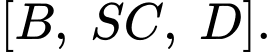
A, 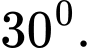
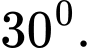
B, 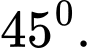
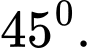
C, 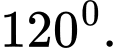
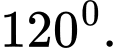
D, 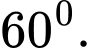
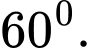
Ta có:  (Vì
(Vì  ).
Trong mặt phẳng
).
Trong mặt phẳng 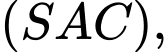 kẻ
kẻ  thì ta có
thì ta có 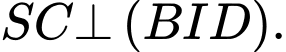

Giao điểm của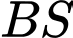 và
và 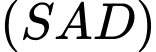 là
là 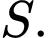
Ta có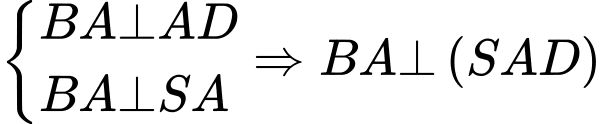

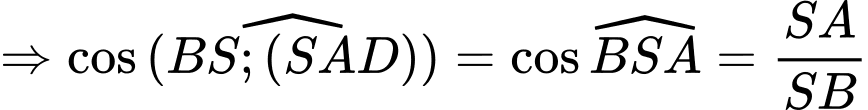 (1)
(1)
Tam giác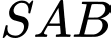 vuông tại
vuông tại 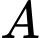
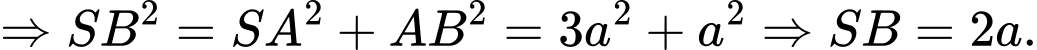
Thế vào (1)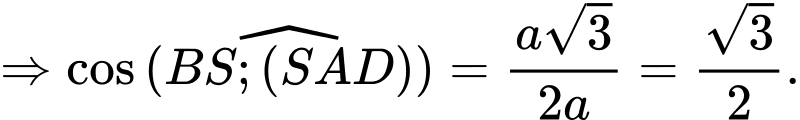 Chọn C.
Đáp án: C
Chọn C.
Đáp án: C
Giao điểm của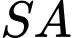 và mặt phẳng
và mặt phẳng 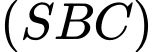 là
là 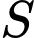
Từ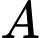 kẻ
kẻ 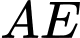 vuông góc với
vuông góc với 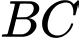 tại
tại 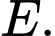
Ta có : và
và 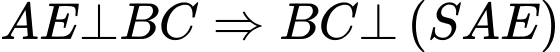 .
.
Dựng ,
,  . Mà
. Mà  .
.
Suy ra
 đều cạnh
đều cạnh 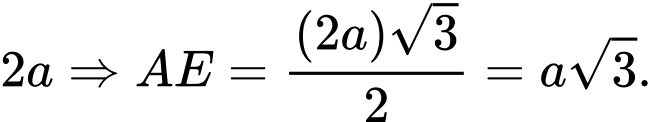
Tam giác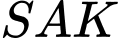 vuông tại
vuông tại 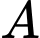 , có
, có 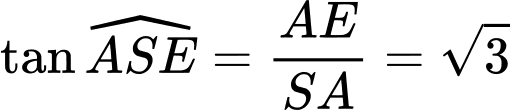
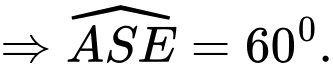 Vậy
Vậy 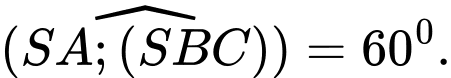 Chọn A.
Đáp án: A
Chọn A.
Đáp án: A
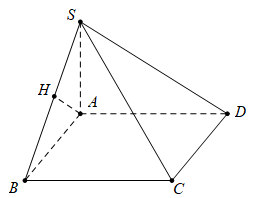
Do ta kẻ
ta kẻ 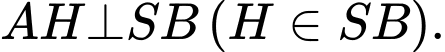
Ta có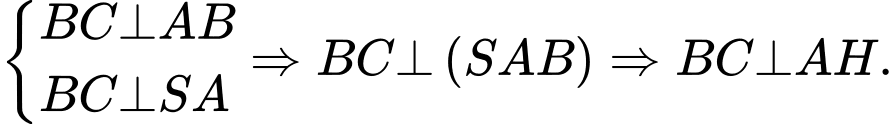
Như vậy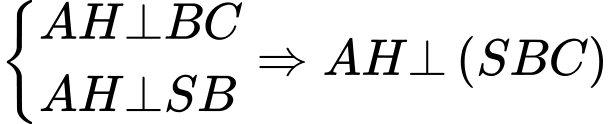
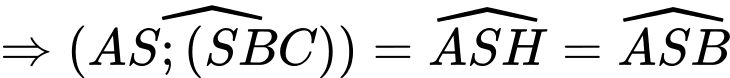
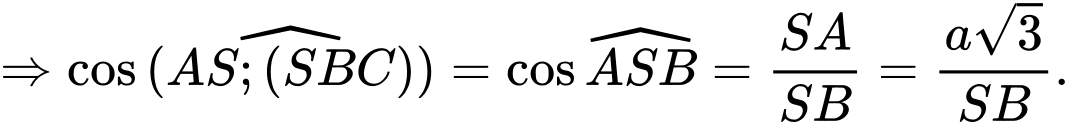
Tam giác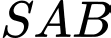 vuông tại
vuông tại 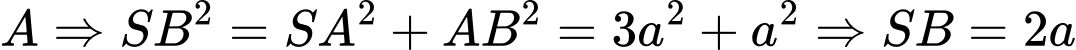
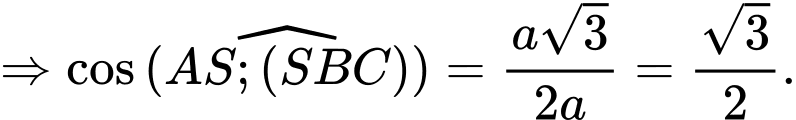 Chọn B.
Chọn B.
Nhận xét: Từ ta xác định được ngay
ta xác định được ngay 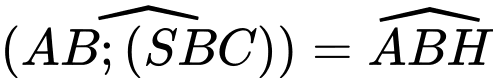 và
và 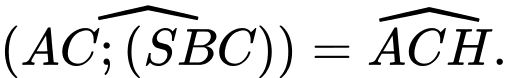 Đáp án: B
Đáp án: B
Do nên ta kẻ
nên ta kẻ 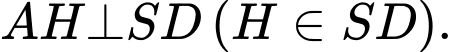
Ta có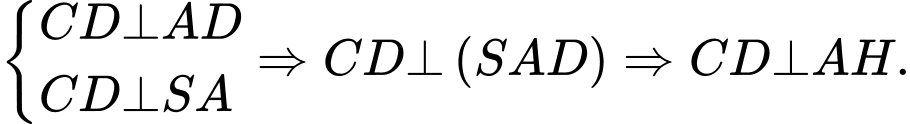
Như vậy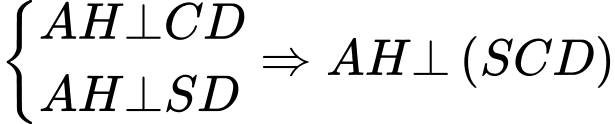
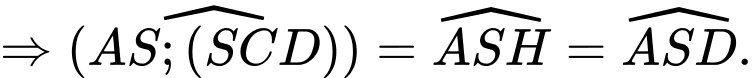
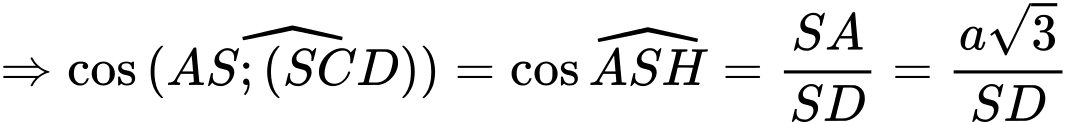 (1)
(1)
Tam giác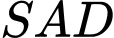 vuông tại
vuông tại 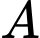
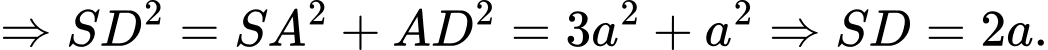
Thế vào (1)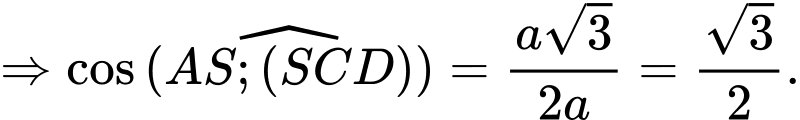 Chọn D
Đáp án: D
Chọn D
Đáp án: D
 Đáp án: B
Đáp án: B
Gọi H là trung điểm của AD ta có:
Lại có: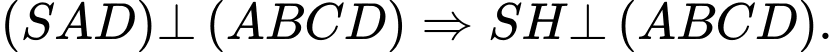
Ta có: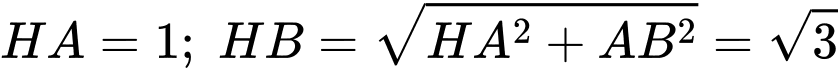
Do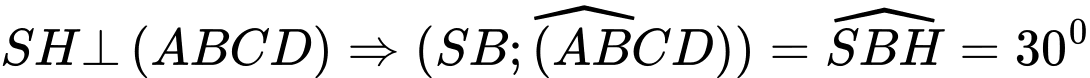
Suy ra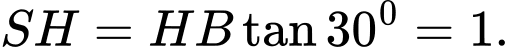
Do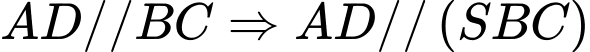 .
.
Do vậy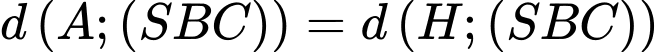 .
.
Dựng ta có:
ta có:  từ đó suy ra
từ đó suy ra 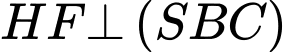
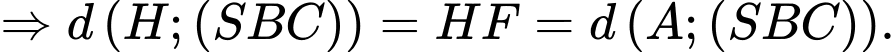 Ta có:
Ta có: 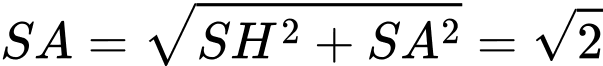
Mặt khác: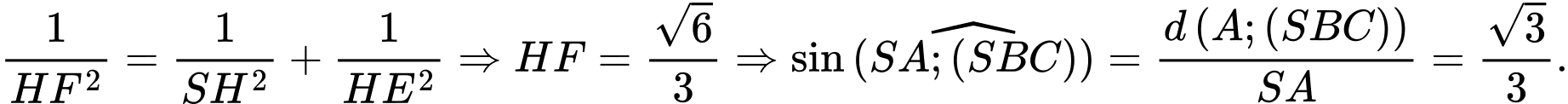 Đáp án: D
Đáp án: D
 Đáp án: C
Đáp án: C
Gọi là tâm của hình vuông
là tâm của hình vuông 
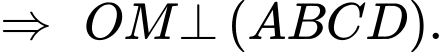
Suy ra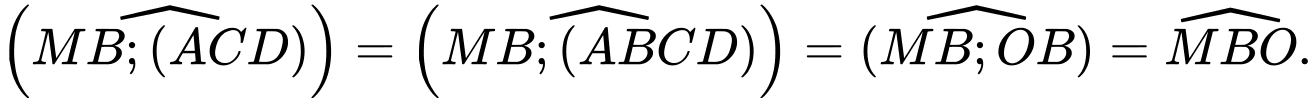
Tam giác vuông tại
vuông tại 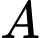

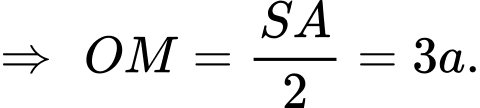
Tam giác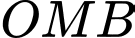 vuông tại
vuông tại  có
có
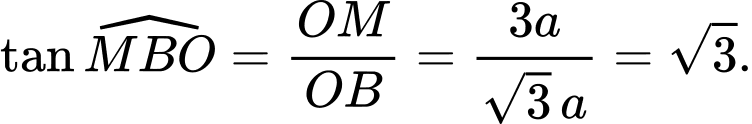
Vậy góc giữa đường thẳng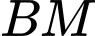 và
và 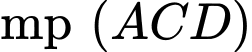 là
là 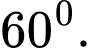
 Đáp án: B
Đáp án: B
Ta có: tại
tại 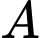 và
và 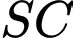 cắt mp
cắt mp 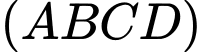 tại
tại 
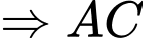 là hình chiếu của
là hình chiếu của 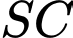 trên mp
trên mp 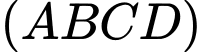

Ta có: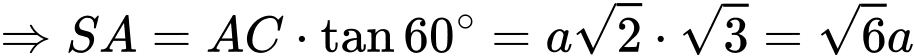
Ta có: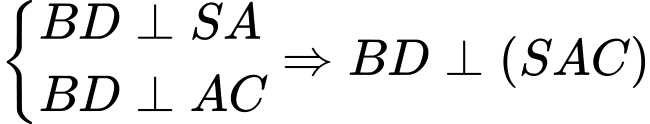
Ta có: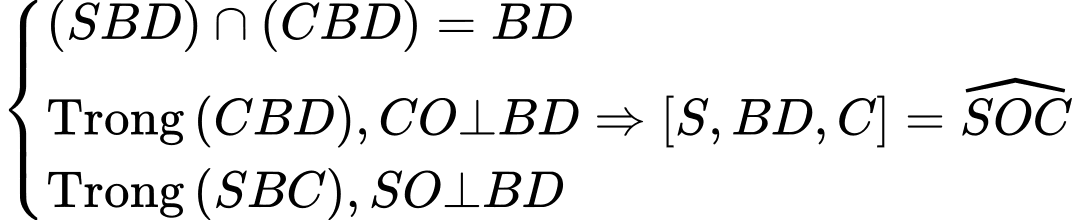
Xét vuông tại
vuông tại 
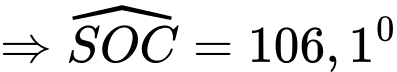

Gọi M là trung điểm BC.
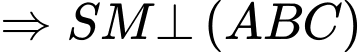 và
và 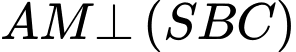
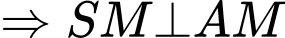
Kẻ đường cao MH.
Có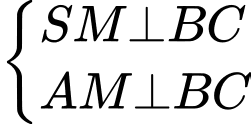
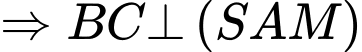

Có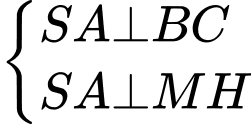
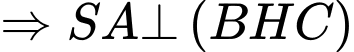
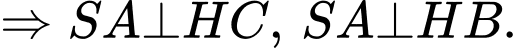
Vậy góc nhị diện
Ta có: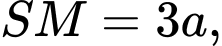

Xét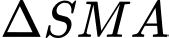 vuông tại
vuông tại 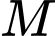 và
và  nên ta có:
nên ta có:
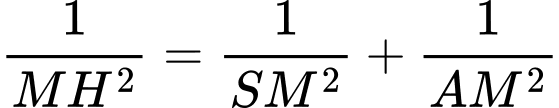
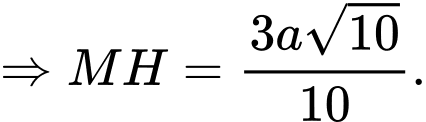
Xét vuông tại
vuông tại 
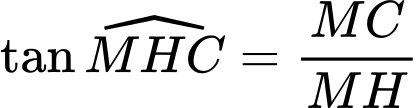
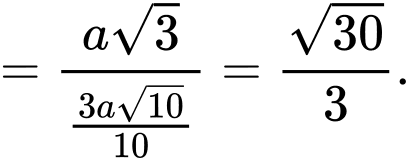
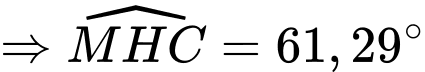
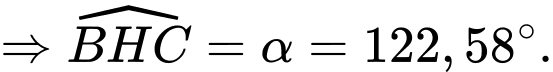
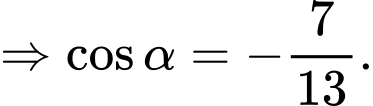
Đáp số: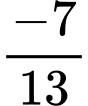 .
.
Vì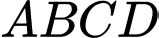 là hình vuông nên
là hình vuông nên 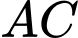 vuông góc với
vuông góc với 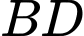 tại
tại 
Suy ra Góc giữa hai mặt phẳng
Góc giữa hai mặt phẳng 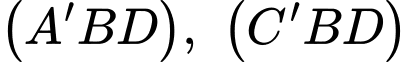 là
là 
Gọi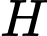 là tâm hình vuông
là tâm hình vuông 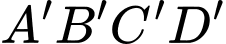 thì
thì 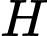 là trung điểm
là trung điểm 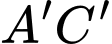 và
và 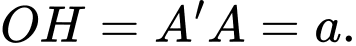
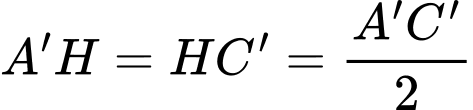
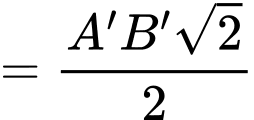
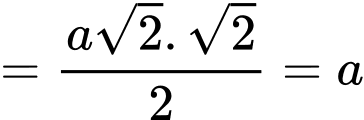
Suy ra các tam giác vuông cân và
vuông cân và 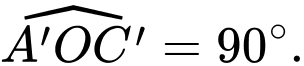
Vậy góc giữa hai mặt phẳng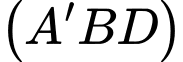 và
và 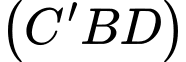 bằng
bằng 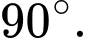
Gọi 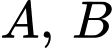 là hai điểm tại hai vị trí chân thang và
là hai điểm tại hai vị trí chân thang và 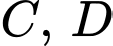 là hai điểm tại hai vị trí ngọn thang,
là hai điểm tại hai vị trí ngọn thang, 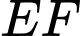 là đường chân tường.
là đường chân tường.
 (Vì
(Vì  ).
Trong mặt phẳng
).
Trong mặt phẳng 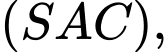 kẻ
kẻ  thì ta có
thì ta có 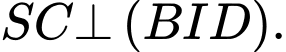
Khi đó, 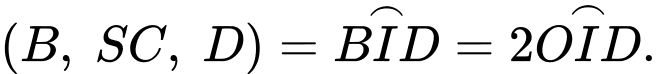
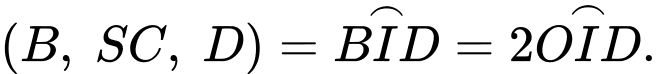
Trong tam giác 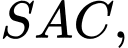 kẻ đường cao
kẻ đường cao  thì
thì 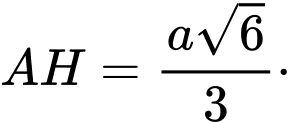
 kẻ đường cao
kẻ đường cao  thì
thì 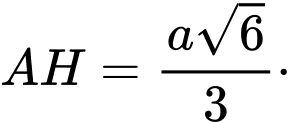
Mà  là trung điểm của
là trung điểm của 
 nên
nên 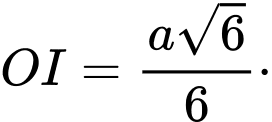
 là trung điểm của
là trung điểm của 
 nên
nên 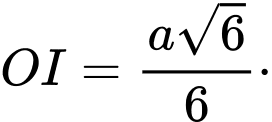
Tam giác 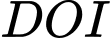 vuông tại
vuông tại  có
có 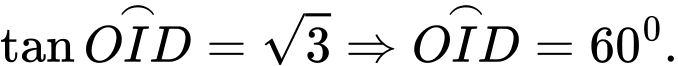
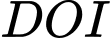 vuông tại
vuông tại  có
có 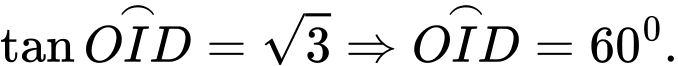
Vậy số đo góc nhị diện 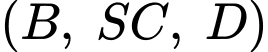 là
là 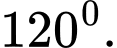 Chọn C.
Chọn C.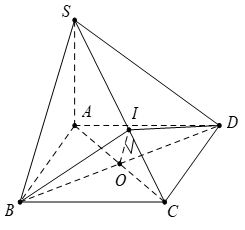 Đáp án: C
Đáp án: C
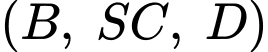 là
là 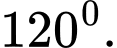 Chọn C.
Chọn C. Đáp án: C
Đáp án: C
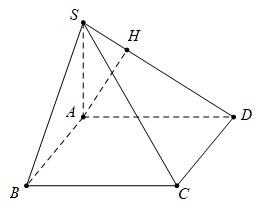
Câu 14 [329060]: Cho hình chóp 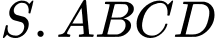 có đáy
có đáy 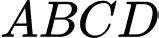 là hình vuông cạnh
là hình vuông cạnh 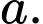 Cạnh
Cạnh  và vuông góc với mặt phẳng đáy. Côsin của góc giữa đường thẳng
và vuông góc với mặt phẳng đáy. Côsin của góc giữa đường thẳng 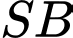 và
và 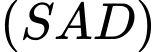 bằng
bằng
 có đáy
có đáy 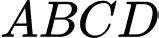 là hình vuông cạnh
là hình vuông cạnh 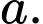 Cạnh
Cạnh  và vuông góc với mặt phẳng đáy. Côsin của góc giữa đường thẳng
và vuông góc với mặt phẳng đáy. Côsin của góc giữa đường thẳng 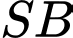 và
và 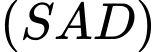 bằng
bằng A, 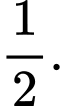
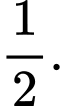
B, 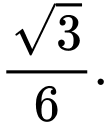
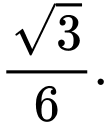
C, 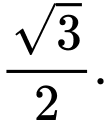
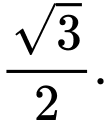
D, 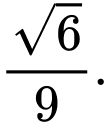
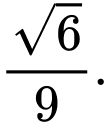

Giao điểm của
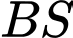 và
và 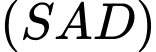 là
là 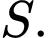
Ta có
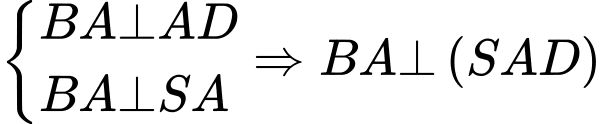

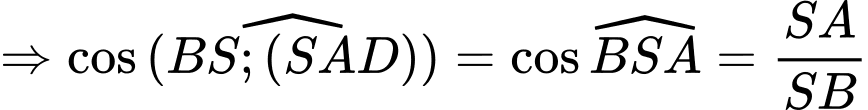 (1)
(1) Tam giác
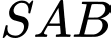 vuông tại
vuông tại 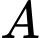
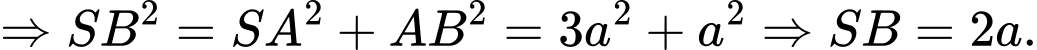
Thế vào (1)
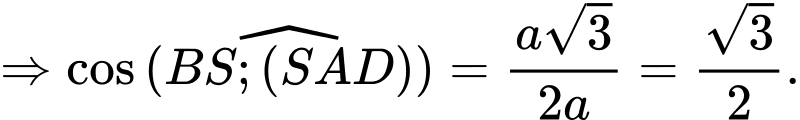 Chọn C.
Đáp án: C
Chọn C.
Đáp án: C
Câu 15 [329063]: Cho hình chóp 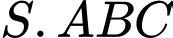 , có đáy
, có đáy 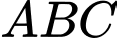 là tam giác đều cạnh
là tam giác đều cạnh 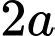 . Cạnh bên
. Cạnh bên  và vuông góc với đáy. Tính góc giữa
và vuông góc với đáy. Tính góc giữa 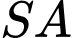 và mặt phẳng
và mặt phẳng 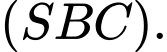
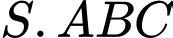 , có đáy
, có đáy 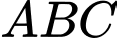 là tam giác đều cạnh
là tam giác đều cạnh 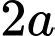 . Cạnh bên
. Cạnh bên  và vuông góc với đáy. Tính góc giữa
và vuông góc với đáy. Tính góc giữa 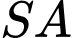 và mặt phẳng
và mặt phẳng 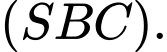
A, 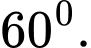
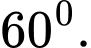
B, 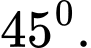
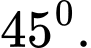
C, 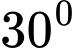
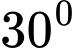
D, 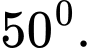
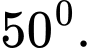

Giao điểm của
 và mặt phẳng
và mặt phẳng 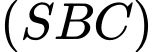 là
là 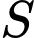
Từ
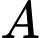 kẻ
kẻ 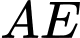 vuông góc với
vuông góc với 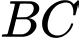 tại
tại 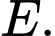
Ta có :
 và
và 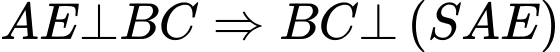 .
.Dựng
 ,
, 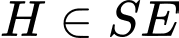 . Mà
. Mà  .
.Suy ra

 đều cạnh
đều cạnh 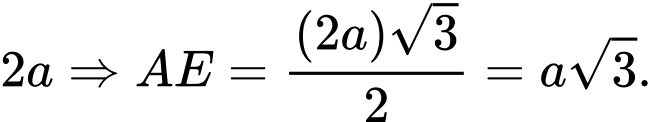
Tam giác
 vuông tại
vuông tại  , có
, có 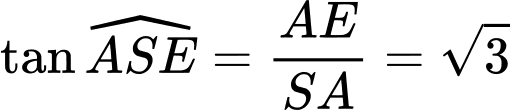
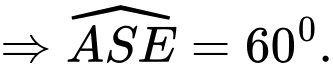 Vậy
Vậy 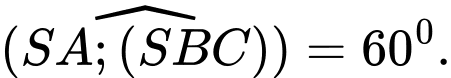 Chọn A.
Đáp án: A
Chọn A.
Đáp án: A
Câu 16 [329065]: Cho hình chóp  có đáy
có đáy 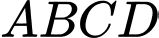 là hình vuông cạnh
là hình vuông cạnh 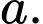 Cạnh
Cạnh  và vuông góc với mặt đáy. Côsin của góc giữa đường thẳng
và vuông góc với mặt đáy. Côsin của góc giữa đường thẳng 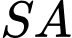 và mặt phẳng
và mặt phẳng 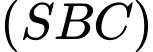 bằng
bằng
 có đáy
có đáy  là hình vuông cạnh
là hình vuông cạnh 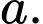 Cạnh
Cạnh  và vuông góc với mặt đáy. Côsin của góc giữa đường thẳng
và vuông góc với mặt đáy. Côsin của góc giữa đường thẳng 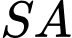 và mặt phẳng
và mặt phẳng 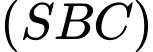 bằng
bằng A, 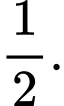
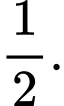
B, 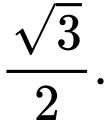
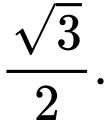
C, 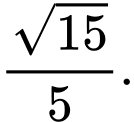
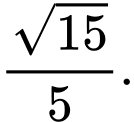
D, 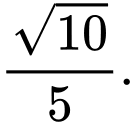
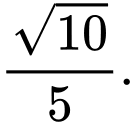

Do
 ta kẻ
ta kẻ 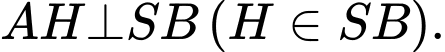
Ta có
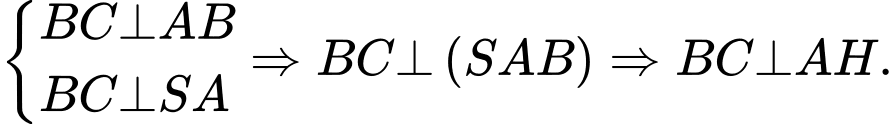
Như vậy
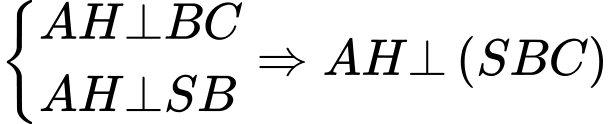
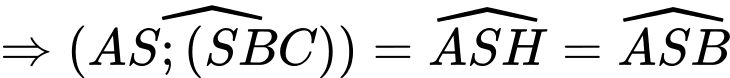
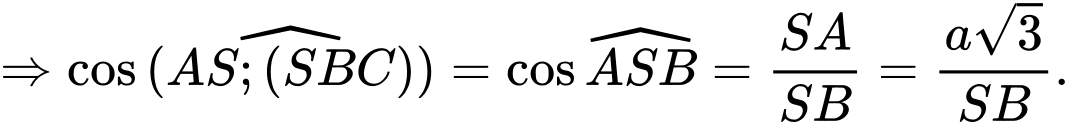
Tam giác
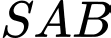 vuông tại
vuông tại 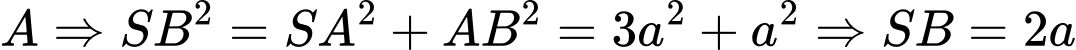
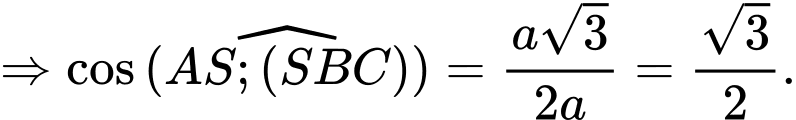 Chọn B.
Chọn B.Nhận xét: Từ
 ta xác định được ngay
ta xác định được ngay 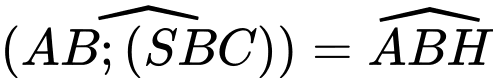 và
và 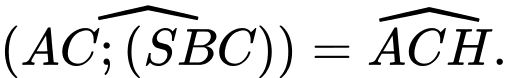 Đáp án: B
Đáp án: B
Câu 17 [280736]: Cho hình chóp  có SA vuông góc với mặt phẳng
có SA vuông góc với mặt phẳng 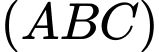 , đáy ABC là tam giác vuông tại B có
, đáy ABC là tam giác vuông tại B có 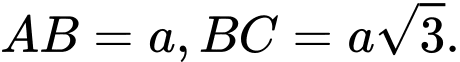 Biết
Biết 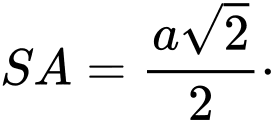 tính số đo góc nhị diện
tính số đo góc nhị diện 
 có SA vuông góc với mặt phẳng
có SA vuông góc với mặt phẳng 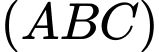 , đáy ABC là tam giác vuông tại B có
, đáy ABC là tam giác vuông tại B có 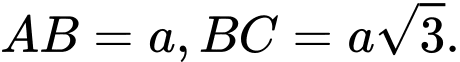 Biết
Biết 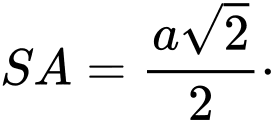 tính số đo góc nhị diện
tính số đo góc nhị diện 
A, 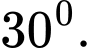
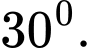
B, 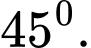
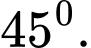
C, 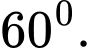
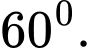
D, 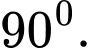
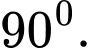
Dựng
Dựng
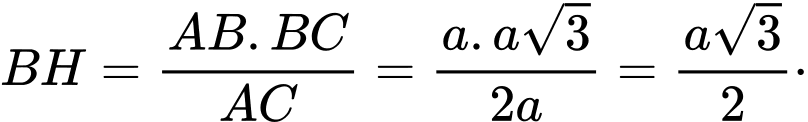
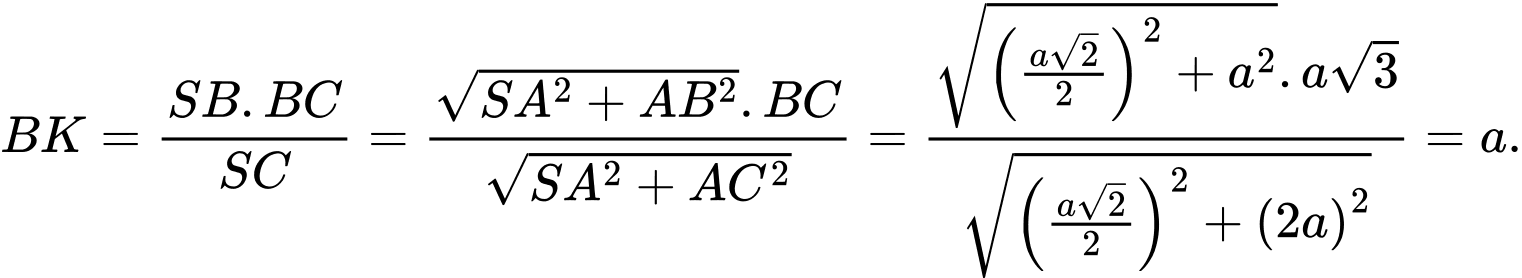
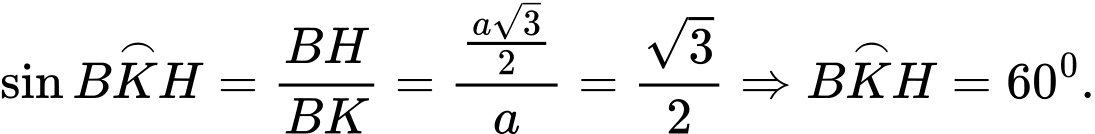

Khi đó, 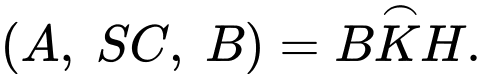
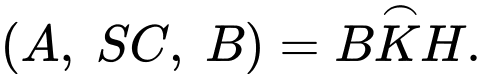
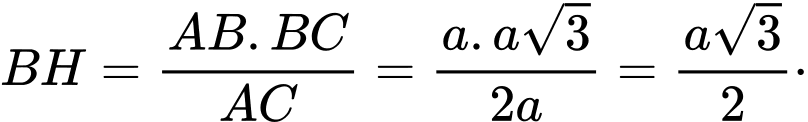
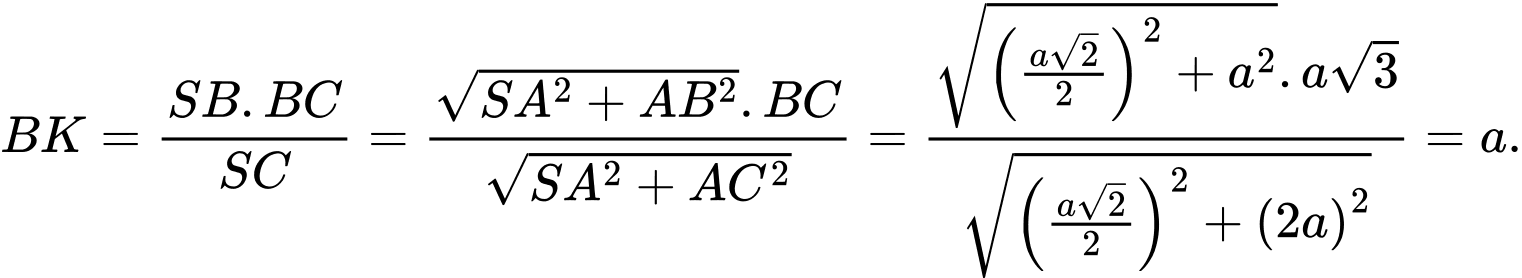
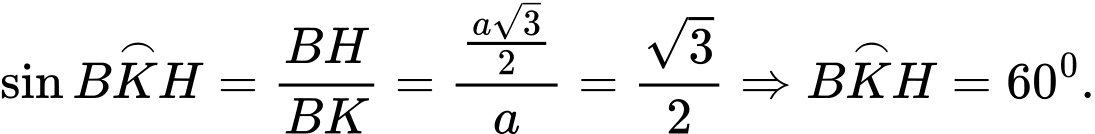
Chọn đáp án C.
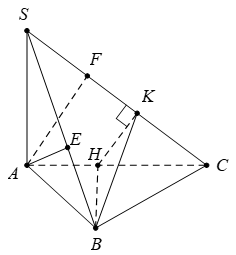
Đáp án: C 
Câu 18 [329066]: Cho hình chóp  có đáy
có đáy  là hình vuông cạnh
là hình vuông cạnh  Cạnh
Cạnh  và vuông góc với mặt đáy. Côsin của góc giữa đường thẳng
và vuông góc với mặt đáy. Côsin của góc giữa đường thẳng  và mặt phẳng
và mặt phẳng  bằng
bằng
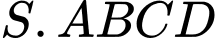 có đáy
có đáy 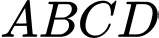 là hình vuông cạnh
là hình vuông cạnh 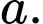 Cạnh
Cạnh  và vuông góc với mặt đáy. Côsin của góc giữa đường thẳng
và vuông góc với mặt đáy. Côsin của góc giữa đường thẳng 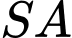 và mặt phẳng
và mặt phẳng  bằng
bằng A, 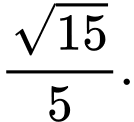
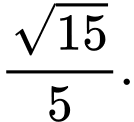
B, 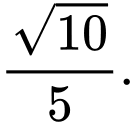
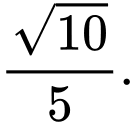
C, 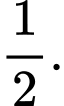
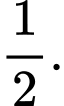
D, 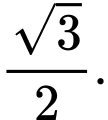
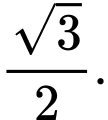

Do
 nên ta kẻ
nên ta kẻ 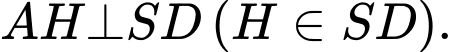
Ta có
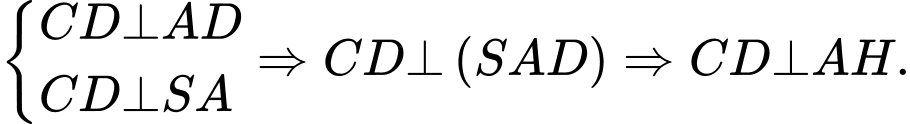
Như vậy
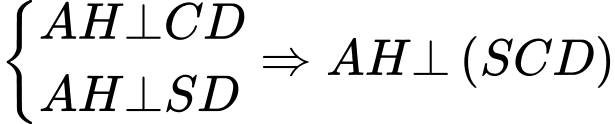
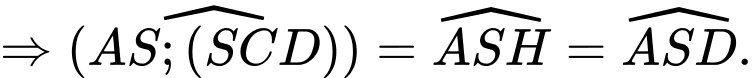
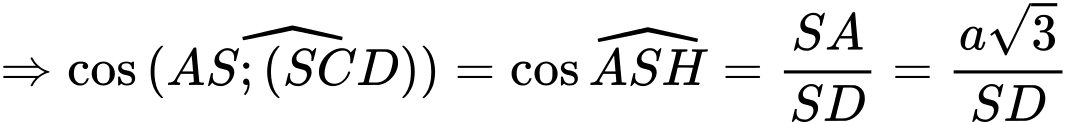 (1)
(1)Tam giác
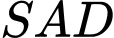 vuông tại
vuông tại 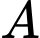
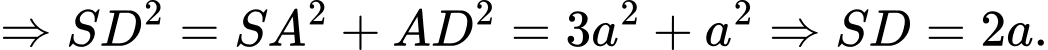
Thế vào (1)
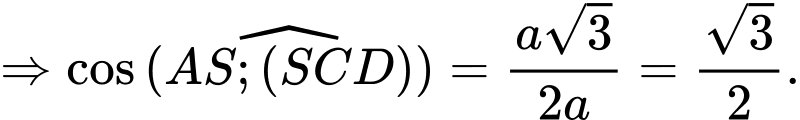 Chọn D
Đáp án: D
Chọn D
Đáp án: D
Câu 19 [7969]: Cho hình chóp 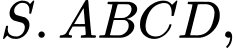 có đáy
có đáy 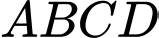 là hình vuông cạnh bằng
là hình vuông cạnh bằng 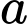 ,
, 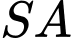 vuông góc với đáy và
vuông góc với đáy và 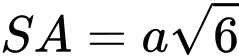 . Góc giữa
. Góc giữa 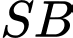 và
và 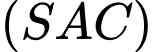 thỏa mãn hệ thức nào sau đây?
thỏa mãn hệ thức nào sau đây?
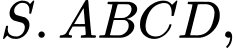 có đáy
có đáy 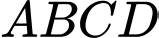 là hình vuông cạnh bằng
là hình vuông cạnh bằng 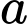 ,
, 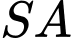 vuông góc với đáy và
vuông góc với đáy và 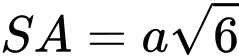 . Góc giữa
. Góc giữa 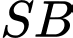 và
và 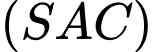 thỏa mãn hệ thức nào sau đây?
thỏa mãn hệ thức nào sau đây? A, 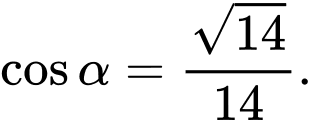
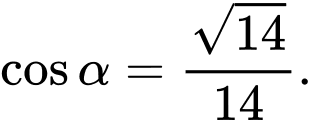
B, 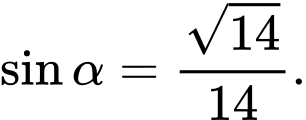
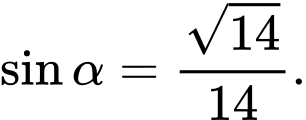
C, 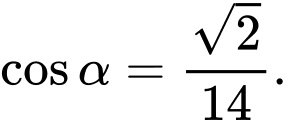
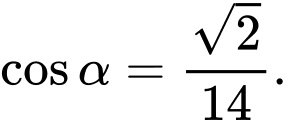
D, 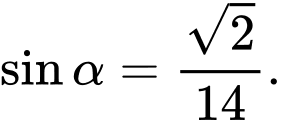
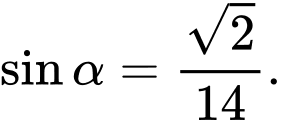
 Đáp án: B
Đáp án: B
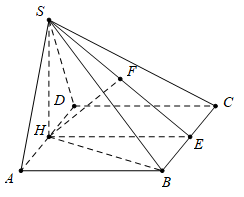
Câu 20 [329069]: Cho hình chóp  có đáy
có đáy 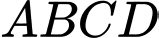 là hình chữ nhật có
là hình chữ nhật có 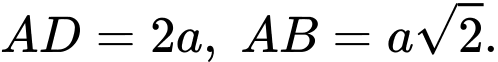 Tam giác
Tam giác 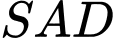 cân tại
cân tại 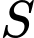 và thuộc mặt phẳng vuông góc với đáy. Đường thẳng
và thuộc mặt phẳng vuông góc với đáy. Đường thẳng 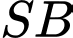 tạo với đáy một góc
tạo với đáy một góc 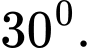 Tính
Tính 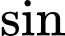 góc
góc 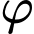 tạo bởi
tạo bởi 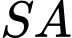 và mặt phẳng
và mặt phẳng 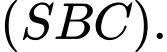
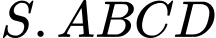 có đáy
có đáy 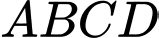 là hình chữ nhật có
là hình chữ nhật có 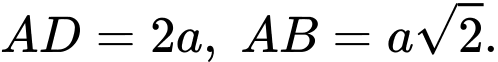 Tam giác
Tam giác 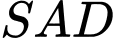 cân tại
cân tại 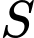 và thuộc mặt phẳng vuông góc với đáy. Đường thẳng
và thuộc mặt phẳng vuông góc với đáy. Đường thẳng 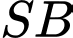 tạo với đáy một góc
tạo với đáy một góc 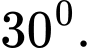 Tính
Tính 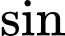 góc
góc 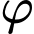 tạo bởi
tạo bởi 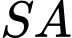 và mặt phẳng
và mặt phẳng 
A, 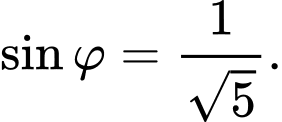
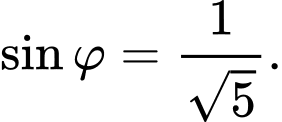
B, 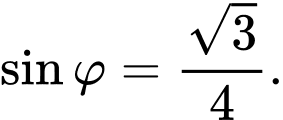
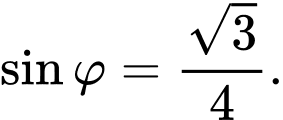
C, 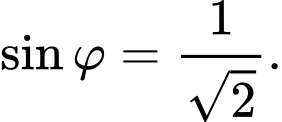
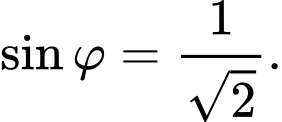
D, 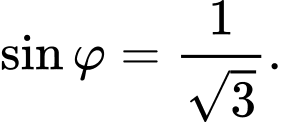
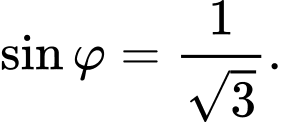

Gọi H là trung điểm của AD ta có:

Lại có:
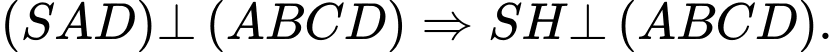
Ta có:
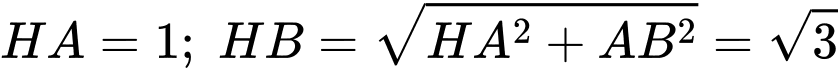
Do
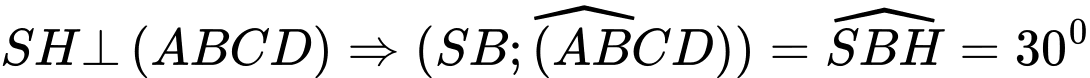
Suy ra
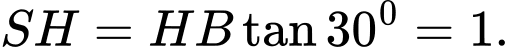
Do
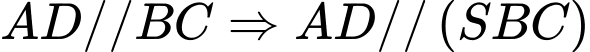 .
.Do vậy
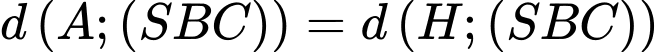 .
.Dựng
 ta có:
ta có:  từ đó suy ra
từ đó suy ra 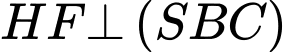
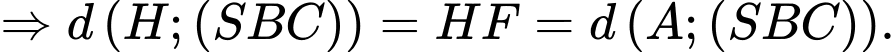 Ta có:
Ta có: 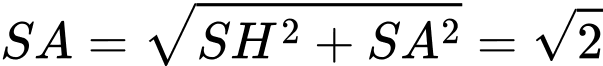
Mặt khác:
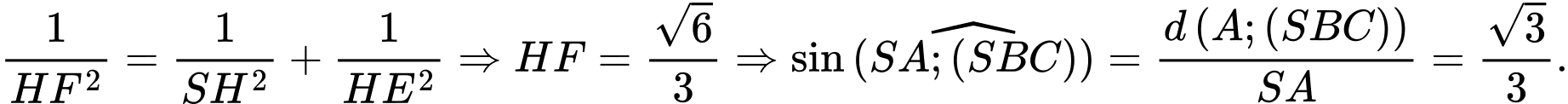 Đáp án: D
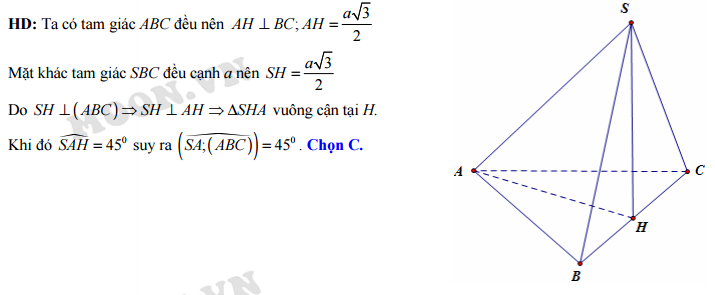
Đáp án: D
Câu 21 [8518]: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên mặt phẳng  trùng với trung điểm H của cạnh
trùng với trung điểm H của cạnh 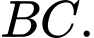 Tam giác
Tam giác 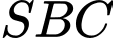 đều. Góc giữa đường thẳng SA và mặt phẳng
đều. Góc giữa đường thẳng SA và mặt phẳng 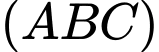 bằng
bằng
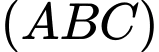 trùng với trung điểm H của cạnh
trùng với trung điểm H của cạnh 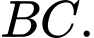 Tam giác
Tam giác 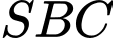 đều. Góc giữa đường thẳng SA và mặt phẳng
đều. Góc giữa đường thẳng SA và mặt phẳng 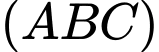 bằng
bằng A, 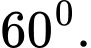
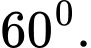
B, 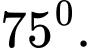
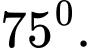
C, 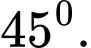
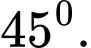
D, 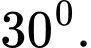
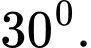
 Đáp án: C
Đáp án: C
Câu 22 [331089]: Giả sử ở những giây đầu tiên sau khi cất cánh, máy bay chuyển động theo một đường thẳng tạo với mặt đất một góc 20° và có tốc độ 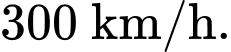 Tính độ cao của máy bay so với mặt đất theo đơn vị mét sau khi máy bay rời khỏi mặt đất 3 giây (làm tròn kết quả đến hàng phần mười).
Tính độ cao của máy bay so với mặt đất theo đơn vị mét sau khi máy bay rời khỏi mặt đất 3 giây (làm tròn kết quả đến hàng phần mười).
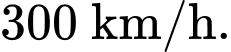 Tính độ cao của máy bay so với mặt đất theo đơn vị mét sau khi máy bay rời khỏi mặt đất 3 giây (làm tròn kết quả đến hàng phần mười).
Tính độ cao của máy bay so với mặt đất theo đơn vị mét sau khi máy bay rời khỏi mặt đất 3 giây (làm tròn kết quả đến hàng phần mười).
Đổi 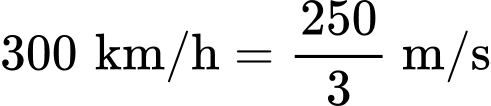
Quãng đường máy bay đi được sau 3 giây là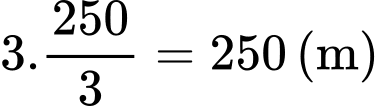
Độ cao của máy bay so với mặt đất là: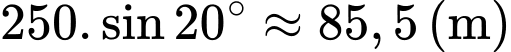
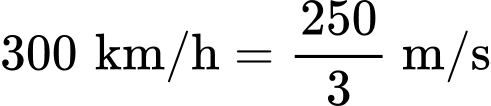
Quãng đường máy bay đi được sau 3 giây là
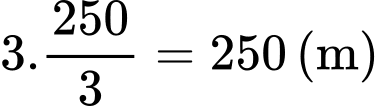
Độ cao của máy bay so với mặt đất là:
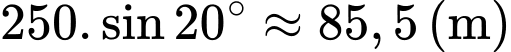
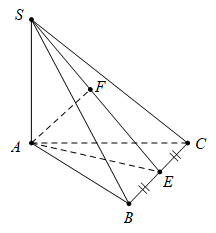
Câu 23 [329056]: Cho hình chóp  có đáy
có đáy 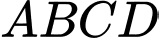 là hình vuông cạnh
là hình vuông cạnh 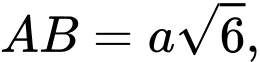 cạnh
cạnh 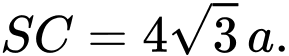 Hai mặt phẳng
Hai mặt phẳng 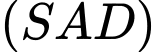 và
và 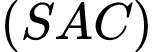 cùng vuông góc với mặt phẳng
cùng vuông góc với mặt phẳng 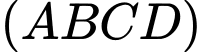 và
và 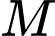 là trung điểm của
là trung điểm của  Tính góc giữa đường thẳng
Tính góc giữa đường thẳng 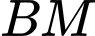 và mặt phẳng
và mặt phẳng 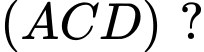
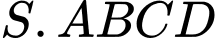 có đáy
có đáy 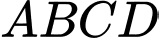 là hình vuông cạnh
là hình vuông cạnh 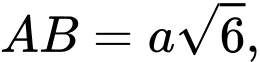 cạnh
cạnh 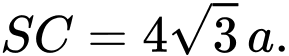 Hai mặt phẳng
Hai mặt phẳng 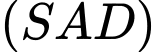 và
và 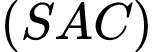 cùng vuông góc với mặt phẳng
cùng vuông góc với mặt phẳng 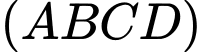 và
và 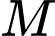 là trung điểm của
là trung điểm của  Tính góc giữa đường thẳng
Tính góc giữa đường thẳng 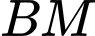 và mặt phẳng
và mặt phẳng 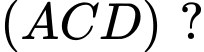

Gọi
 là tâm của hình vuông
là tâm của hình vuông 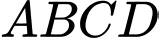
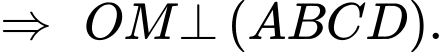
Suy ra
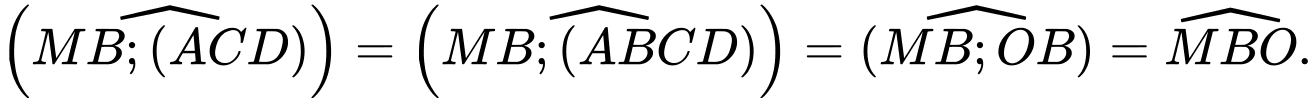
Tam giác
 vuông tại
vuông tại 

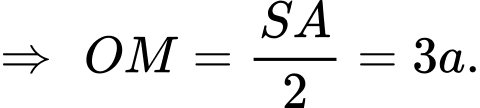
Tam giác
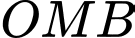 vuông tại
vuông tại  có
có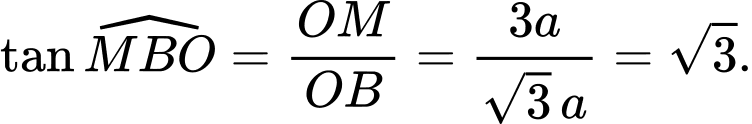
Vậy góc giữa đường thẳng
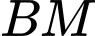 và
và 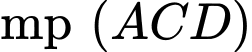 là
là 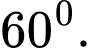
Câu 24 [8642]: Cho hình chóp 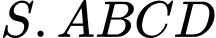 có đáy
có đáy 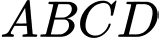 là hình chữ nhật với
là hình chữ nhật với 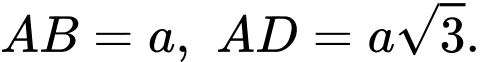 Hình chiếu vuông góc
Hình chiếu vuông góc 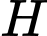 của
của 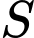 lên mặt đáy trùng với trọng tâm của tam giác
lên mặt đáy trùng với trọng tâm của tam giác 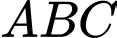 và
và 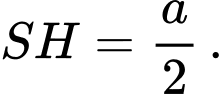 Gọi
Gọi 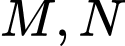 lần lượt là trung điểm của các cạnh
lần lượt là trung điểm của các cạnh 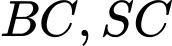 . Tính tan của góc giữa đường thẳng
. Tính tan của góc giữa đường thẳng 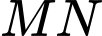 và mặt phẳng
và mặt phẳng 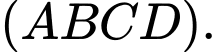
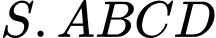 có đáy
có đáy 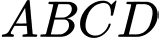 là hình chữ nhật với
là hình chữ nhật với 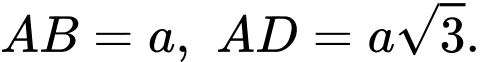 Hình chiếu vuông góc
Hình chiếu vuông góc 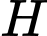 của
của 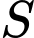 lên mặt đáy trùng với trọng tâm của tam giác
lên mặt đáy trùng với trọng tâm của tam giác 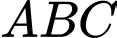 và
và 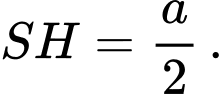 Gọi
Gọi 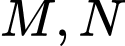 lần lượt là trung điểm của các cạnh
lần lượt là trung điểm của các cạnh 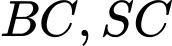 . Tính tan của góc giữa đường thẳng
. Tính tan của góc giữa đường thẳng 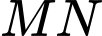 và mặt phẳng
và mặt phẳng 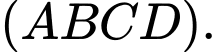
A, 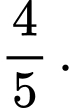
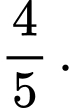
B, 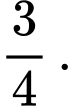
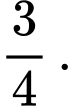
C, 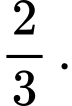
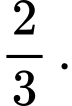
D, 

 Đáp án: B
Đáp án: B
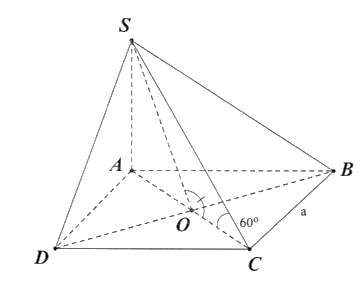
Câu 25 [405474]: Cho hình chóp 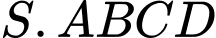 có đáy là hình vuông cạnh
có đáy là hình vuông cạnh 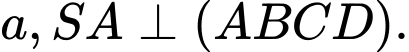 Biết góc giữa
Biết góc giữa 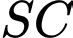 và mặt phẳng
và mặt phẳng 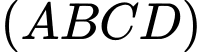 là
là 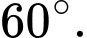 Tính số đo góc nhị diện
Tính số đo góc nhị diện 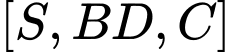 ?
?
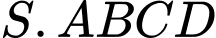 có đáy là hình vuông cạnh
có đáy là hình vuông cạnh 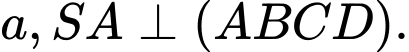 Biết góc giữa
Biết góc giữa 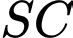 và mặt phẳng
và mặt phẳng 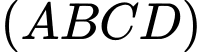 là
là 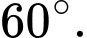 Tính số đo góc nhị diện
Tính số đo góc nhị diện 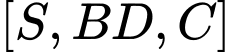 ?
? 
Ta có:
 tại
tại 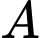 và
và 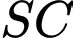 cắt mp
cắt mp 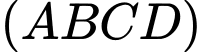 tại
tại 
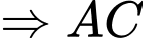 là hình chiếu của
là hình chiếu của 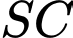 trên mp
trên mp 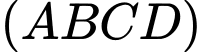

Ta có:
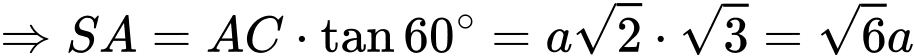
Ta có:
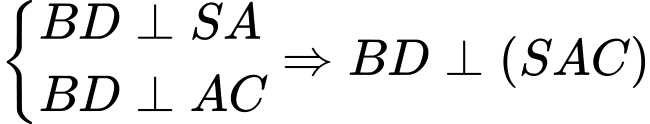
Ta có:
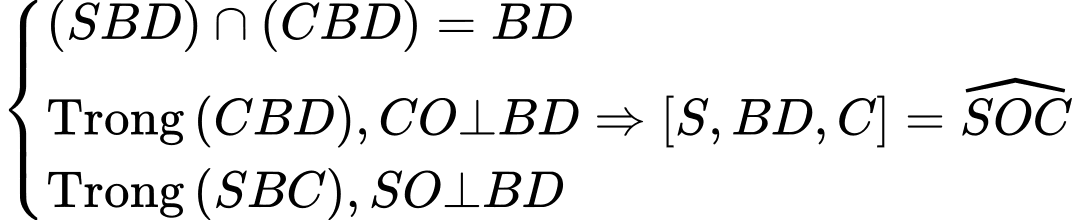
Xét
 vuông tại
vuông tại 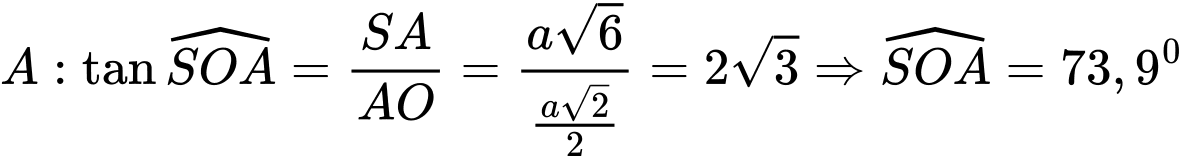
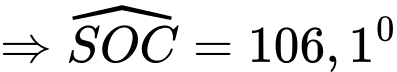
Câu 26 [584400]: Cho hình chóp  có đáy là tam giác ABC vuông tại B có
có đáy là tam giác ABC vuông tại B có 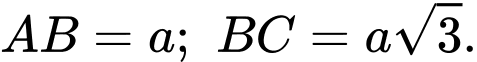 Cạnh bên
Cạnh bên 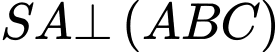 , biết
, biết 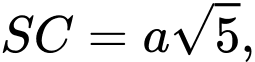 gọi M là trung điểm của AC, tính tan góc giữa hai mặt phẳng
gọi M là trung điểm của AC, tính tan góc giữa hai mặt phẳng 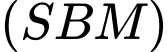 và mặt phẳng đáy
và mặt phẳng đáy 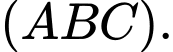 Viết kết quả làm tròn đến hàng phần trăm.
Viết kết quả làm tròn đến hàng phần trăm.
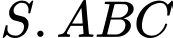 có đáy là tam giác ABC vuông tại B có
có đáy là tam giác ABC vuông tại B có 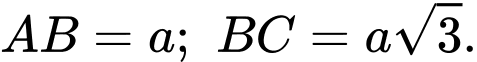 Cạnh bên
Cạnh bên 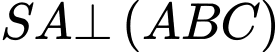 , biết
, biết 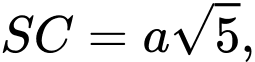 gọi M là trung điểm của AC, tính tan góc giữa hai mặt phẳng
gọi M là trung điểm của AC, tính tan góc giữa hai mặt phẳng 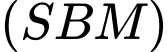 và mặt phẳng đáy
và mặt phẳng đáy 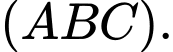 Viết kết quả làm tròn đến hàng phần trăm.
Viết kết quả làm tròn đến hàng phần trăm. 
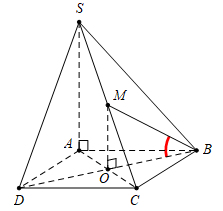
Câu 27 [582123]: Cho khối chóp 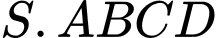 có đáy
có đáy 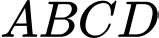 là hình bình hành,
là hình bình hành,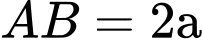 ,
,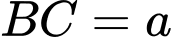 ,
,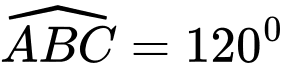 ,
,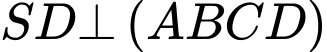 ,
,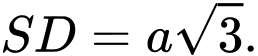 Tính
Tính 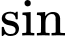 của góc tạo bởi
của góc tạo bởi 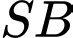 và mặt phẳng
và mặt phẳng 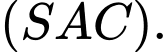
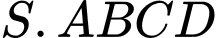 có đáy
có đáy 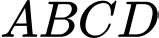 là hình bình hành,
là hình bình hành,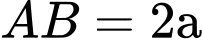 ,
,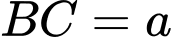 ,
,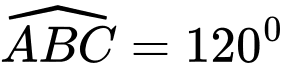 ,
,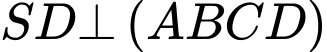 ,
,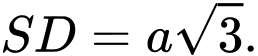 Tính
Tính 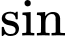 của góc tạo bởi
của góc tạo bởi 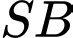 và mặt phẳng
và mặt phẳng 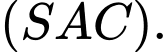
Cách 2: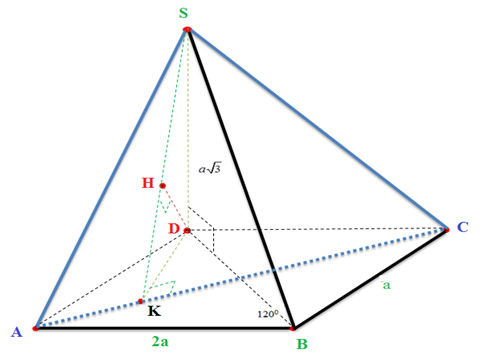
Gọi  lần lượt là hình chiếu của
lần lượt là hình chiếu của  lên
lên 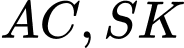 .Từ giả thiết suy ra:
.Từ giả thiết suy ra:
*) 
*) 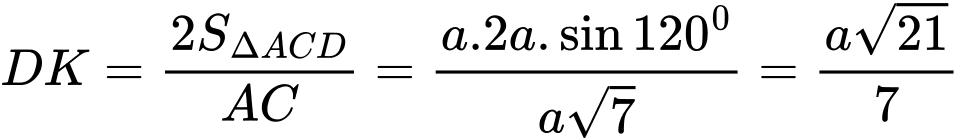
*) 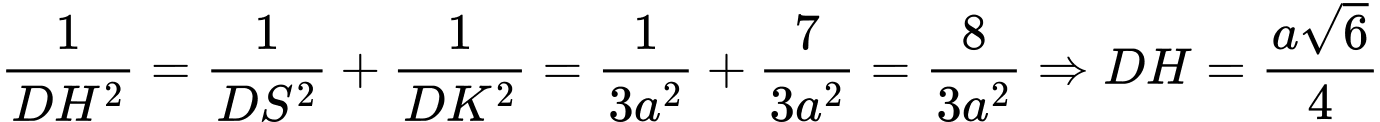
*) 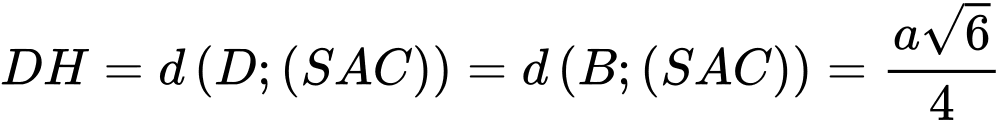
Gọi 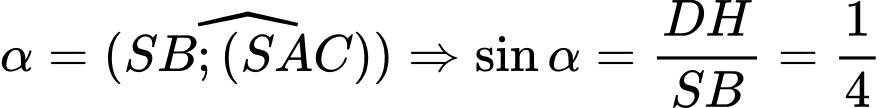
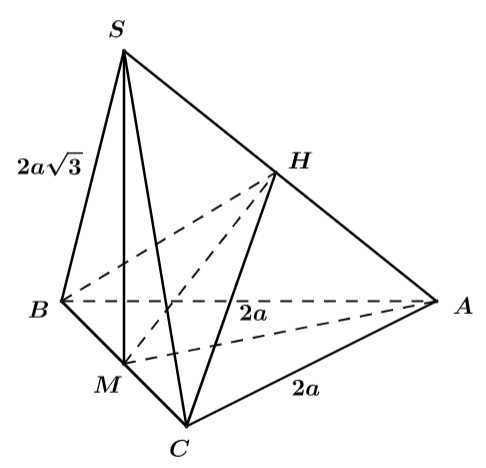
Câu 28 [582124]: Cho hình chóp 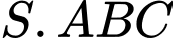 có đáy là tam giác cân tại
có đáy là tam giác cân tại 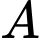 có
có 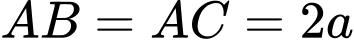 và
và 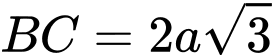 . Tam giác
. Tam giác 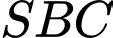 đều và thuộc mặt phẳng vuông góc với đáy. Gọi
đều và thuộc mặt phẳng vuông góc với đáy. Gọi 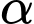 là số đo góc nhị diện
là số đo góc nhị diện  Tính
Tính 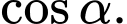
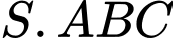 có đáy là tam giác cân tại
có đáy là tam giác cân tại 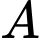 có
có 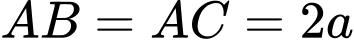 và
và 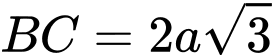 . Tam giác
. Tam giác 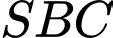 đều và thuộc mặt phẳng vuông góc với đáy. Gọi
đều và thuộc mặt phẳng vuông góc với đáy. Gọi 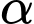 là số đo góc nhị diện
là số đo góc nhị diện  Tính
Tính 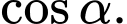

Gọi M là trung điểm BC.
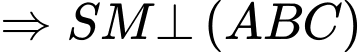 và
và 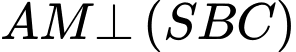
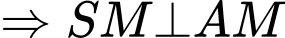
Kẻ đường cao MH.
Có
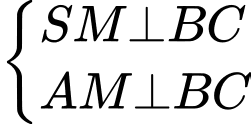
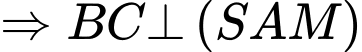

Có
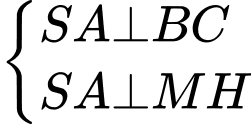
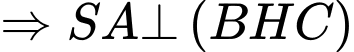
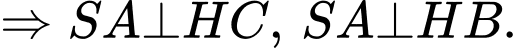
Vậy góc nhị diện

Ta có:
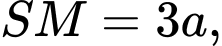

Xét
 vuông tại
vuông tại 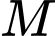 và
và  nên ta có:
nên ta có:
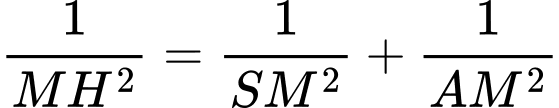
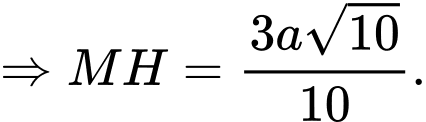
Xét
 vuông tại
vuông tại 
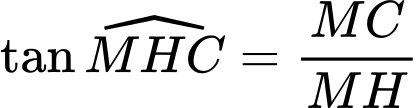
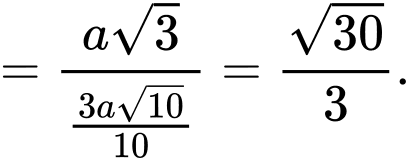
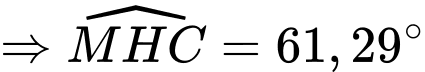
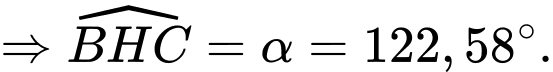
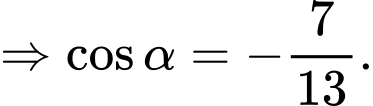
Đáp số:
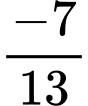 .
.
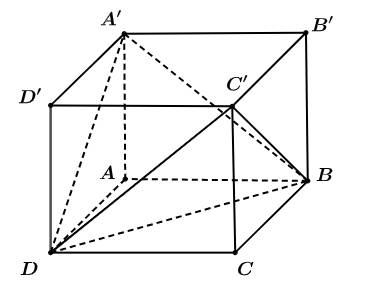
Câu 29 [581412]: Cho hình hộp chữ nhật  có đáy
có đáy 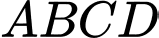 là hình vuông cạnh
là hình vuông cạnh 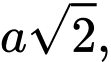 cạnh bên
cạnh bên 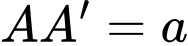 (minh hoạ như hình vẽ). Góc giữa hai mặt phẳng
(minh hoạ như hình vẽ). Góc giữa hai mặt phẳng 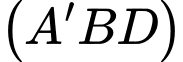 và
và 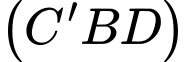 bằng bao nhiêu độ?
bằng bao nhiêu độ?
 có đáy
có đáy 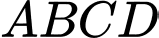 là hình vuông cạnh
là hình vuông cạnh 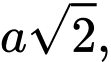 cạnh bên
cạnh bên 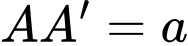 (minh hoạ như hình vẽ). Góc giữa hai mặt phẳng
(minh hoạ như hình vẽ). Góc giữa hai mặt phẳng 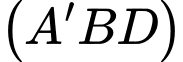 và
và 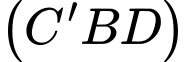 bằng bao nhiêu độ?
bằng bao nhiêu độ? 

Vì
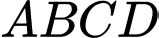 là hình vuông nên
là hình vuông nên 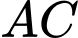 vuông góc với
vuông góc với 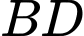 tại
tại 
Suy ra
 Góc giữa hai mặt phẳng
Góc giữa hai mặt phẳng 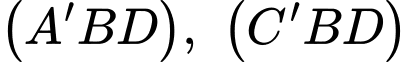 là
là 
Gọi
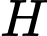 là tâm hình vuông
là tâm hình vuông 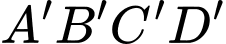 thì
thì 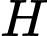 là trung điểm
là trung điểm 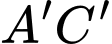 và
và 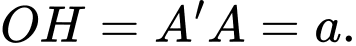
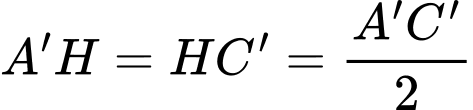
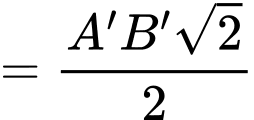
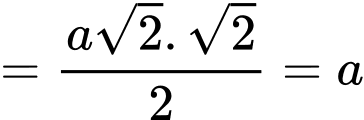
Suy ra các tam giác
 vuông cân và
vuông cân và 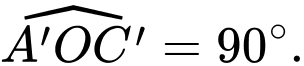
Vậy góc giữa hai mặt phẳng
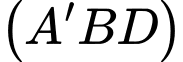 và
và 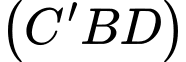 bằng
bằng 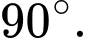
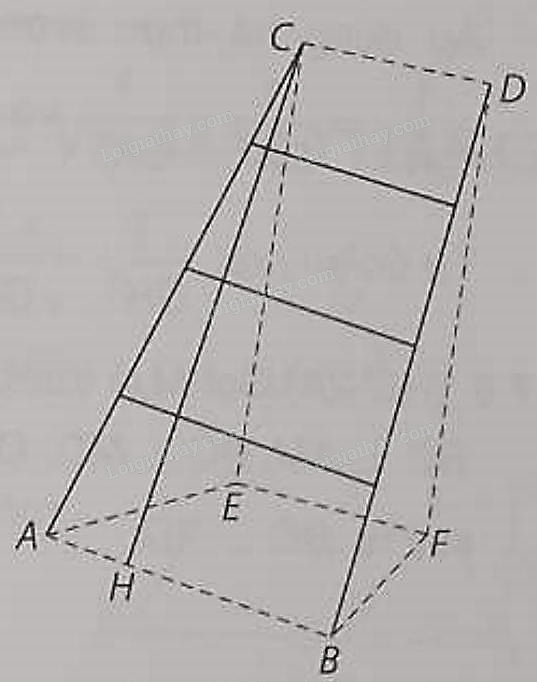
Câu 30 [309020]: Một chiếc thang có dạng hình thang cân cao 6 m, hai chân thang cách nhau 80 cm, hai ngọn thang cách nhau 60 cm. Thang được dựa vào bờ tường như hình bên. Góc tạo giữa đường thẳng chân tường và cạnh cột thang (tính gần đúng theo đơn vị độ, làm tròn kết quả đến chữ số thập phân thứ hai) bằng bao nhiêu?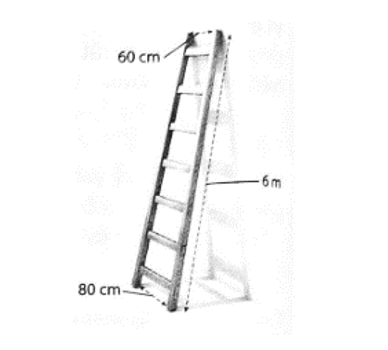


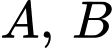 là hai điểm tại hai vị trí chân thang và
là hai điểm tại hai vị trí chân thang và 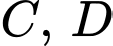 là hai điểm tại hai vị trí ngọn thang,
là hai điểm tại hai vị trí ngọn thang,  là đường chân tường.
là đường chân tường. Ta có: 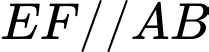 nên
nên 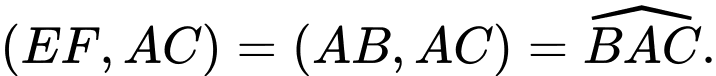 Kẻ
Kẻ  vuông góc với
vuông góc với  tại
tại  ta có
ta có 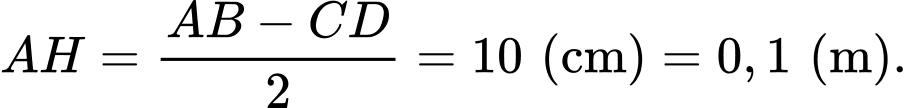
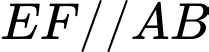 nên
nên 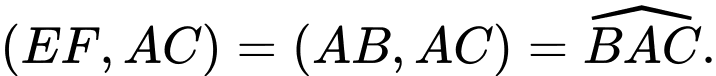 Kẻ
Kẻ 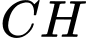 vuông góc với
vuông góc với  tại
tại 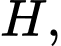 ta có
ta có 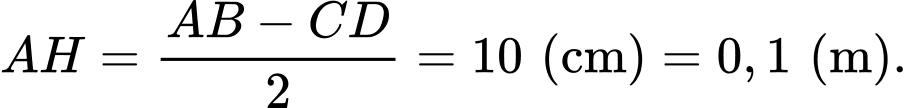
Tam giác  vuông tại
vuông tại  nên
nên 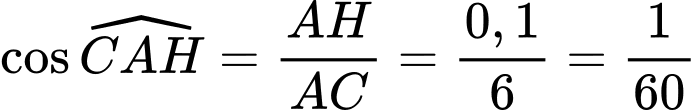
 vuông tại
vuông tại  nên
nên 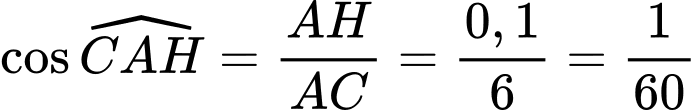
Suy ra 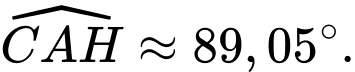
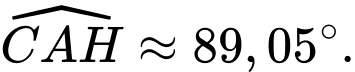
Vậy góc tạo giữa đường thẳng chân tường và cạnh cột thang bằng khoảng