Đáp án Bài tập tự luyện số 2
Câu 1 [378483]: Cho hàm số 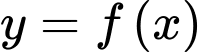 xác định trên
xác định trên 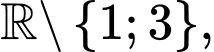 liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau: 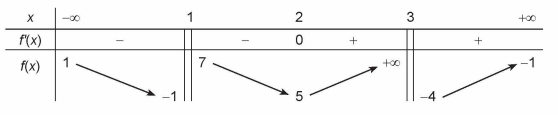
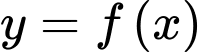 xác định trên
xác định trên 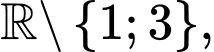 liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau: 
Khẳng định nào sau đây là sai?
A, Đường thẳng 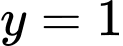 là tiệm cận ngang của đồ thị hàm số đã cho.
là tiệm cận ngang của đồ thị hàm số đã cho.
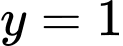 là tiệm cận ngang của đồ thị hàm số đã cho.
là tiệm cận ngang của đồ thị hàm số đã cho.B, Đường thẳng 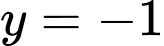 là tiệm cận ngang của đồ thị hàm số đã cho.
là tiệm cận ngang của đồ thị hàm số đã cho.
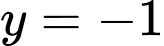 là tiệm cận ngang của đồ thị hàm số đã cho.
là tiệm cận ngang của đồ thị hàm số đã cho.C, Đường thẳng 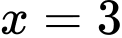 là tiệm cận đứng của đồ thị hàm số đã cho.
là tiệm cận đứng của đồ thị hàm số đã cho.
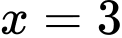 là tiệm cận đứng của đồ thị hàm số đã cho.
là tiệm cận đứng của đồ thị hàm số đã cho.D, Đường thẳng 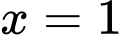 là tiệm cận đứng của đồ thị hàm số đã cho.
là tiệm cận đứng của đồ thị hàm số đã cho.
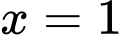 là tiệm cận đứng của đồ thị hàm số đã cho.
là tiệm cận đứng của đồ thị hàm số đã cho.
Từ đồ thị ta thấy 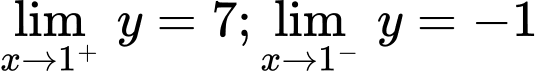
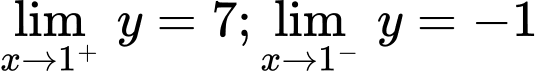
Vậy 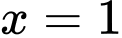 không là tiệm cận đứng của đồ thị hàm số.
không là tiệm cận đứng của đồ thị hàm số.
Đáp án: D  không là tiệm cận đứng của đồ thị hàm số.
không là tiệm cận đứng của đồ thị hàm số.
Câu 2 [132931]: Số tiệm cận đứng của đồ thị hàm số 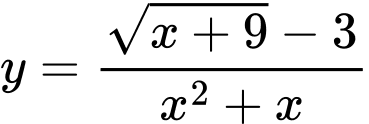 là
là
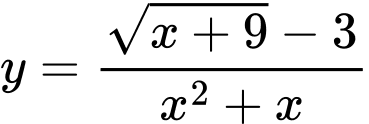 là
là A, 3.
B, 2.
C, 0.
D, 1.
Ta có 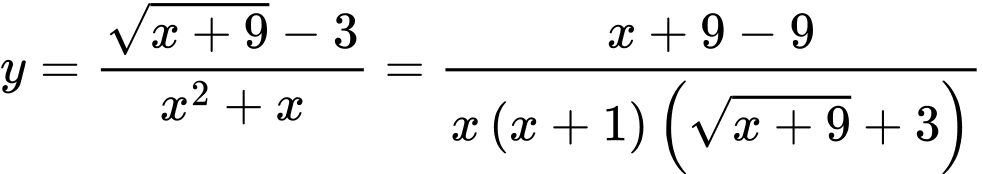
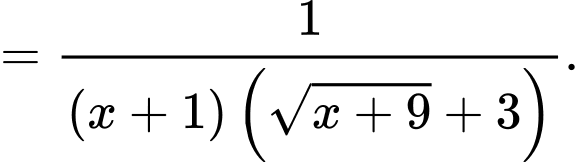
Đồ thị hàm số có đúng 1 tiệm cận đứng là đường thẳng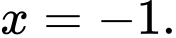 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
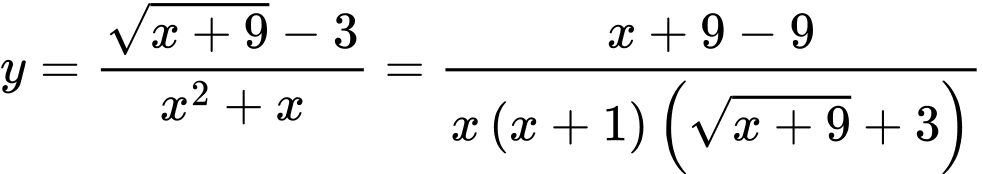
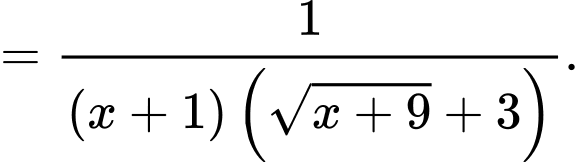
Đồ thị hàm số có đúng 1 tiệm cận đứng là đường thẳng
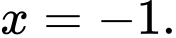 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
Câu 3 [46680]: Tìm giao điểm của trục tung với tiệm cận xiên của đường cong 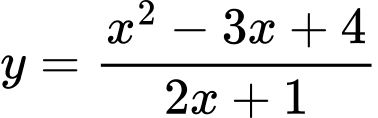 .
.
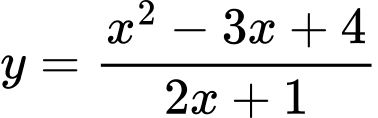 .
. A, 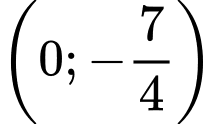
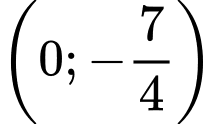
B, (0;4)
C, (0;– 2)
D, 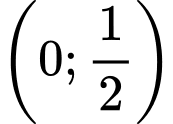
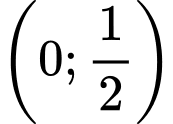
Ta có 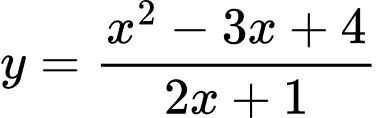
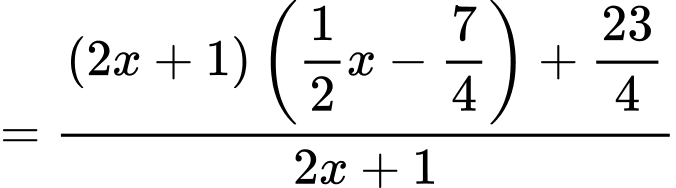
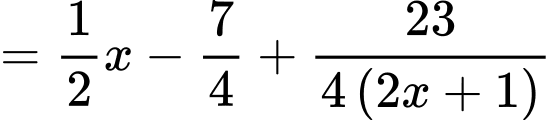
Do đó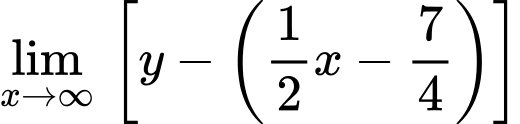
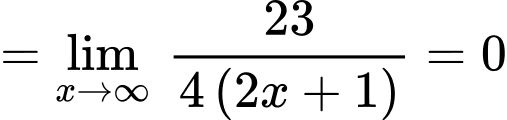
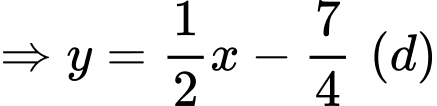 là tiệm cận xiên của đường cong
là tiệm cận xiên của đường cong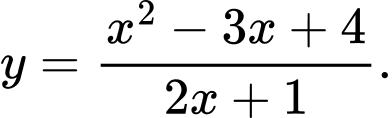
Khi đó
Chọn đáp án A. Đáp án: A
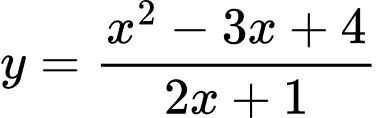
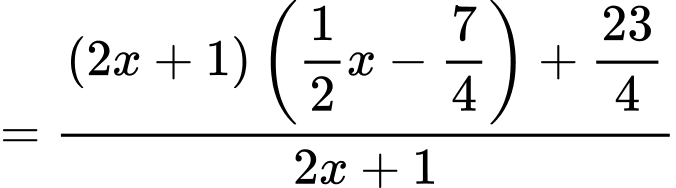
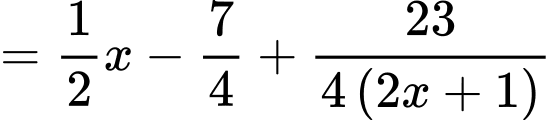
Do đó
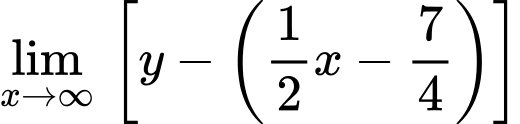
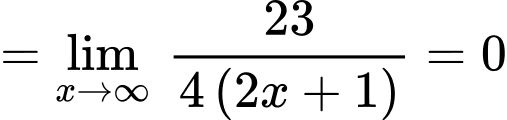
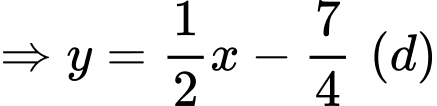 là tiệm cận xiên của đường cong
là tiệm cận xiên của đường cong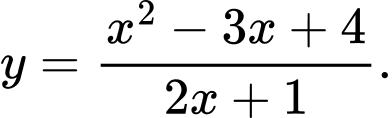
Khi đó

Chọn đáp án A. Đáp án: A
Câu 4 [31248]: Tìm tất cả các đường tiệm cận đứng của đồ thị hàm số 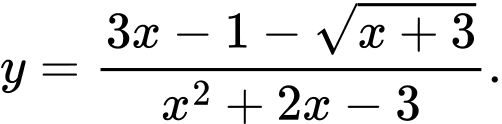
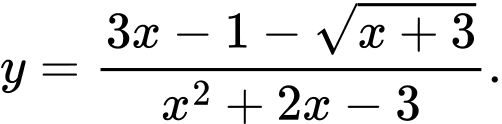
A, 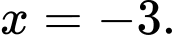
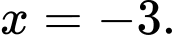
B, 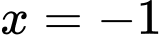 và
và 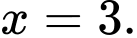
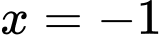 và
và 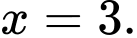
C, 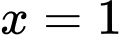 và
và 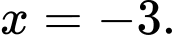
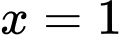 và
và 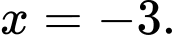
D, 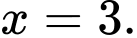
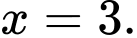
Hàm số có tập xác định 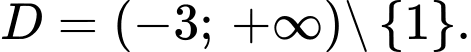
Khi đó,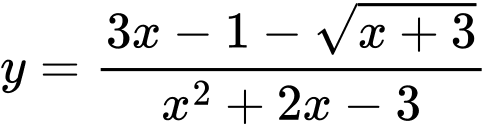
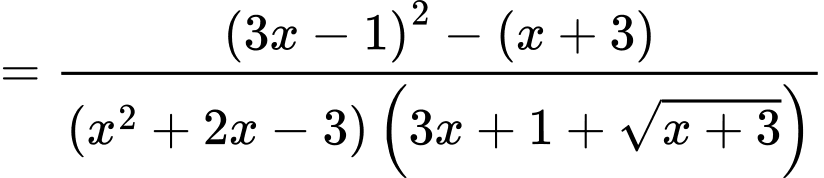
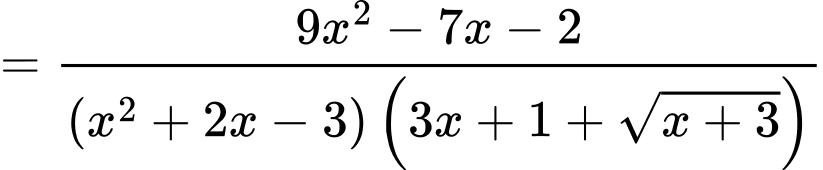
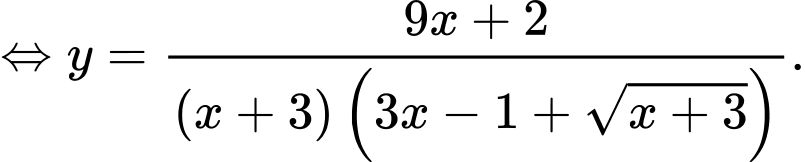
Suy ra,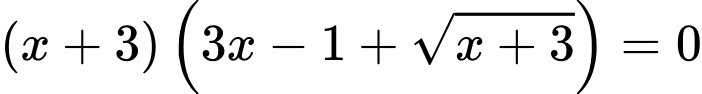
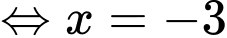
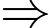 Đồ thị có TCĐ
Đồ thị có TCĐ 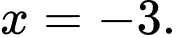
Chọn A. Đáp án: A
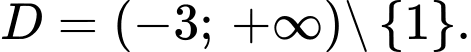
Khi đó,
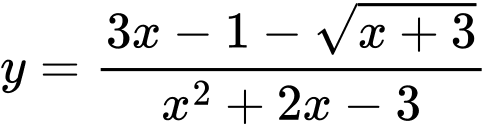
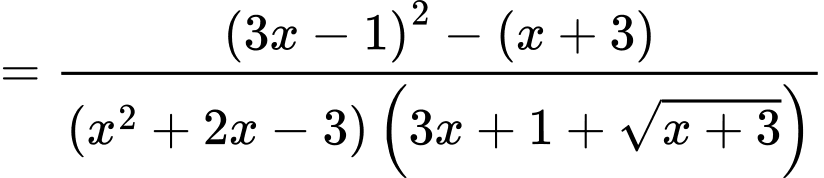
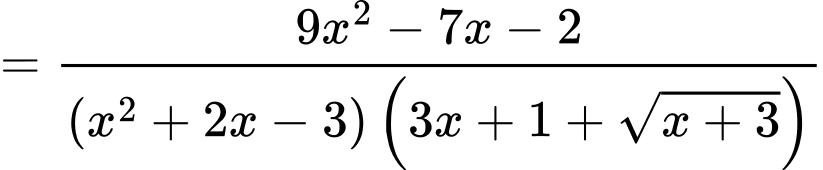
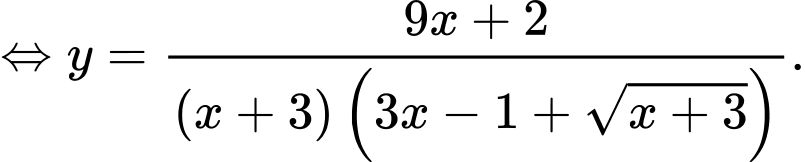
Suy ra,
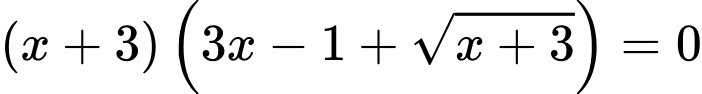
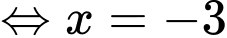
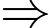 Đồ thị có TCĐ
Đồ thị có TCĐ 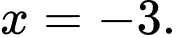
Chọn A. Đáp án: A
Câu 5 [46681]: Tìm đường tiệm cận xiên của đồ thị hàm số 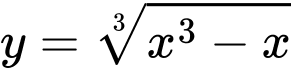 .
.
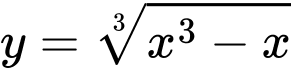 .
. A, 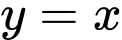
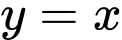
B, 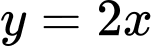
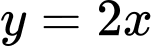
C, 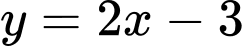
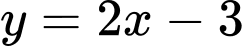
D, 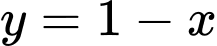
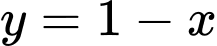
Ta có 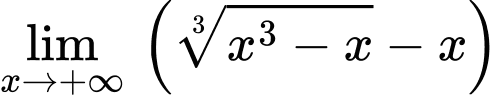
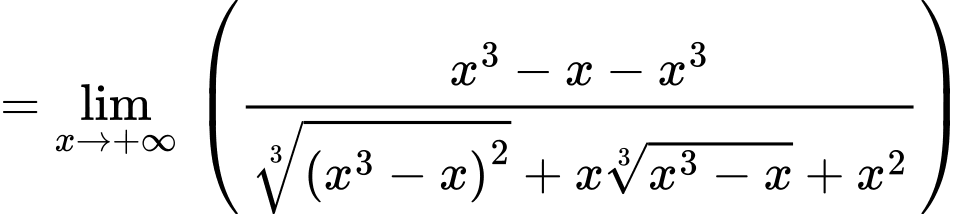
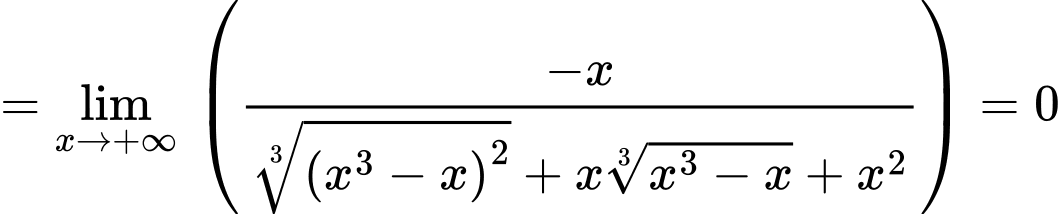
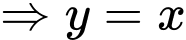 là đường tiệm cận xiên của đồ thị hàm số
là đường tiệm cận xiên của đồ thị hàm số 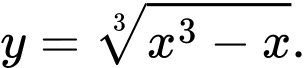
Chọn đáp án A. Đáp án: A
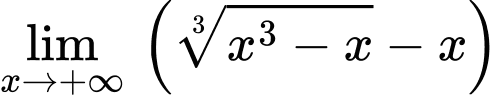
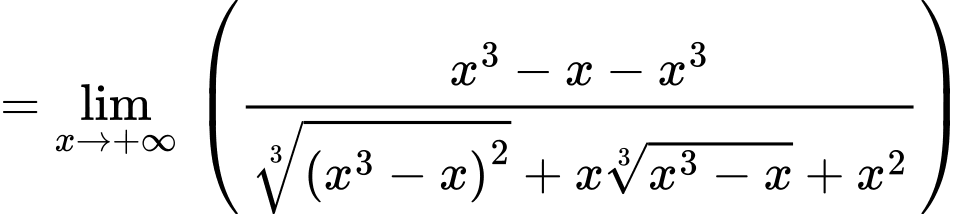
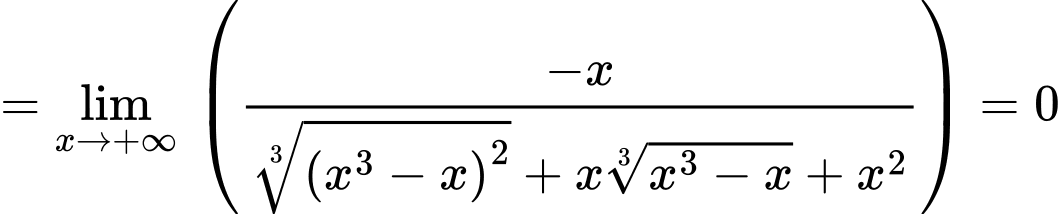
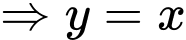 là đường tiệm cận xiên của đồ thị hàm số
là đường tiệm cận xiên của đồ thị hàm số 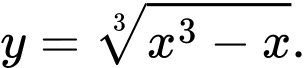
Chọn đáp án A. Đáp án: A
Câu 6 [382482]: Biết đồ thị hàm số 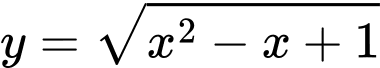 có hai đường tiệm cận xiên. Hỏi chúng cắt nhau tại điểm có hoành độ bằng bao nhiêu
có hai đường tiệm cận xiên. Hỏi chúng cắt nhau tại điểm có hoành độ bằng bao nhiêu
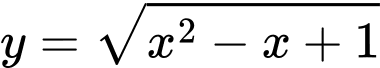 có hai đường tiệm cận xiên. Hỏi chúng cắt nhau tại điểm có hoành độ bằng bao nhiêu
có hai đường tiệm cận xiên. Hỏi chúng cắt nhau tại điểm có hoành độ bằng bao nhiêu A, 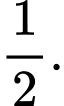
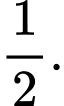
B, 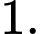
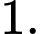
C, 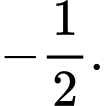
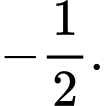
D, 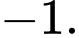
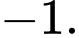
Ta có:
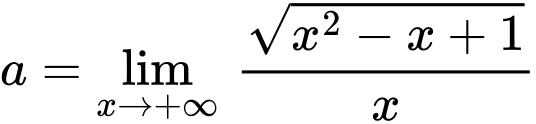
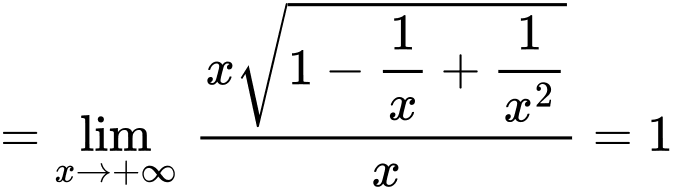
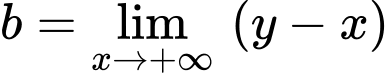
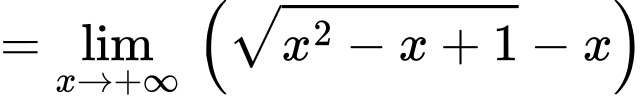
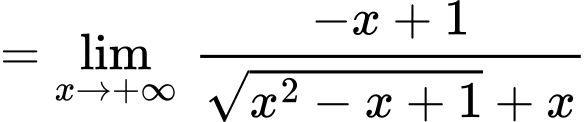
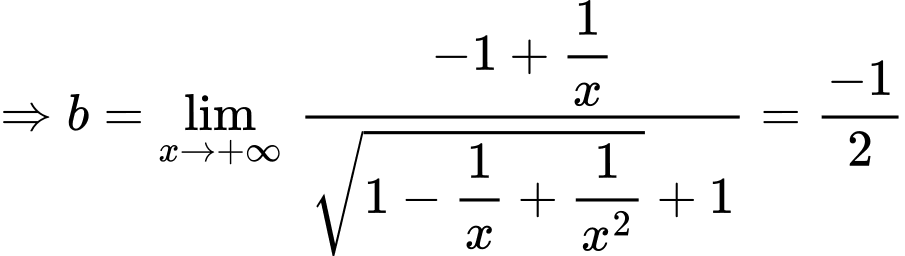
Suy ra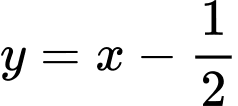 là tiệm cận xiên của đồ thị hàm số khi x tiến về dương vô cùng
là tiệm cận xiên của đồ thị hàm số khi x tiến về dương vô cùng
Lại có: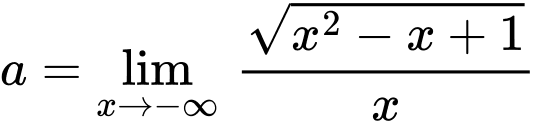
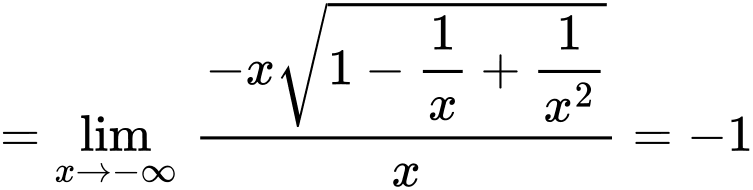
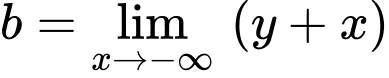
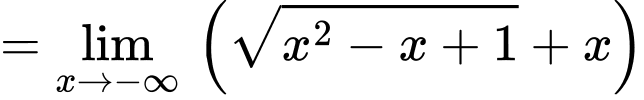
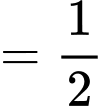 Suy ra
Suy ra 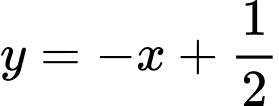 là tiệm cận xiên của đồ thị hàm số khi x tiến về âm vô cùng
là tiệm cận xiên của đồ thị hàm số khi x tiến về âm vô cùng
Vậy 2 đường tiệm cận xiên cắt nhau tại điểm của có hoành độ là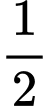 Đáp án: A
Đáp án: A
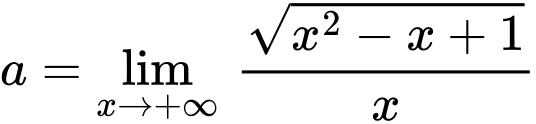
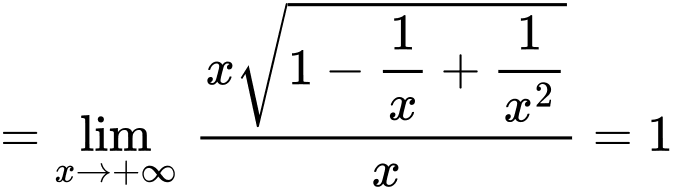
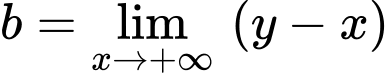
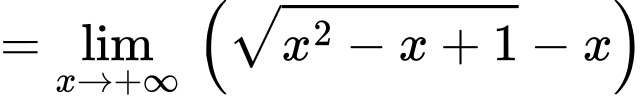
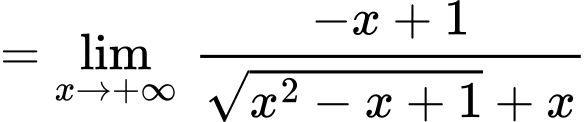
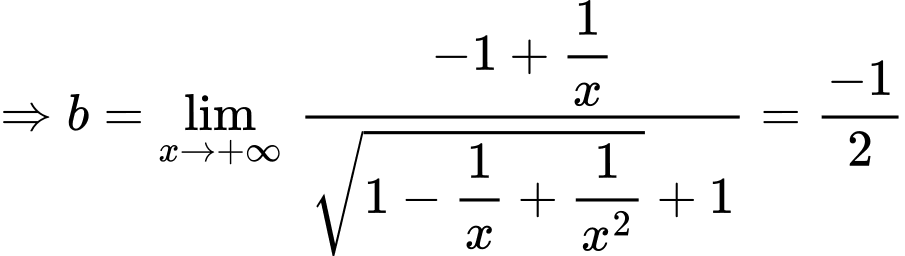
Suy ra
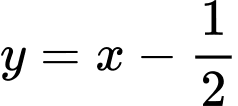 là tiệm cận xiên của đồ thị hàm số khi x tiến về dương vô cùng
là tiệm cận xiên của đồ thị hàm số khi x tiến về dương vô cùng Lại có:
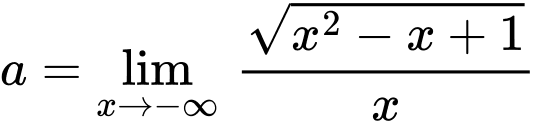
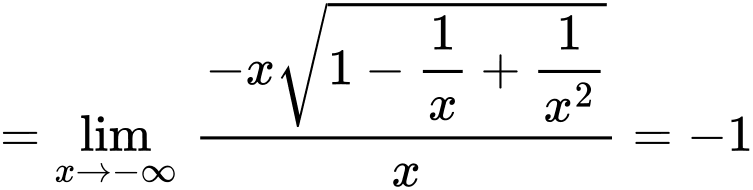
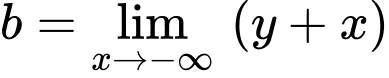
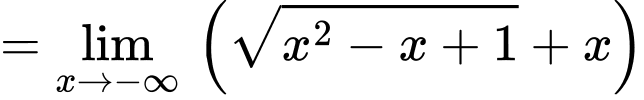
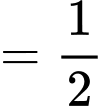 Suy ra
Suy ra 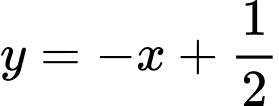 là tiệm cận xiên của đồ thị hàm số khi x tiến về âm vô cùng
là tiệm cận xiên của đồ thị hàm số khi x tiến về âm vô cùng Vậy 2 đường tiệm cận xiên cắt nhau tại điểm của có hoành độ là
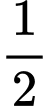 Đáp án: A
Đáp án: A
Câu 7 [31276]: Tìm 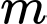 để đồ thị hàm số
để đồ thị hàm số 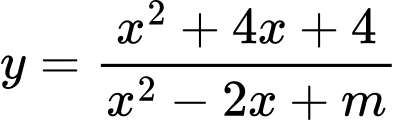 có
có 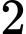 tiệm cận đứng.
tiệm cận đứng.
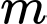 để đồ thị hàm số
để đồ thị hàm số 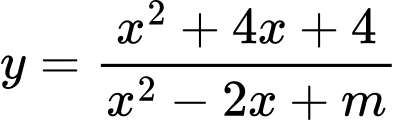 có
có  tiệm cận đứng.
tiệm cận đứng. A,  và
và 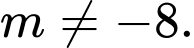
 và
và 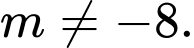
B, 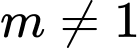 và
và 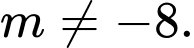
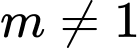 và
và 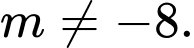
C,  và
và 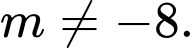
 và
và 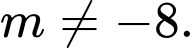
D, 

Ta có 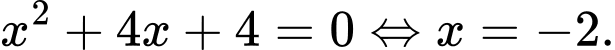
ĐTHS có đúng 2 tiệm cận đứng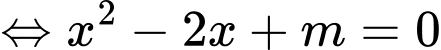 có đúng 2 nghiệm phân biệt khác
có đúng 2 nghiệm phân biệt khác 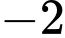
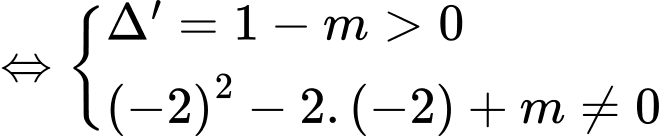
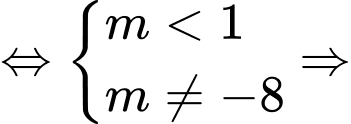 Chọn A Đáp án: A
Chọn A Đáp án: A
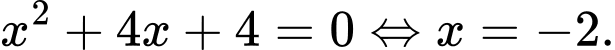
ĐTHS có đúng 2 tiệm cận đứng
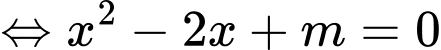 có đúng 2 nghiệm phân biệt khác
có đúng 2 nghiệm phân biệt khác 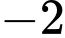
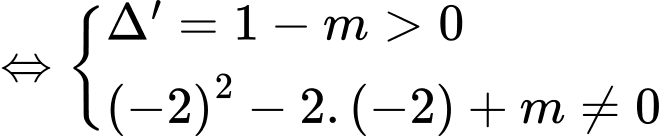
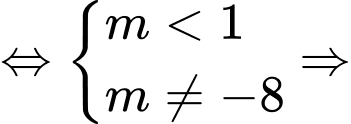 Chọn A Đáp án: A
Chọn A Đáp án: A
Câu 8 [31252]: Tập hợp các giá trị thực của 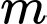 để hàm số
để hàm số 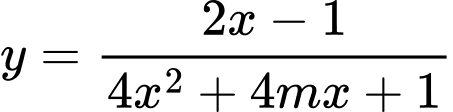 có đúng một đường tiệm cận là
có đúng một đường tiệm cận là
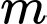 để hàm số
để hàm số 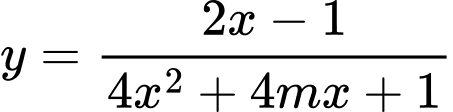 có đúng một đường tiệm cận là
có đúng một đường tiệm cận là A, 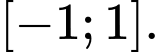
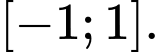
B, 

C, 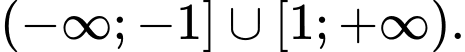
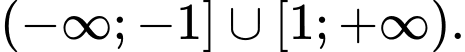
D, 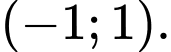
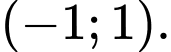
Dễ thấy đồ thị hàm số luôn có TCN 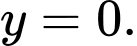 Suy ra hàm số không có tiệm cận đứng.
Suy ra hàm số không có tiệm cận đứng.
Khi đó PT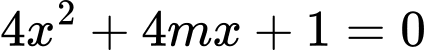 vô nghiệm
vô nghiệm 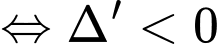
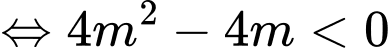

 Chọn D. Đáp án: D
Chọn D. Đáp án: D
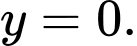 Suy ra hàm số không có tiệm cận đứng.
Suy ra hàm số không có tiệm cận đứng.
Khi đó PT
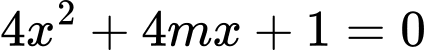 vô nghiệm
vô nghiệm 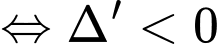
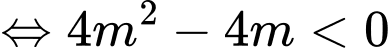

 Chọn D. Đáp án: D
Chọn D. Đáp án: D
Câu 9 [801513]: Tập hợp tất cả các giá trị thực của tham số 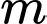 để đồ thị hàm số
để đồ thị hàm số 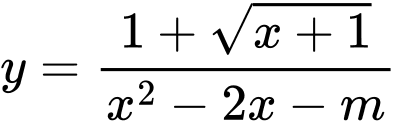 có đúng hai tiệm cận đứng là
có đúng hai tiệm cận đứng là
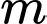 để đồ thị hàm số
để đồ thị hàm số 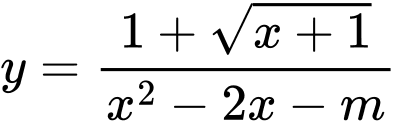 có đúng hai tiệm cận đứng là
có đúng hai tiệm cận đứng là A, 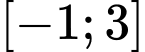 .
.
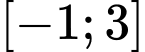 .
.B, 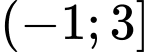 .
.
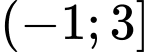 .
.C, 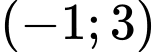 .
.
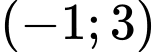 .
.D, 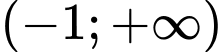 .
.
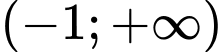 .
.
Đáp án B
Điều kiện . Vì
. Vì 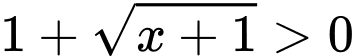 nên đồ thị có đúng 2 tiệm cận đứng khi phương trình
nên đồ thị có đúng 2 tiệm cận đứng khi phương trình 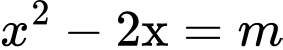 có 2 nghiệm phân biệt lớn hơn – 1.
có 2 nghiệm phân biệt lớn hơn – 1.
Điều kiện
 . Vì
. Vì 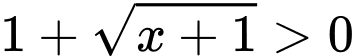 nên đồ thị có đúng 2 tiệm cận đứng khi phương trình
nên đồ thị có đúng 2 tiệm cận đứng khi phương trình 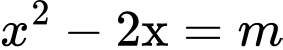 có 2 nghiệm phân biệt lớn hơn – 1.
có 2 nghiệm phân biệt lớn hơn – 1. Khảo sát hàm số như sau
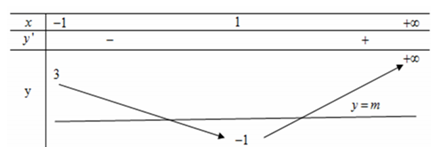
Điều kiện cần là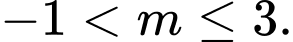
Chọn đáp án B. Đáp án: B 
Điều kiện cần là
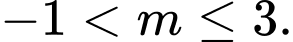
Câu 10 [628768]: Cho hàm số 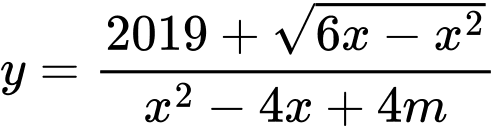 có đồ thị
có đồ thị 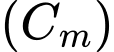 . Tìm tập hợp
. Tìm tập hợp 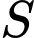 tất cả các giá trị thực của tham số
tất cả các giá trị thực của tham số 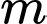 để
để 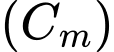 có đúng hai đường tiệm cận đứng.
có đúng hai đường tiệm cận đứng.
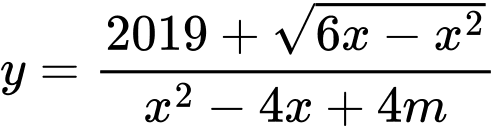 có đồ thị
có đồ thị 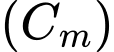 . Tìm tập hợp
. Tìm tập hợp 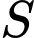 tất cả các giá trị thực của tham số
tất cả các giá trị thực của tham số 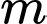 để
để 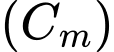 có đúng hai đường tiệm cận đứng.
có đúng hai đường tiệm cận đứng. A, 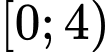 .
.
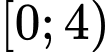 .
.B, 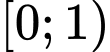 .
.
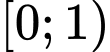 .
.C, 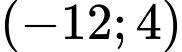 .
.
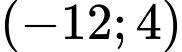 .
.D, 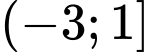 .
.
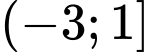 .
.
Đáp án B.
Phương trình
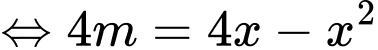 có đúng hai nghiệm thuộc
có đúng hai nghiệm thuộc 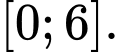
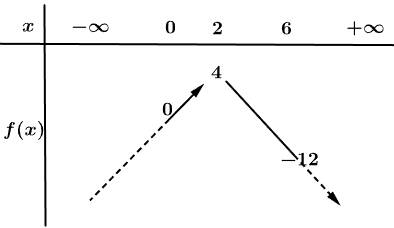
Khảo sát hàm số ta có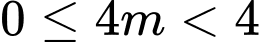
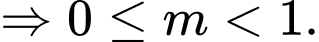 Đáp án: B
Đáp án: B
Phương trình

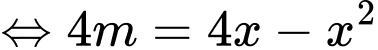 có đúng hai nghiệm thuộc
có đúng hai nghiệm thuộc 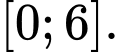

Khảo sát hàm số ta có
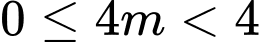
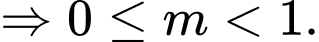 Đáp án: B
Đáp án: B
Câu 11 [31266]: Các giá trị của tham số 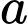 để đồ thị hàm số
để đồ thị hàm số 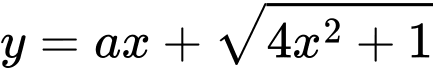 có tiệm cận ngang là
có tiệm cận ngang là
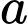 để đồ thị hàm số
để đồ thị hàm số 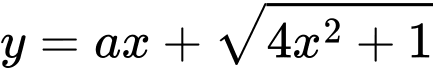 có tiệm cận ngang là
có tiệm cận ngang là A, 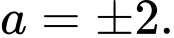
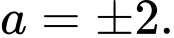
B, 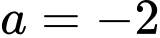 và
và 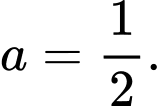
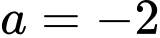 và
và 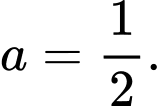
C, 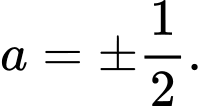
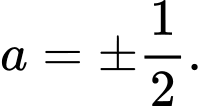
D, 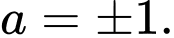
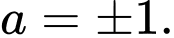
Ta có 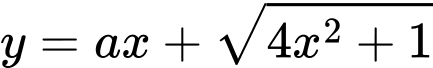
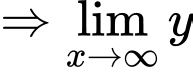
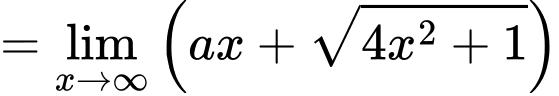
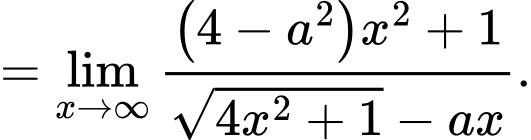
Kí hiệu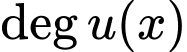 là bậc của hàm số
là bậc của hàm số 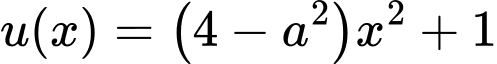 và
và 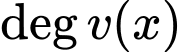 là bậc của hàm số
là bậc của hàm số 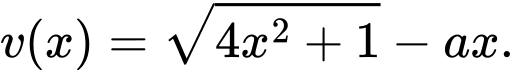
Dễ thấy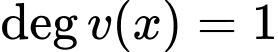 nên đồ thị hàm số có tiệm cận ngang khi
nên đồ thị hàm số có tiệm cận ngang khi 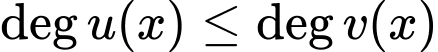
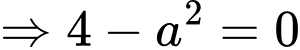
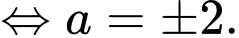
Chọn A. Đáp án: A
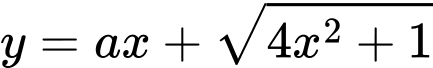
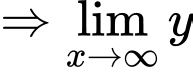
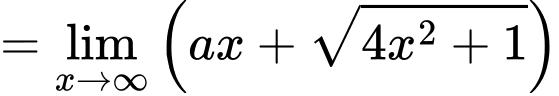
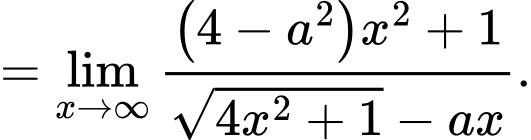
Kí hiệu
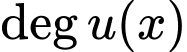 là bậc của hàm số
là bậc của hàm số 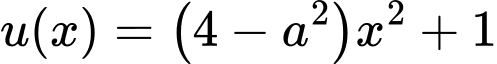 và
và 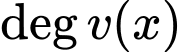 là bậc của hàm số
là bậc của hàm số 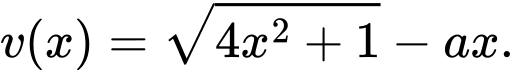
Dễ thấy
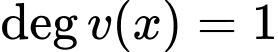 nên đồ thị hàm số có tiệm cận ngang khi
nên đồ thị hàm số có tiệm cận ngang khi 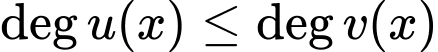
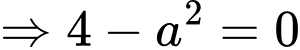
Chọn A. Đáp án: A
Câu 12 [31268]: Biết đồ thị hàm số $y = \frac{{\left( {4a - b} \right){x^2} + ax + 1}}{{{x^2} + ax + b - 12}}$ nhận trục hoành và trục tung làm hai tiệm cận thì giá trị $a + b$ bằng
A,
B,
C,
D,
Do đồ thị nhận trục hoành làm tiệm cận ngang mà $\underset{x\to +\infty }{\mathop{\lim }}\,y=4a-b=0\Rightarrow b=4a.$
Đáp án: D
Do đồ thị nhận trục tung làm tiệm cận đứng $\Rightarrow $ Biểu thức ${{x}^{2}}+ax+b-12$ nhận $x=0$ làm nghiệm $\Rightarrow b=12$ $\Rightarrow a=3$ $\Rightarrow a+b=15.$
Câu 13 [382488]: Đường tiệm đứng và tiệm cận xiên của đồ thị hàm số 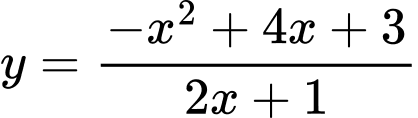 tạo với nhau một góc bao nhiêu độ (làm tròn đến hàng đơn vị của độ)?
tạo với nhau một góc bao nhiêu độ (làm tròn đến hàng đơn vị của độ)?
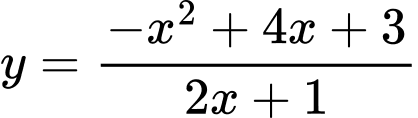 tạo với nhau một góc bao nhiêu độ (làm tròn đến hàng đơn vị của độ)?
tạo với nhau một góc bao nhiêu độ (làm tròn đến hàng đơn vị của độ)?
Ta có:
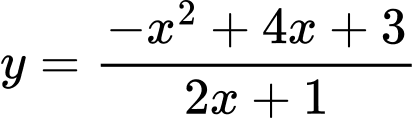
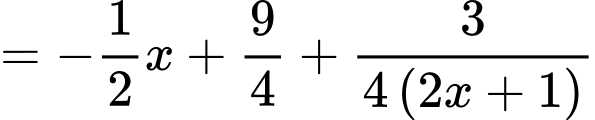
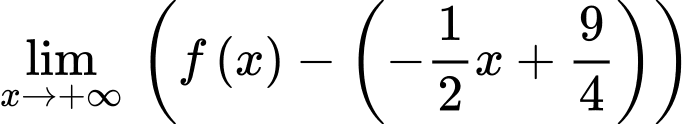
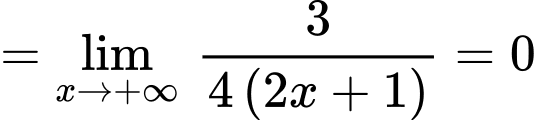
Suy ra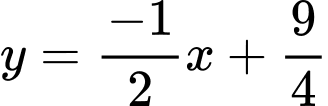 là đường tiệm cận xiên của đồ thị hàm số.
là đường tiệm cận xiên của đồ thị hàm số.
Lại có: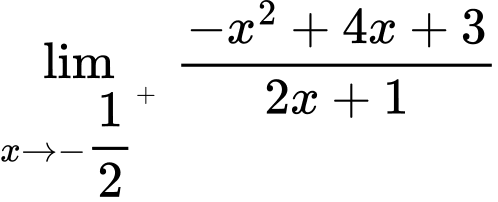
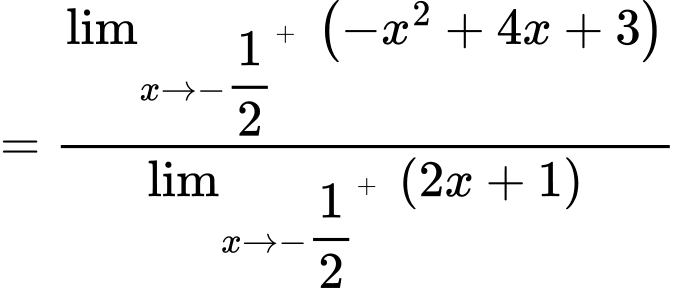

Suy ra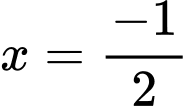 là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số.
Vậy tiệm cận đứng và tiệm cận xiên của đồ thị tạo với nhau 1 góc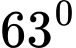
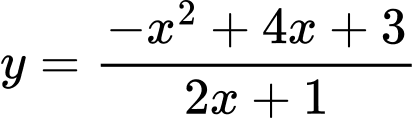
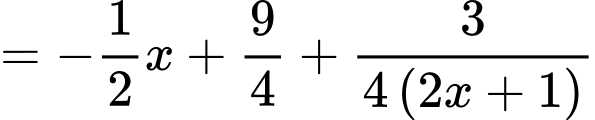
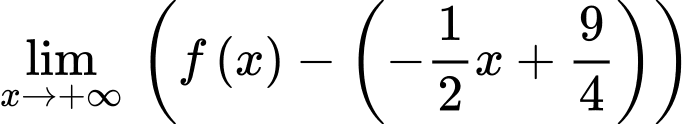
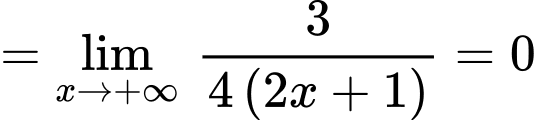
Suy ra
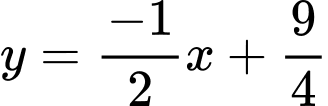 là đường tiệm cận xiên của đồ thị hàm số.
là đường tiệm cận xiên của đồ thị hàm số.Lại có:
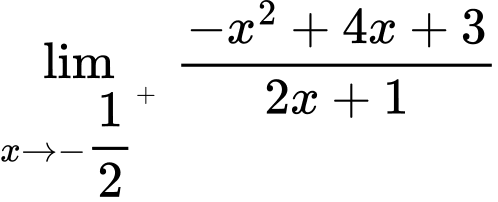
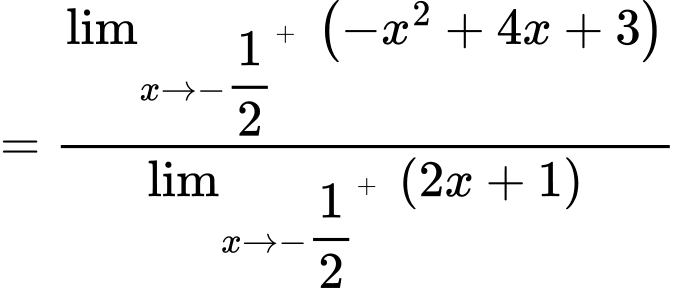

Suy ra
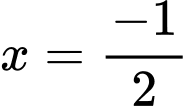 là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số.Vậy tiệm cận đứng và tiệm cận xiên của đồ thị tạo với nhau 1 góc
Câu 14 [801519]: Số các giá trị nguyên dương của tham số 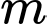 để đồ thị hàm số
để đồ thị hàm số 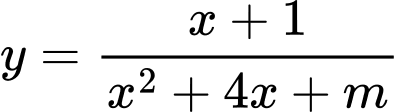 có đúng hai đường tiệm cận là
có đúng hai đường tiệm cận là
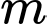 để đồ thị hàm số
để đồ thị hàm số 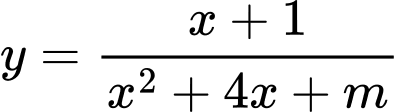 có đúng hai đường tiệm cận là
có đúng hai đường tiệm cận là A, 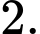
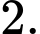
B, 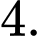
C, vô số.
D, 
Đáp án A
Đồ thị hàm số luôn có 1 tiệm cận ngang là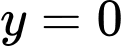 nên để đồ thị có 2 tiệm cận thì đồ thị hàm số phải có duy nhất 1 tiệm cận đứng.
nên để đồ thị có 2 tiệm cận thì đồ thị hàm số phải có duy nhất 1 tiệm cận đứng.
Đồ thị hàm số luôn có 1 tiệm cận ngang là
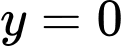 nên để đồ thị có 2 tiệm cận thì đồ thị hàm số phải có duy nhất 1 tiệm cận đứng.
nên để đồ thị có 2 tiệm cận thì đồ thị hàm số phải có duy nhất 1 tiệm cận đứng. Đặt 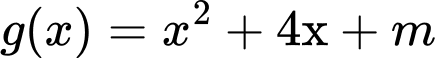 .
.
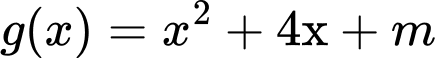 .
. Đồ thị có đúng 1 tiệm cận đứng khi đa thức 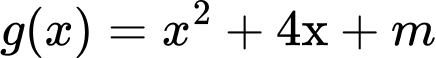 có 2 nghiệm phân biệt trong đó có một nghiệm bằng – 1 hoặc có nghiệm kép.
có 2 nghiệm phân biệt trong đó có một nghiệm bằng – 1 hoặc có nghiệm kép.
Khi đó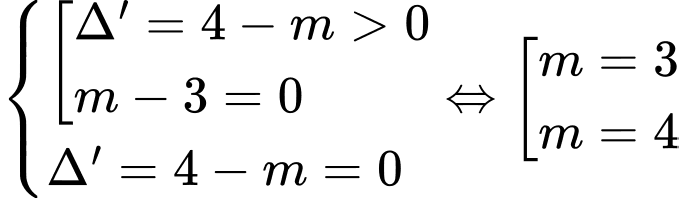
Đáp án: A 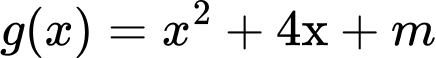 có 2 nghiệm phân biệt trong đó có một nghiệm bằng – 1 hoặc có nghiệm kép.
có 2 nghiệm phân biệt trong đó có một nghiệm bằng – 1 hoặc có nghiệm kép. Khi đó
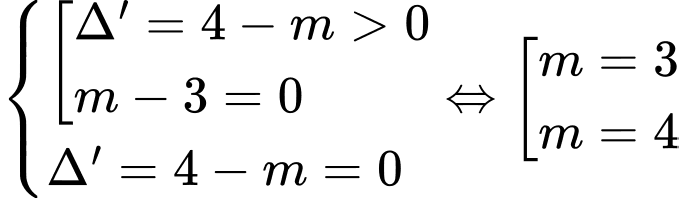
Câu 15 [801763]: Có bao nhiêu số nguyên 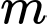 để đồ thị hàm số
để đồ thị hàm số 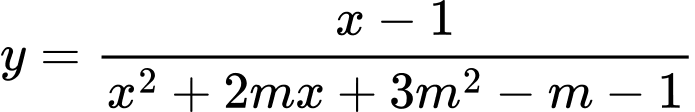 có ba đường tiệm cận?
có ba đường tiệm cận?
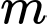 để đồ thị hàm số
để đồ thị hàm số 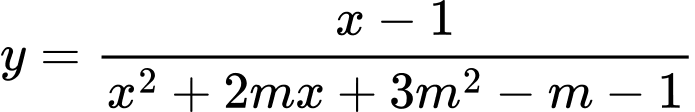 có ba đường tiệm cận?
có ba đường tiệm cận? A, 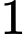 .
.
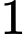 .
.B,  .
.
 .
.C, 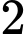 .
.
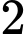 .
.D, 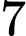 .
.
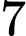 .
.
Chọn B
Ta có: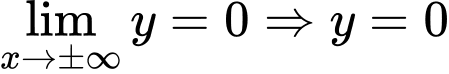 là một tiệm cận ngang của đồ thị hàm số.
là một tiệm cận ngang của đồ thị hàm số.
Do đó để đồ thị hàm số có ba đường tiệm cận thì đồ thị hàm số phải có hai tiệm cận đứng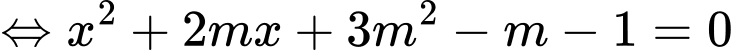 có hai nghiệm phân biệt khác
có hai nghiệm phân biệt khác 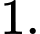
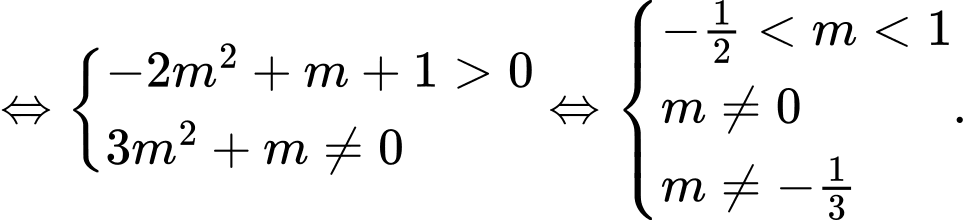
Mà nên không tồn tại giá trị nguyên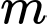 thỏa mãn yêu cầu đề bài. Đáp án: B
thỏa mãn yêu cầu đề bài. Đáp án: B
Ta có:
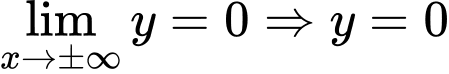 là một tiệm cận ngang của đồ thị hàm số.
là một tiệm cận ngang của đồ thị hàm số. Do đó để đồ thị hàm số có ba đường tiệm cận thì đồ thị hàm số phải có hai tiệm cận đứng
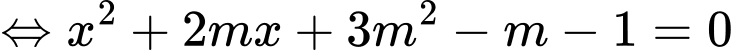 có hai nghiệm phân biệt khác
có hai nghiệm phân biệt khác 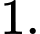
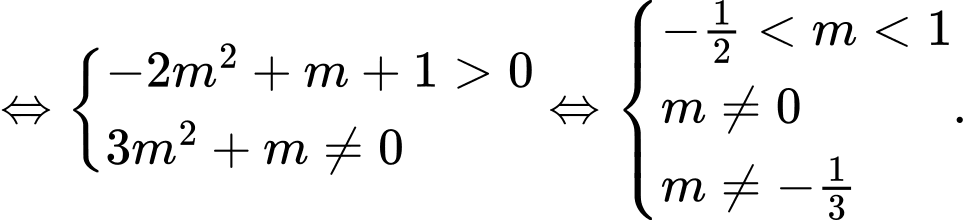
Mà nên không tồn tại giá trị nguyên
 thỏa mãn yêu cầu đề bài.
thỏa mãn yêu cầu đề bài.
Câu 16 [508164]: Cho đồ thị hàm số 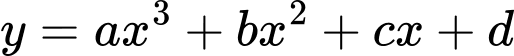 như hình vẽ dưới đây:
như hình vẽ dưới đây:
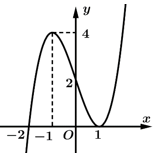
Đồ thị của hàm số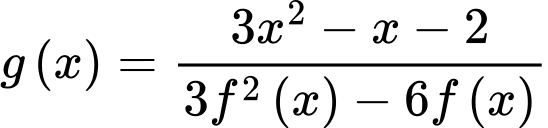 có bao nhiêu đường tiệm cận đứng?
có bao nhiêu đường tiệm cận đứng?
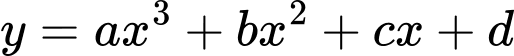 như hình vẽ dưới đây:
như hình vẽ dưới đây:
Đồ thị của hàm số
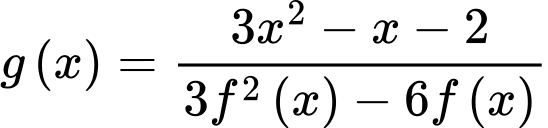 có bao nhiêu đường tiệm cận đứng?
có bao nhiêu đường tiệm cận đứng? A, 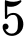 .
.
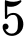 .
.B, 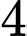 .
.
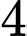 .
.C, 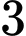 .
.
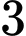 .
.D, 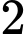 .
.
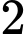 .
.
Chọn A
Xét phương trình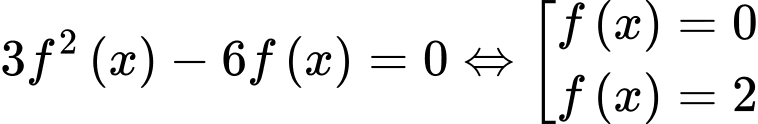
Dựa vào đồ thị, ta có
+) Phương trình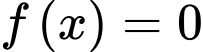
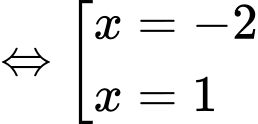 (trong đó
(trong đó 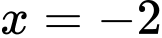 là nghiệm đơn và
là nghiệm đơn và 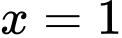 là nghiệm bội 2)
là nghiệm bội 2)
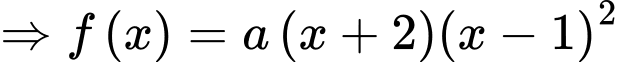 ,
, 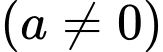 .
.
+) Phương trình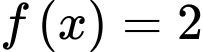
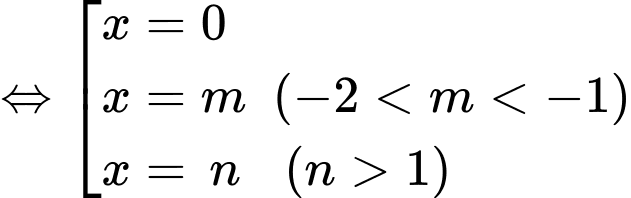 (
(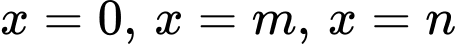 đều là các nghiệm đơn)
đều là các nghiệm đơn) 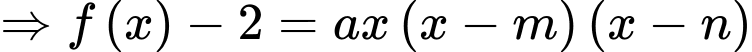 ,
, 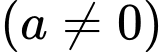 .
.
Suy ra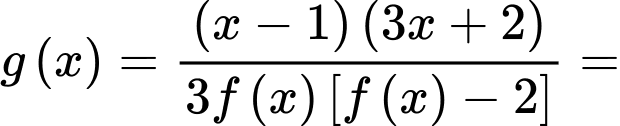
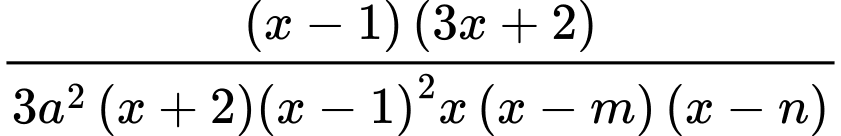 ,
, 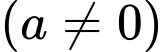 .
.
Vậy đồ thị hàm số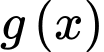 có
có 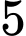 đường tiệm cận đứng. Đáp án: A
đường tiệm cận đứng. Đáp án: A
Xét phương trình
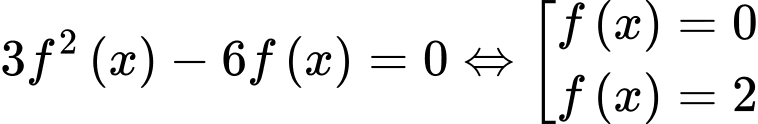
Dựa vào đồ thị, ta có
+) Phương trình
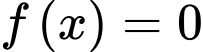
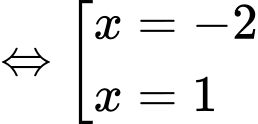 (trong đó
(trong đó 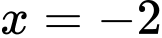 là nghiệm đơn và
là nghiệm đơn và 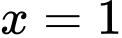 là nghiệm bội 2)
là nghiệm bội 2)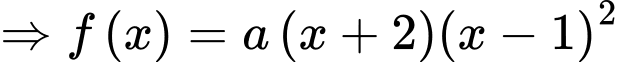 ,
, 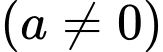 .
.+) Phương trình
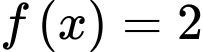
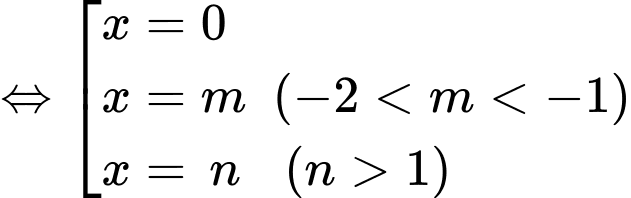 (
(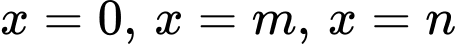 đều là các nghiệm đơn)
đều là các nghiệm đơn) 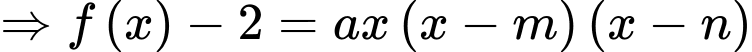 ,
, 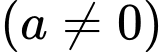 .
.Suy ra
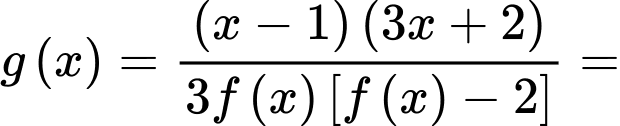
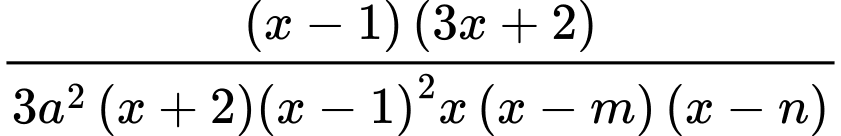 ,
, 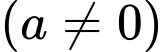 .
.Vậy đồ thị hàm số
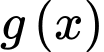 có
có 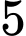 đường tiệm cận đứng. Đáp án: A
đường tiệm cận đứng. Đáp án: A
Câu 17 [679690]: Cho hàm số 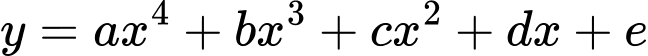 với
với 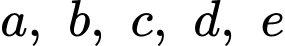 là các số thực và
là các số thực và 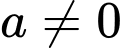 , có bảng biến thiên như sau
, có bảng biến thiên như sau
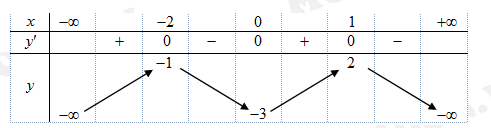
Đồ thị hàm số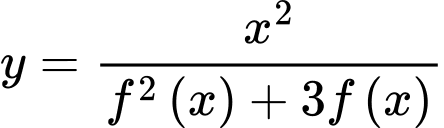 có bao nhiêu tiệm cận đứng?
có bao nhiêu tiệm cận đứng?
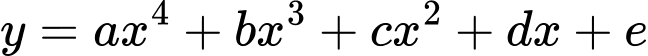 với
với 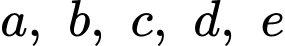 là các số thực và
là các số thực và 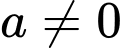 , có bảng biến thiên như sau
, có bảng biến thiên như sau
Đồ thị hàm số
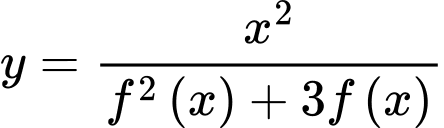 có bao nhiêu tiệm cận đứng?
có bao nhiêu tiệm cận đứng? A, 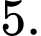
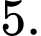
B, 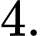
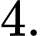
C, 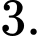
D, 
Xét phương trình 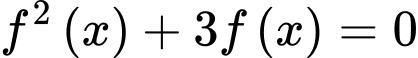
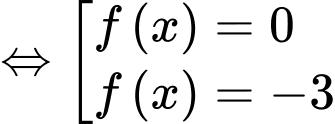
Dựa vào bảng biến thiên ta có
+)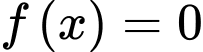
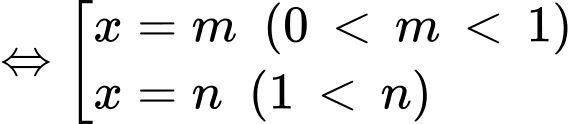 (trong đó:
(trong đó: 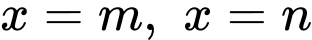 đều là các nghiệm đơn)
đều là các nghiệm đơn)
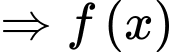
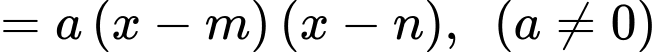
+)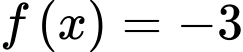
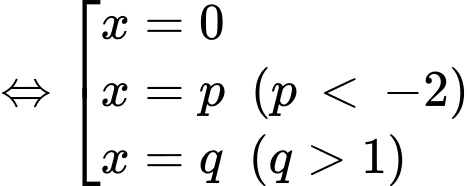 (trong đó,
(trong đó, 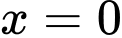 là nghiệm kép;
là nghiệm kép; 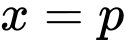 và
và 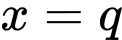 đều là nghiệm đơn)
đều là nghiệm đơn)
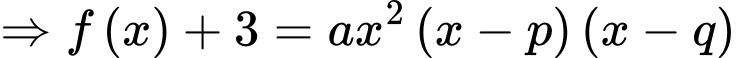
Suy ra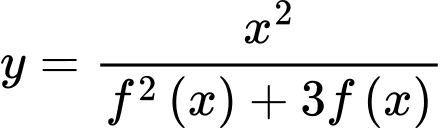
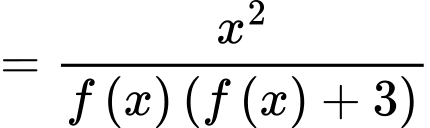
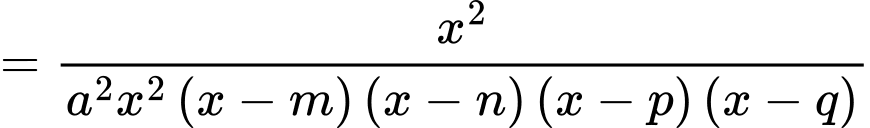
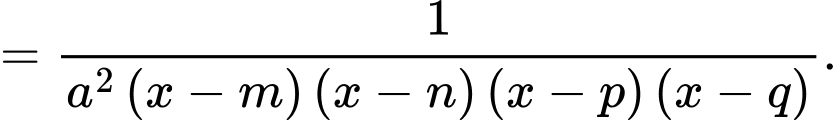
Vậy đồ thị hàm số có 4 tiệm cận đứng.
Chọn đáp án B. Đáp án: B
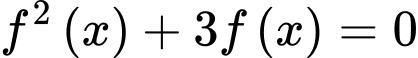
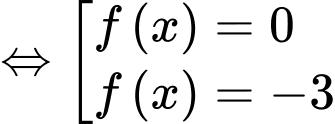
Dựa vào bảng biến thiên ta có
+)
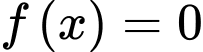
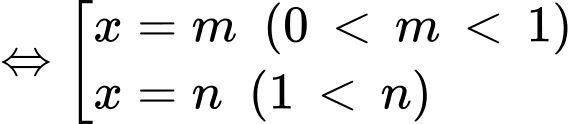 (trong đó:
(trong đó: 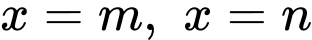 đều là các nghiệm đơn)
đều là các nghiệm đơn) 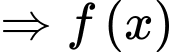
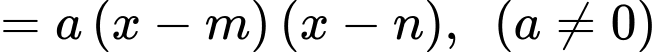
+)
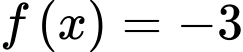
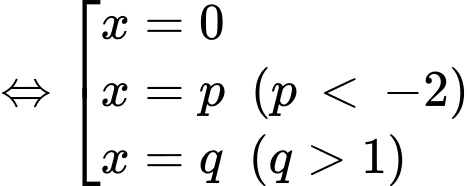 (trong đó,
(trong đó, 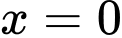 là nghiệm kép;
là nghiệm kép; 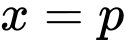 và
và 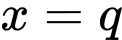 đều là nghiệm đơn)
đều là nghiệm đơn) 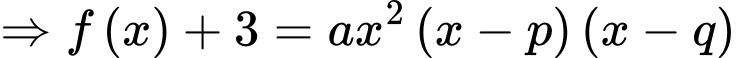
Suy ra
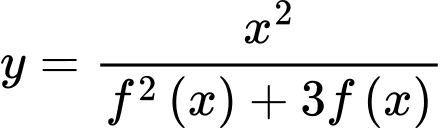
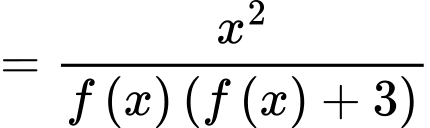
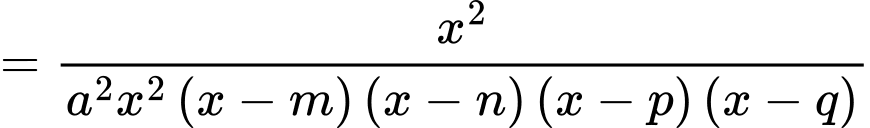
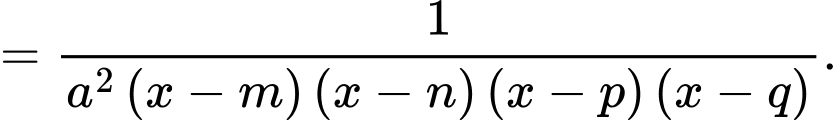
Vậy đồ thị hàm số có 4 tiệm cận đứng.
Chọn đáp án B. Đáp án: B
Câu 18 [31358]: Cho hàm số 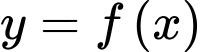 liên tục trên
liên tục trên 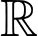 và có bảng biến thiên như dưới đây.
và có bảng biến thiên như dưới đây.
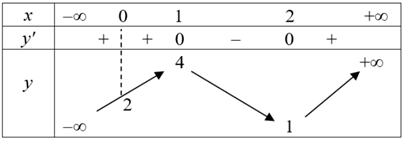
Đồ thị hàm số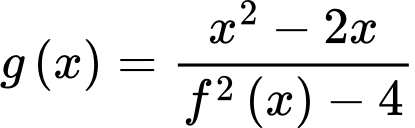 có bao nhiêu tiệm cận đứng?
có bao nhiêu tiệm cận đứng?
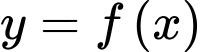 liên tục trên
liên tục trên 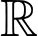 và có bảng biến thiên như dưới đây.
và có bảng biến thiên như dưới đây.
Đồ thị hàm số
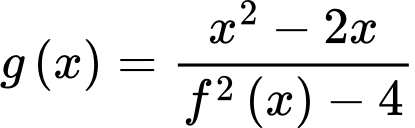 có bao nhiêu tiệm cận đứng?
có bao nhiêu tiệm cận đứng? A, 1.
B, 4.
C, 3.
D, 2.
Ta có:


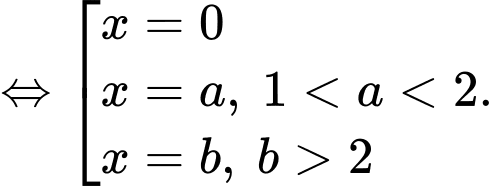

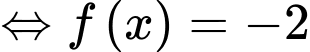
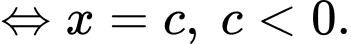
Do đó,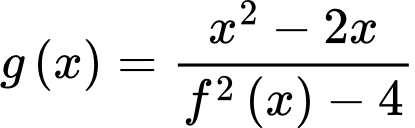
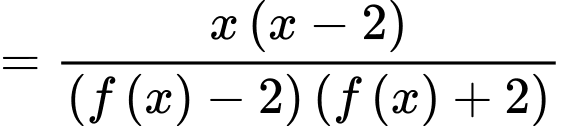
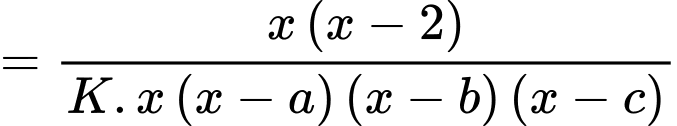
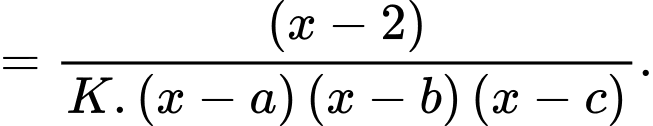
Vậy đồ thị hàm số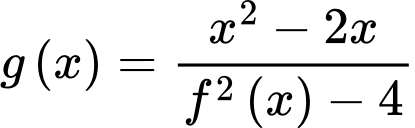 có 3 đường tiệm cận đứng là
có 3 đường tiệm cận đứng là 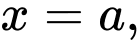
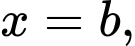
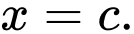 Đáp án: C
Đáp án: C


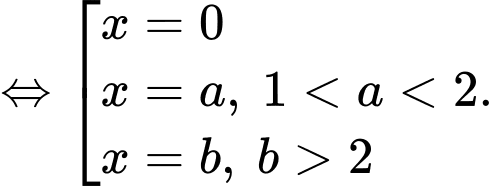

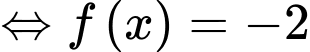
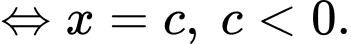
Do đó,
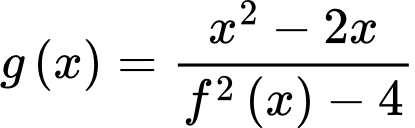
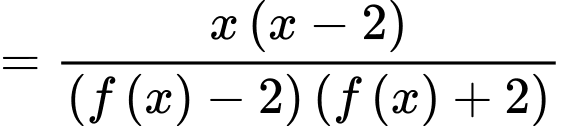
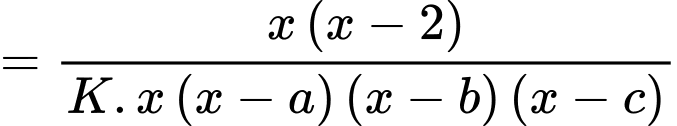
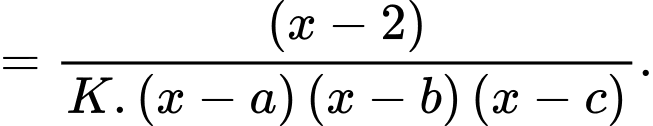
Vậy đồ thị hàm số
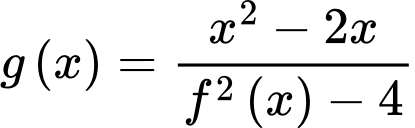 có 3 đường tiệm cận đứng là
có 3 đường tiệm cận đứng là 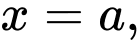
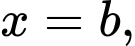
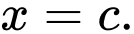 Đáp án: C
Đáp án: C
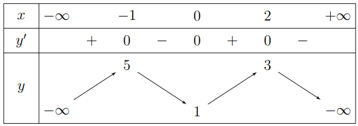
Câu 19 [378257]: Cho hàm số bậc bốn 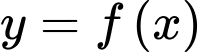 có bảng biến thiên như hình vẽ. Đồ thị hàm số
có bảng biến thiên như hình vẽ. Đồ thị hàm số 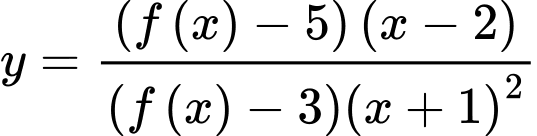 có tất cả bao nhiêu tiệm cận đứng và tiệm cận ngang?
có tất cả bao nhiêu tiệm cận đứng và tiệm cận ngang?
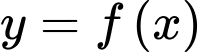 có bảng biến thiên như hình vẽ. Đồ thị hàm số
có bảng biến thiên như hình vẽ. Đồ thị hàm số 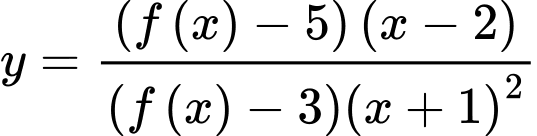 có tất cả bao nhiêu tiệm cận đứng và tiệm cận ngang?
có tất cả bao nhiêu tiệm cận đứng và tiệm cận ngang? 
A, 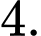
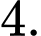
B, 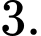
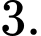
C, 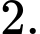
D, 
Chọn A
Điều kiện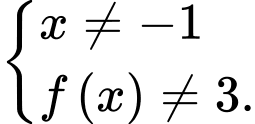
Không mất tính tổng quát, giả sử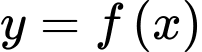 là hàm số bậc bốn.
là hàm số bậc bốn.
Ta có bậc của tử nhỏ hơn bậc của mẫu nên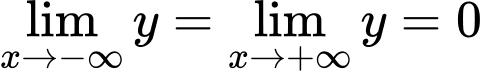 , suy ra
, suy ra 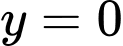 là tiệm cận ngang.
là tiệm cận ngang.
Từ bảng biến thiên, ta thấy đồ thị hàm số tiếp xúc với đường thẳng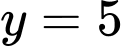 và
và 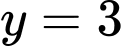 lần lượt tại
lần lượt tại 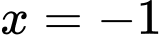 và
và 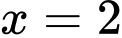 nên
nên 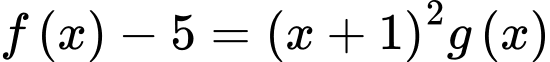 và
và 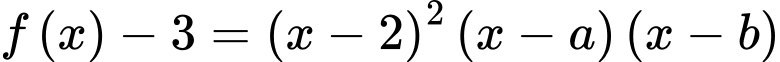 trong đó
trong đó 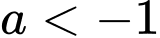 và
và 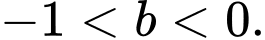
Khi đó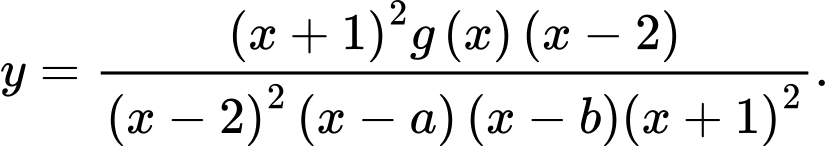 Ta có
Ta có
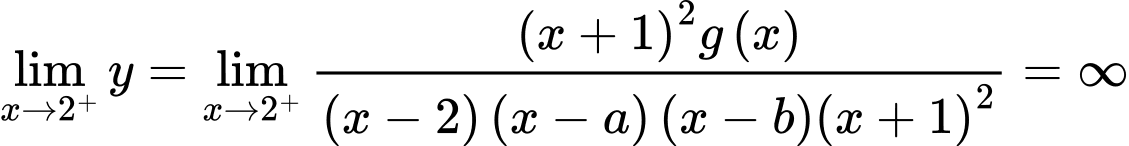 ;
; 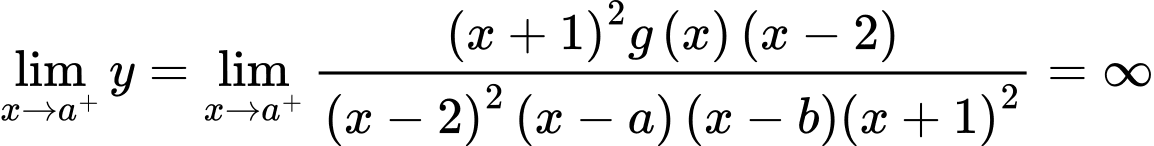 ;
;
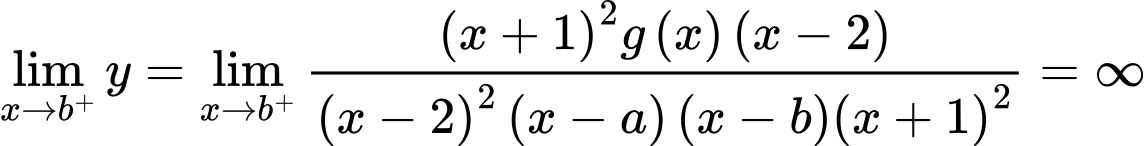 ;
;
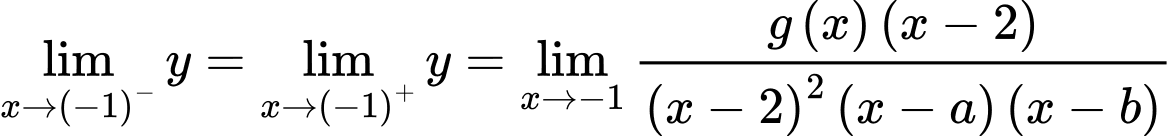
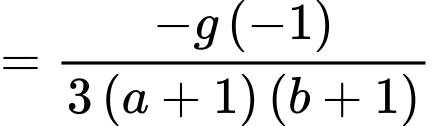 (hằng số).
(hằng số).
Suy ra hàm số có ba đường tiệm cận đứng là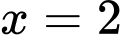 ,
, 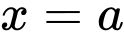 ,
, 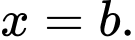
Vậy hàm số đã cho có bốn tiệm cận. Đáp án: A
Điều kiện
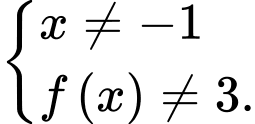
Không mất tính tổng quát, giả sử
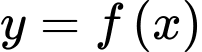 là hàm số bậc bốn.
là hàm số bậc bốn.Ta có bậc của tử nhỏ hơn bậc của mẫu nên
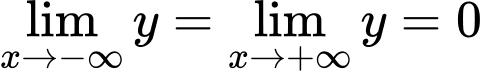 , suy ra
, suy ra 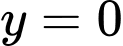 là tiệm cận ngang.
là tiệm cận ngang.Từ bảng biến thiên, ta thấy đồ thị hàm số tiếp xúc với đường thẳng
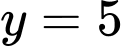 và
và 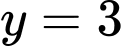 lần lượt tại
lần lượt tại 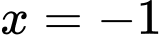 và
và 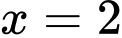 nên
nên 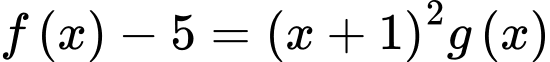 và
và 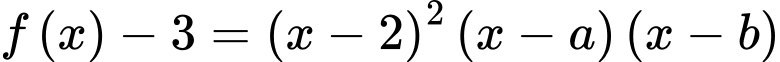 trong đó
trong đó 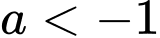 và
và 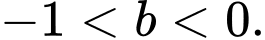
Khi đó
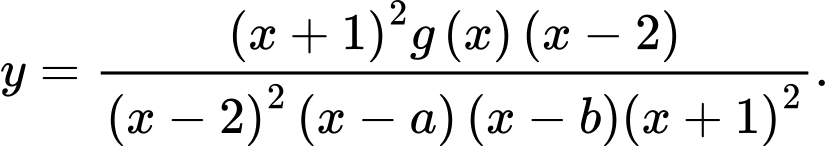 Ta có
Ta có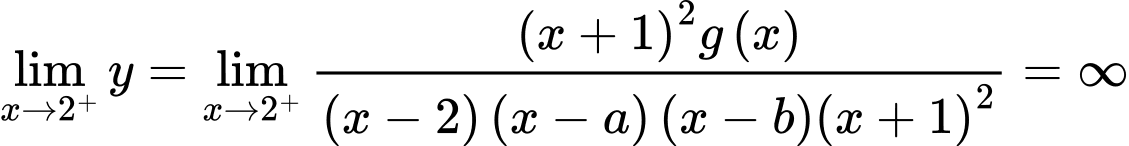 ;
; 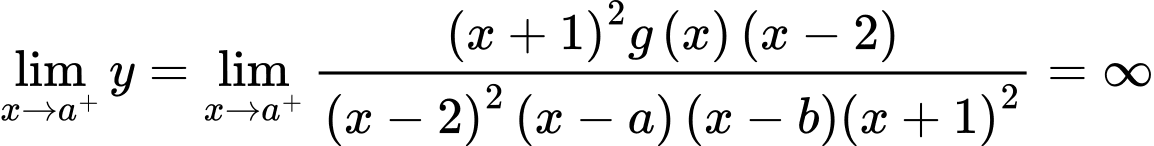 ;
;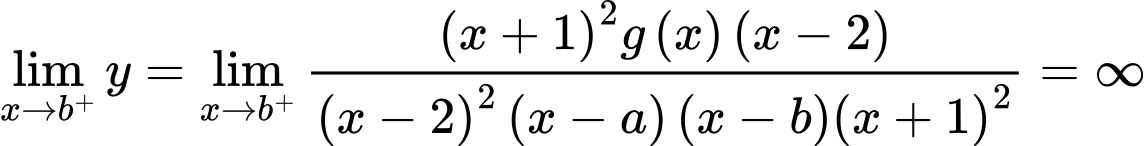 ;
; 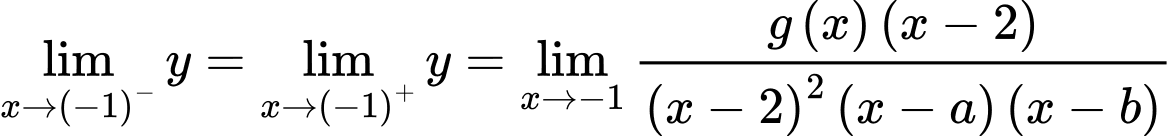
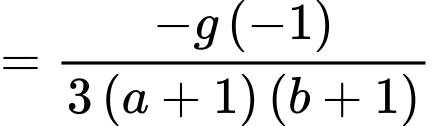 (hằng số).
(hằng số).Suy ra hàm số có ba đường tiệm cận đứng là
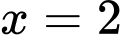 ,
, 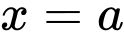 ,
, 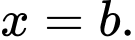
Vậy hàm số đã cho có bốn tiệm cận. Đáp án: A
Câu 20 [311407]: Cho hàm số 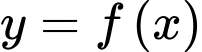 là hàm số bậc ba có bảng biến thiên như hình vẽ
là hàm số bậc ba có bảng biến thiên như hình vẽ
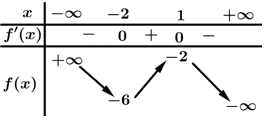
Số đường tiệm cận đứng và ngang của đồ thị hàm số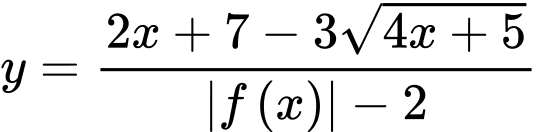 là
là
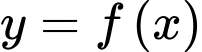 là hàm số bậc ba có bảng biến thiên như hình vẽ
là hàm số bậc ba có bảng biến thiên như hình vẽ
Số đường tiệm cận đứng và ngang của đồ thị hàm số
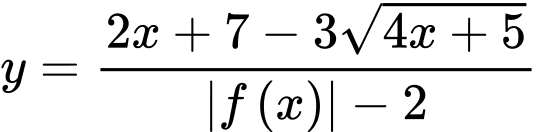 là
là A, 
B, 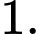
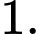
C, 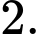
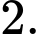
D, 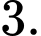
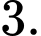
Vì hàm số 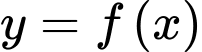 là hàm số bậc ba nên
là hàm số bậc ba nên 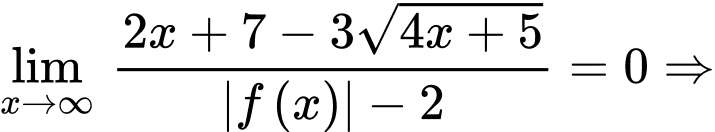 Đồ thị hàm số
Đồ thị hàm số 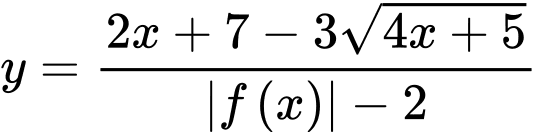 luôn có một đường tiệm cận ngang là
luôn có một đường tiệm cận ngang là 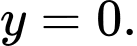
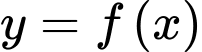 là hàm số bậc ba nên
là hàm số bậc ba nên 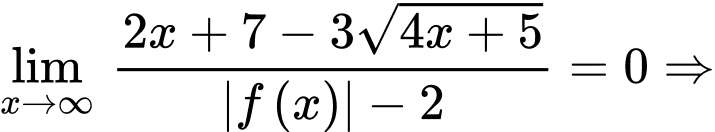 Đồ thị hàm số
Đồ thị hàm số 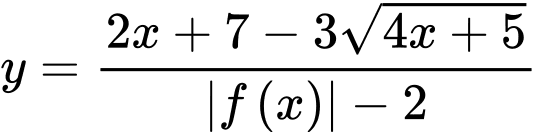 luôn có một đường tiệm cận ngang là
luôn có một đường tiệm cận ngang là 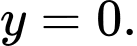
Lại có:
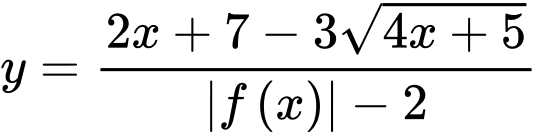
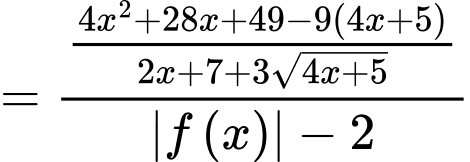
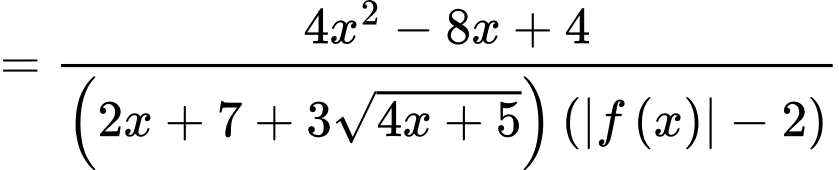
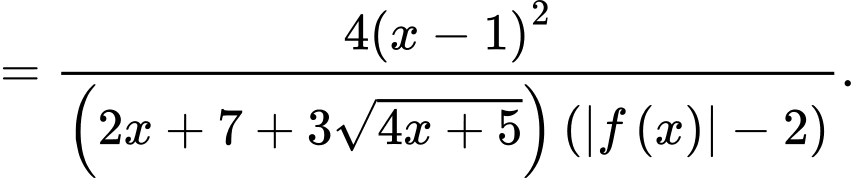
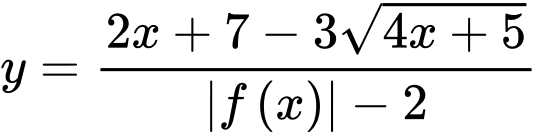
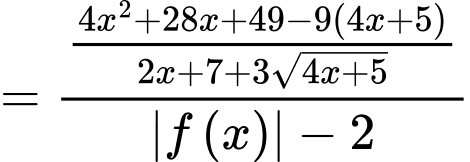
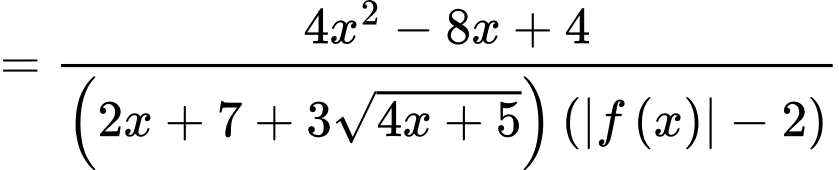
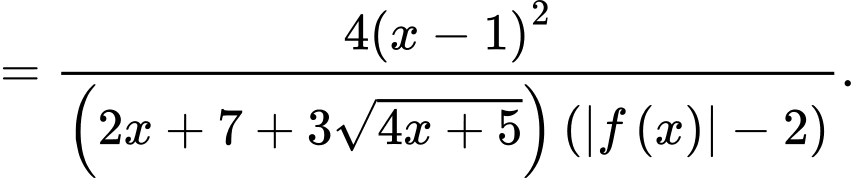
Với điều kiện 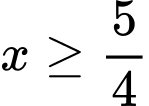 thì phương trình
thì phương trình 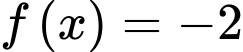 có nghiệm kép
có nghiệm kép 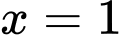 và phương trình
và phương trình 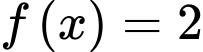 vô nghiệm.
vô nghiệm.
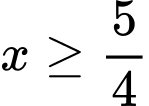 thì phương trình
thì phương trình 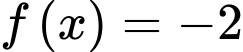 có nghiệm kép
có nghiệm kép 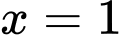 và phương trình
và phương trình 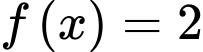 vô nghiệm.
vô nghiệm. Do đó, đồ thị hàm số 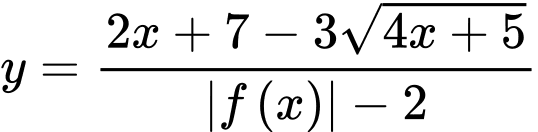 không có tiệm cận đứng.
không có tiệm cận đứng.
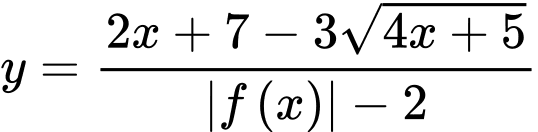 không có tiệm cận đứng.
không có tiệm cận đứng. Vậy đồ thị hàm số 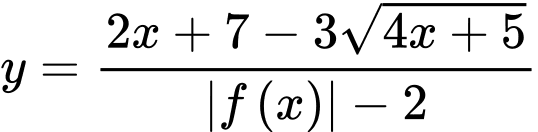 có 1 đường tiệm cận. Chọn B.
có 1 đường tiệm cận. Chọn B.
Đáp án: B 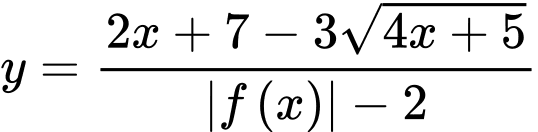 có 1 đường tiệm cận. Chọn B.
có 1 đường tiệm cận. Chọn B.