Đáp án Bài tập tự luyện
Câu 1 [216368]: Đồ thị hàm số 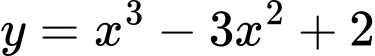 là đường cong trong hình nào dưới đây?
là đường cong trong hình nào dưới đây?
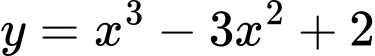 là đường cong trong hình nào dưới đây?
là đường cong trong hình nào dưới đây? A, 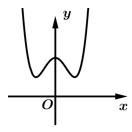

B, 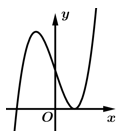

C, 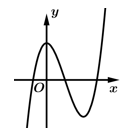

D, 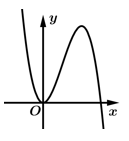

Chọn đáp án C.
+)Vì hàm số đã cho là hàm bậc 3 nên sẽ có nhiều nhất 2 điểm cực trị, suy ra Loại A.
+)Vì hệ số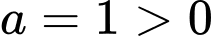 nên phần cuối cùng của đồ thị phải đi lên, suy ra Loại D.
nên phần cuối cùng của đồ thị phải đi lên, suy ra Loại D.
+)Ấn máy tính tìm nghiệm của phương trình giao điểm hoành độ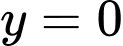 thì được 3 nghiệm đơn. Suy ra Loại B. Vì đồ thị ở hình B có 1 nghiệm kép.
Đáp án: C
thì được 3 nghiệm đơn. Suy ra Loại B. Vì đồ thị ở hình B có 1 nghiệm kép.
Đáp án: C
+)Vì hàm số đã cho là hàm bậc 3 nên sẽ có nhiều nhất 2 điểm cực trị, suy ra Loại A.
+)Vì hệ số
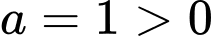 nên phần cuối cùng của đồ thị phải đi lên, suy ra Loại D.
nên phần cuối cùng của đồ thị phải đi lên, suy ra Loại D.
+)Ấn máy tính tìm nghiệm của phương trình giao điểm hoành độ
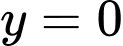 thì được 3 nghiệm đơn. Suy ra Loại B. Vì đồ thị ở hình B có 1 nghiệm kép.
Đáp án: C
thì được 3 nghiệm đơn. Suy ra Loại B. Vì đồ thị ở hình B có 1 nghiệm kép.
Đáp án: C
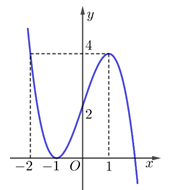
Câu 2 [23326]: Đồ thị sau đây là của hàm số nào?

A, 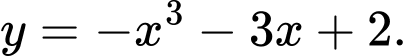
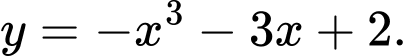
B, 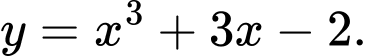
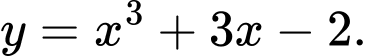
C, 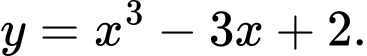
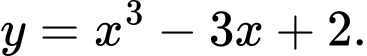
D, 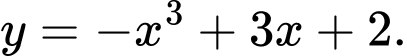
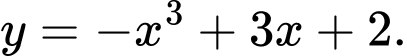
Dựa vào đồ thị hàm số, ta thấy
+)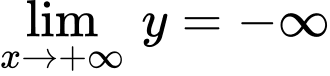 và
và 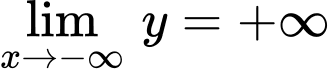 nên hệ số
nên hệ số 
+) Đồ thị hàm số đi qua hai điểm cực trị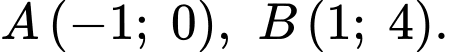
Gọi hàm số cần tìm có dạng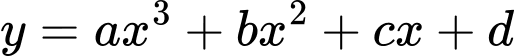
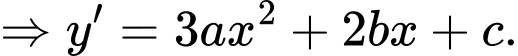
Khi đó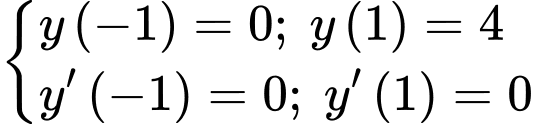
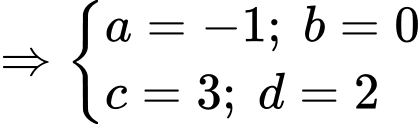
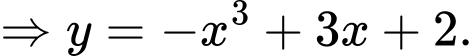
Chọn đáp án D. Đáp án: D
+)
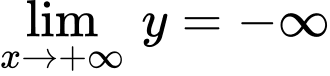 và
và 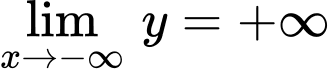 nên hệ số
nên hệ số 
+) Đồ thị hàm số đi qua hai điểm cực trị
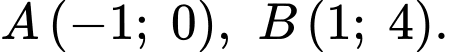
Gọi hàm số cần tìm có dạng
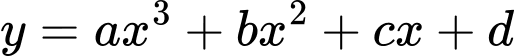
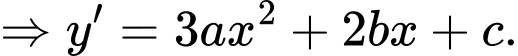
Khi đó
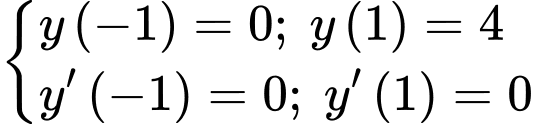
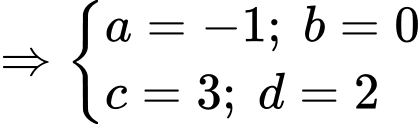
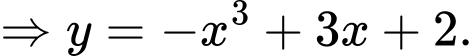
Chọn đáp án D. Đáp án: D
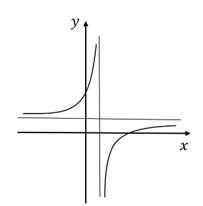
Câu 3 [280774]: Đồ thị hàm số nào dưới đây có dạng đường cong như hình bên?

A, 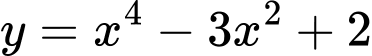 .
.
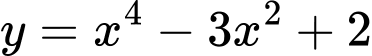 .
.B, 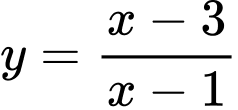 .
.
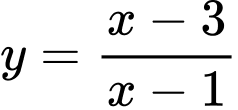 .
.C, 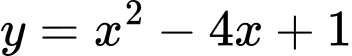 .
.
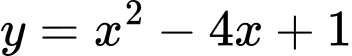 .
.D, 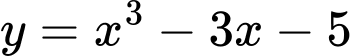 .
.
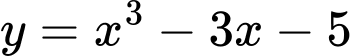 .
.
Chọn B
Đồ thị đã cho thuộc dạng đồ thị hàm phân thức hữa tỷ bậc nhất nên dễ dàng loại 3 đáp án A, C, D (hàm đa thức). Đáp án: B
Đồ thị đã cho thuộc dạng đồ thị hàm phân thức hữa tỷ bậc nhất nên dễ dàng loại 3 đáp án A, C, D (hàm đa thức). Đáp án: B
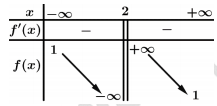
Câu 4 [30671]: Bảng biến thiên ở bên là của hàm số nào?

A, 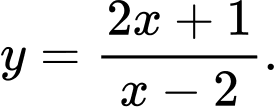
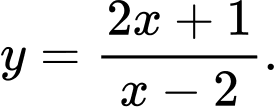
B, 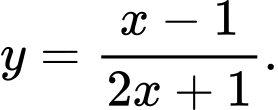
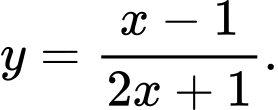
C, 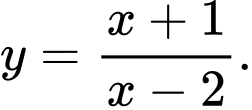
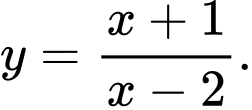
D, 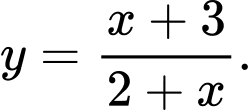
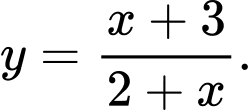
Chọn đáp án C.
Do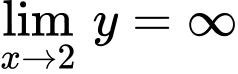
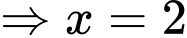 là tiệm cận đứng của hàm số nên loại B, D.
là tiệm cận đứng của hàm số nên loại B, D.
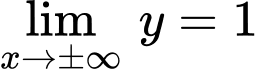
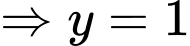 là tiệm cận ngang của hàm số nên loại A. Đáp án: C
là tiệm cận ngang của hàm số nên loại A. Đáp án: C
Do
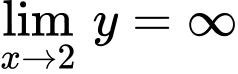
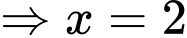 là tiệm cận đứng của hàm số nên loại B, D.
là tiệm cận đứng của hàm số nên loại B, D.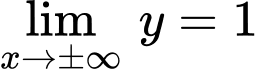
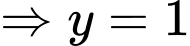 là tiệm cận ngang của hàm số nên loại A. Đáp án: C
là tiệm cận ngang của hàm số nên loại A. Đáp án: C
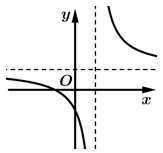
Câu 5 [511897]: Đồ thị trong hình vẽ dưới đây là đồ thị của hàm số nào?

A, 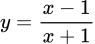 .
.
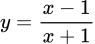 .
.B, 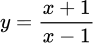 .
.
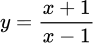 .
.C, 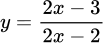 .
.
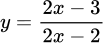 .
.D, 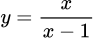 .
.
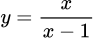 .
.
Chọn B
Đồ thị hàm số nhận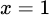 làm đường tiệm cận đứng và
làm đường tiệm cận đứng và 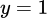 làm đường tiệm cận ngang.
làm đường tiệm cận ngang.
Đồ thị hàm số đi qua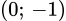 và
và 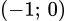 nên là đồ thị của hàm số
nên là đồ thị của hàm số 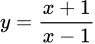 . Đáp án: B
. Đáp án: B
Đồ thị hàm số nhận
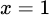 làm đường tiệm cận đứng và
làm đường tiệm cận đứng và 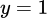 làm đường tiệm cận ngang.
làm đường tiệm cận ngang. Đồ thị hàm số đi qua
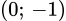 và
và 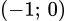 nên là đồ thị của hàm số
nên là đồ thị của hàm số 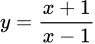 . Đáp án: B
. Đáp án: B
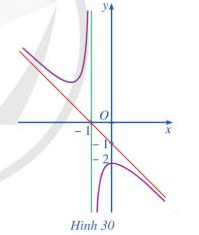
Câu 6 [360115]: Đường cong ở Hình 30 là đồ thị của hàm số:

A, 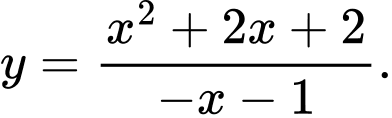
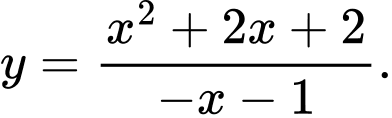
B, 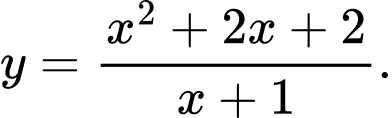
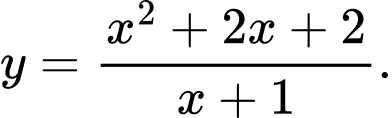
C, 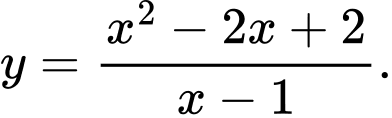
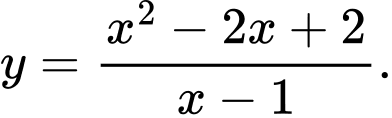
D, 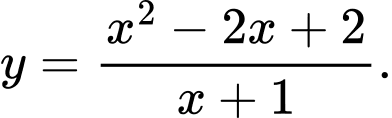
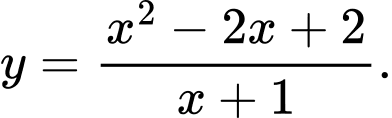
Dựa vào hình dạng đồ thị ta thấy hàm số đã có có 2 cực trị và 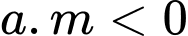 .
.
Chọn đáp án A. Đáp án: A
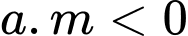 .
.
Chọn đáp án A. Đáp án: A
Câu 7 [383011]: Đồ thị trong hình vẽ là đồ thị của hàm số nào trong các hàm số dưới đây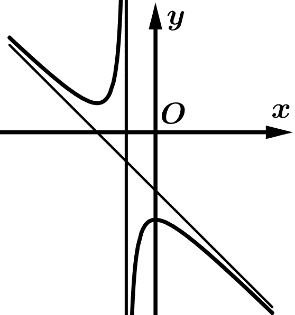

A, 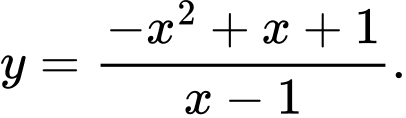
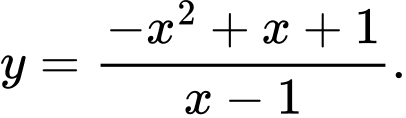
B, 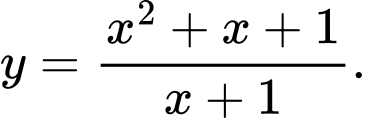
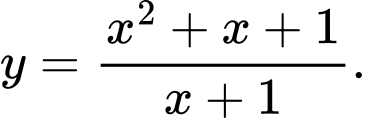
C, 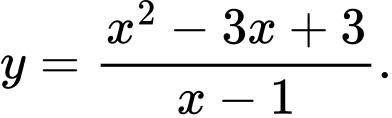
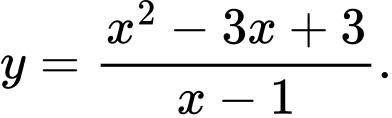
D, 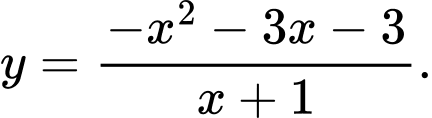
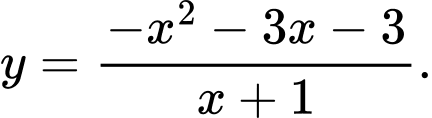
Từ đồ thị ta thấy hàm số đã cho 2 cực trị và 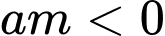 .
.
Xét các đáp án A, B, C, D suy ra loại B, C
Dựa vào đồ thị hàm số ta có hàm số có tiệm cận đứng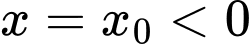 .
.
Suy ra loại đáp án A
Vậy đáp án đúng là D Đáp án: D
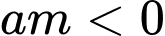 .
.
Xét các đáp án A, B, C, D suy ra loại B, C
Dựa vào đồ thị hàm số ta có hàm số có tiệm cận đứng
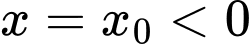 .
.
Suy ra loại đáp án A
Vậy đáp án đúng là D Đáp án: D
Câu 8 [506275]: Tâm đối xứng của đồ thị hàm số 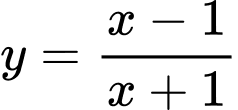 có tọa độ là
có tọa độ là
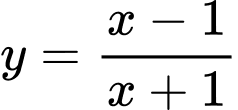 có tọa độ là
có tọa độ là A, 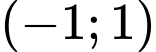 .
.
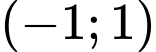 .
.B, 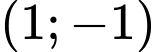 .
.
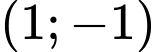 .
.C, 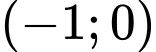 .
.
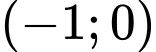 .
.D, 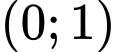 .
.
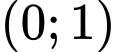 .
.
Chọn đáp án A.
Vì tiệm cận đứng của đồ thị hàm số là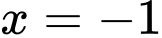 .
.
Tiệm cận ngang của đồ thị hàm số là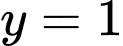 .
.
Tâm đối xứng của đồ thị hàm số là giao điểm của hai đường tiệm cận là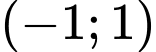 . Đáp án: A
. Đáp án: A
Vì tiệm cận đứng của đồ thị hàm số là
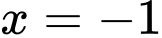 .
.Tiệm cận ngang của đồ thị hàm số là
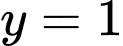 .
.Tâm đối xứng của đồ thị hàm số là giao điểm của hai đường tiệm cận là
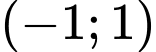 . Đáp án: A
. Đáp án: A
Câu 9 [382491]: Điểm uốn của đồ thị hàm số 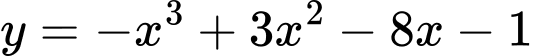 có tung độ bằng:
có tung độ bằng:
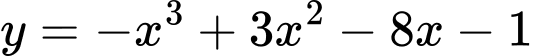 có tung độ bằng:
có tung độ bằng: A, 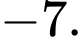
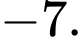
B, 

C, 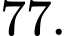
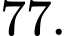
D, 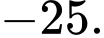
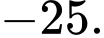
Ta có: 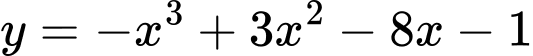
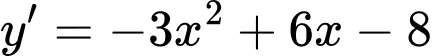
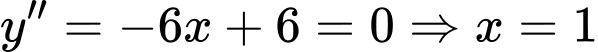
Khi đó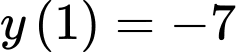
Vậy điểm uốn của đồ thị hàm số có tung độ bằng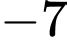 .
Đáp án: A
.
Đáp án: A
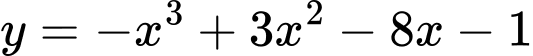
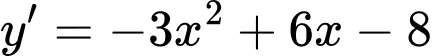
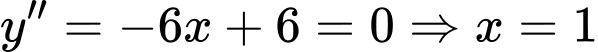
Khi đó
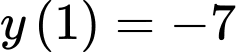
Vậy điểm uốn của đồ thị hàm số có tung độ bằng
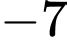 .
Đáp án: A
.
Đáp án: A
Câu 10 [382822]: Tâm đối xứng của đồ thị hàm số 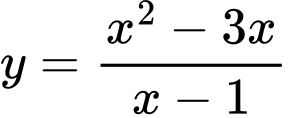 có toạ độ là
có toạ độ là
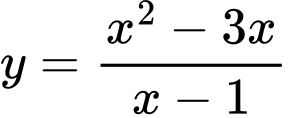 có toạ độ là
có toạ độ là A, 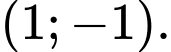
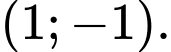
B, 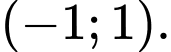
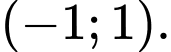
C, 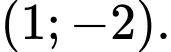
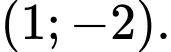
D, 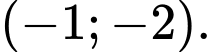
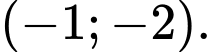
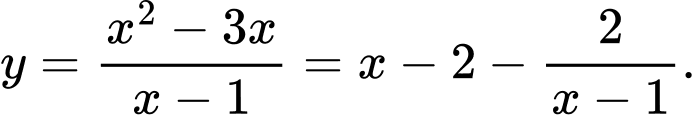
Đồ thị hàm số
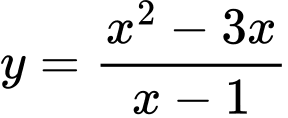 có TCĐ
có TCĐ 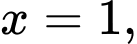 TCX
TCX 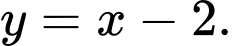
Vậy tâm đối xứng của đồ thị hàm số
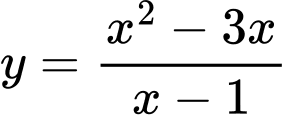 có toạ độ là
có toạ độ là 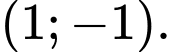 Đáp án: A
Đáp án: A
Câu 11 [601767]: Cho hàm số 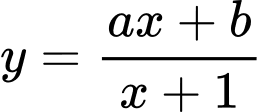 có đồ thị như hình vẽ dưới đây:
có đồ thị như hình vẽ dưới đây:
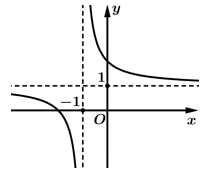
Tìm khẳng định đúng trong các khẳng định sau.
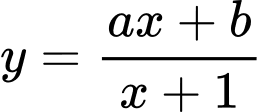 có đồ thị như hình vẽ dưới đây:
có đồ thị như hình vẽ dưới đây: 
Tìm khẳng định đúng trong các khẳng định sau.
A, 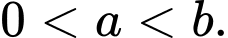
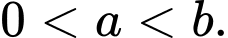
B, 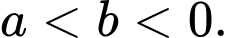
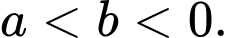
C, 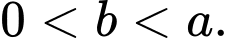
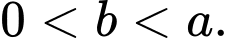
D, 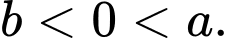
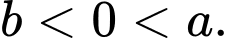
Chọn A
Dựa vào đồ thị, ta có:
+) Tiệm cận ngang: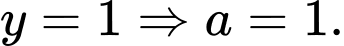
+) Đồ thị cắt trục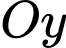 tại điểm có tung độ lớn hơn
tại điểm có tung độ lớn hơn 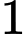 nên
nên 
Vậy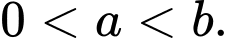 Đáp án: A
Đáp án: A
Dựa vào đồ thị, ta có:
+) Tiệm cận ngang:
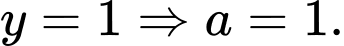
+) Đồ thị cắt trục
 tại điểm có tung độ lớn hơn
tại điểm có tung độ lớn hơn 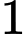 nên
nên 
Vậy
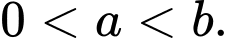 Đáp án: A
Đáp án: A
Câu 12 [801390]: Giá trị của 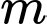 để đường thẳng vuông góc với đường thẳng
để đường thẳng vuông góc với đường thẳng 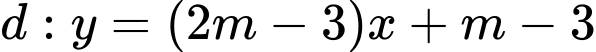 đi qua hai điểm cực trị của đồ thị hàm số
đi qua hai điểm cực trị của đồ thị hàm số 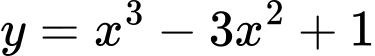 là
là
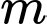 để đường thẳng vuông góc với đường thẳng
để đường thẳng vuông góc với đường thẳng 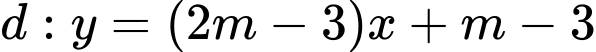 đi qua hai điểm cực trị của đồ thị hàm số
đi qua hai điểm cực trị của đồ thị hàm số 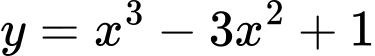 là
là A, 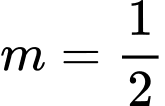 .
.
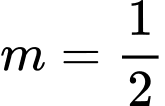 .
.B, 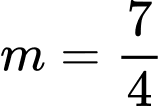 .
.
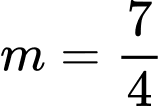 .
.C, 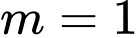 .
.
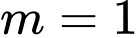 .
.D, 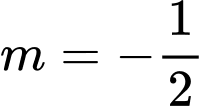 .
.
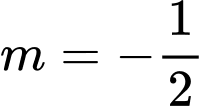 .
.
Chọn B
Tìm đường thẳng đi qua cực trị của đồ thị hàm số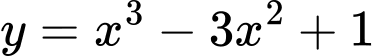 như sau:
như sau:
Cách 1:
Ta có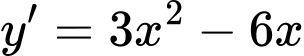
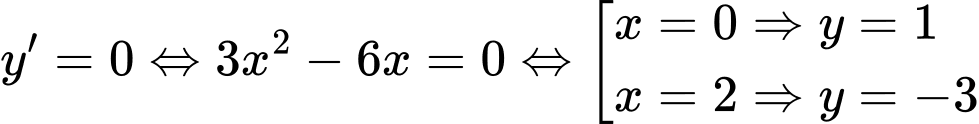
Khi đó các điểm cực trị của đồ thị hàm số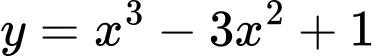 là
là 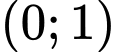 ,
, 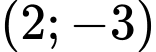
Đường thẳng đi qua hai điểm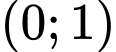 ,
, 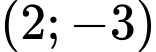 có phương trình
có phương trình 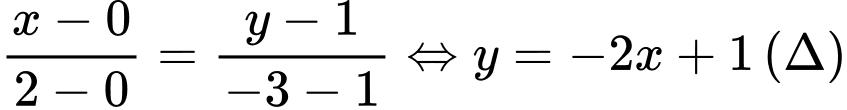
Cách 2:
Ta có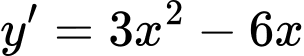
Thực hiện phép chia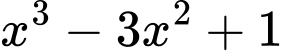 cho
cho 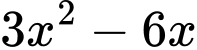 ta được dư là
ta được dư là 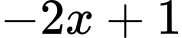 .
.
Do đó, đường thẳng đi qua các điểm cực trị của hàm số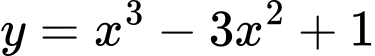 có phương trình
có phương trình 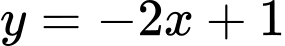 .
.
Theo giả thiết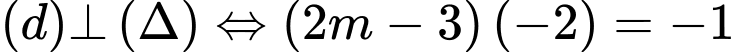
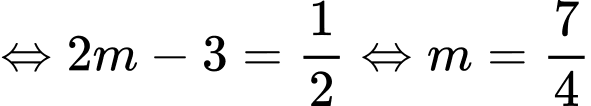
Vậy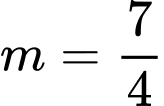 là giá trị cần tìm. Đáp án: B
là giá trị cần tìm. Đáp án: B
Tìm đường thẳng đi qua cực trị của đồ thị hàm số
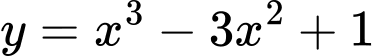 như sau:
như sau: Cách 1:
Ta có
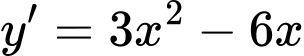
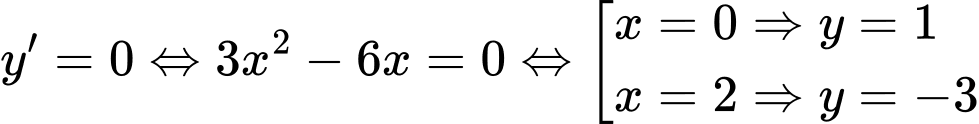
Khi đó các điểm cực trị của đồ thị hàm số
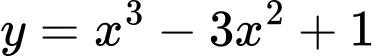 là
là 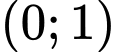 ,
, 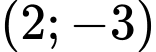
Đường thẳng đi qua hai điểm
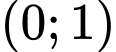 ,
, 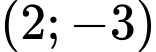 có phương trình
có phương trình 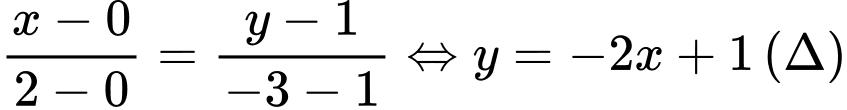
Cách 2:
Ta có
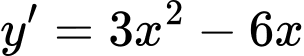
Thực hiện phép chia
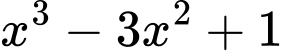 cho
cho 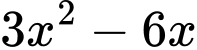 ta được dư là
ta được dư là 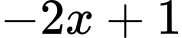 .
.Do đó, đường thẳng đi qua các điểm cực trị của hàm số
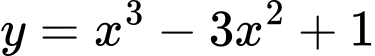 có phương trình
có phương trình 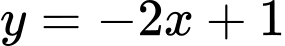 .
.Theo giả thiết
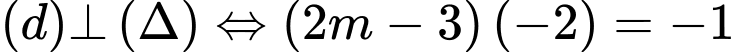
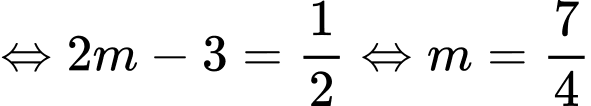
Vậy
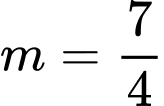 là giá trị cần tìm. Đáp án: B
là giá trị cần tìm. Đáp án: B
Câu 13 [383419]: [Đề Thi ĐGTD ĐH Bách Khoa HN 2022]: Cho hàm số 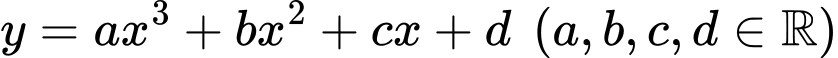 có đồ thị như hình vẽ bên. Khi đó,
có đồ thị như hình vẽ bên. Khi đó, 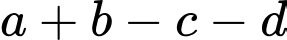 bằng
bằng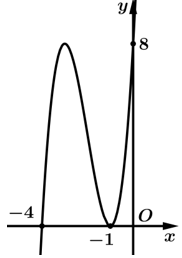
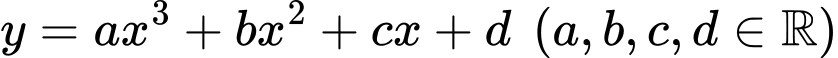 có đồ thị như hình vẽ bên. Khi đó,
có đồ thị như hình vẽ bên. Khi đó, 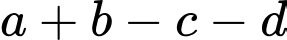 bằng
bằng
A, 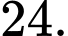
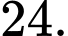
B, 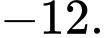
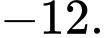
C, 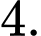
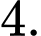
D, 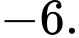
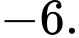
Ta có: 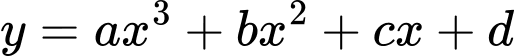
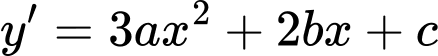
Từ đồ thị hàm số dễ thấy điểm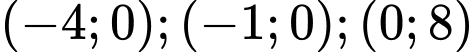 thuộc đồ thị hàm số và điểm
thuộc đồ thị hàm số và điểm 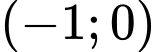 là điểm cực tiểu nên ta có
là điểm cực tiểu nên ta có 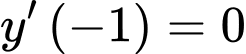 (theo định nghĩa).
(theo định nghĩa).
Suy ra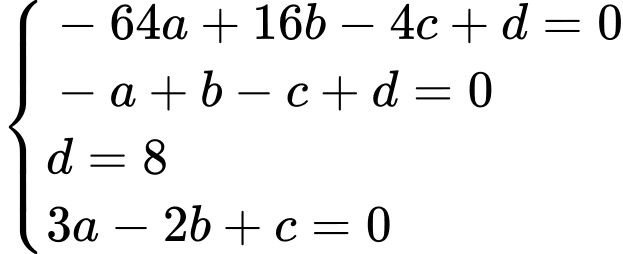
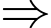
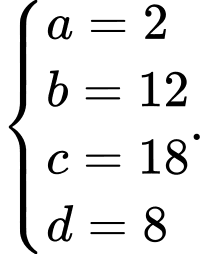
Vậy Đáp án: B
Đáp án: B
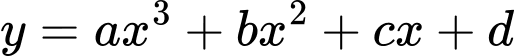
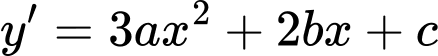
Từ đồ thị hàm số dễ thấy điểm
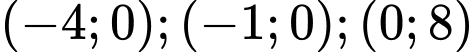 thuộc đồ thị hàm số và điểm
thuộc đồ thị hàm số và điểm 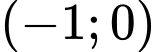 là điểm cực tiểu nên ta có
là điểm cực tiểu nên ta có 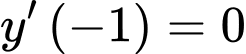 (theo định nghĩa).
(theo định nghĩa).
Suy ra
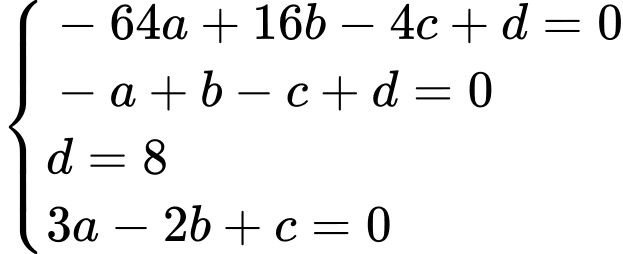
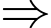
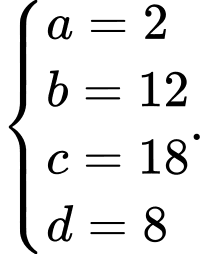
Vậy
 Đáp án: B
Đáp án: B
Câu 14 [526215]: Cho hàm số 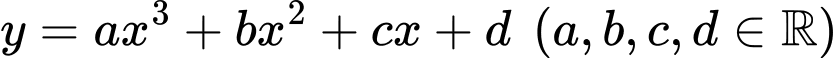 có đồ thị như hình vẽ.
có đồ thị như hình vẽ.
Có bao nhiêu số dương trong các số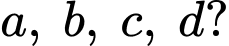
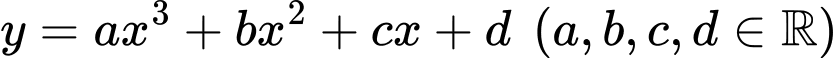 có đồ thị như hình vẽ.
có đồ thị như hình vẽ.
Có bao nhiêu số dương trong các số
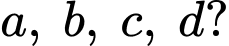
A, 4.
B, 1.
C, 2.
D, 3.
Chọn C.
Ta có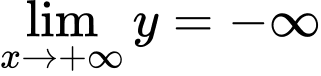
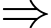
 .
.
Ta có
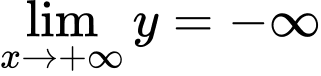
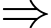
 .
. Gọi 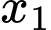 ,
, 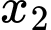 là hoành độ hai điểm cực trị của hàm số suy ra
là hoành độ hai điểm cực trị của hàm số suy ra 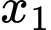 ,
, 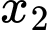 nghiệm phương trình
nghiệm phương trình 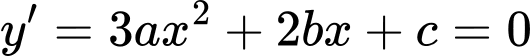 nên theo định lý Viet:
nên theo định lý Viet:
+) Tổng hai nghiệm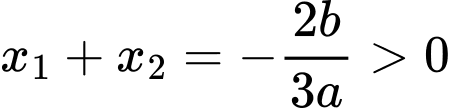
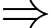
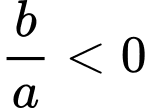
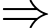
 .
.
+) Tích hai nghiệm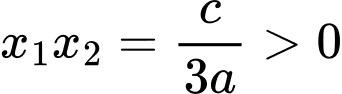
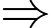
 .
.
Lại có đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên .
.
Vậy có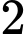 số dương trong các số
số dương trong các số 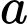 ,
, 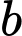 ,
,  ,
, 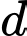 .
.
Đáp án: C 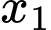 ,
, 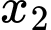 là hoành độ hai điểm cực trị của hàm số suy ra
là hoành độ hai điểm cực trị của hàm số suy ra 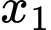 ,
, 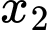 nghiệm phương trình
nghiệm phương trình 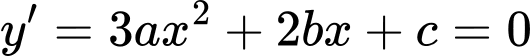 nên theo định lý Viet:
nên theo định lý Viet:+) Tổng hai nghiệm
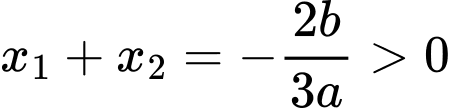
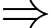
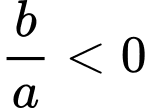
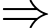
 .
.+) Tích hai nghiệm
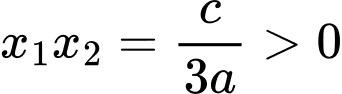
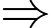
 .
.Lại có đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên
 .
.Vậy có
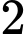 số dương trong các số
số dương trong các số 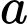 ,
, 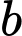 ,
,  ,
, 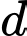 .
.
Câu 15 [526217]: Cho hàm số 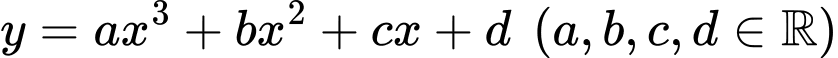 có đồ thị như hình vẽ.
có đồ thị như hình vẽ.
=kphan2de1/30.kslan7thaT.png)
Có bao nhiêu số dương trong các số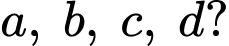
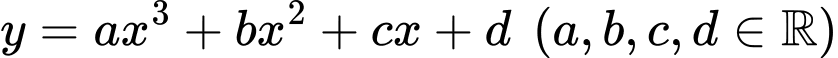 có đồ thị như hình vẽ.
có đồ thị như hình vẽ.=kphan2de1/30.kslan7thaT.png)
Có bao nhiêu số dương trong các số
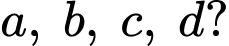
A, 4.
B, 1.
C, 2.
D, 3.
Chọn B.
Ta có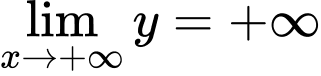
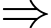
 . Gọi
. Gọi 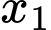 ,
, 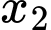 là hoành độ hai điểm cực trị của hàm số suy ra
là hoành độ hai điểm cực trị của hàm số suy ra 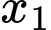 ,
, 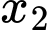 nghiệm phương trình
nghiệm phương trình 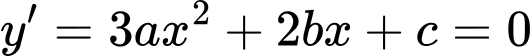 nên theo định lý Viet:
nên theo định lý Viet:
+) Tổng hai nghiệm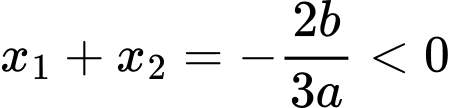
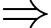
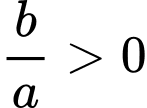
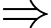
 .
.
+) Tích hai nghiệm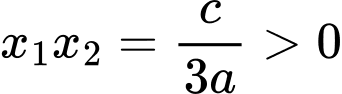
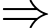
 .
.
Lại có đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên .
.
Vậy có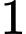 số dương trong các số
số dương trong các số 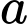 ,
, 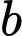 ,
,  ,
, 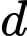 . Đáp án: B
. Đáp án: B
Ta có
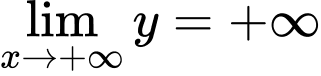
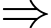
 . Gọi
. Gọi 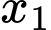 ,
, 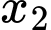 là hoành độ hai điểm cực trị của hàm số suy ra
là hoành độ hai điểm cực trị của hàm số suy ra 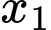 ,
, 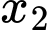 nghiệm phương trình
nghiệm phương trình 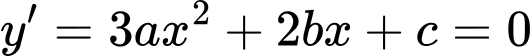 nên theo định lý Viet:
nên theo định lý Viet:+) Tổng hai nghiệm
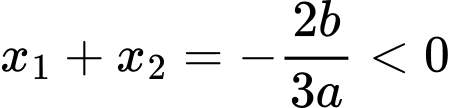
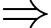
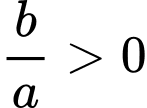
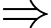
 .
.+) Tích hai nghiệm
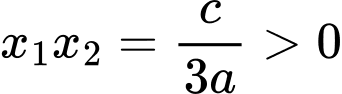
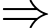
 .
.Lại có đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên
 .
.Vậy có
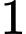 số dương trong các số
số dương trong các số 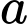 ,
, 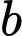 ,
,  ,
, 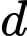 . Đáp án: B
. Đáp án: B
Câu 16 [526213]: Cho hàm số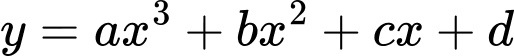 có đồ thị như hình bên. Mệnh đề nào sau đây sai?
có đồ thị như hình bên. Mệnh đề nào sau đây sai?
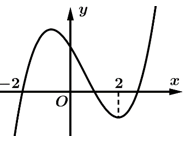
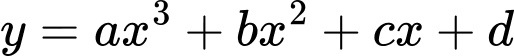 có đồ thị như hình bên. Mệnh đề nào sau đây sai?
có đồ thị như hình bên. Mệnh đề nào sau đây sai?
A, 

B, 

C, 

D, 

Ta có: 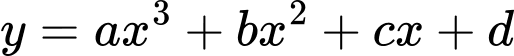
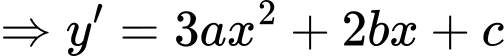
Từ đồ thị ta thấy :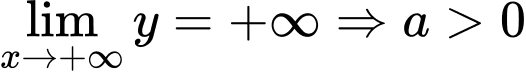 .
.
+ Hàm số có hai điểm cực trị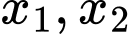 nằm về hai của phía trục
nằm về hai của phía trục 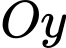
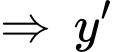 có hai nghiệm
có hai nghiệm 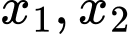 trái dấu
trái dấu 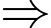
 . Vậy C đúng.
. Vậy C đúng.
Có , mà
, mà 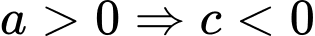 (1).
(1).
+ Ta có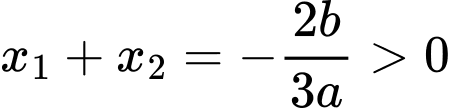 ( vì
( vì 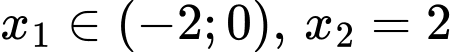 )
)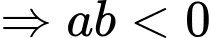 . Vậy A đúng.
. Vậy A đúng.
Có , mà
, mà  (2).
(2).
Từ (1) và (2) suy ra . Vậy B sai, nên chọn
. Vậy B sai, nên chọn 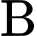 .
.
+ D đúng vì đồ thị cắt trục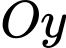 tại điểm nằm phía trên trục hoành nên
tại điểm nằm phía trên trục hoành nên  , mà
, mà 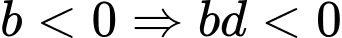 . Chọn B.
Đáp án: B
. Chọn B.
Đáp án: B
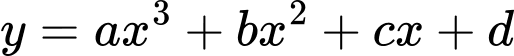
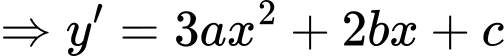
Từ đồ thị ta thấy :
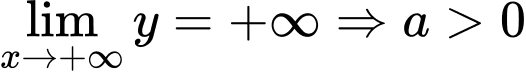 .
.+ Hàm số có hai điểm cực trị
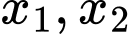 nằm về hai của phía trục
nằm về hai của phía trục 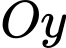
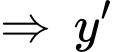 có hai nghiệm
có hai nghiệm 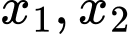 trái dấu
trái dấu 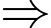
 . Vậy C đúng.
. Vậy C đúng.Có
 , mà
, mà 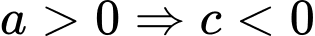 (1).
(1).+ Ta có
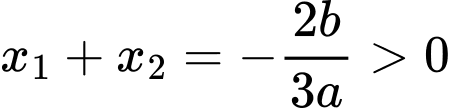 ( vì
( vì 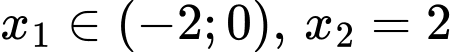 )
)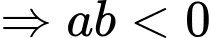 . Vậy A đúng.
. Vậy A đúng.Có
 , mà
, mà  (2).
(2).Từ (1) và (2) suy ra
 . Vậy B sai, nên chọn
. Vậy B sai, nên chọn 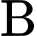 .
.+ D đúng vì đồ thị cắt trục
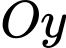 tại điểm nằm phía trên trục hoành nên
tại điểm nằm phía trên trục hoành nên  , mà
, mà 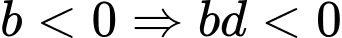 . Chọn B.
Đáp án: B
. Chọn B.
Đáp án: B
Câu 17 [377601]: Cho hàm số 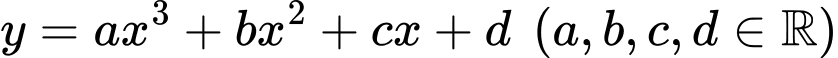 có đồ thị như hình vẽ. Có bao nhiêu số dương trong các số
có đồ thị như hình vẽ. Có bao nhiêu số dương trong các số 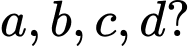
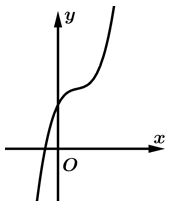
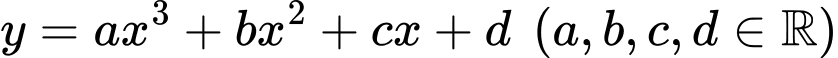 có đồ thị như hình vẽ. Có bao nhiêu số dương trong các số
có đồ thị như hình vẽ. Có bao nhiêu số dương trong các số 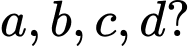

A, 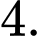
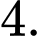
B, 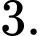
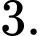
C, 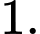
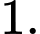
D, 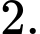
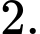
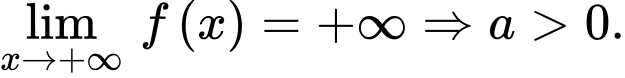 Hoành độ điểm uốn
Hoành độ điểm uốn 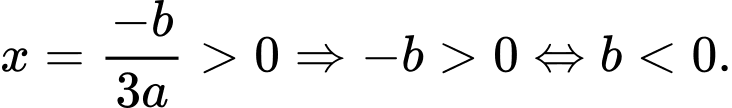
Ta có: 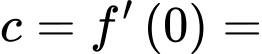 hệ số góc của tiếp tuyến tại điểm có hoành độ
hệ số góc của tiếp tuyến tại điểm có hoành độ 
Chọn đáp án B. Đáp án: B 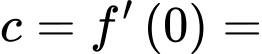 hệ số góc của tiếp tuyến tại điểm có hoành độ
hệ số góc của tiếp tuyến tại điểm có hoành độ 
Giao điểm của đồ thị hàm số với trục tung là điểm 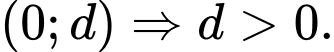
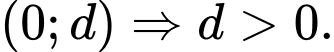
Vậy có 3 số dương trong các số 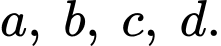
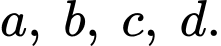
Câu 18 [527758]: Cho hàm số 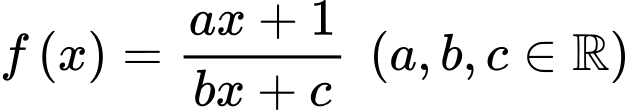 có bảng biến thiên như sau:
có bảng biến thiên như sau:
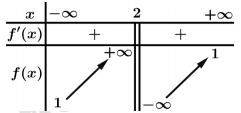
Trong các số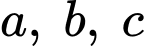 có bao nhiêu số dương
có bao nhiêu số dương
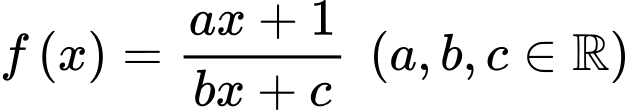 có bảng biến thiên như sau:
có bảng biến thiên như sau:
Trong các số
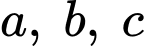 có bao nhiêu số dương
có bao nhiêu số dương A, 2.
B, 3.
C, 1.
D, 0.
Từ bảng biến thiên ta thấy
Đồ thị hàm số cắt trục hoành tại điểm có hoành độ dương nên có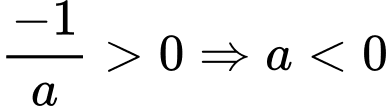
Đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên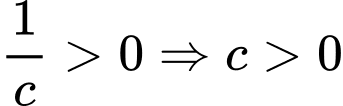
Đồ thị hàm số có đường tiệm cận ngang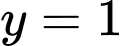 nên
nên 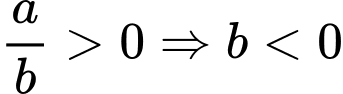 Đáp án: C
Đáp án: C
Đồ thị hàm số cắt trục hoành tại điểm có hoành độ dương nên có
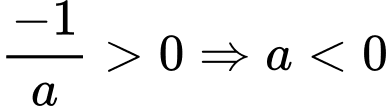
Đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên
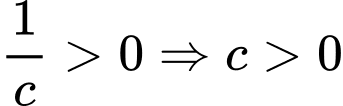
Đồ thị hàm số có đường tiệm cận ngang
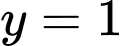 nên
nên 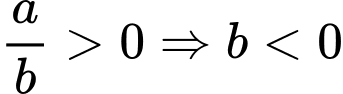 Đáp án: C
Đáp án: C
Câu 19 [30660]: Cho hàm số 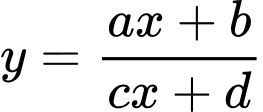 có đồ thị như hình bên dưới. Mệnh đề nào dưới đây đúng?
có đồ thị như hình bên dưới. Mệnh đề nào dưới đây đúng?
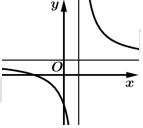
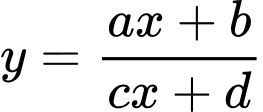 có đồ thị như hình bên dưới. Mệnh đề nào dưới đây đúng?
có đồ thị như hình bên dưới. Mệnh đề nào dưới đây đúng?
A, 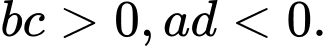
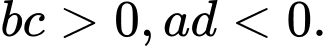
B, 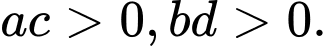
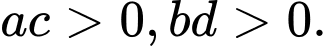
C, 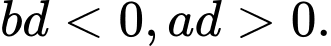
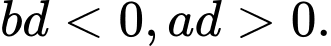
D, 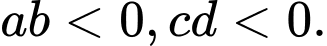
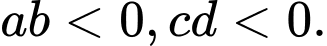
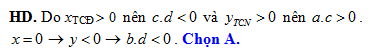 Đáp án: A
Đáp án: A
Câu 20 [30670]: Cho đồ thị hàm số 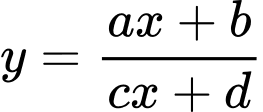 như hình vẽ bên dưới. Khẳng định nào sau đây là đúng?
như hình vẽ bên dưới. Khẳng định nào sau đây là đúng?
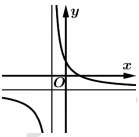
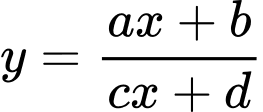 như hình vẽ bên dưới. Khẳng định nào sau đây là đúng?
như hình vẽ bên dưới. Khẳng định nào sau đây là đúng?
A, 

B, 

C, 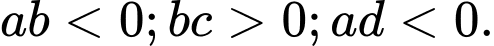
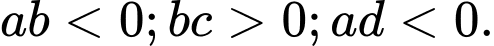
D, 

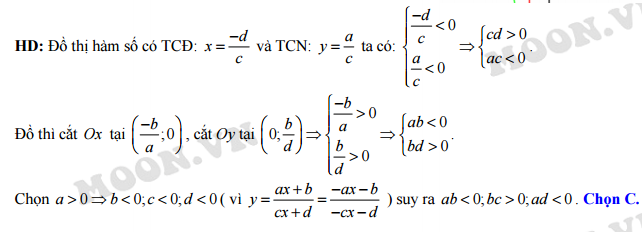 Đáp án: C
Đáp án: C
Câu 21 [527762]: Cho hàm số 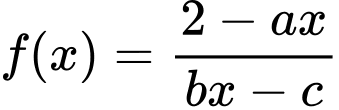
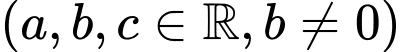 có bảng biến thiên như sau:
có bảng biến thiên như sau:
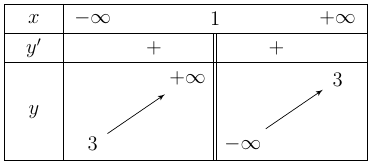
Tổng các số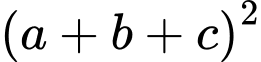 thuộc khoảng nào sau đây?
thuộc khoảng nào sau đây?
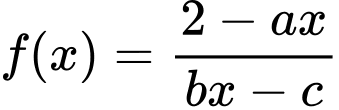
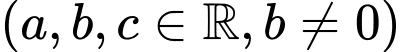 có bảng biến thiên như sau:
có bảng biến thiên như sau:
Tổng các số
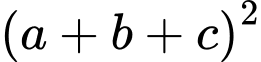 thuộc khoảng nào sau đây?
thuộc khoảng nào sau đây? A, 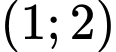 .
.
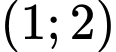 .
.B, 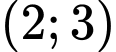 .
.
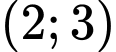 .
.C, 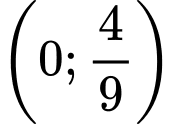 .
.
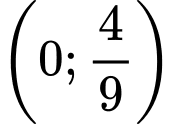 .
.D, 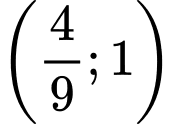 .
.
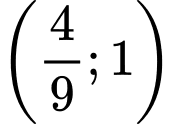 .
.
Chọn C
Ta có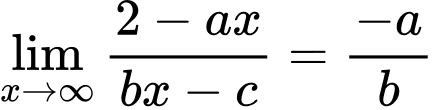 , theo giả thiết suy ra
, theo giả thiết suy ra 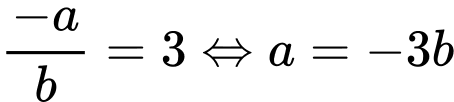
Hàm số không xác định tại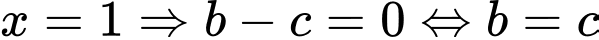
Hàm số đồng biến trên từng khoảng xác định nên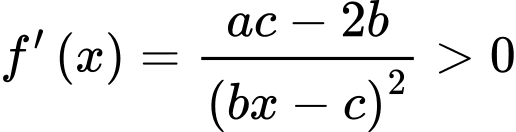 với mọi
với mọi 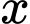 khác 1
khác 1
Suy ra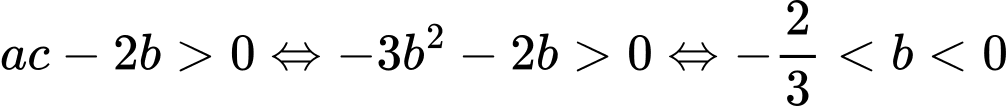
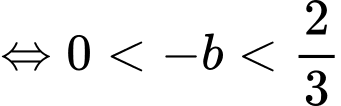
Lại có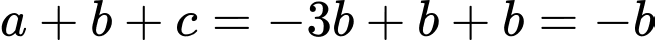 . Suy ra
. Suy ra 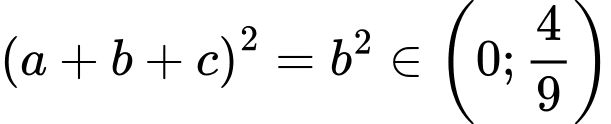
Vậy tổng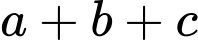 thuộc khoảng
thuộc khoảng 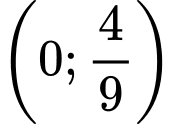 . Đáp án: C
. Đáp án: C
Ta có
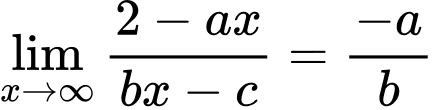 , theo giả thiết suy ra
, theo giả thiết suy ra 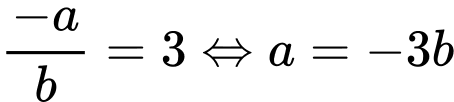
Hàm số không xác định tại
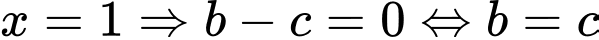
Hàm số đồng biến trên từng khoảng xác định nên
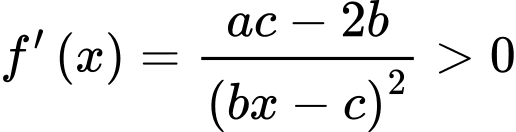 với mọi
với mọi 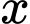 khác 1
khác 1Suy ra
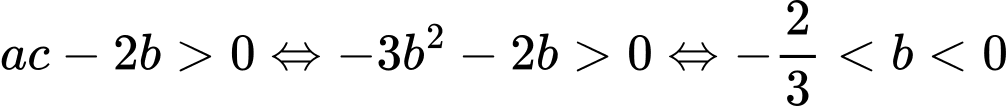
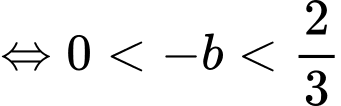
Lại có
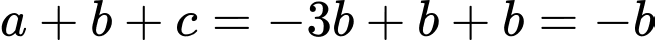 . Suy ra
. Suy ra 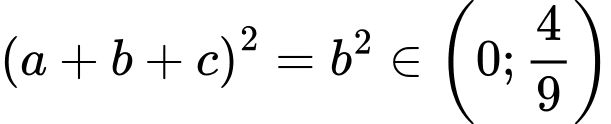
Vậy tổng
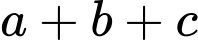 thuộc khoảng
thuộc khoảng 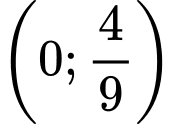 . Đáp án: C
. Đáp án: C
Câu 22 [15767]: Biết 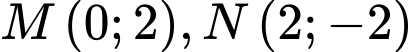 là các điểm cực trị của đồ thị hàm số
là các điểm cực trị của đồ thị hàm số 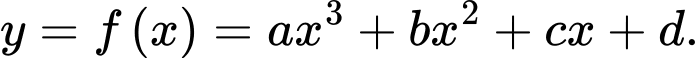 Tính giá trị biểu thức
Tính giá trị biểu thức 
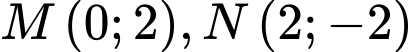 là các điểm cực trị của đồ thị hàm số
là các điểm cực trị của đồ thị hàm số 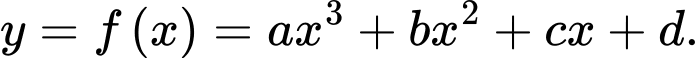 Tính giá trị biểu thức
Tính giá trị biểu thức 
Ta có 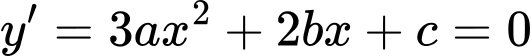
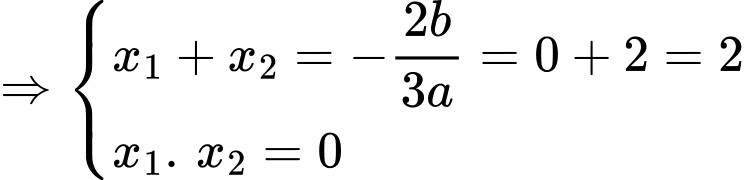
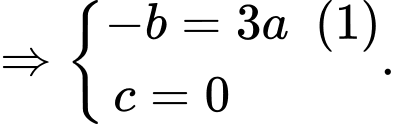
Lại có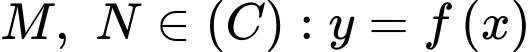
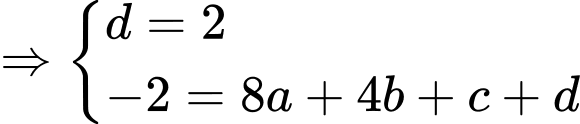
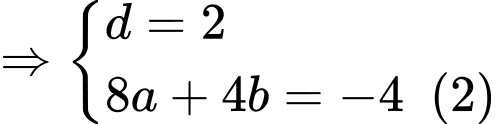
Từ và
và 
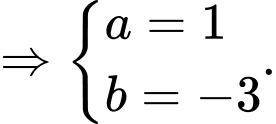
Suy ra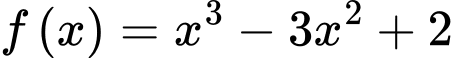
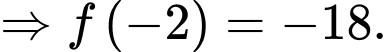
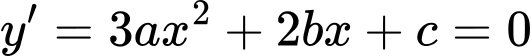
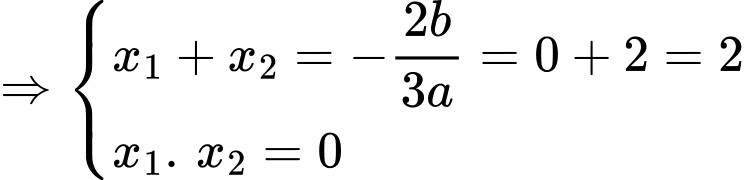
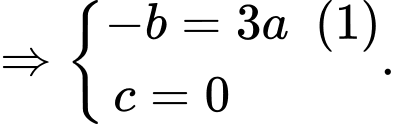
Lại có
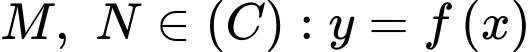
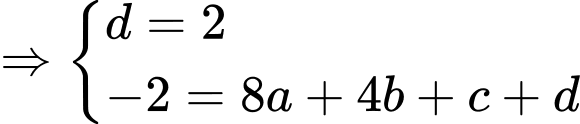
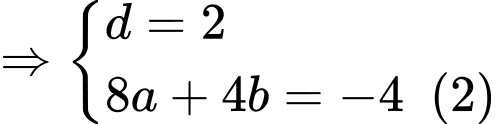
Từ
 và
và 
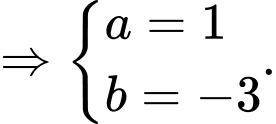
Suy ra
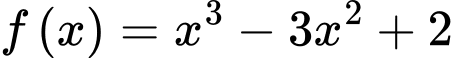
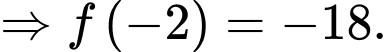
Câu 23 [27355]: Đồ thị của hàm số 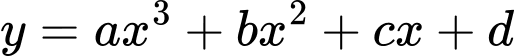 có hai điểm cực trị là
có hai điểm cực trị là 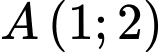 và
và 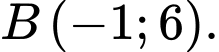 Tính
Tính 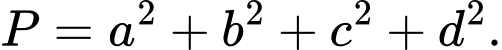
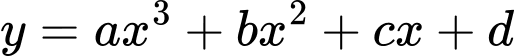 có hai điểm cực trị là
có hai điểm cực trị là 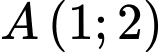 và
và 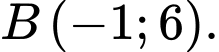 Tính
Tính 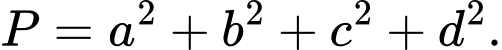
A,
B,
C,
D,
Cách 1: Ta có 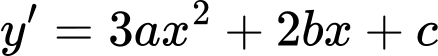
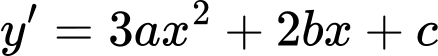
Theo đề bài ta có 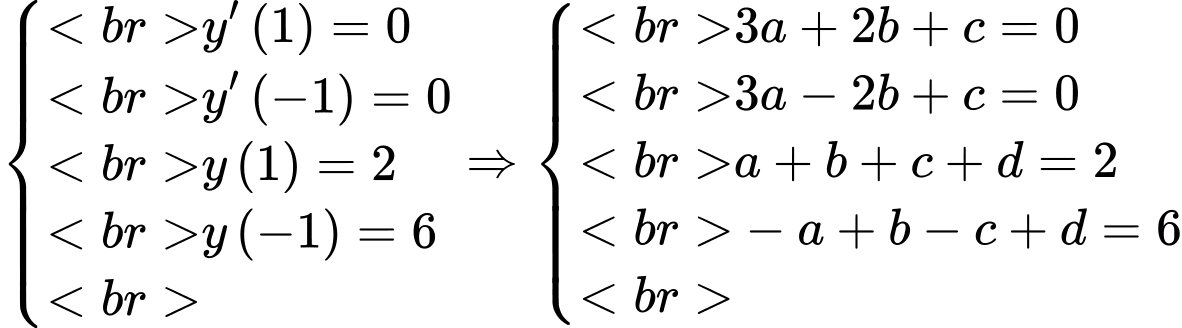
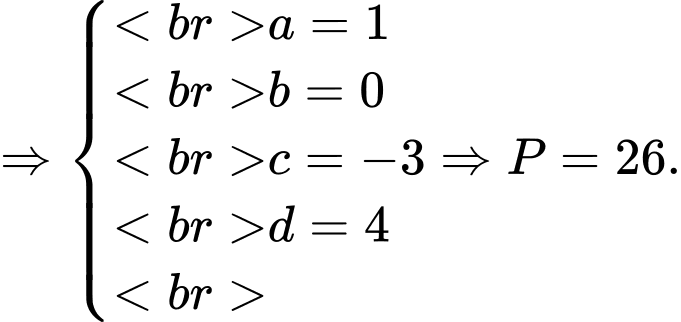
Đáp án: B 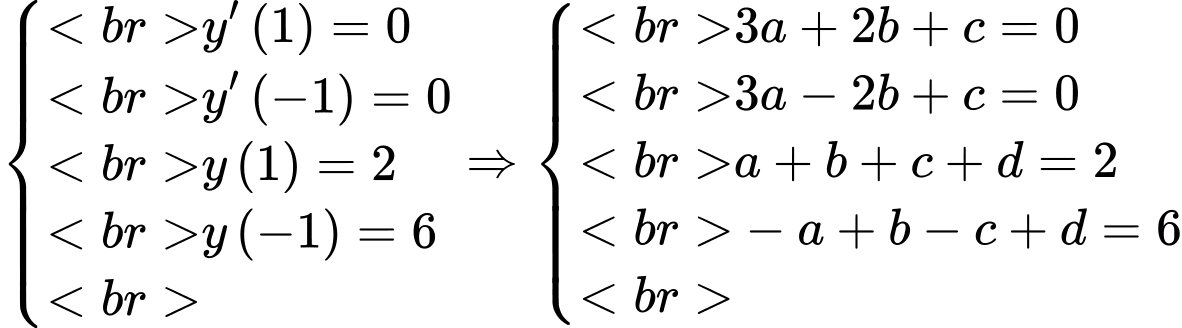
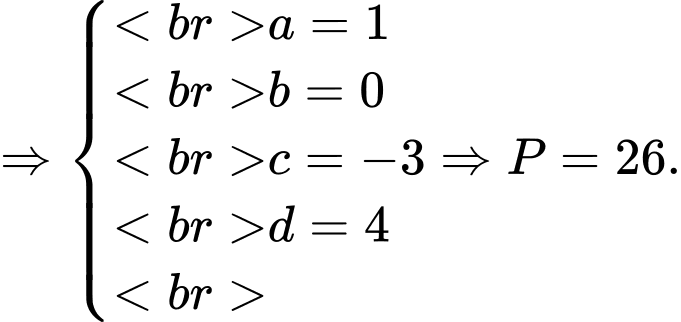
Cách 2: Ta có 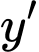 có dạng
có dạng 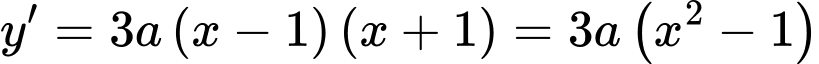
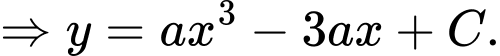
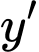 có dạng
có dạng 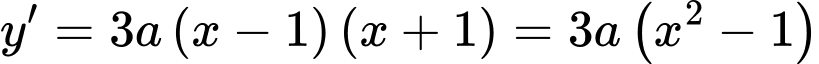
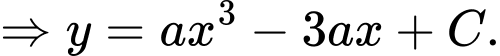
Lại có 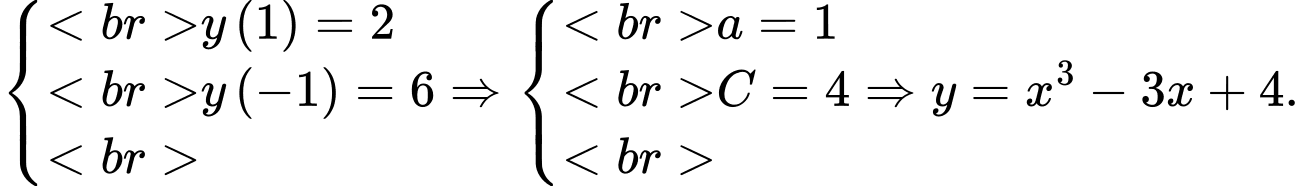
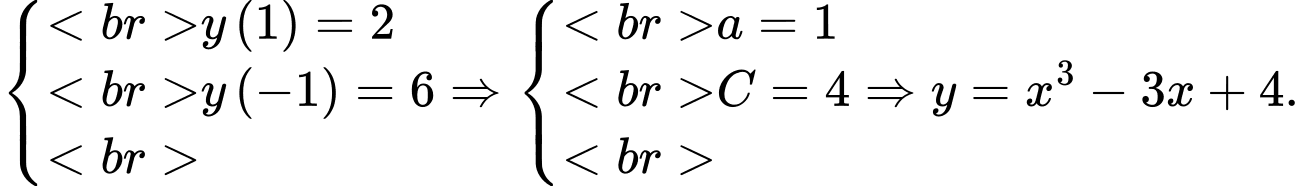
Suy ra 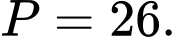
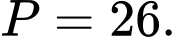
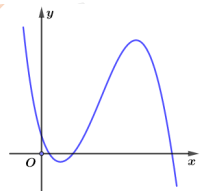
Câu 24 [382493]: [SGK Cùng Khám Phá] Một phần đường ray tàu lượn siêu tốc có dạng đồ thị hàm số bậc ba: 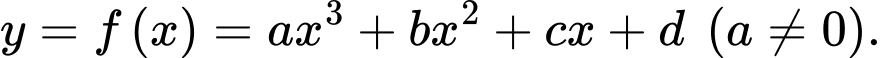 Trục Ox mô tả quãng đường tàu di chuyển theo chiều ngang (tính bằng centimét), trục Oy mô tả chiều cao của đường ray (tính bằng centimét) tại mỗi vị trí x.
Trục Ox mô tả quãng đường tàu di chuyển theo chiều ngang (tính bằng centimét), trục Oy mô tả chiều cao của đường ray (tính bằng centimét) tại mỗi vị trí x.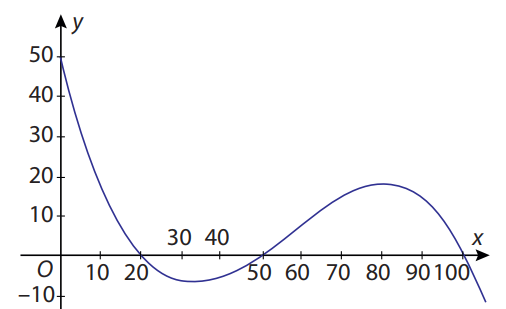
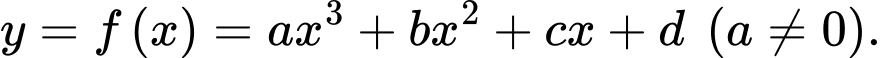 Trục Ox mô tả quãng đường tàu di chuyển theo chiều ngang (tính bằng centimét), trục Oy mô tả chiều cao của đường ray (tính bằng centimét) tại mỗi vị trí x.
Trục Ox mô tả quãng đường tàu di chuyển theo chiều ngang (tính bằng centimét), trục Oy mô tả chiều cao của đường ray (tính bằng centimét) tại mỗi vị trí x.
Chiều cao xuất phát là 50 cm. Tàu xuống dưới mặt đất lần thứ nhất từ vị trí 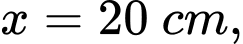 tàu lên khỏi mặt đất ở vị trí
tàu lên khỏi mặt đất ở vị trí 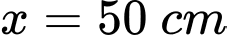 và sau đó xuống dưới mặt đất lần thứ hai ở vị trí
và sau đó xuống dưới mặt đất lần thứ hai ở vị trí 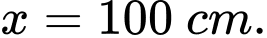
Xét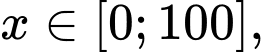 giá trị cực đại của hàm số
giá trị cực đại của hàm số 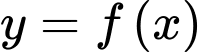 bằng:
bằng:
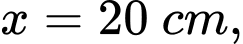 tàu lên khỏi mặt đất ở vị trí
tàu lên khỏi mặt đất ở vị trí 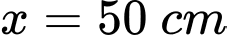 và sau đó xuống dưới mặt đất lần thứ hai ở vị trí
và sau đó xuống dưới mặt đất lần thứ hai ở vị trí 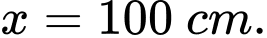
Xét
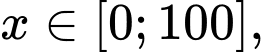 giá trị cực đại của hàm số
giá trị cực đại của hàm số 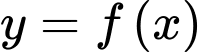 bằng:
bằng:
Ta có: 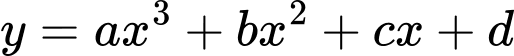 .
.
Vì đồ thị hàm số đi qua các điểm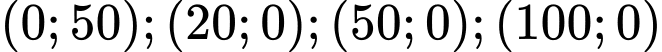
nên ta có hệ phương trình sau
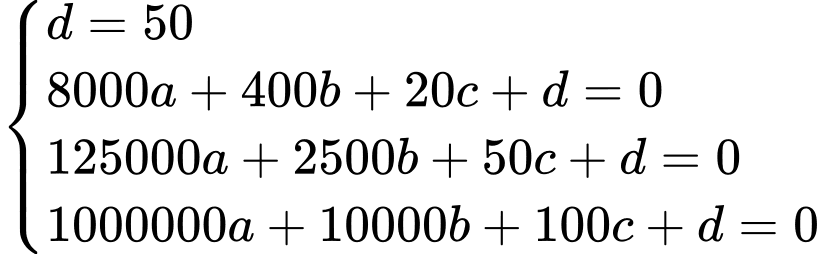
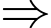
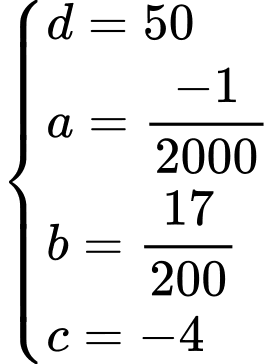
Suy ra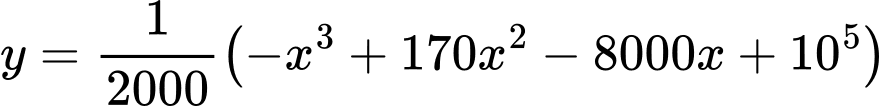 .
.
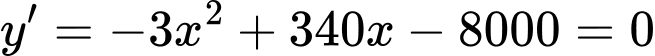
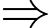
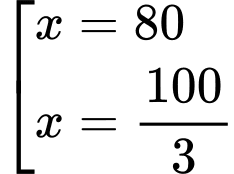
Suy ra giá trị cực đại bằng
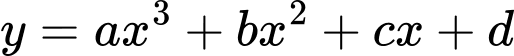 .
.Vì đồ thị hàm số đi qua các điểm
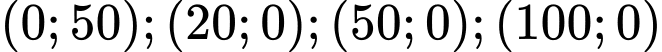
nên ta có hệ phương trình sau
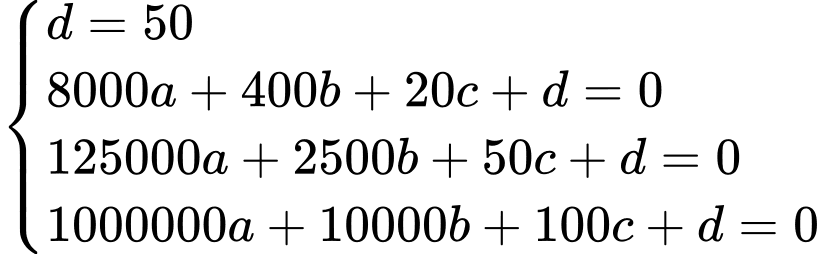
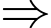
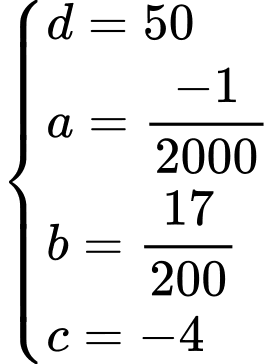
Suy ra
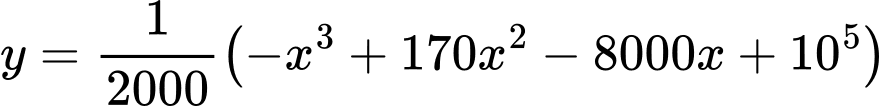 .
.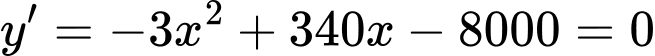
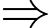
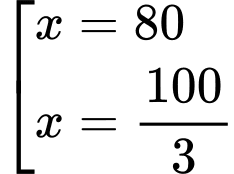
Suy ra giá trị cực đại bằng

Câu 25 [382495]: Đồ thị của hàm số 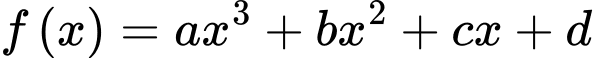 có hai điểm cực trị là
có hai điểm cực trị là 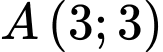 và
và 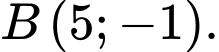 Tính giá trị của
Tính giá trị của 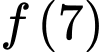 .
.
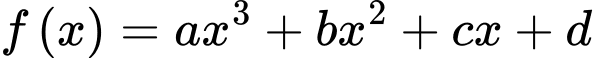 có hai điểm cực trị là
có hai điểm cực trị là 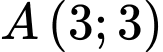 và
và 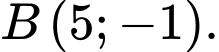 Tính giá trị của
Tính giá trị của 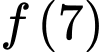 .
.
Ta có 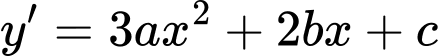
Theo đề bài ta có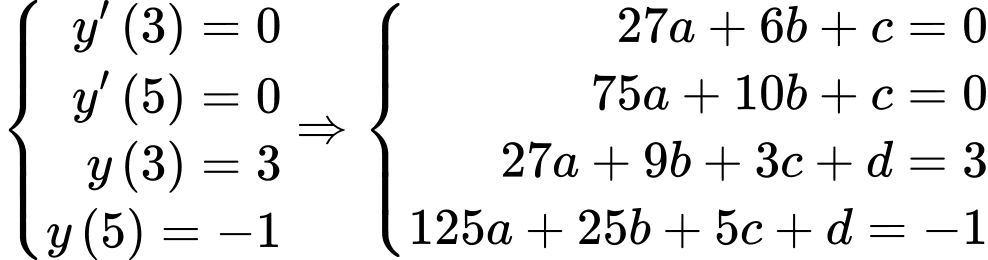
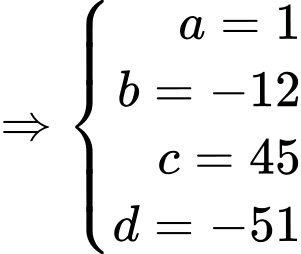
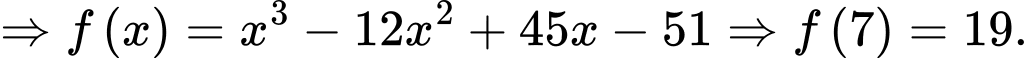
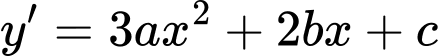
Theo đề bài ta có
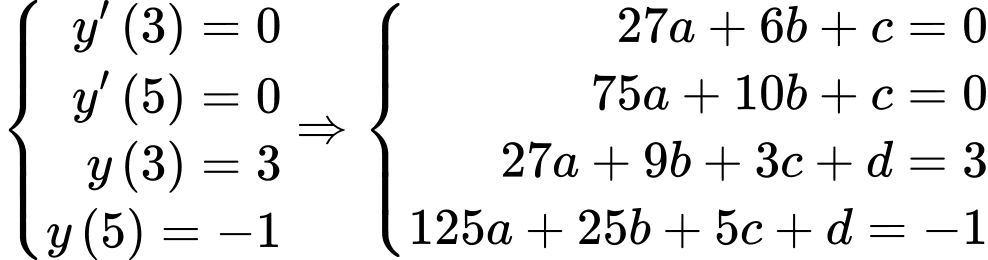
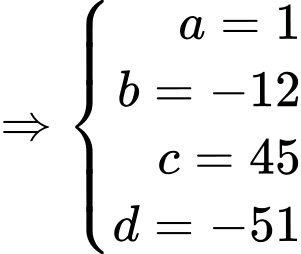
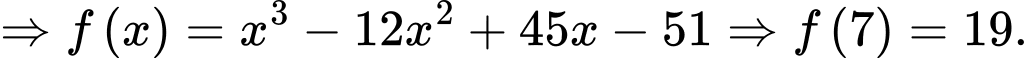
Câu 26 [527764]: Cho hàm số 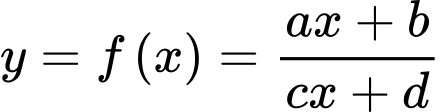 có đồ thị hàm số
có đồ thị hàm số 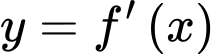 như hình vẽ.
như hình vẽ.
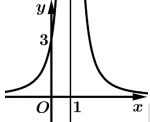
Biết đồ thị hàm số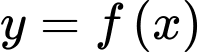 đi qua điểm
đi qua điểm 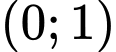 . Giá trị
. Giá trị  bằng
bằng
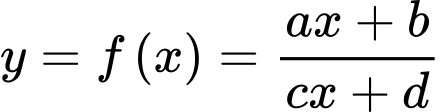 có đồ thị hàm số
có đồ thị hàm số 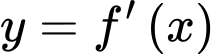 như hình vẽ.
như hình vẽ.
Biết đồ thị hàm số
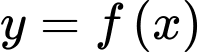 đi qua điểm
đi qua điểm 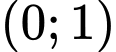 . Giá trị
. Giá trị  bằng
bằng A, 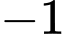 .
.
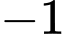 .
.B, 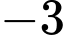 .
.
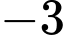 .
.C, 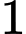 .
.
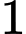 .
.D, 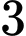 .
.
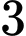 .
.
Chọn A
Điều kiện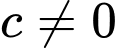 .
.
Ta có đồ thị hàm số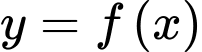 đi qua điểm
đi qua điểm 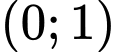
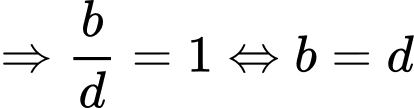 .
.
Từ đồ thị hàm số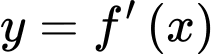 suy ra đường tiệm cận đứng của đồ thị hàm số
suy ra đường tiệm cận đứng của đồ thị hàm số 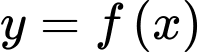 là
là
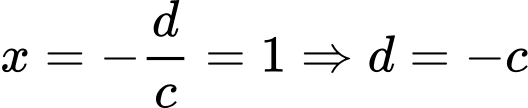
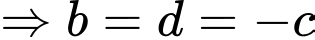 .
.
Lại có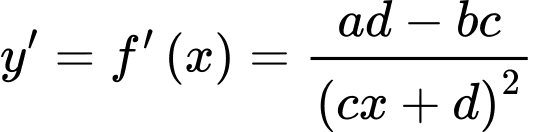 .
.
Mà đồ thị hàm số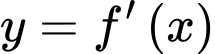 cắt trục
cắt trục 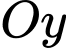 tại điểm
tại điểm 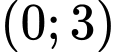
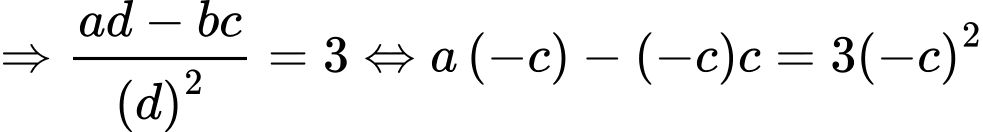
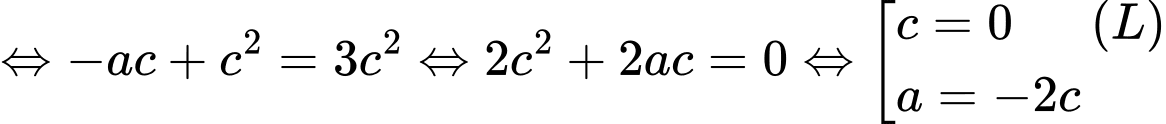 .
.
Do đó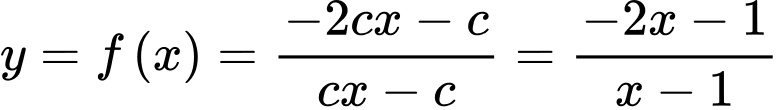 . Vậy
. Vậy 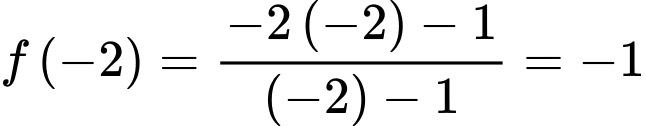 . Đáp án: A
. Đáp án: A
Điều kiện
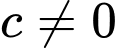 .
.Ta có đồ thị hàm số
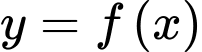 đi qua điểm
đi qua điểm 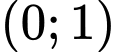
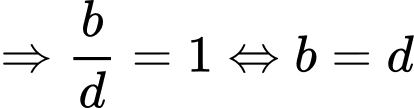 .
.Từ đồ thị hàm số
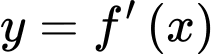 suy ra đường tiệm cận đứng của đồ thị hàm số
suy ra đường tiệm cận đứng của đồ thị hàm số 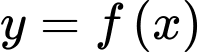 là
là 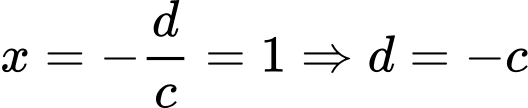
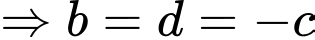 .
.Lại có
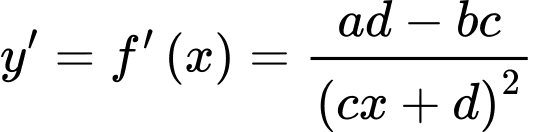 .
.Mà đồ thị hàm số
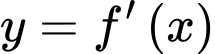 cắt trục
cắt trục 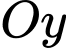 tại điểm
tại điểm 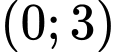
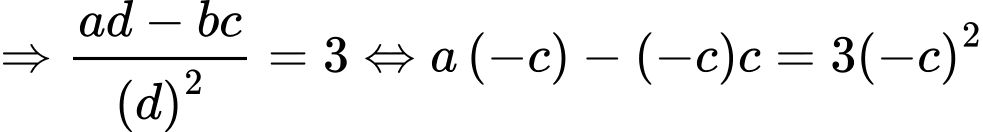
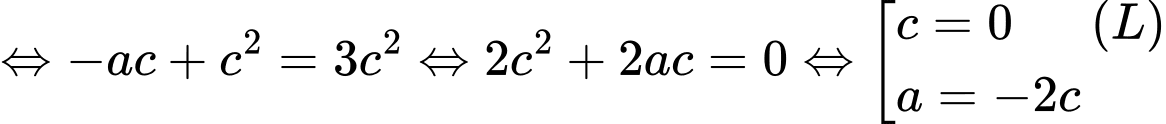 .
.Do đó
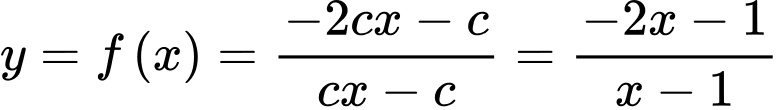 . Vậy
. Vậy 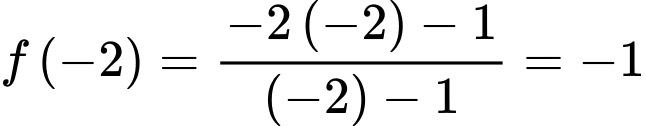 . Đáp án: A
. Đáp án: A
Câu 27 [383019]: Cho hàm số 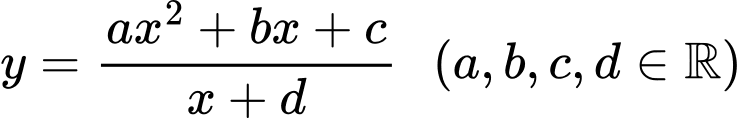 có đồ thị như hình vẽ. Có bao nhiêu số dương trong các số
có đồ thị như hình vẽ. Có bao nhiêu số dương trong các số 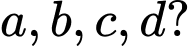
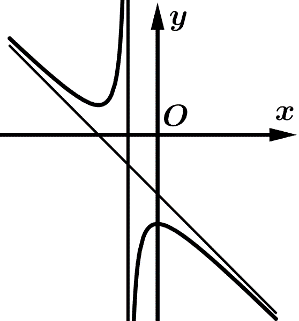
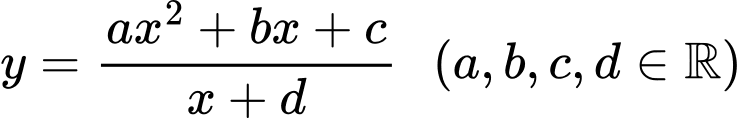 có đồ thị như hình vẽ. Có bao nhiêu số dương trong các số
có đồ thị như hình vẽ. Có bao nhiêu số dương trong các số 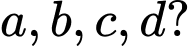

Đáp số: 1
Từ đồ thị hàm số đã cho ta có
Đồ thị hàm số có 1 đường tiệm cận đứng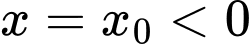 .
.
Suy ra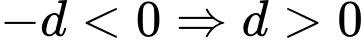 .
.
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm. Nên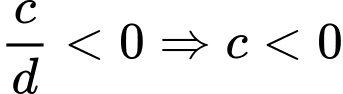 .
.
Dựa vào hình dạng đồ thị dễ thấy hàm số đã cho có 2 cực trị và .
.
Đồ thị hàm số có đường thẳng đi qua 2 điểm cực trị có dạng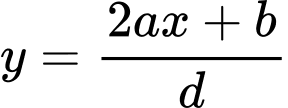 .
.
Mà đường thẳng cắt trục tung tại điểm có tung độ âm nên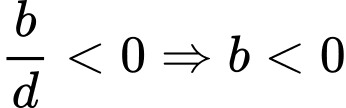 .
.
Vậy có 1 số dương trong các số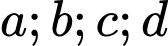 .
.
Từ đồ thị hàm số đã cho ta có
Đồ thị hàm số có 1 đường tiệm cận đứng
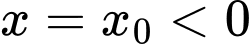 .
.
Suy ra
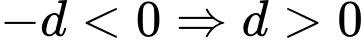 .
.
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm. Nên
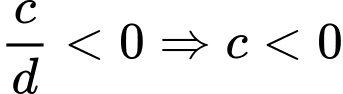 .
.
Dựa vào hình dạng đồ thị dễ thấy hàm số đã cho có 2 cực trị và
 .
.
Đồ thị hàm số có đường thẳng đi qua 2 điểm cực trị có dạng
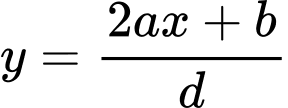 .
.
Mà đường thẳng cắt trục tung tại điểm có tung độ âm nên
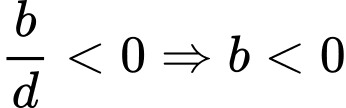 .
.
Vậy có 1 số dương trong các số
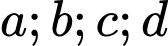 .
.
Câu 28 [383020]: Cho hàm số 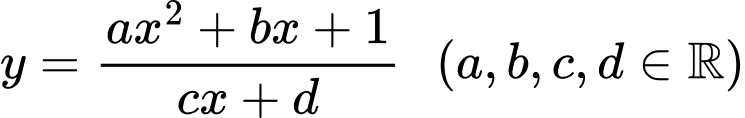 có đồ thị như hình vẽ. Có bao nhiêu số dương trong các số
có đồ thị như hình vẽ. Có bao nhiêu số dương trong các số 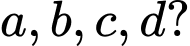
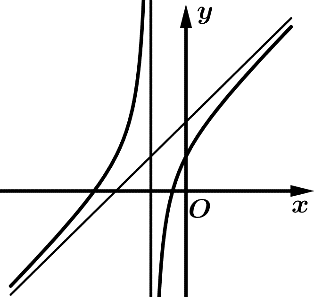
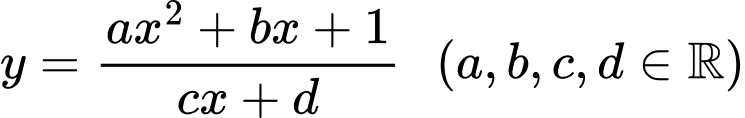 có đồ thị như hình vẽ. Có bao nhiêu số dương trong các số
có đồ thị như hình vẽ. Có bao nhiêu số dương trong các số 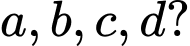

Đáp số: 4
Từ đồ thị hàm số đã cho ta thấy
Đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên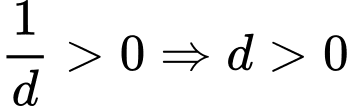 .
.
Đồ thị hàm số có 1 đường tiệm cận đứng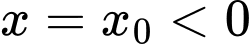 . Suy ra
. Suy ra 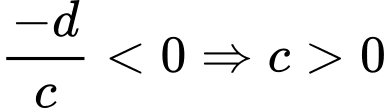 .
.
Dựa vào hình dạng đồ thị hàm số dễ thấy hàm số không có cực trị và . Suy ra
. Suy ra  .
.
Đồ thị hàm số cắt trục hoành tại 2 điểm phân biệt có hoành độ âm.
Nên phương trình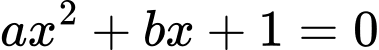 có hai nghiệm phân biệt âm.
có hai nghiệm phân biệt âm.
Suy ra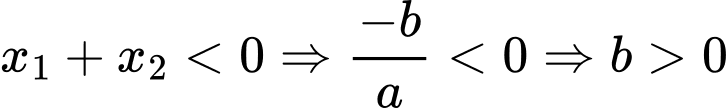 .
.
Vậy có 4 số dương trong các số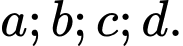
Từ đồ thị hàm số đã cho ta thấy
Đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên
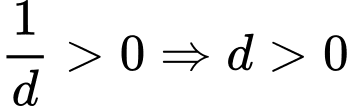 .
.Đồ thị hàm số có 1 đường tiệm cận đứng
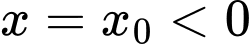 . Suy ra
. Suy ra 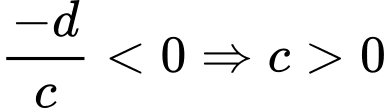 .
.Dựa vào hình dạng đồ thị hàm số dễ thấy hàm số không có cực trị và
 . Suy ra
. Suy ra  .
.Đồ thị hàm số cắt trục hoành tại 2 điểm phân biệt có hoành độ âm.
Nên phương trình
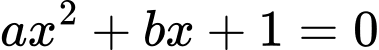 có hai nghiệm phân biệt âm.
có hai nghiệm phân biệt âm.Suy ra
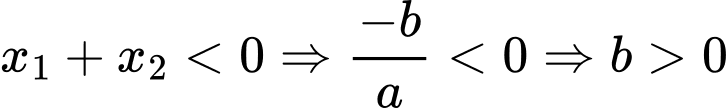 .
.Vậy có 4 số dương trong các số