Đáp án Bài tập tự luyện số 1
Câu 1 [975575]: Cho hàm số 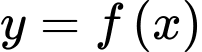 có bảng biến thiên như hình vẽ.
có bảng biến thiên như hình vẽ.
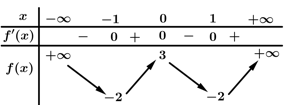
Số nghiệm thực dương phân biệt của phương trình là
là
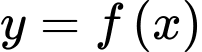 có bảng biến thiên như hình vẽ.
có bảng biến thiên như hình vẽ.
Số nghiệm thực dương phân biệt của phương trình
 là
là A, 
B, 
C, 
D, 
HD: Ta có: 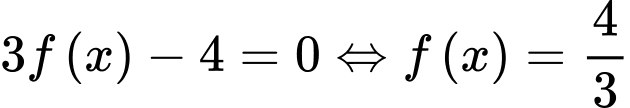
Kẻ đường thẳng nằm ngang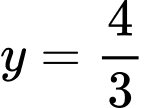 ta thấy đồ thị hàm số
ta thấy đồ thị hàm số 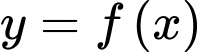 và đường thẳng
và đường thẳng 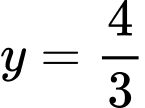 cắt nhau tại 4 điểm phân biệt trong đó có 2 điểm có hoành độ dương (Đọc kỹ đề ko bị lừa :v). Chọn D. Đáp án: D
cắt nhau tại 4 điểm phân biệt trong đó có 2 điểm có hoành độ dương (Đọc kỹ đề ko bị lừa :v). Chọn D. Đáp án: D
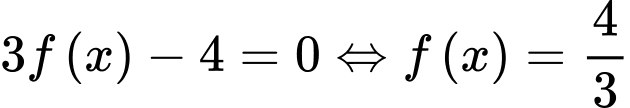
Kẻ đường thẳng nằm ngang
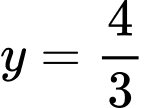 ta thấy đồ thị hàm số
ta thấy đồ thị hàm số 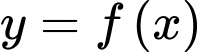 và đường thẳng
và đường thẳng 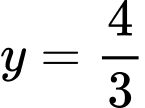 cắt nhau tại 4 điểm phân biệt trong đó có 2 điểm có hoành độ dương (Đọc kỹ đề ko bị lừa :v). Chọn D. Đáp án: D
cắt nhau tại 4 điểm phân biệt trong đó có 2 điểm có hoành độ dương (Đọc kỹ đề ko bị lừa :v). Chọn D. Đáp án: D
Câu 2 [322750]: Tìm số giao điểm của đồ thị hàm số 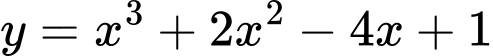 và đường thẳng
và đường thẳng 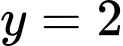 .
.
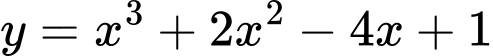 và đường thẳng
và đường thẳng 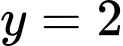 .
. A, 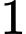 .
.
 .
.B,  .
.
 .
.C,  .
.
 .
.D,  .
.
 .
.
Đáp án C
Phương trình hoành độ giao điểm hai đồ thị là
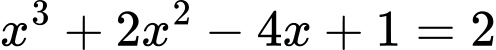
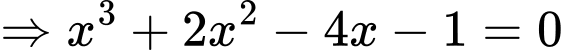 .
.
Sử dụng máy tính ta thấy phương trình này có 3 nghiệm phân biệt.
Ngoài ra các bạn có thể vẽ đồ thị hoặc bảng biến thiên của hàm số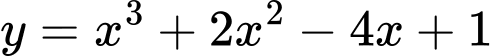 , lấy tương giao với đường thẳng ngang
, lấy tương giao với đường thẳng ngang 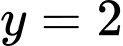 cũng cho 3 giao điểm. Đáp án: C
cũng cho 3 giao điểm. Đáp án: C
Phương trình hoành độ giao điểm hai đồ thị là
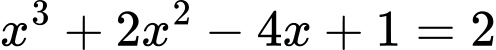
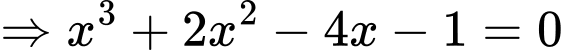 .
.Sử dụng máy tính ta thấy phương trình này có 3 nghiệm phân biệt.
Ngoài ra các bạn có thể vẽ đồ thị hoặc bảng biến thiên của hàm số
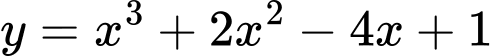 , lấy tương giao với đường thẳng ngang
, lấy tương giao với đường thẳng ngang 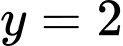 cũng cho 3 giao điểm. Đáp án: C
cũng cho 3 giao điểm. Đáp án: C
Câu 3 [310237]: Cho hàm số 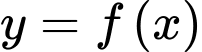 có bảng biến thiên như hình vẽ sau
có bảng biến thiên như hình vẽ sau
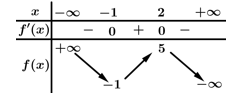
Số nghiệm của phương trình là
là
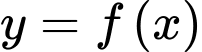 có bảng biến thiên như hình vẽ sau
có bảng biến thiên như hình vẽ sau
Số nghiệm của phương trình
 là
là A, 3.
B, 4.
C, 5.
D, 6.
HD: Phương trình 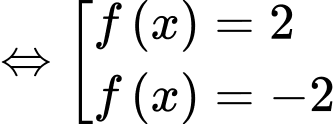
Phương trình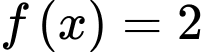 có đúng 3 nghiệm phân biệt và phương trình
có đúng 3 nghiệm phân biệt và phương trình 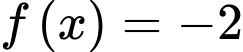 có 1 nghiệm duy nhất.
có 1 nghiệm duy nhất.
Các nghiệm này không trùng nhau.
Vậy phương trình đã cho có đúng 4 nghiệm phân biệt. Chọn B. Đáp án: B
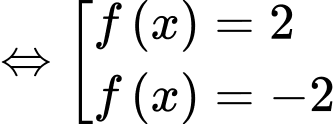
Phương trình
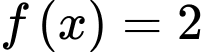 có đúng 3 nghiệm phân biệt và phương trình
có đúng 3 nghiệm phân biệt và phương trình 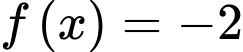 có 1 nghiệm duy nhất.
có 1 nghiệm duy nhất.
Các nghiệm này không trùng nhau.
Vậy phương trình đã cho có đúng 4 nghiệm phân biệt. Chọn B. Đáp án: B
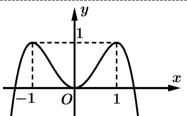
Câu 4 [331233]: Cho hàm số 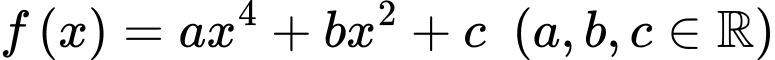 có đồ thị như hình vẽ bên. Số nghiệm thực (phân biệt) của phương trình
có đồ thị như hình vẽ bên. Số nghiệm thực (phân biệt) của phương trình 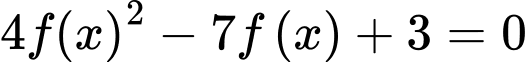 là
là
 có đồ thị như hình vẽ bên. Số nghiệm thực (phân biệt) của phương trình
có đồ thị như hình vẽ bên. Số nghiệm thực (phân biệt) của phương trình 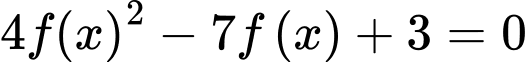 là
là
A, 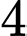 .
.
 .
.B,  .
.
 .
.C,  .
.
 .
.D,  .
.
 .
.
Chọn B
Ta có: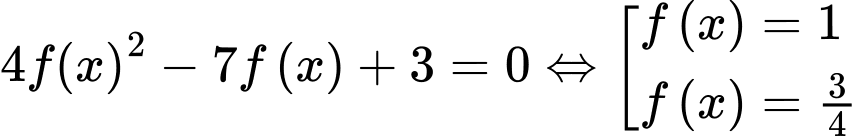 .
.
Dựa vào đồ thị ta có:
+ Đường thẳng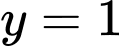 và đồ thị của hàm số
và đồ thị của hàm số 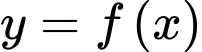 có hai điểm chung phân biệt.
có hai điểm chung phân biệt.
+ Đường thẳng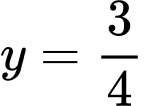 và đồ thị của hàm số
và đồ thị của hàm số 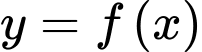 có bốn điểm chung phân biệt.
có bốn điểm chung phân biệt.
+ Mặt khác các giao điểm trên không trùng nhau.
Do đó phương trình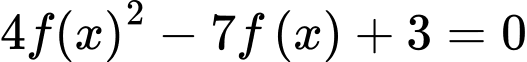 có sáu nghiệm thực phân biệt. Đáp án: B
có sáu nghiệm thực phân biệt. Đáp án: B

Ta có:
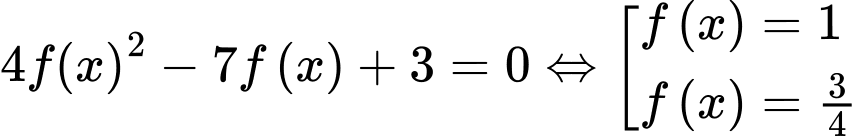 .
.Dựa vào đồ thị ta có:
+ Đường thẳng
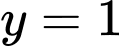 và đồ thị của hàm số
và đồ thị của hàm số 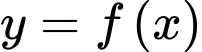 có hai điểm chung phân biệt.
có hai điểm chung phân biệt.+ Đường thẳng
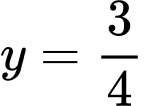 và đồ thị của hàm số
và đồ thị của hàm số 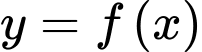 có bốn điểm chung phân biệt.
có bốn điểm chung phân biệt.+ Mặt khác các giao điểm trên không trùng nhau.
Do đó phương trình
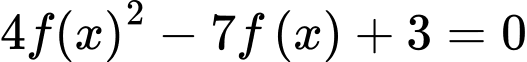 có sáu nghiệm thực phân biệt. Đáp án: B
có sáu nghiệm thực phân biệt. Đáp án: B
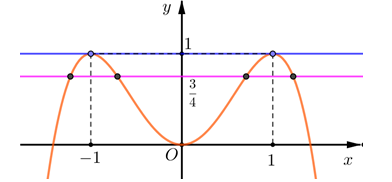
Câu 5 [579663]: [Đề mẫu HSA 2024]: Cho hàm số bậc ba 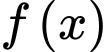 có đồ thị như hình vẽ. Số nghiệm thực của phương trình
có đồ thị như hình vẽ. Số nghiệm thực của phương trình 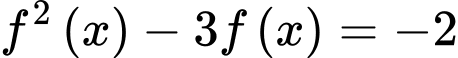 là
là
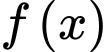 có đồ thị như hình vẽ. Số nghiệm thực của phương trình
có đồ thị như hình vẽ. Số nghiệm thực của phương trình 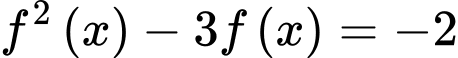 là
là A, 3.
B, 4.
C, 5.
D, 6.
Ta có: 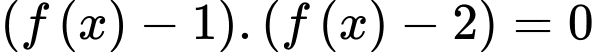
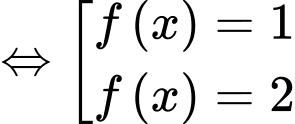
Từ đồ thị, ta thấy
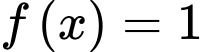 có 3 nghiệm thực phân biệt
có 3 nghiệm thực phân biệt
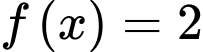 có 2 nghiệm thực phân biệt
có 2 nghiệm thực phân biệt
Vậy phương trình đã cho có 5 nghiệm.
Chọn C. Đáp án: C
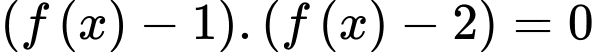
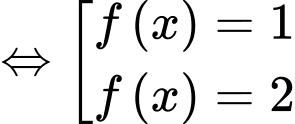
Từ đồ thị, ta thấy
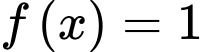 có 3 nghiệm thực phân biệt
có 3 nghiệm thực phân biệt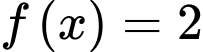 có 2 nghiệm thực phân biệt
có 2 nghiệm thực phân biệtVậy phương trình đã cho có 5 nghiệm.
Chọn C. Đáp án: C
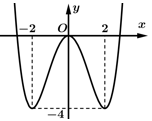
Câu 6 [311579]: Cho hàm số 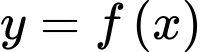 có đồ thị như hình vẽ
có đồ thị như hình vẽ
Số nghiệm của phương trình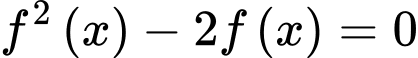 là
là
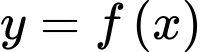 có đồ thị như hình vẽ
có đồ thị như hình vẽ
Số nghiệm của phương trình
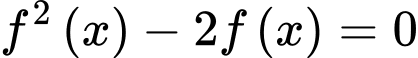 là
là A, 3.
B, 4.
C, 5.
D, 6.
 Đáp án: C
Đáp án: C
Câu 7 [185185]: Biết đường thẳng 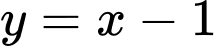 cắt đồ thị hàm số
cắt đồ thị hàm số 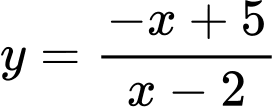 tại hai điểm phân biệt có hoành độ là
tại hai điểm phân biệt có hoành độ là 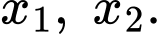 Giá trị của
Giá trị của  bằng
bằng
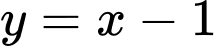 cắt đồ thị hàm số
cắt đồ thị hàm số 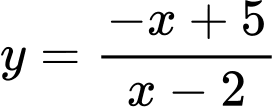 tại hai điểm phân biệt có hoành độ là
tại hai điểm phân biệt có hoành độ là 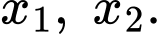 Giá trị của
Giá trị của  bằng
bằng A, 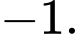
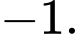
B, 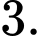
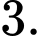
C, 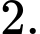
D, 
Phương trình hoành độ giao điểm là:
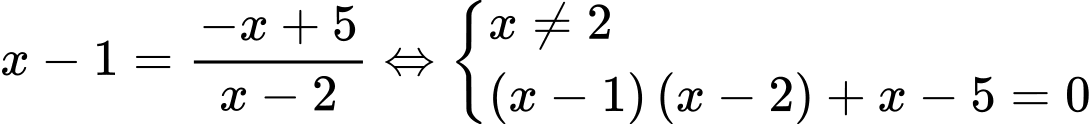
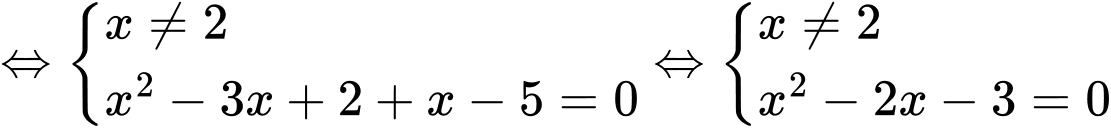
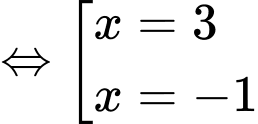
Suy ra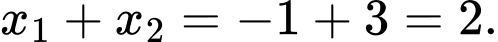 Đáp án: C
Đáp án: C
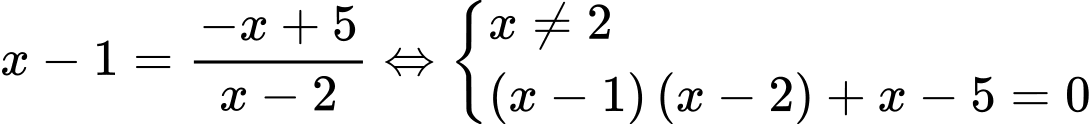
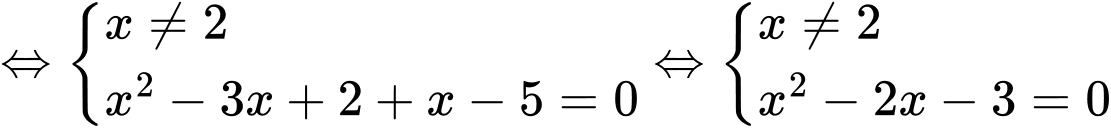
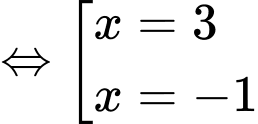
Suy ra
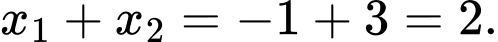 Đáp án: C
Đáp án: C
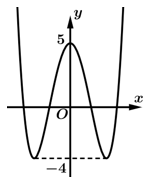
Câu 8 [185148]: Cho hàm số bậc bốn 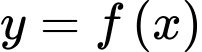 có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị nguyên của
có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị nguyên của 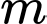 sao cho ứng với mỗi
sao cho ứng với mỗi 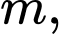 phương trình
phương trình 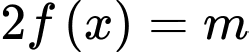 có 4 nghiệm thực phân biệt?
có 4 nghiệm thực phân biệt?
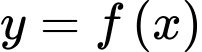 có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị nguyên của
có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị nguyên của 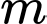 sao cho ứng với mỗi
sao cho ứng với mỗi 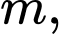 phương trình
phương trình 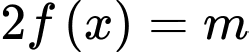 có 4 nghiệm thực phân biệt?
có 4 nghiệm thực phân biệt?
A, 
B, 
C, 
D, 
Ta có: 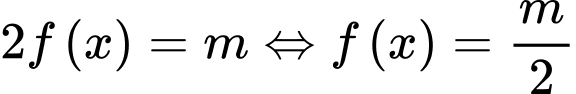 .
.
Để phương trình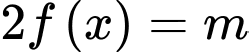 có 4 nghiệm phân biệt thì đồ thị hàm số
có 4 nghiệm phân biệt thì đồ thị hàm số 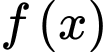 và đường thẳng
và đường thẳng 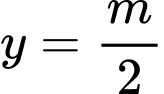 cắt nhau tại 4 điểm phân biệt.
cắt nhau tại 4 điểm phân biệt.
Khi đó: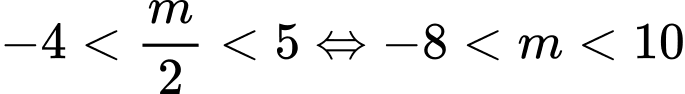 .Mà
.Mà  . Suy ra có 17 giá trị
. Suy ra có 17 giá trị 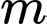 thoả mãn.
thoả mãn.
Vậy có 17 giá trị nguyên của m sao cho ứng với mỗi m, phương trình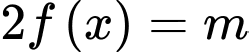 có 4 nghiệm phân biệt.
Đáp án: C
có 4 nghiệm phân biệt.
Đáp án: C
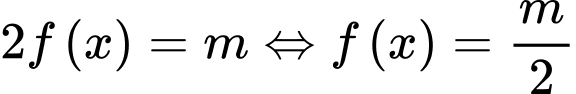 .
.
Để phương trình
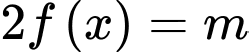 có 4 nghiệm phân biệt thì đồ thị hàm số
có 4 nghiệm phân biệt thì đồ thị hàm số 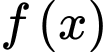 và đường thẳng
và đường thẳng 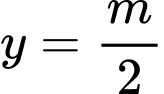 cắt nhau tại 4 điểm phân biệt.
cắt nhau tại 4 điểm phân biệt.
Khi đó:
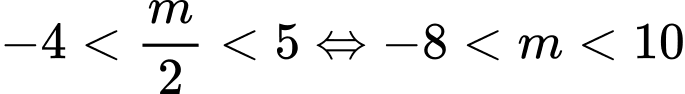 .Mà
.Mà  . Suy ra có 17 giá trị
. Suy ra có 17 giá trị 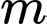 thoả mãn.
thoả mãn.
Vậy có 17 giá trị nguyên của m sao cho ứng với mỗi m, phương trình
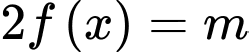 có 4 nghiệm phân biệt.
Đáp án: C
có 4 nghiệm phân biệt.
Đáp án: C
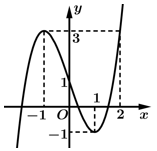
Câu 9 [308190]: Cho hàm số 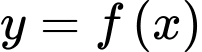 có đồ thị như sau. Tìm tất cả các giá trị của tham số
có đồ thị như sau. Tìm tất cả các giá trị của tham số 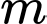 để phương trình
để phương trình 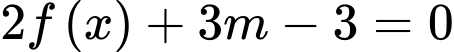 có
có 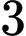 nghiệm phân biệt.
nghiệm phân biệt.
 có đồ thị như sau. Tìm tất cả các giá trị của tham số
có đồ thị như sau. Tìm tất cả các giá trị của tham số 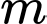 để phương trình
để phương trình 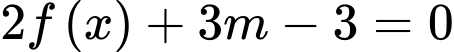 có
có 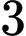 nghiệm phân biệt.
nghiệm phân biệt.
A, 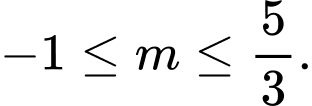
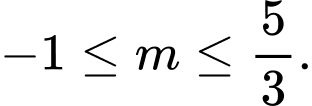
B, 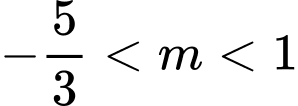
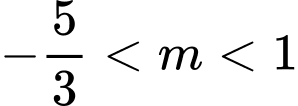
C, 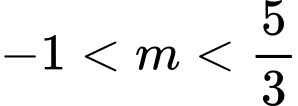
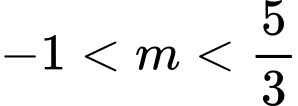
D, 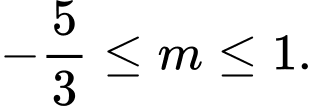
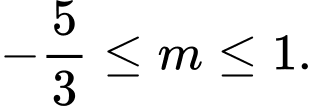
Chọn C
Ta có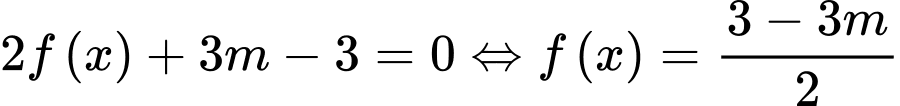
Dựa vào đồ thị, ta thấy phương trình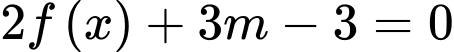 có
có 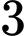 nghiệm phân biệt
nghiệm phân biệt
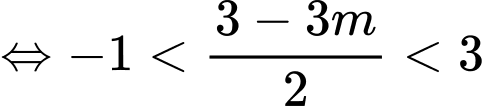
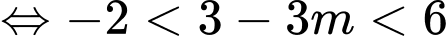
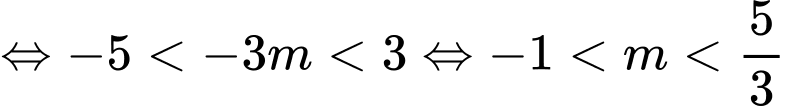 Đáp án: C
Đáp án: C
Ta có
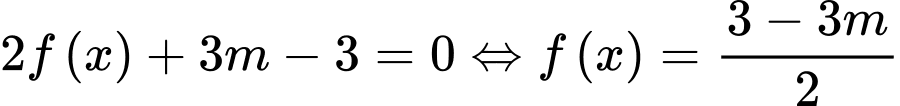
Dựa vào đồ thị, ta thấy phương trình
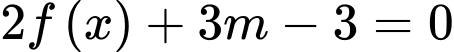 có
có 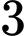 nghiệm phân biệt
nghiệm phân biệt 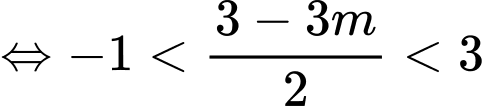
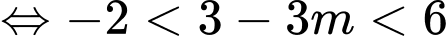
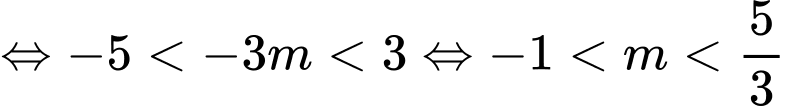 Đáp án: C
Đáp án: C
Câu 10 [29591]: Cho hàm số 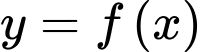 xác định trên
xác định trên 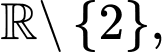 liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ sau.
liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ sau.
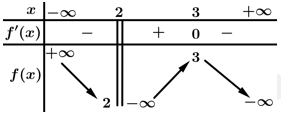
Tìm tập hợp tất cả các giá trị của tham số thực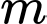 sao cho phương trình
sao cho phương trình 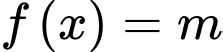 có ba nghiệm phân biệt
có ba nghiệm phân biệt
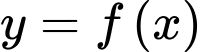 xác định trên
xác định trên 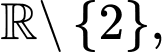 liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ sau.
liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ sau. 
Tìm tập hợp tất cả các giá trị của tham số thực
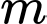 sao cho phương trình
sao cho phương trình 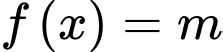 có ba nghiệm phân biệt
có ba nghiệm phân biệt A, 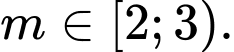
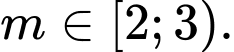
B, 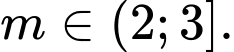
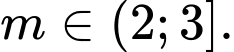
C, 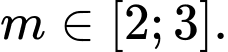
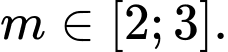
D, 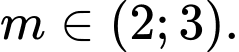
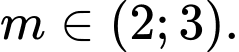
Dựa vào bảng thiên thiên ta có:
Phương trình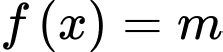 có ba nghiệm phân biệt khi và chỉ khi đường thẳng
có ba nghiệm phân biệt khi và chỉ khi đường thẳng 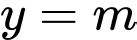 cắt đồ thị hàm số tại 3 điểm phân biệt
cắt đồ thị hàm số tại 3 điểm phân biệt 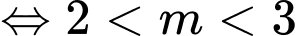 .
.
Chọn D. Đáp án: D
Phương trình
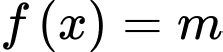 có ba nghiệm phân biệt khi và chỉ khi đường thẳng
có ba nghiệm phân biệt khi và chỉ khi đường thẳng 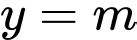 cắt đồ thị hàm số tại 3 điểm phân biệt
cắt đồ thị hàm số tại 3 điểm phân biệt 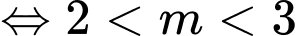 .
. Chọn D. Đáp án: D
Câu 11 [319352]: Đường thẳng 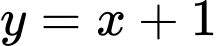 cắt đồ thị hàm số
cắt đồ thị hàm số 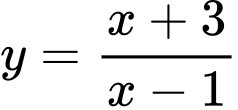 tại hai điểm phân biệt
tại hai điểm phân biệt 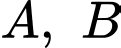 . Tính độ dài đoạn thẳng
. Tính độ dài đoạn thẳng  .
.
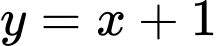 cắt đồ thị hàm số
cắt đồ thị hàm số 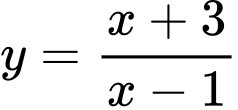 tại hai điểm phân biệt
tại hai điểm phân biệt 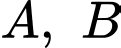 . Tính độ dài đoạn thẳng
. Tính độ dài đoạn thẳng  .
. A, 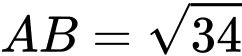 .
.
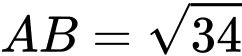 .
.B, 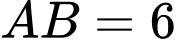 .
.
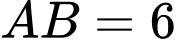 .
.C, 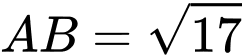 .
.
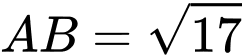 .
.D, 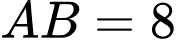 .
.
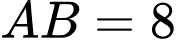 .
.
Chọn A
Ta có phương trình hoành độ giao điểm của 2 đồ thị hàm số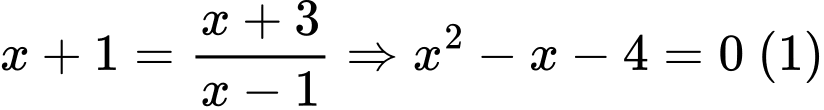
Gọi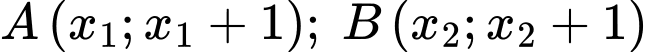 , với
, với 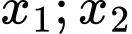 là nghiệm của pt(1), khi đó
là nghiệm của pt(1), khi đó 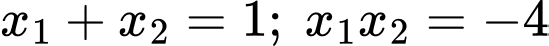
Có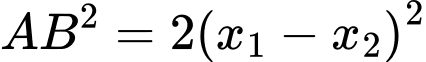
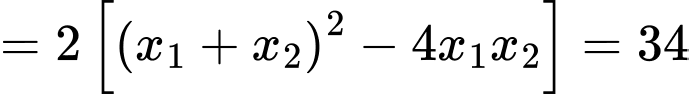
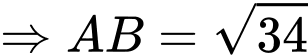 Đáp án: A
Đáp án: A
Ta có phương trình hoành độ giao điểm của 2 đồ thị hàm số
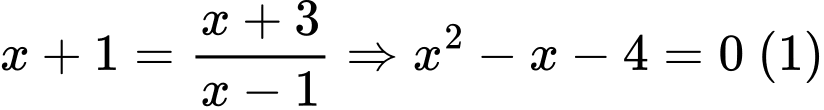
Gọi
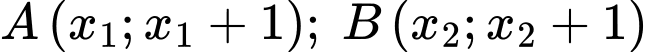 , với
, với 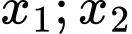 là nghiệm của pt(1), khi đó
là nghiệm của pt(1), khi đó 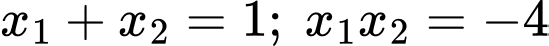
Có
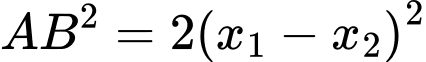
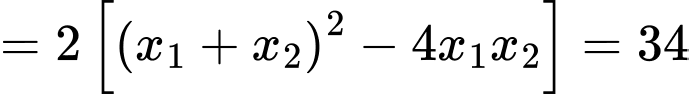
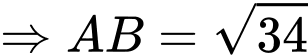 Đáp án: A
Đáp án: A
Câu 12 [29528]: Tìm tất cả các giá trị của tham số 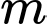 để phương trình
để phương trình 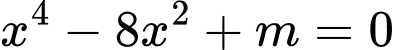 có bốn nghiệm phân biệt.
có bốn nghiệm phân biệt.
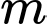 để phương trình
để phương trình 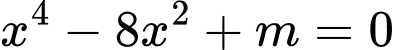 có bốn nghiệm phân biệt.
có bốn nghiệm phân biệt. A, 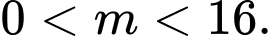
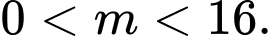
B, 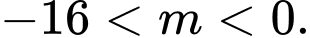
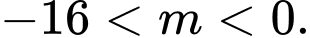
C, 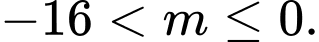
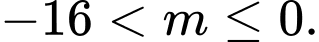
D, 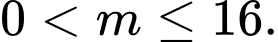
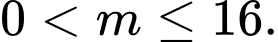
Đặt 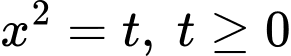 ta thu được phương trình
ta thu được phương trình 
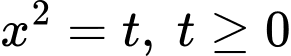 ta thu được phương trình
ta thu được phương trình 
Phương trình này có 2 nghiệm dương khi  do tổng hai nghiệm bằng 8 dương.
do tổng hai nghiệm bằng 8 dương.
 do tổng hai nghiệm bằng 8 dương.
do tổng hai nghiệm bằng 8 dương. Ngoài ra, 

Vậy 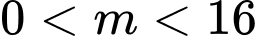
Đáp án: A 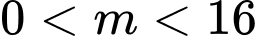
Câu 13 [512250]: Tìm tất cả các giá trị của tham số 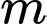 sao cho đồ thị hàm số
sao cho đồ thị hàm số 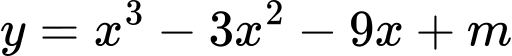 cắt trục hoành tại ba điểm phân biệt
cắt trục hoành tại ba điểm phân biệt
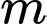 sao cho đồ thị hàm số
sao cho đồ thị hàm số 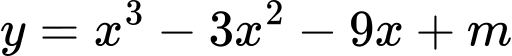 cắt trục hoành tại ba điểm phân biệt
cắt trục hoành tại ba điểm phân biệt A,  .
.
 .
.B, 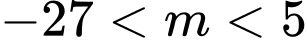 .
.
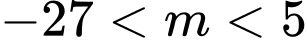 .
.C, 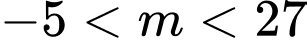 .
.
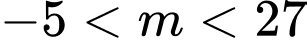 .
.D, 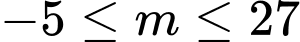 .
.
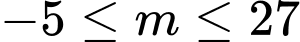 .
.
Chọn C
Đồ thị hàm số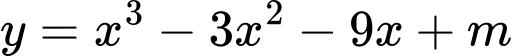 cắt trục hoành tại ba điểm phân biệt khi phương trình
cắt trục hoành tại ba điểm phân biệt khi phương trình
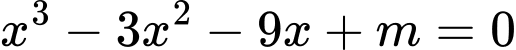
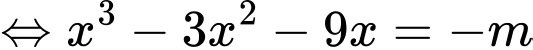 có ba nghiệm phân biệt.
có ba nghiệm phân biệt.
Xét hàm số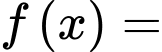
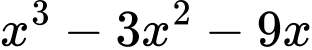
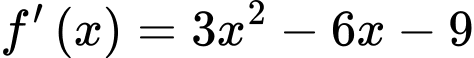
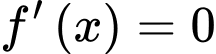
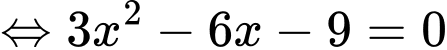
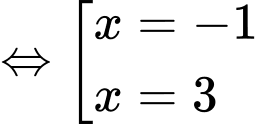 .
.
Bảng biến thiên của hàm số như sau
như sau
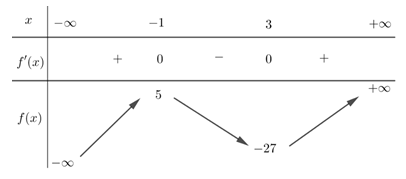
Từ bảng biến thiên suy ra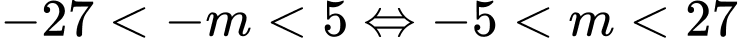 . Đáp án: C
. Đáp án: C
Đồ thị hàm số
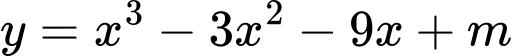 cắt trục hoành tại ba điểm phân biệt khi phương trình
cắt trục hoành tại ba điểm phân biệt khi phương trình
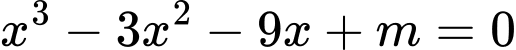
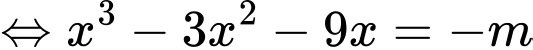 có ba nghiệm phân biệt.
có ba nghiệm phân biệt. Xét hàm số
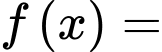
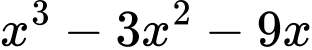
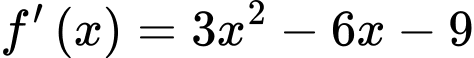
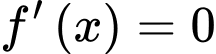
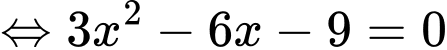
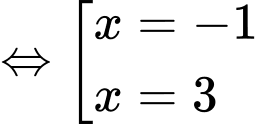 .
.Bảng biến thiên của hàm số
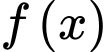 như sau
như sau
Từ bảng biến thiên suy ra
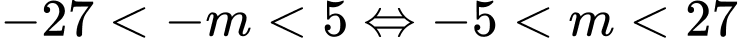 . Đáp án: C
. Đáp án: C
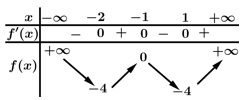
Câu 14 [203311]: Cho hàm số 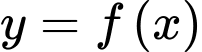 có bảng biến thiên như sau:
có bảng biến thiên như sau:
Số nghiệm của phương trình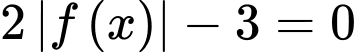 là
là
 có bảng biến thiên như sau:
có bảng biến thiên như sau:
Số nghiệm của phương trình
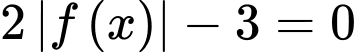 là
là A, 
B, 
C, 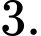
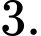
D, 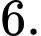
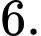
Ta có: 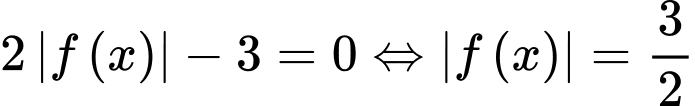

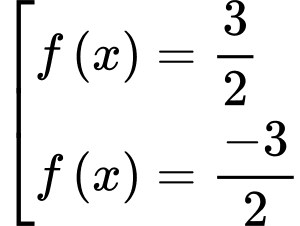
Dựa vào bảng biến thiên
Ta có số nghiệm của phương trình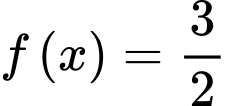 là số giao điểm của đồ thị hàm số
là số giao điểm của đồ thị hàm số 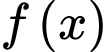 và đường thẳng
và đường thẳng 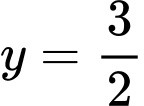 .
.
Dựa vào bảng biến thiên, ta có đồ thị hàm số đồ thị hàm số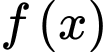 và đường thẳng
và đường thẳng 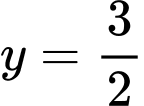 cắt nhau tại 2 điểm phân biệt.
cắt nhau tại 2 điểm phân biệt.
Nên phương trình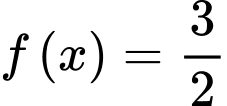 có 2 nghiệm phân biệt.
có 2 nghiệm phân biệt.
Tương tự có, đồ thị hàm số đồ thị hàm số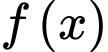 và đường thẳng
và đường thẳng 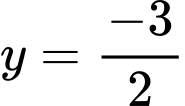 cắt nhau tại 4 điểm phân biệt.
cắt nhau tại 4 điểm phân biệt.
Nên phương trình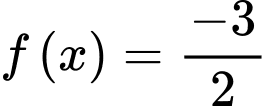 có 4 nghiệm phân biệt.
có 4 nghiệm phân biệt.
Vậy phương trình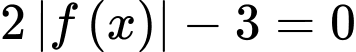 có 6 nghiệm phân biệt.
Đáp án: D
có 6 nghiệm phân biệt.
Đáp án: D
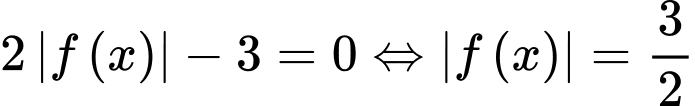

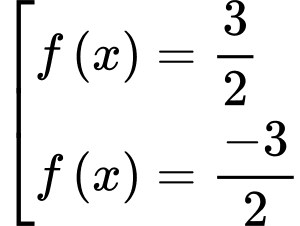
Dựa vào bảng biến thiên
Ta có số nghiệm của phương trình
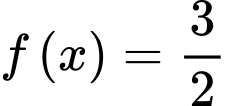 là số giao điểm của đồ thị hàm số
là số giao điểm của đồ thị hàm số 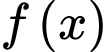 và đường thẳng
và đường thẳng 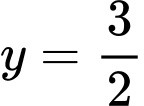 .
.
Dựa vào bảng biến thiên, ta có đồ thị hàm số đồ thị hàm số
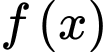 và đường thẳng
và đường thẳng 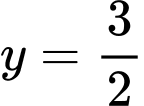 cắt nhau tại 2 điểm phân biệt.
cắt nhau tại 2 điểm phân biệt.
Nên phương trình
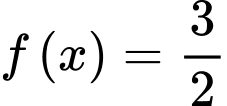 có 2 nghiệm phân biệt.
có 2 nghiệm phân biệt.
Tương tự có, đồ thị hàm số đồ thị hàm số
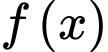 và đường thẳng
và đường thẳng 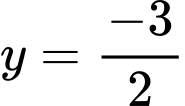 cắt nhau tại 4 điểm phân biệt.
cắt nhau tại 4 điểm phân biệt.
Nên phương trình
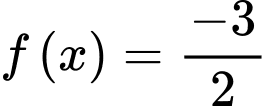 có 4 nghiệm phân biệt.
có 4 nghiệm phân biệt.
Vậy phương trình
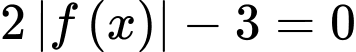 có 6 nghiệm phân biệt.
Đáp án: D
có 6 nghiệm phân biệt.
Đáp án: D
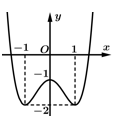
Câu 15 [233390]: Cho hàm số bậc bốn 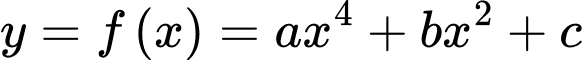 có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên thuộc đoạn
có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên thuộc đoạn 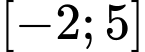 của tham số
của tham số 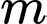 để phương trình
để phương trình 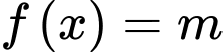 có đúng hai nghiệm thực phân biệt?
có đúng hai nghiệm thực phân biệt?
 có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên thuộc đoạn
có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên thuộc đoạn 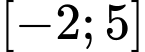 của tham số
của tham số 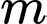 để phương trình
để phương trình 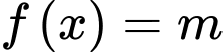 có đúng hai nghiệm thực phân biệt?
có đúng hai nghiệm thực phân biệt?
A, 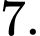
B, 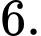
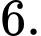
C, 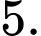
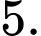
D, 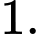
HD: Phương trình đã cho có đúng hai nghiệm thực phân biệt khi 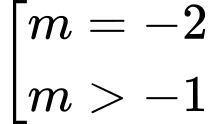
Kết hợp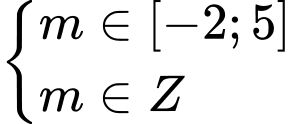
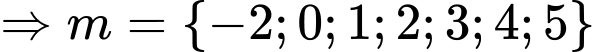 Chọn A. Đáp án: A
Chọn A. Đáp án: A
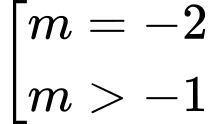
Kết hợp
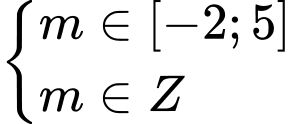
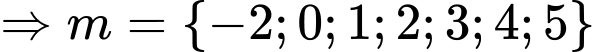 Chọn A. Đáp án: A
Chọn A. Đáp án: A
Câu 16 [28891]: Biết hai đồ thị hàm số 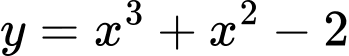 và
và 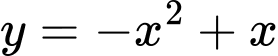 cắt nhau tại ba điểm phân biệt
cắt nhau tại ba điểm phân biệt 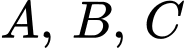 . Khi đó diện tích tam giác
. Khi đó diện tích tam giác 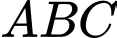 bằng
bằng
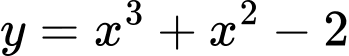 và
và 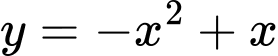 cắt nhau tại ba điểm phân biệt
cắt nhau tại ba điểm phân biệt 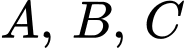 . Khi đó diện tích tam giác
. Khi đó diện tích tam giác 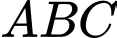 bằng
bằng A, 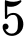 .
.
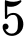 .
.B, 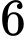 .
.
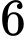 .
.C, 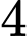 .
.
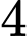 .
.D, 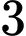 .
.
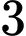 .
.
Chọn D.
Phương trình hoành độ giao điểm là 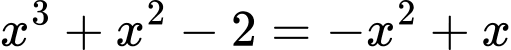
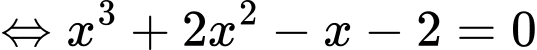
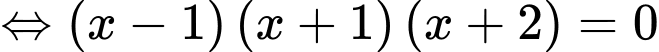
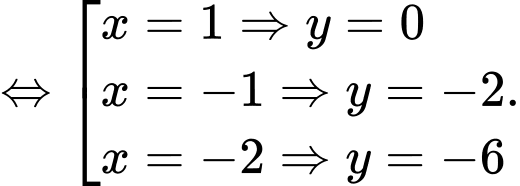
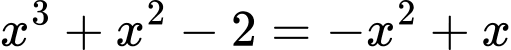
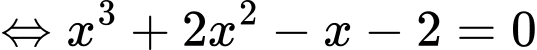
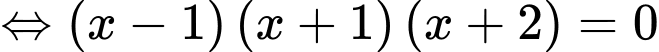
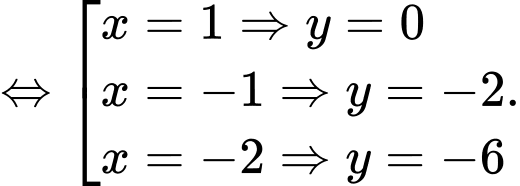
Vậy đồ thị cắt nhau tại 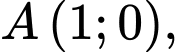
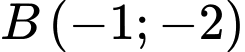 và
và 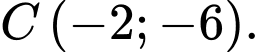
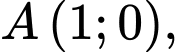
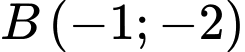 và
và 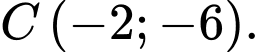
Ta có: 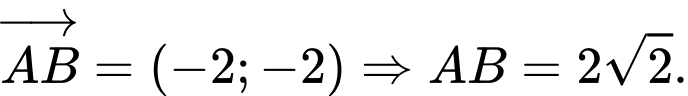 Vectơ pháp tuyến của
Vectơ pháp tuyến của  là
là 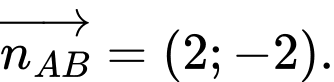
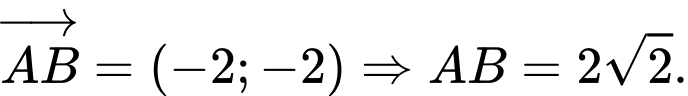 Vectơ pháp tuyến của
Vectơ pháp tuyến của  là
là 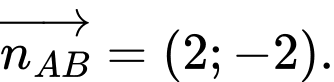
Phương trình đường thẳng  là
là 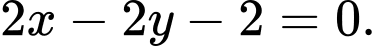
 là
là 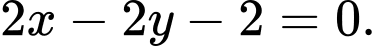
Khoảng cách 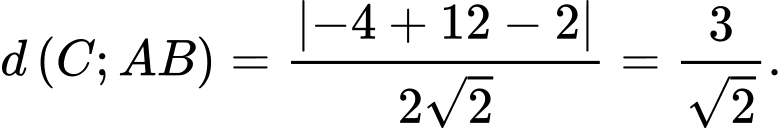
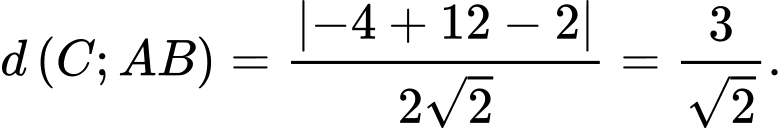
Diện tích tam giác 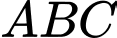 là
là 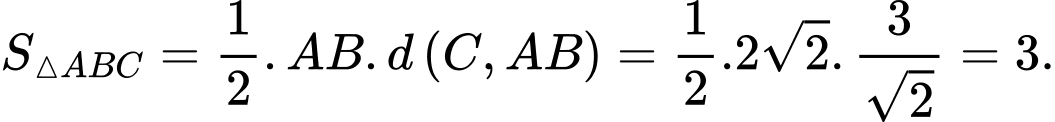
Đáp án: D  là
là 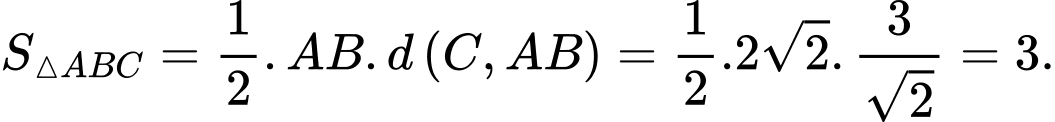
Câu 17 [732584]: [MĐ3] Cho hàm số 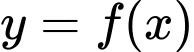 có đồ thị như trong hình vẽ bên
có đồ thị như trong hình vẽ bên
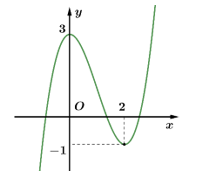
Số nghiệm của phương trình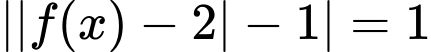 là
là
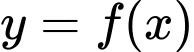 có đồ thị như trong hình vẽ bên
có đồ thị như trong hình vẽ bên
Số nghiệm của phương trình
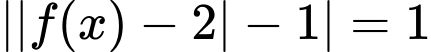 là
là A,  .
.
 .
.B, 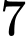 .
.
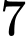 .
.C, 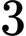 .
.
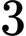 .
.D, 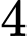 .
.
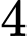 .
.
Ta có 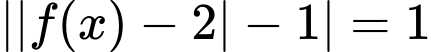



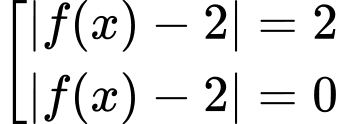

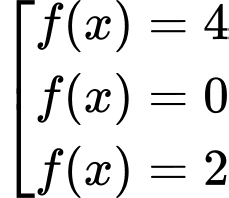 .
.
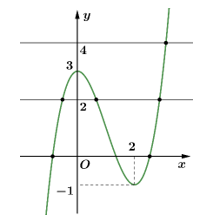
Kết hợp đồ thị ta thấy phương trình đã cho có 7 nghiệm phân biệt. Đáp án: B
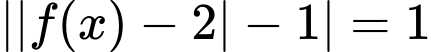



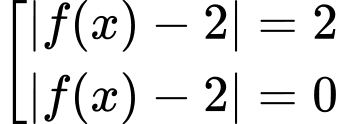

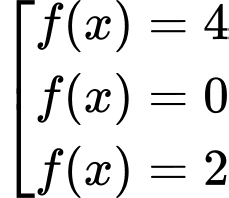 .
.
Kết hợp đồ thị ta thấy phương trình đã cho có 7 nghiệm phân biệt. Đáp án: B
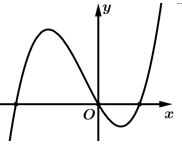
Câu 18 [921319]: [Đề thi THPT QG 2021-Đợt 2]: Cho hàm số 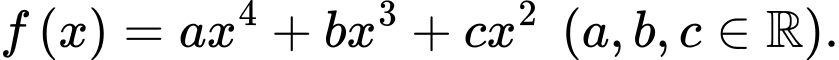 Hàm số
Hàm số 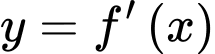 có đồ thị như trong hình vẽ bên. Số nghiệm thực phân biệt của phương trình
có đồ thị như trong hình vẽ bên. Số nghiệm thực phân biệt của phương trình  là
là
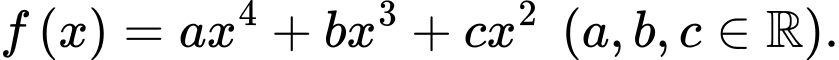 Hàm số
Hàm số 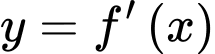 có đồ thị như trong hình vẽ bên. Số nghiệm thực phân biệt của phương trình
có đồ thị như trong hình vẽ bên. Số nghiệm thực phân biệt của phương trình  là
là
A, 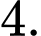
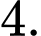
B, 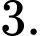
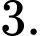
C, 
D, 
Từ đồ thị ta có bảng biến thiên

Dựa vào bảng thiến thiên thì phương trình 
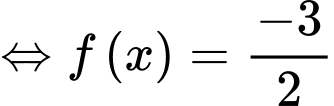 có 2 nghiệm phân biệt. Đáp án: C
có 2 nghiệm phân biệt. Đáp án: C
Câu 19 [382763]: [Trích Đề Mẫu ĐGNL HN]: Số giá trị nguyên của tham số 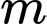 để phương trình
để phương trình 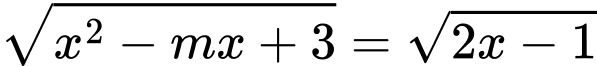 có hai nghiệm phân biệt là
có hai nghiệm phân biệt là
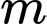 để phương trình
để phương trình 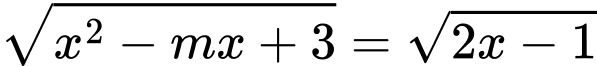 có hai nghiệm phân biệt là
có hai nghiệm phân biệt là
Ta có: 

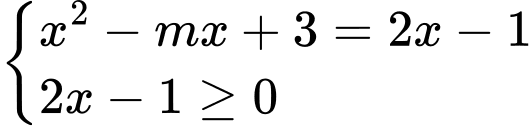

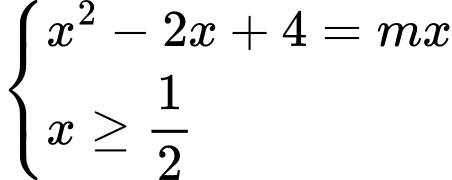

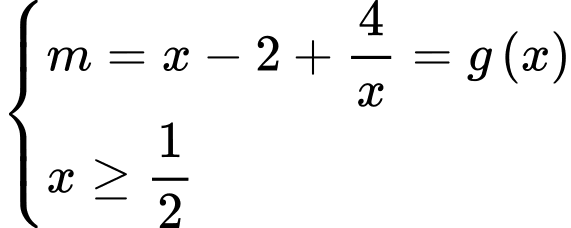
Lập bảng biến thiên của hàm số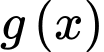 trên
trên 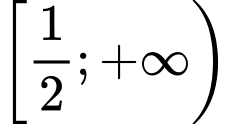

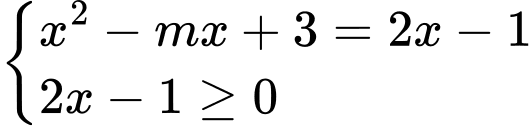

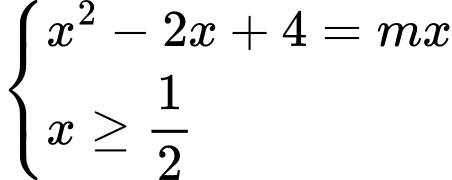

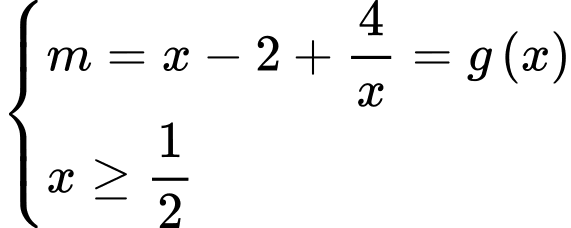
Lập bảng biến thiên của hàm số
 trên
trên 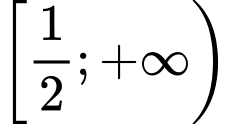
Ta có 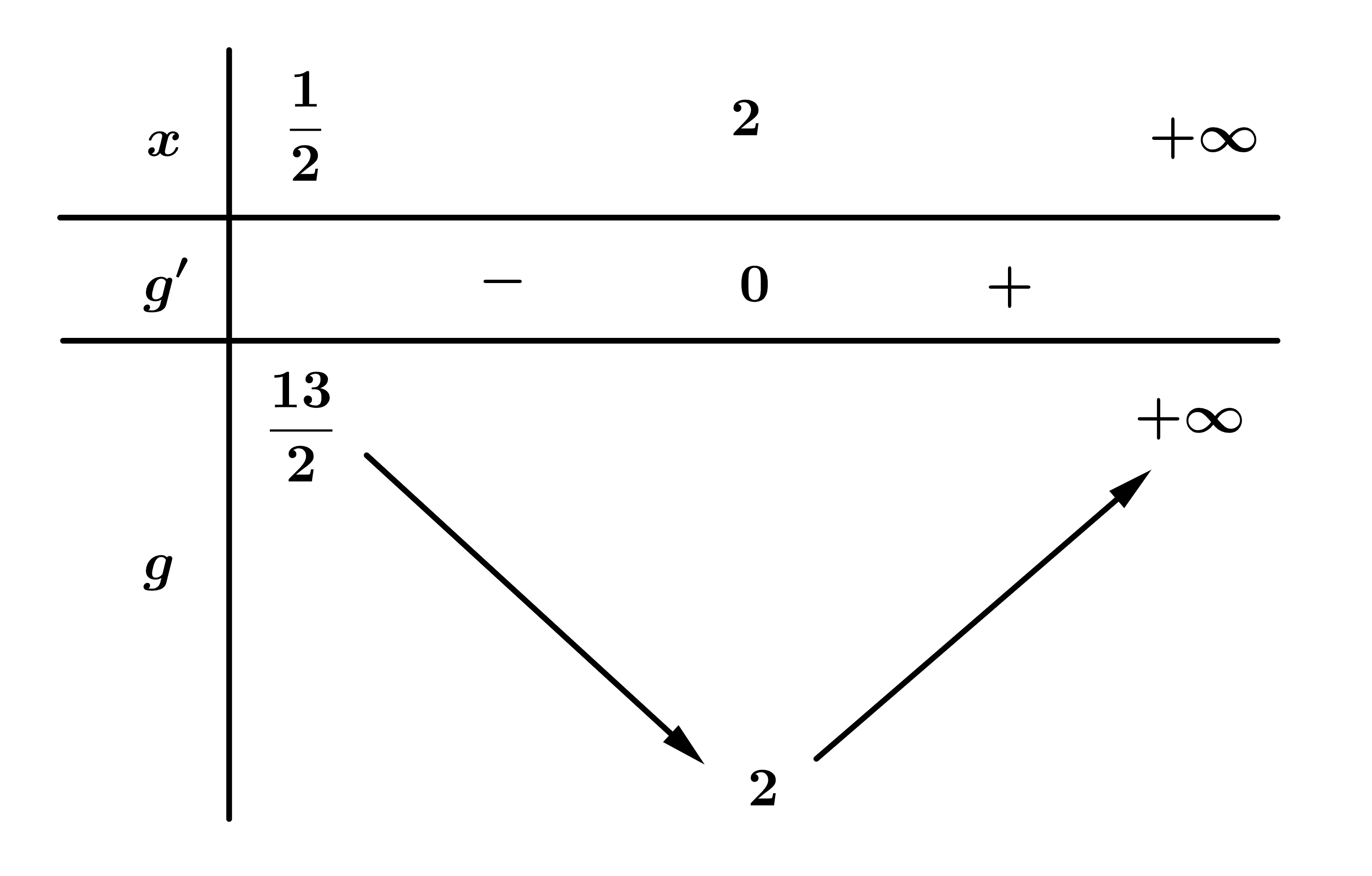

Vậy phương trình có 2 nghiệm phân biệt khi và chỉ khi 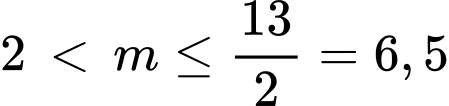
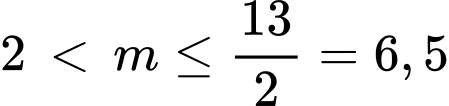
Mà 

Vậy có 4 giá trị của 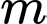 thoả mãn ycbt.
thoả mãn ycbt.
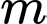 thoả mãn ycbt.
thoả mãn ycbt.
Câu 20 [791427]: Điều kiện để phương trình 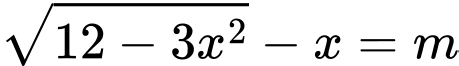 có nghiệm là
có nghiệm là  . Khi đó
. Khi đó 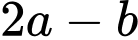 bằng
bằng
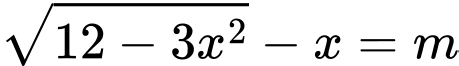 có nghiệm là
có nghiệm là  . Khi đó
. Khi đó 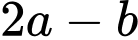 bằng
bằng A, 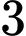 .
.
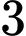 .
.B, 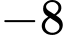 .
.
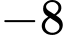 .
.C, 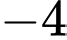 .
.
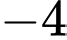 .
.D,  .
.
 .
.
Chọn B
ĐK: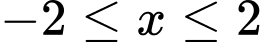 .
.
Xét hàm số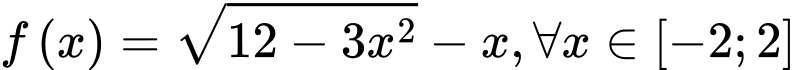 .
.
Ta có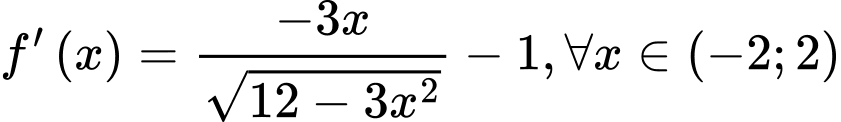 .
.
Cho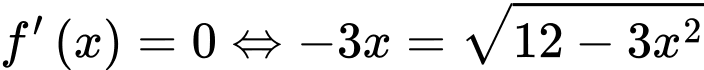
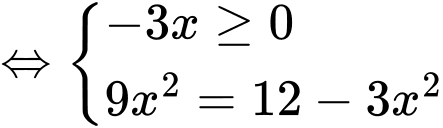
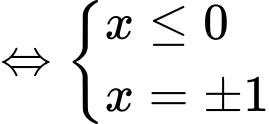
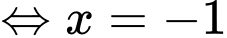 .
.
Bảng biến thiên:
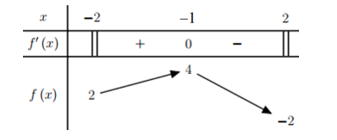
Vậy YCBT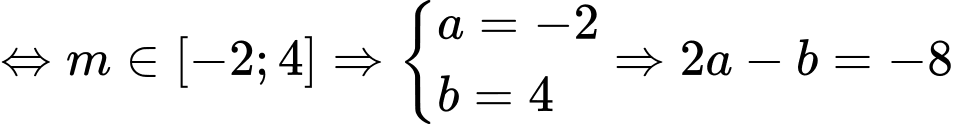 . Đáp án: B
. Đáp án: B
ĐK:
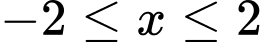 .
.Xét hàm số
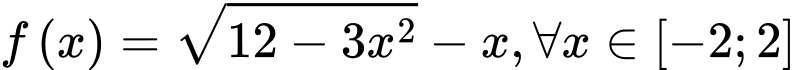 .
.Ta có
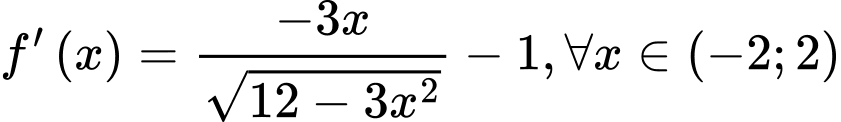 .
.Cho
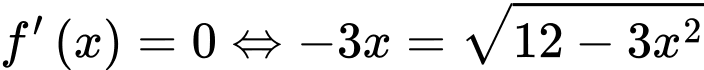
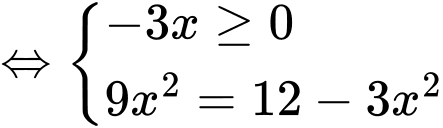
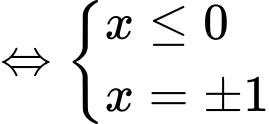
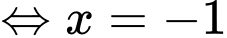 .
.Bảng biến thiên:

Vậy YCBT
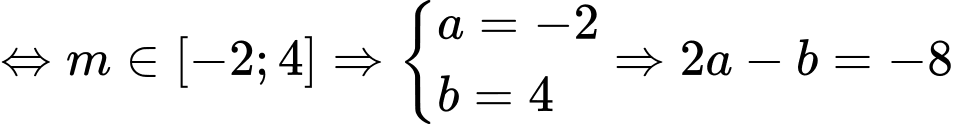 . Đáp án: B
. Đáp án: B
Câu 21 [25531]: Gọi 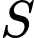 là tập hợp tất cả các giá trị thực của tham số
là tập hợp tất cả các giá trị thực của tham số 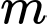 để đồ thị hàm số
để đồ thị hàm số 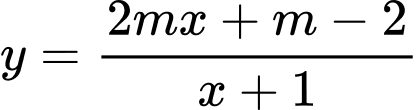 cắt đường thẳng
cắt đường thẳng 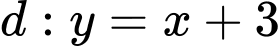 tại hai điểm phân biệt
tại hai điểm phân biệt 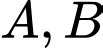 sao cho tam giác
sao cho tam giác 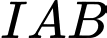 có diện tích bằng 3, với
có diện tích bằng 3, với 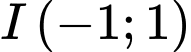 . Tính tổng tất cả các phần tử của
. Tính tổng tất cả các phần tử của 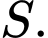
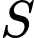 là tập hợp tất cả các giá trị thực của tham số
là tập hợp tất cả các giá trị thực của tham số 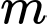 để đồ thị hàm số
để đồ thị hàm số 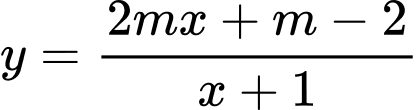 cắt đường thẳng
cắt đường thẳng 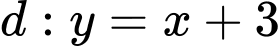 tại hai điểm phân biệt
tại hai điểm phân biệt 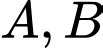 sao cho tam giác
sao cho tam giác 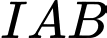 có diện tích bằng 3, với
có diện tích bằng 3, với 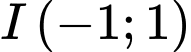 . Tính tổng tất cả các phần tử của
. Tính tổng tất cả các phần tử của 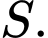
A, 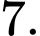
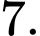
B, 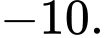
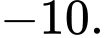
C, 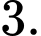
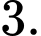
D, 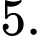
PT hoành độ giao điểm là 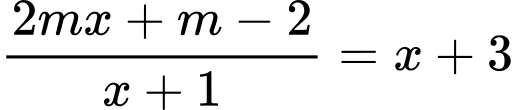
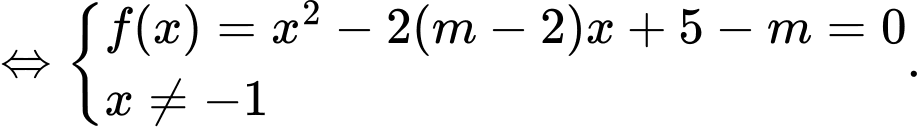
Hai đồ thị có hai giao điểm khi và chỉ khi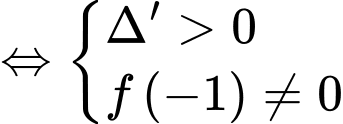
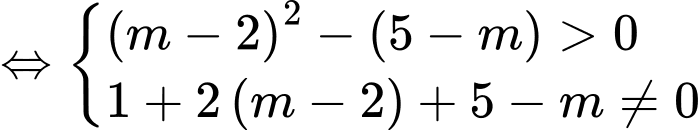
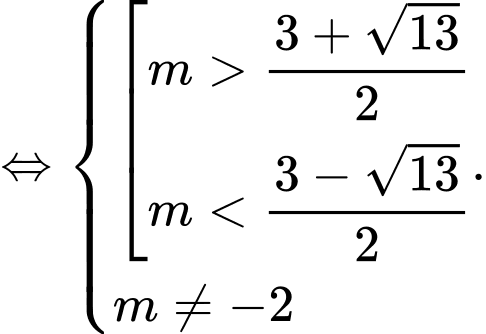
Khi đó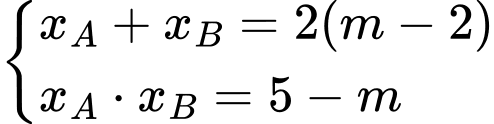
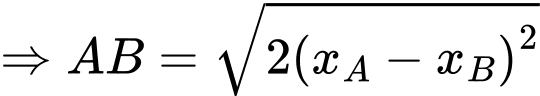
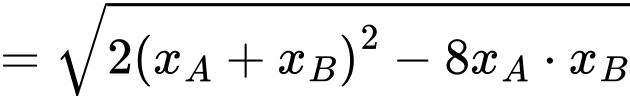
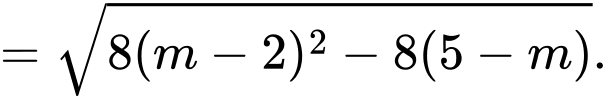
Mặt khác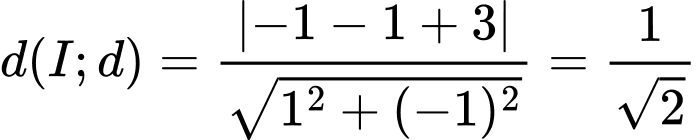
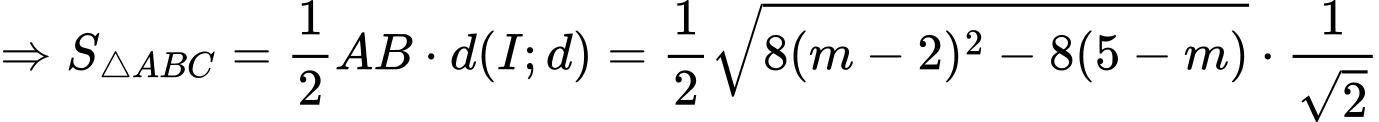
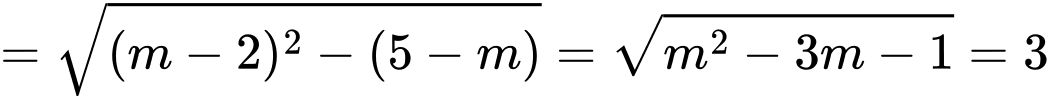
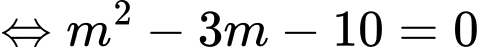
 Chọn C. Đáp án: C
Chọn C. Đáp án: C
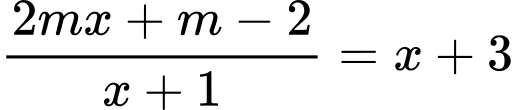
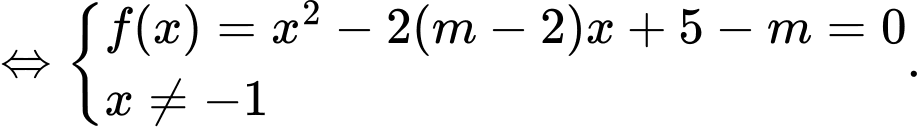
Hai đồ thị có hai giao điểm khi và chỉ khi
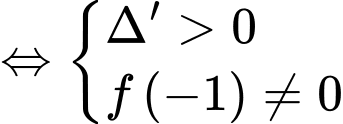
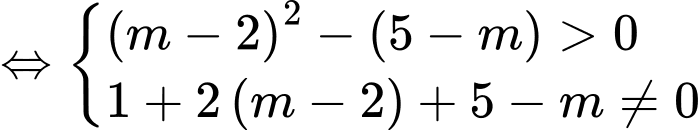
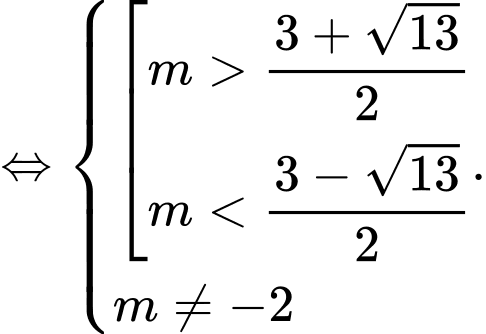
Khi đó
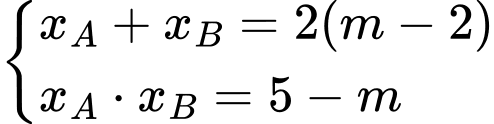
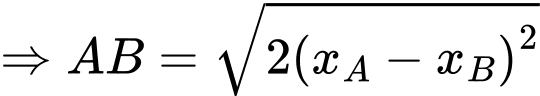
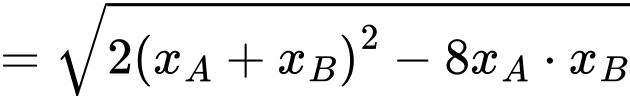
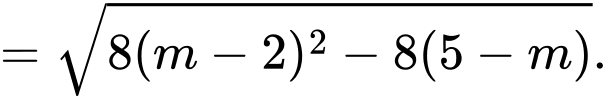
Mặt khác
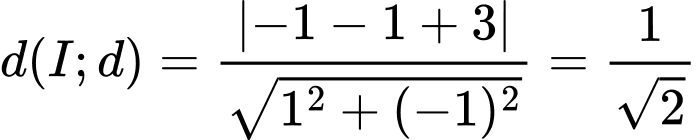
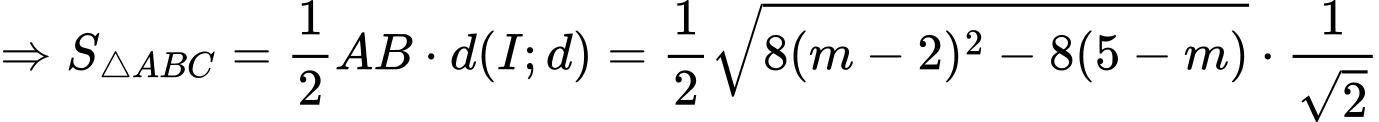
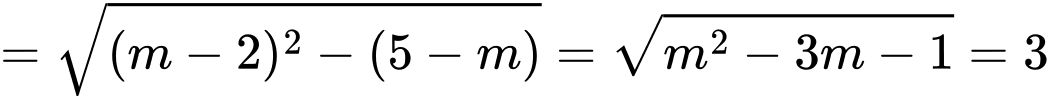
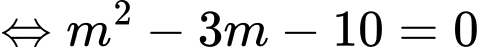
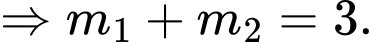 Chọn C. Đáp án: C
Chọn C. Đáp án: C
Câu 22 [28609]: Cho hàm số 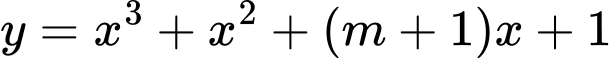 và
và 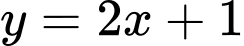 . Có bao nhiêu giá trị nguyên
. Có bao nhiêu giá trị nguyên 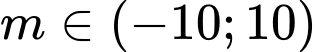 để hai đồ thị của hai hàm số trên cắt nhau tại ba điểm phân biệt?
để hai đồ thị của hai hàm số trên cắt nhau tại ba điểm phân biệt?
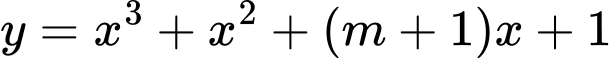 và
và 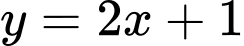 . Có bao nhiêu giá trị nguyên
. Có bao nhiêu giá trị nguyên 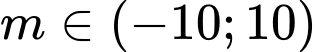 để hai đồ thị của hai hàm số trên cắt nhau tại ba điểm phân biệt?
để hai đồ thị của hai hàm số trên cắt nhau tại ba điểm phân biệt? A, 9.
B, 10.
C, 1.
D, 11.
 Đáp án: B
Đáp án: B
Câu 23 [10305]: Cho phương trình 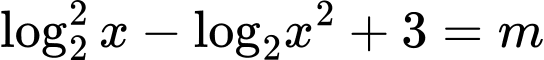 . Điều kiện để để phương trình có nghiệm
. Điều kiện để để phương trình có nghiệm 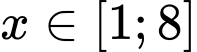 là
là  , tính
, tính 
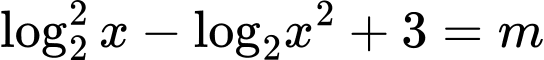 . Điều kiện để để phương trình có nghiệm
. Điều kiện để để phương trình có nghiệm 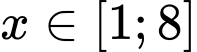 là
là  , tính
, tính 
A, 
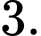
B, 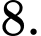
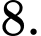
C, 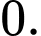
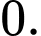
D, 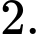
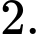
Ta có 
Đặt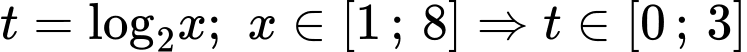
PT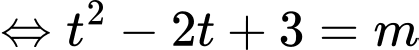
Xét hàm số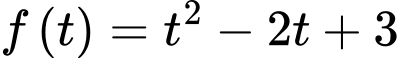 với
với 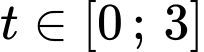
Ta có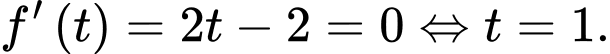
Suy ra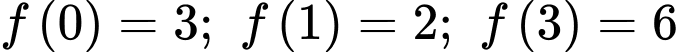
Vậy để phương trình có nghiệm thì
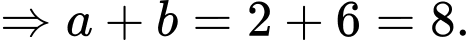 Chọn B. Đáp án: B
Chọn B. Đáp án: B

Đặt
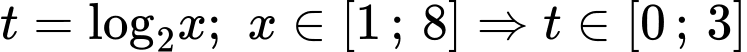
PT
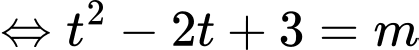
Xét hàm số
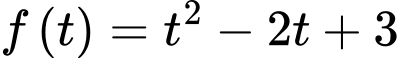 với
với 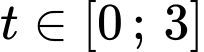
Ta có
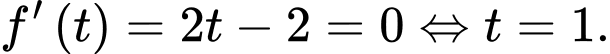
Suy ra
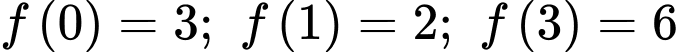
Vậy để phương trình có nghiệm thì

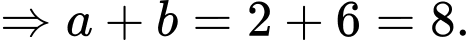 Chọn B. Đáp án: B
Chọn B. Đáp án: B