Đáp án Bài tập tự luyện
Câu 1 [133143]: Một vật chuyển động theo quy luật 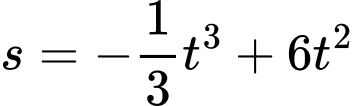 với
với 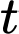 (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và
(giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và 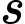 (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 9 giây, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
(mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 9 giây, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
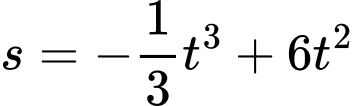 với
với 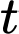 (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và
(giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và 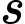 (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 9 giây, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
(mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 9 giây, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu? A, 

B, 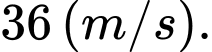
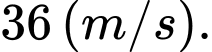
C, 

D, 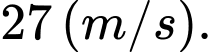
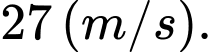
Phương trình vận tốc là : 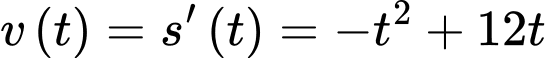
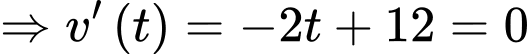
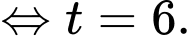
Suy ra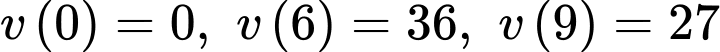
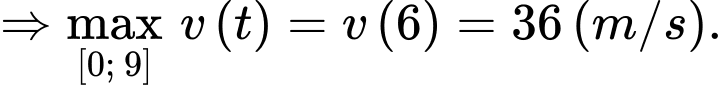 Chọn B.
Đáp án: B
Chọn B.
Đáp án: B
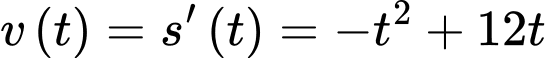
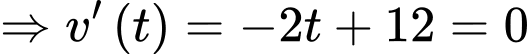
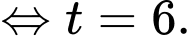
Suy ra
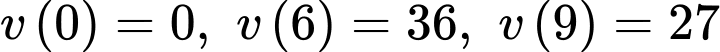
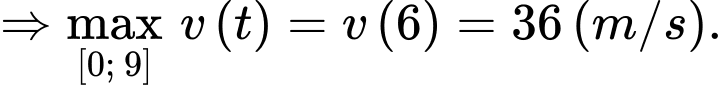 Chọn B.
Đáp án: B
Chọn B.
Đáp án: B
Câu 2 [383478]: Người ta bơm xăng vào bình xăng của một xe ô tô. Biết rằng thể tích  (lít) của lượng xăng trong bình xăng tính theo thòi gian bơm xăng
(lít) của lượng xăng trong bình xăng tính theo thòi gian bơm xăng 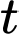 (phút) được cho bởi công thức
(phút) được cho bởi công thức 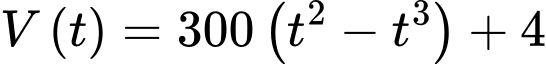 với
với 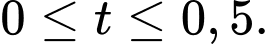 Khi xăng chảy vào bình xăng, gọi
Khi xăng chảy vào bình xăng, gọi 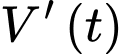 là tốc độ tăng thể tích tại thời điểm
là tốc độ tăng thể tích tại thời điểm 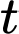 với
với 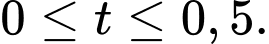 Hỏi xăng chảy vào bình xăng ở thời điểm nào có tốc độ tăng thể tích là lớn nhất?
Hỏi xăng chảy vào bình xăng ở thời điểm nào có tốc độ tăng thể tích là lớn nhất?
 (lít) của lượng xăng trong bình xăng tính theo thòi gian bơm xăng
(lít) của lượng xăng trong bình xăng tính theo thòi gian bơm xăng 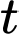 (phút) được cho bởi công thức
(phút) được cho bởi công thức 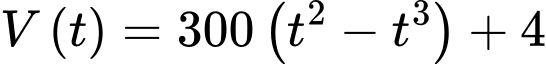 với
với 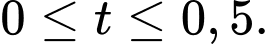 Khi xăng chảy vào bình xăng, gọi
Khi xăng chảy vào bình xăng, gọi 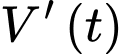 là tốc độ tăng thể tích tại thời điểm
là tốc độ tăng thể tích tại thời điểm 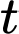 với
với 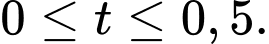 Hỏi xăng chảy vào bình xăng ở thời điểm nào có tốc độ tăng thể tích là lớn nhất?
Hỏi xăng chảy vào bình xăng ở thời điểm nào có tốc độ tăng thể tích là lớn nhất? A, 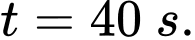
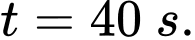
B, 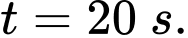
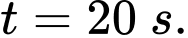
C, 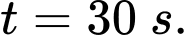
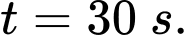
D, 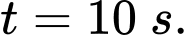
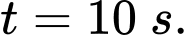
Ta có: 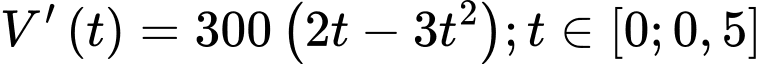
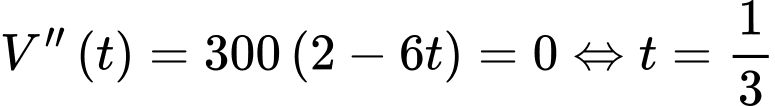 .
.
Lại có: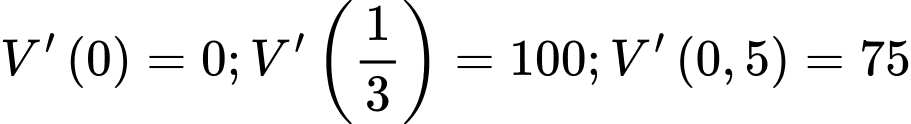 .
.
Do đó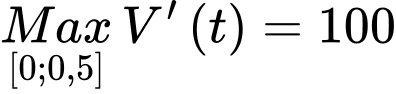 tại
tại 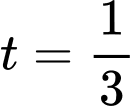 .
Đáp án: B
.
Đáp án: B
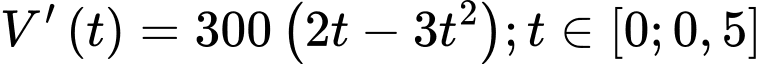
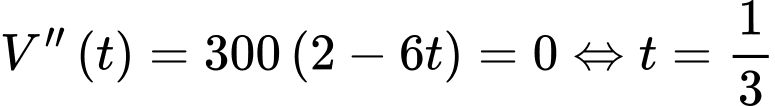 .
.
Lại có:
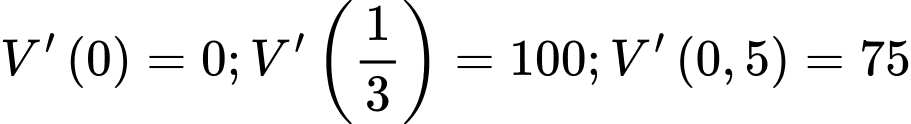 .
.
Do đó
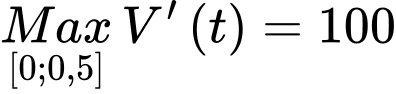 tại
tại 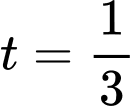 .
Đáp án: B
.
Đáp án: B
Câu 3 [358919]: Ho ép khí quản co lại, ảnh hưởng đến tốc độ của không khí đi vào khí quản. Tốc độ của không khí đi vào khí quản khi ho được cho bởi công thức
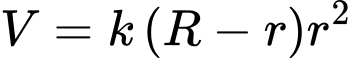 với
với 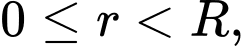 trong đó
trong đó 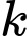 là hằng số,
là hằng số, 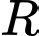 là bán kính bình thường của khí quản,
là bán kính bình thường của khí quản, 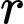 là bán kính khí quản khi ho. Hỏi bán kính của khí quản khi ho bằng bao nhiêu thì tốc độ của không khí đi vào khí quản là lớn nhất?
là bán kính khí quản khi ho. Hỏi bán kính của khí quản khi ho bằng bao nhiêu thì tốc độ của không khí đi vào khí quản là lớn nhất?
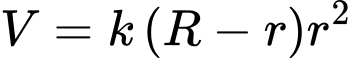 với
với 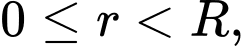 trong đó
trong đó 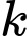 là hằng số,
là hằng số, 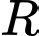 là bán kính bình thường của khí quản,
là bán kính bình thường của khí quản, 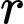 là bán kính khí quản khi ho. Hỏi bán kính của khí quản khi ho bằng bao nhiêu thì tốc độ của không khí đi vào khí quản là lớn nhất?
là bán kính khí quản khi ho. Hỏi bán kính của khí quản khi ho bằng bao nhiêu thì tốc độ của không khí đi vào khí quản là lớn nhất?
Xét hàm số 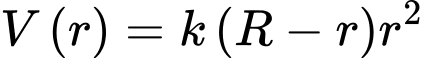 với
với 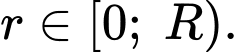
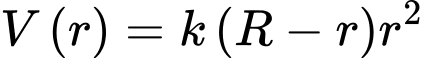 với
với 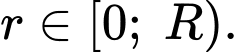
Ta có 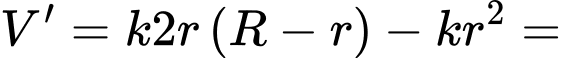
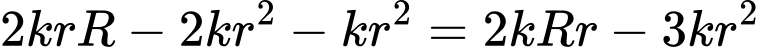
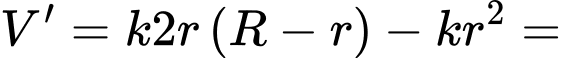
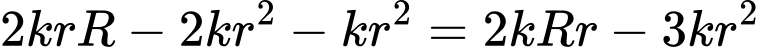
Trong nửa khoảng 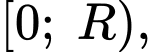
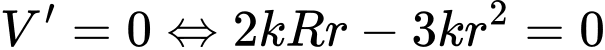
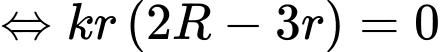
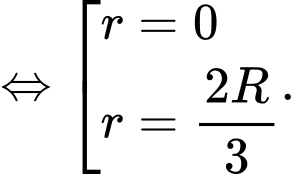
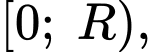
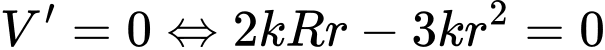
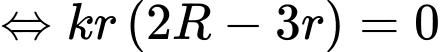
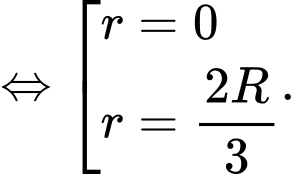
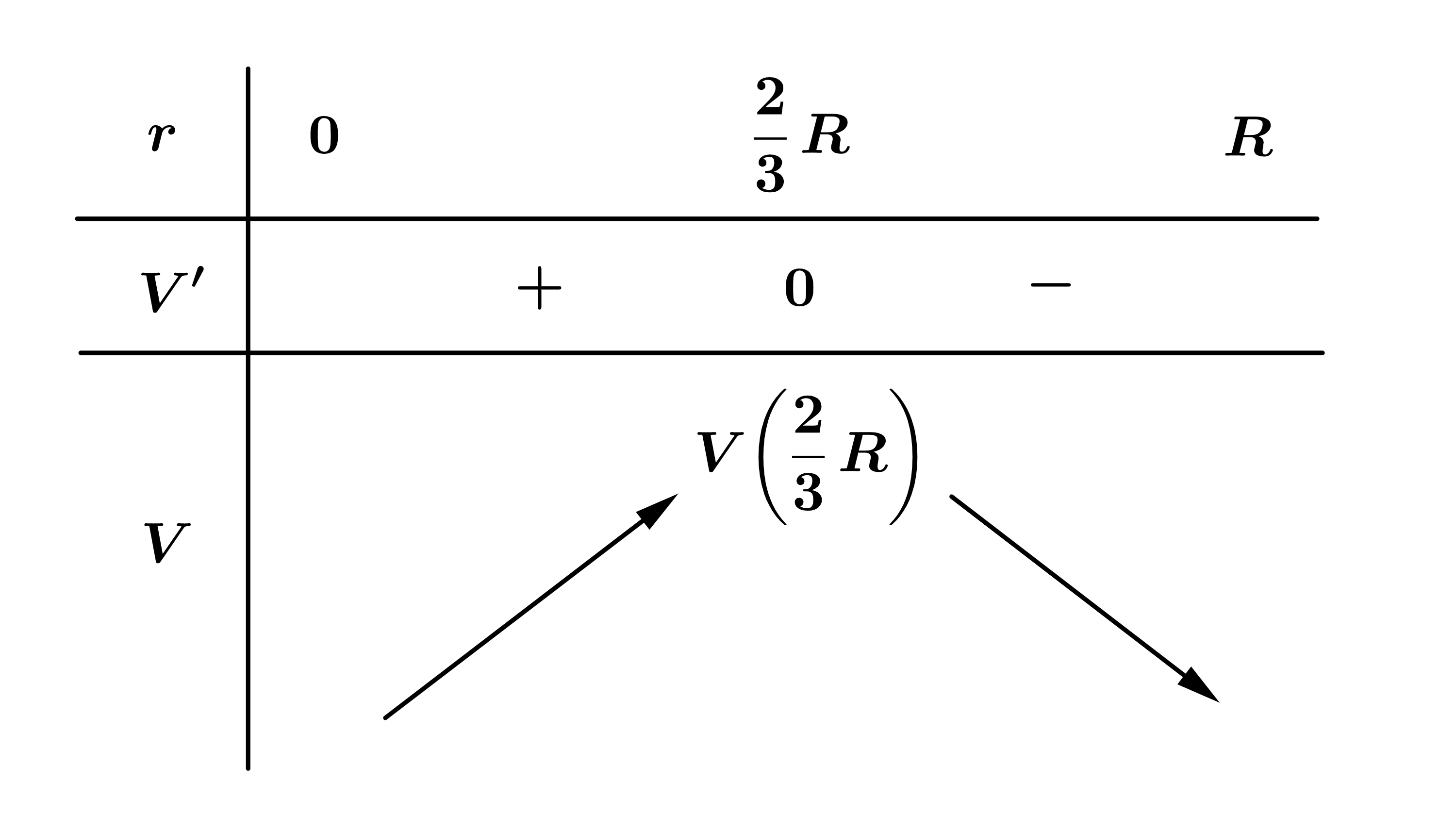
Bảng biến thiên

Vậy bán kính của khí quản khi ho bằng 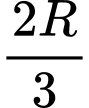 thì tốc độ của không khí đi vào khí quản là lớn nhất.
thì tốc độ của không khí đi vào khí quản là lớn nhất.
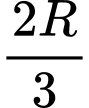 thì tốc độ của không khí đi vào khí quản là lớn nhất.
thì tốc độ của không khí đi vào khí quản là lớn nhất.
Câu 4 [28846]: Một vật chuyển động theo quy luật 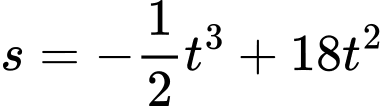 ,
, 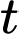 tính bằng giây, được tính là khoảng thời gian kể từ lúc vật bắt đầu chuyển động;
tính bằng giây, được tính là khoảng thời gian kể từ lúc vật bắt đầu chuyển động; 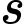 tính bằng
tính bằng 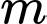 , là quãng đường vật chuyển động trong khoảng thời gian đó. Tính vận tốc lớn nhất vật đạt được trong khoảng thời gian 10 giây kể từ lúc bắt đầu chuyển động.
, là quãng đường vật chuyển động trong khoảng thời gian đó. Tính vận tốc lớn nhất vật đạt được trong khoảng thời gian 10 giây kể từ lúc bắt đầu chuyển động.
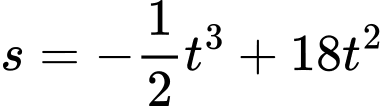 ,
, 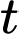 tính bằng giây, được tính là khoảng thời gian kể từ lúc vật bắt đầu chuyển động;
tính bằng giây, được tính là khoảng thời gian kể từ lúc vật bắt đầu chuyển động; 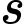 tính bằng
tính bằng 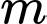 , là quãng đường vật chuyển động trong khoảng thời gian đó. Tính vận tốc lớn nhất vật đạt được trong khoảng thời gian 10 giây kể từ lúc bắt đầu chuyển động.
, là quãng đường vật chuyển động trong khoảng thời gian đó. Tính vận tốc lớn nhất vật đạt được trong khoảng thời gian 10 giây kể từ lúc bắt đầu chuyển động. A, 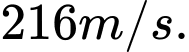
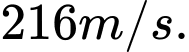
B, 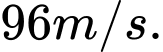
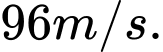
C, 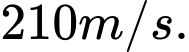
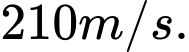
D, 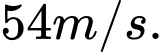
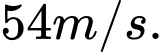
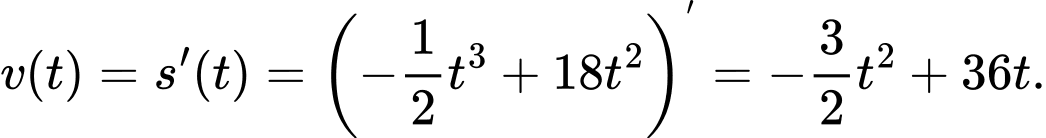
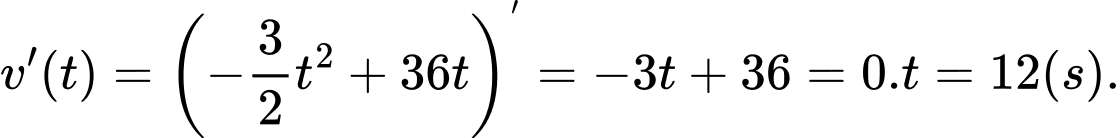
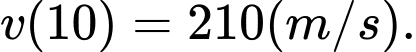
Vậy chọn đáp án C. Đáp án: C
Câu 5 [31128]: Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh ngày càng xuất hiện bệnh nhân đầu tiên đến ngày thứ 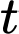 là
là 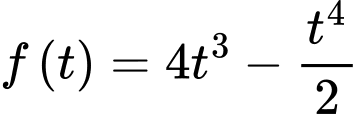 (người). Nếu xem
(người). Nếu xem 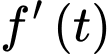 là tốc độ truyền bệnh (người/ngày) tại thời điểm
là tốc độ truyền bệnh (người/ngày) tại thời điểm 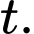 Tốc độ trền bệnh sẽ lớn nhất vào ngày thứ mấy?
Tốc độ trền bệnh sẽ lớn nhất vào ngày thứ mấy?
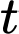 là
là 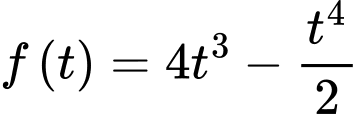 (người). Nếu xem
(người). Nếu xem 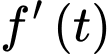 là tốc độ truyền bệnh (người/ngày) tại thời điểm
là tốc độ truyền bệnh (người/ngày) tại thời điểm 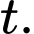 Tốc độ trền bệnh sẽ lớn nhất vào ngày thứ mấy?
Tốc độ trền bệnh sẽ lớn nhất vào ngày thứ mấy? A, 4.
B, 6.
C, 5.
D, 3.
Ta có hàm tốc độ truyền bệnh là g(t)=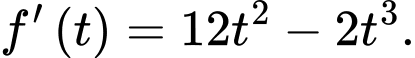
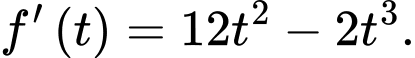
Tốc độ truyền bệnh lớn nhất tính theo: 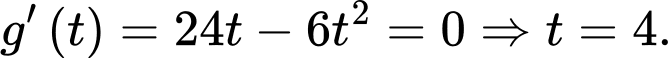
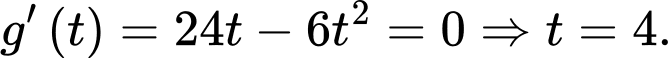
Lập BBT suy ra được tốc độ truyền bệnh lớn nhất vào ngày thứ 4.
Đáp án: A
Câu 6 [28562]: Người ta giới thiệu một loại thuốc kích thích sự sinh sản của một loại vi khuẩn. Sau 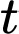 phút, số vi khuẩn được xác định theo công thức
phút, số vi khuẩn được xác định theo công thức 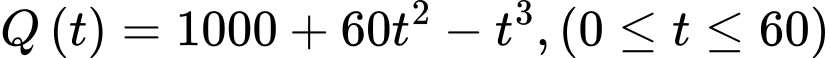 . Hỏi sau bao nhiêu phút thì số vi khuẩn lớn nhất?
. Hỏi sau bao nhiêu phút thì số vi khuẩn lớn nhất?
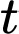 phút, số vi khuẩn được xác định theo công thức
phút, số vi khuẩn được xác định theo công thức 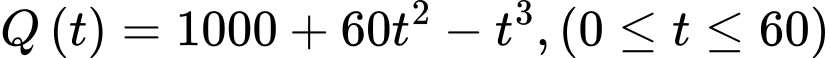 . Hỏi sau bao nhiêu phút thì số vi khuẩn lớn nhất?
. Hỏi sau bao nhiêu phút thì số vi khuẩn lớn nhất? A, 10 phút.
B, 20 phút.
C, 15 phút.
D, 40 phút.
Ta có: 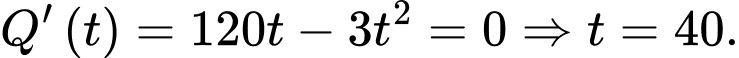 Như vậy tại thời điểm
Như vậy tại thời điểm 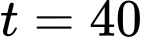 phút thì số vi khuẩn lớn nhất.
Đáp án: D
phút thì số vi khuẩn lớn nhất.
Đáp án: D
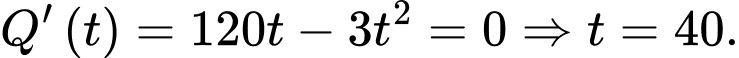 Như vậy tại thời điểm
Như vậy tại thời điểm 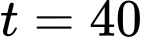 phút thì số vi khuẩn lớn nhất.
Đáp án: D
phút thì số vi khuẩn lớn nhất.
Đáp án: D
Câu 7 [28573]: Giả sử độ giảm huyết áp của một bệnh nhân được cho bởi công thức 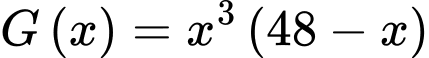 với
với 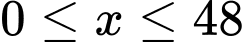 , trong đó
, trong đó 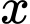 là liều lượng thuốc được tiêm cho bệnh nhân, đơn vị
là liều lượng thuốc được tiêm cho bệnh nhân, đơn vị 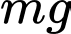 . Tính liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhiều nhất.
. Tính liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhiều nhất.
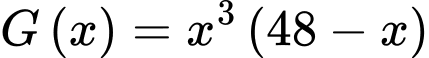 với
với 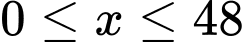 , trong đó
, trong đó 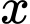 là liều lượng thuốc được tiêm cho bệnh nhân, đơn vị
là liều lượng thuốc được tiêm cho bệnh nhân, đơn vị 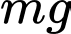 . Tính liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhiều nhất.
. Tính liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhiều nhất. A, 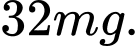
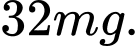
B, 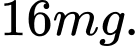
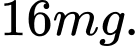
C, 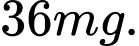
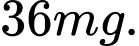
D, 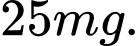
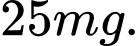
Khảo sát hàm số 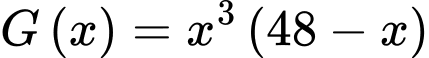
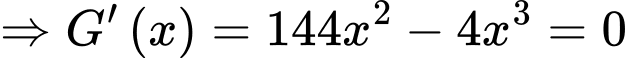
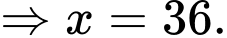
Vậy cần tiêm liều lượng 36mg để huyết áp giảm nhiều nhất. Đáp án: C
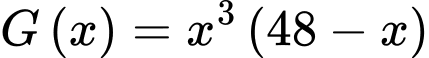
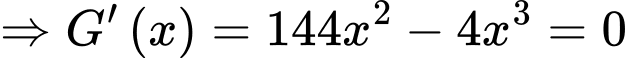
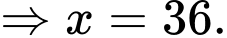
Vậy cần tiêm liều lượng 36mg để huyết áp giảm nhiều nhất. Đáp án: C
Câu 8 [791981]: Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong 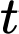 giờ được cho bởi công thức
giờ được cho bởi công thức 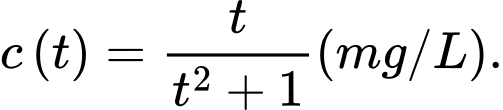 Sau khi tiêm thuốc bao lâu thì nồng độ thuốc trong máu của bệnh nhân cao nhất?
Sau khi tiêm thuốc bao lâu thì nồng độ thuốc trong máu của bệnh nhân cao nhất?
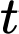 giờ được cho bởi công thức
giờ được cho bởi công thức 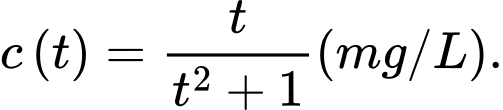 Sau khi tiêm thuốc bao lâu thì nồng độ thuốc trong máu của bệnh nhân cao nhất?
Sau khi tiêm thuốc bao lâu thì nồng độ thuốc trong máu của bệnh nhân cao nhất? A, 4 giờ.
B, 3 giờ.
C, 1 giờ.
D, 2 giờ.
Đáp án C
Hàm nồng độ thuốc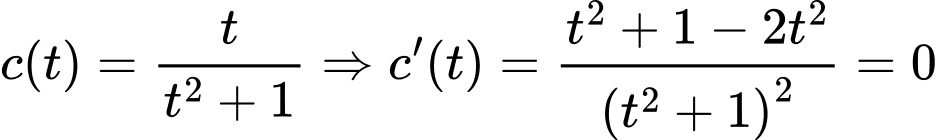
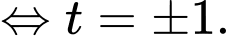
Cực trị là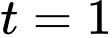 nên sau 1 giờ thì nồng độ thuốc trong máu bệnh nhân cao nhất. Đáp án: C
nên sau 1 giờ thì nồng độ thuốc trong máu bệnh nhân cao nhất. Đáp án: C
Hàm nồng độ thuốc
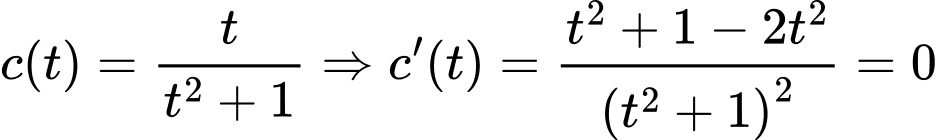
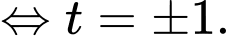
Cực trị là
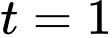 nên sau 1 giờ thì nồng độ thuốc trong máu bệnh nhân cao nhất. Đáp án: C
nên sau 1 giờ thì nồng độ thuốc trong máu bệnh nhân cao nhất. Đáp án: C
Câu 9 [30981]: Một khách sạn có 40 phòng. Tính toán bằng số liệu thống kê với dữ liệu quá khứ người ta ước lượng được rằng nếu đặt ra mức giá cho một phòng là 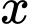 (nghìn đồng/ngày) thì mỗi ngày sẽ cho thuê được số phòng là
(nghìn đồng/ngày) thì mỗi ngày sẽ cho thuê được số phòng là 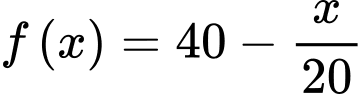 với
với 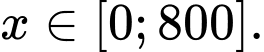 Nếu giá thuê phòng đắt hơn
Nếu giá thuê phòng đắt hơn  nghìn đồng/ngày thì không có khách nào thuê phòng. Với thông tin trên thì khách sạn cần đưa ra mức giá
nghìn đồng/ngày thì không có khách nào thuê phòng. Với thông tin trên thì khách sạn cần đưa ra mức giá 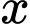 là bao nhiêu để được doanh thu lớn nhất?
là bao nhiêu để được doanh thu lớn nhất?
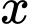 (nghìn đồng/ngày) thì mỗi ngày sẽ cho thuê được số phòng là
(nghìn đồng/ngày) thì mỗi ngày sẽ cho thuê được số phòng là 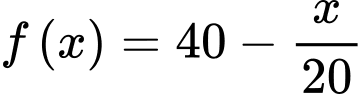 với
với 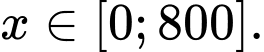 Nếu giá thuê phòng đắt hơn
Nếu giá thuê phòng đắt hơn  nghìn đồng/ngày thì không có khách nào thuê phòng. Với thông tin trên thì khách sạn cần đưa ra mức giá
nghìn đồng/ngày thì không có khách nào thuê phòng. Với thông tin trên thì khách sạn cần đưa ra mức giá 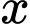 là bao nhiêu để được doanh thu lớn nhất?
là bao nhiêu để được doanh thu lớn nhất? A, 600.
B, 500.
C, 400.
D, 700.
Doanh thu của khách sạn là 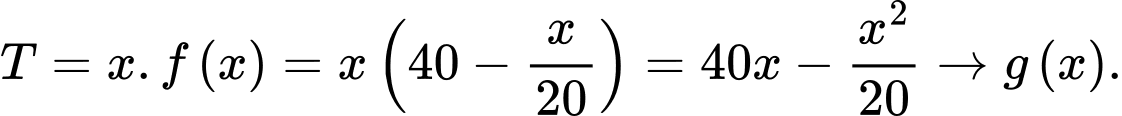
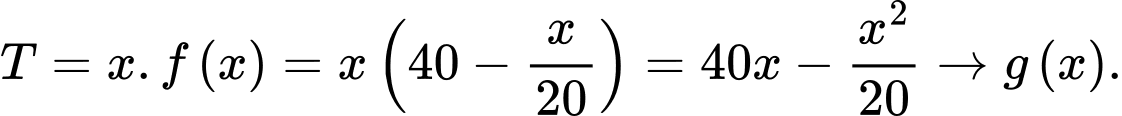
Xét hàm số 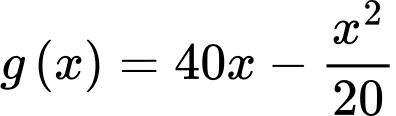 trên
trên 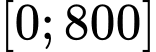 có
có 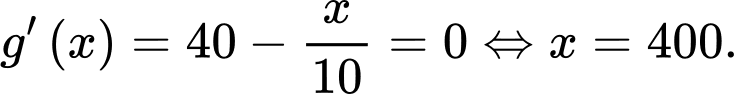
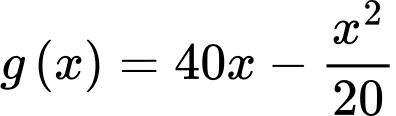 trên
trên 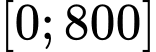 có
có 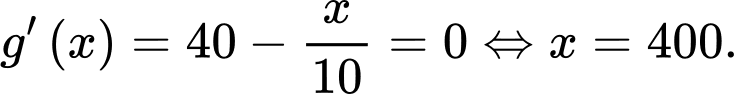
Suy ra 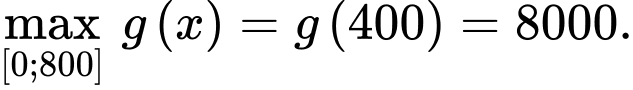
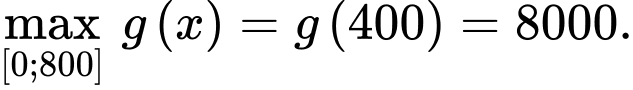
Vậy giá trị 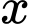 cần tìm là
cần tìm là 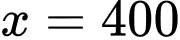 nghìn đồng/ ngày. Chọn C.
nghìn đồng/ ngày. Chọn C.
Đáp án: C 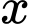 cần tìm là
cần tìm là 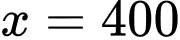 nghìn đồng/ ngày. Chọn C.
nghìn đồng/ ngày. Chọn C.
Câu 10 [30989]: Công ty du lịch Ban Mê dự định tổ chức tour xuyên Việt. Công ty dự định nếu giá tour là 2 triệu đồng thì sẽ có khoảng 150 người tham gia. Để kích thích mọi người tham gia, công ty khuyến mãi theo hình thức cứ thêm 20 người tham gia thì giá tour giảm 100 nghìn đồng. Hỏi công ty phải bán giá tour là bao nhiêu đồng để doanh thu từ tour xuyên Việt là lớn nhất.
A, 1375000.
B, 3781250.
C, 2500000.
D, 3000000.
Nếu 150 người tham gia thì giá là 2 triệu đồng=2000 nghìn đồng
Nếu người tham gia thì giá là
người tham gia thì giá là 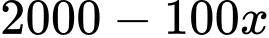 nghìn đồng
nghìn đồng
Doanh thu thu được là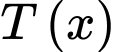
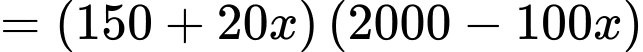
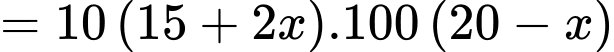
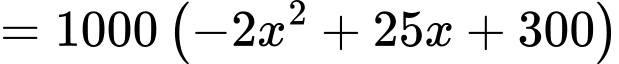
Lại có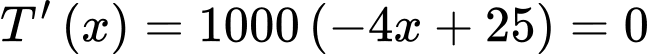

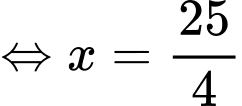
Khi đó ta suy ra được
Vậy công ty phải bán giá tua là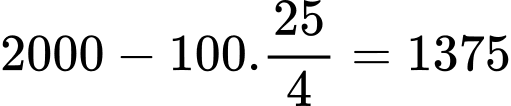 nghìn đồng. Đáp án: A
nghìn đồng. Đáp án: A
Nếu
 người tham gia thì giá là
người tham gia thì giá là 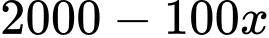 nghìn đồng
nghìn đồngDoanh thu thu được là
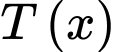
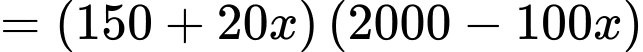
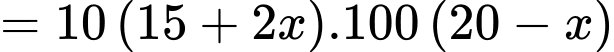
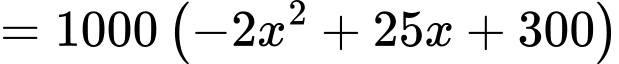
Lại có
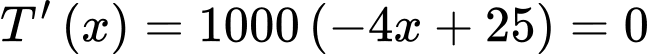

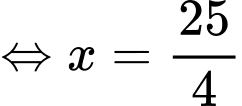
Khi đó ta suy ra được

Vậy công ty phải bán giá tua là
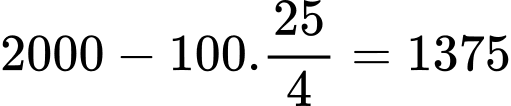 nghìn đồng. Đáp án: A
nghìn đồng. Đáp án: A
Câu 11 [579672]: [Đề mẫu HSA 2024]: Một chiếc lều cắm trại được thiết kế có dạng hình chóp tứ giác đều với thể tích là  Bốn mặt bên của lều được may bằng vải bạt (hình minh họa). Để diện tích vải bạt cần dùng là nhỏ nhất, thì độ dài cạnh đáy gần nhất với giá trị nào sau đây?
Bốn mặt bên của lều được may bằng vải bạt (hình minh họa). Để diện tích vải bạt cần dùng là nhỏ nhất, thì độ dài cạnh đáy gần nhất với giá trị nào sau đây?
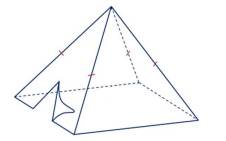
 Bốn mặt bên của lều được may bằng vải bạt (hình minh họa). Để diện tích vải bạt cần dùng là nhỏ nhất, thì độ dài cạnh đáy gần nhất với giá trị nào sau đây?
Bốn mặt bên của lều được may bằng vải bạt (hình minh họa). Để diện tích vải bạt cần dùng là nhỏ nhất, thì độ dài cạnh đáy gần nhất với giá trị nào sau đây? 
A, 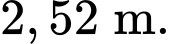
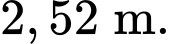
B, 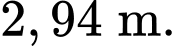
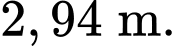
C, 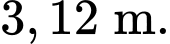
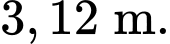
D, 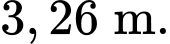
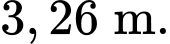
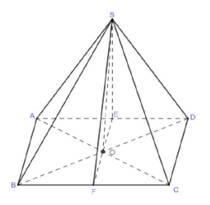
Do chiếc lều có dạng hình chóp tứ giác đều nên 4 mặt bên bằng nhau.
Đặt
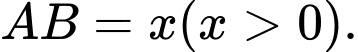
Gọi
 là tâm của hình vuông
là tâm của hình vuông 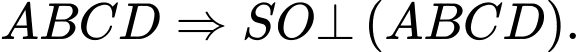
Suy ra
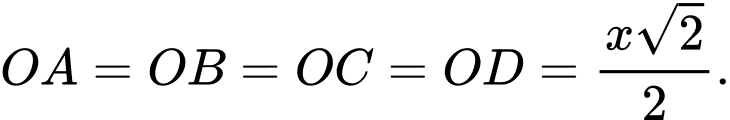
Gọi
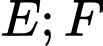 lần lượt là trung điểm
lần lượt là trung điểm 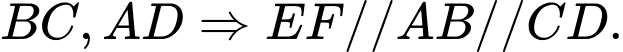
Suy ra
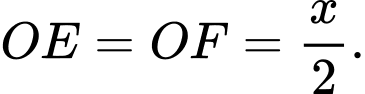
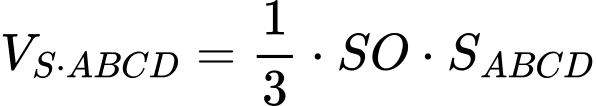
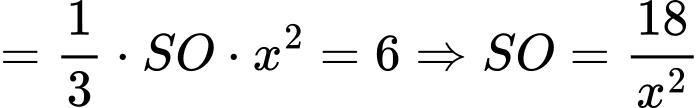
Có
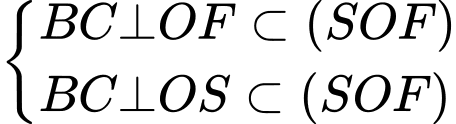
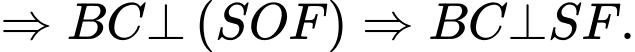
Ta có:
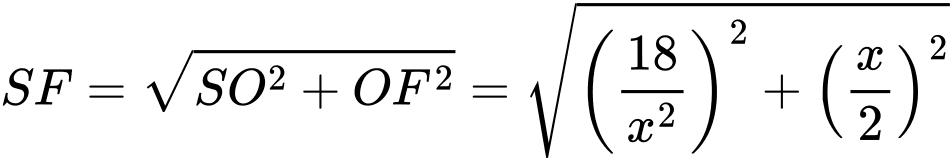
Diện tích vải bạt cần dùng là:
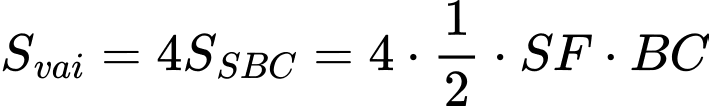
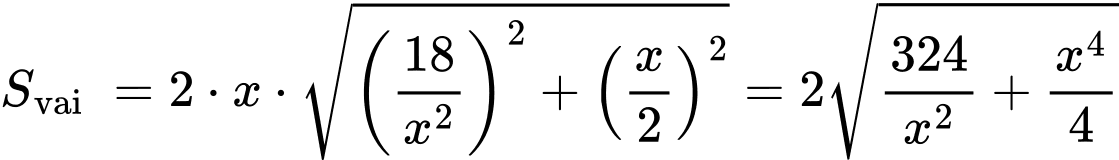
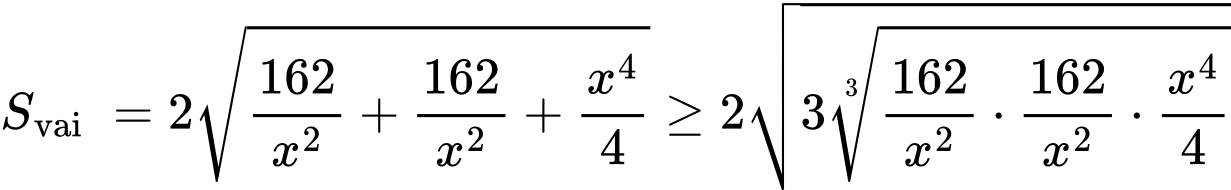
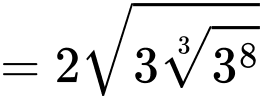
Dấu bằng xảy ra khi
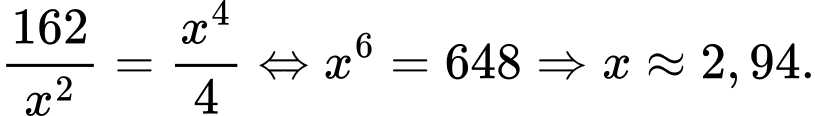
Chọn B. Đáp án: B
Câu 12 [373499]: Trong một thí nghiệm y học, người ta cấy 1000 vi khuẩn vào môi trường dinh dưỡng. Bằng thực nghiệm, người ta xác định số lượng vi khuẩn thay đổi theo thời gian bởi công thức: 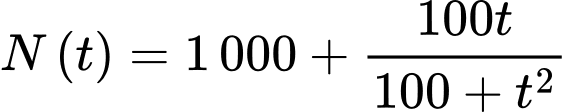 (con), trong đó
(con), trong đó 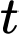 là thời gian tính bằng giây. Tính số lượng vi khuẩn lớn nhất kể từ khi thực hiện cấy vi khuẩn vào môi trường dinh dưỡng.
là thời gian tính bằng giây. Tính số lượng vi khuẩn lớn nhất kể từ khi thực hiện cấy vi khuẩn vào môi trường dinh dưỡng.
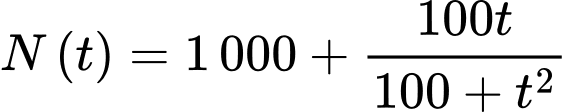 (con), trong đó
(con), trong đó 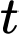 là thời gian tính bằng giây. Tính số lượng vi khuẩn lớn nhất kể từ khi thực hiện cấy vi khuẩn vào môi trường dinh dưỡng.
là thời gian tính bằng giây. Tính số lượng vi khuẩn lớn nhất kể từ khi thực hiện cấy vi khuẩn vào môi trường dinh dưỡng.
Xét hàm số 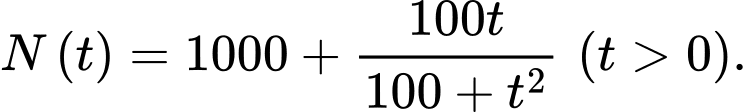

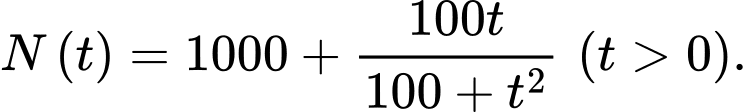
Ta có 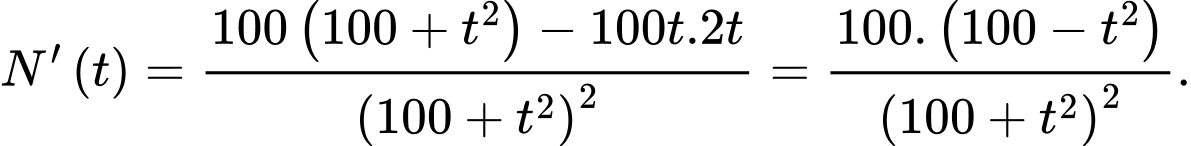
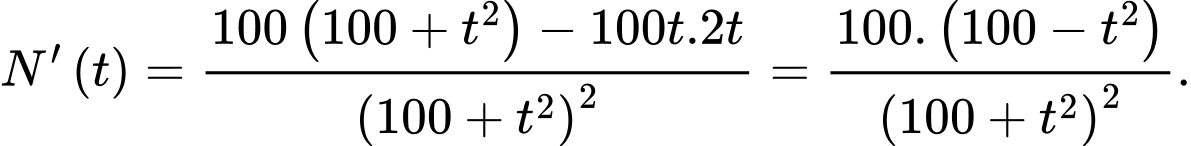
Khi đó, với 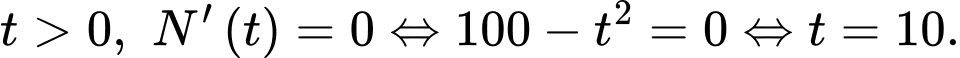
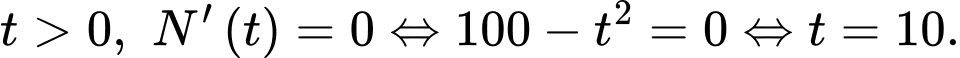
Bảng biến thiên của hàm số như sau

Dựa vào bảng biến thiên, ta thấy hàm số 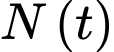 đạt giá trị lớn nhất bằng
đạt giá trị lớn nhất bằng 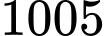 tại
tại 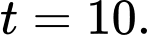
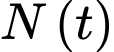 đạt giá trị lớn nhất bằng
đạt giá trị lớn nhất bằng 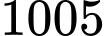 tại
tại 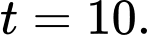
Vậy số lượng vi khuẩn lớn nhất kể từ khi thực hiện cấy vi khuẩn vào môi trường dinh dưỡng là 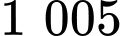 con.
con.
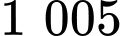 con.
con.
Câu 13 [28250]: Một chuyến xe buýt có sức chứa tối đa 60 hành khách. Giả sử một chuyến xe chở 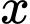 hành khách thì giá cho mỗi hành khách là
hành khách thì giá cho mỗi hành khách là 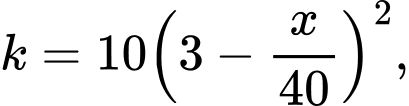 đơn vị nghìn đồng. Xác định doanh thu lớn nhất có thể xảy ra của chuyến xe buýt đó (Viết đáp số với đơn vị triệu đồng và làm tròn đến hàng phần mười).
đơn vị nghìn đồng. Xác định doanh thu lớn nhất có thể xảy ra của chuyến xe buýt đó (Viết đáp số với đơn vị triệu đồng và làm tròn đến hàng phần mười).
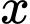 hành khách thì giá cho mỗi hành khách là
hành khách thì giá cho mỗi hành khách là 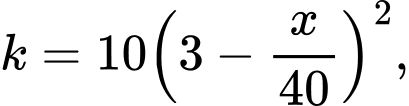 đơn vị nghìn đồng. Xác định doanh thu lớn nhất có thể xảy ra của chuyến xe buýt đó (Viết đáp số với đơn vị triệu đồng và làm tròn đến hàng phần mười).
đơn vị nghìn đồng. Xác định doanh thu lớn nhất có thể xảy ra của chuyến xe buýt đó (Viết đáp số với đơn vị triệu đồng và làm tròn đến hàng phần mười). A,
B,
C,
D,
HD: Ta có doanh thu là 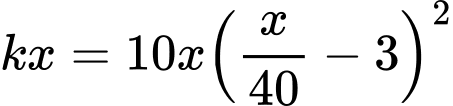
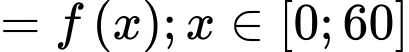
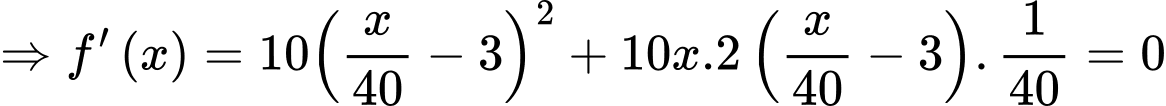
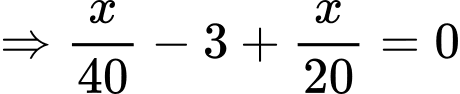
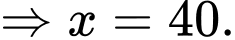
Tính 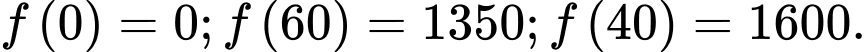
Đáp án: 1,6 triệu đồng.
Câu 14 [30960]: Lưu lượng xe ô tô vào đường hầm được cho bởi công thức: $f(v) = \frac{{290,4v}}{{0,36{v^2} + 13,2v + 264}}$(xe/giây), trong đó $v\,\left( {km/h} \right)$ là vận tốc trung bình của các xe khi vào đường hầm. Tính vận tốc trung bình (đơn vị km/h và làm tròn đến hai chữ số thập phân) của các xe khi vào đường hầm sao cho lưu lượng xe là lớn nhất.
A,
B,
C,
D,
Ta có: $f\left( v \right)=\frac{290,4}{0,36v+13,2+\frac{264}{v}}\le \frac{290,4}{13,2+2\sqrt{0,36v.\frac{264}{v}}}=\frac{290,4}{13,2+\frac{6\sqrt{66}}{5}}.$
Dấu bằng xảy ra khi $\left\{ \begin{align}
& v>0 \\
& 0,36v=\frac{264}{v} \\
\end{align} \right.\Leftrightarrow v=\frac{10\sqrt{66}}{3}.$
& v>0 \\
& 0,36v=\frac{264}{v} \\
\end{align} \right.\Leftrightarrow v=\frac{10\sqrt{66}}{3}.$
Điền đáp án: 27,08
Đáp án: B
Câu 15 [383479]: [Nguồn SGK Kết Nối Tri Thức]: Giả sử doanh số (tính bằng số sản phẩm) của một sản phẩm mới (trong vòng một số năm nhất định) tuân theo quy luật logistic được mô hình hoá bằng hàm số
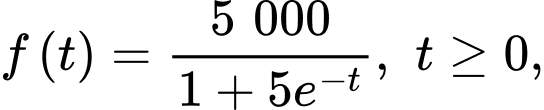
trong đó thời gian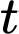 được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm
được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm 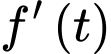 sẽ biểu thị tốc độ bán hàng. Hỏi tốc độ bán hàng lớn nhất bằng bao nhiêu?
sẽ biểu thị tốc độ bán hàng. Hỏi tốc độ bán hàng lớn nhất bằng bao nhiêu?
Đáp số:…………………………………….
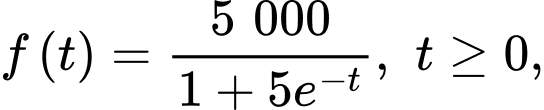
trong đó thời gian
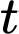 được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm
được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm 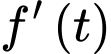 sẽ biểu thị tốc độ bán hàng. Hỏi tốc độ bán hàng lớn nhất bằng bao nhiêu?
sẽ biểu thị tốc độ bán hàng. Hỏi tốc độ bán hàng lớn nhất bằng bao nhiêu?Đáp số:…………………………………….
Ta có: 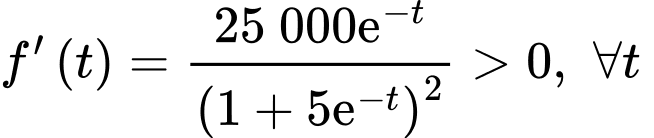 và
và 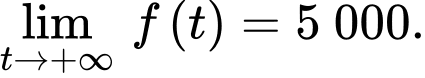
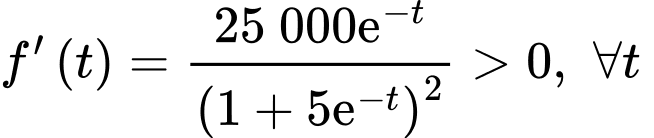 và
và 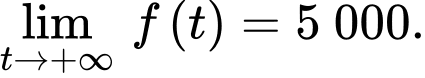
Do đó, doanh số luôn tăng nhưng sẽ không vượt quá 5 000.
Ta có: 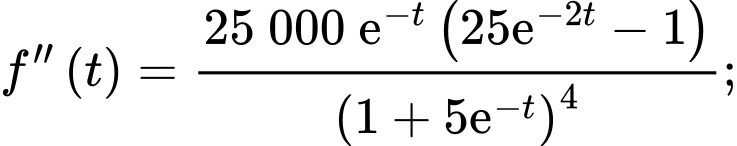
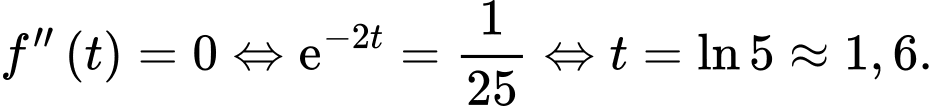
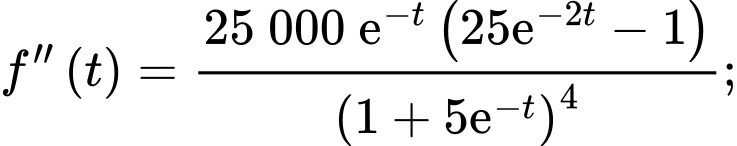
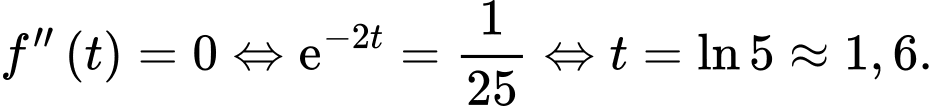
Do 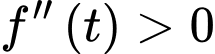 với mọi
với mọi 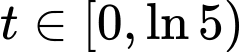 và
và 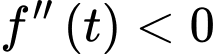 với mọi
với mọi 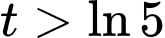 , nên
, nên 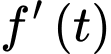 đạt GTLN tại
đạt GTLN tại  và
và 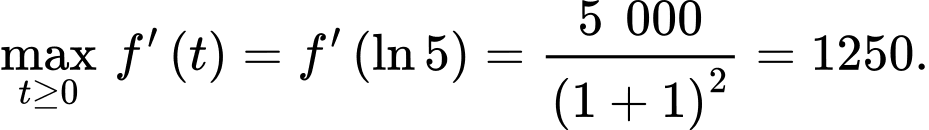
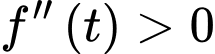 với mọi
với mọi 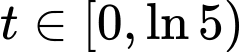 và
và 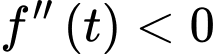 với mọi
với mọi 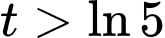 , nên
, nên 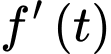 đạt GTLN tại
đạt GTLN tại  và
và 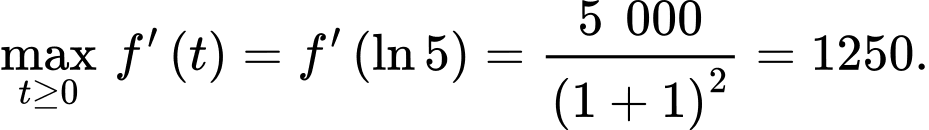
Vậy sau khi phát hành sản phẩm khoảng 1,6 năm thì tốc độ bán hàng lớn nhất.
Câu 16 [390977]: Công ty A chuyên sản xuất một loại sản phẩm, bộ phận sản xuất ước tính rằng với 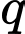 sản phẩm được sản xuất một tháng thì tổng chi phí sẽ là
sản phẩm được sản xuất một tháng thì tổng chi phí sẽ là 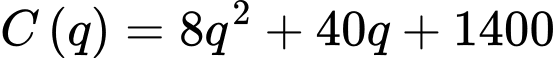 (đơn vị nghìn đồng). Mỗi sản phẩm công ty bán với giá
(đơn vị nghìn đồng). Mỗi sản phẩm công ty bán với giá 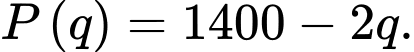 Hãy xác định số sản phẩm công ty A cần sản xuất trong một tháng (giả sử công ty này bán hết được số sản phẩm mình làm ra) để thu về lợi nhuận cao nhất?
Hãy xác định số sản phẩm công ty A cần sản xuất trong một tháng (giả sử công ty này bán hết được số sản phẩm mình làm ra) để thu về lợi nhuận cao nhất?
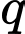 sản phẩm được sản xuất một tháng thì tổng chi phí sẽ là
sản phẩm được sản xuất một tháng thì tổng chi phí sẽ là 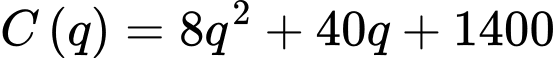 (đơn vị nghìn đồng). Mỗi sản phẩm công ty bán với giá
(đơn vị nghìn đồng). Mỗi sản phẩm công ty bán với giá 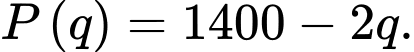 Hãy xác định số sản phẩm công ty A cần sản xuất trong một tháng (giả sử công ty này bán hết được số sản phẩm mình làm ra) để thu về lợi nhuận cao nhất?
Hãy xác định số sản phẩm công ty A cần sản xuất trong một tháng (giả sử công ty này bán hết được số sản phẩm mình làm ra) để thu về lợi nhuận cao nhất? Đáp số:…………………………………….
Gọi 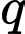
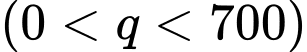 là số sản phẩm mà công ty A cần sản xuất để thu được lợi
nhuận cao nhất.
là số sản phẩm mà công ty A cần sản xuất để thu được lợi
nhuận cao nhất. 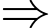 Lợi nhuận mà công ty thu được là:
Lợi nhuận mà công ty thu được là: 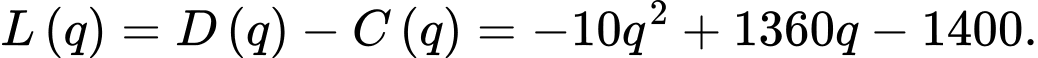
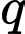
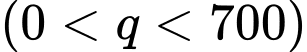 là số sản phẩm mà công ty A cần sản xuất để thu được lợi
nhuận cao nhất.
là số sản phẩm mà công ty A cần sản xuất để thu được lợi
nhuận cao nhất. Khi đó, nếu bán
hết số sản phẩm thì doanh thu là: 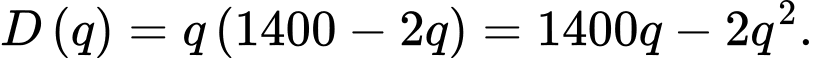
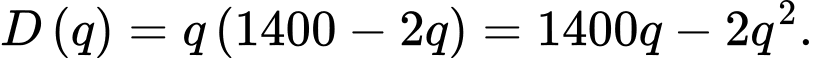
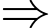 Lợi nhuận mà công ty thu được là:
Lợi nhuận mà công ty thu được là: 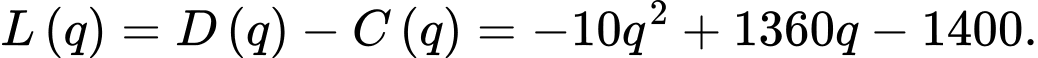
Bài toán trở
thành tìm giá trị lớn nhất của 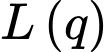 với
với 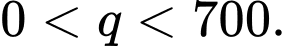 Có:
Có: 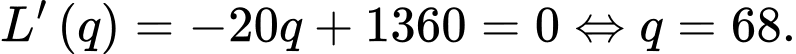
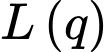 với
với 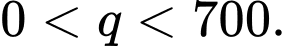 Có:
Có: 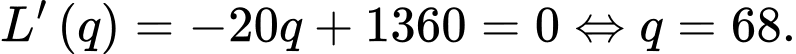
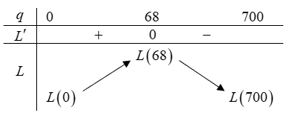
Ta có bảng biến
thiên:

Vậy để thu về lợi
nhuận cao nhất thì công ty cần sản xuất 68 sản phẩm.
Câu 17 [390978]: Công ty B chuyên sản xuất một loại sản phẩm, bộ phận sản xuất ước tính rằng với 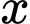 sản phẩm được sản xuất một tháng thì tổng chi phí sẽ là
sản phẩm được sản xuất một tháng thì tổng chi phí sẽ là 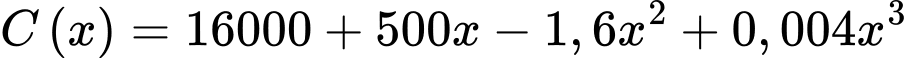 (nghìn đồng). Giá của mỗi sản phẩm được công ty bán với giá
(nghìn đồng). Giá của mỗi sản phẩm được công ty bán với giá 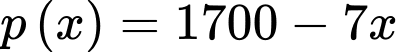 (nghìn đồng). Hãy xác định số sản phẩm công ty B cần sản xuất trong một tháng (giả sử công ty này bán hết được số sản phẩm mình làm ra) để thu về lợi nhuận cao nhất?
(nghìn đồng). Hãy xác định số sản phẩm công ty B cần sản xuất trong một tháng (giả sử công ty này bán hết được số sản phẩm mình làm ra) để thu về lợi nhuận cao nhất?
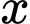 sản phẩm được sản xuất một tháng thì tổng chi phí sẽ là
sản phẩm được sản xuất một tháng thì tổng chi phí sẽ là 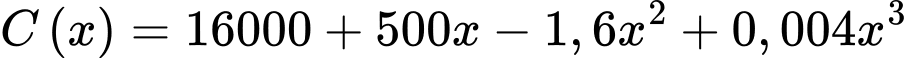 (nghìn đồng). Giá của mỗi sản phẩm được công ty bán với giá
(nghìn đồng). Giá của mỗi sản phẩm được công ty bán với giá 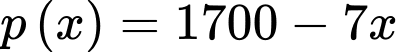 (nghìn đồng). Hãy xác định số sản phẩm công ty B cần sản xuất trong một tháng (giả sử công ty này bán hết được số sản phẩm mình làm ra) để thu về lợi nhuận cao nhất?
(nghìn đồng). Hãy xác định số sản phẩm công ty B cần sản xuất trong một tháng (giả sử công ty này bán hết được số sản phẩm mình làm ra) để thu về lợi nhuận cao nhất? Đáp số:…………………………………….
Gọi 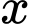
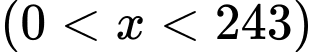 là số sản phẩm mà công ty B cần sản xuất để thu được lợi nhuận cao nhất.
là số sản phẩm mà công ty B cần sản xuất để thu được lợi nhuận cao nhất.
Khi đó, nếu bán hết số sản phẩm thì doanh thu là: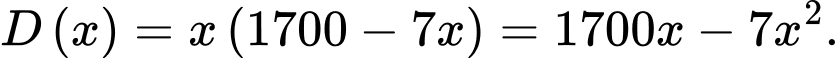
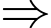 Lợi nhuận mà công ty thu được là:
Lợi nhuận mà công ty thu được là: 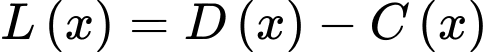
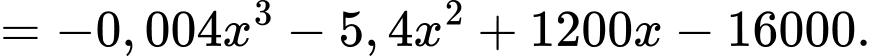
Bài toán trở thành tìm giá trị lớn nhất của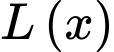 với
với 
Có: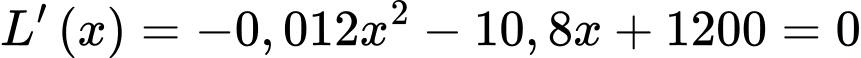
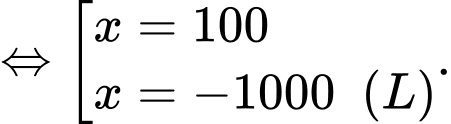
Ta có bảng biến thiên:
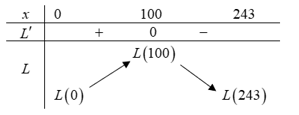
Vậy để thu về lợi nhuận cao nhất thì công ty cần sản xuất 100 sản phẩm.
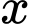
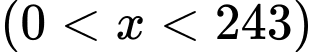 là số sản phẩm mà công ty B cần sản xuất để thu được lợi nhuận cao nhất.
là số sản phẩm mà công ty B cần sản xuất để thu được lợi nhuận cao nhất. Khi đó, nếu bán hết số sản phẩm thì doanh thu là:
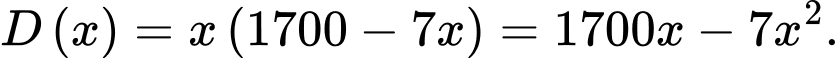
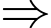 Lợi nhuận mà công ty thu được là:
Lợi nhuận mà công ty thu được là: 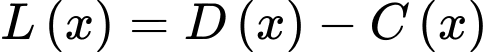
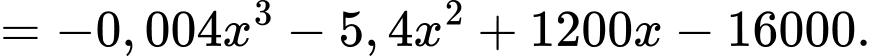
Bài toán trở thành tìm giá trị lớn nhất của
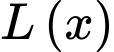 với
với 
Có:
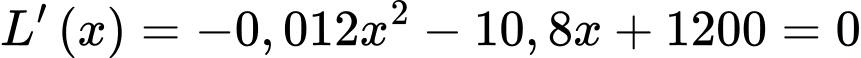
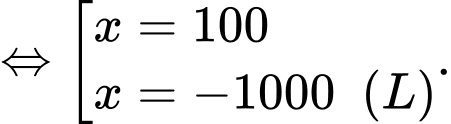
Ta có bảng biến thiên:

Vậy để thu về lợi nhuận cao nhất thì công ty cần sản xuất 100 sản phẩm.
Câu 18 [390979]: Một doanh nghiệp đang tập trung chiến lược vào kinh doanh xe máy với chi phí mua vào một chiếc là 27 (triệu đồng) và bán với giá 40 (triệu đồng) mỗi chiếc. Với giá bán này thì số lượng xe mà khách hàng sẽ mua là 2000 chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá bán và ước tính rằng nếu giảm 1 (triệu đồng) mỗi chiếc thì số lượng xe bán ra sẽ tăng thêm 800 chiếc. Để sau khi đã thực hiện việc giảm giá, lợi nhuận thu được sẽ là cao nhất thì doanh nghiệp phải định giá bán mới là bao nhiêu triệu đồng. Viết kết quả làm tròn đến hàng phần chục.
Đáp số:…………………………………….
Gọi 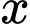 triệu đồng là số tiền mà doanh nghiệp A dự định giảm giá,
triệu đồng là số tiền mà doanh nghiệp A dự định giảm giá, 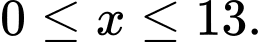
Khi đó: Lợi nhuận thu được khi bán một chiếc xe là: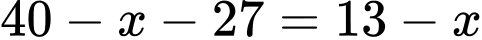 ( đồng).
( đồng).
Số xe mà doanh nghiệp sẽ bán được trong một năm là: (chiếc).
(chiếc).
Lợi nhuận mà doanh nghiệp thu được trong một năm là:
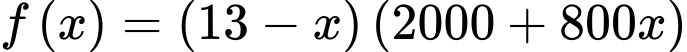
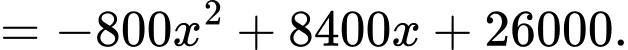
Có: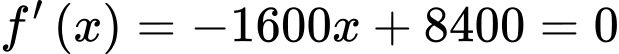
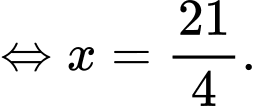
Xét hàm số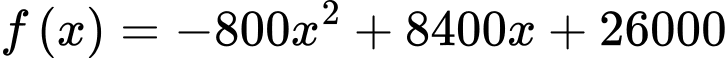 trên đoạn
trên đoạn 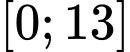 có bảng biến thiên sau:
có bảng biến thiên sau:
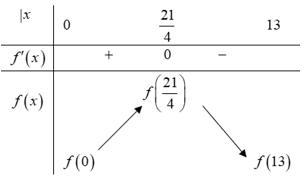
Để sau khi đã thực hiện việc giảm giá, lợi nhuận thu được sẽ là cao nhất thì doanh nghiệp phải định giá bán mới là: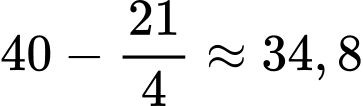 (triệu đồng).
(triệu đồng).
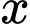 triệu đồng là số tiền mà doanh nghiệp A dự định giảm giá,
triệu đồng là số tiền mà doanh nghiệp A dự định giảm giá, 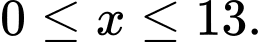
Khi đó: Lợi nhuận thu được khi bán một chiếc xe là:
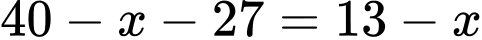 ( đồng).
( đồng). Số xe mà doanh nghiệp sẽ bán được trong một năm là:
 (chiếc).
(chiếc). Lợi nhuận mà doanh nghiệp thu được trong một năm là:
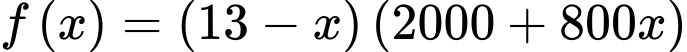
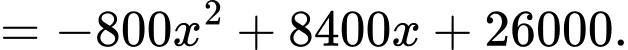
Có:
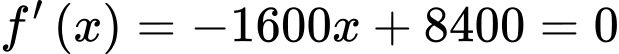
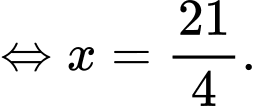
Xét hàm số
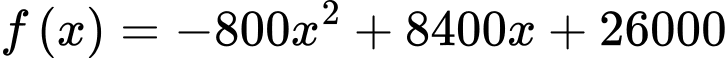 trên đoạn
trên đoạn 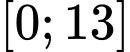 có bảng biến thiên sau:
có bảng biến thiên sau: 
Để sau khi đã thực hiện việc giảm giá, lợi nhuận thu được sẽ là cao nhất thì doanh nghiệp phải định giá bán mới là:
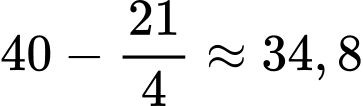 (triệu đồng).
(triệu đồng).
Câu 19 [383480]: [Trích SGK Kết Nối Tri Thức]: Một đội bóng đá thi đấu trong một sân vận động có sức chứa 55 000 khán giả. Với giá mỗi vé là 100 nghìn đồng, số khán giả trung bình là 27 000 người. Qua thăm dò dư luận, người ta thấy rằng mỗi khi giá vé giảm thêm 10 nghìn đồng, sẽ có thêm khoảng 3 000 khán giả. Hỏi ban tổ chức nên đặt giá vé là bao nhiêu (nghìn đồng) để doanh thu từ tiền bán vé là lớn nhất?
Gọi 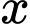
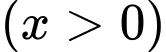 là số lần giảmgiá vé.
là số lần giảmgiá vé.
Khi đó, giá vé sau khi giảm là: (nghìn đồng).
(nghìn đồng).
Sau mỗi lần giảm giá thì có thêm 3000 khán giả.Do đó tổng số khán giả đến xem là:
Vì sân vận động có sức chứa 55000 khán giảnên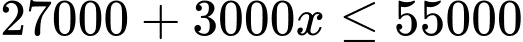
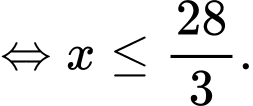
Doanh thu từ tiền bán vé là: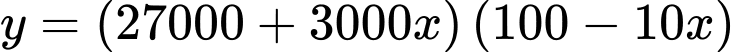
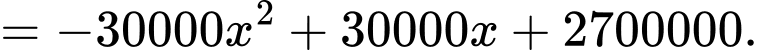
Bài toán trở thành tìm giá trị lớn nhất củahàm số: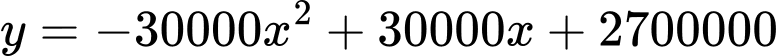
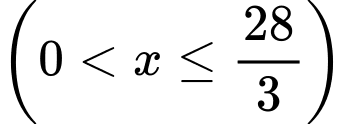
Có: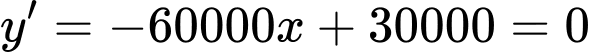
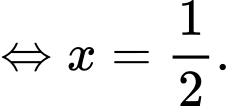
Ta có bảng biến thiên:
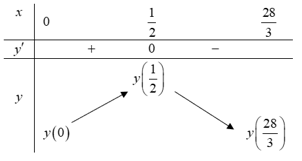
Dể doanh thu từ tiền bán vé là lớn nhất ban tổ chức nên đặt giá vé là: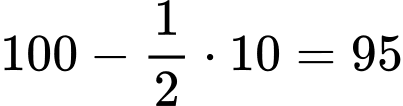 (nghìn đồng).
(nghìn đồng).
 là số lần giảmgiá vé.
là số lần giảmgiá vé. Khi đó, giá vé sau khi giảm là:
 (nghìn đồng).
(nghìn đồng). Sau mỗi lần giảm giá thì có thêm 3000 khán giả.Do đó tổng số khán giả đến xem là:

Vì sân vận động có sức chứa 55000 khán giảnên
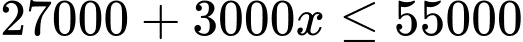
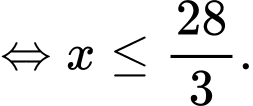
Doanh thu từ tiền bán vé là:
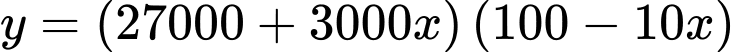
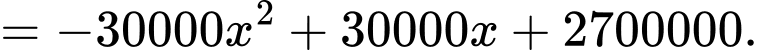
Bài toán trở thành tìm giá trị lớn nhất củahàm số:
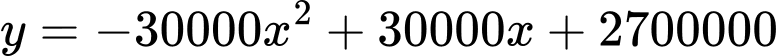
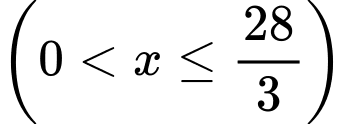
Có:
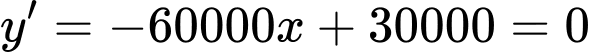
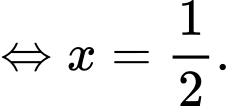
Ta có bảng biến thiên:

Dể doanh thu từ tiền bán vé là lớn nhất ban tổ chức nên đặt giá vé là:
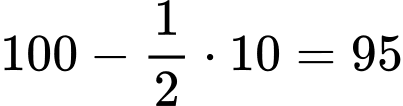 (nghìn đồng).
(nghìn đồng).
Câu 20 [28557]: Anh phong có một cái áo với diện tích 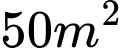 để nuôi cá diêu hồng. Vụ vừa qua, anh nuôi với mật độ 20con/
để nuôi cá diêu hồng. Vụ vừa qua, anh nuôi với mật độ 20con/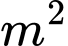 và thu được 1,5 tấn cá thành phẩm. Theo kinh nghiệm nuôi cá của mình anh thấy cứ thả giảm đi 8 con/
và thu được 1,5 tấn cá thành phẩm. Theo kinh nghiệm nuôi cá của mình anh thấy cứ thả giảm đi 8 con/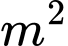 thì mỗi con cá thành phẩm thu được tăng thêm
thì mỗi con cá thành phẩm thu được tăng thêm 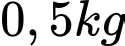 . Để tổng năng suất cao nhất thì vụ anh nên mua bao nhiêu cá giống để thả? (giả sử không có hao hụt trong quá trình nuôi).
. Để tổng năng suất cao nhất thì vụ anh nên mua bao nhiêu cá giống để thả? (giả sử không có hao hụt trong quá trình nuôi).
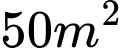 để nuôi cá diêu hồng. Vụ vừa qua, anh nuôi với mật độ 20con/
để nuôi cá diêu hồng. Vụ vừa qua, anh nuôi với mật độ 20con/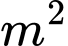 và thu được 1,5 tấn cá thành phẩm. Theo kinh nghiệm nuôi cá của mình anh thấy cứ thả giảm đi 8 con/
và thu được 1,5 tấn cá thành phẩm. Theo kinh nghiệm nuôi cá của mình anh thấy cứ thả giảm đi 8 con/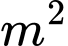 thì mỗi con cá thành phẩm thu được tăng thêm
thì mỗi con cá thành phẩm thu được tăng thêm 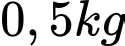 . Để tổng năng suất cao nhất thì vụ anh nên mua bao nhiêu cá giống để thả? (giả sử không có hao hụt trong quá trình nuôi).
. Để tổng năng suất cao nhất thì vụ anh nên mua bao nhiêu cá giống để thả? (giả sử không có hao hụt trong quá trình nuôi).
Điền đáp án: 1100.
Số cá anh Phong thả trong vụ vừa qua là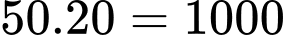 (con)
(con)
Khối lượng trung bình mỗi con cá thành phần là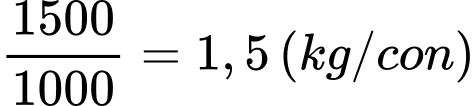
Theo đề bài ta có phương trình: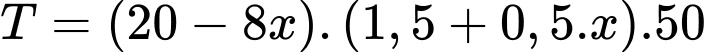
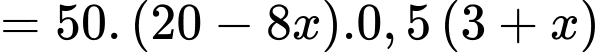
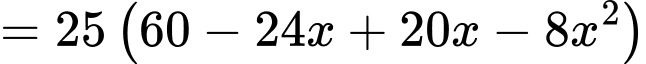
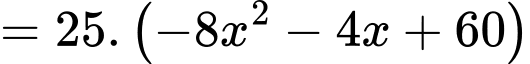
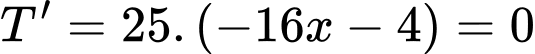
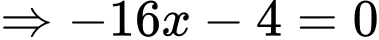
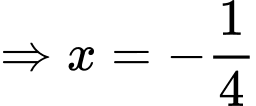
Vậy số cá giống để thả trong lần tiếp theo là: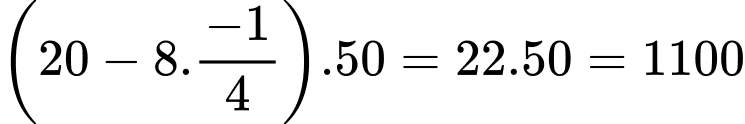 (con) Đáp án: C
(con) Đáp án: C
Số cá anh Phong thả trong vụ vừa qua là
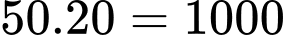 (con)
(con)
Khối lượng trung bình mỗi con cá thành phần là
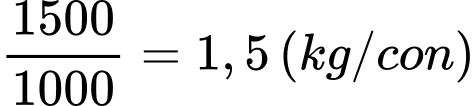
Theo đề bài ta có phương trình:
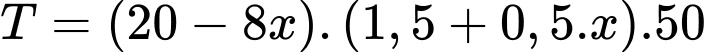
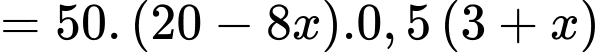
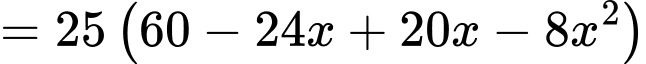
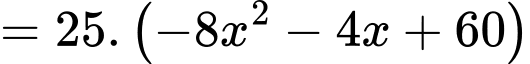
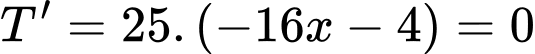
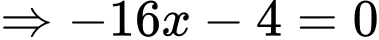
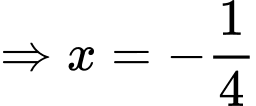
Vậy số cá giống để thả trong lần tiếp theo là:
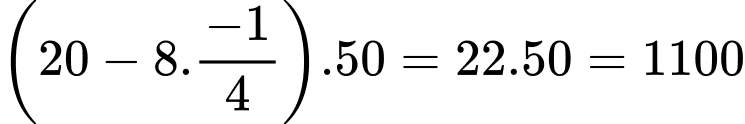 (con) Đáp án: C
(con) Đáp án: C
Câu 21 [30982]: Một công ty bất động sản có 50 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá 2.000.000 đồng một tháng thì mọi căn hộ đều có người thuê và cứ mỗi lần tăng giá cho thuê, mỗi căn hộ thêm 50.000 đồng một tháng thì có thêm một căn hộ bị bỏ trống. Công ty đã tìm ra phương án cho thuê đạt lợi nhuận lớn nhất. Hỏi thu nhập cao nhất công ty có thể đạt được trong một tháng là bao nhiêu?
A, 115.250.000.
B, 101.250.000.
C, 100.00.000.
D, 100.250.000.
50 căn hộ mỗi căn hộ thuê với giá 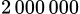 đồng thì mỗi tháng thu được
đồng thì mỗi tháng thu được 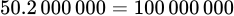 đồng.
đồng.
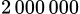 đồng thì mỗi tháng thu được
đồng thì mỗi tháng thu được 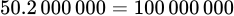 đồng.
đồng. Gọi 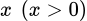 là số căn hộ bị bỏ trống thì số tiền thu thêm là
là số căn hộ bị bỏ trống thì số tiền thu thêm là 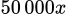 và số căn hộ cho thuế
và số căn hộ cho thuế 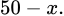
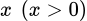 là số căn hộ bị bỏ trống thì số tiền thu thêm là
là số căn hộ bị bỏ trống thì số tiền thu thêm là 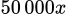 và số căn hộ cho thuế
và số căn hộ cho thuế 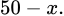
Sau một tháng công ty đó thu được 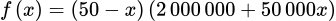 đồng.
đồng.
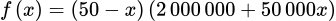 đồng.
đồng. Để được doanh thu cao nhất 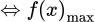 hay
hay 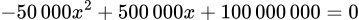 đạt lớn nhất
đạt lớn nhất 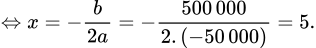
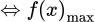 hay
hay 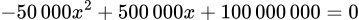 đạt lớn nhất
đạt lớn nhất 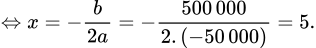
Khi đó số tiền cao nhất công ty thu được là 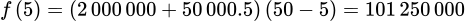 đồng. Chọn B
đồng. Chọn B
Đáp án: B 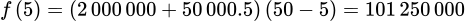 đồng. Chọn B
đồng. Chọn B
Câu 22 [30987]: Một trang trại mỗi ngày thu hoạch được một tấn rau. Mỗi ngày, nếu bán rau với giá 30000 đồng/kg thì hết sạch rau, nếu giá bán cứ tăng thêm 1000 đồng/kg thì số rau thừa lại tăng thêm 20 kg. Số rau thừa này được thu mua làm thức ăn chăn nuôi với giá 2000 đồng/kg. Hỏi số tiền bán rau nhiều nhất mà trang trại có thể thu được mỗi ngày là bao nhiêu?
A, 32420000 đồng.
B, 32400000 đồng.
C, 34400000 đồng.
D, 34240000 đồng.
Gọi 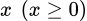 (nghìn đồng) là số tiền tăng lên cho mỗi kg rau.
(nghìn đồng) là số tiền tăng lên cho mỗi kg rau.
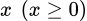 (nghìn đồng) là số tiền tăng lên cho mỗi kg rau.
(nghìn đồng) là số tiền tăng lên cho mỗi kg rau. Số tiền bán mỗi một kg rau sau khi tăng là 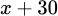 (nghìn đồng).
(nghìn đồng).
Đáp án: A 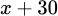 (nghìn đồng).
(nghìn đồng). Số kg rau thừa là 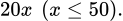
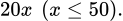
Tổng số kg rau bán được là 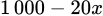 (kg).
(kg).
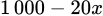 (kg).
(kg). Tổng số tiền thu được là 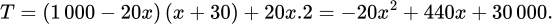
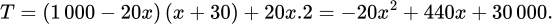
Mà 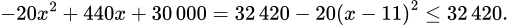
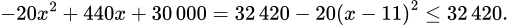
Do đó, 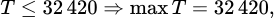 dấu bằng xảy ra khi
dấu bằng xảy ra khi 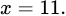
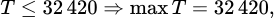 dấu bằng xảy ra khi
dấu bằng xảy ra khi 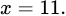
Vậy số tiền nhiều nhất bán được là 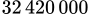 đồng.
Điền đáp án 32
đồng.
Điền đáp án 32
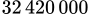 đồng.
Điền đáp án 32
đồng.
Điền đáp án 32
Câu 23 [383482]: [Trích Sách chuyên đề Cánh Diều]: Một cửa hàng nhập bưởi da xanh với giá nhập là 150 000 đồng/1 quả và bán bưởi đó với giá bán là 200 000 đồng/1 quả. Với giá bán này thì cửa hàng dự kiến chỉ bán được 50 quả. Cửa hàng này quyết định giảm giá bán. Biết rằng nếu cửa hàng cứ giảm mỗi quả 10 000 đồng thì số bưởi bán được tăng thêm là 50 quả. Xác định giá bán bưởi để (đơn vị nghìn đồng) cửa hàng đó thu được lợi nhuận lớn nhất.
Đáp số:…………………………………….
Đáp số:…………………………………….
Gọi 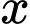 là số lần giảm giá bán bưởi
là số lần giảm giá bán bưởi 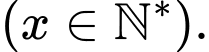
Khi đó số tiền giảm giá cho mỗi quả bưởi là
Suy ra giá bán của mỗi quả bưởi là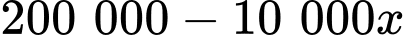 và số bưởi bán được là
và số bưởi bán được là 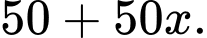
Lợi nhuận cửa hàng thu được là
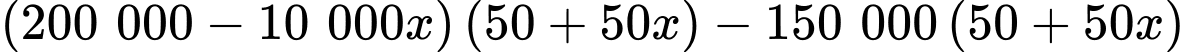
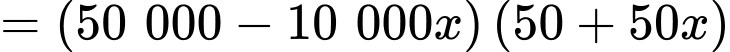
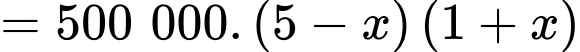
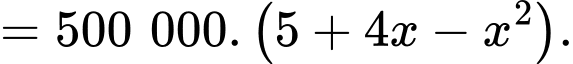
Xét hàm số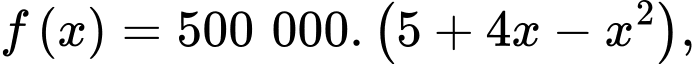 với
với 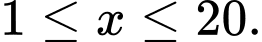
Ta có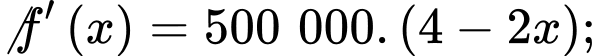
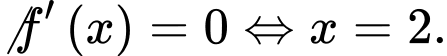
Bảng biến thiên
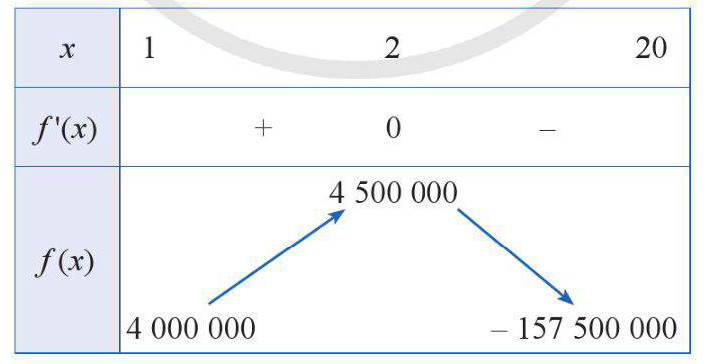
Dựa vào bảng biến thiên, ta có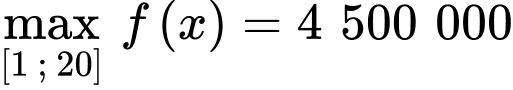 tại
tại 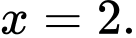
Suy ra giá bán bưởi để cửa hàng đó thu được lợi nhuận lớn nhất là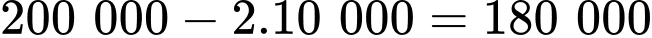 đồng.
đồng.
Vậy cửa hàng cần bán bưởi với giá đồng/ 1 quả để số tiền lãi thu được là lớn nhất.
đồng/ 1 quả để số tiền lãi thu được là lớn nhất.
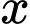 là số lần giảm giá bán bưởi
là số lần giảm giá bán bưởi 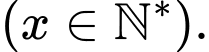
Khi đó số tiền giảm giá cho mỗi quả bưởi là

Suy ra giá bán của mỗi quả bưởi là
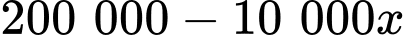 và số bưởi bán được là
và số bưởi bán được là 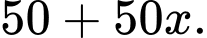
Lợi nhuận cửa hàng thu được là
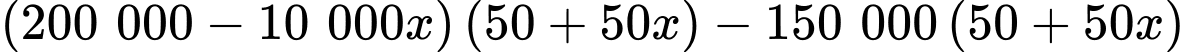
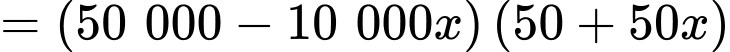
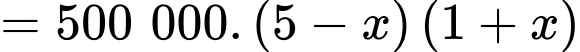
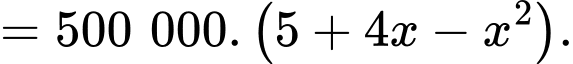
Xét hàm số
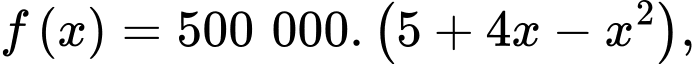 với
với 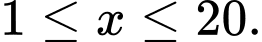
Ta có
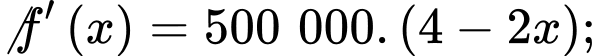
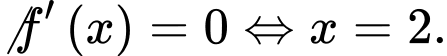
Bảng biến thiên

Dựa vào bảng biến thiên, ta có
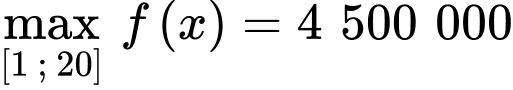 tại
tại 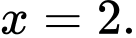
Suy ra giá bán bưởi để cửa hàng đó thu được lợi nhuận lớn nhất là
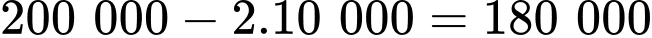 đồng.
đồng.
Vậy cửa hàng cần bán bưởi với giá
 đồng/ 1 quả để số tiền lãi thu được là lớn nhất.
đồng/ 1 quả để số tiền lãi thu được là lớn nhất.
Câu 24 [384376]: Một cửa hàng bán lẻ bán 2500 cái tivi mỗi năm. Chi phí gửi trong kho là 10 USD một cái một năm. Để đặt hàng nhà sản xuất thì mỗi lần chi phí cố định là 20 USD, cộng thêm 9 USD mỗi cái. Biết rằng số lượng tivi trung bình gửi trong kho bằng một nửa số tivi của mỗi lần đặt hàng. Như vậy cửa hàng nên đặt hàng nhà sản xuất bao nhiêu lần mỗi năm để chi phí hàng tồn kho là thấp nhất ?
Đáp số:…………………………………….
Đáp số:…………………………………….
Gọi 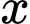 là số tivi mỗi lần đặt hàng, ta có
là số tivi mỗi lần đặt hàng, ta có 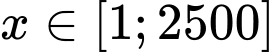
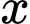 là số tivi mỗi lần đặt hàng, ta có
là số tivi mỗi lần đặt hàng, ta có 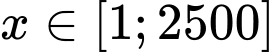
Khi đó, số lượng tivi trung bình gửi trong kho sẽ là 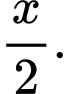
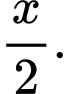
Vì vậy, chi phí gửi hàng trong khi mỗi năm sẽ là: 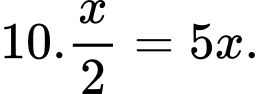
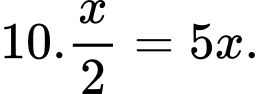
Số lần đặt hàng mỗi năm sẽ là: 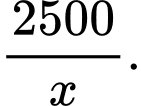
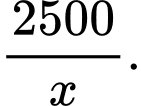
Do đó chi phí đặt hàng mỗi năm sẽ là: 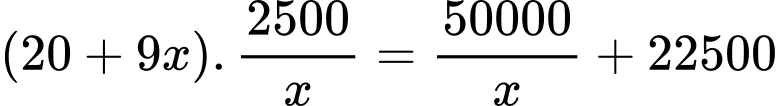
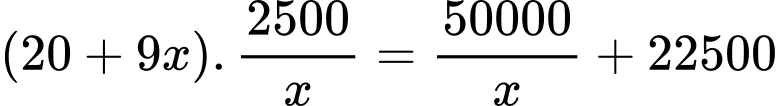
Vậy chi phí hàng tồn kho là: 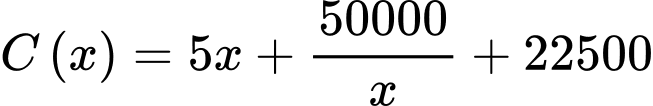
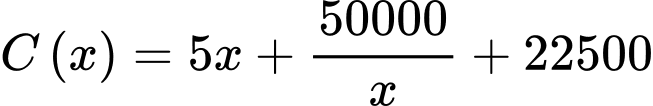
Từ đây, bài toán trở thành tìm giá trị nhỏ nhất của 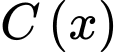 với
với 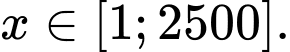
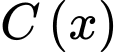 với
với 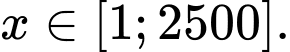
Ta có: 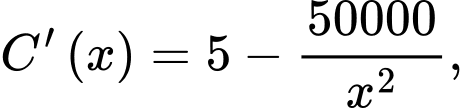
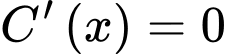
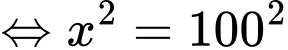
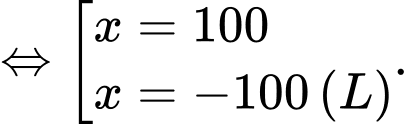
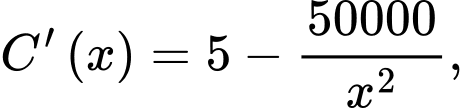
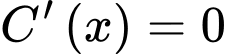
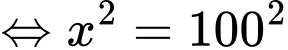
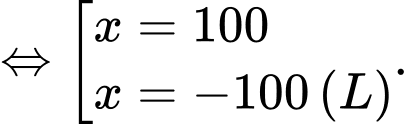
Do 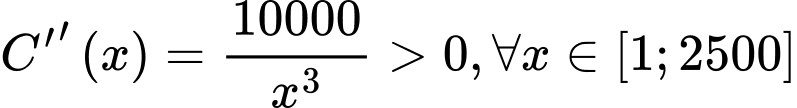 nên
nên 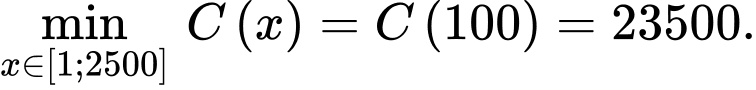
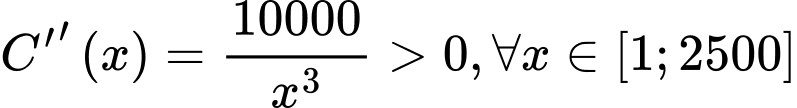 nên
nên 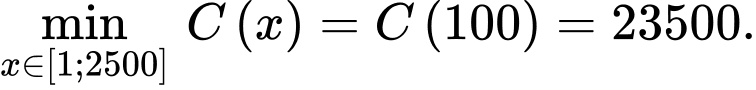
Khi đó số lần đặt hàng mỗi năm sẽ là: 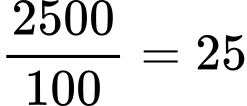 lần.
lần.
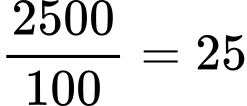 lần.
lần.
Câu 25 [6167]: Một xưởng sản xuất những thùng bằng kẽm hình hộp chữ nhật không có nắp và có các kích thước 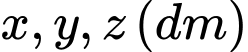 . Biết tỉ số hai cạnh đáy là
. Biết tỉ số hai cạnh đáy là 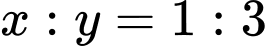 và thể tích của hộp bằng
và thể tích của hộp bằng 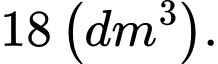 Để tốn ít vật liệu nhất thì tổng
Để tốn ít vật liệu nhất thì tổng 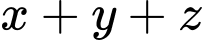 bằng
bằng
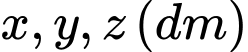 . Biết tỉ số hai cạnh đáy là
. Biết tỉ số hai cạnh đáy là 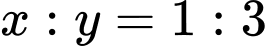 và thể tích của hộp bằng
và thể tích của hộp bằng 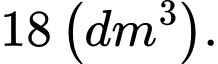 Để tốn ít vật liệu nhất thì tổng
Để tốn ít vật liệu nhất thì tổng 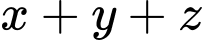 bằng
bằng A,
B,
C,
D,
Đáp án C.
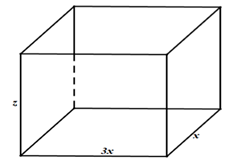
Đáy có kích thước là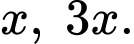 Chiều cao là
Chiều cao là 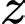 nên thể tích thùng là
nên thể tích thùng là 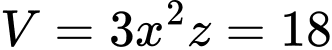
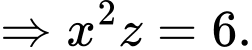
Để tốn ít vật liệu nhất thì diện tích sản xuất phải nhỏ nhất.
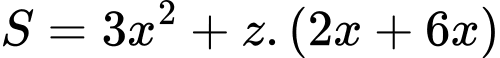
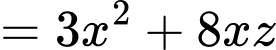
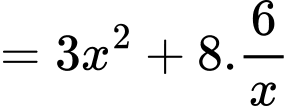
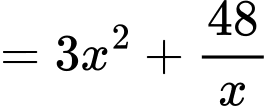
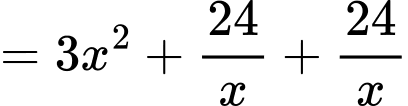
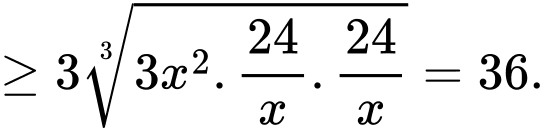
Dấu bằng xảy ra khi và chỉ khi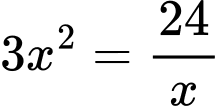
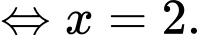
Khi đó,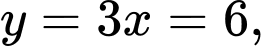
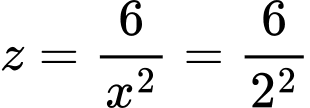
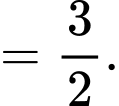
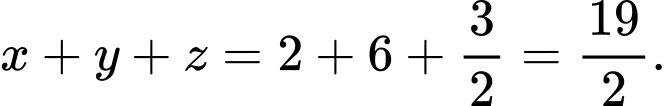 Đáp án: C
Đáp án: C

Đáy có kích thước là
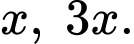 Chiều cao là
Chiều cao là 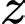 nên thể tích thùng là
nên thể tích thùng là 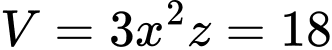
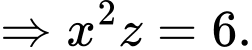
Để tốn ít vật liệu nhất thì diện tích sản xuất phải nhỏ nhất.
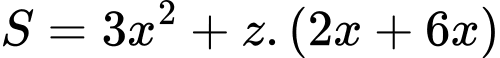
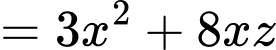
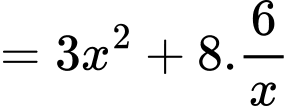
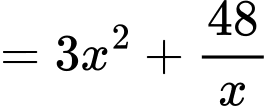
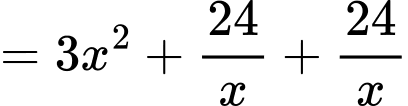
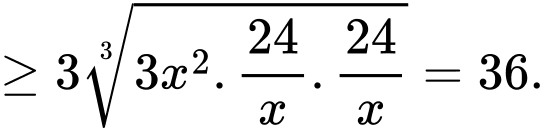
Dấu bằng xảy ra khi và chỉ khi
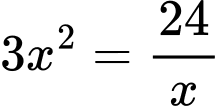
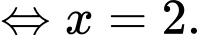
Khi đó,
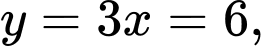
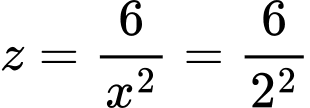
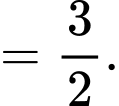
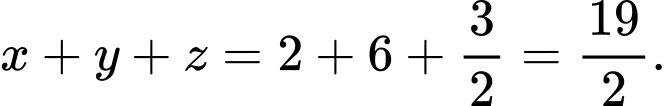 Đáp án: C
Đáp án: C
Câu 26 [327615]: [Đề thi THPT QG năm 2018] Ông  dự định sử dụng hết
dự định sử dụng hết 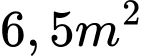 kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
 dự định sử dụng hết
dự định sử dụng hết 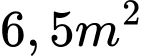 kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)? A, 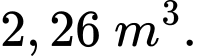
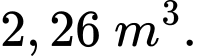
B, 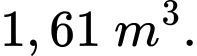
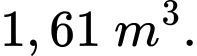
C, 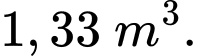
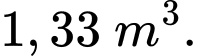
D, 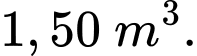
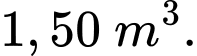
Vì chiều dài bể cá gấp đôi chiều rộng nên ta gọi chiều rộng, chiều dài, chiều cao của bể cá lần lượt là
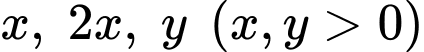
Thể tích của bể cá là:
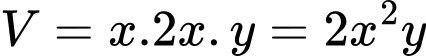
Ta sẽ tìm mối quan hệ giữa
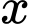 và
và 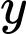 dựa vào diện tích phần lắp kính:
dựa vào diện tích phần lắp kính: 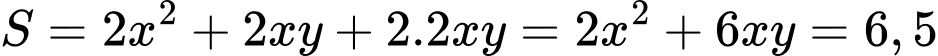
Rút
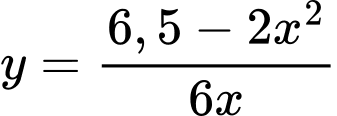 (với
(với 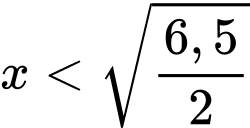 ) ta có:
) ta có: 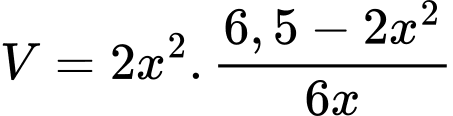
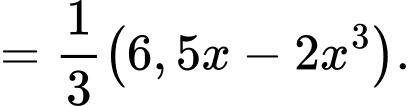
Xét hàm số
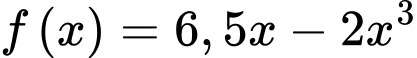 với
với 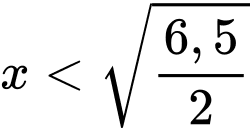 ta có:
ta có: 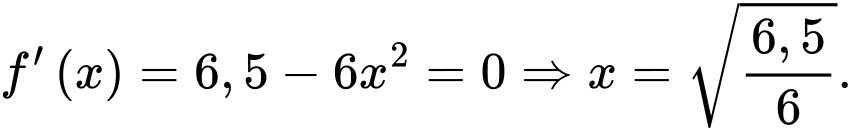
Lập BBT suy ra
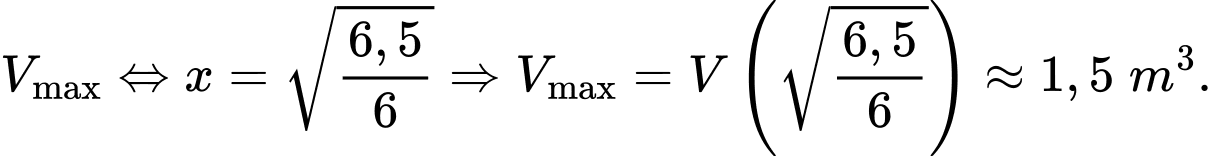 Chọn D. Đáp án: D
Chọn D. Đáp án: D
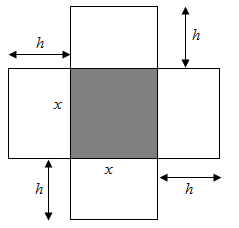
Câu 27 [327622]: Một hộp không nắp được làm từ một mảnh các tông theo hình vẽ. Hộp có đáy là một hình vuông cạnh  chiều cao
chiều cao  và thể tích
và thể tích 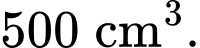 Tính độ dài cạnh hình vuông
Tính độ dài cạnh hình vuông 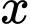 sao cho chiếc hộp làm ra tốn ít bìa cát tông nhất.
sao cho chiếc hộp làm ra tốn ít bìa cát tông nhất.
 chiều cao
chiều cao  và thể tích
và thể tích 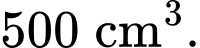 Tính độ dài cạnh hình vuông
Tính độ dài cạnh hình vuông 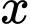 sao cho chiếc hộp làm ra tốn ít bìa cát tông nhất.
sao cho chiếc hộp làm ra tốn ít bìa cát tông nhất.
A, 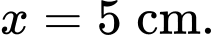
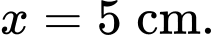
B, 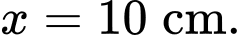
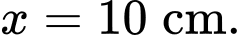
C, 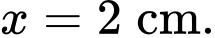
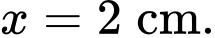
D, 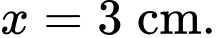
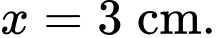
Theo giả thiết ta có thể tích chiếc hộp là 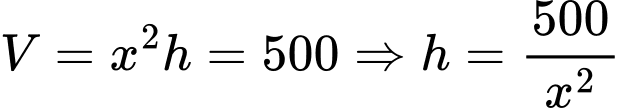
Diện tích các mạnh cát tông là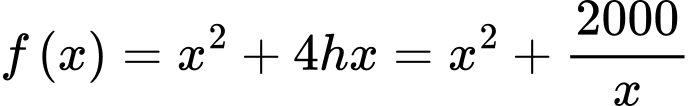
Xét hàm số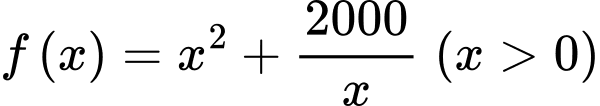 ta có:
ta có: 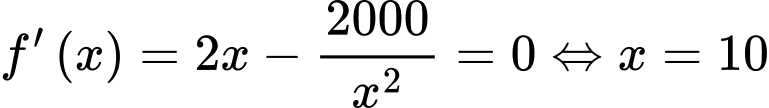
Lập bảng biến thiên ta có: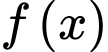 nhỏ nhất khi
nhỏ nhất khi 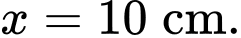 Chọn B.
Đáp án: B
Chọn B.
Đáp án: B
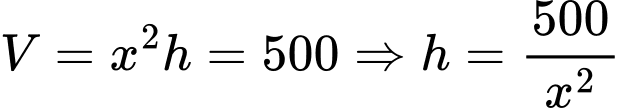
Diện tích các mạnh cát tông là
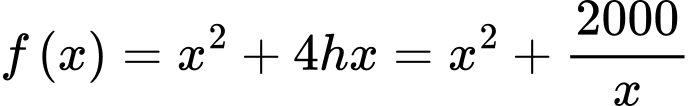
Xét hàm số
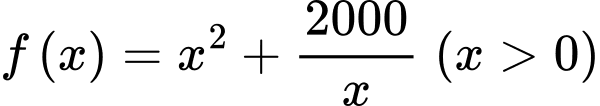 ta có:
ta có: 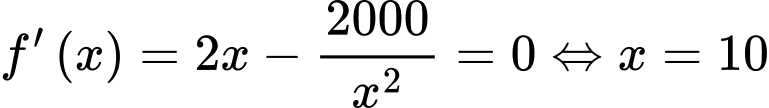
Lập bảng biến thiên ta có:
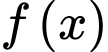 nhỏ nhất khi
nhỏ nhất khi 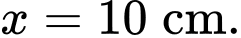 Chọn B.
Đáp án: B
Chọn B.
Đáp án: B
Câu 28 [383949]: Từ một miếng bìa hình chữ nhật với kích thước 20 cm × 10 cm, bạn Lan cắt bỏ hai hình vuông có cạnh là x (cm) và hai hình chữ nhật (phần gạch sọc như hình vẽ) rồi gấp theo đường nét đứt và dán các mép để được một cái hộp có dạng hình hộp chữ nhật. Thể tích lớn nhất của chiếc hộp có thể đạt được là bao nhiêu (làm tròn kết quả đến hàng phần chục)?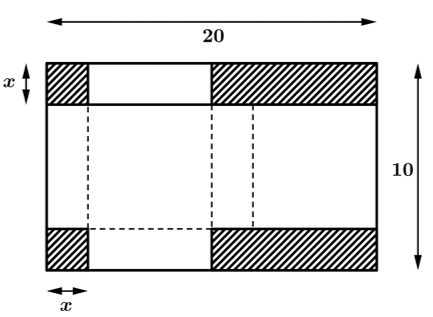

Dựa vào hình minh họa đã cho, ta có kích thước đáy của hộp có dạng hình hộp chữ nhật lần lượt là 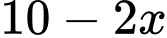 và
và 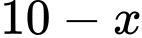 (cm) với
(cm) với 
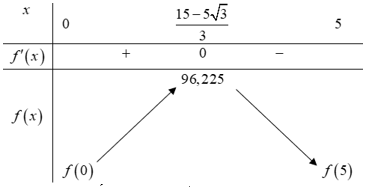
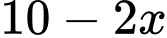 và
và 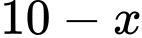 (cm) với
(cm) với 
Hộp có chiều cao là: 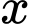 (cm).
(cm).
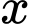 (cm).
(cm). Thể tích của chiếc hộp là: 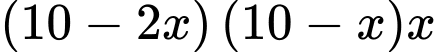 (
(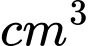 )
)
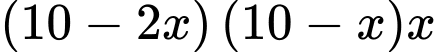 (
(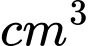 )
) Bài toán trở thành tìm giá trị lớn nhất của hàm số: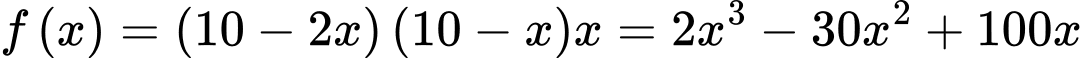 với
với 
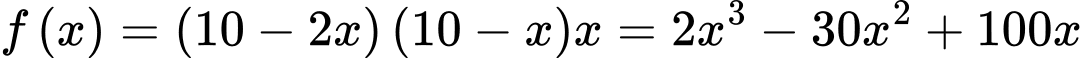 với
với 
Có: 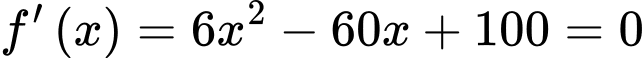
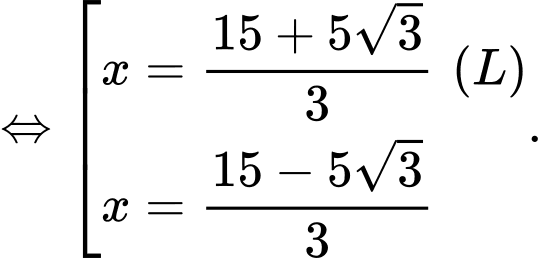
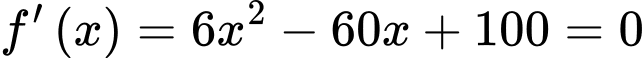
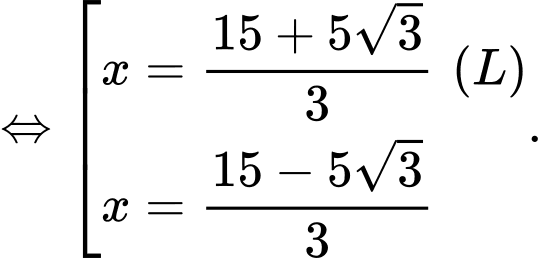
Bảng biến thiên:

Dựa vào bảng biến thiên, ta có: 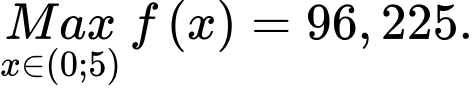
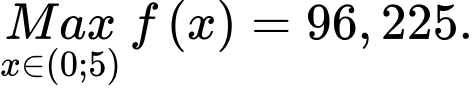
Suy ra thể tích lớn nhất của chiếc hộp có thể đạt được là: 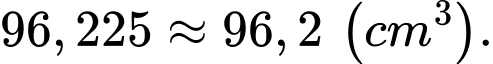
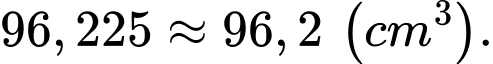
Câu 29 [383951]: [Trích Đề thi mẫu ĐGTD ĐH Bách Khoa HN]: Một người thợ nhôm kính nhận đơn đặt hàng làm một bể cá cảnh bằng kính dạng hình hộp chữ nhật không có nắp với thể tích bằng 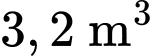 và chiều cao của bể gấp 2 lần chiều rộng của đáy. Biết giá một mét vuông kính để làm bể cá là 1 triệu đồng. Để mua đủ mét vuông kính làm bể cá theo yêu cầu thì người thợ cần tối thiểu số tiền bằng ... triệu đồng. (Coi độ dày của kính là không đáng kể so với kích thước của bể).
và chiều cao của bể gấp 2 lần chiều rộng của đáy. Biết giá một mét vuông kính để làm bể cá là 1 triệu đồng. Để mua đủ mét vuông kính làm bể cá theo yêu cầu thì người thợ cần tối thiểu số tiền bằng ... triệu đồng. (Coi độ dày của kính là không đáng kể so với kích thước của bể).
Đáp số:…………………..
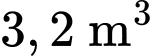 và chiều cao của bể gấp 2 lần chiều rộng của đáy. Biết giá một mét vuông kính để làm bể cá là 1 triệu đồng. Để mua đủ mét vuông kính làm bể cá theo yêu cầu thì người thợ cần tối thiểu số tiền bằng ... triệu đồng. (Coi độ dày của kính là không đáng kể so với kích thước của bể).
và chiều cao của bể gấp 2 lần chiều rộng của đáy. Biết giá một mét vuông kính để làm bể cá là 1 triệu đồng. Để mua đủ mét vuông kính làm bể cá theo yêu cầu thì người thợ cần tối thiểu số tiền bằng ... triệu đồng. (Coi độ dày của kính là không đáng kể so với kích thước của bể).Đáp số:…………………..
Gọi 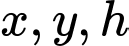
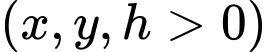 lần lượt là chiều rộng của đáy, chiều dài của đáy và chiều cao của bể.
lần lượt là chiều rộng của đáy, chiều dài của đáy và chiều cao của bể.
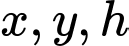
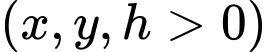 lần lượt là chiều rộng của đáy, chiều dài của đáy và chiều cao của bể.
lần lượt là chiều rộng của đáy, chiều dài của đáy và chiều cao của bể. Từ dữ kiện bài cho, ta có:
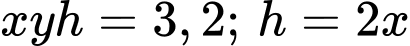
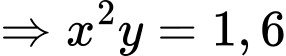
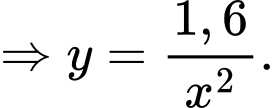
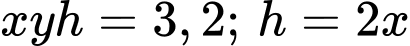
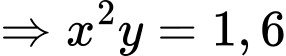
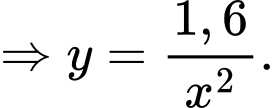
Tổng diện tích 5 mặt của bể cá là:
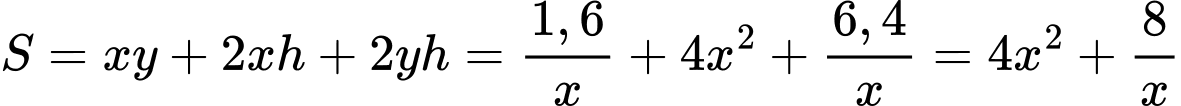
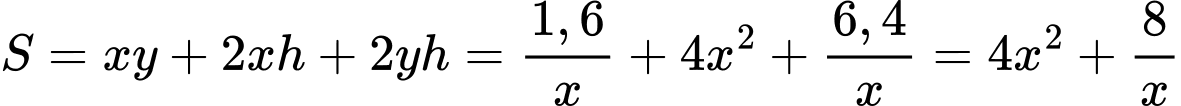
Sử dụng bất đẳng thức Cauchy 3 số dương ta có:
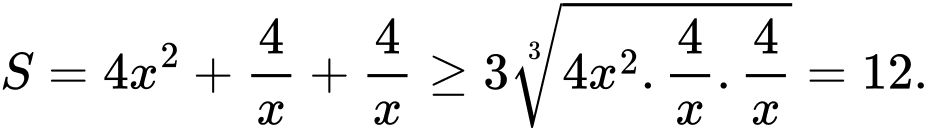
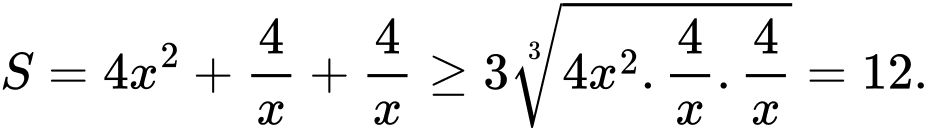
Dấu “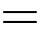 ” xảy ra khi và chỉ khi
” xảy ra khi và chỉ khi 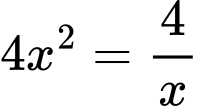
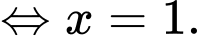
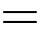 ” xảy ra khi và chỉ khi
” xảy ra khi và chỉ khi 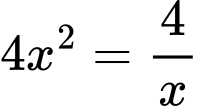
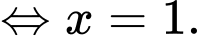
Lúc này chi phí tối thiểu để mua nguyên liệu là: 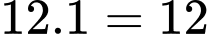 triệu.
triệu.
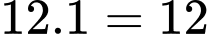 triệu.
triệu.
Câu 30 [390558]: Cần phải đặt một ngọn đèn điện ở phía trên và chính giữa một cái bàn hình tròn có bán kính 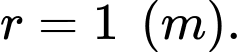 Hỏi phải treo ở độ cao h bằng bao nhiêu mét để mép bàn được nhiều ánh sáng nhất. Biết rằng cường độ sáng C được biểu thị bởi công thức
Hỏi phải treo ở độ cao h bằng bao nhiêu mét để mép bàn được nhiều ánh sáng nhất. Biết rằng cường độ sáng C được biểu thị bởi công thức 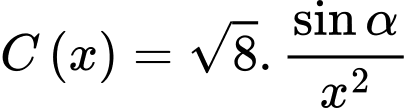 ( là góc nghiêng giữa tia sáng và mép bà và
( là góc nghiêng giữa tia sáng và mép bà và 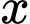 là khoảng cách từ bóng đèn đến mép bàn). Viết kết quả làm tròn đến hàng phần trăm.
là khoảng cách từ bóng đèn đến mép bàn). Viết kết quả làm tròn đến hàng phần trăm.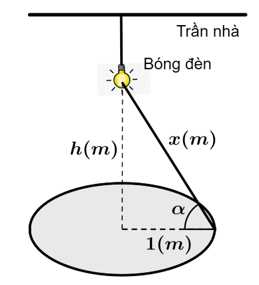
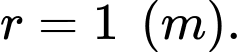 Hỏi phải treo ở độ cao h bằng bao nhiêu mét để mép bàn được nhiều ánh sáng nhất. Biết rằng cường độ sáng C được biểu thị bởi công thức
Hỏi phải treo ở độ cao h bằng bao nhiêu mét để mép bàn được nhiều ánh sáng nhất. Biết rằng cường độ sáng C được biểu thị bởi công thức 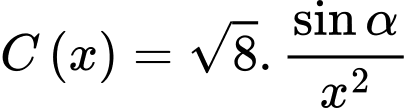 ( là góc nghiêng giữa tia sáng và mép bà và
( là góc nghiêng giữa tia sáng và mép bà và 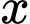 là khoảng cách từ bóng đèn đến mép bàn). Viết kết quả làm tròn đến hàng phần trăm.
là khoảng cách từ bóng đèn đến mép bàn). Viết kết quả làm tròn đến hàng phần trăm.
Đáp số:………………………………
Dựa vào hình ảnh minh họa, ta có: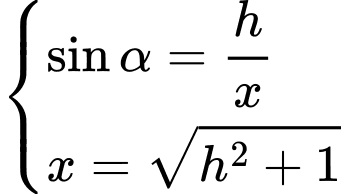
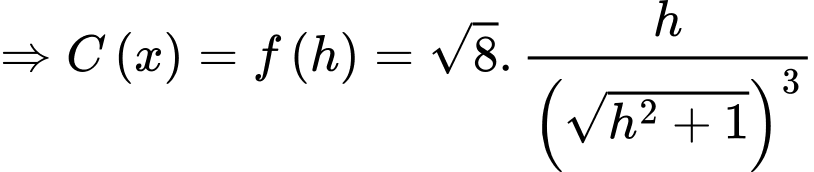
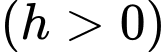
Đặt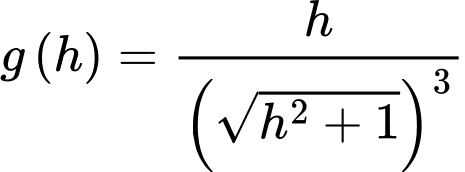
Có: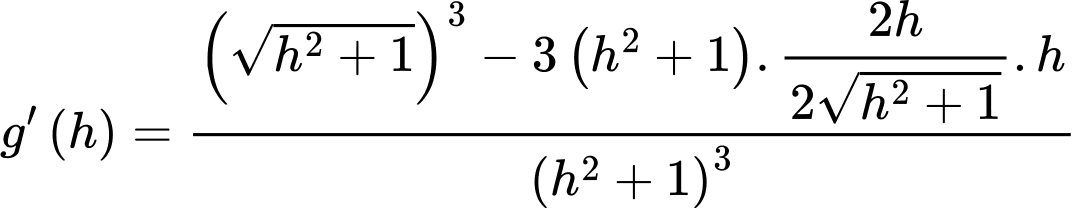
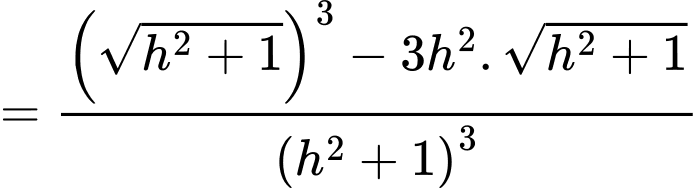
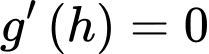
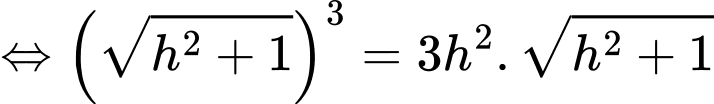
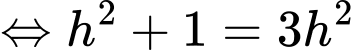
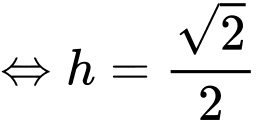
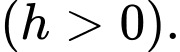
Bảng biến thiên:
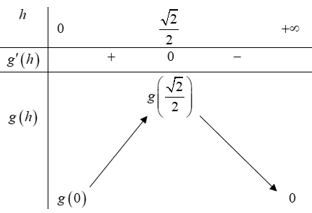
Dựa vào bảng biến thiên, để mép bàn được nhiều ánh sáng nhất thì giá trị của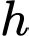 là:
là: 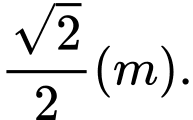
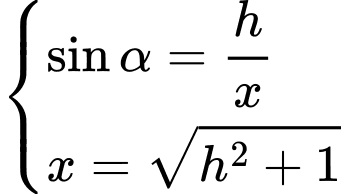
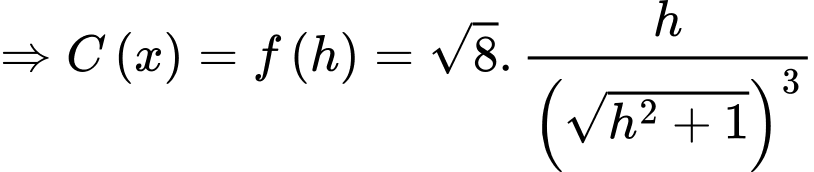
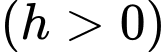
Đặt
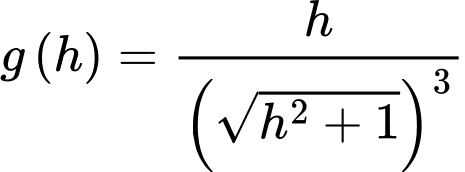
Có:
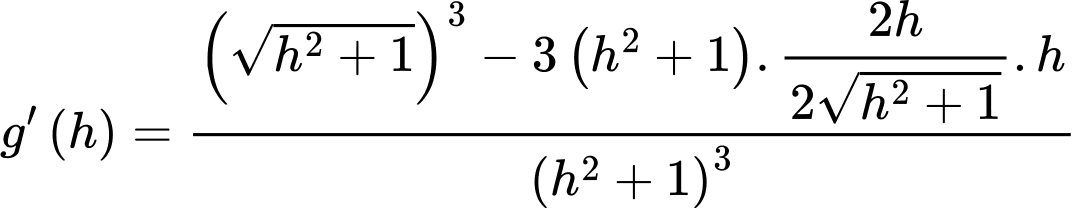
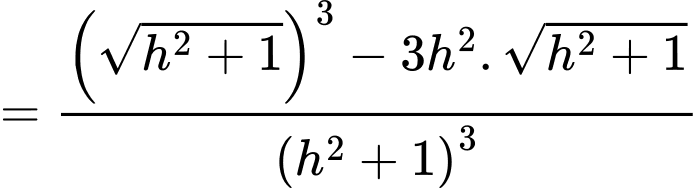
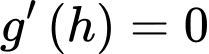
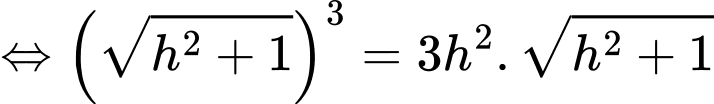
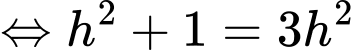
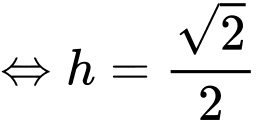
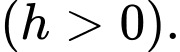
Bảng biến thiên:

Dựa vào bảng biến thiên, để mép bàn được nhiều ánh sáng nhất thì giá trị của
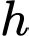 là:
là: 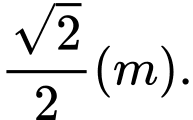
Câu 31 [383952]: [Trích Đề thi mẫu ĐGNL ĐHQG Hà Nội]: Người ta cần chế tạo các món quà lưu niệm bằng đồng có dạng khối chóp tứ giác đều, được mạ vàng bốn mặt bên và có thể tích bằng  Diện tích mạ vàng nhỏ nhất của khối chóp bằng bao nhiêu
Diện tích mạ vàng nhỏ nhất của khối chóp bằng bao nhiêu 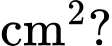
(Kết quả làm tròn đến hàng đơn vị)
Đáp số:…………………………………….
 Diện tích mạ vàng nhỏ nhất của khối chóp bằng bao nhiêu
Diện tích mạ vàng nhỏ nhất của khối chóp bằng bao nhiêu 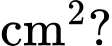
(Kết quả làm tròn đến hàng đơn vị)
Đáp số:…………………………………….
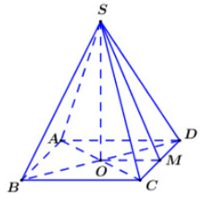
Giả sử chóp tứ giác đều là
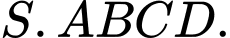 Gọi
Gọi 
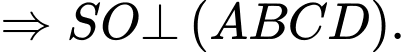
Đặt
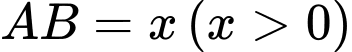 ta có
ta có 
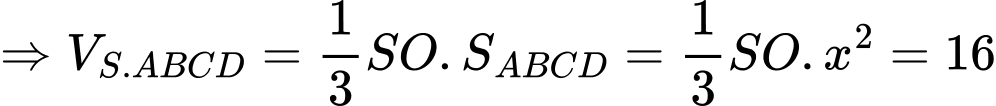
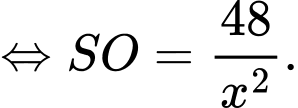
Gọi M là trung điểm của CD ta có:
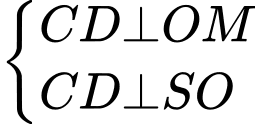
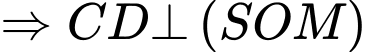
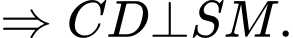
Ta có:
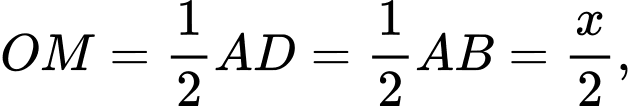 áp dụng định lí Pytago ta có:
áp dụng định lí Pytago ta có: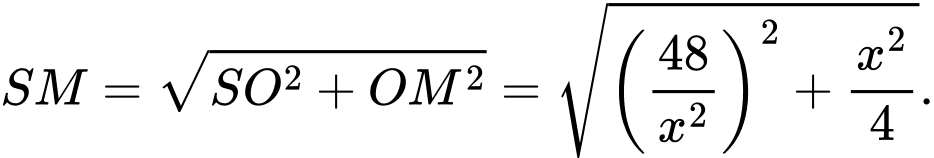
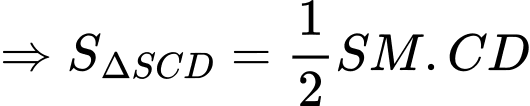
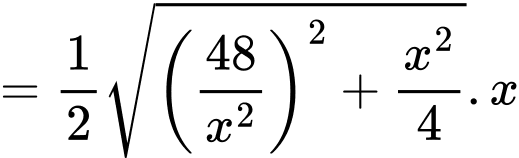
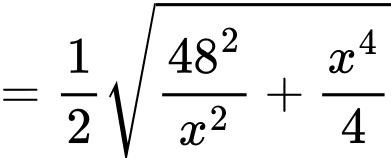
Để diện tích mạ vàng nhỏ nhất thì
 nhỏ nhất
nhỏ nhất 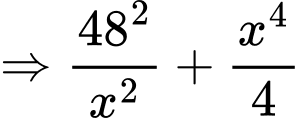 đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất. Ta có:
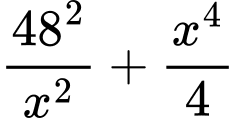
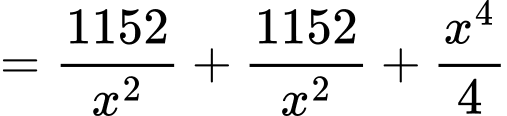
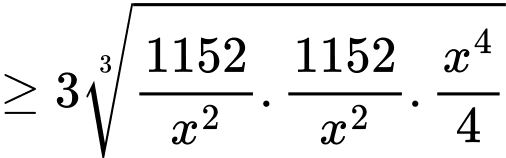
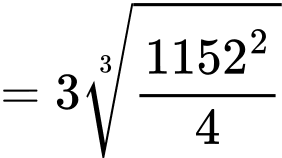 (BĐT Cauchy).
(BĐT Cauchy). Vậy diện tích mạ vàng nhỏ nhất là:
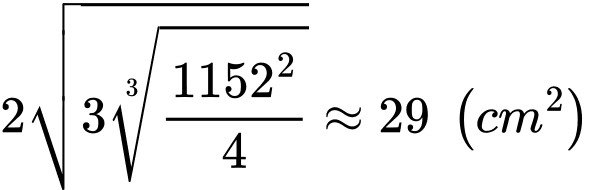
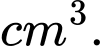
Câu 32 [390559]: Một người thợ thủ công muốn làm một con diều bằng giấy có kích thước 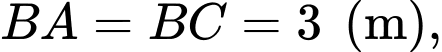
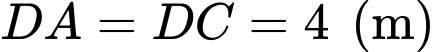 như hình vẽ bên. Khi diện tích con diều lớn nhất, em hãy tính độ dài đường chéo
như hình vẽ bên. Khi diện tích con diều lớn nhất, em hãy tính độ dài đường chéo 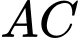 theo đơn vị mét.
theo đơn vị mét. 
Đáp số:…………………….
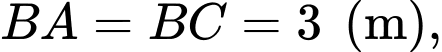
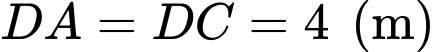 như hình vẽ bên. Khi diện tích con diều lớn nhất, em hãy tính độ dài đường chéo
như hình vẽ bên. Khi diện tích con diều lớn nhất, em hãy tính độ dài đường chéo 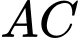 theo đơn vị mét.
theo đơn vị mét. 
Đáp số:…………………….
Cách 1: Xem video bài giảng (cách này sẽ ngắn hơn)
Cách 2: Sử dụng phương pháp hàm số.
Gọi là giao điểm của
là giao điểm của 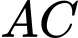 và
và 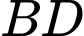 .
.
Gọi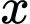 là độ dài của
là độ dài của 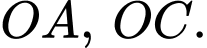

Diện tích của con diều là: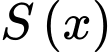 =
= 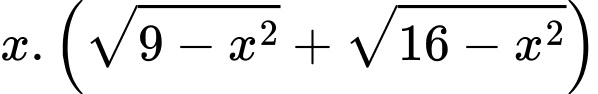 với
với 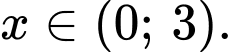
Lại có: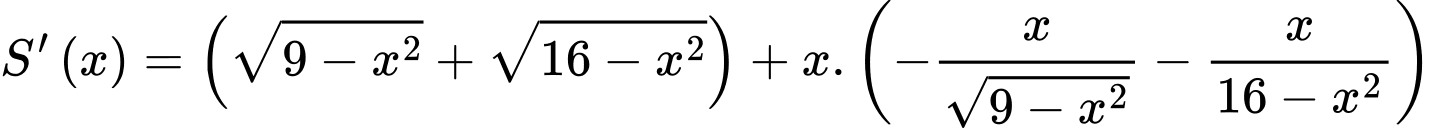
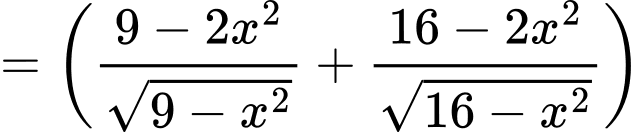
Do vậy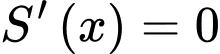
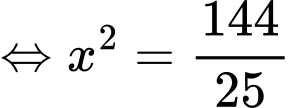
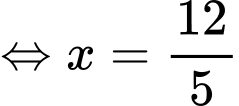
Bảng biến thiên:
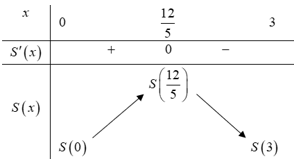 Dựa vào bảng biến thiên, suy ra khi diện tích con diều lớn nhất thì độ dài đường chéo
Dựa vào bảng biến thiên, suy ra khi diện tích con diều lớn nhất thì độ dài đường chéo 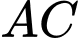 là:
là: 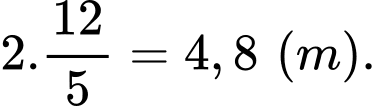
Cách 2: Sử dụng phương pháp hàm số.
Gọi
 là giao điểm của
là giao điểm của 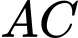 và
và 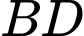 .
.Gọi
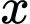 là độ dài của
là độ dài của 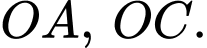

Diện tích của con diều là:
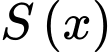 =
= 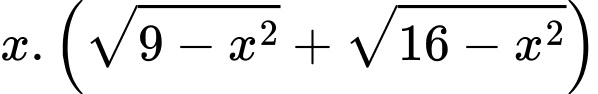 với
với 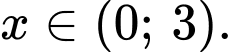
Lại có:
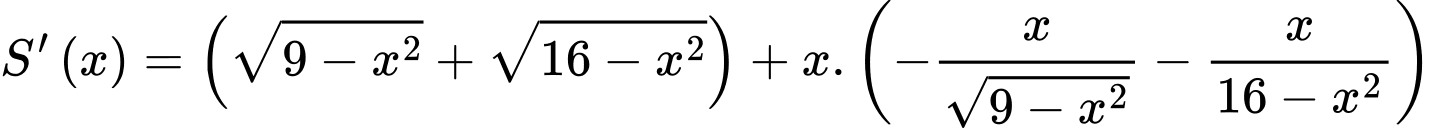
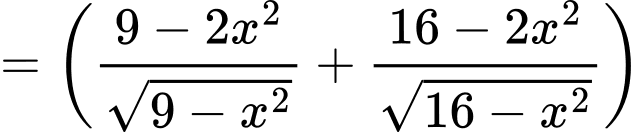
Do vậy
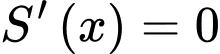
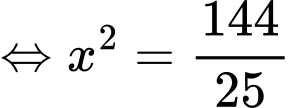
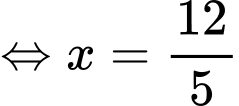
Bảng biến thiên:
 Dựa vào bảng biến thiên, suy ra khi diện tích con diều lớn nhất thì độ dài đường chéo
Dựa vào bảng biến thiên, suy ra khi diện tích con diều lớn nhất thì độ dài đường chéo 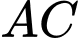 là:
là: