Đáp án Bài tập tự luyện
Câu 1 [510423]: [Học kỳ 2-Chuyên LHP-Nam Định] Xét các số thực 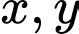 thỏa mãn
thỏa mãn 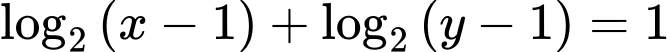 . Khi biểu thức
. Khi biểu thức 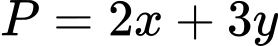 đạt giá trị nhỏ nhất thì
đạt giá trị nhỏ nhất thì 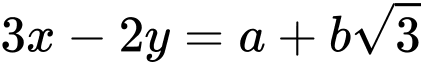 với
với 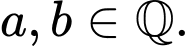 Tính
Tính 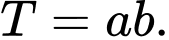
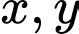 thỏa mãn
thỏa mãn 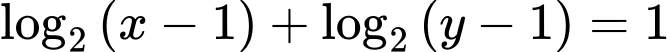 . Khi biểu thức
. Khi biểu thức 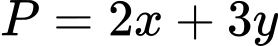 đạt giá trị nhỏ nhất thì
đạt giá trị nhỏ nhất thì 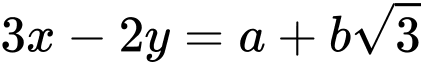 với
với 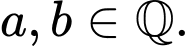 Tính
Tính 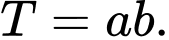
A, 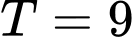 .
.
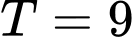 .
.B, 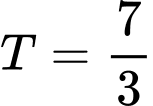 .
.
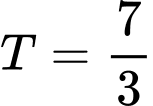 .
.C, 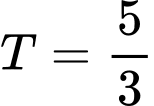 .
.
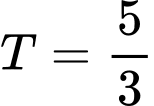 .
.D, 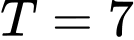 .
.
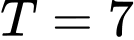 .
.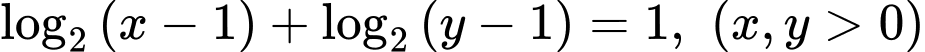
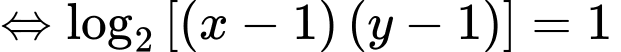
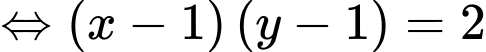
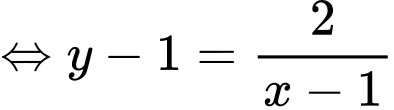
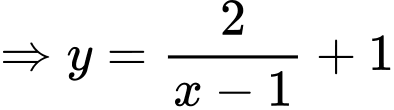
Có:
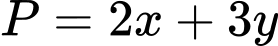
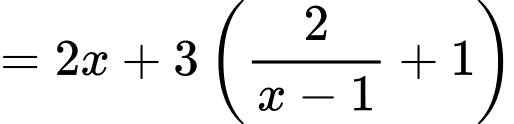
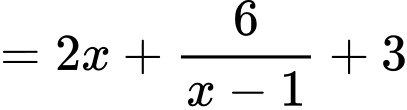
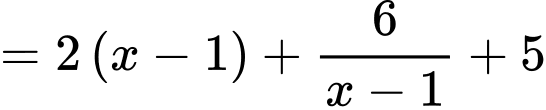
Áp dụng bất đẳng thức Co-si, ta có:
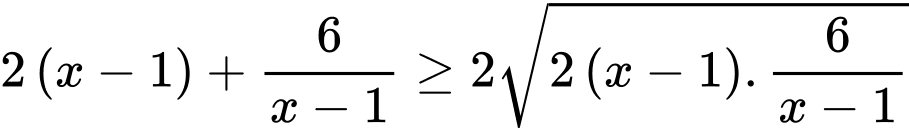
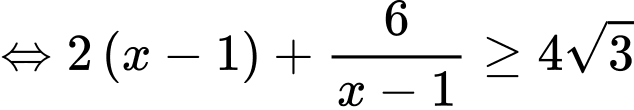
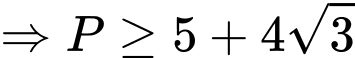
Dấu ‘’=’’ xảy ra khi và chỉ khi:
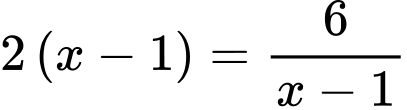
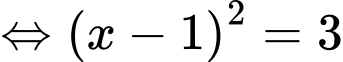
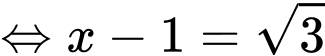
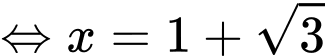
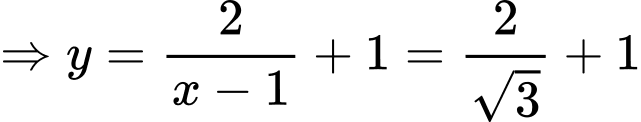
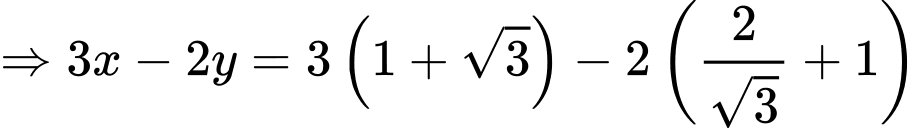
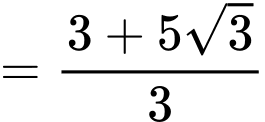
Đáp án: C. Đáp án: C
Câu 2 [789066]: (SỞ GD&ĐT TIỀN GIANG NĂM 2019-2020) Xét các số thực dương 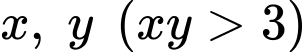 thỏa mãn
thỏa mãn 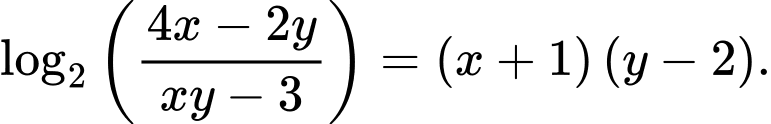 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức 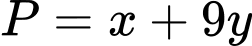 bằng
bằng
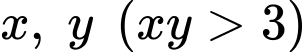 thỏa mãn
thỏa mãn 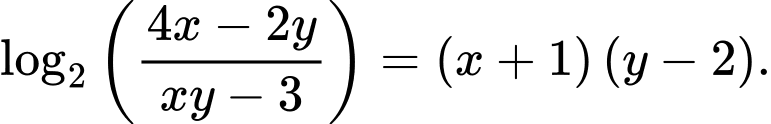 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức 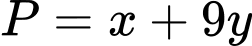 bằng
bằng A, 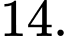
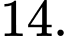
B, 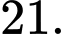
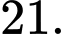
C, 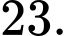
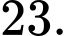
D, 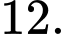
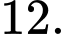
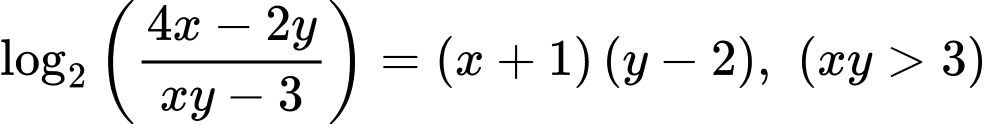
Giả sử:
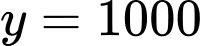 ta bấm máy tính được
ta bấm máy tính được 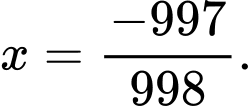
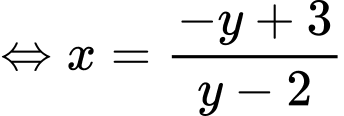
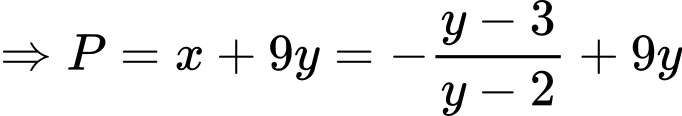
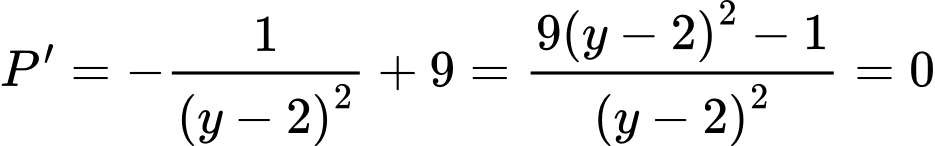
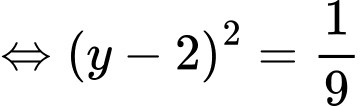
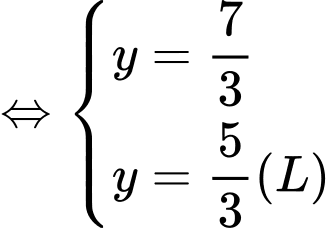 vì
vì 
 tại
tại 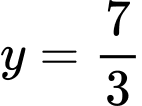
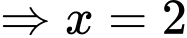
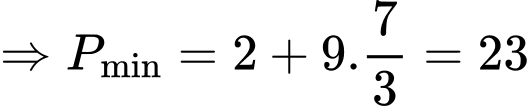
Đáp án: C. Đáp án: C
Câu 3 [79825]: Cho hai số thực dương 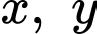 thỏa mãn điều kiện
thỏa mãn điều kiện 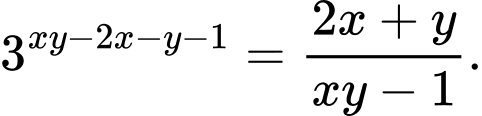 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức 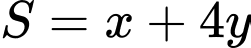 bằng
bằng
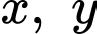 thỏa mãn điều kiện
thỏa mãn điều kiện 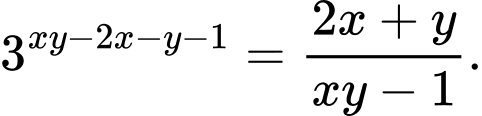 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức 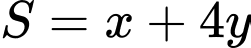 bằng
bằng A, 

B, 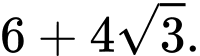
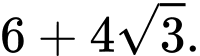
C, 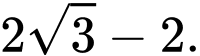
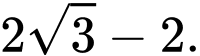
D, 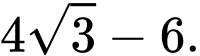
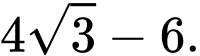
 Đáp án: A
Đáp án: A
Câu 4 [29507]: Xét các số thực 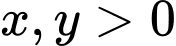 :
: 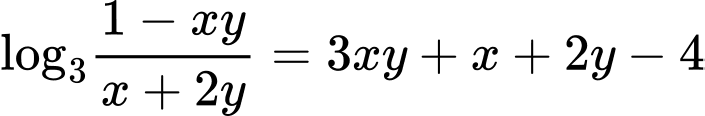 . Tìm giá trị nhỏ nhất của
. Tìm giá trị nhỏ nhất của 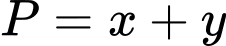
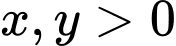 :
: 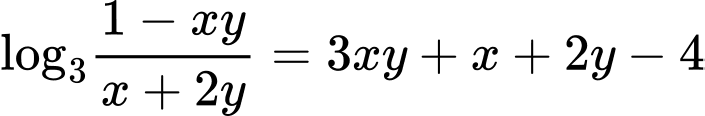 . Tìm giá trị nhỏ nhất của
. Tìm giá trị nhỏ nhất của 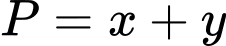
A, 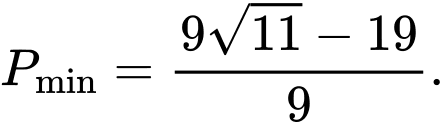
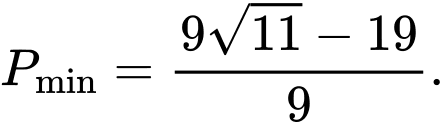
B, 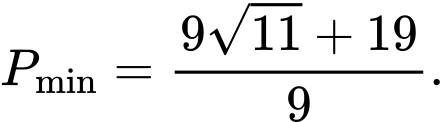
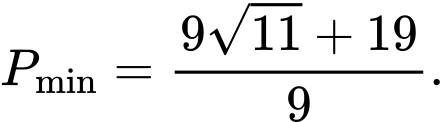
C, 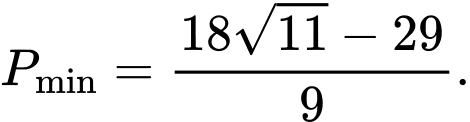
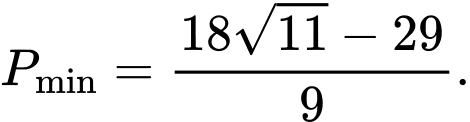
D, 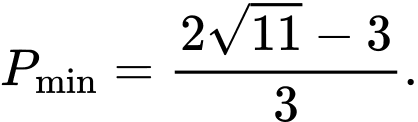
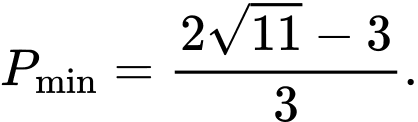
Ta có 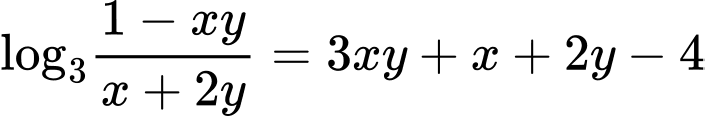
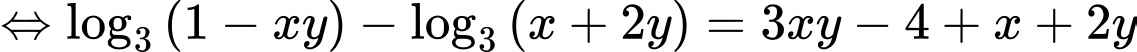
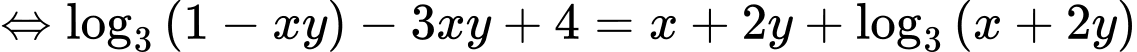


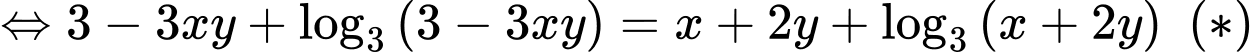
Xét hàm số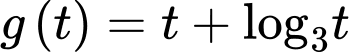 trên khoảng
trên khoảng 
Ta có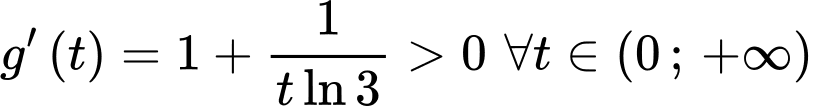
Suy ra hàm số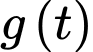 đồng biến trên khoảng
đồng biến trên khoảng 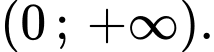
Khi đó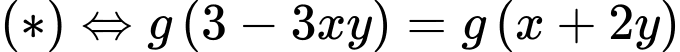
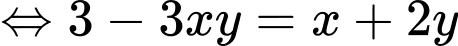
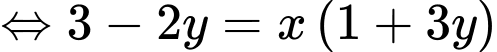
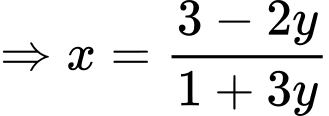
Vì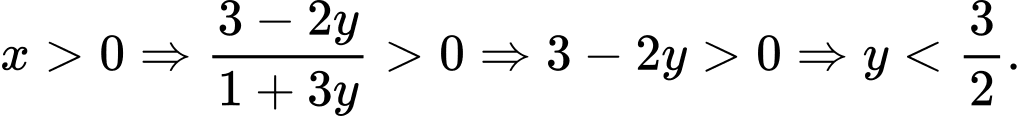
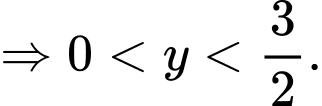
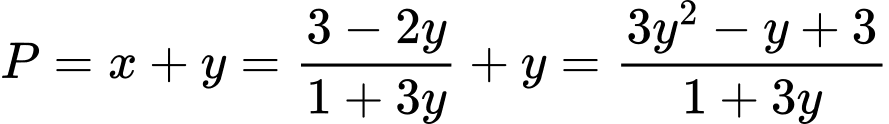
Khảo sát hàm số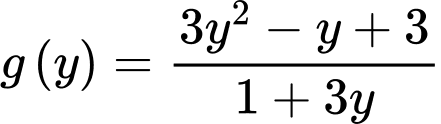 trên khoảng
trên khoảng 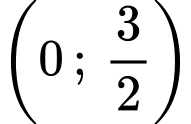
Ta có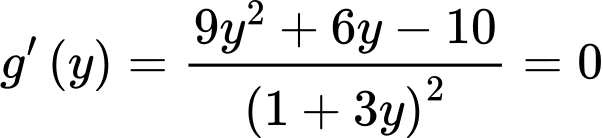
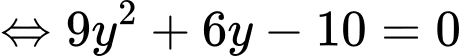
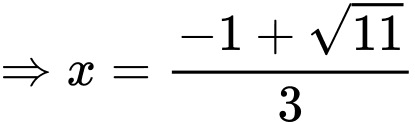
Lại có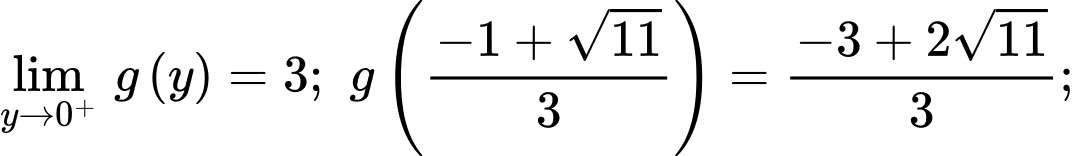
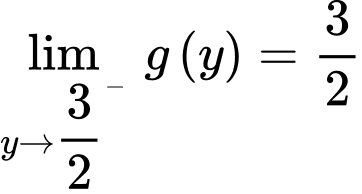
Suy ra giá trị nhỏ nhất của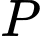 bằng
bằng 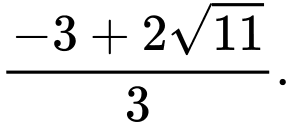
Chọn D.Đáp án: D
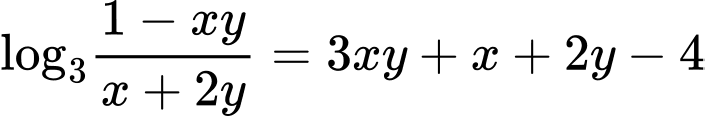
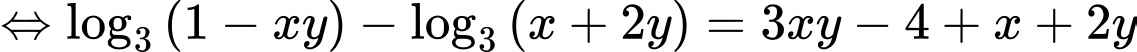
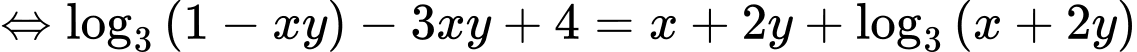


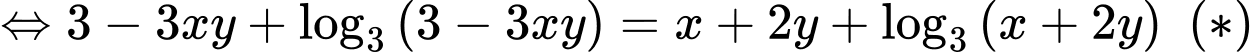
Xét hàm số
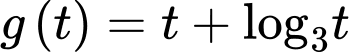 trên khoảng
trên khoảng 
Ta có
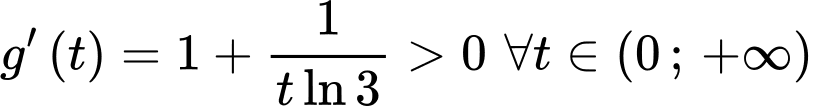
Suy ra hàm số
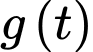 đồng biến trên khoảng
đồng biến trên khoảng 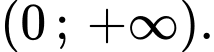
Khi đó
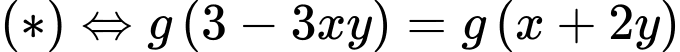
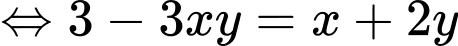
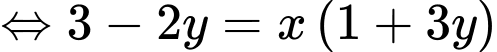
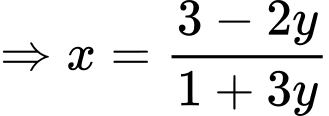
Vì
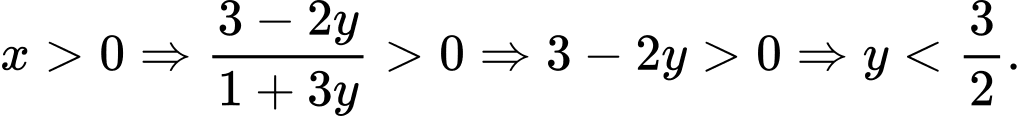
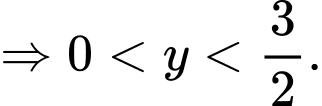
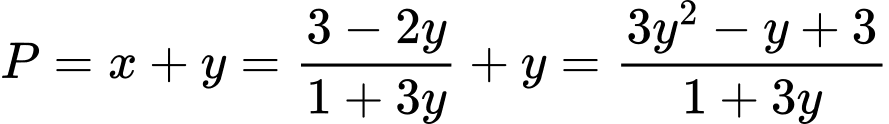
Khảo sát hàm số
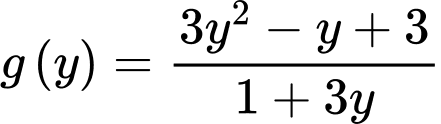 trên khoảng
trên khoảng 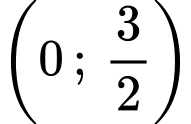
Ta có
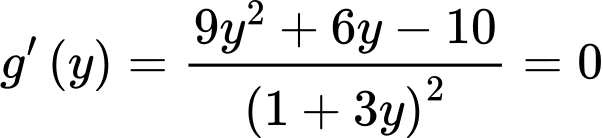
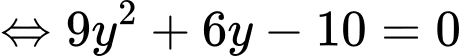
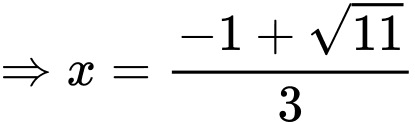
Lại có
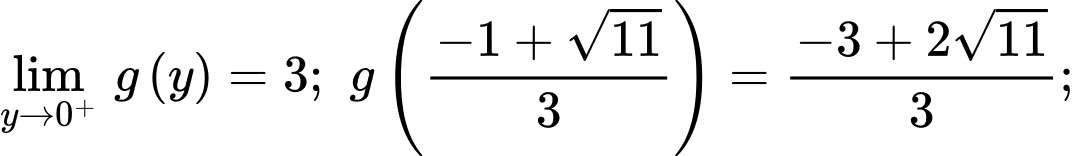
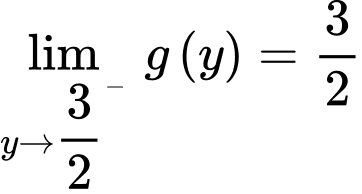
Suy ra giá trị nhỏ nhất của
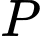 bằng
bằng 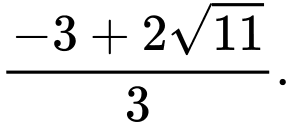
Chọn D.Đáp án: D
Câu 5 [29495]: Cho hai số thực dương 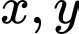 thay đổi thỏa mãn hệ thức
thay đổi thỏa mãn hệ thức 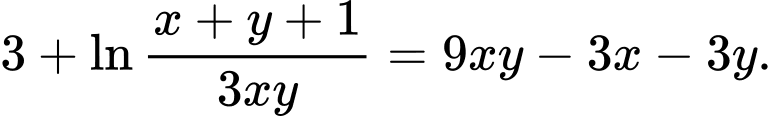 Tìm giá trị nhỏ nhất
Tìm giá trị nhỏ nhất 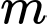 của biểu thức
của biểu thức 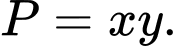
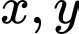 thay đổi thỏa mãn hệ thức
thay đổi thỏa mãn hệ thức 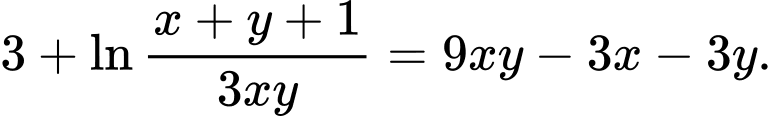 Tìm giá trị nhỏ nhất
Tìm giá trị nhỏ nhất 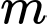 của biểu thức
của biểu thức 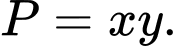
A, 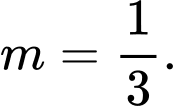
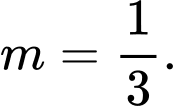
B, 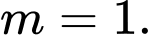
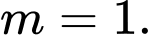
C, 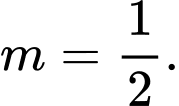
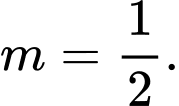
D, 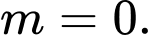
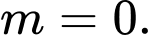
Ta có 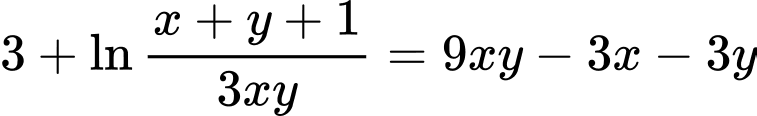
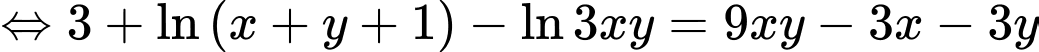
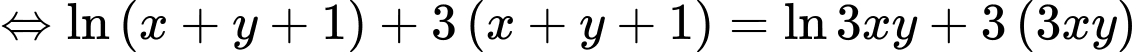
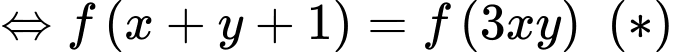
Xét hàm đặc trưng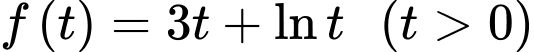
Ta có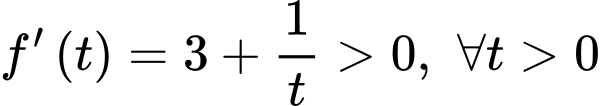
Suy ra hàm số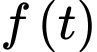 đồng biến.
đồng biến.
Khi đó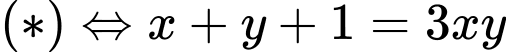
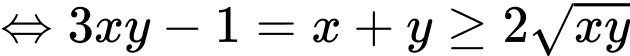 (theo BĐT AM – GM)
(theo BĐT AM – GM)
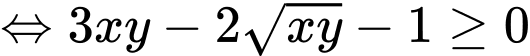
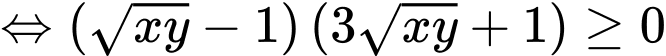
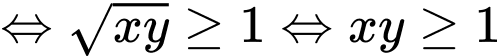
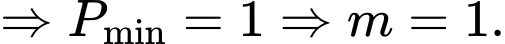
Chọn B. Đáp án: B
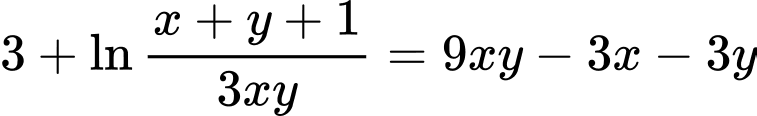
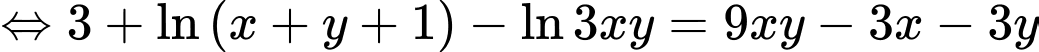
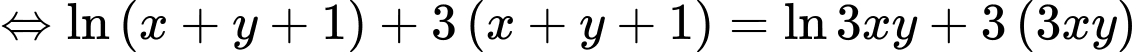
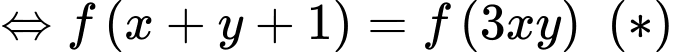
Xét hàm đặc trưng
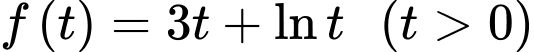
Ta có
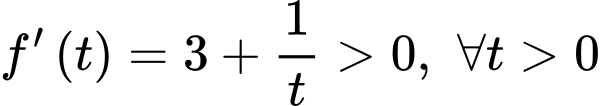
Suy ra hàm số
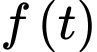 đồng biến.
đồng biến.
Khi đó
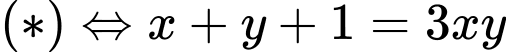
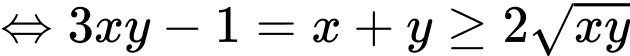 (theo BĐT AM – GM)
(theo BĐT AM – GM)
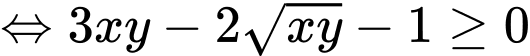
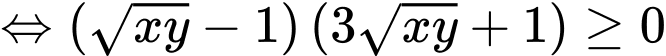
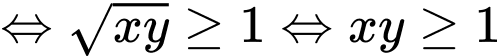
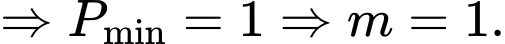
Chọn B. Đáp án: B
Câu 6 [803781]: Xét tất cả các số thực dương 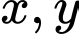 thỏa mãn
thỏa mãn 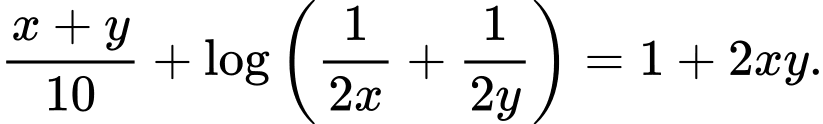 Khi biểu thức
Khi biểu thức 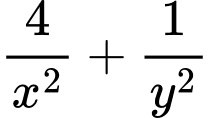 đạt giá trị nhỏ nhất, tích
đạt giá trị nhỏ nhất, tích 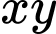 bằng
bằng
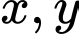 thỏa mãn
thỏa mãn 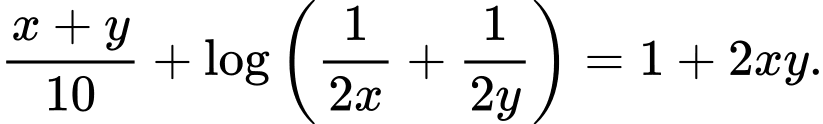 Khi biểu thức
Khi biểu thức 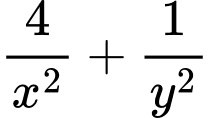 đạt giá trị nhỏ nhất, tích
đạt giá trị nhỏ nhất, tích 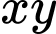 bằng
bằng A, 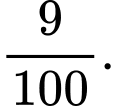
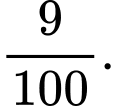
B, 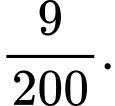
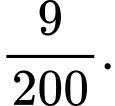
C, 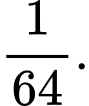
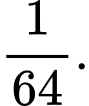
D, 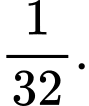
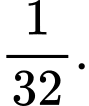
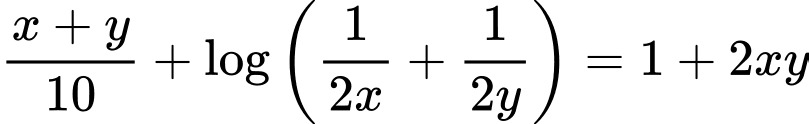
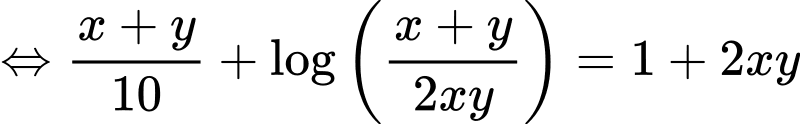
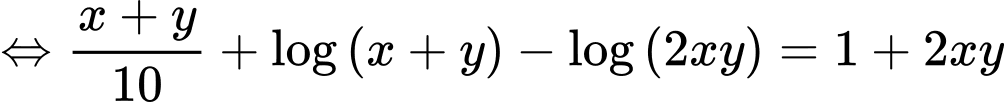
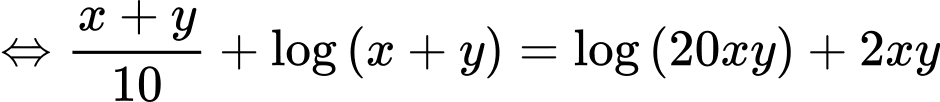
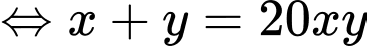
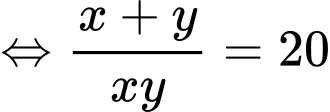
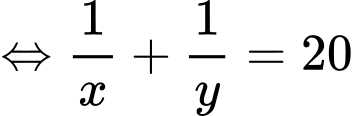
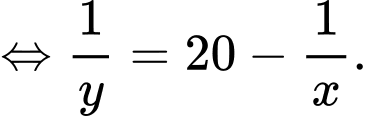
Khi đó:
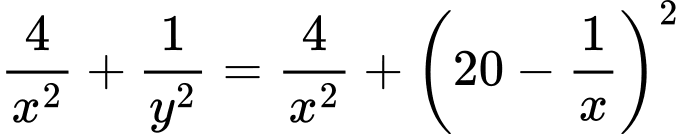
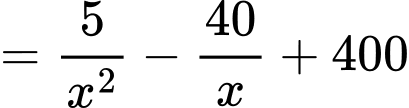
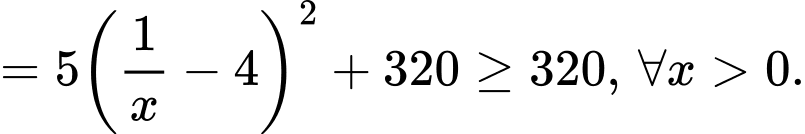
Dấu bằng xảy ra khi:
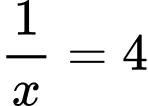
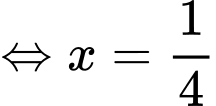
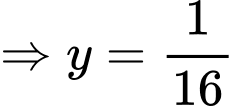
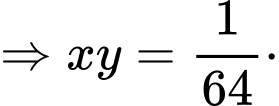
Chọn đáp án C. Đáp án: C
Câu 7 [282753]: Xét các số thực 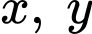 thoả mãn
thoả mãn 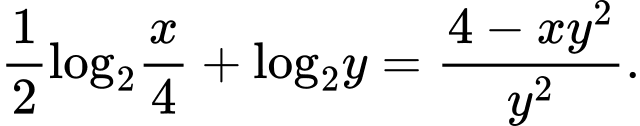 Khi
Khi 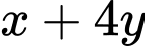 đạt giá trị nhỏ nhất thì giá trị
đạt giá trị nhỏ nhất thì giá trị 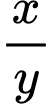 bằng
bằng
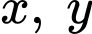 thoả mãn
thoả mãn 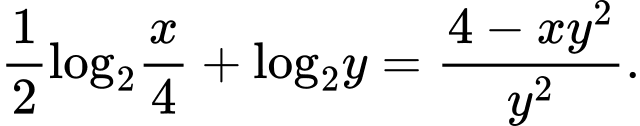 Khi
Khi 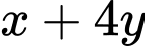 đạt giá trị nhỏ nhất thì giá trị
đạt giá trị nhỏ nhất thì giá trị 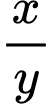 bằng
bằng A, 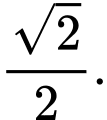
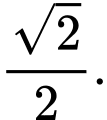
B, 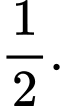
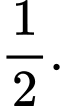
C, 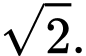
D, 
a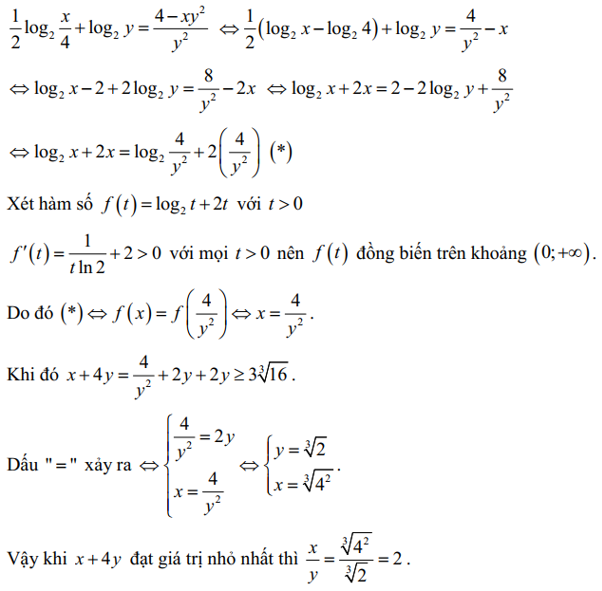 Đáp án: D
Đáp án: D
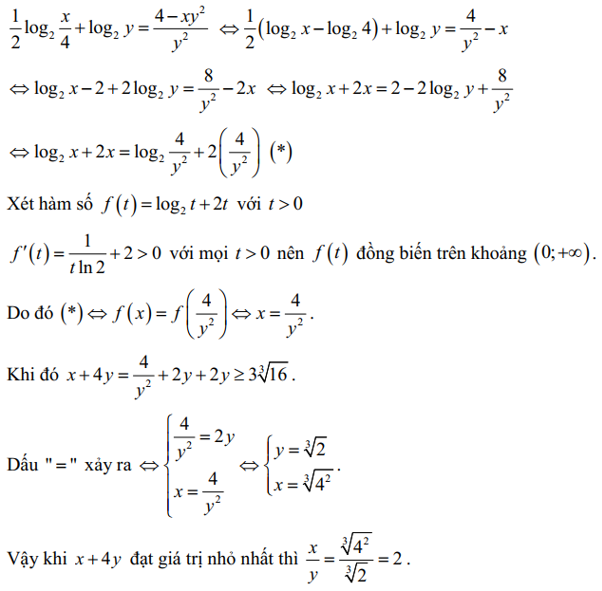 Đáp án: D
Đáp án: D
Câu 8 [789067]: Cho hai số thực dương 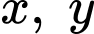 thỏa mãn
thỏa mãn 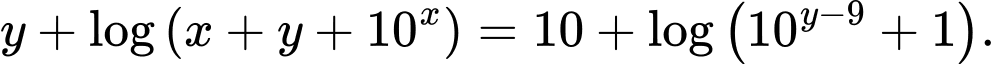 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức  bằng
bằng
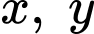 thỏa mãn
thỏa mãn 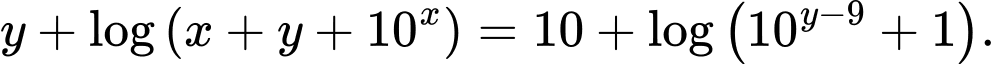 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức  bằng
bằng A, 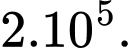
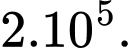
B, 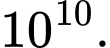
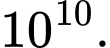
C, 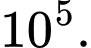
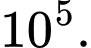
D, 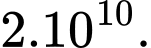
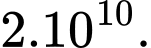
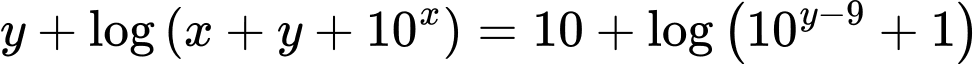
Ta loga 2 vế được:
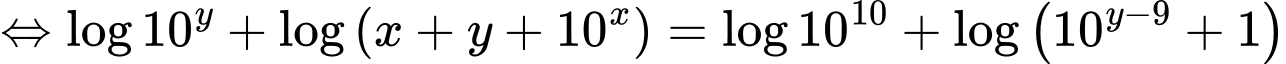
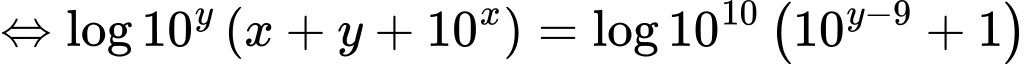
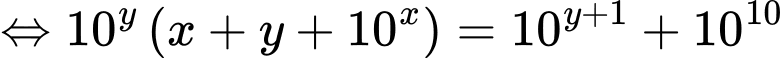
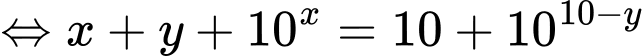
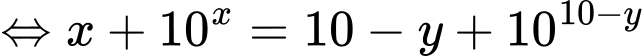
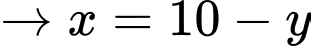
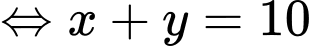
Áp dụng bất đẳng thức Co-si ta có:
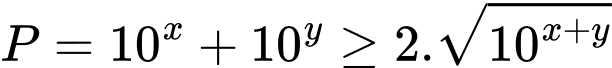

Đáp án: A. Đáp án: A
Câu 9 [789070]: Cho 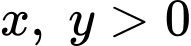 thỏa mãn
thỏa mãn 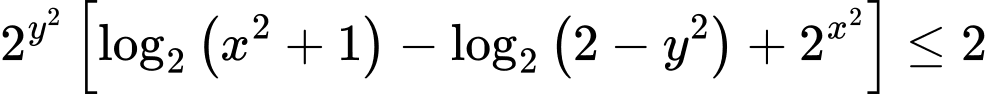 . Giá trị lớn nhất của biểu thức
. Giá trị lớn nhất của biểu thức 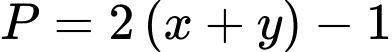 bằng
bằng
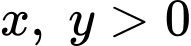 thỏa mãn
thỏa mãn 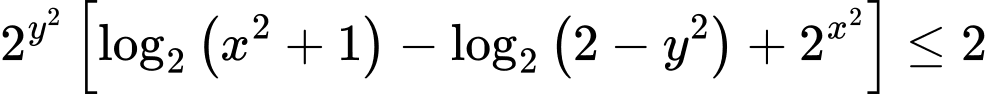 . Giá trị lớn nhất của biểu thức
. Giá trị lớn nhất của biểu thức 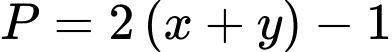 bằng
bằng A, 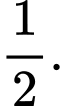
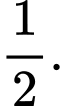
B, 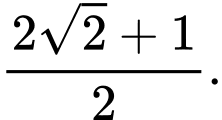
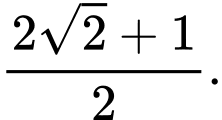
C, 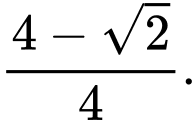
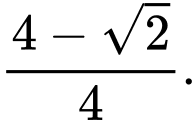
D, 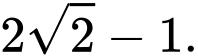
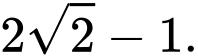
Ta có 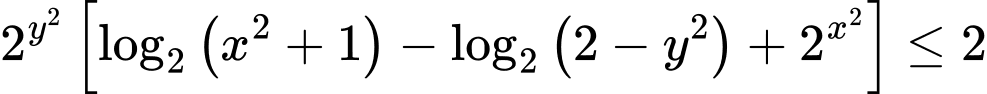
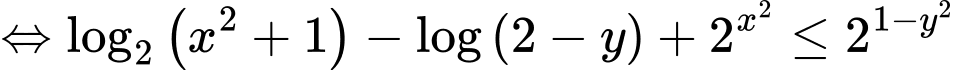
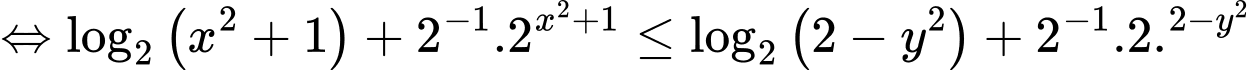
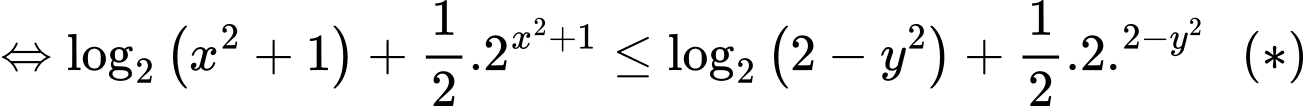
Xét hàm số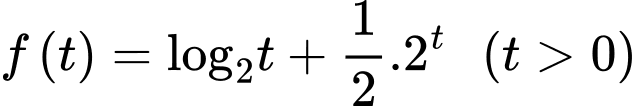
Ta có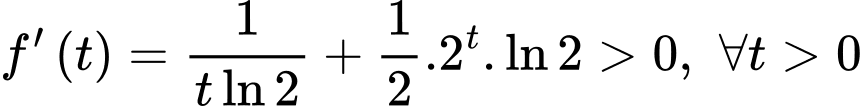
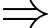 Hàm số
Hàm số 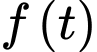 đồng biến trên
đồng biến trên 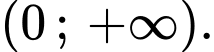
Khi đó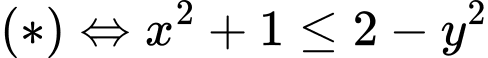
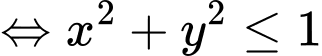
Áp dụng bất đẳng thức Bunhia – Côpxki: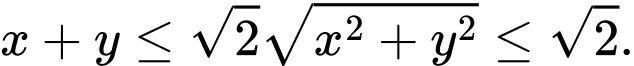
Dấu “=” xảy ra khi và chỉ khi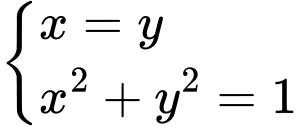
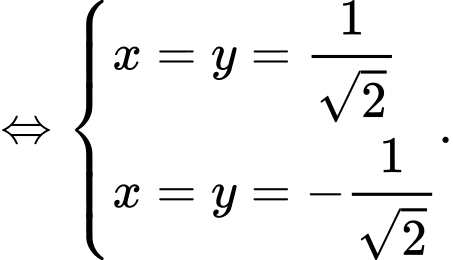
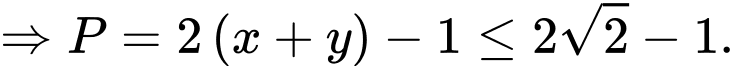
Vậy giá trị lớn nhất của biểu thức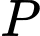 bằng
bằng 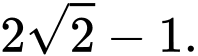
Chọn D. Đáp án: D
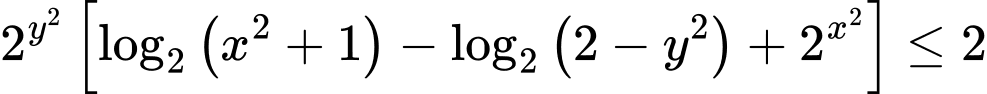
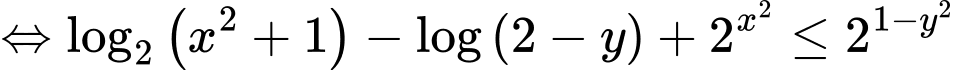
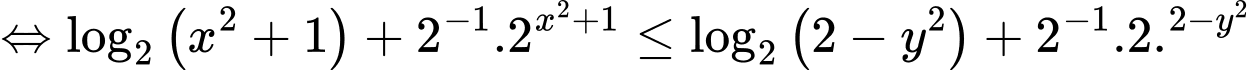
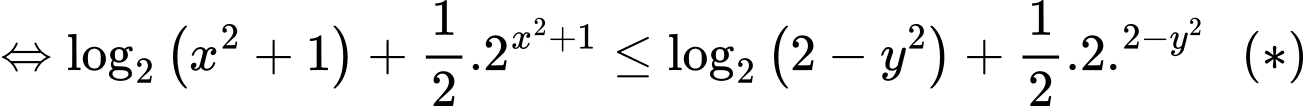
Xét hàm số
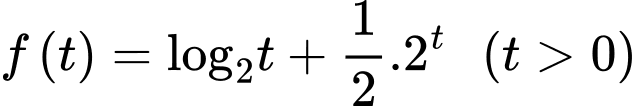
Ta có
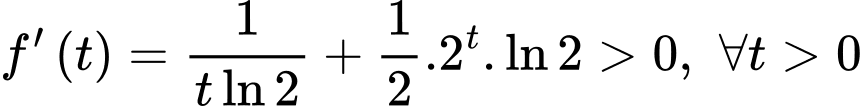
 Hàm số
Hàm số 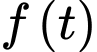 đồng biến trên
đồng biến trên 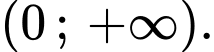
Khi đó
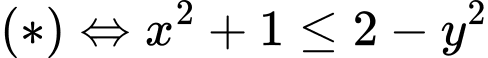
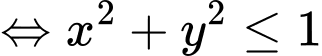
Áp dụng bất đẳng thức Bunhia – Côpxki:
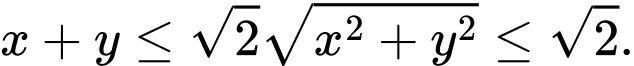
Dấu “=” xảy ra khi và chỉ khi
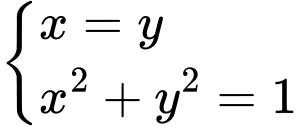
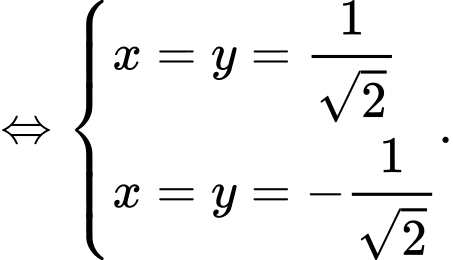
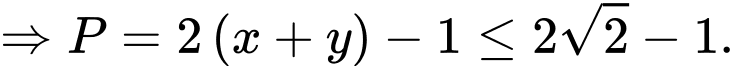
Vậy giá trị lớn nhất của biểu thức
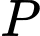 bằng
bằng 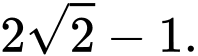
Chọn D. Đáp án: D
Câu 10 [998203]: Xét các số thực dương 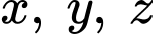 thỏa mãn
thỏa mãn 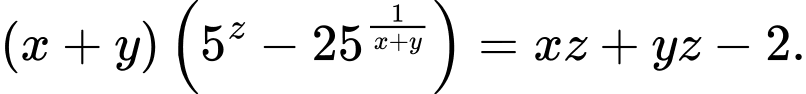 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức 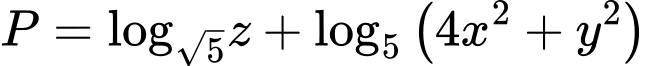
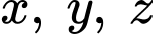 thỏa mãn
thỏa mãn 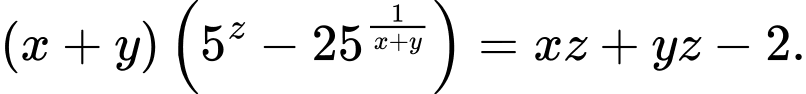 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức 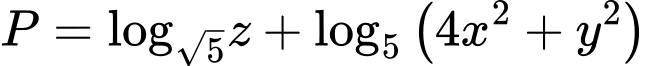
A, 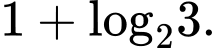
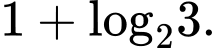
B, 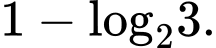
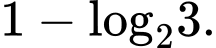
C, 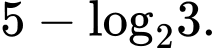
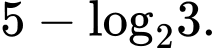
D, 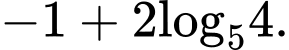
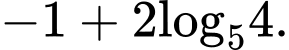
HD: Biến đổi giả thiết ta có: 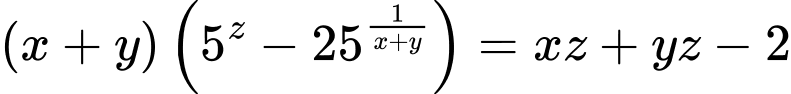
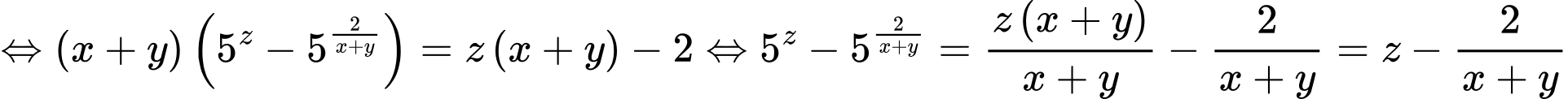
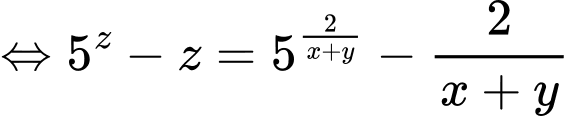
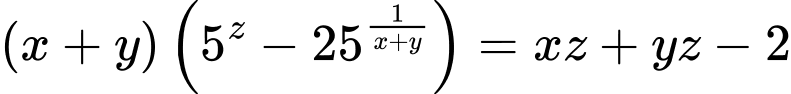
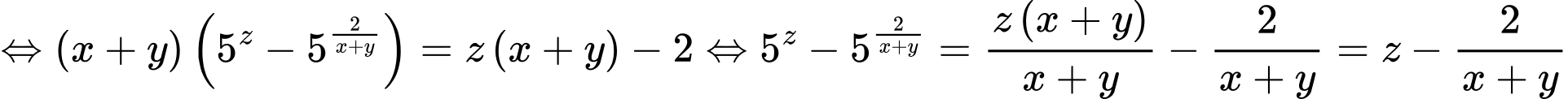
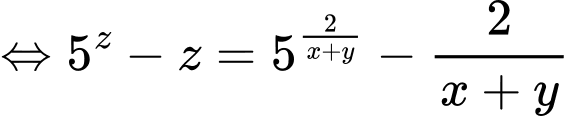
Xét hàm đặc trưng 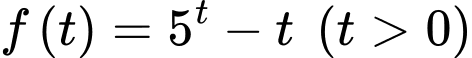 ta có:
ta có: 
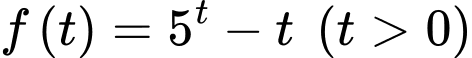 ta có:
ta có: 
Suy ra 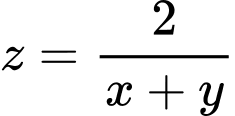 , mặt khác
, mặt khác 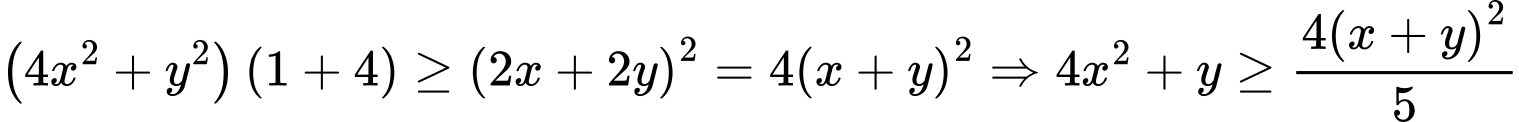 (Bất đẳng thức
(Bất đẳng thức 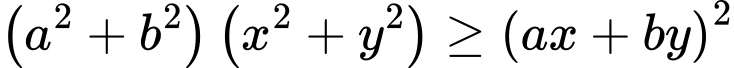 )
)
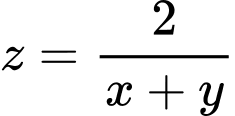 , mặt khác
, mặt khác 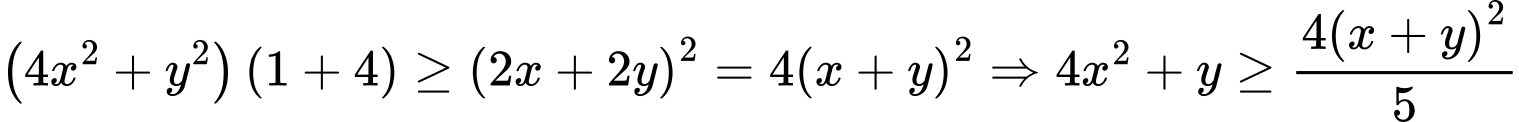 (Bất đẳng thức
(Bất đẳng thức 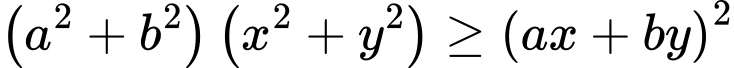 )
) Khi đó 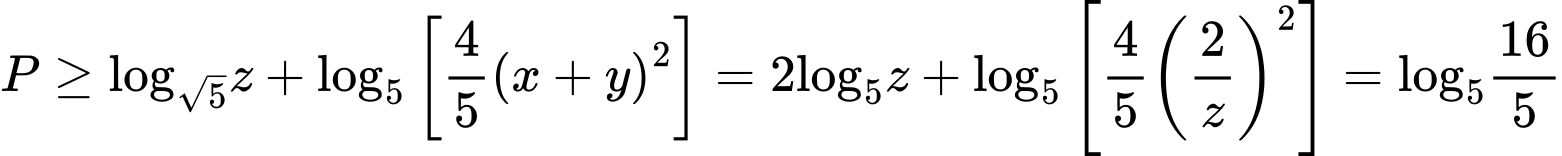
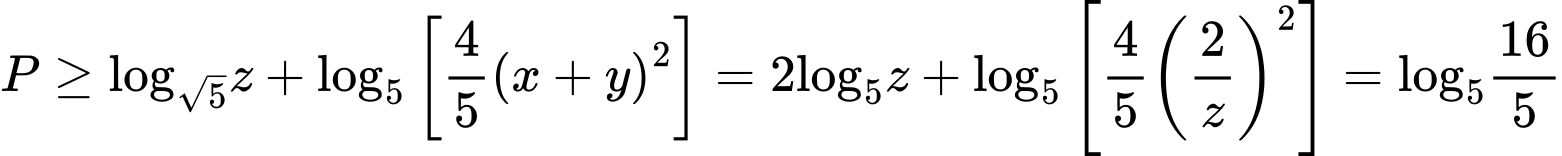
Dấu bằng xảy ra khi 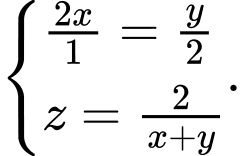 Chọn D. Đáp án: D
Chọn D. Đáp án: D
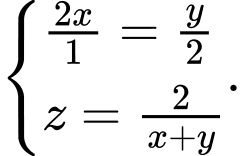 Chọn D. Đáp án: D
Chọn D. Đáp án: D
Câu 11 [581414]: Xét các số thực không âm 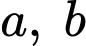 thoả mãn
thoả mãn 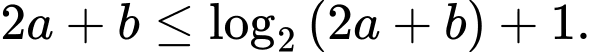 Giá trị nhỏ nhất của
Giá trị nhỏ nhất của  bằng bao nhiêu?
bằng bao nhiêu?
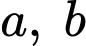 thoả mãn
thoả mãn 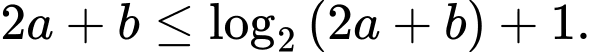 Giá trị nhỏ nhất của
Giá trị nhỏ nhất của  bằng bao nhiêu?
bằng bao nhiêu?
Đặt 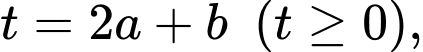 ta có giả thiết đã cho tương đương với
ta có giả thiết đã cho tương đương với 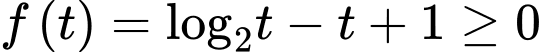
Ta có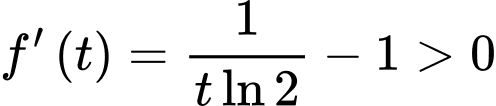
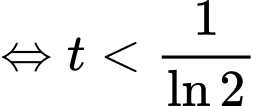
Hàm số đồng biến trên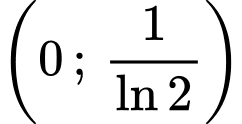
Ta chứng minh Thật vậy giả sử
Thật vậy giả sử  thì
thì 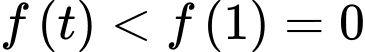 (mâu thuẫn)
(mâu thuẫn)
Vậy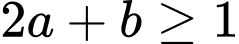
Áp dụng BĐT Cauchy – Schwarz ta có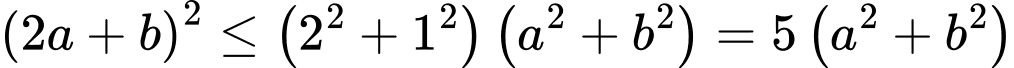
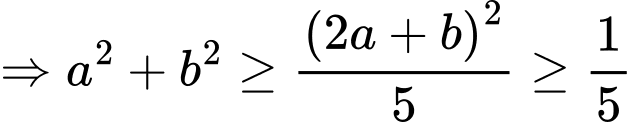
Dấu “=” xảy ra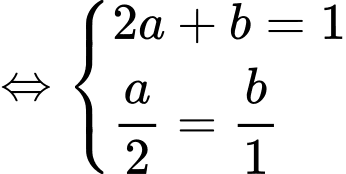
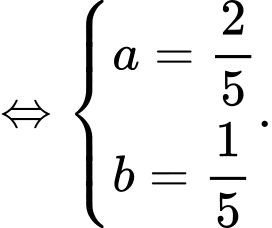
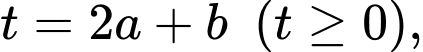 ta có giả thiết đã cho tương đương với
ta có giả thiết đã cho tương đương với 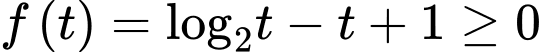
Ta có
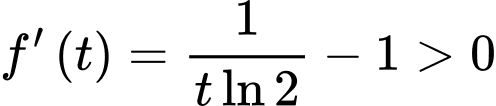
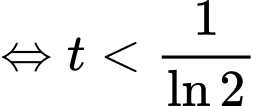
Hàm số đồng biến trên
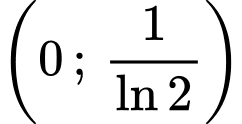
Ta chứng minh
 Thật vậy giả sử
Thật vậy giả sử  thì
thì 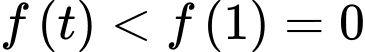 (mâu thuẫn)
(mâu thuẫn)
Vậy
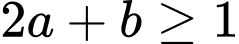
Áp dụng BĐT Cauchy – Schwarz ta có
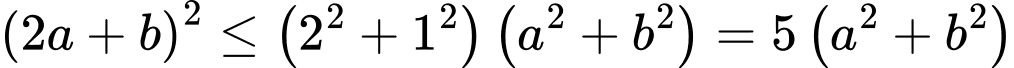
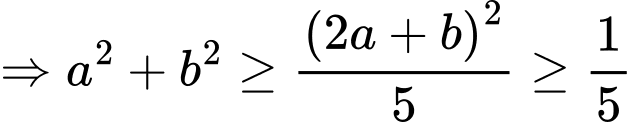
Dấu “=” xảy ra
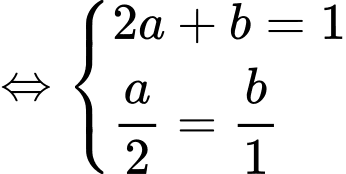
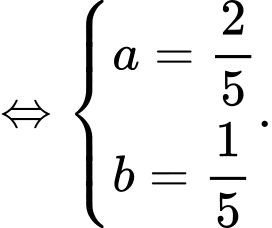
Câu 12 [511326]: Xét các số thực dương 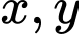 thỏa mãn
thỏa mãn 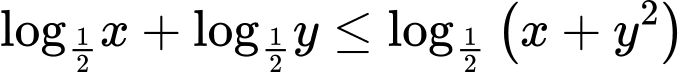 . Tìm giá trị nhỏ nhất
. Tìm giá trị nhỏ nhất  của biểu thức
của biểu thức 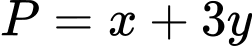 .
.
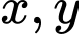 thỏa mãn
thỏa mãn 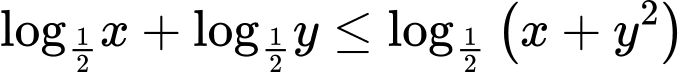 . Tìm giá trị nhỏ nhất
. Tìm giá trị nhỏ nhất  của biểu thức
của biểu thức 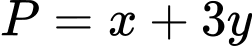 .
. A, 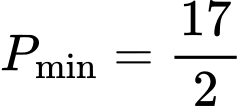
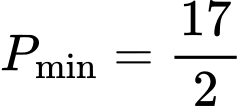
B, 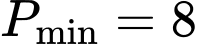 .
.
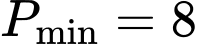 .
.C, 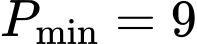 .
.
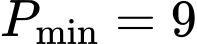 .
.D, 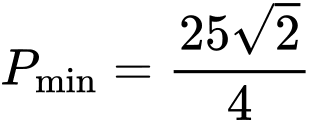 .
.
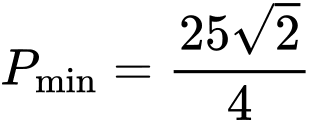 .
.
Chọn C
Với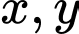 dương, ta có:
dương, ta có:
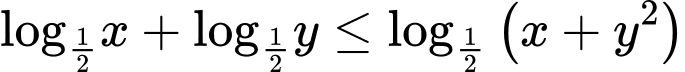
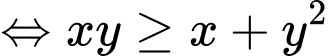
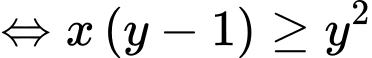
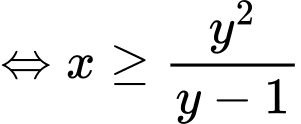 (vì
(vì 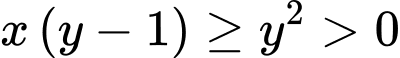 nên
nên 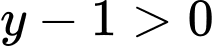 ).
).
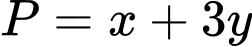
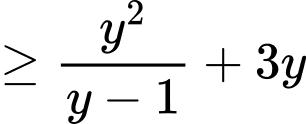
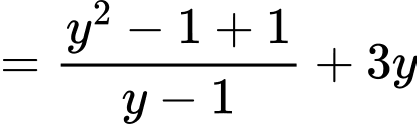
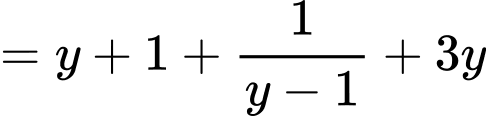
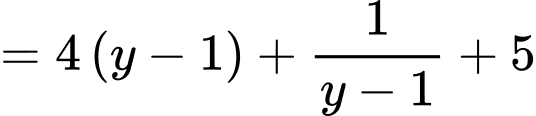
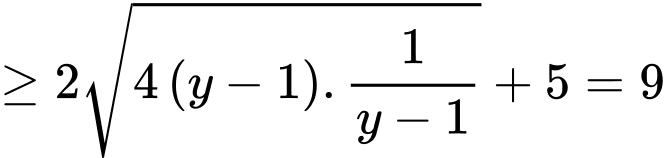 .
.
Đẳng thức xảy ra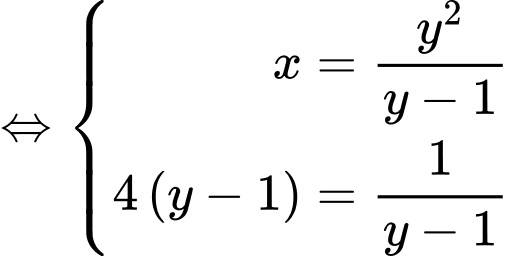
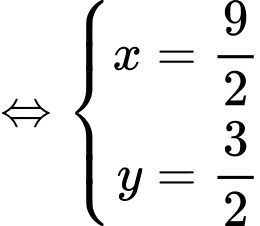 .
.
Vậy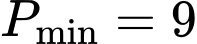 khi
khi 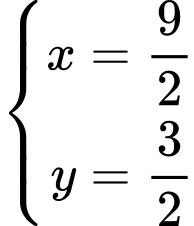 . Đáp án: C
. Đáp án: C
Với
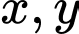 dương, ta có:
dương, ta có: 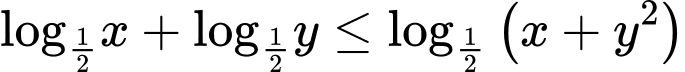
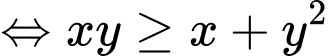
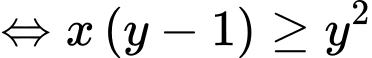
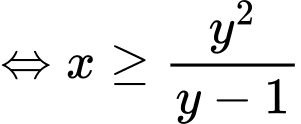 (vì
(vì 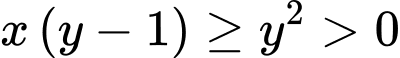 nên
nên 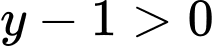 ).
).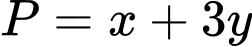
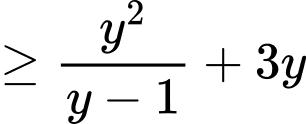
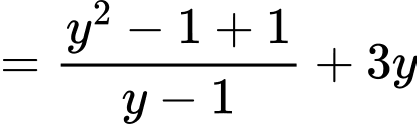
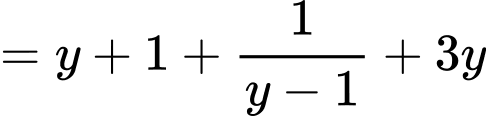
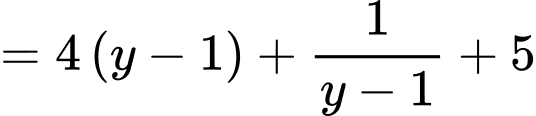
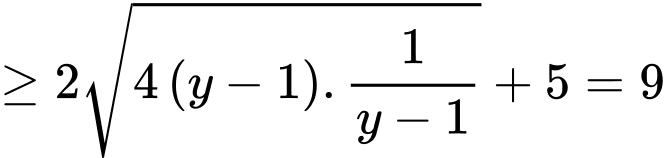 .
.Đẳng thức xảy ra
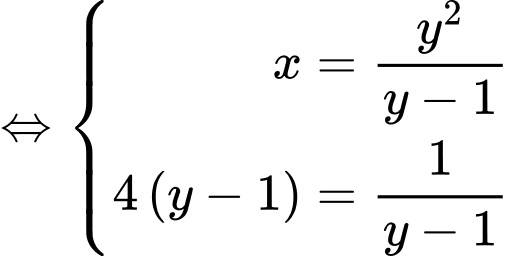
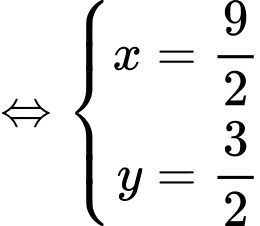 .
.Vậy
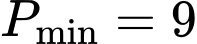 khi
khi 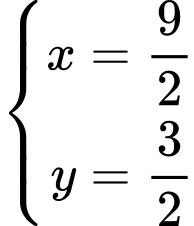 . Đáp án: C
. Đáp án: C
Câu 13 [508791]: Cho hai số thực dương 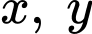 thỏa mãn
thỏa mãn 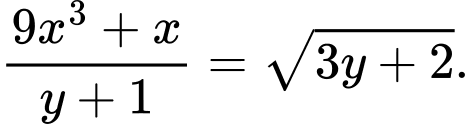 Giá trị lớn nhất của biểu thức
Giá trị lớn nhất của biểu thức 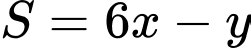 là
là
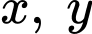 thỏa mãn
thỏa mãn 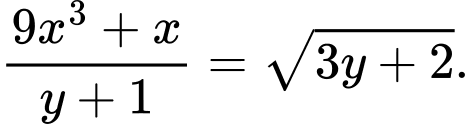 Giá trị lớn nhất của biểu thức
Giá trị lớn nhất của biểu thức 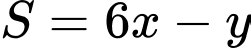 là
là A, 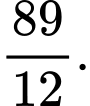
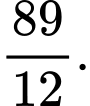
B, 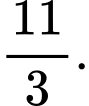
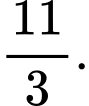
C, 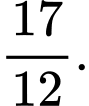
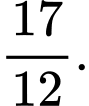
D, 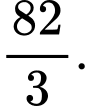
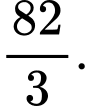
Ta có: 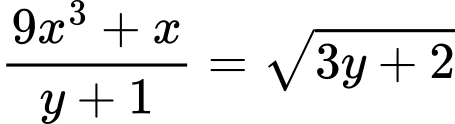
ĐK: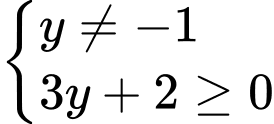
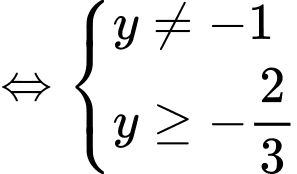
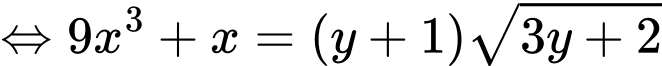
Đặt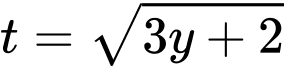
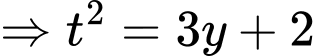
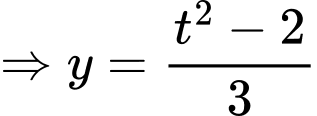
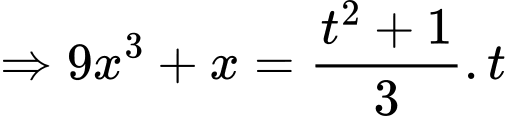
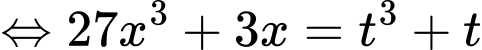
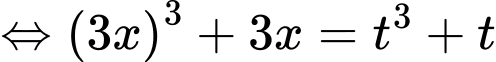
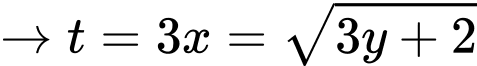
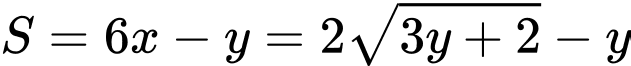
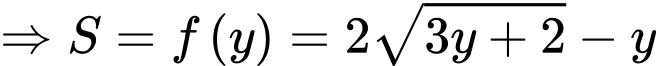
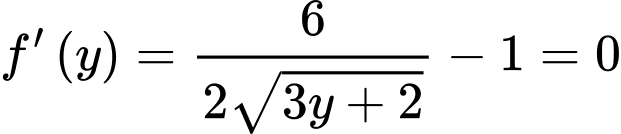
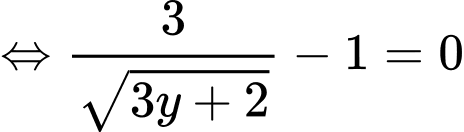
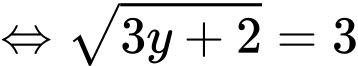

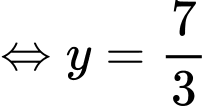
Ta có bảng biến thiên:
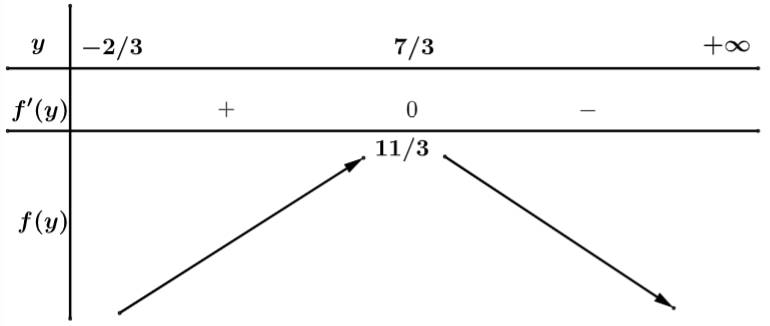
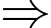 Giá trị lớn nhất của
Giá trị lớn nhất của 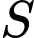 là
là 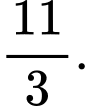
Đáp án: B. Đáp án: B
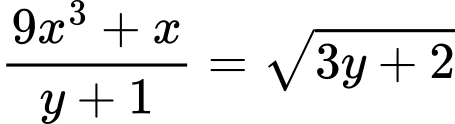
ĐK:
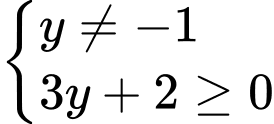
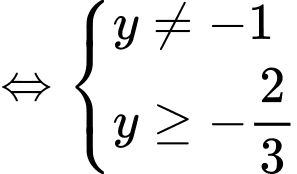
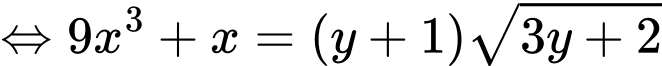
Đặt
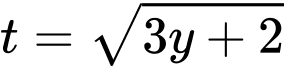
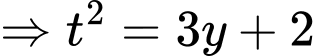
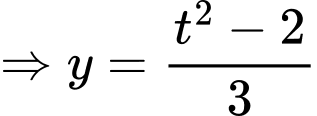
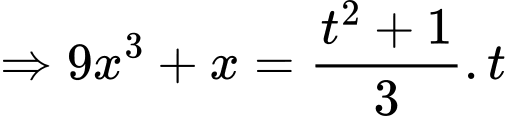
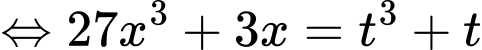
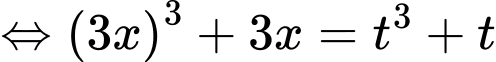
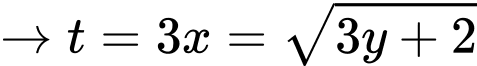
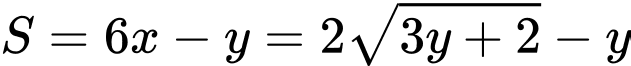
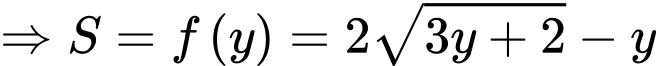
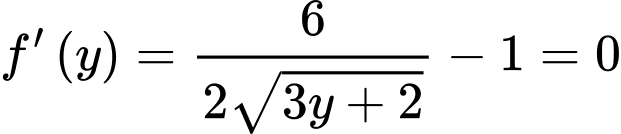
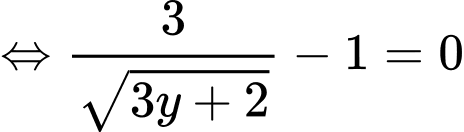
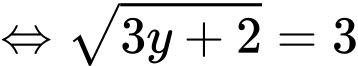

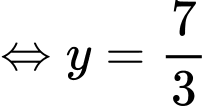
Ta có bảng biến thiên:

 Giá trị lớn nhất của
Giá trị lớn nhất của 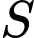 là
là 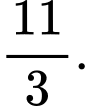
Đáp án: B. Đáp án: B
Câu 14 [25941]: Cho 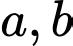 là hai số thực dương thỏa mãn
là hai số thực dương thỏa mãn 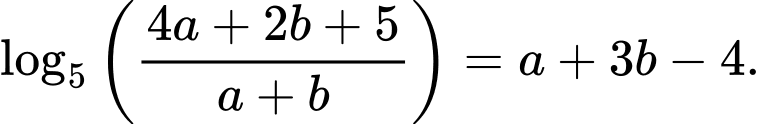 Tìm giá trị nhỏ nhất của biểu thức
Tìm giá trị nhỏ nhất của biểu thức 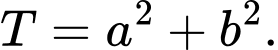
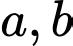 là hai số thực dương thỏa mãn
là hai số thực dương thỏa mãn 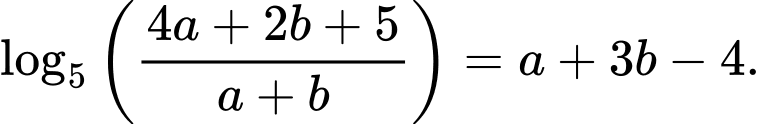 Tìm giá trị nhỏ nhất của biểu thức
Tìm giá trị nhỏ nhất của biểu thức 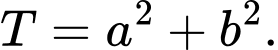
A, 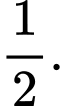
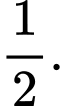
B, 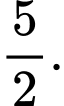
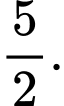
C, 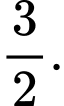
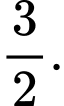
D, 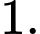
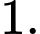
Ta có 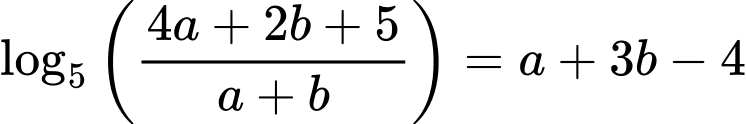

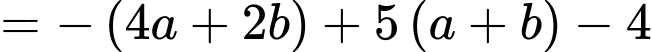

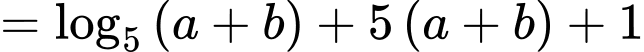

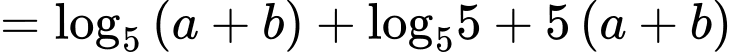

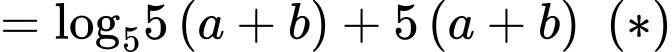
Xét hàm đặc trưng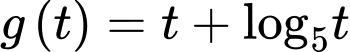 trên khoảng
trên khoảng 
Ta có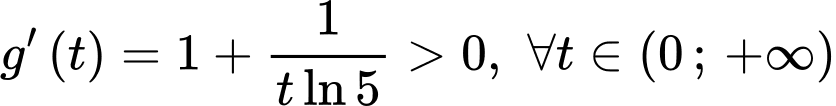
Suy ra hàm số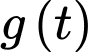 đồng biến trên
đồng biến trên 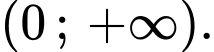
Khi đó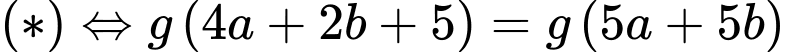
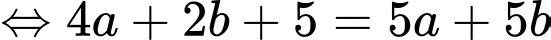
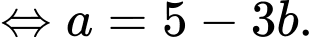
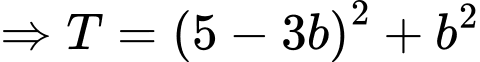
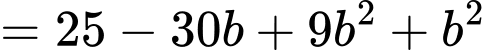
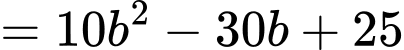
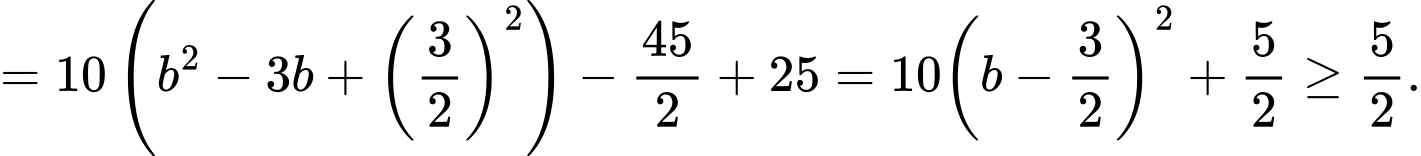
Vậy giá trị nhỏ nhất của biểu thức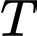 là
là 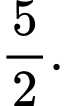 Đáp án: B
Đáp án: B
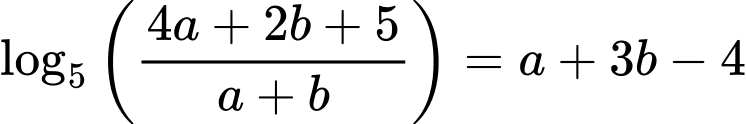

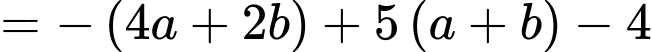

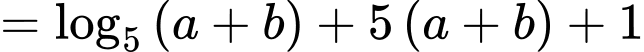

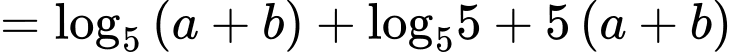

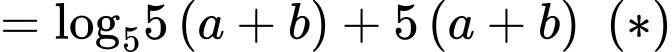
Xét hàm đặc trưng
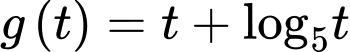 trên khoảng
trên khoảng 
Ta có
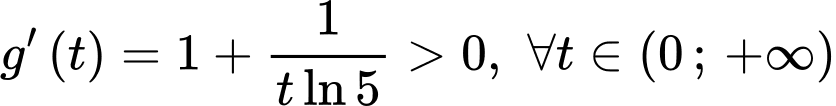
Suy ra hàm số
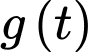 đồng biến trên
đồng biến trên 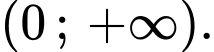
Khi đó
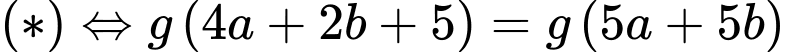
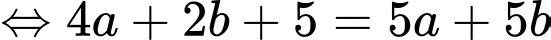
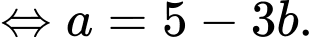
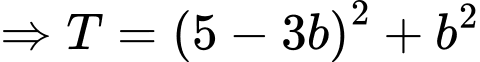
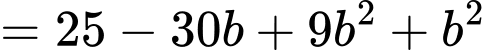
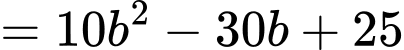
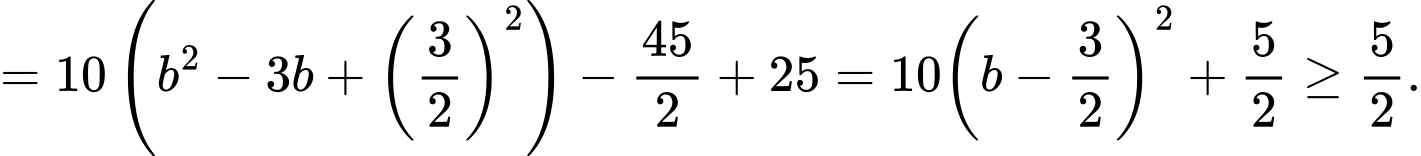
Vậy giá trị nhỏ nhất của biểu thức
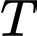 là
là 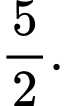 Đáp án: B
Đáp án: B
Câu 15 [203602]: Cho hàm số 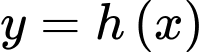 thỏa mãn
thỏa mãn 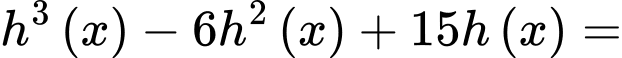
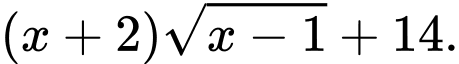 Tìm giá trị nhỏ nhất của biểu thức
Tìm giá trị nhỏ nhất của biểu thức 
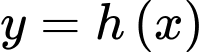 thỏa mãn
thỏa mãn 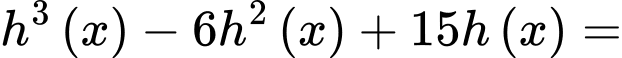
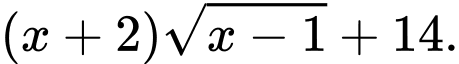 Tìm giá trị nhỏ nhất của biểu thức
Tìm giá trị nhỏ nhất của biểu thức 
A, 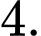
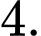
B, 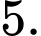
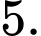
C, 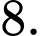
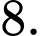
D, 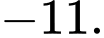
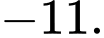
HD: Đặt 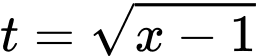 ta có:
ta có: 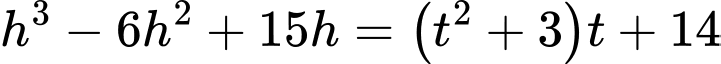 Cho
Cho 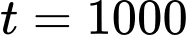 bấm máy CASIO ta được
bấm máy CASIO ta được 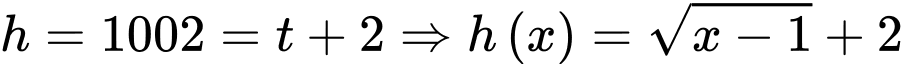 Khi đó
Khi đó 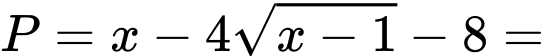
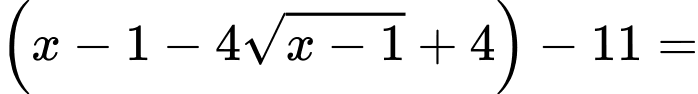
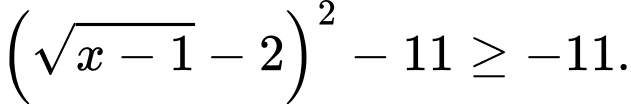 Vậy
Vậy 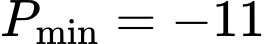 khi
khi 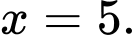 Chọn D. Đáp án: D
Chọn D. Đáp án: D
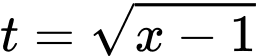 ta có:
ta có: 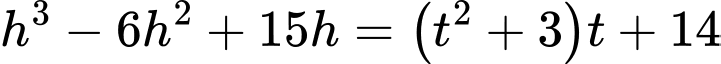 Cho
Cho 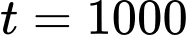 bấm máy CASIO ta được
bấm máy CASIO ta được 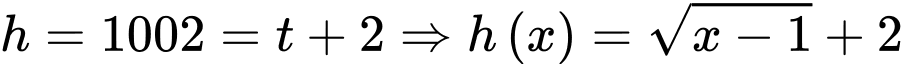 Khi đó
Khi đó 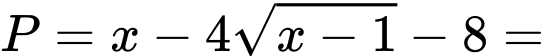
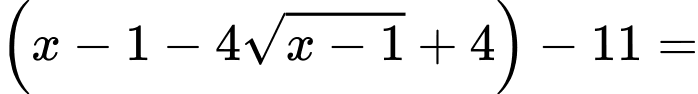
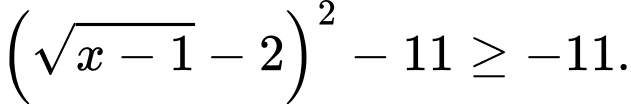 Vậy
Vậy 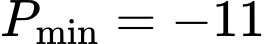 khi
khi 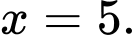 Chọn D. Đáp án: D
Chọn D. Đáp án: D
Câu 16 [79780]: [Đề thi THPTQG năm 2017] Xét các số thực dương 𝑎, 𝑏 thỏa mãn 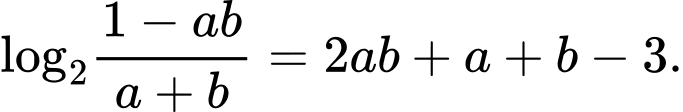 Tìm giá trị nhỏ nhất
Tìm giá trị nhỏ nhất  của
của 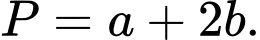
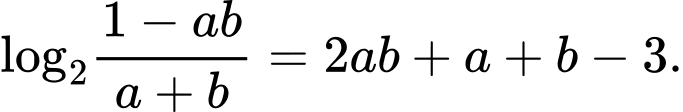 Tìm giá trị nhỏ nhất
Tìm giá trị nhỏ nhất  của
của 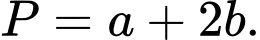
A, 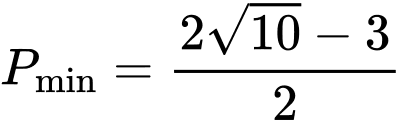 .
.
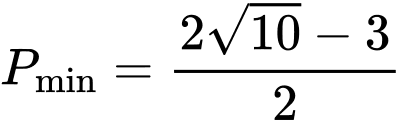 .
.B, 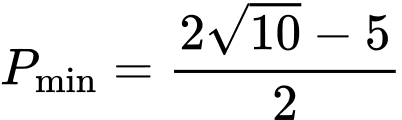 .
.
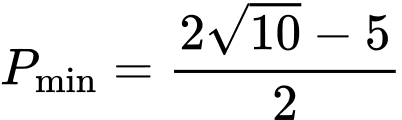 .
.C, 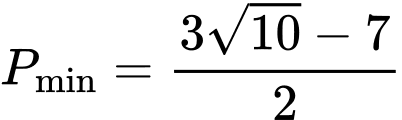 .
.
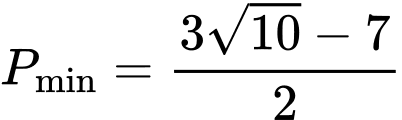 .
.D, 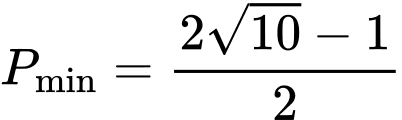 .
.
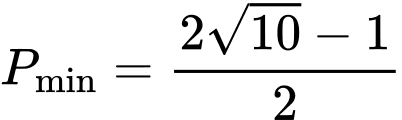 .
.
Ta có 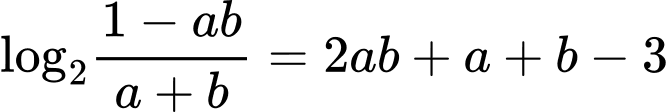
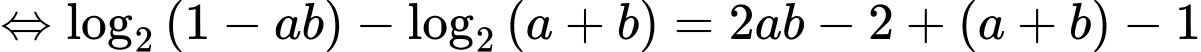
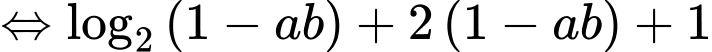
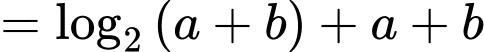
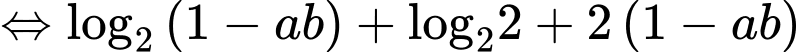
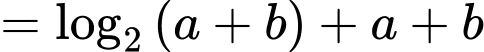
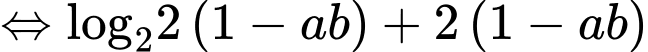
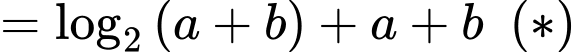
Xét hàm đặc trưng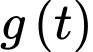
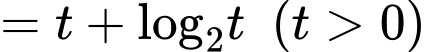
Ta có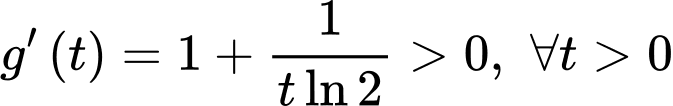
Suy ra hàm số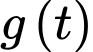 đồng biến trên
đồng biến trên 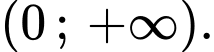
Khi đó
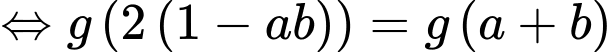
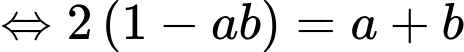
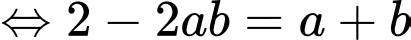
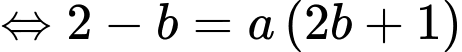
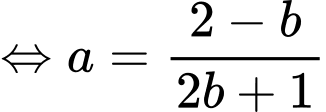
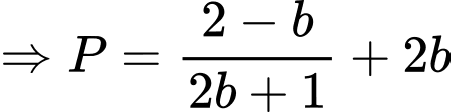
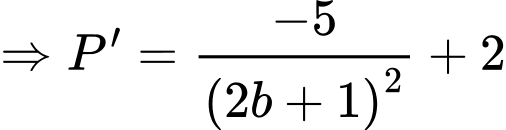
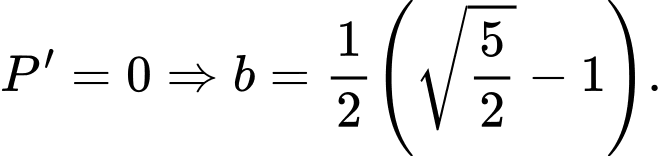
Lại có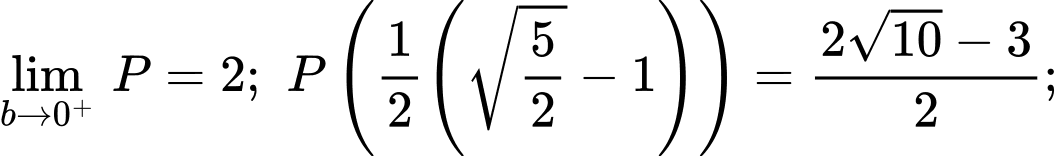
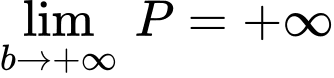
Suy ra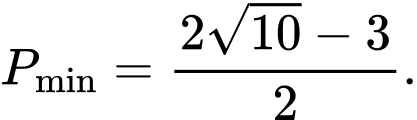 Chọn A. Đáp án: A
Chọn A. Đáp án: A
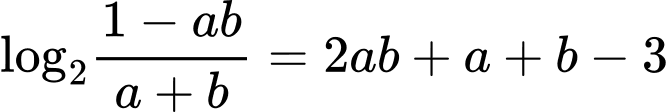
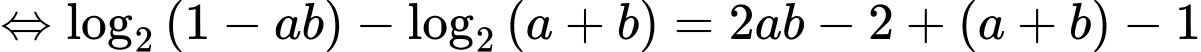
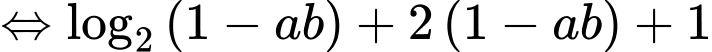
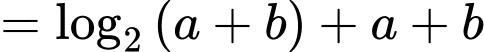
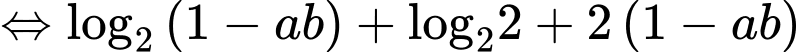
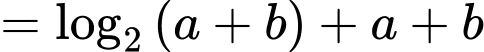
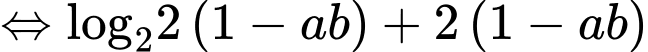
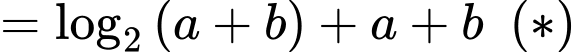
Xét hàm đặc trưng
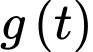
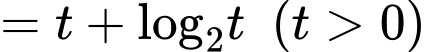
Ta có
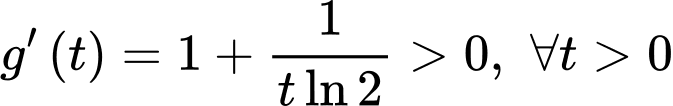
Suy ra hàm số
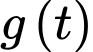 đồng biến trên
đồng biến trên 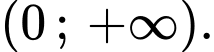
Khi đó

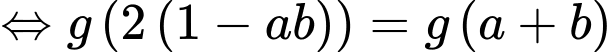
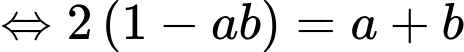
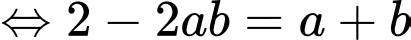
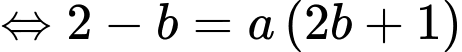
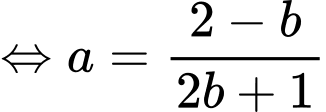
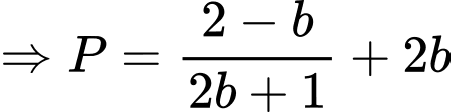
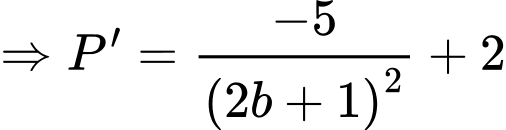
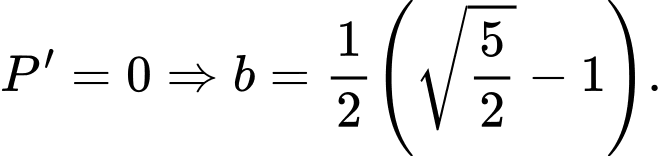
Lại có
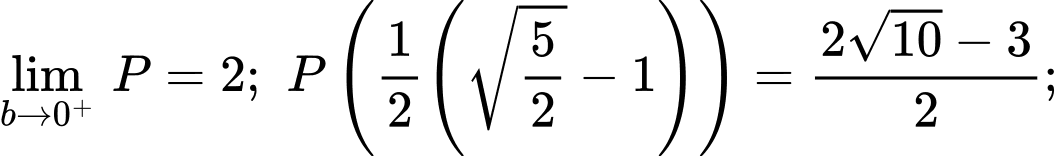
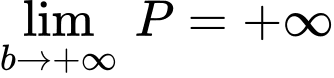
Suy ra
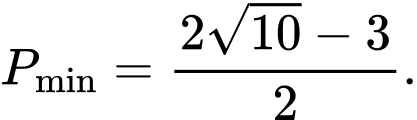 Chọn A. Đáp án: A
Chọn A. Đáp án: A
Câu 17 [509220]: Cho hai số thực 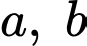 thỏa mãn
thỏa mãn 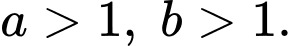 Tìm giá trị nhỏ nhất của biểu thức
Tìm giá trị nhỏ nhất của biểu thức 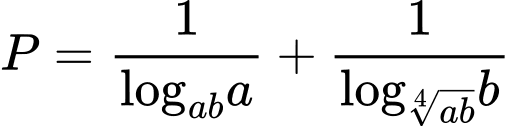
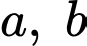 thỏa mãn
thỏa mãn 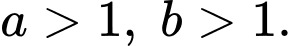 Tìm giá trị nhỏ nhất của biểu thức
Tìm giá trị nhỏ nhất của biểu thức 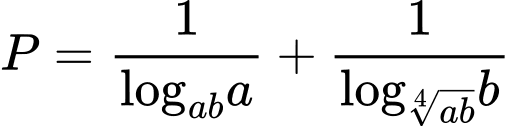
A, 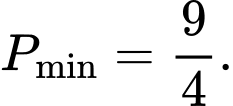
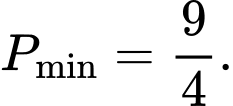
B, 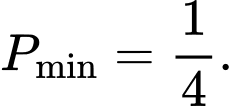
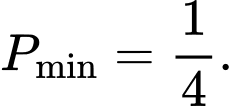
C, 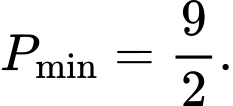
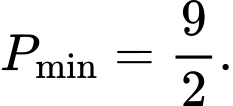
D, 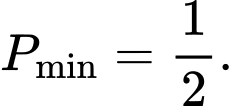
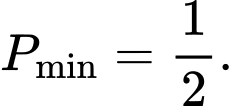
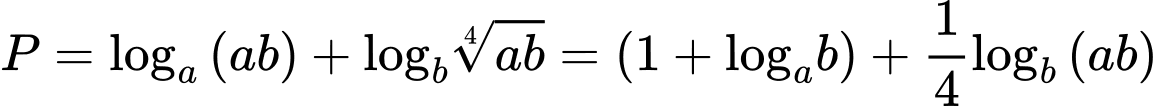
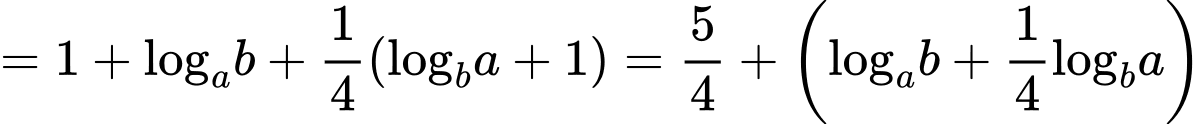
Do 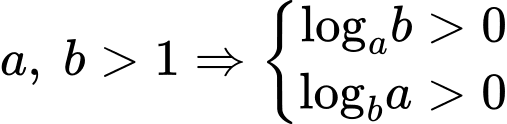 , áp dụng BĐT Cô si cho 2 số dương ta được:
, áp dụng BĐT Cô si cho 2 số dương ta được:
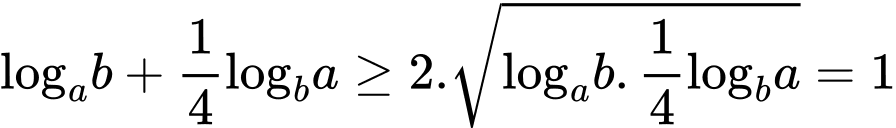
Đáp án: A 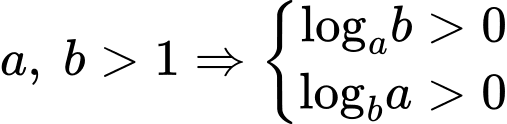 , áp dụng BĐT Cô si cho 2 số dương ta được:
, áp dụng BĐT Cô si cho 2 số dương ta được:
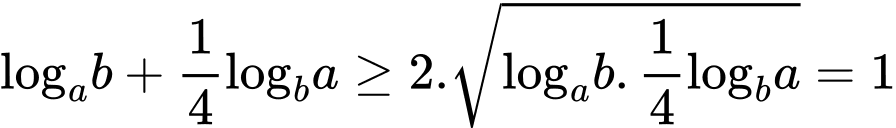
Vậy 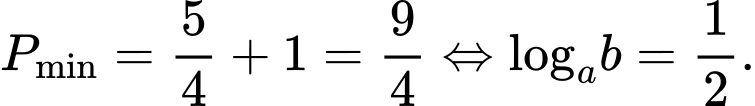 Chọn A.
Chọn A.
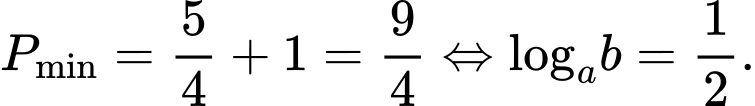 Chọn A.
Chọn A.
Câu 18 [510426]: [Chuyên Đại học Vinh 2020] Xét các số thực dương 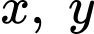 thỏa mãn
thỏa mãn 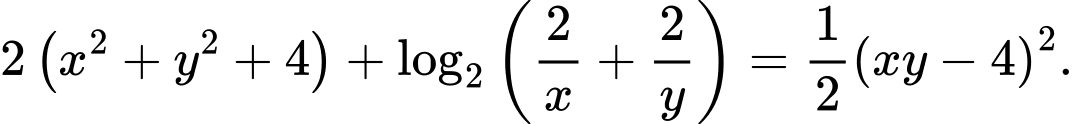 Khi
Khi 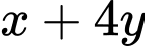 đạt giá trị nhỏ nhất thì
đạt giá trị nhỏ nhất thì 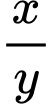 bằng
bằng
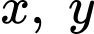 thỏa mãn
thỏa mãn 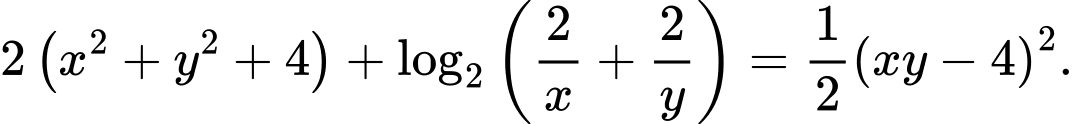 Khi
Khi 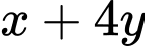 đạt giá trị nhỏ nhất thì
đạt giá trị nhỏ nhất thì 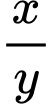 bằng
bằng A, 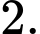
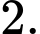
B, 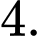
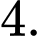
C, 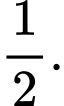
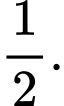
D, 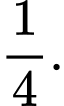
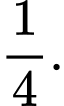
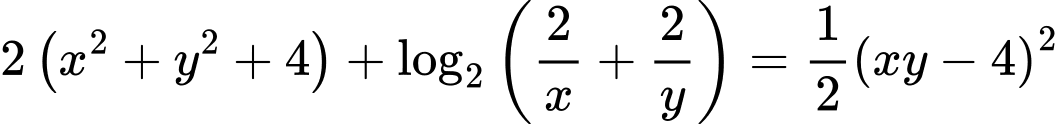
ĐKXĐ:
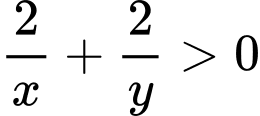
Giả sử:
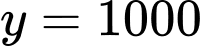 ta bấm máy tính được
ta bấm máy tính được 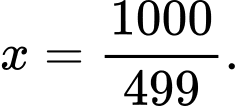
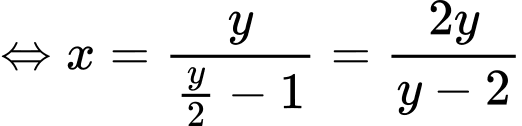
Xét:
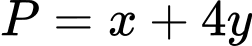
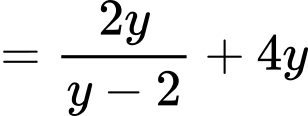
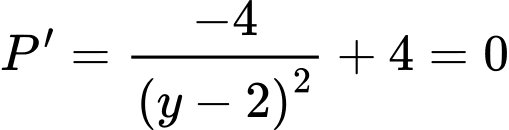
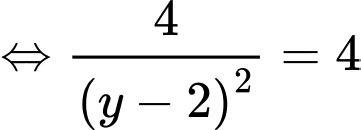
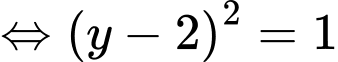
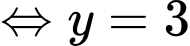
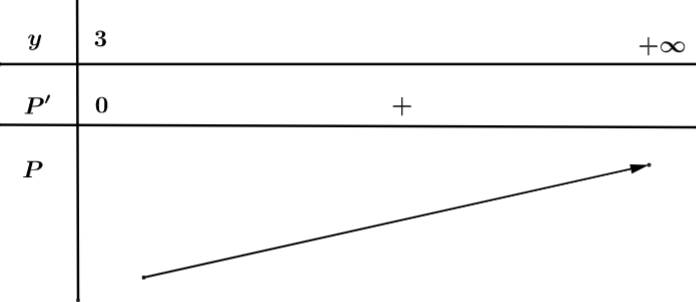
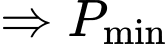 tại
tại 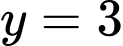
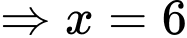
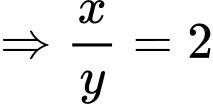
Đáp án: A. Đáp án: A
Câu 19 [510428]: Cho các số thực 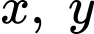 dương và thỏa mãn
dương và thỏa mãn 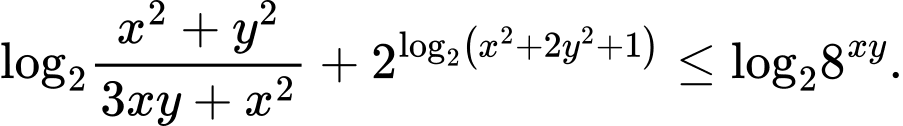 Tìm giá trị nhỏ nhất của biểu thức
Tìm giá trị nhỏ nhất của biểu thức 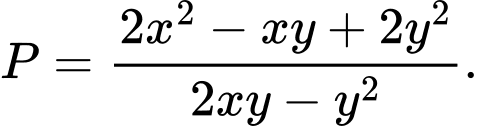
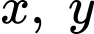 dương và thỏa mãn
dương và thỏa mãn 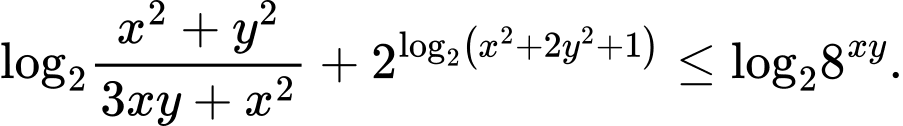 Tìm giá trị nhỏ nhất của biểu thức
Tìm giá trị nhỏ nhất của biểu thức 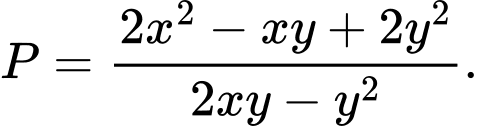
A, 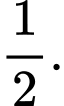
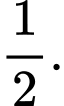
B, 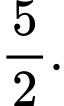
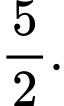
C, 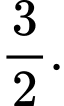
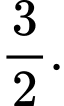
D, 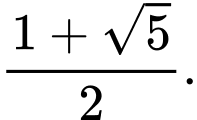
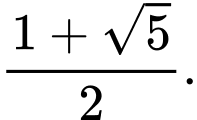
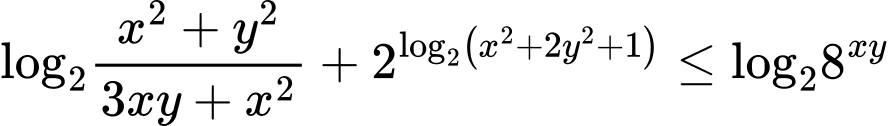
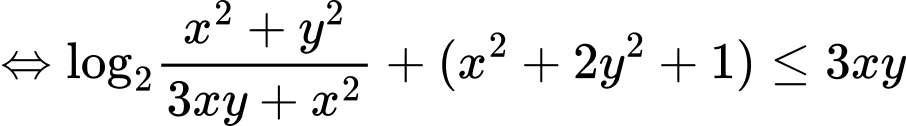
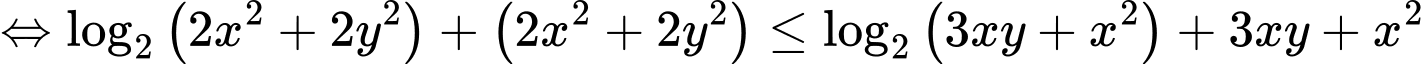
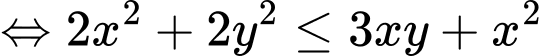
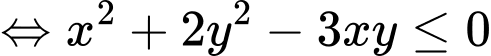
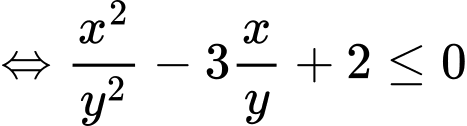
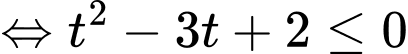
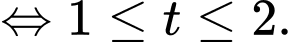
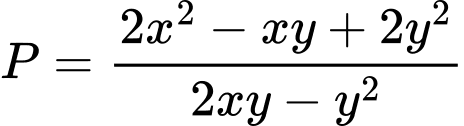
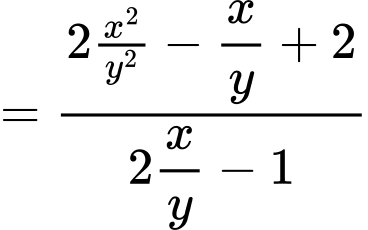
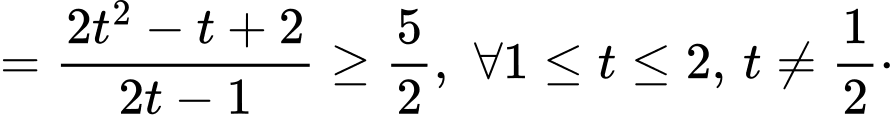
Chọn đáp án B. Đáp án: B
Câu 20 [377855]: Cho các số thực dương 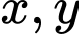 thỏa mãn
thỏa mãn 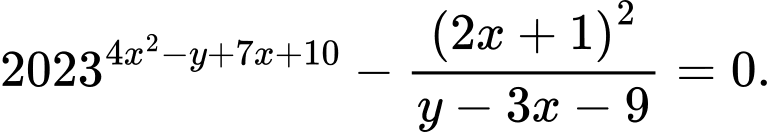 Tìm giá trị nhỏ nhất của biểu thức
Tìm giá trị nhỏ nhất của biểu thức 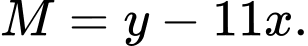
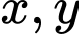 thỏa mãn
thỏa mãn 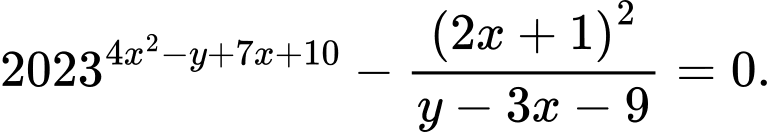 Tìm giá trị nhỏ nhất của biểu thức
Tìm giá trị nhỏ nhất của biểu thức 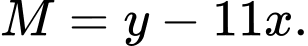
A, 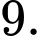
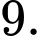
B, 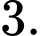
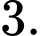
C, 

D, 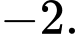
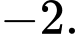
Chọn A
Do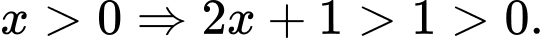
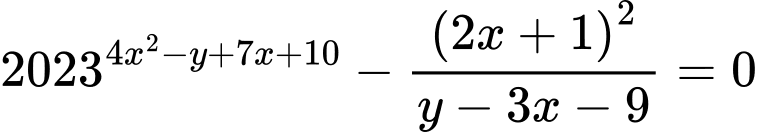
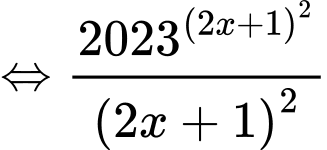
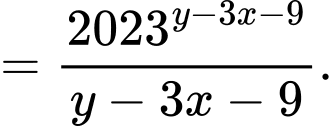
Đặt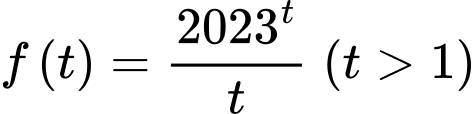
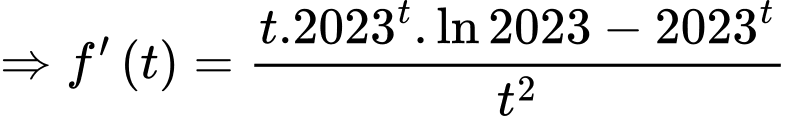
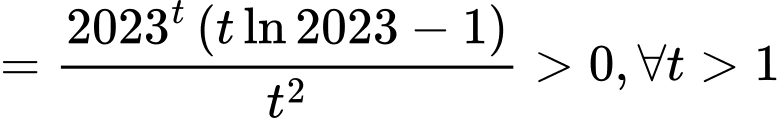
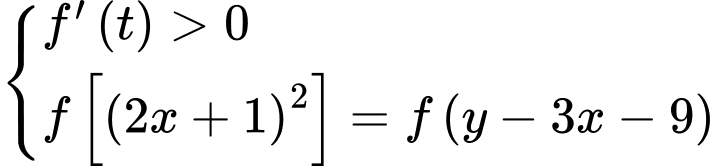
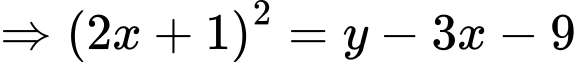
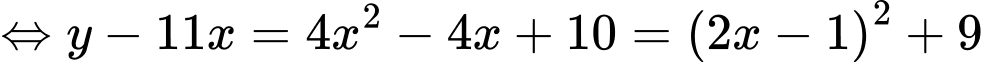
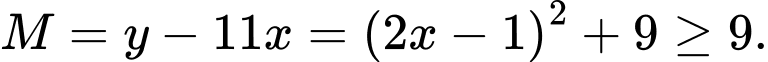
Giá trị nhỏ nhất của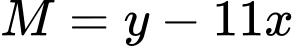 là
là 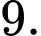 Đáp án: A
Đáp án: A
Do
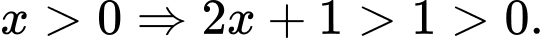
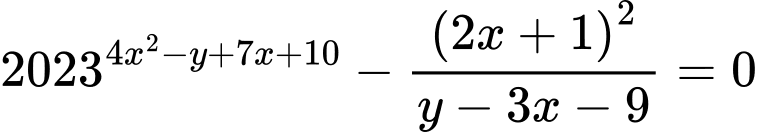
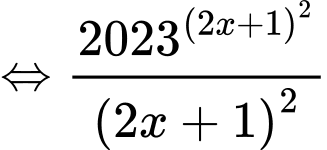
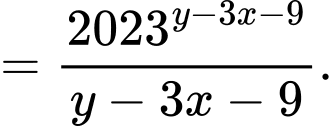
Đặt
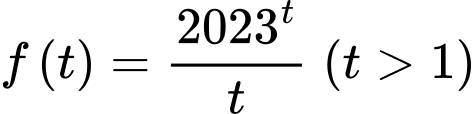
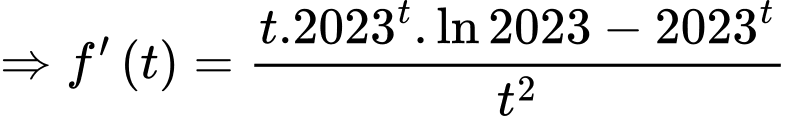
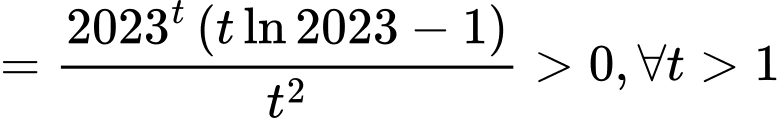
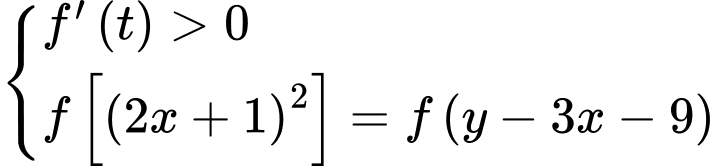
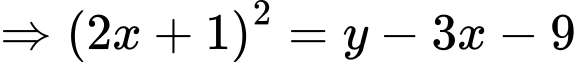
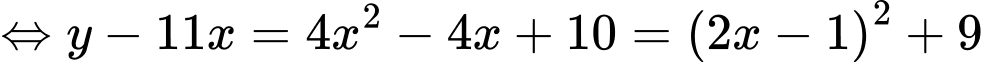
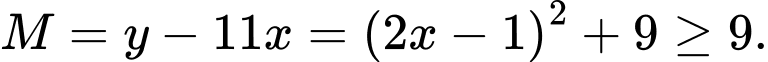
Giá trị nhỏ nhất của
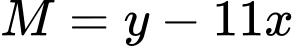 là
là 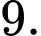 Đáp án: A
Đáp án: A
Câu 21 [677081]: Cho 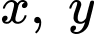 là các số thực dương thỏa mãn
là các số thực dương thỏa mãn 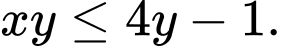 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức 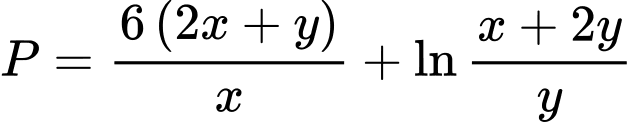 là
là 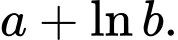 Giá trị của tích
Giá trị của tích 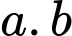 là
là
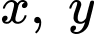 là các số thực dương thỏa mãn
là các số thực dương thỏa mãn 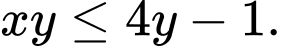 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức 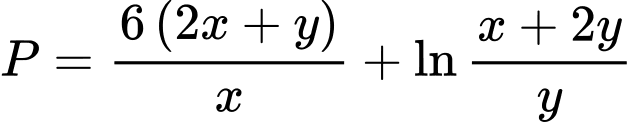 là
là 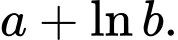 Giá trị của tích
Giá trị của tích 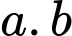 là
là A, 45.
B, 81.
C, 108.
D, 115.
Ta có: 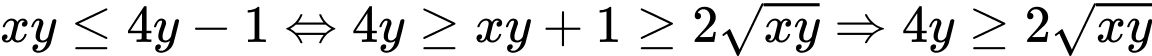 nên:
nên: 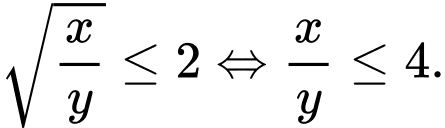
Xét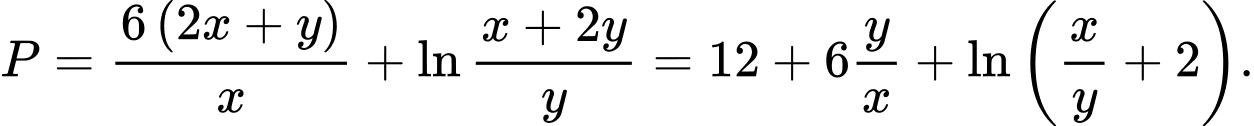
Đặt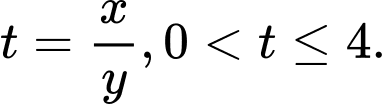 Suy ra:
Suy ra: 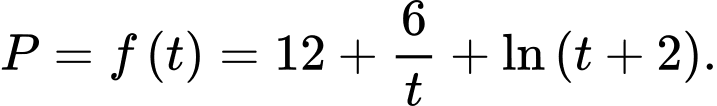
Ta có: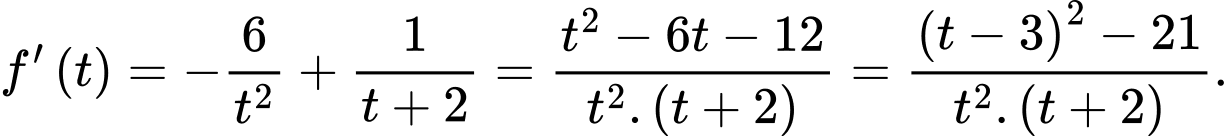
Với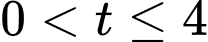 thì
thì 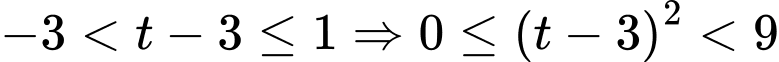 nên
nên 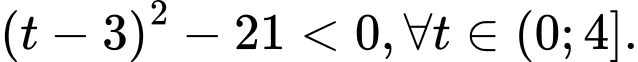
Do đó: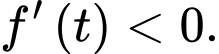 Hàm số
Hàm số 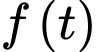 nghịch biến trên
nghịch biến trên 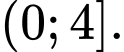
Suy ra: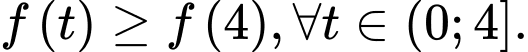 Hay
Hay 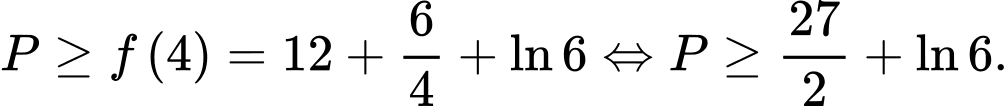
Vậy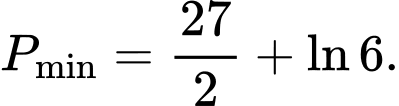 Dấu bằng xảy ra khi và chỉ khi
Dấu bằng xảy ra khi và chỉ khi 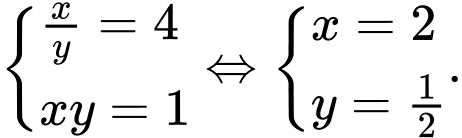
Khi đó: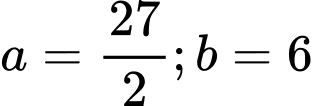 nên
nên 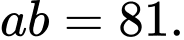 Đáp án: B
Đáp án: B
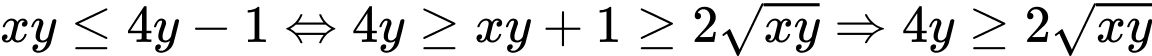 nên:
nên: 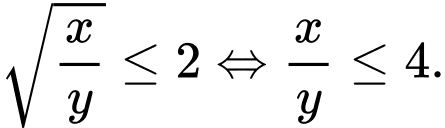
Xét
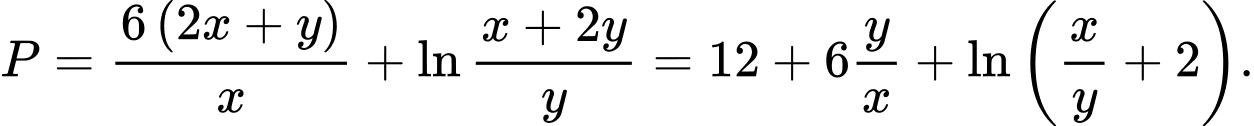
Đặt
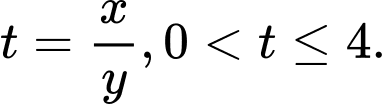 Suy ra:
Suy ra: 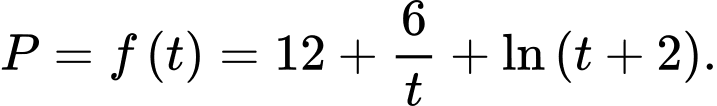
Ta có:
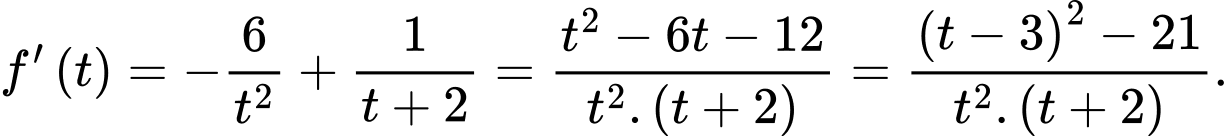
Với
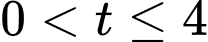 thì
thì 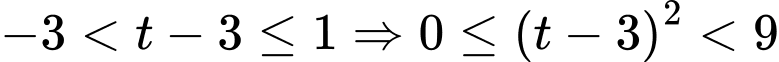 nên
nên 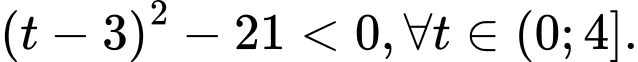
Do đó:
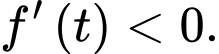 Hàm số
Hàm số 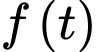 nghịch biến trên
nghịch biến trên 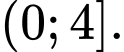
Suy ra:
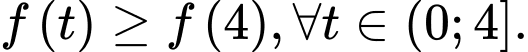 Hay
Hay 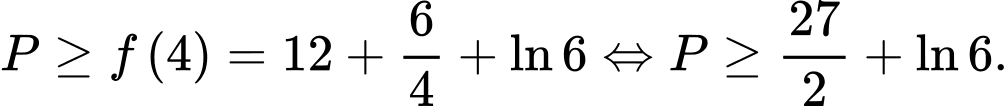
Vậy
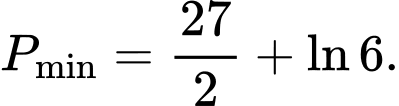 Dấu bằng xảy ra khi và chỉ khi
Dấu bằng xảy ra khi và chỉ khi 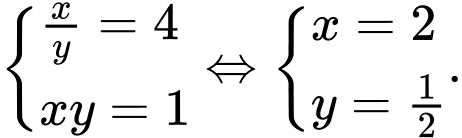
Khi đó:
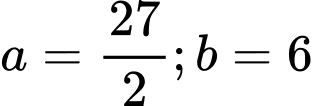 nên
nên 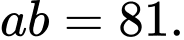 Đáp án: B
Đáp án: B
Câu 22 [333822]: Tính giá trị của biểu thức 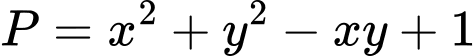 biết rằng
biết rằng 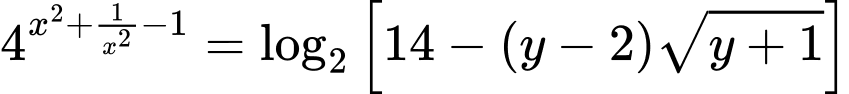 với
với 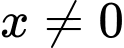 và
và 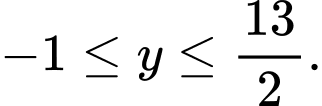
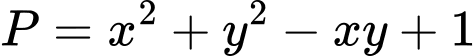 biết rằng
biết rằng 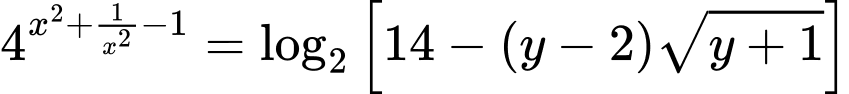 với
với 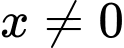 và
và 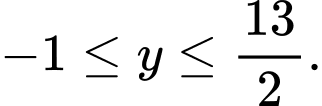
A, 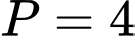 .
.
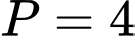 .
.B, 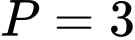 .
.
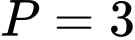 .
.C, 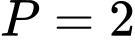 .
.
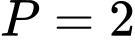 .
.D, 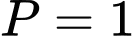 .
.
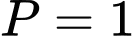 .
.
Đáp án C
Áp dụng bất đẳng thức Cauchy ta có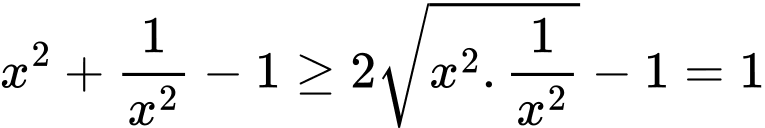
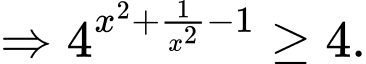
Lại có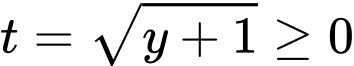
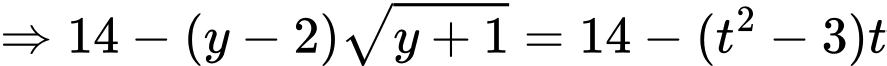
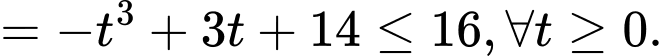
Khi đó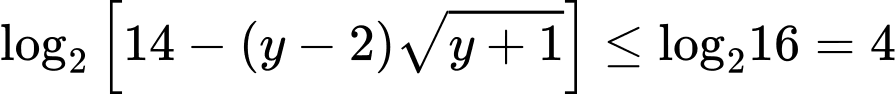 .
.
Các dấu đẳng thức xảy ra khi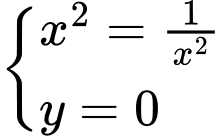
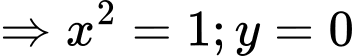
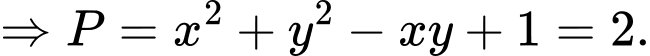 Đáp án: C
Đáp án: C
Áp dụng bất đẳng thức Cauchy ta có
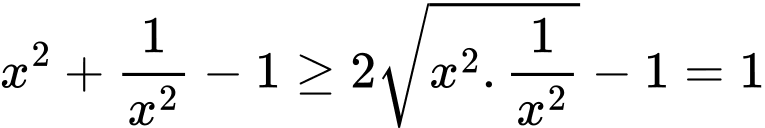
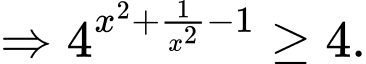
Lại có
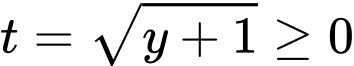
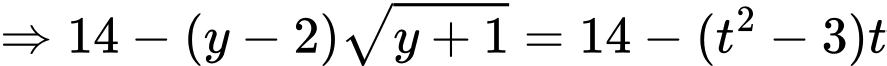
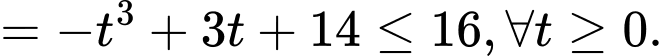
Khi đó
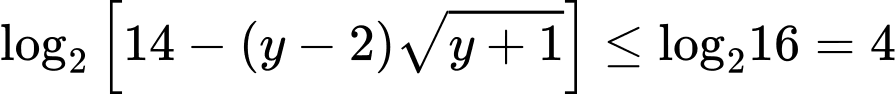 .
.Các dấu đẳng thức xảy ra khi
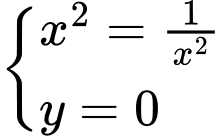
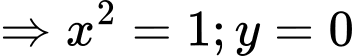
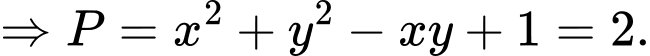 Đáp án: C
Đáp án: C
Câu 23 [502172]: Cho hai số thực 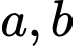 lớn hơn 1 thay đổi thỏa mãn
lớn hơn 1 thay đổi thỏa mãn 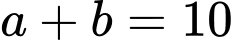 . Gọi
. Gọi 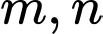 là hai nghiệm của phương trình
là hai nghiệm của phương trình 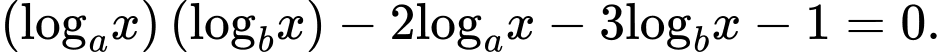 Tìm giá trị lớn nhất của biểu thức
Tìm giá trị lớn nhất của biểu thức 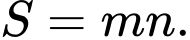
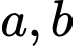 lớn hơn 1 thay đổi thỏa mãn
lớn hơn 1 thay đổi thỏa mãn 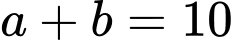 . Gọi
. Gọi 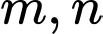 là hai nghiệm của phương trình
là hai nghiệm của phương trình 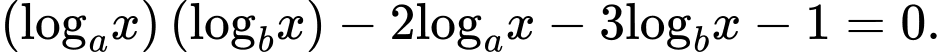 Tìm giá trị lớn nhất của biểu thức
Tìm giá trị lớn nhất của biểu thức 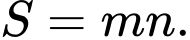
A, 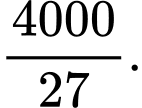
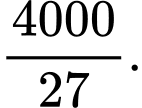
B, 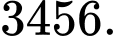
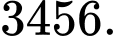
C, 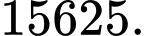
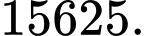
D, 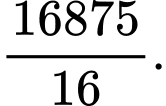
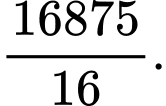
Đáp án B
Sử dụng công thức đổi cơ số ta có
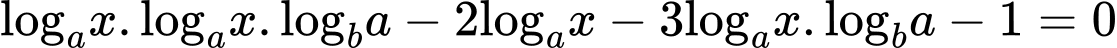
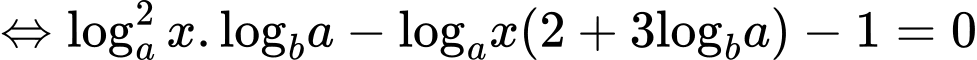
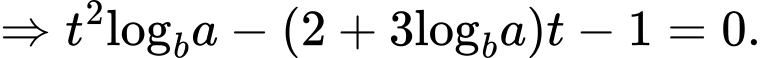
Theo hệ thức Viet thì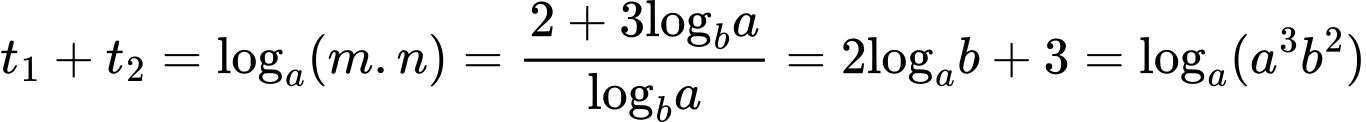
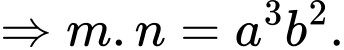
Khi đó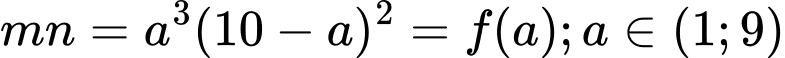
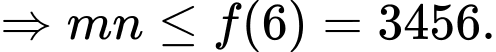 Đáp án: B
Đáp án: B
Sử dụng công thức đổi cơ số ta có
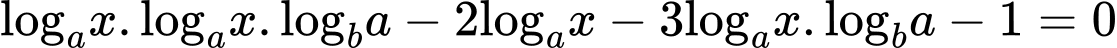
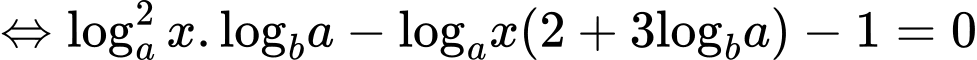
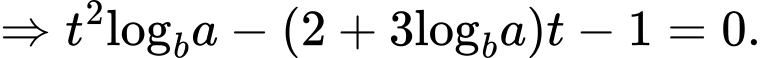
Theo hệ thức Viet thì
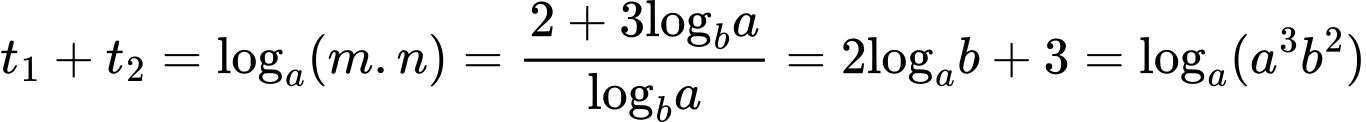
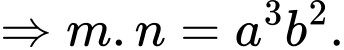
Khi đó
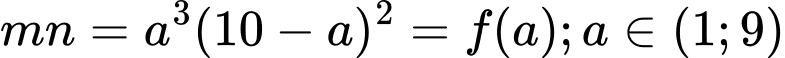
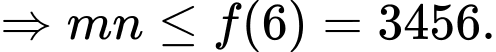 Đáp án: B
Đáp án: B
Câu 24 [677073]: Cho hai số thực 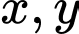 thỏa mãn
thỏa mãn 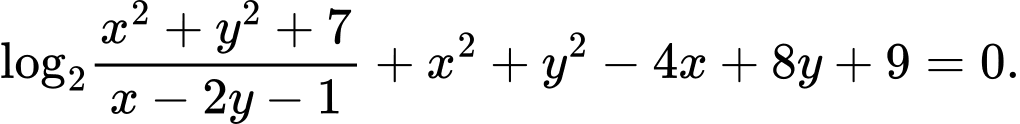 Giá trị lớn nhất của biểu thức
Giá trị lớn nhất của biểu thức 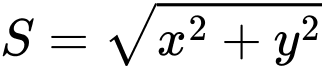 có dạng
có dạng 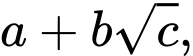 trong đó
trong đó 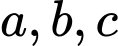 nguyên và
nguyên và  là số nguyên tố. Hỏi
là số nguyên tố. Hỏi 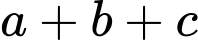 bằng
bằng
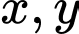 thỏa mãn
thỏa mãn 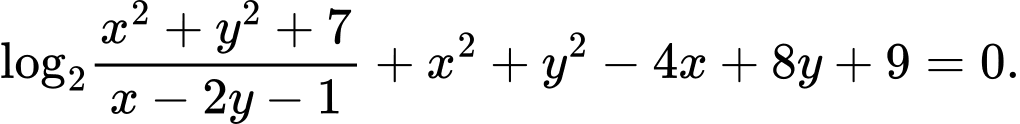 Giá trị lớn nhất của biểu thức
Giá trị lớn nhất của biểu thức 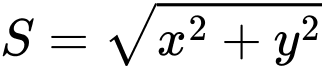 có dạng
có dạng 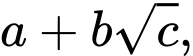 trong đó
trong đó 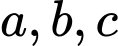 nguyên và
nguyên và  là số nguyên tố. Hỏi
là số nguyên tố. Hỏi 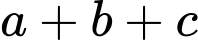 bằng
bằng A, 10.
B, 13.
C, 11.
D, 14.
Đặt 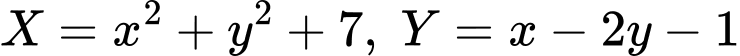
Ta có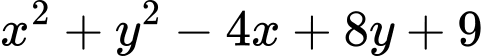
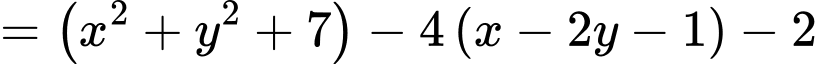
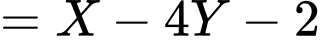
Khi đó ta có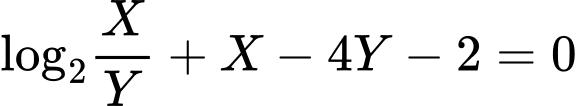
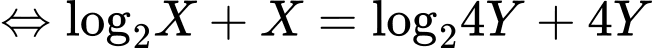

Suy ra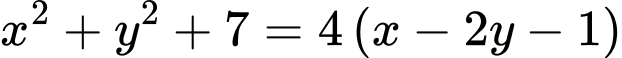
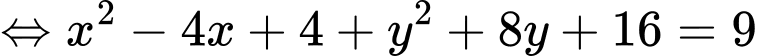
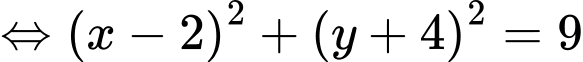
Đặt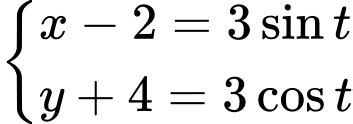
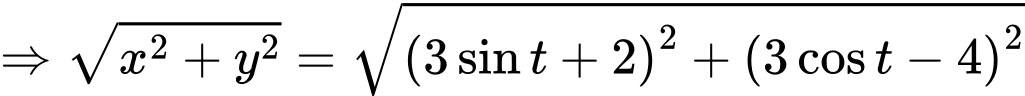
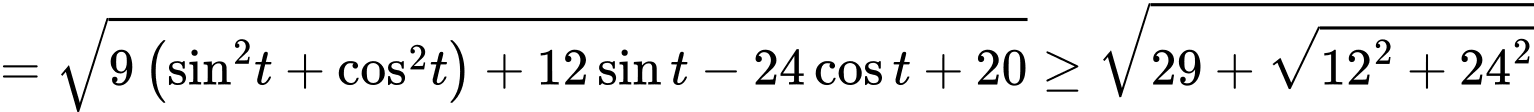
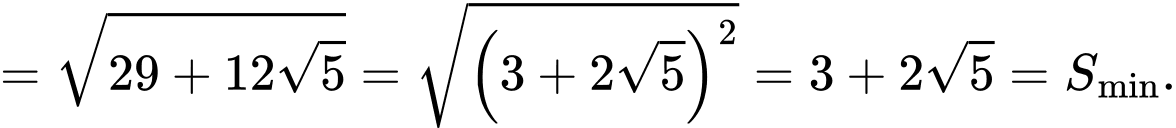 Vậy
Vậy 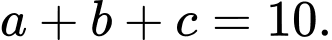 Chọn A. Đáp án: A
Chọn A. Đáp án: A
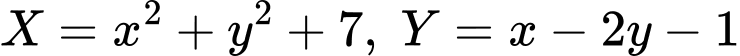
Ta có
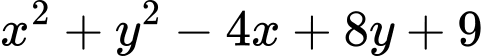
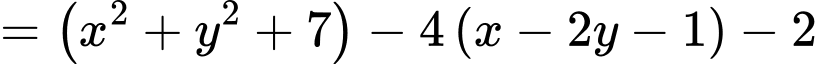
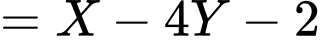
Khi đó ta có
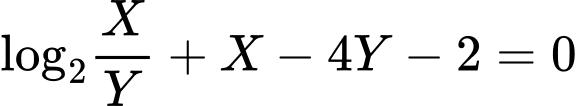
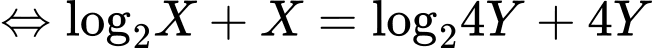

Suy ra
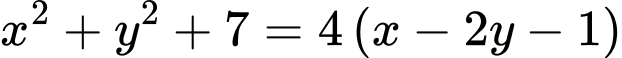
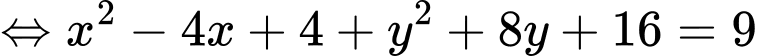
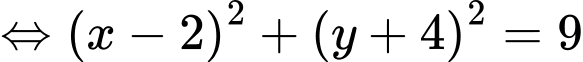
Đặt
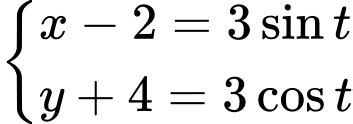
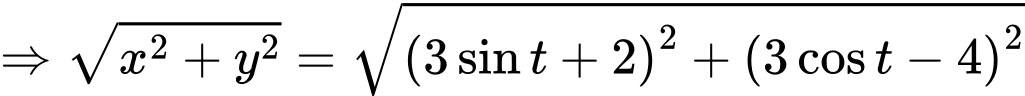
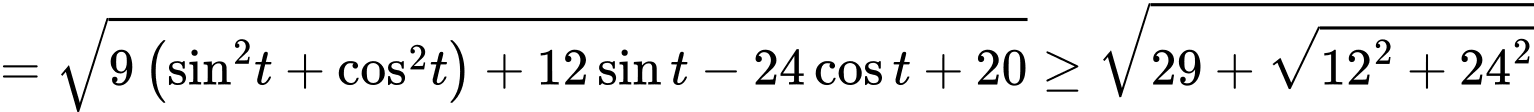
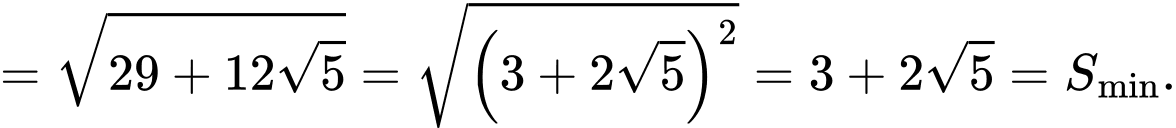 Vậy
Vậy 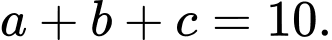 Chọn A. Đáp án: A
Chọn A. Đáp án: A
Câu 25 [234120]: [Đề thi TN THPT 2022]: Xét các số thực 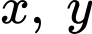 sao cho
sao cho 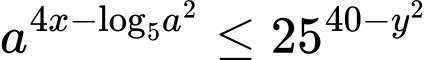 với mọi số thực dương
với mọi số thực dương 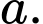 Giá trị lớn nhất của biểu thức
Giá trị lớn nhất của biểu thức 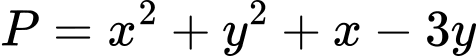 bằng
bằng
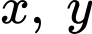 sao cho
sao cho 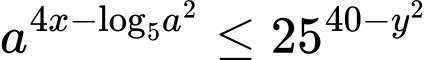 với mọi số thực dương
với mọi số thực dương 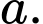 Giá trị lớn nhất của biểu thức
Giá trị lớn nhất của biểu thức 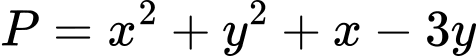 bằng
bằng A, 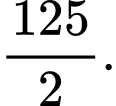
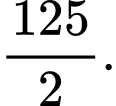
B, 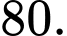
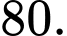
C, 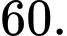
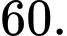
D, 
HD: Ta có: 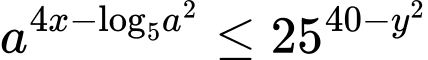
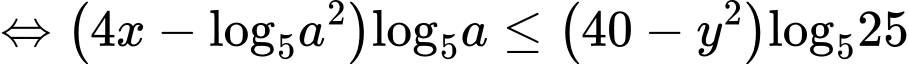 (lấy logarit cơ số 5 cả 2 vế)
(lấy logarit cơ số 5 cả 2 vế)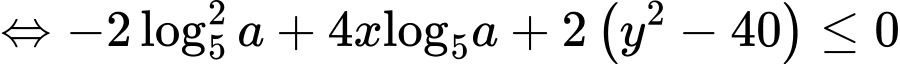
Bất phương trình đúng với mọi khi
khi 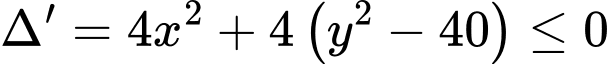
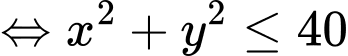
Lại có: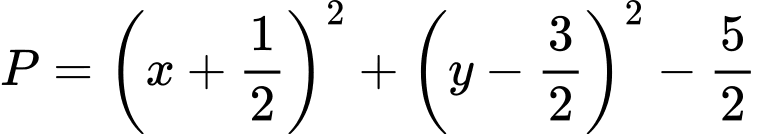
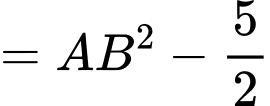
Trong đó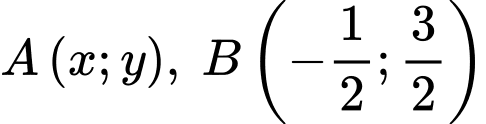 và điểm
và điểm 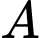 nằm ở miền trong đường tròn
nằm ở miền trong đường tròn 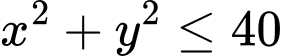 (đường tròn tâm
(đường tròn tâm 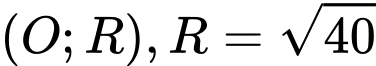 )
)
Lại có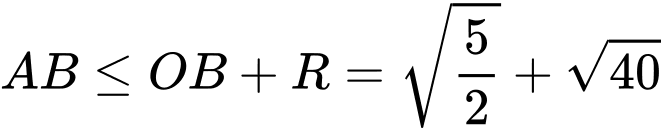
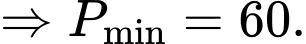
Chọn C. Đáp án: C
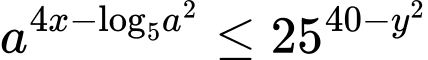
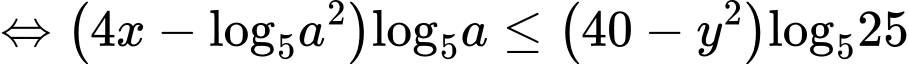 (lấy logarit cơ số 5 cả 2 vế)
(lấy logarit cơ số 5 cả 2 vế)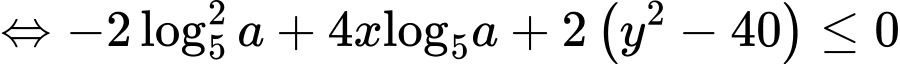
Bất phương trình đúng với mọi
 khi
khi 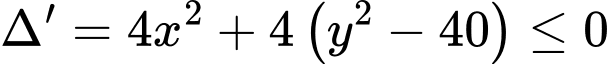
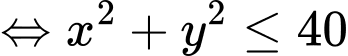
Lại có:
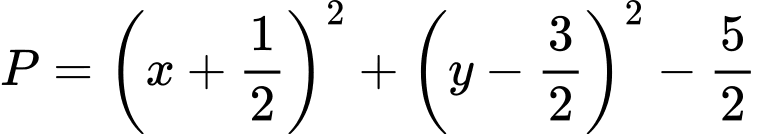
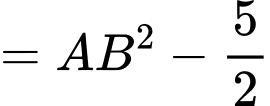
Trong đó
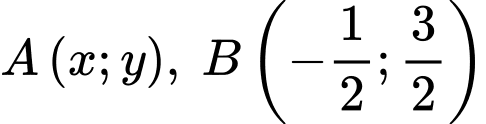 và điểm
và điểm 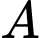 nằm ở miền trong đường tròn
nằm ở miền trong đường tròn 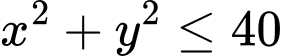 (đường tròn tâm
(đường tròn tâm 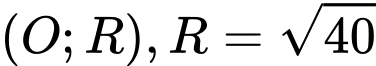 )
) Lại có
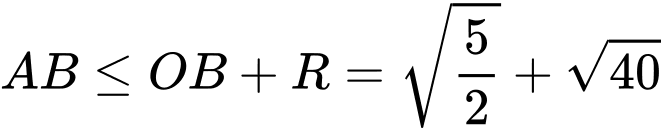
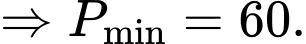
Chọn C. Đáp án: C
Câu 26 [383281]: Xét các số thực không âm 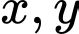 thỏa mãn
thỏa mãn 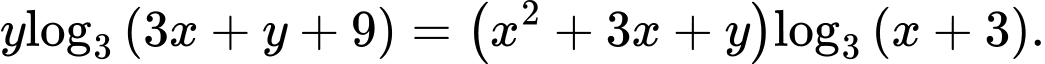 Khi biểu thức
Khi biểu thức 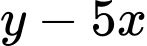 đạt giá trị nhỏ nhất, giá trị của biểu thức
đạt giá trị nhỏ nhất, giá trị của biểu thức 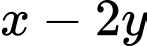 bằng
bằng
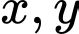 thỏa mãn
thỏa mãn 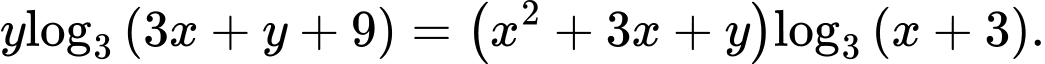 Khi biểu thức
Khi biểu thức 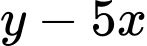 đạt giá trị nhỏ nhất, giá trị của biểu thức
đạt giá trị nhỏ nhất, giá trị của biểu thức 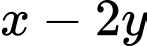 bằng
bằng A, 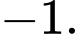
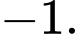
B, 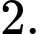
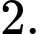
C, 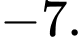
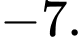
D, 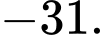
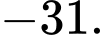
PT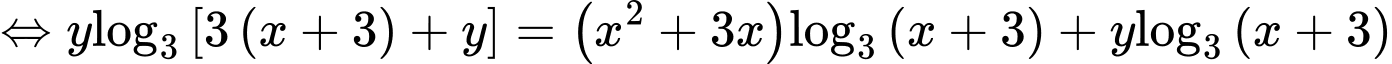
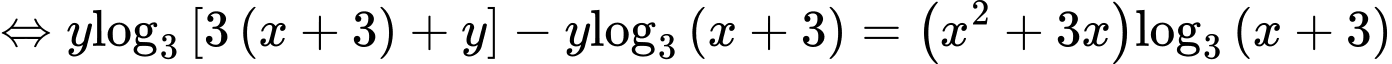
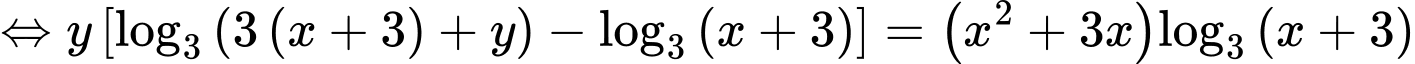
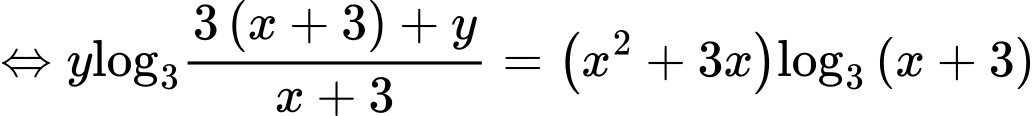
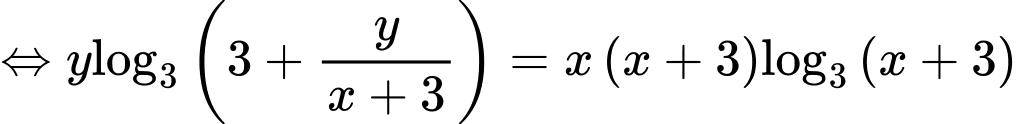
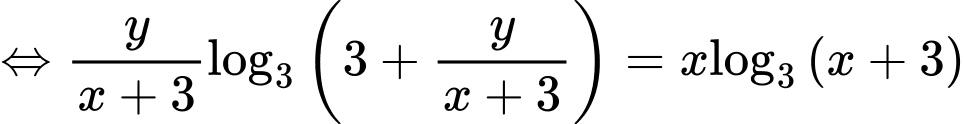
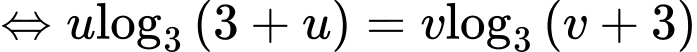
Xét hàm số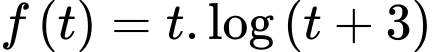 trên khoảng
trên khoảng 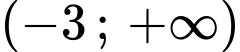
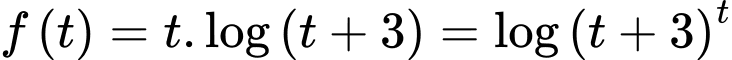
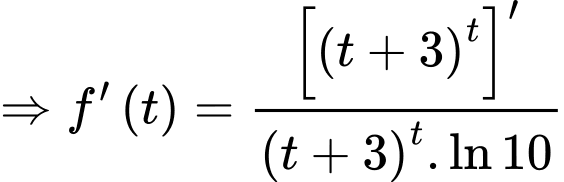
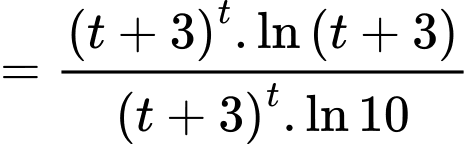
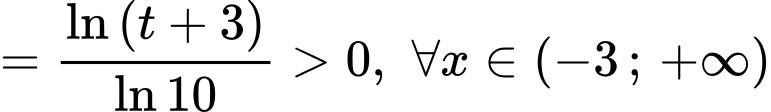
Suy ra hàm số đồng biến.
Suy ra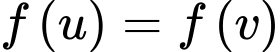
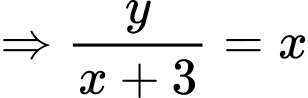
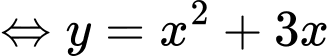
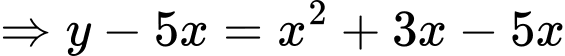
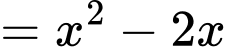
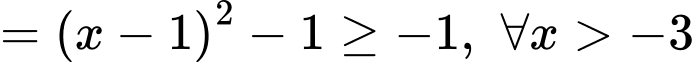
Dấu “=” xảy ra tại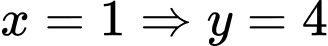
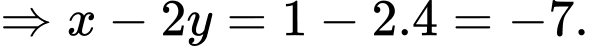
Chọn C.
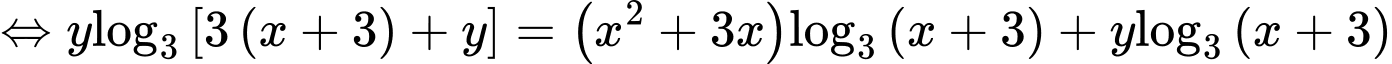
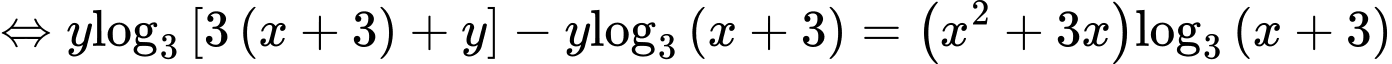
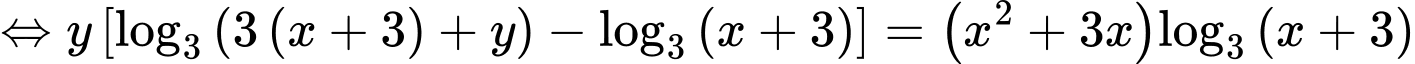
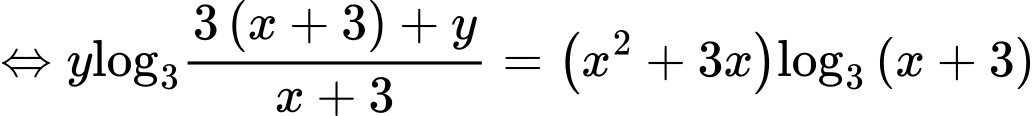
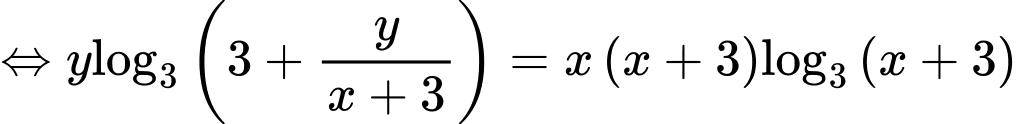
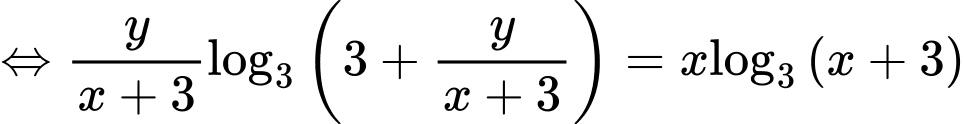
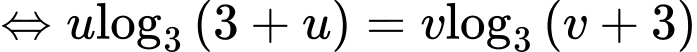
Xét hàm số
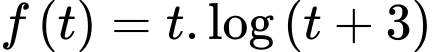 trên khoảng
trên khoảng 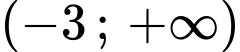
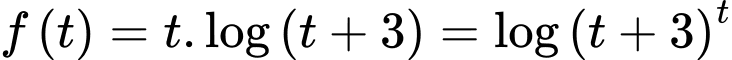
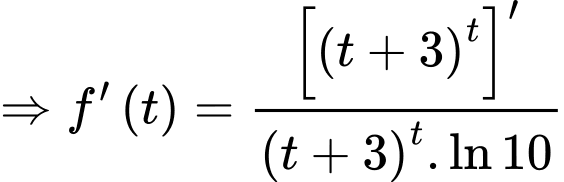
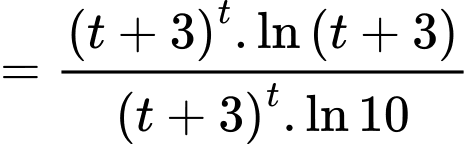
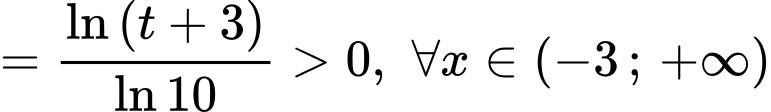
Suy ra hàm số đồng biến.
Suy ra
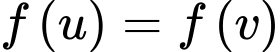
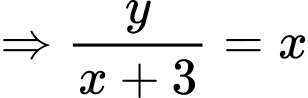
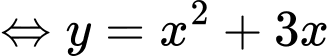
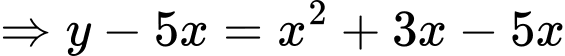
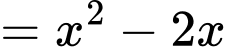
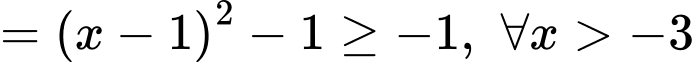
Dấu “=” xảy ra tại
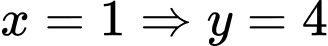
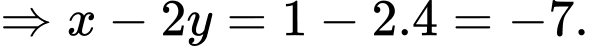
Chọn C.