Đáp án Bài tập tự luyện
Câu 1 [45947]: Cho hàm số 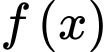 liên tục trên
liên tục trên 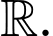 Gọi
Gọi 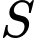 là diện tích hình phẳng giới hạn bởi các đường
là diện tích hình phẳng giới hạn bởi các đường 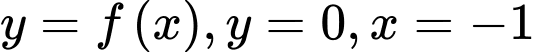 và
và 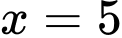 (như hình vẽ bên).
(như hình vẽ bên).
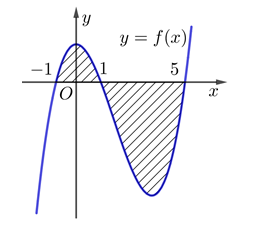
Mệnh đề nào dưới đây đúng?
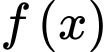 liên tục trên
liên tục trên 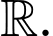 Gọi
Gọi 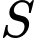 là diện tích hình phẳng giới hạn bởi các đường
là diện tích hình phẳng giới hạn bởi các đường 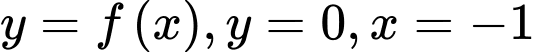 và
và 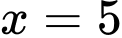 (như hình vẽ bên).
(như hình vẽ bên).
Mệnh đề nào dưới đây đúng?
A, 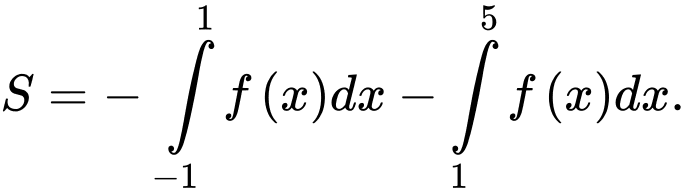
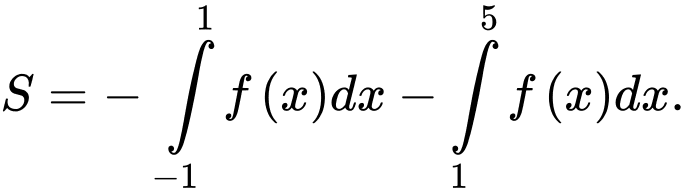
B, 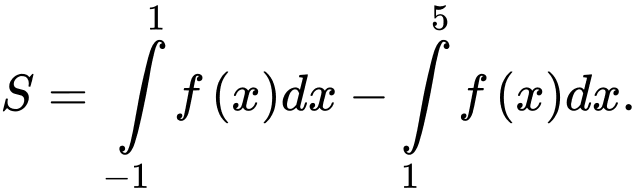
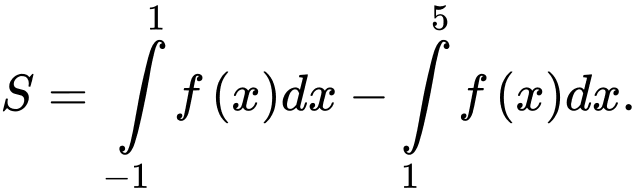
C, 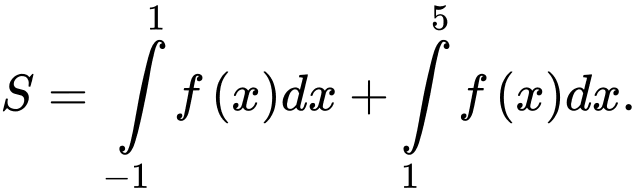
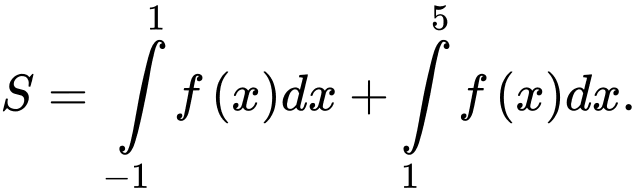
D, 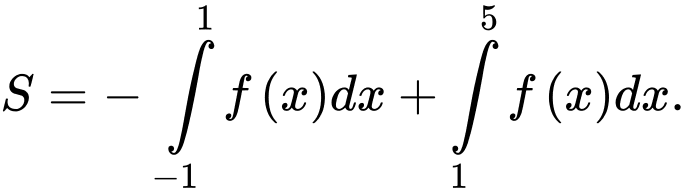
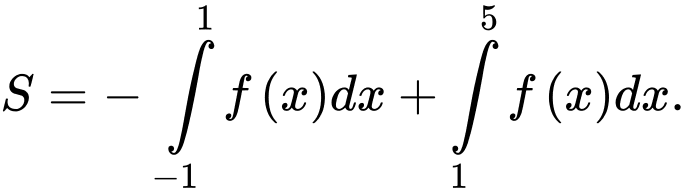
HD: Ta có 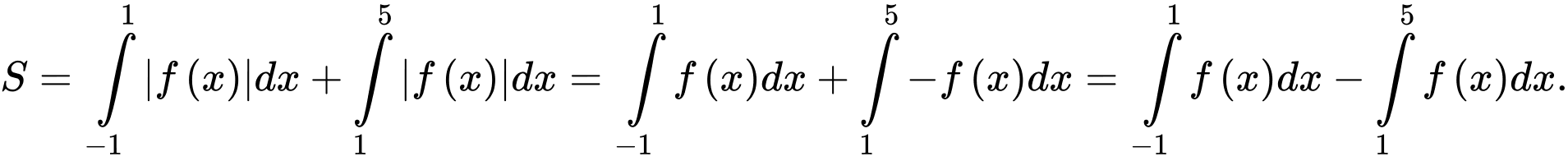
Chọn B. Đáp án: B
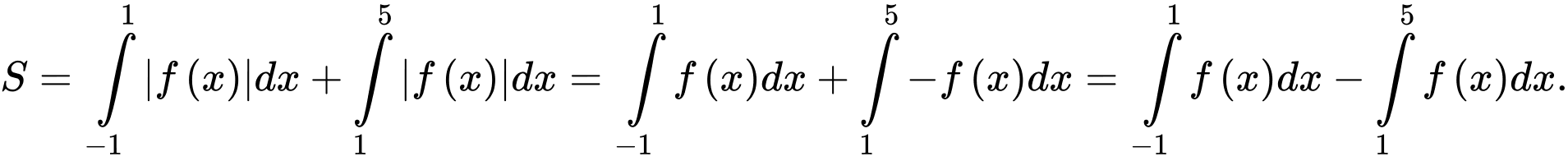
Chọn B. Đáp án: B
Câu 2 [378615]: Cho đồ thị hàm số 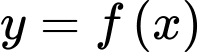 trên đoạn
trên đoạn 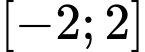 như Hình 4.32.
như Hình 4.32.
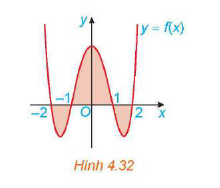
Biết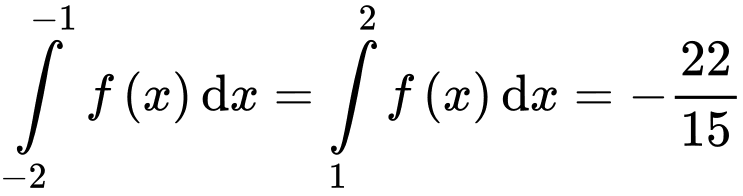 và
và 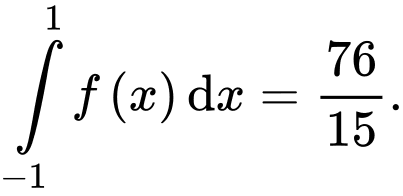 Khi đó, diện tích của hình phẳng được tô màu là
Khi đó, diện tích của hình phẳng được tô màu là
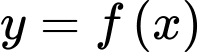 trên đoạn
trên đoạn 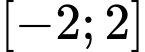 như Hình 4.32.
như Hình 4.32.
Biết
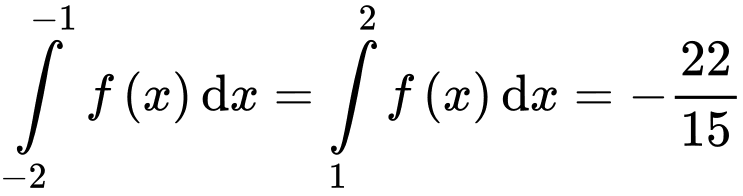 và
và 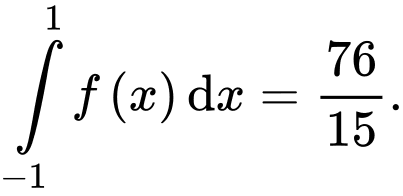 Khi đó, diện tích của hình phẳng được tô màu là
Khi đó, diện tích của hình phẳng được tô màu là A, 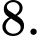
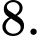
B, 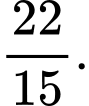
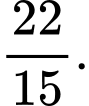
C, 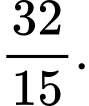
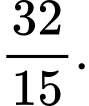
D, 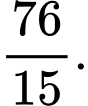
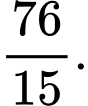
Diện tích phần tô đậm là: 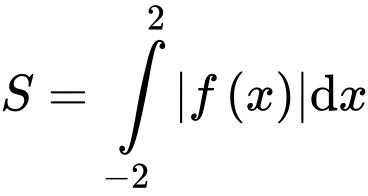
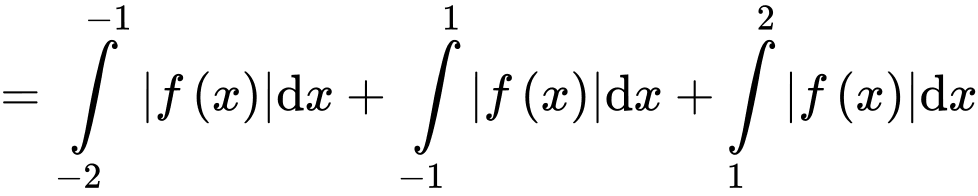
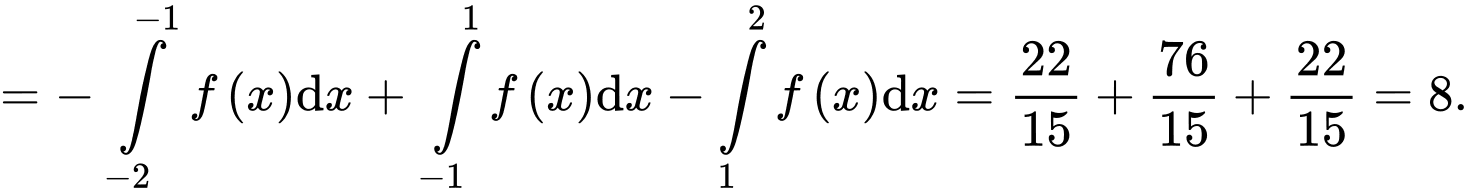 Chọn A. Đáp án: A
Chọn A. Đáp án: A
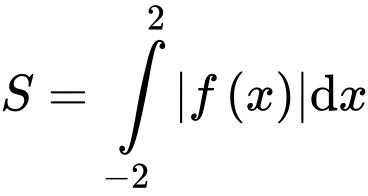
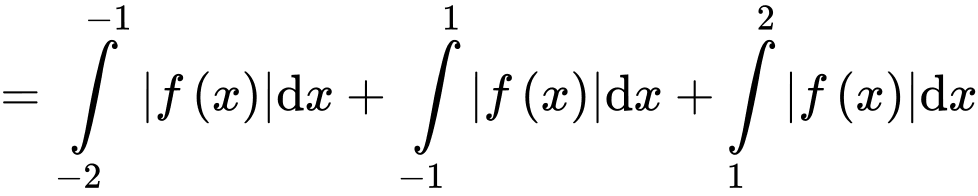
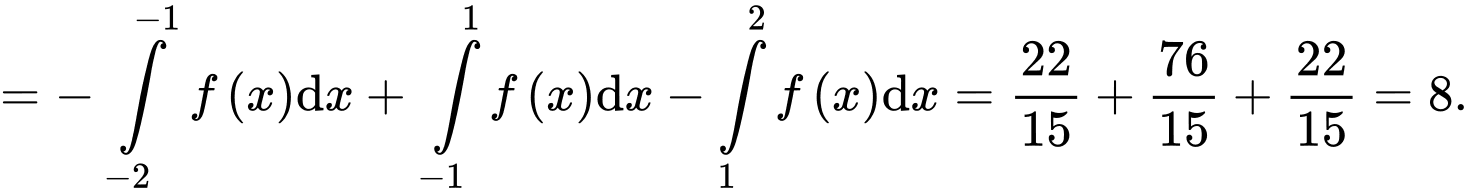 Chọn A. Đáp án: A
Chọn A. Đáp án: A
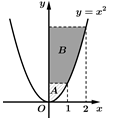
Câu 3 [392137]: Gọi 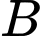 và
và 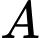 là diện tích hình phẳng mô tả ở hình vẽ bên. Tính tỉ số
là diện tích hình phẳng mô tả ở hình vẽ bên. Tính tỉ số 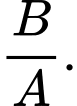
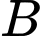 và
và 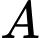 là diện tích hình phẳng mô tả ở hình vẽ bên. Tính tỉ số
là diện tích hình phẳng mô tả ở hình vẽ bên. Tính tỉ số 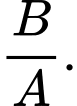

A, 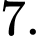
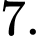
B, 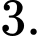
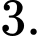
C, 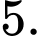
D, 
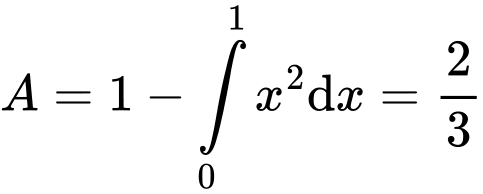
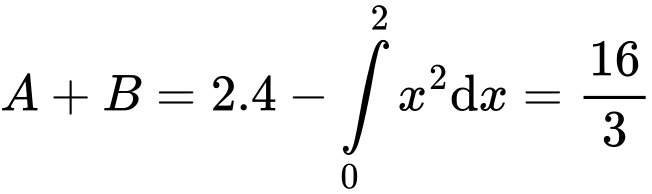
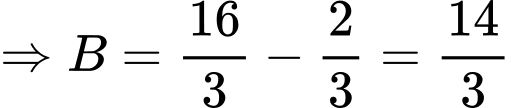
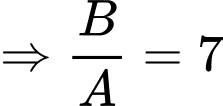
Đáp án A. Đáp án: A
Câu 4 [392134]: Diện tích phần tô đậm trong hình vẽ bên, bằng tích phân nào dưới đây?
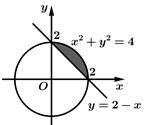

A, 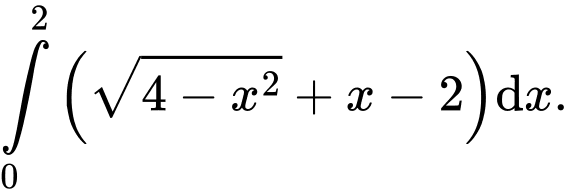
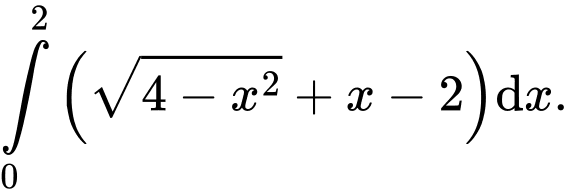
B, 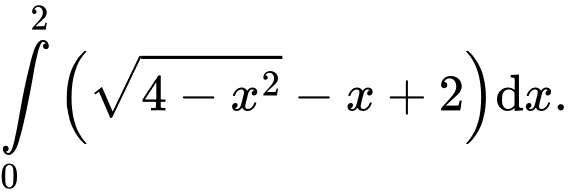
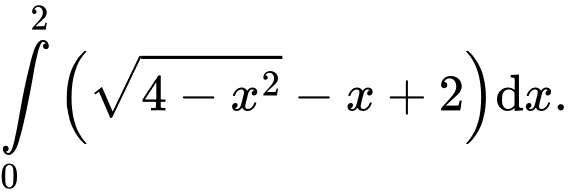
C, 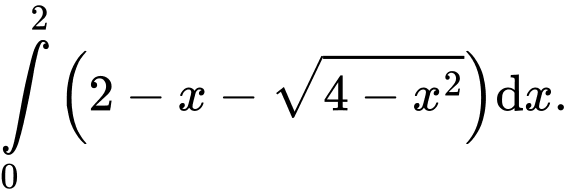
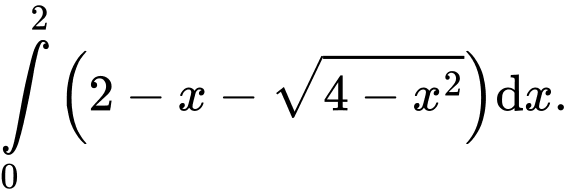
D, 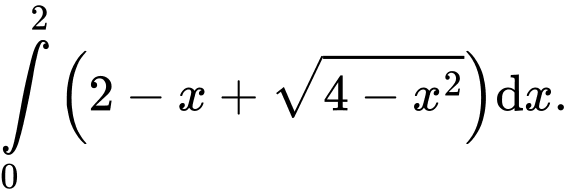
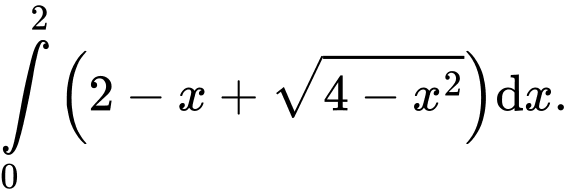
Chọn đáp án A.
Ta có:
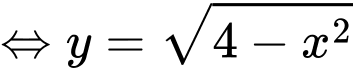
Và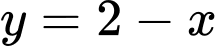
Theo hình vẽ ta có:
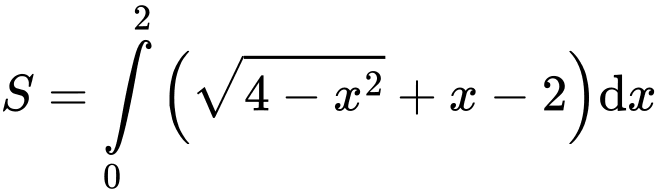
Đáp án: A
Ta có:

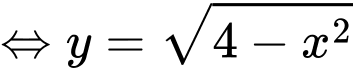
Và
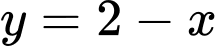
Theo hình vẽ ta có:
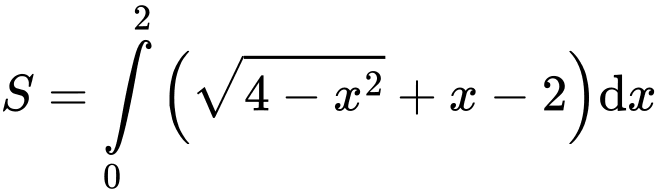
Đáp án: A
Câu 5 [392133]: Diện tích phần tô đậm trong hình vẽ bên, bằng tích phân nào dưới đây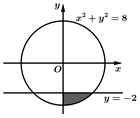

A, 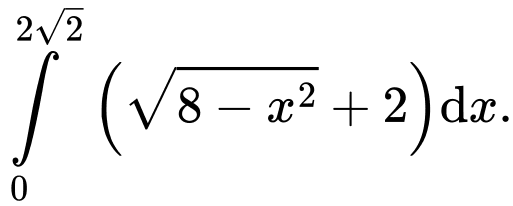
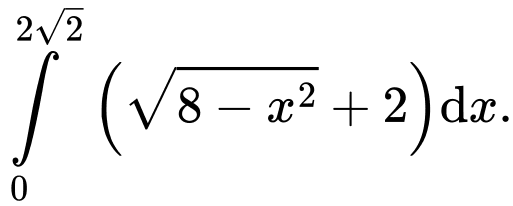
B, 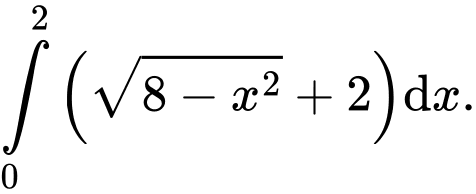
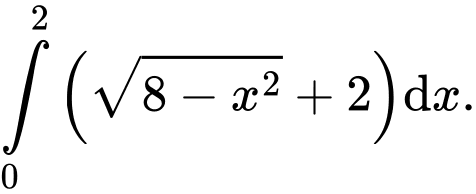
C, 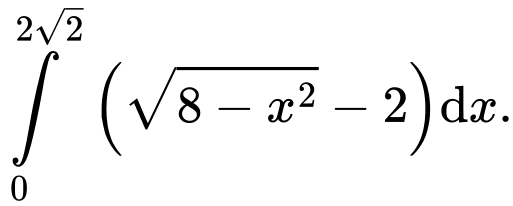
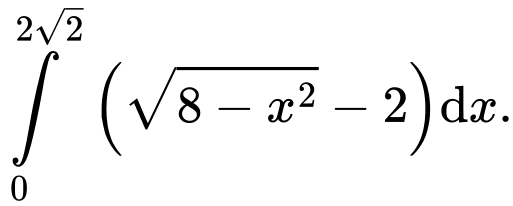
D, 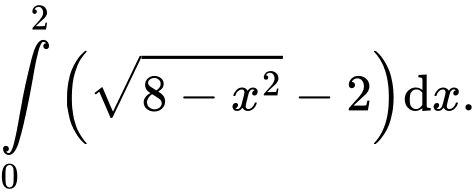
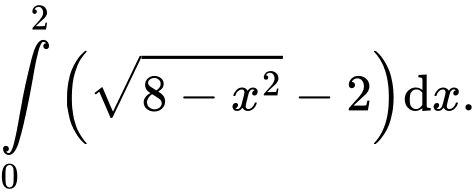
Có: 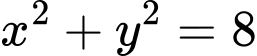
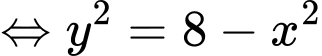
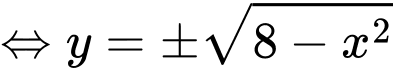
Ta có, từ đồ thị hình vẽ ta có phương hoành độ giao điểm của và
và 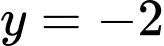 là:
là:
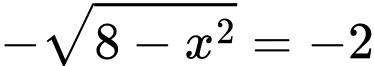

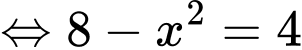
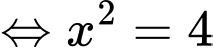
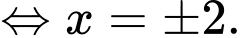
Từ hình vẽ, ta xác định được diện tích phần in đậm là tích phân:
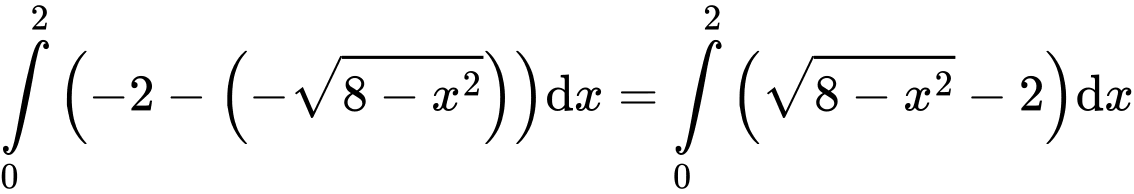
Đáp án: D. Đáp án: D
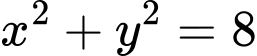
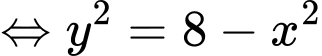
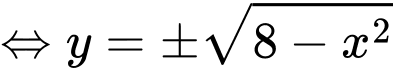
Ta có, từ đồ thị hình vẽ ta có phương hoành độ giao điểm của
 và
và 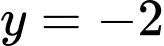 là:
là:
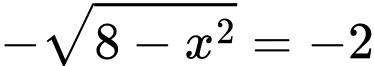

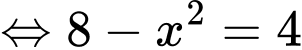
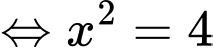
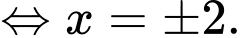
Từ hình vẽ, ta xác định được diện tích phần in đậm là tích phân:
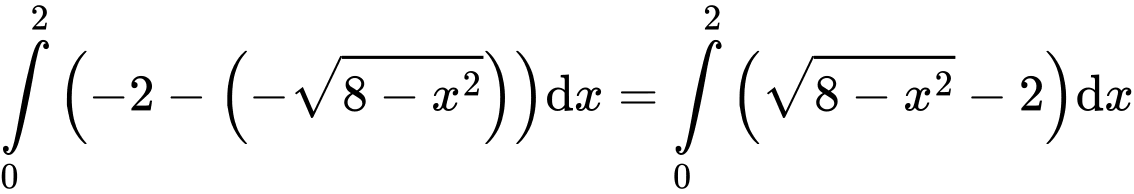
Đáp án: D. Đáp án: D
Câu 6 [151428]: Tính thể tích  của vật thể giới hạn bởi hai mặt phẳng
của vật thể giới hạn bởi hai mặt phẳng 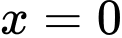 và
và 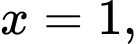 biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục
biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục 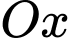 tại điểm có hoành độ
tại điểm có hoành độ 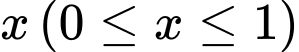 thì được thiết diện là hình vuông có cạnh bằng
thì được thiết diện là hình vuông có cạnh bằng  .
.
 của vật thể giới hạn bởi hai mặt phẳng
của vật thể giới hạn bởi hai mặt phẳng 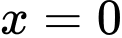 và
và 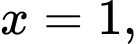 biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục
biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục 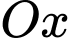 tại điểm có hoành độ
tại điểm có hoành độ 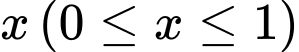 thì được thiết diện là hình vuông có cạnh bằng
thì được thiết diện là hình vuông có cạnh bằng  .
. A, 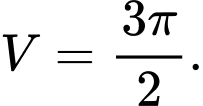
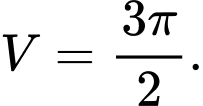
B, 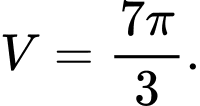
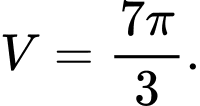
C, 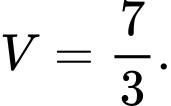
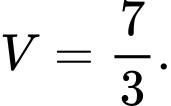
D, 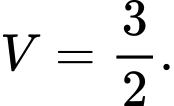
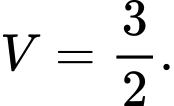
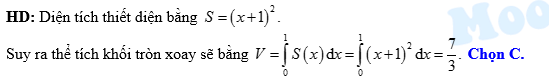 Đáp án: C
Đáp án: C
Câu 7 [151431]: Cho phần vật thể 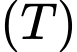 giới hạn bởi hai mặt phẳng có phương trình
giới hạn bởi hai mặt phẳng có phương trình 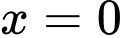 và
và 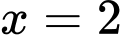 . Cắt phần vật thể
. Cắt phần vật thể 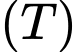 bởi mặt phẳng vuông góc với trục
bởi mặt phẳng vuông góc với trục 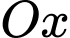 tại điểm có hoành độ
tại điểm có hoành độ 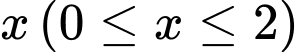 , ta được thiết diện là một tam giác đều có độ dài cạnh bằng
, ta được thiết diện là một tam giác đều có độ dài cạnh bằng 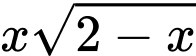 . Tính thể tích
. Tính thể tích  của phần vật thể
của phần vật thể 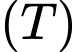 .
.
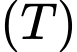 giới hạn bởi hai mặt phẳng có phương trình
giới hạn bởi hai mặt phẳng có phương trình 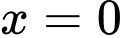 và
và 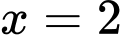 . Cắt phần vật thể
. Cắt phần vật thể 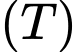 bởi mặt phẳng vuông góc với trục
bởi mặt phẳng vuông góc với trục 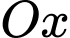 tại điểm có hoành độ
tại điểm có hoành độ 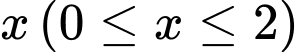 , ta được thiết diện là một tam giác đều có độ dài cạnh bằng
, ta được thiết diện là một tam giác đều có độ dài cạnh bằng 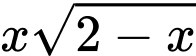 . Tính thể tích
. Tính thể tích  của phần vật thể
của phần vật thể 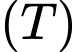 .
. A, 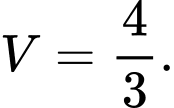
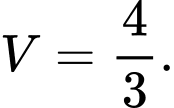
B, 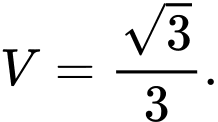
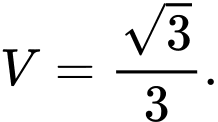
C, 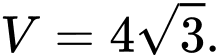
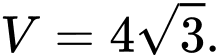
D, 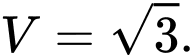
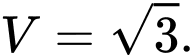
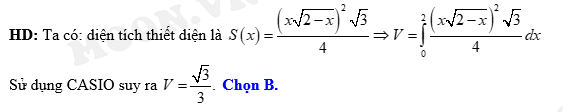 Đáp án: B
Đáp án: B
Câu 8 [151641]: Gọi  là hình phẳng giới hạn bởi đồ thị hàm số
là hình phẳng giới hạn bởi đồ thị hàm số 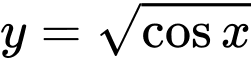 , trục hoành và các đường thẳng
, trục hoành và các đường thẳng 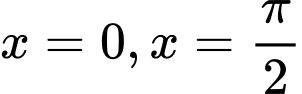 . Tính thể tích
. Tính thể tích  của khối tròn xoay tạo thành khi quay hình
của khối tròn xoay tạo thành khi quay hình  quanh trục
quanh trục 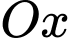 .
.
 là hình phẳng giới hạn bởi đồ thị hàm số
là hình phẳng giới hạn bởi đồ thị hàm số 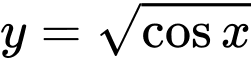 , trục hoành và các đường thẳng
, trục hoành và các đường thẳng 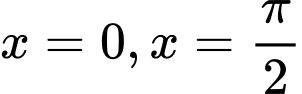 . Tính thể tích
. Tính thể tích  của khối tròn xoay tạo thành khi quay hình
của khối tròn xoay tạo thành khi quay hình  quanh trục
quanh trục 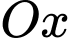 .
. A, 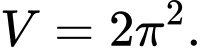
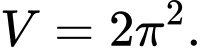
B, 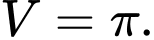
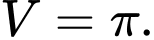
C, 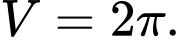
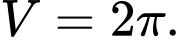
D, 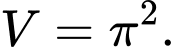
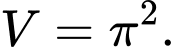
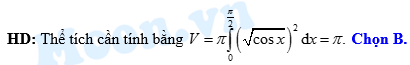 Đáp án: B
Đáp án: B
Câu 9 [151636]: Thể tích vật thể tròn xoay sinh bởi khi quay hình phẳng giới hạn bởi đồ thị hàm số 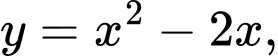 trục hoành, đường thẳng
trục hoành, đường thẳng 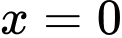 và đường thẳng
và đường thẳng 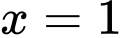 quay quanh trục hoành là
quay quanh trục hoành là
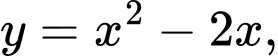 trục hoành, đường thẳng
trục hoành, đường thẳng 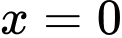 và đường thẳng
và đường thẳng 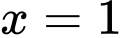 quay quanh trục hoành là
quay quanh trục hoành là A, 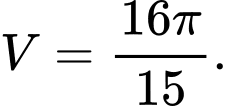
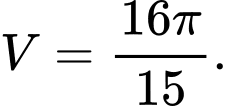
B, 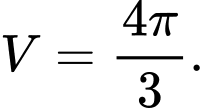
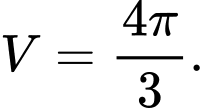
C, 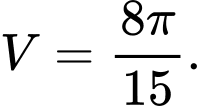
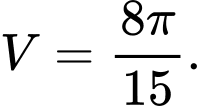
D, 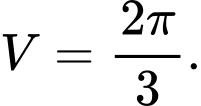
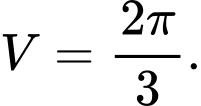
HD: Thể tích cần tính bằng 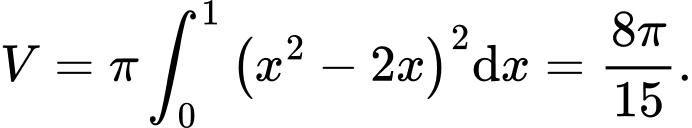 Chọn C. Đáp án: C
Chọn C. Đáp án: C
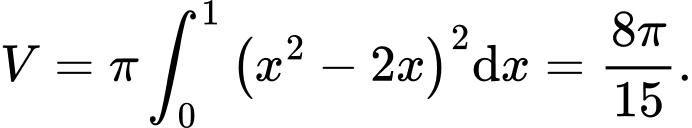 Chọn C. Đáp án: C
Chọn C. Đáp án: C
Câu 10 [153553]: [Đề Mẫu ĐGNL TPHCM]: Diện tích hình phẳng giới hạn bởi hai đường 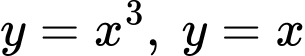 bằng
bằng
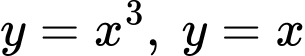 bằng
bằng A, 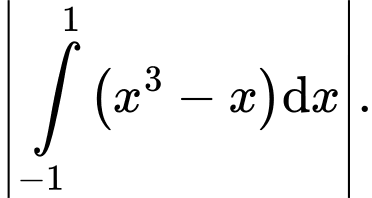
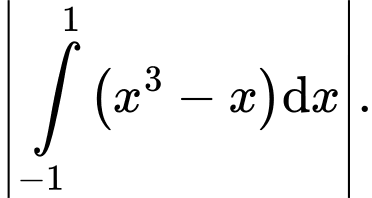
B, 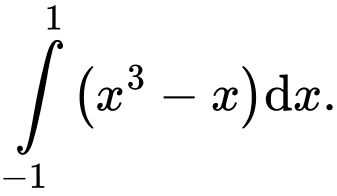
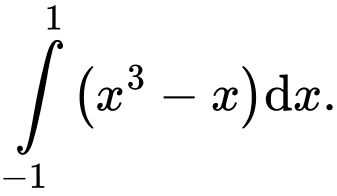
C, 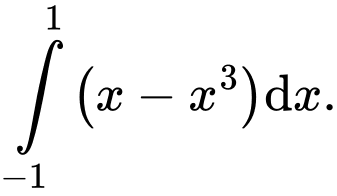
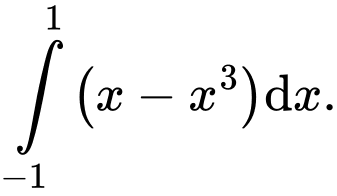
D, 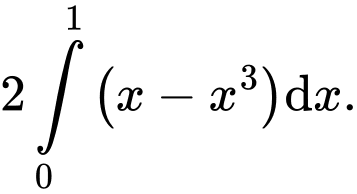
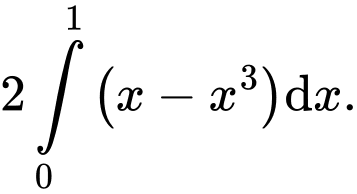
Ta có: 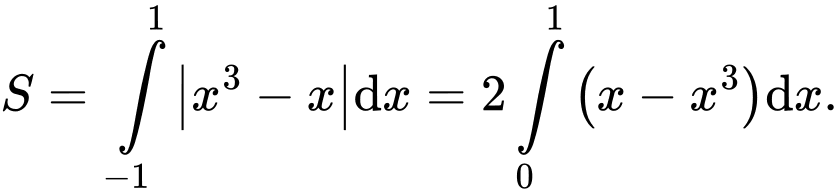
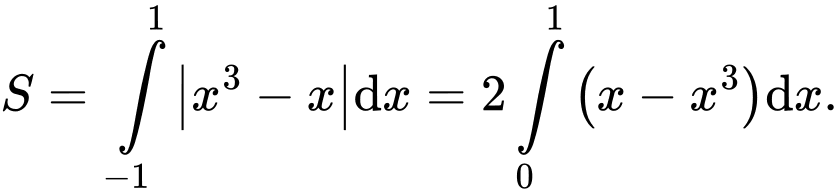
Chọn D.
Đáp án: D
Câu 11 [397899]: [Đề mẫu ĐGNL Hà Nội]: Cho  là hình phẳng giới hạn bởi các đường thẳng
là hình phẳng giới hạn bởi các đường thẳng 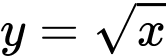 và
và 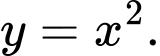 Thể tích của khối tròn xoay tạo thành khi quanh hình
Thể tích của khối tròn xoay tạo thành khi quanh hình  quanh trục
quanh trục 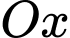 bằng
bằng
 là hình phẳng giới hạn bởi các đường thẳng
là hình phẳng giới hạn bởi các đường thẳng 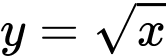 và
và 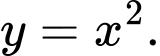 Thể tích của khối tròn xoay tạo thành khi quanh hình
Thể tích của khối tròn xoay tạo thành khi quanh hình  quanh trục
quanh trục 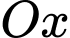 bằng
bằng A, 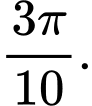
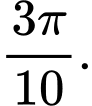
B, 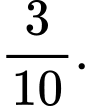
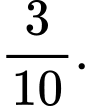
C, 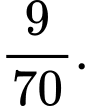
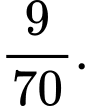
D, 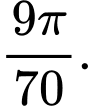
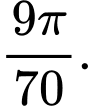
Phương trình hoành độ giao điểm là 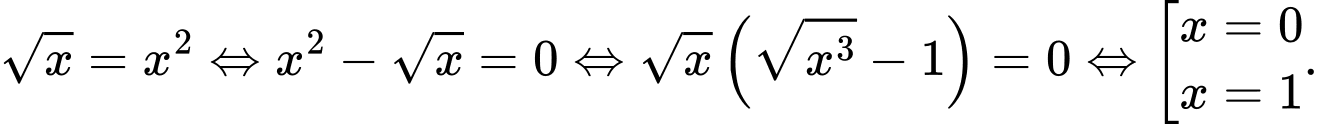
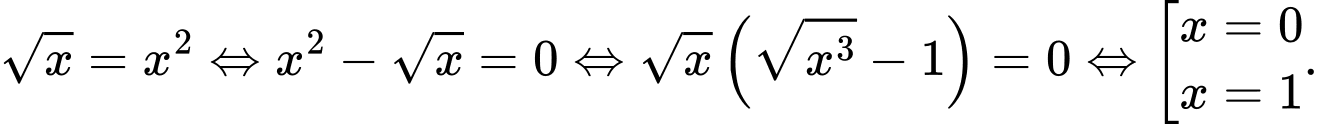
Suy ra thể tích của khối tròn xoay đó là
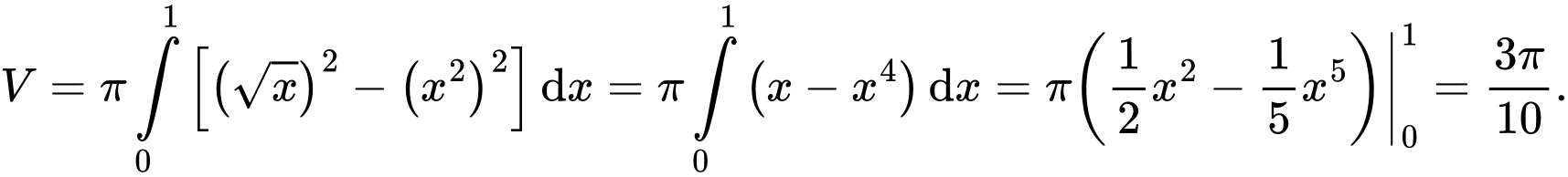
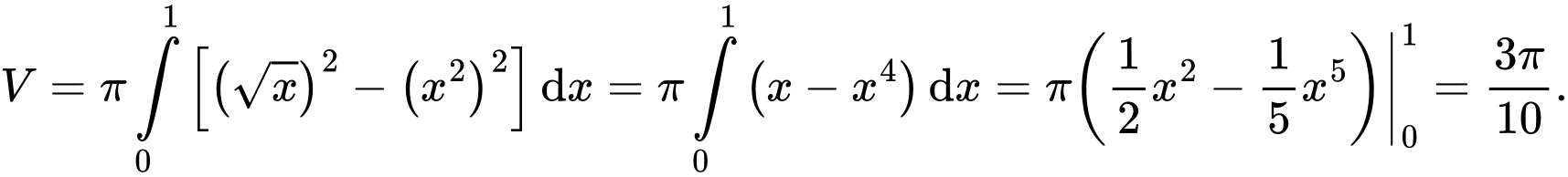
Chọn đáp án A.
Câu 12 [392138]: Đường cong 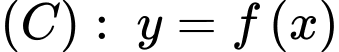 cắt đường thẳng
cắt đường thẳng 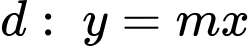 tại hai điểm phân biết như hình bên. Biết rằng
tại hai điểm phân biết như hình bên. Biết rằng 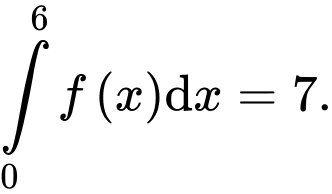 Tính diện tích miền được tô đậm
Tính diện tích miền được tô đậm 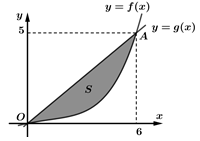
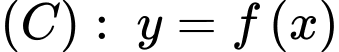 cắt đường thẳng
cắt đường thẳng 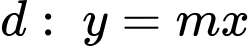 tại hai điểm phân biết như hình bên. Biết rằng
tại hai điểm phân biết như hình bên. Biết rằng 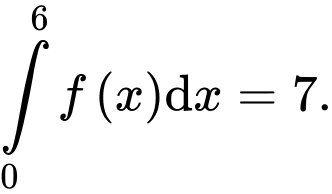 Tính diện tích miền được tô đậm
Tính diện tích miền được tô đậm 
A, 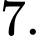
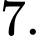
B, 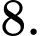
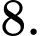
C, 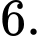
D, 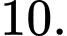
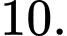
Có: 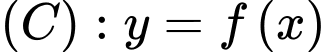 và
và 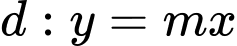
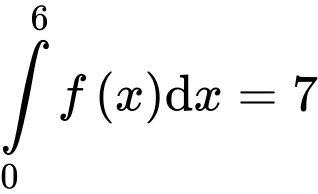
Theo hình vẽ bài cho ta có:
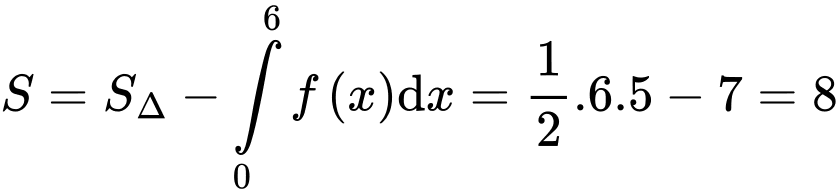
Đáp án B Đáp án: B
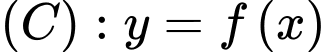 và
và 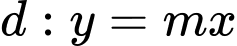
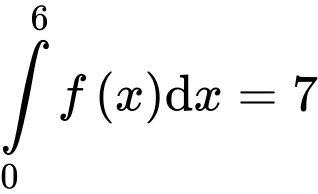
Theo hình vẽ bài cho ta có:
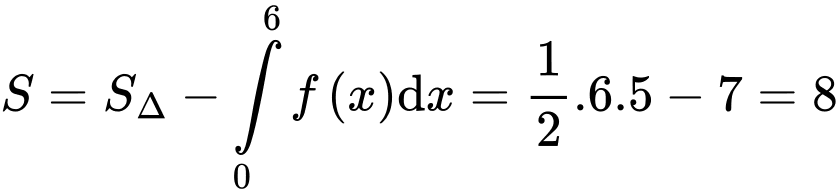
Đáp án B Đáp án: B
Câu 13 [392127]: Cho hàm số 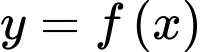 có đồ thị là đường cong như hình vẽ bên. Biết rằng
có đồ thị là đường cong như hình vẽ bên. Biết rằng 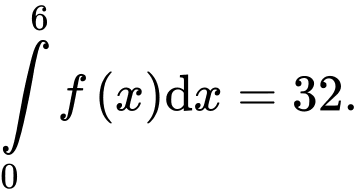 Tính diện hình phần tô đậm
Tính diện hình phần tô đậm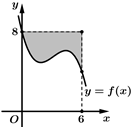
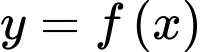 có đồ thị là đường cong như hình vẽ bên. Biết rằng
có đồ thị là đường cong như hình vẽ bên. Biết rằng 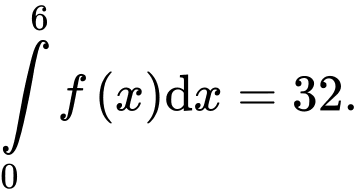 Tính diện hình phần tô đậm
Tính diện hình phần tô đậm
A, 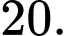
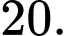
B, 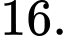
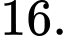
C, 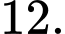
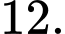
D, 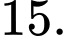
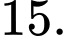
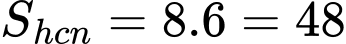
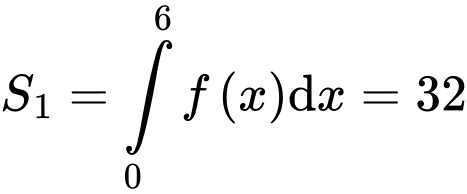
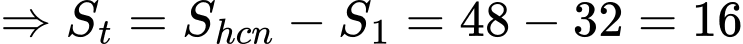
Suy ra, chọn đáp án B. Đáp án: B
Câu 14 [392122]: Cho hai hàm số 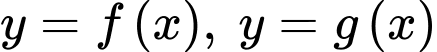 liên tục trên đoạn
liên tục trên đoạn  và có đồ thị như hình vẽ. Biết rằng
và có đồ thị như hình vẽ. Biết rằng 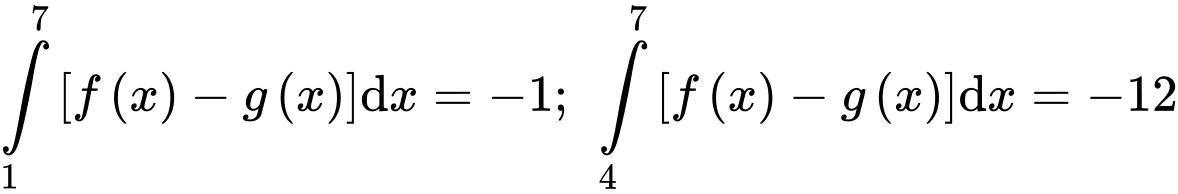 Tính
Tính 
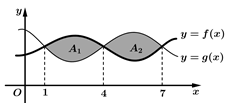
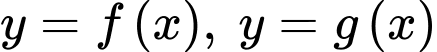 liên tục trên đoạn
liên tục trên đoạn 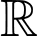 và có đồ thị như hình vẽ. Biết rằng
và có đồ thị như hình vẽ. Biết rằng 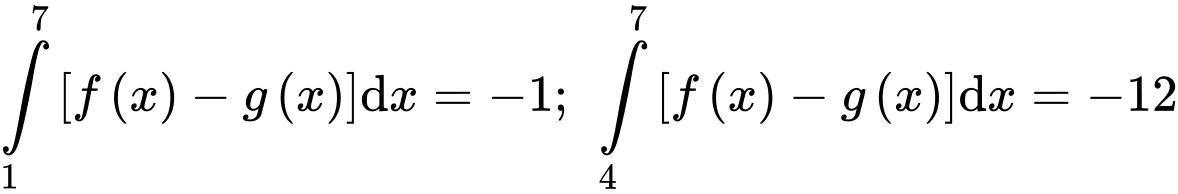 Tính
Tính 

A, 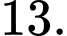
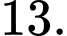
B, 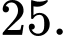
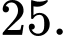
C, 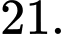
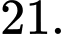
D, 
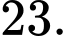
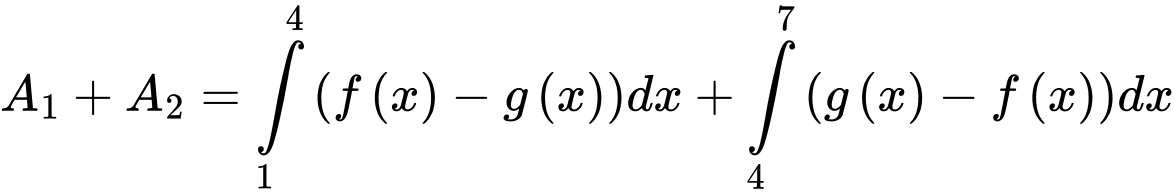
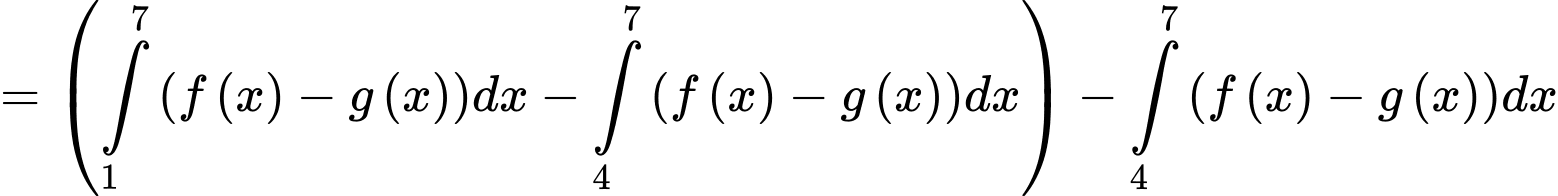
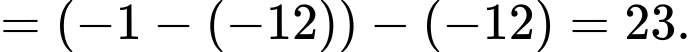 Đáp án: D
Đáp án: D
Câu 15 [392117]: Cho hàm số 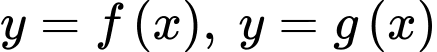 có đồ thị như hình vẽ bên. Tính
có đồ thị như hình vẽ bên. Tính 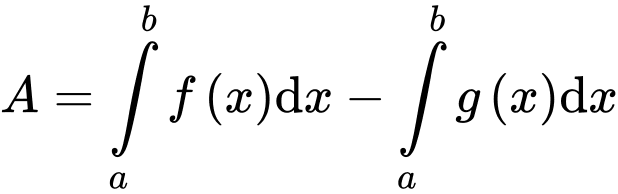 theo
theo 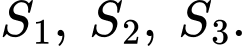
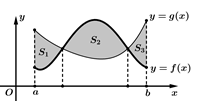
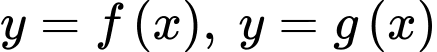 có đồ thị như hình vẽ bên. Tính
có đồ thị như hình vẽ bên. Tính 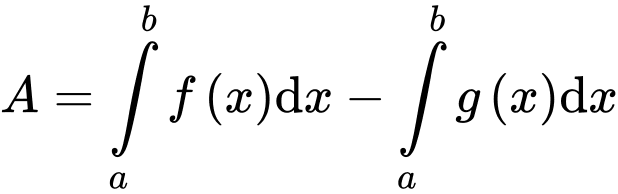 theo
theo 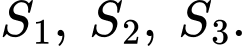

A, 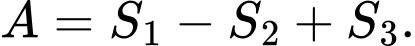
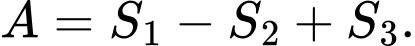
B, 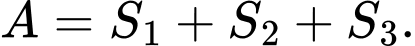
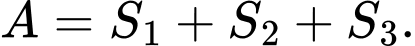
C, 

D, 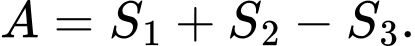
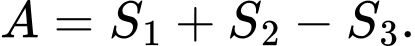
Có: 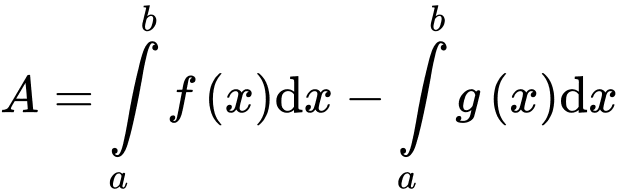
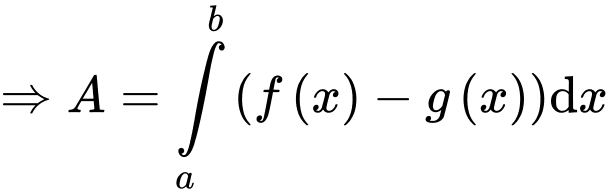
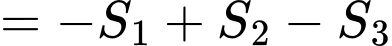
Đáp án: C Đáp án: C
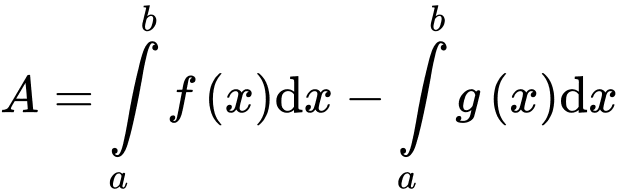
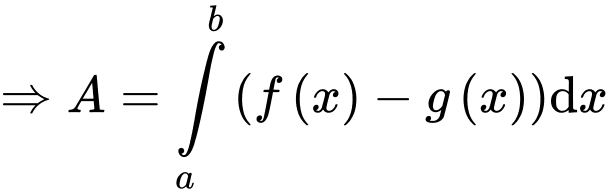
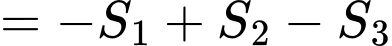
Đáp án: C Đáp án: C
Câu 16 [151234]: Diện tích hình phẳng giới hạn bởi các đường 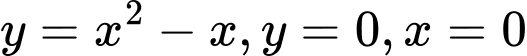 và
và 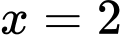 được tính bởi công thức
được tính bởi công thức
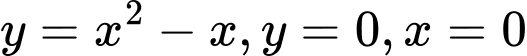 và
và 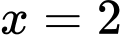 được tính bởi công thức
được tính bởi công thức A, 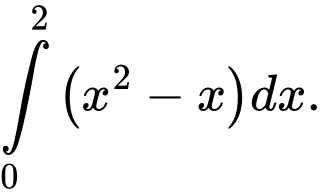
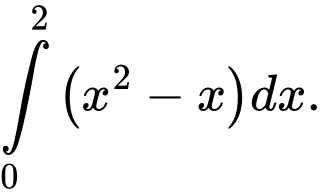
B, 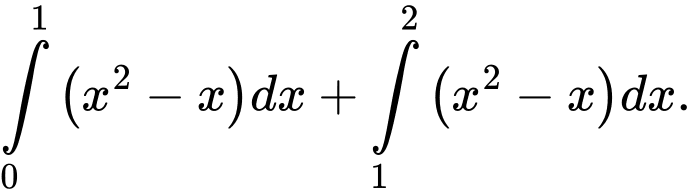
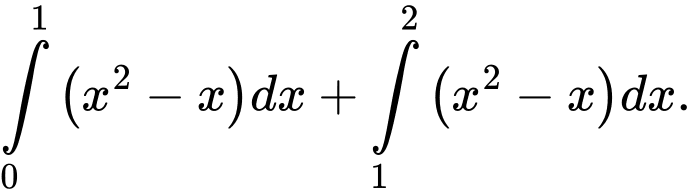
C, 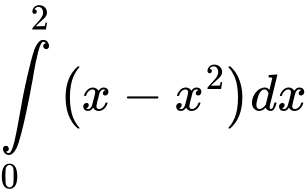
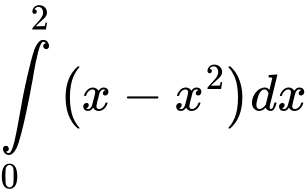
D, 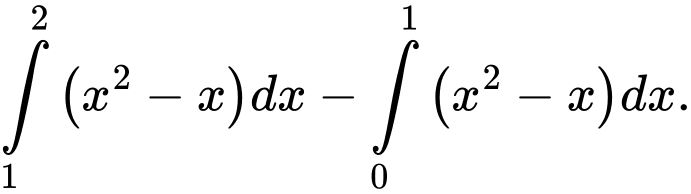
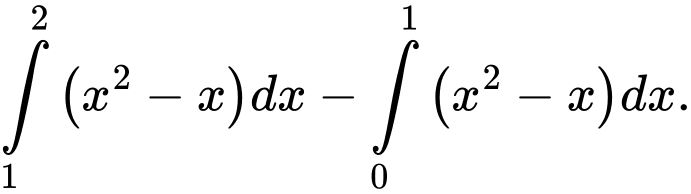
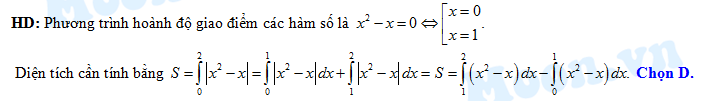 Đáp án: D
Đáp án: D
Câu 17 [140085]: Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số 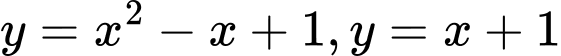 là
là
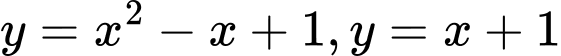 là
là A, 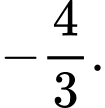
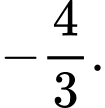
B, 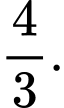
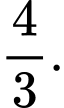
C, 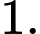
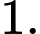
D, 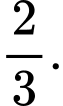
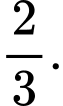
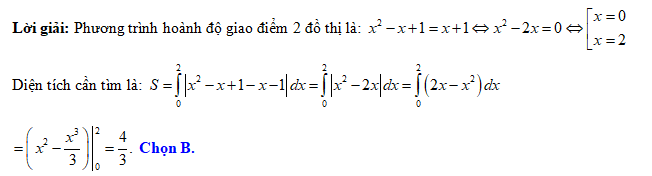 Đáp án: B
Đáp án: B
Câu 18 [392119]: Biết rằng diện tích miền tô đậm trong hình vẽ bên bằng 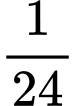 (đvdt). Tìm
(đvdt). Tìm 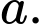
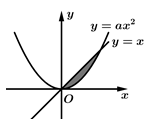
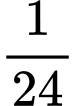 (đvdt). Tìm
(đvdt). Tìm 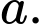

A, 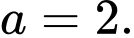
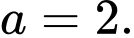
B, 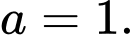
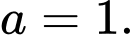
C, 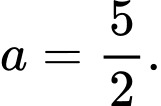
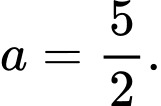
D, 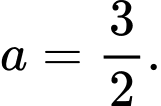
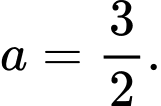
Phương trình hoành độ giao điểm của hai đồ thị là: 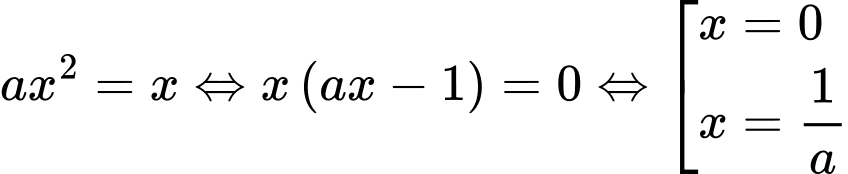
Lại có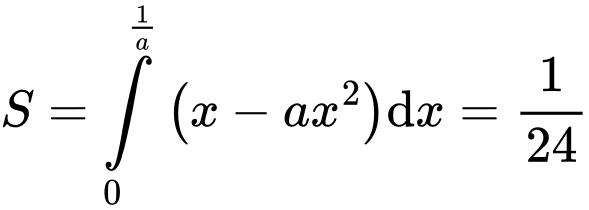
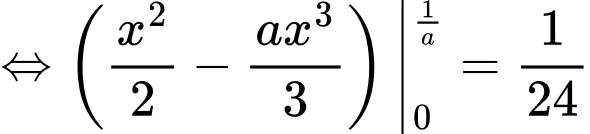
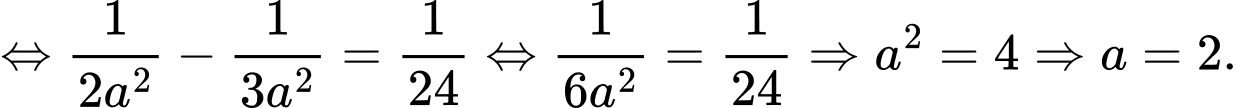 Đáp án: A
Đáp án: A
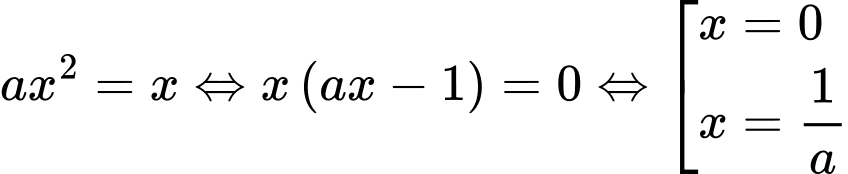
Lại có
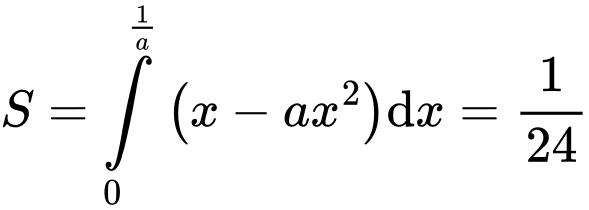
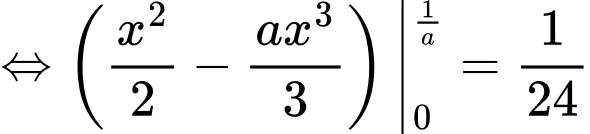
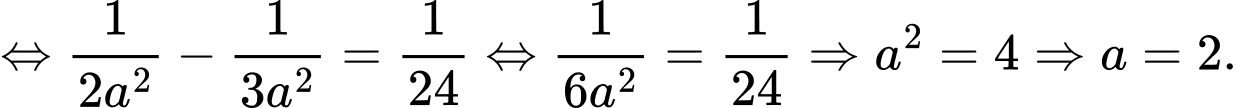 Đáp án: A
Đáp án: A
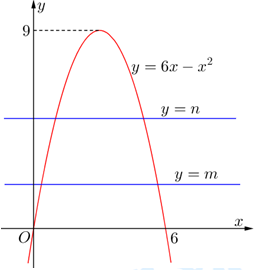
Câu 19 [392129]: Đường thẳng 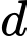 cắt Parabol
cắt Parabol 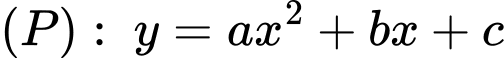 tại hai điểm
tại hai điểm 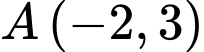 và
và 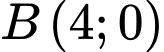 như hình vẽ bên. Diện tích miền được tô đậm trong hình bằng
như hình vẽ bên. Diện tích miền được tô đậm trong hình bằng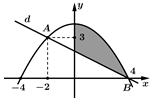
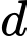 cắt Parabol
cắt Parabol 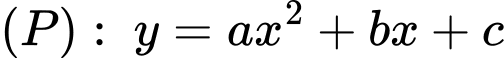 tại hai điểm
tại hai điểm 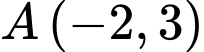 và
và 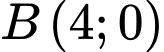 như hình vẽ bên. Diện tích miền được tô đậm trong hình bằng
như hình vẽ bên. Diện tích miền được tô đậm trong hình bằng
A, 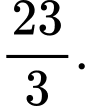
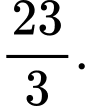
B, 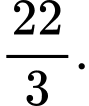
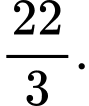
C, 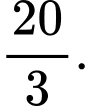
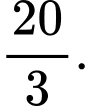
D, 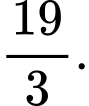
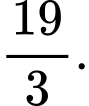
Từ đồ thị hình vẽ ta thấy 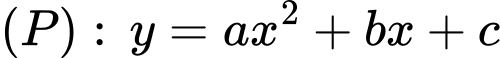 đi qua các điểm
đi qua các điểm 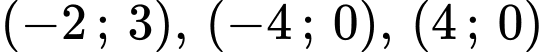 nên ta có hệ Phương trình:
nên ta có hệ Phương trình:
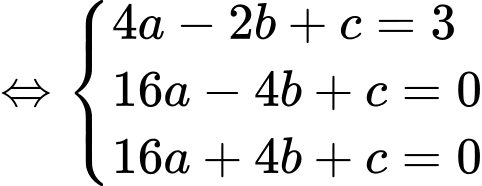
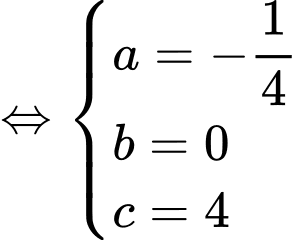
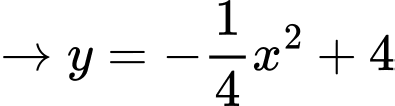
Tương tự, từ đồ thị ta thấy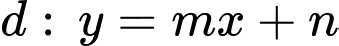 đi qua
đi qua 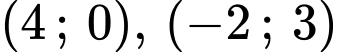 nên ta có hệ:
nên ta có hệ:
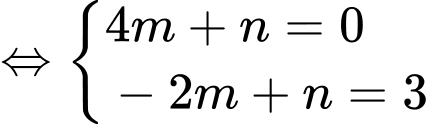
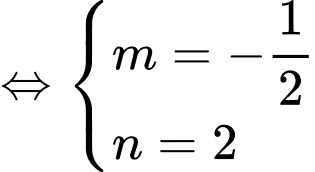
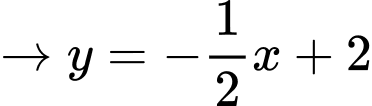
Diện tích phần tô đậm: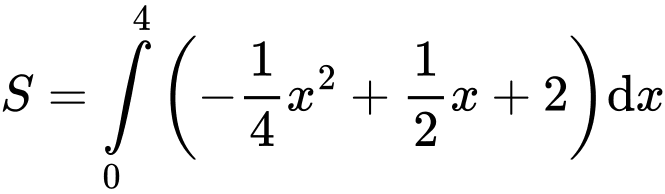
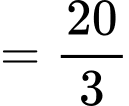
Đáp án: C Đáp án: C
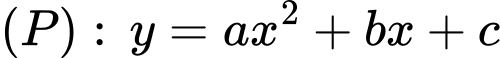 đi qua các điểm
đi qua các điểm 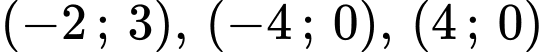 nên ta có hệ Phương trình:
nên ta có hệ Phương trình:
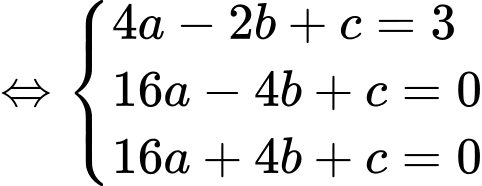
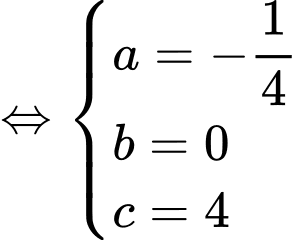
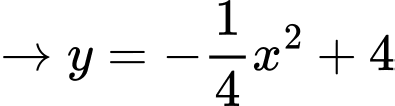
Tương tự, từ đồ thị ta thấy
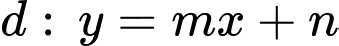 đi qua
đi qua 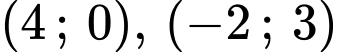 nên ta có hệ:
nên ta có hệ:
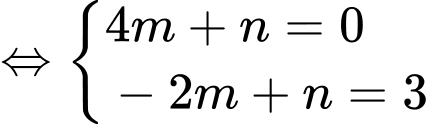
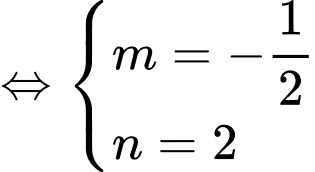
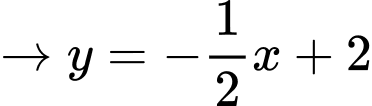
Diện tích phần tô đậm:
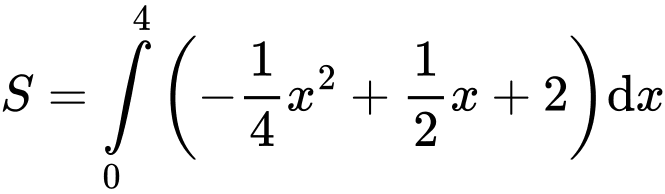
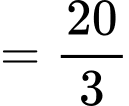
Đáp án: C Đáp án: C
Câu 20 [115844]: Diện tích phần gạch chéo trong hình vẽ bằng bao nhiêu?
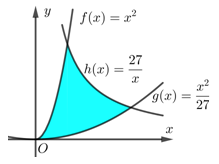

A, 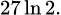
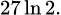
B, 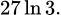
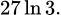
C, 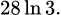
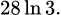
D, 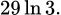
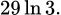
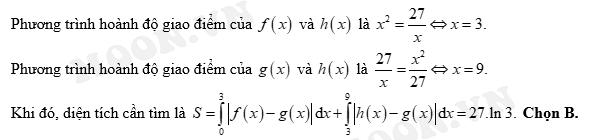 Đáp án: B
Đáp án: B
Câu 21 [579670]: [Đề mẫu HSA 2024]: Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số 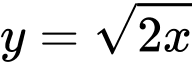 và
và 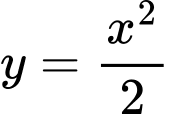 (nhập đáp án vào ô trống).
(nhập đáp án vào ô trống).
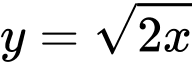 và
và 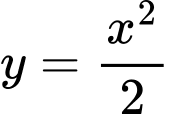 (nhập đáp án vào ô trống).
(nhập đáp án vào ô trống).
ĐKXĐ: 
Xét phương trình hoành độ giao điểm ta có:
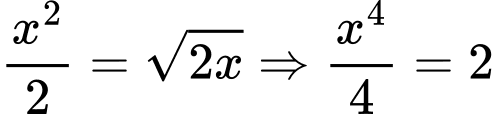
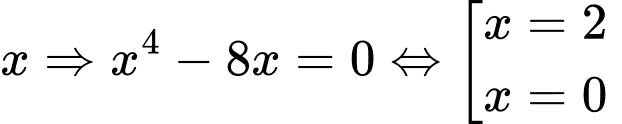 (Thoả mãn)
(Thoả mãn)
Diện tích hình phẳng giới hạn bởi đồ thị của hàm số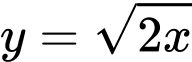 và
và 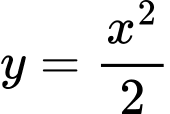 là:
là:
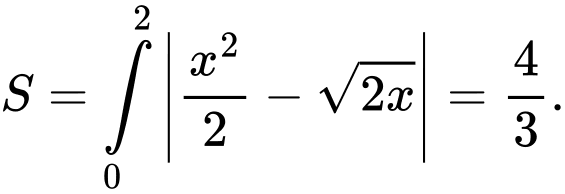
Đáp án: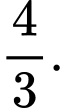

Xét phương trình hoành độ giao điểm ta có:
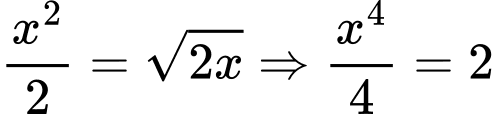
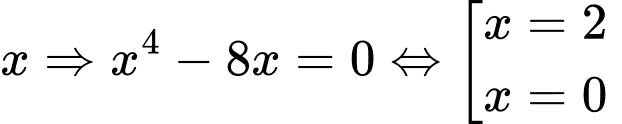 (Thoả mãn)
(Thoả mãn) Diện tích hình phẳng giới hạn bởi đồ thị của hàm số
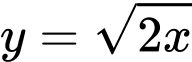 và
và 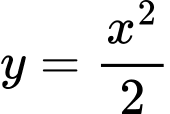 là:
là: 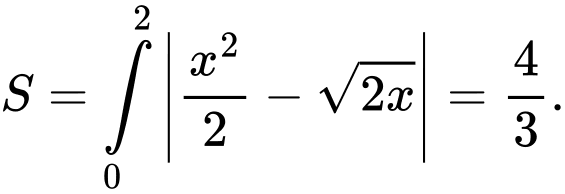
Đáp án:
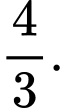
Câu 22 [115854]: Diện tích hình phẳng giới hạn bởi đường cong 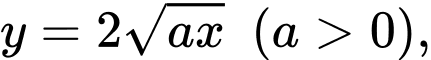 trục hoành và đường thẳng
trục hoành và đường thẳng 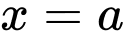 bằng
bằng 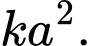 Tính giá trị của tham số
Tính giá trị của tham số 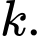
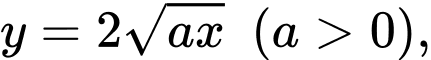 trục hoành và đường thẳng
trục hoành và đường thẳng 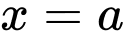 bằng
bằng 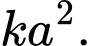 Tính giá trị của tham số
Tính giá trị của tham số 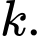
A, 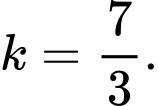
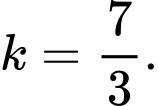
B, 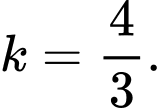
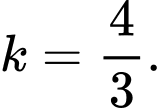
C, 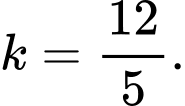
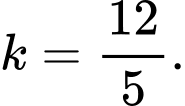
D, 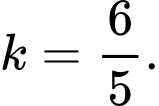
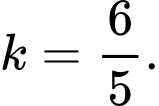
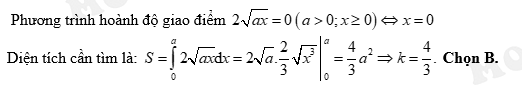 Đáp án: B
Đáp án: B
Câu 23 [151338]: Cho hình  là hình phẳng giới hạn bởi các đường
là hình phẳng giới hạn bởi các đường 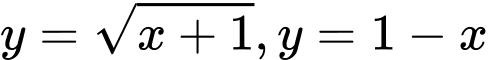 và trục
và trục 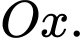 Diện tích của hình
Diện tích của hình  bằng
bằng
 là hình phẳng giới hạn bởi các đường
là hình phẳng giới hạn bởi các đường 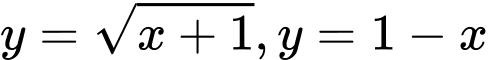 và trục
và trục 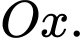 Diện tích của hình
Diện tích của hình  bằng
bằng A, 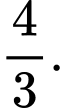
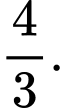
B, 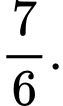
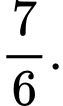
C, 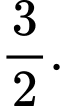
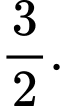
D, 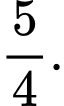
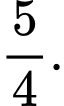
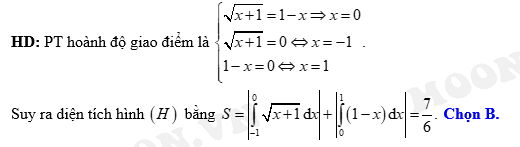 Đáp án: B
Đáp án: B
Câu 24 [371990]: Khi cắt một vật thể hình chiếc nêm bởi mặt phẳng vuông góc với trục 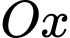 tại điểm có hoành độ
tại điểm có hoành độ 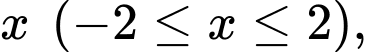 mặt cắt là tam giác vuông có một góc
mặt cắt là tam giác vuông có một góc 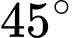 và độ dài một cạnh góc vuông là
và độ dài một cạnh góc vuông là 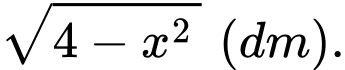 Tính thể tích của vật thể theo đơn vị
Tính thể tích của vật thể theo đơn vị 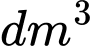 . Làm tròn kết quả đến hàng phần chục.
. Làm tròn kết quả đến hàng phần chục. 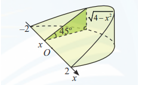
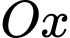 tại điểm có hoành độ
tại điểm có hoành độ 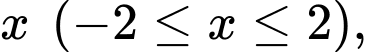 mặt cắt là tam giác vuông có một góc
mặt cắt là tam giác vuông có một góc 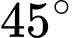 và độ dài một cạnh góc vuông là
và độ dài một cạnh góc vuông là 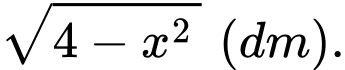 Tính thể tích của vật thể theo đơn vị
Tính thể tích của vật thể theo đơn vị 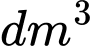 . Làm tròn kết quả đến hàng phần chục.
. Làm tròn kết quả đến hàng phần chục. 
Vì mặt cắt là tam giác vuông có một góc 45° nên mặt cắt là tam giác vuông cân.
Do đó diện tích của mặt cắt là: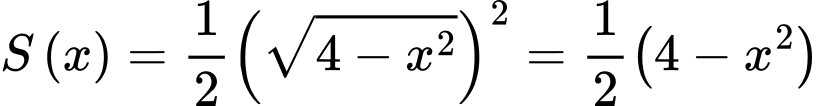
Thể tích vật thể là: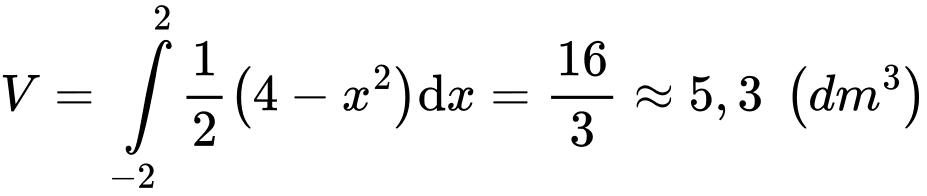
Do đó diện tích của mặt cắt là:
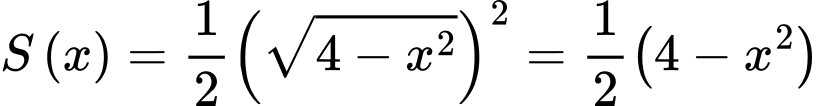
Thể tích vật thể là:
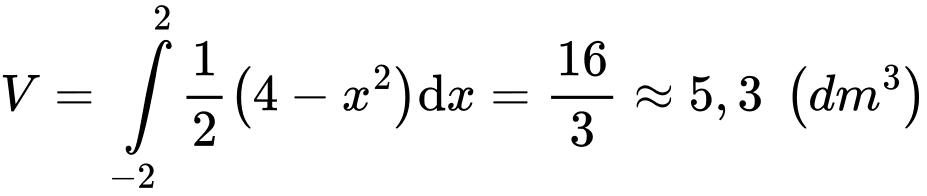
Câu 25 [372588]: Một chiếc lều mái vòm có hình dạng như hình. Nếu cắt lều bằng mặt phẳng song song với mặt đáy và cách mặt đáy một khoảng 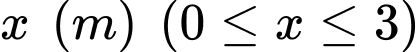 thì được hình vuông có cạnh
thì được hình vuông có cạnh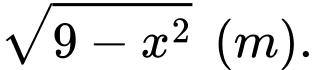 Tính thể tích của lều.
Tính thể tích của lều. 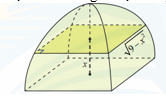
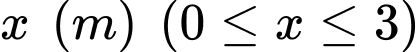 thì được hình vuông có cạnh
thì được hình vuông có cạnh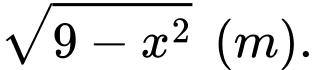 Tính thể tích của lều.
Tính thể tích của lều. 
Vì mặt cắt là hình vuông nên diện tích của mặt cắt là:
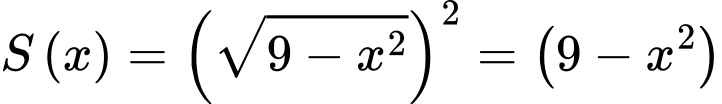
Thể tích vật thể là: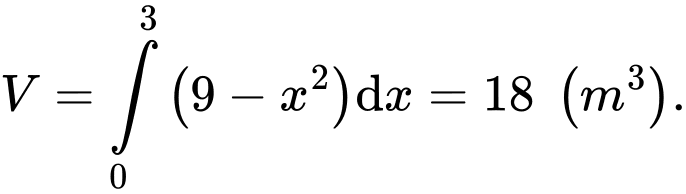
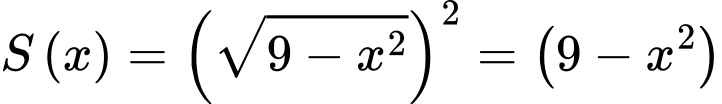
Thể tích vật thể là:
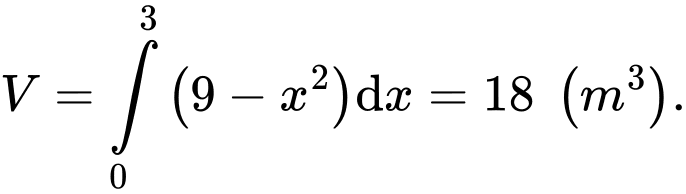
Câu 26 [392141]: Cho 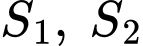 là diện tích các hình phẳng được mô tả trong hình vẽ bên. Biết tỉ số
là diện tích các hình phẳng được mô tả trong hình vẽ bên. Biết tỉ số 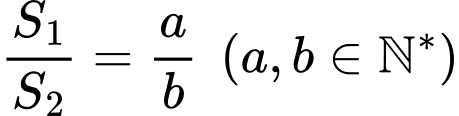 và phân số
và phân số 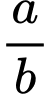 tối giản, tính tổng
tối giản, tính tổng 
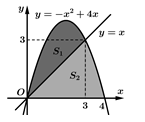
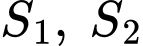 là diện tích các hình phẳng được mô tả trong hình vẽ bên. Biết tỉ số
là diện tích các hình phẳng được mô tả trong hình vẽ bên. Biết tỉ số 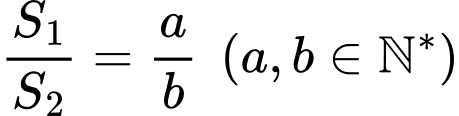 và phân số
và phân số 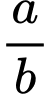 tối giản, tính tổng
tối giản, tính tổng 

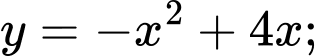
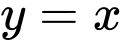
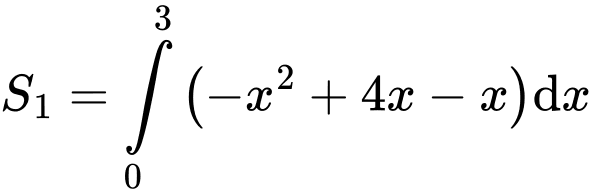
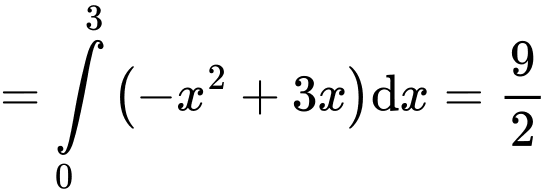
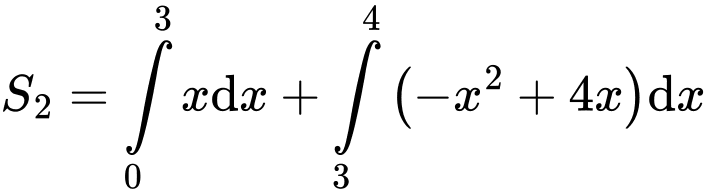
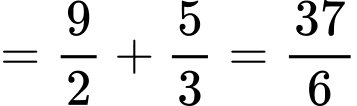
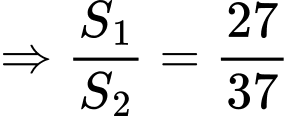
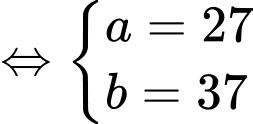
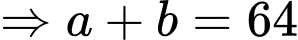
Đáp án: 64
Câu 27 [399916]: Cho hình phẳng  giới hạn bởi đồ thị hàm số
giới hạn bởi đồ thị hàm số 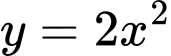 và đường thẳng
và đường thẳng 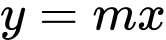 với
với 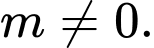 Có bao nhiêu giá trị nguyên dương của
Có bao nhiêu giá trị nguyên dương của 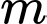 để diện tích hình phẳng
để diện tích hình phẳng  nhỏ hơn 10?
nhỏ hơn 10?
 giới hạn bởi đồ thị hàm số
giới hạn bởi đồ thị hàm số 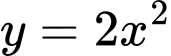 và đường thẳng
và đường thẳng 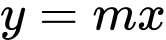 với
với 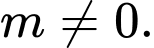 Có bao nhiêu giá trị nguyên dương của
Có bao nhiêu giá trị nguyên dương của 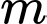 để diện tích hình phẳng
để diện tích hình phẳng  nhỏ hơn 10?
nhỏ hơn 10? A, 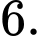
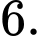
B, 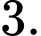
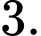
C, 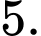
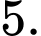
D, 
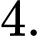
Chọn A
Xét phương trình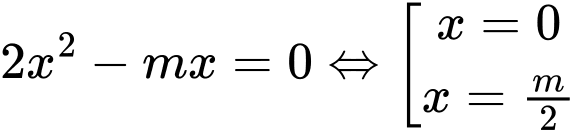
Với ta có diện tích hình phẳng
ta có diện tích hình phẳng  là
là
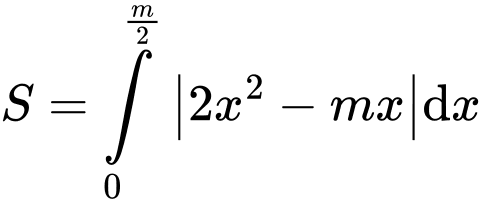
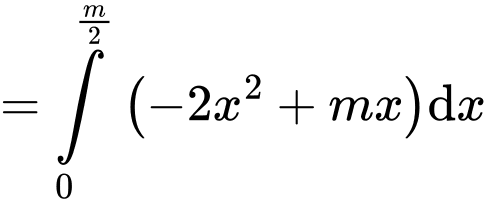
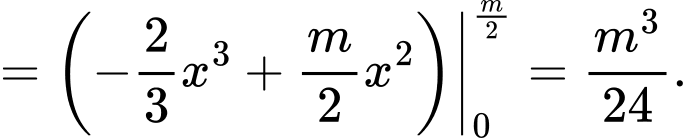
Để thì
thì 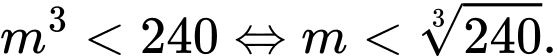 Vì
Vì 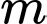 nguyên dương nên
nguyên dương nên 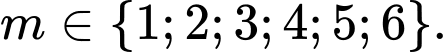 Đáp án: A
Đáp án: A
Xét phương trình
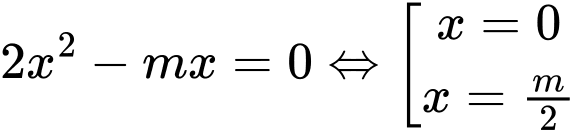
Với
 ta có diện tích hình phẳng
ta có diện tích hình phẳng  là
là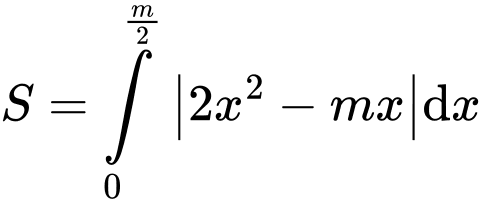
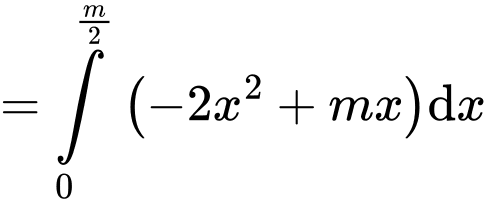
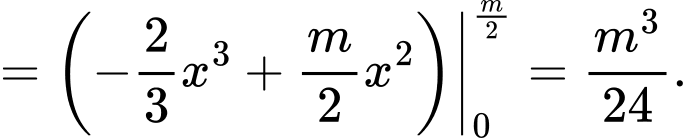
Để
 thì
thì 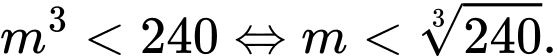 Vì
Vì 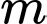 nguyên dương nên
nguyên dương nên 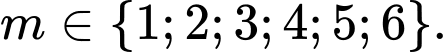 Đáp án: A
Đáp án: A
Câu 28 [392126]: Cho hàm số 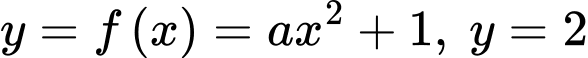 có đồ thị như hình vẽ. Gọi
có đồ thị như hình vẽ. Gọi 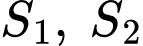 là các diện tích hình phẳng trong hình bên. Biết rằng
là các diện tích hình phẳng trong hình bên. Biết rằng 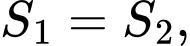 tính diện tích
tính diện tích 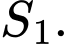 Viết kết quả làm tròn đến hàng phần trăm.
Viết kết quả làm tròn đến hàng phần trăm.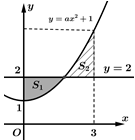
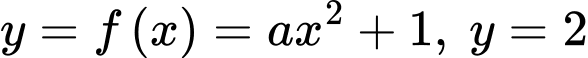 có đồ thị như hình vẽ. Gọi
có đồ thị như hình vẽ. Gọi 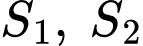 là các diện tích hình phẳng trong hình bên. Biết rằng
là các diện tích hình phẳng trong hình bên. Biết rằng 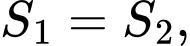 tính diện tích
tính diện tích 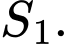 Viết kết quả làm tròn đến hàng phần trăm.
Viết kết quả làm tròn đến hàng phần trăm.
Có: 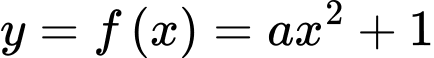 và
và 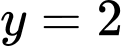
Từ đồ thị ta có:
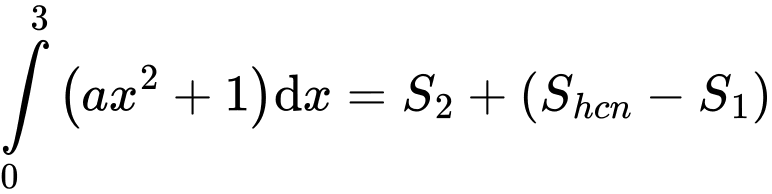
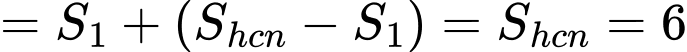
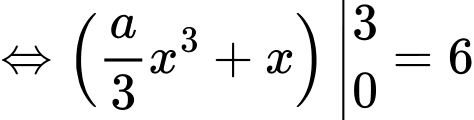

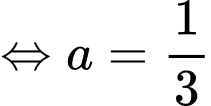
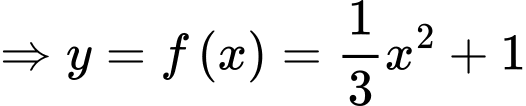
Ta có phương trình hoành độ giao điểm:
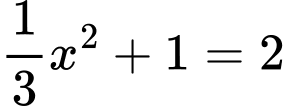
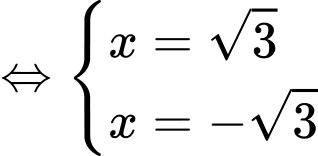
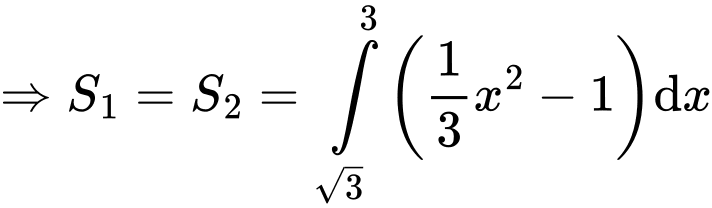
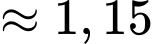
Đáp án: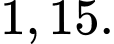
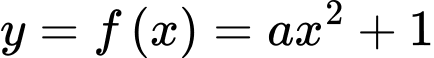 và
và 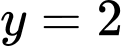
Từ đồ thị ta có:
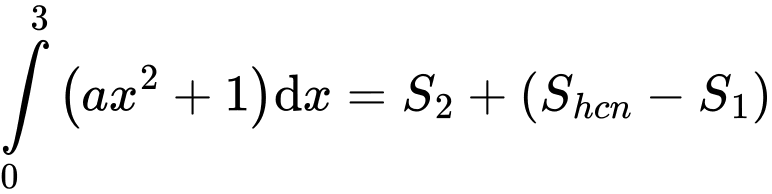
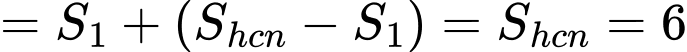
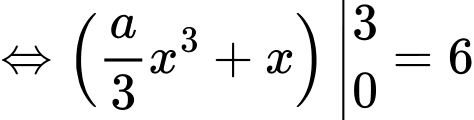

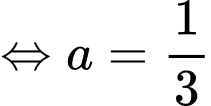
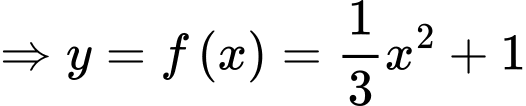
Ta có phương trình hoành độ giao điểm:
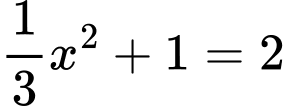
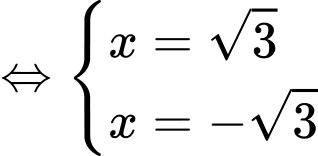
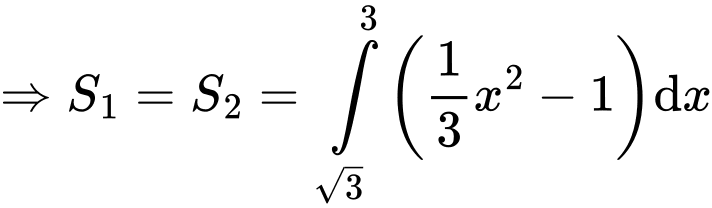
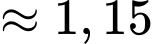
Đáp án:
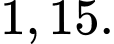
Câu 29 [9656]: Gọi  là phần hình phẳng tô đậm trong hình vẽ dưới đây được giới hạn bởi đồ thị của các hàm số
là phần hình phẳng tô đậm trong hình vẽ dưới đây được giới hạn bởi đồ thị của các hàm số 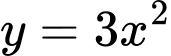 ,
, 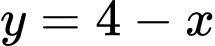 và trục hoành.
và trục hoành.
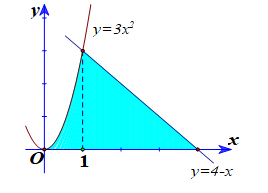
Diện tích của bằng
bằng
 là phần hình phẳng tô đậm trong hình vẽ dưới đây được giới hạn bởi đồ thị của các hàm số
là phần hình phẳng tô đậm trong hình vẽ dưới đây được giới hạn bởi đồ thị của các hàm số 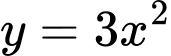 ,
, 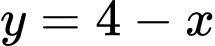 và trục hoành.
và trục hoành.
Diện tích của
 bằng
bằng A, 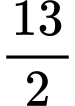 .
.
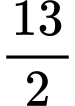 .
.B, 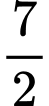 .
.
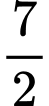 .
.C, 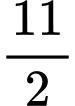 .
.
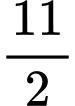 .
.D, 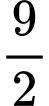 .
.
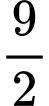 .
. Đáp án: C
Đáp án: C
Câu 30 [392144]: Cho ba hàm số 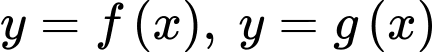 và
và 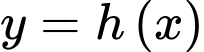 có đồ thị như hình vẽ. Diện tích mỗi miền được ghi bằng số trong hình. Tính
có đồ thị như hình vẽ. Diện tích mỗi miền được ghi bằng số trong hình. Tính 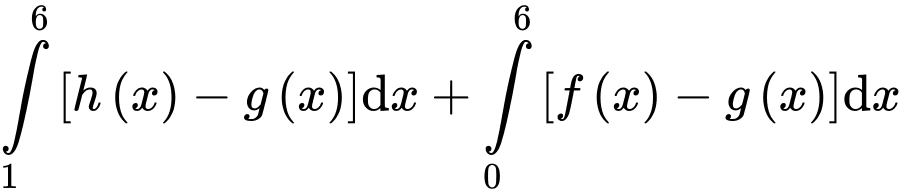
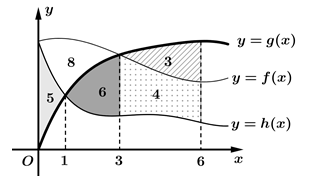
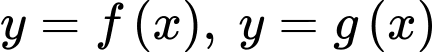 và
và 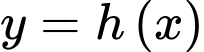 có đồ thị như hình vẽ. Diện tích mỗi miền được ghi bằng số trong hình. Tính
có đồ thị như hình vẽ. Diện tích mỗi miền được ghi bằng số trong hình. Tính 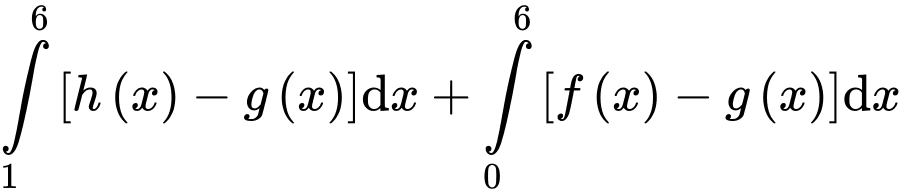

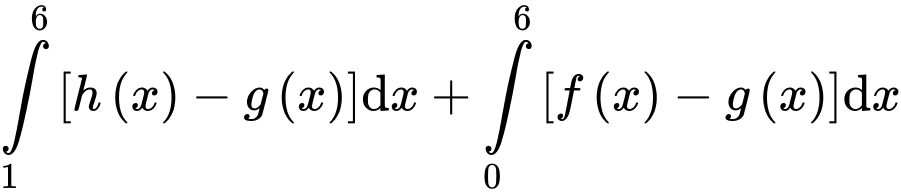
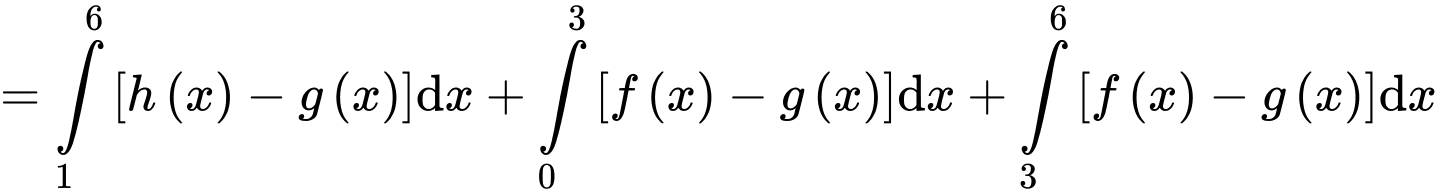
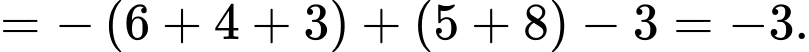
Câu 31 [151377]: Cho hình phẳng  giới hạn bởi các đường
giới hạn bởi các đường 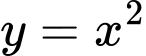 ,
, 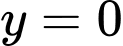 ,
, 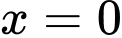 ,
,  . Đường thẳng
. Đường thẳng 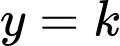 với
với 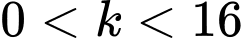 chia hình
chia hình  thành hai phần có diện tích
thành hai phần có diện tích 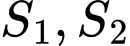 (như hình vẽ). Tìm
(như hình vẽ). Tìm 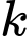 để
để 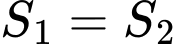 .
.
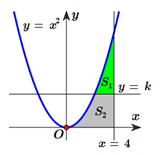
 giới hạn bởi các đường
giới hạn bởi các đường 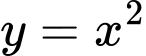 ,
, 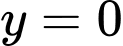 ,
, 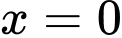 ,
,  . Đường thẳng
. Đường thẳng 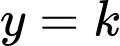 với
với 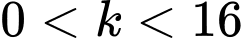 chia hình
chia hình  thành hai phần có diện tích
thành hai phần có diện tích 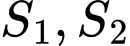 (như hình vẽ). Tìm
(như hình vẽ). Tìm 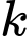 để
để 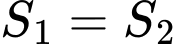 .
.
A, 

B, 

C, 

D, 

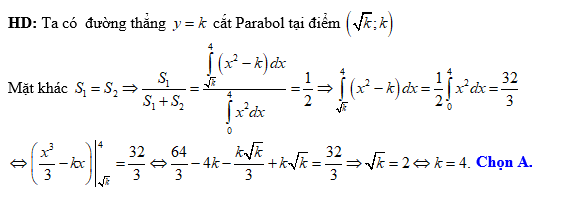 Đáp án: A
Đáp án: A
Câu 32 [151690]: Cho hình thang cong  giới hạn bởi các đường
giới hạn bởi các đường 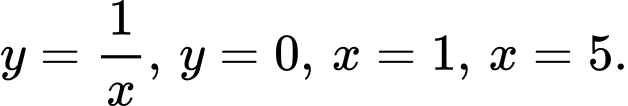 Đường thẳng
Đường thẳng 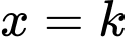 với
với 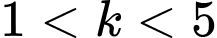 chia
chia  thành hai phần là
thành hai phần là 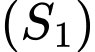 và
và 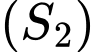 quay quanh trục
quay quanh trục 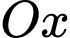 ta thu được hai khối tròn xoay có thể tích lần lượt là
ta thu được hai khối tròn xoay có thể tích lần lượt là 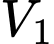 và
và 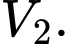 Xác định
Xác định 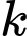 để
để 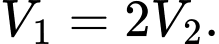
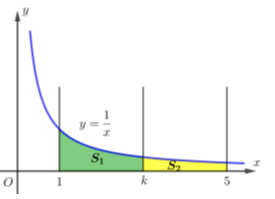
 giới hạn bởi các đường
giới hạn bởi các đường 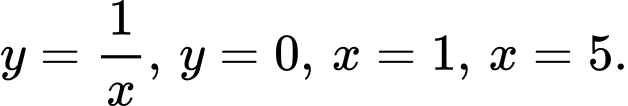 Đường thẳng
Đường thẳng 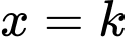 với
với 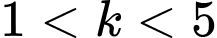 chia
chia  thành hai phần là
thành hai phần là 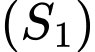 và
và 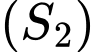 quay quanh trục
quay quanh trục 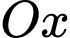 ta thu được hai khối tròn xoay có thể tích lần lượt là
ta thu được hai khối tròn xoay có thể tích lần lượt là 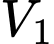 và
và 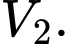 Xác định
Xác định 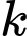 để
để 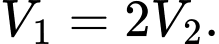

A, 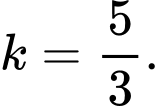
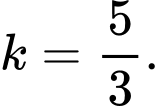
B, 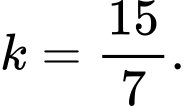
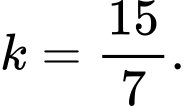
C, 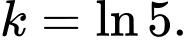
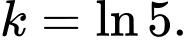
D, 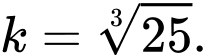
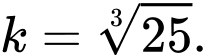
Ta có 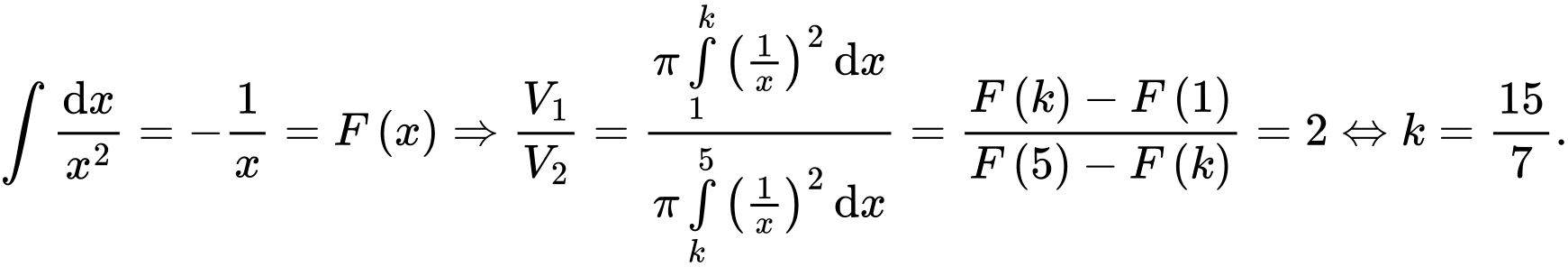
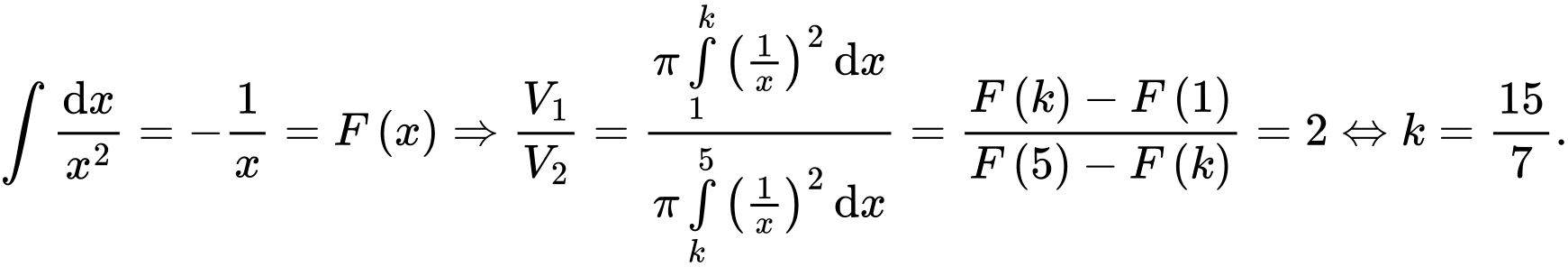
Chọn đáp án B.
Đáp án: B
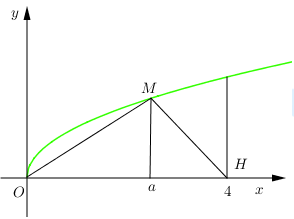
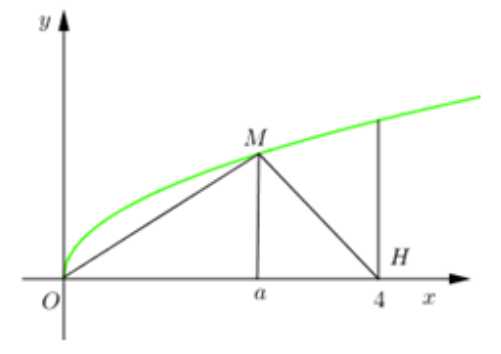
Câu 33 [151693]: Gọi  là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường 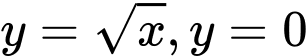 và
và  quanh trục
quanh trục 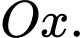 Đường thẳng
Đường thẳng 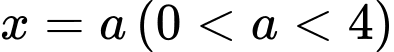 cắt đồ thị hàm số
cắt đồ thị hàm số 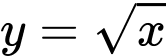 tại
tại 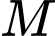 (hình vẽ bên). Gọi
(hình vẽ bên). Gọi 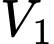 là thể tích khối tròn xoay tạo thành khi quay tam giác
là thể tích khối tròn xoay tạo thành khi quay tam giác 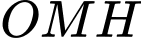 quanh trục
quanh trục 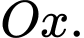 Biết rằng
Biết rằng 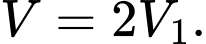 Khi đó
Khi đó 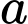 bằng bao nhiêu
bằng bao nhiêu
 là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường 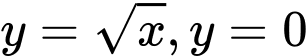 và
và  quanh trục
quanh trục 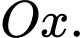 Đường thẳng
Đường thẳng 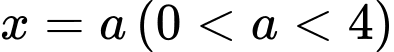 cắt đồ thị hàm số
cắt đồ thị hàm số 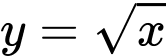 tại
tại 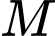 (hình vẽ bên). Gọi
(hình vẽ bên). Gọi 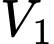 là thể tích khối tròn xoay tạo thành khi quay tam giác
là thể tích khối tròn xoay tạo thành khi quay tam giác 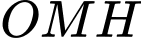 quanh trục
quanh trục 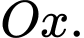 Biết rằng
Biết rằng 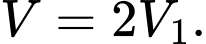 Khi đó
Khi đó 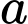 bằng bao nhiêu
bằng bao nhiêu
A, 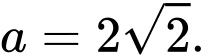
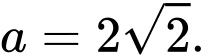
B, 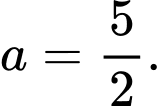
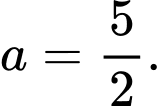
C, 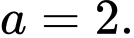
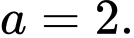
D, 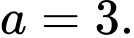
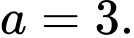
Ta có
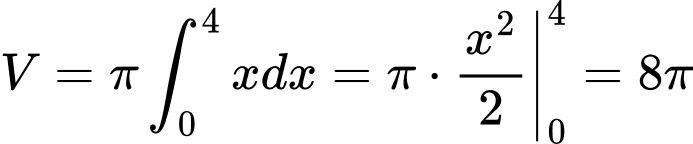
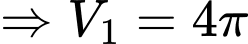 .
.
Gọi
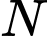 là giao điểm của đường thắng
là giao điểm của đường thắng 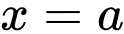 và trục hoành.
và trục hoành.
Khi đó
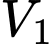 là thể tích tạo được khi xoay hai tam giác
là thể tích tạo được khi xoay hai tam giác 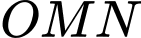 và
và 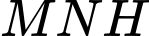 quanh trục
quanh trục 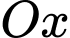 với
với 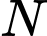 là hình chiếu của
là hình chiếu của 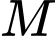 trên
trên 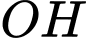 .
.
Ta có
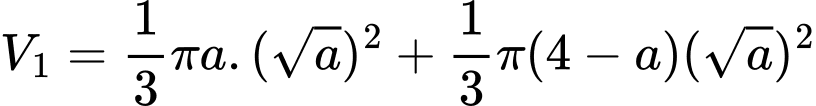
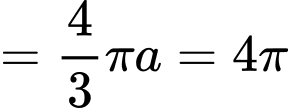
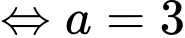 .
.
Chọn đáp án D. Đáp án: D
Câu 34 [234245]: [Đề thi TH THPT 2022]: Biết 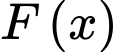 và
và 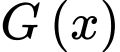 là hai nguyên hàm của hàm số
là hai nguyên hàm của hàm số 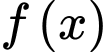 trên
trên 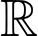 và
và 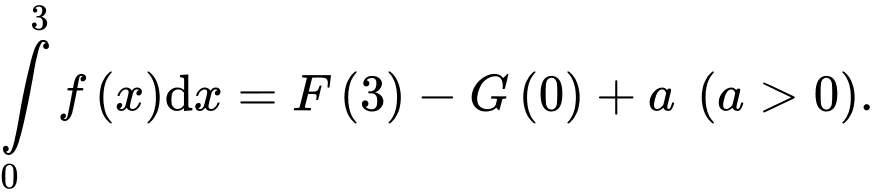 Gọi
Gọi 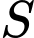 là diện tích hình phẳng giới hạn bởi các đường
là diện tích hình phẳng giới hạn bởi các đường 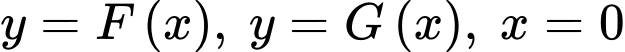 và
và 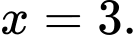 Khi
Khi 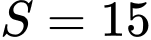 thì
thì 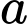 bằng
bằng
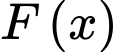 và
và 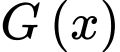 là hai nguyên hàm của hàm số
là hai nguyên hàm của hàm số 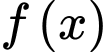 trên
trên 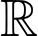 và
và 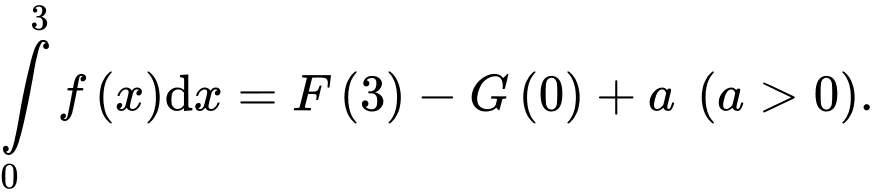 Gọi
Gọi 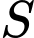 là diện tích hình phẳng giới hạn bởi các đường
là diện tích hình phẳng giới hạn bởi các đường 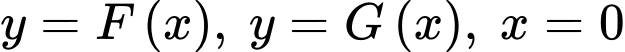 và
và 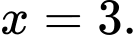 Khi
Khi 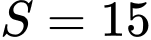 thì
thì 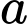 bằng
bằng A, 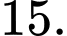
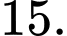
B, 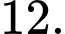
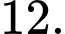
C, 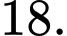
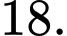
D, 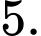
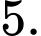
HD: Ta có: 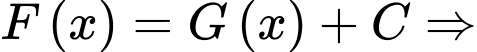
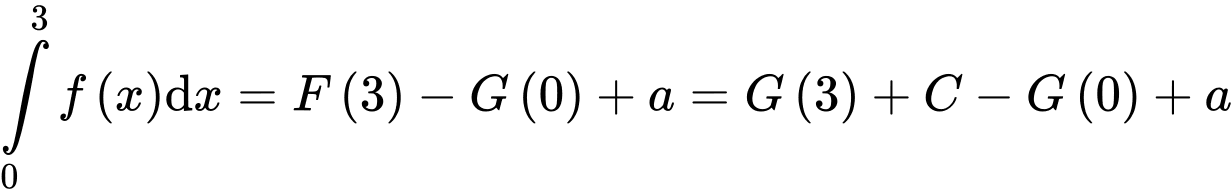
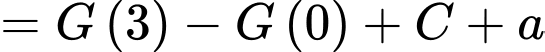 (với
(với  )
Mặt khác
)
Mặt khác 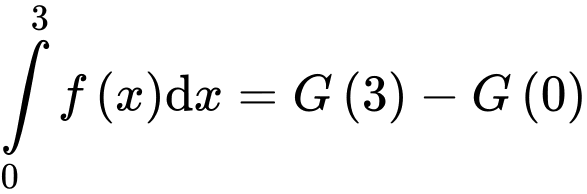 nên
nên 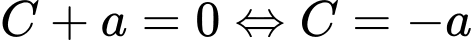
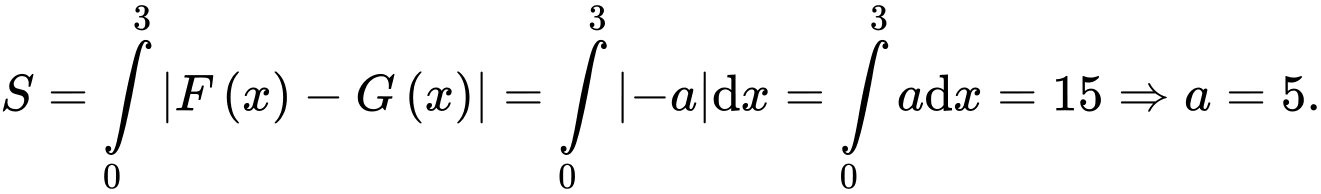 Chọn D. Đáp án: D
Chọn D. Đáp án: D
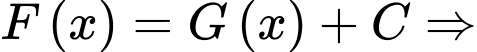
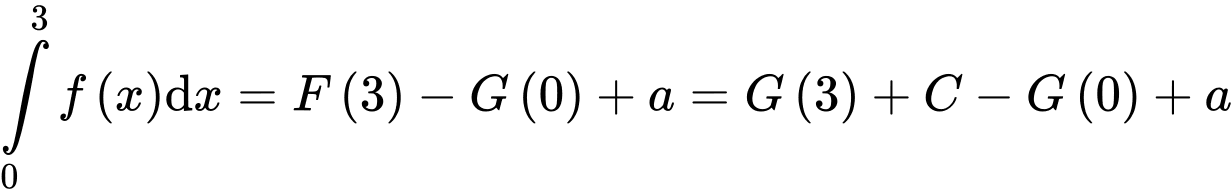
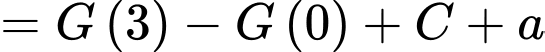 (với
(với  )
Mặt khác
)
Mặt khác 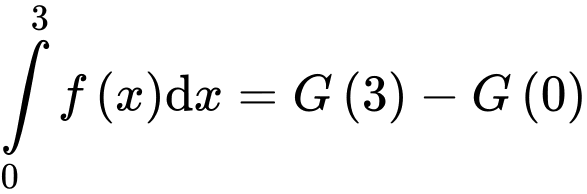 nên
nên 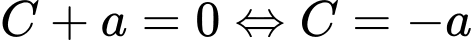
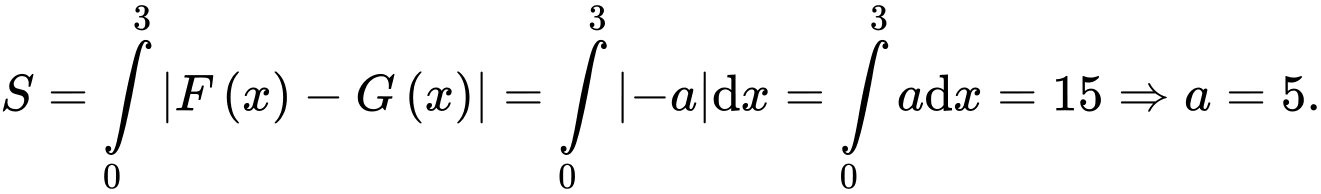 Chọn D. Đáp án: D
Chọn D. Đáp án: D
Câu 35 [151389]: Gọi  là hình phẳng giới hạn bởi đồ thị
là hình phẳng giới hạn bởi đồ thị 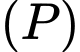 của hàm số
của hàm số 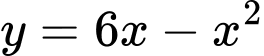 và trục hoành. Hai đường thẳng
và trục hoành. Hai đường thẳng 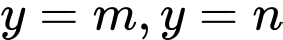 chia hình
chia hình  thành ba phần có diện tích bằng nhau.Tính
thành ba phần có diện tích bằng nhau.Tính 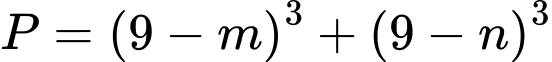 .
.
 là hình phẳng giới hạn bởi đồ thị
là hình phẳng giới hạn bởi đồ thị 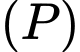 của hàm số
của hàm số 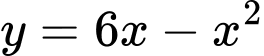 và trục hoành. Hai đường thẳng
và trục hoành. Hai đường thẳng 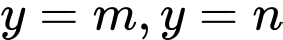 chia hình
chia hình  thành ba phần có diện tích bằng nhau.Tính
thành ba phần có diện tích bằng nhau.Tính 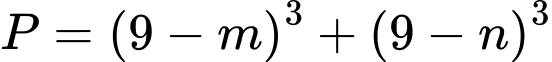 .
.
A, 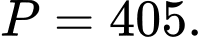
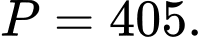
B, 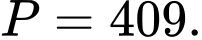
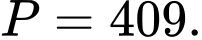
C, 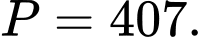
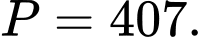
D, 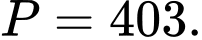
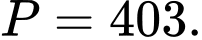
Ta có: 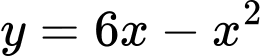
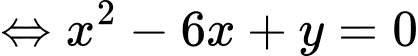
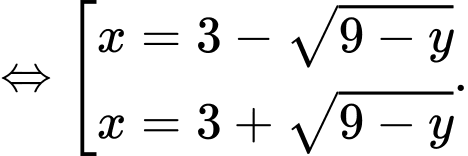
Suy ra diện tích hình bằng
bằng 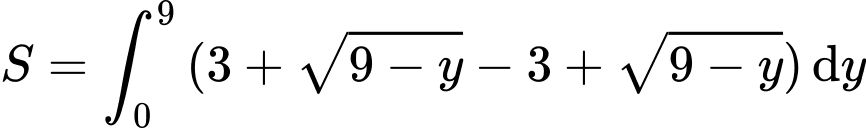
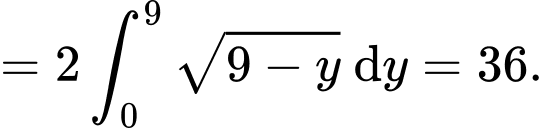
Khi đó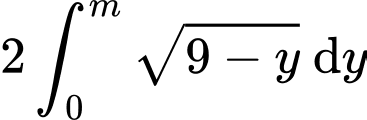
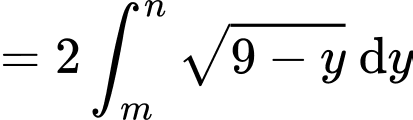
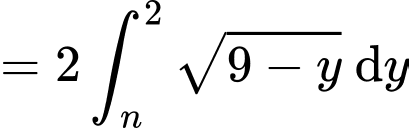
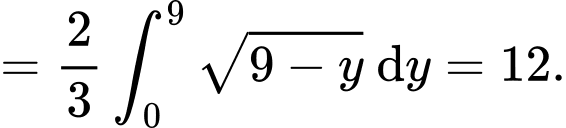
Suy ra: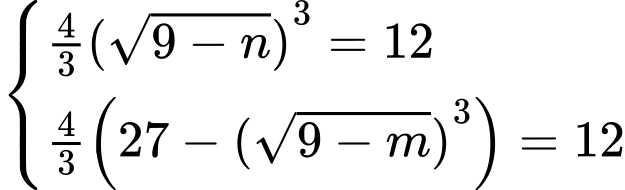
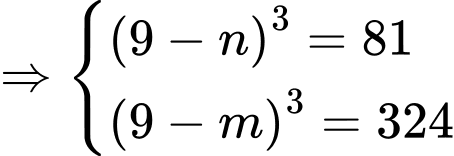
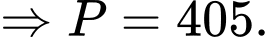
Chọn đáp án A. Đáp án: A
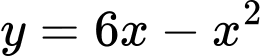
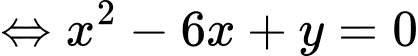
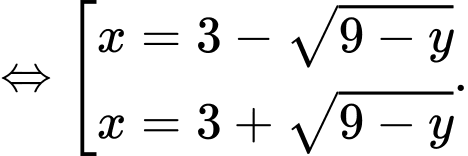
Suy ra diện tích hình
 bằng
bằng 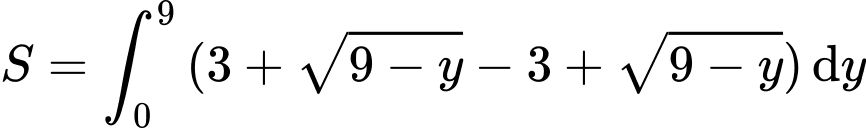
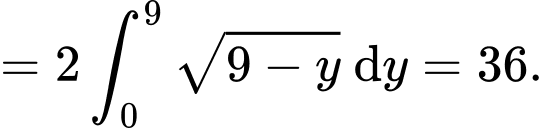
Khi đó
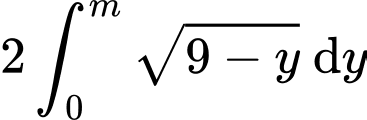
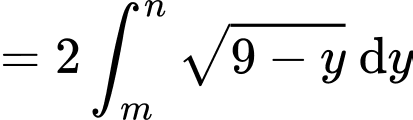
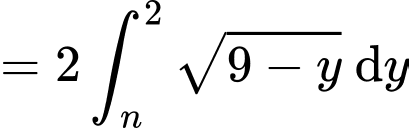
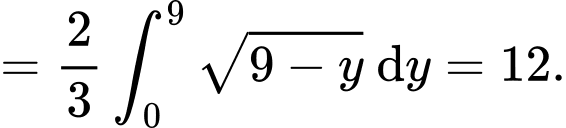
Suy ra:
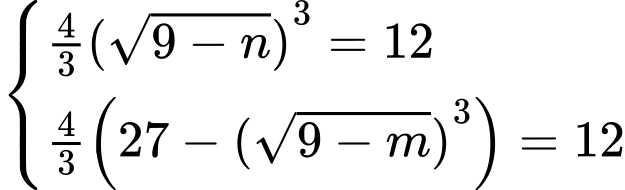
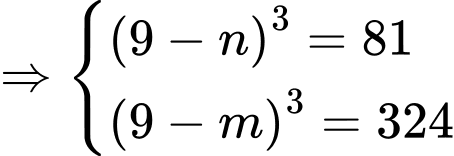
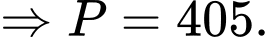
Chọn đáp án A. Đáp án: A