Đáp án Bài tập tự luyện số 1
Câu 1 [153550]: [Đề Mẫu ĐGNL TPHCM]: Gọi 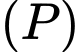 là mặt phẳng chứa điểm
là mặt phẳng chứa điểm 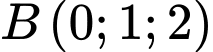 sao cho khoảng cách từ điểm
sao cho khoảng cách từ điểm 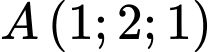 đến
đến 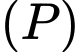 là lớn nhất. Phương trình của
là lớn nhất. Phương trình của 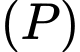 là
là
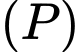 là mặt phẳng chứa điểm
là mặt phẳng chứa điểm 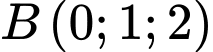 sao cho khoảng cách từ điểm
sao cho khoảng cách từ điểm 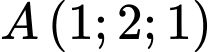 đến
đến 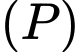 là lớn nhất. Phương trình của
là lớn nhất. Phương trình của 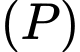 là
là A, 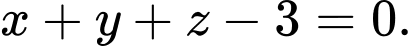
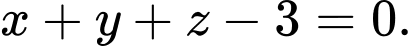
B, 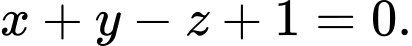
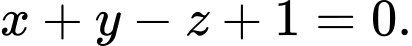
C, 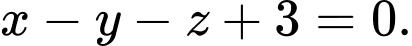
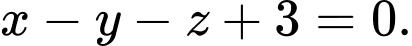
D, 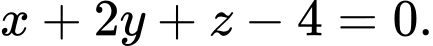
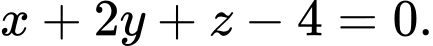
Ta có:  dấu bằng xảy ra khi và chỉ khi
dấu bằng xảy ra khi và chỉ khi 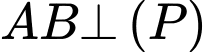
 dấu bằng xảy ra khi và chỉ khi
dấu bằng xảy ra khi và chỉ khi 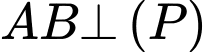
Khi đó 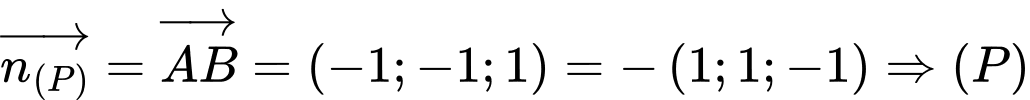
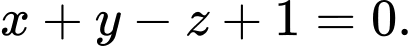
Đáp án: B 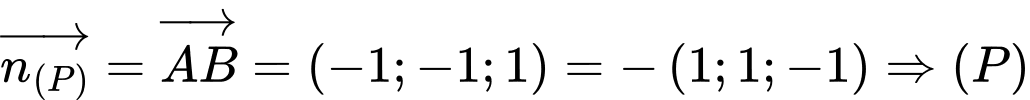
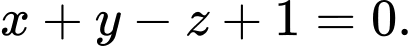
Chọn B.
Câu 2 [234246]: [Đề thi TH THPT 2022]: Trong không gian 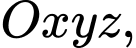 cho điểm
cho điểm 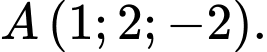 Gọi
Gọi 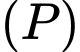 là mặt phẳng chứa trục
là mặt phẳng chứa trục 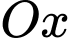 sao cho khoảng cách từ
sao cho khoảng cách từ 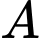 đến
đến 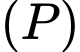 lớn nhất. Phương trình của
lớn nhất. Phương trình của 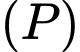 là
là
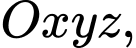 cho điểm
cho điểm 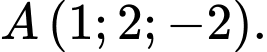 Gọi
Gọi 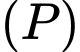 là mặt phẳng chứa trục
là mặt phẳng chứa trục 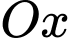 sao cho khoảng cách từ
sao cho khoảng cách từ 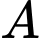 đến
đến 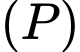 lớn nhất. Phương trình của
lớn nhất. Phương trình của 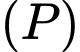 là
là A, 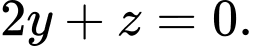
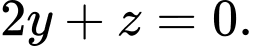
B, 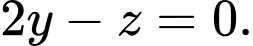
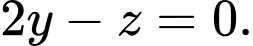
C, 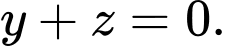
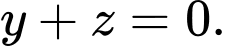
D, 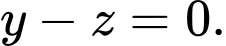
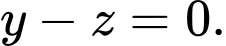
HD: Gọi 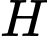 là hình chiếu của
là hình chiếu của 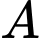 trên trục
trên trục 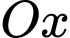 thì
thì 
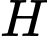 là hình chiếu của
là hình chiếu của 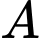 trên trục
trên trục 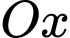 thì
thì 
Khi đó 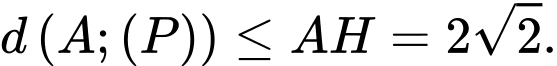
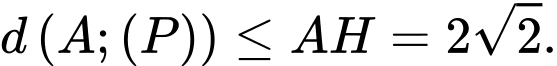
Dấu bằng xảy ra khi 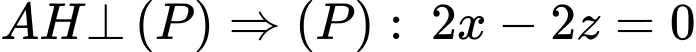 hay
hay 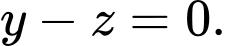
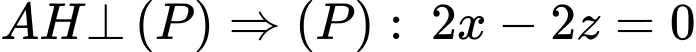 hay
hay 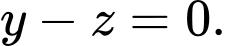
Chọn D.
Đáp án: D
Câu 3 [399915]: Trong không gian 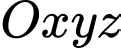 , gọi
, gọi 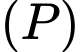 là mặt phẳng đi qua hai điểm
là mặt phẳng đi qua hai điểm 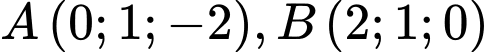 sao cho khoảng cách từ gốc tọa độ
sao cho khoảng cách từ gốc tọa độ  đến
đến 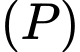 lớn nhất. Phương trình của mặt phẳng
lớn nhất. Phương trình của mặt phẳng 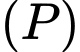 là
là
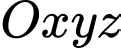 , gọi
, gọi 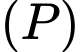 là mặt phẳng đi qua hai điểm
là mặt phẳng đi qua hai điểm 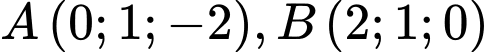 sao cho khoảng cách từ gốc tọa độ
sao cho khoảng cách từ gốc tọa độ  đến
đến 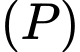 lớn nhất. Phương trình của mặt phẳng
lớn nhất. Phương trình của mặt phẳng 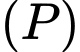 là
là A, 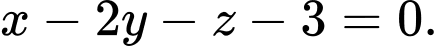
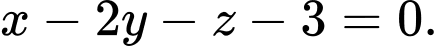
B, 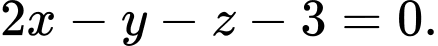
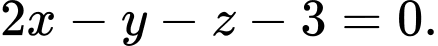
C, 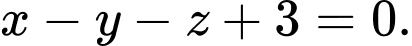
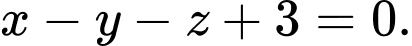
D, 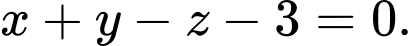
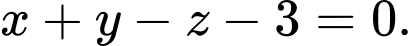
Chọn D
Có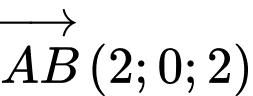 , đường thẳng
, đường thẳng  đi qua điểm
đi qua điểm 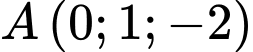 có véc tơ chỉ phương
có véc tơ chỉ phương 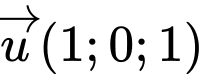 có phương trình tham số là
có phương trình tham số là 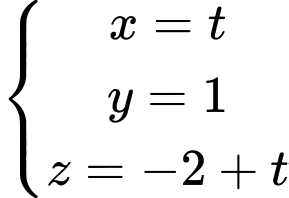
Gọi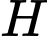 là hình chiếu của
là hình chiếu của  lên đường thẳng
lên đường thẳng  ta có
ta có 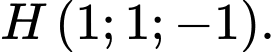
Gọi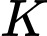 là hình chiếu của
là hình chiếu của  lên
lên 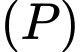 , ta luôn có
, ta luôn có 
Vậy nên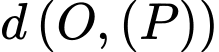 lớn nhất bằng
lớn nhất bằng 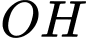 khi
khi 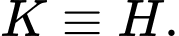
Khi đó mặt phẳng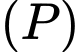 nhận véc tơ
nhận véc tơ 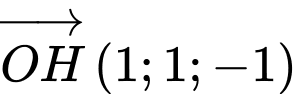 làm véc tơ pháp tuyến và đi qua điểm
làm véc tơ pháp tuyến và đi qua điểm 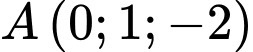 nên có phương trình
nên có phương trình 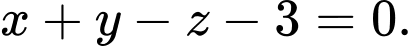 Đáp án: D
Đáp án: D
Có
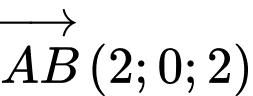 , đường thẳng
, đường thẳng  đi qua điểm
đi qua điểm 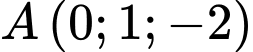 có véc tơ chỉ phương
có véc tơ chỉ phương 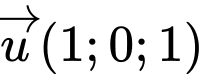 có phương trình tham số là
có phương trình tham số là 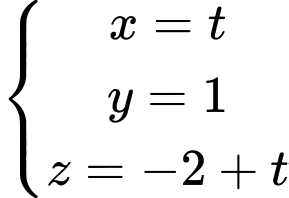
Gọi
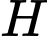 là hình chiếu của
là hình chiếu của  lên đường thẳng
lên đường thẳng  ta có
ta có 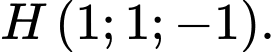
Gọi
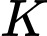 là hình chiếu của
là hình chiếu của  lên
lên 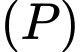 , ta luôn có
, ta luôn có 
Vậy nên
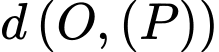 lớn nhất bằng
lớn nhất bằng 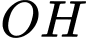 khi
khi 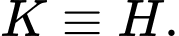
Khi đó mặt phẳng
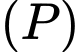 nhận véc tơ
nhận véc tơ 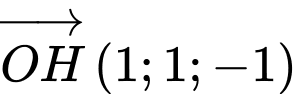 làm véc tơ pháp tuyến và đi qua điểm
làm véc tơ pháp tuyến và đi qua điểm 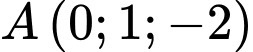 nên có phương trình
nên có phương trình 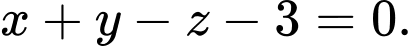 Đáp án: D
Đáp án: D
Câu 4 [579678]: [Đề mẫu HSA 2024]: Trong không gian 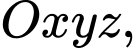 cho điểm
cho điểm 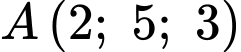 và đường thẳng
và đường thẳng 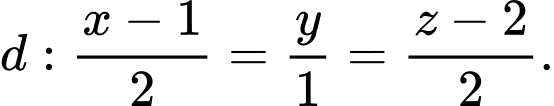
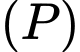 là mặt phẳng chứa đường thẳng
là mặt phẳng chứa đường thẳng 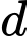 sao cho khoảng cách từ
sao cho khoảng cách từ 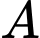 đến
đến 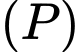 lớn nhất. Phương trình mặt phẳng
lớn nhất. Phương trình mặt phẳng 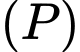 có dạng
có dạng 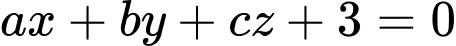 với
với 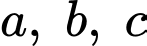 là các số thực. Tổng
là các số thực. Tổng 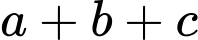 là
là
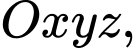 cho điểm
cho điểm 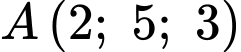 và đường thẳng
và đường thẳng 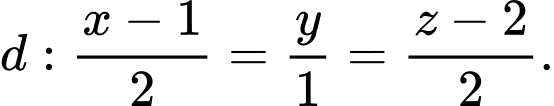
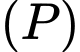 là mặt phẳng chứa đường thẳng
là mặt phẳng chứa đường thẳng 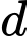 sao cho khoảng cách từ
sao cho khoảng cách từ 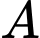 đến
đến 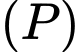 lớn nhất. Phương trình mặt phẳng
lớn nhất. Phương trình mặt phẳng 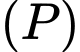 có dạng
có dạng 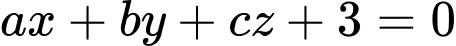 với
với 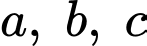 là các số thực. Tổng
là các số thực. Tổng 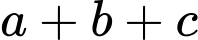 là
là A, - 2.
B, - 4.
C, 2.
D, 4.
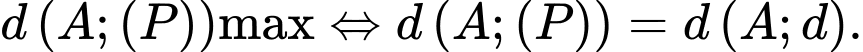
Gọi
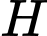 là hình chiếu của
là hình chiếu của 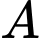 đến
đến 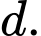
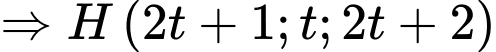
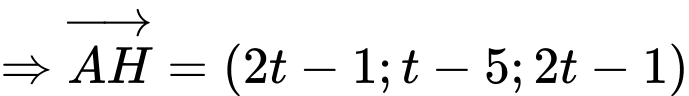
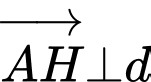
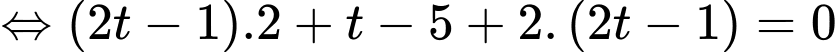
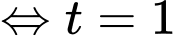
Do
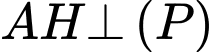 nên
nên 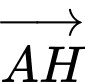 là VTPT của
là VTPT của 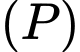
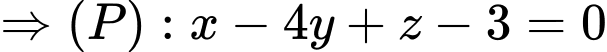 hay
hay 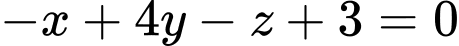
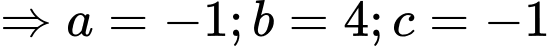
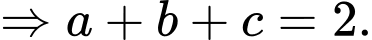
Chọn C. Đáp án: C
Câu 5 [57837]: Trong không gian với hệ trục tọa độ 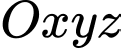 , cho ba điểm
, cho ba điểm 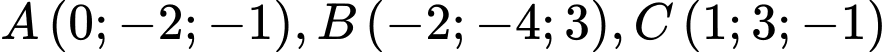 và mặt phẳng
và mặt phẳng 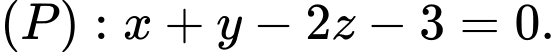 Tìm điểm
Tìm điểm 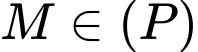 sao cho
sao cho 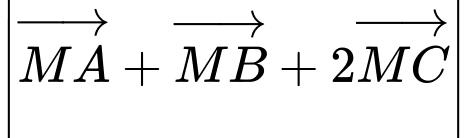 đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất.
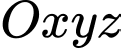 , cho ba điểm
, cho ba điểm 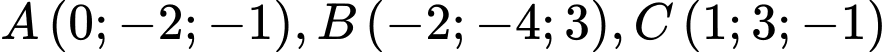 và mặt phẳng
và mặt phẳng 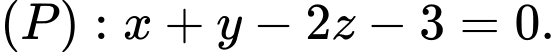 Tìm điểm
Tìm điểm 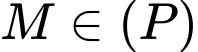 sao cho
sao cho 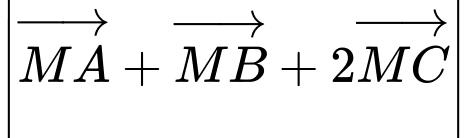 đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất. A, 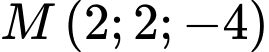 .
.
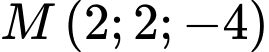 .
.B, 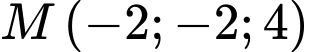 .
.
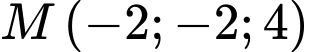 .
.C, 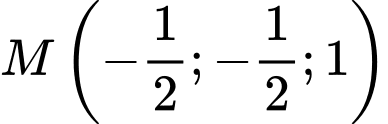 .
.
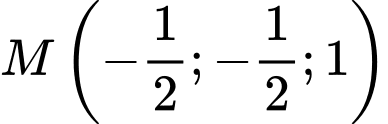 .
.D, 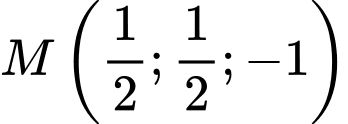 .
.
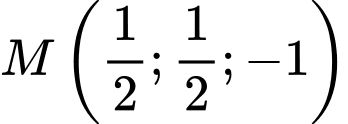 .
. Đáp án: D
Đáp án: D
Câu 6 [153540]: [Đề ĐGNL ĐHSP HN 2024]: Trong không gian với hệ trục tọa độ 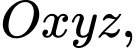 cho các điểm
cho các điểm 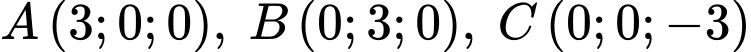 và
và 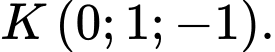 Xét điểm
Xét điểm 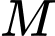 thỏa mãn điều kiện
thỏa mãn điều kiện 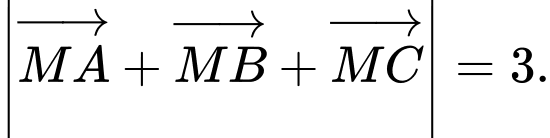 Khi đoạn thẳng
Khi đoạn thẳng 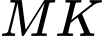 có độ dài lớn nhất, tọa độ của điểm
có độ dài lớn nhất, tọa độ của điểm 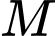 là
là
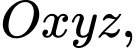 cho các điểm
cho các điểm 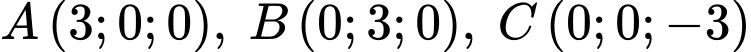 và
và 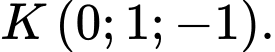 Xét điểm
Xét điểm 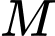 thỏa mãn điều kiện
thỏa mãn điều kiện 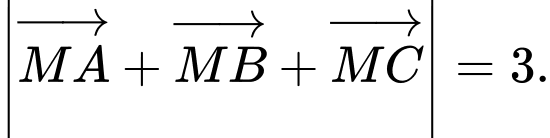 Khi đoạn thẳng
Khi đoạn thẳng 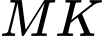 có độ dài lớn nhất, tọa độ của điểm
có độ dài lớn nhất, tọa độ của điểm 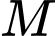 là
là A, 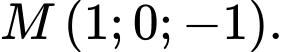
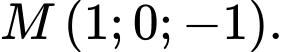
B, 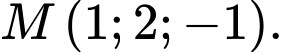
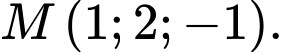
C, 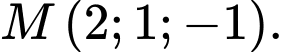
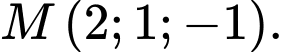
D, 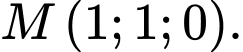
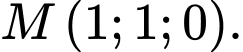
Trọng tâm tam giác 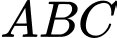 là
là 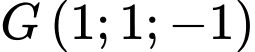
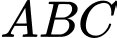 là
là 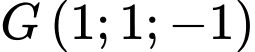
Khi đó 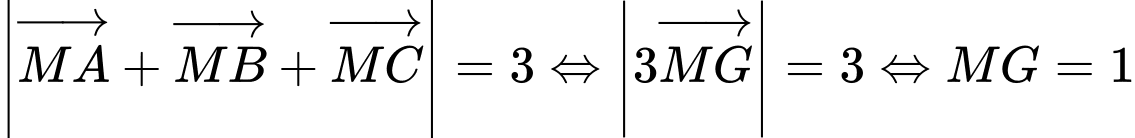
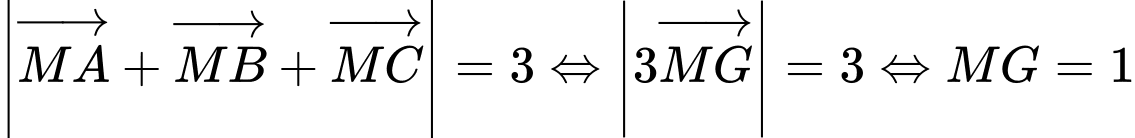
Suy ra 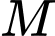 thuộc mặt cầu
thuộc mặt cầu 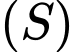 tâm
tâm 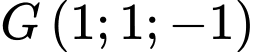 bán kính
bán kính 
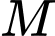 thuộc mặt cầu
thuộc mặt cầu 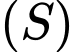 tâm
tâm 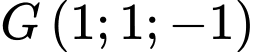 bán kính
bán kính 
Ta có: 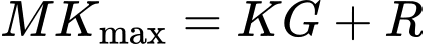 khi
khi 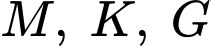 thằng hàng và
thằng hàng và  nằm giữa.
nằm giữa.
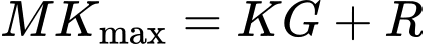 khi
khi 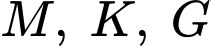 thằng hàng và
thằng hàng và  nằm giữa.
nằm giữa. Lại có:  là trung điểm của
là trung điểm của 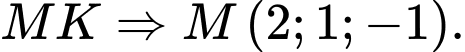
 là trung điểm của
là trung điểm của 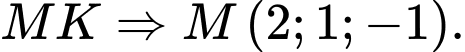
Chọn C.
Câu 7 [899298]: Trong không gian với hệ trục tọa độ 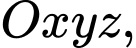 cho
cho 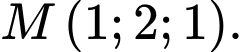 Viết phương trình mặt phẳng
Viết phương trình mặt phẳng 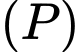 qua
qua 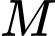 lần lượt cắt các trục
lần lượt cắt các trục 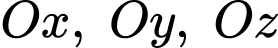 lần lượt tại
lần lượt tại 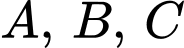 sao cho
sao cho 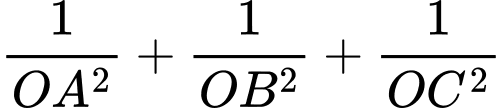 đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất.
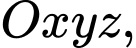 cho
cho 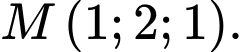 Viết phương trình mặt phẳng
Viết phương trình mặt phẳng 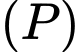 qua
qua 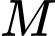 lần lượt cắt các trục
lần lượt cắt các trục 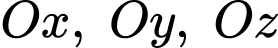 lần lượt tại
lần lượt tại 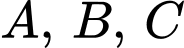 sao cho
sao cho 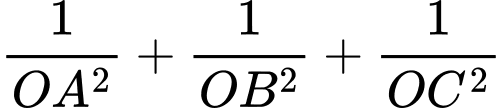 đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất. A, 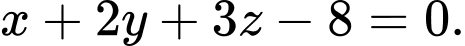
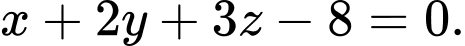
B, 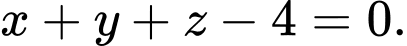
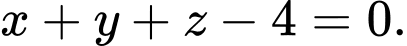
C, 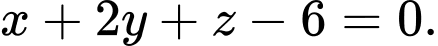
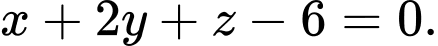
D, 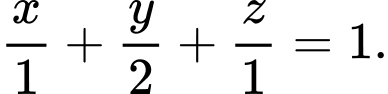
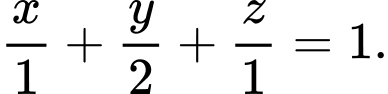
Gọi tọa độ các điểm 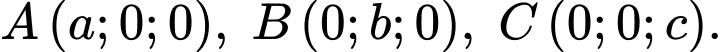
Phương trình đoạn chắn của mặt phẳng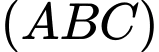 là:
là: 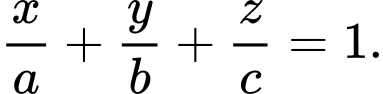
Điểm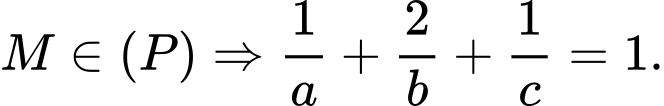 Xét
Xét 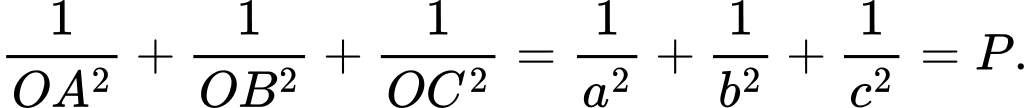
Lại có: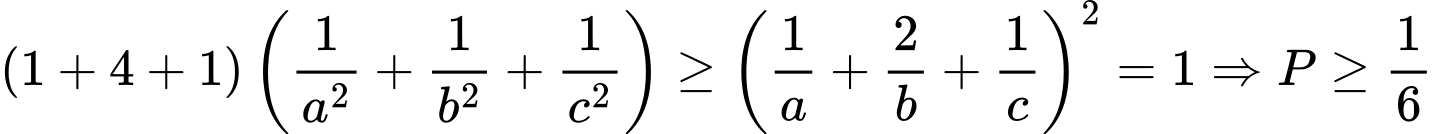 (Theo BĐT Bunhiacopxki).
(Theo BĐT Bunhiacopxki).
Dấu bằng xảy ra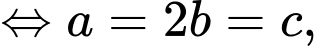 kết hợp
kết hợp 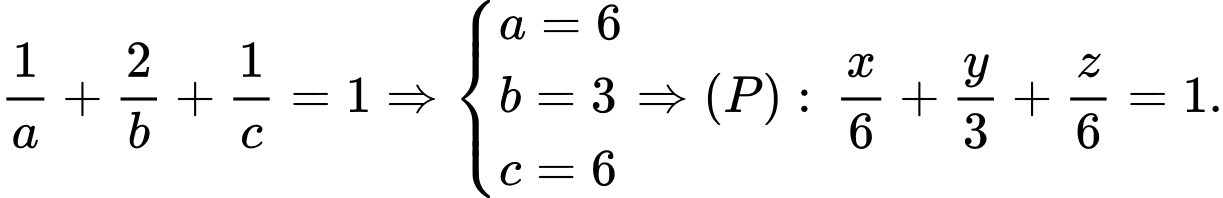
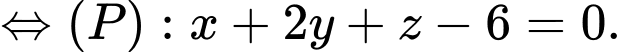 Chọn C.
Đáp án: C
Chọn C.
Đáp án: C
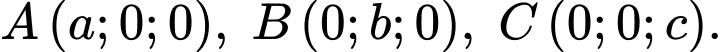
Phương trình đoạn chắn của mặt phẳng
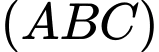 là:
là: 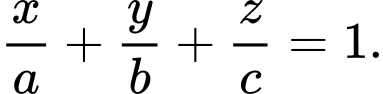
Điểm
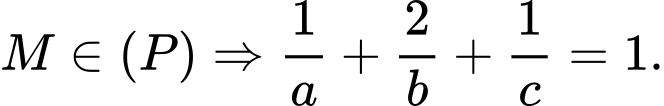 Xét
Xét 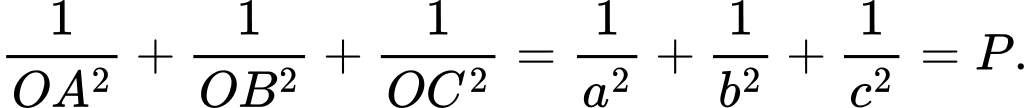
Lại có:
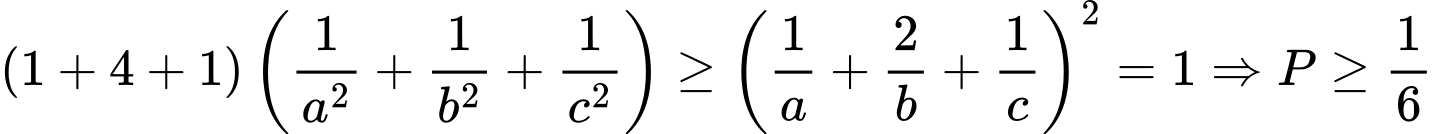 (Theo BĐT Bunhiacopxki).
(Theo BĐT Bunhiacopxki). Dấu bằng xảy ra
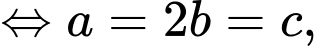 kết hợp
kết hợp 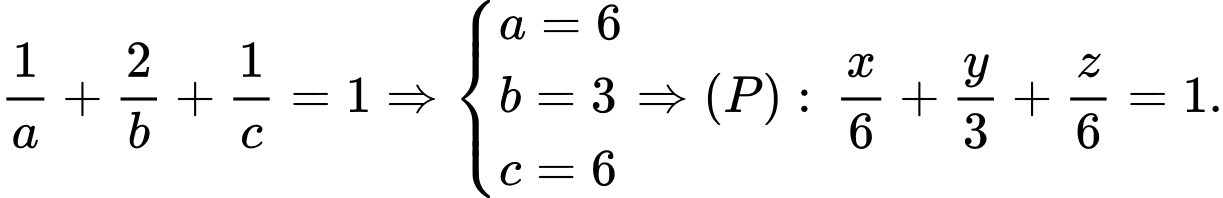
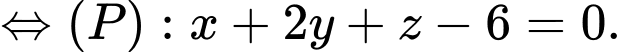 Chọn C.
Đáp án: C
Chọn C.
Đáp án: C
Câu 8 [80461]: [Đề thi Chuyên ĐH Vinh năm 2019] Trong không gian 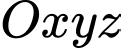 , cho đường thẳng
, cho đường thẳng 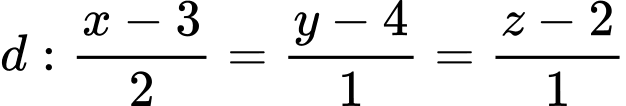 và 2 điểm
và 2 điểm 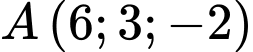 ,
, 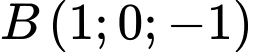 . Gọi
. Gọi  là đường thẳng đi qua
là đường thẳng đi qua 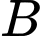 , vuông góc với
, vuông góc với 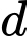 và thỏa mãn khoảng cách từ
và thỏa mãn khoảng cách từ 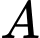 đến
đến  là nhỏ nhất. Một vectơ chỉ phương của
là nhỏ nhất. Một vectơ chỉ phương của  có tọa độ là
có tọa độ là
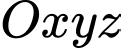 , cho đường thẳng
, cho đường thẳng 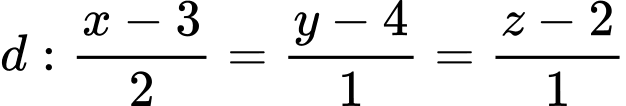 và 2 điểm
và 2 điểm 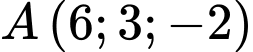 ,
, 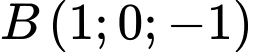 . Gọi
. Gọi  là đường thẳng đi qua
là đường thẳng đi qua 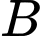 , vuông góc với
, vuông góc với 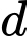 và thỏa mãn khoảng cách từ
và thỏa mãn khoảng cách từ 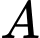 đến
đến  là nhỏ nhất. Một vectơ chỉ phương của
là nhỏ nhất. Một vectơ chỉ phương của  có tọa độ là
có tọa độ là A, 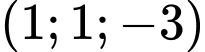 .
.
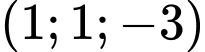 .
.B, 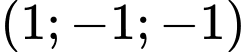 .
.
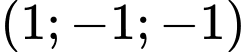 .
.C, 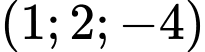 .
.
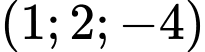 .
.D, 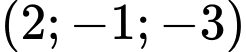 .
.
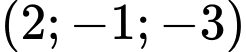 .
.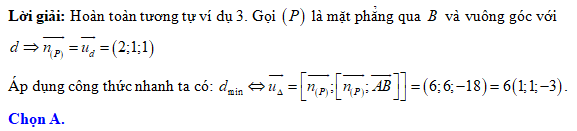 Đáp án: A
Đáp án: A
Câu 9 [80462]: Trong không gian với hệ tọa độ 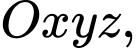 cho đường thẳng
cho đường thẳng 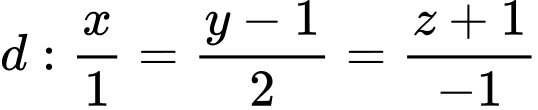 và 2 điểm
và 2 điểm 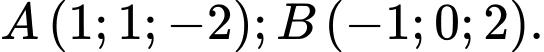 Viết phương trình đường thẳng
Viết phương trình đường thẳng  đi qua
đi qua 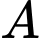 , vuông góc với
, vuông góc với 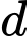 sao cho khoảng cách từ
sao cho khoảng cách từ 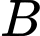 đến
đến  là nhỏ nhất.
là nhỏ nhất.
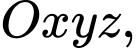 cho đường thẳng
cho đường thẳng 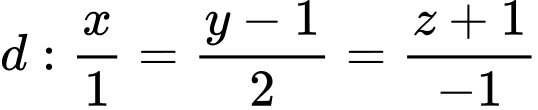 và 2 điểm
và 2 điểm 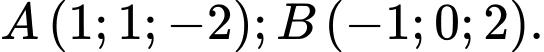 Viết phương trình đường thẳng
Viết phương trình đường thẳng  đi qua
đi qua 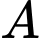 , vuông góc với
, vuông góc với 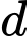 sao cho khoảng cách từ
sao cho khoảng cách từ 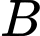 đến
đến  là nhỏ nhất.
là nhỏ nhất. A, 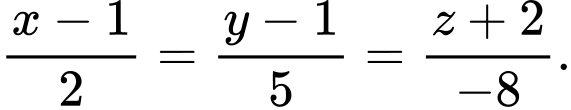
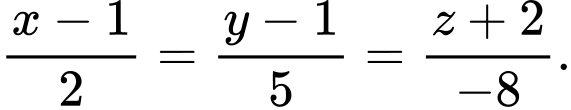
B, 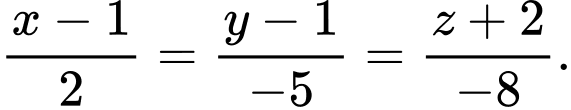
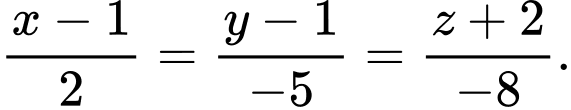
C, 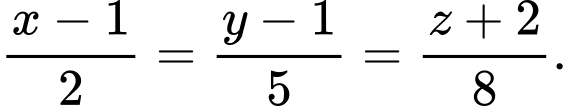
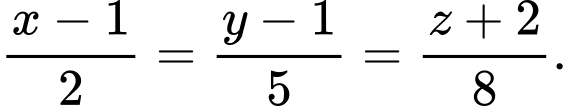
D, 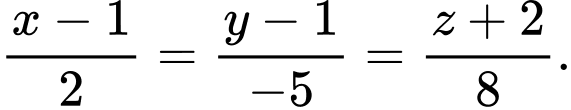
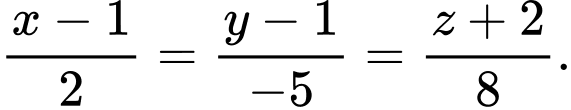
 Đáp án: B
Đáp án: B
Câu 10 [80465]: [Đề thi tham khảo năm 2019] Trong không gian 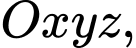 cho điểm
cho điểm 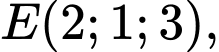 mặt phẳng
mặt phẳng 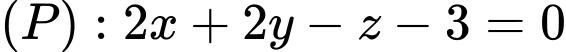 và mặt cầu
và mặt cầu 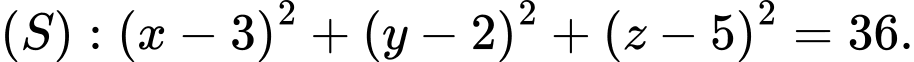 Gọi
Gọi  là đường thẳng đi qua
là đường thẳng đi qua 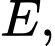 nằm trong
nằm trong 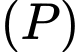 và cắt
và cắt 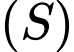 tại hai điểm có khoảng cách nhỏ nhất. Phương trình của
tại hai điểm có khoảng cách nhỏ nhất. Phương trình của  là
là
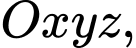 cho điểm
cho điểm 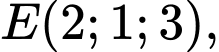 mặt phẳng
mặt phẳng 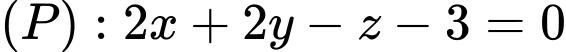 và mặt cầu
và mặt cầu 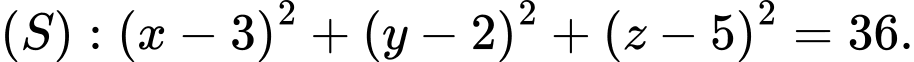 Gọi
Gọi  là đường thẳng đi qua
là đường thẳng đi qua 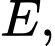 nằm trong
nằm trong 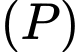 và cắt
và cắt 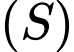 tại hai điểm có khoảng cách nhỏ nhất. Phương trình của
tại hai điểm có khoảng cách nhỏ nhất. Phương trình của  là
là A, 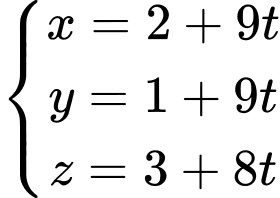
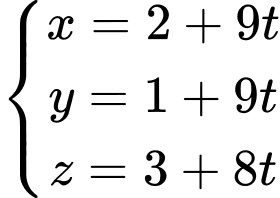
B, 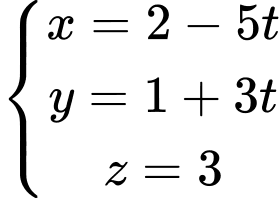
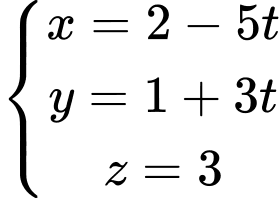
C, 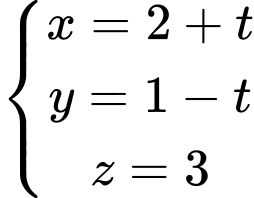
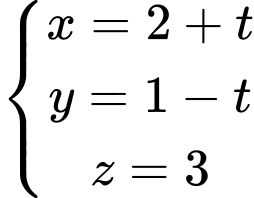
D, 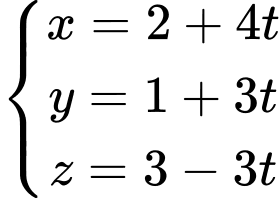
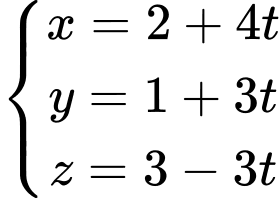
 Đáp án: C
Đáp án: C
Câu 11 [57878]: Cho mặt cầu 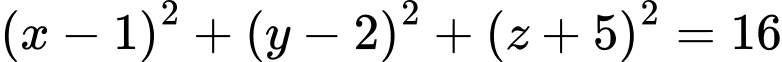 và điểm
và điểm 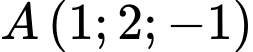 . Tìm tọa độ điểm
. Tìm tọa độ điểm 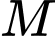 thuộc mặt cầu sao cho độ dài đoạn
thuộc mặt cầu sao cho độ dài đoạn  là lớn nhất.
là lớn nhất.
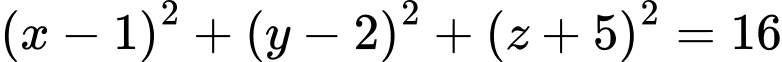 và điểm
và điểm 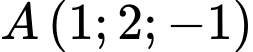 . Tìm tọa độ điểm
. Tìm tọa độ điểm 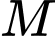 thuộc mặt cầu sao cho độ dài đoạn
thuộc mặt cầu sao cho độ dài đoạn  là lớn nhất.
là lớn nhất. A, 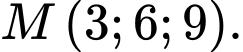
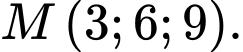
B, 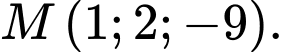
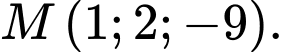
C, 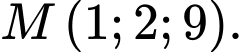
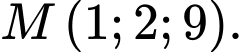
D, 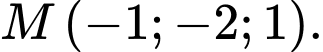
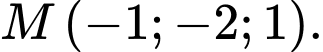
 Đáp án: B
Đáp án: B
Câu 12 [82649]: Trong không gian tọa độ 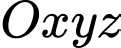 , cho các điểm
, cho các điểm 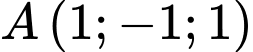 và đường thẳng
và đường thẳng 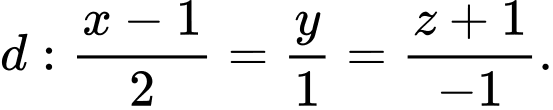 Gọi
Gọi 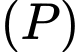 là mặt phẳng chứa d sao cho khoảng cách từ
là mặt phẳng chứa d sao cho khoảng cách từ 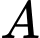 đến
đến 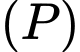 đạt giá trị lớn nhất. Biết
đạt giá trị lớn nhất. Biết 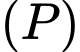 có dạng
có dạng 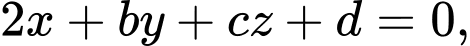 tính
tính 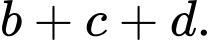
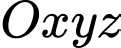 , cho các điểm
, cho các điểm 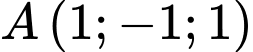 và đường thẳng
và đường thẳng 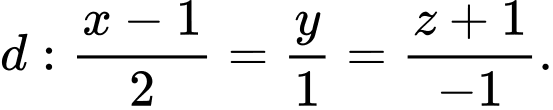 Gọi
Gọi 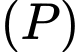 là mặt phẳng chứa d sao cho khoảng cách từ
là mặt phẳng chứa d sao cho khoảng cách từ 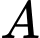 đến
đến 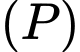 đạt giá trị lớn nhất. Biết
đạt giá trị lớn nhất. Biết 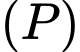 có dạng
có dạng 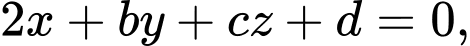 tính
tính 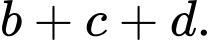
A, 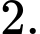
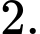
B, 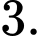
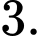
C, 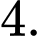
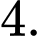
D, 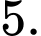
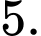
 Đáp án: B
Đáp án: B
Câu 13 [82650]: Trong không gian với hệ tọa độ 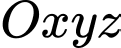 cho cho điểm
cho cho điểm 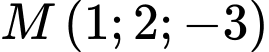 và đường thẳng
và đường thẳng 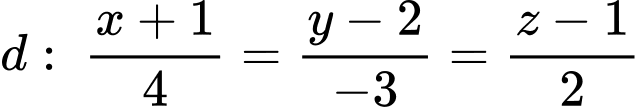 . Mặt phẳng
. Mặt phẳng 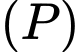 chứa đường thẳng
chứa đường thẳng 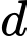 đồng thời cách điểm
đồng thời cách điểm 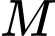 một khoảng lớn nhất có phương trình dạng
một khoảng lớn nhất có phương trình dạng 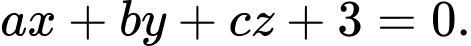 Tính giá trị của biểu thức
Tính giá trị của biểu thức 
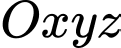 cho cho điểm
cho cho điểm 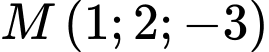 và đường thẳng
và đường thẳng 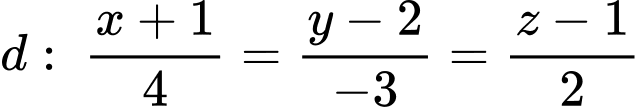 . Mặt phẳng
. Mặt phẳng 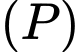 chứa đường thẳng
chứa đường thẳng 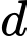 đồng thời cách điểm
đồng thời cách điểm 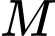 một khoảng lớn nhất có phương trình dạng
một khoảng lớn nhất có phương trình dạng 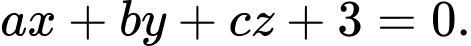 Tính giá trị của biểu thức
Tính giá trị của biểu thức 
A, 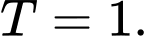
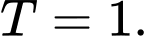
B, 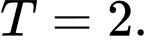
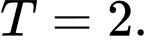
C, 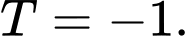
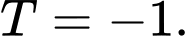
D, 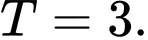
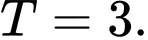
 Đáp án: C
Đáp án: C
Câu 14 [82654]: [Đề thi THPT QG năm 2017] Trong không gian với hệ tọa độ 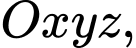 cho hai điểm
cho hai điểm 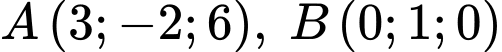 và mặt cầu
và mặt cầu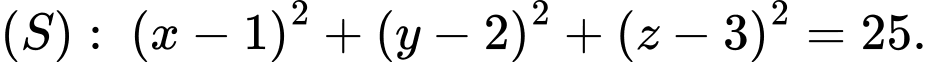 Mặt phẳng
Mặt phẳng 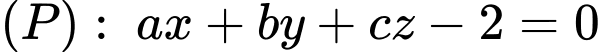 đi qua
đi qua 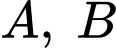 và cắt
và cắt 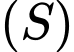 theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính
theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính 
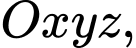 cho hai điểm
cho hai điểm 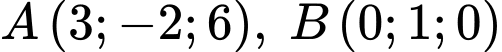 và mặt cầu
và mặt cầu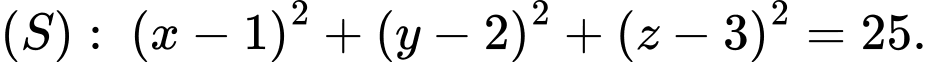 Mặt phẳng
Mặt phẳng 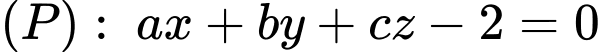 đi qua
đi qua 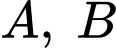 và cắt
và cắt 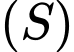 theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính
theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính 
A, 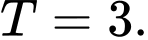
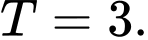
B, 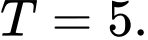
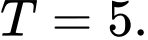
C, 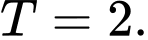
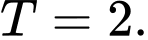
D, 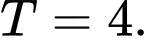
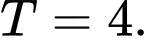
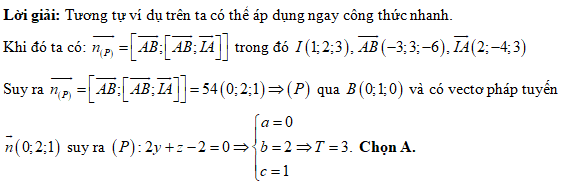 Đáp án: A
Đáp án: A
Câu 15 [80464]: [Đề thi THPT QG năm 2017] Trong không gian 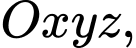 cho mặt cầu
cho mặt cầu 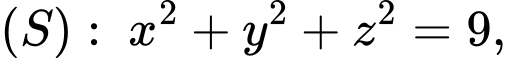 điểm
điểm 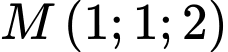 và mặt phẳng
và mặt phẳng 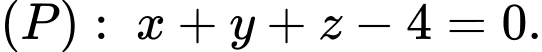 Gọi
Gọi  là đường thẳng qua
là đường thẳng qua 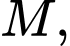 thuộc mặt phẳng
thuộc mặt phẳng 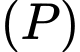 và cắt
và cắt 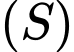 tại hai điểm
tại hai điểm 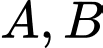 sao cho
sao cho  nhỏ nhất. Biết
nhỏ nhất. Biết  có một vectơ chỉ phương là
có một vectơ chỉ phương là 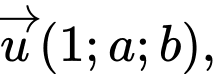 tính
tính 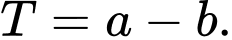
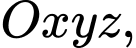 cho mặt cầu
cho mặt cầu 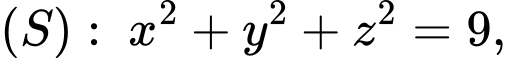 điểm
điểm 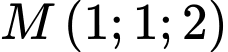 và mặt phẳng
và mặt phẳng 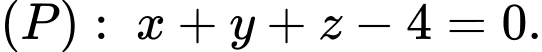 Gọi
Gọi  là đường thẳng qua
là đường thẳng qua 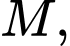 thuộc mặt phẳng
thuộc mặt phẳng 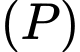 và cắt
và cắt 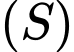 tại hai điểm
tại hai điểm 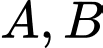 sao cho
sao cho  nhỏ nhất. Biết
nhỏ nhất. Biết  có một vectơ chỉ phương là
có một vectơ chỉ phương là 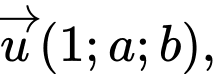 tính
tính 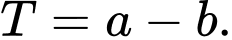
A, 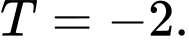
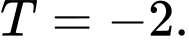
B, 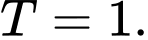
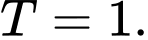
C, 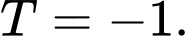
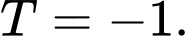
D, 
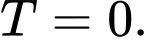
 Đáp án: C
Đáp án: C
Câu 16 [57875]: Trong không gian với hệ tọa độ 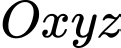 , cho các điểm
, cho các điểm 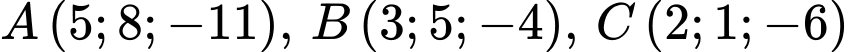 và mặt cầu
và mặt cầu 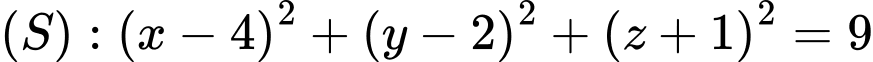 . Gọi
. Gọi 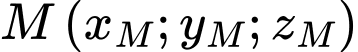 là điểm trên mặt cầu
là điểm trên mặt cầu 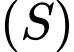 sao cho biểu thức
sao cho biểu thức 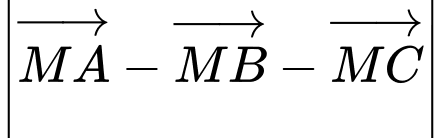 đạt giá trị nhỏ nhất. Tính
đạt giá trị nhỏ nhất. Tính 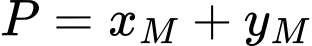 .
.
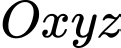 , cho các điểm
, cho các điểm 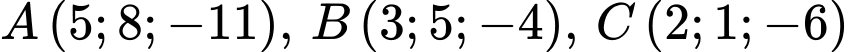 và mặt cầu
và mặt cầu 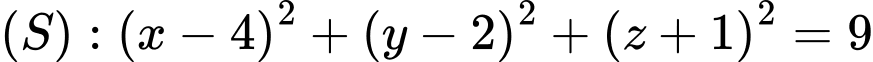 . Gọi
. Gọi 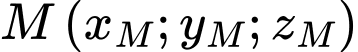 là điểm trên mặt cầu
là điểm trên mặt cầu 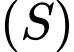 sao cho biểu thức
sao cho biểu thức 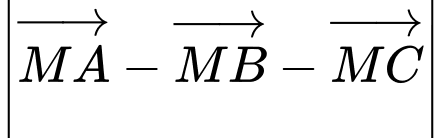 đạt giá trị nhỏ nhất. Tính
đạt giá trị nhỏ nhất. Tính 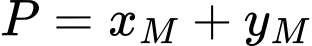 .
. A, 

B, 

C, 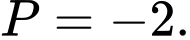
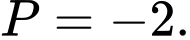
D, 

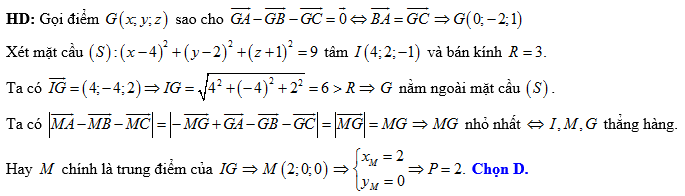 Đáp án: D
Đáp án: D
Câu 17 [322603]: Trong không gian 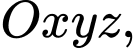 cho hai điểm
cho hai điểm 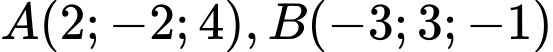 và mặt phẳng
và mặt phẳng 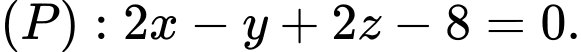 Xét
Xét 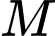 là điểm thay đổi thuộc
là điểm thay đổi thuộc 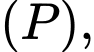 giá trị nhỏ nhất của
giá trị nhỏ nhất của  bằng
bằng
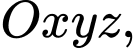 cho hai điểm
cho hai điểm 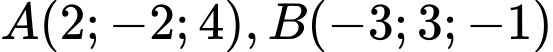 và mặt phẳng
và mặt phẳng 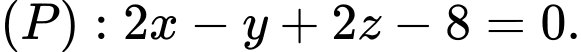 Xét
Xét 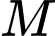 là điểm thay đổi thuộc
là điểm thay đổi thuộc 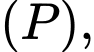 giá trị nhỏ nhất của
giá trị nhỏ nhất của  bằng
bằng A, 135
B, 105
C, 108
D, 145
Gọi 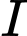 là điểm thỏa mãn
là điểm thỏa mãn 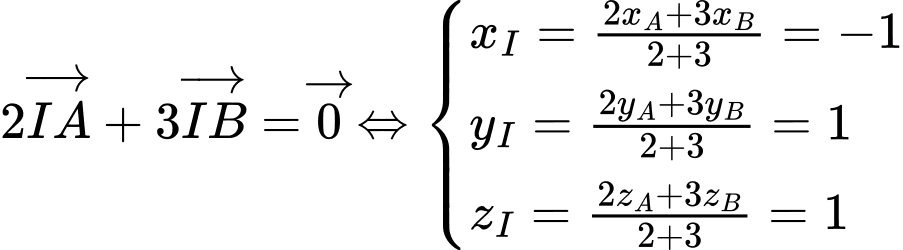
Khi đó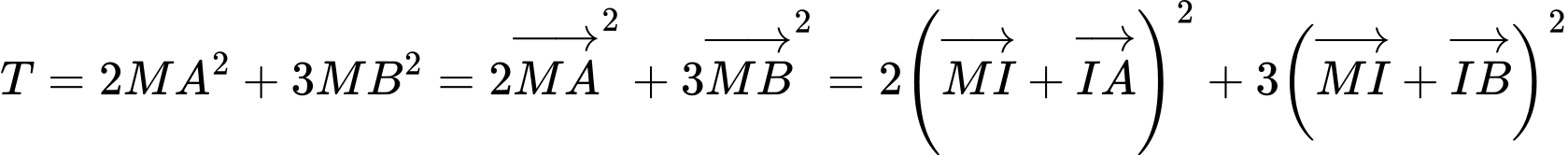
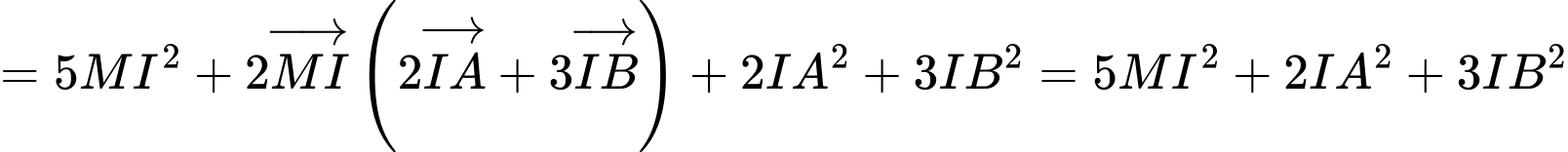 nhỏ nhất
nhỏ nhất 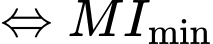 hay M là hình chiếu vuông góc của
hay M là hình chiếu vuông góc của 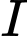 trên
trên 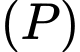
Khi đó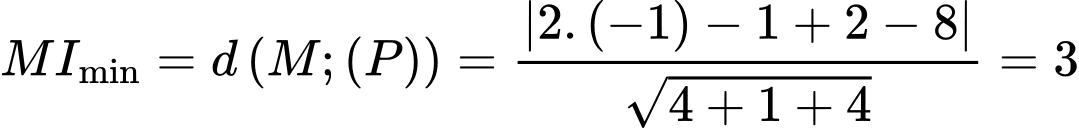
Suy ra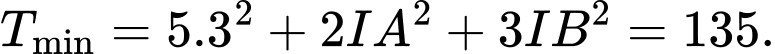 Chọn A.
Đáp án: A
Chọn A.
Đáp án: A
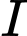 là điểm thỏa mãn
là điểm thỏa mãn 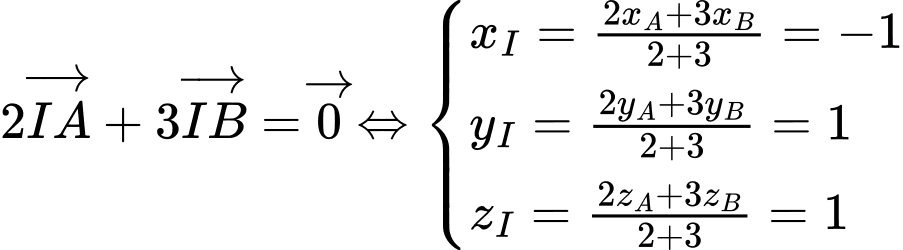
Khi đó
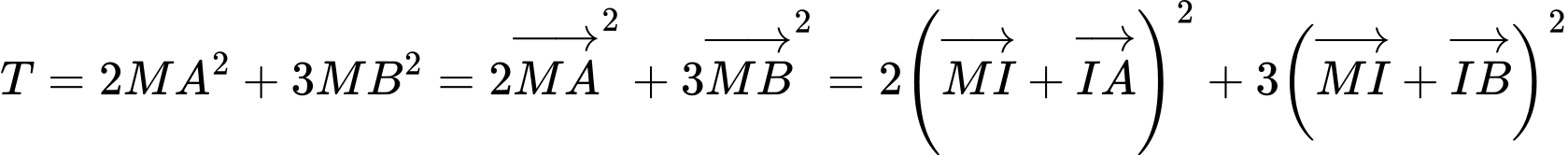
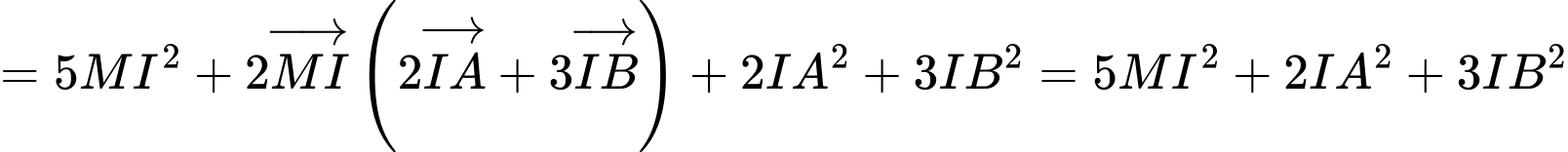 nhỏ nhất
nhỏ nhất 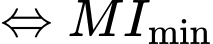 hay M là hình chiếu vuông góc của
hay M là hình chiếu vuông góc của 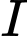 trên
trên 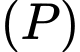
Khi đó
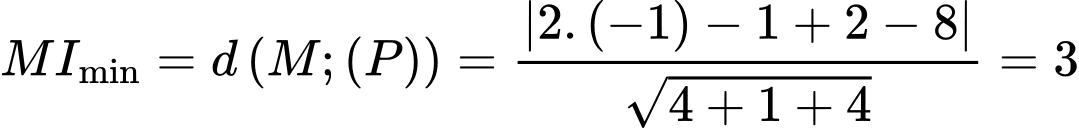
Suy ra
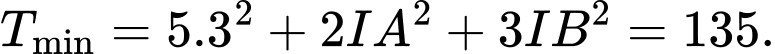 Chọn A.
Đáp án: A
Chọn A.
Đáp án: A
Câu 18 [57854]: Trong không gian với hệ tọa độ 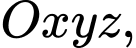 cho hai điểm
cho hai điểm 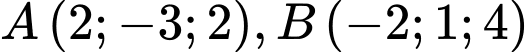 và mặt cầu
và mặt cầu 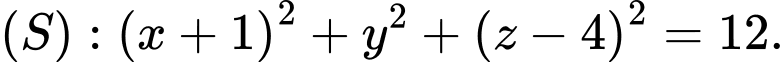 Điểm
Điểm 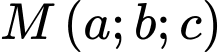 thuộc
thuộc 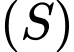 sao cho
sao cho 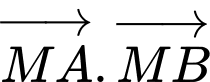 nhỏ nhất, tính
nhỏ nhất, tính 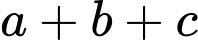 .
.
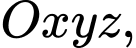 cho hai điểm
cho hai điểm 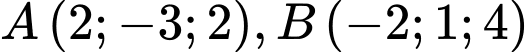 và mặt cầu
và mặt cầu 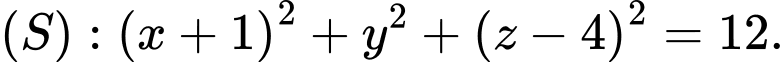 Điểm
Điểm 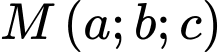 thuộc
thuộc 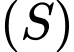 sao cho
sao cho 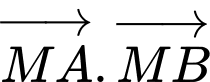 nhỏ nhất, tính
nhỏ nhất, tính 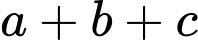 .
. A, 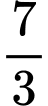 .
.
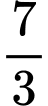 .
.B, 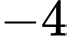 .
.
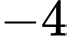 .
.C, 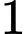 .
.
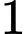 .
.D, 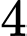 .
.
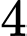 .
. Đáp án: C
Đáp án: C
Câu 19 [58245]: Trong không gian với hệ tọa độ 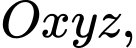 cho mặt cầu
cho mặt cầu 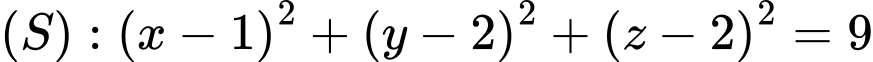 và mặt phẳng
và mặt phẳng 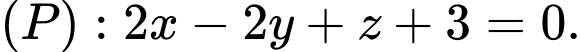 Gọi
Gọi 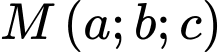 là điểm trên mặt cầu
là điểm trên mặt cầu 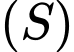 sao cho khoảng cách từ
sao cho khoảng cách từ 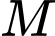 đến mặt phẳng
đến mặt phẳng 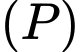 là lớn nhất. Khi đó tính
là lớn nhất. Khi đó tính 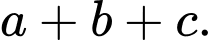
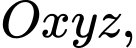 cho mặt cầu
cho mặt cầu 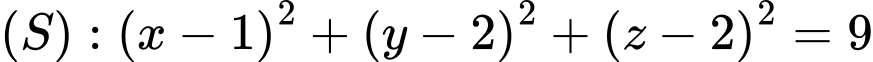 và mặt phẳng
và mặt phẳng 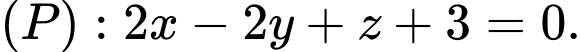 Gọi
Gọi 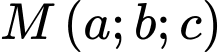 là điểm trên mặt cầu
là điểm trên mặt cầu 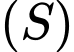 sao cho khoảng cách từ
sao cho khoảng cách từ 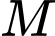 đến mặt phẳng
đến mặt phẳng 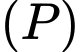 là lớn nhất. Khi đó tính
là lớn nhất. Khi đó tính 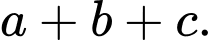
A, 

B, 

C, 

D, 

 Đáp án: C
Đáp án: C
Câu 20 [953306]: Trong không gian tọa độ 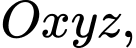 cho các đường thẳng
cho các đường thẳng 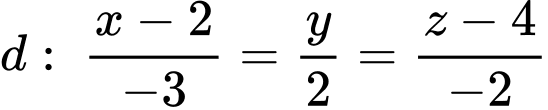 và
và 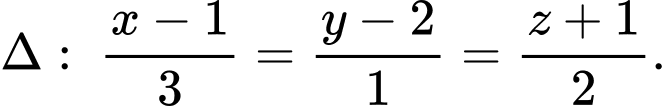 Biết rằng trong tất cả các mặt phẳng chứa
Biết rằng trong tất cả các mặt phẳng chứa  thì mặt phẳng
thì mặt phẳng 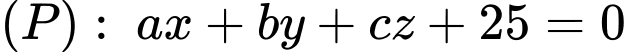 tạo với
tạo với 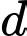 góc lớn nhất. Tính
góc lớn nhất. Tính 
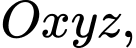 cho các đường thẳng
cho các đường thẳng 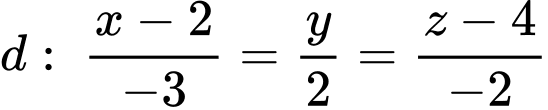 và
và 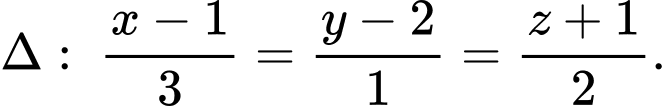 Biết rằng trong tất cả các mặt phẳng chứa
Biết rằng trong tất cả các mặt phẳng chứa  thì mặt phẳng
thì mặt phẳng 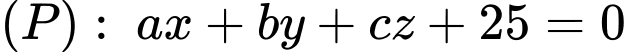 tạo với
tạo với 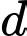 góc lớn nhất. Tính
góc lớn nhất. Tính 
A, 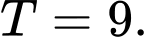
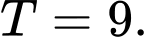
B, 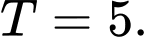
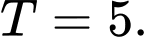
C, 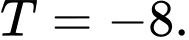
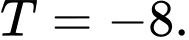
D, 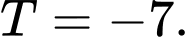
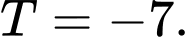
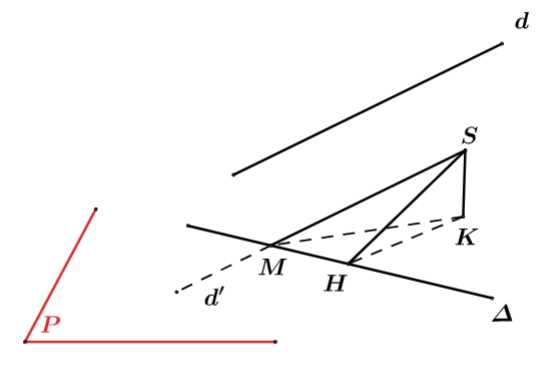
Gọi
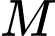 là điểm bất kì thuộc
là điểm bất kì thuộc 
Gọi
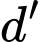 là đường thẳng qua
là đường thẳng qua 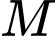 và song song với
và song song với 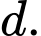 Khi đó ta có
Khi đó ta có 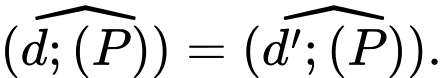
Lấy
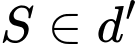 bất kì, kẻ
bất kì, kẻ 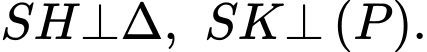
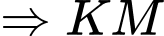 là hình chiếu vuông góc của
là hình chiếu vuông góc của 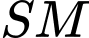 lên
lên 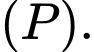

Xét tam giác vuông
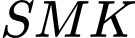 ta có
ta có 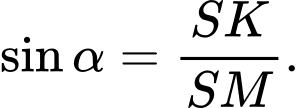
Để
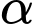 lớn nhất thì
lớn nhất thì 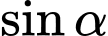 lớn nhất
lớn nhất 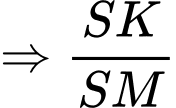 lớn nhất.
lớn nhất.
Ta có:
 (do
(do 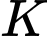 là hình chiếu
là hình chiếu 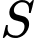 trên
trên 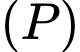 )
)
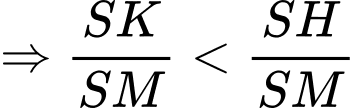 với
với 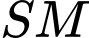 cố định.
cố định.
Ta có:
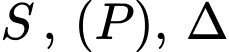 cố định
cố định 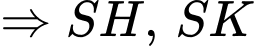 không đổi.
không đổi.
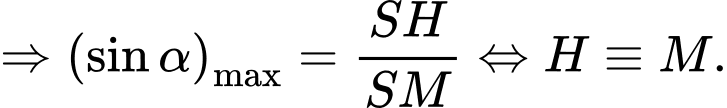
Khi đó
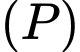 chứa
chứa  và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 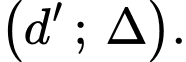
Lấy
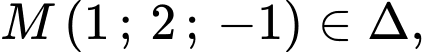 phương trình đường thẳng
phương trình đường thẳng 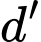 là
là 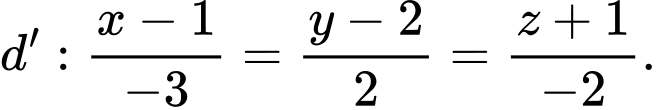
Gọi
 là mặt phẳng chứa
là mặt phẳng chứa 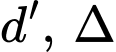
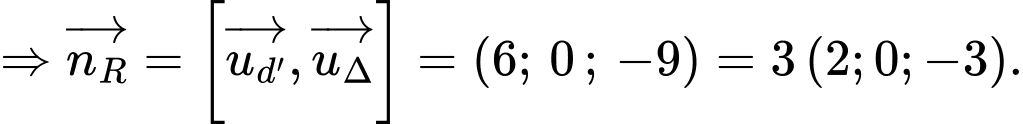
Ta có:
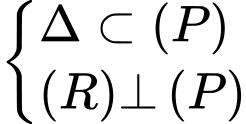
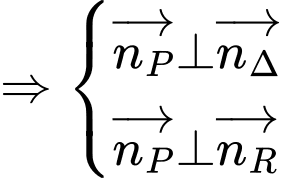
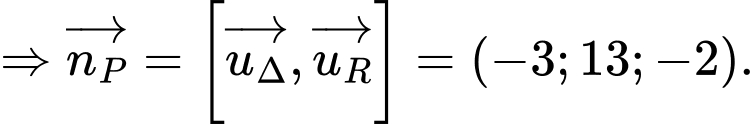
Suy ra, phương trình mặt phẳng
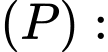


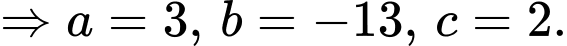
Vậy
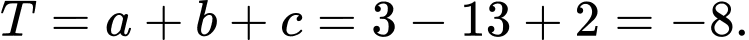
Đáp án: C. Đáp án: C