Đáp án Bài tập tự luyện
Câu 1 [45991]: Trong không gian 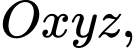 hình chiếu vuông góc của điểm
hình chiếu vuông góc của điểm 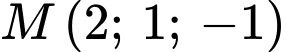 trên trục
trên trục  có tọa độ là
có tọa độ là
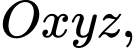 hình chiếu vuông góc của điểm
hình chiếu vuông góc của điểm 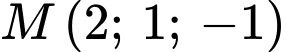 trên trục
trên trục  có tọa độ là
có tọa độ là A, 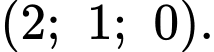
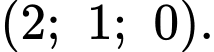
B, 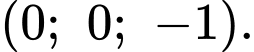
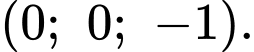
C, 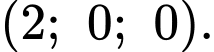
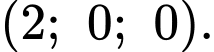
D, 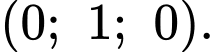
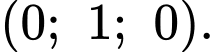
Hình chiếu vuông góc của 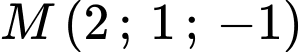 trên trục
trên trục  là
là 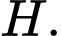
Trong đó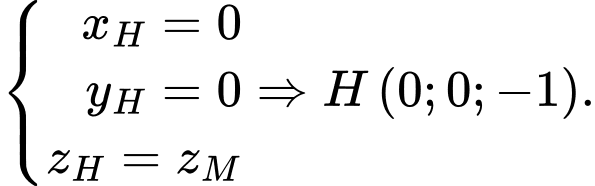 Chọn B.
Đáp án: B
Chọn B.
Đáp án: B
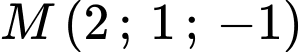 trên trục
trên trục  là
là 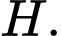
Trong đó
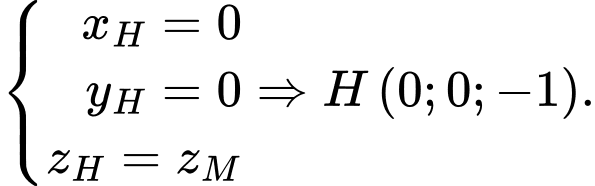 Chọn B.
Đáp án: B
Chọn B.
Đáp án: B
Câu 2 [677443]: Trong không gian 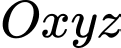 , hình chiếu vuông góc của điểm
, hình chiếu vuông góc của điểm 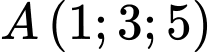 trên mặt phẳng
trên mặt phẳng 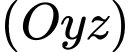 là điểm nào sau đây?
là điểm nào sau đây?
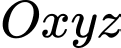 , hình chiếu vuông góc của điểm
, hình chiếu vuông góc của điểm 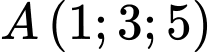 trên mặt phẳng
trên mặt phẳng 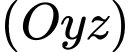 là điểm nào sau đây?
là điểm nào sau đây? A, 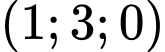 .
.
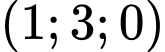 .
.B, 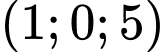 .
.
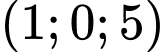 .
.C, 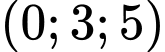 .
.
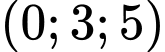 .
.D, 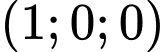 .
.
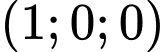 .
.
Chọn C
Vì hình chiếu của điểm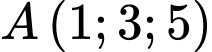 trên mặt phẳng
trên mặt phẳng 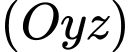 là
là 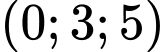 . Đáp án: C
. Đáp án: C
Vì hình chiếu của điểm
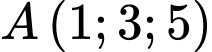 trên mặt phẳng
trên mặt phẳng 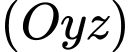 là
là 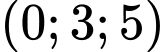 . Đáp án: C
. Đáp án: C
Câu 3 [51359]: Trong không gian với hệ tọa độ 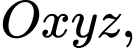 cho
cho 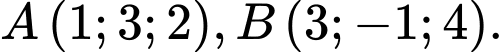 Tìm tọa độ trung điểm
Tìm tọa độ trung điểm 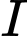 của
của 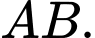
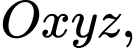 cho
cho 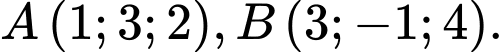 Tìm tọa độ trung điểm
Tìm tọa độ trung điểm 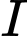 của
của 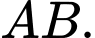
A, 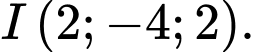
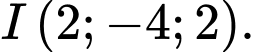
B, 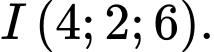
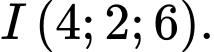
C, 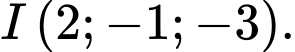
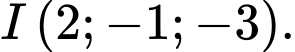
D, 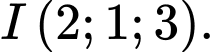
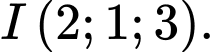
Ta có  tính theo trung bình cộng hai điểm,
tính theo trung bình cộng hai điểm, 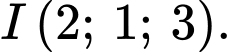
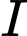 tính theo trung bình cộng hai điểm,
tính theo trung bình cộng hai điểm, 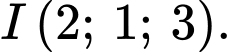
Chọn đáp án D.
Đáp án: D
Câu 4 [358980]: Tích vô hướng của hai vectơ 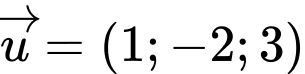 và
và 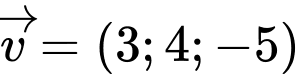 là:
là:
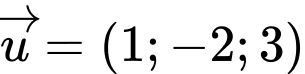 và
và 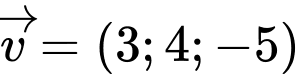 là:
là: A, 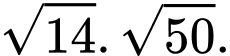
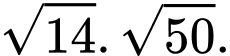
B, 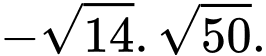
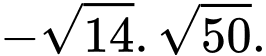
C, 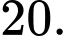
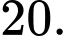
D, 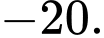
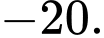
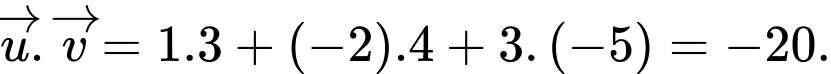 Chọn D. Đáp án: D
Chọn D. Đáp án: D
Câu 5 [384967]: Trong không gian 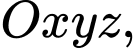 cho điểm
cho điểm 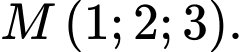 Tìm toạ độ điểm
Tìm toạ độ điểm 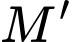 đối xứng với
đối xứng với 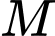 qua trục
qua trục 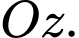
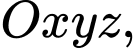 cho điểm
cho điểm 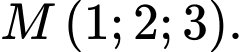 Tìm toạ độ điểm
Tìm toạ độ điểm 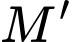 đối xứng với
đối xứng với 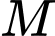 qua trục
qua trục 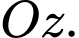
A, 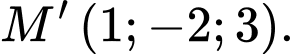
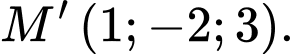
B, 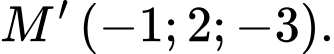
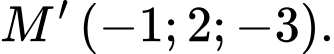
C, 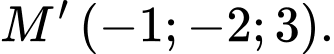
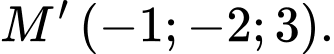
D, 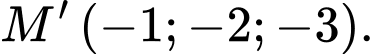
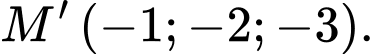
Hình chiếu vuông góc của 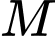 lên trục
lên trục  là
là 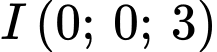
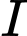 là trung điểm của đoạn thẳng
là trung điểm của đoạn thẳng 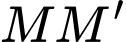
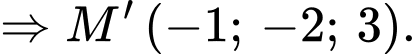 Đáp án: C
Đáp án: C
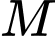 lên trục
lên trục  là
là 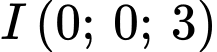
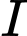 là trung điểm của đoạn thẳng
là trung điểm của đoạn thẳng 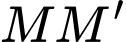
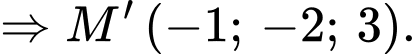
Chọn đáp án C.
Câu 6 [51330]: Trong không gian với hệ tọa độ 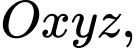 cho hai vectơ
cho hai vectơ 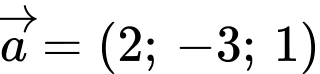 và
và 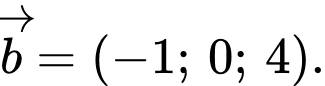 Tìm tọa độ vectơ
Tìm tọa độ vectơ 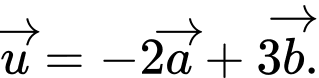
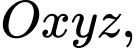 cho hai vectơ
cho hai vectơ 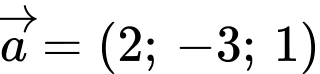 và
và 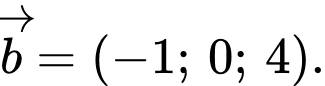 Tìm tọa độ vectơ
Tìm tọa độ vectơ 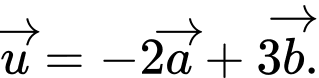
A, 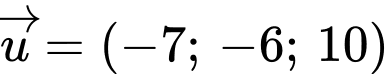 .
.
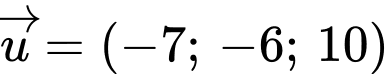 .
.B, 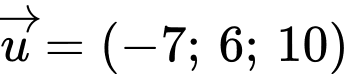 .
.
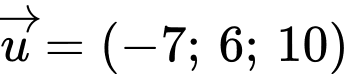 .
.C, 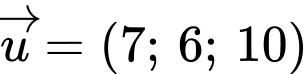 .
.
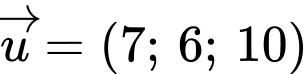 .
.D, 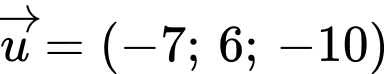 .
.
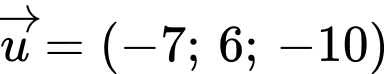 .
.
Ta có 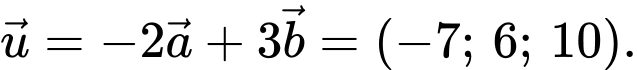 Chọn B. Đáp án: B
Chọn B. Đáp án: B
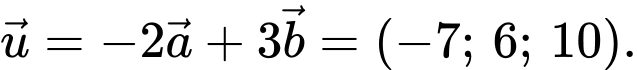 Chọn B. Đáp án: B
Chọn B. Đáp án: B
Câu 7 [51329]: Trong không gian với hệ tọa độ 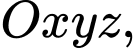 cho
cho 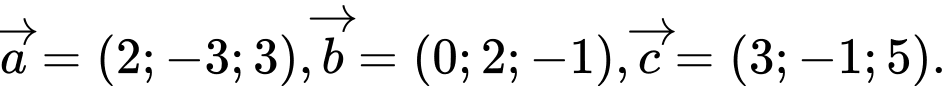 Tìm tọa độ của vectơ
Tìm tọa độ của vectơ 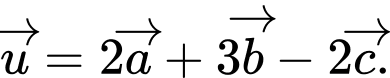
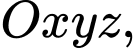 cho
cho 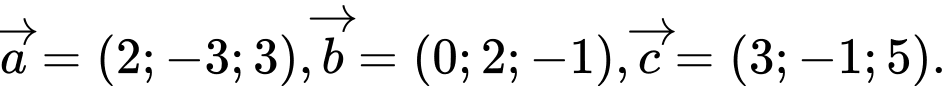 Tìm tọa độ của vectơ
Tìm tọa độ của vectơ 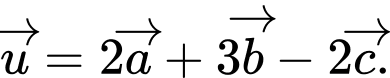
A, 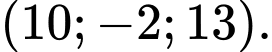
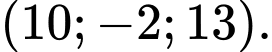
B, 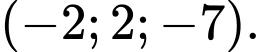
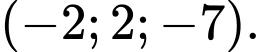
C, 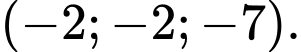
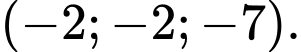
D, 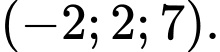
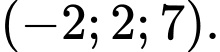
Ta có 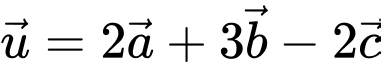
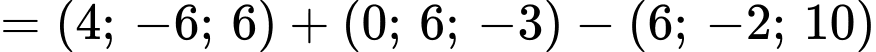
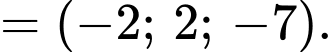 Chọn B. Đáp án: B
Chọn B. Đáp án: B
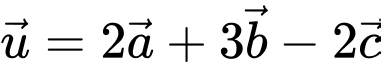
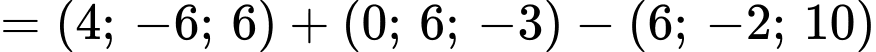
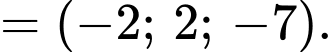 Chọn B. Đáp án: B
Chọn B. Đáp án: B
Câu 8 [51068]: Trong không gian tọa độ 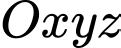 , cho tam giác
, cho tam giác 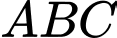 , biết
, biết 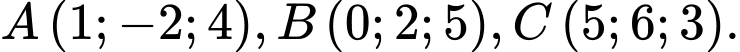 Tọa độ trọng tâm
Tọa độ trọng tâm  của tam giác
của tam giác 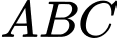 là
là
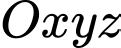 , cho tam giác
, cho tam giác 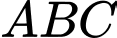 , biết
, biết 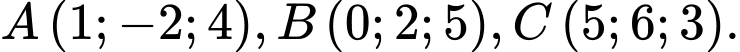 Tọa độ trọng tâm
Tọa độ trọng tâm  của tam giác
của tam giác 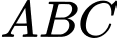 là
là A, 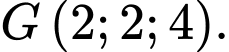
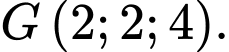
B, 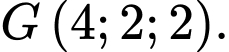
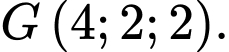
C, 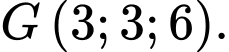
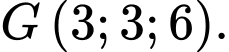
D, 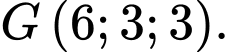
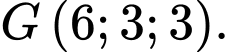
Toạ độ trọng tâm  của tam giác
của tam giác 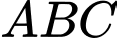 là
là 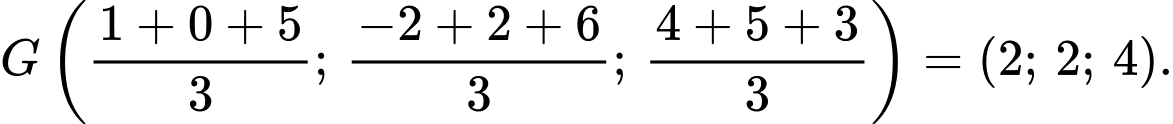 Đáp án: A
Đáp án: A
 của tam giác
của tam giác 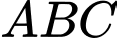 là
là 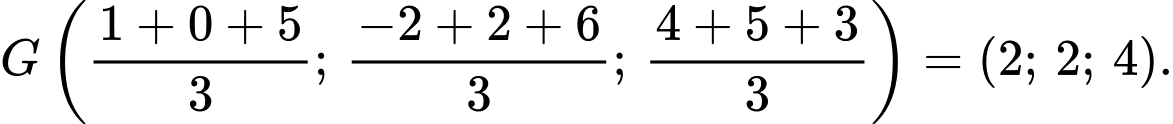
Chọn đáp án A.
Câu 9 [51351]: Trong không gian với hệ toạ độ 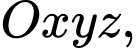 cho ba điểm
cho ba điểm 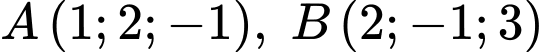 và
và 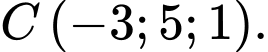 Gọi điểm
Gọi điểm 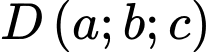 thoả mãn tứ giác
thoả mãn tứ giác 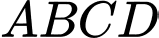 là hình bình hành. Tính tổng
là hình bình hành. Tính tổng 
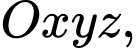 cho ba điểm
cho ba điểm 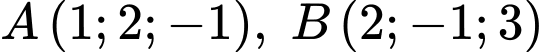 và
và 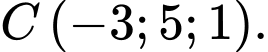 Gọi điểm
Gọi điểm 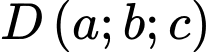 thoả mãn tứ giác
thoả mãn tứ giác 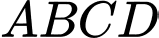 là hình bình hành. Tính tổng
là hình bình hành. Tính tổng 
A, 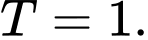
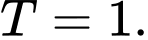
B, 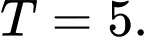
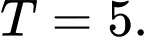
C, 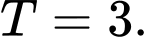
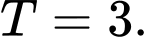
D, 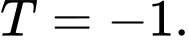
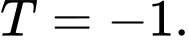

Ta có 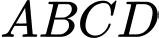 là hình bình hành nên
là hình bình hành nên 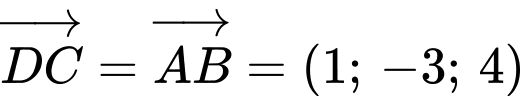
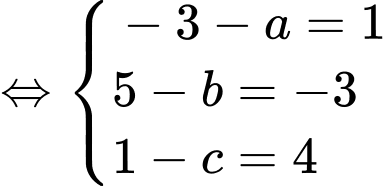
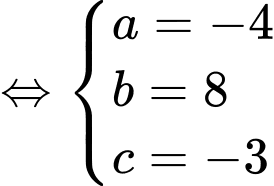
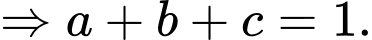
Chọn A. Đáp án: A
Câu 10 [371963]: Cho 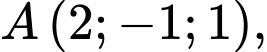
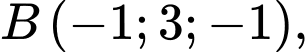
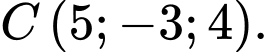 Tích vô hướng
Tích vô hướng 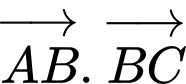 có giá trị là
có giá trị là
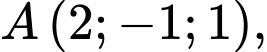
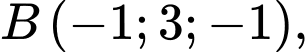
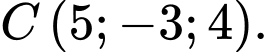 Tích vô hướng
Tích vô hướng 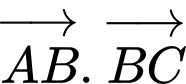 có giá trị là
có giá trị là A, 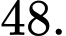
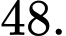
B, 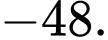
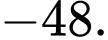
C, 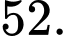
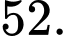
D, 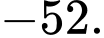
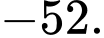
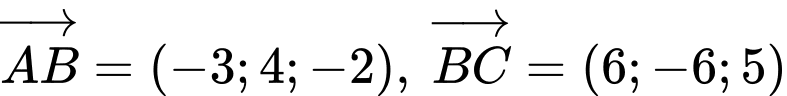
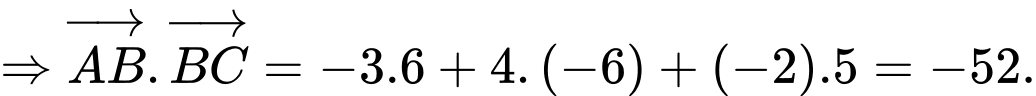 Đáp án: D
Đáp án: D
Câu 11 [898980]: Trong không gian 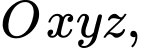 cho hai vectơ
cho hai vectơ 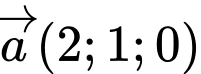 và
và 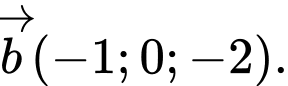 Tính
Tính 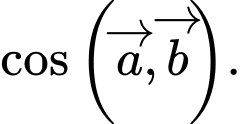
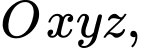 cho hai vectơ
cho hai vectơ 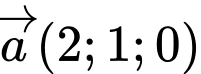 và
và 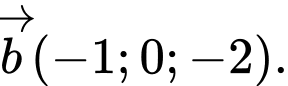 Tính
Tính 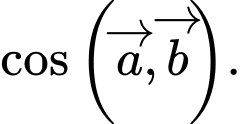
A, 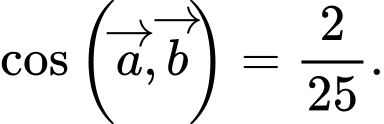
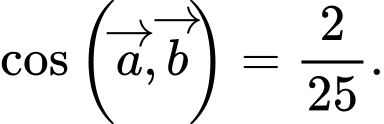
B, 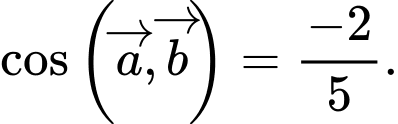
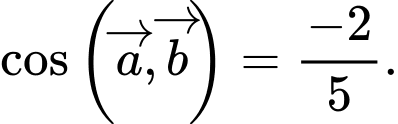
C, 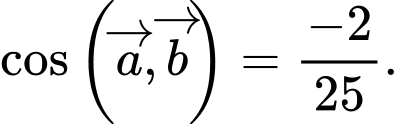
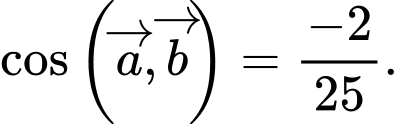
D, 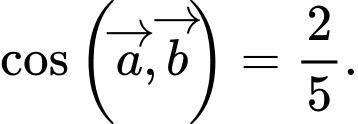
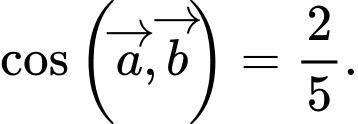
Phương pháp: Góc giữa 2 vectơ: 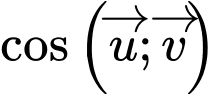
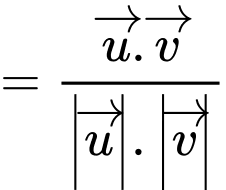
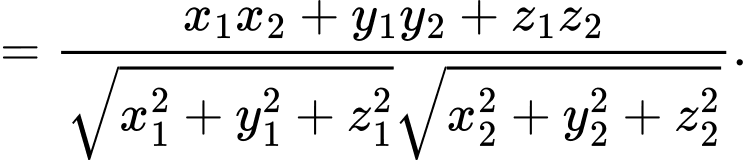
Do đó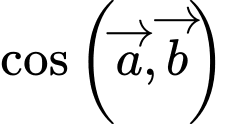
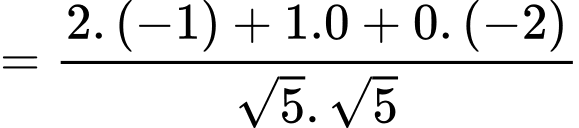
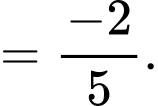 Chọn B. Đáp án: B
Chọn B. Đáp án: B
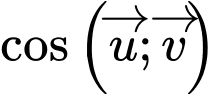
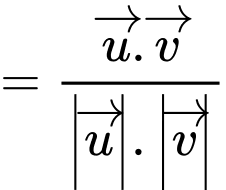
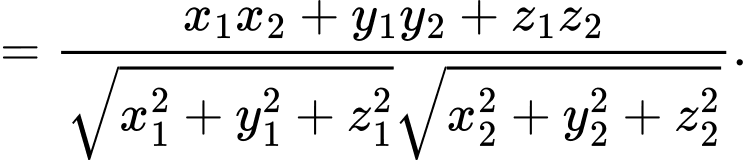
Do đó
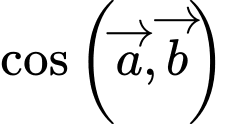
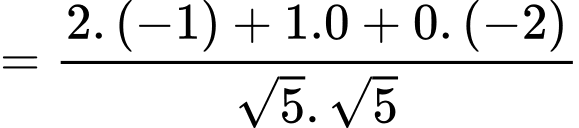
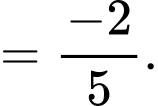 Chọn B. Đáp án: B
Chọn B. Đáp án: B
Câu 12 [51098]: Trong không gian hệ tọa độ 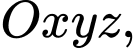 cho các điểm
cho các điểm 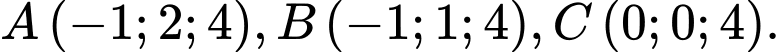 Tìm số đo của
Tìm số đo của 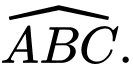
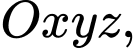 cho các điểm
cho các điểm 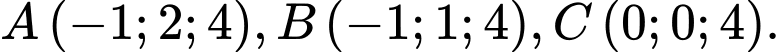 Tìm số đo của
Tìm số đo của 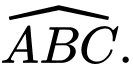
A, 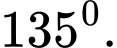
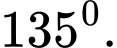
B, 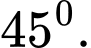
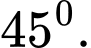
C, 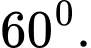
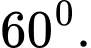
D, 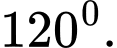
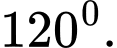
Ta có 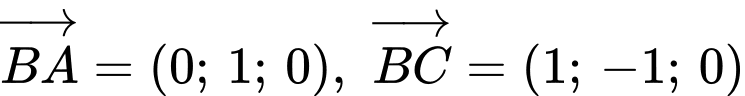
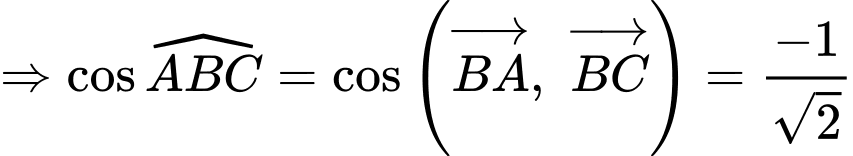
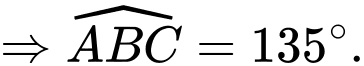 Đáp án: A
Đáp án: A
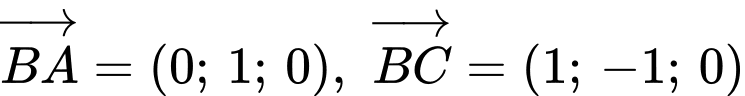
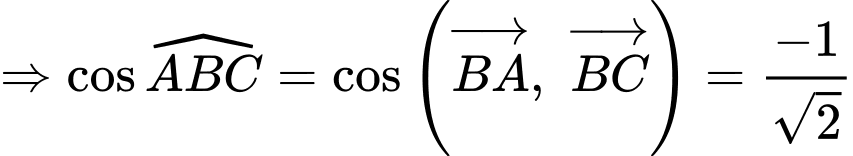
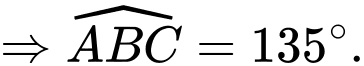
Chọn đáp án A.
Câu 13 [51101]: Cho hai vectơ 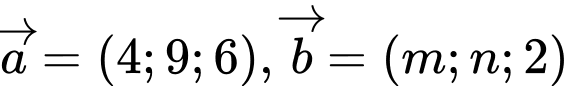 . Với giá trị nào của
. Với giá trị nào của 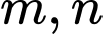 thì
thì 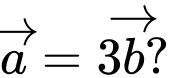
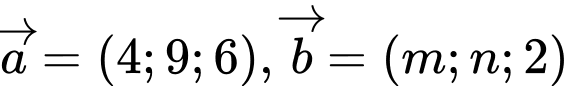 . Với giá trị nào của
. Với giá trị nào của 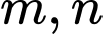 thì
thì 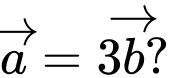
A, 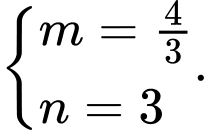
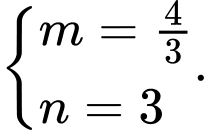
B, 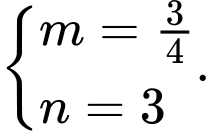
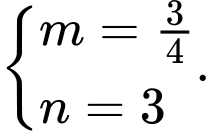
C, 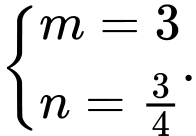
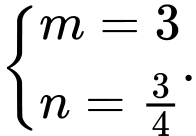
D, 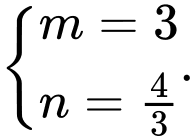
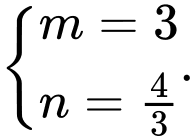
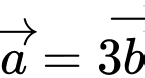
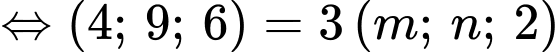
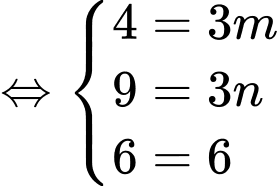
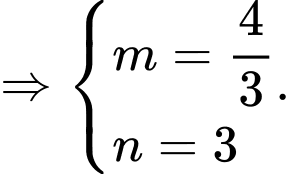 Chọn A. Đáp án: A
Chọn A. Đáp án: A
Câu 14 [51345]: Trong không gian với hệ tọa độ 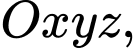 cho hai vectơ
cho hai vectơ 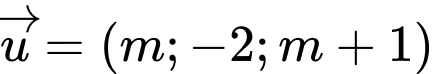 và
và 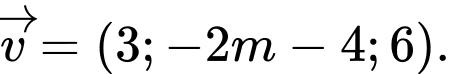 Tìm tất cả các giá trị của
Tìm tất cả các giá trị của 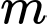 để hai vectơ
để hai vectơ 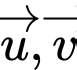 cùng phương.
cùng phương.
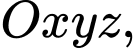 cho hai vectơ
cho hai vectơ 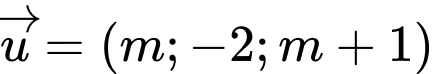 và
và 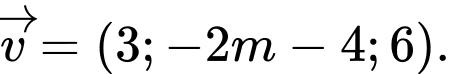 Tìm tất cả các giá trị của
Tìm tất cả các giá trị của 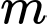 để hai vectơ
để hai vectơ 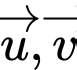 cùng phương.
cùng phương. A, 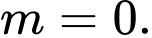
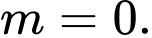
B, 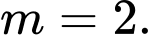
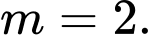
C, 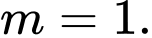
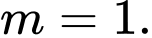
D, 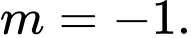
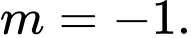
Hai vectơ 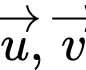 cùng phương
cùng phương 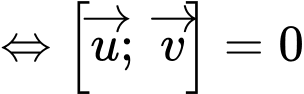
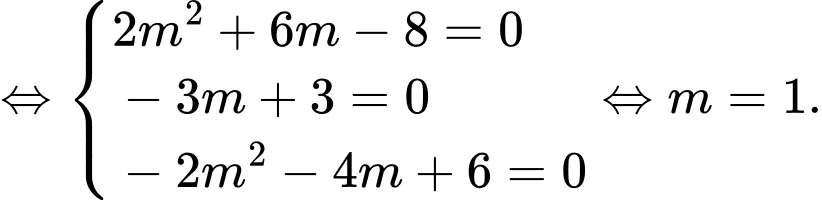 Đáp án: C
Đáp án: C
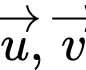 cùng phương
cùng phương 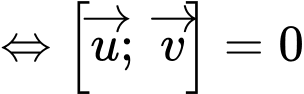
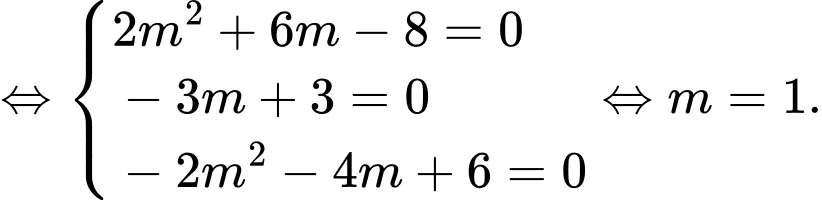
Chọn đáp án C.
Câu 15 [51110]: Trong không gian với hệ tọa độ 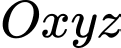 cho hai vectơ
cho hai vectơ 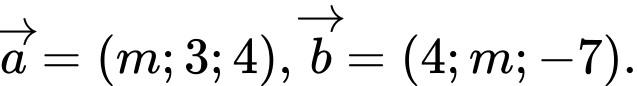 Với giá trị nào của
Với giá trị nào của 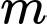 thì
thì 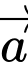 vuông góc với
vuông góc với 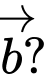
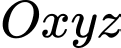 cho hai vectơ
cho hai vectơ 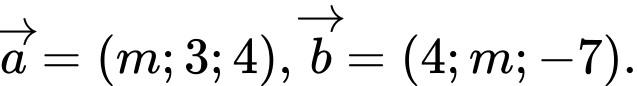 Với giá trị nào của
Với giá trị nào của 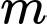 thì
thì 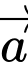 vuông góc với
vuông góc với 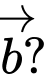
A, 4.
B, 2.
C, 1.
D, 3.
(Hai vectơ vuông góc khi tích vô hướng bằng  )
)
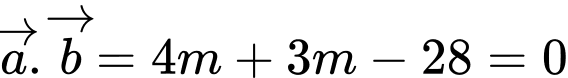
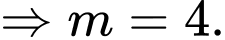
Chọn đáp án A. Đáp án: A
 )
) 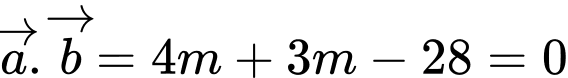
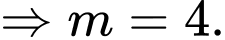
Chọn đáp án A. Đáp án: A
Câu 16 [51377]: Trong không gian với hệ tọa độ 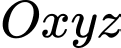 , cho ba điểm
, cho ba điểm 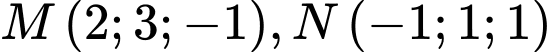 và
và 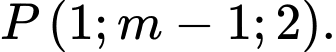 Tìm
Tìm 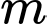 để tam giác
để tam giác 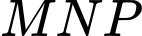 vuông tại
vuông tại 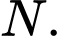
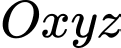 , cho ba điểm
, cho ba điểm 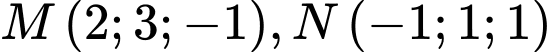 và
và 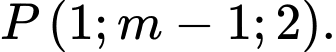 Tìm
Tìm 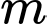 để tam giác
để tam giác 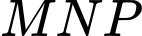 vuông tại
vuông tại 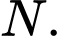
A, 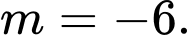
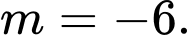
B, 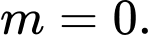
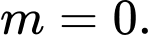
C, 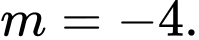
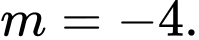
D, 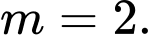
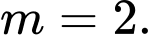
Ta có 
Để tam giác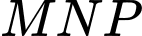 vuông tại
vuông tại 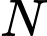 thì
thì 
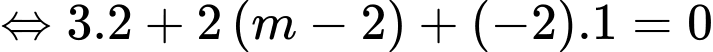
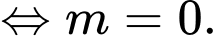
Chọn đáp án B. Đáp án: B

Để tam giác
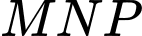 vuông tại
vuông tại 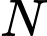 thì
thì 
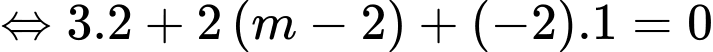
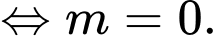
Chọn đáp án B. Đáp án: B
Câu 17 [51105]: Trong không gian 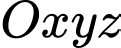 cho hai điểm
cho hai điểm 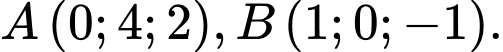 Tìm
Tìm  thuộc tia
thuộc tia 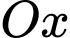 sao cho tam giác
sao cho tam giác 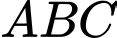 vuông tại
vuông tại 
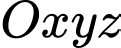 cho hai điểm
cho hai điểm 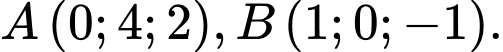 Tìm
Tìm  thuộc tia
thuộc tia 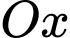 sao cho tam giác
sao cho tam giác 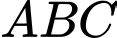 vuông tại
vuông tại 
A, 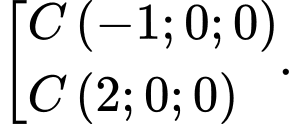
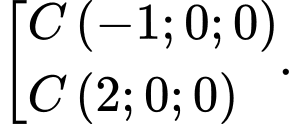
B, 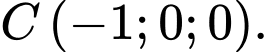
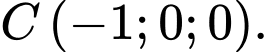
C, 

D, 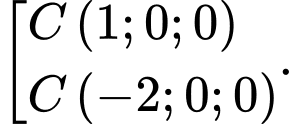
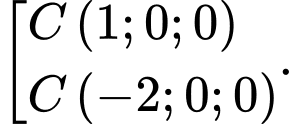
Do 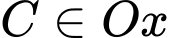
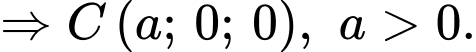
Ta có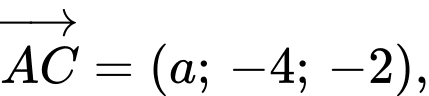
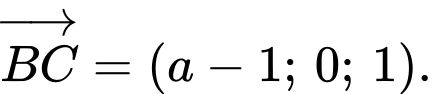
Do tam giác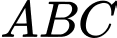 vuông tại
vuông tại 
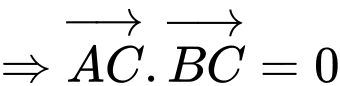
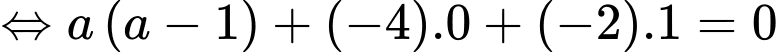
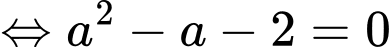
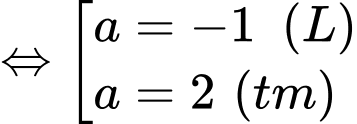
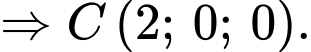
Chọn đáp án C. Đáp án: C
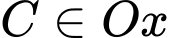
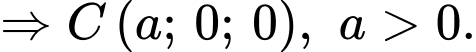
Ta có
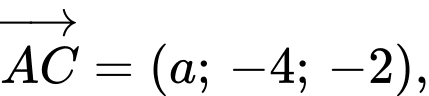
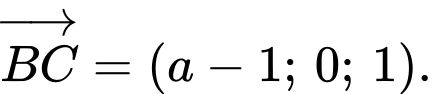
Do tam giác
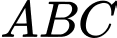 vuông tại
vuông tại 
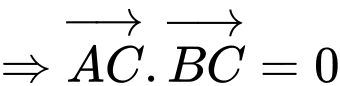
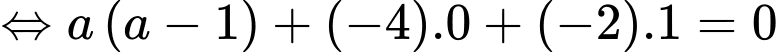
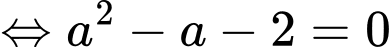
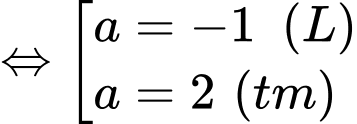
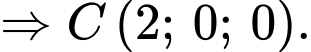
Chọn đáp án C. Đáp án: C
Câu 18 [51338]: Trong không gian với hệ tọa độ 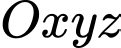 , cho các vectơ
, cho các vectơ 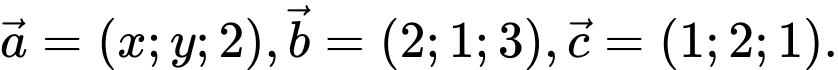 Biết
Biết 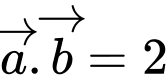 và
và  Tích
Tích 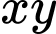 bằng
bằng
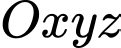 , cho các vectơ
, cho các vectơ 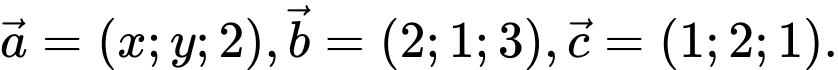 Biết
Biết 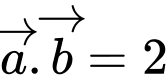 và
và  Tích
Tích 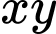 bằng
bằng A, 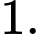
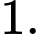
B, 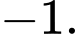
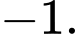
C, 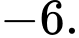
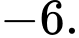
D, 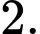
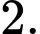
Ta có 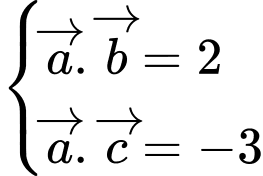
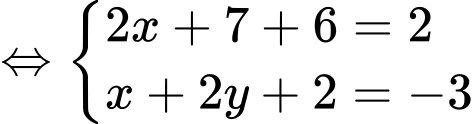
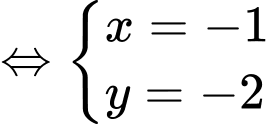
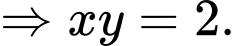
Chọn đáp án D. Đáp án: D
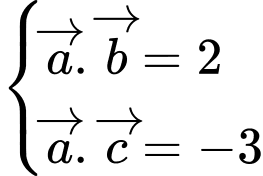
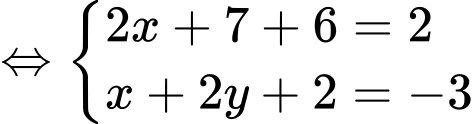
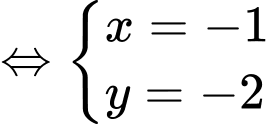
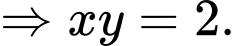
Chọn đáp án D. Đáp án: D
Câu 19 [51366]: Trong không gian với hệ tọa độ 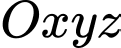 , cho ba điểm
, cho ba điểm 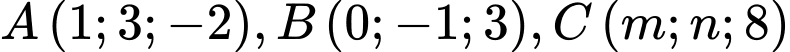 (với
(với 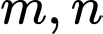 là tham số). Tìm tất cả các giá trị của
là tham số). Tìm tất cả các giá trị của 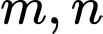 để ba điểm
để ba điểm 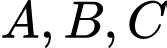 thẳng hàng.
thẳng hàng.
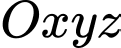 , cho ba điểm
, cho ba điểm 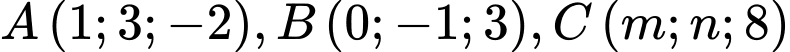 (với
(với 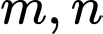 là tham số). Tìm tất cả các giá trị của
là tham số). Tìm tất cả các giá trị của 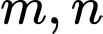 để ba điểm
để ba điểm 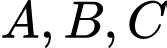 thẳng hàng.
thẳng hàng. A, 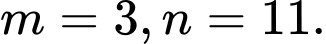
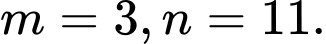
B, 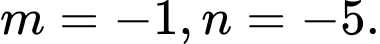
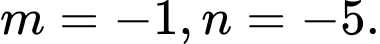
C, 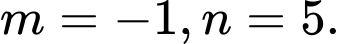
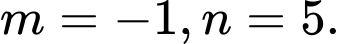
D, 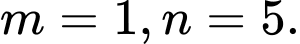
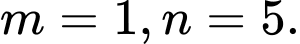
Ta có 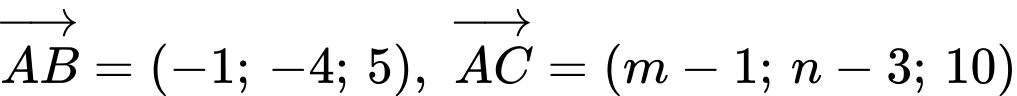
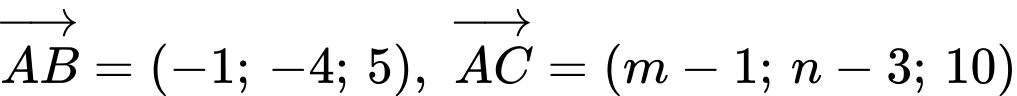
Ba điểm 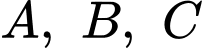 thẳng hàng khi
thẳng hàng khi 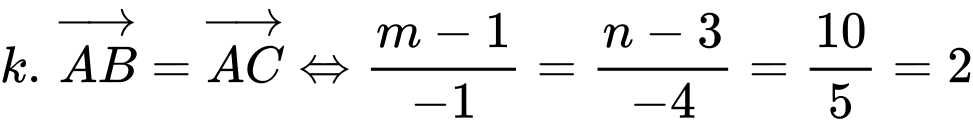
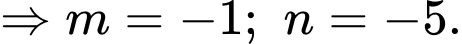 Chọn đáp án B.
Chọn đáp án B.
Đáp án: B 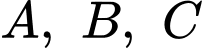 thẳng hàng khi
thẳng hàng khi 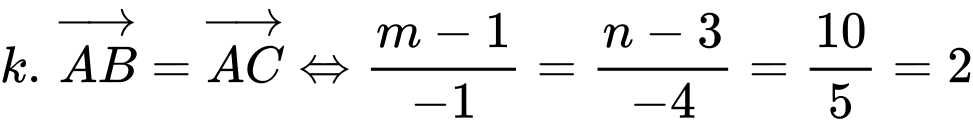
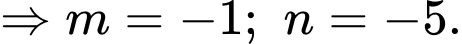 Chọn đáp án B.
Chọn đáp án B.
Câu 20 [51349]: Trong không gian với hệ tọa độ 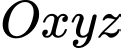 , cho
, cho 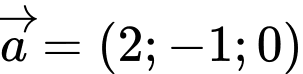 biết
biết 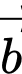 cùng chiều với
cùng chiều với 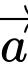 và có
và có 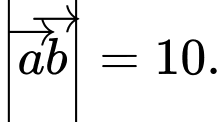 Chọn phương án đúng.
Chọn phương án đúng.
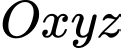 , cho
, cho 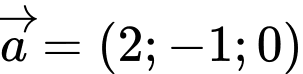 biết
biết 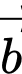 cùng chiều với
cùng chiều với 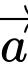 và có
và có 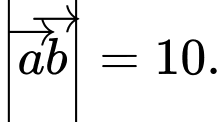 Chọn phương án đúng.
Chọn phương án đúng. A, 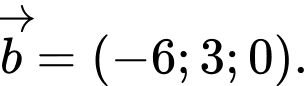
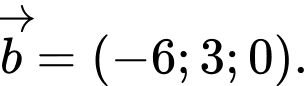
B, 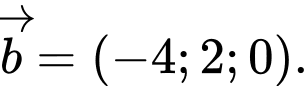
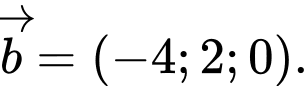
C, 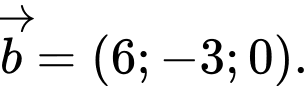
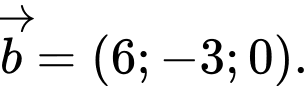
D, 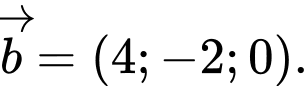
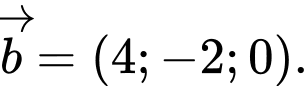
Ta có 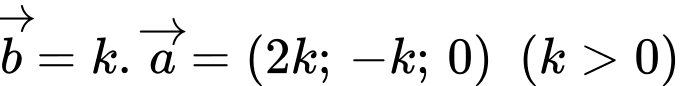
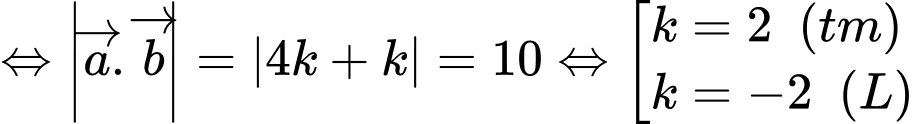
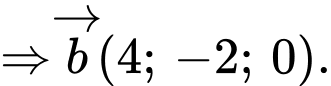 Đáp án: D
Đáp án: D
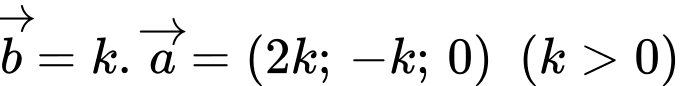
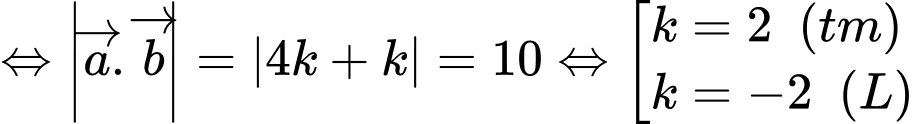
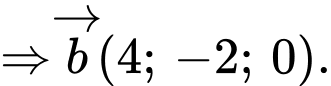
Chọn đáp án D.
Câu 21 [51131]: Trong không gian với hệ tọa độ 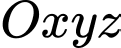 cho
cho 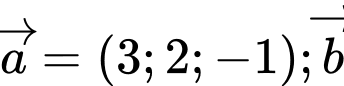 ngược hướng với
ngược hướng với 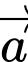 và
và 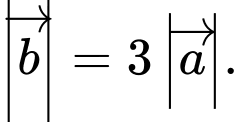 Tọa độ của
Tọa độ của 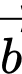 là
là
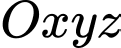 cho
cho 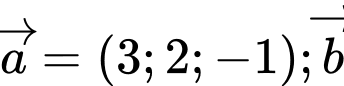 ngược hướng với
ngược hướng với 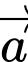 và
và 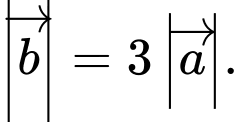 Tọa độ của
Tọa độ của 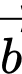 là
là A, 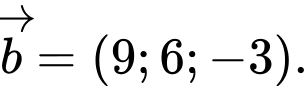
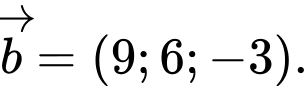
B, 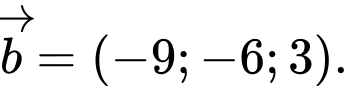
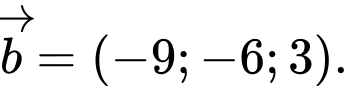
C, 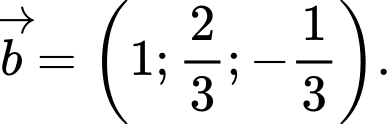
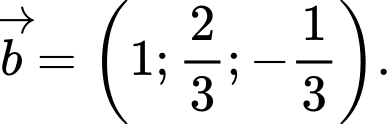
D, 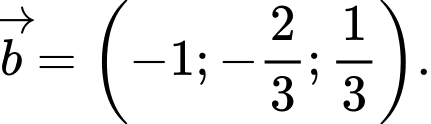
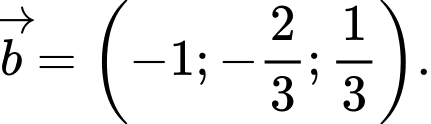
Ta có 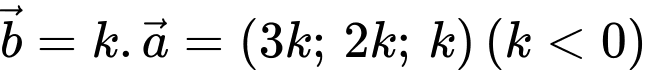

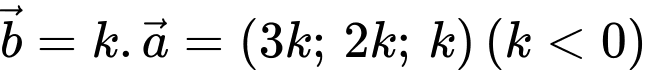

Chọn đáp án B.
Đáp án: B
Câu 22 [51132]: Cho 4 vectơ 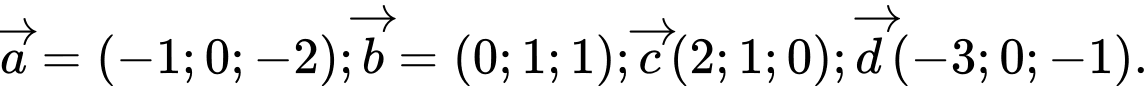 Tìm các số thực
Tìm các số thực 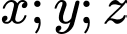 biết rằng
biết rằng 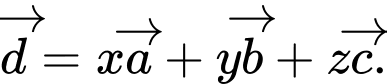
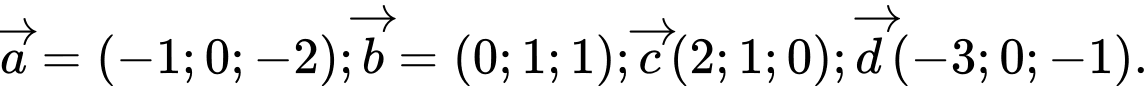 Tìm các số thực
Tìm các số thực 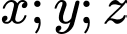 biết rằng
biết rằng 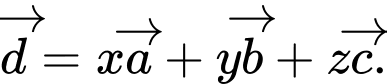
A, 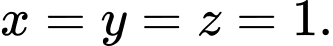
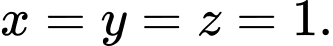
B, 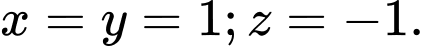
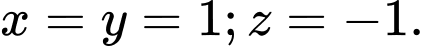
C, 

D, 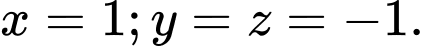
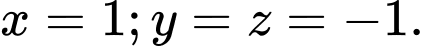
Ta có 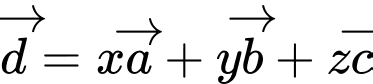
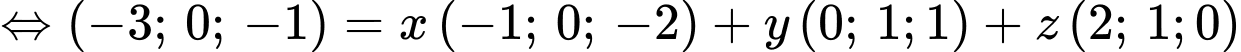
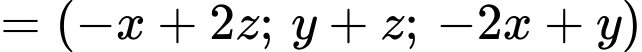
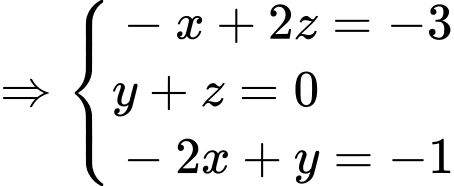
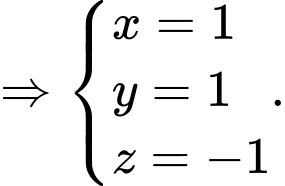
Chọn đáp án B. Đáp án: B
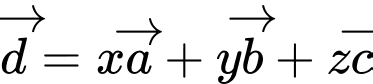
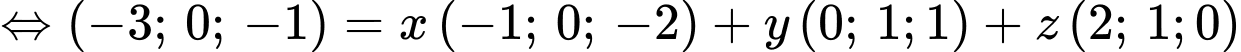
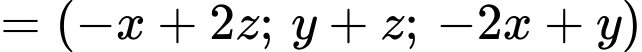
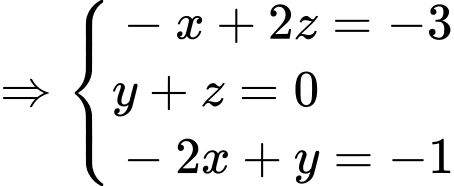
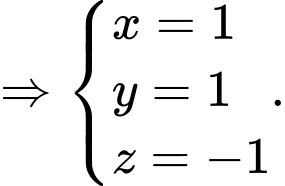
Chọn đáp án B. Đáp án: B
Câu 23 [51079]: Trong không gian với hệ tọa độ 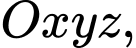 cho hình hộp
cho hình hộp 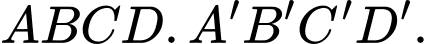 Biết
Biết 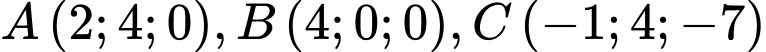 và
và 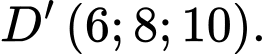 Tọa độ điểm
Tọa độ điểm 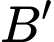 là
là
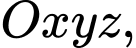 cho hình hộp
cho hình hộp 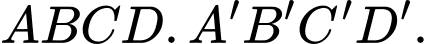 Biết
Biết 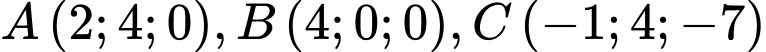 và
và 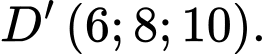 Tọa độ điểm
Tọa độ điểm 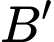 là
là A, 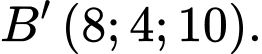
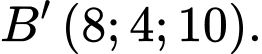
B, 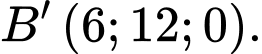
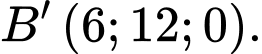
C, 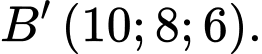
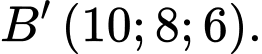
D, 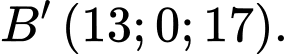
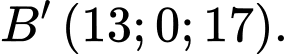

Ta có

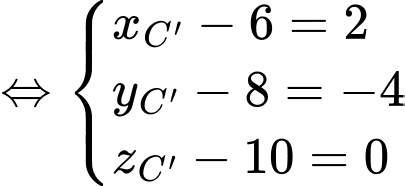
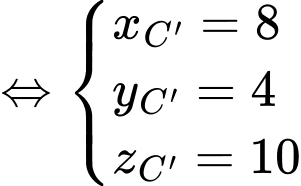
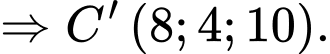
Suy ra
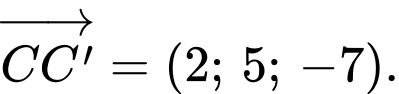
Ta có
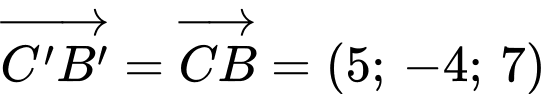
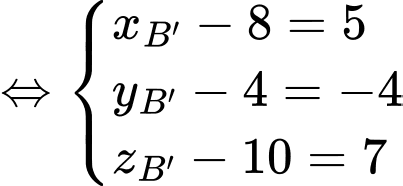
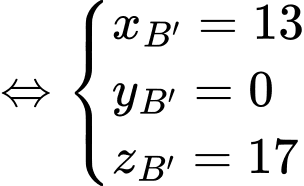
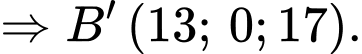
Chọn D. Đáp án: D
Câu 24 [103904]: Trong không gian 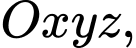 cho hình hộp
cho hình hộp  có
có 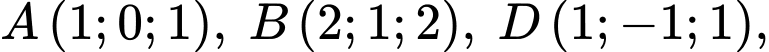
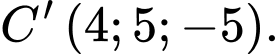 Tính tọa độ đỉnh
Tính tọa độ đỉnh 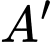 của hình hộp.
của hình hộp.
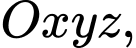 cho hình hộp
cho hình hộp  có
có 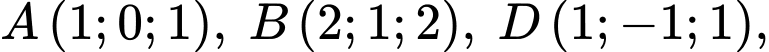
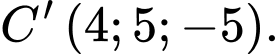 Tính tọa độ đỉnh
Tính tọa độ đỉnh 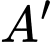 của hình hộp.
của hình hộp. A, 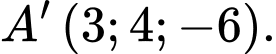
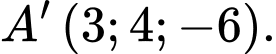
B, 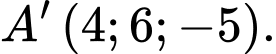
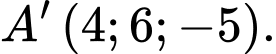
C, 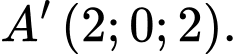
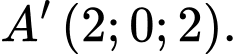
D, 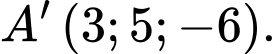
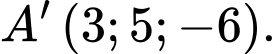

Ta có
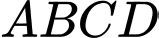 là hình bình hành nên
là hình bình hành nên 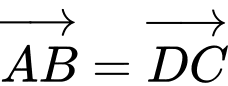
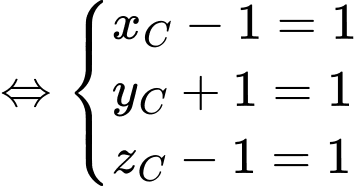
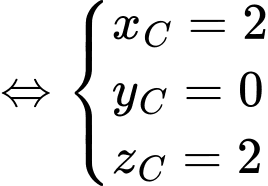
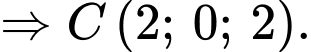
Suy ra
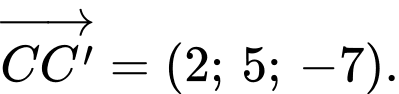
Ta có
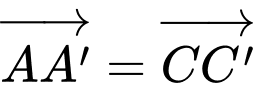
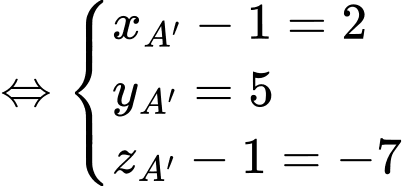
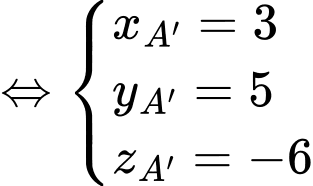
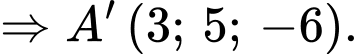
Chọn D. Đáp án: D
Câu 25 [103907]: Trong không gian với hệ tọa độ 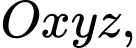 cho hình hộp
cho hình hộp 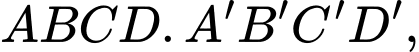 biết rằng
biết rằng 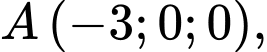
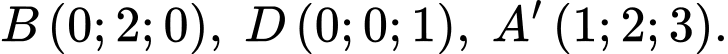 Tìm tọa độ điểm
Tìm tọa độ điểm 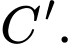
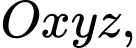 cho hình hộp
cho hình hộp 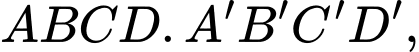 biết rằng
biết rằng 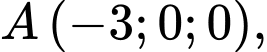
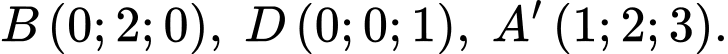 Tìm tọa độ điểm
Tìm tọa độ điểm 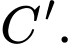
A, 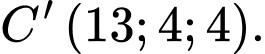
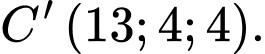
B, 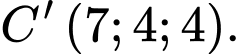
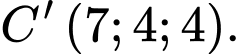
C, 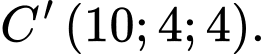
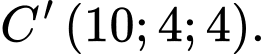
D, 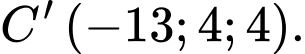
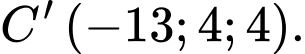

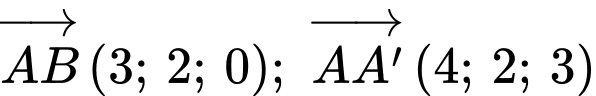
Ta có
 là hình bình hành nên
là hình bình hành nên 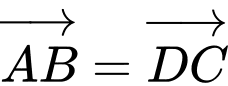
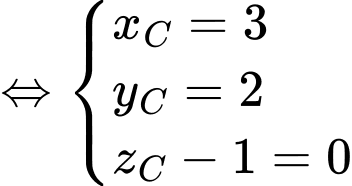
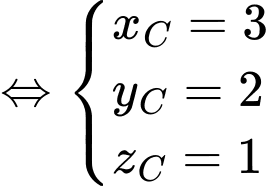
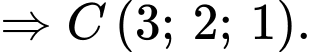
Ta có
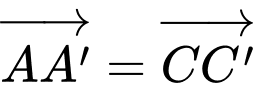
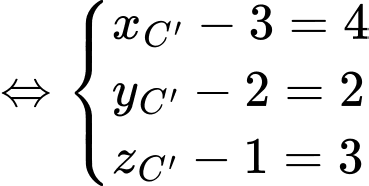
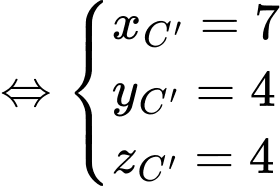
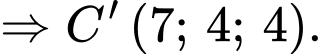
Chọn B. Đáp án: B
Câu 26 [380176]: Trong không gian 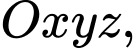 cho hai vectơ
cho hai vectơ 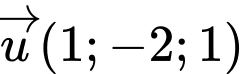 và
và 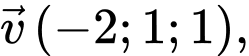 góc giữa hai vectơ đã cho bằng bao nhiêu độ
góc giữa hai vectơ đã cho bằng bao nhiêu độ
Đáp số: ………………….
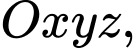 cho hai vectơ
cho hai vectơ 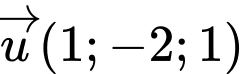 và
và 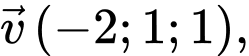 góc giữa hai vectơ đã cho bằng bao nhiêu độ
góc giữa hai vectơ đã cho bằng bao nhiêu độĐáp số: ………………….
Ta có: 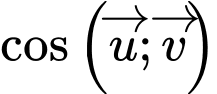
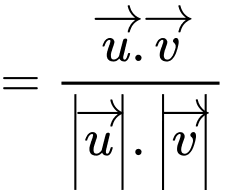
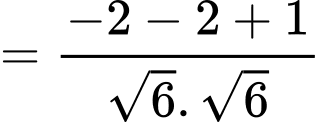
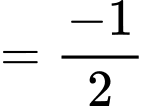
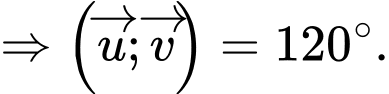
Điền đáp số: 120
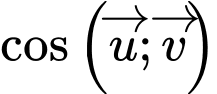
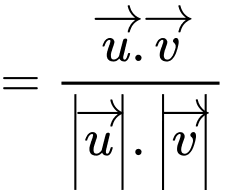
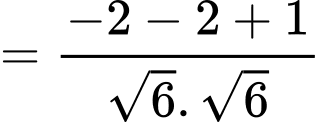
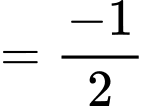
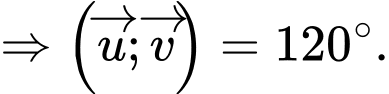
Điền đáp số: 120
Câu 27 [380174]: Trong không gian 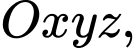 cho các vectơ
cho các vectơ 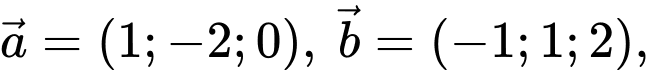
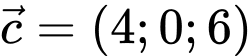 và
và 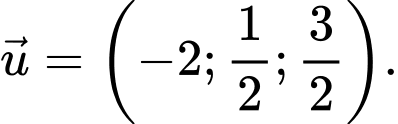 Biết rằng
Biết rằng 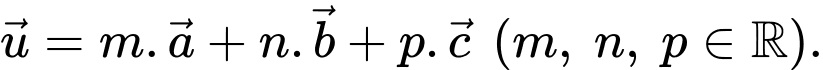 Tính
Tính 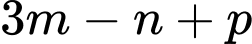 Đáp số: ………………….
Đáp số: ………………….
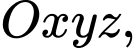 cho các vectơ
cho các vectơ 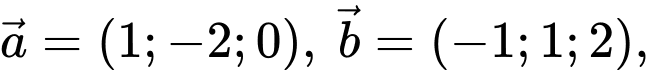
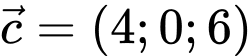 và
và 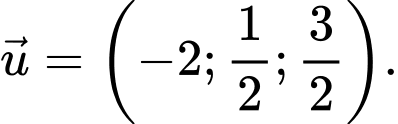 Biết rằng
Biết rằng 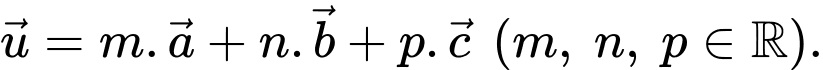 Tính
Tính 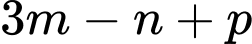 Đáp số: ………………….
Đáp số: …………………. 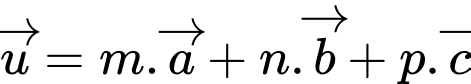
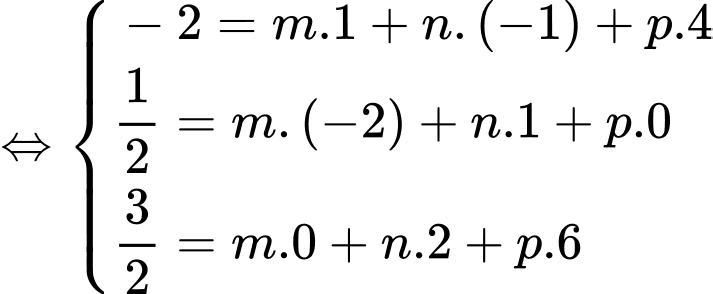
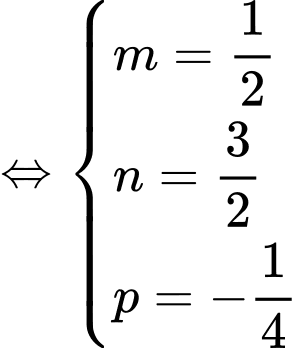
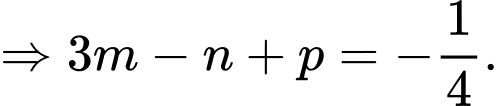
Câu 28 [579677]: [Đề mẫu HSA 2024]: Trong không gian 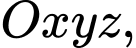 cho điểm
cho điểm 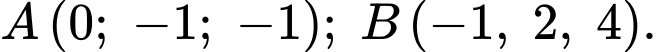 Điểm
Điểm 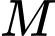 thuộc tia
thuộc tia 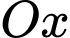 và
và 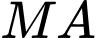 vuông góc với
vuông góc với 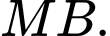 Tìm hoành độ điểm
Tìm hoành độ điểm 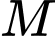 (nhập đáp án vào ô trống).
(nhập đáp án vào ô trống).
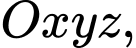 cho điểm
cho điểm 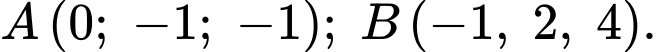 Điểm
Điểm 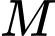 thuộc tia
thuộc tia 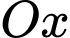 và
và 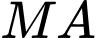 vuông góc với
vuông góc với 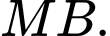 Tìm hoành độ điểm
Tìm hoành độ điểm 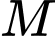 (nhập đáp án vào ô trống).
(nhập đáp án vào ô trống).
Điểm 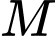 thuộc tia
thuộc tia 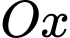 nên
nên 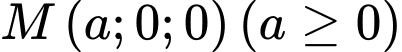
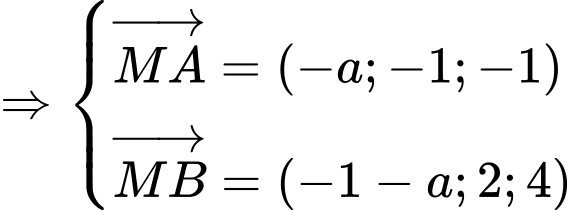
Để thì
thì 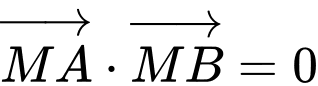
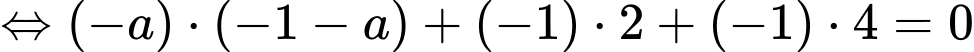

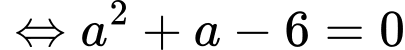
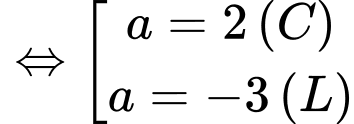
Vậy hoành độ điểm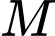 là 2.
là 2.
Đáp án: 2
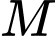 thuộc tia
thuộc tia 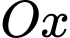 nên
nên 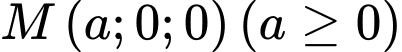
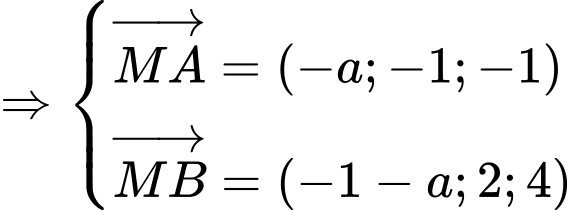
Để
 thì
thì 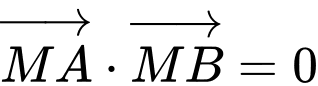
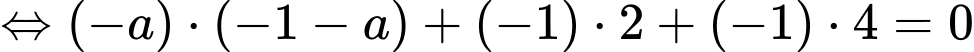

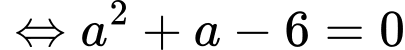
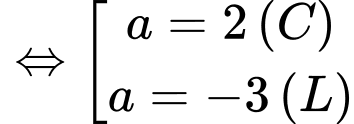
Vậy hoành độ điểm
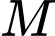 là 2.
là 2. Đáp án: 2
Câu 29 [380175]: Trong không gian tọa độ 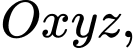 cho 3 vectơ
cho 3 vectơ 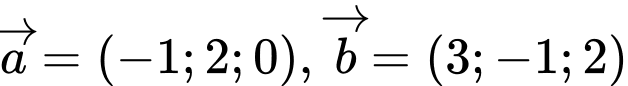 và
và 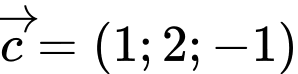 và
và 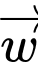 thỏa mãn
thỏa mãn 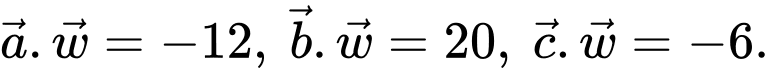 Tính
Tính  Đáp số: ………………….
Đáp số: ………………….
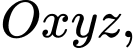 cho 3 vectơ
cho 3 vectơ 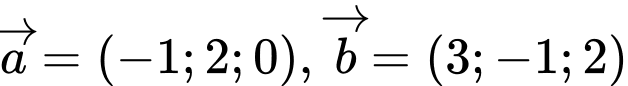 và
và 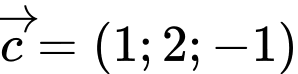 và
và 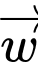 thỏa mãn
thỏa mãn 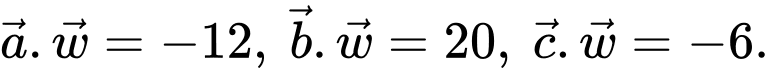 Tính
Tính  Đáp số: ………………….
Đáp số: ………………….
Gọi 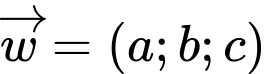 ta có hệ phương trình
ta có hệ phương trình 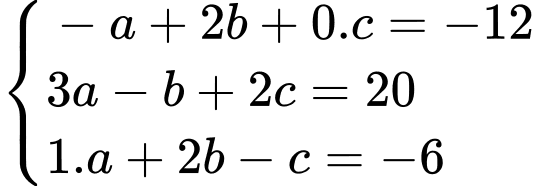
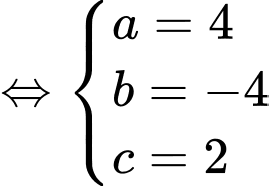
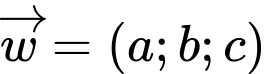 ta có hệ phương trình
ta có hệ phương trình 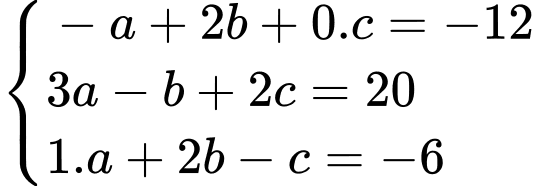
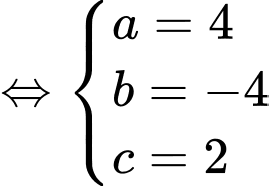
Suy ra 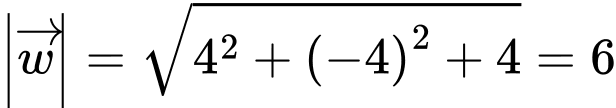
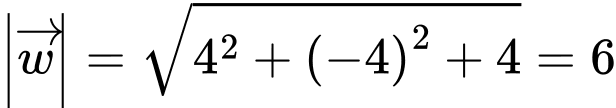
Câu 30 [51091]: Trong không gian với hệ tọa độ 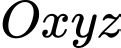 , cho
, cho 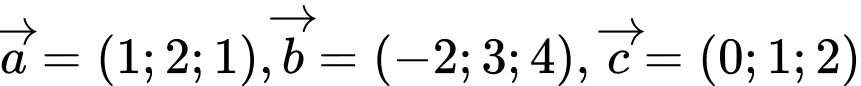 và
và 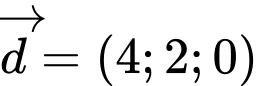 . Biết
. Biết 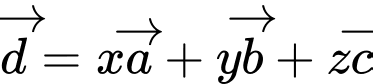 . Tổng
. Tổng 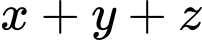 là
là
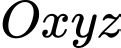 , cho
, cho 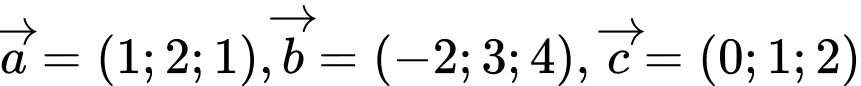 và
và 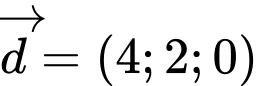 . Biết
. Biết 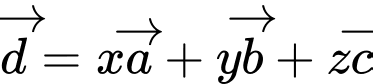 . Tổng
. Tổng 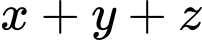 là
là A, 2.
B, 3.
C, 5.
D, 4.
YCBT
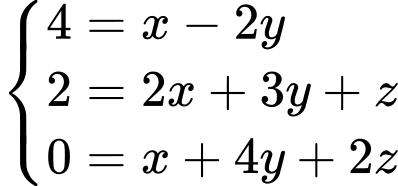
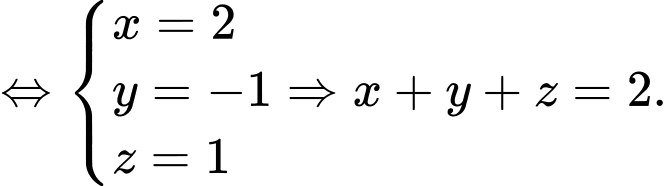

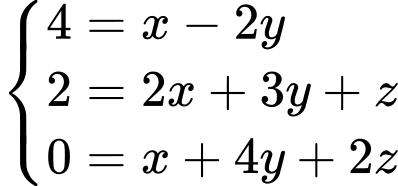
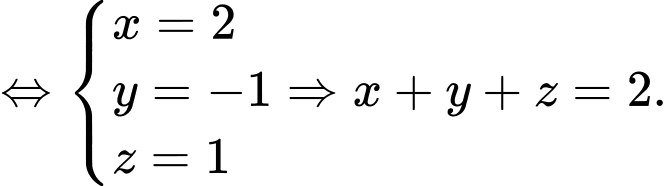
Chọn đáp án A.
Đáp án: A
Câu 31 [380484]: Trong không gian với hệ tọa độ 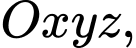 cho hình hộp
cho hình hộp  có
có 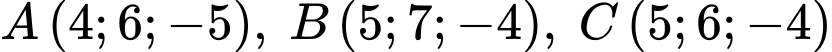 và
và 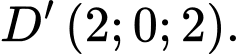 Biết điểm
Biết điểm 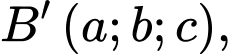 tính
tính 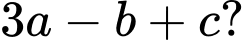
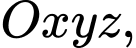 cho hình hộp
cho hình hộp  có
có 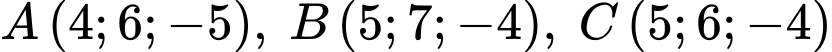 và
và 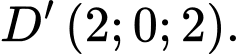 Biết điểm
Biết điểm 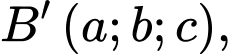 tính
tính 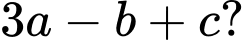
Ta có: 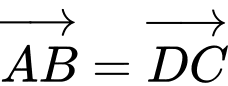
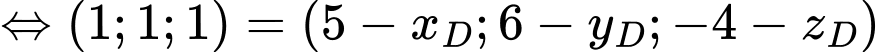
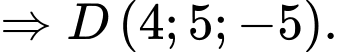
Lại có: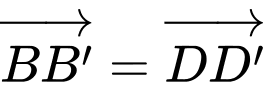
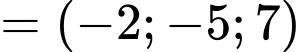
Suy ra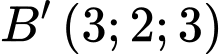
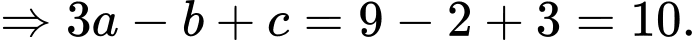
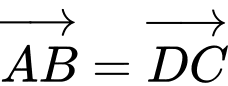
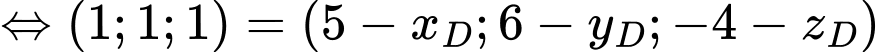
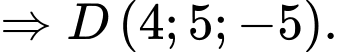
Lại có:
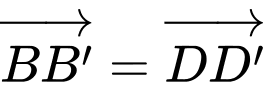
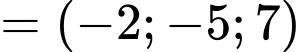
Suy ra
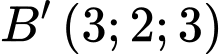
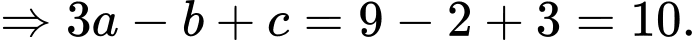
Câu 32 [380485]: Một máy bay đang cất cánh từ phi trường. Với hệ toạ độ 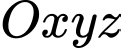 được thiết lập như Hình vẽ, cho biết
được thiết lập như Hình vẽ, cho biết 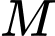 là vị trí của máy bay,
là vị trí của máy bay,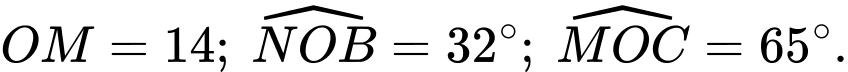 Biết điểm
Biết điểm  Tính tổng
Tính tổng 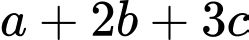 (làm tròn kết quả đến hàng đơn vị)
(làm tròn kết quả đến hàng đơn vị)

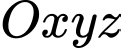 được thiết lập như Hình vẽ, cho biết
được thiết lập như Hình vẽ, cho biết 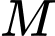 là vị trí của máy bay,
là vị trí của máy bay,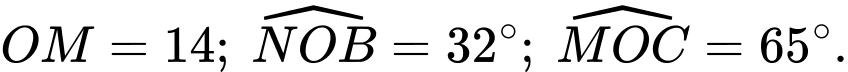 Biết điểm
Biết điểm  Tính tổng
Tính tổng 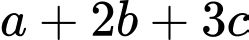 (làm tròn kết quả đến hàng đơn vị)
(làm tròn kết quả đến hàng đơn vị)
Xét 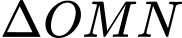 vuông tại
vuông tại 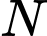 có
có 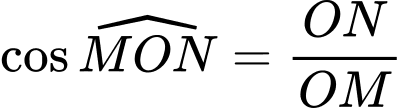

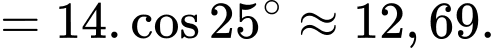
+) Xét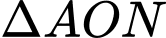 vuông tại
vuông tại 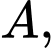 có
có 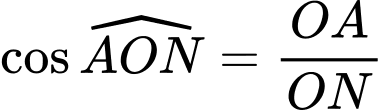

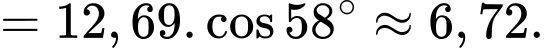
+) Xét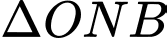 vuông tại
vuông tại 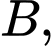 có
có 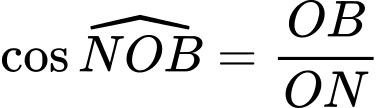

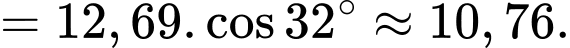
+) Xét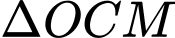 vuông tại
vuông tại 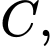 có
có 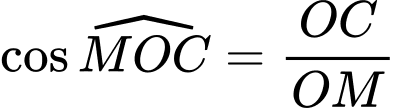

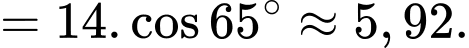
Vì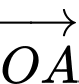 và
và  cùng hướng và
cùng hướng và 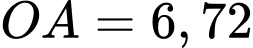 nên
nên 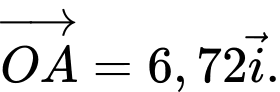
Vì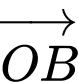 và
và 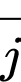 cùng hướng và
cùng hướng và 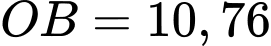 nên
nên 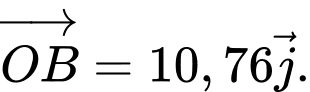
Vì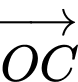 và
và 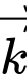 cùng hướng và
cùng hướng và 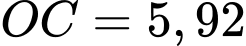 nên
nên 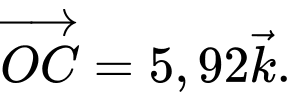
Áp dụng quy tắc hình hộp, ta có:
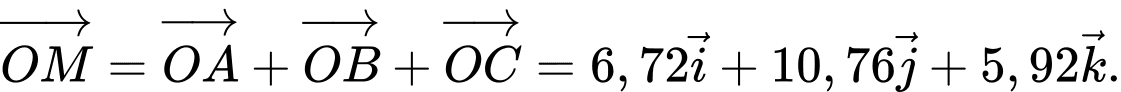
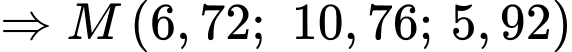
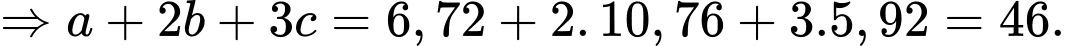
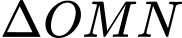 vuông tại
vuông tại 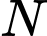 có
có 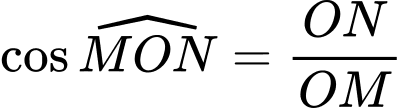

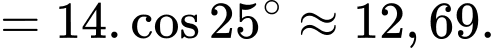
+) Xét
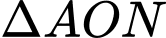 vuông tại
vuông tại 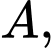 có
có 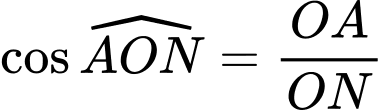

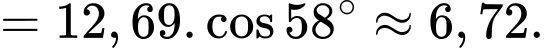
+) Xét
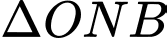 vuông tại
vuông tại 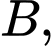 có
có 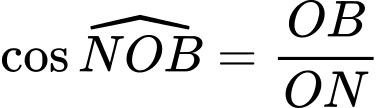

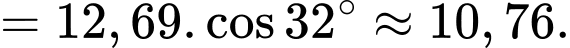
+) Xét
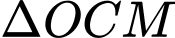 vuông tại
vuông tại 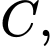 có
có 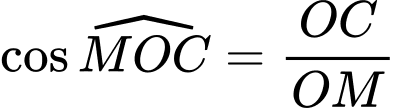

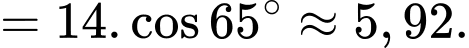
Vì
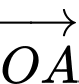 và
và  cùng hướng và
cùng hướng và 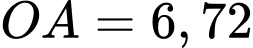 nên
nên 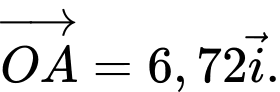
Vì
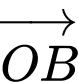 và
và 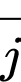 cùng hướng và
cùng hướng và 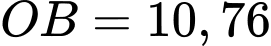 nên
nên 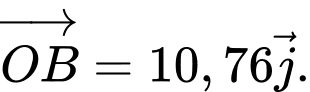
Vì
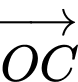 và
và 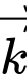 cùng hướng và
cùng hướng và 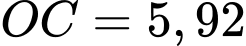 nên
nên 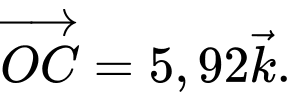
Áp dụng quy tắc hình hộp, ta có:
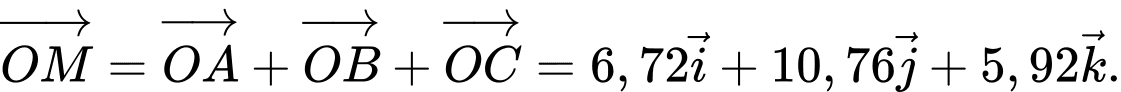
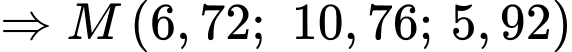
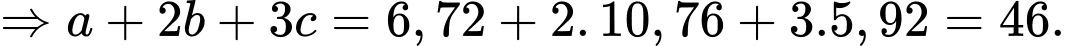
Câu 33 [51354]: Trong không gian với hệ trục tọa độ 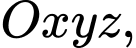 cho ba điểm
cho ba điểm 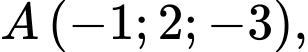
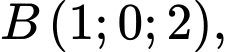
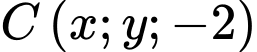 thẳng hàng. Khi đó tính tổng
thẳng hàng. Khi đó tính tổng 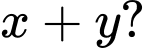
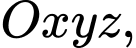 cho ba điểm
cho ba điểm 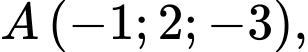
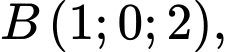
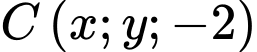 thẳng hàng. Khi đó tính tổng
thẳng hàng. Khi đó tính tổng 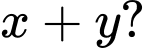
A, 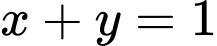 .
.
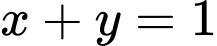 .
.B, 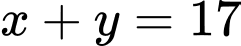 .
.
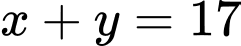 .
.C, 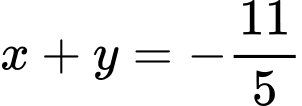 .
.
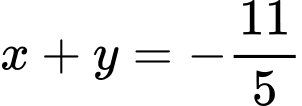 .
.D, 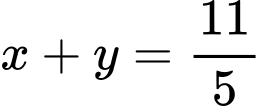 .
.
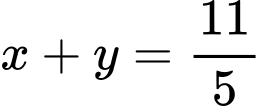 .
.
Ta có 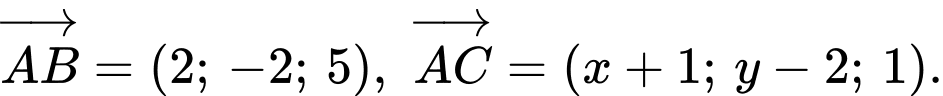
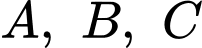 thẳng hàng nên
thẳng hàng nên 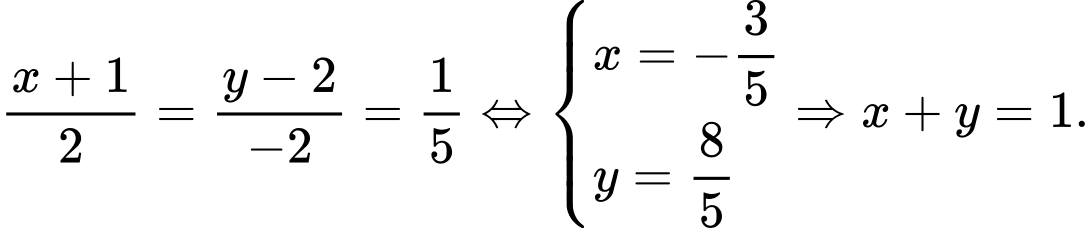 Đáp án: A
Đáp án: A
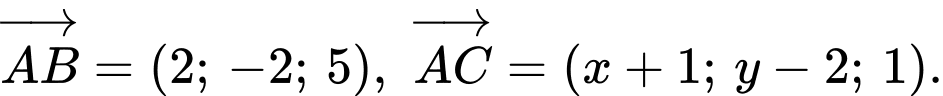
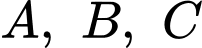 thẳng hàng nên
thẳng hàng nên 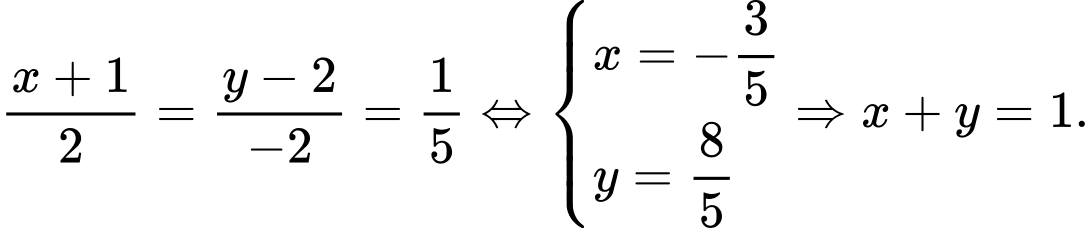
Chọn đáp án A.
Câu 34 [399651]: Cho 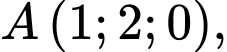
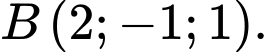 Điểm
Điểm 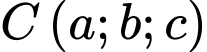 thuộc tia
thuộc tia 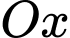 thoả tam giác
thoả tam giác 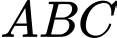 vuông tại
vuông tại  Tính
Tính 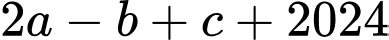
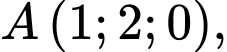
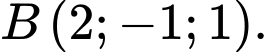 Điểm
Điểm 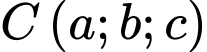 thuộc tia
thuộc tia 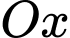 thoả tam giác
thoả tam giác 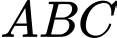 vuông tại
vuông tại  Tính
Tính 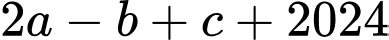
Đáp số: 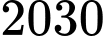
Do có hoành độ dương trên trục
có hoành độ dương trên trục 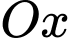 nên
nên 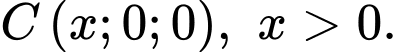
Ta có: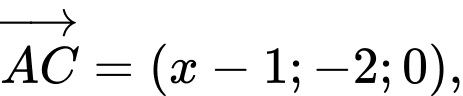
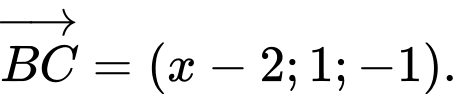
Tam giác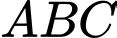 vuông tại
vuông tại 
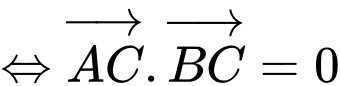
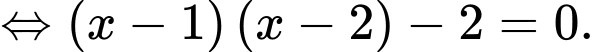
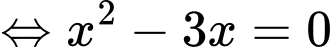
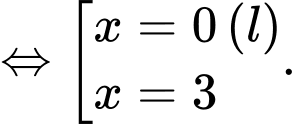
Vậy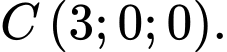
Suy ra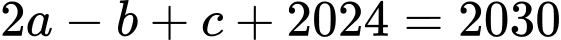
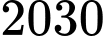
Do
 có hoành độ dương trên trục
có hoành độ dương trên trục 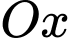 nên
nên 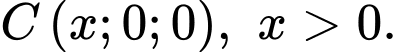
Ta có:
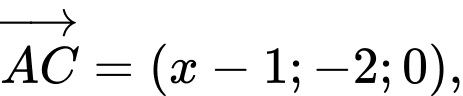
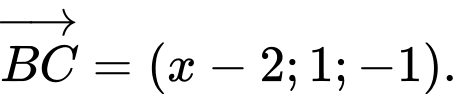
Tam giác
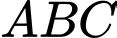 vuông tại
vuông tại 
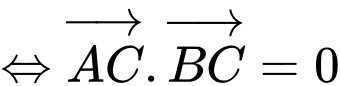
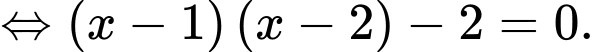
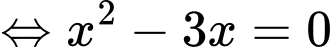
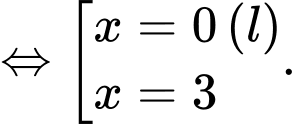
Vậy
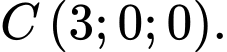
Suy ra
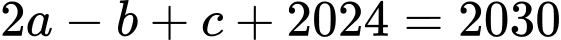
Câu 35 [399650]: Trong không gian với hệ tọa độ 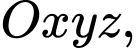 cho ba điểm
cho ba điểm 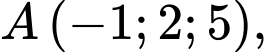
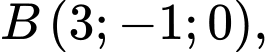
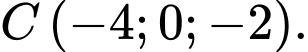 Điểm
Điểm 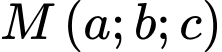 sao cho
sao cho 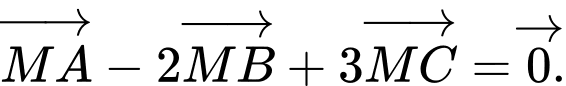 Tính
Tính 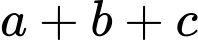
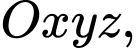 cho ba điểm
cho ba điểm 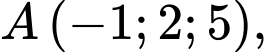
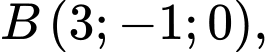
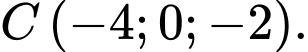 Điểm
Điểm 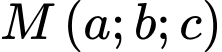 sao cho
sao cho 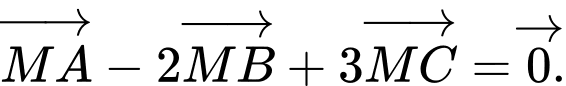 Tính
Tính 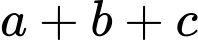
Đáp số: 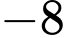
Gọi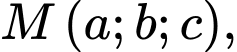 ta có :
ta có :
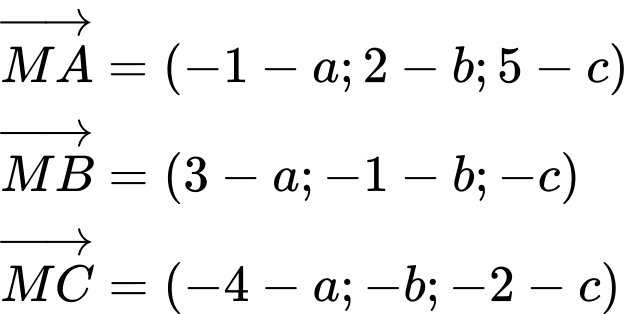
Từ đẳng thức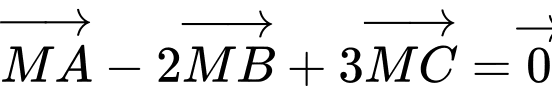
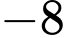
Gọi
 ta có :
ta có :
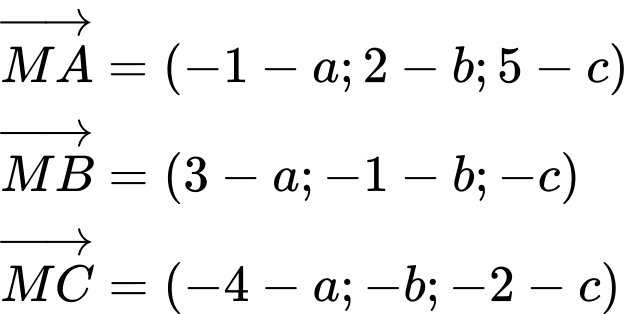
Từ đẳng thức
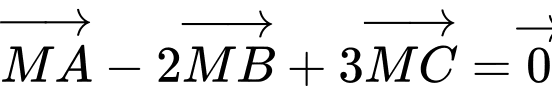
suy ra: 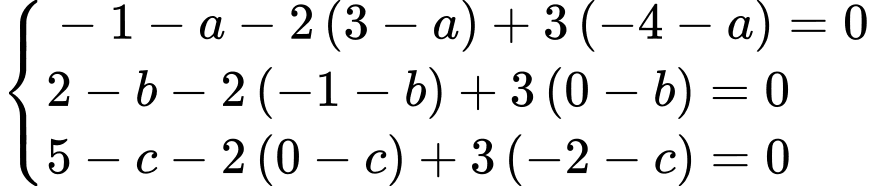

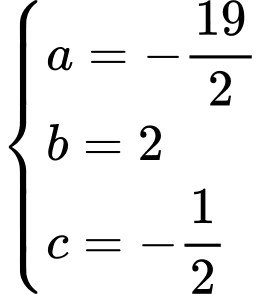
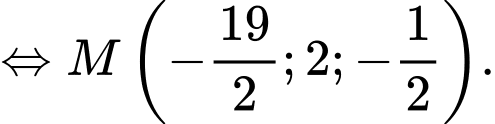 Suy ra
Suy ra 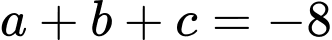
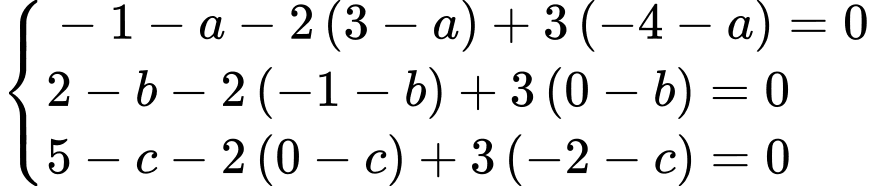

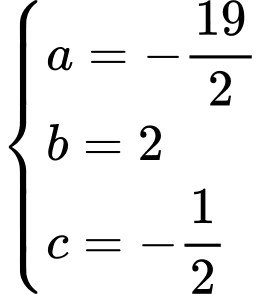
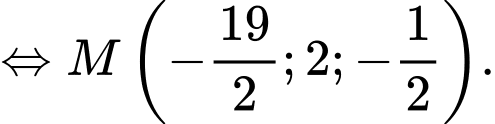 Suy ra
Suy ra 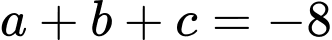
Câu 36 [103908]: Trong không gian với hệ tọa độ 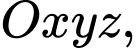 cho hình hộp
cho hình hộp 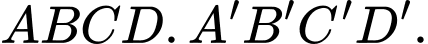 Biết
Biết 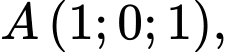
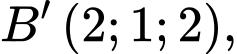
 Gọi tọa độ của đỉnh
Gọi tọa độ của đỉnh 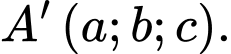 Khi đó
Khi đó 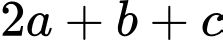 bằng?
bằng?
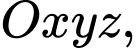 cho hình hộp
cho hình hộp 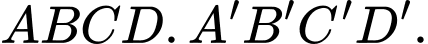 Biết
Biết 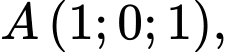
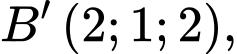
 Gọi tọa độ của đỉnh
Gọi tọa độ của đỉnh 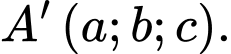 Khi đó
Khi đó 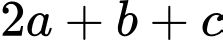 bằng?
bằng? A, 7.
B, 2.
C, 8.
D, 3.
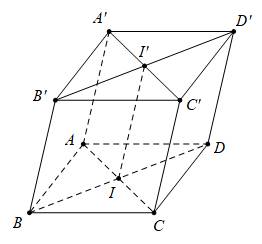
Trung điểm của
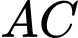 là
là 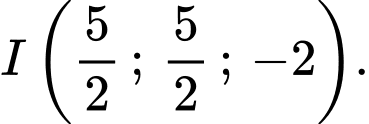
Trung điểm của
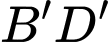 là
là 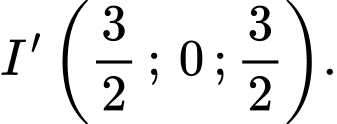
Do
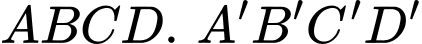 là hình hộp nên
là hình hộp nên 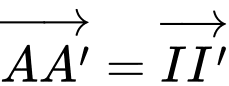
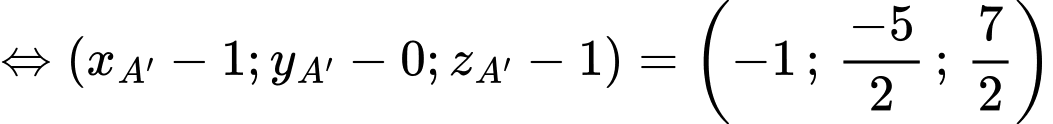
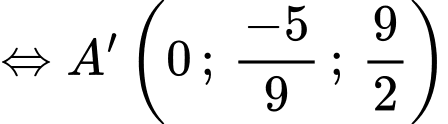
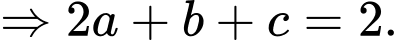
Chọn B. Đáp án: B
Câu 37 [383111]: Trong không gian 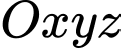 , cho tam giác
, cho tam giác 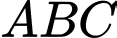 có
có 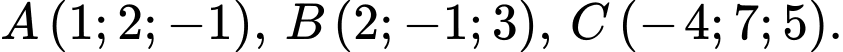 Trong tam giác
Trong tam giác 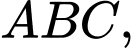 gọi
gọi 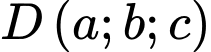 là chân đường phân giác trong góc
là chân đường phân giác trong góc 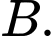 Giá trị của
Giá trị của 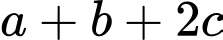 bằng
bằng
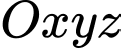 , cho tam giác
, cho tam giác 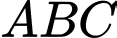 có
có 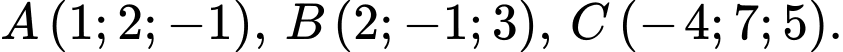 Trong tam giác
Trong tam giác 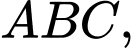 gọi
gọi 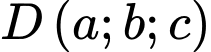 là chân đường phân giác trong góc
là chân đường phân giác trong góc  Giá trị của
Giá trị của 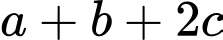 bằng
bằng A, 
B, 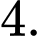
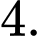
C, 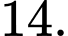
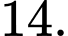
D, 
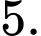
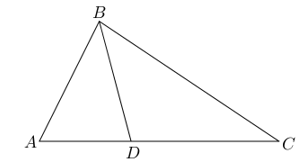
Ta có
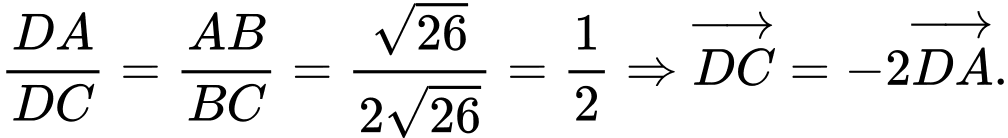
Khi đó
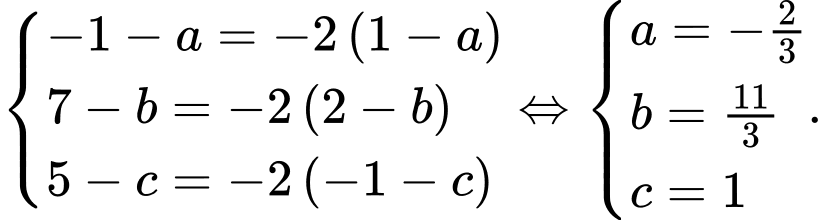
Vậy
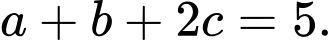 Đáp án: D
Đáp án: D
Câu 38 [399641]: Trong không gian với hệ trục tọa độ 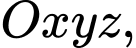 cho
cho 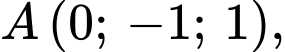
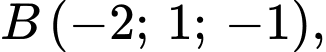
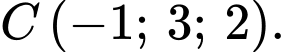
Điểm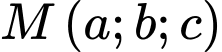 để biểu thức
để biểu thức 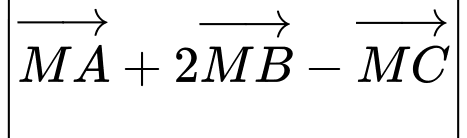 đạt giá trị nhỏ nhất, tổng
đạt giá trị nhỏ nhất, tổng 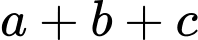 bằng
bằng
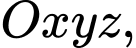 cho
cho 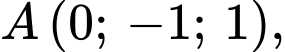
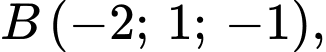
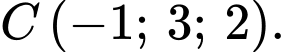
Điểm
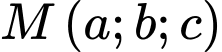 để biểu thức
để biểu thức 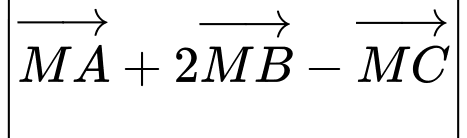 đạt giá trị nhỏ nhất, tổng
đạt giá trị nhỏ nhất, tổng 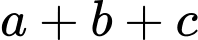 bằng
bằng
Đáp số: 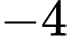
Gọi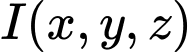 là điểm thỏa mãn
là điểm thỏa mãn
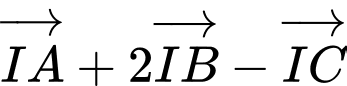
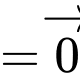 thì tọa độ điểm
thì tọa độ điểm  thỏa mãn
thỏa mãn
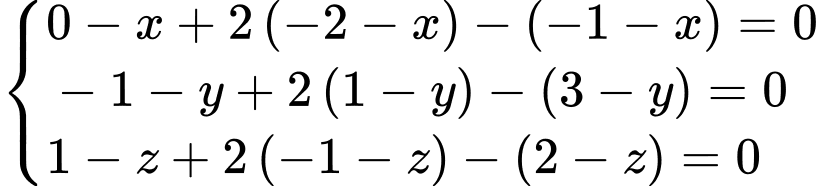

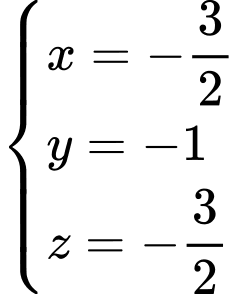
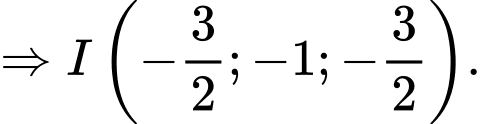
Khi đó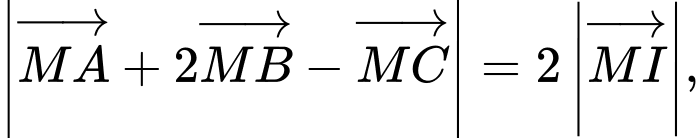 nên
nên
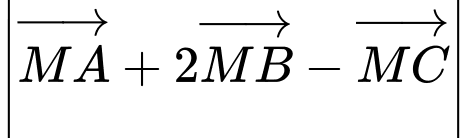 đạt giá trị nhỏ nhất khi và chỉ khi
đạt giá trị nhỏ nhất khi và chỉ khi
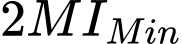
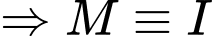
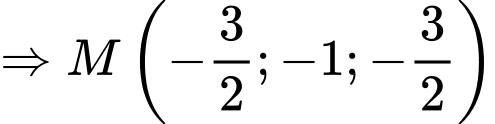
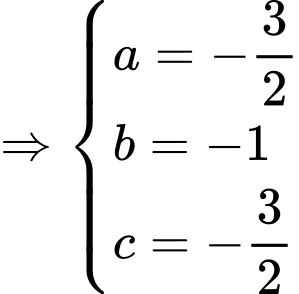

Gọi
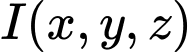 là điểm thỏa mãn
là điểm thỏa mãn 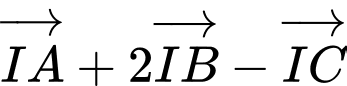
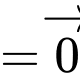 thì tọa độ điểm
thì tọa độ điểm 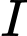 thỏa mãn
thỏa mãn 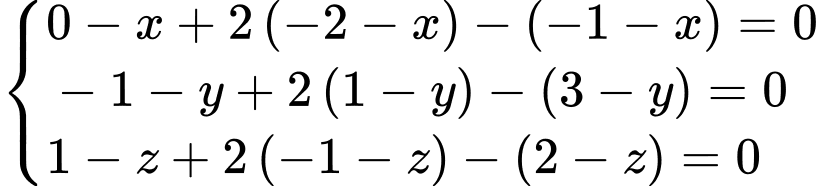

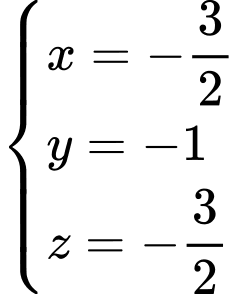
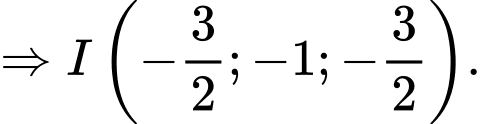
Khi đó
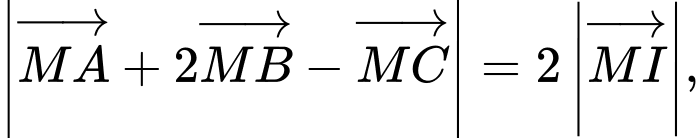 nên
nên 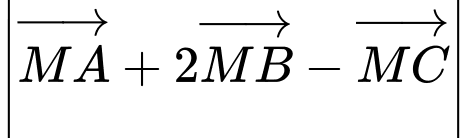 đạt giá trị nhỏ nhất khi và chỉ khi
đạt giá trị nhỏ nhất khi và chỉ khi 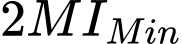
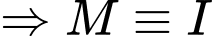
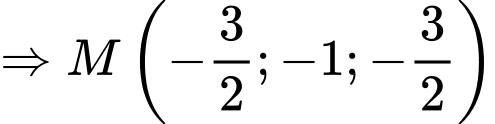
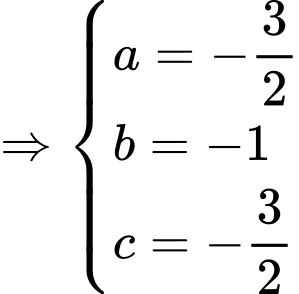

Câu 39 [398657]: Trong không gian 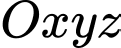 , cho hai điểm
, cho hai điểm 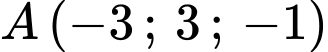 ,
, 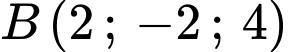 . Xét điểm
. Xét điểm 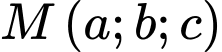 thuộc mặt phẳng
thuộc mặt phẳng 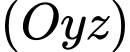 sao cho biểu thức
sao cho biểu thức 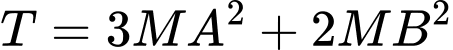 đạt giá trị nhỏ nhất. Khi đó
đạt giá trị nhỏ nhất. Khi đó 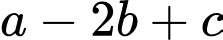 .
.
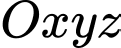 , cho hai điểm
, cho hai điểm 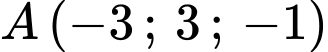 ,
, 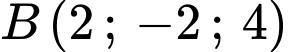 . Xét điểm
. Xét điểm 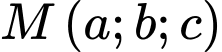 thuộc mặt phẳng
thuộc mặt phẳng 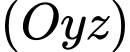 sao cho biểu thức
sao cho biểu thức 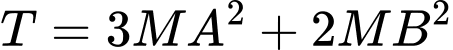 đạt giá trị nhỏ nhất. Khi đó
đạt giá trị nhỏ nhất. Khi đó 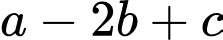 .
. A,  .
.
 .
.B, 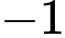 .
.
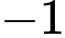 .
.C, 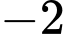 .
.
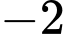 .
.D, 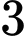 .
.
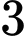 .
.
Chọn B
Xét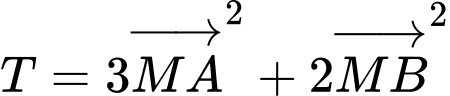
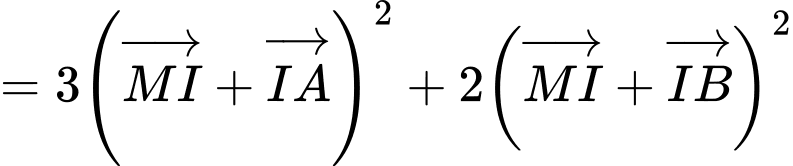
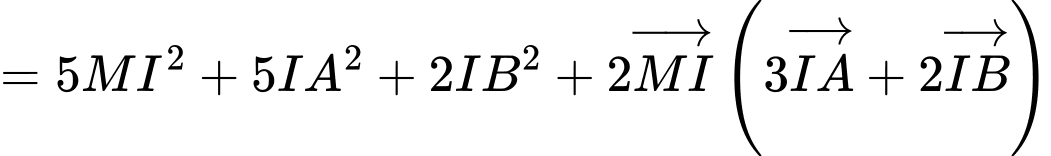
Gọi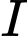 là điểm thỏa mãn
là điểm thỏa mãn 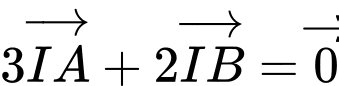
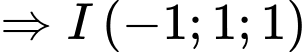
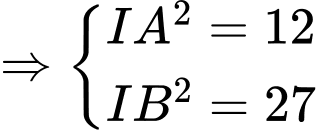
Khi đó: . Do đó
. Do đó 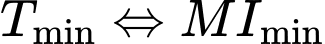 .
.
Gọi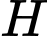 là hình chiếu vuông góc của
là hình chiếu vuông góc của 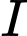 lên mặt phẳng
lên mặt phẳng 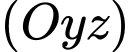
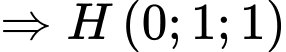
Dễ thấy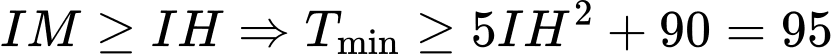
Dấu “=” xảy ra
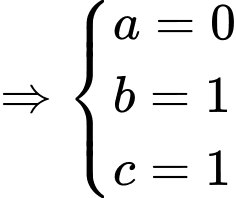
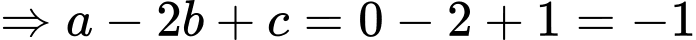 Đáp án: B
Đáp án: B
Xét
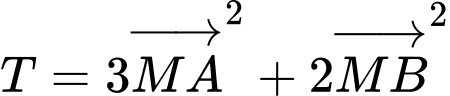
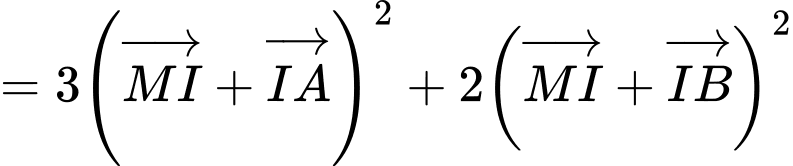
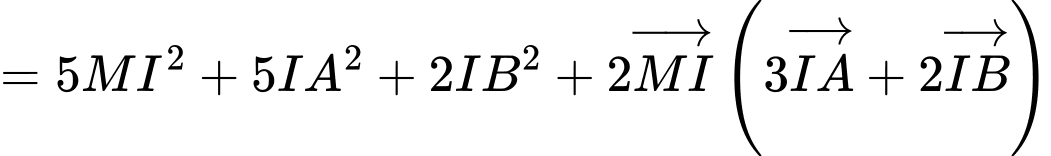
Gọi
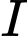 là điểm thỏa mãn
là điểm thỏa mãn 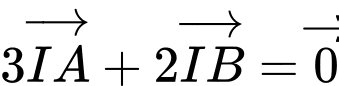
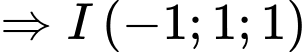
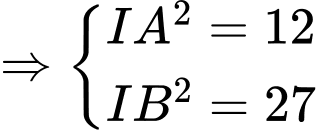
Khi đó:
 . Do đó
. Do đó 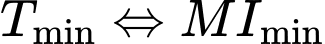 .
.Gọi
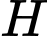 là hình chiếu vuông góc của
là hình chiếu vuông góc của 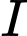 lên mặt phẳng
lên mặt phẳng 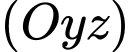
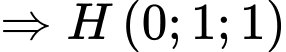
Dễ thấy
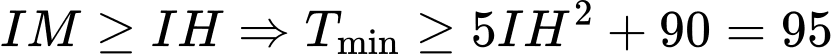
Dấu “=” xảy ra

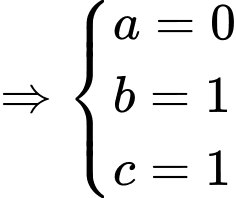
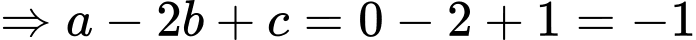 Đáp án: B
Đáp án: B
Câu 40 [384968]: Trong không gian 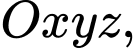 cho hai điểm
cho hai điểm 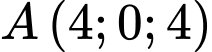 và
và 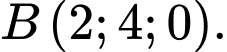 Điểm
Điểm 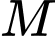 di động trên tia
di động trên tia 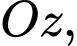 điểm
điểm 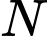 di động trên tia
di động trên tia 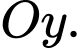 Đường gấp khúc
Đường gấp khúc 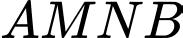 có độ dài nhỏ nhất bằng bao nhiêu? (Kết quả làm tròn đến hàng phần chục).
có độ dài nhỏ nhất bằng bao nhiêu? (Kết quả làm tròn đến hàng phần chục).
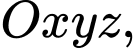 cho hai điểm
cho hai điểm 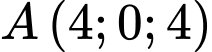 và
và 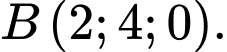 Điểm
Điểm 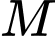 di động trên tia
di động trên tia 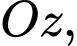 điểm
điểm 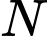 di động trên tia
di động trên tia 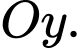 Đường gấp khúc
Đường gấp khúc 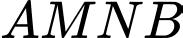 có độ dài nhỏ nhất bằng bao nhiêu? (Kết quả làm tròn đến hàng phần chục).
có độ dài nhỏ nhất bằng bao nhiêu? (Kết quả làm tròn đến hàng phần chục). Đáp số:……………………………..
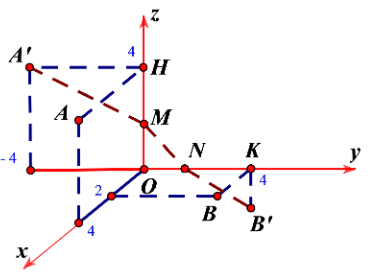
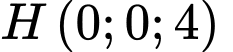 và
và 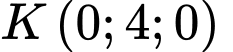 là hình chiếu của
là hình chiếu của 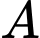 trên
trên  và
và 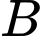 trên
trên 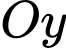
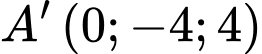 ;
; 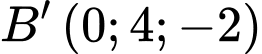
Xét hai tam giác vuông 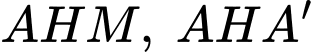 có chung
có chung
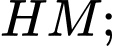
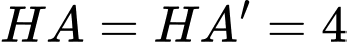
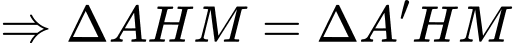 (2 cạnh góc vuông)
(2 cạnh góc vuông)
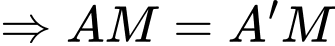
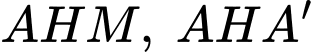 có chung
có chung
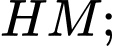
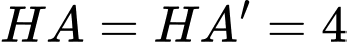
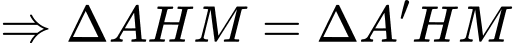 (2 cạnh góc vuông)
(2 cạnh góc vuông)
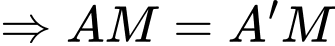
Chứng minh tương tự ta có 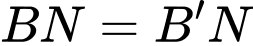
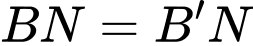
Độ dài đường gấp khúc 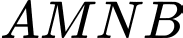 là
là

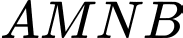 là
là

Vậy đường gấp khúc 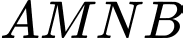 có độ dài nhỏ nhất bằng 10
có độ dài nhỏ nhất bằng 10
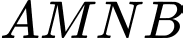 có độ dài nhỏ nhất bằng 10
có độ dài nhỏ nhất bằng 10