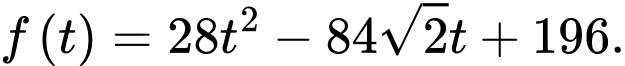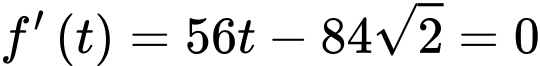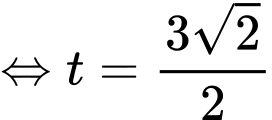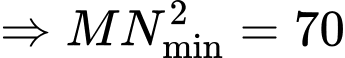Đáp án Bài tập tự luyện
Câu 1 [899367]: Trong không gian 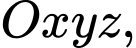 đường thẳng
đường thẳng 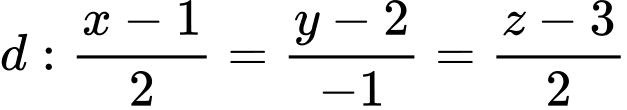 đi qua điểm nào sau đây?
đi qua điểm nào sau đây?
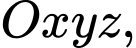 đường thẳng
đường thẳng 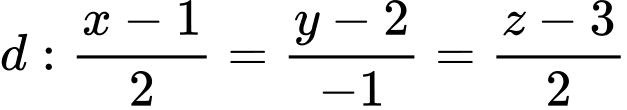 đi qua điểm nào sau đây?
đi qua điểm nào sau đây? A, 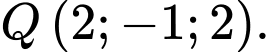
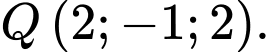
B, 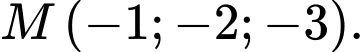
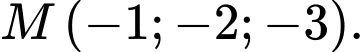
C, 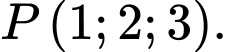
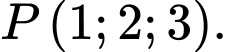
D, 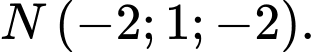
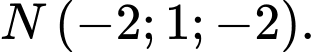
Đường thẳng 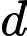 đi qua điểm
đi qua điểm 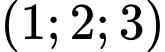 và có vectơ chỉ phương là
và có vectơ chỉ phương là 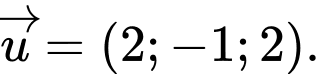 Chọn C. Đáp án: C
Chọn C. Đáp án: C
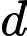 đi qua điểm
đi qua điểm 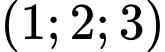 và có vectơ chỉ phương là
và có vectơ chỉ phương là 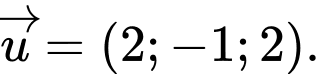 Chọn C. Đáp án: C
Chọn C. Đáp án: C
Câu 2 [899368]: Trong không gian 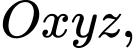 cho ba điểm
cho ba điểm 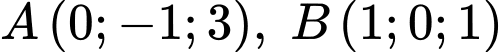 và
và 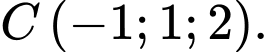 Phương trình nào dưới đây là phương tình chính tắc của đường thẳng đi qua
Phương trình nào dưới đây là phương tình chính tắc của đường thẳng đi qua 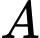 và song song với đường thẳng
và song song với đường thẳng 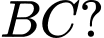
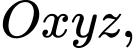 cho ba điểm
cho ba điểm 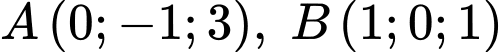 và
và 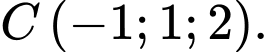 Phương trình nào dưới đây là phương tình chính tắc của đường thẳng đi qua
Phương trình nào dưới đây là phương tình chính tắc của đường thẳng đi qua 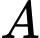 và song song với đường thẳng
và song song với đường thẳng 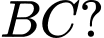
A, 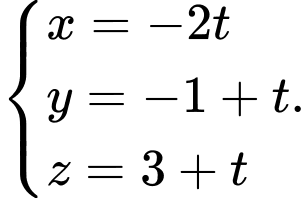
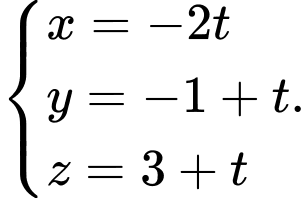
B, 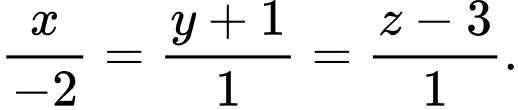
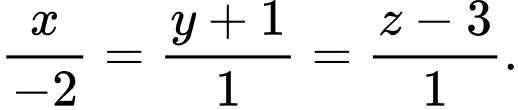
C, 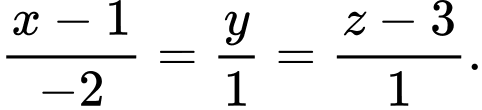
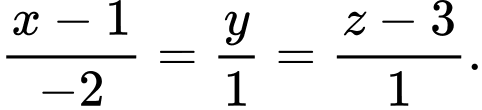
D, 

Tính 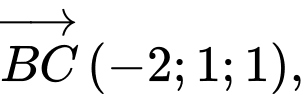 đường thẳng
đường thẳng 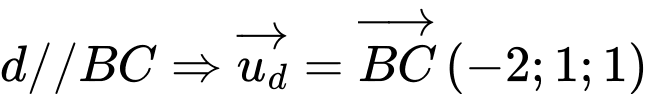
Đường thẳng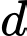 qua
qua 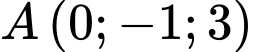 và có vectơ chỉ phương
và có vectơ chỉ phương 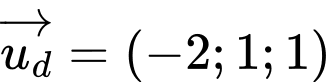 có phương trình là:
có phương trình là: 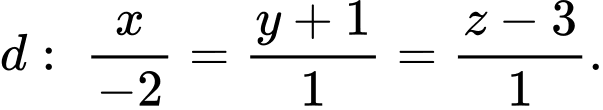 Chọn B.
Đáp án: B
Chọn B.
Đáp án: B
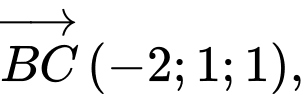 đường thẳng
đường thẳng 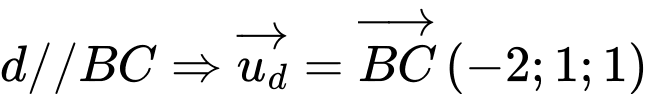
Đường thẳng
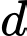 qua
qua 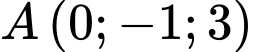 và có vectơ chỉ phương
và có vectơ chỉ phương 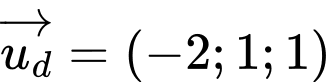 có phương trình là:
có phương trình là: 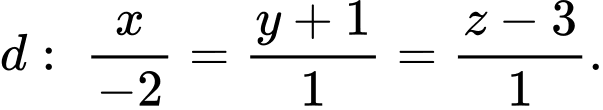 Chọn B.
Đáp án: B
Chọn B.
Đáp án: B
Câu 3 [53268]: Trong không gian với hệ trục tọa độ 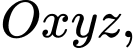 đường thẳng
đường thẳng  đi qua
đi qua 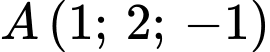 và song song với đường thẳng
và song song với đường thẳng 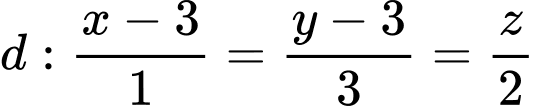 có phương trình là
có phương trình là
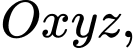 đường thẳng
đường thẳng  đi qua
đi qua 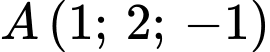 và song song với đường thẳng
và song song với đường thẳng 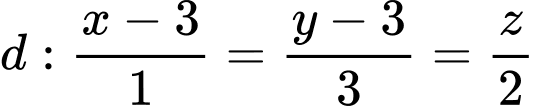 có phương trình là
có phương trình là A, 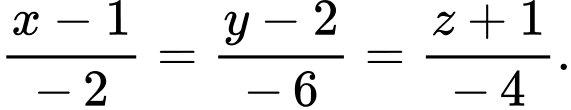
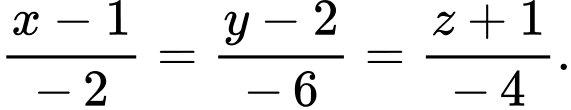
B, 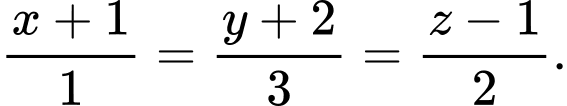
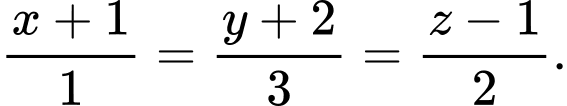
C, 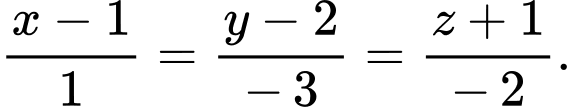
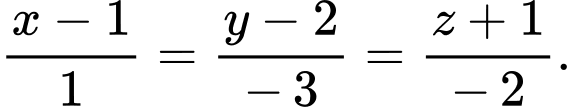
D, 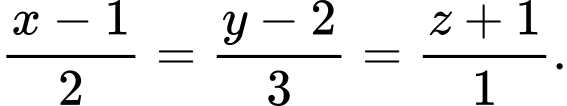
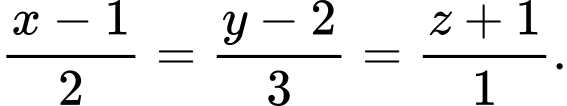
HD: Phương trình đường thẳng  đi qua
đi qua 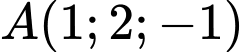 và có VTCP là
và có VTCP là 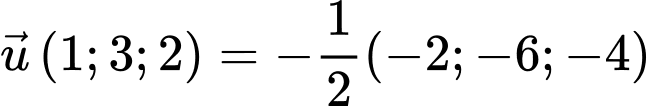
Suy ra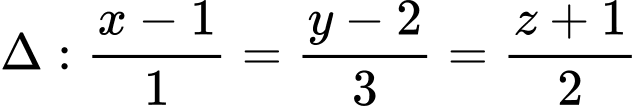 hay
hay 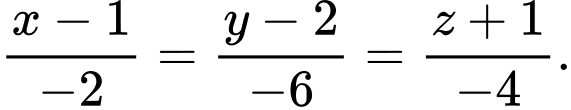 Chọn A. Đáp án: A
Chọn A. Đáp án: A
 đi qua
đi qua 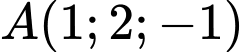 và có VTCP là
và có VTCP là 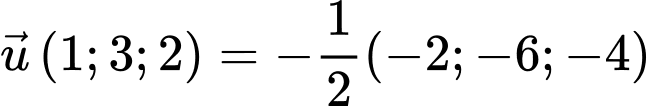
Suy ra
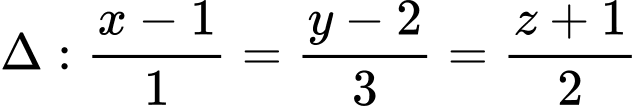 hay
hay 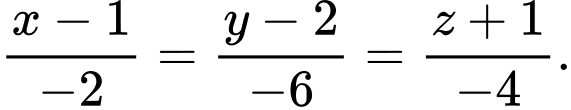 Chọn A. Đáp án: A
Chọn A. Đáp án: A
Câu 4 [53290]: Trong không gian với hệ tọa độ 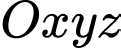 , cho tam giác
, cho tam giác 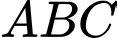 với
với 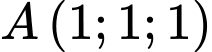 ;
; 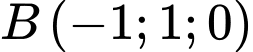 ;
; 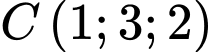 . Đường trung tuyến xuất phát từ đỉnh
. Đường trung tuyến xuất phát từ đỉnh 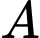 của tam giác
của tam giác 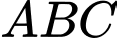 nhận vectơ nào dưới đây là một vectơ chỉ phương?
nhận vectơ nào dưới đây là một vectơ chỉ phương?
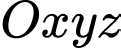 , cho tam giác
, cho tam giác 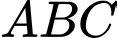 với
với 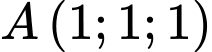 ;
; 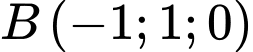 ;
; 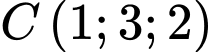 . Đường trung tuyến xuất phát từ đỉnh
. Đường trung tuyến xuất phát từ đỉnh 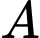 của tam giác
của tam giác 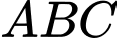 nhận vectơ nào dưới đây là một vectơ chỉ phương?
nhận vectơ nào dưới đây là một vectơ chỉ phương? A, 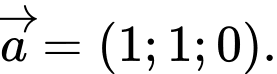
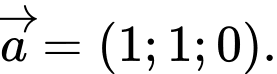
B, 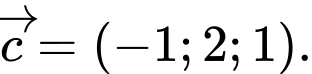
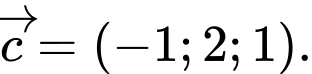
C, 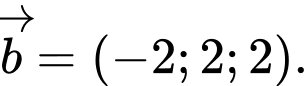
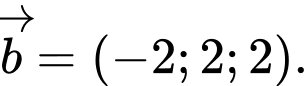
D, 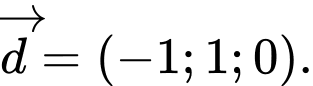
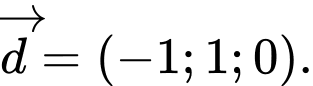
Đáp án D
Gọi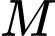 là trung điểm của
là trung điểm của 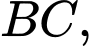 suy ra tọa độ điểm
suy ra tọa độ điểm 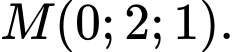
Đường trung tuyến xuất phát từ đỉnh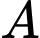 có vectơ chỉ phương là
có vectơ chỉ phương là 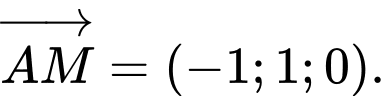 Đáp án: D
Đáp án: D
Gọi
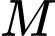 là trung điểm của
là trung điểm của 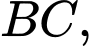 suy ra tọa độ điểm
suy ra tọa độ điểm 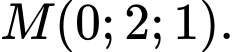
Đường trung tuyến xuất phát từ đỉnh
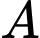 có vectơ chỉ phương là
có vectơ chỉ phương là 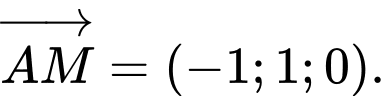 Đáp án: D
Đáp án: D
Câu 5 [899369]: Trong không gian tọa độ 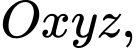 phương trình đường thẳng qua điểm
phương trình đường thẳng qua điểm 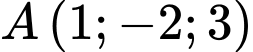 và trung điểm của BC với
và trung điểm của BC với 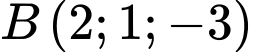 và
và 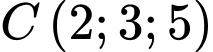 là
là
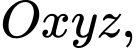 phương trình đường thẳng qua điểm
phương trình đường thẳng qua điểm 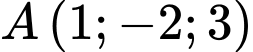 và trung điểm của BC với
và trung điểm của BC với 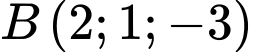 và
và 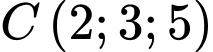 là
là A, 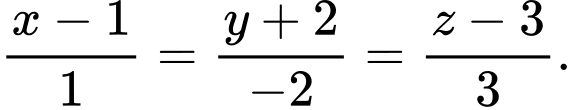
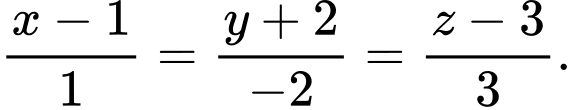
B, 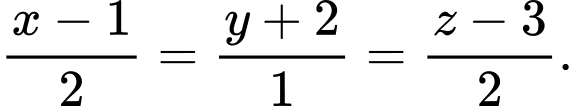
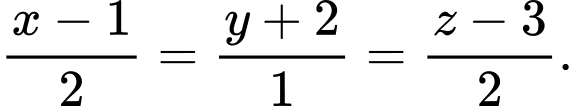
C, 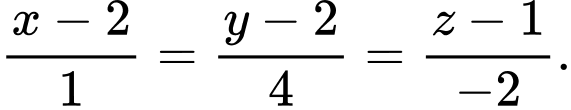
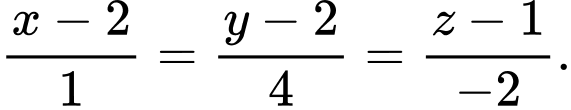
D, 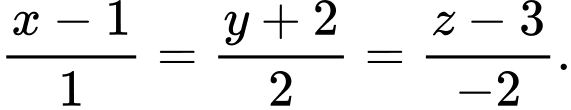
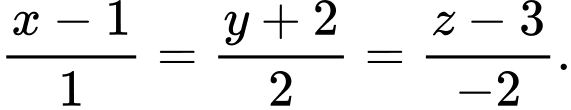
Trung điểm của BC có tọa độ là 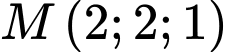
Đường thẳng có một vectơ chỉ phương là
có một vectơ chỉ phương là 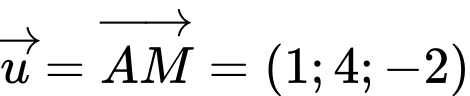
Đường thẳng đi qua
đi qua 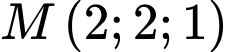 và có vectơ chỉ phương
và có vectơ chỉ phương 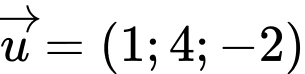
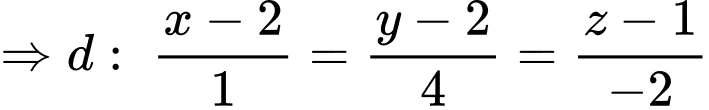 . Chọn C.
Đáp án: C
. Chọn C.
Đáp án: C
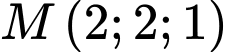
Đường thẳng
 có một vectơ chỉ phương là
có một vectơ chỉ phương là 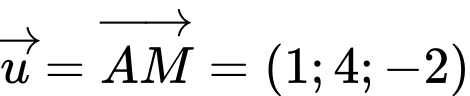
Đường thẳng
 đi qua
đi qua 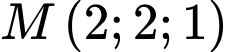 và có vectơ chỉ phương
và có vectơ chỉ phương 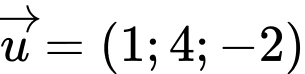
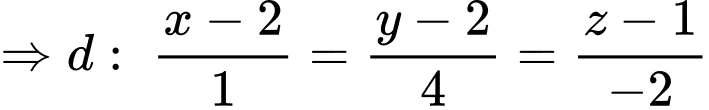 . Chọn C.
Đáp án: C
. Chọn C.
Đáp án: C
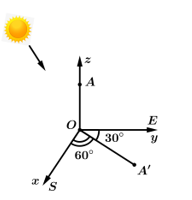
Câu 6 [163889]: Trên mặt đất phẳng, người ta dựng một cây cột thẳng cao 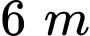 vuông góc với mặt đất, có chân cột đặt tại vị trí
vuông góc với mặt đất, có chân cột đặt tại vị trí  trên mặt đất. Tại một thời điểm, dưới ánh nắng mặt trời, bóng của đỉnh cột dưới mặt đất cách chân cột
trên mặt đất. Tại một thời điểm, dưới ánh nắng mặt trời, bóng của đỉnh cột dưới mặt đất cách chân cột 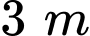 về hướng
về hướng 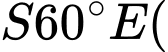 hướng tạo với hướng nam góc
hướng tạo với hướng nam góc 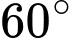 và tạo với hướng đông góc
và tạo với hướng đông góc 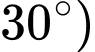 (Hình vẽ). Chọn hệ trục
(Hình vẽ). Chọn hệ trục 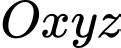 có gốc toạ độ là
có gốc toạ độ là  tia
tia 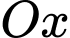 chỉ hướng nam, tia
chỉ hướng nam, tia 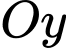 chỉ hướng đông, tia
chỉ hướng đông, tia  chứa cây cột, đơn vị đo là mét. Phương trình đường thẳng chứa tia nắng mặt trời đi qua đỉnh cột tại thời điểm đang xét là
chứa cây cột, đơn vị đo là mét. Phương trình đường thẳng chứa tia nắng mặt trời đi qua đỉnh cột tại thời điểm đang xét là
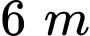 vuông góc với mặt đất, có chân cột đặt tại vị trí
vuông góc với mặt đất, có chân cột đặt tại vị trí  trên mặt đất. Tại một thời điểm, dưới ánh nắng mặt trời, bóng của đỉnh cột dưới mặt đất cách chân cột
trên mặt đất. Tại một thời điểm, dưới ánh nắng mặt trời, bóng của đỉnh cột dưới mặt đất cách chân cột 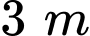 về hướng
về hướng 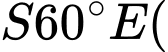 hướng tạo với hướng nam góc
hướng tạo với hướng nam góc 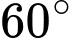 và tạo với hướng đông góc
và tạo với hướng đông góc 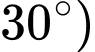 (Hình vẽ). Chọn hệ trục
(Hình vẽ). Chọn hệ trục 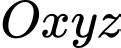 có gốc toạ độ là
có gốc toạ độ là  tia
tia 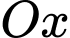 chỉ hướng nam, tia
chỉ hướng nam, tia 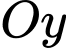 chỉ hướng đông, tia
chỉ hướng đông, tia  chứa cây cột, đơn vị đo là mét. Phương trình đường thẳng chứa tia nắng mặt trời đi qua đỉnh cột tại thời điểm đang xét là
chứa cây cột, đơn vị đo là mét. Phương trình đường thẳng chứa tia nắng mặt trời đi qua đỉnh cột tại thời điểm đang xét là

A, 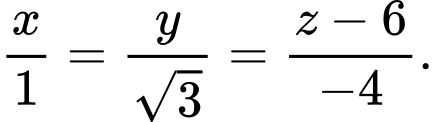
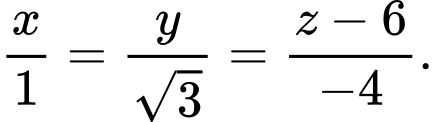
B, 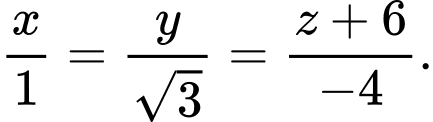
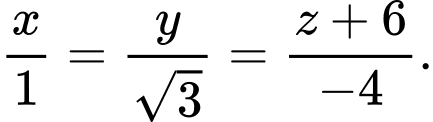
C, 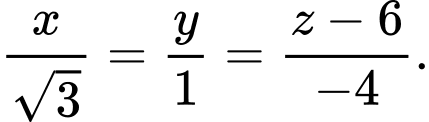
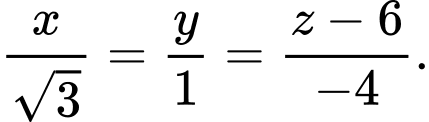
D, 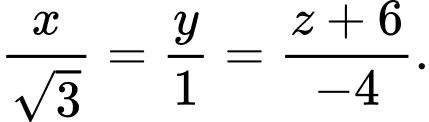
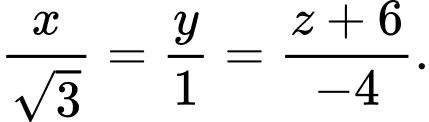
Ta có: 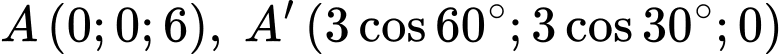
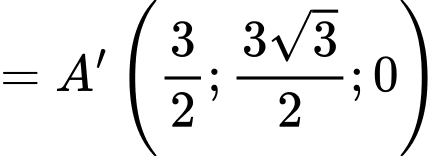
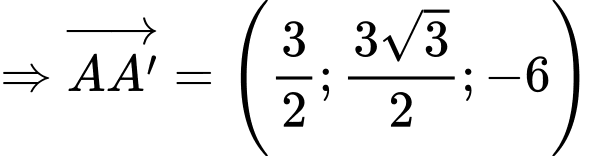
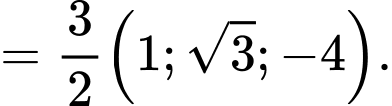
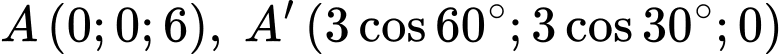
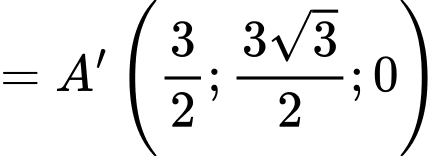
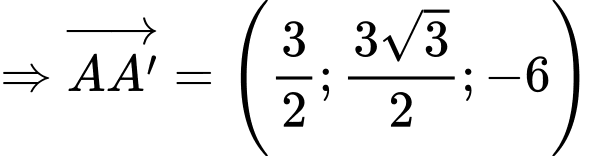
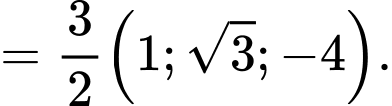
Phương trình đường thẳng 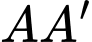 là:
là: 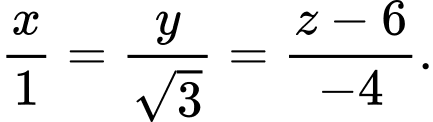
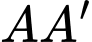 là:
là: 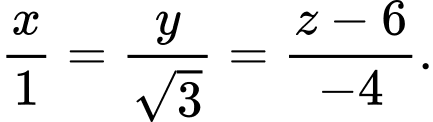
Câu 7 [185147]: Trong không gian 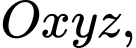 cho điểm
cho điểm 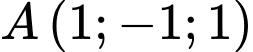 và mặt phẳng
và mặt phẳng 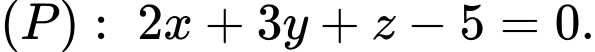 Đường thẳng đi qua
Đường thẳng đi qua 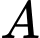 và vuông góc với
và vuông góc với 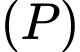 có phương trình là:
có phương trình là:
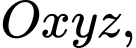 cho điểm
cho điểm 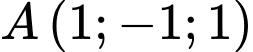 và mặt phẳng
và mặt phẳng 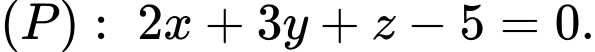 Đường thẳng đi qua
Đường thẳng đi qua 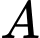 và vuông góc với
và vuông góc với 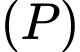 có phương trình là:
có phương trình là: A, 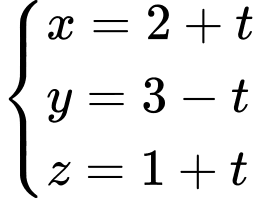
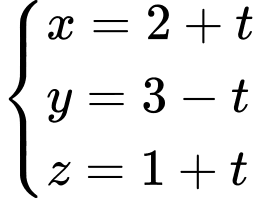
B, 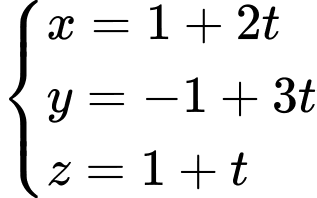
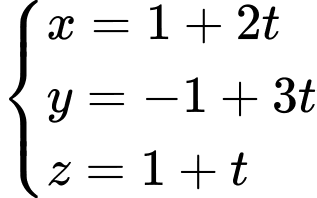
C, 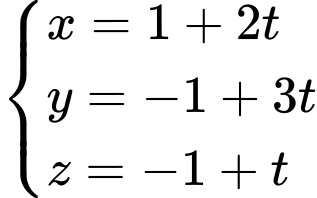
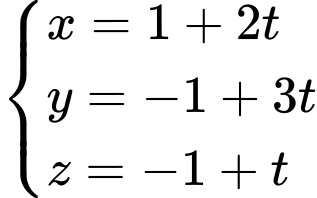
D, 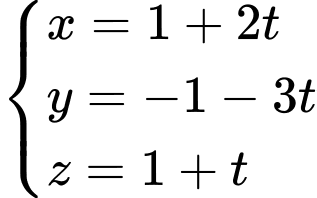
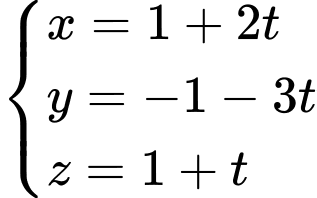
Gọi 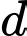 là đường thẳng đi qua
là đường thẳng đi qua 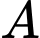 và vuông góc với mp
và vuông góc với mp 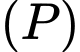
Ta có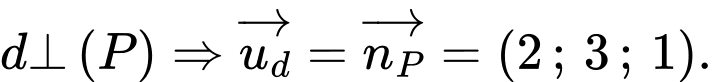
Suy ra phương trình tham số của đường thẳng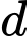 là
là 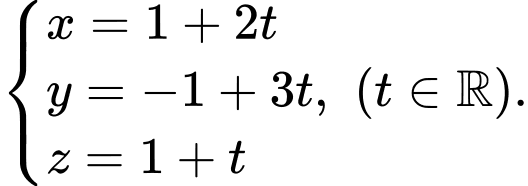
Chọn B. Đáp án: B
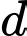 là đường thẳng đi qua
là đường thẳng đi qua 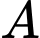 và vuông góc với mp
và vuông góc với mp 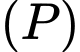
Ta có
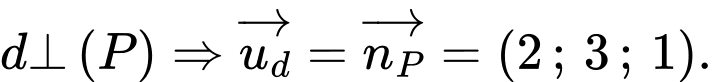
Suy ra phương trình tham số của đường thẳng
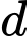 là
là 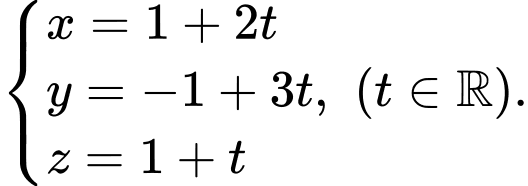
Chọn B. Đáp án: B
Câu 8 [53263]: Trong không gian với hệ tọa độ 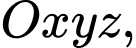 phương trình chính tắc của đường thẳng
phương trình chính tắc của đường thẳng 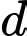 đi qua điểm
đi qua điểm 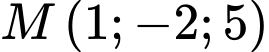 và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 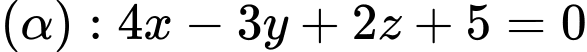 là
là
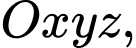 phương trình chính tắc của đường thẳng
phương trình chính tắc của đường thẳng 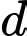 đi qua điểm
đi qua điểm 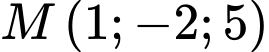 và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 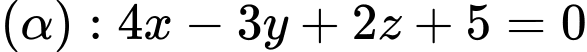 là
là A, 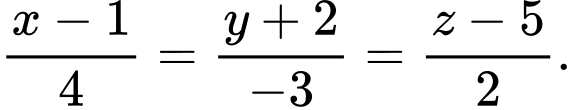
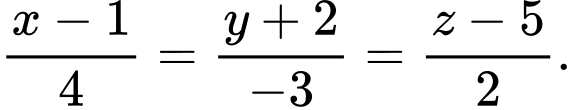
B, 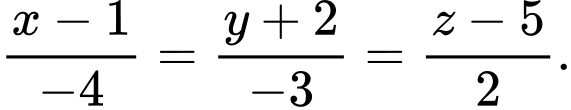
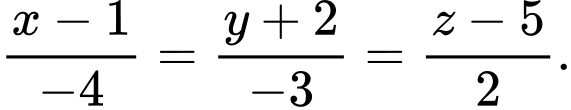
C, 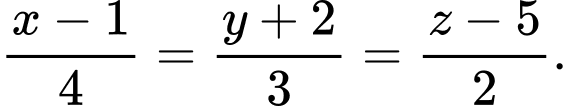
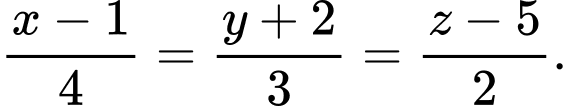
D, 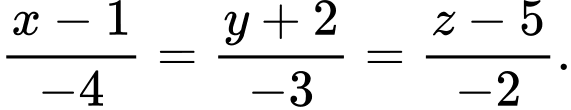
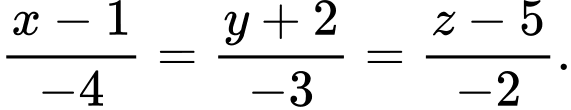
HD: Ta có 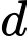 qua
qua 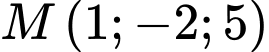 và nhận
và nhận 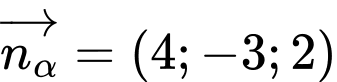 là 1 VTCP
là 1 VTCP
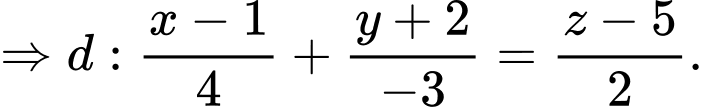 Chọn A. Đáp án: A
Chọn A. Đáp án: A
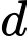 qua
qua 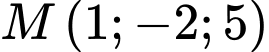 và nhận
và nhận 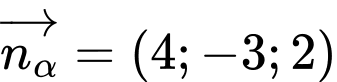 là 1 VTCP
là 1 VTCP
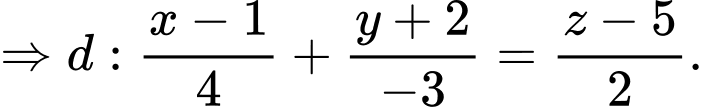 Chọn A. Đáp án: A
Chọn A. Đáp án: A
Câu 9 [899372]: Trong không gian với hệ tọa độ 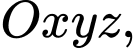 phương trình nào dưới đây là phương trình mặt phẳng đi qua điểm
phương trình nào dưới đây là phương trình mặt phẳng đi qua điểm 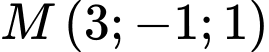 và vuông góc với đường thẳng
và vuông góc với đường thẳng 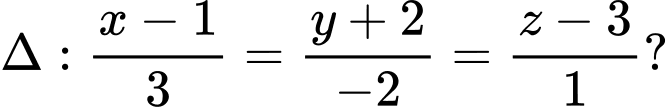
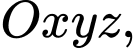 phương trình nào dưới đây là phương trình mặt phẳng đi qua điểm
phương trình nào dưới đây là phương trình mặt phẳng đi qua điểm 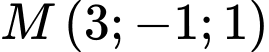 và vuông góc với đường thẳng
và vuông góc với đường thẳng 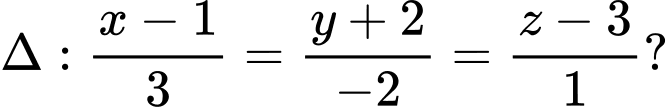
A, 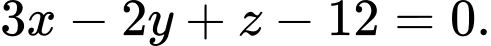
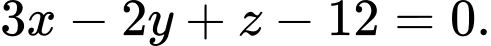
B, 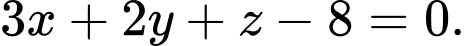
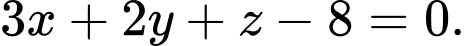
C, 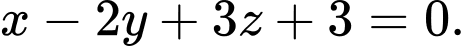
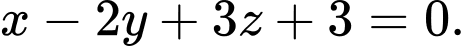
D, 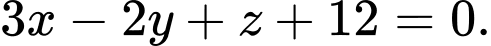
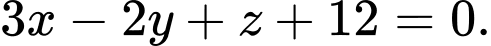
Gọi 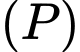 là mặt phẳng cần tìm ta có:
là mặt phẳng cần tìm ta có: 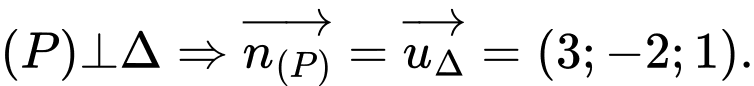
Phương trình mặt phẳng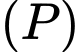 qua
qua 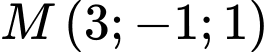 và có vectơ pháp tuyến
và có vectơ pháp tuyến 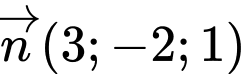 là
là
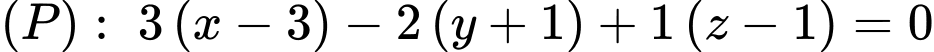 hay
hay 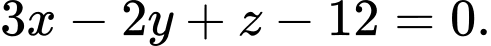 Chọn A. Đáp án: A
Chọn A. Đáp án: A
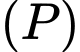 là mặt phẳng cần tìm ta có:
là mặt phẳng cần tìm ta có: 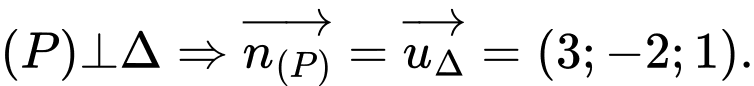
Phương trình mặt phẳng
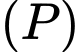 qua
qua 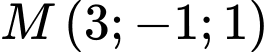 và có vectơ pháp tuyến
và có vectơ pháp tuyến 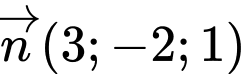 là
là 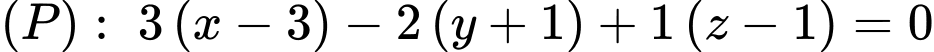 hay
hay 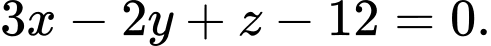 Chọn A. Đáp án: A
Chọn A. Đáp án: A
Câu 10 [899374]: Trong không gian 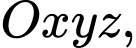 cho điểm
cho điểm 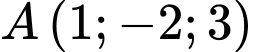 và hai mặt phẳng
và hai mặt phẳng 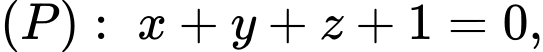
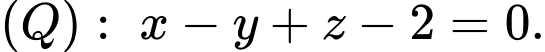 Phương trình nào dưới đây là phương trình đường thẳng đi qua
Phương trình nào dưới đây là phương trình đường thẳng đi qua 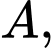 song song với
song song với 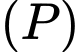 và
và 
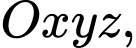 cho điểm
cho điểm 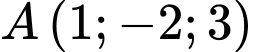 và hai mặt phẳng
và hai mặt phẳng 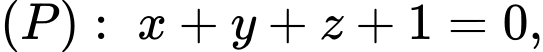
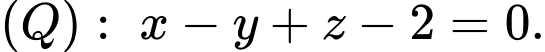 Phương trình nào dưới đây là phương trình đường thẳng đi qua
Phương trình nào dưới đây là phương trình đường thẳng đi qua 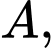 song song với
song song với 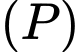 và
và 
A, 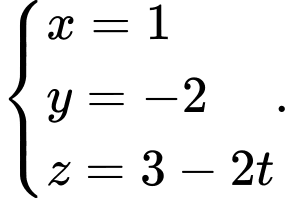
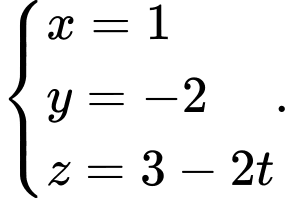
B, 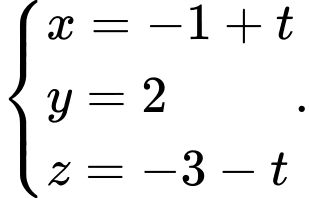
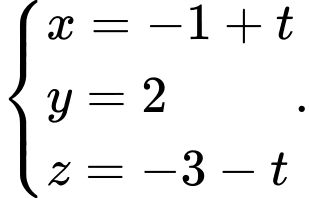
C, 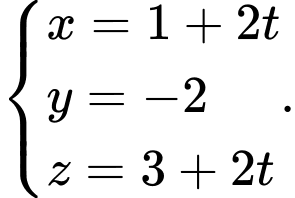
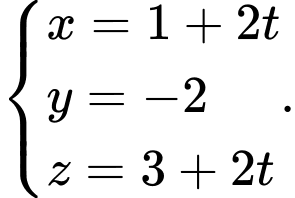
D, 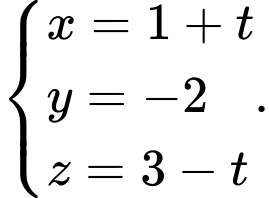
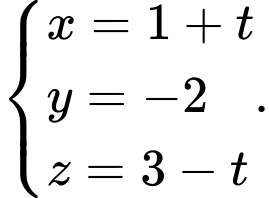
Gọi 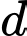 là đường thẳng cần tìm và có vectơ chỉ phương là
là đường thẳng cần tìm và có vectơ chỉ phương là 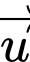
Ta có: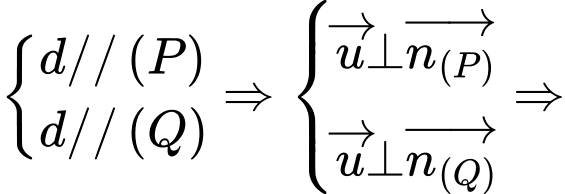 Ta chọn
Ta chọn 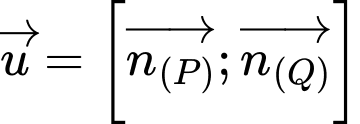 trong đó các vectơ pháp tuyến của mặt phẳng
trong đó các vectơ pháp tuyến của mặt phẳng 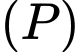 và
và  lần lượt là
lần lượt là 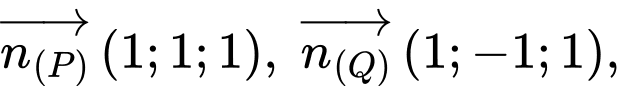
Suy ra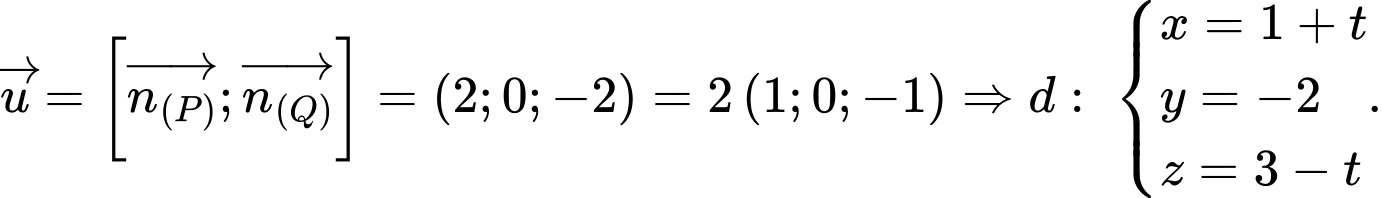 Chọn D. Đáp án: D
Chọn D. Đáp án: D
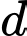 là đường thẳng cần tìm và có vectơ chỉ phương là
là đường thẳng cần tìm và có vectơ chỉ phương là 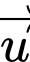
Ta có:
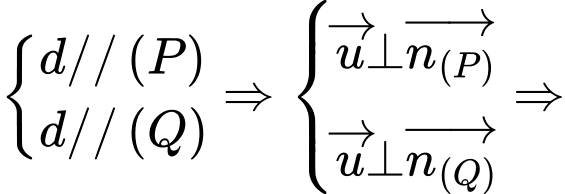 Ta chọn
Ta chọn 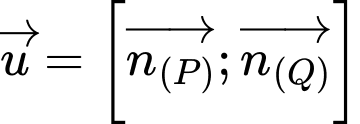 trong đó các vectơ pháp tuyến của mặt phẳng
trong đó các vectơ pháp tuyến của mặt phẳng 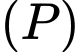 và
và  lần lượt là
lần lượt là 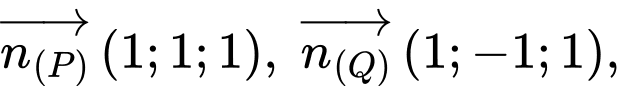
Suy ra
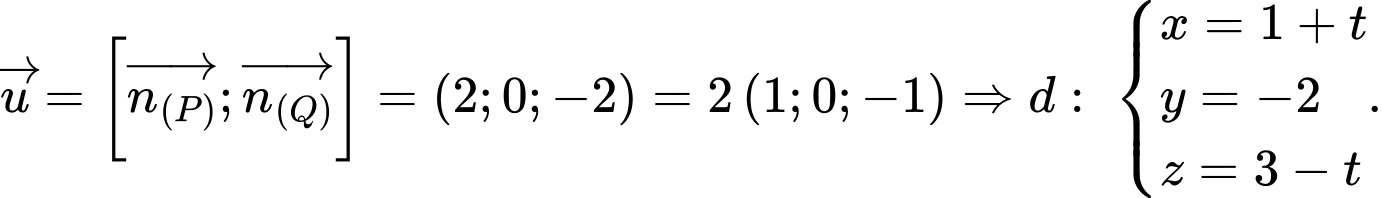 Chọn D. Đáp án: D
Chọn D. Đáp án: D
Câu 11 [234254]: [Đề thi TH THPT 2022]:Trong không gian 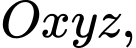 cho ba điểm
cho ba điểm 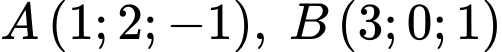 và
và 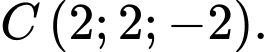 Đường thẳng đi qua
Đường thẳng đi qua 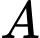 và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 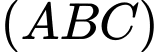 có phương trình là
có phương trình là
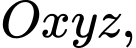 cho ba điểm
cho ba điểm 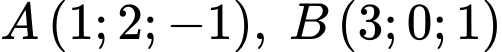 và
và 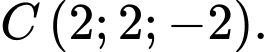 Đường thẳng đi qua
Đường thẳng đi qua 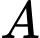 và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 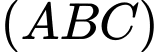 có phương trình là
có phương trình là A, 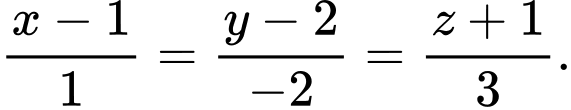
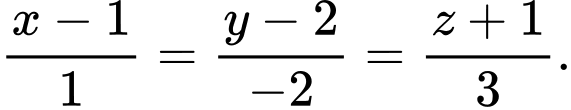
B, 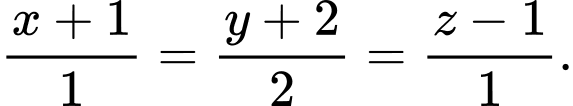
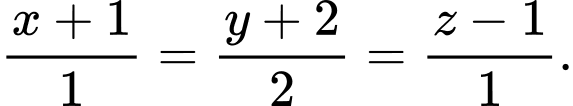
C, 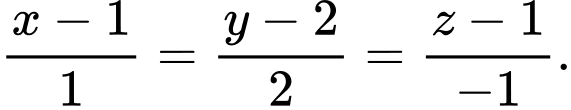
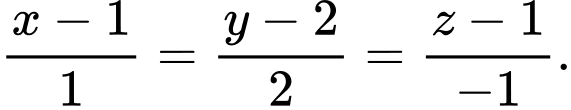
D, 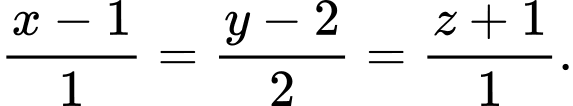
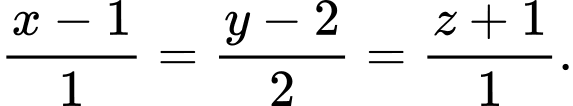
HD: Ta có: 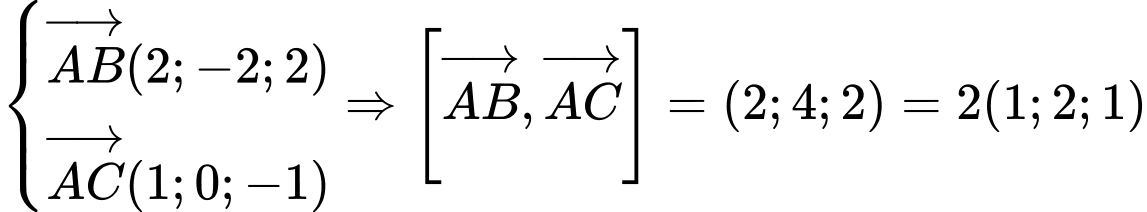 Do đó phương trình đường thẳng cần tìm là
Do đó phương trình đường thẳng cần tìm là 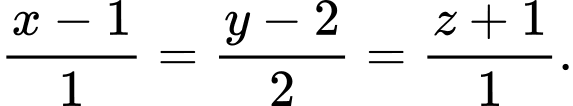 Chọn D. Đáp án: D
Chọn D. Đáp án: D
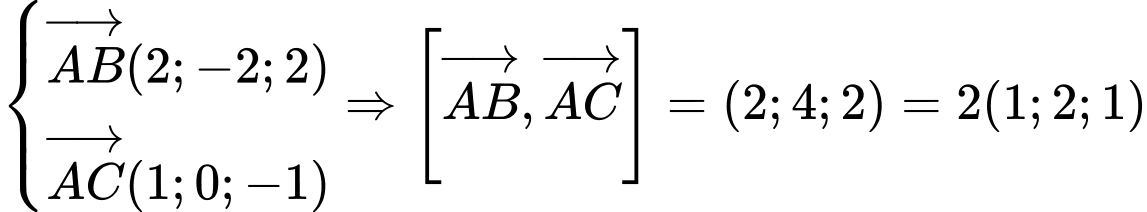 Do đó phương trình đường thẳng cần tìm là
Do đó phương trình đường thẳng cần tìm là 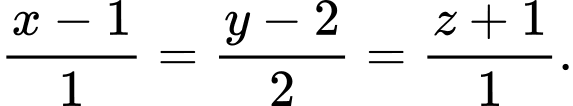 Chọn D. Đáp án: D
Chọn D. Đáp án: D
Câu 12 [899376]: Trong không gian tọa độ 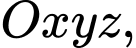 viết phương trình đường thẳng
viết phương trình đường thẳng 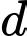 đi qua điểm
đi qua điểm 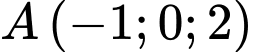 và song song với 2 mặt phẳng
và song song với 2 mặt phẳng 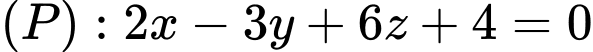 và
và 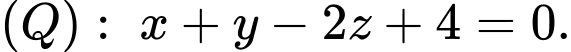
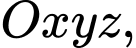 viết phương trình đường thẳng
viết phương trình đường thẳng 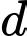 đi qua điểm
đi qua điểm 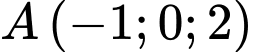 và song song với 2 mặt phẳng
và song song với 2 mặt phẳng 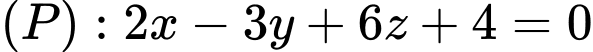 và
và 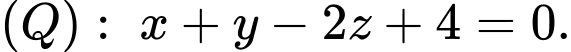
A, 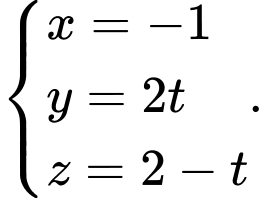
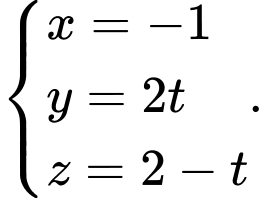
B, 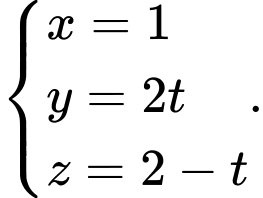
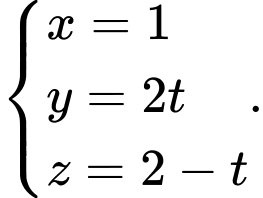
C, 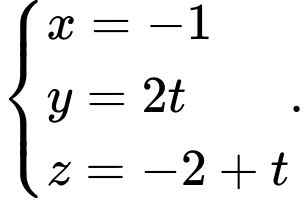
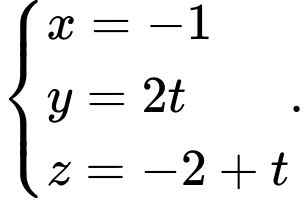
D, 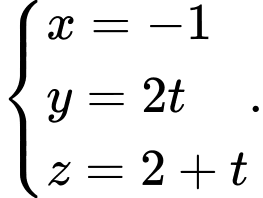
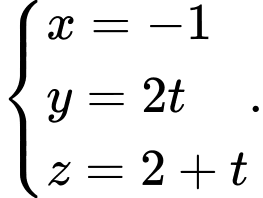
Ta có 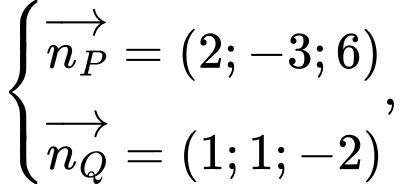 do
do 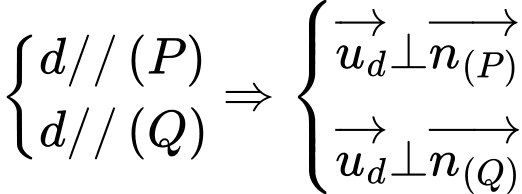
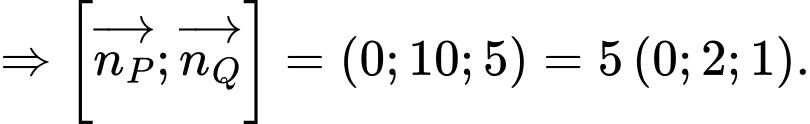
Đường thẳng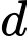 qua
qua 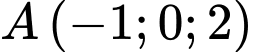 và nhận
và nhận 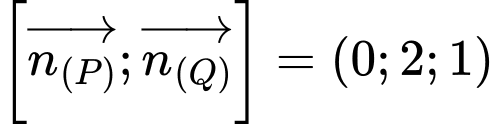 là một vectơ chỉ phương
là một vectơ chỉ phương
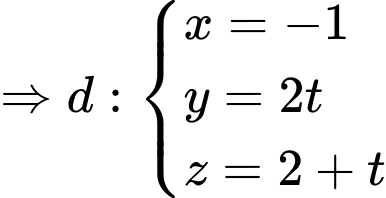
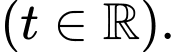 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
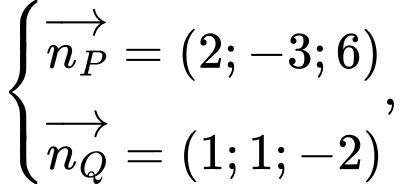 do
do 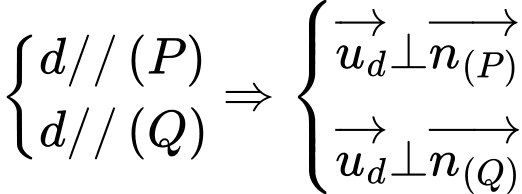
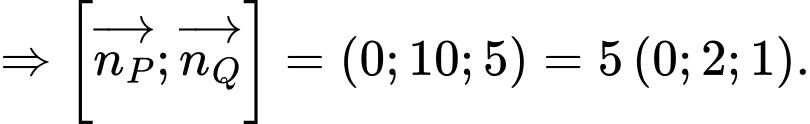
Đường thẳng
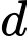 qua
qua 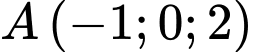 và nhận
và nhận 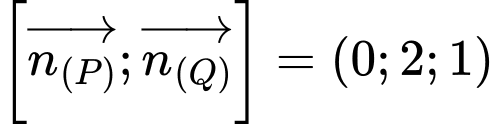 là một vectơ chỉ phương
là một vectơ chỉ phương 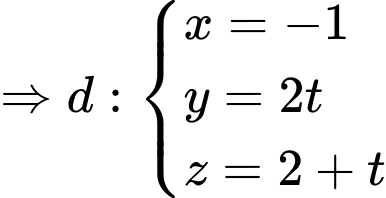
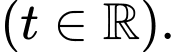 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
Câu 13 [899378]: Trong không gian với hệ tọa độ 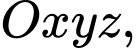 cho điểm
cho điểm 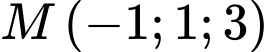 và hai đường thẳng
và hai đường thẳng 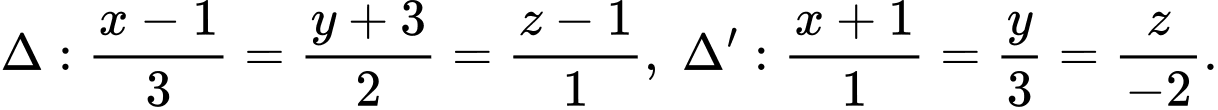 Phương trình nào dưới đây là phương trình đường thẳng đi qua
Phương trình nào dưới đây là phương trình đường thẳng đi qua 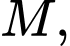 vuông góc với
vuông góc với  và
và 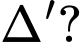
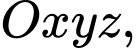 cho điểm
cho điểm 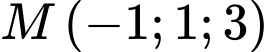 và hai đường thẳng
và hai đường thẳng 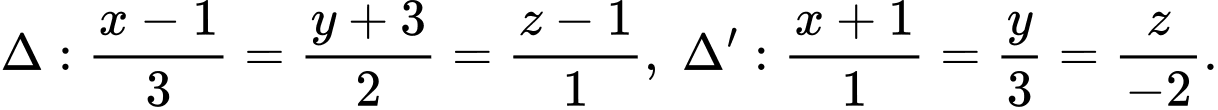 Phương trình nào dưới đây là phương trình đường thẳng đi qua
Phương trình nào dưới đây là phương trình đường thẳng đi qua 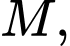 vuông góc với
vuông góc với  và
và 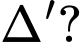
A, 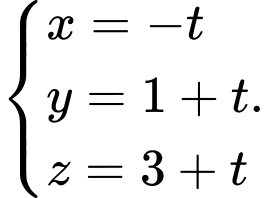
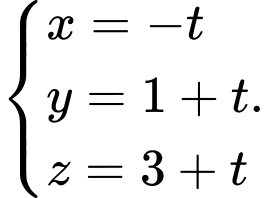
B, 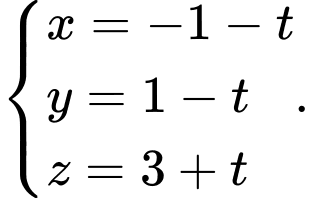
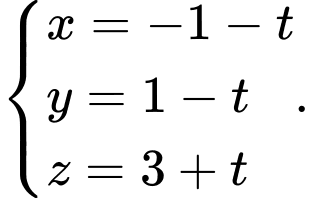
C, 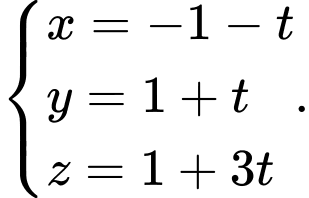
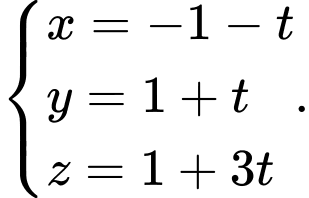
D, 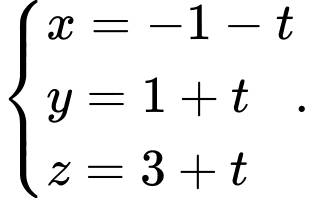
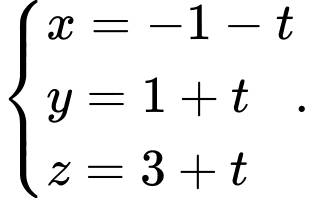
Các vectơ chỉ phương của  và
và  lần lượt là:
lần lượt là: 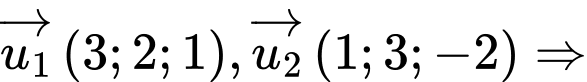 vectơ chỉ phương của đường thẳng cần tìm là:
vectơ chỉ phương của đường thẳng cần tìm là: 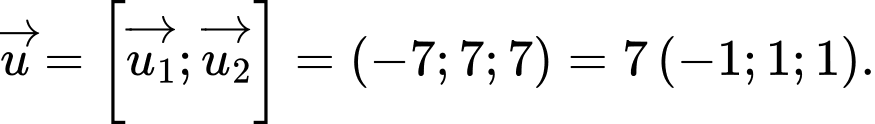 Chọn D. Đáp án: D
Chọn D. Đáp án: D
 và
và 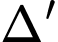 lần lượt là:
lần lượt là: 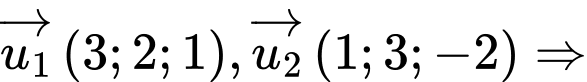 vectơ chỉ phương của đường thẳng cần tìm là:
vectơ chỉ phương của đường thẳng cần tìm là: 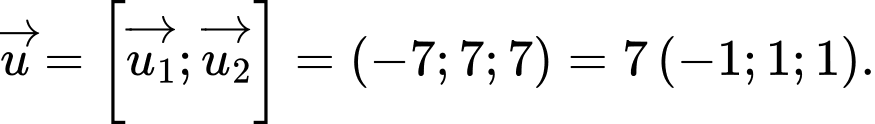 Chọn D. Đáp án: D
Chọn D. Đáp án: D
Câu 14 [55790]: Trong không gian với hệ tọa độ 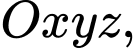 cho đường thẳng
cho đường thẳng 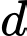 đi qua góc tọa độ, vuông góc với trục
đi qua góc tọa độ, vuông góc với trục 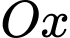 và vuông góc với đường thẳng
và vuông góc với đường thẳng 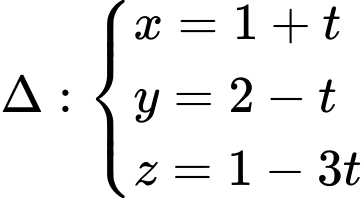 Phương trình của
Phương trình của 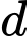 là
là
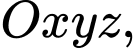 cho đường thẳng
cho đường thẳng 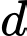 đi qua góc tọa độ, vuông góc với trục
đi qua góc tọa độ, vuông góc với trục 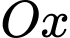 và vuông góc với đường thẳng
và vuông góc với đường thẳng 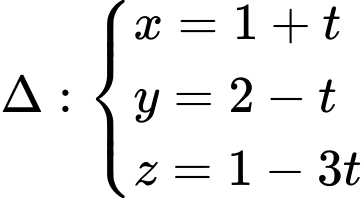 Phương trình của
Phương trình của 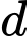 là
là A, 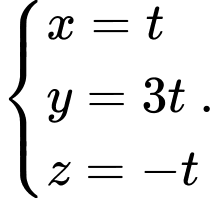
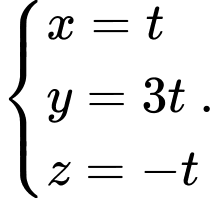
B, 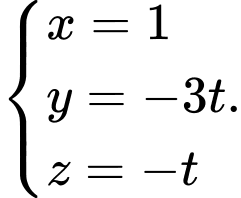
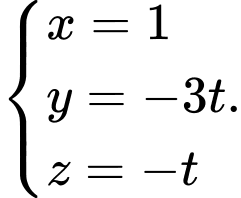
C, 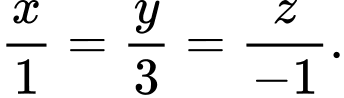
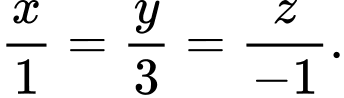
D, 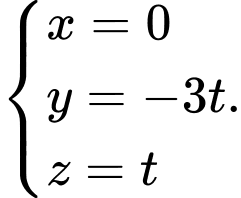
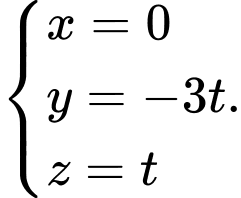
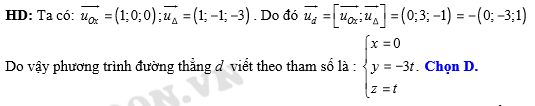 Đáp án: D
Đáp án: D
Câu 15 [55814]: Cho mặt phẳng 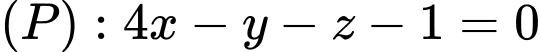 và đường thẳng
và đường thẳng 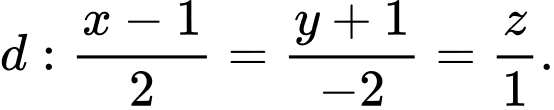 Phương trình đường thẳng qua
Phương trình đường thẳng qua 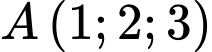 song song với
song song với 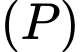 đồng thời vuông góc với
đồng thời vuông góc với 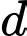 là
là
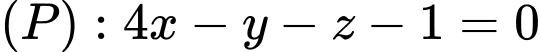 và đường thẳng
và đường thẳng 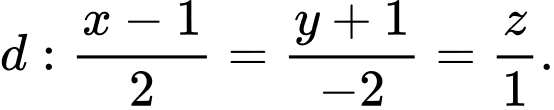 Phương trình đường thẳng qua
Phương trình đường thẳng qua 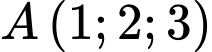 song song với
song song với 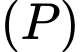 đồng thời vuông góc với
đồng thời vuông góc với 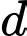 là
là A, 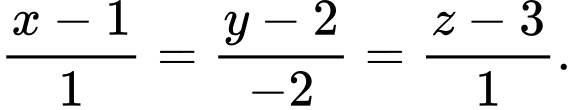
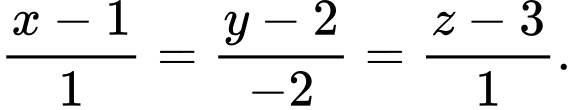
B, 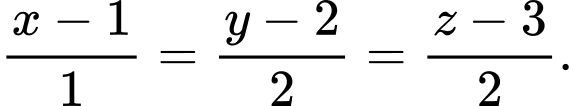
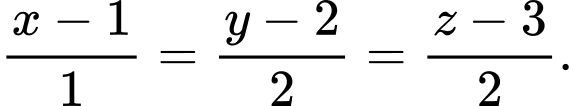
C, 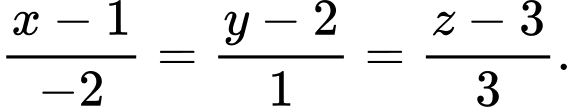
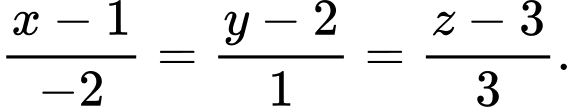
D, 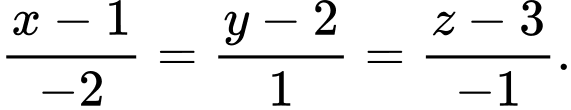
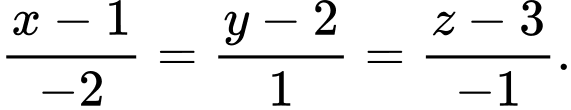
Gọi  là đường thẳng cần tìm.
là đường thẳng cần tìm.
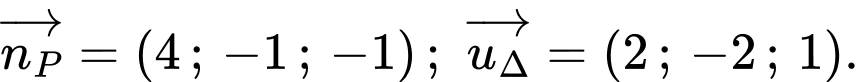
Ta có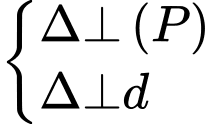
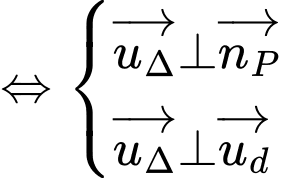
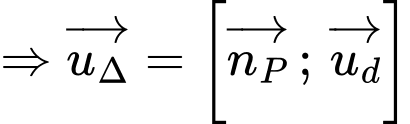

Suy ra phương trình đường thẳng có vectơ chỉ phương và đi qua điểm là
có vectơ chỉ phương và đi qua điểm là
Chọn B. Đáp án: B
 là đường thẳng cần tìm.
là đường thẳng cần tìm.
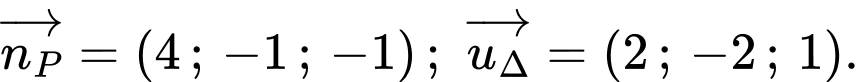
Ta có
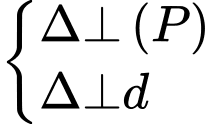
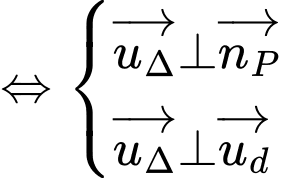
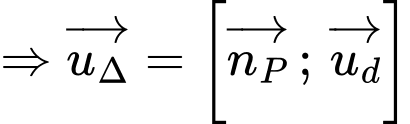

Suy ra phương trình đường thẳng
 có vectơ chỉ phương và đi qua điểm là
có vectơ chỉ phương và đi qua điểm là
Chọn B. Đáp án: B
Câu 16 [55810]: Cho mặt phẳng 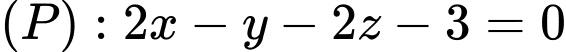 và đường thẳng
và đường thẳng 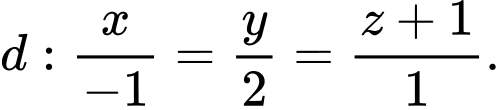 Phương trình tham số của đường thẳng đi qua điểm
Phương trình tham số của đường thẳng đi qua điểm 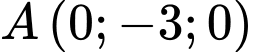 nằm trên mặt phẳng
nằm trên mặt phẳng 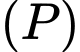 và vuông góc với đường thẳng
và vuông góc với đường thẳng 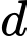 là
là
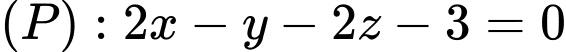 và đường thẳng
và đường thẳng 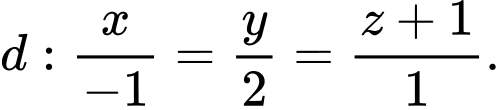 Phương trình tham số của đường thẳng đi qua điểm
Phương trình tham số của đường thẳng đi qua điểm 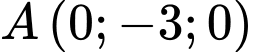 nằm trên mặt phẳng
nằm trên mặt phẳng 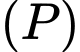 và vuông góc với đường thẳng
và vuông góc với đường thẳng 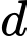 là
là A, 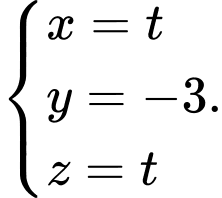
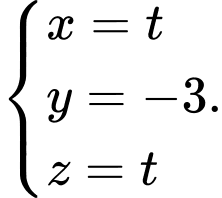
B, 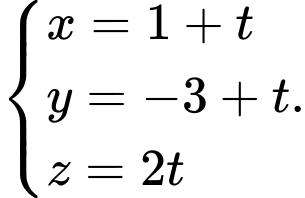
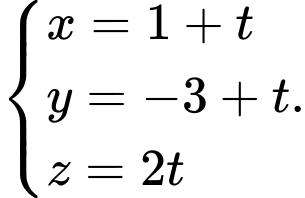
C, 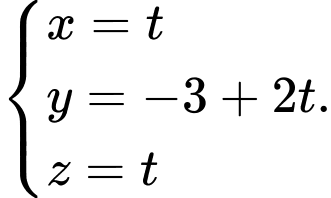
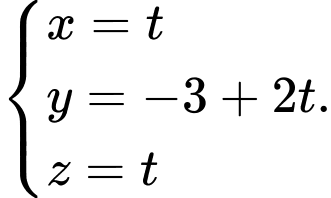
D, 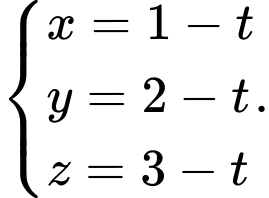
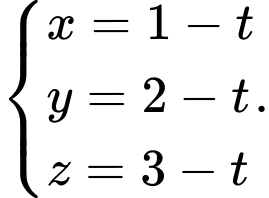
Gọi  là đường thẳng cần tìm, ta có
là đường thẳng cần tìm, ta có  nằm trên
nằm trên 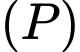 và
và 
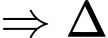 nhận
nhận 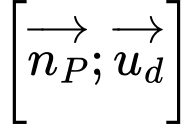 là một VTCP mà
là một VTCP mà 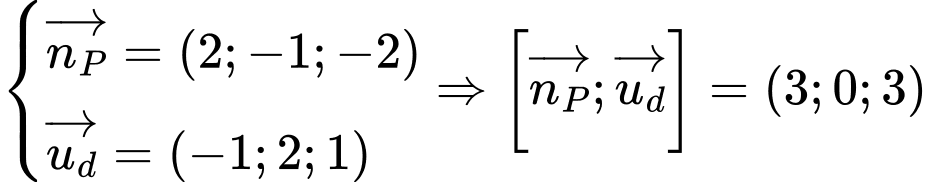
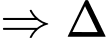 nhận
nhận 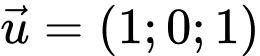 là một VTCP
là một VTCP
mà qua
qua 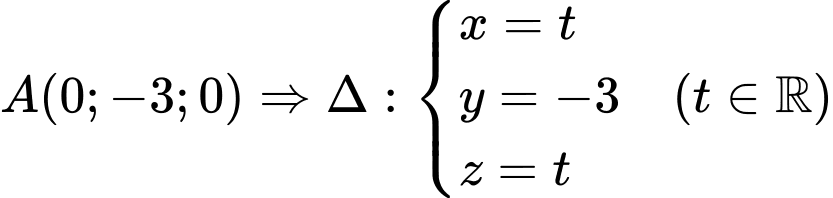
Chọn A. Đáp án: A
 là đường thẳng cần tìm, ta có
là đường thẳng cần tìm, ta có  nằm trên
nằm trên 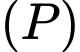 và
và 
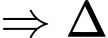 nhận
nhận 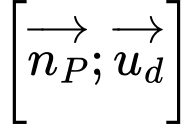 là một VTCP mà
là một VTCP mà 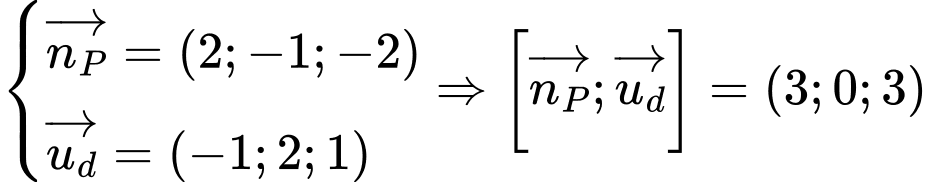
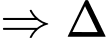 nhận
nhận 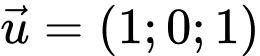 là một VTCP
là một VTCPmà
 qua
qua 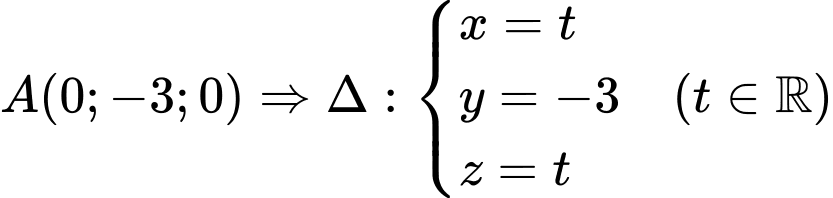
Chọn A. Đáp án: A
Câu 17 [55794]: Trong không gian với hệ tọa độ 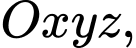 cho tam giác
cho tam giác 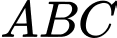 có
có 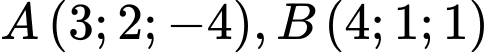 và
và 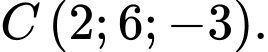 Viết phương trình đường thẳng
Viết phương trình đường thẳng 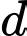 đi qua trọ ng tâm
đi qua trọ ng tâm  của tam giác
của tam giác 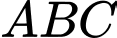 và vuông góc với mặt mặt phẳng
và vuông góc với mặt mặt phẳng 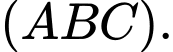
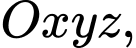 cho tam giác
cho tam giác 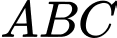 có
có 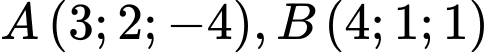 và
và 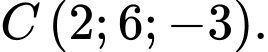 Viết phương trình đường thẳng
Viết phương trình đường thẳng 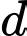 đi qua trọ ng tâm
đi qua trọ ng tâm  của tam giác
của tam giác 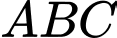 và vuông góc với mặt mặt phẳng
và vuông góc với mặt mặt phẳng 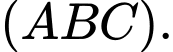
A, 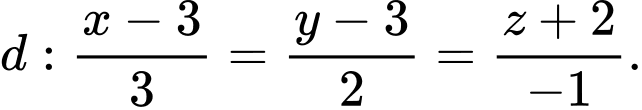
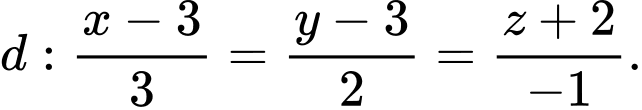
B, 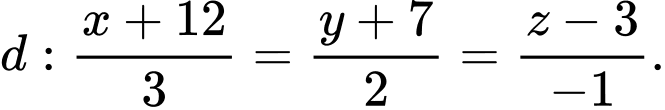
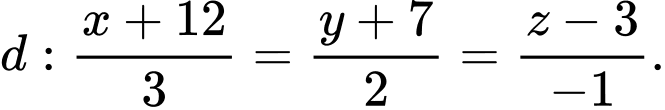
C, 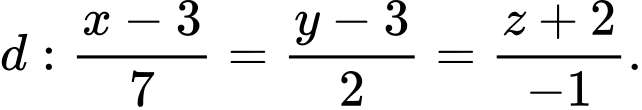
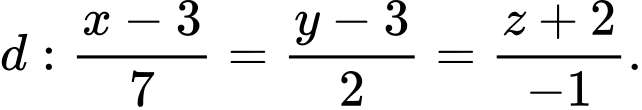
D, 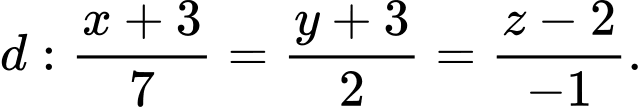
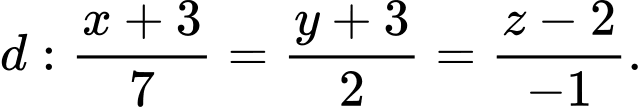
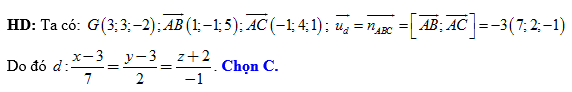 Đáp án: C
Đáp án: C
Câu 18 [55785]: Trong không gian với hệ trục tọa độ 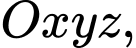 cho đường thẳng
cho đường thẳng 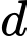 có phương trình
có phương trình 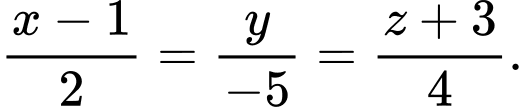 Viết phương trình mặt phẳng
Viết phương trình mặt phẳng  chứa trục
chứa trục 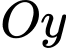 và song song với đường thẳng
và song song với đường thẳng 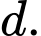
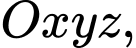 cho đường thẳng
cho đường thẳng 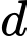 có phương trình
có phương trình 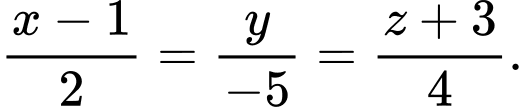 Viết phương trình mặt phẳng
Viết phương trình mặt phẳng  chứa trục
chứa trục 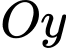 và song song với đường thẳng
và song song với đường thẳng 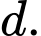
A, 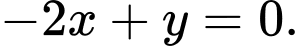
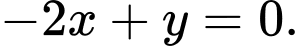
B, 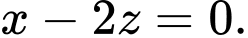
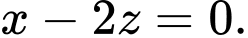
C, 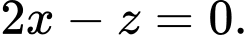
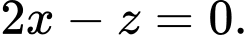
D, 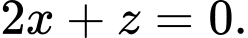
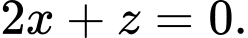
Từ giả thiết ta có: 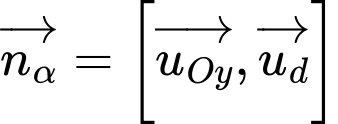
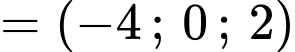
Mặt phẳng đi qua
đi qua  và có vectơ pháp tuyến
và có vectơ pháp tuyến 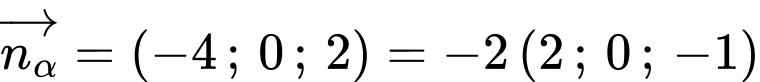
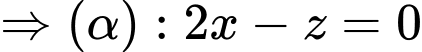
Chọn đáp án C.
Đáp án: C
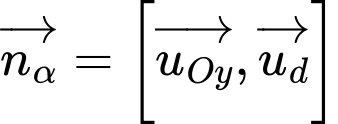
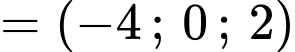
Mặt phẳng
 đi qua
đi qua  và có vectơ pháp tuyến
và có vectơ pháp tuyến 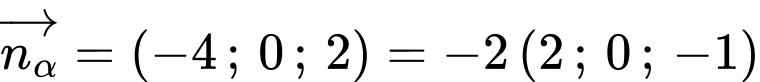
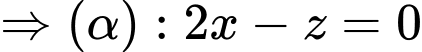
Chọn đáp án C.
Đáp án: C
Câu 19 [579679]: [Đề mẫu HSA 2024]: Trong không gian 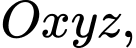 cho đường thẳng
cho đường thẳng 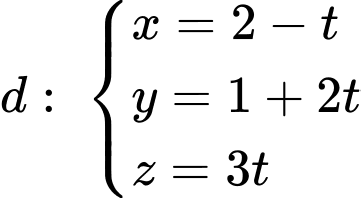 và các điểm
và các điểm 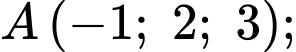
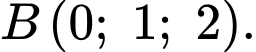 Mặt phẳng
Mặt phẳng 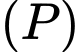 chứa đường thẳng
chứa đường thẳng 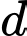 và song song
và song song  có phương trình là
có phương trình là
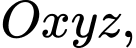 cho đường thẳng
cho đường thẳng 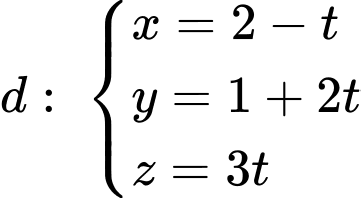 và các điểm
và các điểm 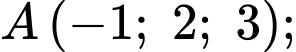
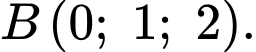 Mặt phẳng
Mặt phẳng 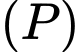 chứa đường thẳng
chứa đường thẳng 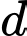 và song song
và song song  có phương trình là
có phương trình là
A, 

B, 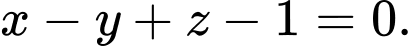
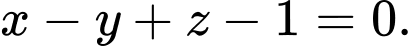
C, 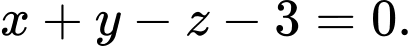
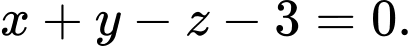
D, 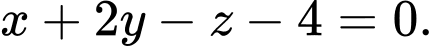
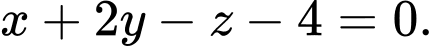
 chứa đường thẳng d và song song với AB
chứa đường thẳng d và song song với AB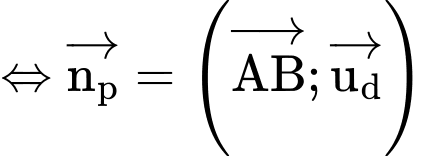
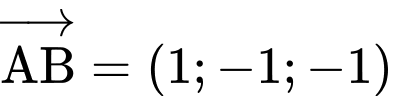
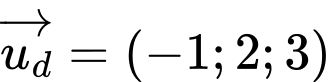
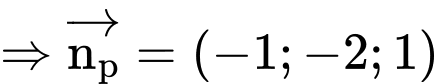
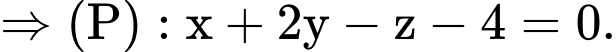
Chọn D. Đáp án: D
Câu 20 [899381]: Trong không gian với hệ tọa độ 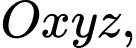 phương trình mặt phẳng song song với đường thẳng
phương trình mặt phẳng song song với đường thẳng 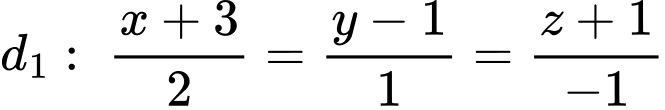 và chứa đường thẳng
và chứa đường thẳng 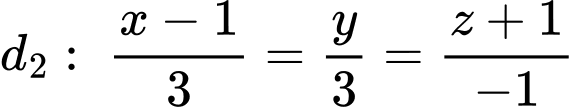 là
là
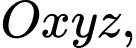 phương trình mặt phẳng song song với đường thẳng
phương trình mặt phẳng song song với đường thẳng 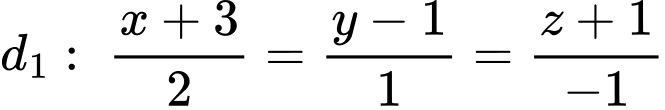 và chứa đường thẳng
và chứa đường thẳng 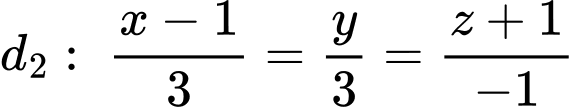 là
là A, 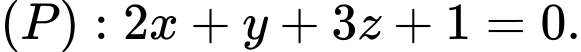
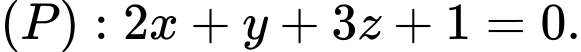
B, 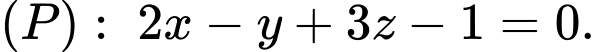
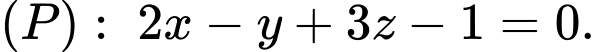
C, 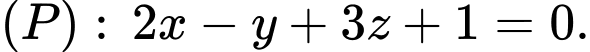
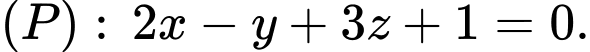
D, 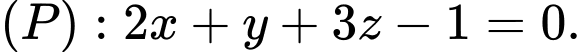
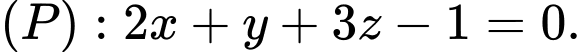
Đường thẳng 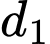 và
và 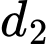 lần lượt có vectơ chỉ phương là
lần lượt có vectơ chỉ phương là 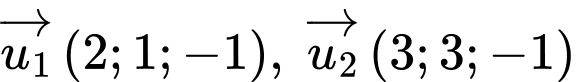
Gọi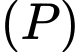 là mặt phẳng cần tìm thì
là mặt phẳng cần tìm thì 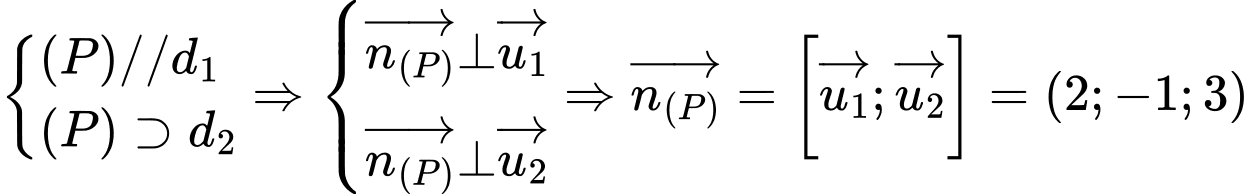
Mặt khác điểm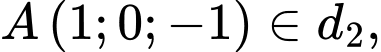 mà
mà 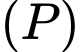 chứa
chứa 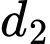 nên
nên 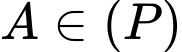 suy ra
suy ra 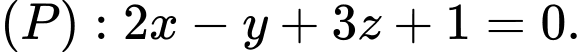
Chọn C. Đáp án: C
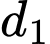 và
và 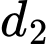 lần lượt có vectơ chỉ phương là
lần lượt có vectơ chỉ phương là 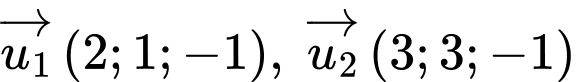
Gọi
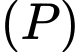 là mặt phẳng cần tìm thì
là mặt phẳng cần tìm thì 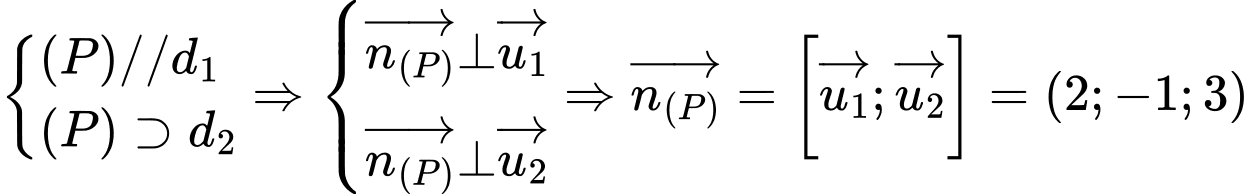
Mặt khác điểm
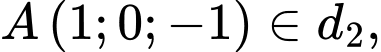 mà
mà 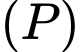 chứa
chứa 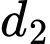 nên
nên 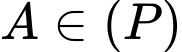 suy ra
suy ra 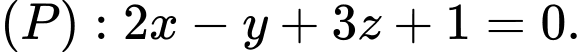
Chọn C. Đáp án: C
Câu 21 [46014]: Trong không gian 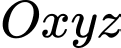 , cho các điểm
, cho các điểm 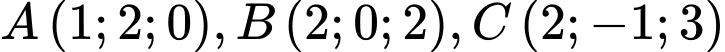 và
và 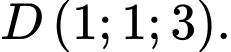 Đường thẳng đi qua
Đường thẳng đi qua  và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 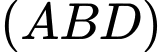 có phương trình là
có phương trình là
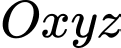 , cho các điểm
, cho các điểm 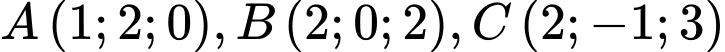 và
và 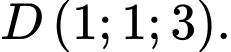 Đường thẳng đi qua
Đường thẳng đi qua  và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 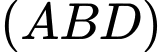 có phương trình là
có phương trình là A, 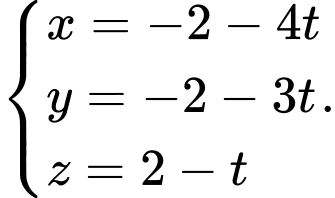
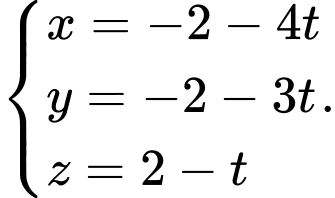
B, 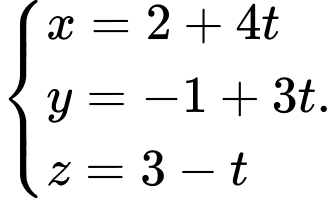
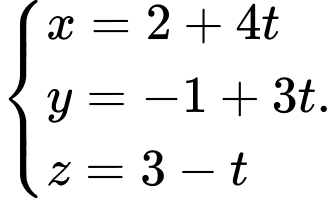
C, 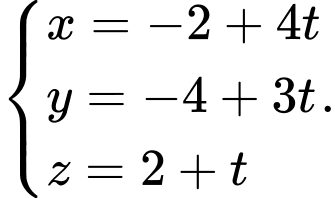
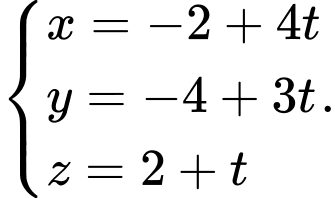
D, 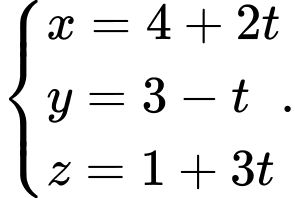
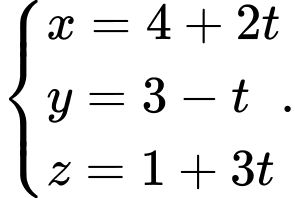
Ta có 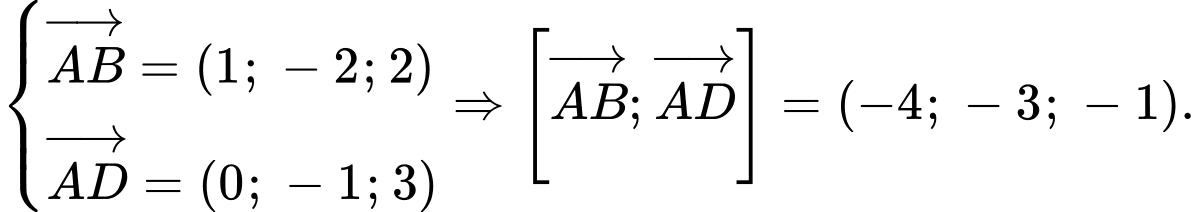
Đường thẳng cần tìm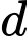 nhận
nhận 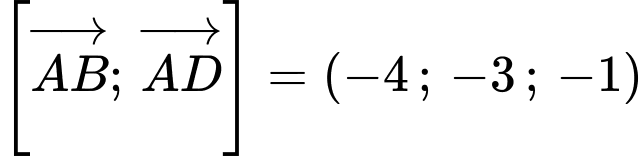 là một VTCP nên nhận
là một VTCP nên nhận 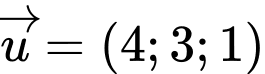 là một VTCP. Kết hợp với
là một VTCP. Kết hợp với 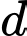 qua
qua 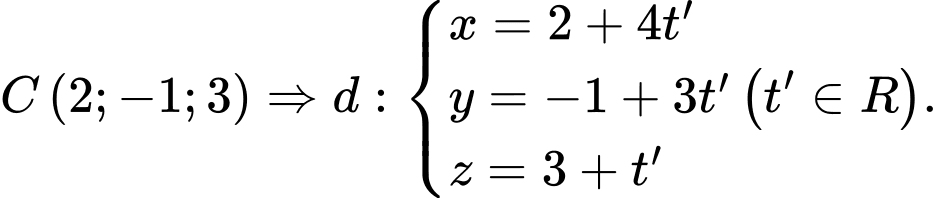
Đặt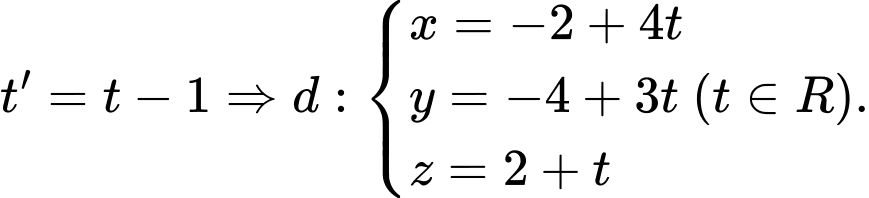 Chọn C.
Đáp án: C
Chọn C.
Đáp án: C
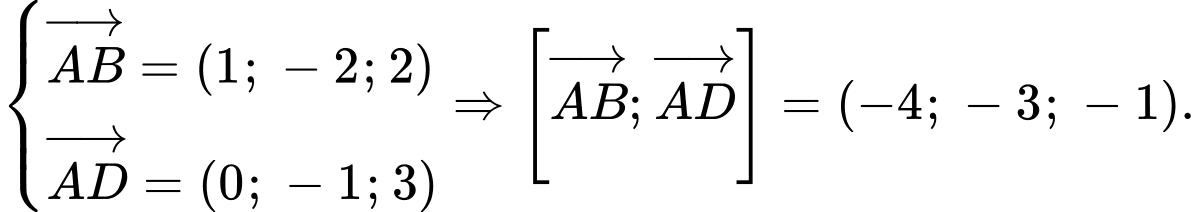
Đường thẳng cần tìm
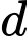 nhận
nhận 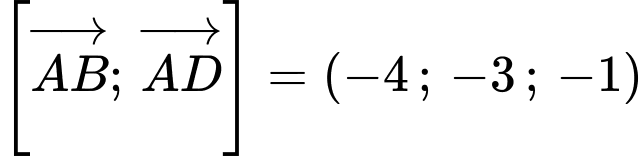 là một VTCP nên nhận
là một VTCP nên nhận 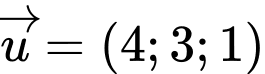 là một VTCP. Kết hợp với
là một VTCP. Kết hợp với 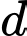 qua
qua 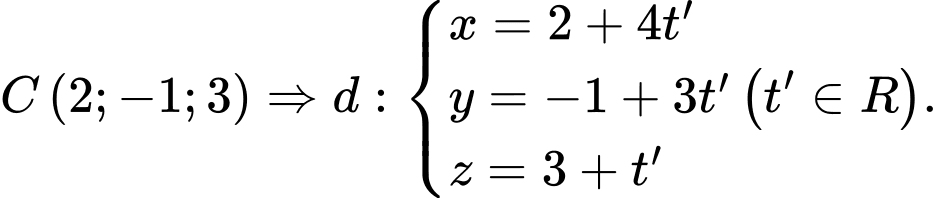
Đặt
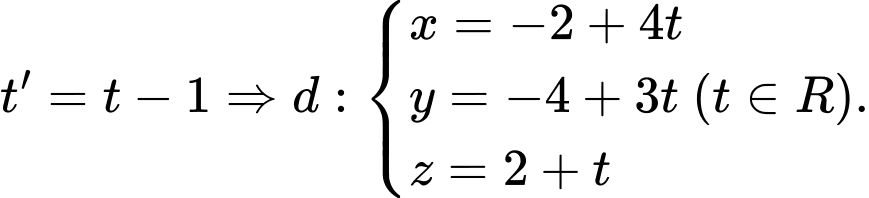 Chọn C.
Đáp án: C
Chọn C.
Đáp án: C
Câu 22 [55797]: Trong không gian tọa độ 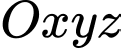 cho
cho 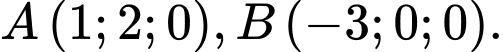 Viết phương trình trung trực
Viết phương trình trung trực  của đoạn
của đoạn  biết
biết  nằm trong mặt phẳng
nằm trong mặt phẳng 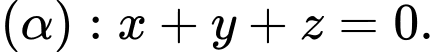
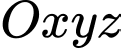 cho
cho 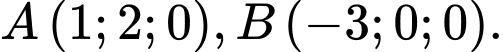 Viết phương trình trung trực
Viết phương trình trung trực  của đoạn
của đoạn  biết
biết  nằm trong mặt phẳng
nằm trong mặt phẳng 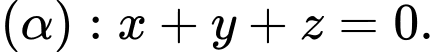
A, 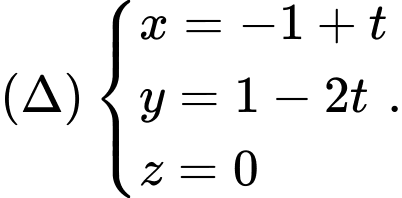
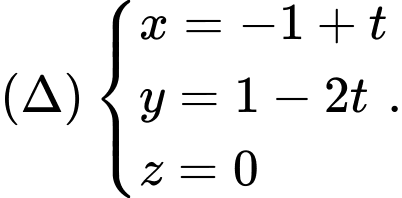
B, 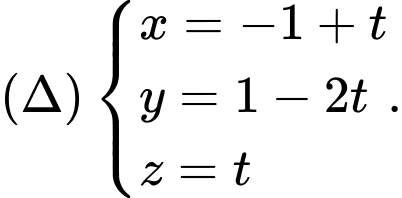
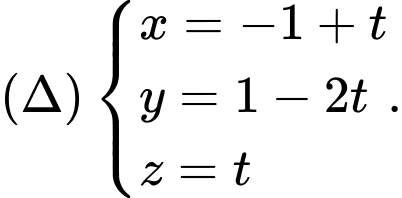
C, 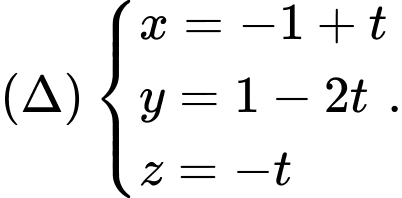
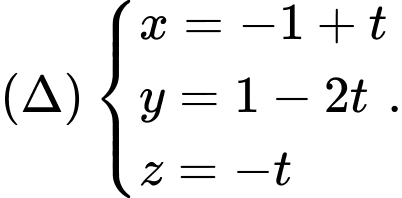
D, 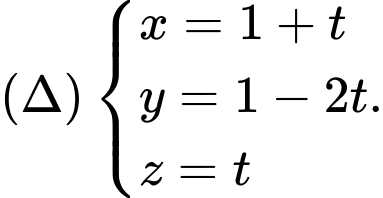
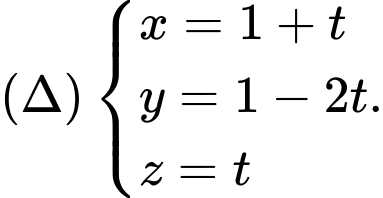
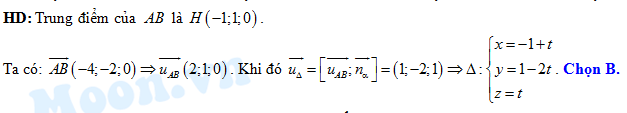 Đáp án: B
Đáp án: B
Câu 23 [163884]: Anh Danh là một nhiếp ảnh gia chuyên săn ảnh chim hoang dã. Giả sử với hệ trục 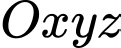 cho trước, anh Danh đang ngắm và ống kính ở vị trí
cho trước, anh Danh đang ngắm và ống kính ở vị trí 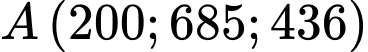 thì có một con gà lôi tía xuất hiện ở vị trí
thì có một con gà lôi tía xuất hiện ở vị trí 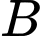 có tọa độ
có tọa độ 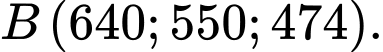 Biết đường thẳng chứa đoạn thẳng nối vị trí ống kính ngắm của anh Danh và con gà lôi tía đi qua điểm
Biết đường thẳng chứa đoạn thẳng nối vị trí ống kính ngắm của anh Danh và con gà lôi tía đi qua điểm 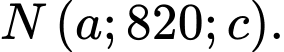 Tính
Tính 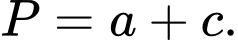
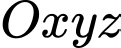 cho trước, anh Danh đang ngắm và ống kính ở vị trí
cho trước, anh Danh đang ngắm và ống kính ở vị trí 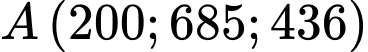 thì có một con gà lôi tía xuất hiện ở vị trí
thì có một con gà lôi tía xuất hiện ở vị trí 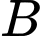 có tọa độ
có tọa độ 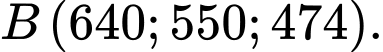 Biết đường thẳng chứa đoạn thẳng nối vị trí ống kính ngắm của anh Danh và con gà lôi tía đi qua điểm
Biết đường thẳng chứa đoạn thẳng nối vị trí ống kính ngắm của anh Danh và con gà lôi tía đi qua điểm 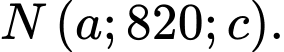 Tính
Tính 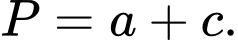
Gọi  là đường thẳng cần tìm.
là đường thẳng cần tìm. 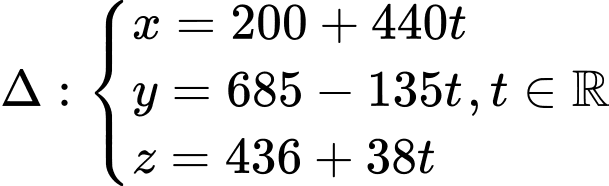
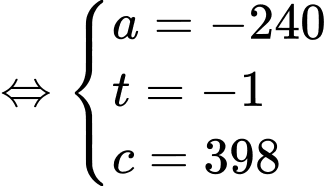
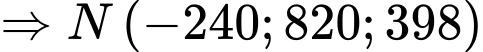 .
.
 là đường thẳng cần tìm.
là đường thẳng cần tìm. Vì  đi qua
đi qua 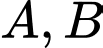 nên có vecto chỉ phương là
nên có vecto chỉ phương là 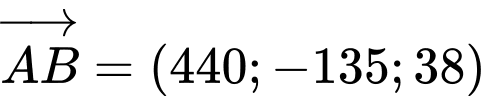 .
.
 đi qua
đi qua 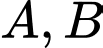 nên có vecto chỉ phương là
nên có vecto chỉ phương là 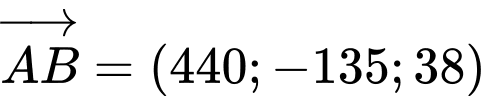 .
. Phương trình đường thẳng  là
là
 là
là 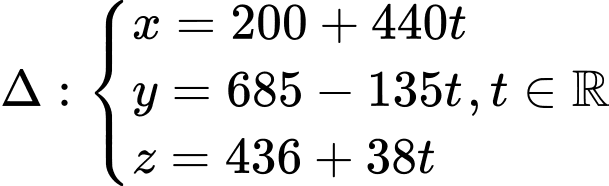
Điểm 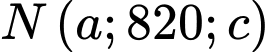 thuộc
thuộc  nên ta có
nên ta có 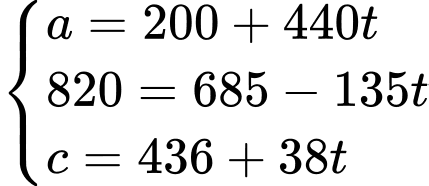
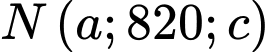 thuộc
thuộc  nên ta có
nên ta có 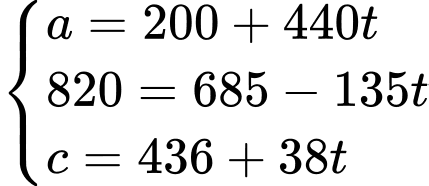
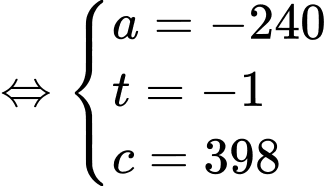
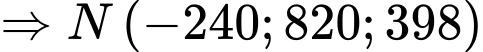 .
. Vậy 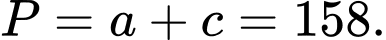
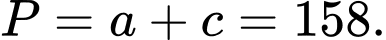
Câu 24 [202978]: Khi gắn hệ toạ độ 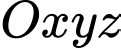 (đơn vị trên mỗi trục tính theo kilômét) vào một sân bay, mặt phẳng
(đơn vị trên mỗi trục tính theo kilômét) vào một sân bay, mặt phẳng 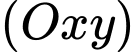 trùng với mặt sân bay. Một máy bay bay theo đường thẳng từ vị trí
trùng với mặt sân bay. Một máy bay bay theo đường thẳng từ vị trí 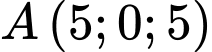 đến vị trí
đến vị trí 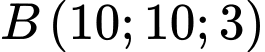 và hạ cánh tại vị trí
và hạ cánh tại vị trí 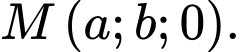 Giá trị của
Giá trị của  bằng bao nhiêu (viết kết quả dưới dạng số thập phân)?
bằng bao nhiêu (viết kết quả dưới dạng số thập phân)?
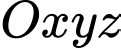 (đơn vị trên mỗi trục tính theo kilômét) vào một sân bay, mặt phẳng
(đơn vị trên mỗi trục tính theo kilômét) vào một sân bay, mặt phẳng 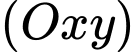 trùng với mặt sân bay. Một máy bay bay theo đường thẳng từ vị trí
trùng với mặt sân bay. Một máy bay bay theo đường thẳng từ vị trí 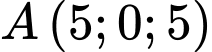 đến vị trí
đến vị trí 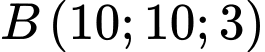 và hạ cánh tại vị trí
và hạ cánh tại vị trí 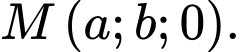 Giá trị của
Giá trị của  bằng bao nhiêu (viết kết quả dưới dạng số thập phân)?
bằng bao nhiêu (viết kết quả dưới dạng số thập phân)?
Phương trình đường thẳng  là:
là: 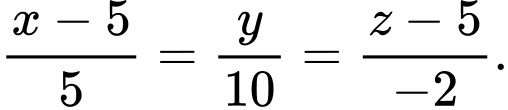
Vì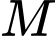 thuộc
thuộc  nên tồn tại số thực
nên tồn tại số thực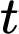 sao cho
sao cho 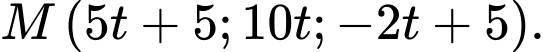
Ngoài ra,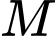 thuộc mặt phẳng
thuộc mặt phẳng 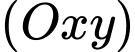 nên
nên 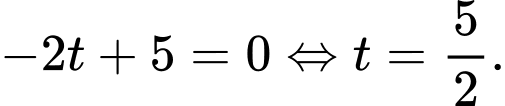
Suy ra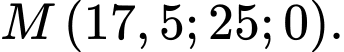 Vậy a+b=17,5+25=42,5.
Vậy a+b=17,5+25=42,5.
 là:
là: 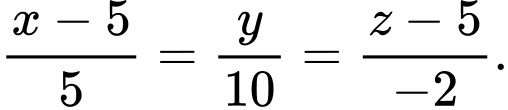
Vì
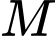 thuộc
thuộc  nên tồn tại số thực
nên tồn tại số thực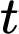 sao cho
sao cho 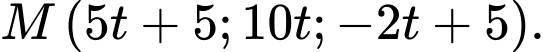
Ngoài ra,
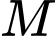 thuộc mặt phẳng
thuộc mặt phẳng 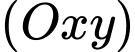 nên
nên 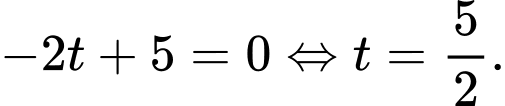
Suy ra
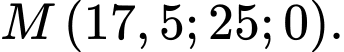 Vậy a+b=17,5+25=42,5.
Vậy a+b=17,5+25=42,5.
Câu 25 [202968]: Trong không gian 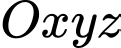 cho trước (1 đơn vị =
cho trước (1 đơn vị =  ), có một chú kiến vàng và một chú kiến đen bò trên hai sợi dây thẳng khác nhau. Giả sử tại thời điểm
), có một chú kiến vàng và một chú kiến đen bò trên hai sợi dây thẳng khác nhau. Giả sử tại thời điểm 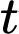 (tính bằng phút), kiến vàng ở tại vị trí
(tính bằng phút), kiến vàng ở tại vị trí 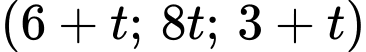 trên đường thẳng
trên đường thẳng 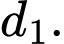 Cùng thời điểm đó, kiến đen ở tại vị trí
Cùng thời điểm đó, kiến đen ở tại vị trí 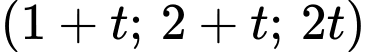 trên đường thẳng
trên đường thẳng 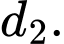 Khoảng cách ngắn nhất giữa hai chú kiến là bao nhiêu
Khoảng cách ngắn nhất giữa hai chú kiến là bao nhiêu 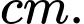 Viết kết quả làm tròn đến hàng phần mười.
Viết kết quả làm tròn đến hàng phần mười.
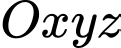 cho trước (1 đơn vị =
cho trước (1 đơn vị =  ), có một chú kiến vàng và một chú kiến đen bò trên hai sợi dây thẳng khác nhau. Giả sử tại thời điểm
), có một chú kiến vàng và một chú kiến đen bò trên hai sợi dây thẳng khác nhau. Giả sử tại thời điểm 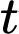 (tính bằng phút), kiến vàng ở tại vị trí
(tính bằng phút), kiến vàng ở tại vị trí 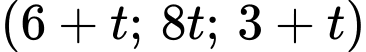 trên đường thẳng
trên đường thẳng 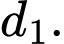 Cùng thời điểm đó, kiến đen ở tại vị trí
Cùng thời điểm đó, kiến đen ở tại vị trí 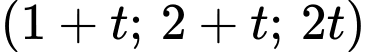 trên đường thẳng
trên đường thẳng 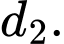 Khoảng cách ngắn nhất giữa hai chú kiến là bao nhiêu
Khoảng cách ngắn nhất giữa hai chú kiến là bao nhiêu 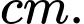 Viết kết quả làm tròn đến hàng phần mười.
Viết kết quả làm tròn đến hàng phần mười.
Khoảng cách giữa hai chú kiến bằng 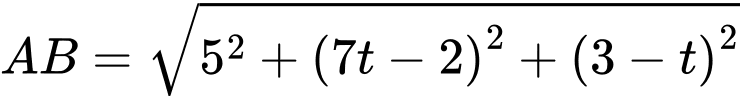
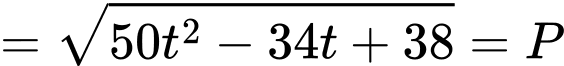
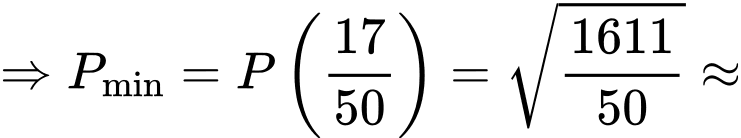
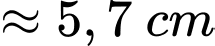
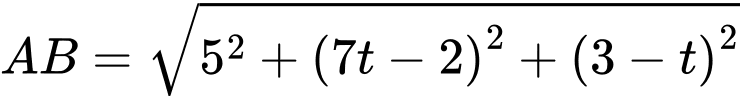
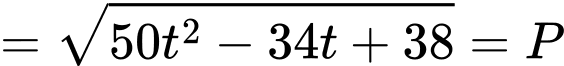
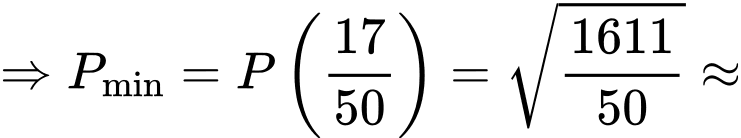
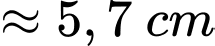
Câu 26 [404934]: Cho đường thẳng 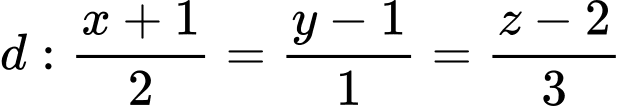 và mặt phẳng
và mặt phẳng 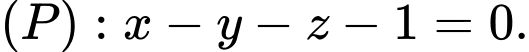 Gọi
Gọi  là đường thẳng đi qua điểm
là đường thẳng đi qua điểm 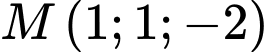 song song với
song song với 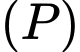 và vuông góc với
và vuông góc với 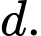 Biết đường thẳng
Biết đường thẳng  đi qua điểm
đi qua điểm 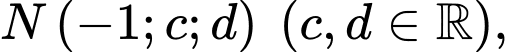 giá trị của
giá trị của  bằng bao nhiêu?
bằng bao nhiêu?
Đáp số: ………………
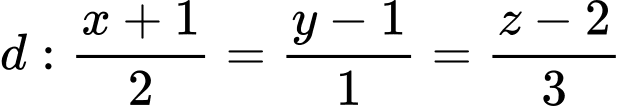 và mặt phẳng
và mặt phẳng 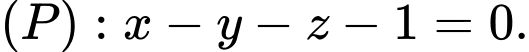 Gọi
Gọi  là đường thẳng đi qua điểm
là đường thẳng đi qua điểm 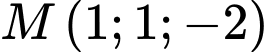 song song với
song song với 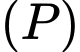 và vuông góc với
và vuông góc với 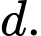 Biết đường thẳng
Biết đường thẳng  đi qua điểm
đi qua điểm 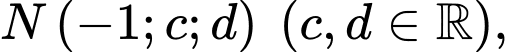 giá trị của
giá trị của  bằng bao nhiêu?
bằng bao nhiêu?Đáp số: ………………
Phương trình tham số của 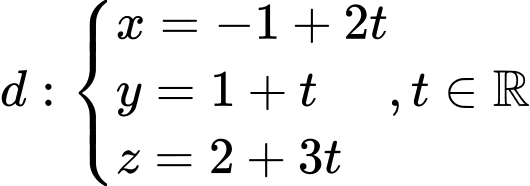 có véc-tơ chỉ phương
có véc-tơ chỉ phương 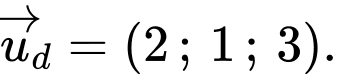
Mặt phẳng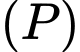 có véc-tơ pháp tuyến
có véc-tơ pháp tuyến 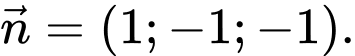
Đường thẳng đi qua điểm
đi qua điểm 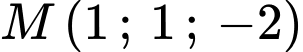 và
và 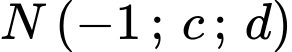
Khi đó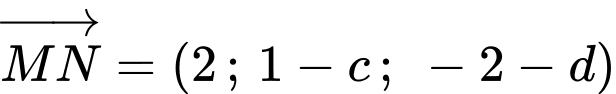 là véc-tơ chỉ phương của
là véc-tơ chỉ phương của 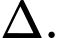 (1)
(1)
Lại có: Đưởng thẳng vuông góc với đường thẳng
vuông góc với đường thẳng 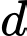 và song song với mặt phẳng
và song song với mặt phẳng 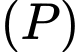
Suy ra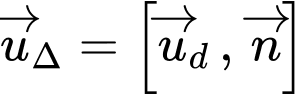
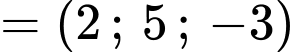 (2)
(2)
Từ (1) và (2) suy ra: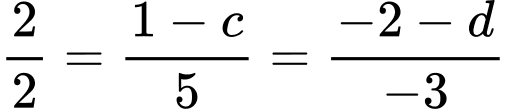
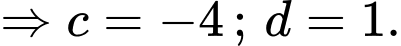
Do đó,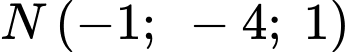
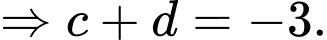
Đáp án: -3.
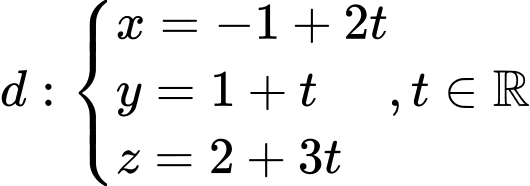 có véc-tơ chỉ phương
có véc-tơ chỉ phương 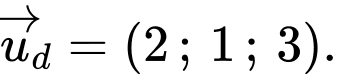
Mặt phẳng
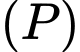 có véc-tơ pháp tuyến
có véc-tơ pháp tuyến 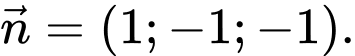
Đường thẳng
 đi qua điểm
đi qua điểm 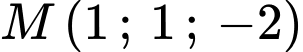 và
và 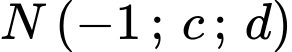
Khi đó
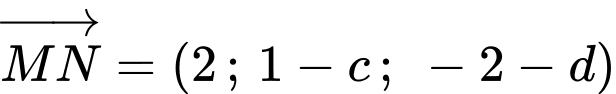 là véc-tơ chỉ phương của
là véc-tơ chỉ phương của 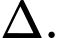 (1)
(1)
Lại có: Đưởng thẳng
 vuông góc với đường thẳng
vuông góc với đường thẳng 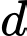 và song song với mặt phẳng
và song song với mặt phẳng 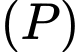
Suy ra
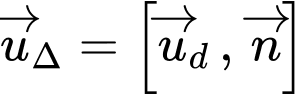
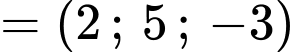 (2)
(2)
Từ (1) và (2) suy ra:
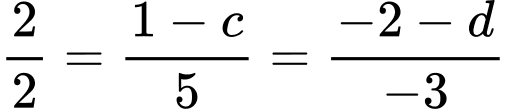
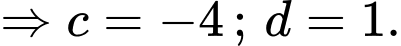
Do đó,
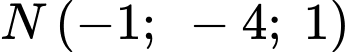
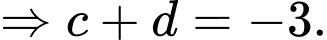
Đáp án: -3.
Câu 27 [404935]: Trong không gian 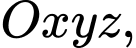 cho điểm
cho điểm 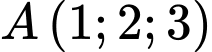 và hai mặt phẳng
và hai mặt phẳng 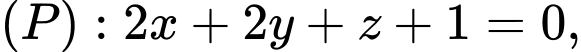
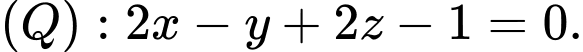 Gọi
Gọi 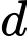 là đường thẳng đi qua
là đường thẳng đi qua 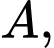 song song với cả
song song với cả 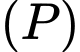 và
và  Biết đường thẳng
Biết đường thẳng 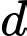 cắt mặt phẳng
cắt mặt phẳng 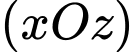 tại điểm
tại điểm 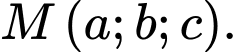 Tính
Tính 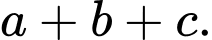
Đáp số: ………………
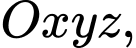 cho điểm
cho điểm 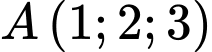 và hai mặt phẳng
và hai mặt phẳng 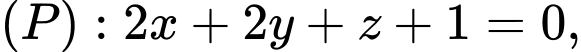
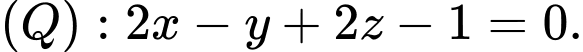 Gọi
Gọi 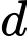 là đường thẳng đi qua
là đường thẳng đi qua 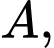 song song với cả
song song với cả 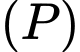 và
và  Biết đường thẳng
Biết đường thẳng 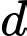 cắt mặt phẳng
cắt mặt phẳng 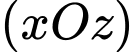 tại điểm
tại điểm 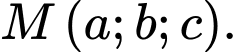 Tính
Tính 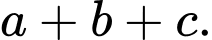
Đáp số: ………………
Ta có:
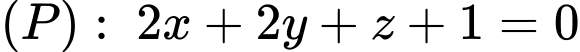 có một vecto pháp tuyến là
có một vecto pháp tuyến là 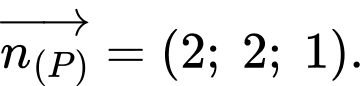
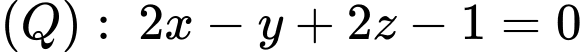 có một vecto pháp tuyến là
có một vecto pháp tuyến là 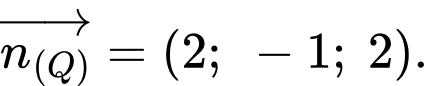
Đường thẳng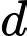 có vecto chỉ phương là
có vecto chỉ phương là 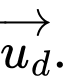
Do đường thẳng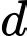 song song với cả
song song với cả 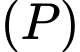 và
và  nên
nên 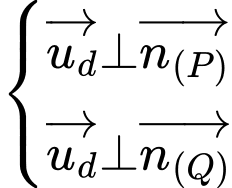
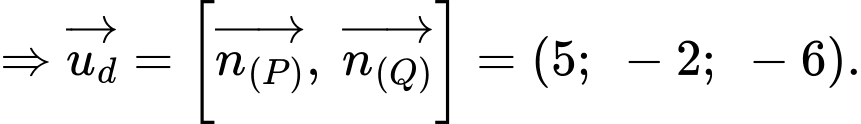
Mặt khác, đường thẳng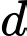 đi qua
đi qua 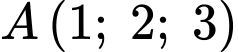 và có vecto chỉ phương
và có vecto chỉ phương 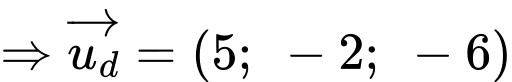 nên phương trình chính tắc của
nên phương trình chính tắc của 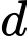 là
là 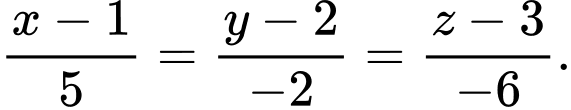
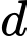 cắt
cắt 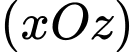 tại điểm
tại điểm 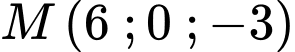
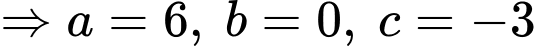
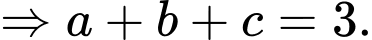
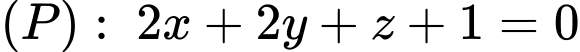 có một vecto pháp tuyến là
có một vecto pháp tuyến là 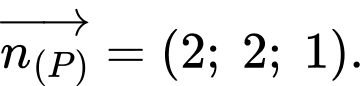
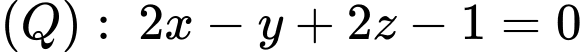 có một vecto pháp tuyến là
có một vecto pháp tuyến là 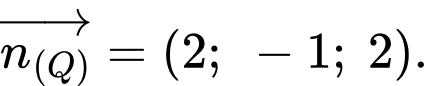
Đường thẳng
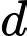 có vecto chỉ phương là
có vecto chỉ phương là 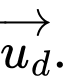
Do đường thẳng
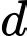 song song với cả
song song với cả 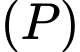 và
và  nên
nên 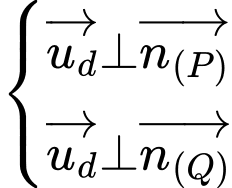
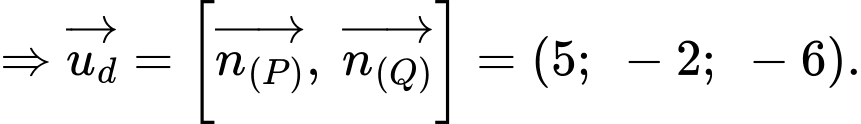
Mặt khác, đường thẳng
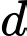 đi qua
đi qua 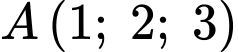 và có vecto chỉ phương
và có vecto chỉ phương 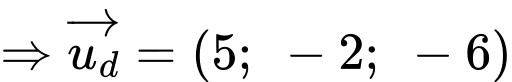 nên phương trình chính tắc của
nên phương trình chính tắc của 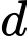 là
là 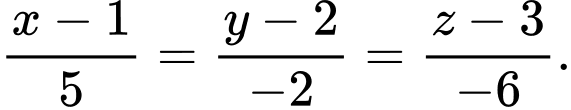
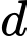 cắt
cắt 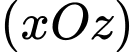 tại điểm
tại điểm 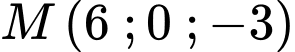
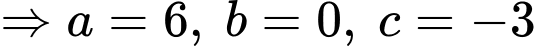
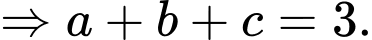
Câu 28 [396431]: Trong không gian với hệ tọa độ 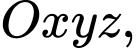 phương trình mặt phẳng chứa đường thẳng
phương trình mặt phẳng chứa đường thẳng 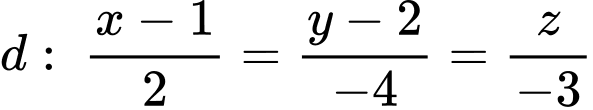 và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 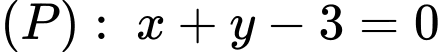 là
là 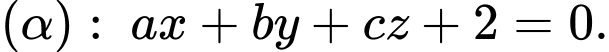 Tính
Tính 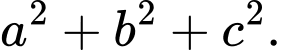
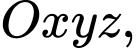 phương trình mặt phẳng chứa đường thẳng
phương trình mặt phẳng chứa đường thẳng 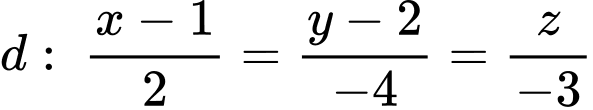 và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 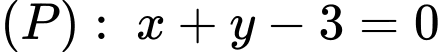 là
là 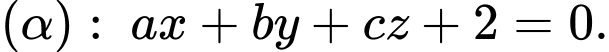 Tính
Tính 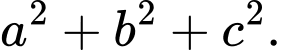
Mặt phẳng  chứa đường thẳng
chứa đường thẳng 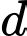 và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 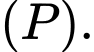
Suy ra có
có 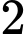 vectơ chỉ phương là
vectơ chỉ phương là 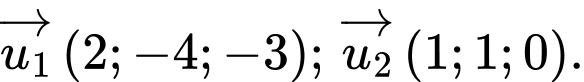
Suy ra một vectơ pháp tuyến của mặt phẳng là
là 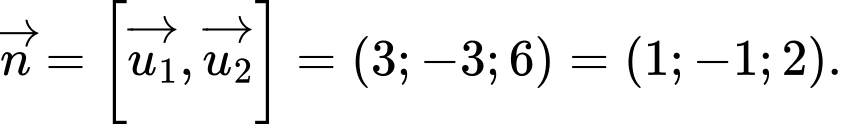
Lấy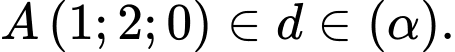
Vậy phương trình mặt phẳng là
là 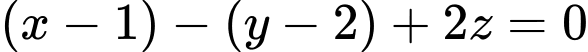
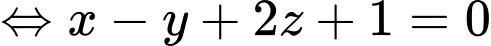

Suy ra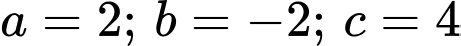
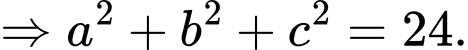
Điền đáp án: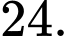
 chứa đường thẳng
chứa đường thẳng 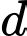 và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 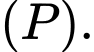
Suy ra
 có
có 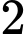 vectơ chỉ phương là
vectơ chỉ phương là 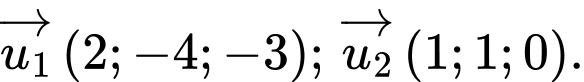
Suy ra một vectơ pháp tuyến của mặt phẳng
 là
là 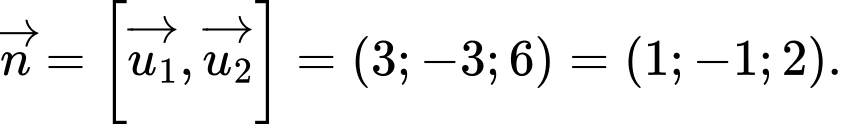
Lấy
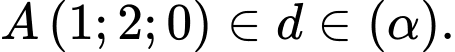
Vậy phương trình mặt phẳng
 là
là 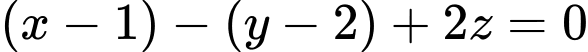
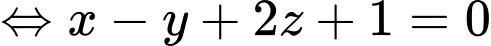

Suy ra
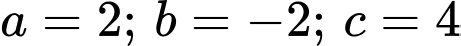
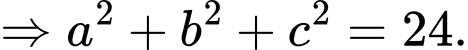
Điền đáp án:
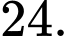
Câu 29 [396432]: Trong không gian với hệ tọa độ 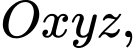 cho hai đường thẳng chéo nhau
cho hai đường thẳng chéo nhau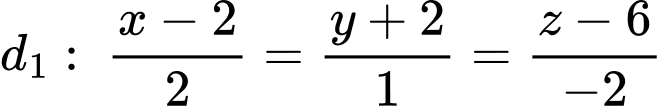 và
và 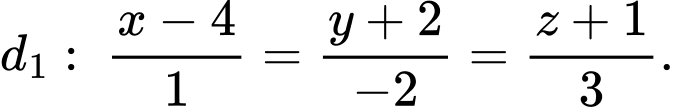 Phương trình mặt phẳng
Phương trình mặt phẳng 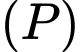 chứa đường thẳng
chứa đường thẳng 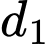 và song song với đường thẳng
và song song với đường thẳng 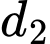 là
là 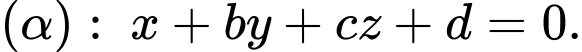 Tính
Tính 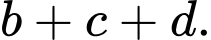
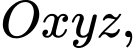 cho hai đường thẳng chéo nhau
cho hai đường thẳng chéo nhau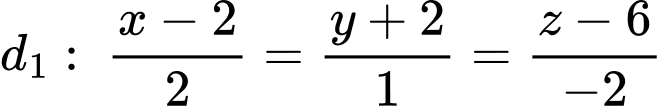 và
và 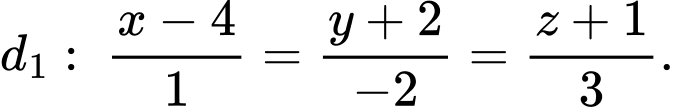 Phương trình mặt phẳng
Phương trình mặt phẳng 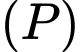 chứa đường thẳng
chứa đường thẳng 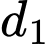 và song song với đường thẳng
và song song với đường thẳng 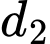 là
là 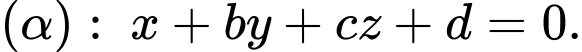 Tính
Tính 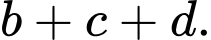
Ta có: 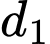 có vectơ chỉ phương
có vectơ chỉ phương 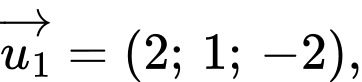
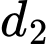 có vectơ chỉ phương
có vectơ chỉ phương 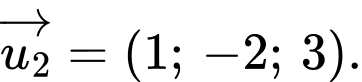
Mặt phẳng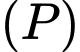 có vectơ pháp tuyến là
có vectơ pháp tuyến là
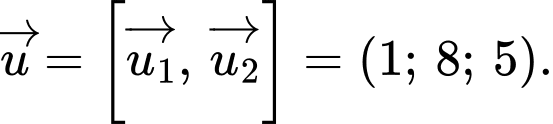
Phương trình mặt phẳng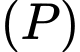 đi qua
đi qua 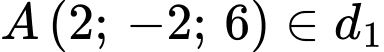 và có vectơ pháp tuyến
và có vectơ pháp tuyến 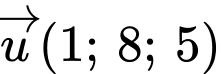 là
là 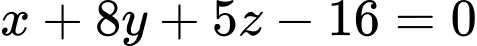
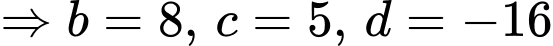

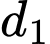 có vectơ chỉ phương
có vectơ chỉ phương 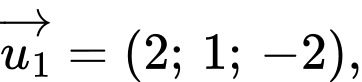
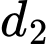 có vectơ chỉ phương
có vectơ chỉ phương 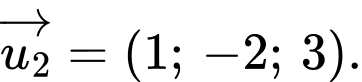
Mặt phẳng
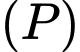 có vectơ pháp tuyến là
có vectơ pháp tuyến là 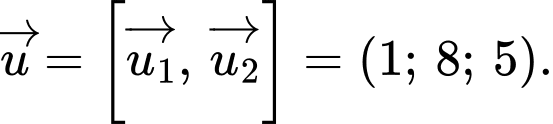
Phương trình mặt phẳng
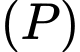 đi qua
đi qua 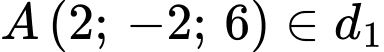 và có vectơ pháp tuyến
và có vectơ pháp tuyến 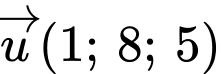 là
là 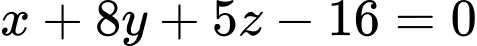
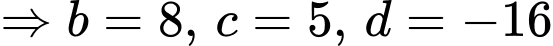

Câu 30 [404892]: Trong không gian 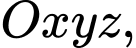 cho mặt phẳng
cho mặt phẳng  vuông góc với
vuông góc với 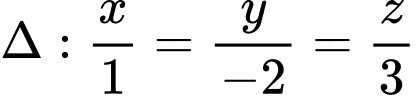 và
và  cắt trục
cắt trục  trục
trục 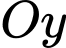 và tia
và tia  lần lượt tại
lần lượt tại 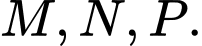 Biết rằng thể tích khối tứ diện
Biết rằng thể tích khối tứ diện 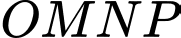 bằng 6. Độ dài đoạn thẳng
bằng 6. Độ dài đoạn thẳng 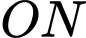 bằng bao nhiêu?
bằng bao nhiêu?
Đáp số: ………………
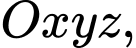 cho mặt phẳng
cho mặt phẳng  vuông góc với
vuông góc với 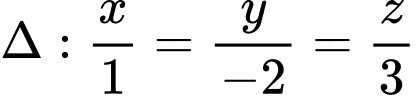 và
và  cắt trục
cắt trục  trục
trục 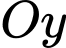 và tia
và tia  lần lượt tại
lần lượt tại 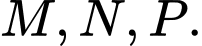 Biết rằng thể tích khối tứ diện
Biết rằng thể tích khối tứ diện 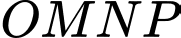 bằng 6. Độ dài đoạn thẳng
bằng 6. Độ dài đoạn thẳng 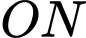 bằng bao nhiêu?
bằng bao nhiêu?Đáp số: ………………
Đường thẳng 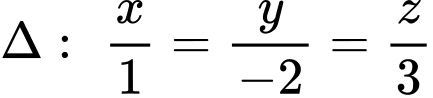 có 1 VTCP là
có 1 VTCP là 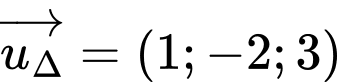 .
.
Vì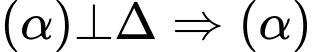 có 1 VTPT là
có 1 VTPT là 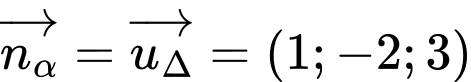 , khi đó phương trình mặt phẳng
, khi đó phương trình mặt phẳng  có dạng:
có dạng: 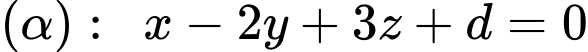 .
.
Ta có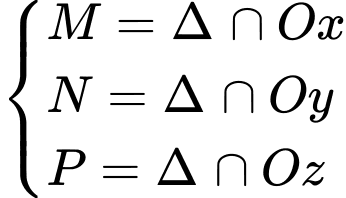
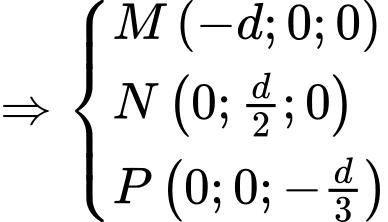
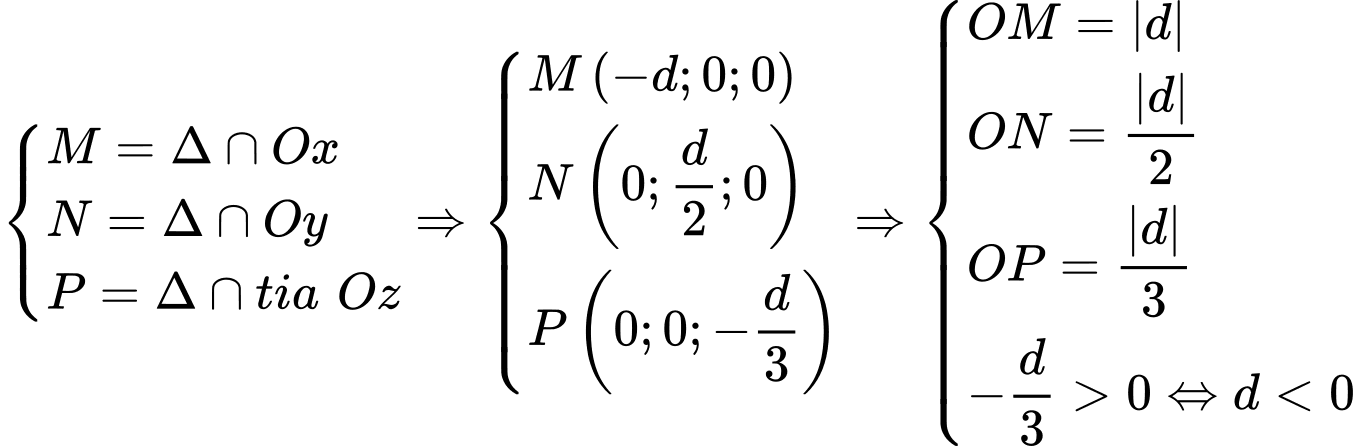 .
.
Vì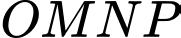 là tứ diện vuông tại
là tứ diện vuông tại  nên
nên
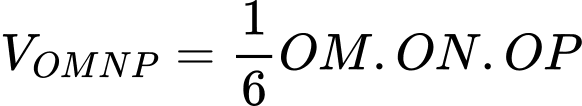
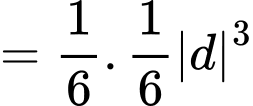
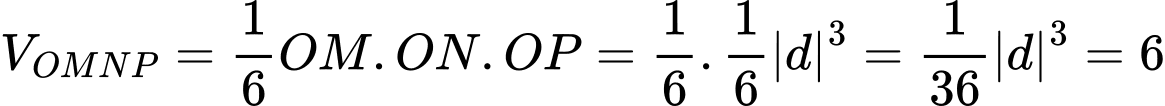
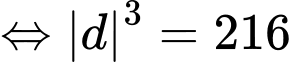
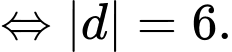 .
.
Vậy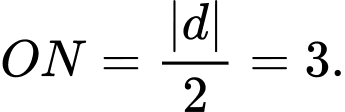
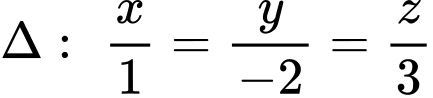 có 1 VTCP là
có 1 VTCP là 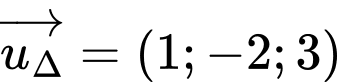 .
. Vì
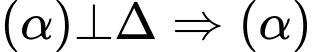 có 1 VTPT là
có 1 VTPT là 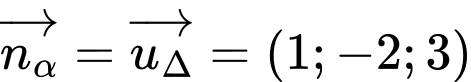 , khi đó phương trình mặt phẳng
, khi đó phương trình mặt phẳng  có dạng:
có dạng: 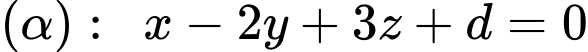 .
. Ta có
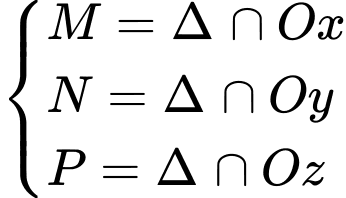
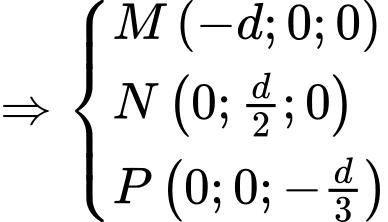
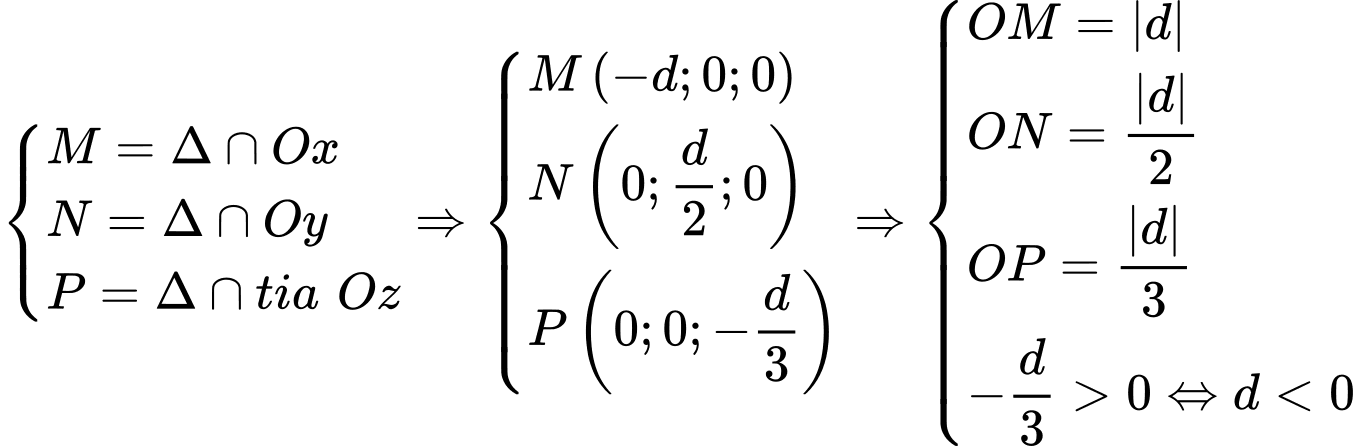 .
.Vì
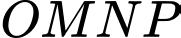 là tứ diện vuông tại
là tứ diện vuông tại  nên
nên
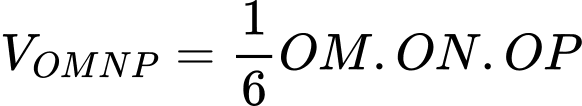
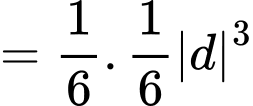
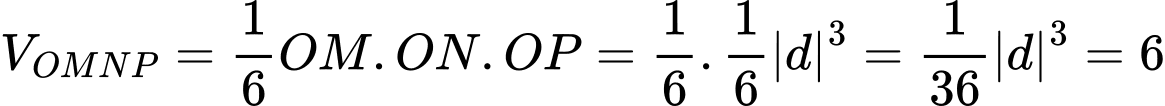
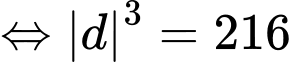
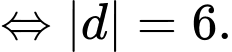 .
. Vậy
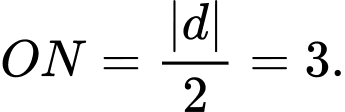
Câu 31 [202973]: Một tháp phát sóng cao 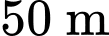 đặt ở góc
đặt ở góc  của sân hình chữ nhật
của sân hình chữ nhật  Để giữ cho tháp không bị đổ, người ta có cột rất nhiều dây cáp quanh tháp và cố định tại các vị trí trên mặt đất. Hai chú kiến vàng và kiến đen bắt đầu leo lên hai dây cáp
Để giữ cho tháp không bị đổ, người ta có cột rất nhiều dây cáp quanh tháp và cố định tại các vị trí trên mặt đất. Hai chú kiến vàng và kiến đen bắt đầu leo lên hai dây cáp 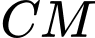 và
và 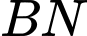 (từ
(từ  và
và 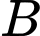 ) với vận tốc lần lượt là
) với vận tốc lần lượt là 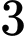 m/phút và
m/phút và 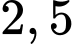 m/phút (xem hình vẽ). Hỏi sau 10 phút thì hai chú kiến cách nhau bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?
m/phút (xem hình vẽ). Hỏi sau 10 phút thì hai chú kiến cách nhau bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?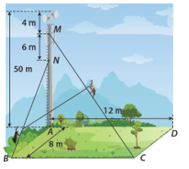
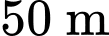 đặt ở góc
đặt ở góc 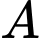 của sân hình chữ nhật
của sân hình chữ nhật 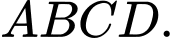 Để giữ cho tháp không bị đổ, người ta có cột rất nhiều dây cáp quanh tháp và cố định tại các vị trí trên mặt đất. Hai chú kiến vàng và kiến đen bắt đầu leo lên hai dây cáp
Để giữ cho tháp không bị đổ, người ta có cột rất nhiều dây cáp quanh tháp và cố định tại các vị trí trên mặt đất. Hai chú kiến vàng và kiến đen bắt đầu leo lên hai dây cáp 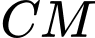 và
và 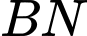 (từ
(từ  và
và 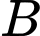 ) với vận tốc lần lượt là
) với vận tốc lần lượt là 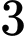 m/phút và
m/phút và 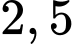 m/phút (xem hình vẽ). Hỏi sau 10 phút thì hai chú kiến cách nhau bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?
m/phút (xem hình vẽ). Hỏi sau 10 phút thì hai chú kiến cách nhau bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?
Điền đáp án: 6,15 m.
* Đặt gốc toạ độ tại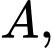 trục
trục 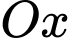 chứa cạnh
chứa cạnh  trục
trục 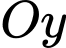 chứa cạnh
chứa cạnh 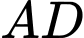 và trục
và trục  chứa cạnh
chứa cạnh 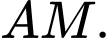
- Toạ độ các điểm là: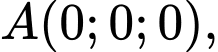
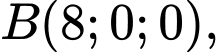
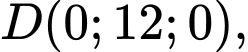
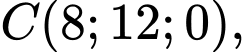
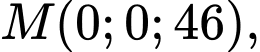
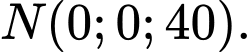
* Tính chiều dài của dây cáp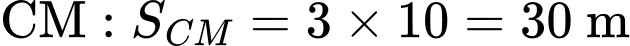 và
và 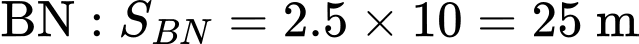 :
:
- Dây cáp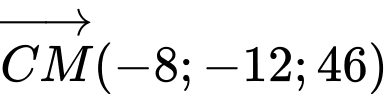 :
:
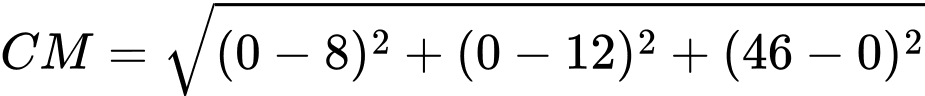
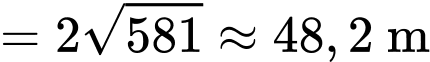
- Dây cáp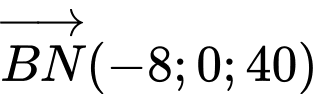 :
: 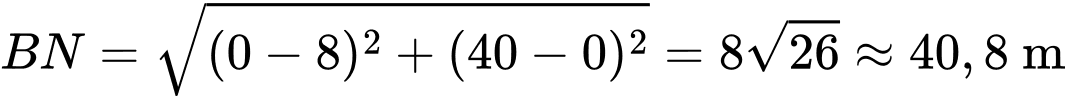
* Tính quãng đường hai chú kiến leo lên sau 10 phút:
- Quãng đường chú kiến vàng leo lên dây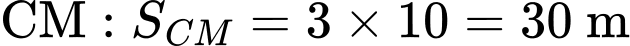
- Quãng đường chú kiến đen leo lên dây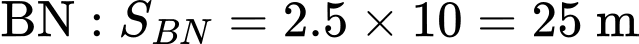
* Xác định vị trí của hai chú kiến trên các dây cáp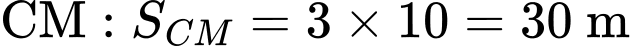 và
và 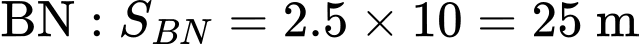 sau 10 phút:
sau 10 phút:
- Tỉ lệ vị trí của chú kiến vàng trên dây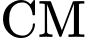 :
: 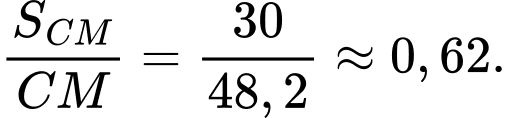
- Tọa độ của chú kiến vàng sau 10 phút là: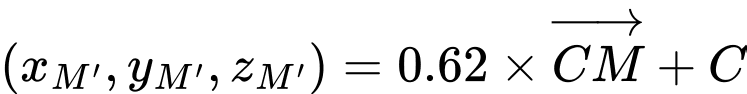
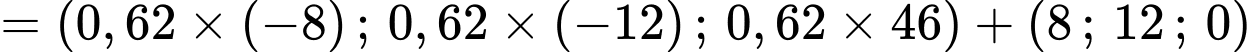
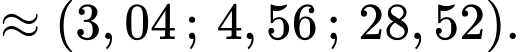
- Tỉ lệ vị trí của chú kiến đen trên dây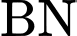 :
: 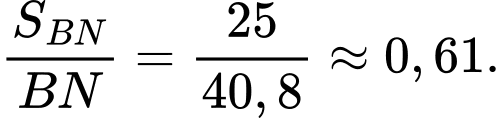
- Tọa độ của chú kiến đen sau 10 phút là:

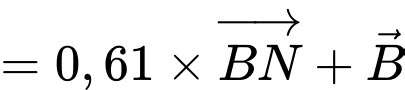
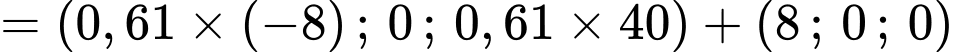
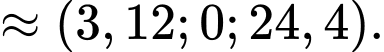
* Tính khoảng cách giữa hai chú kiến Khoảng cách giữa hai chú kiến là:
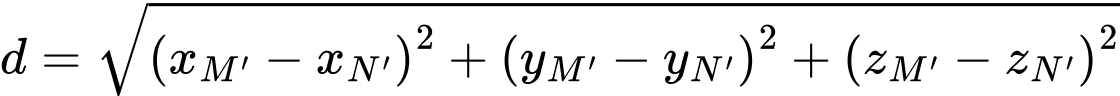
Thay các giá trị vào:
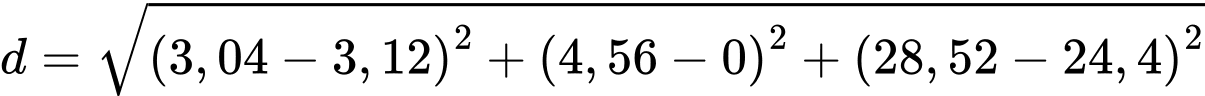
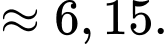
Vậy sau 10 phút, khoảng cách giữa hai chú kiến là khoảng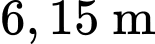 (làm tròn đến hàng phần trăm).
(làm tròn đến hàng phần trăm).
* Đặt gốc toạ độ tại
 trục
trục 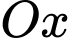 chứa cạnh
chứa cạnh  trục
trục 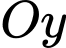 chứa cạnh
chứa cạnh 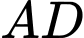 và trục
và trục  chứa cạnh
chứa cạnh 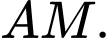
- Toạ độ các điểm là:
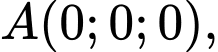
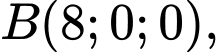
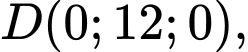
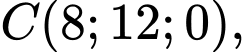
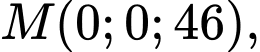
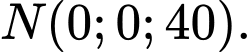
* Tính chiều dài của dây cáp
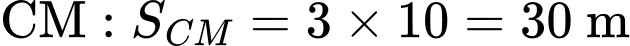 và
và 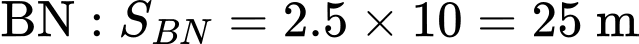 :
:
- Dây cáp
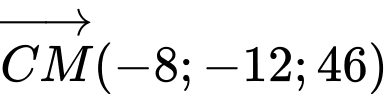 :
:
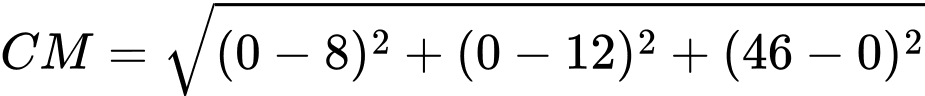
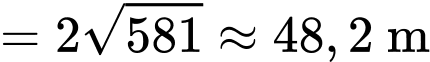
- Dây cáp
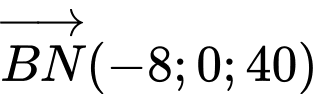 :
: 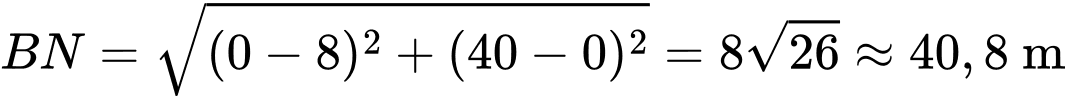
* Tính quãng đường hai chú kiến leo lên sau 10 phút:
- Quãng đường chú kiến vàng leo lên dây
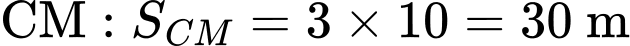
- Quãng đường chú kiến đen leo lên dây
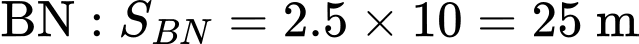
* Xác định vị trí của hai chú kiến trên các dây cáp
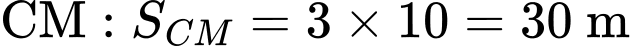 và
và 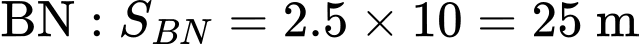 sau 10 phút:
sau 10 phút:
- Tỉ lệ vị trí của chú kiến vàng trên dây
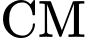 :
: 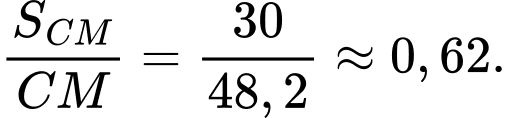
- Tọa độ của chú kiến vàng sau 10 phút là:
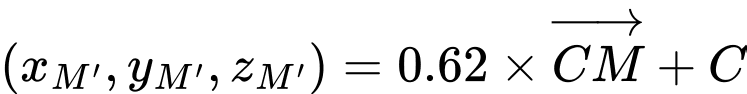
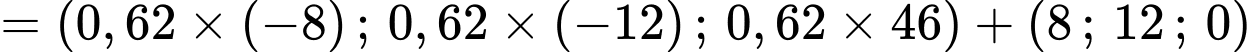
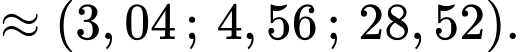
- Tỉ lệ vị trí của chú kiến đen trên dây
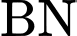 :
: 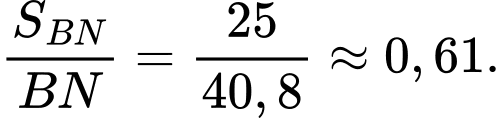
- Tọa độ của chú kiến đen sau 10 phút là:

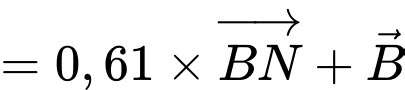
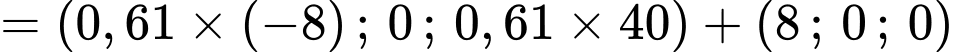
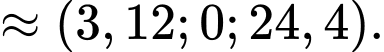
* Tính khoảng cách giữa hai chú kiến Khoảng cách giữa hai chú kiến là:
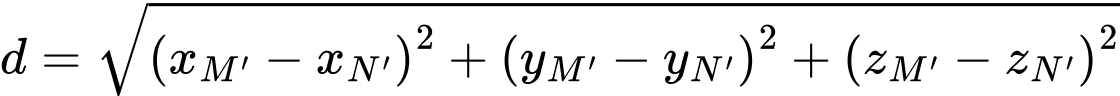
Thay các giá trị vào:
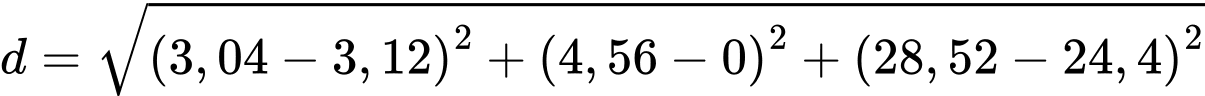
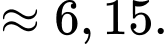
Vậy sau 10 phút, khoảng cách giữa hai chú kiến là khoảng
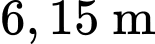 (làm tròn đến hàng phần trăm).
(làm tròn đến hàng phần trăm).
Câu 32 [301829]: Cho hình lập phương  có cạnh bằng
có cạnh bằng 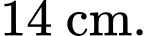 Hai chú kiến vàng và đen xuất phát cùng một lúc tại các vị trí
Hai chú kiến vàng và đen xuất phát cùng một lúc tại các vị trí 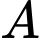 và
và 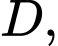 kiến vàng đi từ
kiến vàng đi từ 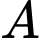 đến
đến 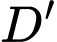 với vận tốc
với vận tốc 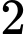 cm/s và kiến đen đi từ
cm/s và kiến đen đi từ 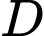 đến
đến 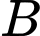 với vận tốc
với vận tốc 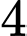 cm/s. Hỏi khoảng cách ngắn giữa hai chú kiến là bao nhiêu cm. Viết kết quả làm tròn đến hàng phần chục.
cm/s. Hỏi khoảng cách ngắn giữa hai chú kiến là bao nhiêu cm. Viết kết quả làm tròn đến hàng phần chục.
 có cạnh bằng
có cạnh bằng  Hai chú kiến vàng và đen xuất phát cùng một lúc tại các vị trí
Hai chú kiến vàng và đen xuất phát cùng một lúc tại các vị trí  và
và  kiến vàng đi từ
kiến vàng đi từ  đến
đến 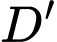 với vận tốc
với vận tốc 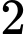 cm/s và kiến đen đi từ
cm/s và kiến đen đi từ 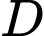 đến
đến 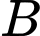 với vận tốc
với vận tốc  cm/s. Hỏi khoảng cách ngắn giữa hai chú kiến là bao nhiêu cm. Viết kết quả làm tròn đến hàng phần chục.
cm/s. Hỏi khoảng cách ngắn giữa hai chú kiến là bao nhiêu cm. Viết kết quả làm tròn đến hàng phần chục. 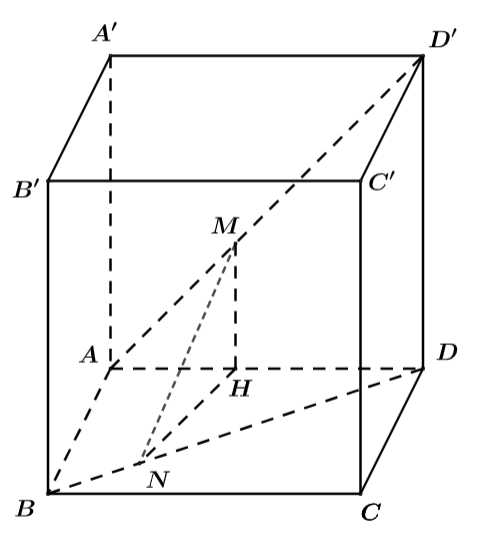
Giả sử trong thời gian t kiến vàng đi được đến điểm M, kiên đen đi được đến điểm N; Và kiến vàng đi với vận tốc
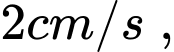 kiến đen đi với vận tốc
kiến đen đi với vận tốc 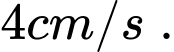
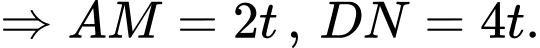
Ta có:
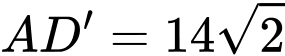 là đường chéo của hình vuông
là đường chéo của hình vuông 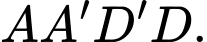
Ta kẻ

Xét
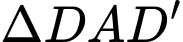 có:
có: 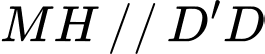
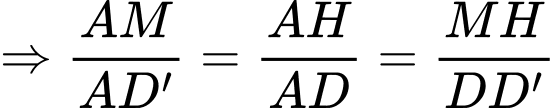
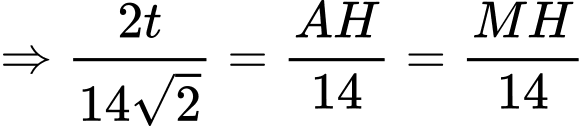

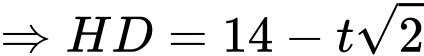
Xét
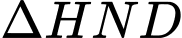 có:
có:
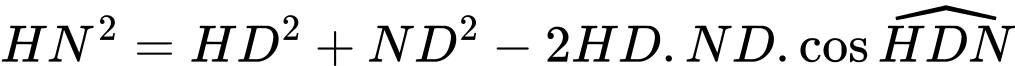
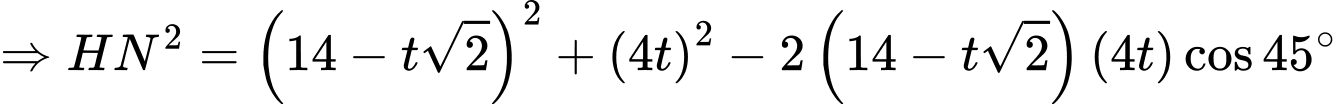
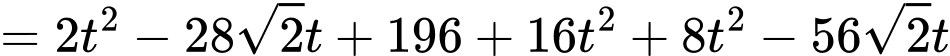
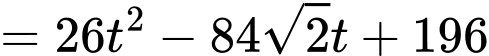
Khoảng cách hai con kiến là:
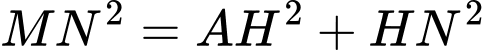

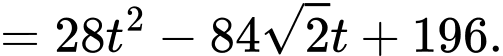
Khoảng cách ngắn nhất
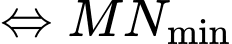
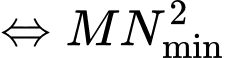
Xét hàm số